Thuật Toán Dijkstra và Ứng Dụng | Tiểu luận Môn Cấu trúc rời rạc - Trường Cao đẳng Công thương Thành phố Hồ Chí Minh

lOMoAR cPSD| 58797173 BỘ CÔNG THƯƠNG
TRƯỜNG ĐẠI HỌC CÔNG THƯƠNG TP. HỒ CHÍ MINH
KHOA CÔNG NGHỆ THÔNG TIN
TIỂU LUẬN HỌC PHẦN
MÔN: CẤU TRÚC RỜI RẠC
Giảng viên hướng dẫn: ThS Nguyễn Hải Yến Thành viên: MSSV:
1. Cao Đình Triệu Vĩ 2033225842
2. Trần Hoàng Huyền Trân 2033225505 3. Dư Quốc Vinh 2033225864 4. Lê Văn Quân 2033223965 5. Tô Kim Phụng 2033223803
Thành phố Hồ Chí Minh, tháng 12, năm 2023 lOMoAR cPSD| 58797173 MỤC LỤC
KHÁI QUÁT VỀ THUẬT TOÁN DIJKSTRA..............................................................0
1. Lịch Sử....................................................................................................................0
2. Khái niệm................................................................................................................0
3. Định Nghĩa:.............................................................................................................0
4. Đặc điểm của Dijkstra: .............................................................................................. 1
5. Cách hoạt động: ......................................................................................................... 1
6. Ứng dụng thực tế của thuật toán Dijkstra ............................................................... 3
7. Ưu và nhược điểm của thuật toán Dijkstra ............................................................. 4
8. Kết luận ....................................................................................................................... 5 1
BÁO CÁO KẾT QUẢ BÀI TẬP NHÓM Thành Vi ên Tỷ Lệ Đóng Góp Họ tên MSSV Cao Đình Triệu Vĩ 2033225842 20% Trần Hoàng Huyền Trân 2033225505 20% Lê Văn Quân 2033223965 20% Dư Quốc Vinh 2033225864 20% Tô Kim Phụng 2033223803 20% 2
KHÁI QUÁT VỀ THUẬT TOÁN DIJKSTRA 1. Lịch Sử
- Thuật toán Dijkstra được phát triển bởi nhà toán học người Hà Lan Edsger W. Dijkstra
vào năm 1956 và được sử dụng rộng rãi trong việc tìm đường đi ngắn nhất trong đồ thị
có trọng số dương từ một đỉnh gốc đến tất cả các đỉnh còn lại trong một đồ thị có hướng không vòng 2. Khái niệm. lOMoAR cPSD| 58797173
- Thuật toán Dijkstra là một thuật toán giải quyết bài toán đường đi ngắn nhất nguồn
đơn trong một đồ thị có hướng không có cạnh mang trọng số âm. Thuật toán thường
được sử dụng trong định tuyến với một chương trình con trong các thuật toán đồ thị
hay trong công nghệ hệ thống định vị toàn cầu (GPS). 3. Định Nghĩa:
Thành phố Hồ Chí Minh, tháng 12, năm 2023 lOMoAR cPSD| 58797173 -
Cho đồ thị có hướng không vòng G = (V, E) với trọng số trên các cạnh. Thuật toán
Dijkstra tìm đường đi ngắn nhất từ một đỉnh gốc s đến tất cả các đỉnh còn lại trong
G. Đường đi ngắn nhất được định nghĩa là đường đi có tổng trọng số của các cạnh
trên đường đi đó là nhỏ nhất.
4. Đặc điểm của Dijkstra:
- Chỉ áp dụng cho đồ thị có trọng số dương: Thuật toán Dijkstra thích hợp cho các đồ
thị có trọng số dương, nghĩa là các cạnh (edges) của đồ thị có giá trị không âm. Nếu
có trọng số âm, thuật toán có thể bị lặp vô hạn hoặc không hoạt động chính xác.
- Thuật toán Dijkstra sử dụng tìm kiếm theo chiều rộng (Breadth-First Search) hoặc
tìm kiếm theo độ ưu tiên (Priority Queue) để đảm bảo rằng nó luôn tìm ra đường đi
ngắn nhất từ đỉnh bắt đầu đến tất cả các đỉnh khác.
- Độ phức tạp thời gian của thuật toán Dijkstra là O(V^2) trong trường hợp sử dụng
ma trận kề (adjacency matrix) và O((V + E) * log(V)) trong trường hợp sử dụng danh
sách kề (adjacency list), với V là số lượng đỉnh và E là số lượng cạnh trong đồ thị.
- Không thể tối ưu hóa động: Thuật toán Dijkstra tính toán đường đi ngắn nhất dựa
trên thông tin tại thời điểm ban đầu và không thể tối ưu hóa nếu động thay đổi trọng số của các cạnh.
5. Cách hoạt động:
1. Khởi tạo một tập hợp con chứa các đỉnh mà chúng ta đã biết đường đi ngắn nhất từ
đỉnh bắt đầu đến nó. Ban đầu, tập hợp này chứa chỉ đỉnh bắt đầu với khoảng cách là
0, và các đỉnh khác với khoảng cách vô cùng (Infinity).
2. Lặp qua các đỉnh chưa được thêm vào tập hợp con và chọn đỉnh có khoảng cách ngắn
nhất để thêm vào tập hợp.
3. Cập nhật khoảng cách từ đỉnh bắt đầu đến các đỉnh kết nối với đỉnh vừa chọn thông
qua đỉnh vừa chọn đó. Nếu khoảng cách mới tới một đỉnh nhỏ hơn khoảng cách hiện
tại, thì cập nhật lại khoảng cách đó.
4. Lặp lại bước 2 và 3 cho đến khi chúng ta đã thêm tất cả các đỉnh vào tập hợp con
hoặc chúng ta đã thêm đỉnh đích vào tập hợp con.
5. Kết quả là tập hợp các đỉnh với khoảng cách ngắn nhất từ đỉnh bắt đầu đến chúng.
Để tìm đường đi ngắn nhất từ đỉnh bắt đầu đến đỉnh đích, chúng ta có thể theo dấu
vết từ đỉnh đích về đỉnh bắt đầu. lOMoAR cPSD| 58797173
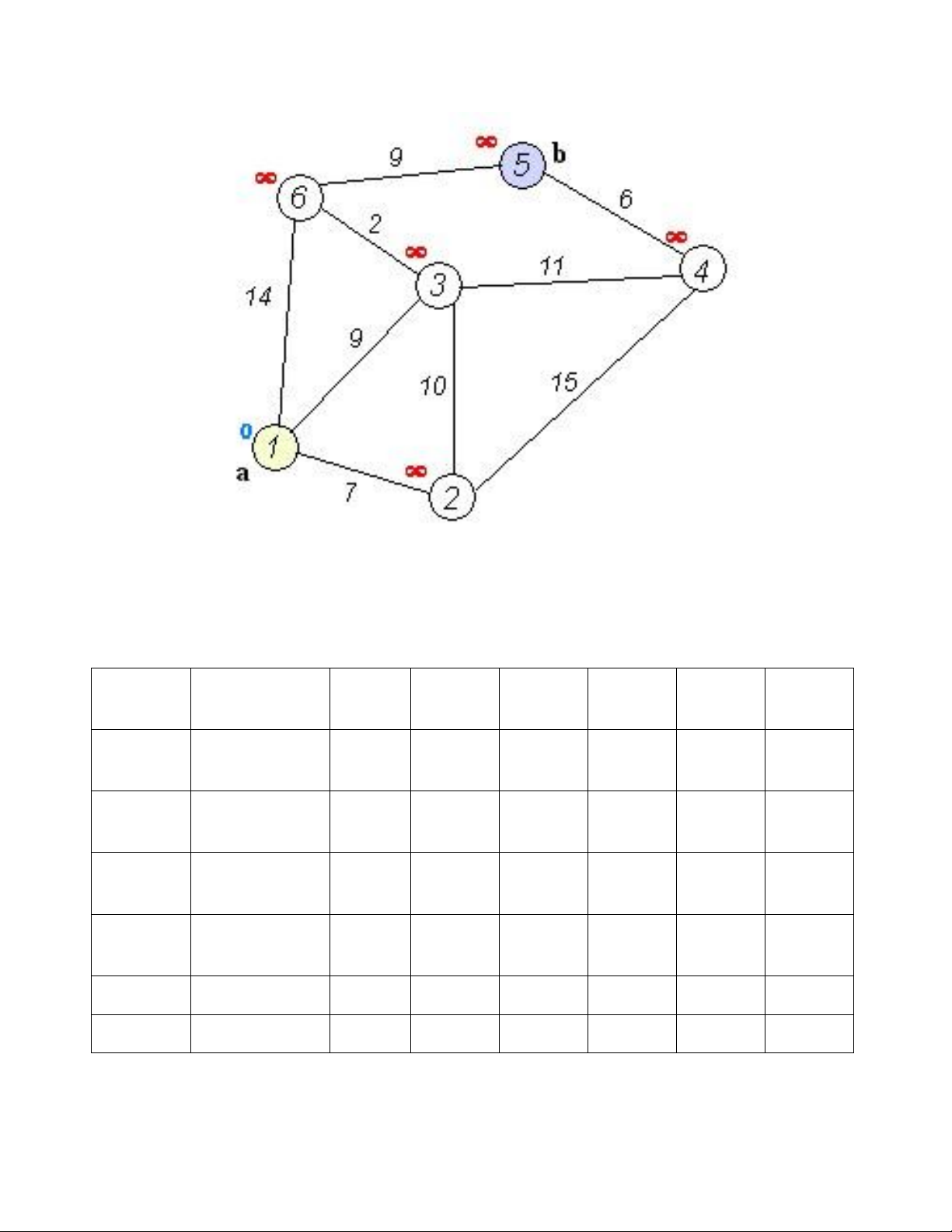
Ví dụ bài toán mẫu: Bướ Đỉnh đã D D2 D3 D4 D5 D6 c thăm 1 1 0 0 IN IN IN IN IN F F F F F 2 1 0 7 9 IN IN 14 F F 3 1,2 0 7 9 22 IN 14 F 4 1,2,3 0 7 9 20 IN 11 F 5 1,2,3,6 0 7 9 22 20 11 6 1,2,3,5,6 0 7 9 22 20 11 lOMoAR cPSD| 58797173 7 1,2,3,4,5, 0 7 9 22 20 11 6
Vậy khoảng các ngắn nhất từ a (Đỉnh 1) đến b (Đỉnh 5) là 20 .
6. Ứng dụng thực tế của thuật toán Dijkstra.
- Định tuyến mạng: Dijkstra được sử dụng trong việc xác định đường đi ngắn nhất
giữa hai điểm trên mạng, chẳng hạn như giao thông đường bộ hoặc mạng máy tính.
- Tìm đường đi trong bản đồ: Ứng dụng điều hướng GPS sử dụng thuật toán Dijkstra
để tìm đường đi ngắn nhất từ vị trí hiện tại đến điểm đến.
- Mô phỏng hệ thống vận chuyển: Dijkstra giúp tối ưu hóa quá trình vận chuyển hàng
hóa hoặc người trong các hệ thống giao thông. lOMoAR cPSD| 58797173
7. Ưu và nhược điểm của thuật toán Dijkstra - Ưu điểm:
• Tìm đường đi ngắn nhất: Dijkstra đảm bảo tìm ra đường đi ngắn nhất từ một đỉnh
bắt đầu đến tất cả các đỉnh khác trong đồ thị với trọng số không âm.
• Dễ hiểu và triển khai: Thuật toán Dijkstra có cấu trúc đơn giản và dễ hiểu, dễ triển
khai bằng cả mã nguồn hoặc bằng các thư viện có sẵn.
• Áp dụng rộng rãi: Dijkstra được sử dụng trong nhiều ứng dụng thực tế như tìm
đường đi trên bản đồ, định tuyến mạng, quản lý vận tải, và nhiều lĩnh vực khác.
• Độ phức tạp thời gian tốt: Trong trường hợp sử dụng danh sách kề, Dijkstra có độ
phức tạp thời gian là O((V + E) * log(V)), với V là số đỉnh và E là số cạnh. Điều này
làm cho nó hiệu quả đối với đồ thị lớn.
- Nhược điểm:
• Không xử lý trọng số âm: Dijkstra không thể xử lý các đồ thị có trọng số âm. Nếu
có trọng số âm, thuật toán có thể không cho kết quả đúng hoặc lặp vô hạn.
• Độ phức tạp không phải lúc nào cũng tốt: Trong trường hợp sử dụng ma trận kề,
Dijkstra có độ phức tạp thời gian là O(V^2), là một độ phức tạp tương đối lớn đối với
đồ thị lớn với số đỉnh lớn.
• Không tối ưu hóa động: Dijkstra không tối ưu hóa được nếu trọng số của các cạnh
thay đổi sau khi tính toán đã bắt đầu. Điều này đặc biệt quan trọng trong các ứng
dụng yêu cầu quản lý động của các yếu tố.
• Yêu cầu lưu trữ nhiều thông tin phụ: Dijkstra yêu cầu lưu trữ thông tin về khoảng
cách từ đỉnh bắt đầu đến tất cả các đỉnh khác, điều này có thể làm tăng yêu cầu lưu
trữ đối với đồ thị lớn.
• Có thể không tối ưu trong trường hợp đường đi gần nhau: Trong trường hợp
đường đi gần nhau, thuật toán Dijkstra có thể tốn thời gian và tài nguyên không cần
thiết do không sử dụng được tính chất tối ưu toàn cục. lOMoAR cPSD| 58797173 8. Kết luận.
Thuật toán Dijkstra là một công cụ quan trọng trong lĩnh vực khoa học máy
tính và toán học, giúp giải quyết nhiều vấn đề thực tế liên quan đến tìm đường đi
ngắn nhất. Hiểu cách hoạt động của thuật toán này có thể giúp bạn xây dựng và ứng
dụng nó trong các dự án thực tế. Tuy nhiên, Dijkstra cũng có một số hạn chế và độ
phức tạp nhất định. Vì thế tùy vào từng trường hợp, các nhà phát triển cũng sẽ thay
thế bằng các thuật toán tìm đường đi ngắn nhất khác.