














































Preview text:
1
C¸c kh¸i niÖm c¬ b¶n vÒ biÕn cè ngÉu nhiªn 1. Kh«ng gian x¸c suÊt
Tr−íc hÕt chóng ta ®−a vo kh¸i niÖm mét hä c¸c tËp con no ®ã cña kh«ng gian c¸c biÕn cè ngÉu nhiªn c¬
b¶n ®−îc gäi l σ&®¹i sè nÕu: 1. ∈ 2. A ∈ suy ra \A ∈ 3.
NÕu A1, A2, ... l d1y c¸c tËp hîp thuéc , khi ®ã A i i còng thuéc .
Trong lÝ thuyÕt x¸c xuÊt, tËp c¸c biÕn cè ngÉu nhiªn l mét σ&®¹i sè . Mét ¸nh x¹ P tõ vo tËp c¸c sè thùc R P : → R tho¶ m1n c¸c tiªn ®Ò sau: 1.
Víi mäi A ∈ 0 P (A) 1 2. P () = 1 3.
NÕu A1, A2, ..., Ai, ... l c¸c biÕn cè ngÉu nhiªn ®«i mét xung kh¾c nhau thuéc , khi ®ã P Ai = P (Ai) P (A) kh«ng gian x¸c suÊt. TÝnh chÊt cña x¸c suÊt (A) P (∅) = 0. (B) A ⊂ B ⇒ P (A) P (B). (C) P (A) = 1 − P (A). (D)
P (A + B) = P (A) + P (B) − P (AB). (E)
P (A + B + C) = P (A) + P (B) + P (C) − P (BC) − P (AB) − P (AC) + P (ABC). (F)
P (A1 + A2 + ... + An) P (A1) + P (A2) + + P (An). (G)
Víi d1y c¸c biÕn cè gi¶m dÇn A1 ⊃ A2 ⊃ A3 ⊃ ... (hoÆc t¨ng dÇn A1 ⊂ A2 ⊂ ...), khi ®ã
2. ng dông ®Ó tÝnh x¸c suÊt c¸c biÕn cè ngÉu nhiªn
Kh«ng gian c¸c biÕn cè ngÉu nhiªn c¬ b¶n gåm n biÕn cè ®ång kh¶ n¨ng = {ω1, ω2, ..., ωn},
P (ω1) = P (ω2) = ... = P (ωn)
Khi ®ã do P () = 1, suy ra P (ωi) = 1 víi mäi i v( nÕu n m
A = {ωn , ωn , ..., ωn } ⇒ P (A) = . m n http://www.ebook.edu.vn 1 CuuDuongThanCong.com
https://fb.com/tailieudientucntt Ta cßn nãi
Sè tr−êng hîp thuËn lîi cho biÕn cè A P (A) = .
Sè tr−êng hîp ®ång kh¶ n¨ng
Tr−êng hîp kh«ng gian c¸c biÕn cè ngÉu nhiªn c¬ b¶n l( mét miÒn h×nh häc, gi¶ thiÕt r»ng x¸c suÊt ®Ó
biÕn cè ngÉu nhiªn c¬ b¶n thuéc miÒn A tØ lÖ víi ®é ®o cña A, khi ®ã ®é ®o cña A P (A) = . ®é ®o cña
(§é ®o ë ®©y ®−îc hiÓu nh− l( ®é d(i, diÖn tÝch hoÆc thÓ tÝch tïy theo ®−îc nh¾c ®Õn l( miÒn h×nh häc n(o). B%i tËp 1
1. Gieo liªn tiÕp mét xóc x¾c, kÝ hiÖu Ak l biÕn cè: lÇn gieo thø k l lÇn ®Çu tiªn mÆt 6 chÊm xuÊt hiÖn. a. H1y tÝnh P (Ak).
b. T×m x¸c suÊt ®Ó mÆt 6 chÊm xuÊt hiÖn ë mét lÇn gieo no ®ã.
c. H1y t×m x¸c suÊt ®Ó sau mét sè lÎ lÇn gieo, mÆt 6 chÊm xuÊt hiÖn.
2. Mét tËp 10 vÐ trong ®ã cã 3 vÐ cã th−ëng. Chän ngÉu nhiªn 5 vÐ, t×m x¸c suÊt ®Ó trong ®ã cã ®óng 2 vÐ cã th−ëng.
3. Mét hép ®ùng 3 bi ®á, 3 bi tr¾ng, 3 bi xanh. Chän ngÉu nhiªn ra 6 viªn bi, t×m x¸c suÊt ®Ó cã ®ñ 3 mu
trong sè 6 viªn bi ®−îc chän ra. 4. Chøng minh r»ng N −n+1 Cn N = Cn−1 (n N) N −k k=1
5. Mét chÊt ®iÓm xuÊt ph¸t tõ 0, lang thang ngÉu nhiªn trªn trôc sè, nã dÞch chuyÓn sang ph¶i hoÆc sang tr¸i 1
®¬n vÞ víi x¸c suÊt b»ng 1. T×m x¸c suÊt ®Ó sau n b−íc, chÊt ®iÓm tíi vÞ trÝ k trªn trôc sè. 6. Bi
3. X¸c suÊt cã ®iÒu kiÖn v% sù ®éc lËp cña c¸c biÕn cè ngÉu nhiªn
X¸c suÊt cña A víi ®iÒu kiÖn B x¶y ra, kÝ hiÖu P (AB) P (A/B) = P(B)
Tõ ®Þnh nghÜa x¸c suÊt cã ®iÒu kiÖn, suy ra c«ng thøc nh©n x¸c suÊt P (AB) = P (A/B)P (B)
P (A1A2 An) = P (An/A1A2 An A /A A A A /A −1)P ( n−1 1 2 n−2) P ( 2 1)P (A1)
NhËn xÐt r»ng víi kÝ hiÖu P ∗(A) = P (A/B) l( x¸c suÊt cã ®iÒu kiÖn cña biÕn cè A víi ®iÒu kiÖn B (B cè
®Þnh), khi ®ã (, , P ∗) còng l( kh«ng gian x¸c suÊt.
Hai biÕn cè A v B ®éc lËp nhau nÕu
C¸c biÕn cè A1, A2, ..., An ®éc lËp, nÕu víi bÊt k× k biÕn cè ®«i mét kh¸c nhau Ai , A , ..., A k = 2, 3, ...n i ik trong d1y c¸c biÕn cè trªn
P (Ai A Ai ) = P (A )P (A ) P (A ) i k i i ik
Trong øng dông thùc tÕ hÖ c¸c biÕn cè m( mçi biÕn cè liªn quan tíi mét phÐp thö ngÉu nhiªn trong dMy c¸c
phÐp thö ®−îc tiÕn h(nh ®éc lËp nhau t¹o th(nh hÖ c¸c biÕn cè ®éc lËp.
§Þnh lÝ 1 (®Þnh lÝ x¸c suÊt ®Çy ®ñ) NÕu A1, A2, ..., An, ... l( hÖ ®Çy ®ñ c¸c biÕn cè ngÉu nhiªn, A l( biÕn cè
ngÉu nhiªn bÊt k×, khi ®ã ∞ P (A) = P (A/Ai)P (Ai). i=1 http://www.ebook.edu.vn 2 CuuDuongThanCong.com
https://fb.com/tailieudientucntt B%i tËp 2
1. Mét chÊt ®iÓm xuÊt ph¸t tõ x = k, lang thang ngÉu nhiªn trªn trôc sè, nã dÞch chuyÓn sang ph¶i hoÆc sang
tr¸i 1 ®¬n vÞ víi x¸c suÊt b»ng 1 . ChÊt ®iÓm dõng l¹i nÕu nã ®¹t tíi c¸c vÞ trÝ hót x = 0 hoÆc x = n. T×m x¸c 2
suÊt ®Ó mét lóc no ®ã nã dÞch chuyÓn tíi tr¹ng th¸i hót x = 0. (XÝch Markov).
2. R¶i ngÉu nhiªn N viªn bi vo n hép. Víi ®iÒu kiÖn mét hép x¸c ®Þnh tõ tr−íc (vÝ dô hép thø nhÊt) kh«ng
rçng, t×m x¸c suÊt ®Ó hép ®ã cã ®óng K viªn bi (K ≥ 1).
3. Mét x¹ thñ b¾n bia, x¸c suÊt tróng bia cña x¹ thñ b»ng p. T×m x¸c suÊt ®Ó sau n lÇn b¾n liªn tôc, lÇn b¾n
thø n l lÇn ®Çu tiªn x¹ thñ b¾n tróng bia.
4. A v B ch¬i mét trß ch¬i nh− sau: A gieo xóc x¾c, kÕt qu¶ gi¶ sö mÆt k chÊm xuÊt hiÖn. A gieo tiÕp ®ång
thêi 2 ®ång xu k lÇn. NÕu Ýt nhÊt cã mét lÇn x¶y ra biÕn cè c¶ hai ®ång xu cïng xuÊt hiÖn mÆt ngöa, khi ®ã A
th¾ng cuéc, ng−îc l¹i A bÞ thua. Hái trß ch¬i ®ã cã lîi cho A hay B?
5. A v B ch¬i mét trß ch¬i nh− sau: A gieo ®ång thêi 2 xóc x¾c. NÕu tæng b»ng 7 hoÆc 11, A th¾ng cuéc,
nÕu tæng b»ng 2,3 hoÆc 12, A thua cuéc. C¸c tr−êng hîp cßn l¹i, A lÆp l¹i trß ch¬i cho ®Õn khi cã ng−êi th¾ng
ng−êi thua. T×m x¸c suÊt ®Ó A th¾ng. (§S: 2) 3
6. Cho n hép, mçi hép chøa ®óng a bi tr¾ng v b bi ®á. LÊy ngÉu nhiªn 1 viªn bi tõ hép thø nhÊt v bá sang
hép thø hai, sau ®ã lÊy tiÕp 1 viªn bi tõ hép thø hai v bá sang hép thø ba,... Cuèi cïng lÊy 1 viªn bi tõ hép
thø n. Gäi A l biÕn cè viªn bi lÊy tõ hép thø nhÊt bá sang hép thø hai l viªn bi tr¾ng, B l biÕn cè viªn bi
lÊy tõ hép thø n l viªn bi tr¾ng. KÝ hiÖu pn = P (B/A). Chøng minh r»ng a b pn = + (a + b + 1)1−n. a + b a + b
7. C¸c hép ®−îc ®¸nh sè 0, 1, 2, ..., N v hép mang sè k chøa k bi ®á, N − k bi tr¾ng (k = 0, 1, 2, ..., N).
Chän ngÉu nhiªn mét hép v tõ hép ny chän lÇn l−ît cã hon l¹i tõng viªn bi. Gäi An l l biÕn cè lÇn chän
thø n lÊy ®−îc viªn bi ®á. a. TÝnh P (A3/A1A2)
b. Gi¶ sö tõ hép ®1 chän ngÉu nhiªn chän lÇn l−ît hai viªn bi kh«ng hon l¹i. T×m x¸c suÊt ®Ó c¶ hai bi ®1 chän l 4. C«ng thøc Bernoulli
Gi¶ sö x¸c suÊt x¶y ra biÕn cè A l p. Khi ®ã x¸c suÊt ®Ó trong n lÇn tiÕn hnh phÐp thö ngÉu nhiªn ®éc
lËp nhau cã ®óng k lÇn x¶y ra A b»ng
Pk;n = Cknpkqn−k (trong ®ã p + q = 1). B%i tËp 3
1. T×m x¸c suÊt ®Ó mét gia ®×nh 5 ng−êi con cã ®óng 3 trai, 2 g¸i.
2. BiÕt x¸c suÊt ®Ó ®Êu thñ bãng bn A th¾ng B ë mçi sÐc l p. Hai ®Êu thñ ®Êu víi nhau tèi ®a 5 sÐc, ng−êi
no th¾ng tr−íc 3 sÐc l ng−êi th¾ng chung cuéc. T×m x¸c suÊt ®Ó ®Êu thñ A th¾ng chung cuéc. p
X¸c suÊt cÇn t×m: P (A) = p3(1 + 3q + 6q2) 0,6 0,68256 0,7 0,83692 2
§¹i l−îng ngÉu nhiªn v% ph©n bè x¸c suÊt 1. Kh¸i niÖm c¬ b¶n
Mét ¸nh x¹ X : → R trªn kh«ng gian x¸c suÊt (, , P ) tháa m1n
{ω : X(ω) < x} ∈ víi mäi x ∈ R http://www.ebook.edu.vn 3 CuuDuongThanCong.com
https://fb.com/tailieudientucntt
®−îc gäi l ®¹i l−îng ngÉu nhiªn X. Hm F (x) = P (X < x) víi mäi x ∈ R
®−îc gäi l hm ph©n bè x¸c suÊt cña ®¹i l−îng ngÉu nhiªn X. HiÓn nhiªn
P (a X < b) = F (b) − F (a)
NÕu tån t¹i mét hm kh«ng ©m f : R → [0, +∞) sao cho hm ph©n bè F (x) cña ®¹i l−îng ngÉu nhiªn X tho¶ m1n b
F (b) − F (a) = P (a X < b) = f (x) dx víi mäi a < b ∈ R, a
khi ®ã hm f ®−îc gäi l mËt ®é x¸c suÊt cña ®¹i l−îng ngÉu nhiªn X. §¹i l−îng ngÉu nhiªn cã hm mËt ®é
®−îc gäi l ®¹i l−îng ngÉu nhiªn liªn tôc. §Æc biÖt x F (x) = f (x) dx víi mäi x ∈ R. −∞
T¹i c¸c ®iÓm hm mËt ®é liªn tôc F ′(x) = f (x). Chó ý r»ng ®¹i l−îng ngÉu nhiªn rêi r¹c (®¹i l−îng ngÉu
nhiªn m miÒn gi¸ trÞ l tËp kh«ng qu¸ ®Õm ®−îc) kh«ng cã hm mËt ®é, ph©n bè cña nã th−êng ®−îc cho d−íi d¹ng pn = P (X = xn), n = 0, 1, 2, ... trong ®ã pn = 1 n hoÆc d−íi d¹ng b¶ng X x1 x2 ... xn ... trong ®ã p P p n n = 1. 1 p2 ... pn ...
TÝnh chÊt h(m ph©n bè, h(m mËt ®é 1. 2.
Hm ph©m bè ®¬n ®iÖu t¨ng v liªn tôc tr¸i trªn R. 3.
+∞ f(x) dx = F (+∞) − F(−∞) = 1. −∞ 4.
Víi ®¹i l−îng ngÉu nhiªn liªn tôc, x¸c suÊt ®Ó X nhËn c¸c gi¸ trÞ trong mét tËp h÷u h¹n hoÆc v« h¹n
®Õm ®−îc lu«n b»ng 0. Suy ra
P (a X < b) = P (a < b) = P (a X b) = F (b) − F (a). B%i tËp 4
1. X l sè lçi in sai trong mét trang s¸ch gi¸o khoa NXB Gi¸o dôc. Ng−êi ta biÕt r»ng P (X = 0) = 0.85, P (X = 1) = 0.1, P (X = 2) = 0.05
Nh− vËy X l ®¹i l−îng ngÉu nhiªn rêi r¹c nhËn c¸c gi¸ trÞ 0, 1, 2 v b¶ng ph©n bè cña X th−êng ®−îc viÕt d−íi d
Hm ph©n bè cña X khi ®ã b»ng 0 nÕu x 0 0.85 nÕu 0 < x 1 F (x) = nÕu 0.95 1 < x 2 1 nÕu 2 < x
2. Gäi X l sè lÇn b¾n liªn tôc vo bia cho ®Õn khi tróng bia, p l x¸c suÊt tróng bia cña mçi lÇn b¾n. Gi¶ thiÕt
c¸c lÇn b¾n ®éc lËp nhau, khi ®ã b¶ng ph©n bè cña X X 1 2 ... n ... (p + q = 1) P p qp ... pqn−1 ... http://www.ebook.edu.vn 4 CuuDuongThanCong.com
https://fb.com/tailieudientucntt
3. X l ®iÓm chän ngÉu nhiªn trªn ®o¹n [a, b] (gi¶ thiÕt r»ng x¸c suÊt ®Ó X thuéc kho¶ng (u, v) ⊂ [a, b] tØ lÖ
víi ®é di ®o¹n [u, v]). Khi ®ã X l ®¹i l−îng ngÉu nhiªn liªn tôc víi hm mËt ®é 1 nÕu a < x b f (x) = b−a 0 nÕu x a hoÆc x > b
(X ®−îc gäi l ®¹i l−îng ngÉu nhiªn cã ph©n bè ®Òu trªn ®o¹n [a, b].)
4. NÕu f (x) l hm mËt ®é cña X, khi ®ã hm mËt ®é cña Y = aX + b b»ng 1 y − b g(y) = f |a| a
5. T×m hm mËt ®é cña ξ2, biÕt ξ ph©n bè ®Òu trªn ®o¹n [−1, 1].
2. K× väng, ph−¬ng sai cña ®¹i l−îng ngÉu nhiªn
Víi c¸c ®¹i l−îng ngÉu nhiªn rêi r¹c cã ph©n bè X x1 x2 ... xn ... P p1 p2 ... pn ...
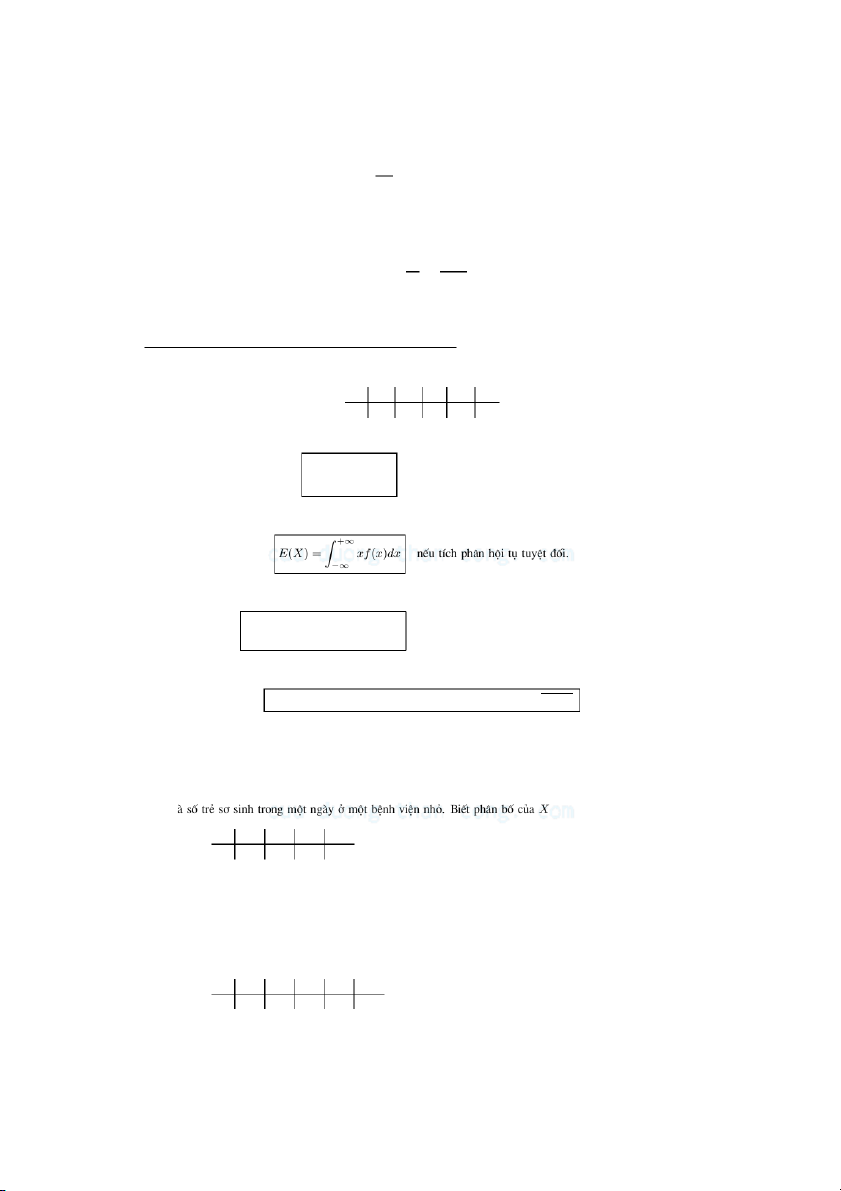
K× väng cña X, kÝ hiÖu E(X) b»ng ∞ E(X) = xipi
nÕu chuçi héi tô tuyÖt ®èi. i=1
Tr−êng hîp X l ®¹i l−îng ngÉu nhiªn liªn tôc cã f (x) l hm mËt ®é
Chó ý r»ng k× väng l to¸n tö tuyÕn tÝnh v +∞ E(ϕ(X)) = ϕ(x)f (x)dx
trong ®ã f (x) l hm mËt ®é cña X. −∞
Ph−¬ng sai D(X) v ®é lÖch tiªu chuÈn σX cña X
D(X) = E(X − EX)2 = EX2 − (EX)2, σX = D(X).
HiÓn nhiªn ph−¬ng sai cña h»ng sè b»ng 0 v D(αX) = α2D(X). B%i tËp 5 1. X l X 0 1 2 3 P 0.3 0.4 0.2 0.1
Khi ®ã trung b×nh sè trÎ em míi sinh trong mét ngy b»ng
EX = 0 × 0.3 + 1 × 0.4 + 2 × 0.2 + 3 × 0.1 = 1.1
2. Gäi X l sè lÇn gieo xóc x¾c liªn tôc cho ®Õn khi mÆt 6 chÊm xuÊt hiÖn. H1y tÝnh sè lÇn gieo trung b×nh.
3. Mét c«ng viÖc trong x©y dùng dù tÝnh sÏ ®−îc hon thnh trong kho¶ng thêi gian tõ 10 ®Õn 14 ngy. Gi¶ sö
X l sè ngy c«ng ®Ó hon thnh c«ng viÖc ®ã, ph©n bè cña X ®−îc dù tÝnh nh− sau X 10 11 12 13 14 X) = 1. P 0.1 0.3 0.3 0.2 0.1 ⇒ E(X) = 11.9 ngy, D( 29 http://www.ebook.edu.vn 5 CuuDuongThanCong.com
https://fb.com/tailieudientucntt
Nh thÇu −íc l−îng chi phÝ ton bé cho c«ng tr×nh gåm 85 triÖu tiÒn vËt liÖu x©y dùng v tiÒn nh©n c«ng l 1.6
triÖu ®ång mét ngy c«ng. Khi ®ã chi phÝ ton bé cho c«ng tr×nh b»ng Y = 85 + 1.5X (triÖu ®ång)
VËy k× väng hay gi¸ trÞ trung b×nh cña ton bé chi phÝ l
E(Y ) = 85 + 1.5E(X) = 85 + 1.5 × 11.9 = 102.85 (triÖu ®ång) √
D(Y ) = 1.52 × D(X) = 1.52 × 1.29 = 2.9025 ⇒ σY = 2.9025 = 1.7037
4. K× väng v ph−¬ng sai cña ph©n bè ®Òu trªn [a, b] a + b (a − b)2 EX = , DX = 2 12
3. C¸c ph©n bè th−êng gÆp 1. Ph©n bè nhÞ thøc X 0 1 ... k ... n P p0 p1 ... pk ... pn
trong ®ã pk = P (X = k) = Cknpkqn−k, p + q = 1, k = 0, 1, ..., n
NhËn xÐt r»ng ®¹i l−îng ngÉu nhiªn cã ph©n bè nhÞ thøc cã thÓ biÓu diÔn d−íi d¹ng n X = Xi i=1
trong ®ã Xi ghi l¹i kÕt qu¶ cña viÖc xuÊt hiÖn hay kh«ng xuÊt hiÖn biÕn cè A trong d1y c¸c phÐp thö ngÉu nhiªn 1
nÕu A x¶y ra trong phÐp thö thø i Xi = 0
nÕu A kh«ng x¶y ra trong phÐp thö thø i 2. Ph©n bè Poisson X 0 1 2 ... k ... P p0 p1 p2 ... pk ... trong ®ã λk p −λ k = P (X = k) = e , λ > 0, k = 0, 1, 2, ... k! 3. Ph©n bè h×nh häc X 1 2 ... n ... P p qp ... qn−1p ... trong ® 4. Ph©n bè mò
X l ®¹i l−îng ngÉu nhiªn cã ph©n bè mò, nÕu hm mËt ®é cña X b»ng λe−λx nÕu x > 0 f (x) = víi λ > 0 0 nÕu x 0 5. Ph©n bè chuÈn
X l ®¹i l−îng ngÉu nhiªn cã ph©n bè chuÈn, kÝ hiÖu X ∈ N(m, σ2) nÕu hm mËt ®é cña X b»ng 1 − f (x) = √ e− x m σ trong ®ã σ > 0, m ∈ R. 2πσ http://www.ebook.edu.vn 6 CuuDuongThanCong.com
https://fb.com/tailieudientucntt Sö dông ∞ √π I = e−x dx = 0 2
ta dÔ dng chøng minh hm f (x) nãi trªn l hm mËt ®é v EX = m, DX = σ2.
NhËn xÐt r»ng X ∈ N(m, σ2) khi v( chØ khi Z = X−m ∈ N(0, 1). Ng−êi ta th−êng kÝ hiÖu hm ph©n bè cña σ X ∈ N(0, 1) 1 x Φ(x) = √ e− u du. 2π −∞
Tra b¶ng ph©n bè chuÈn, ta cã
Quy t¾c σ NÕu X ∈ N(m, σ2), khi ®ã X − m 1 3
P (m − 3σ X m + 3σ) = P ( √ e− x dx = 2Φ(3) − 1 = 0, 9973 σ 3) = 2π −3
3 §¹i l−îng ngÉu nhiªn nhiÒu chiÒu
1. H%m ph©n bè v% h%m mËt ®é chung
XÐt mét cÆp hai ®¹i l−îng ngÉu nhiªn (ξ, η). NÕu chóng ta ®ång thêi kh¶o s¸t hai ®¹i l−îng ngÉu nhiªn ξ
v η, chóng ta sÏ coi chóng nh− c¸c to¹ ®é cña mét vÐc t¬ ngÉu nhiªn (hay mét ®iÓm ngÉu nhiªn) (ξ, η). C¸c
gi¸ trÞ cã thÓ cã cña nã l c¸c ®iÓm (x, y) trong mÆt ph¼ng to¹ ®é xOy. Gäi tËp E l mét miÒn ph¼ng bÊt k× E ⊂ R ξ,η (E), víi mä §Þnh nghÜa 1 H(m
H(x, y) = P (ξ < x, η < y) = P ({ξ ∈ (−∞, x)} {η ∈ (−∞, y)})
víi mäi x, y ∈ R l( h(m ph©n bè chung cña hai ®¹i l−îng ngÉu nhiªn ξ v( η (hay cßn gäi l( h(m ph©n bè
®ång thêi cña vÐc t¬ ngÉu nhiªn (ξ, η)).
NÕu tån t¹i mét h(m kh«ng ©m h(x, y) ≥ 0 sao cho P ((ξ, η) ∈ E) = h(x, y) dxdy E
víi mäi miÒn E cña mÆt ph¼ng. Khi ®ã ta nãi h(x, y) l( h(m mËt ®é cña vÐc t¬ ngÉu nhiªn (ξ, η) (hay cßn gäi
l( h(m mËt ®é chung cña ξ v( η).
§èi víi c¸c ®¹i l−îng ngÉu nhiªn rêi r¹c, thay cho hm ph©n bè ®ång thêi H(x, y) l c¸c x¸c suÊt Chóng
§¹i l−îng ngÉu nhiªn X ®o møc ®é hi lßng cña ng−êi d©n sèng trong mét khu chung c− míi x©y dùng v Y
biÓu thÞ sè n¨m ng−êi d©n sèng trong khu chung c− ®ã. Gi¶ sö møc ®é hi lßng cña ng−êi ë biÓu thÞ qua c¸c
gi¸ trÞ X = 1, X = 2, X = 3 hoÆc X = 4 (gi¸ trÞ X cng lín t−¬ng øng víi møc hi lßng cng cao). §¹i l−îng
ngÉu nhiªn Y nhËn c¸c gi¸ trÞ 1 nÕu ng−êi d©n sèng kh«ng qu¸ 1 n¨m trong khu chung c− ®ã v nhËn gi¸ trÞ 2
trong tr−êng hîp ng−îc l¹i. X 1 2 3 4 Tæng Y 1 0.04 0.17 0.18 0.1 0.49 2 0.06 0.15 0.2 0.1 0.51 Tæng 0.1 0.32 0.38 0.2 1 http://www.ebook.edu.vn 7 CuuDuongThanCong.com
https://fb.com/tailieudientucntt
B¶ng ph©n bè trªn cho biÕt, ch¼ng h¹n
P (3, 2) = P (X = 3, Y = 2) = 0.2
l x¸c suÊt ®Ó khi chän ngÉu nhiªn mét ng−êi sèng ë khu chung c−, ng−êi ®ã cã møc hi lßng 3 v sèng trªn
1 n¨m trong khu chung c− ®ã. Cét tæng cho ph©n bè cña Y
P (Y = 1) = 0.49, P (Y = 2) = 0.51
Hng tæng x¸c ®Þnh ph©n bè cña X
P (X = 1) = 0.1, P (X = 2) = 0.32, P (X = 3) = 0.38, P (X = 4) = 0.2
Tr−êng hîp tån t¹i h(m mËt ®é chung, hiÓn nhiªn P ((X, Y ) ∈ E) = h(x, y) dxdy víi mäi tËp E ⊂ R2. E x y ∂2H
H(x, y) = P (X < x, Y < y) = h(u, v) dudv, = h(x, y) −∞ ∂x∂y −∞ x +∞ F (x) = H(x, +∞) =
h(u, v) dv du l hm ph©n bè cña X. −∞ −∞ y +∞ G(y) = H(+∞, y) = h(u, v) du dv l hm ph©n bè cña Y. −∞ −∞
Hm mËt ®é cña X, Y t−¬ng øng l −∞ −∞
§Þnh nghÜa 2 C¸c ®¹i l−îng ngÉu nhiªn ξ v( η ®−îc gäi l( ®éc lËp nhau nÕu víi mäi x, y ∈ R
H(x, y) = P (ξ < x, η < y) = P (ξ < x)P (η < y) = F (x)G(y) ⇔ h(x, y) = f(x)g(y)
§Þnh lÝ 2 Gi¶ sö X, Y cã h(m mËt ®é chung h(x, y), khi ®ã ∞ ∞ E (ϕ(X, Y )) = ϕ(x, y)h(x, y) dxdy. −∞ −∞
§Æc biÖt nÕu X, Y l( c¸c ®¹i l−îng ngÉu nhiªn ®éc lËp nhau, khi ®ã E(XY ) = EX EY, D(X + Y ) = DX + DY. Gi¶ sö
(x + y ) nÕu 0 < x < 1, 0 < y < 1 h(x, y) = 5 0
trong tr−êng hîp ng−îc l¹i
Sö dông f (x) = ∞ h(x, y) dy, hm mËt ®é cña X −∞ 6
1(x + y2) dy = 6 (x + 1) nÕu 0 < x < 1 f (x) = 5 0 5 3 0 nÕu x / ∈ (0, 1) hm mËt ®é cña Y 6
1(x + y2) dx = 6(1 + y2) nÕu 0 < y < 1 g(y) = 5 0 5 2 0 nÕu y / ∈ (0, 1) http://www.ebook.edu.vn 8 CuuDuongThanCong.com
https://fb.com/tailieudientucntt
(X, Y ) ph©n bè ®Òu trªn h×nh trßn t©m (0, 1) b¸n kÝnh b»ng 1. Hm mËt ®é chung cña X v Y
1 nÕu x2 + (y − 1)2 < 1 h(x, y) = π 0
trong tr−êng hîp ng−îc l¹i Hm mËt ®é Y b»ng √ ∞ 2 2y−y nÕu g(y) = h(x, y) dx = 0 < y < 2 π −∞ 0 nÕu y / ∈ (0, 2) 1 E(Y ) = 1, D(Y ) = 4 B%i tËp
1. Gi¶ sö X v Y l hai ®¹i l−îng ngÉu nhiªn ®éc lËp cã cïng ph©n bè chuÈn N(0, 1). H1y t×m hm mËt ®é cña Z = |X|signY .
2. Chän ngÉu nhiªn 2 ®iÓm M v N trªn ®o¹n [0, 1], 2 ®iÓm M, N ®ã chia ®o¹n [0, 1] thnh 3 phÇn, gäi c¸c
®é di cña 3 ®o¹n th¼ng ®ã t−¬ng øng l c¸c ®¹i l−îng ngÉu nhiªn X1, X2 v X3.
a) H1y t×m c¸c hm mËt ®é cña X1, X2 v X3.
b) H1y tÝnh c¸c k× väng E(X1), E(X2) v E(X3). 2. Ph©n bè cã ®iÒu kiÖn Gi¶ u
§Þnh nghÜa 3 Ng−êi ta gäi h(m
F (x/A) = P (X < x/A) víi ∀x
l( h(m ph©n bè cã ®iÒu kiÖn cña X víi ®iÒu kiÖn biÕn cè A x¶y ra. NÕu F (x/A) kh¶ vi, kÝ hiÖu f(x/A) = F ′(x/A) v( x F (x/A) = P (X < x/A) = f (t/A) dt víi ∀x −∞
khi ®ã f(x/A) ®−îc gäi l( h(m mËt ®é cã ®iÒu kiÖn cña X víi ®iÒu kiÖn biÕn cè A x¶y ra (hoÆc nãi t¾t l( h(m
mËt ®é cña X víi ®iÒu kiÖn A).
Ta cã nhËn xÐt r»ng nÕu Ai, i = 1, 2, ... l mét hÖ ®Çy ®ñ c¸c biÕn cè. Khi ®ã theo c«ng thøc x¸c suÊt ®Çy
®ñ, hm ph©n bè cña X cã thÓ biÓu diÔn theo c¸c hm ph©n bè cã ®iÒu kiÖn: F (x) = P (X < x) = P (X < x/Ai)P (Ai) = F (x/Ai)P (Ai) i i ®¹o h f (x) = f (x/Ai)P (Ai). i B%i tËp
Mçi ngy sè ca cÊp cøu tíi mét bÖnh viÖn l ®¹i l−îng ngÉu nhiªn N tu©n theo luËt Poisson víi tham sè λ.
Ng−êi ta ph©n ra hai lo¹i cÊp cøu: cÊp cøu do tai n¹n giao th«ng (lo¹i A) v cÊp cøu v× c¸c lÝ do kh¸c (lo¹i B).
Gi¶ thiÕt r»ng p l x¸c suÊt ®Ó mét ca cÊp cøu thuéc lo¹i A, cÊp cøu do tai n¹n giao th«ng. KÝ hiÖu XA l ®¹i
l−îng ngÉu nhiªn biÓu thÞ sè ca cÊp cøu thuéc lo¹i A, XB l sè ca cÊp cøu thuéc lo¹i B trong ngy.
1. Víi k, n l hai sè nguyªn, h1y tÝnh P (XA = k/N = n).
2. X¸c ®Þnh luËt ph©n bè ®ång thêi cña (N, XA). http://www.ebook.edu.vn 9 CuuDuongThanCong.com
https://fb.com/tailieudientucntt
3. X¸c ®Þnh luËt ph©n bè, k× väng v ph−¬ng sai cña XA.
4. X¸c ®Þnh luËt ph©n bè cña XB.
5. XA v XB cã ®éc lËp víi nhau kh«ng?
Gi¶i b%i tËp: N cã ph©n bè Poisson víi tham sè λ. λn P (N = n) = e−λ n!
1. Víi k, n l hai sè nguyªn, P (XA = k/N = n) = Cknpkqn−k.
2. X¸c ®Þnh luËt ph©n bè ®ång thêi cña (N, XA)
P (N = n, XA = k) = P (XA = k/N = n)P (N = n) = Ck n pkqn−k e−λ λn = n! 1 1 =
e−λλnpkqn−k = e−λ(λp)k(λq)n−k víi n ≥ k. k!(n − k)! k!(n − k)!
3. X¸c ®Þnh luËt ph©n bè, k× väng v ph−¬ng sai cña XA. ∞ ∞ 1 P (X −λ A = k) = P (XA = k, N = n) = e (λp)k(λq)n−k = k!(n − k)! n=k n=k (λp)k ∞ (λq)n−k λp k ∞ (λq)i = e−λ = e−λ ( )
= e−λ (λp)k eλq = e−λp (λp)k k! (n − k)! k! i! k! k! n=k i=0
4. T−¬ng tù luËt ph©n bè cña XB i
5. XA v XB ®éc lËp víi nhau. ThËt vËy xÐt P (XA = k, XB = i), kÝ hiÖu n = k + i, khi ®ã 1 P (X k
A = k, XB = i) = P (XA = k, N = n) = e−λ(λp) (λq)n−k = k!(n − k)! (λp)k (λq)i = e−λp e−λq = P (XA = k)P (XB = i), víi mäi k, i ≥ 0. k! i!
Gi¶ thiÕt (X, Y ) l vÐc t¬ ngÉu nhiªn cã h(x, y) l hm mËt ®é chung. Khi ®ã Y l ®¹i l−îng ngÉu nhiªn
liªn tôc, hm mËt ®é cña Y l ∞ g(y) = h(x, y) dx. −∞
Ta ®Þnh nghÜa x¸c suÊt cã ®iÒu kiÖn cña biÕn cè {X < x} víi ®iÒu kiÖn Y = y nh− l giíi h¹n cña P (X <
x/y Y < y + ∆y) khi ∆y dÇn tíi 0. Hm
®−îc gäi l h(m ph©n bè cã ®iÒu kiÖn cña X víi ®iÒu kiÖn Y = y, tÊt nhiªn víi gi¶ thiÕt tån t¹i giíi h¹n trªn.
Do ®Þnh nghÜa x¸c suÊt cã ®iÒu kiÖn v tÝnh chÊt cña hm ph©n bè chung
P (X < x, y Y < y + ∆y) H(x, y + ∆y) − H(x, y)
P (X < x/y Y < y + ∆y) = = P (y Y < y + ∆y) G(y + ∆y) − G(y)
(H(x, y) l hm ph©n bè chung cña X v Y , G(y) l hm ph©n bè cña Y ). Chia c¶ tö v mÉu cho ∆y, chuyÓn
qua giíi h¹n khi ∆y → 0 ta ®−îc ∂ H(x, y) ∂ ∂ H(x, y) h(x, y) F (x/y) = ∂y ⇒ f (x/y) = F (x/y) = ∂x∂y = . g(y) ∂x g(y) g(y)
f (x/y) ®−îc gäi l h(m mËt ®é cã ®iÒu kiÖn cña X víi ®iÒu kiÖn Y = y. http://www.ebook.edu.vn 10 CuuDuongThanCong.com
https://fb.com/tailieudientucntt
Chó ý r»ng c¸c hm mËt ®é cã ®iÒu kiÖn còng nh− ph©n bè cã ®iÒu kiÖn ë ®©y chØ ®−îc x¸c ®Þnh t¹i y sao
cho g(y) > 0. T¹i nh÷ng ®iÓm m g(y) = 0, hm mËt ®é f (x/y) ®−îc x¸c ®Þnh tïy ý (®Ó ®¬n gi¶n, t¹i ®ã
ng−êi ta th−êng g¸n cho f(x/y) gi¸ trÞ 0). ViÕt chÝnh x¸c h¬n, mËt ®é cã ®iÒu kiÖn h(x,y) nÕu g(y) > 0 f (x/y) = g(y) 0 nÕu g(y) = 0
T−¬ng tù hm mËt ®é cã ®iÒu kiÖn cña Y víi ®iÒu kiÖn X = x h(x,y) nÕu f(x) > 0 g(y/x) = f (x) 0 nÕu f(x) = 0
Suy ra h(x, y) = f (x/y)g(y) = g(y/x)f (x). Tõ ®ã ta nhËn ®−îc c¸c c«ng thøc t−¬ng tù nh− c«ng thøc x¸c suÊt ®Çy ®ñ ∞ ∞ f (x) = h(x, y) dy = f (x/y)g(y) dy −∞ −∞ ∞ ∞ g(y) = h(x, y) dx = g(y/x)f (x) dx −∞ −∞
Chó ý r»ng nÕu X, Y l c¸c ®¹i l−îng ngÉu nhiªn ®éc lËp nhau khi ®ã c¸c hm mËt ®é cã ®iÒu kiÖn
f (x/y) = f (x) kh«ng phô thuéc vo y còng nh− g(y/x) = g(y) kh«ng phô thuéc vo x.
§Þnh lÝ 3 Gi¶ sö ϕ l( mét song ¸nh
ϕ : D → T D ⊂ R2, T ⊂ R2
kh¶ vi t¹i mäi ®iÓm thuéc D. (X, Y ) l( vÐc t¬ ngÉu nhiªn nhËn c¸c gi¸ trÞ trong D v( h(x, y) l( h(m mËt ®é
®ång thêi cña vÐc t¬ ngÉu nhiªn ®ã. Khi ®ã h(m mËt ®é cña (U, V ) = ϕ(X, Y ) b»ng
g(u, v) = h ϕ−1(u, v) |J(u, v)| trong ®
KÝ hiÖu (x, y) = ϕ−1(u, v), khi ®ã Jacobien cña ϕ−1b»ng J(u, v) = ∂u ∂v ∂y ∂y = − ∂u ∂v ∂v ∂u ∂u ∂v
NhËn xÐt 1 Gi¶ sö h(x, y) l( h(m mËt ®é chung cña (X, Y ). C¸c ®¹i l−îng ngÉu nhiªn U v( V ®−îc x¸c ®Þnh X = a11U + a12V Y = a21U + a22V
Khi ®ã mËt ®é chung cña (U, V ) b»ng
g(u, v) = h (a11u + a12v, a21u + a22v) |det(A)| a trong ®ã A = 11 a12 l( ma trËn kh«ng suy biÕn. a21 a22
X v Y l hai ®¹i l−îng ngÉu nhiªn ®éc lËp thuéc N (0, 1). Khi ®ã ξ = X + Y v η = X − Y còng √
®éc lËp v cã cïng ph©n bè chuÈn (∈ N(0, ( 2)2)). ThËt vËy X 1 Y Suy ra 1 1 g(u, v) = √ √ e− u √ √ e− u 2π 2 2π 2 NhËn xÐt 2
1. NÕu X v( Y l( hai ®¹i l−îng ngÉu nhiªn ®éc lËp, khi ®ã h(m ph©n bè cã ®iÒu kiÖn cña X víi ®iÒu kiÖn
Y = y trïng víi h(m ph©n bè cña X, (kh«ng phô thuéc v(o ®iÒu kiÖn Y = y)
F (x/Y = y) = P (X < x/Y = y) = P (X < x) = F (x).
2. Tæng qu¸t h¬n, gi¶ sö ϕ(x, y) l( mét h(m hai biÕn bÊt k×, X v( Y l( hai ®¹i l−îng ngÉu nhiªn ®éc lËp.
Khi ®ã h(m ph©n bè cã ®iÒu kiÖn cña ϕ(X, Y ) víi ®iÒu kiÖn Y = y trïng víi h(m ph©n bè cña ϕ(X, y)
P (ϕ(X, Y ) < x/Y = y) = P (ϕ(X, y) < x. http://www.ebook.edu.vn 11 CuuDuongThanCong.com
https://fb.com/tailieudientucntt
Ch¼ng h¹n ®Ó tÝnh hm mËt ®é cña tæng hai ®¹i l−îng ngÉu nhiªn ®éc lËp X v Y , cã thÓ suy ra tõ nhËn xÐt trªn nh− sau:
XÐt Z = ϕ(X, Y ) = X + Y , hm ph©n bè cã ®iÒu kiÖn cña Z víi ®iÒu kiÖn Y = y (kÝ hiÖu H(z/y)), theo
nhËn xÐt trªn b»ng hm ph©n bè cña ϕ(X, y)(= X + y)
H(z/y) = P (X + y < z) = F (z − y)
®¹o hm hai vÕ theo z ®Ó x¸c ®Þnh hm mËt ®é, ta ®−îc mËt ®é cã ®iÒu kiÖn cña Z víi ®iÒu kiÖn Y = y (kÝ hiÖu h(z/y)) h(z/y) = f (z − y).
¸p dông c«ng thøc ”x¸c suÊt ®Çy ®ñ më réng” ®Ó tÝnh hm mËt ®é cña Z (kÝ hiÖu r(z)), ta ®−îc ∞ ∞ r(z) = h(z/y)g(y) dy = f (z − y)g(y) dy. −∞ −∞
§©y chÝnh l c«ng thøc x¸c ®Þnh hm mËt ®é cña tæng hai ®¹i l−îng ngÉu nhiªn ®éc lËp.
Hon ton t−¬ng tù ta cã thÓ thiÕt lËp ®−îc c¸c hm mËt ®é cña XY v X/Y , nÕu X, Y ®éc lËp nhau. B¹n
®äc tù chøng minh c¸c kÕt qu¶ sau:
a. Hm mËt ®é cña XY b»ng ∞ 1 z s(z) = f ( )g(y) dy −∞ |y| y
b. Hm mËt ®é cña X b»ng Y ∞ t(z) = |y|f(zy))g(y) dy −∞ Ch m hm ph©n b cã ®iÒu
kiÖn ®ã b»ng hm ph©n bè cña y X (kh«ng ®iÒu kiÖn), suy ra, hm mËt ®é cña y X b»ng 1 f( z ), vËy hm |y| y mËt ®é cña XY ∞ 1 z s(z) = f ( )g(y) dy. y −∞ |y| B%i tËp
1. Gi¶ sö X v Y l hai ®¹i l−îng ngÉu nhiªn ®éc lËp cã cïng ph©n bè ®Òu trªn (−1, 1). H1y tÝnh hm mËt ®é cña X + Y .
2. Gi¶ sö X v Y l hai ®¹i l−îng ngÉu nhiªn ®éc lËp cã cïng ph©n bè ®Òu trªn (a, b) (®Ó ®¬n gi¶n ta gi¶ thiÕt
a, b l c¸c sè d−¬ng 0 < a < b). H1y tÝnh hm mËt ®é cña ®¹i l−îng ngÉu nhiªn tÝch XY .
3. Gi¶ sö X v Y l hai ®¹i l−îng ngÉu nhiªn ®éc lËp cã cïng ph©n bè mò víi tham sè λ. H1y tÝnh hm mËt ®é cña |X − Y |. 4. Gä y/x) l hm m y. H1y
x¸c ®Þnh c¸c hm mËt cã ®iÒu kiÖn g(y/x) v f(x/y).
4’. Kh¸c mét chót víi bi tËp 4, gi¶ sö X v Y l hai ®¹i l−îng ngÉu nhiªn ®éc lËp, X cã ph©n bè mò víi
tham sè λ, trong khi Y cã ph©n bè mò víi tham sè ;, (; = λ). KÝ hiÖu g(y/x) l hm mËt ®é cña X + Y víi
®iÒu kiÖn X = x v f(x/y) l hm mËt ®é cña X víi ®iÒu kiÖn X + Y = y. H1y x¸c ®Þnh c¸c hm mËt cã
®iÒu kiÖn g(y/x) v f (x/y).
5. Gi¶ sö X = (X1, X2) v Y = (Y1, Y2) l hai ®iÓm chän ngÉu nhiªn (theo ph©n bè ®Òu) ®éc lËp nhau trªn ®−êng trßn ®¬n vÞ: x2 + y2 = 1
H1y t×m hm mËt ®é cña ®¹i l−îng ngÉu nhiªn X Z = 1 X2 Y 1 Y2 http://www.ebook.edu.vn 12 CuuDuongThanCong.com
https://fb.com/tailieudientucntt 3. K× väng cã ®iÒu kiÖn
Gi¶ sö A l biÕn cè cã x¸c suÊt P (A) > 0 v X l ®¹i l−îng ngÉu nhiªn tïy ý. T−¬ng tù nh− ®Þnh nghÜa
k× väng cña ®¹i l−îng ngÉu nhiªn, ta cã ®Þnh nghÜa sau
§Þnh nghÜa 4 NÕu X l( ®¹i l−îng ngÉu nhiªn rêi r¹c chØ nhËn c¸c gi¸ trÞ xi, i = 1, 2, ..., khi ®ã E(X/A) = xiP (X = xi/A) i
®−îc gäi l( k× väng cã ®iÒu kiÖn cña X víi ®iÒu kiÖn biÕn cè A x¶y ra.
Tr−êng hîp X l( ®¹i l−îng ngÉu nhiªn liªn tôc víi f (x/A) l( h(m mËt ®é cã ®iÒu kiÖn, khi ®ã ∞ E(X/A) = xf(x/A) dx −∞
®−îc gäi l( k× väng cã ®iÒu kiÖn cña X víi ®iÒu kiÖn biÕn cè A x¶y ra.
NÕu X v( Y l( hai ®¹i l−îng ngÉu nhiªn liªn tôc víi f (x) v( g(x) l( c¸c h(m mËt ®é cña chóng. Gäi
f (x/y) l( h(m mËt ®é cã ®iÒu kiÖn cña X víi ®iÒu kiÖn Y = y K× väng cña X víi ®iÒu kiÖn Y = y, ®−îc kÝ
hiÖu E(X/Y = y) l( tÝch ph©n ∞ E(X/Y = y) = xf(x/y) dx, −∞
nÕu tÝch ph©n tån t¹i v( héi tô tuyÖt ®èi. §Þnh l X ®èi víi Y , E(X) = E(E(X/Y )). Chøng minh
KÝ hiÖu h(y) = E(X/Y = y) (ng−êi ta gäi h(y) l hm håi quy cña X víi ®iÒu kiÖn Y = y) ∞ ∞ E(h(Y )) = h(y)g(y) dy = E(X/Y = y)g(y) dy = −∞ −∞ ∞ ∞ ∞ ∞ = xf(x/y) dx g(y) dy = x f (x/y)g(y)dy dx −∞ −∞ −∞ −∞
MÆt kh¸c f (x) = ∞ f(x/y)g(y) dy nªn −∞ ∞ E(h(Y )) = E(E(X/Y )) = xf(x) dx = E(X) ®.p.c.m. −∞
4. T−¬ng quan v% hÖ sè t−¬ng quan
§Þnh nghÜa 5 NÕu X v( Y l( hai ®¹i l−îng ngÉu nhiªn tån t¹i k× väng E(X) v( E(Y ), khi ®ã
cov(X, Y ) = E[(X − E(X))(Y − E(Y ))]
®−îc gäi l( covarian (hay cßn gäi l( m« men t−¬ng quan) cña X v( Y .
HiÓn nhiªn nÕu X v Y ®éc lËp , khi ®ã
cov(X, Y ) = E[(X − E(X))(Y − E(Y ))] = E(X − E(X)) E(Y − E(Y )) = 0 http://www.ebook.edu.vn 13 CuuDuongThanCong.com
https://fb.com/tailieudientucntt
Tr−êng hîp X = Y , khi ®ã covarian cov(X, X) = D(X).
M« men t−¬ng quan cña hai ®¹i l−îng ngÉu nhiªn cã c¸c tÝnh chÊt sau
i) cov(X, Y ) = E[(X − E(X))(Y − E(Y ))] = E(XY ) − E(X)E(Y )
ii) cov(αX, Y ) = cov(X, αY ) = αcov(X, Y ) iii) KÝ hiÖu σx = D(X) v σy =
D(Y ) l c¸c ®é lÖch tiªu chuÈn cña X v Y . Khi ®ã |cov(X, Y )| σxσy. ThËt vËy xÐt
E[(Y − tX)2] = E(Y 2 − 2tXY + t2Y 2) = E(Y 2) − 2E(XY )t + E(Y 2)t2 ≥ 0 víi mäi t.
§©y l tam thøc bËc hai kh«ng ©m víi mäi t, suy ra
[E(XY )]2 E(X2)E(Y 2)hay |E(XY )| E(X2) E(Y 2)
¸p dông bÊt ®¼ng thøc trªn víi X − E(X) v Y − E(Y ) thay cho X v Y
|cov(X, Y )| = |E[(X − E(X))(Y − E(Y ))]| D(X) D(X) = σxσy.
NhËn xÐt r»ng tõ chøng minh trªn suy ra |cov(X, Y )| = σxσy ⇔
Y l mét hm bËc nhÊt cña X : Y = aX + b. §Þnh nghÜa 6 cov(X, Y ) E[(X − E(X))(Y − E(Y ))] >(X, Y ) = = σxσy D(X) D(X)
®−îc gäi l( hÖ sè t−¬ng quan cña X v( Y .
HiÓn nhiªn hÖ sè t−¬ng quan cã c¸c tÝnh chÊt i) −
ii) NÕu X v Y ®éc lËp, khi ®ã hÖ sè t−¬ng quan >(X, Y ) = 0
HÖ sè t−¬ng quan ®o møc ®é phô thuéc tuyÕn tÝnh gi÷a Y v X. NÕu |>(X, Y )| xÊp xØ 1 khi ®ã c¸c ®iÓm
ngÉu nhiªn (X, Y ) gÇn nh− t¹o thnh mét ®−êng th¼ng trªn mÆt ph¼ng to¹ ®é. Khi >(X, Y ) = 0 ta nãi X v
Y kh«ng t−¬ng quan. Chó ý r»ng nÕu X v Y ®éc lËp khi ®ã chóng kh«ng t−¬ng quan, ng−îc l¹i tõ sù kh«ng
t−¬ng quan cña X v Y kh«ng suy ra chóng ®éc lËp víi nhau.
§Þnh nghÜa 7 KÝ hiÖu c = cov(X, Y ) l( m« men t−¬ng quan cña X v( Y . Khi ®ã ma trËn D(X) c C = c D(Y )
®−îc gäi l( ma trËn covarian (ma trËn t−¬ng quan) cña X v( Y .
Duy tr× c¸c kÝ hiÖu σx, σy l c¸c ®é lÖch tiªu chuÈn cña X v Y , > l hÖ sè t−¬ng quan cña X v Y . Tõ
®Þnh nghÜa hÖ sè t−¬ng quan suy ra c = >σxσy. Khi ®ã ma trËn covarian cã thÓ viÕt d−íi d¹ng Do |>| 1 nªn σ2 det(C) = x >σxσy >σ = (1 − >2)σ2 xσ2 x ≥ 0 xσy σ2 y
Ph−¬ng sai cña ®¹i l−îng ngÉu nhiªn cho ta biÕt ®é lÖch ®¹i l−îng ngÉu nhiªn v gi¸ trÞ trung b×nh cña ®¹i
l−îng ngÉu nhiªn ®ã. Ma trËn c¸c hÖ sè t−¬ng quan còng ®ãng vai trß t−¬ng tù nh− ph−¬ng sai khi xÐt ®é dao
®éng cña vÐc t¬ ngÉu nhiªn.
Gi¶ sö d l ®−êng th¼ng ®i qua (EX, EY ) (gi¸ trÞ trung b×nh cña vÐc t¬ ngÉu nhiªn (X, Y )) v − → n (α, β) l
vÐc t¬ ®¬n vÞ chØ ph−¬ng cña d. Gäi
Z = α(X − EX) + β(Y − EY ) http://www.ebook.edu.vn 14 CuuDuongThanCong.com
https://fb.com/tailieudientucntt
l h×nh chiÕu vu«ng gãc cña (X − EX, Y − EY ) lªn ®−êng th¼ng d. Ph−¬ng sai cña Z sÏ ®−îc tÝnh th«ng qua ma trËn covarian C nh− sau
D(Z) = α2E(X − EX)2 + β2(Y − EY )2 + 2αβE(X − EX)E(Y − EY ) =
= α2σ2x + β2σ2y + 2αβ>σxσy
NhËn xÐt r»ng ph−¬ng sai cña Z l d¹ng ton ph−¬ng víi ma trËn covarian C l ma trËn cña d¹ng ton ph−¬ng
®ã. Do det(C) ≥ 0, nãi chung C l ma trËn b¸n x¸c ®Þnh d−¬ng. NÕu X v Y ®éc lËp tuyÕn tÝnh (|>| < 1),
khi ®ã C l ma trËn x¸c ®Þnh d−¬ng thùc sù.
NhËn xÐt 3 Sö dông c¸c phÐp to¸n ®èi víi ma trËn, ta cã thÓ më réng kh¸i niÖm ma trËn covarian cho nhiÒu ®¹i l−îng ngÉu nhiªn
Xi, E(Xi) = mi, cov(Xi, Xj) = σij, i, j = 1, 2, ..., n
Khi ®ã ma trËn covarian cña (X1, X2, ..., Xn) l( σ11 σ12 σ1n σ 21 σ C(X) = 22 σ2n σn1 σn2 σnn
Gi¶ sö ai, i = 1, 2, ...n l( c¸c sè thùc bÊt k×. Khi ®ã n n 2 D( aiXi) = E ai(Xi − mi) = i=1 i=1 = aiajσij i j T−¬ng cov( aiXi, biXi) = aibjσij i=1 i=1 i j
KÝ hiÖu l( c¸c vÐc t¬ cét víi c¸c th(nh phÇn ai, bi, Xi, mi t−¬ng øng. l( ma trËn covarian cña
. Tõ c¸c ®¼ng thøc trªn suy ra E(AT X) = AT E(X) = AT M D(AT X) = AT C(X)A
cov(AT X, BT X) = AT C(X)B = BT C(X)A. 4 H%m ®Æc tr−ng
1. §¹i l−îng ngÉu nhiªn phøc
Trong lÝ thuyÕt x¸c suÊt ng−êi ta sö dông h(m ®Æc tr−ng nh− l mét c«ng cô quan träng ®Ó chøng minh c¸c ®Þnh lÝ Tr−íc khi dÉ
Gäi ξ v η l hai ®¹i l−îng ngÉu nhiªn, khi ®ã ζ = ξ + iη ®−îc gäi l ®¹i l−îng ngÉu nhiªn phøc. Nã thùc
chÊt l mét hm víi gi¸ trÞ phøc ®−îc x¸c ®Þnh trªn kh«ng gian c¸c biÕn cè ngÉu nhiªn c¬ b¶n . K× väng v
ph−¬ng sai cña ζ ®−îc x¸c ®ônh nh− sau E(ζ) = E(ξ) + iE(η) D(ζ) = E(|ζ − E(ζ)|2)
Hai ®¹i l−îng ngÉu nhiªn phøc ζ1 = ξ1 + iη2 v ζ2 = ξ2 + iη2 ®éc lËp nhau nÕu c¸c vÐct¬ ngÉu nhiªn (ξ1, η1)
v (ξ2, η2) ®éc lËp nhau. Sù ®éc lËp cña nhiÒu ®¹i l−îng ngÉu nhiªn phøc còng l sù ®éc lËp cña c¸c ®¹i l−îng
ngÉu nhiªn 2 chiÒu. DÔ dng chøng minh ®−îc khi ®ã E(ζ1ζ2) = E(ζ1) + E(ζ2) D(ζ1 + ζ2) = D(ζ1) + D(ζ2) http://www.ebook.edu.vn 15 CuuDuongThanCong.com
https://fb.com/tailieudientucntt
KÕt qu¶ ny còng më réng cho tr−êng hîp nhiÒu h¬n hai ®¹i l−îng ngÉu nhiªn ®éc lËp.
2. H%m ®Æc tr−ng v% c¸c tÝnh chÊt cña h%m ®Æc tr−ng
H(m ®Æc tr−ng cña ®¹i l−îng ngÉu nhiªn ξ ®−îc x¸c ®Þnh trªn R
ϕ(t) = E(eitξ) = E(cos tξ) + iE(sin tξ) ξ x
Tr−êng hîp ξ l ®¹i l−îng ngÉu nhiªn rêi r¹c 1 x2 ... xn ... P p1 p2 ... pn ... khi ®ã +∞ +∞ +∞ ϕ(t) = pn cos txn + i pn sin txn = pneitxn. n=1 n=1 n=1
NÕu ξ l ®¹i l−îng ngÉu nhiªn liªn tôc víi f(x) l hm mËt ®é, hm ®Æc tr−ng cña ξ +∞ +∞ +∞ ϕ(t) = f (x) cos tx dx + i f (x) sin tx dx = f (x)eitxdx. −∞ −∞ −∞
Hm ®Æc tr−ng lu«n lu«n tån t¹i v chóng cã c¸c tÝnh chÊt sau
1. Gi¸ trÞ h(m ®Æc tr−ng t¹i t = 0 lu«n b»ng 1, ϕ(0) = 1 v( |ϕ(t)| 1 víi mäi t ∈ R.
ThËt vËy, ϕ(0) = 1 l hiÓn nhiªn. ¸p dông bÊt ®¼ng thøc E2(X) E(X2) víi bÊt k× X
|ϕ(t)|2 = E2(cos tξ) + E2(sin tξ) E(cos2 tξ) + E(sin2 tξ) = 1. 2. Víi mäi t ∈ R −itξ m ®Æc
tr−ng cña ξ nhËn c¸c gi¸ trÞ thùc v ϕ(t) l hm ch½n.
3. Víi c¸c sè thùc bÊt k× a v( b, h(m ®Æc tr−ng cña ®¹i l−îng ngÉu nhiªn X = aξ + b b»ng E(itX) = eibtϕ(at).
4. H(m ®Æc tr−ng ϕ(t) liªn tôc ®Òu trªn to(n bé R.
Chän ε > 0 tïy ý. KÝ hiÖu Aλ l biÕn cè |ξ| > λ sao cho P (Aλ) = P (|ξ| > λ) < ε. Khi ®ã 3
ϕ(t) = E(eitξ/Aλ)P (Aλ) + E(eitξ/Aλ)P (Aλ). Suy ra ε
|ϕ(t) − E(eitξ/Aλ)P (Aλ)| = |E(eitξ/Aλ)P (Aλ)| 1 |P (Aλ)| 3 Tõ ®©y ta suy ra 2ε 2ε |ϕ(t ξ 1) − ϕ(t2)| E(|eit it − e ξ|/Aλ)P (Aλ) + E(|(t1 − t 3 2)ξ|/Aλ) + 3
5. H(m ®Æc tr−ng cã tÝnh chÊt ®Æc biÖt quan träng sau ®©y: Gi¶ sö ξ1, ξ2, ..., ξn l( c¸c ®¹i l−îng ngÉu nhiªn
ho(n to(n ®éc lËp, khi ®ã h(m ®Æc tr−ng cña tæng X = ξ1 + ξ2 + ξn b»ng n ϕ (t) = ϕ (t) X ξi i=1
Do nhËn xÐt sù ®éc lËp cña nhiÒu ®¹i l−îng ngÉu nhiªn phøc còng l sù ®éc lËp cña c¸c ®¹i l−îng ngÉu
nhiªn nhiÒu chiÒu, nªn kÕt qu¶ trªn ®−îc suy ra tõ ®Þnh lÝ k× väng cña tÝch c¸c ®¹i l−îng ngÉu nhiªn ®éc
lËp b»ng tÝch c¸c k× väng. http://www.ebook.edu.vn 16 CuuDuongThanCong.com
https://fb.com/tailieudientucntt
6. NÕu tån t¹i c¸c m«ment cÊp k, (k = 1, 2, ..., n) cña ξ, khi ®ã h(m ®Æc tr−ng ϕξ(t) kh¶ vi cÇp n v(
ϕ(k)(0) = ikE(ξk) (k = 1, 2, ..., n). ξ
Theo gi¶ thiÕt +∞ f (x)|x| dx tån t¹i v h÷u h¹n nªn +∞ xeitxf(x) dx héi tô ®Òu theo t, suy ra −∞ −∞ +∞ +∞ ′ ′ ϕ itx xf(x) dx = iE(ξ) ξ (t) = ixe f (x) dx ⇒ ϕ ξ(0) = i −∞ −∞
LËp luËn t−¬ng tù víi k = 2, ..., n.
7. Ta c«ng nhËn kÕt qu¶ rÊt m¹nh sau ®©y cña hm ®Æc tr−ng: C¸c h(m ph©n bè ®−îc x¸c ®Þnh duy nhÊt
bëi h(m ®Æc tr−ng cña nã. Ngo(i ra nÕu gi¶ thiÕt tÝch ph©n
+∞ |ϕ(t)| dt < +∞ khi ®ã h(m mËt ®é −∞ f (x) liªn tôc, v( 1 +∞ f (x) = ϕ(t)e−itx dt 2π −∞
8. Cho mét d1y c¸c hm ph©n bè F (x), F1(x), F1(x), ... cïng víi c¸c hm ®Æc tr−ng t−¬ng øng ϕ(t), ϕ1(t), ϕ2(t), ...
§iÒu kiÖn cÇn v ®ñ ®Ó
lim Fn(x) = F (x) t¹i mäi ®iÓm liªn tôc cña F (x) n→∞
l, víi mäi sè thùc t ∈ R lim ϕn(t) = ϕ(t). n→∞ B%i tËp 6
1. Hm ®Æc tr−ng cña ξk(k = 1, 2, ..., n) ph©n bè theo luËt 0, 1
Suy ra hm ®Æc tr−ng cña ph©n bè nhÞ thøc ξ = ξ i=1 i
(do ξ l tæng cña c¸c ®¹i l−îng ngÉu nhiªn ®éc lËp ξi)
ϕ(t) = E(eitξ) = (1 + p(eit − 1))n
2. Hm ®Æc tr−ng cña ph©n bè Poisson ∞ λk ∞ (λeit)k it ϕ(t) = eitke−λ = e−λ = eλ(e −1) k! k! k=0 k=0
3. Hm ®Æc tr−ng cña ph©n bè mò +∞ 1 ϕ(t) = λ e−x(λ−it)dx = 0 1 − it λ
4. Hm ®Æc tr−ng cña ph©n bè ®Òu trªn (−1, 1)
Chó ý r»ng t−¬ng tù nh− h(m ®Æc tr−ng cña ®¹i l−îng ngÉu nhiªn ξ víi f (x) l( h(m mËt ®é, ng−êi ta cßn
®−a v(o mét h(m kh¸c ®−îc ®Þnh nghÜa nh− sau +∞ G(t) = E(etξ) = etxf (x) dx −∞
Kh¸c víi h(m h(m ®Æc tr−ng, h(m G(t) kh«ng ph¶i lu«n lu«n tån t¹i. §èi víi ph©n bè chuÈn ξ ∈ N(0, 1) 1 +∞ 1 +∞ 1 +∞ x−t t t G(t) = √ etxe− x + t dx = √ e− x−t dx = √ e− e dx = e 2π −∞ 2π −∞ 2π −∞
Sö dông nã ta cã thÓ tÝnh hm ®Æc tr−ng cña ph©n bè chuÈn http://www.ebook.edu.vn 17 CuuDuongThanCong.com
https://fb.com/tailieudientucntt
5. Hm ®Æc tr−ng cña ph©n bè chuÈn ξ ∈ N(0, 1) it ϕ(t) = G(it) = e = e− t
6. Sö dông tÝnh chÊt 3. hm ®Æc tr−ng cña ph©n bè chuÈn ξ ∈ N(m, σ2) ϕ(t) = eimt−σ t
7. Hm ®Æc tr−ng cña ph©n bè χ2n = ξ21 + ξ22 + + ξ2 . §©y l tæng cña n ®¹i l−îng ngÉu nhiªn ®éc lËp n
cã cïng ph©n bè χ2 víi mét bËc tù do. Ta ®1 biÕt r»ng hm mËt ®é cña mçi sè h¹ng b»ng 1 √ e− x nÕu x > 0, h(x) = 2πx 0 nÕu x < 0
Hm ®Æc tr−ng cña χ2 b»ng 1 ∞ 1 ∞ 1 ϕ (1−2it) ξ (t) = eitx √ e− xdx = √ e− x dx = k 0 2πx 0 2πx ∞ 2 1 = e− u (1−2it) du = √ 0 π 1 − 2it
VËy hm ®Æc tr−ng cña ph©n bè χ2 víi n n bËc tù do ϕ(t) = (1 − 2it)− n
Chó ý r»ng tõ tÝnh chÊt 6. cã thÓ tÝnh k× väng, ph−¬ng sai v( m«ment c¸c cÊp cña c¸c ®¹i l−îng ngÉu nhiªn
dùa v(o h(m ®Æc trung cña c¸c ®¹i l−îng ngÉu nhiªn ®ã. Ch¼ng h¹n ph−¬ng sai cña ®¹i l−îng ngÉu nhiªn ph©n bè χ2n B% a) ϕ(t) = 1 1+t
XÐt h(m mËt ®é f(x) = e−|x| . H(m ®Æc tr−ng cña ph©n bè ®ã b»ng ϕ(t) = 1 . NÕu ¸p dông tÝch ph©n 2 1+t trong tÝnh chÊt 7. e−|x| 1 +∞ 1 +∞ 1 = e−itx dt ⇔ e−|u| = eiux dx 2 2π π(1 + x2) −∞ 1 + t2 −∞
VËy ϕ(t) = e−|t| l( h(m ®Æc tr−ng cña ph©n bè Cauchy.
b) ϕ(t) = e−t kh«ng l hm ®Æc tr−ng.
Do ϕ′′(0) = 0 suy ra D(ξ) = 0, v« lÝ.
c) ϕ(t) = sin t kh«ng l hm ®Æc tr−ng.
d) ϕ(t) = cos t l hm ®Æc tr−ng cña ξ víi ph©n bè cña ξ : P (ξ = 1) = P (ξ = −1) = 1 . e) ) = 1 , 4 P (ξ = 0) = 1 . 2
f) T×m hm ®Æc tr−ng cña ®¹i l−îng ngÉu nhiªn cã hm mËt ®é f (x) = 1 − |x|, víi |x| 1 1 2 t 2 ϕ(t) = eitx(1 − |x|)dx = sin t 2 −1
Ta còng cã thÓ ®¹t ®−îc kÕt qu¶ trªn b»ng c¸ch chøng minh f (x) = 1 − |x| l( h(m mËt ®é cña tæng hai
®¹i l−îng ngÉu nhiªn ®éc lËp ph©n bè ®Òu trªn ®o¹n [−1, 1 2 ]. 2 http://www.ebook.edu.vn 18 CuuDuongThanCong.com
https://fb.com/tailieudientucntt
B%i tËp 2. Chøng tá r»ng nÕu ϕ(t) l hm ®Æc tr−ng, khi ®ã 1
còng l hm ®Æc tr−ng. 2−ϕ(t)
Gi¶ sö ξ1, ξ2, ... l d1y c¸c ®¹i l−îng ngÉu nhiªn ®éc lËp cïng cã ϕ(t) l hm ®Æc tr−ng. Gäi ν l ®¹i l−îng
ngÉu nhiªn ®éc lËp víi d1y trªn v 1 P (ν = n) = (n = 0, 1, ...). 2n+1 XÐt ξ ξ = 1 + ξ2 + + ξν nÕu ν > 0, 0 nÕu ν = 0
¸p dông ®Þnh lÝ k× väng ®Çy ®ñ ∞ ∞ (ϕ(t))n 1 ϕξ(t) = E(eitξ) = E(eitξ/{ν = n})P (ν = n) = = 2n+1 2 − ϕ(t) n=0 n=0
B%i tËp 3. Chøng minh r»ng tæng cña hai ®¹i l−îng ngÉu nhiªn ®éc lËp cã ph©n bè chuÈn (víi c¸c tham sè tïy
ý) còng l ®¹i l−îng ngÉu nhiªn cã ph©n bè chuÈn.
ThËt vËy hm ®Æc tr−ng cña tæng hai ®¹i l−îng ngÉu nhiªn ®éc lËp cã d¹ng hm ®Æc tr−ng cña ph©n bè chuÈn ϕ im t t t−σ 1(t)ϕ2(t) = e
eimt−σ = ei(m+m)t−(σ+σ) t . 5
LuËt sè lín v% ®Þnh lÝ giíi h¹n trung t©m
1. C¸c d¹ng héi tô v% kh¸i niÖm vÒ luËt sè lín Sù æn g−êi ta gäi ch u nhiªn
Y1 + Y2 + + Yn → C khi n → ∞ n l luËt sè lín.
§Þnh nghÜa 8 Cho dMy Yn, n = 1, 2, ... c¸c ®¹i l−îng ngÉu nhiªn. Ta nãi Yn héi tô theo x¸c suÊt tíi ®¹i l−îng ngÉu nhiªn P
Y , kÝ hiÖu Yn → Y , nÕu víi bÊt k× ǫ > 0
lim P (|Yn − Y | > ǫ) = 0. n→∞
Ta nãi dMy c¸c ®¹i l−îng ngÉu nhiªn X h.c.c n,
n = 1, 2, ... héi tô hÇu ch¾c ch¾n tíi X, kÝ hiÖu Xn → X, nÕu P ( lim Xn = X) = 1. n→∞
Ta cã thÓ chøng minh héi tô hÇu ch¾c ch¾n kÐo theo héi tô theo x¸c suÊt. §iÒu ng−îc l¹i nãi chung kh«ng ®óng. ThËt vËy ∞ ∞ ∞ Gi¶ sö h.c.c
Xn → X, suy ra víi mäi ε > 0 ∞ ∞ ∞ P {|Xm − X| < ǫ} = lim P {|Xm − X| < ǫ} = 1. n→∞ n=1 m=n m=n Do vËy P
lim P (|Xm − X| < ε) = 1 hay Xn → X. n→∞ NhËn xÐt r»ng X h.c.c n → X t−¬ng ®−¬ng víi ∞ lim P
{|Xm − X| < ǫ} = 1 víi mäi ε > 0 ⇔ sup |Xm − X| P → 0. n→∞ m=n m≥n http://www.ebook.edu.vn 19 CuuDuongThanCong.com
https://fb.com/tailieudientucntt
§Þnh lÝ 5 (Trªb−sÐp) Gi¶ sö X l( ®¹i l−îng ngÉu nhiªn tån t¹i k× väng m = E(X) v( ph−¬ng sai σ2 = D(X).
Khi ®ã víi mäi ǫ > 0 ta cã: σ2 P (|X − m| ≥ ǫ) ǫ2
Chøng minh Víi ®¹i l−îng ngÉu nhiªn kh«ng ©m Y , ta biÕt r»ng P (Y ≥ ǫ) E(Y ) . Do ®ã ǫ E(|X − m|2) σ2
P (|X − m| ≥ ǫ) = P (|X − m|2 ≥ ǫ2) = . ǫ2 ǫ2
2. LuËt sè lín v% ®Þnh lÝ giíi h¹n trung t©m
B©y giê ta ph¸t biÓu v chøng minh ®Þnh lÝ sau vÒ luËt sè lín
§Þnh lÝ 6 (LuËt yÕu sè lín) Gi¶ sö X
l( c¸c ®¹i l−îng ngÉu nhiªn ®éc lËp cã cïng k× väng v( ph−¬ng 1, X2, ... sai E(Xi) = m, D(Xi) = σ2, i = 1, 2, ...
Khi ®ã X+X+...+Xn héi tô theo x¸c suÊt tíi m n X1 + X2 + ... + Xn P → m n Chøng minh Ta cã X X σ2 E 1 + X2 + ... + Xn = m, D 1 + X2 + ... + Xn = n n n
¸p dông ®Þnh lÝ Trªb−sÐp ta ®−îc ®.p.c.m.
NhËn xÐt r»ng ®Þnh lÝ trªn vÉn ®óng nÕu ta thay gi¶ thiÕt sù ®éc lËp b»ng sù kh«ng t−¬ng quan cña c¸c ®¹i
l−îng ngÉu nhiªn X1, X2, ...
Cuèi cïng ta ph¸t biÓu, kh«ng chøng minh ®Þnh lÝ sau cña Kolgomorov
§Þnh lÝ 7 (LuËt m¹nh sè lín) Gi¶ sö X1, X2, ... l( c¸c ®¹i l−îng ngÉu nhiªn ®éc lËp cã cïng h(m ph©n bè.
Khi ®ã ®iÒu kiÖn cÇn v( ®ñ ®Ó X+X+...+Xn héi tô hÇu ch¾c ch¾n tíi ; n X1 + X2 + ... + Xn h.c.c → ; n
l( tån t¹i k× väng E(Xi) v( E(Xi) = ;.
Sö dông c¸c kÕt qu¶ vÒ hm ®Æc tr−ng ta cã thÓ chøng minh ®Þnh lÝ giíi h¹n sau
§Þnh lÝ 8 Cho mét dMy c¸c ®¹i l−îng ngÉu nhiªn ®éc lËp cïng ph©n bè X1, X2, X3, ..., Xn, ... víi E(Xk) =
m, D(X ) = σ2 víi mäi k = 1, 2, ... Khi ®ã n→∞ σ n 2π −∞
Chøng minh KÝ hiÖu ϕ(t) l hm ®Æc tr−ng cña X t
k − m, khi ®ã hm ®Æc tr−ng cña Xk−m √ b»ng ϕ √ . øng σ n σ n
dông tÝnh chÊt 6 cña hm ®Æc tr−ng v khai triÓn Taylo ®Õn cÊp 2 t t2 1 ϕ √ = 1 − + o σ n 2n n ! "n Do tÝnh ®éc lËp cña X X +Xn−nm t
1, X2, ..., Xn hm ®Æc tr−ng cña X+ + √ b»ng ϕ √ . Suy ra σ n σ n · $ · $ t n t2 1 n lim ϕ √ = lim 1 − + o = e− t . n→∞ σ n n→∞ 2n n http://www.ebook.edu.vn 20 CuuDuongThanCong.com
https://fb.com/tailieudientucntt
§©y chÝnh l hm ®Æc tr−ng cña ph©n bè chuÈn thuéc líp N (0, 1), tõ tÝnh chÊt cuèi cïng cña hm ®Æc tr−ng,
suy ra ®iÒu ph¶i chøng minh.
§Æc biÖt khi X cã ph©n bè nhÞ thøc
P (X = k) = Cknpkqn−k, 0 < p < 1, q = 1 − p, 0 k n,
ng−êi ta chøng minh ®−îc r»ng B − np + 1 A − np − 1 P (A X B) ≈ Φ 2 √ − Φ 2 √ . npq npq
(Φ(.) l hm ph©n bè chuÈn thuéc líp N (0, 1))
C«ng thøc ny cßn ®−îc gäi l ®Þnh lÝ MoivrejLaplace.
TØ lÖ häc sinh giái trong mét tr−êng phæ th«ng b»ng 25%.
1. T×m x¸c suÊt ®Ó khi chän ngÉu nhiªn 100 em, sè häc sinh giái dao ®éng tõ 10 ®Õn 20.
2. H1y t×m x¸c suÊt ®Ó khi chän ngÉu nhiªn 500 em, sè häc sinh giái kh«ng Ýt h¬n 120 em. Gi¶i:
1. Gäi X l sè häc sinh giái trong sè 100 em chän ra, X cã ph©n bè nhÞ thøc víi p =0,25 n = 100. P (X = k) = Ck k 100−k npkqn−k = Ck 100(0, 25) (0, 75)
trong ®ã 0 k 100. Suy ra x¸c suÊt cÇn t×m 20
§Ó tÝnh gÇn ®óng x¸c suÊt trªn, ¸p dông c«ng thøc Moivre&Laplace
P (10 X 20) ≈ Φ(b) − Φ(a). trong ®ã 10 − 100 0, 25 − 1 a = 2 √
= −3, 58 v Φ(a) = Φ(−3, 58) = 0, 000172 100 0, 25 0, 75 20 − 100 0, 25 + 1 b = 2 √
= −1, 04 v Φ(b) = Φ(−1, 04) = 0, 14917 100 0, 25 0, 75 VËy
P (10 X 20) ≈ 0, 14917 − 0, 000172 = 0, 148998.
2. T−¬ng tù nh− phÇn 1, x¸c suÊt cÇn t×m xÊp xØ
Chó ý r»ng nÕu X cã ph©n bè nhÞ thøc m( n kh¸ lín v( p ®ñ nhá, cïng víi gi¶ thiÕt limn 0 →∞ np = λ > , khi
®ã c¸c sè h¹ng cña ph©n bè nhÞ thøc tiÕn dÇn tíi c¸c sè h¹ng t−¬ng øng cña ph©n bè Poisson lim Ck k = e λ λk . n→∞ npk(1 − p)n− − k!
Nãi c¸ch kh¸c trong tr−êng hîp n(y np k Ck n pk(1 − p)n−k ∼ = e−np ( ) . k! http://www.ebook.edu.vn 21 CuuDuongThanCong.com
https://fb.com/tailieudientucntt
TØ lÖ phÕ phÈm ë mét c«ng ty may mÆc b»ng 1,2%. H1y t×m x¸c suÊt ®Ó trong mét l« hng 500 chiÕc
¸o s¬ mi, sè ¸o bÞ lçi kh«ng v−ît qu¸ 11 chiÕc.
p = 0.012 kh¸ nhá, ¸p dông c«ng thøc gÇn ®óng nªu trªn 11 (np)k P (X 11) ≈ e−np = 0, 98. k! k=0
Ta cã thÓ minh häa sù xÊp xØ cña ph©n bè nhÞ thøc víi ph©n bè Poisson t−¬ng øng trong tr−êng hîp 1 p = , n = 64. 32
b»ng b¶ng so s¸nh d−íi ®©y Ph©n bè nhÞ thøc Ph©n bè Poisson k Ck k n pk(1 − p)n− − e np (np)k k! 0 0,131 0,135 1 0,271 0,271 2 0,275 0,271 3 0,183 0,180 4 0,090 0,090 5 0,035 0,036 6 0,011 0,012 7 0,003 0,003 8 0,001 0,001 9 0,000 0,000
(C¸c kÕt qu¶ trªn ®−îc tÝnh b»ng Mathematica 4.0) http://www.ebook.edu.vn 22 CuuDuongThanCong.com
https://fb.com/tailieudientucntt
1
MÉu ngÉu nhiªn v% ph©n bè mÉu XÐt mét mÉu ngÉu nhiªn (X1, X2, ..., Xn)
t−¬ng øng víi ®¹i l−îng ngÉu nhiªn X E(X) = m, D(X) = σ2.
Gäi ξ l ®¹i l−îng ngÉu nhiªn: 1 P (ξ = xi) = víi mäi i = 1, 2, ..., n. n
Khi ®ã E(ξ), D(ξ) ®−îc gäi l c¸c ®Æc tr−ng mÉu. Ng−êi ta kÝ hiÖu X = E(ξ) l k× väng mÉu v S2 = D(ξ)
l ph−¬ng sai mÉu. HiÓn nhiªn n X 1 X = 1 + X2 + ... + Xn = X n n i i=1 v n n 1 1 2 S2 = (X X2 . n i − X )2 = n i − X i=1 i=1 n n 1 1 σ2 E(X) = E(X D(X . n i) = m, D(X ) = n2 i) = n §Ó tÝn n n 1 1 (X 2 X2 . n i − X)2 = n i − X i=1 i=1 Suy ra 1 n 1 n E(S2) = 2 E (Xi − X)2 = E(X2 ) = n n i ) − E(X i=1 i=1 1 n σ2 n − 1 = (m2 + σ2) − m2 + = σ2. n n n i=1 KÝ hiÖu n n 1 S∗2 = S2 = (X n − 1 n − 1 i − X )2. i=1 Khi ®ã
S∗2 ®−îc gäi l l ph−¬ng sai mÉu ®iÒu chØnh.
E(X) = m = E(X), E(S∗2) = σ2 = D(X), NhËn xÐt 4
1. X kh«ng nh÷ng héi tô theo x¸c suÊt m( héi tô hÇu ch¾c ch¾n tíi m = E(X).
2. S2, S∗2 héi tô hÇu ch¾c ch¾n (suy ra còng héi tô theo x¸c suÊt) tíi σ2 khi n → ∞. http://www.ebook.edu.vn 23 CuuDuongThanCong.com
https://fb.com/tailieudientucntt
2 C¸c h%m ph©n bè th−êng gÆp trong thèng kª
H%m Gamma, Beta v% tÝnh chÊt h%m Gamma, Beta
A. TÝch ph©n sau héi tô víi mäi x > 0, y > 0 +∞ 1 Γ(x) = e−ttx−1dt, B(x, y) = tx−1(1 − t)y−1dt. 0 0
T¸ch Γ(x) thnh hai tÝch ph©n +∞ 1 +∞ Γ(x) = e−ttx−1dt = e−ttx−1dt + e−ttx−1dt = I1 + I2. 0 0 1
TÝch ph©n I1 héi tô v× víi 0 < x < 1, 0 < t 1, ta cã e−ttx−1 < 1 . t−x
TÝch ph©n I2 héi tô v× limt→+∞ e−ttx+1 = 0, suy ra víi t ®ñ lín e−ttx−1 < 1 . t
B. TÝch ph©n sau héi tô víi mäi x > 0, y > 0. 1 B(x, y) = tx−1(1 − t)y−1dt. 0
T¸ch Γ(x) thnh hai tÝch ph©n 1 c 1 B(x, y) = tx−1(1 − t)y−1dt = tx−1(1 − t)y−1dt + tx−1(1 − t)y−1dt. 0 0 c 1. Γ(1) = 1. 2. +∞ +∞ +∞ Γ(x + 1) = e−ttxdt = − txde−t = −txe−t|+∞ x−1 0 + xt e−tdt = xΓ(x) 0 0 0 3. lim Γ(x+1) x→0+ Γ(x) = limx→0+ = +∞. x
4. Víi x − k > 0, k l sè tù nhiªn bÊt k×
Γ(x) = (x − 1)(x − 2) (x − k)Γ(x − k) ⇒ suy ra Γ(n) = (n − 1)! √ 5. Chó ý r»ng Γ( 1) = π, suy ra 2 1
1 3 (2n − 1) √ (2n − 1)!! √ Γ(n + ) = π = π 2 2n 2n
6. Ta c«ng nhËn kÕt qu¶ sau ®óng víi mäi sè thùc x > 0, y > 0 Ph©n bè Gamma, Beta
1. NÕu Xi ∈ N(mi, σ2i ), i = 1, 2, ..., n ®éc lËp, khi ®ã trung b×nh mÉu X X =
1 + X2 + + Xn ∈ N(m, σ2) n trong ®ã m m σ2 σ2 m = 1 + m2 + + n , σ2 1 + σ2 2 + + n . n i = n http://www.ebook.edu.vn 24 CuuDuongThanCong.com
https://fb.com/tailieudientucntt
2. Ph©n bè cña Y = X2 víi X ∈ N(m, σ2). Hm mËt ®é cña Y √ −ym y √y g(y) = (2σ 2πy)−1e σ em σ + e−m σ . NÕu m = 0 1 −y − g(y) = √ e σ y . 2σ 2π
Ph©n bè cña Y = X2 l tr−êng hîp ®Æc biÖt cña ph©n bè Gamma: G(y, α, p) = const e−αyyp−1.
3. Ph©n bè Gamma l ph©n bè cã hm mËt ®é αp G(x, α, p) = e−αxxp−1, α > 0, p > 0, x > 0. Γ(p)
M« men cÊp k cña ph©n bè Gamma +∞ αp +∞ αp Γ(p + k) mk = xk e−αxxp−1dx = e−αxxk+p−1dx = . 0 Γ(p) 0 Γ(p) αkΓ(p)
V× vËy k× väng v ph−¬ng sai cña ph©n bè Gamma lÇn l−ît b»ng p Γ(p + 2) p2 p m = , σ2 = m − = . (1) α 2 − m21 = α2Γ(p) α2 α2
B%i tËp Gi¶ sö X ph©n bè ®Òu trªn ®o¹n [0, 1]. Chøng minh r»ng Y = − ln X cã ph©n bè Gamma víi c¸c tham sè α = 1, p = 1.
4. Ph©n bè Beta l ph©n bè cã hm mËt ®é Γ(α + β)
B(x, α, β) = [B(α, β)]−1 xα−1(1 − x)β−1 =
xα−1(1 − x)β−1, 0 < x < 1. Γ(α)Γ(β)
§Æc biÖt B(x, 1, 1) = x l hm mËt ®é cña ph©n bè ®Òu trªn ®o¹n [0, 1]. B%i tË
Tõ ®ã suy ra k× väng v ph−¬ng sai cña nã. (m = α , σ2 = αβ ). α+β (α+β)(α+β+1)
B%i tËp 2. Gi¶ sö X v Y ®éc lËp cã ph©n bè Beta víi c¸c tham sè (α1, β1) v (α2, β2) t−¬ng øng. Chøng
minh r»ng XY còng cã cã ph©n bè Beta víi c¸c tham sè (α2, β1 + β2), nÕu α1 = α2 + β2.
H−íng dÉn: XÐt phÐp biÕn ®æi u = xy, v = x. Khi ®ã Jac«biªn b»ng 1. TÝch ph©n h(m mËt ®é chung cña v
(U, V ) theo v tõ u ®Õn 1 ta ®−îc mËt ®é cña XY .
B%i tËp 3. Gi¶ sö X ∈ G(α1, 1) v Y ∈ G(α2, 1) ®éc lËp cã ph©n bè Gamma. Khi ®ã u = X cã ph©n bè X+Y
Beta víi c¸c tham sè (α1, α2).
H−íng dÉn: XÐt phÐp biÕn ®æi u = x , v = y. TÝch ph©n h(m mËt ®é chung theo v tõ 0 ®Õn ∞. x+y
§Þnh lÝ 9 NÕu X ∈ G(α, p1), Y ∈ G(α, p2) ®éc lËp, khi ®ã r = X + Y v( f = X còng ®éc lËp. Ngo(i ra Y
r ∈ G(α, p1 + p2) v( h(m mËt ®é cña f b»ng Γ(p1 + p2) f p−1 . Γ(p1)Γ(p2) (1 + f )p+p Chøng
§æi biÕn x = r sin2 ϕ, y = r cos2 ϕ,
0 < r < +∞, 0 < ϕ < π , khi ®ã Jacobien cña (x, y) b»ng J(r, ϕ) = 2
r sin 2ϕ. MËt ®é cña (r, ϕ) b»ng
c′ e−αrrp+p−1(sin ϕ)2p−1(cos ϕ)2p−1, (2)
®iÒu ®ã chøng tá r v ϕ ®éc lËp. Suy ra r = X + Y v f = X = tg2ϕ còng ®éc lËp. Tõ biÓu thøc (2) hiÓn Y nhiªn r ∈ G(α, p1 + p2). √
§Ó x¸c ®Þnh hm mËt ®é cña f, ta sö dông phÐp ®æi biÕn ϕ = arctg f, ta thu ®−îc kÕt qu¶ Γ(p1 + p2) f p−1 . Γ(p1)Γ(p2) (1 + f )p+p
Chó ý r»ng víi phÐp biÕn ®æi 1 u = 1 , khi ®ã up ∞ f p− −1(1 df . 1+f − u)p−1du = 0 0 (1+f )p p http://www.ebook.edu.vn 25 CuuDuongThanCong.com
https://fb.com/tailieudientucntt 1. Ph©n bè χ2.
NÕu Xi ∈ N(0, 1), i = 1, 2, ..., n ®éc lËp, khi ®ã ph©n bè cña X21 + X22 + + X2 ®−îc gäi l ph©n n
bè χ2 víi n bËc tù do. Ng−êi ta th−êng kÝ hiÖu χ2(n) l líp c¸c ®¹i l−îng ngÉu nhiªn cã ph©n bè χ2 víi
n bËc tù do. §©y l tr−êng hîp ®Æc biÖt cña ph©n bè Gamma (α = 1, p = n ) víi hm mËt ®é 2 2 1 n 1 n G(x, , ) =
e− x x −1, x > 0. 2 2 2 nΓ( n ) 2
Do ®¼ng thøc (1), k× väng v ph−¬ng sai cña ph©n bè χ2(n) lÇn l−ît b»ng m = n, σ2 = 2n. 2. Ph©n bè F .
NÕu X1 ∈ χ2(m), X2 ∈ χ2(n) ®éc lËp, khi ®ã ph©n bè cña 1 X1 F = m 1 X n 2
®−îc gäi l ph©n bè F víi (m, n) bËc tù do. MËt ®é cña X b»ng X Γ( m+n) m f −1 2 . Γ( m )Γ( n ) mn 2 2 (1 + f )
MËt ®é cña ph©n bè F víi (m, n) bËc tù do b»ng m m m Γ( m+n) x −1 2 . n Γ( m)Γ( n ) mn 2 2 (1 + mx) n 3. Y √ T = √ n X
®−îc gäi l ph©n bè T (hay ph©n bè Student) víi n bËc tù do. Ph©n bè ®ång thêi cña (Y, X) b»ng c e− y n e− x x −1.
§æi biÕn y = r sin ϕ, x = r2 cos2 ϕ,
0 < r < +∞, − π < ϕ < π , khi ®ã Jacobien cña (x, y) b»ng 2 2
J(r, ϕ) = 2r2 cos ϕ. MËt ®é cña (r, ϕ) b»ng
c′ e− r rn(cos ϕ)n−1,
®iÒu ®ã chøng tá r v ϕ ®éc lËp. Chó ý r»ng hÖ sè c cña c(cos ϕ)n−1 b»ng c = [B( 1, n )]−1 . §Ó x¸c 2 2
®Þnh hm mËt ®é cña T , ta sö dông phÐp ®æi biÕn √
ta ®−îc hm mËt ®é cña ph©n bè T víi n bËc tù do · $ √ 1 n −1 t2 − n Γ( n+1) t2 − n S(t, n) = nB , 1 + = 2 √ 1 + . 2 2 n nΓ(n )Γ( 1 ) n 2 2 NÕu X
n) v Y ∈ N m, σ2) ®éc lËp, khi ®ã σ ∈ χ2( ( Y − m√ T = √ n X
cã ph©n bè Student víi n bËc tù do.
KÝ hiÖu S(n) l líp c¸c ®¹i l−îng ngÉu nhiªn cã ph©n bè Student víi n bËc tù do. http://www.ebook.edu.vn 26 CuuDuongThanCong.com
https://fb.com/tailieudientucntt
4. Ph©n bè cña trung b×nh mÉu v% ph−¬ng sai mÉu.
NÕu Xi ∈ N(m, σ2), i = 1, 2, ..., n ®éc lËp, khi ®ã X X σ2 n n − 1 X = 1 + X2 + + n ∈ N m, v S2 = S∗2 ∈ χ2(n − 1). n n σ2 σ2
ThËt vËy, kÝ hiÖu = (X1, ..., Xn)T v xÐt phÐp biÕn ®æi trùc giao = víi ( 1 √ , 1 √ , , 1 √ ) l n n n
hng thø nhÊt cña . Khi ®ã √ (a) Y1 = X n (b) Y 2 2 1 + + Y 2 n = X 2 1 + + X 2 Y 2 n = (Xi − X)2 + nX ⇔ Y 2 2 + + n = (n − 1)S∗2 √ √
(c) Víi vÐc t¬ = (m, m, ..., m), ta cã ( − ) = − (m n, 0, ..., 0) = (Y1 − m n, Y2, ..., Yn). Suy ra √
(Y1 − m n)2 + Y2 + + Y 2n = (X1 − m)2 + (X2 − m)2 + + (Xn − m)2.
BiÕt hm mËt ®é cña b»ng xi−m c e− σ . VËy mËt ®é cña b»ng √ y−m ny y c e− n σ . √ √ §iÒu ®ã chøng tá Y 2 1 = X
n ∈ N(m n, σ ), Yi ∈ N(0, σ2), i = 2, ..., n ®éc lËp v (n − 1)S∗2 Y 2 Y 2 = 2 + + n ∈ χ2(n − 1). σ2 σ2
B©y giê ta suy ra hÖ qu¶ quan träng: T cã ph©n bè Student víi n − 1 bËc tù do, víi S S
ThËt vËy T b»ng th−¬ng cña 2 ®¹i l−îng ngÉu nhiªn √ √ X − m√ S n T = n − 1 n : σ σ √ trong ®ã X−m n = (n−1)S∗ σ ∈ N(0, 1) v nS σ σ ∈ χ2(n − 1). http://www.ebook.edu.vn 27 CuuDuongThanCong.com
https://fb.com/tailieudientucntt
3 Kho¶ng tin cËy cho gi¸ trÞ trung b×nh
(a) MÉu cã ph©n bè chuÈn víi ph−¬ng sai σ2 ®1 cho. Kho¶ng tin cËy cho gi¸
trÞ trung b×nh, víi ®é tin cËy 1 − α σ σ
X − uα√ < m < X + u √ , n α n
trong ®ã uα ®−îc x¸c ®Þnh tõ hÖ thøc P (|u| ≥ uα) = α, u ∈ N(0, 1).
(b) MÉu cã ph©n bè chuÈn víi ph−¬ng sai ch−a biÕt. Kho¶ng tin cËy cho gi¸ trÞ
trung b×nh, víi ®é tin cËy 1 − α S∗ S∗
X − tα√ < m < X + t √ , n α n
trong ®ã tα ®−îc x¸c ®Þnh tõ hÖ thøc P (|t| ≥ tα) = α (t
cã ph©n bè Student víi n − 1 bËc tù do.)
NÕu kÝch th−íc mÉu ®ñ lín (n ≥ 30), mÆc dï ph©n bè mÉu cã thÓ kh«ng
l( ph©n bè chuÈn, tuy nhiªn ¸p dông luËt giíi h¹n trung t©m ta cã thÓ
sö dông c«ng thøc sau ®Ó tÝnh kho¶ng tin cËy cho gi¸ trÞ trung b×nh, ®é tin cËy 1 − α S∗ S∗
X − uα√ < m < X + u √ , n α n
trong ®ã uα ®−îc x¸c ®Þnh tõ hÖ thøc P (|u| ≥ uα) = α, u ∈ N(0, 1).
4 Kho¶ng tin cËy cho x¸c suÊt
Cho biÕn cè ngÉu nhiªn víi x¸c suÊt p cÊn ph¶i −íc l−îng. Gi¶ thiÕt % p = kn
l tÇn suÊt xuÊt hiÖn cña biÕn cè ®ã. (KÝch th−íc mÉu ®ñ lín & th«ng th−êng
n ≥ 40). Khi ®ã víi ®é tin cËy 1 − α, kho¶ng tin cËy cho x¸c suÊt u u % p − α √ % p(1 − % p) < p < % p + α √ % p(1 − % p), n n
trong ®ã uα ®−îc x¸c ®Þnh tõ hÖ thøc P (|u| ≥ uα) = α, u ∈ N(0, 1). 5 K
MÉu cã ph©n bè chuÈn víi ph−¬ng sai σ2 cÊn ph¶i −íc l−îng. Víi ®é tin cËy
1 − α, kho¶ng tin cËy cho σ2 nS2 nS2 < σ2 < χ2α χ2 1− α
trong ®ã χ2 ®−îc x¸c ®Þnh tõ hÖ thøc α P (χ2 > χ2α) = α,
(χ2l ®¹i l−îng ngÉu nhiªn cã ph©n bè χ2 víi (n − 1) bËc tù do). http://www.ebook.edu.vn 28 CuuDuongThanCong.com
https://fb.com/tailieudientucntt
6 Kho¶ng tin cËy cho hiÖu c¸c gi¸ trÞ trung b×nh cña ph©n bè chuÈn
6.1 Tr−êng hîp ph−¬ng sai ®Z biÕt
Gäi (X1, X2, ..., Xm) l mÉu ngÉu nhiªn t−¬ng øng víi ®¹i l−îng ngÉu nhiªn X ∈ N(m1, σ21), (Y1, Y2, ..., Yn)
l mÉu ngÉu nhiªn t−¬ng øng víi ®¹i l−îng ngÉu nhiªn Y ∈ N(m2, σ22). C¸c tham sè m1, m2 ch−a biÕt v
σ21, σ2 l c¸c tham sè ®1 biÕt. Gi¶ thiÕt tiÕp c¸c ®¹i l−îng ngÉu nhiªn 2 X1, X2, ..., Xm, Y1, Y2, ..., Yn ®éc lËp nhau. DÔ dng nhËn thÊy E(X − Y ) = m1 − m2 σ2 σ2
D(X − Y ) = D(X) + D(Y ) = 1 + 2 m n Suy ra (X − Y ) − (m u = 1 − m2) & σ + σ m n
cã ph©n bè chuÈn, thuéc líp N(0,1).
Kho¶ng tin cËy cho hiÖu c¸c gi¸ trÞ trung b×nh m1 − m2 víi ®é tin cËy 1 − α σ2 σ2 σ2 σ2 (X − Y ) − u 1 2 1 2 α + < m + , m n 1 − m2 < (X − Y ) + uα m n
NÕu n1, n2 ®ñ lín (≥ 30), ta xÊp xØ c«ng thøc trªn cho hiÖu c¸c gi¸ trÞ
trung b×nh m1 −m2 c¶ trong tr−êng hîp c¸c mÉu ®M cho kh«ng tu©n theo
ph©n bè chuÈn, sö dông S∗ v( thay cho 1 S∗ 2
σ1, σ2 t−¬ng øng trong c«ng thøc trªn.
6.2 Tr−êng hîp c¸c ph−¬ng sai ch−a biÕt v% b»ng nhau
Gäi (X1, X2, ..., Xm) l mÉu ngÉu nhiªn t−¬ng øng víi ®¹i l−îng ngÉu nhiªn X ∈ N(m1, σ2), (Y1, Y2, ..., Yn)
l mÉu ngÉu nhiªn t−¬ng øng víi ®¹i l−îng ngÉu nhiªn Y ∈ N(m2, σ2). (Chóng cã ph−¬ng sai b»ng nhau). C¸c tham sè m 2 1, m2, σ
ch−a biÕt v gi¶ thiÕt r»ng c¸c ®¹i l−îng ngÉu nhiªn X1, X2, ..., Xm, Y1, Y2, ..., Yn ®éc lËp nhau. DÔ 2 σ2 σ2 m + n D(X − Y ) = D(X) + D(Y ) = + = σ m n mn Suy ra (X − Y ) − (m u = 1 − m2) & σ m+n mn
cã ph©n bè chuÈn, thuéc líp N(0,1). DÔ dng chøng minh ®−îc mS2X + nS2Y m + n − 2 http://www.ebook.edu.vn 29 CuuDuongThanCong.com
https://fb.com/tailieudientucntt
l −íc l−îng kh«ng chÖch cña σ2. Ng−êi ta chøng minh ®−îc r»ng (thay σ2 trong thèng kª trªn b»ng −íc l−îng cña nã) (X − Y ) − (m
mn(m + n − 2) (X − Y ) − (m t = 1 − m2) & & = 1 − m2) mS +nS m + n mS2 + nS2 X Y m+n X Y m+n−2 mn
cã ph©n bè Student víi m + n − 2 bËc tù do.
§Æc biÖt khi hai gi¸ trÞ trung b×nh b»ng nhau m1 = m2 mn(m + n − 2) X − Y t = m + n mS2 + nS2 X Y
còng cã ph©n bè Student víi m + n − 2 bËc tù do.
Kho¶ng tin cËy cho hiÖu c¸c gi¸ trÞ trung b×nh m1 − m2 víi ®é tin cËy 1 − α b»ng MÉu {X m i}i=1 ∈ N (m1, σ2)
{Yi}ni=1 ∈ N(m2, σ2), cã ph©n bè chuÈn víi
ph−¬ng sai σ2 ch−a biÕt. Gi¶ thiÕt c¸c phÇn tö mÉu ®ã ®éc lËp nhau. m + n m + n (X − Y ) − S.tα < m , mn
1 − m2 < (X − Y ) + S.tα mn mS2 + nS2 trong ®ã kÝ hiÖu S2 = X Y v t m + n − 2 α
®−îc x¸c ®Þnh tõ hÖ thøc
P (|t| ≥ tα) = α (t cã ph©n bè Student víi m + n − 2 bËc tù do.) 7 K )
B%i to¸n 1 v quy t¾c kiÓm ®Þnh
MÉu cã ph©n bè chuÈn víi ph−¬ng sai σ2 ®1 cho. KiÓm ®Þnh gi¶ thiÕt vÒ k× väng mÉu, møc ý nghÜa α (H) : m = m0, víi ®èi thiÕt (K) : m = m0. X − m √ Quy t¾c: B¸c bá (H) nÕu 0 n σ = |uqs| > uα,
trong ®ã uα ®−îc x¸c ®Þnh tõ hÖ thøc P (|u| ≥ uα) = α, u ∈ N(0, 1). B%i to
MÉu cã ph©n bè chuÈn víi ph−¬ng sai σ2 ®1 cho. KiÓm ®Þnh gi¶ thiÕt vÒ k× väng mÉu, møc ý nghÜa α (H) : m = m0, víi ®èi thiÕt (K) : m > m0. X − m √ Quy t¾c: B¸c bá (H) nÕu 0 n = u σ qs > uα,
trong ®ã uα ®−îc x¸c ®Þnh tõ hÖ thøc P ((u ≥ uα) = α, u ∈ N(0, 1). http://www.ebook.edu.vn 30 CuuDuongThanCong.com
https://fb.com/tailieudientucntt
MÉu cã ph©n bè chuÈn víi ph−¬ng sai σ2 ®1 cho. KiÓm ®Þnh gi¶ thiÕt vÒ k× väng mÉu, møc ý nghÜa α (H) : m m0, víi ®èi thiÕt (K) : m > m0. X − m √ Quy t¾c: B¸c bá (H) nÕu 0 n = u σ qs > uα,
trong ®ã uα ®−îc x¸c ®Þnh tõ hÖ thøc P ((u ≥ uα) = α, u ∈ N(0, 1).
MÉu cã ph©n bè chuÈn víi ph−¬ng sai σ2 ®1 cho. KiÓm ®Þnh gi¶ thiÕt vÒ k× väng mÉu, møc ý nghÜa α
(H) : m = m0 hoÆc (H) : m m0 víi ®èi thiÕt (K) : m > m0. X − m √ Quy t¾c: B¸c bá (H) nÕu 0 n = u σ qs > uα,
trong ®ã uα ®−îc x¸c ®Þnh tõ hÖ thøc P ((u ≥ uα) = α, u ∈ N(0, 1).
Hon ton t−¬ng tù, chóng ta sÏ xÐt bi to¸n kiÓm ®Þnh 1 phÝa n÷a B%i to¸n 3
MÉu cã ph©n bè chuÈn víi ph−¬ng sai σ2 ®1 cho. KiÓm ®Þnh gi¶ thiÕt vÒ k× väng mÉu, møc ý nghÜa α
(H) : m = m0 hoÆc (H) : m ≥ m0 víi ®èi thiÕt (K) : m < m0. X − m √ Quy t¾c: B¸c bá (H) nÕu 0 n = u σ qs < −uα, http://www.ebook.edu.vn 31 CuuDuongThanCong.com
https://fb.com/tailieudientucntt
8 KiÓm ®Þnh gi¶ thiÕt vÒ gi¸ trÞ trung b×nh (tr−êng hîp σ2 ch−a biÕt)
MÉu cã ph©n bè chuÈn víi ph−¬ng sai σ2 ch−a biÕt. KiÓm ®Þnh gi¶ thiÕt vÒ k× väng mÉu, møc ý nghÜa α (a) B%i to¸n 1 (H) : m = m0 víi ®èi thiÕt (K) : m = m0. X √ Quy t¾c: − m B¸c bá (H) nÕu 0 n S∗ > tα,
trong ®ã tα ®−îc x¸c ®Þnh tõ hÖ thøc P (|t| ≥ tα) = α (t
cã ph©n bè Student víi n − 1 bËc tù do.) (b) B%i to¸n 2
(H) : m = m0 hoÆc (H) : m m0 víi ®èi thiÕt (K) : m > m0. X − m √ Quy t¾c: B¸c bá (H) nÕu t 0 qs = n > t S∗ α,
trong ®ã tα ®−îc x¸c ®Þnh tõ hÖ thøc P (t ≥ tα) = α (t
cã ph©n bè Student víi n − 1 bËc tù do.)
(H) : m = m0 hoÆc (H) : m ≥ m0 víi ®èi thiÕt (K) : m < m0. X − m √ Quy t¾c: B¸c bá (H) nÕu t 0 qs = n < −tα, S∗
trong ®ã tα ®−îc x¸c ®Þnh tõ hÖ thøc P (t ≥ tα) = α (t
cã ph©n bè Student víi n − 1 bËc tù do.) http://www.ebook.edu.vn 32 CuuDuongThanCong.com
https://fb.com/tailieudientucntt
9 KiÓm ®Þnh gi¶ thiÕt vÒ sù b»ng nhau cña c¸c gi¸ trÞ trung b×nh
9.1 Tr−êng hîp ph−¬ng sai ®Z biÕt MÉu {X m i}i=1 ∈ N (m1, σ2 1 )
{Yi}ni=1 ∈ N(m2, σ22), cã ph©n bè chuÈn víi
ph−¬ng sai σ21, σ2 ®1 biÕt. KiÓm ®Þnh gi¶ thiÕt vÒ k× väng mÉu, møc ý nghÜa 2 α (a) B%i to¸n 1 (H) : m1 = m2 víi ®èi thiÕt (K) : m1 = m2. X Quy t¾c: B¸c bá (H) nÕu − Y & > uα, σ + σ m n
trong ®ã uα ®−îc x¸c ®Þnh tõ hÖ thøc P ((|u| ≥ uα) = α, u ∈ N(0, 1). (b) B%i to¸n 2
(H) : m1 = m2 hoÆc (H) : m1 m2 víi ®èi thiÕt (K) : m1 > m2. X − Y Quy t¾c: B¸c bá (H) nÕu & > uα, σ + σ (c) B%i to¸n 3
(H) : m1 = m2 hoÆc (H) : m1 ≥ m2 víi ®èi thiÕt (K) : m1 < m2. X − Y Quy t¾c: B¸c bá (H) nÕu & < −uα, σ + σ m n
trong ®ã uα ®−îc x¸c ®Þnh tõ hÖ thøc P ((u ≥ uα) = α, u ∈ N(0, 1).
NÕu mÉu cã kÝch th−íc ®ñ lín (m, n > 30), mét c¸ch xÊp xØ kh¸ tèt l(
¸p dông quy t¾c nªu trªn ®Ó kiÓm ®Þnh gi¶ thiÕt kh«ng, kÓ c¶ tr−êng hîp
ph©n bè mÉu kh«ng cã ph©n bè chuÈn, thay c¸c ph−¬ng sai σ2 trong 1 , σ2 2
thèng kª u b»ng c¸c ph−¬ng sai mÉu ®iÒu chØnh S∗2 v( S∗2 . X Y http://www.ebook.edu.vn 33 CuuDuongThanCong.com
https://fb.com/tailieudientucntt
9.2 Tr−êng hîp c¸c ph−¬ng sai ch−a biÕt v% b»ng nhau MÉu {X m i}i=1 ∈ N (m1, σ2)
{Yi}ni=1 ∈ N(m2, σ2), cã ph©n bè chuÈn víi
ph−¬ng sai σ2 ch−a biÕt. KiÓm ®Þnh gi¶ thiÕt vÒ k× väng mÉu, møc ý nghÜa α (a) B%i to¸n 1 (H) : m1 = m2 víi ®èi thiÕt (K) : m1 = m2. mn(m + n − 2) X − Y Quy t¾c: B¸c bá (H) nÕu > t m + n α, mS2 + nS2 X Y
trong ®ã tα ®−îc x¸c ®Þnh tõ hÖ thøc P (|t| ≥ tα) = α (t
cã ph©n bè Student víi m + n − 2 bËc tù do.) (b) B%i to¸n 2
(H) : m1 = m2 hoÆc (H) : m1 m2 víi ®èi thiÕt (K) : m1 > m2. mn(m + n − 2) X Quy t¾c: B¸c bá (H) nÕu − Y > tα, m + n mS2 + nS2 X Y (t
cã ph©n bè Student víi m + n − 2 bËc tù do.) (c) B%i to¸n 3
(H) : m1 = m2 hoÆc (H) : m1 ≥ m2 víi ®èi thiÕt (K) : m1 < m2. mn(m + n − 2) X Quy t¾c: B¸c bá (H) nÕu − Y < −tα, m + n mS2 + nS2 X Y
trong ®ã tα ®−îc x¸c ®Þnh tõ hÖ thøc P (t ≥ tα) = α (t
cã ph©n bè Student víi m + n − 2 bËc tù do.) http://www.ebook.edu.vn 34 CuuDuongThanCong.com
https://fb.com/tailieudientucntt
10 KiÓm ®Þnh gi¶ thiÕt vÒ sù b»ng nhau cña c¸c ph−¬ng sai Gi¶ sö {Xi}m ) {Y ) l c¸c mÉu hon ton i=1 ∈ N (m1, σ2 X i}n i=1 ∈ N (m2, σ2 Y
®éc lËp, cã ph©n bè chuÈn. KiÓm ®Þnh gi¶ thiÕt vÒ c¸c ph−¬ng sai, víi møc ý
nghÜa α. Ta s¾p xÕp sao cho S∗ 2 > S∗ 2 X Y (a) B%i to¸n 1 (H) : σ2 X = σ2 Y víi ®èi thiÕt (K) : σ2 X = σ2 Y . S∗ 2 Quy t¾c: B¸c bá (H) nÕu X > Fα/2, S∗ 2 Y α
trong ®ã Fα/2 ®−îc x¸c ®Þnh tõ hÖ thøc P (F ≥ Fα/2) = 2 (F
l ®¹i l−îng ngÉu nhiªn ph©n bè F víi m − 1, n − 1 bËc tù do.) (b) B%i to¸n 2 (H) : σ2 hoÆc X = σ2 Y (H) : σ2X σ2Y víi ®èi thiÕt (K) : σ2 X > σ2 Y . S∗ 2
trong ®ã Fα ®−îc x¸c ®Þnh tõ hÖ thøc P (F ≥ Fα) = α (F
l ®¹i l−îng ngÉu nhiªn ph©n bè F víi m − 1, n − 1 bËc tù do.)
11 KiÓm ®Þnh gi¶ thiÕt vÒ x¸c suÊt cña biÕn cè ngÉu nhiªn
Gi¶ söA l biÕn cè ngÉu nhiªn cã x¸c suÊt P (A) = p ch−a biÕt. Ta sö dông −íc l−îng X X % p = X = 1 + X2 + + n n
trong ®ã Xi b»ng 1 hoÆc 0 tïy theo biÕn cè A x¶y ra hoÆc kh«ng x¶y ra ë phÐp thö ngÉu nhiªn thø i, i = 1, 2, ..., n. (%
p thùc chÊt l tÇn suÊt xuÊt hiÖn cña biÕn cè A). Khi ®ã n%
p cã ph©n bè nhÞ thøc víi E(n% p) = np, D(n% p) = npq, q = 1 − p víi mø
Ta ®1 biÕt, theo ®Þnh lÝ giíi h¹n trung t©m n% p − np √ %p− p √ = n √ npq pq
cã ph©n bè xÊp xØ chuÈn (≈ N(0, 1)) khi n ®ñ lín. V× vËy sö dông thèng kª √ % p − p u = u 0 qs = n , p0(1 − p0)
u cã ph©n bè xÊp xØ chuÈn N(0,1), khi gi¶ thiÕt (H): p = p0 ®óng. http://www.ebook.edu.vn 35 CuuDuongThanCong.com
https://fb.com/tailieudientucntt
KiÓm ®Þnh gi¶ thiÕt vÒ x¸c suÊt cña biÕn cè ngÉu nhiªn.
Gi¶ thiÕt kÝch th−íc mÉu n ®ñ lín (n ≥ 40). KiÓm ®Þnh gi¶ thiÕt vÒ x¸c suÊt, møc ý nghÜa α (a) B%i to¸n 1 (H) : p = p0 víi ®èi thiÕt (K) : p = p0. √ % p − p Quy t¾c: B¸c bá (H) nÕu 0 n > uα, p0(1 − p0)
trong ®ã uα ®−îc x¸c ®Þnh tõ hÖ thøc P (|u| ≥ uα) = α (u
cã ph©n bè chuÈn u ∈ N(0, 1).) (b) B%i to¸n 2
(H) : p = p0 hoÆc (H) : p p0 víi ®èi thiÕt (K) : p > p0. √ % p − p Quy t¾c: B¸c bá (H) nÕu n 0 > uα, p0(1 − p0)
trong ®ã uα ®−îc x¸c ®Þnh tõ hÖ thøc P (u ≥ uα) = α (c) B%i to¸n 3
(H) : p = p0 hoÆc (H) : p ≥ p0 víi ®èi thiÕt (K) : p < p0. √ % p − p Quy t¾c: B¸c bá (H) nÕu n 0 < −uα, p0(1 − p0)
trong ®ã uα ®−îc x¸c ®Þnh tõ hÖ thøc P (u ≥ uα) = α (u
cã ph©n bè chuÈn u ∈ N(0, 1).)
Trong b(i to¸n 2, b(i to¸n 3, uα ®−îc x¸c ®Þnh tõ hÖ thøc P (u > uα) = α α http://www.ebook.edu.vn 36 CuuDuongThanCong.com
https://fb.com/tailieudientucntt
12 KiÓm ®Þnh gi¶ thiÕt vÒ tÝnh phï hîp cña h%m ph©n bè
Gi¶ thiÕt mÉu ngÉu nhiªn gåm n phÇn tö mÉu. C¸c phÇn tö mÉu ®−îc ph©n lo¹i
thnh r nhãm: mçi nhãm chøa ni phÇn tö mÉu, mçi phÇn tö mÉu chØ thuéc mét nhãm duy nhÊt r n = n1 + n2 + ... + nr = ni. i=1
XÐt bi to¸n kiÓm ®Þnh møc ý nghÜa α, gi¶ thiÕt kh«ng sau ®©y:
(H) : X¸c suÊt ®Ó mçi phÇn tö mÉu thuéc nhãm thø i b»ng pi r víi mäi i = 1, 2, ..., r ( pi = 1). i=1 r (ni − np
Quy t¾c: B¸c bá (H) nÕu Q2 = i)2 > χ2 np α, i=1 i
trong ®ã χ2 ®−îc x¸c ®Þnh tõ hÖ thøc α P (χ2 > χ2α) = α,
(χ2l ®¹i l−îng ngÉu nhiªn cã ph©n bè χ2 víi r − 1 bËc tù do).
Ng−êi ta còng sö dông ph©n bè χ2 ®Ó kiÓm ®Þnh c¸c bi to¸n vÒ tÝnh phï hîp cña hm ph©n bè. XÐt bi
to¸n kiÓm ®Þnh gi¶ thiÕt:
(H): Mét ®¹i l−îng ngÉu nhiªn X no ®ã cã ph©n bè d¹ng F (x, Θ) víi ®èi thiÕt ng−îc l¹i. Gi¶ h©n bè chuÈn
§Ó gi¶i bi to¸n ®ã, ng−êi ta chän mét mÉu ngÉu nhiªn (X1, X2, ..., Xn)
t−¬ng øng víi ®¹i l−îng ngÉu nhiªn X v chia c¸c phÇn tö mÉu vo r nhãm: mçi nhãm chøa ni phÇn tö mÉu,
mçi phÇn tö mÉu chØ thuéc mét nhãm duy nhÊt r n = n1 + n2 + ... + nr = ni. i=1
Gi¶ sö pi l x¸c suÊt ®Ó ®¹i l−îng ngÉu nhiªn X nhËn c¸c gi¸ trÞ thuéc nhãm thø i, i = 1, 2, ..., r víi ®iÒu kiÖn
gi¶ thiÕt (H) ®óng. Khi ®ã 1 = p1 + p2 + ... + pr
HiÓn nhiªn ni l ®¹i l−îng ngÉu nhiªn cã ph©n bè nhÞ thøc víi k× väng E(ni) = npi. XÐt thèng kª i=1 i trong ®ã %
pi, i = 1, 2, ..., r l x¸c suÊt ®Ó X nhËn c¸c gi¸ trÞ thuéc nhãm thø i, x¸c suÊt ®ã ®−îc tÝnh th«ng qua hm ph©n bè F (x, % Θ) m % Θ = (' Θ1, ' Θ2, ..., '
Θk) l c¸c −íc l−îng hîp lÝ cùc ®¹i cña c¸c tham sè Θ1, Θ2, ..., Θk.
Ng−êi ta ®1 chøng minh ®−îc r»ng víi n ®ñ lín v gi¶ thiÕt (H) l ®óng khi ®ã Q2 sÏ cã ph©n bè xÊp xØ
ph©n bè χ2 víi r − k − 1 bËc tù do, k l sè tham sè cña ph©n bè F (x, Θ) trong gi¶ thiÕt (H).
(Gi¶ sö ph©n bè F (x, Θ) l ph©n bè chuÈn N (m, σ2), Θ ®−îc coi nh− vÐc t¬ (m, σ2) v sè tham sè cña
ph©n bè b»ng k = 2, tr−êng hîp F (x, λ) l ph©n bè mò ch¼ng h¹n sè tham sè cña ph©n bè l k = 1,...)
MiÒn b¸c bá cña kiÓm ®Þnh do vËy l r (n W = {(X i − n % pi)2 1, X2, ..., Xn) ∈ Rn/ > χ2 n % p α}. i=1 i http://www.ebook.edu.vn 37 CuuDuongThanCong.com
https://fb.com/tailieudientucntt
trong ®ã χ2 ®−îc x¸c ®Þnh tõ hÖ thøc α
P (χ2 > χ2α) = α, (χ2 l ®¹i l−îng ngÉu nhiªn cã ph©n bè χ2 víi r −k −1
bËc tù do). Ta tãm t¾t quy t¾c trªn trong b¶ng sau
KiÓm ®Þnh sù phï hîp víi h%m ph©n bè chøa tham sè ch−a biÕt.
Gi¶ thiÕt mÉu ngÉu nhiªn gåm n phÇn tö mÉu. C¸c phÇn tö mÉu ®−îc ph©n lo¹i
thnh r nhãm: mçi nhãm chøa ni phÇn tö mÉu, mçi phÇn tö mÉu chØ thuéc mét nhãm duy nhÊt r n = n1 + n2 + ... + nr = ni. i=1
XÐt bi to¸n kiÓm ®Þnh møc ý nghÜa α, gi¶ thiÕt kh«ng sau ®©y:
(H) : MÉu ngÉu nhiªn cã ph©n bè d¹ng F (x, Θ) r (n
Quy t¾c: B¸c bá (H) nÕu Q2 = i − n % pi)2 > χ2 n % p α, i i=1 trong ®ã %
pi, i = 1, 2, ..., r l x¸c suÊt ®Ó X nhËn c¸c gi¸ trÞ thuéc nhãm thø i,
x¸c suÊt ®ã ®−îc tÝnh th«ng qua hm ph©n bè F (x, % Θ) m % Θ = (' Θ1, ' Θ2, ..., ' Θk)
l c¸c −íc l−îng hîp lÝ cùc ®¹i cña c¸c tham sè Θ1, Θ2, ..., Θk.
Ph©n vÞ χ2 ®−îc x¸c ®Þnh tõ hÖ thøc α P (χ2 > χ2α) = α,
(χ2l ®¹i l−îng ngÉu nhiªn cã ph©n bè χ2 víi r − k − 1 bËc tù do). 13
KiÓm ®Þnh vÒ tÝnh ®éc lËp
Ng−êi ta cã thÓ kiÓm ®Þnh vÒ tÝnh ®éc lËp cña c¸c biÕn cè ngÉu nhiªn, c¸c ®¹i l−îng ngÉu nhiªn. Chóng ta tr×nh
by vÊn ®Ò d−íi d¹ng sau ®©y:
Cho hai hÖ ®Çy ®ñ c¸c biÕn cè A1, A2, ..., Ar; B1, B2, ..., Bs.
H1y kiÓm ®Þnh gi¶ thiÕt hai hÖ ®ã ®éc lËp:
(H): P (AiBj) = P (Ai)P (Bj) víi mäi i = 1, 2, ..., r; j = 1, 2, ..., s.
XÐt mét mÉu ngÉu nhiªn cì n (mÉu gåm n phÇn tö mÉu). Ta ®−a vo c¸c kÝ hiÖu sau:
nij l sè lÇn x¶y ra biÕn cè tÝch AiBj trong tËp hîp c¸c phÇn tö mÉu. n s i. = n j=1
ij l sè lÇn x¶y ra biÕn cè Ai. n r .j = n i=1
ij l sè lÇn x¶y ra biÕn cè Bj . HiÓ i=1 j=1 v r s nij = n. i=1 j=1 http://www.ebook.edu.vn 38 CuuDuongThanCong.com
https://fb.com/tailieudientucntt
C¸c sè nij ®−îc xÕp vo b¶ng sau ®©y: j 1 2 . . . s Tæng i 1 n11 n12 n1s n1. 2 n21 n22 n2s n2. . . . . . . r nr1 nr2 nrs nr. Tæng n.1 n.2 n.s n
Ta tãm t¾t quy t¾c kiÓm ®Þnh trong b¶ng sau
KiÓm ®Þnh vÒ tÝnh ®éc lËp.
Cho hai hÖ ®Çy ®ñ c¸c biÕn cè A1, A2, ..., Ar; B1, B2, ..., Bs.
H1y kiÓm ®Þnh gi¶ thiÕt hai hÖ ®ã ®éc lËp, víi møc ý nghÜa b»ng α: (H) :
P (AiBj) = P (Ai)P (Bj) víi mäi i = 1, 2, ..., r; j = 1, 2, ..., s. r s 2 n Quy t¾c: B¸c bá (H) nÕu ij − ni.n.j n n > χ2 i.n.j α, i=1 j=1 n
(χ2l ®¹i l−îng ngÉu nhiªn cã ph©n bè χ2 víi (r − 1)(s − 1) bËc tù do).
Chó ý r»ng xÊp xØ t−¬ng ®èi tèt nÕu ni.n.j i, j n ≥ 5 víi mäi . http://www.ebook.edu.vn 39 CuuDuongThanCong.com
https://fb.com/tailieudientucntt 14 HÖ sè t−¬ng quan mÉu
Trong lÝ thuyÕt x¸c suÊt, chóng ta biÕt r»ng ®Ó ®o mèi quan hÖ gi÷a hai hoÆc nhiÒu ®¹i l−îng ngÉu nhiªn, ng−êi
ta th−êng tÝnh c¸c hÖ sè t−¬ng quan gi÷a chóng. cov(X, Y ) E[(X − E(X))(Y − E(Y ))] >(X, Y ) = = . σxσy D(X) D(X)
NÕu X v Y l hai ®¹i l−îng ngÉu nhiªn ®éc lËp khi ®ã hÖ sè t−¬ng quan >(X, Y ) = 0. Tr−êng hîp
|>(X, Y )| = 1, gi÷a X v Y cã mèi quan hÖ phô thuéc tuyÕn tÝnh Y = aX + b. Trong thèng kª, thay v× hai
®¹i l−îng ngÉu nhiªn X, Y ta xÐt mÉu ngÉu nhiªn
(X1, Y1), (X2, Y2), ..., (Xn, Yn)
Cã thÓ coi chóng nh− c¸c ®iÓm ngÉu nhiªn trªn mÆt ph¼ng to¹ ®é. HÖ sè t−¬ng quan mÉu ®−îc ®Þnh nghÜa 1 n (x )( 1 n x r = n i=1 i − x
Yi − Y ) = n i=1 iYi − x Y . SxSY SxSY S2 , S2 X
l ph−¬ng sai mÉu cña X, Y t−¬ng øng Y 1 n 1 n n n 2 1 1 2 S2X = (Xi − X)2 = X2 , S2 (Yi − Y )2 = Y 2 . n n i − X Y = n n i − Y i=1 i=1 i=1 i=1
DÔ dng chøng minh ®−îc 1 n (x n i − x)(Yi − Y ) x r = n−1 i=1 iYi − nx Y = i=1 S∗ . xS∗ Y n 2 2 X2 n Y 2 i=1 i − nX i=1 i − nY Ch sè liÖu
hng n¨m vÒ l−îng m−a trong th¸ng S¸u trªn th−îng nguån s«ng Hång (Xi) v ®Ønh lò t−¬ng øng víi n¨m ®ã
t¹i H néi (Yi). C¸c sè liÖu gi¶ ®Þnh nh»m gióp ®éc gi¶ nghiªn cøu c¸ch sö dông håi quy trong c«ng viÖc dù
b¸o ®−îc cho trong b¶ng d−íi ®©y STT N¨m L−îng m−a (X) §Ønh lò (Y ) STT N¨m L−îng m−a (X) §Ønh lò (Y ) 1 1969 720 1405 13 1981 690 1337 2 1970 720 1405 14 1982 500 960 3 1971 730 1439 15 1983 460 879 4 1972 590 1133 16 1984 610 1176 5 1973 660 1272 17 1985 710 1382 6 1974 780 1519 18 1986 620 1178 7 1975 770 1524 19 1987 660 1271 8 1976 710 1364 20 1988 620 1194 9 1977 640 1253 21 1989 590 1161 10 1978 670 1324 22 1990 740 1449 1 1
NÕu ta minh ho¹ c¸c cÆp sè liÖu (xi, yi), i = 1, 2, ..., 24 trong b¶ng trªn b»ng c¸c ®iÓm trªn mÆt ph¼ng,
chóng ta c¶m nhËn thÊy mét mèi liªn hÖ gi÷a l−îng m−a (X) hng n¨m v ®Ønh lò t¹i H néi (Y ), l−îng m−a
cng lín th× lò do m−a g©y nªn cng cao. HÖ sè t−¬ng quan mÉu sÏ gi¶i thÝch mèi quan hÖ gi÷a hai ®¹i l−îng:
l−îng m−a hng n¨m v ®Ønh lò t¹i H néi. §Ó tÝnh hÖ sè t−¬ng quan mÉu gi÷a chóng, ta tÝnh c¸c ®Æc tr−ng k×
väng mÉu v ph−¬ng sai mÉu cña X v Y x y S2 x S2y 1 n x 1 n y 1 n (x n (y n i=1 i n i=1 i n i=1 i − x)2 1 n i=1 i − y)2 658,95833 1272,16667 85, 024252 163, 50712 http://www.ebook.edu.vn 40 CuuDuongThanCong.com
https://fb.com/tailieudientucntt
HÖ sè t−¬ng quan mÉu do vËy b»ng 1 n (xi − x)(yi − y) r = n i=1 = 0, 97045. SxSy
Dùa vo hÖ sè t−¬ng quan mÉu, sau ny ng−êi ta gi¶i thÝch ®−îc møc ®é liªn hÖ gi÷a hai ®¹i l−îng ngÉu
nhiªn X v Y khi biÓu diÔn chóng th«ng qua mèi quan hÖ tuyÕn tÝnh.
15 Håi quy b×nh ph−¬ng trung b×nh tuyÕn tÝnh Gi¶ sö
(X1, Y1), (X2, Y2), ..., (Xn, Yn)
l mÉu ngÉu nhiªn t−¬ng øng víi hai ®¹i l−îng ngÉu nhiªn X v Y . Ch¼ng h¹n khi xÐt bi to¸n dù b¸o ®Ønh
lò hng n¨m trªn s«ng Hång t¹i H néi ®1 nãi trong môc tr−íc. Chóng ta c¶m nhËn ®−îc mèi liªn hÖ gi÷a
l−îng m−a (X) hng n¨m v ®Ønh lò t¹i H néi (Y ), tuy nhiªn kh«ng cã th«ng tin no h¬n vÒ mèi liªn hÖ thùc
gi÷a X v Y , khi ®ã ta gi¶ thiÕt gi÷a chóng cã mèi quan hÖ tuyÕn tÝnh (bËc nhÊt). MÆt kh¸c do chóng ta
xem l−îng m−a v ®Ønh lò l c¸c ®¹i l−îng ngÉu nhiªn, v× vËy khi dù b¸o l−îng m−a Y víi ®iÒu kiÖn l−îng
m−a X b»ng mét gi¸ trÞ x no ®ã, ta chØ cã thÓ kh¶o s¸t hm ph©n bè cã ®iÒu kiÖn cña Y . (X cßn gäi l
biÕn ®éc lËp v Y ®−îc gäi l biÕn phô thuéc). §Æc tr−ng quan träng cña ph©n bè cã ®iÒu kiÖn l k× väng cã
®iÒu kiÖn E(Y /X = x). V× vËy trong ch−¬ng ny chóng ta h¹n chÕ chØ xÐt tr−êng hîp k× väng cã ®iÒu kiÖn
E(Y/X = x) l( h(m tuyÕn tÝnh ®èi víi X E(Y/X = x) = αx + β.
Chó ý r»ng khi X t¨ng 1 ®¬n vÞ, k× väng cã ®iÒu kiÖn cña Y sÏ t¨ng α
E(Y/X = x + 1) = α(x + 1) + β = αx + β + α = E(Y/X = x) + α. §Ó chØ ong bi
to¸n håi quy ng−êi ta coi xi l c¸c biÓu hiÖn cô thÓ cña biÕn ngÉu nhiªn X, yi l c¸c biÓu hiÖn cô thÓ cña biÕn
ngÉu nhiªn phô thuéc Yi t−¬ng øng. Do ®¼ng thøc trªn, k× väng cã ®iÒu kiÖn cña Yi tho¶ m1n E(Yi/X = xi) = αxi + β i = 1, 2, ..., n.
Nh− vËy sai sè gi÷a Yi v k× väng cã ®iÒu kiÖn E(Yi/X = xi), kÝ hiÖu
εi = Yi − E(Yi/X = xi) = Yi − (αxi + β)
l ®¹i l−îng ngÉu nhiªn cã k× väng b»ng 0
E(εi) = E(Yi) − E(E(Yi/X = xi)) = E(Yi) − E(Yi) = 0.
VËy mÉu håi quy tuyÕn tÝnh cña Y ®èi víi X ®−îc tãm t¾t nh− sau: §¹ Yi = αxi + β + εi i = 1, 2, ..., n. (3)
trong ®ã α, β l% c¸c hÖ sè cÇn −íc l−îng, y = αx + β ®−îc gäi l% ®−êng th¼ng håi quy, εi l% ®¹i l−îng
ngÉu nhiªn cã k× väng E(εi) = 0.
Ta gäi a, b l c¸c −íc l−îng bÊt k× cña c¸c hÖ sè α, β t−¬ng øng. Khi ®ã ®−êng th¼ng håi quy ®−îc −íc l−îng l ®−êng th¼ng y = ax + b.
§é lÖch (hay t¹m gäi l sai sè) gi÷a yi víi ®−êng th¼ng trªn t¹i ®iÓm xi, kÝ hiÖu ei b»ng ei = yi − (axi + b). http://www.ebook.edu.vn 41 CuuDuongThanCong.com
https://fb.com/tailieudientucntt
§é lÖch ny cã thÓ d−¬ng hoÆc ©m tuú theo gi¸ trÞ mÉu (xi, yi) l ®iÓm n»m trªn hoÆc n»m d−íi ®−êng th¼ng
−íc l−îng y = ax + b. Mét trong c¸c ph−¬ng ph¸p −íc l−îng cã nhiÒu −u ®iÓm l t×m c¸c −íc l−îng a, b cña
α, β sao cho tæng b×nh ph−¬ng c¸c ®é lÖch ei ®¹t gi¸ trÞ nhá nhÊt. Ng−êi ta gäi ph−¬ng ph¸p −íc l−îng nh−
vËy l ph−¬ng ph¸p b×nh ph−¬ng bÐ nhÊt. §−êng th¼ng håi quy nhËn ®−îc tõ ph−¬ng ph¸p b×nh ph−¬ng bÐ
nhÊt cßn ®−îc gäi l håi quy b×nh ph−¬ng trung b×nh tuyÕn tÝnh.
C¸c −íc l−îng a, b cña α v β dùa trªn ph−¬ng ph¸p b×nh ph−¬ng bÐ nhÊt, tøc l lm cùc tiÓu hm n u(a, b) = (Yi − axi − b)2. i=1
Bi to¸n trªn cã thÓ gi¶i mét c¸ch dÔ dng b»ng c¸ch t×m ®iÓm dõng cña hm u(a, b) : ∂u = −2 n (Y ∂a i=1 i − axi − b)xi = 0 ∂u = −2 n ∂b (Y i=1 i − axi − b) = 0
Tõ ph−¬ng tr×nh thø hai suy ra b = Y − ax. (4)
Thay b vo ph−¬ng tr×nh thø nhÊt, khi ®ã n n
[(Yi − Y ) − a(xi − x)]xi =
[(Yi − Y ) − a(xi − x)](xi − x) = 0. i=1 i=1 Suy ra n n (x x S a = i=1 i − x)(Yi − Y ) i=1 iYi − nxY Y n = = r , (5) (x n S i=1 i − x)2 x2 i=1 i − nx2 x
trong ®ã r l hÖ sè t−¬ng quan mÉu (6) SxSY SxSY
S2 , S2 l ph−¬ng sai mÉu cña X, Y t−¬ng øng X Y 1 n n 1 2 S2 X = (X X2 , n i − X)2 = n i − X i=1 i=1 1 n 1 n 2 S2 Y = (Y Y 2 . (7) n i − Y )2 = n i − Y i=1 i=1
VËy hm håi quy b×nh ph−¬ng trung b×nh tuyÕn tÝnh cã d¹ng S
y = ax + b = y + r y (x − x). Sx
Trë l¹i vÝ dô vÒ dù b¸o lò, ta ®1 tÝnh
HÖ sè t−¬ng quan mÉu r = 0, 97045. ¸p dông c«ng thøc ®Ó tÝnh c¸c hÖ sè a v b cña ®−êng th¼ng håi quy y = ax + b S a = r y = 1, 86623 Sx S b = y − rx y = 42, 39808. Sx
VËy ®−êng th¼ng håi quy cña Y ®èi víi X y = 1, 86623x + 42, 39808. Ta ph¸t biÓu ®Þnh lÝ sau http://www.ebook.edu.vn 42 CuuDuongThanCong.com
https://fb.com/tailieudientucntt
§Þnh lÝ 10 [§Þnh lÝ GaussjMarkov]
Gi¶ thiÕt r»ng theo (3) mÉu håi quy tuyÕn tÝnh cña Y ®èi víi X : Yi = αxi + β + εi i = 1, 2, ..., n tho¶ mMn E(εi) = 0, D(εi) = σ2, E(εiεj) = 0, víi mäi i = j, i, j = 1...n
Khi ®ã c¸c −íc l−îng a, b cña α v( β theo ph−¬ng ph¸p b×nh ph−¬ng bÐ nhÊt l( c¸c −íc l−îng kh«ng chÖch
cã ph−¬ng sai nhá nhÊt. H¬n n÷a víi mäi sè thùc u v( v, ua + vb còng l( −íc l−îng cã ph−¬ng sai nhá nhÊt
trong sè tÊt c¶ c¸c −íc l−îng tuyÕn tÝnh
piYi = P ′Y kh«ng chÖch cña uα + vβ.
Theo (4) v (5) a v b l c¸c hm tuyÕn tÝnh cña Yi n (xi − x)(Yi − Y ) a = i=1 n , b = Y − ax. (x i=1 i − x)2 VËy n (x )( n (x n (x )α( E(a) = E i=1 i − x Yi − Y ) i=1 i − x)(E(Yi) − E(Y )) i=1 i − x xi − x) n = = = α (x n n (x i (x =1 i − x)2 i=1 i − x)2 i=1 i − x)2
E(b) = E(Y − ax) = ax + β − ax = β.
Hay a, b l c¸c −íc l−îng kh«ng chÖch cña α v β. E(b) = β, E(a) = α. Nh n nSx
§Þnh lÝ 11 Víi c¸c ®iÒu kiÖn cña ®Þnh lÝ GaussjMarkov, k× väng cña tæng b×nh ph−¬ng sai sè n E(SSE) = (n − 2)σ2 (SSE = [y 2 i − (axi + b)] .) i=1
Nãi c¸ch kh¸c nÕu kÝ hiÖu SSE nS2 (1 − r2) σ∗2 = = Y , n − 2 n − 2
khi ®ã σ∗2 l( −íc l−îng kh«ng chÖch cña σ2, σ∗ cßn ®−îc gäi l( sai sè chuÈn (Standard Error).
−íc l−îng cho ph−¬ng sai cña α ®−îc tÝnh nh− sau: n n S 1 (x − x)(Y − Y ) x − x
§Æt Ci = xi−x, víi mçi gi¸ trÞ cè ®Þnh cña x nS
i, ph−¬ng sai cña hÖ sè a b»ng x n n n x σ2 D(a) = D i − x Y = D( CiY C2 . nS2 i i) = σ2 i = nS2 i=1 x i=1 i=1 x
Sö dông ®Þnh lÝ trªn, kÝ hiÖu σ∗2 SSE s2a = = nS2x n(n − 2)S2x
ta cã s2 l −íc l−îng kh«ng chÖch cña a
D(a), do vËy sa ®−îc coi l sai sè trung b×nh cña hÖ sè gãc α cña
ph−¬ng tr×nh ®−êng th¼ng håi quy. http://www.ebook.edu.vn 43 CuuDuongThanCong.com
https://fb.com/tailieudientucntt
Chó ý r»ng nÕu cïng víi c¸c ®iÒu kiÖn cña ®Þnh lÝ Gauss&Markov, ta gi¶ thiÕt thªm εi (sai sè trong mÉu håi
quy) cã ph©n bè chuÈn, khi ®ã thèng kª a − α t = sa
cã ph©n bè Student víi n − 2 bËc tù do. Do vËy kho¶ng tin cËy cña α cßn cã thÓ viÕt d−íi d¹ng
a − tǫsa < α < a + tǫsa. (8)
Còng dùa trªn c¬ së t cã ph©n bè Student víi n − 2 bËc tù do, ta cã thÓ kiÓm ®Þnh c¸c gi¶ thiÕt H0 : α = α0 hoÆc H0 : α α0 víi ®èi thiÕt H1 : α > α0, a − α theo quy t¾c b¸c bá H 0 0 nÕu tqs = > tǫ. sa
(C¸c kiÓm ®Þnh mét phÝa kh¸c hoÆc kiÓm ®Þnh 2 phÝa còng theo quy t¾c t−¬ng tù ®1 biÕt).
§Æc biÖt nÕu gi¶ thiÕt α = 0,
Yi = α + εi khi ®ã E(Yi) = α kh«ng bÞ ¶nh h−ëng bëi biÕn ®éc lËp X. Nãi
c¸ch kh¸c sù biÕn thiªn cña biÕn phô thuéc Y hon ton kh«ng mét phÇn no cã thÓ gi¶i thÝch b»ng mèi quan hÖ tuyÕn tÝnh víi X.
NhËn xÐt r»ng khi α = 0, tqs = a l( gi¸ trÞ quan s¸t (t Stat) øng víi hÖ sè gãc α trong b¶ng sa ANOVA ph©n tÝch håi quy.
T−¬ng tù xÐt hÖ sè tù do cña håi quy trung b×nh tuyÕn tÝnh thùc nghiÖm n n n S 1 (x )( 1 x b = Y − rx Y = Y − x n i=1 i − x Yi − Y ) = Y i − x Y S i − i x. x S2x n nS2 i=1 i=1 x §Æt Ci = xi−x, khi ®ã nS x n 1
Suy ra víi mçi gi¸ trÞ cè ®Þnh cña xi, ph−¬ng sai cña hÖ sè b b»ng n 1 2 n 1 C n i 1 x2 D(b) = σ2 − C = σ2 − 2 x + C2 = σ2 + . n ix n2 n i x2 n nS2 i=1 i=1 i=1 x KÝ hiÖu n 1 n x2 (1 − r2)S2 (S2 σ∗2( x2 s2 Y x + x2) = i=1 i ) b = σ∗2 + = , n nS2 (n − 2)S2 n2S2 i=1 x x x
ta cã s2 l −íc l−îng kh«ng chÖch cña D(b), s b
b ®−îc coi l sai sè trung b×nh cña hÖ sè tù do β cña ph−¬ng
tr×nh ®−êng th¼ng håi quy.
Còng nh− hÖ sè gãc cña ®−êng th¼ng håi quy, ng−êi ta chøng minh ®−îc r»ng nÕu εi cã ph©n bè chuÈn, khi ®ã thèng kª b − β t = sb
cã ph©n bè Student víi n − 2 bËc tù do. Do vËy ¸p dông ph−¬ng ph¸p −íc l−îng kho¶ng tin cËy cho gi¸ trÞ trung b ǫ b ǫ b (9)
Khi β = 0, tqs = b l( gi¸ trÞ quan s¸t (t Stat) øng víi hÖ sè tù do β trong b¶ng ANOVA ph©n tÝch sb håi quy. VÝ dô 1
Trong vÝ dô ë môc tr−íc, ®−êng th¼ng håi quy cña Y ®èi víi X y = 1, 86623x + 42, 39808. Sai sè trung b×nh √ n SSE 37363, 89302 σ∗ = √ SY 1 − r2 = = = 41, 21115. n − 2 n − 2 22 http://www.ebook.edu.vn 44 CuuDuongThanCong.com
https://fb.com/tailieudientucntt 1.
Sai sè khi −íc l−îng c¸c hÖ sè a v( b cña ®−êng håi quy Ta biÕt r»ng S2(1 − r2) s2 Y a = (n − 2)S2X 2 (1 − r2)S2 (S2 + X ) s2 Y X b = . (n − 2)S2X
Thay vo tÝnh ta sÏ ®−îc c¸c sai sè khi −íc l−îng a v b. Sai sè trung b×nh cña a sa = 0, 098939 Sai sè cña b sb = 65, 73696 2.
KiÓm ®Þnh quan hÖ tuyÕn tÝnh cña h(m håi quy
Nh− ®1 tr×nh by ë trªn, kiÓm ®Þnh vÒ mèi liªn quan tuyÕn tÝnh t−¬ng ®−¬ng víi kiÓm ®Þnh gi¶ thuyÕt
(H): α = 0 víi ®èi thiÕt (K): α = 0
Khi gi¶ thiÕt (H): α = 0 ®óng, gi¸ trÞ quan s¸t cña thèng kª a − α 1, 86623 t 0 = qs = = 18, 86 sa 0, 098939
tra b¶ng ph©n vÞ ph©n bè Student víi n − 2 = 22 bËc tù do, møc ý nghÜa ǫ = 0, 05 ta cã ph©n vÞ
t0,05 = 2, 405468. Gi¸ trÞ quan s¸t lín h¬n nhiÒu so víi ph©n vÞ t0,05 = 2, 405468. Ta b¸c bá gi¶ thiÕt
α = 0, mèi quan hÖ gi÷a Y v X l quan hÖ tuyÕn tÝnh.
NhËn xÐt r»ng t−¬ng ®−¬ng víi kiÓm ®Þnh trªn, ta cã thÓ sö dông thèng kª F .
Víi møc ý nghÜa ǫ = 0, 05 tra b¶ng ph©n vÞ ph©n bè F víi 1 v n − 2 = 22 bËc tù do, ta x¸c ®Þnh F2 = 5, 78632
Gi¸ trÞ quan s¸t Fqs = 355, 7938 lín h¬n rÊt nhiÒu so víi F2 = 5, 78632, ta b¸c bá gi¶ thiÕt (H): α = 0,
tøc l mèi quan hÖ tuyÕn tÝnh gi÷a Y v X kh¸ chÆt. 3.
Kho¶ng tin cËy cho hÖ sè gãc α cña ®−êng håi quy Thèng kª a − α t = sa
cã ph©n bè Student víi 22 bËc tù do. ¸p dông c«ng thøc (8) t×m kho¶ng tin cËy víi ®é tin cËy 95% cho
hÖ sè gãc α: a − tǫsa < α < a + tǫsa (ph©n vÞ t0,05 = 2, 405468) ta ®−îc kho¶ng tin cËy cho hÖ sè gãc α l (1, 628237 ; 2, 104225) http://www.ebook.edu.vn 45 CuuDuongThanCong.com
https://fb.com/tailieudientucntt VÝ dô 2
H1y ph©n tÝch hiÖu qu¶ cña viÖc ®Çu t− qu¶ng c¸o (X) v doanh thu cña mét c«ng ty (Y ) trong kho¶ng thêi
gian mét n¨m. C¸c sè liÖu ®−îc cho trong b¶ng d−íi ®©y: X 7 5 2 4 9 4 Y 14,99 12,08 5,55 9,79 16,38 9,68 X 9 6 3 4 7 5 Y 18,61 14,25 5,52 12,49 15,94 12,54
Sö dông lÖnh {= LIN EST (Y, X, 1, 1)} trong EXCEL (nhÊn ®ång thêi c¸c phÝm CT RL + SHIF T +
ENT ER) ta thu ®−îc b¶ng sau 1.72676783 2.965007587 0.199411812 1.161334855 0.882330203 1.47775679 74.98357456 10 163.7465154 21.83765129
Hng thø nhÊt l c¸c hÖ sè håi quy a = 1.72676783, b = 2.965007587 ⇒ y = 1.72676783x + 2.965007587
Sai sè trung b×nh cña c¸c hÖ sè håi quy a v b trong hng thø hai. D(α) = 0.199411812 D(β) = 1.161334855.
Hng thø ba l hÖ sè sè t−¬ng quan r2 = 0.882330203 v sai sè chuÈn (standard error) b»ng σ∗ = 1.47775679. H H 154 v Y phÇn d− R2
) trong b¶ng ph©n tÝch ph−¬ng sai
0 = 21.83765129 (kÝ hiÖu l SSR SUMMARY OUTPUT Regression Statistics Multiple R 0.939324333 R Square 0.882330203 Adjusted R Square 0.870563223 Standard Error 1.47775679 Observations 12 ANOVA df SS MS F Significance F Regression 1 163.7465154 163.7465154 74.98357456 5.84643E&06 Residual 10 21.83765129 2.183765129 Intercept 2.965007587 1.161335 2.5531 0.028710768 0.377392 5.552623 X Variable 1 1.72676783 0.199412 8.6593 5.84643E&06 1.282451 2.171085
¸p dông c«ng thøc (8) ta ®−îc 2 cËn trªn, cËn d−íi (1.282451; 2.171085) cña hÖ sè gãc cña ®−êng th¼ng
håi quy víi ®é tin cËy 95%. C¸c nhËn xÐt sau c«ng thøc (8) v (9): a b tqs = , tqs = D(a) D(b)
cho ta c¸c gi¸ trÞ quan s¸t t Stat 8.6593 v 2.5531. C«ng thøc (9) ®Ó tÝnh kho¶ng tin cËy cho hÖ sè tù do b cña
®−êng th¼ng håi quy víi ®é tin cËy 95% (0.377392; 5.552623). http://www.ebook.edu.vn 46 CuuDuongThanCong.com
https://fb.com/tailieudientucntt 16 Håi quy nhiÒu chiÒu
Bi to¸n håi quy nhiÒu chiÒu l bi to¸n xÐt t¸c ®éng cña nhiÒu biÕn ngÉu nhiªn (X1, X2, ...) tíi mét biÕn ngÉu
nhiªn kh¸c (Y ). Ch¼ng h¹n khi muèn t×m hiÓu l1i suÊt hng n¨m cña c¸c c«ng ty ti chÝnh, ng−êi ta thÊy l1i
suÊt ®ã tØ lÖ thuËn víi tæng thu (tõ thuÕ cña nh n−íc, ®¬n vÞ cña tæng thu ny tÝnh theo % v kÝ hiÖu l X1),
®ång thêi còng tØ lÖ nghÞch víi sè v¨n phßng giao dÞch (X2). (Do sù c¹nh tranh gi÷a c¸c c«ng ty, sè v¨n phßng
giao dÞch ®−îc më ngy mét t¨ng). Gäi Y l tØ lÖ l1i suÊt hng n¨m cña c«ng ty (®¬n vÞ %).
B¶ng sau cho ta sè liÖu quan s¸t ®−îc vÒ c¸c ®¹i l−îng ny trong vßng 25 n¨m. STT X1 X2 Y STT X1 X2 Y 1 3.92 7298 0.75 14 3.78 6672 0.84 2 3.61 6855 0.71 15 3.82 6890 0.79 3 3.32 6636 0.66 16 3.97 7115 0.7 4 3.07 6506 0.61 17 4.07 7327 0.68 5 3.06 6450 0.7 18 4.25 7546 0.72 6 3.11 6402 0.72 19 4.41 7931 0.55 7 3.21 6368 0.77 20 4.49 8097 0.63 8 3.26 6340 0.74 21 4.7 8468 0.56 9 3.42 6349 0.9 22 4.58 8717 0.41 10 3.42 6352 0.82 23 4.69 8991 0.51 11 3.45 6361 0.75 24 4.71 9179 0.47 12 3.58 6369 0.77 25 4.78 9318 0.32 13 3.66 6546 0.78 MÉu håi quy nhiÒu chiÒu
E(Yi/X1 = x1i, X2 = x2i, ..., Xk = xki) = α + β1x1i + β2x2i + ... + βkxki, i = 1, 2, ..., n. hay
Yi = α + β1x1i + β2x2i + ... + βkxki + εi,
trong ®ã βi l c¸c h»ng sè cÇn −íc l−îng v εi l biÕn ngÉu nhiªn cã k× väng b»ng 0. C¸c mÉu ngÉu nhiªn l c¸c ®iÓm quan s¸t (x1i, x2i, ..., xki, yi), i = 1, 2, ..., n. Do mÉu håi quy nhiÒu chiÒu
E(Yi/X1 = x1i, X2 = x2i, ..., Xk = xki) = α + β1x1i + β2x2i + ... + βkxki, i = 1, 2, ..., n. Suy ra
E(Yi/X1 = x1i + 1, X2 = x2i, ..., Xk = xki) − E(Yi/X1 = x1i, X2 = x2i, ..., Xk = xki) = β1
(NghÜa l( trong vÝ dô trªn nÕu tæng thu t¨ng thªm 1%, víi sè v¨n phßng giao dÞch X2 kh«ng ®æi, khi
®ã tØ lÖ lMi suÊt h(ng n¨m t¨ng thªm β1.)
Gäi a, b1, b2, ..., bk l c¸c −íc l−îng t−¬ng øng, khi ®ã mÉu dù b¸o cña biÕn ngÉu nhiªn Y l ˆ
y = a + b x + b x + ... + b x . Theo ®
ei = yi − (a + b1x1i + b2x2i + ... + bkxki), i = 1, 2, ..., n.
§èi víi mÉu håi quy tuyÕn tÝnh nhiÒu chiÒu, c¸c −íc l−îng a, b1, b2, ..., bk cÇn x¸c ®Þnh theo ph−¬ng ph¸p b×nh
ph−¬ng bÐ nhÊt, tøc l tæng b×nh ph−¬ng c¸c ®é lÖch n n SS = e2 (y i =
i − a − b1x1i − b2x2i − ... − bkxki)2 i=1 i=1 ®¹t gi¸ trÞ nhá nhÊt. Ph−¬ng tr×nh
y = a + b1x1 + b2x2 + ... + bkxk
®−îc gäi l mÆt ph¼ng håi quy cña Y ®èi víi X1, X2, ..., Xk.
Tr−íc hÕt ta ph¸t biÓu ®Þnh lÝ sau http://www.ebook.edu.vn 47 CuuDuongThanCong.com
https://fb.com/tailieudientucntt §Þnh lÝ 12
Gi¶ thiÕt r»ng mÉu håi quy tuyÕn tÝnh cña Y ®èi víi X : 1, X2, ..., Xk
Yi = α + β1x1i + β2x2i + ... + βkxki + εi, trong ®ã
1. x1i, x2i, ..., xki l( c¸c thÓ hiÖn cña X1i, X2i, ..., Xki. C¸c biÕn ngÉu nhiªn ®ã ®éc lËp víi εi. 2. E(εi) = 0, D(εi) = σ2, E(εiεj) = 0, víi mäi i = j, i, j = 1...n
3. H¹ng cña ma trËn (xij) b»ng k.
Khi ®ã c¸c −íc l−îng a, b1, b2, ..., bk x¸c ®Þnh theo ph−¬ng ph¸p b×nh ph−¬ng bÐ nhÊt cña α v( β1, β2, ..., βk
l( c¸c −íc l−îng kh«ng chÖch cã ph−¬ng sai nhá nhÊt. H¬n n÷a víi mäi sè thùc d0, d1, d2, ..., dk, −íc l−îng
d0 + d1b1 + d2b2 + + dkbk còng l( −íc l−îng cã ph−¬ng sai nhá nhÊt trong sè tÊt c¶ c¸c −íc l−îng tuyÕn tÝnh kh«ng chÖch cña
d0 + d1β1 + d2β2 + + dkβk. Tõ hÖ thøc yi − y = (ˆyi − y) + ei,
b×nh ph−¬ng c¶ hai vÕ ®¼ng thøc trªn v céng chóng l¹i theo i ta ®−îc n n n (y 2 2 i − y) = (ˆ yi − y) + e2i. i=1 i=1 i=1
§¼ng thøc cã ý nghÜa nh− sau: vÕ tr¸i l tæng b×nh ph−¬ng c¸c ®é lÖch gi÷a c¸c phÇn tö mÉu cña Y víi gi¸ trÞ
trung b×nh mÉu y, kÝ hiÖu SST (total sum of squares) ®−îc ph©n tÝch thnh tæng cña hai phÇn: phÇn thø nhÊt
l tæng b×nh ph−¬ng c¸c ®é lÖch gi÷a håi quy ˆ
yi víi trung b×nh mÉu y v phÇn thø hai l phÇn d−: tæng b×nh
ph−¬ng c¸c sai sè. KÝ hiÖu i=1 n SSR = (ˆ
yi − y)2 (Tæng b×nh ph−¬ng håi quy) i=1 n SSE = e2
(Tæng b×nh ph−¬ng sai sè) i . i=1
Theo ®¼ng thøc: SST = SSR + SSE, khi ®ã tØ sè SSR SSE R2 = = 1 − SST SST
®−îc gäi l hÖ sè x¸c ®Þnh biÓu diÔn lùc cña håi quy. 0 R2 1 v khi R2 cng gÇn víi 1, phÇn d− SSE
(tæng b×nh ph−¬ng c¸c sai sè) cng nhá so víi tæng b×nh ph−¬ng c¸c ®é lÖch chung cña Y .
Chó ý: hÖ sè x¸c ®Þnh ®iÒu chØnh
Ng−êi ta chøng minh ®−îc r»ng víi c¸c ®iÒu kiÖn cña ®Þnh lÝ trªn n e2 SSE s2 i=1 i e = = n − k − 1 n − k − 1
l −íc l−îng kh«ng chÖch cña σ2. Ta gäi se = s2 l sai sè chuÈn. e
ViÖc tÝnh sai sè chuÈn cña c¸c hÖ sè håi quy bk, bk , b , a −1, ..., b2 1
phøc t¹p h¬n (xem phÇn håi quy ®¬n
gi¶n, mét chiÒu). C¸c ch−¬ng tr×nh phÇn mÒm thèng kª sÏ tÝnh gióp ta c¸c sai sè ®ã. Thùc h%nh trªn EXCEL
XÐt vÝ dô vÒ l1i suÊt hng n¨m cña c¸c c«ng ty ti chÝnh, sö dông lÖnh {= LIN EST (Y, X, 1, 1)}, ta ®−îc b¶ng sau http://www.ebook.edu.vn 48 CuuDuongThanCong.com
https://fb.com/tailieudientucntt &0.000249079 0.237197475 1.564496771 3.20485E&05 0.055559366 0.079395981 0.865296068 0.053302217 70.66057082 22 0.40151122 0.06250478
Hng thø nhÊt l c¸c hÖ sè håi quy viÕt theo ®óng thø tù y = bkxk + bk x b
−1 k−1 + ... + 2x2 + b1x1 + a
Hay y = −0.00025x2 + 0.2372x1 + 1.5645.
Sai sè trung b×nh (c¨n bËc hai cña ph−¬ng sai) cña c¸c hÖ sè håi quy bk, bk , b , a −1, ..., b2 1 cho trong hng thø hai. D(b2) = 3.20485E − 05, D(b1) = 0.055559, D(a) = 0.079396.
Hng thø ba l hÖ sè x¸c ®Þnh gi¶i thÝch lùc cña håi quy R2 = 0.865296068 v sai sè chuÈn (standard error) se = 0.053302217.
Hng thø t− cho gi¸ trÞ quan s¸t Fqs = 70.66057082 cña ph©n bè F víi (k, 22) bËc tù do. (Trong vÝ dô ny k = 2).
Hng thø n¨m l c¸c tæng b×nh ph−¬ng SSR = 0.40151122 v phÇn d− SSE = 0.06250478.
Chó ý r»ng håi quy tuyÕn tÝnh nhiÒu chiÒu th−êng xuyªn ®−îc sö dông h¬n håi quy ®¬n gi¶n (mét chiÒu),
nÕu cßn c¸c biÕn ®éc lËp t¸c ®éng ®¸ng kÓ tíi biÕn phô thuéc. Ch¼ng h¹n trong vÝ dô trªn , biÕn phô thuéc
(lMi suÊt y) tØ lÖ thuËn víi tæng thu (x1). Trong khi nÕu ta chØ quan t©m tíi lMi suÊt v( tæng thu, håi quy ®¬n gi¶n cho ta kÕt qu¶ y = 1.326 − 0.169x1
lMi suÊt gi¶m khi x1 t¨ng(!) T−
Ta nhÊn m¹nh r»ng t−¬ng øng víi mÉu quan s¸t yi, i = 1, 2, ..., n l mÉu dù b¸o ˆ
yi = a + b1x1i + b2x2i + ... + bkxki, i = 1, 2, ..., n.
HÖ sè t−¬ng quan gi÷a chóng ®−îc gäi l hÖ sè t−¬ng quan béi, nã ®o møc ®é t¸c dông tuyÕn tÝnh cña
X = (X1, , Xk) lªn Y . (DÔ dng chøng minh ®−îc: Y − ˆ
Y kh«ng t−¬ng quan (trùc giao) víi X1, , Xk.
Thùc chÊt cña ph−¬ng ph¸p b×nh ph−¬ng nhá nhÊt l( sau khi tÞnh tiÕn hÖ trôc to¹ ®é tíi ®iÓm
(EY, EX1, ..., EXk) ∈ Rk+1, ˆ
Y l( phÐp chiÕu vu«ng gãc Y xuèng L2(X1, ..., Xk)). Suy ra, nh− ®1 biÕt
trong lÝ thuyÕt vÒ kh«ng gian Hilbert hÖ sè t−¬ng quan ch¼ng qua l( c«sin cña gãc gi÷a hai vÐc t¬, hÖ sè
t−¬ng quan béi b»ng c¨n bËc hai cña hÖ sè x¸c ®Þnh √ R = R2. √
Trong vÝ dô cña chóng ta R = 0.8652 = 0.93.
Khi kh¶o s¸t mèi t−¬ng quan ta tÝnh hÖ sè t−¬ng quan gi÷a c¸c ®¹i l−îng ngÉu nhiªn, ch¼ng h¹n >ij = >ij(Xi ¸c biÕn ngÉu n æng cña
hai ®¹i l−îng ngÉu nhiªn kh«ng t−¬ng quan (chiÕu vu«ng gãc xuèng L2(X2, ..., Xk)) Y = ˆ YY ′2...k + (Y − ˆ YY ′2...k) = ˆ YY ′2...k + ηY ′2...k, X1 = ˆ X1 + (X1 − ˆ X1) = ˆ X1 + η1′2...k
Cã thÓ coi ηY ′2...k = Y − ˆ
YY ′2...k l phÇn cßn l¹i cña Y sau khi ®1 lo¹i ®i c¸c t¸c ®éng tuyÕn tÝnh cña X2, ..., Xk
vo Y . T−¬ng tù η1′2...k = X1 − ˆ
X1 l phÇn cßn l¹i cña X1 sau khi ®1 lo¹i ®i c¸c t¸c ®éng tuyÕn tÝnh cña
X2, ..., Xk vo X1. Khi ®ã hÖ sè t−¬ng quan gi÷a hai phÇn d− ηY ′2...k = Y − ˆ
YY ′2...k v η1′2...k = X1 − ˆ X1
®−îc gäi l hÖ sè t−¬ng quan riªng (mèi quan hÖ néi t¹i, kh«ng phô thuéc vo c¸c ®¹i l−îng ngÉu nhiªn kh¸c:
X2, ..., Xk) gi÷a Y v X1. KÝ hiÖu >Y.1 = >(ηY ′2...k, η1′2...k).
Quay trë l¹i vÝ dô trªn, ta tÝnh hÖ hÖ sè t−¬ng quan riªng gi÷a l1i suÊt (Y ) v sè v¨n phßng giao dÞch ®−îc
më ra (X2). Ta lËp b¶ng sau m c¸c cét d÷ liÖu l håi quy cña Y theo X1 v håi quy cña Y theo X2. http://www.ebook.edu.vn 49 CuuDuongThanCong.com
https://fb.com/tailieudientucntt STT ηY ′2...k η1′2...k = X1 − ˆ X1 STT ηY ′2...k η1′2...k = X1 − ˆ X1 1 0.086830251 &53.63957787 14 0.153152011 &451.2549257 2 &0.005600136 9.06929472 15 0.109917223 &298.5076835 3 &0.104647917 263.1517884 16 0.045286765 &318.2055251 4 &0.196930487 540.9815244 17 0.042199793 &269.3374194 5 &0.10862179 501.2947138 18 0.112643243 &343.9748293 6 &0.080165276 371.7287666 19 &0.030295912 &219.9858604 7 &0.013252248 174.5968723 20 0.06323451 &184.4913759 8 &0.034795734 65.03092506 21 0.028751869 &156.0683541 9 0.152265111 &186.980106 22 &0.141543765 288.6899192 10 0.072265111 &183.980106 23 &0.022939434 383.2448354 11 0.007339019 &223.9196743 24 &0.059556828 538.6184565 12 0.049325955 &427.991137 25 &0.197717709 563.4261304 13 0.072856378 &381.4966525
HÖ sè t−¬ng quan riªng gi÷a l1i suÊt (Y ) v sè v¨n phßng giao dÞch ®−îc më ra (X2) khi ®ã b»ng >Y.1 =
−0.85617. (Sö dông lÖnh CORREL).
B×nh ph−¬ng hÖ sè t−¬ng quan riªng (−0.85617)2 = 0.73, vËy 73% phÇn biÕn ®éng cña l1i suÊt (Y ) ®−îc
gi¶i thÝch bëi sù phô thuéc tuyÕn tÝnh (tØ lÖ nghÞch) vo sè l−îng v¨n phßng giao dÞch ®−îc më.
T−¬ng tù hÖ sè t−¬ng quan riªng gi÷a l1i suÊt (Y ) v (X1) b»ng >Y.2 = 0.6731. (TØ lÖ thuËn).
Ta còng cã thÓ tÝnh t−¬ng quan riªng gi÷a lMi suÊt (Y ) v( (X1) b»ng c¸ch sö dông c¸c c«ng thøc (??j??) −C 5.929936871 > 10 01.(23...n) = √ = √ = 0.673126. C00C11 3.10432981 × 25
Kho¶ng tin cËy v% kiÓm ®Þnh gi¶ thiÕt cho c¸c tham sè cña håi quy.
C¸c vÊn ®Ò vÒ kho¶ng tin cËy v kiÓm ®Þnh gi¶ thiÕt cho c¸c tham sè cña håi quy dùa trªn ®Þnh lÝ sau §Þnh l Ví i h©n bè chuÈn. KÝ hiÖu sb , s , ..., s , s s k bk− b
b a l( c¸c sai sè chuÈn cña c¸c hÖ sè håi quy bk, bk , b , a −1, ..., b2 1 , khi ®ã a − α b t i − βi a = , t = , i = 1, 2, ..., k s bi a sbi
l( c¸c ®¹i l−îng ngÉu nhiªn cã ph©n bè Student víi n − k − 1 bËc tù do.
Ch¼ng h¹n trong vÝ dô l1i suÊt cña c¸c c«ng ty ti chÝnh, víi ®é tin cËy 99% 0.081 < β2 < 0.394,
−0.000339 < β1 < −0.000159. (s −5 b tǫ − b1 β1 sb t 81876 = 3.2 × 10 , b1 = −0.000249) ǫ + b1, tǫ = t0.01 = 2. , sb Do mÉu håi quy nhiÒu chiÒu
E(Yi/X1 = x1i, X2 = x2i, ..., Xk = xki) = α + β1x1i + β2x2i + ... + βkxki, i = 1, 2, ..., n. Suy ra
E(Yi/X1 = x1i + 1, X2 = x2i, ..., Xk = xki) − E(Yi/X1 = x1i, X2 = x2i, ..., Xk = xki) = β1
NghÜa l trong vÝ dô ®1 nªu nÕu sè v¨n phßng giao dÞch t¨ng thªm 1000, (víi tæng thu X1 kh«ng ®æi), khi ®ã
tØ lÖ l1i suÊt hng n¨m gi¶m tõ 0.159 tíi 0.339.
KiÓm ®Þnh gi¶ thiÕt cho mçi tham sè cña håi quy.
Còng dùa trªn c¬ së tb cã ph©n bè Student víi n − k − 1 bËc tù do, ta cã thÓ kiÓm ®Þnh c¸c gi¶ thiÕt i H0 : βi = βi,0 hoÆc H0 : βi βi,0 víi ®èi thiÕt H1 : βi > βi,0, http://www.ebook.edu.vn 50 CuuDuongThanCong.com
https://fb.com/tailieudientucntt β theo quy t¾c b¸c bá H i − βi,0 0 nÕu tqs = > tǫ. sbi
(C¸c kiÓm ®Þnh mét phÝa kh¸c hoÆc kiÓm ®Þnh 2 phÝa còng theo quy t¾c t−¬ng tù ®1 biÕt).
§Æc biÖt nÕu gi¸ trÞ thùc cña β1 = 0
Yi = α + β2x2i + ... + βkxki + εi
kh«ng bÞ ¶nh h−ëng bëi biÕn ®éc lËp X1 khi c¸c biÕn X2, ..., Xk nhËn c¸c gi¸ trÞ cè ®Þnh cho tr−íc. Nãi c¸ch
kh¸c X1 kh«ng gãp phÇn vo gi¶i thÝch mèi quan hÖ tuyÕn tÝnh gi÷a biÕn phô thuéc víi c¸c biÕn ®éc lËp.
Trong vÝ dô trªn kiÓm ®Þnh H0 : β1 = 0 víi ®èi thiÕt H1 : β1 > 0 b 0.237 t i − βi,0 qs = = = 4.27 sb 0.0555 i
NhËn xÐt r»ng khi βi = 0, tqs = bi l( gi¸ trÞ quan s¸t (t Stat) øng víi hÖ sè gãc β s i trong b¶ng ANOVA bi ph©n tÝch håi quy.
NÕu møc ý nghÜa rÊt bÐ 0.5%, tra b¶ng 22 bËc tù do (1 phÝa) tǫ = 2.81876, ta vÉn b¸c bá H0 : β1 = 0.
T−¬ng tù xÐt bi to¸n kiÓm ®Þnh H0 : β2 = 0 víi ®èi thiÕt H1 : β2 < 0 b −0.000249 t 2 − 0 qs = =
= −7.78 < −tǫ = −2.81876, sb 0.0000320 ta b¸c bá H0 : β2 = 0 ë møc 0.5%.
Ta cã thÓ kiÓm ®Þnh B(i to¸n (2): gi¶ thiÕt H0 : βi = βi,0 hoÆc H0 : βi ≥ βi,0 víi ®èi thiÕt theo quy t¾c b¸c bá H0 nÕu tqs = i i,0 < −t s ǫ. bi B(i to¸n (3): H0 : βi = βi,0 víi ®èi thiÕt H1 : βi = βi,0, theo quy t¾c b¸c bá βi − β H i,0 0 nÕu |tqs| = s > tǫ/2. bi
KiÓm ®Þnh gi¶ thiÕt ®ång thêi cho c¸c tham sè cña håi quy. H0 :
β1 = β2 = = βk = 0 víi ®è
NÕu gi¶ thiÕt H0 ®óng, Yi = α + εi, nªn E(Yi/X) = α l h»ng sè. C¸c biÕn ®éc lËp Xi kh«ng cã ¶nh h−ëng
(tuyÕn tÝnh) tíi Y . KiÓm ®Þnh gi¶ thiÕt H0 thùc chÊt nh»m b¸c bá tÝnh phô thuéc tuyÕn tÝnh gi÷a c¸c biÕn. Ta
biÕt r»ng SST = SSR + SSE, trong ®ã SSR nh»m gi¶i thÝch sù biÕn ®éng cña håi quy (sù phô thuéc tuyÕn
tÝnh cña biÕn phô thuéc vo c¸c biÕn ®éc lËp), cßn SSE l phÇn biÕn ®éng ngoi håi quy. Do vËy nÕu gi÷a c¸c
biÕn ngÉu nhiªn kh«ng tån t¹i quan hÖ tuyÕn tÝnh khi ®ã SSR t−¬ng ®èi nhá so víi SSE, nãi c¸ch kh¸c tØ sè
gi÷a SSR v SSE cng lín, kh¶ n¨ng b¸c bá gi¶ thiÕt kh«ng (quan hÖ tuyÕn tÝnh) cng cao. V× thÕ ®Ó t¹o ra
mét thèng kª nh− vËy ng−êi ta sö dông kÕt qu¶ sau: NÕu gi¶ thiÕt H0 :
β1 = β2 = = βk = 0 ®óng v εi cã ph©n bè chuÈn, khi ®ã SSR/k F = SSE/(n − k − 1) http://www.ebook.edu.vn 51 CuuDuongThanCong.com
https://fb.com/tailieudientucntt
cã ph©n bè F víi (k, n − k − 1) bËc tù do. VËy ta cã quy t¾c ë møc α SSR/k B¸c bá H0 nÕu Fqs = > F , SSE/(n − k − 1) k,n−k−1,α trong ®ã
P (Fk,n−k−1 > Fk,n−k−1,α) = α.
NhËn xÐt r»ng do R2 = SSR = 1 − SSE, suy ra SST SST SSR/k n − k − 1 R2 F = = . SSE/(n − k − 1) k 1 − R2
Trë l¹i vÝ dô l1i suÊt tiÕt kiÖm v cho vay SSR/k 0.40151122/2 Fqs = = = 70.66057082 SSE/(n − k − 1) 0.06250478/22
Víi møc ý nghÜa 1%, Fk,n−k−1,α = 5.719, nhá h¬n rÊt nhiÒu so víi Fqs = 70.66057082, ta b¸c bá gi¶ thiÕt H0.
KiÓm ®Þnh gi¶ thiÕt ®ång thêi cho mét tËp con c¸c tham sè cña håi quy.
Gi¶ thiÕt r»ng ta cÇn kiÓm ®Þnh k1 tham sè ®Çu tiªn cña håi quy b»ng 0. H0 :
β1 = β2 = = βk = 0 (Víi ®èi thiÕt H1 :
Tån t¹i Ýt nhÊt mét i, 1 i k1 : βi = 0.)
NÕu gi¶ thiÕt H0 ®óng, c¸c biÕn X1, X2, ..., Xk kh«ng cã ¶nh h−ëng g× tíi Y , do vËy ta tiÕn hnh −íc l−îng håi qu Yi = α + βk β +1xk+1,i + + kxki + εi
Khi ®ã ta hy väng SSE cña mÉu håi quy cò kh¸c nhiÒu so víi SSE∗ cña mÉu håi quy míi. Thèng kª (SSR∗ − SSE)/k F = 1 SSE/(n − k − 1)
cã ph©n bè F víi (k1, n − k − 1) bËc tù do. VËy ta cã quy t¾c ë møc α (SSE∗ − SSE)/k B¸c bá H 1 0 nÕu Fqs = > F . SSE/(n − k − 1) k,n−k−1,α Dù b¸o.
Víi mÉu håi quy nh− ®1 nãi ë trªn, kÝ hiÖu a, b1, b2, ..., bk l c¸c −íc l−îng theo ph−¬ng ph¸p b×nh ph−¬ng bÐ nhÊ 1,n+1 2,n+1 k,n+1
dù b¸o cña biÕn phô thuéc (Yn+1 = α + β1x1,n+1 + + βkxk,n+1 + εn+1) ˆ
Yn+1 = a + b1x1,n+1 + b2x2,n+1 + + bkxk,n+1
l −íc l−îng tuyÕn tÝnh kh«ng chÖch tèt nhÊt cña Yn+1.
Trë l¹i vÝ dô quen thuéc nÕu x1,n+1 = 4.50 v sè l−îng c¸c v¨n phßng x2,n+1 = 9000 khi ®ã ˆ
Yn+1 = a + b1x1,n+1 + b2x2,n+1 = 0, 39.
Ngo(i ra nÕu gi¶ thiÕt εi cã ph©n bè chuÈn khi ®ã chóng ta cã thÓ tÝnh c¸c kho¶ng tin cËy cho c¸c dù b¸o ˆ Yn+1. http://www.ebook.edu.vn 52 CuuDuongThanCong.com
https://fb.com/tailieudientucntt




