Cây quyết định
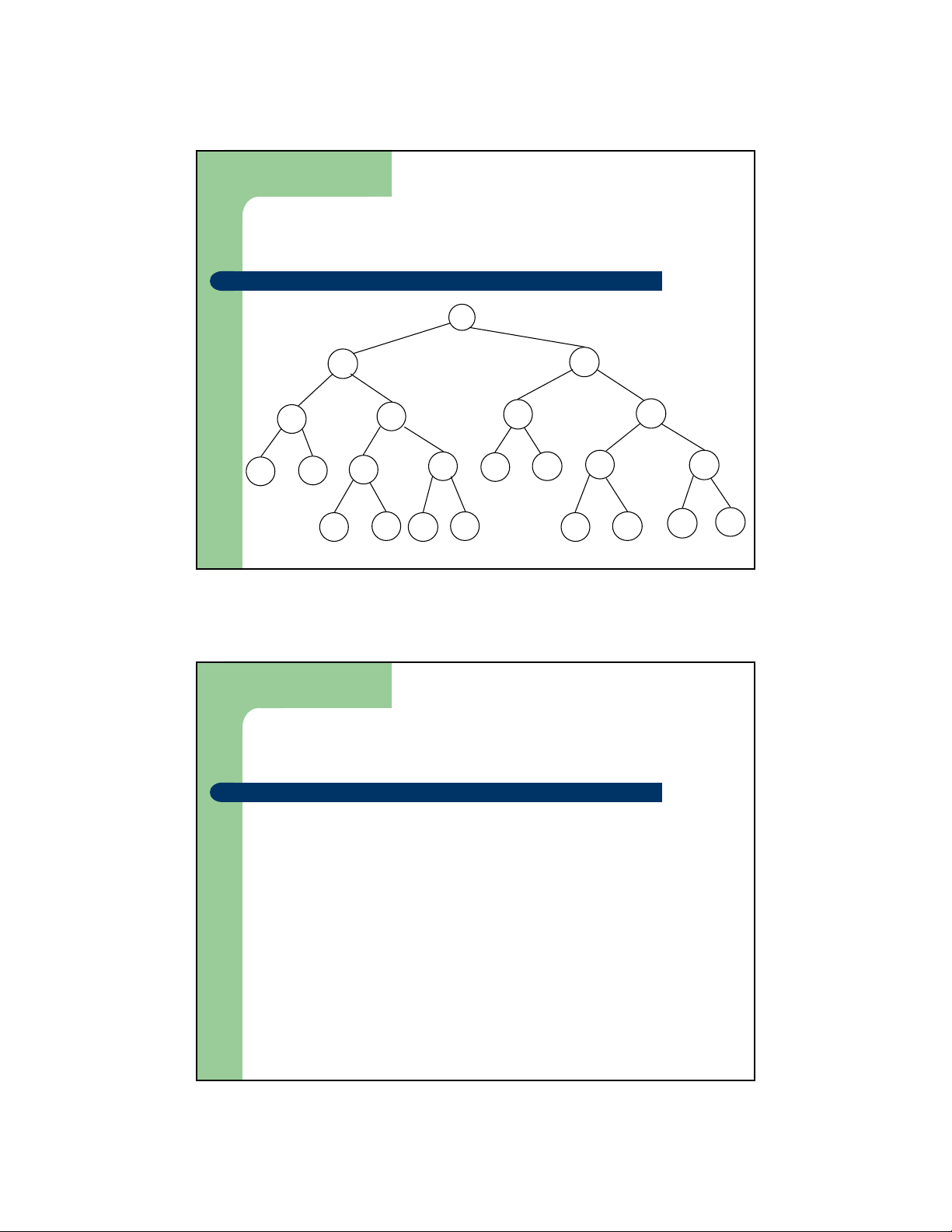
– Cây quyết định là cây:
z Mỗi nút trong tương ứng với một câu hỏi trên dữ liệu
z Mỗi nhánh của cây tương ứng với một khả năng trả lời cho một câu hỏi
z Mỗi nút lá của cây tương ứng với một kết luận
– Khi tính toán trên cây quyết định
z Xác định một kết luận bằng việc bắt đầu từ nút gốc, xác
định một đường đi đến một nút lá
z Tại các nút trung gian, việc chọn khả năng trả lời với dữ
liệu sẽ dẫn ta đến một nút ở mức tiếp theo Cây quyết định
– Ví dụ : Bài toán tìm kiếm
z Cho một mảng A gồm n số được sắp xếp. Xác định xem
một giá trị X có xuất hiện trong A không, nếu có cho biết
vị trí trong mảng A của X
– Cây quyết định để giải bài toán z Là cây nhị phân
z Mỗi nút trong biểu diễn một câu hỏi dạng X < k ?
z Mỗi nút sát lá biểu diễn câu hỏi dạng X = A[i] ?
– Mỗi nút lá tương ứng là một giá trị về vị trí i hoặc giá trị 0
thể hiện sự không xuất hiện 1
Cây quyết định – Bài toán tìm kiếm
z A = { 2, 4, 5, 7, 9, 12} x<7 ? x<4 ? x<9? x =7 ? x<12? x =2? x<5 ? x=4 ? x=5 ? x =9 ? x =12? 1 0 4 0 2 0 3 0 5 0 6 0 Mã hóa văn bản
z Bài toán mã hóa văn bản :
– Cho một văn bản D trên bảng chữ cái C. Cần mã hóa văn bản đã cho
z Mã hóa văn bản với ASCII
z Mã hóa văn bản với độ dài cố định
z Mã hóa văn bản với mã phi tiền tố 2
Mã hóa với độ dài cố định
– Ví dụ: Bảng chữ cái tiếng Anh gồm 26 chữ cái,
mã hóa sử dụng mã nhị phân độ dài cố định
z Mã hóa một chữ cái sử dụng 5 bit, không phân biệt chữ hoa chữ thường – A Æ 00001 – B Æ 00010 – C Æ 00011 – D Æ 00100 – E Æ 00101 – F Æ 00110 – G Æ 00111 – … z 000110000110100 ÅÆ CAT Mã Huffman
– Thuộc dạng mã phi tiền tố
z Mã hóa mỗi ký tự c sao cho mã của một ký tự bất kỳ
không phải là đoạn đầu của mã của một ký tự nào trong số các ký tự còn lại
– Mã hóa các ký tự sử dụng đoạn mã có độ dài khác nhau
z Ký tự có tần suất xuất hiện lớn hơn thì được mã hóa sử dụng đoạn mã ngắn hơn 3 Mã Huffman
– Một mã phi tiền tố được biểu diễn bằng một cây nhị phân
z Các nút lá biểu diễn các ký tự và tần suất xuất hiện của ký tự trong văn bản
z Các nút trong có 2 nhánh tương ứng với : 0 – nhánh
bên trái và 1 – nhánh bên phải. Các nút này chứa tổng
tần suất xuất hiện của các nút trong các nhánh con của nó
z Một đường đi từ nút gốc đến nút lá chính là một mã nhị
phân biểu diễn ký tự ở nút lá
z Ký tự có tần suất lớn sẽ xuất hiện ở mức thấp hơn, ký
tự có tần suất nhỏ sẽ xuất hiện ở mức cao hơn trong cây mã Huffman Mã Huffman 100 0 1 a: 45 55 0 1 0 25 30 0 0 1 1 c: b: 14 d: 12 13 0 1 16 111 100 101 f :5 e: 9 1100 1101 4
Thiết lập mã Huffman
– Đầu vào: Bảng chữ cái C. Tần suất xuất hiện của các ký tự trong C
– Đầu ra: Cây mã hóa Huffman – Ý tưởng:
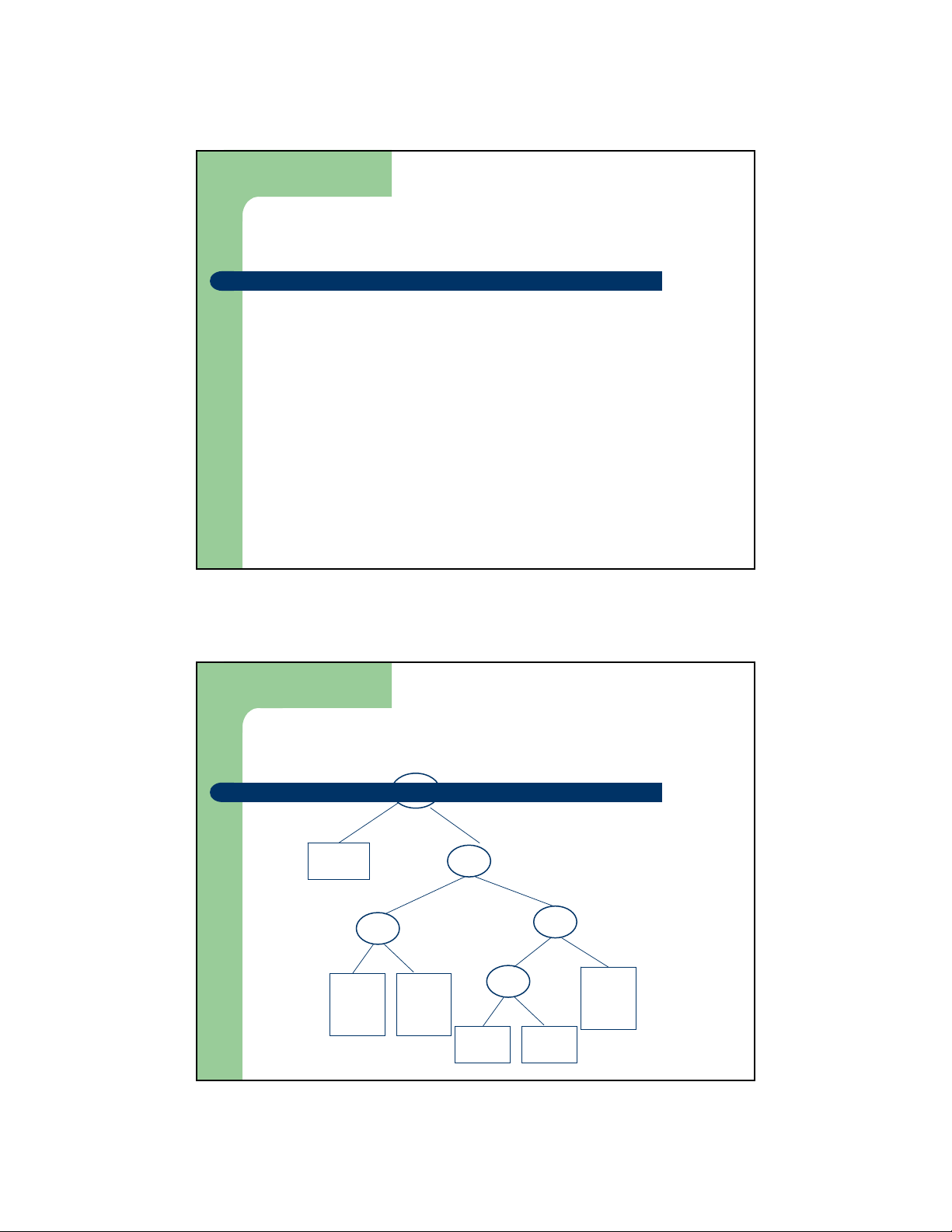
z Dựng cây từ dưới lên, xuất phát với các nút lá
z Tạo lập một nút nhánh (nút trong) bằng cách nhóm hai
nhánh đã có sẵn mà tần suất của hai nhánh đó là nhỏ nhất
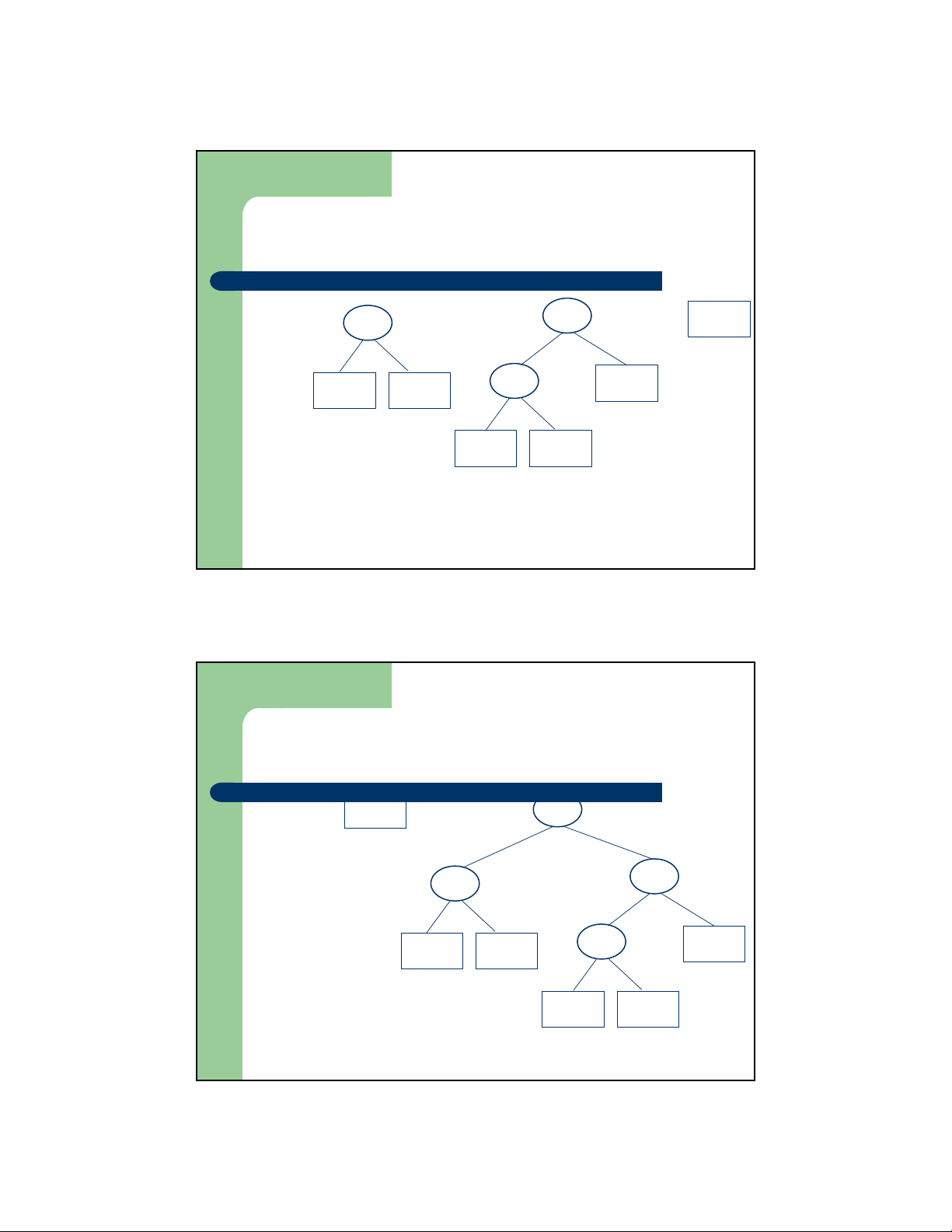
Thiết lập mã Huffman – Ví dụ Bắt đầu: f: 5 e :9 c: 12 b: 13 d: 16 a: 45 Bước 1 c: 12 b: 13 14 d: 16 a: 45 0 1 f: 5 e :9 Bước 2 14 d: 16 25 a: 45 0 1 0 1 f: 5 e: 9 c: 12 b: 13 5
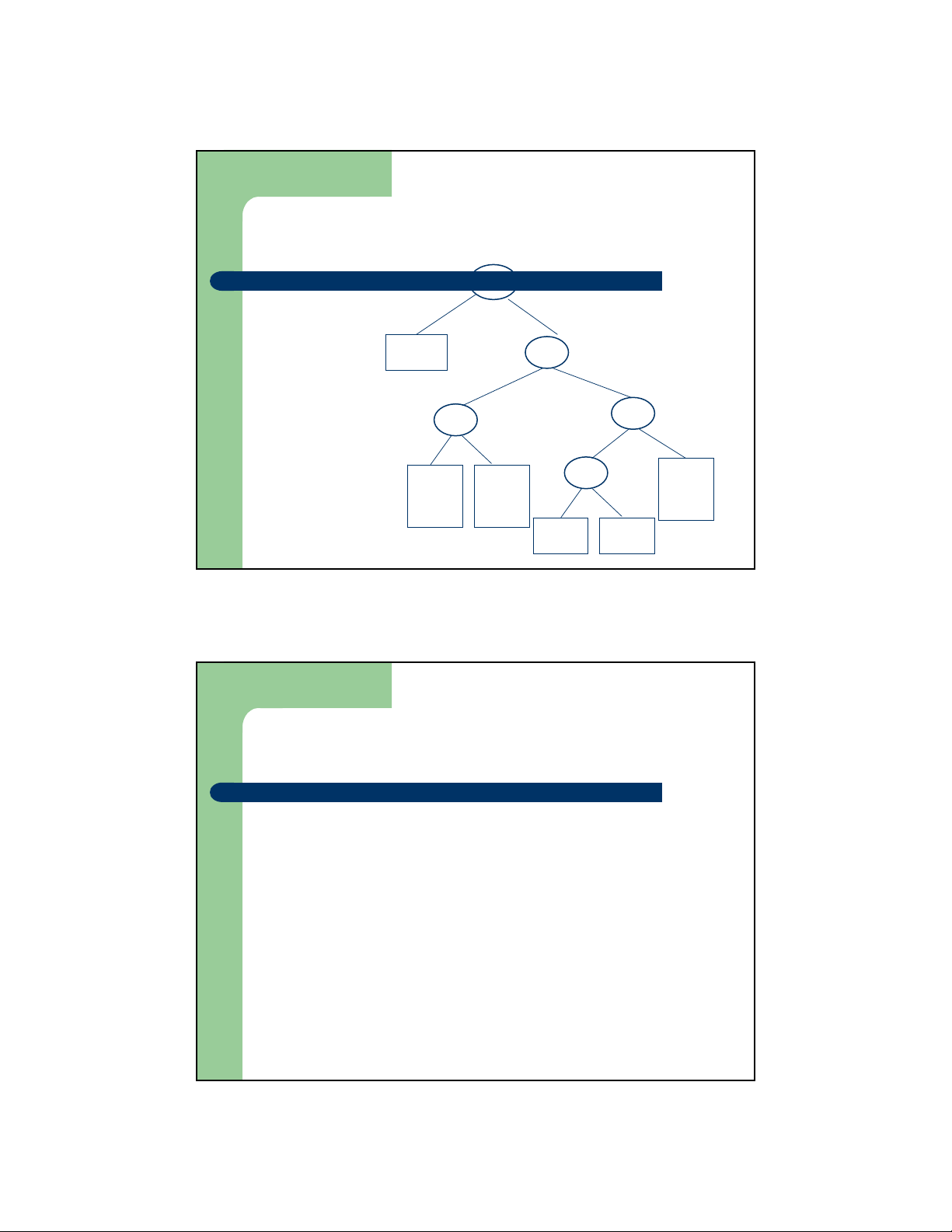
Thiết lập mã Huffman – Ví dụ Bước 3 25 30 a: 45 0 0 1 1 c: 12 b: 13 14 d: 16 0 1 f :5 e: 9
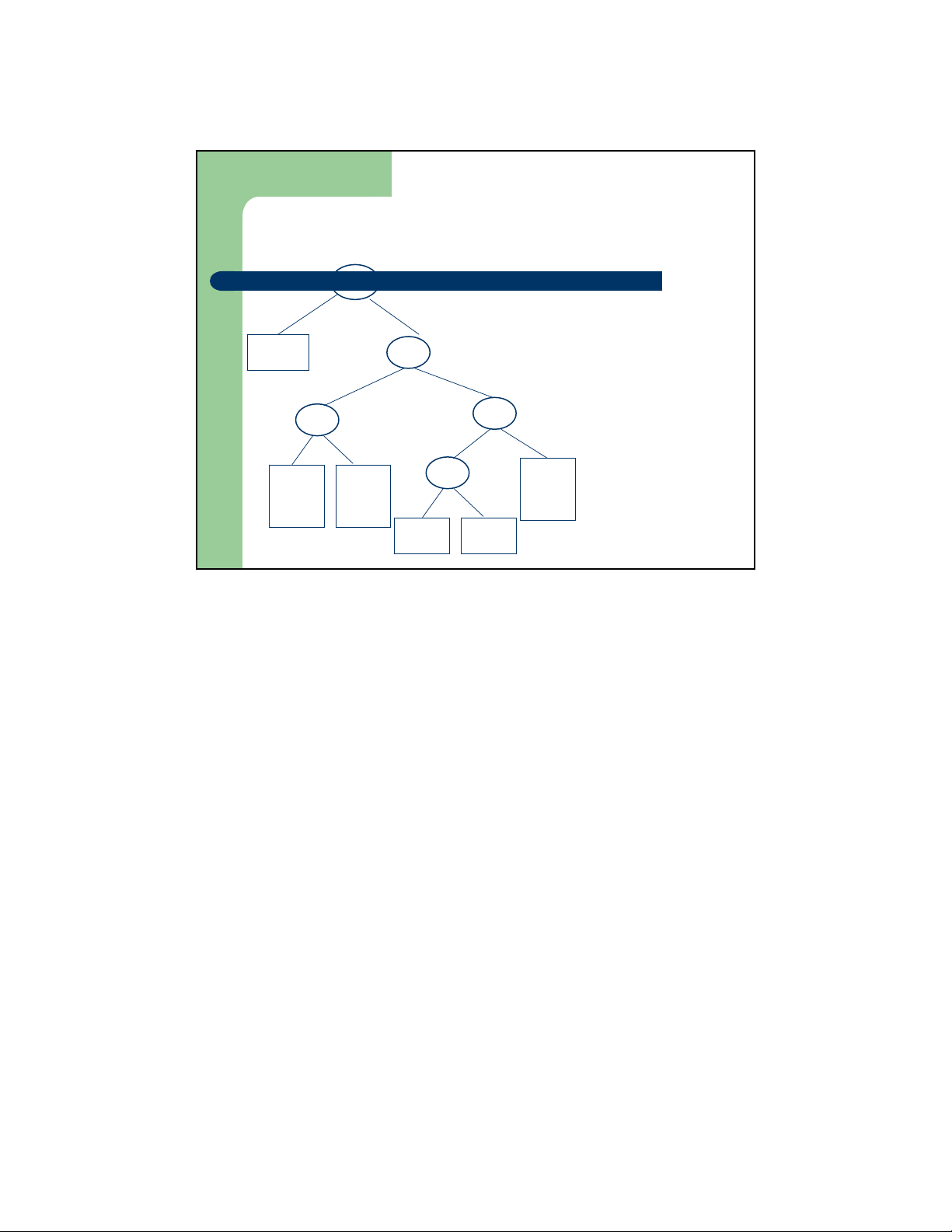
Thiết lập mã Huffman – Ví dụ Bước 4 a: 45 55 0 1 25 30 0 0 1 1 c: 12 b: 13 14 d: 16 0 1 f :5 e: 9 6
Thiết lập mã Huffman – Ví dụ Bước 5: 100 0 1 a: 45 55 0 1 0 25 30 0 0 1 1 c: b: 14 d: 12 13 0 1 16 111 100 101 f :5 e: 9 1100 1101 Giải mã Huffman
– Xuất phát từ gốc của cây mã hóa
– Đọc lần lượt từng ký tự trong xâu mã hóa z Nếu là 0 : đi sang trái z Nếu là 1: đi sang phải
– Nếu chạm tới một nút lá ghi ký tự chứa tại nút lá
ra, sau đó quay lại nút gốc của cây mã hóa. 7 Giải mã Huffman 100
Xâu ký tự cần giải mã theo cây 0 ở bên 1 111110101100 Æ deaf a: 45 55 0 1 0 25 30 0 0 1 1 c: b: 14 d: 12 13 0 1 16 111 100 101 f :5 e: 9 1100 1101 8