



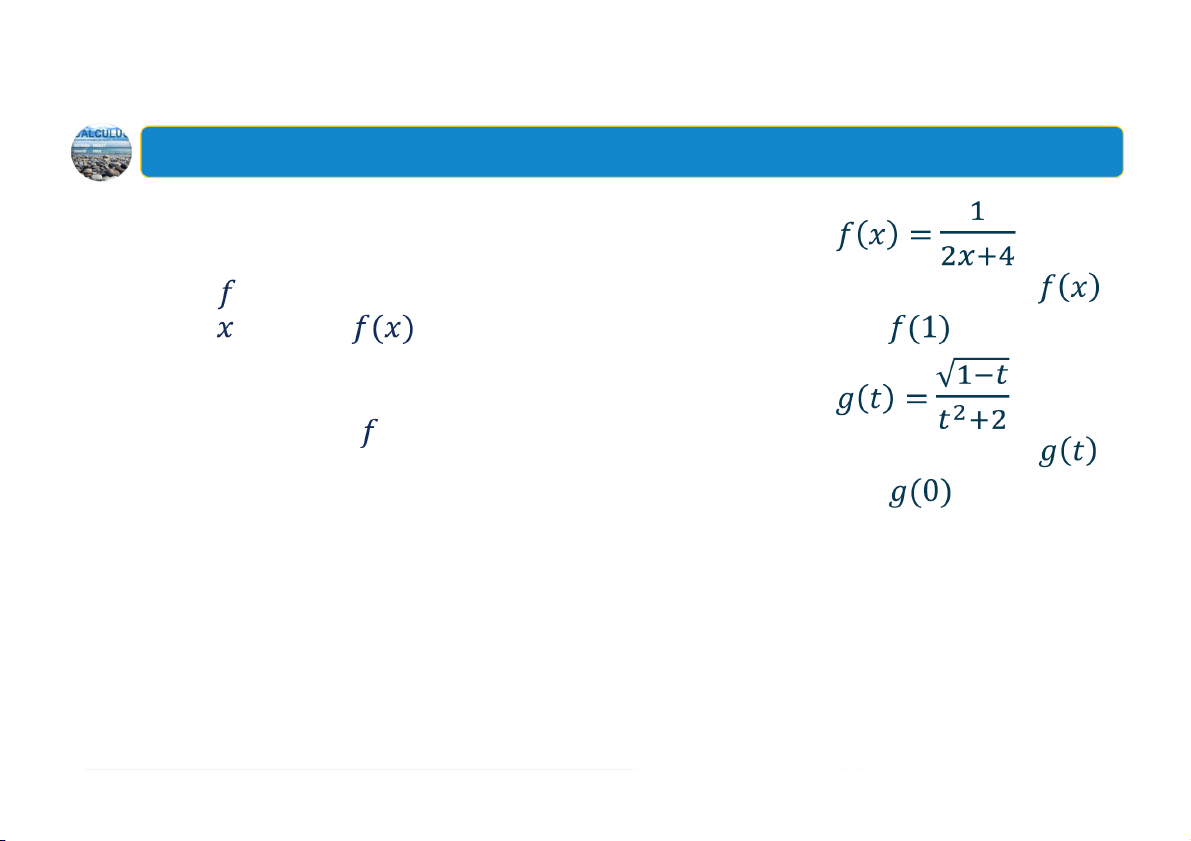
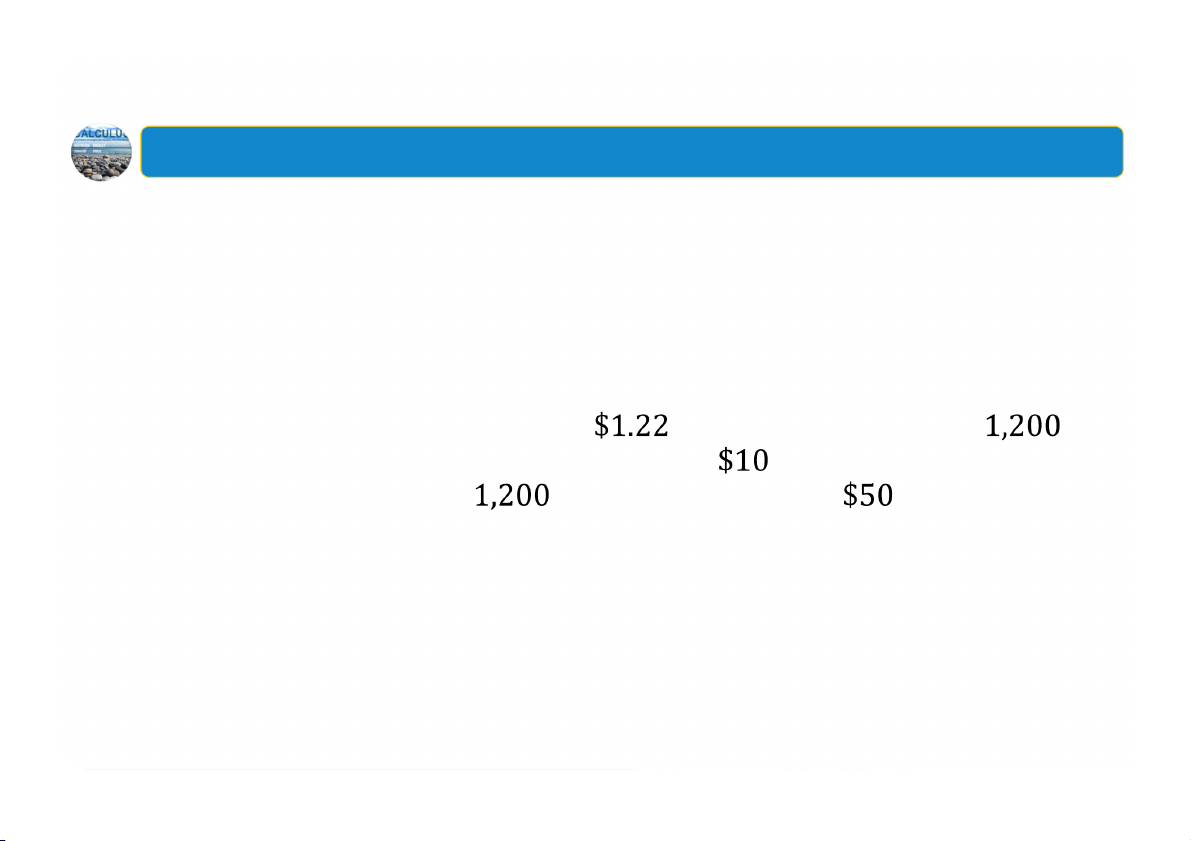
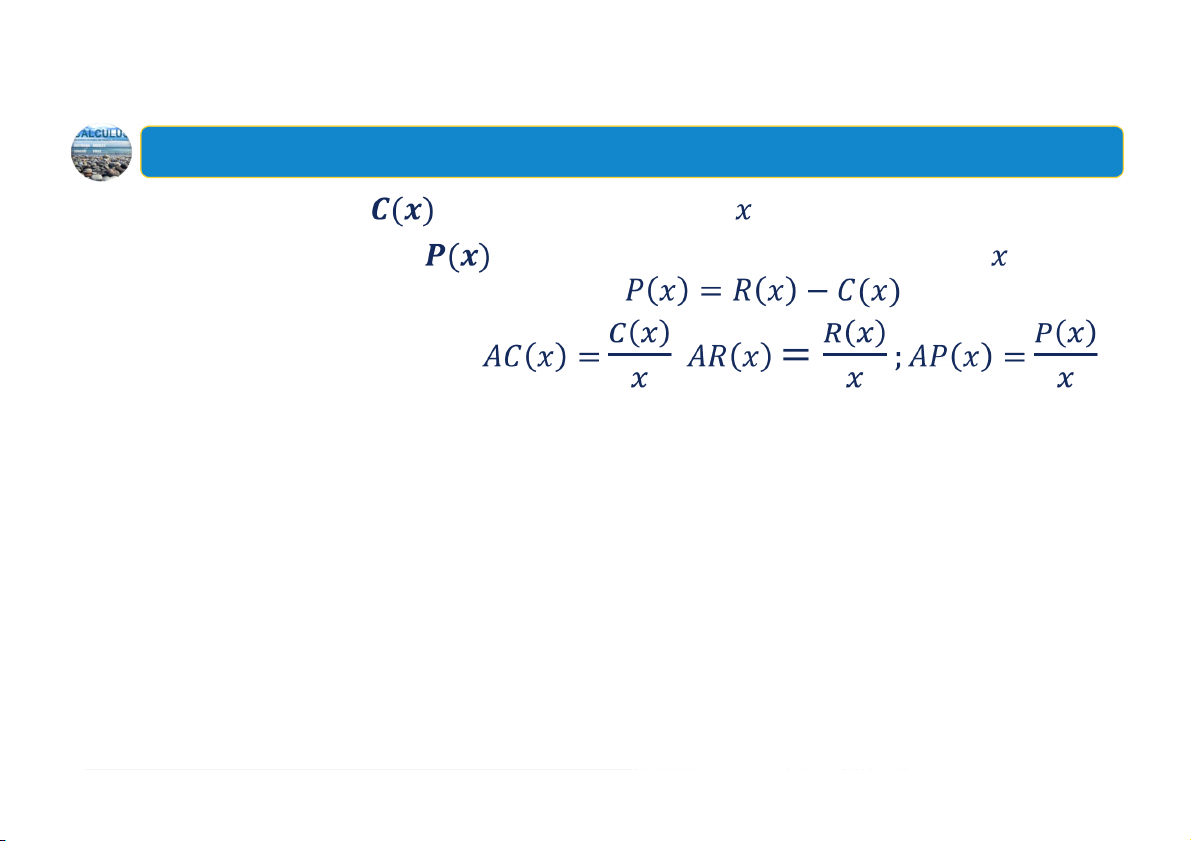



























Preview text:
KHOA TOÁN KINH TẾ
BỘ MÔN TOÁN CƠ BẢN Bài giảng
TOÁN CHO CÁC NHÀ KINH TẾ
Chương 1: HÀM SỐ, ĐỒ THỊ VÀ GIỚI HẠN Mục êu chương 1 Mục tiêu:
Giới thiệu các khái niệm cơ bản về hàm số, giới hạn và tính liên tục của hàm số.
Đề cập các ứng dụng của hàm số trong phân tích kinh doanh, kinh tế
và các bài toán khoa học xã hội. Nội dung: 1. Hàm số 2. Đồ thị hàm số 3. Các mô hình hàm số 4. Giới hạn
5. Các giới hạn một phía và sự liên tục 2 KHOA TOÁN KINH TẾ
BỘ MÔN TOÁN CƠ BẢN Bài giảng
TOÁN CHO CÁC NHÀ KINH TẾ
Chương 1: HÀM SỐ, ĐỒ THỊ VÀ GIỚI HẠN Bài 1: Hàm số Mục êu bài 1
Khái niệm biến số, khái niệm hàm số, miền xác định của hàm số và
tính giá trị hàm số từ một phương trình
Làm quen với hàm xác định từng khúc
Giới thiệu và minh họa các hàm số được sử dụng trong kinh tế học
Thiết lập và sử dụng hàm hợp trong các bài toán ứng dụng 4
1. Khái niệm biến số và hàm số Biến số là:
một đại lượng được đo bằng một số chưa biết trong tập .
một ký hiệu có thể được gán bằng một số bất kỳ trong tập , thường là .
Nếu chỉ có một giá trị thì ta gọi ký hiệu đó là hằng số. Ví dụ:
1) Ngày mai tôi đi mua quần áo, chuẩn bị mang theo 2 triệu. Khi đó số
tiền để mua sẽ là một biến trong miền xác định [0, 2,000,000].
2) Hôm qua tôi vừa mua quần áo xong. Số tiền để mua là một hằng số dù tôi chưa xác định. 5
1. Khái niệm biến số và hàm số Định nghĩa
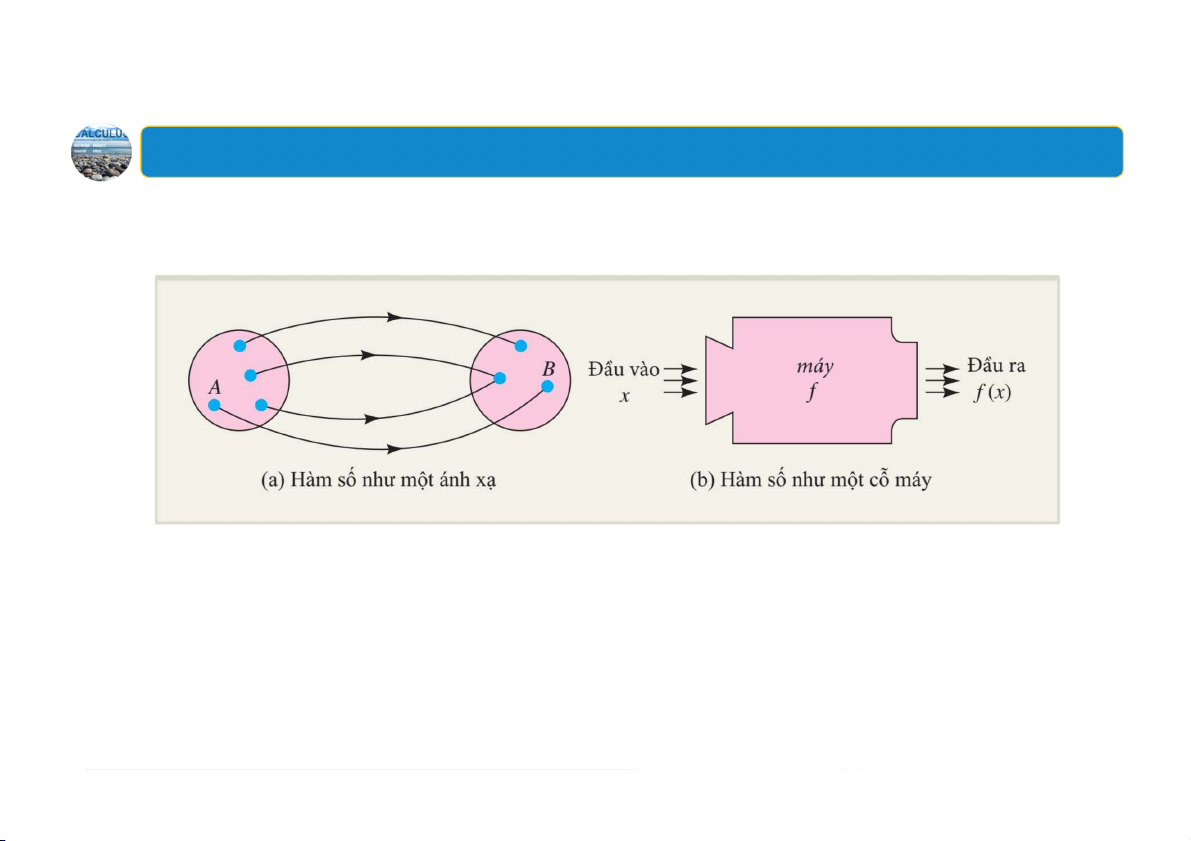
Hàm số là một quy tắc cho tương ứng mỗi phần tử thuộc tập hợp A
với một và chỉ một phần tử thuộc tập hợp B.
Tập A gọi là miền xác định của hàm số
Tập B gọi là miền giá trị
Chúng ta chủ yếu xem xét các hàm số có miền xác định và miền giá
trị là tập hợp số thực. Ký hiệu , trong đó
gọi là biến độc lập
gọi là biến phụ thuộc 6
1. Khái niệm hàm số Minh họa 7
1. Khái niệm biến số và hàm số Ví dụ
Nếu không được chỉ định cụ thể 1. Cho hàm số
thì ta sẽ coi miền xác định của hàm
là tập hợp tất cả các số
a) Tìm miền xác định của thực sao cho có thể được b) Tính giá trị
xác định là một số thực, còn
được gọi là miền xác định tự 2. Cho hàm số nhiên của hàm .
a) Tìm miền xác định của b) Tính giá trị . 8
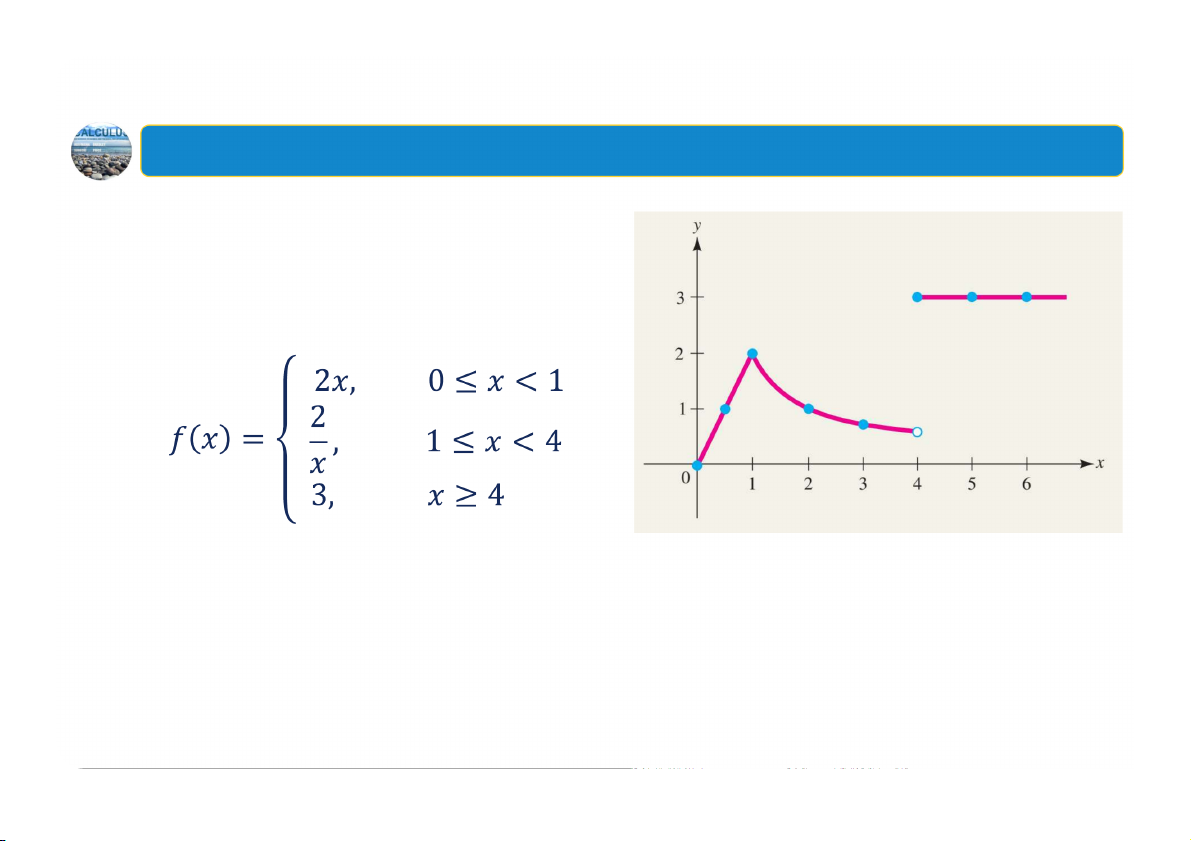
1. Khái niệm biến số và hàm số Ví dụ: Hàm xác định từng khúc Hàm xác định
Trong khoảng thời gian xảy ra hạn hán, người từng khúc
dân ở quận Marin, California phải đối mặt với (piecewise-defined
sự thiếu hụt nước trầm trọng. Để ngăn việc sử function) là hàm số
dụng lãng phí nguồn nước, chính quyền nơi đây có nhiều hơn một
đã áp dụng cách tính giá nước như sau: giá biểu thức trên các
nước hàng tháng đối với một gia đình bốn khoảng rời nhau. người là mỗi trăm feet khối cho feet khối đầu tiên, mỗi trăm feet khối cho feet khối tiếp theo và mỗi trăm feet
khối cho các feet khối sau đó.
Hãy biểu diễn hóa đơn tiền nước hàng tháng
đối với một gia đình bốn người dưới dạng một
hàm theo lượng nước đã sử dụng. 9
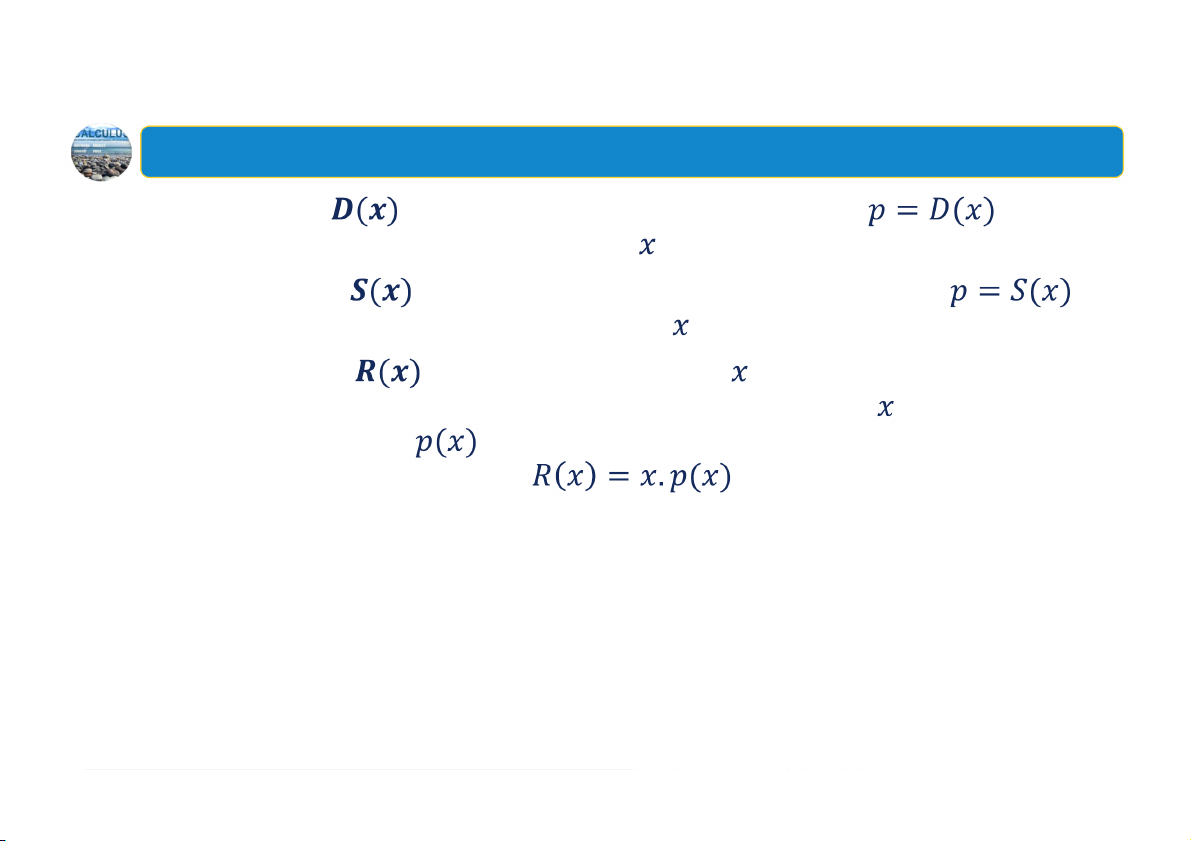
2. Các hàm số được sử dụng trong kinh tế học Hàm cầu
đối với một loại hàng hóa là giá phải trả
cho mỗi đơn vị hàng hóa đó nếu đơn vị hàng hóa có nhu cầu. Hàm cung
đối với một loại hàng hóa là đơn giá để
các nhà sản xuất sẵn sàng cung cấp đơn vị hàng hóa ra thị trường Doanh thu
thu được từ việc bán đơn vị hàng hóa được xác
định bởi tích giữa số đơn vị hàng hóa bán được và đơn giá mỗi đơn vị hàng hóa 10
2. Các hàm số được sử dụng trong kinh tế học Hàm chi phí
là chi phí để sản xuất đơn vị hàng hóa Hàm lợi nhuận
là lợi nhuận thu được từ việc bán đơn vị
hàng hóa và được xác định bởi:
Các hàm bình quân: ; 11
2. Các hàm số được sử dụng trong kinh tế học - Ví dụ
Ví dụ 1: Nghiên cứu cho thấy người tiêu
Ví dụ 2: Giả sử tổng chi phí để
dùng sẽ mua nghìn đơn vị một loại
sản xuất chiếc máy chạy bộ
máy pha cà phê khi đơn giá là được cho bởi hàm số (đô la)
Chi phí sản xuất nghìn đơn vị đó là (đô la) (nghìn đô la) a) Tìm chi phí sản xuất chiếc
a) Chi phí bình quân để sản xuất
máy chạy bộ. Chi phí bình quân
máy pha cà phê là bao nhiêu? để sản xuất máy chạy bộ đó
b) Tìm doanh thu và lợi nhuận từ việc là bao nhiêu?
bán nghìn đơn vị máy pha cà phê.
b) Tính chi phí sản xuất chiếc
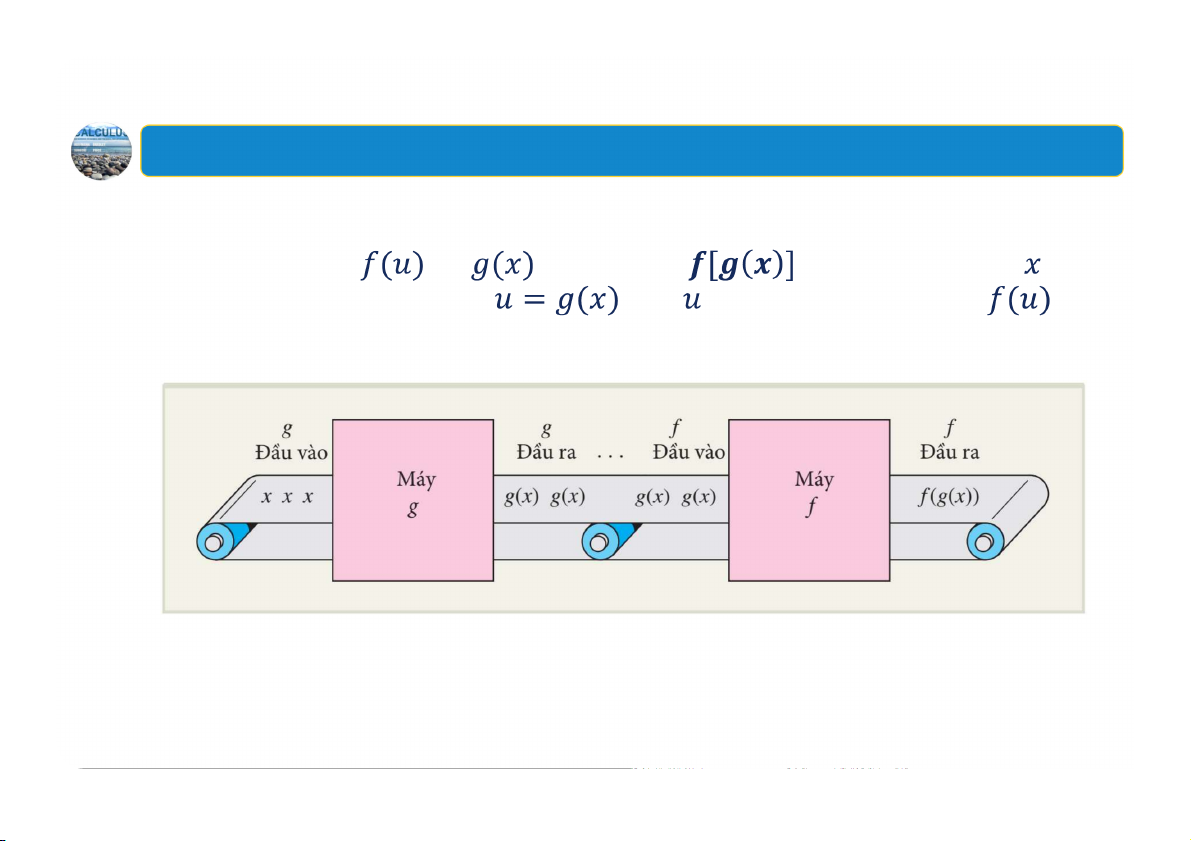
c) Tìm để việc sản xuất máy pha cà phê máy chạy bộ thứ . là có lợi nhuận? 12 3. Hàm hợp Định nghĩa Cho hai hàm số và , hàm hợp là hàm của biến được tạo thành bằng cách thay vào trong công thức của . Minh họa 13
3. Hàm hợp - Ví dụ
Ví dụ 1: Tìm hàm hợp , trong đó và 14
3. Hàm hợp - Tỉ số của các số gia
Tỉ số của các số gia
Ví dụ: Tìm tỉ số của các số gia đối với hàm .
Tỉ số của các số gia đối với hàm là hàm hợp có dạng Với là hằng số. 15
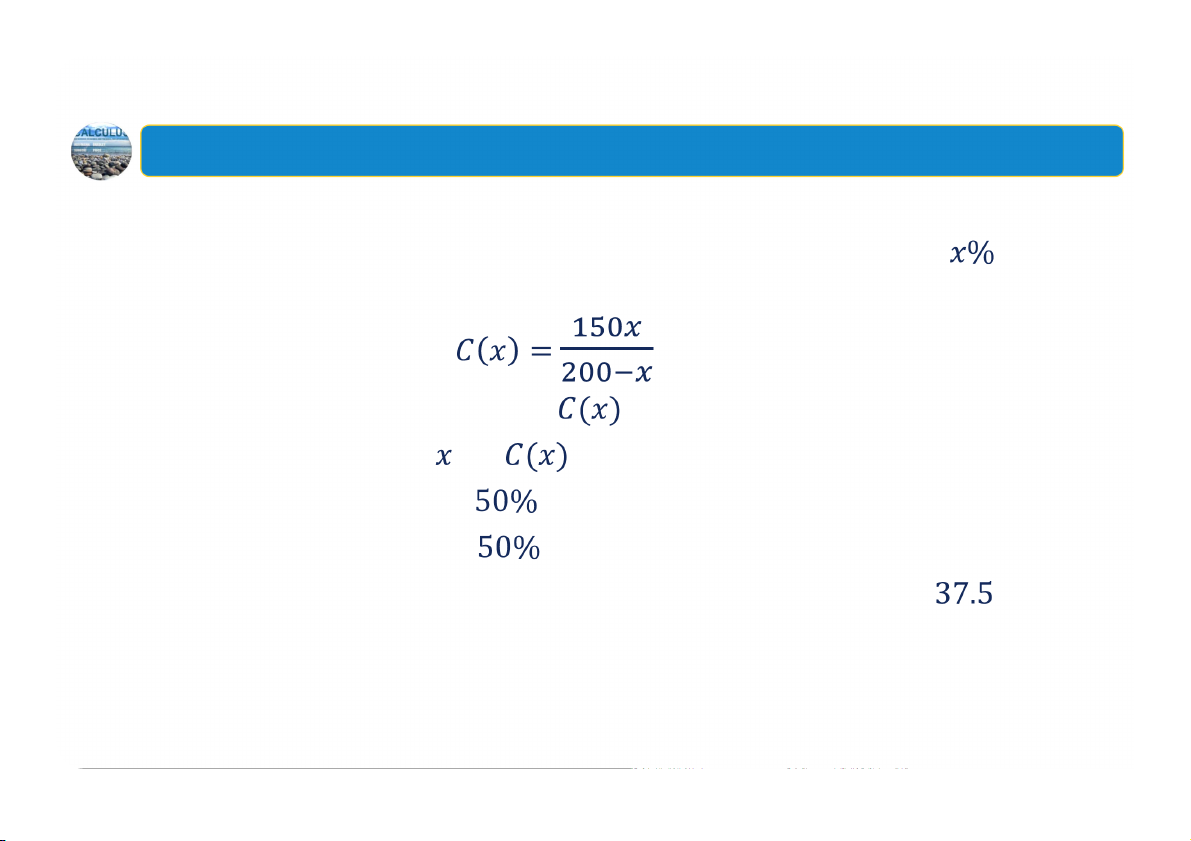
Ví dụ: Quá trình miễn dịch
Trong một chương trình quốc gia giúp tăng cường hệ miễn dịch của
người dân, cơ quan y tế ước tính rằng chi phí để tiêm chủng dân số xấp xỉ là triệu đô la
a) Tìm miền xác định của hàm
b) Với giá trị nào của thì phù hợp với thực tế?
c) Chi phí để tiêm chủng
dân số đầu tiên là bao nhiêu?
d) Chi phí để tiêm chủng
dân số còn lại là bao nhiêu?
e) Phần trăm dân số đã được tiêm chủng khi đã chi phí hết triệu đô la là bao nhiêu? 16 KHOA TOÁN KINH TẾ
BỘ MÔN TOÁN CƠ BẢN Bài giảng
TOÁN CHO CÁC NHÀ KINH TẾ
Chương 1: HÀM SỐ, ĐỒ THỊ VÀ GIỚI HẠN
Bài 2: Đồ thị của hàm số Mục êu bài 2
Ôn tập hệ tọa độ vuông góc Vẽ đồ thị hàm số
Tìm giao điểm của các đồ thị
Kiểm tra theo đường thẳng đứng Hệ số chặn
Các hàm lũy thừa, đa thức và phân thức
Phác họa và sử dụng đồ thị hàm bậc hai trong ứng dụng 18 Ví dụ dẫn nhập
Đồ thị mô tả trực quan về những thông tin của một hàm số 19
1. Hệ tọa độ vuông góc
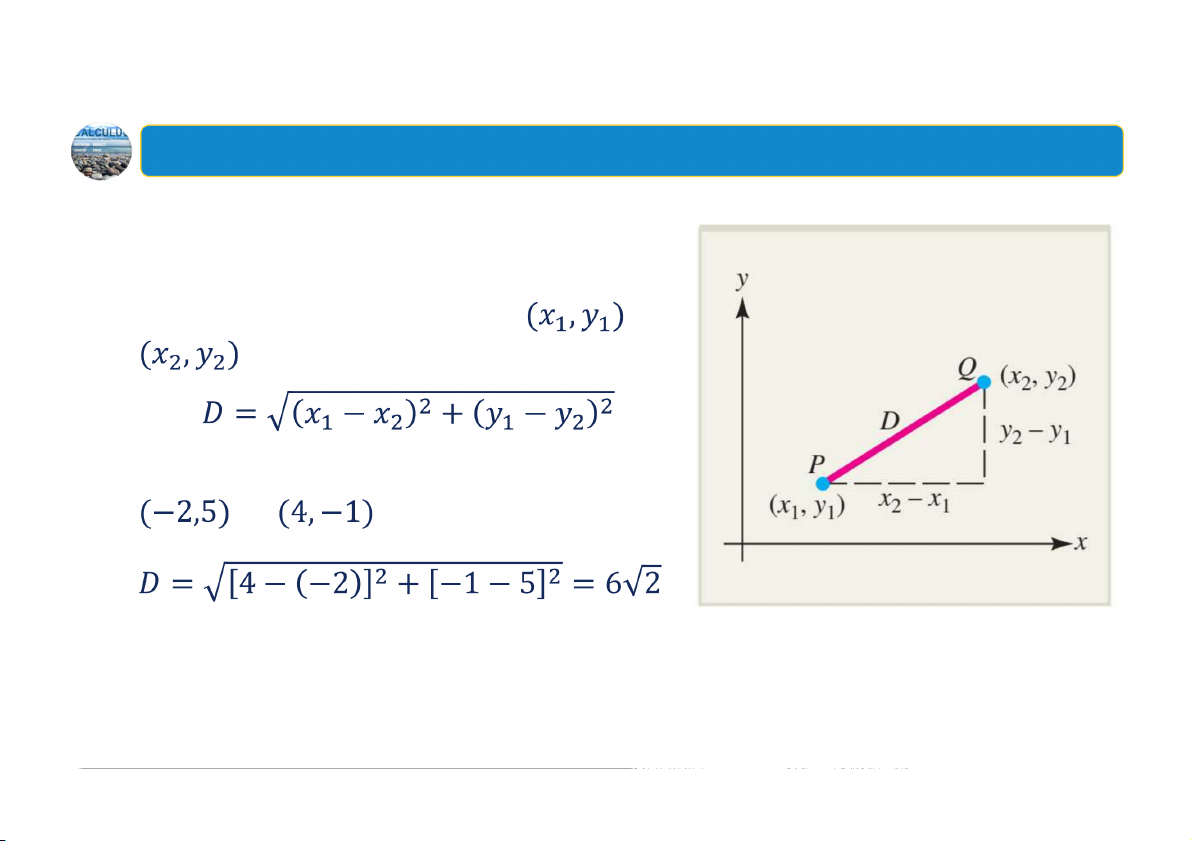
2. Công thức khoảng cách
Sinh viên tự đọc định nghĩa hệ tọa độ
vuông góc trong sách
Khoảng cách giữa hai điểm và được cho bởi
Ví dụ: Khoảng cách giữa hai điểm và là 20
3. Đồ thị của hàm số
Sinh viên tự đọc định nghĩa trong sách (trang 18)
Ví dụ: Vẽ đồ thị hàm số 21
3. Đồ thị của hàm số
Ví dụ: Thương hiệu giầy Ugg của hãng Deckers Outdoor có mặt trên
thị trường từ năm 1979, đến năm 2003 doanh số bán hàng tăng nhanh
làm cho giá cổ phiếu tăng mạnh. Gọi
là giá cổ phiếu của hãng lúc năm sau kể từ ngày 1 tháng 1
năm 2000, người ta ước lượng được Hãy vẽ đồ thị hàm 22
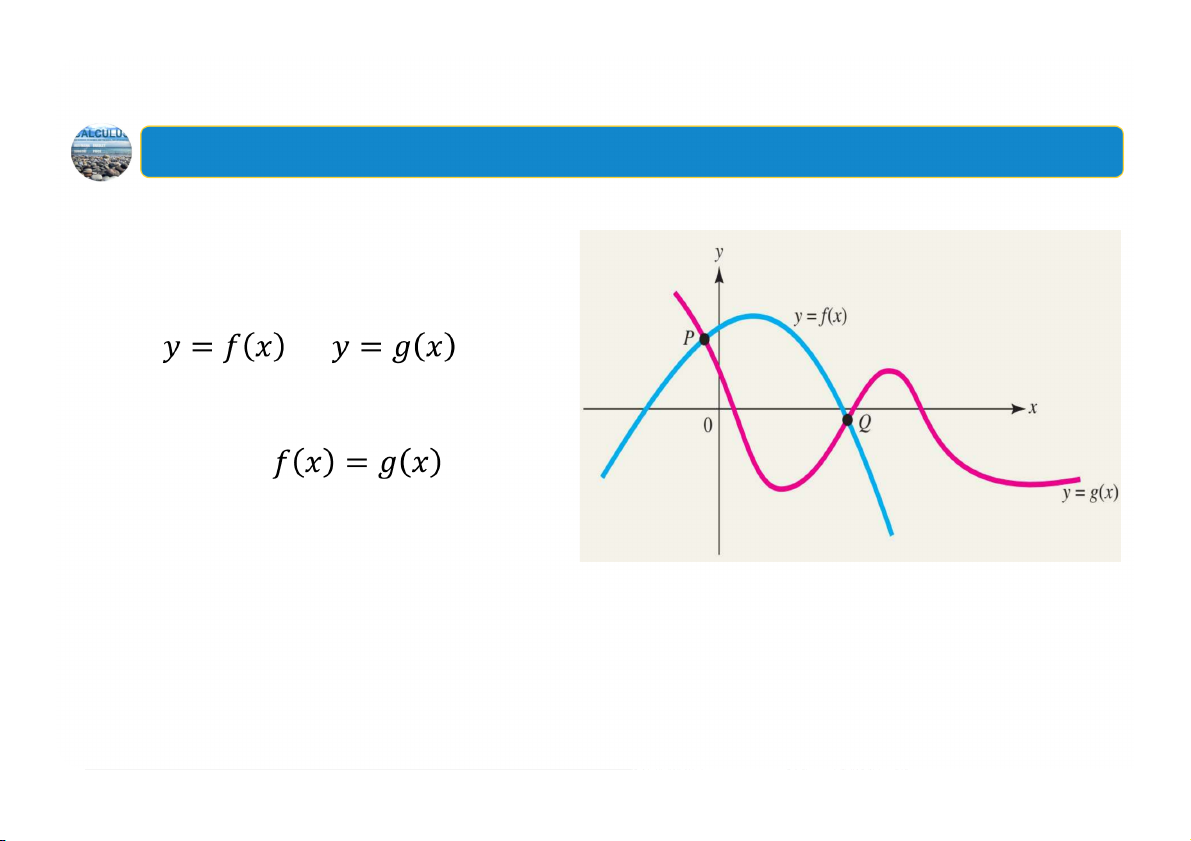
4. Giao điểm của các đồ thị
Sinh viên tự đọc định nghĩa trong sách (trang 20)
Để tìm giao điểm 2 đồ thị và ,
chúng ta phải giải phương trình 23
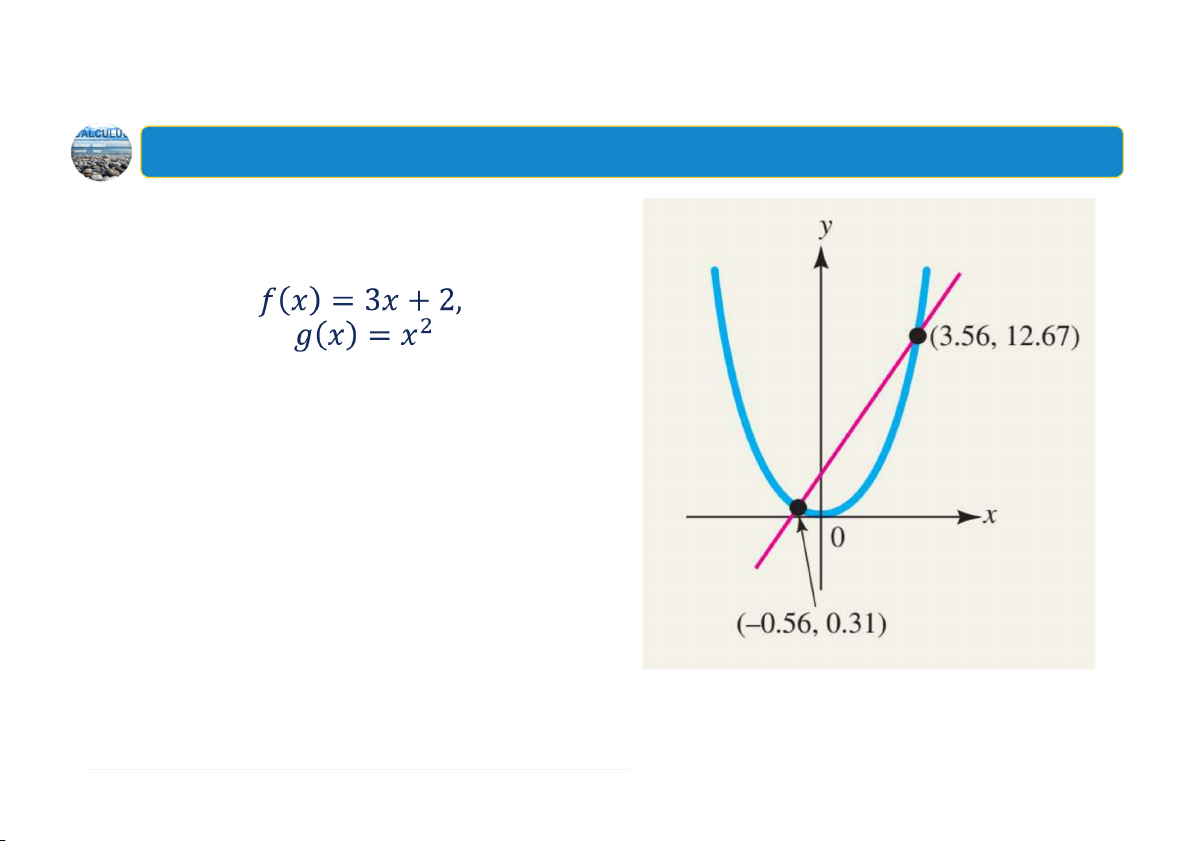
4. Giao điểm của các đồ thị
Ví dụ: Tìm giao điểm của các đồ thị 24
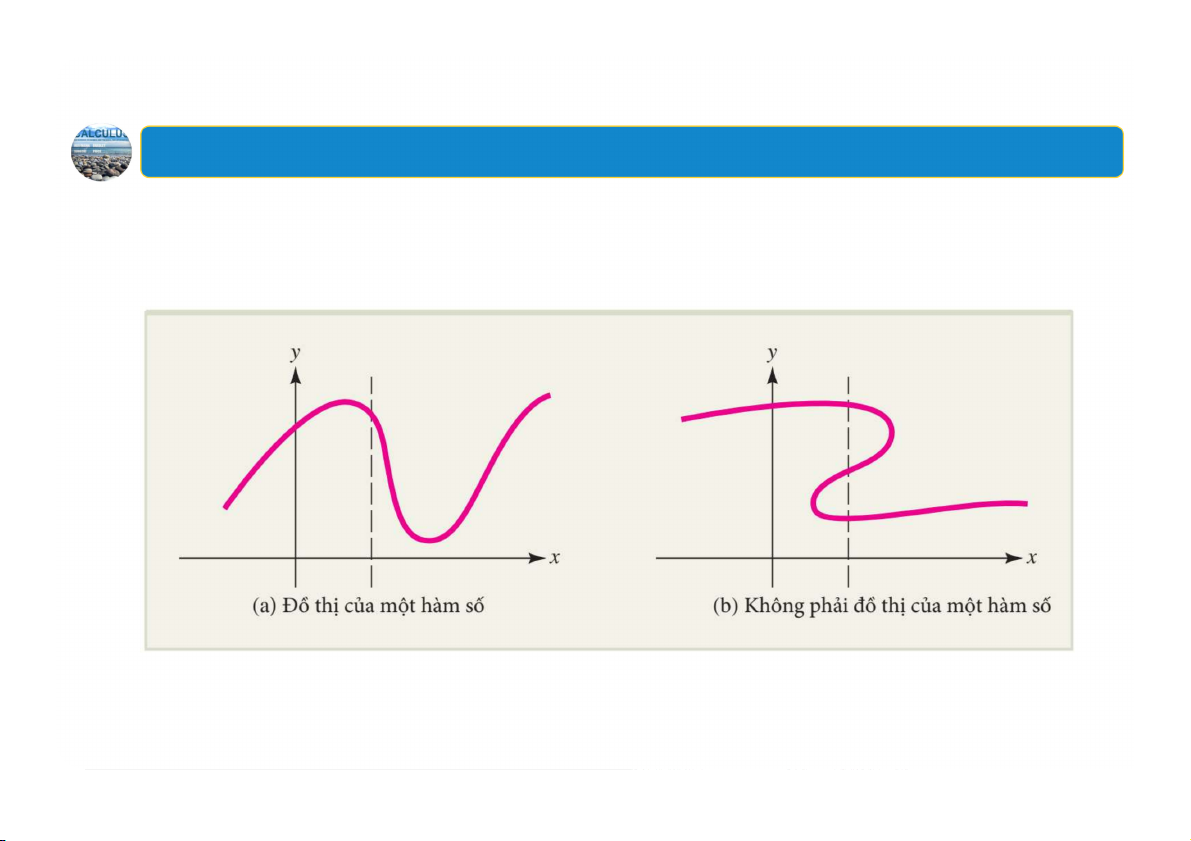
5. Kiểm tra theo đường thẳng đứng
Một đường cong là đồ thị của một hàm số khi và chỉ khi không có
đường thẳng đứng nào cắt đường cong đó tại nhiều hơn một điểm 25 6. Hệ số chặn
Các điểm (nếu có) tại đó đồ thị
Ví dụ: Tìm hệ số chặn của đồ
của hàm số giao với trục được thị các hàm số:
gọi là hệ số chặn Các điểm a)
(nếu có) tại đó đồ thị của hàm số b)
giao với trục được gọi là hệ số chặn
Đồ thị của một hàm số có thể có
nhiều hệ số chặn , nhưng có
nhiều nhất một hệ số chặn .
Với đồ thị hàm số , để
tìm hệ số chặn , ta đặt ;
để tìm hệ số chặn ta đặt 26
7. Các hàm lũy thừa, đa thức và phân thức
Hàm lũy thừa là hàm có dạng: là một số thực
Đa thức là hàm có dạng: là số nguyên không âm Nếu
thì gọi là bậc của đa thức
Phân thức là hàm có dạng: , với là các đa thức 27
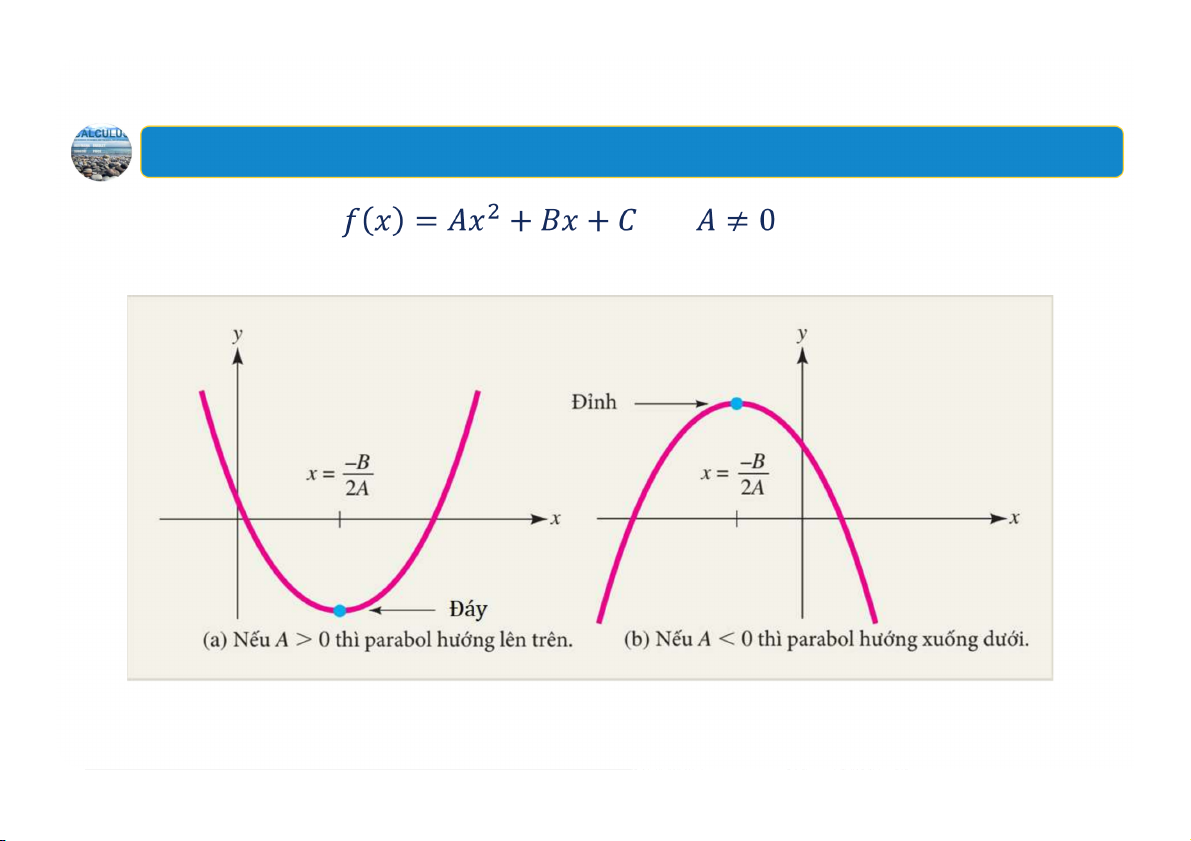
8. Phác họa và ứng dụng đồ thị của hàm bậc hai Đa thức bậc hai với được gọi là hàm bậc hai. 28
8. Phác họa và ứng dụng đồ thị của hàm bậc hai
Một nhà sản xuất xác định được Đa thức bậc hai
đơn giá bán của 1 sản phẩm được cho bởi hàm cầu với được gọi là hàm (đô-la). bậc hai.
khi trăm đơn vị sản phẩm được • : Hàm số đạt giá trị sản xuất lớn nhất tại .
Tại mức sản xuất nào thì doanh • : Hàm số đạt giá trị
thu của sản phẩm này đạt tối đa?
Doanh thu tối đa đó bằng bao nhỏ nhất tại . nhiêu? 29 Ví dụ
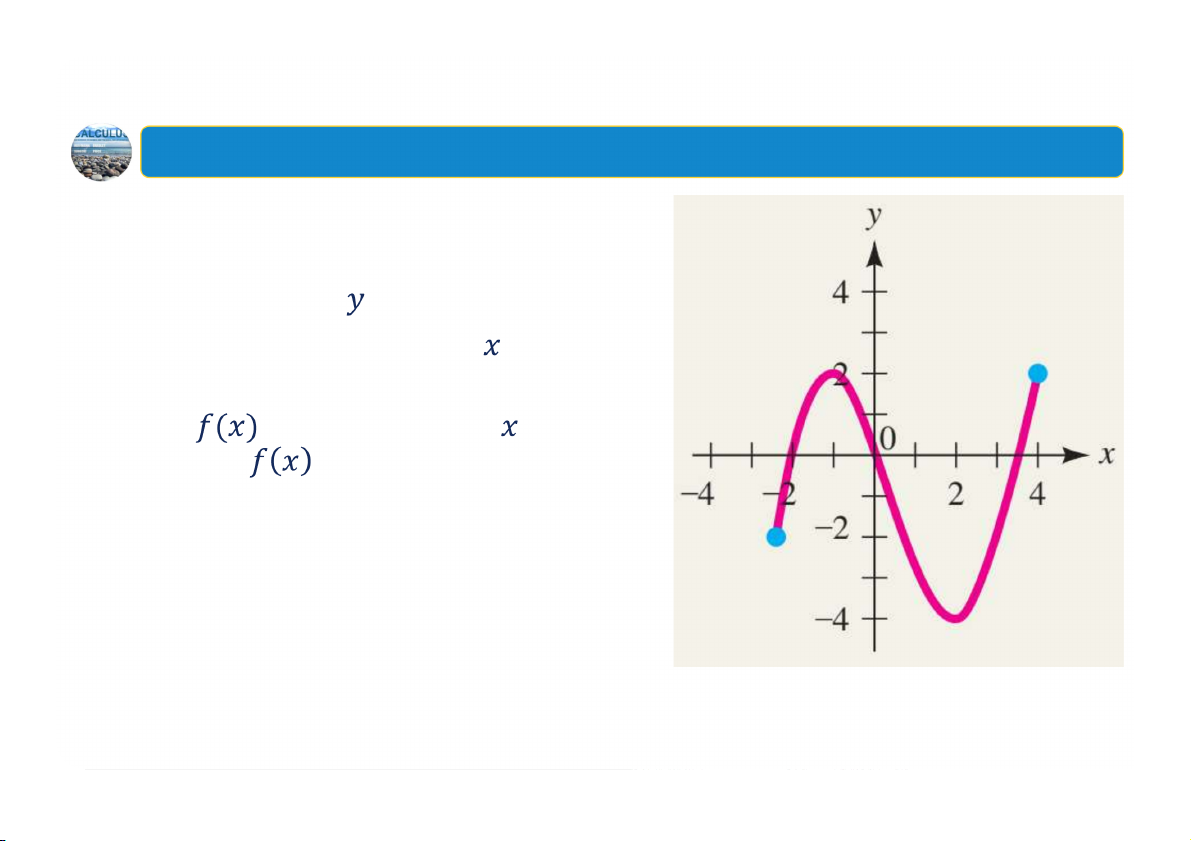
Cho hàm số với đồ thị như hình bên, hãy tìm: a) Hệ số chặn ;
b) Tất cả các hệ số chặn ;
c) Giá trị lớn nhất (nhỏ nhất) của và các giá trị của sao cho lớn nhất (nhỏ nhất) 30 Ví dụ
Yuri quản lý 150 căn hộ tại Irvine, California. Tất cả các căn hộ đều có thể được thuê với giá
mỗi tháng mỗi căn, nhưng với mỗi lần tăng giá thuê hàng tháng thêm
thì sẽ có thêm căn hộ bỏ trống.
a. Biểu diễn tổng doanh thu hàng tháng thu được từ việc cho thuê căn
hộ dưới hạng hàm của giá cho thuê mỗi căn hộ hàng tháng .
b. Phác họa đồ thị của hàm doanh thu tìm được trong phần (a).
c. Yuri nên đặt mức giá cho thuê hàng tháng là bao nhiêu để tối đa
doanh thu? Doanh thu tối đa là bao nhiêu? 31 KHOA TOÁN KINH TẾ
BỘ MÔN TOÁN CƠ BẢN Bài giảng
TOÁN CHO CÁC NHÀ KINH TẾ
Chương 1: HÀM SỐ, ĐỒ THỊ VÀ GIỚI HẠN
Bài 3: Các mô hình hàm số Mục êu học tập
Nghiên cứu phương pháp lập mô hình tổng quát
Khám phá các mô hình ứng dụng
Trạng thái cân bằng thị trường và phân tích hòa vốn trong kinh tế học 33
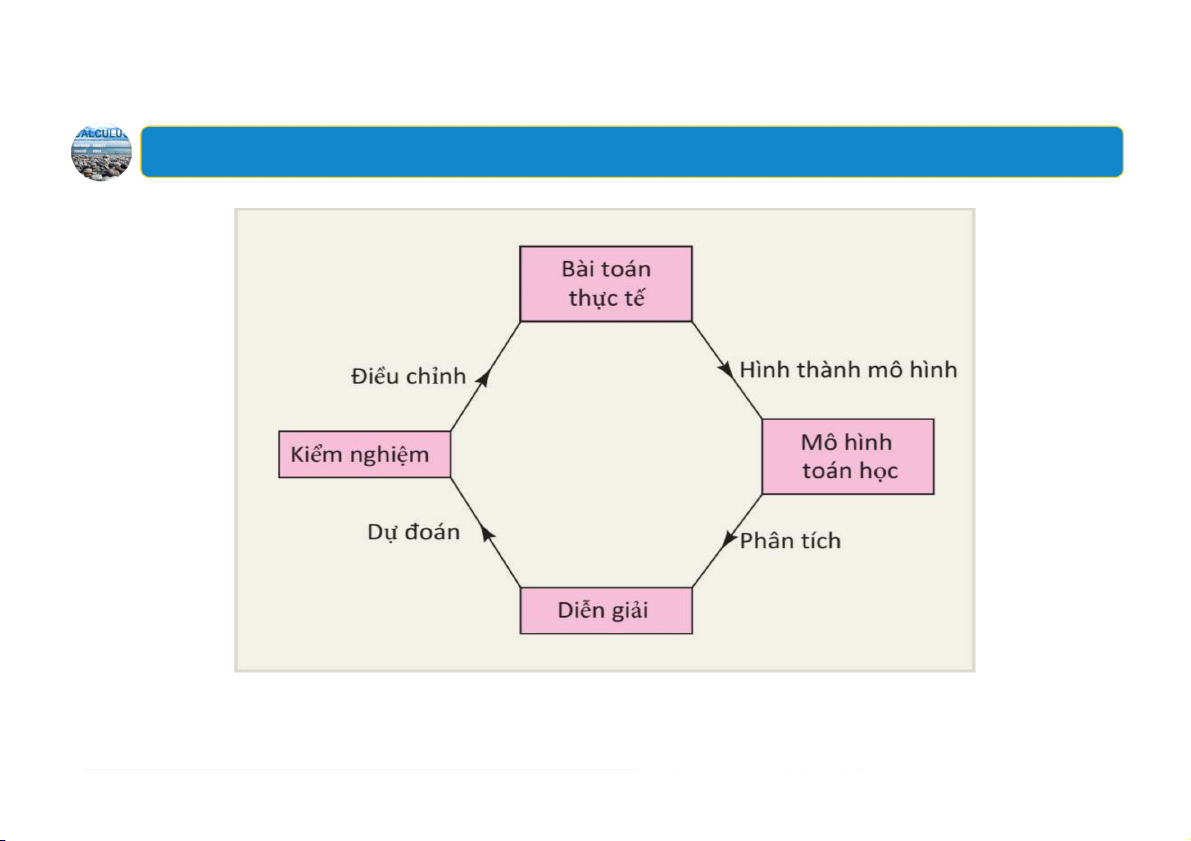
1. Quy trình lập mô hình toán học 34
1. Quy trình lập mô hình toán học - Ví dụ: Tìm lợi nhuận tối đa
Một nhà máy có thể sản xuất giấy in với chi phí mỗi ream giấy. Giá bán hiện tại là
mỗi ream giấy, và với mức giá đó thì người tiêu dùng mua
reams giấy mỗi tháng. Nhà sản xuất dự định nâng mức giá
bán lên và ước tính rằng với mỗi lần tăng giá thêm thì số giấy bán
được mỗi tháng sẽ giảm đi reams.
Tìm mức giá để nhà máy thu lợi nhuận tối đa, lợi nhuận tối đa bằng bao nhiêu? 35
1. Quy trình lập mô hình toán học
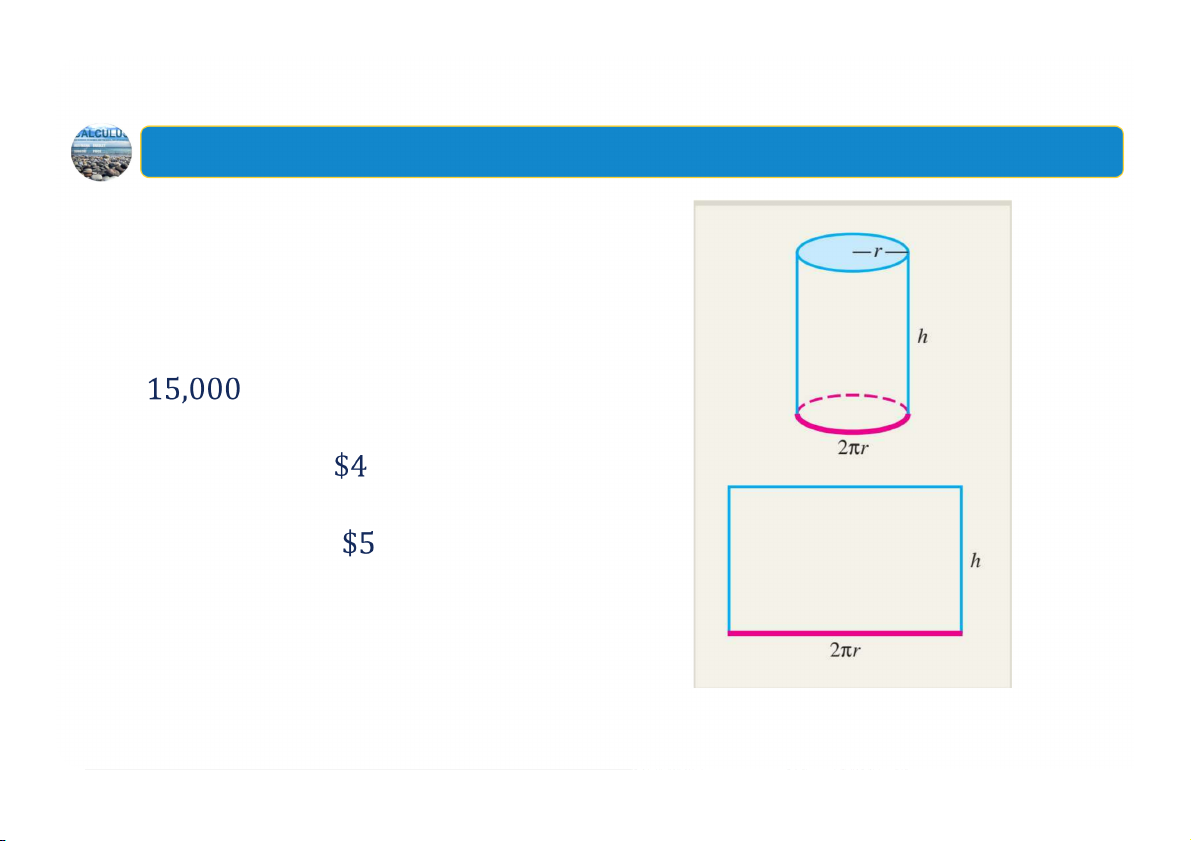
Ví dụ: Lập mô hình chi phí xây dựng
Armando muốn làm một bể chứa
nước hình trụ kín có sức chứa là
feet khối cho trang trại của
anh ấy. Chi phí cho vật liệu sử dụng làm nắp bể là mỗi foot vuông, chi
phí cho vật liệu sử dụng làm đáy bể và thành bể là mỗi foot vuông.
Hãy biểu diễn tổng chi phí xây dựng
bể nước của Armando như một hàm
của bán kính bể nước. 36 2. Tỷ lệ
Các mối quan hệ tỷ lệ là yếu tố quan trọng, thường được xét đến khi lập
các mô hình toán học từ bài toán thực tế, bao gồm: Đại lượng
gọi là tỉ lệ thuận với nếu: , là hằng số Đại lượng
gọi là tỉ lệ nghịch với nếu: , là hằng số Đại lượng
gọi là tỉ lệ đồng thời với và nếu: , là hằng số
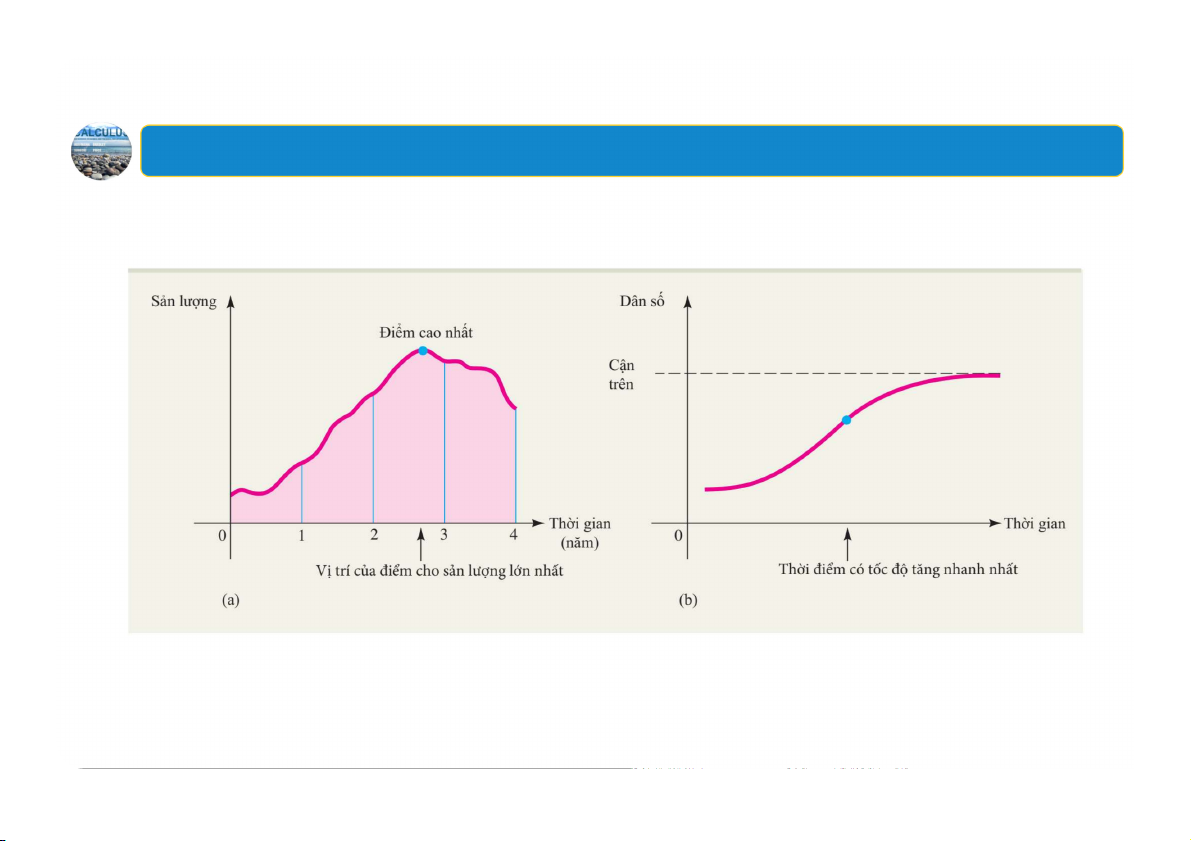
Ví dụ: Lập mô hình có các đại lượng tỉ lệ
Khi các nhân tố môi trường giới hạn một cận trên lên quy mô dân số, dân số
tăng với tốc độ tỷ lệ đồng thời với quy mô dân số hiện tại và độ chênh lệch
giữa quy mô dân số hiện tại và cận trên của nó.
Biểu diễn tốc độ tăng dân số dưới dạng một hàm của quy mô dân số. 37
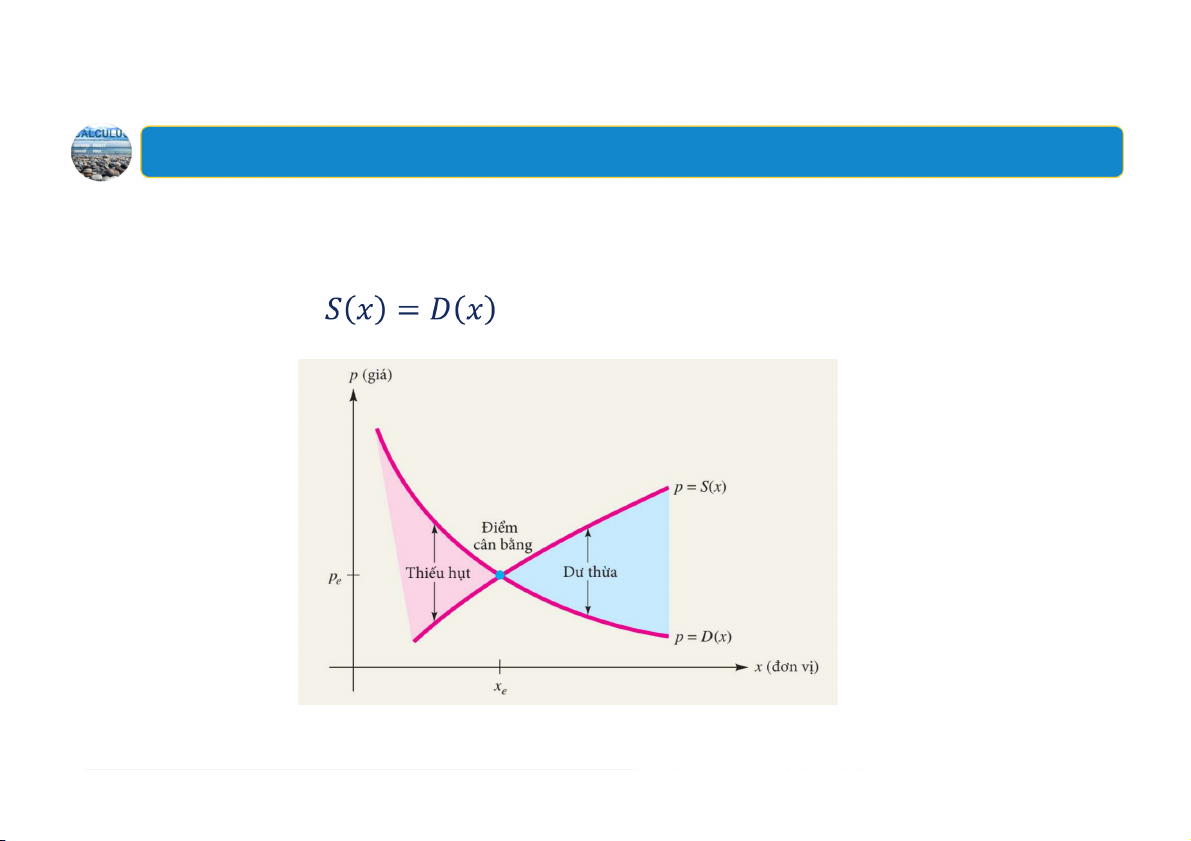
3. Cân bằng thị trường Quy luật cung-cầu:
Trong một thị trường cạnh tranh, cung thường có xu hướng bằng cầu, nghĩa là
, được gọi là trạng thái cân bằng. 38
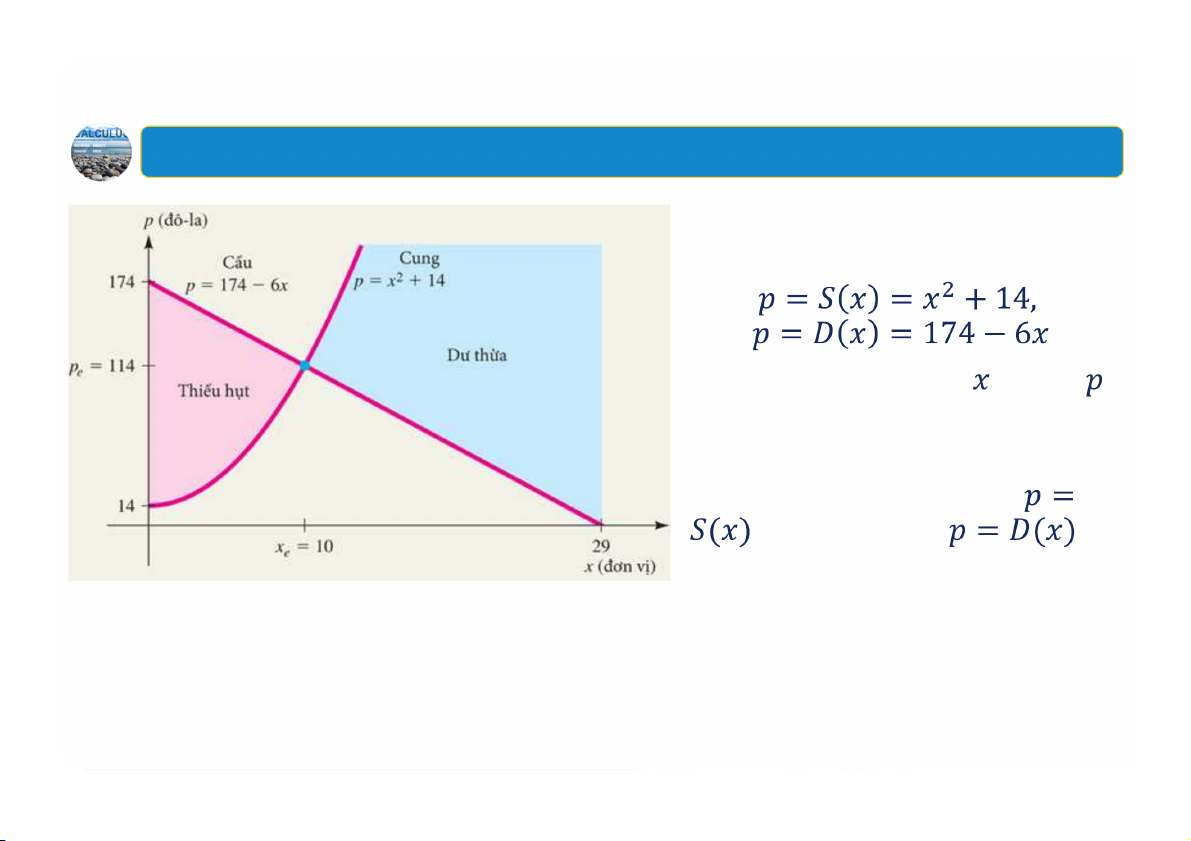
3. Cân bằng thị trường - Ví dụ: Lập mô hình
Cho hàm cung và cầu đối với một loại hàng hóa là:
a) Tìm mức sản xuất và giá
khi thị trường đạt trạng thái cân bằng b) Phác họa đường cung và đường cầu
trên cùng một hệ trục tọa độ và
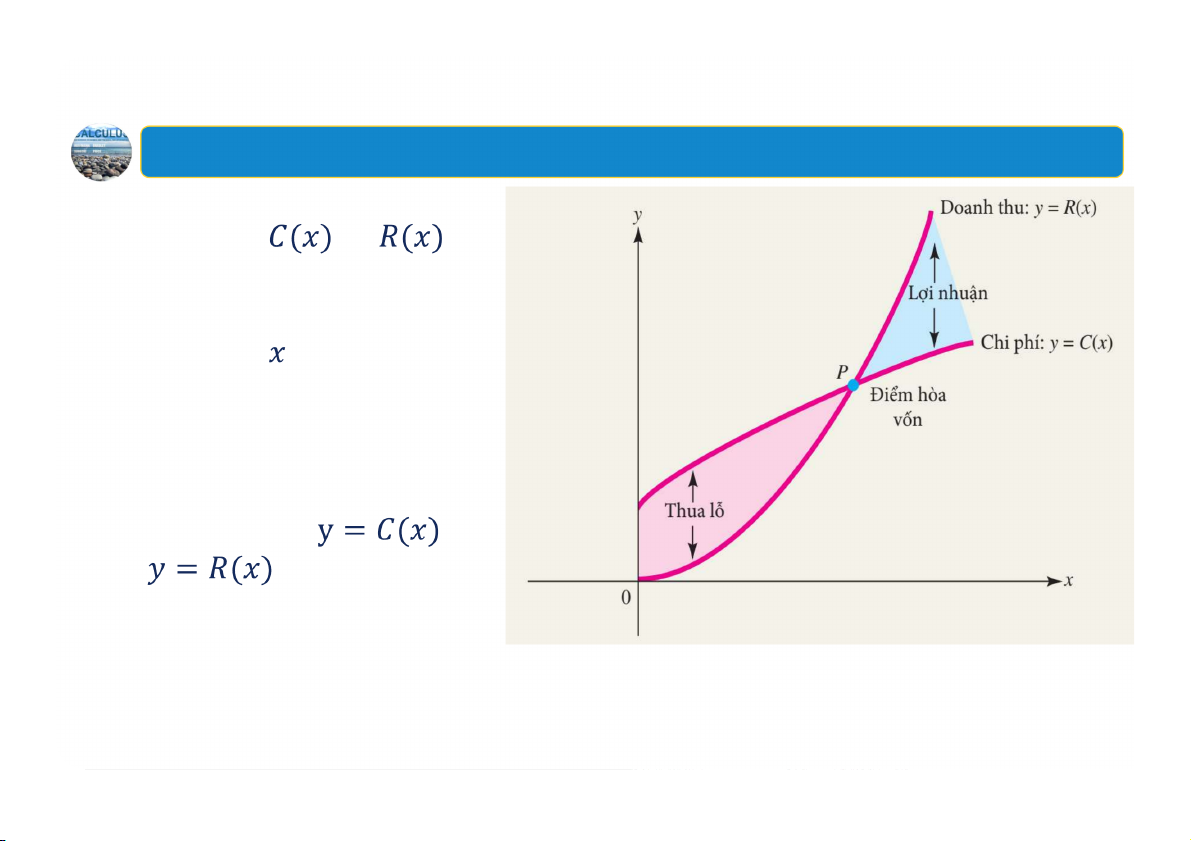
giải thích về trạng thái cân bằng. 39 4. Phân ch hòa vốn Giả sử và lần
lượt là tổng chi phí và tổng doanh thu tại mức sản xuất đơn vị hàng hóa Định nghĩa: Điểm mà tại đó hai đường cong và giao nhau được
gọi là điểm hòa vốn. 40
3. Phân ch hòa vốn - Ví dụ
Ví dụ 1: Một đại lý cho
Ví dụ 2: Một nhà sản xuất có thể bán
thuê xe với mức phí cố định
một sản phẩm nhất định với giá 80 cộng thêm cent cho
USD/đơn vị. Tổng chi phí bao gồm chi phí
mỗi mile. Một đại lý khác
chung cố định là 4,500 USD cộng với chi thu mức phí cộng thêm
phí sản xuất là 50 USD cho mỗi đơn vị. cho mỗi mile.
a. Nhà sản xuất phải bán bao nhiêu sản Hợp đồng thuê xe với phẩm để hòa vốn?
đại lý nào sẽ lợi hơn cho
b. Nhà sản xuất lãi hoặc lỗ bao nhiêu nếu khách hàng? bán được 200 chiếc?
c. Nhà sản xuất phải bán bao nhiêu sản
phẩm để đạt được lợi nhuận 900$? 41 KHOA TOÁN KINH TẾ
BỘ MÔN TOÁN CƠ BẢN Bài giảng
TOÁN CHO CÁC NHÀ KINH TẾ
Chương 1: HÀM SỐ, ĐỒ THỊ VÀ GIỚI HẠN Bài 4: Giới hạn Mục êu học tập
Tìm hiểu khái niệm giới hạn và các tính chất tổng quát của giới hạn
Tính giới hạn bằng các kỹ thuật khác nhau
Tìm hiểu các giới hạn liên quan đến vô hạn 43
1. Giới thiệu trực quan về giới hạn
Giả sử giám đốc một công ty bất động sản xác định được rằng, năm
sau kể từ bây giờ, sẽ có khoảng căn hộ ở một địa phương bán được, trong đó
Hỏi doanh số sau một năm dự kiến bằng bao nhiêu? Phân tích Kết luận: “
có giá trị giới hạn bằng 4 khi tiến đến ”, ta viết: 44
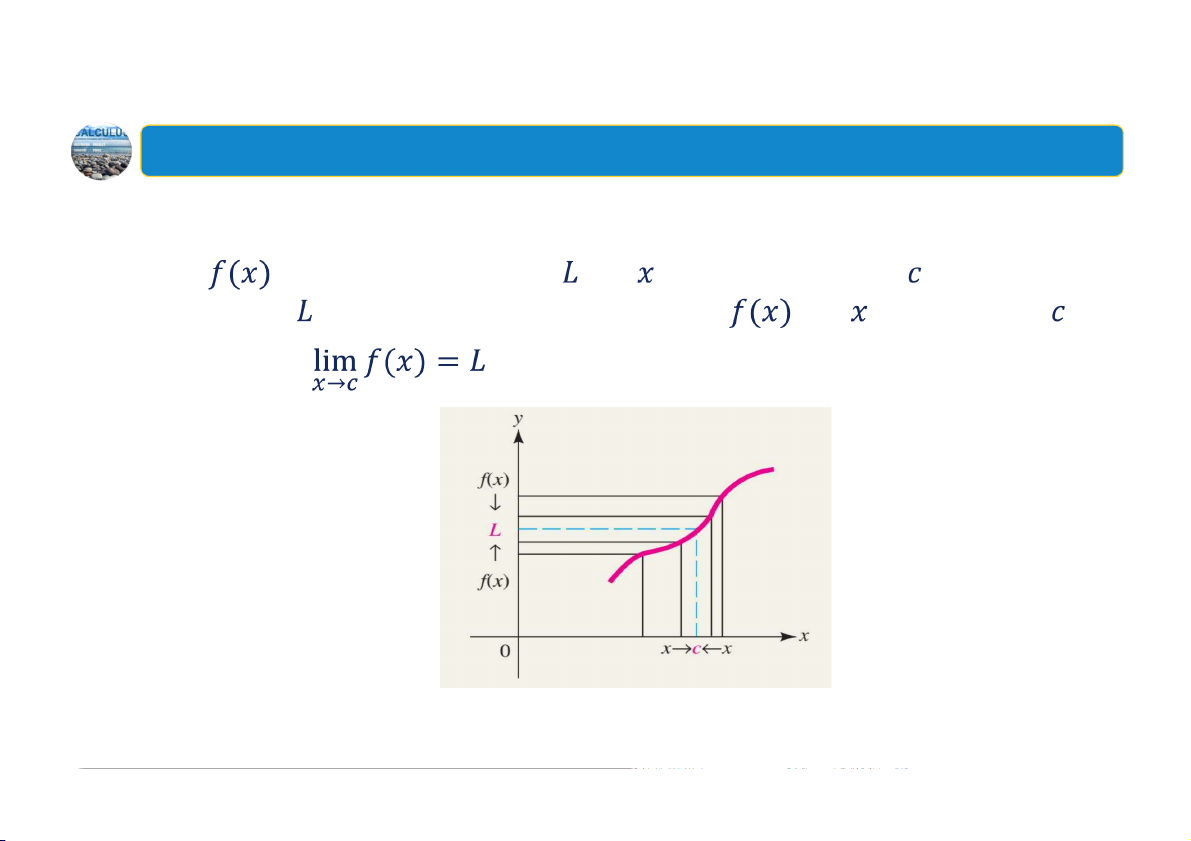
1. Giới thiệu trực quan về giới hạn Định nghĩa: Nếu
ngày càng gần tới số khi ngày càng gần tới từ cả hai
phía thì số được gọi là giới hạn của hàm khi tiến gần đến . Ký hiệu: 45
1. Giới thiệu trực quan về giới hạn
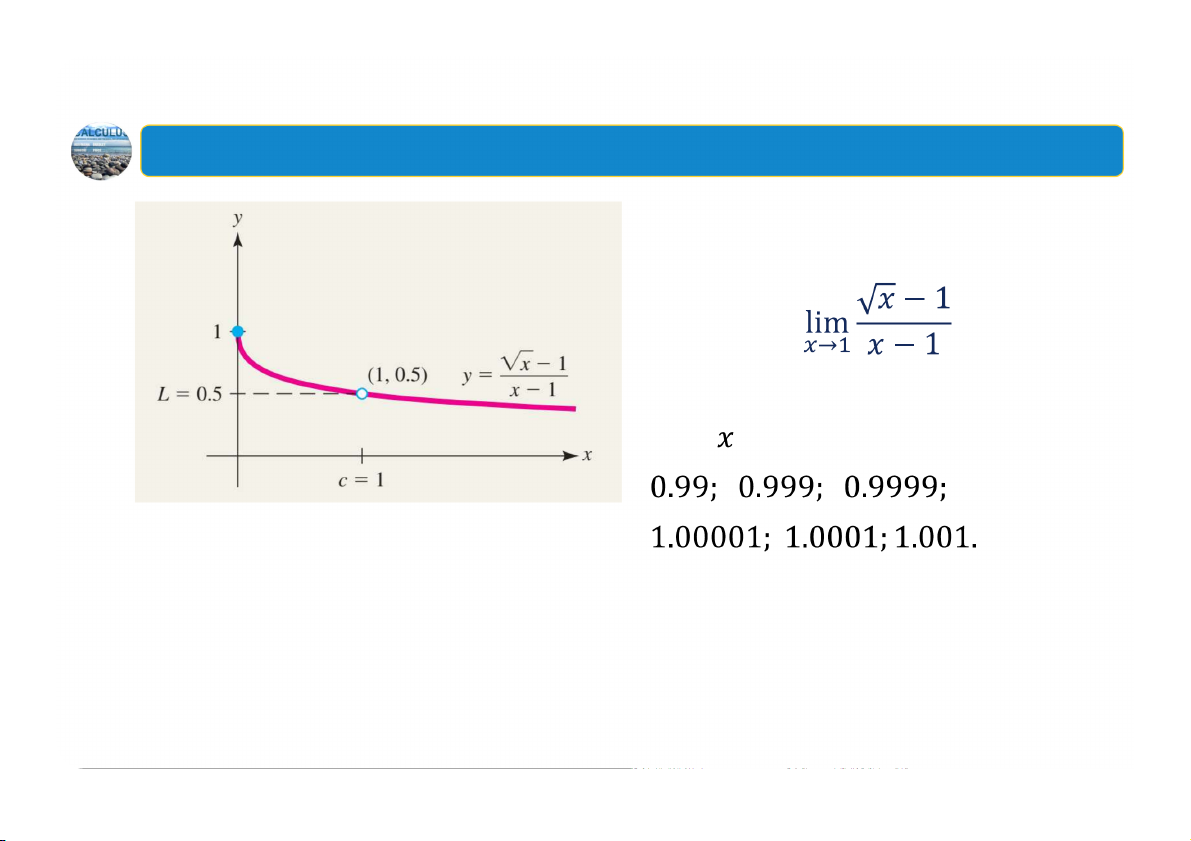
Ví dụ: Sử dụng bảng giá trị để ước lượng giới hạn sau: Thay bởi 46
1. Giới thiệu trực quan về giới hạn –Một số lưu ý
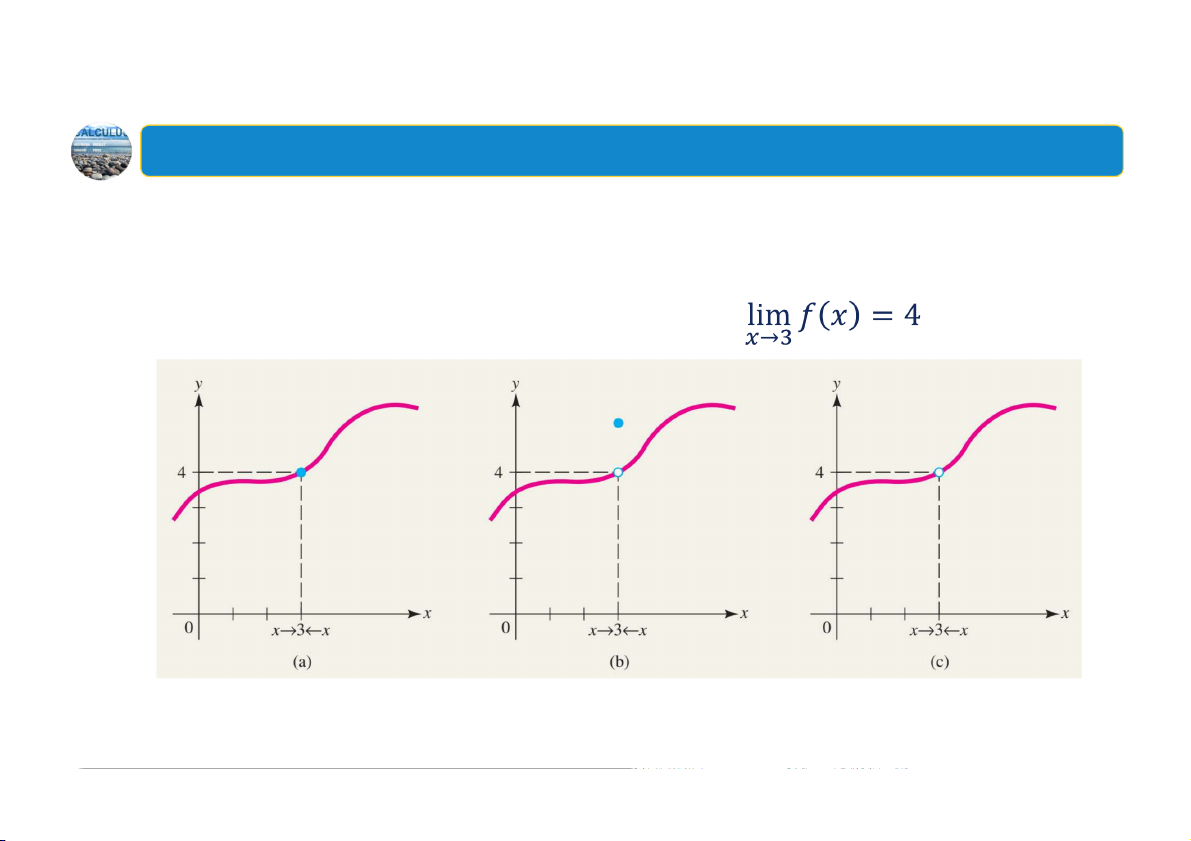
Giới hạn mô tả hành vi của hàm số gần một điểm cụ thể, không nhất
thiết phải tại chính điểm đó.
Dưới đây là ví dụ về 3 hàm đều thỏa mãn 47
1. Giới thiệu trực quan về giới hạn –Một số lưu ý
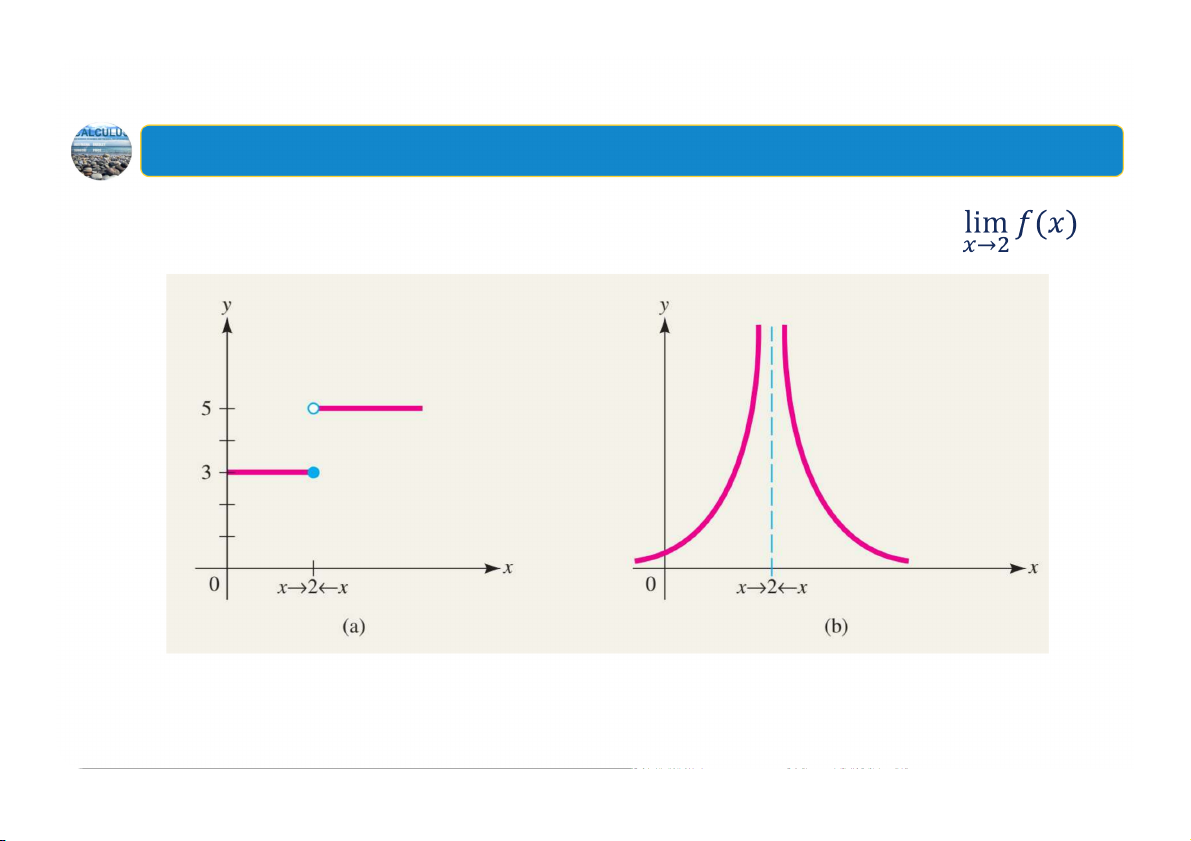
Hình vẽ dưới đây minh họa hai trường hợp không tồn tại 48
2. Các nh chất của giới hạn Nếu và tồn tại thì
với là hằng số bất kỳ nếu nếu tồn tại 49
2. Các nh chất của giới hạn
Giới hạn của hàm tuyến tính:
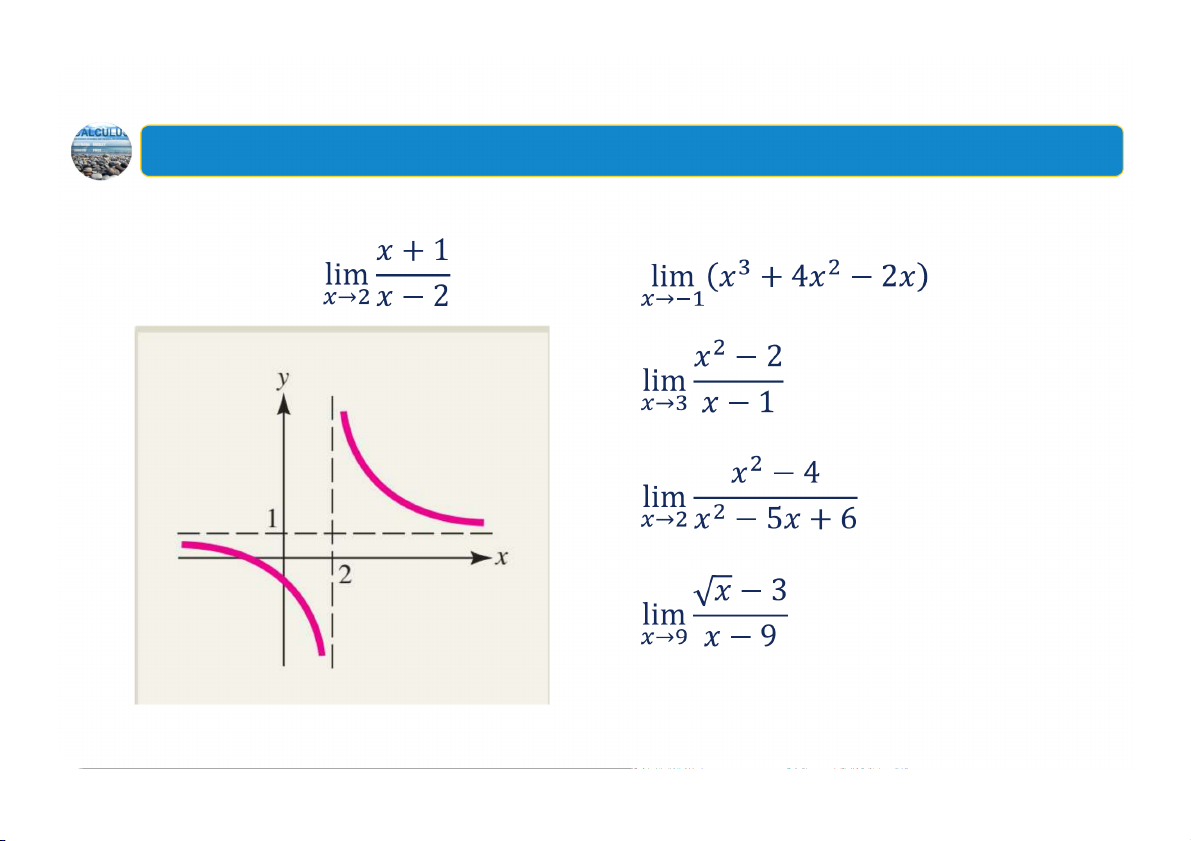
Giới hạn của đa thức và phân thức: Nếu và là các đa thức thì nếu Nếu còn
thì không tồn tại giới hạn 50
2. Các nh chất của giới hạn
Ví dụ: Tính giới hạn: Tính các giới hạn sau: 51
3. Các giới hạn liên quan đến vô hạn - Giới hạn tại vô hạn
Giới hạn tại vô hạn (Limits at Infinity):
Nếu các giá trị của hàm
tiến gần đến số khi tăng không bị chặn thì ta viết
Nếu các giá trị của hàm tiến gần đến số khi giảm không bị chặn thì ta viết Chú ý:
Nếu và là các hằng số với và xác định với mọi thì và 52
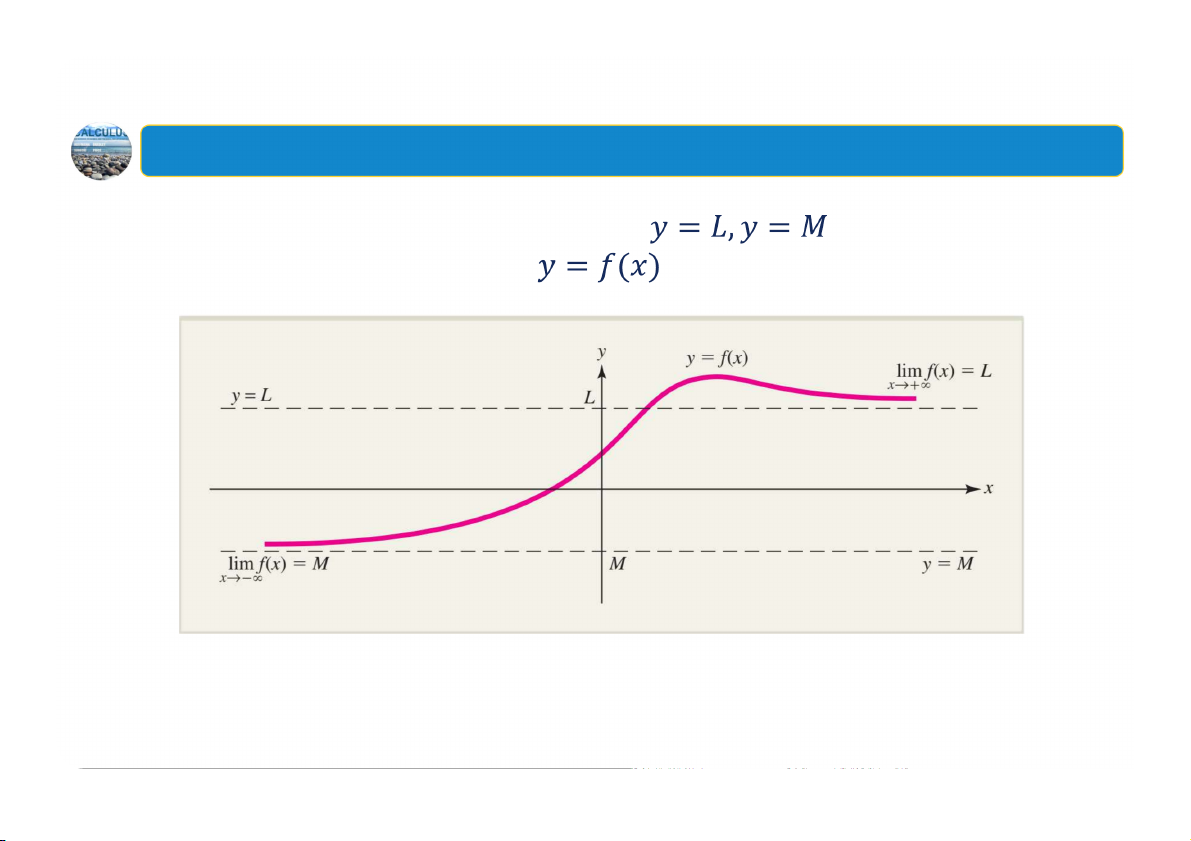
3. Các giới hạn liên quan đến vô hạn - Giới hạn tại vô hạn
Về mặt hình học: Các đường thẳng được gọi là các tiệm
cận ngang của đồ thị hàm số . 53
3. Các giới hạn liên quan đến vô hạn - Ví dụ Tính giới hạn:
Nếu hàm lượng Ni-tơ có trong một thửa đất là thì sản lượng của
vụ mùa trồng trên thửa đất được
tính bởi công thức của Michalelis- Menten: Trong đó và là các hằng số dương.
Điều gì sẽ xảy ra với sản lượng
của vụ mùa nếu lượng Ni-tơ trong
đất tăng không bị chặn? 54
3. Các giới hạn liên quan đến vô hạn
Giới hạn vô hạn (infinite limit):
Ví dụ: Phân tích lợi ích – chi phí Hàm
được gọi là có giới hạn vô hạn nếu tăng hoặc
Giả sử rằng để loại bỏ % giảm không bị chặn khi .
ô nhiễm từ một vụ tràn dầu thì
phải tiêu tốn ngàn đô la, Ký hiệu: trong đó nếu tăng không bị chặn khi nếu Chuyện gì xảy ra khi ? giảm không bị chặn khi
Liệu có thể loại bỏ toàn bộ ô nhiễm? 55 KHOA TOÁN KINH TẾ
BỘ MÔN TOÁN CƠ BẢN Bài giảng
TOÁN CHO CÁC NHÀ KINH TẾ
Chương 1: HÀM SỐ, ĐỒ THỊ VÀ GIỚI HẠN
Bài 5: Các giới hạn một phía và sự liên tục Mục êu học tập
Tính toán và sử dụng các giới hạn một phía
Tìm hiểu khái niệm liên tục và kiểm tra tính liên tục của một hàm số
Tìm hiểu định lý giá trị trung gian 57
1. Các giới hạn một phía Định nghĩa
Sự tồn tại giới hạn Nếu tiến dần đến khi Giới hạn hai phía tồn tại
tiến gần đến từ bên trái (khi
khi và chỉ khi cả hai giới hạn một ) thì ta viết phía và đều
tồn tại và bằng nhau, khi đó Nếu tiến dần đến khi
tiến gần đến từ bên phải (khi ) thì ta viết 58
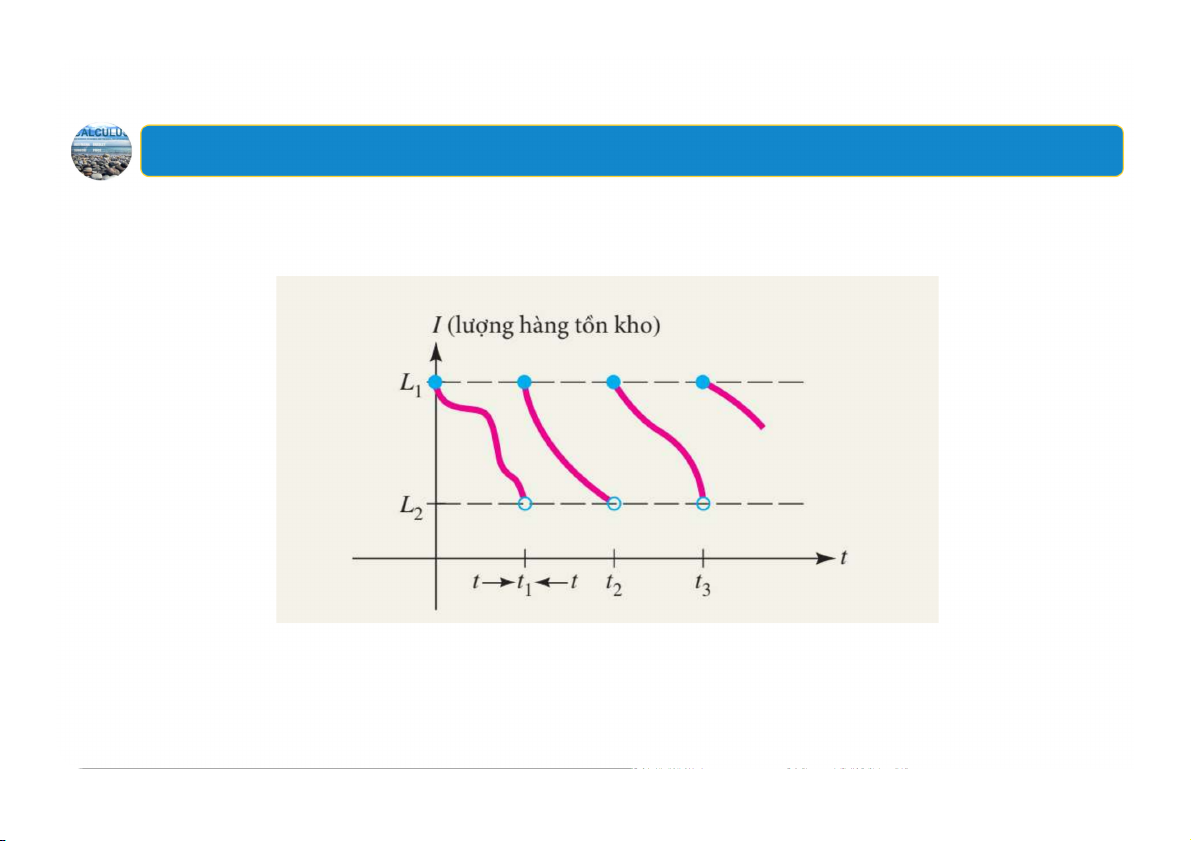
1. Các giới hạn một phía
Giới hạn một phía trong bài toán ứng dụng 59
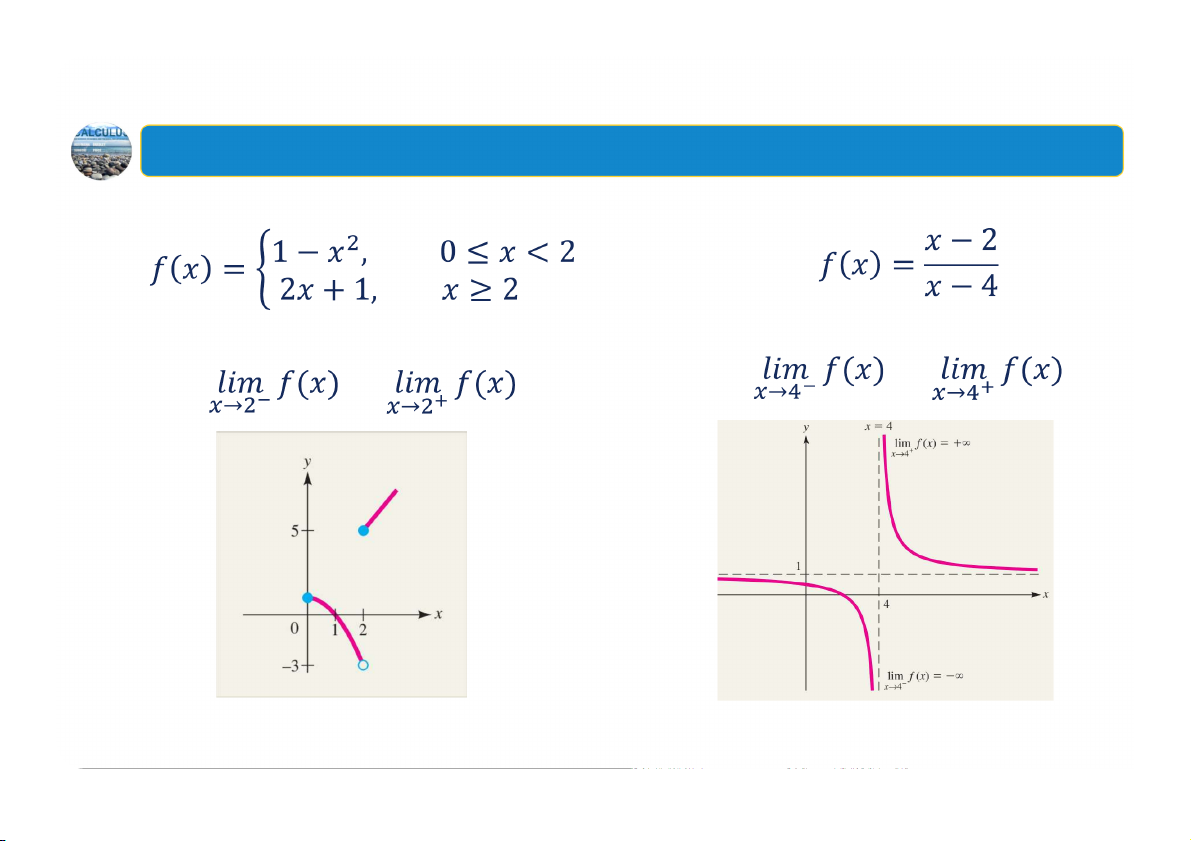
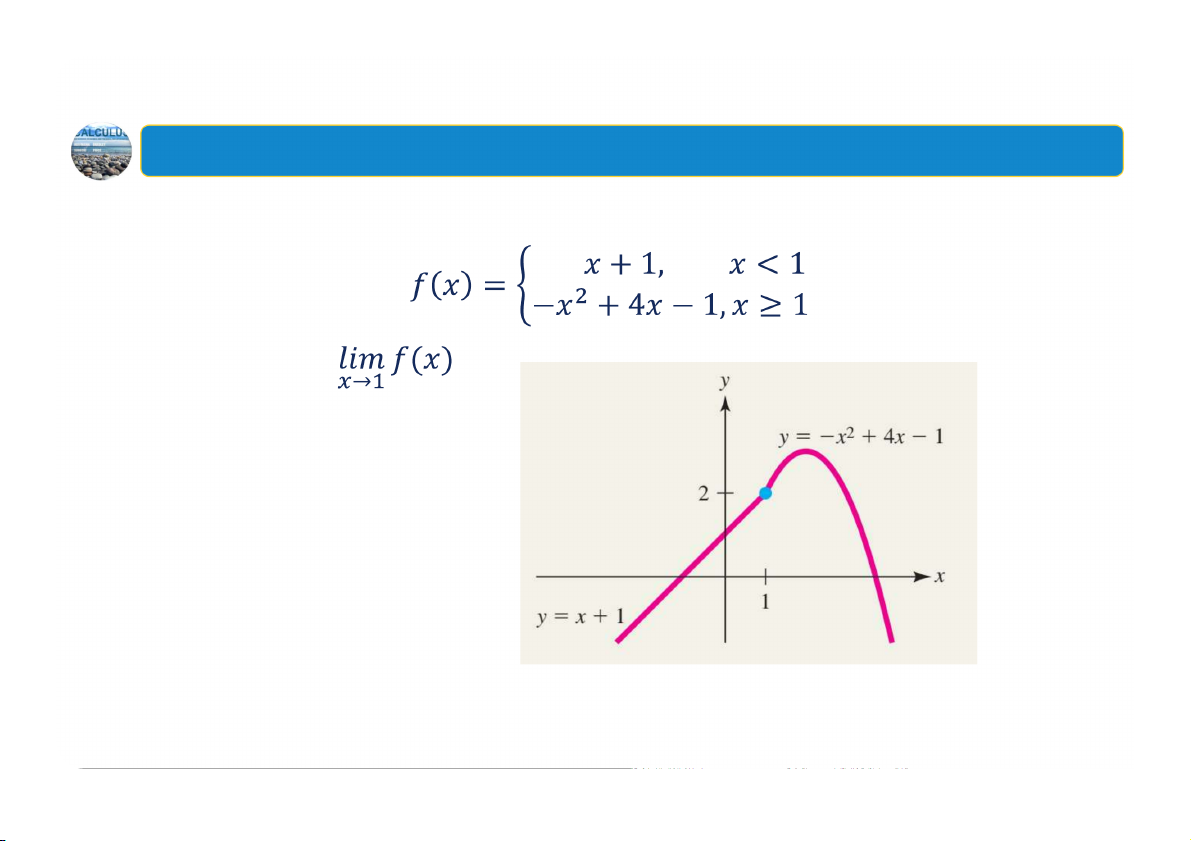
1. Các giới hạn một phía Ví dụ: Cho hàm số Ví dụ: Cho hàm số
Tính các giới hạn một phía
Tính các giới hạn một phía và và 60
Ví dụ: Sử dụng các giới hạn một phía để tìm giới hạn hai phía Cho hàm số Tính giới hạn 61 2. Tính liên tục Định nghĩa:
Hàm số liên tục tại
nếu nó thỏa mãn ba điều kiện sau đây: 1. xác định 2. tồn tại 3. Nếu không liên tục tại
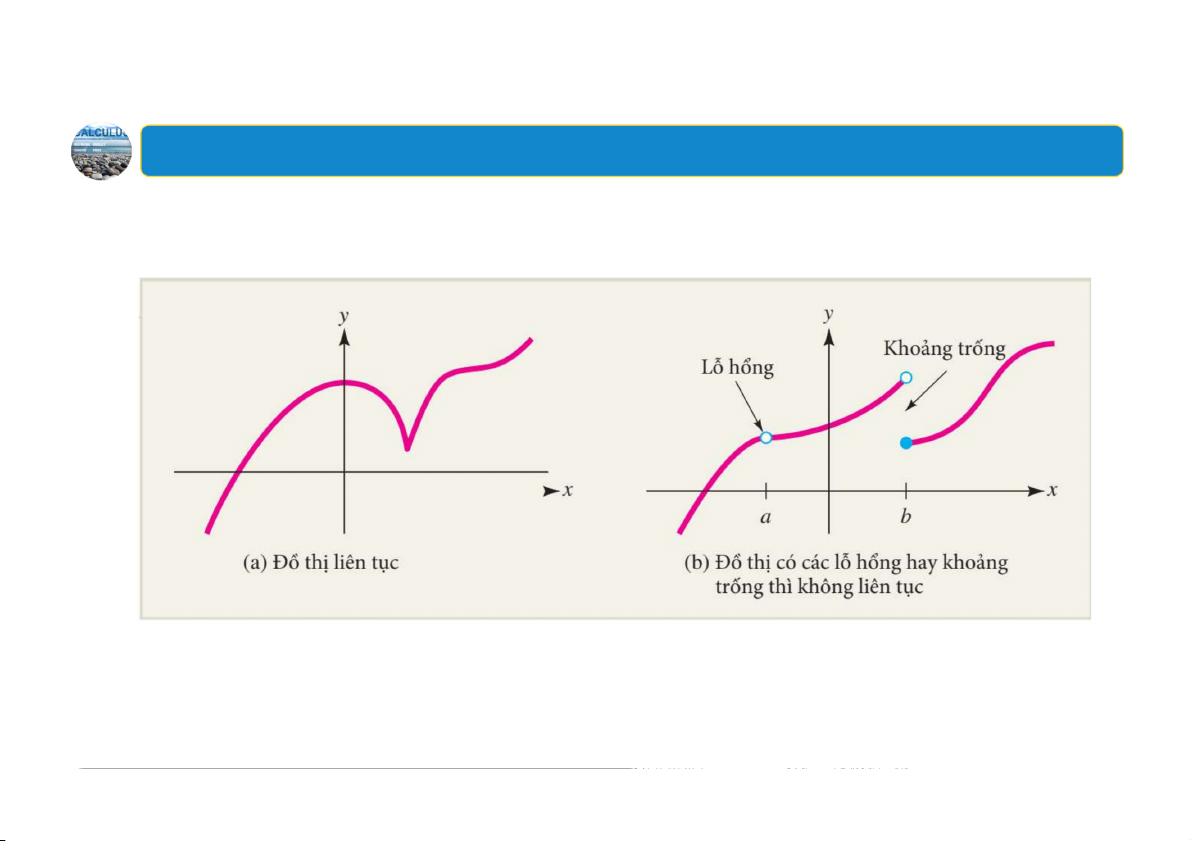
thì hàm số được gọi là gián đoạn tại 62 2. Tính liên tục
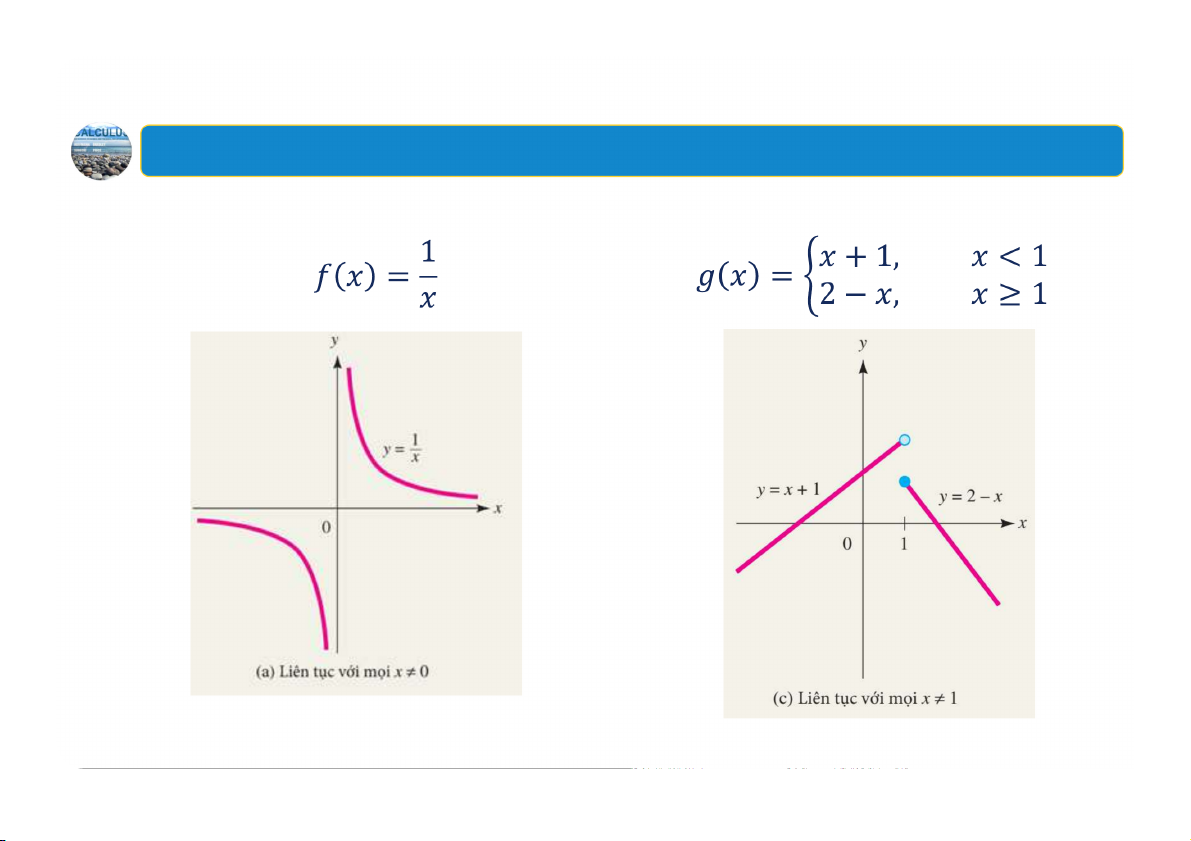
Sự liên tục và gián đoạn 63 2. Tính liên tục
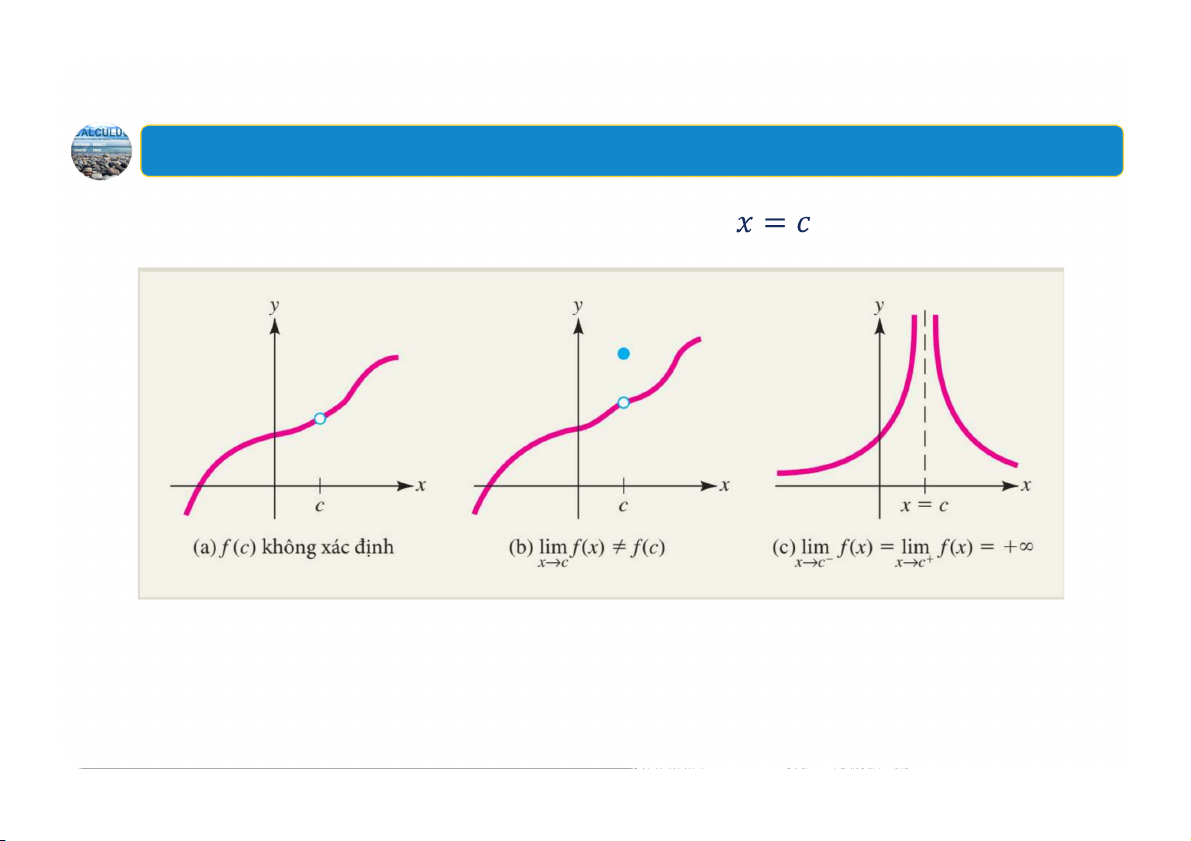
Ba trường hợp đồ thị hàm số có lỗ hổng tại 64 2. Tính liên tục
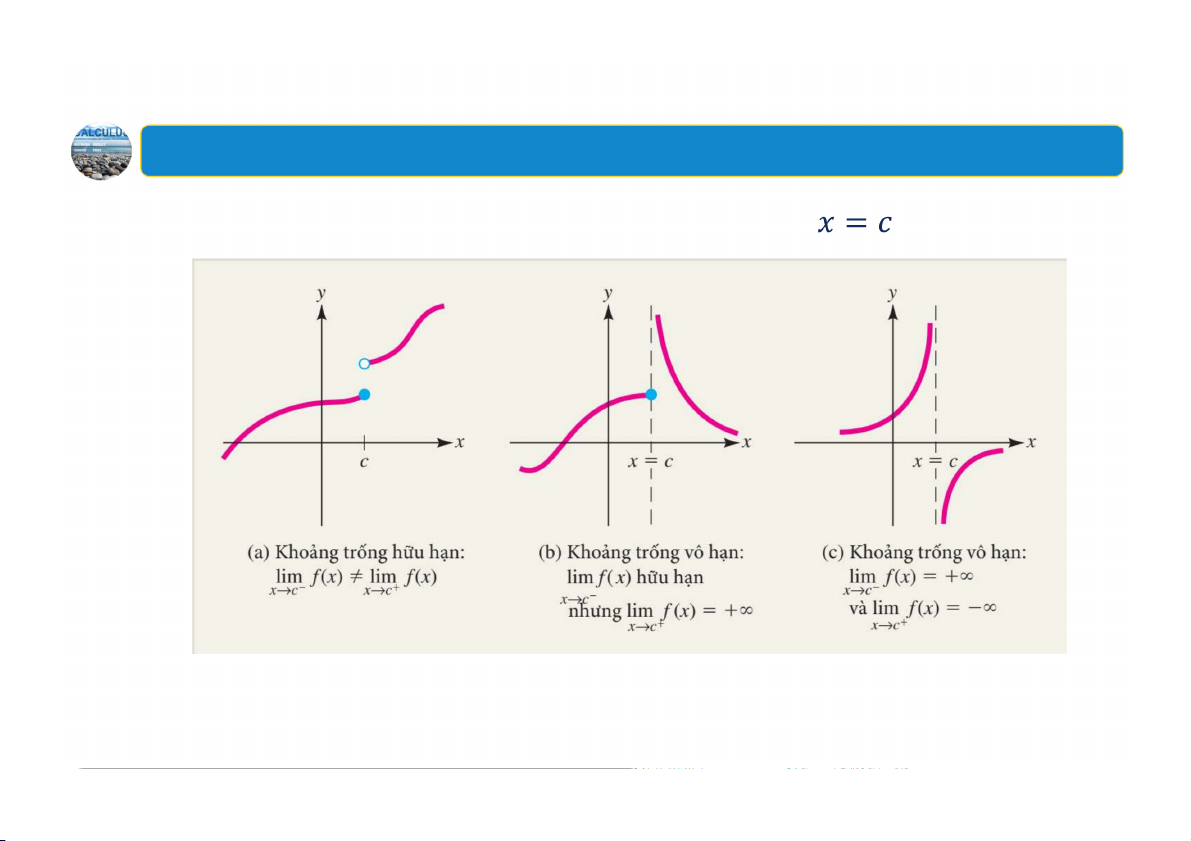
Ba trường hợp đồ thị hàm số có khoảng trống tại 65
3. Tính liên tục của hàm đa thức và hàm phân thức Tính chất: Ví dụ:
1. Chứng minh rằng đa thức liên tục tại .
Do đó, các hàm đa thức và hàm
2. Chứng minh rằng phân thức
phân thức liên tục tại tất cả các điểm mà nó xác định. liên tục tại . 66
3. Tính liên tục của hàm đa thức và hàm phân thức
Ví dụ: Xét sự liên tục của hàm số:
Xét sự liên tục của hàm số 67
4. Hàm số liên tục trên một khoảng Định nghĩa:
Ví dụ: Xét sự liên tục của hàm số Hàm được gọi là liên tục trên khoảng mở nếu
nó liên tục tại mọi điểm trên khoảng mở và trong khoảng đó khoảng đóng . Hàm liên tục trên khoảng đóng nếu nó liên tục trên khoảng mở và và 68
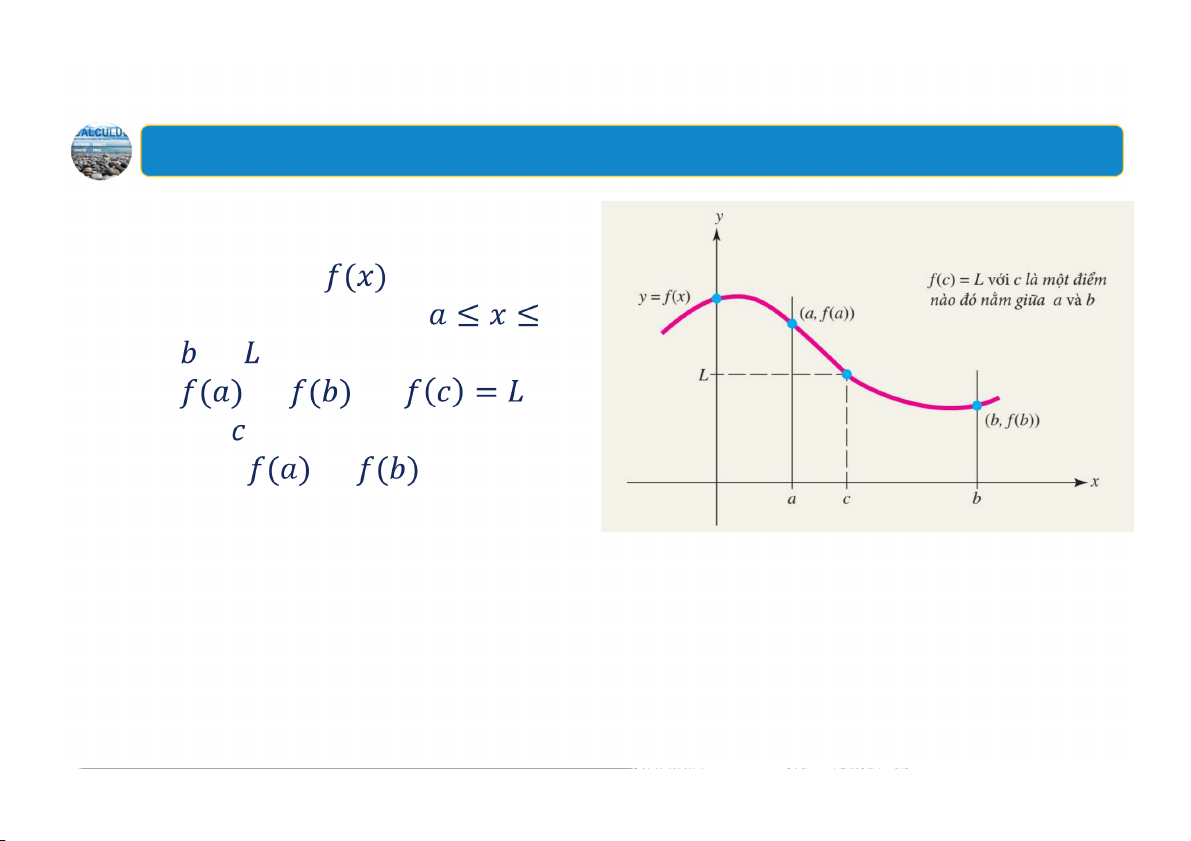
5. Định lý giá trị trung gian Định lý: Nếu hàm liên tục trên khoảng đóng
và là một số nằm giữa và thì
với là một số nào đó nằm giữa và . 69
5. Định lý giá trị trung gian
Ví dụ: Ở tuổi 15, Michaela cao gấp đôi em trai Juan 5 tuổi của cô,
nhưng vào sinh nhật thứ 21 của Juan, mọi người phát hiện ra rằng cậu
đã cao hơn cô 6 inch. Giải thích tại sao chắc hẳn đã có lúc Michaela và
Juan có chiều cao hoàn toàn giống nhau. 70




