Bài giảng môn Vật lý đại cương chương 3: Động lực học chất điểm

lOMoARcPSD|36442750 NỘI DUNG CHƯƠNG TRÌNH PHẦ T N à 1: i l C iệ Ơ u H Ọ h
C ọc tập: Vật lý đại c PHẦN 2: NHI ương ỆT HỌC CHƯƠ t N ậ G 1p . M 1 ở đ, ầutập 2 (Giáo t C r H ì Ư n Ơ h NG + 7. b Thà u i yế tt đ ậ ộn p g h)ọ,c phân tử CHƯƠNG 2. N Đ X ộn B g h G ọc chD ất , đi ểLmương cD ác u ch y ất ê khín B và đị ìnn h l h uật phân bố
CHƯƠNG 3. Động lực học chất điểm
CHƯƠNG 8. Nguyên lý thứ nhất của
CHƯƠNG 4. Cơ năng và trường lực thế nhiệt động lực học
CHƯƠNG 5. Chuyển động quay của vật
CHƯƠNG 9. Nguyên lý thứ hai của nhiệt rắn động lực học
CHƯƠNG 6. Dao động và sóng cơ CHƯƠNG 10. Khí thực
Downloaded by v?n ti?n Lê (vantienle525@gmail.com) lOMoARcPSD|36442750 CHƯƠNG 3
ĐỘNG HỌC LỰC CHẤT ĐIỂM
1. Phát biểu các định luật Newton ( Định luật 1, 2, 3)
2. Nguyên lý tương đối Galileo ( Không gian và thời gian, Phép biến đổi Galileo,
Tổng hợp vận tốc và gia tốc, Hệ quy chiếu và nguyên lý tương đối)
3. Một số loại lực cơ học ( Trọng lực, lực hướng tâm, Lực ly tâm, Lực quán tính…)
4. Động lượng của chất điểm (Định lý 1,2 về động lượng, …)
5. Định luật bảo toàn động lượng của hệ chất điểm
6. Mô men động lượng của chất điểm và một hệ chất điểm
Downloaded by v?n ti?n Lê (vantienle525@gmail.com) lOMoARcPSD|36442750 CHƯƠNG 3
ĐỘNG HỌC LỰC CHẤT ĐIỂM
3. 1. Phát biểu các định luật Newton 3.1.1 Định luật I Newton vPhát biểu:
Khi một chất điểm cô lập nếu đang đứng yên, nó sẽ tiếp tục
đứng yên, nếu đang chuyển động thì chuyển động của nó là thẳng đều. Issac Newton (1643-1727) =const (3.1) (Định luật quán tính)
v Hệ quy chiếu quán tính:
Nếu hợp lực tác dụng lên vật (chất điểm) bằng 0 thì tồn tại 1 hệ quy chiếu trong đó ậ
. Đây được gọi là hệ quy chiếu quán tính.
Downloaded by v?n ti?n Lê (vantienle525@gmail.com) lOMoARcPSD|36442750 CHƯƠNG 3
ĐỘNG HỌC LỰC CHẤT ĐIỂM
3. 1. Phát biểu các định luật Newton 3.1.2 Định luật II Newton vPhát biểu:
1/ Chuyển động của một chất điểm chịu tác dụng của các
lực có tổng hợp  0 là một chuyển động có gia tốc.
2/ Gia tốc chuyển động của chất điểm tỉ lệ với tổng hợp lực
tác dụng và tỉ lệ nghịch với khối lượng của chất điểm ấy Issac Newton (1643-1727) 𝑭 (3.2) Đơn vị: m/s2 𝒎
Downloaded by v?n ti?n Lê (vantienle525@gmail.com) lOMoARcPSD|36442750 CHƯƠNG 3
ĐỘNG HỌC LỰC CHẤT ĐIỂM
3. 1. Phát biểu các định luật Newton 3.1.2 Định luật II Newton v Phát biểu: Lưu ý: 𝑭 (3.2) 𝒎 Công thức 3.2: Trong hệ SI: k=1 nên 𝐹 ∑𝑖 với Issac Newton (1643-1727) 𝑚 𝑚 𝑖 Hay
(3.3) (Phương trình cơ bản của động lực học chất điểm) 𝑖 § Khi  Định luật thứ nhất § Khi  ∑ 𝐹 Định luật thứ hai 𝑚
Downloaded by v?n ti?n Lê (vantienle525@gmail.com) lOMoARcPSD|36442750 CHƯƠNG 3
ĐỘNG HỌC LỰC CHẤT ĐIỂM
3. 1. Phát biểu các định luật Newton
3.1.2 Định luật III Newton v Phát biểu:
Khi chất điểm A tác dụng lên chất điểm B một lực thì chất điểm B
cũng tác dụng lên chất điểm A một lực hai lực và tồn tại đồng
thời cùng phương, ngược chiều và cùng cường độ.
Nói cách khác: tổng hình học các lực tương tác giữa hai chất điểm =0 Issac Newton (1643-1727) (3.4)
Ø Tổng quát: Tổng các nội lực của một hệ chất điểm cô lập (còn gọi là hệ kín) bằng không
Downloaded by v?n ti?n Lê (vantienle525@gmail.com) lOMoARcPSD|36442750 CHƯƠNG 3
ĐỘNG HỌC LỰC CHẤT ĐIỂM
3. 2. Nguyên lý tương đối Galileo
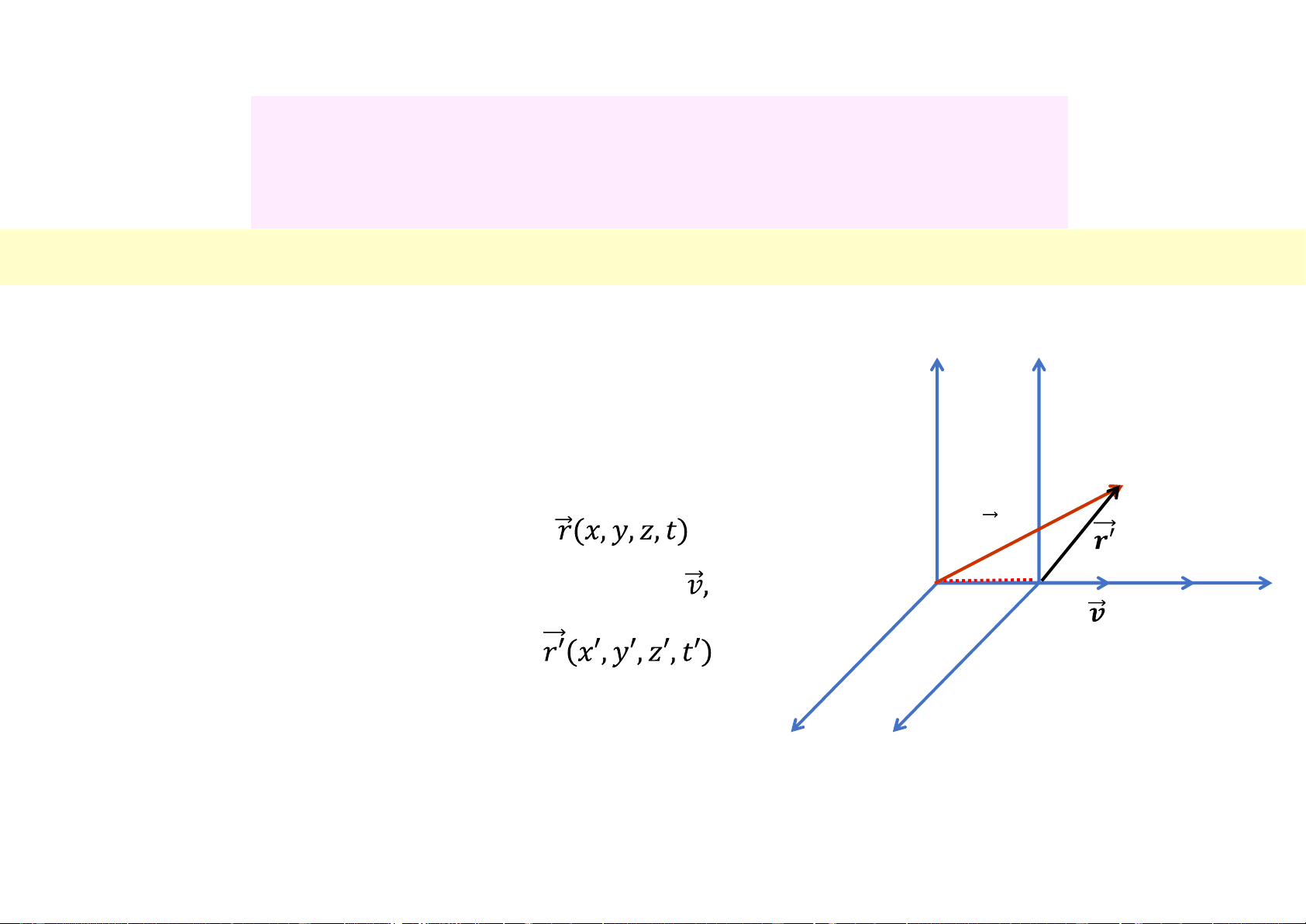
3.1.1 Không gian và thời gian trong cơ học cổ điển y y’
* Xét 2 hệ tọa độ Oxyz và O’x’y’z’ + Hệ Oxyz đứng yên. M
M được xác định bởi 𝒓
+ Hệ O’x’y’z’: trượt dọc theo Ox với vận tốc O O’ x x’
M được xác định bởi z z’
Downloaded by v?n ti?n Lê (vantienle525@gmail.com) lOMoARcPSD|36442750 CHƯƠNG 3
ĐỘNG HỌC LỰC CHẤT ĐIỂM
3. 2. Nguyên lý tương đối Galileo
* Theo quan điểm của cơ học cổ điển Newton
+ Thời gian có tính tuyệt đối không phụ thuộc vào hệ quy chiếu: t=t’ y y’
+ Vị trí không gian có tính tương đối phụ thuộc vào hệ quy chiếu: x=x’+v.t’ ; y=y’; z=z’ (3.5)
Do đó: chuyển động có tính tương đối phụ thuộc hệ quy chiếu O O
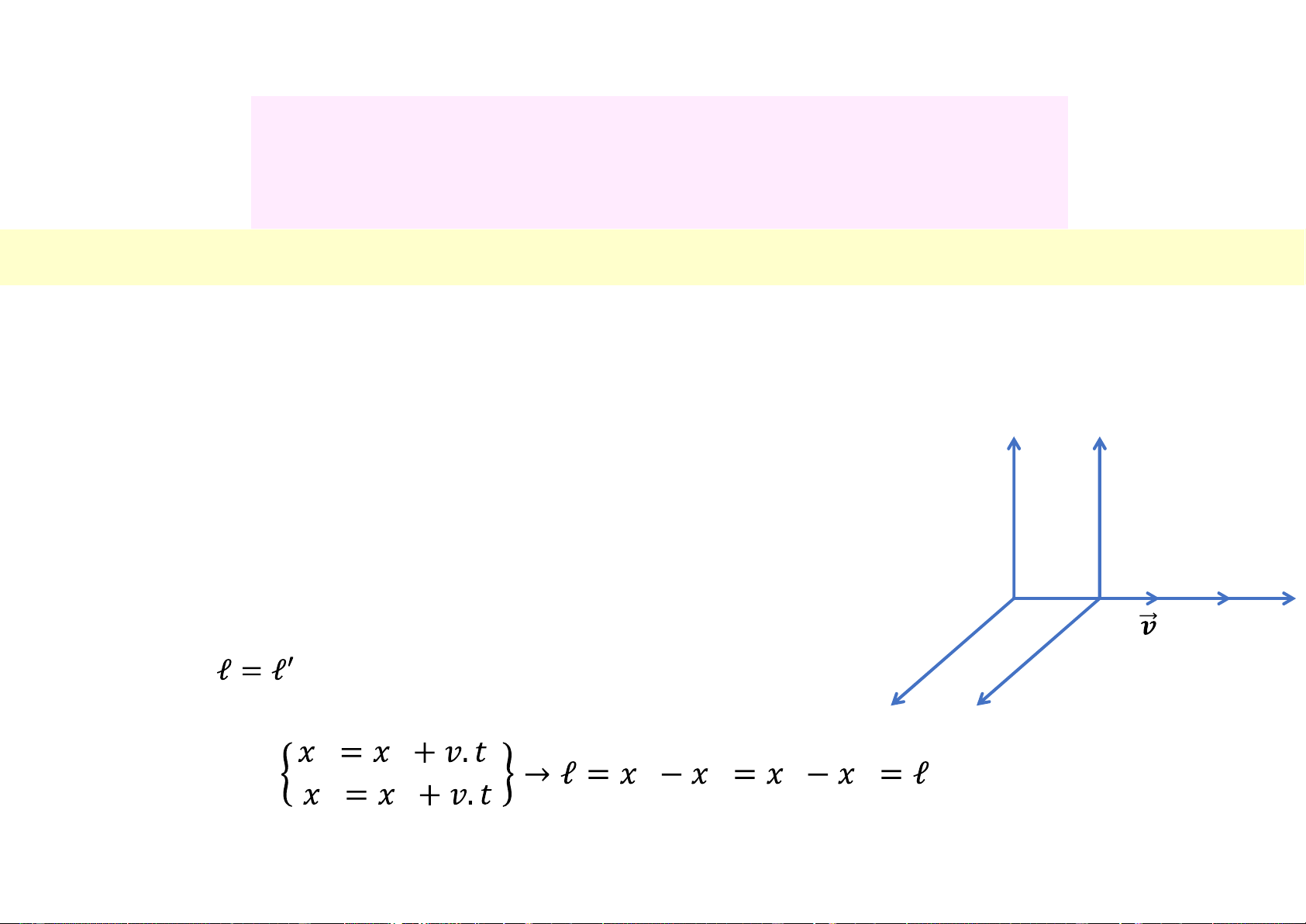
+ Khoảng không gian có tính tuyệt đối, không phụ thuộc hệ ’ x x’ quy chiếu ( ) z z’ (3.6)
Downloaded by v?n ti?n Lê (vantienle525@gmail.com) lOMoARcPSD|36442750 CHƯƠNG 3
ĐỘNG HỌC LỰC CHẤT ĐIỂM
3. 2. Nguyên lý tương đối Galileo y y’ M
3.1.2 Phép biến đổi Galileo
* Xét 2 hệ quy chiếu quán tính O và O’.
+ Giả sử Hệ O đứng yên, O’ chuyển động với vận tốc so với O O O’
+ Ở thời điểm ban đầu O  O’ x x’
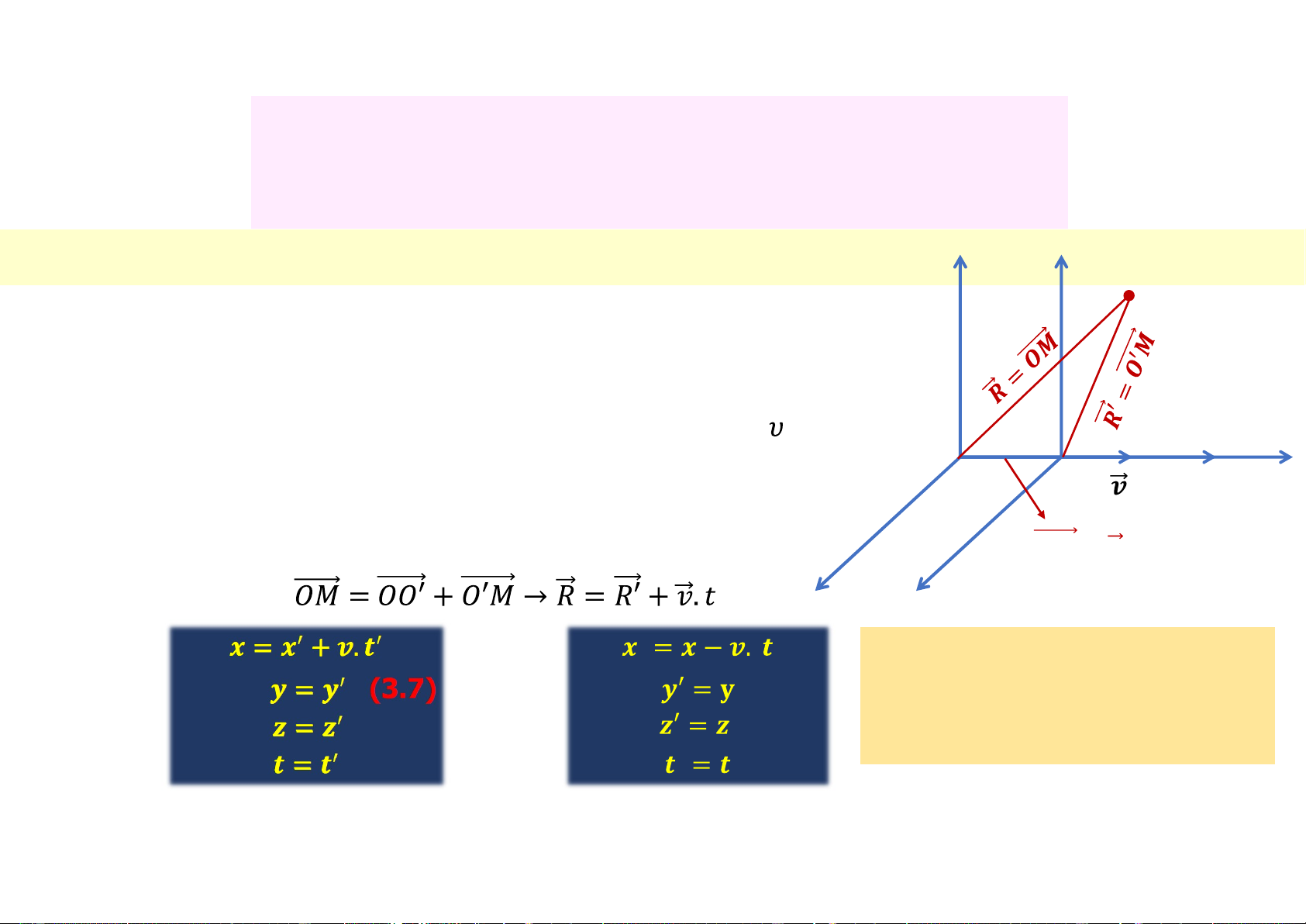
+ Sau thời gian t thì O (x,y,z,t) và O’ (x’,y’,z’,t’) 𝑶𝑶 = 𝝊. 𝒕 Cộng vận tốc z z’ • Ta có: • Và ngược Ø Phép biến đổi Galileo (3.7) (3.8) lại:
(Chuyển các tọa độ không gian, thời
gian từ hqc O’ sang O và ngược lại)
Downloaded by v?n ti?n Lê (vantienle525@gmail.com) lOMoARcPSD|36442750 CHƯƠNG 3
ĐỘNG HỌC LỰC CHẤT ĐIỂM
3. 2. Nguyên lý tương đối Galileo
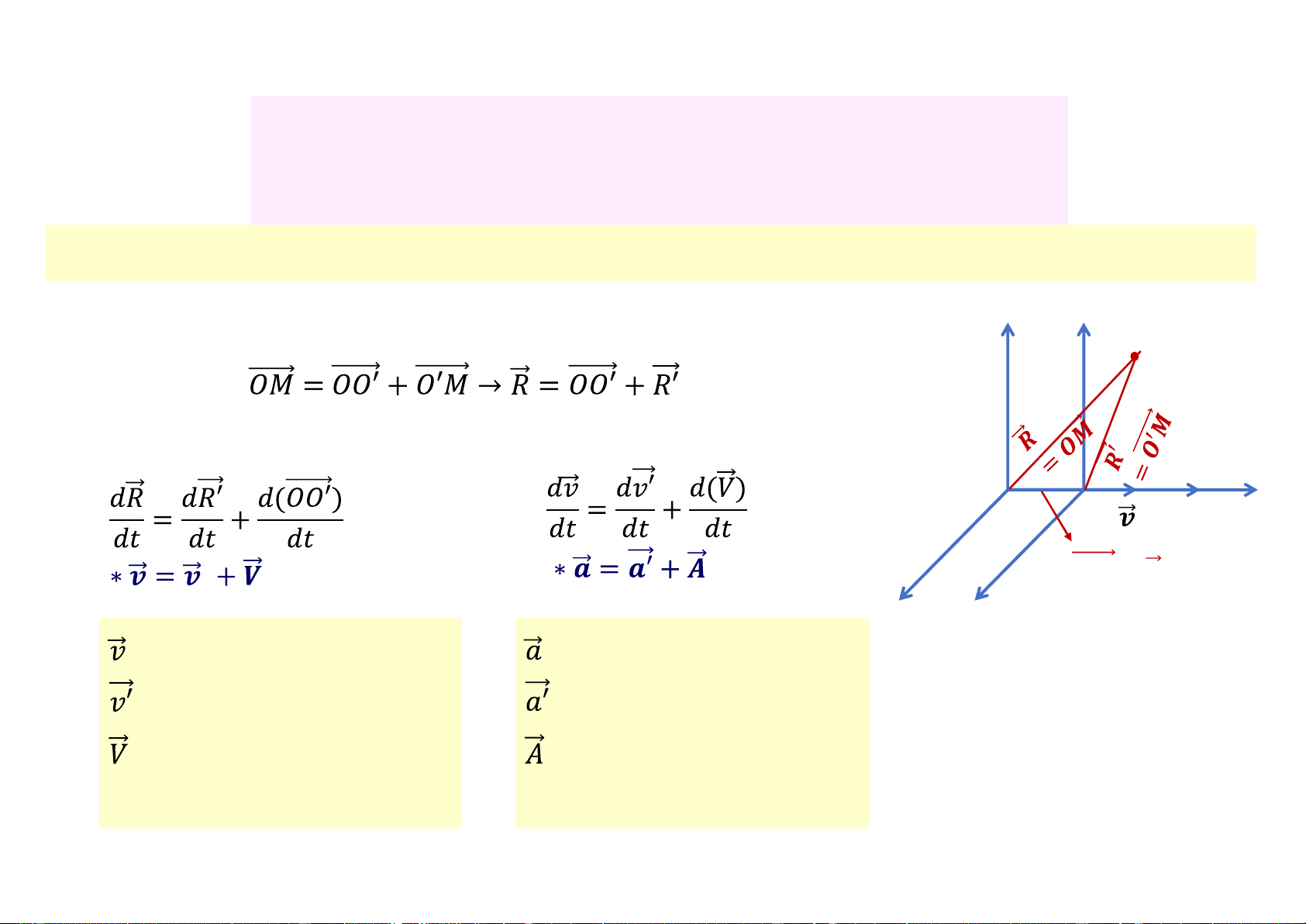
3.1.3 Tổng hợp vận tốc và gia tốc y y’ M + Ta có:
+ Đạo hàm 2 vế theo thời gian: O O’ x x’ (3.10) 𝑶𝑶 = 𝝊. 𝒕 (3.9) z z’
: vận tốc của M đối với O
: gia tốc của M đối với O
: vận tốc của M đối với O’
: gia tốc của M đối với O’
: vận tốc tịnh tiến của hệ
: gia tốc tịnh tiến của hệ O’ đối với O O’ đối với O
Downloaded by v?n ti?n Lê (vantienle525@gmail.com) lOMoARcPSD|36442750 CHƯƠNG 3
ĐỘNG HỌC LỰC CHẤT ĐIỂM
3. 2. Nguyên lý tương đối Galileo
3.1.4 Hệ quy chiếu quán tính và nguyên lý tương đối Galileo
a. Hệ quy chiếu quán tính
+ Hệ quy chiếu trong đó định luật quán tính (định luật I Niu tơn) được nghiệm
đúng.( Trong tự nhiên không có hệ quy chiếu quán tính)
+ Hệ quy chiếu gắn với trái đất có thể coi là h.q.c quán tính khi bỏ qua chuyển động
quay của Trái đất quanh Mặt trời và quanh trục của nó ( Hqc không đòi hỏi có độ chính xác cao)
+ Các hệ quy chiếu đứng yên hoặc chuyển động thẳng đều đối với h.q.c quán tính.
Downloaded by v?n ti?n Lê (vantienle525@gmail.com) lOMoARcPSD|36442750 CHƯƠNG 3
ĐỘNG HỌC LỰC CHẤT ĐIỂM
3. 2. Nguyên lý tương đối Galileo
3.1.4 Hệ quy chiếu quán tính và nguyên lý tương đối Galileo b. Nguyên lý Galileo:
Các thí nghiệm cơ học thực hiện trên một hệ quy chiếu đang chuyển động thẳng đều
với một hệ qui chiếu lấy làm mốc khác, người ta không thể phát hiện được hệ qui
chiếu của mình đứng yên hay chuyển động thẳng đều so với hệ quy chiếu mốc.
+ Xét chất điểm chuyển động trong 2 hệ quy chiếu:
+ Nếu hệ O’ c/đ thẳng đều đối với hqc quán tính O thì:
(3.11)  O’ cũng là hệ quy chiếu quán tính
Downloaded by v?n ti?n Lê (vantienle525@gmail.com) lOMoARcPSD|36442750 CHƯƠNG 3
ĐỘNG HỌC LỰC CHẤT ĐIỂM
3. 2. Nguyên lý tương đối Galileo
PB nguyên lý: Các hiện tượng, các quá trình cơ học trong các hệ quy chiếu quán
tính khác nhau đều xảy ra giống nhau. Các phương trình cơ học bất biến đối với phép biến đổi Galileo.
Ø Mọi hệ quy chiếu chuyển động thẳng đều đối với 1 hệ quy chiếu quán tính cũng là hệ quy chiếu quán tính
Ø Các định luật Newton được nghiệm đúng trong hệ quy chiếu chuyển động thẳng
đều đối với hệ quy chiếu quán tính
Ø Các phương trình động lực học trong các hệ quy chiếu quán tính có dạng như nhau.
Downloaded by v?n ti?n Lê (vantienle525@gmail.com) lOMoARcPSD|36442750 CHƯƠNG 3
ĐỘNG HỌC LỰC CHẤT ĐIỂM
3. 2. Nguyên lý tương đối Galileo
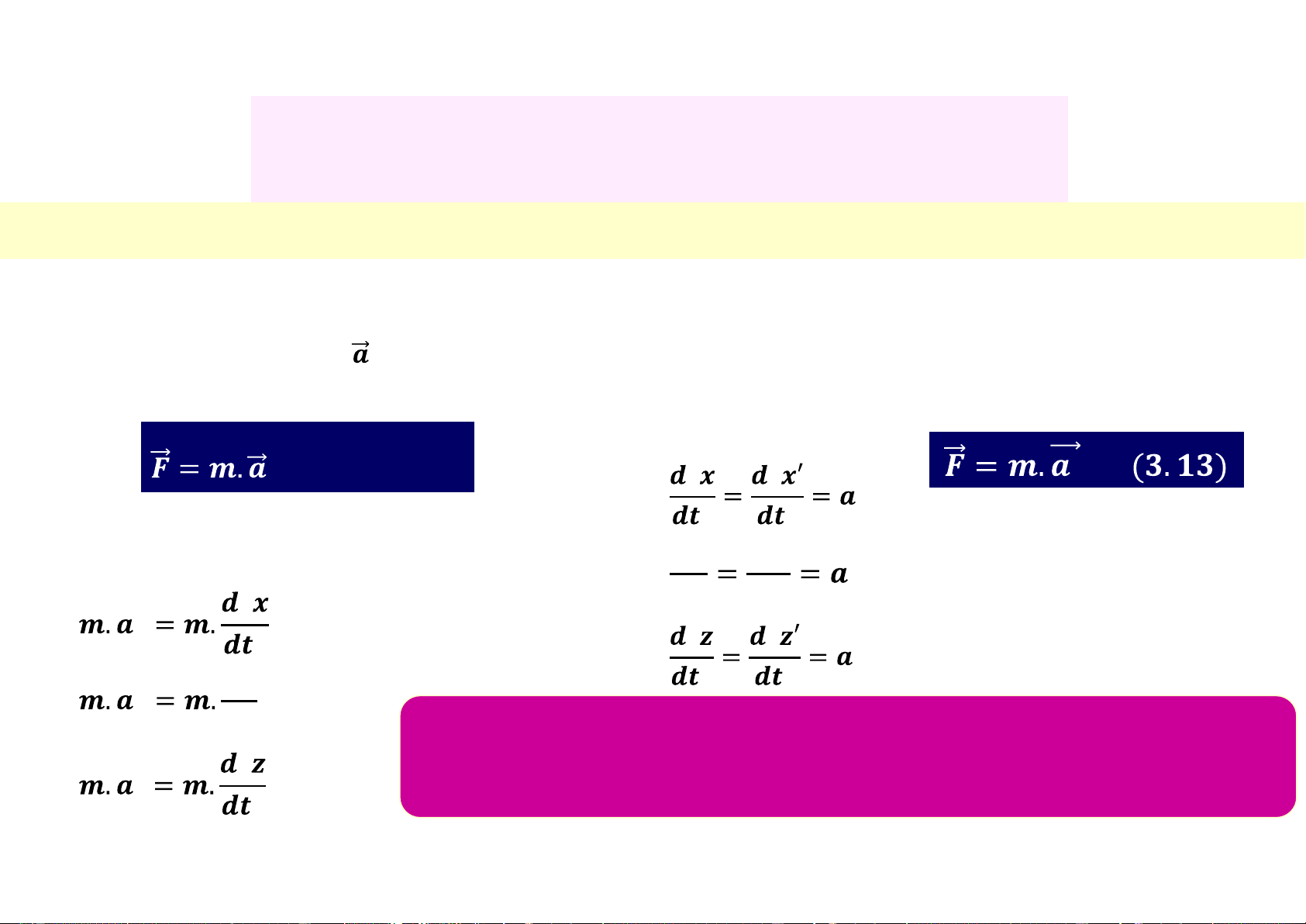
v Sự bất biến của các phương trình cơ học
+ Xét chất điểm m, F, trong hệ quy chiếu quán tính O
Phương trình chuyển động của chất điểm m: (3.12) 𝟐 𝟐 𝟐 𝟐 𝒙
Chiếu xuống các trục Ox, Oy, Oz Do có: 𝒅𝟐𝒚 𝒅𝟐𝒚′ Ø Phương trình c.động trong hệ O’ 𝟐 𝒅𝒕𝟐 𝒅𝒕𝟐 𝒚 (3.15) 𝒙 𝟐 𝟐 𝟐 𝟐 𝟐 𝒛 𝒅𝟐𝒚 𝒚 ( 3.14) 𝒅𝒕𝟐
Ø Các phương trình cơ học bất biến qua phép biến đổi Galileo 𝟐
(H.q.c O’ c.động thẳng đều đ.với h.q.c q. tính O cũng là h.q.c quán tính) 𝒛 𝟐
Downloaded by v?n ti?n Lê (vantienle525@gmail.com) lOMoARcPSD|36442750 CHƯƠNG 3
ĐỘNG HỌC LỰC CHẤT ĐIỂM
3. 3. Một số lực cơ học 3.3.1 Trọng lực
Ø Lực tác dụng lên chất điểm bởi sức hút của trái đất (gia
tốc trọng trường), theo ĐL 2 Newton có: m (3.16)
Ø Trọng lực luôn hướng thẳng góc xuống phía dưới
Downloaded by v?n ti?n Lê (vantienle525@gmail.com) lOMoARcPSD|36442750 CHƯƠNG 3
ĐỘNG HỌC LỰC CHẤT ĐIỂM
3. 3. Một số lực cơ học
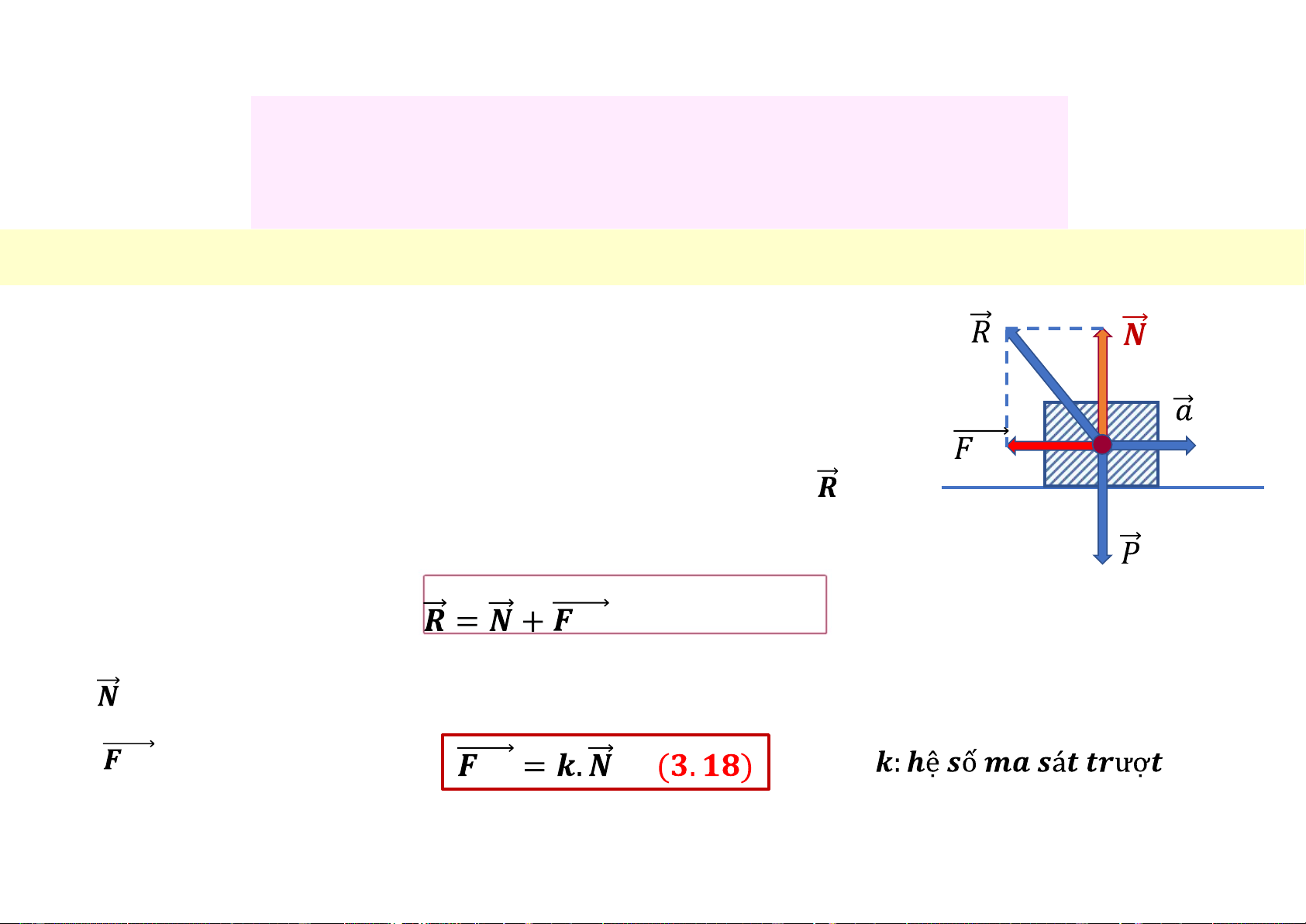
3.3.2 Phản lực và lực ma sát
Ø Khi vật thể c.động (trượt) trên một bề mặt  tác dung lên m bề mặt một lực nén.
Ø Theo định luật III Newton có phản lực của bề mặt ( ) tác
dụng trở lại  xác định bởi: 𝒎𝒔 (3.17) • : Phản lực pháp tuyến • 𝒎𝒔 : Lực ma sát 𝒎𝒔
Downloaded by v?n ti?n Lê (vantienle525@gmail.com) lOMoARcPSD|36442750 CHƯƠNG 3
ĐỘNG HỌC LỰC CHẤT ĐIỂM
3. 3. Một số lực cơ học
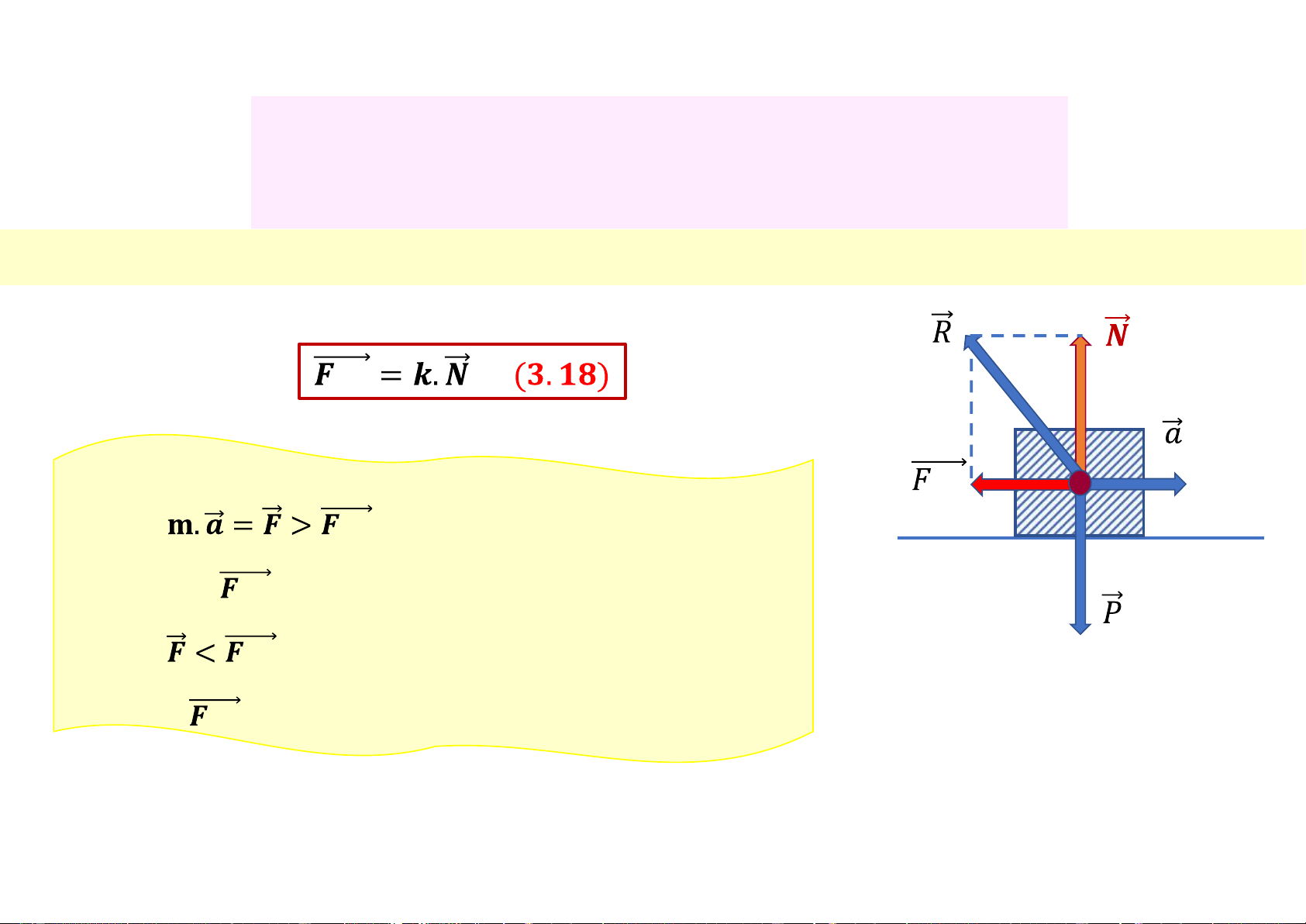
3.3.2 Phản lực và lực ma sát Lực ma sát 𝒎𝒔 m v Nếu
𝒎𝒔: vật sẽ trượt hoặc chuyển động
v  𝒎𝒔 : Lực ma sát động v Nếu
𝒎𝒔: vật sẽ đứng yên
 𝒎𝒔 : Lực ma sát tĩnh
Downloaded by v?n ti?n Lê (vantienle525@gmail.com) lOMoARcPSD|36442750 CHƯƠNG 3
ĐỘNG HỌC LỰC CHẤT ĐIỂM
3. 3. Một số lực cơ học
3.3.2 Phản lực và lực ma sát v Lực ma sát nhớt v Lực ma sát lăn
Xuất hiện ở mặt tiếp xúc giữa 2 lớp chất
Xuất hiện ở mặt tiếp xúc giữa 1 vật lăn
lưu (lỏng hay khí) c.động đối với nhau
trên mặt của 1 vật khác 𝒎𝒔 (3.20) • : hệ số ma sát nhớt 𝒎𝒔.𝒍ă𝒏 (3.19)
• : vận tốc của vật c.động trong chất lưu
• r: bán kính của vật lăn
v Nếu vật có dạng hình cầu, đường kính d. Fms nhớt
được x.định theo công thức Stokes:
• : hệ số ma sát lăn 𝒎𝒔 (3.21) . ă . ượ
hệ số nhớt của chất lưu
Downloaded by v?n ti?n Lê (vantienle525@gmail.com) lOMoARcPSD|36442750 CHƯƠNG 3
ĐỘNG HỌC LỰC CHẤT ĐIỂM
3. 3. Một số lực cơ học 3.3.3 Lực căng dây
Ø Lực căng tại điểm A trên dây là lực tương tác giữa 2
nhánh dây 2 bên điểm A, tuân theo định luật III Newton (3.22)
Downloaded by v?n ti?n Lê (vantienle525@gmail.com) lOMoARcPSD|36442750 CHƯƠNG 3
ĐỘNG HỌC LỰC CHẤT ĐIỂM
3. 3. Một số lực cơ học
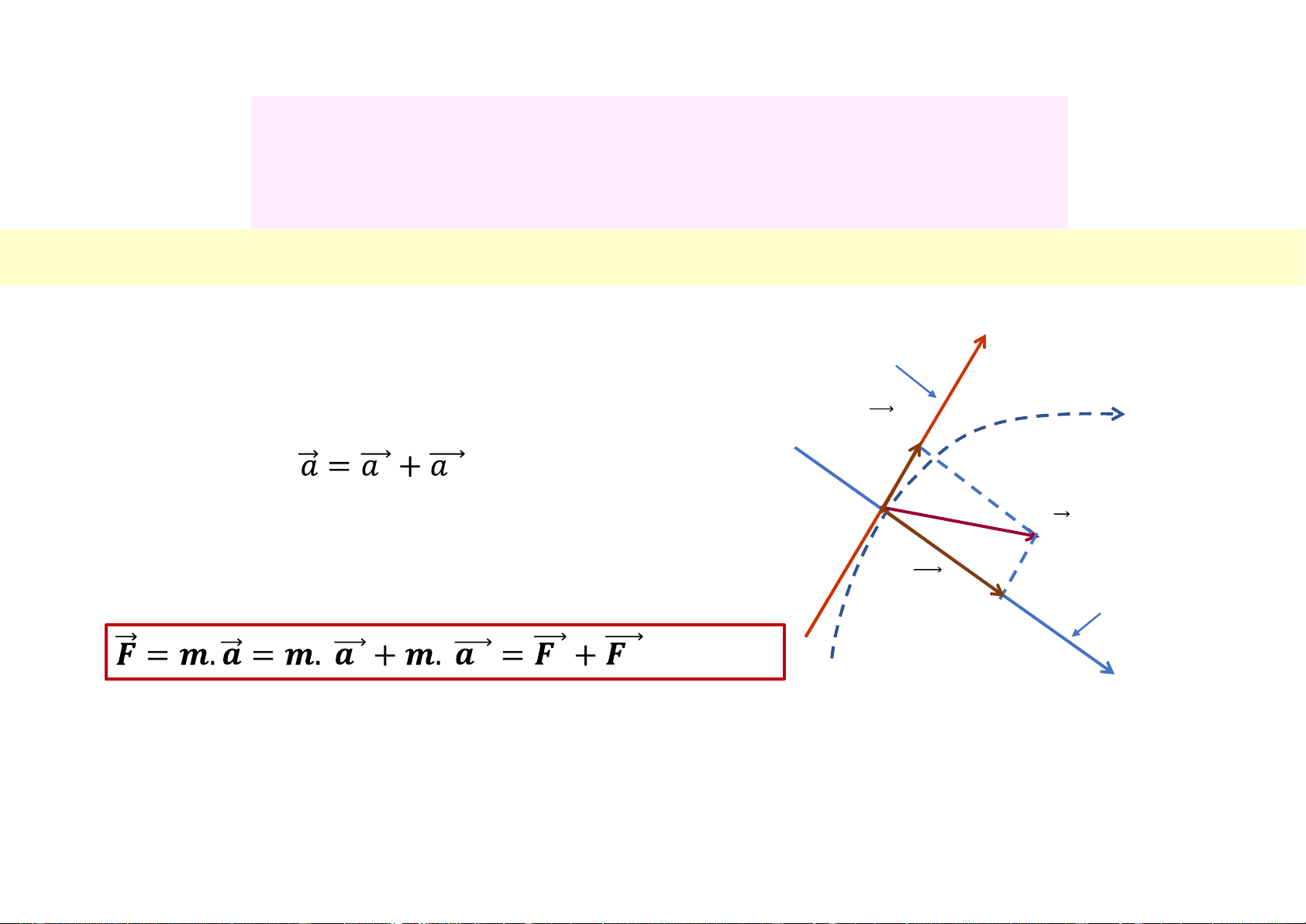
3.3.4 Lực hướng tâm, ly tâm
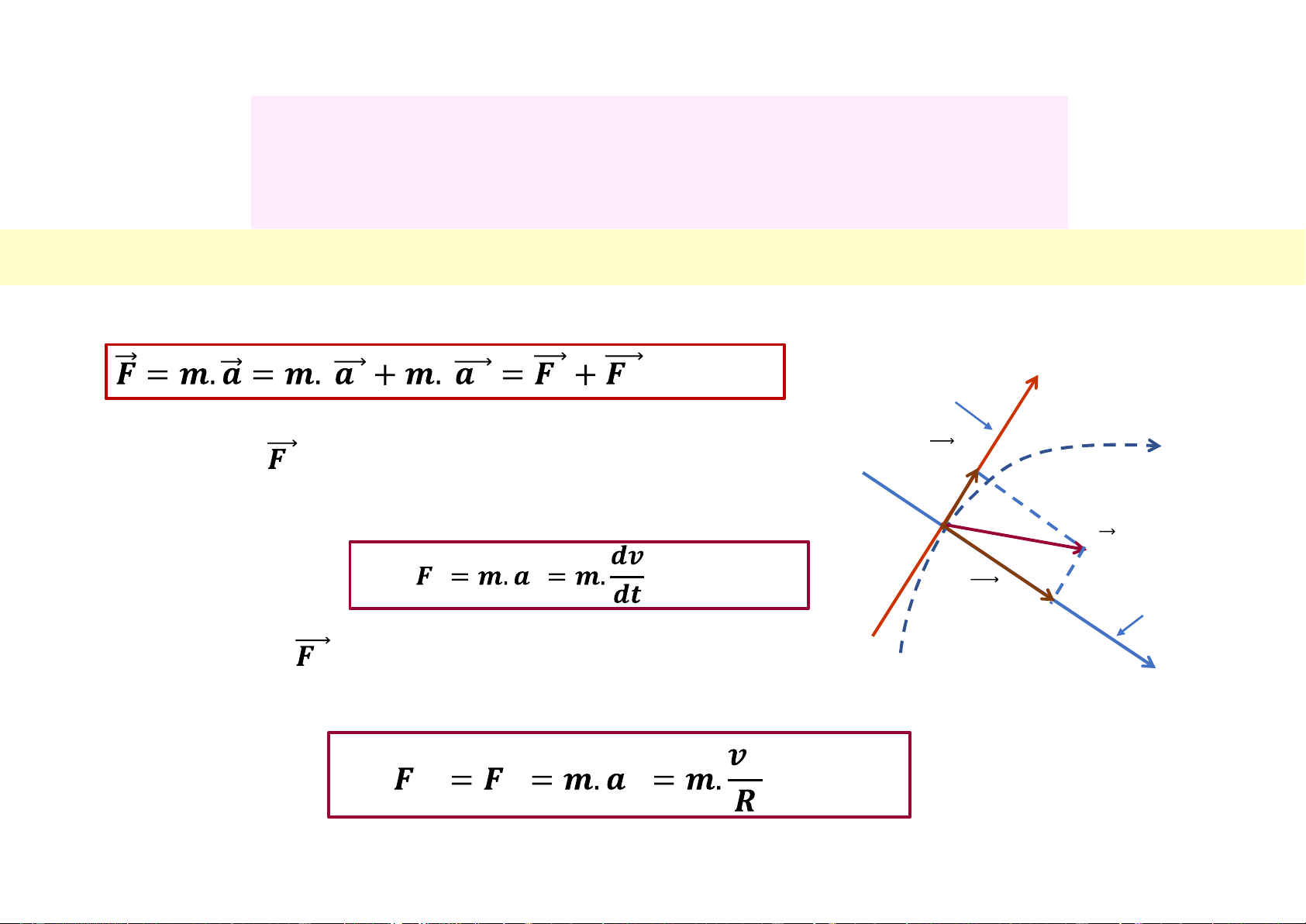
Tiếp tuyến với quỹ đạo CĐ tại M (C)
+ Khi chất điểm c.động trên quỹ đạo cong (C): 𝒂𝒕  Gia tốc CĐ: M
+ Phương trình động lực của chất điểm CĐ trên quỹ đạo: 𝒂 𝒂𝒏 Vuông góc với quỹ đạo CĐ tại M 𝒕 𝒏 𝒕 𝒏 (3.23)
Downloaded by v?n ti?n Lê (vantienle525@gmail.com) lOMoARcPSD|36442750 CHƯƠNG 3
ĐỘNG HỌC LỰC CHẤT ĐIỂM
3. 3. Một số lực cơ học
3.3.4 Lực hướng tâm, ly tâm Tiếp tuyến với quỹ 𝒕 𝒏 𝒕 𝒏 (3.23) đạo CĐ tại M (C) v Thành phần 𝒂
𝒕 sinh ra gia tốc tiếp tuyến, thay đổi độ 𝒕
lớn của véc tơ vận tốc, gọi là lực tiếp tuyến, được M 𝒂 xác định bởi: Vuông góc với 𝒕 𝒕 (3.24) 𝒂𝒏 quỹ đạo CĐ tại M
v Thành phần 𝒏 sinh ra gia tốc pháp tuyến, thay đổi
phương của véc tơ vận tốc, gọi là lực pháp tuyến  lực hướng tâm (F 𝟐 ht). 𝒉𝒕 𝒏 𝒏 (3.25)
Downloaded by v?n ti?n Lê (vantienle525@gmail.com) lOMoARcPSD|36442750 CHƯƠNG 3
ĐỘNG HỌC LỰC CHẤT ĐIỂM
3. 3. Một số lực cơ học
3.3.4 Lực hướng tâm, ly tâm Tiếp tuyến với quỹ đạo CĐ tại M (C)
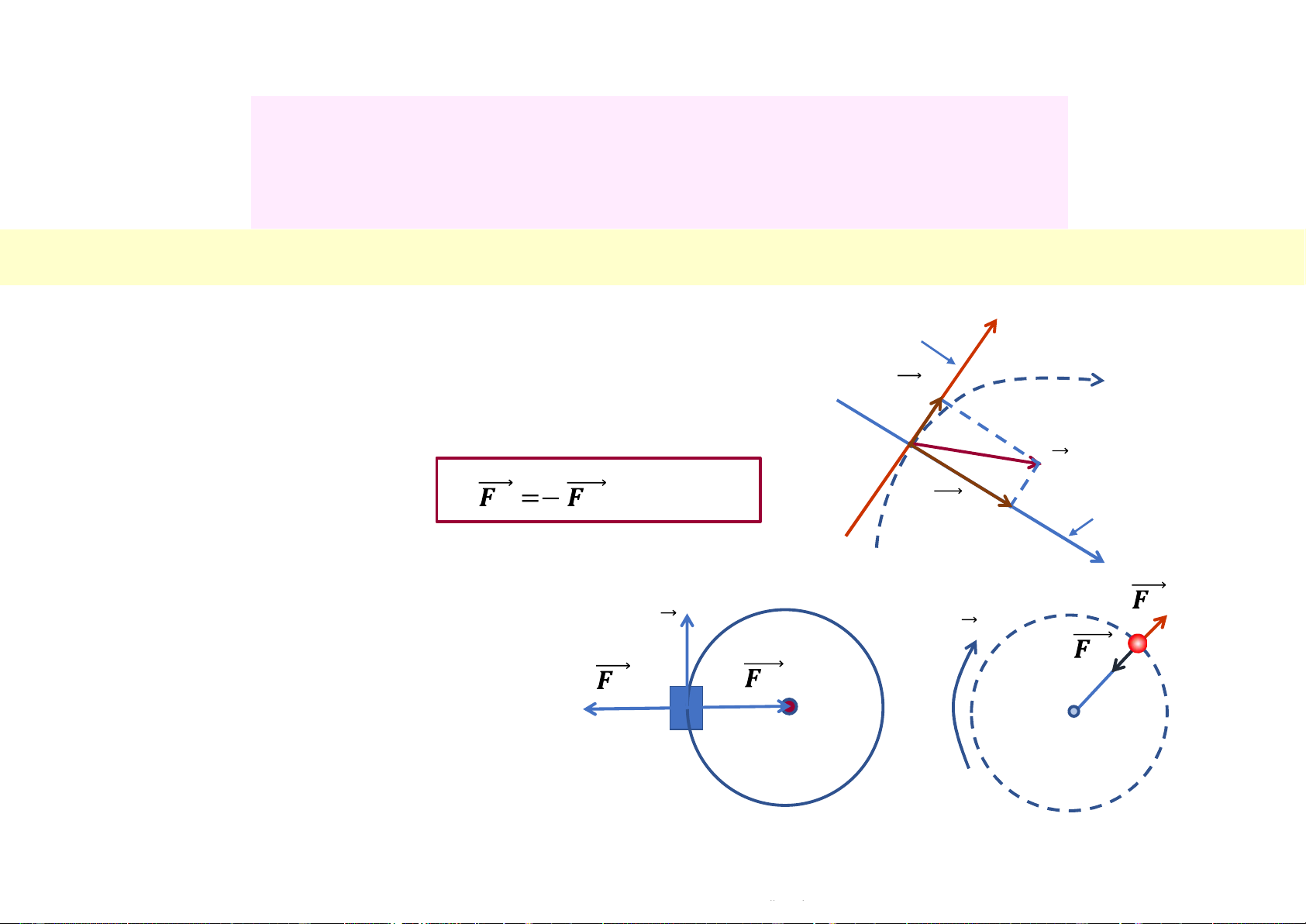
v Theo định luật III Newton, tồn tại phản lực bằng 𝒂𝒕
và ngược chiều giữ cho vật duy trì phương c.động M gọi là Lực ly tâm (F 𝒂 lt), tức là: (3.26) 𝒍𝒕 𝒉𝒕 𝒂𝒏 Vuông góc với quỹ đạo CĐ tại M
q Cặp lực liên kết này luôn tồn tại khi
vật c. động trên quỹ đạo tròn có liên 𝝊 𝒍𝒕 𝝊 𝒉𝒕
kết với vật khác (sợi dây, thanh nối, 𝒍𝒕 𝒉𝒕 mặt cong…) Sợi dây
Downloaded by v?n ti?n Lê (vantienle525@gmail.com) lOMoARcPSD|36442750 CHƯƠNG 3
ĐỘNG HỌC LỰC CHẤT ĐIỂM
3. 3. Một số lực cơ học
3.3.5 Lực quán tính và lực quán tính ly tâm
a. Hệ quy chiếu phi quán tính là hệ quy chiếu trong đó định luật Niu tơn không được nghiệm đúng
Hay Hệ quy chiếu chuyển động có gia tốc đối với hệ quy chiếu quán tính là hệ quy chiếu phi quán tính
b. Lực quán tính bản chất không phải là một lực cơ học, nó là một lực ảo, không
có nguồn gốc tương tác, chỉ quan sát được trong hệ quy chiếu phi quán tính
Downloaded by v?n ti?n Lê (vantienle525@gmail.com) lOMoARcPSD|36442750 CHƯƠNG 3
ĐỘNG HỌC LỰC CHẤT ĐIỂM
3. 3. Một số lực cơ học y y’
3.3.5 Lực quán tính và lực quán tính ly tâm
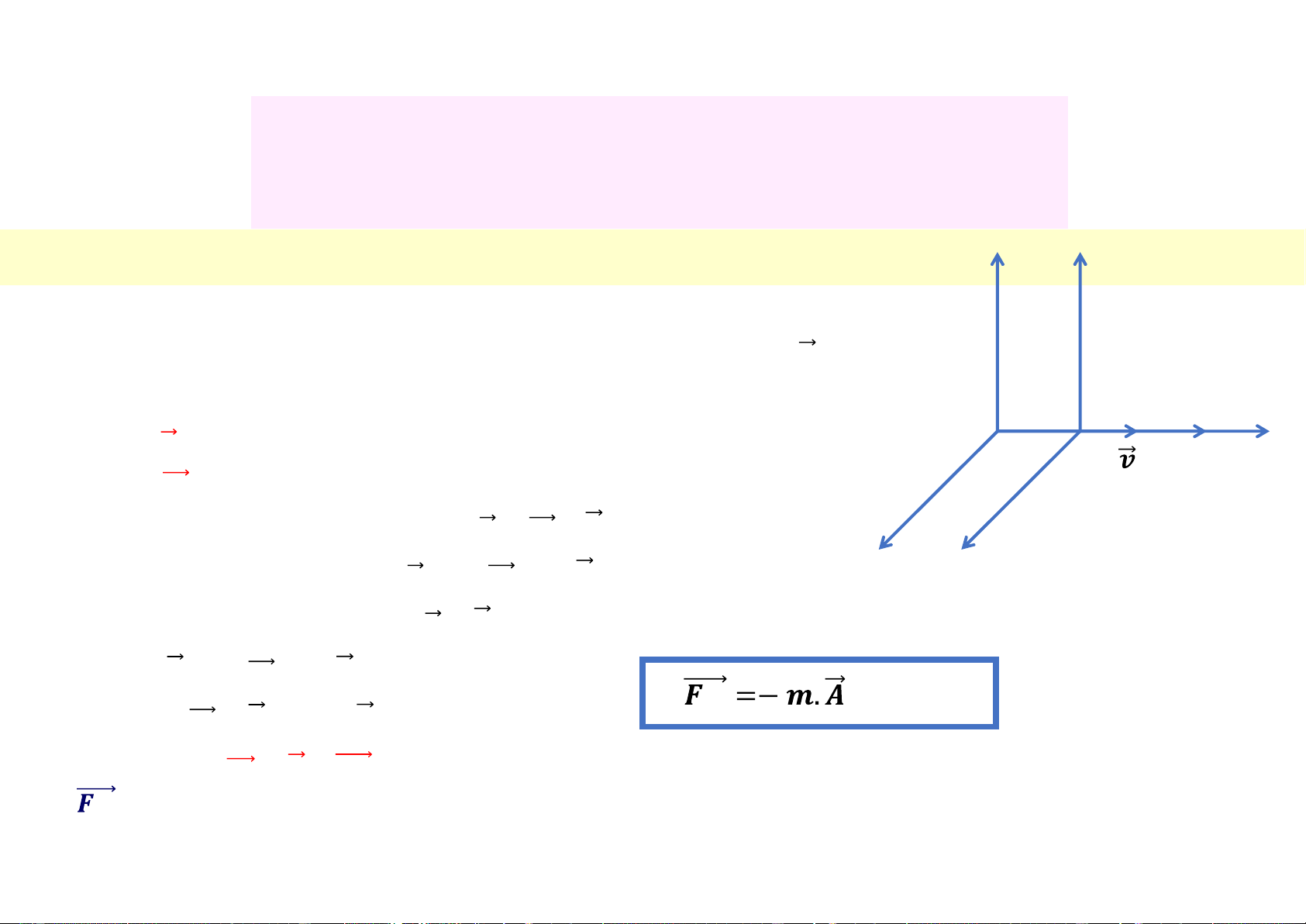
* Xét hệ quy chiếu phi quán tính O’ c.động tịnh tiến với gia tốc 𝐴 so với O (hệ quán tính) O O
+ Gọi 𝑎 là gia tốc của chuyển động c/điểm đối với hệ O, ’ x x’
𝑎 là g.tốc chuyển động của c/điểm đối với hệ phi quán tính O’.
+ Áp dụng phép tổng hợp gia tốc: 𝑎 = 𝑎 + 𝐴 (3.27) z z’
+ Nhân 2 vế với m ta có: m. 𝑎 = 𝑚. 𝑎 + 𝑚. 𝐴
+ Vì O là hệ q.tính nên có: m. 𝑎 = 𝐹
Do đó: 𝐹 = 𝑚. 𝑎 + 𝑚. 𝐴 (3.28)
Hay 𝑚. 𝑎 = 𝐹 + (−𝑚. 𝐴) (3.28’) Đặt 𝒒𝒕 (3.29)
Nên: 𝒎. 𝒂𝟏 = 𝑭 + 𝑭𝒒𝒕
𝒒𝒕 là lực quán tính (cùng phương, ngược chiều vecto gia tốc của hệ qui chiếu O’
Downloaded by v?n ti?n Lê (vantienle525@gmail.com) lOMoARcPSD|36442750 CHƯƠNG 3
ĐỘNG HỌC LỰC CHẤT ĐIỂM
3. 3. Một số lực cơ học
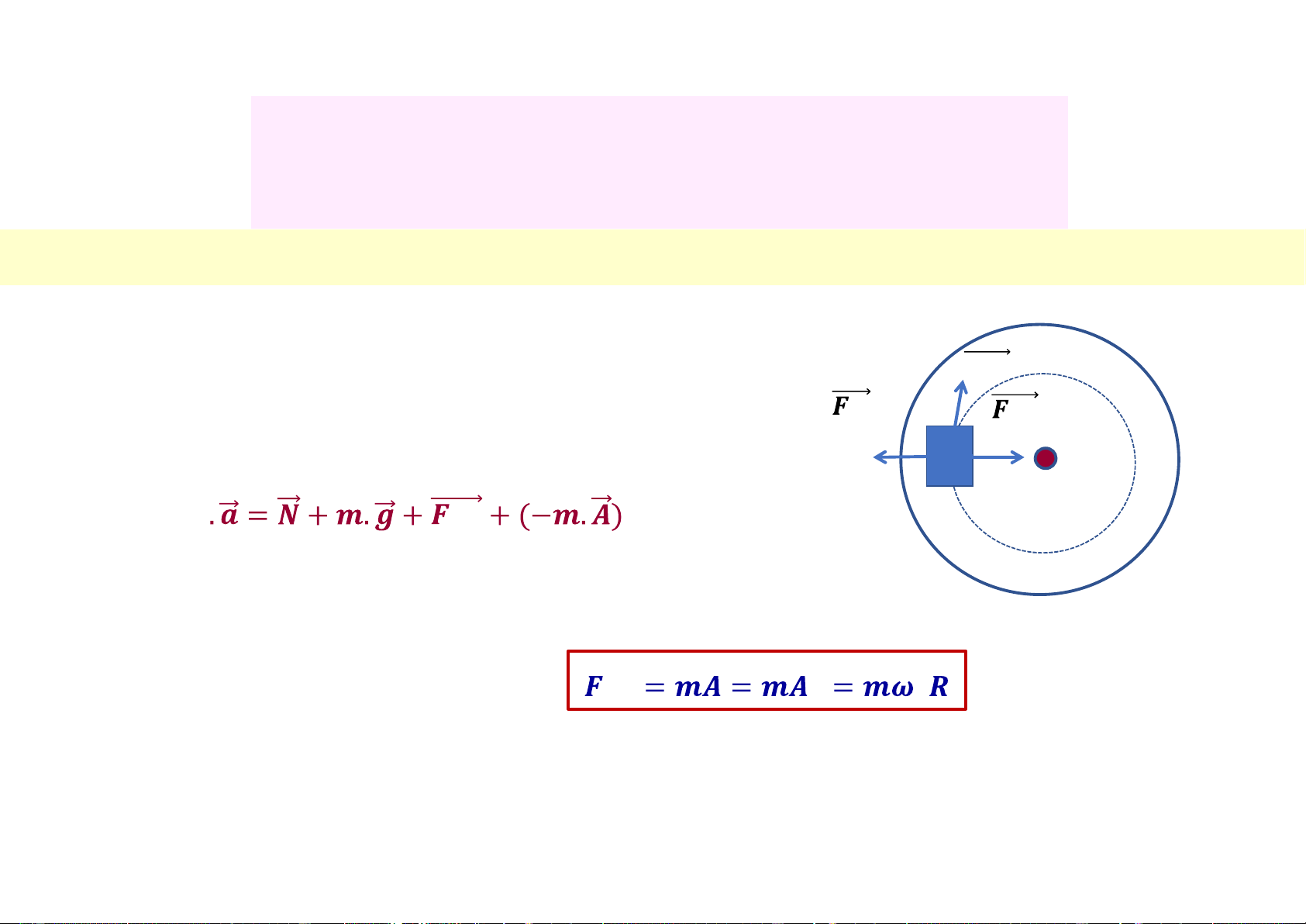
3.3.5 Lực quán tính và lực quán tính ly tâm
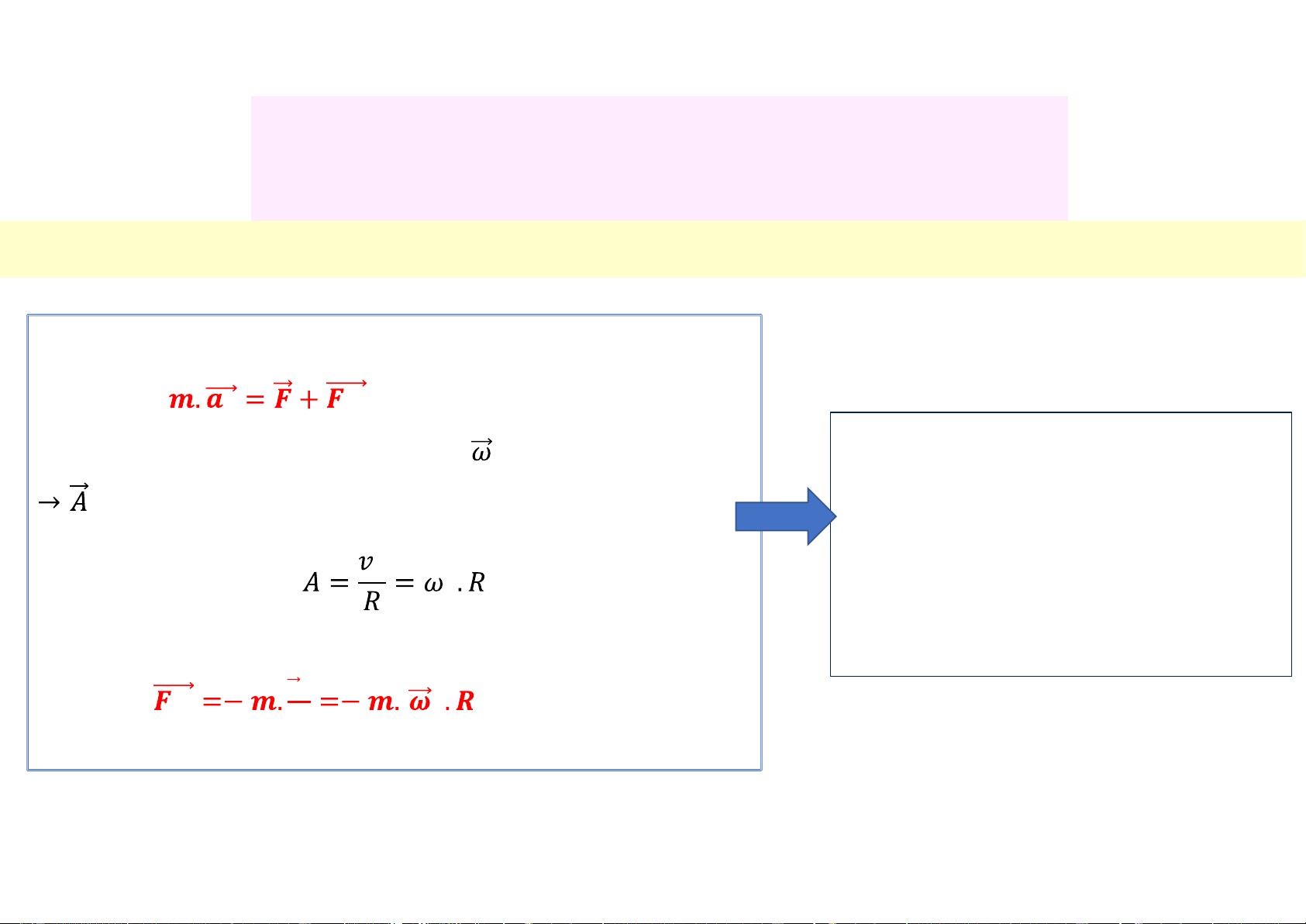
*Phương trình động lực học của chất điểm trong hệ O’: (3.30) 𝟏 𝒒𝒕
• Nếu hệ O’ quay với vận tốc góc so với O
ü Thang máy (lực căng cáp treo)
chính là gia tốc pháp tuyến, có độ lớn:
ü Lực ma sát để giữ vật trong chuyển động quay
Thay vào biểu thức tính lực quán tính
ü Lực nén lên ghế của phi công 𝒗𝟐 (3.31) 𝒒𝒕 𝟐 𝑹  Lực quán tính ly tâm
Downloaded by v?n ti?n Lê (vantienle525@gmail.com) lOMoARcPSD|36442750 CHƯƠNG 3
ĐỘNG HỌC LỰC CHẤT ĐIỂM
3. 3. Một số lực cơ học
3.3.5 Lực quán tính và lực quán tính ly tâm 𝝎đĩ𝒂
v Lực ma sát để giữ m trong chuyển động quay 𝒒𝒕 𝒎𝒔
• Phương trình ĐLH cho m: m 𝒎𝒔
• Chiếu theo chiều quay của đĩa (coi m là
không chuyển động nên a=0): 𝟐 𝒎𝒔 𝒏
Downloaded by v?n ti?n Lê (vantienle525@gmail.com) lOMoARcPSD|36442750 CHƯƠNG 3
ĐỘNG HỌC LỰC CHẤT ĐIỂM
3. 3. Một số lực cơ học
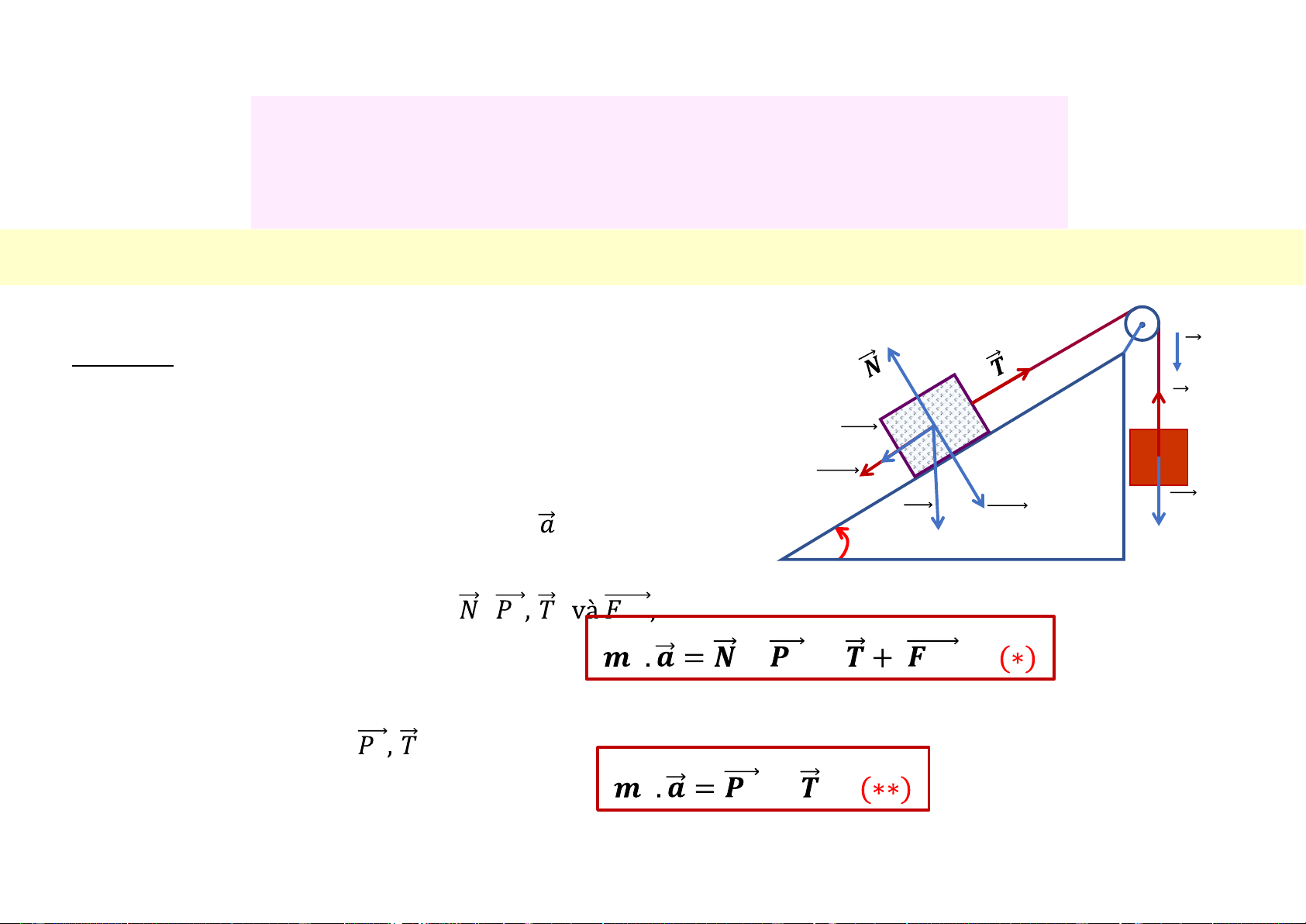
v Chuyển động trên mặt phẳng nghiêng Bài toán 𝒂
§ m1 và m2 liên kết với nhau qua sợi dây (T) m1 𝑇
§ m1 chuyển động trượt trên bề mặt nghiêng góc  𝑷𝟏𝒕 m2
§ m2 chuyển động rơi thẳng đứng 𝑭𝒎𝒔 𝑃 § m 𝑷 𝑷
1 và m2 chuyển động cùng gia tốc 𝟏 𝟏𝒏 Phân tích 
* m1 chịu tác dụng của các lực: , ,
Phương trình động lực học với m1: 𝟏 + 𝟏 + 𝒎𝒔 * m2 chịu tác dụng của
Phương trình động lực học với m2: 𝟐 𝟐 +
Downloaded by v?n ti?n Lê (vantienle525@gmail.com) lOMoARcPSD|36442750 CHƯƠNG 3
ĐỘNG HỌC LỰC CHẤT ĐIỂM
3. 3. Một số lực cơ học
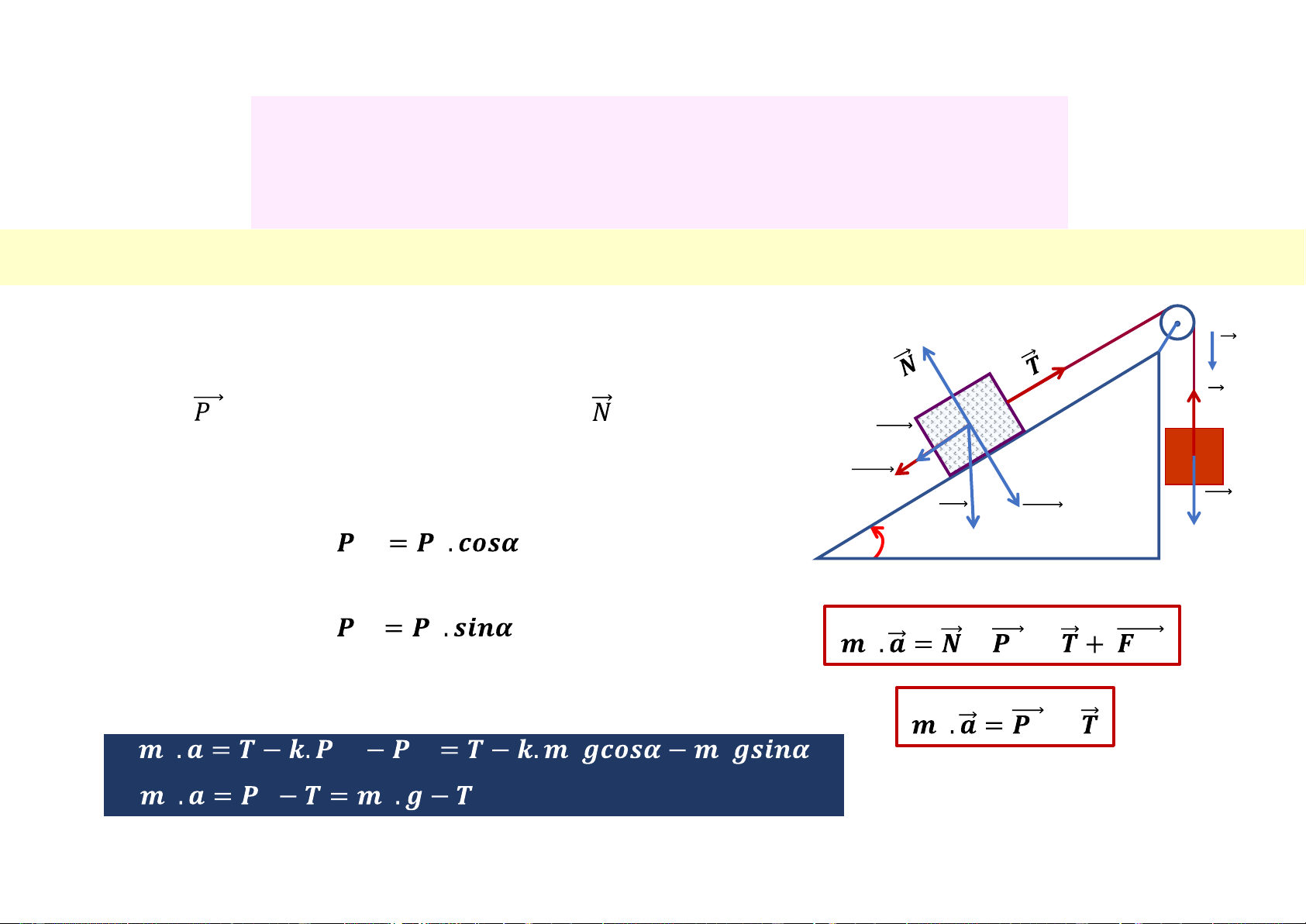
v Chuyển động trên mặt phẳng nghiêng 𝒂 Đặc điểm riêng m
§ Trọng lực hợp với phương của phản lực góc  được 1 𝑇
phân tích thành 2 thành phần: 𝑷𝟏𝒕 m2 𝑭
ü Thành phần  với bề mặt nghiêng = trọng lực pháp 𝒎𝒔 𝑷 𝑃 𝑷 tuyển 𝟏 𝟏𝒏 𝟏𝒏 𝟏 
ü Thành phần // với bề mặt nghiêng = trọng lực tiếp tuyển 𝟏𝒕 𝟏 (∗) 𝟏 + 𝟏 + 𝒎𝒔 Phương pháp giải
• Chiếu các phương trình (*) và (**) lên phương chuyển động, có: (∗∗) 𝟐 𝟐 + 𝟏 𝟏𝒏 𝟏𝒕 𝟏 𝟏 𝟐 𝟐 𝟐
Downloaded by v?n ti?n Lê (vantienle525@gmail.com) lOMoARcPSD|36442750 CHƯƠNG 3
ĐỘNG HỌC LỰC CHẤT ĐIỂM
3. 4. Động lượng của chất điểm
3.4.1. Các định lý về động lượng 
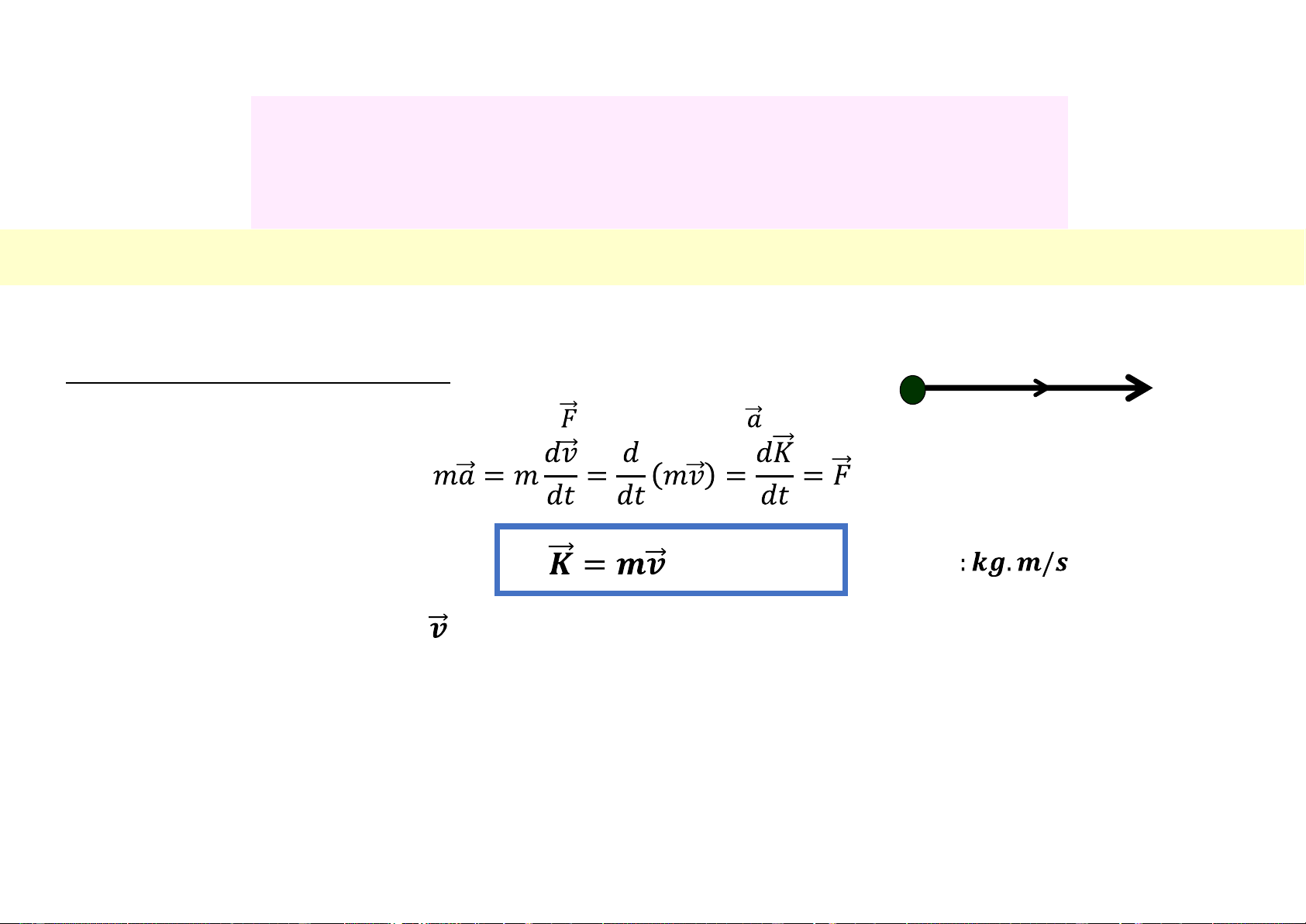
a. Định nghĩa về động lượng m v K
* Xét chất điểm m chịu tác dụng của lực và có gia tốc
Theo định luật II Newton:
Véc tơ động lượng của chất điểm (3.32) Đơn vị + Cùng hướng với
+ Độ lớn phụ thuộc vào cả vận tốc và khối lượng
ØĐặc trưng cho trạng thái chuyển động của vật thể về mặt động lực học
Downloaded by v?n ti?n Lê (vantienle525@gmail.com) lOMoARcPSD|36442750 CHƯƠNG 3
ĐỘNG HỌC LỰC CHẤT ĐIỂM
3. 4. Động lượng của chất điểm
3.4.1. Các định lý về động lượng
Ví dụ về vận tốc liên quan đến khối lượng:
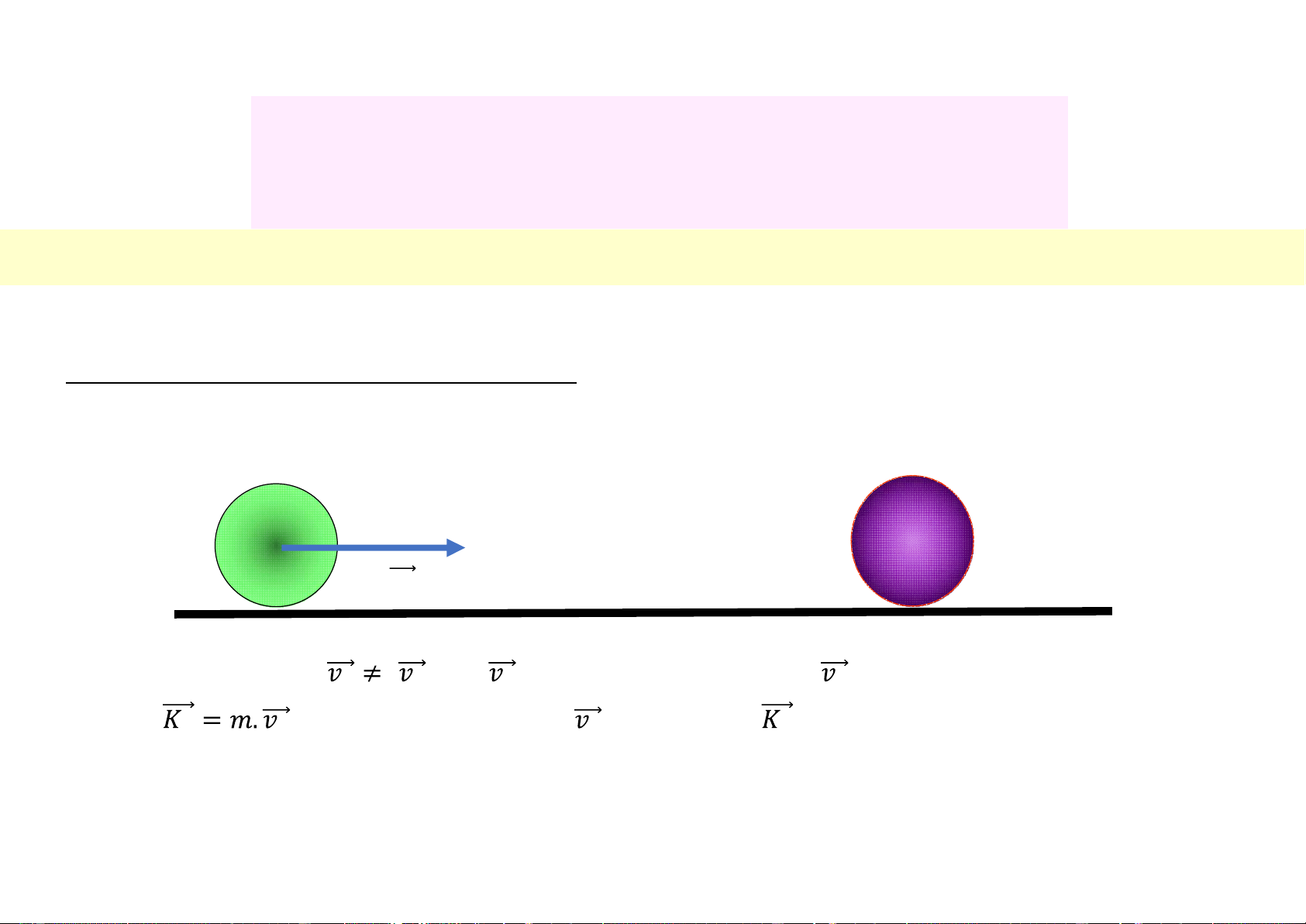
Giả sử quả cầu 1 có khối lượng m1, c.động với vận tốc v1 đến đập vào quả cầu 2 có k.lượng m2
đang đứng yên. Sau va chạm quả cầu 2 c.động với vận tốc v2. m1 m2 𝒗𝟏 Thực nghiệm chứng tỏ:
và : không những phụ thuộc mà còn phụ thuộc m1 hay phụ thuộc vào
của quả cầu 1. Cụ thể càng lớn khi càng lớn.
Ø Trong hiện tượng va chạm động lượng là một đại lượng đặc trưng cho khả năng truyền chuyển động
Downloaded by v?n ti?n Lê (vantienle525@gmail.com) lOMoARcPSD|36442750 CHƯƠNG 3
ĐỘNG HỌC LỰC CHẤT ĐIỂM
3. 4. Động lượng của chất điểm
b. Các định lý về động lượng  vĐịnh lý 1 m v K
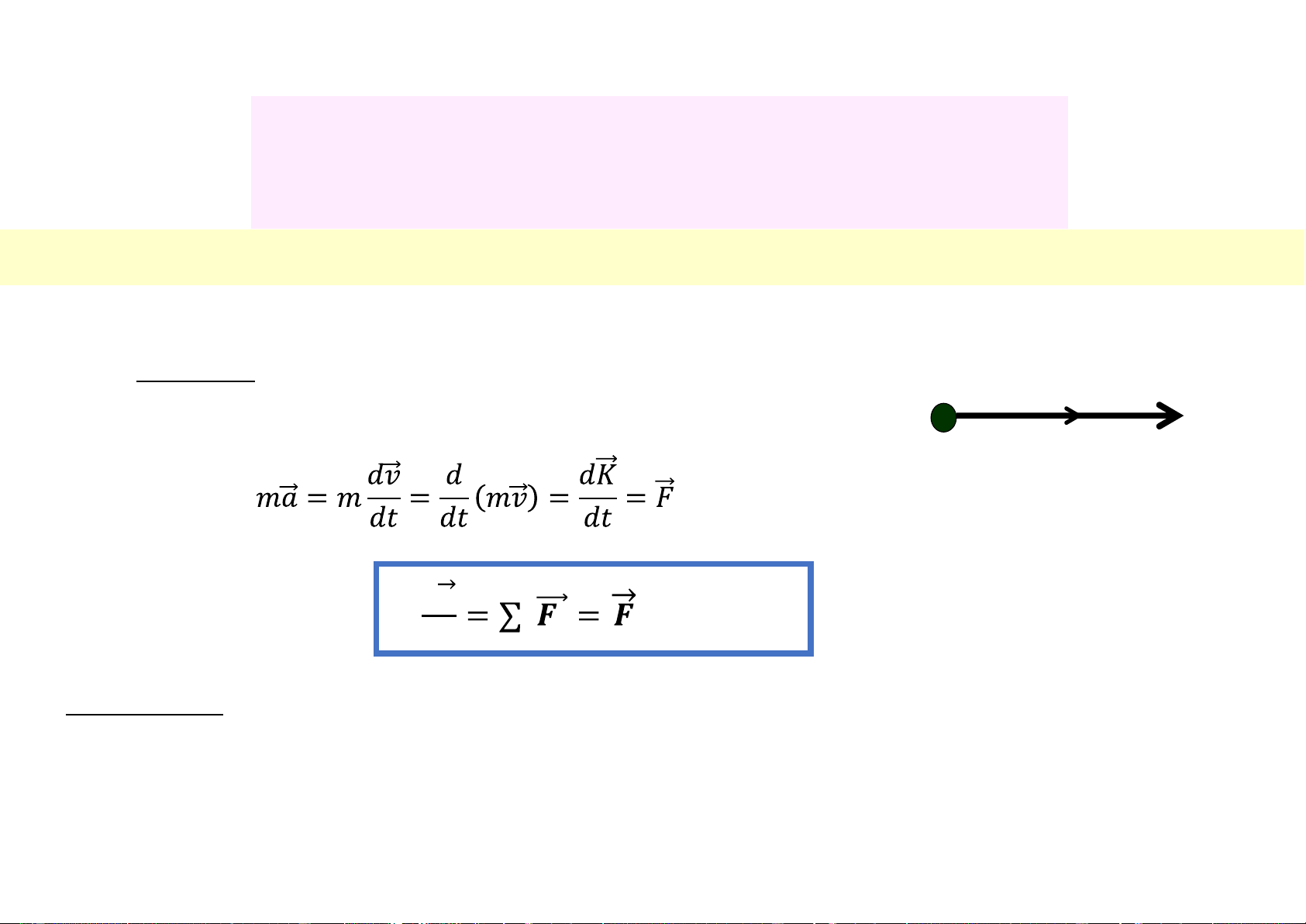
+ Từ PT định luật 2 Niu tơn 𝒅𝑲 𝒅𝒕 𝒊 𝒊 (3.33) Biểu thức
Phát biểu: Đạo hàm theo thời gian của vecto động lượng chất điểm chuyển động
có giá trị bằng tổng hợp các ngoại lực tác dụng lên chất điểm đó.
Downloaded by v?n ti?n Lê (vantienle525@gmail.com) lOMoARcPSD|36442750 CHƯƠNG 3
ĐỘNG HỌC LỰC CHẤT ĐIỂM
3. 4. Động lượng của chất điểm
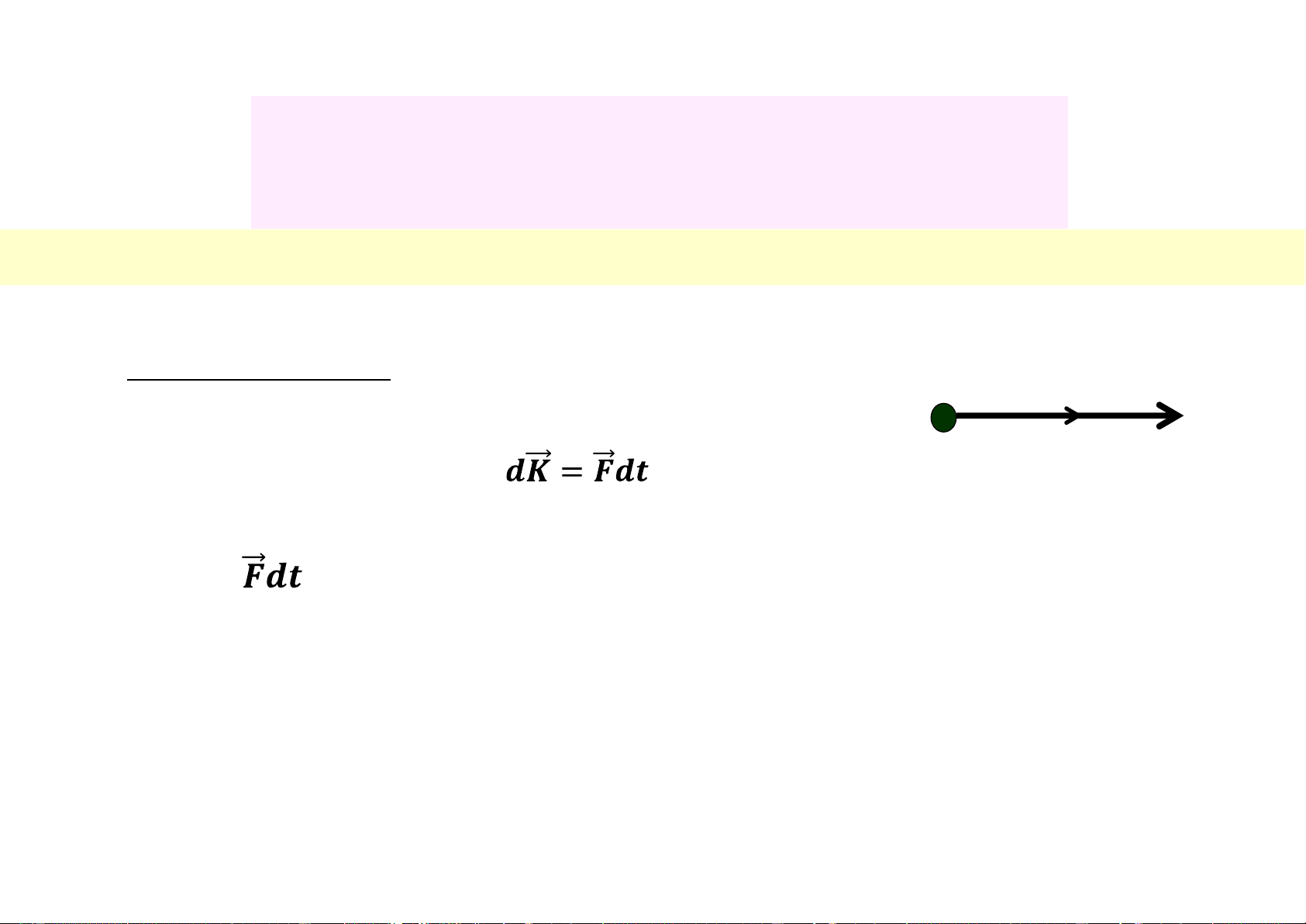
b. Các định lý về động lượng  vXung lượng của lực m v K Từ định lý 1 có: (3.34) Trong đó:
là véc tơ xung lượng của lực tác dụng lên chất điểm trong
khoảng thời gian vô cùng nhỏ dt.
Downloaded by v?n ti?n Lê (vantienle525@gmail.com) lOMoARcPSD|36442750 CHƯƠNG 3
ĐỘNG HỌC LỰC CHẤT ĐIỂM
3. 4. Động lượng của chất điểm
3.4.1. Các định lý về động lượng  m v K Từ định lý 1 có: 𝒅𝑲 = 𝑭𝒅𝒕
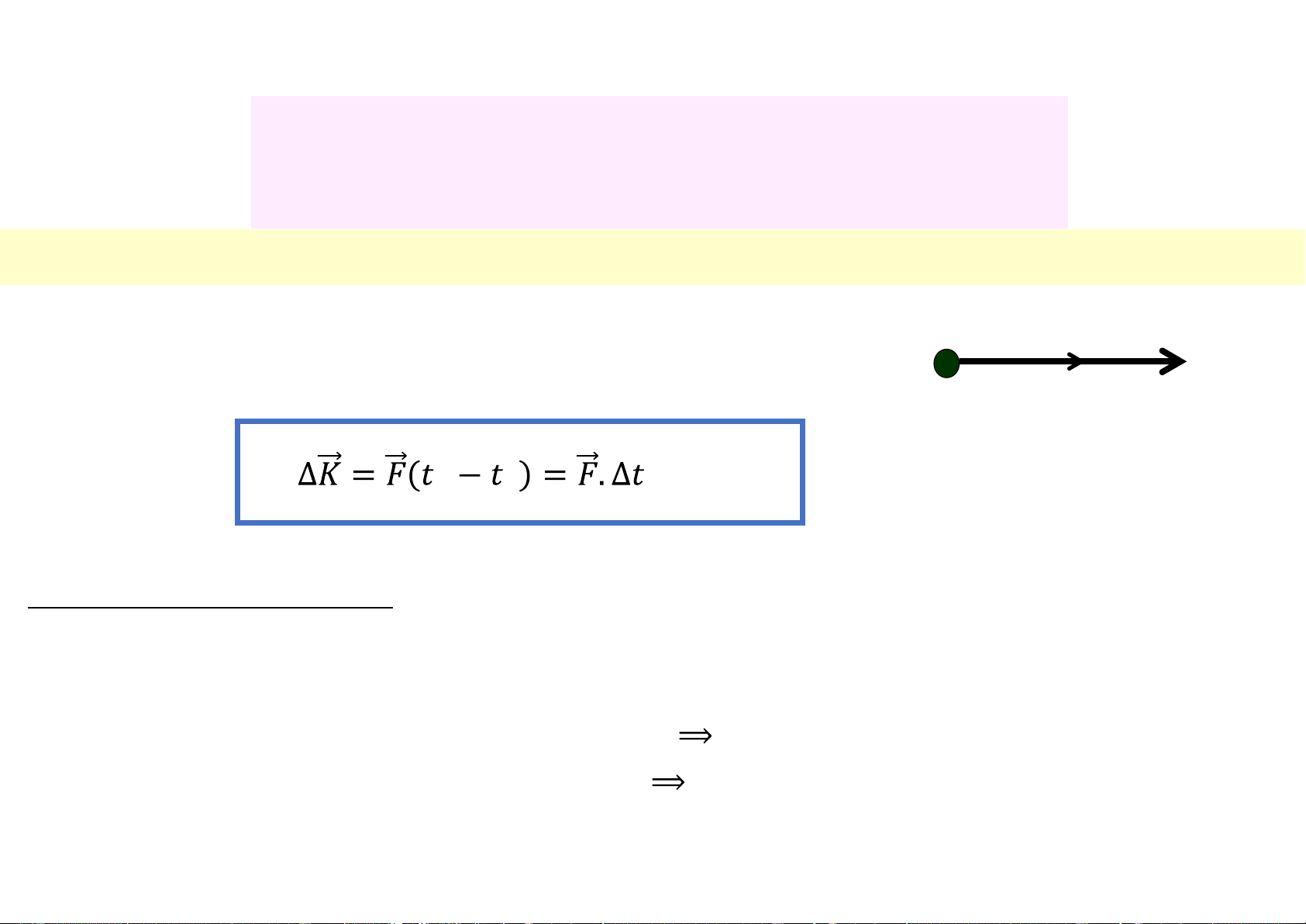
+ Nếu thay đổi trong khoảng thời gian từ t1 đến t2, có: 𝑲𝟐 𝒕𝟐 𝒕𝟐 𝟐 𝟏 𝑲 𝒕 𝒕 𝟏 𝟏 𝟏 + Nếu (3.36)
Ø Phát biểu: Độ biến thiên vectơ động lượng của 1 chất điểm chuyển động trong một khoảng
thời gian xác định, có giá trị bằng xung lượng của lực (hay tổng hợp lực) tác dụng lên chất
điểm trong khoảng thời gian đó.
Downloaded by v?n ti?n Lê (vantienle525@gmail.com) lOMoARcPSD|36442750 CHƯƠNG 3
ĐỘNG HỌC LỰC CHẤT ĐIỂM
3. 4. Động lượng của chất điểm
3.4.1. Các định lý về động lượng  m v K (3.36) Ý nghĩa của xung lượng:
* Xung lượng của lực trong khoảng thời gian đặc trưng cho lực tác dụng trong khoảng thời gian đó.
* Với cùng một lực, thời gian tác động lâu động lượng biến thiên nhiều
Ngược lại, nếu thời gian tác dụng ngắn động lượng biến thiên ít dù lực lớn.
Downloaded by v?n ti?n Lê (vantienle525@gmail.com)