Bài giảng phần cơ học | Môn Vật lý kỹ thuật - Đại học Xây Dựng Hà Nội

lOMoAR cPSD| 59054137 PHẦN I CƠ HỌC ĐỘNG HỌC
ĐỘNG LỰC HỌC CHẤT ĐIỂM
CÔNG SUẤT VÀ NĂNG LƯỢNG TRONG HỆ QUI CHIẾU GALILEO
HỆ CHẤT ĐIỂM. VẬT RẮN TRƯỜNG HẤP DẪN CHƯƠNG 1. ĐỘNG HỌC
1.1. CHUYỂN ĐỘNG CỦA MỘT ĐIỂM
1.1.1. Chuyển động cơ
Chuyển động cơ là sự thay đổi vị trí của vật này đối với vật khác hoặc của phần này đối với
phần khác của cùng một vật.
Chuyển động cơ là đối tượng nghiên cứu của môn cơ học. Trong cơ học, phần nghiên cứu
tính chất chuyển động mà không xét đến các nguyên nhân gây ra các chuyển động đ được gọi
là Động học. Như vậy, động học chỉ nghiên cứu những tính chất hình học của chuyển động, tức là sự
thay đổi vị trí tương đối của các vật.
Chuyển động cơ có mặt khắp nơi xung quanh chúng ta: Người đi bộ, chuyển động của đu
quay,… Tuy nhiên, chuyển động hay đứng yên là một khái niệm có tính tương đối. Ví dụ: Đối
với người quan sát đứng trên mặt đất, ngôi nhà bên đường đứng yên, còn đối với người ngồi
trên chiếc xe máy chạy qua, ng i nh chuyển động về phía sau người đó...
Như vậy, một vật chuyển động theo những cách khÆc nhau đối với hai người quan sát
chuyển động tương đối với nhau. Do đó, các đại lượng động học có t nh tương đối, phụ thuộc vào người quan sát.
Trong cơ học cổ điển, thời gian trôi qua như nhau với mọi người quan sát. Khoảng thời
gian giữa hai biến cố không phụ thuộc vào người quan sát. Như vậy, thời gian có tính tuyệt lOMoAR cPSD| 59054137
đối. Để xác định thời gian, ta thường chọn một thời điểm gốc và một đơn vị đo. Khi đó, mọi
thời điểm được xác định bởi một số thực t biểu diễn số đơn vị thời gian đã trôi qua kể từ thời điểm gốc.
1.1.2. Hệ qui chiếu
Từ phần trên ta thấy, chuyển động có tính tương đối. Vì vậy, khi xét chuyển động của một
điểm ta cần xác định rõ điểm ấy chuyển động so với những vật nào mà ta chọn làm mốc.
Một tập hợp các điểm cố định đối với người quan sát và một đồng hồ tạo thành hệ qui chiếu của người quan sát đó.
Khi khảo sát chuyển động ta có thể chọn các hệ qui chiếu khác nhau, và chuyển động sẽ được
mô tả theo những cách khÆc nhau trong các hệ qui chiếu đó.
Ví dụ: Xét chuyển động của điểm M trŒn v nh bÆnh xe đạp đang chạy. Nếu ta chọn hệ
qui chiếu l xe th M thực hiện một chuyển động tròn; nếu chọn hệ qui chiếu là mặt đường thì
chuyển động của M là tổng hợp của hai chuyển động: Chuyển động tròn đối với xe và chuyển
động của xe đối với mặt đường.
1.1.3. Hệ tọa độ
1.1.3.1. Véctơ vị trí u 3
Trong không gian ba chiều của hình học Euclide, để xác định vị
trí của một điểm, ta chọn điểm O tuỳ ý làm gốc, khi đó vị trí của một M
điểm M sẽ được xác định bởi véctơ vị trí (H nh 1.01) r 3 e O 2 e u r OM. 2 1 e
1.1.3.2. Cơ sở véctơ u1
Trong vật lý, ta dùng các cơ sở véctơ trực chuẩn thuận. Đó là
H nh 1.01. Véctơ vị trí.
một tập hợp ba véctơ đơn vị e1 , e2 , e3 vuông góc với nhau từng đôi một sao cho:
e3 e1 e2 hay e2 e3 e1 hay e1 e2 e .3 1 e cái trỏ giữa 2 e
H nh 1.02 mô tả cách xác định cơ sở véctơ trực chuẩn thuận bằng 3 e
các ngón tay của bàn tay phải. cái trỏ 2 e giữa 3 e Nếu cơ sở B e ,e ,e1 2 3
được xác định thì véctơ u sẽ được phân 1 e
tích trong cơ sở đó một cách duy nhất: u u e1 1 u e2 2 u e .3 3 Ba số thực u ,u ,u1 2 3
là các thành phần của véctơ u trong cơ
H nh 1.02. Cơ sở véctơ lOMoAR cPSD| 59054137 sở B . trực chuẩn.
1.1.3.3. Góc ở trong một mặt phẳng
Phép đo góc trên một mặt phẳng P trong không gian phụ thuộc vào chiều dương qui ước.
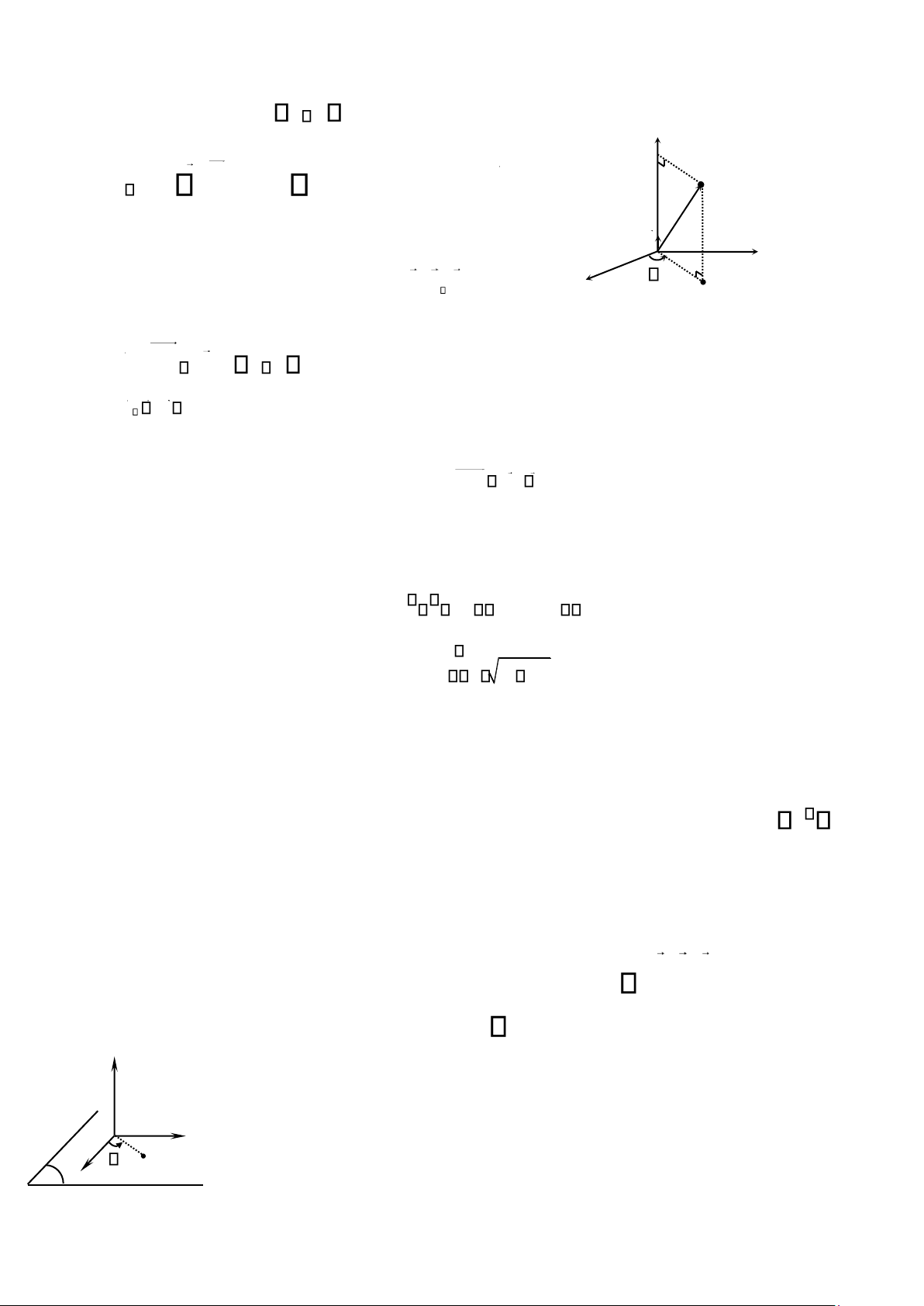
Trong mọi lĩnh vực của vật lý, người ta qui ước chiều dương được xác định bởi pháp tuyến n
của mặt phẳng như sau: một chiếc vặn nút chai thông thường, khi tiến theo chiều n , sẽ quay
theo chiều dương (hình 1.03). Theo đó, trŒn h nh 1.03 g c
1 có giá trị dương và góc 2 có giá trị âm,
không phụ thuộc vào việc ta nhìn các góc đó từ phía trên hay từ phía H nh 1.03. Sự định hướng
dưới của mặt phẳng.
góc trên mặt phẳng n + 1 2
1.1.3.4. Hệ tọa độ P
Một hệ tọa độ trong không gian O; e ,e ,e1 2 3 được xác định bởi điểm gốc O và một cơ
sở véctơ trực chuẩn thuận B e ,e ,e1 2 3 . Khi đã xác định được một hệ tọa độ thì chỉ cần ba
tọa độ là đủ để xác định vị trí của một điểm và ngược lại vị trí một điểm trong không gian xác
định một tập hợp của ba tọa độ.
Có nhiều qui ước để xác định chính xác vị trí của một điểm bằng ba số thực.
Dưới đây chúng ta sẽ xét một số hệ tọa độ thường dùng trong cơ học cũng như trong vật l n i chung. z
Tọa độ Descartes z
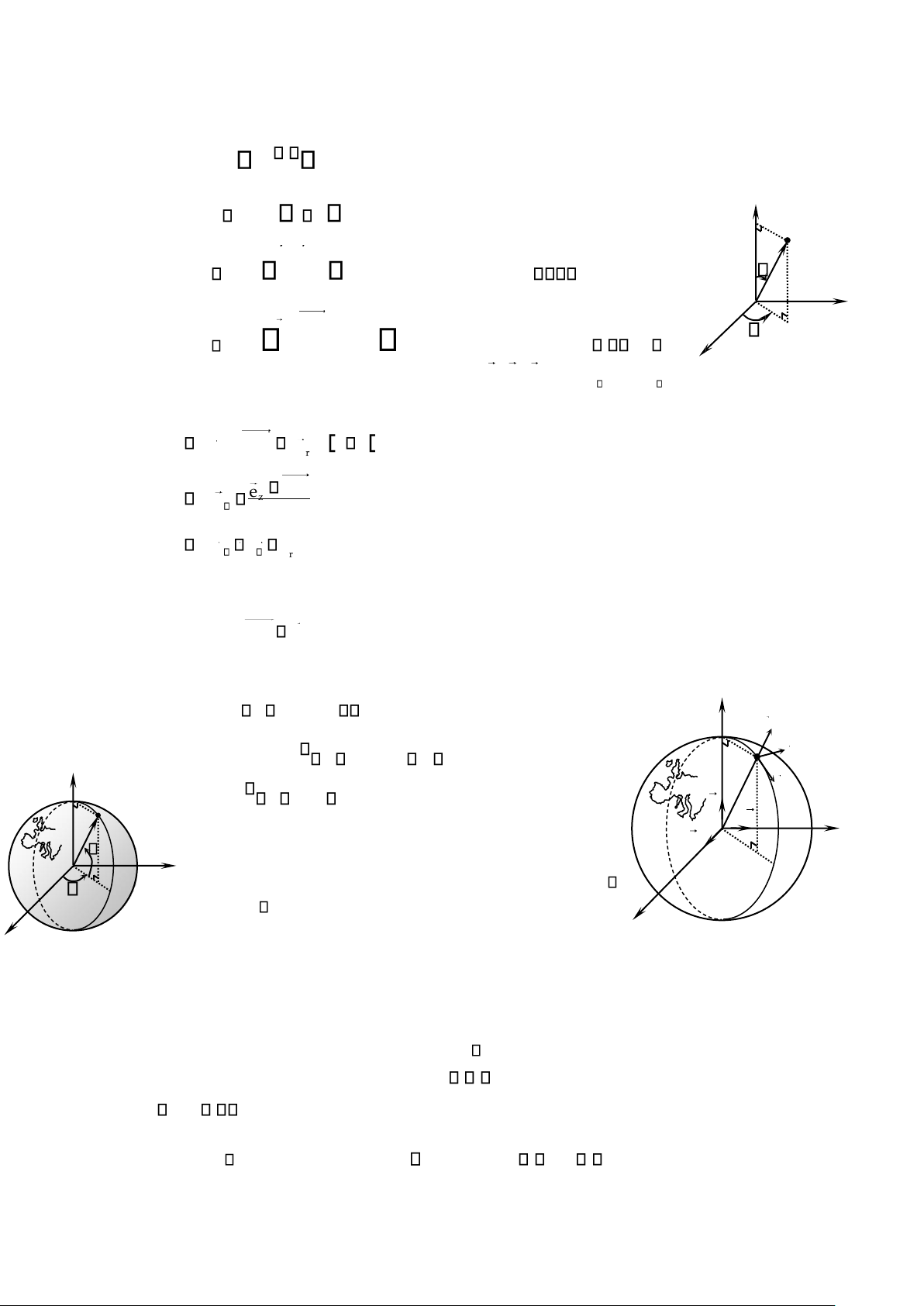
Hệ tọa độ Descartes Oxyz là hệ tọa độ trực chuẩn thuận được M ez r
xÆc định bởi điểm gốc O và một cơ sở trực chuẩn thuận O; e ,e ,ex y O e e y y z (h nh 1.04). x
Các tọa độ Descartes (x, y, z) của điểm M l cÆc th nh phần y H
của véctơ vị trí: x r OM xe x yey ze .z x
H nh 1.04. Tọa độ Descartes
Tọa độ trụ
Cho một hệ tọa độ Descartes O; e ,e ,ex y z
. Gọi H là hình chiếu vuông góc của M lŒn mặt
phẳng (Oxy) (h nh 1.05). Vị trí của điểm M được xác định bởi các tọa độ trụ r, ,z : lOMoAR cPSD| 59054137 •
r : khoảng cách OH r 0 ; z M • : g c e ,OHx
, chiều dương được xác định bởi ez ; e • z
z : tọa độ Descartes thứ ba. O z r y
Các véctơ đơn vị trong hệ tọa độ trụ là e ,e ,er z được xác định x H như sau:
Hnh 1.05. Tọa độ trụ • er : OH rer r 0 ; • e e z e .r
Như vậy, một điểm M trong tọa độ trụ được xác định bởi véctơ vị tr : OM re r ze .z
Mối liên hệ giữa toạ độ trụ và toạ độ Descartes xy rcosrsin 2 r x y2
Tọa độ cực
Khi điểm M chuyển động trong một mặt phẳng P chỉ cần hai
tọa độ để xác định vị trí của nó. Trong mặt phẳng (Oxy), ta có thể
sử dụng các tọa độ Descartes (x,y) hay các tọa độ cực r, . C
thể coi tọa độ cực là trường hợp riêng của tọa độ trụ khi z = 0 (h nh 1.06).
Tọa độ cầu
Cho một hệ toạ độ Descartes O, e ,e ,ex y z , một điểm M v z O r y x P M lOMoAR cPSD| 59054137
H nh 1.06. Tọa độ cực
hình chiếu H của nó lên mặt phẳng (Oxy) (h nh 1.07). Vị trí của điểm M được xác định bởi các tọa độ cầu r, , với : • r OM r 0 ; z M • : g c e ,e z r
có giá trị trong khoảng 0 ; O y • H : g c e ,OHx
có giá trị trong khoảng 0 2 .
Các véctơ đơn vị trong hệ tọa độ cầu là e ,e ,er được xác định như sau: x e OM re r : r r 0 ; ez OH e ; OH e e r e.
H nh 1.07. Tọa độ cầu
Như vậy, một điểm M trong tọa độ cầu được xác định bởi véctơ vị trí: OM re .r
Mối liên hệ giữa toạ độ cầu và Descartes x rsin cos z ez e y rsin sin y Pa z ex z rcos ez M e O y
Các tọa độ địa lí (vĩ độ và kinh độ) e y x H y
Vị trí địa lí của một điểm được xác định bởi kinh độ H
và vĩ độ . Các toạ độ này được suy ra từ các tọa độ cầu x
• (Oz): trục cực Nam - cực Bắc; x
• (Ox): trục cắt xích đạo và kinh tuyến Greenwich.
H nh 1.08. Tọa độ địa lí.
(hình 1.08). Hai trong số ba trục của hệ toạ độ địa lí l :
Khi đó kinh độ của một điểm là tọa độ có giá trị trong khoảng -180o v 180o. Người ta
còn phân biệt kinh độ Đ ng khi 00 1800 v kinh độ T y khi 1800 0 .0
Vĩ độ liên hệ với toạ độ cầu bởi hệ thức 900 . Người ta cũng phân biệt vĩ độ Bắc khi lOMoAR cPSD| 59054137 00
900 v vĩ độ Nam khi 900 0 .0 Ví dụ:
• H Nội có vị trí trong khoảng từ 20 25’ đến 21 23’ vĩ Bắc, 105 15’ đến 106 03’ kinh
Đông. H nh 1.09. Thí dụ về các hệ tọa độ
gắn vào mặt đất.
• Vệ tinh địa tĩnh VINASAT-I quay trong mặt
phẳng xích đạo (vĩ độ = 0 ) ở độ cao 35768 km và = 132 kinh Đông. Nhận xét:
Tồn tại vô số các hệ tọa độ gắn vào một hệ qui chiếu cho trước của người quan sát.
Thí dụ: Ta thường sử dụng hệ qui chiếu Trái Đất, kí hiệu là RT gắn vào mặt đất mà ta
giả định là cứng. Trong vô số các hệ tọa độ, ta có thể sử dụng hai hệ tọa độ Descartes
R1 v R2 đều gắn với RT (h nh 1.09) như sau: O :t©mTr¸i§Êt 1 x y z R O, e ,e ,e Oz : trôccùc Nam- cùc B¾c
Ox : trôc ®i qua giao ®iÓm cña ®-êng xÝch ®¹o víi kinh tuyÕn Greenwich
P :®iÓm g¾n vµo mÆt ®Êt 2 x y z
ez :h-íng theo b¸n kÝnh Tr¸i §Êt ®i qua P R P, e ,e ,e ex :h-íng vÒ phÝa Nam ey :h-íng vÒ phÝa §«ng
1.1.4. Quĩ đạo v phương trình chuyển động của một điểm
Cho R là một hệ qui chiếu và M là một động điểm, thì ở mỗi thời điểm luôn tồn tại một
điểm cố định của R có vị trí trùng với M. Điểm đó gọi là điểm trùng hợp, kí hiệu l MR . Tập hợp
các điểm trùng hợp đó trong R tạo thành một đường liên tục gọi là quĩ đạo của M. Quĩ đạo có
tính tương đối, phụ thuộc vào hệ qui chiếu.
Khi M chuyển động, véctơ vị trí của nó biến thiên theo thời gian, tức là: r r(t)
Phương trình này được gọi là phương trình chuyển động của điểm M. lOMoAR cPSD| 59054137 1.2. TOẠ ĐỘ CONG
1.2.1. Phép tính đạo hàm của một véctơ
1.2.1.1. Định nghĩa Cho U
là một đại lượng véctơ phụ thuộc vào biến số . Khi đó, đạo hàm của U đối
với được định nghĩa là: dU limU U . (1.01) d 0
Chœ : Đạo hàm của một đại lượng véctơ phụ thuộc hệ qui chiếu.
1.2.1.2. T nh chất Cho U , W , V
là các đại lượng véctơ phụ thuộc vào biến số v
là một đại lượng vô hướng phụ thuộc vào . Khi đó, từ định nghĩa của đạo hàm một véctơ
ta suy ra các tính chất sau: • Nếu W .U th (1.02) dW d dU U . d d d • Nếu W U V th (1.03) dW dU dV . d d d • Nếu W U .V dW dU dV th (1.04) V U . d d d • Nếu W U V th V U dW dU dV. (1.05) d d d
1.2.1.3. Đạo hàm của một véctơ có độ dài không đổi Cho U
là một véctơ có độ dài không đổi nhưng hướng của U có thể thay đổi. M’ d U Vì tích vô hướng U 2
U2 là một hằng số nên ta có: U d M U O dU2 d U.U 0. lOMoAR cPSD| 59054137 d d Mặt khác: 2 dU dU U dU U 2 dU U. d d d d
H nh 1.10. Đạo hàm của một
véctơ có độ dài không đổi.
Vậy, kết hợp hai kết quả trên ta được: dU 0, tức là dU U. (1.06) U d d
Kết luận: Đạo hàm của một véctơ có độ dài không đổi là một véctơ trực giao với véctơ đó (h nh 1.10).
1.2.1.4. Đạo hàm của đại lượng véctơ trong tọa độ Descartes
Trong hệ tọa độ Descartes, hàm véctơ U
được biểu diễn như sau: U U ex x U ey y U e .z z V e ,e ,ex y
z đều không đổi trong R nŒn:
dU dUx ex dUy ey dUz e .z (1.07) d d d d
1.2.2. Hoành độ cong ( ) M’ +
Cho một đường cong C cố định trong hệ qui chiếu R ; chọn
điểm A thuộc C làm gốc và một chiều dương (h nh 1.11). Khi
đó, vị trí của một điểm M thuộc C có thể xác định bằng một số M
thực s duy nhất với: A ( M ) •
s là độ dài của cung AM ; H nh 1.11. Hoành độ cong. •
s > 0 nếu sự chuyển dời từ A đến M tiến hành theo chiều dương và s < 0 trong trường hợp ngược lại.
Hoành độ cong của điểm M trên C bằng số đo đại số của cung AM . lOMoAR cPSD| 59054137
1.2.3. Véctơ đơn vị tiếp tuyến
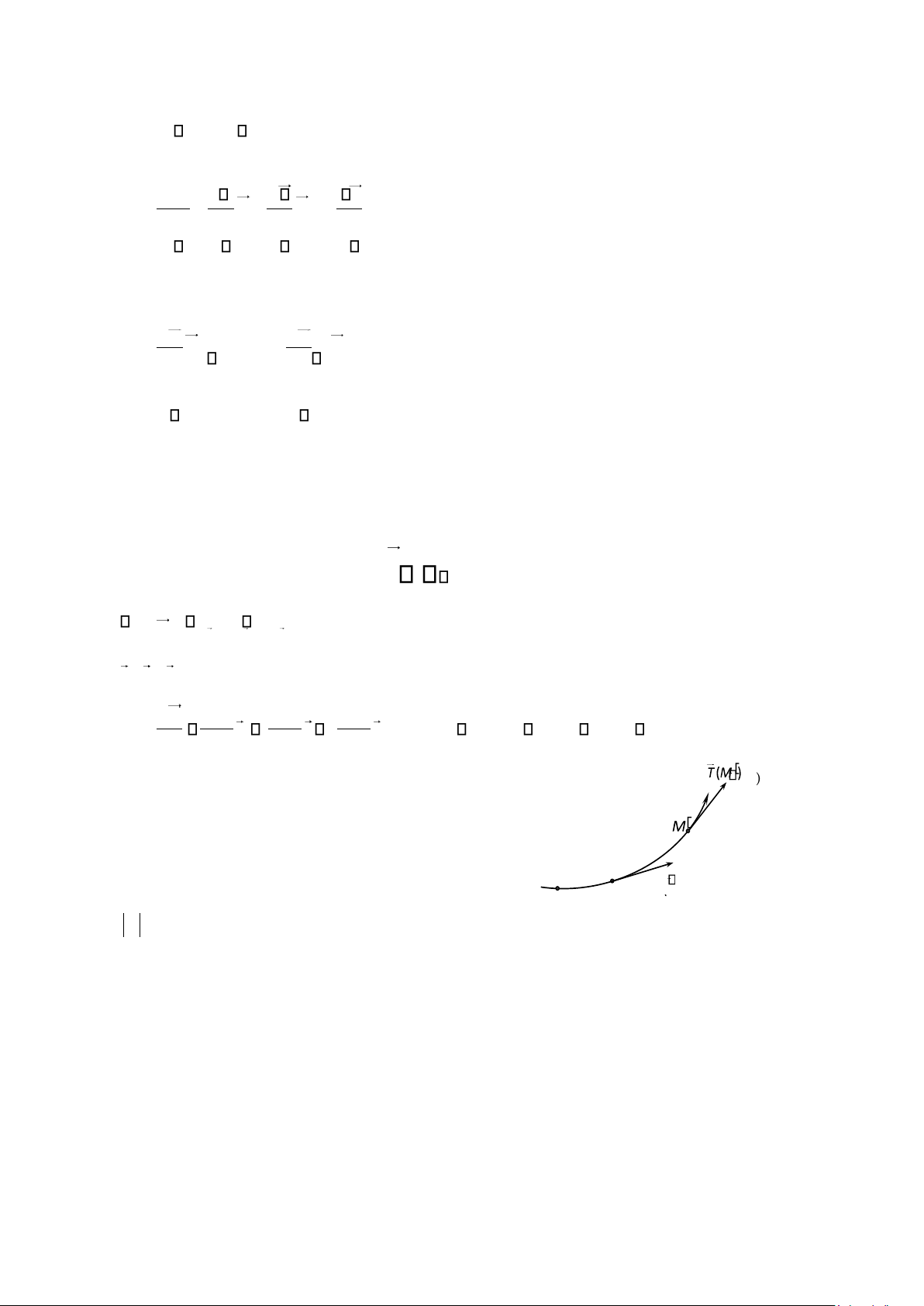
Véctơ có độ dài đơn vị, tiếp tuyến với C và luôn định hướng theo
chiều dương qui ước (hình 1.12), gọi là véctơ đơn vị tiếp tuyến, kí hiệu là . M ’
Xét một điểm O cố định trong R . Khi đó: O •
dOM OM’ OM gọi là véctơ độ dời nguyên tố; M •
ds biểu diễn số đo của cung MM’ m dOM l d y cung.
H nh 1.12. Véctơ đơn vị tiếp tuyến.
Ta thừa nhận dOM ds. và do đó véctơ đơn vị tiếp tuyến được xác định bởi: dOM (1.2.8) ds
Vậy: Véctơ đơn vị tiếp tuyến là đạo hàm của véctơ vị trí theo toạ độ cong.
1.2.4. Bán kính cong của C
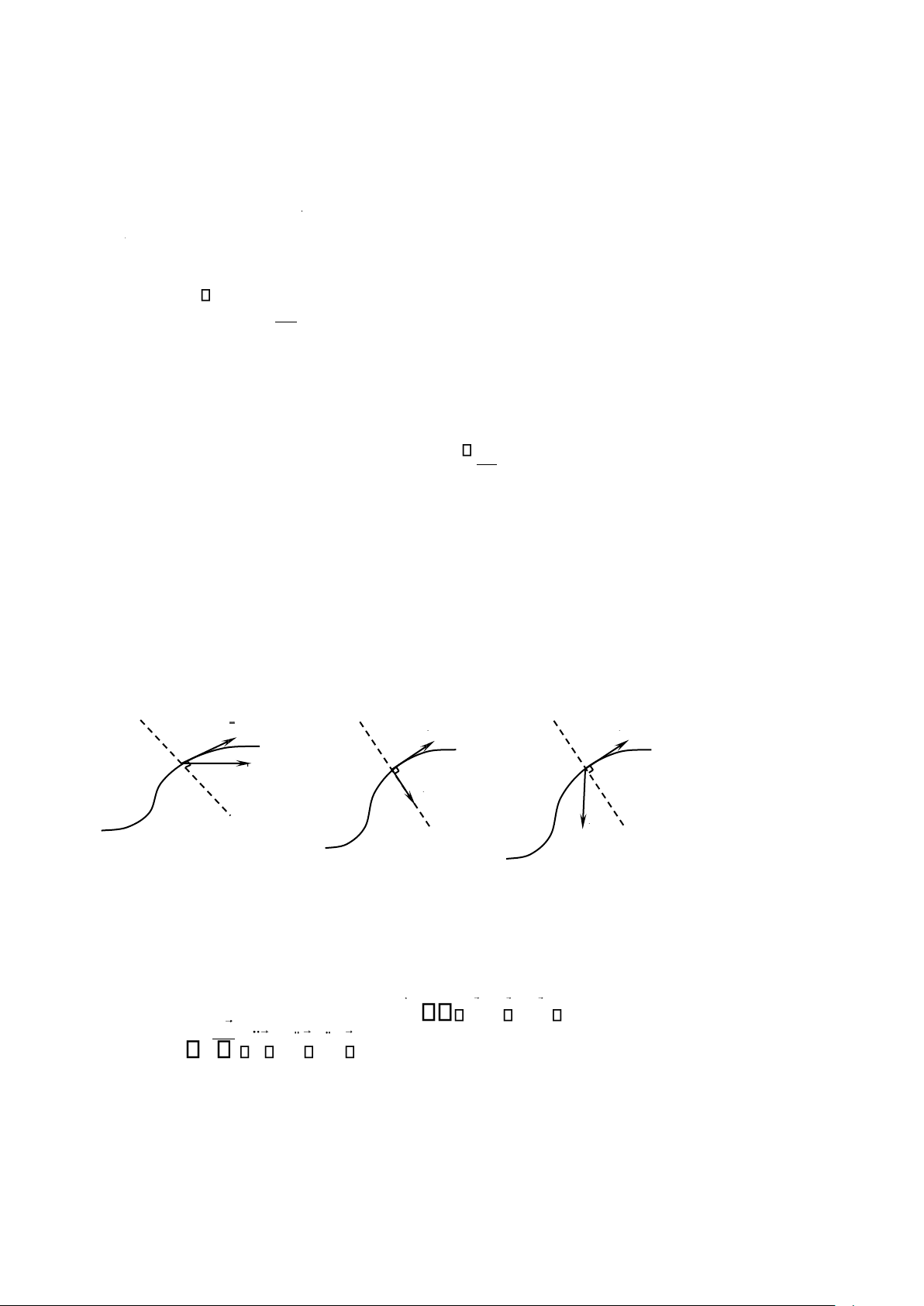
Cho một đường cong C cố định trong hệ qui chiếu R . Khi đó, người ta định nghĩa bÆn
k nh cong R của C là bán kính của đường tròn mật tiếp với C tại M (h nh 1.13). M C
Ta định nghĩa véctơ đơn vị pháp tuyến n l vØctơ có độ dài n
đơn vị, vuông góc với . Mặt khác, đạo hàm của véctơ d O
đơn vị tiếp tuyến theo hoành độ cong là một véctơ ds
vuông góc với . Do đó, bÆn k nh cong R của quĩ đạo tại điểm
Hình 1.13. Đường tròn mật tiếp
M có thể xác định theo hệ thức: d 1 n. (1.08) ds R
Đặt R 0. Với qui ước này thì véctơ n luôn hướng vào chiều lõm của đường cong C.
1.3. VÉCTƠ VẬN TỐC. VÉCTƠ GIA TỐC
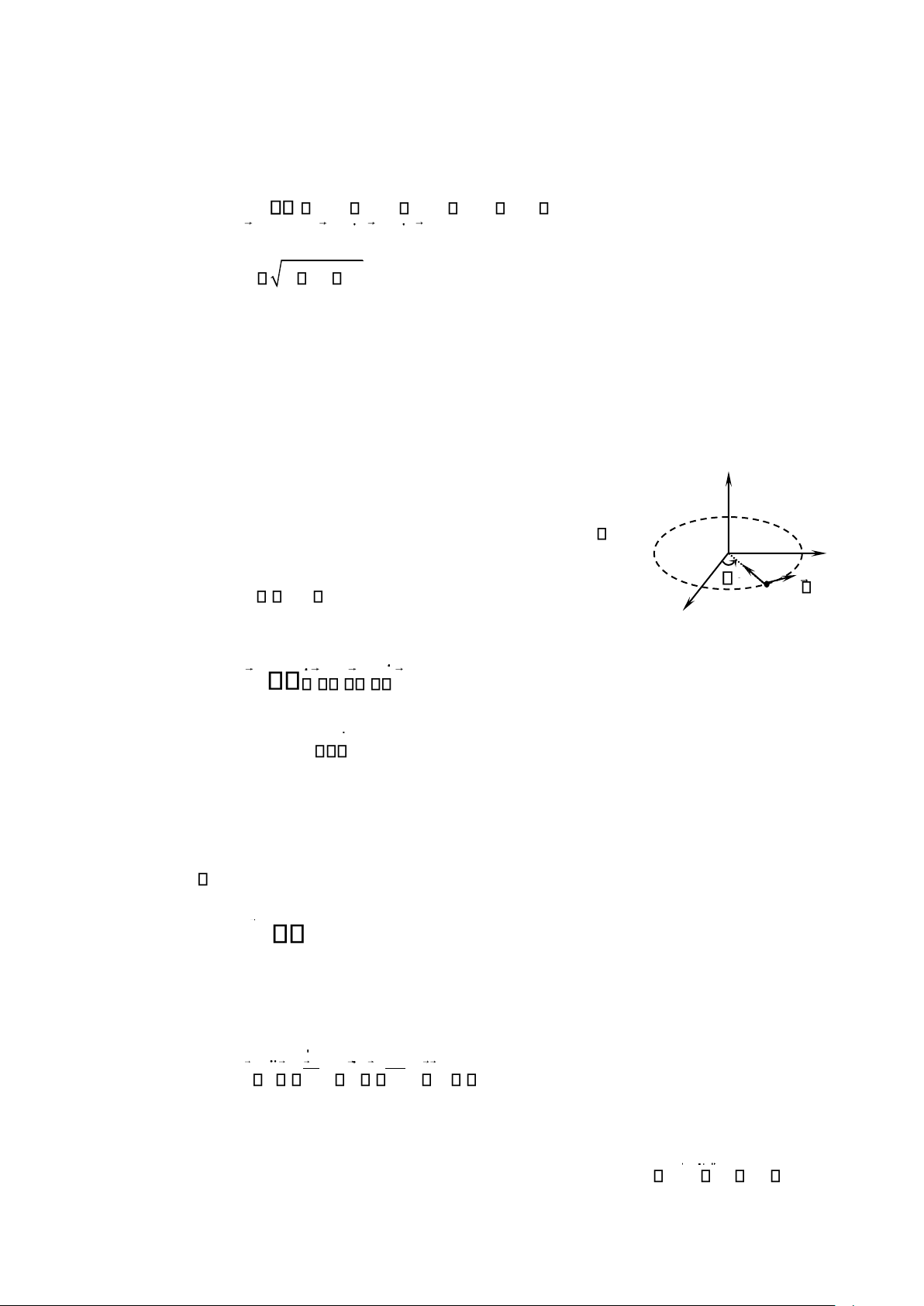
1.3.1. Véctơ vận tốc B
1.3.1.1. Định nghĩa M
Véctơ vận tốc là một đại lượng đặc trưng cho phương, chiều và sự O C
nhanh chậm của chuyển động. A lOMoAR cPSD| 59054137
Cho một điểm O cố định trong hệ qui chiếu R , véctơ vận tốc của M trong hệ qui chiếu
đó, được định nghĩa, bằng đạo hàm H nh 1.14. Véctơ vận tốc. của véctơ vị trí theo thời gian (h nh 1.14): v M dOM (1.09) dt
Đơn vị của vận tốc trong hệ SI là m/s.
1.3.1.2. Biểu thức của véctơ vận tốc trong tọa độ cong
Nếu đường cong C là quĩ đạo của điểm M thì vị trí của M là hàm số của s s AM ,
v s là một hàm số của thời gian t.
Khi đó, theo định nghĩa của véctơ vận tốc ta có: v M dOM dOM ds s (1.10) dt ds dt dOM
là véctơ đơn vị tiếp tuyến với quĩ đạo; s là đạo hàm của s theo thời trong đó ds
ds s v là giá trị đại số của vận tốc. Nếu M chuyển động theo chiều dương thì v 0; gian; dt
nếu M chuyển động ngược chiều dương thì v 0. Vậy
trong tọa độ cong, véctơ vận tốc có biểu thức: v M s v . (1.11)
1.3.1.3. Biểu thức của véctơ vận tốc trong hệ tọa độ Descartes:
Trong tọa độ Descartes, véctơ vị trí là OM xe x yey ze .z
Theo định nghĩa v có biểu thức v M dOM xe x yey zez dt hay: lOMoAR cPSD| 59054137 v M v e x x v ey y v e .z z (1.12) Độ lớn: v v2x v2y vz2 (1.13)
1.3.2. Véctơ gia tốc
1.3.2.1. Định nghĩa
Ta nhận thấy trong trường hợp tổng quát, véctơ vận tốc của một điểm có thể biến đổi cả
về độ lớn lẫn phương chiều. Để đặc trưng cho sự biến thiên của véctơ vận tốc người ta đưa ra khái
niệm véctơ gia tốc.
Véctơ gia tốc của M đối với hệ qui chiếu R là đạo hàm của véctơ vận tốc theo thời gian: dv M a M d OM2 2 . (1.14) dt dt
Đơn vị của gia tốc trong hệ SI là m / s2 .
1.3.2.2. Biểu thức của véctơ gia tốc trong tọa độ cong
Trong phần trên ta biết rằng, biểu thức của véctơ vận tốc trong toạ độ cong l :
V là hàm số của s m s thay đổi theo thời gian nên: (1.15) lOMoAR cPSD| 59054137 Hay: (1.16) (1.17)
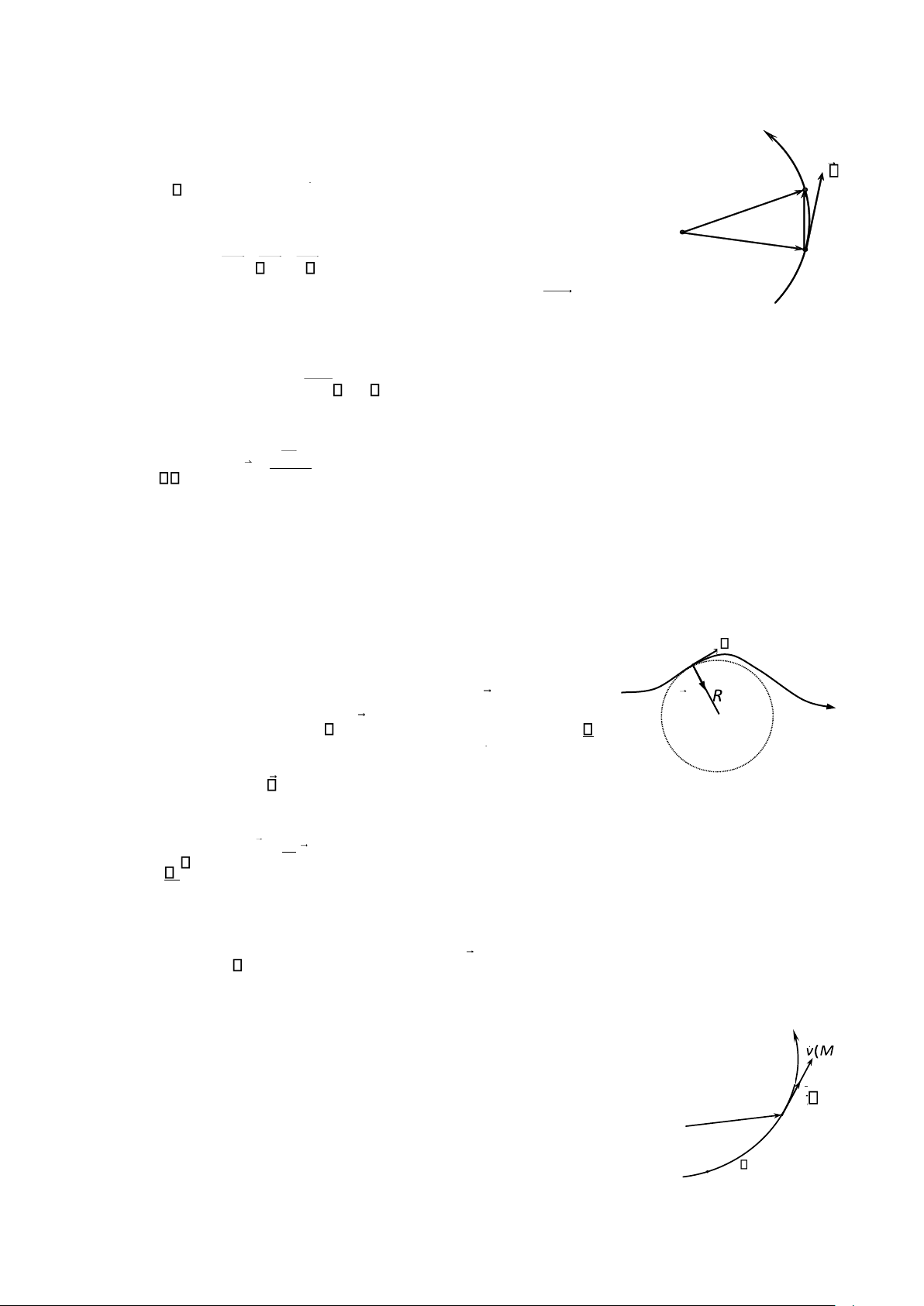
Như vậy, véctơ gia tốc có thể phân tích thành hai thành phần:
• Thành phần tiếp tuyến at đặc trưng cho sự biến thiŒn độ lớn của véctơ vận tốc. Véctơ
at có phương trùng với phương của véctơ đơn vị tiếp tuyến tại M; có độ lớn t nh bằng công thức a dv t . dt
• Thành phần pháp tuyến an đặc trưng cho sự biến thiŒn về hướng của vectơ vận tốc.
Véctơ an bao giờ cũng hướng về chiều lõm của quĩ đạo; có phương là phương của
véctơ đơn vị pháp tuyến tại M; có độ lớn l a v n 2 . R Chœ :
• Thành phần gia tốc tiếp tuyến chỉ bằng không khi chuẩn của véctơ vận tốc không thay
đổi theo thời gian tức l khi điểm M chuyển động cong đều.
• Thành phần pháp tuyến chỉ bằng không khi véctơ vận tốc không thay đổi phương, tức
l điểm M chuyển động theo đường thẳng.
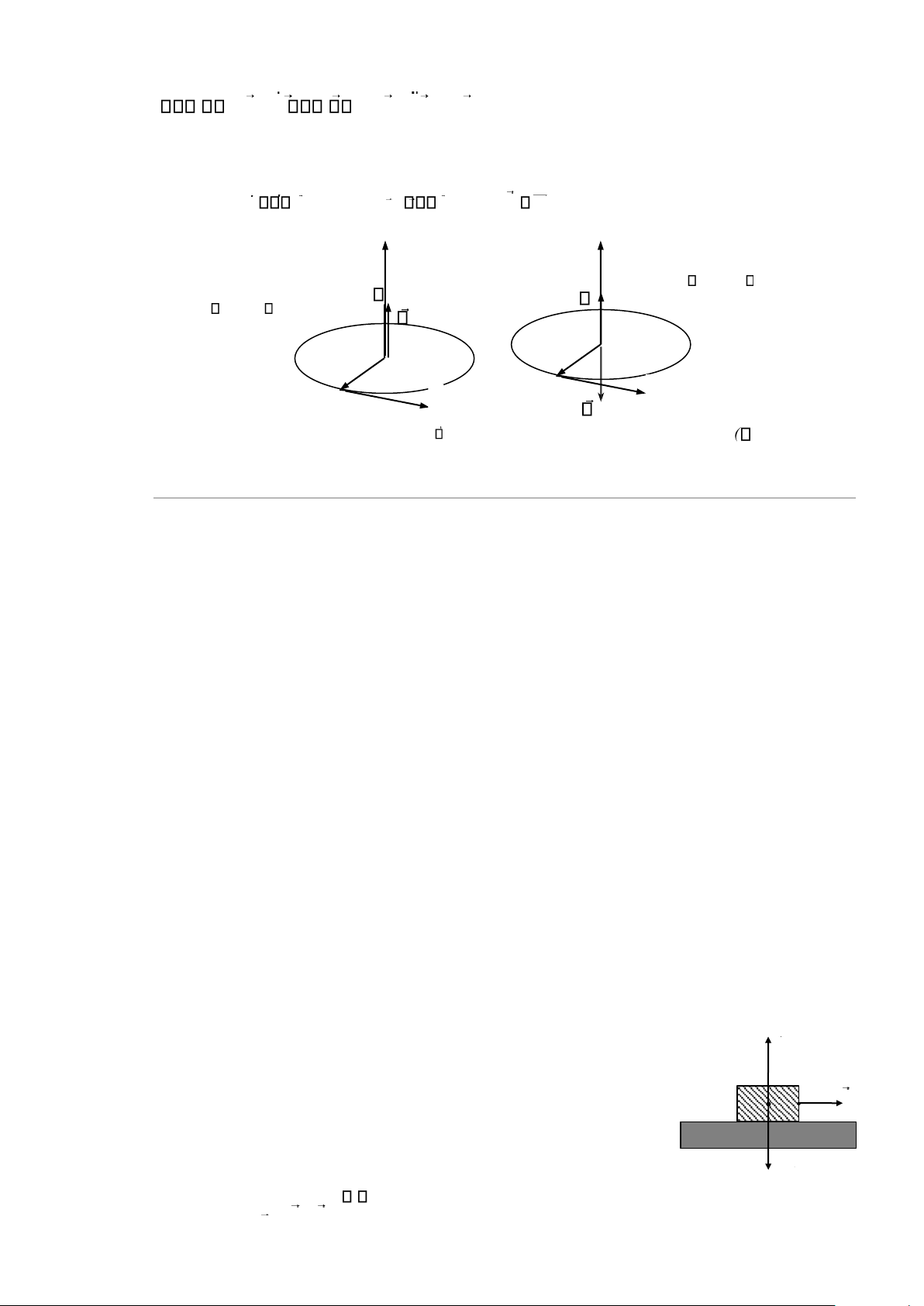
• Gia tốc của M chỉ bằng không trong chuyển động thẳng đều. Nếu là chuyển động cong
thì gia tốc bao giờ cũng khác không (hình 1.15). v v v M a M M a a a b c
H nh 1.15. a: Chuyển động nhanh dần; b: Chuyển động đều; c: Chuyển động chậm dần
1.3.2.3. Biểu thức của véctơ gia tốc trong tọa độ Descartes:
Trong tọa độ Descartes véctơ vận tốc là v M v e xx
v eyy v ezz , theo định nghĩa: (1.18) a M xe x yey ze .z dt Hay: lOMoAR cPSD| 59054137 dv a M v e xx
v eyy v ezz a exx a eyy a e .z z (1.19) Độ lớn: a a2 x a2y a .2z (1.20)
1.4. CHUYỂN ĐỘNG TRÒN
Trong phần này, chúng ta sẽ áp dụng các kết quả đã thu được ở trên để khảo sát một dạng
chuyển động rất phổ biến: chuyển động tròn.
Xét chuyển động của M trên đường tròn tâm O, bÆn k nh R và trong mặt phẳng (Oxy) (h
nh 1.16). Bán kính cong của quĩ đạo chính là bán kính của đường tròn. z
1.4.1. Véctơ vận tốc
Trong chuyển động tròn, tọa độ cong s và tọa độ góc liên
hệ với nhau theo hệ thức: O y R n s R ( đo bằng radian). (1.21) M
Từ biểu thức (1.11) ta có biểu thức của vận tốc: x v M s v R . (1.22) H nh
1.16.. Chuyển động tròn Theo định nghĩa,
l vận tốc góc trong chuyển động tròn: Vận tốc góc có giá trị bằng đạo
hàm của tọa độ góc theo thời gian.
Đơn vị vận tốc góc là rad/s.
Như vậy, từ biểu thức (1.22) ta được biểu thức liên hệ giữa vận tốc dài v vận tốc góc: v = R. (1.23) Vận tốc v M
có phương tiếp tuyến với quĩ đạo và có chiều phụ thuộc dấu của s.
1.4.2. Véctơ gia tốc
Từ (1.15) v (1.22) ta suy ra véctơ gia tốc: a s s2 n v v2 n a t a n.n (1.24) R R
Do M chuyển động trŒn quĩ đạo tr n t m O bÆn k nh R nŒn s R ; s R . Biểu thức của lOMoAR cPSD| 59054137 gia tốc có dạng: v2 a R R 2 n v n. R (1.25)
Theo định nghĩa, l gia tốc góc của điểm M trong chuyển động tròn. Biểu thức (1.25)
có thể viết lại như sau: a R R 2n v v2 n R 2Rn R Hay: a R 2Rn a t an (1.26)
Như vậy: Trong chuyển động tròn véctơ gia tốc có thể phân tích thành hai thành phần:
• Thành phần tiếp tuyến a
t có độ lớn liên hệ với gia tốc góc bởi at R . (1.27)
• Thành phần pháp tuyến an (còn gọi là gia tốc hướng tâm) có độ lớn liên hệ với vận tốc góc bởi a n 2R (1.28)
• Trong trường hợp chuyển động tròn đều
là hằng số thì véctơ gia tốc có dạng: a an R 2n v2 n R 2n (1.29) R
Vậy, trong chuyển động tròn đều gia tốc toàn phần bằng gia tốc pháp tuyến v lu n hướng vào tâm đường tròn.
Trong trường hợp chuyển động tròn đều người ta còn định nghĩa chu k T là thời gian điểm
M quay được một vòng: T 2 (1.30)
và tần số f là số vòng mà điểm M quay được trong một đơn vị thời gian: f 1 (1.31) T 2
1.4.3. Véctơ vận tốc góc và véctơ gia tốc góc
Trong chuyển động tròn, véctơ vận tốc góc và véctơ gia tốc góc (h nh 1.17) được định nghĩa bởi: lOMoAR cPSD| 59054137 ez ez v ez ez (1.32)
Khi đó, từ các biểu thức (1.22) v (1.26) ta suy ra mối liên hệ giữa các đại lượng, viết dưới dạng véctơ, như sau: v R v a R t R ( với OM ) (1.33) z z   giảm ( < 0) tăng ( > 0)   R O R O M   v M v
Hình 1.17. Véctơ vận tốc góc ( )và
véctơ gia tốc góc trong chuyển ộng tròn ( ) CHƯƠNG 2.
ĐỘNG LỰC HỌC CHẤT ĐIỂM
2.1. C`C ĐỊNH LUẬT NEWTON
2.1.1. Một số khái niệm mở đầu
2.1.1.1. Chất điểm
Định nghĩa: Chất điểm là một vật thể điểm mà kích thước có thể bỏ qua so với những khoảng cách mà ta nghiên cứu.
Ví dụ: Các hạt sơ cấp (electron, neutron, proton...) có thể coi là các chất điểm.
Vì chất điểm là một vật thể điểm nên để xác định vị trí của nó ta chỉ cần biết ba tọa độ.
Chất điểm được gọi là cô lập nếu nó không chịu bất kì một tác dụng cơ học nào.
Trong thực tế không tồn tại một chất điểm hoàn toàn cô lập mà nó lu n lu n chịu cÆc tÆc
dụng cơ học khác nhau. Chất điểm cô lập là một sự lí tưởng hóa. Tuy
nhiên, có những trường hợp mà các tác dụng cơ học lên một chất N
điểm bù trừ chính xác cho nhau. Khi đó, chất điểm được gọi là giả cô lập. v
Ví dụ: Đặt một vật có khối lượng m trên một cái bàn nằm ngang
có đệm không khí. Vật đó là giả cô lập vì phản lực của bàn bù trừ với mg
trọng lượng của vật: mg N 0.
H nh 2.01. Lực bù trừ. lOMoAR cPSD| 59054137
2.1.1.2. Khối lượng của chất điểm
Quán tính cơ học
Để có khái niệm về quán tính, ta xét thí dụ sau:
Trên mặt đường nằm ngang có một xe đẩy tr 攃ऀ em và một xe ôtô nhỏ đang đứng yên.
Ta hãy dùng sức đẩy các xe đó làm cho chúng chuyển động. Ta nhận thấy rằng, để hai xe có
cùng một vận tốc thì ta phải đẩy xe ôtô mạnh hơn và lâu hơn. Sau đó, khi đã hai xe đã chuyển
động thì việc cho xe ôtô dừng lại cũng khó hơn.
Trong trường hợp này ta n i: Quán tính của ôtô lớn hơn quán tính của chiếc xe đẩy. Vậy ta c thể định nghĩa:
Quán tính của một vật là khả năng chống lại sự biến đổi vận tốc của vật đó .
Khối lượng của một chất điểm
Đối với chất điểm, quán tính được biểu diễn bằng một yếu tố vô hướng có giá trị dương,
kí hiệu là m, gọi là khối lượng.
Theo định nghĩa quÆn t nh ta suy ra: Khối lượng của một chất điểm càng lớn thì càng khó thay
đổi vận tốc của nó.
Trong cơ học phi tương đối tính, khối lượng bất biến theo thời gian và không phụ thuộc vào hệ
qui chiếu. Đy là một đặc trưng nội tại của chất điểm.
Đơn vị của khối lượng trong hệ SI là kilogram (kí hiệu: kg).
Tính cộng được của khối lượng
Trong cơ học phi tương đối tính, khối lượng có tính cộng được.
Cho hai chất điểm có khối lượng là m1 và m2 . Nếu chúng được hợp lại để tạo thành một
chất điểm duy nhất c khối lượng m thì: m m 1 m .2 (2.01)
2.1.1.3. Lực cơ học
Khái niệm v lực cơ học Tác dụng cơ học của
một vật thể S lên một chất điểm M được đặc trưng bởi một véctơ
gọi là lực mà ta ký hiệu là FS M .
Lực cơ học là một đại lượng vật l đặc trưng cho tương tác cơ học giữa các vật.
Lực cơ học chính là nguyên nhân vật lý làm biến dạng hay làm thay đổi trạng thái chuyển
động của các vật. Ta thừa nhận rằng lực không phụ thuộc hệ qui chiếu, n là một đại lượng nội tại,
đặc trưng cho tương tác giữa S và M.
Tương tác giữa các vật có thể xảy ra khi chœng tiếp xúc với nhau (người đẩy xe, mặt
đường tác dụng vào bánh xe,…) hoặc khi các vật không tiếp xúc trực tiếp với nhau (tương tác
hấp dẫn, tương tác điện từ,…). Do đó, người ta ph n biệt hai loại lực : Loại thứ nhất gồm các
lực xuất hiện khi có tiếp xúc trực tiếp giữa các vật tương tác như lực đàn hồi, lực ma sát,…Loại lOMoAR cPSD| 59054137
thứ hai gồm các lực xuất hiện khi các vật tương tác không tiếp xúc trực tiếp với nhau như lực
hấp dẫn, lực điện từ,…
Tính cộng được của các lực
Lực là một đại lượng có tính cộng được: Lực tổng hợp của nhiều tác dụng cơ học bằng tổng
véctơ của các lực do các tác dụng cơ học đó gây ra.
Gọi S là tập hợp các vật thể Si , FSi M là lực tác dụng của vật thể Si lên chất điểm M. Khi đó,
lực tổng hợp do tập hợp S tác dụng lên chất điểm M là: FS M FSi M . (2.02) i
2.1.2. Các định luật Newton
2.1.2.1. Định luật I Newton
Tồn tại một lớp các hệ qui chiếu, gọi là hệ qui chiếu Galileo, mà đối với ch 甃 Āng thì một chất điểm
cô lập s 攃̀ đứng yên hoặc chuyển động thẳng đều.
Hệ qui chiếu Galileo (kí hiệu Rg ) còn gọi là hệ qui chiếu quán tính.
Trong phần lớn các thí nghiệm thường ngày, hệ qui chiếu gắn với mặt đất có thể coi là hệ qui chiếu Galileo.
2.1.2.2. Định luật II Newton
Định luật II Newton xét chất điểm ở trạng thái không cô lập, nghĩa là chất điểm chịu tÆc
dụng của những ngoại lực.
Cho Rg là hệ qui chiếu quán tính Galileo, M là một chất điểm khối lượng m và E là toàn thể
vũ trụ ngoại trừ M. Khi đó, tổng các lực tác dụng lên M và gia tốc của nó liên kết với nhau bởi
hệ thức cơ bản của động lực học hay định luật II Newton (hình 2.02): F E M ma. (2.03)
trong đó FE M là tổng các lực tác dụng lên M của tất cả các vật thể khác trong
vũ trụ. Trong thực tế, đối với một bài toán cho trước ta chỉ xét đến một vài lực M(m)
Chú ý rằng, nếu bây giờ ta định nghĩa đại lượng động
lượng đối với một hệ qui chiếu Rg của chất điểm M có khối
H nh 2.02. Lực và gia tốc
lượng m, chuyển động với vận tốc v là: p mv. (2.04)
và bỏ qua các lực khác. thì khi đó, định luật II Newton có thể
được biểu diễn dưới dạng khác như sau: lOMoAR cPSD| 59054137 dp FE M . (2.05) dt
Hệ thức (2.05) chính là nội dung của định lí về động lượng. Nhận xét:
• Có thể định nghĩa E là toàn thể vũ trụ, với qui ước như một tiên đề rằng một chất điểm
không tác dụng lên chính nó.
• Hệ thức cơ bản của động lực học phù hợp với định luật quán tính. Thật vật một chất
điểm chịu tác dụng của một lực bằng không, sẽ có gia tốc bằng không tức là có không đổi.
• Nếu M cân bằng thì gia tốc của nó bằng không và tổng các lực tác dụng lên M cũng bằng không.
• Trong hệ đơn vị SI lực được biểu thị bằng Newton (N), nó được suy ra từ các đơn vị
cơ bản khối lượng (kg), chiều dài (m) và thời gian (s).
Từ hệ thức F ma suy ra 1N = 1 kg.m.s-2.
• Đơn vị của động lượng không có tên gọi riêng. Từ biểu thức (2.04) ta suy ra đơn vị của động lượng là kg.m/s.
2.1.2.3. Định luật III Newton
Thực nghiệm xác nhận rằng không bao giờ có tác dụng một phía. Trong thực tế, mọi sự
thay đổi trạng thái chuyển động trong các hệ qui chiếu Galileo đều xảy ra do kết quả tương
tác giữa các vật. Định luật các tác dụng tương hỗ hay định luật III Newton xét đến sự tương tác
giữa các vật và được phát biểu như sau:
Cho hai chất điểm M1 và M2 tương tác với nhau. Các lực tương tác F
M M1 2 và FM M2 1 là các lực đối nhau và cùng trên một M 2 đường thẳng M 1M2 (hình 2.03).
Định luật III Newton c n được gọi là định luật “tác dụng”
và “phản lực tác dụng”, được thể hiện bởi: M1
H nh 2.03. Tác dụng tương h . F FM1 M2 M2 M1 ; FM 2 M1 M M1 2 0.
Tên gọi “tác dụng” và “phản lực tác dụng” chỉ có tính chất qui ước mà không hề có sự phân
biệt có tính chất nguyên tắc nào giữa chúng. Nếu “tác dụng” là lực biến dạng thì “phản lực
tác dụng” cũng là lực biến dạng; nếu “tác dụng” là lực hấp dẫn thì “phản lực tác dụng” cũng là lực hấp dẫn;… lOMoAR cPSD| 59054137
Chú ý rằng, tuy các lực FM1 M2 , FM2 M1 có tổng bằng không nhưng tác dụng của chúng không
khử nhau vì điểm đặt của ch 甃 Āng là khác nhau.
Các định luật II và III Newton lập thành những định luật cơ bản động lực học chất điểm.
 Xem bài tập 1, 2 và 4.
2.2. MOMENT ĐỘNG LƯỢNG dp
Định lí về động lượng FE M
là một trong những định luật cơ bản của cơ học chất dt
điểm. Trong nhiều trường hợp (nhất là khi xét chuyển động tr n của chất điểm) người ta
thường diễn tả định l trên đây dưới dạng khác, đó là định lí về moment động lượng.
2.2.1. Moment động lượng của chất điểm LO
2.2.1.1. Moment động lượng đối với một điểm
Cho hệ qui chiếu R v một điểm O trong không
gian. Moment động lượng đối với điểm O trong hệ qui v
chiếu R của một chất điểm M có khối lượng m xác định O M bởi: P d LO OM pOM mv mOM v. (2.06)
H nh 2.04. Moment động lượng.
Đơn vị của moment động lượng là kg.m2/s.
Giả sử là một đường thẳng đi qua M và song song với véctơ vận tốc v ; (P) là mặt phẳng
xác định bởi đường thẳng và điểm O. Gọi d là khoảng cách giữa O và (hình 2.04). Khi đó,
moment động lượng LO của chất điểm M đối với điểm O là một véctơ nằm trên đường thẳng
vuông góc với mặt phẳng (P) v có độ lớn: L O d.mv. (2.07) z
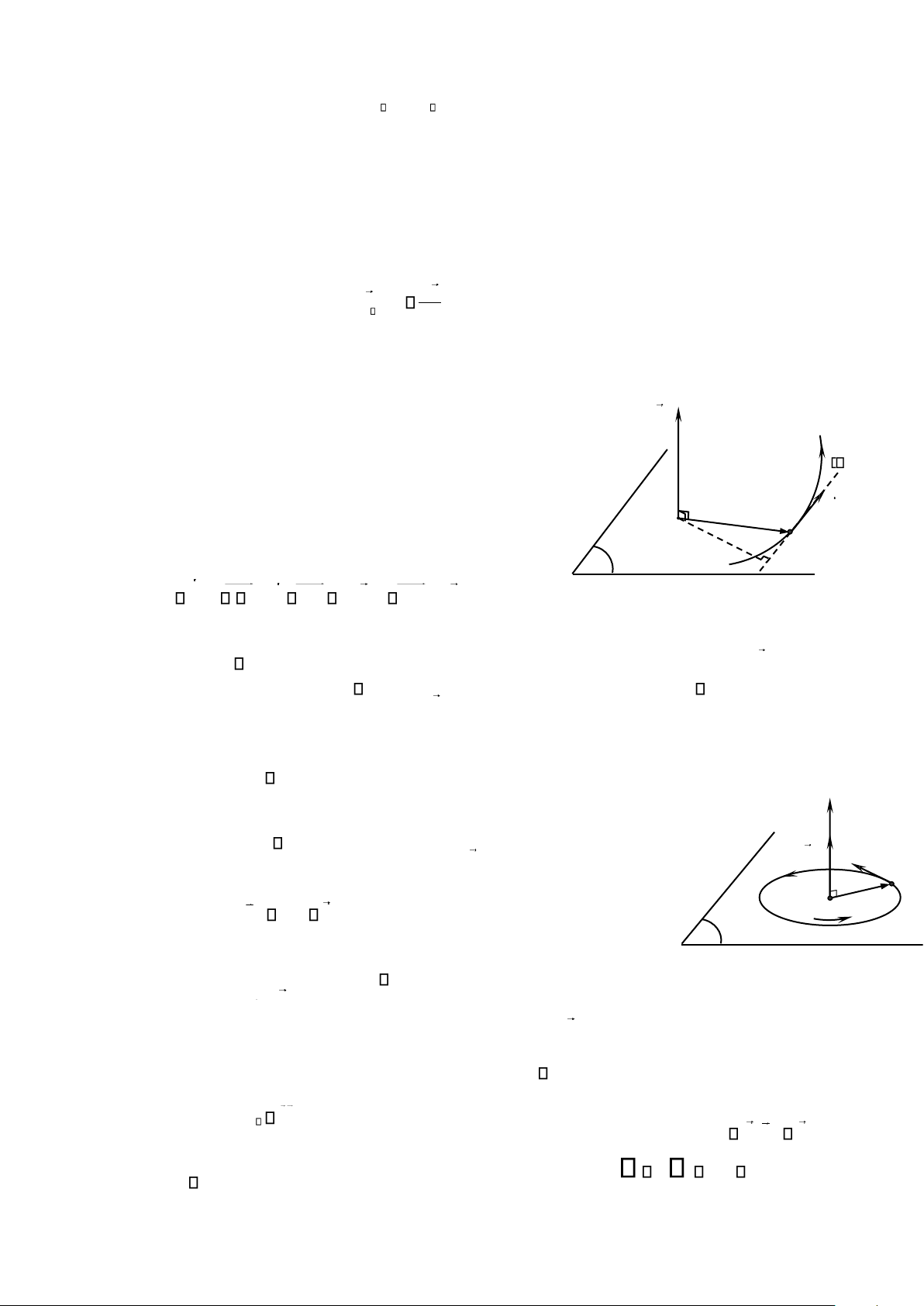
Trường hợp M chuyển động trên đường tròn tâm O, bán kính r
với vận tốc góc (hình 2.05) trong mặt phẳng (P) xác định bởi véctơ L đơn vị pháp tuyến e O v z th ta c : M r L O mr2 e .z (2.08) O
2.2.1.2. Moment động lượng đối với một trục P
Thí dụ: Trong trường
Cho một trục định hướng xác định bởi điểm O và véctơ hợp chất điểm chuyển
đơn vị e , LO là moment động lượng của chất điểm động tròn trong mặt
M đối với điểm O (h nh 2.06). Khi đó, hình chiếu của L phẳng (Oxy), moment O lên
động lượng của chất điểm
trục này được gọi là moment động lượng đối với trục .
M đối với trục Oz là: L eL .O (2.09) L Z e Lz O e . mrz
Như vậy, moment động lượng của chất điểm M đối với 2 e z mr2 . (2.10)
trục là một đại lượng vô hướng. lOMoAR cPSD| 59054137
2.2.2. Moment của lực
H nh 2.06. Moment động lượng đối với một trục.
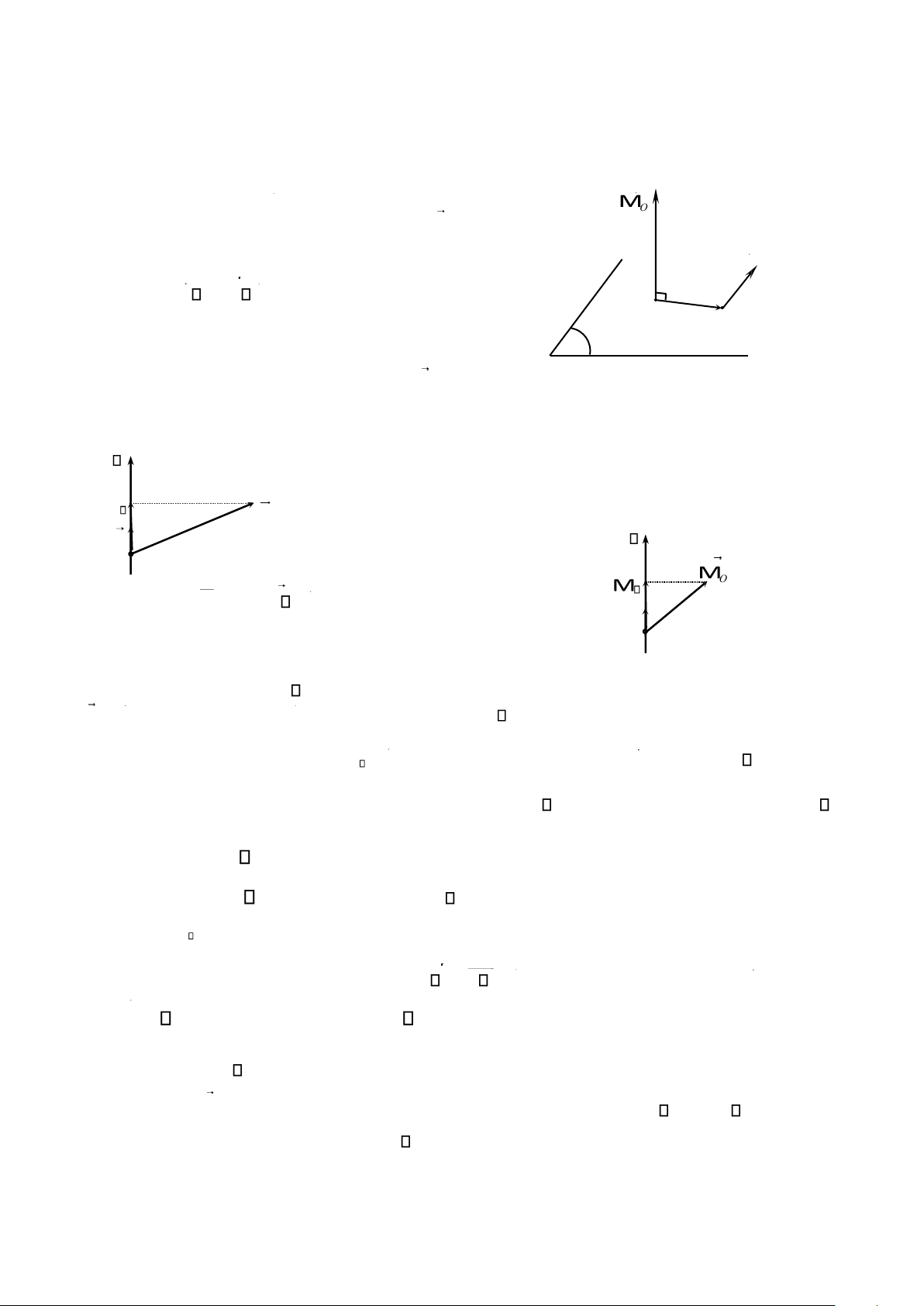
2.2.2.1. Moment của một lực đối với một điểm
Moment của một lực F có điểm đặt tại M đối với điểm O
O, theo định nghĩa, là một véctơ, kí hiệu là MO , được xác định bởi (h nh 2.07): F M O OM F. (2.11) O
Đơn vị của moment lực đối với một điểm là N.m. M P
H nh 2.05. Chuyển động tròn.
H nh 2.07. Moment của một lực
đối với một điểm. L LO e Từ bi
O ểu thức ( 2.11 ) ta nhậ n thấy, nếu lực F nằm trên cùng một O
đường thẳng với OM thì M O 0. e
2.2.2.2. Moment của một lực đối với một trục O
Cho một trục định hướng xác định bởi điểm O và véctơ đơn H nh 2.08. Moment của vị e , MO là moment
của lực F có điểm đặt tại M đối với điểm O lực đối với trục .
(h nh 2.08). Khi đó, tích vô hướng M=M
O.e được gọi là moment của lực F đối với trục .
Có thể chứng minh rằng, moment của một lực đối với trục không phụ thuộc điểm O trên trục .
Lực song song với trục
Moment đối với trục của một lực song song với thì bằng không. M = 0. (2.12)
Thật vậy, moment của lực này đối với O: M O
OM F là một véctơ vuông góc với F, do đó MO vuông
góc với trục . Vì vậy hình chiếu của nó lên sẽ bằng không.
Lực trực giao với trục
Cho một lực F có điểm đặt tại M, nằm trên đường thẳng (D), trực giao với . Gọi d H H1 2 là chiều
dài đường vuông góc chung của (D) và trục (cánh tay đòn) (h nh 2.09):