













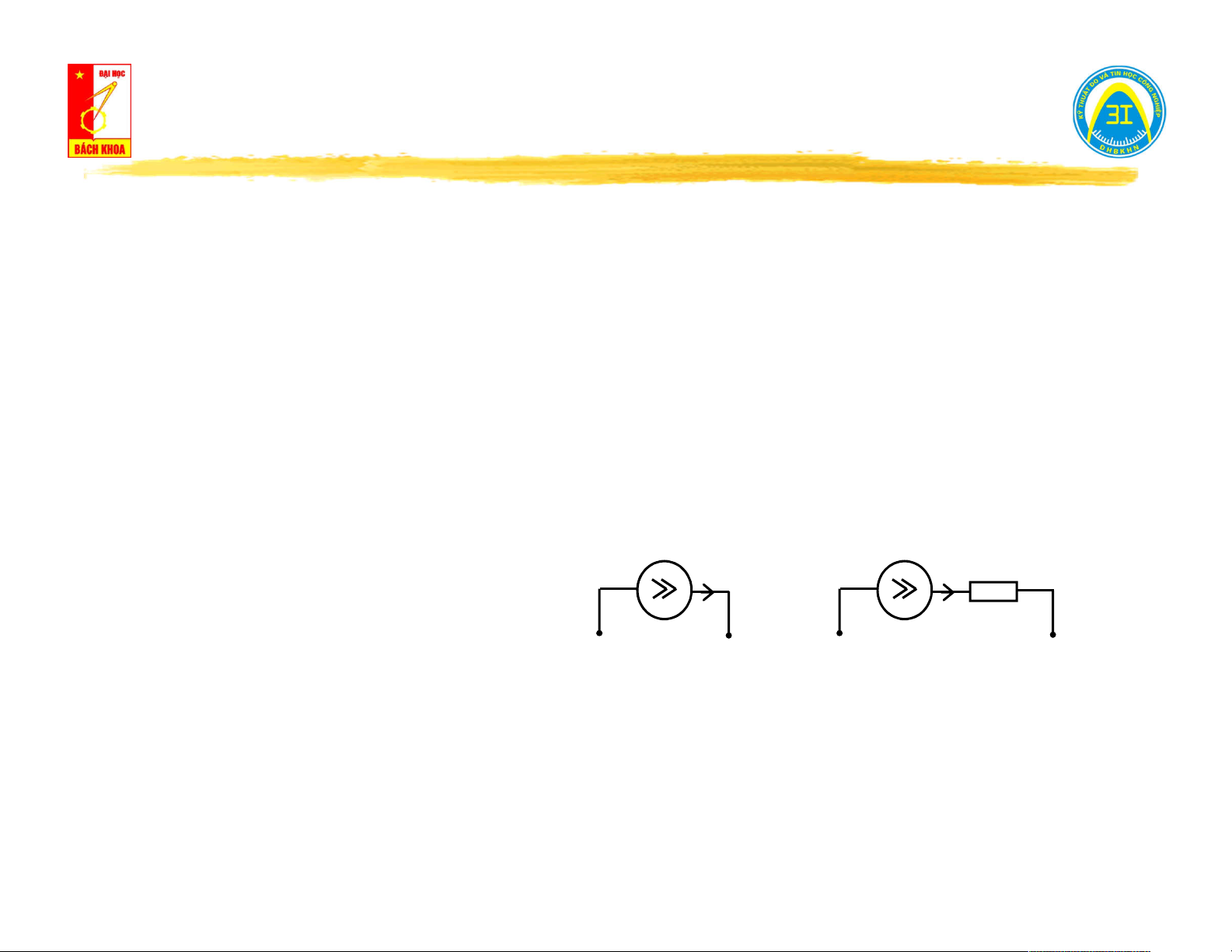








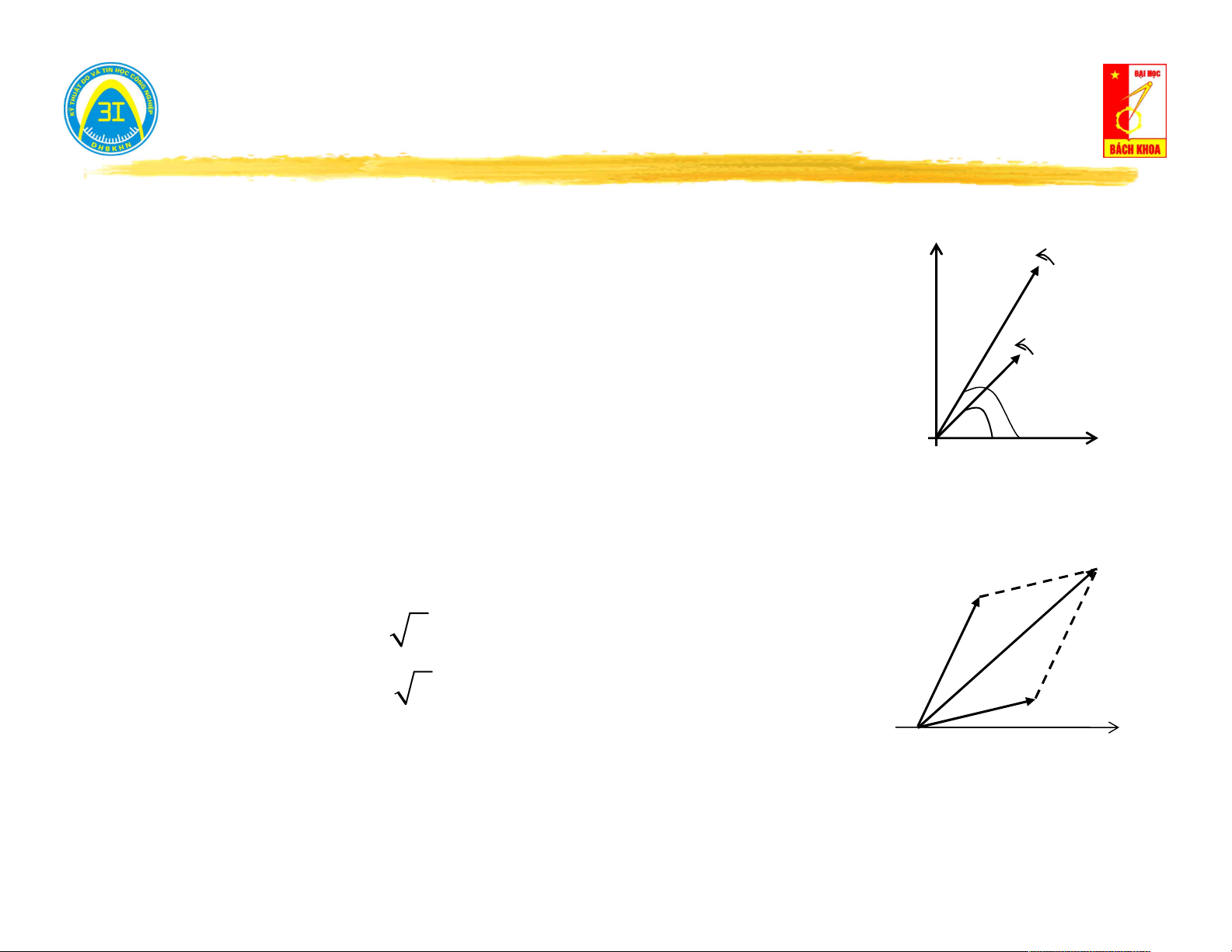

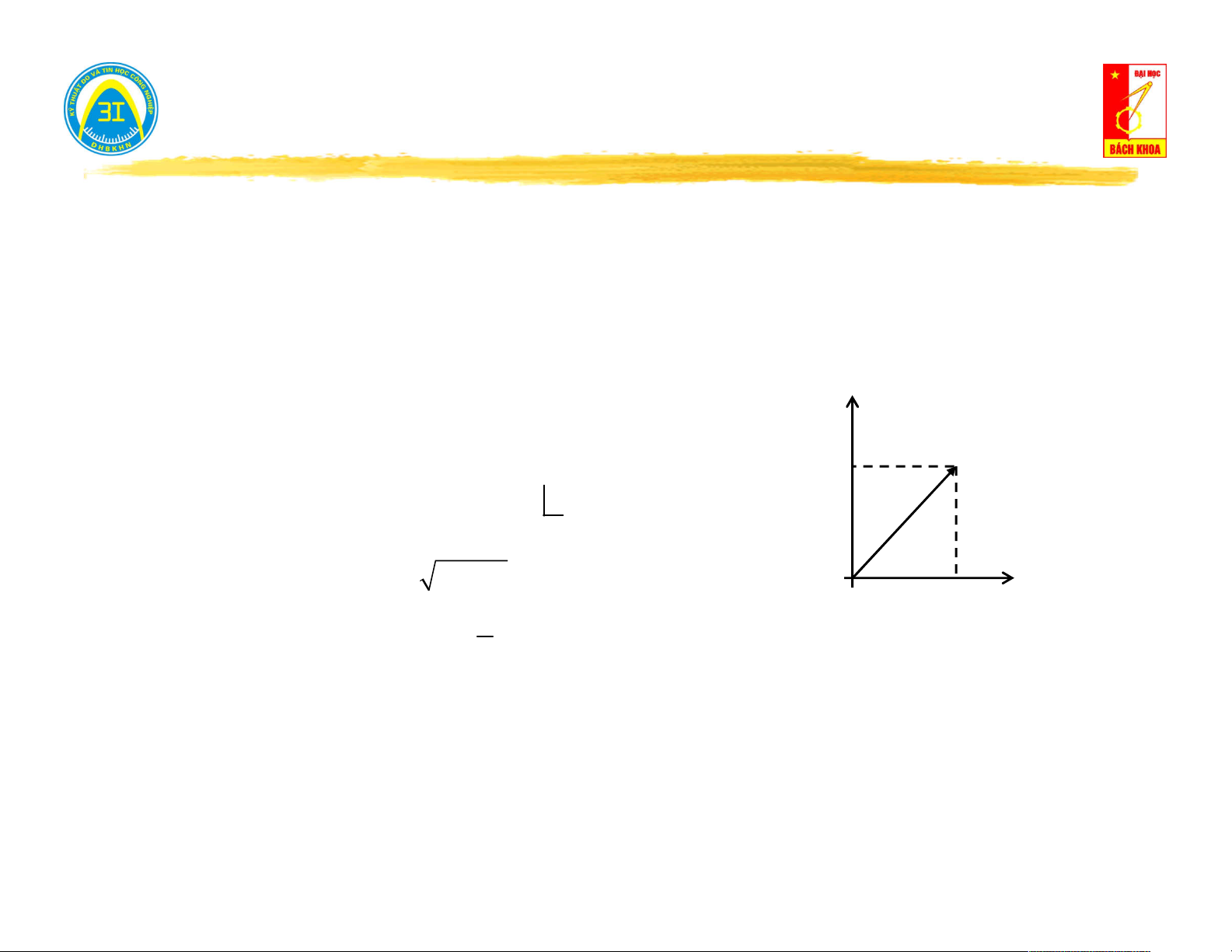







































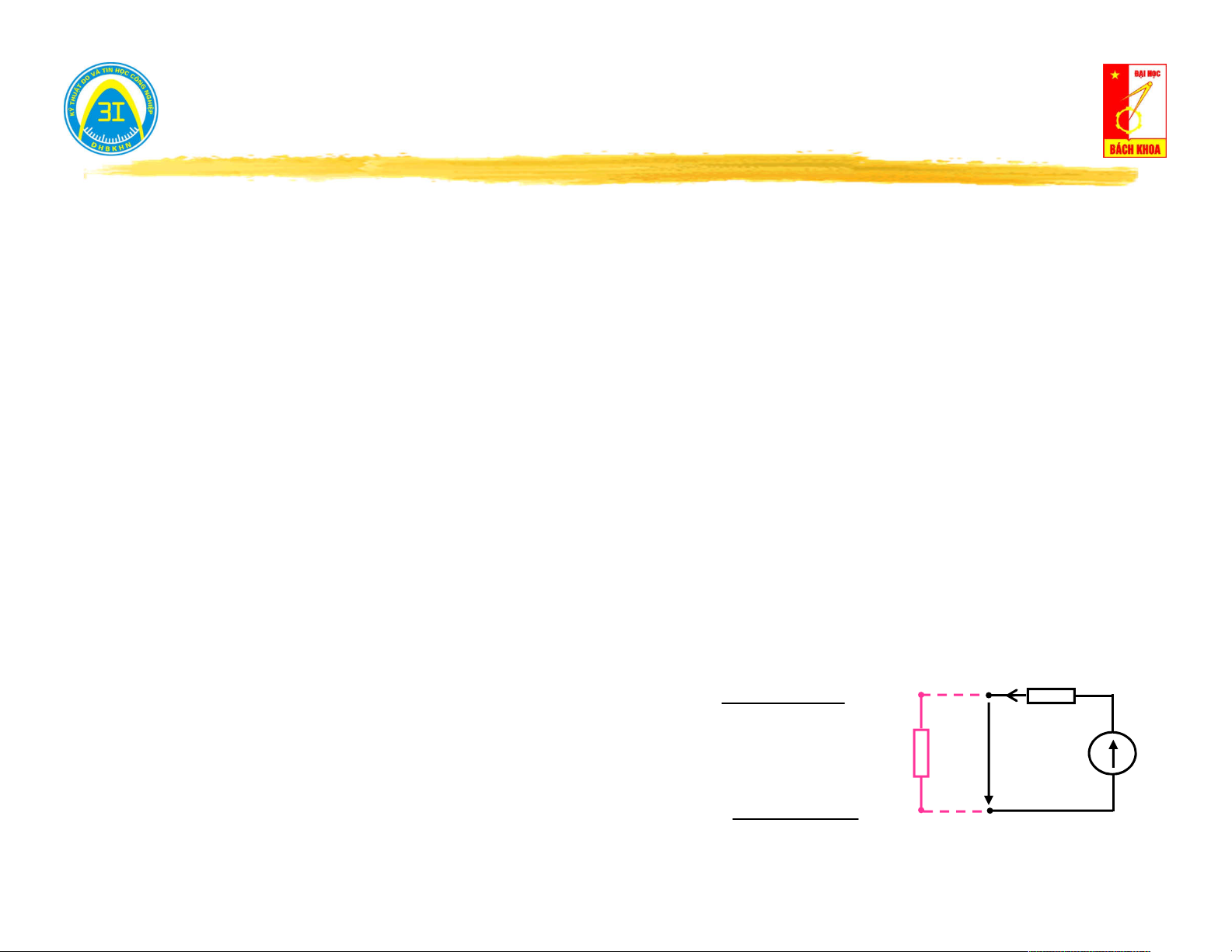





































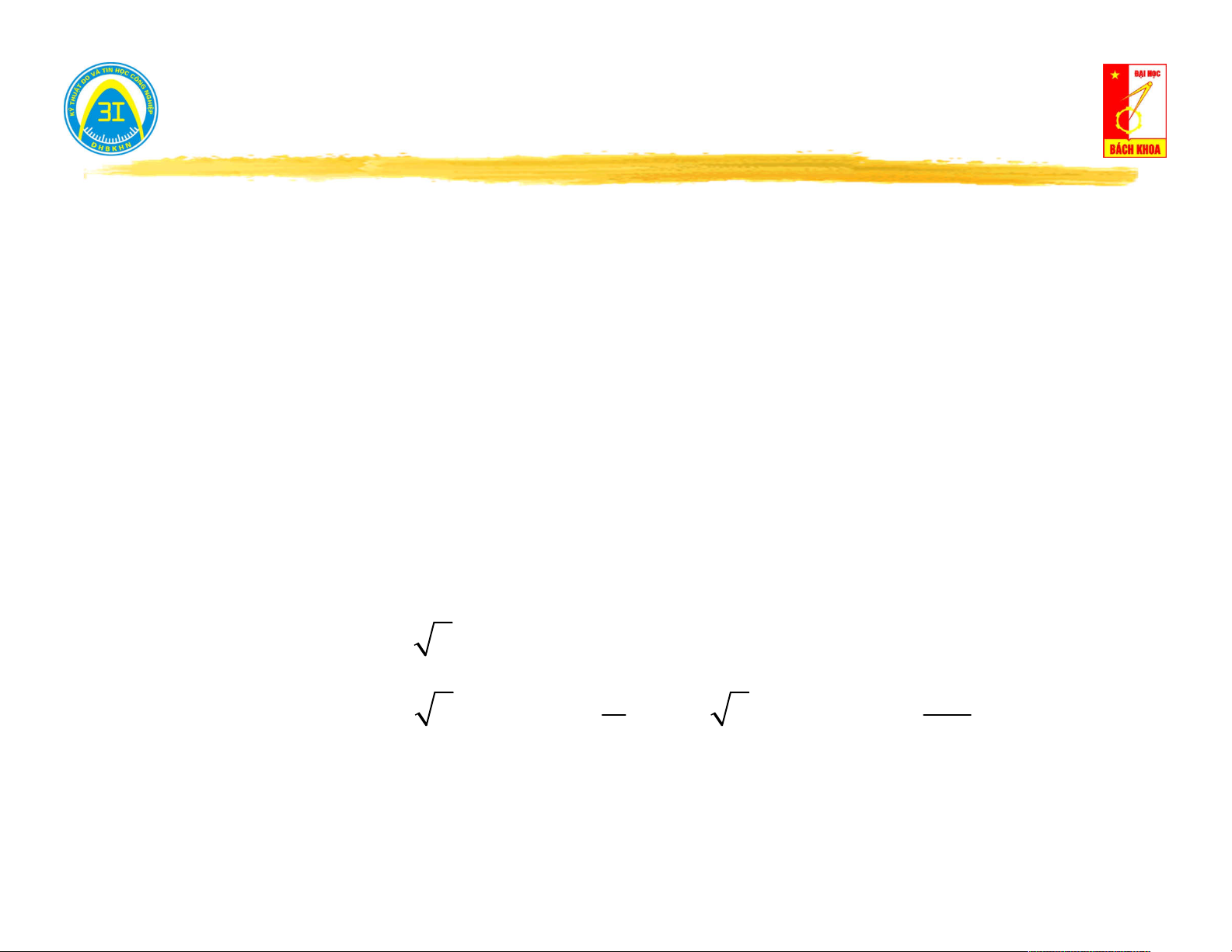
Preview text:
LÝ THUYẾT MẠCH ĐIỆN 1 HP: EE2020
Giáo viên: TS. Nguyễn Việt Sơn
Bộ môn: Kỹ thuật đo & Tin học công nghiệp
Viện Điện - Đại học Bách Khoa Hà Nội
Email: son.nguyenviet@hust.edu.vn Năm 2018
LÝ THUYẾT MẠCH ĐIỆN 1
Tài liệu tham khảo:
1. Cơ sở kỹ thuật điện 1 & 2 - Nguyễn Bình Thành - 1971.
2. Cơ sở kỹ thuật điện - Quyển 1 - Bộ môn Kỹ thuật đo & THCN - 2004
3. Giáo trình lý thuyết mạch điện - PGS - TS. Lê Văn Bảng - 2005.
4. Fundamentals of electric circuits - David A.Bell - Prentice Hall - 1990.
5. Electric circuits - Norman Blabanian - Mc Graw-Hill - 1994.
6. Methodes d’etudes des circuit electriques - Fancois Mesa - 1987.
7. An introduction to circuit analysis a system approach - Donald E.Scott - 1994.
8. Electric circuits - Schaum - McGraw-Hill - 2003 (*)
9. Fundamentals of Electric Circuits - Charles K. Alexander - 2012 (*)
(*) http://www.mica.edu.vn/perso/Nguyen-Viet-Son/courses.html
2018 - Lý thuyết mạch điện 1 - Nguyễn Việt Sơn 2
LÝ THUYẾT MẠCH ĐIỆN 1
Nội dung chương trình:
Chương 1: Khái niệm về mô hình mạch Kirchhoff.
I. Khái niệm về mô hình trường - mô hình hệ thống.
II. Các hiện tượng cơ bản trong mô hình mạch Kirchhoff.
III. Các luật cơ bản trong mô hình mạch Kirchhoff.
IV. Nội dung bài toán mạch.
Chương 2: Mạch tuyến tính ở chế độ xác lập điều hòa.
I. Hàm điều hòa & các đại lượng đặc trưng.
II. Số phức - Biểu diễn hàm điều hòa trong miền ảnh phức
III. Phản ứng của một nhánh với kích thích điều hòa.
IV. Dạng phức các luật cơ bản trong mạch Kirchhoff.
2018 - Lý thuyết mạch điện 1 - Nguyễn Việt Sơn 3
LÝ THUYẾT MẠCH ĐIỆN 1
Nội dung chương trình:
Chương 3: Phương pháp cơ bản tính mạch tuyến tính ở chế độ xác lập điều hòa - Graph Kirchhoff I. Phương pháp dòng nhánh II. Phương pháp thế nút
III. Phương pháp dòng vòng
IV. Khái niệm về graph Kirchhoff
V. Các định lý về lập phương trình Kirchhoff VI. Ma trận cấu trúc A, B
VII. Lập phương trình bằng ma trận cấu trúc
2018 - Lý thuyết mạch điện 1 - Nguyễn Việt Sơn 4
LÝ THUYẾT MẠCH ĐIỆN 1
Nội dung chương trình:
Chương 4: Tính chất cơ bản của mạch điện tuyến tính. I. Khái niệm.
II. Tính chất tuyến tính.
III. Khái niệm hàm truyền đạt.
IV. Truyền đạt tương hỗ và không tương hỗ.
Chương 5: Mạch điện tuyến tính có kích thích chu kỳ I. Khái niệm
II. Cách phân tích mạch điện tuyến tính có kích thích chu kỳ.
III. Trị hiệu dụng - công suất dòng chu kỳ
IV. Hàm truyền đạt và đặc tính tần số.
2018 - Lý thuyết mạch điện 1 - Nguyễn Việt Sơn 5
LÝ THUYẾT MẠCH ĐIỆN 1
Nội dung chương trình:
Chương 6: Mạng một cửa Kirchhoff tuyến tính. I. Khái niệm
II. Phương trình & sơ đồ tương đương mạng một cửa có nguồn.
III. Điều kiện đưa công suất cực đại ra khỏi mạng một cửa.
Chương 7: Mạng hai cửa tuyến tính I. Khái niệm
II. Mô hình mạng hai cửa - Phương pháp tính bộ số đặc trưng.
III. Tính chất mạng 2 cửa tuyến tính tương.
IV. Hàm truyền đạt dòng - áp. Tổng trở vào của mạng hai cửa.
Vấn đề hòa hợp nguồn và tải bằng mạng hai cửa. V. Mạng hai cửa phi hỗ.
VI. Khuếch đại thuật toán
2018 - Lý thuyết mạch điện 1 - Nguyễn Việt Sơn 6
LÝ THUYẾT MẠCH ĐIỆN 1
Nội dung chương trình:
Chương 8: Mạch điện 3 pha. I. Khái niệm.
II. Mạch 3 pha đối xứng và không đối xứng tải tĩnh.
III. Tính và đo công suất mạch điện 3 pha.
IV. Mạch 3 pha có tải động - Phương pháp thành phần đối xứng
V. Một số sự cố trong mạch điện 3 pha.
2018 - Lý thuyết mạch điện 1 - Nguyễn Việt Sơn 7
LÝ THUYẾT MẠCH ĐIỆN 1
PHƯƠNG PHÁP HỌC TẬP
Download tài liệu www.mica.edu.vn/perso/Nguyen-Viet-Son/courses.html
Bài giảng + bài tập + sách tham khảo (Tiếng Anh)
Nắm vững lý thuyết làm nhiều bài tập
Tích cực trao đổi thảo luận Sử dụng
Kết hợp Bài giảng + nghe giảng trên lớp
Đọc tài liệu tham khảo (khuyến khích đọc tài liệu Tiếng Anh)
Sử dụng thành thạo Calculator + phần mềm mô phỏng
Calculator FX570ES (Plus)
Matlab, Circuit Maker, Proteus, Altium Designer
2018 - Lý thuyết mạch điện 1 - Nguyễn Việt Sơn 8
LÝ THUYẾT MẠCH ĐIỆN 1 THI GIỮA KỲ:
Thông báo trước 2 tuần.
Thi viết ~40 phút (bài tập)
Không được sử dụng tài liệu THI CUỐI KỲ:
Thi 2 chung: Thời gian thi + Bộ đề thi
Thi viết 90 phút (bài tập)
Được sử dụng tài liệu
2018 - Lý thuyết mạch điện 1 - Nguyễn Việt Sơn 9
LÝ THUYẾT MẠCH ĐIỆN 1
Chương 1: Khái niệm về mô hình mạch Kirchhoff
I. Khái niệm về mô hình trường - mô hình hệ thống.
II. Các hiện tượng cơ bản trong mô hình mạch Kirchhoff.
III. Các luật cơ bản trong mô hình mạch Kirchhoff.
IV. Nội dung bài toán mạch. Bài tập: 7 - 16
2014 - Lý thuyết mạch điện 1 - Nguyễn Việt Sơn 1
Chương 1: Khái niệm về mô hình mạch Kirchhoff
I. Khái niệm về mô hình trường - mô hình hệ thống.
Mạch điện gồm một hệ thống các thiết bị nối ghép với nhau cho phép trao đổi năng lượng và tín hiệu. Mạch điện u(t), i(t), p(t) …
E(x, y, z, t), H(x,y,z,t) c … 6000(km) Mô hình hệ thống f Mô hình trường Mô hình mạch tín hiệu Hình vẽ mô phỏng thiết bị điện Mạch hóa Luật Mô hình mạch Phương trình Sơ đồ mạch Kirchhoff l << λ toán học Luật Ohm
Xét truyền đạt năng lượng g >> g tb moi truong
Luật Kirchhoff 1, 2
giữa các thiết bị điện
Hữu hạn các trạng thái.
Luật bảo toàn công suất
2014 - Lý thuyết mạch điện 1 - Nguyễn Việt Sơn 2
LÝ THUYẾT MẠCH ĐIỆN 1
Chương 1: Khái niệm về mô hình mạch Kirchhoff.
I. Khái niệm về mô hình trường - mô hình hệ thống.
II. Các hiện tượng cơ bản trong mô hình mạch Kirchhoff. II.1. Nguồn điện.
II.2. Phần tử tiêu tán trong mạch điện R.
II.3. Kho điện. Điện dung C.
II.4. Kho từ. Điện cảm L.
III. Các luật cơ bản trong mô hình mạch Kirchhoff.
IV. Nội dung bài toán mạch.
2014 - Lý thuyết mạch điện 1 - Nguyễn Việt Sơn 3
Chương 1: Khái niệm về mô hình mạch Kirchhoff
II. Các hiện tượng cơ bản trong mạch Kirchhoff.
Mô hình mạch Kirchhoff được xem xét trên phương diện truyền đạt năng lượng giữa các
thiết bị trong một mạch điện.
Có rất nhiều hiện tượng trong các thiết bị điện: Tiêu tán, Tích phóng điện từ, Tạo sóng,
phát sóng, Khuếch đại, Chỉnh lưu, Điều chế … tồn tại một nhóm đủ hiện tượng cơ bản,
từ đó hợp thành mọi hiện tượng khác:
Hiện tượng tiêu tán: Năng lượng điện từ đưa vào một vùng và chuyển thành dạng
năng lượng khác tiêu tán đi, không hoàn nguyên lại nữa.
Ví dụ : Bếp điện, bóng đèn neon, động cơ kéo …
Hiện tượng phát: Là hiện tượng biến các dạng năng lượng khác thành dạng năng
lượng điện từ. Hiện tượng phát tương ứng với một nguồn phát.
Ví dụ : Pin, acqui, nhà máy thủy điện, nhiệt điện, cối xay gió …
Hiện tượng tích phóng của kho điện: Năng lượng điện từ tích vào một vùng tập trung
điện trường như lân cận các bản tụ điện hoặc đưa từ vùng đó trả lại trường điện từ.
Hiện tượng tích phóng của kho từ: Năng lượng điện từ tích vào một vùng tập trung từ
trường như lân cận một cuộn dây có dòng điện hoặc đưa trả từ vùng đó.
2014 - Lý thuyết mạch điện 1 - Nguyễn Việt Sơn 4
Chương 1: Khái niệm về mô hình mạch Kirchhoff
II. Các hiện tượng cơ bản trong mạch Kirchhoff.
Mô hình mạch Kirchhoff nghiên cứu quá trình truyền đạt năng lượng và tìm cách
mô hình hóa các hiện tượng trao đổi năng lượng bằng những phần tử sao cho
quan hệ giữa các biến trạng thái trên chúng cho phép biểu diễn quá trình truyền
đạt năng lượng tại vùng mà chúng được thay thế.
Với 4 quá trình năng lượng cơ bản, mạch Kirchhoff sẽ có 4 phần tử cơ bản:
Nguồn điện (nguồn suất điện động, nguồn dòng) ↔ Hiện tượng phát
Phần tử tiêu tán (điện trở R, điện dẫn g) ↔ Hiện tượng tiêu tán
Phần tử kho điện (điện dung C) ↔ Hiện tượng tích phóng của kho điện
Phần tử kho từ (điện cảm L, hỗ cảm M) ↔ Hiện tượng tích phóng của kho từ
2014 - Lý thuyết mạch điện 1 - Nguyễn Việt Sơn 5
Chương 1: Khái niệm về mô hình mạch Kirchhoff II.1. Nguồn điện.
Định nghĩa: Các thiết bị thực hiện quá trình chuyển hóa các dạng năng lượng khác thành
điện năng được gọi là nguồn điện.
Quy ước: Chiều dòng điện chảy trong nguồn chảy từ nơi có điện áp thấp đến nơi có
điện áp cao. P
= u . i < 0 → phát công suất nguon P
= u . i > 0 → nhận công suất nguon Phân loại:
Nguồn độc lập: Các thông số của nguồn (biên độ, tần số, hình dáng, góc pha …) chỉ
tùy thuộc vào quy luật riêng của nguồn mà không phụ thuộc vào trạng thái bất kỳ trong mạch.
Ví dụ: Nguồn áp độc lập, nguồn dòng độc lập
Nguồn phụ thuộc: Các trạng thái của nguồn bị phụ thuộc (điều khiển) bởi một trạng
thái nào đó trong mạch điện.
Ví dụ: Nguồn áp bị điều khiển bởi dòng, nguồn áp bị điều khiển bởi áp; nguồn dòng bị
điều khiển bởi dòng, nguồn dòng bị điều khiển bởi áp …
2014 - Lý thuyết mạch điện 1 - Nguyễn Việt Sơn 6
Chương 1: Khái niệm về mô hình mạch Kirchhoff II.1. Nguồn điện
Nguồn áp độc lập
Định nghĩa: Nguồn áp e(t) là một phần tử sơ đồ mạch Kirchhoff có đặc tính duy trì
trên hai cực của nó một hàm điện áp, còn gọi là sức điện động xác định theo thời
gian, và không phụ thuộc vào dòng điện chảy qua nó.
Biến trạng thái: Điện áp trên hai cực của nguồn. Đối với một nguồn áp lý tưởng, giá trị
của điện áp trên hai cực của nguồn không phụ thuộc vào giá trị của tải nối với nguồn.
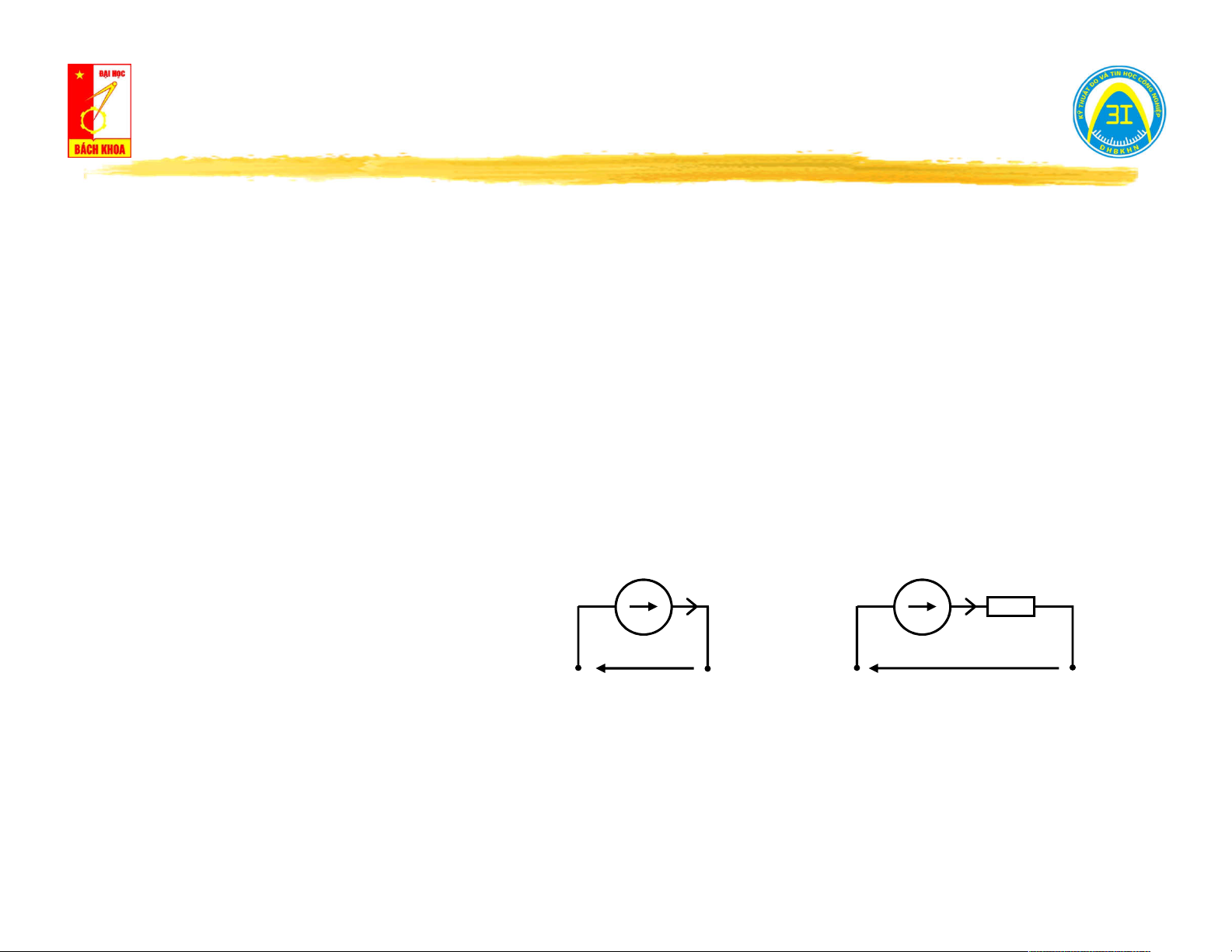
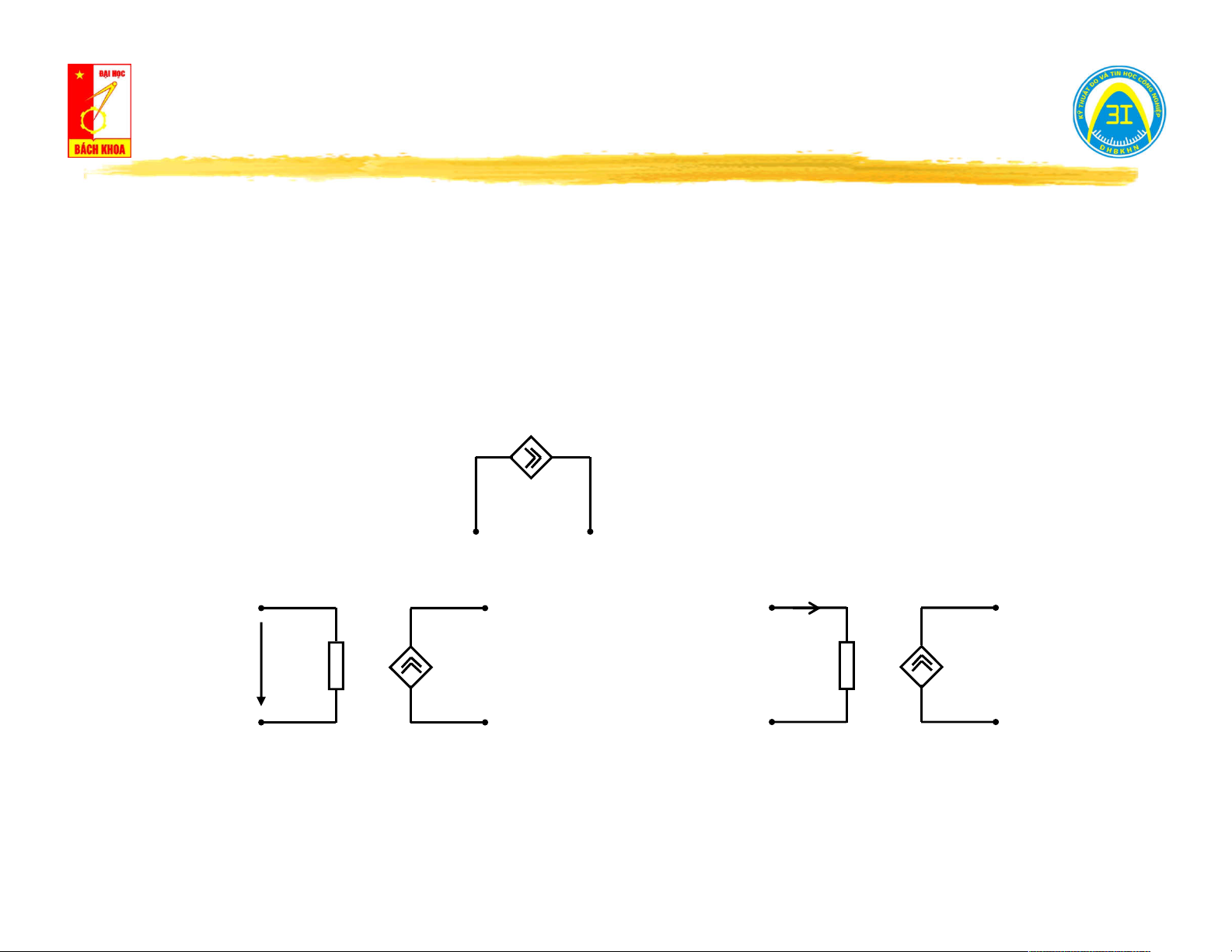
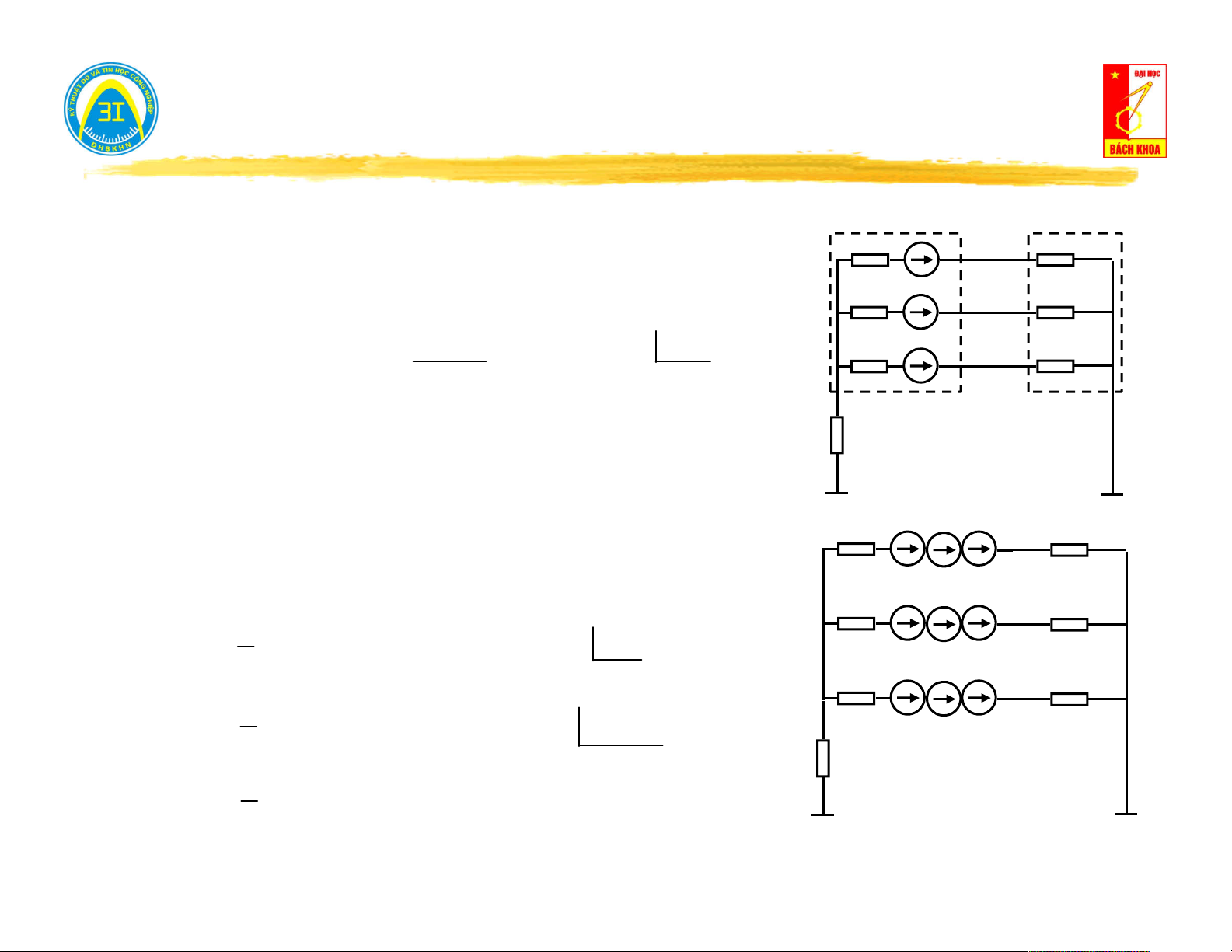
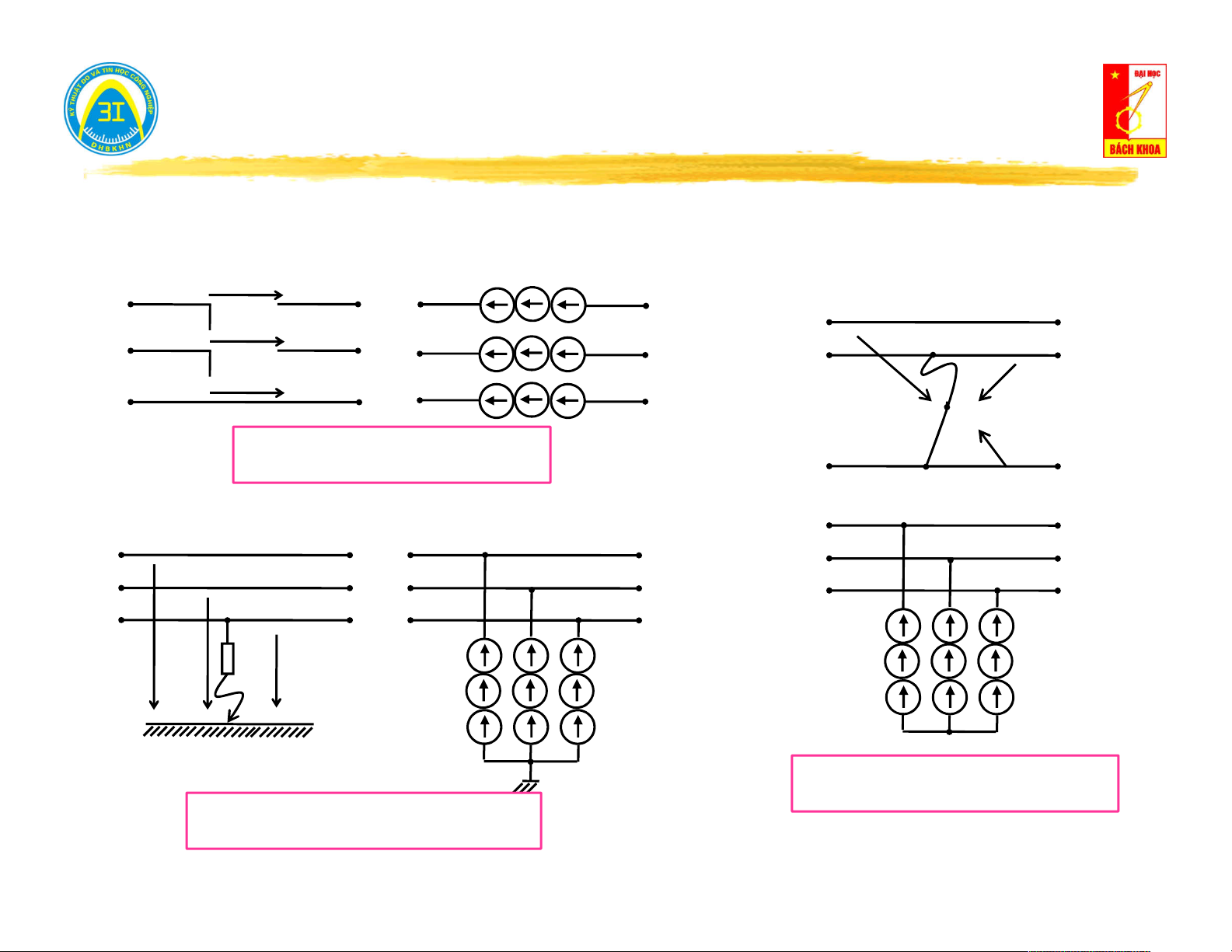
Phương trình trạng thái: u(t) = - e(t) e(t) e(t) R i(t) ng Ký hiệu: i(t) u(t) u(t) Nguồn lý tưởng Nguồn thực (R = 0) (R ≠ 0) ng ng
(Chiều của mũi tên là chiều dương quy ước của dòng điện sinh ra bởi nguồn)
Cách nối: Tránh ngắn mạch nguồn áp
2014 - Lý thuyết mạch điện 1 - Nguyễn Việt Sơn 7
Chương 1: Khái niệm về mô hình mạch Kirchhoff II.1. Nguồn điện
Nguồn áp phụ thuộc (nguồn áp bị điều khiển)
Định nghĩa: Nguồn áp phụ thuộc là nguồn áp mà trạng thái điện áp (suất
điện động) của nó phụ thuộc vào trạng thái (dòng điện, điện áp) của một nhánh khác trong mạch. e(t)
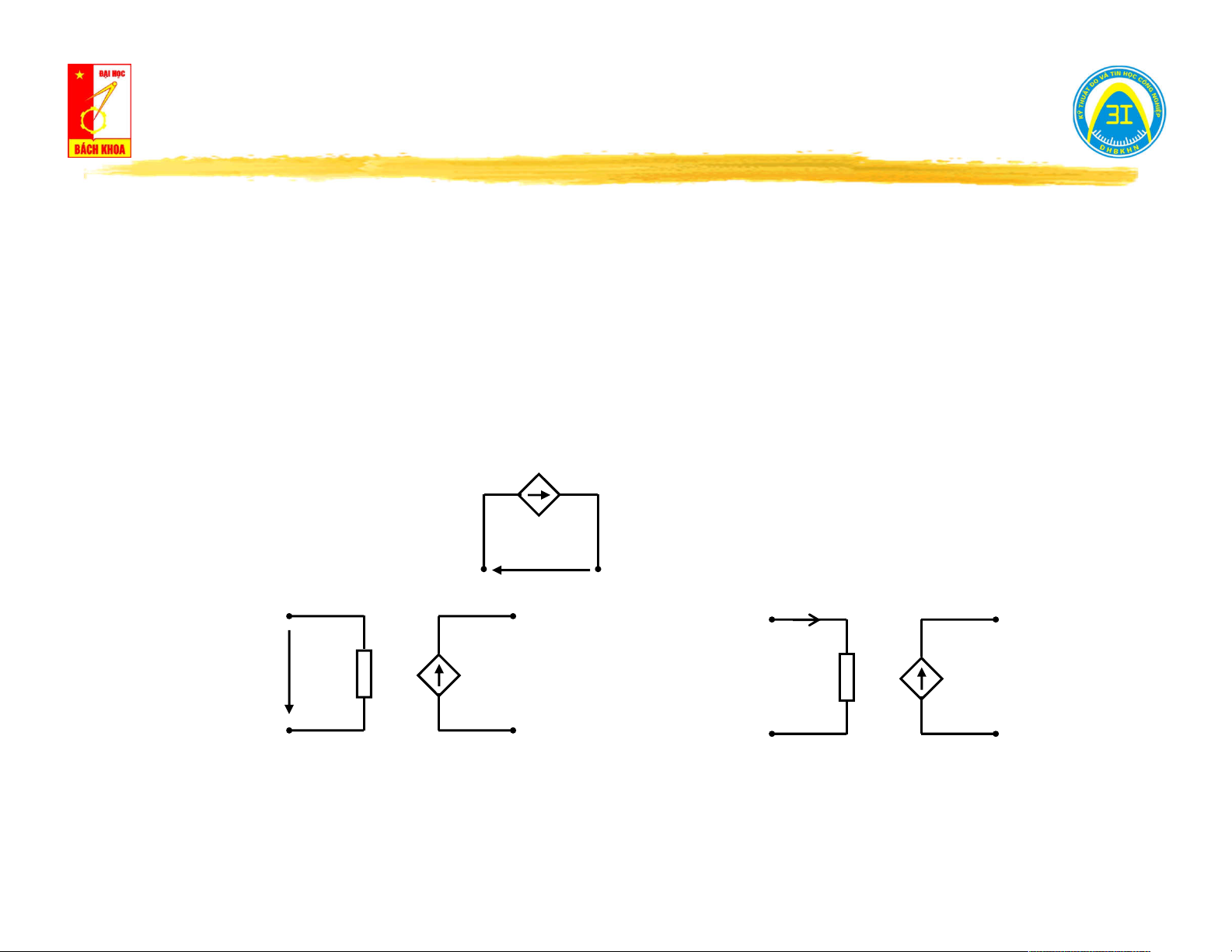
Ký hiệu: u(t) = - e(t) u(t) Phân loại: i (t) 1 u (t) 1 e (t) = k.u (t) 2 1 e (t) = R.i (t) 2 1
Nguồn áp bị điều khiển bởi áp
Nguồn áp bị điều khiển bởi dòng
(voltage-cotrolled voltage source)
(current-controlled voltage source)
2014 - Lý thuyết mạch điện 1 - Nguyễn Việt Sơn 8
Chương 1: Khái niệm về mô hình mạch Kirchhoff II.1. Nguồn điện
Nguồn dòng độc lập:
Định nghĩa: Nguồn dòng j(t) là một phần tử sơ đồ mạch Kirchhoff có đặc tính bơm
qua nó một hàm dòng điện i(t) xác định, không tùy thuộc vào điện áp trên hai
cực của nó.
Biến trạng thái: Dòng điện chảy qua nguồn. Đối với một nguồn dòng lý tưởng, giá trị
của dòng điện sinh ra bởi nguồn không phụ thuộc vào giá trị của tải nối với nguồn.
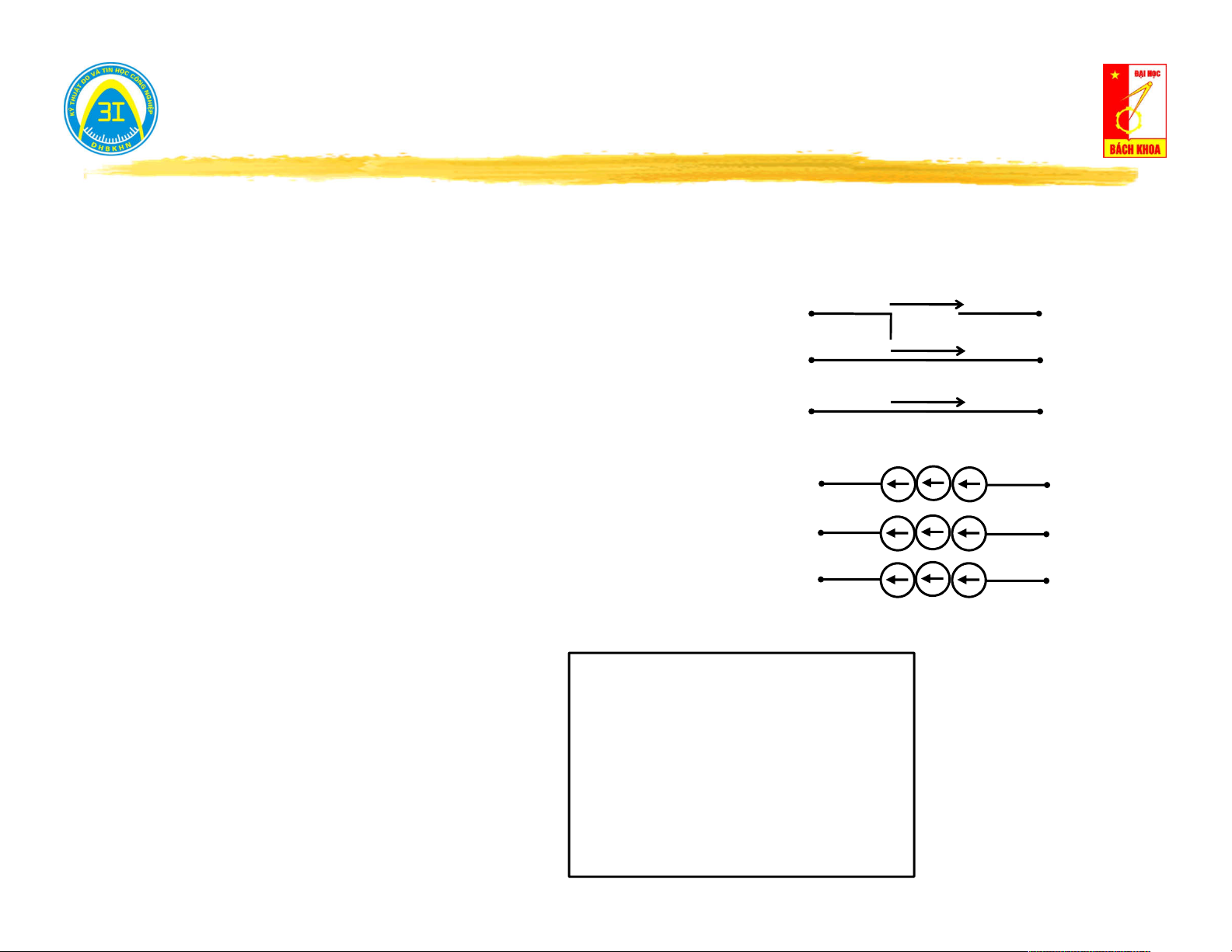
Phương trình trạng thái: i(t) = j(t) j(t) j(t) i(t) i(t) Rng Ký hiệu: Nguồn lý tưởng Nguồn thực (R = ∞) (R < ∞) ng ng
(Chiều của mũi tên là chiều dương quy ước của dòng điện sinh ra bởi nguồn)
Cách nối: Tránh hở mạch nguồn dòng
2014 - Lý thuyết mạch điện 1 - Nguyễn Việt Sơn 9
Chương 1: Khái niệm về mô hình mạch Kirchhoff II.1. Nguồn điện
Nguồn dòng phụ thuộc (nguồn dòng bị điều khiển)
Định nghĩa: Nguồn dòng phụ thuộc là nguồn dòng mà trạng thái dòng điện
của nó phụ thuộc vào trạng thái (dòng điện, điện áp) của một nhánh khác trong mạch.
Ký hiệu: i(t) = j(t) i(t) = j(t) Phân loại: i (t) 1 u (t) 1 j (t) = Y.u (t) j (t) = α.i (t) 2 1 2 1
nguồn dòng bị điều khiển bởi áp
nguồn dòng bị điều khiển bởi dòng
(voltage-controlled current source)
(current-controlled current source)
2014 - Lý thuyết mạch điện 1 - Nguyễn Việt Sơn 10
Chương 1: Khái niệm về mô hình mạch Kirchhoff
II.2. Phần tử tiêu tán - Điện trở R - Điện dẫn g.
Hiện tượng: Khi có một dòng điện chạy qua một vật dẫn điện → vật dẫn nóng
lên do có sự chuyển hóa điện năng thành nhiệt năng. Ví dụ: Bếp điện, bàn là …
Định nghĩa: Điện trở (điện dẫn) là đại lượng đo khả năng cản trở (dẫn) dòng điện của vật dẫn.
Biến trạng thái: u(t), i(t) u (t) i (t) r g
Phương trình trạng thái: i (t) u (t) [V] [ ] A r [] g [S ] [A] [V ] Thứ nguyên: [Ω]
Đơn vị dẫn xuất: 1KΩ = 103Ω, 1MΩ = 106Ω
2014 - Lý thuyết mạch điện 1 - Nguyễn Việt Sơn 11
Chương 1: Khái niệm về mô hình mạch Kirchhoff
II.2. Phần tử tiêu tán - Điện trở R - Điện dẫn g. Phân loại:
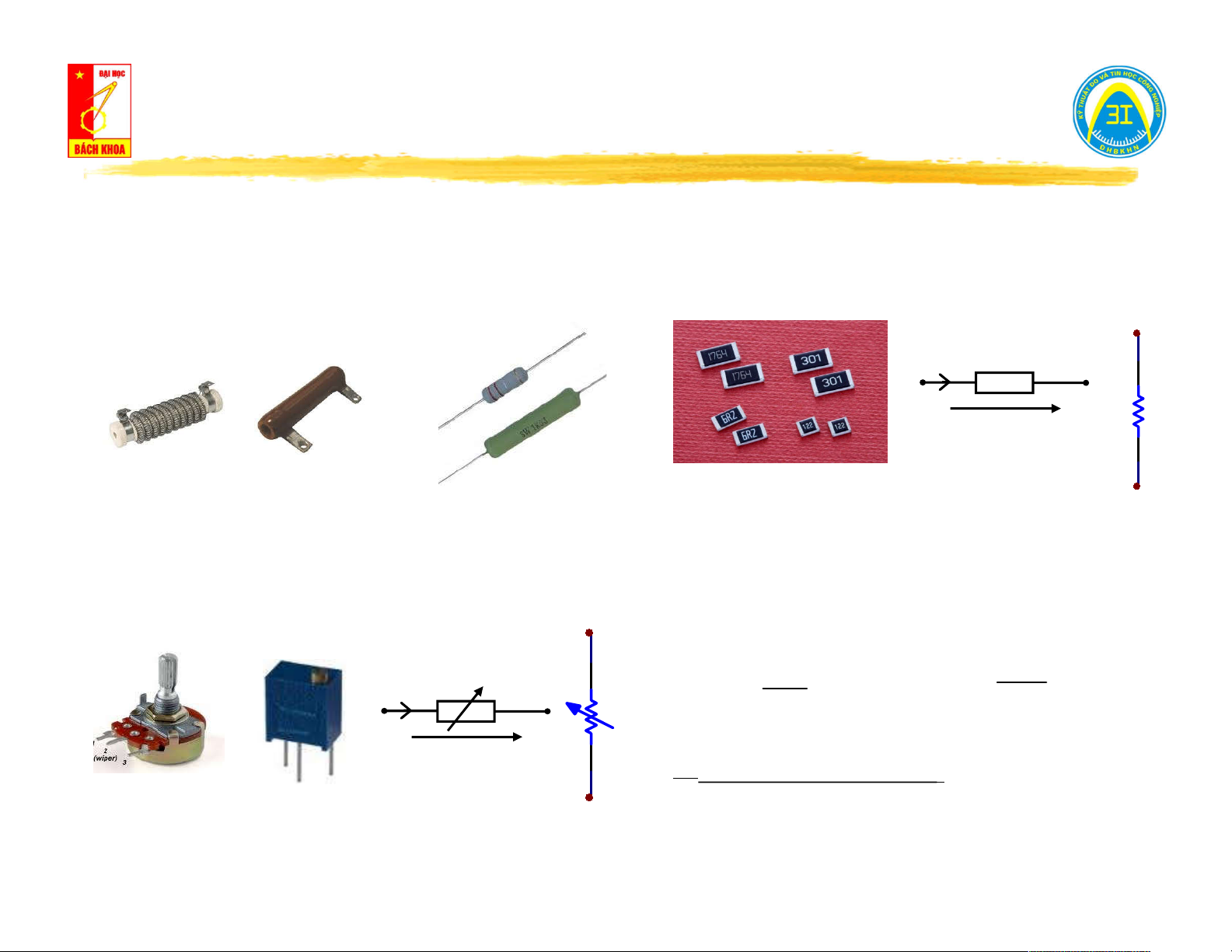
Điện trở (fixed resistor): i(t) R R u(t) Điện trở dây quấn Điện trở composition Điện trở dán Ký hiệu (giá trị nhỏ) (giá trị lớn) (độ chính xác cao)
Biến trở (variable resistor):
Điện trở tuyến tính: ( u t) ( i t) i(t) R r const g const R ( i t) ( u t) u(t) Điện trở phi tuyến: Ký hiệu
r R(u,i)
g G(u, i)
2014 - Lý thuyết mạch điện 1 - Nguyễn Việt Sơn 12
Chương 1: Khái niệm về mô hình mạch Kirchhoff
II.3. Kho điện - Điện dung C.
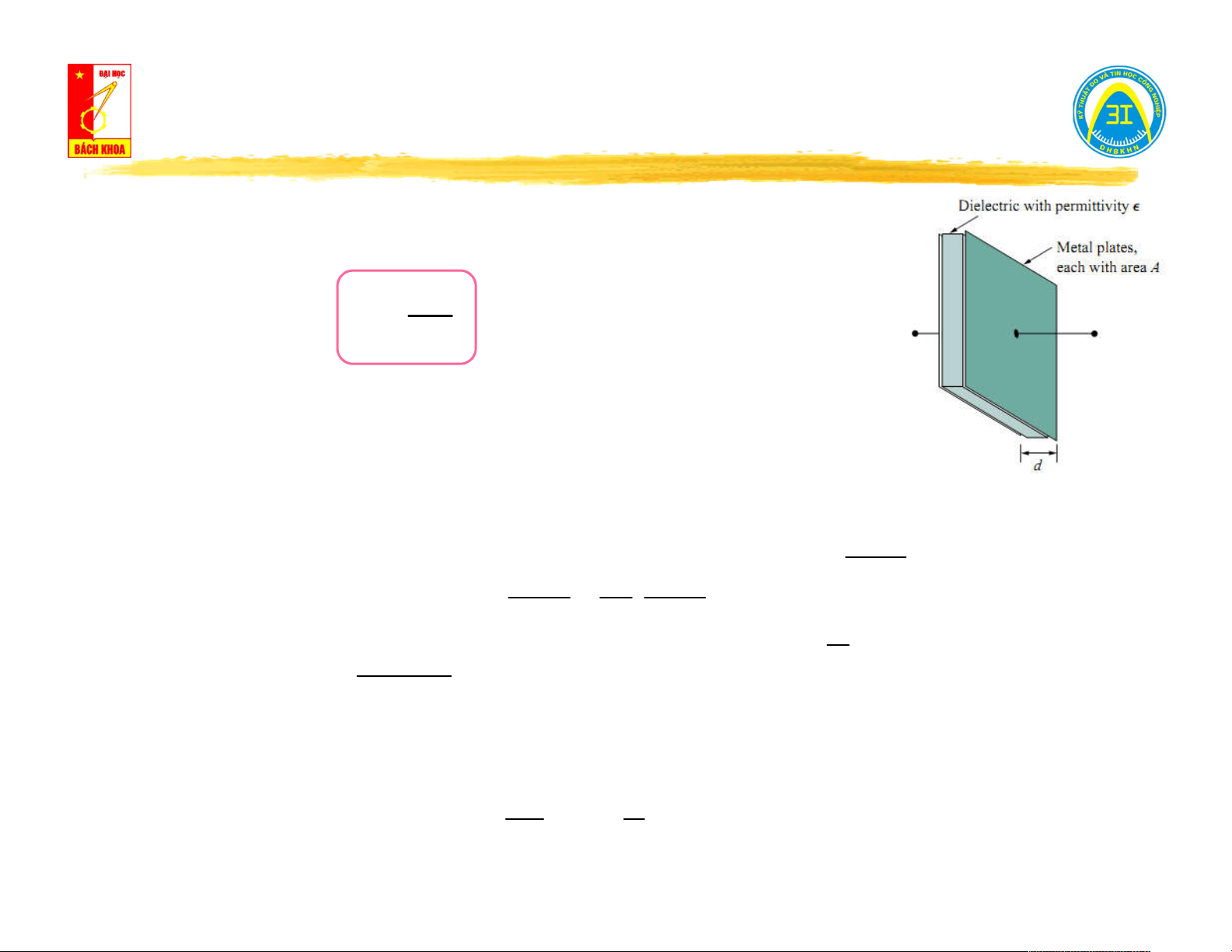
A: diện tích bề mặt bản cực Hiện tượng: A C
d: khoảng cách 2 bản cực d
ɛ: hệ số điện môi
Định nghĩa: Điện dung C là thông số đặc trưng cho khả năng
tích lũy điện tích của kho điện.
Biến trạng thái: u(t), i(t) d ( u ) t ( i ) t C d ( q t) q ( u t)
Phương trình trạng thái: ( i t) . dt dt u t 1 ( u t) ( i t)dt [Culon]
Thứ nguyên: C [F ] C [V]
Đơn vị dẫn xuất: 1µF = 10-6F 1nF = 10-9F 1pF = 10-12F q 1 2
Năng lượng: dw . u dq u .du .C.du E u 2
2014 - Lý thuyết mạch điện 1 - Nguyễn Việt Sơn 13
Chương 1: Khái niệm về mô hình mạch Kirchhoff
II.3. Kho điện - Điện dung C. Phân loại:
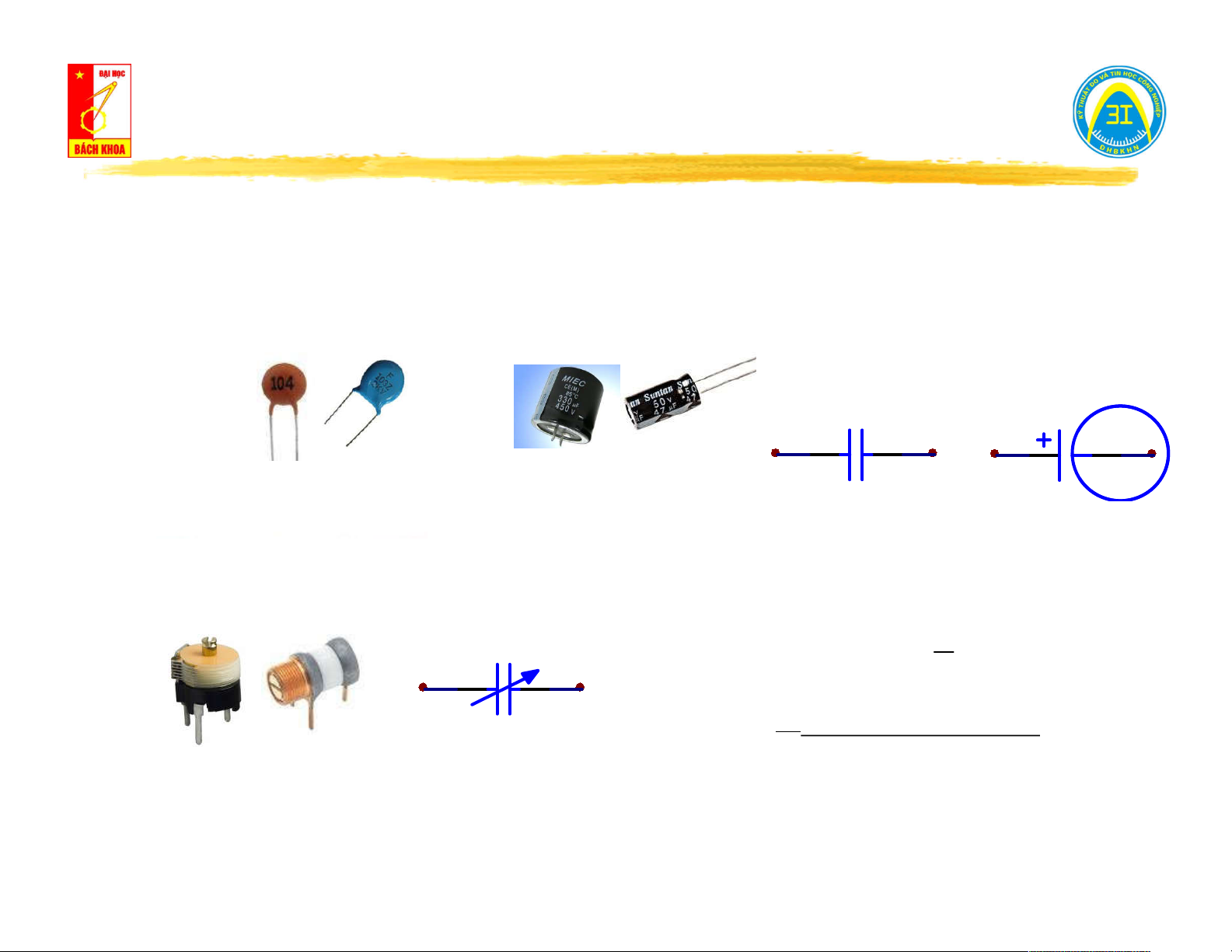
Tụ điện (fixed capacitor): C C Tụ gốm Tụ hóa
(nhỏ, không phân cực)
(lớn, phân cực) Ký hiệu
Tụ điện biến thiên (variable capacitor):
Tụ điện tuyến tính: q C C const u Tụ điện phi tuyến: Ký hiệu Trimmer capacitor
C C(q, u)
2014 - Lý thuyết mạch điện 1 - Nguyễn Việt Sơn 14
Chương 1: Khái niệm về mô hình mạch Kirchhoff
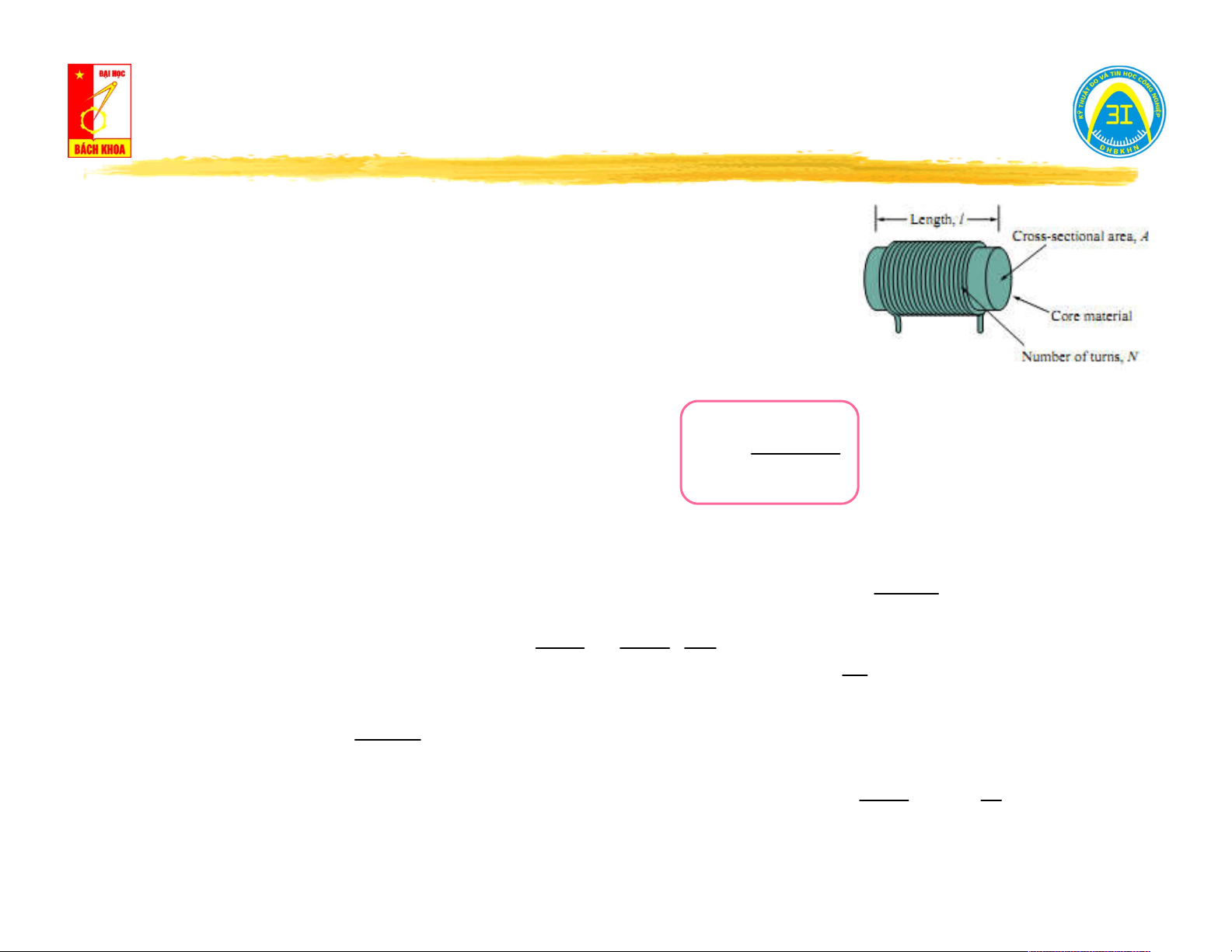
II.4. Kho từ - Điện cảm L - Hỗ cảm M.
Hiện tượng: Khi dây dẫn (cuộn dây) có dòng điện biến
thiên chảy qua trong vùng lân cận của vật dẫn tập
trung một từ trường (kho từ).
Định nghĩa: Điện cảm L là thông số đặc
N: số vòng dây cuốn N 2 A l: chiều dài lõi
trưng cho khả năng tích lũy năng lượng L l
A: tiết diện ngang lõi
từ trường của cuộn dây.
μ: độ từ thẩm của lõi
Biến trạng thái: u(t), i(t) di(t) u(t) . L d i dt
Phương trình trạng thái: u(t) . 1 dt i t i(t) u(t).dt L [Wb]
Thứ nguyên: L [H ] Năng lượng: [A] 1 2 dw . i d i .di . . L di
Đơn vị dẫn xuất: 1mH = 10-3H L i 2
2014 - Lý thuyết mạch điện 1 - Nguyễn Việt Sơn 15
Chương 1: Khái niệm về mô hình mạch Kirchhoff
II.4. Kho từ - Điện cảm L - Hỗ cảm M. Phân loại:
Cuộn dây lõi sắt từ
Cuộn dây lõi không khí L i(t)
Cuộn dây tuyến tính: L =const I u(t)
Cuộn dây phi tuyến: L L( , I )
2014 - Lý thuyết mạch điện 1 - Nguyễn Việt Sơn 16
Chương 1: Khái niệm về mô hình mạch Kirchhoff
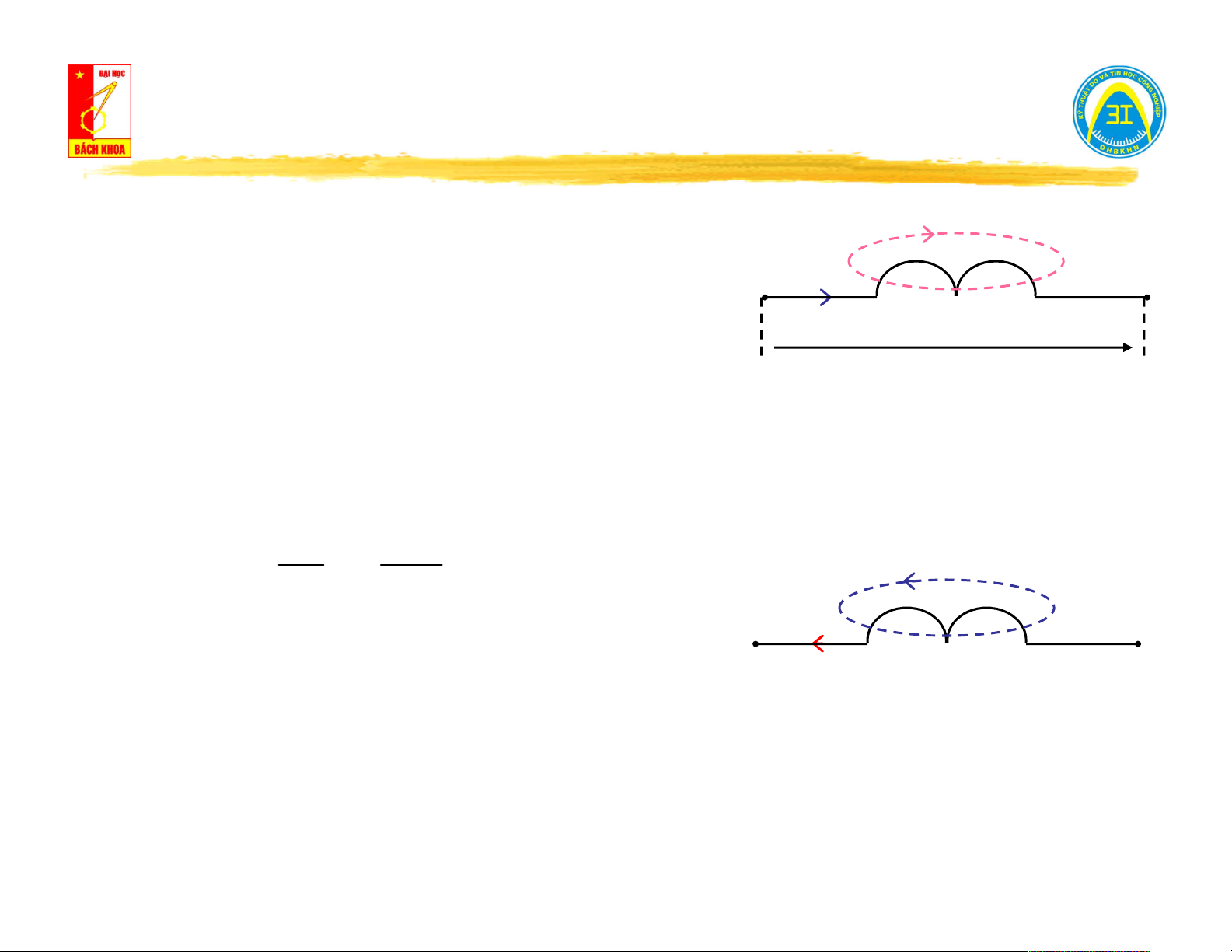
II.4. Kho từ - Điện cảm L - Hỗ cảm M. Ψ(t) L
Hiện tượng tự cảm: i(t)
Xét cuộn dây L, có dòng điện biến thiên i(t). u (t) tc
Luật Lenx: i(t) sinh ra từ thông ψ(t) biến thiên, chống lại sự biến thiên của
i(t) (chiều ψ(t) xác định theo quy tắc vặn nút chai (quy tắc bàn tay phải).
Từ thông ψ(t) sinh ra suất điện động tự cảm u (t) trên cuộn dây. tc d di(t) u (t) L Ψ(t)
L : hệ số tự cảm tc dt dt L
Ngược lại: xét cuộn dây đặt trong không i(t)
gian có từ thông ψ(t) biến thiên.
Từ thông ψ(t) sinh ra suất điện trên cuộn dây sinh ra dòng điện tự cảm
i (t), chống lại sự biến thiên của ψ(t) (chiều của dòng điện tự cảm được xác tc
định theo quy tắc vặn nút chai).
2014 - Lý thuyết mạch điện 1 - Nguyễn Việt Sơn 17
Chương 1: Khái niệm về mô hình mạch Kirchhoff
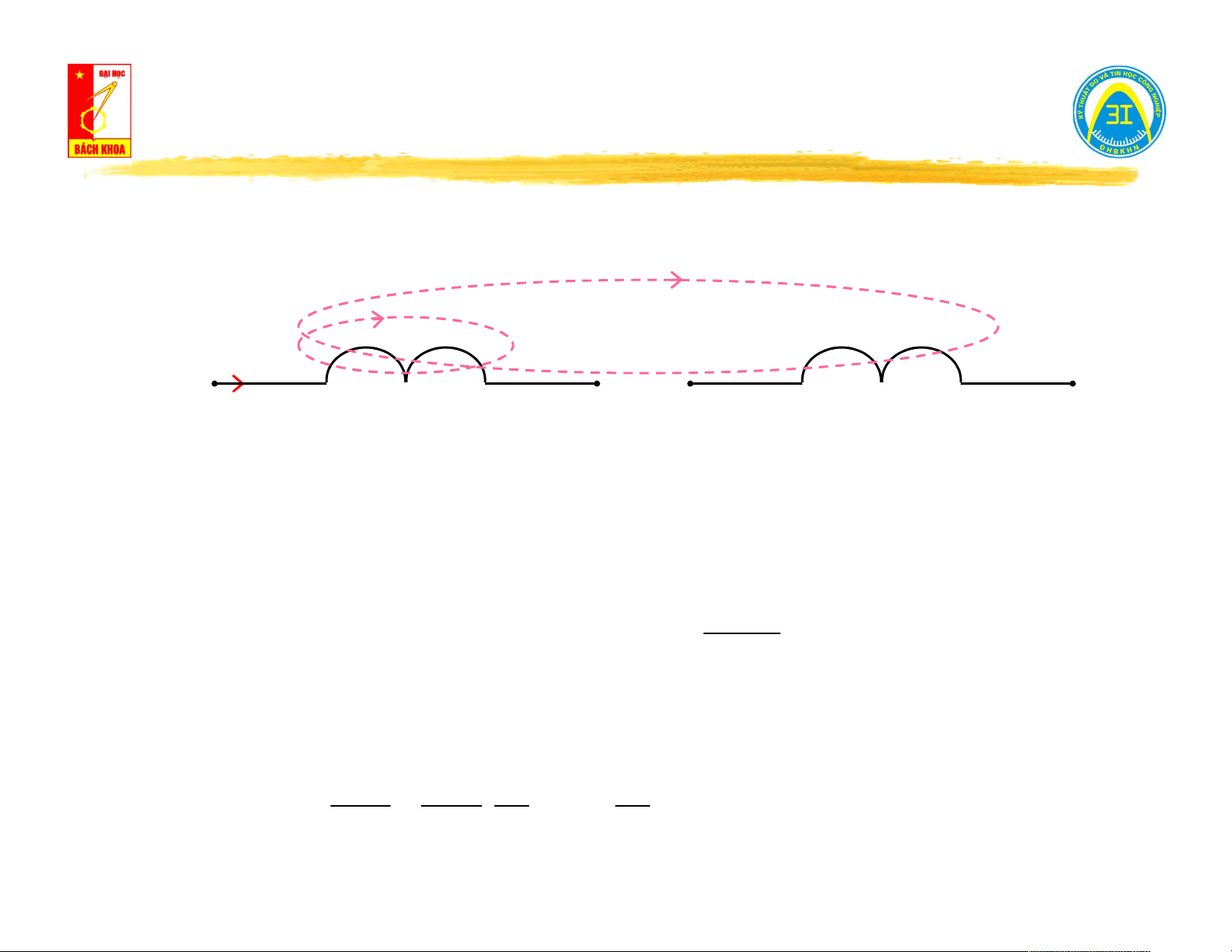
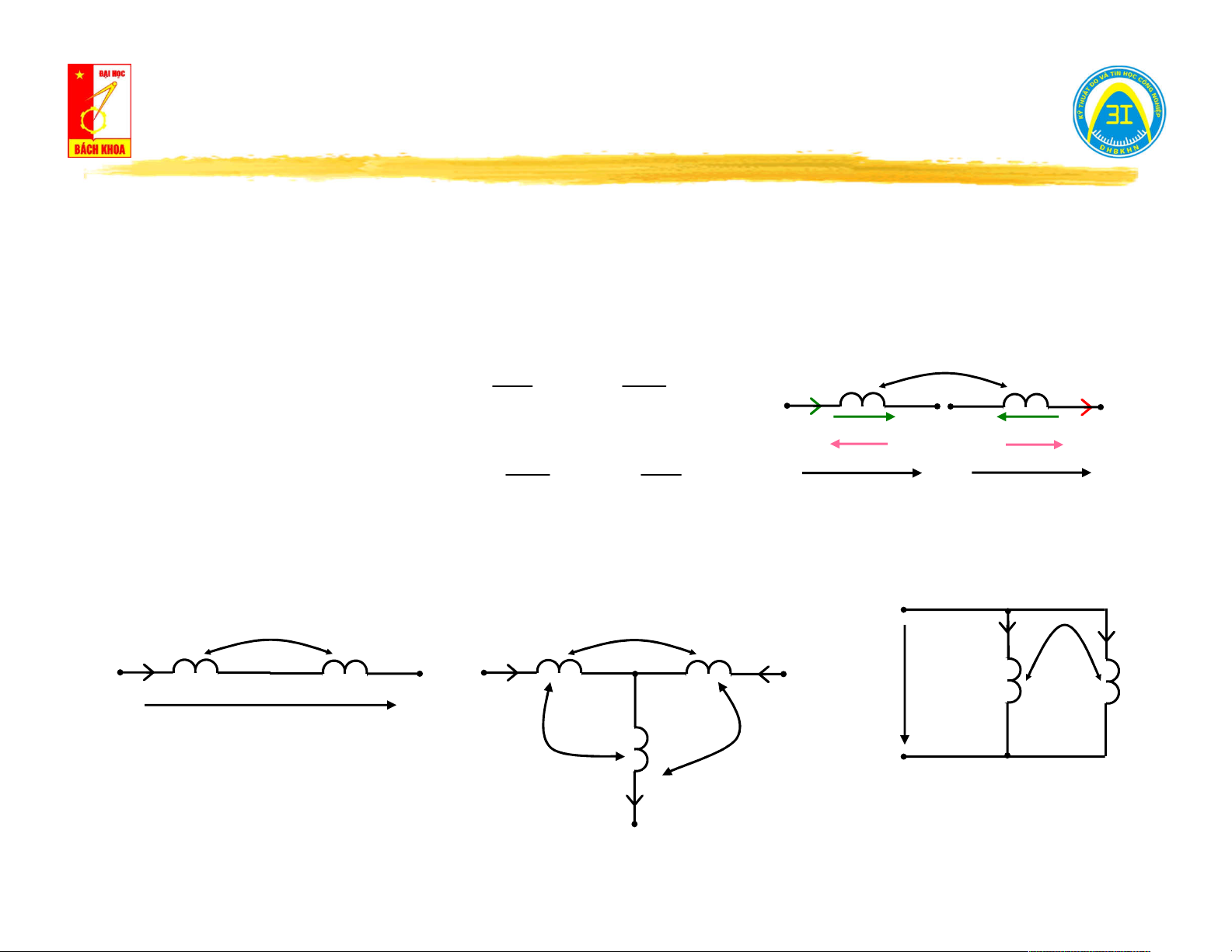
II.4. Kho từ - Điện cảm L - Hỗ cảm M. Ψ (t)
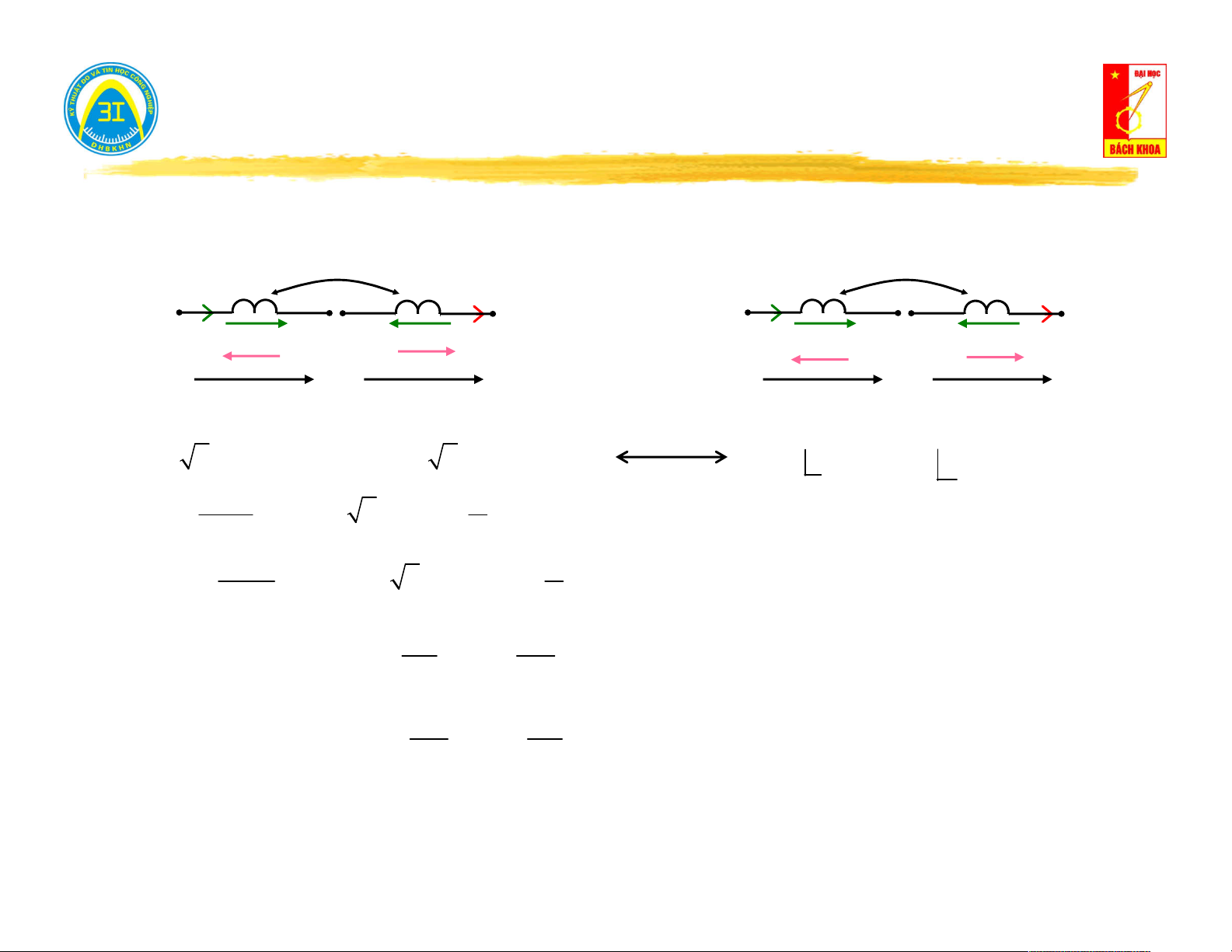
Hiện tượng hỗ cảm: 21 Ψ (t) 11 L1 L2 i (t) 1 u (t) u (t) 11 21
Xét cuộn dây L và L đặt gần nhau trong không gian, cuộn dây L có dòng 1 2 1
điện biến thiên i (t). 1
Luật Lenx: i (t) sinh ra từ thông ψ (t) biến thiên qua cuộn L → sinh ra điện 1 11 1 áp tự cảm u (t). 11 di (t) 1
u (t) L . 11 1 dt
Do L đặt gần L , một phần từ thông ψ (t) biến thiên qua cuộn dây L → 2 1 21 2
sinh ra sức điện động cảm ứng u (t). 21 d di di 21 21 1 1 u (t) . M .
M : hệ số hỗ cảm 21 21 21 dt i dt dt 1
2014 - Lý thuyết mạch điện 1 - Nguyễn Việt Sơn 18
Chương 1: Khái niệm về mô hình mạch Kirchhoff
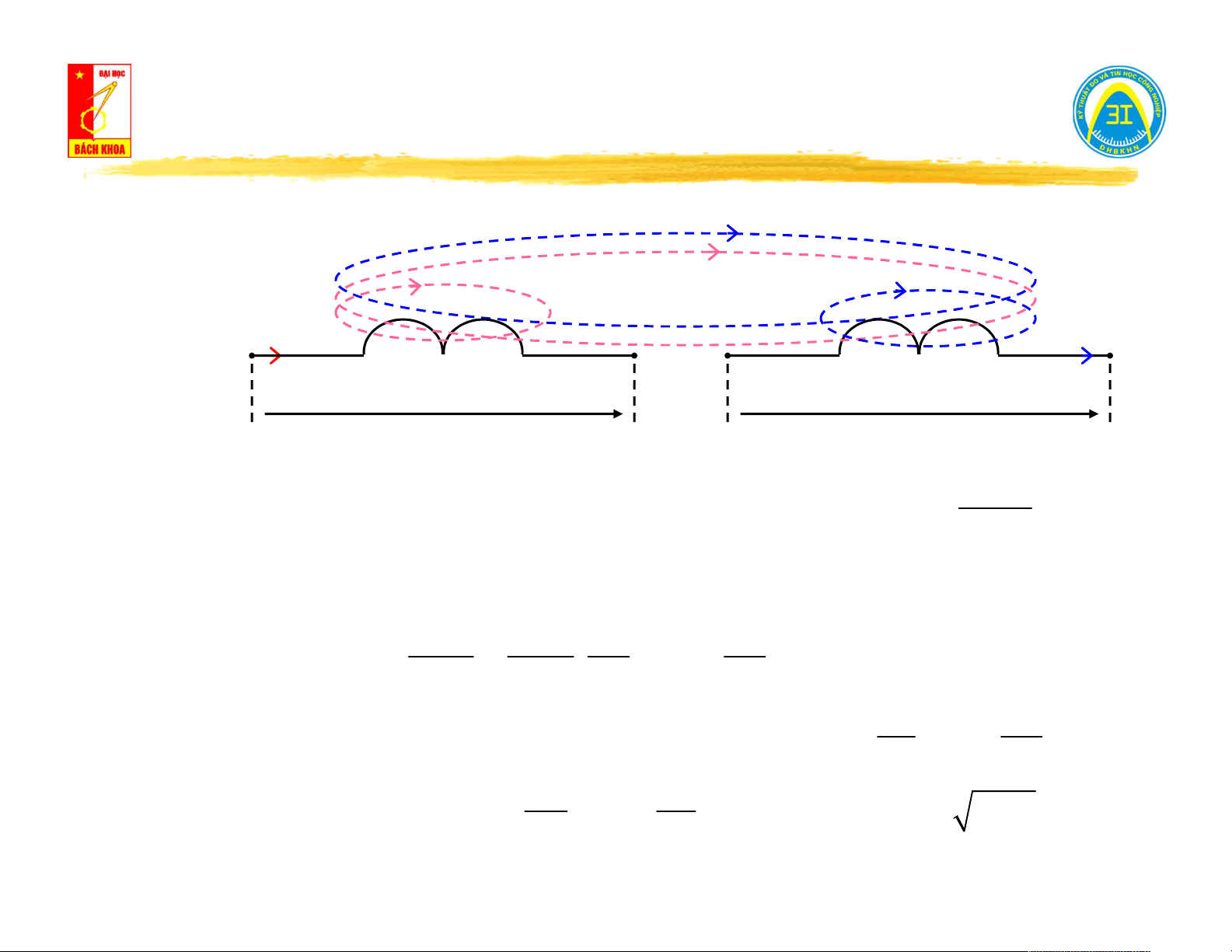
II.4. Kho từ - Điện cảm L - Hỗ cảm M. Ψ (t) 12
Hiện tượng hỗ cảm: Ψ (t) Ψ (t) 21 Ψ (t) 11 22 L1 L2 i (t) i (t) 1 2 u (t) u (t) u (t) u (t) 11 12 21 22 u (t) u (t) 1 2
Nếu L có i (t) chạy qua → sinh ra ψ (t) móc 2 2 22 di (t) 2
u (t) L . 22 2
vòng qua L → sinh ra điện áp cảm ứng u (t) 2 22 dt
Phần ψ (t) móc vòng qua L → sinh ra suất điện động cảm ứng u (t) trên 12 1 12 cuộn L1 d di di 12 12 2 2 u (t) . M . 12 12
M : hệ số hỗ cảm dt i dt dt 12 2 di di
Điện áp tổng trên 2 cuộn dây: 1 2
u (t) u (t) u (t) L . M 1 11 12 1 12 dt dt di di 2 1
u (t) u (t) u (t) L . M M M
k. L .L 2 22 21 2 21 dt dt 12 21 1 2
2014 - Lý thuyết mạch điện 1 - Nguyễn Việt Sơn
k: hệ số quan hệ giữa L và L 19 1 2
Chương 1: Khái niệm về mô hình mạch Kirchhoff
II.4. Kho từ - Điện cảm L - Hỗ cảm M.
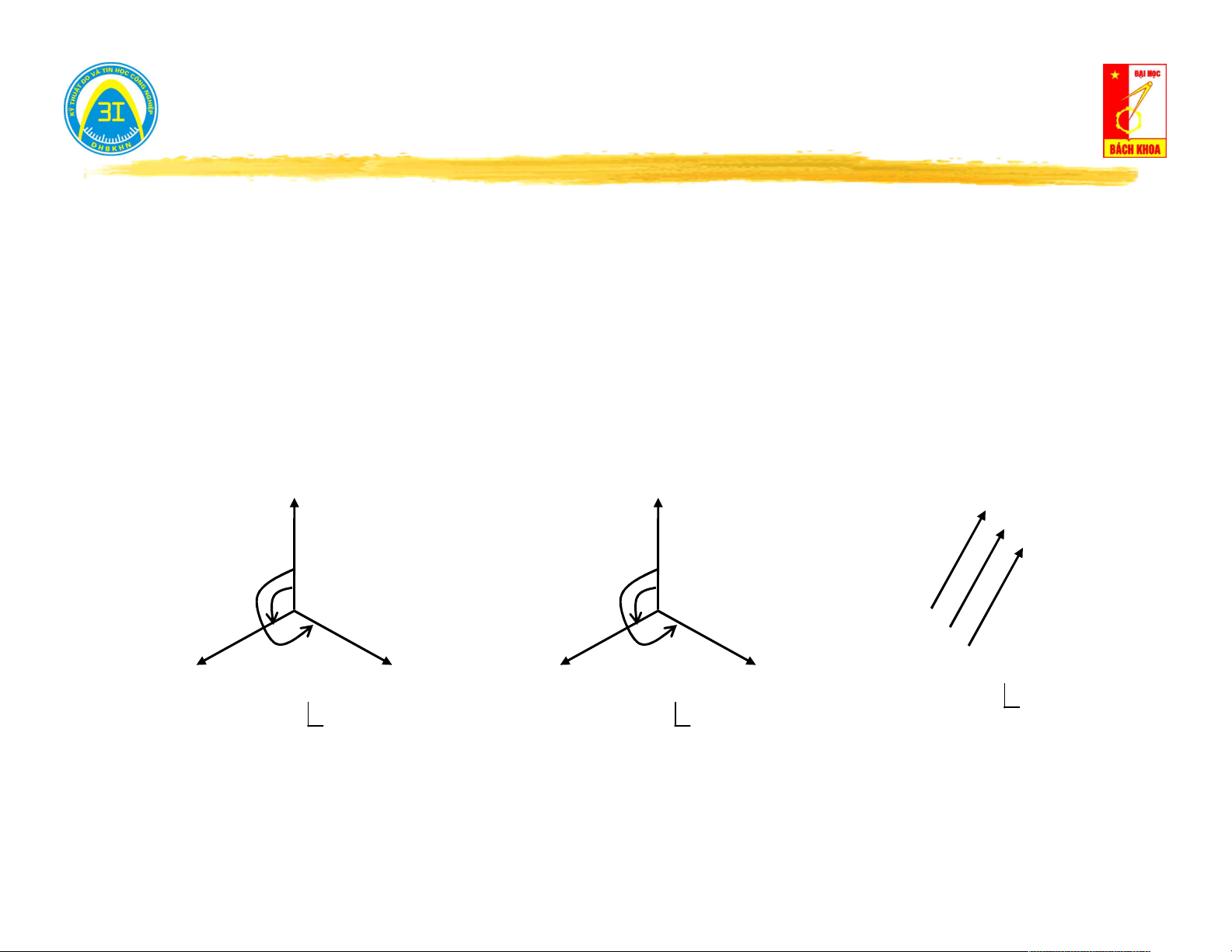
Cực tính của cuộn dây:
Thực tế: Cuộn dây không có cực tính. Để xác định chiều điện áp tự cảm & hỗ
cảm sử dụng khái niệm cực tính của cuộn dây
Trong không gian: Chiều của từ thông được xác định theo quy tắc vặn nút
chai (quy tắc bàn tay phải): Nếu biết chiều dòng điện so với chiều cuốn của
cuộn dây xác định được chiều điện áp
Trong sơ đồ: Mất thông tin chiều quấn của cuộn dây → dùng dấu * để đánh
dấu và quy ước: Chiều điện áp tự cảm và điện áp hỗ cảm sẽ luôn cùng
chiều với chiều của dòng điện sinh ra nó.
2014 - Lý thuyết mạch điện 1 - Nguyễn Việt Sơn 20
Chương 1: Khái niệm về mô hình mạch Kirchhoff
II.4. Kho từ - Điện cảm L - Hỗ cảm M.
Ví dụ 1.1: Xét cuộn dây L và L đặt cạnh nhau, giữa chúng có hỗ cảm M = M . 1 2 12 21 Tính u (t), u (t). 1 2 M di di 1 2 i (t) L L 1 1 2 i (t) 2
u (t) u (t) u (t) L M * * 1 11 12 1 12 dt dt u (t) 11 u (t) u (t) u (t) 12 21 22 di di 2 1
u (t) u (t) u (t) L M 2 22 21 2 21 u (t) u (t) 1 2 dt dt
Ví dụ 1.2: Tính điện áp trong các trường hợp sau. i (t) M 2 L M L 12 i (t) i(t) 1 L 1 L u(t) 2 * 2 1 i (t) i (t) M * * 1 * * 2 = L2 u (t) = ? u (t) = ? 1 2 ? L * 1 * u(t) = ? M12 L M23 3 u (t) = ? 3 i (t) 3
2014 - Lý thuyết mạch điện 1 - Nguyễn Việt Sơn 21
LÝ THUYẾT MẠCH ĐIỆN 1
Chương 1: Khái niệm về mô hình mạch Kirchhoff
I. Khái niệm về mô hình trường - mô hình hệ thống.
II. Các hiện tượng cơ bản trong mô hình mạch Kirchhoff.
III. Các luật cơ bản trong mô hình mạch Kirchhoff. III.1. Luật Ohm.
III.2. Luật Kirchhoff 1 & 2.
III.3. Luật cân bằng công suất.
IV. Nội dung bài toán mạch.
2014 - Lý thuyết mạch điện 1 - Nguyễn Việt Sơn 22
Chương 1: Khái niệm về mô hình mạch Kirchhoff III.1. Luật Ohm.
Phát biểu: Luật Ohm biểu diễn mối quan hệ giữa hai biến trạng thái dòng điện
và điện áp trên cùng một nhánh.
Số phương trình: Mạch Kirchhoff có n nhánh → Có (n) phương trình luật Ohm.
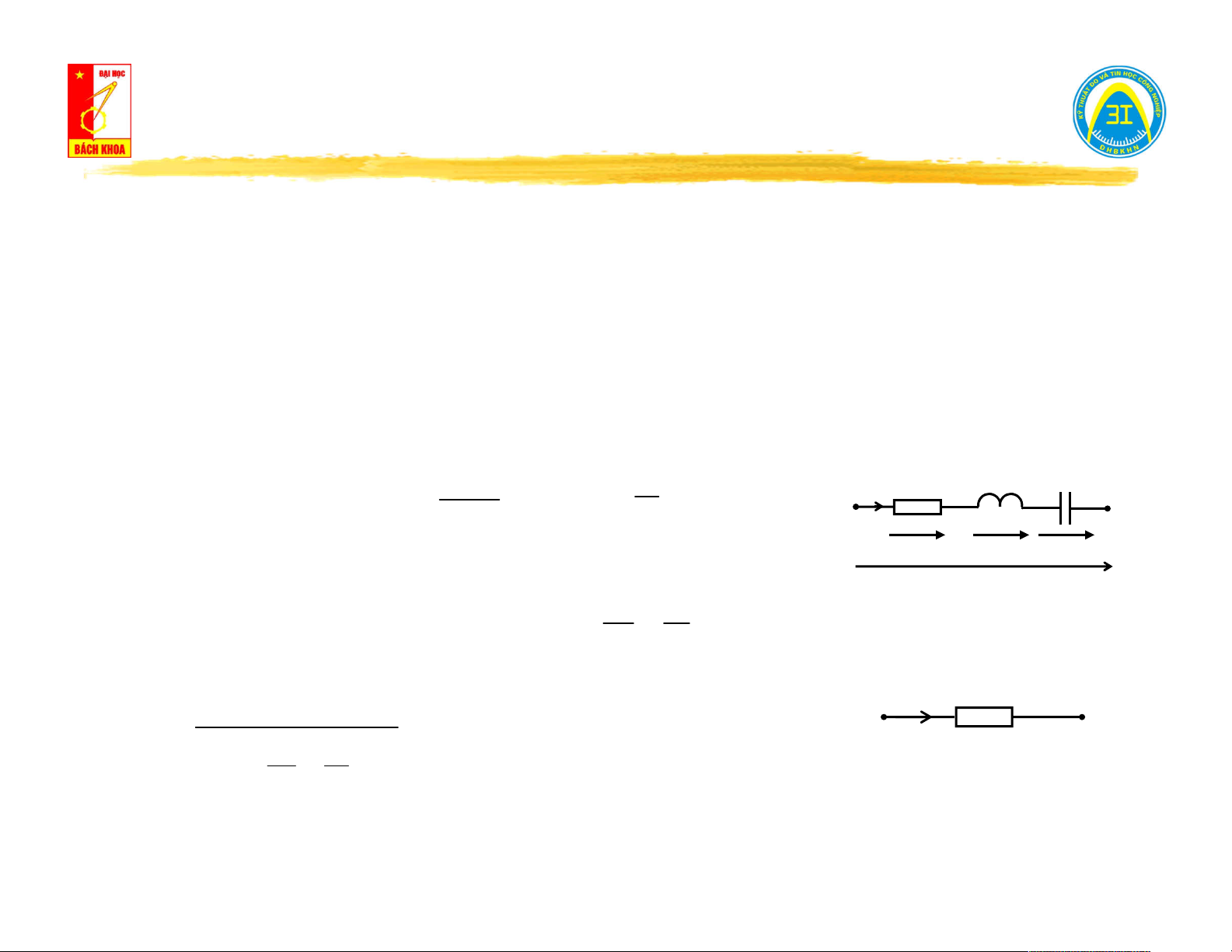
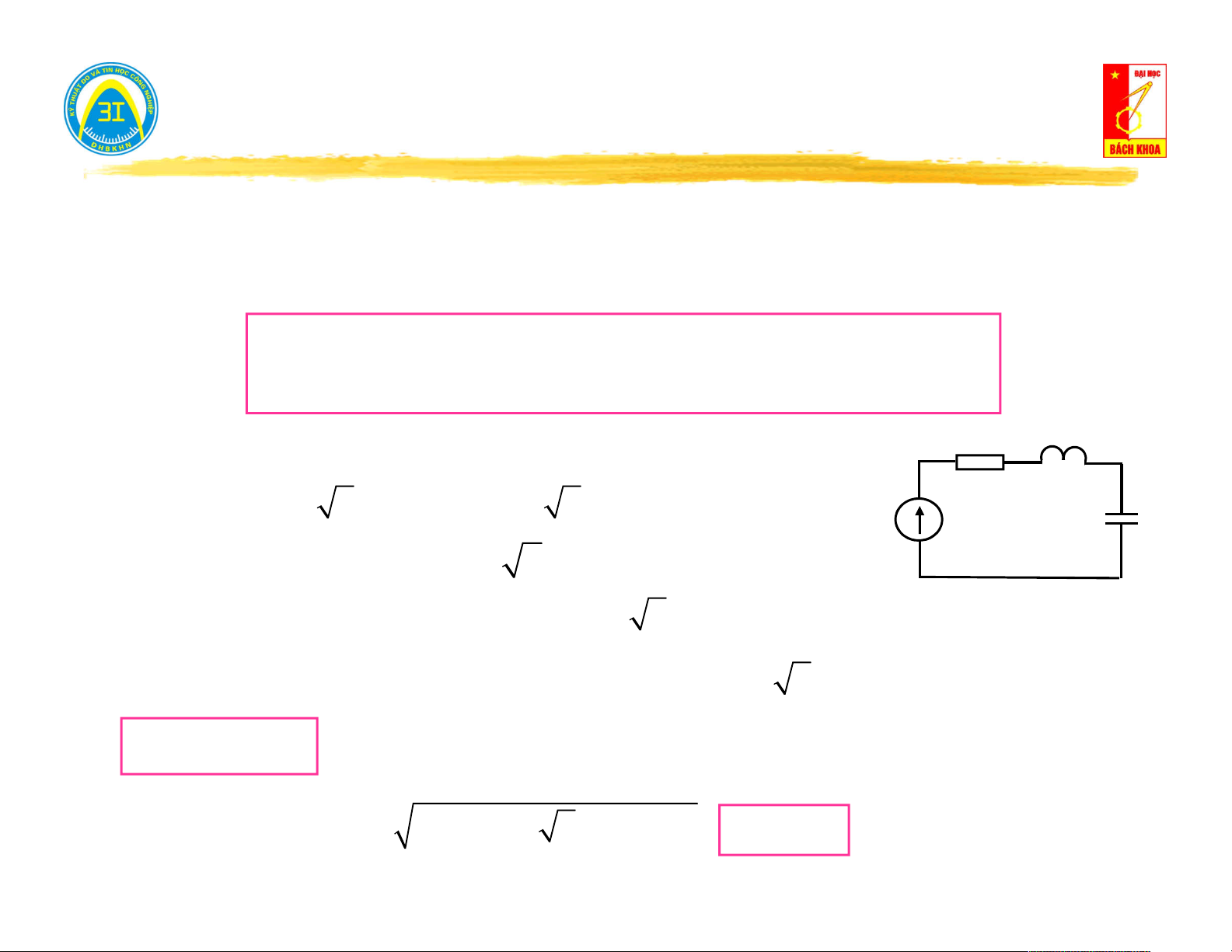
Ví dụ 1.3: Xét mạch điện như hình vẽ. Viết phương trình luật Ohm. di(t) 1 L R C i(t) u (t) . R i(t)
u (t) L u (t) i(t).dt R L C A B dt C u u u R L C u (t) AB d 1
u (t) u (t) u (t) u (t) R L
dt .i(t) Z .i(t) AB R L C AB dt C Z i(t) AB A B 1 i(t)
u (t) Y .u (t) d 1 AB AB AB u (t) AB R L dt dt C
Z : Tổng trở tương đương nhánh AB AB
Y : Tổng dẫn tương đương nhánh AB AB
2014 - Lý thuyết mạch điện 1 - Nguyễn Việt Sơn 23
Chương 1: Khái niệm về mô hình mạch Kirchhoff III.1. Luật Ohm.
Ví dụ 1.4: Viết phương trình luật Ohm cho mạch điện. 1
i (t) g.u (t) du (t) i (t) u (t).dt g AB L AB
i (t) C. AB L C dt A i(t) ig i i L C 1 d u (t) AB g
i(t) i (t) i (t) i (t) g dt C .u (t) L C g L C AB L dt
i(t) Y .u (t) AB AB B i(t) 1 A u (t)
.i(t) Z .i(t) AB 1 AB d g dt C L dt u (t) AB YAB
Y : Tổng dẫn tương đương nhánh AB B AB
Z : Tổng trở tương đương nhánh AB AB
2014 - Lý thuyết mạch điện 1 - Nguyễn Việt Sơn 24
Chương 1: Khái niệm về mô hình mạch Kirchhoff
III.2. Luật Kirchhoff 1 và Kirchhoff 2.
Luật Kirchhoff 1: Tổng các dòng điện tại một nút bằng không, với quy ước:
Dòng điện đi vào nút mang dấu âm. i (t) 0 k
Dòng điện đi ra nút mang dấu dương. nut
Luật Kirchhoff 2: Tổng điện áp trong một vòng kín bằng không, với quy ước:
Điện áp cùng chiều vòng kín mang dấu dương u (t) 0 k
Điện áp ngược chiều vòng kín mang dấu âm. vong
Chú ý: Mạch Kirchhoff có n nhánh và d đỉnh → Số phương trình cần và đủ:
Luật K1: d-1 phương trình.
Luật K2: n-d+1 phương trình
Luật cân bằng công suất: Tổng công suất p (t) 0 k
trong một hệ kín bằng không hekin
2014 - Lý thuyết mạch điện 1 - Nguyễn Việt Sơn 25
Chương 1: Khái niệm về mô hình mạch Kirchhoff
III.2. Luật Kirchhoff 1 và Kirchhoff 2.
Ví dụ 1.5: Lập phương trình theo luật K1 & K2 cho mạch điện. j (t) 4 Luật Ohm: L C R 1 1 i (t) 1 R4 4 d 1 d 1
u (t) (R L dt).i (t)
u (t) (R L dt).i (t) 1 1 1 1 dt C 2 2 2 2 dt C 1 2 C i (t) 2 1 d 1 L3
u (t) (L dt).i (t)
u (t) R .i (t) 3 3 3 4 4 4 dt C3 L2 C3 i
(t) i (t) i (t) j (t) 0 i (t) 2 i (t) Luật K1: 1 2 4 4 e (t) 3 1 i
(t) i (t) j (t) 0 R 3 4 4 2 e (t) 3
u (t) u (t) e (t) 1 2 1
Luật K2: u (t) u (t) u (t) e (t) 2 3 4 3
Số đỉnh: d = 3. Số nhánh: n = 4 i
i i j 0 Số pt luật Ohm: n = 4 pt Biến là dòng 1 2 4 4 các nhánh: i
i j 0 3 4 4
Số pt luật K1: d - 1 = 2 pt. d 1 d 1
Số pt luật K2: n - d + 1 = 2 pt (R L
dt).i (R L
dt).i e (t) 1 1 1 2 2 2 1 dt C dt C 1 2
2n pt ↔ 2n biến (i , u ) nh nh d 1 d 1 (R L
dt).i (L
dt).i R .i e (t) 2 2 2 3 3 4 4 3 dt C dt C 2 3
2014 - Lý thuyết mạch điện 1 - Nguyễn Việt Sơn 26
LÝ THUYẾT MẠCH ĐIỆN 1
Chương 1: Khái niệm về mô hình mạch Kirchhoff
I. Khái niệm về mô hình trường - mô hình hệ thống.
II. Các hiện tượng cơ bản trong mô hình mạch Kirchhoff.
III. Các luật cơ bản trong mô hình mạch Kirchhoff.
IV. Nội dung bài toán mạch.
2014 - Lý thuyết mạch điện 1 - Nguyễn Việt Sơn 27
Chương 1: Khái niệm về mô hình mạch Kirchhoff
V. Nội dung bài toán mạch.
Sơ đồ mạch Kirchhoff mô tả với các biến nhánh cùng các luật K1, K2, luật Ohm được sử
dụng nhằm nghiên cứu các quá trình năng lượng trên các thiết bị điện.
Có hai loại bài toán mạch:
Bài toán tổng hợp: Là bài toán cho biết tính quy luật của quan hệ giữa các tín hiệu
dòng, áp hoặc cho biết những nghiệm dòng, áp cần có ứng với những kích thích cụ
thể. Yêu cầu cần lập phương trình của hệ hoặc thiết kế mạch với kết cấu và thông số
cụ thể cho phép thực hiện được những quy luật đó.
Bài toán phân tích mạch: Là bài toán cho một thiết bị điện hoặc sơ đồ mạch của nó
với kết cấu và thông số đã biết, cần lập phương trình mạch, dựa vào đó khảo sát các
hiện tượng và quan hệ giữa các biến hoặc tìm lời giải về một số biến, dòng áp cụ thể.
Bài toán phân tích liên quan tới việc khảo sát định tính, định lượng một hệ phương
trình vi tích phân hoặc giải nghiệm cụ thể.
Học phần này chú trọng xét bài toán phân tích và chỉ nêu sơ lược về bài toán tổng hợp.
2014 - Lý thuyết mạch điện 1 - Nguyễn Việt Sơn 28
LÝ THUYẾT MẠCH ĐIỆN 1
Chương 2: Mạch tuyến tính ở chế độ xác lập điều hòa I.
Hàm điều hòa & các đại lượng đặc trưng II.
Số phức - Biểu diễn hàm điều hòa trong miền ảnh phức
III. Phản ứng của một nhánh với kích thích điều hòa.
IV. Dạng phức các luật cơ bản trong mạch Kirchhoff.
2014 - Lý thuyết mạch điện 1 - Nguyễn Việt Sơn 1
Chương 2: Mạch tuyến tính ở chế độ xác lập điều hòa
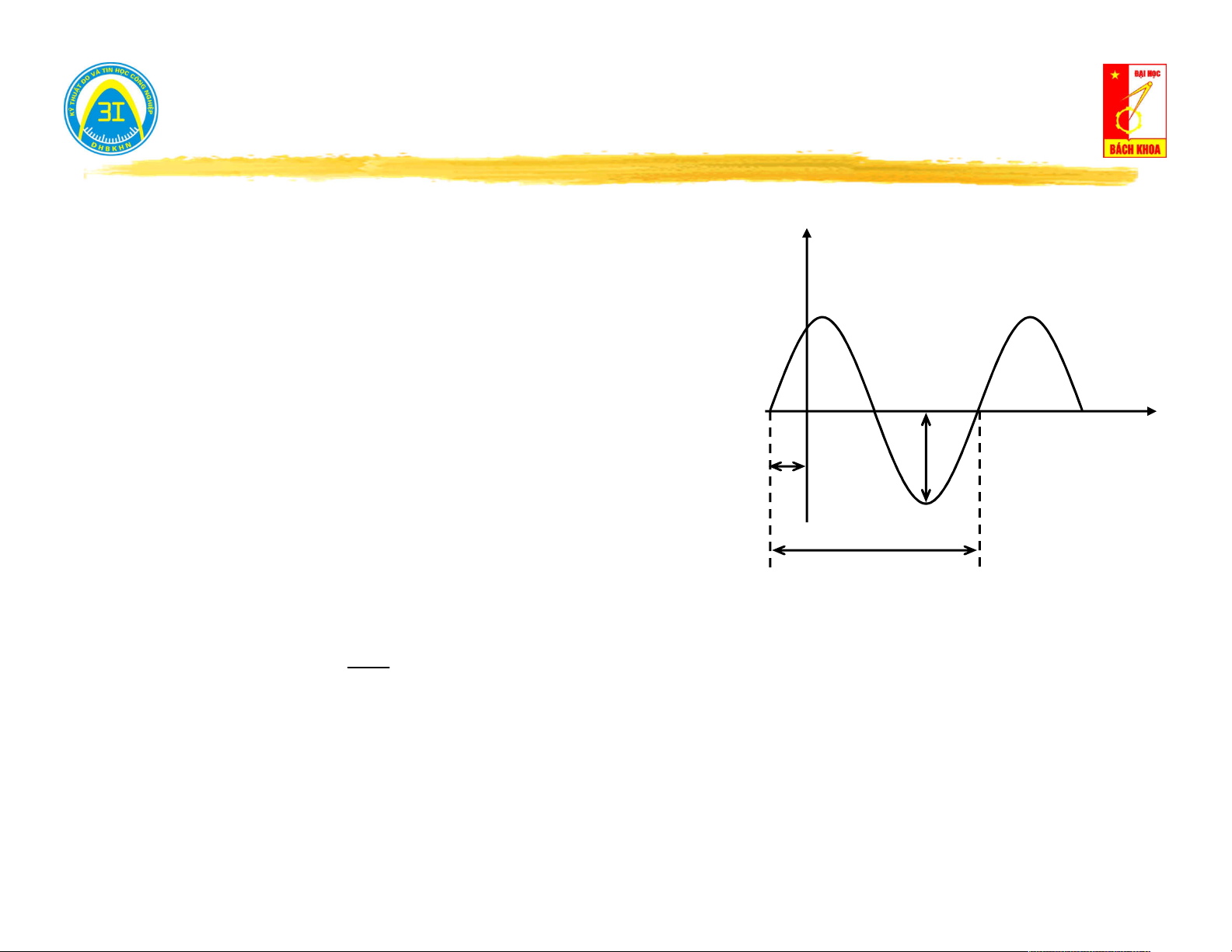
I. Hàm điều hòa và các đại lượng đặc trưng. e(t)
Hàm điều hòa là hàm sin (cos) của biến thời gian t.
Các thông số đặc trưng: t
Giá trị cực đại (hiệu dụng): I , E (I, E) m m φ Em Góc pha: ωt + φ (rad) Góc pha ban đầu: φ [rad] T Tần số góc: ω [rad/s]
Các hàm điều hòa cùng tần số 2
được phân biệt bởi 2 thông số: Chu kỳ: T [s]
Biên độ - Pha ban đầu
Biên độ - pha là cặp thông số đặc trưng của hàm điều hòa.
2014 - Lý thuyết mạch điện 1 - Nguyễn Việt Sơn 2
Chương 2: Mạch tuyến tính ở chế độ xác lập điều hòa
I. Hàm điều hòa và các đại lượng đặc trưng. 2
Biểu diễn bằng đồ thị vector: I2 I2
Độ dài vector tỷ lệ với trị hiệu dụng I 1 1 I
Góc giữa vector với trục hoành tỷ lệ với góc pha 1 1 2 0
Thực hiện các phép toán trên các hàm điều hòa cùng
tần số tương ứng việc thực hiện phép toán trên đồ I thị vector. I2
i (t) I . 2.sin(t ) 1 1 1 Ví dụ 2.1:
i(t) i (t) i (t) 1 2
i (t) I . 2.sin(t ) 2 2 2 I1
2014 - Lý thuyết mạch điện 1 - Nguyễn Việt Sơn 3
LÝ THUYẾT MẠCH ĐIỆN 1
Chương 2: Mạch tuyến tính ở chế độ xác lập điều hòa I.
Hàm điều hòa & các đại lượng đặc trưng. II.
Số phức - Biểu diễn hàm điều hòa trong miền ảnh phức II.1. Khái niệm.
II.2. Các phép toán cơ bản.
III.3. Biểu diễn các hàm điều hòa trong miền ảnh phức.
III. Phản ứng của một nhánh với kích thích điều hòa.
IV. Dạng phức các luật cơ bản trong mạch Kirchhoff.
2014 - Lý thuyết mạch điện 1 - Nguyễn Việt Sơn 4
Chương 2: Mạch tuyến tính ở chế độ xác lập điều hòa II.1. Khái niệm
Nguồn gốc: Giải phương trình bậc 2, có Deltal âm.
Số phức là một cặp 2 thành phần, số thực a, và số ảo j.b, với định nghĩa nó là tổng a + j.b,
trong đó j2 = -1, và a, b là những số thực. Im
Biểu diễn trên mặt phẳng phức: Dạng đại số:
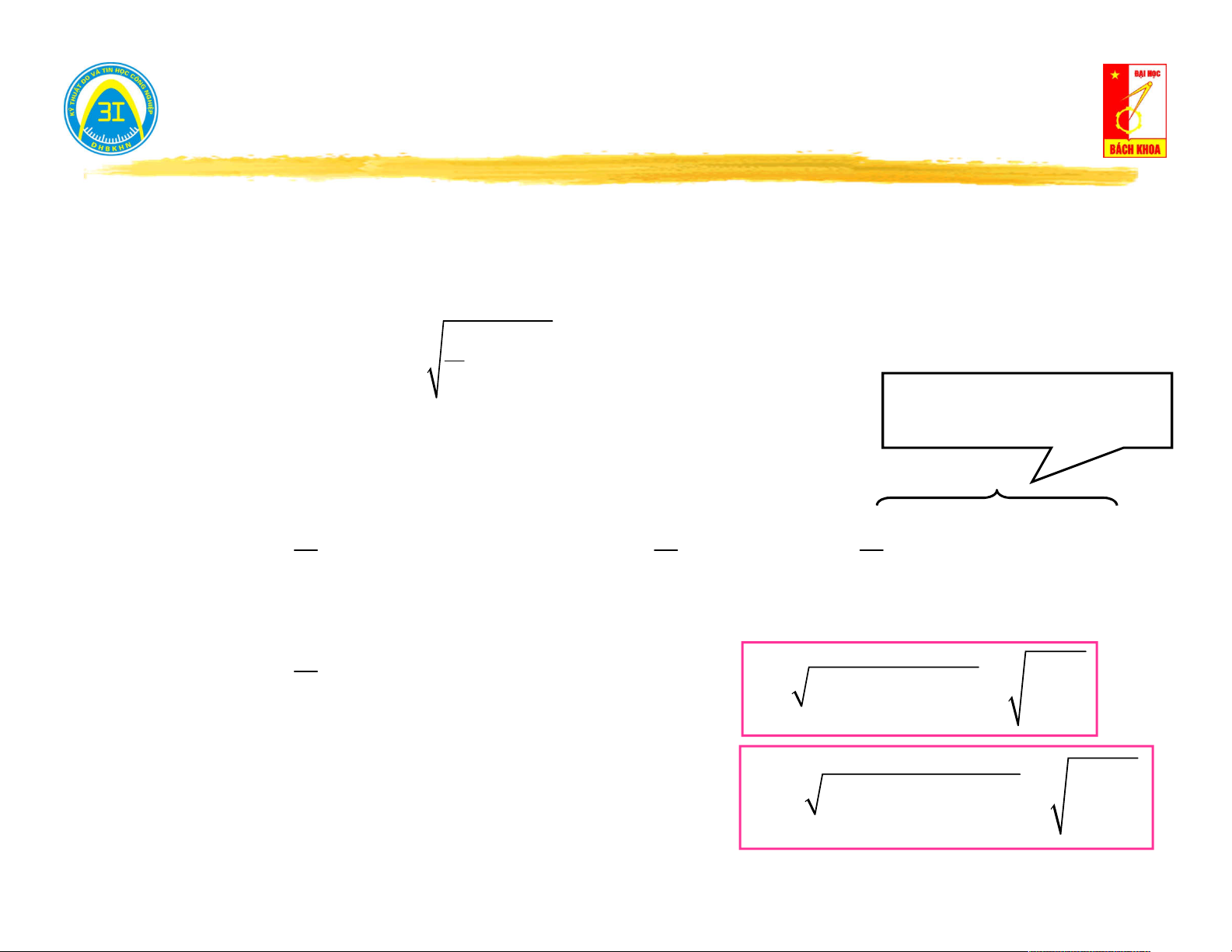
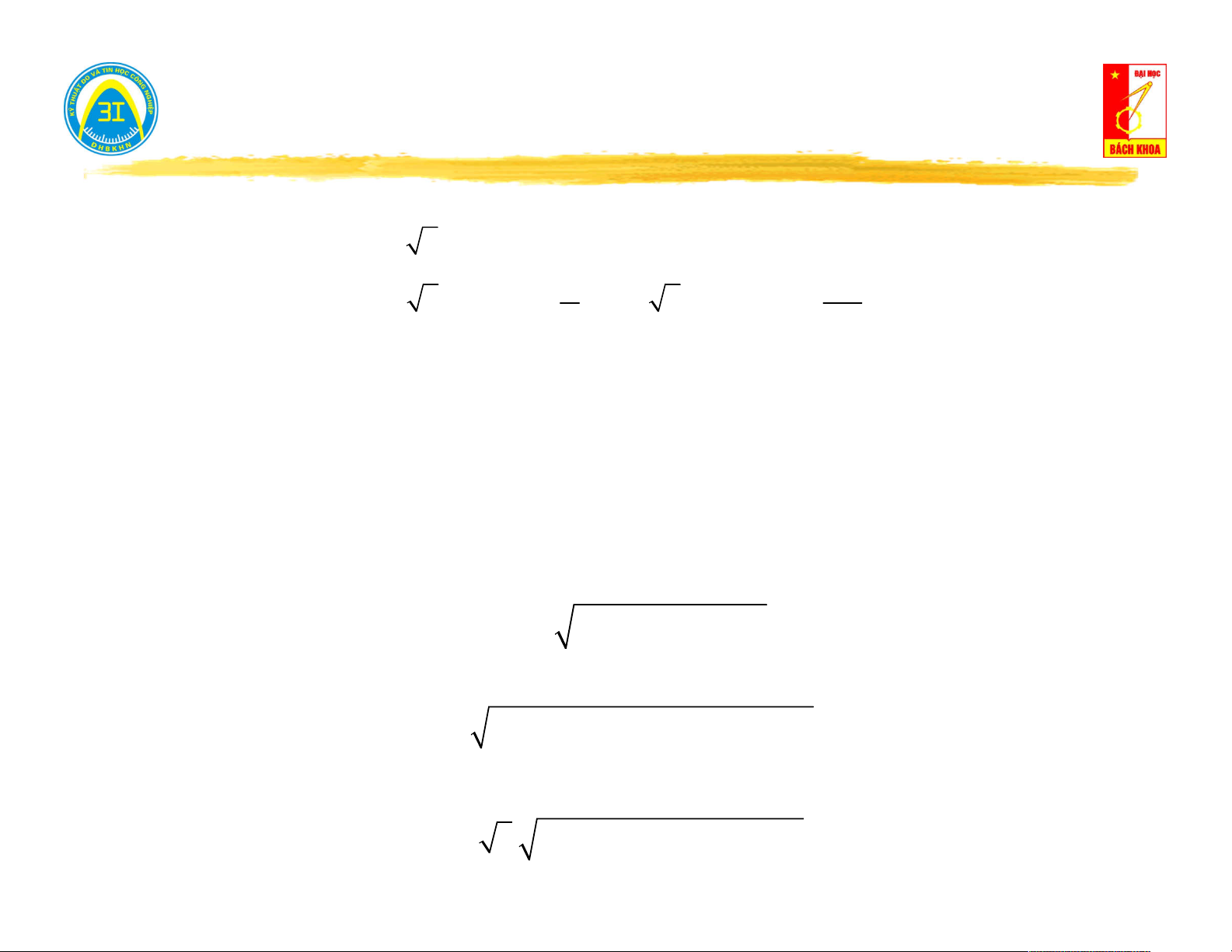
V a j.b V b Dạng modul-góc: . . j V
V e V V Quan hệ: 2 2
V a b a V .cos 0 a Re b b V .sin arctg a Số phức liên hợp:
V a j.b V và V là 2 số a a 1 1 1 1 2 1 2 b b
V a j.b phức liên hợp nếu 1 2 2 2 2
2014 - Lý thuyết mạch điện 1 - Nguyễn Việt Sơn 5
Chương 2: Mạch tuyến tính ở chế độ xác lập điều hòa
II.2. Các phép toán cơ bản.
V V V (a a ) j.(b b )
Phép cộng - trừ. 3 1 2 1 2 1 2 V a . j b V 1 1 1 1 1 Phép nhân - chia. V a . j b V
V V .V V .V 4 1 2 1 2 1 2 2 2 2 2 2
Phép nghịch đảo. V V 1 1 1 1 ... V V 5 1 2 6 V 1 V 2 V 2 1 V1 Chú ý:
Nhân j với một số phức góc quay ngược chiều kim đồng hồ 900 j 2
A 10 30 j. A 1.e .10 30 10 120
Chia một số phức cho j góc quay thuận chiều kim đồng hồ 900. A A 10 30
j. A j.10 30 10 6 0 j j3 = -j
2014 - Lý thuyết mạch điện 1 - Nguyễn Việt Sơn 6
Chương 2: Mạch tuyến tính ở chế độ xác lập điều hòa
II.3. Biểu diễn các hàm điều hòa trong miền ảnh phức.
Có thể biểu diễn các hàm điều hòa cùng tần số bằng những số phức:
Modul = Trị hiệu dụng
Pha = Góc pha ban đầu
e(t) E 2.sin(wt ) E E
Nếu số phức là ảnh của hàm điều hòa
E 2.sin(t ) E E thì e(t) = hoặc
E 2.cos(t )
2014 - Lý thuyết mạch điện 1 - Nguyễn Việt Sơn 7
Chương 2: Mạch tuyến tính ở chế độ xác lập điều hòa
II.3. Biểu diễn các hàm điều hòa trong miền ảnh phức.
Xét hàm điều hòa: i(t) I. 2.sin(t ) I I di(t)
.I. 2.cos(t ) .I. 2.sin(t ) j.. I dt 2 1 1 1
i(t).dt
.I 2.cos(t )
.I. 2.sin(t ) . I 2 j Miền thời gian Miền ảnh phức Hàm điều hòa Ảnh phức d j.ω dt 1 dt j.
Hệ phương trình vi tích phân
Hệ phương trình đại số ảnh phức
2014 - Lý thuyết mạch điện 1 - Nguyễn Việt Sơn 8
LÝ THUYẾT MẠCH ĐIỆN 1
Chương 2: Mạch tuyến tính ở chế độ xác lập điều hòa. I.
Hàm điều hòa & các đại lượng đặc trưng. II.
Số phức - Biểu diễn hàm điều hòa trong miền ảnh phức III.
Phản ứng của một nhánh với kích thích điều hòa.
III.1. Kích thích điều hòa.
III.2. Mạch thuần trở.
III.3. Mạch thuần cảm.
III.4. Mạch thuần dung.
III.5. Mạch nối tiếp R-L-C
III.6. Mạch song song R//L//C
IV. Dạng phức các luật cơ bản trong mạch Kirchhoff.
2014 - Lý thuyết mạch điện 1 - Nguyễn Việt Sơn 9
Chương 2: Mạch tuyến tính ở chế độ xác lập điều hòa
III.1. Kích thích điều hòa.
Xét mạch Kirchhoff có nguồn xoay chiều điều hòa
III.2. Mạch thuần trở. i (t) I U R R R R I R R u (t) R U dòng - áp cùng pha R u(t) . R i(t)
i(t) I 2 sin t( ) A j.0 I I.e I 0( ) A u(t) . R I 2 sin t U R . R I . R I 0 2
Công suất tác dụng:
p(t) u(t).i(t) P . R I 2 = .
R I (1 cos 2t) 1 T 2 P=
p(t)dt . R I T 0
2014 - Lý thuyết mạch điện 1 - Nguyễn Việt Sơn 10
Chương 2: Mạch tuyến tính ở chế độ xác lập điều hòa
III.3. Mạch thuần cảm. U L IL L i (t) L L u (t) U I L L L di (t)
Điện áp sớm pha π/2 u (t) L L L dt I I 0( ) A
i (t) I. 2 sin t( ) A L L di (t) U . . L I / 2 .
j X . I Z. I u (t) L L .
L I. 2..cost L L L L L dt
Z j..L L =. .
L I 2 sin(t ) 2
Công suất phản kháng: Đo cường độ quá trình 2
Q X .I
dao động năng lượng trong kho từ. L L L
2014 - Lý thuyết mạch điện 1 - Nguyễn Việt Sơn 11
Chương 2: Mạch tuyến tính ở chế độ xác lập điều hòa
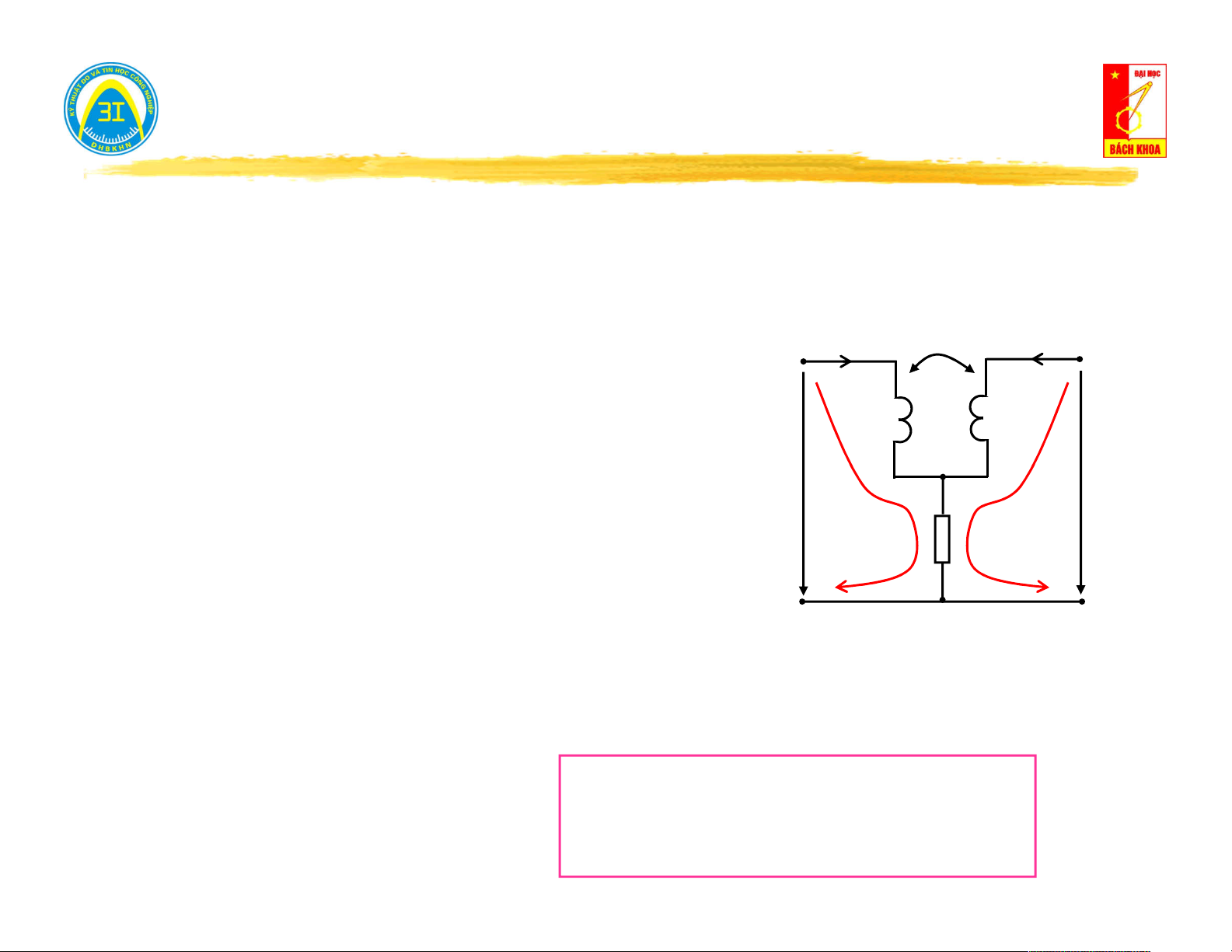
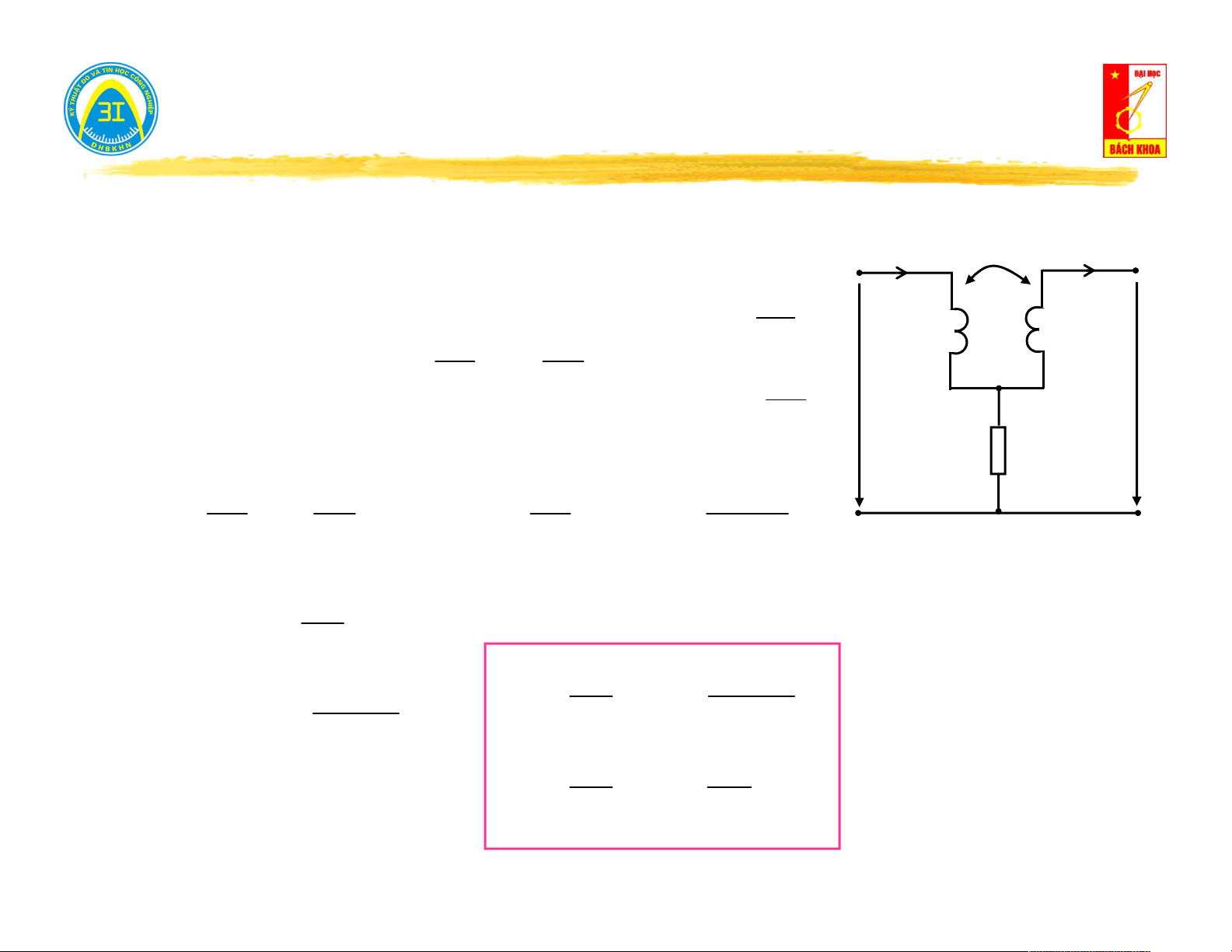
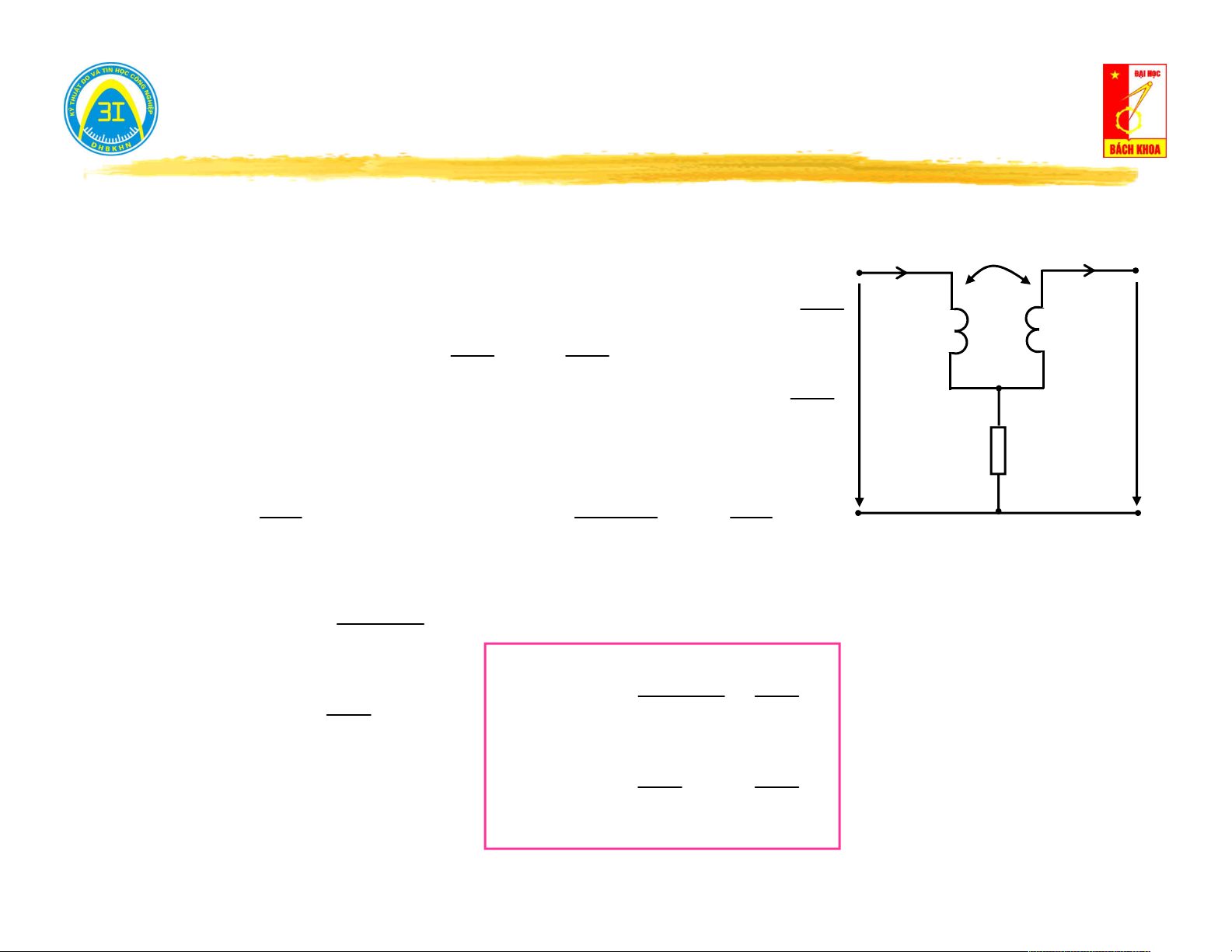
Mạch có hỗ cảm: M M i (t) L L L L I 1 1 2 i (t) 2 * * 1 2 1 * * I2 u (t) u (t) I 11 u (t) u (t) 21 1 U U 12 22 11 21 U U 12 22 u (t) 1 u (t 2 U U ) 1 2
i (t) I 2 sin(t)( )
A ; i (t) I 2 sin(t )( ) A I I 0( )
A ; I I ( ) A 1 1 2 2 1 1 2 2 di (t) 1
u (t) L
.L .I . 2.sin(t ) 11 1 1 1
U j..L . I dt 2 11 1 1 di (t) 2
u (t) M
.M .I . 2 sin(t ) U
j..M . I 12 12 12 2 12 12 2 dt 2 di di
U U U
j..L . I j..M . I 1 2
u (t) u (t) u (t) L M 1 11 12 1 1 12 2 1 11 12 1 12 dt dt
U U U
j..L . I j..M . I 2 22 21 2 2 21 1 di di 2 1
u (t) u (t) u (t) L M 2 22 21 2 21 dt dt
2014 - Lý thuyết mạch điện 1 - Nguyễn Việt Sơn 12
Chương 2: Mạch tuyến tính ở chế độ xác lập điều hòa
III.4. Mạch thuần dung. IC C C i (t) IC C U C u (t) C UC 1
Điện áp chậm pha π/2 u (t) i (t).dt C C C
i (t) I. 2 sin t( ) A I I 0( ) A C C 1 1 j u (t)
i (t).dt .I. 2.cost 1 1 2 U . I .e j . I C C C C C . C C . C C I. 2 1 =
. I j.X . I = .sin(t ) j.. C C C C .C 2
Công suất phản kháng: Đo cường độ của quá 2
Q X .I C C C
trình dao động năng lượng trong kho điện.
2014 - Lý thuyết mạch điện 1 - Nguyễn Việt Sơn 13
Chương 2: Mạch tuyến tính ở chế độ xác lập điều hòa
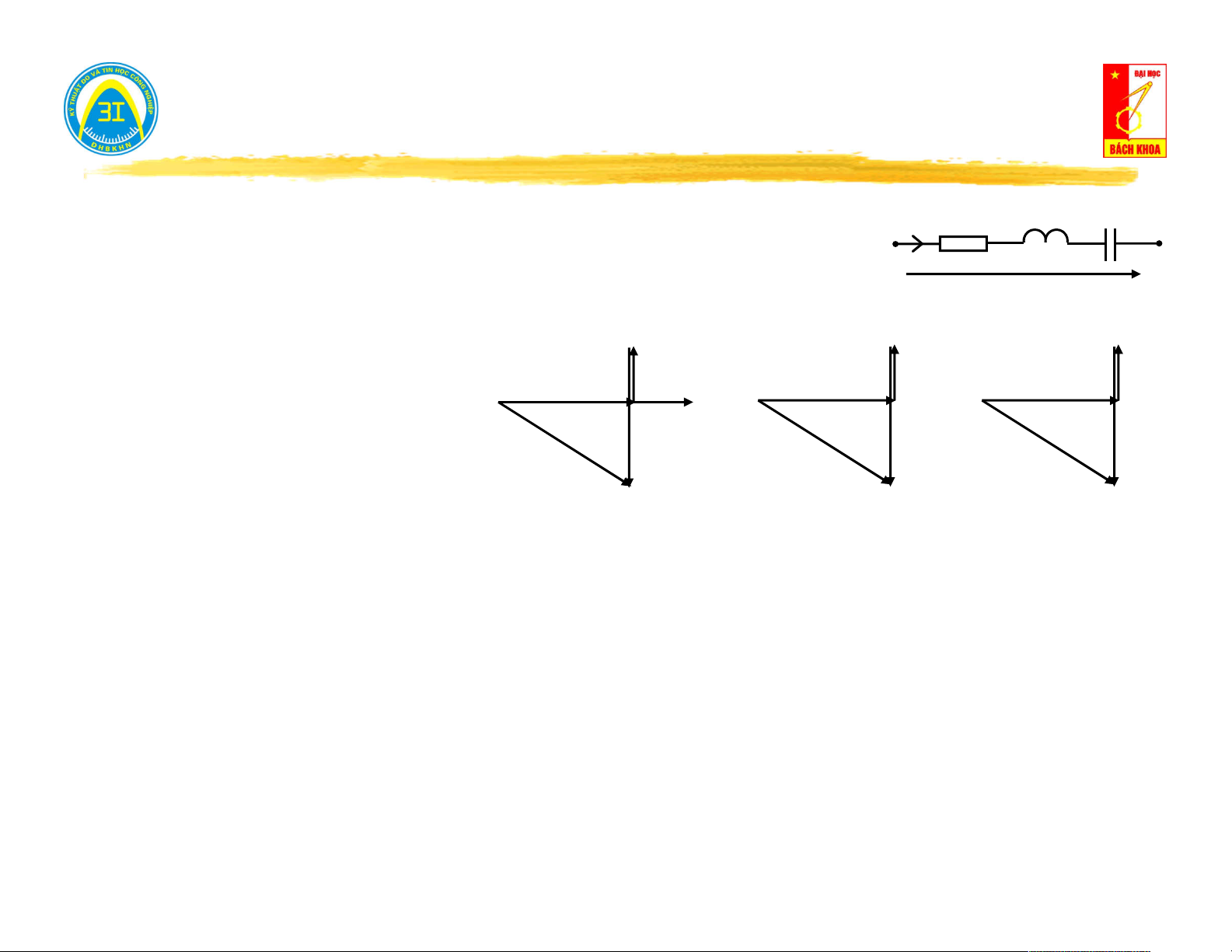
III.5. Mạch nối tiếp R - L - C. U U U L C I R R L C
U U U U R L C Tam giác điện áp Tam giác trở kháng Tam giác công suất jX U jQ L L L U .
R I j.X . I ( j.X ). I L C U I R R P φ φ φ ~
U [R j( X X )]. I Z. I L C Z S -jX C -jQ
Z R j( X X ) R jX U C U L C C R = |Z|.cosφ X = |Z|.sinφ
Công suất: ĐỒNG DẠNG
Công suất tác dụng: P = R.I2 = U.I.cosφ [W].
Công suất phản kháng: Q = X.I2 = U. I.sinφ [Var]. ~
Công suất toàn phần: S P j(Q Q ) [ ] VA L C ~ 2 2 *
S [R j( X X )].I Z.I U . I L C
2014 - Lý thuyết mạch điện 1 - Nguyễn Việt Sơn 14
Chương 2: Mạch tuyến tính ở chế độ xác lập điều hòa
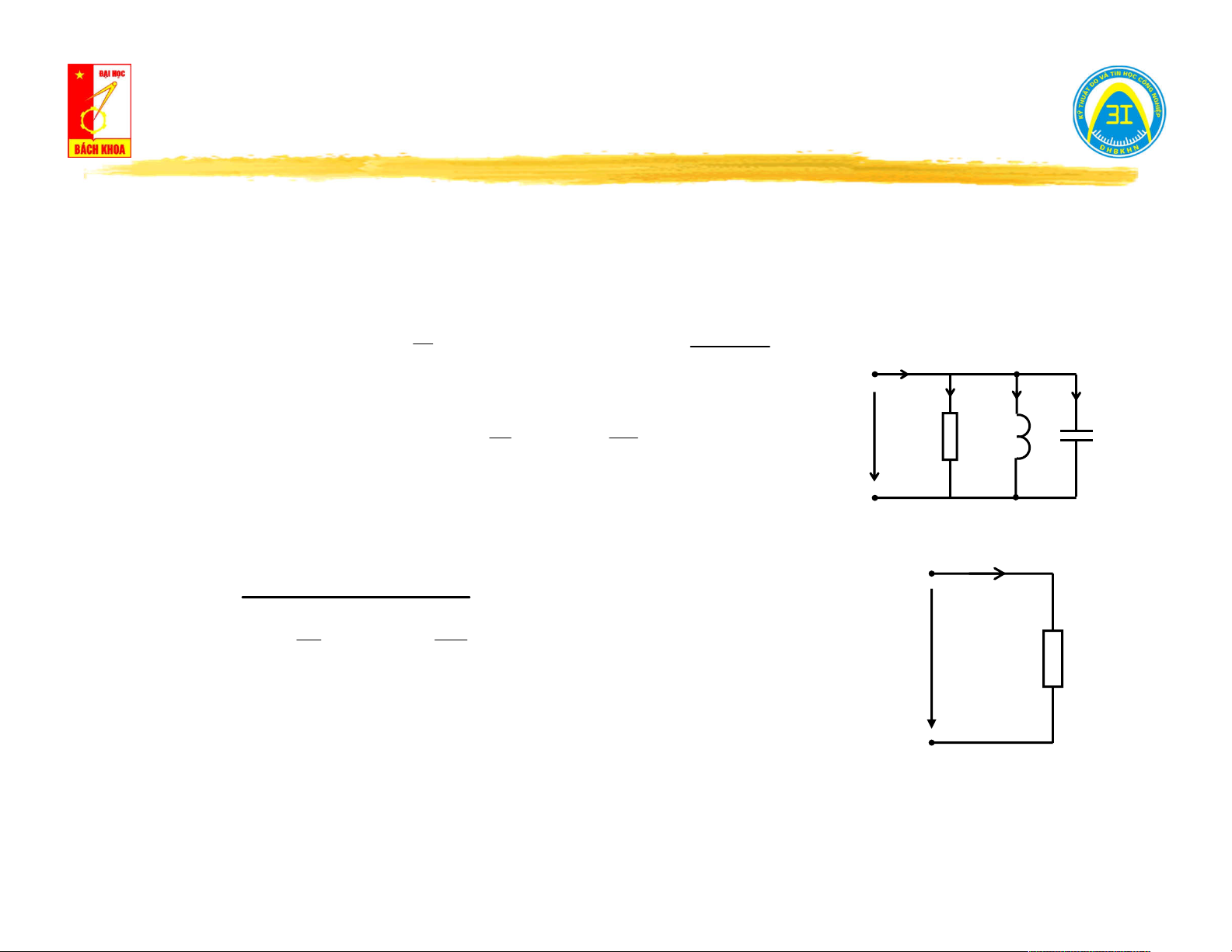
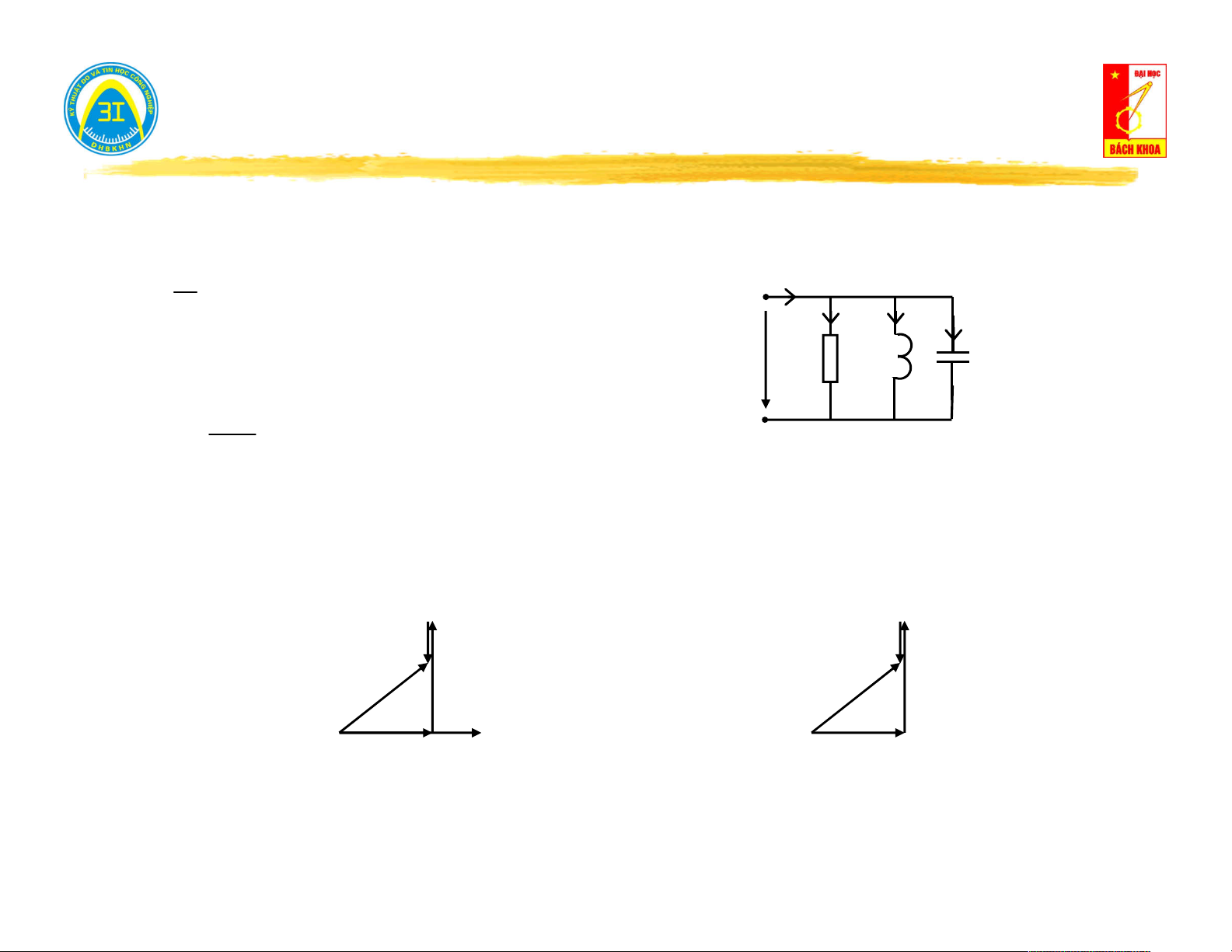
III.6. Mạch song song R // L // C. . . . 1 I I
.U g.U R R I I I R L C . . . U R L
I j..C.U j.b .U C C C . . . 1 I j
.U j.b .U L . L L . . . . . .
I I I I [g j(b b )].U Y.U R L C C L Tam giác dòng điện Tam giác tổng dẫn I j.b j.b L I L C C I ĐỒNG DẠNG Y φ I φ R g U
2014 - Lý thuyết mạch điện 1 - Nguyễn Việt Sơn 15
LÝ THUYẾT MẠCH ĐIỆN 1
Chương 2: Mạch tuyến tính ở chế độ xác lập điều hòa. I.
Hàm điều hòa & các đại lượng đặc trưng. II.
Số phức - Biểu diễn hàm điều hòa trong miền ảnh phức
III. Phản ứng của một nhánh với kích thích điều hòa.
IV. Dạng phức các luật cơ bản trong mạch Kirchhoff. IV.1. Luật Ohm.
IV.2. Luật Kirchhoff 1.
IV.3. Luật Kirchhoff 2.
IV.4. Luật cân bằng công suất.
2014 - Lý thuyết mạch điện 1 - Nguyễn Việt Sơn 16
Chương 2: Mạch tuyến tính ở chế độ xác lập điều hòa IV.1. Luật Ohm. U Z. I
Z: tổng trở phức tương đương của nhánh với
Y: tổng dẫn phức tương đương của nhánh I Y.U
IV.2. Luật Kirchhoff 1.
IV.3. Luật Kirchhoff 2. I 0 U E nut vong vong
(đi vào âm, đi ra dương) (cùng chiều dương)
IV.4. Luật cân bằng công suất. P 0 ~ S 0 kin kin Q 0 kin
2014 - Lý thuyết mạch điện 1 - Nguyễn Việt Sơn 17
LÝ THUYẾT MẠCH ĐIỆN 1
Chương 3: Phương pháp cơ bản tính mạch tuyến tính ở
chế độ xác lập điều hòa - Graph Kirchhoff
I. Phương pháp dòng nhánh.
II. Phương pháp thế nút.
III. Phương pháp dòng vòng.
IV. Khái niệm về graph Kirchhoff.
V. Các định lý về lập phương trình Kirchhoff.
VI. Ma trận cấu trúc A, B.
VII. Lập phương trình bằng ma trận cấu trúc.
Bài tập: 7, 8, 11 - 25, bài thêm.
2014 – Lý thuyết mạch điện 1 - Nguyễn Việt Sơn 1
Chương 3: Phương pháp cơ bản tính mạch tuyến tính
ở chế độ xác lập điều hòa - Graph Kirchhoff
I. Phương pháp dòng nhánh.
Phương pháp dòng nhánh là phương pháp lập phương trình mạch với biến là
dòng điện chảy trong các nhánh, sử dụng luật K1, K2
Nội dung phương pháp:
Đặt ẩn là ảnh phức của dòng điện trong các nhánh của mạch điện.
Lập hệ phương trình theo luật K1 và K2.
Số phương trình luật K1: d - 1.
Tổng số: (n)
(n) biến dòng
Số phương trình luật K2: n - d + 1. pt điện
2014 – Lý thuyết mạch điện 1 - Nguyễn Việt Sơn 2
Chương 3: Phương pháp cơ bản tính mạch tuyến tính
ở chế độ xác lập điều hòa - Graph Kirchhoff
I. Phương pháp dòng nhánh.
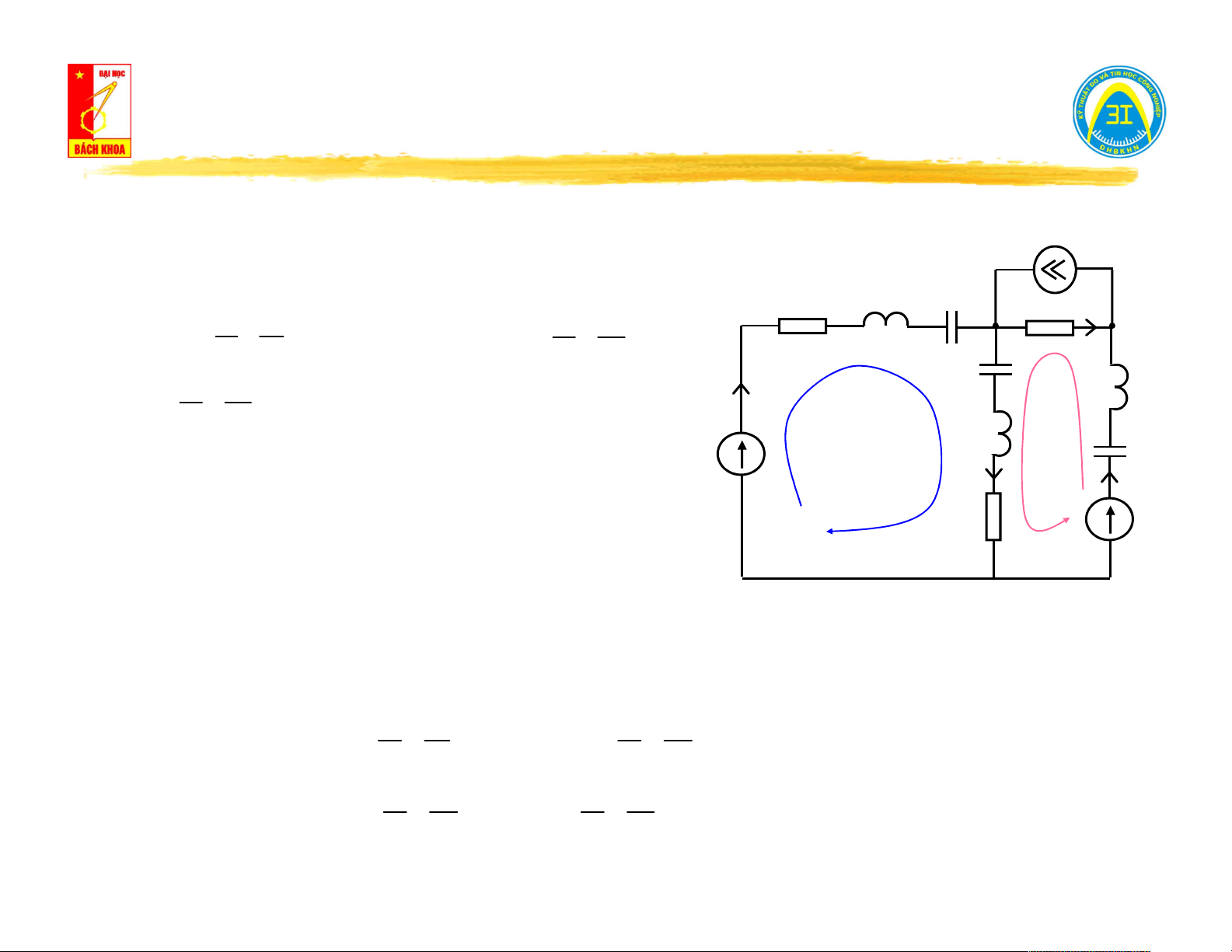
Ví dụ 3.1: Lập phương trình mạch theo phương pháp dòng nhánh cho mạch điện.
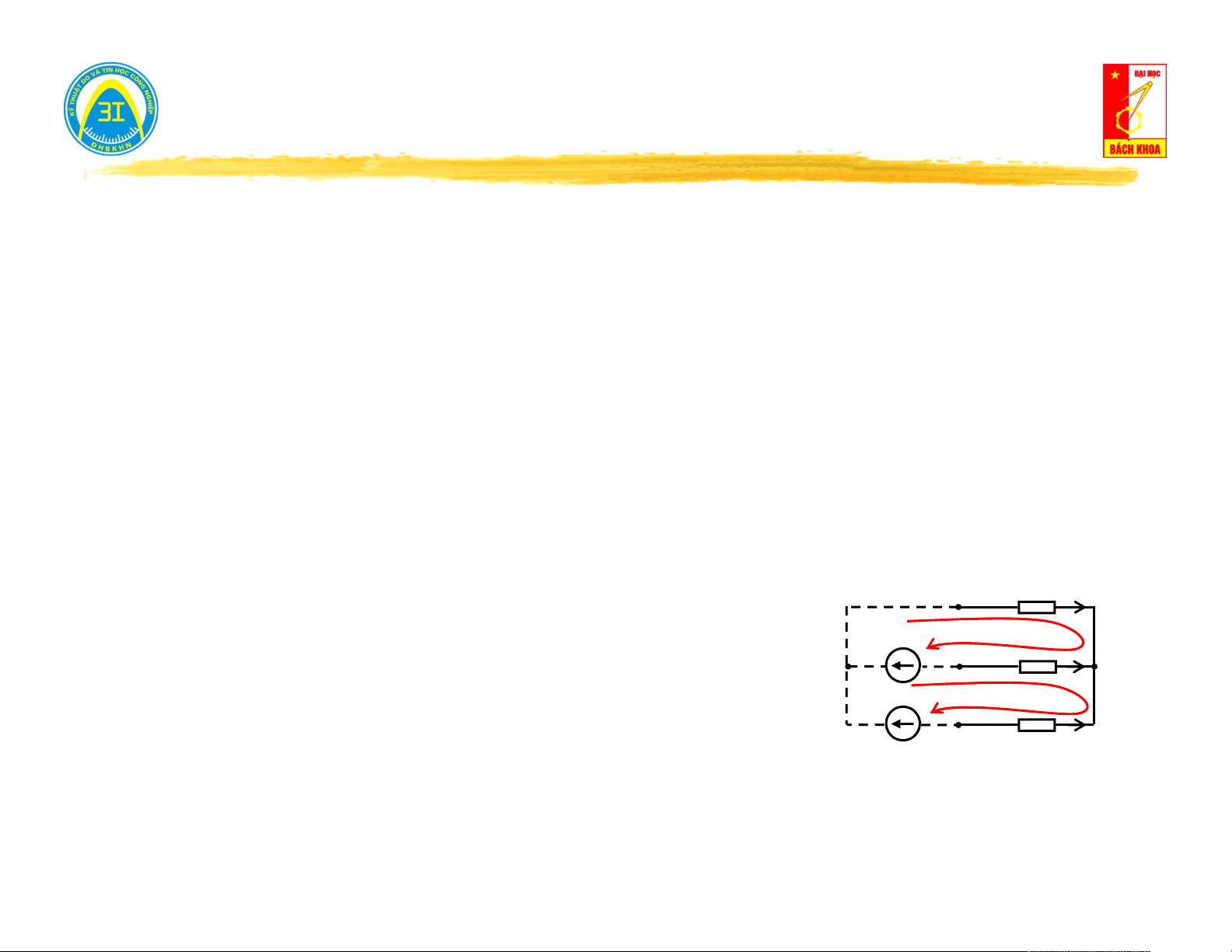
Chọn chiều dòng điện trong các nhánh. J Luật K1: I Z 1 1 I I 3 5 A B
I I I J Nút A: E 1 2 3 5 I Z3 I 2 4
Nút B: I I I J 3 4 5 I Z Z 2 4 II III Z Áp dụng luật K2: E 5 1 C
Vòng 1: I .Z I .Z E 1 1 2 2 1
Vòng 2: I .Z I .Z I .Z 0 3 3 4 4 2 2
Vòng 3: I .Z I .Z E 5 5 4 4 5 Nhận xét:
Nguồn dòng chỉ viết ở luật K1, nguồn áp chỉ viết ở luật K2.
Phương pháp dòng nhánh áp dụng với mạch có số nhánh & số đỉnh nhỏ.
2014 – Lý thuyết mạch điện 1 - Nguyễn Việt Sơn 3
LÝ THUYẾT MẠCH ĐIỆN 1
Chương 3: Phương pháp cơ bản tính mạch tuyến tính ở
chế độ xác lập điều hòa - Graph Kirchhoff
I. Phương pháp dòng nhánh.
II. Phương pháp thế nút.
III. Phương pháp dòng vòng.
IV. Khái niệm về graph Kirchhoff.
V. Các định lý về lập phương trình Kirchhoff.
VI. Ma trận cấu trúc A, B.
VII. Lập phương trình bằng ma trận cấu trúc.
2014 – Lý thuyết mạch điện 1 - Nguyễn Việt Sơn 4
Chương 3: Phương pháp cơ bản tính mạch tuyến tính
ở chế độ xác lập điều hòa - Graph Kirchhoff
II. Phương pháp thế nút.
Phương pháp thế nút (đỉnh) là phương pháp lập phương trình mạch với biến là
điện thế của các nút trong mạch, sử dụng luật K1.
Nội dung phương pháp:
Giữ lại nguồn dòng, (nguồn áp → đổi thành nguồn dòng tương đương):
Nguồn dòng tương đương cùng chiều với nguồn áp. E Độ lớn: J TD Z
Coi một đỉnh bất kỳ có điện thế bằng 0 (ground).
Lập phương trình mạch với biến là điện thế của (d-1) đỉnh còn lại trong
mạch, sử dụng luật K1 ((d-1) phương trình)
2014 – Lý thuyết mạch điện 1 - Nguyễn Việt Sơn 5
Chương 3: Phương pháp cơ bản tính mạch tuyến tính
ở chế độ xác lập điều hòa - Graph Kirchhoff
II. Phương pháp thế nút.
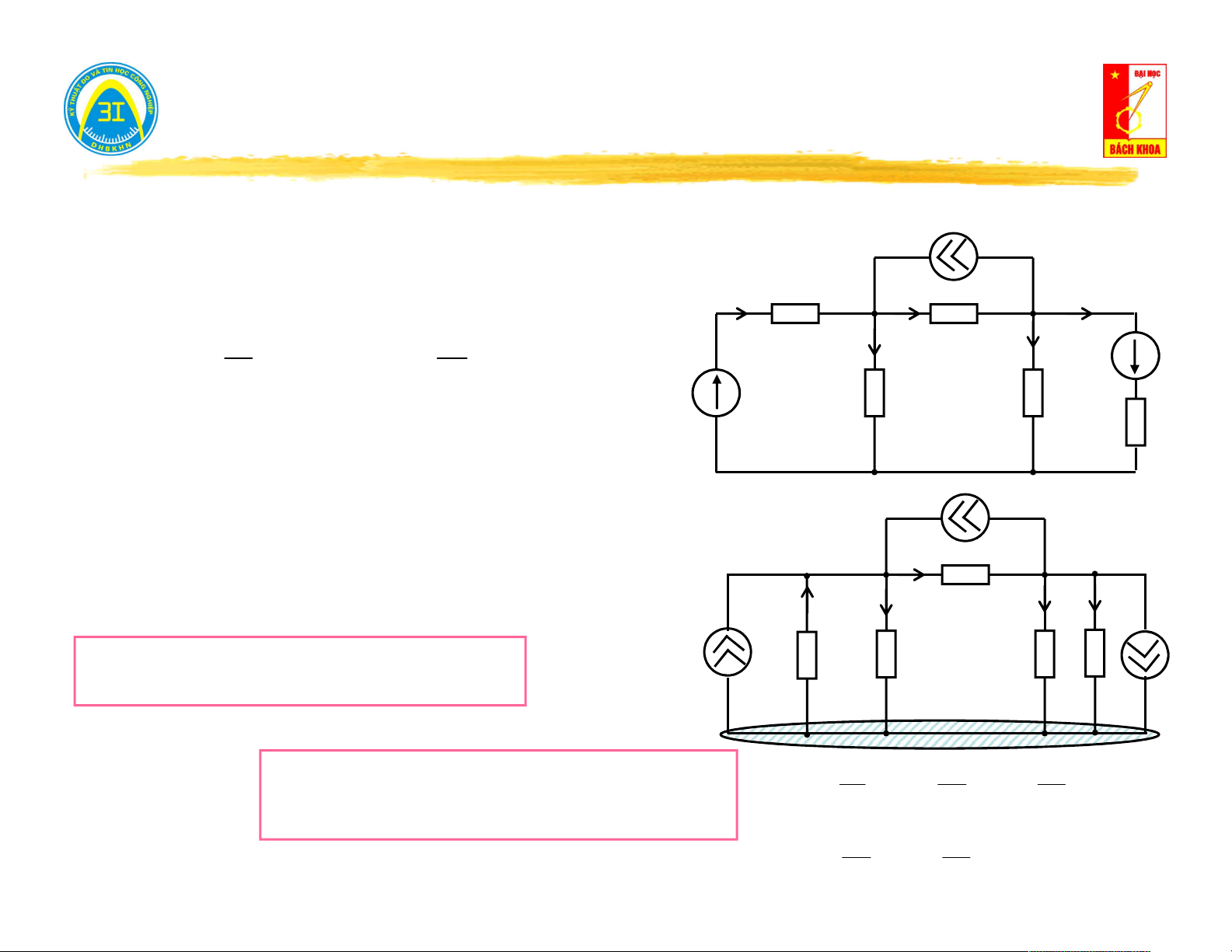
Ví dụ 3.2: Lập phương trình theo phương pháp thế nút. J I Z Biến đổi nguồn áp: 1 1 I I 3 5 A B E5 E E 1 5 I Z3 I 2 4 J
E .Y ; J E .Y 1 1 1 5 5 5 Z Z 1 5 Z Z 2 4 Z
Chọn đỉnh C là đất E 5 1 C Áp dụng luật K1: J Nút A: I
J I I I J J k k 1 2 3 1 nut nut A I3 B Y I I 3 I I (
).Y ( ).Y ( ).Y J E .Y C A 1 A C 2 A B 3 1 1 J 1 2 4 5 1 Y Y 1 Y2 4
(Y Y Y ). Y . J E .Y 1 2 3 A 3 B 1 1 Y C 5 J5 1 1 1 Y ; Y ; Y ; Nút B: Y
. (Y Y Y ). JE .Y 1 2 3 3 A 3 4 5 B 5 Z Z Z 1 2 3 1 1 Y ; Y ;
2014 – Lý thuyết mạch điện 1 - Nguyễn Việt Sơn 4 5 6 Z Z 4 5
Chương 3: Phương pháp cơ bản tính mạch tuyến tính
ở chế độ xác lập điều hòa - Graph Kirchhoff J
II. Phương pháp thế nút. A I3 B
Y Y Y Y J J 1 2 3 3 1 Y I I 3 I I . A J 1 2 4 5 1 Y
Y Y Y 3 3 4 5 Y Y J J 1 Y2 4 B 5 Y C 5 J5 Nhận xét:
Giải hệ phương trình tính được: , A B
I ( ).Y 3 A B 3
→ Cần tìm dòng điện trong các nhánh:
Nhánh không biến đổi nguồn: I .Y I .Y 2 A 2 4 B 4
Nhánh có biến đổi nguồn: I Z I 1 1 5 A B E5 (E ) (E ) 1 A 5 B I I 1 5 Z Z5 Z 1 5 E1 0 C 0 C
2014 – Lý thuyết mạch điện 1 - Nguyễn Việt Sơn 7
Chương 3: Phương pháp cơ bản tính mạch tuyến tính
ở chế độ xác lập điều hòa - Graph Kirchhoff J
II. Phương pháp thế nút A I3 B
Y Y Y Y J J 1 2 3 3 1 Y . A I I 3 I I J 1 2 4 5 1 Y
Y Y Y 3 3 4 5
J J B 5 Y Y 1 Y2 4 Y Nhận xét: C 5 J5 Ma trận tổng dẫn:
Y = Σ các tổng dẫn nối với đỉnh k. kk
Y = Σ các tổng dẫn nối đỉnh k với đỉnh l kl En (luôn âm). Z J 1 E n 2 Z Ma trận nguồn dòng: 3 Z Z 2 n J
= Σ các nguồn dòng nối với đỉnh k E kk . 1
Đi vào đỉnh → dương.
Đi ra đỉnh → âm.
Số phương trình: (d-1) → phù hợp với mạch có số đỉnh ít.
Phương pháp thế nút ít sử dụng khi mạch có hỗ cảm.
2014 – Lý thuyết mạch điện 1 - Nguyễn Việt Sơn 8
LÝ THUYẾT MẠCH ĐIỆN 1
Chương 3: Phương pháp cơ bản tính mạch tuyến tính ở
chế độ xác lập điều hòa - Graph Kirchhoff
I. Phương pháp dòng nhánh
II. Phương pháp thế nút
III. Phương pháp dòng vòng
IV. Khái niệm về graph Kirchhoff
V. Các định lý về lập phương trình Kirchhoff
VI. Ma trận cấu trúc A, B
VII. Lập phương trình bằng ma trận cấu trúc
2014 – Lý thuyết mạch điện 1 - Nguyễn Việt Sơn 9
Chương 3: Phương pháp cơ bản tính mạch tuyến tính
ở chế độ xác lập điều hòa - Graph Kirchhoff
III. Phương pháp dòng vòng
Phương pháp dòng vòng là phương pháp lập phương trình mạch với biến là
dòng điện vòng quy ước chảy trong các vòng kín, sử dụng luật K2.
Nội dung phương pháp:
Giữ lại nguồn áp. (nguồn dòng → biến đổi thành nguồn áp tương đương)
Nguồn áp tương đương cùng chiều với nguồn dòng.
Độ lớn: E J .Z td nh nh
Chọn (n-d+1) vòng và chọn chiều dòng điện trong các vòng tương ứng.
Lập phương trình mạch với biến là dòng điện vòng đã chọn, sử dụng luật
K2 (n-d+1 phương trình).
2014 – Lý thuyết mạch điện 1 - Nguyễn Việt Sơn 10
Chương 3: Phương pháp cơ bản tính mạch tuyến tính
ở chế độ xác lập điều hòa - Graph Kirchhoff
III. Phương pháp dòng vòng
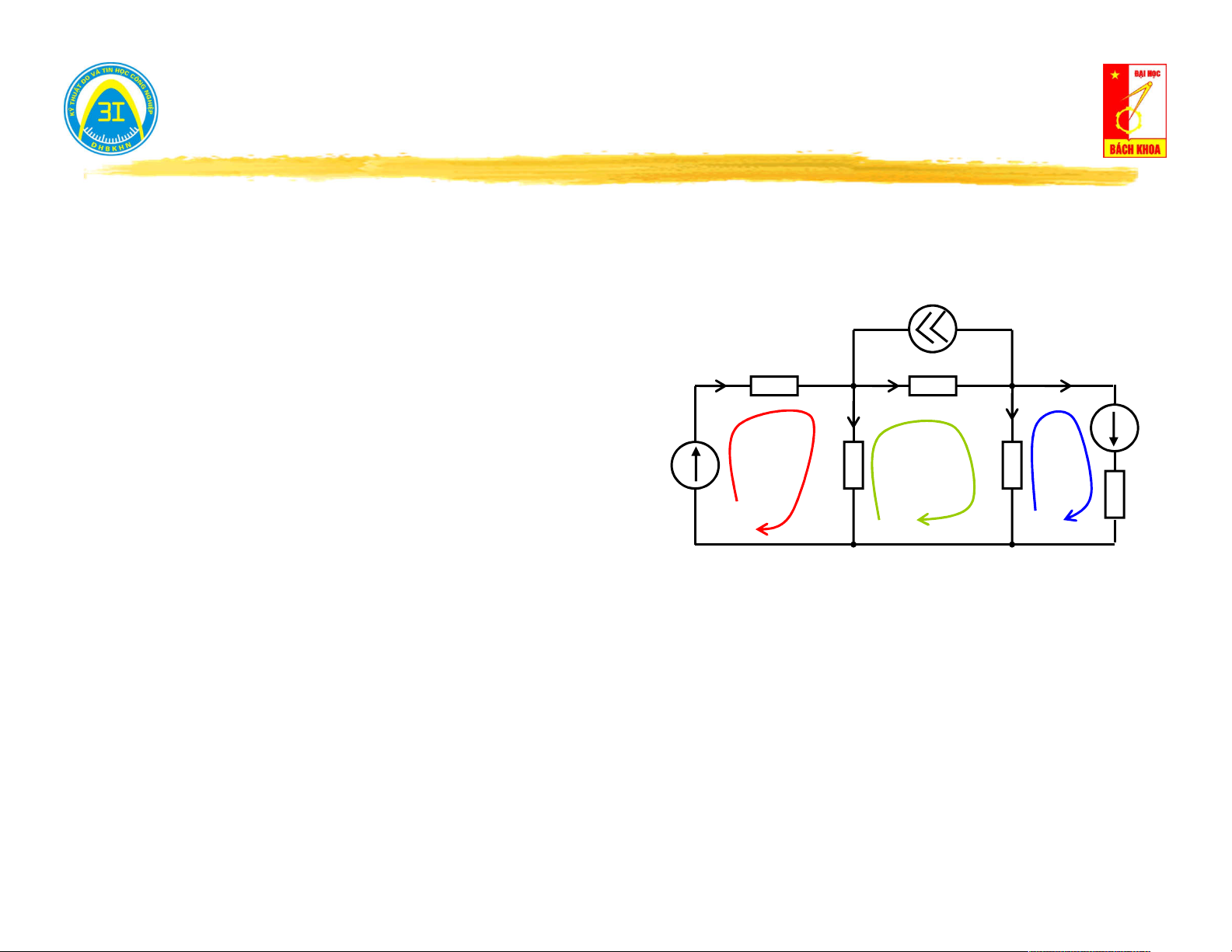
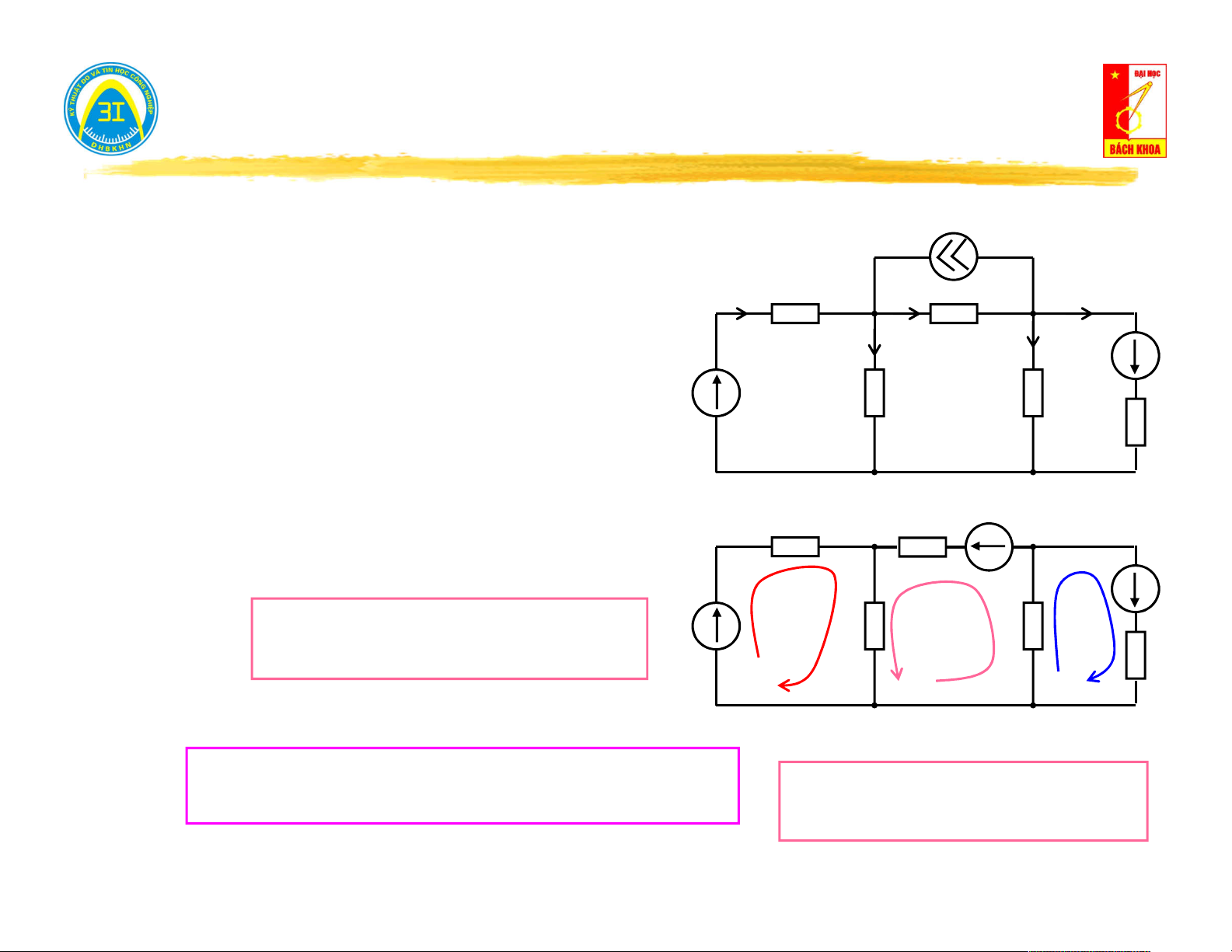
Ví dụ 3.3: Lập phương trình mạch theo phương pháp dòng vòng J I Z 1 1 I I
Biến đổi nguồn dòng: 3 5
E Z . J A B 3 3 E5 I Z3 I 2 4
Chọn (n-d+1) dòng điện vòng: Z Z 2 4 Áp dụng luật K2: Z E 5 1 C Vòng 1: U
E U U E 1 Z Z k k 2 1 vong vong E Z Z 3 1 A 3 B E5
IV1 .Z IV1 .Z IV 2 .Z E 1 2 2 1 I V 1 Z Z 2 I 4 V 2 I V 3
(Z Z ). IV1 Z . IV 2 E 1 2 2 1 Z E 5 1 Vòng 2: C Vòng 3: Z . I V 1 (Z
Z Z ). I V 2 Z . I V 3 E 2 2 3 4 4 3
Z . I V 2 (Z Z ). I V 3 E 4 4 5 5
2014 – Lý thuyết mạch điện 1 - Nguyễn Việt Sơn 11
Chương 3: Phương pháp cơ bản tính mạch tuyến tính
ở chế độ xác lập điều hòa - Graph Kirchhoff
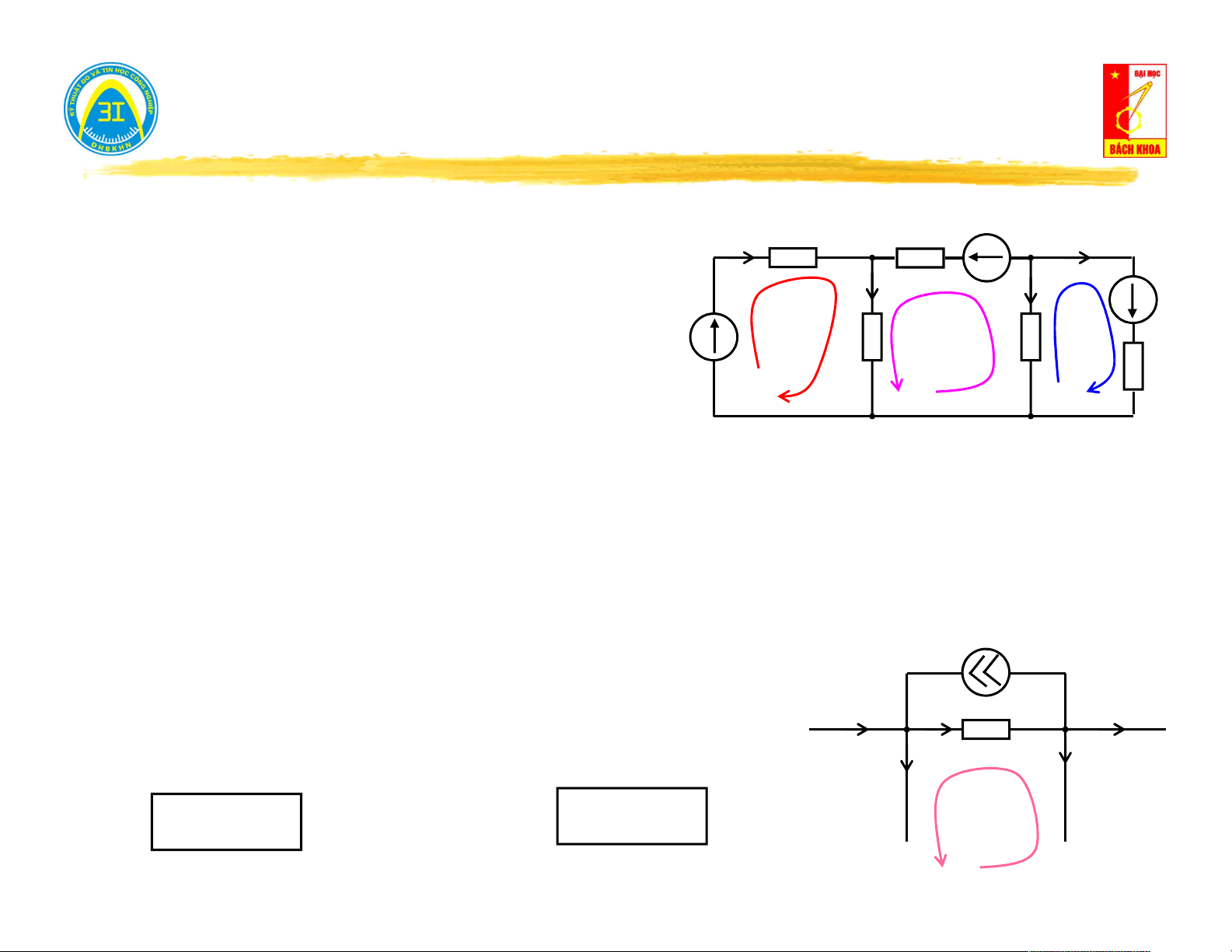
III. Phương pháp dòng vòng E I Z Z 3 I 1 1 A 3 B 5 IV1 E E 1 Z Z Z 0 5 1 2 2 I 2 I 4 Z
Z Z Z Z . IV 2 E 2 2 3 4 4 3 IV1 Z Z 2 4 I V 2 I V 3 0 Z Z Z Z 4 4 5 5 IV 3 E E 5 1 C Nhận xét:
Giải hệ phương trình tính được nghiệm: I V1, I V 2 , I V 3
→ Cần tìm dòng điện trong các nhánh.
I (IV 2 IV 3 ) 4
Nhánh không biến đổi nguồn:
I I 1 I I I I I 1 V 1 2 2 V V 3 5 V
Nhánh có biến đổi nguồn: J
I I I J 0 I
Nút A: I I I J 0 Nút B: 3 4 5 I I 1 3 5 1 2 3 A B I Z3 I hoặc
I J I V 2 I V 3 IV 3 2 4
I J I V1 I V1 IV 2 3 3
I J I V 2 I V 2
I J IV 2 3 3
2014 – Lý thuyết mạch điện 1 - Nguyễn Việt Sơn 12
Chương 3: Phương pháp cơ bản tính mạch tuyến tính
ở chế độ xác lập điều hòa - Graph Kirchhoff
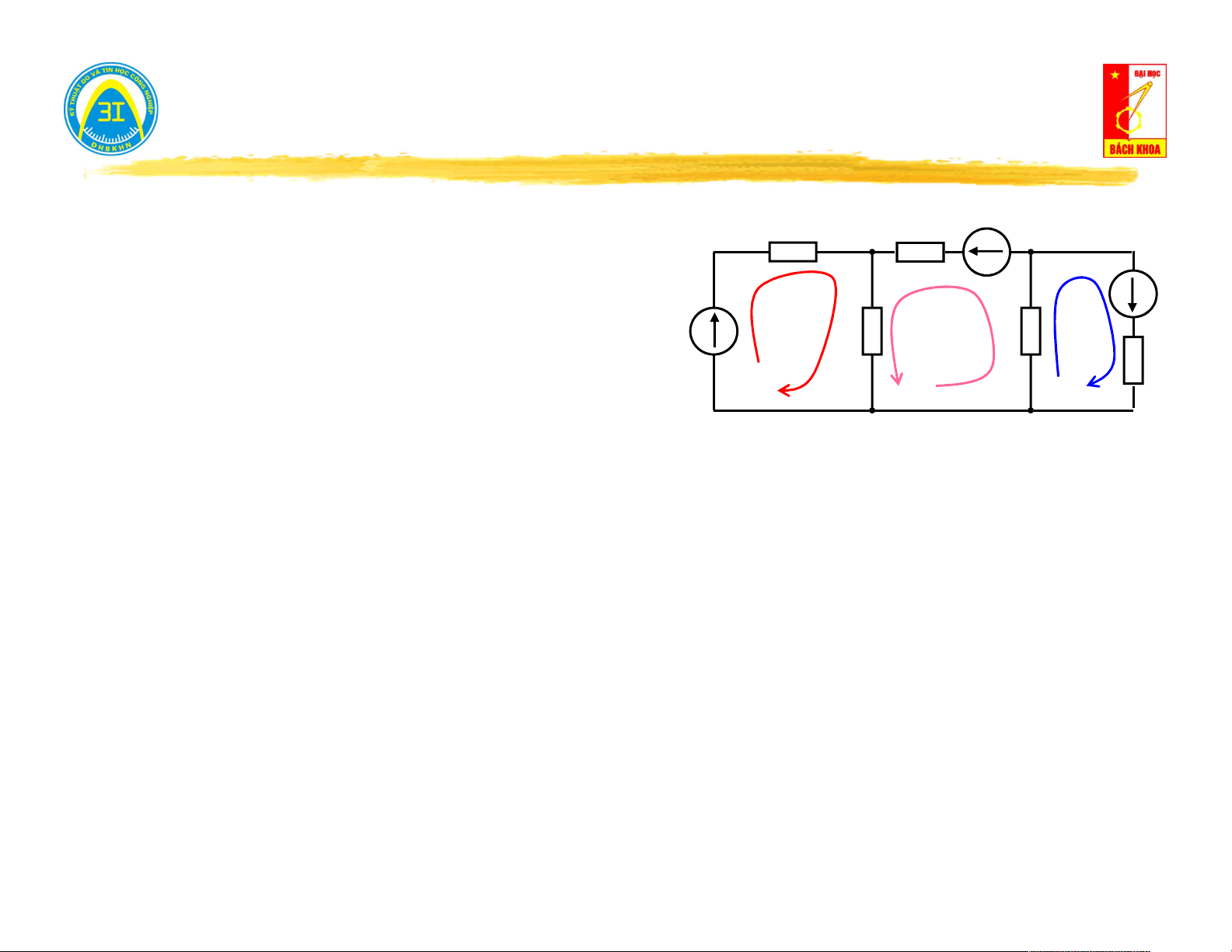
III. Phương pháp dòng vòng E Z Z 3 1 A 3 B IV1 E E5 1 Z Z Z 0 1 2 2 Z
Z Z Z Z . IV 2 E 2 2 3 4 4 3 I V 1 Z Z 2 4 I V 2 I V 3 Z 0 Z Z Z 4 4 5 E 5 IV 3 E 1 5 C Nhận xét: Ma trận tổng trở vòng Z : Ma trận nguồn áp vòng: vong Z
= Σ tổng trở có trong vòng thứ k E
= Σ nguồn áp có trong vòng k kk kk .
Z = Σ tổng trở chung (hỗ cảm) giữa
Dương: nguồn áp cùng chiều vòng kl
vòng k và vòng l.
Âm: nguồn áp ngược chiều vòng Dương: I và I cùng chiều. vong k vong l Âm: I và I ngược chiều. vong k vong l
Số phương trình: (n–d+1) → phù hợp với mạch có số vòng ít
2014 – Lý thuyết mạch điện 1 - Nguyễn Việt Sơn 13
LÝ THUYẾT MẠCH ĐIỆN 1
Chương 3: Phương pháp cơ bản tính mạch tuyến tính ở
chế độ xác lập điều hòa - Graph Kirchhoff
I. Phương pháp dòng nhánh.
II. Phương pháp thế nút.
III. Phương pháp dòng vòng.
IV. Khái niệm về graph Kirchhoff.
V. Các định lý về lập phương trình Kirchhoff.
VI. Ma trận cấu trúc A, B.
VII. Lập phương trình bằng ma trận cấu trúc.
2014 – Lý thuyết mạch điện 1 - Nguyễn Việt Sơn 14
Chương 3: Phương pháp cơ bản tính mạch tuyến tính
ở chế độ xác lập điều hòa - Graph Kirchhoff
IV. Khái niệm về Graph Kirchhoff.
Graph là tập (d) đỉnh, (n) nhánh (cung) nối giữa các đỉnh đó.
Graph Kirchhoff là graph mô tả ghép nối gavanic giữa các vật dẫn, sự phân bố
các vùng năng lượng & sự phân bố các cặp biến dòng, áp nhánh của hệ. I Ví dụ 3.4: 1 Z Z 1 2 2 5 Z5 3 II 4 III Z Z 3 4 IV Z e(t) 6 6
Sơ đồ mạch Kirchhoff = Cấu trúc + thông số
Graph Kirchhoff = Cấu trúc Nhánh: 2
Vật lý: Đặc trưng cho một vùng năng lượng.
Hình học: Cung nối giữa 2 đỉnh, có định chiều.
Đỉnh: Là chỗ chắp nối của 3 nhánh trở lên. 1
2014 – Lý thuyết mạch điện 1 - Nguyễn Việt Sơn 15
Chương 3: Phương pháp cơ bản tính mạch tuyến tính
ở chế độ xác lập điều hòa - Graph Kirchhoff
IV. Khái niệm về Graph Kirchhoff.
Cây: Tập hợp các nhánh của graph, nối đủ các đỉnh, không tạo thành vòng kín.
Cành: Tập hợp các nhánh của cây. Một graph có thể có nhiều cây khác nhau. Ví dụ 3.5: I I 1 I 2 1 1 5 2 2 5 3 5 II 4 III 3 3 II 4 III II 4 III IV 6 IV IV 6 6
Số cành trong 1 cây: (d – 1)
Bù cây: Tập các nhánh cùng với cây tạo thành graph đã cho.
Bù cành: Tập hợp các nhánh tạo nên bù cây. Mỗi bù cành + cành = vòng kín.
Số bù cành trong 1 graph: (n - d + 1)
2014 – Lý thuyết mạch điện 1 - Nguyễn Việt Sơn 16
LÝ THUYẾT MẠCH ĐIỆN 1
Chương 3: Phương pháp cơ bản tính mạch tuyến tính ở chế độ xác
lập điều hòa - Graph Kirchhoff
I. Phương pháp dòng nhánh
II. Phương pháp thế nút
III. Phương pháp dòng vòng
IV. Khái niệm về graph Kirchhoff
V. Các định lý về lập phương trình Kirchhoff
V.1. Định lý về lập phương trình Kirchhoff 2
V.2. Định lý về lập phương trình Kirchhoff 1
VI. Ma trận cấu trúc A, B
VII. Lập phương trình bằng ma trận cấu trúc
2014 – Lý thuyết mạch điện 1 - Nguyễn Việt Sơn 17
Chương 3: Phương pháp cơ bản tính mạch tuyến tính
ở chế độ xác lập điều hòa - Graph Kirchhoff
V.1. Định lý về lập phương trình Kirchhoff 2.
Định lý 1: Các áp cành trên một cây làm thành 1 tập đủ áp nhánh độc lập. Chứng minh:
Các áp cành trên 1 cây không tạo thành vòng kín → độc lập tuyến tính
Các áp bù cành + áp cành = vòng kín → phụ thuộc vào áp cành theo luật K2
Số phương trình độc lập viết theo luật K2 là: (n-d+1)
Định lý 2: Các hệ phương trình cân bằng áp trên các vòng kín khép bởi
mỗi bù cành làm thành một hệ đủ phương trình độc lập Chứng minh:
Mỗi vòng chứa duy nhất một áp bù cành, phụ thuộc vào các áp cành → độc lập tuyến tính.
Các phương trình cân bằng áp trên các vòng kín tạo thành hệ đủ và độc lập.
2014 – Lý thuyết mạch điện 1 - Nguyễn Việt Sơn 18
Chương 3: Phương pháp cơ bản tính mạch tuyến tính
ở chế độ xác lập điều hòa - Graph Kirchhoff
V.2. Định lý về lập phương trình Kirchhoff 1.
Định lý 1: Các dòng bù cành trên một bù cây tạo thành một tập dòng
nhánh độc lập. Chứng minh:
Bù cành không chứa tập cắt đỉnh không bị ràng buộc bởi luật K1 → độc lập tuyến tính
Số phương trình độc lập viết theo luật K11: (d–1).
Định lý 2: Phương trình cân bằng dòng trên các tập cắt ứng với mỗi cành
làm thành hệ đủ và độc lập. Chứng minh:
Do mỗi tập cắt chứa riêng một dòng nhánh.
2014 – Lý thuyết mạch điện 1 - Nguyễn Việt Sơn 19
LÝ THUYẾT MẠCH ĐIỆN 1
Chương 3: Phương pháp cơ bản tính mạch tuyến tính ở
chế độ xác lập điều hòa - Graph Kirchhoff
I. Phương pháp dòng nhánh
II. Phương pháp thế nút
III. Phương pháp dòng vòng
IV. Khái niệm về graph Kirchhoff
V. Các định lý về lập phương trình Kirchhoff
VI. Ma trận cấu trúc A, B
VI.1. Ma trận đỉnh - nhánh A
VI.2. Ma trận bù - nhánh B
VII. Lập phương trình bằng ma trận cấu trúc
2014 – Lý thuyết mạch điện 1 - Nguyễn Việt Sơn 20
Chương 3: Phương pháp cơ bản tính mạch tuyến tính
ở chế độ xác lập điều hòa - Graph Kirchhoff
VI. Ma trận cấu trúc A. Graph Mạch điện Ma trận cấu trúc Kirchhoff
VI.1. Ma trận đỉnh - nhánh A.
1 nếu nhánh j đi ra nút i
a 0 nếu nhánh j không dính với nút i ij 1
nếu nhánh j đi vào nút i
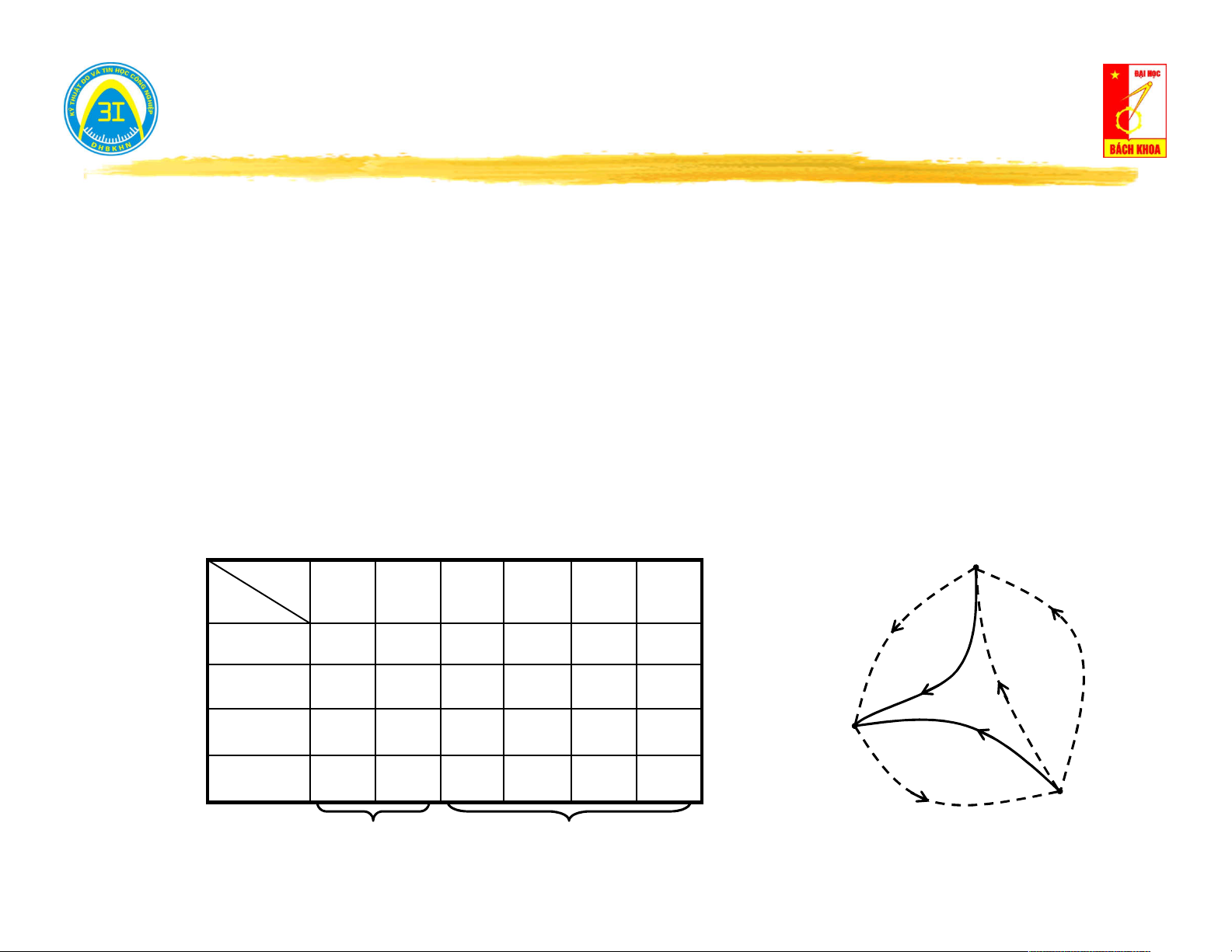
Ví dụ 3.5: Lập ma trận đỉnh - nhánh A của graph cho bởi hình bên. II Nhánh 1 1 2 3 4 5 6 Đỉnh 3 2 I -1 0 0 1 0 -1 4 I 5 III II 1 1 1 0 0 0 III 0 0 -1 0 -1 1 IV 6 IV 0 -1 0 -1 1 0
2014 – Lý thuyết mạch điện 1 - Nguyễn Việt Sơn 21
Chương 3: Phương pháp cơ bản tính mạch tuyến tính
ở chế độ xác lập điều hòa - Graph Kirchhoff
VI.1. Ma trận đỉnh - nhánh A Ma trận A = Ma trận A - 1 hàng Tính chất: đủ thừa
Cột: Nhánh thứ i nối 2 đỉnh nào với nhau, và chiều dương của nhánh.
Hàng: Đỉnh thứ j có những nhánh nào và chiều của mỗi nhánh tại đỉnh đó.
Mỗi hàng của A là tổ hợp tuyến tính của các hàng còn lại → Athừa Ví dụ 3.6: 1 0 0 1 0 1 A 0 1 0 1 1 0 du 0 0 1 0 1 1 Nhánh 1 2 3 4 5 6 cây bù cành Đỉnh II I -1 0 0 1 0 -1 1 II 3 1 1 1 0 0 0 2 III 0 0 -1 0 -1 1 4 I 5 III IV 0 -1 0 -1 1 0 IV 6
2014 – Lý thuyết mạch điện 1 - Nguyễn Việt Sơn 22
Chương 3: Phương pháp cơ bản tính mạch tuyến tính
ở chế độ xác lập điều hòa - Graph Kirchhoff
VI.1. Ma trận đỉnh - nhánh A. Ứng dụng:
Lập phương trình theo luật Kirchhoff 1: I 1 . A I
0 trong đó I ... nh nh I n 1 xn
Lập phương trình quan hệ giữa điện áp các nhánh và điện thế nút: U 1 1 t U A . ... ; U ... trong đó nut nh nh nut U 1 n d 1x( d-1) 1 xn bỏ đi đỉnh có thế bằng 0
2014 – Lý thuyết mạch điện 1 - Nguyễn Việt Sơn 23
Chương 3: Phương pháp cơ bản tính mạch tuyến tính
ở chế độ xác lập điều hòa - Graph Kirchhoff
VI.1. Ma trận đỉnh - nhánh A. Chú ý: Từ ma trận A
có thể khôi phục lại được cấu trúc của graph bằng cách: đủ
Khôi phục lại ma trận Athừa
Số hàng của ma trận bằng số đỉnh của graph II
Số cột của ma trận bằng số nhánh của graph.
Ví dụ 3.7: Cho ma trận A Vẽ lại graph. đủ. 1 1 1 1 1 0 2 5 A du 1 1 0 0 1 4 I 1 1 1 1 0 I 3 III A 1 1 0 0 1 II thua 0 0 1 1 1 III 1 2 3 4 5
2014 – Lý thuyết mạch điện 1 - Nguyễn Việt Sơn 24
Chương 3: Phương pháp cơ bản tính mạch tuyến tính
ở chế độ xác lập điều hòa - Graph Kirchhoff
VI.2. Ma trận bù - nhánh B.
Một graph hoàn toàn xác định nếu chỉ rõ tập các nhánh có định chiều & tập các
bù cành khép kín qua một cây & chỉ rõ mỗi vòng kín gồm các nhánh nào.
1 nếu nhánh i tham gia vòng & cùng chiều bù cành j
b 0 nếu nhánh i không không tham gia vòng với bù cành j ij 1
nếu nhánh i tham gia vòng & ngược chiều với bù cành j
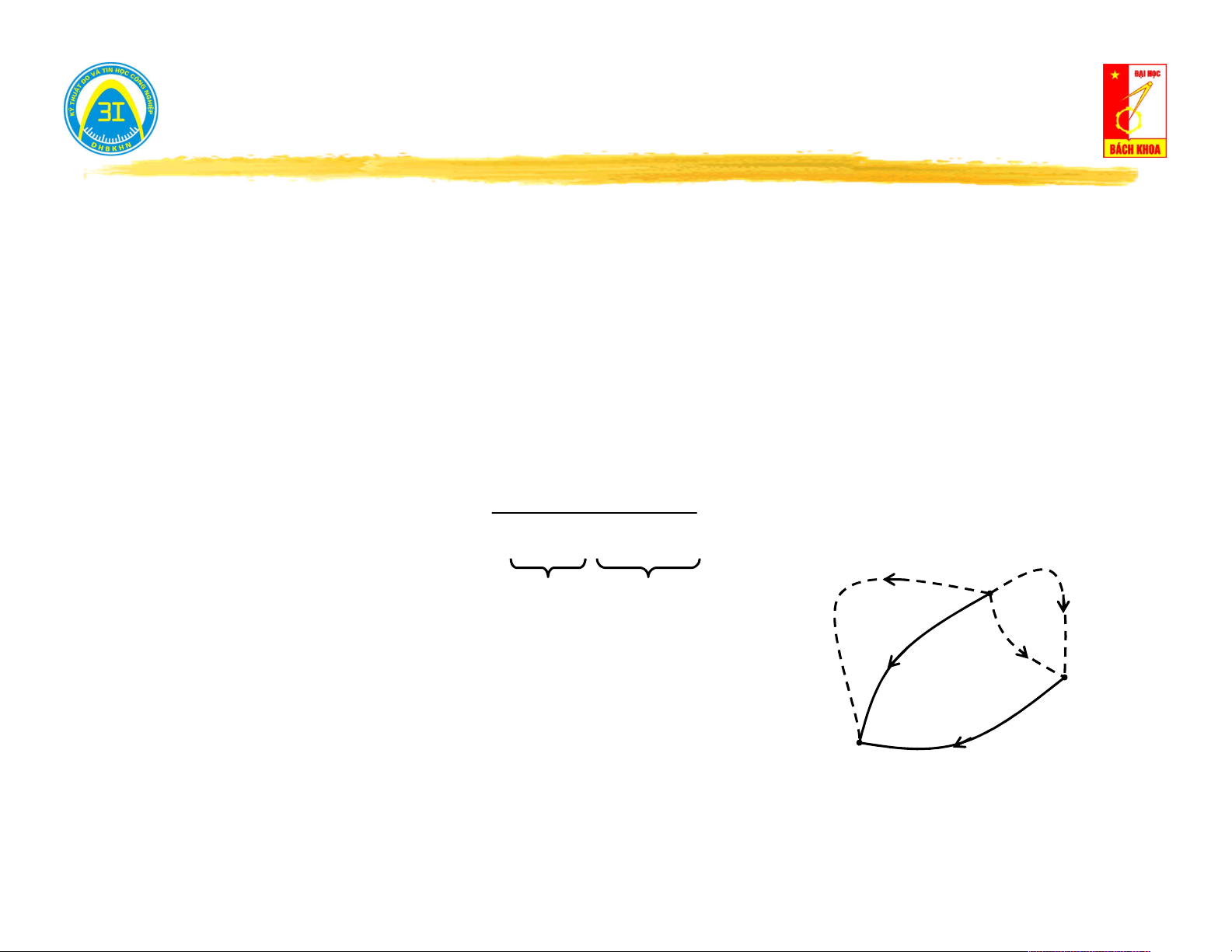
Ví dụ 3.8: Lập ma trận bù - nhánh B của graph cho bởi hình bên. II Nhánh 1 2 3 4 5 6 6 Bù 5 3 -1 1 1 0 0 0 2 3 4 1 0 0 1 0 0 1 5 0 -1 0 0 1 0 I 6 4 -1 1 0 0 0 1 III Cành Bù cành
2014 – Lý thuyết mạch điện 1 - Nguyễn Việt Sơn 25
Chương 3: Phương pháp cơ bản tính mạch tuyến tính
ở chế độ xác lập điều hòa - Graph Kirchhoff
VI.2. Ma trận bù - nhánh B. Tính chất:
Cột: Nhánh j tham gia vòng nào, chiều của j so với chiều vòng (quy ước
chiều vòng là chiều của bù cành).
Bù cành chỉ tham gia vào vòng của mình, không tham gia vào vòng khác.
Hàng: Số vòng của graph, số nhánh và chiều của nhánh trong mỗi vòng. B = (B | B ) = (B | I) cành bù cành Ứng dụng: U 1
Phương trình theo luật K1: . B U trong đó: nh 0 U nh ... U n 1 xn
Phương trình quan hệ giữa dòng điện nhánh & dòng điện bù: I1 I 1 bu t
I nh B . I bu trong đó: I nh ... ; I bu ... I n I bu 1 k xn 1 xk
2014 – Lý thuyết mạch điện 1 - Nguyễn Việt Sơn 26
Chương 3: Phương pháp cơ bản tính mạch tuyến tính
ở chế độ xác lập điều hòa - Graph Kirchhoff
VI.2. Ma trận bù - nhánh B.
Chú ý: Từ ma trận B, có thể vẽ lại được graph đã cho. Ví dụ 3.9: 1 1 0 0 0 1 0 1 0 0 3 B 1 0 1 0 1 1 1 0 1 0 4 1 0 0 1 1 1 1 0 0 1 5 1 2 3 4 5 3 II cành bù cành 5
Số nhánh: 5 (1, 2, 3, 4, 5). 1 4 Số bù cành: 3 (4, 5, 6) III
Số cành: 5 – 3 = 2 → Số đỉnh: I 3 2
2014 – Lý thuyết mạch điện 1 - Nguyễn Việt Sơn 27
LÝ THUYẾT MẠCH ĐIỆN 1
Chương 3: Phương pháp cơ bản tính mạch tuyến tính ở
chế độ xác lập điều hòa - Graph Kirchhoff
I. Phương pháp dòng nhánh
II. Phương pháp thế nút
III. Phương pháp dòng vòng
IV. Khái niệm về graph Kirchhoff
V. Các định lý về lập phương trình Kirchhoff
VI. Ma trận cấu trúc A, B
VII. Lập phương trình bằng ma trận cấu trúc
VII.1. Luật Ohm theo nghĩa rộng
VII.2. Lập phương trình
2014 – Lý thuyết mạch điện 1 - Nguyễn Việt Sơn 28
Chương 3: Phương pháp cơ bản tính mạch tuyến tính
ở chế độ xác lập điều hòa - Graph Kirchhoff
VII.1. Luật Ohm theo nghĩa rộng. I Z nh nh
Nhánh không nguồn: 1 U nh Z . I nh Z Y nh nh nh U nh I nh Y .U nh nh I nh Znh
Nhánh có nguồn áp: U Enh
nh U Z E nh Unh I nh .Z Enh U Z nh U nh U nh E nh I nh
I nh Y .(U nh Enh ) nh Z nh J nh
Nhánh có nguồn dòng: Znh I nh I Z
I nh Y .U nh J nh
I I J nh I
I J nh nh Z nh nh Z
U nh Z (I nh J nh ) U nh nh J nh
Nhánh có nguồn dòng - nguồn áp: Z
U nh U Z Enh U nh (I nh J nh ).Z Enh I Enh nh nh I Z nh
I nh Y .(U nh Enh ) J nh nh U nh
2014 – Lý thuyết mạch điện 1 - Nguyễn Việt Sơn 29
Chương 3: Phương pháp cơ bản tính mạch tuyến tính
ở chế độ xác lập điều hòa - Graph Kirchhoff
VII.2. Lập phương trình. Ma trận thông số.
Ma trận tổng trở nhánh: Z ... Z 11 1n Z : Tổng trở nhánh k kk Z ... Z ...
Z : Tổng trở tương hỗ nhánh k & l nh kk kl Z ... Z 1 n nn nxn E1
Ma trận nguồn áp nhánh: E nh ...
Ei: là giá trị nguồn áp nhánh i E n 1 xn J 1
Ma trận nguồn dòng nhánh: J nh ...
J i : là giá trị nguồn dòng nhánh i J n 1 xn
2014 – Lý thuyết mạch điện 1 - Nguyễn Việt Sơn 30
Chương 3: Phương pháp cơ bản tính mạch tuyến tính
ở chế độ xác lập điều hòa - Graph Kirchhoff
VII.2. Lập phương trình.
a. Lập phương trình với ma trận A.
Trình tự tính toán bằng Matlab: Từ phương trình: . A I nh 0 Vào số liệu: ,
A Z , Enh , J nh . nh
Mặt khác có: I nh Y .(U nh Enh ) J nh nh
Tính các ma trận: Suy ra: . A Y .U nh . A Y . Enh . A J nh 0 nh nh
Y inv(Z ) Y . AY . t A nh nh nut nh . A Y . t A . .( A J nh Y . Enh ) nh nut nh J nut .(
A J nh Y . Enh ) nh Đặt: Y . A Y . t A . nut nh J nut \ Y nut nut J nut .(
A J nh Y . Enh ) nh Kết quả: J nut Mà: J nut Y . nut nut nut Y t U nh A . nut nut t Tính được: U
I nh Y .(U nh Enh ) J nh nh A . nh nut
I nh Y .(U nh Enh ) J nh nh
2014 – Lý thuyết mạch điện 1 - Nguyễn Việt Sơn 31
Chương 3: Phương pháp cơ bản tính mạch tuyến tính
ở chế độ xác lập điều hòa - Graph Kirchhoff
VII.2. Lập phương trình.
b. Lập phương trình với ma trận B.
Trình tự tính toán bằng Matlab: Từ phương trình: . B U nh 0
Vào số liệu: B, Z , Enh , J nh . nh
Mặt khác có: U nh (I nh J nh ).Z Enh nh
Tính các ma trận: Suy ra: . B Z . I nh . B Z . J nh . B Enh 0 nh nh Z . B Z . t B vong nh B.Z . t B . I bu .(
B Enh Z . J nh ) nh nh Evong .(
B Enh Z . J nh ) nh Đặt: Z . B Z . t B . vong nh
I bu Evong \ Zvong Evong .(
B Enh Z . J nh ) nh Kết quả: Evong Vậy ta có: Z
. I bu Evong I bu t vong
I nh B . I Z bu vong
U nh Z .(I nh J nh ) E t Như vậy tính được: nh I nh
nh B . I bu
U nh Z .(I nh J nh ) Enh nh
2014 – Lý thuyết mạch điện 1 - Nguyễn Việt Sơn 32
LÝ THUYẾT MẠCH ĐIỆN 1
Chương 4: Tính chất cơ bản của mạch điện tuyến tính. I. Khái niệm chung.
II. Tính chất tuyến tính.
III. Khái niệm hàm truyền đạt.
IV. Truyền đạt tương hỗ và không tương hỗ.
Bài tập: 1, 2, 3, 4, 5, 8 + bài thêm. 1
2014 – Lý thuyết mạch điện 1 - Nguyễn Việt Sơn
Chương 4: Tính chất cơ bản của mạch điện tuyến tính I. Khái niệm chung.
Mạch điện tuyến tính là mạch điện có mô hình toán học gồm hữu hạn các biến
trạng thái với tính chất:
Các thông số của mạch (R, L, C) là hằng số.
Quan hệ giữa các biến trạng thái trên cùng 1 phần tử là phương trình vi tích
phân tuyến tính, hệ số hằng. Miền thời gian
Phương trình vi tích phân
Mạch điện tuyến tính
tuyến tính, hệ số hằng Miền ảnh phức
Các thông số của mạch là hằng số. Phương trình đại
Quan hệ giữa các biến trạng thái số ảnh phức
trên 1 phân tử là tuyến tính.
Kích thích điều hòa 2
2014 – Lý thuyết mạch điện 1 - Nguyễn Việt Sơn
LÝ THUYẾT MẠCH ĐIỆN 1
Chương 4: Tính chất cơ bản của mạch điện tuyến tính. I. Khái niệm chung
II. Tính chất tuyến tính.
II.1. Quan hệ tuyến tính giữa kích thích và đáp ứng.
II.2. Quan hệ tuyến tính giữa các đáp ứng.
III. Khái niệm hàm truyền đạt.
IV. Truyền đạt tương hỗ và không tương hỗ. 3
2014 – Lý thuyết mạch điện 1 - Nguyễn Việt Sơn
Chương 4: Tính chất cơ bản của mạch điện tuyến tính
II.1. Quan hệ tuyến tính giữa kích thích và đáp ứng:
Phát biểu 1: Nếu trong mạch có một kích thích thì mỗi đáp ứng của mạch đều có
quan hệ tuyến tính với kích thích đó.
X k : ảnh phức của đáp ứng thứ k
X k T . F F
: ảnh phức của kích thích trong mạch k T
: hàm truyền đạt biểu diễn mối quan k
hệ giữa đáp ứng thứ k và kích thích Ví dụ: Z E Z Z 1 2 3 I1 . E Z .Z 2 3
Z .Z Z .Z Z .Z 1 2 1 3 2 3 Z 1 I I Z Z 1 2 2 3 T1 Z2 Z3 E Z Z Z Z 2 3 3 3 I . . E . E 2
Z .Z Z .Z Z .Z Z Z
Z .Z Z .Z Z .Z 1 2 1 3 2 3 2 3 1 2 1 3 2 3 T2 4
2014 – Lý thuyết mạch điện 1 - Nguyễn Việt Sơn
Chương 4: Tính chất cơ bản của mạch điện tuyến tính
II.1. Quan hệ tuyến tính giữa kích thích và đáp ứng:
Phát biểu 2: Nếu trong mạch có nhiều kích thích cùng tần số tác động đồng thời thì
mỗi đáp ứng của mạch đều có quan hệ tuyến tính với mỗi kích thích đó. (tính chất xếp chồng) X
: ảnh phức của đáp ứng thứ k k
X k T . F T . F ... T . F
F , F ,..., F : ảnh phức của các kích thích trong mạch 1k 1 2k 2 nk n 1 2 n
T ,T ,...,T
: hàm truyền đạt biểu diễn mối quan hệ 1k 2k nk
giữa đáp ứng thứ k và các kích thích
Nếu các kích thích không cùng tần số thì ta phải xếp chồng các đáp ứng trong
miền thời gian (tính chất xếp chồng)
Phát biểu 3: Nếu trong mạch có nhiều kích thích cùng tác động nhưng chỉ có một
kích thích biến động thì quan hệ giữa mỗi đáp ứng với kích thích biến động đấy có dạng:
X k : ảnh phức của đáp ứng thứ k
F1 : ảnh phức của kích thích biến động
X k T . F X 0 1 k k T
: hàm truyền đạt biểu diễn mối quan hệ giữa 1k
đáp ứng thứ k và kích thích biến động
X 0k : tổng của những số hạng khác 5
2014 – Lý thuyết mạch điện 1 - Nguyễn Việt Sơn
Chương 4: Tính chất cơ bản của mạch điện tuyến tính
II.2. Quan hệ tuyến tính giữa các đáp ứng:
Phát biểu: Trong mạch tuyến tính, mỗi đáp ứng của mạch luôn có một quan hệ
tuyến tính với ít nhất một đáp ứng khác trong mạch theo dạng:
X k , X j: ảnh phức của 2 đáp ứng bất kỳ trong mạch
X k A . X j B jk
A , B : hàm truyền đạt biểu diễn mối jk quan hệ giữa 2 đáp ứng Z1
Ví dụ: Tìm quan hệ tuyến tính giữa I1 và I 2 khi Z biến thiên từ 0 đến ∞. 3 I1 I 2
Quan hệ tuyến tính giữa I1 và I 2 có dạng: I1 . A I 2 B Z2 E E
Z = 0 → ∞ 3 Khi Z = 0: 3
I 2 0 I1 B Z1 E Khi Z = ∞: 3
I1 I 2 Z Z 1 2 Z E E E E Z 2 2 Vậy ta có: I . I . A A 1 2 Z Z Z Z Z Z Z Z 1 1 1 2 1 2 1 1 6
2014 – Lý thuyết mạch điện 1 - Nguyễn Việt Sơn
LÝ THUYẾT MẠCH ĐIỆN 1
Chương 4: Tính chất cơ bản của mạch điện tuyến tính. I. Khái niệm chung.
II. Tính chất tuyến tính.
III. Khái niệm hàm truyền đạt.
IV. Truyền đạt tương hỗ và không tương hỗ. 7
2014 – Lý thuyết mạch điện 1 - Nguyễn Việt Sơn
Chương 4: Tính chất cơ bản của mạch điện tuyến tính
III. Khái niệm hàm truyền đạt.
Hàm truyền đạt là những hàm đặc tính tần phức đặc trưng cho hành vi của mạch tuyến
tính hệ số hằng dưới tác dụng kích thích của một phổ tần điều hòa.
Hàm truyền đạt được định nghĩa là tỷ số riêng hoặc đạo hàm riêng của ảnh đáp ứng trên ảnh kích thích.
X k () : ảnh phức đáp ứng trên nhánh thứ k của mạch. X k () T ()
: ảnh phức kích thích trên nhánh thứ m của mạch. mk F m () F m () T () mk
: hàm đặc tính tần phức giữa nhánh thứ k và nhánh thứ m
Mạch Kirchhoff có 4 hàm truyền đạt chính: U k
Hàm truyền đạt áp: Đo khả năng cung cấp áp trên nhánh k từ riêng K Umk
một nguồn áp ở nhánh m. Em
Hàm truyền đạt dòng: Đo khả năng cung cấp dòng điện trên nhánh I k K
k từ riêng một nguồn dòng ở nhánh m. Imk J m
Hàm truyền đạt tổng dẫn: Đo khả năng truyền dòng điện thứ k từ I k Y
riêng một nguồn áp ở nhánh m. mk Em
Hàm truyền đạt tổng trở: Đo khả năng truyền áp thứ k từ riêng một U k Z mk nguồn dòng ở nhánh m. J m 8
2014 – Lý thuyết mạch điện 1 - Nguyễn Việt Sơn
LÝ THUYẾT MẠCH ĐIỆN 1
Chương 4: Tính chất cơ bản của mạch điện tuyến tính. I. Khái niệm chung.
II. Tính chất tuyến tính.
III. Khái niệm hàm truyền đạt.
IV. Truyền đạt tương hỗ và không tương hỗ. 9
2014 – Lý thuyết mạch điện 1 - Nguyễn Việt Sơn
Chương 4: Tính chất cơ bản của mạch điện tuyến tính
IV. Truyền đạt tương hỗ và không tương hỗ.
Mạch điện Kirchhoff tuyến tính được gọi là tương hỗ nếu những hàm truyền đạt tổng trở,
tổng dẫn trong mạch là tuyến tính và thuận nghịch. Z Z KL LK U U I I K K trong đó: L Z ; Z và L Y ; Y Y Y KL LK KL LK KL LK I K I L U K U L Ví dụ:
Truyền đạt áp giữa 2 cuộn dây đặt gần nhau có hỗ cảm là một truyền đạt tương hỗ. M M
k. L .L 12 21 1 2
Truyền đạt áp (dòng) trong máy biến áp (biến dòng), trong khuếch đại thuật toán ...,
hàm truyền đạt tổng trở (tổng dẫn) trong transistor ... không có tính tương hỗ. Tính chất:
Mạch tuyến tính tương hỗ có ma trận Z và Y
đối xứng với nhau qua đường chéo vòng nút
chính → chỉ cần tìm một nửa các hàm truyền đạt tổng trở, tổng dẫn.
Nhìn chung các hàm truyền đạt dòng, áp không có tính tương hỗ. 10
2014 – Lý thuyết mạch điện 1 - Nguyễn Việt Sơn
Chương 4: Tính chất cơ bản của mạch điện tuyến tính
IV. Truyền đạt tương hỗ và không tương hỗ.
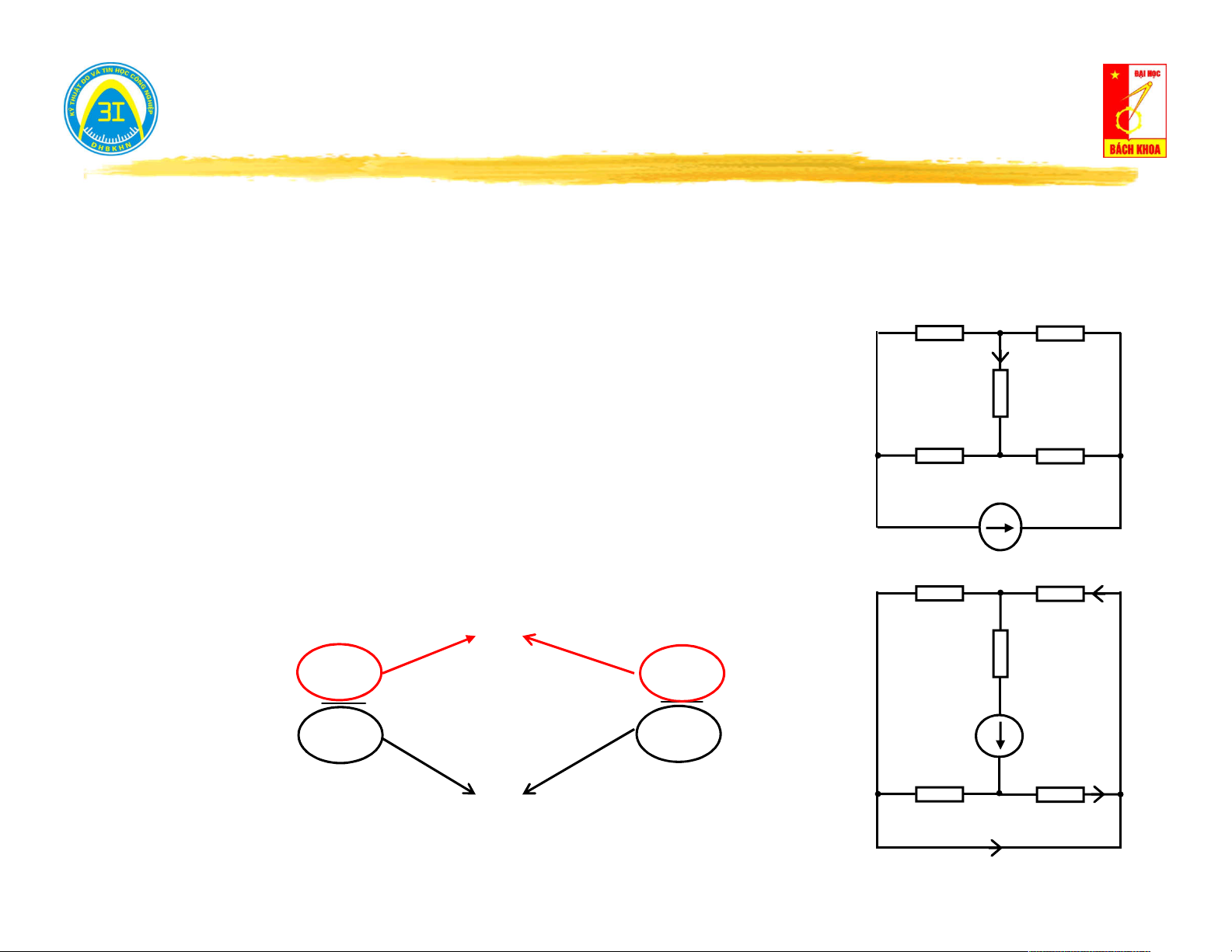
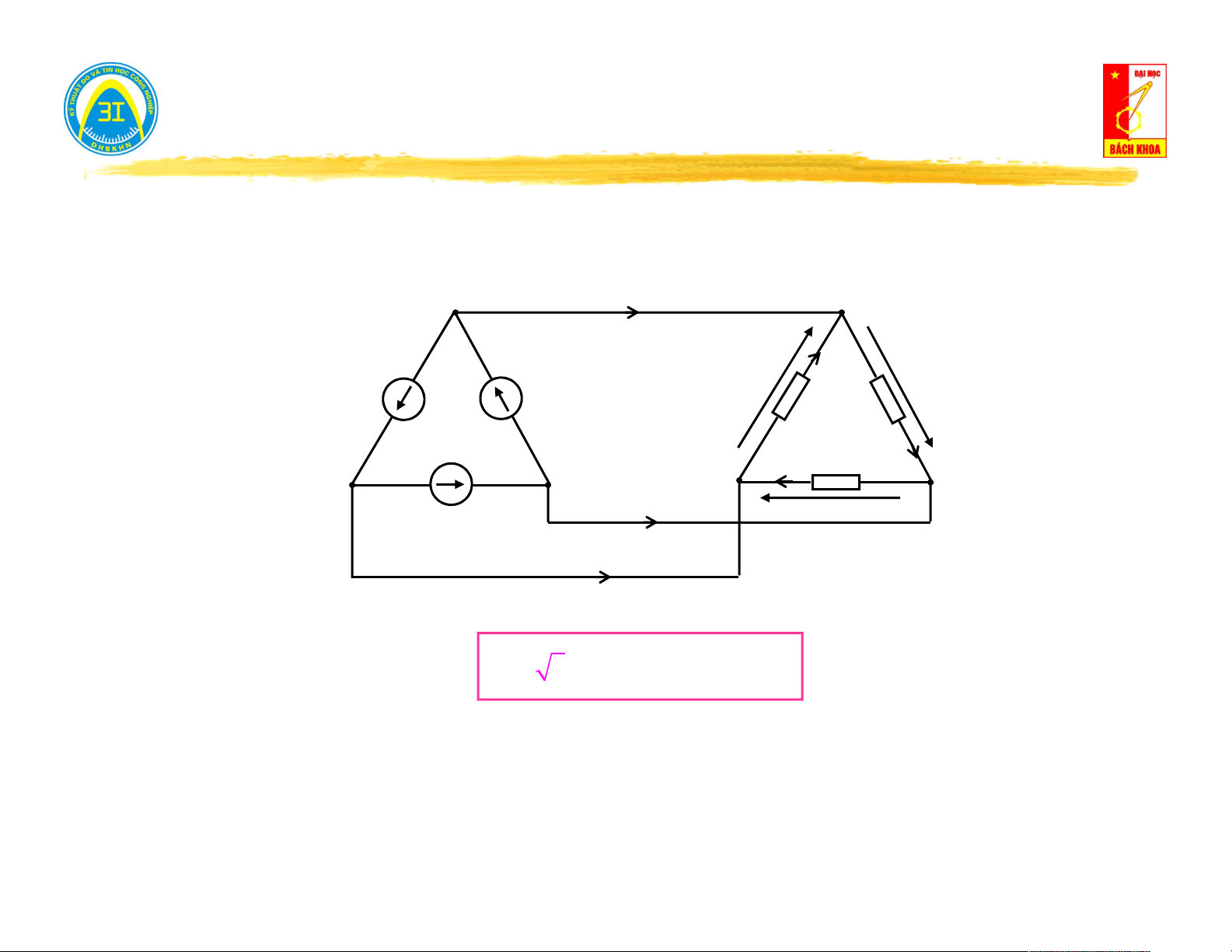
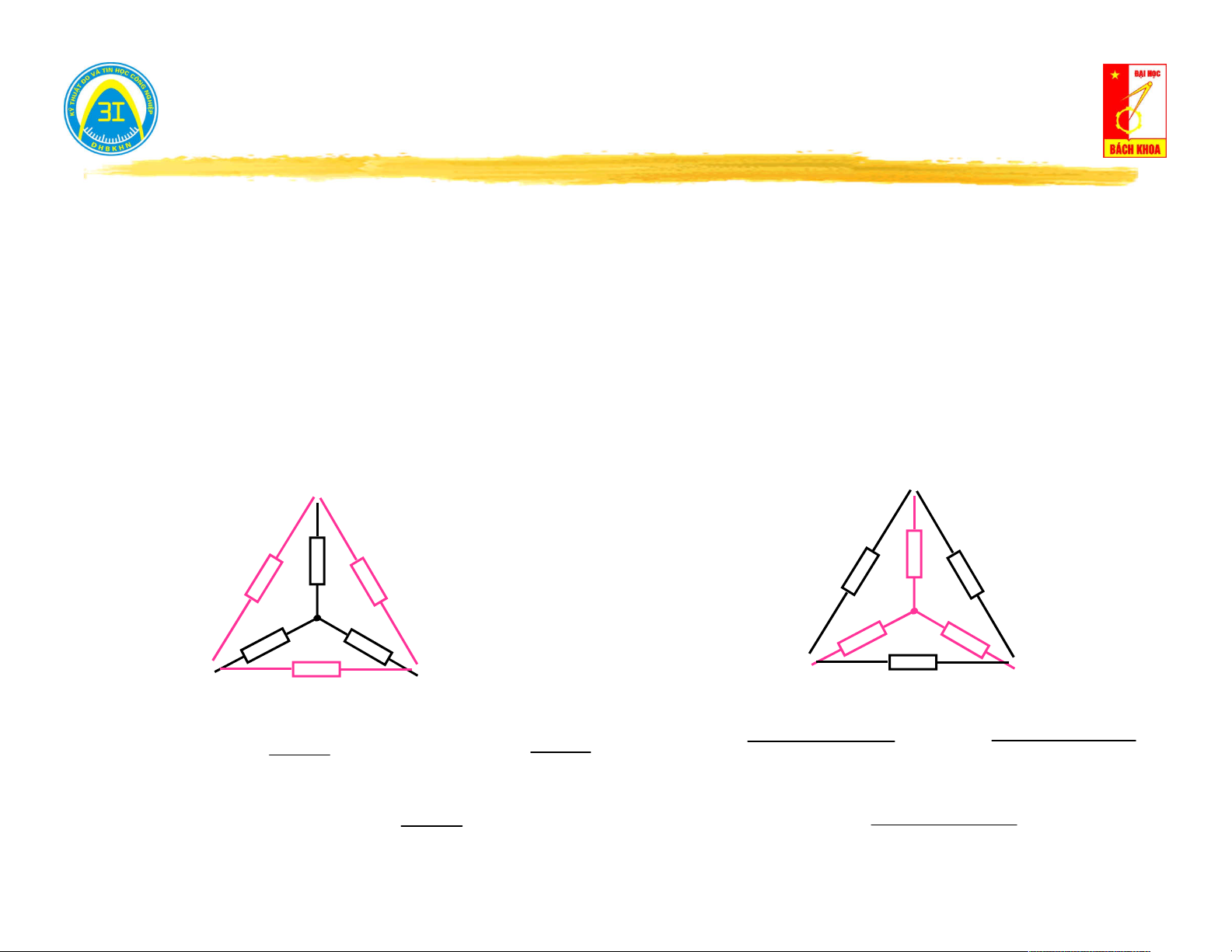
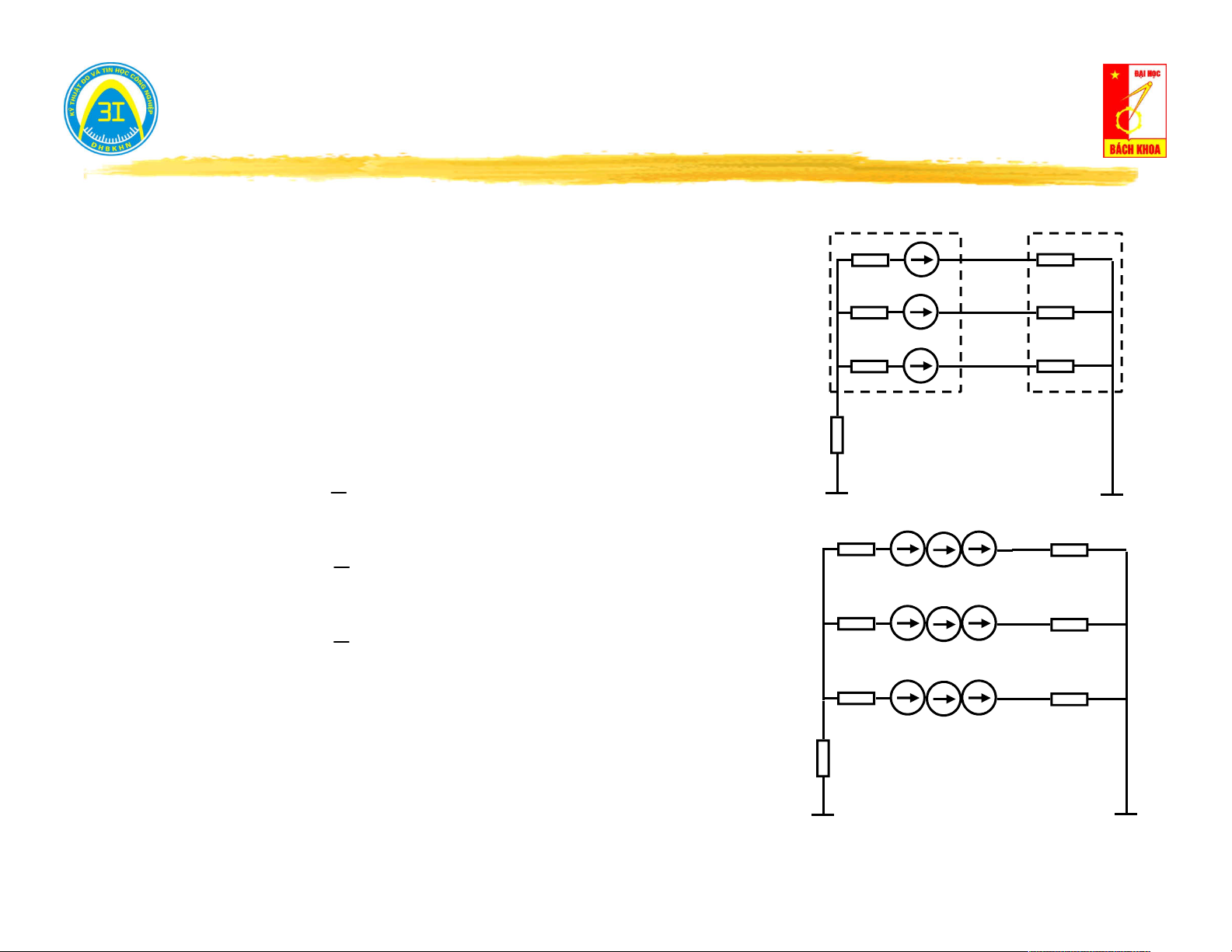
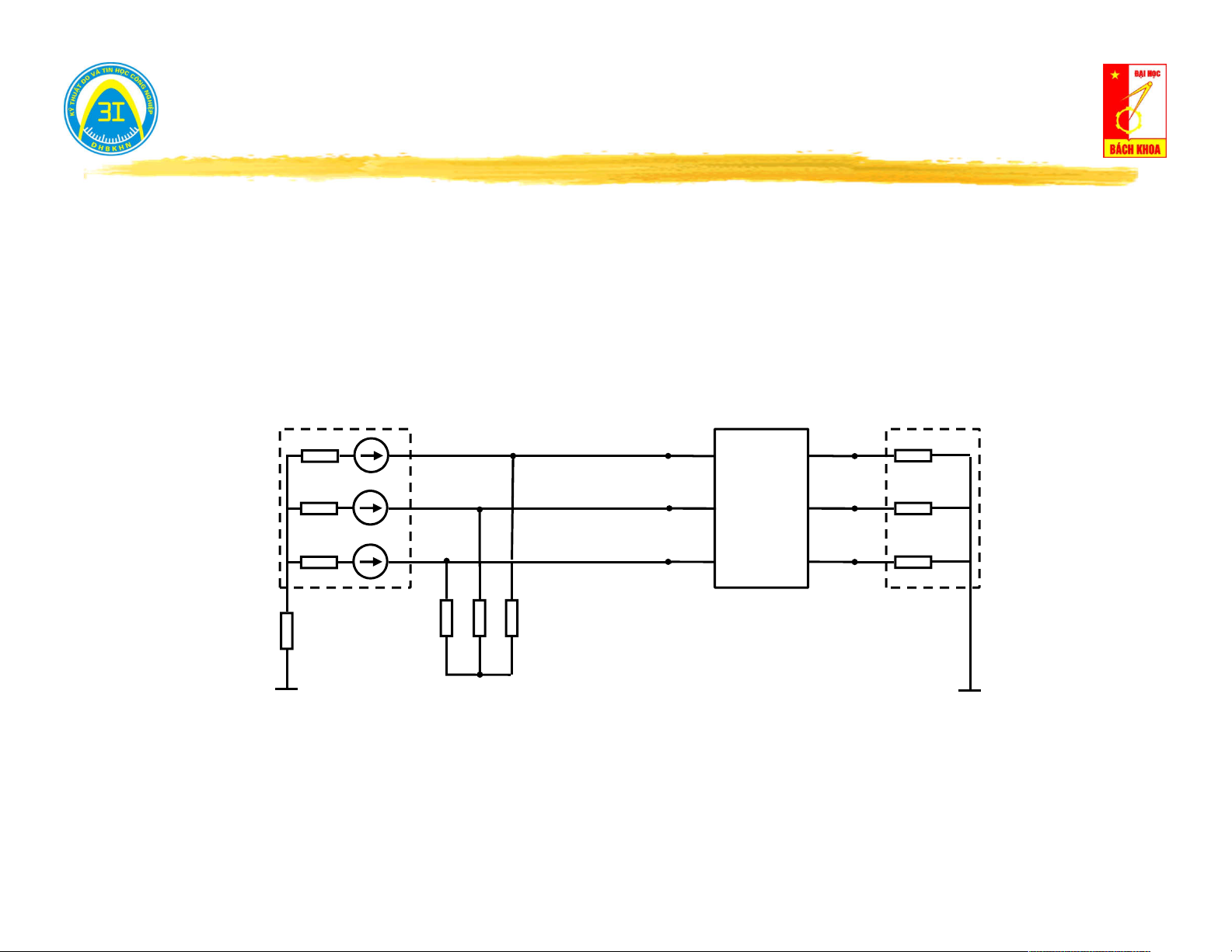
Ví dụ: Cho mạch điện tuyến tính tương hỗ. Hãy tính dòng điện trong nhánh 5 khi nguồn kích thích đặt trong nhánh 6. R =20Ω 1 R =20Ω 3
Với mạch hình (a) → ta có thể tính I theo các phương pháp dòng 5 I
nhánh, dòng vòng, thế đỉnh, tuy nhiên dù giải bằng phương pháp 5
nào ta cũng phải giải với ít nhất 3 phương trình. R =8Ω 5 R =20Ω R =30Ω (a) 2 4
Áp dụng tính chất tương hỗ: Dòng điện I trong hình (a) sẽ bằng 5
dòng điện I trong hình (b). Thật vậy, vì mạch là tuyến tính tương E=6V 6 hỗ nên: R1 R3 I3 Y Y 56 65 = R5 I I 6 Y 5 Y (b) 56 65 E E E 5 6 R R I 2 4 4 = I6 11
2014 – Lý thuyết mạch điện 1 - Nguyễn Việt Sơn
Chương 4: Tính chất cơ bản của mạch điện tuyến tính
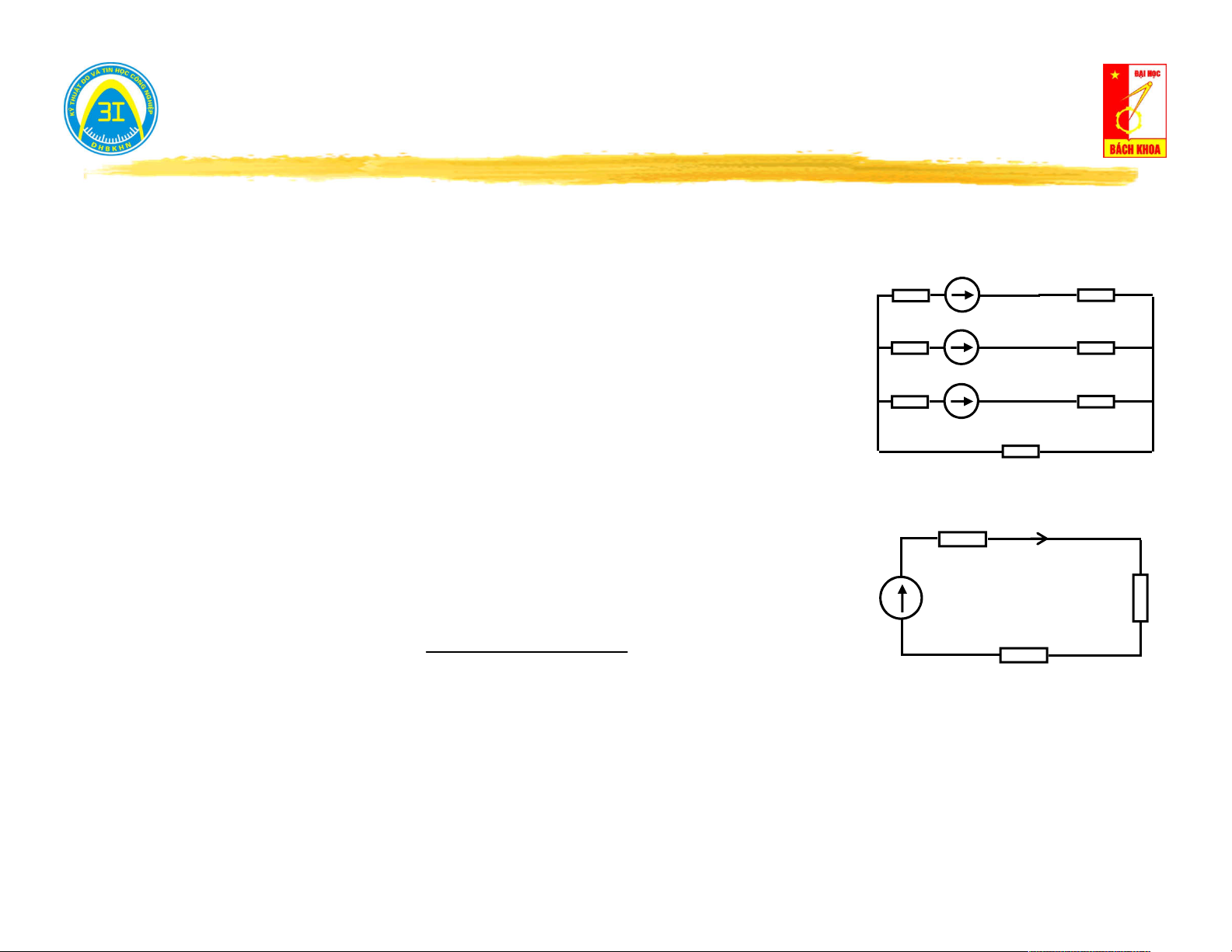
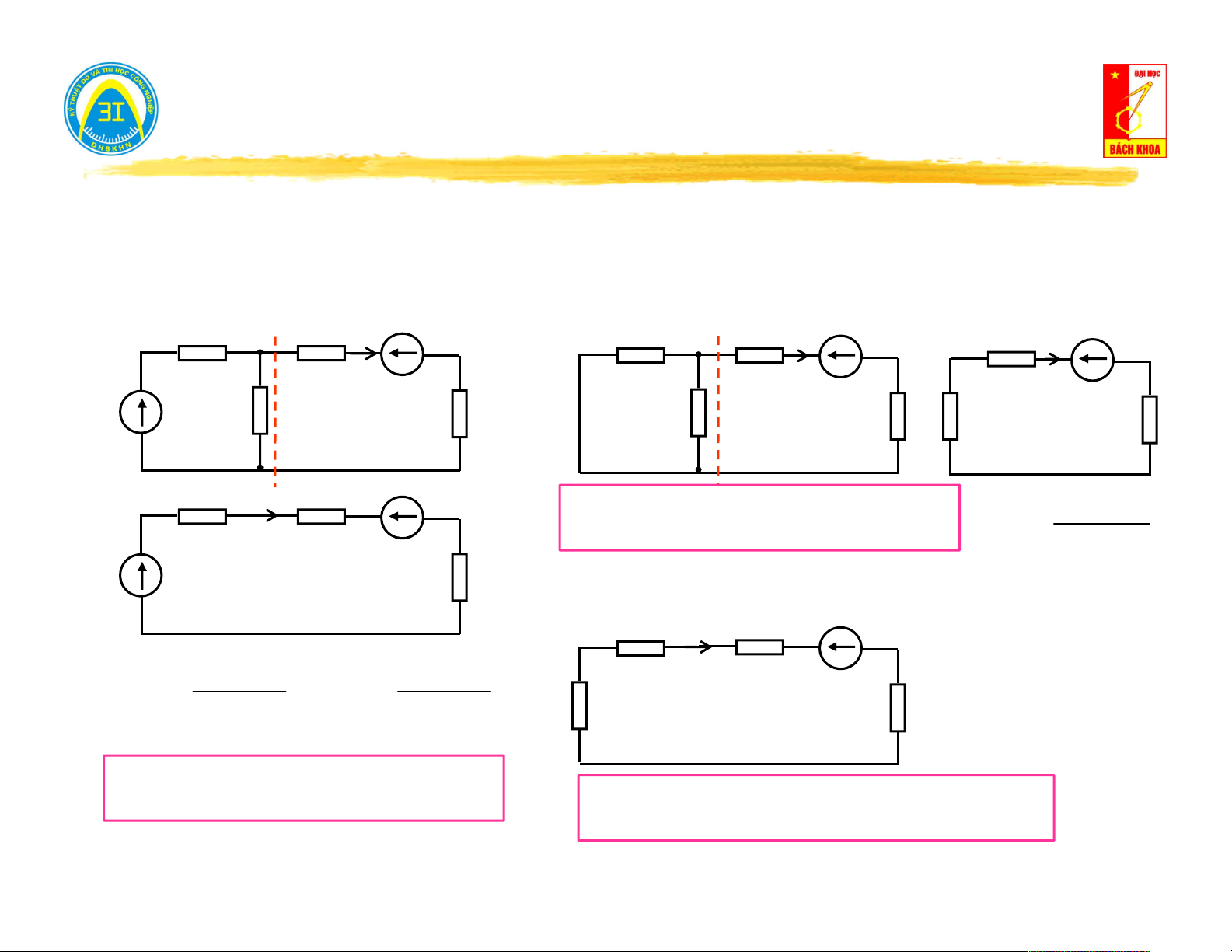
IV. Truyền đạt tương hỗ và không tương hỗ. R =20Ω 1 R =20Ω 3 Ví dụ: I5 E R =8Ω I 0.2( ) A 5 ng
R (R // R ) (R // R ) R =20Ω R =30Ω (a) 5 2 4 1 3 2 4 E=6V R2 I I . 0.08( ) A 4 ng R R 2 4 R R =20Ω R =20Ω 1 3 1 I I . 0.1( ) A 3 ng R R 1 3 I3 R =8Ω 5 Ing
I I I 0.1 0.08 0.02( ) A 6 3 4 (b) E=6V R =20Ω R =30Ω Vậy: I = 0.02(A) 2 4 5 I I 4 6 12
2014 – Lý thuyết mạch điện 1 - Nguyễn Việt Sơn
LÝ THUYẾT MẠCH ĐIỆN 1
Chương 5: Mạch điện tuyến tính có kích thích chu kỳ I. Khái niệm.
II. Cách phân tích mạch tuyến tính có kích thích chu kỳ.
III. Giá trị hiệu dụng - công suất dòng chu kỳ.
IV. Hàm truyền đạt và đặc tính tần số.
Bài tập: 3, 4, 7, 8, 9, 10, 11, 12 + Bài thêm 1
2014 – Lý thuyết mạch điện 1 - Nguyễn Việt Sơn
Chương 5: Mạch điện tuyến tính có kích thích chu kỳ I. Khái niệm.
Định nghĩa: Tín hiệu chu kỳ là tín hiệu mà dáng điệu của nó lặp lại sau một
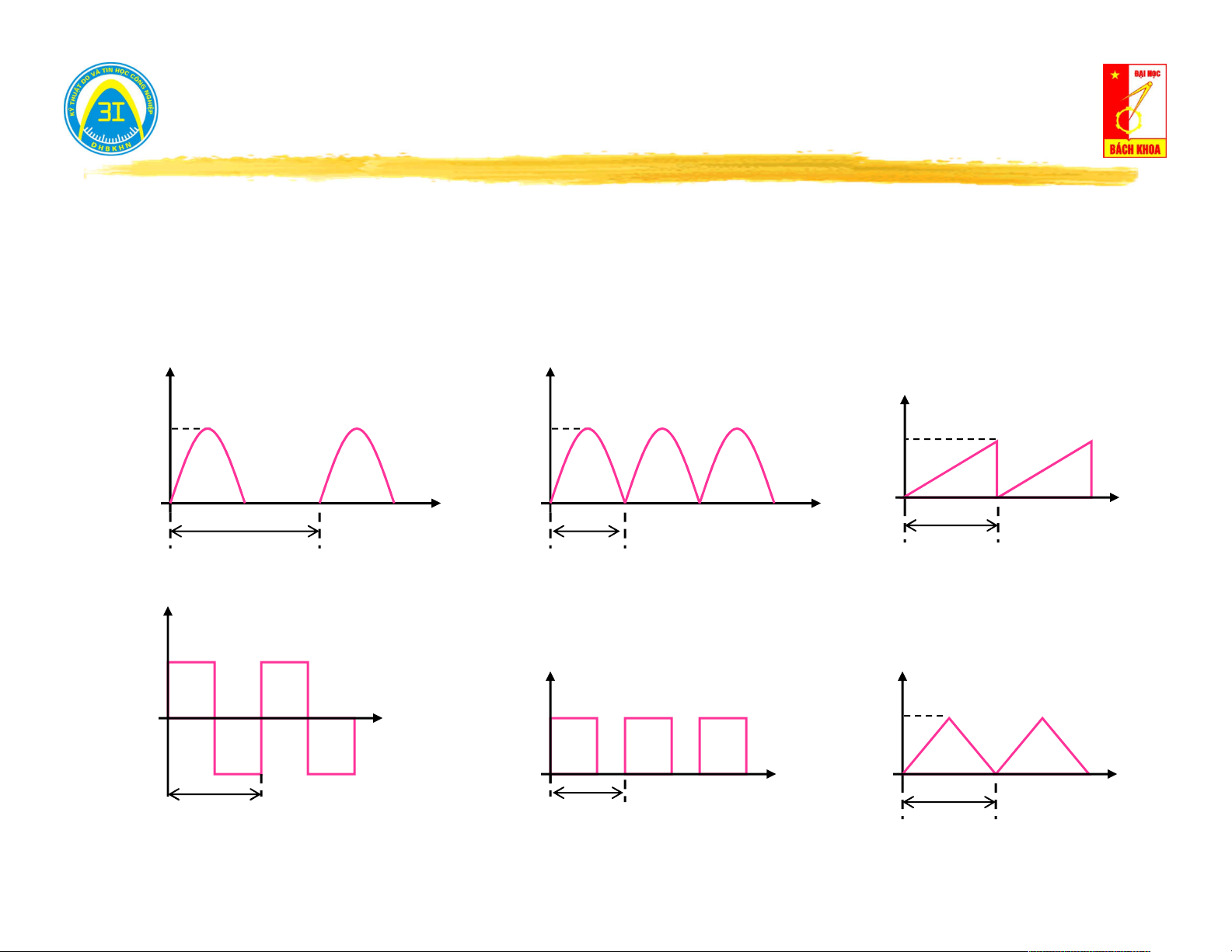
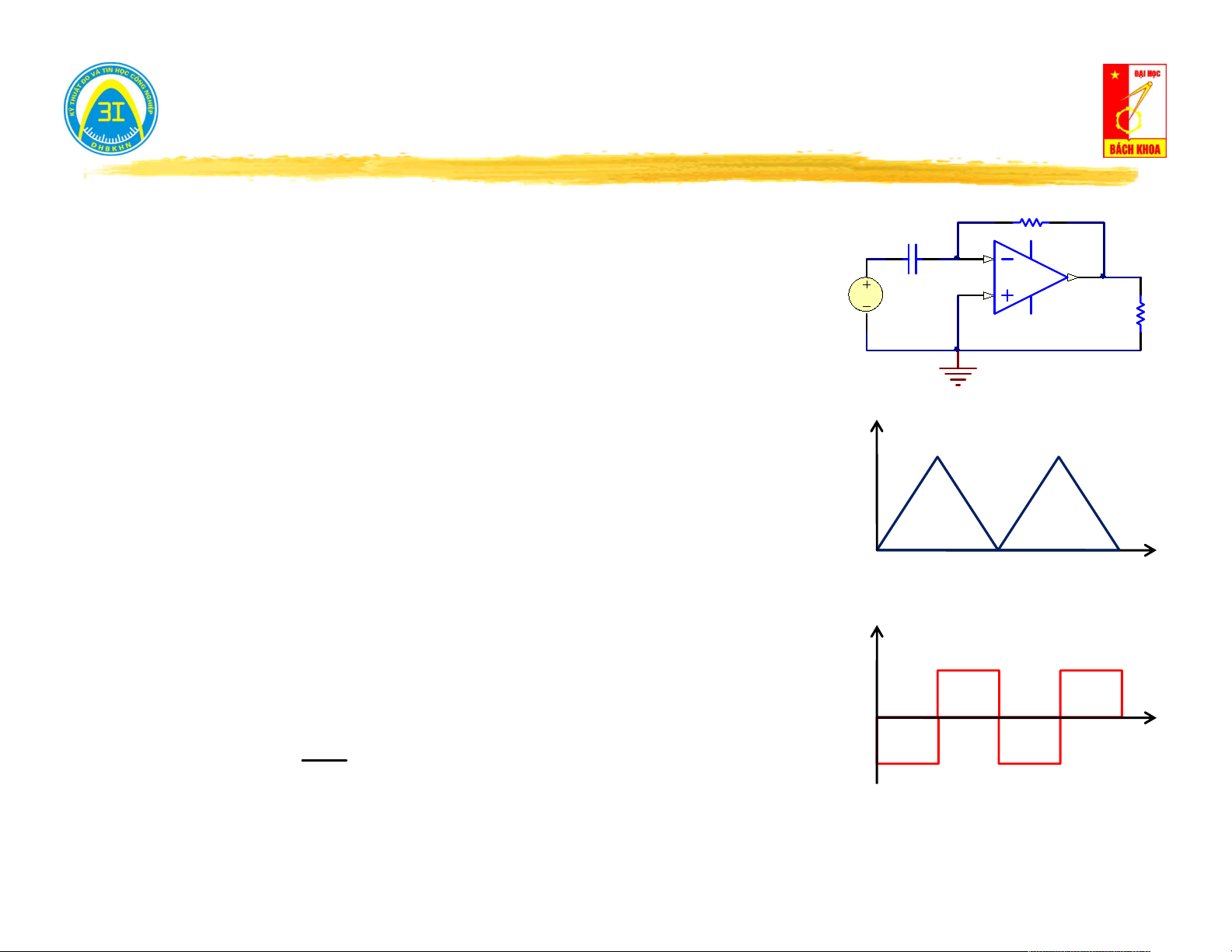
khoảng thời gian, khoảng thời gian đó gọi là chu kỳ của tín hiệu. Ví dụ: U U U t t α t T T T Xung răng cưa
Chỉnh lưu nửa chu kỳ
Chỉnh lưu 2 nửa chu kỳ Ton U t Ton U U T T off off t α t T T T Xung vuông Xung vuông Xung tam giác 2
2014 – Lý thuyết mạch điện 1 - Nguyễn Việt Sơn
Chương 5: Mạch điện tuyến tính có kích thích chu kỳ I. Khái niệm.
Khai triển chuỗi Furiê: Hàm chu kỳ có thể phân tích thành tổng các hàm điều
hòa bậc 0, 1, 2, 3, ... dạng:
f (t) f
F .cos(k.t ) 0 km k k 1 hoặc
f (t) f
F .sin(k.t ) 0 km k k 1 Do chuỗi hội tụ:
Những thành phần điều hòa bậc cao có biên độ nhỏ.
Chỉ lấy một vài số hạng đầu. 3
2014 – Lý thuyết mạch điện 1 - Nguyễn Việt Sơn
LÝ THUYẾT MẠCH ĐIỆN 1
Chương 5: Mạch điện tuyến tính có kích thích chu kỳ I. Khái niệm.
II. Cách phân tích mạch tuyến tính có kích thích chu kỳ.
III. Giá trị hiệu dụng - công suất dòng chu kỳ.
IV. Hàm truyền đạt và đặc tính tần số. 4
2014 – Lý thuyết mạch điện 1 - Nguyễn Việt Sơn
Chương 5: Mạch điện tuyến tính có kích thích chu kỳ
II. Cách phân tích mạch tuyến tính có kích thích chu kỳ.
Mạch tuyến tính có kích thích chu kỳ không điều hòa giải theo phương pháp số phức:
Phân tích nguồn chu kỳ không điều hòa thành tổng các nguồn điều hòa có tần số khác nhau.
Tính đáp ứng của mạch với từng thành phần tần số.
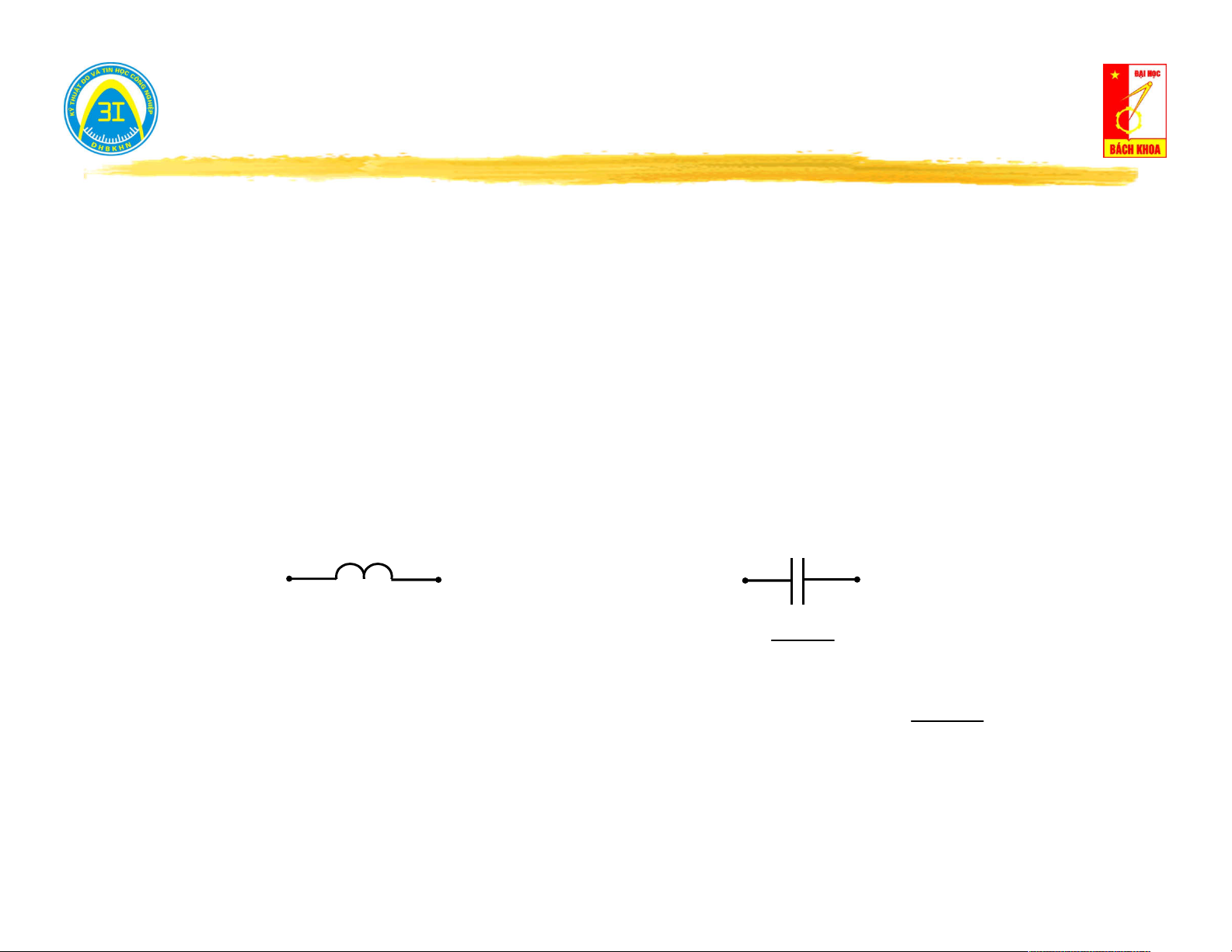
Thành phần 1 chiều (có thể thay đổi cấu trúc của mạch): L C ngắn mạch hở mạch U j.. . L I 0 L 1 U . I C C j..C 1
Thành phần xoay chiều tần số kω: Z j..L ; Z L C j..C
Xếp chồng trong miền thời gian 5
2014 – Lý thuyết mạch điện 1 - Nguyễn Việt Sơn
Chương 5: Mạch điện tuyến tính có kích thích chu kỳ
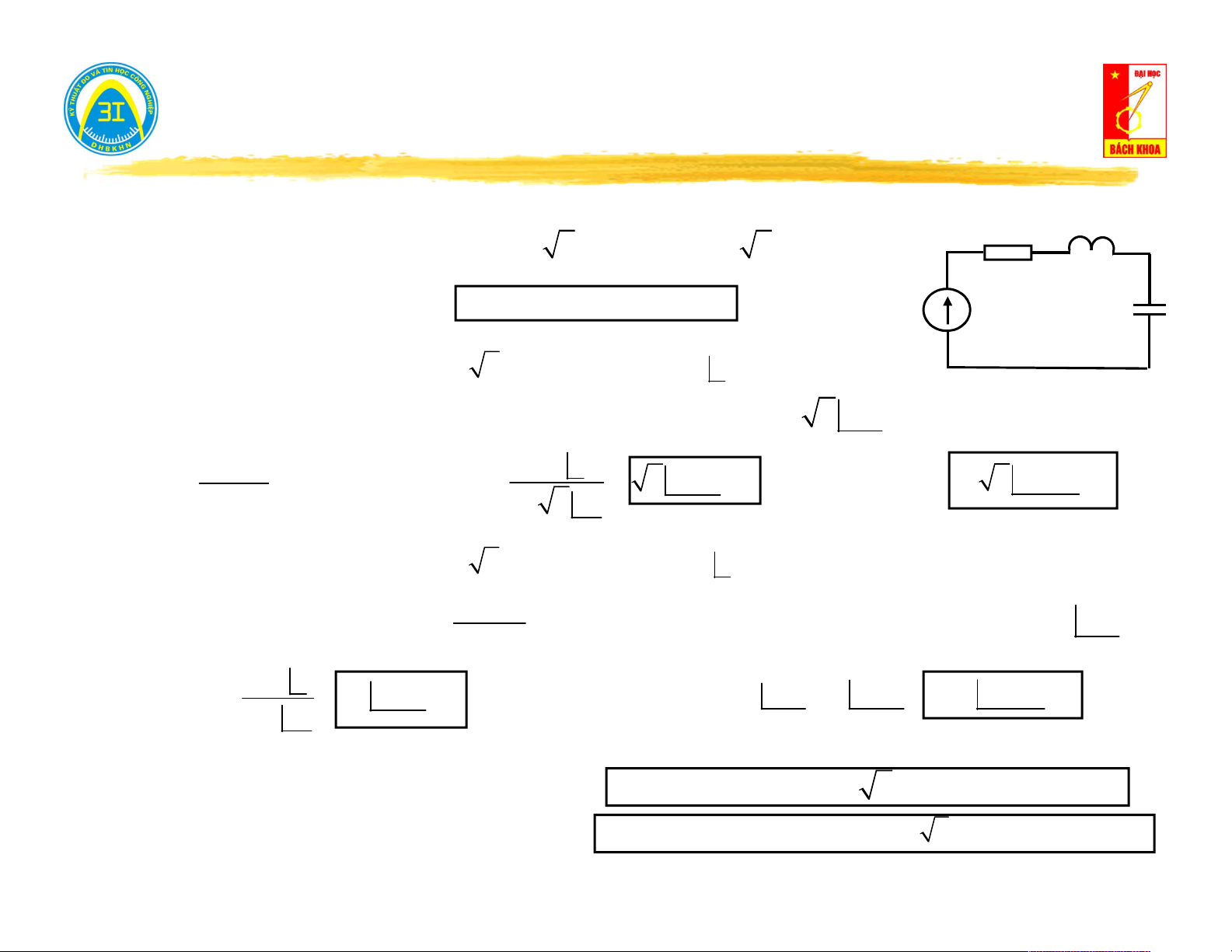
II. Cách phân tích mạch tuyến tính có kích thích chu kỳ. R = 50Ω L = 0.1H
Ví dụ: Tính i(t), u (t) biết: C
e(t) 100 100 2 sin1000t 200 2 sin 2000t(V )
Xét 1 chiều: E = 100(V) I = 0(A) ; u = 100(V) 0 0 C0 e(t) C = 20μF
Xét ω =1000 rad/s: 1
e(t) 100 2 sin1000t E 100 0(V )
Z j. .L 100 j () 0
Z R Z Z 50 j50 50 2 45 () L 1 L C 1 100 0 Z j50() 0 I 2 4 5 ( ) A 0
U C I .Z 50 2 13 5 (V ) C 1 1 1 C j. .C 50 2 45 1
Xét ω =2000 rad/s: 1
e(t) 200 2 sin 2000t E 200 0(V ) 1
Z j. .L j200() Z j25() 0
Z R Z Z 50 175 j 182 74 () L 2 C j. .C L C 2 200 0 0 0 I 0 0 2 1.1 7 4 ( ) A
U C2 I 2 .Z 1.1 74 .25 90 27.5 164 (V ) C 182 74
Xếp chồng: 0 0
i(t) i (t) i (t) i (t) 0 2 sin(1000t 45 ) 1.1 2 sin(2000t 74 )( ) A 0 1 2 0 0
u (t) u (t) u (t) u (t) 100 100 sin(1000t 135 ) 27.5 2 sin(2000t 164 )(V ) C C 0 C1 C 2 6
2014 – Lý thuyết mạch điện 1 - Nguyễn Việt Sơn
LÝ THUYẾT MẠCH ĐIỆN 1
Chương 5: Mạch điện tuyến tính có kích thích chu kỳ I. Khái niệm.
II. Cách phân tích mạch tuyến tính có kích thích chu kỳ.
III. Giá trị hiệu dụng - công suất dòng chu kỳ.
III.1. Giá trị hiệu dụng.
III.2. Công suất dòng chu kỳ.
IV. Hàm truyền đạt và đặc tính tần số. 7
2014 – Lý thuyết mạch điện 1 - Nguyễn Việt Sơn
Chương 5: Mạch điện tuyến tính có kích thích chu kỳ
III.1. Giá trị hiệu dụng.
Để đo khả năng sinh công của dòng điện chu kỳ dùng khái niệm giá trị hiệu dụng I với định nghĩa: 1 T
T: chu kỳ của dòng điện chu kỳ. 2 (*) I i (t)dt T i(t): dòng điện chu kỳ. 0
Tích phân hàm điều hòa
trong 1 chu kỳ thì bằng 0
Áp dụng khai triển chuỗi Furie: i(t) i (t) k k 0 0 2 1 T 1 T 1 T 2 2 2 (*) I .
i (t) .dt I .
i (t).dt .
i (t).i (t).dt k k k l T T T k 0 k 0 k l 0 0 0 0 1 T 2 2 2 I
. i (t).dt I n k k Vậy ta có: 2 2 2 2 I
I I ... I I T k 0 k 0 0 1 n k 0 k 0
Giá trị hiệu dụng dòng, áp bằng căn bậc 2 n
tổng bình phương các giá trị hiệu dụng 2 2 2 2
U U U ... U U 0 1 n k thành phần. k 0 8
2014 – Lý thuyết mạch điện 1 - Nguyễn Việt Sơn
Chương 5: Mạch điện tuyến tính có kích thích chu kỳ
III.2. Công suất dòng chu kỳ.
Công suất tác dụng bằng tổng
Công suất trung bình trong một chu kỳ:
công suất tác dụng các thành phần 2 2 2 P . R I . R I . R I
P P P P ... k k k 0 1 2 k 0 k 0 k 0 R = 50Ω L = 0.1H
Ví dụ: Tính công suất nguồn và số chỉ vôn kế đo điện áp trên tụ
e(t) 100 100 2 sin1000t 200 2 sin 2000t(V ) e(t) C = 20μF 0 0
i(t) 2 sin(1000t 45 ) 1.1 2 sin(2000t 74 )( ) A 0 0
u (t) 100 100 sin(1000t 135 ) 27.5 2 sin(2000t 164 )(V ) C
P P P P P 0 0
P E .I .cos 100. 2.cos(45 ) 100(W ). 0 1 2 0 1 1 1 1 0 P 160.64(W )
P E .I .cos 200.1,1.cos(74 ) 60.64(W ) 2 2 2 2 Số chỉ vôn mét: 2 2 2
U 100 (50 2) 27, 5 125, 52V 9
2014 – Lý thuyết mạch điện 1 - Nguyễn Việt Sơn
LÝ THUYẾT MẠCH ĐIỆN 1
Chương 5: Mạch điện tuyến tính có kích thích chu kỳ
I. Khái niệm về nguồn kích thích chu kỳ.
II. Cách phân tích mạch điện tuyến tính có kích thích chu kỳ.
III. Trị hiệu dụng - công suất dòng chu kỳ.
IV. Hàm truyền đạt và đặc tính tần số. 10
2014 – Lý thuyết mạch điện 1 - Nguyễn Việt Sơn
Chương 5: Mạch điện tuyến tính có kích thích chu kỳ
IV. Hàm truyền đạt và đặc tính tần số.
Hàm truyền đạt là tỷ số riêng (đạo hàm riêng) của ảnh đáp ứng trên ảnh kích thích
T () Đặc tính tần biên độ: Mô tả quan hệ biên độ (hiệu X () j ( ) T () T () .e
dụng) giữa các phổ tần kích thích và đáp ứng. F ()
() Đặc tính tần pha: Mô tả độ lệch pha giữa phổ
đáp ứng và phổ kích thích
Hàm truyền đạt K (ω), K (ω), Z(ω), Y(ω) của mạch Kirchhoff có dạng: u i 2
a a s a s ... n a s F (s) 0 1 2 n 1 T (s) ; s j 2
b b s b s ... m b s F (s) 0 1 2 m 2
n, m: Phụ thuộc vào kết cấu của mạch.
a , b : phụ thuộc vào kết cấu của mạch và các thông số R, L, C. k k
Điểm cực: Nghiệm của đa thức F (s) = 0. 2
Điểm không: Nghiệm của đa thức F (s) = 0. 1 Đặc trưng Điểm cực Hàm truyền đạt Dựng lại Điểm không 11
2014 – Lý thuyết mạch điện 1 - Nguyễn Việt Sơn
LÝ THUYẾT MẠCH ĐIỆN 1
Chương 6: Mạng một cửa Kirchhoff tuyến tính.
I. Khái niệm mạng một cửa Kirchhoff.
II. Phương trình - Sơ đồ tương đương mạng một cửa có nguồn.
III. Điều kiện đưa công suất cực đại ra khỏi mạng một cửa.
Bài tập: 1 - 7, bài thêm 1
2014 – Lý thuyết mạch điện 1 - Nguyễn Việt Sơn
Chương 6: Mạng một cửa Kirchhoff tuyến tính I.1. Khái niệm.
Thực tế có những thiết bị điện làm nhiệm vụ trao đổi năng lượng, tín hiệu
điện từ ra/vào ở một cửa ngõ.
Ví dụ: Máy phát điện; một máy thu; một đường dây truyền tin; vôn mét, ampe
mét, đồng hồ đo công suất …
Các thiết bị có cấu trúc bên trong khác nhau, nhưng hệ thống được coi như một
vùng năng lượng và được quan sát dựa trên quá trình phản ứng và hành vi trên
cửa ngõ, và không quan tâm đến kết cấu và tính năng các vùng bên trong của hệ.
Để mô tả quá trình ấy ta định nghĩa phần tử phức hợp mạng một cửa Kirchhoff. 2
2014 – Lý thuyết mạch điện 1 - Nguyễn Việt Sơn
Chương 6: Mạng một cửa Kirchhoff tuyến tính I.1. Khái niệm.
Định nghĩa: Mạng một cửa Kirchhoff là kết cấu mạch có một cửa ngõ để
trao đổi năng lượng, tín hiệu điện với những phần khác của mạch.
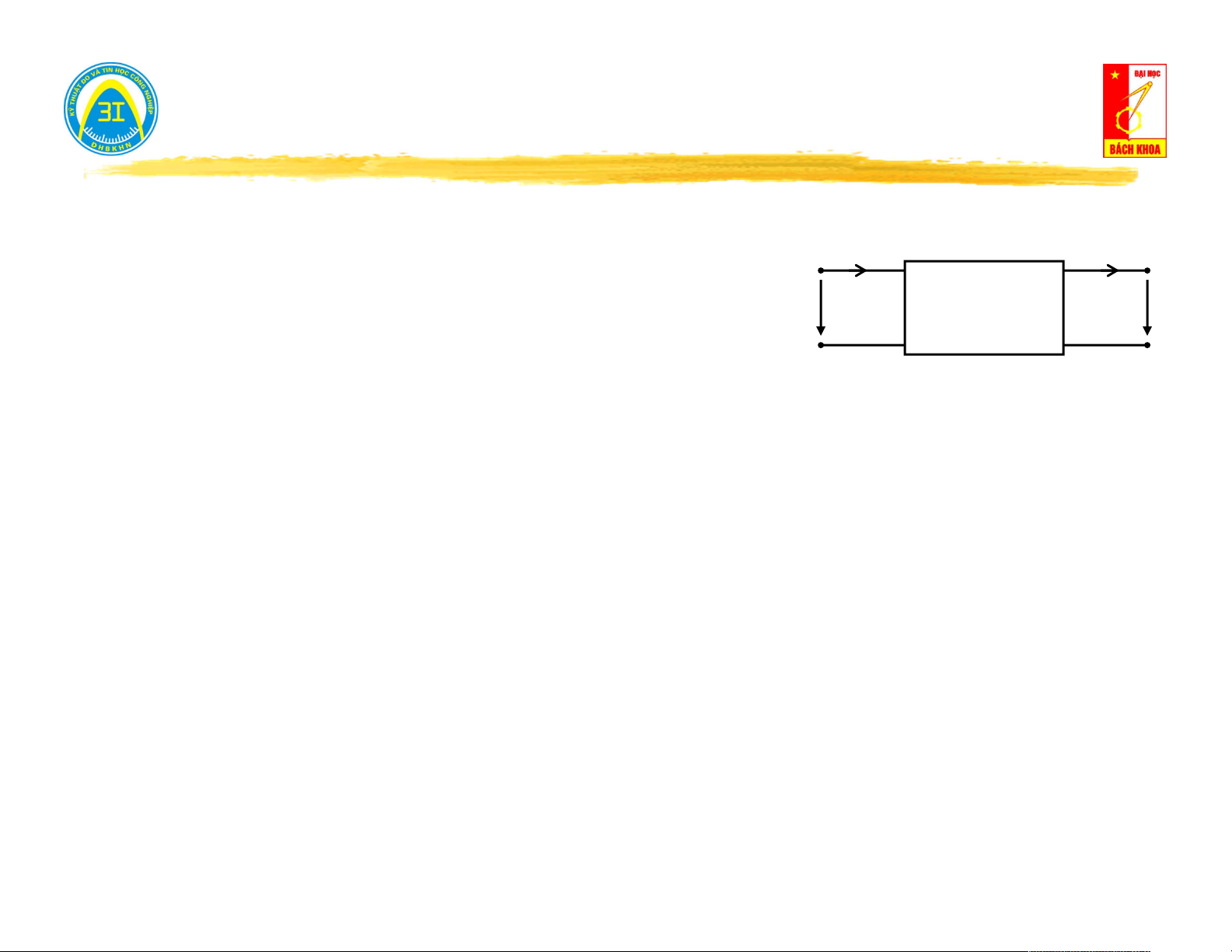
Biến trạng thái trên cửa: i(t), u(t). i(t)
Điều kiện mạng một cửa: Dòng điện chảy vào cực u(t)
này bằng dòng điện chảy ra ở cực kia. Mô hình toán học:
Quá trình năng lượng tín hiệu thể hiện ở quan hệ giữa u(t) và i(t).
Mạch Kirchhoff: Phương trình vi tích phân thường trong miền thời gian.
f (u, u ', u ' ,..., i, i ', i ' ,..., t) 0 3
2014 – Lý thuyết mạch điện 1 - Nguyễn Việt Sơn
Chương 6: Mạng một cửa Kirchhoff tuyến tính I.2. Phân loại.
Mạng 1 cửa tuyến tính.
Theo phương trình trạng thái: Mạng 1 cửa phi tuyến.
Theo khả năng trao đổi năng lượng:
Mạng 1 cửa không nguồn: Không thể đưa năng lượng ra cửa ngõ.
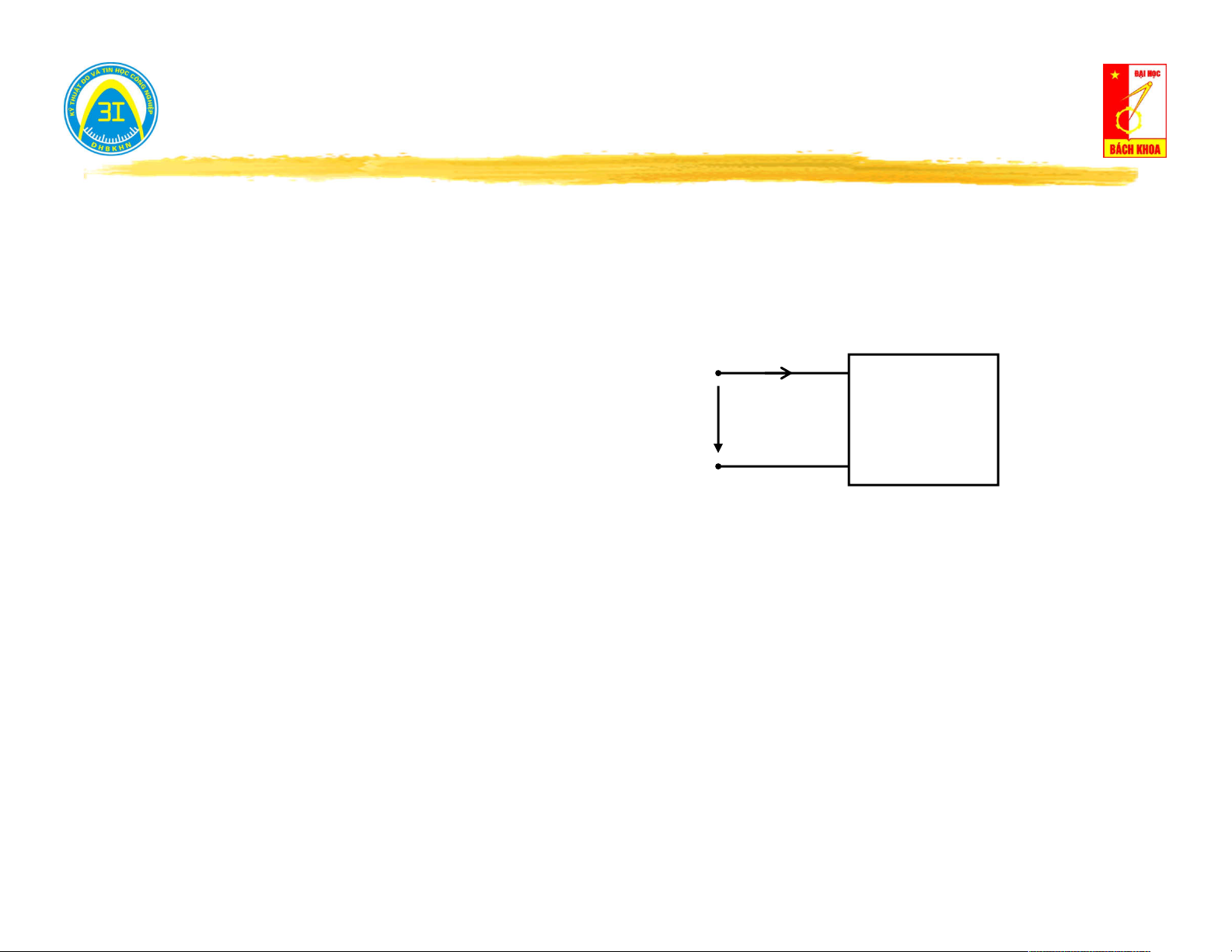
Chú ý: Kết cấu bên trong mạng 1 cửa có thể chứa i
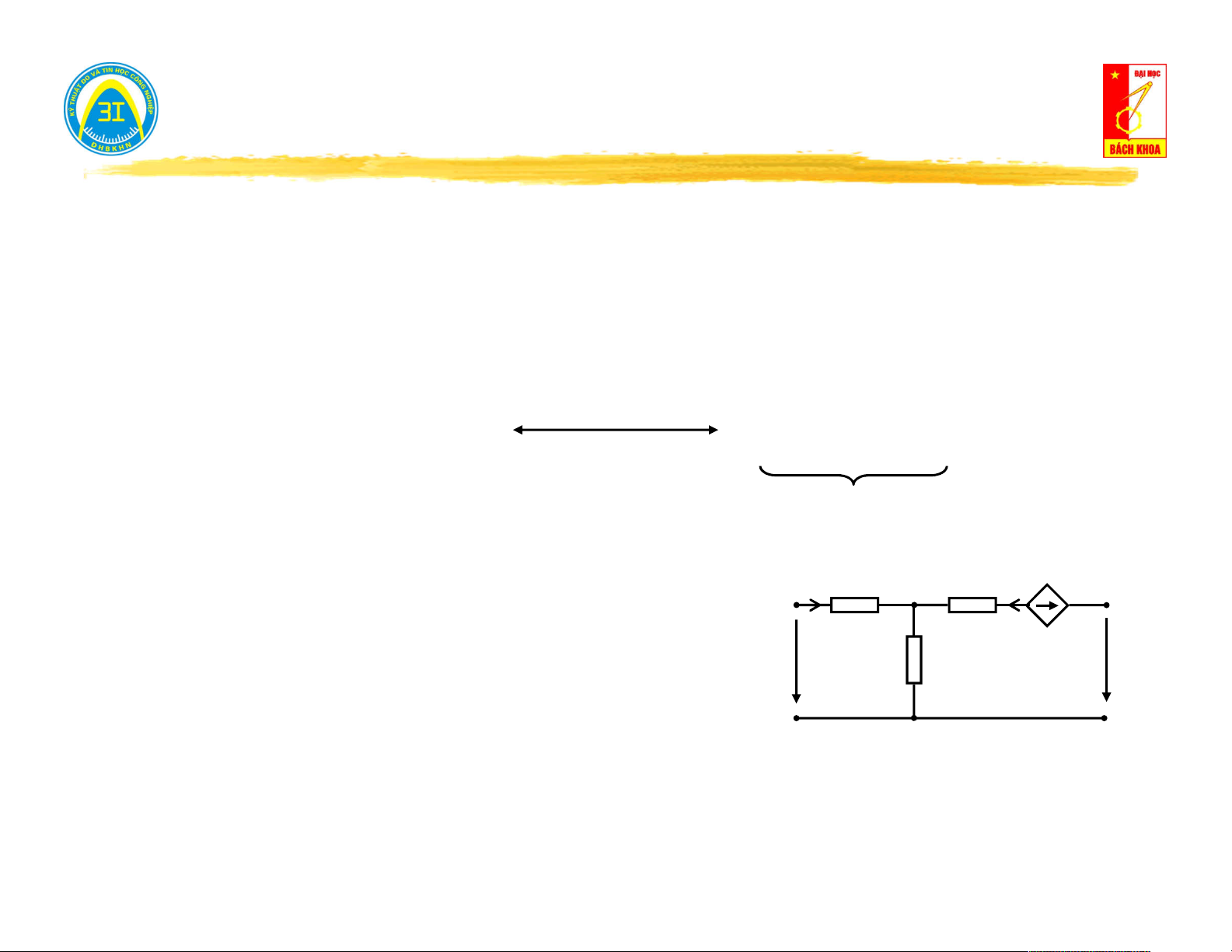
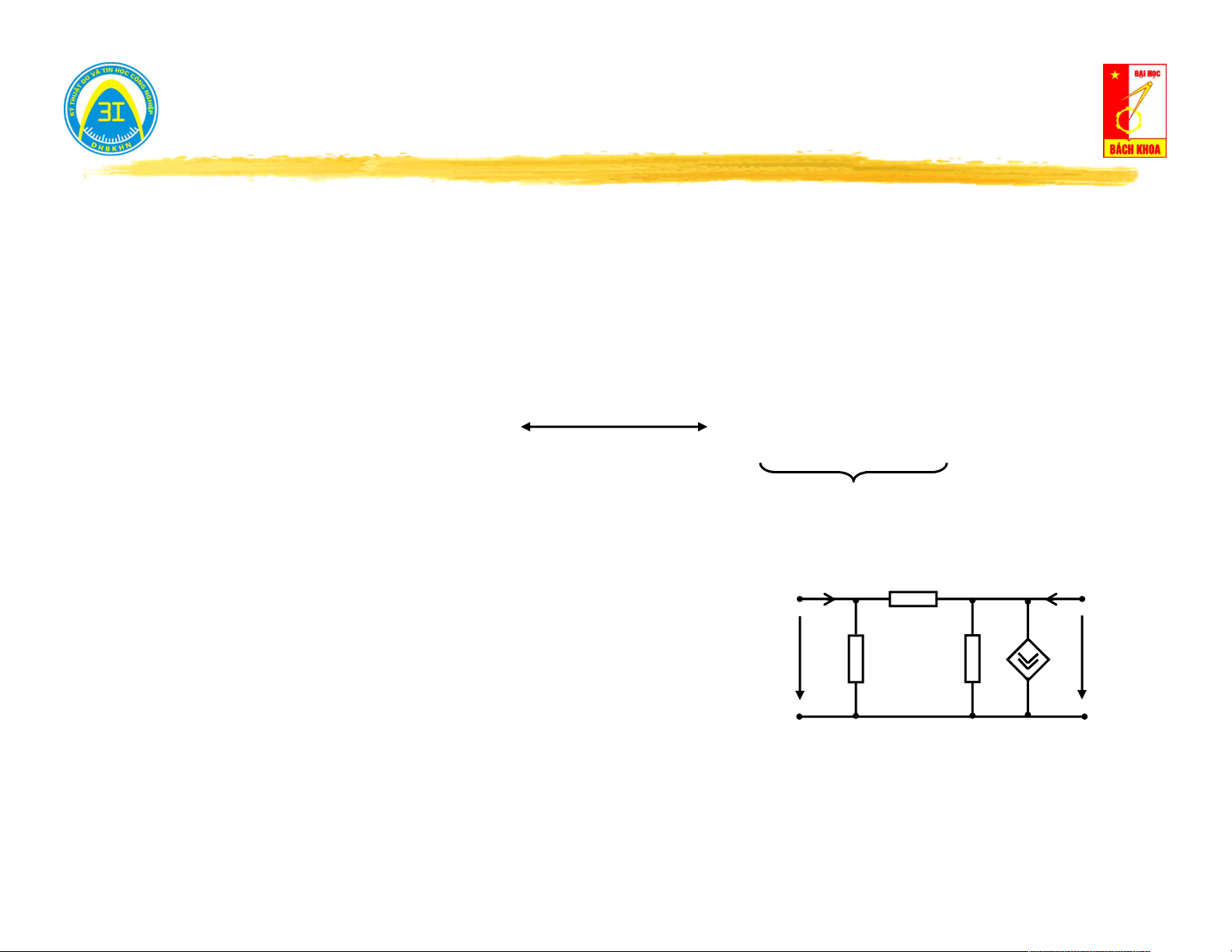
nguồn e(t), j(t) nhưng nếu chúng không có khả u
năng trao năng lượng ra bên ngoài thì coi là mạng một cửa không nguồn. i
Mạng 1 cửa có nguồn: Có thể đưa năng lượng u ra cửa ngõ. 4
2014 – Lý thuyết mạch điện 1 - Nguyễn Việt Sơn
Chương 6: Mạng một cửa Kirchhoff tuyến tính I.2. Phân loại.
Cách xác định mạng 1 cửa có nguồn/không nguồn:
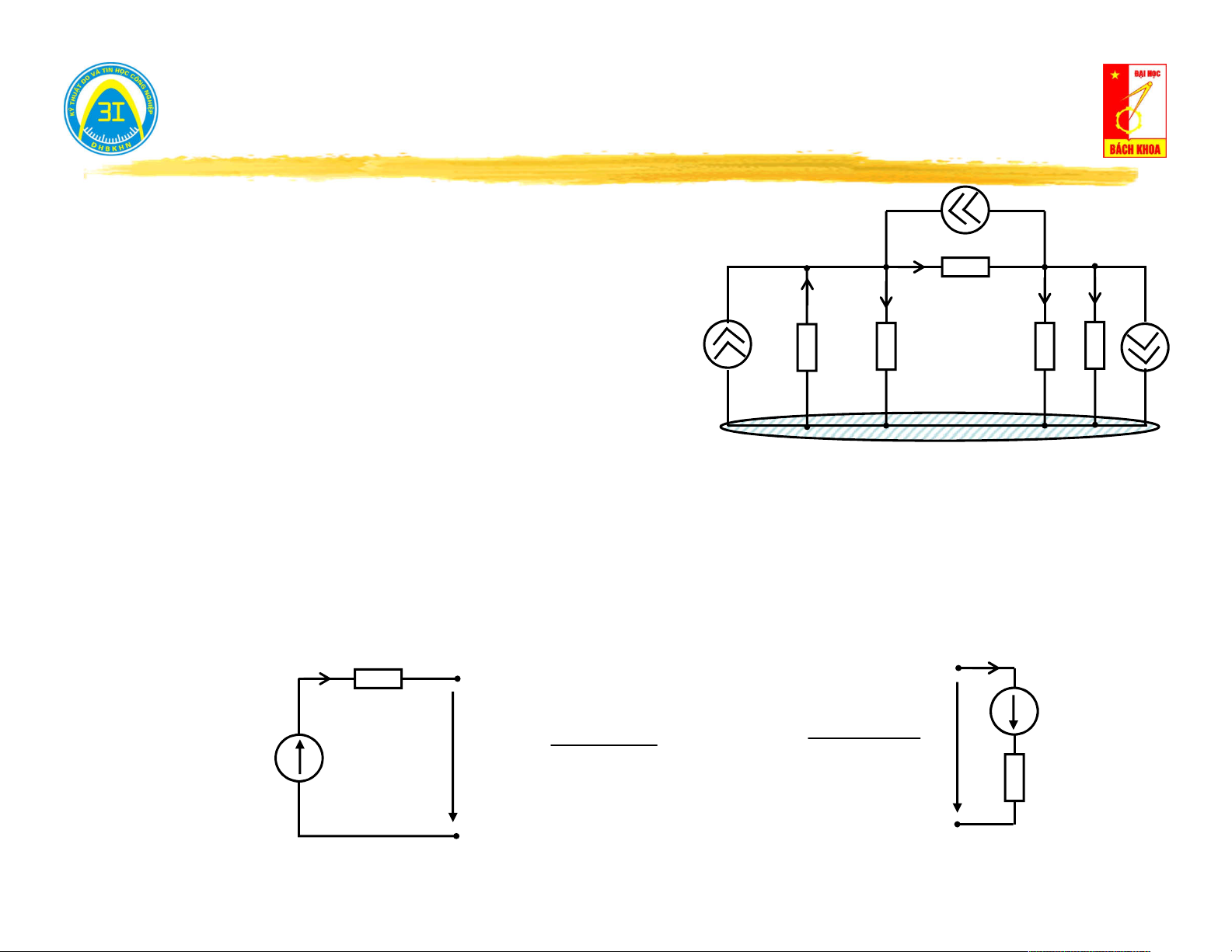
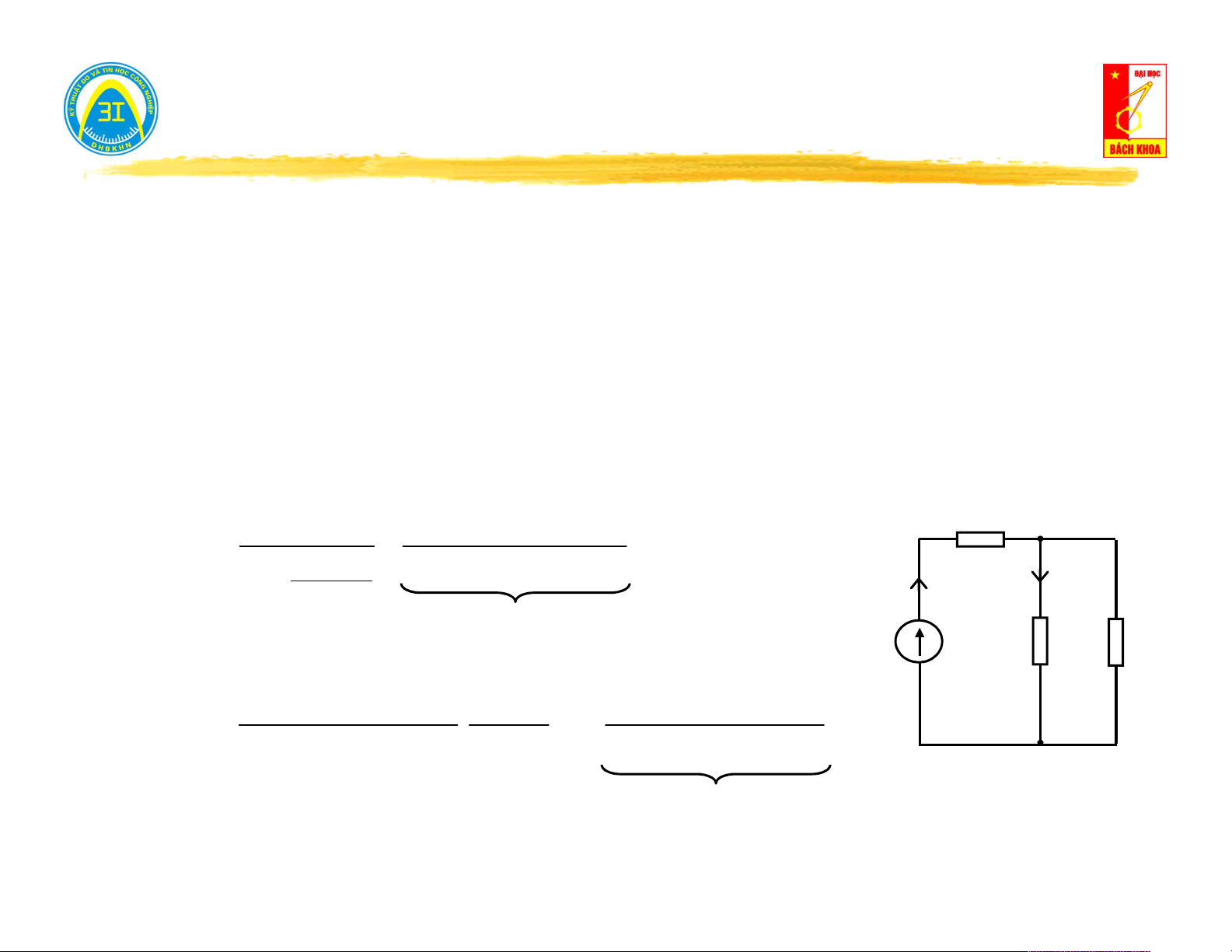
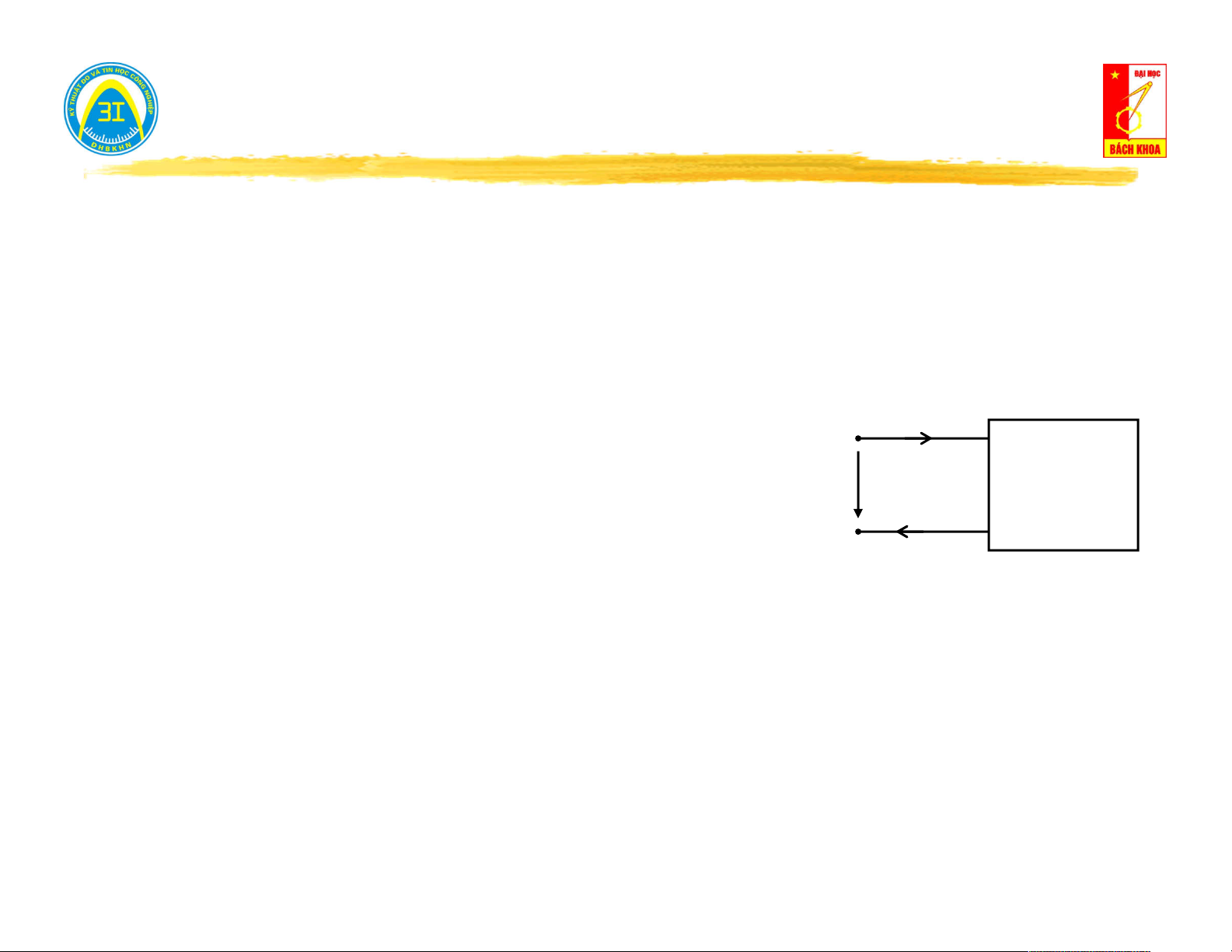
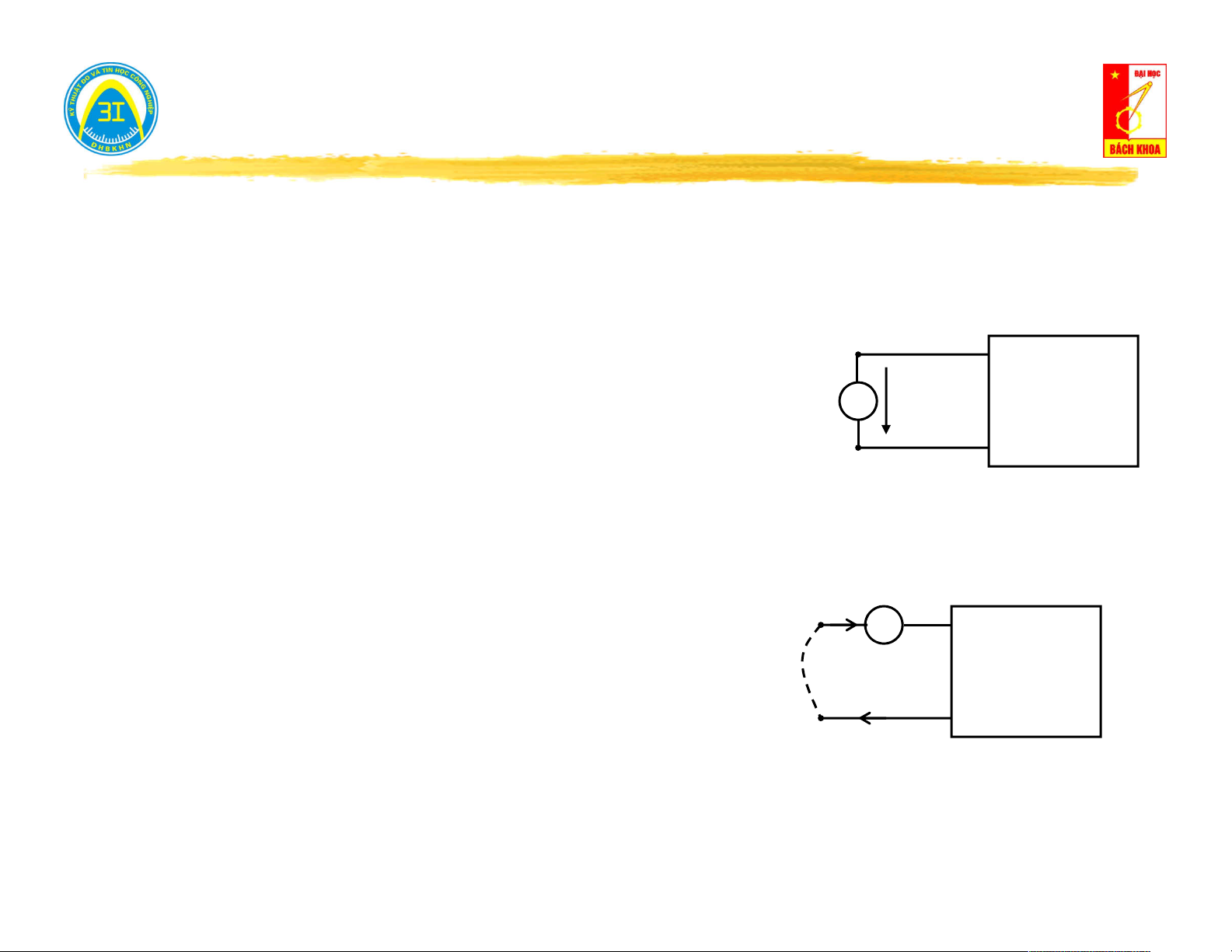
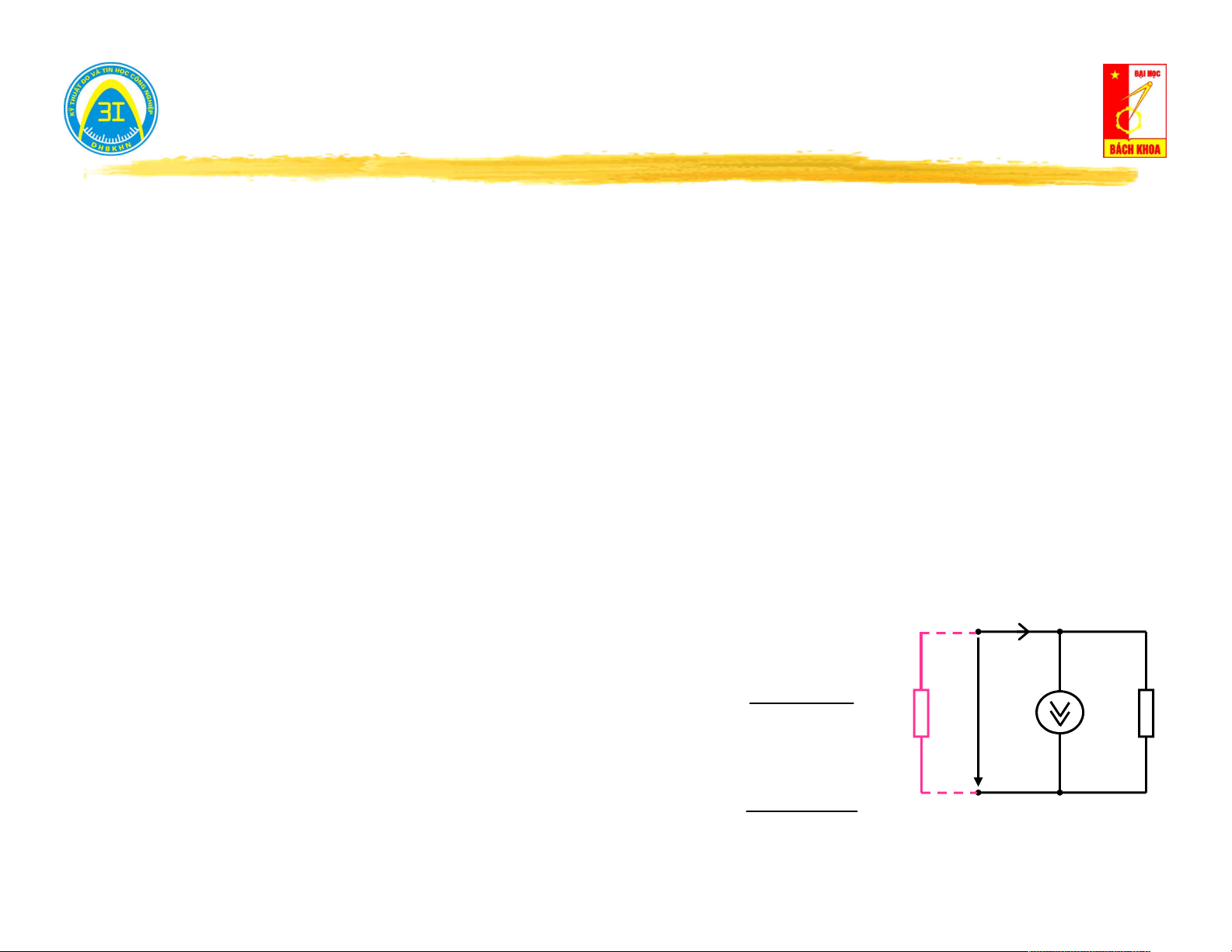
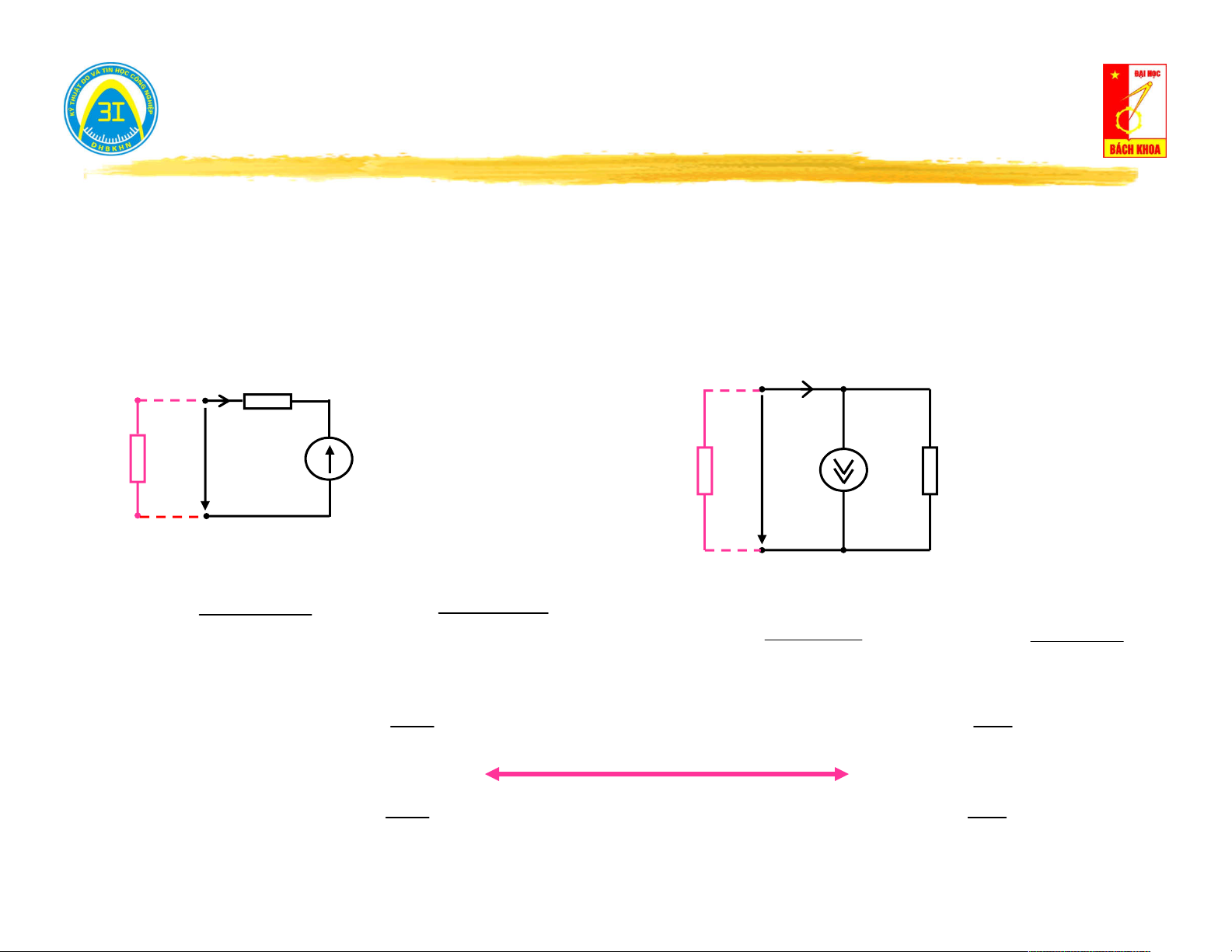
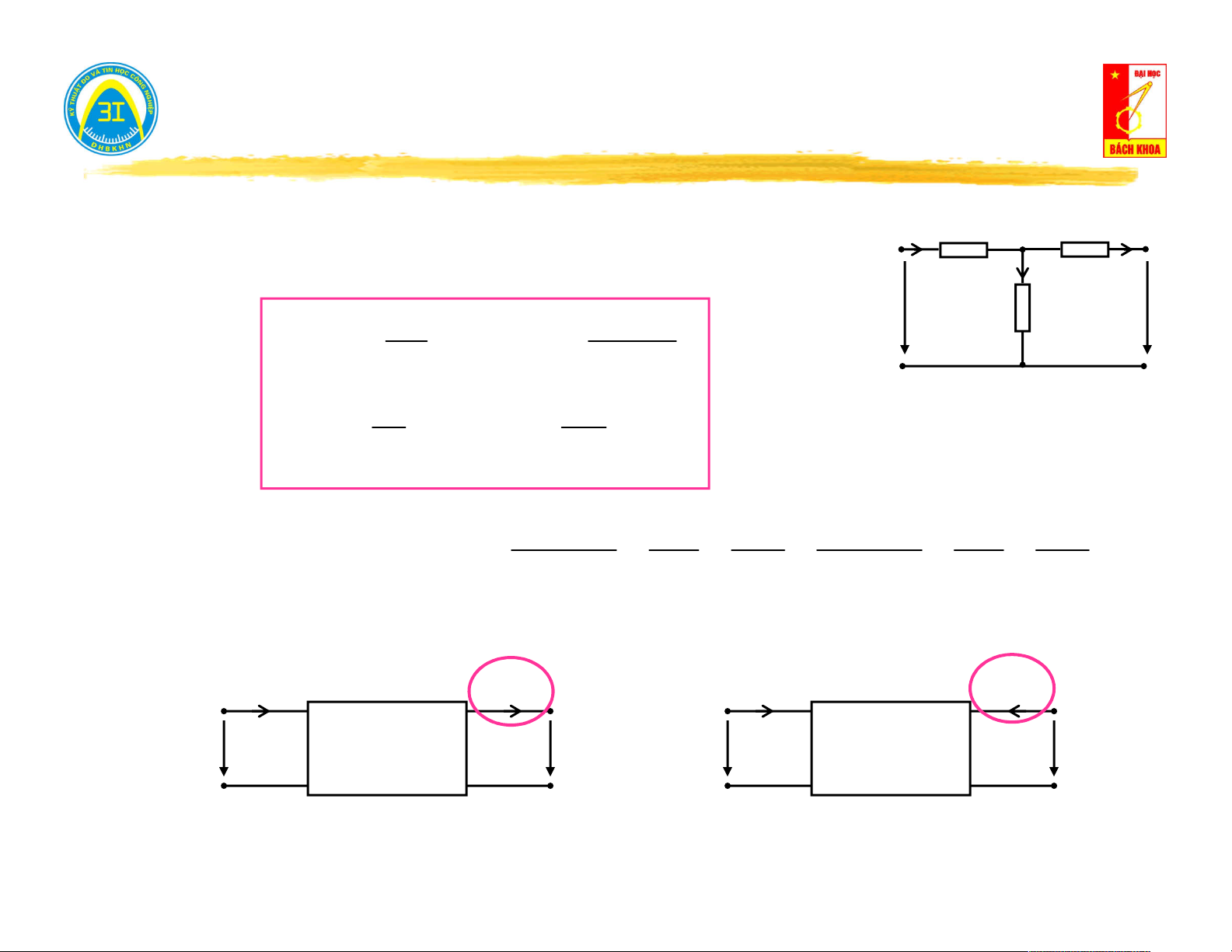
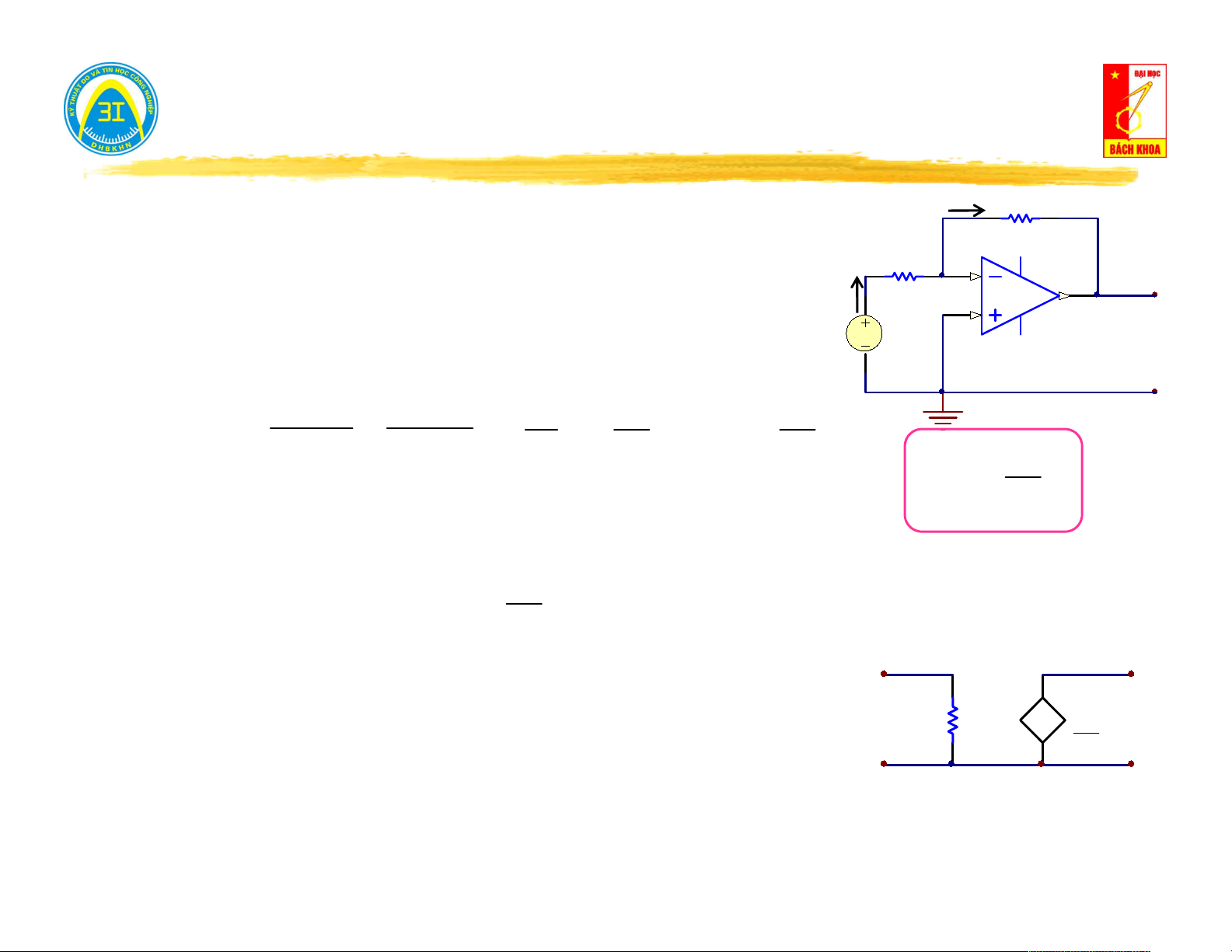
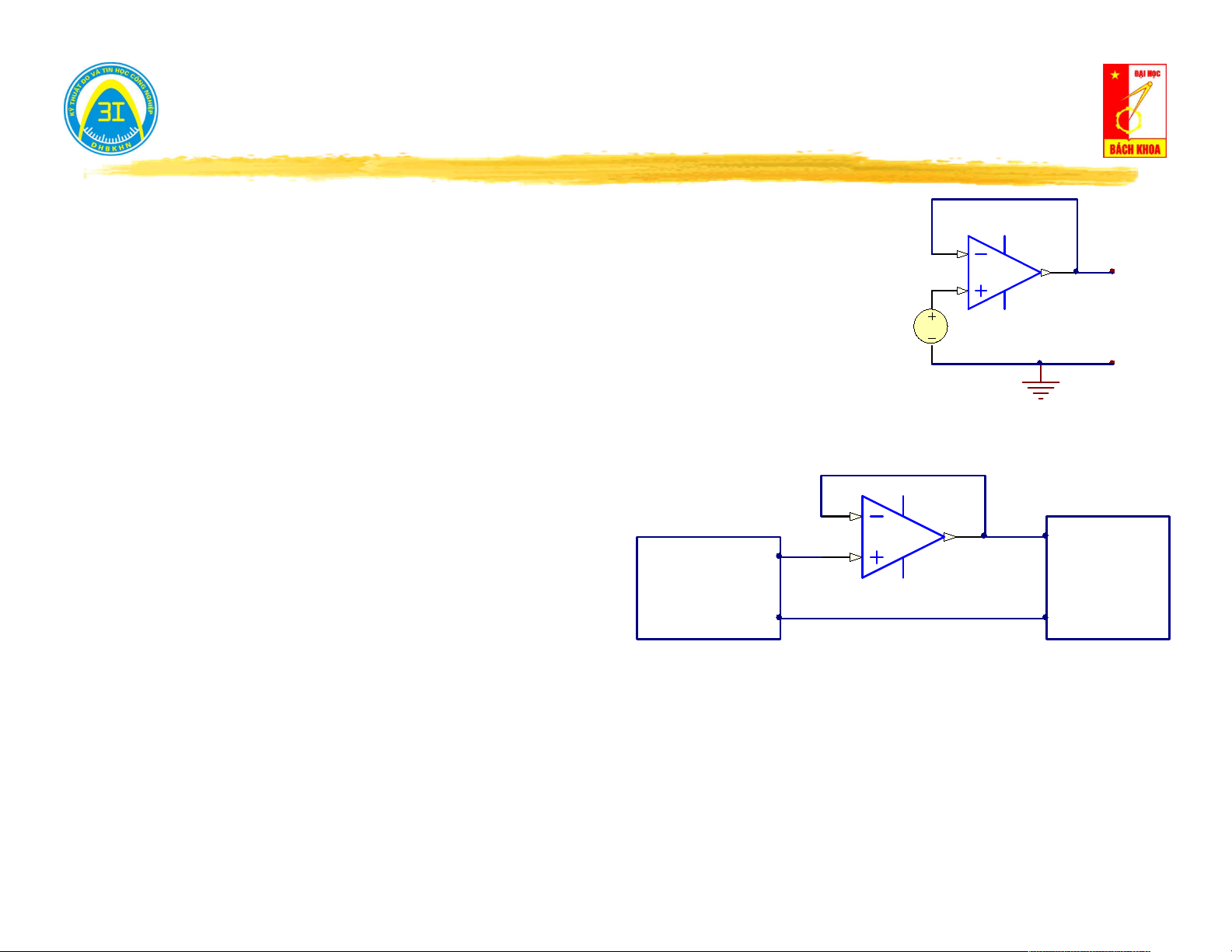
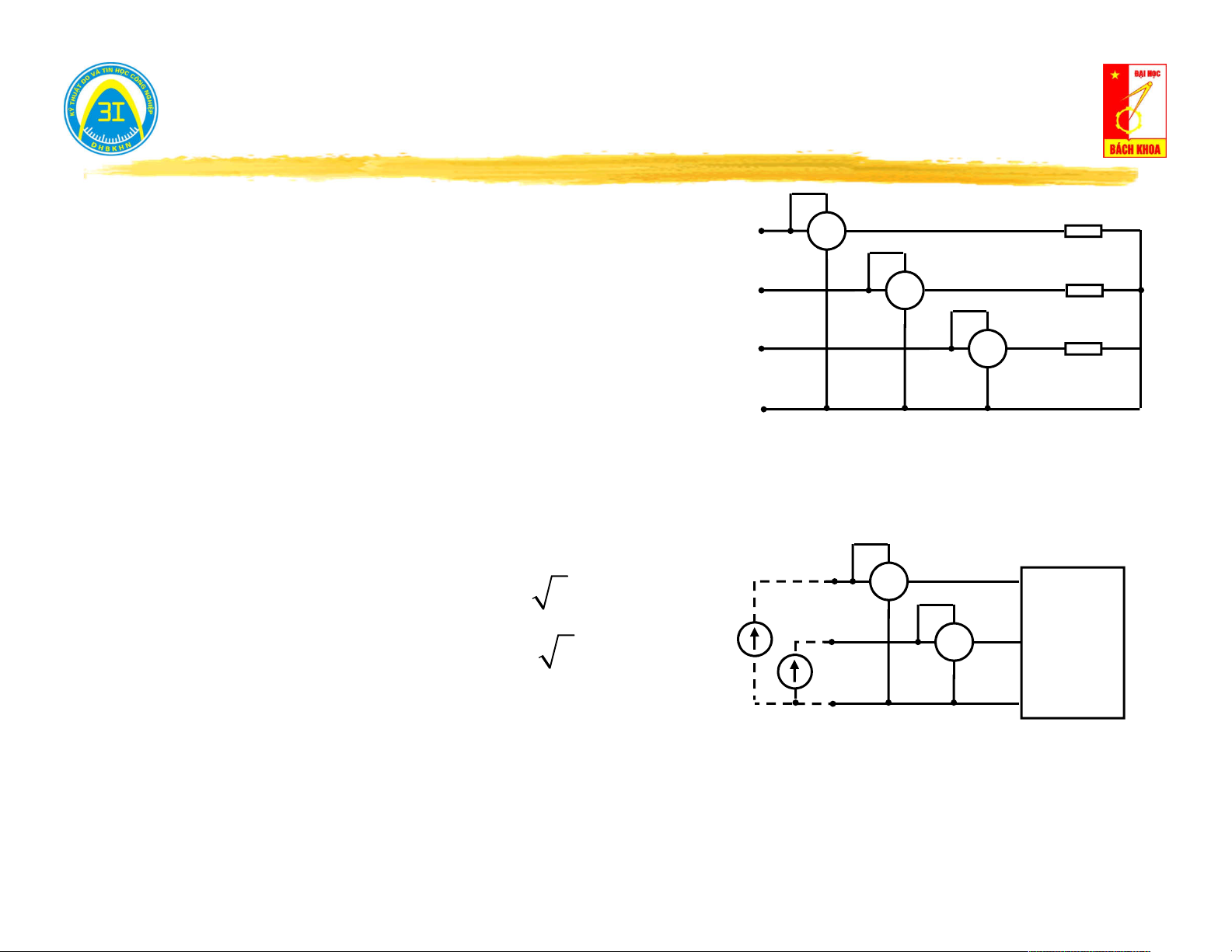
Hở mạch cửa (i = 0) → đo điện áp trên cửa u (t): i(t) = 0 0
Nếu u (t) = 0 → mạng một cửa không nguồn. 0 V u (t) 0
Nếu u (t) ≠ 0 → mạng một cửa có nguồn. 0
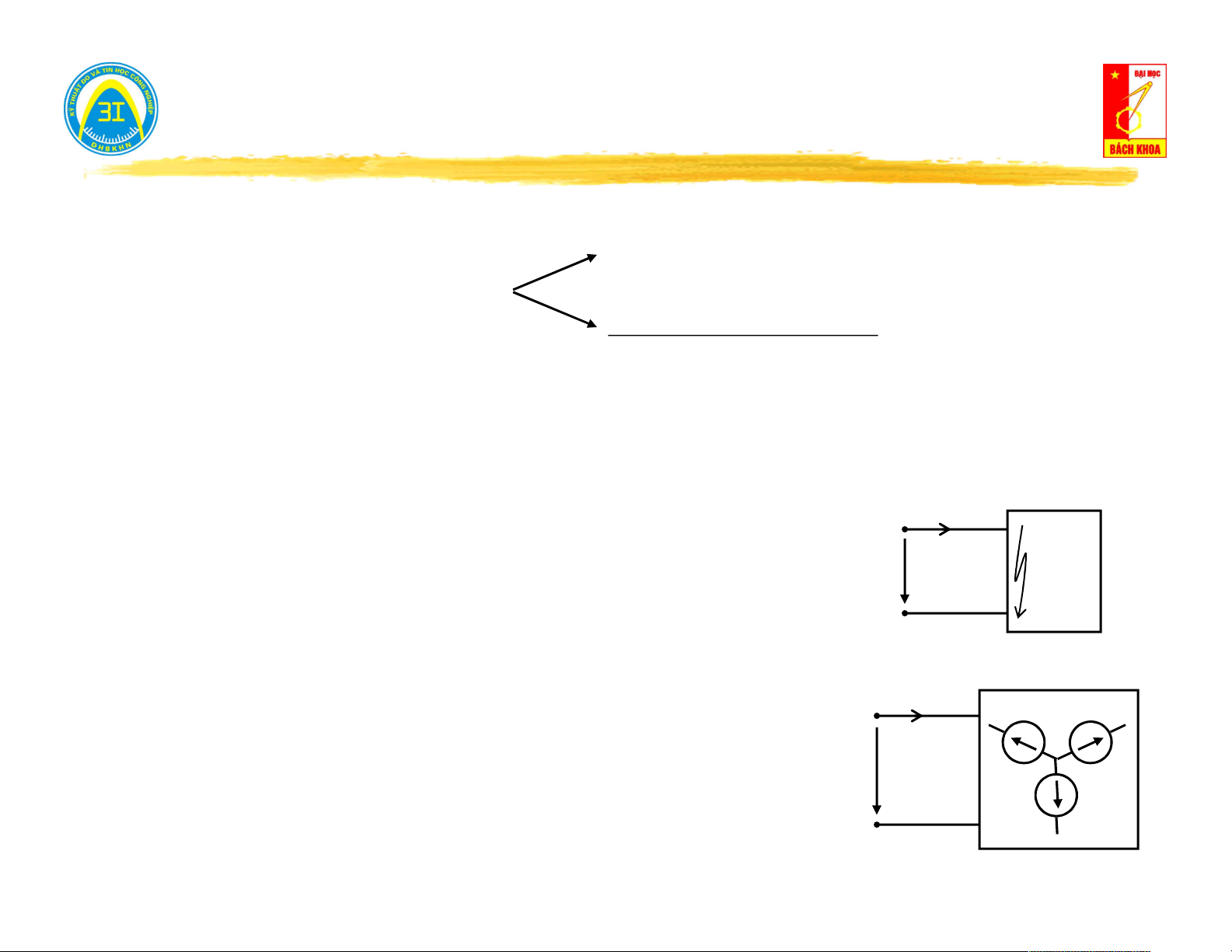
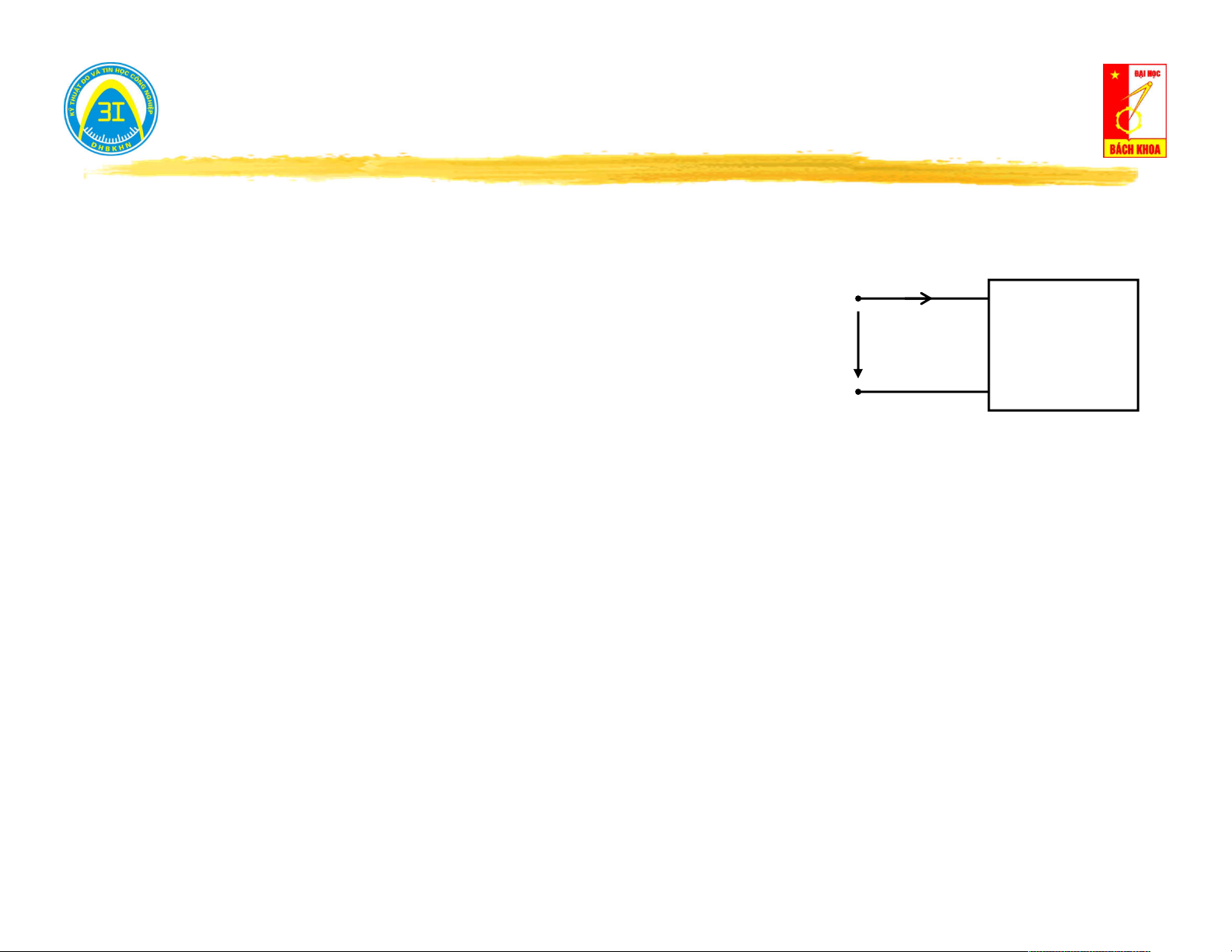
Ngắn mạch cửa (u = 0) → đo dòng điện trên cửa i (t): 0
Nếu i (t) = 0 → mạng một cửa không nguồn. i (t) 0 0 A
Nếu i (t) ≠ 0 → mạng một cửa có nguồn. 0 u(t) = 0 5
2014 – Lý thuyết mạch điện 1 - Nguyễn Việt Sơn
LÝ THUYẾT MẠCH ĐIỆN 1
Chương 6: Mạng một cửa Kirchhoff tuyến tính.
I. Khái niệm mạng một cửa Kirchhoff.
II. Phương trình - Sơ đồ tương đương mạng một cửa có nguồn.
II.1. Phương trình trạng thái mạng 1 cửa Kirchhoff tuyến tính.
II.2. Sơ đồ tương đương mạng 1 cửa có nguồn.
III. Điều kiện đưa công suất cực đại ra khỏi mạng một cửa. 6
2014 – Lý thuyết mạch điện 1 - Nguyễn Việt Sơn
Chương 6: Mạng một cửa Kirchhoff tuyến tính
II.1. Phương trình trạng thái mạng 1 cửa Kirchhoff tuyến tính.
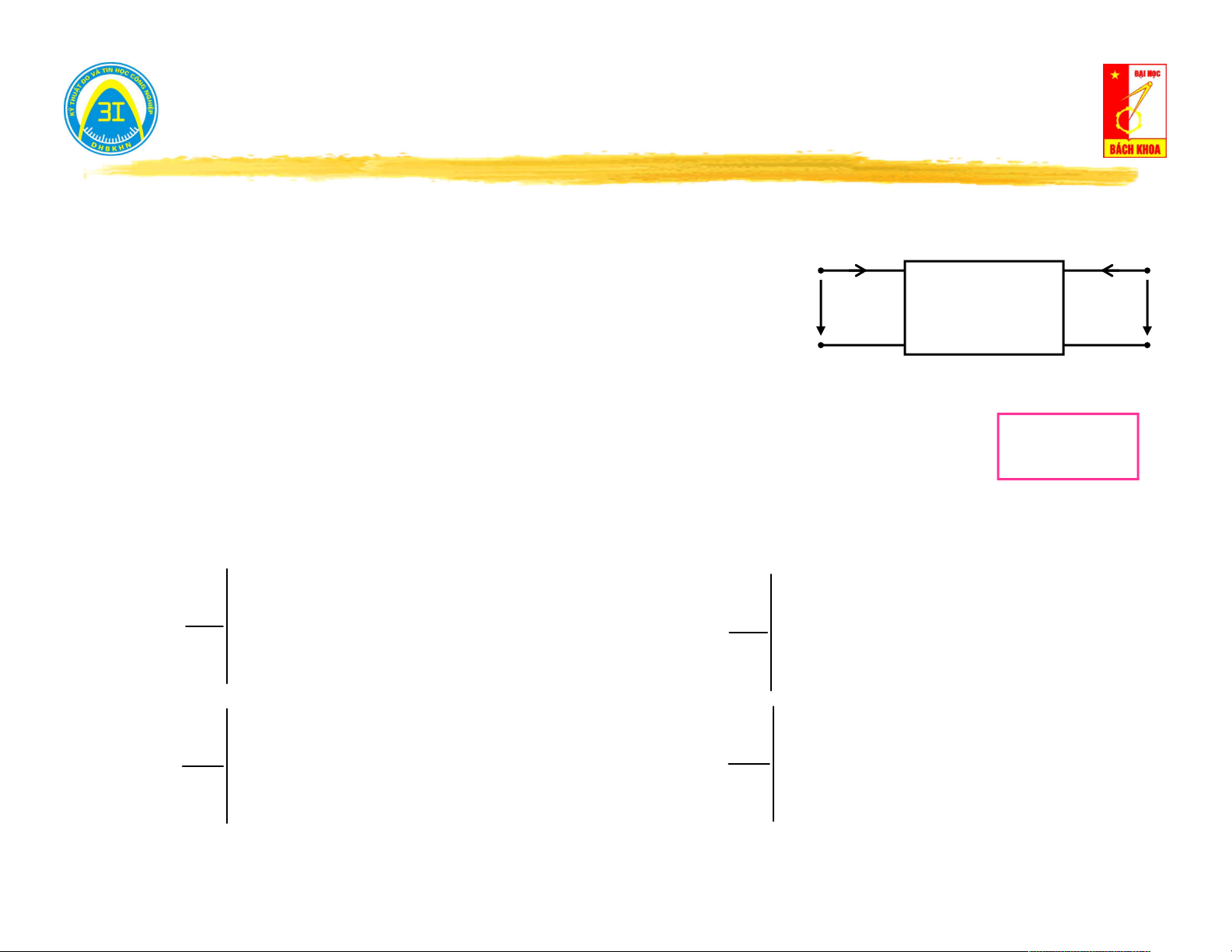
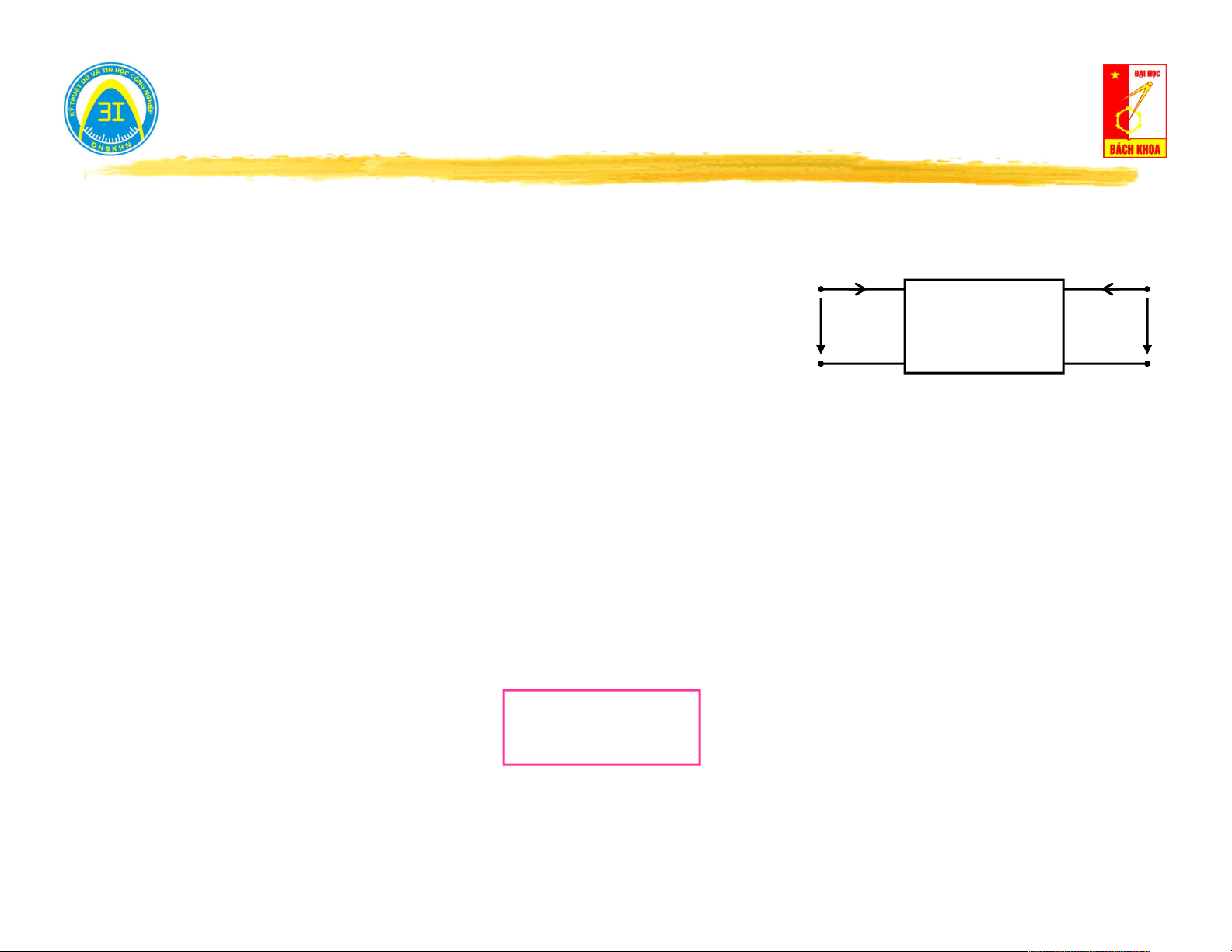
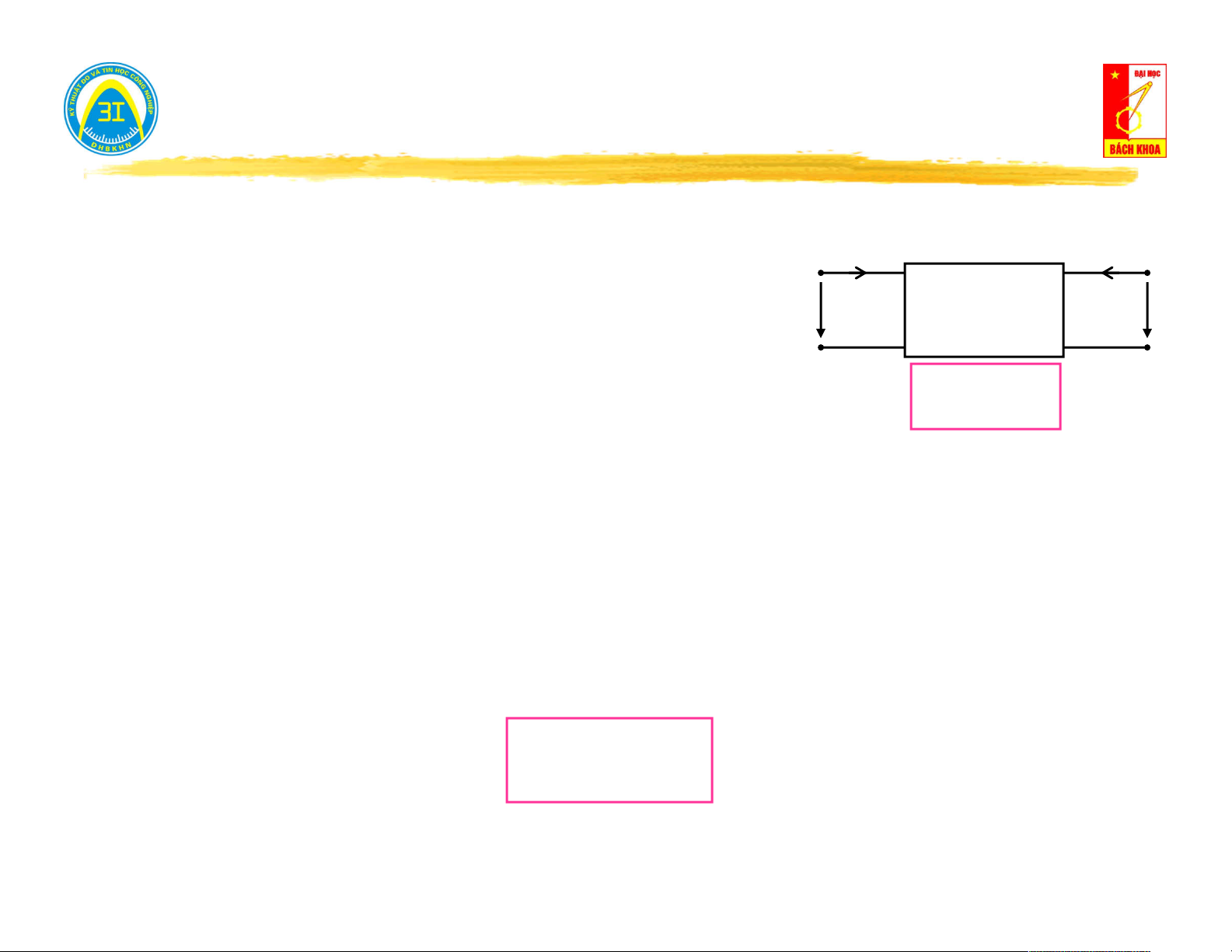
Xét mạng 1 cửa tuyến tính làm việc ở chế độ xác lập điều hòa. I
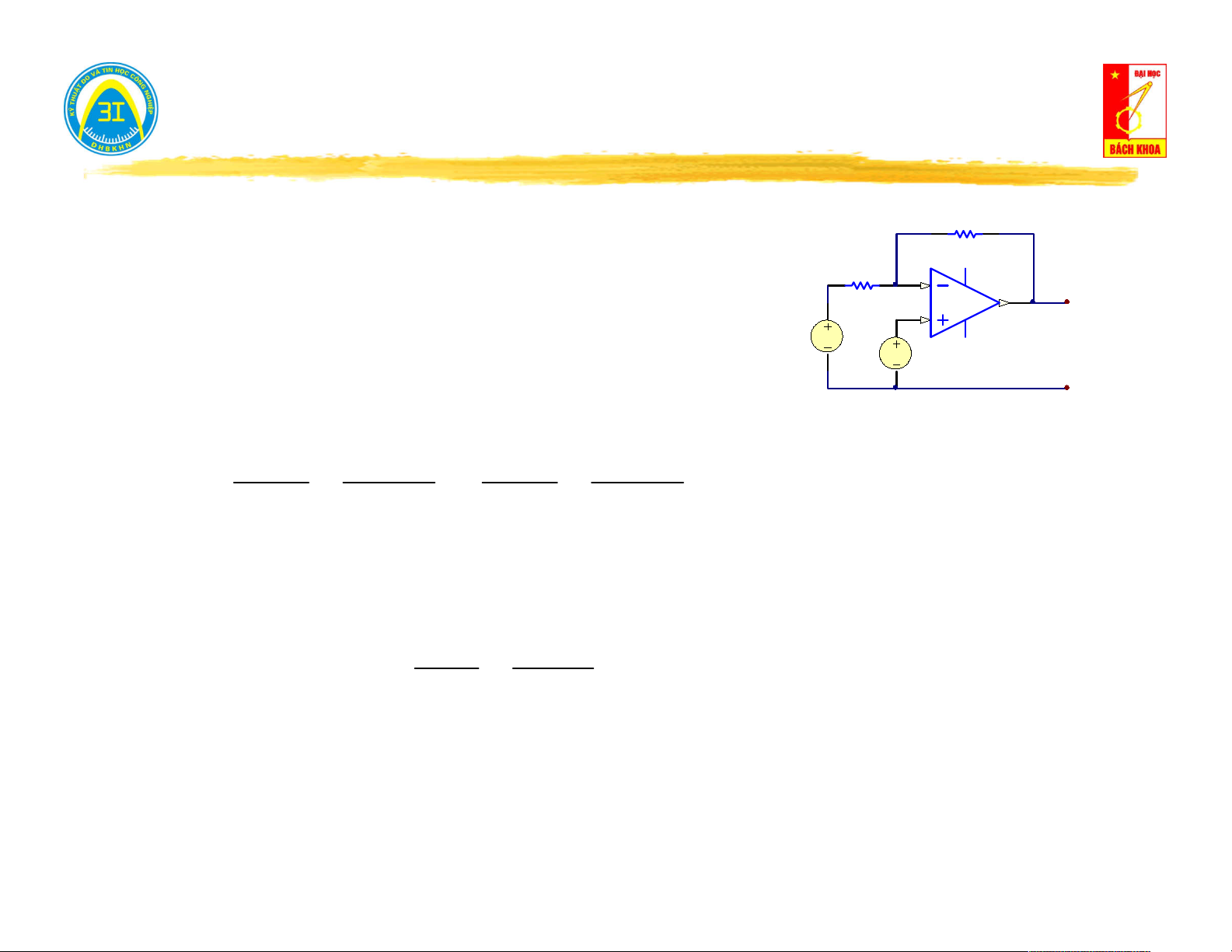
Theo tính chất tuyến tính, quan hệ dòng - áp trên cửa U có dạng: U . A I B (1)
I C.U D (2)
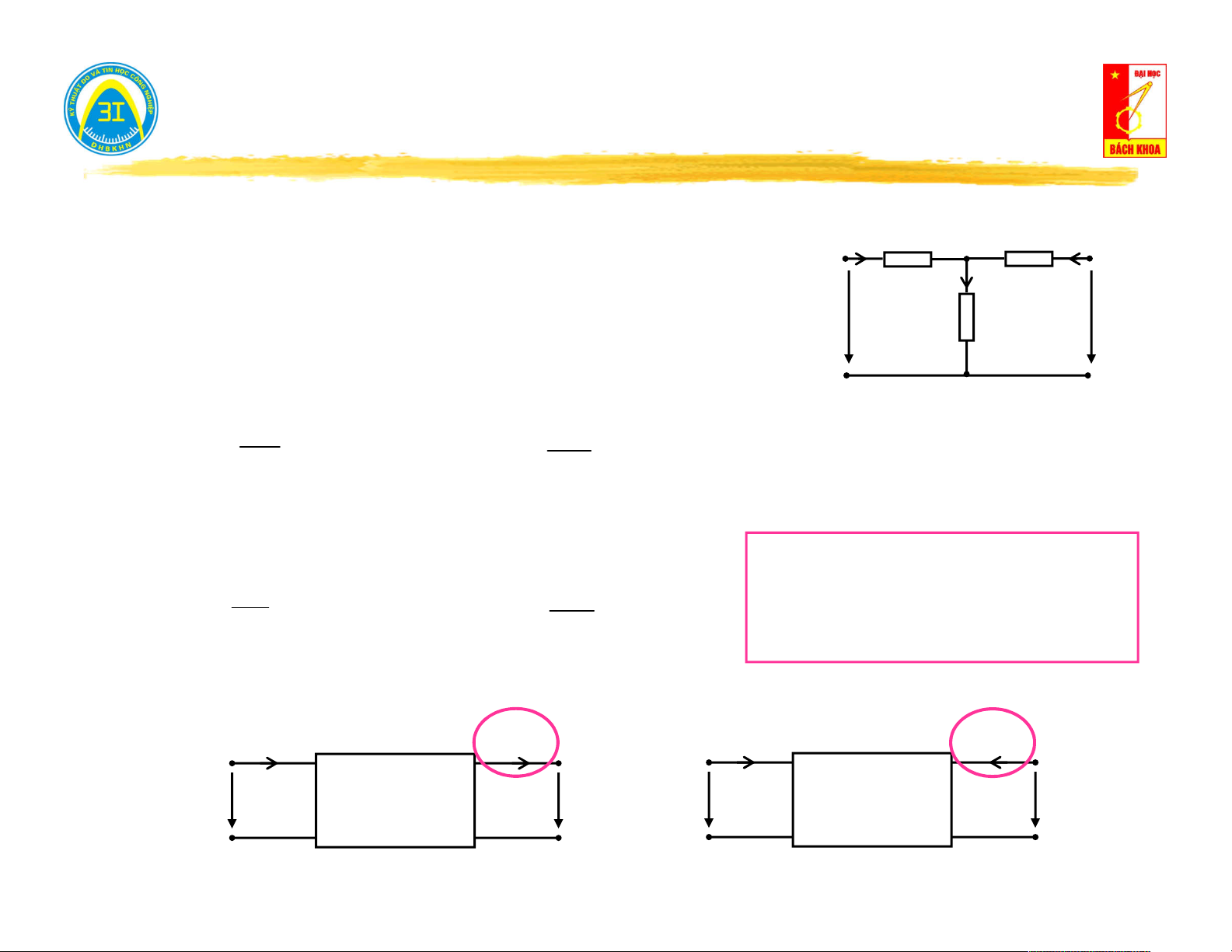
Xét phương trình (1):
Xét phương trình (2):
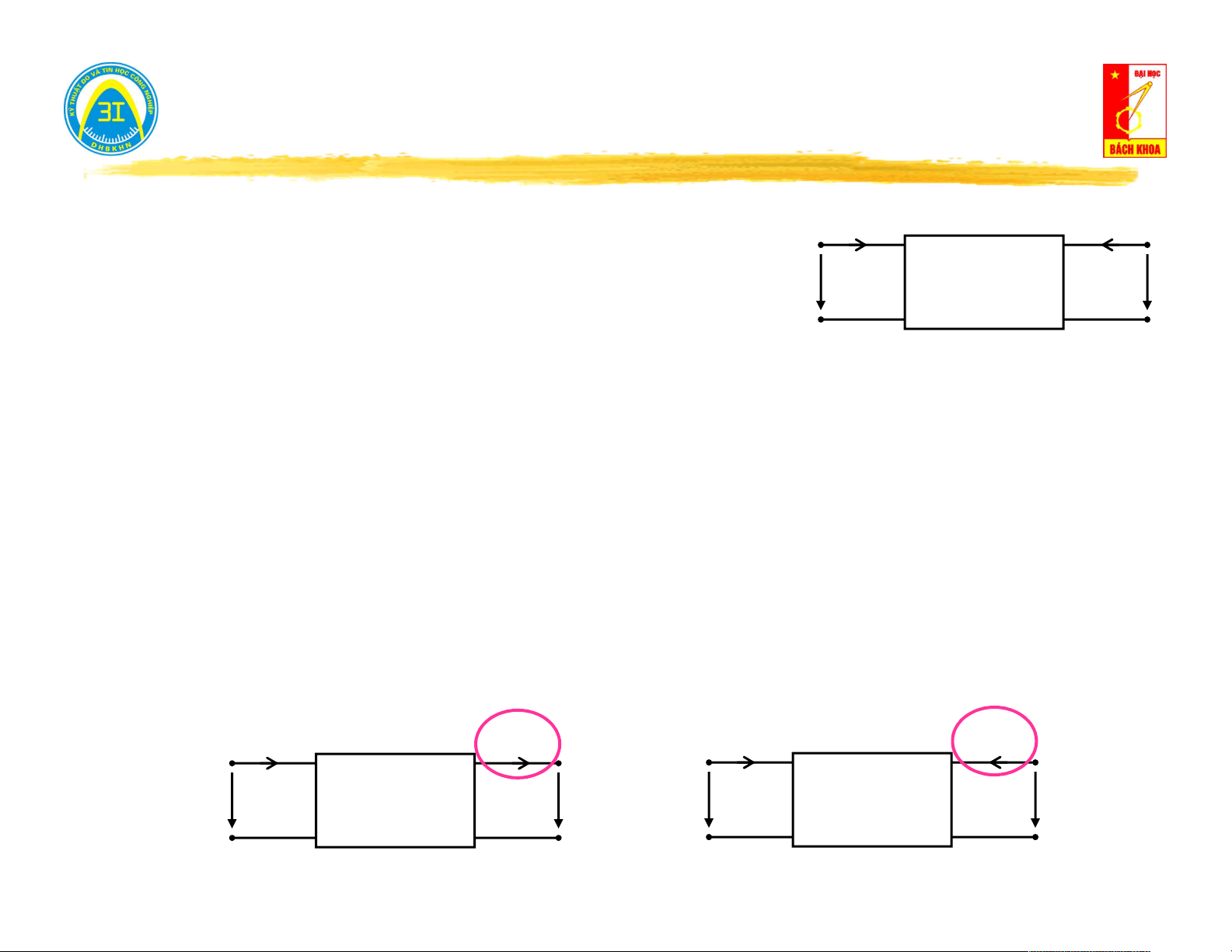
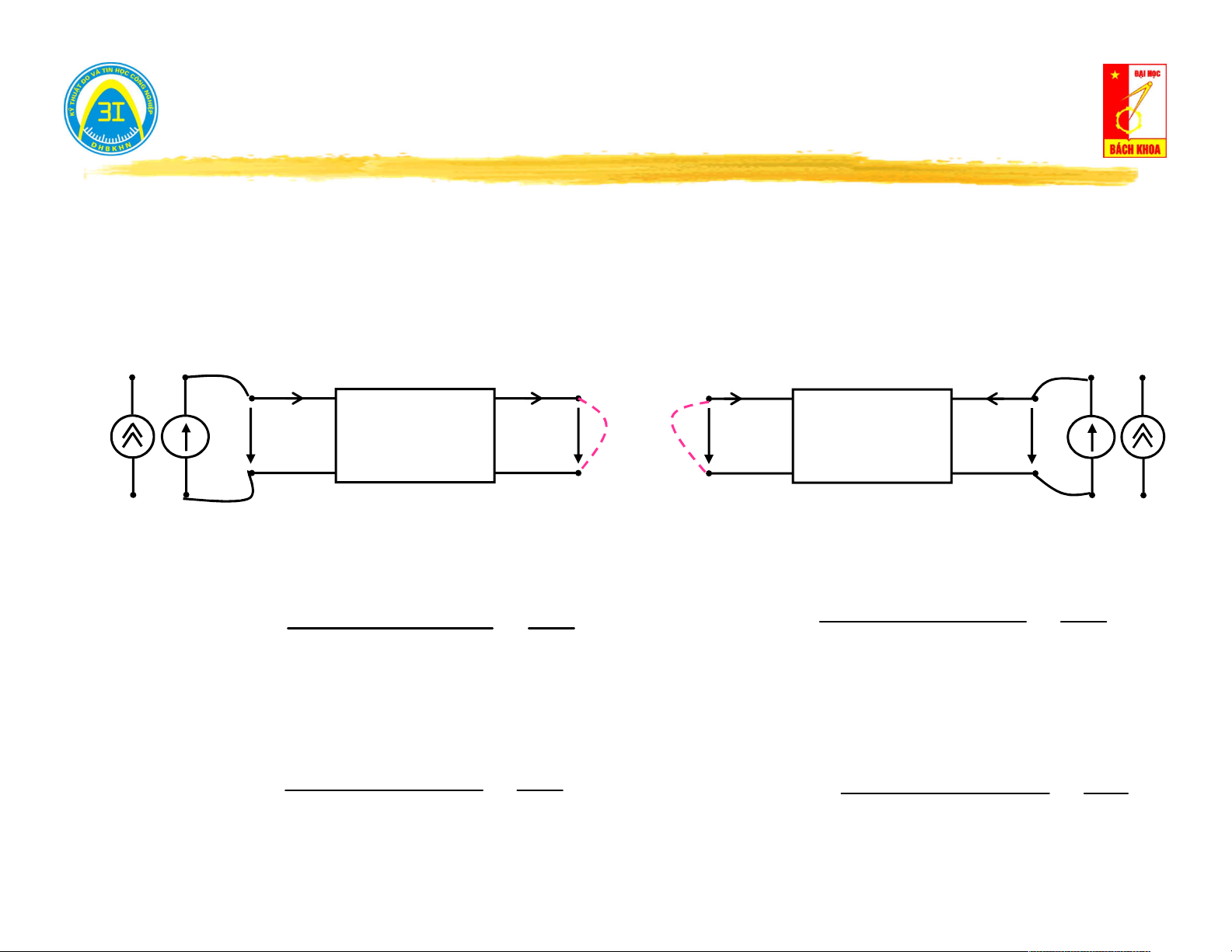
Khi I 0 (hở mạch cửa) → B U [V ] Khi
(ngắn mạch cửa) → U 0 D I [ ] A h N
B [V]: điện áp hở mạch trên cửa
D [A]: dòng điện ngắn mạch trên cửa.
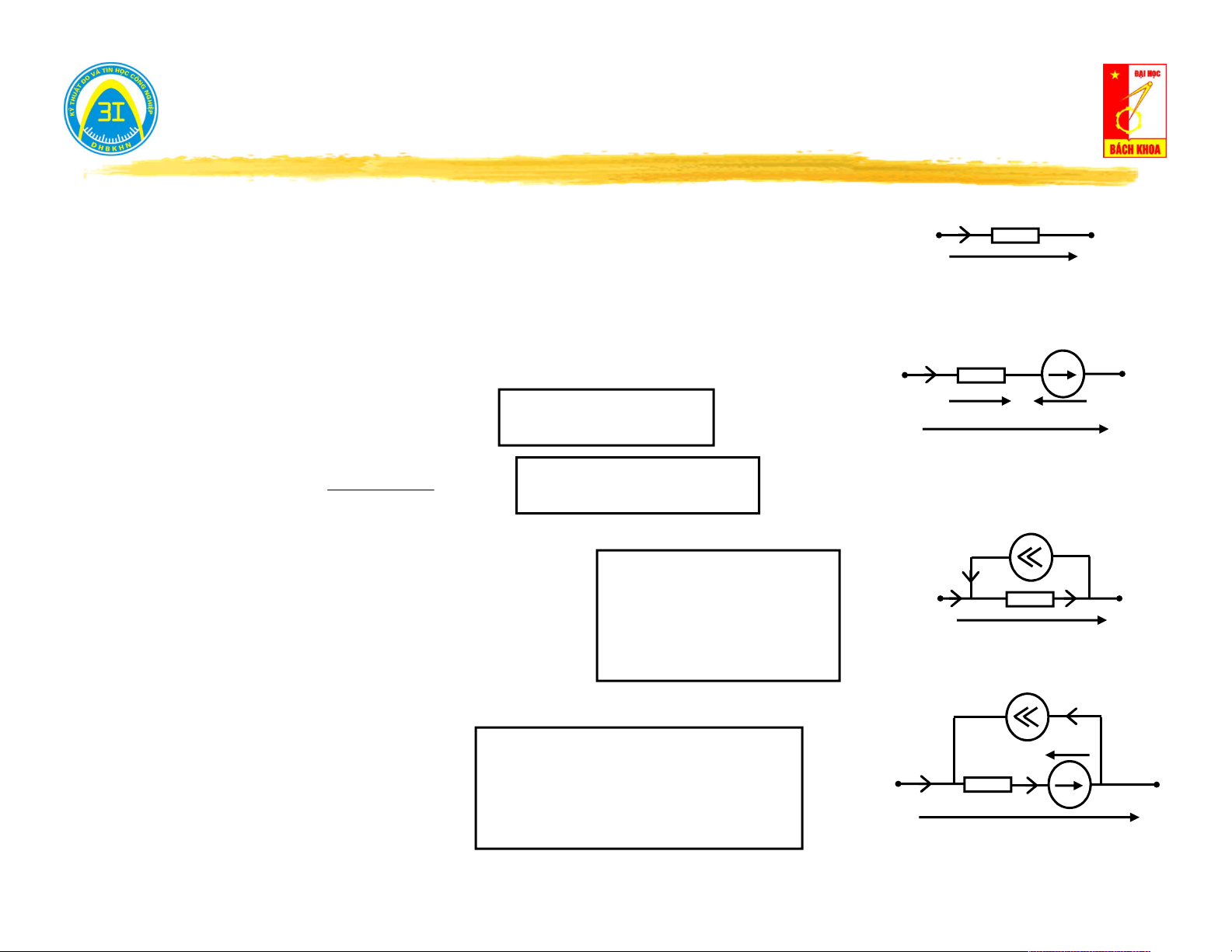
0 Mạng 1 cửa không nguồn
0 Mạng 1 cửa không nguồn D I N B U h
0 Mạng 1 cửa có nguồn 0 Mạng 1 cửa có nguồn (1) [V ] .[ A ] A [V ] (2) [ ]
A C.[V ] [ ] A
A [Ω]: tổng trở vào
C [S]: tổng dẫn vào 7
2014 – Lý thuyết mạch điện 1 - Nguyễn Việt Sơn
Chương 6: Mạng một cửa Kirchhoff tuyến tính
II.1. Phương trình trạng thái mạng 1 cửa Kirchhoff tuyến tính.
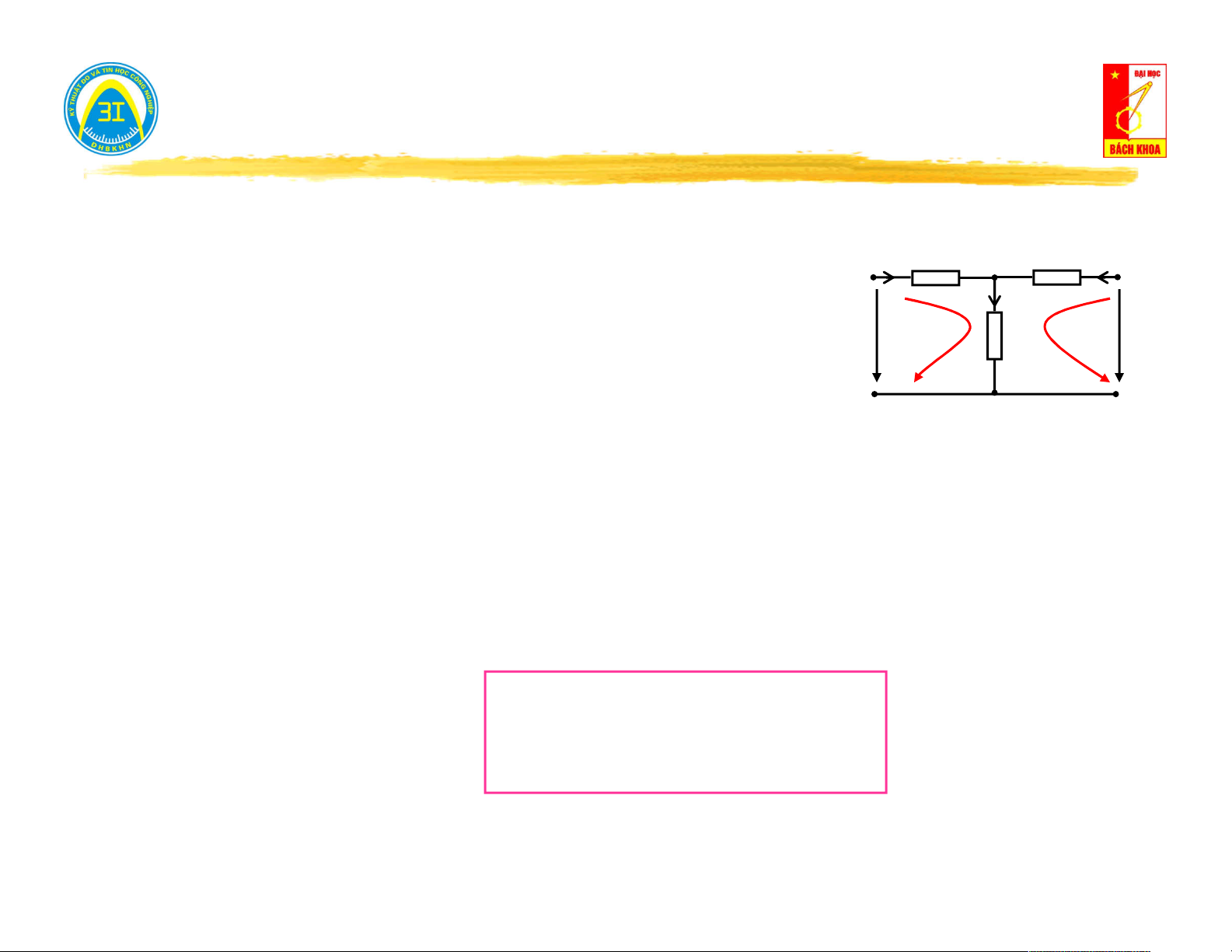
Mô hình toán học của mạng 1 cửa Kirchhoff tuyến tính: I
U Z .IU h vao U
I Y .U I N vao
Mạng 1 cửa tuyến tính có nguồn có thể đặc trưng bởi một cặp thông số (Z
, U h ) hoặc (Y , I N ) vao vao 8
2014 – Lý thuyết mạch điện 1 - Nguyễn Việt Sơn
Chương 6: Mạng một cửa Kirchhoff tuyến tính
II.2. Sơ đồ tương đương mạng 1 cửa có nguồn.
a. Định lý Thévenin.
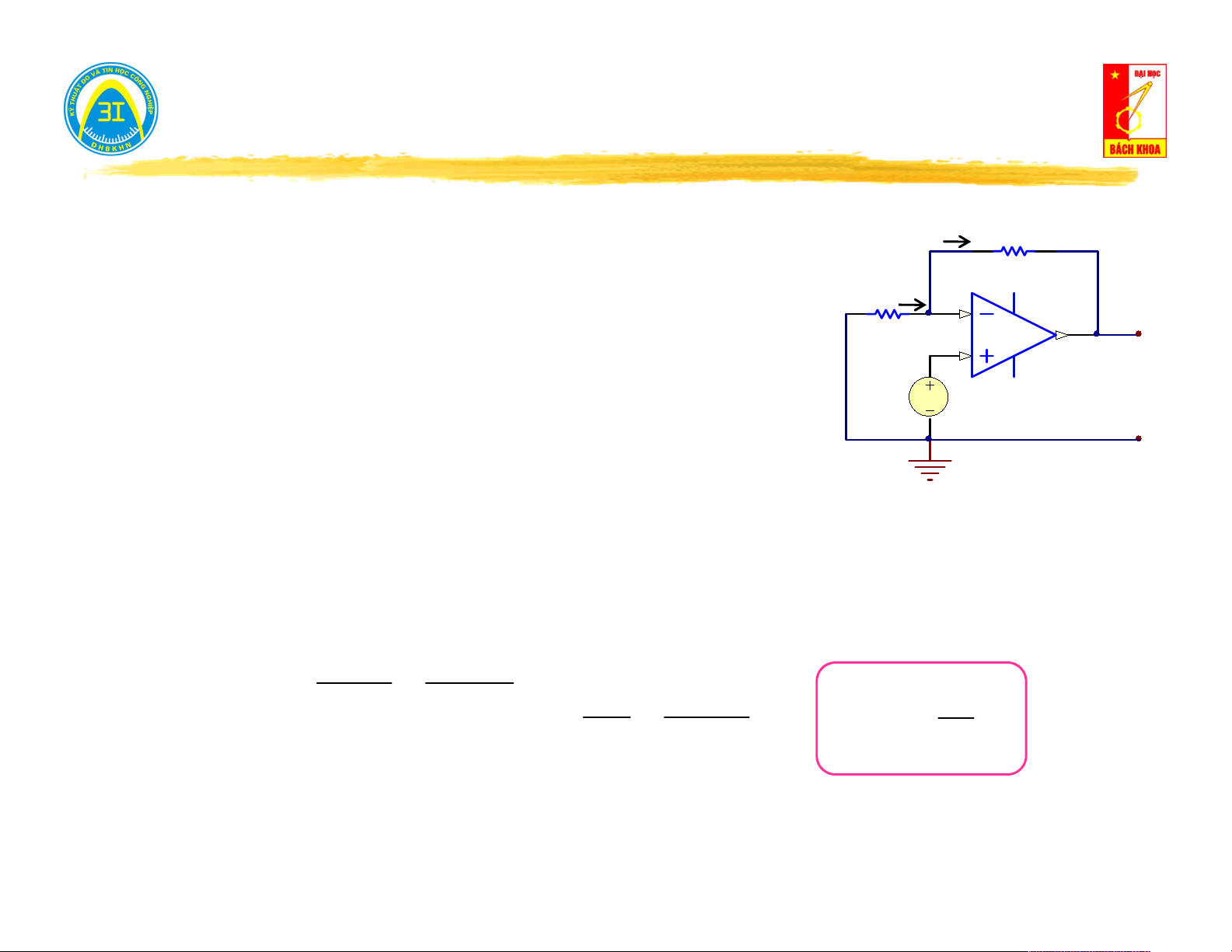
Xét phương trình: U Z . I U h vao
Phương trình có dạng luật K2, ứng với sơ đồ gồm: Tổng trở Z
(tổng trở vào của mạng một cửa) mắc nối tiếp với, vao
Nguồn áp U h (điện áp hở tại cửa)
Phát biểu: Có thể thay thế mạng 1 cửa tuyến tính bằng một nguồn áp (có suất
điện động bằng điện áp trên cửa khi hở mạch) mắc nối tiếp với một tổng trở (có
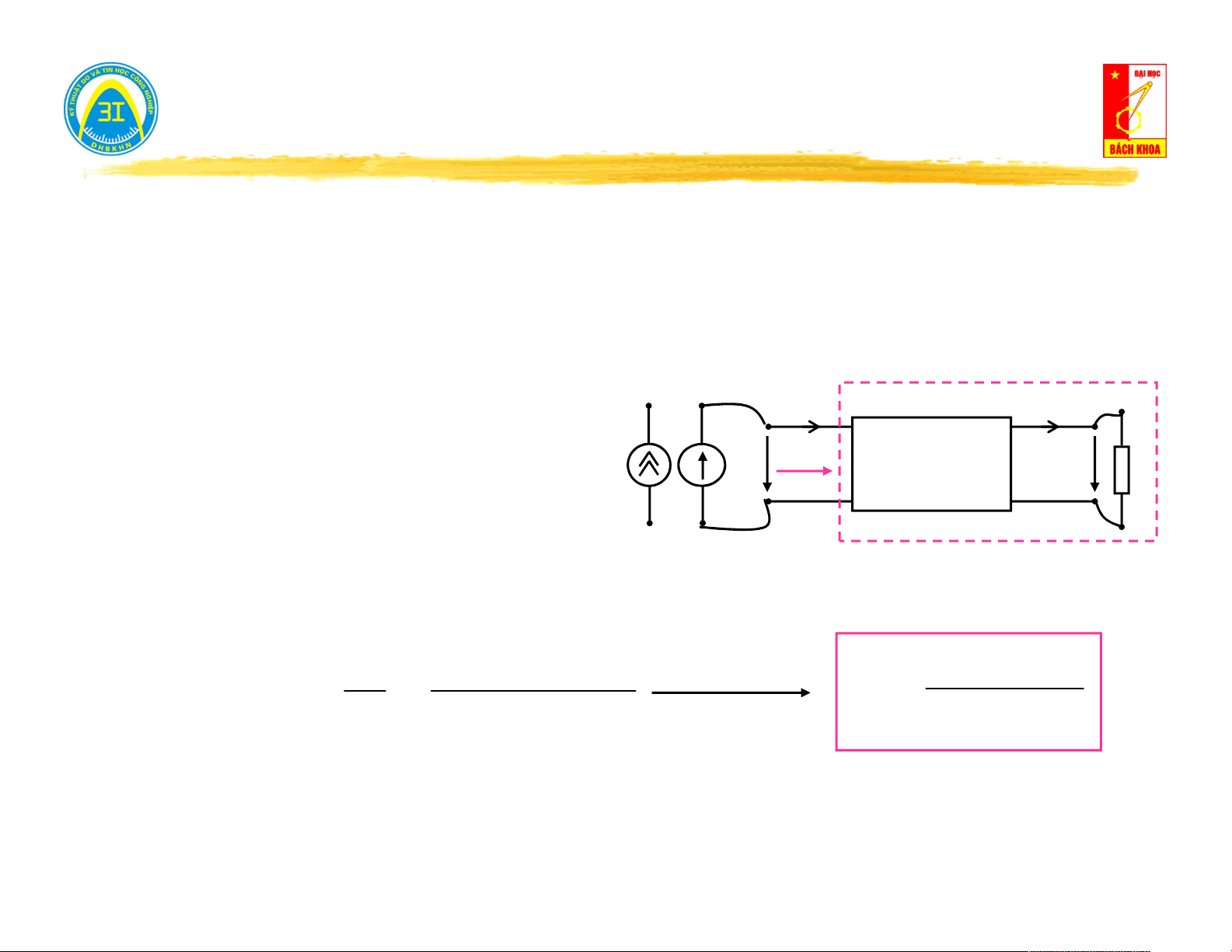
giá trị bằng tổng trở vào của mạng một cửa.) Z
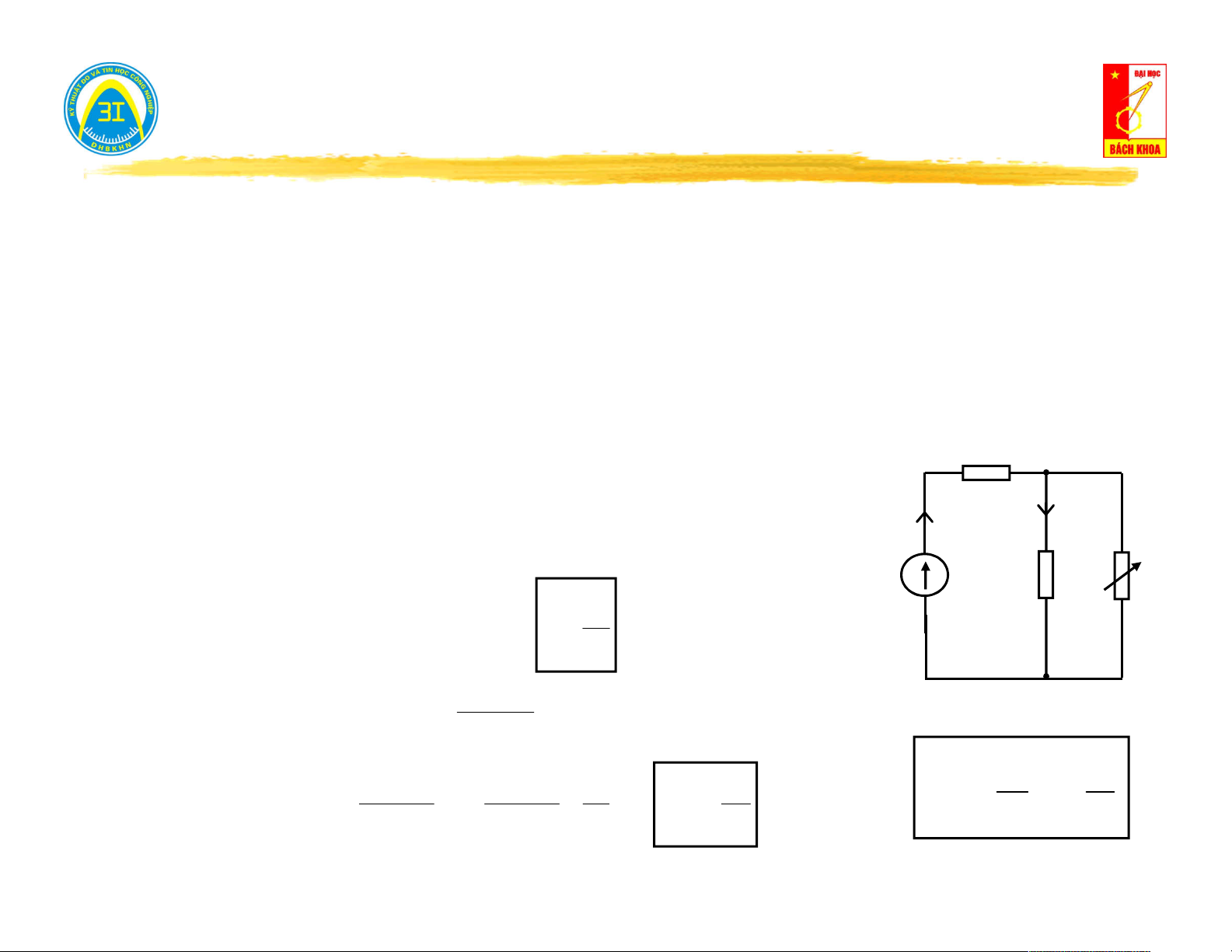
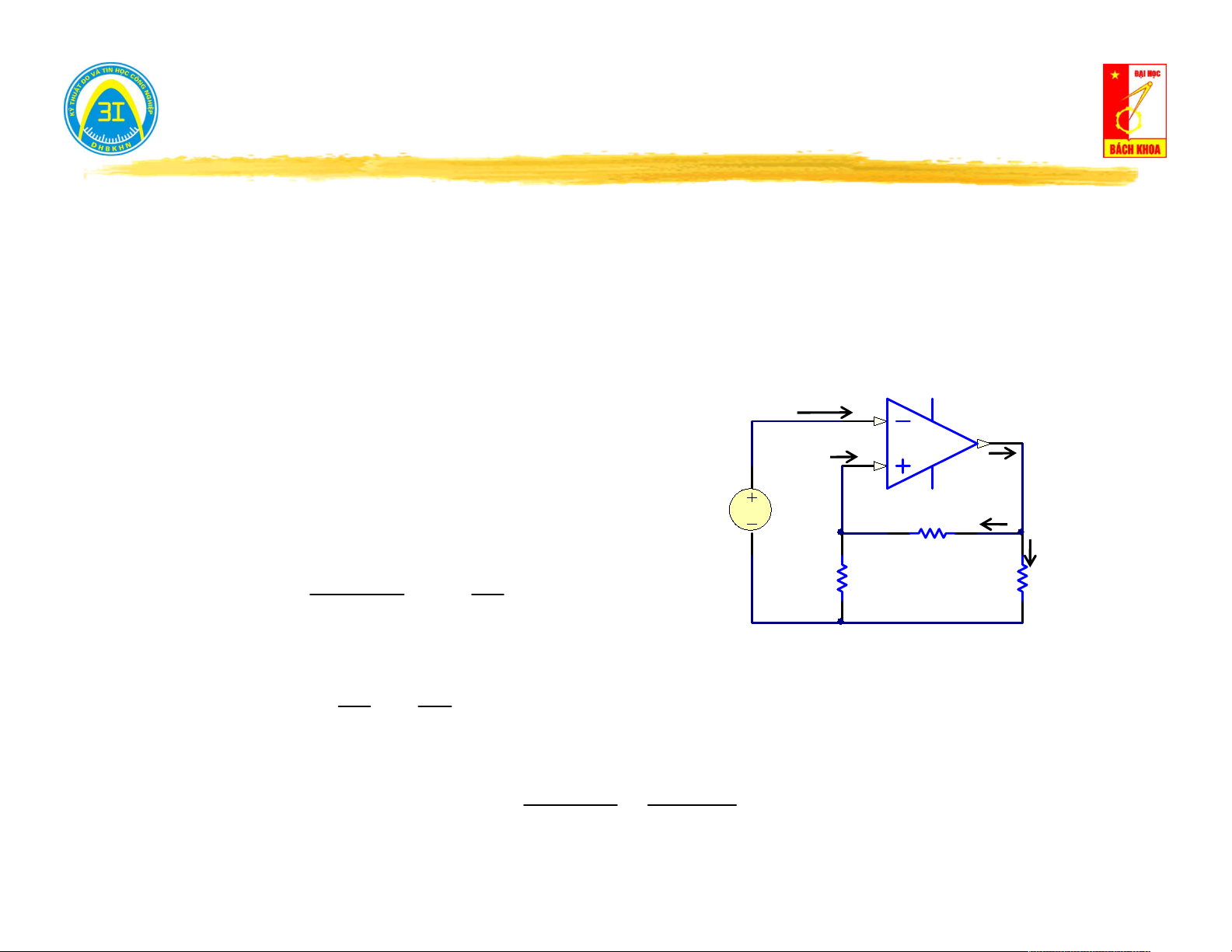
Cách tính Z : I vao vao U h I tai
Triệt tiêu nguồn độc lập: Ngắn mạch Z Z vao tai Ztai U U h
nguồn áp, hở mạch nguồn dòng. U h
Tính tổng trở tương đương. U tai .Ztai Z Z vao tai 9
2014 – Lý thuyết mạch điện 1 - Nguyễn Việt Sơn
Chương 6: Mạng một cửa Kirchhoff tuyến tính
II.2. Sơ đồ tương đương mạng 1 cửa có nguồn.
b. Định lý Norton.
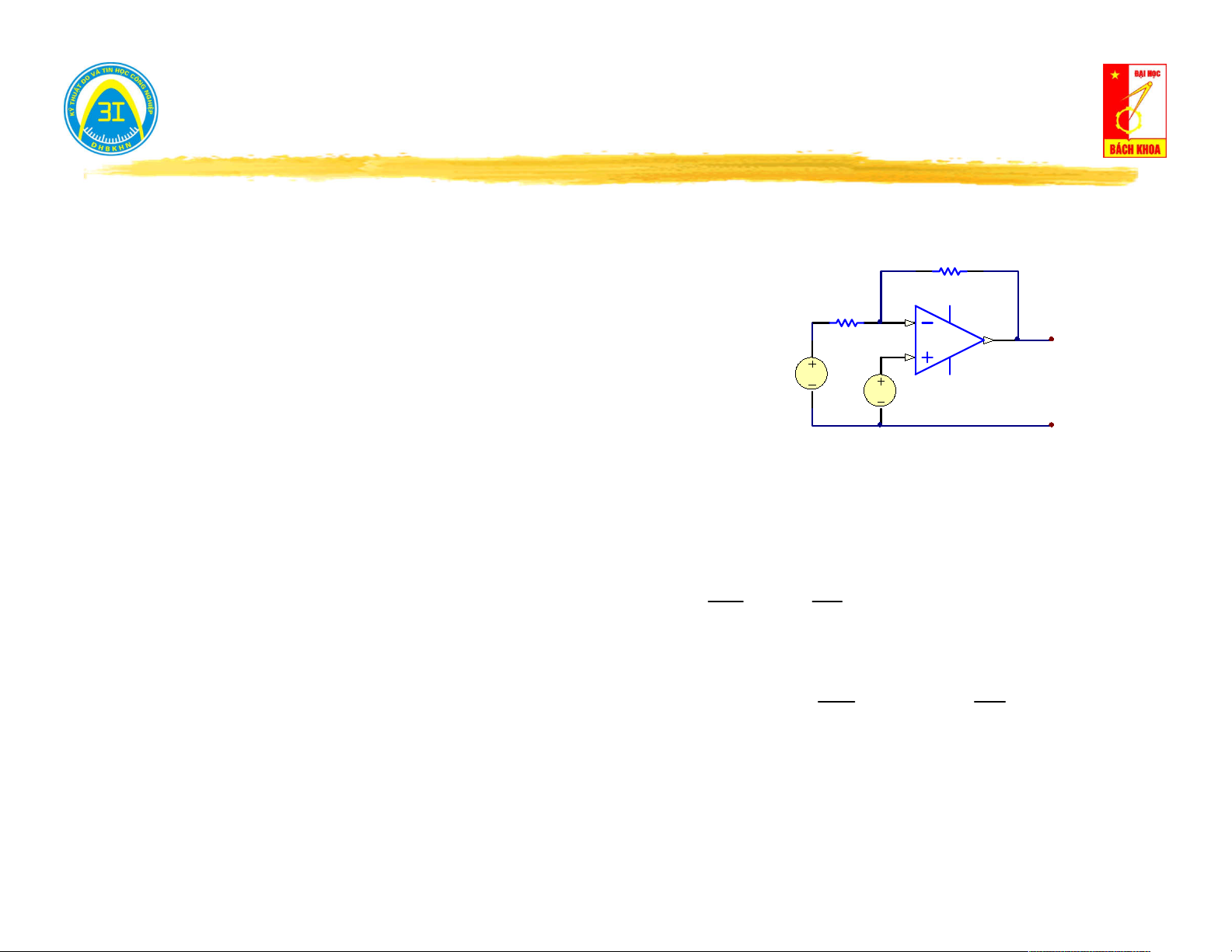
Xét phương trình: I Y .U I N vao
Phương trình có dạng luật K1, ứng với sơ đồ gồm: Tổng dẫn Y
(tổng dẫn vào của mạng một cửa), mắc song song với, vao
Nguồn dòng J N (dòng điện ngắn mạch trên cửa)
Phát biểu: Có thể thay thế mạng 1 cửa tuyến tính bằng một nguồn dòng (có giá
trị bằng giá trị dòng điện ngắn mạch trên cửa) mắc song song với một tổng dẫn
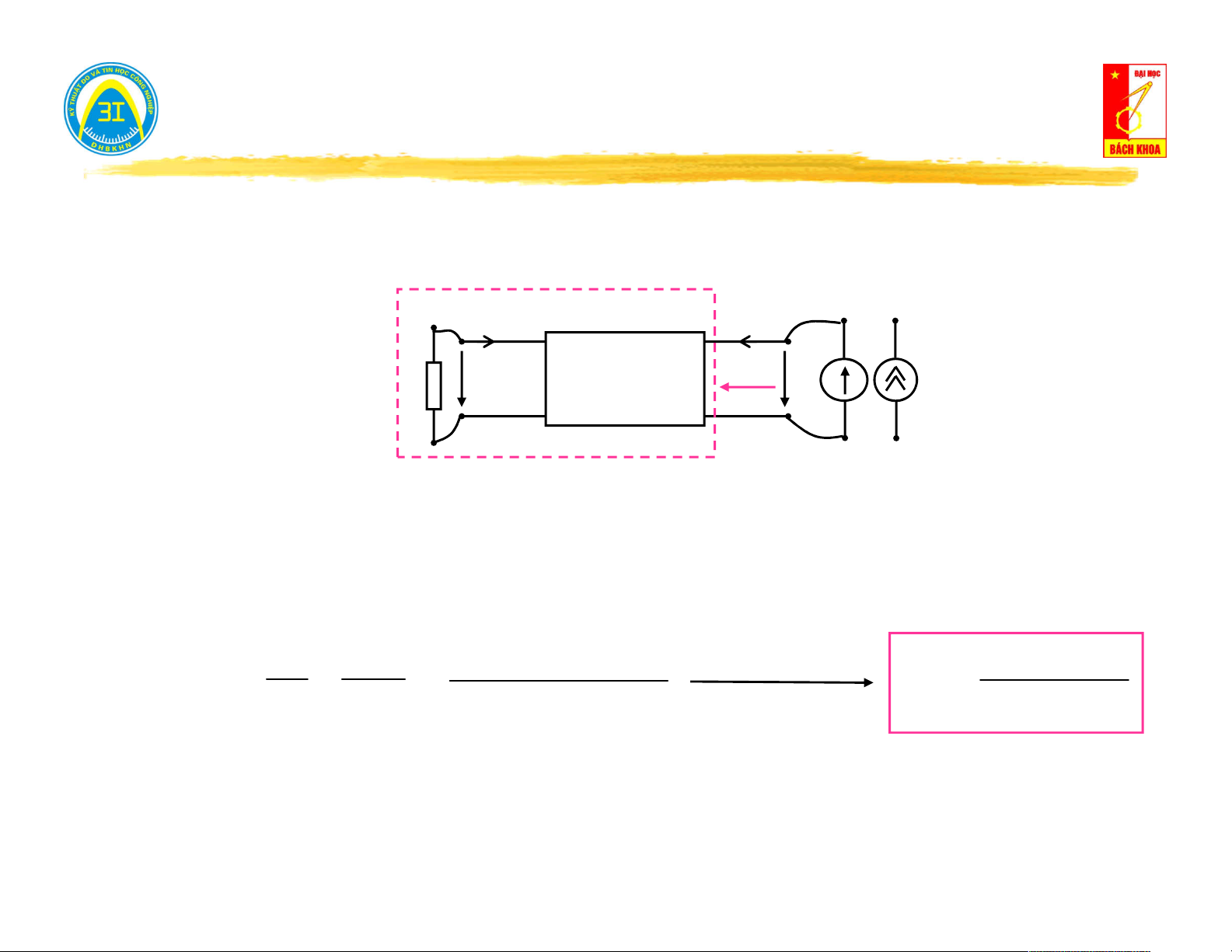
(có giá trị bằng tổng dẫn vào của mạng một cửa). I
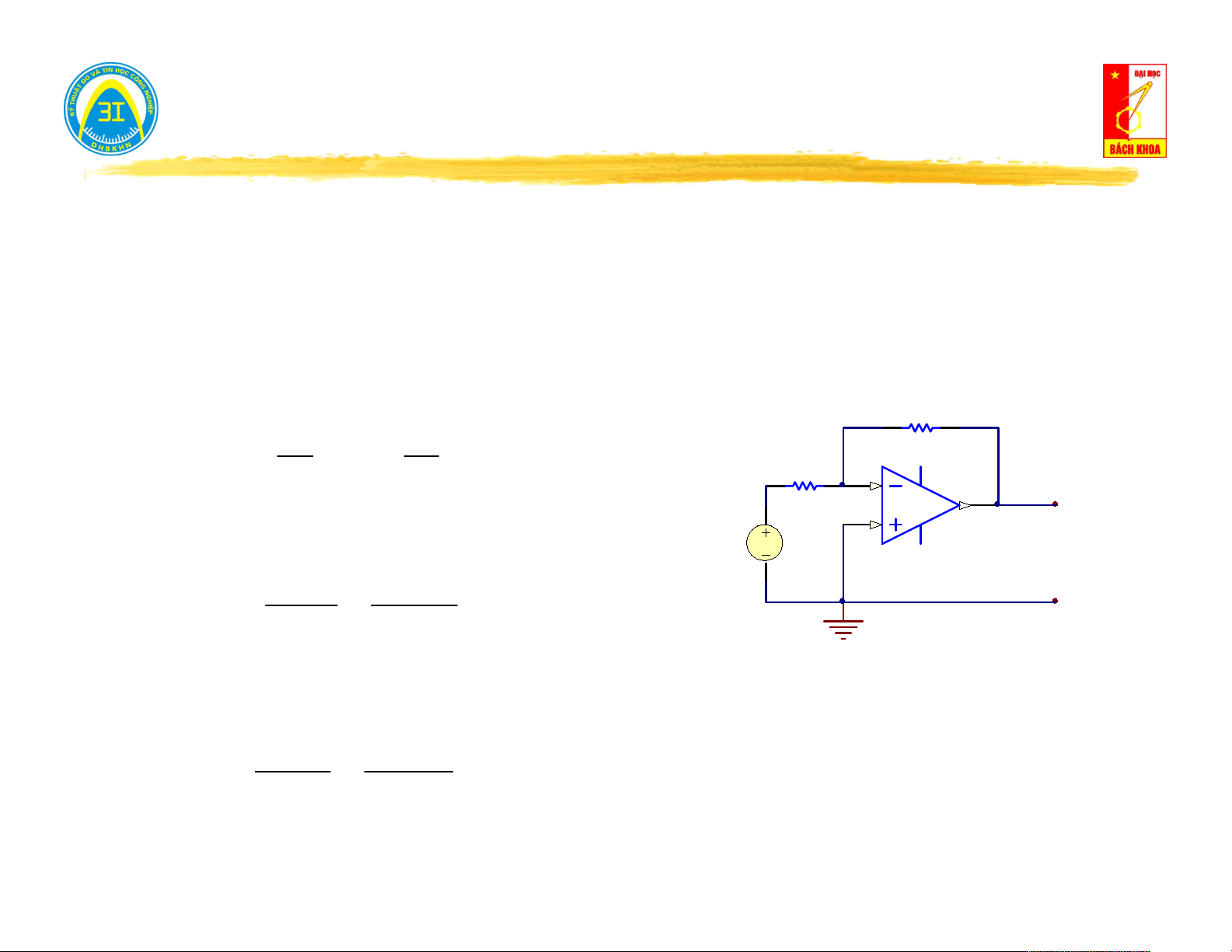
Cách tính Y : vao I N U tai Y Y U
Triệt tiêu nguồn độc lập: Ngắn mạch vao tai Y Y vao tai J N
nguồn áp, hở mạch nguồn dòng. I N I tai .Y
Tính tổng dẫn tương đương. tai Y Y vao tai 10
2014 – Lý thuyết mạch điện 1 - Nguyễn Việt Sơn
Chương 6: Mạng một cửa Kirchhoff tuyến tính
II.2. Sơ đồ tương đương mạng 1 cửa có nguồn.
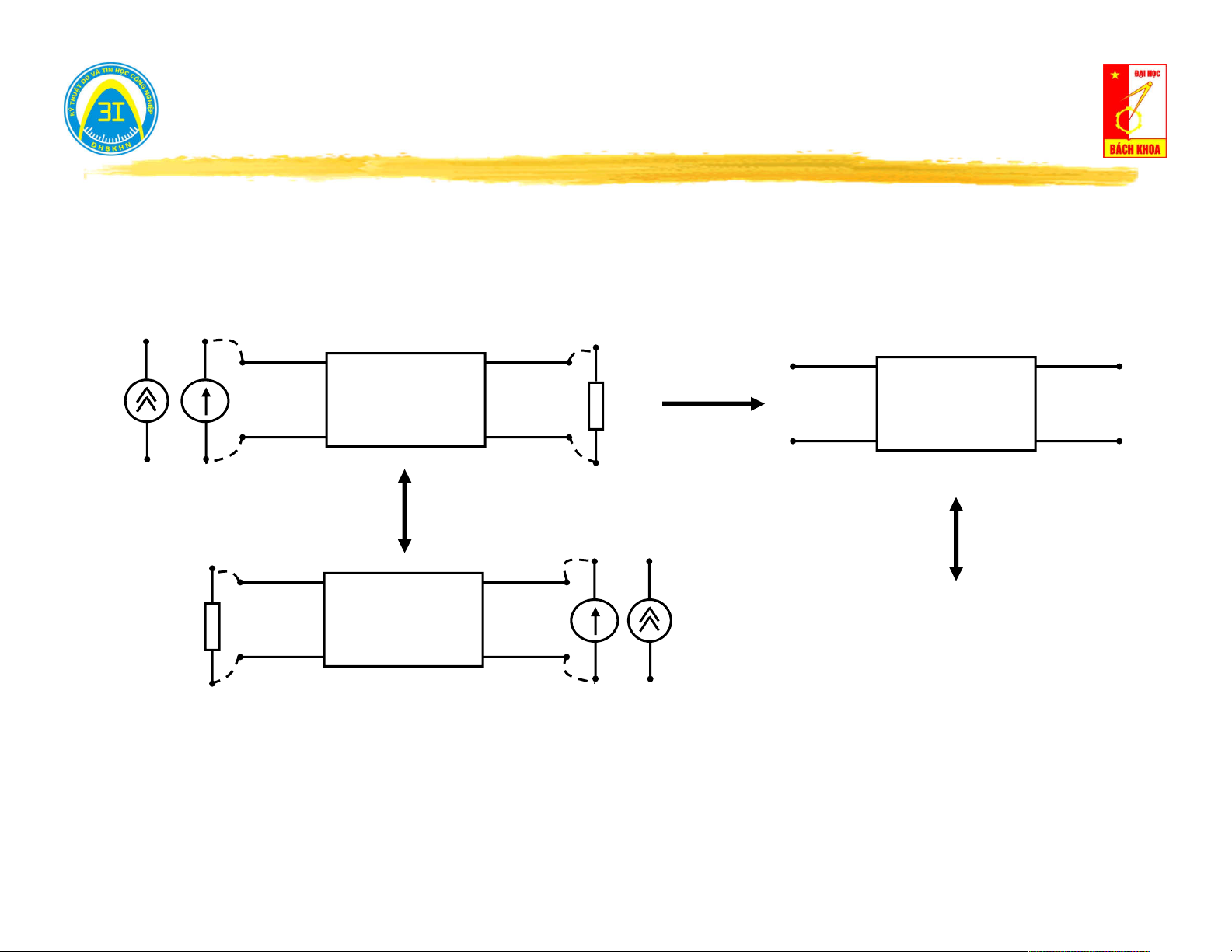
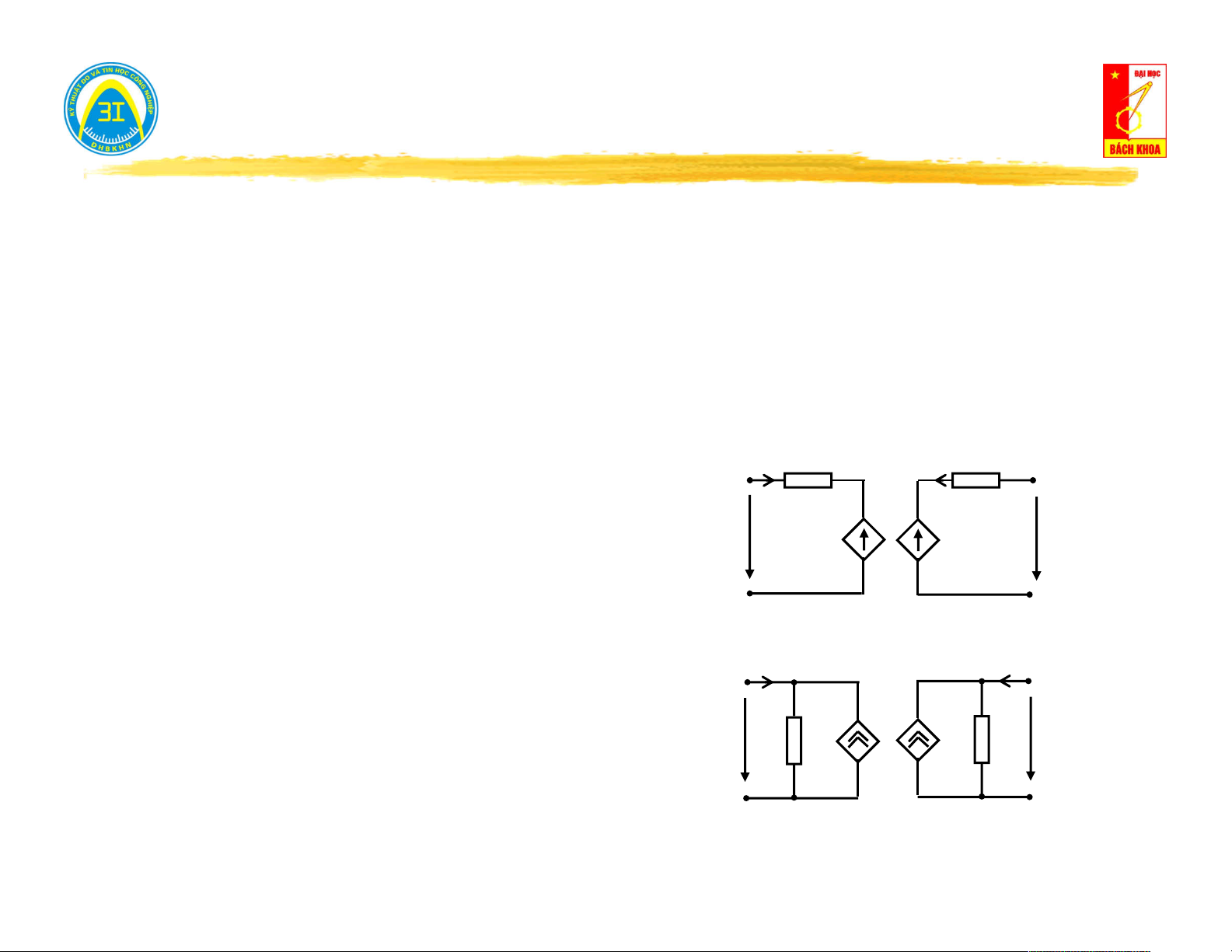
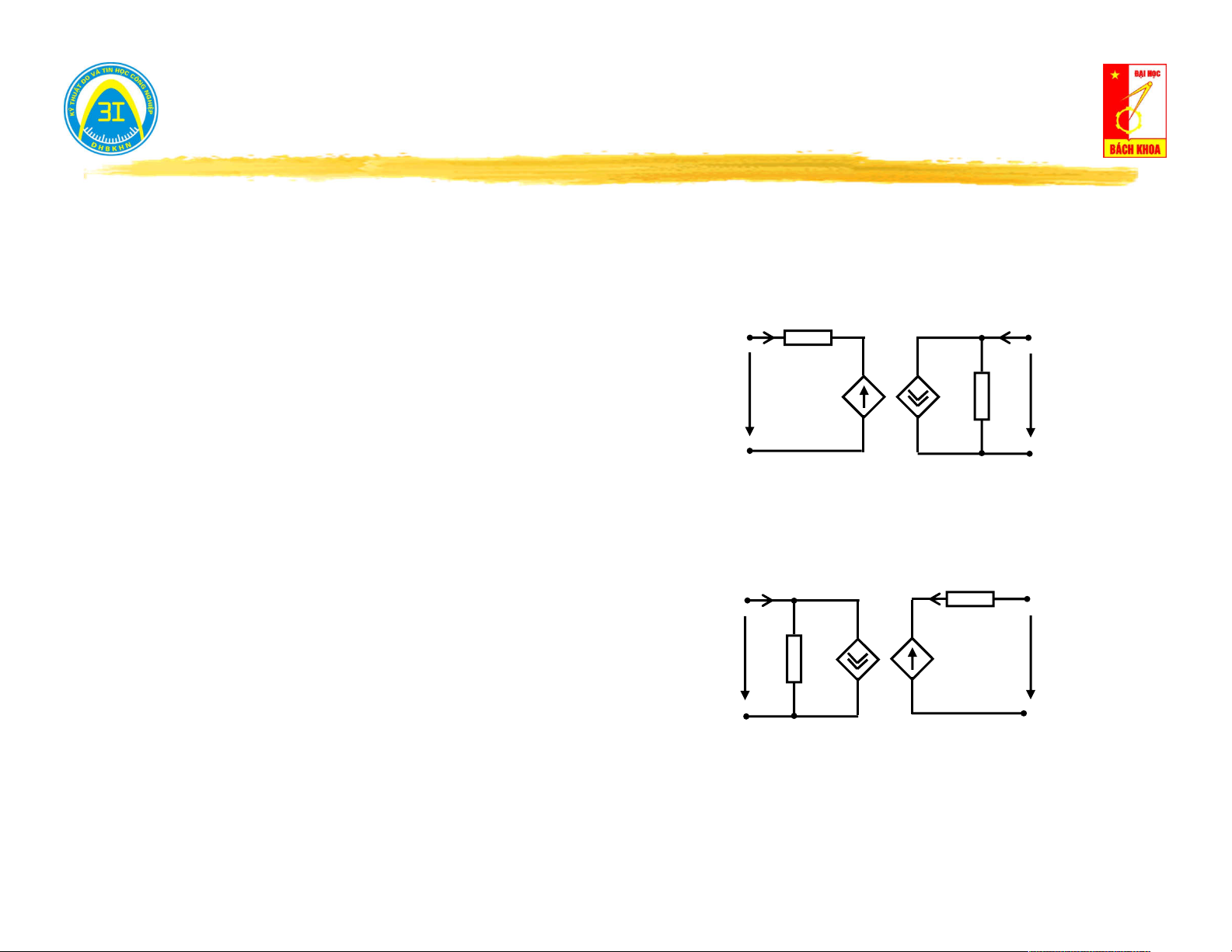
c. Quan hệ giữa sơ đồ Thévenin và Norton. Sơ đồ Sơ đồ Norton Thévenin Z I vao I Z tai U U h U Z . I U h Y vao vao Y U tai
I Y .U J N vao J N U h U h I tai U tai .Ztai I Z Z Z Z N I N vao tai vao tai I tai .Y U tai tai Y Y Y Y vao tai vao tai 1 1 Y Z vao Z vao Y vao vao Công thức liên hệ U I h I N U N Z h Y vao vao 11
2014 – Lý thuyết mạch điện 1 - Nguyễn Việt Sơn
Chương 6: Mạng một cửa Kirchhoff tuyến tính
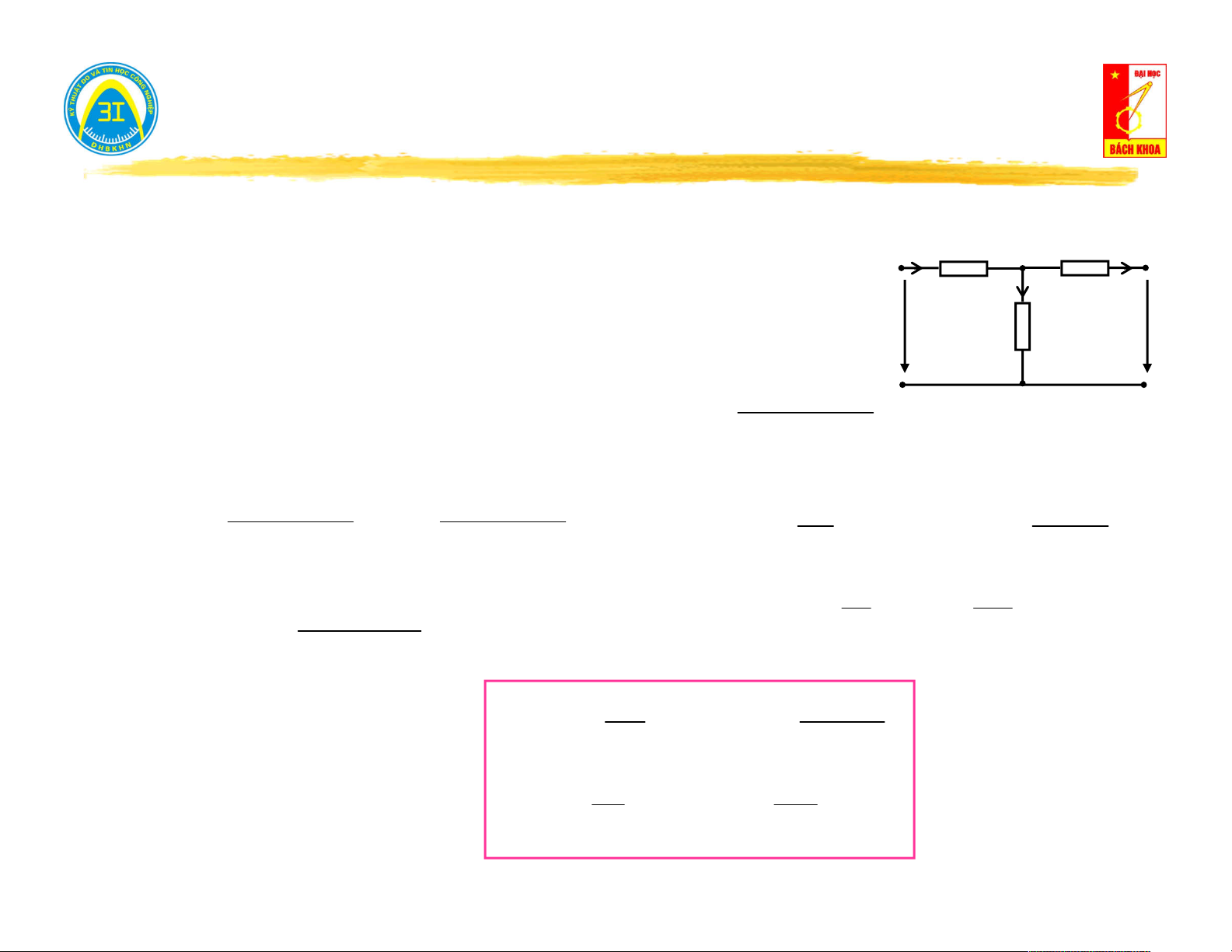
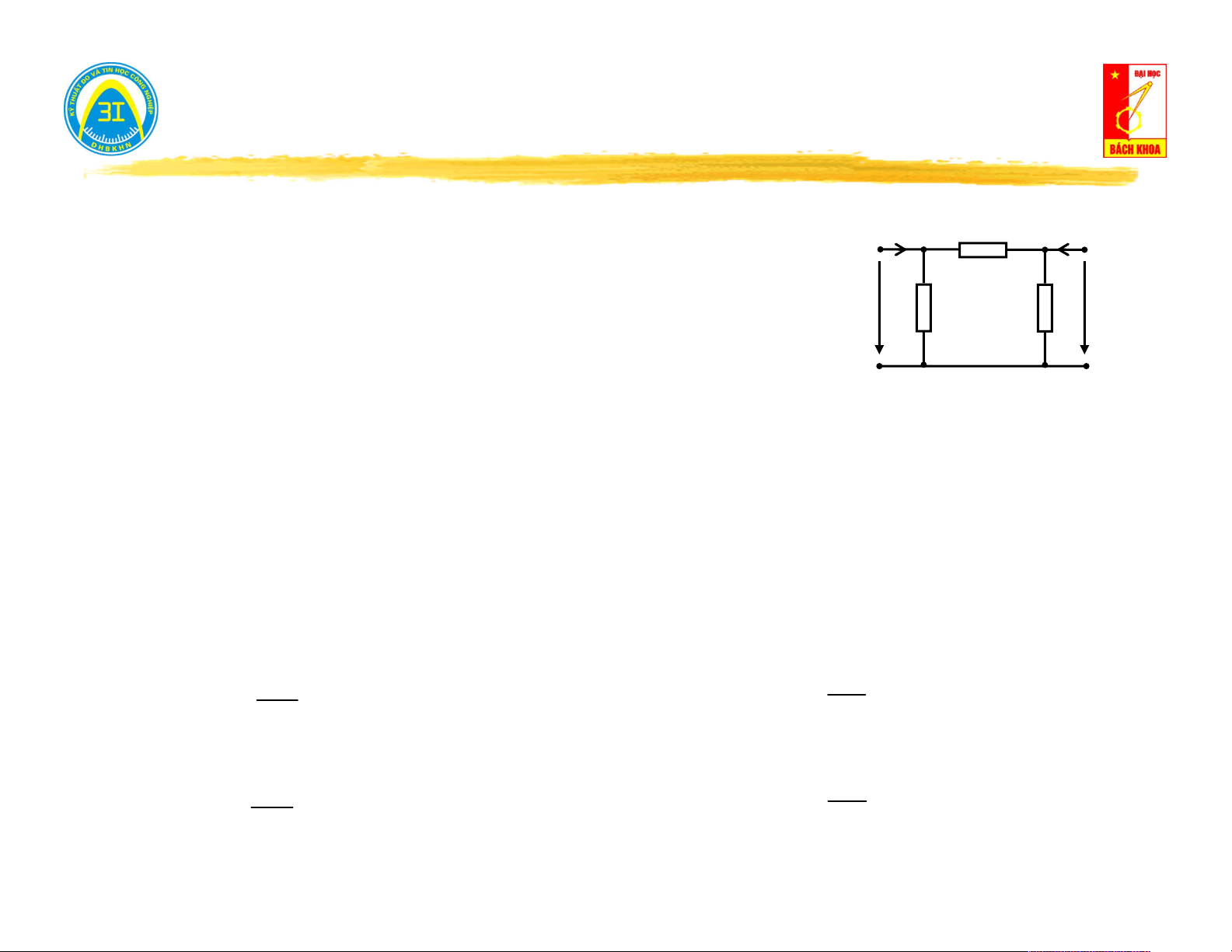
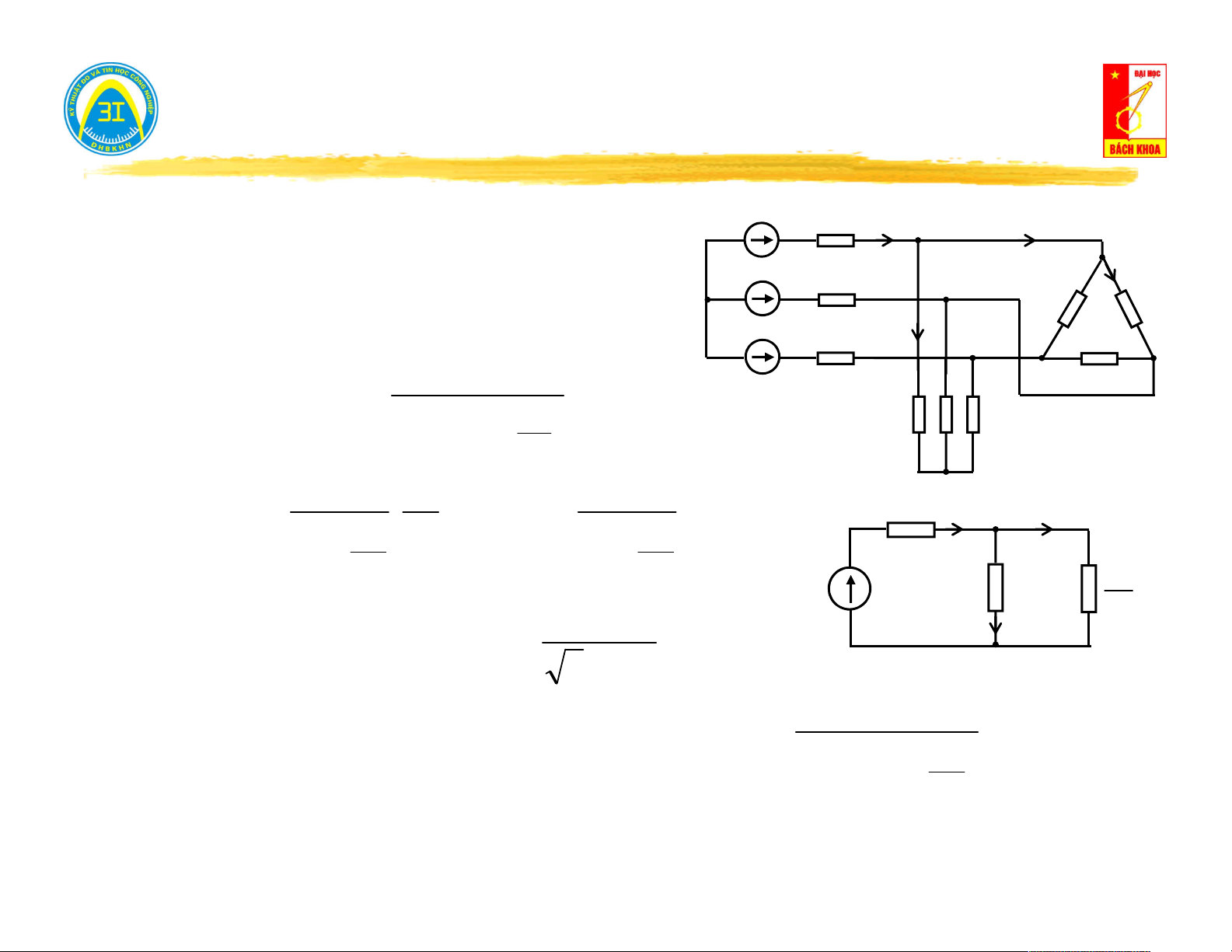
II.2. Sơ đồ tương đương mạng 1 cửa có nguồn. Z J 1 Z2
Ví dụ: Tính dòng điện và điện áp trên Z I 3 3 Z E Cắt nhánh 3: E 3 2 1
Tính U h theo phương pháp thế nút.
E .Y E .Y J 1 1 1 1 2 2 trong đó: Y ; Y A U h A 1 2 Y Y Z Z 1 2 1 2 Z Z 1 2 Z .Z 1 2 J
Tính tổng trở vào: Z Z // Z vao 1 2 E E 1 2 Z Z 1 2
Thay mạng 1 cửa bằng sơ đồ Thévenin: 0 U
E .Y E .Y J h Zvao Suy ra: 1 1 2 2 I I3 3 Z Z
(Y Y ).(Z Z ) vao 3 1 2 vao 3 U Z h 3
E .Y E .Y J 1 1 2 2
U Z . I .Z 3 3 3 3
(Y Y ).(Z Z ) 1 2 vao 3 12
2014 – Lý thuyết mạch điện 1 - Nguyễn Việt Sơn
Chương 6: Mạng một cửa Kirchhoff tuyến tính
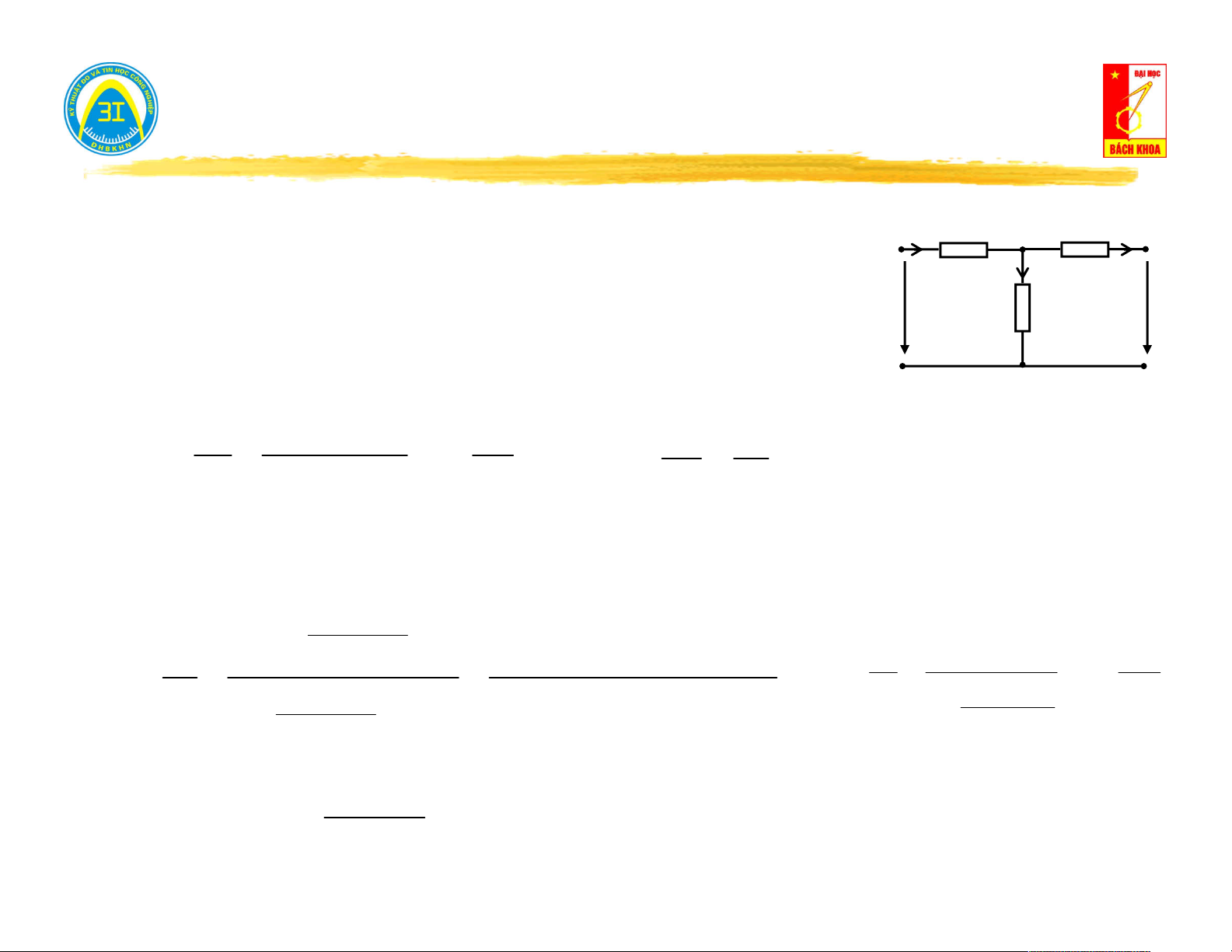
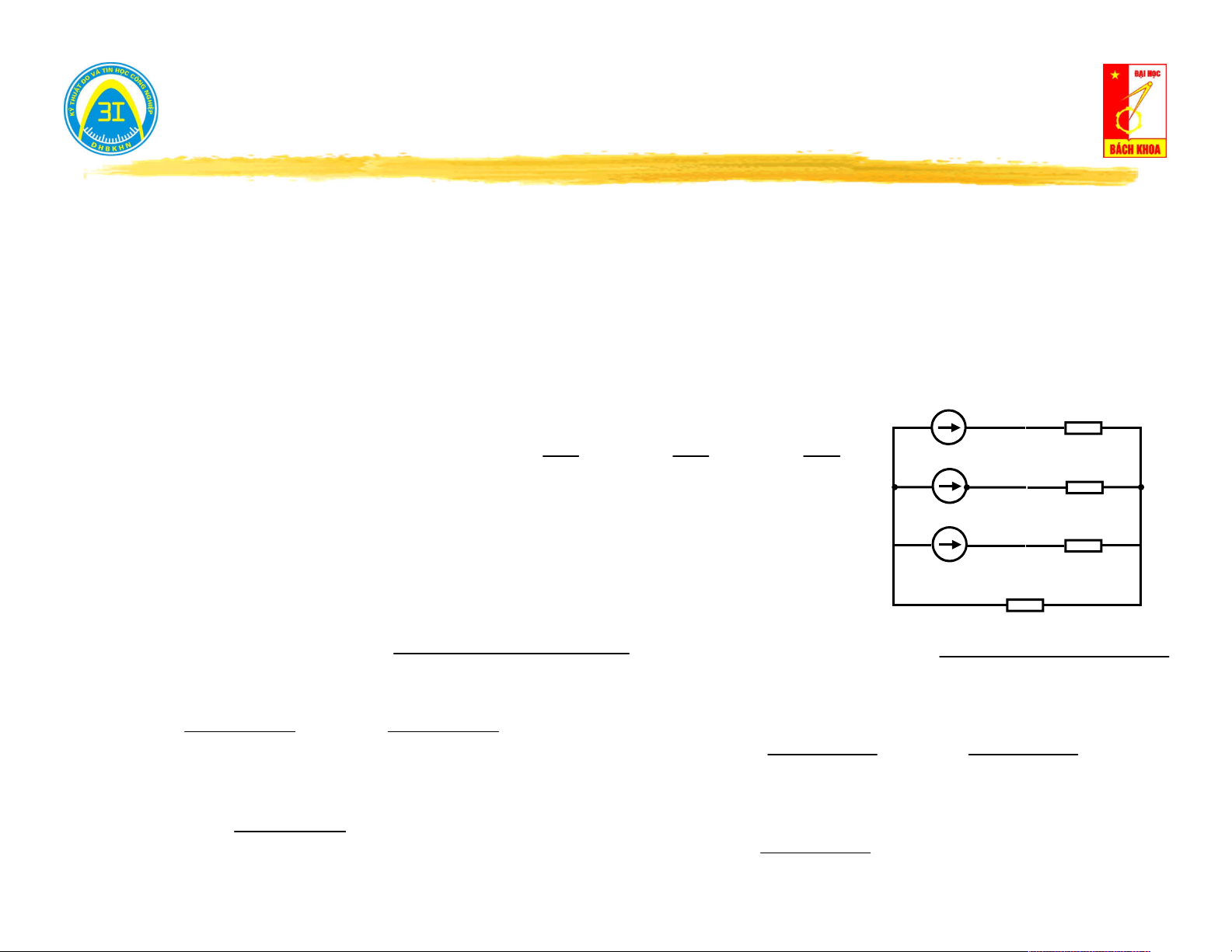
II.2. Sơ đồ tương đương mạng 1 cửa có nguồn. Z J 1 Z2
Ví dụ: Tính dòng điện và điện áp trên Z I 3 3 Z E E 3 2 1 Cắt nhánh 3: Tính I N 1 1 I trong đó: Y ; Y
N J Y . E1 Y . E 2 1 2 1 2 Z Z 1 2 Z Z 1 2
Tính tổng dẫn vào: Y
Y // Y Y Y vao 1 2 1 2 J E E I N 1 2
Thay mạng 1 cửa bằng sơ đồ Norton: Suy ra: I3 I N I 3 I N I .Y ; U 3 3 3 Y Y Y Y Y J 3 vao 3 3 vao N Y Y vao 3 13
2014 – Lý thuyết mạch điện 1 - Nguyễn Việt Sơn
LÝ THUYẾT MẠCH ĐIỆN 1
Chương 6: Mạng một cửa Kirchhoff tuyến tính.
I. Khái niệm mạng một cửa Kirchhoff.
II. Phương trình - Sơ đồ tương đương mạng một cửa có nguồn.
III. Điều kiện đưa công suất cực đại ra khỏi mạng một cửa. 14
2014 – Lý thuyết mạch điện 1 - Nguyễn Việt Sơn
Chương 6: Mạng một cửa Kirchhoff tuyến tính
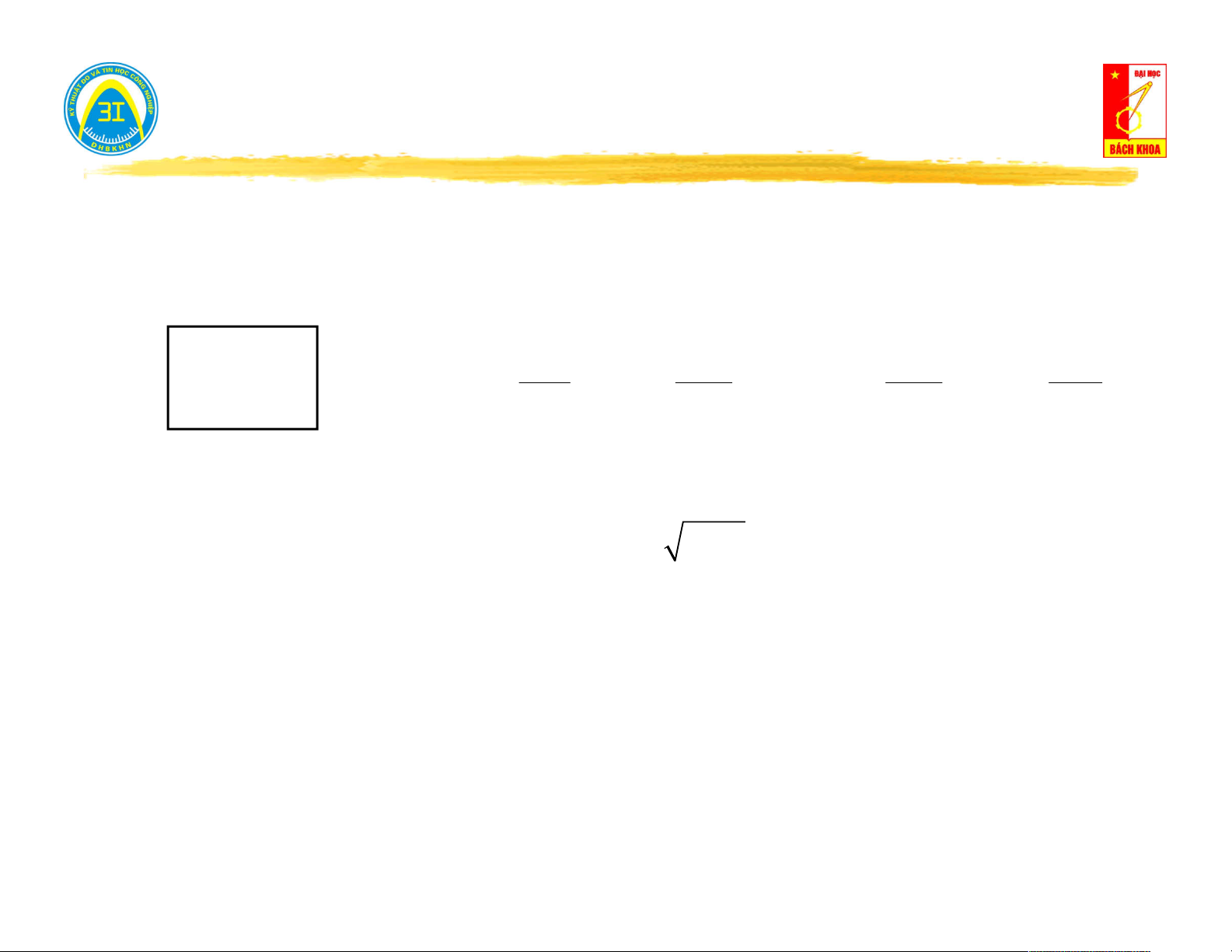
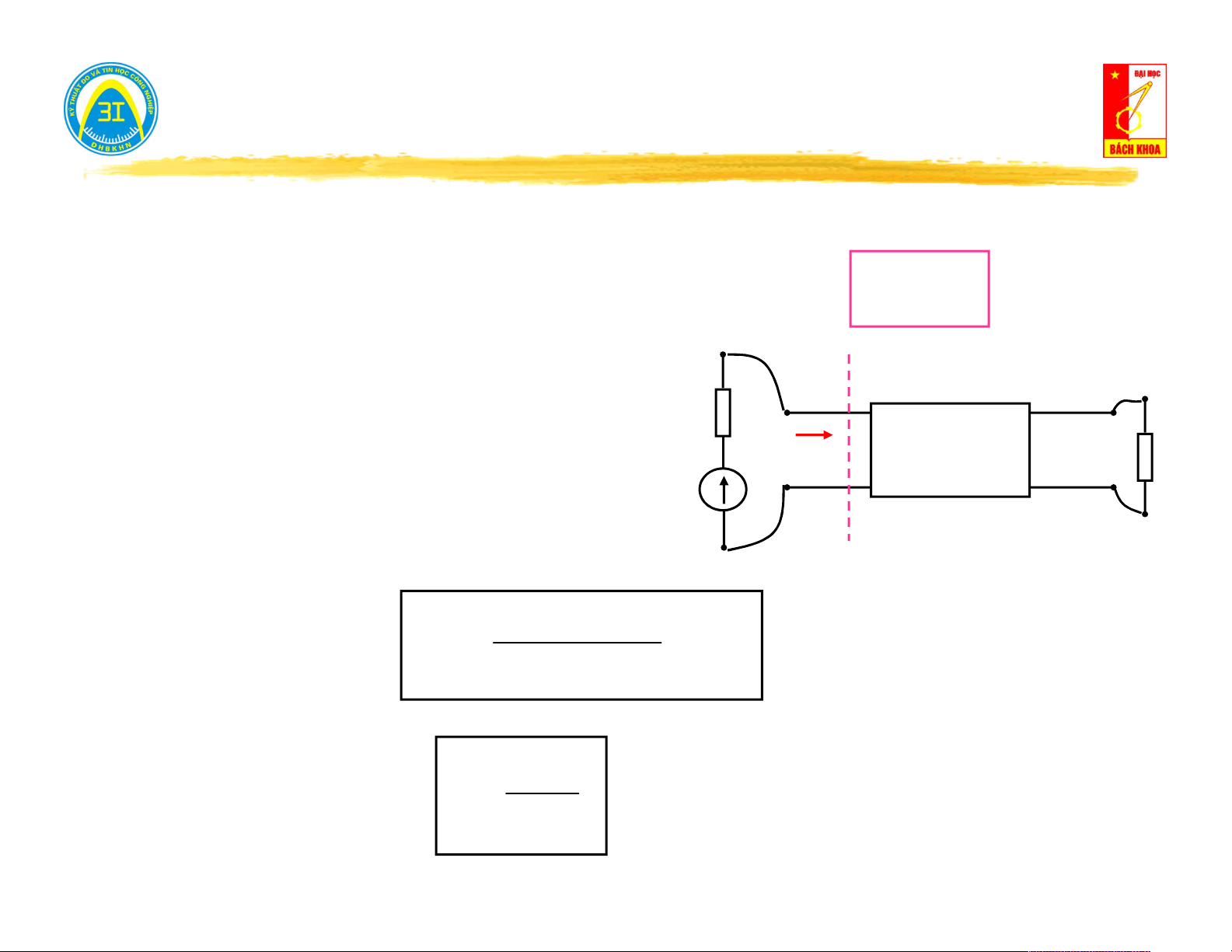
III. Điều kiện đưa công suất cực đại ra khỏi mạng một cửa. I
Mạng 1 cửa có nguồn cung cấp cho tải Z biến động. t Nguồn Tải Zt
Theo định lý Thévenin: Thay thế mạng 1 cửa bằng một
nguồn tương đương (U h , Z ) . ng Zng I , P
Khi đó công suất đưa đến tải: 2 U R 2 h 2 t U Z h t
P R .I R . U . t t t 2 h 2 2 Z
(R R ) ( X X ) ng t ng t
Để công suất đến tải đạt cực đại: X X 0 X X 0 ng t ng t X X R =const ng t R ng t max d Rt R R 2 0 (R R ) 2 ng t ng t dR (R R ) t ng t 15
2014 – Lý thuyết mạch điện 1 - Nguyễn Việt Sơn
Chương 6: Mạng một cửa Kirchhoff tuyến tính
III. Điều kiện đưa công suất cực đại ra khỏi mạng một cửa.
Điều kiện đưa công suất cực đại ra mạng 1 cửa là: I ^ Nguồn Tải Zt Z Z ng t
Công suất cực đại đưa ra tải là: 2 2 2 Z U .R U .R ng I , P h ng U h t h P t 2 2 (R R ) (2.R ) 4.R ng t ng ng U Z h t
Hiệu suất truyền năng lượng đến tải: 2 P R .I t t 50% 2 P
(R R ).I ng ng t Thực tế Z
& R không thỏa mãn điều kiện trên → cần nối thêm một bộ phận ng t
trung gian có thông số thích hợp giữa nguồn & tải (hòa hợp nguồn với tải). 16
2014 – Lý thuyết mạch điện 1 - Nguyễn Việt Sơn
LÝ THUYẾT MẠCH ĐIỆN 1
Chương 7: Mạng hai cửa tuyến tính I. Khái niệm.
II. Mô hình toán học mạng hai cửa - Phương pháp tính bộ số
III. Tính chất mạng 2 cửa tuyến tính tương hỗ.
IV. Hàm truyền đạt dòng - áp. Tổng trở vào mạng hai cửa.
Vấn đề hòa hợp nguồn và tải bằng mạng hai cửa.
V. Mạng hai cửa phi hỗ.
VI. Khuếch đại thuật toán.
Bài tập: 1 - 9, bài thêm 1
2017 – Lý thuyết mạch điện 1 - Nguyễn Việt Sơn
Chương 7: Mạng hai cửa tuyến tính I.1. Đặt vấn đề.
Các chương trước đã trình bày:
Phương pháp xét mạch tuyến tính hệ số hằng ở chế độ xác lập điều hòa:
Phương pháp dòng nhánh.
Phương pháp dòng vòng.
Phương pháp thế đỉnh.
Phương pháp xét mạch tuyến tính có kích thích chu kỳ không điều hòa.
Phương pháp mạng một cửa Kirchhoff tuyến tính.
Chương này sẽ trình bày sơ đồ cấu trúc mới, mô hình mạng hai cửa Kirchhoff.
Thế nào là mạng 2 cửa ???
Tại sao ta phải xây dựng mô hình mạng 2 cửa ??? 2
2017 – Lý thuyết mạch điện 1 - Nguyễn Việt Sơn
Chương 7: Mạng hai cửa tuyến tính
I.1. Đặt vấn đề.
Thực tế có những thiết bị điện (có cấu trúc bên trong khác nhau)
làm nhiệm vụ nhận năng lượng / tín hiệu đưa vào một cửa ngõ và
truyền ra một cửa ngõ khác.
Hệ thống đo lường điều khiển tạo bởi nhiều khối, mỗi khối
có 2 cửa ngõ, tác động lên tín hiệu ở cửa vào, để cho một
tín hiệu khác ở cửa ra. Việc phân tích theo sơ đồ khối dễ
dàng nhìn thấy cấu trúc của hệ thống, hiểu được chức
năng của từng khối trong hệ thống đó.
Để mô tả quan hệ các quá trình năng lượng/tín hiệu trên hai
cửa ngõ sử dụng mô hình mạng hai cửa. 3
2017 – Lý thuyết mạch điện 1 - Nguyễn Việt Sơn
Chương 7: Mạng hai cửa tuyến tính
I.1. Đặt vấn đề.
Định nghĩa: Mô hình mạng hai cửa là kết cấu sơ đồ mạch có hai cửa ngõ để
truyền đạt, trao đổi năng lượng / tín hiệu điện với các mạch khác. Nếu quá trình
năng lượng trên các cửa được đo bằng cặp biến trạng thái dòng, áp u (t), i (t), 1 1
u (t), i (t) mạng hai cửa Kirchhoff. 2 2 i (t) 1 i (t) 2
Theo tính chất tuyến tính, mỗi biến trạng thái có u (t) u (t) 1 2
quan hệ tuyến tính với 2 biến trạng thái khác: Mô hình toán học: ' ' ' '
f (u ,u ,...i ,i ,..., u ,u ,..., i , i ,..., t) 0 1 1 1 1 1 2 2 2 2 ' ' ' '
f (u , u ,...i , i ,..., u , u ,..., i , i ,..., t) 0 2 1 1 1 1 2 2 2 2
Có 06 hệ phương trình tuyến tính ứng với 06 bộ số A, Z, Y, B, G, H 4
2017 – Lý thuyết mạch điện 1 - Nguyễn Việt Sơn
Chương 7: Mạng hai cửa tuyến tính I.2. Phân loại.
Theo tính chất của mô hình toán học:
Theo tính chất tương hỗ:
Mạng hai cửa tuyến tính.
Mạng hai cửa tương hỗ.
Mạng hai cửa phi tuyến Mạng hai cửa phi hỗ.
Theo cấu trúc của mạng hai cửa:
Theo năng lượng:
Mạng hai cửa đối xứng.
Mạng hai cửa có nguồn.
Mạng hai cửa không đối xứng.
Mạng hai cửa không nguồn. 5
2017 – Lý thuyết mạch điện 1 - Nguyễn Việt Sơn
Chương 7: Mạng hai cửa tuyến tính I.2. Phân loại.
Cách xác định mạng 2 cửa có nguồn / không nguồn:
Hở mạch 2 cửa (i = i = 0) → đo điện áp hở mạch: 1 2 Nếu u = u
= 0 → mạng 2 cửa không nguồn 10 20 Nếu u ≠ 0 hoặc u
≠ 0 → mạng 2 cửa có nguồn 10 20
Ngắn mạch 2 cửa (u = u = 0) → đo dòng điện ngắn mạch: 1 2 Nếu i = i
= 0 → mạng 2 cửa không nguồn 10 20 Nếu i ≠ 0 hoặc i
≠ 0 → mạng 2 cửa có nguồn 10 20 i (t) i (t) 10 20 i (t) = 0 i (t) = 0 1 2 A A 1 2 V u (t) u (t) u (t) = 0 20 V u (t) = 0 1 10 2 1 2 6
2017 – Lý thuyết mạch điện 1 - Nguyễn Việt Sơn
Chương 7: Mạng hai cửa tuyến tính I.2. Phân loại.
Thực tế có nhiều loại mạng hai cửa khác nhau:
Mạng hai cửa phi tuyến có nguồn / không nguồn.
Mạng hai cửa tuyến tính có nguồn / không nguồn.
Mạng hai cửa tuyến tính tương hỗ.
Mạng hai cửa tuyến tính phi hỗ. …
Chương này chỉ việc mô tả & phân tích mạng hai cửa tuyến tính, không
nguồn, có hệ số hằng ở chế độ xác lập điều hòa.
→ Sử dụng phương pháp số phức. 7
2017 – Lý thuyết mạch điện 1 - Nguyễn Việt Sơn
LÝ THUYẾT MẠCH ĐIỆN 1
Chương 7: Mạng hai cửa tuyến tính I. Khái niệm.
II. Mô hình toán học mạng hai cửa - Phương pháp tính bộ số.
II.1. Hệ phương trình trạng thái dạng A.
II.2. Hệ phương trình trạng thái dạng B.
II.3. Hệ phương trình trạng thái dạng Z.
II.4. Hệ phương trình trạng thái dạng Y.
II.5. Hệ phương trình trạng thái dạng H.
II.6. Hệ phương trình trạng thái dạng G.
II.7. Ma trận của hệ các mạng hai cửa.
II.8. Các phương pháp tính bộ số đặc trưng.
III. Tính chất mạng 2 cửa tuyến tính tương hỗ.
IV. Hàm truyền đạt dòng - áp. Tổng trở vào mạng hai cửa. Vấn đề hòa hợp
nguồn và tải bằng mạng hai cửa.
V. Mạng hai cửa phi hỗ.
VI. Khuếch đại thuật toán. 8
2017 – Lý thuyết mạch điện 1 - Nguyễn Việt Sơn
Chương 7: Mạng hai cửa tuyến tính
II.1. Hệ phương trình trạng thái dạng A.
Xét mạng hai cửa Kirchhoff ở chế độ xác lập điều hòa:
Theo tính chất tuyến tính, mỗi biến trạng thái có quan hệ tuyến tính với 2 biến trạng thái khác I1 I 2
Xét quan hệ tuyến tính giữa (U 1, I1) và (U 2, I 2 ) U 1 A U 2 U1
A .U 2 A . I 2 U 10 11 12
I1 A .U 2 A . I 2 I10 21 22
Do mạng 2 cửa không nguồn, nếu U U 0 và I I 0 U I 0 1 2 1 2 10 10
Vậy phương trình trạng thái dạng A của mạng 2 cửa tuyến tính không nguồn là: U 1
A .U 2 A . I 2 11 12 U 1 A A U 2 11 12 Dạng ma trận: . A A I 21 22
1 A .U 2 A . I 2 I I 21 22 1 2 9
2017 – Lý thuyết mạch điện 1 - Nguyễn Việt Sơn
Chương 7: Mạng hai cửa tuyến tính
II.1. Hệ phương trình trạng thái dạng A. U1
A .U 2 A . I 2 11 12
Bộ số A đặc trưng cho quan hệ dòng - áp giữa cửa 1 và cửa ij
2 (đặc trưng cho sự truyền đạt).
I1 A .U 2 A .I 2 21 22
Các mạng 2 cửa có cấu trúc khác nhau nhưng có cùng bộ số A tương đương ij
nhau về truyền đạt năng lượng và tín hiệu.
Ý nghĩa của bộ số A (công thức định nghĩa):
Hở mạch cửa 2: I 2 0
Ngắn mạch cửa 2: U 2 0
Đo độ biến thiên điện U U 1 U 1 1 U 1
Đo độ biến thiên điện áp áp trên cửa 1 theo A A [] 12 11
trên cửa 1 theo kích thích kích thích dòng trên U I 2 I 2 2 U 2 áp trên cửa 2. cửa 2. Đo độ biến thiên dòng Đo độ biến thiên dòng I I1 I1 1 I1 A
[Si] trên cửa 1 theo kích A 22 trên cửa 1 theo kích 21 thích dòng trên cửa 2. U thích áp trên cửa 2. I 2 I 2 2 U 2 10
2017 – Lý thuyết mạch điện 1 - Nguyễn Việt Sơn
Chương 7: Mạng hai cửa tuyến tính
II.1. Hệ phương trình trạng thái dạng A.
Bộ số A được tính trong điều kiện đặc biệt của mạng 2 cửa (hở mạch & ngắn ij
mạch cửa 2) không phụ thuộc vào các phần tử ngoài bộ số A đặc trưng & ij
thể hiện tính truyền đạt giữa 2 cửa.
Cách xác định thông số A : ịj
Lập phương trình mạch:
Từ sơ đồ mạch lập phương trình mạch theo các phương pháp
Rút gọn về quan hệ giữa (U 1, I1) và (U 2 , I 2 )
Dùng công thức định nghĩa:
Đo dòng, áp trên 2 cửa trong điều kiện ngắn mạch & hở mạch cửa 2.
Dùng công thức định nghĩa tính giá trị A . ij 11
2017 – Lý thuyết mạch điện 1 - Nguyễn Việt Sơn
Chương 7: Mạng hai cửa tuyến tính
II.1. Hệ phương trình trạng thái dạng A. Z Z I1 d1 d2 I 2
Ví dụ: Tính bộ số A của mạng 2 cửa có sơ đồ hình T. I
Cách 1: Lập phương trình mạch n Z U U n 2 1 U 1
I1 .Z I n .Z d1 n
U I .Z 2 2 2
U 2 I .Z I 2 .Z d n I n n d 2
I1 I n I 2 Zn U 2 I 2 .Z
U 2 I 2 .Z d 2 d 2 Z Z .Z U d1 d1 d 2 1 Z . I 2 .Z d1 n U 1
.U Z Z . I 1 2 Z Z d1 d 2 2 n n Z Z n n 1 Z d 2 U I .U 1 . I 2 I .Z 1 2 2 2 d 2 I Z Z 1 I2 n n Z n Z Z .Z
Bộ số A của mạch hình T: d1 d1 d 2 1 Z Z d1 d 2 Z Z n n A T 1 Z d 2 1 Z Z n n 12
2017 – Lý thuyết mạch điện 1 - Nguyễn Việt Sơn
Chương 7: Mạng hai cửa tuyến tính
II.1. Hệ phương trình trạng thái dạng A. Z Z I1 d1 d2 I 2
Ví dụ: Tính bộ số A của mạng 2 cửa có sơ đồ hình T. I n
Cách 2: Tính bộ số A theo công thức định nghĩa. Z U U n 2 1
Hở mạch cửa 2: I 2 0 U 1
A .U 2 A . I 2 11 12 U 1 Z Z I Z d1 n 1 I 1 d1 A 1 1 11 A Z 21
I1 A .U 2 A . I 2 U Z 21 22 2 Z . I1 n n U 2 n
Ngắn mạch cửa 2: U 2 0 Z .Z n d 2 Z . I1 d1 U I I Z 1 Z Z Z Z Z Z Z Z 1 1 n d . . . 2 d1 d 2 d1 n d 2 n A d 2 A 1 12 22 Z Z Z n Z n I I I . n 2 . n I 2 1 1 Z Z Z Z n d 2 n d 2 Z .Z d1 d 2
A Z Z 12 d1 d 2 Zn 13
2017 – Lý thuyết mạch điện 1 - Nguyễn Việt Sơn
Chương 7: Mạng hai cửa tuyến tính
II.1. Hệ phương trình trạng thái dạng A. Z Z I1 d1 d2 I 2
Ví dụ: Tính bộ số A của mạng 2 cửa có sơ đồ hình T. I n Z U U n 2 1 Z Z .Z d1 d1 d 2 1 Z Z d1 d 2 Z Z n n A T 1 Z U 1
A .U 2 A . I 2 11 12 d 2 1 Z Z n n
I1 A .U 2 A . I 2 21 22 Z .Z Z Z Z .Z Z Z d1 d 2 d1 d 2 d1 d 2 d1 d 2
det A A .A A .A 1 1 11 22 12 21 2 2 Z Z Z Z Z Z n n n n n n
Chú ý: Mạng 2 cửa tuyến tính tương hỗ det A = ± 1 I1 I 2 I1 I 2 U 1 A U U 1 A U 2 2 det A = 1 det A = - 1 14
2017 – Lý thuyết mạch điện 1 - Nguyễn Việt Sơn
Chương 7: Mạng hai cửa tuyến tính
II.2. Hệ phương trình trạng thái dạng B. I1 I 2
Xét quan hệ tuyến tính giữa (U 2 , I 2 ) và (U1, I1) U 1 B U 2
Ta có hệ phương trình trạng thái dạng B của
mạng 2 cửa tuyến tính không nguồn: U 2
B .U 1 B . I1 Dạng ma trận: U B B U 11 12 2 1 11 12 . B B I 21 22
2 B .U 1 B . I1 I 2 I1 21 22 1
Như vậy ta có: B A det B 1
Quan hệ giữa các thông số B và A : ij ij
A B A B 11 22 12 12
A B A B 21 21 22 11 15
2017 – Lý thuyết mạch điện 1 - Nguyễn Việt Sơn
Chương 7: Mạng hai cửa tuyến tính
II.3. Hệ phương trình trạng thái dạng Z. I1 I 2
Xét quan hệ tuyến tính giữa (U (I , I ) 1 ,U 2 ) và 1 2 U 1 Z U 2
Ta có hệ phương trình trạng thái dạng Z của
mạng 2 cửa tuyến tính không nguồn: Dạng ma trận:
U 1 Z . I1 Z . I 2 U1 Z Z I1 11 12 11 12 . Z Z U 21 22 U I 2 Z
. I1 Z . I 2 2 2 21 22
Ý nghĩa bộ số Z (công thức định nghĩa): U 1 U 2 Z
[] Tổng trở vào cửa 1 Z
[] Tổng trở tương hỗ 11 khi cửa 2 hở mạch 21 khi hở mạch cửa 2 I1 I1 I 2 0 I 2 0 U 1 Tổng trở tương hỗ Z [] U 2 Tổng trở vào cửa 2 12 khi hở mạch cửa 1 Z [] 22 I khi cửa 1 hở mạch 2 I I 1 0 2 I1 0 16
2017 – Lý thuyết mạch điện 1 - Nguyễn Việt Sơn
Chương 7: Mạng hai cửa tuyến tính
II.3. Hệ phương trình trạng thái dạng Z. I1 I 2
Cách xác định thông số Z : ịj U 1 Z U 2
Lập phương trình mạch:
Từ sơ đồ mạch lập phương trình mạch theo các phương pháp
Rút gọn về dạng quan hệ giữa (U1,U 2 ) và (I1, I 2 )
Dùng công thức định nghĩa:
Đo dòng, áp trên 2 cửa trong các điều kiện hở mạch cửa 1 & cửa 2.
Dùng công thức định nghĩa tính giá trị Z . ij 17
2017 – Lý thuyết mạch điện 1 - Nguyễn Việt Sơn
Chương 7: Mạng hai cửa tuyến tính
II.3. Hệ phương trình trạng thái dạng Z. Z Z
Ví dụ: Tính bộ số Z của mạng 2 cửa có sơ đồ hình T. I1 d1 d2 I 2 I n
Cách 1: Lập phương trình mạch Z I v2 U U I 1 v n 2 1
Chọn dòng điện vòng có chiều như hình vẽ.
Lập phương trình mạch theo phương pháp dòng vòng. Mặt khác có: U
U (Z Z ). I Z . I 1 (Z Z ). I 1
v Z . I v2 I1 I 1 v 1 1 2 d1 n n d1 n n U I I U
2 Z .I1 (Z Z ).I 2 2 Z . I 1 v (Z Z ). I v2 2 v 2 n d 2 n n d 2 n
Ma trận Z của mạch hình T: Z Z Z d1 n n Z T Z Z Z n d 2 n 18
2017 – Lý thuyết mạch điện 1 - Nguyễn Việt Sơn
Chương 7: Mạng hai cửa tuyến tính
II.3. Hệ phương trình trạng thái dạng Z. Z Z I1 d1 d2 I 2
Ví dụ: Tính bộ số Z của mạng 2 cửa có sơ đồ hình T. I n
Cách 2: Dùng công thức định nghĩa. Z U U n 2 1
Hở mạch cửa 1: I1 0 U 1 U
U 1 Z . I1 Z . I 2 Z Z 2 11 12 12 Z Z Z n 22 d 2 n I 2 I 2
U 2 Z . I1 Z . I 2 21 22
Hở mạch cửa 2: I 2 0 Z Z Z d1 n n U 1 U 2 Z Z Z Z T 11 Z Z d1 n 21 n Z Z Z n d 2 n I1 I1
Chú ý: Mạng 2 cửa tuyến tính tương hỗ: I1 I 2 I1 I 2 Z Z U Z Z U 1 12 21 U 2 U 1 2 12 21 19
2017 – Lý thuyết mạch điện 1 - Nguyễn Việt Sơn
Chương 7: Mạng hai cửa tuyến tính
II.4. Hệ phương trình trạng thái dạng Y.
Xét quan hệ tuyến tính giữa(I1, I 2 ) và (U1,U 2 ) I1 I 2
Khi đó ta có hệ phương trình trạng thái dạng Y U 1 Y U 2
của mạng 2 cửa tuyến tính không nguồn: I Dạng ma trận:
1 Y .U 1 Y .U 2 I1 Y Y U 11 12 1 11 12 . 1 Y Z Y Y I 21 22 I U
2 Y .U 1 Y .U 2 2 2 21 22
Ý nghĩa bộ số Y (công thức định nghĩa): I1 Y
[Si] Tổng dẫn vào cửa 1 I 2 Tổng dẫn tương hỗ 11 Y [Si] 21 U khi cửa 2 ngắn mạch khi ngắn mạch cửa 2 1 U U 1 2 0 U 2 0 I1 I 2 Y [Si] Tổng dẫn tương hỗ Y
[Si] Tổng dẫn vào cửa 2 12 22 khi cửa 1 ngắn mạch U khi ngắn mạch cửa 1 2 U 2 U1 0 U1 0 20
2017 – Lý thuyết mạch điện 1 - Nguyễn Việt Sơn
Chương 7: Mạng hai cửa tuyến tính
II.4. Hệ phương trình trạng thái dạng Y. I1 I 2
Cách xác định thông số Y : ịj U 1 Y U 2
Lập phương trình mạch:
Từ sơ đồ mạch lập phương trình mạch theo cách phương pháp
Rút gọn về dạng quan hệ giữa (I1, I 2 ) và (U 1,U 2 )
Dùng công thức định nghĩa:
Đo dòng, áp trên 2 cửa trong các điều kiện ngắn mạch cửa 1 & cửa 2.
Dùng công thức định nghĩa tính các giá trị Y . ij
Chú ý: Mạng 2 cửa tuyến tính tương hỗ: I1 I 2 I1 I 2 Y Y U Y Y U 1 12 21 U 2 U 1 2 12 21 21
2017 – Lý thuyết mạch điện 1 - Nguyễn Việt Sơn
Chương 7: Mạng hai cửa tuyến tính
II.4. Hệ phương trình trạng thái dạng Y. Y I1 d I 2 A B
Ví dụ: Tính bộ số Y của mạng 2 cửa có sơ đồ hình π U1 Y Y n1 U
Cách 1: Lập phương trình mạch n2 2
Lập phương trình mạch theo phương pháp thế đỉnh. Mặt khác có: I 1 (Y
Y ). Y . 1 n d A d B U
I (Y Y ).U Y .U 1 A 1 1 2 1 n d d I 2 Y
. (Y Y ). d A n 2 d B U 2 B I 2 Y
.U 1 (Y Y ).U 2 d n2 d
Cách 2: Dùng công thức định nghĩa.
Ngắn mạch cửa 1: U Ngắn mạch cửa 2: 1 0 U 2 0 I I 1 1 Y Y Y Y Y 12 d 11 1 n d U U 2 1 I I 2 2 Y Y Y Y Y 22 n2 d 21 d U U 2 1 22
2017 – Lý thuyết mạch điện 1 - Nguyễn Việt Sơn
Chương 7: Mạng hai cửa tuyến tính
II.5. Hệ phương trình trạng thái dạng H. I1 I 2
Xét quan hệ tuyến tính giữa (U 1, I 2 ) và (I1,U 2 ) U 1 H U 2
Khi đó ta có hệ phương trình trạng thái dạng H của
mạng 2 cửa tuyến tính không nguồn: U Dạng ma trận: 1
H . I1 H .U 2 U H H I 11 12 1 1 11 12 . H H I 21 22 2 H
. I1 H .U 2 I 2 U 2 21 22
Chú ý: Mạng 2 cửa tuyến tính tương hỗ: H H 12 21 23
2017 – Lý thuyết mạch điện 1 - Nguyễn Việt Sơn
Chương 7: Mạng hai cửa tuyến tính
II.6. Hệ phương trình trạng thái dạng G. I1 I 2
Xét quan hệ tuyến tính giữa (I1,U 2 ) và (U 1, I 2 ) U 1 G U 2
Khi đó ta có hệ phương trình trạng thái dạng G 1
của mạng 2 cửa tuyến tính không nguồn: G H Dạng ma trận:
I1 G .U 1 G . I 2 11 12 I1 G G U 1 11 12 . U G G 21 22 2 G
.U 1 G . I 2 21 22 U 2 I 2
Chú ý: Mạng 2 cửa tuyến tính tương hỗ: G G 12 21 24
2017 – Lý thuyết mạch điện 1 - Nguyễn Việt Sơn
Chương 7: Mạng hai cửa tuyến tính
II.7. Ma trận của hệ các mạng hai cửa.
a. Mạng hai cửa nối xâu chuỗi (cascade connection). n A A A A A 1 2 n k k 1
Ví dụ: Tính bộ số A của mạng 2 cửa hình π. Zd I Z 1 d I 2 U 1 1 Z U 2 d Z Z U n1 n2 1 U . 2 0 1 I 1 I 2 A A A n1 d n2 I
A A .A .A 1 I 2 1 n d n2 1 0 Z U 1 U 2 d U 1 Z Z U 1 . d 1 n1 2 1 Z I n2 1 Z I 2 A 1 n 1 1 Z Z d d 1 Z Z Z .Z Z 1 n n 2 1 n n 2 1 n 25
2017 – Lý thuyết mạch điện 1 - Nguyễn Việt Sơn
Chương 7: Mạng hai cửa tuyến tính
II.7. Ma trận của hệ các mạng hai cửa.
b. Mạng hai cửa ghép nối tiếp.
Các mạng 2 cửa ghép nối tiếp nếu có cùng dòng điện trên các cửa. Z1
Z Z Z 1 2 Z2
c. Mạng hai cửa ghép song song.
Các mạng 2 cửa ghép ghép song song nếu có cùng điện áp trên các cửa. Y1
Y Y Y 1 2 Y2 26
2017 – Lý thuyết mạch điện 1 - Nguyễn Việt Sơn
Chương 7: Mạng hai cửa tuyến tính
II.7. Ma trận của hệ các mạng hai cửa.
d. Mạng hai cửa ghép nối tiếp - song song. H1
H H H 1 2 H2
e. Mạng hai cửa ghép song song - nối tiếp. G1
G G G 1 2 G2 27
2017 – Lý thuyết mạch điện 1 - Nguyễn Việt Sơn
Chương 7: Mạng hai cửa tuyến tính
II.8. Các phương pháp tính bộ số đặc trưng.
Dùng công thức định nghĩa.
Lập phương trình mạch I1 M I 2
Từ bộ số này tính ra bộ số khác. R * * R 1 2 L L
Phương pháp tổng hợp toán học. 1 2 U 1 U 2 R
Ví dụ: Tính các bộ số của sơ đồ hình bên.
Tính bộ Z.
Lập phương trình dòng vòng
(R R jL ). I1 (R jM ). I 2 U 1 (1) 1 1
(R jM ).I1 (R R jL ).I 2 U 2 (2) 2 2
R R jL
R jM 1 1 Z
R jM
R R jL 2 2 28
2017 – Lý thuyết mạch điện 1 - Nguyễn Việt Sơn
Chương 7: Mạng hai cửa tuyến tính
II.8. Các phương pháp tính bộ số đặc trưng.
Ví dụ: Tính các bộ số của sơ đồ hình bên. I1 M I 2
Tính bộ A. 1 R * * R A 1 2 21 1 Z Z21 L L 1 2 Từ phương trình (2): 22 I1 .U 2 . I 2 Z Z Z 21 21 22 A 22 U 1 U 2 R Z 21 Thay vào phương trình (1): 1 Z Z Z .Z 22 11 11 22 U 1 Z . .U . I Z . I U Z . I 11 2 2 12 2 2 12 2 Z Z Z Z 21 21 21 21 U1
A .U 2 A . I 2 11 12 Z11 A 11
I1 A .U 2 A . I 2 21 22 Z21 Z Z .Z 11 11 22 Z .Z 11 22 Z 12 A Z 12 12 Z Z 21 21 Z 21 A 1 Z 22 Z Z 21 21 29
2017 – Lý thuyết mạch điện 1 - Nguyễn Việt Sơn
Chương 7: Mạng hai cửa tuyến tính
II.8. Các phương pháp tính bộ số đặc trưng.
Ví dụ: Tính các bộ số của sơ đồ hình bên. I1 M I 2 Z
Tính bộ H. 21 H R * * R 21 1 2 1 Z Z22 L L 1 2 Từ phương trình (2): 21 I 2 .U 2 . I1 Z Z 1 22 22 H 22 U 1 U 2 R Z 22 Thay vào phương trình (1): Z Z .Z Z 12 21 12 12
U 1 Z . I1
. U 2 Z . I1 Z . I1 .U 2 11 21 11 Z Z Z 22 22 22 U1
H . I1 H .U 2 11 12 Z .Z 12 21 H Z 11 11
I 2 H . I1 H .U 2 21 22 Z22 Z .Z Z 12 21 12 Z Z 12 11 H 12 Z Z 22 22 Z 22 H Z 1 21 Z Z 22 22 30
2017 – Lý thuyết mạch điện 1 - Nguyễn Việt Sơn
LÝ THUYẾT MẠCH ĐIỆN 1
Chương 7: Mạng hai cửa tuyến tính I. Khái niệm.
II. Mô hình toán học mạng hai cửa - Phương pháp tính bộ số
III. Tính chất mạng 2 cửa tuyến tính tương hỗ.
IV. Hàm truyền đạt dòng - áp. Tổng trở vào mạng hai cửa. Vấn
đề hòa hợp nguồn - tải bằng mạng hai cửa.
V. Mạng hai cửa phi hỗ.
VI. Khuếch đại thuật toán. 31
2017 – Lý thuyết mạch điện 1 - Nguyễn Việt Sơn
Chương 7: Mạng hai cửa tuyến tính
III. Tính chất mạng 2 cửa tuyến tính tương hỗ.
Mạng 2 cửa là tuyến tính tương hỗ khi và chỉ khi: det A 1 Z Z H H 12 21 12 21 det B 1 Y Y G G 12 21 12 21
Bộ số của mạng 2 cửa tuyến tính tương hỗ luôn có 1 ràng buộc mạch chỉ có
3 thông số độc lập tuyến tính → Sơ đồ tương đương của mạng 2 cửa tuyến
tính tương hỗ gồm 3 phần tử mắc theo sơ đồ hình T (π) Zd Z Z Sơ đồ hình π n1 n2 I1 I 2 tuyến tính U 1 tương hỗ U 2 Z Z d1 d2 Sơ đồ hình T Zn 32
2017 – Lý thuyết mạch điện 1 - Nguyễn Việt Sơn
Chương 7: Mạng hai cửa tuyến tính
III. Tính chất mạng 2 cửa tuyến tính tương hỗ.
Mạng 2 cửa đối xứng là mạng 2 cửa khi thay đổi chiều truyền đạt trên các cửa,
tính chất và phương trình truyền đạt vẫn không thay đổi. A, Z, G A, Z, G J E 1 2 Z 1 2 t (B, Y, H) (B, Y, H)
Mạng 2 cửa đối xứng A, Z, G A A Z Z 11 22 11 22 Z 1 2 E J t (B, Y, H) B B Y Y 11 22 11 22 det H = 1 det G = 1
Mạng 2 cửa tuyến tính tương hỗ & đối xứng chỉ có 2 thông số độc lập
tuyến tính Sơ đồ gồm 02 phần tử 33
2017 – Lý thuyết mạch điện 1 - Nguyễn Việt Sơn
LÝ THUYẾT MẠCH ĐIỆN 1
Chương 7: Mạng hai cửa tuyến tính I. Khái niệm.
II. Mô hình toán học mạng hai cửa - Phương pháp tính bộ số.
III. Tính chất mạng 2 cửa tuyến tính tương hỗ.
IV. Hàm truyền đạt dòng - áp. Tổng trở vào mạng hai cửa. Vấn
đề hòa hợp nguồn và tải bằng mạng hai cửa.
IV.1. Hàm truyền đạt dòng áp.
IV.2. Tổng trở vào mạng hai cửa.
IV.3. Tổng trở vào ngắn mạch và hở mạch
IV.4. Vấn đề hòa hợp nguồn và tải bằng mạng hai cửa.
V. Mạng hai cửa phi hỗ.
VI. Khuếch đại thuật toán. 34
2017 – Lý thuyết mạch điện 1 - Nguyễn Việt Sơn
Chương 7: Mạng hai cửa tuyến tính
IV.1. Hàm truyền đạt dòng - áp.
Đối với các hệ thống truyền tin, đo lường, điều khiển, chỉ quan tâm:
Trạng thái dòng, áp trên mỗi cửa tính & xét hàm
Truyền đạt năng lượng giữa các cửa truyền đạt
Xét mạng 2 cửa tuyến tính, không nguồn: Cửa 1 nối nguồn
Truyền tín hiệu, năng Cửa 2 nối tải
lượng từ nguồn đến tải U 2 I 2
Hàm truyền đạt điện áp: K K U
Hàm truyền đạt dòng điện: I U 1 I1 ~ S 2
Hàm truyền đạt công suất: K S ~ S1 35
2017 – Lý thuyết mạch điện 1 - Nguyễn Việt Sơn
Chương 7: Mạng hai cửa tuyến tính
IV.2. Tổng trở vào của mạng 2 cửa.
Quá trình năng lượng/tín hiệu đưa vào một cửa và truyền đến tải có mô hình
tương tự khi xét mô hình mạng một cửa trao đổi năng lượng/tín hiệu với tải.
Quá trình trên cửa đặc trưng bởi I1 I 2 J E Z A, Z, G
cặp dòng – áp đặc trưng bởi một 1 v U 1 U 2 Zt (B, Y, H) hàm Z (hoặc Y ). v v
Mạng 2 cửa truyền đạt như hình vẽ được mô tả bởi hàm tổng trở vào. U 1
A .U A . I 2 U Z I
A .Z A Z 11 2 12 2 . 2 t 11 t 12 Z 1 v 1 v
A .Z A I 21 t 22 1
A .U 2 A . I 2 21 22
Mạng 2 cửa thực hiện phép biến đổi tổng trở Z Z . t v1 36
2017 – Lý thuyết mạch điện 1 - Nguyễn Việt Sơn
Chương 7: Mạng hai cửa tuyến tính
IV.2. Tổng trở vào của mạng 2 cửa. ' I I I 2 1 2 E J A, Z, G Z Z U 1 v 2 U 2 t (B, Y, H)
Xét mạng 2 cửa truyền đạt từ cửa 2 đến Z quá trình năng lượng, tín hiệu t
ở cửa 2 đặc trưng bởi hàm tổng trở vào cửa 2. U 2 U 2
A .U 1 A . I1
U 1 Z . I1
A .Z A Z 22 12 t 22 t 12 Z v 2 v 2 '
A .Z A I I 21 t 11 2
A .U A . I 2 1 21 1 11
Mạng 2 cửa thực hiện phép biến đổi tổng trở Z Z . t v2 37
2017 – Lý thuyết mạch điện 1 - Nguyễn Việt Sơn
Chương 7: Mạng hai cửa tuyến tính
IV.3. Tổng trở vào ngắn mạch và hở mạch.
Xét tải ngắn mạch (hở mạch) trên cửa 2 chỉ còn một tín hiệu (điện áp hoặc
dòng điện) tổng trở vào là những hàm đặc trưng riêng của mạng 2 cửa. ' I1 I I 2 1 I 2 J E E J A, Z, G A, Z, G U 1 U 2 U U 2 (B, Y, H) 1 (B, Y, H)
Xét cửa 2 hở mạch: I 2 0
Xét cửa 1 hở mạch: I1 0
A .U A . I
A .U A . I A 2 A 1 11 2 12 11 Z 22 1 12 22 Z 1ho 2ho A A 21 A .U 21
A .U A . I 2 A . I 2 1 1 21 22 21 11
Xét cửa 2 ngắn mạch: U
Xét cửa 1 ngắn mạch: 2 0 U 1 0
A .U A . I 2 A
A .U A . I A 11 2 12 12 Z 1 22 1 12 12 Z 1ng A 2ng 22 A .U A 2 A . I 2 11 21 22
A .U 1 A . I1 21 11 38
2017 – Lý thuyết mạch điện 1 - Nguyễn Việt Sơn
Chương 7: Mạng hai cửa tuyến tính
IV.3. Tổng trở vào ngắn mạch và hở mạch. Các hàm Z , Z , Z , Z
đặc trưng cho mạng 2 cửa cho phép tính giá trị 1hở 1ng 2hở 2ng các bộ số.
Ví dụ: Ta có thể tính bộ số A từ các giá trị của Z , Z , Z theo công thức sau. 1hở 1ng 2ng Z .Z 1ng 1ho A
A A .Z 11 12 11 2ng Z .(Z Z ) 2ng 1ho 1ng A A 11 A 12 A 21 22 Z Z 1ho 1ng
Thực tế các công thức này thường được sử dụng khi thực hiện các phép đo giá
trị tổng trở vào trên cửa trong các điều kiện ngắn mạch và hở mạch đối với
mạng 2 cửa khi chưa biết sơ đồ. 39
2017 – Lý thuyết mạch điện 1 - Nguyễn Việt Sơn
Chương 7: Mạng hai cửa tuyến tính
IV.4. Vấn đề hòa hợp nguồn và tải bằng mạng 2 cửa. ^
Điều kiện để truyền công suất lớn nhất từ nguồn đến tải: Z Z ng t Thực tế, Z
và Z không thỏa mãn điều ng t Z
kiện hòa hợp cần nối mạng 2 cửa để ng A Z ij Zt e(t)
biến đổi tổng trở. 1 v
Chọn mạng 2 cửa thuần kháng cửa Có thông số: ^
A .Z A 11 t 12 Z Z 1 ng v
A .Z A 21 t 22 2 Eng Công suất cực đại: P 4.Rng 40
2017 – Lý thuyết mạch điện 1 - Nguyễn Việt Sơn
LÝ THUYẾT MẠCH ĐIỆN 1
Chương 7: Mạng hai cửa tuyến tính I. Khái niệm.
II. Mô hình toán học của mạng hai cửa - Phương pháp tính bộ số.
III. Tính chất mạng 2 cửa tuyến tính tương hỗ.
IV. Hàm truyền đạt dòng - áp. Tổng trở vào mạng hai cửa. Vấn
đề hòa hợp nguồn và tải bằng mạng hai cửa.
V. Mạng hai cửa phi hỗ.
VI. Khuếch đại thuật toán. 41
2017 – Lý thuyết mạch điện 1 - Nguyễn Việt Sơn
Chương 7: Mạng hai cửa tuyến tính
V. Mạng hai cửa phi hỗ
Mạng hai cửa phi hỗ là mạng hai cửa mà quan hệ giữa các biến dòng, áp trên
các cửa không có quan hệ tương hỗ với nhau.
Các bộ số có 4 tham số độc lập tuyến tính → sơ đồ tương đương có 4 phần tử.
Sơ đồ 2 trở kháng + 2 nguồn bị điều khiển. i (t) i (t) 1 2
u Z .i Z .i Z Z 1 11 1 12 2 11 22 Xét bộ Z: u (t) u (t)
u Z .i Z .i 1 2 2 21 1 22 2 e = Z .i e = Z .i 1 12 2 2 21 1 i (t) i (t) 1 2
i Y .u Y .u 1 11 1 12 2 Xét bộ Y: u (t) u (t)
i Y .u Y .u 1 Y j j Y 2 11 1 2 22 2 21 1 22 2 j = Y .u 1 12 2 j = Y .u 2 21 1 42
2017 – Lý thuyết mạch điện 1 - Nguyễn Việt Sơn
Chương 7: Mạng hai cửa tuyến tính
V. Mạng hai cửa phi hỗ
Sơ đồ 2 trở kháng + 2 nguồn bị điều khiển. i (t) 1 i (t) 2 u
H .i H .u H11 1 11 1 12 2 Xét bộ H: u (t) 1 e u (t)
i H .i H .u 1 j H 2 2 22 2 21 1 22 2 e = H .u 1 12 2 j = H .i 2 21 1 i (t) i (t) 1 2
i G .u G .i G22 Xét bộ G: 1 11 1 12 2 u (t) u (t) 1 G j e 2
u G .u G .i 11 1 2 2 21 1 22 2 j = G .i e = G .u 1 12 2 2 21 1 43
2017 – Lý thuyết mạch điện 1 - Nguyễn Việt Sơn
Chương 7: Mạng hai cửa tuyến tính
V. Mạng hai cửa phi hỗ
Sơ đồ 3 trở kháng + 1 nguồn bị điều khiển. Xét bộ Z:
u Z .i Z .i
Z Z Z
u Z .i Z .i 1 11 1 12 2 1 11 1 12 2 21 12
u Z .i Z .i
u Z .i Z .i Z .i 2 21 1 22 2 2 12 1 22 2 1 Sơ đồ hình T
tính được Z , Z , Z theo công thức: d1 d2 n i (t) i (t) 1 2
Z Z Z Z Z Z Z n 12 d 2 22 12 d1
d2 e Z .i u (t) Z 1 u (t) 1 n 2 Z
Z Z Z Z Z d1 11 12 21 12 44
2017 – Lý thuyết mạch điện 1 - Nguyễn Việt Sơn
Chương 7: Mạng hai cửa tuyến tính
V. Mạng hai cửa phi hỗ
Sơ đồ 3 trở kháng + 1 nguồn bị điều khiển. Xét bộ Y:
i Y .u Y .u 1 11 1 12 2 Y Y Y
i Y .u Y .u 1 11 1 12 2 21 12
i Y .u Y .u
i Y .u Y .u Y .u 2 21 1 22 2 2 12 1 22 2 1 Sơ đồ hình π
tính Y , Y , và Y theo công thức: n1 n2 d i (t) i (t) 1 2 Y Y Y Y Y d 12 n2 22 12 Yd j(t)
Y Y Y Y Y Y u (t) Y u (t) 1 n1 Yn2 2 1 n 11 12 21 12
j(t) Y .u (t) 1 45
2017 – Lý thuyết mạch điện 1 - Nguyễn Việt Sơn
LÝ THUYẾT MẠCH ĐIỆN 1
Chương 7: Mạng hai cửa tuyến tính I. Khái niệm.
II. Mô hình toán học của mạng hai cửa - Phương pháp tính bộ số.
III. Tính chất mạng 2 cửa tuyến tính tương hỗ.
IV. Hàm truyền đạt dòng - áp. Tổng trở vào mạng hai cửa. Vấn
đề hòa hợp nguồn và tải bằng mạng hai cửa.
V. Mạng hai cửa phi hỗ.
VI. Khuếch đại thuật toán. 46
2017 – Lý thuyết mạch điện 1 - Nguyễn Việt Sơn
Chương 7: Mạng hai cửa tuyến tính
VI. Khuếch đại thuật toán 1. Khái niệm
Khuếch đại thuật toán (Operational Amplifier – OP AMP) là một phần tử phức
hợp của mạch điện, có 2 cửa ngõ, cho phép thực hiện các phép toán: cộng, trừ,
nhân, chia, vi phân, tích phân
Các chân tín hiệu của OP AMP: Đầu vào đảo (2)
Đầu vào không đảo (3) Đầu ra (6) Nguồn cung cấp (4, 7) 47
2017 – Lý thuyết mạch điện 1 - Nguyễn Việt Sơn
Chương 7: Mạng hai cửa tuyến tính
VI. Khuếch đại thuật toán
2. Sơ đồ tương đương. R : Điện trở vào. i
Nguồn áp bị điều khiển A.Vd R : Điện trở ra O
Điện áp ra: V = A.(V – V ) A: hệ số khuếch đại vòng hở (open loop gain) O 2 1 Thông số Giá trị thực Giá trị lý tưởng
Hệ số khuếch đại vòng hở, A 105 - 108 ∞
Điện trở vào, R 106 - 1013 Ω ∞ Ω i
Điện trở ra, R 10 - 100 Ω 0 Ω 0
Nguồn cung cấp, V 5 - 24 V -- cc
Chế độ làm việc của OP APM48
2017 – Lý thuyết mạch điện 1 - Nguyễn Việt Sơn
Chương 7: Mạng hai cửa tuyến tính
VI. Khuếch đại thuật toán
3. Khuếch đại thuật toán lý tưởng. OP AMP lý tưởng: i = 0 1 -3 V 7 + i = 0 d
Hệ số khuếch đại vòng hở A = ∞ 2 4 + V + + 1 V R = 0 V =V 0 2 1 O - - - R = ∞ i GND
Tính chất cơ bản của OP AMP lý tưởng:
Dòng điện tại cửa vào bằng 0: i = i = 0 1 2
Điện áp vi sai giữa 2 cửa vào bằng 0: V = V 2 1 49
2017 – Lý thuyết mạch điện 1 - Nguyễn Việt Sơn
Chương 7: Mạng hai cửa tuyến tính
VI. Khuếch đại thuật toán
3. Khuếch đại thuật toán lý tưởng.
Ví dụ: Cho OP AMP lý tưởng. Tính hệ số khuếch đại điện áp V /V . Tính dòng O S
điện i nếu V = 1V 0 S i = 0 2 V2 3 7
Vì OP AMP là lý tưởng, ta có i = 0 1 4 i0 V1 741 V
i = 0 R mắc nối tiếp với R S 1 1 2 R2 0 1 40kΩ R1 + V V 20kΩ 0 0 V0 5kΩ V R - 1 R R 1 9 1 2 V V
Vậy ta có: V 0 0 9 S 9 VS V V V 9V
Áp dụng luật K1 tại nút 0: i 0 0 V 1 0 S 0 R R 3 20.10 i 0, mA 65 1 2 0 50
2017 – Lý thuyết mạch điện 1 - Nguyễn Việt Sơn
Chương 7: Mạng hai cửa tuyến tính i2 R2
VI. Khuếch đại thuật toán R1 V1 3
4. Khuếch đại đảo. 1 7 i1 4 + V2 V
Áp dụng luật K1 tại nút 1: i 741 V0 - V V V V V V R
i i i 1 1 0
i 0 V 2 V 1 2 R R 0 i R R R R 1 2 1 2 1 V 2 V 0 i
Do OP AMP lý tưởng: V = V R 1 2 1
Chú ý: R
Hệ số khuếch đại A 2 phụ thuộc vào điện trở nối ngoài OP AMP. V R1
Đặc điểm nhận dạng mạch KĐ đảo: + + R1
Tín hiệu đưa vào chân đảo - V R V i + 0 f Vi - R - 1 Phản hồi âm
Mạch KĐ đảo thường dùng trong bộ biến đổi dòng - áp. 51
2017 – Lý thuyết mạch điện 1 - Nguyễn Việt Sơn
Chương 7: Mạng hai cửa tuyến tính
VI. Khuếch đại thuật toán
4. Khuếch đại đảo
Ví dụ: Tính điện áp V và dòng điện chảy qua điện trở R và R nếu v = 0,5V O 1 2 i
Áp dụng công thức của mạch khuếch đại đảo R2 R 25
V 2 .V .0, 5 1, V 25 25kΩ 0 i R1 3 R 10 1 7 10kΩ 4 +
Dòng điện chảy qua điện trở R1 Vi 741 V0 V 0 0,5 - i i 50 A R1 R 3 10.10 1
Dòng điện chảy qua điện trở R2 V 0 1.25 i 0 50 A R2 R 3 25.10 2 52
2017 – Lý thuyết mạch điện 1 - Nguyễn Việt Sơn
Chương 7: Mạng hai cửa tuyến tính
VI. Khuếch đại thuật toán R2 10kΩ
4. Khuếch đại đảo R1 3 7 4kΩ 4 +
Ví dụ: Tính giá trị điện áp VO 6 V 4V 0 - V
Áp dụng luật K1 tại nút 3: 6 V V V 6 V V V 3 3 O 3 3 O R R 4 10 1 2
Vì khuếch đại thuật toán lý tưởng, ta có V = V = 4V 3 4 6 4 4 V
O V V 1 O 4 10 53
2017 – Lý thuyết mạch điện 1 - Nguyễn Việt Sơn
Chương 7: Mạng hai cửa tuyến tính
VI. Khuếch đại thuật toán i2 R2
5. Khuếch đại không đảo i1 R1 3 7
Khuếch đại thuật toán không đảo là mạch khuếch đại 4 + V
cung cấp hệ số khuếch đại dương: V 0 i -
Tín hiệu điện áp vào V được cấp tại chân không i đảo của OP AMP.
Mạch có phản hồi âm. 0 V V V i i 3 3 0 1 2 R R V V V R i i 0 2 1 2 V 1 0 V R R i R 1 2 1
V V V 3 4 i 54
2017 – Lý thuyết mạch điện 1 - Nguyễn Việt Sơn
Chương 7: Mạng hai cửa tuyến tính
VI. Khuếch đại thuật toán
5. Khuếch đại không đảo 3 7 4 + Chú ý: V V = V 0 i i -
Nếu R = 0 hoặc R = ∞ hệ số khuếch đại bằng 1 2 1
Mạch lặp điện áp (voltage follower, hoặc unity gain amplifier) Tính chất: 3 7 Trở kháng vào lớn 4 Second First stage stage
Dùng nối tầng để cách ly 2 phần
Mạch lặp điện áp dùng để cách ly giữa 2
của mạch điện (buffer). tầng của mạch điện
Giảm thiểu sự ảnh hưởng giữa 2 tầng khác nhau của mạch điện, tránh sự
ảnh hưởng qua lại giữa các tầng. 55
2017 – Lý thuyết mạch điện 1 - Nguyễn Việt Sơn
Chương 7: Mạng hai cửa tuyến tính
VI. Khuếch đại thuật toán
5. Khuếch đại không đảo R2 10kΩ R1
Ví dụ: Tính điện áp V 3 0 7 4kΩ 4 +
Áp dụng tính chất tuyến tính: V V V 6 V 4V 0 O O1 O2 - V V
là điện áp do nguồn 6V tạo ra O1 V
là điện áp do nguồn 4V tạo ra O2 R 10
Tính V : Ta có mạch khuếch đại đảo V 2 6 6 V 15 O1 O1 R 4 1 R 10 2
Tính V : Ta có mạch khuếch đại không đảo V 1 4 1 4 14V O2 O2 R 4 1
Tổng hợp nghiệm: V V V 1 V O 1 O O 2 56
2017 – Lý thuyết mạch điện 1 - Nguyễn Việt Sơn
Chương 7: Mạng hai cửa tuyến tính R2
VI. Khuếch đại thuật toán 5kΩ
5. Khuếch đại không đảo R1 3 7 2kΩ R3 4 +
Ví dụ: Tính điện áp V0 4kΩ R4 V 3V 0 8kΩ - 57
2017 – Lý thuyết mạch điện 1 - Nguyễn Việt Sơn
Chương 7: Mạng hai cửa tuyến tính
VI. Khuếch đại thuật toán
5. Khuếch đại không đảo
Ví dụ: Tính i , v , v , i . So sánh với S 1 2 l
trường hợp nguồn và tải nối trực tiếp.
Áp dụng tính chất OP AMP lí tưởng: v
i 0; v v v ; i S S 1 2 S l Rl
Mạch lặp điện áp không tiêu tốn công suất của nguồn vS
Mạch lặp điện áp truyền tín hiệu, công suất từ
nguồn đến tải nhưng không gây tổn hao (dòng
điện trên tải được cấp bởi OP AMP). v R Cách ly nguồn và tải i i S ; v v l v S l 1 2 R R R S R l S l S 58
2017 – Lý thuyết mạch điện 1 - Nguyễn Việt Sơn
Chương 7: Mạng hai cửa tuyến tính
VI. Khuếch đại thuật toán
6. Mạch cộng điện áp
Mạch cộng điện áp là mạch OP AMP trong đó điện áp đầu ra là tổng của các giá
trị điện áp đầu vào theo các giá trị trọng số.
Mạch cộng điện áp là một mạch khuếch đại đảo với V i1 i 1 R1 Rf nhiều đầu vào V i 0 R2 2 2 3 a 7 i i 4 +
Áp dụng luật K1 tại nút 0 ta có: V R3 3 3 0 V0 V V V V V V V V a O 1 a 2 a 3 a -
i i i i 1 2 3 R R R R f 1 2 3
Vì khuếch đại thuật toán lý tưởng V = 0 a R R R V
f V f V f V O 1 2 3 R R R 1 2 3 59
2017 – Lý thuyết mạch điện 1 - Nguyễn Việt Sơn
Chương 7: Mạng hai cửa tuyến tính
VI. Khuếch đại thuật toán R15kΩ Rf 10kΩ
6. Mạch cộng điện áp 2V R2 a 3 7 2,5kΩ + 4
Ví dụ: Tính giá trị V và i b i0 0 0 1V 2kΩ VO -
Áp dụng công thức tính của mạch cộng điện áp R R f f 10 10 V V V .2 8V O 1 2 R R 5 2, 5 1 2
Áp dụng luật K1 tại cửa ra của OP AMP, ta có: V V V V 8 8 i O a O b 4,8mA 0 10 2 10 2 60
2017 – Lý thuyết mạch điện 1 - Nguyễn Việt Sơn
Chương 7: Mạng hai cửa tuyến tính
VI. Khuếch đại thuật toán
7. Mạch khuếch đại vi sai
Mạch khuếch đại vi sai là mạch OP AMP cho phép khuếch đại điện áp vi sai giữa
hai đầu vào và triệt tiêu các tín hiệu đồng pha giữa chúng. R2
Áp dụng luật K1 tại nút a: 0 R1 Va 3 V V V V R R 7 1 a a 0 2 2 R3 V 1 V V 0 4 + 0 a 1 V1 V R R R R b 1 2 1 1 R4 V0
Áp dụng luật K1 tại nút b V2 - V V V R 2 b b V 4 V b R R R R 2 3 4 3 4
Vì OP AMP lí tưởng V = V a b R 1 1 R R R R 2 3 2 2 R2 R V 1 V V V V 2 0 V R R R 2 R 1 0 R 2 1 R 1 R 3 4 1 1 1 3 1 R 61
2017 – Lý thuyết mạch điện 1 - Nguyễn Việt Sơn 4
Chương 7: Mạng hai cửa tuyến tính
VI. Khuếch đại thuật toán
7. Mạch khuếch đại vi sai R R Nếu
1 3 và V = V V = 0 (triệt tiêu các tín hiệu vào đồng pha) 1 2 O R R 2 4 R2 R 0
Khi đó ta có: V 2 R1 Va 3 0 V V 2 1 R 7 1 R3 0 4 + V1 Vb
Nếu R = R , và R = R R4 V 2 1 3 4 0 V2 -
V V V (bộ trừ điện áp) 0 2 1 Nhận xét:
Mạch khuếch đại vi sai có thể sử dụng để thiết kế mạch trừ điện áp
Mạch khuếch đại vi sai thường được dùng trong các mạch khuếch đại đo
lường (Instrumentation Amplifier (IA)) 62
2017 – Lý thuyết mạch điện 1 - Nguyễn Việt Sơn
Chương 7: Mạng hai cửa tuyến tính
VI. Khuếch đại thuật toán
7. Mạch khuếch đại vi sai
Ví dụ: Thiết kế mạch OP AMP với 2 đầu vàoV and V trong đó V = -5V + 3V 1 2 0 1 2
Cách 1: Sử dụng 1 OP AMP 3
Biến đổi:V 5V 3V 5 V V 0 1 2 2 1 5 R R
Áp dụng công thức mạch khuếch đại vi sai: V 2 5 0 V V 2 1 2 R R 1 1 R 1 1 1 1 R 5 2 R2 R2 Mặt khác: V V V 5 V 5V 0 R 2 1 2 1 R R R 1 1 3 1 1 3 1 R4 R4 1 5 3 R Chọn:
2 1 3 R R 3 4 R 5 R
R 10k ; R 50k 1 2 1 3 4 R
R R 20k 4 3 4 63
2017 – Lý thuyết mạch điện 1 - Nguyễn Việt Sơn
Chương 7: Mạng hai cửa tuyến tính
VI. Khuếch đại thuật toán
7. Mạch khuếch đại vi sai
Ví dụ: Thiết kế mạch OP AMP với 2 đầu vàoV and V trong đó V = -5V + 3V 1 2 0 1 2
Cách 2: Sử dụng 02 OP AMP khuếch đại đảo + mạch cộng điện áp. 3R1
Mạch cộng áp: V V 5V 5R1 0 a 1 R1 3 5R1 V 7 3 2 4 7 V
Mạch khuếch đại đảo: V V 3 a 4 a 2 V R1 0 V1
Kết hợp 2 mạch khuếch đại: V = 3V - 5V 0 2 1
Lựa chọn thông số thiết kế: R 10k; 1 64
2017 – Lý thuyết mạch điện 1 - Nguyễn Việt Sơn
Chương 7: Mạng hai cửa tuyến tính
VI. Khuếch đại thuật toán
7. Mạch khuếch đại vi sai
Ví dụ: Tính điện áp V của mạch khuếch đại đo lường 0 4 V 7 R O1 1 R2 A 3
Vì OP AMP là lý tưởng, dòng điện i chỉ 1 R3 V1 0 chảy qua 3 điện trở Va 3 R4 7 i A 4
V V i(2R R ) 0 3 V0 01 02 3 4 Vb R3 3 V V a b R1 7 Mặt khác: i
; V V ; V V A a b 4 2 R 1 2 VO2 R2 4 V2 V V Do đó: i 1 2 R4 Ta có công thức: R 2R V 2 1 3 0 V V 2 1 R1 R4 65
2017 – Lý thuyết mạch điện 1 - Nguyễn Việt Sơn
Chương 7: Mạng hai cửa tuyến tính
VI. Khuếch đại thuật toán
7. Mạch khuếch đại vi sai
Ví dụ: Tính giá trị i trong mạch khuếch đại đo lường 0 4 7 R2 40kΩ 3 20kΩ 8V R1 3 7 R1 4 R3 i0 20kΩ 3 R2 7 40kΩ 10kΩ 4 8,01V 66
2017 – Lý thuyết mạch điện 1 - Nguyễn Việt Sơn
Chương 7: Mạng hai cửa tuyến tính
VI. Khuếch đại thuật toán i C C 8. Mạch tích phân R1 + 3 + 7
Mạch tích phân là mạch OP AMP có đầu ra quan hệ tích iR 4 v v i 0
phân với tín hiệu vào. - - GND
Áp dụng luật K1 tại nút 3: v dv t 1
i i i i i C 0
v (t) v (0) v (t)dt R C R C 0 0 R dt i RC 0 t 1 v (t) ( ) 0 v t dt i RC 0 Nhận xét:
Mạch tích phân thường có điện trở phản hồi để giảm hệ số khuếch đại một
chiều và tránh trạng thái bão hòa (saturation)
Mạch tích phân hoạt động trong vùng tuyến tính, tránh trạng thái bão hòa 67
2017 – Lý thuyết mạch điện 1 - Nguyễn Việt Sơn
Chương 7: Mạng hai cửa tuyến tính
VI. Khuếch đại thuật toán 8. Mạch vi phân
Mạch vi phân là mạch OP AMP trong đó đầu ra của mạch khuếch đại tỉ lệ tuyến
tính với sự biên thiên của tín hiệu vào. i R R C iC 3
Áp dụng luật K1 tại đỉnh a: 7 a + + 4 v dv v 0 i v0 i i i i i C - R C R C R dt - GND dv v (t) i RC 0 dt Nhận xét:
Nhìn chung, đầu ra của mạch vi phân là không ổn định do nó biến thiên tỉ lệ
với độ biến thiên của tín hiện vào.
Do sự không ổn định, mạch vi phân ít được ứng dụng trong thực tế. 68
2017 – Lý thuyết mạch điện 1 - Nguyễn Việt Sơn
Chương 7: Mạng hai cửa tuyến tính R15kΩ
VI. Khuếch đại thuật toán 0,2μF C 3 8. Mạch vi phân 7 4 v + R2
Ví dụ: Tính điện áp ra của mạch vi phân. i v-0
Áp dụng công thức của mạch vi phân:: GND 3 6 RC 3 5.10 .0, 2.10 10 vi 4
Trong khoảng 0 < t < 4ms hoặc 4 < t < 8ms, điện áp t (ms) ra có dạng 0 2 4 6 8 v 2t
0 t 2ms, 4 t 6ms i v i
8 2t 2 t 4ms,6 t 8ms 2 t (ms) 0 dv
2mV 0 t 2ms, 4 t 6ms 2 4 6 8 v i RC O -2 dt 2mV
2 t 4ms,6 t 8ms 69
2017 – Lý thuyết mạch điện 1 - Nguyễn Việt Sơn
Chương 7: Mạng hai cửa tuyến tính 4
VI. Khuếch đại thuật toán 7 a 4 3 7
9. Nối xâu chuỗi (nối tầng) các OP AMP 3 + i R112kΩ 0
Ví dụ: Tìm V và i trong mạch điện 0 0 R3 10kΩ 20mV b R2 VO
Mạch điện gồm 2 tầng khuếch đại 3kΩ R4 4kΩ
Xét tại đầu ra của tầng 1 - R
V 1 1 20 100mV a R2 R
Xét tại đầu ra của tầng 2: V 1 3 V 350mV O a R4
Giá trị dòng điện i0 V V 3 (350 100).10 O b V V i b a i 25 A 0 R 0 3 10.10 3 70
2017 – Lý thuyết mạch điện 1 - Nguyễn Việt Sơn
Chương 7: Mạng hai cửa tuyến tính
VI. Khuếch đại thuật toán
9. Nối xâu chuỗi (nối tầng) các OP AMP R2 6kΩ Ví dụ: Tìm V R1 0 3 V =1V 1 R5 5kΩ 7 C 2kΩ 4 a R7 10kΩ A 3 R4 8kΩ 7 4 V R3 3 O V =2V 2 R6 7 4kΩ 4 b 15kΩ B
Mạch điện gồm 2 mạch KĐ đảo A và B và mạch cộng áp C R R
V 2 V V 3
V 4 V 4V a b 2 R 1 R 1 3
Áp dụng công thức của mạch cộng áp R R 2 7 7 V V V 2.(3) (4) 8.333V O a b R R 3 5 6 71
2017 – Lý thuyết mạch điện 1 - Nguyễn Việt Sơn
Chương 7: Mạng hai cửa tuyến tính
VI. Khuếch đại thuật toán
9. Nối xâu chuỗi (nối tầng) các OP AMP
Ví dụ: Tìm V nếu V = 2V, V = 1,5V 0 1 2 R5 80kΩ 3 V1 7 R1 30kΩ 3 4 7 4 VO R4 R2 50kΩ 20kΩ R3 3 7 15kΩ 4 V2 72
2017 – Lý thuyết mạch điện 1 - Nguyễn Việt Sơn
Chương 7: Mạng hai cửa tuyến tính
VI. Khuếch đại thuật toán 10. Ứng dụng
OP AMP được sử dụng rất nhiều trong thực tế:
Bộ đảo, bộ cộng, bộ trừ, mạch tích phân, mạch vi phân, mạch logarit.
Mạch khuếch đại đo lường, mạch hiệu chỉnh (calibration)
Bộ biến đổi số - tương tự (Digital – analog converter), bộ biến đổi áp- dòng,
mạch biến đổi dòng – áp. Máy tính tương tự
Bộ lọc, bộ chỉnh lưu, bộ dịch pha, …
Bộ so sánh, bộ dao động … 73
2017 – Lý thuyết mạch điện 1 - Nguyễn Việt Sơn
Chương 7: Mạng hai cửa tuyến tính
VI. Khuếch đại thuật toán 10. Ứng dụng
Mạch DAC có chức năng biến đổi tín hiệu số sang tín hiệu tương tự
Mạch DAC có thể tạo bằng các sử dụng mạch
trọng số nhị phân (binary weighted ladder): DAC 4 bits
Các bit nhị phân được đánh trọng số theo vị trí.V V V 1 V2 3 4 Rf
Trọng số nhị phân quyết định bởi giá trị R /R f n R1 R2 R3 R4 R R R R 3 V
f V f V f V f V 7 O MSB LSB R 1 R 2 R 3 R 4 4 V 1 2 3 4 O
V1, … V4 là các điện áp nhị phân (0, 1) (binary
Binary weighted ladder type
code) đầu ra của DAC có quan hệ tỉ lệ tuyến
tính với các giá trị đầu vào 74
2017 – Lý thuyết mạch điện 1 - Nguyễn Việt Sơn
Chương 7: Mạng hai cửa tuyến tính
VI. Khuếch đại thuật toán V V V 1 V2 3 4 10. Ứng dụng Rf 10kΩ R1 R2 R3 R4
Ví dụ: Tính điện áp đầu ra của mạch DAC. 10K 20K 40K 80K 3 V V V V [B] Giá trị [D] -V 7 1 2 3 4 0 MSB LSB 4 VO 0000 0 0 0001 1 0.125 0010 2 0.25 R R R R 0011 3 0.375 V
f V f V f V f V O R 1 R 2 R 3 R 4 1 2 3 4 0100 4 0.5
V V 0, 5V 0, 2 V 5 0,125V 0101 5 0.625 0 1 2 3 4 0110 6 0.75 0111 7 0.875
Mỗi bit có giá trị tương ứng 0.125V không 1000 8 1.0
thể biểu diễn giá trị điện áp trong khoảng (1V, 1001 9 1.125
1.125V) (DAC resolution). … 1111 15 1.875 75
2017 – Lý thuyết mạch điện 1 - Nguyễn Việt Sơn
Chương 7: Mạng hai cửa tuyến tính
VI. Khuếch đại thuật toán 10. Ứng dụng
Khuếch đại đo lường (IA) được sử dụng nhiều trong các mạch khuếch đại cách
ly, mạch đo nhiệt độ, mạch thu thập dữ liệu (data acquisition systems). Quan hệ điện áp: V1 4 Inverted input 7 R R 1 3 2R Gain set V 1 0 V V 2 1 R 3 7 Output R R G G 3 R 4 V0 3 Gain set 7 R R 4 2 Non-inverted input V2 Đặc điểm:
Khuếch đại tín hiệu vi sai đầu vào nhỏ
Triệt tiêu tín hiệu đồng pha ở đầu vào Sơ đồ nguyên lý 76
2017 – Lý thuyết mạch điện 1 - Nguyễn Việt Sơn
Chương 7: Mạng hai cửa tuyến tính
VI. Khuếch đại thuật toán 10. Ứng dụng Tính chất của IA:
Hệ số khuếch đại điện áp có thể thay đổi bằng điện trở ngoài RG
Điện trở vào rất lớn và không bị thay đổi khi thay đổi hệ số khuếch đại.
Điện áp ra V chỉ phụ thuộc vào thành phần điện áp vi sai giữa 2 tín hiệu O
vào V , V , không phụ thuộc vào thành phần điện áp đồng pha giữa chúng. 1 2 77
2017 – Lý thuyết mạch điện 1 - Nguyễn Việt Sơn
Chương 7: Mạng hai cửa tuyến tính
VI. Khuếch đại thuật toán 10. Ứng dụng
Ex: A precision Intrumentation amplifier Product highlight:
Input noise is less than 4 nV/√Hz at 1 kHz.
Pin programmable gains of 1, 100, 200, 500 and
1000 provided on the chip. Using a single
external resistor for other gains.
The offset voltage, offset voltage drift, gain
accuracy and gain temperature coefficients are
guaranteed for all pretrimmed gains.
Provides totally independent input and output
offset for high precision applications.
A sense terminal is provided to enable the user
to minimize the errors induced through long
leads. A reference terminal is also provided to
permit level shifting at the output. Price (100 - 499) Price (1000) $4.82 $4.09 78
2017 – Lý thuyết mạch điện 1 - Nguyễn Việt Sơn
Chương 7: Mạng hai cửa tuyến tính
VI. Khuếch đại thuật toán 10. Ứng dụng
Ex: LT167 – Single resistor gain, programmable, precision intrumentation amplifier Price (1 - 99) Price (1000)
Datasheet: http://cds.linear.com/docs/Datasheet/1167fc.pdf $6.45 $5.55 79
2017 – Lý thuyết mạch điện 1 - Nguyễn Việt Sơn
LÝ THUYẾT MẠCH ĐIỆN 1
Chương 8: Mạch điện ba pha. I. Khái niệm.
II. Mạch ba pha đối xứng và không đối xứng tải tĩnh.
III. Tính và đo công suất mạch điện ba pha.
IV. Mạch ba pha có tải động - Phương pháp thành phần đối xứng
V. Phân tích mạch ba pha không đối xứng bằng phương pháp
thành phần đối xứng.
Bài tập: 10.1 - 10.5, 11.1 - 11.5, bài thêm 1
2017 – Lý thuyết mạch điện 1 - Nguyễn Việt Sơn
Chương 8: Mạch điện ba pha I.1. Định nghĩa.
Mạch điện ba pha là mạch điện làm việc với nguồn kích thích ba pha. V
Nguồn điện ba pha gồm 3 nguồn điện 1 pha: e (t)
e (t) e (t) A C
Cùng biên độ hiệu dụng. B Cùng tần số. t
Pha ban đầu lệch nhau 1200 0
e (t) E .sin t(V ).
E A E 0 (V ) A m 0
e (t) E .sin(t 120 )(V ). 0 B m
EB E 120 (V ) 0
e (t) E .sin(t 120 )(V ). E A C m 0
EC E 120 (V ) Nhận xét: 0 0 120 1 20
Tổng các suất điện động của 3 dây quấn đều triệt tiêu. EC E B
e (t) e (t) e (t) 0 E E E 0 A B C A B C
Thứ tự thuận (ngược): Pha B (C) chậm hơn pha A góc 1200; pha C (B) sớm hơn pha A góc 1200. 2
2017 – Lý thuyết mạch điện 1 - Nguyễn Việt Sơn
Chương 8: Mạch điện ba pha
I.2. Cách tạo nguồn điện ba pha.
Sử dụng máy phát điện xoay chiều đồng bộ ba pha đối xứng. Cấu tạo :
Stator: Hình trụ, gắn cố định với thân máy, đặt 3 cuộn dây AX, BY, CZ giống
nhau, lệch nhau trong không gian 1200.
Rotor: Hình trụ, đặt trong stator, trục rotor được gắn với tuốc bin.
Nguyên lý hoạt động:
Rotor được từ hóa bằng dòng điện 1 chiều (lấy từ nguồn kích thích ngoài) nam châm điện.
Rotor quay đều với vận tốc ω (do lực ngoài tác động của hơi nước, thủy
điện, động cơ kéo …) từ trường của rotor quét qua các dây quấn stator
suất điện động cảm ứng trên các cuộn dây AX, BY, CZ. 3
2017 – Lý thuyết mạch điện 1 - Nguyễn Việt Sơn
Chương 8: Mạch điện ba pha
I.3. Động cơ không đồng bộ ba pha. i
(t) I .cost. A m a. Từ trường quay. 0 i
(t) I .cos(t 120 ). B m
Xét 3 cuộn dây stator cấp bởi dòng điện 3 pha đối xứng. 0
i (t) I .cos(t 240 ). C m C Y Y Y C C A X A X X A Z B B Z Z B I
Tại t 0 i I ; m i i A m B C
Quy ước: Dòng điện dương là dòng đi ra 2
khỏi đầu cuộn dây, đi vào cuối cuộn dây. T I Tại t i I ; m i i 3 B m A C 2
→ áp dụng quy tắc vặn nút chai 2T Im Tạit
i I ; i i 3 C m A B 2
→ Từ trường trong máy điện là từ 4
2017 – Lý thuyết mạch điện 1 - Nguyễn Việt Sơn trường quay.
Chương 8: Mạch điện ba pha
I.3. Động cơ không đồng bộ ba pha.
b. Động cơ không đồng bộ ba pha. Cấu tạo:
Stator: Gồm các cuộn dây tạo ra từ trường quay.
Rotor: Cấu tạo kiểu lồng sóc đoản mạch, các thanh
dẫn lắp xiên so với đường sinh của lồng sóc.
Nguyên lý hoạt động:
Từ trường quay do cuộn dây stator tạo ra cắt các thanh
dẫn dây quấn rotor sinh ra suất điện động cảm ứng.
Dây quấn rotor nối ngắn mạch các suất điện động
cảm ứng sinh ra các dòng điện cảm ứng trong các thanh dẫn.
Lực tác dụng tương hỗ giữa dòng điện trong thanh dẫn với từ trường quay
làm rotor quay cùng chiều với chiều quay của từ trường. 5
2017 – Lý thuyết mạch điện 1 - Nguyễn Việt Sơn
Chương 8: Mạch điện ba pha
I.4. Cách đấu dây mạch ba pha.
Mỗi dây quấn stator có một cực đầu và một cực cuối (cực đầu là cực ở đấy
chiều dương dòng điện đi ra, cực còn lại là cực cuối).
Có 2 cách đấu dây nguồn ba pha: Nối hình sao Y:
Nối 3 cực cuối X, Y, Z chụm một điểm O (điểm trung tính của nguồn). A Pha A e (t) A Pha A e (t) e (t) A B Pha B
Sơ đồ tương đương O Dây trung tính X ≡ Y ≡ Z ≡ O e (t) C Pha C B Pha B C e (t) C e (t) Dây trung tính B Pha C
Sơ đồ 3 pha - 4 dây
Sơ đồ 3 pha - 4 dây thường dùng cung cấp cho mạng điện sinh hoạt với tải đấu hình sao. 6
2017 – Lý thuyết mạch điện 1 - Nguyễn Việt Sơn
Chương 8: Mạch điện ba pha
I.4. Cách đấu dây mạch ba pha. Nối tam giác Δ:
Đầu dây của cuộn trước nối với điểm cuối của cuộn sau. A≡Z Pha A Pha A e (t) e (t) C C e (t) e (t) A
Sơ đồ tương đương A e (t) e (t) B B C≡Y Pha B Pha B B≡X Pha C Pha C
Sơ đồ 3 pha - 3 dây
Sơ đồ 3 pha - 3 dây, nguồn, tải nối theo sơ đồ tam giác thường cung cấp
cho tải công nghiệp (động cơ 3 pha) 7
2017 – Lý thuyết mạch điện 1 - Nguyễn Việt Sơn
Chương 8: Mạch điện ba pha
I.4. Cách đấu dây mạch ba pha.
Tải 3 pha có thể được đấu theo 2 cách: Y và Δ Pha A Pha A Z A Z A ZB O’ Trung tính tải ZC Pha B Z Z Pha B B C Pha C Pha C
Sơ đồ hình Y - 3 pha - 4 dây
Sơ đồ hình Δ - 3 pha - 3 dây
Nguồn & tải có thể đấu khác nhau. e (t) Z A d O e (t) Z B d e (t) Z C d Zd
Tải nối Y 3 pha - 4 dây Tải nối Y
Tải nối Δ 3 pha - 3 dây 3 pha - 3 dây 8
2017 – Lý thuyết mạch điện 1 - Nguyễn Việt Sơn
LÝ THUYẾT MẠCH ĐIỆN 1
Chương 8: Mạch điện ba pha. I. Khái niệm.
II. Mạch ba pha đối xứng và không đối xứng tải tĩnh.
II.1. Khái niệm mạch ba pha đối xứng.
II.2. Đặc điểm mạch ba pha đối xứng.
II.3. Cách phân tích mạch ba pha đối xứng.
II.4. Mạch ba pha không đối xứng tải tĩnh.
III. Tính và đo công suất mạch điện ba pha.
IV. Mạch ba pha có tải động - Phương pháp thành phần đối xứng
V. Phân tích mạch ba pha không đối xứng bằng phương pháp
thành phần đối xứng. 9
2017 – Lý thuyết mạch điện 1 - Nguyễn Việt Sơn
Chương 8: Mạch điện ba pha
II.1. Khái niệm mạch ba pha đối xứng.
Có thể coi: Mạch ba pha gồm ba mạch điện 01 pha.
Ví dụ: Máy phát điện có 3 dây quấn, đường dây truyền tải có 3 dây, tải 3 ba gồm
3 tải một pha hợp thành.
Mạch điện ba pha đối xứng là mạch điện ba pha có nguồn đối xứng và tải đối xứng:
Nguồn ba pha đối xứng:
Tải ba pha đối xứng là tải có Biên độ bằng nhau. Biên độ bằng nhau. Tần số bằng nhau. Pha bằng nhau.
Pha ban đầu lệch nhau 1200
Đại lượng pha - đại lượng dây.
Dòng điện chảy trên dây dẫn từ nguồn đến tải & điện áp giữa các dây ấy gọi
là dòng điện dây & điện áp dây
Dòng điện & điện áp trên các pha của nguồn (tải) được gọi là dòng điện
pha & điện áp pha. 10
2017 – Lý thuyết mạch điện 1 - Nguyễn Việt Sơn
Chương 8: Mạch điện ba pha
II.2. Đặc điểm mạch ba pha đối xứng. E I A Z
a. Mạch nối hình sao Y. A A O O’
Xét điện áp giữa 2 điểm trung tính nguồn và tải: E B Z I B B
Y . E Y . E Y . E
Vì mạch ba pha đối xứng A A B B C C EC I C ZC U O'O I
Y Y Y
Y Y Y Y N A B C A B C A
Y. E Y. E Y . E
E E E Trung tính nguồn A B C A B C U O 'O 0 3.Y 3 và tải trùng nhau E U AB A U CA H
Áp dụng luật K2 cho vòng OAO’O: O E E B
A U A U O 'O U A
Hệ thống điện áp EC C B
pha trên tải đối xứng U Tương tự: E BC
B U B ; E C U C 0 j.30
I d I f ;U d 3.U f .e Xét tam giác OAH: 0 0 U
2.U .cos 30 3.U .30 U I N 0 AB 3.U A . j e AB A A Hệ thống dòng
Hệ thống dòng điện:
I A Y.U A ; I B Y.U B ; I C Y.U C
điện pha đối xứng
Dòng điện dây trung tính: I N I A I B I C 0 11
2017 – Lý thuyết mạch điện 1 - Nguyễn Việt Sơn
Chương 8: Mạch điện ba pha
II.2. Đặc điểm mạch ba pha đối xứng.
b. Mạch nối tam giác Δ A A I A I CA U CA U AB Z Z I BC Z I AB C C B B I B U BC I C 0 j.30 I d 3 I f .e ; U d U f 12
2017 – Lý thuyết mạch điện 1 - Nguyễn Việt Sơn
Chương 8: Mạch điện ba pha
II.3. Cách phân tích mạch ba pha đối xứng.
Việc phân tích mạch 3 pha đối xứng có thể đưa phân tích trên một pha (trạng
thái trên 2 pha còn lại giống như trên pha đang xét nhưng lệch 1/3 chu kỳ)
Quá trình phân tích thường thực hiện trên sơ đồ nối Y
Công thức biến đổi tổng trở
Công thức chuyển Y Δ
Công thức chuyển Δ Y Z Z12 12 Z Z Z Z 13 13 1 1 Z Z Z Z 2 3 2 3 Z Z23 23 Z .Z Z .Z Z .Z Z .Z 12 13 12 23 1 2 Z Z
Z Z Z 1 3
Z Z Z 1 2 12 1 2 13 1 3
Z Z Z
Z Z Z Z Z 12 13 23 12 13 23 3 2 Z .Z Z .Z 2 3 Z Z Z 13 23 Z 23 2 3 3 Z
Z Z Z 1 12 13 23 13
2017 – Lý thuyết mạch điện 1 - Nguyễn Việt Sơn
Chương 8: Mạch điện ba pha
II.3. Cách phân tích mạch ba pha đối xứng.
Quá trình phân tích thường thực hiện trên sơ đồ nối Y
Công thức biến đổi nguồn V AB 0 V 3 0 a n 3 V AB 0 V 1 5 0 b n 3 V A B 0 V 9 0 c n 3 14
2017 – Lý thuyết mạch điện 1 - Nguyễn Việt Sơn
Chương 8: Mạch điện ba pha
II.3. Cách phân tích mạch ba pha đối xứng. I A A
Ví dụ 8.1 : Xét mạch 3 pha đối xứng. E A Z I Z d 2 I B 2 A O Z 2 Z
Chuyển Δ - Y, xét riêng pha A. E 2 B Zd I 1A C E A E Z
Dòng điện dây: I C Zd 2 A Z Z Z 2 Z (Z // ) 1 1 d 1 3 Z1 I A Z I 2 A I A . ; I A .Z I A I A 2 A 1 2 1 Z Z 2 3 2 Z Z Zd 1 1 3 3 Z Z . E 2 A 1 . . 3 I 2 A I 1A
Dòng điện pha tải Z : I I 2 Z f 2 0 j 30 . 3.e Sơ đồ pha A E A
Tổn thất dọc đường dây: U d Z . I d Z . I A Z . d d d Z2 Z (Z // ) d 1 3
Trạng thái dòng - áp ở pha B (C) sẽ quay đi một góc tương ứng 15
2017 – Lý thuyết mạch điện 1 - Nguyễn Việt Sơn
Chương 8: Mạch điện ba pha
II.4. Mạch ba pha không đối xứng tải tĩnh.
Nguồn ba pha cung cấp cho tải thắp sáng, tải sinh hoạt, động cơ một pha, biến
áp hàn, lò hồ quang … làm việc ở trạng thái không đối xứng.
Coi mạch ba pha là một mạch có 3 nguồn 1 pha → sử dụng tất cả các phương
pháp xét: Dòng vòng, thế nút, dòng nhánh, xếp chồng, … Xét mạch 3 pha hình Y E E E A I ; B A I B ; C I C E A YA
Nếu Z 0 U O'O 0 Z Z Z N A B C O O’ E B YB
I N I A I B I C
Nếu đứt, chập 1 pha không ảnh hưởng đến các pha khác. EC YC YN
Y . E Y . E Y . E
Y . E Y . E Y . E Nếu Z A A B B C C U Nếu Z 0 N O 'O A A B B C C U O'O
Y Y Y N A B C
Y Y Y Y A B C N E U O 'O
E U O'O A I ; B A I B E U E U Z Z O 'O O 'O A I ; B A I B A B Z Z A B E U O 'O C I C ; I N 0 E U O 'O Z C I C ; I
I I I C N A B C 16
2017 – Lý thuyết mạch điện 1 - Nguyễn Việt Sơn ZC
Chương 8: Mạch điện ba pha
II.4. Mạch ba pha không đối xứng tải tĩnh.
Thực tế ta biết điện áp dây mà không biết điện áp từng pha của nguồn
Thay thế hệ thống điện áp dây bằng hệ thống ba (hoặc hai) nguồn áp tương
đương, đảm bảo điện áp dây đã cho.
Ví dụ 8.2: Cho mạch ba pha có hệ thống điện áp dây không đối xứng U AB;U AC , tải mắc hình sao đối xứng.
Thay hệ thống điện áp dây không đối xứng bằng 2 nguồn áp: EB U AB ; EC U AC
Chọn chiều dòng vòng như hình vẽ. Z A A I ZA
Lập phương trình mạch theo phương pháp dòng vòng E I 1 v B Z B B O I Z I B Z I 1 v A E I v2 C
(Z Z ). I 1
v Z . I v2 E B A B B I I I C Z v 2 1 v B Z C I Z C Z . I 1 v (Z
Z ). I v2 EC E B B B C I Z I v2 C 17
2017 – Lý thuyết mạch điện 1 - Nguyễn Việt Sơn
LÝ THUYẾT MẠCH ĐIỆN 1
Chương 8: Mạch điện ba pha. I. Khái niệm.
II. Mạch ba pha đối xứng và không đối xứng tải tĩnh.
III. Tính và đo công suất mạch điện ba pha.
IV. Mạch ba pha có tải động - Phương pháp thành phần đối xứng
V. Phân tích mạch ba pha không đối xứng bằng phương pháp
thành phần đối xứng. 18
2017 – Lý thuyết mạch điện 1 - Nguyễn Việt Sơn
Chương 8: Mạch điện ba pha
III. Tính và đo công suất mạch ba pha. * P Z A A A W * Tổng quát:. * P Z * * * B ~ B W B S *
3 fa U A . I A U B . I B U C . I C * P ZC P
P P P C W C 3 fa A B C * Q
Q Q Q N 3 fa A B C
Sơ đồ đo công suất 3 pha - 3 phần tử
Mạch 3 pha đối xứng: Công suất các pha bằng nhau → đo công suất 1 pha. * ~
S 3 fa 3.U A . I A * A P1 W P 3.P
3.U .I .cos 3.U .I .cos * 3 fa 1 fa f f d d E Tải nối 1 * B P2 Y hoặc Q 3.Q
3.U .I .sin 3.U .I .sin W * 3 fa 1 fa f f d d E2 Δ C
Mạch 3 pha không đối xứng: Thay bằng 2
Sơ đồ đo công suất 3 pha - 2 phần tử nguồn tương đương: ^ ^ P
P P P Re{U AC . I A} Re{U BC . I B} 3 fa tai 1 E 2 E 19
2017 – Lý thuyết mạch điện 1 - Nguyễn Việt Sơn
LÝ THUYẾT MẠCH ĐIỆN 1
Chương 8: Mạch điện ba pha. I. Khái niệm.
II. Mạch ba pha đối xứng và không đối xứng tải tĩnh.
III. Tính và đo công suất mạch điện ba pha.
IV. Mạch ba pha có tải động - Phương pháp thành phần đối xứng IV.1. Khái niệm.
IV.2. Hệ điện áp cơ sở.
IV.3. Công thức phân tích - tổng hợp.
IV.4. Tính chất các thành phần đối xứng trong mạch 3 pha.
V. Phân tích mạch ba pha không đối xứng bằng phương pháp
thành phần đối xứng. 20
2017 – Lý thuyết mạch điện 1 - Nguyễn Việt Sơn
Chương 8: Mạch điện ba pha IV.1. Khái niệm.
Trong mạch điện 3 pha, thực tế có tải hỗ cảm, tự cảm tổng trở các pha tải
không cố định (tải động), thay đổi phức tạp theo mức độ không đối xứng của dòng điện.
Coi hệ thống là tuyến tính, một trạng thái dòng, áp không đối xứng có thể phân
tích thành các thành phần đối xứng sao cho với mỗi hệ thành phần dòng đối
xứng, tổng trở cuộn dây là không đổi.
Áp dụng tính chất xếp chồng để giải bài toán mạch không đối xứng:
Phân tích nguồn ba pha không đối xứng ra những thành phần đối xứng.
Tìm đáp ứng đối với mỗi thành phần và xếp chồng lại.
Phương pháp thành phần đối xứng của Fortescue dựa trên sự phân tích chính
tắc những hệ dòng áp ba pha thành những thành phần đối xứng thuận, nghịch và không. 21
2017 – Lý thuyết mạch điện 1 - Nguyễn Việt Sơn
Chương 8: Mạch điện ba pha
IV.2. Hệ điện áp cơ sở của phương pháp thành phần đối xứng.
Phương pháp thành phần đối xứng của Fortescue là phương pháp xét mạch
điện ba pha không đối xứng bằng cách phân tích chính tắc những hệ dòng áp
ba pha thành những thành phần đối xứng thuận, nghịch và không.
Hệ thành phần đối xứng thuận, nghịch và không chính là hệ điện áp cơ sở : Thứ tự thuận:
Thứ tự ngược: Thứ tự không: U 1 A U A2 U A0 U B0 U C0 a a U C1 U 1 B U B2 U C2 a2 a2
U A0 A 0 (V ) U 1 A A 0 (V )
U A A 0 (V ) 2 U B0 U A0 2 U 1 B a .U 1 A U B2 . a U A2 U C0 U A0 U 2 C1 . a U 1 A U
C2 a .U A2 22
2017 – Lý thuyết mạch điện 1 - Nguyễn Việt Sơn
Chương 8: Mạch điện ba pha
IV.3. Công thức phân tích và tổng hợp.
Nếu biết vector của pha chuẩn ( U 1 A , U A 2 , U
A0 ) tìm được vector của pha B, C.
Khi phân tích hệ thống điện áp không đối xứng U A,U B ,U cần tìm C U 1
A ,U A2 ,U A0
Công thức tổng hợp: U A U 1
A U A2 U A0 U A U 1
A U A2 U A0 2 U B U 1
B U B 2 U B0 U B a .U 1 A . a U A2 U A0 2 U
C U C1 U C2 U C0 U C . a U 1
A a .U A2 U A0 1
Công thức phân tích: 2 U 1 A (U A .
a U B a .U C ) 3 Tính U 1
A ,U A2 ,U A0 theo 1 2 U A2
(U A a .U B . a U C ) 3 U
A ,U B ,U C 1 U A0
(U A U B U C ) 3 23
2017 – Lý thuyết mạch điện 1 - Nguyễn Việt Sơn
Chương 8: Mạch điện ba pha
IV.3. Công thức phân tích và tổng hợp.
Ví dụ 8.3: Phân tích hệ thống điện áp không đối xứng thành các thành phần đối xứng. 0
U A 120(V ) ; U B 120 120
(V ) ; U C 0.
Theo công thức phân tích, các thành phần đối xứng của điện áp pha A là: 1 1 2 0 0 U 1 A (U A .
a U B a .U C ) (120 120 1
20 120 ) 80(V ) 3 3 1 1 2 0 0 0 U A2
(U A a .U B . a U C )
(120 120 120 240 ) 40 60 (V ) 3 3 1 0 U A0
(U A U B U C ) 40 60 (V ). 3
Từ đó ta có thể tính được các thành phần đối xứng của U B ,U C : 0 0 U 1 B 80 1 20 (V )
U C1 80 120 (V ) 0 0 U B2
40 180 (V ) ; U C2 40 6 0 (V ) 0 0 U
B0 40 60 (V ). U C0 40 6 0 (V ). 24
2017 – Lý thuyết mạch điện 1 - Nguyễn Việt Sơn
Chương 8: Mạch điện ba pha
IV.3. Công thức phân tích và tổng hợp.
Ví dụ 8.4: Tìm dòng điện trong các pha nếu đã biết các thành phần đối xứng 0 0 I 1 A 5 90 ( )
A ; I A2 5 90 ( ) A ; I A0 0.
Theo công thức tổng hợp ta có: 0 0 I A I 1
A I A2 I A0 5 90 5 90 0( ) A 2 0 0
I B a . I 1 A .
a I A2 I A0 5 30 5 30 5. 3( ) A 2 0 0 0 I C . a I 1
A a . I A2 I A0 5 150 5 150 5. 3.180 ( ) A 25
2017 – Lý thuyết mạch điện 1 - Nguyễn Việt Sơn
Chương 8: Mạch điện ba pha
IV.4. Tính chất các thành phần đối xứng trong mạch 3 pha.
Từ công thức tổng hợp, ta có: 2 2
A B C (1 a a). 1
A (1 a a ). A2 3. A0 A 1
A A2 A0 2
A B C 3. A B a . 0 1 A . a A2 0 A 2
Tổng ba lượng pha bằng ba lần giá trị C . a 1
A a . A2 0 A
thành phần thứ tự không.
Xét hiệu 2 trạng thái: A B ( 1
A A2 A0 ) ( 1
B B2 B0 ) ( 1 A 1
B ) ( A2 B2 )
Hiệu hai lượng pha của hệ không chứa thành phần thứ tự không.
Từ 2 tính chất trên ta có thể suy ra một số tính chất sau:
Dòng điện dây trung tính bằng ba lần thành
phần thứ tự không của dòng điện dây.
I N I A I B I C 3. I 0
Điện áp dây luôn không có thành phần thứ tự không. 26
2017 – Lý thuyết mạch điện 1 - Nguyễn Việt Sơn
LÝ THUYẾT MẠCH ĐIỆN 1
Chương 8: Mạch điện ba pha. I. Khái niệm.
II. Mạch ba pha đối xứng và không đối xứng tải tĩnh.
III. Tính và đo công suất mạch điện ba pha.
IV. Mạch ba pha có tải động - Phương pháp thành phần đối xứng
V. Phân tích mạch ba pha không đối xứng bằng phương pháp
thành phần đối xứng.
V.1. Mạch ba pha có nguồn không đối xứng.
V.2. Các sự cố ngắn mạch, đứt dây trong mạch ba pha.
V.3. Các điều hòa cao của dòng - áp trong mạch ba pha. 27
2017 – Lý thuyết mạch điện 1 - Nguyễn Việt Sơn
Chương 8: Mạch điện ba pha
V.1. Mạch ba pha có nguồn không đối xứng. Nguồn Tải Z A 1ng Z
Xét nguồn 3 pha không đối xứng tìm dòng 1t B Z
điện xác lập trong các pha của tải. 2ng Z2t C Z
Phân tích hệ suất điện động không đối xứng 0ng Z0t
thành theo thành phần thuận, nghịch không. ZN 1 2 U 1 A (U A .
a U B a .U C ) 3 E 1 A E A2 E A0 1 A 2 U A2
(U A a .U B . a U C ) 3 E 1 B E B2 E B0 1 B U A0
(U A U B U C ) 3
EC1 EC2 EC0 C
Thay thế các nguồn suất điện động → áp dụng
tính chất xếp chồng, tách thành 3 bài toán đối ZN xứng 28
2017 – Lý thuyết mạch điện 1 - Nguyễn Việt Sơn
Chương 8: Mạch điện ba pha
V.1. Mạch ba pha có nguồn không đối xứng.
Bài toán 1: I 1 A Z1ng
Nguồn: hệ suất điện động thứ tự thuận E 1 A , E 1 B , . EC1 E Z 1 A 1t
Khi đó mạch điện hoàn toàn đối xứng.
Cách giải giống hoàn toàn bài toán mạch điện Sơ đồ thứ tự thuận
ba pha đối xứng: Dùng sơ đồ tách riêng pha A, ta có: E 1 A I 1 A Z Z Bài toán 2: 1ng 1t I A2
Nguồn tác dụng là hệ suất điện động thứ tự ngược Z2ng E Z
A2 , E B 2 , E C 2 . E A2 2t
Tương tự như trên, ta cũng có sơ đồ tính toán cho Sơ đồ thứ tự
mạch ba pha đối xứng khi xét riêng pha A. ngược E A2
I A2 Z Z 2ng 2t 29
2017 – Lý thuyết mạch điện 1 - Nguyễn Việt Sơn
Chương 8: Mạch điện ba pha
V.1. Mạch ba pha có nguồn không đối xứng.
Bài toán 3: Z Z
Nguồn tác dụng là một hệ suất điện động thứ tự không 0ng 0t E A0 E Z A Z
0 , E B0 , E C 0 , tổng trở tải Z và tổng nguồn Z đều đối 0ng E 0t 0ng B0 0t xứng. Z0ng Z0t EC0 ZN
Lúc này mạch điện có dây trung tính, dòng điện trong dây
trung tính bằng 3 lần dòng điện thứ tự không. Z Xét riêng pha A ta có: 0ng I A0 Z E A0 0t E A0 3Z I N
A0 Z Z 3.Z 0ng 0t N
Sơ đồ thứ tự không
Chú ý: Với sơ đồ thứ tự không, nếu không có dây trung tính, dòng điện trong các pha
sẽ bằng không. 30
2017 – Lý thuyết mạch điện 1 - Nguyễn Việt Sơn
Chương 8: Mạch điện ba pha
V.1. Mạch ba pha có nguồn không đối xứng.
Sau khi tính được các thành phần dòng điện do từng hệ thống ba pha thuận, nghịch,
không tác dụng riêng rẽ, áp dụng công thức tổng hợp, ta tính được dòng điện trong mỗi pha:
I A I 1A I A2 I A0 2
I B a . I 1 A . a I A2 I A0 2 I C . a I 1
A a . I A2 I A0
Các bước giải bài toán mạch ba pha có nguồn không đối xứng:
Phân tích nguồn đối xứng thành tổng của các thành phần thuận, nghịch, không.
Lập và tính các giá trị dòng áp cần thiết trên các sơ đồ thuận, nghịch, không. (Sơ đồ
thuận và nghịch có kết cấu giống nhau; sơ đồ thứ tự không có thêm tổng trở dây
trung tính với giá trị tăng gấp 3 lần)
Áp dụng công thức tổng hợp để tính toán các giá trị dòng, áp cần tìm. 31
2017 – Lý thuyết mạch điện 1 - Nguyễn Việt Sơn
Chương 8: Mạch điện ba pha
V.1. Mạch ba pha có nguồn không đối xứng. Nguồn Tải
Ví dụ 8.5: Tính dòng điện trong các pha của mạch 3 pha không Z A 1ng Z1t
đối xứng như hình bên, biết: B Z2ng Z2t 0 0
E A 6500(V ); E B 6800 135
(V ); EC 6300 130 (V ) C Z0ng Z0t Z Z j.14(); Z
j.1(); Z j.10(); 1ng 2ng 0ng N ZN
Z 40 j.45(); Z 2 j.8(); Z j.3(); 1t 2t 0t Giải: E 1 A E A2 E A0
Phân tích hệ thống suất điện động không đối xứng thành A
các thành phần thứ tự thuận nghịch không. E 1 B
E B2 E B0 B 1 2 0 E 1 A (E A .
a E B a . EC ) 6420 2 (V ) 3
EC1 EC2 EC0 C 1 2 0 E A2
(E A a . E B .
a EC ) 800 13, 50 (V ) 3 ZN 1 E A0
(E A E B EC ) 783(V ) 3 32
2017 – Lý thuyết mạch điện 1 - Nguyễn Việt Sơn
Chương 8: Mạch điện ba pha
V.1. Mạch ba pha có nguồn không đối xứng.
Xét sơ đồ thuận:
Xét sơ đồ ngược: Z1ng I Z 1 A 2ng I A2 E Z Z 1 A 1t E A2 2t
Sơ đồ thứ tự thuận
Sơ đồ thứ tự ngược E 1 A 0 E I A2 0 1 A 90, 2 57, 50 ( ) A I A2 40.5 71 ( ) A Z Z 1ng 1t Z Z 2ng 2t
Xét sơ đồ không: Z
Áp dụng công thức tổng hợp ta có: 0ng I A0 E Z A0 0t 0 3Z
I I I I A N A 1 A A2 A0 111 56, 20 ( )
Sơ đồ thứ tự không 2 0
I B a . I 1 A .
a I A2 I A0 81, 2 141, 50 ( ) A E A0 0 I 2 0 A0 23 90 ( ) A I C . a I 1
A a . I A2 I A0 111 82, 45 ( ) A Z Z 3.Z 0ng 0t N 33
2017 – Lý thuyết mạch điện 1 - Nguyễn Việt Sơn
Chương 8: Mạch điện ba pha
V.2. Các sự cố ngắn mạch, đứt dây trong mạch ba pha.
Khi mạch ba pha đối xứng bị sự cố (sự cố đứt dây, ngắn mạch …), phần mạch ở nơi sự cố sẽ không
đối xứng nữa. Điện áp tại phần mạch sự cố lập thành một hệ điện áp không đối xứng.
Phương pháp xét bài toán mạch điện ba pha sự cố:
Phân tích thành phần điện áp không đối xứng tại vị trí sự cố thành các thành phần đối xứng thuận, nghịch, không.
Áp dụng phương pháp xét mạch ba pha đối xứng.
Có 2 loại sự cố trong mạch ba pha:
Sự cố dọc đường dây: Ví dụ: Sự cố đứt dây 1 pha, đứt dây 2 pha …
Làm thay đổi tổng trở pha của đường dây.
Thay thế vị trí sự cố bằng hệ thống dòng, áp mắc nối tiếp vào đường dây.
Sự cố ngang đường dây: Ví dụ: Sự cố ngắn mạch 2 pha, chạm đất 1 pha …
Làm thay đổi tổng trở cách điện giữa các pha đường dây với nhau và với đất.
Thay thế vị trí sự cố bằng hệ thống dòng, áp mắc song song vào đường dây. 34
2017 – Lý thuyết mạch điện 1 - Nguyễn Việt Sơn
Chương 8: Mạch điện ba pha
V.2. Các sự cố ngắn mạch, đứt dây trong mạch ba pha.
a. Sự cố đứt dây 1 pha. A U A A’ Hiện tượng: Z fa A U
Tổng trở tại vị trí sự cố: B Z 0 B B’ fa B Z 0 C U C C’ fa C U A A’ A 0 B B’
Điện áp tại ví trí sự cố: U B 0 C C’ U C 0 Phương trình sự cố: I A 0 I 1
A I A2 I A0 0 U 2 B 0 a .U 1 A .
a U A2 U A0 0 U 2 C 0 . a U 1
A a .U 1 A U A0 0 35
2017 – Lý thuyết mạch điện 1 - Nguyễn Việt Sơn
Chương 8: Mạch điện ba pha
V.2. Các sự cố ngắn mạch, đứt dây trong mạch ba pha.
a. Sự cố đứt dây 1 pha.
Ví dụ 8.6: Cho mạch điện 3 pha đơn giản, cho đường dây bị đứt pha A làm thành một bộ phận không
đối xứng biểu diễn bằng một hình chữ nhật. Tìm các dòng áp trong mạch. Phần mạch Nguồn sự cố Tải đối xứng Z Đường dây A A’ 1ng Z1t Z , Z , Z 1d 2d 0d B B’ Z2ng Z2t C C’ Z0ng Z0t Tải đối ZN xứng Z
Trừ phần sự cố ra, mạch điện còn lại hoàn toàn đối xứng.
Muốn đưa bài toán này về đối xứng → cần thay thế hệ thống điện áp không đối xứng ở phần sự cố
bằng những thành phần đối xứng thuận, nghịch, không. 36
2017 – Lý thuyết mạch điện 1 - Nguyễn Việt Sơn
Chương 8: Mạch điện ba pha
V.2. Các sự cố ngắn mạch, đứt dây trong mạch ba pha.
a. Sự cố đứt dây 1 pha. Ví dụ 8.6: Nguồn Tải đối xứng Z Đường dây A A’ 1ng Z1t Z , Z , Z 1d 2d 0d B B’ Z2ng Z2t C C’ Z0ng Z0t Tải đối ZN xứng Z Z Z U 1 A U A2 U A0 1ng 1d Z Z 2ng 2d Z Z 0ng 0d E Z I Z 1 A 1 A Z1t I A2 Z 3Z 2t I N A0 Z0t
Sơ đồ thứ tự thuận
Sơ đồ thứ tự ngược
Sơ đồ thứ tự không
Thứ tự không chỉ chạy trong mạch có dây trung tính 37
2017 – Lý thuyết mạch điện 1 - Nguyễn Việt Sơn
Chương 8: Mạch điện ba pha
V.2. Các sự cố ngắn mạch, đứt dây trong mạch ba pha.
a. Sự cố đứt dây 1 pha. Ví dụ:
Sơ đồ thứ tự thuận:
Sơ đồ thứ tự ngược: Z Z 1ng 1d I Z Z 2ng 2d Z 1 A I 2d U A2 I A2 E Z 1 A Z U A2 U 1 A Z A2 Z td2 1t Z2t Z2t Z .Z 2ng
U A2 I A2 .(Z Z Z ) 0 Z Z Z td 2 2d 2t td 2 td1 1d Z Z I 1 A U 2ng 1 A Etd1 Z1t
Sơ đồ thứ tự không: E Z Z Z A . . Z Z 1 0ng 1ng I 0d A0 U A0 Etd1 ; Z td1 3ZN Z0t Z Z Z Z 1ng 1ng U 1 A I 1 A .(Z
Z Z ) Etd1 td1 1d 1t
U A0 I A0 .(3.Z Z Z Z ) 0 N 0ng 0d 0t 38
2017 – Lý thuyết mạch điện 1 - Nguyễn Việt Sơn
Chương 8: Mạch điện ba pha
V.2. Các sự cố ngắn mạch, đứt dây trong mạch ba pha.
a. Sự cố đứt dây 1 pha. Ví dụ 8.6:
Vậy có 6 phương trình = 3 phương trình sự cố + 3 phương trình lập từ sơ đồ thuận, nghịch, không.
Giải 6 phương trình này ta tìm được: U 1 A I 1 A .(Z
Z Z ) Etd1 td1 1d 1t I 1
A , I A2 , I A0 ,U 1
A ,U A2 ,U A0 U
A2 I A2 .(Z Z Z ) 0 Thay U 1
A ,U A2 ,U A0 vào sơ đồ thuận, td 2 2d 2t
nghịch, không → tìm được dòng áp thứ tự U
A0 I A0 .(3.Z Z Z Z ) 0 N 0ng 0d 0t
thuận, nghịch, không ở mọi nhánh trong I 1
A I A2 I A0 0 mạch. 2
Để tìm dòng áp trên các nhánh của mạch a .U 1 A .
a U A2 U A0 0
điện, tao dùng công thức tổng hợp: . a U 2 1
A a .U A2 U A0 0 U A U 1
A U A2 U A0 2
I B a . I 1 A . a I A2 I A0 2 I C . a I 1
A a . I A2 I A0 39
2017 – Lý thuyết mạch điện 1 - Nguyễn Việt Sơn
Chương 8: Mạch điện ba pha
V.2. Các sự cố ngắn mạch, đứt dây trong mạch ba pha.
b. Sự cố đứt dây 2 pha.
d. Sự cố ngắn mạch 2 pha. A U A A’ A A’ A A’ B U B B’ B B’ B B’ C U C C’ C C’ U A U B M C U C C’
I A 0 ; I B 0 ; U C 0
c. Sự cố chạm đất 1 pha. A A’ A A’ A A’ B B’ B B’ B B’ C C’ C C’ C C’ Z U A U B U C
I A 0 ; U B 0 ; U C 0
I A 0 ; I B 0 ; U C Z. I C 40
2017 – Lý thuyết mạch điện 1 - Nguyễn Việt Sơn
Chương 8: Mạch điện ba pha
V.3. Các điều hòa cao của dòng - áp trong mạch ba pha.
Có nhiều nguyên nhân sinh ra các điều hòa cao của suất điện động và dòng ba pha:
Máy phát điện chế tạo không hoàn hảo → sinh ra các suất điện động không sin …
Phân tích suất điện động đó thành chuỗi Furie, ngoài sóng cơ bản có tần số ω, còn chứa nhiều sóng
bậc cao có tần số 3ω, 5ω, 7ω …
Do máy phát điện có cấu tạo đối xứng, nên suất điện động các pha hoàn toàn giống nhau, và lệch
nhau về thời gian 1/3 chu kỳ nên:
e (t) E . 2.sin k..t kA k T 2.
e (t) E . 2.sin k.(t
) E . 2.sin(k..t k. ) kB k 3 k 3 41
2017 – Lý thuyết mạch điện 1 - Nguyễn Việt Sơn
Chương 8: Mạch điện ba pha
V.3. Các điều hòa cao của dòng - áp trong mạch ba pha.
e (t) E . 2.sin k..t kA k T 2.
e (t) E . 2.sin k.(t
) E . 2.sin(k..t k. ) kB k 3 k 3 Nhận xét:
Các sóng điều hòa có k = 3n → φ = n.2.π → tạo thành hệ thống thứ tự không. k
Các sóng điều hòa có k = 3n + 1 → φ = n.2.π + 2.π/3 → tạo thành hệ thống thứ tự thuận. k
Các sóng điều hòa có k = 3n + 2 → φ = n.2.π + 4.π/3 → tạo thành hệ thống thứ tự ngược. k Suy ra:
Dòng điện trong dây trung tính chỉ chứa các sóng điều hòa bậc 3.n của dòng pha. 2 2 2
I 3. I I I ... N 3 9 15
Điện áp pha bao gồm tất cả các sóng điều hòa: 2 2 2 2 2
U U U U U U ... f 1 3 5 7 9
Điện áp dây không chứa thành phần thứ tự không (3n) 2 2 2 2
U 3. U U U U ... d 1 5 7 11 42
2017 – Lý thuyết mạch điện 1 - Nguyễn Việt Sơn



