-
Thông tin
-
Hỏi đáp
Bài giảng thống kê Xã hội học 2022│Đại học Sư phạm Hà Nội
Bài giảng thống kê Xã hội học 2022│Đại học Sư phạm Hà Nội được biên soạn theo phân phối chương trình học. Bao gồm các thông tin được sắp xếp theo trật tự logic nhằm cung cấp cho người học kiến thức và kỹ năng nhất định, sẽ làm tăng tính sinh động của môn học, từ đó giúp sinh viên có thể tiếp thu kiến thức một cách dễ dàng và linh hoạt hơn.
Môn:
Thống kê xã hội học 96 tài liệu
Trường:
Đại học Sư Phạm Hà Nội 2.1 K tài liệu
Thông tin:
65 trang
4 tháng trước
Tác giả:
Bài giảng thống kê Xã hội học 2022│Đại học Sư phạm Hà Nội
Bài giảng thống kê Xã hội học 2022│Đại học Sư phạm Hà Nội được biên soạn theo phân phối chương trình học. Bao gồm các thông tin được sắp xếp theo trật tự logic nhằm cung cấp cho người học kiến thức và kỹ năng nhất định, sẽ làm tăng tính sinh động của môn học, từ đó giúp sinh viên có thể tiếp thu kiến thức một cách dễ dàng và linh hoạt hơn.
240
120 lượt tải
Tải xuống
Môn: Thống kê xã hội học
96 tài liệu
Trường: Đại học Sư Phạm Hà Nội
2.1 K tài liệu
Thông tin:
65 trang
4 tháng trước
Tác giả:
Bài giảng Thống kê Xã hội học
Khoa Toán Tin
Trường Đại học Sư phạm Hà Nội
2020
Mục
lục
1
MỘT SỐ KIẾN THỨC XÁC SUẤT CƠ SỞ
6
1.1 Định nghĩa xác suất . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 7
1.1.1 Phép thử ngẫu nhiên . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 7
1.1.2 Không gian mẫu và Biến cố sơ cấp . . . . . . . . . . . . . . . . . . . . . . . .
7
1.1.3 Biến cố . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 8
1.1.4 Phép toán trên các biến cố . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 9
1.1.5 Mối quan hệ giữa các biến cố . . . . . . . . . . . . . . . . . . . . . . . . . . . 9
1.1.6 Định nghĩa xác suất cổ điển
. . . . . . . . . . . . . . . . . . . . . . . . . . . . 10
1.1.7 Tính chất của xác suất . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 10
1.1.8 Định nghĩa xác suất theo thống kê . . . . . . . . . . . . . . . . . . . . . . . . 10
1.2 Sự độc lập . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 11
1.2.1 Hai biến cố độc lập
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 11
1.2.2 Dãy biến cố độc lập . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 11
1.2.3 Dãy phép thử Bernoulli . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
11
1.2.4 Công thức xác suất nhị thức . . . . . . . . . . . . . . . . . . . . . . . . . . . . 12
1.3 Biến ngẫu nhiên rời rạc . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
13
1.3.1 Định nghĩa . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 13
1.3.2 Phân phối của biến ngẫu nhiên . . . . . . . . . . . . . . . . . . . . . . . . . . 14
1.3.3 Các số đặc trưng . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 14
1.3.4 Ý nghĩa của kỳ vọng và phương sai . . . . . . . . . . . . . . . . . . . . . . . . 14
1.3.5 Phân phối nhị thức
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 15
1.3.6 Tính chất của kỳ vọng và phương sai
. . . . . . . . . . . . . . . . . . . . . . . 15
1.4 Biến ngẫu nhiên liên tục và Phân phối chuẩn
. . . . . . . . . . . . . . . . . . . . . .
15
1.4.1 Biến ngẫu nhiên liên tục . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 15
1.4.2 Hàm mật độ
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 15
1.4.3 Các số đặc trưng . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 16
1.4.4 Phân phối chuẩn . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 16
1.4.5 Tính chất của phân phối chuẩn . . . . . . . . . . . . . . . . . . . . . . . . . . 17
1.4.6 Xấp xỉ phân phối nhị thức bằng phân phối chuẩn . . . . . . . . . . . . . . .
18
2
MẪU NGẪU NHIÊN
20
2.1 Giới thiệu về Thống kê . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
21
2.1.1 Mẫu và quần thể . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 21
2.1.2 Quy trình nghiên cứu thống kê . . . . . . . . . . . . . . . . . . . . . . . . . . 21
2.1.3 Các bài toán thống kê sẽ học: . . . . . . . . . . . . . . . . . . . . . . . . . . . 21
2.2 Thu thập dữ liệu . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
22
2.2.1 Xác định dữ liệu cần thu thập
. . . . . . . . . . . . . . . . . . . . . . . . . . . 22
1
2.2.2
Dữ liệu sơ cấp và thứ cấp
............................................................................................
22
2.2.3
Lấy mẫu hoàn lại và không hoàn lại
..........................................................................
23
2.2.4
Quy tắc lấy mẫu
............................................................................................................
23
2.2.5
Phương pháp lấy mẫu giản đơn
..................................................................................
23
2.2.6
Các phương pháp lấy mẫu khác
.................................................................................
23
2.3
Trình bày dữ liệu bằng bảng và biểu đồ
................................................................................
24
2.3.1
Biểu đồ thân-lá (stem-and-leaf diagram)
..................................................................
24
2.3.2
Tần số
.............................................................................................................................
25
2.3.3
Bảng tần số
....................................................................................................................
26
2.4
Biểu đồ tần số
............................................................................................................................
26
2.4.1
Biểu đồ tần suất
............................................................................................................
27
2.5
Số liệu và các số đặc trưng
......................................................................................................
28
2.5.1
Biến
số
...........................................................................................................................
28
2.5.2
Phân loại biến số
..........................................................................................................
28
2.5.3
Các số đo giá trị trung tâm
..........................................................................................
28
2.5.4
Các số đo độ phân tán
................................................................................................
29
2.5.5
Thống kê
........................................................................................................................
30
3 KHOẢNG ƯỚC LƯỢNG 31
3.1
Khoảng ước lượng cho trung bình
..........................................................................................
31
3.1.1
Đặt vấn đề
.....................................................................................................................
31
3.1.2 Khoảng ước lượng.........................................................................................................32
3.1.3
Khoảng ước lượng cho trung bình µ khi σ
2
đã biết
.................................................
32
3.1.4
Khoảng ước lượng cho trung bình µ của mẫu cỡ lớn
..............................................
34
3.1.5
Khoảng ước lượng cho mẫu nhỏ có phân phối chuẩn với σ
2
chưa biết
................
36
3.1.6
Vấn đề xác định cỡ mẫu
..............................................................................................
37
3.2
Khoảng ước lượng cho tỷ lệ
....................................................................................................
37
3.2.1
Đặt vấn đề
.....................................................................................................................
37
3.2.2
Công thức khoảng ước lượng cho tỷ lệ
.....................................................................
37
3.2.3
Vấn đề xác định cỡ mẫu
..............................................................................................
38
4 KIỂM ĐỊNH GIẢ THUYẾT THỐNG KÊ 40
4.1
Tình huống thực tế
...................................................................................................................
41
4.2
Bài toán kiểm định giả thuyết tổng quát
................................................................................
41
4.2.1
Miền tiêu chuẩn
............................................................................................................
42
4.2.2
Các loại sai lầm
............................................................................................................
42
4.3
Bài toán kiểm định giả thuyết cho giá trị trung bình một mẫu
...........................................
43
4.3.1
Bài toán 1: So sánh trung bình của mẫu có phân phối chuẩn với phương sai
σ
2
đã biết
.......................................................................................................................
43
4.3.2
Bài toán 2: So sánh giá trị trung bình của mẫu cỡ lớn với phương sai chưa biết 44
4.3.3
Bài toán 3: So sánh giá trị trung bình của mẫu có phân phối chuẩn với
phương sai chưa biết
....................................................................................................
45
4.4
Bài toán kiểm định giả thuyết về tỉ lệ
....................................................................................
48
4.4.1
Tình huống thực tế
.......................................................................................................
48
4.4.2
Bài toán kiểm định giả thuyết cho tỉ lệ
......................................................................
49
4.4.3
Tiêu chuẩn kiểm định
..................................................................................................
49
4.5
Bài toán so sánh hai giá trị trung bình
....................................................................................
51
4.5.1
Tình huống thực tế
.......................................................................................................
51
4.5.2
So sánh hai giá trị trung bình
......................................................................................
51
4.5.3
Bài toán 1: So sánh giá trị trung bình của hai mẫu có phân phối chuẩn với
phương sai đã biết
.......................................................................................................
52
4.5.4
Bài toán 2: So sánh hai giá trị trung bình của hai mẫu có phân phối chuẩn
với phương sai σ
X
= σ
Y
= σ
2
chưa biết
..................................................................
53
4.6
Bài toán so sánh hai tỉ lệ
..........................................................................................................
54
4.6.1
Tình huống thực tế
.......................................................................................................
54
4.6.2
So sánh hai tỉ lệ
............................................................................................................
54
5 Hồi quy tuyến tính đơn 58
5.1
Tình huống thực tế
...................................................................................................................
58
5.2
Mô hình hồi quy tuyến tính đơn
.............................................................................................
59
5.2.1
Khoảng tin cậy cho σ
2
.........................................................................................................................................
60
5.2.2
Khoảng tin cậy cho β
1
.........................................................................................................................................
60
5.2.3
Khoảng tin cậy cho β
0
.........................................................................................................................................
60
5.2.4
Khoảng dự báo
..............................................................................................................
61
Giới thiệu học phần
Thống kê Xã hội học
Một số vấn đề thực tế
•
Làm thế nào để biết cân nặng trung bình của trẻ sơ sinh ở một địa phương?
–
Một nhà điều tra thử tính cân nặng trung bình của 50 trẻ sơ sinh ở một địa phương
thì được kết quả là 3,1kg. Có thể nói gì về cân nặng của trẻ sơ sinh toàn địa
phương đó?
–
Một nhà quản lý cho rằng cân nặng trung bình của tất cả các trẻ sơ sinh ở địa
phương đó là 3,3kg. Tuyên bố của nhà quản lý có đúng không?
•
Làm thế nào để so sánh hiệu quả của hai phác đồ điều trị cho một bệnh nào đó?
–
Có hai phác đồ điều trị cho cùng một bệnh. Trong 200 bệnh nhân điều trị theo phác đồ
1 có 150 khỏi bệnh. Trong 50 người điều trị theo phác đồ 2 thì có 40 người khỏi bệnh.
Hỏi phác đồ 2 có thực sự tốt hơn phác đồ 1 hay không?
•
Con của bạn sẽ cao bao nhiêu cm?
–
Chiều cao của con bị ảnh hưởng bởi chiều cao của bố hay chiều cao của mẹ?
–
Chiều cao của bố/mẹ và con liên quan như thế nào đến nhau?
–
Biết chiều cao của bố/mẹ thì có thể dự đoán được chiều cao của con không?
Thống kê là gì?
Thống kê là khoa học về việc thu thập, xử lý, biểu diễn, phân tích mẫu số liệu thu thập được
từ một quần thể để rút ra được các kết luận có độ tin cậy cho toàn bộ quần thể đó.
Cơ sở khoa học của Thống kê là Lý thuyết xác suất.
4
MỤC LỤC 5
Nội dung học phần
1.
Chương 1: Một số kiến thức xác suất cơ sở
2.
Chương 2: Mẫu ngẫu nhiên
3. Chương 3: Khoảng ước lượng
4.
Chương 4: Kiểm định giả thuyết thống kê
5. Chương 5: Hồi quy
Mục tiêu của học phần
1.
Hiểu được ý nghĩa và tính được xác suất, kì vọng, phương sai trong một số trường hợp đơn
giản.
2.
Vận dụng phân phối nhị thức và phân phối chuẩn giải quyết một số bài toán thực tế.
3.
Hiểu được phương pháp lấy mẫu ngẫu nhiên.
4.
Biết phân loại số liệu và tính toán các đặc trưng của mẫu số liệu. Trình bày số liệu dưới
dạng
biểu đồ cột, biểu đồ quạt.
5.
Hiểu được ý nghĩa và tính khoảng ước lượng cho trung bình và tỉ lệ.
6.
Hiểu được ý nghĩa bài toán kiểm định giả thuyết. Vận dụng để so sánh tỉ lệ và trung bình.
7.
Hiểu được ý nghĩa và giải quyết được bài toán hồi quy tuyến tính đơn.
Chương
1
MỘT SỐ KIẾN THỨC XÁC SUẤT CƠ SỞ
Nội dung của chương:
1.
Định nghĩa xác suất cổ điển và định nghĩa xác suất theo thống kê.
2. Sự độc lập
3.
Biến ngẫu nhiên rời rạc.
4.
Biến ngẫu nhiên liên tục
5.
Phân phối nhị thức và Phân phối chuẩn
6.
Các số đặc trưng của biến ngẫu nhiên.
Mục tiêu của chương
1.
Hiểu được các khái niệm cơ bản của xác suất: phép thử ngẫu nhiên, không gian mẫu,
biến cố, mối quan hệ giữa các biến cố.
2.
Hiểu được ý nghĩa của khái niệm độc lập.
3.
Hiểu được ý nghĩa và tính được xác suất, kì vọng, phương sai trong một số trường hợp đơn
giản.
4.
Vận dụng phân phối nhị thức và phân phối chuẩn giải quyết một số bài toán thực tế.
6
1.1
Định nghĩa xác suất
1.1.1
Phép thử ngẫu nhiên
•
Phép thử: việc thực hiện một tổ hợp các hành động nào đó.
•
Phép thử ngẫu nhiên: phép thử mà ta không biết trước được kết quả của nó
1.1.2 Không gian mẫu và Biến cố sơ cấp
Không gian mẫu là tập hợp tất cả các kết quả có thể xảy ra của phép thử. Ta thường kí hiệu
không gian mẫu bởi Ω.
•
Biến cố sơ cấp là một phần tử của không gian mẫu.
Ví dụ 1.1.1. Trong hộp có 1 bi xanh, 1 bi đỏ và 1 bi vàng. Hãy xác định không gian mẫu và số biến
cố sơ cấp của các phép thử sau:
a)
Lấy ra ngẫu nhiên 1 bi từ hộp.
b)
Lấy ra ngẫu nhiên đồng thời 2 bi từ hộp.
c)
Lấy ra lần lượt 2 bi từ hộp.
d)
Lấy ra ngẫu nhiên 1 bi từ hộp, xem màu, trả lại hộp rồi lại lấy ra ngẫu nhiên 1 bi nữa.
Lời giải. a) Lấy ra ngẫu nhiên 1 bi từ hộp
Ω =
n
X, Đ, V
,
.
b)
Lấy ra ngẫu nhiên đồng thời 2 bi từ hộp
Ω =
n
{X, Đ}, {X, V }, {Đ, V }
,
.
c)
Lấy ra lần lượt 2 bi từ hộp
Ω =
n
XĐ, XV, ĐX, ĐV, V X, V Đ
,
=
n
(X, Đ), (X, V ), (Đ, X),
(Đ, V ), (V, X), (V, Đ)
,
•
d)
Lấy ra ngẫu nhiên 1 bi từ hộp, xem màu, trả lại hộp rồi lại lấy ra ngẫu nhiên 1 bi nữa
Ω =
n
XX, XĐ, XV, ĐX, ĐV, ĐĐ, V X, V Đ, V V
,
=
n
(X, X), (X, Đ), (X, V ), (Đ, X),
(Đ, Đ), (Đ, V ), (V, X), (V, Đ), (V, V )
,
.
1.1.3 Biến cố
Biến cố là một sự kiện liên quan đến phép thử. Một biến cố có thể xảy ra hoặc không xảy
ra
sau khi phép thử được thực hiện. Mỗi biến cố là một tập con của không gian mẫu.
•
Biến cố chắc chắn là biến cố luôn xảy ra.
•
Biến cố rỗng (trống) là biến cố luôn không xảy ra.
Ví dụ 1.1.2. Xét phép thử gieo hai con xúc xắc cân đối. Hãy xác định không gian mẫu và biểu
diễn các biến cố sau dưới dạng tập hợp.
•
A là b/c xuất hiện hai mặt 1 chấm.
•
B là b/c xuất hiện hai mặt 4 chấm.
•
C là b/c xuất hiện hai mặt cùng chấm.
•
D là b/c tổng số chấm bằng 8.
•
E là b/c tích số chấm xuất hiện là số lẻ.
Lời giải.
Ω = {(1, 1), (1, 2), . . . , (6, 6)}
= {(i, j) : 1 ≤ i, j ≤
6}
•
A = {(1, 1)}.
•
B = {(4, 4)}.
•
•
C là b/c xuất hiện hai mặt cùng chấm
C = {(1, 1), (2, 2), (3, 3), (4, 4), (5, 5), (6, 6)}.
•
D là b/c tổng số chấm bằng 8
D = {(2, 6), (3, 5), (4, 4), (5, 3), (6, 2)}.
•
E là b/c tích số chấm xuất hiện là số lẻ
E = {(1, 1), (1, 3), (1, 5), (3, 1), (3, 3), (3, 5), (5, 1), (5, 3), (5, 5)}.
1.1.4
Phép toán trên các biến cố
•
A ∪ B: Hợp của hai biến cố A và B.
•
A ∩ B = AB: Giao của hai biến cố A và B.
•
A \ B: Hiệu của hai biến cố A cho B.
Ví dụ 1.1.3. Trong phép thử gieo hai con xúc xắc, hãy xác định biến cố hợp, giao và hiệu của
các biến cố C và D.
1.1.5 Mối quan hệ giữa các biến cố
•
Biến cố A được gọi là thuận lợi cho biến cố B nếu khi A xảy ra thì B cũng xảy ra. Kí hiệu là
A ⊂ B.
•
Biến cố A được gọi là xung khắc với biến cố B nếu khi A xảy ra thì B không xảy ra và
ngược lại. Hai biến cố xung khắc không thể đồng thời cùng xảy ra. Kí hiệu là A ∩ B = ∅.
Ví dụ 1.1.4. Trong các biến cố A, B, C, D, E ở phép thử gieo hai con xúc xắc
•
hãy chỉ ra biến cố nào thuận lợi cho biến cố nào;
•
hãy chỉ ra các cặp biến cố xung khắc.
•
Biến cố A và B là đối nhau nếu luôn chỉ có đúng một trong hai biến cố xảy ra.
A ∩ B =
∅
A ∪ B =
Ω
Kí hiệu biến cố đối của biến cố A là
A
¯
.
⇔ A = Ω \ B.
Hai biến cố A và B được gọi là đồng khả năng nếu chúng có khả năng xuất hiện như
nhau trong mỗi phép thử.
Ví dụ 1.1.5. Trong phép thử gieo hai con xúc xắc, hãy xác định biến cố đối của các biến cố C, D, E.
1.1.6
Định nghĩa xác suất cổ điển
Giả sử một phép thử có n kết quả khác nhau và có cùng khả năng xảy ra, trong đó có m
kết quả thuận lợi cho biến cố A. Khi đó xác suất để biến cố A xảy ra là
P(
A
) =
Số kết quả thuận lợi cho A
=
m
.
Tổng số kết quả
n
Ví dụ 1.1.6. Giả sử hai con xúc xắc là cân đối và đồng chất.
1.
Tính xác suất của các biến cố A, B, C, D, E.
2.
Tính xác suất của các biến cố C ∩ D, C ∪ D, C \ D, D \ C.
1.1.7 Tính chất của xác suất
•
Với mọi biến cố A:
0 ≤ P(A) ≤ 1.
•
Với mọi biến cố xung khắc A và B:
•
Với mọi biến cố A:
P(A ∪ B) = P(A) + P(B).
P
(
A
¯
)
= 1 − P(A).
1.1.8
Định nghĩa xác suất theo thống kê
Thực hiện lặp đi lặp lại phép thử n lần và gọi m là số lần biến cố A xuất hiện trong n lần thử.
m
• Tỉ
số
được gọi là xác suất thực nghiệm của biến cố A trong n lần thử.
n
m
•
Nếu xác suất thực
nghiệm
hội tụ đến một giá trị p
0
nào đó thì ta nói p
0
là xác suất của
n
iến cố A theo nghĩa thống kê.
(
•
1.2
Sự độc lập
Tung một đồng xu hai lần. Nếu biết được kết quả lần gieo thứ nhất thì có đoán được kết quả
lần gieo thứ hai hay không?
1.2.1
Hai biến cố độc lập
Hai biến cố A và B được gọi là độc lập nếu việc A có xảy ra hay không cũng không ảnh
hưởng tới khả năng xảy ra của B và ngược lại. Theo xác suất thì
P(A ∩ B) = P(A)P(B).
Ví dụ 1.2.1. Tung một đồng xu hai lần. Gọi A và B lần lượt là biến cố lần tung thứ nhất và thứ
hai xuất hiện mặt sấp thì A và B là hai biến cố độc lập.
Mệnh đề 1.2.2. Nếu A và B độc lập thì các cặp biến cố sau cũng độc lập:
•
A
¯
và B;
•
A và
B
¯
;
•
A
¯
và
B
¯
.
1.2.2
Dãy biến cố độc lập
Dãy biến cố A
1
, A
2
, . . . , A
n
được gọi là độc lập nếu việc một biến cố A
i
nào đó trong dãy có
xảy ra hay không cũng không ảnh hưởng tới khả năng xảy ra của các biến cố còn lại và ngược
lại. Theo xác suất thì
P(A
i
1
∩ A
i
2
∩ . . . ∩ A
i
k
) = P(A
i
1
)P(A
i
2
) . . . P(A
i
k
),
với mọi 2 ≤ k ≤ n, mọi 1 ≤ i
1
< i
2
< . . . < i
k
≤ n.
Ví dụ 1.2.3. Gieo hú hoạ một con xúc xắc n lần, gọi A
k
là biến cố lần gieo thứ k được mặt 6
chấm. Khi đó A
1
, A
2
, . . . , A
n
là dãy các biến cố độc lập.
1.2.3 Dãy phép thfi Bernoulli
Một dãy phép thử được gọi là dãy phép thử Bernoulli nếu
•
Kết quả của mỗi phép thử hoặc là thành công, hoặc là thất bại.
•
Xác suất thành công của mỗi lần thử đều bằng nhau.
•
Kết quả của từng lần thử là dãy biến cố độc lập.
0,
8
Ví
dụ:
•
Gieo 3 hạt giống và quan sát sự nảy mầm của mỗi hạt.
Lần lượt chọn ngẫu nhiên hồ sơ sức khoẻ của 10 trẻ 4 tuổi và kiểm tra xem trẻ có bị suy
dinh dưỡng hay không?
Ví dụ 1.2.4. Gieo 3 hạt giống. Xác suất nảy mầm của mỗi hạt là 0,8. Tính xác suất để
1.
Cả 3 hạt đều nảy mầm.
2.
Cả 3 hạt đều không nảy mầm.
3.
Có đúng 2 hạt nảy mầm.
Lời giải. Gọi A
k
là biến cố hạt thứ k này mầm, k = 1, 2, 3.
1.
Xác suất cả 3 hạt đều nảy mầm là
P(A
1
A
2
A
3
) = P(A
1
)P(A
2
)P(A
3
) = 0, 8
3
.
2.
Xác suất cả 3 hạt đều không nảy mầm là
P
(
A
¯
1
A
¯
2
A
¯
3
)
=
P
(
A
¯
1
)
P
(
A
¯
2
)
P
(
A
¯
3
)
= 0, 2
3
.
3.
Xác suất có đúng 2 hạt nảy mầm là
P
(
A
¯
1
A
2
A
3
)
+
P
(
A
1
A
¯
2
A
3
)
+
P
(
A
1
A
2
A
¯
3
)
= 3 ×
2
× 0, 2.
1.2.4 Công thfíc xác suất nhị thfíc
Gọi p là xác suất thành công trong mỗi lần thử.
Xác suất để có đúng k lần thành công trong n lần thử độc lập là
Luyện
tập
k
k
C
n
p
(1 −
p)
n−
k
, 0 ≤ k ≤ n.
1.2.1.
Tỉ lệ trẻ 4 tuổi bị suy dinh dưỡng trong một cộng đồng là 5%. Lần lượt chọn ngẫu nhiên
hồ sơ sức khoẻ của 10 trẻ 4 tuổi. Tính xác suất của các biến cố
1.
Cả 10 trẻ đều không bị suy dinh dưỡng.
2.
Có đúng 2 trẻ bị suy dinh dưỡng.
3.
Có ít nhất 2 trẻ bị suy dinh dưỡng.
1.2.2.
Trong trò chơi "Bầu, cua, cá, cọp, gà, tôm" nhà cái sẽ gieo ba con xúc xắc. Mỗi con xúc
xắc
sáu mặt được dán bởi sáu hình "Bầu, cua, cá, cọp, gà, tôm". Người chơi sẽ chọn một hình
để đặt cược (chẳng hạn hình cá).
1.
Tính xác suất để có 3 mặt cá xuất hiện.
•
2.
Tính xác suất để không có mặt cá nào.
3.
Tính xác suất để có ít nhất 1 mặt cá.
1.3
Biến ngẫu nhiên rời rạc
1.3.1
Định nghĩa
Biến ngẫu nhiên là một quan sát nhận giá trị bằng số kết quả của phép thử.
Ví dụ 1.3.1.
1. Tung hai đồng xu, số mặt sấp xuất hiện là một biến ngẫu nhiên.
2.
Gieo hai con xúc xắc, tổng số chấm xuất hiện là một biến ngẫu nhiên.
3.
Gieo hai con xúc xắc, tích số chấm xuất hiện là một biến ngẫu nhiên.
4.
Một người đi thi cho đến khi đỗ thì số lần thi của người này cũng là biến ngẫu nhiên.
Ví dụ 1.3.2. Gieo hai đồng xu cân đối và đồng chất. Gọi X là số mặt sấp xuất hiện.
1.
Biến ngẫu nhiên X nhận các giá trị nào?
2.
Hãy tính xác suất để X nhận mỗi giá trị chỉ ra ở trên.
Lời
giải. 1. Biến ngẫu nhiên X nhận các giá 0, 1, 2
2.
Không gian mẫu
ta có
Ω = {SS, SN, NS, NN }.
P[X = 0] =
1
, P[X = 1] =
2
=
1
, P[X = 2] =
1
.
4 4 2 4
3.
Do kết quả của hai đồng xu là độc lập và xác suất để xuất hiện mặt sấp là 1/2 nên ta
cũng có thể tính các xác suất trên bằng công thức xác suất nhị thức.
Ta có bảng sau gọi là bảng phân phối xác suất của X.
x
P[X = x]
0 1 2
1 1 1
4 2 4
2
√
1 2
+
x
k
p
2
1.3.2
Phân phối của biến ngẫu nhiên
X được gọi là bnn rời rạc nếu nó nhận các giá trị x
1
, x
2
, . . .
Kí hiệu p
k
= P[X = x
k
] với k = 1, 2, . . .
Bảng phân phối của X:
Chú ý:
1.3.3 Các số đặc trưng
p
1
+ p
2
+ . . . + p
k
= 1.
Để đánh giá biến ngẫu nhiên X, ta thường dùng các giá trị sau
1.
Kỳ
vọng:
E[X] = x
1
p
1
+ x
2
p
2
+ · · · + x
k
p
k
.
2.
Phương sai: V ar(X) = x
2
p
1
+ x
2
p
2
+ · · ·
k
− (E[X]) .
3.
σ(X) = V ar(X) là độ lệch chuẩn của X.
Với mỗi hàm số ϕ : R → R ta có
E[ϕ(X)] = ϕ(x
1
)p
1
+ ϕ(x
2
)p
2
+ · · · + ϕ(x
k
)p
k
.
Ví dụ 1.3.3. Cho biến ngẫu nhiên X và Y có phân phối xác suất như sau:
X
-2 -1
1 2
P 0, 2 0, 3 0, 3 0, 2
Y
-
20
-1
1 20
P 0, 2 0, 3 0, 3 0, 2
1.
Hãy tính kì vọng và phương sai của X và của Y .
2.
Tính xác suất X ≥ 0 và xác suất Y ≤ 1.
Lời giải. E[X] = E[Y ] = 0, V ar(X) = 2, 2, V ar(Y ) = 320, 6. Nhận xét: X và Y có giá trị trung
bình
như nhau nhưng độ phân tán của Y cao hơn so với độ phân tán của X.
P[X ≥ 0] = P[X = 1] + P[X = 2] = 0, 5.
P[Y ≤ 1] = 1 − P[Y > 1] = 1 − P[Y = 20] = 0, 8.
1.3.4
Ý nghĩa của kỳ vọng và phương sai
•
Kỳ vọng đặc trưng cho giá trị trung bình mà biến ngẫu nhiên có thể nhận.
Phương sai đặc trưng cho độ phân tán của giá trị của biến ngẫu nhiên xung quanh giá
trị trung bình của nó. Độ phân tán của biến ngẫu nhiên càng rộng thì phương sai càng
lớn.
xx
1
x
2
P[X = x]p
1
p
2
· ·
·
· ·
·
x
k
p
k
•
n
2 2
2
2
∫
b
1.3.5
Phân phối nhị thfíc
Gọi X là số phép thử thành công trong dãy n phép thử Bernoulli.
P[X = k] = C
k
p
k
(1 − p)
n−k
, k = 0, 1, . . . , n.
X có phân phối nhị thức, kí hiệu là B(n, p).
E[X] = np, V ar(X) = np(1 − p).
1.3.6 Tính chất của kỳ vọng và phương sai
Với mọi số thực a, b, c và mọi bnn X và Y :
• E[c] = c.
• E[aX + bY ] = aE[X] + bE[Y ].
•
Nếu X ≥ Y thì E[X] ≥ E[Y ].
•
V ar(X) = E[(X − E[X]) ] = E[X ] − (E[X]) .
• V ar(X + c) = V ar(X).
•
V ar(aX) = a V ar(X).
1.4
Biến ngẫu nhiên liên tục và Phân phối chuẩn
1.4.1
Biến ngẫu nhiên liên tục
Trên thực tế có nhiều đại lượng ngẫu nhiên nhận giá trị là các số thực
•
Cân nặng của một trẻ sơ sinh.
•
Thời gian bạn đi từ nhà đến trường mỗi ngày.
•
Chiều cao của cây bạch đàn 1 năm tuổi.
Ta gọi mỗi đại lượng trên là một biến ngẫu nhiên liên tục.
1.4.2 Hàm mật độ
Hàm
f
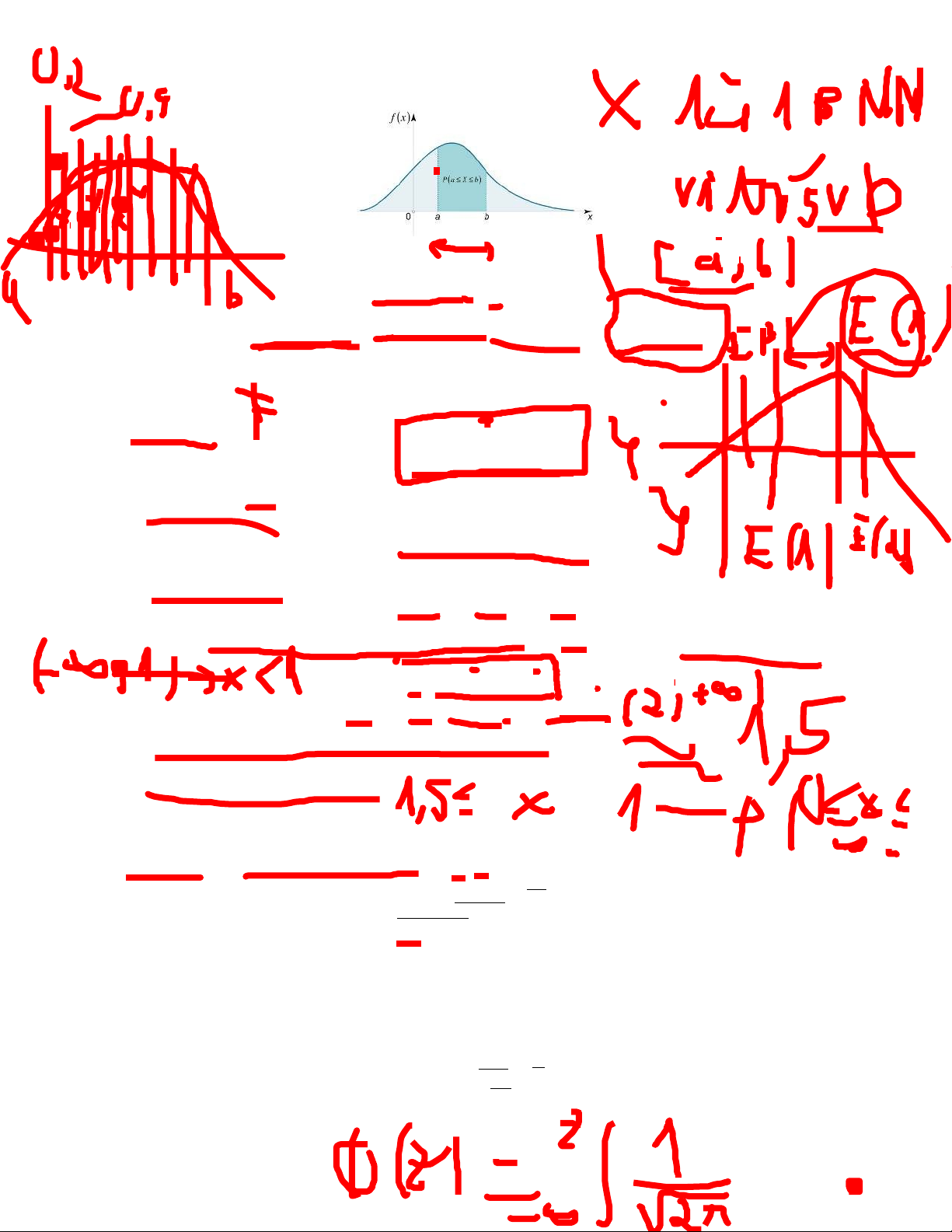
: R → [0, ∞) được gọi là hàm mật độ của biến ngẫu nhiên liên tục X nếu
với mọi số thực a <
b.
P[a < X < b]
=
f
(x)dx,
a
(
(µ, σ
)
√
√
P[a ≤ X ≤ b] = P[a < X ≤ b] = P[a ≤ X
< b] =
1.4.3 Các số đặc trưng
b
f
(x)dx.
a
•
Kỳ
vọng
E[X]
=
∞
xf (x)dx.
−∞
• Kỳ vọng của X
E[X
2
]
=
∞
2
x
f
(x)dx.
−∞
•
Phương sai
2 2
V ar(X) = E[X ] − (E[X]) .
Ví dụ 1.4.1. Thời gian mỗi lần Lan đi từ nhà đến quê nội (đơn vị: giờ) là một đại lượng ngẫu nhiên
X có hàm mật độ
f
(
x
) =
1
nếu 1 ≤ x ≤ 2,
0 nếu x < 1 hoặc x > 2.
1.
Tính xác suất để Lan đi từ nhà đến quê nội hết hơn 90 phút.
2.
Tính kì vọng và phương sai của X.
1.4.4
Phân phối chuẩn
Bnn X được gọi là có phân phối chuẩn N
2
nếu hàm mật độ của X xác định bởi
Ta tính được
1
f (x) =
e
2πσ
2
E[X] = µ và
—
x
2
2σ
2
.
2
V ar(X) = σ .
Khi µ = 0 và σ = 1 thì ta nói X có phân phối chuẩn tắc.
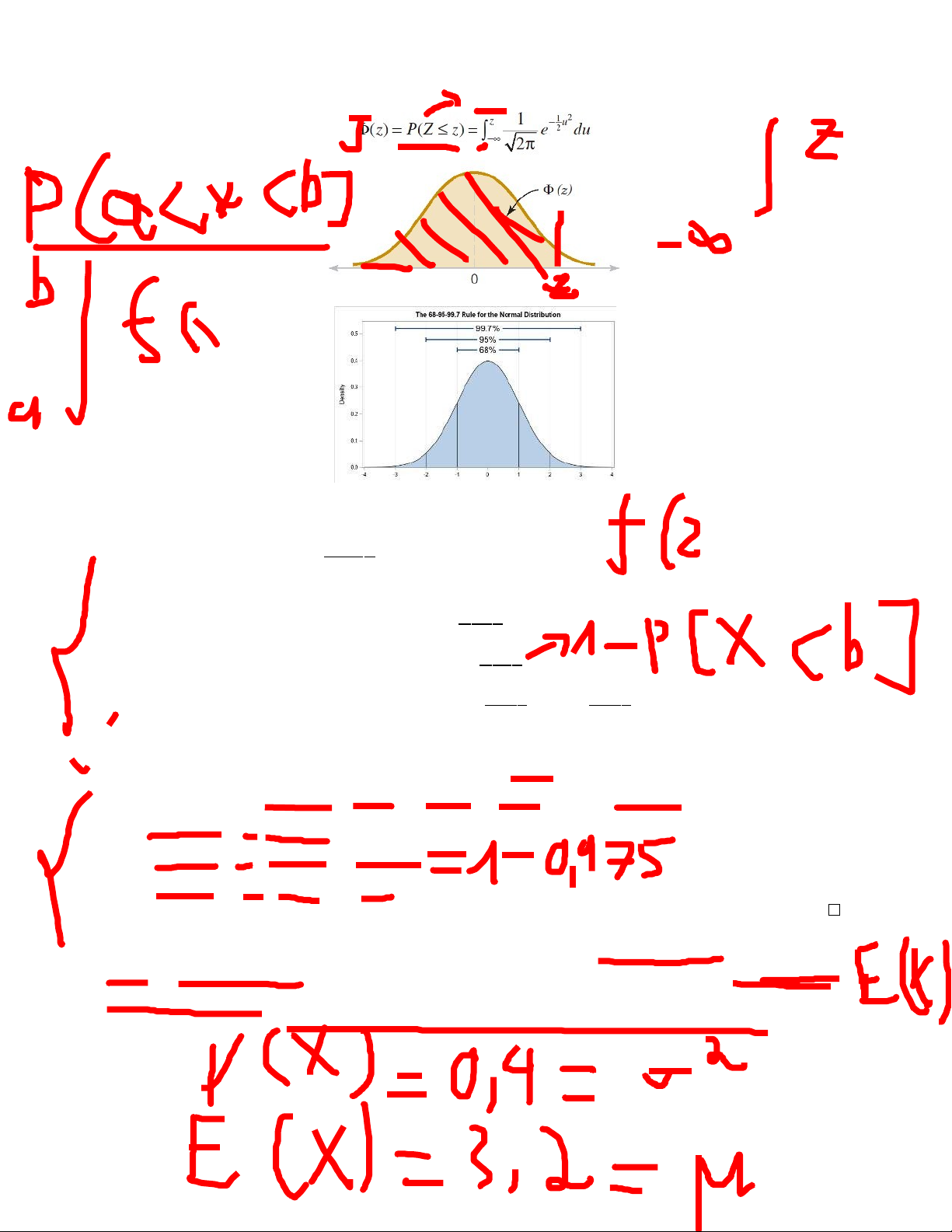
Hàm Φ xác định như sau được gọi là hàm phân phối chuẩn tắc
Φ(z) =
z
1
e
−∞
2π
—
x
2
2
dx.
Hàm Φ đóng vai trò quan trọng trong thống kê. Tuy nhiên vì không tính được trực tiếp nên
ta sẽ dùng bảng để tra giá trị của nó.
∫
∫
2
∫
∫
—
1.4.5
Tính chất của phân phối chuẩn
1)
Nếu X ∼
N
Do đó
(µ,
σ
2
)
thì
X
−
µ
sẽ có phân phối chuẩn tắc.
σ
P[X < a] = Φ(
a
−
µ
)
σ
P[X > b] = 1 Φ(
b
−
µ
)
σ
P[a <
X
< b] = Φ(
b
−
µ
) − Φ(
a
−
µ
)
σ σ
2)Φ(−x) = 1 − Φ(x).
Ví dụ 1.4.2. Cho biết Φ(1, 96) = 0, 975 và Φ(2, 58) = 0, 995, hãy tính Φ(−1, 96) và Φ(−2, 58).
Lời giải. Ta sử dụng tính chất của phân phối chuẩn tắc Φ(−x) = 1 − Φ(x) thì
• Φ(−1, 96) = 1 − Φ(1, 96) = 0, 025.
• Φ(−2, 58) = 1 − Φ(2, 58) = 0, 005.
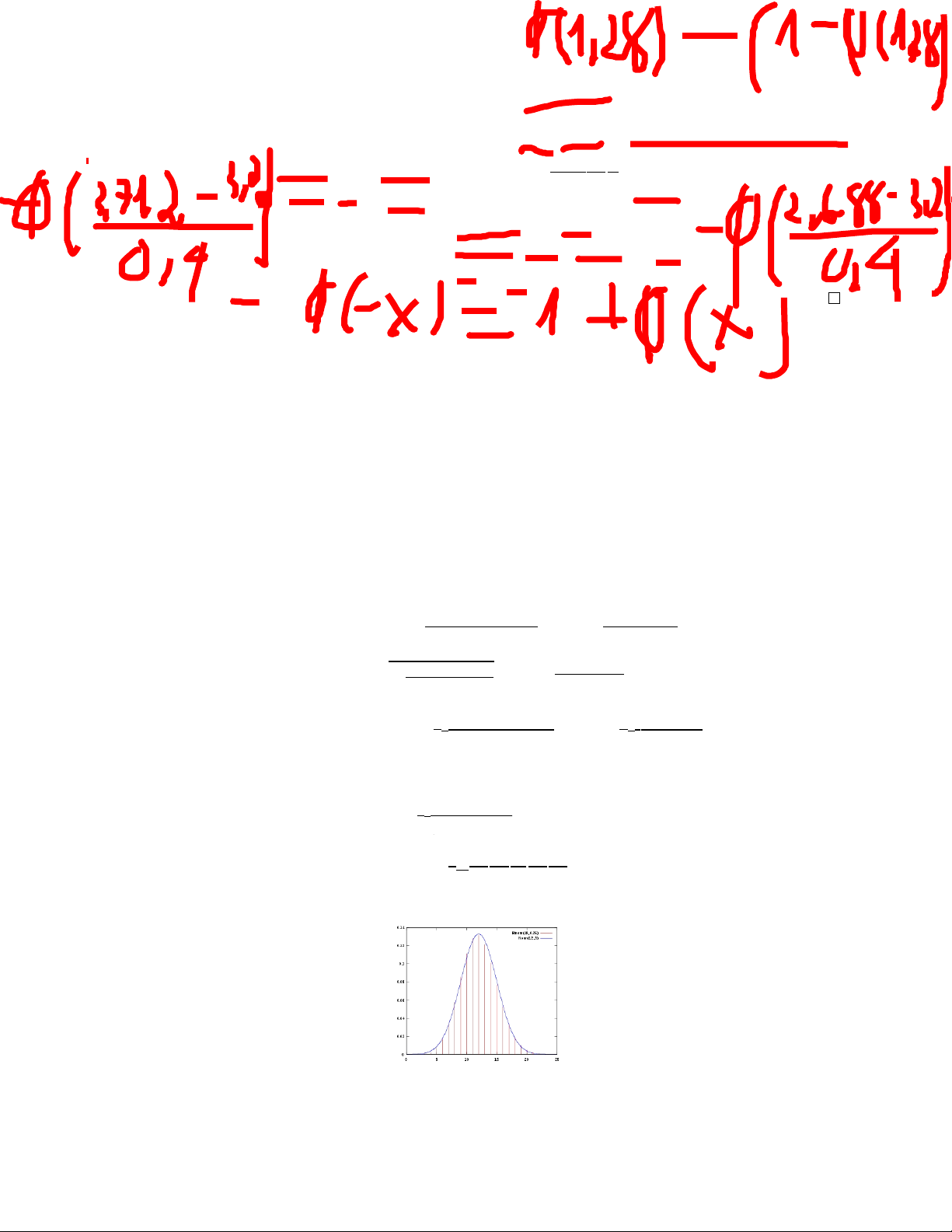
Ví dụ 1.4.3. Trọng lượng trẻ sơ sinh là một biến ngẫu nhiên có phân phối chuẩn với trung
bình
3,2kg và độ lệch tiêu chuẩn 0,4kg. Một trẻ sơ sinh được gọi là bình thường nếu có trọng
lượng từ
2,688kg đến 3,712kg. Tính xác suất để một đứa trẻ sơ sinh có trọng lượng bình
thường.
√np(1 − p)
2
−
30
0
30
0
√
P[
X
=
k
] ≈ Φ
k + 0 , 5
−
np
!
−
Φ
k
−
0 , 5
−
np
!
√
P[
k
1
≤
X
≤
k
2
] ≈ Φ
k
2
+ 0 , 5
−
np
!
−
Φ
k
1
−
0 ,
5
−
np
!
k
2
+ 0 , 5 −
np
!
Lời giải. Gọi X là trọng lượng một trẻ sơ sinh, X
là
N (3, 2; (0, 4) ). Xác suất để 1 trẻ bình thường
P(2, 688 < X < 3, 712) = P1, 28 <
X
− 3
,
2
< 1, 28
0, 4
= Φ(1, 28) − Φ(−1, 28)
= 2Φ(1, 28) − 1 = 2 × 0, 9 − 1
= 0, 8.
1.4.6
Xấp xỉ phân phối nhị thfíc bằng phân phối chuẩn
Ví dụ 1.4.4. Trong một thành phố có 40% người dân có mức thu nhập cao. Chọn ngẫu nhiên
300 người (chọn từng người).Tính xác xuất để trong 300 người được chọn có đúng 140 người
lương cao?
Theo công thức của phân phối nhị thức, xác suất để có 140 người thu nhập cao trong 300
người là
C
140
(0, 4)
140
(0, 6)
160
Khi sử dụng máy tính bỏ túi thông thường, kết quả sẽ hiện là error! Có điều này là do C
140
là số
quá lớn còn (0, 4)
140
lại là số quá nhỏ nên máy tính không hiển thị được.
Mệnh đề 1.4.5. Giả sử X có phân phối nhị thức B(n, p). Khi n lớn thì
np(1 − p)
1
np(1 − p)
(k − np)
2
≈
√
2πnp(1 − p)
exp
−
np(1 −
p)
,
P[X ≤
k
2
] ≈
Φ
√
np(1 − p)
√
np(1 − p)
,
√
np(1 − p)
P[X ≥ k
1
] ≈ 1
−
Φ
k
1
−
0
,
5
−
np
!
.
~
−
−
−
√
2
1
Ví dụ 1.4.6. Gọi X là số người có mức lương cao trong 300 người được chọn. Ta có np = 300 ×
0, 4 = 120 và np(1 − p) = 72. Xác suất để X nhận giá trị 140 là
P(X = 140) = P(139, 5 ≤ X < 140, 5)
140 , 5 120
≈ Φ
√
72
139 , 5 120
—
Φ
√
72
≈ Φ(2, 42) − Φ(2, 30)
≈ 0, 9920 − 0, 9893 = 0, 0027.
Ví dụ 1.4.7. Một loại hạt giống có xác suất nảy mầm là 0,7. Tìm xác suất để trong 100 hạt giống
có
1.
Có hơn 65 hạt nảy mầm.
2.
Ít hơn 72 hạt nảy mầm.
3.
Có đúng 70 hạt nảy mầm.
Lời giải. Gọi X là số hạt nảy mầm trong 100 hạt, X có phân phối B(n = 100; p = 0, 7). Ta có
np = 70 và np(1 − p) = 21.
65 , 5 −
70
2.
P[X < 72] ≈
Φ
71 , 5
70
√
21
≈ Φ(0, 33).
3. P[X = 70] = P[69, 5 ≤
X
< 70, 5] ≈ 2Φ(0, 11) − 1.
1. P[X > 65] ≈ 1
−
Φ
= Φ(0,
98).
Bấm Tải xuống để xem toàn bộ.