











Preview text:
BÀI TẬP XÁC SUẤT & THỐNG KÊ XÃ HỘI HỌC
Khoa Toán tin
Trường Đại học Sư Phạm Hà Nội Hà Nội, tháng 01 năm 2020
MỤC LỤC
- Bài tập xác suất 3
- Bài tập thống kê 7
BÀI TẬP XÁC SUẤT
Định nghĩa xác suất
Bài 1. Gieo ngẫu nhiên một con xúc xắc cân đối và đồng chất. Tính xác suất của các biến cố sau:
A: "Mặt chẵn xuất hiện";
B: "Xuất hiện mặt có số chấm chia hết cho 3"; C: "Xuất hiện mặt có số chấm không bé hơn 3".
Bài 2. Gieo ngẫu nhiên một con xúc xắc cân đối và đồng chất hai lần một cách độc lập. Tính xác suất của các biến cố sau:
A: "Số chấm trong hai lần gieo bằng nhau"; B: "Tổng số chấm trong hai lần gieo bằng 8".
Bài 3. Từ một hộp chứa ba quả cầu trắng và hai quả cầu đen, lấy ngẫu nhiên đồng thời hai quả. Hãy tính xác suất sao cho hai quả lấy ra cùng màu.
Bài 4. Một khách sạn có 6 phòng đơn. Có 10 khách đến thuê phòng trong đó có 6 nam và 4 nữ. Người quản lí chọn ngẫu nhiên 6 người. Tính xác suất để:
- Cả 6 người đều là nam.
- Có 4 nam và 2 nữ.
- Có ít nhất 2 nữ.
Bài 5. Lấy ngẫu nhiên ra 6 lá bài từ bộ bài 52 con. Tìm xác suất của các biến cố sau:
- Lấy được 4 lá bài màu đỏ
- Lấy được 1 lá cơ
- Lấy được 1 lá Át, 3 lá K và 2 lá chín.
Bài tập Xác suất - Thống kê xã hội học
Sự độc lập
Bài 6. Gieo ngẫu nhiên một con xúc xắc cân đối đồng chất hai lần. Gọi A là biến cố lần thứ nhất xuất hiện mặt 6 và B là biến cố lần thứ hai xuất hiện mặt 6. Hai biến cố A và B có độc lập với nhau hay không?
Bài 7. Hai sinh viên An và Bình thi môn Thống kê xã hội học. Khả năng đạt của mỗi người tương ứng là 0,85 và 0,95. Tìm xác suất để xảy ra các tình huống sau:
- Cả hai cùng đạt.
- Không ai đạt.
- Có đúng 1 người đạt.
- Có ít nhất một người đạt.
Bài 8. Một bài thi trắc nghiệm gồm 10 câu hỏi, mỗi câu hỏi cho 4 câu trả lời, trong đó chỉ có 1 câu đúng. Giả sử mỗi câu trả lời đúng được 1 điểm, trả lời sai hoặc không trả lời không có điểm. Một học sinh kém làm bài bằng cách chọn hú họa. Tính xác suất để học sinh này:
- Được 10 điểm.
- Được 0 điểm
- Được ít nhất 9 điểm.
- Được không quá 2 điểm.
Biến ngẫu nhiên rời rạc
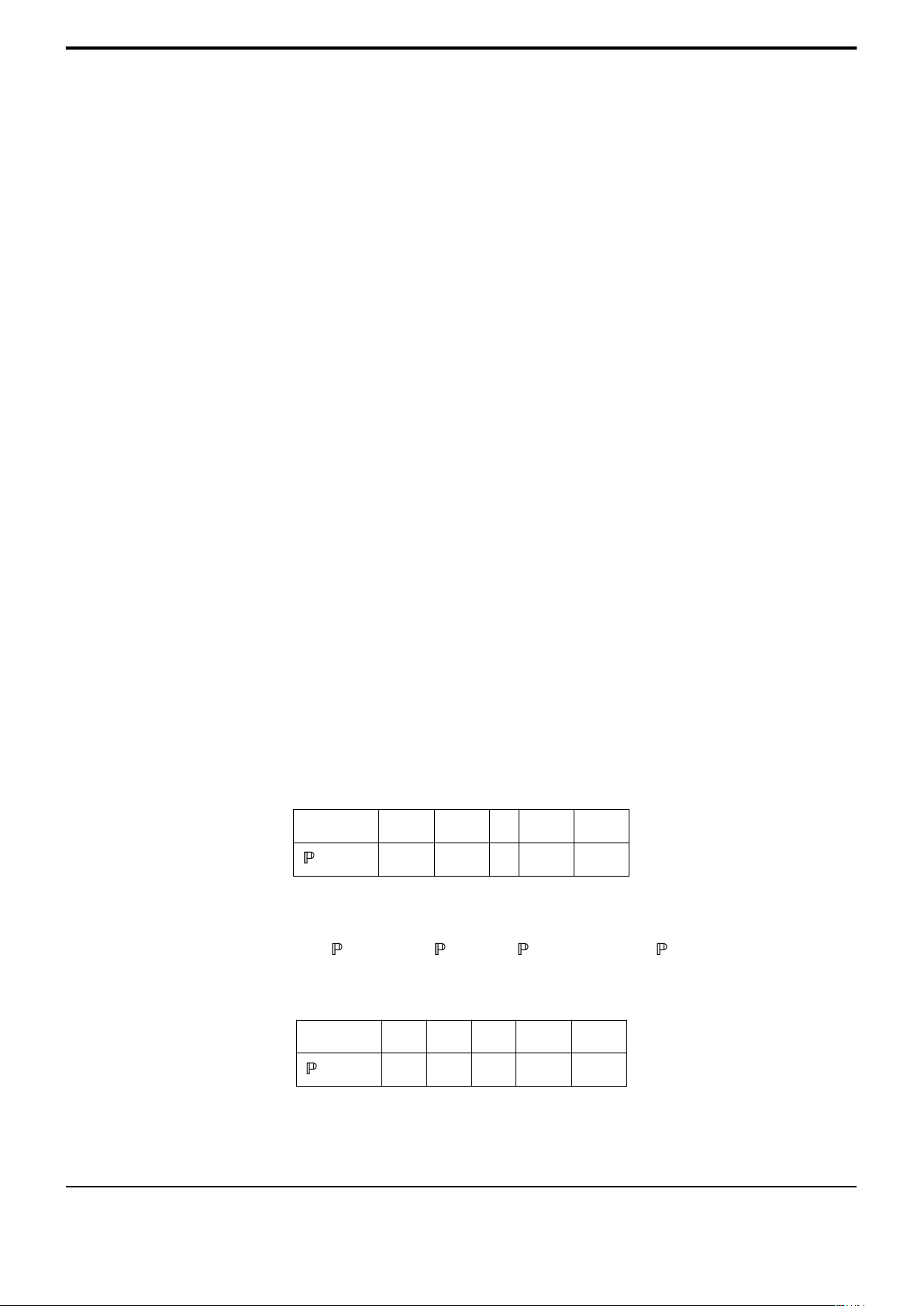
Bài 9. Cho biến ngẫu nhiên X có bảng phân phối xác suất:
X | 4 | 5 | 6 | 7 | 8 |
| 0,15 | 0,35 | a | 0,25 | 0,15 |
- Hãy tìm giá trị của a.
- Hãy tính các xác suất sau:
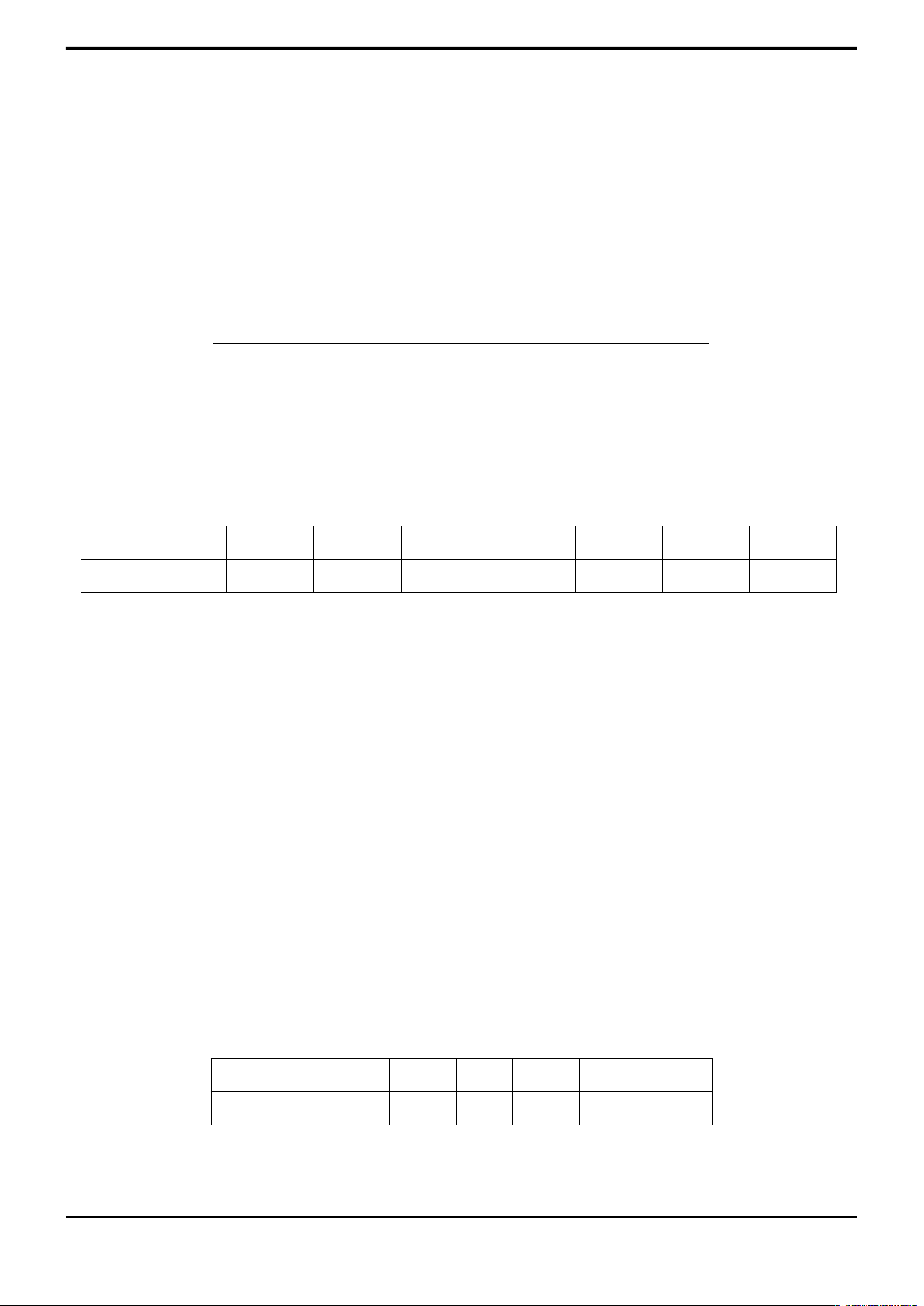
 [X < 7, 5];
[X < 7, 5];  [X > 8];
[X > 8];  [4 ≤ X ≤ 6, 5];
[4 ≤ X ≤ 6, 5]; 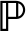 [5 < X < 6].
[5 < X < 6].
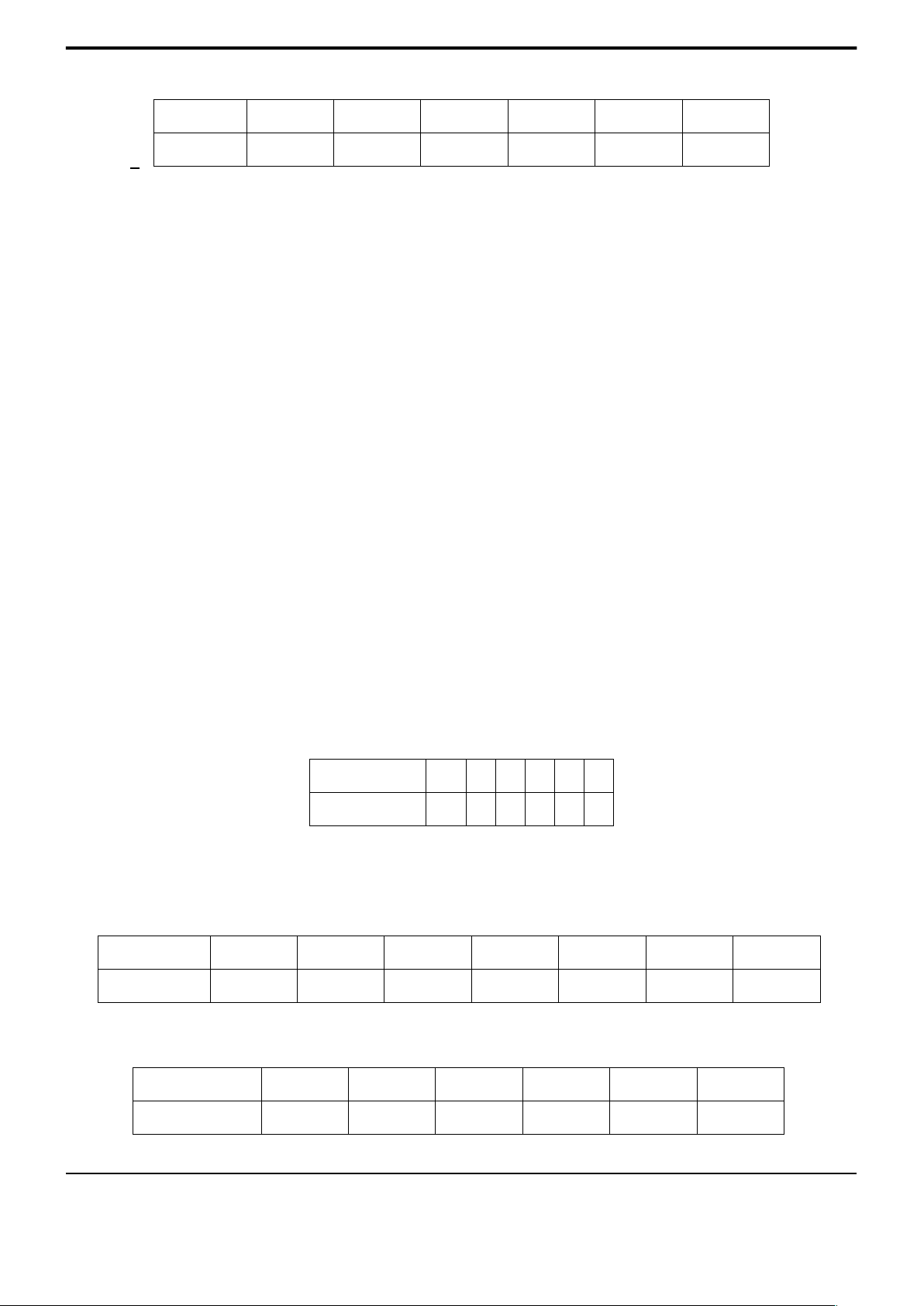
Bài 10. Cho biến ngẫu nhiên X có bảng phân phối xác suất:
X | 0 | 1 | 2 | 3 | 4 |
| 0,1 | 0,2 | 0,3 | 0,25 | 0,15 |
- Tìm kì vọng và phương sai của X .
- Tìm kì vọng của Y = X 2 + 3.
4
Bài tập Xác suất - Thống kê xã hội học
Bài 11. Xạ thủ 1 có khả năng bắn trúng bia là 0,8; xạ thủ 2 có khả năng bắn trúng bia là 0,7. Mỗi người bắn vào bia 1 lần. Gọi X là tổng số phát bắn trúng của cả 2 người. Lập bảng phân phối của X . Tính E[X ], V ar(X ).
Bài 12. Một người đi từ nhà đến cơ quan phải qua 3 ngã tư. Xác suất gặp đèn đỏ tương ứng tại các ngã tư này là 0,2; 0,25 và 0,3. Giả sử mỗi lần gặp đèn đỏ, người đó phải dừng chờ trên đường mất 2 phút. Hỏi khi đi từ nhà đến cơ quan, người đó phải dừng chờ trên đường trung bình mất bao nhiêu phút?
Bài 13. Trung bình trong 100 người thì có 7 người mang nhóm máu O âm tính. Chọn ra ngẫu nhiên 6 người. Tính xác suất:
- Có đúng 2 người mang nhóm máu O âm tính.
- Có không ít hơn 2 người mang nhóm máu O âm tính.
Bài 14. Trung bình gieo 1000 hạt giống thì có 650 hạt nảy mầm. Chọn ngẫu nhiên ra 12 hạt giống để gieo thử nghiệm. Tìm số hạt nảy mầm có xác suất xảy ra cao nhất?
Bài 15. Một nhà máy sản suất sản phẩm với tỉ lệ phế phẩm là 7%. Quan sát ngẫu nhiên n sản phẩm do máy làm ra. Gọi X là số phế phẩm trong số n sản phẩm này. Xác định phân phối xác suất của X . Cần chọn n ít nhất là bao nhiêu để biến cố "có ít nhất 1 phế phẩm trong n sản phẩm quan sát" có xác suất không thấp hơn 0,9?
Phân phối chuẩn
Bài 16. Chiều cao của nam giới đã trưởng thành là một biến ngẫu nhiên X có phân phối chuẩn N (163; 25).
- Tính tỉ lệ nam giới trưởng thành cao từ 160cm đến 170cm.
- Chọn ngẫu nhiên 1 nam giới, tìm xác suất để chọn được nam giới cao trên 165cm.
- Tìm xác suất để khi chọn ngẫu nhiên ra 5 nam giới thì có ít nhất 1 người cao trên 165cm.
Cho biết Φ(0, 4) = 0, 6554; Φ(0, 6) = 0, 7257; Φ(1, 4) = 0, 9192.
Bài 17. Chiều cao của học sinh nam (tính theo đơn vị cm) ở một trường học là biến ngẫu nhiên có phân phối chuẩn với độ lệch tiêu chuẩn 5,25 cm. Chọn ngẫu nhiên 200 học sinh nam của trường, đo chiều cao thấy có 57 học sinh có chiều cao trên 170 cm. Xác định chiều cao trung bình của học sinh nam trường trung học trên.
Bài 18. Thời gian đi từ nhà tới trường của sinh viên An là 1 bnn T (đơn vị là phút) có phân phối chuẩn. Biết rằng 65% số ngày An đến trường mất hơn 20 phút và 8% số ngày mất hơn 30 phút.
- Tính thời gian đến trường trung bình của An và độ lệch chuẩn biết Φ(0, 3853) = 0, 65;
Φ(1, 405) = 0, 92.
Bài tập Xác suất - Thống kê xã hội học
- Giả sử An xuất phát từ nhà trước giờ vào học 25 phút. Tính xác suất để An bị muộn học biết Φ(0, 51) = 0, 695.
Bài 19. Chiều cao của 1 loại cây là 1 biến ngẫu nhiên có phân phối chuẩn. Trong 1 mẫu gồm 640 cây có 25 cây thấp hơn 18m và 110 cây cao hơn 24m.
- Tính chiều cao trung bình của cây và độ lệch chuẩn biết Φ(0, 9463) = 0, 8281; Φ(1, 762) =
0, 961.
- Ước lượng số cây có chiều cao trong khoảng từ 16m đến 20m trong 640 cây nói trên biết
Φ(0, 859) = 0, 8051; Φ(2, 665) = 0, 9964.
Bài 20. Một khách sạn có 200 phòng. Với mỗi khách đã đặt phòng, giả thuyết xác suất hủy phòng là 0,2. Lễ tân của khách sạn nên chấp nhận nhiều nhất bao nhiêu đề nghị đặt phòng để khi khách đã đặt phòng đến, xác suất không còn phòng không vượt quá 0,025.
6
BÀI TẬP THỐNG KÊ
Mẫu và các số đặc trưng mẫu
Bài 21. Một mẫu số liệu gồm n = 20 quan sát được cho trong bảng tần số sau:
x | 1 | 2 | 3 | 4 |
f | 3 | a | 2 | 1 |
Tìm giá trị của a.
Bài 22. Một mẫu số liệu được cho trong bảng tần suất như sau:
x | 1 | 2 | 3 | 4 |
fn | 0,3 | p | 0,2 | 0,1 |
Tìm giá trị của p.
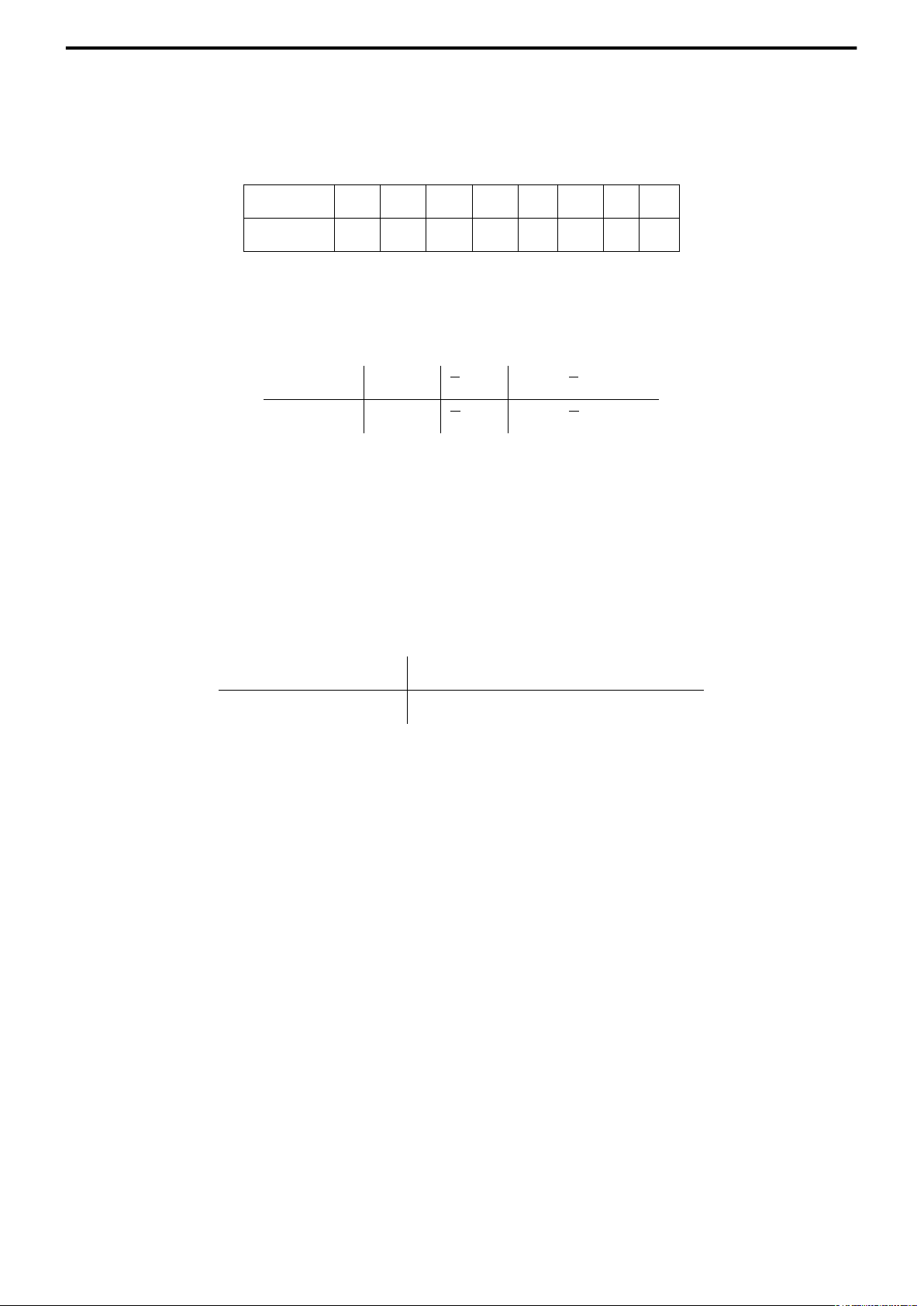
Bài 23. Cho mẫu số liệu gồm {1, 2, 6}. Hãy tính: X xi, X x2, X(xi − 3), X(xi − 3)2. Bài 24. Cho mẫu số liệu gồm {−1, 0, 1, 4}. Hãy tính: X xi, X x2, X(xi − 1), X(xi − 1)2. Bài 25. Đo lượng huyết tương của 8 người mạnh khỏe, ta được:
i
i
Tính n, x, s.
2, 86 3, 37 2, 75 2, 62 3, 50 3, 25 3, 12 3, 15
Bài 26. Kết quả thi môn xác suất-thống kê của sinh viên một khoa như sau:
X (điểm) | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
Số sinh viên | 20 | 10 | 25 | 30 | 60 | 20 | 20 | 8 | 5 | 2 |
Tính n, x, s.
Bài 27. Đo chiều cao ngẫu nhiên 35 cây bạch đàn trong rừng thu được kết quả:
Khoảng chiều cao (m) | 6,5-7,0 | 7,0-7,5 | 7,5-8,0 | 8,0-8,5 | 8,5-9,0 | 9,0-9,5 |
Số cây | 2 | 4 | 10 | 11 | 5 | 3 |
Tính n, x, s.
Bài tập Xác suất - Thống kê xã hội học
Bài 28. Đo lượng cholesterlemie (đơn vị mg%) của một số người, ta được
X (mg%) | 150-160 | 160-170 | 170-180 | 180-190 | 190-200 | 200-210 |
Số người | 2 | 4 | 5 | 6 | 4 | 3 |
Tính n, x, s.
Bài toán ước lượng tham số
Ước lượng khoảng cho giá trị trung bình (trường hợp mẫu lớn)
Bài 29. Hãy xây dựng một khoảng tin cậy 90% cho giá trị trung bình của quần thể dựa trên thông tin về một mẫu ngẫu nhiên cho trước như sau:
- n = 36; x¯ = 105, 2; s = 11, 2.
- n = 100; x¯ = 105, 2; s = 11, 2.
Giả sử phương sai quần thể đã biết là 11, 3.
Bài 30. Hãy xây dựng một khoảng tin cậy 99% cho giá trị trung bình của quần thể dựa trên thông tin về một mẫu ngẫu nhiên cho trước như sau:
- n = 49; x¯ = 17, 1; s = 2, 1.
- n = 169; x¯ = 17, 1; s = 2, 2.
Giả sử phương sai quần thể chưa xác định.
Bài 31. Để nghiên cứu tình trạng nghỉ học của học sinh ở một trường A vào năm học trước, người ta điều tra 40 học sinh và thu được bảng số liệu như sau:
X (ngày) | 0 | 1 | 2 | 3 | 4 | 5 |
Số học sinh | 24 | 7 | 5 | 2 | 1 | 1 |
Hãy xây dựng một khoảng tin cậy 90% về trung bình số ngày nghỉ học của học sinh trường này.
Bài 32. Theo dõi trọng lượng X của một giống Cam ta có bảng số liệu:
X ( gram) | 135-155 | 155-175 | 175-195 | 195-215 | 215-235 | 235-255 | 255-275 |
Số quả (ni) | 5 | 10 | 23 | 35 | 32 | 10 | 5 |
Với độ tin cậy 99%, xác định khoảng tin cậy cho trọng lượng trung bình của giống cam trên.
Bài 33. Quan sát chiều cao X (cm) của một số người, ta ghi nhận:
X (cm) | 140-145 | 145-150 | 150-155 | 155-160 | 160-165 | 165-170 |
Số người (ni) | 1 | 3 | 7 | 9 | 5 | 2 |
Với độ tin cậy 95%, xác định khoảng tin cậy cho chiều cao trung bình.
8
Bài tập Xác suất - Thống kê xã hội học
Bài 34. Số liệu định lượng của mẫu thuốc tiêm vitamin B12 tại một cơ sở thu được như sau:
Hàm lượng (γ/ml) | 94-96 | 96-98 | 98-100 | 100-102 | 102-104 |
Số ống | 4 | 8 | 15 | 12 | 3 |
Hãy xác định khoảng tin cậy về hàm lượng trung bình của lô thuốc trên với độ tin cậy 95%.
Bài 35. Khảo sát khối lượng của bộ óc người trên 50 tuổi, người ta thu được các số liệu sau:
KL (g) | 1175-1225 | 1225-1275 | 1275-1325 | 1325-1375 | 1375-1425 | 1425-1475 | 1475-1525 |
SL | 6 | 15 | 27 | 25 | 28 | 14 | 8 |
Tính khoảng tin cậy của trọng lượng trung bình bộ óc của người trên 50 tuổi với độ tin cậy 95%.
Ước lượng khoảng cho giá trị trung bình (trường hợp mẫu bé)
Bài 36. Một mẫu ngẫu nhiên được lấy từ một quần thể có phân phối chuẩn với độ lệch chuẩn là 5. Hãy xây dựng khoảng tin cậy 95% cho giá trị trung bình của quần txhể dựa trên các thông tin về mẫu số liệu như sau:
- n = 16; x¯ = 98; s = 5, 6.
- n = 9; x¯ = 98; s = 5, 6.
Bài 37. Một mẫu ngẫu nhiên được lấy từ một quần thể có phân phối chuẩn với phương sai chưa biết. Hãy xây dựng khoảng tin cậy 99% cho giá trị trung bình của quần thể dựa trên các thông tin về mẫu số liệu như sau:
- n = 18; x¯ = 386; s = 24.
- n = 7; x¯ = 386; s = 24.
Bài 38. Đo sức bền chịu lực của một loại ống thí nghiệm, người ta thu được bộ số liệu sau: 4500 6500 5200 4800 4900 5125 6200 5375
Từ kinh nghiệm nghề nghiệp người ta cũng biết rằng sức bền đó có phân phối chuẩn với độ lệch tiêu chuẩn σ = 300. Hãy xác định khoảng tin cậy 90% cho sức bền trung bình của loại ống trên.
Bài 39. Theo dõi huyết áp của 10 bệnh nhân bị choáng thu được kết quả (tính theo mmHg) như sau:
75 90 85 65 95 75 60 85 85 65
Giả sử huyết áp của người bệnh là biến ngẫu nhiên có phân phối chuẩn. Với độ tin cậy 95%, hãy xác định khoảng ước lượng cho giá trị trung bình về huyết áp của nhóm bệnh trên.
Ước lượng khoảng cho tỉ lệ
Bài 40. Hãy xây dựng khoảng tin cậy 90% cho tỉ lệ quần thể dựa trên thông tin về mẫu số liệu như sau:
Bài tập Xác suất - Thống kê xã hội học
b) n = 50; fn = 0, 7.
Bài 41. Để xác định tỉ lệ này mầm của một loại hạt giống, người ta gieo thử 300 hạt, thấy có 276 hạt nảy mầm. Với độ tin cậy 95% ta có thể nói tỉ lệ nảy mầm của lô hạt tối đa là bao nhiêu?
Bài 42. Trước bầu cử người ta phỏng vấn ngẫu nhiên 2000 cử tri thì thấy có 1380 người ủng hộ ứng cử viên K. Với độ tin cậy 95% hỏi ứng cử viên đó thu được tối thiểu bao nhiêu phần trăm phiếu bầu?
Bài 43. Cân thử 100 quả cam ta có bộ số liệu sau:
Khối lượng (g)
Số cam
32 33 34 35 36 37 38 39 40
2
3
15 26 28
6
8
8
4
- Hãy ước lượng khối lượng trung bình các quả cam với độ tin cậy 95%.
- Cam có khối lượng dưới 34g được coi là cam loại 2. Hãy xác định khoảng ước lượng cho tỉ lệ số cam loại 2 với độ tin cậy 90%.
Bài 44. Tiến hành đo chiều cao của các học sinh lớp 2 trường Kim Đồng ta có bảng số liệu:
Chiều cao (cm) | 112-114 | 114-116 | 116-118 | 118-120 | 120-122 | 122-124 | 124-126 |
Số học sinh | 8 | 12 | 20 | 26 | 30 | 14 | 10 |
- Với độ tin cậy 95%, tìm khoảng ước lượng chiều cao trung bình của học sinh lớp 2 trường Kim Đồng.
- Chọn ngẫu nhiên 250 học sinh lớp 2 trường Kim Đồng. Từ số liệu trên, với độ tin cậy 95%, có thể dự báo nhiều nhất bao nhiêu học sinh trong nhóm được chọn có chiều cao trên 120 cm?
Bài 45. Để xác định số cá trong một cái ao, người ta bắt lên 200 con, đánh dấu chúng rồi thả lại xuống hồ. Sau một thời gian, người ta lại bắt lên 500 con và thấy có 20 con cá đánh dấu của lần bắt trước. Dựa vào số liệu đó hãy ước lượng số cá có trong hồ với độ tin cậy 95%.
Bài 46. Để có thể dự đoán được số lượng chim thường nghỉ tại nhà mình, người chủ bắt 89 con, đem đeo khuyên cho chúng rồi thả đi. Sau một thời gian, ông bắt ngẫu nhiên được 120 con và thấy có 7 con có đeo khuyên. Hãy dự đoán số chim giúp ông chủ vườn với độ tin cậy 99%.
Vấn đề xác định cỡ mẫu
Bài 47. Tiến hành điều tra ngẫu nhiên trên 100 con bò, kết quả như sau:
X (sản lượng/ngày) | 7-9kg | 9-11 | 11-13 | 13-15 | 15-17 |
Số con bò | 10 | 24 | 42 | 16 | 8 |
- Sản lượng sữa trung bình một ngày của một con bò là bao nhiêu?
- Bao nhiêu % đàn bò cho sản lượng sữa trên 11kg trong ngày?
10
Bài tập Xác suất - Thống kê xã hội học
- Muốn độ tin cậy của kết luận là 99%, sai số khi nghiên cứu sản lượng trung bình không vượt quá 0,5kg thì cần phải điều tra bao nhiêu con bò?
- Muốn độ tin cậy của kết luận là 99%, sai số khi nghiên cứu tỉ lệ bò cho sản lượng trên 11kg/ngày không vượt quá 12% thì cần phải điều tra bao nhiêu con bò?
Bài 48. Để ước lượng xác suất mắc bệnh gan với độ tin cậy 90% và sai số không vượt quá 2% thì cần phải khám cho ít nhất bao nhiêu người, biết rằng tỉ lệ mắc bệnh gan thực nghiệm đã cho bằng 0,9.
Bài 49. Giả sử quan sát 100 người thấy có 20 người bị bệnh sốt xuất huyết. Hãy ước lượng tỉ lệ bệnh sốt xuất huyết với độ tin cậy 97%. Nếu muốn sai số ước lượng không quá 3% với độ tin cậy 95% thì phải quan sát ít nhất bao nhiêu người?
Bài 50. Một loại thuốc mới được đem thử điều trị cho 50 người bị bệnh B, kết quả có 40 người khỏi bệnh.
- Hãy ước lượng tỉ lệ khỏi bệnh nếu dùng thuốc đó điều trị với độ tin cậy 99%.
- Nếu ta muốn sai số ước lượng không quá 0,02 với độ tin cậy 95% thì cần quan sát bao nhiêu bệnh nhân?
Bài 51. Khảo sát về chiều cao X (cm) của trẻ em lứa tuổi 14-15 thu được số liệu sau:
X (cm) | dưới 137 | 137-139 | 139-141 | 141-143 | 143-145 | 145-147 | trên 147 |
Số trẻ (ni) | 56 | 112 | 93 | 155 | 121 | 82 | 57 |
Với độ tin cậy 95%, ước lượng chiều cao trung bình của đứa trẻ lứa tuổi 14-15. Muốn ước lượng này có độ chính xác tăng lên gấp 2 lần thì cần lấy một mẫu kích thước là bao nhiêu?
Bài 52. Tuổi thọ của một loại bóng đèn được biết theo phân phối chuẩn với độ lệch tiêu chuẩn là 100 giờ.
- Chọn ngẫu nhiên 100 bóng đèn để thử nghiệm, thấy mỗi bóng có tuổi thọ trung bình là 100 giờ. Hãy ước lượng tuổi thọ trung bình của bóng đèn do xí nghiệp A sản xuất với độ tin cậy là 95%.
- Với sai số của ước lượng tuổi thọ trung bình là 15 giờ, hãy xác định độ tin cậy.
- Để sai số của ước lượng tuổi thọ trung bình không quá 25 giờ với độ tin cậy là 95% thì cần phải thử nghiệm ít nhất bao nhiêu bóng?
Bài 53. Đo đường kính của một chi tiết máy do một máy tiện tự động sản xuất ta ghi nhận được số liệu sau:
X (mm) | 12.00 | 12.05 | 12.10 | 12.15 | 12.20 | 12.25 | 12.30 | 12.35 | 12.40 |
n | 2 | 3 | 7 | 9 | 10 | 8 | 6 | 5 | 3 |
- Hãy ước lượng đường kính trung bình với độ tin cậy 0,95.
- Nếu muốn sai số của ước lượng không quá 0,02 mm với độ tin cậy là 95% thì cần phải đo ít nhất bao nhiêu chi tiết máy?
Bài tập Xác suất - Thống kê xã hội học
Bài 54. Đem cân một số trái cây vừa thu hoạch, ta được kết quả sau:
X ( gam) | 200-210 | 210-220 | 220-230 | 230-240 | 240-250 |
Số trái | 12 | 17 | 20 | 18 | 15 |
- Hãy ước lượng trọng lượng trung bình với độ tin cậy 0,95 và 0,99. Nếu muốn sai số không quá 2gam với độ tin cậy 99% thì phải cân ít nhất bao nhiêu trái cây?
- Trái cây có trọng lượng lớn hơn 230 gam được xếp loại A. Hãy tìm khoảng ước lượng cho tỉ lệ trái cây loại A với độ tin cậy 0,95 và 0,99. Nếu muốn sai số ước lượng không quá 0,04 với độ tin cậy 0,99 thì phải cân ít nhất bao nhiêu trái cây?
12
Bài tập Xác suất - Thống kê xã hội học
Bài toán kiểm định giả thuyết
Bài toán kiểm định giả thuyết cho giá trị trung bình một mẫu
Bài 55. Đo lượng cholesterolemie (X mg%) trên một số người bình thường ta được bảng kết quả sau:
X | 125-149 | 150-174 | 175-199 | 200-224 | 225-249 | 250-274 | 275-299 | 300-324 |
n | 2 | 5 | 5 | 7 | 10 | 10 | 8 | 3 |
Cho hằng số sinh học trung bình về cholesterolemie là 225 mg%. Hỏi với mức ý nghĩa 5%, kết quả thực nghiệm trên có khác hằng số sinh học về cholesterolemie không?
Bài 56. Trong thập niên 80, trọng lượng trung bình của thanh niên là 48kg. Hiện nay, để xác định lại trọng lượng đó, người ta chọn ngẫu nhiên 100 thanh niên và đo được trọng lượng trung bình là 50kg với độ lệch tiêu chuẩn mẫu là 10kg. Với mức ý nghĩa 5%, có thể cho rằng trọng lượng thanh niên hiện nay phải chăng đã thay đổi?
Bài 57. Khảo sát trọng lượng X của trẻ em 6 tuổi ở một khu vực được kết quả:
X (kg) | 14-16 | 16-18 | 18-20 | 20-22 | 22-24 | 24-26 | 26-28 |
Số trẻ (ni) | 25 | 60 | 120 | 105 | 42 | 30 | 18 |
- Ở mức ý nghĩa 5% có thể kết luận rằng trọng lượng trung bình của trẻ em 6 tuổi ở khu vực này đạt trên 20,5 (kg) không?
- Với độ tin cậy 95%, hãy ước lượng xem có tối đa bao nhiêu trẻ em 6 tuối với trọng lượng không quá 20 (kg) khi ta tiến hành khảo sát 3000 trẻ em ở khu vực trên?
Bài 58. Đối với người Việt Nam, lượng huyết sắc tố trung bình là 138,3 g/l. Khám cho 80 công nhân ở nhà máy có tiếp xúc với hóa chất, thấy huyết sắc tố trung bình là 120g/l và độ lệch tiêu chuẩn là 15g/l. Từ kết quả trên, có thể kết luận lượng huyết sắc tố trung bình của công nhân nhà máy hóa chất này thấp hơn mức chung hay không? Cho mức ý nghĩa là α = 0, 05.
Bài 59. Theo dõi năng suất của giống ngô mới LVN9860 ta có bảng số liệu:
Năng suất (tạ/ha) | 48-50 | 50-52 | 52-54 | 54-56 | 56-58 | 58-60 | 60-62 |
Số thửa ruộng | 7 | 10 | 18 | 22 | 35 | 17 | 11 |
- Cho trồng giống Ngô mới LVN9860 trên 250 thửa ruộng khác nhau có cùng diện tích. Từ số liệu trên, với độ tin cậy 95%, có thể dự báo ít nhất bao nhiêu thửa ruộng sẽ cho năng suất đạt trên 56 tạ/ha?
- Có thông tin cho rằng năng suất trung bình của giống Ngô mới LVN9860 đạt 55 tạ/ha. Với mức ý nghĩa α = 0, 05, ta có thể chấp nhận thông tin đã nêu ra như trên không?
Bài 60. Trong điều kiện chăn nuôi bình thường, lượng sữa trung bình của một con bò là 14kg/ngày. Nghi ngờ điều kiện chăn nuôi kém đi làm cho lượng sữa giảm xuống, người ta điều tra ngẫu nhiên 25 con và tính được lượng sữa trung bình của 1 con trong 1 ngày là 12,5kg và độ lệch chuẩn là 2,5kg. Với mức ý nghĩa α = 0, 05, hãy kết luận điều nghi ngờ nói trên với giả thuyết lượng sữa bò là một biến ngẫu nhiên có phân phối chuẩn.
Bài tập Xác suất - Thống kê xã hội học
Bài 61. Trọng lượng trung bình khi xuất chuồng ở một trại chăn nuôi gà trước đây là 3,3kg/con. Năm nay người ta sử dụng một loại thức ăn mới, cân thử 14 con khi xuất chuồng ta được bảng số liệu sau:
3,25 2,50 4,00 3,75 3,80 3,90 4,02 3,60 3,80 3,82 3,40 3,75 4,00 3,50
Giả sử trọng lượng gà là biến ngẫu nhiên có phân phối chuẩn.
- Với mức ý nghĩa α = 0, 05, hãy cho kết luận về tác dụng của loại thức ăn này?
- Nếu trại chăn nuôi báo cáo trọng lượng trung bình khi xuất chuồng là 3,5kg/con thì có chấp nhận được không, với mức ý nghĩa là α = 0, 05.
Bài 62. Quan sát số hoa hồng bán ra trong một ngày của một cửa hàng hoa sau một thời gian, người ta ghi được số liệu sau:
Số hoa hồng
Số ngày
12 13 15 16 17 18 19
3
2
7
7
3
2
1
Giả sử số hoa bán ra trong ngày có phân phối chuẩn.
- Giả sử những ngày bán được từ 13 đến 17 đóa hồng là những ngày "bình thường". Hãy ước lượng tỉ lệ của những ngày bình thường của cửa hàng với độ tin cậy 90%.
- Sau khi tính toán, ông chủ của hàng nói rằng nếu trung bình một ngày không bán được 15 đóa hồng thì phải đóng cửa hàng. Dựa vào số liệu trên, hãy kết luận giúp ông chủ cửa hàng xem có nên tiếp tục bán hay không ở mức ý nghĩa α = 0, 05.
Bài toán kiểm định giả thuyết cho tỉ lệ một mẫu
Bài 63. Khám lao cho 100.000 người thấy 89 người bị lao. Xác suất bị lao là 0,001 có đúng không? Kiểm định 1 phía với α = 0, 05.
Bài 64. Kiểm tra chẩn đoán cho 500 người thấy 440 người được chẩn đoán đúng. Xác suất chẩn đoán đúng là 0,9 có đúng không? Kiểm định một phía với α = 0, 05.
Bài 65. Đo huyết sắc tố cho 50 công nhân nông trường thấy có 60% ở mức dưới 110g/l. Số liệu chung của khu vực này là 30% ở mức dưới 110g/l. Với mức ý nghĩa α = 0, 05, có thể kết luận công nhân nông trường có tỉ lệ huyết sắc tố dưới 110g/l cao hơn mức chung hay không?
Bài 66. Đầu năm bệnh viện A đưa ra một số cải tiến về phương pháp điều trị. Cuối năm tổng kết thấy số tử vong là 45 người. Trong khi đó, những năm trước số tử vong trung bình là 65 người. Hỏi với mức ý nghĩa α = 0, 05 cải tiến về phương pháp điều trị có đem lại kết quả không? Biết mỗi năm bệnh viện A điều trị khoảng 2000 ca.
14
Bài tập Xác suất - Thống kê xã hội học
Bài toán kiểm định giả thuyết cho giá trị trung bình hai mẫu
Bài 67. Hai loại thuốc A và B làm tim đập chậm được thử nghiệm trên 16 con mèo. Mỗi loại thuốc được thử trên 8 con. Kết quả về hiệu số nhịp đập của tim sau và trước khi dùng thuốc thu được:
Thuốc A | -22 | -14 | -36 | -28 | -8 | -22 | -8 | 2 |
Thuốc B | -14 | -12 | -22 | -30 | 10 | 0 | -8 | 24 |
Với mức ý nghĩa α = 0, 05, tác dụng của hai loại thuốc trên có khác nhau không?
Bài 68. Để so sánh điểm môn Toán của học sinh ở hai trường A và B, người ta lấy hai mẫu ngẫu nhiên gồm học sinh của hai trường để làm cùng một đề thi Toán. Kết quả được cho theo bảng sau:
Trường A n1 = 20 x = 43 X(x − x)2 = 1296
Trường B n2 = 17 y = 36 X( y − y)2 = 1388
Giả sử điểm thi Toán của học sinh cả hai trường đều tuân theo phân phối chuẩn với phương sai bằng nhau. Với mức ý nghĩa 5%, hãy kiểm định liệu có sự khác nhau về chất lượng học Toán của học sinh hai trường A và B không?
Bài 69. Các khách hàng của một chi nhánh ngân hàng được mời tham gia đánh giá chất lượng một dịch vụ chăm sóc mới. Các đánh giá của họ được qui ra theo "điểm hài lòng". Điểm số này tuân theo phân phối chuẩn. Hai mẫu ngẫu nhiên được lấy từ ngân hàng này cho kết quả điểm trước và sau chương trình chăm sóc như sau:
Trước khi thực hiện 126 93 114 107 98
Sau khi thực hiện 124 107 117 136 120 122
Kiểm định với mức ý nghĩa 5% cho giả thuyết "điểm trung bình của trước và và sau khi thực hiện chương trình là như nhau", với đối thuyết "điểm trung bình sau khi thực hiện chương trình là cao hơn".
Bài 70. Mỗi khóa diễn viên của một trường sân khấu sẽ được đánh giá bởi một nhóm các diễn viên có kinh nghiệm thông qua tổng điểm đánh giá. Gần đây, trường đưa vào thử nghiệm phương pháp đào tạo mới nhằm nâng cao chất lượng diễn xuất. Kết thúc đợt thử nghiệm, một mẫu ngẫu nhiên gồm 6 học viên đào tạo theo phương pháp cũ có điểm số là
243, 228, 220, 206, 230, 198,
và điểm số của mẫu ngẫu nhiên gồm 8 học viên đào tạo theo phương pháp mới là
235, 259, 227, 242, 238, 253, 221, 217.
Sử dụng tiêu chuẩn phù hợp, với mức ý nghĩa 5%, hãy kiểm định xem phương pháp mới có làm tăng điểm số trung bình của học viên hay không?
Bài 71. Để so sánh chất lượng hai loại bóng gôn, người ta đánh năm quả bóng mỗi loại bởi cùng một loại máy. Khoảng cách (đơn vị: mét) mà mỗi bóng đi được như sau:
Bài tập Xác suất - Thống kê xã hội học
Loại 1: 275, 286, 287, 271, 283.
Loại 2: 278, 274, 263, 265, 273.
Giả sử khoảng cách mà các bóng đi được tuân theo phân phối chuẩn với phương sai bằng nhau. Hãy kiểm định giả thuyết độ dài quãng đường trung bình hai loại bóng đi được là như nhau ở mức j nghĩa α = 0.05.
Bài toán kiểm định giả thuyết cho tỉ lệ hai mẫu
Bài 72. Người ta điều tra 250 người ở xã A thấy có 40 nữ và điều tra 160 người ở xã B thấy có 80 nữ. Hãy so sánh tỉ lệ nữ ở hai xã với mức j nghĩa 5%.
Bài 73. Để đánh giá tác dụng điều trị một loại bệnh bằng hai thuốc A,B, người ta cho 220 bệnh nhân dùng thuốc A và 140 bệnh nhân dùng thuốc B. Kết quả điều trị cho bởi bảng sau:
Kết quả điều trị | Thuốc A | Thuốc B |
Khỏi hoặc đã đỡ bệnh | 190 | 130 |
Không khỏi bệnh | 30 | 10 |
Với mức j nghĩa α = 5%, có thể khẳng định thuốc A có dụng điều trị tốt hơn thuốc B không?
Bài 74. Trong 90 người dùng DDT để ngừa bệnh ngoài da thì có 10 người nhiễm bệnh; trong 100 người không dùng DDT thì có 26 người mắc bệnh. Hỏi rằng với mức j nghĩa α = 0, 05, thuốc DDT có tác dụng ngừa bệnh ngoài da không?
Bài 75. Áp dụng hai phương pháp gieo hạt ta thấy: theo phương pháp A gieo 180 hạt thì có 150 hạt nảy mầm; theo phương pháp B gieo 250 hạt thì có 160 hạt nảy mầm. Hãy so sánh hiệu quả của hai phương pháp này với mức j nghĩa α = 5%.
Bài 76. Theo dõi trọng lượng của một số trẻ sơ sinh tại một số nhà hộ sinh thành phố và nông thôn, người ta thấy rằng trong số 150 trẻ sơ sinh ở thành phố có 100 cháu nặng hơn 3kg và trong số 200 trẻ sơ sinh ở nông thôn có 98 cháu nặng hơn 3kg. Từ kết quả đó, hãy so sánh tỉ lệ trẻ sơ sinh có trọng lượng trên 3kg ở thành phố và nông thôn với mức j nghĩa 5%.
Bài 77. Một báo cáo cho biết ở tỉnh A có 11% trẻ em bị suy dinh dưỡng nặng, 13% trẻ bị suy dinh dưỡng và 56% trẻ em thuộc diện không suy dinh dưỡng. Trong khi đó, điều tra trẻ em ở tỉnh B thấy có 300 trẻ bị suy dinh dưỡng nặng, 1500 trẻ bị suy dinh dưỡng và 2200 trẻ không bị suy dinh dưỡng.
- Với độ tin cậy 95%, ước lượng tỉ lệ trẻ bị suy dinh dưỡng nói chung ở tỉnh B.
- Ở mức j nghĩa 5% có thể khẳng định tình hình dinh dưỡng của trẻ em ở tỉnh A và B là như nhau được không?
16
Bài tập Xác suất - Thống kê xã hội học
Bài toán hồi quy và dự báo
Bài 78. Bảng dưới đây cung cấp số liệu về tuổi và số giờ ngủ vào ban đêm của 5 người.
Tuổi (X)
Số giờ ngủ (Y)
35 40 45 50 55
7
7
6
5.5
5
Viết phương trình hồi quy tuyến tính đơn giữa Y và X . Dựa và dữ liệu trên hãy ước lượng thời gian ngủ của một người 52 tuổi với độ tin cậy 95%.
Bài 79. Một đội bóng rổ đang thử nghiệm một chương trình khởi động mới để giảm chấn thương khi thi đấu. Dữ liệu dưới đây cho thấy số phút hàng ngày thực hiện các bài tập khởi động và số lần chấn thương trong suốt giải đấu.
Số phút khởi động (X )
Số chấn thương (Y )
0 30 10 15 5 25 35 40
4
1
2
2
3
1
0
1
Hãy viết phương trình hồi quy tuyến tính đơn thể hiện số lần chấn thương phụ thuộc vào thời gian khởi động. Dựa vào dữ liệu trên hãy ước lượng số lần chấn thương của một vận động viên khởi động trong một giờ với độ tin cậy 95%?
Bài 80. Một nghiên cứu đã được thực hiện để xác định sự mất mất hiệu quả của một loại thuốc. Bảng dưới đây cho thấy kết quả của thí nghiệm.
Thời gian (theo năm) (X ) 1 2 3 4 5
Hiệu quả (%) (Y ) 96 84 70 58 52
- Xây dựng mô hình hồi quy tuyến tính cho tính hiệu quả theo thời gian.
- Theo mô hình trên, khi nào hiệu quả sẽ là 80 %? Khi nào thuốc sẽ mất hết tác dụng?
Bài 81. Một dữ liệu cho biết mối liên quan đến việc sản xuất lúa mì tính theo tấn (X ) và giá của một kg bột mì trong pesetas (đơn vị tiền Tây Ban Nha thời đó) (Y ) trong thập niên 1980 của Tây Ban Nha là:
Sản lượng lúa mì 30 28 32 25 25 25 22 24 35 40
Giá bột mì 25 30 27 40 42 40 50 45 30 25
Xây dựng mô hình hồi quy tuyến tính của giá bột mì theo sản lượng lúa mì.
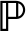 [X = x]
[X = x]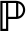 [X = x]
[X = x]


