






































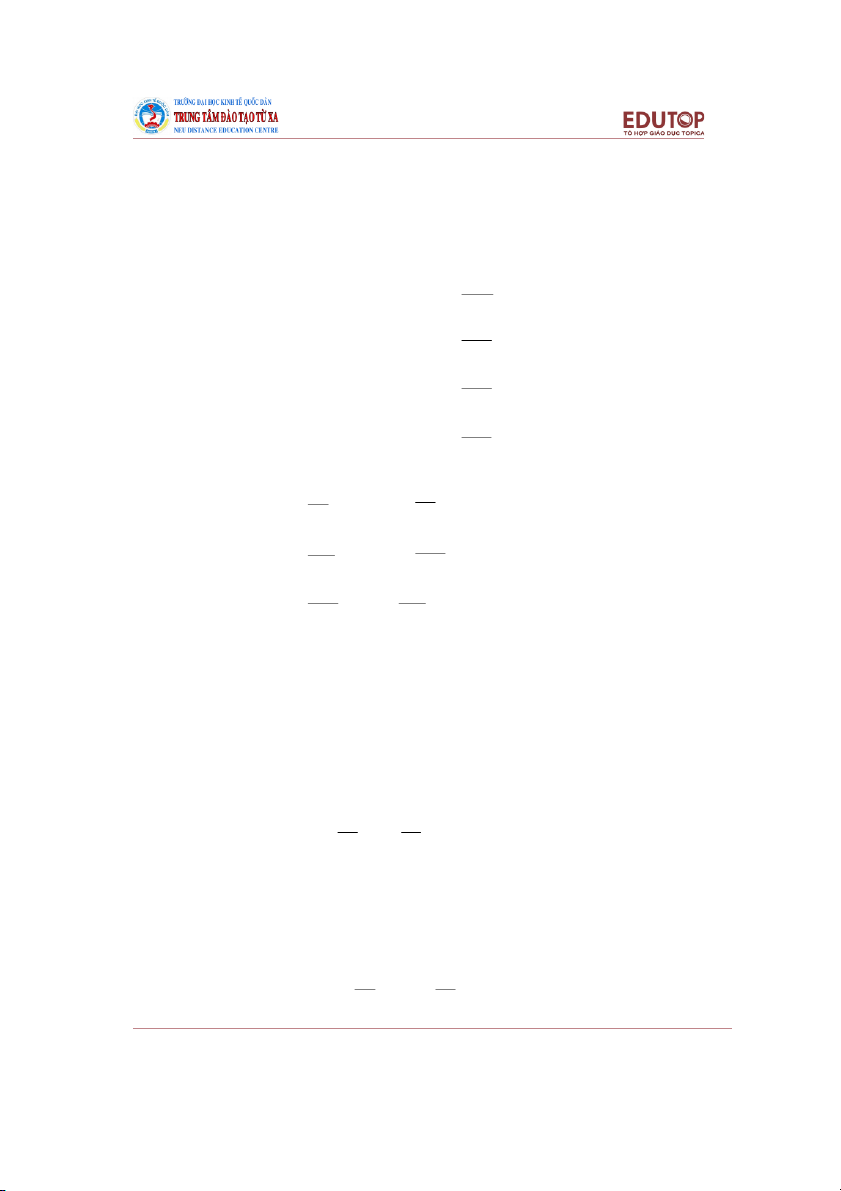
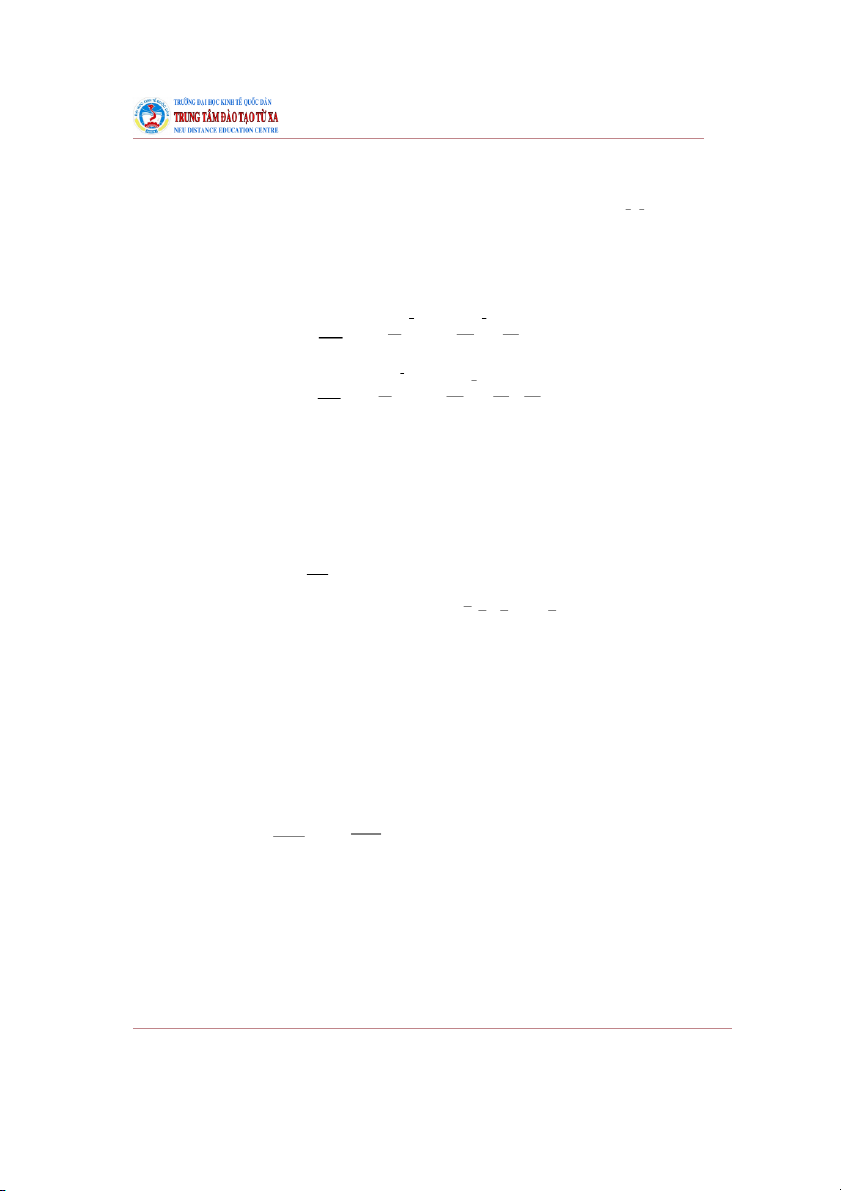


















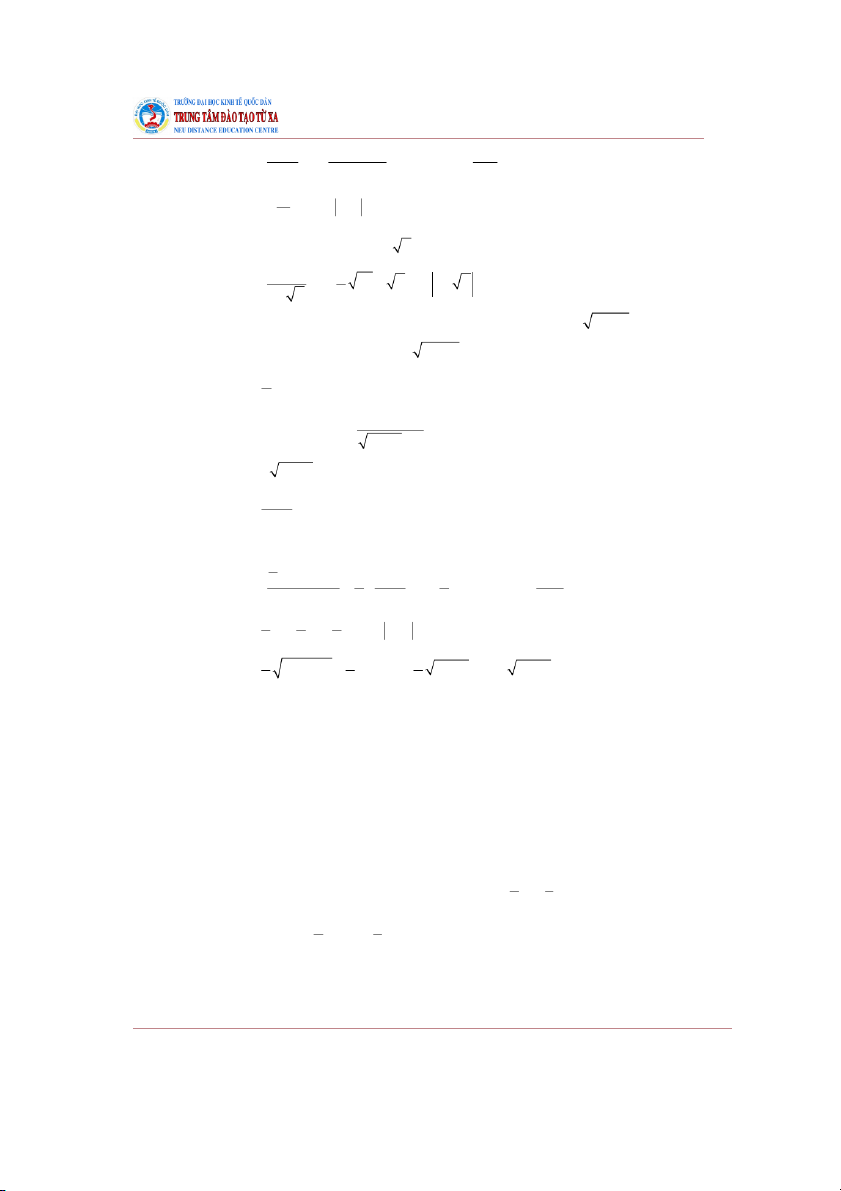









Preview text:
Bài 1: Các khái niệm cơ bản về hàm số một biến số BÀI 1
CÁC KHÁI NIỆM CƠ BẢN VỀ HÀM SỐ MỘT BIẾN SỐ Hướng dẫn học
Để học tốt bài này, sinh viên cần tham khảo các phương pháp học s au:
Học đúng lịch trình của môn học theo tuần, làm các bài luyện tập đầy đủ và
tham gia thảo luận trên diễn đàn. Đọc tài liệu:
1. BỘ MÔN TOÁN CƠ BẢN, 2009, Bài tập toán cao cấp cho các nhà kinh tế, NXB Thống kê.
2. NGUYỄN ĐÌNH TRÍ, TẠ VĂN ĐĨNH, NGUYỄN HỒ QUỲNH, 2008, Toán cao cấp 2, NXB Giáo dục.
3. NGUYỄN ĐÌNH TRÍ, TẠ VĂN ĐĨNH, NGUYỄN HỒ QUỲNH, 2008, Toán cao cấp 3, NXB Giáo dục.
4. ALPHA C. CHIANG,1995, Fundamental Methods of Mathematical Economics,
Third edition, Mc. Graw–Hill, Inc.
5. MICHAEL HOY,JOHN LIVERNOIS, CHRIS MC KENNA, RAY REES,
THANASIS STENGOS, 2001, Mathematics for Economics, The MIT Press
Cambrige, Massachusetts, London, England.
Sinh viên làm việc theo nhóm và trao đổi với giảng viên trực tiếp tại lớp học hoặc qua email.
Tham khảo các thông tin từ trang Web môn học. Nội dung Biến số; Quan hệ hàm số; Đồ thị của hàm số; Khái niệm hàm ngược;
Một số đặc trưng của hàm số;
Các hàm số cơ bản và các phép toán sơ cấp đối với hàm số;
Các mô hình hàm số trong phân tích kinh tế. Mục tiêu
Nắm được các khái niệm cơ bản về hàm 1 biến: biến số, quan hệ hàm số…
Bước đầu làm quen với các mô hình hàm số trong phân tích kinh tế. TXTOCB01_Bai1_v1.0014105205 1
Bài 1: Các khái niệm cơ bản về hàm số một biến số Tình huống dẫn nhập
Một nhà sản xuất hoạt động trong môi trường độc quyền, lượng cầu đối với sản phẩm ở mỗi mức giá p là: Q 2 00 0,25p
Biết rằng lượng chi phí cần bỏ ra để sản xuất Q sản phẩm là: 3 2 TC Q 7Q 30Q 20
Hãy tính lợi nhuận của nhà sản xuất theo mức sản lượng Q? 2 TXTOCB01_Bai1_v1.0014105205
Bài 1: Các khái niệm cơ bản về hàm số một biến số 1. Biến số 2.
Khái niệm biến số
Trong các lĩnh vực khoa học, chúng ta thường gặp các đại lượng đo được bằng số. Khi nghiên cứu
quy luật thay đổi trị số của các đại lượng đó, người ta thường dùng chữ để ký hiệu số đo của chúng.
Chẳng hạn, trong hình học, chúng ta thường dùng chữ V để ký hiệu thể tích. Với mỗi khối hình học
trong không gian, V là một số thực. Trong kinh tế học, để xem xét sự thay đổi của mức sản lượng,
ta ký hiệu mức sản lượng là . Khi đó với ý nghĩa thực tế là một số thực lớn hơn hoặc bằng không.
Trong ngôn ngữ hình thức của toán học, từ “biến số” được hiểu theo nghĩa như sau:
Định nghĩa: Biến số là một ký hiệu mà ta có thể gán cho nó một số bất kỳ thuộc một tập số cho
trước (X R). Tập hợp X được gọi là miền biến thiên và mỗi số thực x 0
X được gọi là một giá
trị của biến số đó.
Từ biến số nhiều khi được gọi tắt là biến. Các biến số thường được ký hiệu bằng các chữ cái: x, y,
z… Thông thường người ta chỉ xét các biến số mà miền biến thiên của nó có ít nhất hai số. Một
biến số chỉ nhận một giá trị duy nhất được gọi là hằng số.
Trong giải tích toán học ta thường xét các biến số thay đổi giá trị một cách liên tục, với miền biến
thiên là một khoảng số. Các khoảng số được ký hiệu như sau: Khoảng đóng (đoạn): [a, b] = {x: a ≤ x ≤ b} Khoảng mở: (a, b) = {x: a < x < b} Các khoảng nửa mở: [a, b) = {x: a ≤ x < b} (a, b] = {x: a < x ≤ b} 3.
Các biến số kinh tế
Trong lĩnh vực kinh tế người ta thường quan tâm đến các đại lượng như: giá cả, lượng cung, lượng
cầu, doanh thu, chi phí, thu nhập quốc dân, tỷ lệ lạm phát, tỷ lệ thất nghiệp… Khi phân tích xu
hướng thay đổi trị số của các đại lượng đó theo không gian, thời gian và theo các điều kiện khác
nhau, các nhà kinh tế xem chúng như các biến số. Các biến số đó được gọi là biến số kinh tế.
Trong các tài liệu kinh tế, người ta thường ký hiệu các biến số kinh tế bằng các chữ cái đầu các từ
tiếng Anh liên quan đến ý nghĩa của các biến số đó. Sau đây là một số ký hiệu thường gặp: P: giá hàng hoá (price)
Qs: Lượng cung (Quantity Supplied)
Qd: Lượng cầu (Quantity Demanded) U: Lợi ích (Untility)
TC: Tổng chi phí (Total Cost)
TR: Tổng doanh thu (Total Revenue) Lợi nhuận (Profit)
Y: thu nhập quốc dân (National Income) C: Tiêu dùng (Consumption) I: Đầu tư (Investment); S: Tiết kiệm (Saving) TXTOCB01_Bai1_v1.0014105205 3
Bài 1: Các khái niệm cơ bản về hàm số một biến số 4. Quan hệ hàm số 5. Khái niệm hàm số
Khái niệm hàm số được sử dụng rộng rãi trong nhiều lĩnh vực để biểu diễn quan hệ chi phối lẫn nhau giữa các
biến số. Ví dụ, mỗi bao gạo trong cửa hàng sẽ tương ứng với một mức cân nặng nào đó hoặc mỗi số lượng gạo
sẽ tương ứng với một số tiền (phải trả để mua số gạo đó).
Định nghĩa hàm số bằng ngôn ngữ hình thức của toán học có nội dung như sau:
Định nghĩa: Một hàm số f xác định trên một tập hợp (X
R) là một quy tắc đặt tương ứng mỗi số thực
x X với một và chỉ một số thực y.
Tập hợp X được gọi là miền xác định của hàm số f. Số y tương ứng với số x, theo quy tắc f, được gọi là giá trị
của hàm số f tại điểm x. Giá trị của hàm số f tại điểm x được ký hiệu là f(x)
Định nghĩa: Miền giá trị của một hàm số f là tập hợp tất cả các số thực là giá trị của hàm số đó tại
ít nhất một điểm thuộc miền xác định của nó.
Miền giá trị của hàm số f xác định trên miền X được ký hiệu là f(X): f (X) y R : x
X sao cho f (x) y 6.
Hàm số cho dưới dạng biểu thức
Ở bậc học phổ thông, bạn đã được làm quen với các biểu thức chức biến số, từ những biểu thức có
một phép toán đến những biển thức có nhiều phép toán phối hợp, chẳng hạn như: n n x
x , x,a ,log x,sin x, cos x, a 2 2 ax bx c 3x 1 ax bx c, ,log , 2 px q 5 x
Ta gọi miền xác định tự nhiên của một biểu thức f(x) là tập hợp tất cả các số thực mà khi gán cho x
thì biểu thức đó có nghĩa. Mỗi biểu thức f(x) là một hàm số xác định trên một tập con X bất kỳ của
miền xác định tự nhiên của nó: mỗi số thực x X 0
được đặt tương ứng với giá trị tính toán của
biểu thức đó khi gán x = x0.
Ví dụ: Với hàm số được xác định bởi biểu thức Để tìm giá trị của hàm số tại một điểm nào đó, ta
sẽ thay các vị trí của bởi giá trị đó. Chẳng hạn:
Ví dụ: Biểu thức xác định một hàm số. Miền xác định tự nhiên của biểu thức này là tập tất cả các
giá trị của mà mẫu số của biểu thức khác 0. Như vậy, miền xác định của hàm số là Ví dụ: Biểu thức 3x 1 f (x) l og2 5 x
là một hàm số với miền xác định tự nhiên là tập hợp tất cả các số thực x thỏa mãn điều kiện 3x 1 1 0 x 5. 5 x 3 4 TXTOCB01_Bai1_v1.0014105205
Bài 1: Các khái niệm cơ bản về hàm số một biến số
Theo biểu thức đó ta dễ dàng tính giá trị của hàm số tại một điểm bất kỳ thuộc miền xác định, chẳng hạn: 3.1 1 1 f (1) log log 1 3.3 1 f (3) l og l og 4 2 . 2 2 5 1 2 2 2 ; 5 3
Ví dụ: Kiểm tra xem giá trị có nằm trong tập giá trị của hàm số hay không?
Theo định nghĩa, nằm trong tập giá trị của hàm số khi và chỉ khi tồn tại giá trị (vì tập xác định
của hàm số là toàn bộ ) thỏa mãn: Điều này tương đương với việc phương trình có nghiệm Ta xét
Dễ thấy phương trình cuối có 2 nghiệm và .
Như vậy, giá trị nằm trong tập giá trị của hàm số
Phương pháp xác định hàm số bằng biểu thức là một phương pháp phổ biến trong toán học cũng
như trong các lĩnh vực ứng dụng toán học. Khi xem xét các hàm số cho bằng biểu thức, bạn cần lưu ý những điều sau đây:
Về nguyên tắc, miền xác định của một hàm số là một tập số thực cho trước, còn biểu thức giữ vai
trò quy tắc tương ứng f trong định nghĩa hàm số. Do đó, khi một hàm số xác định trên tập X R
được cho bằng một biểu thức f(x), tập X có thể chỉ là một tập con nào đó của miền xác định tự
nhiên của biểu thức đó. Tuy nhiên, trong toán học nhiều khi người ta cho trước một biểu thức f(x)
và xét biểu thức đó như một hàm số. Trong trường hợp này ta đồng nhất miền xác định của hàm số
với miền xác định tự nhiên của biểu thức f(x).
Một hàm số có thể được cho dưới dạng phân rã miền xác định thành các tập con rời nhau và trên
mỗi tập con đó quy tắc xác định giá trị tương ứng của hàm số tại mỗi điểm được biểu diễn bằng một biểu thức riêng. Ví dụ: 2 x 1 khi x 0 f (x) 1 2x khi x 0
là một hàm số xác định trên .
Trong khoảng [0; + ∞), giá trị của hàm số tại mỗi điểm x được tính theo công thức f(x) = x2 + 1,
còn trong khoảng (–∞; 0) giá trị của hàm số tại mỗi điểm x được tính theo công thức f(x) = 1 – 2x. 7.
Quan hệ hàm số giữa các biến số
Trong các lĩnh vực khoa học, người ta phân tích quy luật thay đổi giá trị của các đại lượng đo được
bằng số dưới dạng các biến số có quan hệ với nhau: sự thay đổi giá trị của biến số này kéo theo sự
thay đổi giá trị của biến số kia theo một quy luật nhất định. Chẳng hạn, trong kinh tế chúng ta thấy
khi giá hàng hóa thay đổi thì lượng hàng hóa mà người sản xuất muốn bán ra thị trường và lượng
hàng hóa mà người mua bằng lòng mua cũng thay đổi theo; khi thu nhập của các hộ gia đình thay
đổi thì lượng tiêu dùng của họ cũng thay đổi… Sự phụ thuộc của một biến số này vào một biến số
khác thường được biểu diễn dưới dạng hàm số.
Cho hai biến số x và y với miền biến thiên là các tập hợp số thực X và Y, trong đó biến x có thể
nhận giá trị tùy ý trong miền biến thiên X của nó. Ta gọi x là biến độc lập, hay đối số. Định nghĩa:
Ta nói biến số y phụ thuộc hàm số vào biến số x, hay biến số y là hàm số của biến số x, khi và chỉ
khi tồn tại một quy tắc hoặc quy luật f sao cho mỗi giá trị của biến số x trong miền biến thiên X của TXTOCB01_Bai1_v1.0014105205 5
Bài 1: Các khái niệm cơ bản về hàm số một biến số
nó được đặt tương ứng với một và chỉ một giá trị của biến số y.
Theo định nghĩa thì quy tắc f chính là một hàm số xác định trên miền biến thiên X của biến số x và
giá trị của hàm số f tại điểm x chính là giá trị tương ứng của biến số y. x y f (x)
Để nói một cách khái quát rằng y là hàm số của x (y phụ thuộc hàm số vào x) ta có thể viết: y = y(x).
Chú ý: Hai định nghĩa hàm số trên đây tương đương với nhau. Khi cho một hàm số f với miền xác
định là tập hợp X, các cách diễn đạt sau đây có nghĩa như sau:
1. Cho hàm số f xác định trên tập X (X là một tập số cho trước) 2. Cho hàm số f(x), x X
3. Cho hàm số y = f(x), x X
Chú ý rằng khi viết hàm số dưới dạng y = f(x), các ký hiệu x và y chỉ mang ý nghĩa hình thức, dùng
để gọi tên các biến số. Một hàm số được xác định bởi hai yếu tố: miền xác định X (miền biến thiên
của biến độc lập x) và quy tắc f cho phép ta xác định được giá trị của hàm số tại mỗi điểm x R .
Chẳng hạn, dưới giác độ toán học ta không phân biệt các hàm số y = x2 và v = u2 khi miền biến
thiên của x và miền biến thiên của u trùng nhau. ). Khi nói đến các hàm số khác nhau, ta sử dụng
các ký hiệu khác nhau: f, g, φ…
8. Đồ thị của hàm số
Quan hệ hàm số y = f(x) liên kết các cặp số thực (x0, y0), trong đó x0 là một số bất kỳ thuộc miền
xác định X của hàm số và y0 = f(x0). Mỗi cặp số như vậy là một điểm của mặt phẳng tọa độ.
Định nghĩa: Đồ thị của hàm số f là tập hợp tất cả các điểm M(x, y) của mặt phẳng tọa độ có hoành
độ x là một số thực bất kỳ lấy từ miền xác định của hàm số và tung độ y là giá trị tương ứng của hàm số tại điểm x.
Việc lập đồ thị của một hàm số f với miền xác định là một khoảng số thực thường được thực hiện theo trình tự như sau:
Lấy các số x1, x2,…, xn từ miền xác định của hàm số (càng gần nhau càng tốt)
Tính các giá trị tương ứng của hàm số tại các điểm đó:
y1 = f(x1), y2 = f(x2),…, yn = f(xn)
Định vị các điểm M1(x1, y1), M2(x2, y2),…,Mn(xn, yn)
Nối các điểm M1, M2,…,Mn ta được hình ảnh đồ thị của hàm số. 6 TXTOCB01_Bai1_v1.0014105205
Bài 1: Các khái niệm cơ bản về hàm số một biến số y y = f(x) yn Mn y2 y1 M2 M1 0 x1 x2 xn x
Phương pháp đồ thị không phải là phương pháp chính xác. Tuy nhiên, người ta thường sử dụng đồ
thị để minh họa bằng hình ảnh các đặc trưng cơ bản của sự phụ thuộc hàm số giữa các biến số.
Nhìn vào đồ thị ta dễ dàng quan sát xu hướng biến thiên của hàm số khi biến độc lập thay đổi giá trị.
9. Khái niệm hàm ngược
Xét một hàm số y = f(x) với miền xác định X và miền giá trị Y = f(X). Nếu với mỗi giá trị y0 Y
chỉ tồn tại duy nhất một giá trị x0 X sao cho f(x0) = y0, tức là phương trình f(x) = y0 có một
nghiệm duy nhất x0 trong miền X, thì 1 y f x x
f y (x X, y Y) Trong đó ký hiệu x –1
0 = f (y0) chỉ nhiệm duy nhất của phương trình f(x) = 0 như đã nói ở trên.
Như vậy, trong trường hợp này quan hệ hàm số y = f(x) biểu diễn sự phụ thuộc của y vào x có thể
đảo ngược để biểu diễn sự phụ thuộc của x vào y thông qua hàm số 1 x f y
Định nghĩa: Với giả thiết và quy ước về ký hiệu nêu trên, ta gọi hàm số x = f–1(y)
là hàm ngược của hàm số y = f(x). Nói cách khác, hàm số f–1 (xác định trên miền
Y = f(X) là hàm ngược của hàm số f (xác định trên miền X).
Ví dụ: Hàm ngược của hàm số là hàm , ta có thể viết hàm ngược dạng Ví dụ: 3
Hàm số y = x3 với miền xác định X = R có hàm ngược là hàm số x y 3 3 y x x y (x X, y Y)
Hàm ngược của hàm số mũ y = ax là hàm số logarit x = logay: x y a x l og y (x X, y 0) a
Chú ý: Hàm số y = f(x) và hàm ngược x = f–1(y) cùng đồ thị, bởi vì y = f(x) và
x = f–1(y) là các phương trình tương đương. Tuy nhiên, trong toán học người ta thường dùng ký
hiệu x để chỉ biến độc lập và ký hiệu y để chỉ biến phụ thuộc, do đó thay cho cách viết hàm ngược
dưới dạng x = f–1(y) người ta có thể tráo ký hiệu biến số và viết hàm ngược của hàm số y = f(x)
dưới dạng y = f–1(x). Chẳng hạn, ta có thể nói: hàm số y = log x
ax là hàm ngược của hàm số a , hay đơn giản hơn: logax là hàm ngược của hàm số ax.
Do tráo ký hiệu biến số nên điểm M(x, y) thuộc đồ thị y = f–1(x) khi và chỉ khi điểm M’(y, x) thuộc
đồ thị y = f(x). Trên mặt phẳng tọa độ hai điểm M(x, y) và M’(y, x) đối xứng nhau qua đường phân TXTOCB01_Bai1_v1.0014105205 7
Bài 1: Các khái niệm cơ bản về hàm số một biến số
giác thứ nhất. Như vậy, nếu biểu diễn hai đồ thị y = f(x) và y = f–1(x) trên cùng một hệ tọa độ trực
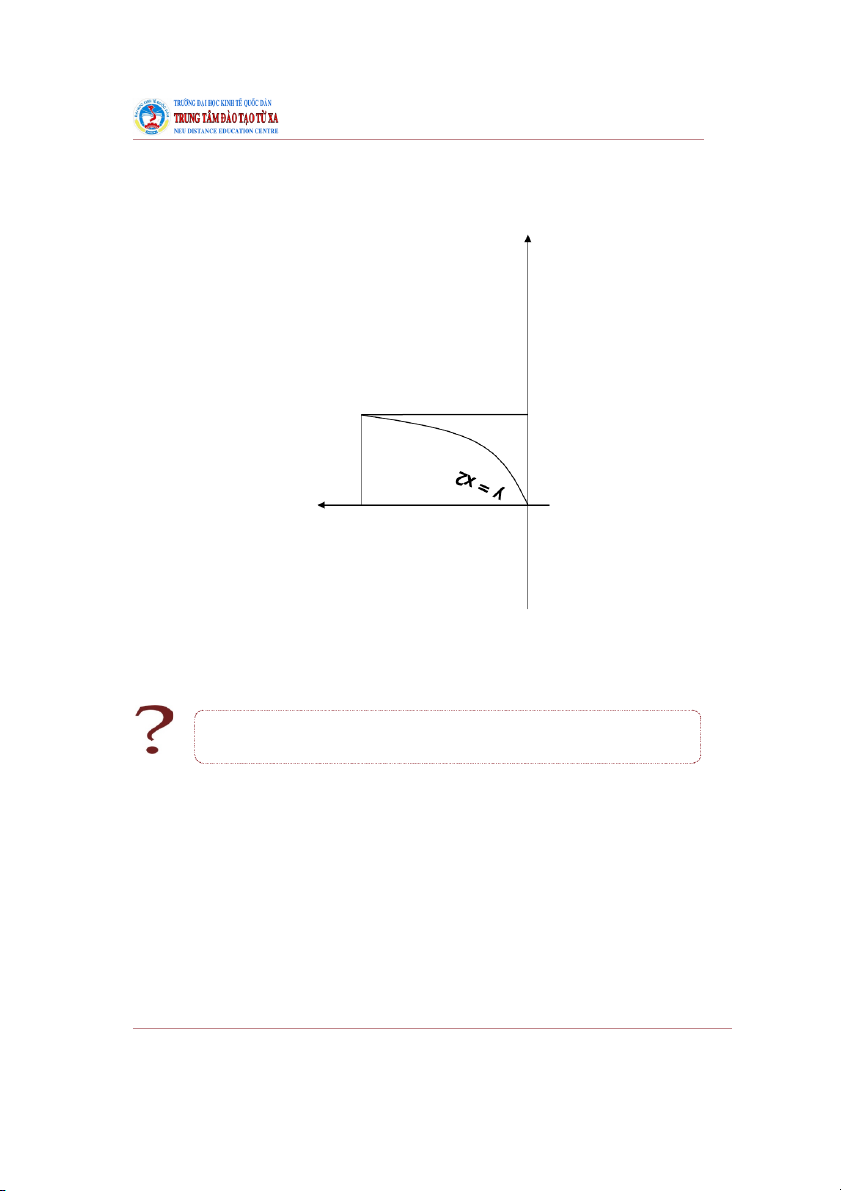
chuẩn thì chúng đối xứng nhau qua đường thẳng y = x (đường phân giác của góc phần tư thứ nhất). Chẳng hạn, hai đường cong
y = ax và y = logax có dạng như hình vẽ dưới đây. y y = ax y = x y = logax 1 0 1 x
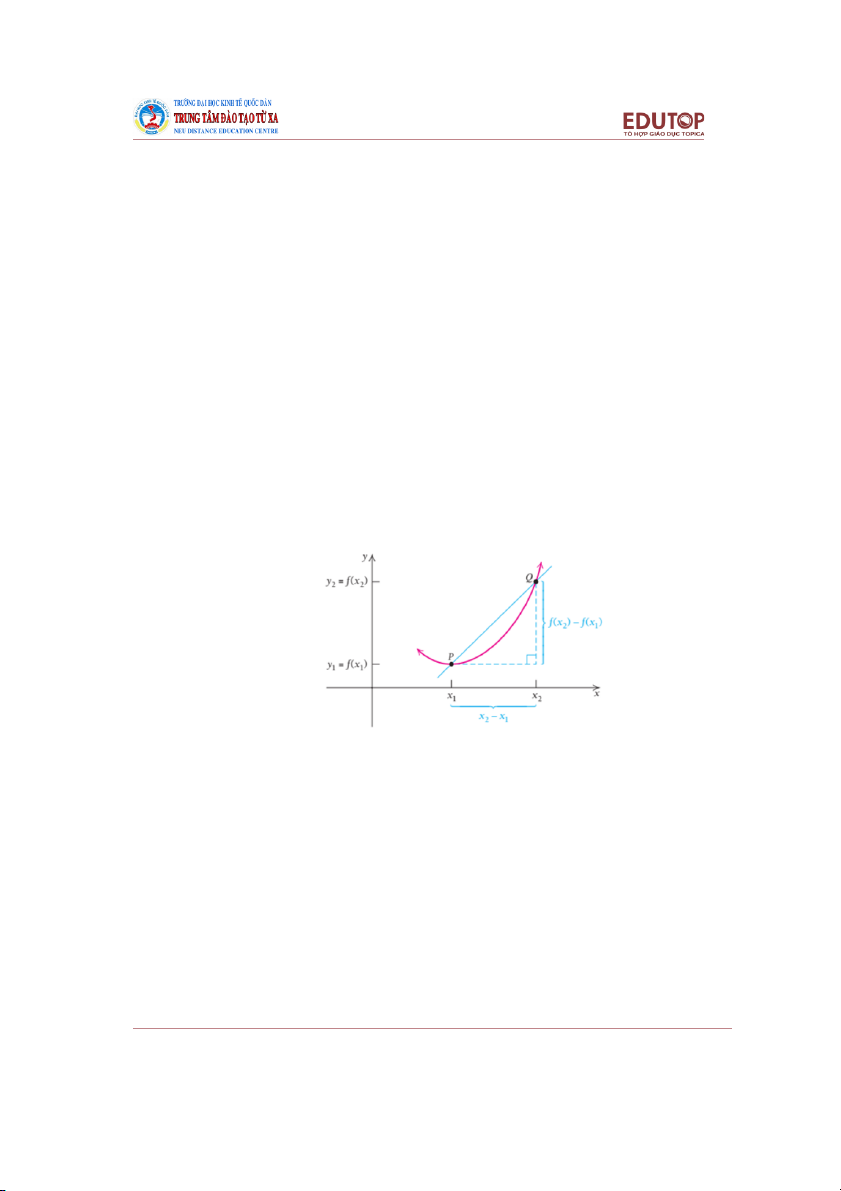
10.Một số đặc trưng hàm số 11. Hàm số đơn điệu
Định nghĩa: Ta nói rằng hàm số y = f(x) đơn điệu tăng (đơn điệu giảm) trên một khoảng K nếu với
mọi cặp điểm x1, x2 (x1 ≠ x2) thuộc K, hiệu số f(x2) – f(x1) luôn cùng dấu (trái dấu) với x2 – x1. Nói cách khác:
Hàm số f(x) là hàm đơn điệu tăng trên khoảng K nếu x x f (x ) f (x ) ( x ,x K) 1 2 1 2 1 2
Hàm số f(x) là hàm đơn điệu giảm trên khoảng K nếu x x f (x ) f (x ) ( x , x K) 1 2 1 2 1 2
Hàm số đơn điệu tăng (đơn điệu giảm) còn được gọi là hàm số đồng biến (hàm số nghịch biến).
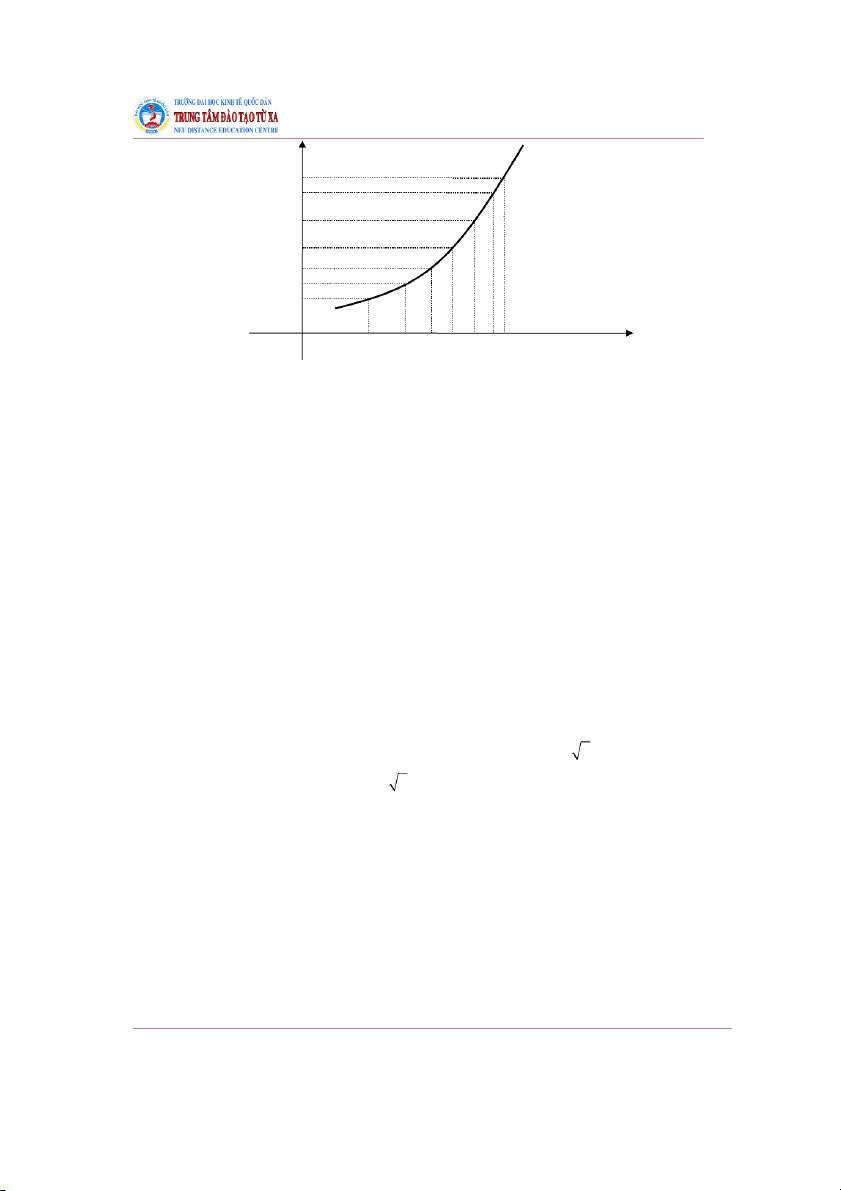
Ví dụ: Xét mối quan hệ giữa chi phí sản xuất (TC) với mức sản lượng (Q) của một nhà sản xuất:
Dễ thấy rằng, khi mức sản lượng tăng lên thì chi phí cũng tăng lên. Hàm chi phí này tăng trong miền Ví dụ:
Hàm số f(x) = x2 là hàm đơn điệu tăng trên khoảng [0; +∞) và đơn điệu giảm trên khoảng (–∞; 0]: 2 2 x 1, x 2 [0; ) : x1 x 2 x1 x 2 2 2 x 1, x 2 ( ;0]: x1 x 2 x1 x 2 1 f (x) Hàm số
x đơn điệu giảm trong khoảng (0; +∞): 1 1 x , x (0; ) : x x 1 2 1 2 x x 1 2
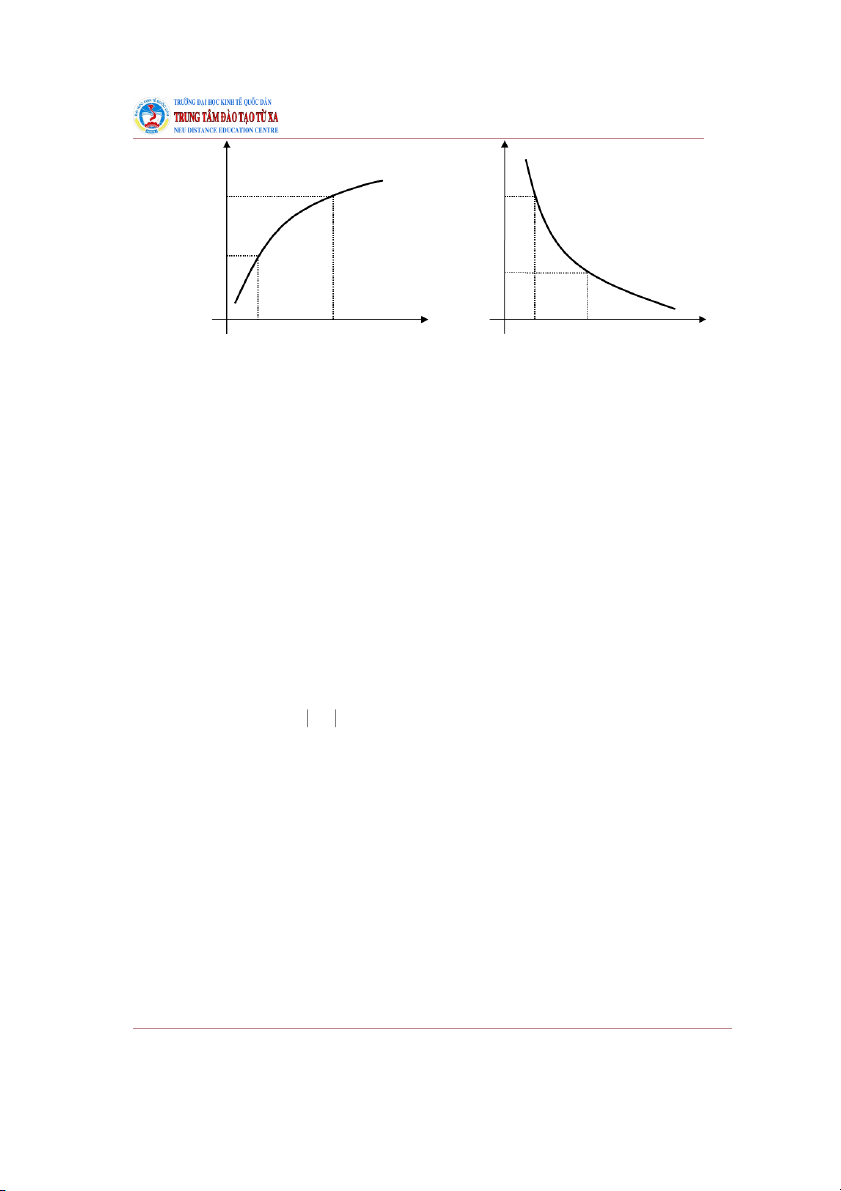
Nếu quan sát đồ thị của hàm số theo hướng từ trái sang phải thì đồ thị của hàm số đơn điệu tăng có
dáng dốc lên và đồ thị của hàm số đơn điệu giảm có dáng dốc xuống. 8 TXTOCB01_Bai1_v1.0014105205
Bài 1: Các khái niệm cơ bản về hàm số một biến số y y y = f(x) f(x2) f(x2) f(x1) f(x1) y = f(x) 0 x1 x2 x 0 x1 x2 x
Hàm số đơn điệu tăng
Hàm số đơn điệu giảm 12. Hàm số bị chặn Định nghĩa:
Hàm số f(x) được gọi là hàm bị chặn trong một miền X nếu giá trị của hàm số chỉ thay đổi trong
phạm vi một tập con của một khoảng số hữu hạn khi x biến thiên trên miền X, tức là tồn tại các hằng số m và M sao cho: m f (x) M x X
Hàm số f(x) được gọi là hàm bị chặn trên trong một miền X nếu tồn tại hằng số M sao cho: f (x) M x X
Hằng số M được gọi là cận trên của hàm số f(x) trong miền X
Hàm số f(x) được gọi là hàm bị chặn dưới trong một miền X nếu tồn tại hằng số m sao cho: f (x) m x X
Hằng số m được gọi là cận dưới của hàm số f(x) trong miền X.
Chú ý rằng tính bị chặn bao hàm cả bị chặn trên và bị chặn dưới. Dễ dàng thấy rằng hàm số f(x) bị
chặn trong miền X khi và chỉ khi tồn tại hằng số K > 0 sao cho: f (x) K ( x X) Ví dụ:
Hàm số f(x) = x2 + a (x R) là hàm bị chặn dưới: f(x) = x2 + a ≥ a, x R
Hàm số f(x) = –x2 + a (x R) là hàm bị chặn trên: f(x) = –x2 + a ≤ a, x R
Hàm số f(x) = sin x (x R) là hàm bị chặn:
–1 ≤ sin x ≤ 1, x R 13.
Hàm số chẵn và hàm số lẻ Định nghĩa:
Hàm số f(x) xác định trên miền X được gọi là hàm chẵn nếu với mọi x X ta luôn có x X và f(–x) = f(x). TXTOCB01_Bai1_v1.0014105205 9
Bài 1: Các khái niệm cơ bản về hàm số một biến số
Hàm số f(x) xác định trên miền X được gọi là hàm lẻ nếu với mọi x X ta luôn có; và f(–x) = – f(x).
Ví dụ 1: Các hàm số f(x) = x2, g(x) = cosx (x R) là các hàm số chẵn:
f(–x) = (–x)2 = x2 = f(x), x R
g(–x) = cos(–x) = cos(x) = g(x), x R
Ví dụ 2: Các hàm số f(x) = x3, g(x) = sinx (x R) là các hàm số lẻ:
f(–x) = (–x)3 = –x3 = –f(x), x R
g(–x) = sin(–x) = –sinx = –g(x), x R
Đồ thị của hàm số chẵn và hàm số lẻ có tính chất đối xứng: đồ thị của hàm số chẵn nhận trục tung
làm trục đối xứng, còn đồ thị của hàm số lẻ nhận gốc tọa độ làm tâm đối xứng. 14. Hàm số tuần hoàn
Định nghĩa: Hàm số f(x) xác định trên miền X được gọi là hàm tuần hoàn với chu kỳ T nếu với
mọi x X ta luôn có x T X và: f(x + T) = f(x)
Dễ dàng thấy rằng nếu hàm số f(x) tuần hoàn với chu kỳ T thì nó cũng tuần hoàn với chu kỳ mT (m là số nguyên bất kỳ): F(x + mT) = f(x), x X
Để cho xác định, khi nói đến chu kỳ của hàm số tuần hoàn người ta thường lấy chu kỳ dương nhỏ nhất. Ví dụ:
Các hàm số sinx, cosx là các hàm tuần hoàn với chu kỳ T = 2π:
sin(x + 2π) = sinx; cos(x + 2π) = cosx, x R
Các hàm số tgx, cotgx là các hàm tuần hoàn với chu kỳ T = π: x k tan(x + π) = tanx, 2 ; cot(x + π) = cotx, x k
15.Các hàm số cơ bản và các phép toán sơ cấp đối với hàm số 16.
Các hàm số sơ cấp cơ bản
Thông thường một hàm số y = f(x) được cho dưới dạng một biểu thức hữu hạn. Các biểu thức hữu
hạn được hợp thành từ các biểu thức hàm số cơ bản.
Chúng ta sẽ xem xét những quy luật hàm số cơ bản thường gặp.
Các hàm số sau đây được gọi là các hàm số sơ cấp cơ bản (bỏ qua các hàm lượng giác ngược).
F(x) = C (hàm số nhận giá trị không đổi C với mọi x)
Hàm số lũy thừa: f(x) = xα (α = const.)
Hàm số mũ: f(x) = ax (a > 0 và a ≠ 1)
Hàm số logarit: f(x) = logax (a > 0 và a ≠ 1).
Các hàm số lượng giác:
f(x) = sinx, f(x) = cosx, f(x) = tan x, f(x) = cotx.
Chú ý: Trong giải tích toán học cung và góc luôn luôn được đo bằng radian. 10 TXTOCB01_Bai1_v1.0014105205
Bài 1: Các khái niệm cơ bản về hàm số một biến số 17.
Các phép toán sơ cấp đối với hàm số
Ta gọi các phép toán sơ cấp là các phép toán: phép cộng, phép trừ, phép nhân, phép chia và phép hợp hàm.
Các phép toán cộng, trừ, nhân, chia đối với các biểu thức hàm số được thực hiện giống như đối với
các biểu thức đại số. Nếu f(x) và g(x) là các hàm số cho dưới dạng biểu thức thì các biểu thức f(x) f x
g x , f x – g x , f x g x , g(x)
Được gọi tương ứng là tổng, hiệu, tích, thương của f(x) và g(x). Các hàm số này đặt tương ứng
mỗi giá trị của biến độc lập x với tổng hiệu, tích, thương các giá trị của hàm số f và g tại điểm x: f(x) + g(x): x y f (x) g(x) f(x) – g(x): x y f (x) g(x) f(x).g(x): x y f (x).g(x) f (x) f (x) : x y g(x) g(x)
Ví dụ: Hàm số y = x + sinx là tổng của hai hàm số: f(x) = x, g(x) = sinx
Hàm số là tích của hai hàm số
Phép hợp hàm là phép lập hàm số của hàm số. Giả sử ta có hai hàm số:
y = f(u): biểu diễn sự phụ thuộc của y vào u
u = φ(x): biếu diễn sự phụ thuộc của u vào x
Giả sử khi x thay đổi trong miền X, các giá trị của hàm số u = φ(x) luôn luôn thuộc miền xác
định của hàm số y = f(u). Khi đó, mỗi giá trị của biến số x được đặt tương ứng với một và chỉ
một giá trị của biến số y theo quy tắc như sau: f x u ( x) y f [ ( x)] g (x)
Hàm số y = g(x) = f[φ(x)] đặt tương ứng mỗi giá trị của biến số x với một giá trị duy nhất của
biến y theo quy tắc nêu trên được gọi là hàm hợp của các hàm số y = f(u) và u = φ(x). Hàm hợp
còn được gọi là hàm
kép. Bỏ qua vai trò hình thức của các ký hiệu biến số ta có thể nói: g(x) =
f[φ(x)] là hàm hợp của hai hàm số f(x) và φ(x). Ví dụ 1:
Hàm số y = sin5x là hàm hợp của hai hàm số y = u5 và u = sinx. Ta cũng có thể nói: g(x) = sin5x
là hàm hợp của hai hàm số f(x) = x5, φ(x) = sinx Ví dụ 2:
Hàm số khi được viết dưới dạng có thể coi là hàm hợp của hàm số và 18.
Các hàm số sơ cấp
Ta gọi hàm số sơ cấp là hàm số được cho dưới dạng một biểu thức hữu hạn, tức là một biểu thức
được hợp thành từ các hàm số sơ cấp cơ bản nói trên thông qua một số hữu hạn các phép toán sơ cấp đối với hàm số.
Phạm vi của tập hợp các hàm sơ cấp khá rộng. Trong kinh tế học người ta thường hay sử dụng các dạng hàm số sau: Hàm số f(x) = axα
(a và α là các hằng số) TXTOCB01_Bai1_v1.0014105205 11
Bài 1: Các khái niệm cơ bản về hàm số một biến số
Hàm số mũ và hàm số logarit: f(x) = ax, f(x) = logax (a > 0 và a ≠ 1)
Hàm đa thức, hay hàm nguyên:
f(x) = a0 + a1x + a2x2 +…+ anxn
Hàm phân thức, hay hàm hữu tỷ: P(x) f (x) Q(x)
trong đó P(x) và Q(x) là các đa thức.
19.Các mô hình hàm số trong phân tích kinh tế 20.
Hàm cung và hàm cầu
Khi phân tích thị trường hàng hóa và dịch vụ, các nhà kinh tế sử dụng khái niệm hàm cung (supply
function) và hàm cầu (demand
function) để biểu diễn sự phụ thuộc của lượng cung và lượng cầu
đối với một loại hàng hóa vào giá của hàng hóa đó. Hàm cung và hàm cầu có dạng: Hàm cung: Qs = S(p) Hàm cầu: Qd = D(p)
trong đó: p là giá hàng hóa; Qs là lượng cung (quantity supplied), tức là lượng hàng hóa mà người
bán bằng lòng bán ở mỗi mức giá; Qd là lượng cầu (quantity demanded), tức là lượng hàng hóa mà
người mua bằng lòng mua ở mỗi mức giá. Trong mô hình phân tích thị trường một loại hàng hóa,
lượng cung của thị trường là tổng lượng cầu của tất cả những người tiêu dùng.
Tất nhiên, lượng cung và lượng cầu hàng hóa không chỉ phụ thuộc vào giá của hàng hóa đó mà còn
chịu ảnh hưởng của nhiều yếu tố khác, chẳng hạn như thu nhập và giá của các hàng hóa liên quan.
Khi xem xét các mô hình hàm cung và hàm cầu ở dạng nêu trên người ta giả thiết rằng các yếu tố
khác không thay đổi. Quy luật thị trường trong kinh tế học nói rằng, đối với các hàng hóa thông
thường, hàm cung là hàm đơn điệu tăng, còn hàm cầu là hàm đơn điệu giảm. Điều này có nghĩa là,
với các yếu tố khác giữ nguyên, khi giá hàng hóa tăng lên thì người bán sẽ muốn bán nhiều hơn và
người mua sẽ mua ít đi. Các nhà kinh tế gọi đồ thị của hàm cung và hàm cầu là đường cung và
đường cầu. Giao điểm của đường cung và đường cầu được gọi là điểm cân bằng của thị trường. Ở
mức giá cân bằng p ta có Q Q Q s d
, tức là người bán bán hết và người mua mua đủ, thị trường
không có hiện tượng dư thừa hoặc khan hiếm hàng hóa.
Chú ý: Trong các tài liệu kinh tế người ta thường sử dụng trục hoành để biểu diễn lượng Q và trục
tung để biểu diễn giá p. Cách biểu diễn như vậy tương ứng với việc đảo ngược hàm cung và hàm
cầu ở dạng nói trên. Trong kinh tế học nhiều khi người ta vẫn gọi hàm ngược của hàm Qs = S(p) là
hàm cung và hàm ngược của hàm Qd = D(p) là hàm cầu: Q S p 1 p S Q s s Q D p 1 p D Q d d
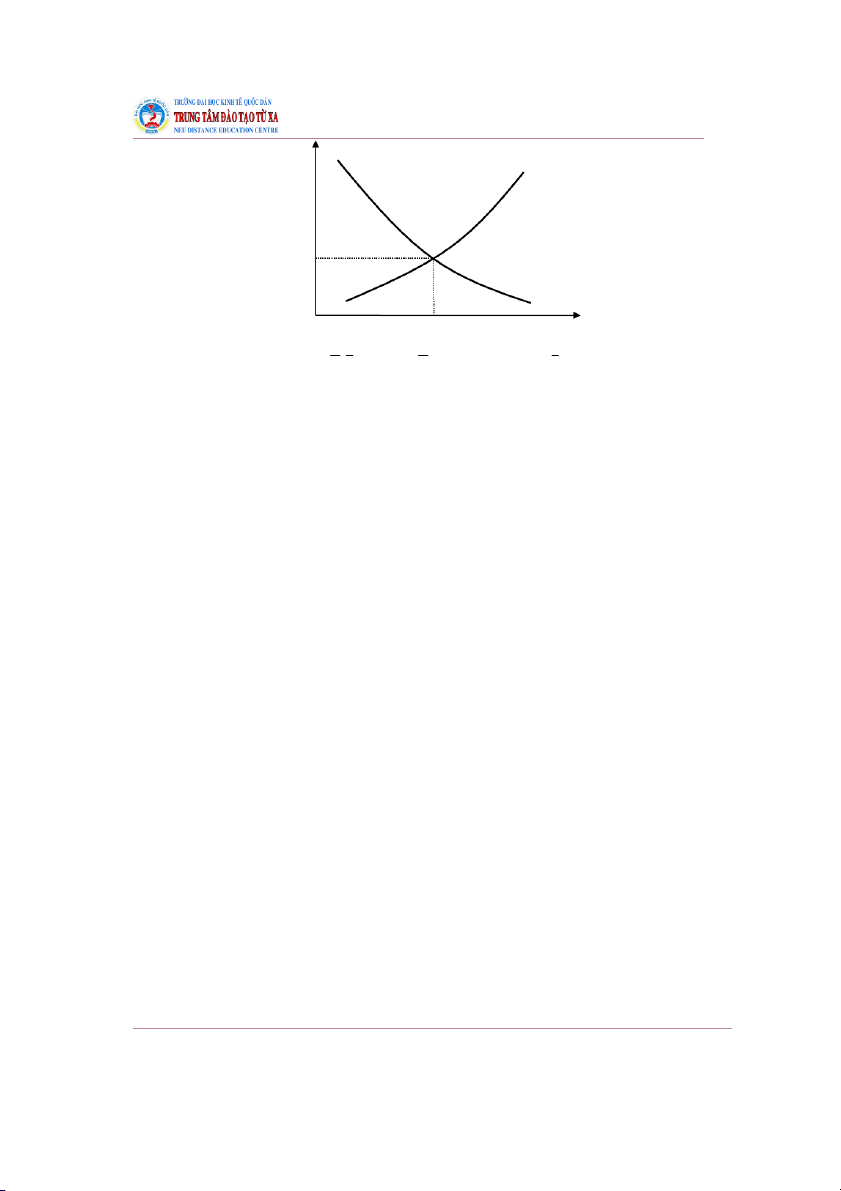
Đồ thị của hàm cung và hàm cầu (đường cung và đường cầu) có dạng như hình vẽ 12 TXTOCB01_Bai1_v1.0014105205
Bài 1: Các khái niệm cơ bản về hàm số một biến số p p = S–1(Q) p = D–1(Q) 0 0
Điểm cân bằng là điểm (Q,p) , trong đó Q là lượng cân bằng và p là giá cân bằng. 21.
Hàm sản xuất ngắn hạn
Các nhà kinh tế học sử dụng khái niệm hàm sản xuất để
mô tả sự phụ thuộc của sản lượng hàng
hóa (tổng số lượng sản phẩm hiện vật) của một nhà sản xuất vào các yếu tố đầu vào của sản xuất,
gọi là các yếu tố sản xuất, như vốn và lao động…
Trong kinh tế học khái niệm ngắn hạn và dài hạn không được xác định bằng một khoảng thời gia
cụ thể, mà được hiểu theo nghĩa như sau:
Ngắn hạn là khoảng thời gian mà ít nhất một trong các yếu tố sản xuất không thể thay đổi. Dài hạn
là khoảng thời gian mà tất cả các yếu tố sản xuất có thể thay đổi.
Khi phân tích sản xuất, người ta thường quan tâm đến hai yếu tố sản xuất quan trọng là vốn
(Capital) và lao động (Labor), được ký hiệu tương ứng là K và L.
Trong ngắn hạn thì K không thay đổi, do đó hàm sản xuất ngắn hạn có dạng: Q = f(L)
Trong đó L là lượng lao động được sử dụng và Q là mức sản lượng tương ứng. Chú ý rằng khi xét
hàm sản xuất sản lượng Q và các yếu tố sản xuất K, L được đo theo luồng (flow), tức là đo định kỳ
(hàng ngày, hàng tuần, hàng tháng, hàng năm…). 22.
Hàm doanh thu, hàm chi phí và hàm lợi nhuận
Tổng doanh thu (total revenue), tổng chi phí (total cost) và tổng lợi nhuận (total profit) của nhà sản
xuất phụ thuộc vào sản lượng hàng hóa. Khi phân tích hoạt động sản xuất, cùng với hàm sản xuất
các nhà kinh tế học còn sử dụng các hàm số:
Hàm doanh thu là hàm số biểu diễn sự phụ thuộc của tổng doanh thu (ký hiệu là TR) vào sản lượng (ký hiệu là Q): TR = TR(Q)
Chẳng hạn, tổng doanh thu của nhà sản xuất cạnh tranh là hàm bậc nhất: TR = pQ
Trong đó p là giá sản phẩm trên thị trường.
Hàm chi phí là hàm số biểu diễn sự phụ thuộc của tổng chi phí sản xuất (ký hiệu là TC) vào sản lượng (ký hiệu là Q): TC = TC(Q)
Hàm lợi nhuận là hàm số biểu diễn sự phụ thuộc của tổng lợi nhuận (ký hiệu là π)vào sản lượng (ký hiệu là Q): π = π(Q)
Hàm lợi nhuận có thể được xác định thông qua hàm doanh thu và hàm chi phí: π = TR(Q) – TC(Q) TXTOCB01_Bai1_v1.0014105205 13
Bài 1: Các khái niệm cơ bản về hàm số một biến số
Ví dụ: Cho biết chi phí của một doanh nghiệp ứng với mức sản lượng được xác định bởi và giá
bán của một đơn vị sản phẩm đó là , hãy xác định mức lợi nhuận của doanh nghiệp khi sản xuất đơn vị sản phẩm. Giải:
Hàm doanh thu của doanh nghiệp là
Do đó hàm lợi nhuận của doanh nghiệp là
Mức lợi nhuận của doanh nghiệp khi sản xuất đơn vị sản phẩm được tìm bằng cách thay 23.
Hàm tiêu dùng và hàm tiết kiệm
Lượng tiền mà người tiêu dùng dành để mua sắm hàng hóa và dịch vụ phụ thuộc vào thu nhập. Các
nhà kinh tế sử dụng hàm tiêu
dùng để biểu diễn sự phụ thuộc của biến tiêu dùng C (Consumption)
vào biến thu nhập Y (Income): C = f(Y)
Theo quy luật chung, khi thu nhập tăng người ta có xu hướng tiêu dùng nhiều hơn, do đó hàm tiêu dùng là hàm đồng biến.
Hàm tiết kiệm là hàm số biểu diễn sự phụ thuộc của biến tiết kiệm S (Saving) vào biến thu nhập: S = S(Y)
Tóm lược cuối bài
Biến số là một ký hiệu mà ta có thể gán cho nó một số bất kỳ thuộc một tập số x ≠ Ø cho trước.
Hàm số là một quy tắc đặt tương ứng mỗi x X với 1 và chỉ 1 số thực y.
Ta thường cho hàm số dưới dạng một biểu thức, khi hàm số được cho dưới dạng biểu thức –
nếu không nói gì thêm thì tập xác định của hàm số được hiểu là tập xác định tự nhiên của biểu thức đó.
Một số hàm số thường gặp trong phân tích kinh tế: Hàm cung: Q = S(p) s Hàm cầu: Q = D(p) d
Hàm sản xuất ngắn hạn: Q = f(L) Hàm doanh thu: TR = TR(Q) Hàm chi phí: TC = TC(Q)
Hàm lợi nhuận: = TR(Q) – TC(Q) Hàm tiêu dùng: C = f(Y) Hàm tiết kiệm: S = S(Y) 14 TXTOCB01_Bai1_v1.0014105205
Bài 1: Các khái niệm cơ bản về hàm số một biến số Câu hỏi ôn tập 1.
Nêu định nghĩa biến số, hàm số. 2.
Gọi tên các biến số thường gặp trong kinh tế. 3.
Định nghĩa hàm số đồng biến, nghịch biến? Hàm số chẵn, hàm số lẻ? Hàm tuần hoàn? 4.
Hãy cho nhận xét về hình dáng đồ thị của hàm số đồng biến, nghịch biến trên một khoảng. 5.
Hàm số là hàm hợp của những hàm nào? 6.
Hàm số là hàm hợp của những hàm nào? 7. Hàm sơ cấp là gì? 8.
Hãy nêu các hàm số cơ bản trong phân tích kinh tế? Thế nào là điểm cân
bằng của thị trường (với thị trường chỉ gồm một hàng hóa)? TXTOCB01_Bai1_v1.0014105205 15
Bài 1: Các khái niệm cơ bản về hàm số một biến số BÀI 2
ĐẠO HÀM VÀ VI PHÂN CỦA HÀM SỐ Hướng dẫn học
Để học tốt bài này, sinh viên cần tham khảo các phương pháp học s au:
Học đúng lịch trình của môn học theo tuần, làm các bài luyện tập đầy đủ và
tham gia thảo luận trên diễn đàn. Đọc tài liệu:
6. BỘ MÔN TOÁN CƠ BẢN, 2009, Bài tập toán cao cấp cho các nhà kinh tế, NXB Thống kê.
7. NGUYỄN ĐÌNH TRÍ, TẠ VĂN ĐĨNH, NGUYỄN HỒ QUỲNH, 2008, Toán cao cấp 2, NXB Giáo dục.
8. NGUYỄN ĐÌNH TRÍ, TẠ VĂN ĐĨNH, NGUYỄN HỒ QUỲNH, 2008, Toán cao cấp 3, NXB Giáo dục.
9. ALPHA C. CHIANG,1995, Fundamental Methods of Mathematical Economics,
Third edition, Mc. Graw–Hill, Inc.
10. MICHAEL HOY,JOHN LIVERNOIS, CHRIS MC KENNA, RAY REES,
THANASIS STENGOS, 2001, Mathematics for Economics, The MIT Press
Cambrige, Massachusetts, London, England.
Sinh viên làm việc theo nhóm và trao đổi với giảng viên trực tiếp tại lớp học hoặc qua email.
Tham khảo các thông tin từ trang Web môn học. Nội dung Khái niệm đạo hàm;
Đạo hàm của các hàm sơ cấp cơ bản;
Các quy tắc tính đạo hàm; Vi phân của hàm số;
Đạo hàm cấp cao và vi phân cấp cao. Mục tiêu
Trình bày được khái niệm đạo hàm: đạo hàm tại 1 điểm, đạo hàm trên một miền;
Áp dụng các quy tắc tính đạo hàm để tính được đạo hàm của một hàm số cụ
thể (quy tắc đạo hàm của tổng, hiệu, tích, thương và đạo hàm của hàm hợp);
Biết sử dụng phương pháp mũ hóa hoặc logarit hóa để tính đạo hàm của biểu thức lũy thừa mũ;
Hiểu được khái niệm, cách tính vi phân tại 1 điểm, biểu thức vi phân; 16 TXTOCB01_Bai1_v1.0014105205
Bài 1: Các khái niệm cơ bản về hàm số một biến số Tình huống dẫn nhập
Giả sử lượng cung đối với một loại sản phẩm có dạng:
trong đó là lượng cung, là giá của sản phẩm.
Qua biểu thức quan hệ giữa lượng cung và giá p ta thấy rằng hàm cung là hàm
đơn điệu tăng – nghĩa là khi giá p tăng thì lượng cung cũng tăng theo, bạn hãy
ước lượng “tốc độ tăng tức thời” của lượng cung tại mức giá cho trước? TXTOCB01_Bai1_v1.0014105205 17
Bài 1: Các khái niệm cơ bản về hàm số một biến số
24.Khái niệm đạo hàm
25. Đạo hàm của hàm số tại một điểm
Một chiếc xe đi được 110 km sau 2 giờ, vận tốc trung bình của chiếc xe sẽ là kmgiờ hay km/giờ.
Nói chung, để tìm vận tốc trung bình của một chiếc xe trong khoảng thời gian thì ta sẽ lấy quãng
đường đi được trong khoảng thời gian đó chia cho thời gian đã đi:
Câu hỏi đặt ra là làm thế nào để tìm được vận tốc (vận tốc tức thời) của chiếc xe tại một thời điểm
cụ thể, chẳng hạn thời điểm chiếc xe đó va chạm với một vật khác, tức là ta sẽ phải xem xét vận tốc
trung bình trong khoảng thời gian bé nhất có thể. Khái niệm vận tốc tức thời được tổng quát và
phát biểu theo ngôn ngữ toán học như sau.
Giả sử hàm số xác định trong khoảng . Nếu xuất phát từ điểm ta cho biến độc lập thay đổi giá trị
đến điểm thì biến phụ thuộc y sẽ thay đổi giá trị từ đến . Hiệu số chỉ lượng thay đổi giá trị của
biến độc lập, được gọi là số gia của đối số, còn hiệu số
Chỉ lượng thay đổi giá trị tương ứng của y, được gọi là số gia tương ứng của hàm số (ta sử dụng ký
hiệu Δ để chỉ số gia, hay lượng thay đổi trị số của các biến số). Với , tỷ số
biểu diễn tốc độ biến thiên trung bình của biến số y khi biến số x thay đổi giá trị từ x0 đến x. Nếu tỷ
số này có giới hạn hữu hạn khi thì con số giới hạn cho biết tốc độ biến thiên tức thời của hàm số tại điểm .
Định nghĩa: Nếu tỷ số (2.1) có giới hạn hữu hạn khi Δx→0
thì số k được gọi là đạo hàm của hàm số y = f(x) tại điểm x0.
Đạo hàm của hàm số y = f(x) tại điểm x0 được biểu diễn bằng một trong các ký hiệu sau: Theo định nghĩa ta có:
Ví dụ 1: Xét hàm số f(x) = x2 tại điểm x0 bất kỳ, ta có
Theo định nghĩa đạo hàm, ta có:
Ví dụ 2: Xét hàm số f(x) = sinx tại điểm x0 bất kỳ, ta có 18 TXTOCB01_Bai1_v1.0014105205
Bài 1: Các khái niệm cơ bản về hàm số một biến số
Chú ý: Nếu giới hạn của tỷ số (2.1) khi Δx → 0 được tính riêng từng phía (, ) tức là luôn lớn hơn
(nhỏ hơn) thì các giới hạn tương ứng được gọi là đạo hàm một phía (đạo hàm bên phải, đạo hàm
bên trái) của hàm số tại điểm x0. Các đạo hàm một phía được ký hiệu như sau: Đạo hàm bên phải: Đạo hàm bên trái:
Hàm số y = f(x) có đạo hàm tại điểm x0 khi và chỉ khi tại điểm đó đạo hàm bên phải và đạo hàm
bên trái cùng tồn tại và bằng nhau:
Ví dụ: Xét hàm số f(x) = |x| tại điểm x0 = 0, ta có Đạo hàm bên phải: Đạo hàm bên trái:
Tại điểm 0 hàm số không có đạo hàm vì các đạo hàm một phía không bằng nhau.
26. Tính liên tục của hàm số có đạo hàm
Định lý: Nếu hàm số f(x) có đạo hàm tại điểm x0 thì nó liên tục tại điểm đó.
Chứng minh: Thật vậy, nếu tồn tại thì Từ đây suy ra:
Điều này chứng tỏ hàm số liên tục tại .
Chú ý: Định lý khẳng định rằng một hàm số liên tục tại tất cả các điểm mà tại đó hàm số đó có đạo
hàm. Tuy nhiên, một hàm số liên tục tại một điểm chưa chắc có đạo hàm tại điểm đó. Chẳng hạn,
hàm số liên tục tại điểm , nhưng không có đạo hàm tại điểm đó.
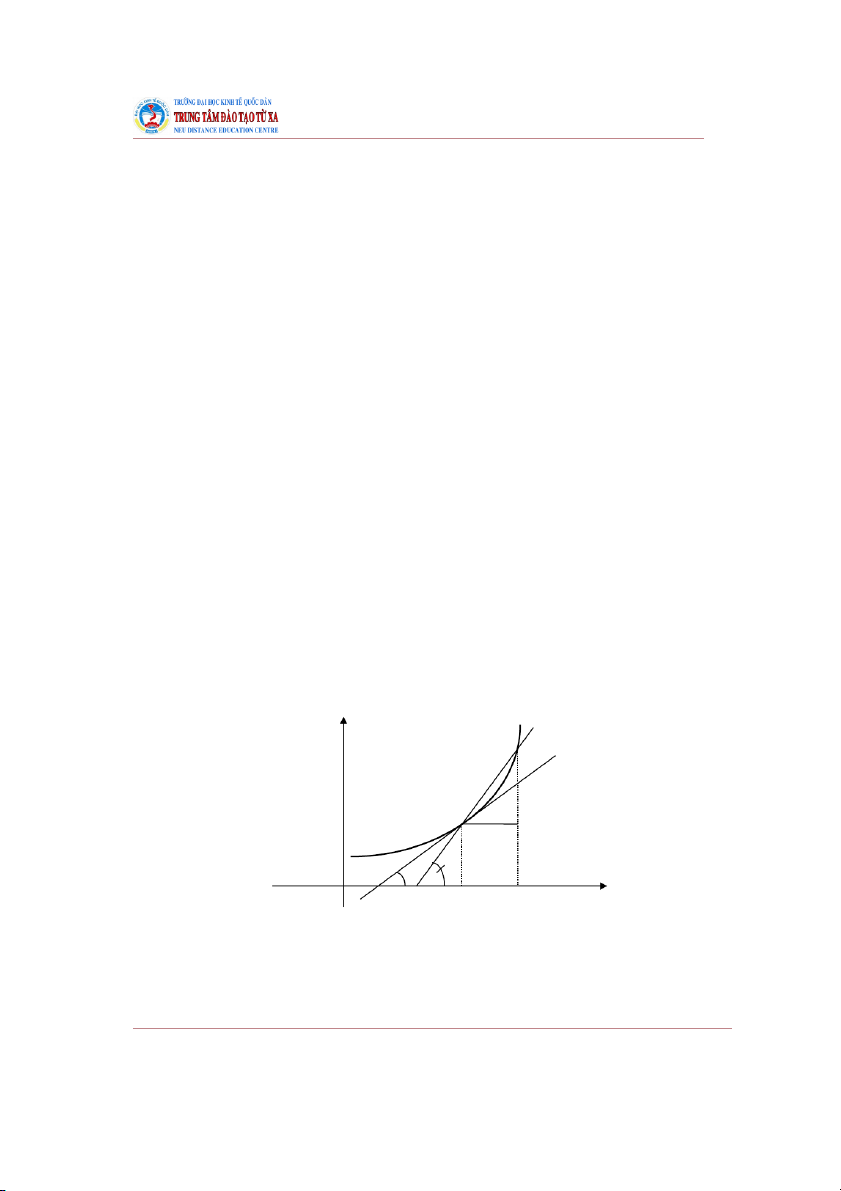
27. Đạo hàm và độ dốc của đường cong
Như ta đã biết, hệ số góc của một đường thẳng biểu thị độ dốc của đường thẳng đó so với trục Ox.
Độ dốc của đường cong tại điểm M0 được đo bởi hệ số góc của tiếp tuyến kẻ tại điểm đó. y M T M0 N y = f(x) 0 x0 x0+x x
Nếu thay đổi giá trị của biến độc lập từ đến thì điểm tương ứng trên đồ thị xê dịch từ vị trí đến vị
trí . Số gia có giá trị tuyệt đối càng nhỏ thì điểm càng gần điểm . Gọi là góc nghiêng của đường
thẳng và là góc nghiêng của tiếp tuyến với trục hoành, ta có: TXTOCB01_Bai1_v1.0014105205 19
Bài 1: Các khái niệm cơ bản về hàm số một biến số
Với x0 cố định và Δx→0 thì điểm M tiến dần đến vị trí M0 và đường thẳng M0M tiến dần tới vị trí
giới hạn là tiếp tuyến M0T, đồng thời φ → α. Từ đẳng thức (2.2) suy ra:
Từ đây suy ra: Đạo hàm của hàm số y = f(x) tại điểm x0 là hệ số góc của tiếp tuyến của đồ thị hàm
số tại điểm M0 có hoành độ x = x0.
Như vậy, đạo hàm f’(x0) là số đo độ dốc của đường cong y = f(x) tại điểm M0[x0, f(x0)].
28. Đạo hàm của hàm số trên một miền
Theo định nghĩa thì đạo hàm của hàm số tại một điểm x0 là một số thực xác định. Nếu hàm số có
đạo hàm tại mọi điểm thuộc một miền X thì mỗi giá trị
cho tương ứng một giá trị xác định của đạo hàm , do đó ta có hàm số:
Ta gọi hàm số này là đạo hàm của hàm số trên miền Ví dụ:
Đạo hàm của hàm số là hàm số , (ở đây được thay bởi
Đạo hàm của hàm số là hàm số ,
29.Đạo hàm của các hàm sơ cấp cơ bản
Để thực hiện việc tính toán đạo hàm, trước hết bạn cần ghi nhớ các công thức đạo hàm của các hàm
số sơ cấp cơ bản. Các công thức sau đây được thiết lập trực tiếp theo định nghĩa. Ví dụ:
30.Các quy tắc tính đạo hàm
31. Đạo hàm của tổng, hiệu, tích, thương các hàm số
Định lý 1: Nếu các hàm số u = u(x) và v = v(x) có đạo hàm tại điểm x0 thì tại điểm đó: ( là hằng số bất kỳ)
Ví dụ 1: Tính đạo hàm của hàm số
Giải: Sử dụng các quy tắc 1 và 2 trong định lý 1, ta được 20 TXTOCB01_Bai1_v1.0014105205
Bài 1: Các khái niệm cơ bản về hàm số một biến số
Ví dụ 2: Tính đạo hàm của hàm số
Giải: Để dễ sử dụng công thức đạo hàm của hàm lũy thừa, ta viết biểu thức hàm số dưới dạng:
Sử dụng các quy tắc 1 và 2 trong định lý 1, ta được
Ví dụ 3: Tính đạo hàm của hàm số
Giải: Sử dụng quy tắc 3 về đạo hàm của tích (với ), ta có
Ví dụ 4: Tính đạo hàm của hàm số
Sử dụng quy tắc 4 về đạo hàm của thương (với u = lnx, v = x4), ta có
Ví dụ 5: Tính đạo hàm của hàm số Giải: Đặt , ta có
32. Đạo hàm của hàm hợp
Định lý 2: Nếu hàm số u = φ(x) có đạo hàm tại điểm x0 và hàm số y = f(u) có đạo hàm tại điểm
tương ứng u0 = φ(x0) thì hàm hợp y = g(x) = f[φ(x)] có đạo hàm tại điểm x0 và đạo hàm của hàm
hợp (đạo hàm của y theo x) được tính theo công thức:
Công thức (2.3) có thể viết dưới dạng:
Ví dụ 1: Hàm số là hàm hợp của hai hàm cơ bản và . Theo quy tắc nói trên ta có Chú ý:
Áp dụng quy tắc đạo hàm của hàm hợp, nếu u = φ(x) là một hàm số có đạo hàm thì các công thức
đạo hàm cơ bản được sử dụng như sau:
Ví dụ 2: Sử dụng các công thức 2’, 4, 5 với u = kx ta có:
Ví dụ 3: Tính đạo hàm của hàm số
Giải: Sử dụng công thức 1 với u = 3x + 2, ta có
Ví dụ 4: Tính đạo hàm của hàm số
Giải: Sử dụng công thức 2’, với , ta có TXTOCB01_Bai1_v1.0014105205 21
Bài 1: Các khái niệm cơ bản về hàm số một biến số
Ví dụ 5: Tính đạo hàm của hàm số
Giải: Sử dụng công thức 1’ với u = x2 + m, ta có
Ví dụ 6: Tính đạo hàm của hàm số Giải:
Ví dụ 7: Tính đạo hàm của hàm số
Giải: Sử dụng phối hợp các quy tắc tính đạo hàm, ta có
33. Đạo hàm của biểu thức lũy thừa mũ và phương pháp logarit hóa
Ví dụ 1: Tính đạo hàm của hàm số Ta thấy
Khi đó, lấy đạo hàm 2 vế ta dễ dàng có:
Với dạng đặc biệt của hàm số, việc lấy logarit có thể giúp đơn giản việc tính toán.
Biểu thức lũy thừa mũ là biểu thức dạng y = uv, trong đó u = u(x), v = v(x) là các hàm số đối số x
và u(x) > 0. Do cả cơ số u và lũy thừa v đều phụ thuộc x, khi tính đạo hàm của biểu thức loại này ta
không thể áp dụng trực tiếp các công thức đạo hàm của hàm số mũ và hàm lũy thừa. Để tính đạo
hàm, ta viết lại biểu thức hàm số dưới dạng:
Với giả thiết các hàm số u = u(x), v = v(x) có đạo hàm, ta có
Ta cũng có thể tính đạo hàm của hàm số y = uv bằng phương pháp logarit hóa như sau:
Lấy logarit của y (cơ số e): lny = vlnu;
Lấy đạo hàm hai vế ta được từ đây suy ra:
Ví dụ 2: Tính đạo hàm của hàm số Giải: Ta có
34.Vi phân của hàm số
35. Khái niệm hàm khả vi và vi phân
Trong khái niệm đạo hàm của hàm số tại một điểm, ta thấy đại lượng , khi là một giá trị xác định
đủ nhỏ thì ta sẽ tính được xấp xỉ sự thay đổi của hàm số ứng với sự thay đổi của đối số. 22 TXTOCB01_Bai1_v1.0014105205
Bài 1: Các khái niệm cơ bản về hàm số một biến số
Định nghĩa: Hàm số f(x) được gọi là hàm khả vi tại điểm x0 chỉ khi nó có đạo hàm tại điểm đó.
Tích của đạo hàm f’(x0) với số gia Δx của biến độc lập được gọi là vi phân của hàm số f(x) tại điểm
x0 và được ký hiệu là df(x0):
Ví dụ: Hàm số f(x) = x3 khả vi tại điểm x bất kỳ vì nó có đạo hàm tại mọi điểm
Vi phân của hàm số này tại điểm x0 bất kỳ là:
Ý nghĩa của giá trị đó như sau: , chẳng hạn thì
36. Biểu thức vi phân
Nếu hàm số y = f(x) khả vi tại mọi điểm thuộc khoảng X thì biểu thức vi phân
là một hàm số đối số x, xác định trên khoảng X (Δx là số gia bất kỳ, không phụ thuộc vào x):
Áp dụng công thức trên cho hàm số f(x) = x ta có
Như vậy, vi phân của biến độc lập x bằng số gia của nó, do đó trong biểu thức (2.4) người ta
thường viết dx thay vì Δx. Biểu thức vi phân của hàm số y = f(x) thường được viết dưới dạng: hoặc:
Để tính vi phân của một hàm số ta tính đạo hàm của nó, sau đó nhân với vi phân của biến độc lập. Ví dụ:
37. Các quy tắc tính vi phân
Vi phân của tổng, hiệu, tích, thương các hàm số:
Định lý: Nếu các hàm số u = u(x) và v = v(x) khả vi tại điểm x thì tại điểm đó ta có: ( là hằng số bất kỳ)
Các quy tắc trên suy ra trực tiếp từ các quy tắc tính đạo hàm. Chẳng hạn, quy tắc tính vi phân
của tích được chứng minh như sau:
Tính bất biến của biểu thức vi phân:
Nếu y = f(x) là hàm số khả vi của biến độc lập x thì vi phân của nó được tính theo công thức
(2.5). Ta hãy xét trường hợp x là hàm số khả vi của một biến độc lập t nào đó: x = φ(t). Khi đó
y là hàm số của biến độc lập t:
Theo công thức tính vi phân và theo quy tắc tính đạo hàm của hàm hợp, ta có: TXTOCB01_Bai1_v1.0014105205 23
Bài 1: Các khái niệm cơ bản về hàm số một biến số
Như vậy: Biểu thức vi phân (2.5) vẫn giữ nguyên dạng trong trường hợp biểu thức x không
phải là biến độc lập, mà phụ thuộc vào biến độc lập khác. Nói cách khác, biểu thức vi phân
(2.5) bất biến đổi với phép biến đổi biến số x= φ(t).
Chú ý: Trong trường hợp x là biến phụ thuộc, dx trong biểu thức vi phân
không còn là gia số Δx, mà là vi phân của hàm số x= φ(t):
38.Đạo hàm và vi phân cấp cao
39. Đạo hàm cấp cao
Như ta đã biết, nếu hàm số có đạo hàm tại mọi điểm thuộc miền thì đạo hàm là một hàm số đối số
x, xác định trong miền X, do đó ta có thể lấy đạo hàm của hàm số Đạo hàm của hàm số được gọi
là đạo hàm cấp hai của hàm số đó. Tiếp theo ta lại có thể xét đạo hàm cấp hai của hàm số y = f(x)
như một hàm số đối số x và tiếp tục lấy đạo hàm của nó để nhận được đạo hàm cấp ba …
Định nghĩa: Đạo hàm của đạo hàm cấp n – 1 của hàm số được gọi là đạo hàm cấp n của hàm số đó.
Các đạo hàm cấp cao của hàm số được ký hiệu như sau: Đạo hàm cấp 2: hoặc Đạo hàm cấp 3: hoặc … Đạo hàm cấp n: hoặc
Đạo hàm cấp cao của hàm số còn được gọi là đạo hàm l .
ặp Để tính đạo hàm cấp n của hàm số y =
f(x), ta thực hiện phép toán đạo hàm liên tiếp n lần:
Ví dụ 1: Tính đạo hàm cấp 2 của hàm số Giải:
Ví dụ 2: Tính đạo hàm cấp 3 của hàm số: Giải:
Ví dụ 3: Tính đạo hàm cấp n của hàm số y = ekx Giải: Ta có:
Bằng phương pháp quy nạp bạn có thể chứng minh được rằng
Trong thực hành, chúng ta thường chỉ sử dụng đến đạo hàm cấp 2. 40. Vi phân cấp cao
Nếu hàm số khả vi tại mọi điểm thuộc một miền X thì vi phân là một hàm số của biến x:
trong đó vi phân dx của biến độc lập x là số gia Δx, không phụ thuộc x. Khái niệm vi phân cấp cao
được định nghĩa tương tự như đạo hàm cấp cao: 24 TXTOCB01_Bai1_v1.0014105205
Bài 1: Các khái niệm cơ bản về hàm số một biến số
Định nghĩa: Vi phân cấp n của hàm số là vi phân của vi phân cấp của hàm số đó (ta gọi vi phân dy là vi phân cấp 1).
Vi phân cấp n của hàm số được ký hiệu là :
Trong công thức vi phân đạo hàm phụ thuộc , còn là số gia bất kỳ của biến độc lập , không phụ
thuộc . Do đó, khi xem như một hàm số của thì được xem như hằng số. Ta có:
Bằng phương pháp quy nạp ta có thể chứng minh công thức tính vi phân cấp n của một hàm số theo đạo hàm cấp n của nó: hoặc
Chú ý rằng biểu thức vi phân cấp cao không có tính bất biến như biểu thức vi phân cấp một, tức là
với n > 1 công thức này chỉ đúng khi x là biến độc lập. Ví dụ: TXTOCB01_Bai1_v1.0014105205 25
Bài 1: Các khái niệm cơ bản về hàm số một biến số
Tóm lược cuối bài
Đạo hàm tại 1 điểm:
Hàm số đạo hàm (đạo hàm trên một miền):
Đạo hàm của tổng, hiệu, tích, thương:
Đạo hàm của hàm hợp: Vi phân tại 1 điểm: Biểu thức vi phân: 26 TXTOCB01_Bai1_v1.0014105205
Bài 1: Các khái niệm cơ bản về hàm số một biến số Câu hỏi ôn tập 9.
Nêu định nghĩa đạo hàm tại một điểm. 10.
Nêu công thức đạo hàm của các hàm cơ bản. 11.
Nêu công thức đạo hàm của tổng, hiệu, tích, thương. 12.
Nêu công thức đạo hàm của hàm hợp. 13.
Nêu công thức tính vi phân. 14. Tính đạo hàm của: 15. Tính đạo hàm của: 16. Tính đạo hàm của: 17. Tính đạo hàm của: 18. Tính đạo hàm của: 19.
Viết biểu thức vi phân của hàm số: 20.
Tính đạo hàm cấp 2 của: 21.
Tính đạo hàm cấp 2 của: BÀI 3
ỨNG DỤNG CỦA ĐẠO HÀM TRONG TOÁN HỌC VÀ TRONG PHÂN TÍCH KINH TẾ TXTOCB01_Bai1_v1.0014105205 27
Bài 1: Các khái niệm cơ bản về hàm số một biến số Hướng dẫn học
Để học tốt bài này, sinh viên cần tham khảo các phương pháp học s au:
Học đúng lịch trình của môn học theo tuần, làm các bài luyện tập đầy đủ và
tham gia thảo luận trên diễn đàn. Đọc tài liệu:
11. BỘ MÔN TOÁN CƠ BẢN, 2009, Bài tập toán cao cấp cho các nhà kinh tế, NXB Thống kê.
12. NGUYỄN ĐÌNH TRÍ, TẠ VĂN ĐĨNH, NGUYỄN HỒ QUỲNH, 2008, Toán cao cấp 2, NXB Giáo dục.
13. NGUYỄN ĐÌNH TRÍ, TẠ VĂN ĐĨNH, NGUYỄN HỒ QUỲNH, 2008, Toán cao cấp 3, NXB Giáo dục.
14. ALPHA C. CHIANG,1995, Fundamental Methods of Mathematical Economics,
Third edition, Mc. Graw–Hill, Inc.
15. MICHAEL HOY,JOHN LIVERNOIS, CHRIS MC KENNA, RAY REES,
THANASIS STENGOS, 2001, Mathematics for Economics, The MIT Press
Cambrige, Massachusetts, London, England.
Sinh viên làm việc theo nhóm và trao đổi với giảng viên trực tiếp tại lớp học hoặc qua email.
Tham khảo các thông tin từ trang Web môn học. Nội dung
Đạo hàm và xu hướng biến thiên của hàm số;
Tìm các điểm cực trị của hàm số;
Ý nghĩa của đạo hàm trong kinh tế;
Tính hệ số co dãn của cung và cầu theo giá;
Sự lựa chọn tối ưu trong kinh tế. Mục tiêu
Trình bày ứng dụng của đạo hàm để tìm các khoảng tăng, giảm và cực trị của hàm số;
Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số trên đoạn [a, b];
Tính và nêu được ý nghĩa kinh tế của ;
Tính và nêu được ý nghĩa kinh tế của hệ số co dãn của cung, cầu theo giá;
Giải quyết được bài toán tối ưu lợi nhuận (theo mức sản lượng tối ưu hoặc sử
dụng mức lao động tối ưu). 28 TXTOCB01_Bai1_v1.0014105205
Bài 1: Các khái niệm cơ bản về hàm số một biến số Tình huống dẫn nhập
Cho biết hàm lợi nhuận của nhà sản xuất ứng với mức sản lượng được xác định như sau: trong đó:
là lợi nhuận của nhà sản xuất
Q là mức sản lượng cho lợi nhuận
Hãy chọn mức sản lượng cho lợi nhuận tối đa? TXTOCB01_Bai1_v1.0014105205 29
Bài 1: Các khái niệm cơ bản về hàm số một biến số
41. Đạo hàm và xu hướng biến thiên của hàm số
42. Liên hệ giữa đạo hàm và xu hướng biến thiên của hàm số
Xin nhắc lại rằng hàm số được gọi là đơn điệu tăng (đơn điệu giảm) trên một khoảng nếu với mọi
cặp điểm thuộc , hiệu số luôn cùng dấu (trái dấu) với . Nói cách khác, hàm số đơn điệu tăng (đơn
điệu giảm) trong khoảng khi và chỉ khi
Trong nhiều tình huống chúng ta cần biết khi nào thì hàm số đang có xu hướng tăng hoặc giảm,
chẳng hạn nếu lợi nhuận của doanh nghiệp đang tăng thì doanh nghiệp đó sẽ tăng mức sản lượng để đạt lợi nhuận cao hơn.
Định lý sau đây cho biết điều kiện cần để hàm số đơn điệu tăng (đơn điệu giảm) trong một khoảng.
Định lý 1: Giả sử hàm số có đạo hàm tại mọi điểm thuộc khoảng . Nếu đơn điệu tăng (đơn điệu giảm) trong khoảng thì
Điều kiện đủ để hàm số đơn điệu tăng (đơn điệu giảm) trong một khoảng có nội dung như sau:
Định lý 2: Giả sử hàm số có đạo hàm trong khoảng .
Nếu tại mọi điểm thì hàm số đơn điệu tăng (đơn điệu giảm) trong khoảng .
Nếu tại mọi điểm thì hàm số nhận giá trị không đổi trong khoảng .
Định lý 2 có thể mở rộng như sau:
Định lý 3: Nếu hàm số liên tục và có đạo hàm trên khoảng và
với mọi , trong đó là một tập con rời rạc của khoảng , thì hàm số đơn điệu tăng (đơn điệu giảm) trên toàn bộ khoảng .
43. Xác định các khoảng tăng, giảm của hàm số
Để xác định các khoảng tăng, giảm của hàm số ta lần lượt thực hiện như sau:
Tìm miền xác định của hàm số Tính đạo hàm
Xét dấu của đạo hàm theo
Căn cứ vào dấu của (dựa theo điều kiện đủ nên trên) để xác định các khoảng tăng, giảm của hàm số .
Ví dụ 1: Xác định các khoảng tăng, giảm của hàm số
Giải: Hàm số đã cho xác định và liên tục tại mọi điểm và
Dấu của như dấu của nhị thức (1 – x), do đó
Theo định lý 2, hàm số tăng trong khoảng và giảm trong khoảng
Ví dụ 2: Xác định các khoảng tăng, giảm của hàm số
Giải: Hàm số đã cho xác định và liên tục tại mọi điểm và
Dấu của là dấu của tam thức bậc hai , do đó trong khoảng trong các khoảng và
Như vậy, hàm số tăng trên khoảng , hàm số giảm trên các khoảng và
Ví dụ 3: Xác định các khoảng tăng, giảm của hàm số: 30 TXTOCB01_Bai1_v1.0014105205
Bài 1: Các khái niệm cơ bản về hàm số một biến số
Giải: Hàm số đã cho xác định và liên tục tại mọi điểm và
Đạo hàm là một phân thức có mẫu số dương với mọi , do đó dấu của nó như dấu của tử số. Theo
quy tắc dấu của nhị thức bậc nhất ta dễ dàng xác định được dấu của như sau: với mọi
với mọi , trừ một điểm .
Theo định lý 2, hàm số giảm trong khoảng và, theo định lý 3, hàm số tăng trong khoảng
Ví dụ 4: Xác định khoảng tăng, giảm của hàm số:
Giải: Hàm số xác định trên miền (điều kiện để ).
Trên miền xác định, mẫu số của luôn dương nên dấu của trùng với dấu của
Ta có thể kết luận được rằng hàm số tăng trên khoảng và hàm số giảm trên khoảng
44.Tìm các điểm cực trị của hàm số
Câu hỏi tiếp theo của doanh nghiệp là mức sản lượng nào sẽ cho lợi nhuận tối đa.
45. Khái niệm cực trị địa phương
Giả sử hàm số xác định và liên tục trong khoảng
Định nghĩa: Ta nói rằng hàm số đạt giá trị cực đại (giá trị cực tiểu) tại điểm nếu tồn tại số đủ nhỏ sao cho bất đẳng thức
luôn luôn được thỏa mãn khi
Điểm mà tại đó hàm số nhận giá trị cực đại (giá trị cực tiểu) được gọi là
điểm cực đại (điểm cực tiểu) cuả nó.
Điểm cực đại và điểm cực tiểu được gọi chung là điểm cực trị của hàm số.
Việc hạn chế , với đủ nhỏ có nghĩa là khái niệm cực trị (giá trị cực đại hoặc giá trị cực tiểu) được
hiểu theo nghĩa cực trị địa phương (còn gọi là cực trị tương đối): giá trị là giá trị cực đại (cực tiểu)
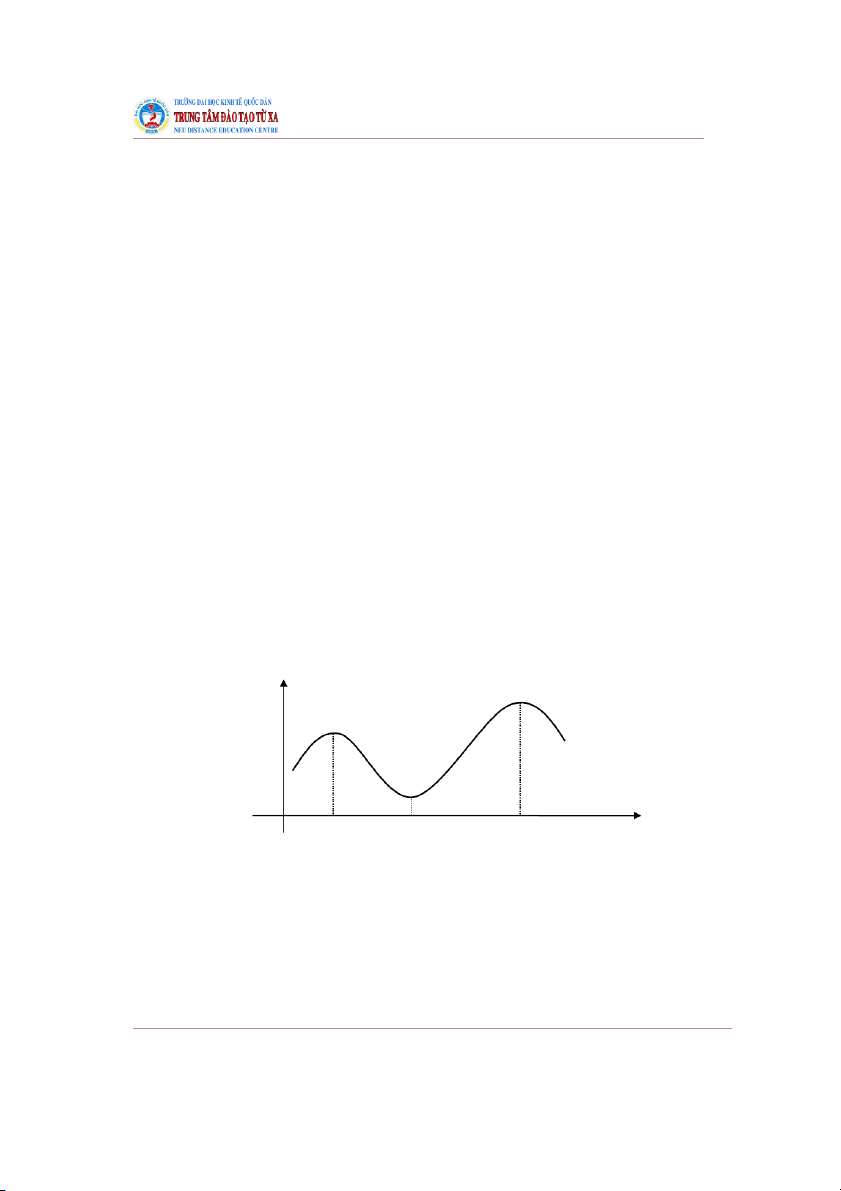
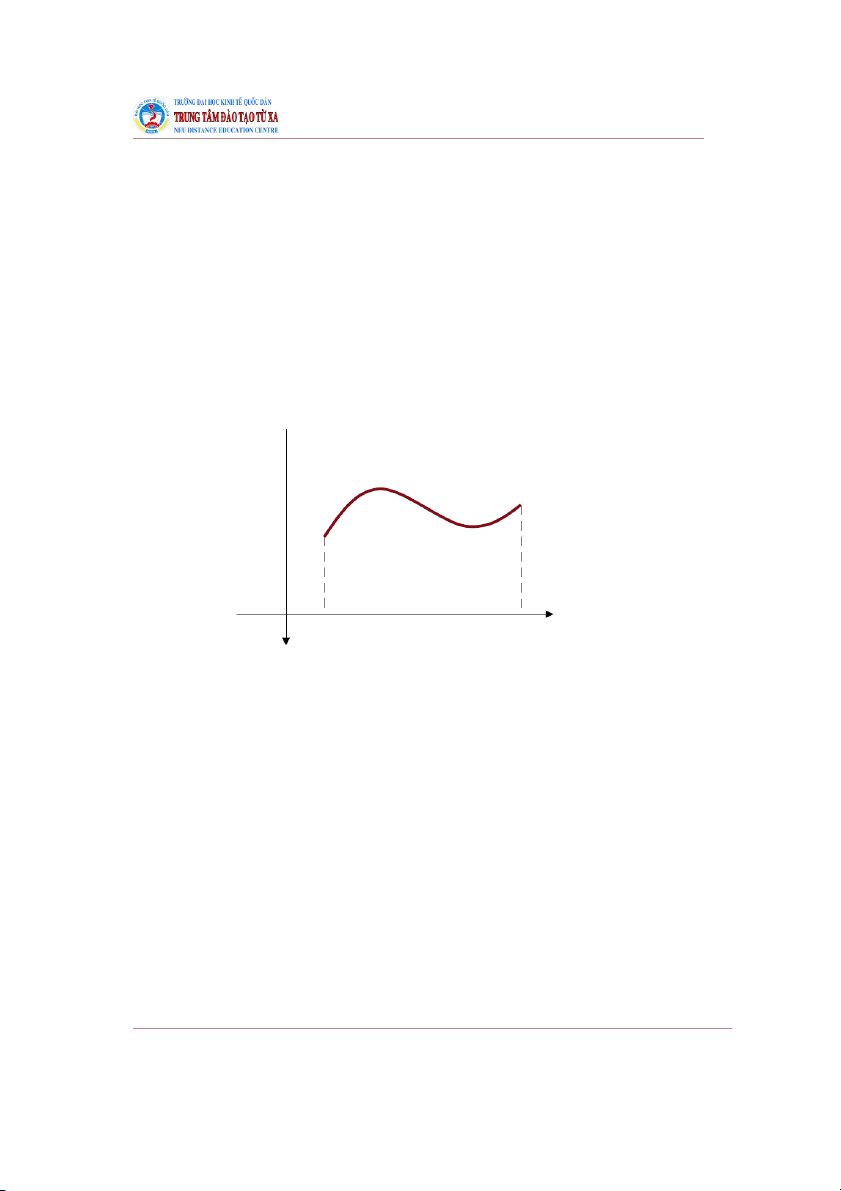
nếu nó lớn hơn (nhỏ hơn) tất cả các giá trị khác tại những điểm gần . y y = f(x) 0 x1 x2 x3 x
Nhìn trên đồ thị thì thứ tự cực đại (cực tiểu) là các đỉnh nhô lên (đỉnh thụt xuống) của đường cong .
Trên hình vẽ, và là các điểm cực đại, còn là điểm cực tiểu của hàm số
46. Điều kiện cần của cực trị
Định lý về điều kiện cần có nội dung như sau:
Định lý: Nếu hàm số đạt giá trị cực đại hoặc cực tiểu tại điểm và tại điểm đó hàm số có đạo hàm thì
Định lý cho biết hàm số chỉ có thể đạt cực trị tại các điểm thuộc một trong hai loại sau đây:
Điểm mà tại đó đạo hàm triệt tiêu (gọi là điểm dừng); TXTOCB01_Bai1_v1.0014105205 31
Bài 1: Các khái niệm cơ bản về hàm số một biến số
Điểm mà tại đó hàm số liên tục nhưng không có đạo hàm;
Các điểm thuộc cả hai loại nói trên được gọi là điểm tới hạn của hàm số
Để tìm các điểm cực trị của một hàm số, trước hết ta phải tìm tất cả các điểm tới hạn của nó. Tuy
nhiên, các điểm tới hạn mới chỉ là những điểm thỏa mãn điều kiện cần. Muốn có kết luận cuối cùng
về các điểm tới hạn ta phải tiếp tục xét điều kiện đủ.
47. Điều kiện đủ
Định lý sau đây dùng để xét một điểm tới hạn bất kỳ dựa vào dấu của đạo hàm cấp 1:
Định lý 1: Giả sử điểm là một điểm tới hạn của hàm số và giả sử hàm số có đạo hàm mang dấu
xác định trong mỗi khoảng và . Khi đó:
Nếu qua điểm đạo hàm đổi dấu thì hàm số đạt cực trị tại điểm đó: o
là điểm cực đại nếu đổi dấu từ + sang – o
là điểm cực tiểu nếu đổi dấu từ – sang +
Nếu qua điểm đạo hàm không đổi dấu thì hàm số không đạt cực trị tại điểm đó.
Để xét điều kiện đủ đối với các điểm dừng, ta còn có thể sử dụng đạo hàm cấp cao:
Định lý 2: Giả sử tồn tại số tự nhiên sao cho Khi đó:
Nếu n là số chẵn thì là một điểm cực trị của hàm số là điểm cực đại nếu ; x0 là điểm cực tiểu nếu .
Nếu lẻ thì không phải là điểm cực trị của hàm số
Trường hợp ta có quy tắc sau: o
Nếu và thì x0 là điểm cực đại của hàm số o
Nếu và thì x0 là điểm cực tiểu của hàm số
48. Tìm các điểm cực trị của hàm số
Để tìm các điểm cực trị (địa phương) của một hàm số ta thực hiện như sau:
Tìm miền xác định của hàm số Tính đạo hàm
Giải điều kiện cần để tìm các điểm tới hạn: o
Giải phương trình để tìm các điểm dừng o
Chỉ ra những điểm thuộc miền xác định mà tại đó hàm số liên tục nhưng không có đạo hàm (đạo hàm không xác định).
Xét điều kiện đủ đối với từng điểm tới hạn và kết luận.
Ví dụ 1: Tìm các điểm cực trị của hàm số
Giải: Hàm số này xác định và liên tục trên toàn bộ trục số. Ta có:
Hàm số đã cho có 2 điểm tới hạn: khi và không tồn tại khi
Dấu của đạo hàm y’ như dấu của biểu thức x – 3/5 1 + + 0 – ║ +
Sử dụng định lý 1 về điều kiện đủ ta đi đến kết luận: là điểm cực đại và là điểm cực tiểu. 32 TXTOCB01_Bai1_v1.0014105205
Bài 1: Các khái niệm cơ bản về hàm số một biến số
Ví dụ 2: Tìm các điểm cực trị của hàm số
Giải: Hàm số đã cho xác định trên toàn bộ trục số và có đạo hàm như sau
Hàm số có đạo hàm tại mọi điểm và phương trình chỉ có một nghiệm Đó là điểm dừng và là điểm
tới hạn duy nhất. Để xét điều kiện đủ ta sử dụng đạo hàm cấp 2:
Tại điểm dừng x = 2 ta có . Theo định lý 2 thì là điểm cực tiểu và đó là điểm cực trị duy nhất của hàm số đã cho.
Ví dụ 3: Tìm các điểm cực trị của hàm số
Giải: Hàm số xác định trong khoảng (0; +) và Ta thấy , đồng thời
Vậy hàm số đã cho đạt cực đại tại điểm và đó là điểm cực trị duy nhất của nó.
49. Bài toán cực trị toàn thể
Như ta đã biết, nếu hàm số liên tục trên khoảng đóng thì trên khoảng đó hàm số có giá trị lớn nhất
và giá trị nhỏ nhất. Nếu hàm số đạt giá trị lớn nhất (giá trị nhỏ nhất) tại một điểm bên trong
khoảng thì là một giá trị cực đại (giá trị cực tiểu). Ngoài ra, các giá trị tại đầu mút a và b cũng có
thể là giá trị lớn nhất hoặc giá trị nhỏ nhất của hàm số. Như vậy, để tìm giá trị lớn nhất (giá trị nhỏ
nhất) của hàm số trước hết ta phải tìm tất cả các giá trị cực đại (giá trị cực tiểu) địa phương,
sau đó so sánh các giá trị đó cùng với các giá trị và để chọn ra số lớn nhất (số nhỏ nhất).
Ta cũng có thể tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số trên khoảng bằng cách tính giá trị
của nó tại tất cả các điểm tới hạn và tại hai đầu mút, sau đó chọn ra số lớn nhất và số nhỏ nhất.
Ví dụ: Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số trên đoạn Giải: Ta có tại các điểm và
So sánh các giá trị ta tìm được:
Giá trị lớn nhất: tại điểm
Giá trị nhỏ nhất: tại điểm
Trong thực hành ta thường gặp trường hợp hàm số liên tục trong khoảng và chỉ có một điểm cực
trị duy nhất . Khi đó nếu điểm là điểm cực đại (điểm cực tiểu) thì chính là giá trị lớn nhất (giá trị
nhỏ nhất) của hàm số trong khoảng
Ví dụ: Dựa theo kết quả tìm các điểm cực trị ở ví dụ 2 và ví dụ 3 trên đây ta có thể kết luận:
Giá trị nhỏ nhất của hàm số trên là:
Giá trị lớn nhất của hàm số trong khoảng là TXTOCB01_Bai1_v1.0014105205 33
Bài 1: Các khái niệm cơ bản về hàm số một biến số 50.
Ý nghĩa của đạo hàm trong kinh tế
51. Đạo hàm và giá trị cận biên trong kinh tế Xét mô hình hàm số:
trong đó x và y là các biến số kinh tế (ta coi biến độc lập x là biến số đầu vào và biến phụ thuộc y
là biến số đầu ra). Trong kinh tế học người ta quan tâm đến xu hướng biến thiên của biến phụ thuộc
y tại một điểm khi biến độc lập x thay đổi một lượng nhỏ. Chẳng hạn, khi xét mô hình hàm sản
xuất người ta thường quan tâm đến số lượng sản phẩm hiện vật tăng thêm khi sử dụng thêm một đơn vị lao động.
Theo định nghĩa đạo hàm:
Khi x có giá trị tuyệt đối đủ nhỏ ta có:
Khi ta có Như vậy, đạo hàm biểu diễn xấp xỉ lượng thay đổi giá trị của biến phụ thuộc y khi biến
độc lập x tăng thêm một đơn vị.
Khi xét mô hình biểu diễn ảnh thưởng của biến số kinh tế x đối vói biến số kinh tế y, các nhà kinh
tế gọi là giá trị y – cận biên của x tại điểm
Đối với mỗi hàm kinh tế, giá trị cận biên có tên gọi cụ thể như sau:
Đối với mô hình hàm sản xuất thì được gọi là sản phẩm hiện vật cận biên của lao động tại điểm
Sản phẩm hiện vật cận biên của lao động được ký hiệu là (Marginal physical product of labor):
Tại mỗi điểm cho biết xấp xỉ lượng sản phẩm hiện vật gia tăng khi sử dụng thêm một đơn vị lao động.
Đối với mô hình hàm doanh thu thì được gọi là doanh thu cận biên tại điểm Doanh thu cận biên
được ký hiệu là MR (Marginal Revenue):
Tại mỗi mức sản lượng cho biết xấp xỉ lượng doanh thu tăng thêm khi sản xuất thêm một đơn
vị sản phẩm. Đối với doanh nghiệp cạnh tranh, ta có:
( là giá sản phẩm trên thị trường)
Đối với mô hình hàm chi phí thì được gọi là chi phí cận biên tại điểm Chi phí cận biên được ký hiệu là (Marginal Cost):
Tại mỗi mức sản lượng cho biết xấp xỉ lượng chi phí tăng thêm khi sản xuất thêm một đơn vị sản phẩm.
Đối với hàm tiêu dùng thì được gọi là xu hướng tiêu dùng cận biên và được ký hiệu là MPC
(Marginal Propensity to Consume):
Tại mỗi mức thu nhập là số đo xấp xỉ lượng tiêu dùng gia tăng khi người ta có thêm $1 thu nhập.
Đối với hàm tiết kiệm thì được gọi là xu hướng tiết kiệm cận biên và được ký hiệu là MPS (Marginal Propensity to Save):
Tại mỗi mức thu nhập là số đo xấp xỉ lượng tiết kiệm gia tăng khi người ta có thêm $1 thu nhập. Ví dụ:
Giả sử hàm sản xuất của một doanh nghiệp là 34 TXTOCB01_Bai1_v1.0014105205
Bài 1: Các khái niệm cơ bản về hàm số một biến số
Ở mức sử dụng đơn vị lao động (chẳng hạn, 100 giờ lao động một tuần), mức sản lượng tương ứng
là sản phẩm. Sản phẩm cận biên của lao động tại điểm L = 100 là
Điều này có nghĩa là khi tăng mức sử dụng lao động hàng tuần từ 100 lên 101 thì sản lượng hàng
tuần sẽ tăng thêm khoảng 0,25 đơn vị hiện vật.
52. Đạo hàm cấp hai và quy luật lợi ích cận biên giảm dần
Xét mô hình , trong đó y là biến số biểu diễn lợi ích (chẳng hạn như thu nhập, doanh thu, lợi
nhuận…) và x là biến số mô tả yếu tố đem lại lợi ích y. Quy luật lợi ích cận biên giảm dần (the Law
of deminishing returns) nói rằng khi x càng lớn thì giá trị y– cận biên càng nhỏ, tức là là hàm số
đơn điệu giảm (ít nhất theo nghĩa rộng). Dưới giác độ toán học, điều kiện để giảm dần theo x là:
Ví dụ: Nếu hàm sản xuất ngắn hạn được ước lượng dưới dạng ( và là các hằng số dương) thì quy
luật lợi ích cận biên giảm dần đòi hỏi:
53. Tính hệ số co dãn của cung và cầu theo giá
Một vấn đề được quan tâm trong kinh tế là phản ứng của cung và cầu đối với sự biến động giá cả
trên thị trường. Với giả thiết các yếu tố khác không thay đổi, sự phụ thuộc của lượng cầu vào giá p
được biểu diễn bằng hàm cầu:
Trong mô hình hàm cầu biến số p được đo bằng đơn vị tiền tệ, còn biến số Q được đo bằng đơn vị
hiện vật. Nếu gọi Qd là mức thay đổi lượng cầu khi giá thay đổi một đơn vị thì ý nghĩa của con số
đó còn phụ thuộc vào đơn vị đo. Hơn nữa, đối với các hàng hóa khác nhau thì sự thay đổi giá thêm
$1 mang ý nghĩa khác nhau. Chẳng hạn, nếu giá một chiếc ô tô tăng $1 thì có thể xem như giá ô tô
không thay đổi. Trong khi đó nếu giá 1 kg cà phê tăng $1 thì chắc hẳn đó làm một biến động lớn
trên thị trường cà phê. Để đánh giá độ nhạy cảm của cầu hàng hóa đối với sự biến động giá cả, các
nhà kinh tế sử dụng khái niệm hệ số co dãn.
Hệ số co dãn của cầu theo giá (tính ở mỗi mức giá) là số đo mức thay đổi tính bằng phần trăm của
lượng cầu khi giá tăng 1%.
Tại mức giá p, nếu giá thay đổi một lượng p thì lượng cầu thay đổi tương ứng một lượng Qd. Mức
phần trăm thay đổi của lượng cầu tính bình quân cho 1% thay đổi giá là:
Chuyển qua giới hạn khi p 0 ta được công thức tín hệ số co dãn của cầu theo giá tại điểm p:
Tương tự: Hệ số co dãn của cung theo giá là
số đo mức thay đổi tính bằng phần trăm của lượng
cung khi giá tăng 1%. Nếu biết hàm cung thì hệ số co dãn của cung theo giá tại điểm p được tính theo công thức
Ví dụ 1: Nếu hàm cầu là thì hệ số co dãn tại điểm p là
Tại điểm ta có Điều này có nghĩa là, tại mức giá , nếu giá tăng 1% thì cầu sẽ giảm khoảng 0,8%.
Ví dụ 2: Nếu hàm cầu có dạng bậc nhất thì hệ số co dãn tại điểm p là TXTOCB01_Bai1_v1.0014105205 35
Bài 1: Các khái niệm cơ bản về hàm số một biến số
54.Sự lựa chọn tối ưu trong kinh tế
Trong lĩnh vực hoạt động kinh tế việc ra quyết định gắn liền với việc tối ưu hóa một hàm mục tiêu
Bài toán đặt ra là: lựa chọn x để y đạt giá trị lớn nhất hoặc giá trị nhỏ nhất. Đối với một doanh
nghiệp sản xuất, mục tiêu thường được đặt ra là tối đa hóa lợi nhuận.
55.Chọn mức sản lượng tối ưu
Giả sử doanh nghiệp có hàm tổng chi phí và hàm tổng doanh thu . Tổng lợi nhuận của doanh
nghiệp là hàm số của biến số Q:
Bài toán đặt ra là: chọn mức sản lượng để thu lợi nhuận tối đa. Điều kiện cần để đạt cực đại tại điểm là:
Bằng ngôn ngữ của kinh tế học, điều kiện cần để đạt lợi nhuận tối đa là: doanh thu cận biên bằng chi phí cận biên.
Tại điểm mà , điều kiện đủ để đạt cực đại là:
Ví dụ: Một nhà sản xuất có hàm doanh thu và hàm chi phí như sau và
Hãy xác định mức sản lượng tối ưu. Giải: Ta có
Điều kiện cần để đạt lợi nhuận tối đa là:
MR = MC 400 – 15Q = 3Q2 – 12Q + 140
3Q2 + 3Q – 1260 = 0 Q2 + Q – 420 = 0
Từ phương trình này ta xác định được Q = 20 (loại Q = – 21 do Q > 0). Tại điểm Q = 20 ta có :
Điều kiện đủ thỏa mãn, do đó là điểm cực đại.
Chú ý rằng trong khoảng (0; ) hàm lợi nhuận chỉ có một điểm cực trị duy nhất, do đó mức sản
lượng tối ưu là Q = 20 và lợi nhuận tối đa là:
56. Lựa chọn tối ưu mức sử dụng yếu tố đầu vào
Xét trường hợp doanh nghiệp cạnh tranh tiến hành sản xuất với hàm sản xuất ngắn hạn , trong điều
kiện giá sản phẩm trên thị trường là p và giá lao động (tiền công) là . Khi đó tổng lợi nhuận là hàm số của biến số L (lượng lao động được sử dụng):
Bài toán đặt ra là: chọn L để đạt cực đại. Điều kiện cần để thu lợi nhuận tối đa là:
Như vậy, điều kiện cần để đạt lợi nhuận tối đa là: giá trị bằng tiền của sản phẩm hiện vật cận biên
của lao động bằng giá lao động.
Tại điểm L0 mà điều kiện cần đã được thỏa mãn, điều kiện đủ để đạt lợi nhuận tối đa là: 36 TXTOCB01_Bai1_v1.0014105205
Bài 1: Các khái niệm cơ bản về hàm số một biến số
Theo quy luật lợi ích cận biên giảm dần thì sản phẩm hiện vật cận biên của lao động giảm dần khi
L tăng, do đó , tức là điều kiện đủ được đảm bảo.
Ví dụ: Giả sử doanh nghiệp cạnh tranh có hàm sản xuất ngắn hạn và giá sản phẩm là $4 và giá lao
động là $5. Hãy xác định mức sử dụng lao động tối ưu.
Giải: Sản phẩm cận biên của lao động là:
Điều kiện cần để đạt lợi nhuận tối đa là:
Điều kiện đủ luôn thỏa mãn:
Để đạt lợi nhuận tối đa, doanh nghiệp phải sử dụng 400 đơn vị lao động. TXTOCB01_Bai1_v1.0014105205 37
Bài 1: Các khái niệm cơ bản về hàm số một biến số
Tóm lược cuối bài Trên một khoảng :
Nếu đạo hàm thì hàm số đó đơn điệu tăng;
Nếu thì hàm số đơn điệu giảm.
Hàm số chỉ có thể đạt cực trị tại các điểm tới hạn. Điểm tới hạn là điểm thỏa mãn 1 trong 2 điều kiện:
Điểm mà tại đó đạo hàm của hàm số bằng 0 (). Điểm này còn được gọi là điểm dừng;
Điểm mà tại đó hàm liên tục nhưng không có đạo hàm.
Xét 1 điểm tới hạn, nếu thay đổi qua điểm đó đạo hàm đổi dấu thì điểm tới hạn đó là điểm cực trị:
+ → – điểm cực đại
– → + điểm cực tiểu
Nếu qua điểm tới hạn, hàm số không đổi dấu điểm tới hạn đó không là điểm cực trị.
Với các biến số kinh tế và là giá trị – cận biên của tại .
Hệ số co dãn của cung, cầu theo giá:
Bài toán tối ưu trong kinh tế: Tối đa hóa lợi nhuận 38 TXTOCB01_Bai1_v1.0014105205
Bài 1: Các khái niệm cơ bản về hàm số một biến số Câu hỏi ôn tập 22.
Nêu điều kiện để hàm số đơn điệu tăng, đơn điệu giảm trên khoảng ; 23.
Nêu điều kiện đủ (theo đạo hàm cấp 1) để điểm tới hạn là điểm cực trị; 24.
Nêu điều kiện đủ (theo đạo hàm cấp cao) để điểm dừng là điểm cực trị; 25.
Nêu công thức tính hệ số co dãn của cung, cầu theo giá? 26.
Tìm các khoảng tăng, giảm và cực trị của hàm số: 27.
Tìm các khoảng tăng, giảm và cực trị của hàm số: 28.
Tìm các khoảng tăng, giảm và cực trị của hàm số: 29.
Tìm các khoảng tăng, giảm và cực trị của hàm số: 30.
Tìm các khoảng tăng, giảm và cực trị của hàm số: 31.
Cho hàm cung Tính hệ số co dãn của cung tại mức giá p = 20 và nêu ý nghĩa
kinh tế của giá trị tìm được. BÀI 4 HÀM SỐ NHIỀU BIẾN SỐ TXTOCB01_Bai1_v1.0014105205 39
Bài 1: Các khái niệm cơ bản về hàm số một biến số Hướng dẫn học
Để học tốt bài này, sinh viên cần tham khảo các phương pháp học s au:
Học đúng lịch trình của môn học theo tuần, làm các bài luyện tập đầy đủ và
tham gia thảo luận trên diễn đàn. Đọc tài liệu:
16. BỘ MÔN TOÁN CƠ BẢN, 2009, Bài tập toán cao cấp cho các nhà kinh tế, NXB Thống kê.
17. NGUYỄN ĐÌNH TRÍ, TẠ VĂN ĐĨNH, NGUYỄN HỒ QUỲNH, 2008, Toán cao cấp 1, NXB Giáo dục.
18. ALPHA C. CHIANG, 1995, Fundamental Methods of Mathematical Economics,
Third edition, Mc. Graw-Hill, Inc.
19. MICHAEL HOY, JOHN LIVERNOIS, CHRIS MC KENNA, RAY REES,
THANASIS STENGOS, 2001, Mathematics for Economics, The MIT Press
Cambrige, Massachusetts, London, England.
Sinh viên làm việc theo nhóm và trao đổi với giảng viên trực tiếp tại lớp học hoặc qua email.
Tham khảo các thông tin từ trang Web môn học. Nội dung
Trong bài số 4 “Hàm số nhiều biến số” chúng ta sẽ xem xét các khái niệm cơ bản về
hàm số được bao gồm từ hai biến độc lập trở lên, tìm hiểu quy luật quan hệ giữa các
biến độc lập và biến phụ thuộc, miền xác định của hàm nhiều biến, tìm giá trị tương
ứng của biến phụ thuộc khi đã xác định được giá trị của các biến độc lập,… Ngoài ra,
một số mô hình hàm nhiều biến thường gặp trong kinh tế học sẽ được giới thiệu cùng
với một số tình huống ứng dụng khác.
Các khái niệm đạo hàm riêng, vi phân toàn phần của hàm nhiều biến sẽ được giới thiệu
để phân tích tác động của một hoặc tất cả các biến độc lập đến biến phụ thuộc. Trong
đó, đạo hàm riêng được sử dụng để đánh giá tác động riêng của một biến độc lập cụ thể,
trong khi vi phân toàn phần được sử dụng để đánh giá tác động gộp từ sự thay đổi của
tất cả các biến độc lập đến biến phụ thuộc. Cuối cùng, tương tự như hàm nhiều biến, hai
ứng dụng cơ bản của đạo hàm trong phân tích kinh tế sẽ được đề cập là giá trị cận biên 40 TXTOCB01_Bai1_v1.0014105205
Bài 1: Các khái niệm cơ bản về hàm số một biến số Mục tiêu
Sau khi học xong bài học, sinh viên phải thực hiện được những yêu cầu sau:
Hiểu được khái niệm hàm số n biến số và sự cần thiết của việc sử dụng hàm
nhiều biến trong các nghiên cứu định lượng về các vấn đề kinh tế xã hội;
Tìm và biểu diễn được miền xác định và đường mức của hàm số 2 biến số trên mặt phẳng;
Tính được đạo hàm riêng của hàm số tại một điểm theo định nghĩa;
Tính được đạo hàm riêng bằng cách sử dụng các quy tắc tìm đạo hàm;
Viết được biểu thức vi phần toàn phần của hàm 2 biến số;
Tìm được các đạo hàm riêng cấp 2 của hàm số 2 biến số;
Tính được giá trị cận biên của hàm số và nêu được ý nghĩa trong một số tình huống ứng dụng;
Nêu được biểu hiện toán học của quy luật lợi ích cận biên giảm dần. TXTOCB01_Bai1_v1.0014105205 41
Bài 1: Các khái niệm cơ bản về hàm số một biến số Tình huống dẫn nhập
Một doanh nghiệp sử dụng một hệ thống máy móc để sản xuất sản phẩm, với hai đầu vào sản xuất là lao động
và tư bản. Theo thiết kế, ứng với mỗi lượng kết hợp lao động (L) và tư bản (K), doanh nghiệp sẽ nhận được
một lượng sản phẩm Q tương ứng. 1.
Hãy lập mô hình toán học để mô tả mối quan hệ giữa sản lượng Q và các
đầu vào, bao gồm K và L? 2.
Khi một đầu vào có sự thay đổi nhỏ, trong khi đầu vào còn lại không đổi
thì sản lượng đầu ra thay đổi như thế nào? 3.
Khi cả hai đầu vào đều thay đổi nhỏ thì sản lượng đầu ra thay đổi như thế nào? 42 TXTOCB01_Bai1_v1.0014105205
Bài 1: Các khái niệm cơ bản về hàm số một biến số 4.1. Một số ví dụ
Khái niệm hàm số một biến số phản ánh sự phụ thuộc hàm số của một đại lượng vào một đại lượng
khác, chẳng hạn diện tích của hình vuông phụ thuộc vào độ dài cạnh của hình vuông đó: S = x2 (1)
Trong thực tế, một đại lượng có thể phụ thuộc đồng thời vào nhiều đại lượng khác. Chẳng hạn, diện
tích hình chữ nhật sẽ phụ thuộc vào chiều dài và chiều rộng của hình chữ nhật đó: S = xy (2)
Một ví dụ trong kinh tế học: nếu một người bán ra 3 loại sản phẩm với giá tương ứng là $3, $5 và
$6. Số tiền người đó thu về phụ thuộc vào số lượng các sản phẩm bán được. Nếu số lượng sản
phẩm người đó bán được tương ứng là x, y và z thì số tiền người đó nhận được là: T = 3x + 5y + 6z (3)
Ta gọi (2) và (3) là những hàm số nhiều biến, thể hiện được sử dụng để phản ánh sự phụ thuộc hàm
số của một biến số theo từ hai biến số khác trở lên.
Trong tình huống dẫn nhập của bài, mô hình toán học mô tả sự phụ thuộc của sản lượng đầu ra Q
theo các đầu vào, bao gồm tư bản K và lao động L cũng cho ta một ví dụ về hàm nhiều biến thường
được đề cập trong kinh tế học, có dạng như sau: Q = f(K, L)
57. Khái niệm hàm số 2 biến số
Cho một cặp biến số có thứ tự (x, y). Ta có thể đồng nhất mỗi cặp số thực có thứ tự (x 0, y0) với một
điểm M0(x0, y0) của mặt phẳng. Mặt phẳng toạ độ được gọi là không gian hai chiều và được ký hiệu
là R2. Theo cách như vậy, một cặp biến số (x, y) được xem như một biến điểm M(x, y) với miền biến
thiên là một tập hợp D của không gian R2.
Định nghĩa: Một hàm số f của biến điểm M(x, y), với miền biến thiên D R2, là một quy tắc (quy
luật) đặt tương ứng mỗi điểm M(x, y)D với một và chỉ một số thực w. Miền D được
gọi là miền xác định của hàm số f, còn số thực w tương ứng với điểm M(x, y) được
gọi là giá trị của hàm số f tại điểm M(x, y) và được ký hiệu là f(M), hoặc f(x, y).
Một hàm số của biến điểm hai chiều M(x, y) còn được gọi là hàm số của hai biến số x và y.
Khi nghiên cứu sự phụ thuộc của một biến số vào các biến số khác, để nói rằng biến số w là một
hàm số của hai biến x và y ta dùng ký hiệu w = f(x, y), trong đó f là một quy tắc cho phép ta xác
định được giá trị tương ứng của w khi biết giá trị của x và y. Trong trường hợp này người ta còn nói
rằng biến số w phụ thuộc hàm số vào các biến số x, y. Các biến số x, y được gọi là các biến số độc
lập, hay các đối số của hàm số.
Trong toán học, các ký hiệu biến số chỉ mang ý nghĩa hình thức. Khi nói đến các hàm số khác nhau
người ta có thể vẫn dùng các ký hiệu biến số như nhau, nhưng phân biệt ở ký hiệu biểu diễn quy
luật hàm số: w = f(x, y), w = g(x, y), w = h(x, y),...
Khi cho một hàm hai biến, các cách diễn đạt sau đây có nghĩa như nhau:
Hàm số f xác định trên miền D R2;
Hàm số f(M), M D;
Hàm số f(x, y), (x, y) D;
Hàm số w = f(x, y), (x, y) D.
58. Miền xác định của hàm số cho dưới dạng biểu thức
Theo định nghĩa, miền xác định (MXĐ) của hàm hai biến w = f(x, y) là miền biến thiên của biến
điểm M(x, y). Nếu biểu diễn hình học thì đó là một tập hợp điểm của mặt phẳng toạ độ. Về nguyên
tắc, khi cho một hàm số ta phải cho trước miền xác định D và chỉ rõ quy tắc f đặt tương ứng mỗi
điểm M(x, y) D với một số thực w nhất định. TXTOCB01_Bai1_v1.0014105205 43
Bài 1: Các khái niệm cơ bản về hàm số một biến số
Quy tắc f gán cặp 2 giá trị (x, y) với giá trị w = f(x, y) thường được cho dưới dạng biểu thức. Hàm
số cho dưới dạng một biểu thức hai biến f(x, y) đặt tương ứng mỗi điểm M0(x0, y0) với giá trị tính
toán của biểu thức khi gán x = x0, y = y0. Người ta gọi tập hợp tất cả các cặp số thực (x0, y0) mà
biểu thức đó có nghĩa khi ta gán x = x0 và
y = y0 là miền xác định tự nhiên của biểu thức. Nói chung MXĐ của một hàm hai biến cho dưới
dạng biểu thức có thể là tập con D bất kỳ của MXĐ tự nhiên của biểu thức đó (tuỳ theo ý nghĩa của
các biến số). Tuy nhiên, trong toán học người ta thường xét biểu thức hàm số trong toàn bộ MXĐ tự nhiên của nó. 2 2
Ví dụ 4.1: Cho hàm số w f (x, y) x 3xy 2y .
Miền xác định của hàm số là R2
Theo cách tính giá trị của biểu thức, giá trị của hàm số tại điểm (2, 1) là: 2 2 f (2,1) 2 3.2.1 2.1 0. 2 2 w f (x, y) 9 x y .
Ví dụ 4.2: Cho hàm số 2 2 2 2 (x, y) : 9 x y
0 (x, y) : x y 9 . Trong mặt phẳng
Miền xác định của hàm số là
Oxy, miền xác định này là một hình tròn, tâm là gốc tọa độ, bán kính bằng 3. 2 2 9 2 2 1 .
Giá trị của hàm số tại điểm (2, 2) là f(2, 2) = 59. Miền giá trị
Ứng với mỗi điểm M(x, y) thuộc MXĐ ta tìm được một giá trị của hàm số. Ta sẽ quan tâm tới các
giá trị của hàm số khi M(x, y) thay đổi trong MXĐ.
Định nghĩa: Miền giá trị (MGT) của hàm số w = f(x, y) là tập hợp tất cả các giá trị của hàm số khi
điểm M(x,y) thay đổi trong miền xác định. 2 2 x y
Ví dụ 4.3: Miền giá trị của hàm số f(x, y) =
, (x, y)R2, là khoảng [0; +).
60. Đồ thị của hàm hai biến
Để biểu diễn hình học quan hệ hàm số w = f(x, y), w
trong không gian ba chiều ta dùng hệ toạ độ vuông
góc Oxyw, trong đó trục hoành Ox biểu diễn biến số 2
x, trục tung Oy biểu diễn biến số y và trục cao Ow
biểu diễn biến phụ thuộc w.
Miền xác định D của hàm số w = f(x, y) là một tập 0
hợp điểm trên mặt phẳng (0xy). Theo quy tắc tương y 2
ứng f, mỗi điểm M(x, y) cho tương ứng một số w là
giá trị của hàm số tại điểm M(x, y), theo đó ta có 2
tương ứng một điểm P(x, y, w) trong không gian với x cao độ bằng w.
Định nghĩa: Đồ thị của hàm số w = f(x, y) là tập hợp tất cả các điểm P(x, y, w) trong không gian,
trong đó M(x, y) là điểm bất kỳ thuộc miền xác định D và w là giá trị của hàm số tại điểm đó.
Thông thường, đồ thị của một hàm hai biến là một mặt trong không gian 3 chiều. x y
Ví dụ: Đồ thị hàm số w = 4 2 2
là nửa mặt cầucó tâm ở gốc toạ độ và bán kính R = 2, bao
gồm những điểm trên mặt cầu có cao độ không âm. 44 TXTOCB01_Bai1_v1.0014105205
Bài 1: Các khái niệm cơ bản về hàm số một biến số 61. Đường mức
Cho w = f(x, y) là một hàm số xác định trong miền D và w0 là một giá trị cố định của hàm số đó.
Định nghĩa: Đường mức của hàm số w = f(x, y) ta xét tập hợp tất cả các điểm M(x,y) thoả mãn điều kiện: f(x, y) = w0.
Nói cách khác, đường mức của hàm hai biến w= f(x, y) là tập hợp tất cả các điểm của mặt phẳng
(0xy) mà khi điểm M(x, y) biến thiên trên tập hợp đó, hàm số nhận một giá trị w0 cố định.
Thông thường đường mức của một hàm hai biến là một y
đường trên mặt phẳng. Mỗi giá trị w0 cố định cho tương ứng một đường mức. Ví dụ 4.4:
Các đường mức của hàm số w = 2x + 3y là các đường thẳng 0 x 2x
+ 3y = w0, với w0 là hằng số. 62. Hàm số n biến số
Không gian điểm n chiều
Định nghĩa: Mỗi bộ n số thực có thứ tự (x1, x2,..., xn) được gọi là một điểm n chiều.
Để gán tên cho một điểm n chiều (x1, x2,..., xn) ta dùng một chữ cái in hoa. Nếu gọi tên điểm đó là X thì ta viết:
X = (x1, x2,..., xn), hoặc X(x1, x2,..., xn)
Không gian n chiều được ký hiệu là Rn.
Khái niệm hàm số n biến số
Ta có thể xem mỗi bộ n biến số có thứ tự (x1, x2,..., xn) như một biến điểm X(x1, x2,..., xn) của
không gian n chiều. Khái niệm hàm số n biến số được định nghĩa tương tự như hàm số hai biến số. Định nghĩa:
Một hàm số f của biến điểm n chiều X(x1, x2,..., xn), với miền biến thiên D Rn, là một quy tắc
đặt tương ứng mỗi điểm X(x1, x2,..., xn) D với một và chỉ một số thực w. Miền D được gọi là
miền xác định của hàm số f và số w được gọi là giá trị của hàm số f tại điểm X(x1, x2,..., xn) và
được ký hiệu là f(x1, x2,..., xn), hoặc f(X).
Hàm số f của biến điểm n chiều X(x1, x2,..., xn) còn được gọi là hàm số của n biến số x1, x2,...,
xn. Khi dùng quan hệ hàm số f để biểu diễn sự phụ thuộc của một biến số w vào n biến số x1,
x2,..., xn ta dùng ký hiệu: w = f(x1, x2,..., xn)
Thông thường một hàm n biến được cho dưới dạng một biểu thức n biến f(x1, x2,..., xn). Các
khái niệm MXĐ, MGT của hàm số n biến số được hiểu theo nghĩa tương tự như đã định nghĩa
cho hàm số hai biến số. Tập hợp tất cả các điểm n chiều X(x1, x2,..., xn) mà tại đó hàm số f(x1,
x2,..., xn) nhận cùng một giá trị w0 cố định được gọi là tập mức của hàm số đó. Phương trình của
tập mức tương ứng với mỗi giá trị w0 cho trước có dạng: f(x1, x2,..., xn) = w0. 63.
Một số hàm số trong phân tích kinh tế
Mục này giới thiệu một số hàm nhiều biến được sử dụng trong các môn học Kinh tế học trong
chương trình đào tạo bậc Đại học. Để tiện cho người đọc, các ký hiệu biến số kinh tế đưa ra ở đây
đã được thống nhất với các ký hiệu tương ứng trong các tài liệu về kinh tế học, thường là lấy chữ
cái đầu của từ tiếng Anh tương ứng. TXTOCB01_Bai1_v1.0014105205 45
Bài 1: Các khái niệm cơ bản về hàm số một biến số 64. Hàm sản xuất
Hàm sản xuất là hàm số biểu diễn sự phụ thuộc của mức sản lượng tiềm năng của một doanh
nghiệp vào mức sử dụng các yếu tố sản xuất. Khi phân tích hoạt động sản xuất, các nhà kinh tế
thường quan tâm đến hai yếu tố sản xuất quan trọng nhất là tư bản (capital) và lao động (labor), bởi
về căn bản thì hai yếu tố này sẽ quyết định mức sản lượng đầu ra tương ứng. Gọi K là lượng tư bản
và L là lượng lao động được sử dụng. Với trình độ công nghệ của mình, khi sử dụng K đơn vị tư
bản và L đơn vị lao động, doanh nghiệp đó có khả năng sản xuất một lượng sản phẩm tối đa ký
hiệu là Q (gọi là sản lượng tiềm năng). Hàm sản xuất có dạng: Q = f(K, L). (4.1)
Hàm số (4.1) cho biết số lượng sản phẩm mà doanh nghiệp có khả năng sản xuất được ở mỗi mức
sử dụng kết hợp vốn và lao động. Khi phân tích sản xuất người ta giả thiết rằng các doanh nghiệp
khai thác hết khả năng công nghệ, tức là Q luôn luôn là sản lượng tiềm năng, do đó hàm sản xuất f
là do công nghệ xác định.
Dạng hàm sản xuất mà các nhà kinh tế học hay sử dụng là hàm Cobb-Douglas: Q = aK L
trong đó , , a là các hằng số dương.
Đường mức của hàm sản xuất có phương trình:
f(K, L) = Q0 (Q0 = const > 0)
Trong kinh tế học thuật ngữ "đường mức " của hàm sản xuất có tên gọi là đường đồng lượng, hay
đường đẳng lượng (isoquant). Đường đồng lượng là tập hợp các tổ hợp yếu tố sản xuất (K, L) cho
cùng một mức sản lượng Q0 cố định.
65. Hàm chi phí và hàm lợi nhuận theo các yếu tố sản xuất
Như ta đã biết, hàm chi phí sản xuất, trong đó tổng chi phí TC (total cost) phụ thuộc vào sản lượng Q có dạng như sau: TC = TC(Q)
Nếu tính theo các yếu tố sản xuất thì hàm chi phí là hàm số của các yếu tố sản xuất TC = wKK + wLL + C0
trong đó wK là giá thuê một đơn vị tư bản (chẳng hạn thuê toàn bộ xưởng máy trong một giờ); wL là
giá thuê một đơn vị lao động (chẳng hạn một giờ làm việc của một công nhân); C0 là chi phí cố định.
Nếu doanh nghiệp cạnh tranh có hàm sản xuất Q = f(K, L) và giá thị trường của sản phẩm là p thì
tổng doanh thu của doanh nghiệp phụ thuộc vào K và L: TR = pQ = pf(K, L)
Tổng lợi nhuận của một doanh nghiệp cạnh tranh là hàm số của các yếu tố sản xuất:
= pf(K, L) (wKK + wLL + C0)
66. Hàm chi phí kết hợp
Trên thực tế có nhiều doanh nghiệp sản xuất kết hợp nhiều loại sản phẩm. Giả sử doanh nghiệp sản
xuất n sản phẩm. Với trình độ công nghệ nhất định, để sản xuất Q1 đơn vị sản phẩm 1, Q2 đơn vị
sản phẩm 2,..., Qn đơn vị sản phẩm n, doanh nghiệp phải bỏ ra một khoản chi phí TC. Như vậy TC
là hàm số của n biến số: TC = TC(Q1, Q2,..., Qn). (4.2)
Hàm số (4.2) được gọi là hàm chi phí kết hợp. 46 TXTOCB01_Bai1_v1.0014105205
Bài 1: Các khái niệm cơ bản về hàm số một biến số 67. Hàm lợi ích
Sở thích của người tiêu dùng là một trong các yếu tố quan trọng chi phối quyết định mua sắm, tức
là ảnh hưởng tới phía cầu của hoạt động kinh tế. Các nhà kinh tế học dùng biến số lợi ích U (utility)
để biểu diễn mức độ ưa thích của người tiêu dùng đối với mỗi tổ hợp hàng hoá trong cơ cấu tiêu
dùng. Ta gọi mỗi tổ hợp hàng hoá là một túi hàng. Giả sử cơ cấu tiêu dùng gồm có n mặt hàng. Mỗi túi hàng là một bộ n số thực
X = (x1,x2,..., xn), trong đó x1 là lượng hàng hoá T1, x2 là lượng hàng hoá T2,..., xn là lượng hàng hoá
Tn. Hàm lợi ích là hàm số đặt tương ứng mỗi túi hàng X = (x1,x2,..., xn) với một giá trị lợi ích U
nhất định theo quy tắc: túi hàng nào được ưa chuộng hơn thì có giá trị lợi ích lớn hơn. Hàm lợi ích
có dạng tổng quát như sau: U = U(x1,x2,..., xn)
Một trong những dạng hàm lợi ích hay được sử dụng là hàm Cobb-Douglas: 1 α 2 α n U a x x ....x α 1 2
n (a, 1, 2,...., n là các hằng số dương).
Tập mức của hàm lợi ích có phương trình:
U(x1, x2,..., xn) = U0 (với U0 là hằng số dương)
Trong kinh tế học tập mức của hàm lợi ích được gọi là tập bàng quan (indifferent set). Tập bàng
quan là tập hợp tất cả các túi hàng đem lại cùng một mức lợi ích cho người tiêu dùng (tập hợp các
túi hàng được ưa chuộng như nhau). Trường hợp n = 2 tập bàng quan được gọi là đường bàng quan
(indifferent curve). Phương trình của đường bàng quan là phương trình hai biến số: U(x1, x2) = U0.
68. Hàm cung và hàm cầu trên thị trường nhiều loại hàng hoá liên quan
Hàm cung (hàm cầu) biểu diễn lượng hàng hoá mà người bán bằng lòng bán (người mua bằng lòng
mua) ở mỗi mức giá. Lượng cung và lượng cầu đối với một loại hàng hoá trên thị trường không
những phụ thuộc vào giá của hàng hoá đó mà còn bị chi phối bởi nhiều yếu tố, trong đó phụ thuộc
vào giá của các hàng hoá liên quan và thu nhập của người tiêu dùng. Trên thị trường n hàng hoá
liên quan hàm cung hàng hoá i và hàm cầu đối với hàng hoá i có dạng (với giả thiết các yếu tố khác không thay đổi): Qsi = Si(p1, p2...., pn) Qdi = Di(p1, p2,..., pn)
trong đó Qsi là lượng cung hàng hoá i, Qdi là lượng cầu đối với hàng hoá i, pi là giá hàng hoá i (i =1,
2,..., n). Mô hình cân bằng của thị trường gồm n loại hàng hoá liên quan có dạng: Q Q si di Q S (p , p , , p ) si i 1 2 n Q D (p , p , , p ) di i 1 2 n i 1 , 2, ..., n 69.Đạo hàm riêng
70. Đạo hàm riêng tại một điểm
Xét hàm số w = f(x, y) xác định trên miền D và điểm M0(x0, y0) thuộc D.
Gán y = y0, khi đó w = f(x, y0) = g(x) là hàm số của chỉ 1 biến số x.
Nếu hàm số g(x) có đạo hàm tại điểm x0 thì giá trị đạo hàm g’(x0) được gọi là đạo hàm riêng
theo biến x của hàm số f tại điểm M0(x0, y0). Ta có thể sử dụng một trong các ký hiệu sau để ký
hiệu cho giá trị đạo hàm riêng: TXTOCB01_Bai1_v1.0014105205 47
Bài 1: Các khái niệm cơ bản về hàm số một biến số f w f(x , y );w (x , y ) (x0 , 0 y ); (x0, y0). x 0 0 x 0 0 x x hay
Tương tự, gán x = x0: hàm số w = f(x0, y) = h(y) là hàm số của chỉ 1 biến số y.
Nếu hàm số h(y) có đạo hàm tại điểm y0 thì giá trị đạo hàm h’(y0) được gọi là đạo hàm riêng
theo biến y của hàm số f tại điểm M0(x0, y0). Ta có thể sử dụng một trong các ký hiệu sau để ký
hiệu cho giá trị đạo hàm riêng: f w f(x , y );w (x , y ) (x , y ); (x , y ). 0 0 0 0 y 0 0 y 0 0 y y hay
Ví dụ 4.5: Hàm số w = f(x, y) = x3 + 2x2y + y2, điểm M0(1, –2).
Ta có f(x, –2) = x3 – 4x2 + 4 = g(x); g’(x) = 3x2 – 8x; g’(1) = 3 – 8 = –5.
Hàm số f(x, y) có đạo hàm riêng theo biến x tại điểm M0(1,–2) và f’x(1,–2) = –5.
f(1, y) = 1 + 2y + y2 = h(y); h’(y) = 2y + 2; h’(–2) = –4 + 2 = –2.
Hàm số f(x, y) có đạo hàm riêng theo biến y tại điểm M0(1,–2) và f’y(1,–2) = –2.
Ví dụ 4.6: Tìm đạo hàm của hàm số f(x, y) tại điểm M0(0,0) ì 3 3 ï x - 2xy - ï 3y 2 2 ï khi x +2y ¹ 0 ï 2 2 f (x, y) = í x +2y ïïï 0 khi x = y = ïî 0 Giải: 3 2 3 f (x,0) f (0,0) (x / x ) 0 x lim lim lim 1 f ' (0,0) 1 3 x x 0 x 0 x 0 x 0 x x 3 2 3 f (0, y) f (0,0) ( 3y / 2y ) 0 3y 3 3 lim li m lim f ' (0,0) . 3 y y 0 y 0 y 0 y 0 y 2y 2 2
71. Đạo hàm riêng trên một miền
Nếu hàm số w = f(x, y) có các đạo hàm riêng tại mọi điểm thuộc miền X thì ta sẽ có các hàm số w ;w.
đạo hàm riêng xác định trên miền X là: x y
Chú ý: Đạo hàm riêng theo một biến thực chất là đạo hàm theo quan điểm một biến số, khi ta coi
một trong các biến độc lập là đối số, còn các biến còn lại được cố định giá trị (xem như các hằng số).
Ví dụ 4.7: w = x3 + 2x2y + y2.
Xem w như là hàm số của biến x và y là hằng số ta dễ dàng tính đạo hàm riêng theo x: w wx = x = 3x2 + 4xy.
Tương tự, xem w là hàm số của một biến y và x là hằng số ta có: w wy = y = 2x2 + 2y.
72. Đạo hàm riêng của hàm số n biến số M (x , x ,..., x ) Xét hàm số w = f(x 0 1 2 n
1 , x2,..., xn) xác định trên miền D và điểm thuộc D. 48 TXTOCB01_Bai1_v1.0014105205
Bài 1: Các khái niệm cơ bản về hàm số một biến số x
Tương tự hàm số 2 biến số, để xét đạo hàm riêng theo biến i của hàm số tại điểm M0 ta sẽ gán x x , k i
các biến số còn lại bằng các giá trị tương ứng của M k k 0: , khi đó hàm số w f
(x1, x 2,..., xi1, x , xi 1,..., x n) x i
chỉ phụ thuộc vào 1 biến i . Nếu hàm số này có đạo hàm tại x x
điểm i thì ta gọi giá trị đạo hàm này là đạo hàm riêng theo biến i của hàm số w tại điểm M0, ký w ' (x ,x ,..., x ).
hiệu được sử dụng là: i x 1 2 n
Tương tự như vậy đối với đạo hàm riêng của các biến còn lại và hàm số n biến có tất cả n giá trị
đạo hàm riêng theo n biến tương ứng.
Ví dụ 4.8: Hàm số w = f(x, y, z) = 2x2y – 5y2z3
Tại M0(1, –1, 2): để tìm đạo hàm riêng của hàm số theo biến x ta gán y = –1, z = : 2 f(x, –1, 2) = –
2x2 – 40 = g(x). Hàm g(x) có đạo hàm g’(x) = –4x và g’(1) = –4 từ đó ta kết luận đạo hàm riêng của
hàm số w theo biến x tại điểm M0 có giá trị là –4. 2 2
Biểu thức đạo hàm riêng của hàm số theo biến z có dạng: w ' 15y z w ' z (lưu ý rằng khi tính z ta coi x, y là hằng số). 73. Vi phân
Giả sử hàm số w = f(x, y) xác định trong miền D và có các đạo hàm riêng liên tục tại điểm M0(x0,
y0) thuộc miền D. Xét số gia toàn phần của hàm số:
f(x0, y0) = f(x0 + x, y0 + y) f(x0, y0)
Khi x, y có giá trị tuyệt đối đủ nhỏ ta có f f(x f
0, y0) x (x0, y0).x + y (x0, y0).y (4.3)
Định nghĩa: Nếu hàm số w = f(x, y) xác định trong miền D và có các đạo hàm riêng liên tục tại
điểm M0(x0, y0) D thì biểu thức ở vế phải của công thức gần đúng (4.3) được gọi là giá trị vi
phân toàn phần của hàm số w = f(x, y) tại điểm M0(x0, y0) và được ký hiệu là dw(x0, y0) hoặc df(x0, y0). Theo định nghĩa: df(x f f
0, y0) = x (x0, y0).x + y (x0, y0).y (4.4)
Về ý nghĩa, giá trị vi phân toàn phần trong công thức (4.4) biểu thị một cách xấp xỉ giá trị thay đổi
của biến phụ thuộc w khi các biến độc lập (x,y) đồng thời thay đổi giá trị tương ứng là x và y tại điểm (x0, y0) cho trước.
Với x và y là các biến số độc lập, ta có dx = x, dy = y. Biểu thức vi phân toàn phần (4.4) được viết dưới dạng: f df = f xdx + y dy hoặc: w w dw = x dx + y dy
Ví dụ 4.9: Vi phân toàn phần của hàm số w = x3y4 tại một điểm (x, y) bất kỳ được tính như sau: w w dw = x dx + y dy = 3x2y4dx + 4x3y3dy TXTOCB01_Bai1_v1.0014105205 49
Bài 1: Các khái niệm cơ bản về hàm số một biến số 74.
Đạo hàm riêng cấp 2
Giả sử hàm số w = f(x, y) có đạo hàm riêng theo các biến tại mọi điểm thuộc miền
D Rn. Khi đó các đạo hàm riêng như đã biết, bao gồm w’x và w’y, còn được gọi là các đạo hàm
riêng cấp 1 của w = f(x, y) trong miền D.
Đạo hàm riêng của w’x, w’y (nếu tồn tại) được gọi là các đạo hàm riêng cấp hai của hàm số đó.
Hàm số 2 biến w = f(x, y) có thể có tới 4 đạo hàm riêng cấp 2 tại một điểm (x,y) cho trước, cụ thể như sau: 2 w Đạo hàm riêng (w’ xx
x)’x được ký hiệu là w”xx hoặc ; 2 w Đạo hàm riêng (w’ xy
x)’y được ký hiệu là w”xy hoặc ; 2 w Đạo hàm riêng (w’ yx
y)’x được ký hiệu là w”yx hoặc ; 2 w Đạo hàm riêng (w’ yy
y)’y được ký hiệu là w”yy hoặc .
Ví dụ 4.10: Với w = x3y4, ta có các đạo hàm riêng cấp 1 là: w w x = 3x2y4; y = 4x3y3; 2 w 2 w 2 x = 6xy4; xy = 12x2y3, 2 w 2 w y x 2 = 12x2y3; y = 12x3y2.
75.Ứng dụng của đạo hàm riêng trong kinh tế học
76. Đạo hàm riêng và giá trị cận biên
Xét hàm số w = f(x1, x2,...,xn) biểu diễn sự phụ thuộc của biến số kinh tế w vào n biến số kinh tế x1,
x2,...,xn. Trong kinh tế học đạo hàm riêng của w theo xi tại điểm X(x1, x2,..., xn) được gọi là giá trị w
– cận biên của xi tại điểm đó. Giá trị w – cận biên của xi biểu diễn xấp xỉ lượng thay đổi giá trị của
biến phụ thuộc w khi biến xi tăng thêm một đơn vị, trong khi các biến độc lập còn lại không thay
đổi giá trị. Đối với mỗi hàm kinh tế người ta dùng các thuật ngữ tương ứng tuỳ theo tên gọi của các biến số kinh tế.
Đối với hàm sản xuất Q = f(K, L), các đạo hàm riêng Q Q Q K L K = , QL =
được gọi tương ứng là sản phẩm hiện vật cận biên của tư bản và sản phẩm hiện vật cận biên
của lao động tại điểm (K, L). Để cho gọn, đôi khi người ta bỏ từ hiện vật và gọi tắt là sản phẩm
cận biên của tư bản và sản phẩm cận biên của lao động.
Trong kinh tế học sản phẩm hiện vật cận biên của tư bản và sản phẩm hiện vật cận biên của lao
động được ký hiệu là MPPK (Marginal Physical Product of Capital) và MPPL (Marginal Physical Product of Labor): Q Q MPP K L K = , MPPL = 50 TXTOCB01_Bai1_v1.0014105205
Bài 1: Các khái niệm cơ bản về hàm số một biến số
Tại điểm (K0, L0) giá trị MPPK biểu diễn xấp xỉ lượng sản phảm hiện vật gia tăng khi sử dụng
thêm một đơn vị tư bản và giữ nguyên mức sử dụng lao động; MPPL biểu diễn xấp xỉ lượng sản
phẩm gia tăng khi sử dụng thêm một đơn vị lao động và giữ nguyên mức sử dụng tư bản. 2 1
Ví dụ 4.11: Giả sử hàm sản xuất của một doanh nghiệp có dạng: Q = 30 3 3 K L , trong đó K, L,
Q là mức sử dụng lao động, mức sử dụng tư bản và sản lượng hàng ngày.
Giả sử doanh nghiệp đó đang sử dụng 27 đơn vị tư bản và 64 đơn vị lao động trong một ngày,
tức là K = 27 và L = 64. Sản lượng cận biên của tư bản và của lao động là: 1 1 Q 3 3 L 64 80 20. 2 0. MPP K K 27 3 K = = 26,7; 2 3 2 Q 3 K 27 90 45 10. 1 0. MPP L L 64 16 8 L = = 5,6
Điều này có nghĩa là nếu doanh nghiệp tăng mức sử dụng tư bản lên 28 và giữ nguyên mức sử
dụng 64 lao động trong một ngày thì sản lượng hàng ngày của nó sẽ tăng thêm khoảng 26,7 đơn
vị sản phẩm hiện vật; nếu doanh nghiệp nâng mức sử dụng lao động lên 65 đơn vị và giữ
nguyên mức sử dụng 27 đơn vị tư bản trong một ngày thì sản lượng hàng ngày sẽ tăng thêm
khoảng 5,6 đơn vị sản phẩm hiện vật.
Đối với hàm lợi ích U = U (x1, x2,..., xn) U thì đạo hàm U x i i =
được gọi là lợi ích cận biên của hàng hoá thứ i đối với người tiêu dùng và được ký hiệu là MU X( 1 x , x2, ... , xn ) i. Con số MUi tại điểm
biểu diễn xấp xỉ lợi ích tăng
thêm khi người tiêu dùng có thêm 1 đơn vị hàng hoá thứ i và lượng các hàng hoá khác không đổi.
77. Đạo hàm riêng cấp hai và quy luật lợi ích cận biên giảm dần Xét mô hình hàm số: U = f(x, y),
trong đó biến số u biểu diễn lợi ích kinh tế và x, y là các yếu tố đem lại lợi ích U. Quy luật lợi ích
cận biên giảm dần (lợi ích tăng chậm dần) nói rằng, khi yếu tố còn lại không thay đổi, giá trị U –
cận biên của một biến số giảm dần khi biến số đó tăng. Dưới giác độ toán học, quy luật này biểu hiện dưới dạng 2 f 2 f 0 0. xx và y y Ví dụ 4.12:
Đối với hàm lợi ích U = f(x, y), trong đó x là lượng hàng hoá thứ nhất, y là lượng hàng hoá thứ hai
và U là lợi ích của người tiêu dùng đối với túi hàng (x, y), quy luật lợi ích cận biên giảm dần trong
kinh tế nói rằng lợi ích cận biên của hàng hoá thứ nhất giảm dần khi x tăng và y không đối và lợi
ích cận biên của hàng hoá thứ hai giảm dần khi y tăng và x không đổi. Quy luật lợi ích cận biên
giảm dần biểu hiện ở các đạo hàm riêng cấp hai của hàm lợi ích như sau: Uxx 0 MU Ux x =
giảm khi x tăng và y không đổi; TXTOCB01_Bai1_v1.0014105205 51
Bài 1: Các khái niệm cơ bản về hàm số một biến số U U yy 0 MU y y =
giảm khi y tăng và x không đổi.
Đối với hàm sản xuất, quy luật lợi ích cận biên giảm dần có nghĩa là ở mức sử dụng một yếu tố sản
xuất càng lớn (trong khi lượng sử dụng các yếu tố khác không thay đổi) thì sản lượng gia tăng do
sử dụng thêm một đơn vị yếu tố sản xuất đó đem lại càng nhỏ. Nói cách khác, sản phẩm hiện vật
cận biên của mỗi yếu tố giảm dần khi lượng sử dụng yếu tố đó tăng (trong khi lượng sử dụng các
yếu tố khác không thay đổi). Quy luật này biểu hiện thông qua đạo hàm riêng cấp hai của hàm sản xuất Q = f (K, L) như sau: 2 2 Q Q (MPP ) 0, (MPP ) 0 K K 2 L L 2 K L .
Chẳng hạn, đối với hàm sản xuất dạng Cobb-Douglas
Q = a KL (a, , > 0) ta có: (MPP ) (MPP ) K K 2 = a ( 1)K K, L L = a( 1)L K 2.
Biểu hiện của quy luật lợi ích cận biên giảm dần là:
1 và 1 (để (MPP ) (MPP ) K K 0 và L L 0).
Tóm lược cuối bài
Hàm số nhiều biến số mô tả sự phụ thuộc của một biến số vào các biến số khác.
Miền xác định tự nhiên của biểu thức là miền các điểm mà khi thay giá trị biến số trong biểu
thức bởi các giá trị tương ứng thì ta nhận được một giá trị xác định.
Khi hàm số cho bởi biểu thức, ta thường đồng nhất miền xác định của hàm số với miền xác
định tự nhiên của biểu thức.
Đạo hàm riêng của hàm số theo một biến có thể hiểu là đạo hàm của hàm số theo biến đó khi
coi các biến còn lại là hằng số. Các quy tắc và công thức tìm đạo hàm vẫn áp dụng được khi tìm đạo hàm riêng.
Sau khi đã tính đạo hàm riêng của hàm số theo một biến ta nhận được một hàm số, nếu hàm số
đó lại có đạo hàm riêng thì đạo hàm riêng tính sau này được gọi là đạo hàm riêng cấp 2 của hàm số ban đầu.
Trong kinh tế học đạo hàm riêng của hàm số theo một biến được gọi là giá trị cận biên của hàm số theo biến đó.
Quy luật lợi ích cận biên khẳng định rằng với biến số phụ thuộc là biến lợi ích thì giá trị lợi ích
cận biên theo một biến sẽ giảm dần khi giá trị của biến đó tăng. 52 TXTOCB01_Bai1_v1.0014105205
Bài 1: Các khái niệm cơ bản về hàm số một biến số Câu hỏi ôn tập 32.
Hàm số nhiều biến số là quy luật như thế nào? 33.
Hãy đưa ra một ví dụ về hàm số biểu diễn quan hệ giữa một đại lượng vào các đại lượng khác. 34.
Khi hàm số cho bởi biểu thức, miền xác định tự nhiên của hàm số là gì? 35.
Khi hàm số cho bởi biểu thức f(x, y), để tìm giá trị của hàm số tại điểm (x0,
y0) thuộc miền xác định của hàm số ta sẽ làm gì? 36.
Hàm sản xuất được sử dụng biểu diễn sự phụ thuộc của sản lượng vào những
yếu tố sản xuất cơ bản nào? 37.
Hàm số cho bởi biểu thức f(x, y), để tìm biểu thức f(x, y0) ta sẽ làm như thế nào? 38.
Hãy phát biểu khái niệm đạo hàm riêng của hàm số 2 biến số tại điểm (x0, y0). 39.
Đạo hàm riêng theo biến x của tổng hai hàm số có bằng tổng hai đạo hàm
riêng theo biến x của hai hàm số đó hay không? 40.
Đạo hàm riêng theo biến x của tích hai hàm số có bằng tích hai đạo hàm
riêng theo biến x của hai hàm số đó hay không? 41.
Để tìm đạo hàm riêng của hàm số theo một biến số theo quy tắc, ta sẽ coi
những biến số nào là hằng số? 42.
Hãy phát biểu công thức vi phân của hàm số 2 biến số tại một điểm. 43.
Hãy phát biểu dạng tổng quát của biểu thức vi phân của hàm số 2 biến số. 44.
Hàm số 2 biến số có thể có bao nhiêu đạo hàm riêng cấp 2? Các đạo hàm
riêng hỗn hợp cấp 2 là đạo hàm như thế nào? 45.
Để tìm giá trị sản phẩm (hiện vật) cận biên của lao động tại mức sử dụng kết
hợp (K0, L0) ta phải tính giá trị nào? 46.
Hàm lợi ích u = f(x, y) dạng Cobb – Douglas có dạng tổng quát như thế nào? 47.
Theo quy luật lợi ích cận biên giảm dần, giá trị u – cận biên của x sẽ tăng hay giảm khi x tăng? 48.
Biểu hiện toán học của quy luật lợi ích cận biên giảm dần đó là gì? TXTOCB01_Bai1_v1.0014105205 53
Bài 1: Các khái niệm cơ bản về hàm số một biến số BÀI 5
CỰC TRỊ CỦA HÀM SỐ NHIỀU BIẾN SỐ Hướng dẫn học
Trong bài 5 “Cực trị của hàm số nhiều biến số” chúng ta sẽ tìm hiểu về cách tìm các
điểm cực trị của hàm số và tìm các điểm cực trị của hàm số mà các điểm này phải thỏa
mãn một phương trình nào đó, được gọi là điều
kiện ràng buộc. Trong giới hạn bài học chúng ta sẽ chỉ hàm số 2 biến số. đề cập đến
Để có thể giải quyết được những vấn đề nêu ra của bài học, sinh viên cần có kỹ năng
tính đạo hàm riêng tới cấp 2 của hàm 2 biến số; kỹ năng giải hệ phương trình; kỹ năng
tính định thức cấp 1 và cấp 2.
Để học tốt bài này, sinh viên cần tham khảo các phương pháp học s au:
Học đúng lịch trình của môn học theo tuần, làm các bài luyện tập đầy đủ và
tham gia thảo luận trên diễn đàn. Đọc tài liệu:
20. BỘ MÔN TOÁN CƠ BẢN, 2009, Bài tập toán cao cấp cho các nhà kinh tế, NXB Thống kê.
21. NGUYỄN ĐÌNH TRÍ, TẠ VĂN ĐĨNH, NGUYỄN HỒ QUỲNH, 2008, Toán cao cấp 1, NXB Giáo dục.
22. ALPHA C. CHIANG,1995, Fundamental Methods of Mathematical Economics,
Third edition, Mc. Graw-Hill, Inc.
23. MICHAEL HOY,JOHN LIVERNOIS, CHRIS MC KENNA, RAY REES,
THANASIS STENGOS, 2001, Mathematics for Economics, The MIT Press
Cambrige, Massachusetts, London, England.
Sinh viên làm việc theo nhóm và trao đổi với giảng viên trực tiếp tại lớp học hoặc qua email.
Tham khảo các thông tin từ trang Web môn học. Nội dung
Bài toán cực trị không có điều kiện và ứng dụng trong phân tích kinh tế;
Bài toán cực trị có điều kiện ràng buộc và ứng dụng trong phân tích kinh tế. Mục tiêu
Sau khi học xong bài học sinh viên cần phải thực hiện được những yêu cầu sau:
Phân biệt được bài toán cực trị không có điều kiện và cực trị có điều kiện ràng buộc.
Tìm được điểm dừng của hàm số đối với bài toán cực trị không có điều kiện.
Kiểm tra điểm dừng của hàm số có là điểm cực trị của hàm số đối với bài toán
cực trị không có điều kiện.
Lập được hàm Lagrange từ bài toán cực trị có điều kiện ràng buộc.
Tìm được điểm dừng của hàm số đối với bài toán cực trị có điều kiện ràng buộc. ể ề ố ề 54 TXTOCB01_Bai1_v1.0014105205
Bài 1: Các khái niệm cơ bản về hàm số một biến số Tình huống dẫn nhập
Lựa chọn tối ưu trong kinh tế
Trong doanh nghiệp cạnh tranh thuần túy sản xuất 2 loại sản phẩm với hàm chi phí kết hợp: 2 2 TC 3 Q 2Q Q 2Q 10 1 1 2 2
Với giá thị trường của sản phẩm 1 là $160 và giá của sản phẩm 2 là $120.
Hãy chọn một cơ cấu sản lượng (Q , Q ) để doanh nghiệp đạt lợi nhuận tối đa? 1 2 TXTOCB01_Bai1_v1.0014105205 55
Bài 1: Các khái niệm cơ bản về hàm số một biến số 5.1
Bài toán cực trị không có điều kiện ràng buộc 78. Khái niệm cực trị
Khái niệm cực trị địa phương của hàm số n biến số được định nghĩa hoàn toàn tương tự như cực trị
của hàm số một biến số.
Xét hàm số 2 biến w = f(x, y) = f(M) xác định và liên tục trong miền
D = {M(x, y) : a x b,c y d}
Định nghĩa: Ta nói rằng hàm số w = f(x, y) đạt giá trị cực đại tại điểm M0(x0, y0) thuộc D nếu tồn f (M) f (M )
tại số r > 0 đủ nhỏ sao cho bất đẳng thức 0
được thoả mãn tại mọi điểm M(x, y) của
miền D có khoảng cách đến điểm M0(x0, y0) nhỏ hơn r: 0 < d(M, M0) < r.
Ta nói rằng hàm số w = f(x, y) đạt giá trị cực tiểu tại điểm M0(x0, y0) thuộc D nếu tồn tại số r > 0
đủ nhỏ sao cho bất đẳng thức f (M) f (M )
0 được thoả mãn tại mọi điểm M(x, y) của miền D có
khoảng cách đến điểm M0(x0, y0) nhỏ hơn r: 0 < d(M, M0) < r.
Điểm M0(x0, y0) mà tại đó hàm số f(M) đạt giá trị cực đại (cực tiểu) được gọi là điểm cực đại (điểm
cực tiểu) của hàm số đó. Giá trị cực đại, giá trị cực tiểu của hàm số được gọi chung là cực trị của hàm số.
Ví dụ 5.1: Hàm số w = x2 + y2 đạt giá trị cực tiểu tại điểm O(0,0) vì x2 + y2 > 0 với mọi điểm (x, y)
khác (0, 0) thuộc lân cận của điểm (0, 0).
79. Quy tắc tìm cực trị
Sau đây là một số định lý là cơ sở cho thuật toán tìm cực trị không có điều kiện đối với hàm số hai biến số.
Định lý 1 (Điều kiện cần)
Hàm số w = f(x, y) = f(M) xác định, liên tục và có các đạo hàm riêng trên miền D:
D = {M(x, y) : a x b,c y d}
Khi đó, Nếu điểm M0(x0, y0) là điểm cực trị của hàm số thì tại điểm M0(x0, y0)
tất cả các đạo hàm riêng cấp 1 của hàm số triệt tiêu. w (x , y ) 0 x 0 0 w y(x0, y0) 0 (*) w x 0 w 0 Điểm M y
0(x0, y0) thỏa mãn điều kiện ( ), tức là nghiệm của hệ:
được gọi là điểm dừng của hàm số w = f(x, y). Lưu ý:
Hàm số chỉ có thể đạt cực trị tại các điểm dừng của nó, nên các điểm dừng còn được
gọi là điểm “nghi ngờ cực trị” của hàm số.
Một điểm là điểm dừng của hàm số thì cũng chưa chắc là điểm cực trị. Cho nên cần xét
điều kiện đủ để một điểm dừng là điểm cực trị.
Định lý 2 (điều kiện đủ)
Giả sử hàm số w = f(x y) = f(M) có điểm dừng M0(x0,y0) và các đạo hàm riêng cấp 2 của hàm
số xác định, liên tục tại M0(x0,y0). a a n n a w (x , y ); a w (x , y ) 11 12 D 11 xx 0 0 12 xy 0 0 a a n n a w (x , y ); a w (x , y ) Xét: 21 22 với 21 yx 0 0 22 yy 0 0 56 TXTOCB01_Bai1_v1.0014105205
Bài 1: Các khái niệm cơ bản về hàm số một biến số o
Nếu D < 0 thì điểm M0(x0,y0) không phải là điểm cực trị của hàm số w f (x, y) w f (x, y) o
Nếu D > 0 thì điểm M0(x0,y0) là điểm cực trị của hàm số a 0 11
thì điểm M0(x0,y0) là điểm cực tiểu của hàm số. a 0 11
thì điểm M0(x0,y0) là điểm cực đại của hàm số.
Từ các định lý nêu trên, ta đưa ra quy tắc sau đây:
Quy tắc tìm các điểm cực trị của hàm số w f (x, y) :
Bước 1: Tìm điểm dừng o
Tìm các đạo hàm riêng cấp 1 và 2 của hàm số w f (x, y) , bao gồm các giá trị: ' ' " " " " w , w , w , w w , w x y xx xy yx yy ' w 0 x ' w 0 y M (x , y ) o Giải hệ
nghiệm 0 0 0 được gọi là điểm dừng của hàm số
Bước 2: Kiểm tra điều kiện đủ " " a a w w 11 12 xx xy D D (x, y) " " a a w w 21 22 yx yy o Tính định thức cấp 2: M (x , y ) x x , y y D(x , y ) o
Tại điểm dừng 0 0 0 thay 0 0 vào D(x, y) ta được 0 0 Nếu D(x , y ) 0 M (x , y ) 0 0
thì 0 0 0 không phải là điểm cực trị. Nếu D(x , y ) 0 a 0 M (x , y ) 0 0 và 11
thì 0 0 0 là điểm tiểu Nếu D(x , y ) 0 a 0 M (x , y ) 0 0 và 11 thì 0 0 0 là điểm đại M (x , y )
Chú ý: Nếu hàm số w f (x, y) có duy nhất một điểm dừng 0 0 0 và điều kiện đủ
thỏa mãn tại mọi điểm (x, y) mà hàm số xác định thì cực trị sẽ mang ý nghĩa toàn thể, nghĩa là w f (x, y) M (x , y )
đạt giá trị lớn nhất tại 0 0 0 nếu đó là điểm cực đại; hoặc đạt giá trị nhỏ nhất tại M (x , y ) 0 0
0 nếu đó là điểm cực tiểu.
Ví dụ 5.2: Tìm các điểm cực trị của hàm số: 3 4 2
w x 2y 6x 9x 8y Giải:
Bước 1: Tìm các điểm dừng o
Tìm các đạo hàm riêng cấp 1 và 2: ' 3 " "
w 3x 12x 9 w 6x 12, w 0 x xx xy ' 3 " " 2 w y 8y 8 w yx 0, w yy 24y ' 2 w 0 3x 12x 9 0 x ' 3 w 0 8y 8 0 y o Giải hệ :
Giải hệ ta tìm được 2 nghiệm: (x, y) ( 1, 1),(3, 1)
Hàm số có 2 điểm dừng là M1(1, 1) và M2(3, 1).
Bước 2: Kiểm tra điều kiện đủ TXTOCB01_Bai1_v1.0014105205 57
Bài 1: Các khái niệm cơ bản về hàm số một biến số o Tính định thức cấp 2: " " a a w w 6x 1 2 0 11 12 xx xy 2 D 2 4y ( 6x 12) " " 2 a a w w 0 24y 21 22 yx yy o
Xét tại từng điểm dừng: 2 Tại M (1, 1) 1
Ta có M(1, 1) 24( 1) ( 6.112) 144 0 a 6.112 6 0 M (1, 1) và 11 nên 1 là điểm cực tiểu. 2 Tại M (3, 1)
D(3, 1) 24( 1) ( 6.312) 144 0 2 Ta có nên M (3, 1) 2
không phải là điểm cực trị.
Ví dụ 5.3: Tìm các điểm cực trị của hàm số: 2 2 w 11
x 7y 12xy 8x 18y 36 Giải:
Bước 1: Tìm các điểm dừng o
Tìm các đạo hàm riêng cấp 1 và 2: ' " " w 2 2x 12y 8 w 2 2, w 12 x xx xy ' " "
w 12x 14y 18 w 12,w 1 4 y yx yy ' w 0 22x 12y 8 0 22x 12y 8 x ' w 0 12x 14y 180 12x 14y 1 8 y o Giải hệ .
Giải hệ ta tìm được 1 nghiệm duy nhất: (x, y) ( 2,3)
Hàm số có 1 điểm dừng duy nhất là M(2, 3).
Bước 2: Kiểm tra điều kiện đủ o Tính định thức cấp 2: " " a a w w 22 12 11 12 xx xy D 1 64 0 x , y " " a a w w 12 14 21 22 yx yy D 0 x, y a 0 o Nhận xét: 11
nên điểm dừng duy nhất M(2, 3) là điểm cực tiểu.
80.Ứng dụng trong kinh tế: bài toán tối đa hoá lợi nhuận
Các kết quả trên đây tạo cơ sở toán học cho việc giải các bài toán tối ưu. Dưới góc độ định lượng
bài toán tối ưu đặt ra mục tiêu tối đa hoá hoặc tối thiểu hoá giá trị của một hàm số, gọi là hàm mục tiêu: w = f(x1, x2,...., xn)
Các biến độc lập x1, x2,..., xn được gọi là các biến chọn: ta phải lựa chọn các giá trị thích hợp của
chúng để mục tiêu đề ra đạt được một cách tốt nhất.
Một trong những tiên đề của kinh tế học thị trường là: các nhà sản xuất theo đuổi mục tiêu tối đa
hoá lợi nhuận. Dưới đây là một số ví dụ phân tích hành vi tối đa hoá lợi nhuận của các doanh nghiệp. 58 TXTOCB01_Bai1_v1.0014105205
Bài 1: Các khái niệm cơ bản về hàm số một biến số
81. Chọn mức sản lượng tối ưu
Xét doanh nghiệp cạnh tranh thuần tuý sản xuất 2 loại sản phẩm với hàm chi phí kết hợp: TC = TC
(Q1, Q2), Q1 là số lượng sản phẩm thứ nhất, Q2 là số lượng sản phẩm thứ hai. Vì là môi trường cạnh
tranh nên doanh nghiệp phải chấp nhận giá thị trường của các loại sản phẩm. Với p1, p2 là giá thị
trường của 2 loại sản phẩm, hàm lợi nhuận có dạng: p Q p Q TC(Q ,Q ) 1 1 2 2 1 2
Bài toán đặt ra: Chọn một cơ cấu sản lượng (Q1, Q2) để hàm lợi nhuận đạt tối đa. Về bản chất, bài
toán này là một trường hợp cụ thể của bài toán cực trị tự do đã đề cập ở trên.
Ví dụ 5.4. Xét doanh nghiệp cạnh tranh thuần tuý sản xuất 2 loại sản phẩm với hàm chi phí kết hợp: 2 2 TC 3 Q 2Q Q 2Q 10 1 1 2 2
Với giá thị trường của sản phẩm 1 là $160 và giá của sản phẩm 2 là $120.
Hãy chọn một cơ cấu sản lượng (Q1, Q2) để hàm lợi nhuận đạt giá trị tối đa. Giải. p Q p Q TC(Q ,Q )
Bước 1: Lập hàm tổng lợi nhuận: 1 1 2 2 1 2 2 2 1 60Q 1 120Q2 (3Q1 2Q1Q2 2Q2 10) 2 2 3 1 Q 2Q2 2 1 Q Q2 160 1 Q 120Q2 10)
Bước 2: Bài toán trở thành: Tìm (Q max 1, Q2) = ? Để
Vấn đề trên được quy về bài toán cực trị không có điều kiện ràng buộc: Tìm điểm dừng:
Tìm các đạo hàm riêng cấp 1 và 2:
6Q 2Q 160 6, 2 Q 1 1 2 Q 1Q 1 Q 1Q 2 Q 4Q 2Q 120 2, 4 2 2 1 Q2Q1 Q 2Q 2 ' 0 6Q 2Q 160 0 6Q 2Q 160 1 Q 1 2 1 2 ' 0 2Q 4Q 120 0 2Q 4Q 120 Giải hệ: Q 1 2 1 2 2 (Q ,Q ) ( 20,20)
Giải hệ ta tìm được 1 nghiệm duy nhất: 1 2
Hàm số có 1 điểm dừng duy nhất là M(20, 20).
Kiểm tra điều kiện đủ:
Tính định thức cấp 2: " " a a 6 2 11 12 1 Q 1 Q 1 Q Q2 D 20 0 x , y " " a a 2 4 21 22 Q 2Q1 Q2Q 2 D 0 x , y a 0 Nhận xét: 11
; nên điểm dừng duy nhất M(20, 20) là điểm cực đại, cũng đồng thời là
điểm mà tại đó hàm số đạt giá trị lớn nhất. (Q ,Q ) ( 20,20) Kết luận: Khi 1 2 thì max. TXTOCB01_Bai1_v1.0014105205 59
Bài 1: Các khái niệm cơ bản về hàm số một biến số 82.
Trường hợp doanh nghiệp độc quyền
Xét trường hợp một doanh nghiệp độc quyền sản xuất hai loại sản phẩm với hàm chi phí kết hợp: TC = TC(Q1, Q2) .
Doanh nghiệp độc quyền định giá sản phẩm của mình căn cứ vào chi phí sản xuất và cầu của thị trường:
Giả sử cầu đối với các các sản phẩm là: 1 Q D1 1 = D1(p1) ↔ p1 = (Q1) 1 Q D 2 = D2(p2) ↔ p2 = 2 (Q2)
Hàm lợi nhuận có dạng: p Q p Q TC Q ,Q 1 1 2 2 1 2 1 D Q 1 .Q D Q .Q TC Q ,Q 1 1 1 2 2 2 1 2 Q ,Q ? 1 2
Câu hỏi đặt ra là chọn cơ cấu sản xuất
để lợi nhuận của doanh nghiệp đạt giá trị tối đa (cực đại)?
Nhận xét: Dưới góc độ toán học, đây là bài toán cực trị tự do của hàm 2 biến. Theo phương pháp Q , Q
giải bài toán cực trị của hàm hai biến ta xác định được mức sản lượng 1
2 để đạt cực đại, từ 1 p D Q 1 , p D Q . 1 1 1 2 2 2 đó suy ra giá tối ưu:
Ví dụ: Một doanh nghiệp độc quyền sản xuất hai loại sản phẩm với hàm chi phí kết hợp 2 2 TC Q 2Q Q Q 20. 1 1 2 2
Cho biết hàm cầu đối với các sản phẩm đó như sau: Q 25 0,5p , Q 30 p 1 1 2
2 . Hãy cho biết mức sản lượng Q1, Q2 cho lợi nhuận tối đa. Giải.
Lập hàm lợi nhuận: = p1Q1 + p2Q2 – TC
Từ giả thiết ta có: p1 = 50 – 2Q1; p2 = 30 – Q2
50 2Q .Q 30 Q .Q 2 2 Q 2Q Q Q 20 1 1 2 2 1 1 2 2 Từ đó suy ra, 2 2 3 1 Q 2Q2 2 1 Q Q2 50 1 Q 30Q2 20
Giải điều kiện cần: o
Các đạo hàm riêng cấp 1 và 2: ' ' '
6Q 2Q 50 6; ' 2 Q 1 1 2 Q1Q1 Q1Q 2 ' ' '
2Q 4Q 30 ' 2; ' 4 Q2 1 2 Q2Q1 Q 2Q 2 ' 0 6Q 2Q 50 0 1 Q 1 2 ' 0 2Q 4Q 30 0 Q 1 2 o Giải hệ: 2 6Q 2Q 5 0 Q 7 1 2 1 2Q 4Q 3 0 Q 4 1 2 2 Q ,Q 7,4 1 2
Hàm số có một điểm dừng duy nhất: 60 TXTOCB01_Bai1_v1.0014105205
Bài 1: Các khái niệm cơ bản về hàm số một biến số
Kiểm tra điều kiện đủ o Tính định thức cấp 2: ' '' a a 6 2 11 12 1 Q 1 Q 1 Q Q2 D 20 0 Q ,Q 0 ' '' 1 2 a a 2 4 21 22 Q 2Q1 Q 2Q 2 D 0 Q ,Q 0 1 2 a 0 Q ,Q 7,4 1 2 o Như vậy, 11
nên điểm dừng duy nhất là điểm cực đại. Q 7 p 36 1 max , 1 Q 4 p 2 6 Kết luận: 2
giá cho lợi nhuận tối đa: 2
83. Bài toán cực trị có điều kiện ràng buộc
Một người tiêu dùng phải ra quyết định mua sắm hai loại hàng hoá và giả sử hàm lợi ích (hay hàm
thoả dụng) của người đó là: U = U(x, y), trong đó biến số U chỉ lợi ích (độ thoả mãn) của người đó
khi có x đơn vị hàng hoá thứ nhất và y đơn vị hàng hoá thứ hai. Tâm lý chung của người tiêu dùng
là nhiều hơn ít, tức là khi x và y càng lớn thì U càng lớn. Tuy nhiên, do túi tiền có hạn nên muốn
mua được nhiều hơn thứ này thì người tiêu dùng phải bớt thứ kia.
Giả sử, giá thị trường của các loại hàng hoá mà người tiêu dùng muốn mua là p1, p2 và người đó chỉ
có số tiền là b. Khi đó, để tối đa hoá độ thoả dụng U, người đó chỉ được phép lựa chọn x và y trong
khuôn khổ ràng buộc về ngân sách: p1x + p2y = b. 84.
Bài toán cực trị có điều kiện
‘‘Tìm các điểm cực trị của hàm số w = f(x, y) thỏa mãn điều kiện g(x, y) = b”
Trong mô hình bài toán trên:
x, y được gọi là các biến chọn.
w được gọi là biến mục tiêu; f(x, y) được gọi là hàm mục tiêu.
g(x, y) = b được gọi là phương trình ràng buộc.
85. Phương pháp nhân tử lagrange
Các bước giải bài toán bằng phương pháp nhân tử Lagrange
Bước 1: Lập hàm Lagrange L f (x, y) [ b g(x, y)]
Bước 2: Giải điều kiện cần
Tìm các đạo hàm riêng cấp 1 và 2: L ,L ,L , L L ,L L , L L ,L L ;g g ,g g x y 11 xx 12 xy 21 yx 22 yy 1 x 2 y
Giải hệ (Tìm điểm dừng) nghiệm L 0 x L 0 y L 0 g(x, y) b nghiệm M (x , y , ) 0 0 0 0
Bước 3: Kiểm tra điều kiện đủ tại từng điểm dừng rồi kết luận
Tính định thức cấp 3: TXTOCB01_Bai1_v1.0014105205 61
Bài 1: Các khái niệm cơ bản về hàm số một biến số ' ' 0 g1 g2 0 gx gy __ __ ' " " D g L L g L L D (x, y, ) 1 11 12 x xx xy ' " " g L L g L L 2 21 22 y yx yy __ __
Xét tại điểm dừng M (x , y , ) D D (x , y , ) 0 0 0 0 , ta có: 0 0 0 __ D 0 M (x , y ) o Nếu thì điểm 0 0 0 là điểm cực đại. __ D 0 M (x , y ) o Nếu thì điểm 0 0 0 là điểm cực tiểu.
Chú ý: Giá trị 0 , được gọi là nhân tử Lagrange, có ý nghĩa như sau: Nếu giá trị b trong điều kiện
ràng buộc tăng thêm 1 đơn vị thì giá trị cực trị của hàm số sẽ tăng thêm xấp xỉ 0 đơn vị so với giá trị hiện tại.
Ví dụ 5.5: Sử dụng phương pháp nhân tử Lagrange tìm các điểm cực trị của hàm số 2 w 3x 5xy
với điều kiện: x y 16 . Giải: 2
Trước hết ta chú ý: f (x, y) 3x 5xy; g(x, y) x y; b 16 2 Lập hàm Lagrange: L 3x
5xy (16 x y) o Giải điều kiện cần
Tìm các đạo hàm riêng cấp 1 và 2: " " " x L 6x 5y 1 L 1 x L x 6, 1 L 2 x L y 5 " " " L 5 x L L 5 , L L 0 y 21 yx 22 yy " L 16 x y;g g 1,g g 1 1 x 2 y
Giải hệ (Tìm điểm dừng) ' L 6 x 5y 0 6 x 5y x ' L 5x 0 5x y ' L x y 0
Từ 2 phương trình đầu ta suy ra: 6x 5y 5
x x 5y thế vào phương trình thứ 3 ta được: 5y y 1 6 y 4 x 2 0 1 00
Vậy hàm số có một điểm dừng duy nhất: M(20, 4); 1 00 o
Kiểm tra điều kiện đủ (tại từng điểm dừng) Tính định thức cấp 3: ' ' 0 g g 0 g g 0 1 1 1 2 x y __ ' " " D 1 g 11 L 12 L x g xx L xy L 1 6 5 4 0 x, y, ' " " g2 L21 L22 gy Lyx Lyy 1 5 0 2 Vậy hàm số w 3x
5xy với điều kiện x y 1
6 đạt cực đại tại điểm M(20, 4)
và giá trị cực đại của w là 800. 62 TXTOCB01_Bai1_v1.0014105205
Bài 1: Các khái niệm cơ bản về hàm số một biến số 86.
Ứng dụng trong kinh tế: bài toán tối đa hóa lợi ích tiêu dùng
Giả sử người tiêu dùng lựa chọn hai mặt hàng với số lượng mỗi loại lần lượt là x và y, giá mỗi sản
phẩm lần lượt là p1, p2. Biết rằng số tiền dành cho mua sắm của người tiêu dùng là b. Khi đó, người
tiêu dùng cần tối đa hoá độ thoả dụng U = U(x, y) trong điều kiện bị ràng buộc về ngân sách: p1x + p2y = b.
Bài toán: Chọn (x, y) để hàm lợi ích U = U(x, y) đạt cực đại với điều kiện p1x + p2y = b.
Ví dụ 5.7: Giả sử người tiêu dùng có hàm lợi ích U = x0,4.y0,9. Trong điều kiện giá của hàng hóa thứ
nhất là $8, giá của hàng hóa thứ hai là $3 và thu nhập dành cho tiêu dùng là $260 hãy xác định giỏ
hàng đem lại lợi ích tối đa cho người tiêu dùng.
Giải: Bài toán trên được chuyển về bài toán cực trị có điều kiện, cụ thể như sau: 0,4 0,9
Tìm (x, y) sao cho hàm số u x y đạt cực đại với điều kiện: 8x 3y 2 60
Lập hàm Lagrange: L = x0,4.y0,9 + (260 – 8x – 3y).
Giải điều kiện cần o
Tính các đạo hàm riêng cấp 1 và 2: ' 0,6 0,9 " 1,6 0,9 " 0,6 0,1 L 0,4x
y 8 L L 0,24x y ;L L 0,36x y x 11 xx 12 xy ' 0,4 0,1 " 0,6 0,1 " 0,4 1,1 L 0 ,9x y
3 L L 0,36x y ;L L 0,09x y y 21 yx 22 yy ' L 260 8x 3y;g g 8;g g 3 1 x 2 y ' 0,6 0,9 0,6 0,9 L 0 0,4.x .y 8 0 0,4.x .y 8 x ' 0,4 0,1 0,4 0,1 L 0 0,9.x .y
3 0 0,9.x .y 3 y ' L 0 8x 3y 260 8x 3y 260 o Giải hệ:
Chia theo vế hai phương trình đầu trong hệ, ta được: y = 6x.
Thay y = 6x vào PT thứ 3, ta được: 8x + 3.6x = 260 0,4 0,1 x 10; y 60; 0,3.10 .60 0 0,4 0,1
Vậy có một điểm dừng duy nhất là: M(10,60); 0,3.10 .60 0
Kiểm tra điều kiện đủ: o Tính định thức cấp 3: 0 g g 0 8 3 1 2 __ D g L L 8 L L 4 8L 9L 64L 1 11 12 11 12 12 11 22 g L L 3 L L 2 21 22 21 22 Vì L 0;L 0;L 0 x , y, 0 12 11 22 nên __ D 4 8L 9L 64L 0 x , y, 12 11 22 .
Như vậy, điểm dừng M(10,60) là điểm cực đại.
Kết luận: Giỏ hàng cho lợi ích tối đa là (x, y) ( 10,60). TXTOCB01_Bai1_v1.0014105205 63
Bài 1: Các khái niệm cơ bản về hàm số một biến số
Tóm lược cuối bài
Bài toán cực trị tự do của hàm số là bài toán tìm các giá trị của biến chọn trên miền xác định
của hàm số mà tại đó hàm số đạt giá trị lớn nhất (nhỏ nhất) trong phạm vi lân cận đủ nhỏ của điểm đó.
Để tìm cực trị tự do của hàm số, ta tiến hành tìm các điểm dừng, hay còn gọi là các điểm nghi
ngờ cực trị của hàm số. Sau đó, sử dụng điều kiện đủ kiểm tra các điểm dừng tìm được có là
điểm cực trị hay không.
Bài toán tối đa hóa lợi ích của nhà sản xuất được giới thiệu với 2 bài toán cơ bản là lựa chọn
mức sản lượng tối ưu và lựa chọn mức sử dụng yếu tố đầu vào tối ưu.
Đối với cực trị có điều kiện ràng buộc ta phải tiến hành tìm cực trị của hàm số trong điều kiện
các biến chọn thỏa mãn 1 phương trình ràng buộc.
Phương pháp nhân tử Lagrange được sử dụng để tìm cực trị có điều kiện ràng buộc. Nhân tử
Lagrange là một biến số phụ được đưa thêm vào trong khi lập hàm Lagrang. Chúng ta thực
hiện tìm cực trị của hàm Lagrang và sử dụng điều kiện đủ kiểm tra hàm số có đạt cực trị tại
điểm tìm được hay không.
Trong phương pháp nhân tử Lagrange, khi giá trị b trong điều kiện ràng buộc tăng thêm 1 đơn
vị, ta không cần giải lại bài toán mà dựa vào ý nghĩa của nhân tử Lagrang để biết lượng thay
đổi của giá trị cực trị của hàm số.
Bài toán tối đa hóa lợi ích khi có ràng buộc ngân sách đưa ra là một minh họa cho việc sử dụng
bài toán cực trị có điều kiện trong phân tích kinh tế. 64 TXTOCB01_Bai1_v1.0014105205
Bài 1: Các khái niệm cơ bản về hàm số một biến số Câu hỏi ôn tập 49.
Theo định nghĩa hàm số w = f(x, y) đạt giá trị cực đại tại điểm M0(x0, y0) nếu
giá trị của hàm số tại điểm M0 là lớn hơn hay nhỏ hơn giá trị của hàm số tại những điểm gần M(x, y) gần M0(x0, y0)? 50.
Cực trị của hàm số là gì? 51.
Để tìm điểm dừng của hàm số ta phải làm gì? 52.
Hàm số có chắc chắn đạt cực trị tại điểm dừng của hàm số hay không? 53.
Hãy phát biểu quy tắc kiểm tra điều kiện đủ của cực trị của hàm số 2 biến số. 54.
Hàm Lagrange trong bài toán cực trị của hàm số với 2 biến chọn và 1
phương trình ràng buộc được lập như thế nào? 55. Nhân tử Lagrange là gì? 56.
Để tìm điểm dừng của hàm số Lagrange ta cần phải làm gì? 57.
Hãy phát biểu quy tắc kiểm tra điều kiện đủ của cực trị của bài toán cực trị
có điều kiện với 2 biến chọn và 1 phương trình ràng buộc. 58.
Hãy nêu ý nghĩa của nhân tử Lagrange. BÀI 6 T 105205
NGUYÊN HÀM VÀ TÍCH PHÂN BẤT ĐỊNH 65
Bài 1: Các khái niệm cơ bản về hàm số một biến số Hướng dẫn học
Để học tốt bài này, sinh viên cần tham khảo các phương pháp học s au:
Học đúng lịch trình của môn học theo tuần, làm các bài luyện tập đầy đủ và
tham gia thảo luận trên diễn đàn. Đọc tài liệu:
24. BỘ MÔN TOÁN CƠ BẢN, 2009, Bài tập toán cao cấp cho các nhà kinh tế, NXB Thống kê.
25. NGUYỄN ĐÌNH TRÍ, TẠ VĂN ĐĨNH, NGUYỄN HỒ QUỲNH, 2008, Toán cao cấp 1, NXB Giáo dục.
26. ALPHA C. CHIANG,1995, Fundamental Methods of Mathematical Economics,
Third edition, Mc. Graw–Hill, Inc.
27. MICHAEL HOY, JOHN LIVERNOIS, CHRIS MC KENNA, RAY REES,
THANASIS STENGOS, 2001, Mathematics for Economics, The MIT Press
Cambrige, Massachusetts, London, England.
Sinh viên làm việc theo nhóm và trao đổi với giảng viên trực tiếp tại lớp học hoặc qua email.
Tham khảo các thông tin từ trang Web môn học. Nội dung Nguyên hàm của hàm số; Tích phân bất định;
Các công thức tích phân cơ bản;
Các phương pháp tính tích phân. Mục tiêu
Nắm vững được định nghĩa tích phân bất định và các tính chất cơ bản;
Hiểu, nhớ và áp dụng được tích phân các hàm cơ bản;
Nắm được 4 phương pháp tính tích phân;
Nhớ các dạng tích phân cơ bản. 66 TXTOCB01_Bai1_v1.0014105205
Bài 1: Các khái niệm cơ bản về hàm số một biến số Tình huống dẫn nhập
Giả sử hàm chi phí cận biên (MC) ở mỗi mức sản lượng Q là: MC = 25 – 30Q + 9Q2
và chi phí cố định FC = 55.
Hãy lập hàm tổng chi phí. TXTOCB01_Bai1_v1.0014105205 67
Bài 1: Các khái niệm cơ bản về hàm số một biến số
6.1. Nguyên hàm của hàm số
87. Khái niệm nguyên hàm
Bài này đề cập đến phép toán ngược của phép tính đạo hàm và vi phân của hàm số. Ta xét bài toán
sau đây: Tìm tất cả các hàm số có đạo hàm là một hàm số f(x) cho trước.
Định nghĩa: Hàm số F(x) được gọi là nguyên hàm của hàm số f(x) trên một khoảng X nếu: F’(x) = f(x), xX Ví dụ:
Hàm số sinx là nguyên hàm của hàm số cosx trên R, vì: (sinx)’ = cosx, xR
Hàm số x4 là một nguyên hàm của hàm số 4x3 trên R, vì: (x4)’ = 4x3, xR
88. Biểu thức nguyên hàm tổng quát
Định lý: Nếu F(x) là một nguyên hàm của hàm số f(x) trên khoảng X thì:
Hàm số F(x) + C, với C là một hằng số bất kỳ, cũng là nguyên hàm của hàm số f(x).
Ngược lại, mọi nguyên hàm của hàm số f(x) đều biểu diễn được dưới dạng
F(x) + C, với C là một hằng số.
Chứng minh: Với C là hằng số bất kỳ ta luôn có [F(x) + C]’ = F’(x), do đó nếu
F’(x) = f(x), xX thì [F(x) + C]’ = f(x) xX.
Ngược lại, với (x) là một nguyên hàm bất kỳ của hàm số f(x), ta có:
[(x) – F(x)]’ = ’(x) – F’(x) = f(x) – f(x) = 0, (xX)
Từ đây suy ra rằng hàm số (x) – F(x) nhận giá trị không đổi trên khoảng X:
(x) – F(x) = C, xX (x) = F(x) + C, xX
Định lý nêu trên cho thấy biểu thức F(x) + C bao quát tất cả các nguyên hàm của hàm số f(x): mỗi
hằng số C cho tương ứng một nguyên hàm. 89.
Tích phân bất định
90. Định nghĩa tích phân
Định nghĩa: Tích phân bất định của hàm số f(x) là biểu thức nguyên hàm tổng quát F(x) + C, trong
đó F(x) là một nguyên hàm của hàm số f(x) và C là hằng số bất kỳ.
Để biểu diễn tích phân bất định của hàm số f(x) người ta dùng ký hiệu: ∫f(x)dx
[đọc là: tích phân của f(x)dx].
Biểu thức f(x)dx được gọi là biểu thức dưới dấu tích phân và hàm số f(x) được gọi là hàm số dưới dấu tích phân.
Theo ký hiệu nói trên ta có: ∫f(x)dx = F(x) + C Ví dụ: ∫cosxdx = sinx + C ∫4x3dx = x4 + C
91. Các tính chất cơ bản của tích phân bất định
Tích phân bất định có các tính chất cơ bản sau đây: 68 TXTOCB01_Bai1_v1.0014105205
Bài 1: Các khái niệm cơ bản về hàm số một biến số ' 1. f (x)dx f (x) d f (x)dx f (x)dx hay 2. F'(x)dx F (x) C dF(x) F (x) C hay 3. [f (x) g
(x)]dx f (x)dx g(x)dx 4. kf (x)dx k f (x)dx (k là hằng số)
92.Các công thức tích phân cơ bản
Để tính tích phân bất định, trước hết bạn cần ghi nhớ các công thức sau đây: 1. 1.dx dx x C 1 x 2. x dx C ( 1) 1 dx 3. l n x C x x x a 4. a dx C ln a x x e dx e C 5. sin xdx cos x C 6. cos xdx s in x C dx 7. cot x C 2 sin x dx 8. tan x C 2 cos x
93.Các phương pháp tính tích phân 94.
Phương pháp khai triển
Để tính tích phân ta cần phải sử dụng các phương pháp thích hợp để chuyển về các tích phân đã có
trong bảng công thức tích phân cơ bản. Một cách đơn giản là khai triển tích phân của tổng (hiệu)
thành tổng (hiệu) các tích phân và đưa hằng số nhân ra ngoài dấu tích phân: [af (x) bg(x) c ( x)]dx a f (x)dx b g(x)dx c ( x)dx
Ví dụ 1: Tính tích phân 5 3 I (3x 5x 2sin x)dx
Giải: Sử dụng quy tắc khai triển ta dễ dàng đưa về các tích phân cơ bản 5 3 I 3 x dx5 x dx 2 s in xdx 6 4 x 5x 2cos x C 2 4 3 (1 2x) dx I 3
Ví dụ 2: Tính tích phân x TXTOCB01_Bai1_v1.0014105205 69
Bài 1: Các khái niệm cơ bản về hàm số một biến số Giải: Ta có: 2 3 1 2 5 8 (16x 12x 8x )dx 3 3 3 3 I x 6x 12x 8x dx 3 x
Sử dụng phương pháp khai triển và công thức tích phân của hàm lũy thừa (công thức 2) ta được: 1 2 5 8 3 3 3 3
I x dx 6 x dx 12 x dx 8 x dx 2 5 8 11 3 3 3 3 3 3 3 3
x 6 x 12 x 8 x C 2 5 8 11 3 3 2 18 3 5 9 3 8 24 3 11 x x x x C 2 5 2 11 3 2 (1 x ) dx I
Ví dụ 3: Tính tích phân x Giải: 3 3 2 (1 2 x x )dx 1 2 1 I dx 3 2 3 x x x x 2 1 1 2 dx 3 3 3 3 3 2 x dx x dx ln x 2 3x x C x 2 3 3 3 2 ln x 6 x x C 2 2 I tan x.dx
Ví dụ 4: Tính tích phân 2 1 1 tan x
Giải: Sử dụng công thức lượng giác 2 cos x , ta có 1 dx I 1 dx dx tan x x C 2 2 cos x cos x dx I 2 2
Ví dụ 5: Tính tích phân sin x.cos x
Giải: Sử dụng công thức lượng giác sin2x + cos2x = 1, ta có 2 2 sin x cos x 1 1 I dx dx 2 2 2 2 sin x.cos x cos x sin x
Sử dụng quy tắc khai triển ta được: I = tanx – cotx + C
95. Sử dụng tính bất biến của biểu thức tích phân
Tính bất biến của biểu thức tích phân có nội dung như sau:
Nếu ∫f(x)dx = F(x) + C thì ∫f(u)du = F(u) + C, trong đó u = (x) là một biểu thức hàm số có đạo hàm liên tục. du dx
Trường hợp u = kx + b ta có du = kdx, hay
k . Sử dụng tính chất trên, ta có quy tắc như sau: 70 TXTOCB01_Bai1_v1.0014105205
Bài 1: Các khái niệm cơ bản về hàm số một biến số 1
f (kx b)dx F(kx b) C
Nếu ∫f(x)dx = F(x) + C thì k
Ví dụ 1: Áp dụng quy tắc về tính bất biến của biểu thức tích phân trong trường hợp
u = kx + b, từ các công thức 2, 3, 6, 7, 8 trong bảng tích phân cơ bản ta suy ra: 1 (kx b) (kx b) C, 1 k( 1) dx 1 ln kx b C kx b k kx 1 kx e dx e C k 1 sin kxdx cos kx C k 1 cos kxdx sin kx C k
Chú ý: Sử dụng công thức thứ nhất trong ví dụ 1 trên đây ta dễ dàng tính tích phân của phân thức
hữu tỷ với mẫu số bậc nhất P(x) dx kxb
Với P(x) là đa thức, bởi vì bằng cách thực hiện phép chia đa thức P(x) cho nhị thức bậc nhất ta dễ
dàng đưa được tích phân này về dạng: P(x) m dx Q(x) dx kx b kx b
với Q(x) là một đa thức có bậc nhỏ hơn bậc của đa thức P(x) 1 đơn vị và m là phần dư của phép chia. 2 3x 2x I dx
Ví dụ 2: Tính tích phân x 1
Giải: Bằng cách chia đa thức P(x) = 3x2 + 2x cho x + 1 ta có: 2 3x 2x 1 3x 1 x 1 x 1
Bằng phương pháp khai triển ta dễ dàng tính được: 2 1 3x I 3x 1 dx x ln x 1 C x 1 2 2 9 x(1 x ) dx
Ví dụ 3: Tính tích phân 1 2 xdx d(1 x )
Giải: Biểu thức xdx có thể viết dưới dạng 2 , do đó 1 2 9 2 1 2 10 2 (1 x ) d(1 x ) (1 x ) C (u 1 x ) 2 20 cos x I sin x.e dx
Ví dụ 4: Tính tích phân
Giải: Biểu thức sinxdx có thể viết dưới dạng sinxdx = –d(cosx), do đó TXTOCB01_Bai1_v1.0014105205 71
Bài 1: Các khái niệm cơ bản về hàm số một biến số cos x cosx I e d(cos x) e C (u c os x) 4 I tan x.dx
Ví dụ 5: Tính tích phân Giải: 2 2 2 1 I tan x.tan xdx tan x. 1 dx 2 cos x 2 dx 2 tan x. tan x.dx 2 cos x 2 1 1 3 tan x.d(tan x)
1 dx tan x (tan x x) C 2 cos x 3 dx I
Ví dụ 6: Tính tích phân sin x.cos x
Giải: Biểu thức ở mẫu số có thể viết dưới dạng sin x 2 2 sin x.cos x cos x tan x.cos x cos x Do đó dx dx d(tan x) l n tan x C 2 sin x.cos x tan x.cos x tan x I cot x.dx
Ví dụ 7: Tính tích phân Giải cos x.dx d(sin x) cot x.dx l n sin x C sin x sin x
96. Phương pháp đổi biến số
Xét tích phân I = ∫f(x)dx, trong đó f(x) là một hàm số liên tục. Để tính tích phân này ta có thể
chuyển sang một tích phân khác bằng cách thay x = (t). Với giả thiết hàm số
x = (t) đơn điệu và có đạo hàm liên tục, ta có
dx '(t)dt I f (x).dx f[ ( t)]'(t)dt g(t)dt
Khi phép đổi biến được lựa chọn phù hợp thì tích phân theo biến số t sẽ đơn giản hơn. Nếu ta tính
được ∫g(t)dt = G(t) + C thì I f (x).dx G [h(x)] C
Trong đó t = h(x) là hàm ngược của hàm số x = (t) dx I 3
Ví dụ 1: Tính tích phân 1 x
Giải: Trong trường hợp này ta có thể đổi biến như sau 3 2 x t , dx 3t dt 72 TXTOCB01_Bai1_v1.0014105205
Bài 1: Các khái niệm cơ bản về hàm số một biến số 2 2 3t dt (t 1) 1 1 I 3 dt 3 t 1 dt 1 t 1 t 1 t 2 t 3 t ln 1 t C 2
Hàm ngược của hàm số x = t3 là 3 t x , do đó dx 1 3 2 3 3 I 3 x x ln 1 x C 3 1 x 2 n
Chú ý: Khi tính tích phân của biểu thức chứa căn của nhị thức bậc nhất kx b n
Ta có thể loại bỏ căn bằng cách đặt t kx b , từ đó chọn phép đổi biến: 1 x nt b k x.dx I
Ví dụ 2: Tính tích phân 2x 1 2
Giải: Đặt t 2x 1 và đổi ngược x theo t ta chọn được phép đổi biến làm mất căn: 2 t 1 x , dx tdt 2
Sau khi đổi biến ta được 1 2 (t 1)t.dt 3 2 1 t t 1 2 10 I dt t 2t 5 dt t 2 2 t 2 2 t 2 1 3 1 2 5
t t t 5ln t 2 C 6 2 2 1 3 1 5 (2x 1) (2x 1)
2x 1 5ln( 2x 1 2) C 6 2 2
Chú ý: nếu biểu thức f(x)dx dưới dấu tích phân có thể biểu diễn dưới dạng f(x)dx = g[(x)]d(x)
Thì ta có thể đặt t = (x) để chuyển sang tích phân của biểu thức g(t)dt nếu tích phân đó dễ tính hơn 5 I sin x.dx
Ví dụ 3: Tính tích phân Giải: Ta có 5 4 2 2 sin x si n x.(sin x.dx) ( 1 cos x) [ d(cos x)] Đặt t = cosx ta được 2 2 2 4 2 3 1 5
I (1 t ) .( dt) (1 2t t )dt t t t 3 5 2 3 1 5
cos x cos x cos x C 3 5
Nhận xét: Tương tự như ví dụ 2 ta dễ dàng tính các tích phân sau đây TXTOCB01_Bai1_v1.0014105205 73
Bài 1: Các khái niệm cơ bản về hàm số một biến số
Với n là một số nguyên dương.
Tích phân J dễ dàng đổi qua biến t = cosx:
Tích phân K dễ dàng đổi qua biến t = sinx: 6 3 K sin x.cos x.dx
Ví dụ 4: Tính tích phân
Giải: Trong trường hợp này ta có 6 3 6 2 sin x.cos x s in x.cos x(cos x.dx) 6 2 s in x(1 sin x).d(sin x) Đặt t = sinx ta được 2x e .dx I 4
Ví dụ 5: Tính tích phân x e 1 Giải: Ta có x x x x e .(e dx) e d(e ) I 4 x x e 1 e 1 Đặt t = ex, ta được tdt 1 I 1 dt t ln t 1 C 4 t 1 t 1 x x e ln(e 1 ) C 5 x .dx I 5 3 3
Ví dụ 6: Tính tích phân 1 x Giải: Ta có 5 3 3 x .dx 1 [(1 x ) 1].d(1 x ) I 5 3 3 3 3 1 x 3 1 x Đặt t = 1 + x3 ta được 5 2 1 (t 1).dt 1 1 1 3 3 3 2 3 3 I t .dt t t C 5 3 3 3 t 3 t 3 5 2 3 2 3 3 2 t 3 3 (1 x ) 3 3 9 t C x C 3 5 2 3 5 10
97. Phương pháp tích phân từng phần
Công thức tính tích phân từng phần
Giả sử u = u(x) và v = v(x) là các hàm số có đạo hàm liên tục. Ta có:
d(uv) = vdu + udv udv = d(uv) – vdu Từ đây suy ra: 74 TXTOCB01_Bai1_v1.0014105205
Bài 1: Các khái niệm cơ bản về hàm số một biến số udv d(uv) vdu udv u v vdu
Công thức này được gọi là công thức tích phân từng phần. Áp dụng
Để tính tích phân I = ∫f(x)dx bằng phương pháp tích phân từng phần ta cần phải biểu diễn biểu
thức dưới dấu tích phân dưới dạng: f(x)dx = g(x).[h(x)dx] = udv
trong đó u = g(x) và dv = h(x)dx. Với u và dv là các biểu thức đã biết ta tìm được du u d x g
(x)dx, v dv h(x)dx
sau đó sử dụng công thức tích phân từng phần. 2x I xe dx
Ví dụ 1: Tính tích phân 2x 1 2x v e dx e
Giải: Với u = x, dv = e–2xdx, ta có du = dx, 2
Thay vào công thức tích phân từng phần ta được x 2x 1 2x I udv uv vdu e e dx 2 2 x 2x 1 2x x 2x 1 2x e e dx e e C 2 2 2 4 2 I x sin 3xdx
Ví dụ 2: Tính tích phân 1 v cos3x
Giải: Với u = x2, dv = sin3xdx, ta có du = 2x.dx, 3 2 x 2 I cos3x x cos3xdx 3 3
Tiếp tục sử dụng công thức tích phân từng phần đối với tích phân ở vế phải với u = x, dv = cos3x.dx ta có 2 x 2 x 1 I cos3x sin 3x sin 3xdx 3 3 3 3 2 x 2x 2 cos3x sin 3x cos3x C 3 9 27
Chú ý: Tương tự như ví dụ 1 và ví dụ 2, ta có thể tính các tích phân sau đây bằng phương pháp tích phân từng phần n kx n n
x e dx; x sin kxdx; x cos kx.dx (n nguyên dương)
Với u = xn và dv là phần còn lại của biểu thức dưới dấu tích phân. 2 I x ln x.dx
Ví dụ 3: Tính tích phân 3 dx x du , v
Giải: Với u = lnx, dv = x2dx, ta có x 3 TXTOCB01_Bai1_v1.0014105205 75
Bài 1: Các khái niệm cơ bản về hàm số một biến số 3 3 3 x ln x 1 x ln x x 2 I x dx C 3 3 3 9 2 I x ln xdx
Ví dụ 4: Tính tích phân dx 2x x du 2 ln x , v xdx
Giải: Với u = ln2x, dv x , ta có x 3
Sử dụng công thức tích phân từng phần ta được 2 2x x ln x 4 I x ln xdx 3 3
Tiếp tục sử dụng công thức tích phân từng phần đối với tích phân ở vế phải với u = lnx, dv xdx ta có dx 2x x du , v x 3 2 2x x ln x 4 2x x ln x 2 I xdx 3 3 3 3 2
2x x ln x 4 2x x ln x 4x x C 3 3 3 9 2x x 2 9ln x 12ln x 8 C 27
Chú ý: Tương tự như ví dụ 3 và ví dụ 4, ta có thể tính tích phân sau đây n x ln x.dx
(n nguyên dương, ≠ –1)
Bằng phương pháp tích phân từng phần với u = lnnx và dv là phần còn lại của biểu thức dưới dấu tích phân. 2 I x tan x.dx
Ví dụ 5: Tính tích phân
Giải: Với u = x, dv = tan2x.dx, ta có 2 1 du d x, v tan xdx 1 dx t an x x 2 cos x
I x(tan x x) (tan x x).dx d(cos x) x (tan x x) xdx cos x 1 2 x
tan x x ln cos x C 2 x xe .dx I 2
Ví dụ 6: Tính tích phân (x 1) x dx u xe , dv x 1 2 du (1 x)e , v Giải: Đặt (1 x) , ta có
1 x . Sử dụng công thức tích phân từng phần ta được 76 TXTOCB01_Bai1_v1.0014105205
Bài 1: Các khái niệm cơ bản về hàm số một biến số x x x xe xe e x x I e dx e C C 1 x 1 x 1 x TXTOCB01_Bai1_v1.0014105205 77
Bài 1: Các khái niệm cơ bản về hàm số một biến số
Tóm lược cuối bài
Nguyên hàm của hàm số f(x) trên X là hàm F(x) thỏa mãn: F’(x) = f(x) trên X. f (x)dx F (x) C
Tích phân bất định:
với F(x) là một nguyên hàm của f(x).
Các tính chất cơ bản nhất: f(x) g (x ) dx f(x)dx g(x)dx k.f (x)dx k f (x)dx
Có 4 phương pháp tính tích phân bất định: Phương pháp khai triển, phương pháp sử dụng tính
bất biến của biểu thức tích phân, phương pháp đổi biến, phương pháp tích phân từng phần. Câu hỏi ôn tập 59.
Nêu các tính chất cơ bản của tích phân bất định? 60.
Nêu các tích phân cơ bản? 61.
Sử dụng phương pháp khai triển, tính tích phân I 5 3 3x 4x x sin x dx 1 I 5x x dx 2 2 2 3 62.
Sử dụng phương pháp khai triển, tính tích phân I x 3x 4 .dx 3 20 2 63.
Sử dụng phương pháp bất biến, tính tích phân 3 2 x I x e .dx 64.
Sử dụng phương pháp bất biến, tính tích phân 4 2x 3 I dx 5 65.
Sử dụng phương pháp đổi biến, tính tích phân 1 5x 1 3 I x. 4x 3.dx 66.
Sử dụng phương pháp đổi biến, tính tích phân 6 67.
Sử dụng phương pháp tích phân từng phần, tính tích phân I 2x e 2 3x 7 dx 68.
Sử dụng phương pháp tích phân từng phần, tính tích phân I 3x 1 sin 5x.dx 8 78 TXTOCB01_Bai1_v1.0014105205
Bài 1: Các khái niệm cơ bản về hàm số một biến số TXTOCB01_Bai1_v1.0014105205 79
Bài 1: Các khái niệm cơ bản về hàm số một biến số BÀI 7 TÍCH PHÂN XÁC ĐỊNH Hướng dẫn học
Để học tốt bài này, sinh viên cần tham khảo các phương pháp học s au:
Học đúng lịch trình của môn học theo tuần, làm các bài luyện tập đầy đủ và
tham gia thảo luận trên diễn đàn. Đọc tài liệu:
28. BỘ MÔN TOÁN CƠ BẢN, 2009, Bài tập toán cao cấp cho các nhà kinh tế, NXB Thống kê.
29. NGUYỄN ĐÌNH TRÍ, TẠ VĂN ĐĨNH, NGUYỄN HỒ QUỲNH, 2008, Toán cao cấp 1, NXB Giáo dục.
30. ALPHA C. CHIANG,1995, Fundamental Methods of Mathematical Economics,
Third edition, Mc. Graw-Hill, Inc.
31. MICHAEL HOY, JOHN LIVERNOIS, CHRIS MC KENNA, RAY REES,
THANASIS STENGOS, 2001, Mathematics for Economics, The MIT Press
Cambrige, Massachusetts, London, England.
Sinh viên làm việc theo nhóm và trao đổi với giảng viên trực tiếp tại lớp học hoặc qua email.
Tham khảo các thông tin từ trang Web môn học. Nội dung
Khái niệm tích phân xác định và ý nghĩa hình học;
Các tính chất cơ bản của tích phân xác định;
Phương pháp đổi biến số;
Phương pháp tích phân từng phần. Mục tiêu
Nắm được định nghĩa tích phân xác định qua công thức Newton – Leibnitz;
Nắm được ý nghĩa hình học của tích phân xác định;
Đổi biến thành thạo các dạng tích phân cơ bản, đặc biệt là tích phân các hàm chứa căn;
Sử dụng tốt phương pháp tích phân từng phần. 80 TXTOCB01_Bai1_v1.0014105205
Bài 1: Các khái niệm cơ bản về hàm số một biến số
Tình huống dẫn nhập
Giả sử một cái hồ nước có hình dạng một tam giác cong như sau: x A B y 4 0
Trong đó điểm B có hoành độ x = 20 (m), cạnh cong OA có phương trình y = x2.
Hãy tính diện tích của cái hồ hình tam giác cong này. TXTOCB01_Bai1_v1.0014105205 81
Bài 1: Các khái niệm cơ bản về hàm số một biến số 7.1.
Khái niệm tích phân xác định và ý nghĩa hình học
98. Tích phân xác định của hàm số liên tục
Cho hàm số f(x) xác định và liên tục trong một khoảng X và cho a, b là hai số thực thuộc khoảng
X. Với F(x) và G(x) là hai nguyên hàm bất kỳ của f(x) ta luôn có: G(x) = F(x) + C, do đó G(b) G(a) [
F(b) C] [F(a) C] F (b) F(a)
Như vậy, với f(x) là một hàm số liên tục cho trước và a, b là các số cho trước, hiệu số F(b) – F(a)
là một hằng số, không phụ thuộc vào việc lựa chọn nguyên hàm F(x).
Định nghĩa: Tích phân xác định từ a đến b của hàm số f(x) là hiệu số b F(x) F (b) F(a) a
Với F(x) là một nguyên hàm bất kỳ của f(x). b f (x)dx
Tích phân xác định được ký hiệu là a
(đọc là: tích phân từ a đến b của f(x)dx). Các số a và
b được gọi tương ứng là cận dưới và cận trên của tích phân; f(x) được gọi là hàm số dưới dấu tích
phân; f(x)dx được gọi là biểu thức dưới dấu tích phân.
Theo định nghĩa ta có: b b f (x)dx F (b) F(a) F (x) a a
Với F(x) là một nguyên hàm bất kỳ của f(x)
Ví dụ 1: Theo định nghĩa trên ta có /2 / 2 sin xdx ( cos x) cos ( cos 0) 1 0 2 0 1 x x 1 1 0 e dx e 0 e e e 1 0 /4 dx / 4 t an x t an tan 0 1 2 0 cos x 4 0 /4 xdx I 2 cos x
Ví dụ 2: Tính tích phân 0
Giải: Để tính tích phân này, trước hết ta tìm nguyên hàm của hàm số dưới dấu tích phân xdx F(x) 2 cos x
Áp dụng phương pháp tích phân từng phần với dx u x, dv 2 cos x
Ta dễ dàng tìm được (chỉ cần lấy một nguyên hàm ứng với C = 0): 82 TXTOCB01_Bai1_v1.0014105205
Bài 1: Các khái niệm cơ bản về hàm số một biến số Kết quả là: Chú ý:
Định nghĩa nêu trên chỉ áp dụng cho hàm số liên tục;
Tích phân xác định là một số xác định, không phụ thuộc biến lấy tích phân b b b
f (x)dx f (y)dy f (t)dt a a a
99. Ý nghĩa hình học của tích phân xác định
Trong trường hợp a < b và f(x) 0 trên đoạn [a; b], tích phân xác định của hàm số f(x) trên đoạn
[a; b] là số đo diện tích S của hình thang cong aABb với cạnh cong phía trên là đồ thị của hàm số y = f(x) trên đoạn đó: b S f (x)dx a y ) x ( f = y B A b S f(x).dx a a b x 100.
Các tính chất cơ bản của tích phân xác định
Tích phân xác định của hàm số liên tục thỏa mãn các tính chất sau đây: a f (x)dx 0 a a b f (x)dx f (x)dx b a b c b
f (x)dx f (x)dx f (x)dx a a c
(a, b, c là ba số bất kỳ) b b b f(x) g (x) dx f(x)dx g(x)dx a a a b b kf (x)dx k f (x)dx a a
(k là hằng số bất kỳ)
Nếu a < b và f(x) g(x), x[a; b] thì TXTOCB01_Bai1_v1.0014105205 83
Bài 1: Các khái niệm cơ bản về hàm số một biến số b b f (x)dx g (x)dx a a
Nói cách khác: ta có thể lấy tích phân hai vế của một bất đẳng thức hàm số nếu cận dưới nhỏ hơn cận trên.
Nếu hàm số f(x) liên tục trên đoạn [a; b] thì tồn tại ít nhất một điểm trong khoảng giữa hai cận a và b sao cho: b f (x)dx f ( ).(b a) ξ a
Mệnh đề này khẳng định rằng số
là một trong các giá trị của f(x) trên đoạn [a; b]. Số được gọi là giá trị trung bình của hàm số f(x) trên đoạn [a; b]. 101.
Phương pháp đổi biến số
Phương pháp đổi biến số có thể áp dụng trực tiếp đối với tích phân xác định như sau:
Giả sử ta phải tính tích phân b f (x)dx a
Thay x = (t), dx = ’(t)dt với giả thiết hàm số (t) thỏa mãn các điều kiện:
(t) xác định, liên tục, đơn điệu và có đạo hàm liên tục
() = a, (β) = b, tức là cận x = a tương ứng với cận t = và cận x = b tương ứng với cận t = β. Khi đó 10 dx I 3
Ví dụ 1: Tính tích phân 2 1 x 2 Giải: Đặt 3 t x 2 , ta có 3 x t 2 và dx = 3t2dt
Đổi cận theo t: x = 2 ↔ t = 0; x = 10 ↔ t = 2
Theo công thức đổi biến: 2 2 2 2 2 3t dt 1 t I 3 t 1 dt 3 t ln 1 t 3 ln 3 1 t 1 t 2 0 0 0 π /2 3 8 I sin x cos xdx
Ví dụ 2: Tính tích phân 0
Giải: Viết lại biểu thức dưới dấu tích phân dưới dạng 3 8 2 8
sin x.cos x.dx sin x.cos x.(sin xdx) 2 8
(1 cos x)cos x.d(cos x) x
Đặt t = cosx ta có dt = -sinx.dx; x = 0 t = 1, 2 t = 0 84 TXTOCB01_Bai1_v1.0014105205
Bài 1: Các khái niệm cơ bản về hàm số một biến số 2 4 2 I x 4 x dx
Ví dụ 3: Tính tích phân 0 (0 t ) Giải: Thay x = 2sint 2 , ta có 2 dx 2 cos tdt, 4 x 2 cos t x 0 t 0, x 2 t 2 102.
Phương pháp tích phân từng phần
Công thức tích phân từng phần đối với tích phân bất định được chuyển sang tích phân xác định dưới dạng: b b b udv u v vdu a a a
Trong đó u = u(x) và v = v(x) là các hàm số có đạo hàm liên tục.
Phương pháp áp dụng công thức này hoàn toàn tương tự như đối với tích phân bất định. 1 3x I x.e dx
Ví dụ 1: Tính tích phân 0 1 3x v e
Giải: Đặt u = x, dv = e3xdx, ta có du = dx, 3 1 1 1 3x 1 3x I xe e dx 0 3 3 0 3 1 1 3 1 3x 1 3 1 3 2e 1 e e e (e 1) 0 3 9 3 9 9 π x I x cos dx 2
Ví dụ 2: Tính tích phân 0 x dv cos dx Giải: Đặt u = x, 2 , ta có x du d x, v 2sin 2 x x x I 2x sin 2 sin dx 2 4 cos 2 4 2 0 2 2 0 0 TXTOCB01_Bai1_v1.0014105205 85
Bài 1: Các khái niệm cơ bản về hàm số một biến số e I x ln xdx
Ví dụ 3: Tính tích phân 1
Giải: Đặt u = lnx, dv = xdx ta có 2 dx x du ; v x 2 e e 2 e 2 e 2 x ln x 1 e 1 2 e 1 I x ln xdx xdx x 2 2 2 4 4 1 1 1 1
Tóm lược cuối bài b b f (x)dx F (x) F (b) F(a) a Tích phân xác định a
với F(X) là một nguyên hàm của f(x).
Các tính chất của tích phân xác định giống như tích phân bất định.
Khi sử dụng phương pháp đổi biến, đổi biến phải kèm theo đổi cận tính tích phân. b b b udv u v vdu a
Công thức tích phân từng phần: a a
Các dạng tích được bằng tích phân từng phần: b b α x P(x)e dx P(x)cos ax dx a a b b α n P (x)sinaxdx x ln (kx)dx a a Câu hỏi ôn tập 69.
Nêu các tính chất cơ bản của tích phân xác định. 1 3 2x x 5 I .dx 1 2x1 70. Tính tích phân 0 4 3x 1 I .dx 2 71. Tính tích phân 1 2x 1 0 86 TXTOCB01_Bai1_v1.0014105205
Bài 1: Các khái niệm cơ bản về hàm số một biến số 2 2 x I .dx 3 3 72. Tính tích phân 2 3x 2 1 1 I x.ln 2x 1 .dx 4 73. Tính tích phân 0 π 4 5 2 I sin x.cos x.dx 5 74. Tính tích phân 0 π 12 I 3x 1 sin 3x.dx 6 75. Tính tích phân 0 TXTOCB01_Bai1_v1.0014105205 87




