
I.THEMICROSCOPE
I.A.PRINCIPLESOFTHETRANSMISSIONELECTRONMICROSCOPE(TEM)
I.A.1.OriginoftheTransmissionElectronMicroscope
I.A.2.ComparisonofLight(LM)andElectronMicroscopes(Fig.I.1)
a.Similarities(Arrangementandfunctionofcomponentsaresimilar)
1)Illuminationsystem:producesrequiredradiationanddirectsitontothespecimen.Consistsofasource,whichemitstheradiation,anda
condenserlens,whichfocusestheilluminatingbeam(allowingvariationsofintensitytobemade)onthespecimen.
2)Specimenstage:situatedbetweentheilluminationandimagingsystems.
3)Imagingsystem:Lenseswhichtogetherproducethefinalmagnifiedimageofthespecimen.Consistsofi)anobjectivelenswhichfocusesthe
beamafteritpassesthroughthespecimenandformsanintermediateimageofthespecimenandii)theprojectorlens(es)whichmagnifiesa
portionoftheintermediateimagetoformthefinalimage.
4)Imagerecordingsystem:Convertstheradiationintoapermanentimage(typicallyonaphotographicemulsion)thatcanbeviewed.
b.Differences
1)Opticallensesaregenerallymadeofglasswithfixedfocallengthswhereasmagneticlensesareconstructedwithferromagneticmaterialsand
windingsofcopperwireproducingafocallengthwhichcanbechangedbyvaryingthecurrentthroughthecoil.
2)MagnificationintheLMisgenerallychangedbyswitchingbetweendifferentpowerobjectivelensesmountedonarotatingturretabovethe
specimen.Itcanalsobechangedifoculars(eyepieces)ofdifferentpowerareused.IntheTEMthemagnification(focallength)oftheobjective
remainsfixedwhilethefocallengthoftheprojectorlensischangedtovarymagnification.
3)TheLMhasasmalldepthoffield,thusdifferentfocallevelscanbeseeninthespecimen.Thelarge(relative)depthoffieldintheTEMmeans
thattheentire(thin)specimenisinfocussimultaneously.
4)Mechanismsofimageformationvary(phaseandamplitudecontrast).
5)TEMsaregenerallyconstructedwiththeradiationsourceatthetopoftheinstrument:thesourceisgenerallysituatedatthebottomofLMs.
6)TEMisoperatedathighvacuum(sincethemeanfreepathofelectronsinairisverysmall)somostspecimens(biological)mustbedehydrated
(i.e.dead!!).
7)TEMspecimens(biological)arerapidlydamagedbytheelectronbeam.
8)TEMscanachievehighermagnificationandbetterresolutionthanLMs.
9)Pricetag!!!(100xmorethanLM)
I.A.3.Photons/Electrons
a.Dualconceptofwaveandparticle(Fig.I.4)
Lighthaspropertiesbothofaparticleandawave.Thisdualnatureisrequiredtosatisfactorilyexplaintheresultsofvariousphysicalexperiments.
Thediffractionoflight(bendingaroundcorners)illustratesthewavenature.TheWAVETHEORYisbasedonthestatisticalnatureofeventsand
haslittlemeaningwithrespecttothebehaviorofsingleparticles.ThewavetheorywasdevelopedandexpoundedbyHuygens(16291695)and
Hooke(16381703).TheCORPUSCULARTHEORYwasproposedbyNewton(16421727)andbecamethemoreacceptedtheoryevenafter
demonstrationofdiffractionbyYoung(17731829)andinterferencebyFresnel(17881827).Atabout1850,thewavetheorycamebackinto
favoruntilabout1900whenmoreevidenceforthecorpusculartheorywasdiscovered.
QUANTUMTHEORY(PlanckandEinstein)providesthebasisforexplainingthephenomenaofINTERFERENCE,DIFFRACTIONandthe
PHOTOELECTRICeffect(lightfallingoncertainmetalscausethemtoemitelectrons)andthusformsacommonbasisforexplainingthenatureof
actionoflight.Thetransferofenergybetweenlightandmatteroccursonlyindiscretequantitiesproportionaltothefrequencyofthe
lightwave.
E=hJ
where
E=energyofphoton(joules)
h=Planck'sconstant(6.624
•
10
34
joulesec)
J=frequency(cycles/sec)
b.Electronvelocityandwavelength
Therelationbetweenthewavelength(l )ofaparticleofmass,m,movingatavelocity,v,isgivenbytheDeBrogliewaveequation:
(1)
Anelectronofchargee(1.6
•
10
19
coulomb),andmassm(9.11
•
10
28
gm),whenpassingthroughapotentialdifferenceofVvolts(expressedin
joules/coulomb),hasakineticenergy:
(2)
Solvingforvelocity:
(3)
substitutingintotheDeBroglieequation(1):
(4)
Since1joule=10
7
dyne
•
cm=10
7
cm
2
•
gm/sec
2
(5)
Thus,forexample,ifV=60,000volts,l =0.005nm.
Fromequation(3)theelectronvelocitycanbecalculatedifVisknown:
(6)
Thefollowingtableillustratesthat,athighvoltage,electronvelocityiscomparabletothespeedoflightinavacuum(c=3
•
10
10
cm/sec).
Theequationbreaksdownwhenthevelocityoftheelectronapproachesthespeedoflightbecausearelativisticcorrectionmustbemadeforthe
valueofthemasswhere:
(7)
Therelationbetweenl andVismorecorrectlygivenby:(seeHall(1966)pp.3334)
(8)
Thefollowingtableisobtainedwhenrelativityeffectsareincluded:
c.Interference/diffraction/coherence
Anideallenssystemobtainsanexactimageoftheobject(eachpointfaithfullyreproduced).Thephenomenaofdiffractionmakesthis
unattainable(Figs.I.5,I.6).
Diffractionphenomenainvolvesthebendingofthepathofradiationpassingclosetoanobstacle(Fig.I.6).Thisresultsinaspreadingofthe
radiationintotheregionbehindtheobstructionthatthewavespassed.Thediffractionatedgescontributestothecontrastatwhichanedgecan
beobserved.Diffractionalsolimitstheresolvingpowerofthemicroscopesincetheimagepointproducedbyalensisadiffractionimageofthe
openingofthelensortheaperturerestrictingtheeffectiveopeningofthelens(Fig.I.5).
Ifthelightsourceandtheplaneatwhichthediffractionpatternisobservedareatfinitedistancesfromtheedge,thephenomenoniscalled
Fresneldiffraction.Thepatternisdescribedasduetointerferencebetweenthenondiffractedlightandawaveoflightdiffractedattheedge.
Theresultingsuperpositiongivesrisetoaseriesofdiffractionfringesorientedparalleltotheedgeandrepresentingperiodicallyvaryingbrightness,
maximaandminima.(Figs.I.7,1.8,I.9).
Coherence:Aprerequisiteforinterferenceisasuperpositionofwavesystemswhosephasedifferenceremainsconstantintime.Twobeams
arecoherentif,whencombined,theyproduceaninterferencepattern.Thebeamsareincoherentwhentheyareincapableofproducingan
interferencepattern.Twobeamsoflightfromselfluminoussourcesareincoherent.Iflightfromthetwosourcesfallsonascreen,theresultant
intensityissimplythesumofthetwointensitieswhichwouldoccurfromeachsourceseparately(Figs.I.10,I.11).Inpracticeanemittingsource
hasfiniteextentandeachpointofthesourcecanbeconsideredtogeneratelight.EachsourcegivesrisetoasystemofFresnelfringesatthe
edge.Thesuperpositionofthesefringesystemsisfairlygoodforthefirstmaximaandminimabutfartherawayfromtheedgeshadowtheoverlap
ofthefringepatternsbecomessufficientlyrandomtomakethefringesdisappear.Thenatureofwaves,phase,amplitude,andinterferenceare
illustratedinFigs.I.12andI.13.
d.Resolution
1)Definitions:
RESOLUTION:abilitytodistinguishcloselyspacedpointsasseparatepoints.
RESOLUTIONLIMIT:smallestseparationofpointswhichcanberecognizedasdistinct.
RESOLVINGPOWER:resolutionachievedbyaparticularinstrumentunderoptimumviewingconditions.
2)Distinctionbetweenresolutionandresolvingpower:
Notethedistinctionbetweenresolutionandresolvingpower.Resolvingpowerisapropertyoftheinstrumentandisaquantitythatmaybe
estimatedontheoreticalgrounds.Resolutionisequaltoorpoorerthantheresolvingpowerandisthequantityobservedunderanygivenset
ofexperimentalconditions.IntheTEM,especiallywithbiologicalsamples,theresolutionachievedmaybeconsiderablyinferiortothetheoretical
resolvingpoweroftheinstrument.
Microscopyisthescienceofseeingtheverysmall.Underidealconditions,theeyeresolvesabout1minuteofarc(=1/60degree=2.9x10
4
radian;recallthereare2p radiansin360°)andsinceitcanfocusdowntoabout250mm,thesmallestobjectwecanresolveisabout0.07mm
(70mm)(Fig.I.14).Thislimitisrelatedtothesizeofthereceptorsintheretinaoftheeye.Thefunctionofamicroscopeistomagnifytheimage
fallingontheretina(Fig.I.15).Theadvantageoflightandelectronmicroscopesisthattheyeffectivelygettheobjectclosertotheeyesoa
magnifiedimageisobtainedandmoredetailcanbediscerned.
TENNISBALLANALOGY:Eyecanresolve3cmat100meters,thusatennisballisclearlyvisible.Butifthetennisballisheldupagainstawhite
background,thevisibilitydecreases(becauseofthedecreaseincontrast).
3)Abbecriteriaofresolution:
Thefundamentalnatureoflightposeslimitsonthedetailthatcanberesolved(Fig.I.16).Abbe(1893)showedthatthesmallestresolvable
distanceisabout1/2thewavelengthoflightused.Thus,1/2thewavelengthoftheradiationusedistheultimateresolvingpowerofany
instrument.Thislimitstheusablemagnificationofopticalmicroscopesto<1000X.Atfirstitwasthoughtthatxraymicroscopeswouldbeuseful
buttherefractiveindexofsubstancesforxraysisnearly=1,thusrefractinglensescannotbemadeforxrays,andconsequently,xrayscannot
beeasilyfocusedtoformimages.
4)Magnificationlimits:
Themaximummagnificationofaninstrumentislimitedaccordingtothefollowingrelationship:
Thus,fortheLM,witharesolvingpowerofapproximately0.25µm,themaximum(useful)magnificationisabout250µm/0.25µm=1000X.Thevalue
usedfortheresolvingpoweroftheeyeinthisexample(250µm)representsamorerealisticviewingcondition.Anymagnificationabovethevalue
givenbytheaboveformularepresentsemptymagnification,sincesuchmagnificationleadstonomoreusefulinformationbutratheramagnified
blur.
AccordingtotheAbbecriteria,at60,000volts,theTEMshouldhavearesolvingpowerofabout0.0025nm.Thisshouldallowamaximumuseful
magnificationofabout100milliontimes!!!Inpractice,themaximumusefulmagnificationoftheTEMoperatedat60kVislimitedtomuchlessthan
1,000,000X.Thus,althoughtheLMnearlyobeystheAbbecriteria,theTEMfallsshortbyaconsiderableamount.Themainlimitingfactorinthe
TEM,withrespecttoachievingthetheoreticalresolvingpoweroftheinstrument,concernsthenatureoftheimaginglensesandtheprocessof
imageformation.
5)Rayleighcriteria(practicalbutarbitrary):(Fig.I.17).
Itistheabilityofmicroscopestomakeobjectpointswhichareclosetogetherappearintheimageasseparatepoints.Anideallenstakeseach
objectpointandrepresentsitexactlyasapointintheimage.Areallenstakeseachobjectpointandspreadsitoutintoacirculardisk(Airy
disk)intheimageplanewhosediameterdependsontheangularapertureofthelens.
Theshortestdistancebetween2disksatwhichthetwodisksappearpartiallyseparatedcorrespondstoabout1/2thewidthofthedisks.The
distance,d,inobjectspaceisgivenby:
d=0.61l /n
•
sina
where
l =wavelenghtoftheradiation
n=refractiveindexofthemedia
a=semiangularapertureofthelens
NOTE:n
•
sina=thenumericalaperture(N.A.)ofthelens.
Thus,tomaximizeresolvingpower,l mustbedecreased,nincreased,oraincreased.Recallthatweareconcernedatthemomentwithan
aberrationfreeopticalsystem.Thevaluefortheconstant(0.61)iscontroversialbecauseitdependsonthecoherenceoftheradiationanda
criteriaofvisibility.
FortheLM,usingoilimmersionoptics(n=1.5),sina=0.87,andvioletlight(l =400nm),d=0.2µm.Theonlywaytoimprovetheresolutionisto
uselightofshorterwavelengthsinceN.A.cannotbeincreasedbeyond~1.5.FortheTEM,n=1(vacuum),sina=10
2
andl =0.005nmfor60kV
electrons,thusd=0.3nm.
I.A.4.Optics(LensTheory)
a.Basiclawsofclassicalgeometricaloptics
1)Rectilinearpropagationoflightwhenn(refractiveindex)isconstant.
2)Lawofreflection:
3)Lawofrefraction(Snell'sLaw):
4)Independenceofrays.Theassumptionismadethatlightraystravelindependentlythroughspace.
Theselawsholdforelectrons,except#4,ifthecurrentdensityistoohighwhennegativechargedelectronscaninterfere.
b.Classicalvs.electronoptics
1)Classicaloptics:Therefractiveindexchangesabruptlyatasurfaceandisconstantbetweenthesurfaces.Therefractionoflightatsurfaces
separatingmediaofdifferentrefractiveindicesmakesitpossibletoconstructimaginglenses.Glasssurfacescanbeshaped.
2)Electronoptics:Here,changesintherefractiveindexaregradualsoraysarecontinuouscurvesratherthanbrokenstraightlines.Refraction
ofelectronsmustbeaccomplishedbyfieldsinspacearoundchargedelectrodesorsolenoids,andthesefieldscanassumeonlycertaindistributions
consistentwithfieldtheory.
c.Geometricalandphysicaloptics
Thefundamentalprinciplesofopticsgovernthedesignandoperationofboththelightandelectronmicroscopes.Thebasicopticalprinciples
involvingtheuseofrefractileelementsorlensesinordertoformmagnifiedimagesareidenticalinboththeLMandTEM.TheTEMdiffersfromthe
LMonlyintheradiationitusesandinthewayinwhichtheradiationisbentorrefracted.
Geometricalopticsdealswiththestudyofthepathsfollowedby'rays'oflightorelectronsthroughlensesandapertures,andthegeometrical
constructionsusedtofindtherelativepositionsandsizesofobjectsandtheirimages.Arayoflightorelectronsisdefinedasaninfinitelythin
pencilorbeam.Physicalopticsshowsthatthisanabstractionandcannotphysicallyexistbecauseof'diffraction'whichdealswiththewave
natureoflightandelectrons.Allresultsobtainedingeometricalopticscanbederivedfromtheprinciplesofphysicaloptics,alongwithother
phenomenasuchasinterferenceanddiffractionwhicharenotexplicableinsimplegeometricalterms.
d.Idealversesreallenses:
Lensesareusedtobendraysoflightorelectronssotheyaredeflectedinapredictablewayfromtheiroriginalpaths.Thepropertiesofanideal
lens,possessinganaxisofrotationalsymmetryare:
1)Eachrayofthebundleofrayswhichpassesfromanobjectpointwillberefractedbytheideallenstomeetinoneimagepoint.
2)Raysoriginatingfrompointswhichlieonaplaneperpendiculartotheaxis,mustbeimagedinaplanewhichisalsoperpendiculartotheaxis.
3)Theimageappearsliketheobjectirrespectiveofthemagnification,sotherelativelineardimensionsoftheobjectarepreservedintheimage.
Inpractice,theimagingbyanyreallensdoesnotcorrespondtothatoftheideallensowingtothefactthatanobjectpointisrepresentedbya
diffractionimage(Airydisc)ofthelensopeningortheapertureusedforrestrictingtheeffectiveopeningofthelens.Thisisaresultofthewave
likepropertiesoflight.Lensaberrationsalsocontributetomoreorlesspronounceddeviationsfromthepropertiesoftheideallens.
Thesinglerefractingsurfaceofsphericalcurvatureisthefundamentalunitoffocusingactionbyglasslenses.Sphericalrefractingsurfacesactas
lensesforparaxialrayswhicharethoseraysthatpassclosetotheprincipalaxisofthelens.RayswithlargeangleswillNOTobeyideallens
action.
Afundamentaldifferencebetweenlightandmagneticlensesisthattheelectronbeamdoesnotchangeinforwardvelocityasitpassesthrough
themagneticfield(lightraysslowdownwhenpassingintoamediumofhigherrefractiveindex).Refractioniscontinuouswithelectronswhenthey
areinthemagneticfield:lightisrefractedonlyattheinterfacebetweenmediaofdifferingrefractiveindex.Theelectronsalsofollowspiral
trajectoriesthroughthemagneticfield(seealsoSec.I.A.5.c(Magneticfieldsandmagneticlenses)
e.Raydiagrams:(Figs.I.20I.28)
Themethodofconstructionofraydiagramsisbasedonthreesimpleprinciples:
1)Allraysenteringthelensparalleltotheaxisarebroughttoacommonpointontheaxis,thefocalpoint.
2)Allrayspassingthroughthegeometricalcenterofthelensareundeviatedandpassstraighton,nomatterfromwhichdirectiontheycome.
3)Principleofreversibility:ifthedirectionofarayisreversedinanysystemtherayexactlyretracesitspaththroughthesystem.Thisapplies
onlytothelocationoflightpathsandnottotheintensityofthelight.
Theaboveprinciplesarebasedontheassumptionsthatwearedealingwithathinlensandconcernedwiththepathsofparaxialrays.The
standardconventionistodrawdiagramswithraysthattravelfromlefttoright.Theobjectistotheleft(infront)ofthelensandtheimageisto
theright(behind)ofthelens.
f.Definitions:
Realimage:oneatwhichlightraysphysicallyreunite,sothataphotographicplateplacedatthepositionofarealimageisexposed.
VirtualImage:onefromwhichlightraysappeartodiverge;raysarenotinfactconcentratedatthepositionofavirtualimage,sothata
photographicplateplacedatthepositionoftheimageisnotexposed(byfocusedrays).Placinganopticalsystemsuchastheeyebehindthe
lens,willenablethedivergentraystobefocusedtoformarealimage.TheintermediatelensofanTEMissometimesusedthiswayinorderto
reducethefinalsizeoftherealimageformedbytheprojectorlens(es).
Converging(positive)lens:bendsraystowardtheaxis.Ithasapositivefocallength.Formsarealinvertedimageofanobjectplacedtothe
leftofthefirstfocalpointandanerectvirtualimageofanobjectplacedbetweenthefirstfocalpointandthelens.
Diverging(negative)lens:bendsthelightraysawayfromtheaxis.Ithasanegativefocallength.Anobjectplacedanywheretotheleftofa
diverginglensresultsinanerectvirtualimage.Itisnotpossibletoconstructanegativemagneticlensalthoughnegativeelectrostaticlensescan
bemade.
g.Lensformula(thinlensequation):
where
f=focallengthofthethinlens(sameradiusofcurvatureforboth
sphericalsurfaces)
o=distanceofobjectfromlens(positivetotheleft)
i=distanceofimagefromthelens(positivetotheright)
NOTE:Foravirtualimage,ihasanegativevalue.
h.Magnification:
Foraconverginglens,iftheobjectismorethantwicethefocallengthfromthelens,thentheimageformedisreal,inverted,andsmallerinsize
thantheobject(M<1).Whentheobjectisatadistance=2f,theimageandobjectarethesamesize(M=1);whenitisbetweenfand2f,
theimageislargerthantheobject(M>1),andwhenitis<f,theimageisvirtual,erect,andlargerthantheobject(M>1).
i.Angularapertureofthelens(2a)(Fig.I.29)
Theaperturedeterminesthetotalamountofradiationarrivingfromtheobjectwhichcanbefocusedto
formanimage.Theaperturethuscontrolstheabilityofthelenstogatherinformationabouttheobject.
Thisdependsontheangleoftheconeofraysitisabletoacceptfromtheobject.Bringinganobject
closertotheeyeincreasestheangularaperture,butthereisalimittotheclosenessthattheobjectcan
bebroughttotheeye(~25cmcorrespondingtoanangleofabout0.9°fora4mmexitpupildiameterof
theeyelens;atypicalLMwithanoilimmersionobjectivelenshas2aof~175°).
j.Simplevs.compoundmicroscope(Figs.I.30I.32)
Inprinciple,arealimageofanydesiredmagnificationcanbeobtainedfromasinglepositivelens,butin
practicethisiscumbersomebecauseofthelonglensimagedistance.Oneormorelensescanbeusedto
magnifytheimageinstages(totalmagnificationequalingtheproductofthemagnificationsofeachlens).
Theimageformedbyonelensconstitutestheobjectforthesubsequentlens,whetherornotareal
intermediateimageisformed.
Comparisonofoneversestwostagemagnification:
Thefollowingdescriptionillustrateshowdifferentpathlengthsarerequiredtoachieveamagnificationof10,000Xusingeitheroneortwolenses
withf=2.0cm.
OneStageSystem:
TwoStageSystem:
Assumebothlenseshavef=2.0cmandarearrangedsoeachgives100Xmagnification.
Thus,M=100=x
i
/x
o
foreachstage.
FirstStage:
x
o
=2.02cm
x
i
=202.00cm
Therealimageformedinthefirststagebecomestheobjectforthesecondlens.
SecondStage:x
o
,x
i
sameasinthefirststage.
Totallengthofsystem
=lengthoffirststage+lengthofsecondstage
=(x
o
+x
i
)+(x
o
+x
i
)
=2(x
o
+x
i
)
=2(2.02+202.00)=408.04cm(4.08meters)
k.Problemset
Thefollowingproblemsareforyourownedificationtotesthowwellyouunderstandthebasicsoflensoptics.
1.Foreachsituationbelow,drawanaccurate(usegraphpaper)raydiagramshowingthepathof(atleasttwo)raysfromtheobjecttoimage.
Indicatewhethertheimageisrealorvirtualandspecifythedistanceoftheimagefromthelensandthemagnificationoftheimagewithrespect
totheobject.Ineachexample,thelensisconverging,withidenticalfrontandbackfocalpoints.Distancesareinarbitraryunits.Letf=lens
focallength,x
o
=distanceofobjectinfrontofthelens,andx
i
=distanceofimagebehindthelens.Theobjectmaybeanysize.
2.Inthefollowingexamples,therearetwoconverginglensesinsuccession.Drawraydiagramsshowingtheformationofboththeintermediate
andfinalimagesandgiveappropriateinformationaboutthenature(real/virtual),positions,andsizesoftheintermediateandfinalimages.What
isthemagnificationateachstageofimageformationandwhatisthemagnificationofthefinalimage?Thedistancefromthecenteroflens1(L1)
tothecenteroflens2(L2)equalsD.
I.A.5.ElectronOptics/ElectronLenses
a.Electronemission
Innershellelectronsinmetalatomsshieldtheelectricfieldofthenucleusthroughtherepulsiveforcestheyexertontheoutershell(valence)
electrons.Thustheattractionbetweenthevalenceelectronsandthenucleusisreduced.Metalatomsarecharacterizedashavingtwoloosely
boundvalenceelectronswhichmigratefreely(thisiswhymetalsaregoodelectricalconductors)andcanescapefromthemetalcompletelyif
sufficientadditionalenergyisimpartedtothem.Asthetemperatureofametalisincreased,thekineticenergyoftheelectronsincreasesbecause
ofincreasedthermalvibrationsofthemetalions,whichcollidemorefrequentlywiththeelectrons.Thermionicemissionisthetermusedto
describetheprocessbywhichthermalenergyissuppliedtolooselyboundelectronsinordertoformasourceofelectrons.
Atroomtemperatureelectronsareeffectivelypreventedfromescapingthesurfaceofthemetalowingtotheattractiveforceofthepositively
chargedions.Asthetemperatureisincreasedsomeelectronsacquiresufficientenergytoovercometheattractionandleavethemetal
temporarily.Metal,shapedasathinwire,caneasilybeheatedbypassinganelectriccurrentthroughit.Sincethemetalsurfacebecomes
positivelycharged,acertainlevelofenergy(workfunction)mustbesuppliedtoallowelectronstoescapefromthesurface.Eachmetalhasa
characteristicworkfunction.Tungsten,withalowworkfunction,emitsmoreelectronsthanmetalswithhigherworkfunctions(seealsopp.2930
andFig.I.59).
Ifastrongelectrostaticfieldisappliedinavacuumbetweenthewire(givenanegative,cathode,potential)andananode,theelectricfieldwill
causeelectronstoaccelerateawayfromthewiretowardstheanodesurface(Fig.I.33).Thespeedoftheelectronsdependsonthestrengthof
theelectrostaticfield(voltage)betweenthecathodeandanode(equation(3),Sec.I.A.3.b)Thenumberofelectronswhichleavethewire
dependsonthetemperaturetowhichthewireisheated,whichdependsonhowmuchfilamentcurrentpassesthroughthewire.
A"V"shapedwirewillhavethehighesttemperatureatthetip.Electronswithdrawnfromthefilamenttipcarryelectricchargestotheanode.This
electriccurrent,whichflowsbetweenthefilamentandtheanode,iscalledthebeamcurrent.
1)Electricfield/Equipotentials
Anelectricallychargedobjecthasassociatedwithitanelectricfield.Thus,anelectricallychargedparticle,whenbroughtnearachargedobject,
isinfluencedbyanelectricalforceinthevicinityoftheobject.Theforceisdirectedtowardthechargedobjectifthechargesareofopposite
signsandawayfromtheobjectiftheyareofsimilarsign.DEFINITION:Thedirectionofanelectricfieldisdefinedasthedirectionoftheforce
actingonapositivecharge.(Figs.I.3435)
Alongthelinesofforceconnectingthetwocharges,theelectricpotentialwillchangegraduallybetweentheextremevaluesrepresentedbythe
twocharges.DEFINITION:Equipotentiallinesdefinethepointsalongthelinesofforcewithidenticalelectricalpotential.Theseequipotential
surfacesarealwaysorientedperpendiculartothelinesofforce.Thechangesintheelectricpotentialaregradualinspace.
Electronswhichenterafieldbetweentwoparallelplatesinadirectionparalleltotheplatesareaffectedbytheforcedirectedperpendicularto
theplates(FigI.36).Theelectronswillbeattractedtowardthepositiveplate.Thepathchangesinaseriesofgradualstepsattheequipotential
surfaces.
FigureI.37showshowtheelectronpathis"refracted"attheequipotentialsurface.TheresultisfundamentallythesameasthatgivenbySnell's
Lawofrefractioninlightoptics.Aconsequenceofthisisthatasphericallycurvedequipotentialsurfaceexhibitsthepropertiesofalens.
FiguresI.38andI.39showhowbothpositive(converging)andnegative(diverging)electrostaticlensescanbeformed.Thisfeatureof
electrostaticlensesdiffersfromelectromagneticlenseswhichcanonlyactasconverginglenses.
2)Advantages/Disadvantagesofelectronlenses:
Thefactthattherefractiveindexdoesnotchangeabruptlyinelectronlenseshasoneadvantageinthattherearenotroublesomereflectionsat
equipotentialsasatglassinterfaces.Thereisaseriousdisadvantageinthatequipotentialscannotbeshapedandcombinedinarbitraryfashionto
correctforchromaticaberrationandothererrors.
Althoughelectronmicroscopeswhichemployelectrostaticlenseshavebeenmade,mostmicroscopesuseelectromagneticlenses.Amajorreason
isthatelectrostaticlensesaremoresensitivetothequalityofthevacuumandcleanlinessofthecomponentsthanareelectromagneticlenses.
Somelensaberrationsaremoresevereforelectrostaticlensescomparedtoelectromagneticlenses.Electrostaticlensesrequireverypowerful
electrostaticfieldswhichcanleadtoelectricalbreakdownor"arcingover"insidethecolumn,especiallyunderpoorvacuumconditions.Forthis
reason,electrostaticlensescannotbemadewithfocallengthsasshortasmagneticlenses.
b.Electrostaticlens
Abasicunderstandingofelectrostaticlensesisimportantfortwomainreasons:i)theelectrongunuseselectrostaticlensactiontoformthe
primarybeamsource,andii)itisquitecommonforachargetodeveloponthenonconductingcontaminationwhichmayaccumulateonphysical
apertures(suchastheobjectiveaperture)andtransformthemintoweakelectrostaticlenseswhichcandistorttheelectronimage.
3)Propertiesofelectrostaticlenses:
a)Anyaxiallysymmetricalelectrostaticfieldhasthepropertiesofalensforraysconfinedtotheparaxialregion.Alltheideallensformulasapply
toelectrostaticlenses.
b)Forelectronlenses,replaceÃ(f)forrefractiveindexinthelensequations(f=valueofthepotentialontheaxis).Intheimageformingsystem
ofmostTEMs,fisthesameonbothsidesofthelens(SeeSec.I.A.5.c).
c)Ifboundedbyregionswherefisconstant,anelectrostaticlensisalwaysconvergent.
c.Magneticfieldsandmagneticlenses
1)Magneticfield
Anelectriccurrentpassingthroughaconductorgivesrisetoamagneticfield.TheconventionisthatNisthedirectioninwhichthelinesofthe
magneticfieldpoint(Fig.I.40).Themagneticfluxisthetotalnumberoflinesandthefluxdensityisthenumberoflinesperunitareaofasurface.
UsetheRIGHThandruletodeterminethedirectionofthefield(thumbpointstowardcurrentdirectionandfingerscurlindirectionoffield.NOTE:
Byconvention,thedirectionofelectronflowisoppositetothatofcurrentflow.
Fluxdensitydependsonthepropertiesofthematerialsurroundingtheconductor.Ironinducesahigherfluxdensitythanairoravacuum.The
propertyofthematerialwhichaffectsthefluxdensityiscalledthepermeability,m,ofthematerial.Forairandvacuum,m=1.0.For
ferromagneticmaterialsitcanbeaslargeasseveralhundredthousand.
Iftheconductorhastheshapeofacircularloop,thelinesofforceformcirclesaroundtheloop.Thefluxdensityisgreatestatthecenterofthe
loop.Themagnetinthecenteroftheloopisorientedperpendiculartotheplaneoftheloopifthecurrentthroughtheloopissufficientlystrongto
eliminatetheinfluenceoftheearth'sfield.ThesideoftheloopatwhichthelinesofforceleavetheloopistheNorth(N)poleofthemagnet(Figs.
I.41,I.42).
Ifthewireiswoundinseveralturnsaroundacylindricalsurface(solenoid),eachturnwillcontributetotheinducedmagneticfield.Theflux
densityinthecenterofthecoilisgivenby:
Inthecaseofairandnonmagneticmaterials,µ=1.0andB=H.
Thepermeabilityofirondependsonthefieldstrength,H,anddecreasestounityathighfieldstrengthorwhenthefluxdensity,B=H(Fig.I.43).
Thehighpermeabilityofironisduetotheinducedmagneticfieldorientingmicroscopiccrystalregionsactingastinymagnetsintheiron.Allthese
tinymagnetsaddtheirmagneticfieldstotheinducedfield(Fig.I.44).Whenallmicromagnetsarenearlyoriented,theironwillaffecttheflux
densitytoadecreasingamountsincethereorientationofmicromagnetsisnearingcompletion.Thus,thepermeabilityofironathighfieldstrengths
approachesthatofemptyspace.Atthispointtheironreachesmagneticsaturation.
2)Hysteresis
Thestrengthofthelensdependstosomeextentonthepreviousmagnetichistoryof
thelens.Whenthecurrentinalensisreduced,thedecreaseinmagnetizationdoes
notretracethesamepathobtainedwhenthecurrentwasincreased(Fig.I.45).
Inductionofmagnetizationinvolvesaphysicalmovementwithinthemagnetized
material,requiringtheovercomeofacertaindegreeofinertia.Asaresult,
magnetizationtendstolagbehindthemagnetizingforceapplied.Inducedmagnetic
fluxcanonlybereturnedtozerobyapplicationofacurrentintheoppositedirection.
Aconsequenceofhysteresisisthatthelevelofcurrentusedtoenergizeamagnetic
lensDOESNOTpreciselyspecifythelensstrength(i.e.focallength).
NormalizationofTEMlensesisaccomplishedbyreducingthelenscurrenttozero
somepredeterminednumberoftimes.Hysteresismayalsobeminimizedbytakinga
lenstosaturationandthenreturningittotheworkingcurrentwithoutovershooting.
Whenthefieldstrengthisreducedtozero,somemagnetizationstillremainsintheiron
(residualmagnetizationorremanence).Anadvantageofsoftironisthefactthat,
whenusedinanelectromagnet,hysteresisislow.
Introductionofpiecesofironinamagneticfielddrasticallyaffectsthefluxdensity.
Magneticmaterialhasashieldingeffect,theeffectbeinggreaterthegreaterthe
permeability.Permalloy(mmetal)hasamaximumpermeabilityof80,000140,000
comparedtoironusedintransformers(~7000).mmetalpermeabilityislimitedtolower
fieldstrengthsthanthatatwhichironstillretainshighpermeability.Thismetalis
thereforeusefulforshieldingtheTEMfromexternalmagneticfields.
d.Theelectromagneticlens
1)Lensdesigndevelopment(Figs.I.46I.48)
Theefficiencyofthemagneticfieldproducedbyashortsolenoidwasfirstimproved
byencasingtheenergizingcoilinasheathofsoftironwhichhasthepropertyofconcentratingthelinesofforceinamagneticfieldandthus
becomingmagnetizedbyinduction.Inthiswayamuchmorepowerfulaxialmagneticfieldisobtainedforthesameamountofcurrentflowing
throughthesolenoid.Furtherdevelopmentinvolvedencasingtheentirecoilwithsoftironexceptatanarrowannulargapintheinsideofthecoil.
Thisproducesagreaterconcentrationofthemagneticfieldalongashortaxialdistance.Toachieveshorterfocallengthlenses(andobtaingreater
magnifications)asoftironpolepiecewithanopenaxialborewasintroducedatthepositionoftheannulargap.
MagneticlensesusedinTEMsarealwaysconstructedwithanironcircuittoproduceahighfieldstrengthacrossashortgap.Themagneticfields
forTEMlensesareintherangeof10,00020,000gauss.
2)Forcesactingonacurrentinamagneticfield
Theforceonanelectroninamagneticfieldisalwaysatrightanglestothevelocityandthedirectionofthefield(Figs.I.49,I.50,andI.52).The
fieldonlyactsonthevelocitycomponentwhichisdirectedperpendiculartothelinesofforce.Usethelefthandrule(Fig.I.51:firstfingerfor
fielddirection,middlefingerforcurrentdirection,andthumbfordirectionofforce).Rayspassingthroughthelensareturnedthroughanangle
whichdoesNOTdependonthedistanceoftheraysfromtheaxis.Allelectronscontainedinagivenmeridionalplanebeforeenteringthefieldare
containedinarotatingmeridionalplaneastheypassthroughthelens,andthentheyleavethelenscoplanar.
Whenelectronsenterthelenstheyencounterasidewaysforcewhichcausestheelectrontorotate
asitcontinuesthroughthelens(Figs.I.53I.57).Sincetheradialcomponentofthemagneticfield
reversesafterthecenterofthelens,therotationalvelocitysetupinthefirsthalfofthelensis
countered.Theelectronenteredthelenswithoutangularmomentumabouttheaxisandleaves
withoutangularmomentum.Theneteffectisadeflectiontowardtheaxis,whichitmustcrossatthe
focalpointf
2
.Theanglebetweentheobjectvectorandtheimagevectoris180°+q,whereas,for
glasslensesandelectrostaticlenses,theanglebetweenarealobjectandtheimageisexactly180°.
Sincetheradialforceisdirectedtowardtheaxis,thelensisconvergentnomatterwhatthedirection
ofthefield.
3)Propertiesofamagneticlens:
Anyaxiallysymmetricmagneticfieldhasthepropertiesofanideallens.Alltheformulasfortheideallensmaybeapplied.
Magneticlensesarealwaysconvergent.Theconventional,axiallysymmetriclensisalwaysboundedbyregionswhicharefieldfree,the
consequencebeingthatthenetactionofelectronlensesisinevitablyconvergent.Limitedregionsmaybedivergentbutnotthelensasawhole.
Theseriousconsequenceofthisisthatneithersphericalorchromaticaberrationscanbecorrectedasisdoneinlightopticsbytheusedoublets
ofpositiveandnegativelenses.
Intheabsenceofelectrostaticfields,therefractiveindexisthesameinobjectandimagespace,thereforef
1
=f
2
.
Electronstravelingthroughaxiallysymmetricfieldsexperienceaspiraltrajectoryofdiminishingradius.Theimagevectorisatanangle180°+qto
theobjectvector.
Thedeflectionoftheelectrontowardstheaxismeansthatanelectronenteringthelensparalleltoitsaxiswillcrosstheaxisafterhavingpassed
thelens.Thedeflectionwillincreasewiththedistancefromtheaxis.Thus,abeamofelectronsinparallelpathsparalleltotheaxisofthelenswill
befocusedtoanimagepointontheaxiswhichrepresentsthesecond(back)focalpointofthelens(f
2
).Notethatmagneticlensesarehighly
inefficientinthatonlyaminorportionofthetotalfieldstrengthisactuallyeffectiveinfocusingtheelectron.
4)Magneticlensfocallength
Inamagneticelectronlensthefocallengthisdeterminedbythefieldstrengthinthelensgapandbythespeedoftheelectrons(determinedby
theacceleratingvoltage).
Formagneticlenses,focusingisachievedbyvaryingthecurrentwhichpassesthroughtheelectromagnet.Thisinturnchangesthestrengthof
themagneticfieldandtherebyaltersthefocallengthofthelensandisequivalenttoacombinedchangeinboththe"refractiveindex"and
"curvatureofsurface".Forabeamofmoreenergeticelectrons,thelenscurrenthastobeincreasedinordertokeepthefocallengthconstant.
FocallengthandcurrentareNOTlinearlyrelated:strengthincreasesinasigmoidfashion(Fig.I.45)ascurrentincreasesuntilapointisreached
wherethelensissaturatedandnofurtherincreaseinlensstrengthcanbeachieved.
Sincethefocallengthofthelensisdirectlyproportionaltotheacceleratingvoltage,avariationinthevelocityoftheelectronsintheimaging
beamaffectsimagequalitybyeliminatingperfectfocus(chromaticaberration).
5)Magneticlensdesign:(Figs.I.46,I.47).
Condenserlensesusuallyhavearelativelylargeboreandspacingwhichresultsinalongfieldandlongfocallength.
Typicalconstructionoftheobjectivelensproducesastrongfieldofshortaxialextent(i.e.shortfocallengthbetween(1.53mm)necessaryfor
formationofimagesathighmagnification.Thespecimenisplacedwithinthemagneticfieldoftheobjectivelens.Thus,anyfieldintroducedby
contaminantsinthespecimencandistortthefieldofthelens.Notethatthisalsomeansthatpartofthelensfield("prefield")isonthefrontside
oftheobjectandaffectstheelectronbeambeforeitpassesthroughtheobject.
Mostofatypicalmagneticlensliesoutsidethevacuumofthemicroscope.Onlythoseregionsthroughwhichtheelectronbeampassesareinhigh
vacuum.Magneticlensesmustbewatercooledtodissipatethelargeamountsofheatproducedbythecurrentsintheelectromagnetcoils.
DATE NAME EVENT
1897 J.J.Thompson Discoverstheelectron
1924 LouisdeBroglie Identifiesawavelengthtomovingelectrons
l =h/mv
where
l =wavelength
h=Planck'sconstant
m=mass
v=velocity
(Foranelectronat60kVl=0.005nm)
1926 H.Busch Magneticorelectricfieldsactaslensesforelectrons
1929 E.Ruska Ph.Dthesisonmagneticlenses
1931 Knoll&Ruska Firstelectronmicroscopebuilt
1931 Davisson&Calbrick Propertiesofelectrostaticlenses
1934 Driest&Muller SurpassresolutionoftheLM
1938 vonBorries&Ruska FirstpracticalEM(Siemens)10nmresolution
1940 RCA CommercialEMwith2.4nmresolution
1945 1.0nmresolution
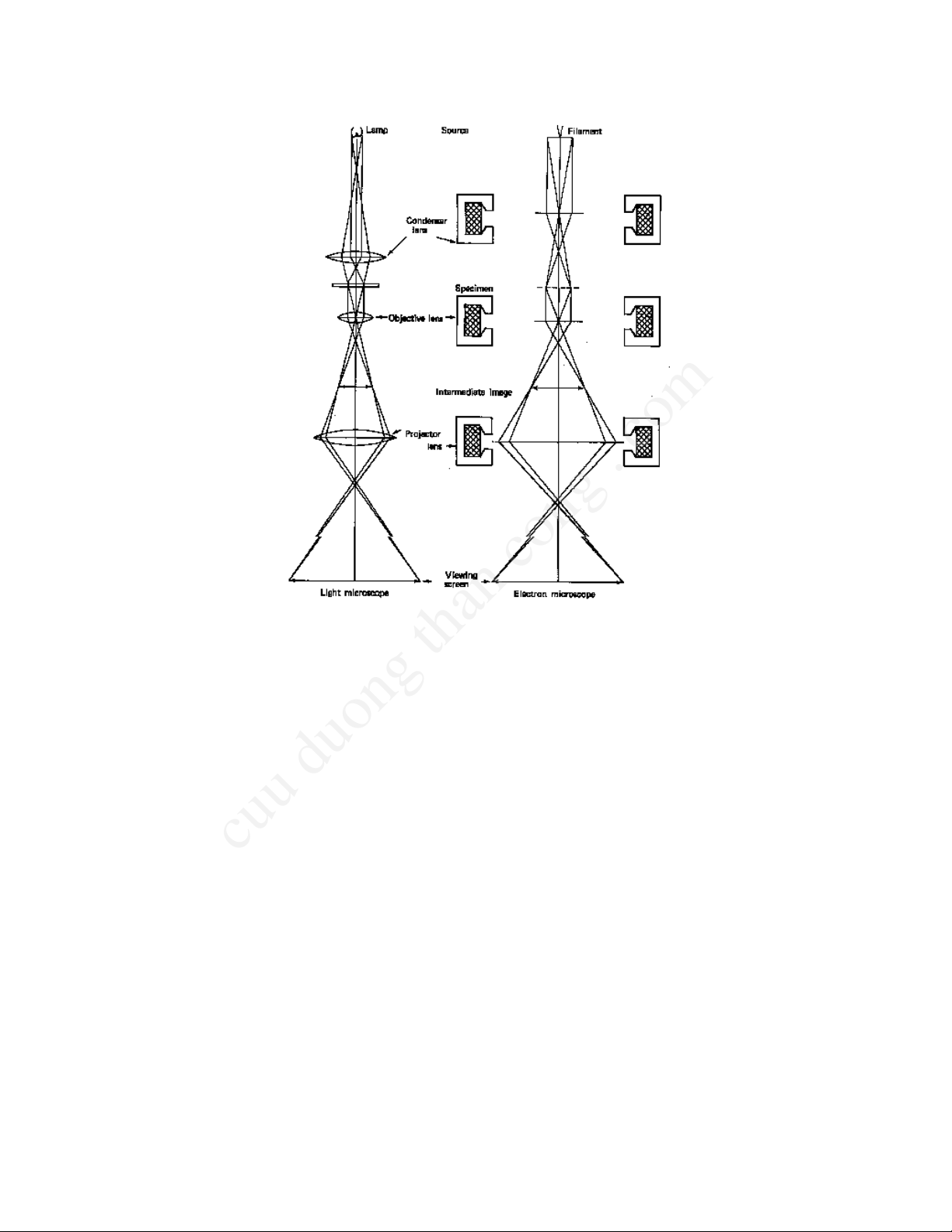
Fig.I.1Comparisonoflightandelectronmicroscopes.Ineach
instrument,illuminationfromthesource(lamp,filamentinthe
electrongun)isfocusedbythecondenserlensontothespecimen.
Afirstmagnifiedimageisformedbytheobjectivelens.Thisimage
isfurthermagnifiedbytheprojectorlensontoagroundglass
screen(light)orfluorescentscreen(electrons).(FromAgar,p.8)
Fig.I.2CrosssectionalviewofthePhilipsEM300.(FromAgar,p.40)
Toviewtheanimatedmicroscope,clickhere.
Note:QuickTimePlugInrequired
(Thiscanbedownloadedathttp://apple.com/quicktime/download)
Fig.I.3Sectionthroughacomplex
doublecondenser6lensPhilips
EM200electronmicroscope.(From
Meek,p.99)
Fig.I.4Thestatisticalnatureofdiffraction
patterns.(FromHall,p.13)
"Theprecisenatureof'electronwaves'or'matterwaves'isverydifficulttounderstandordescribeinmaterialterms.Electronwavesarenot
electromagneticradiationofthekindtowhichlight,Xraysandradiowavesbelong.Theyconstituteasortofquantumor'packet'ofradiationwhich
accompanieseachindividualelectron,followingitspathandnotradiatingoutwardsfromit."(Meek,1976,pp.4849).
V l (nm)
v(
•
10
10
cm/sec)
v/c
10,000 0.0123 0.593 0.198
50,000 0.0055 1.326 0.442
100,000 0.0039 1.875 0.625
1,000,000 0.0012 5.930 1.977!
V l (nm)
v(
•
10
10
cm/sec)
v/c
10,000 0.0123 0.593 0.195
50,000 0.0055 1.326 0.414
100,000 0.0039 1.875 0.548
1,000,000 0.0012 5.930 0.941
FigI.5Aperfectpointsourcecannotbe
imagedbyalensasaperfectpointimagedue
tothepresenceoftheapertureAB(which
maybetheedgeofthelens).Diffractionat
thisaperturegivesrisetoaseriesoffringes,
whichsurroundtheimageformedofthepoint
source.Thepatternproducediscalledan'Airy'
disk.(FromMeek1sted.,p.35)
Fig.I.6Wheneverawavefrontstrikesa
barrier,itcanbendaroundthecorner'by
givingrisetoasecondarywavefrontatthe
edge,sinceeachpointonthewavefrontcan
giverisetoanewsourceofwaves.This
phenomenoniscalled'diffraction'.(FromMeek
1sted.,p.22)
Fig.I.7Diffractionpattern(right)formedbyanirregularlyshapedaperture
(left).(FromYoung,p.95)
Fig.I.8(a)
Photographof
theedgeofa
razorblade
illuminatedby
monochromatic
(blue)light
rendered
coherentby
passing
througha
narrowslit.(b)
Microdensitometer
tracingofthe
negativefrom
whichthe
photograph
wasmade.
FourFresnel
fringescanbe
distinguished.
(FromMeek1st
ed.,p.27)
(a)
(b)
(a) (c)
(b)
Fig.I.9(a)Fresnelfringesformed
byelectrons.Thesefringesare
formedoutsidetheedgeofahole
(white)inacarbonfilm(black).(b)
Amicrodensitometertracingofthe
fringesystem;thepatternis
identicalwiththeFresnelfringe
systemformedbyvisiblelight(see
Fig.I.8).(c)Anunderfocusedimage
ofaholeinafilm,showinga
completesystemofabout40
Fresnelfringesinsidethehole.
(FromMeek1sted.,pp.2930)
Fig.I.10Diffractionimagesoftwo
easilyresolvedpoints.(From
Slayter,p.243)
Fig.I.11Imagesoftwo
incoherentlyilluminatedpointsat
thelimitofresolution.(a)individual
intensities;(b)summedintensities.
(FromSlayter,p.244)
Fig.I.12Examplesofwhatoccurswhentwo
wavesofthesamewavelengthandequal
amplitudeadd.Ineachexample,thetwo
separatewavesareshownontheleftand
theirsumorresultantwaveontheright.The
differentexamplesarecharacterizedbyvarying
phasedifferences.Thephaseofawave
(usuallyexpressedasafractionofthe
wavelengthorindegrees)isthepositionofa
crestrelativetosomearbitrarypoint.Although
thephaseofagivenwavevarieswithtimeas
thewavetravels,thedifferenceinphaseofthe
twowavesofthesamewavelengthwiththe
samevelocity,isindependentoftime.Such
wavescaninterferewithoneanother.The
resultantwavehasthesamewavelength,l .
(a)Phasedifferencezero.Thewavestotally
reinforceandaresaidtobe"inphase"orto
showconstructiveinterference.
(b)Phasedifferencel /4.Partialreinforcement,
givingawaveofamplitude1.4(intensity2.0).
(c)Phasedifferencel /2.Thewavesare"outof
phase"andthereistotaldestructive
interferencetogivenoresultantwaveora
wavewithamplitude0(intensity0).(From
GluskerandTrueblood,p.19)
Fig.I.13Photographofan
interferencepatterninwater
wavesformedbythe
superpositionofwavesfromtwo
sourcesoscillatinginphasewith
thesamefrequency.(FromYoung,
p.22)
Fig.I.14Theangularapertureofthe
eyeisrelativelysmall.(FromMeek,
1sted.,p.13)
Fig.I.15Increasingtheangular
apertureoftheeyewithalens.The
lensallowstheobjecttobeheld
closertotheeye,whichisthereby
enabledtogathermoreinformation.
(FromMeek1sted.,p.14)
Fig.I.16Theinteractionofwaves
withanobstacle.Theboatridesthe
longwavelengthoceanwave,but
reflectsthesmallwavelength
surfaceripple.Anobserverwho
wishestodetectthepresenceof
theboatcandosoonlyby
observingwaveswhichhave
wavelengthssmallerthan,or
comparableto,thelengthofthe
boat.(FromSherwood,p.19)
Maximummagnification=
resolvingpoweroftheeye
resolvingpowerofthemicroscope
(a)
Fig.I.17(a)TwoAiry
disksrepresenting
twoimagepoints
shownatincreasing
separationfromleft
toright.Inthe
pictureatthe
extremerightthe
twodiskscanbe
distinguishedas
separatedisks.
(b)Theintensity
distributionatanAiry
disk.R,halfwidthof
thecentralmaximum
representedbya
bellshapedcurve.
(c)TheRayleigh
criteriaforresolution.
(FromSjostrand,
p.115)
i=r
Fig.I.18Reflection.(FromSlayter,
p.4)
Fig.I.19Refraction.(FromSlayter,
p.6)
Fig.I.20Principalraydiagramsshowing
imageformationbyaconvexlens.
(a)Whentheobjectdistanceisgreater
thanthefocallength,areal,inverted
imageisformed.
(b)Whentheobjectdistanceisless
thanthefocallength,avirtual,erect
imageisformed;itspositionis
obtainedbyprojectingtheprincipal
raysbackward.Theraysappearto
comefrompointQ.(FromYoung,
p.127)
Fig.I.21Definitionof
principalfocus,F,inimage
spaceofalens.(From
Sjostrand,p.20)
Fig.I.22Focusingeffectoflenson
raysoriginatingfrompointson
principalaxislocatedatdifferent
distancesfromthelens.(From
Sjostrand,p.21)
Fig.I.23Definitionofprincipal
focusinobjectspaceF1ofa
lens.(FromSjostrand,p.21)
Fig.I.24VirtualimageQof
objectpointlocatedbetween
principalfocusinobjectspace
andthelens.(FromSjostrand,
p.21)
Fig.I.25Constructionoftheimage
ofanobjectbymeansofray
tracing.(FromSjostrand,p.22)
Fig.I.26Magnifyingeffectof
apositivelens.(From
Sjostrand,p.22)
Fig.I.27Virtualmagnified
imageofobjectlocated
betweenprincipalfocusin
objectspaceandthelens.
(FromSjostrand,p.22)
Fig.I.28Amagnifyingglassformsan
enlarged,erectvirtualimage.The
angularsizeofthisimageis
approximately4"/15"or4/15.The
angularsizeoftheobjectatthe
closestdistanceforcomfortable
viewingis1"/10"or1/10.The
magnificationinthissituationis(4/15)/
(1/10),or22/3.(FromYoung,p.130)
Fig.I.29Theangularapertureofa
lens.Theangle2a isthe
acceptanceangleofthelens,and
thelargeritcanbemade,themore
informationcanthelenstransmit.A
largelensofhighaperturecan
thereforetellusmoreaboutan
objectthanasmalllensoflow
power.(FromMeek1sted.,p.12)
Fig.I.30Raydiagramforhighmagnification
modeofoperation.Notethateachlens
formsarealimage,withimageinversion.
I0istheimageformedbytheobjective
lensO,I1isformedbythefirstprojector
lensP1andI2bythesecondprojectorP2,
onthescreen.(FromAgar,p.30)
Fig.I.31Left:raydiagramofthe3realimagemediumandhighmagnificationimagingsystemofa3lens
microscope.Center:2realimageverylowor'scan'magnificationrangeofa3lensmicroscope.Right:2real
imagelowmagnificationsystemofa3lensmicroscope.(FromMeek1sted.,pp.118,120121)
Fig.I.32Raydiagramforacompleteelectron
microscope.FilamentF,condenser1lensC1,
condenser2lensC2,condenserapertureCA,
specimenS,objectivelensO,objectiveaperture
OA(inbackfocalplane).1stintermediateimage
andselectorapertureSA.IntermediatelensP1,
secondintermediateimageI2,projectorlensP2
andfinalimageonthefluorescentscreenFC.
(FromAgar,p.35)
a)f=2.0
x
o
=5.0
e)f=4.0
x
o
=3.0
b)f=10.5
x
o
=21.0
f)f=13.3
x
o
=13.3
c)f=3.5
x
o
=3.0
g)f=3.142
x
o
=0.0
d)f=5.0
x
o
=2.5
a)D=8.0
L1:f=2.0
x
o
=4.0
L2:f=3.0
b)D=8.0
L1:f=2.0
x
o
=6.0
L2:f=3.0
c)D=4.0
L1:f=2.0
x
o
=3.0
L2:f=2.0
FigI.33Accelerationofelectronin
electricfield.(FromSjostrand,p.26)
Fig.I.34Linesofforceatapositively
chargedsphericalbody.(FromSjostrand,
p.32)
Fig.I.35Linesofforceandequipotential
surfaces(stippledlines)associatedwith
twoequalchargesofoppositesign.
(FromSjostrand,p.32)
Fig.I.36Equipotentialsurfacesattwoparallel
platesofoppositechargeswiththepathofan
electronindicatedwithinthehomogeneous
partofthefield.(FromSjostrand,p.33)
Fig.I.37Refractionofelectronatan
equipotentialsurface.(FromSjostrand,p.33)
Fig.I.38.Negativelensactionof
electrostaticfieldatanaperturewhen
V2V1>V3V2.(FromSjostrand,
p.34)
Fig.I.39.Positivelensactionatan
aperturewhenV2V1<V3V2.
(FromSjostrand,p.34)
Fig.I.40Magneticfieldinducedbycurrent
passingthroughaconductor.(From
Sjostrand,p.35)
Fig.I.41Magneticfieldinducedbycurrent
passingthroughasolenoid.(From
Sjostrand,p.37)
Fig.I.42Solenoidwithironcore.(From
Sjostrand,p.40)
Fig.I.43a.Dependenceofpermeabilityonfluxdensity,B.
b.RelationshipbetweenfluxdensityBandfieldstrength.
(FromSjostrand,p.38).
Fig.I.44Magnetization.(FromSlayter,
p.361)
Fig.I.45Curves
showinghowthe
magnetizationof
softiron(lens
strength)is
relatedtothe
magnetizing
force(lens
current).An
unmagnetized
lensstartsfrom
thepointOand
followsthepath
OAaslens
current
increases.Atthe
pointA,further
increaseinlens
currentproduces
nofurther
increaseinlens
strength;thelensissaidtobe'saturated'.Whenlenscurrent
isreduced,thepathOAisnotretraced;adifferentpathABis
followed.Thisdisplacementiscalled'hysteresis'.Atzero
current(pointB),someresiduallensstrengthremains;thisis
called'remanence'.Tobringthelensbacktozerostrength,a
reversecurrentOCmustbeapplied.Lensstrengththen
increaseswithincreasingreversecurrent,followingthepath
CD.Thepolarityofthelenschanges,butthisdoesnotaffect
itsfocusingpower;onlythespiralelectronpathisreversed.
Becauseofhysteresis,itisnotpossibletocalibratealens
currentmeteraccuratelyintermsoflensstrengthor
magnification.
Fig.I.46Evolutionofmagneticelectron
lenses.(A)Shortsolenoidusedasa
magneticlens.(B)Softironcasing
enclosingoutersurfaceofthesolenoid,
thusconcentratingthefield.(C)Soft
ironencasingthesolenoidexceptata
narrowannulargaptherebyreducing
themagneticfieldtoaveryshortregion
alongthelensaxis.(D)Modern
objectivelensconsistingofasoftiron
encasedsolenoidandsoftironpole
piecessoastohaveanenormously
concentratedfieldatthelevelofthe
annulargap.(FromWischnizter2nded.,
p.33)
Fig.I.47(a)Amagneticlensconsisting
ofatightlywoundcoilandasoftiron
shroudsurroundingthecoilexceptfor
asmallgap.Thefieldisconcentratedin
thatgap.(b)Shortfocallength
electromagneticlenswithpolepieces.
(FromSjostrand,p.50)
Fig.I.48Fieldstrengthdistribution
curves.ThecurvesADcorrespondto
therespectivelensesillustratedinFig.
I.46.Eachrepresentsthefieldstrength
alongthelongaxisofthelens.The
changesintheshapeofthecurves
representtheshorteningor
concentrationofthefieldovera
shorteraxialdistance.Hz=
longitudinalmagneticfield.Z=
distancealongtheaxisofsymmetry.
(FromWischnizter2nded.,p.33)
Fig.I.49TheforceFactingon
astraightconductorina
homogeneousmagneticfield
offluxdensityBwhencurrent
Iispassedthroughthe
conductor.(FromSjostrand,
p.43)
Fig.I.50Pathofanelectronina
magneticfield.(A)Inalarge,uniform
magneticfield.(B)Inasmall,uniform
magneticfield.(FromWischnitzer2nd
ed.,p.25)
Fig.I.51Lefthandthumbrule.
(FromSjostrand,p.43)
Fig.I.52Thompson'sexperiment.A
streamofelectronsoriginatingfroma
sourceandpassing,invacuo,through
amagneticfieldproducedbyapairof
magnetswillbedeflected.The
directionofdeflectiondemonstrates
thatelectronsarenegativelycharged
particlesofmatter.(FromWischnitzer
2nded.,p.25)
Fig.I.53Actionofasolenoidonan
electronbeam.Anelectriccurrent
passingthroughthecoilproducesan
axialmagneticfield.Thisisthe
refractingmediumfortheelectrons.An
electronstartingatapointontheaxisA
andatanangletoitfollowsaspiral
path,returningtotheaxisatthepoint
B.Theactionisbasicallysimilartothat
oftheconverginglightlensshownin
Fig.I.20.(FromMeek1sted.,p.8)
Fig.I.54Actionofthemagnetic
lens.(a)Inperspective.(b)
Electrontrajectoryin
projection,alongdirectionof
propagation.(c)Electron
trajectoryinprojection,side
view.(FromSlayter,p.358)
Fig.I.55Componentsofthe
vectorHneartheaxisoffields
withaxialsymmetry.His
representedbytwo
components,Hz,the
componentinthez(axial)
direction,andHr,the
compnentinther(radial)
direction.(FromHall,p.85)
Fig.I.56Theycomponentof
themagneticfieldina
magneticlensisoriented
perpendiculartothedirection
ofanelectronenteringthe
lensalongapathparallelto
thelensaxis.Thisy
componentwillaffectthe
electron,deflectingitinthex
directionasindicatedbythe
arrowmarkedvx.(From
Sjostrand,p.48)
Fig.I.57Thezcomponentofthemagneticfield
andthexvelocitycomponentoftheelectron
inamagneticlensinteract,deflectingthe
electronintheydirectiontowardthelens
axis.(FromSjostrand,p.49)
CuuDuongThanCong.com https://fb.com/tailieudientucntt
cuu duong than cong . com
I.THEMICROSCOPE
I.A.PRINCIPLESOFTHETRANSMISSIONELECTRONMICROSCOPE(TEM)
I.A.1.OriginoftheTransmissionElectronMicroscope
I.A.2.ComparisonofLight(LM)andElectronMicroscopes(Fig.I.1)
a.Similarities(Arrangementandfunctionofcomponentsaresimilar)
1)Illuminationsystem:producesrequiredradiationanddirectsitontothespecimen.Consistsofasource,whichemitstheradiation,anda
condenserlens,whichfocusestheilluminatingbeam(allowingvariationsofintensitytobemade)onthespecimen.
2)Specimenstage:situatedbetweentheilluminationandimagingsystems.
3)Imagingsystem:Lenseswhichtogetherproducethefinalmagnifiedimageofthespecimen.Consistsofi)anobjectivelenswhichfocusesthe
beamafteritpassesthroughthespecimenandformsanintermediateimageofthespecimenandii)theprojectorlens(es)whichmagnifiesa
portionoftheintermediateimagetoformthefinalimage.
4)Imagerecordingsystem:Convertstheradiationintoapermanentimage(typicallyonaphotographicemulsion)thatcanbeviewed.
b.Differences
1)Opticallensesaregenerallymadeofglasswithfixedfocallengthswhereasmagneticlensesareconstructedwithferromagneticmaterialsand
windingsofcopperwireproducingafocallengthwhichcanbechangedbyvaryingthecurrentthroughthecoil.
2)MagnificationintheLMisgenerallychangedbyswitchingbetweendifferentpowerobjectivelensesmountedonarotatingturretabovethe
specimen.Itcanalsobechangedifoculars(eyepieces)ofdifferentpowerareused.IntheTEMthemagnification(focallength)oftheobjective
remainsfixedwhilethefocallengthoftheprojectorlensischangedtovarymagnification.
3)TheLMhasasmalldepthoffield,thusdifferentfocallevelscanbeseeninthespecimen.Thelarge(relative)depthoffieldintheTEMmeans
thattheentire(thin)specimenisinfocussimultaneously.
4)Mechanismsofimageformationvary(phaseandamplitudecontrast).
5)TEMsaregenerallyconstructedwiththeradiationsourceatthetopoftheinstrument:thesourceisgenerallysituatedatthebottomofLMs.
6)TEMisoperatedathighvacuum(sincethemeanfreepathofelectronsinairisverysmall)somostspecimens(biological)mustbedehydrated
(i.e.dead!!).
7)TEMspecimens(biological)arerapidlydamagedbytheelectronbeam.
8)TEMscanachievehighermagnificationandbetterresolutionthanLMs.
9)Pricetag!!!(100xmorethanLM)
I.A.3.Photons/Electrons
a.Dualconceptofwaveandparticle(Fig.I.4)
Lighthaspropertiesbothofaparticleandawave.Thisdualnatureisrequiredtosatisfactorilyexplaintheresultsofvariousphysicalexperiments.
Thediffractionoflight(bendingaroundcorners)illustratesthewavenature.TheWAVETHEORYisbasedonthestatisticalnatureofeventsand
haslittlemeaningwithrespecttothebehaviorofsingleparticles.ThewavetheorywasdevelopedandexpoundedbyHuygens(16291695)and
Hooke(16381703).TheCORPUSCULARTHEORYwasproposedbyNewton(16421727)andbecamethemoreacceptedtheoryevenafter
demonstrationofdiffractionbyYoung(17731829)andinterferencebyFresnel(17881827).Atabout1850,thewavetheorycamebackinto
favoruntilabout1900whenmoreevidenceforthecorpusculartheorywasdiscovered.
QUANTUMTHEORY(PlanckandEinstein)providesthebasisforexplainingthephenomenaofINTERFERENCE,DIFFRACTIONandthe
PHOTOELECTRICeffect(lightfallingoncertainmetalscausethemtoemitelectrons)andthusformsacommonbasisforexplainingthenatureof
actionoflight.Thetransferofenergybetweenlightandmatteroccursonlyindiscretequantitiesproportionaltothefrequencyofthe
lightwave.
E=hJ
where
E=energyofphoton(joules)
h=Planck'sconstant(6.624
•
10
34
joulesec)
J=frequency(cycles/sec)
b.Electronvelocityandwavelength
Therelationbetweenthewavelength(l )ofaparticleofmass,m,movingatavelocity,v,isgivenbytheDeBrogliewaveequation:
(1)
Anelectronofchargee(1.6
•
10
19
coulomb),andmassm(9.11
•
10
28
gm),whenpassingthroughapotentialdifferenceofVvolts(expressedin
joules/coulomb),hasakineticenergy:
(2)
Solvingforvelocity:
(3)
substitutingintotheDeBroglieequation(1):
(4)
Since1joule=10
7
dyne
•
cm=10
7
cm
2
•
gm/sec
2
(5)
Thus,forexample,ifV=60,000volts,l =0.005nm.
Fromequation(3)theelectronvelocitycanbecalculatedifVisknown:
(6)
Thefollowingtableillustratesthat,athighvoltage,electronvelocityiscomparabletothespeedoflightinavacuum(c=3
•
10
10
cm/sec).
Theequationbreaksdownwhenthevelocityoftheelectronapproachesthespeedoflightbecausearelativisticcorrectionmustbemadeforthe
valueofthemasswhere:
(7)
Therelationbetweenl andVismorecorrectlygivenby:(seeHall(1966)pp.3334)
(8)
Thefollowingtableisobtainedwhenrelativityeffectsareincluded:
c.Interference/diffraction/coherence
Anideallenssystemobtainsanexactimageoftheobject(eachpointfaithfullyreproduced).Thephenomenaofdiffractionmakesthis
unattainable(Figs.I.5,I.6).
Diffractionphenomenainvolvesthebendingofthepathofradiationpassingclosetoanobstacle(Fig.I.6).Thisresultsinaspreadingofthe
radiationintotheregionbehindtheobstructionthatthewavespassed.Thediffractionatedgescontributestothecontrastatwhichanedgecan
beobserved.Diffractionalsolimitstheresolvingpowerofthemicroscopesincetheimagepointproducedbyalensisadiffractionimageofthe
openingofthelensortheaperturerestrictingtheeffectiveopeningofthelens(Fig.I.5).
Ifthelightsourceandtheplaneatwhichthediffractionpatternisobservedareatfinitedistancesfromtheedge,thephenomenoniscalled
Fresneldiffraction.Thepatternisdescribedasduetointerferencebetweenthenondiffractedlightandawaveoflightdiffractedattheedge.
Theresultingsuperpositiongivesrisetoaseriesofdiffractionfringesorientedparalleltotheedgeandrepresentingperiodicallyvaryingbrightness,
maximaandminima.(Figs.I.7,1.8,I.9).
Coherence:Aprerequisiteforinterferenceisasuperpositionofwavesystemswhosephasedifferenceremainsconstantintime.Twobeams
arecoherentif,whencombined,theyproduceaninterferencepattern.Thebeamsareincoherentwhentheyareincapableofproducingan
interferencepattern.Twobeamsoflightfromselfluminoussourcesareincoherent.Iflightfromthetwosourcesfallsonascreen,theresultant
intensityissimplythesumofthetwointensitieswhichwouldoccurfromeachsourceseparately(Figs.I.10,I.11).Inpracticeanemittingsource
hasfiniteextentandeachpointofthesourcecanbeconsideredtogeneratelight.EachsourcegivesrisetoasystemofFresnelfringesatthe
edge.Thesuperpositionofthesefringesystemsisfairlygoodforthefirstmaximaandminimabutfartherawayfromtheedgeshadowtheoverlap
ofthefringepatternsbecomessufficientlyrandomtomakethefringesdisappear.Thenatureofwaves,phase,amplitude,andinterferenceare
illustratedinFigs.I.12andI.13.
d.Resolution
1)Definitions:
RESOLUTION:abilitytodistinguishcloselyspacedpointsasseparatepoints.
RESOLUTIONLIMIT:smallestseparationofpointswhichcanberecognizedasdistinct.
RESOLVINGPOWER:resolutionachievedbyaparticularinstrumentunderoptimumviewingconditions.
2)Distinctionbetweenresolutionandresolvingpower:
Notethedistinctionbetweenresolutionandresolvingpower.Resolvingpowerisapropertyoftheinstrumentandisaquantitythatmaybe
estimatedontheoreticalgrounds.Resolutionisequaltoorpoorerthantheresolvingpowerandisthequantityobservedunderanygivenset
ofexperimentalconditions.IntheTEM,especiallywithbiologicalsamples,theresolutionachievedmaybeconsiderablyinferiortothetheoretical
resolvingpoweroftheinstrument.
Microscopyisthescienceofseeingtheverysmall.Underidealconditions,theeyeresolvesabout1minuteofarc(=1/60degree=2.9x10
4
radian;recallthereare2p radiansin360°)andsinceitcanfocusdowntoabout250mm,thesmallestobjectwecanresolveisabout0.07mm
(70mm)(Fig.I.14).Thislimitisrelatedtothesizeofthereceptorsintheretinaoftheeye.Thefunctionofamicroscopeistomagnifytheimage
fallingontheretina(Fig.I.15).Theadvantageoflightandelectronmicroscopesisthattheyeffectivelygettheobjectclosertotheeyesoa
magnifiedimageisobtainedandmoredetailcanbediscerned.
TENNISBALLANALOGY:Eyecanresolve3cmat100meters,thusatennisballisclearlyvisible.Butifthetennisballisheldupagainstawhite
background,thevisibilitydecreases(becauseofthedecreaseincontrast).
3)Abbecriteriaofresolution:
Thefundamentalnatureoflightposeslimitsonthedetailthatcanberesolved(Fig.I.16).Abbe(1893)showedthatthesmallestresolvable
distanceisabout1/2thewavelengthoflightused.Thus,1/2thewavelengthoftheradiationusedistheultimateresolvingpowerofany
instrument.Thislimitstheusablemagnificationofopticalmicroscopesto<1000X.Atfirstitwasthoughtthatxraymicroscopeswouldbeuseful
buttherefractiveindexofsubstancesforxraysisnearly=1,thusrefractinglensescannotbemadeforxrays,andconsequently,xrayscannot
beeasilyfocusedtoformimages.
4)Magnificationlimits:
Themaximummagnificationofaninstrumentislimitedaccordingtothefollowingrelationship:
Thus,fortheLM,witharesolvingpowerofapproximately0.25µm,themaximum(useful)magnificationisabout250µm/0.25µm=1000X.Thevalue
usedfortheresolvingpoweroftheeyeinthisexample(250µm)representsamorerealisticviewingcondition.Anymagnificationabovethevalue
givenbytheaboveformularepresentsemptymagnification,sincesuchmagnificationleadstonomoreusefulinformationbutratheramagnified
blur.
AccordingtotheAbbecriteria,at60,000volts,theTEMshouldhavearesolvingpowerofabout0.0025nm.Thisshouldallowamaximumuseful
magnificationofabout100milliontimes!!!Inpractice,themaximumusefulmagnificationoftheTEMoperatedat60kVislimitedtomuchlessthan
1,000,000X.Thus,althoughtheLMnearlyobeystheAbbecriteria,theTEMfallsshortbyaconsiderableamount.Themainlimitingfactorinthe
TEM,withrespecttoachievingthetheoreticalresolvingpoweroftheinstrument,concernsthenatureoftheimaginglensesandtheprocessof
imageformation.
5)Rayleighcriteria(practicalbutarbitrary):(Fig.I.17).
Itistheabilityofmicroscopestomakeobjectpointswhichareclosetogetherappearintheimageasseparatepoints.Anideallenstakeseach
objectpointandrepresentsitexactlyasapointintheimage.Areallenstakeseachobjectpointandspreadsitoutintoacirculardisk(Airy
disk)intheimageplanewhosediameterdependsontheangularapertureofthelens.
Theshortestdistancebetween2disksatwhichthetwodisksappearpartiallyseparatedcorrespondstoabout1/2thewidthofthedisks.The
distance,d,inobjectspaceisgivenby:
d=0.61l /n
•
sina
where
l =wavelenghtoftheradiation
n=refractiveindexofthemedia
a=semiangularapertureofthelens
NOTE:n
•
sina=thenumericalaperture(N.A.)ofthelens.
Thus,tomaximizeresolvingpower,l mustbedecreased,nincreased,oraincreased.Recallthatweareconcernedatthemomentwithan
aberrationfreeopticalsystem.Thevaluefortheconstant(0.61)iscontroversialbecauseitdependsonthecoherenceoftheradiationanda
criteriaofvisibility.
FortheLM,usingoilimmersionoptics(n=1.5),sina=0.87,andvioletlight(l =400nm),d=0.2µm.Theonlywaytoimprovetheresolutionisto
uselightofshorterwavelengthsinceN.A.cannotbeincreasedbeyond~1.5.FortheTEM,n=1(vacuum),sina=10
2
andl =0.005nmfor60kV
electrons,thusd=0.3nm.
I.A.4.Optics(LensTheory)
a.Basiclawsofclassicalgeometricaloptics
1)Rectilinearpropagationoflightwhenn(refractiveindex)isconstant.
2)Lawofreflection:
3)Lawofrefraction(Snell'sLaw):
4)Independenceofrays.Theassumptionismadethatlightraystravelindependentlythroughspace.
Theselawsholdforelectrons,except#4,ifthecurrentdensityistoohighwhennegativechargedelectronscaninterfere.
b.Classicalvs.electronoptics
1)Classicaloptics:Therefractiveindexchangesabruptlyatasurfaceandisconstantbetweenthesurfaces.Therefractionoflightatsurfaces
separatingmediaofdifferentrefractiveindicesmakesitpossibletoconstructimaginglenses.Glasssurfacescanbeshaped.
2)Electronoptics:Here,changesintherefractiveindexaregradualsoraysarecontinuouscurvesratherthanbrokenstraightlines.Refraction
ofelectronsmustbeaccomplishedbyfieldsinspacearoundchargedelectrodesorsolenoids,andthesefieldscanassumeonlycertaindistributions
consistentwithfieldtheory.
c.Geometricalandphysicaloptics
Thefundamentalprinciplesofopticsgovernthedesignandoperationofboththelightandelectronmicroscopes.Thebasicopticalprinciples
involvingtheuseofrefractileelementsorlensesinordertoformmagnifiedimagesareidenticalinboththeLMandTEM.TheTEMdiffersfromthe
LMonlyintheradiationitusesandinthewayinwhichtheradiationisbentorrefracted.
Geometricalopticsdealswiththestudyofthepathsfollowedby'rays'oflightorelectronsthroughlensesandapertures,andthegeometrical
constructionsusedtofindtherelativepositionsandsizesofobjectsandtheirimages.Arayoflightorelectronsisdefinedasaninfinitelythin
pencilorbeam.Physicalopticsshowsthatthisanabstractionandcannotphysicallyexistbecauseof'diffraction'whichdealswiththewave
natureoflightandelectrons.Allresultsobtainedingeometricalopticscanbederivedfromtheprinciplesofphysicaloptics,alongwithother
phenomenasuchasinterferenceanddiffractionwhicharenotexplicableinsimplegeometricalterms.
d.Idealversesreallenses:
Lensesareusedtobendraysoflightorelectronssotheyaredeflectedinapredictablewayfromtheiroriginalpaths.Thepropertiesofanideal
lens,possessinganaxisofrotationalsymmetryare:
1)Eachrayofthebundleofrayswhichpassesfromanobjectpointwillberefractedbytheideallenstomeetinoneimagepoint.
2)Raysoriginatingfrompointswhichlieonaplaneperpendiculartotheaxis,mustbeimagedinaplanewhichisalsoperpendiculartotheaxis.
3)Theimageappearsliketheobjectirrespectiveofthemagnification,sotherelativelineardimensionsoftheobjectarepreservedintheimage.
Inpractice,theimagingbyanyreallensdoesnotcorrespondtothatoftheideallensowingtothefactthatanobjectpointisrepresentedbya
diffractionimage(Airydisc)ofthelensopeningortheapertureusedforrestrictingtheeffectiveopeningofthelens.Thisisaresultofthewave
likepropertiesoflight.Lensaberrationsalsocontributetomoreorlesspronounceddeviationsfromthepropertiesoftheideallens.
Thesinglerefractingsurfaceofsphericalcurvatureisthefundamentalunitoffocusingactionbyglasslenses.Sphericalrefractingsurfacesactas
lensesforparaxialrayswhicharethoseraysthatpassclosetotheprincipalaxisofthelens.RayswithlargeangleswillNOTobeyideallens
action.
Afundamentaldifferencebetweenlightandmagneticlensesisthattheelectronbeamdoesnotchangeinforwardvelocityasitpassesthrough
themagneticfield(lightraysslowdownwhenpassingintoamediumofhigherrefractiveindex).Refractioniscontinuouswithelectronswhenthey
areinthemagneticfield:lightisrefractedonlyattheinterfacebetweenmediaofdifferingrefractiveindex.Theelectronsalsofollowspiral
trajectoriesthroughthemagneticfield(seealsoSec.I.A.5.c(Magneticfieldsandmagneticlenses)
e.Raydiagrams:(Figs.I.20I.28)
Themethodofconstructionofraydiagramsisbasedonthreesimpleprinciples:
1)Allraysenteringthelensparalleltotheaxisarebroughttoacommonpointontheaxis,thefocalpoint.
2)Allrayspassingthroughthegeometricalcenterofthelensareundeviatedandpassstraighton,nomatterfromwhichdirectiontheycome.
3)Principleofreversibility:ifthedirectionofarayisreversedinanysystemtherayexactlyretracesitspaththroughthesystem.Thisapplies
onlytothelocationoflightpathsandnottotheintensityofthelight.
Theaboveprinciplesarebasedontheassumptionsthatwearedealingwithathinlensandconcernedwiththepathsofparaxialrays.The
standardconventionistodrawdiagramswithraysthattravelfromlefttoright.Theobjectistotheleft(infront)ofthelensandtheimageisto
theright(behind)ofthelens.
f.Definitions:
Realimage:oneatwhichlightraysphysicallyreunite,sothataphotographicplateplacedatthepositionofarealimageisexposed.
VirtualImage:onefromwhichlightraysappeartodiverge;raysarenotinfactconcentratedatthepositionofavirtualimage,sothata
photographicplateplacedatthepositionoftheimageisnotexposed(byfocusedrays).Placinganopticalsystemsuchastheeyebehindthe
lens,willenablethedivergentraystobefocusedtoformarealimage.TheintermediatelensofanTEMissometimesusedthiswayinorderto
reducethefinalsizeoftherealimageformedbytheprojectorlens(es).
Converging(positive)lens:bendsraystowardtheaxis.Ithasapositivefocallength.Formsarealinvertedimageofanobjectplacedtothe
leftofthefirstfocalpointandanerectvirtualimageofanobjectplacedbetweenthefirstfocalpointandthelens.
Diverging(negative)lens:bendsthelightraysawayfromtheaxis.Ithasanegativefocallength.Anobjectplacedanywheretotheleftofa
diverginglensresultsinanerectvirtualimage.Itisnotpossibletoconstructanegativemagneticlensalthoughnegativeelectrostaticlensescan
bemade.
g.Lensformula(thinlensequation):
where
f=focallengthofthethinlens(sameradiusofcurvatureforboth
sphericalsurfaces)
o=distanceofobjectfromlens(positivetotheleft)
i=distanceofimagefromthelens(positivetotheright)
NOTE:Foravirtualimage,ihasanegativevalue.
h.Magnification:
Foraconverginglens,iftheobjectismorethantwicethefocallengthfromthelens,thentheimageformedisreal,inverted,andsmallerinsize
thantheobject(M<1).Whentheobjectisatadistance=2f,theimageandobjectarethesamesize(M=1);whenitisbetweenfand2f,
theimageislargerthantheobject(M>1),andwhenitis<f,theimageisvirtual,erect,andlargerthantheobject(M>1).
i.Angularapertureofthelens(2a)(Fig.I.29)
Theaperturedeterminesthetotalamountofradiationarrivingfromtheobjectwhichcanbefocusedto
formanimage.Theaperturethuscontrolstheabilityofthelenstogatherinformationabouttheobject.
Thisdependsontheangleoftheconeofraysitisabletoacceptfromtheobject.Bringinganobject
closertotheeyeincreasestheangularaperture,butthereisalimittotheclosenessthattheobjectcan
bebroughttotheeye(~25cmcorrespondingtoanangleofabout0.9°fora4mmexitpupildiameterof
theeyelens;atypicalLMwithanoilimmersionobjectivelenshas2aof~175°).
j.Simplevs.compoundmicroscope(Figs.I.30I.32)
Inprinciple,arealimageofanydesiredmagnificationcanbeobtainedfromasinglepositivelens,butin
practicethisiscumbersomebecauseofthelonglensimagedistance.Oneormorelensescanbeusedto
magnifytheimageinstages(totalmagnificationequalingtheproductofthemagnificationsofeachlens).
Theimageformedbyonelensconstitutestheobjectforthesubsequentlens,whetherornotareal
intermediateimageisformed.
Comparisonofoneversestwostagemagnification:
Thefollowingdescriptionillustrateshowdifferentpathlengthsarerequiredtoachieveamagnificationof10,000Xusingeitheroneortwolenses
withf=2.0cm.
OneStageSystem:
TwoStageSystem:
Assumebothlenseshavef=2.0cmandarearrangedsoeachgives100Xmagnification.
Thus,M=100=x
i
/x
o
foreachstage.
FirstStage:
x
o
=2.02cm
x
i
=202.00cm
Therealimageformedinthefirststagebecomestheobjectforthesecondlens.
SecondStage:x
o
,x
i
sameasinthefirststage.
Totallengthofsystem
=lengthoffirststage+lengthofsecondstage
=(x
o
+x
i
)+(x
o
+x
i
)
=2(x
o
+x
i
)
=2(2.02+202.00)=408.04cm(4.08meters)
k.Problemset
Thefollowingproblemsareforyourownedificationtotesthowwellyouunderstandthebasicsoflensoptics.
1.Foreachsituationbelow,drawanaccurate(usegraphpaper)raydiagramshowingthepathof(atleasttwo)raysfromtheobjecttoimage.
Indicatewhethertheimageisrealorvirtualandspecifythedistanceoftheimagefromthelensandthemagnificationoftheimagewithrespect
totheobject.Ineachexample,thelensisconverging,withidenticalfrontandbackfocalpoints.Distancesareinarbitraryunits.Letf=lens
focallength,x
o
=distanceofobjectinfrontofthelens,andx
i
=distanceofimagebehindthelens.Theobjectmaybeanysize.
2.Inthefollowingexamples,therearetwoconverginglensesinsuccession.Drawraydiagramsshowingtheformationofboththeintermediate
andfinalimagesandgiveappropriateinformationaboutthenature(real/virtual),positions,andsizesoftheintermediateandfinalimages.What
isthemagnificationateachstageofimageformationandwhatisthemagnificationofthefinalimage?Thedistancefromthecenteroflens1(L1)
tothecenteroflens2(L2)equalsD.
I.A.5.ElectronOptics/ElectronLenses
a.Electronemission
Innershellelectronsinmetalatomsshieldtheelectricfieldofthenucleusthroughtherepulsiveforcestheyexertontheoutershell(valence)
electrons.Thustheattractionbetweenthevalenceelectronsandthenucleusisreduced.Metalatomsarecharacterizedashavingtwoloosely
boundvalenceelectronswhichmigratefreely(thisiswhymetalsaregoodelectricalconductors)andcanescapefromthemetalcompletelyif
sufficientadditionalenergyisimpartedtothem.Asthetemperatureofametalisincreased,thekineticenergyoftheelectronsincreasesbecause
ofincreasedthermalvibrationsofthemetalions,whichcollidemorefrequentlywiththeelectrons.Thermionicemissionisthetermusedto
describetheprocessbywhichthermalenergyissuppliedtolooselyboundelectronsinordertoformasourceofelectrons.
Atroomtemperatureelectronsareeffectivelypreventedfromescapingthesurfaceofthemetalowingtotheattractiveforceofthepositively
chargedions.Asthetemperatureisincreasedsomeelectronsacquiresufficientenergytoovercometheattractionandleavethemetal
temporarily.Metal,shapedasathinwire,caneasilybeheatedbypassinganelectriccurrentthroughit.Sincethemetalsurfacebecomes
positivelycharged,acertainlevelofenergy(workfunction)mustbesuppliedtoallowelectronstoescapefromthesurface.Eachmetalhasa
characteristicworkfunction.Tungsten,withalowworkfunction,emitsmoreelectronsthanmetalswithhigherworkfunctions(seealsopp.2930
andFig.I.59).
Ifastrongelectrostaticfieldisappliedinavacuumbetweenthewire(givenanegative,cathode,potential)andananode,theelectricfieldwill
causeelectronstoaccelerateawayfromthewiretowardstheanodesurface(Fig.I.33).Thespeedoftheelectronsdependsonthestrengthof
theelectrostaticfield(voltage)betweenthecathodeandanode(equation(3),Sec.I.A.3.b)Thenumberofelectronswhichleavethewire
dependsonthetemperaturetowhichthewireisheated,whichdependsonhowmuchfilamentcurrentpassesthroughthewire.
A"V"shapedwirewillhavethehighesttemperatureatthetip.Electronswithdrawnfromthefilamenttipcarryelectricchargestotheanode.This
electriccurrent,whichflowsbetweenthefilamentandtheanode,iscalledthebeamcurrent.
1)Electricfield/Equipotentials
Anelectricallychargedobjecthasassociatedwithitanelectricfield.Thus,anelectricallychargedparticle,whenbroughtnearachargedobject,
isinfluencedbyanelectricalforceinthevicinityoftheobject.Theforceisdirectedtowardthechargedobjectifthechargesareofopposite
signsandawayfromtheobjectiftheyareofsimilarsign.DEFINITION:Thedirectionofanelectricfieldisdefinedasthedirectionoftheforce
actingonapositivecharge.(Figs.I.3435)
Alongthelinesofforceconnectingthetwocharges,theelectricpotentialwillchangegraduallybetweentheextremevaluesrepresentedbythe
twocharges.DEFINITION:Equipotentiallinesdefinethepointsalongthelinesofforcewithidenticalelectricalpotential.Theseequipotential
surfacesarealwaysorientedperpendiculartothelinesofforce.Thechangesintheelectricpotentialaregradualinspace.
Electronswhichenterafieldbetweentwoparallelplatesinadirectionparalleltotheplatesareaffectedbytheforcedirectedperpendicularto
theplates(FigI.36).Theelectronswillbeattractedtowardthepositiveplate.Thepathchangesinaseriesofgradualstepsattheequipotential
surfaces.
FigureI.37showshowtheelectronpathis"refracted"attheequipotentialsurface.TheresultisfundamentallythesameasthatgivenbySnell's
Lawofrefractioninlightoptics.Aconsequenceofthisisthatasphericallycurvedequipotentialsurfaceexhibitsthepropertiesofalens.
FiguresI.38andI.39showhowbothpositive(converging)andnegative(diverging)electrostaticlensescanbeformed.Thisfeatureof
electrostaticlensesdiffersfromelectromagneticlenseswhichcanonlyactasconverginglenses.
2)Advantages/Disadvantagesofelectronlenses:
Thefactthattherefractiveindexdoesnotchangeabruptlyinelectronlenseshasoneadvantageinthattherearenotroublesomereflectionsat
equipotentialsasatglassinterfaces.Thereisaseriousdisadvantageinthatequipotentialscannotbeshapedandcombinedinarbitraryfashionto
correctforchromaticaberrationandothererrors.
Althoughelectronmicroscopeswhichemployelectrostaticlenseshavebeenmade,mostmicroscopesuseelectromagneticlenses.Amajorreason
isthatelectrostaticlensesaremoresensitivetothequalityofthevacuumandcleanlinessofthecomponentsthanareelectromagneticlenses.
Somelensaberrationsaremoresevereforelectrostaticlensescomparedtoelectromagneticlenses.Electrostaticlensesrequireverypowerful
electrostaticfieldswhichcanleadtoelectricalbreakdownor"arcingover"insidethecolumn,especiallyunderpoorvacuumconditions.Forthis
reason,electrostaticlensescannotbemadewithfocallengthsasshortasmagneticlenses.
b.Electrostaticlens
Abasicunderstandingofelectrostaticlensesisimportantfortwomainreasons:i)theelectrongunuseselectrostaticlensactiontoformthe
primarybeamsource,andii)itisquitecommonforachargetodeveloponthenonconductingcontaminationwhichmayaccumulateonphysical
apertures(suchastheobjectiveaperture)andtransformthemintoweakelectrostaticlenseswhichcandistorttheelectronimage.
3)Propertiesofelectrostaticlenses:
a)Anyaxiallysymmetricalelectrostaticfieldhasthepropertiesofalensforraysconfinedtotheparaxialregion.Alltheideallensformulasapply
toelectrostaticlenses.
b)Forelectronlenses,replaceÃ(f)forrefractiveindexinthelensequations(f=valueofthepotentialontheaxis).Intheimageformingsystem
ofmostTEMs,fisthesameonbothsidesofthelens(SeeSec.I.A.5.c).
c)Ifboundedbyregionswherefisconstant,anelectrostaticlensisalwaysconvergent.
c.Magneticfieldsandmagneticlenses
1)Magneticfield
Anelectriccurrentpassingthroughaconductorgivesrisetoamagneticfield.TheconventionisthatNisthedirectioninwhichthelinesofthe
magneticfieldpoint(Fig.I.40).Themagneticfluxisthetotalnumberoflinesandthefluxdensityisthenumberoflinesperunitareaofasurface.
UsetheRIGHThandruletodeterminethedirectionofthefield(thumbpointstowardcurrentdirectionandfingerscurlindirectionoffield.NOTE:
Byconvention,thedirectionofelectronflowisoppositetothatofcurrentflow.
Fluxdensitydependsonthepropertiesofthematerialsurroundingtheconductor.Ironinducesahigherfluxdensitythanairoravacuum.The
propertyofthematerialwhichaffectsthefluxdensityiscalledthepermeability,m,ofthematerial.Forairandvacuum,m=1.0.For
ferromagneticmaterialsitcanbeaslargeasseveralhundredthousand.
Iftheconductorhastheshapeofacircularloop,thelinesofforceformcirclesaroundtheloop.Thefluxdensityisgreatestatthecenterofthe
loop.Themagnetinthecenteroftheloopisorientedperpendiculartotheplaneoftheloopifthecurrentthroughtheloopissufficientlystrongto
eliminatetheinfluenceoftheearth'sfield.ThesideoftheloopatwhichthelinesofforceleavetheloopistheNorth(N)poleofthemagnet(Figs.
I.41,I.42).
Ifthewireiswoundinseveralturnsaroundacylindricalsurface(solenoid),eachturnwillcontributetotheinducedmagneticfield.Theflux
densityinthecenterofthecoilisgivenby:
Inthecaseofairandnonmagneticmaterials,µ=1.0andB=H.
Thepermeabilityofirondependsonthefieldstrength,H,anddecreasestounityathighfieldstrengthorwhenthefluxdensity,B=H(Fig.I.43).
Thehighpermeabilityofironisduetotheinducedmagneticfieldorientingmicroscopiccrystalregionsactingastinymagnetsintheiron.Allthese
tinymagnetsaddtheirmagneticfieldstotheinducedfield(Fig.I.44).Whenallmicromagnetsarenearlyoriented,theironwillaffecttheflux
densitytoadecreasingamountsincethereorientationofmicromagnetsisnearingcompletion.Thus,thepermeabilityofironathighfieldstrengths
approachesthatofemptyspace.Atthispointtheironreachesmagneticsaturation.
2)Hysteresis
Thestrengthofthelensdependstosomeextentonthepreviousmagnetichistoryof
thelens.Whenthecurrentinalensisreduced,thedecreaseinmagnetizationdoes
notretracethesamepathobtainedwhenthecurrentwasincreased(Fig.I.45).
Inductionofmagnetizationinvolvesaphysicalmovementwithinthemagnetized
material,requiringtheovercomeofacertaindegreeofinertia.Asaresult,
magnetizationtendstolagbehindthemagnetizingforceapplied.Inducedmagnetic
fluxcanonlybereturnedtozerobyapplicationofacurrentintheoppositedirection.
Aconsequenceofhysteresisisthatthelevelofcurrentusedtoenergizeamagnetic
lensDOESNOTpreciselyspecifythelensstrength(i.e.focallength).
NormalizationofTEMlensesisaccomplishedbyreducingthelenscurrenttozero
somepredeterminednumberoftimes.Hysteresismayalsobeminimizedbytakinga
lenstosaturationandthenreturningittotheworkingcurrentwithoutovershooting.
Whenthefieldstrengthisreducedtozero,somemagnetizationstillremainsintheiron
(residualmagnetizationorremanence).Anadvantageofsoftironisthefactthat,
whenusedinanelectromagnet,hysteresisislow.
Introductionofpiecesofironinamagneticfielddrasticallyaffectsthefluxdensity.
Magneticmaterialhasashieldingeffect,theeffectbeinggreaterthegreaterthe
permeability.Permalloy(mmetal)hasamaximumpermeabilityof80,000140,000
comparedtoironusedintransformers(~7000).mmetalpermeabilityislimitedtolower
fieldstrengthsthanthatatwhichironstillretainshighpermeability.Thismetalis
thereforeusefulforshieldingtheTEMfromexternalmagneticfields.
d.Theelectromagneticlens
1)Lensdesigndevelopment(Figs.I.46I.48)
Theefficiencyofthemagneticfieldproducedbyashortsolenoidwasfirstimproved
byencasingtheenergizingcoilinasheathofsoftironwhichhasthepropertyofconcentratingthelinesofforceinamagneticfieldandthus
becomingmagnetizedbyinduction.Inthiswayamuchmorepowerfulaxialmagneticfieldisobtainedforthesameamountofcurrentflowing
throughthesolenoid.Furtherdevelopmentinvolvedencasingtheentirecoilwithsoftironexceptatanarrowannulargapintheinsideofthecoil.
Thisproducesagreaterconcentrationofthemagneticfieldalongashortaxialdistance.Toachieveshorterfocallengthlenses(andobtaingreater
magnifications)asoftironpolepiecewithanopenaxialborewasintroducedatthepositionoftheannulargap.
MagneticlensesusedinTEMsarealwaysconstructedwithanironcircuittoproduceahighfieldstrengthacrossashortgap.Themagneticfields
forTEMlensesareintherangeof10,00020,000gauss.
2)Forcesactingonacurrentinamagneticfield
Theforceonanelectroninamagneticfieldisalwaysatrightanglestothevelocityandthedirectionofthefield(Figs.I.49,I.50,andI.52).The
fieldonlyactsonthevelocitycomponentwhichisdirectedperpendiculartothelinesofforce.Usethelefthandrule(Fig.I.51:firstfingerfor
fielddirection,middlefingerforcurrentdirection,andthumbfordirectionofforce).Rayspassingthroughthelensareturnedthroughanangle
whichdoesNOTdependonthedistanceoftheraysfromtheaxis.Allelectronscontainedinagivenmeridionalplanebeforeenteringthefieldare
containedinarotatingmeridionalplaneastheypassthroughthelens,andthentheyleavethelenscoplanar.
Whenelectronsenterthelenstheyencounterasidewaysforcewhichcausestheelectrontorotate
asitcontinuesthroughthelens(Figs.I.53I.57).Sincetheradialcomponentofthemagneticfield
reversesafterthecenterofthelens,therotationalvelocitysetupinthefirsthalfofthelensis
countered.Theelectronenteredthelenswithoutangularmomentumabouttheaxisandleaves
withoutangularmomentum.Theneteffectisadeflectiontowardtheaxis,whichitmustcrossatthe
focalpointf
2
.Theanglebetweentheobjectvectorandtheimagevectoris180°+q,whereas,for
glasslensesandelectrostaticlenses,theanglebetweenarealobjectandtheimageisexactly180°.
Sincetheradialforceisdirectedtowardtheaxis,thelensisconvergentnomatterwhatthedirection
ofthefield.
3)Propertiesofamagneticlens:
Anyaxiallysymmetricmagneticfieldhasthepropertiesofanideallens.Alltheformulasfortheideallensmaybeapplied.
Magneticlensesarealwaysconvergent.Theconventional,axiallysymmetriclensisalwaysboundedbyregionswhicharefieldfree,the
consequencebeingthatthenetactionofelectronlensesisinevitablyconvergent.Limitedregionsmaybedivergentbutnotthelensasawhole.
Theseriousconsequenceofthisisthatneithersphericalorchromaticaberrationscanbecorrectedasisdoneinlightopticsbytheusedoublets
ofpositiveandnegativelenses.
Intheabsenceofelectrostaticfields,therefractiveindexisthesameinobjectandimagespace,thereforef
1
=f
2
.
Electronstravelingthroughaxiallysymmetricfieldsexperienceaspiraltrajectoryofdiminishingradius.Theimagevectorisatanangle180°+qto
theobjectvector.
Thedeflectionoftheelectrontowardstheaxismeansthatanelectronenteringthelensparalleltoitsaxiswillcrosstheaxisafterhavingpassed
thelens.Thedeflectionwillincreasewiththedistancefromtheaxis.Thus,abeamofelectronsinparallelpathsparalleltotheaxisofthelenswill
befocusedtoanimagepointontheaxiswhichrepresentsthesecond(back)focalpointofthelens(f
2
).Notethatmagneticlensesarehighly
inefficientinthatonlyaminorportionofthetotalfieldstrengthisactuallyeffectiveinfocusingtheelectron.
4)Magneticlensfocallength
Inamagneticelectronlensthefocallengthisdeterminedbythefieldstrengthinthelensgapandbythespeedoftheelectrons(determinedby
theacceleratingvoltage).
Formagneticlenses,focusingisachievedbyvaryingthecurrentwhichpassesthroughtheelectromagnet.Thisinturnchangesthestrengthof
themagneticfieldandtherebyaltersthefocallengthofthelensandisequivalenttoacombinedchangeinboththe"refractiveindex"and
"curvatureofsurface".Forabeamofmoreenergeticelectrons,thelenscurrenthastobeincreasedinordertokeepthefocallengthconstant.
FocallengthandcurrentareNOTlinearlyrelated:strengthincreasesinasigmoidfashion(Fig.I.45)ascurrentincreasesuntilapointisreached
wherethelensissaturatedandnofurtherincreaseinlensstrengthcanbeachieved.
Sincethefocallengthofthelensisdirectlyproportionaltotheacceleratingvoltage,avariationinthevelocityoftheelectronsintheimaging
beamaffectsimagequalitybyeliminatingperfectfocus(chromaticaberration).
5)Magneticlensdesign:(Figs.I.46,I.47).
Condenserlensesusuallyhavearelativelylargeboreandspacingwhichresultsinalongfieldandlongfocallength.
Typicalconstructionoftheobjectivelensproducesastrongfieldofshortaxialextent(i.e.shortfocallengthbetween(1.53mm)necessaryfor
formationofimagesathighmagnification.Thespecimenisplacedwithinthemagneticfieldoftheobjectivelens.Thus,anyfieldintroducedby
contaminantsinthespecimencandistortthefieldofthelens.Notethatthisalsomeansthatpartofthelensfield("prefield")isonthefrontside
oftheobjectandaffectstheelectronbeambeforeitpassesthroughtheobject.
Mostofatypicalmagneticlensliesoutsidethevacuumofthemicroscope.Onlythoseregionsthroughwhichtheelectronbeampassesareinhigh
vacuum.Magneticlensesmustbewatercooledtodissipatethelargeamountsofheatproducedbythecurrentsintheelectromagnetcoils.
DATE NAME EVENT
1897 J.J.Thompson Discoverstheelectron
1924 LouisdeBroglie Identifiesawavelengthtomovingelectrons
l =h/mv
where
l =wavelength
h=Planck'sconstant
m=mass
v=velocity
(Foranelectronat60kVl=0.005nm)
1926 H.Busch Magneticorelectricfieldsactaslensesforelectrons
1929 E.Ruska Ph.Dthesisonmagneticlenses
1931 Knoll&Ruska Firstelectronmicroscopebuilt
1931 Davisson&Calbrick Propertiesofelectrostaticlenses
1934 Driest&Muller SurpassresolutionoftheLM
1938 vonBorries&Ruska FirstpracticalEM(Siemens)10nmresolution
1940 RCA CommercialEMwith2.4nmresolution
1945 1.0nmresolution
Fig.I.1Comparisonoflightandelectronmicroscopes.Ineach
instrument,illuminationfromthesource(lamp,filamentinthe
electrongun)isfocusedbythecondenserlensontothespecimen.
Afirstmagnifiedimageisformedbytheobjectivelens.Thisimage
isfurthermagnifiedbytheprojectorlensontoagroundglass
screen(light)orfluorescentscreen(electrons).(FromAgar,p.8)
Fig.I.2CrosssectionalviewofthePhilipsEM300.(FromAgar,p.40)
Toviewtheanimatedmicroscope,clickhere.
Note:QuickTimePlugInrequired
(Thiscanbedownloadedathttp://apple.com/quicktime/download)
Fig.I.3Sectionthroughacomplex
doublecondenser6lensPhilips
EM200electronmicroscope.(From
Meek,p.99)
Fig.I.4Thestatisticalnatureofdiffraction
patterns.(FromHall,p.13)
"Theprecisenatureof'electronwaves'or'matterwaves'isverydifficulttounderstandordescribeinmaterialterms.Electronwavesarenot
electromagneticradiationofthekindtowhichlight,Xraysandradiowavesbelong.Theyconstituteasortofquantumor'packet'ofradiationwhich
accompanieseachindividualelectron,followingitspathandnotradiatingoutwardsfromit."(Meek,1976,pp.4849).
V l (nm)
v(
•
10
10
cm/sec)
v/c
10,000 0.0123 0.593 0.198
50,000 0.0055 1.326 0.442
100,000 0.0039 1.875 0.625
1,000,000 0.0012 5.930 1.977!
V l (nm)
v(
•
10
10
cm/sec)
v/c
10,000 0.0123 0.593 0.195
50,000 0.0055 1.326 0.414
100,000 0.0039 1.875 0.548
1,000,000 0.0012 5.930 0.941
FigI.5Aperfectpointsourcecannotbe
imagedbyalensasaperfectpointimagedue
tothepresenceoftheapertureAB(which
maybetheedgeofthelens).Diffractionat
thisaperturegivesrisetoaseriesoffringes,
whichsurroundtheimageformedofthepoint
source.Thepatternproducediscalledan'Airy'
disk.(FromMeek1sted.,p.35)
Fig.I.6Wheneverawavefrontstrikesa
barrier,itcanbendaroundthecorner'by
givingrisetoasecondarywavefrontatthe
edge,sinceeachpointonthewavefrontcan
giverisetoanewsourceofwaves.This
phenomenoniscalled'diffraction'.(FromMeek
1sted.,p.22)
Fig.I.7Diffractionpattern(right)formedbyanirregularlyshapedaperture
(left).(FromYoung,p.95)
Fig.I.8(a)
Photographof
theedgeofa
razorblade
illuminatedby
monochromatic
(blue)light
rendered
coherentby
passing
througha
narrowslit.(b)
Microdensitometer
tracingofthe
negativefrom
whichthe
photograph
wasmade.
FourFresnel
fringescanbe
distinguished.
(FromMeek1st
ed.,p.27)
(a)
(b)
(a) (c)
(b)
Fig.I.9(a)Fresnelfringesformed
byelectrons.Thesefringesare
formedoutsidetheedgeofahole
(white)inacarbonfilm(black).(b)
Amicrodensitometertracingofthe
fringesystem;thepatternis
identicalwiththeFresnelfringe
systemformedbyvisiblelight(see
Fig.I.8).(c)Anunderfocusedimage
ofaholeinafilm,showinga
completesystemofabout40
Fresnelfringesinsidethehole.
(FromMeek1sted.,pp.2930)
Fig.I.10Diffractionimagesoftwo
easilyresolvedpoints.(From
Slayter,p.243)
Fig.I.11Imagesoftwo
incoherentlyilluminatedpointsat
thelimitofresolution.(a)individual
intensities;(b)summedintensities.
(FromSlayter,p.244)
Fig.I.12Examplesofwhatoccurswhentwo
wavesofthesamewavelengthandequal
amplitudeadd.Ineachexample,thetwo
separatewavesareshownontheleftand
theirsumorresultantwaveontheright.The
differentexamplesarecharacterizedbyvarying
phasedifferences.Thephaseofawave
(usuallyexpressedasafractionofthe
wavelengthorindegrees)isthepositionofa
crestrelativetosomearbitrarypoint.Although
thephaseofagivenwavevarieswithtimeas
thewavetravels,thedifferenceinphaseofthe
twowavesofthesamewavelengthwiththe
samevelocity,isindependentoftime.Such
wavescaninterferewithoneanother.The
resultantwavehasthesamewavelength,l .
(a)Phasedifferencezero.Thewavestotally
reinforceandaresaidtobe"inphase"orto
showconstructiveinterference.
(b)Phasedifferencel /4.Partialreinforcement,
givingawaveofamplitude1.4(intensity2.0).
(c)Phasedifferencel /2.Thewavesare"outof
phase"andthereistotaldestructive
interferencetogivenoresultantwaveora
wavewithamplitude0(intensity0).(From
GluskerandTrueblood,p.19)
Fig.I.13Photographofan
interferencepatterninwater
wavesformedbythe
superpositionofwavesfromtwo
sourcesoscillatinginphasewith
thesamefrequency.(FromYoung,
p.22)
Fig.I.14Theangularapertureofthe
eyeisrelativelysmall.(FromMeek,
1sted.,p.13)
Fig.I.15Increasingtheangular
apertureoftheeyewithalens.The
lensallowstheobjecttobeheld
closertotheeye,whichisthereby
enabledtogathermoreinformation.
(FromMeek1sted.,p.14)
Fig.I.16Theinteractionofwaves
withanobstacle.Theboatridesthe
longwavelengthoceanwave,but
reflectsthesmallwavelength
surfaceripple.Anobserverwho
wishestodetectthepresenceof
theboatcandosoonlyby
observingwaveswhichhave
wavelengthssmallerthan,or
comparableto,thelengthofthe
boat.(FromSherwood,p.19)
Maximummagnification=
resolvingpoweroftheeye
resolvingpowerofthemicroscope
(a)
Fig.I.17(a)TwoAiry
disksrepresenting
twoimagepoints
shownatincreasing
separationfromleft
toright.Inthe
pictureatthe
extremerightthe
twodiskscanbe
distinguishedas
separatedisks.
(b)Theintensity
distributionatanAiry
disk.R,halfwidthof
thecentralmaximum
representedbya
bellshapedcurve.
(c)TheRayleigh
criteriaforresolution.
(FromSjostrand,
p.115)
i=r
Fig.I.18Reflection.(FromSlayter,
p.4)
Fig.I.19Refraction.(FromSlayter,
p.6)
Fig.I.20Principalraydiagramsshowing
imageformationbyaconvexlens.
(a)Whentheobjectdistanceisgreater
thanthefocallength,areal,inverted
imageisformed.
(b)Whentheobjectdistanceisless
thanthefocallength,avirtual,erect
imageisformed;itspositionis
obtainedbyprojectingtheprincipal
raysbackward.Theraysappearto
comefrompointQ.(FromYoung,
p.127)
Fig.I.21Definitionof
principalfocus,F,inimage
spaceofalens.(From
Sjostrand,p.20)
Fig.I.22Focusingeffectoflenson
raysoriginatingfrompointson
principalaxislocatedatdifferent
distancesfromthelens.(From
Sjostrand,p.21)
Fig.I.23Definitionofprincipal
focusinobjectspaceF1ofa
lens.(FromSjostrand,p.21)
Fig.I.24VirtualimageQof
objectpointlocatedbetween
principalfocusinobjectspace
andthelens.(FromSjostrand,
p.21)
Fig.I.25Constructionoftheimage
ofanobjectbymeansofray
tracing.(FromSjostrand,p.22)
Fig.I.26Magnifyingeffectof
apositivelens.(From
Sjostrand,p.22)
Fig.I.27Virtualmagnified
imageofobjectlocated
betweenprincipalfocusin
objectspaceandthelens.
(FromSjostrand,p.22)
Fig.I.28Amagnifyingglassformsan
enlarged,erectvirtualimage.The
angularsizeofthisimageis
approximately4"/15"or4/15.The
angularsizeoftheobjectatthe
closestdistanceforcomfortable
viewingis1"/10"or1/10.The
magnificationinthissituationis(4/15)/
(1/10),or22/3.(FromYoung,p.130)
Fig.I.29Theangularapertureofa
lens.Theangle2a isthe
acceptanceangleofthelens,and
thelargeritcanbemade,themore
informationcanthelenstransmit.A
largelensofhighaperturecan
thereforetellusmoreaboutan
objectthanasmalllensoflow
power.(FromMeek1sted.,p.12)
Fig.I.30Raydiagramforhighmagnification
modeofoperation.Notethateachlens
formsarealimage,withimageinversion.
I0istheimageformedbytheobjective
lensO,I1isformedbythefirstprojector
lensP1andI2bythesecondprojectorP2,
onthescreen.(FromAgar,p.30)
Fig.I.31Left:raydiagramofthe3realimagemediumandhighmagnificationimagingsystemofa3lens
microscope.Center:2realimageverylowor'scan'magnificationrangeofa3lensmicroscope.Right:2real
imagelowmagnificationsystemofa3lensmicroscope.(FromMeek1sted.,pp.118,120121)
Fig.I.32Raydiagramforacompleteelectron
microscope.FilamentF,condenser1lensC1,
condenser2lensC2,condenserapertureCA,
specimenS,objectivelensO,objectiveaperture
OA(inbackfocalplane).1stintermediateimage
andselectorapertureSA.IntermediatelensP1,
secondintermediateimageI2,projectorlensP2
andfinalimageonthefluorescentscreenFC.
(FromAgar,p.35)
a)f=2.0
x
o
=5.0
e)f=4.0
x
o
=3.0
b)f=10.5
x
o
=21.0
f)f=13.3
x
o
=13.3
c)f=3.5
x
o
=3.0
g)f=3.142
x
o
=0.0
d)f=5.0
x
o
=2.5
a)D=8.0
L1:f=2.0
x
o
=4.0
L2:f=3.0
b)D=8.0
L1:f=2.0
x
o
=6.0
L2:f=3.0
c)D=4.0
L1:f=2.0
x
o
=3.0
L2:f=2.0
FigI.33Accelerationofelectronin
electricfield.(FromSjostrand,p.26)
Fig.I.34Linesofforceatapositively
chargedsphericalbody.(FromSjostrand,
p.32)
Fig.I.35Linesofforceandequipotential
surfaces(stippledlines)associatedwith
twoequalchargesofoppositesign.
(FromSjostrand,p.32)
Fig.I.36Equipotentialsurfacesattwoparallel
platesofoppositechargeswiththepathofan
electronindicatedwithinthehomogeneous
partofthefield.(FromSjostrand,p.33)
Fig.I.37Refractionofelectronatan
equipotentialsurface.(FromSjostrand,p.33)
Fig.I.38.Negativelensactionof
electrostaticfieldatanaperturewhen
V2V1>V3V2.(FromSjostrand,
p.34)
Fig.I.39.Positivelensactionatan
aperturewhenV2V1<V3V2.
(FromSjostrand,p.34)
Fig.I.40Magneticfieldinducedbycurrent
passingthroughaconductor.(From
Sjostrand,p.35)
Fig.I.41Magneticfieldinducedbycurrent
passingthroughasolenoid.(From
Sjostrand,p.37)
Fig.I.42Solenoidwithironcore.(From
Sjostrand,p.40)
Fig.I.43a.Dependenceofpermeabilityonfluxdensity,B.
b.RelationshipbetweenfluxdensityBandfieldstrength.
(FromSjostrand,p.38).
Fig.I.44Magnetization.(FromSlayter,
p.361)
Fig.I.45Curves
showinghowthe
magnetizationof
softiron(lens
strength)is
relatedtothe
magnetizing
force(lens
current).An
unmagnetized
lensstartsfrom
thepointOand
followsthepath
OAaslens
current
increases.Atthe
pointA,further
increaseinlens
currentproduces
nofurther
increaseinlens
strength;thelensissaidtobe'saturated'.Whenlenscurrent
isreduced,thepathOAisnotretraced;adifferentpathABis
followed.Thisdisplacementiscalled'hysteresis'.Atzero
current(pointB),someresiduallensstrengthremains;thisis
called'remanence'.Tobringthelensbacktozerostrength,a
reversecurrentOCmustbeapplied.Lensstrengththen
increaseswithincreasingreversecurrent,followingthepath
CD.Thepolarityofthelenschanges,butthisdoesnotaffect
itsfocusingpower;onlythespiralelectronpathisreversed.
Becauseofhysteresis,itisnotpossibletocalibratealens
currentmeteraccuratelyintermsoflensstrengthor
magnification.
Fig.I.46Evolutionofmagneticelectron
lenses.(A)Shortsolenoidusedasa
magneticlens.(B)Softironcasing
enclosingoutersurfaceofthesolenoid,
thusconcentratingthefield.(C)Soft
ironencasingthesolenoidexceptata
narrowannulargaptherebyreducing
themagneticfieldtoaveryshortregion
alongthelensaxis.(D)Modern
objectivelensconsistingofasoftiron
encasedsolenoidandsoftironpole
piecessoastohaveanenormously
concentratedfieldatthelevelofthe
annulargap.(FromWischnizter2nded.,
p.33)
Fig.I.47(a)Amagneticlensconsisting
ofatightlywoundcoilandasoftiron
shroudsurroundingthecoilexceptfor
asmallgap.Thefieldisconcentratedin
thatgap.(b)Shortfocallength
electromagneticlenswithpolepieces.
(FromSjostrand,p.50)
Fig.I.48Fieldstrengthdistribution
curves.ThecurvesADcorrespondto
therespectivelensesillustratedinFig.
I.46.Eachrepresentsthefieldstrength
alongthelongaxisofthelens.The
changesintheshapeofthecurves
representtheshorteningor
concentrationofthefieldovera
shorteraxialdistance.Hz=
longitudinalmagneticfield.Z=
distancealongtheaxisofsymmetry.
(FromWischnizter2nded.,p.33)
Fig.I.49TheforceFactingon
astraightconductorina
homogeneousmagneticfield
offluxdensityBwhencurrent
Iispassedthroughthe
conductor.(FromSjostrand,
p.43)
Fig.I.50Pathofanelectronina
magneticfield.(A)Inalarge,uniform
magneticfield.(B)Inasmall,uniform
magneticfield.(FromWischnitzer2nd
ed.,p.25)
Fig.I.51Lefthandthumbrule.
(FromSjostrand,p.43)
Fig.I.52Thompson'sexperiment.A
streamofelectronsoriginatingfroma
sourceandpassing,invacuo,through
amagneticfieldproducedbyapairof
magnetswillbedeflected.The
directionofdeflectiondemonstrates
thatelectronsarenegativelycharged
particlesofmatter.(FromWischnitzer
2nded.,p.25)
Fig.I.53Actionofasolenoidonan
electronbeam.Anelectriccurrent
passingthroughthecoilproducesan
axialmagneticfield.Thisisthe
refractingmediumfortheelectrons.An
electronstartingatapointontheaxisA
andatanangletoitfollowsaspiral
path,returningtotheaxisatthepoint
B.Theactionisbasicallysimilartothat
oftheconverginglightlensshownin
Fig.I.20.(FromMeek1sted.,p.8)
Fig.I.54Actionofthemagnetic
lens.(a)Inperspective.(b)
Electrontrajectoryin
projection,alongdirectionof
propagation.(c)Electron
trajectoryinprojection,side
view.(FromSlayter,p.358)
Fig.I.55Componentsofthe
vectorHneartheaxisoffields
withaxialsymmetry.His
representedbytwo
components,Hz,the
componentinthez(axial)
direction,andHr,the
compnentinther(radial)
direction.(FromHall,p.85)
Fig.I.56Theycomponentof
themagneticfieldina
magneticlensisoriented
perpendiculartothedirection
ofanelectronenteringthe
lensalongapathparallelto
thelensaxis.Thisy
componentwillaffectthe
electron,deflectingitinthex
directionasindicatedbythe
arrowmarkedvx.(From
Sjostrand,p.48)
Fig.I.57Thezcomponentofthemagneticfield
andthexvelocitycomponentoftheelectron
inamagneticlensinteract,deflectingthe
electronintheydirectiontowardthelens
axis.(FromSjostrand,p.49)
CuuDuongThanCong.com https://fb.com/tailieudientucntt
cuu duong than cong . com

I.THEMICROSCOPE
I.A.PRINCIPLESOFTHETRANSMISSIONELECTRONMICROSCOPE(TEM)
I.A.1.OriginoftheTransmissionElectronMicroscope
I.A.2.ComparisonofLight(LM)andElectronMicroscopes(Fig.I.1)
a.Similarities(Arrangementandfunctionofcomponentsaresimilar)
1)Illuminationsystem:producesrequiredradiationanddirectsitontothespecimen.Consistsofasource,whichemitstheradiation,anda
condenserlens,whichfocusestheilluminatingbeam(allowingvariationsofintensitytobemade)onthespecimen.
2)Specimenstage:situatedbetweentheilluminationandimagingsystems.
3)Imagingsystem:Lenseswhichtogetherproducethefinalmagnifiedimageofthespecimen.Consistsofi)anobjectivelenswhichfocusesthe
beamafteritpassesthroughthespecimenandformsanintermediateimageofthespecimenandii)theprojectorlens(es)whichmagnifiesa
portionoftheintermediateimagetoformthefinalimage.
4)Imagerecordingsystem:Convertstheradiationintoapermanentimage(typicallyonaphotographicemulsion)thatcanbeviewed.
b.Differences
1)Opticallensesaregenerallymadeofglasswithfixedfocallengthswhereasmagneticlensesareconstructedwithferromagneticmaterialsand
windingsofcopperwireproducingafocallengthwhichcanbechangedbyvaryingthecurrentthroughthecoil.
2)MagnificationintheLMisgenerallychangedbyswitchingbetweendifferentpowerobjectivelensesmountedonarotatingturretabovethe
specimen.Itcanalsobechangedifoculars(eyepieces)ofdifferentpowerareused.IntheTEMthemagnification(focallength)oftheobjective
remainsfixedwhilethefocallengthoftheprojectorlensischangedtovarymagnification.
3)TheLMhasasmalldepthoffield,thusdifferentfocallevelscanbeseeninthespecimen.Thelarge(relative)depthoffieldintheTEMmeans
thattheentire(thin)specimenisinfocussimultaneously.
4)Mechanismsofimageformationvary(phaseandamplitudecontrast).
5)TEMsaregenerallyconstructedwiththeradiationsourceatthetopoftheinstrument:thesourceisgenerallysituatedatthebottomofLMs.
6)TEMisoperatedathighvacuum(sincethemeanfreepathofelectronsinairisverysmall)somostspecimens(biological)mustbedehydrated
(i.e.dead!!).
7)TEMspecimens(biological)arerapidlydamagedbytheelectronbeam.
8)TEMscanachievehighermagnificationandbetterresolutionthanLMs.
9)Pricetag!!!(100xmorethanLM)
I.A.3.Photons/Electrons
a.Dualconceptofwaveandparticle(Fig.I.4)
Lighthaspropertiesbothofaparticleandawave.Thisdualnatureisrequiredtosatisfactorilyexplaintheresultsofvariousphysicalexperiments.
Thediffractionoflight(bendingaroundcorners)illustratesthewavenature.TheWAVETHEORYisbasedonthestatisticalnatureofeventsand
haslittlemeaningwithrespecttothebehaviorofsingleparticles.ThewavetheorywasdevelopedandexpoundedbyHuygens(16291695)and
Hooke(16381703).TheCORPUSCULARTHEORYwasproposedbyNewton(16421727)andbecamethemoreacceptedtheoryevenafter
demonstrationofdiffractionbyYoung(17731829)andinterferencebyFresnel(17881827).Atabout1850,thewavetheorycamebackinto
favoruntilabout1900whenmoreevidenceforthecorpusculartheorywasdiscovered.
QUANTUMTHEORY(PlanckandEinstein)providesthebasisforexplainingthephenomenaofINTERFERENCE,DIFFRACTIONandthe
PHOTOELECTRICeffect(lightfallingoncertainmetalscausethemtoemitelectrons)andthusformsacommonbasisforexplainingthenatureof
actionoflight.Thetransferofenergybetweenlightandmatteroccursonlyindiscretequantitiesproportionaltothefrequencyofthe
lightwave.
E=hJ
where
E=energyofphoton(joules)
h=Planck'sconstant(6.624
•
10
34
joulesec)
J=frequency(cycles/sec)
b.Electronvelocityandwavelength
Therelationbetweenthewavelength(l )ofaparticleofmass,m,movingatavelocity,v,isgivenbytheDeBrogliewaveequation:
(1)
Anelectronofchargee(1.6
•
10
19
coulomb),andmassm(9.11
•
10
28
gm),whenpassingthroughapotentialdifferenceofVvolts(expressedin
joules/coulomb),hasakineticenergy:
(2)
Solvingforvelocity:
(3)
substitutingintotheDeBroglieequation(1):
(4)
Since1joule=10
7
dyne
•
cm=10
7
cm
2
•
gm/sec
2
(5)
Thus,forexample,ifV=60,000volts,l =0.005nm.
Fromequation(3)theelectronvelocitycanbecalculatedifVisknown:
(6)
Thefollowingtableillustratesthat,athighvoltage,electronvelocityiscomparabletothespeedoflightinavacuum(c=3
•
10
10
cm/sec).
Theequationbreaksdownwhenthevelocityoftheelectronapproachesthespeedoflightbecausearelativisticcorrectionmustbemadeforthe
valueofthemasswhere:
(7)
Therelationbetweenl andVismorecorrectlygivenby:(seeHall(1966)pp.3334)
(8)
Thefollowingtableisobtainedwhenrelativityeffectsareincluded:
c.Interference/diffraction/coherence
Anideallenssystemobtainsanexactimageoftheobject(eachpointfaithfullyreproduced).Thephenomenaofdiffractionmakesthis
unattainable(Figs.I.5,I.6).
Diffractionphenomenainvolvesthebendingofthepathofradiationpassingclosetoanobstacle(Fig.I.6).Thisresultsinaspreadingofthe
radiationintotheregionbehindtheobstructionthatthewavespassed.Thediffractionatedgescontributestothecontrastatwhichanedgecan
beobserved.Diffractionalsolimitstheresolvingpowerofthemicroscopesincetheimagepointproducedbyalensisadiffractionimageofthe
openingofthelensortheaperturerestrictingtheeffectiveopeningofthelens(Fig.I.5).
Ifthelightsourceandtheplaneatwhichthediffractionpatternisobservedareatfinitedistancesfromtheedge,thephenomenoniscalled
Fresneldiffraction.Thepatternisdescribedasduetointerferencebetweenthenondiffractedlightandawaveoflightdiffractedattheedge.
Theresultingsuperpositiongivesrisetoaseriesofdiffractionfringesorientedparalleltotheedgeandrepresentingperiodicallyvaryingbrightness,
maximaandminima.(Figs.I.7,1.8,I.9).
Coherence:Aprerequisiteforinterferenceisasuperpositionofwavesystemswhosephasedifferenceremainsconstantintime.Twobeams
arecoherentif,whencombined,theyproduceaninterferencepattern.Thebeamsareincoherentwhentheyareincapableofproducingan
interferencepattern.Twobeamsoflightfromselfluminoussourcesareincoherent.Iflightfromthetwosourcesfallsonascreen,theresultant
intensityissimplythesumofthetwointensitieswhichwouldoccurfromeachsourceseparately(Figs.I.10,I.11).Inpracticeanemittingsource
hasfiniteextentandeachpointofthesourcecanbeconsideredtogeneratelight.EachsourcegivesrisetoasystemofFresnelfringesatthe
edge.Thesuperpositionofthesefringesystemsisfairlygoodforthefirstmaximaandminimabutfartherawayfromtheedgeshadowtheoverlap
ofthefringepatternsbecomessufficientlyrandomtomakethefringesdisappear.Thenatureofwaves,phase,amplitude,andinterferenceare
illustratedinFigs.I.12andI.13.
d.Resolution
1)Definitions:
RESOLUTION:abilitytodistinguishcloselyspacedpointsasseparatepoints.
RESOLUTIONLIMIT:smallestseparationofpointswhichcanberecognizedasdistinct.
RESOLVINGPOWER:resolutionachievedbyaparticularinstrumentunderoptimumviewingconditions.
2)Distinctionbetweenresolutionandresolvingpower:
Notethedistinctionbetweenresolutionandresolvingpower.Resolvingpowerisapropertyoftheinstrumentandisaquantitythatmaybe
estimatedontheoreticalgrounds.Resolutionisequaltoorpoorerthantheresolvingpowerandisthequantityobservedunderanygivenset
ofexperimentalconditions.IntheTEM,especiallywithbiologicalsamples,theresolutionachievedmaybeconsiderablyinferiortothetheoretical
resolvingpoweroftheinstrument.
Microscopyisthescienceofseeingtheverysmall.Underidealconditions,theeyeresolvesabout1minuteofarc(=1/60degree=2.9x10
4
radian;recallthereare2p radiansin360°)andsinceitcanfocusdowntoabout250mm,thesmallestobjectwecanresolveisabout0.07mm
(70mm)(Fig.I.14).Thislimitisrelatedtothesizeofthereceptorsintheretinaoftheeye.Thefunctionofamicroscopeistomagnifytheimage
fallingontheretina(Fig.I.15).Theadvantageoflightandelectronmicroscopesisthattheyeffectivelygettheobjectclosertotheeyesoa
magnifiedimageisobtainedandmoredetailcanbediscerned.
TENNISBALLANALOGY:Eyecanresolve3cmat100meters,thusatennisballisclearlyvisible.Butifthetennisballisheldupagainstawhite
background,thevisibilitydecreases(becauseofthedecreaseincontrast).
3)Abbecriteriaofresolution:
Thefundamentalnatureoflightposeslimitsonthedetailthatcanberesolved(Fig.I.16).Abbe(1893)showedthatthesmallestresolvable
distanceisabout1/2thewavelengthoflightused.Thus,1/2thewavelengthoftheradiationusedistheultimateresolvingpowerofany
instrument.Thislimitstheusablemagnificationofopticalmicroscopesto<1000X.Atfirstitwasthoughtthatxraymicroscopeswouldbeuseful
buttherefractiveindexofsubstancesforxraysisnearly=1,thusrefractinglensescannotbemadeforxrays,andconsequently,xrayscannot
beeasilyfocusedtoformimages.
4)Magnificationlimits:
Themaximummagnificationofaninstrumentislimitedaccordingtothefollowingrelationship:
Thus,fortheLM,witharesolvingpowerofapproximately0.25µm,themaximum(useful)magnificationisabout250µm/0.25µm=1000X.Thevalue
usedfortheresolvingpoweroftheeyeinthisexample(250µm)representsamorerealisticviewingcondition.Anymagnificationabovethevalue
givenbytheaboveformularepresentsemptymagnification,sincesuchmagnificationleadstonomoreusefulinformationbutratheramagnified
blur.
AccordingtotheAbbecriteria,at60,000volts,theTEMshouldhavearesolvingpowerofabout0.0025nm.Thisshouldallowamaximumuseful
magnificationofabout100milliontimes!!!Inpractice,themaximumusefulmagnificationoftheTEMoperatedat60kVislimitedtomuchlessthan
1,000,000X.Thus,althoughtheLMnearlyobeystheAbbecriteria,theTEMfallsshortbyaconsiderableamount.Themainlimitingfactorinthe
TEM,withrespecttoachievingthetheoreticalresolvingpoweroftheinstrument,concernsthenatureoftheimaginglensesandtheprocessof
imageformation.
5)Rayleighcriteria(practicalbutarbitrary):(Fig.I.17).
Itistheabilityofmicroscopestomakeobjectpointswhichareclosetogetherappearintheimageasseparatepoints.Anideallenstakeseach
objectpointandrepresentsitexactlyasapointintheimage.Areallenstakeseachobjectpointandspreadsitoutintoacirculardisk(Airy
disk)intheimageplanewhosediameterdependsontheangularapertureofthelens.
Theshortestdistancebetween2disksatwhichthetwodisksappearpartiallyseparatedcorrespondstoabout1/2thewidthofthedisks.The
distance,d,inobjectspaceisgivenby:
d=0.61l /n
•
sina
where
l =wavelenghtoftheradiation
n=refractiveindexofthemedia
a=semiangularapertureofthelens
NOTE:n
•
sina=thenumericalaperture(N.A.)ofthelens.
Thus,tomaximizeresolvingpower,l mustbedecreased,nincreased,oraincreased.Recallthatweareconcernedatthemomentwithan
aberrationfreeopticalsystem.Thevaluefortheconstant(0.61)iscontroversialbecauseitdependsonthecoherenceoftheradiationanda
criteriaofvisibility.
FortheLM,usingoilimmersionoptics(n=1.5),sina=0.87,andvioletlight(l =400nm),d=0.2µm.Theonlywaytoimprovetheresolutionisto
uselightofshorterwavelengthsinceN.A.cannotbeincreasedbeyond~1.5.FortheTEM,n=1(vacuum),sina=10
2
andl =0.005nmfor60kV
electrons,thusd=0.3nm.
I.A.4.Optics(LensTheory)
a.Basiclawsofclassicalgeometricaloptics
1)Rectilinearpropagationoflightwhenn(refractiveindex)isconstant.
2)Lawofreflection:
3)Lawofrefraction(Snell'sLaw):
4)Independenceofrays.Theassumptionismadethatlightraystravelindependentlythroughspace.
Theselawsholdforelectrons,except#4,ifthecurrentdensityistoohighwhennegativechargedelectronscaninterfere.
b.Classicalvs.electronoptics
1)Classicaloptics:Therefractiveindexchangesabruptlyatasurfaceandisconstantbetweenthesurfaces.Therefractionoflightatsurfaces
separatingmediaofdifferentrefractiveindicesmakesitpossibletoconstructimaginglenses.Glasssurfacescanbeshaped.
2)Electronoptics:Here,changesintherefractiveindexaregradualsoraysarecontinuouscurvesratherthanbrokenstraightlines.Refraction
ofelectronsmustbeaccomplishedbyfieldsinspacearoundchargedelectrodesorsolenoids,andthesefieldscanassumeonlycertaindistributions
consistentwithfieldtheory.
c.Geometricalandphysicaloptics
Thefundamentalprinciplesofopticsgovernthedesignandoperationofboththelightandelectronmicroscopes.Thebasicopticalprinciples
involvingtheuseofrefractileelementsorlensesinordertoformmagnifiedimagesareidenticalinboththeLMandTEM.TheTEMdiffersfromthe
LMonlyintheradiationitusesandinthewayinwhichtheradiationisbentorrefracted.
Geometricalopticsdealswiththestudyofthepathsfollowedby'rays'oflightorelectronsthroughlensesandapertures,andthegeometrical
constructionsusedtofindtherelativepositionsandsizesofobjectsandtheirimages.Arayoflightorelectronsisdefinedasaninfinitelythin
pencilorbeam.Physicalopticsshowsthatthisanabstractionandcannotphysicallyexistbecauseof'diffraction'whichdealswiththewave
natureoflightandelectrons.Allresultsobtainedingeometricalopticscanbederivedfromtheprinciplesofphysicaloptics,alongwithother
phenomenasuchasinterferenceanddiffractionwhicharenotexplicableinsimplegeometricalterms.
d.Idealversesreallenses:
Lensesareusedtobendraysoflightorelectronssotheyaredeflectedinapredictablewayfromtheiroriginalpaths.Thepropertiesofanideal
lens,possessinganaxisofrotationalsymmetryare:
1)Eachrayofthebundleofrayswhichpassesfromanobjectpointwillberefractedbytheideallenstomeetinoneimagepoint.
2)Raysoriginatingfrompointswhichlieonaplaneperpendiculartotheaxis,mustbeimagedinaplanewhichisalsoperpendiculartotheaxis.
3)Theimageappearsliketheobjectirrespectiveofthemagnification,sotherelativelineardimensionsoftheobjectarepreservedintheimage.
Inpractice,theimagingbyanyreallensdoesnotcorrespondtothatoftheideallensowingtothefactthatanobjectpointisrepresentedbya
diffractionimage(Airydisc)ofthelensopeningortheapertureusedforrestrictingtheeffectiveopeningofthelens.Thisisaresultofthewave
likepropertiesoflight.Lensaberrationsalsocontributetomoreorlesspronounceddeviationsfromthepropertiesoftheideallens.
Thesinglerefractingsurfaceofsphericalcurvatureisthefundamentalunitoffocusingactionbyglasslenses.Sphericalrefractingsurfacesactas
lensesforparaxialrayswhicharethoseraysthatpassclosetotheprincipalaxisofthelens.RayswithlargeangleswillNOTobeyideallens
action.
Afundamentaldifferencebetweenlightandmagneticlensesisthattheelectronbeamdoesnotchangeinforwardvelocityasitpassesthrough
themagneticfield(lightraysslowdownwhenpassingintoamediumofhigherrefractiveindex).Refractioniscontinuouswithelectronswhenthey
areinthemagneticfield:lightisrefractedonlyattheinterfacebetweenmediaofdifferingrefractiveindex.Theelectronsalsofollowspiral
trajectoriesthroughthemagneticfield(seealsoSec.I.A.5.c(Magneticfieldsandmagneticlenses)
e.Raydiagrams:(Figs.I.20I.28)
Themethodofconstructionofraydiagramsisbasedonthreesimpleprinciples:
1)Allraysenteringthelensparalleltotheaxisarebroughttoacommonpointontheaxis,thefocalpoint.
2)Allrayspassingthroughthegeometricalcenterofthelensareundeviatedandpassstraighton,nomatterfromwhichdirectiontheycome.
3)Principleofreversibility:ifthedirectionofarayisreversedinanysystemtherayexactlyretracesitspaththroughthesystem.Thisapplies
onlytothelocationoflightpathsandnottotheintensityofthelight.
Theaboveprinciplesarebasedontheassumptionsthatwearedealingwithathinlensandconcernedwiththepathsofparaxialrays.The
standardconventionistodrawdiagramswithraysthattravelfromlefttoright.Theobjectistotheleft(infront)ofthelensandtheimageisto
theright(behind)ofthelens.
f.Definitions:
Realimage:oneatwhichlightraysphysicallyreunite,sothataphotographicplateplacedatthepositionofarealimageisexposed.
VirtualImage:onefromwhichlightraysappeartodiverge;raysarenotinfactconcentratedatthepositionofavirtualimage,sothata
photographicplateplacedatthepositionoftheimageisnotexposed(byfocusedrays).Placinganopticalsystemsuchastheeyebehindthe
lens,willenablethedivergentraystobefocusedtoformarealimage.TheintermediatelensofanTEMissometimesusedthiswayinorderto
reducethefinalsizeoftherealimageformedbytheprojectorlens(es).
Converging(positive)lens:bendsraystowardtheaxis.Ithasapositivefocallength.Formsarealinvertedimageofanobjectplacedtothe
leftofthefirstfocalpointandanerectvirtualimageofanobjectplacedbetweenthefirstfocalpointandthelens.
Diverging(negative)lens:bendsthelightraysawayfromtheaxis.Ithasanegativefocallength.Anobjectplacedanywheretotheleftofa
diverginglensresultsinanerectvirtualimage.Itisnotpossibletoconstructanegativemagneticlensalthoughnegativeelectrostaticlensescan
bemade.
g.Lensformula(thinlensequation):
where
f=focallengthofthethinlens(sameradiusofcurvatureforboth
sphericalsurfaces)
o=distanceofobjectfromlens(positivetotheleft)
i=distanceofimagefromthelens(positivetotheright)
NOTE:Foravirtualimage,ihasanegativevalue.
h.Magnification:
Foraconverginglens,iftheobjectismorethantwicethefocallengthfromthelens,thentheimageformedisreal,inverted,andsmallerinsize
thantheobject(M<1).Whentheobjectisatadistance=2f,theimageandobjectarethesamesize(M=1);whenitisbetweenfand2f,
theimageislargerthantheobject(M>1),andwhenitis<f,theimageisvirtual,erect,andlargerthantheobject(M>1).
i.Angularapertureofthelens(2a)(Fig.I.29)
Theaperturedeterminesthetotalamountofradiationarrivingfromtheobjectwhichcanbefocusedto
formanimage.Theaperturethuscontrolstheabilityofthelenstogatherinformationabouttheobject.
Thisdependsontheangleoftheconeofraysitisabletoacceptfromtheobject.Bringinganobject
closertotheeyeincreasestheangularaperture,butthereisalimittotheclosenessthattheobjectcan
bebroughttotheeye(~25cmcorrespondingtoanangleofabout0.9°fora4mmexitpupildiameterof
theeyelens;atypicalLMwithanoilimmersionobjectivelenshas2aof~175°).
j.Simplevs.compoundmicroscope(Figs.I.30I.32)
Inprinciple,arealimageofanydesiredmagnificationcanbeobtainedfromasinglepositivelens,butin
practicethisiscumbersomebecauseofthelonglensimagedistance.Oneormorelensescanbeusedto
magnifytheimageinstages(totalmagnificationequalingtheproductofthemagnificationsofeachlens).
Theimageformedbyonelensconstitutestheobjectforthesubsequentlens,whetherornotareal
intermediateimageisformed.
Comparisonofoneversestwostagemagnification:
Thefollowingdescriptionillustrateshowdifferentpathlengthsarerequiredtoachieveamagnificationof10,000Xusingeitheroneortwolenses
withf=2.0cm.
OneStageSystem:
TwoStageSystem:
Assumebothlenseshavef=2.0cmandarearrangedsoeachgives100Xmagnification.
Thus,M=100=x
i
/x
o
foreachstage.
FirstStage:
x
o
=2.02cm
x
i
=202.00cm
Therealimageformedinthefirststagebecomestheobjectforthesecondlens.
SecondStage:x
o
,x
i
sameasinthefirststage.
Totallengthofsystem
=lengthoffirststage+lengthofsecondstage
=(x
o
+x
i
)+(x
o
+x
i
)
=2(x
o
+x
i
)
=2(2.02+202.00)=408.04cm(4.08meters)
k.Problemset
Thefollowingproblemsareforyourownedificationtotesthowwellyouunderstandthebasicsoflensoptics.
1.Foreachsituationbelow,drawanaccurate(usegraphpaper)raydiagramshowingthepathof(atleasttwo)raysfromtheobjecttoimage.
Indicatewhethertheimageisrealorvirtualandspecifythedistanceoftheimagefromthelensandthemagnificationoftheimagewithrespect
totheobject.Ineachexample,thelensisconverging,withidenticalfrontandbackfocalpoints.Distancesareinarbitraryunits.Letf=lens
focallength,x
o
=distanceofobjectinfrontofthelens,andx
i
=distanceofimagebehindthelens.Theobjectmaybeanysize.
2.Inthefollowingexamples,therearetwoconverginglensesinsuccession.Drawraydiagramsshowingtheformationofboththeintermediate
andfinalimagesandgiveappropriateinformationaboutthenature(real/virtual),positions,andsizesoftheintermediateandfinalimages.What
isthemagnificationateachstageofimageformationandwhatisthemagnificationofthefinalimage?Thedistancefromthecenteroflens1(L1)
tothecenteroflens2(L2)equalsD.
I.A.5.ElectronOptics/ElectronLenses
a.Electronemission
Innershellelectronsinmetalatomsshieldtheelectricfieldofthenucleusthroughtherepulsiveforcestheyexertontheoutershell(valence)
electrons.Thustheattractionbetweenthevalenceelectronsandthenucleusisreduced.Metalatomsarecharacterizedashavingtwoloosely
boundvalenceelectronswhichmigratefreely(thisiswhymetalsaregoodelectricalconductors)andcanescapefromthemetalcompletelyif
sufficientadditionalenergyisimpartedtothem.Asthetemperatureofametalisincreased,thekineticenergyoftheelectronsincreasesbecause
ofincreasedthermalvibrationsofthemetalions,whichcollidemorefrequentlywiththeelectrons.Thermionicemissionisthetermusedto
describetheprocessbywhichthermalenergyissuppliedtolooselyboundelectronsinordertoformasourceofelectrons.
Atroomtemperatureelectronsareeffectivelypreventedfromescapingthesurfaceofthemetalowingtotheattractiveforceofthepositively
chargedions.Asthetemperatureisincreasedsomeelectronsacquiresufficientenergytoovercometheattractionandleavethemetal
temporarily.Metal,shapedasathinwire,caneasilybeheatedbypassinganelectriccurrentthroughit.Sincethemetalsurfacebecomes
positivelycharged,acertainlevelofenergy(workfunction)mustbesuppliedtoallowelectronstoescapefromthesurface.Eachmetalhasa
characteristicworkfunction.Tungsten,withalowworkfunction,emitsmoreelectronsthanmetalswithhigherworkfunctions(seealsopp.2930
andFig.I.59).
Ifastrongelectrostaticfieldisappliedinavacuumbetweenthewire(givenanegative,cathode,potential)andananode,theelectricfieldwill
causeelectronstoaccelerateawayfromthewiretowardstheanodesurface(Fig.I.33).Thespeedoftheelectronsdependsonthestrengthof
theelectrostaticfield(voltage)betweenthecathodeandanode(equation(3),Sec.I.A.3.b)Thenumberofelectronswhichleavethewire
dependsonthetemperaturetowhichthewireisheated,whichdependsonhowmuchfilamentcurrentpassesthroughthewire.
A"V"shapedwirewillhavethehighesttemperatureatthetip.Electronswithdrawnfromthefilamenttipcarryelectricchargestotheanode.This
electriccurrent,whichflowsbetweenthefilamentandtheanode,iscalledthebeamcurrent.
1)Electricfield/Equipotentials
Anelectricallychargedobjecthasassociatedwithitanelectricfield.Thus,anelectricallychargedparticle,whenbroughtnearachargedobject,
isinfluencedbyanelectricalforceinthevicinityoftheobject.Theforceisdirectedtowardthechargedobjectifthechargesareofopposite
signsandawayfromtheobjectiftheyareofsimilarsign.DEFINITION:Thedirectionofanelectricfieldisdefinedasthedirectionoftheforce
actingonapositivecharge.(Figs.I.3435)
Alongthelinesofforceconnectingthetwocharges,theelectricpotentialwillchangegraduallybetweentheextremevaluesrepresentedbythe
twocharges.DEFINITION:Equipotentiallinesdefinethepointsalongthelinesofforcewithidenticalelectricalpotential.Theseequipotential
surfacesarealwaysorientedperpendiculartothelinesofforce.Thechangesintheelectricpotentialaregradualinspace.
Electronswhichenterafieldbetweentwoparallelplatesinadirectionparalleltotheplatesareaffectedbytheforcedirectedperpendicularto
theplates(FigI.36).Theelectronswillbeattractedtowardthepositiveplate.Thepathchangesinaseriesofgradualstepsattheequipotential
surfaces.
FigureI.37showshowtheelectronpathis"refracted"attheequipotentialsurface.TheresultisfundamentallythesameasthatgivenbySnell's
Lawofrefractioninlightoptics.Aconsequenceofthisisthatasphericallycurvedequipotentialsurfaceexhibitsthepropertiesofalens.
FiguresI.38andI.39showhowbothpositive(converging)andnegative(diverging)electrostaticlensescanbeformed.Thisfeatureof
electrostaticlensesdiffersfromelectromagneticlenseswhichcanonlyactasconverginglenses.
2)Advantages/Disadvantagesofelectronlenses:
Thefactthattherefractiveindexdoesnotchangeabruptlyinelectronlenseshasoneadvantageinthattherearenotroublesomereflectionsat
equipotentialsasatglassinterfaces.Thereisaseriousdisadvantageinthatequipotentialscannotbeshapedandcombinedinarbitraryfashionto
correctforchromaticaberrationandothererrors.
Althoughelectronmicroscopeswhichemployelectrostaticlenseshavebeenmade,mostmicroscopesuseelectromagneticlenses.Amajorreason
isthatelectrostaticlensesaremoresensitivetothequalityofthevacuumandcleanlinessofthecomponentsthanareelectromagneticlenses.
Somelensaberrationsaremoresevereforelectrostaticlensescomparedtoelectromagneticlenses.Electrostaticlensesrequireverypowerful
electrostaticfieldswhichcanleadtoelectricalbreakdownor"arcingover"insidethecolumn,especiallyunderpoorvacuumconditions.Forthis
reason,electrostaticlensescannotbemadewithfocallengthsasshortasmagneticlenses.
b.Electrostaticlens
Abasicunderstandingofelectrostaticlensesisimportantfortwomainreasons:i)theelectrongunuseselectrostaticlensactiontoformthe
primarybeamsource,andii)itisquitecommonforachargetodeveloponthenonconductingcontaminationwhichmayaccumulateonphysical
apertures(suchastheobjectiveaperture)andtransformthemintoweakelectrostaticlenseswhichcandistorttheelectronimage.
3)Propertiesofelectrostaticlenses:
a)Anyaxiallysymmetricalelectrostaticfieldhasthepropertiesofalensforraysconfinedtotheparaxialregion.Alltheideallensformulasapply
toelectrostaticlenses.
b)Forelectronlenses,replaceÃ(f)forrefractiveindexinthelensequations(f=valueofthepotentialontheaxis).Intheimageformingsystem
ofmostTEMs,fisthesameonbothsidesofthelens(SeeSec.I.A.5.c).
c)Ifboundedbyregionswherefisconstant,anelectrostaticlensisalwaysconvergent.
c.Magneticfieldsandmagneticlenses
1)Magneticfield
Anelectriccurrentpassingthroughaconductorgivesrisetoamagneticfield.TheconventionisthatNisthedirectioninwhichthelinesofthe
magneticfieldpoint(Fig.I.40).Themagneticfluxisthetotalnumberoflinesandthefluxdensityisthenumberoflinesperunitareaofasurface.
UsetheRIGHThandruletodeterminethedirectionofthefield(thumbpointstowardcurrentdirectionandfingerscurlindirectionoffield.NOTE:
Byconvention,thedirectionofelectronflowisoppositetothatofcurrentflow.
Fluxdensitydependsonthepropertiesofthematerialsurroundingtheconductor.Ironinducesahigherfluxdensitythanairoravacuum.The
propertyofthematerialwhichaffectsthefluxdensityiscalledthepermeability,m,ofthematerial.Forairandvacuum,m=1.0.For
ferromagneticmaterialsitcanbeaslargeasseveralhundredthousand.
Iftheconductorhastheshapeofacircularloop,thelinesofforceformcirclesaroundtheloop.Thefluxdensityisgreatestatthecenterofthe
loop.Themagnetinthecenteroftheloopisorientedperpendiculartotheplaneoftheloopifthecurrentthroughtheloopissufficientlystrongto
eliminatetheinfluenceoftheearth'sfield.ThesideoftheloopatwhichthelinesofforceleavetheloopistheNorth(N)poleofthemagnet(Figs.
I.41,I.42).
Ifthewireiswoundinseveralturnsaroundacylindricalsurface(solenoid),eachturnwillcontributetotheinducedmagneticfield.Theflux
densityinthecenterofthecoilisgivenby:
Inthecaseofairandnonmagneticmaterials,µ=1.0andB=H.
Thepermeabilityofirondependsonthefieldstrength,H,anddecreasestounityathighfieldstrengthorwhenthefluxdensity,B=H(Fig.I.43).
Thehighpermeabilityofironisduetotheinducedmagneticfieldorientingmicroscopiccrystalregionsactingastinymagnetsintheiron.Allthese
tinymagnetsaddtheirmagneticfieldstotheinducedfield(Fig.I.44).Whenallmicromagnetsarenearlyoriented,theironwillaffecttheflux
densitytoadecreasingamountsincethereorientationofmicromagnetsisnearingcompletion.Thus,thepermeabilityofironathighfieldstrengths
approachesthatofemptyspace.Atthispointtheironreachesmagneticsaturation.
2)Hysteresis
Thestrengthofthelensdependstosomeextentonthepreviousmagnetichistoryof
thelens.Whenthecurrentinalensisreduced,thedecreaseinmagnetizationdoes
notretracethesamepathobtainedwhenthecurrentwasincreased(Fig.I.45).
Inductionofmagnetizationinvolvesaphysicalmovementwithinthemagnetized
material,requiringtheovercomeofacertaindegreeofinertia.Asaresult,
magnetizationtendstolagbehindthemagnetizingforceapplied.Inducedmagnetic
fluxcanonlybereturnedtozerobyapplicationofacurrentintheoppositedirection.
Aconsequenceofhysteresisisthatthelevelofcurrentusedtoenergizeamagnetic
lensDOESNOTpreciselyspecifythelensstrength(i.e.focallength).
NormalizationofTEMlensesisaccomplishedbyreducingthelenscurrenttozero
somepredeterminednumberoftimes.Hysteresismayalsobeminimizedbytakinga
lenstosaturationandthenreturningittotheworkingcurrentwithoutovershooting.
Whenthefieldstrengthisreducedtozero,somemagnetizationstillremainsintheiron
(residualmagnetizationorremanence).Anadvantageofsoftironisthefactthat,
whenusedinanelectromagnet,hysteresisislow.
Introductionofpiecesofironinamagneticfielddrasticallyaffectsthefluxdensity.
Magneticmaterialhasashieldingeffect,theeffectbeinggreaterthegreaterthe
permeability.Permalloy(mmetal)hasamaximumpermeabilityof80,000140,000
comparedtoironusedintransformers(~7000).mmetalpermeabilityislimitedtolower
fieldstrengthsthanthatatwhichironstillretainshighpermeability.Thismetalis
thereforeusefulforshieldingtheTEMfromexternalmagneticfields.
d.Theelectromagneticlens
1)Lensdesigndevelopment(Figs.I.46I.48)
Theefficiencyofthemagneticfieldproducedbyashortsolenoidwasfirstimproved
byencasingtheenergizingcoilinasheathofsoftironwhichhasthepropertyofconcentratingthelinesofforceinamagneticfieldandthus
becomingmagnetizedbyinduction.Inthiswayamuchmorepowerfulaxialmagneticfieldisobtainedforthesameamountofcurrentflowing
throughthesolenoid.Furtherdevelopmentinvolvedencasingtheentirecoilwithsoftironexceptatanarrowannulargapintheinsideofthecoil.
Thisproducesagreaterconcentrationofthemagneticfieldalongashortaxialdistance.Toachieveshorterfocallengthlenses(andobtaingreater
magnifications)asoftironpolepiecewithanopenaxialborewasintroducedatthepositionoftheannulargap.
MagneticlensesusedinTEMsarealwaysconstructedwithanironcircuittoproduceahighfieldstrengthacrossashortgap.Themagneticfields
forTEMlensesareintherangeof10,00020,000gauss.
2)Forcesactingonacurrentinamagneticfield
Theforceonanelectroninamagneticfieldisalwaysatrightanglestothevelocityandthedirectionofthefield(Figs.I.49,I.50,andI.52).The
fieldonlyactsonthevelocitycomponentwhichisdirectedperpendiculartothelinesofforce.Usethelefthandrule(Fig.I.51:firstfingerfor
fielddirection,middlefingerforcurrentdirection,andthumbfordirectionofforce).Rayspassingthroughthelensareturnedthroughanangle
whichdoesNOTdependonthedistanceoftheraysfromtheaxis.Allelectronscontainedinagivenmeridionalplanebeforeenteringthefieldare
containedinarotatingmeridionalplaneastheypassthroughthelens,andthentheyleavethelenscoplanar.
Whenelectronsenterthelenstheyencounterasidewaysforcewhichcausestheelectrontorotate
asitcontinuesthroughthelens(Figs.I.53I.57).Sincetheradialcomponentofthemagneticfield
reversesafterthecenterofthelens,therotationalvelocitysetupinthefirsthalfofthelensis
countered.Theelectronenteredthelenswithoutangularmomentumabouttheaxisandleaves
withoutangularmomentum.Theneteffectisadeflectiontowardtheaxis,whichitmustcrossatthe
focalpointf
2
.Theanglebetweentheobjectvectorandtheimagevectoris180°+q,whereas,for
glasslensesandelectrostaticlenses,theanglebetweenarealobjectandtheimageisexactly180°.
Sincetheradialforceisdirectedtowardtheaxis,thelensisconvergentnomatterwhatthedirection
ofthefield.
3)Propertiesofamagneticlens:
Anyaxiallysymmetricmagneticfieldhasthepropertiesofanideallens.Alltheformulasfortheideallensmaybeapplied.
Magneticlensesarealwaysconvergent.Theconventional,axiallysymmetriclensisalwaysboundedbyregionswhicharefieldfree,the
consequencebeingthatthenetactionofelectronlensesisinevitablyconvergent.Limitedregionsmaybedivergentbutnotthelensasawhole.
Theseriousconsequenceofthisisthatneithersphericalorchromaticaberrationscanbecorrectedasisdoneinlightopticsbytheusedoublets
ofpositiveandnegativelenses.
Intheabsenceofelectrostaticfields,therefractiveindexisthesameinobjectandimagespace,thereforef
1
=f
2
.
Electronstravelingthroughaxiallysymmetricfieldsexperienceaspiraltrajectoryofdiminishingradius.Theimagevectorisatanangle180°+qto
theobjectvector.
Thedeflectionoftheelectrontowardstheaxismeansthatanelectronenteringthelensparalleltoitsaxiswillcrosstheaxisafterhavingpassed
thelens.Thedeflectionwillincreasewiththedistancefromtheaxis.Thus,abeamofelectronsinparallelpathsparalleltotheaxisofthelenswill
befocusedtoanimagepointontheaxiswhichrepresentsthesecond(back)focalpointofthelens(f
2
).Notethatmagneticlensesarehighly
inefficientinthatonlyaminorportionofthetotalfieldstrengthisactuallyeffectiveinfocusingtheelectron.
4)Magneticlensfocallength
Inamagneticelectronlensthefocallengthisdeterminedbythefieldstrengthinthelensgapandbythespeedoftheelectrons(determinedby
theacceleratingvoltage).
Formagneticlenses,focusingisachievedbyvaryingthecurrentwhichpassesthroughtheelectromagnet.Thisinturnchangesthestrengthof
themagneticfieldandtherebyaltersthefocallengthofthelensandisequivalenttoacombinedchangeinboththe"refractiveindex"and
"curvatureofsurface".Forabeamofmoreenergeticelectrons,thelenscurrenthastobeincreasedinordertokeepthefocallengthconstant.
FocallengthandcurrentareNOTlinearlyrelated:strengthincreasesinasigmoidfashion(Fig.I.45)ascurrentincreasesuntilapointisreached
wherethelensissaturatedandnofurtherincreaseinlensstrengthcanbeachieved.
Sincethefocallengthofthelensisdirectlyproportionaltotheacceleratingvoltage,avariationinthevelocityoftheelectronsintheimaging
beamaffectsimagequalitybyeliminatingperfectfocus(chromaticaberration).
5)Magneticlensdesign:(Figs.I.46,I.47).
Condenserlensesusuallyhavearelativelylargeboreandspacingwhichresultsinalongfieldandlongfocallength.
Typicalconstructionoftheobjectivelensproducesastrongfieldofshortaxialextent(i.e.shortfocallengthbetween(1.53mm)necessaryfor
formationofimagesathighmagnification.Thespecimenisplacedwithinthemagneticfieldoftheobjectivelens.Thus,anyfieldintroducedby
contaminantsinthespecimencandistortthefieldofthelens.Notethatthisalsomeansthatpartofthelensfield("prefield")isonthefrontside
oftheobjectandaffectstheelectronbeambeforeitpassesthroughtheobject.
Mostofatypicalmagneticlensliesoutsidethevacuumofthemicroscope.Onlythoseregionsthroughwhichtheelectronbeampassesareinhigh
vacuum.Magneticlensesmustbewatercooledtodissipatethelargeamountsofheatproducedbythecurrentsintheelectromagnetcoils.
DATE NAME EVENT
1897 J.J.Thompson Discoverstheelectron
1924 LouisdeBroglie Identifiesawavelengthtomovingelectrons
l =h/mv
where
l =wavelength
h=Planck'sconstant
m=mass
v=velocity
(Foranelectronat60kVl=0.005nm)
1926 H.Busch Magneticorelectricfieldsactaslensesforelectrons
1929 E.Ruska Ph.Dthesisonmagneticlenses
1931 Knoll&Ruska Firstelectronmicroscopebuilt
1931 Davisson&Calbrick Propertiesofelectrostaticlenses
1934 Driest&Muller SurpassresolutionoftheLM
1938 vonBorries&Ruska FirstpracticalEM(Siemens)10nmresolution
1940 RCA CommercialEMwith2.4nmresolution
1945 1.0nmresolution
Fig.I.1Comparisonoflightandelectronmicroscopes.Ineach
instrument,illuminationfromthesource(lamp,filamentinthe
electrongun)isfocusedbythecondenserlensontothespecimen.
Afirstmagnifiedimageisformedbytheobjectivelens.Thisimage
isfurthermagnifiedbytheprojectorlensontoagroundglass
screen(light)orfluorescentscreen(electrons).(FromAgar,p.8)
Fig.I.2CrosssectionalviewofthePhilipsEM300.(FromAgar,p.40)
Toviewtheanimatedmicroscope,clickhere.
Note:QuickTimePlugInrequired
(Thiscanbedownloadedathttp://apple.com/quicktime/download)
Fig.I.3Sectionthroughacomplex
doublecondenser6lensPhilips
EM200electronmicroscope.(From
Meek,p.99)
Fig.I.4Thestatisticalnatureofdiffraction
patterns.(FromHall,p.13)
"Theprecisenatureof'electronwaves'or'matterwaves'isverydifficulttounderstandordescribeinmaterialterms.Electronwavesarenot
electromagneticradiationofthekindtowhichlight,Xraysandradiowavesbelong.Theyconstituteasortofquantumor'packet'ofradiationwhich
accompanieseachindividualelectron,followingitspathandnotradiatingoutwardsfromit."(Meek,1976,pp.4849).
V l (nm)
v(
•
10
10
cm/sec)
v/c
10,000 0.0123 0.593 0.198
50,000 0.0055 1.326 0.442
100,000 0.0039 1.875 0.625
1,000,000 0.0012 5.930 1.977!
V l (nm)
v(
•
10
10
cm/sec)
v/c
10,000 0.0123 0.593 0.195
50,000 0.0055 1.326 0.414
100,000 0.0039 1.875 0.548
1,000,000 0.0012 5.930 0.941
FigI.5Aperfectpointsourcecannotbe
imagedbyalensasaperfectpointimagedue
tothepresenceoftheapertureAB(which
maybetheedgeofthelens).Diffractionat
thisaperturegivesrisetoaseriesoffringes,
whichsurroundtheimageformedofthepoint
source.Thepatternproducediscalledan'Airy'
disk.(FromMeek1sted.,p.35)
Fig.I.6Wheneverawavefrontstrikesa
barrier,itcanbendaroundthecorner'by
givingrisetoasecondarywavefrontatthe
edge,sinceeachpointonthewavefrontcan
giverisetoanewsourceofwaves.This
phenomenoniscalled'diffraction'.(FromMeek
1sted.,p.22)
Fig.I.7Diffractionpattern(right)formedbyanirregularlyshapedaperture
(left).(FromYoung,p.95)
Fig.I.8(a)
Photographof
theedgeofa
razorblade
illuminatedby
monochromatic
(blue)light
rendered
coherentby
passing
througha
narrowslit.(b)
Microdensitometer
tracingofthe
negativefrom
whichthe
photograph
wasmade.
FourFresnel
fringescanbe
distinguished.
(FromMeek1st
ed.,p.27)
(a)
(b)
(a) (c)
(b)
Fig.I.9(a)Fresnelfringesformed
byelectrons.Thesefringesare
formedoutsidetheedgeofahole
(white)inacarbonfilm(black).(b)
Amicrodensitometertracingofthe
fringesystem;thepatternis
identicalwiththeFresnelfringe
systemformedbyvisiblelight(see
Fig.I.8).(c)Anunderfocusedimage
ofaholeinafilm,showinga
completesystemofabout40
Fresnelfringesinsidethehole.
(FromMeek1sted.,pp.2930)
Fig.I.10Diffractionimagesoftwo
easilyresolvedpoints.(From
Slayter,p.243)
Fig.I.11Imagesoftwo
incoherentlyilluminatedpointsat
thelimitofresolution.(a)individual
intensities;(b)summedintensities.
(FromSlayter,p.244)
Fig.I.12Examplesofwhatoccurswhentwo
wavesofthesamewavelengthandequal
amplitudeadd.Ineachexample,thetwo
separatewavesareshownontheleftand
theirsumorresultantwaveontheright.The
differentexamplesarecharacterizedbyvarying
phasedifferences.Thephaseofawave
(usuallyexpressedasafractionofthe
wavelengthorindegrees)isthepositionofa
crestrelativetosomearbitrarypoint.Although
thephaseofagivenwavevarieswithtimeas
thewavetravels,thedifferenceinphaseofthe
twowavesofthesamewavelengthwiththe
samevelocity,isindependentoftime.Such
wavescaninterferewithoneanother.The
resultantwavehasthesamewavelength,l .
(a)Phasedifferencezero.Thewavestotally
reinforceandaresaidtobe"inphase"orto
showconstructiveinterference.
(b)Phasedifferencel /4.Partialreinforcement,
givingawaveofamplitude1.4(intensity2.0).
(c)Phasedifferencel /2.Thewavesare"outof
phase"andthereistotaldestructive
interferencetogivenoresultantwaveora
wavewithamplitude0(intensity0).(From
GluskerandTrueblood,p.19)
Fig.I.13Photographofan
interferencepatterninwater
wavesformedbythe
superpositionofwavesfromtwo
sourcesoscillatinginphasewith
thesamefrequency.(FromYoung,
p.22)
Fig.I.14Theangularapertureofthe
eyeisrelativelysmall.(FromMeek,
1sted.,p.13)
Fig.I.15Increasingtheangular
apertureoftheeyewithalens.The
lensallowstheobjecttobeheld
closertotheeye,whichisthereby
enabledtogathermoreinformation.
(FromMeek1sted.,p.14)
Fig.I.16Theinteractionofwaves
withanobstacle.Theboatridesthe
longwavelengthoceanwave,but
reflectsthesmallwavelength
surfaceripple.Anobserverwho
wishestodetectthepresenceof
theboatcandosoonlyby
observingwaveswhichhave
wavelengthssmallerthan,or
comparableto,thelengthofthe
boat.(FromSherwood,p.19)
Maximummagnification=
resolvingpoweroftheeye
resolvingpowerofthemicroscope
(a)
Fig.I.17(a)TwoAiry
disksrepresenting
twoimagepoints
shownatincreasing
separationfromleft
toright.Inthe
pictureatthe
extremerightthe
twodiskscanbe
distinguishedas
separatedisks.
(b)Theintensity
distributionatanAiry
disk.R,halfwidthof
thecentralmaximum
representedbya
bellshapedcurve.
(c)TheRayleigh
criteriaforresolution.
(FromSjostrand,
p.115)
i=r
Fig.I.18Reflection.(FromSlayter,
p.4)
Fig.I.19Refraction.(FromSlayter,
p.6)
Fig.I.20Principalraydiagramsshowing
imageformationbyaconvexlens.
(a)Whentheobjectdistanceisgreater
thanthefocallength,areal,inverted
imageisformed.
(b)Whentheobjectdistanceisless
thanthefocallength,avirtual,erect
imageisformed;itspositionis
obtainedbyprojectingtheprincipal
raysbackward.Theraysappearto
comefrompointQ.(FromYoung,
p.127)
Fig.I.21Definitionof
principalfocus,F,inimage
spaceofalens.(From
Sjostrand,p.20)
Fig.I.22Focusingeffectoflenson
raysoriginatingfrompointson
principalaxislocatedatdifferent
distancesfromthelens.(From
Sjostrand,p.21)
Fig.I.23Definitionofprincipal
focusinobjectspaceF1ofa
lens.(FromSjostrand,p.21)
Fig.I.24VirtualimageQof
objectpointlocatedbetween
principalfocusinobjectspace
andthelens.(FromSjostrand,
p.21)
Fig.I.25Constructionoftheimage
ofanobjectbymeansofray
tracing.(FromSjostrand,p.22)
Fig.I.26Magnifyingeffectof
apositivelens.(From
Sjostrand,p.22)
Fig.I.27Virtualmagnified
imageofobjectlocated
betweenprincipalfocusin
objectspaceandthelens.
(FromSjostrand,p.22)
Fig.I.28Amagnifyingglassformsan
enlarged,erectvirtualimage.The
angularsizeofthisimageis
approximately4"/15"or4/15.The
angularsizeoftheobjectatthe
closestdistanceforcomfortable
viewingis1"/10"or1/10.The
magnificationinthissituationis(4/15)/
(1/10),or22/3.(FromYoung,p.130)
Fig.I.29Theangularapertureofa
lens.Theangle2a isthe
acceptanceangleofthelens,and
thelargeritcanbemade,themore
informationcanthelenstransmit.A
largelensofhighaperturecan
thereforetellusmoreaboutan
objectthanasmalllensoflow
power.(FromMeek1sted.,p.12)
Fig.I.30Raydiagramforhighmagnification
modeofoperation.Notethateachlens
formsarealimage,withimageinversion.
I0istheimageformedbytheobjective
lensO,I1isformedbythefirstprojector
lensP1andI2bythesecondprojectorP2,
onthescreen.(FromAgar,p.30)
Fig.I.31Left:raydiagramofthe3realimagemediumandhighmagnificationimagingsystemofa3lens
microscope.Center:2realimageverylowor'scan'magnificationrangeofa3lensmicroscope.Right:2real
imagelowmagnificationsystemofa3lensmicroscope.(FromMeek1sted.,pp.118,120121)
Fig.I.32Raydiagramforacompleteelectron
microscope.FilamentF,condenser1lensC1,
condenser2lensC2,condenserapertureCA,
specimenS,objectivelensO,objectiveaperture
OA(inbackfocalplane).1stintermediateimage
andselectorapertureSA.IntermediatelensP1,
secondintermediateimageI2,projectorlensP2
andfinalimageonthefluorescentscreenFC.
(FromAgar,p.35)
a)f=2.0
x
o
=5.0
e)f=4.0
x
o
=3.0
b)f=10.5
x
o
=21.0
f)f=13.3
x
o
=13.3
c)f=3.5
x
o
=3.0
g)f=3.142
x
o
=0.0
d)f=5.0
x
o
=2.5
a)D=8.0
L1:f=2.0
x
o
=4.0
L2:f=3.0
b)D=8.0
L1:f=2.0
x
o
=6.0
L2:f=3.0
c)D=4.0
L1:f=2.0
x
o
=3.0
L2:f=2.0
FigI.33Accelerationofelectronin
electricfield.(FromSjostrand,p.26)
Fig.I.34Linesofforceatapositively
chargedsphericalbody.(FromSjostrand,
p.32)
Fig.I.35Linesofforceandequipotential
surfaces(stippledlines)associatedwith
twoequalchargesofoppositesign.
(FromSjostrand,p.32)
Fig.I.36Equipotentialsurfacesattwoparallel
platesofoppositechargeswiththepathofan
electronindicatedwithinthehomogeneous
partofthefield.(FromSjostrand,p.33)
Fig.I.37Refractionofelectronatan
equipotentialsurface.(FromSjostrand,p.33)
Fig.I.38.Negativelensactionof
electrostaticfieldatanaperturewhen
V2V1>V3V2.(FromSjostrand,
p.34)
Fig.I.39.Positivelensactionatan
aperturewhenV2V1<V3V2.
(FromSjostrand,p.34)
Fig.I.40Magneticfieldinducedbycurrent
passingthroughaconductor.(From
Sjostrand,p.35)
Fig.I.41Magneticfieldinducedbycurrent
passingthroughasolenoid.(From
Sjostrand,p.37)
Fig.I.42Solenoidwithironcore.(From
Sjostrand,p.40)
Fig.I.43a.Dependenceofpermeabilityonfluxdensity,B.
b.RelationshipbetweenfluxdensityBandfieldstrength.
(FromSjostrand,p.38).
Fig.I.44Magnetization.(FromSlayter,
p.361)
Fig.I.45Curves
showinghowthe
magnetizationof
softiron(lens
strength)is
relatedtothe
magnetizing
force(lens
current).An
unmagnetized
lensstartsfrom
thepointOand
followsthepath
OAaslens
current
increases.Atthe
pointA,further
increaseinlens
currentproduces
nofurther
increaseinlens
strength;thelensissaidtobe'saturated'.Whenlenscurrent
isreduced,thepathOAisnotretraced;adifferentpathABis
followed.Thisdisplacementiscalled'hysteresis'.Atzero
current(pointB),someresiduallensstrengthremains;thisis
called'remanence'.Tobringthelensbacktozerostrength,a
reversecurrentOCmustbeapplied.Lensstrengththen
increaseswithincreasingreversecurrent,followingthepath
CD.Thepolarityofthelenschanges,butthisdoesnotaffect
itsfocusingpower;onlythespiralelectronpathisreversed.
Becauseofhysteresis,itisnotpossibletocalibratealens
currentmeteraccuratelyintermsoflensstrengthor
magnification.
Fig.I.46Evolutionofmagneticelectron
lenses.(A)Shortsolenoidusedasa
magneticlens.(B)Softironcasing
enclosingoutersurfaceofthesolenoid,
thusconcentratingthefield.(C)Soft
ironencasingthesolenoidexceptata
narrowannulargaptherebyreducing
themagneticfieldtoaveryshortregion
alongthelensaxis.(D)Modern
objectivelensconsistingofasoftiron
encasedsolenoidandsoftironpole
piecessoastohaveanenormously
concentratedfieldatthelevelofthe
annulargap.(FromWischnizter2nded.,
p.33)
Fig.I.47(a)Amagneticlensconsisting
ofatightlywoundcoilandasoftiron
shroudsurroundingthecoilexceptfor
asmallgap.Thefieldisconcentratedin
thatgap.(b)Shortfocallength
electromagneticlenswithpolepieces.
(FromSjostrand,p.50)
Fig.I.48Fieldstrengthdistribution
curves.ThecurvesADcorrespondto
therespectivelensesillustratedinFig.
I.46.Eachrepresentsthefieldstrength
alongthelongaxisofthelens.The
changesintheshapeofthecurves
representtheshorteningor
concentrationofthefieldovera
shorteraxialdistance.Hz=
longitudinalmagneticfield.Z=
distancealongtheaxisofsymmetry.
(FromWischnizter2nded.,p.33)
Fig.I.49TheforceFactingon
astraightconductorina
homogeneousmagneticfield
offluxdensityBwhencurrent
Iispassedthroughthe
conductor.(FromSjostrand,
p.43)
Fig.I.50Pathofanelectronina
magneticfield.(A)Inalarge,uniform
magneticfield.(B)Inasmall,uniform
magneticfield.(FromWischnitzer2nd
ed.,p.25)
Fig.I.51Lefthandthumbrule.
(FromSjostrand,p.43)
Fig.I.52Thompson'sexperiment.A
streamofelectronsoriginatingfroma
sourceandpassing,invacuo,through
amagneticfieldproducedbyapairof
magnetswillbedeflected.The
directionofdeflectiondemonstrates
thatelectronsarenegativelycharged
particlesofmatter.(FromWischnitzer
2nded.,p.25)
Fig.I.53Actionofasolenoidonan
electronbeam.Anelectriccurrent
passingthroughthecoilproducesan
axialmagneticfield.Thisisthe
refractingmediumfortheelectrons.An
electronstartingatapointontheaxisA
andatanangletoitfollowsaspiral
path,returningtotheaxisatthepoint
B.Theactionisbasicallysimilartothat
oftheconverginglightlensshownin
Fig.I.20.(FromMeek1sted.,p.8)
Fig.I.54Actionofthemagnetic
lens.(a)Inperspective.(b)
Electrontrajectoryin
projection,alongdirectionof
propagation.(c)Electron
trajectoryinprojection,side
view.(FromSlayter,p.358)
Fig.I.55Componentsofthe
vectorHneartheaxisoffields
withaxialsymmetry.His
representedbytwo
components,Hz,the
componentinthez(axial)
direction,andHr,the
compnentinther(radial)
direction.(FromHall,p.85)
Fig.I.56Theycomponentof
themagneticfieldina
magneticlensisoriented
perpendiculartothedirection
ofanelectronenteringthe
lensalongapathparallelto
thelensaxis.Thisy
componentwillaffectthe
electron,deflectingitinthex
directionasindicatedbythe
arrowmarkedvx.(From
Sjostrand,p.48)
Fig.I.57Thezcomponentofthemagneticfield
andthexvelocitycomponentoftheelectron
inamagneticlensinteract,deflectingthe
electronintheydirectiontowardthelens
axis.(FromSjostrand,p.49)
CuuDuongThanCong.com https://fb.com/tailieudientucntt
cuu duong than cong . com
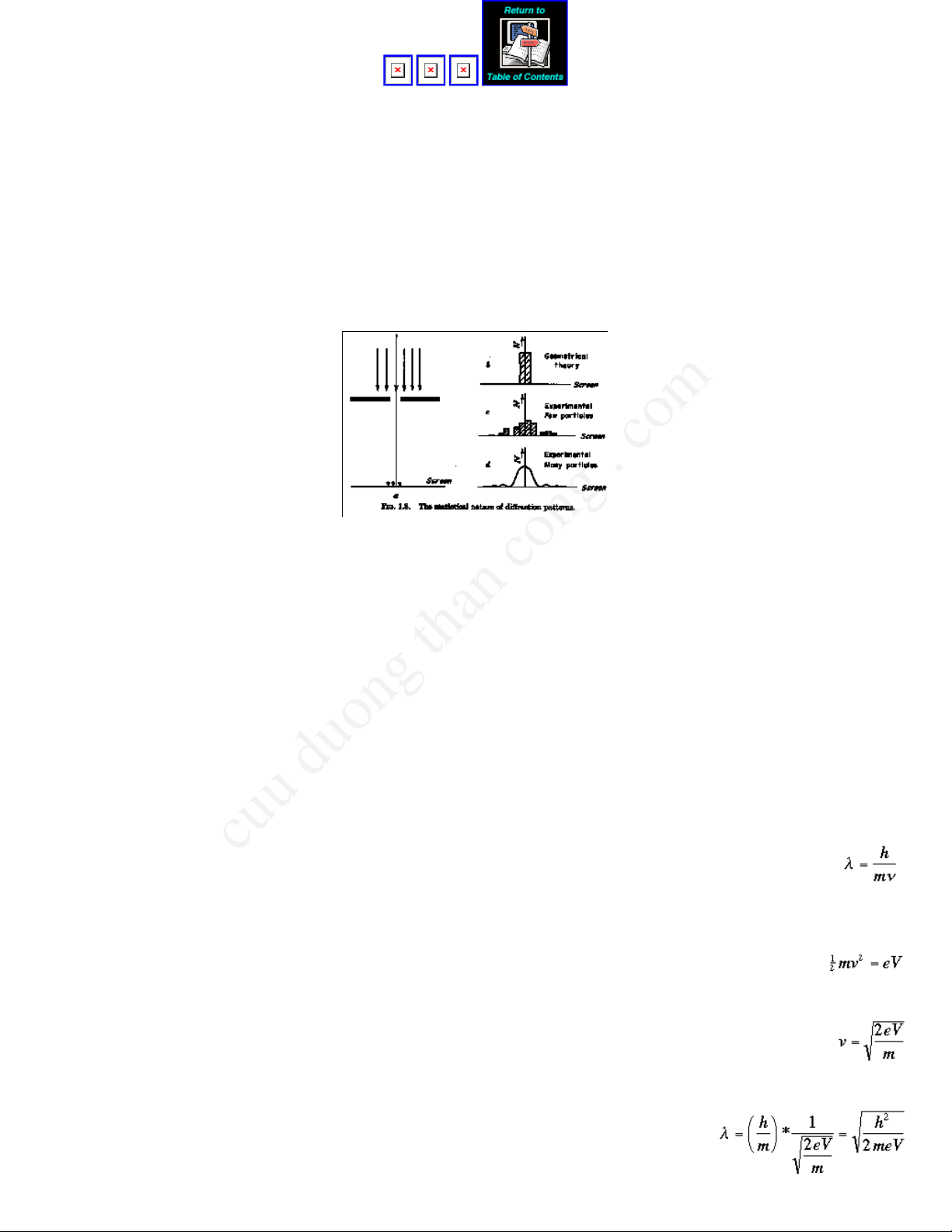
I.THEMICROSCOPE
I.A.PRINCIPLESOFTHETRANSMISSIONELECTRONMICROSCOPE(TEM)
I.A.1.OriginoftheTransmissionElectronMicroscope
I.A.2.ComparisonofLight(LM)andElectronMicroscopes(Fig.I.1)
a.Similarities(Arrangementandfunctionofcomponentsaresimilar)
1)Illuminationsystem:producesrequiredradiationanddirectsitontothespecimen.Consistsofasource,whichemitstheradiation,anda
condenserlens,whichfocusestheilluminatingbeam(allowingvariationsofintensitytobemade)onthespecimen.
2)Specimenstage:situatedbetweentheilluminationandimagingsystems.
3)Imagingsystem:Lenseswhichtogetherproducethefinalmagnifiedimageofthespecimen.Consistsofi)anobjectivelenswhichfocusesthe
beamafteritpassesthroughthespecimenandformsanintermediateimageofthespecimenandii)theprojectorlens(es)whichmagnifiesa
portionoftheintermediateimagetoformthefinalimage.
4)Imagerecordingsystem:Convertstheradiationintoapermanentimage(typicallyonaphotographicemulsion)thatcanbeviewed.
b.Differences
1)Opticallensesaregenerallymadeofglasswithfixedfocallengthswhereasmagneticlensesareconstructedwithferromagneticmaterialsand
windingsofcopperwireproducingafocallengthwhichcanbechangedbyvaryingthecurrentthroughthecoil.
2)MagnificationintheLMisgenerallychangedbyswitchingbetweendifferentpowerobjectivelensesmountedonarotatingturretabovethe
specimen.Itcanalsobechangedifoculars(eyepieces)ofdifferentpowerareused.IntheTEMthemagnification(focallength)oftheobjective
remainsfixedwhilethefocallengthoftheprojectorlensischangedtovarymagnification.
3)TheLMhasasmalldepthoffield,thusdifferentfocallevelscanbeseeninthespecimen.Thelarge(relative)depthoffieldintheTEMmeans
thattheentire(thin)specimenisinfocussimultaneously.
4)Mechanismsofimageformationvary(phaseandamplitudecontrast).
5)TEMsaregenerallyconstructedwiththeradiationsourceatthetopoftheinstrument:thesourceisgenerallysituatedatthebottomofLMs.
6)TEMisoperatedathighvacuum(sincethemeanfreepathofelectronsinairisverysmall)somostspecimens(biological)mustbedehydrated
(i.e.dead!!).
7)TEMspecimens(biological)arerapidlydamagedbytheelectronbeam.
8)TEMscanachievehighermagnificationandbetterresolutionthanLMs.
9)Pricetag!!!(100xmorethanLM)
I.A.3.Photons/Electrons
a.Dualconceptofwaveandparticle(Fig.I.4)
Lighthaspropertiesbothofaparticleandawave.Thisdualnatureisrequiredtosatisfactorilyexplaintheresultsofvariousphysicalexperiments.
Thediffractionoflight(bendingaroundcorners)illustratesthewavenature.TheWAVETHEORYisbasedonthestatisticalnatureofeventsand
haslittlemeaningwithrespecttothebehaviorofsingleparticles.ThewavetheorywasdevelopedandexpoundedbyHuygens(16291695)and
Hooke(16381703).TheCORPUSCULARTHEORYwasproposedbyNewton(16421727)andbecamethemoreacceptedtheoryevenafter
demonstrationofdiffractionbyYoung(17731829)andinterferencebyFresnel(17881827).Atabout1850,thewavetheorycamebackinto
favoruntilabout1900whenmoreevidenceforthecorpusculartheorywasdiscovered.
QUANTUMTHEORY(PlanckandEinstein)providesthebasisforexplainingthephenomenaofINTERFERENCE,DIFFRACTIONandthe
PHOTOELECTRICeffect(lightfallingoncertainmetalscausethemtoemitelectrons)andthusformsacommonbasisforexplainingthenatureof
actionoflight.Thetransferofenergybetweenlightandmatteroccursonlyindiscretequantitiesproportionaltothefrequencyofthe
lightwave.
E=hJ
where
E=energyofphoton(joules)
h=Planck'sconstant(6.624
•
10
34
joulesec)
J=frequency(cycles/sec)
b.Electronvelocityandwavelength
Therelationbetweenthewavelength(l )ofaparticleofmass,m,movingatavelocity,v,isgivenbytheDeBrogliewaveequation:
(1)
Anelectronofchargee(1.6
•
10
19
coulomb),andmassm(9.11
•
10
28
gm),whenpassingthroughapotentialdifferenceofVvolts(expressedin
joules/coulomb),hasakineticenergy:
(2)
Solvingforvelocity:
(3)
substitutingintotheDeBroglieequation(1):
(4)
Since1joule=10
7
dyne
•
cm=10
7
cm
2
•
gm/sec
2
(5)
Thus,forexample,ifV=60,000volts,l =0.005nm.
Fromequation(3)theelectronvelocitycanbecalculatedifVisknown:
(6)
Thefollowingtableillustratesthat,athighvoltage,electronvelocityiscomparabletothespeedoflightinavacuum(c=3
•
10
10
cm/sec).
Theequationbreaksdownwhenthevelocityoftheelectronapproachesthespeedoflightbecausearelativisticcorrectionmustbemadeforthe
valueofthemasswhere:
(7)
Therelationbetweenl andVismorecorrectlygivenby:(seeHall(1966)pp.3334)
(8)
Thefollowingtableisobtainedwhenrelativityeffectsareincluded:
c.Interference/diffraction/coherence
Anideallenssystemobtainsanexactimageoftheobject(eachpointfaithfullyreproduced).Thephenomenaofdiffractionmakesthis
unattainable(Figs.I.5,I.6).
Diffractionphenomenainvolvesthebendingofthepathofradiationpassingclosetoanobstacle(Fig.I.6).Thisresultsinaspreadingofthe
radiationintotheregionbehindtheobstructionthatthewavespassed.Thediffractionatedgescontributestothecontrastatwhichanedgecan
beobserved.Diffractionalsolimitstheresolvingpowerofthemicroscopesincetheimagepointproducedbyalensisadiffractionimageofthe
openingofthelensortheaperturerestrictingtheeffectiveopeningofthelens(Fig.I.5).
Ifthelightsourceandtheplaneatwhichthediffractionpatternisobservedareatfinitedistancesfromtheedge,thephenomenoniscalled
Fresneldiffraction.Thepatternisdescribedasduetointerferencebetweenthenondiffractedlightandawaveoflightdiffractedattheedge.
Theresultingsuperpositiongivesrisetoaseriesofdiffractionfringesorientedparalleltotheedgeandrepresentingperiodicallyvaryingbrightness,
maximaandminima.(Figs.I.7,1.8,I.9).
Coherence:Aprerequisiteforinterferenceisasuperpositionofwavesystemswhosephasedifferenceremainsconstantintime.Twobeams
arecoherentif,whencombined,theyproduceaninterferencepattern.Thebeamsareincoherentwhentheyareincapableofproducingan
interferencepattern.Twobeamsoflightfromselfluminoussourcesareincoherent.Iflightfromthetwosourcesfallsonascreen,theresultant
intensityissimplythesumofthetwointensitieswhichwouldoccurfromeachsourceseparately(Figs.I.10,I.11).Inpracticeanemittingsource
hasfiniteextentandeachpointofthesourcecanbeconsideredtogeneratelight.EachsourcegivesrisetoasystemofFresnelfringesatthe
edge.Thesuperpositionofthesefringesystemsisfairlygoodforthefirstmaximaandminimabutfartherawayfromtheedgeshadowtheoverlap
ofthefringepatternsbecomessufficientlyrandomtomakethefringesdisappear.Thenatureofwaves,phase,amplitude,andinterferenceare
illustratedinFigs.I.12andI.13.
d.Resolution
1)Definitions:
RESOLUTION:abilitytodistinguishcloselyspacedpointsasseparatepoints.
RESOLUTIONLIMIT:smallestseparationofpointswhichcanberecognizedasdistinct.
RESOLVINGPOWER:resolutionachievedbyaparticularinstrumentunderoptimumviewingconditions.
2)Distinctionbetweenresolutionandresolvingpower:
Notethedistinctionbetweenresolutionandresolvingpower.Resolvingpowerisapropertyoftheinstrumentandisaquantitythatmaybe
estimatedontheoreticalgrounds.Resolutionisequaltoorpoorerthantheresolvingpowerandisthequantityobservedunderanygivenset
ofexperimentalconditions.IntheTEM,especiallywithbiologicalsamples,theresolutionachievedmaybeconsiderablyinferiortothetheoretical
resolvingpoweroftheinstrument.
Microscopyisthescienceofseeingtheverysmall.Underidealconditions,theeyeresolvesabout1minuteofarc(=1/60degree=2.9x10
4
radian;recallthereare2p radiansin360°)andsinceitcanfocusdowntoabout250mm,thesmallestobjectwecanresolveisabout0.07mm
(70mm)(Fig.I.14).Thislimitisrelatedtothesizeofthereceptorsintheretinaoftheeye.Thefunctionofamicroscopeistomagnifytheimage
fallingontheretina(Fig.I.15).Theadvantageoflightandelectronmicroscopesisthattheyeffectivelygettheobjectclosertotheeyesoa
magnifiedimageisobtainedandmoredetailcanbediscerned.
TENNISBALLANALOGY:Eyecanresolve3cmat100meters,thusatennisballisclearlyvisible.Butifthetennisballisheldupagainstawhite
background,thevisibilitydecreases(becauseofthedecreaseincontrast).
3)Abbecriteriaofresolution:
Thefundamentalnatureoflightposeslimitsonthedetailthatcanberesolved(Fig.I.16).Abbe(1893)showedthatthesmallestresolvable
distanceisabout1/2thewavelengthoflightused.Thus,1/2thewavelengthoftheradiationusedistheultimateresolvingpowerofany
instrument.Thislimitstheusablemagnificationofopticalmicroscopesto<1000X.Atfirstitwasthoughtthatxraymicroscopeswouldbeuseful
buttherefractiveindexofsubstancesforxraysisnearly=1,thusrefractinglensescannotbemadeforxrays,andconsequently,xrayscannot
beeasilyfocusedtoformimages.
4)Magnificationlimits:
Themaximummagnificationofaninstrumentislimitedaccordingtothefollowingrelationship:
Thus,fortheLM,witharesolvingpowerofapproximately0.25µm,themaximum(useful)magnificationisabout250µm/0.25µm=1000X.Thevalue
usedfortheresolvingpoweroftheeyeinthisexample(250µm)representsamorerealisticviewingcondition.Anymagnificationabovethevalue
givenbytheaboveformularepresentsemptymagnification,sincesuchmagnificationleadstonomoreusefulinformationbutratheramagnified
blur.
AccordingtotheAbbecriteria,at60,000volts,theTEMshouldhavearesolvingpowerofabout0.0025nm.Thisshouldallowamaximumuseful
magnificationofabout100milliontimes!!!Inpractice,themaximumusefulmagnificationoftheTEMoperatedat60kVislimitedtomuchlessthan
1,000,000X.Thus,althoughtheLMnearlyobeystheAbbecriteria,theTEMfallsshortbyaconsiderableamount.Themainlimitingfactorinthe
TEM,withrespecttoachievingthetheoreticalresolvingpoweroftheinstrument,concernsthenatureoftheimaginglensesandtheprocessof
imageformation.
5)Rayleighcriteria(practicalbutarbitrary):(Fig.I.17).
Itistheabilityofmicroscopestomakeobjectpointswhichareclosetogetherappearintheimageasseparatepoints.Anideallenstakeseach
objectpointandrepresentsitexactlyasapointintheimage.Areallenstakeseachobjectpointandspreadsitoutintoacirculardisk(Airy
disk)intheimageplanewhosediameterdependsontheangularapertureofthelens.
Theshortestdistancebetween2disksatwhichthetwodisksappearpartiallyseparatedcorrespondstoabout1/2thewidthofthedisks.The
distance,d,inobjectspaceisgivenby:
d=0.61l /n
•
sina
where
l =wavelenghtoftheradiation
n=refractiveindexofthemedia
a=semiangularapertureofthelens
NOTE:n
•
sina=thenumericalaperture(N.A.)ofthelens.
Thus,tomaximizeresolvingpower,l mustbedecreased,nincreased,oraincreased.Recallthatweareconcernedatthemomentwithan
aberrationfreeopticalsystem.Thevaluefortheconstant(0.61)iscontroversialbecauseitdependsonthecoherenceoftheradiationanda
criteriaofvisibility.
FortheLM,usingoilimmersionoptics(n=1.5),sina=0.87,andvioletlight(l =400nm),d=0.2µm.Theonlywaytoimprovetheresolutionisto
uselightofshorterwavelengthsinceN.A.cannotbeincreasedbeyond~1.5.FortheTEM,n=1(vacuum),sina=10
2
andl =0.005nmfor60kV
electrons,thusd=0.3nm.
I.A.4.Optics(LensTheory)
a.Basiclawsofclassicalgeometricaloptics
1)Rectilinearpropagationoflightwhenn(refractiveindex)isconstant.
2)Lawofreflection:
3)Lawofrefraction(Snell'sLaw):
4)Independenceofrays.Theassumptionismadethatlightraystravelindependentlythroughspace.
Theselawsholdforelectrons,except#4,ifthecurrentdensityistoohighwhennegativechargedelectronscaninterfere.
b.Classicalvs.electronoptics
1)Classicaloptics:Therefractiveindexchangesabruptlyatasurfaceandisconstantbetweenthesurfaces.Therefractionoflightatsurfaces
separatingmediaofdifferentrefractiveindicesmakesitpossibletoconstructimaginglenses.Glasssurfacescanbeshaped.
2)Electronoptics:Here,changesintherefractiveindexaregradualsoraysarecontinuouscurvesratherthanbrokenstraightlines.Refraction
ofelectronsmustbeaccomplishedbyfieldsinspacearoundchargedelectrodesorsolenoids,andthesefieldscanassumeonlycertaindistributions
consistentwithfieldtheory.
c.Geometricalandphysicaloptics
Thefundamentalprinciplesofopticsgovernthedesignandoperationofboththelightandelectronmicroscopes.Thebasicopticalprinciples
involvingtheuseofrefractileelementsorlensesinordertoformmagnifiedimagesareidenticalinboththeLMandTEM.TheTEMdiffersfromthe
LMonlyintheradiationitusesandinthewayinwhichtheradiationisbentorrefracted.
Geometricalopticsdealswiththestudyofthepathsfollowedby'rays'oflightorelectronsthroughlensesandapertures,andthegeometrical
constructionsusedtofindtherelativepositionsandsizesofobjectsandtheirimages.Arayoflightorelectronsisdefinedasaninfinitelythin
pencilorbeam.Physicalopticsshowsthatthisanabstractionandcannotphysicallyexistbecauseof'diffraction'whichdealswiththewave
natureoflightandelectrons.Allresultsobtainedingeometricalopticscanbederivedfromtheprinciplesofphysicaloptics,alongwithother
phenomenasuchasinterferenceanddiffractionwhicharenotexplicableinsimplegeometricalterms.
d.Idealversesreallenses:
Lensesareusedtobendraysoflightorelectronssotheyaredeflectedinapredictablewayfromtheiroriginalpaths.Thepropertiesofanideal
lens,possessinganaxisofrotationalsymmetryare:
1)Eachrayofthebundleofrayswhichpassesfromanobjectpointwillberefractedbytheideallenstomeetinoneimagepoint.
2)Raysoriginatingfrompointswhichlieonaplaneperpendiculartotheaxis,mustbeimagedinaplanewhichisalsoperpendiculartotheaxis.
3)Theimageappearsliketheobjectirrespectiveofthemagnification,sotherelativelineardimensionsoftheobjectarepreservedintheimage.
Inpractice,theimagingbyanyreallensdoesnotcorrespondtothatoftheideallensowingtothefactthatanobjectpointisrepresentedbya
diffractionimage(Airydisc)ofthelensopeningortheapertureusedforrestrictingtheeffectiveopeningofthelens.Thisisaresultofthewave
likepropertiesoflight.Lensaberrationsalsocontributetomoreorlesspronounceddeviationsfromthepropertiesoftheideallens.
Thesinglerefractingsurfaceofsphericalcurvatureisthefundamentalunitoffocusingactionbyglasslenses.Sphericalrefractingsurfacesactas
lensesforparaxialrayswhicharethoseraysthatpassclosetotheprincipalaxisofthelens.RayswithlargeangleswillNOTobeyideallens
action.
Afundamentaldifferencebetweenlightandmagneticlensesisthattheelectronbeamdoesnotchangeinforwardvelocityasitpassesthrough
themagneticfield(lightraysslowdownwhenpassingintoamediumofhigherrefractiveindex).Refractioniscontinuouswithelectronswhenthey
areinthemagneticfield:lightisrefractedonlyattheinterfacebetweenmediaofdifferingrefractiveindex.Theelectronsalsofollowspiral
trajectoriesthroughthemagneticfield(seealsoSec.I.A.5.c(Magneticfieldsandmagneticlenses)
e.Raydiagrams:(Figs.I.20I.28)
Themethodofconstructionofraydiagramsisbasedonthreesimpleprinciples:
1)Allraysenteringthelensparalleltotheaxisarebroughttoacommonpointontheaxis,thefocalpoint.
2)Allrayspassingthroughthegeometricalcenterofthelensareundeviatedandpassstraighton,nomatterfromwhichdirectiontheycome.
3)Principleofreversibility:ifthedirectionofarayisreversedinanysystemtherayexactlyretracesitspaththroughthesystem.Thisapplies
onlytothelocationoflightpathsandnottotheintensityofthelight.
Theaboveprinciplesarebasedontheassumptionsthatwearedealingwithathinlensandconcernedwiththepathsofparaxialrays.The
standardconventionistodrawdiagramswithraysthattravelfromlefttoright.Theobjectistotheleft(infront)ofthelensandtheimageisto
theright(behind)ofthelens.
f.Definitions:
Realimage:oneatwhichlightraysphysicallyreunite,sothataphotographicplateplacedatthepositionofarealimageisexposed.
VirtualImage:onefromwhichlightraysappeartodiverge;raysarenotinfactconcentratedatthepositionofavirtualimage,sothata
photographicplateplacedatthepositionoftheimageisnotexposed(byfocusedrays).Placinganopticalsystemsuchastheeyebehindthe
lens,willenablethedivergentraystobefocusedtoformarealimage.TheintermediatelensofanTEMissometimesusedthiswayinorderto
reducethefinalsizeoftherealimageformedbytheprojectorlens(es).
Converging(positive)lens:bendsraystowardtheaxis.Ithasapositivefocallength.Formsarealinvertedimageofanobjectplacedtothe
leftofthefirstfocalpointandanerectvirtualimageofanobjectplacedbetweenthefirstfocalpointandthelens.
Diverging(negative)lens:bendsthelightraysawayfromtheaxis.Ithasanegativefocallength.Anobjectplacedanywheretotheleftofa
diverginglensresultsinanerectvirtualimage.Itisnotpossibletoconstructanegativemagneticlensalthoughnegativeelectrostaticlensescan
bemade.
g.Lensformula(thinlensequation):
where
f=focallengthofthethinlens(sameradiusofcurvatureforboth
sphericalsurfaces)
o=distanceofobjectfromlens(positivetotheleft)
i=distanceofimagefromthelens(positivetotheright)
NOTE:Foravirtualimage,ihasanegativevalue.
h.Magnification:
Foraconverginglens,iftheobjectismorethantwicethefocallengthfromthelens,thentheimageformedisreal,inverted,andsmallerinsize
thantheobject(M<1).Whentheobjectisatadistance=2f,theimageandobjectarethesamesize(M=1);whenitisbetweenfand2f,
theimageislargerthantheobject(M>1),andwhenitis<f,theimageisvirtual,erect,andlargerthantheobject(M>1).
i.Angularapertureofthelens(2a)(Fig.I.29)
Theaperturedeterminesthetotalamountofradiationarrivingfromtheobjectwhichcanbefocusedto
formanimage.Theaperturethuscontrolstheabilityofthelenstogatherinformationabouttheobject.
Thisdependsontheangleoftheconeofraysitisabletoacceptfromtheobject.Bringinganobject
closertotheeyeincreasestheangularaperture,butthereisalimittotheclosenessthattheobjectcan
bebroughttotheeye(~25cmcorrespondingtoanangleofabout0.9°fora4mmexitpupildiameterof
theeyelens;atypicalLMwithanoilimmersionobjectivelenshas2aof~175°).
j.Simplevs.compoundmicroscope(Figs.I.30I.32)
Inprinciple,arealimageofanydesiredmagnificationcanbeobtainedfromasinglepositivelens,butin
practicethisiscumbersomebecauseofthelonglensimagedistance.Oneormorelensescanbeusedto
magnifytheimageinstages(totalmagnificationequalingtheproductofthemagnificationsofeachlens).
Theimageformedbyonelensconstitutestheobjectforthesubsequentlens,whetherornotareal
intermediateimageisformed.
Comparisonofoneversestwostagemagnification:
Thefollowingdescriptionillustrateshowdifferentpathlengthsarerequiredtoachieveamagnificationof10,000Xusingeitheroneortwolenses
withf=2.0cm.
OneStageSystem:
TwoStageSystem:
Assumebothlenseshavef=2.0cmandarearrangedsoeachgives100Xmagnification.
Thus,M=100=x
i
/x
o
foreachstage.
FirstStage:
x
o
=2.02cm
x
i
=202.00cm
Therealimageformedinthefirststagebecomestheobjectforthesecondlens.
SecondStage:x
o
,x
i
sameasinthefirststage.
Totallengthofsystem
=lengthoffirststage+lengthofsecondstage
=(x
o
+x
i
)+(x
o
+x
i
)
=2(x
o
+x
i
)
=2(2.02+202.00)=408.04cm(4.08meters)
k.Problemset
Thefollowingproblemsareforyourownedificationtotesthowwellyouunderstandthebasicsoflensoptics.
1.Foreachsituationbelow,drawanaccurate(usegraphpaper)raydiagramshowingthepathof(atleasttwo)raysfromtheobjecttoimage.
Indicatewhethertheimageisrealorvirtualandspecifythedistanceoftheimagefromthelensandthemagnificationoftheimagewithrespect
totheobject.Ineachexample,thelensisconverging,withidenticalfrontandbackfocalpoints.Distancesareinarbitraryunits.Letf=lens
focallength,x
o
=distanceofobjectinfrontofthelens,andx
i
=distanceofimagebehindthelens.Theobjectmaybeanysize.
2.Inthefollowingexamples,therearetwoconverginglensesinsuccession.Drawraydiagramsshowingtheformationofboththeintermediate
andfinalimagesandgiveappropriateinformationaboutthenature(real/virtual),positions,andsizesoftheintermediateandfinalimages.What
isthemagnificationateachstageofimageformationandwhatisthemagnificationofthefinalimage?Thedistancefromthecenteroflens1(L1)
tothecenteroflens2(L2)equalsD.
I.A.5.ElectronOptics/ElectronLenses
a.Electronemission
Innershellelectronsinmetalatomsshieldtheelectricfieldofthenucleusthroughtherepulsiveforcestheyexertontheoutershell(valence)
electrons.Thustheattractionbetweenthevalenceelectronsandthenucleusisreduced.Metalatomsarecharacterizedashavingtwoloosely
boundvalenceelectronswhichmigratefreely(thisiswhymetalsaregoodelectricalconductors)andcanescapefromthemetalcompletelyif
sufficientadditionalenergyisimpartedtothem.Asthetemperatureofametalisincreased,thekineticenergyoftheelectronsincreasesbecause
ofincreasedthermalvibrationsofthemetalions,whichcollidemorefrequentlywiththeelectrons.Thermionicemissionisthetermusedto
describetheprocessbywhichthermalenergyissuppliedtolooselyboundelectronsinordertoformasourceofelectrons.
Atroomtemperatureelectronsareeffectivelypreventedfromescapingthesurfaceofthemetalowingtotheattractiveforceofthepositively
chargedions.Asthetemperatureisincreasedsomeelectronsacquiresufficientenergytoovercometheattractionandleavethemetal
temporarily.Metal,shapedasathinwire,caneasilybeheatedbypassinganelectriccurrentthroughit.Sincethemetalsurfacebecomes
positivelycharged,acertainlevelofenergy(workfunction)mustbesuppliedtoallowelectronstoescapefromthesurface.Eachmetalhasa
characteristicworkfunction.Tungsten,withalowworkfunction,emitsmoreelectronsthanmetalswithhigherworkfunctions(seealsopp.2930
andFig.I.59).
Ifastrongelectrostaticfieldisappliedinavacuumbetweenthewire(givenanegative,cathode,potential)andananode,theelectricfieldwill
causeelectronstoaccelerateawayfromthewiretowardstheanodesurface(Fig.I.33).Thespeedoftheelectronsdependsonthestrengthof
theelectrostaticfield(voltage)betweenthecathodeandanode(equation(3),Sec.I.A.3.b)Thenumberofelectronswhichleavethewire
dependsonthetemperaturetowhichthewireisheated,whichdependsonhowmuchfilamentcurrentpassesthroughthewire.
A"V"shapedwirewillhavethehighesttemperatureatthetip.Electronswithdrawnfromthefilamenttipcarryelectricchargestotheanode.This
electriccurrent,whichflowsbetweenthefilamentandtheanode,iscalledthebeamcurrent.
1)Electricfield/Equipotentials
Anelectricallychargedobjecthasassociatedwithitanelectricfield.Thus,anelectricallychargedparticle,whenbroughtnearachargedobject,
isinfluencedbyanelectricalforceinthevicinityoftheobject.Theforceisdirectedtowardthechargedobjectifthechargesareofopposite
signsandawayfromtheobjectiftheyareofsimilarsign.DEFINITION:Thedirectionofanelectricfieldisdefinedasthedirectionoftheforce
actingonapositivecharge.(Figs.I.3435)
Alongthelinesofforceconnectingthetwocharges,theelectricpotentialwillchangegraduallybetweentheextremevaluesrepresentedbythe
twocharges.DEFINITION:Equipotentiallinesdefinethepointsalongthelinesofforcewithidenticalelectricalpotential.Theseequipotential
surfacesarealwaysorientedperpendiculartothelinesofforce.Thechangesintheelectricpotentialaregradualinspace.
Electronswhichenterafieldbetweentwoparallelplatesinadirectionparalleltotheplatesareaffectedbytheforcedirectedperpendicularto
theplates(FigI.36).Theelectronswillbeattractedtowardthepositiveplate.Thepathchangesinaseriesofgradualstepsattheequipotential
surfaces.
FigureI.37showshowtheelectronpathis"refracted"attheequipotentialsurface.TheresultisfundamentallythesameasthatgivenbySnell's
Lawofrefractioninlightoptics.Aconsequenceofthisisthatasphericallycurvedequipotentialsurfaceexhibitsthepropertiesofalens.
FiguresI.38andI.39showhowbothpositive(converging)andnegative(diverging)electrostaticlensescanbeformed.Thisfeatureof
electrostaticlensesdiffersfromelectromagneticlenseswhichcanonlyactasconverginglenses.
2)Advantages/Disadvantagesofelectronlenses:
Thefactthattherefractiveindexdoesnotchangeabruptlyinelectronlenseshasoneadvantageinthattherearenotroublesomereflectionsat
equipotentialsasatglassinterfaces.Thereisaseriousdisadvantageinthatequipotentialscannotbeshapedandcombinedinarbitraryfashionto
correctforchromaticaberrationandothererrors.
Althoughelectronmicroscopeswhichemployelectrostaticlenseshavebeenmade,mostmicroscopesuseelectromagneticlenses.Amajorreason
isthatelectrostaticlensesaremoresensitivetothequalityofthevacuumandcleanlinessofthecomponentsthanareelectromagneticlenses.
Somelensaberrationsaremoresevereforelectrostaticlensescomparedtoelectromagneticlenses.Electrostaticlensesrequireverypowerful
electrostaticfieldswhichcanleadtoelectricalbreakdownor"arcingover"insidethecolumn,especiallyunderpoorvacuumconditions.Forthis
reason,electrostaticlensescannotbemadewithfocallengthsasshortasmagneticlenses.
b.Electrostaticlens
Abasicunderstandingofelectrostaticlensesisimportantfortwomainreasons:i)theelectrongunuseselectrostaticlensactiontoformthe
primarybeamsource,andii)itisquitecommonforachargetodeveloponthenonconductingcontaminationwhichmayaccumulateonphysical
apertures(suchastheobjectiveaperture)andtransformthemintoweakelectrostaticlenseswhichcandistorttheelectronimage.
3)Propertiesofelectrostaticlenses:
a)Anyaxiallysymmetricalelectrostaticfieldhasthepropertiesofalensforraysconfinedtotheparaxialregion.Alltheideallensformulasapply
toelectrostaticlenses.
b)Forelectronlenses,replaceÃ(f)forrefractiveindexinthelensequations(f=valueofthepotentialontheaxis).Intheimageformingsystem
ofmostTEMs,fisthesameonbothsidesofthelens(SeeSec.I.A.5.c).
c)Ifboundedbyregionswherefisconstant,anelectrostaticlensisalwaysconvergent.
c.Magneticfieldsandmagneticlenses
1)Magneticfield
Anelectriccurrentpassingthroughaconductorgivesrisetoamagneticfield.TheconventionisthatNisthedirectioninwhichthelinesofthe
magneticfieldpoint(Fig.I.40).Themagneticfluxisthetotalnumberoflinesandthefluxdensityisthenumberoflinesperunitareaofasurface.
UsetheRIGHThandruletodeterminethedirectionofthefield(thumbpointstowardcurrentdirectionandfingerscurlindirectionoffield.NOTE:
Byconvention,thedirectionofelectronflowisoppositetothatofcurrentflow.
Fluxdensitydependsonthepropertiesofthematerialsurroundingtheconductor.Ironinducesahigherfluxdensitythanairoravacuum.The
propertyofthematerialwhichaffectsthefluxdensityiscalledthepermeability,m,ofthematerial.Forairandvacuum,m=1.0.For
ferromagneticmaterialsitcanbeaslargeasseveralhundredthousand.
Iftheconductorhastheshapeofacircularloop,thelinesofforceformcirclesaroundtheloop.Thefluxdensityisgreatestatthecenterofthe
loop.Themagnetinthecenteroftheloopisorientedperpendiculartotheplaneoftheloopifthecurrentthroughtheloopissufficientlystrongto
eliminatetheinfluenceoftheearth'sfield.ThesideoftheloopatwhichthelinesofforceleavetheloopistheNorth(N)poleofthemagnet(Figs.
I.41,I.42).
Ifthewireiswoundinseveralturnsaroundacylindricalsurface(solenoid),eachturnwillcontributetotheinducedmagneticfield.Theflux
densityinthecenterofthecoilisgivenby:
Inthecaseofairandnonmagneticmaterials,µ=1.0andB=H.
Thepermeabilityofirondependsonthefieldstrength,H,anddecreasestounityathighfieldstrengthorwhenthefluxdensity,B=H(Fig.I.43).
Thehighpermeabilityofironisduetotheinducedmagneticfieldorientingmicroscopiccrystalregionsactingastinymagnetsintheiron.Allthese
tinymagnetsaddtheirmagneticfieldstotheinducedfield(Fig.I.44).Whenallmicromagnetsarenearlyoriented,theironwillaffecttheflux
densitytoadecreasingamountsincethereorientationofmicromagnetsisnearingcompletion.Thus,thepermeabilityofironathighfieldstrengths
approachesthatofemptyspace.Atthispointtheironreachesmagneticsaturation.
2)Hysteresis
Thestrengthofthelensdependstosomeextentonthepreviousmagnetichistoryof
thelens.Whenthecurrentinalensisreduced,thedecreaseinmagnetizationdoes
notretracethesamepathobtainedwhenthecurrentwasincreased(Fig.I.45).
Inductionofmagnetizationinvolvesaphysicalmovementwithinthemagnetized
material,requiringtheovercomeofacertaindegreeofinertia.Asaresult,
magnetizationtendstolagbehindthemagnetizingforceapplied.Inducedmagnetic
fluxcanonlybereturnedtozerobyapplicationofacurrentintheoppositedirection.
Aconsequenceofhysteresisisthatthelevelofcurrentusedtoenergizeamagnetic
lensDOESNOTpreciselyspecifythelensstrength(i.e.focallength).
NormalizationofTEMlensesisaccomplishedbyreducingthelenscurrenttozero
somepredeterminednumberoftimes.Hysteresismayalsobeminimizedbytakinga
lenstosaturationandthenreturningittotheworkingcurrentwithoutovershooting.
Whenthefieldstrengthisreducedtozero,somemagnetizationstillremainsintheiron
(residualmagnetizationorremanence).Anadvantageofsoftironisthefactthat,
whenusedinanelectromagnet,hysteresisislow.
Introductionofpiecesofironinamagneticfielddrasticallyaffectsthefluxdensity.
Magneticmaterialhasashieldingeffect,theeffectbeinggreaterthegreaterthe
permeability.Permalloy(mmetal)hasamaximumpermeabilityof80,000140,000
comparedtoironusedintransformers(~7000).mmetalpermeabilityislimitedtolower
fieldstrengthsthanthatatwhichironstillretainshighpermeability.Thismetalis
thereforeusefulforshieldingtheTEMfromexternalmagneticfields.
d.Theelectromagneticlens
1)Lensdesigndevelopment(Figs.I.46I.48)
Theefficiencyofthemagneticfieldproducedbyashortsolenoidwasfirstimproved
byencasingtheenergizingcoilinasheathofsoftironwhichhasthepropertyofconcentratingthelinesofforceinamagneticfieldandthus
becomingmagnetizedbyinduction.Inthiswayamuchmorepowerfulaxialmagneticfieldisobtainedforthesameamountofcurrentflowing
throughthesolenoid.Furtherdevelopmentinvolvedencasingtheentirecoilwithsoftironexceptatanarrowannulargapintheinsideofthecoil.
Thisproducesagreaterconcentrationofthemagneticfieldalongashortaxialdistance.Toachieveshorterfocallengthlenses(andobtaingreater
magnifications)asoftironpolepiecewithanopenaxialborewasintroducedatthepositionoftheannulargap.
MagneticlensesusedinTEMsarealwaysconstructedwithanironcircuittoproduceahighfieldstrengthacrossashortgap.Themagneticfields
forTEMlensesareintherangeof10,00020,000gauss.
2)Forcesactingonacurrentinamagneticfield
Theforceonanelectroninamagneticfieldisalwaysatrightanglestothevelocityandthedirectionofthefield(Figs.I.49,I.50,andI.52).The
fieldonlyactsonthevelocitycomponentwhichisdirectedperpendiculartothelinesofforce.Usethelefthandrule(Fig.I.51:firstfingerfor
fielddirection,middlefingerforcurrentdirection,andthumbfordirectionofforce).Rayspassingthroughthelensareturnedthroughanangle
whichdoesNOTdependonthedistanceoftheraysfromtheaxis.Allelectronscontainedinagivenmeridionalplanebeforeenteringthefieldare
containedinarotatingmeridionalplaneastheypassthroughthelens,andthentheyleavethelenscoplanar.
Whenelectronsenterthelenstheyencounterasidewaysforcewhichcausestheelectrontorotate
asitcontinuesthroughthelens(Figs.I.53I.57).Sincetheradialcomponentofthemagneticfield
reversesafterthecenterofthelens,therotationalvelocitysetupinthefirsthalfofthelensis
countered.Theelectronenteredthelenswithoutangularmomentumabouttheaxisandleaves
withoutangularmomentum.Theneteffectisadeflectiontowardtheaxis,whichitmustcrossatthe
focalpointf
2
.Theanglebetweentheobjectvectorandtheimagevectoris180°+q,whereas,for
glasslensesandelectrostaticlenses,theanglebetweenarealobjectandtheimageisexactly180°.
Sincetheradialforceisdirectedtowardtheaxis,thelensisconvergentnomatterwhatthedirection
ofthefield.
3)Propertiesofamagneticlens:
Anyaxiallysymmetricmagneticfieldhasthepropertiesofanideallens.Alltheformulasfortheideallensmaybeapplied.
Magneticlensesarealwaysconvergent.Theconventional,axiallysymmetriclensisalwaysboundedbyregionswhicharefieldfree,the
consequencebeingthatthenetactionofelectronlensesisinevitablyconvergent.Limitedregionsmaybedivergentbutnotthelensasawhole.
Theseriousconsequenceofthisisthatneithersphericalorchromaticaberrationscanbecorrectedasisdoneinlightopticsbytheusedoublets
ofpositiveandnegativelenses.
Intheabsenceofelectrostaticfields,therefractiveindexisthesameinobjectandimagespace,thereforef
1
=f
2
.
Electronstravelingthroughaxiallysymmetricfieldsexperienceaspiraltrajectoryofdiminishingradius.Theimagevectorisatanangle180°+qto
theobjectvector.
Thedeflectionoftheelectrontowardstheaxismeansthatanelectronenteringthelensparalleltoitsaxiswillcrosstheaxisafterhavingpassed
thelens.Thedeflectionwillincreasewiththedistancefromtheaxis.Thus,abeamofelectronsinparallelpathsparalleltotheaxisofthelenswill
befocusedtoanimagepointontheaxiswhichrepresentsthesecond(back)focalpointofthelens(f
2
).Notethatmagneticlensesarehighly
inefficientinthatonlyaminorportionofthetotalfieldstrengthisactuallyeffectiveinfocusingtheelectron.
4)Magneticlensfocallength
Inamagneticelectronlensthefocallengthisdeterminedbythefieldstrengthinthelensgapandbythespeedoftheelectrons(determinedby
theacceleratingvoltage).
Formagneticlenses,focusingisachievedbyvaryingthecurrentwhichpassesthroughtheelectromagnet.Thisinturnchangesthestrengthof
themagneticfieldandtherebyaltersthefocallengthofthelensandisequivalenttoacombinedchangeinboththe"refractiveindex"and
"curvatureofsurface".Forabeamofmoreenergeticelectrons,thelenscurrenthastobeincreasedinordertokeepthefocallengthconstant.
FocallengthandcurrentareNOTlinearlyrelated:strengthincreasesinasigmoidfashion(Fig.I.45)ascurrentincreasesuntilapointisreached
wherethelensissaturatedandnofurtherincreaseinlensstrengthcanbeachieved.
Sincethefocallengthofthelensisdirectlyproportionaltotheacceleratingvoltage,avariationinthevelocityoftheelectronsintheimaging
beamaffectsimagequalitybyeliminatingperfectfocus(chromaticaberration).
5)Magneticlensdesign:(Figs.I.46,I.47).
Condenserlensesusuallyhavearelativelylargeboreandspacingwhichresultsinalongfieldandlongfocallength.
Typicalconstructionoftheobjectivelensproducesastrongfieldofshortaxialextent(i.e.shortfocallengthbetween(1.53mm)necessaryfor
formationofimagesathighmagnification.Thespecimenisplacedwithinthemagneticfieldoftheobjectivelens.Thus,anyfieldintroducedby
contaminantsinthespecimencandistortthefieldofthelens.Notethatthisalsomeansthatpartofthelensfield("prefield")isonthefrontside
oftheobjectandaffectstheelectronbeambeforeitpassesthroughtheobject.
Mostofatypicalmagneticlensliesoutsidethevacuumofthemicroscope.Onlythoseregionsthroughwhichtheelectronbeampassesareinhigh
vacuum.Magneticlensesmustbewatercooledtodissipatethelargeamountsofheatproducedbythecurrentsintheelectromagnetcoils.
DATE NAME EVENT
1897 J.J.Thompson Discoverstheelectron
1924 LouisdeBroglie Identifiesawavelengthtomovingelectrons
l =h/mv
where
l =wavelength
h=Planck'sconstant
m=mass
v=velocity
(Foranelectronat60kVl=0.005nm)
1926 H.Busch Magneticorelectricfieldsactaslensesforelectrons
1929 E.Ruska Ph.Dthesisonmagneticlenses
1931 Knoll&Ruska Firstelectronmicroscopebuilt
1931 Davisson&Calbrick Propertiesofelectrostaticlenses
1934 Driest&Muller SurpassresolutionoftheLM
1938 vonBorries&Ruska FirstpracticalEM(Siemens)10nmresolution
1940 RCA CommercialEMwith2.4nmresolution
1945 1.0nmresolution
Fig.I.1Comparisonoflightandelectronmicroscopes.Ineach
instrument,illuminationfromthesource(lamp,filamentinthe
electrongun)isfocusedbythecondenserlensontothespecimen.
Afirstmagnifiedimageisformedbytheobjectivelens.Thisimage
isfurthermagnifiedbytheprojectorlensontoagroundglass
screen(light)orfluorescentscreen(electrons).(FromAgar,p.8)
Fig.I.2CrosssectionalviewofthePhilipsEM300.(FromAgar,p.40)
Toviewtheanimatedmicroscope,clickhere.
Note:QuickTimePlugInrequired
(Thiscanbedownloadedathttp://apple.com/quicktime/download)
Fig.I.3Sectionthroughacomplex
doublecondenser6lensPhilips
EM200electronmicroscope.(From
Meek,p.99)
Fig.I.4Thestatisticalnatureofdiffraction
patterns.(FromHall,p.13)
"Theprecisenatureof'electronwaves'or'matterwaves'isverydifficulttounderstandordescribeinmaterialterms.Electronwavesarenot
electromagneticradiationofthekindtowhichlight,Xraysandradiowavesbelong.Theyconstituteasortofquantumor'packet'ofradiationwhich
accompanieseachindividualelectron,followingitspathandnotradiatingoutwardsfromit."(Meek,1976,pp.4849).
V l (nm)
v(
•
10
10
cm/sec)
v/c
10,000 0.0123 0.593 0.198
50,000 0.0055 1.326 0.442
100,000 0.0039 1.875 0.625
1,000,000 0.0012 5.930 1.977!
V l (nm)
v(
•
10
10
cm/sec)
v/c
10,000 0.0123 0.593 0.195
50,000 0.0055 1.326 0.414
100,000 0.0039 1.875 0.548
1,000,000 0.0012 5.930 0.941
FigI.5Aperfectpointsourcecannotbe
imagedbyalensasaperfectpointimagedue
tothepresenceoftheapertureAB(which
maybetheedgeofthelens).Diffractionat
thisaperturegivesrisetoaseriesoffringes,
whichsurroundtheimageformedofthepoint
source.Thepatternproducediscalledan'Airy'
disk.(FromMeek1sted.,p.35)
Fig.I.6Wheneverawavefrontstrikesa
barrier,itcanbendaroundthecorner'by
givingrisetoasecondarywavefrontatthe
edge,sinceeachpointonthewavefrontcan
giverisetoanewsourceofwaves.This
phenomenoniscalled'diffraction'.(FromMeek
1sted.,p.22)
Fig.I.7Diffractionpattern(right)formedbyanirregularlyshapedaperture
(left).(FromYoung,p.95)
Fig.I.8(a)
Photographof
theedgeofa
razorblade
illuminatedby
monochromatic
(blue)light
rendered
coherentby
passing
througha
narrowslit.(b)
Microdensitometer
tracingofthe
negativefrom
whichthe
photograph
wasmade.
FourFresnel
fringescanbe
distinguished.
(FromMeek1st
ed.,p.27)
(a)
(b)
(a) (c)
(b)
Fig.I.9(a)Fresnelfringesformed
byelectrons.Thesefringesare
formedoutsidetheedgeofahole
(white)inacarbonfilm(black).(b)
Amicrodensitometertracingofthe
fringesystem;thepatternis
identicalwiththeFresnelfringe
systemformedbyvisiblelight(see
Fig.I.8).(c)Anunderfocusedimage
ofaholeinafilm,showinga
completesystemofabout40
Fresnelfringesinsidethehole.
(FromMeek1sted.,pp.2930)
Fig.I.10Diffractionimagesoftwo
easilyresolvedpoints.(From
Slayter,p.243)
Fig.I.11Imagesoftwo
incoherentlyilluminatedpointsat
thelimitofresolution.(a)individual
intensities;(b)summedintensities.
(FromSlayter,p.244)
Fig.I.12Examplesofwhatoccurswhentwo
wavesofthesamewavelengthandequal
amplitudeadd.Ineachexample,thetwo
separatewavesareshownontheleftand
theirsumorresultantwaveontheright.The
differentexamplesarecharacterizedbyvarying
phasedifferences.Thephaseofawave
(usuallyexpressedasafractionofthe
wavelengthorindegrees)isthepositionofa
crestrelativetosomearbitrarypoint.Although
thephaseofagivenwavevarieswithtimeas
thewavetravels,thedifferenceinphaseofthe
twowavesofthesamewavelengthwiththe
samevelocity,isindependentoftime.Such
wavescaninterferewithoneanother.The
resultantwavehasthesamewavelength,l .
(a)Phasedifferencezero.Thewavestotally
reinforceandaresaidtobe"inphase"orto
showconstructiveinterference.
(b)Phasedifferencel /4.Partialreinforcement,
givingawaveofamplitude1.4(intensity2.0).
(c)Phasedifferencel /2.Thewavesare"outof
phase"andthereistotaldestructive
interferencetogivenoresultantwaveora
wavewithamplitude0(intensity0).(From
GluskerandTrueblood,p.19)
Fig.I.13Photographofan
interferencepatterninwater
wavesformedbythe
superpositionofwavesfromtwo
sourcesoscillatinginphasewith
thesamefrequency.(FromYoung,
p.22)
Fig.I.14Theangularapertureofthe
eyeisrelativelysmall.(FromMeek,
1sted.,p.13)
Fig.I.15Increasingtheangular
apertureoftheeyewithalens.The
lensallowstheobjecttobeheld
closertotheeye,whichisthereby
enabledtogathermoreinformation.
(FromMeek1sted.,p.14)
Fig.I.16Theinteractionofwaves
withanobstacle.Theboatridesthe
longwavelengthoceanwave,but
reflectsthesmallwavelength
surfaceripple.Anobserverwho
wishestodetectthepresenceof
theboatcandosoonlyby
observingwaveswhichhave
wavelengthssmallerthan,or
comparableto,thelengthofthe
boat.(FromSherwood,p.19)
Maximummagnification=
resolvingpoweroftheeye
resolvingpowerofthemicroscope
(a)
Fig.I.17(a)TwoAiry
disksrepresenting
twoimagepoints
shownatincreasing
separationfromleft
toright.Inthe
pictureatthe
extremerightthe
twodiskscanbe
distinguishedas
separatedisks.
(b)Theintensity
distributionatanAiry
disk.R,halfwidthof
thecentralmaximum
representedbya
bellshapedcurve.
(c)TheRayleigh
criteriaforresolution.
(FromSjostrand,
p.115)
i=r
Fig.I.18Reflection.(FromSlayter,
p.4)
Fig.I.19Refraction.(FromSlayter,
p.6)
Fig.I.20Principalraydiagramsshowing
imageformationbyaconvexlens.
(a)Whentheobjectdistanceisgreater
thanthefocallength,areal,inverted
imageisformed.
(b)Whentheobjectdistanceisless
thanthefocallength,avirtual,erect
imageisformed;itspositionis
obtainedbyprojectingtheprincipal
raysbackward.Theraysappearto
comefrompointQ.(FromYoung,
p.127)
Fig.I.21Definitionof
principalfocus,F,inimage
spaceofalens.(From
Sjostrand,p.20)
Fig.I.22Focusingeffectoflenson
raysoriginatingfrompointson
principalaxislocatedatdifferent
distancesfromthelens.(From
Sjostrand,p.21)
Fig.I.23Definitionofprincipal
focusinobjectspaceF1ofa
lens.(FromSjostrand,p.21)
Fig.I.24VirtualimageQof
objectpointlocatedbetween
principalfocusinobjectspace
andthelens.(FromSjostrand,
p.21)
Fig.I.25Constructionoftheimage
ofanobjectbymeansofray
tracing.(FromSjostrand,p.22)
Fig.I.26Magnifyingeffectof
apositivelens.(From
Sjostrand,p.22)
Fig.I.27Virtualmagnified
imageofobjectlocated
betweenprincipalfocusin
objectspaceandthelens.
(FromSjostrand,p.22)
Fig.I.28Amagnifyingglassformsan
enlarged,erectvirtualimage.The
angularsizeofthisimageis
approximately4"/15"or4/15.The
angularsizeoftheobjectatthe
closestdistanceforcomfortable
viewingis1"/10"or1/10.The
magnificationinthissituationis(4/15)/
(1/10),or22/3.(FromYoung,p.130)
Fig.I.29Theangularapertureofa
lens.Theangle2a isthe
acceptanceangleofthelens,and
thelargeritcanbemade,themore
informationcanthelenstransmit.A
largelensofhighaperturecan
thereforetellusmoreaboutan
objectthanasmalllensoflow
power.(FromMeek1sted.,p.12)
Fig.I.30Raydiagramforhighmagnification
modeofoperation.Notethateachlens
formsarealimage,withimageinversion.
I0istheimageformedbytheobjective
lensO,I1isformedbythefirstprojector
lensP1andI2bythesecondprojectorP2,
onthescreen.(FromAgar,p.30)
Fig.I.31Left:raydiagramofthe3realimagemediumandhighmagnificationimagingsystemofa3lens
microscope.Center:2realimageverylowor'scan'magnificationrangeofa3lensmicroscope.Right:2real
imagelowmagnificationsystemofa3lensmicroscope.(FromMeek1sted.,pp.118,120121)
Fig.I.32Raydiagramforacompleteelectron
microscope.FilamentF,condenser1lensC1,
condenser2lensC2,condenserapertureCA,
specimenS,objectivelensO,objectiveaperture
OA(inbackfocalplane).1stintermediateimage
andselectorapertureSA.IntermediatelensP1,
secondintermediateimageI2,projectorlensP2
andfinalimageonthefluorescentscreenFC.
(FromAgar,p.35)
a)f=2.0
x
o
=5.0
e)f=4.0
x
o
=3.0
b)f=10.5
x
o
=21.0
f)f=13.3
x
o
=13.3
c)f=3.5
x
o
=3.0
g)f=3.142
x
o
=0.0
d)f=5.0
x
o
=2.5
a)D=8.0
L1:f=2.0
x
o
=4.0
L2:f=3.0
b)D=8.0
L1:f=2.0
x
o
=6.0
L2:f=3.0
c)D=4.0
L1:f=2.0
x
o
=3.0
L2:f=2.0
FigI.33Accelerationofelectronin
electricfield.(FromSjostrand,p.26)
Fig.I.34Linesofforceatapositively
chargedsphericalbody.(FromSjostrand,
p.32)
Fig.I.35Linesofforceandequipotential
surfaces(stippledlines)associatedwith
twoequalchargesofoppositesign.
(FromSjostrand,p.32)
Fig.I.36Equipotentialsurfacesattwoparallel
platesofoppositechargeswiththepathofan
electronindicatedwithinthehomogeneous
partofthefield.(FromSjostrand,p.33)
Fig.I.37Refractionofelectronatan
equipotentialsurface.(FromSjostrand,p.33)
Fig.I.38.Negativelensactionof
electrostaticfieldatanaperturewhen
V2V1>V3V2.(FromSjostrand,
p.34)
Fig.I.39.Positivelensactionatan
aperturewhenV2V1<V3V2.
(FromSjostrand,p.34)
Fig.I.40Magneticfieldinducedbycurrent
passingthroughaconductor.(From
Sjostrand,p.35)
Fig.I.41Magneticfieldinducedbycurrent
passingthroughasolenoid.(From
Sjostrand,p.37)
Fig.I.42Solenoidwithironcore.(From
Sjostrand,p.40)
Fig.I.43a.Dependenceofpermeabilityonfluxdensity,B.
b.RelationshipbetweenfluxdensityBandfieldstrength.
(FromSjostrand,p.38).
Fig.I.44Magnetization.(FromSlayter,
p.361)
Fig.I.45Curves
showinghowthe
magnetizationof
softiron(lens
strength)is
relatedtothe
magnetizing
force(lens
current).An
unmagnetized
lensstartsfrom
thepointOand
followsthepath
OAaslens
current
increases.Atthe
pointA,further
increaseinlens
currentproduces
nofurther
increaseinlens
strength;thelensissaidtobe'saturated'.Whenlenscurrent
isreduced,thepathOAisnotretraced;adifferentpathABis
followed.Thisdisplacementiscalled'hysteresis'.Atzero
current(pointB),someresiduallensstrengthremains;thisis
called'remanence'.Tobringthelensbacktozerostrength,a
reversecurrentOCmustbeapplied.Lensstrengththen
increaseswithincreasingreversecurrent,followingthepath
CD.Thepolarityofthelenschanges,butthisdoesnotaffect
itsfocusingpower;onlythespiralelectronpathisreversed.
Becauseofhysteresis,itisnotpossibletocalibratealens
currentmeteraccuratelyintermsoflensstrengthor
magnification.
Fig.I.46Evolutionofmagneticelectron
lenses.(A)Shortsolenoidusedasa
magneticlens.(B)Softironcasing
enclosingoutersurfaceofthesolenoid,
thusconcentratingthefield.(C)Soft
ironencasingthesolenoidexceptata
narrowannulargaptherebyreducing
themagneticfieldtoaveryshortregion
alongthelensaxis.(D)Modern
objectivelensconsistingofasoftiron
encasedsolenoidandsoftironpole
piecessoastohaveanenormously
concentratedfieldatthelevelofthe
annulargap.(FromWischnizter2nded.,
p.33)
Fig.I.47(a)Amagneticlensconsisting
ofatightlywoundcoilandasoftiron
shroudsurroundingthecoilexceptfor
asmallgap.Thefieldisconcentratedin
thatgap.(b)Shortfocallength
electromagneticlenswithpolepieces.
(FromSjostrand,p.50)
Fig.I.48Fieldstrengthdistribution
curves.ThecurvesADcorrespondto
therespectivelensesillustratedinFig.
I.46.Eachrepresentsthefieldstrength
alongthelongaxisofthelens.The
changesintheshapeofthecurves
representtheshorteningor
concentrationofthefieldovera
shorteraxialdistance.Hz=
longitudinalmagneticfield.Z=
distancealongtheaxisofsymmetry.
(FromWischnizter2nded.,p.33)
Fig.I.49TheforceFactingon
astraightconductorina
homogeneousmagneticfield
offluxdensityBwhencurrent
Iispassedthroughthe
conductor.(FromSjostrand,
p.43)
Fig.I.50Pathofanelectronina
magneticfield.(A)Inalarge,uniform
magneticfield.(B)Inasmall,uniform
magneticfield.(FromWischnitzer2nd
ed.,p.25)
Fig.I.51Lefthandthumbrule.
(FromSjostrand,p.43)
Fig.I.52Thompson'sexperiment.A
streamofelectronsoriginatingfroma
sourceandpassing,invacuo,through
amagneticfieldproducedbyapairof
magnetswillbedeflected.The
directionofdeflectiondemonstrates
thatelectronsarenegativelycharged
particlesofmatter.(FromWischnitzer
2nded.,p.25)
Fig.I.53Actionofasolenoidonan
electronbeam.Anelectriccurrent
passingthroughthecoilproducesan
axialmagneticfield.Thisisthe
refractingmediumfortheelectrons.An
electronstartingatapointontheaxisA
andatanangletoitfollowsaspiral
path,returningtotheaxisatthepoint
B.Theactionisbasicallysimilartothat
oftheconverginglightlensshownin
Fig.I.20.(FromMeek1sted.,p.8)
Fig.I.54Actionofthemagnetic
lens.(a)Inperspective.(b)
Electrontrajectoryin
projection,alongdirectionof
propagation.(c)Electron
trajectoryinprojection,side
view.(FromSlayter,p.358)
Fig.I.55Componentsofthe
vectorHneartheaxisoffields
withaxialsymmetry.His
representedbytwo
components,Hz,the
componentinthez(axial)
direction,andHr,the
compnentinther(radial)
direction.(FromHall,p.85)
Fig.I.56Theycomponentof
themagneticfieldina
magneticlensisoriented
perpendiculartothedirection
ofanelectronenteringthe
lensalongapathparallelto
thelensaxis.Thisy
componentwillaffectthe
electron,deflectingitinthex
directionasindicatedbythe
arrowmarkedvx.(From
Sjostrand,p.48)
Fig.I.57Thezcomponentofthemagneticfield
andthexvelocitycomponentoftheelectron
inamagneticlensinteract,deflectingthe
electronintheydirectiontowardthelens
axis.(FromSjostrand,p.49)
CuuDuongThanCong.com https://fb.com/tailieudientucntt
cuu duong than cong . com
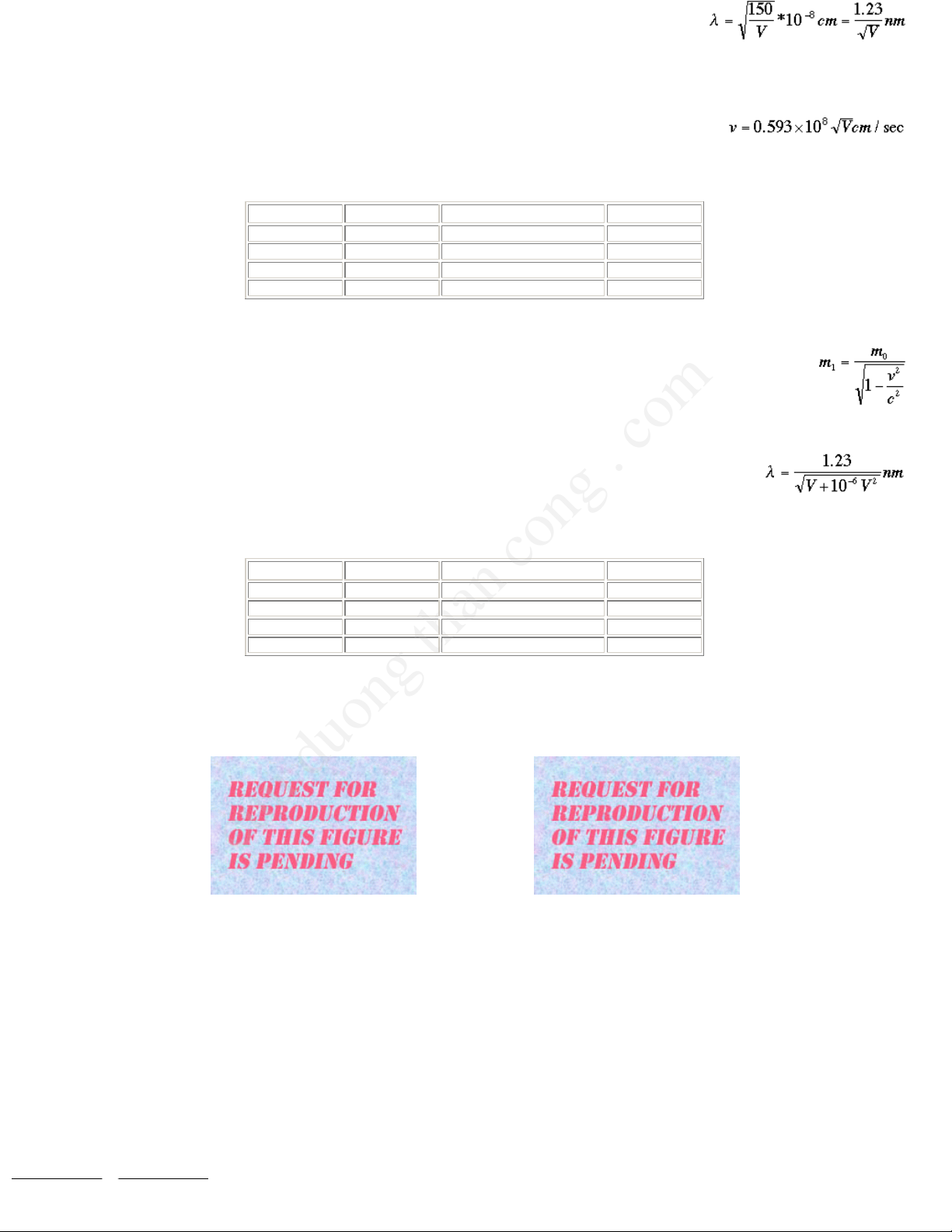
I.THEMICROSCOPE
I.A.PRINCIPLESOFTHETRANSMISSIONELECTRONMICROSCOPE(TEM)
I.A.1.OriginoftheTransmissionElectronMicroscope
I.A.2.ComparisonofLight(LM)andElectronMicroscopes(Fig.I.1)
a.Similarities(Arrangementandfunctionofcomponentsaresimilar)
1)Illuminationsystem:producesrequiredradiationanddirectsitontothespecimen.Consistsofasource,whichemitstheradiation,anda
condenserlens,whichfocusestheilluminatingbeam(allowingvariationsofintensitytobemade)onthespecimen.
2)Specimenstage:situatedbetweentheilluminationandimagingsystems.
3)Imagingsystem:Lenseswhichtogetherproducethefinalmagnifiedimageofthespecimen.Consistsofi)anobjectivelenswhichfocusesthe
beamafteritpassesthroughthespecimenandformsanintermediateimageofthespecimenandii)theprojectorlens(es)whichmagnifiesa
portionoftheintermediateimagetoformthefinalimage.
4)Imagerecordingsystem:Convertstheradiationintoapermanentimage(typicallyonaphotographicemulsion)thatcanbeviewed.
b.Differences
1)Opticallensesaregenerallymadeofglasswithfixedfocallengthswhereasmagneticlensesareconstructedwithferromagneticmaterialsand
windingsofcopperwireproducingafocallengthwhichcanbechangedbyvaryingthecurrentthroughthecoil.
2)MagnificationintheLMisgenerallychangedbyswitchingbetweendifferentpowerobjectivelensesmountedonarotatingturretabovethe
specimen.Itcanalsobechangedifoculars(eyepieces)ofdifferentpowerareused.IntheTEMthemagnification(focallength)oftheobjective
remainsfixedwhilethefocallengthoftheprojectorlensischangedtovarymagnification.
3)TheLMhasasmalldepthoffield,thusdifferentfocallevelscanbeseeninthespecimen.Thelarge(relative)depthoffieldintheTEMmeans
thattheentire(thin)specimenisinfocussimultaneously.
4)Mechanismsofimageformationvary(phaseandamplitudecontrast).
5)TEMsaregenerallyconstructedwiththeradiationsourceatthetopoftheinstrument:thesourceisgenerallysituatedatthebottomofLMs.
6)TEMisoperatedathighvacuum(sincethemeanfreepathofelectronsinairisverysmall)somostspecimens(biological)mustbedehydrated
(i.e.dead!!).
7)TEMspecimens(biological)arerapidlydamagedbytheelectronbeam.
8)TEMscanachievehighermagnificationandbetterresolutionthanLMs.
9)Pricetag!!!(100xmorethanLM)
I.A.3.Photons/Electrons
a.Dualconceptofwaveandparticle(Fig.I.4)
Lighthaspropertiesbothofaparticleandawave.Thisdualnatureisrequiredtosatisfactorilyexplaintheresultsofvariousphysicalexperiments.
Thediffractionoflight(bendingaroundcorners)illustratesthewavenature.TheWAVETHEORYisbasedonthestatisticalnatureofeventsand
haslittlemeaningwithrespecttothebehaviorofsingleparticles.ThewavetheorywasdevelopedandexpoundedbyHuygens(16291695)and
Hooke(16381703).TheCORPUSCULARTHEORYwasproposedbyNewton(16421727)andbecamethemoreacceptedtheoryevenafter
demonstrationofdiffractionbyYoung(17731829)andinterferencebyFresnel(17881827).Atabout1850,thewavetheorycamebackinto
favoruntilabout1900whenmoreevidenceforthecorpusculartheorywasdiscovered.
QUANTUMTHEORY(PlanckandEinstein)providesthebasisforexplainingthephenomenaofINTERFERENCE,DIFFRACTIONandthe
PHOTOELECTRICeffect(lightfallingoncertainmetalscausethemtoemitelectrons)andthusformsacommonbasisforexplainingthenatureof
actionoflight.Thetransferofenergybetweenlightandmatteroccursonlyindiscretequantitiesproportionaltothefrequencyofthe
lightwave.
E=hJ
where
E=energyofphoton(joules)
h=Planck'sconstant(6.624
•
10
34
joulesec)
J=frequency(cycles/sec)
b.Electronvelocityandwavelength
Therelationbetweenthewavelength(l )ofaparticleofmass,m,movingatavelocity,v,isgivenbytheDeBrogliewaveequation:
(1)
Anelectronofchargee(1.6
•
10
19
coulomb),andmassm(9.11
•
10
28
gm),whenpassingthroughapotentialdifferenceofVvolts(expressedin
joules/coulomb),hasakineticenergy:
(2)
Solvingforvelocity:
(3)
substitutingintotheDeBroglieequation(1):
(4)
Since1joule=10
7
dyne
•
cm=10
7
cm
2
•
gm/sec
2
(5)
Thus,forexample,ifV=60,000volts,l =0.005nm.
Fromequation(3)theelectronvelocitycanbecalculatedifVisknown:
(6)
Thefollowingtableillustratesthat,athighvoltage,electronvelocityiscomparabletothespeedoflightinavacuum(c=3
•
10
10
cm/sec).
Theequationbreaksdownwhenthevelocityoftheelectronapproachesthespeedoflightbecausearelativisticcorrectionmustbemadeforthe
valueofthemasswhere:
(7)
Therelationbetweenl andVismorecorrectlygivenby:(seeHall(1966)pp.3334)
(8)
Thefollowingtableisobtainedwhenrelativityeffectsareincluded:
c.Interference/diffraction/coherence
Anideallenssystemobtainsanexactimageoftheobject(eachpointfaithfullyreproduced).Thephenomenaofdiffractionmakesthis
unattainable(Figs.I.5,I.6).
Diffractionphenomenainvolvesthebendingofthepathofradiationpassingclosetoanobstacle(Fig.I.6).Thisresultsinaspreadingofthe
radiationintotheregionbehindtheobstructionthatthewavespassed.Thediffractionatedgescontributestothecontrastatwhichanedgecan
beobserved.Diffractionalsolimitstheresolvingpowerofthemicroscopesincetheimagepointproducedbyalensisadiffractionimageofthe
openingofthelensortheaperturerestrictingtheeffectiveopeningofthelens(Fig.I.5).
Ifthelightsourceandtheplaneatwhichthediffractionpatternisobservedareatfinitedistancesfromtheedge,thephenomenoniscalled
Fresneldiffraction.Thepatternisdescribedasduetointerferencebetweenthenondiffractedlightandawaveoflightdiffractedattheedge.
Theresultingsuperpositiongivesrisetoaseriesofdiffractionfringesorientedparalleltotheedgeandrepresentingperiodicallyvaryingbrightness,
maximaandminima.(Figs.I.7,1.8,I.9).
Coherence:Aprerequisiteforinterferenceisasuperpositionofwavesystemswhosephasedifferenceremainsconstantintime.Twobeams
arecoherentif,whencombined,theyproduceaninterferencepattern.Thebeamsareincoherentwhentheyareincapableofproducingan
interferencepattern.Twobeamsoflightfromselfluminoussourcesareincoherent.Iflightfromthetwosourcesfallsonascreen,theresultant
intensityissimplythesumofthetwointensitieswhichwouldoccurfromeachsourceseparately(Figs.I.10,I.11).Inpracticeanemittingsource
hasfiniteextentandeachpointofthesourcecanbeconsideredtogeneratelight.EachsourcegivesrisetoasystemofFresnelfringesatthe
edge.Thesuperpositionofthesefringesystemsisfairlygoodforthefirstmaximaandminimabutfartherawayfromtheedgeshadowtheoverlap
ofthefringepatternsbecomessufficientlyrandomtomakethefringesdisappear.Thenatureofwaves,phase,amplitude,andinterferenceare
illustratedinFigs.I.12andI.13.
d.Resolution
1)Definitions:
RESOLUTION:abilitytodistinguishcloselyspacedpointsasseparatepoints.
RESOLUTIONLIMIT:smallestseparationofpointswhichcanberecognizedasdistinct.
RESOLVINGPOWER:resolutionachievedbyaparticularinstrumentunderoptimumviewingconditions.
2)Distinctionbetweenresolutionandresolvingpower:
Notethedistinctionbetweenresolutionandresolvingpower.Resolvingpowerisapropertyoftheinstrumentandisaquantitythatmaybe
estimatedontheoreticalgrounds.Resolutionisequaltoorpoorerthantheresolvingpowerandisthequantityobservedunderanygivenset
ofexperimentalconditions.IntheTEM,especiallywithbiologicalsamples,theresolutionachievedmaybeconsiderablyinferiortothetheoretical
resolvingpoweroftheinstrument.
Microscopyisthescienceofseeingtheverysmall.Underidealconditions,theeyeresolvesabout1minuteofarc(=1/60degree=2.9x10
4
radian;recallthereare2p radiansin360°)andsinceitcanfocusdowntoabout250mm,thesmallestobjectwecanresolveisabout0.07mm
(70mm)(Fig.I.14).Thislimitisrelatedtothesizeofthereceptorsintheretinaoftheeye.Thefunctionofamicroscopeistomagnifytheimage
fallingontheretina(Fig.I.15).Theadvantageoflightandelectronmicroscopesisthattheyeffectivelygettheobjectclosertotheeyesoa
magnifiedimageisobtainedandmoredetailcanbediscerned.
TENNISBALLANALOGY:Eyecanresolve3cmat100meters,thusatennisballisclearlyvisible.Butifthetennisballisheldupagainstawhite
background,thevisibilitydecreases(becauseofthedecreaseincontrast).
3)Abbecriteriaofresolution:
Thefundamentalnatureoflightposeslimitsonthedetailthatcanberesolved(Fig.I.16).Abbe(1893)showedthatthesmallestresolvable
distanceisabout1/2thewavelengthoflightused.Thus,1/2thewavelengthoftheradiationusedistheultimateresolvingpowerofany
instrument.Thislimitstheusablemagnificationofopticalmicroscopesto<1000X.Atfirstitwasthoughtthatxraymicroscopeswouldbeuseful
buttherefractiveindexofsubstancesforxraysisnearly=1,thusrefractinglensescannotbemadeforxrays,andconsequently,xrayscannot
beeasilyfocusedtoformimages.
4)Magnificationlimits:
Themaximummagnificationofaninstrumentislimitedaccordingtothefollowingrelationship:
Thus,fortheLM,witharesolvingpowerofapproximately0.25µm,themaximum(useful)magnificationisabout250µm/0.25µm=1000X.Thevalue
usedfortheresolvingpoweroftheeyeinthisexample(250µm)representsamorerealisticviewingcondition.Anymagnificationabovethevalue
givenbytheaboveformularepresentsemptymagnification,sincesuchmagnificationleadstonomoreusefulinformationbutratheramagnified
blur.
AccordingtotheAbbecriteria,at60,000volts,theTEMshouldhavearesolvingpowerofabout0.0025nm.Thisshouldallowamaximumuseful
magnificationofabout100milliontimes!!!Inpractice,themaximumusefulmagnificationoftheTEMoperatedat60kVislimitedtomuchlessthan
1,000,000X.Thus,althoughtheLMnearlyobeystheAbbecriteria,theTEMfallsshortbyaconsiderableamount.Themainlimitingfactorinthe
TEM,withrespecttoachievingthetheoreticalresolvingpoweroftheinstrument,concernsthenatureoftheimaginglensesandtheprocessof
imageformation.
5)Rayleighcriteria(practicalbutarbitrary):(Fig.I.17).
Itistheabilityofmicroscopestomakeobjectpointswhichareclosetogetherappearintheimageasseparatepoints.Anideallenstakeseach
objectpointandrepresentsitexactlyasapointintheimage.Areallenstakeseachobjectpointandspreadsitoutintoacirculardisk(Airy
disk)intheimageplanewhosediameterdependsontheangularapertureofthelens.
Theshortestdistancebetween2disksatwhichthetwodisksappearpartiallyseparatedcorrespondstoabout1/2thewidthofthedisks.The
distance,d,inobjectspaceisgivenby:
d=0.61l /n
•
sina
where
l =wavelenghtoftheradiation
n=refractiveindexofthemedia
a=semiangularapertureofthelens
NOTE:n
•
sina=thenumericalaperture(N.A.)ofthelens.
Thus,tomaximizeresolvingpower,l mustbedecreased,nincreased,oraincreased.Recallthatweareconcernedatthemomentwithan
aberrationfreeopticalsystem.Thevaluefortheconstant(0.61)iscontroversialbecauseitdependsonthecoherenceoftheradiationanda
criteriaofvisibility.
FortheLM,usingoilimmersionoptics(n=1.5),sina=0.87,andvioletlight(l =400nm),d=0.2µm.Theonlywaytoimprovetheresolutionisto
uselightofshorterwavelengthsinceN.A.cannotbeincreasedbeyond~1.5.FortheTEM,n=1(vacuum),sina=10
2
andl =0.005nmfor60kV
electrons,thusd=0.3nm.
I.A.4.Optics(LensTheory)
a.Basiclawsofclassicalgeometricaloptics
1)Rectilinearpropagationoflightwhenn(refractiveindex)isconstant.
2)Lawofreflection:
3)Lawofrefraction(Snell'sLaw):
4)Independenceofrays.Theassumptionismadethatlightraystravelindependentlythroughspace.
Theselawsholdforelectrons,except#4,ifthecurrentdensityistoohighwhennegativechargedelectronscaninterfere.
b.Classicalvs.electronoptics
1)Classicaloptics:Therefractiveindexchangesabruptlyatasurfaceandisconstantbetweenthesurfaces.Therefractionoflightatsurfaces
separatingmediaofdifferentrefractiveindicesmakesitpossibletoconstructimaginglenses.Glasssurfacescanbeshaped.
2)Electronoptics:Here,changesintherefractiveindexaregradualsoraysarecontinuouscurvesratherthanbrokenstraightlines.Refraction
ofelectronsmustbeaccomplishedbyfieldsinspacearoundchargedelectrodesorsolenoids,andthesefieldscanassumeonlycertaindistributions
consistentwithfieldtheory.
c.Geometricalandphysicaloptics
Thefundamentalprinciplesofopticsgovernthedesignandoperationofboththelightandelectronmicroscopes.Thebasicopticalprinciples
involvingtheuseofrefractileelementsorlensesinordertoformmagnifiedimagesareidenticalinboththeLMandTEM.TheTEMdiffersfromthe
LMonlyintheradiationitusesandinthewayinwhichtheradiationisbentorrefracted.
Geometricalopticsdealswiththestudyofthepathsfollowedby'rays'oflightorelectronsthroughlensesandapertures,andthegeometrical
constructionsusedtofindtherelativepositionsandsizesofobjectsandtheirimages.Arayoflightorelectronsisdefinedasaninfinitelythin
pencilorbeam.Physicalopticsshowsthatthisanabstractionandcannotphysicallyexistbecauseof'diffraction'whichdealswiththewave
natureoflightandelectrons.Allresultsobtainedingeometricalopticscanbederivedfromtheprinciplesofphysicaloptics,alongwithother
phenomenasuchasinterferenceanddiffractionwhicharenotexplicableinsimplegeometricalterms.
d.Idealversesreallenses:
Lensesareusedtobendraysoflightorelectronssotheyaredeflectedinapredictablewayfromtheiroriginalpaths.Thepropertiesofanideal
lens,possessinganaxisofrotationalsymmetryare:
1)Eachrayofthebundleofrayswhichpassesfromanobjectpointwillberefractedbytheideallenstomeetinoneimagepoint.
2)Raysoriginatingfrompointswhichlieonaplaneperpendiculartotheaxis,mustbeimagedinaplanewhichisalsoperpendiculartotheaxis.
3)Theimageappearsliketheobjectirrespectiveofthemagnification,sotherelativelineardimensionsoftheobjectarepreservedintheimage.
Inpractice,theimagingbyanyreallensdoesnotcorrespondtothatoftheideallensowingtothefactthatanobjectpointisrepresentedbya
diffractionimage(Airydisc)ofthelensopeningortheapertureusedforrestrictingtheeffectiveopeningofthelens.Thisisaresultofthewave
likepropertiesoflight.Lensaberrationsalsocontributetomoreorlesspronounceddeviationsfromthepropertiesoftheideallens.
Thesinglerefractingsurfaceofsphericalcurvatureisthefundamentalunitoffocusingactionbyglasslenses.Sphericalrefractingsurfacesactas
lensesforparaxialrayswhicharethoseraysthatpassclosetotheprincipalaxisofthelens.RayswithlargeangleswillNOTobeyideallens
action.
Afundamentaldifferencebetweenlightandmagneticlensesisthattheelectronbeamdoesnotchangeinforwardvelocityasitpassesthrough
themagneticfield(lightraysslowdownwhenpassingintoamediumofhigherrefractiveindex).Refractioniscontinuouswithelectronswhenthey
areinthemagneticfield:lightisrefractedonlyattheinterfacebetweenmediaofdifferingrefractiveindex.Theelectronsalsofollowspiral
trajectoriesthroughthemagneticfield(seealsoSec.I.A.5.c(Magneticfieldsandmagneticlenses)
e.Raydiagrams:(Figs.I.20I.28)
Themethodofconstructionofraydiagramsisbasedonthreesimpleprinciples:
1)Allraysenteringthelensparalleltotheaxisarebroughttoacommonpointontheaxis,thefocalpoint.
2)Allrayspassingthroughthegeometricalcenterofthelensareundeviatedandpassstraighton,nomatterfromwhichdirectiontheycome.
3)Principleofreversibility:ifthedirectionofarayisreversedinanysystemtherayexactlyretracesitspaththroughthesystem.Thisapplies
onlytothelocationoflightpathsandnottotheintensityofthelight.
Theaboveprinciplesarebasedontheassumptionsthatwearedealingwithathinlensandconcernedwiththepathsofparaxialrays.The
standardconventionistodrawdiagramswithraysthattravelfromlefttoright.Theobjectistotheleft(infront)ofthelensandtheimageisto
theright(behind)ofthelens.
f.Definitions:
Realimage:oneatwhichlightraysphysicallyreunite,sothataphotographicplateplacedatthepositionofarealimageisexposed.
VirtualImage:onefromwhichlightraysappeartodiverge;raysarenotinfactconcentratedatthepositionofavirtualimage,sothata
photographicplateplacedatthepositionoftheimageisnotexposed(byfocusedrays).Placinganopticalsystemsuchastheeyebehindthe
lens,willenablethedivergentraystobefocusedtoformarealimage.TheintermediatelensofanTEMissometimesusedthiswayinorderto
reducethefinalsizeoftherealimageformedbytheprojectorlens(es).
Converging(positive)lens:bendsraystowardtheaxis.Ithasapositivefocallength.Formsarealinvertedimageofanobjectplacedtothe
leftofthefirstfocalpointandanerectvirtualimageofanobjectplacedbetweenthefirstfocalpointandthelens.
Diverging(negative)lens:bendsthelightraysawayfromtheaxis.Ithasanegativefocallength.Anobjectplacedanywheretotheleftofa
diverginglensresultsinanerectvirtualimage.Itisnotpossibletoconstructanegativemagneticlensalthoughnegativeelectrostaticlensescan
bemade.
g.Lensformula(thinlensequation):
where
f=focallengthofthethinlens(sameradiusofcurvatureforboth
sphericalsurfaces)
o=distanceofobjectfromlens(positivetotheleft)
i=distanceofimagefromthelens(positivetotheright)
NOTE:Foravirtualimage,ihasanegativevalue.
h.Magnification:
Foraconverginglens,iftheobjectismorethantwicethefocallengthfromthelens,thentheimageformedisreal,inverted,andsmallerinsize
thantheobject(M<1).Whentheobjectisatadistance=2f,theimageandobjectarethesamesize(M=1);whenitisbetweenfand2f,
theimageislargerthantheobject(M>1),andwhenitis<f,theimageisvirtual,erect,andlargerthantheobject(M>1).
i.Angularapertureofthelens(2a)(Fig.I.29)
Theaperturedeterminesthetotalamountofradiationarrivingfromtheobjectwhichcanbefocusedto
formanimage.Theaperturethuscontrolstheabilityofthelenstogatherinformationabouttheobject.
Thisdependsontheangleoftheconeofraysitisabletoacceptfromtheobject.Bringinganobject
closertotheeyeincreasestheangularaperture,butthereisalimittotheclosenessthattheobjectcan
bebroughttotheeye(~25cmcorrespondingtoanangleofabout0.9°fora4mmexitpupildiameterof
theeyelens;atypicalLMwithanoilimmersionobjectivelenshas2aof~175°).
j.Simplevs.compoundmicroscope(Figs.I.30I.32)
Inprinciple,arealimageofanydesiredmagnificationcanbeobtainedfromasinglepositivelens,butin
practicethisiscumbersomebecauseofthelonglensimagedistance.Oneormorelensescanbeusedto
magnifytheimageinstages(totalmagnificationequalingtheproductofthemagnificationsofeachlens).
Theimageformedbyonelensconstitutestheobjectforthesubsequentlens,whetherornotareal
intermediateimageisformed.
Comparisonofoneversestwostagemagnification:
Thefollowingdescriptionillustrateshowdifferentpathlengthsarerequiredtoachieveamagnificationof10,000Xusingeitheroneortwolenses
withf=2.0cm.
OneStageSystem:
TwoStageSystem:
Assumebothlenseshavef=2.0cmandarearrangedsoeachgives100Xmagnification.
Thus,M=100=x
i
/x
o
foreachstage.
FirstStage:
x
o
=2.02cm
x
i
=202.00cm
Therealimageformedinthefirststagebecomestheobjectforthesecondlens.
SecondStage:x
o
,x
i
sameasinthefirststage.
Totallengthofsystem
=lengthoffirststage+lengthofsecondstage
=(x
o
+x
i
)+(x
o
+x
i
)
=2(x
o
+x
i
)
=2(2.02+202.00)=408.04cm(4.08meters)
k.Problemset
Thefollowingproblemsareforyourownedificationtotesthowwellyouunderstandthebasicsoflensoptics.
1.Foreachsituationbelow,drawanaccurate(usegraphpaper)raydiagramshowingthepathof(atleasttwo)raysfromtheobjecttoimage.
Indicatewhethertheimageisrealorvirtualandspecifythedistanceoftheimagefromthelensandthemagnificationoftheimagewithrespect
totheobject.Ineachexample,thelensisconverging,withidenticalfrontandbackfocalpoints.Distancesareinarbitraryunits.Letf=lens
focallength,x
o
=distanceofobjectinfrontofthelens,andx
i
=distanceofimagebehindthelens.Theobjectmaybeanysize.
2.Inthefollowingexamples,therearetwoconverginglensesinsuccession.Drawraydiagramsshowingtheformationofboththeintermediate
andfinalimagesandgiveappropriateinformationaboutthenature(real/virtual),positions,andsizesoftheintermediateandfinalimages.What
isthemagnificationateachstageofimageformationandwhatisthemagnificationofthefinalimage?Thedistancefromthecenteroflens1(L1)
tothecenteroflens2(L2)equalsD.
I.A.5.ElectronOptics/ElectronLenses
a.Electronemission
Innershellelectronsinmetalatomsshieldtheelectricfieldofthenucleusthroughtherepulsiveforcestheyexertontheoutershell(valence)
electrons.Thustheattractionbetweenthevalenceelectronsandthenucleusisreduced.Metalatomsarecharacterizedashavingtwoloosely
boundvalenceelectronswhichmigratefreely(thisiswhymetalsaregoodelectricalconductors)andcanescapefromthemetalcompletelyif
sufficientadditionalenergyisimpartedtothem.Asthetemperatureofametalisincreased,thekineticenergyoftheelectronsincreasesbecause
ofincreasedthermalvibrationsofthemetalions,whichcollidemorefrequentlywiththeelectrons.Thermionicemissionisthetermusedto
describetheprocessbywhichthermalenergyissuppliedtolooselyboundelectronsinordertoformasourceofelectrons.
Atroomtemperatureelectronsareeffectivelypreventedfromescapingthesurfaceofthemetalowingtotheattractiveforceofthepositively
chargedions.Asthetemperatureisincreasedsomeelectronsacquiresufficientenergytoovercometheattractionandleavethemetal
temporarily.Metal,shapedasathinwire,caneasilybeheatedbypassinganelectriccurrentthroughit.Sincethemetalsurfacebecomes
positivelycharged,acertainlevelofenergy(workfunction)mustbesuppliedtoallowelectronstoescapefromthesurface.Eachmetalhasa
characteristicworkfunction.Tungsten,withalowworkfunction,emitsmoreelectronsthanmetalswithhigherworkfunctions(seealsopp.2930
andFig.I.59).
Ifastrongelectrostaticfieldisappliedinavacuumbetweenthewire(givenanegative,cathode,potential)andananode,theelectricfieldwill
causeelectronstoaccelerateawayfromthewiretowardstheanodesurface(Fig.I.33).Thespeedoftheelectronsdependsonthestrengthof
theelectrostaticfield(voltage)betweenthecathodeandanode(equation(3),Sec.I.A.3.b)Thenumberofelectronswhichleavethewire
dependsonthetemperaturetowhichthewireisheated,whichdependsonhowmuchfilamentcurrentpassesthroughthewire.
A"V"shapedwirewillhavethehighesttemperatureatthetip.Electronswithdrawnfromthefilamenttipcarryelectricchargestotheanode.This
electriccurrent,whichflowsbetweenthefilamentandtheanode,iscalledthebeamcurrent.
1)Electricfield/Equipotentials
Anelectricallychargedobjecthasassociatedwithitanelectricfield.Thus,anelectricallychargedparticle,whenbroughtnearachargedobject,
isinfluencedbyanelectricalforceinthevicinityoftheobject.Theforceisdirectedtowardthechargedobjectifthechargesareofopposite
signsandawayfromtheobjectiftheyareofsimilarsign.DEFINITION:Thedirectionofanelectricfieldisdefinedasthedirectionoftheforce
actingonapositivecharge.(Figs.I.3435)
Alongthelinesofforceconnectingthetwocharges,theelectricpotentialwillchangegraduallybetweentheextremevaluesrepresentedbythe
twocharges.DEFINITION:Equipotentiallinesdefinethepointsalongthelinesofforcewithidenticalelectricalpotential.Theseequipotential
surfacesarealwaysorientedperpendiculartothelinesofforce.Thechangesintheelectricpotentialaregradualinspace.
Electronswhichenterafieldbetweentwoparallelplatesinadirectionparalleltotheplatesareaffectedbytheforcedirectedperpendicularto
theplates(FigI.36).Theelectronswillbeattractedtowardthepositiveplate.Thepathchangesinaseriesofgradualstepsattheequipotential
surfaces.
FigureI.37showshowtheelectronpathis"refracted"attheequipotentialsurface.TheresultisfundamentallythesameasthatgivenbySnell's
Lawofrefractioninlightoptics.Aconsequenceofthisisthatasphericallycurvedequipotentialsurfaceexhibitsthepropertiesofalens.
FiguresI.38andI.39showhowbothpositive(converging)andnegative(diverging)electrostaticlensescanbeformed.Thisfeatureof
electrostaticlensesdiffersfromelectromagneticlenseswhichcanonlyactasconverginglenses.
2)Advantages/Disadvantagesofelectronlenses:
Thefactthattherefractiveindexdoesnotchangeabruptlyinelectronlenseshasoneadvantageinthattherearenotroublesomereflectionsat
equipotentialsasatglassinterfaces.Thereisaseriousdisadvantageinthatequipotentialscannotbeshapedandcombinedinarbitraryfashionto
correctforchromaticaberrationandothererrors.
Althoughelectronmicroscopeswhichemployelectrostaticlenseshavebeenmade,mostmicroscopesuseelectromagneticlenses.Amajorreason
isthatelectrostaticlensesaremoresensitivetothequalityofthevacuumandcleanlinessofthecomponentsthanareelectromagneticlenses.
Somelensaberrationsaremoresevereforelectrostaticlensescomparedtoelectromagneticlenses.Electrostaticlensesrequireverypowerful
electrostaticfieldswhichcanleadtoelectricalbreakdownor"arcingover"insidethecolumn,especiallyunderpoorvacuumconditions.Forthis
reason,electrostaticlensescannotbemadewithfocallengthsasshortasmagneticlenses.
b.Electrostaticlens
Abasicunderstandingofelectrostaticlensesisimportantfortwomainreasons:i)theelectrongunuseselectrostaticlensactiontoformthe
primarybeamsource,andii)itisquitecommonforachargetodeveloponthenonconductingcontaminationwhichmayaccumulateonphysical
apertures(suchastheobjectiveaperture)andtransformthemintoweakelectrostaticlenseswhichcandistorttheelectronimage.
3)Propertiesofelectrostaticlenses:
a)Anyaxiallysymmetricalelectrostaticfieldhasthepropertiesofalensforraysconfinedtotheparaxialregion.Alltheideallensformulasapply
toelectrostaticlenses.
b)Forelectronlenses,replaceÃ(f)forrefractiveindexinthelensequations(f=valueofthepotentialontheaxis).Intheimageformingsystem
ofmostTEMs,fisthesameonbothsidesofthelens(SeeSec.I.A.5.c).
c)Ifboundedbyregionswherefisconstant,anelectrostaticlensisalwaysconvergent.
c.Magneticfieldsandmagneticlenses
1)Magneticfield
Anelectriccurrentpassingthroughaconductorgivesrisetoamagneticfield.TheconventionisthatNisthedirectioninwhichthelinesofthe
magneticfieldpoint(Fig.I.40).Themagneticfluxisthetotalnumberoflinesandthefluxdensityisthenumberoflinesperunitareaofasurface.
UsetheRIGHThandruletodeterminethedirectionofthefield(thumbpointstowardcurrentdirectionandfingerscurlindirectionoffield.NOTE:
Byconvention,thedirectionofelectronflowisoppositetothatofcurrentflow.
Fluxdensitydependsonthepropertiesofthematerialsurroundingtheconductor.Ironinducesahigherfluxdensitythanairoravacuum.The
propertyofthematerialwhichaffectsthefluxdensityiscalledthepermeability,m,ofthematerial.Forairandvacuum,m=1.0.For
ferromagneticmaterialsitcanbeaslargeasseveralhundredthousand.
Iftheconductorhastheshapeofacircularloop,thelinesofforceformcirclesaroundtheloop.Thefluxdensityisgreatestatthecenterofthe
loop.Themagnetinthecenteroftheloopisorientedperpendiculartotheplaneoftheloopifthecurrentthroughtheloopissufficientlystrongto
eliminatetheinfluenceoftheearth'sfield.ThesideoftheloopatwhichthelinesofforceleavetheloopistheNorth(N)poleofthemagnet(Figs.
I.41,I.42).
Ifthewireiswoundinseveralturnsaroundacylindricalsurface(solenoid),eachturnwillcontributetotheinducedmagneticfield.Theflux
densityinthecenterofthecoilisgivenby:
Inthecaseofairandnonmagneticmaterials,µ=1.0andB=H.
Thepermeabilityofirondependsonthefieldstrength,H,anddecreasestounityathighfieldstrengthorwhenthefluxdensity,B=H(Fig.I.43).
Thehighpermeabilityofironisduetotheinducedmagneticfieldorientingmicroscopiccrystalregionsactingastinymagnetsintheiron.Allthese
tinymagnetsaddtheirmagneticfieldstotheinducedfield(Fig.I.44).Whenallmicromagnetsarenearlyoriented,theironwillaffecttheflux
densitytoadecreasingamountsincethereorientationofmicromagnetsisnearingcompletion.Thus,thepermeabilityofironathighfieldstrengths
approachesthatofemptyspace.Atthispointtheironreachesmagneticsaturation.
2)Hysteresis
Thestrengthofthelensdependstosomeextentonthepreviousmagnetichistoryof
thelens.Whenthecurrentinalensisreduced,thedecreaseinmagnetizationdoes
notretracethesamepathobtainedwhenthecurrentwasincreased(Fig.I.45).
Inductionofmagnetizationinvolvesaphysicalmovementwithinthemagnetized
material,requiringtheovercomeofacertaindegreeofinertia.Asaresult,
magnetizationtendstolagbehindthemagnetizingforceapplied.Inducedmagnetic
fluxcanonlybereturnedtozerobyapplicationofacurrentintheoppositedirection.
Aconsequenceofhysteresisisthatthelevelofcurrentusedtoenergizeamagnetic
lensDOESNOTpreciselyspecifythelensstrength(i.e.focallength).
NormalizationofTEMlensesisaccomplishedbyreducingthelenscurrenttozero
somepredeterminednumberoftimes.Hysteresismayalsobeminimizedbytakinga
lenstosaturationandthenreturningittotheworkingcurrentwithoutovershooting.
Whenthefieldstrengthisreducedtozero,somemagnetizationstillremainsintheiron
(residualmagnetizationorremanence).Anadvantageofsoftironisthefactthat,
whenusedinanelectromagnet,hysteresisislow.
Introductionofpiecesofironinamagneticfielddrasticallyaffectsthefluxdensity.
Magneticmaterialhasashieldingeffect,theeffectbeinggreaterthegreaterthe
permeability.Permalloy(mmetal)hasamaximumpermeabilityof80,000140,000
comparedtoironusedintransformers(~7000).mmetalpermeabilityislimitedtolower
fieldstrengthsthanthatatwhichironstillretainshighpermeability.Thismetalis
thereforeusefulforshieldingtheTEMfromexternalmagneticfields.
d.Theelectromagneticlens
1)Lensdesigndevelopment(Figs.I.46I.48)
Theefficiencyofthemagneticfieldproducedbyashortsolenoidwasfirstimproved
byencasingtheenergizingcoilinasheathofsoftironwhichhasthepropertyofconcentratingthelinesofforceinamagneticfieldandthus
becomingmagnetizedbyinduction.Inthiswayamuchmorepowerfulaxialmagneticfieldisobtainedforthesameamountofcurrentflowing
throughthesolenoid.Furtherdevelopmentinvolvedencasingtheentirecoilwithsoftironexceptatanarrowannulargapintheinsideofthecoil.
Thisproducesagreaterconcentrationofthemagneticfieldalongashortaxialdistance.Toachieveshorterfocallengthlenses(andobtaingreater
magnifications)asoftironpolepiecewithanopenaxialborewasintroducedatthepositionoftheannulargap.
MagneticlensesusedinTEMsarealwaysconstructedwithanironcircuittoproduceahighfieldstrengthacrossashortgap.Themagneticfields
forTEMlensesareintherangeof10,00020,000gauss.
2)Forcesactingonacurrentinamagneticfield
Theforceonanelectroninamagneticfieldisalwaysatrightanglestothevelocityandthedirectionofthefield(Figs.I.49,I.50,andI.52).The
fieldonlyactsonthevelocitycomponentwhichisdirectedperpendiculartothelinesofforce.Usethelefthandrule(Fig.I.51:firstfingerfor
fielddirection,middlefingerforcurrentdirection,andthumbfordirectionofforce).Rayspassingthroughthelensareturnedthroughanangle
whichdoesNOTdependonthedistanceoftheraysfromtheaxis.Allelectronscontainedinagivenmeridionalplanebeforeenteringthefieldare
containedinarotatingmeridionalplaneastheypassthroughthelens,andthentheyleavethelenscoplanar.
Whenelectronsenterthelenstheyencounterasidewaysforcewhichcausestheelectrontorotate
asitcontinuesthroughthelens(Figs.I.53I.57).Sincetheradialcomponentofthemagneticfield
reversesafterthecenterofthelens,therotationalvelocitysetupinthefirsthalfofthelensis
countered.Theelectronenteredthelenswithoutangularmomentumabouttheaxisandleaves
withoutangularmomentum.Theneteffectisadeflectiontowardtheaxis,whichitmustcrossatthe
focalpointf
2
.Theanglebetweentheobjectvectorandtheimagevectoris180°+q,whereas,for
glasslensesandelectrostaticlenses,theanglebetweenarealobjectandtheimageisexactly180°.
Sincetheradialforceisdirectedtowardtheaxis,thelensisconvergentnomatterwhatthedirection
ofthefield.
3)Propertiesofamagneticlens:
Anyaxiallysymmetricmagneticfieldhasthepropertiesofanideallens.Alltheformulasfortheideallensmaybeapplied.
Magneticlensesarealwaysconvergent.Theconventional,axiallysymmetriclensisalwaysboundedbyregionswhicharefieldfree,the
consequencebeingthatthenetactionofelectronlensesisinevitablyconvergent.Limitedregionsmaybedivergentbutnotthelensasawhole.
Theseriousconsequenceofthisisthatneithersphericalorchromaticaberrationscanbecorrectedasisdoneinlightopticsbytheusedoublets
ofpositiveandnegativelenses.
Intheabsenceofelectrostaticfields,therefractiveindexisthesameinobjectandimagespace,thereforef
1
=f
2
.
Electronstravelingthroughaxiallysymmetricfieldsexperienceaspiraltrajectoryofdiminishingradius.Theimagevectorisatanangle180°+qto
theobjectvector.
Thedeflectionoftheelectrontowardstheaxismeansthatanelectronenteringthelensparalleltoitsaxiswillcrosstheaxisafterhavingpassed
thelens.Thedeflectionwillincreasewiththedistancefromtheaxis.Thus,abeamofelectronsinparallelpathsparalleltotheaxisofthelenswill
befocusedtoanimagepointontheaxiswhichrepresentsthesecond(back)focalpointofthelens(f
2
).Notethatmagneticlensesarehighly
inefficientinthatonlyaminorportionofthetotalfieldstrengthisactuallyeffectiveinfocusingtheelectron.
4)Magneticlensfocallength
Inamagneticelectronlensthefocallengthisdeterminedbythefieldstrengthinthelensgapandbythespeedoftheelectrons(determinedby
theacceleratingvoltage).
Formagneticlenses,focusingisachievedbyvaryingthecurrentwhichpassesthroughtheelectromagnet.Thisinturnchangesthestrengthof
themagneticfieldandtherebyaltersthefocallengthofthelensandisequivalenttoacombinedchangeinboththe"refractiveindex"and
"curvatureofsurface".Forabeamofmoreenergeticelectrons,thelenscurrenthastobeincreasedinordertokeepthefocallengthconstant.
FocallengthandcurrentareNOTlinearlyrelated:strengthincreasesinasigmoidfashion(Fig.I.45)ascurrentincreasesuntilapointisreached
wherethelensissaturatedandnofurtherincreaseinlensstrengthcanbeachieved.
Sincethefocallengthofthelensisdirectlyproportionaltotheacceleratingvoltage,avariationinthevelocityoftheelectronsintheimaging
beamaffectsimagequalitybyeliminatingperfectfocus(chromaticaberration).
5)Magneticlensdesign:(Figs.I.46,I.47).
Condenserlensesusuallyhavearelativelylargeboreandspacingwhichresultsinalongfieldandlongfocallength.
Typicalconstructionoftheobjectivelensproducesastrongfieldofshortaxialextent(i.e.shortfocallengthbetween(1.53mm)necessaryfor
formationofimagesathighmagnification.Thespecimenisplacedwithinthemagneticfieldoftheobjectivelens.Thus,anyfieldintroducedby
contaminantsinthespecimencandistortthefieldofthelens.Notethatthisalsomeansthatpartofthelensfield("prefield")isonthefrontside
oftheobjectandaffectstheelectronbeambeforeitpassesthroughtheobject.
Mostofatypicalmagneticlensliesoutsidethevacuumofthemicroscope.Onlythoseregionsthroughwhichtheelectronbeampassesareinhigh
vacuum.Magneticlensesmustbewatercooledtodissipatethelargeamountsofheatproducedbythecurrentsintheelectromagnetcoils.
DATE NAME EVENT
1897 J.J.Thompson Discoverstheelectron
1924 LouisdeBroglie Identifiesawavelengthtomovingelectrons
l =h/mv
where
l =wavelength
h=Planck'sconstant
m=mass
v=velocity
(Foranelectronat60kVl=0.005nm)
1926 H.Busch Magneticorelectricfieldsactaslensesforelectrons
1929 E.Ruska Ph.Dthesisonmagneticlenses
1931 Knoll&Ruska Firstelectronmicroscopebuilt
1931 Davisson&Calbrick Propertiesofelectrostaticlenses
1934 Driest&Muller SurpassresolutionoftheLM
1938 vonBorries&Ruska FirstpracticalEM(Siemens)10nmresolution
1940 RCA CommercialEMwith2.4nmresolution
1945 1.0nmresolution
Fig.I.1Comparisonoflightandelectronmicroscopes.Ineach
instrument,illuminationfromthesource(lamp,filamentinthe
electrongun)isfocusedbythecondenserlensontothespecimen.
Afirstmagnifiedimageisformedbytheobjectivelens.Thisimage
isfurthermagnifiedbytheprojectorlensontoagroundglass
screen(light)orfluorescentscreen(electrons).(FromAgar,p.8)
Fig.I.2CrosssectionalviewofthePhilipsEM300.(FromAgar,p.40)
Toviewtheanimatedmicroscope,clickhere.
Note:QuickTimePlugInrequired
(Thiscanbedownloadedathttp://apple.com/quicktime/download)
Fig.I.3Sectionthroughacomplex
doublecondenser6lensPhilips
EM200electronmicroscope.(From
Meek,p.99)
Fig.I.4Thestatisticalnatureofdiffraction
patterns.(FromHall,p.13)
"Theprecisenatureof'electronwaves'or'matterwaves'isverydifficulttounderstandordescribeinmaterialterms.Electronwavesarenot
electromagneticradiationofthekindtowhichlight,Xraysandradiowavesbelong.Theyconstituteasortofquantumor'packet'ofradiationwhich
accompanieseachindividualelectron,followingitspathandnotradiatingoutwardsfromit."(Meek,1976,pp.4849).
V l (nm)
v(
•
10
10
cm/sec)
v/c
10,000 0.0123 0.593 0.198
50,000 0.0055 1.326 0.442
100,000 0.0039 1.875 0.625
1,000,000 0.0012 5.930 1.977!
V l (nm)
v(
•
10
10
cm/sec)
v/c
10,000 0.0123 0.593 0.195
50,000 0.0055 1.326 0.414
100,000 0.0039 1.875 0.548
1,000,000 0.0012 5.930 0.941
FigI.5Aperfectpointsourcecannotbe
imagedbyalensasaperfectpointimagedue
tothepresenceoftheapertureAB(which
maybetheedgeofthelens).Diffractionat
thisaperturegivesrisetoaseriesoffringes,
whichsurroundtheimageformedofthepoint
source.Thepatternproducediscalledan'Airy'
disk.(FromMeek1sted.,p.35)
Fig.I.6Wheneverawavefrontstrikesa
barrier,itcanbendaroundthecorner'by
givingrisetoasecondarywavefrontatthe
edge,sinceeachpointonthewavefrontcan
giverisetoanewsourceofwaves.This
phenomenoniscalled'diffraction'.(FromMeek
1sted.,p.22)
Fig.I.7Diffractionpattern(right)formedbyanirregularlyshapedaperture
(left).(FromYoung,p.95)
Fig.I.8(a)
Photographof
theedgeofa
razorblade
illuminatedby
monochromatic
(blue)light
rendered
coherentby
passing
througha
narrowslit.(b)
Microdensitometer
tracingofthe
negativefrom
whichthe
photograph
wasmade.
FourFresnel
fringescanbe
distinguished.
(FromMeek1st
ed.,p.27)
(a)
(b)
(a) (c)
(b)
Fig.I.9(a)Fresnelfringesformed
byelectrons.Thesefringesare
formedoutsidetheedgeofahole
(white)inacarbonfilm(black).(b)
Amicrodensitometertracingofthe
fringesystem;thepatternis
identicalwiththeFresnelfringe
systemformedbyvisiblelight(see
Fig.I.8).(c)Anunderfocusedimage
ofaholeinafilm,showinga
completesystemofabout40
Fresnelfringesinsidethehole.
(FromMeek1sted.,pp.2930)
Fig.I.10Diffractionimagesoftwo
easilyresolvedpoints.(From
Slayter,p.243)
Fig.I.11Imagesoftwo
incoherentlyilluminatedpointsat
thelimitofresolution.(a)individual
intensities;(b)summedintensities.
(FromSlayter,p.244)
Fig.I.12Examplesofwhatoccurswhentwo
wavesofthesamewavelengthandequal
amplitudeadd.Ineachexample,thetwo
separatewavesareshownontheleftand
theirsumorresultantwaveontheright.The
differentexamplesarecharacterizedbyvarying
phasedifferences.Thephaseofawave
(usuallyexpressedasafractionofthe
wavelengthorindegrees)isthepositionofa
crestrelativetosomearbitrarypoint.Although
thephaseofagivenwavevarieswithtimeas
thewavetravels,thedifferenceinphaseofthe
twowavesofthesamewavelengthwiththe
samevelocity,isindependentoftime.Such
wavescaninterferewithoneanother.The
resultantwavehasthesamewavelength,l .
(a)Phasedifferencezero.Thewavestotally
reinforceandaresaidtobe"inphase"orto
showconstructiveinterference.
(b)Phasedifferencel /4.Partialreinforcement,
givingawaveofamplitude1.4(intensity2.0).
(c)Phasedifferencel /2.Thewavesare"outof
phase"andthereistotaldestructive
interferencetogivenoresultantwaveora
wavewithamplitude0(intensity0).(From
GluskerandTrueblood,p.19)
Fig.I.13Photographofan
interferencepatterninwater
wavesformedbythe
superpositionofwavesfromtwo
sourcesoscillatinginphasewith
thesamefrequency.(FromYoung,
p.22)
Fig.I.14Theangularapertureofthe
eyeisrelativelysmall.(FromMeek,
1sted.,p.13)
Fig.I.15Increasingtheangular
apertureoftheeyewithalens.The
lensallowstheobjecttobeheld
closertotheeye,whichisthereby
enabledtogathermoreinformation.
(FromMeek1sted.,p.14)
Fig.I.16Theinteractionofwaves
withanobstacle.Theboatridesthe
longwavelengthoceanwave,but
reflectsthesmallwavelength
surfaceripple.Anobserverwho
wishestodetectthepresenceof
theboatcandosoonlyby
observingwaveswhichhave
wavelengthssmallerthan,or
comparableto,thelengthofthe
boat.(FromSherwood,p.19)
Maximummagnification=
resolvingpoweroftheeye
resolvingpowerofthemicroscope
(a)
Fig.I.17(a)TwoAiry
disksrepresenting
twoimagepoints
shownatincreasing
separationfromleft
toright.Inthe
pictureatthe
extremerightthe
twodiskscanbe
distinguishedas
separatedisks.
(b)Theintensity
distributionatanAiry
disk.R,halfwidthof
thecentralmaximum
representedbya
bellshapedcurve.
(c)TheRayleigh
criteriaforresolution.
(FromSjostrand,
p.115)
i=r
Fig.I.18Reflection.(FromSlayter,
p.4)
Fig.I.19Refraction.(FromSlayter,
p.6)
Fig.I.20Principalraydiagramsshowing
imageformationbyaconvexlens.
(a)Whentheobjectdistanceisgreater
thanthefocallength,areal,inverted
imageisformed.
(b)Whentheobjectdistanceisless
thanthefocallength,avirtual,erect
imageisformed;itspositionis
obtainedbyprojectingtheprincipal
raysbackward.Theraysappearto
comefrompointQ.(FromYoung,
p.127)
Fig.I.21Definitionof
principalfocus,F,inimage
spaceofalens.(From
Sjostrand,p.20)
Fig.I.22Focusingeffectoflenson
raysoriginatingfrompointson
principalaxislocatedatdifferent
distancesfromthelens.(From
Sjostrand,p.21)
Fig.I.23Definitionofprincipal
focusinobjectspaceF1ofa
lens.(FromSjostrand,p.21)
Fig.I.24VirtualimageQof
objectpointlocatedbetween
principalfocusinobjectspace
andthelens.(FromSjostrand,
p.21)
Fig.I.25Constructionoftheimage
ofanobjectbymeansofray
tracing.(FromSjostrand,p.22)
Fig.I.26Magnifyingeffectof
apositivelens.(From
Sjostrand,p.22)
Fig.I.27Virtualmagnified
imageofobjectlocated
betweenprincipalfocusin
objectspaceandthelens.
(FromSjostrand,p.22)
Fig.I.28Amagnifyingglassformsan
enlarged,erectvirtualimage.The
angularsizeofthisimageis
approximately4"/15"or4/15.The
angularsizeoftheobjectatthe
closestdistanceforcomfortable
viewingis1"/10"or1/10.The
magnificationinthissituationis(4/15)/
(1/10),or22/3.(FromYoung,p.130)
Fig.I.29Theangularapertureofa
lens.Theangle2a isthe
acceptanceangleofthelens,and
thelargeritcanbemade,themore
informationcanthelenstransmit.A
largelensofhighaperturecan
thereforetellusmoreaboutan
objectthanasmalllensoflow
power.(FromMeek1sted.,p.12)
Fig.I.30Raydiagramforhighmagnification
modeofoperation.Notethateachlens
formsarealimage,withimageinversion.
I0istheimageformedbytheobjective
lensO,I1isformedbythefirstprojector
lensP1andI2bythesecondprojectorP2,
onthescreen.(FromAgar,p.30)
Fig.I.31Left:raydiagramofthe3realimagemediumandhighmagnificationimagingsystemofa3lens
microscope.Center:2realimageverylowor'scan'magnificationrangeofa3lensmicroscope.Right:2real
imagelowmagnificationsystemofa3lensmicroscope.(FromMeek1sted.,pp.118,120121)
Fig.I.32Raydiagramforacompleteelectron
microscope.FilamentF,condenser1lensC1,
condenser2lensC2,condenserapertureCA,
specimenS,objectivelensO,objectiveaperture
OA(inbackfocalplane).1stintermediateimage
andselectorapertureSA.IntermediatelensP1,
secondintermediateimageI2,projectorlensP2
andfinalimageonthefluorescentscreenFC.
(FromAgar,p.35)
a)f=2.0
x
o
=5.0
e)f=4.0
x
o
=3.0
b)f=10.5
x
o
=21.0
f)f=13.3
x
o
=13.3
c)f=3.5
x
o
=3.0
g)f=3.142
x
o
=0.0
d)f=5.0
x
o
=2.5
a)D=8.0
L1:f=2.0
x
o
=4.0
L2:f=3.0
b)D=8.0
L1:f=2.0
x
o
=6.0
L2:f=3.0
c)D=4.0
L1:f=2.0
x
o
=3.0
L2:f=2.0
FigI.33Accelerationofelectronin
electricfield.(FromSjostrand,p.26)
Fig.I.34Linesofforceatapositively
chargedsphericalbody.(FromSjostrand,
p.32)
Fig.I.35Linesofforceandequipotential
surfaces(stippledlines)associatedwith
twoequalchargesofoppositesign.
(FromSjostrand,p.32)
Fig.I.36Equipotentialsurfacesattwoparallel
platesofoppositechargeswiththepathofan
electronindicatedwithinthehomogeneous
partofthefield.(FromSjostrand,p.33)
Fig.I.37Refractionofelectronatan
equipotentialsurface.(FromSjostrand,p.33)
Fig.I.38.Negativelensactionof
electrostaticfieldatanaperturewhen
V2V1>V3V2.(FromSjostrand,
p.34)
Fig.I.39.Positivelensactionatan
aperturewhenV2V1<V3V2.
(FromSjostrand,p.34)
Fig.I.40Magneticfieldinducedbycurrent
passingthroughaconductor.(From
Sjostrand,p.35)
Fig.I.41Magneticfieldinducedbycurrent
passingthroughasolenoid.(From
Sjostrand,p.37)
Fig.I.42Solenoidwithironcore.(From
Sjostrand,p.40)
Fig.I.43a.Dependenceofpermeabilityonfluxdensity,B.
b.RelationshipbetweenfluxdensityBandfieldstrength.
(FromSjostrand,p.38).
Fig.I.44Magnetization.(FromSlayter,
p.361)
Fig.I.45Curves
showinghowthe
magnetizationof
softiron(lens
strength)is
relatedtothe
magnetizing
force(lens
current).An
unmagnetized
lensstartsfrom
thepointOand
followsthepath
OAaslens
current
increases.Atthe
pointA,further
increaseinlens
currentproduces
nofurther
increaseinlens
strength;thelensissaidtobe'saturated'.Whenlenscurrent
isreduced,thepathOAisnotretraced;adifferentpathABis
followed.Thisdisplacementiscalled'hysteresis'.Atzero
current(pointB),someresiduallensstrengthremains;thisis
called'remanence'.Tobringthelensbacktozerostrength,a
reversecurrentOCmustbeapplied.Lensstrengththen
increaseswithincreasingreversecurrent,followingthepath
CD.Thepolarityofthelenschanges,butthisdoesnotaffect
itsfocusingpower;onlythespiralelectronpathisreversed.
Becauseofhysteresis,itisnotpossibletocalibratealens
currentmeteraccuratelyintermsoflensstrengthor
magnification.
Fig.I.46Evolutionofmagneticelectron
lenses.(A)Shortsolenoidusedasa
magneticlens.(B)Softironcasing
enclosingoutersurfaceofthesolenoid,
thusconcentratingthefield.(C)Soft
ironencasingthesolenoidexceptata
narrowannulargaptherebyreducing
themagneticfieldtoaveryshortregion
alongthelensaxis.(D)Modern
objectivelensconsistingofasoftiron
encasedsolenoidandsoftironpole
piecessoastohaveanenormously
concentratedfieldatthelevelofthe
annulargap.(FromWischnizter2nded.,
p.33)
Fig.I.47(a)Amagneticlensconsisting
ofatightlywoundcoilandasoftiron
shroudsurroundingthecoilexceptfor
asmallgap.Thefieldisconcentratedin
thatgap.(b)Shortfocallength
electromagneticlenswithpolepieces.
(FromSjostrand,p.50)
Fig.I.48Fieldstrengthdistribution
curves.ThecurvesADcorrespondto
therespectivelensesillustratedinFig.
I.46.Eachrepresentsthefieldstrength
alongthelongaxisofthelens.The
changesintheshapeofthecurves
representtheshorteningor
concentrationofthefieldovera
shorteraxialdistance.Hz=
longitudinalmagneticfield.Z=
distancealongtheaxisofsymmetry.
(FromWischnizter2nded.,p.33)
Fig.I.49TheforceFactingon
astraightconductorina
homogeneousmagneticfield
offluxdensityBwhencurrent
Iispassedthroughthe
conductor.(FromSjostrand,
p.43)
Fig.I.50Pathofanelectronina
magneticfield.(A)Inalarge,uniform
magneticfield.(B)Inasmall,uniform
magneticfield.(FromWischnitzer2nd
ed.,p.25)
Fig.I.51Lefthandthumbrule.
(FromSjostrand,p.43)
Fig.I.52Thompson'sexperiment.A
streamofelectronsoriginatingfroma
sourceandpassing,invacuo,through
amagneticfieldproducedbyapairof
magnetswillbedeflected.The
directionofdeflectiondemonstrates
thatelectronsarenegativelycharged
particlesofmatter.(FromWischnitzer
2nded.,p.25)
Fig.I.53Actionofasolenoidonan
electronbeam.Anelectriccurrent
passingthroughthecoilproducesan
axialmagneticfield.Thisisthe
refractingmediumfortheelectrons.An
electronstartingatapointontheaxisA
andatanangletoitfollowsaspiral
path,returningtotheaxisatthepoint
B.Theactionisbasicallysimilartothat
oftheconverginglightlensshownin
Fig.I.20.(FromMeek1sted.,p.8)
Fig.I.54Actionofthemagnetic
lens.(a)Inperspective.(b)
Electrontrajectoryin
projection,alongdirectionof
propagation.(c)Electron
trajectoryinprojection,side
view.(FromSlayter,p.358)
Fig.I.55Componentsofthe
vectorHneartheaxisoffields
withaxialsymmetry.His
representedbytwo
components,Hz,the
componentinthez(axial)
direction,andHr,the
compnentinther(radial)
direction.(FromHall,p.85)
Fig.I.56Theycomponentof
themagneticfieldina
magneticlensisoriented
perpendiculartothedirection
ofanelectronenteringthe
lensalongapathparallelto
thelensaxis.Thisy
componentwillaffectthe
electron,deflectingitinthex
directionasindicatedbythe
arrowmarkedvx.(From
Sjostrand,p.48)
Fig.I.57Thezcomponentofthemagneticfield
andthexvelocitycomponentoftheelectron
inamagneticlensinteract,deflectingthe
electronintheydirectiontowardthelens
axis.(FromSjostrand,p.49)
CuuDuongThanCong.com https://fb.com/tailieudientucntt
cuu duong than cong . com
I.THEMICROSCOPE
I.A.PRINCIPLESOFTHETRANSMISSIONELECTRONMICROSCOPE(TEM)
I.A.1.OriginoftheTransmissionElectronMicroscope
I.A.2.ComparisonofLight(LM)andElectronMicroscopes(Fig.I.1)
a.Similarities(Arrangementandfunctionofcomponentsaresimilar)
1)Illuminationsystem:producesrequiredradiationanddirectsitontothespecimen.Consistsofasource,whichemitstheradiation,anda
condenserlens,whichfocusestheilluminatingbeam(allowingvariationsofintensitytobemade)onthespecimen.
2)Specimenstage:situatedbetweentheilluminationandimagingsystems.
3)Imagingsystem:Lenseswhichtogetherproducethefinalmagnifiedimageofthespecimen.Consistsofi)anobjectivelenswhichfocusesthe
beamafteritpassesthroughthespecimenandformsanintermediateimageofthespecimenandii)theprojectorlens(es)whichmagnifiesa
portionoftheintermediateimagetoformthefinalimage.
4)Imagerecordingsystem:Convertstheradiationintoapermanentimage(typicallyonaphotographicemulsion)thatcanbeviewed.
b.Differences
1)Opticallensesaregenerallymadeofglasswithfixedfocallengthswhereasmagneticlensesareconstructedwithferromagneticmaterialsand
windingsofcopperwireproducingafocallengthwhichcanbechangedbyvaryingthecurrentthroughthecoil.
2)MagnificationintheLMisgenerallychangedbyswitchingbetweendifferentpowerobjectivelensesmountedonarotatingturretabovethe
specimen.Itcanalsobechangedifoculars(eyepieces)ofdifferentpowerareused.IntheTEMthemagnification(focallength)oftheobjective
remainsfixedwhilethefocallengthoftheprojectorlensischangedtovarymagnification.
3)TheLMhasasmalldepthoffield,thusdifferentfocallevelscanbeseeninthespecimen.Thelarge(relative)depthoffieldintheTEMmeans
thattheentire(thin)specimenisinfocussimultaneously.
4)Mechanismsofimageformationvary(phaseandamplitudecontrast).
5)TEMsaregenerallyconstructedwiththeradiationsourceatthetopoftheinstrument:thesourceisgenerallysituatedatthebottomofLMs.
6)TEMisoperatedathighvacuum(sincethemeanfreepathofelectronsinairisverysmall)somostspecimens(biological)mustbedehydrated
(i.e.dead!!).
7)TEMspecimens(biological)arerapidlydamagedbytheelectronbeam.
8)TEMscanachievehighermagnificationandbetterresolutionthanLMs.
9)Pricetag!!!(100xmorethanLM)
I.A.3.Photons/Electrons
a.Dualconceptofwaveandparticle(Fig.I.4)
Lighthaspropertiesbothofaparticleandawave.Thisdualnatureisrequiredtosatisfactorilyexplaintheresultsofvariousphysicalexperiments.
Thediffractionoflight(bendingaroundcorners)illustratesthewavenature.TheWAVETHEORYisbasedonthestatisticalnatureofeventsand
haslittlemeaningwithrespecttothebehaviorofsingleparticles.ThewavetheorywasdevelopedandexpoundedbyHuygens(16291695)and
Hooke(16381703).TheCORPUSCULARTHEORYwasproposedbyNewton(16421727)andbecamethemoreacceptedtheoryevenafter
demonstrationofdiffractionbyYoung(17731829)andinterferencebyFresnel(17881827).Atabout1850,thewavetheorycamebackinto
favoruntilabout1900whenmoreevidenceforthecorpusculartheorywasdiscovered.
QUANTUMTHEORY(PlanckandEinstein)providesthebasisforexplainingthephenomenaofINTERFERENCE,DIFFRACTIONandthe
PHOTOELECTRICeffect(lightfallingoncertainmetalscausethemtoemitelectrons)andthusformsacommonbasisforexplainingthenatureof
actionoflight.Thetransferofenergybetweenlightandmatteroccursonlyindiscretequantitiesproportionaltothefrequencyofthe
lightwave.
E=hJ
where
E=energyofphoton(joules)
h=Planck'sconstant(6.624
•
10
34
joulesec)
J=frequency(cycles/sec)
b.Electronvelocityandwavelength
Therelationbetweenthewavelength(l )ofaparticleofmass,m,movingatavelocity,v,isgivenbytheDeBrogliewaveequation:
(1)
Anelectronofchargee(1.6
•
10
19
coulomb),andmassm(9.11
•
10
28
gm),whenpassingthroughapotentialdifferenceofVvolts(expressedin
joules/coulomb),hasakineticenergy:
(2)
Solvingforvelocity:
(3)
substitutingintotheDeBroglieequation(1):
(4)
Since1joule=10
7
dyne
•
cm=10
7
cm
2
•
gm/sec
2
(5)
Thus,forexample,ifV=60,000volts,l =0.005nm.
Fromequation(3)theelectronvelocitycanbecalculatedifVisknown:
(6)
Thefollowingtableillustratesthat,athighvoltage,electronvelocityiscomparabletothespeedoflightinavacuum(c=3
•
10
10
cm/sec).
Theequationbreaksdownwhenthevelocityoftheelectronapproachesthespeedoflightbecausearelativisticcorrectionmustbemadeforthe
valueofthemasswhere:
(7)
Therelationbetweenl andVismorecorrectlygivenby:(seeHall(1966)pp.3334)
(8)
Thefollowingtableisobtainedwhenrelativityeffectsareincluded:
c.Interference/diffraction/coherence
Anideallenssystemobtainsanexactimageoftheobject(eachpointfaithfullyreproduced).Thephenomenaofdiffractionmakesthis
unattainable(Figs.I.5,I.6).
Diffractionphenomenainvolvesthebendingofthepathofradiationpassingclosetoanobstacle(Fig.I.6).Thisresultsinaspreadingofthe
radiationintotheregionbehindtheobstructionthatthewavespassed.Thediffractionatedgescontributestothecontrastatwhichanedgecan
beobserved.Diffractionalsolimitstheresolvingpowerofthemicroscopesincetheimagepointproducedbyalensisadiffractionimageofthe
openingofthelensortheaperturerestrictingtheeffectiveopeningofthelens(Fig.I.5).
Ifthelightsourceandtheplaneatwhichthediffractionpatternisobservedareatfinitedistancesfromtheedge,thephenomenoniscalled
Fresneldiffraction.Thepatternisdescribedasduetointerferencebetweenthenondiffractedlightandawaveoflightdiffractedattheedge.
Theresultingsuperpositiongivesrisetoaseriesofdiffractionfringesorientedparalleltotheedgeandrepresentingperiodicallyvaryingbrightness,
maximaandminima.(Figs.I.7,1.8,I.9).
Coherence:Aprerequisiteforinterferenceisasuperpositionofwavesystemswhosephasedifferenceremainsconstantintime.Twobeams
arecoherentif,whencombined,theyproduceaninterferencepattern.Thebeamsareincoherentwhentheyareincapableofproducingan
interferencepattern.Twobeamsoflightfromselfluminoussourcesareincoherent.Iflightfromthetwosourcesfallsonascreen,theresultant
intensityissimplythesumofthetwointensitieswhichwouldoccurfromeachsourceseparately(Figs.I.10,I.11).Inpracticeanemittingsource
hasfiniteextentandeachpointofthesourcecanbeconsideredtogeneratelight.EachsourcegivesrisetoasystemofFresnelfringesatthe
edge.Thesuperpositionofthesefringesystemsisfairlygoodforthefirstmaximaandminimabutfartherawayfromtheedgeshadowtheoverlap
ofthefringepatternsbecomessufficientlyrandomtomakethefringesdisappear.Thenatureofwaves,phase,amplitude,andinterferenceare
illustratedinFigs.I.12andI.13.
d.Resolution
1)Definitions:
RESOLUTION:abilitytodistinguishcloselyspacedpointsasseparatepoints.
RESOLUTIONLIMIT:smallestseparationofpointswhichcanberecognizedasdistinct.
RESOLVINGPOWER:resolutionachievedbyaparticularinstrumentunderoptimumviewingconditions.
2)Distinctionbetweenresolutionandresolvingpower:
Notethedistinctionbetweenresolutionandresolvingpower.Resolvingpowerisapropertyoftheinstrumentandisaquantitythatmaybe
estimatedontheoreticalgrounds.Resolutionisequaltoorpoorerthantheresolvingpowerandisthequantityobservedunderanygivenset
ofexperimentalconditions.IntheTEM,especiallywithbiologicalsamples,theresolutionachievedmaybeconsiderablyinferiortothetheoretical
resolvingpoweroftheinstrument.
Microscopyisthescienceofseeingtheverysmall.Underidealconditions,theeyeresolvesabout1minuteofarc(=1/60degree=2.9x10
4
radian;recallthereare2p radiansin360°)andsinceitcanfocusdowntoabout250mm,thesmallestobjectwecanresolveisabout0.07mm
(70mm)(Fig.I.14).Thislimitisrelatedtothesizeofthereceptorsintheretinaoftheeye.Thefunctionofamicroscopeistomagnifytheimage
fallingontheretina(Fig.I.15).Theadvantageoflightandelectronmicroscopesisthattheyeffectivelygettheobjectclosertotheeyesoa
magnifiedimageisobtainedandmoredetailcanbediscerned.
TENNISBALLANALOGY:Eyecanresolve3cmat100meters,thusatennisballisclearlyvisible.Butifthetennisballisheldupagainstawhite
background,thevisibilitydecreases(becauseofthedecreaseincontrast).
3)Abbecriteriaofresolution:
Thefundamentalnatureoflightposeslimitsonthedetailthatcanberesolved(Fig.I.16).Abbe(1893)showedthatthesmallestresolvable
distanceisabout1/2thewavelengthoflightused.Thus,1/2thewavelengthoftheradiationusedistheultimateresolvingpowerofany
instrument.Thislimitstheusablemagnificationofopticalmicroscopesto<1000X.Atfirstitwasthoughtthatxraymicroscopeswouldbeuseful
buttherefractiveindexofsubstancesforxraysisnearly=1,thusrefractinglensescannotbemadeforxrays,andconsequently,xrayscannot
beeasilyfocusedtoformimages.
4)Magnificationlimits:
Themaximummagnificationofaninstrumentislimitedaccordingtothefollowingrelationship:
Thus,fortheLM,witharesolvingpowerofapproximately0.25µm,themaximum(useful)magnificationisabout250µm/0.25µm=1000X.Thevalue
usedfortheresolvingpoweroftheeyeinthisexample(250µm)representsamorerealisticviewingcondition.Anymagnificationabovethevalue
givenbytheaboveformularepresentsemptymagnification,sincesuchmagnificationleadstonomoreusefulinformationbutratheramagnified
blur.
AccordingtotheAbbecriteria,at60,000volts,theTEMshouldhavearesolvingpowerofabout0.0025nm.Thisshouldallowamaximumuseful
magnificationofabout100milliontimes!!!Inpractice,themaximumusefulmagnificationoftheTEMoperatedat60kVislimitedtomuchlessthan
1,000,000X.Thus,althoughtheLMnearlyobeystheAbbecriteria,theTEMfallsshortbyaconsiderableamount.Themainlimitingfactorinthe
TEM,withrespecttoachievingthetheoreticalresolvingpoweroftheinstrument,concernsthenatureoftheimaginglensesandtheprocessof
imageformation.
5)Rayleighcriteria(practicalbutarbitrary):(Fig.I.17).
Itistheabilityofmicroscopestomakeobjectpointswhichareclosetogetherappearintheimageasseparatepoints.Anideallenstakeseach
objectpointandrepresentsitexactlyasapointintheimage.Areallenstakeseachobjectpointandspreadsitoutintoacirculardisk(Airy
disk)intheimageplanewhosediameterdependsontheangularapertureofthelens.
Theshortestdistancebetween2disksatwhichthetwodisksappearpartiallyseparatedcorrespondstoabout1/2thewidthofthedisks.The
distance,d,inobjectspaceisgivenby:
d=0.61l /n
•
sina
where
l =wavelenghtoftheradiation
n=refractiveindexofthemedia
a=semiangularapertureofthelens
NOTE:n
•
sina=thenumericalaperture(N.A.)ofthelens.
Thus,tomaximizeresolvingpower,l mustbedecreased,nincreased,oraincreased.Recallthatweareconcernedatthemomentwithan
aberrationfreeopticalsystem.Thevaluefortheconstant(0.61)iscontroversialbecauseitdependsonthecoherenceoftheradiationanda
criteriaofvisibility.
FortheLM,usingoilimmersionoptics(n=1.5),sina=0.87,andvioletlight(l =400nm),d=0.2µm.Theonlywaytoimprovetheresolutionisto
uselightofshorterwavelengthsinceN.A.cannotbeincreasedbeyond~1.5.FortheTEM,n=1(vacuum),sina=10
2
andl =0.005nmfor60kV
electrons,thusd=0.3nm.
I.A.4.Optics(LensTheory)
a.Basiclawsofclassicalgeometricaloptics
1)Rectilinearpropagationoflightwhenn(refractiveindex)isconstant.
2)Lawofreflection:
3)Lawofrefraction(Snell'sLaw):
4)Independenceofrays.Theassumptionismadethatlightraystravelindependentlythroughspace.
Theselawsholdforelectrons,except#4,ifthecurrentdensityistoohighwhennegativechargedelectronscaninterfere.
b.Classicalvs.electronoptics
1)Classicaloptics:Therefractiveindexchangesabruptlyatasurfaceandisconstantbetweenthesurfaces.Therefractionoflightatsurfaces
separatingmediaofdifferentrefractiveindicesmakesitpossibletoconstructimaginglenses.Glasssurfacescanbeshaped.
2)Electronoptics:Here,changesintherefractiveindexaregradualsoraysarecontinuouscurvesratherthanbrokenstraightlines.Refraction
ofelectronsmustbeaccomplishedbyfieldsinspacearoundchargedelectrodesorsolenoids,andthesefieldscanassumeonlycertaindistributions
consistentwithfieldtheory.
c.Geometricalandphysicaloptics
Thefundamentalprinciplesofopticsgovernthedesignandoperationofboththelightandelectronmicroscopes.Thebasicopticalprinciples
involvingtheuseofrefractileelementsorlensesinordertoformmagnifiedimagesareidenticalinboththeLMandTEM.TheTEMdiffersfromthe
LMonlyintheradiationitusesandinthewayinwhichtheradiationisbentorrefracted.
Geometricalopticsdealswiththestudyofthepathsfollowedby'rays'oflightorelectronsthroughlensesandapertures,andthegeometrical
constructionsusedtofindtherelativepositionsandsizesofobjectsandtheirimages.Arayoflightorelectronsisdefinedasaninfinitelythin
pencilorbeam.Physicalopticsshowsthatthisanabstractionandcannotphysicallyexistbecauseof'diffraction'whichdealswiththewave
natureoflightandelectrons.Allresultsobtainedingeometricalopticscanbederivedfromtheprinciplesofphysicaloptics,alongwithother
phenomenasuchasinterferenceanddiffractionwhicharenotexplicableinsimplegeometricalterms.
d.Idealversesreallenses:
Lensesareusedtobendraysoflightorelectronssotheyaredeflectedinapredictablewayfromtheiroriginalpaths.Thepropertiesofanideal
lens,possessinganaxisofrotationalsymmetryare:
1)Eachrayofthebundleofrayswhichpassesfromanobjectpointwillberefractedbytheideallenstomeetinoneimagepoint.
2)Raysoriginatingfrompointswhichlieonaplaneperpendiculartotheaxis,mustbeimagedinaplanewhichisalsoperpendiculartotheaxis.
3)Theimageappearsliketheobjectirrespectiveofthemagnification,sotherelativelineardimensionsoftheobjectarepreservedintheimage.
Inpractice,theimagingbyanyreallensdoesnotcorrespondtothatoftheideallensowingtothefactthatanobjectpointisrepresentedbya
diffractionimage(Airydisc)ofthelensopeningortheapertureusedforrestrictingtheeffectiveopeningofthelens.Thisisaresultofthewave
likepropertiesoflight.Lensaberrationsalsocontributetomoreorlesspronounceddeviationsfromthepropertiesoftheideallens.
Thesinglerefractingsurfaceofsphericalcurvatureisthefundamentalunitoffocusingactionbyglasslenses.Sphericalrefractingsurfacesactas
lensesforparaxialrayswhicharethoseraysthatpassclosetotheprincipalaxisofthelens.RayswithlargeangleswillNOTobeyideallens
action.
Afundamentaldifferencebetweenlightandmagneticlensesisthattheelectronbeamdoesnotchangeinforwardvelocityasitpassesthrough
themagneticfield(lightraysslowdownwhenpassingintoamediumofhigherrefractiveindex).Refractioniscontinuouswithelectronswhenthey
areinthemagneticfield:lightisrefractedonlyattheinterfacebetweenmediaofdifferingrefractiveindex.Theelectronsalsofollowspiral
trajectoriesthroughthemagneticfield(seealsoSec.I.A.5.c(Magneticfieldsandmagneticlenses)
e.Raydiagrams:(Figs.I.20I.28)
Themethodofconstructionofraydiagramsisbasedonthreesimpleprinciples:
1)Allraysenteringthelensparalleltotheaxisarebroughttoacommonpointontheaxis,thefocalpoint.
2)Allrayspassingthroughthegeometricalcenterofthelensareundeviatedandpassstraighton,nomatterfromwhichdirectiontheycome.
3)Principleofreversibility:ifthedirectionofarayisreversedinanysystemtherayexactlyretracesitspaththroughthesystem.Thisapplies
onlytothelocationoflightpathsandnottotheintensityofthelight.
Theaboveprinciplesarebasedontheassumptionsthatwearedealingwithathinlensandconcernedwiththepathsofparaxialrays.The
standardconventionistodrawdiagramswithraysthattravelfromlefttoright.Theobjectistotheleft(infront)ofthelensandtheimageisto
theright(behind)ofthelens.
f.Definitions:
Realimage:oneatwhichlightraysphysicallyreunite,sothataphotographicplateplacedatthepositionofarealimageisexposed.
VirtualImage:onefromwhichlightraysappeartodiverge;raysarenotinfactconcentratedatthepositionofavirtualimage,sothata
photographicplateplacedatthepositionoftheimageisnotexposed(byfocusedrays).Placinganopticalsystemsuchastheeyebehindthe
lens,willenablethedivergentraystobefocusedtoformarealimage.TheintermediatelensofanTEMissometimesusedthiswayinorderto
reducethefinalsizeoftherealimageformedbytheprojectorlens(es).
Converging(positive)lens:bendsraystowardtheaxis.Ithasapositivefocallength.Formsarealinvertedimageofanobjectplacedtothe
leftofthefirstfocalpointandanerectvirtualimageofanobjectplacedbetweenthefirstfocalpointandthelens.
Diverging(negative)lens:bendsthelightraysawayfromtheaxis.Ithasanegativefocallength.Anobjectplacedanywheretotheleftofa
diverginglensresultsinanerectvirtualimage.Itisnotpossibletoconstructanegativemagneticlensalthoughnegativeelectrostaticlensescan
bemade.
g.Lensformula(thinlensequation):
where
f=focallengthofthethinlens(sameradiusofcurvatureforboth
sphericalsurfaces)
o=distanceofobjectfromlens(positivetotheleft)
i=distanceofimagefromthelens(positivetotheright)
NOTE:Foravirtualimage,ihasanegativevalue.
h.Magnification:
Foraconverginglens,iftheobjectismorethantwicethefocallengthfromthelens,thentheimageformedisreal,inverted,andsmallerinsize
thantheobject(M<1).Whentheobjectisatadistance=2f,theimageandobjectarethesamesize(M=1);whenitisbetweenfand2f,
theimageislargerthantheobject(M>1),andwhenitis<f,theimageisvirtual,erect,andlargerthantheobject(M>1).
i.Angularapertureofthelens(2a)(Fig.I.29)
Theaperturedeterminesthetotalamountofradiationarrivingfromtheobjectwhichcanbefocusedto
formanimage.Theaperturethuscontrolstheabilityofthelenstogatherinformationabouttheobject.
Thisdependsontheangleoftheconeofraysitisabletoacceptfromtheobject.Bringinganobject
closertotheeyeincreasestheangularaperture,butthereisalimittotheclosenessthattheobjectcan
bebroughttotheeye(~25cmcorrespondingtoanangleofabout0.9°fora4mmexitpupildiameterof
theeyelens;atypicalLMwithanoilimmersionobjectivelenshas2aof~175°).
j.Simplevs.compoundmicroscope(Figs.I.30I.32)
Inprinciple,arealimageofanydesiredmagnificationcanbeobtainedfromasinglepositivelens,butin
practicethisiscumbersomebecauseofthelonglensimagedistance.Oneormorelensescanbeusedto
magnifytheimageinstages(totalmagnificationequalingtheproductofthemagnificationsofeachlens).
Theimageformedbyonelensconstitutestheobjectforthesubsequentlens,whetherornotareal
intermediateimageisformed.
Comparisonofoneversestwostagemagnification:
Thefollowingdescriptionillustrateshowdifferentpathlengthsarerequiredtoachieveamagnificationof10,000Xusingeitheroneortwolenses
withf=2.0cm.
OneStageSystem:
TwoStageSystem:
Assumebothlenseshavef=2.0cmandarearrangedsoeachgives100Xmagnification.
Thus,M=100=x
i
/x
o
foreachstage.
FirstStage:
x
o
=2.02cm
x
i
=202.00cm
Therealimageformedinthefirststagebecomestheobjectforthesecondlens.
SecondStage:x
o
,x
i
sameasinthefirststage.
Totallengthofsystem
=lengthoffirststage+lengthofsecondstage
=(x
o
+x
i
)+(x
o
+x
i
)
=2(x
o
+x
i
)
=2(2.02+202.00)=408.04cm(4.08meters)
k.Problemset
Thefollowingproblemsareforyourownedificationtotesthowwellyouunderstandthebasicsoflensoptics.
1.Foreachsituationbelow,drawanaccurate(usegraphpaper)raydiagramshowingthepathof(atleasttwo)raysfromtheobjecttoimage.
Indicatewhethertheimageisrealorvirtualandspecifythedistanceoftheimagefromthelensandthemagnificationoftheimagewithrespect
totheobject.Ineachexample,thelensisconverging,withidenticalfrontandbackfocalpoints.Distancesareinarbitraryunits.Letf=lens
focallength,x
o
=distanceofobjectinfrontofthelens,andx
i
=distanceofimagebehindthelens.Theobjectmaybeanysize.
2.Inthefollowingexamples,therearetwoconverginglensesinsuccession.Drawraydiagramsshowingtheformationofboththeintermediate
andfinalimagesandgiveappropriateinformationaboutthenature(real/virtual),positions,andsizesoftheintermediateandfinalimages.What
isthemagnificationateachstageofimageformationandwhatisthemagnificationofthefinalimage?Thedistancefromthecenteroflens1(L1)
tothecenteroflens2(L2)equalsD.
I.A.5.ElectronOptics/ElectronLenses
a.Electronemission
Innershellelectronsinmetalatomsshieldtheelectricfieldofthenucleusthroughtherepulsiveforcestheyexertontheoutershell(valence)
electrons.Thustheattractionbetweenthevalenceelectronsandthenucleusisreduced.Metalatomsarecharacterizedashavingtwoloosely
boundvalenceelectronswhichmigratefreely(thisiswhymetalsaregoodelectricalconductors)andcanescapefromthemetalcompletelyif
sufficientadditionalenergyisimpartedtothem.Asthetemperatureofametalisincreased,thekineticenergyoftheelectronsincreasesbecause
ofincreasedthermalvibrationsofthemetalions,whichcollidemorefrequentlywiththeelectrons.Thermionicemissionisthetermusedto
describetheprocessbywhichthermalenergyissuppliedtolooselyboundelectronsinordertoformasourceofelectrons.
Atroomtemperatureelectronsareeffectivelypreventedfromescapingthesurfaceofthemetalowingtotheattractiveforceofthepositively
chargedions.Asthetemperatureisincreasedsomeelectronsacquiresufficientenergytoovercometheattractionandleavethemetal
temporarily.Metal,shapedasathinwire,caneasilybeheatedbypassinganelectriccurrentthroughit.Sincethemetalsurfacebecomes
positivelycharged,acertainlevelofenergy(workfunction)mustbesuppliedtoallowelectronstoescapefromthesurface.Eachmetalhasa
characteristicworkfunction.Tungsten,withalowworkfunction,emitsmoreelectronsthanmetalswithhigherworkfunctions(seealsopp.2930
andFig.I.59).
Ifastrongelectrostaticfieldisappliedinavacuumbetweenthewire(givenanegative,cathode,potential)andananode,theelectricfieldwill
causeelectronstoaccelerateawayfromthewiretowardstheanodesurface(Fig.I.33).Thespeedoftheelectronsdependsonthestrengthof
theelectrostaticfield(voltage)betweenthecathodeandanode(equation(3),Sec.I.A.3.b)Thenumberofelectronswhichleavethewire
dependsonthetemperaturetowhichthewireisheated,whichdependsonhowmuchfilamentcurrentpassesthroughthewire.
A"V"shapedwirewillhavethehighesttemperatureatthetip.Electronswithdrawnfromthefilamenttipcarryelectricchargestotheanode.This
electriccurrent,whichflowsbetweenthefilamentandtheanode,iscalledthebeamcurrent.
1)Electricfield/Equipotentials
Anelectricallychargedobjecthasassociatedwithitanelectricfield.Thus,anelectricallychargedparticle,whenbroughtnearachargedobject,
isinfluencedbyanelectricalforceinthevicinityoftheobject.Theforceisdirectedtowardthechargedobjectifthechargesareofopposite
signsandawayfromtheobjectiftheyareofsimilarsign.DEFINITION:Thedirectionofanelectricfieldisdefinedasthedirectionoftheforce
actingonapositivecharge.(Figs.I.3435)
Alongthelinesofforceconnectingthetwocharges,theelectricpotentialwillchangegraduallybetweentheextremevaluesrepresentedbythe
twocharges.DEFINITION:Equipotentiallinesdefinethepointsalongthelinesofforcewithidenticalelectricalpotential.Theseequipotential
surfacesarealwaysorientedperpendiculartothelinesofforce.Thechangesintheelectricpotentialaregradualinspace.
Electronswhichenterafieldbetweentwoparallelplatesinadirectionparalleltotheplatesareaffectedbytheforcedirectedperpendicularto
theplates(FigI.36).Theelectronswillbeattractedtowardthepositiveplate.Thepathchangesinaseriesofgradualstepsattheequipotential
surfaces.
FigureI.37showshowtheelectronpathis"refracted"attheequipotentialsurface.TheresultisfundamentallythesameasthatgivenbySnell's
Lawofrefractioninlightoptics.Aconsequenceofthisisthatasphericallycurvedequipotentialsurfaceexhibitsthepropertiesofalens.
FiguresI.38andI.39showhowbothpositive(converging)andnegative(diverging)electrostaticlensescanbeformed.Thisfeatureof
electrostaticlensesdiffersfromelectromagneticlenseswhichcanonlyactasconverginglenses.
2)Advantages/Disadvantagesofelectronlenses:
Thefactthattherefractiveindexdoesnotchangeabruptlyinelectronlenseshasoneadvantageinthattherearenotroublesomereflectionsat
equipotentialsasatglassinterfaces.Thereisaseriousdisadvantageinthatequipotentialscannotbeshapedandcombinedinarbitraryfashionto
correctforchromaticaberrationandothererrors.
Althoughelectronmicroscopeswhichemployelectrostaticlenseshavebeenmade,mostmicroscopesuseelectromagneticlenses.Amajorreason
isthatelectrostaticlensesaremoresensitivetothequalityofthevacuumandcleanlinessofthecomponentsthanareelectromagneticlenses.
Somelensaberrationsaremoresevereforelectrostaticlensescomparedtoelectromagneticlenses.Electrostaticlensesrequireverypowerful
electrostaticfieldswhichcanleadtoelectricalbreakdownor"arcingover"insidethecolumn,especiallyunderpoorvacuumconditions.Forthis
reason,electrostaticlensescannotbemadewithfocallengthsasshortasmagneticlenses.
b.Electrostaticlens
Abasicunderstandingofelectrostaticlensesisimportantfortwomainreasons:i)theelectrongunuseselectrostaticlensactiontoformthe
primarybeamsource,andii)itisquitecommonforachargetodeveloponthenonconductingcontaminationwhichmayaccumulateonphysical
apertures(suchastheobjectiveaperture)andtransformthemintoweakelectrostaticlenseswhichcandistorttheelectronimage.
3)Propertiesofelectrostaticlenses:
a)Anyaxiallysymmetricalelectrostaticfieldhasthepropertiesofalensforraysconfinedtotheparaxialregion.Alltheideallensformulasapply
toelectrostaticlenses.
b)Forelectronlenses,replaceÃ(f)forrefractiveindexinthelensequations(f=valueofthepotentialontheaxis).Intheimageformingsystem
ofmostTEMs,fisthesameonbothsidesofthelens(SeeSec.I.A.5.c).
c)Ifboundedbyregionswherefisconstant,anelectrostaticlensisalwaysconvergent.
c.Magneticfieldsandmagneticlenses
1)Magneticfield
Anelectriccurrentpassingthroughaconductorgivesrisetoamagneticfield.TheconventionisthatNisthedirectioninwhichthelinesofthe
magneticfieldpoint(Fig.I.40).Themagneticfluxisthetotalnumberoflinesandthefluxdensityisthenumberoflinesperunitareaofasurface.
UsetheRIGHThandruletodeterminethedirectionofthefield(thumbpointstowardcurrentdirectionandfingerscurlindirectionoffield.NOTE:
Byconvention,thedirectionofelectronflowisoppositetothatofcurrentflow.
Fluxdensitydependsonthepropertiesofthematerialsurroundingtheconductor.Ironinducesahigherfluxdensitythanairoravacuum.The
propertyofthematerialwhichaffectsthefluxdensityiscalledthepermeability,m,ofthematerial.Forairandvacuum,m=1.0.For
ferromagneticmaterialsitcanbeaslargeasseveralhundredthousand.
Iftheconductorhastheshapeofacircularloop,thelinesofforceformcirclesaroundtheloop.Thefluxdensityisgreatestatthecenterofthe
loop.Themagnetinthecenteroftheloopisorientedperpendiculartotheplaneoftheloopifthecurrentthroughtheloopissufficientlystrongto
eliminatetheinfluenceoftheearth'sfield.ThesideoftheloopatwhichthelinesofforceleavetheloopistheNorth(N)poleofthemagnet(Figs.
I.41,I.42).
Ifthewireiswoundinseveralturnsaroundacylindricalsurface(solenoid),eachturnwillcontributetotheinducedmagneticfield.Theflux
densityinthecenterofthecoilisgivenby:
Inthecaseofairandnonmagneticmaterials,µ=1.0andB=H.
Thepermeabilityofirondependsonthefieldstrength,H,anddecreasestounityathighfieldstrengthorwhenthefluxdensity,B=H(Fig.I.43).
Thehighpermeabilityofironisduetotheinducedmagneticfieldorientingmicroscopiccrystalregionsactingastinymagnetsintheiron.Allthese
tinymagnetsaddtheirmagneticfieldstotheinducedfield(Fig.I.44).Whenallmicromagnetsarenearlyoriented,theironwillaffecttheflux
densitytoadecreasingamountsincethereorientationofmicromagnetsisnearingcompletion.Thus,thepermeabilityofironathighfieldstrengths
approachesthatofemptyspace.Atthispointtheironreachesmagneticsaturation.
2)Hysteresis
Thestrengthofthelensdependstosomeextentonthepreviousmagnetichistoryof
thelens.Whenthecurrentinalensisreduced,thedecreaseinmagnetizationdoes
notretracethesamepathobtainedwhenthecurrentwasincreased(Fig.I.45).
Inductionofmagnetizationinvolvesaphysicalmovementwithinthemagnetized
material,requiringtheovercomeofacertaindegreeofinertia.Asaresult,
magnetizationtendstolagbehindthemagnetizingforceapplied.Inducedmagnetic
fluxcanonlybereturnedtozerobyapplicationofacurrentintheoppositedirection.
Aconsequenceofhysteresisisthatthelevelofcurrentusedtoenergizeamagnetic
lensDOESNOTpreciselyspecifythelensstrength(i.e.focallength).
NormalizationofTEMlensesisaccomplishedbyreducingthelenscurrenttozero
somepredeterminednumberoftimes.Hysteresismayalsobeminimizedbytakinga
lenstosaturationandthenreturningittotheworkingcurrentwithoutovershooting.
Whenthefieldstrengthisreducedtozero,somemagnetizationstillremainsintheiron
(residualmagnetizationorremanence).Anadvantageofsoftironisthefactthat,
whenusedinanelectromagnet,hysteresisislow.
Introductionofpiecesofironinamagneticfielddrasticallyaffectsthefluxdensity.
Magneticmaterialhasashieldingeffect,theeffectbeinggreaterthegreaterthe
permeability.Permalloy(mmetal)hasamaximumpermeabilityof80,000140,000
comparedtoironusedintransformers(~7000).mmetalpermeabilityislimitedtolower
fieldstrengthsthanthatatwhichironstillretainshighpermeability.Thismetalis
thereforeusefulforshieldingtheTEMfromexternalmagneticfields.
d.Theelectromagneticlens
1)Lensdesigndevelopment(Figs.I.46I.48)
Theefficiencyofthemagneticfieldproducedbyashortsolenoidwasfirstimproved
byencasingtheenergizingcoilinasheathofsoftironwhichhasthepropertyofconcentratingthelinesofforceinamagneticfieldandthus
becomingmagnetizedbyinduction.Inthiswayamuchmorepowerfulaxialmagneticfieldisobtainedforthesameamountofcurrentflowing
throughthesolenoid.Furtherdevelopmentinvolvedencasingtheentirecoilwithsoftironexceptatanarrowannulargapintheinsideofthecoil.
Thisproducesagreaterconcentrationofthemagneticfieldalongashortaxialdistance.Toachieveshorterfocallengthlenses(andobtaingreater
magnifications)asoftironpolepiecewithanopenaxialborewasintroducedatthepositionoftheannulargap.
MagneticlensesusedinTEMsarealwaysconstructedwithanironcircuittoproduceahighfieldstrengthacrossashortgap.Themagneticfields
forTEMlensesareintherangeof10,00020,000gauss.
2)Forcesactingonacurrentinamagneticfield
Theforceonanelectroninamagneticfieldisalwaysatrightanglestothevelocityandthedirectionofthefield(Figs.I.49,I.50,andI.52).The
fieldonlyactsonthevelocitycomponentwhichisdirectedperpendiculartothelinesofforce.Usethelefthandrule(Fig.I.51:firstfingerfor
fielddirection,middlefingerforcurrentdirection,andthumbfordirectionofforce).Rayspassingthroughthelensareturnedthroughanangle
whichdoesNOTdependonthedistanceoftheraysfromtheaxis.Allelectronscontainedinagivenmeridionalplanebeforeenteringthefieldare
containedinarotatingmeridionalplaneastheypassthroughthelens,andthentheyleavethelenscoplanar.
Whenelectronsenterthelenstheyencounterasidewaysforcewhichcausestheelectrontorotate
asitcontinuesthroughthelens(Figs.I.53I.57).Sincetheradialcomponentofthemagneticfield
reversesafterthecenterofthelens,therotationalvelocitysetupinthefirsthalfofthelensis
countered.Theelectronenteredthelenswithoutangularmomentumabouttheaxisandleaves
withoutangularmomentum.Theneteffectisadeflectiontowardtheaxis,whichitmustcrossatthe
focalpointf
2
.Theanglebetweentheobjectvectorandtheimagevectoris180°+q,whereas,for
glasslensesandelectrostaticlenses,theanglebetweenarealobjectandtheimageisexactly180°.
Sincetheradialforceisdirectedtowardtheaxis,thelensisconvergentnomatterwhatthedirection
ofthefield.
3)Propertiesofamagneticlens:
Anyaxiallysymmetricmagneticfieldhasthepropertiesofanideallens.Alltheformulasfortheideallensmaybeapplied.
Magneticlensesarealwaysconvergent.Theconventional,axiallysymmetriclensisalwaysboundedbyregionswhicharefieldfree,the
consequencebeingthatthenetactionofelectronlensesisinevitablyconvergent.Limitedregionsmaybedivergentbutnotthelensasawhole.
Theseriousconsequenceofthisisthatneithersphericalorchromaticaberrationscanbecorrectedasisdoneinlightopticsbytheusedoublets
ofpositiveandnegativelenses.
Intheabsenceofelectrostaticfields,therefractiveindexisthesameinobjectandimagespace,thereforef
1
=f
2
.
Electronstravelingthroughaxiallysymmetricfieldsexperienceaspiraltrajectoryofdiminishingradius.Theimagevectorisatanangle180°+qto
theobjectvector.
Thedeflectionoftheelectrontowardstheaxismeansthatanelectronenteringthelensparalleltoitsaxiswillcrosstheaxisafterhavingpassed
thelens.Thedeflectionwillincreasewiththedistancefromtheaxis.Thus,abeamofelectronsinparallelpathsparalleltotheaxisofthelenswill
befocusedtoanimagepointontheaxiswhichrepresentsthesecond(back)focalpointofthelens(f
2
).Notethatmagneticlensesarehighly
inefficientinthatonlyaminorportionofthetotalfieldstrengthisactuallyeffectiveinfocusingtheelectron.
4)Magneticlensfocallength
Inamagneticelectronlensthefocallengthisdeterminedbythefieldstrengthinthelensgapandbythespeedoftheelectrons(determinedby
theacceleratingvoltage).
Formagneticlenses,focusingisachievedbyvaryingthecurrentwhichpassesthroughtheelectromagnet.Thisinturnchangesthestrengthof
themagneticfieldandtherebyaltersthefocallengthofthelensandisequivalenttoacombinedchangeinboththe"refractiveindex"and
"curvatureofsurface".Forabeamofmoreenergeticelectrons,thelenscurrenthastobeincreasedinordertokeepthefocallengthconstant.
FocallengthandcurrentareNOTlinearlyrelated:strengthincreasesinasigmoidfashion(Fig.I.45)ascurrentincreasesuntilapointisreached
wherethelensissaturatedandnofurtherincreaseinlensstrengthcanbeachieved.
Sincethefocallengthofthelensisdirectlyproportionaltotheacceleratingvoltage,avariationinthevelocityoftheelectronsintheimaging
beamaffectsimagequalitybyeliminatingperfectfocus(chromaticaberration).
5)Magneticlensdesign:(Figs.I.46,I.47).
Condenserlensesusuallyhavearelativelylargeboreandspacingwhichresultsinalongfieldandlongfocallength.
Typicalconstructionoftheobjectivelensproducesastrongfieldofshortaxialextent(i.e.shortfocallengthbetween(1.53mm)necessaryfor
formationofimagesathighmagnification.Thespecimenisplacedwithinthemagneticfieldoftheobjectivelens.Thus,anyfieldintroducedby
contaminantsinthespecimencandistortthefieldofthelens.Notethatthisalsomeansthatpartofthelensfield("prefield")isonthefrontside
oftheobjectandaffectstheelectronbeambeforeitpassesthroughtheobject.
Mostofatypicalmagneticlensliesoutsidethevacuumofthemicroscope.Onlythoseregionsthroughwhichtheelectronbeampassesareinhigh
vacuum.Magneticlensesmustbewatercooledtodissipatethelargeamountsofheatproducedbythecurrentsintheelectromagnetcoils.
DATE NAME EVENT
1897 J.J.Thompson Discoverstheelectron
1924 LouisdeBroglie Identifiesawavelengthtomovingelectrons
l =h/mv
where
l =wavelength
h=Planck'sconstant
m=mass
v=velocity
(Foranelectronat60kVl=0.005nm)
1926 H.Busch Magneticorelectricfieldsactaslensesforelectrons
1929 E.Ruska Ph.Dthesisonmagneticlenses
1931 Knoll&Ruska Firstelectronmicroscopebuilt
1931 Davisson&Calbrick Propertiesofelectrostaticlenses
1934 Driest&Muller SurpassresolutionoftheLM
1938 vonBorries&Ruska FirstpracticalEM(Siemens)10nmresolution
1940 RCA CommercialEMwith2.4nmresolution
1945 1.0nmresolution
Fig.I.1Comparisonoflightandelectronmicroscopes.Ineach
instrument,illuminationfromthesource(lamp,filamentinthe
electrongun)isfocusedbythecondenserlensontothespecimen.
Afirstmagnifiedimageisformedbytheobjectivelens.Thisimage
isfurthermagnifiedbytheprojectorlensontoagroundglass
screen(light)orfluorescentscreen(electrons).(FromAgar,p.8)
Fig.I.2CrosssectionalviewofthePhilipsEM300.(FromAgar,p.40)
Toviewtheanimatedmicroscope,clickhere.
Note:QuickTimePlugInrequired
(Thiscanbedownloadedathttp://apple.com/quicktime/download)
Fig.I.3Sectionthroughacomplex
doublecondenser6lensPhilips
EM200electronmicroscope.(From
Meek,p.99)
Fig.I.4Thestatisticalnatureofdiffraction
patterns.(FromHall,p.13)
"Theprecisenatureof'electronwaves'or'matterwaves'isverydifficulttounderstandordescribeinmaterialterms.Electronwavesarenot
electromagneticradiationofthekindtowhichlight,Xraysandradiowavesbelong.Theyconstituteasortofquantumor'packet'ofradiationwhich
accompanieseachindividualelectron,followingitspathandnotradiatingoutwardsfromit."(Meek,1976,pp.4849).
V l (nm)
v(
•
10
10
cm/sec)
v/c
10,000 0.0123 0.593 0.198
50,000 0.0055 1.326 0.442
100,000 0.0039 1.875 0.625
1,000,000 0.0012 5.930 1.977!
V l (nm)
v(
•
10
10
cm/sec)
v/c
10,000 0.0123 0.593 0.195
50,000 0.0055 1.326 0.414
100,000 0.0039 1.875 0.548
1,000,000 0.0012 5.930 0.941
FigI.5Aperfectpointsourcecannotbe
imagedbyalensasaperfectpointimagedue
tothepresenceoftheapertureAB(which
maybetheedgeofthelens).Diffractionat
thisaperturegivesrisetoaseriesoffringes,
whichsurroundtheimageformedofthepoint
source.Thepatternproducediscalledan'Airy'
disk.(FromMeek1sted.,p.35)
Fig.I.6Wheneverawavefrontstrikesa
barrier,itcanbendaroundthecorner'by
givingrisetoasecondarywavefrontatthe
edge,sinceeachpointonthewavefrontcan
giverisetoanewsourceofwaves.This
phenomenoniscalled'diffraction'.(FromMeek
1sted.,p.22)
Fig.I.7Diffractionpattern(right)formedbyanirregularlyshapedaperture
(left).(FromYoung,p.95)
Fig.I.8(a)
Photographof
theedgeofa
razorblade
illuminatedby
monochromatic
(blue)light
rendered
coherentby
passing
througha
narrowslit.(b)
Microdensitometer
tracingofthe
negativefrom
whichthe
photograph
wasmade.
FourFresnel
fringescanbe
distinguished.
(FromMeek1st
ed.,p.27)
(a)
(b)
(a) (c)
(b)
Fig.I.9(a)Fresnelfringesformed
byelectrons.Thesefringesare
formedoutsidetheedgeofahole
(white)inacarbonfilm(black).(b)
Amicrodensitometertracingofthe
fringesystem;thepatternis
identicalwiththeFresnelfringe
systemformedbyvisiblelight(see
Fig.I.8).(c)Anunderfocusedimage
ofaholeinafilm,showinga
completesystemofabout40
Fresnelfringesinsidethehole.
(FromMeek1sted.,pp.2930)
Fig.I.10Diffractionimagesoftwo
easilyresolvedpoints.(From
Slayter,p.243)
Fig.I.11Imagesoftwo
incoherentlyilluminatedpointsat
thelimitofresolution.(a)individual
intensities;(b)summedintensities.
(FromSlayter,p.244)
Fig.I.12Examplesofwhatoccurswhentwo
wavesofthesamewavelengthandequal
amplitudeadd.Ineachexample,thetwo
separatewavesareshownontheleftand
theirsumorresultantwaveontheright.The
differentexamplesarecharacterizedbyvarying
phasedifferences.Thephaseofawave
(usuallyexpressedasafractionofthe
wavelengthorindegrees)isthepositionofa
crestrelativetosomearbitrarypoint.Although
thephaseofagivenwavevarieswithtimeas
thewavetravels,thedifferenceinphaseofthe
twowavesofthesamewavelengthwiththe
samevelocity,isindependentoftime.Such
wavescaninterferewithoneanother.The
resultantwavehasthesamewavelength,l .
(a)Phasedifferencezero.Thewavestotally
reinforceandaresaidtobe"inphase"orto
showconstructiveinterference.
(b)Phasedifferencel /4.Partialreinforcement,
givingawaveofamplitude1.4(intensity2.0).
(c)Phasedifferencel /2.Thewavesare"outof
phase"andthereistotaldestructive
interferencetogivenoresultantwaveora
wavewithamplitude0(intensity0).(From
GluskerandTrueblood,p.19)
Fig.I.13Photographofan
interferencepatterninwater
wavesformedbythe
superpositionofwavesfromtwo
sourcesoscillatinginphasewith
thesamefrequency.(FromYoung,
p.22)
Fig.I.14Theangularapertureofthe
eyeisrelativelysmall.(FromMeek,
1sted.,p.13)
Fig.I.15Increasingtheangular
apertureoftheeyewithalens.The
lensallowstheobjecttobeheld
closertotheeye,whichisthereby
enabledtogathermoreinformation.
(FromMeek1sted.,p.14)
Fig.I.16Theinteractionofwaves
withanobstacle.Theboatridesthe
longwavelengthoceanwave,but
reflectsthesmallwavelength
surfaceripple.Anobserverwho
wishestodetectthepresenceof
theboatcandosoonlyby
observingwaveswhichhave
wavelengthssmallerthan,or
comparableto,thelengthofthe
boat.(FromSherwood,p.19)
Maximummagnification=
resolvingpoweroftheeye
resolvingpowerofthemicroscope
(a)
Fig.I.17(a)TwoAiry
disksrepresenting
twoimagepoints
shownatincreasing
separationfromleft
toright.Inthe
pictureatthe
extremerightthe
twodiskscanbe
distinguishedas
separatedisks.
(b)Theintensity
distributionatanAiry
disk.R,halfwidthof
thecentralmaximum
representedbya
bellshapedcurve.
(c)TheRayleigh
criteriaforresolution.
(FromSjostrand,
p.115)
i=r
Fig.I.18Reflection.(FromSlayter,
p.4)
Fig.I.19Refraction.(FromSlayter,
p.6)
Fig.I.20Principalraydiagramsshowing
imageformationbyaconvexlens.
(a)Whentheobjectdistanceisgreater
thanthefocallength,areal,inverted
imageisformed.
(b)Whentheobjectdistanceisless
thanthefocallength,avirtual,erect
imageisformed;itspositionis
obtainedbyprojectingtheprincipal
raysbackward.Theraysappearto
comefrompointQ.(FromYoung,
p.127)
Fig.I.21Definitionof
principalfocus,F,inimage
spaceofalens.(From
Sjostrand,p.20)
Fig.I.22Focusingeffectoflenson
raysoriginatingfrompointson
principalaxislocatedatdifferent
distancesfromthelens.(From
Sjostrand,p.21)
Fig.I.23Definitionofprincipal
focusinobjectspaceF1ofa
lens.(FromSjostrand,p.21)
Fig.I.24VirtualimageQof
objectpointlocatedbetween
principalfocusinobjectspace
andthelens.(FromSjostrand,
p.21)
Fig.I.25Constructionoftheimage
ofanobjectbymeansofray
tracing.(FromSjostrand,p.22)
Fig.I.26Magnifyingeffectof
apositivelens.(From
Sjostrand,p.22)
Fig.I.27Virtualmagnified
imageofobjectlocated
betweenprincipalfocusin
objectspaceandthelens.
(FromSjostrand,p.22)
Fig.I.28Amagnifyingglassformsan
enlarged,erectvirtualimage.The
angularsizeofthisimageis
approximately4"/15"or4/15.The
angularsizeoftheobjectatthe
closestdistanceforcomfortable
viewingis1"/10"or1/10.The
magnificationinthissituationis(4/15)/
(1/10),or22/3.(FromYoung,p.130)
Fig.I.29Theangularapertureofa
lens.Theangle2a isthe
acceptanceangleofthelens,and
thelargeritcanbemade,themore
informationcanthelenstransmit.A
largelensofhighaperturecan
thereforetellusmoreaboutan
objectthanasmalllensoflow
power.(FromMeek1sted.,p.12)
Fig.I.30Raydiagramforhighmagnification
modeofoperation.Notethateachlens
formsarealimage,withimageinversion.
I0istheimageformedbytheobjective
lensO,I1isformedbythefirstprojector
lensP1andI2bythesecondprojectorP2,
onthescreen.(FromAgar,p.30)
Fig.I.31Left:raydiagramofthe3realimagemediumandhighmagnificationimagingsystemofa3lens
microscope.Center:2realimageverylowor'scan'magnificationrangeofa3lensmicroscope.Right:2real
imagelowmagnificationsystemofa3lensmicroscope.(FromMeek1sted.,pp.118,120121)
Fig.I.32Raydiagramforacompleteelectron
microscope.FilamentF,condenser1lensC1,
condenser2lensC2,condenserapertureCA,
specimenS,objectivelensO,objectiveaperture
OA(inbackfocalplane).1stintermediateimage
andselectorapertureSA.IntermediatelensP1,
secondintermediateimageI2,projectorlensP2
andfinalimageonthefluorescentscreenFC.
(FromAgar,p.35)
a)f=2.0
x
o
=5.0
e)f=4.0
x
o
=3.0
b)f=10.5
x
o
=21.0
f)f=13.3
x
o
=13.3
c)f=3.5
x
o
=3.0
g)f=3.142
x
o
=0.0
d)f=5.0
x
o
=2.5
a)D=8.0
L1:f=2.0
x
o
=4.0
L2:f=3.0
b)D=8.0
L1:f=2.0
x
o
=6.0
L2:f=3.0
c)D=4.0
L1:f=2.0
x
o
=3.0
L2:f=2.0
FigI.33Accelerationofelectronin
electricfield.(FromSjostrand,p.26)
Fig.I.34Linesofforceatapositively
chargedsphericalbody.(FromSjostrand,
p.32)
Fig.I.35Linesofforceandequipotential
surfaces(stippledlines)associatedwith
twoequalchargesofoppositesign.
(FromSjostrand,p.32)
Fig.I.36Equipotentialsurfacesattwoparallel
platesofoppositechargeswiththepathofan
electronindicatedwithinthehomogeneous
partofthefield.(FromSjostrand,p.33)
Fig.I.37Refractionofelectronatan
equipotentialsurface.(FromSjostrand,p.33)
Fig.I.38.Negativelensactionof
electrostaticfieldatanaperturewhen
V2V1>V3V2.(FromSjostrand,
p.34)
Fig.I.39.Positivelensactionatan
aperturewhenV2V1<V3V2.
(FromSjostrand,p.34)
Fig.I.40Magneticfieldinducedbycurrent
passingthroughaconductor.(From
Sjostrand,p.35)
Fig.I.41Magneticfieldinducedbycurrent
passingthroughasolenoid.(From
Sjostrand,p.37)
Fig.I.42Solenoidwithironcore.(From
Sjostrand,p.40)
Fig.I.43a.Dependenceofpermeabilityonfluxdensity,B.
b.RelationshipbetweenfluxdensityBandfieldstrength.
(FromSjostrand,p.38).
Fig.I.44Magnetization.(FromSlayter,
p.361)
Fig.I.45Curves
showinghowthe
magnetizationof
softiron(lens
strength)is
relatedtothe
magnetizing
force(lens
current).An
unmagnetized
lensstartsfrom
thepointOand
followsthepath
OAaslens
current
increases.Atthe
pointA,further
increaseinlens
currentproduces
nofurther
increaseinlens
strength;thelensissaidtobe'saturated'.Whenlenscurrent
isreduced,thepathOAisnotretraced;adifferentpathABis
followed.Thisdisplacementiscalled'hysteresis'.Atzero
current(pointB),someresiduallensstrengthremains;thisis
called'remanence'.Tobringthelensbacktozerostrength,a
reversecurrentOCmustbeapplied.Lensstrengththen
increaseswithincreasingreversecurrent,followingthepath
CD.Thepolarityofthelenschanges,butthisdoesnotaffect
itsfocusingpower;onlythespiralelectronpathisreversed.
Becauseofhysteresis,itisnotpossibletocalibratealens
currentmeteraccuratelyintermsoflensstrengthor
magnification.
Fig.I.46Evolutionofmagneticelectron
lenses.(A)Shortsolenoidusedasa
magneticlens.(B)Softironcasing
enclosingoutersurfaceofthesolenoid,
thusconcentratingthefield.(C)Soft
ironencasingthesolenoidexceptata
narrowannulargaptherebyreducing
themagneticfieldtoaveryshortregion
alongthelensaxis.(D)Modern
objectivelensconsistingofasoftiron
encasedsolenoidandsoftironpole
piecessoastohaveanenormously
concentratedfieldatthelevelofthe
annulargap.(FromWischnizter2nded.,
p.33)
Fig.I.47(a)Amagneticlensconsisting
ofatightlywoundcoilandasoftiron
shroudsurroundingthecoilexceptfor
asmallgap.Thefieldisconcentratedin
thatgap.(b)Shortfocallength
electromagneticlenswithpolepieces.
(FromSjostrand,p.50)
Fig.I.48Fieldstrengthdistribution
curves.ThecurvesADcorrespondto
therespectivelensesillustratedinFig.
I.46.Eachrepresentsthefieldstrength
alongthelongaxisofthelens.The
changesintheshapeofthecurves
representtheshorteningor
concentrationofthefieldovera
shorteraxialdistance.Hz=
longitudinalmagneticfield.Z=
distancealongtheaxisofsymmetry.
(FromWischnizter2nded.,p.33)
Fig.I.49TheforceFactingon
astraightconductorina
homogeneousmagneticfield
offluxdensityBwhencurrent
Iispassedthroughthe
conductor.(FromSjostrand,
p.43)
Fig.I.50Pathofanelectronina
magneticfield.(A)Inalarge,uniform
magneticfield.(B)Inasmall,uniform
magneticfield.(FromWischnitzer2nd
ed.,p.25)
Fig.I.51Lefthandthumbrule.
(FromSjostrand,p.43)
Fig.I.52Thompson'sexperiment.A
streamofelectronsoriginatingfroma
sourceandpassing,invacuo,through
amagneticfieldproducedbyapairof
magnetswillbedeflected.The
directionofdeflectiondemonstrates
thatelectronsarenegativelycharged
particlesofmatter.(FromWischnitzer
2nded.,p.25)
Fig.I.53Actionofasolenoidonan
electronbeam.Anelectriccurrent
passingthroughthecoilproducesan
axialmagneticfield.Thisisthe
refractingmediumfortheelectrons.An
electronstartingatapointontheaxisA
andatanangletoitfollowsaspiral
path,returningtotheaxisatthepoint
B.Theactionisbasicallysimilartothat
oftheconverginglightlensshownin
Fig.I.20.(FromMeek1sted.,p.8)
Fig.I.54Actionofthemagnetic
lens.(a)Inperspective.(b)
Electrontrajectoryin
projection,alongdirectionof
propagation.(c)Electron
trajectoryinprojection,side
view.(FromSlayter,p.358)
Fig.I.55Componentsofthe
vectorHneartheaxisoffields
withaxialsymmetry.His
representedbytwo
components,Hz,the
componentinthez(axial)
direction,andHr,the
compnentinther(radial)
direction.(FromHall,p.85)
Fig.I.56Theycomponentof
themagneticfieldina
magneticlensisoriented
perpendiculartothedirection
ofanelectronenteringthe
lensalongapathparallelto
thelensaxis.Thisy
componentwillaffectthe
electron,deflectingitinthex
directionasindicatedbythe
arrowmarkedvx.(From
Sjostrand,p.48)
Fig.I.57Thezcomponentofthemagneticfield
andthexvelocitycomponentoftheelectron
inamagneticlensinteract,deflectingthe
electronintheydirectiontowardthelens
axis.(FromSjostrand,p.49)
CuuDuongThanCong.com https://fb.com/tailieudientucntt
cuu duong than cong . com

I.THEMICROSCOPE
I.A.PRINCIPLESOFTHETRANSMISSIONELECTRONMICROSCOPE(TEM)
I.A.1.OriginoftheTransmissionElectronMicroscope
I.A.2.ComparisonofLight(LM)andElectronMicroscopes(Fig.I.1)
a.Similarities(Arrangementandfunctionofcomponentsaresimilar)
1)Illuminationsystem:producesrequiredradiationanddirectsitontothespecimen.Consistsofasource,whichemitstheradiation,anda
condenserlens,whichfocusestheilluminatingbeam(allowingvariationsofintensitytobemade)onthespecimen.
2)Specimenstage:situatedbetweentheilluminationandimagingsystems.
3)Imagingsystem:Lenseswhichtogetherproducethefinalmagnifiedimageofthespecimen.Consistsofi)anobjectivelenswhichfocusesthe
beamafteritpassesthroughthespecimenandformsanintermediateimageofthespecimenandii)theprojectorlens(es)whichmagnifiesa
portionoftheintermediateimagetoformthefinalimage.
4)Imagerecordingsystem:Convertstheradiationintoapermanentimage(typicallyonaphotographicemulsion)thatcanbeviewed.
b.Differences
1)Opticallensesaregenerallymadeofglasswithfixedfocallengthswhereasmagneticlensesareconstructedwithferromagneticmaterialsand
windingsofcopperwireproducingafocallengthwhichcanbechangedbyvaryingthecurrentthroughthecoil.
2)MagnificationintheLMisgenerallychangedbyswitchingbetweendifferentpowerobjectivelensesmountedonarotatingturretabovethe
specimen.Itcanalsobechangedifoculars(eyepieces)ofdifferentpowerareused.IntheTEMthemagnification(focallength)oftheobjective
remainsfixedwhilethefocallengthoftheprojectorlensischangedtovarymagnification.
3)TheLMhasasmalldepthoffield,thusdifferentfocallevelscanbeseeninthespecimen.Thelarge(relative)depthoffieldintheTEMmeans
thattheentire(thin)specimenisinfocussimultaneously.
4)Mechanismsofimageformationvary(phaseandamplitudecontrast).
5)TEMsaregenerallyconstructedwiththeradiationsourceatthetopoftheinstrument:thesourceisgenerallysituatedatthebottomofLMs.
6)TEMisoperatedathighvacuum(sincethemeanfreepathofelectronsinairisverysmall)somostspecimens(biological)mustbedehydrated
(i.e.dead!!).
7)TEMspecimens(biological)arerapidlydamagedbytheelectronbeam.
8)TEMscanachievehighermagnificationandbetterresolutionthanLMs.
9)Pricetag!!!(100xmorethanLM)
I.A.3.Photons/Electrons
a.Dualconceptofwaveandparticle(Fig.I.4)
Lighthaspropertiesbothofaparticleandawave.Thisdualnatureisrequiredtosatisfactorilyexplaintheresultsofvariousphysicalexperiments.
Thediffractionoflight(bendingaroundcorners)illustratesthewavenature.TheWAVETHEORYisbasedonthestatisticalnatureofeventsand
haslittlemeaningwithrespecttothebehaviorofsingleparticles.ThewavetheorywasdevelopedandexpoundedbyHuygens(16291695)and
Hooke(16381703).TheCORPUSCULARTHEORYwasproposedbyNewton(16421727)andbecamethemoreacceptedtheoryevenafter
demonstrationofdiffractionbyYoung(17731829)andinterferencebyFresnel(17881827).Atabout1850,thewavetheorycamebackinto
favoruntilabout1900whenmoreevidenceforthecorpusculartheorywasdiscovered.
QUANTUMTHEORY(PlanckandEinstein)providesthebasisforexplainingthephenomenaofINTERFERENCE,DIFFRACTIONandthe
PHOTOELECTRICeffect(lightfallingoncertainmetalscausethemtoemitelectrons)andthusformsacommonbasisforexplainingthenatureof
actionoflight.Thetransferofenergybetweenlightandmatteroccursonlyindiscretequantitiesproportionaltothefrequencyofthe
lightwave.
E=hJ
where
E=energyofphoton(joules)
h=Planck'sconstant(6.624
•
10
34
joulesec)
J=frequency(cycles/sec)
b.Electronvelocityandwavelength
Therelationbetweenthewavelength(l )ofaparticleofmass,m,movingatavelocity,v,isgivenbytheDeBrogliewaveequation:
(1)
Anelectronofchargee(1.6
•
10
19
coulomb),andmassm(9.11
•
10
28
gm),whenpassingthroughapotentialdifferenceofVvolts(expressedin
joules/coulomb),hasakineticenergy:
(2)
Solvingforvelocity:
(3)
substitutingintotheDeBroglieequation(1):
(4)
Since1joule=10
7
dyne
•
cm=10
7
cm
2
•
gm/sec
2
(5)
Thus,forexample,ifV=60,000volts,l =0.005nm.
Fromequation(3)theelectronvelocitycanbecalculatedifVisknown:
(6)
Thefollowingtableillustratesthat,athighvoltage,electronvelocityiscomparabletothespeedoflightinavacuum(c=3
•
10
10
cm/sec).
Theequationbreaksdownwhenthevelocityoftheelectronapproachesthespeedoflightbecausearelativisticcorrectionmustbemadeforthe
valueofthemasswhere:
(7)
Therelationbetweenl andVismorecorrectlygivenby:(seeHall(1966)pp.3334)
(8)
Thefollowingtableisobtainedwhenrelativityeffectsareincluded:
c.Interference/diffraction/coherence
Anideallenssystemobtainsanexactimageoftheobject(eachpointfaithfullyreproduced).Thephenomenaofdiffractionmakesthis
unattainable(Figs.I.5,I.6).
Diffractionphenomenainvolvesthebendingofthepathofradiationpassingclosetoanobstacle(Fig.I.6).Thisresultsinaspreadingofthe
radiationintotheregionbehindtheobstructionthatthewavespassed.Thediffractionatedgescontributestothecontrastatwhichanedgecan
beobserved.Diffractionalsolimitstheresolvingpowerofthemicroscopesincetheimagepointproducedbyalensisadiffractionimageofthe
openingofthelensortheaperturerestrictingtheeffectiveopeningofthelens(Fig.I.5).
Ifthelightsourceandtheplaneatwhichthediffractionpatternisobservedareatfinitedistancesfromtheedge,thephenomenoniscalled
Fresneldiffraction.Thepatternisdescribedasduetointerferencebetweenthenondiffractedlightandawaveoflightdiffractedattheedge.
Theresultingsuperpositiongivesrisetoaseriesofdiffractionfringesorientedparalleltotheedgeandrepresentingperiodicallyvaryingbrightness,
maximaandminima.(Figs.I.7,1.8,I.9).
Coherence:Aprerequisiteforinterferenceisasuperpositionofwavesystemswhosephasedifferenceremainsconstantintime.Twobeams
arecoherentif,whencombined,theyproduceaninterferencepattern.Thebeamsareincoherentwhentheyareincapableofproducingan
interferencepattern.Twobeamsoflightfromselfluminoussourcesareincoherent.Iflightfromthetwosourcesfallsonascreen,theresultant
intensityissimplythesumofthetwointensitieswhichwouldoccurfromeachsourceseparately(Figs.I.10,I.11).Inpracticeanemittingsource
hasfiniteextentandeachpointofthesourcecanbeconsideredtogeneratelight.EachsourcegivesrisetoasystemofFresnelfringesatthe
edge.Thesuperpositionofthesefringesystemsisfairlygoodforthefirstmaximaandminimabutfartherawayfromtheedgeshadowtheoverlap
ofthefringepatternsbecomessufficientlyrandomtomakethefringesdisappear.Thenatureofwaves,phase,amplitude,andinterferenceare
illustratedinFigs.I.12andI.13.
d.Resolution
1)Definitions:
RESOLUTION:abilitytodistinguishcloselyspacedpointsasseparatepoints.
RESOLUTIONLIMIT:smallestseparationofpointswhichcanberecognizedasdistinct.
RESOLVINGPOWER:resolutionachievedbyaparticularinstrumentunderoptimumviewingconditions.
2)Distinctionbetweenresolutionandresolvingpower:
Notethedistinctionbetweenresolutionandresolvingpower.Resolvingpowerisapropertyoftheinstrumentandisaquantitythatmaybe
estimatedontheoreticalgrounds.Resolutionisequaltoorpoorerthantheresolvingpowerandisthequantityobservedunderanygivenset
ofexperimentalconditions.IntheTEM,especiallywithbiologicalsamples,theresolutionachievedmaybeconsiderablyinferiortothetheoretical
resolvingpoweroftheinstrument.
Microscopyisthescienceofseeingtheverysmall.Underidealconditions,theeyeresolvesabout1minuteofarc(=1/60degree=2.9x10
4
radian;recallthereare2p radiansin360°)andsinceitcanfocusdowntoabout250mm,thesmallestobjectwecanresolveisabout0.07mm
(70mm)(Fig.I.14).Thislimitisrelatedtothesizeofthereceptorsintheretinaoftheeye.Thefunctionofamicroscopeistomagnifytheimage
fallingontheretina(Fig.I.15).Theadvantageoflightandelectronmicroscopesisthattheyeffectivelygettheobjectclosertotheeyesoa
magnifiedimageisobtainedandmoredetailcanbediscerned.
TENNISBALLANALOGY:Eyecanresolve3cmat100meters,thusatennisballisclearlyvisible.Butifthetennisballisheldupagainstawhite
background,thevisibilitydecreases(becauseofthedecreaseincontrast).
3)Abbecriteriaofresolution:
Thefundamentalnatureoflightposeslimitsonthedetailthatcanberesolved(Fig.I.16).Abbe(1893)showedthatthesmallestresolvable
distanceisabout1/2thewavelengthoflightused.Thus,1/2thewavelengthoftheradiationusedistheultimateresolvingpowerofany
instrument.Thislimitstheusablemagnificationofopticalmicroscopesto<1000X.Atfirstitwasthoughtthatxraymicroscopeswouldbeuseful
buttherefractiveindexofsubstancesforxraysisnearly=1,thusrefractinglensescannotbemadeforxrays,andconsequently,xrayscannot
beeasilyfocusedtoformimages.
4)Magnificationlimits:
Themaximummagnificationofaninstrumentislimitedaccordingtothefollowingrelationship:
Thus,fortheLM,witharesolvingpowerofapproximately0.25µm,themaximum(useful)magnificationisabout250µm/0.25µm=1000X.Thevalue
usedfortheresolvingpoweroftheeyeinthisexample(250µm)representsamorerealisticviewingcondition.Anymagnificationabovethevalue
givenbytheaboveformularepresentsemptymagnification,sincesuchmagnificationleadstonomoreusefulinformationbutratheramagnified
blur.
AccordingtotheAbbecriteria,at60,000volts,theTEMshouldhavearesolvingpowerofabout0.0025nm.Thisshouldallowamaximumuseful
magnificationofabout100milliontimes!!!Inpractice,themaximumusefulmagnificationoftheTEMoperatedat60kVislimitedtomuchlessthan
1,000,000X.Thus,althoughtheLMnearlyobeystheAbbecriteria,theTEMfallsshortbyaconsiderableamount.Themainlimitingfactorinthe
TEM,withrespecttoachievingthetheoreticalresolvingpoweroftheinstrument,concernsthenatureoftheimaginglensesandtheprocessof
imageformation.
5)Rayleighcriteria(practicalbutarbitrary):(Fig.I.17).
Itistheabilityofmicroscopestomakeobjectpointswhichareclosetogetherappearintheimageasseparatepoints.Anideallenstakeseach
objectpointandrepresentsitexactlyasapointintheimage.Areallenstakeseachobjectpointandspreadsitoutintoacirculardisk(Airy
disk)intheimageplanewhosediameterdependsontheangularapertureofthelens.
Theshortestdistancebetween2disksatwhichthetwodisksappearpartiallyseparatedcorrespondstoabout1/2thewidthofthedisks.The
distance,d,inobjectspaceisgivenby:
d=0.61l /n
•
sina
where
l =wavelenghtoftheradiation
n=refractiveindexofthemedia
a=semiangularapertureofthelens
NOTE:n
•
sina=thenumericalaperture(N.A.)ofthelens.
Thus,tomaximizeresolvingpower,l mustbedecreased,nincreased,oraincreased.Recallthatweareconcernedatthemomentwithan
aberrationfreeopticalsystem.Thevaluefortheconstant(0.61)iscontroversialbecauseitdependsonthecoherenceoftheradiationanda
criteriaofvisibility.
FortheLM,usingoilimmersionoptics(n=1.5),sina=0.87,andvioletlight(l =400nm),d=0.2µm.Theonlywaytoimprovetheresolutionisto
uselightofshorterwavelengthsinceN.A.cannotbeincreasedbeyond~1.5.FortheTEM,n=1(vacuum),sina=10
2
andl =0.005nmfor60kV
electrons,thusd=0.3nm.
I.A.4.Optics(LensTheory)
a.Basiclawsofclassicalgeometricaloptics
1)Rectilinearpropagationoflightwhenn(refractiveindex)isconstant.
2)Lawofreflection:
3)Lawofrefraction(Snell'sLaw):
4)Independenceofrays.Theassumptionismadethatlightraystravelindependentlythroughspace.
Theselawsholdforelectrons,except#4,ifthecurrentdensityistoohighwhennegativechargedelectronscaninterfere.
b.Classicalvs.electronoptics
1)Classicaloptics:Therefractiveindexchangesabruptlyatasurfaceandisconstantbetweenthesurfaces.Therefractionoflightatsurfaces
separatingmediaofdifferentrefractiveindicesmakesitpossibletoconstructimaginglenses.Glasssurfacescanbeshaped.
2)Electronoptics:Here,changesintherefractiveindexaregradualsoraysarecontinuouscurvesratherthanbrokenstraightlines.Refraction
ofelectronsmustbeaccomplishedbyfieldsinspacearoundchargedelectrodesorsolenoids,andthesefieldscanassumeonlycertaindistributions
consistentwithfieldtheory.
c.Geometricalandphysicaloptics
Thefundamentalprinciplesofopticsgovernthedesignandoperationofboththelightandelectronmicroscopes.Thebasicopticalprinciples
involvingtheuseofrefractileelementsorlensesinordertoformmagnifiedimagesareidenticalinboththeLMandTEM.TheTEMdiffersfromthe
LMonlyintheradiationitusesandinthewayinwhichtheradiationisbentorrefracted.
Geometricalopticsdealswiththestudyofthepathsfollowedby'rays'oflightorelectronsthroughlensesandapertures,andthegeometrical
constructionsusedtofindtherelativepositionsandsizesofobjectsandtheirimages.Arayoflightorelectronsisdefinedasaninfinitelythin
pencilorbeam.Physicalopticsshowsthatthisanabstractionandcannotphysicallyexistbecauseof'diffraction'whichdealswiththewave
natureoflightandelectrons.Allresultsobtainedingeometricalopticscanbederivedfromtheprinciplesofphysicaloptics,alongwithother
phenomenasuchasinterferenceanddiffractionwhicharenotexplicableinsimplegeometricalterms.
d.Idealversesreallenses:
Lensesareusedtobendraysoflightorelectronssotheyaredeflectedinapredictablewayfromtheiroriginalpaths.Thepropertiesofanideal
lens,possessinganaxisofrotationalsymmetryare:
1)Eachrayofthebundleofrayswhichpassesfromanobjectpointwillberefractedbytheideallenstomeetinoneimagepoint.
2)Raysoriginatingfrompointswhichlieonaplaneperpendiculartotheaxis,mustbeimagedinaplanewhichisalsoperpendiculartotheaxis.
3)Theimageappearsliketheobjectirrespectiveofthemagnification,sotherelativelineardimensionsoftheobjectarepreservedintheimage.
Inpractice,theimagingbyanyreallensdoesnotcorrespondtothatoftheideallensowingtothefactthatanobjectpointisrepresentedbya
diffractionimage(Airydisc)ofthelensopeningortheapertureusedforrestrictingtheeffectiveopeningofthelens.Thisisaresultofthewave
likepropertiesoflight.Lensaberrationsalsocontributetomoreorlesspronounceddeviationsfromthepropertiesoftheideallens.
Thesinglerefractingsurfaceofsphericalcurvatureisthefundamentalunitoffocusingactionbyglasslenses.Sphericalrefractingsurfacesactas
lensesforparaxialrayswhicharethoseraysthatpassclosetotheprincipalaxisofthelens.RayswithlargeangleswillNOTobeyideallens
action.
Afundamentaldifferencebetweenlightandmagneticlensesisthattheelectronbeamdoesnotchangeinforwardvelocityasitpassesthrough
themagneticfield(lightraysslowdownwhenpassingintoamediumofhigherrefractiveindex).Refractioniscontinuouswithelectronswhenthey
areinthemagneticfield:lightisrefractedonlyattheinterfacebetweenmediaofdifferingrefractiveindex.Theelectronsalsofollowspiral
trajectoriesthroughthemagneticfield(seealsoSec.I.A.5.c(Magneticfieldsandmagneticlenses)
e.Raydiagrams:(Figs.I.20I.28)
Themethodofconstructionofraydiagramsisbasedonthreesimpleprinciples:
1)Allraysenteringthelensparalleltotheaxisarebroughttoacommonpointontheaxis,thefocalpoint.
2)Allrayspassingthroughthegeometricalcenterofthelensareundeviatedandpassstraighton,nomatterfromwhichdirectiontheycome.
3)Principleofreversibility:ifthedirectionofarayisreversedinanysystemtherayexactlyretracesitspaththroughthesystem.Thisapplies
onlytothelocationoflightpathsandnottotheintensityofthelight.
Theaboveprinciplesarebasedontheassumptionsthatwearedealingwithathinlensandconcernedwiththepathsofparaxialrays.The
standardconventionistodrawdiagramswithraysthattravelfromlefttoright.Theobjectistotheleft(infront)ofthelensandtheimageisto
theright(behind)ofthelens.
f.Definitions:
Realimage:oneatwhichlightraysphysicallyreunite,sothataphotographicplateplacedatthepositionofarealimageisexposed.
VirtualImage:onefromwhichlightraysappeartodiverge;raysarenotinfactconcentratedatthepositionofavirtualimage,sothata
photographicplateplacedatthepositionoftheimageisnotexposed(byfocusedrays).Placinganopticalsystemsuchastheeyebehindthe
lens,willenablethedivergentraystobefocusedtoformarealimage.TheintermediatelensofanTEMissometimesusedthiswayinorderto
reducethefinalsizeoftherealimageformedbytheprojectorlens(es).
Converging(positive)lens:bendsraystowardtheaxis.Ithasapositivefocallength.Formsarealinvertedimageofanobjectplacedtothe
leftofthefirstfocalpointandanerectvirtualimageofanobjectplacedbetweenthefirstfocalpointandthelens.
Diverging(negative)lens:bendsthelightraysawayfromtheaxis.Ithasanegativefocallength.Anobjectplacedanywheretotheleftofa
diverginglensresultsinanerectvirtualimage.Itisnotpossibletoconstructanegativemagneticlensalthoughnegativeelectrostaticlensescan
bemade.
g.Lensformula(thinlensequation):
where
f=focallengthofthethinlens(sameradiusofcurvatureforboth
sphericalsurfaces)
o=distanceofobjectfromlens(positivetotheleft)
i=distanceofimagefromthelens(positivetotheright)
NOTE:Foravirtualimage,ihasanegativevalue.
h.Magnification:
Foraconverginglens,iftheobjectismorethantwicethefocallengthfromthelens,thentheimageformedisreal,inverted,andsmallerinsize
thantheobject(M<1).Whentheobjectisatadistance=2f,theimageandobjectarethesamesize(M=1);whenitisbetweenfand2f,
theimageislargerthantheobject(M>1),andwhenitis<f,theimageisvirtual,erect,andlargerthantheobject(M>1).
i.Angularapertureofthelens(2a)(Fig.I.29)
Theaperturedeterminesthetotalamountofradiationarrivingfromtheobjectwhichcanbefocusedto
formanimage.Theaperturethuscontrolstheabilityofthelenstogatherinformationabouttheobject.
Thisdependsontheangleoftheconeofraysitisabletoacceptfromtheobject.Bringinganobject
closertotheeyeincreasestheangularaperture,butthereisalimittotheclosenessthattheobjectcan
bebroughttotheeye(~25cmcorrespondingtoanangleofabout0.9°fora4mmexitpupildiameterof
theeyelens;atypicalLMwithanoilimmersionobjectivelenshas2aof~175°).
j.Simplevs.compoundmicroscope(Figs.I.30I.32)
Inprinciple,arealimageofanydesiredmagnificationcanbeobtainedfromasinglepositivelens,butin
practicethisiscumbersomebecauseofthelonglensimagedistance.Oneormorelensescanbeusedto
magnifytheimageinstages(totalmagnificationequalingtheproductofthemagnificationsofeachlens).
Theimageformedbyonelensconstitutestheobjectforthesubsequentlens,whetherornotareal
intermediateimageisformed.
Comparisonofoneversestwostagemagnification:
Thefollowingdescriptionillustrateshowdifferentpathlengthsarerequiredtoachieveamagnificationof10,000Xusingeitheroneortwolenses
withf=2.0cm.
OneStageSystem:
TwoStageSystem:
Assumebothlenseshavef=2.0cmandarearrangedsoeachgives100Xmagnification.
Thus,M=100=x
i
/x
o
foreachstage.
FirstStage:
x
o
=2.02cm
x
i
=202.00cm
Therealimageformedinthefirststagebecomestheobjectforthesecondlens.
SecondStage:x
o
,x
i
sameasinthefirststage.
Totallengthofsystem
=lengthoffirststage+lengthofsecondstage
=(x
o
+x
i
)+(x
o
+x
i
)
=2(x
o
+x
i
)
=2(2.02+202.00)=408.04cm(4.08meters)
k.Problemset
Thefollowingproblemsareforyourownedificationtotesthowwellyouunderstandthebasicsoflensoptics.
1.Foreachsituationbelow,drawanaccurate(usegraphpaper)raydiagramshowingthepathof(atleasttwo)raysfromtheobjecttoimage.
Indicatewhethertheimageisrealorvirtualandspecifythedistanceoftheimagefromthelensandthemagnificationoftheimagewithrespect
totheobject.Ineachexample,thelensisconverging,withidenticalfrontandbackfocalpoints.Distancesareinarbitraryunits.Letf=lens
focallength,x
o
=distanceofobjectinfrontofthelens,andx
i
=distanceofimagebehindthelens.Theobjectmaybeanysize.
2.Inthefollowingexamples,therearetwoconverginglensesinsuccession.Drawraydiagramsshowingtheformationofboththeintermediate
andfinalimagesandgiveappropriateinformationaboutthenature(real/virtual),positions,andsizesoftheintermediateandfinalimages.What
isthemagnificationateachstageofimageformationandwhatisthemagnificationofthefinalimage?Thedistancefromthecenteroflens1(L1)
tothecenteroflens2(L2)equalsD.
I.A.5.ElectronOptics/ElectronLenses
a.Electronemission
Innershellelectronsinmetalatomsshieldtheelectricfieldofthenucleusthroughtherepulsiveforcestheyexertontheoutershell(valence)
electrons.Thustheattractionbetweenthevalenceelectronsandthenucleusisreduced.Metalatomsarecharacterizedashavingtwoloosely
boundvalenceelectronswhichmigratefreely(thisiswhymetalsaregoodelectricalconductors)andcanescapefromthemetalcompletelyif
sufficientadditionalenergyisimpartedtothem.Asthetemperatureofametalisincreased,thekineticenergyoftheelectronsincreasesbecause
ofincreasedthermalvibrationsofthemetalions,whichcollidemorefrequentlywiththeelectrons.Thermionicemissionisthetermusedto
describetheprocessbywhichthermalenergyissuppliedtolooselyboundelectronsinordertoformasourceofelectrons.
Atroomtemperatureelectronsareeffectivelypreventedfromescapingthesurfaceofthemetalowingtotheattractiveforceofthepositively
chargedions.Asthetemperatureisincreasedsomeelectronsacquiresufficientenergytoovercometheattractionandleavethemetal
temporarily.Metal,shapedasathinwire,caneasilybeheatedbypassinganelectriccurrentthroughit.Sincethemetalsurfacebecomes
positivelycharged,acertainlevelofenergy(workfunction)mustbesuppliedtoallowelectronstoescapefromthesurface.Eachmetalhasa
characteristicworkfunction.Tungsten,withalowworkfunction,emitsmoreelectronsthanmetalswithhigherworkfunctions(seealsopp.2930
andFig.I.59).
Ifastrongelectrostaticfieldisappliedinavacuumbetweenthewire(givenanegative,cathode,potential)andananode,theelectricfieldwill
causeelectronstoaccelerateawayfromthewiretowardstheanodesurface(Fig.I.33).Thespeedoftheelectronsdependsonthestrengthof
theelectrostaticfield(voltage)betweenthecathodeandanode(equation(3),Sec.I.A.3.b)Thenumberofelectronswhichleavethewire
dependsonthetemperaturetowhichthewireisheated,whichdependsonhowmuchfilamentcurrentpassesthroughthewire.
A"V"shapedwirewillhavethehighesttemperatureatthetip.Electronswithdrawnfromthefilamenttipcarryelectricchargestotheanode.This
electriccurrent,whichflowsbetweenthefilamentandtheanode,iscalledthebeamcurrent.
1)Electricfield/Equipotentials
Anelectricallychargedobjecthasassociatedwithitanelectricfield.Thus,anelectricallychargedparticle,whenbroughtnearachargedobject,
isinfluencedbyanelectricalforceinthevicinityoftheobject.Theforceisdirectedtowardthechargedobjectifthechargesareofopposite
signsandawayfromtheobjectiftheyareofsimilarsign.DEFINITION:Thedirectionofanelectricfieldisdefinedasthedirectionoftheforce
actingonapositivecharge.(Figs.I.3435)
Alongthelinesofforceconnectingthetwocharges,theelectricpotentialwillchangegraduallybetweentheextremevaluesrepresentedbythe
twocharges.DEFINITION:Equipotentiallinesdefinethepointsalongthelinesofforcewithidenticalelectricalpotential.Theseequipotential
surfacesarealwaysorientedperpendiculartothelinesofforce.Thechangesintheelectricpotentialaregradualinspace.
Electronswhichenterafieldbetweentwoparallelplatesinadirectionparalleltotheplatesareaffectedbytheforcedirectedperpendicularto
theplates(FigI.36).Theelectronswillbeattractedtowardthepositiveplate.Thepathchangesinaseriesofgradualstepsattheequipotential
surfaces.
FigureI.37showshowtheelectronpathis"refracted"attheequipotentialsurface.TheresultisfundamentallythesameasthatgivenbySnell's
Lawofrefractioninlightoptics.Aconsequenceofthisisthatasphericallycurvedequipotentialsurfaceexhibitsthepropertiesofalens.
FiguresI.38andI.39showhowbothpositive(converging)andnegative(diverging)electrostaticlensescanbeformed.Thisfeatureof
electrostaticlensesdiffersfromelectromagneticlenseswhichcanonlyactasconverginglenses.
2)Advantages/Disadvantagesofelectronlenses:
Thefactthattherefractiveindexdoesnotchangeabruptlyinelectronlenseshasoneadvantageinthattherearenotroublesomereflectionsat
equipotentialsasatglassinterfaces.Thereisaseriousdisadvantageinthatequipotentialscannotbeshapedandcombinedinarbitraryfashionto
correctforchromaticaberrationandothererrors.
Althoughelectronmicroscopeswhichemployelectrostaticlenseshavebeenmade,mostmicroscopesuseelectromagneticlenses.Amajorreason
isthatelectrostaticlensesaremoresensitivetothequalityofthevacuumandcleanlinessofthecomponentsthanareelectromagneticlenses.
Somelensaberrationsaremoresevereforelectrostaticlensescomparedtoelectromagneticlenses.Electrostaticlensesrequireverypowerful
electrostaticfieldswhichcanleadtoelectricalbreakdownor"arcingover"insidethecolumn,especiallyunderpoorvacuumconditions.Forthis
reason,electrostaticlensescannotbemadewithfocallengthsasshortasmagneticlenses.
b.Electrostaticlens
Abasicunderstandingofelectrostaticlensesisimportantfortwomainreasons:i)theelectrongunuseselectrostaticlensactiontoformthe
primarybeamsource,andii)itisquitecommonforachargetodeveloponthenonconductingcontaminationwhichmayaccumulateonphysical
apertures(suchastheobjectiveaperture)andtransformthemintoweakelectrostaticlenseswhichcandistorttheelectronimage.
3)Propertiesofelectrostaticlenses:
a)Anyaxiallysymmetricalelectrostaticfieldhasthepropertiesofalensforraysconfinedtotheparaxialregion.Alltheideallensformulasapply
toelectrostaticlenses.
b)Forelectronlenses,replaceÃ(f)forrefractiveindexinthelensequations(f=valueofthepotentialontheaxis).Intheimageformingsystem
ofmostTEMs,fisthesameonbothsidesofthelens(SeeSec.I.A.5.c).
c)Ifboundedbyregionswherefisconstant,anelectrostaticlensisalwaysconvergent.
c.Magneticfieldsandmagneticlenses
1)Magneticfield
Anelectriccurrentpassingthroughaconductorgivesrisetoamagneticfield.TheconventionisthatNisthedirectioninwhichthelinesofthe
magneticfieldpoint(Fig.I.40).Themagneticfluxisthetotalnumberoflinesandthefluxdensityisthenumberoflinesperunitareaofasurface.
UsetheRIGHThandruletodeterminethedirectionofthefield(thumbpointstowardcurrentdirectionandfingerscurlindirectionoffield.NOTE:
Byconvention,thedirectionofelectronflowisoppositetothatofcurrentflow.
Fluxdensitydependsonthepropertiesofthematerialsurroundingtheconductor.Ironinducesahigherfluxdensitythanairoravacuum.The
propertyofthematerialwhichaffectsthefluxdensityiscalledthepermeability,m,ofthematerial.Forairandvacuum,m=1.0.For
ferromagneticmaterialsitcanbeaslargeasseveralhundredthousand.
Iftheconductorhastheshapeofacircularloop,thelinesofforceformcirclesaroundtheloop.Thefluxdensityisgreatestatthecenterofthe
loop.Themagnetinthecenteroftheloopisorientedperpendiculartotheplaneoftheloopifthecurrentthroughtheloopissufficientlystrongto
eliminatetheinfluenceoftheearth'sfield.ThesideoftheloopatwhichthelinesofforceleavetheloopistheNorth(N)poleofthemagnet(Figs.
I.41,I.42).
Ifthewireiswoundinseveralturnsaroundacylindricalsurface(solenoid),eachturnwillcontributetotheinducedmagneticfield.Theflux
densityinthecenterofthecoilisgivenby:
Inthecaseofairandnonmagneticmaterials,µ=1.0andB=H.
Thepermeabilityofirondependsonthefieldstrength,H,anddecreasestounityathighfieldstrengthorwhenthefluxdensity,B=H(Fig.I.43).
Thehighpermeabilityofironisduetotheinducedmagneticfieldorientingmicroscopiccrystalregionsactingastinymagnetsintheiron.Allthese
tinymagnetsaddtheirmagneticfieldstotheinducedfield(Fig.I.44).Whenallmicromagnetsarenearlyoriented,theironwillaffecttheflux
densitytoadecreasingamountsincethereorientationofmicromagnetsisnearingcompletion.Thus,thepermeabilityofironathighfieldstrengths
approachesthatofemptyspace.Atthispointtheironreachesmagneticsaturation.
2)Hysteresis
Thestrengthofthelensdependstosomeextentonthepreviousmagnetichistoryof
thelens.Whenthecurrentinalensisreduced,thedecreaseinmagnetizationdoes
notretracethesamepathobtainedwhenthecurrentwasincreased(Fig.I.45).
Inductionofmagnetizationinvolvesaphysicalmovementwithinthemagnetized
material,requiringtheovercomeofacertaindegreeofinertia.Asaresult,
magnetizationtendstolagbehindthemagnetizingforceapplied.Inducedmagnetic
fluxcanonlybereturnedtozerobyapplicationofacurrentintheoppositedirection.
Aconsequenceofhysteresisisthatthelevelofcurrentusedtoenergizeamagnetic
lensDOESNOTpreciselyspecifythelensstrength(i.e.focallength).
NormalizationofTEMlensesisaccomplishedbyreducingthelenscurrenttozero
somepredeterminednumberoftimes.Hysteresismayalsobeminimizedbytakinga
lenstosaturationandthenreturningittotheworkingcurrentwithoutovershooting.
Whenthefieldstrengthisreducedtozero,somemagnetizationstillremainsintheiron
(residualmagnetizationorremanence).Anadvantageofsoftironisthefactthat,
whenusedinanelectromagnet,hysteresisislow.
Introductionofpiecesofironinamagneticfielddrasticallyaffectsthefluxdensity.
Magneticmaterialhasashieldingeffect,theeffectbeinggreaterthegreaterthe
permeability.Permalloy(mmetal)hasamaximumpermeabilityof80,000140,000
comparedtoironusedintransformers(~7000).mmetalpermeabilityislimitedtolower
fieldstrengthsthanthatatwhichironstillretainshighpermeability.Thismetalis
thereforeusefulforshieldingtheTEMfromexternalmagneticfields.
d.Theelectromagneticlens
1)Lensdesigndevelopment(Figs.I.46I.48)
Theefficiencyofthemagneticfieldproducedbyashortsolenoidwasfirstimproved
byencasingtheenergizingcoilinasheathofsoftironwhichhasthepropertyofconcentratingthelinesofforceinamagneticfieldandthus
becomingmagnetizedbyinduction.Inthiswayamuchmorepowerfulaxialmagneticfieldisobtainedforthesameamountofcurrentflowing
throughthesolenoid.Furtherdevelopmentinvolvedencasingtheentirecoilwithsoftironexceptatanarrowannulargapintheinsideofthecoil.
Thisproducesagreaterconcentrationofthemagneticfieldalongashortaxialdistance.Toachieveshorterfocallengthlenses(andobtaingreater
magnifications)asoftironpolepiecewithanopenaxialborewasintroducedatthepositionoftheannulargap.
MagneticlensesusedinTEMsarealwaysconstructedwithanironcircuittoproduceahighfieldstrengthacrossashortgap.Themagneticfields
forTEMlensesareintherangeof10,00020,000gauss.
2)Forcesactingonacurrentinamagneticfield
Theforceonanelectroninamagneticfieldisalwaysatrightanglestothevelocityandthedirectionofthefield(Figs.I.49,I.50,andI.52).The
fieldonlyactsonthevelocitycomponentwhichisdirectedperpendiculartothelinesofforce.Usethelefthandrule(Fig.I.51:firstfingerfor
fielddirection,middlefingerforcurrentdirection,andthumbfordirectionofforce).Rayspassingthroughthelensareturnedthroughanangle
whichdoesNOTdependonthedistanceoftheraysfromtheaxis.Allelectronscontainedinagivenmeridionalplanebeforeenteringthefieldare
containedinarotatingmeridionalplaneastheypassthroughthelens,andthentheyleavethelenscoplanar.
Whenelectronsenterthelenstheyencounterasidewaysforcewhichcausestheelectrontorotate
asitcontinuesthroughthelens(Figs.I.53I.57).Sincetheradialcomponentofthemagneticfield
reversesafterthecenterofthelens,therotationalvelocitysetupinthefirsthalfofthelensis
countered.Theelectronenteredthelenswithoutangularmomentumabouttheaxisandleaves
withoutangularmomentum.Theneteffectisadeflectiontowardtheaxis,whichitmustcrossatthe
focalpointf
2
.Theanglebetweentheobjectvectorandtheimagevectoris180°+q,whereas,for
glasslensesandelectrostaticlenses,theanglebetweenarealobjectandtheimageisexactly180°.
Sincetheradialforceisdirectedtowardtheaxis,thelensisconvergentnomatterwhatthedirection
ofthefield.
3)Propertiesofamagneticlens:
Anyaxiallysymmetricmagneticfieldhasthepropertiesofanideallens.Alltheformulasfortheideallensmaybeapplied.
Magneticlensesarealwaysconvergent.Theconventional,axiallysymmetriclensisalwaysboundedbyregionswhicharefieldfree,the
consequencebeingthatthenetactionofelectronlensesisinevitablyconvergent.Limitedregionsmaybedivergentbutnotthelensasawhole.
Theseriousconsequenceofthisisthatneithersphericalorchromaticaberrationscanbecorrectedasisdoneinlightopticsbytheusedoublets
ofpositiveandnegativelenses.
Intheabsenceofelectrostaticfields,therefractiveindexisthesameinobjectandimagespace,thereforef
1
=f
2
.
Electronstravelingthroughaxiallysymmetricfieldsexperienceaspiraltrajectoryofdiminishingradius.Theimagevectorisatanangle180°+qto
theobjectvector.
Thedeflectionoftheelectrontowardstheaxismeansthatanelectronenteringthelensparalleltoitsaxiswillcrosstheaxisafterhavingpassed
thelens.Thedeflectionwillincreasewiththedistancefromtheaxis.Thus,abeamofelectronsinparallelpathsparalleltotheaxisofthelenswill
befocusedtoanimagepointontheaxiswhichrepresentsthesecond(back)focalpointofthelens(f
2
).Notethatmagneticlensesarehighly
inefficientinthatonlyaminorportionofthetotalfieldstrengthisactuallyeffectiveinfocusingtheelectron.
4)Magneticlensfocallength
Inamagneticelectronlensthefocallengthisdeterminedbythefieldstrengthinthelensgapandbythespeedoftheelectrons(determinedby
theacceleratingvoltage).
Formagneticlenses,focusingisachievedbyvaryingthecurrentwhichpassesthroughtheelectromagnet.Thisinturnchangesthestrengthof
themagneticfieldandtherebyaltersthefocallengthofthelensandisequivalenttoacombinedchangeinboththe"refractiveindex"and
"curvatureofsurface".Forabeamofmoreenergeticelectrons,thelenscurrenthastobeincreasedinordertokeepthefocallengthconstant.
FocallengthandcurrentareNOTlinearlyrelated:strengthincreasesinasigmoidfashion(Fig.I.45)ascurrentincreasesuntilapointisreached
wherethelensissaturatedandnofurtherincreaseinlensstrengthcanbeachieved.
Sincethefocallengthofthelensisdirectlyproportionaltotheacceleratingvoltage,avariationinthevelocityoftheelectronsintheimaging
beamaffectsimagequalitybyeliminatingperfectfocus(chromaticaberration).
5)Magneticlensdesign:(Figs.I.46,I.47).
Condenserlensesusuallyhavearelativelylargeboreandspacingwhichresultsinalongfieldandlongfocallength.
Typicalconstructionoftheobjectivelensproducesastrongfieldofshortaxialextent(i.e.shortfocallengthbetween(1.53mm)necessaryfor
formationofimagesathighmagnification.Thespecimenisplacedwithinthemagneticfieldoftheobjectivelens.Thus,anyfieldintroducedby
contaminantsinthespecimencandistortthefieldofthelens.Notethatthisalsomeansthatpartofthelensfield("prefield")isonthefrontside
oftheobjectandaffectstheelectronbeambeforeitpassesthroughtheobject.
Mostofatypicalmagneticlensliesoutsidethevacuumofthemicroscope.Onlythoseregionsthroughwhichtheelectronbeampassesareinhigh
vacuum.Magneticlensesmustbewatercooledtodissipatethelargeamountsofheatproducedbythecurrentsintheelectromagnetcoils.
DATE NAME EVENT
1897 J.J.Thompson Discoverstheelectron
1924 LouisdeBroglie Identifiesawavelengthtomovingelectrons
l =h/mv
where
l =wavelength
h=Planck'sconstant
m=mass
v=velocity
(Foranelectronat60kVl=0.005nm)
1926 H.Busch Magneticorelectricfieldsactaslensesforelectrons
1929 E.Ruska Ph.Dthesisonmagneticlenses
1931 Knoll&Ruska Firstelectronmicroscopebuilt
1931 Davisson&Calbrick Propertiesofelectrostaticlenses
1934 Driest&Muller SurpassresolutionoftheLM
1938 vonBorries&Ruska FirstpracticalEM(Siemens)10nmresolution
1940 RCA CommercialEMwith2.4nmresolution
1945 1.0nmresolution
Fig.I.1Comparisonoflightandelectronmicroscopes.Ineach
instrument,illuminationfromthesource(lamp,filamentinthe
electrongun)isfocusedbythecondenserlensontothespecimen.
Afirstmagnifiedimageisformedbytheobjectivelens.Thisimage
isfurthermagnifiedbytheprojectorlensontoagroundglass
screen(light)orfluorescentscreen(electrons).(FromAgar,p.8)
Fig.I.2CrosssectionalviewofthePhilipsEM300.(FromAgar,p.40)
Toviewtheanimatedmicroscope,clickhere.
Note:QuickTimePlugInrequired
(Thiscanbedownloadedathttp://apple.com/quicktime/download)
Fig.I.3Sectionthroughacomplex
doublecondenser6lensPhilips
EM200electronmicroscope.(From
Meek,p.99)
Fig.I.4Thestatisticalnatureofdiffraction
patterns.(FromHall,p.13)
"Theprecisenatureof'electronwaves'or'matterwaves'isverydifficulttounderstandordescribeinmaterialterms.Electronwavesarenot
electromagneticradiationofthekindtowhichlight,Xraysandradiowavesbelong.Theyconstituteasortofquantumor'packet'ofradiationwhich
accompanieseachindividualelectron,followingitspathandnotradiatingoutwardsfromit."(Meek,1976,pp.4849).
V l (nm)
v(
•
10
10
cm/sec)
v/c
10,000 0.0123 0.593 0.198
50,000 0.0055 1.326 0.442
100,000 0.0039 1.875 0.625
1,000,000 0.0012 5.930 1.977!
V l (nm)
v(
•
10
10
cm/sec)
v/c
10,000 0.0123 0.593 0.195
50,000 0.0055 1.326 0.414
100,000 0.0039 1.875 0.548
1,000,000 0.0012 5.930 0.941
FigI.5Aperfectpointsourcecannotbe
imagedbyalensasaperfectpointimagedue
tothepresenceoftheapertureAB(which
maybetheedgeofthelens).Diffractionat
thisaperturegivesrisetoaseriesoffringes,
whichsurroundtheimageformedofthepoint
source.Thepatternproducediscalledan'Airy'
disk.(FromMeek1sted.,p.35)
Fig.I.6Wheneverawavefrontstrikesa
barrier,itcanbendaroundthecorner'by
givingrisetoasecondarywavefrontatthe
edge,sinceeachpointonthewavefrontcan
giverisetoanewsourceofwaves.This
phenomenoniscalled'diffraction'.(FromMeek
1sted.,p.22)
Fig.I.7Diffractionpattern(right)formedbyanirregularlyshapedaperture
(left).(FromYoung,p.95)
Fig.I.8(a)
Photographof
theedgeofa
razorblade
illuminatedby
monochromatic
(blue)light
rendered
coherentby
passing
througha
narrowslit.(b)
Microdensitometer
tracingofthe
negativefrom
whichthe
photograph
wasmade.
FourFresnel
fringescanbe
distinguished.
(FromMeek1st
ed.,p.27)
(a)
(b)
(a) (c)
(b)
Fig.I.9(a)Fresnelfringesformed
byelectrons.Thesefringesare
formedoutsidetheedgeofahole
(white)inacarbonfilm(black).(b)
Amicrodensitometertracingofthe
fringesystem;thepatternis
identicalwiththeFresnelfringe
systemformedbyvisiblelight(see
Fig.I.8).(c)Anunderfocusedimage
ofaholeinafilm,showinga
completesystemofabout40
Fresnelfringesinsidethehole.
(FromMeek1sted.,pp.2930)
Fig.I.10Diffractionimagesoftwo
easilyresolvedpoints.(From
Slayter,p.243)
Fig.I.11Imagesoftwo
incoherentlyilluminatedpointsat
thelimitofresolution.(a)individual
intensities;(b)summedintensities.
(FromSlayter,p.244)
Fig.I.12Examplesofwhatoccurswhentwo
wavesofthesamewavelengthandequal
amplitudeadd.Ineachexample,thetwo
separatewavesareshownontheleftand
theirsumorresultantwaveontheright.The
differentexamplesarecharacterizedbyvarying
phasedifferences.Thephaseofawave
(usuallyexpressedasafractionofthe
wavelengthorindegrees)isthepositionofa
crestrelativetosomearbitrarypoint.Although
thephaseofagivenwavevarieswithtimeas
thewavetravels,thedifferenceinphaseofthe
twowavesofthesamewavelengthwiththe
samevelocity,isindependentoftime.Such
wavescaninterferewithoneanother.The
resultantwavehasthesamewavelength,l .
(a)Phasedifferencezero.Thewavestotally
reinforceandaresaidtobe"inphase"orto
showconstructiveinterference.
(b)Phasedifferencel /4.Partialreinforcement,
givingawaveofamplitude1.4(intensity2.0).
(c)Phasedifferencel /2.Thewavesare"outof
phase"andthereistotaldestructive
interferencetogivenoresultantwaveora
wavewithamplitude0(intensity0).(From
GluskerandTrueblood,p.19)
Fig.I.13Photographofan
interferencepatterninwater
wavesformedbythe
superpositionofwavesfromtwo
sourcesoscillatinginphasewith
thesamefrequency.(FromYoung,
p.22)
Fig.I.14Theangularapertureofthe
eyeisrelativelysmall.(FromMeek,
1sted.,p.13)
Fig.I.15Increasingtheangular
apertureoftheeyewithalens.The
lensallowstheobjecttobeheld
closertotheeye,whichisthereby
enabledtogathermoreinformation.
(FromMeek1sted.,p.14)
Fig.I.16Theinteractionofwaves
withanobstacle.Theboatridesthe
longwavelengthoceanwave,but
reflectsthesmallwavelength
surfaceripple.Anobserverwho
wishestodetectthepresenceof
theboatcandosoonlyby
observingwaveswhichhave
wavelengthssmallerthan,or
comparableto,thelengthofthe
boat.(FromSherwood,p.19)
Maximummagnification=
resolvingpoweroftheeye
resolvingpowerofthemicroscope
(a)
Fig.I.17(a)TwoAiry
disksrepresenting
twoimagepoints
shownatincreasing
separationfromleft
toright.Inthe
pictureatthe
extremerightthe
twodiskscanbe
distinguishedas
separatedisks.
(b)Theintensity
distributionatanAiry
disk.R,halfwidthof
thecentralmaximum
representedbya
bellshapedcurve.
(c)TheRayleigh
criteriaforresolution.
(FromSjostrand,
p.115)
i=r
Fig.I.18Reflection.(FromSlayter,
p.4)
Fig.I.19Refraction.(FromSlayter,
p.6)
Fig.I.20Principalraydiagramsshowing
imageformationbyaconvexlens.
(a)Whentheobjectdistanceisgreater
thanthefocallength,areal,inverted
imageisformed.
(b)Whentheobjectdistanceisless
thanthefocallength,avirtual,erect
imageisformed;itspositionis
obtainedbyprojectingtheprincipal
raysbackward.Theraysappearto
comefrompointQ.(FromYoung,
p.127)
Fig.I.21Definitionof
principalfocus,F,inimage
spaceofalens.(From
Sjostrand,p.20)
Fig.I.22Focusingeffectoflenson
raysoriginatingfrompointson
principalaxislocatedatdifferent
distancesfromthelens.(From
Sjostrand,p.21)
Fig.I.23Definitionofprincipal
focusinobjectspaceF1ofa
lens.(FromSjostrand,p.21)
Fig.I.24VirtualimageQof
objectpointlocatedbetween
principalfocusinobjectspace
andthelens.(FromSjostrand,
p.21)
Fig.I.25Constructionoftheimage
ofanobjectbymeansofray
tracing.(FromSjostrand,p.22)
Fig.I.26Magnifyingeffectof
apositivelens.(From
Sjostrand,p.22)
Fig.I.27Virtualmagnified
imageofobjectlocated
betweenprincipalfocusin
objectspaceandthelens.
(FromSjostrand,p.22)
Fig.I.28Amagnifyingglassformsan
enlarged,erectvirtualimage.The
angularsizeofthisimageis
approximately4"/15"or4/15.The
angularsizeoftheobjectatthe
closestdistanceforcomfortable
viewingis1"/10"or1/10.The
magnificationinthissituationis(4/15)/
(1/10),or22/3.(FromYoung,p.130)
Fig.I.29Theangularapertureofa
lens.Theangle2a isthe
acceptanceangleofthelens,and
thelargeritcanbemade,themore
informationcanthelenstransmit.A
largelensofhighaperturecan
thereforetellusmoreaboutan
objectthanasmalllensoflow
power.(FromMeek1sted.,p.12)
Fig.I.30Raydiagramforhighmagnification
modeofoperation.Notethateachlens
formsarealimage,withimageinversion.
I0istheimageformedbytheobjective
lensO,I1isformedbythefirstprojector
lensP1andI2bythesecondprojectorP2,
onthescreen.(FromAgar,p.30)
Fig.I.31Left:raydiagramofthe3realimagemediumandhighmagnificationimagingsystemofa3lens
microscope.Center:2realimageverylowor'scan'magnificationrangeofa3lensmicroscope.Right:2real
imagelowmagnificationsystemofa3lensmicroscope.(FromMeek1sted.,pp.118,120121)
Fig.I.32Raydiagramforacompleteelectron
microscope.FilamentF,condenser1lensC1,
condenser2lensC2,condenserapertureCA,
specimenS,objectivelensO,objectiveaperture
OA(inbackfocalplane).1stintermediateimage
andselectorapertureSA.IntermediatelensP1,
secondintermediateimageI2,projectorlensP2
andfinalimageonthefluorescentscreenFC.
(FromAgar,p.35)
a)f=2.0
x
o
=5.0
e)f=4.0
x
o
=3.0
b)f=10.5
x
o
=21.0
f)f=13.3
x
o
=13.3
c)f=3.5
x
o
=3.0
g)f=3.142
x
o
=0.0
d)f=5.0
x
o
=2.5
a)D=8.0
L1:f=2.0
x
o
=4.0
L2:f=3.0
b)D=8.0
L1:f=2.0
x
o
=6.0
L2:f=3.0
c)D=4.0
L1:f=2.0
x
o
=3.0
L2:f=2.0
FigI.33Accelerationofelectronin
electricfield.(FromSjostrand,p.26)
Fig.I.34Linesofforceatapositively
chargedsphericalbody.(FromSjostrand,
p.32)
Fig.I.35Linesofforceandequipotential
surfaces(stippledlines)associatedwith
twoequalchargesofoppositesign.
(FromSjostrand,p.32)
Fig.I.36Equipotentialsurfacesattwoparallel
platesofoppositechargeswiththepathofan
electronindicatedwithinthehomogeneous
partofthefield.(FromSjostrand,p.33)
Fig.I.37Refractionofelectronatan
equipotentialsurface.(FromSjostrand,p.33)
Fig.I.38.Negativelensactionof
electrostaticfieldatanaperturewhen
V2V1>V3V2.(FromSjostrand,
p.34)
Fig.I.39.Positivelensactionatan
aperturewhenV2V1<V3V2.
(FromSjostrand,p.34)
Fig.I.40Magneticfieldinducedbycurrent
passingthroughaconductor.(From
Sjostrand,p.35)
Fig.I.41Magneticfieldinducedbycurrent
passingthroughasolenoid.(From
Sjostrand,p.37)
Fig.I.42Solenoidwithironcore.(From
Sjostrand,p.40)
Fig.I.43a.Dependenceofpermeabilityonfluxdensity,B.
b.RelationshipbetweenfluxdensityBandfieldstrength.
(FromSjostrand,p.38).
Fig.I.44Magnetization.(FromSlayter,
p.361)
Fig.I.45Curves
showinghowthe
magnetizationof
softiron(lens
strength)is
relatedtothe
magnetizing
force(lens
current).An
unmagnetized
lensstartsfrom
thepointOand
followsthepath
OAaslens
current
increases.Atthe
pointA,further
increaseinlens
currentproduces
nofurther
increaseinlens
strength;thelensissaidtobe'saturated'.Whenlenscurrent
isreduced,thepathOAisnotretraced;adifferentpathABis
followed.Thisdisplacementiscalled'hysteresis'.Atzero
current(pointB),someresiduallensstrengthremains;thisis
called'remanence'.Tobringthelensbacktozerostrength,a
reversecurrentOCmustbeapplied.Lensstrengththen
increaseswithincreasingreversecurrent,followingthepath
CD.Thepolarityofthelenschanges,butthisdoesnotaffect
itsfocusingpower;onlythespiralelectronpathisreversed.
Becauseofhysteresis,itisnotpossibletocalibratealens
currentmeteraccuratelyintermsoflensstrengthor
magnification.
Fig.I.46Evolutionofmagneticelectron
lenses.(A)Shortsolenoidusedasa
magneticlens.(B)Softironcasing
enclosingoutersurfaceofthesolenoid,
thusconcentratingthefield.(C)Soft
ironencasingthesolenoidexceptata
narrowannulargaptherebyreducing
themagneticfieldtoaveryshortregion
alongthelensaxis.(D)Modern
objectivelensconsistingofasoftiron
encasedsolenoidandsoftironpole
piecessoastohaveanenormously
concentratedfieldatthelevelofthe
annulargap.(FromWischnizter2nded.,
p.33)
Fig.I.47(a)Amagneticlensconsisting
ofatightlywoundcoilandasoftiron
shroudsurroundingthecoilexceptfor
asmallgap.Thefieldisconcentratedin
thatgap.(b)Shortfocallength
electromagneticlenswithpolepieces.
(FromSjostrand,p.50)
Fig.I.48Fieldstrengthdistribution
curves.ThecurvesADcorrespondto
therespectivelensesillustratedinFig.
I.46.Eachrepresentsthefieldstrength
alongthelongaxisofthelens.The
changesintheshapeofthecurves
representtheshorteningor
concentrationofthefieldovera
shorteraxialdistance.Hz=
longitudinalmagneticfield.Z=
distancealongtheaxisofsymmetry.
(FromWischnizter2nded.,p.33)
Fig.I.49TheforceFactingon
astraightconductorina
homogeneousmagneticfield
offluxdensityBwhencurrent
Iispassedthroughthe
conductor.(FromSjostrand,
p.43)
Fig.I.50Pathofanelectronina
magneticfield.(A)Inalarge,uniform
magneticfield.(B)Inasmall,uniform
magneticfield.(FromWischnitzer2nd
ed.,p.25)
Fig.I.51Lefthandthumbrule.
(FromSjostrand,p.43)
Fig.I.52Thompson'sexperiment.A
streamofelectronsoriginatingfroma
sourceandpassing,invacuo,through
amagneticfieldproducedbyapairof
magnetswillbedeflected.The
directionofdeflectiondemonstrates
thatelectronsarenegativelycharged
particlesofmatter.(FromWischnitzer
2nded.,p.25)
Fig.I.53Actionofasolenoidonan
electronbeam.Anelectriccurrent
passingthroughthecoilproducesan
axialmagneticfield.Thisisthe
refractingmediumfortheelectrons.An
electronstartingatapointontheaxisA
andatanangletoitfollowsaspiral
path,returningtotheaxisatthepoint
B.Theactionisbasicallysimilartothat
oftheconverginglightlensshownin
Fig.I.20.(FromMeek1sted.,p.8)
Fig.I.54Actionofthemagnetic
lens.(a)Inperspective.(b)
Electrontrajectoryin
projection,alongdirectionof
propagation.(c)Electron
trajectoryinprojection,side
view.(FromSlayter,p.358)
Fig.I.55Componentsofthe
vectorHneartheaxisoffields
withaxialsymmetry.His
representedbytwo
components,Hz,the
componentinthez(axial)
direction,andHr,the
compnentinther(radial)
direction.(FromHall,p.85)
Fig.I.56Theycomponentof
themagneticfieldina
magneticlensisoriented
perpendiculartothedirection
ofanelectronenteringthe
lensalongapathparallelto
thelensaxis.Thisy
componentwillaffectthe
electron,deflectingitinthex
directionasindicatedbythe
arrowmarkedvx.(From
Sjostrand,p.48)
Fig.I.57Thezcomponentofthemagneticfield
andthexvelocitycomponentoftheelectron
inamagneticlensinteract,deflectingthe
electronintheydirectiontowardthelens
axis.(FromSjostrand,p.49)
CuuDuongThanCong.com https://fb.com/tailieudientucntt
cuu duong than cong . com

I.THEMICROSCOPE
I.A.PRINCIPLESOFTHETRANSMISSIONELECTRONMICROSCOPE(TEM)
I.A.1.OriginoftheTransmissionElectronMicroscope
I.A.2.ComparisonofLight(LM)andElectronMicroscopes(Fig.I.1)
a.Similarities(Arrangementandfunctionofcomponentsaresimilar)
1)Illuminationsystem:producesrequiredradiationanddirectsitontothespecimen.Consistsofasource,whichemitstheradiation,anda
condenserlens,whichfocusestheilluminatingbeam(allowingvariationsofintensitytobemade)onthespecimen.
2)Specimenstage:situatedbetweentheilluminationandimagingsystems.
3)Imagingsystem:Lenseswhichtogetherproducethefinalmagnifiedimageofthespecimen.Consistsofi)anobjectivelenswhichfocusesthe
beamafteritpassesthroughthespecimenandformsanintermediateimageofthespecimenandii)theprojectorlens(es)whichmagnifiesa
portionoftheintermediateimagetoformthefinalimage.
4)Imagerecordingsystem:Convertstheradiationintoapermanentimage(typicallyonaphotographicemulsion)thatcanbeviewed.
b.Differences
1)Opticallensesaregenerallymadeofglasswithfixedfocallengthswhereasmagneticlensesareconstructedwithferromagneticmaterialsand
windingsofcopperwireproducingafocallengthwhichcanbechangedbyvaryingthecurrentthroughthecoil.
2)MagnificationintheLMisgenerallychangedbyswitchingbetweendifferentpowerobjectivelensesmountedonarotatingturretabovethe
specimen.Itcanalsobechangedifoculars(eyepieces)ofdifferentpowerareused.IntheTEMthemagnification(focallength)oftheobjective
remainsfixedwhilethefocallengthoftheprojectorlensischangedtovarymagnification.
3)TheLMhasasmalldepthoffield,thusdifferentfocallevelscanbeseeninthespecimen.Thelarge(relative)depthoffieldintheTEMmeans
thattheentire(thin)specimenisinfocussimultaneously.
4)Mechanismsofimageformationvary(phaseandamplitudecontrast).
5)TEMsaregenerallyconstructedwiththeradiationsourceatthetopoftheinstrument:thesourceisgenerallysituatedatthebottomofLMs.
6)TEMisoperatedathighvacuum(sincethemeanfreepathofelectronsinairisverysmall)somostspecimens(biological)mustbedehydrated
(i.e.dead!!).
7)TEMspecimens(biological)arerapidlydamagedbytheelectronbeam.
8)TEMscanachievehighermagnificationandbetterresolutionthanLMs.
9)Pricetag!!!(100xmorethanLM)
I.A.3.Photons/Electrons
a.Dualconceptofwaveandparticle(Fig.I.4)
Lighthaspropertiesbothofaparticleandawave.Thisdualnatureisrequiredtosatisfactorilyexplaintheresultsofvariousphysicalexperiments.
Thediffractionoflight(bendingaroundcorners)illustratesthewavenature.TheWAVETHEORYisbasedonthestatisticalnatureofeventsand
haslittlemeaningwithrespecttothebehaviorofsingleparticles.ThewavetheorywasdevelopedandexpoundedbyHuygens(16291695)and
Hooke(16381703).TheCORPUSCULARTHEORYwasproposedbyNewton(16421727)andbecamethemoreacceptedtheoryevenafter
demonstrationofdiffractionbyYoung(17731829)andinterferencebyFresnel(17881827).Atabout1850,thewavetheorycamebackinto
favoruntilabout1900whenmoreevidenceforthecorpusculartheorywasdiscovered.
QUANTUMTHEORY(PlanckandEinstein)providesthebasisforexplainingthephenomenaofINTERFERENCE,DIFFRACTIONandthe
PHOTOELECTRICeffect(lightfallingoncertainmetalscausethemtoemitelectrons)andthusformsacommonbasisforexplainingthenatureof
actionoflight.Thetransferofenergybetweenlightandmatteroccursonlyindiscretequantitiesproportionaltothefrequencyofthe
lightwave.
E=hJ
where
E=energyofphoton(joules)
h=Planck'sconstant(6.624
•
10
34
joulesec)
J=frequency(cycles/sec)
b.Electronvelocityandwavelength
Therelationbetweenthewavelength(l )ofaparticleofmass,m,movingatavelocity,v,isgivenbytheDeBrogliewaveequation:
(1)
Anelectronofchargee(1.6
•
10
19
coulomb),andmassm(9.11
•
10
28
gm),whenpassingthroughapotentialdifferenceofVvolts(expressedin
joules/coulomb),hasakineticenergy:
(2)
Solvingforvelocity:
(3)
substitutingintotheDeBroglieequation(1):
(4)
Since1joule=10
7
dyne
•
cm=10
7
cm
2
•
gm/sec
2
(5)
Thus,forexample,ifV=60,000volts,l =0.005nm.
Fromequation(3)theelectronvelocitycanbecalculatedifVisknown:
(6)
Thefollowingtableillustratesthat,athighvoltage,electronvelocityiscomparabletothespeedoflightinavacuum(c=3
•
10
10
cm/sec).
Theequationbreaksdownwhenthevelocityoftheelectronapproachesthespeedoflightbecausearelativisticcorrectionmustbemadeforthe
valueofthemasswhere:
(7)
Therelationbetweenl andVismorecorrectlygivenby:(seeHall(1966)pp.3334)
(8)
Thefollowingtableisobtainedwhenrelativityeffectsareincluded:
c.Interference/diffraction/coherence
Anideallenssystemobtainsanexactimageoftheobject(eachpointfaithfullyreproduced).Thephenomenaofdiffractionmakesthis
unattainable(Figs.I.5,I.6).
Diffractionphenomenainvolvesthebendingofthepathofradiationpassingclosetoanobstacle(Fig.I.6).Thisresultsinaspreadingofthe
radiationintotheregionbehindtheobstructionthatthewavespassed.Thediffractionatedgescontributestothecontrastatwhichanedgecan
beobserved.Diffractionalsolimitstheresolvingpowerofthemicroscopesincetheimagepointproducedbyalensisadiffractionimageofthe
openingofthelensortheaperturerestrictingtheeffectiveopeningofthelens(Fig.I.5).
Ifthelightsourceandtheplaneatwhichthediffractionpatternisobservedareatfinitedistancesfromtheedge,thephenomenoniscalled
Fresneldiffraction.Thepatternisdescribedasduetointerferencebetweenthenondiffractedlightandawaveoflightdiffractedattheedge.
Theresultingsuperpositiongivesrisetoaseriesofdiffractionfringesorientedparalleltotheedgeandrepresentingperiodicallyvaryingbrightness,
maximaandminima.(Figs.I.7,1.8,I.9).
Coherence:Aprerequisiteforinterferenceisasuperpositionofwavesystemswhosephasedifferenceremainsconstantintime.Twobeams
arecoherentif,whencombined,theyproduceaninterferencepattern.Thebeamsareincoherentwhentheyareincapableofproducingan
interferencepattern.Twobeamsoflightfromselfluminoussourcesareincoherent.Iflightfromthetwosourcesfallsonascreen,theresultant
intensityissimplythesumofthetwointensitieswhichwouldoccurfromeachsourceseparately(Figs.I.10,I.11).Inpracticeanemittingsource
hasfiniteextentandeachpointofthesourcecanbeconsideredtogeneratelight.EachsourcegivesrisetoasystemofFresnelfringesatthe
edge.Thesuperpositionofthesefringesystemsisfairlygoodforthefirstmaximaandminimabutfartherawayfromtheedgeshadowtheoverlap
ofthefringepatternsbecomessufficientlyrandomtomakethefringesdisappear.Thenatureofwaves,phase,amplitude,andinterferenceare
illustratedinFigs.I.12andI.13.
d.Resolution
1)Definitions:
RESOLUTION:abilitytodistinguishcloselyspacedpointsasseparatepoints.
RESOLUTIONLIMIT:smallestseparationofpointswhichcanberecognizedasdistinct.
RESOLVINGPOWER:resolutionachievedbyaparticularinstrumentunderoptimumviewingconditions.
2)Distinctionbetweenresolutionandresolvingpower:
Notethedistinctionbetweenresolutionandresolvingpower.Resolvingpowerisapropertyoftheinstrumentandisaquantitythatmaybe
estimatedontheoreticalgrounds.Resolutionisequaltoorpoorerthantheresolvingpowerandisthequantityobservedunderanygivenset
ofexperimentalconditions.IntheTEM,especiallywithbiologicalsamples,theresolutionachievedmaybeconsiderablyinferiortothetheoretical
resolvingpoweroftheinstrument.
Microscopyisthescienceofseeingtheverysmall.Underidealconditions,theeyeresolvesabout1minuteofarc(=1/60degree=2.9x10
4
radian;recallthereare2p radiansin360°)andsinceitcanfocusdowntoabout250mm,thesmallestobjectwecanresolveisabout0.07mm
(70mm)(Fig.I.14).Thislimitisrelatedtothesizeofthereceptorsintheretinaoftheeye.Thefunctionofamicroscopeistomagnifytheimage
fallingontheretina(Fig.I.15).Theadvantageoflightandelectronmicroscopesisthattheyeffectivelygettheobjectclosertotheeyesoa
magnifiedimageisobtainedandmoredetailcanbediscerned.
TENNISBALLANALOGY:Eyecanresolve3cmat100meters,thusatennisballisclearlyvisible.Butifthetennisballisheldupagainstawhite
background,thevisibilitydecreases(becauseofthedecreaseincontrast).
3)Abbecriteriaofresolution:
Thefundamentalnatureoflightposeslimitsonthedetailthatcanberesolved(Fig.I.16).Abbe(1893)showedthatthesmallestresolvable
distanceisabout1/2thewavelengthoflightused.Thus,1/2thewavelengthoftheradiationusedistheultimateresolvingpowerofany
instrument.Thislimitstheusablemagnificationofopticalmicroscopesto<1000X.Atfirstitwasthoughtthatxraymicroscopeswouldbeuseful
buttherefractiveindexofsubstancesforxraysisnearly=1,thusrefractinglensescannotbemadeforxrays,andconsequently,xrayscannot
beeasilyfocusedtoformimages.
4)Magnificationlimits:
Themaximummagnificationofaninstrumentislimitedaccordingtothefollowingrelationship:
Thus,fortheLM,witharesolvingpowerofapproximately0.25µm,themaximum(useful)magnificationisabout250µm/0.25µm=1000X.Thevalue
usedfortheresolvingpoweroftheeyeinthisexample(250µm)representsamorerealisticviewingcondition.Anymagnificationabovethevalue
givenbytheaboveformularepresentsemptymagnification,sincesuchmagnificationleadstonomoreusefulinformationbutratheramagnified
blur.
AccordingtotheAbbecriteria,at60,000volts,theTEMshouldhavearesolvingpowerofabout0.0025nm.Thisshouldallowamaximumuseful
magnificationofabout100milliontimes!!!Inpractice,themaximumusefulmagnificationoftheTEMoperatedat60kVislimitedtomuchlessthan
1,000,000X.Thus,althoughtheLMnearlyobeystheAbbecriteria,theTEMfallsshortbyaconsiderableamount.Themainlimitingfactorinthe
TEM,withrespecttoachievingthetheoreticalresolvingpoweroftheinstrument,concernsthenatureoftheimaginglensesandtheprocessof
imageformation.
5)Rayleighcriteria(practicalbutarbitrary):(Fig.I.17).
Itistheabilityofmicroscopestomakeobjectpointswhichareclosetogetherappearintheimageasseparatepoints.Anideallenstakeseach
objectpointandrepresentsitexactlyasapointintheimage.Areallenstakeseachobjectpointandspreadsitoutintoacirculardisk(Airy
disk)intheimageplanewhosediameterdependsontheangularapertureofthelens.
Theshortestdistancebetween2disksatwhichthetwodisksappearpartiallyseparatedcorrespondstoabout1/2thewidthofthedisks.The
distance,d,inobjectspaceisgivenby:
d=0.61l /n
•
sina
where
l =wavelenghtoftheradiation
n=refractiveindexofthemedia
a=semiangularapertureofthelens
NOTE:n
•
sina=thenumericalaperture(N.A.)ofthelens.
Thus,tomaximizeresolvingpower,l mustbedecreased,nincreased,oraincreased.Recallthatweareconcernedatthemomentwithan
aberrationfreeopticalsystem.Thevaluefortheconstant(0.61)iscontroversialbecauseitdependsonthecoherenceoftheradiationanda
criteriaofvisibility.
FortheLM,usingoilimmersionoptics(n=1.5),sina=0.87,andvioletlight(l =400nm),d=0.2µm.Theonlywaytoimprovetheresolutionisto
uselightofshorterwavelengthsinceN.A.cannotbeincreasedbeyond~1.5.FortheTEM,n=1(vacuum),sina=10
2
andl =0.005nmfor60kV
electrons,thusd=0.3nm.
I.A.4.Optics(LensTheory)
a.Basiclawsofclassicalgeometricaloptics
1)Rectilinearpropagationoflightwhenn(refractiveindex)isconstant.
2)Lawofreflection:
3)Lawofrefraction(Snell'sLaw):
4)Independenceofrays.Theassumptionismadethatlightraystravelindependentlythroughspace.
Theselawsholdforelectrons,except#4,ifthecurrentdensityistoohighwhennegativechargedelectronscaninterfere.
b.Classicalvs.electronoptics
1)Classicaloptics:Therefractiveindexchangesabruptlyatasurfaceandisconstantbetweenthesurfaces.Therefractionoflightatsurfaces
separatingmediaofdifferentrefractiveindicesmakesitpossibletoconstructimaginglenses.Glasssurfacescanbeshaped.
2)Electronoptics:Here,changesintherefractiveindexaregradualsoraysarecontinuouscurvesratherthanbrokenstraightlines.Refraction
ofelectronsmustbeaccomplishedbyfieldsinspacearoundchargedelectrodesorsolenoids,andthesefieldscanassumeonlycertaindistributions
consistentwithfieldtheory.
c.Geometricalandphysicaloptics
Thefundamentalprinciplesofopticsgovernthedesignandoperationofboththelightandelectronmicroscopes.Thebasicopticalprinciples
involvingtheuseofrefractileelementsorlensesinordertoformmagnifiedimagesareidenticalinboththeLMandTEM.TheTEMdiffersfromthe
LMonlyintheradiationitusesandinthewayinwhichtheradiationisbentorrefracted.
Geometricalopticsdealswiththestudyofthepathsfollowedby'rays'oflightorelectronsthroughlensesandapertures,andthegeometrical
constructionsusedtofindtherelativepositionsandsizesofobjectsandtheirimages.Arayoflightorelectronsisdefinedasaninfinitelythin
pencilorbeam.Physicalopticsshowsthatthisanabstractionandcannotphysicallyexistbecauseof'diffraction'whichdealswiththewave
natureoflightandelectrons.Allresultsobtainedingeometricalopticscanbederivedfromtheprinciplesofphysicaloptics,alongwithother
phenomenasuchasinterferenceanddiffractionwhicharenotexplicableinsimplegeometricalterms.
d.Idealversesreallenses:
Lensesareusedtobendraysoflightorelectronssotheyaredeflectedinapredictablewayfromtheiroriginalpaths.Thepropertiesofanideal
lens,possessinganaxisofrotationalsymmetryare:
1)Eachrayofthebundleofrayswhichpassesfromanobjectpointwillberefractedbytheideallenstomeetinoneimagepoint.
2)Raysoriginatingfrompointswhichlieonaplaneperpendiculartotheaxis,mustbeimagedinaplanewhichisalsoperpendiculartotheaxis.
3)Theimageappearsliketheobjectirrespectiveofthemagnification,sotherelativelineardimensionsoftheobjectarepreservedintheimage.
Inpractice,theimagingbyanyreallensdoesnotcorrespondtothatoftheideallensowingtothefactthatanobjectpointisrepresentedbya
diffractionimage(Airydisc)ofthelensopeningortheapertureusedforrestrictingtheeffectiveopeningofthelens.Thisisaresultofthewave
likepropertiesoflight.Lensaberrationsalsocontributetomoreorlesspronounceddeviationsfromthepropertiesoftheideallens.
Thesinglerefractingsurfaceofsphericalcurvatureisthefundamentalunitoffocusingactionbyglasslenses.Sphericalrefractingsurfacesactas
lensesforparaxialrayswhicharethoseraysthatpassclosetotheprincipalaxisofthelens.RayswithlargeangleswillNOTobeyideallens
action.
Afundamentaldifferencebetweenlightandmagneticlensesisthattheelectronbeamdoesnotchangeinforwardvelocityasitpassesthrough
themagneticfield(lightraysslowdownwhenpassingintoamediumofhigherrefractiveindex).Refractioniscontinuouswithelectronswhenthey
areinthemagneticfield:lightisrefractedonlyattheinterfacebetweenmediaofdifferingrefractiveindex.Theelectronsalsofollowspiral
trajectoriesthroughthemagneticfield(seealsoSec.I.A.5.c(Magneticfieldsandmagneticlenses)
e.Raydiagrams:(Figs.I.20I.28)
Themethodofconstructionofraydiagramsisbasedonthreesimpleprinciples:
1)Allraysenteringthelensparalleltotheaxisarebroughttoacommonpointontheaxis,thefocalpoint.
2)Allrayspassingthroughthegeometricalcenterofthelensareundeviatedandpassstraighton,nomatterfromwhichdirectiontheycome.
3)Principleofreversibility:ifthedirectionofarayisreversedinanysystemtherayexactlyretracesitspaththroughthesystem.Thisapplies
onlytothelocationoflightpathsandnottotheintensityofthelight.
Theaboveprinciplesarebasedontheassumptionsthatwearedealingwithathinlensandconcernedwiththepathsofparaxialrays.The
standardconventionistodrawdiagramswithraysthattravelfromlefttoright.Theobjectistotheleft(infront)ofthelensandtheimageisto
theright(behind)ofthelens.
f.Definitions:
Realimage:oneatwhichlightraysphysicallyreunite,sothataphotographicplateplacedatthepositionofarealimageisexposed.
VirtualImage:onefromwhichlightraysappeartodiverge;raysarenotinfactconcentratedatthepositionofavirtualimage,sothata
photographicplateplacedatthepositionoftheimageisnotexposed(byfocusedrays).Placinganopticalsystemsuchastheeyebehindthe
lens,willenablethedivergentraystobefocusedtoformarealimage.TheintermediatelensofanTEMissometimesusedthiswayinorderto
reducethefinalsizeoftherealimageformedbytheprojectorlens(es).
Converging(positive)lens:bendsraystowardtheaxis.Ithasapositivefocallength.Formsarealinvertedimageofanobjectplacedtothe
leftofthefirstfocalpointandanerectvirtualimageofanobjectplacedbetweenthefirstfocalpointandthelens.
Diverging(negative)lens:bendsthelightraysawayfromtheaxis.Ithasanegativefocallength.Anobjectplacedanywheretotheleftofa
diverginglensresultsinanerectvirtualimage.Itisnotpossibletoconstructanegativemagneticlensalthoughnegativeelectrostaticlensescan
bemade.
g.Lensformula(thinlensequation):
where
f=focallengthofthethinlens(sameradiusofcurvatureforboth
sphericalsurfaces)
o=distanceofobjectfromlens(positivetotheleft)
i=distanceofimagefromthelens(positivetotheright)
NOTE:Foravirtualimage,ihasanegativevalue.
h.Magnification:
Foraconverginglens,iftheobjectismorethantwicethefocallengthfromthelens,thentheimageformedisreal,inverted,andsmallerinsize
thantheobject(M<1).Whentheobjectisatadistance=2f,theimageandobjectarethesamesize(M=1);whenitisbetweenfand2f,
theimageislargerthantheobject(M>1),andwhenitis<f,theimageisvirtual,erect,andlargerthantheobject(M>1).
i.Angularapertureofthelens(2a)(Fig.I.29)
Theaperturedeterminesthetotalamountofradiationarrivingfromtheobjectwhichcanbefocusedto
formanimage.Theaperturethuscontrolstheabilityofthelenstogatherinformationabouttheobject.
Thisdependsontheangleoftheconeofraysitisabletoacceptfromtheobject.Bringinganobject
closertotheeyeincreasestheangularaperture,butthereisalimittotheclosenessthattheobjectcan
bebroughttotheeye(~25cmcorrespondingtoanangleofabout0.9°fora4mmexitpupildiameterof
theeyelens;atypicalLMwithanoilimmersionobjectivelenshas2aof~175°).
j.Simplevs.compoundmicroscope(Figs.I.30I.32)
Inprinciple,arealimageofanydesiredmagnificationcanbeobtainedfromasinglepositivelens,butin
practicethisiscumbersomebecauseofthelonglensimagedistance.Oneormorelensescanbeusedto
magnifytheimageinstages(totalmagnificationequalingtheproductofthemagnificationsofeachlens).
Theimageformedbyonelensconstitutestheobjectforthesubsequentlens,whetherornotareal
intermediateimageisformed.
Comparisonofoneversestwostagemagnification:
Thefollowingdescriptionillustrateshowdifferentpathlengthsarerequiredtoachieveamagnificationof10,000Xusingeitheroneortwolenses
withf=2.0cm.
OneStageSystem:
TwoStageSystem:
Assumebothlenseshavef=2.0cmandarearrangedsoeachgives100Xmagnification.
Thus,M=100=x
i
/x
o
foreachstage.
FirstStage:
x
o
=2.02cm
x
i
=202.00cm
Therealimageformedinthefirststagebecomestheobjectforthesecondlens.
SecondStage:x
o
,x
i
sameasinthefirststage.
Totallengthofsystem
=lengthoffirststage+lengthofsecondstage
=(x
o
+x
i
)+(x
o
+x
i
)
=2(x
o
+x
i
)
=2(2.02+202.00)=408.04cm(4.08meters)
k.Problemset
Thefollowingproblemsareforyourownedificationtotesthowwellyouunderstandthebasicsoflensoptics.
1.Foreachsituationbelow,drawanaccurate(usegraphpaper)raydiagramshowingthepathof(atleasttwo)raysfromtheobjecttoimage.
Indicatewhethertheimageisrealorvirtualandspecifythedistanceoftheimagefromthelensandthemagnificationoftheimagewithrespect
totheobject.Ineachexample,thelensisconverging,withidenticalfrontandbackfocalpoints.Distancesareinarbitraryunits.Letf=lens
focallength,x
o
=distanceofobjectinfrontofthelens,andx
i
=distanceofimagebehindthelens.Theobjectmaybeanysize.
2.Inthefollowingexamples,therearetwoconverginglensesinsuccession.Drawraydiagramsshowingtheformationofboththeintermediate
andfinalimagesandgiveappropriateinformationaboutthenature(real/virtual),positions,andsizesoftheintermediateandfinalimages.What
isthemagnificationateachstageofimageformationandwhatisthemagnificationofthefinalimage?Thedistancefromthecenteroflens1(L1)
tothecenteroflens2(L2)equalsD.
I.A.5.ElectronOptics/ElectronLenses
a.Electronemission
Innershellelectronsinmetalatomsshieldtheelectricfieldofthenucleusthroughtherepulsiveforcestheyexertontheoutershell(valence)
electrons.Thustheattractionbetweenthevalenceelectronsandthenucleusisreduced.Metalatomsarecharacterizedashavingtwoloosely
boundvalenceelectronswhichmigratefreely(thisiswhymetalsaregoodelectricalconductors)andcanescapefromthemetalcompletelyif
sufficientadditionalenergyisimpartedtothem.Asthetemperatureofametalisincreased,thekineticenergyoftheelectronsincreasesbecause
ofincreasedthermalvibrationsofthemetalions,whichcollidemorefrequentlywiththeelectrons.Thermionicemissionisthetermusedto
describetheprocessbywhichthermalenergyissuppliedtolooselyboundelectronsinordertoformasourceofelectrons.
Atroomtemperatureelectronsareeffectivelypreventedfromescapingthesurfaceofthemetalowingtotheattractiveforceofthepositively
chargedions.Asthetemperatureisincreasedsomeelectronsacquiresufficientenergytoovercometheattractionandleavethemetal
temporarily.Metal,shapedasathinwire,caneasilybeheatedbypassinganelectriccurrentthroughit.Sincethemetalsurfacebecomes
positivelycharged,acertainlevelofenergy(workfunction)mustbesuppliedtoallowelectronstoescapefromthesurface.Eachmetalhasa
characteristicworkfunction.Tungsten,withalowworkfunction,emitsmoreelectronsthanmetalswithhigherworkfunctions(seealsopp.2930
andFig.I.59).
Ifastrongelectrostaticfieldisappliedinavacuumbetweenthewire(givenanegative,cathode,potential)andananode,theelectricfieldwill
causeelectronstoaccelerateawayfromthewiretowardstheanodesurface(Fig.I.33).Thespeedoftheelectronsdependsonthestrengthof
theelectrostaticfield(voltage)betweenthecathodeandanode(equation(3),Sec.I.A.3.b)Thenumberofelectronswhichleavethewire
dependsonthetemperaturetowhichthewireisheated,whichdependsonhowmuchfilamentcurrentpassesthroughthewire.
A"V"shapedwirewillhavethehighesttemperatureatthetip.Electronswithdrawnfromthefilamenttipcarryelectricchargestotheanode.This
electriccurrent,whichflowsbetweenthefilamentandtheanode,iscalledthebeamcurrent.
1)Electricfield/Equipotentials
Anelectricallychargedobjecthasassociatedwithitanelectricfield.Thus,anelectricallychargedparticle,whenbroughtnearachargedobject,
isinfluencedbyanelectricalforceinthevicinityoftheobject.Theforceisdirectedtowardthechargedobjectifthechargesareofopposite
signsandawayfromtheobjectiftheyareofsimilarsign.DEFINITION:Thedirectionofanelectricfieldisdefinedasthedirectionoftheforce
actingonapositivecharge.(Figs.I.3435)
Alongthelinesofforceconnectingthetwocharges,theelectricpotentialwillchangegraduallybetweentheextremevaluesrepresentedbythe
twocharges.DEFINITION:Equipotentiallinesdefinethepointsalongthelinesofforcewithidenticalelectricalpotential.Theseequipotential
surfacesarealwaysorientedperpendiculartothelinesofforce.Thechangesintheelectricpotentialaregradualinspace.
Electronswhichenterafieldbetweentwoparallelplatesinadirectionparalleltotheplatesareaffectedbytheforcedirectedperpendicularto
theplates(FigI.36).Theelectronswillbeattractedtowardthepositiveplate.Thepathchangesinaseriesofgradualstepsattheequipotential
surfaces.
FigureI.37showshowtheelectronpathis"refracted"attheequipotentialsurface.TheresultisfundamentallythesameasthatgivenbySnell's
Lawofrefractioninlightoptics.Aconsequenceofthisisthatasphericallycurvedequipotentialsurfaceexhibitsthepropertiesofalens.
FiguresI.38andI.39showhowbothpositive(converging)andnegative(diverging)electrostaticlensescanbeformed.Thisfeatureof
electrostaticlensesdiffersfromelectromagneticlenseswhichcanonlyactasconverginglenses.
2)Advantages/Disadvantagesofelectronlenses:
Thefactthattherefractiveindexdoesnotchangeabruptlyinelectronlenseshasoneadvantageinthattherearenotroublesomereflectionsat
equipotentialsasatglassinterfaces.Thereisaseriousdisadvantageinthatequipotentialscannotbeshapedandcombinedinarbitraryfashionto
correctforchromaticaberrationandothererrors.
Althoughelectronmicroscopeswhichemployelectrostaticlenseshavebeenmade,mostmicroscopesuseelectromagneticlenses.Amajorreason
isthatelectrostaticlensesaremoresensitivetothequalityofthevacuumandcleanlinessofthecomponentsthanareelectromagneticlenses.
Somelensaberrationsaremoresevereforelectrostaticlensescomparedtoelectromagneticlenses.Electrostaticlensesrequireverypowerful
electrostaticfieldswhichcanleadtoelectricalbreakdownor"arcingover"insidethecolumn,especiallyunderpoorvacuumconditions.Forthis
reason,electrostaticlensescannotbemadewithfocallengthsasshortasmagneticlenses.
b.Electrostaticlens
Abasicunderstandingofelectrostaticlensesisimportantfortwomainreasons:i)theelectrongunuseselectrostaticlensactiontoformthe
primarybeamsource,andii)itisquitecommonforachargetodeveloponthenonconductingcontaminationwhichmayaccumulateonphysical
apertures(suchastheobjectiveaperture)andtransformthemintoweakelectrostaticlenseswhichcandistorttheelectronimage.
3)Propertiesofelectrostaticlenses:
a)Anyaxiallysymmetricalelectrostaticfieldhasthepropertiesofalensforraysconfinedtotheparaxialregion.Alltheideallensformulasapply
toelectrostaticlenses.
b)Forelectronlenses,replaceÃ(f)forrefractiveindexinthelensequations(f=valueofthepotentialontheaxis).Intheimageformingsystem
ofmostTEMs,fisthesameonbothsidesofthelens(SeeSec.I.A.5.c).
c)Ifboundedbyregionswherefisconstant,anelectrostaticlensisalwaysconvergent.
c.Magneticfieldsandmagneticlenses
1)Magneticfield
Anelectriccurrentpassingthroughaconductorgivesrisetoamagneticfield.TheconventionisthatNisthedirectioninwhichthelinesofthe
magneticfieldpoint(Fig.I.40).Themagneticfluxisthetotalnumberoflinesandthefluxdensityisthenumberoflinesperunitareaofasurface.
UsetheRIGHThandruletodeterminethedirectionofthefield(thumbpointstowardcurrentdirectionandfingerscurlindirectionoffield.NOTE:
Byconvention,thedirectionofelectronflowisoppositetothatofcurrentflow.
Fluxdensitydependsonthepropertiesofthematerialsurroundingtheconductor.Ironinducesahigherfluxdensitythanairoravacuum.The
propertyofthematerialwhichaffectsthefluxdensityiscalledthepermeability,m,ofthematerial.Forairandvacuum,m=1.0.For
ferromagneticmaterialsitcanbeaslargeasseveralhundredthousand.
Iftheconductorhastheshapeofacircularloop,thelinesofforceformcirclesaroundtheloop.Thefluxdensityisgreatestatthecenterofthe
loop.Themagnetinthecenteroftheloopisorientedperpendiculartotheplaneoftheloopifthecurrentthroughtheloopissufficientlystrongto
eliminatetheinfluenceoftheearth'sfield.ThesideoftheloopatwhichthelinesofforceleavetheloopistheNorth(N)poleofthemagnet(Figs.
I.41,I.42).
Ifthewireiswoundinseveralturnsaroundacylindricalsurface(solenoid),eachturnwillcontributetotheinducedmagneticfield.Theflux
densityinthecenterofthecoilisgivenby:
Inthecaseofairandnonmagneticmaterials,µ=1.0andB=H.
Thepermeabilityofirondependsonthefieldstrength,H,anddecreasestounityathighfieldstrengthorwhenthefluxdensity,B=H(Fig.I.43).
Thehighpermeabilityofironisduetotheinducedmagneticfieldorientingmicroscopiccrystalregionsactingastinymagnetsintheiron.Allthese
tinymagnetsaddtheirmagneticfieldstotheinducedfield(Fig.I.44).Whenallmicromagnetsarenearlyoriented,theironwillaffecttheflux
densitytoadecreasingamountsincethereorientationofmicromagnetsisnearingcompletion.Thus,thepermeabilityofironathighfieldstrengths
approachesthatofemptyspace.Atthispointtheironreachesmagneticsaturation.
2)Hysteresis
Thestrengthofthelensdependstosomeextentonthepreviousmagnetichistoryof
thelens.Whenthecurrentinalensisreduced,thedecreaseinmagnetizationdoes
notretracethesamepathobtainedwhenthecurrentwasincreased(Fig.I.45).
Inductionofmagnetizationinvolvesaphysicalmovementwithinthemagnetized
material,requiringtheovercomeofacertaindegreeofinertia.Asaresult,
magnetizationtendstolagbehindthemagnetizingforceapplied.Inducedmagnetic
fluxcanonlybereturnedtozerobyapplicationofacurrentintheoppositedirection.
Aconsequenceofhysteresisisthatthelevelofcurrentusedtoenergizeamagnetic
lensDOESNOTpreciselyspecifythelensstrength(i.e.focallength).
NormalizationofTEMlensesisaccomplishedbyreducingthelenscurrenttozero
somepredeterminednumberoftimes.Hysteresismayalsobeminimizedbytakinga
lenstosaturationandthenreturningittotheworkingcurrentwithoutovershooting.
Whenthefieldstrengthisreducedtozero,somemagnetizationstillremainsintheiron
(residualmagnetizationorremanence).Anadvantageofsoftironisthefactthat,
whenusedinanelectromagnet,hysteresisislow.
Introductionofpiecesofironinamagneticfielddrasticallyaffectsthefluxdensity.
Magneticmaterialhasashieldingeffect,theeffectbeinggreaterthegreaterthe
permeability.Permalloy(mmetal)hasamaximumpermeabilityof80,000140,000
comparedtoironusedintransformers(~7000).mmetalpermeabilityislimitedtolower
fieldstrengthsthanthatatwhichironstillretainshighpermeability.Thismetalis
thereforeusefulforshieldingtheTEMfromexternalmagneticfields.
d.Theelectromagneticlens
1)Lensdesigndevelopment(Figs.I.46I.48)
Theefficiencyofthemagneticfieldproducedbyashortsolenoidwasfirstimproved
byencasingtheenergizingcoilinasheathofsoftironwhichhasthepropertyofconcentratingthelinesofforceinamagneticfieldandthus
becomingmagnetizedbyinduction.Inthiswayamuchmorepowerfulaxialmagneticfieldisobtainedforthesameamountofcurrentflowing
throughthesolenoid.Furtherdevelopmentinvolvedencasingtheentirecoilwithsoftironexceptatanarrowannulargapintheinsideofthecoil.
Thisproducesagreaterconcentrationofthemagneticfieldalongashortaxialdistance.Toachieveshorterfocallengthlenses(andobtaingreater
magnifications)asoftironpolepiecewithanopenaxialborewasintroducedatthepositionoftheannulargap.
MagneticlensesusedinTEMsarealwaysconstructedwithanironcircuittoproduceahighfieldstrengthacrossashortgap.Themagneticfields
forTEMlensesareintherangeof10,00020,000gauss.
2)Forcesactingonacurrentinamagneticfield
Theforceonanelectroninamagneticfieldisalwaysatrightanglestothevelocityandthedirectionofthefield(Figs.I.49,I.50,andI.52).The
fieldonlyactsonthevelocitycomponentwhichisdirectedperpendiculartothelinesofforce.Usethelefthandrule(Fig.I.51:firstfingerfor
fielddirection,middlefingerforcurrentdirection,andthumbfordirectionofforce).Rayspassingthroughthelensareturnedthroughanangle
whichdoesNOTdependonthedistanceoftheraysfromtheaxis.Allelectronscontainedinagivenmeridionalplanebeforeenteringthefieldare
containedinarotatingmeridionalplaneastheypassthroughthelens,andthentheyleavethelenscoplanar.
Whenelectronsenterthelenstheyencounterasidewaysforcewhichcausestheelectrontorotate
asitcontinuesthroughthelens(Figs.I.53I.57).Sincetheradialcomponentofthemagneticfield
reversesafterthecenterofthelens,therotationalvelocitysetupinthefirsthalfofthelensis
countered.Theelectronenteredthelenswithoutangularmomentumabouttheaxisandleaves
withoutangularmomentum.Theneteffectisadeflectiontowardtheaxis,whichitmustcrossatthe
focalpointf
2
.Theanglebetweentheobjectvectorandtheimagevectoris180°+q,whereas,for
glasslensesandelectrostaticlenses,theanglebetweenarealobjectandtheimageisexactly180°.
Sincetheradialforceisdirectedtowardtheaxis,thelensisconvergentnomatterwhatthedirection
ofthefield.
3)Propertiesofamagneticlens:
Anyaxiallysymmetricmagneticfieldhasthepropertiesofanideallens.Alltheformulasfortheideallensmaybeapplied.
Magneticlensesarealwaysconvergent.Theconventional,axiallysymmetriclensisalwaysboundedbyregionswhicharefieldfree,the
consequencebeingthatthenetactionofelectronlensesisinevitablyconvergent.Limitedregionsmaybedivergentbutnotthelensasawhole.
Theseriousconsequenceofthisisthatneithersphericalorchromaticaberrationscanbecorrectedasisdoneinlightopticsbytheusedoublets
ofpositiveandnegativelenses.
Intheabsenceofelectrostaticfields,therefractiveindexisthesameinobjectandimagespace,thereforef
1
=f
2
.
Electronstravelingthroughaxiallysymmetricfieldsexperienceaspiraltrajectoryofdiminishingradius.Theimagevectorisatanangle180°+qto
theobjectvector.
Thedeflectionoftheelectrontowardstheaxismeansthatanelectronenteringthelensparalleltoitsaxiswillcrosstheaxisafterhavingpassed
thelens.Thedeflectionwillincreasewiththedistancefromtheaxis.Thus,abeamofelectronsinparallelpathsparalleltotheaxisofthelenswill
befocusedtoanimagepointontheaxiswhichrepresentsthesecond(back)focalpointofthelens(f
2
).Notethatmagneticlensesarehighly
inefficientinthatonlyaminorportionofthetotalfieldstrengthisactuallyeffectiveinfocusingtheelectron.
4)Magneticlensfocallength
Inamagneticelectronlensthefocallengthisdeterminedbythefieldstrengthinthelensgapandbythespeedoftheelectrons(determinedby
theacceleratingvoltage).
Formagneticlenses,focusingisachievedbyvaryingthecurrentwhichpassesthroughtheelectromagnet.Thisinturnchangesthestrengthof
themagneticfieldandtherebyaltersthefocallengthofthelensandisequivalenttoacombinedchangeinboththe"refractiveindex"and
"curvatureofsurface".Forabeamofmoreenergeticelectrons,thelenscurrenthastobeincreasedinordertokeepthefocallengthconstant.
FocallengthandcurrentareNOTlinearlyrelated:strengthincreasesinasigmoidfashion(Fig.I.45)ascurrentincreasesuntilapointisreached
wherethelensissaturatedandnofurtherincreaseinlensstrengthcanbeachieved.
Sincethefocallengthofthelensisdirectlyproportionaltotheacceleratingvoltage,avariationinthevelocityoftheelectronsintheimaging
beamaffectsimagequalitybyeliminatingperfectfocus(chromaticaberration).
5)Magneticlensdesign:(Figs.I.46,I.47).
Condenserlensesusuallyhavearelativelylargeboreandspacingwhichresultsinalongfieldandlongfocallength.
Typicalconstructionoftheobjectivelensproducesastrongfieldofshortaxialextent(i.e.shortfocallengthbetween(1.53mm)necessaryfor
formationofimagesathighmagnification.Thespecimenisplacedwithinthemagneticfieldoftheobjectivelens.Thus,anyfieldintroducedby
contaminantsinthespecimencandistortthefieldofthelens.Notethatthisalsomeansthatpartofthelensfield("prefield")isonthefrontside
oftheobjectandaffectstheelectronbeambeforeitpassesthroughtheobject.
Mostofatypicalmagneticlensliesoutsidethevacuumofthemicroscope.Onlythoseregionsthroughwhichtheelectronbeampassesareinhigh
vacuum.Magneticlensesmustbewatercooledtodissipatethelargeamountsofheatproducedbythecurrentsintheelectromagnetcoils.
DATE NAME EVENT
1897 J.J.Thompson Discoverstheelectron
1924 LouisdeBroglie Identifiesawavelengthtomovingelectrons
l =h/mv
where
l =wavelength
h=Planck'sconstant
m=mass
v=velocity
(Foranelectronat60kVl=0.005nm)
1926 H.Busch Magneticorelectricfieldsactaslensesforelectrons
1929 E.Ruska Ph.Dthesisonmagneticlenses
1931 Knoll&Ruska Firstelectronmicroscopebuilt
1931 Davisson&Calbrick Propertiesofelectrostaticlenses
1934 Driest&Muller SurpassresolutionoftheLM
1938 vonBorries&Ruska FirstpracticalEM(Siemens)10nmresolution
1940 RCA CommercialEMwith2.4nmresolution
1945 1.0nmresolution
Fig.I.1Comparisonoflightandelectronmicroscopes.Ineach
instrument,illuminationfromthesource(lamp,filamentinthe
electrongun)isfocusedbythecondenserlensontothespecimen.
Afirstmagnifiedimageisformedbytheobjectivelens.Thisimage
isfurthermagnifiedbytheprojectorlensontoagroundglass
screen(light)orfluorescentscreen(electrons).(FromAgar,p.8)
Fig.I.2CrosssectionalviewofthePhilipsEM300.(FromAgar,p.40)
Toviewtheanimatedmicroscope,clickhere.
Note:QuickTimePlugInrequired
(Thiscanbedownloadedathttp://apple.com/quicktime/download)
Fig.I.3Sectionthroughacomplex
doublecondenser6lensPhilips
EM200electronmicroscope.(From
Meek,p.99)
Fig.I.4Thestatisticalnatureofdiffraction
patterns.(FromHall,p.13)
"Theprecisenatureof'electronwaves'or'matterwaves'isverydifficulttounderstandordescribeinmaterialterms.Electronwavesarenot
electromagneticradiationofthekindtowhichlight,Xraysandradiowavesbelong.Theyconstituteasortofquantumor'packet'ofradiationwhich
accompanieseachindividualelectron,followingitspathandnotradiatingoutwardsfromit."(Meek,1976,pp.4849).
V l (nm)
v(
•
10
10
cm/sec)
v/c
10,000 0.0123 0.593 0.198
50,000 0.0055 1.326 0.442
100,000 0.0039 1.875 0.625
1,000,000 0.0012 5.930 1.977!
V l (nm)
v(
•
10
10
cm/sec)
v/c
10,000 0.0123 0.593 0.195
50,000 0.0055 1.326 0.414
100,000 0.0039 1.875 0.548
1,000,000 0.0012 5.930 0.941
FigI.5Aperfectpointsourcecannotbe
imagedbyalensasaperfectpointimagedue
tothepresenceoftheapertureAB(which
maybetheedgeofthelens).Diffractionat
thisaperturegivesrisetoaseriesoffringes,
whichsurroundtheimageformedofthepoint
source.Thepatternproducediscalledan'Airy'
disk.(FromMeek1sted.,p.35)
Fig.I.6Wheneverawavefrontstrikesa
barrier,itcanbendaroundthecorner'by
givingrisetoasecondarywavefrontatthe
edge,sinceeachpointonthewavefrontcan
giverisetoanewsourceofwaves.This
phenomenoniscalled'diffraction'.(FromMeek
1sted.,p.22)
Fig.I.7Diffractionpattern(right)formedbyanirregularlyshapedaperture
(left).(FromYoung,p.95)
Fig.I.8(a)
Photographof
theedgeofa
razorblade
illuminatedby
monochromatic
(blue)light
rendered
coherentby
passing
througha
narrowslit.(b)
Microdensitometer
tracingofthe
negativefrom
whichthe
photograph
wasmade.
FourFresnel
fringescanbe
distinguished.
(FromMeek1st
ed.,p.27)
(a)
(b)
(a) (c)
(b)
Fig.I.9(a)Fresnelfringesformed
byelectrons.Thesefringesare
formedoutsidetheedgeofahole
(white)inacarbonfilm(black).(b)
Amicrodensitometertracingofthe
fringesystem;thepatternis
identicalwiththeFresnelfringe
systemformedbyvisiblelight(see
Fig.I.8).(c)Anunderfocusedimage
ofaholeinafilm,showinga
completesystemofabout40
Fresnelfringesinsidethehole.
(FromMeek1sted.,pp.2930)
Fig.I.10Diffractionimagesoftwo
easilyresolvedpoints.(From
Slayter,p.243)
Fig.I.11Imagesoftwo
incoherentlyilluminatedpointsat
thelimitofresolution.(a)individual
intensities;(b)summedintensities.
(FromSlayter,p.244)
Fig.I.12Examplesofwhatoccurswhentwo
wavesofthesamewavelengthandequal
amplitudeadd.Ineachexample,thetwo
separatewavesareshownontheleftand
theirsumorresultantwaveontheright.The
differentexamplesarecharacterizedbyvarying
phasedifferences.Thephaseofawave
(usuallyexpressedasafractionofthe
wavelengthorindegrees)isthepositionofa
crestrelativetosomearbitrarypoint.Although
thephaseofagivenwavevarieswithtimeas
thewavetravels,thedifferenceinphaseofthe
twowavesofthesamewavelengthwiththe
samevelocity,isindependentoftime.Such
wavescaninterferewithoneanother.The
resultantwavehasthesamewavelength,l .
(a)Phasedifferencezero.Thewavestotally
reinforceandaresaidtobe"inphase"orto
showconstructiveinterference.
(b)Phasedifferencel /4.Partialreinforcement,
givingawaveofamplitude1.4(intensity2.0).
(c)Phasedifferencel /2.Thewavesare"outof
phase"andthereistotaldestructive
interferencetogivenoresultantwaveora
wavewithamplitude0(intensity0).(From
GluskerandTrueblood,p.19)
Fig.I.13Photographofan
interferencepatterninwater
wavesformedbythe
superpositionofwavesfromtwo
sourcesoscillatinginphasewith
thesamefrequency.(FromYoung,
p.22)
Fig.I.14Theangularapertureofthe
eyeisrelativelysmall.(FromMeek,
1sted.,p.13)
Fig.I.15Increasingtheangular
apertureoftheeyewithalens.The
lensallowstheobjecttobeheld
closertotheeye,whichisthereby
enabledtogathermoreinformation.
(FromMeek1sted.,p.14)
Fig.I.16Theinteractionofwaves
withanobstacle.Theboatridesthe
longwavelengthoceanwave,but
reflectsthesmallwavelength
surfaceripple.Anobserverwho
wishestodetectthepresenceof
theboatcandosoonlyby
observingwaveswhichhave
wavelengthssmallerthan,or
comparableto,thelengthofthe
boat.(FromSherwood,p.19)
Maximummagnification=
resolvingpoweroftheeye
resolvingpowerofthemicroscope
(a)
Fig.I.17(a)TwoAiry
disksrepresenting
twoimagepoints
shownatincreasing
separationfromleft
toright.Inthe
pictureatthe
extremerightthe
twodiskscanbe
distinguishedas
separatedisks.
(b)Theintensity
distributionatanAiry
disk.R,halfwidthof
thecentralmaximum
representedbya
bellshapedcurve.
(c)TheRayleigh
criteriaforresolution.
(FromSjostrand,
p.115)
i=r
Fig.I.18Reflection.(FromSlayter,
p.4)
Fig.I.19Refraction.(FromSlayter,
p.6)
Fig.I.20Principalraydiagramsshowing
imageformationbyaconvexlens.
(a)Whentheobjectdistanceisgreater
thanthefocallength,areal,inverted
imageisformed.
(b)Whentheobjectdistanceisless
thanthefocallength,avirtual,erect
imageisformed;itspositionis
obtainedbyprojectingtheprincipal
raysbackward.Theraysappearto
comefrompointQ.(FromYoung,
p.127)
Fig.I.21Definitionof
principalfocus,F,inimage
spaceofalens.(From
Sjostrand,p.20)
Fig.I.22Focusingeffectoflenson
raysoriginatingfrompointson
principalaxislocatedatdifferent
distancesfromthelens.(From
Sjostrand,p.21)
Fig.I.23Definitionofprincipal
focusinobjectspaceF1ofa
lens.(FromSjostrand,p.21)
Fig.I.24VirtualimageQof
objectpointlocatedbetween
principalfocusinobjectspace
andthelens.(FromSjostrand,
p.21)
Fig.I.25Constructionoftheimage
ofanobjectbymeansofray
tracing.(FromSjostrand,p.22)
Fig.I.26Magnifyingeffectof
apositivelens.(From
Sjostrand,p.22)
Fig.I.27Virtualmagnified
imageofobjectlocated
betweenprincipalfocusin
objectspaceandthelens.
(FromSjostrand,p.22)
Fig.I.28Amagnifyingglassformsan
enlarged,erectvirtualimage.The
angularsizeofthisimageis
approximately4"/15"or4/15.The
angularsizeoftheobjectatthe
closestdistanceforcomfortable
viewingis1"/10"or1/10.The
magnificationinthissituationis(4/15)/
(1/10),or22/3.(FromYoung,p.130)
Fig.I.29Theangularapertureofa
lens.Theangle2a isthe
acceptanceangleofthelens,and
thelargeritcanbemade,themore
informationcanthelenstransmit.A
largelensofhighaperturecan
thereforetellusmoreaboutan
objectthanasmalllensoflow
power.(FromMeek1sted.,p.12)
Fig.I.30Raydiagramforhighmagnification
modeofoperation.Notethateachlens
formsarealimage,withimageinversion.
I0istheimageformedbytheobjective
lensO,I1isformedbythefirstprojector
lensP1andI2bythesecondprojectorP2,
onthescreen.(FromAgar,p.30)
Fig.I.31Left:raydiagramofthe3realimagemediumandhighmagnificationimagingsystemofa3lens
microscope.Center:2realimageverylowor'scan'magnificationrangeofa3lensmicroscope.Right:2real
imagelowmagnificationsystemofa3lensmicroscope.(FromMeek1sted.,pp.118,120121)
Fig.I.32Raydiagramforacompleteelectron
microscope.FilamentF,condenser1lensC1,
condenser2lensC2,condenserapertureCA,
specimenS,objectivelensO,objectiveaperture
OA(inbackfocalplane).1stintermediateimage
andselectorapertureSA.IntermediatelensP1,
secondintermediateimageI2,projectorlensP2
andfinalimageonthefluorescentscreenFC.
(FromAgar,p.35)
a)f=2.0
x
o
=5.0
e)f=4.0
x
o
=3.0
b)f=10.5
x
o
=21.0
f)f=13.3
x
o
=13.3
c)f=3.5
x
o
=3.0
g)f=3.142
x
o
=0.0
d)f=5.0
x
o
=2.5
a)D=8.0
L1:f=2.0
x
o
=4.0
L2:f=3.0
b)D=8.0
L1:f=2.0
x
o
=6.0
L2:f=3.0
c)D=4.0
L1:f=2.0
x
o
=3.0
L2:f=2.0
FigI.33Accelerationofelectronin
electricfield.(FromSjostrand,p.26)
Fig.I.34Linesofforceatapositively
chargedsphericalbody.(FromSjostrand,
p.32)
Fig.I.35Linesofforceandequipotential
surfaces(stippledlines)associatedwith
twoequalchargesofoppositesign.
(FromSjostrand,p.32)
Fig.I.36Equipotentialsurfacesattwoparallel
platesofoppositechargeswiththepathofan
electronindicatedwithinthehomogeneous
partofthefield.(FromSjostrand,p.33)
Fig.I.37Refractionofelectronatan
equipotentialsurface.(FromSjostrand,p.33)
Fig.I.38.Negativelensactionof
electrostaticfieldatanaperturewhen
V2V1>V3V2.(FromSjostrand,
p.34)
Fig.I.39.Positivelensactionatan
aperturewhenV2V1<V3V2.
(FromSjostrand,p.34)
Fig.I.40Magneticfieldinducedbycurrent
passingthroughaconductor.(From
Sjostrand,p.35)
Fig.I.41Magneticfieldinducedbycurrent
passingthroughasolenoid.(From
Sjostrand,p.37)
Fig.I.42Solenoidwithironcore.(From
Sjostrand,p.40)
Fig.I.43a.Dependenceofpermeabilityonfluxdensity,B.
b.RelationshipbetweenfluxdensityBandfieldstrength.
(FromSjostrand,p.38).
Fig.I.44Magnetization.(FromSlayter,
p.361)
Fig.I.45Curves
showinghowthe
magnetizationof
softiron(lens
strength)is
relatedtothe
magnetizing
force(lens
current).An
unmagnetized
lensstartsfrom
thepointOand
followsthepath
OAaslens
current
increases.Atthe
pointA,further
increaseinlens
currentproduces
nofurther
increaseinlens
strength;thelensissaidtobe'saturated'.Whenlenscurrent
isreduced,thepathOAisnotretraced;adifferentpathABis
followed.Thisdisplacementiscalled'hysteresis'.Atzero
current(pointB),someresiduallensstrengthremains;thisis
called'remanence'.Tobringthelensbacktozerostrength,a
reversecurrentOCmustbeapplied.Lensstrengththen
increaseswithincreasingreversecurrent,followingthepath
CD.Thepolarityofthelenschanges,butthisdoesnotaffect
itsfocusingpower;onlythespiralelectronpathisreversed.
Becauseofhysteresis,itisnotpossibletocalibratealens
currentmeteraccuratelyintermsoflensstrengthor
magnification.
Fig.I.46Evolutionofmagneticelectron
lenses.(A)Shortsolenoidusedasa
magneticlens.(B)Softironcasing
enclosingoutersurfaceofthesolenoid,
thusconcentratingthefield.(C)Soft
ironencasingthesolenoidexceptata
narrowannulargaptherebyreducing
themagneticfieldtoaveryshortregion
alongthelensaxis.(D)Modern
objectivelensconsistingofasoftiron
encasedsolenoidandsoftironpole
piecessoastohaveanenormously
concentratedfieldatthelevelofthe
annulargap.(FromWischnizter2nded.,
p.33)
Fig.I.47(a)Amagneticlensconsisting
ofatightlywoundcoilandasoftiron
shroudsurroundingthecoilexceptfor
asmallgap.Thefieldisconcentratedin
thatgap.(b)Shortfocallength
electromagneticlenswithpolepieces.
(FromSjostrand,p.50)
Fig.I.48Fieldstrengthdistribution
curves.ThecurvesADcorrespondto
therespectivelensesillustratedinFig.
I.46.Eachrepresentsthefieldstrength
alongthelongaxisofthelens.The
changesintheshapeofthecurves
representtheshorteningor
concentrationofthefieldovera
shorteraxialdistance.Hz=
longitudinalmagneticfield.Z=
distancealongtheaxisofsymmetry.
(FromWischnizter2nded.,p.33)
Fig.I.49TheforceFactingon
astraightconductorina
homogeneousmagneticfield
offluxdensityBwhencurrent
Iispassedthroughthe
conductor.(FromSjostrand,
p.43)
Fig.I.50Pathofanelectronina
magneticfield.(A)Inalarge,uniform
magneticfield.(B)Inasmall,uniform
magneticfield.(FromWischnitzer2nd
ed.,p.25)
Fig.I.51Lefthandthumbrule.
(FromSjostrand,p.43)
Fig.I.52Thompson'sexperiment.A
streamofelectronsoriginatingfroma
sourceandpassing,invacuo,through
amagneticfieldproducedbyapairof
magnetswillbedeflected.The
directionofdeflectiondemonstrates
thatelectronsarenegativelycharged
particlesofmatter.(FromWischnitzer
2nded.,p.25)
Fig.I.53Actionofasolenoidonan
electronbeam.Anelectriccurrent
passingthroughthecoilproducesan
axialmagneticfield.Thisisthe
refractingmediumfortheelectrons.An
electronstartingatapointontheaxisA
andatanangletoitfollowsaspiral
path,returningtotheaxisatthepoint
B.Theactionisbasicallysimilartothat
oftheconverginglightlensshownin
Fig.I.20.(FromMeek1sted.,p.8)
Fig.I.54Actionofthemagnetic
lens.(a)Inperspective.(b)
Electrontrajectoryin
projection,alongdirectionof
propagation.(c)Electron
trajectoryinprojection,side
view.(FromSlayter,p.358)
Fig.I.55Componentsofthe
vectorHneartheaxisoffields
withaxialsymmetry.His
representedbytwo
components,Hz,the
componentinthez(axial)
direction,andHr,the
compnentinther(radial)
direction.(FromHall,p.85)
Fig.I.56Theycomponentof
themagneticfieldina
magneticlensisoriented
perpendiculartothedirection
ofanelectronenteringthe
lensalongapathparallelto
thelensaxis.Thisy
componentwillaffectthe
electron,deflectingitinthex
directionasindicatedbythe
arrowmarkedvx.(From
Sjostrand,p.48)
Fig.I.57Thezcomponentofthemagneticfield
andthexvelocitycomponentoftheelectron
inamagneticlensinteract,deflectingthe
electronintheydirectiontowardthelens
axis.(FromSjostrand,p.49)
CuuDuongThanCong.com https://fb.com/tailieudientucntt
cuu duong than cong . com

I.THEMICROSCOPE
I.A.PRINCIPLESOFTHETRANSMISSIONELECTRONMICROSCOPE(TEM)
I.A.1.OriginoftheTransmissionElectronMicroscope
I.A.2.ComparisonofLight(LM)andElectronMicroscopes(Fig.I.1)
a.Similarities(Arrangementandfunctionofcomponentsaresimilar)
1)Illuminationsystem:producesrequiredradiationanddirectsitontothespecimen.Consistsofasource,whichemitstheradiation,anda
condenserlens,whichfocusestheilluminatingbeam(allowingvariationsofintensitytobemade)onthespecimen.
2)Specimenstage:situatedbetweentheilluminationandimagingsystems.
3)Imagingsystem:Lenseswhichtogetherproducethefinalmagnifiedimageofthespecimen.Consistsofi)anobjectivelenswhichfocusesthe
beamafteritpassesthroughthespecimenandformsanintermediateimageofthespecimenandii)theprojectorlens(es)whichmagnifiesa
portionoftheintermediateimagetoformthefinalimage.
4)Imagerecordingsystem:Convertstheradiationintoapermanentimage(typicallyonaphotographicemulsion)thatcanbeviewed.
b.Differences
1)Opticallensesaregenerallymadeofglasswithfixedfocallengthswhereasmagneticlensesareconstructedwithferromagneticmaterialsand
windingsofcopperwireproducingafocallengthwhichcanbechangedbyvaryingthecurrentthroughthecoil.
2)MagnificationintheLMisgenerallychangedbyswitchingbetweendifferentpowerobjectivelensesmountedonarotatingturretabovethe
specimen.Itcanalsobechangedifoculars(eyepieces)ofdifferentpowerareused.IntheTEMthemagnification(focallength)oftheobjective
remainsfixedwhilethefocallengthoftheprojectorlensischangedtovarymagnification.
3)TheLMhasasmalldepthoffield,thusdifferentfocallevelscanbeseeninthespecimen.Thelarge(relative)depthoffieldintheTEMmeans
thattheentire(thin)specimenisinfocussimultaneously.
4)Mechanismsofimageformationvary(phaseandamplitudecontrast).
5)TEMsaregenerallyconstructedwiththeradiationsourceatthetopoftheinstrument:thesourceisgenerallysituatedatthebottomofLMs.
6)TEMisoperatedathighvacuum(sincethemeanfreepathofelectronsinairisverysmall)somostspecimens(biological)mustbedehydrated
(i.e.dead!!).
7)TEMspecimens(biological)arerapidlydamagedbytheelectronbeam.
8)TEMscanachievehighermagnificationandbetterresolutionthanLMs.
9)Pricetag!!!(100xmorethanLM)
I.A.3.Photons/Electrons
a.Dualconceptofwaveandparticle(Fig.I.4)
Lighthaspropertiesbothofaparticleandawave.Thisdualnatureisrequiredtosatisfactorilyexplaintheresultsofvariousphysicalexperiments.
Thediffractionoflight(bendingaroundcorners)illustratesthewavenature.TheWAVETHEORYisbasedonthestatisticalnatureofeventsand
haslittlemeaningwithrespecttothebehaviorofsingleparticles.ThewavetheorywasdevelopedandexpoundedbyHuygens(16291695)and
Hooke(16381703).TheCORPUSCULARTHEORYwasproposedbyNewton(16421727)andbecamethemoreacceptedtheoryevenafter
demonstrationofdiffractionbyYoung(17731829)andinterferencebyFresnel(17881827).Atabout1850,thewavetheorycamebackinto
favoruntilabout1900whenmoreevidenceforthecorpusculartheorywasdiscovered.
QUANTUMTHEORY(PlanckandEinstein)providesthebasisforexplainingthephenomenaofINTERFERENCE,DIFFRACTIONandthe
PHOTOELECTRICeffect(lightfallingoncertainmetalscausethemtoemitelectrons)andthusformsacommonbasisforexplainingthenatureof
actionoflight.Thetransferofenergybetweenlightandmatteroccursonlyindiscretequantitiesproportionaltothefrequencyofthe
lightwave.
E=hJ
where
E=energyofphoton(joules)
h=Planck'sconstant(6.624
•
10
34
joulesec)
J=frequency(cycles/sec)
b.Electronvelocityandwavelength
Therelationbetweenthewavelength(l )ofaparticleofmass,m,movingatavelocity,v,isgivenbytheDeBrogliewaveequation:
(1)
Anelectronofchargee(1.6
•
10
19
coulomb),andmassm(9.11
•
10
28
gm),whenpassingthroughapotentialdifferenceofVvolts(expressedin
joules/coulomb),hasakineticenergy:
(2)
Solvingforvelocity:
(3)
substitutingintotheDeBroglieequation(1):
(4)
Since1joule=10
7
dyne
•
cm=10
7
cm
2
•
gm/sec
2
(5)
Thus,forexample,ifV=60,000volts,l =0.005nm.
Fromequation(3)theelectronvelocitycanbecalculatedifVisknown:
(6)
Thefollowingtableillustratesthat,athighvoltage,electronvelocityiscomparabletothespeedoflightinavacuum(c=3
•
10
10
cm/sec).
Theequationbreaksdownwhenthevelocityoftheelectronapproachesthespeedoflightbecausearelativisticcorrectionmustbemadeforthe
valueofthemasswhere:
(7)
Therelationbetweenl andVismorecorrectlygivenby:(seeHall(1966)pp.3334)
(8)
Thefollowingtableisobtainedwhenrelativityeffectsareincluded:
c.Interference/diffraction/coherence
Anideallenssystemobtainsanexactimageoftheobject(eachpointfaithfullyreproduced).Thephenomenaofdiffractionmakesthis
unattainable(Figs.I.5,I.6).
Diffractionphenomenainvolvesthebendingofthepathofradiationpassingclosetoanobstacle(Fig.I.6).Thisresultsinaspreadingofthe
radiationintotheregionbehindtheobstructionthatthewavespassed.Thediffractionatedgescontributestothecontrastatwhichanedgecan
beobserved.Diffractionalsolimitstheresolvingpowerofthemicroscopesincetheimagepointproducedbyalensisadiffractionimageofthe
openingofthelensortheaperturerestrictingtheeffectiveopeningofthelens(Fig.I.5).
Ifthelightsourceandtheplaneatwhichthediffractionpatternisobservedareatfinitedistancesfromtheedge,thephenomenoniscalled
Fresneldiffraction.Thepatternisdescribedasduetointerferencebetweenthenondiffractedlightandawaveoflightdiffractedattheedge.
Theresultingsuperpositiongivesrisetoaseriesofdiffractionfringesorientedparalleltotheedgeandrepresentingperiodicallyvaryingbrightness,
maximaandminima.(Figs.I.7,1.8,I.9).
Coherence:Aprerequisiteforinterferenceisasuperpositionofwavesystemswhosephasedifferenceremainsconstantintime.Twobeams
arecoherentif,whencombined,theyproduceaninterferencepattern.Thebeamsareincoherentwhentheyareincapableofproducingan
interferencepattern.Twobeamsoflightfromselfluminoussourcesareincoherent.Iflightfromthetwosourcesfallsonascreen,theresultant
intensityissimplythesumofthetwointensitieswhichwouldoccurfromeachsourceseparately(Figs.I.10,I.11).Inpracticeanemittingsource
hasfiniteextentandeachpointofthesourcecanbeconsideredtogeneratelight.EachsourcegivesrisetoasystemofFresnelfringesatthe
edge.Thesuperpositionofthesefringesystemsisfairlygoodforthefirstmaximaandminimabutfartherawayfromtheedgeshadowtheoverlap
ofthefringepatternsbecomessufficientlyrandomtomakethefringesdisappear.Thenatureofwaves,phase,amplitude,andinterferenceare
illustratedinFigs.I.12andI.13.
d.Resolution
1)Definitions:
RESOLUTION:abilitytodistinguishcloselyspacedpointsasseparatepoints.
RESOLUTIONLIMIT:smallestseparationofpointswhichcanberecognizedasdistinct.
RESOLVINGPOWER:resolutionachievedbyaparticularinstrumentunderoptimumviewingconditions.
2)Distinctionbetweenresolutionandresolvingpower:
Notethedistinctionbetweenresolutionandresolvingpower.Resolvingpowerisapropertyoftheinstrumentandisaquantitythatmaybe
estimatedontheoreticalgrounds.Resolutionisequaltoorpoorerthantheresolvingpowerandisthequantityobservedunderanygivenset
ofexperimentalconditions.IntheTEM,especiallywithbiologicalsamples,theresolutionachievedmaybeconsiderablyinferiortothetheoretical
resolvingpoweroftheinstrument.
Microscopyisthescienceofseeingtheverysmall.Underidealconditions,theeyeresolvesabout1minuteofarc(=1/60degree=2.9x10
4
radian;recallthereare2p radiansin360°)andsinceitcanfocusdowntoabout250mm,thesmallestobjectwecanresolveisabout0.07mm
(70mm)(Fig.I.14).Thislimitisrelatedtothesizeofthereceptorsintheretinaoftheeye.Thefunctionofamicroscopeistomagnifytheimage
fallingontheretina(Fig.I.15).Theadvantageoflightandelectronmicroscopesisthattheyeffectivelygettheobjectclosertotheeyesoa
magnifiedimageisobtainedandmoredetailcanbediscerned.
TENNISBALLANALOGY:Eyecanresolve3cmat100meters,thusatennisballisclearlyvisible.Butifthetennisballisheldupagainstawhite
background,thevisibilitydecreases(becauseofthedecreaseincontrast).
3)Abbecriteriaofresolution:
Thefundamentalnatureoflightposeslimitsonthedetailthatcanberesolved(Fig.I.16).Abbe(1893)showedthatthesmallestresolvable
distanceisabout1/2thewavelengthoflightused.Thus,1/2thewavelengthoftheradiationusedistheultimateresolvingpowerofany
instrument.Thislimitstheusablemagnificationofopticalmicroscopesto<1000X.Atfirstitwasthoughtthatxraymicroscopeswouldbeuseful
buttherefractiveindexofsubstancesforxraysisnearly=1,thusrefractinglensescannotbemadeforxrays,andconsequently,xrayscannot
beeasilyfocusedtoformimages.
4)Magnificationlimits:
Themaximummagnificationofaninstrumentislimitedaccordingtothefollowingrelationship:
Thus,fortheLM,witharesolvingpowerofapproximately0.25µm,themaximum(useful)magnificationisabout250µm/0.25µm=1000X.Thevalue
usedfortheresolvingpoweroftheeyeinthisexample(250µm)representsamorerealisticviewingcondition.Anymagnificationabovethevalue
givenbytheaboveformularepresentsemptymagnification,sincesuchmagnificationleadstonomoreusefulinformationbutratheramagnified
blur.
AccordingtotheAbbecriteria,at60,000volts,theTEMshouldhavearesolvingpowerofabout0.0025nm.Thisshouldallowamaximumuseful
magnificationofabout100milliontimes!!!Inpractice,themaximumusefulmagnificationoftheTEMoperatedat60kVislimitedtomuchlessthan
1,000,000X.Thus,althoughtheLMnearlyobeystheAbbecriteria,theTEMfallsshortbyaconsiderableamount.Themainlimitingfactorinthe
TEM,withrespecttoachievingthetheoreticalresolvingpoweroftheinstrument,concernsthenatureoftheimaginglensesandtheprocessof
imageformation.
5)Rayleighcriteria(practicalbutarbitrary):(Fig.I.17).
Itistheabilityofmicroscopestomakeobjectpointswhichareclosetogetherappearintheimageasseparatepoints.Anideallenstakeseach
objectpointandrepresentsitexactlyasapointintheimage.Areallenstakeseachobjectpointandspreadsitoutintoacirculardisk(Airy
disk)intheimageplanewhosediameterdependsontheangularapertureofthelens.
Theshortestdistancebetween2disksatwhichthetwodisksappearpartiallyseparatedcorrespondstoabout1/2thewidthofthedisks.The
distance,d,inobjectspaceisgivenby:
d=0.61l /n
•
sina
where
l =wavelenghtoftheradiation
n=refractiveindexofthemedia
a=semiangularapertureofthelens
NOTE:n
•
sina=thenumericalaperture(N.A.)ofthelens.
Thus,tomaximizeresolvingpower,l mustbedecreased,nincreased,oraincreased.Recallthatweareconcernedatthemomentwithan
aberrationfreeopticalsystem.Thevaluefortheconstant(0.61)iscontroversialbecauseitdependsonthecoherenceoftheradiationanda
criteriaofvisibility.
FortheLM,usingoilimmersionoptics(n=1.5),sina=0.87,andvioletlight(l =400nm),d=0.2µm.Theonlywaytoimprovetheresolutionisto
uselightofshorterwavelengthsinceN.A.cannotbeincreasedbeyond~1.5.FortheTEM,n=1(vacuum),sina=10
2
andl =0.005nmfor60kV
electrons,thusd=0.3nm.
I.A.4.Optics(LensTheory)
a.Basiclawsofclassicalgeometricaloptics
1)Rectilinearpropagationoflightwhenn(refractiveindex)isconstant.
2)Lawofreflection:
3)Lawofrefraction(Snell'sLaw):
4)Independenceofrays.Theassumptionismadethatlightraystravelindependentlythroughspace.
Theselawsholdforelectrons,except#4,ifthecurrentdensityistoohighwhennegativechargedelectronscaninterfere.
b.Classicalvs.electronoptics
1)Classicaloptics:Therefractiveindexchangesabruptlyatasurfaceandisconstantbetweenthesurfaces.Therefractionoflightatsurfaces
separatingmediaofdifferentrefractiveindicesmakesitpossibletoconstructimaginglenses.Glasssurfacescanbeshaped.
2)Electronoptics:Here,changesintherefractiveindexaregradualsoraysarecontinuouscurvesratherthanbrokenstraightlines.Refraction
ofelectronsmustbeaccomplishedbyfieldsinspacearoundchargedelectrodesorsolenoids,andthesefieldscanassumeonlycertaindistributions
consistentwithfieldtheory.
c.Geometricalandphysicaloptics
Thefundamentalprinciplesofopticsgovernthedesignandoperationofboththelightandelectronmicroscopes.Thebasicopticalprinciples
involvingtheuseofrefractileelementsorlensesinordertoformmagnifiedimagesareidenticalinboththeLMandTEM.TheTEMdiffersfromthe
LMonlyintheradiationitusesandinthewayinwhichtheradiationisbentorrefracted.
Geometricalopticsdealswiththestudyofthepathsfollowedby'rays'oflightorelectronsthroughlensesandapertures,andthegeometrical
constructionsusedtofindtherelativepositionsandsizesofobjectsandtheirimages.Arayoflightorelectronsisdefinedasaninfinitelythin
pencilorbeam.Physicalopticsshowsthatthisanabstractionandcannotphysicallyexistbecauseof'diffraction'whichdealswiththewave
natureoflightandelectrons.Allresultsobtainedingeometricalopticscanbederivedfromtheprinciplesofphysicaloptics,alongwithother
phenomenasuchasinterferenceanddiffractionwhicharenotexplicableinsimplegeometricalterms.
d.Idealversesreallenses:
Lensesareusedtobendraysoflightorelectronssotheyaredeflectedinapredictablewayfromtheiroriginalpaths.Thepropertiesofanideal
lens,possessinganaxisofrotationalsymmetryare:
1)Eachrayofthebundleofrayswhichpassesfromanobjectpointwillberefractedbytheideallenstomeetinoneimagepoint.
2)Raysoriginatingfrompointswhichlieonaplaneperpendiculartotheaxis,mustbeimagedinaplanewhichisalsoperpendiculartotheaxis.
3)Theimageappearsliketheobjectirrespectiveofthemagnification,sotherelativelineardimensionsoftheobjectarepreservedintheimage.
Inpractice,theimagingbyanyreallensdoesnotcorrespondtothatoftheideallensowingtothefactthatanobjectpointisrepresentedbya
diffractionimage(Airydisc)ofthelensopeningortheapertureusedforrestrictingtheeffectiveopeningofthelens.Thisisaresultofthewave
likepropertiesoflight.Lensaberrationsalsocontributetomoreorlesspronounceddeviationsfromthepropertiesoftheideallens.
Thesinglerefractingsurfaceofsphericalcurvatureisthefundamentalunitoffocusingactionbyglasslenses.Sphericalrefractingsurfacesactas
lensesforparaxialrayswhicharethoseraysthatpassclosetotheprincipalaxisofthelens.RayswithlargeangleswillNOTobeyideallens
action.
Afundamentaldifferencebetweenlightandmagneticlensesisthattheelectronbeamdoesnotchangeinforwardvelocityasitpassesthrough
themagneticfield(lightraysslowdownwhenpassingintoamediumofhigherrefractiveindex).Refractioniscontinuouswithelectronswhenthey
areinthemagneticfield:lightisrefractedonlyattheinterfacebetweenmediaofdifferingrefractiveindex.Theelectronsalsofollowspiral
trajectoriesthroughthemagneticfield(seealsoSec.I.A.5.c(Magneticfieldsandmagneticlenses)
e.Raydiagrams:(Figs.I.20I.28)
Themethodofconstructionofraydiagramsisbasedonthreesimpleprinciples:
1)Allraysenteringthelensparalleltotheaxisarebroughttoacommonpointontheaxis,thefocalpoint.
2)Allrayspassingthroughthegeometricalcenterofthelensareundeviatedandpassstraighton,nomatterfromwhichdirectiontheycome.
3)Principleofreversibility:ifthedirectionofarayisreversedinanysystemtherayexactlyretracesitspaththroughthesystem.Thisapplies
onlytothelocationoflightpathsandnottotheintensityofthelight.
Theaboveprinciplesarebasedontheassumptionsthatwearedealingwithathinlensandconcernedwiththepathsofparaxialrays.The
standardconventionistodrawdiagramswithraysthattravelfromlefttoright.Theobjectistotheleft(infront)ofthelensandtheimageisto
theright(behind)ofthelens.
f.Definitions:
Realimage:oneatwhichlightraysphysicallyreunite,sothataphotographicplateplacedatthepositionofarealimageisexposed.
VirtualImage:onefromwhichlightraysappeartodiverge;raysarenotinfactconcentratedatthepositionofavirtualimage,sothata
photographicplateplacedatthepositionoftheimageisnotexposed(byfocusedrays).Placinganopticalsystemsuchastheeyebehindthe
lens,willenablethedivergentraystobefocusedtoformarealimage.TheintermediatelensofanTEMissometimesusedthiswayinorderto
reducethefinalsizeoftherealimageformedbytheprojectorlens(es).
Converging(positive)lens:bendsraystowardtheaxis.Ithasapositivefocallength.Formsarealinvertedimageofanobjectplacedtothe
leftofthefirstfocalpointandanerectvirtualimageofanobjectplacedbetweenthefirstfocalpointandthelens.
Diverging(negative)lens:bendsthelightraysawayfromtheaxis.Ithasanegativefocallength.Anobjectplacedanywheretotheleftofa
diverginglensresultsinanerectvirtualimage.Itisnotpossibletoconstructanegativemagneticlensalthoughnegativeelectrostaticlensescan
bemade.
g.Lensformula(thinlensequation):
where
f=focallengthofthethinlens(sameradiusofcurvatureforboth
sphericalsurfaces)
o=distanceofobjectfromlens(positivetotheleft)
i=distanceofimagefromthelens(positivetotheright)
NOTE:Foravirtualimage,ihasanegativevalue.
h.Magnification:
Foraconverginglens,iftheobjectismorethantwicethefocallengthfromthelens,thentheimageformedisreal,inverted,andsmallerinsize
thantheobject(M<1).Whentheobjectisatadistance=2f,theimageandobjectarethesamesize(M=1);whenitisbetweenfand2f,
theimageislargerthantheobject(M>1),andwhenitis<f,theimageisvirtual,erect,andlargerthantheobject(M>1).
i.Angularapertureofthelens(2a)(Fig.I.29)
Theaperturedeterminesthetotalamountofradiationarrivingfromtheobjectwhichcanbefocusedto
formanimage.Theaperturethuscontrolstheabilityofthelenstogatherinformationabouttheobject.
Thisdependsontheangleoftheconeofraysitisabletoacceptfromtheobject.Bringinganobject
closertotheeyeincreasestheangularaperture,butthereisalimittotheclosenessthattheobjectcan
bebroughttotheeye(~25cmcorrespondingtoanangleofabout0.9°fora4mmexitpupildiameterof
theeyelens;atypicalLMwithanoilimmersionobjectivelenshas2aof~175°).
j.Simplevs.compoundmicroscope(Figs.I.30I.32)
Inprinciple,arealimageofanydesiredmagnificationcanbeobtainedfromasinglepositivelens,butin
practicethisiscumbersomebecauseofthelonglensimagedistance.Oneormorelensescanbeusedto
magnifytheimageinstages(totalmagnificationequalingtheproductofthemagnificationsofeachlens).
Theimageformedbyonelensconstitutestheobjectforthesubsequentlens,whetherornotareal
intermediateimageisformed.
Comparisonofoneversestwostagemagnification:
Thefollowingdescriptionillustrateshowdifferentpathlengthsarerequiredtoachieveamagnificationof10,000Xusingeitheroneortwolenses
withf=2.0cm.
OneStageSystem:
TwoStageSystem:
Assumebothlenseshavef=2.0cmandarearrangedsoeachgives100Xmagnification.
Thus,M=100=x
i
/x
o
foreachstage.
FirstStage:
x
o
=2.02cm
x
i
=202.00cm
Therealimageformedinthefirststagebecomestheobjectforthesecondlens.
SecondStage:x
o
,x
i
sameasinthefirststage.
Totallengthofsystem
=lengthoffirststage+lengthofsecondstage
=(x
o
+x
i
)+(x
o
+x
i
)
=2(x
o
+x
i
)
=2(2.02+202.00)=408.04cm(4.08meters)
k.Problemset
Thefollowingproblemsareforyourownedificationtotesthowwellyouunderstandthebasicsoflensoptics.
1.Foreachsituationbelow,drawanaccurate(usegraphpaper)raydiagramshowingthepathof(atleasttwo)raysfromtheobjecttoimage.
Indicatewhethertheimageisrealorvirtualandspecifythedistanceoftheimagefromthelensandthemagnificationoftheimagewithrespect
totheobject.Ineachexample,thelensisconverging,withidenticalfrontandbackfocalpoints.Distancesareinarbitraryunits.Letf=lens
focallength,x
o
=distanceofobjectinfrontofthelens,andx
i
=distanceofimagebehindthelens.Theobjectmaybeanysize.
2.Inthefollowingexamples,therearetwoconverginglensesinsuccession.Drawraydiagramsshowingtheformationofboththeintermediate
andfinalimagesandgiveappropriateinformationaboutthenature(real/virtual),positions,andsizesoftheintermediateandfinalimages.What
isthemagnificationateachstageofimageformationandwhatisthemagnificationofthefinalimage?Thedistancefromthecenteroflens1(L1)
tothecenteroflens2(L2)equalsD.
I.A.5.ElectronOptics/ElectronLenses
a.Electronemission
Innershellelectronsinmetalatomsshieldtheelectricfieldofthenucleusthroughtherepulsiveforcestheyexertontheoutershell(valence)
electrons.Thustheattractionbetweenthevalenceelectronsandthenucleusisreduced.Metalatomsarecharacterizedashavingtwoloosely
boundvalenceelectronswhichmigratefreely(thisiswhymetalsaregoodelectricalconductors)andcanescapefromthemetalcompletelyif
sufficientadditionalenergyisimpartedtothem.Asthetemperatureofametalisincreased,thekineticenergyoftheelectronsincreasesbecause
ofincreasedthermalvibrationsofthemetalions,whichcollidemorefrequentlywiththeelectrons.Thermionicemissionisthetermusedto
describetheprocessbywhichthermalenergyissuppliedtolooselyboundelectronsinordertoformasourceofelectrons.
Atroomtemperatureelectronsareeffectivelypreventedfromescapingthesurfaceofthemetalowingtotheattractiveforceofthepositively
chargedions.Asthetemperatureisincreasedsomeelectronsacquiresufficientenergytoovercometheattractionandleavethemetal
temporarily.Metal,shapedasathinwire,caneasilybeheatedbypassinganelectriccurrentthroughit.Sincethemetalsurfacebecomes
positivelycharged,acertainlevelofenergy(workfunction)mustbesuppliedtoallowelectronstoescapefromthesurface.Eachmetalhasa
characteristicworkfunction.Tungsten,withalowworkfunction,emitsmoreelectronsthanmetalswithhigherworkfunctions(seealsopp.2930
andFig.I.59).
Ifastrongelectrostaticfieldisappliedinavacuumbetweenthewire(givenanegative,cathode,potential)andananode,theelectricfieldwill
causeelectronstoaccelerateawayfromthewiretowardstheanodesurface(Fig.I.33).Thespeedoftheelectronsdependsonthestrengthof
theelectrostaticfield(voltage)betweenthecathodeandanode(equation(3),Sec.I.A.3.b)Thenumberofelectronswhichleavethewire
dependsonthetemperaturetowhichthewireisheated,whichdependsonhowmuchfilamentcurrentpassesthroughthewire.
A"V"shapedwirewillhavethehighesttemperatureatthetip.Electronswithdrawnfromthefilamenttipcarryelectricchargestotheanode.This
electriccurrent,whichflowsbetweenthefilamentandtheanode,iscalledthebeamcurrent.
1)Electricfield/Equipotentials
Anelectricallychargedobjecthasassociatedwithitanelectricfield.Thus,anelectricallychargedparticle,whenbroughtnearachargedobject,
isinfluencedbyanelectricalforceinthevicinityoftheobject.Theforceisdirectedtowardthechargedobjectifthechargesareofopposite
signsandawayfromtheobjectiftheyareofsimilarsign.DEFINITION:Thedirectionofanelectricfieldisdefinedasthedirectionoftheforce
actingonapositivecharge.(Figs.I.3435)
Alongthelinesofforceconnectingthetwocharges,theelectricpotentialwillchangegraduallybetweentheextremevaluesrepresentedbythe
twocharges.DEFINITION:Equipotentiallinesdefinethepointsalongthelinesofforcewithidenticalelectricalpotential.Theseequipotential
surfacesarealwaysorientedperpendiculartothelinesofforce.Thechangesintheelectricpotentialaregradualinspace.
Electronswhichenterafieldbetweentwoparallelplatesinadirectionparalleltotheplatesareaffectedbytheforcedirectedperpendicularto
theplates(FigI.36).Theelectronswillbeattractedtowardthepositiveplate.Thepathchangesinaseriesofgradualstepsattheequipotential
surfaces.
FigureI.37showshowtheelectronpathis"refracted"attheequipotentialsurface.TheresultisfundamentallythesameasthatgivenbySnell's
Lawofrefractioninlightoptics.Aconsequenceofthisisthatasphericallycurvedequipotentialsurfaceexhibitsthepropertiesofalens.
FiguresI.38andI.39showhowbothpositive(converging)andnegative(diverging)electrostaticlensescanbeformed.Thisfeatureof
electrostaticlensesdiffersfromelectromagneticlenseswhichcanonlyactasconverginglenses.
2)Advantages/Disadvantagesofelectronlenses:
Thefactthattherefractiveindexdoesnotchangeabruptlyinelectronlenseshasoneadvantageinthattherearenotroublesomereflectionsat
equipotentialsasatglassinterfaces.Thereisaseriousdisadvantageinthatequipotentialscannotbeshapedandcombinedinarbitraryfashionto
correctforchromaticaberrationandothererrors.
Althoughelectronmicroscopeswhichemployelectrostaticlenseshavebeenmade,mostmicroscopesuseelectromagneticlenses.Amajorreason
isthatelectrostaticlensesaremoresensitivetothequalityofthevacuumandcleanlinessofthecomponentsthanareelectromagneticlenses.
Somelensaberrationsaremoresevereforelectrostaticlensescomparedtoelectromagneticlenses.Electrostaticlensesrequireverypowerful
electrostaticfieldswhichcanleadtoelectricalbreakdownor"arcingover"insidethecolumn,especiallyunderpoorvacuumconditions.Forthis
reason,electrostaticlensescannotbemadewithfocallengthsasshortasmagneticlenses.
b.Electrostaticlens
Abasicunderstandingofelectrostaticlensesisimportantfortwomainreasons:i)theelectrongunuseselectrostaticlensactiontoformthe
primarybeamsource,andii)itisquitecommonforachargetodeveloponthenonconductingcontaminationwhichmayaccumulateonphysical
apertures(suchastheobjectiveaperture)andtransformthemintoweakelectrostaticlenseswhichcandistorttheelectronimage.
3)Propertiesofelectrostaticlenses:
a)Anyaxiallysymmetricalelectrostaticfieldhasthepropertiesofalensforraysconfinedtotheparaxialregion.Alltheideallensformulasapply
toelectrostaticlenses.
b)Forelectronlenses,replaceÃ(f)forrefractiveindexinthelensequations(f=valueofthepotentialontheaxis).Intheimageformingsystem
ofmostTEMs,fisthesameonbothsidesofthelens(SeeSec.I.A.5.c).
c)Ifboundedbyregionswherefisconstant,anelectrostaticlensisalwaysconvergent.
c.Magneticfieldsandmagneticlenses
1)Magneticfield
Anelectriccurrentpassingthroughaconductorgivesrisetoamagneticfield.TheconventionisthatNisthedirectioninwhichthelinesofthe
magneticfieldpoint(Fig.I.40).Themagneticfluxisthetotalnumberoflinesandthefluxdensityisthenumberoflinesperunitareaofasurface.
UsetheRIGHThandruletodeterminethedirectionofthefield(thumbpointstowardcurrentdirectionandfingerscurlindirectionoffield.NOTE:
Byconvention,thedirectionofelectronflowisoppositetothatofcurrentflow.
Fluxdensitydependsonthepropertiesofthematerialsurroundingtheconductor.Ironinducesahigherfluxdensitythanairoravacuum.The
propertyofthematerialwhichaffectsthefluxdensityiscalledthepermeability,m,ofthematerial.Forairandvacuum,m=1.0.For
ferromagneticmaterialsitcanbeaslargeasseveralhundredthousand.
Iftheconductorhastheshapeofacircularloop,thelinesofforceformcirclesaroundtheloop.Thefluxdensityisgreatestatthecenterofthe
loop.Themagnetinthecenteroftheloopisorientedperpendiculartotheplaneoftheloopifthecurrentthroughtheloopissufficientlystrongto
eliminatetheinfluenceoftheearth'sfield.ThesideoftheloopatwhichthelinesofforceleavetheloopistheNorth(N)poleofthemagnet(Figs.
I.41,I.42).
Ifthewireiswoundinseveralturnsaroundacylindricalsurface(solenoid),eachturnwillcontributetotheinducedmagneticfield.Theflux
densityinthecenterofthecoilisgivenby:
Inthecaseofairandnonmagneticmaterials,µ=1.0andB=H.
Thepermeabilityofirondependsonthefieldstrength,H,anddecreasestounityathighfieldstrengthorwhenthefluxdensity,B=H(Fig.I.43).
Thehighpermeabilityofironisduetotheinducedmagneticfieldorientingmicroscopiccrystalregionsactingastinymagnetsintheiron.Allthese
tinymagnetsaddtheirmagneticfieldstotheinducedfield(Fig.I.44).Whenallmicromagnetsarenearlyoriented,theironwillaffecttheflux
densitytoadecreasingamountsincethereorientationofmicromagnetsisnearingcompletion.Thus,thepermeabilityofironathighfieldstrengths
approachesthatofemptyspace.Atthispointtheironreachesmagneticsaturation.
2)Hysteresis
Thestrengthofthelensdependstosomeextentonthepreviousmagnetichistoryof
thelens.Whenthecurrentinalensisreduced,thedecreaseinmagnetizationdoes
notretracethesamepathobtainedwhenthecurrentwasincreased(Fig.I.45).
Inductionofmagnetizationinvolvesaphysicalmovementwithinthemagnetized
material,requiringtheovercomeofacertaindegreeofinertia.Asaresult,
magnetizationtendstolagbehindthemagnetizingforceapplied.Inducedmagnetic
fluxcanonlybereturnedtozerobyapplicationofacurrentintheoppositedirection.
Aconsequenceofhysteresisisthatthelevelofcurrentusedtoenergizeamagnetic
lensDOESNOTpreciselyspecifythelensstrength(i.e.focallength).
NormalizationofTEMlensesisaccomplishedbyreducingthelenscurrenttozero
somepredeterminednumberoftimes.Hysteresismayalsobeminimizedbytakinga
lenstosaturationandthenreturningittotheworkingcurrentwithoutovershooting.
Whenthefieldstrengthisreducedtozero,somemagnetizationstillremainsintheiron
(residualmagnetizationorremanence).Anadvantageofsoftironisthefactthat,
whenusedinanelectromagnet,hysteresisislow.
Introductionofpiecesofironinamagneticfielddrasticallyaffectsthefluxdensity.
Magneticmaterialhasashieldingeffect,theeffectbeinggreaterthegreaterthe
permeability.Permalloy(mmetal)hasamaximumpermeabilityof80,000140,000
comparedtoironusedintransformers(~7000).mmetalpermeabilityislimitedtolower
fieldstrengthsthanthatatwhichironstillretainshighpermeability.Thismetalis
thereforeusefulforshieldingtheTEMfromexternalmagneticfields.
d.Theelectromagneticlens
1)Lensdesigndevelopment(Figs.I.46I.48)
Theefficiencyofthemagneticfieldproducedbyashortsolenoidwasfirstimproved
byencasingtheenergizingcoilinasheathofsoftironwhichhasthepropertyofconcentratingthelinesofforceinamagneticfieldandthus
becomingmagnetizedbyinduction.Inthiswayamuchmorepowerfulaxialmagneticfieldisobtainedforthesameamountofcurrentflowing
throughthesolenoid.Furtherdevelopmentinvolvedencasingtheentirecoilwithsoftironexceptatanarrowannulargapintheinsideofthecoil.
Thisproducesagreaterconcentrationofthemagneticfieldalongashortaxialdistance.Toachieveshorterfocallengthlenses(andobtaingreater
magnifications)asoftironpolepiecewithanopenaxialborewasintroducedatthepositionoftheannulargap.
MagneticlensesusedinTEMsarealwaysconstructedwithanironcircuittoproduceahighfieldstrengthacrossashortgap.Themagneticfields
forTEMlensesareintherangeof10,00020,000gauss.
2)Forcesactingonacurrentinamagneticfield
Theforceonanelectroninamagneticfieldisalwaysatrightanglestothevelocityandthedirectionofthefield(Figs.I.49,I.50,andI.52).The
fieldonlyactsonthevelocitycomponentwhichisdirectedperpendiculartothelinesofforce.Usethelefthandrule(Fig.I.51:firstfingerfor
fielddirection,middlefingerforcurrentdirection,andthumbfordirectionofforce).Rayspassingthroughthelensareturnedthroughanangle
whichdoesNOTdependonthedistanceoftheraysfromtheaxis.Allelectronscontainedinagivenmeridionalplanebeforeenteringthefieldare
containedinarotatingmeridionalplaneastheypassthroughthelens,andthentheyleavethelenscoplanar.
Whenelectronsenterthelenstheyencounterasidewaysforcewhichcausestheelectrontorotate
asitcontinuesthroughthelens(Figs.I.53I.57).Sincetheradialcomponentofthemagneticfield
reversesafterthecenterofthelens,therotationalvelocitysetupinthefirsthalfofthelensis
countered.Theelectronenteredthelenswithoutangularmomentumabouttheaxisandleaves
withoutangularmomentum.Theneteffectisadeflectiontowardtheaxis,whichitmustcrossatthe
focalpointf
2
.Theanglebetweentheobjectvectorandtheimagevectoris180°+q,whereas,for
glasslensesandelectrostaticlenses,theanglebetweenarealobjectandtheimageisexactly180°.
Sincetheradialforceisdirectedtowardtheaxis,thelensisconvergentnomatterwhatthedirection
ofthefield.
3)Propertiesofamagneticlens:
Anyaxiallysymmetricmagneticfieldhasthepropertiesofanideallens.Alltheformulasfortheideallensmaybeapplied.
Magneticlensesarealwaysconvergent.Theconventional,axiallysymmetriclensisalwaysboundedbyregionswhicharefieldfree,the
consequencebeingthatthenetactionofelectronlensesisinevitablyconvergent.Limitedregionsmaybedivergentbutnotthelensasawhole.
Theseriousconsequenceofthisisthatneithersphericalorchromaticaberrationscanbecorrectedasisdoneinlightopticsbytheusedoublets
ofpositiveandnegativelenses.
Intheabsenceofelectrostaticfields,therefractiveindexisthesameinobjectandimagespace,thereforef
1
=f
2
.
Electronstravelingthroughaxiallysymmetricfieldsexperienceaspiraltrajectoryofdiminishingradius.Theimagevectorisatanangle180°+qto
theobjectvector.
Thedeflectionoftheelectrontowardstheaxismeansthatanelectronenteringthelensparalleltoitsaxiswillcrosstheaxisafterhavingpassed
thelens.Thedeflectionwillincreasewiththedistancefromtheaxis.Thus,abeamofelectronsinparallelpathsparalleltotheaxisofthelenswill
befocusedtoanimagepointontheaxiswhichrepresentsthesecond(back)focalpointofthelens(f
2
).Notethatmagneticlensesarehighly
inefficientinthatonlyaminorportionofthetotalfieldstrengthisactuallyeffectiveinfocusingtheelectron.
4)Magneticlensfocallength
Inamagneticelectronlensthefocallengthisdeterminedbythefieldstrengthinthelensgapandbythespeedoftheelectrons(determinedby
theacceleratingvoltage).
Formagneticlenses,focusingisachievedbyvaryingthecurrentwhichpassesthroughtheelectromagnet.Thisinturnchangesthestrengthof
themagneticfieldandtherebyaltersthefocallengthofthelensandisequivalenttoacombinedchangeinboththe"refractiveindex"and
"curvatureofsurface".Forabeamofmoreenergeticelectrons,thelenscurrenthastobeincreasedinordertokeepthefocallengthconstant.
FocallengthandcurrentareNOTlinearlyrelated:strengthincreasesinasigmoidfashion(Fig.I.45)ascurrentincreasesuntilapointisreached
wherethelensissaturatedandnofurtherincreaseinlensstrengthcanbeachieved.
Sincethefocallengthofthelensisdirectlyproportionaltotheacceleratingvoltage,avariationinthevelocityoftheelectronsintheimaging
beamaffectsimagequalitybyeliminatingperfectfocus(chromaticaberration).
5)Magneticlensdesign:(Figs.I.46,I.47).
Condenserlensesusuallyhavearelativelylargeboreandspacingwhichresultsinalongfieldandlongfocallength.
Typicalconstructionoftheobjectivelensproducesastrongfieldofshortaxialextent(i.e.shortfocallengthbetween(1.53mm)necessaryfor
formationofimagesathighmagnification.Thespecimenisplacedwithinthemagneticfieldoftheobjectivelens.Thus,anyfieldintroducedby
contaminantsinthespecimencandistortthefieldofthelens.Notethatthisalsomeansthatpartofthelensfield("prefield")isonthefrontside
oftheobjectandaffectstheelectronbeambeforeitpassesthroughtheobject.
Mostofatypicalmagneticlensliesoutsidethevacuumofthemicroscope.Onlythoseregionsthroughwhichtheelectronbeampassesareinhigh
vacuum.Magneticlensesmustbewatercooledtodissipatethelargeamountsofheatproducedbythecurrentsintheelectromagnetcoils.
DATE NAME EVENT
1897 J.J.Thompson Discoverstheelectron
1924 LouisdeBroglie Identifiesawavelengthtomovingelectrons
l =h/mv
where
l =wavelength
h=Planck'sconstant
m=mass
v=velocity
(Foranelectronat60kVl=0.005nm)
1926 H.Busch Magneticorelectricfieldsactaslensesforelectrons
1929 E.Ruska Ph.Dthesisonmagneticlenses
1931 Knoll&Ruska Firstelectronmicroscopebuilt
1931 Davisson&Calbrick Propertiesofelectrostaticlenses
1934 Driest&Muller SurpassresolutionoftheLM
1938 vonBorries&Ruska FirstpracticalEM(Siemens)10nmresolution
1940 RCA CommercialEMwith2.4nmresolution
1945 1.0nmresolution
Fig.I.1Comparisonoflightandelectronmicroscopes.Ineach
instrument,illuminationfromthesource(lamp,filamentinthe
electrongun)isfocusedbythecondenserlensontothespecimen.
Afirstmagnifiedimageisformedbytheobjectivelens.Thisimage
isfurthermagnifiedbytheprojectorlensontoagroundglass
screen(light)orfluorescentscreen(electrons).(FromAgar,p.8)
Fig.I.2CrosssectionalviewofthePhilipsEM300.(FromAgar,p.40)
Toviewtheanimatedmicroscope,clickhere.
Note:QuickTimePlugInrequired
(Thiscanbedownloadedathttp://apple.com/quicktime/download)
Fig.I.3Sectionthroughacomplex
doublecondenser6lensPhilips
EM200electronmicroscope.(From
Meek,p.99)
Fig.I.4Thestatisticalnatureofdiffraction
patterns.(FromHall,p.13)
"Theprecisenatureof'electronwaves'or'matterwaves'isverydifficulttounderstandordescribeinmaterialterms.Electronwavesarenot
electromagneticradiationofthekindtowhichlight,Xraysandradiowavesbelong.Theyconstituteasortofquantumor'packet'ofradiationwhich
accompanieseachindividualelectron,followingitspathandnotradiatingoutwardsfromit."(Meek,1976,pp.4849).
V l (nm)
v(
•
10
10
cm/sec)
v/c
10,000 0.0123 0.593 0.198
50,000 0.0055 1.326 0.442
100,000 0.0039 1.875 0.625
1,000,000 0.0012 5.930 1.977!
V l (nm)
v(
•
10
10
cm/sec)
v/c
10,000 0.0123 0.593 0.195
50,000 0.0055 1.326 0.414
100,000 0.0039 1.875 0.548
1,000,000 0.0012 5.930 0.941
FigI.5Aperfectpointsourcecannotbe
imagedbyalensasaperfectpointimagedue
tothepresenceoftheapertureAB(which
maybetheedgeofthelens).Diffractionat
thisaperturegivesrisetoaseriesoffringes,
whichsurroundtheimageformedofthepoint
source.Thepatternproducediscalledan'Airy'
disk.(FromMeek1sted.,p.35)
Fig.I.6Wheneverawavefrontstrikesa
barrier,itcanbendaroundthecorner'by
givingrisetoasecondarywavefrontatthe
edge,sinceeachpointonthewavefrontcan
giverisetoanewsourceofwaves.This
phenomenoniscalled'diffraction'.(FromMeek
1sted.,p.22)
Fig.I.7Diffractionpattern(right)formedbyanirregularlyshapedaperture
(left).(FromYoung,p.95)
Fig.I.8(a)
Photographof
theedgeofa
razorblade
illuminatedby
monochromatic
(blue)light
rendered
coherentby
passing
througha
narrowslit.(b)
Microdensitometer
tracingofthe
negativefrom
whichthe
photograph
wasmade.
FourFresnel
fringescanbe
distinguished.
(FromMeek1st
ed.,p.27)
(a)
(b)
(a) (c)
(b)
Fig.I.9(a)Fresnelfringesformed
byelectrons.Thesefringesare
formedoutsidetheedgeofahole
(white)inacarbonfilm(black).(b)
Amicrodensitometertracingofthe
fringesystem;thepatternis
identicalwiththeFresnelfringe
systemformedbyvisiblelight(see
Fig.I.8).(c)Anunderfocusedimage
ofaholeinafilm,showinga
completesystemofabout40
Fresnelfringesinsidethehole.
(FromMeek1sted.,pp.2930)
Fig.I.10Diffractionimagesoftwo
easilyresolvedpoints.(From
Slayter,p.243)
Fig.I.11Imagesoftwo
incoherentlyilluminatedpointsat
thelimitofresolution.(a)individual
intensities;(b)summedintensities.
(FromSlayter,p.244)
Fig.I.12Examplesofwhatoccurswhentwo
wavesofthesamewavelengthandequal
amplitudeadd.Ineachexample,thetwo
separatewavesareshownontheleftand
theirsumorresultantwaveontheright.The
differentexamplesarecharacterizedbyvarying
phasedifferences.Thephaseofawave
(usuallyexpressedasafractionofthe
wavelengthorindegrees)isthepositionofa
crestrelativetosomearbitrarypoint.Although
thephaseofagivenwavevarieswithtimeas
thewavetravels,thedifferenceinphaseofthe
twowavesofthesamewavelengthwiththe
samevelocity,isindependentoftime.Such
wavescaninterferewithoneanother.The
resultantwavehasthesamewavelength,l .
(a)Phasedifferencezero.Thewavestotally
reinforceandaresaidtobe"inphase"orto
showconstructiveinterference.
(b)Phasedifferencel /4.Partialreinforcement,
givingawaveofamplitude1.4(intensity2.0).
(c)Phasedifferencel /2.Thewavesare"outof
phase"andthereistotaldestructive
interferencetogivenoresultantwaveora
wavewithamplitude0(intensity0).(From
GluskerandTrueblood,p.19)
Fig.I.13Photographofan
interferencepatterninwater
wavesformedbythe
superpositionofwavesfromtwo
sourcesoscillatinginphasewith
thesamefrequency.(FromYoung,
p.22)
Fig.I.14Theangularapertureofthe
eyeisrelativelysmall.(FromMeek,
1sted.,p.13)
Fig.I.15Increasingtheangular
apertureoftheeyewithalens.The
lensallowstheobjecttobeheld
closertotheeye,whichisthereby
enabledtogathermoreinformation.
(FromMeek1sted.,p.14)
Fig.I.16Theinteractionofwaves
withanobstacle.Theboatridesthe
longwavelengthoceanwave,but
reflectsthesmallwavelength
surfaceripple.Anobserverwho
wishestodetectthepresenceof
theboatcandosoonlyby
observingwaveswhichhave
wavelengthssmallerthan,or
comparableto,thelengthofthe
boat.(FromSherwood,p.19)
Maximummagnification=
resolvingpoweroftheeye
resolvingpowerofthemicroscope
(a)
Fig.I.17(a)TwoAiry
disksrepresenting
twoimagepoints
shownatincreasing
separationfromleft
toright.Inthe
pictureatthe
extremerightthe
twodiskscanbe
distinguishedas
separatedisks.
(b)Theintensity
distributionatanAiry
disk.R,halfwidthof
thecentralmaximum
representedbya
bellshapedcurve.
(c)TheRayleigh
criteriaforresolution.
(FromSjostrand,
p.115)
i=r
Fig.I.18Reflection.(FromSlayter,
p.4)
Fig.I.19Refraction.(FromSlayter,
p.6)
Fig.I.20Principalraydiagramsshowing
imageformationbyaconvexlens.
(a)Whentheobjectdistanceisgreater
thanthefocallength,areal,inverted
imageisformed.
(b)Whentheobjectdistanceisless
thanthefocallength,avirtual,erect
imageisformed;itspositionis
obtainedbyprojectingtheprincipal
raysbackward.Theraysappearto
comefrompointQ.(FromYoung,
p.127)
Fig.I.21Definitionof
principalfocus,F,inimage
spaceofalens.(From
Sjostrand,p.20)
Fig.I.22Focusingeffectoflenson
raysoriginatingfrompointson
principalaxislocatedatdifferent
distancesfromthelens.(From
Sjostrand,p.21)
Fig.I.23Definitionofprincipal
focusinobjectspaceF1ofa
lens.(FromSjostrand,p.21)
Fig.I.24VirtualimageQof
objectpointlocatedbetween
principalfocusinobjectspace
andthelens.(FromSjostrand,
p.21)
Fig.I.25Constructionoftheimage
ofanobjectbymeansofray
tracing.(FromSjostrand,p.22)
Fig.I.26Magnifyingeffectof
apositivelens.(From
Sjostrand,p.22)
Fig.I.27Virtualmagnified
imageofobjectlocated
betweenprincipalfocusin
objectspaceandthelens.
(FromSjostrand,p.22)
Fig.I.28Amagnifyingglassformsan
enlarged,erectvirtualimage.The
angularsizeofthisimageis
approximately4"/15"or4/15.The
angularsizeoftheobjectatthe
closestdistanceforcomfortable
viewingis1"/10"or1/10.The
magnificationinthissituationis(4/15)/
(1/10),or22/3.(FromYoung,p.130)
Fig.I.29Theangularapertureofa
lens.Theangle2a isthe
acceptanceangleofthelens,and
thelargeritcanbemade,themore
informationcanthelenstransmit.A
largelensofhighaperturecan
thereforetellusmoreaboutan
objectthanasmalllensoflow
power.(FromMeek1sted.,p.12)
Fig.I.30Raydiagramforhighmagnification
modeofoperation.Notethateachlens
formsarealimage,withimageinversion.
I0istheimageformedbytheobjective
lensO,I1isformedbythefirstprojector
lensP1andI2bythesecondprojectorP2,
onthescreen.(FromAgar,p.30)
Fig.I.31Left:raydiagramofthe3realimagemediumandhighmagnificationimagingsystemofa3lens
microscope.Center:2realimageverylowor'scan'magnificationrangeofa3lensmicroscope.Right:2real
imagelowmagnificationsystemofa3lensmicroscope.(FromMeek1sted.,pp.118,120121)
Fig.I.32Raydiagramforacompleteelectron
microscope.FilamentF,condenser1lensC1,
condenser2lensC2,condenserapertureCA,
specimenS,objectivelensO,objectiveaperture
OA(inbackfocalplane).1stintermediateimage
andselectorapertureSA.IntermediatelensP1,
secondintermediateimageI2,projectorlensP2
andfinalimageonthefluorescentscreenFC.
(FromAgar,p.35)
a)f=2.0
x
o
=5.0
e)f=4.0
x
o
=3.0
b)f=10.5
x
o
=21.0
f)f=13.3
x
o
=13.3
c)f=3.5
x
o
=3.0
g)f=3.142
x
o
=0.0
d)f=5.0
x
o
=2.5
a)D=8.0
L1:f=2.0
x
o
=4.0
L2:f=3.0
b)D=8.0
L1:f=2.0
x
o
=6.0
L2:f=3.0
c)D=4.0
L1:f=2.0
x
o
=3.0
L2:f=2.0
FigI.33Accelerationofelectronin
electricfield.(FromSjostrand,p.26)
Fig.I.34Linesofforceatapositively
chargedsphericalbody.(FromSjostrand,
p.32)
Fig.I.35Linesofforceandequipotential
surfaces(stippledlines)associatedwith
twoequalchargesofoppositesign.
(FromSjostrand,p.32)
Fig.I.36Equipotentialsurfacesattwoparallel
platesofoppositechargeswiththepathofan
electronindicatedwithinthehomogeneous
partofthefield.(FromSjostrand,p.33)
Fig.I.37Refractionofelectronatan
equipotentialsurface.(FromSjostrand,p.33)
Fig.I.38.Negativelensactionof
electrostaticfieldatanaperturewhen
V2V1>V3V2.(FromSjostrand,
p.34)
Fig.I.39.Positivelensactionatan
aperturewhenV2V1<V3V2.
(FromSjostrand,p.34)
Fig.I.40Magneticfieldinducedbycurrent
passingthroughaconductor.(From
Sjostrand,p.35)
Fig.I.41Magneticfieldinducedbycurrent
passingthroughasolenoid.(From
Sjostrand,p.37)
Fig.I.42Solenoidwithironcore.(From
Sjostrand,p.40)
Fig.I.43a.Dependenceofpermeabilityonfluxdensity,B.
b.RelationshipbetweenfluxdensityBandfieldstrength.
(FromSjostrand,p.38).
Fig.I.44Magnetization.(FromSlayter,
p.361)
Fig.I.45Curves
showinghowthe
magnetizationof
softiron(lens
strength)is
relatedtothe
magnetizing
force(lens
current).An
unmagnetized
lensstartsfrom
thepointOand
followsthepath
OAaslens
current
increases.Atthe
pointA,further
increaseinlens
currentproduces
nofurther
increaseinlens
strength;thelensissaidtobe'saturated'.Whenlenscurrent
isreduced,thepathOAisnotretraced;adifferentpathABis
followed.Thisdisplacementiscalled'hysteresis'.Atzero
current(pointB),someresiduallensstrengthremains;thisis
called'remanence'.Tobringthelensbacktozerostrength,a
reversecurrentOCmustbeapplied.Lensstrengththen
increaseswithincreasingreversecurrent,followingthepath
CD.Thepolarityofthelenschanges,butthisdoesnotaffect
itsfocusingpower;onlythespiralelectronpathisreversed.
Becauseofhysteresis,itisnotpossibletocalibratealens
currentmeteraccuratelyintermsoflensstrengthor
magnification.
Fig.I.46Evolutionofmagneticelectron
lenses.(A)Shortsolenoidusedasa
magneticlens.(B)Softironcasing
enclosingoutersurfaceofthesolenoid,
thusconcentratingthefield.(C)Soft
ironencasingthesolenoidexceptata
narrowannulargaptherebyreducing
themagneticfieldtoaveryshortregion
alongthelensaxis.(D)Modern
objectivelensconsistingofasoftiron
encasedsolenoidandsoftironpole
piecessoastohaveanenormously
concentratedfieldatthelevelofthe
annulargap.(FromWischnizter2nded.,
p.33)
Fig.I.47(a)Amagneticlensconsisting
ofatightlywoundcoilandasoftiron
shroudsurroundingthecoilexceptfor
asmallgap.Thefieldisconcentratedin
thatgap.(b)Shortfocallength
electromagneticlenswithpolepieces.
(FromSjostrand,p.50)
Fig.I.48Fieldstrengthdistribution
curves.ThecurvesADcorrespondto
therespectivelensesillustratedinFig.
I.46.Eachrepresentsthefieldstrength
alongthelongaxisofthelens.The
changesintheshapeofthecurves
representtheshorteningor
concentrationofthefieldovera
shorteraxialdistance.Hz=
longitudinalmagneticfield.Z=
distancealongtheaxisofsymmetry.
(FromWischnizter2nded.,p.33)
Fig.I.49TheforceFactingon
astraightconductorina
homogeneousmagneticfield
offluxdensityBwhencurrent
Iispassedthroughthe
conductor.(FromSjostrand,
p.43)
Fig.I.50Pathofanelectronina
magneticfield.(A)Inalarge,uniform
magneticfield.(B)Inasmall,uniform
magneticfield.(FromWischnitzer2nd
ed.,p.25)
Fig.I.51Lefthandthumbrule.
(FromSjostrand,p.43)
Fig.I.52Thompson'sexperiment.A
streamofelectronsoriginatingfroma
sourceandpassing,invacuo,through
amagneticfieldproducedbyapairof
magnetswillbedeflected.The
directionofdeflectiondemonstrates
thatelectronsarenegativelycharged
particlesofmatter.(FromWischnitzer
2nded.,p.25)
Fig.I.53Actionofasolenoidonan
electronbeam.Anelectriccurrent
passingthroughthecoilproducesan
axialmagneticfield.Thisisthe
refractingmediumfortheelectrons.An
electronstartingatapointontheaxisA
andatanangletoitfollowsaspiral
path,returningtotheaxisatthepoint
B.Theactionisbasicallysimilartothat
oftheconverginglightlensshownin
Fig.I.20.(FromMeek1sted.,p.8)
Fig.I.54Actionofthemagnetic
lens.(a)Inperspective.(b)
Electrontrajectoryin
projection,alongdirectionof
propagation.(c)Electron
trajectoryinprojection,side
view.(FromSlayter,p.358)
Fig.I.55Componentsofthe
vectorHneartheaxisoffields
withaxialsymmetry.His
representedbytwo
components,Hz,the
componentinthez(axial)
direction,andHr,the
compnentinther(radial)
direction.(FromHall,p.85)
Fig.I.56Theycomponentof
themagneticfieldina
magneticlensisoriented
perpendiculartothedirection
ofanelectronenteringthe
lensalongapathparallelto
thelensaxis.Thisy
componentwillaffectthe
electron,deflectingitinthex
directionasindicatedbythe
arrowmarkedvx.(From
Sjostrand,p.48)
Fig.I.57Thezcomponentofthemagneticfield
andthexvelocitycomponentoftheelectron
inamagneticlensinteract,deflectingthe
electronintheydirectiontowardthelens
axis.(FromSjostrand,p.49)
CuuDuongThanCong.com https://fb.com/tailieudientucntt
cuu duong than cong . com
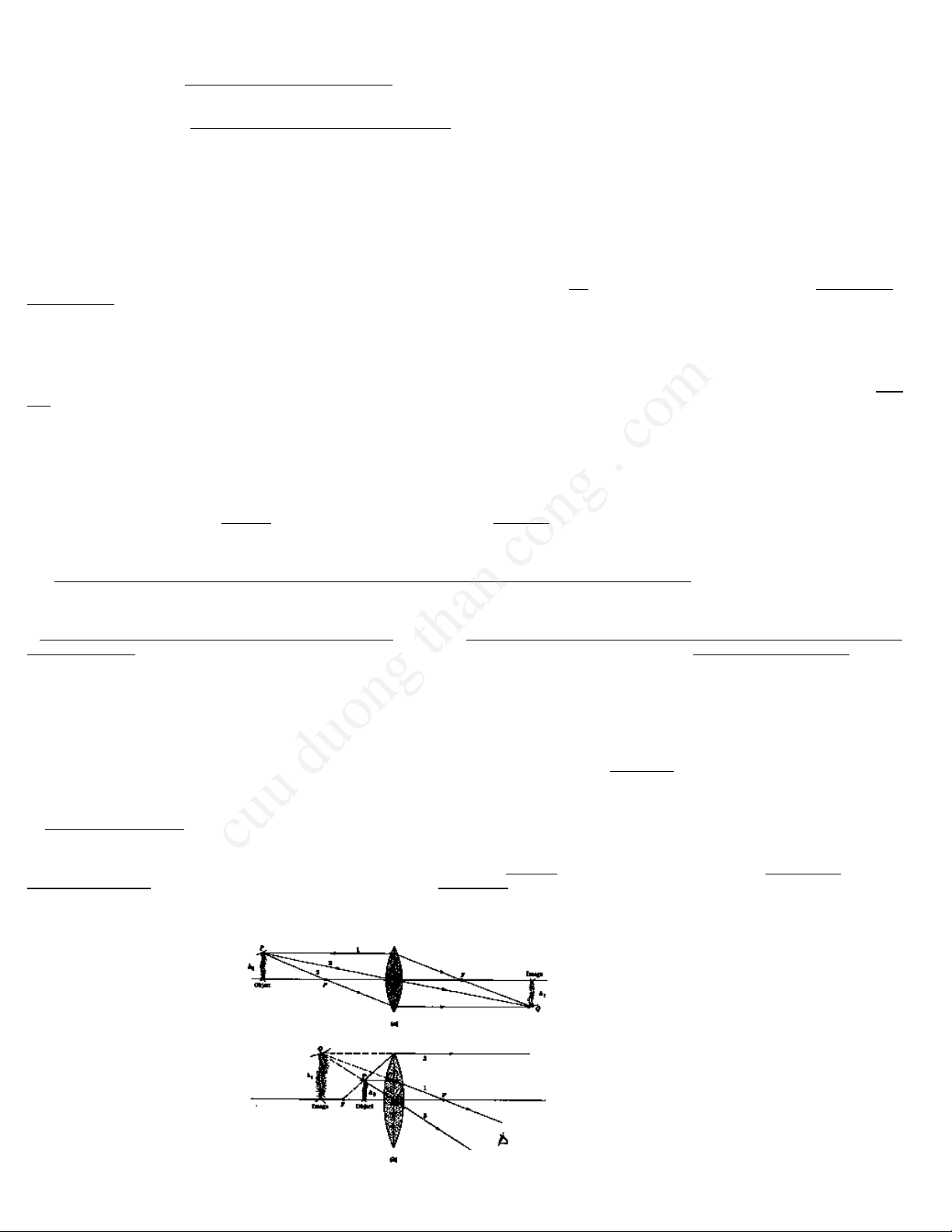
I.THEMICROSCOPE
I.A.PRINCIPLESOFTHETRANSMISSIONELECTRONMICROSCOPE(TEM)
I.A.1.OriginoftheTransmissionElectronMicroscope
I.A.2.ComparisonofLight(LM)andElectronMicroscopes(Fig.I.1)
a.Similarities(Arrangementandfunctionofcomponentsaresimilar)
1)Illuminationsystem:producesrequiredradiationanddirectsitontothespecimen.Consistsofasource,whichemitstheradiation,anda
condenserlens,whichfocusestheilluminatingbeam(allowingvariationsofintensitytobemade)onthespecimen.
2)Specimenstage:situatedbetweentheilluminationandimagingsystems.
3)Imagingsystem:Lenseswhichtogetherproducethefinalmagnifiedimageofthespecimen.Consistsofi)anobjectivelenswhichfocusesthe
beamafteritpassesthroughthespecimenandformsanintermediateimageofthespecimenandii)theprojectorlens(es)whichmagnifiesa
portionoftheintermediateimagetoformthefinalimage.
4)Imagerecordingsystem:Convertstheradiationintoapermanentimage(typicallyonaphotographicemulsion)thatcanbeviewed.
b.Differences
1)Opticallensesaregenerallymadeofglasswithfixedfocallengthswhereasmagneticlensesareconstructedwithferromagneticmaterialsand
windingsofcopperwireproducingafocallengthwhichcanbechangedbyvaryingthecurrentthroughthecoil.
2)MagnificationintheLMisgenerallychangedbyswitchingbetweendifferentpowerobjectivelensesmountedonarotatingturretabovethe
specimen.Itcanalsobechangedifoculars(eyepieces)ofdifferentpowerareused.IntheTEMthemagnification(focallength)oftheobjective
remainsfixedwhilethefocallengthoftheprojectorlensischangedtovarymagnification.
3)TheLMhasasmalldepthoffield,thusdifferentfocallevelscanbeseeninthespecimen.Thelarge(relative)depthoffieldintheTEMmeans
thattheentire(thin)specimenisinfocussimultaneously.
4)Mechanismsofimageformationvary(phaseandamplitudecontrast).
5)TEMsaregenerallyconstructedwiththeradiationsourceatthetopoftheinstrument:thesourceisgenerallysituatedatthebottomofLMs.
6)TEMisoperatedathighvacuum(sincethemeanfreepathofelectronsinairisverysmall)somostspecimens(biological)mustbedehydrated
(i.e.dead!!).
7)TEMspecimens(biological)arerapidlydamagedbytheelectronbeam.
8)TEMscanachievehighermagnificationandbetterresolutionthanLMs.
9)Pricetag!!!(100xmorethanLM)
I.A.3.Photons/Electrons
a.Dualconceptofwaveandparticle(Fig.I.4)
Lighthaspropertiesbothofaparticleandawave.Thisdualnatureisrequiredtosatisfactorilyexplaintheresultsofvariousphysicalexperiments.
Thediffractionoflight(bendingaroundcorners)illustratesthewavenature.TheWAVETHEORYisbasedonthestatisticalnatureofeventsand
haslittlemeaningwithrespecttothebehaviorofsingleparticles.ThewavetheorywasdevelopedandexpoundedbyHuygens(16291695)and
Hooke(16381703).TheCORPUSCULARTHEORYwasproposedbyNewton(16421727)andbecamethemoreacceptedtheoryevenafter
demonstrationofdiffractionbyYoung(17731829)andinterferencebyFresnel(17881827).Atabout1850,thewavetheorycamebackinto
favoruntilabout1900whenmoreevidenceforthecorpusculartheorywasdiscovered.
QUANTUMTHEORY(PlanckandEinstein)providesthebasisforexplainingthephenomenaofINTERFERENCE,DIFFRACTIONandthe
PHOTOELECTRICeffect(lightfallingoncertainmetalscausethemtoemitelectrons)andthusformsacommonbasisforexplainingthenatureof
actionoflight.Thetransferofenergybetweenlightandmatteroccursonlyindiscretequantitiesproportionaltothefrequencyofthe
lightwave.
E=hJ
where
E=energyofphoton(joules)
h=Planck'sconstant(6.624
•
10
34
joulesec)
J=frequency(cycles/sec)
b.Electronvelocityandwavelength
Therelationbetweenthewavelength(l )ofaparticleofmass,m,movingatavelocity,v,isgivenbytheDeBrogliewaveequation:
(1)
Anelectronofchargee(1.6
•
10
19
coulomb),andmassm(9.11
•
10
28
gm),whenpassingthroughapotentialdifferenceofVvolts(expressedin
joules/coulomb),hasakineticenergy:
(2)
Solvingforvelocity:
(3)
substitutingintotheDeBroglieequation(1):
(4)
Since1joule=10
7
dyne
•
cm=10
7
cm
2
•
gm/sec
2
(5)
Thus,forexample,ifV=60,000volts,l =0.005nm.
Fromequation(3)theelectronvelocitycanbecalculatedifVisknown:
(6)
Thefollowingtableillustratesthat,athighvoltage,electronvelocityiscomparabletothespeedoflightinavacuum(c=3
•
10
10
cm/sec).
Theequationbreaksdownwhenthevelocityoftheelectronapproachesthespeedoflightbecausearelativisticcorrectionmustbemadeforthe
valueofthemasswhere:
(7)
Therelationbetweenl andVismorecorrectlygivenby:(seeHall(1966)pp.3334)
(8)
Thefollowingtableisobtainedwhenrelativityeffectsareincluded:
c.Interference/diffraction/coherence
Anideallenssystemobtainsanexactimageoftheobject(eachpointfaithfullyreproduced).Thephenomenaofdiffractionmakesthis
unattainable(Figs.I.5,I.6).
Diffractionphenomenainvolvesthebendingofthepathofradiationpassingclosetoanobstacle(Fig.I.6).Thisresultsinaspreadingofthe
radiationintotheregionbehindtheobstructionthatthewavespassed.Thediffractionatedgescontributestothecontrastatwhichanedgecan
beobserved.Diffractionalsolimitstheresolvingpowerofthemicroscopesincetheimagepointproducedbyalensisadiffractionimageofthe
openingofthelensortheaperturerestrictingtheeffectiveopeningofthelens(Fig.I.5).
Ifthelightsourceandtheplaneatwhichthediffractionpatternisobservedareatfinitedistancesfromtheedge,thephenomenoniscalled
Fresneldiffraction.Thepatternisdescribedasduetointerferencebetweenthenondiffractedlightandawaveoflightdiffractedattheedge.
Theresultingsuperpositiongivesrisetoaseriesofdiffractionfringesorientedparalleltotheedgeandrepresentingperiodicallyvaryingbrightness,
maximaandminima.(Figs.I.7,1.8,I.9).
Coherence:Aprerequisiteforinterferenceisasuperpositionofwavesystemswhosephasedifferenceremainsconstantintime.Twobeams
arecoherentif,whencombined,theyproduceaninterferencepattern.Thebeamsareincoherentwhentheyareincapableofproducingan
interferencepattern.Twobeamsoflightfromselfluminoussourcesareincoherent.Iflightfromthetwosourcesfallsonascreen,theresultant
intensityissimplythesumofthetwointensitieswhichwouldoccurfromeachsourceseparately(Figs.I.10,I.11).Inpracticeanemittingsource
hasfiniteextentandeachpointofthesourcecanbeconsideredtogeneratelight.EachsourcegivesrisetoasystemofFresnelfringesatthe
edge.Thesuperpositionofthesefringesystemsisfairlygoodforthefirstmaximaandminimabutfartherawayfromtheedgeshadowtheoverlap
ofthefringepatternsbecomessufficientlyrandomtomakethefringesdisappear.Thenatureofwaves,phase,amplitude,andinterferenceare
illustratedinFigs.I.12andI.13.
d.Resolution
1)Definitions:
RESOLUTION:abilitytodistinguishcloselyspacedpointsasseparatepoints.
RESOLUTIONLIMIT:smallestseparationofpointswhichcanberecognizedasdistinct.
RESOLVINGPOWER:resolutionachievedbyaparticularinstrumentunderoptimumviewingconditions.
2)Distinctionbetweenresolutionandresolvingpower:
Notethedistinctionbetweenresolutionandresolvingpower.Resolvingpowerisapropertyoftheinstrumentandisaquantitythatmaybe
estimatedontheoreticalgrounds.Resolutionisequaltoorpoorerthantheresolvingpowerandisthequantityobservedunderanygivenset
ofexperimentalconditions.IntheTEM,especiallywithbiologicalsamples,theresolutionachievedmaybeconsiderablyinferiortothetheoretical
resolvingpoweroftheinstrument.
Microscopyisthescienceofseeingtheverysmall.Underidealconditions,theeyeresolvesabout1minuteofarc(=1/60degree=2.9x10
4
radian;recallthereare2p radiansin360°)andsinceitcanfocusdowntoabout250mm,thesmallestobjectwecanresolveisabout0.07mm
(70mm)(Fig.I.14).Thislimitisrelatedtothesizeofthereceptorsintheretinaoftheeye.Thefunctionofamicroscopeistomagnifytheimage
fallingontheretina(Fig.I.15).Theadvantageoflightandelectronmicroscopesisthattheyeffectivelygettheobjectclosertotheeyesoa
magnifiedimageisobtainedandmoredetailcanbediscerned.
TENNISBALLANALOGY:Eyecanresolve3cmat100meters,thusatennisballisclearlyvisible.Butifthetennisballisheldupagainstawhite
background,thevisibilitydecreases(becauseofthedecreaseincontrast).
3)Abbecriteriaofresolution:
Thefundamentalnatureoflightposeslimitsonthedetailthatcanberesolved(Fig.I.16).Abbe(1893)showedthatthesmallestresolvable
distanceisabout1/2thewavelengthoflightused.Thus,1/2thewavelengthoftheradiationusedistheultimateresolvingpowerofany
instrument.Thislimitstheusablemagnificationofopticalmicroscopesto<1000X.Atfirstitwasthoughtthatxraymicroscopeswouldbeuseful
buttherefractiveindexofsubstancesforxraysisnearly=1,thusrefractinglensescannotbemadeforxrays,andconsequently,xrayscannot
beeasilyfocusedtoformimages.
4)Magnificationlimits:
Themaximummagnificationofaninstrumentislimitedaccordingtothefollowingrelationship:
Thus,fortheLM,witharesolvingpowerofapproximately0.25µm,themaximum(useful)magnificationisabout250µm/0.25µm=1000X.Thevalue
usedfortheresolvingpoweroftheeyeinthisexample(250µm)representsamorerealisticviewingcondition.Anymagnificationabovethevalue
givenbytheaboveformularepresentsemptymagnification,sincesuchmagnificationleadstonomoreusefulinformationbutratheramagnified
blur.
AccordingtotheAbbecriteria,at60,000volts,theTEMshouldhavearesolvingpowerofabout0.0025nm.Thisshouldallowamaximumuseful
magnificationofabout100milliontimes!!!Inpractice,themaximumusefulmagnificationoftheTEMoperatedat60kVislimitedtomuchlessthan
1,000,000X.Thus,althoughtheLMnearlyobeystheAbbecriteria,theTEMfallsshortbyaconsiderableamount.Themainlimitingfactorinthe
TEM,withrespecttoachievingthetheoreticalresolvingpoweroftheinstrument,concernsthenatureoftheimaginglensesandtheprocessof
imageformation.
5)Rayleighcriteria(practicalbutarbitrary):(Fig.I.17).
Itistheabilityofmicroscopestomakeobjectpointswhichareclosetogetherappearintheimageasseparatepoints.Anideallenstakeseach
objectpointandrepresentsitexactlyasapointintheimage.Areallenstakeseachobjectpointandspreadsitoutintoacirculardisk(Airy
disk)intheimageplanewhosediameterdependsontheangularapertureofthelens.
Theshortestdistancebetween2disksatwhichthetwodisksappearpartiallyseparatedcorrespondstoabout1/2thewidthofthedisks.The
distance,d,inobjectspaceisgivenby:
d=0.61l /n
•
sina
where
l =wavelenghtoftheradiation
n=refractiveindexofthemedia
a=semiangularapertureofthelens
NOTE:n
•
sina=thenumericalaperture(N.A.)ofthelens.
Thus,tomaximizeresolvingpower,l mustbedecreased,nincreased,oraincreased.Recallthatweareconcernedatthemomentwithan
aberrationfreeopticalsystem.Thevaluefortheconstant(0.61)iscontroversialbecauseitdependsonthecoherenceoftheradiationanda
criteriaofvisibility.
FortheLM,usingoilimmersionoptics(n=1.5),sina=0.87,andvioletlight(l =400nm),d=0.2µm.Theonlywaytoimprovetheresolutionisto
uselightofshorterwavelengthsinceN.A.cannotbeincreasedbeyond~1.5.FortheTEM,n=1(vacuum),sina=10
2
andl =0.005nmfor60kV
electrons,thusd=0.3nm.
I.A.4.Optics(LensTheory)
a.Basiclawsofclassicalgeometricaloptics
1)Rectilinearpropagationoflightwhenn(refractiveindex)isconstant.
2)Lawofreflection:
3)Lawofrefraction(Snell'sLaw):
4)Independenceofrays.Theassumptionismadethatlightraystravelindependentlythroughspace.
Theselawsholdforelectrons,except#4,ifthecurrentdensityistoohighwhennegativechargedelectronscaninterfere.
b.Classicalvs.electronoptics
1)Classicaloptics:Therefractiveindexchangesabruptlyatasurfaceandisconstantbetweenthesurfaces.Therefractionoflightatsurfaces
separatingmediaofdifferentrefractiveindicesmakesitpossibletoconstructimaginglenses.Glasssurfacescanbeshaped.
2)Electronoptics:Here,changesintherefractiveindexaregradualsoraysarecontinuouscurvesratherthanbrokenstraightlines.Refraction
ofelectronsmustbeaccomplishedbyfieldsinspacearoundchargedelectrodesorsolenoids,andthesefieldscanassumeonlycertaindistributions
consistentwithfieldtheory.
c.Geometricalandphysicaloptics
Thefundamentalprinciplesofopticsgovernthedesignandoperationofboththelightandelectronmicroscopes.Thebasicopticalprinciples
involvingtheuseofrefractileelementsorlensesinordertoformmagnifiedimagesareidenticalinboththeLMandTEM.TheTEMdiffersfromthe
LMonlyintheradiationitusesandinthewayinwhichtheradiationisbentorrefracted.
Geometricalopticsdealswiththestudyofthepathsfollowedby'rays'oflightorelectronsthroughlensesandapertures,andthegeometrical
constructionsusedtofindtherelativepositionsandsizesofobjectsandtheirimages.Arayoflightorelectronsisdefinedasaninfinitelythin
pencilorbeam.Physicalopticsshowsthatthisanabstractionandcannotphysicallyexistbecauseof'diffraction'whichdealswiththewave
natureoflightandelectrons.Allresultsobtainedingeometricalopticscanbederivedfromtheprinciplesofphysicaloptics,alongwithother
phenomenasuchasinterferenceanddiffractionwhicharenotexplicableinsimplegeometricalterms.
d.Idealversesreallenses:
Lensesareusedtobendraysoflightorelectronssotheyaredeflectedinapredictablewayfromtheiroriginalpaths.Thepropertiesofanideal
lens,possessinganaxisofrotationalsymmetryare:
1)Eachrayofthebundleofrayswhichpassesfromanobjectpointwillberefractedbytheideallenstomeetinoneimagepoint.
2)Raysoriginatingfrompointswhichlieonaplaneperpendiculartotheaxis,mustbeimagedinaplanewhichisalsoperpendiculartotheaxis.
3)Theimageappearsliketheobjectirrespectiveofthemagnification,sotherelativelineardimensionsoftheobjectarepreservedintheimage.
Inpractice,theimagingbyanyreallensdoesnotcorrespondtothatoftheideallensowingtothefactthatanobjectpointisrepresentedbya
diffractionimage(Airydisc)ofthelensopeningortheapertureusedforrestrictingtheeffectiveopeningofthelens.Thisisaresultofthewave
likepropertiesoflight.Lensaberrationsalsocontributetomoreorlesspronounceddeviationsfromthepropertiesoftheideallens.
Thesinglerefractingsurfaceofsphericalcurvatureisthefundamentalunitoffocusingactionbyglasslenses.Sphericalrefractingsurfacesactas
lensesforparaxialrayswhicharethoseraysthatpassclosetotheprincipalaxisofthelens.RayswithlargeangleswillNOTobeyideallens
action.
Afundamentaldifferencebetweenlightandmagneticlensesisthattheelectronbeamdoesnotchangeinforwardvelocityasitpassesthrough
themagneticfield(lightraysslowdownwhenpassingintoamediumofhigherrefractiveindex).Refractioniscontinuouswithelectronswhenthey
areinthemagneticfield:lightisrefractedonlyattheinterfacebetweenmediaofdifferingrefractiveindex.Theelectronsalsofollowspiral
trajectoriesthroughthemagneticfield(seealsoSec.I.A.5.c(Magneticfieldsandmagneticlenses)
e.Raydiagrams:(Figs.I.20I.28)
Themethodofconstructionofraydiagramsisbasedonthreesimpleprinciples:
1)Allraysenteringthelensparalleltotheaxisarebroughttoacommonpointontheaxis,thefocalpoint.
2)Allrayspassingthroughthegeometricalcenterofthelensareundeviatedandpassstraighton,nomatterfromwhichdirectiontheycome.
3)Principleofreversibility:ifthedirectionofarayisreversedinanysystemtherayexactlyretracesitspaththroughthesystem.Thisapplies
onlytothelocationoflightpathsandnottotheintensityofthelight.
Theaboveprinciplesarebasedontheassumptionsthatwearedealingwithathinlensandconcernedwiththepathsofparaxialrays.The
standardconventionistodrawdiagramswithraysthattravelfromlefttoright.Theobjectistotheleft(infront)ofthelensandtheimageisto
theright(behind)ofthelens.
f.Definitions:
Realimage:oneatwhichlightraysphysicallyreunite,sothataphotographicplateplacedatthepositionofarealimageisexposed.
VirtualImage:onefromwhichlightraysappeartodiverge;raysarenotinfactconcentratedatthepositionofavirtualimage,sothata
photographicplateplacedatthepositionoftheimageisnotexposed(byfocusedrays).Placinganopticalsystemsuchastheeyebehindthe
lens,willenablethedivergentraystobefocusedtoformarealimage.TheintermediatelensofanTEMissometimesusedthiswayinorderto
reducethefinalsizeoftherealimageformedbytheprojectorlens(es).
Converging(positive)lens:bendsraystowardtheaxis.Ithasapositivefocallength.Formsarealinvertedimageofanobjectplacedtothe
leftofthefirstfocalpointandanerectvirtualimageofanobjectplacedbetweenthefirstfocalpointandthelens.
Diverging(negative)lens:bendsthelightraysawayfromtheaxis.Ithasanegativefocallength.Anobjectplacedanywheretotheleftofa
diverginglensresultsinanerectvirtualimage.Itisnotpossibletoconstructanegativemagneticlensalthoughnegativeelectrostaticlensescan
bemade.
g.Lensformula(thinlensequation):
where
f=focallengthofthethinlens(sameradiusofcurvatureforboth
sphericalsurfaces)
o=distanceofobjectfromlens(positivetotheleft)
i=distanceofimagefromthelens(positivetotheright)
NOTE:Foravirtualimage,ihasanegativevalue.
h.Magnification:
Foraconverginglens,iftheobjectismorethantwicethefocallengthfromthelens,thentheimageformedisreal,inverted,andsmallerinsize
thantheobject(M<1).Whentheobjectisatadistance=2f,theimageandobjectarethesamesize(M=1);whenitisbetweenfand2f,
theimageislargerthantheobject(M>1),andwhenitis<f,theimageisvirtual,erect,andlargerthantheobject(M>1).
i.Angularapertureofthelens(2a)(Fig.I.29)
Theaperturedeterminesthetotalamountofradiationarrivingfromtheobjectwhichcanbefocusedto
formanimage.Theaperturethuscontrolstheabilityofthelenstogatherinformationabouttheobject.
Thisdependsontheangleoftheconeofraysitisabletoacceptfromtheobject.Bringinganobject
closertotheeyeincreasestheangularaperture,butthereisalimittotheclosenessthattheobjectcan
bebroughttotheeye(~25cmcorrespondingtoanangleofabout0.9°fora4mmexitpupildiameterof
theeyelens;atypicalLMwithanoilimmersionobjectivelenshas2aof~175°).
j.Simplevs.compoundmicroscope(Figs.I.30I.32)
Inprinciple,arealimageofanydesiredmagnificationcanbeobtainedfromasinglepositivelens,butin
practicethisiscumbersomebecauseofthelonglensimagedistance.Oneormorelensescanbeusedto
magnifytheimageinstages(totalmagnificationequalingtheproductofthemagnificationsofeachlens).
Theimageformedbyonelensconstitutestheobjectforthesubsequentlens,whetherornotareal
intermediateimageisformed.
Comparisonofoneversestwostagemagnification:
Thefollowingdescriptionillustrateshowdifferentpathlengthsarerequiredtoachieveamagnificationof10,000Xusingeitheroneortwolenses
withf=2.0cm.
OneStageSystem:
TwoStageSystem:
Assumebothlenseshavef=2.0cmandarearrangedsoeachgives100Xmagnification.
Thus,M=100=x
i
/x
o
foreachstage.
FirstStage:
x
o
=2.02cm
x
i
=202.00cm
Therealimageformedinthefirststagebecomestheobjectforthesecondlens.
SecondStage:x
o
,x
i
sameasinthefirststage.
Totallengthofsystem
=lengthoffirststage+lengthofsecondstage
=(x
o
+x
i
)+(x
o
+x
i
)
=2(x
o
+x
i
)
=2(2.02+202.00)=408.04cm(4.08meters)
k.Problemset
Thefollowingproblemsareforyourownedificationtotesthowwellyouunderstandthebasicsoflensoptics.
1.Foreachsituationbelow,drawanaccurate(usegraphpaper)raydiagramshowingthepathof(atleasttwo)raysfromtheobjecttoimage.
Indicatewhethertheimageisrealorvirtualandspecifythedistanceoftheimagefromthelensandthemagnificationoftheimagewithrespect
totheobject.Ineachexample,thelensisconverging,withidenticalfrontandbackfocalpoints.Distancesareinarbitraryunits.Letf=lens
focallength,x
o
=distanceofobjectinfrontofthelens,andx
i
=distanceofimagebehindthelens.Theobjectmaybeanysize.
2.Inthefollowingexamples,therearetwoconverginglensesinsuccession.Drawraydiagramsshowingtheformationofboththeintermediate
andfinalimagesandgiveappropriateinformationaboutthenature(real/virtual),positions,andsizesoftheintermediateandfinalimages.What
isthemagnificationateachstageofimageformationandwhatisthemagnificationofthefinalimage?Thedistancefromthecenteroflens1(L1)
tothecenteroflens2(L2)equalsD.
I.A.5.ElectronOptics/ElectronLenses
a.Electronemission
Innershellelectronsinmetalatomsshieldtheelectricfieldofthenucleusthroughtherepulsiveforcestheyexertontheoutershell(valence)
electrons.Thustheattractionbetweenthevalenceelectronsandthenucleusisreduced.Metalatomsarecharacterizedashavingtwoloosely
boundvalenceelectronswhichmigratefreely(thisiswhymetalsaregoodelectricalconductors)andcanescapefromthemetalcompletelyif
sufficientadditionalenergyisimpartedtothem.Asthetemperatureofametalisincreased,thekineticenergyoftheelectronsincreasesbecause
ofincreasedthermalvibrationsofthemetalions,whichcollidemorefrequentlywiththeelectrons.Thermionicemissionisthetermusedto
describetheprocessbywhichthermalenergyissuppliedtolooselyboundelectronsinordertoformasourceofelectrons.
Atroomtemperatureelectronsareeffectivelypreventedfromescapingthesurfaceofthemetalowingtotheattractiveforceofthepositively
chargedions.Asthetemperatureisincreasedsomeelectronsacquiresufficientenergytoovercometheattractionandleavethemetal
temporarily.Metal,shapedasathinwire,caneasilybeheatedbypassinganelectriccurrentthroughit.Sincethemetalsurfacebecomes
positivelycharged,acertainlevelofenergy(workfunction)mustbesuppliedtoallowelectronstoescapefromthesurface.Eachmetalhasa
characteristicworkfunction.Tungsten,withalowworkfunction,emitsmoreelectronsthanmetalswithhigherworkfunctions(seealsopp.2930
andFig.I.59).
Ifastrongelectrostaticfieldisappliedinavacuumbetweenthewire(givenanegative,cathode,potential)andananode,theelectricfieldwill
causeelectronstoaccelerateawayfromthewiretowardstheanodesurface(Fig.I.33).Thespeedoftheelectronsdependsonthestrengthof
theelectrostaticfield(voltage)betweenthecathodeandanode(equation(3),Sec.I.A.3.b)Thenumberofelectronswhichleavethewire
dependsonthetemperaturetowhichthewireisheated,whichdependsonhowmuchfilamentcurrentpassesthroughthewire.
A"V"shapedwirewillhavethehighesttemperatureatthetip.Electronswithdrawnfromthefilamenttipcarryelectricchargestotheanode.This
electriccurrent,whichflowsbetweenthefilamentandtheanode,iscalledthebeamcurrent.
1)Electricfield/Equipotentials
Anelectricallychargedobjecthasassociatedwithitanelectricfield.Thus,anelectricallychargedparticle,whenbroughtnearachargedobject,
isinfluencedbyanelectricalforceinthevicinityoftheobject.Theforceisdirectedtowardthechargedobjectifthechargesareofopposite
signsandawayfromtheobjectiftheyareofsimilarsign.DEFINITION:Thedirectionofanelectricfieldisdefinedasthedirectionoftheforce
actingonapositivecharge.(Figs.I.3435)
Alongthelinesofforceconnectingthetwocharges,theelectricpotentialwillchangegraduallybetweentheextremevaluesrepresentedbythe
twocharges.DEFINITION:Equipotentiallinesdefinethepointsalongthelinesofforcewithidenticalelectricalpotential.Theseequipotential
surfacesarealwaysorientedperpendiculartothelinesofforce.Thechangesintheelectricpotentialaregradualinspace.
Electronswhichenterafieldbetweentwoparallelplatesinadirectionparalleltotheplatesareaffectedbytheforcedirectedperpendicularto
theplates(FigI.36).Theelectronswillbeattractedtowardthepositiveplate.Thepathchangesinaseriesofgradualstepsattheequipotential
surfaces.
FigureI.37showshowtheelectronpathis"refracted"attheequipotentialsurface.TheresultisfundamentallythesameasthatgivenbySnell's
Lawofrefractioninlightoptics.Aconsequenceofthisisthatasphericallycurvedequipotentialsurfaceexhibitsthepropertiesofalens.
FiguresI.38andI.39showhowbothpositive(converging)andnegative(diverging)electrostaticlensescanbeformed.Thisfeatureof
electrostaticlensesdiffersfromelectromagneticlenseswhichcanonlyactasconverginglenses.
2)Advantages/Disadvantagesofelectronlenses:
Thefactthattherefractiveindexdoesnotchangeabruptlyinelectronlenseshasoneadvantageinthattherearenotroublesomereflectionsat
equipotentialsasatglassinterfaces.Thereisaseriousdisadvantageinthatequipotentialscannotbeshapedandcombinedinarbitraryfashionto
correctforchromaticaberrationandothererrors.
Althoughelectronmicroscopeswhichemployelectrostaticlenseshavebeenmade,mostmicroscopesuseelectromagneticlenses.Amajorreason
isthatelectrostaticlensesaremoresensitivetothequalityofthevacuumandcleanlinessofthecomponentsthanareelectromagneticlenses.
Somelensaberrationsaremoresevereforelectrostaticlensescomparedtoelectromagneticlenses.Electrostaticlensesrequireverypowerful
electrostaticfieldswhichcanleadtoelectricalbreakdownor"arcingover"insidethecolumn,especiallyunderpoorvacuumconditions.Forthis
reason,electrostaticlensescannotbemadewithfocallengthsasshortasmagneticlenses.
b.Electrostaticlens
Abasicunderstandingofelectrostaticlensesisimportantfortwomainreasons:i)theelectrongunuseselectrostaticlensactiontoformthe
primarybeamsource,andii)itisquitecommonforachargetodeveloponthenonconductingcontaminationwhichmayaccumulateonphysical
apertures(suchastheobjectiveaperture)andtransformthemintoweakelectrostaticlenseswhichcandistorttheelectronimage.
3)Propertiesofelectrostaticlenses:
a)Anyaxiallysymmetricalelectrostaticfieldhasthepropertiesofalensforraysconfinedtotheparaxialregion.Alltheideallensformulasapply
toelectrostaticlenses.
b)Forelectronlenses,replaceÃ(f)forrefractiveindexinthelensequations(f=valueofthepotentialontheaxis).Intheimageformingsystem
ofmostTEMs,fisthesameonbothsidesofthelens(SeeSec.I.A.5.c).
c)Ifboundedbyregionswherefisconstant,anelectrostaticlensisalwaysconvergent.
c.Magneticfieldsandmagneticlenses
1)Magneticfield
Anelectriccurrentpassingthroughaconductorgivesrisetoamagneticfield.TheconventionisthatNisthedirectioninwhichthelinesofthe
magneticfieldpoint(Fig.I.40).Themagneticfluxisthetotalnumberoflinesandthefluxdensityisthenumberoflinesperunitareaofasurface.
UsetheRIGHThandruletodeterminethedirectionofthefield(thumbpointstowardcurrentdirectionandfingerscurlindirectionoffield.NOTE:
Byconvention,thedirectionofelectronflowisoppositetothatofcurrentflow.
Fluxdensitydependsonthepropertiesofthematerialsurroundingtheconductor.Ironinducesahigherfluxdensitythanairoravacuum.The
propertyofthematerialwhichaffectsthefluxdensityiscalledthepermeability,m,ofthematerial.Forairandvacuum,m=1.0.For
ferromagneticmaterialsitcanbeaslargeasseveralhundredthousand.
Iftheconductorhastheshapeofacircularloop,thelinesofforceformcirclesaroundtheloop.Thefluxdensityisgreatestatthecenterofthe
loop.Themagnetinthecenteroftheloopisorientedperpendiculartotheplaneoftheloopifthecurrentthroughtheloopissufficientlystrongto
eliminatetheinfluenceoftheearth'sfield.ThesideoftheloopatwhichthelinesofforceleavetheloopistheNorth(N)poleofthemagnet(Figs.
I.41,I.42).
Ifthewireiswoundinseveralturnsaroundacylindricalsurface(solenoid),eachturnwillcontributetotheinducedmagneticfield.Theflux
densityinthecenterofthecoilisgivenby:
Inthecaseofairandnonmagneticmaterials,µ=1.0andB=H.
Thepermeabilityofirondependsonthefieldstrength,H,anddecreasestounityathighfieldstrengthorwhenthefluxdensity,B=H(Fig.I.43).
Thehighpermeabilityofironisduetotheinducedmagneticfieldorientingmicroscopiccrystalregionsactingastinymagnetsintheiron.Allthese
tinymagnetsaddtheirmagneticfieldstotheinducedfield(Fig.I.44).Whenallmicromagnetsarenearlyoriented,theironwillaffecttheflux
densitytoadecreasingamountsincethereorientationofmicromagnetsisnearingcompletion.Thus,thepermeabilityofironathighfieldstrengths
approachesthatofemptyspace.Atthispointtheironreachesmagneticsaturation.
2)Hysteresis
Thestrengthofthelensdependstosomeextentonthepreviousmagnetichistoryof
thelens.Whenthecurrentinalensisreduced,thedecreaseinmagnetizationdoes
notretracethesamepathobtainedwhenthecurrentwasincreased(Fig.I.45).
Inductionofmagnetizationinvolvesaphysicalmovementwithinthemagnetized
material,requiringtheovercomeofacertaindegreeofinertia.Asaresult,
magnetizationtendstolagbehindthemagnetizingforceapplied.Inducedmagnetic
fluxcanonlybereturnedtozerobyapplicationofacurrentintheoppositedirection.
Aconsequenceofhysteresisisthatthelevelofcurrentusedtoenergizeamagnetic
lensDOESNOTpreciselyspecifythelensstrength(i.e.focallength).
NormalizationofTEMlensesisaccomplishedbyreducingthelenscurrenttozero
somepredeterminednumberoftimes.Hysteresismayalsobeminimizedbytakinga
lenstosaturationandthenreturningittotheworkingcurrentwithoutovershooting.
Whenthefieldstrengthisreducedtozero,somemagnetizationstillremainsintheiron
(residualmagnetizationorremanence).Anadvantageofsoftironisthefactthat,
whenusedinanelectromagnet,hysteresisislow.
Introductionofpiecesofironinamagneticfielddrasticallyaffectsthefluxdensity.
Magneticmaterialhasashieldingeffect,theeffectbeinggreaterthegreaterthe
permeability.Permalloy(mmetal)hasamaximumpermeabilityof80,000140,000
comparedtoironusedintransformers(~7000).mmetalpermeabilityislimitedtolower
fieldstrengthsthanthatatwhichironstillretainshighpermeability.Thismetalis
thereforeusefulforshieldingtheTEMfromexternalmagneticfields.
d.Theelectromagneticlens
1)Lensdesigndevelopment(Figs.I.46I.48)
Theefficiencyofthemagneticfieldproducedbyashortsolenoidwasfirstimproved
byencasingtheenergizingcoilinasheathofsoftironwhichhasthepropertyofconcentratingthelinesofforceinamagneticfieldandthus
becomingmagnetizedbyinduction.Inthiswayamuchmorepowerfulaxialmagneticfieldisobtainedforthesameamountofcurrentflowing
throughthesolenoid.Furtherdevelopmentinvolvedencasingtheentirecoilwithsoftironexceptatanarrowannulargapintheinsideofthecoil.
Thisproducesagreaterconcentrationofthemagneticfieldalongashortaxialdistance.Toachieveshorterfocallengthlenses(andobtaingreater
magnifications)asoftironpolepiecewithanopenaxialborewasintroducedatthepositionoftheannulargap.
MagneticlensesusedinTEMsarealwaysconstructedwithanironcircuittoproduceahighfieldstrengthacrossashortgap.Themagneticfields
forTEMlensesareintherangeof10,00020,000gauss.
2)Forcesactingonacurrentinamagneticfield
Theforceonanelectroninamagneticfieldisalwaysatrightanglestothevelocityandthedirectionofthefield(Figs.I.49,I.50,andI.52).The
fieldonlyactsonthevelocitycomponentwhichisdirectedperpendiculartothelinesofforce.Usethelefthandrule(Fig.I.51:firstfingerfor
fielddirection,middlefingerforcurrentdirection,andthumbfordirectionofforce).Rayspassingthroughthelensareturnedthroughanangle
whichdoesNOTdependonthedistanceoftheraysfromtheaxis.Allelectronscontainedinagivenmeridionalplanebeforeenteringthefieldare
containedinarotatingmeridionalplaneastheypassthroughthelens,andthentheyleavethelenscoplanar.
Whenelectronsenterthelenstheyencounterasidewaysforcewhichcausestheelectrontorotate
asitcontinuesthroughthelens(Figs.I.53I.57).Sincetheradialcomponentofthemagneticfield
reversesafterthecenterofthelens,therotationalvelocitysetupinthefirsthalfofthelensis
countered.Theelectronenteredthelenswithoutangularmomentumabouttheaxisandleaves
withoutangularmomentum.Theneteffectisadeflectiontowardtheaxis,whichitmustcrossatthe
focalpointf
2
.Theanglebetweentheobjectvectorandtheimagevectoris180°+q,whereas,for
glasslensesandelectrostaticlenses,theanglebetweenarealobjectandtheimageisexactly180°.
Sincetheradialforceisdirectedtowardtheaxis,thelensisconvergentnomatterwhatthedirection
ofthefield.
3)Propertiesofamagneticlens:
Anyaxiallysymmetricmagneticfieldhasthepropertiesofanideallens.Alltheformulasfortheideallensmaybeapplied.
Magneticlensesarealwaysconvergent.Theconventional,axiallysymmetriclensisalwaysboundedbyregionswhicharefieldfree,the
consequencebeingthatthenetactionofelectronlensesisinevitablyconvergent.Limitedregionsmaybedivergentbutnotthelensasawhole.
Theseriousconsequenceofthisisthatneithersphericalorchromaticaberrationscanbecorrectedasisdoneinlightopticsbytheusedoublets
ofpositiveandnegativelenses.
Intheabsenceofelectrostaticfields,therefractiveindexisthesameinobjectandimagespace,thereforef
1
=f
2
.
Electronstravelingthroughaxiallysymmetricfieldsexperienceaspiraltrajectoryofdiminishingradius.Theimagevectorisatanangle180°+qto
theobjectvector.
Thedeflectionoftheelectrontowardstheaxismeansthatanelectronenteringthelensparalleltoitsaxiswillcrosstheaxisafterhavingpassed
thelens.Thedeflectionwillincreasewiththedistancefromtheaxis.Thus,abeamofelectronsinparallelpathsparalleltotheaxisofthelenswill
befocusedtoanimagepointontheaxiswhichrepresentsthesecond(back)focalpointofthelens(f
2
).Notethatmagneticlensesarehighly
inefficientinthatonlyaminorportionofthetotalfieldstrengthisactuallyeffectiveinfocusingtheelectron.
4)Magneticlensfocallength
Inamagneticelectronlensthefocallengthisdeterminedbythefieldstrengthinthelensgapandbythespeedoftheelectrons(determinedby
theacceleratingvoltage).
Formagneticlenses,focusingisachievedbyvaryingthecurrentwhichpassesthroughtheelectromagnet.Thisinturnchangesthestrengthof
themagneticfieldandtherebyaltersthefocallengthofthelensandisequivalenttoacombinedchangeinboththe"refractiveindex"and
"curvatureofsurface".Forabeamofmoreenergeticelectrons,thelenscurrenthastobeincreasedinordertokeepthefocallengthconstant.
FocallengthandcurrentareNOTlinearlyrelated:strengthincreasesinasigmoidfashion(Fig.I.45)ascurrentincreasesuntilapointisreached
wherethelensissaturatedandnofurtherincreaseinlensstrengthcanbeachieved.
Sincethefocallengthofthelensisdirectlyproportionaltotheacceleratingvoltage,avariationinthevelocityoftheelectronsintheimaging
beamaffectsimagequalitybyeliminatingperfectfocus(chromaticaberration).
5)Magneticlensdesign:(Figs.I.46,I.47).
Condenserlensesusuallyhavearelativelylargeboreandspacingwhichresultsinalongfieldandlongfocallength.
Typicalconstructionoftheobjectivelensproducesastrongfieldofshortaxialextent(i.e.shortfocallengthbetween(1.53mm)necessaryfor
formationofimagesathighmagnification.Thespecimenisplacedwithinthemagneticfieldoftheobjectivelens.Thus,anyfieldintroducedby
contaminantsinthespecimencandistortthefieldofthelens.Notethatthisalsomeansthatpartofthelensfield("prefield")isonthefrontside
oftheobjectandaffectstheelectronbeambeforeitpassesthroughtheobject.
Mostofatypicalmagneticlensliesoutsidethevacuumofthemicroscope.Onlythoseregionsthroughwhichtheelectronbeampassesareinhigh
vacuum.Magneticlensesmustbewatercooledtodissipatethelargeamountsofheatproducedbythecurrentsintheelectromagnetcoils.
DATE NAME EVENT
1897 J.J.Thompson Discoverstheelectron
1924 LouisdeBroglie Identifiesawavelengthtomovingelectrons
l =h/mv
where
l =wavelength
h=Planck'sconstant
m=mass
v=velocity
(Foranelectronat60kVl=0.005nm)
1926 H.Busch Magneticorelectricfieldsactaslensesforelectrons
1929 E.Ruska Ph.Dthesisonmagneticlenses
1931 Knoll&Ruska Firstelectronmicroscopebuilt
1931 Davisson&Calbrick Propertiesofelectrostaticlenses
1934 Driest&Muller SurpassresolutionoftheLM
1938 vonBorries&Ruska FirstpracticalEM(Siemens)10nmresolution
1940 RCA CommercialEMwith2.4nmresolution
1945 1.0nmresolution
Fig.I.1Comparisonoflightandelectronmicroscopes.Ineach
instrument,illuminationfromthesource(lamp,filamentinthe
electrongun)isfocusedbythecondenserlensontothespecimen.
Afirstmagnifiedimageisformedbytheobjectivelens.Thisimage
isfurthermagnifiedbytheprojectorlensontoagroundglass
screen(light)orfluorescentscreen(electrons).(FromAgar,p.8)
Fig.I.2CrosssectionalviewofthePhilipsEM300.(FromAgar,p.40)
Toviewtheanimatedmicroscope,clickhere.
Note:QuickTimePlugInrequired
(Thiscanbedownloadedathttp://apple.com/quicktime/download)
Fig.I.3Sectionthroughacomplex
doublecondenser6lensPhilips
EM200electronmicroscope.(From
Meek,p.99)
Fig.I.4Thestatisticalnatureofdiffraction
patterns.(FromHall,p.13)
"Theprecisenatureof'electronwaves'or'matterwaves'isverydifficulttounderstandordescribeinmaterialterms.Electronwavesarenot
electromagneticradiationofthekindtowhichlight,Xraysandradiowavesbelong.Theyconstituteasortofquantumor'packet'ofradiationwhich
accompanieseachindividualelectron,followingitspathandnotradiatingoutwardsfromit."(Meek,1976,pp.4849).
V l (nm)
v(
•
10
10
cm/sec)
v/c
10,000 0.0123 0.593 0.198
50,000 0.0055 1.326 0.442
100,000 0.0039 1.875 0.625
1,000,000 0.0012 5.930 1.977!
V l (nm)
v(
•
10
10
cm/sec)
v/c
10,000 0.0123 0.593 0.195
50,000 0.0055 1.326 0.414
100,000 0.0039 1.875 0.548
1,000,000 0.0012 5.930 0.941
FigI.5Aperfectpointsourcecannotbe
imagedbyalensasaperfectpointimagedue
tothepresenceoftheapertureAB(which
maybetheedgeofthelens).Diffractionat
thisaperturegivesrisetoaseriesoffringes,
whichsurroundtheimageformedofthepoint
source.Thepatternproducediscalledan'Airy'
disk.(FromMeek1sted.,p.35)
Fig.I.6Wheneverawavefrontstrikesa
barrier,itcanbendaroundthecorner'by
givingrisetoasecondarywavefrontatthe
edge,sinceeachpointonthewavefrontcan
giverisetoanewsourceofwaves.This
phenomenoniscalled'diffraction'.(FromMeek
1sted.,p.22)
Fig.I.7Diffractionpattern(right)formedbyanirregularlyshapedaperture
(left).(FromYoung,p.95)
Fig.I.8(a)
Photographof
theedgeofa
razorblade
illuminatedby
monochromatic
(blue)light
rendered
coherentby
passing
througha
narrowslit.(b)
Microdensitometer
tracingofthe
negativefrom
whichthe
photograph
wasmade.
FourFresnel
fringescanbe
distinguished.
(FromMeek1st
ed.,p.27)
(a)
(b)
(a) (c)
(b)
Fig.I.9(a)Fresnelfringesformed
byelectrons.Thesefringesare
formedoutsidetheedgeofahole
(white)inacarbonfilm(black).(b)
Amicrodensitometertracingofthe
fringesystem;thepatternis
identicalwiththeFresnelfringe
systemformedbyvisiblelight(see
Fig.I.8).(c)Anunderfocusedimage
ofaholeinafilm,showinga
completesystemofabout40
Fresnelfringesinsidethehole.
(FromMeek1sted.,pp.2930)
Fig.I.10Diffractionimagesoftwo
easilyresolvedpoints.(From
Slayter,p.243)
Fig.I.11Imagesoftwo
incoherentlyilluminatedpointsat
thelimitofresolution.(a)individual
intensities;(b)summedintensities.
(FromSlayter,p.244)
Fig.I.12Examplesofwhatoccurswhentwo
wavesofthesamewavelengthandequal
amplitudeadd.Ineachexample,thetwo
separatewavesareshownontheleftand
theirsumorresultantwaveontheright.The
differentexamplesarecharacterizedbyvarying
phasedifferences.Thephaseofawave
(usuallyexpressedasafractionofthe
wavelengthorindegrees)isthepositionofa
crestrelativetosomearbitrarypoint.Although
thephaseofagivenwavevarieswithtimeas
thewavetravels,thedifferenceinphaseofthe
twowavesofthesamewavelengthwiththe
samevelocity,isindependentoftime.Such
wavescaninterferewithoneanother.The
resultantwavehasthesamewavelength,l .
(a)Phasedifferencezero.Thewavestotally
reinforceandaresaidtobe"inphase"orto
showconstructiveinterference.
(b)Phasedifferencel /4.Partialreinforcement,
givingawaveofamplitude1.4(intensity2.0).
(c)Phasedifferencel /2.Thewavesare"outof
phase"andthereistotaldestructive
interferencetogivenoresultantwaveora
wavewithamplitude0(intensity0).(From
GluskerandTrueblood,p.19)
Fig.I.13Photographofan
interferencepatterninwater
wavesformedbythe
superpositionofwavesfromtwo
sourcesoscillatinginphasewith
thesamefrequency.(FromYoung,
p.22)
Fig.I.14Theangularapertureofthe
eyeisrelativelysmall.(FromMeek,
1sted.,p.13)
Fig.I.15Increasingtheangular
apertureoftheeyewithalens.The
lensallowstheobjecttobeheld
closertotheeye,whichisthereby
enabledtogathermoreinformation.
(FromMeek1sted.,p.14)
Fig.I.16Theinteractionofwaves
withanobstacle.Theboatridesthe
longwavelengthoceanwave,but
reflectsthesmallwavelength
surfaceripple.Anobserverwho
wishestodetectthepresenceof
theboatcandosoonlyby
observingwaveswhichhave
wavelengthssmallerthan,or
comparableto,thelengthofthe
boat.(FromSherwood,p.19)
Maximummagnification=
resolvingpoweroftheeye
resolvingpowerofthemicroscope
(a)
Fig.I.17(a)TwoAiry
disksrepresenting
twoimagepoints
shownatincreasing
separationfromleft
toright.Inthe
pictureatthe
extremerightthe
twodiskscanbe
distinguishedas
separatedisks.
(b)Theintensity
distributionatanAiry
disk.R,halfwidthof
thecentralmaximum
representedbya
bellshapedcurve.
(c)TheRayleigh
criteriaforresolution.
(FromSjostrand,
p.115)
i=r
Fig.I.18Reflection.(FromSlayter,
p.4)
Fig.I.19Refraction.(FromSlayter,
p.6)
Fig.I.20Principalraydiagramsshowing
imageformationbyaconvexlens.
(a)Whentheobjectdistanceisgreater
thanthefocallength,areal,inverted
imageisformed.
(b)Whentheobjectdistanceisless
thanthefocallength,avirtual,erect
imageisformed;itspositionis
obtainedbyprojectingtheprincipal
raysbackward.Theraysappearto
comefrompointQ.(FromYoung,
p.127)
Fig.I.21Definitionof
principalfocus,F,inimage
spaceofalens.(From
Sjostrand,p.20)
Fig.I.22Focusingeffectoflenson
raysoriginatingfrompointson
principalaxislocatedatdifferent
distancesfromthelens.(From
Sjostrand,p.21)
Fig.I.23Definitionofprincipal
focusinobjectspaceF1ofa
lens.(FromSjostrand,p.21)
Fig.I.24VirtualimageQof
objectpointlocatedbetween
principalfocusinobjectspace
andthelens.(FromSjostrand,
p.21)
Fig.I.25Constructionoftheimage
ofanobjectbymeansofray
tracing.(FromSjostrand,p.22)
Fig.I.26Magnifyingeffectof
apositivelens.(From
Sjostrand,p.22)
Fig.I.27Virtualmagnified
imageofobjectlocated
betweenprincipalfocusin
objectspaceandthelens.
(FromSjostrand,p.22)
Fig.I.28Amagnifyingglassformsan
enlarged,erectvirtualimage.The
angularsizeofthisimageis
approximately4"/15"or4/15.The
angularsizeoftheobjectatthe
closestdistanceforcomfortable
viewingis1"/10"or1/10.The
magnificationinthissituationis(4/15)/
(1/10),or22/3.(FromYoung,p.130)
Fig.I.29Theangularapertureofa
lens.Theangle2a isthe
acceptanceangleofthelens,and
thelargeritcanbemade,themore
informationcanthelenstransmit.A
largelensofhighaperturecan
thereforetellusmoreaboutan
objectthanasmalllensoflow
power.(FromMeek1sted.,p.12)
Fig.I.30Raydiagramforhighmagnification
modeofoperation.Notethateachlens
formsarealimage,withimageinversion.
I0istheimageformedbytheobjective
lensO,I1isformedbythefirstprojector
lensP1andI2bythesecondprojectorP2,
onthescreen.(FromAgar,p.30)
Fig.I.31Left:raydiagramofthe3realimagemediumandhighmagnificationimagingsystemofa3lens
microscope.Center:2realimageverylowor'scan'magnificationrangeofa3lensmicroscope.Right:2real
imagelowmagnificationsystemofa3lensmicroscope.(FromMeek1sted.,pp.118,120121)
Fig.I.32Raydiagramforacompleteelectron
microscope.FilamentF,condenser1lensC1,
condenser2lensC2,condenserapertureCA,
specimenS,objectivelensO,objectiveaperture
OA(inbackfocalplane).1stintermediateimage
andselectorapertureSA.IntermediatelensP1,
secondintermediateimageI2,projectorlensP2
andfinalimageonthefluorescentscreenFC.
(FromAgar,p.35)
a)f=2.0
x
o
=5.0
e)f=4.0
x
o
=3.0
b)f=10.5
x
o
=21.0
f)f=13.3
x
o
=13.3
c)f=3.5
x
o
=3.0
g)f=3.142
x
o
=0.0
d)f=5.0
x
o
=2.5
a)D=8.0
L1:f=2.0
x
o
=4.0
L2:f=3.0
b)D=8.0
L1:f=2.0
x
o
=6.0
L2:f=3.0
c)D=4.0
L1:f=2.0
x
o
=3.0
L2:f=2.0
FigI.33Accelerationofelectronin
electricfield.(FromSjostrand,p.26)
Fig.I.34Linesofforceatapositively
chargedsphericalbody.(FromSjostrand,
p.32)
Fig.I.35Linesofforceandequipotential
surfaces(stippledlines)associatedwith
twoequalchargesofoppositesign.
(FromSjostrand,p.32)
Fig.I.36Equipotentialsurfacesattwoparallel
platesofoppositechargeswiththepathofan
electronindicatedwithinthehomogeneous
partofthefield.(FromSjostrand,p.33)
Fig.I.37Refractionofelectronatan
equipotentialsurface.(FromSjostrand,p.33)
Fig.I.38.Negativelensactionof
electrostaticfieldatanaperturewhen
V2V1>V3V2.(FromSjostrand,
p.34)
Fig.I.39.Positivelensactionatan
aperturewhenV2V1<V3V2.
(FromSjostrand,p.34)
Fig.I.40Magneticfieldinducedbycurrent
passingthroughaconductor.(From
Sjostrand,p.35)
Fig.I.41Magneticfieldinducedbycurrent
passingthroughasolenoid.(From
Sjostrand,p.37)
Fig.I.42Solenoidwithironcore.(From
Sjostrand,p.40)
Fig.I.43a.Dependenceofpermeabilityonfluxdensity,B.
b.RelationshipbetweenfluxdensityBandfieldstrength.
(FromSjostrand,p.38).
Fig.I.44Magnetization.(FromSlayter,
p.361)
Fig.I.45Curves
showinghowthe
magnetizationof
softiron(lens
strength)is
relatedtothe
magnetizing
force(lens
current).An
unmagnetized
lensstartsfrom
thepointOand
followsthepath
OAaslens
current
increases.Atthe
pointA,further
increaseinlens
currentproduces
nofurther
increaseinlens
strength;thelensissaidtobe'saturated'.Whenlenscurrent
isreduced,thepathOAisnotretraced;adifferentpathABis
followed.Thisdisplacementiscalled'hysteresis'.Atzero
current(pointB),someresiduallensstrengthremains;thisis
called'remanence'.Tobringthelensbacktozerostrength,a
reversecurrentOCmustbeapplied.Lensstrengththen
increaseswithincreasingreversecurrent,followingthepath
CD.Thepolarityofthelenschanges,butthisdoesnotaffect
itsfocusingpower;onlythespiralelectronpathisreversed.
Becauseofhysteresis,itisnotpossibletocalibratealens
currentmeteraccuratelyintermsoflensstrengthor
magnification.
Fig.I.46Evolutionofmagneticelectron
lenses.(A)Shortsolenoidusedasa
magneticlens.(B)Softironcasing
enclosingoutersurfaceofthesolenoid,
thusconcentratingthefield.(C)Soft
ironencasingthesolenoidexceptata
narrowannulargaptherebyreducing
themagneticfieldtoaveryshortregion
alongthelensaxis.(D)Modern
objectivelensconsistingofasoftiron
encasedsolenoidandsoftironpole
piecessoastohaveanenormously
concentratedfieldatthelevelofthe
annulargap.(FromWischnizter2nded.,
p.33)
Fig.I.47(a)Amagneticlensconsisting
ofatightlywoundcoilandasoftiron
shroudsurroundingthecoilexceptfor
asmallgap.Thefieldisconcentratedin
thatgap.(b)Shortfocallength
electromagneticlenswithpolepieces.
(FromSjostrand,p.50)
Fig.I.48Fieldstrengthdistribution
curves.ThecurvesADcorrespondto
therespectivelensesillustratedinFig.
I.46.Eachrepresentsthefieldstrength
alongthelongaxisofthelens.The
changesintheshapeofthecurves
representtheshorteningor
concentrationofthefieldovera
shorteraxialdistance.Hz=
longitudinalmagneticfield.Z=
distancealongtheaxisofsymmetry.
(FromWischnizter2nded.,p.33)
Fig.I.49TheforceFactingon
astraightconductorina
homogeneousmagneticfield
offluxdensityBwhencurrent
Iispassedthroughthe
conductor.(FromSjostrand,
p.43)
Fig.I.50Pathofanelectronina
magneticfield.(A)Inalarge,uniform
magneticfield.(B)Inasmall,uniform
magneticfield.(FromWischnitzer2nd
ed.,p.25)
Fig.I.51Lefthandthumbrule.
(FromSjostrand,p.43)
Fig.I.52Thompson'sexperiment.A
streamofelectronsoriginatingfroma
sourceandpassing,invacuo,through
amagneticfieldproducedbyapairof
magnetswillbedeflected.The
directionofdeflectiondemonstrates
thatelectronsarenegativelycharged
particlesofmatter.(FromWischnitzer
2nded.,p.25)
Fig.I.53Actionofasolenoidonan
electronbeam.Anelectriccurrent
passingthroughthecoilproducesan
axialmagneticfield.Thisisthe
refractingmediumfortheelectrons.An
electronstartingatapointontheaxisA
andatanangletoitfollowsaspiral
path,returningtotheaxisatthepoint
B.Theactionisbasicallysimilartothat
oftheconverginglightlensshownin
Fig.I.20.(FromMeek1sted.,p.8)
Fig.I.54Actionofthemagnetic
lens.(a)Inperspective.(b)
Electrontrajectoryin
projection,alongdirectionof
propagation.(c)Electron
trajectoryinprojection,side
view.(FromSlayter,p.358)
Fig.I.55Componentsofthe
vectorHneartheaxisoffields
withaxialsymmetry.His
representedbytwo
components,Hz,the
componentinthez(axial)
direction,andHr,the
compnentinther(radial)
direction.(FromHall,p.85)
Fig.I.56Theycomponentof
themagneticfieldina
magneticlensisoriented
perpendiculartothedirection
ofanelectronenteringthe
lensalongapathparallelto
thelensaxis.Thisy
componentwillaffectthe
electron,deflectingitinthex
directionasindicatedbythe
arrowmarkedvx.(From
Sjostrand,p.48)
Fig.I.57Thezcomponentofthemagneticfield
andthexvelocitycomponentoftheelectron
inamagneticlensinteract,deflectingthe
electronintheydirectiontowardthelens
axis.(FromSjostrand,p.49)
CuuDuongThanCong.com https://fb.com/tailieudientucntt
cuu duong than cong . com
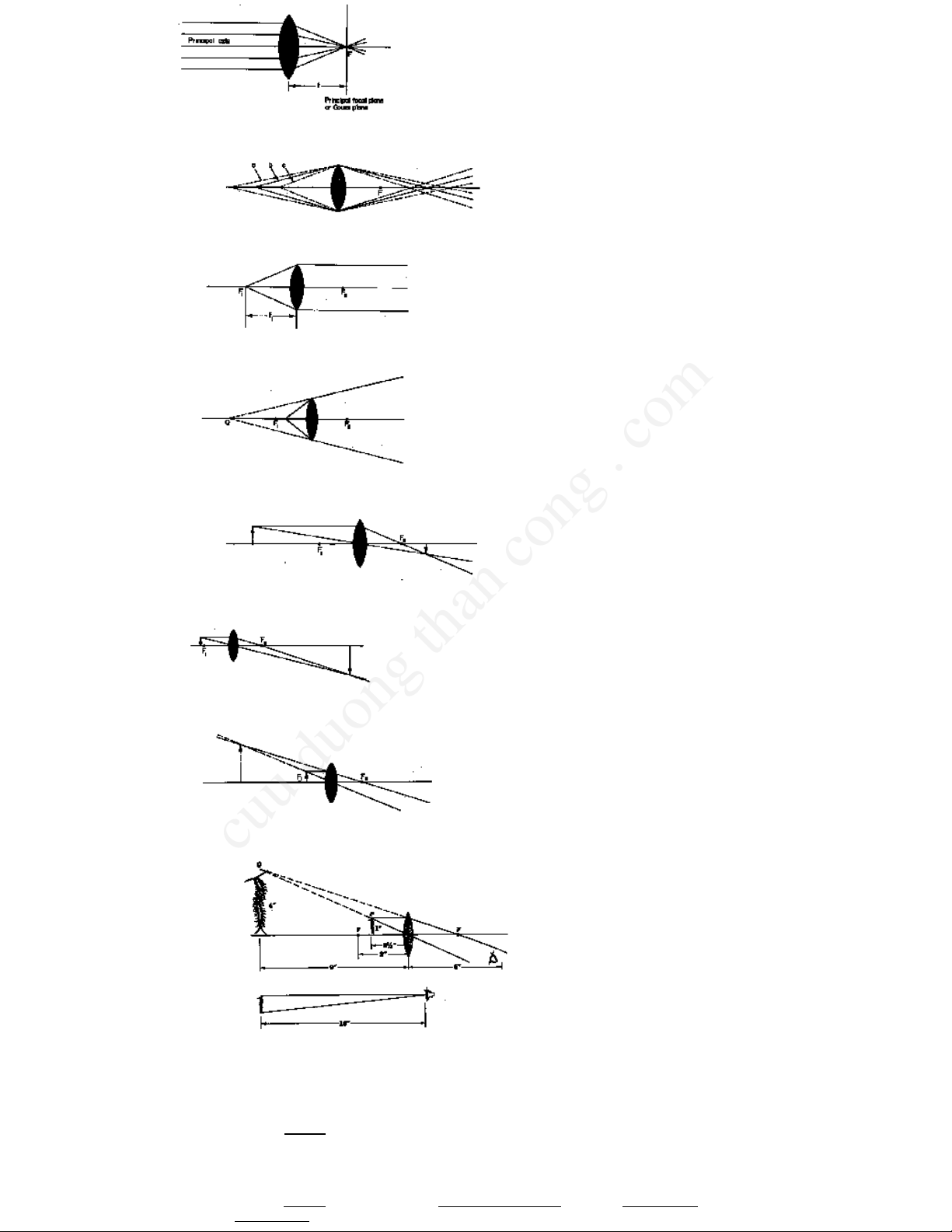
I.THEMICROSCOPE
I.A.PRINCIPLESOFTHETRANSMISSIONELECTRONMICROSCOPE(TEM)
I.A.1.OriginoftheTransmissionElectronMicroscope
I.A.2.ComparisonofLight(LM)andElectronMicroscopes(Fig.I.1)
a.Similarities(Arrangementandfunctionofcomponentsaresimilar)
1)Illuminationsystem:producesrequiredradiationanddirectsitontothespecimen.Consistsofasource,whichemitstheradiation,anda
condenserlens,whichfocusestheilluminatingbeam(allowingvariationsofintensitytobemade)onthespecimen.
2)Specimenstage:situatedbetweentheilluminationandimagingsystems.
3)Imagingsystem:Lenseswhichtogetherproducethefinalmagnifiedimageofthespecimen.Consistsofi)anobjectivelenswhichfocusesthe
beamafteritpassesthroughthespecimenandformsanintermediateimageofthespecimenandii)theprojectorlens(es)whichmagnifiesa
portionoftheintermediateimagetoformthefinalimage.
4)Imagerecordingsystem:Convertstheradiationintoapermanentimage(typicallyonaphotographicemulsion)thatcanbeviewed.
b.Differences
1)Opticallensesaregenerallymadeofglasswithfixedfocallengthswhereasmagneticlensesareconstructedwithferromagneticmaterialsand
windingsofcopperwireproducingafocallengthwhichcanbechangedbyvaryingthecurrentthroughthecoil.
2)MagnificationintheLMisgenerallychangedbyswitchingbetweendifferentpowerobjectivelensesmountedonarotatingturretabovethe
specimen.Itcanalsobechangedifoculars(eyepieces)ofdifferentpowerareused.IntheTEMthemagnification(focallength)oftheobjective
remainsfixedwhilethefocallengthoftheprojectorlensischangedtovarymagnification.
3)TheLMhasasmalldepthoffield,thusdifferentfocallevelscanbeseeninthespecimen.Thelarge(relative)depthoffieldintheTEMmeans
thattheentire(thin)specimenisinfocussimultaneously.
4)Mechanismsofimageformationvary(phaseandamplitudecontrast).
5)TEMsaregenerallyconstructedwiththeradiationsourceatthetopoftheinstrument:thesourceisgenerallysituatedatthebottomofLMs.
6)TEMisoperatedathighvacuum(sincethemeanfreepathofelectronsinairisverysmall)somostspecimens(biological)mustbedehydrated
(i.e.dead!!).
7)TEMspecimens(biological)arerapidlydamagedbytheelectronbeam.
8)TEMscanachievehighermagnificationandbetterresolutionthanLMs.
9)Pricetag!!!(100xmorethanLM)
I.A.3.Photons/Electrons
a.Dualconceptofwaveandparticle(Fig.I.4)
Lighthaspropertiesbothofaparticleandawave.Thisdualnatureisrequiredtosatisfactorilyexplaintheresultsofvariousphysicalexperiments.
Thediffractionoflight(bendingaroundcorners)illustratesthewavenature.TheWAVETHEORYisbasedonthestatisticalnatureofeventsand
haslittlemeaningwithrespecttothebehaviorofsingleparticles.ThewavetheorywasdevelopedandexpoundedbyHuygens(16291695)and
Hooke(16381703).TheCORPUSCULARTHEORYwasproposedbyNewton(16421727)andbecamethemoreacceptedtheoryevenafter
demonstrationofdiffractionbyYoung(17731829)andinterferencebyFresnel(17881827).Atabout1850,thewavetheorycamebackinto
favoruntilabout1900whenmoreevidenceforthecorpusculartheorywasdiscovered.
QUANTUMTHEORY(PlanckandEinstein)providesthebasisforexplainingthephenomenaofINTERFERENCE,DIFFRACTIONandthe
PHOTOELECTRICeffect(lightfallingoncertainmetalscausethemtoemitelectrons)andthusformsacommonbasisforexplainingthenatureof
actionoflight.Thetransferofenergybetweenlightandmatteroccursonlyindiscretequantitiesproportionaltothefrequencyofthe
lightwave.
E=hJ
where
E=energyofphoton(joules)
h=Planck'sconstant(6.624
•
10
34
joulesec)
J=frequency(cycles/sec)
b.Electronvelocityandwavelength
Therelationbetweenthewavelength(l )ofaparticleofmass,m,movingatavelocity,v,isgivenbytheDeBrogliewaveequation:
(1)
Anelectronofchargee(1.6
•
10
19
coulomb),andmassm(9.11
•
10
28
gm),whenpassingthroughapotentialdifferenceofVvolts(expressedin
joules/coulomb),hasakineticenergy:
(2)
Solvingforvelocity:
(3)
substitutingintotheDeBroglieequation(1):
(4)
Since1joule=10
7
dyne
•
cm=10
7
cm
2
•
gm/sec
2
(5)
Thus,forexample,ifV=60,000volts,l =0.005nm.
Fromequation(3)theelectronvelocitycanbecalculatedifVisknown:
(6)
Thefollowingtableillustratesthat,athighvoltage,electronvelocityiscomparabletothespeedoflightinavacuum(c=3
•
10
10
cm/sec).
Theequationbreaksdownwhenthevelocityoftheelectronapproachesthespeedoflightbecausearelativisticcorrectionmustbemadeforthe
valueofthemasswhere:
(7)
Therelationbetweenl andVismorecorrectlygivenby:(seeHall(1966)pp.3334)
(8)
Thefollowingtableisobtainedwhenrelativityeffectsareincluded:
c.Interference/diffraction/coherence
Anideallenssystemobtainsanexactimageoftheobject(eachpointfaithfullyreproduced).Thephenomenaofdiffractionmakesthis
unattainable(Figs.I.5,I.6).
Diffractionphenomenainvolvesthebendingofthepathofradiationpassingclosetoanobstacle(Fig.I.6).Thisresultsinaspreadingofthe
radiationintotheregionbehindtheobstructionthatthewavespassed.Thediffractionatedgescontributestothecontrastatwhichanedgecan
beobserved.Diffractionalsolimitstheresolvingpowerofthemicroscopesincetheimagepointproducedbyalensisadiffractionimageofthe
openingofthelensortheaperturerestrictingtheeffectiveopeningofthelens(Fig.I.5).
Ifthelightsourceandtheplaneatwhichthediffractionpatternisobservedareatfinitedistancesfromtheedge,thephenomenoniscalled
Fresneldiffraction.Thepatternisdescribedasduetointerferencebetweenthenondiffractedlightandawaveoflightdiffractedattheedge.
Theresultingsuperpositiongivesrisetoaseriesofdiffractionfringesorientedparalleltotheedgeandrepresentingperiodicallyvaryingbrightness,
maximaandminima.(Figs.I.7,1.8,I.9).
Coherence:Aprerequisiteforinterferenceisasuperpositionofwavesystemswhosephasedifferenceremainsconstantintime.Twobeams
arecoherentif,whencombined,theyproduceaninterferencepattern.Thebeamsareincoherentwhentheyareincapableofproducingan
interferencepattern.Twobeamsoflightfromselfluminoussourcesareincoherent.Iflightfromthetwosourcesfallsonascreen,theresultant
intensityissimplythesumofthetwointensitieswhichwouldoccurfromeachsourceseparately(Figs.I.10,I.11).Inpracticeanemittingsource
hasfiniteextentandeachpointofthesourcecanbeconsideredtogeneratelight.EachsourcegivesrisetoasystemofFresnelfringesatthe
edge.Thesuperpositionofthesefringesystemsisfairlygoodforthefirstmaximaandminimabutfartherawayfromtheedgeshadowtheoverlap
ofthefringepatternsbecomessufficientlyrandomtomakethefringesdisappear.Thenatureofwaves,phase,amplitude,andinterferenceare
illustratedinFigs.I.12andI.13.
d.Resolution
1)Definitions:
RESOLUTION:abilitytodistinguishcloselyspacedpointsasseparatepoints.
RESOLUTIONLIMIT:smallestseparationofpointswhichcanberecognizedasdistinct.
RESOLVINGPOWER:resolutionachievedbyaparticularinstrumentunderoptimumviewingconditions.
2)Distinctionbetweenresolutionandresolvingpower:
Notethedistinctionbetweenresolutionandresolvingpower.Resolvingpowerisapropertyoftheinstrumentandisaquantitythatmaybe
estimatedontheoreticalgrounds.Resolutionisequaltoorpoorerthantheresolvingpowerandisthequantityobservedunderanygivenset
ofexperimentalconditions.IntheTEM,especiallywithbiologicalsamples,theresolutionachievedmaybeconsiderablyinferiortothetheoretical
resolvingpoweroftheinstrument.
Microscopyisthescienceofseeingtheverysmall.Underidealconditions,theeyeresolvesabout1minuteofarc(=1/60degree=2.9x10
4
radian;recallthereare2p radiansin360°)andsinceitcanfocusdowntoabout250mm,thesmallestobjectwecanresolveisabout0.07mm
(70mm)(Fig.I.14).Thislimitisrelatedtothesizeofthereceptorsintheretinaoftheeye.Thefunctionofamicroscopeistomagnifytheimage
fallingontheretina(Fig.I.15).Theadvantageoflightandelectronmicroscopesisthattheyeffectivelygettheobjectclosertotheeyesoa
magnifiedimageisobtainedandmoredetailcanbediscerned.
TENNISBALLANALOGY:Eyecanresolve3cmat100meters,thusatennisballisclearlyvisible.Butifthetennisballisheldupagainstawhite
background,thevisibilitydecreases(becauseofthedecreaseincontrast).
3)Abbecriteriaofresolution:
Thefundamentalnatureoflightposeslimitsonthedetailthatcanberesolved(Fig.I.16).Abbe(1893)showedthatthesmallestresolvable
distanceisabout1/2thewavelengthoflightused.Thus,1/2thewavelengthoftheradiationusedistheultimateresolvingpowerofany
instrument.Thislimitstheusablemagnificationofopticalmicroscopesto<1000X.Atfirstitwasthoughtthatxraymicroscopeswouldbeuseful
buttherefractiveindexofsubstancesforxraysisnearly=1,thusrefractinglensescannotbemadeforxrays,andconsequently,xrayscannot
beeasilyfocusedtoformimages.
4)Magnificationlimits:
Themaximummagnificationofaninstrumentislimitedaccordingtothefollowingrelationship:
Thus,fortheLM,witharesolvingpowerofapproximately0.25µm,themaximum(useful)magnificationisabout250µm/0.25µm=1000X.Thevalue
usedfortheresolvingpoweroftheeyeinthisexample(250µm)representsamorerealisticviewingcondition.Anymagnificationabovethevalue
givenbytheaboveformularepresentsemptymagnification,sincesuchmagnificationleadstonomoreusefulinformationbutratheramagnified
blur.
AccordingtotheAbbecriteria,at60,000volts,theTEMshouldhavearesolvingpowerofabout0.0025nm.Thisshouldallowamaximumuseful
magnificationofabout100milliontimes!!!Inpractice,themaximumusefulmagnificationoftheTEMoperatedat60kVislimitedtomuchlessthan
1,000,000X.Thus,althoughtheLMnearlyobeystheAbbecriteria,theTEMfallsshortbyaconsiderableamount.Themainlimitingfactorinthe
TEM,withrespecttoachievingthetheoreticalresolvingpoweroftheinstrument,concernsthenatureoftheimaginglensesandtheprocessof
imageformation.
5)Rayleighcriteria(practicalbutarbitrary):(Fig.I.17).
Itistheabilityofmicroscopestomakeobjectpointswhichareclosetogetherappearintheimageasseparatepoints.Anideallenstakeseach
objectpointandrepresentsitexactlyasapointintheimage.Areallenstakeseachobjectpointandspreadsitoutintoacirculardisk(Airy
disk)intheimageplanewhosediameterdependsontheangularapertureofthelens.
Theshortestdistancebetween2disksatwhichthetwodisksappearpartiallyseparatedcorrespondstoabout1/2thewidthofthedisks.The
distance,d,inobjectspaceisgivenby:
d=0.61l /n
•
sina
where
l =wavelenghtoftheradiation
n=refractiveindexofthemedia
a=semiangularapertureofthelens
NOTE:n
•
sina=thenumericalaperture(N.A.)ofthelens.
Thus,tomaximizeresolvingpower,l mustbedecreased,nincreased,oraincreased.Recallthatweareconcernedatthemomentwithan
aberrationfreeopticalsystem.Thevaluefortheconstant(0.61)iscontroversialbecauseitdependsonthecoherenceoftheradiationanda
criteriaofvisibility.
FortheLM,usingoilimmersionoptics(n=1.5),sina=0.87,andvioletlight(l =400nm),d=0.2µm.Theonlywaytoimprovetheresolutionisto
uselightofshorterwavelengthsinceN.A.cannotbeincreasedbeyond~1.5.FortheTEM,n=1(vacuum),sina=10
2
andl =0.005nmfor60kV
electrons,thusd=0.3nm.
I.A.4.Optics(LensTheory)
a.Basiclawsofclassicalgeometricaloptics
1)Rectilinearpropagationoflightwhenn(refractiveindex)isconstant.
2)Lawofreflection:
3)Lawofrefraction(Snell'sLaw):
4)Independenceofrays.Theassumptionismadethatlightraystravelindependentlythroughspace.
Theselawsholdforelectrons,except#4,ifthecurrentdensityistoohighwhennegativechargedelectronscaninterfere.
b.Classicalvs.electronoptics
1)Classicaloptics:Therefractiveindexchangesabruptlyatasurfaceandisconstantbetweenthesurfaces.Therefractionoflightatsurfaces
separatingmediaofdifferentrefractiveindicesmakesitpossibletoconstructimaginglenses.Glasssurfacescanbeshaped.
2)Electronoptics:Here,changesintherefractiveindexaregradualsoraysarecontinuouscurvesratherthanbrokenstraightlines.Refraction
ofelectronsmustbeaccomplishedbyfieldsinspacearoundchargedelectrodesorsolenoids,andthesefieldscanassumeonlycertaindistributions
consistentwithfieldtheory.
c.Geometricalandphysicaloptics
Thefundamentalprinciplesofopticsgovernthedesignandoperationofboththelightandelectronmicroscopes.Thebasicopticalprinciples
involvingtheuseofrefractileelementsorlensesinordertoformmagnifiedimagesareidenticalinboththeLMandTEM.TheTEMdiffersfromthe
LMonlyintheradiationitusesandinthewayinwhichtheradiationisbentorrefracted.
Geometricalopticsdealswiththestudyofthepathsfollowedby'rays'oflightorelectronsthroughlensesandapertures,andthegeometrical
constructionsusedtofindtherelativepositionsandsizesofobjectsandtheirimages.Arayoflightorelectronsisdefinedasaninfinitelythin
pencilorbeam.Physicalopticsshowsthatthisanabstractionandcannotphysicallyexistbecauseof'diffraction'whichdealswiththewave
natureoflightandelectrons.Allresultsobtainedingeometricalopticscanbederivedfromtheprinciplesofphysicaloptics,alongwithother
phenomenasuchasinterferenceanddiffractionwhicharenotexplicableinsimplegeometricalterms.
d.Idealversesreallenses:
Lensesareusedtobendraysoflightorelectronssotheyaredeflectedinapredictablewayfromtheiroriginalpaths.Thepropertiesofanideal
lens,possessinganaxisofrotationalsymmetryare:
1)Eachrayofthebundleofrayswhichpassesfromanobjectpointwillberefractedbytheideallenstomeetinoneimagepoint.
2)Raysoriginatingfrompointswhichlieonaplaneperpendiculartotheaxis,mustbeimagedinaplanewhichisalsoperpendiculartotheaxis.
3)Theimageappearsliketheobjectirrespectiveofthemagnification,sotherelativelineardimensionsoftheobjectarepreservedintheimage.
Inpractice,theimagingbyanyreallensdoesnotcorrespondtothatoftheideallensowingtothefactthatanobjectpointisrepresentedbya
diffractionimage(Airydisc)ofthelensopeningortheapertureusedforrestrictingtheeffectiveopeningofthelens.Thisisaresultofthewave
likepropertiesoflight.Lensaberrationsalsocontributetomoreorlesspronounceddeviationsfromthepropertiesoftheideallens.
Thesinglerefractingsurfaceofsphericalcurvatureisthefundamentalunitoffocusingactionbyglasslenses.Sphericalrefractingsurfacesactas
lensesforparaxialrayswhicharethoseraysthatpassclosetotheprincipalaxisofthelens.RayswithlargeangleswillNOTobeyideallens
action.
Afundamentaldifferencebetweenlightandmagneticlensesisthattheelectronbeamdoesnotchangeinforwardvelocityasitpassesthrough
themagneticfield(lightraysslowdownwhenpassingintoamediumofhigherrefractiveindex).Refractioniscontinuouswithelectronswhenthey
areinthemagneticfield:lightisrefractedonlyattheinterfacebetweenmediaofdifferingrefractiveindex.Theelectronsalsofollowspiral
trajectoriesthroughthemagneticfield(seealsoSec.I.A.5.c(Magneticfieldsandmagneticlenses)
e.Raydiagrams:(Figs.I.20I.28)
Themethodofconstructionofraydiagramsisbasedonthreesimpleprinciples:
1)Allraysenteringthelensparalleltotheaxisarebroughttoacommonpointontheaxis,thefocalpoint.
2)Allrayspassingthroughthegeometricalcenterofthelensareundeviatedandpassstraighton,nomatterfromwhichdirectiontheycome.
3)Principleofreversibility:ifthedirectionofarayisreversedinanysystemtherayexactlyretracesitspaththroughthesystem.Thisapplies
onlytothelocationoflightpathsandnottotheintensityofthelight.
Theaboveprinciplesarebasedontheassumptionsthatwearedealingwithathinlensandconcernedwiththepathsofparaxialrays.The
standardconventionistodrawdiagramswithraysthattravelfromlefttoright.Theobjectistotheleft(infront)ofthelensandtheimageisto
theright(behind)ofthelens.
f.Definitions:
Realimage:oneatwhichlightraysphysicallyreunite,sothataphotographicplateplacedatthepositionofarealimageisexposed.
VirtualImage:onefromwhichlightraysappeartodiverge;raysarenotinfactconcentratedatthepositionofavirtualimage,sothata
photographicplateplacedatthepositionoftheimageisnotexposed(byfocusedrays).Placinganopticalsystemsuchastheeyebehindthe
lens,willenablethedivergentraystobefocusedtoformarealimage.TheintermediatelensofanTEMissometimesusedthiswayinorderto
reducethefinalsizeoftherealimageformedbytheprojectorlens(es).
Converging(positive)lens:bendsraystowardtheaxis.Ithasapositivefocallength.Formsarealinvertedimageofanobjectplacedtothe
leftofthefirstfocalpointandanerectvirtualimageofanobjectplacedbetweenthefirstfocalpointandthelens.
Diverging(negative)lens:bendsthelightraysawayfromtheaxis.Ithasanegativefocallength.Anobjectplacedanywheretotheleftofa
diverginglensresultsinanerectvirtualimage.Itisnotpossibletoconstructanegativemagneticlensalthoughnegativeelectrostaticlensescan
bemade.
g.Lensformula(thinlensequation):
where
f=focallengthofthethinlens(sameradiusofcurvatureforboth
sphericalsurfaces)
o=distanceofobjectfromlens(positivetotheleft)
i=distanceofimagefromthelens(positivetotheright)
NOTE:Foravirtualimage,ihasanegativevalue.
h.Magnification:
Foraconverginglens,iftheobjectismorethantwicethefocallengthfromthelens,thentheimageformedisreal,inverted,andsmallerinsize
thantheobject(M<1).Whentheobjectisatadistance=2f,theimageandobjectarethesamesize(M=1);whenitisbetweenfand2f,
theimageislargerthantheobject(M>1),andwhenitis<f,theimageisvirtual,erect,andlargerthantheobject(M>1).
i.Angularapertureofthelens(2a)(Fig.I.29)
Theaperturedeterminesthetotalamountofradiationarrivingfromtheobjectwhichcanbefocusedto
formanimage.Theaperturethuscontrolstheabilityofthelenstogatherinformationabouttheobject.
Thisdependsontheangleoftheconeofraysitisabletoacceptfromtheobject.Bringinganobject
closertotheeyeincreasestheangularaperture,butthereisalimittotheclosenessthattheobjectcan
bebroughttotheeye(~25cmcorrespondingtoanangleofabout0.9°fora4mmexitpupildiameterof
theeyelens;atypicalLMwithanoilimmersionobjectivelenshas2aof~175°).
j.Simplevs.compoundmicroscope(Figs.I.30I.32)
Inprinciple,arealimageofanydesiredmagnificationcanbeobtainedfromasinglepositivelens,butin
practicethisiscumbersomebecauseofthelonglensimagedistance.Oneormorelensescanbeusedto
magnifytheimageinstages(totalmagnificationequalingtheproductofthemagnificationsofeachlens).
Theimageformedbyonelensconstitutestheobjectforthesubsequentlens,whetherornotareal
intermediateimageisformed.
Comparisonofoneversestwostagemagnification:
Thefollowingdescriptionillustrateshowdifferentpathlengthsarerequiredtoachieveamagnificationof10,000Xusingeitheroneortwolenses
withf=2.0cm.
OneStageSystem:
TwoStageSystem:
Assumebothlenseshavef=2.0cmandarearrangedsoeachgives100Xmagnification.
Thus,M=100=x
i
/x
o
foreachstage.
FirstStage:
x
o
=2.02cm
x
i
=202.00cm
Therealimageformedinthefirststagebecomestheobjectforthesecondlens.
SecondStage:x
o
,x
i
sameasinthefirststage.
Totallengthofsystem
=lengthoffirststage+lengthofsecondstage
=(x
o
+x
i
)+(x
o
+x
i
)
=2(x
o
+x
i
)
=2(2.02+202.00)=408.04cm(4.08meters)
k.Problemset
Thefollowingproblemsareforyourownedificationtotesthowwellyouunderstandthebasicsoflensoptics.
1.Foreachsituationbelow,drawanaccurate(usegraphpaper)raydiagramshowingthepathof(atleasttwo)raysfromtheobjecttoimage.
Indicatewhethertheimageisrealorvirtualandspecifythedistanceoftheimagefromthelensandthemagnificationoftheimagewithrespect
totheobject.Ineachexample,thelensisconverging,withidenticalfrontandbackfocalpoints.Distancesareinarbitraryunits.Letf=lens
focallength,x
o
=distanceofobjectinfrontofthelens,andx
i
=distanceofimagebehindthelens.Theobjectmaybeanysize.
2.Inthefollowingexamples,therearetwoconverginglensesinsuccession.Drawraydiagramsshowingtheformationofboththeintermediate
andfinalimagesandgiveappropriateinformationaboutthenature(real/virtual),positions,andsizesoftheintermediateandfinalimages.What
isthemagnificationateachstageofimageformationandwhatisthemagnificationofthefinalimage?Thedistancefromthecenteroflens1(L1)
tothecenteroflens2(L2)equalsD.
I.A.5.ElectronOptics/ElectronLenses
a.Electronemission
Innershellelectronsinmetalatomsshieldtheelectricfieldofthenucleusthroughtherepulsiveforcestheyexertontheoutershell(valence)
electrons.Thustheattractionbetweenthevalenceelectronsandthenucleusisreduced.Metalatomsarecharacterizedashavingtwoloosely
boundvalenceelectronswhichmigratefreely(thisiswhymetalsaregoodelectricalconductors)andcanescapefromthemetalcompletelyif
sufficientadditionalenergyisimpartedtothem.Asthetemperatureofametalisincreased,thekineticenergyoftheelectronsincreasesbecause
ofincreasedthermalvibrationsofthemetalions,whichcollidemorefrequentlywiththeelectrons.Thermionicemissionisthetermusedto
describetheprocessbywhichthermalenergyissuppliedtolooselyboundelectronsinordertoformasourceofelectrons.
Atroomtemperatureelectronsareeffectivelypreventedfromescapingthesurfaceofthemetalowingtotheattractiveforceofthepositively
chargedions.Asthetemperatureisincreasedsomeelectronsacquiresufficientenergytoovercometheattractionandleavethemetal
temporarily.Metal,shapedasathinwire,caneasilybeheatedbypassinganelectriccurrentthroughit.Sincethemetalsurfacebecomes
positivelycharged,acertainlevelofenergy(workfunction)mustbesuppliedtoallowelectronstoescapefromthesurface.Eachmetalhasa
characteristicworkfunction.Tungsten,withalowworkfunction,emitsmoreelectronsthanmetalswithhigherworkfunctions(seealsopp.2930
andFig.I.59).
Ifastrongelectrostaticfieldisappliedinavacuumbetweenthewire(givenanegative,cathode,potential)andananode,theelectricfieldwill
causeelectronstoaccelerateawayfromthewiretowardstheanodesurface(Fig.I.33).Thespeedoftheelectronsdependsonthestrengthof
theelectrostaticfield(voltage)betweenthecathodeandanode(equation(3),Sec.I.A.3.b)Thenumberofelectronswhichleavethewire
dependsonthetemperaturetowhichthewireisheated,whichdependsonhowmuchfilamentcurrentpassesthroughthewire.
A"V"shapedwirewillhavethehighesttemperatureatthetip.Electronswithdrawnfromthefilamenttipcarryelectricchargestotheanode.This
electriccurrent,whichflowsbetweenthefilamentandtheanode,iscalledthebeamcurrent.
1)Electricfield/Equipotentials
Anelectricallychargedobjecthasassociatedwithitanelectricfield.Thus,anelectricallychargedparticle,whenbroughtnearachargedobject,
isinfluencedbyanelectricalforceinthevicinityoftheobject.Theforceisdirectedtowardthechargedobjectifthechargesareofopposite
signsandawayfromtheobjectiftheyareofsimilarsign.DEFINITION:Thedirectionofanelectricfieldisdefinedasthedirectionoftheforce
actingonapositivecharge.(Figs.I.3435)
Alongthelinesofforceconnectingthetwocharges,theelectricpotentialwillchangegraduallybetweentheextremevaluesrepresentedbythe
twocharges.DEFINITION:Equipotentiallinesdefinethepointsalongthelinesofforcewithidenticalelectricalpotential.Theseequipotential
surfacesarealwaysorientedperpendiculartothelinesofforce.Thechangesintheelectricpotentialaregradualinspace.
Electronswhichenterafieldbetweentwoparallelplatesinadirectionparalleltotheplatesareaffectedbytheforcedirectedperpendicularto
theplates(FigI.36).Theelectronswillbeattractedtowardthepositiveplate.Thepathchangesinaseriesofgradualstepsattheequipotential
surfaces.
FigureI.37showshowtheelectronpathis"refracted"attheequipotentialsurface.TheresultisfundamentallythesameasthatgivenbySnell's
Lawofrefractioninlightoptics.Aconsequenceofthisisthatasphericallycurvedequipotentialsurfaceexhibitsthepropertiesofalens.
FiguresI.38andI.39showhowbothpositive(converging)andnegative(diverging)electrostaticlensescanbeformed.Thisfeatureof
electrostaticlensesdiffersfromelectromagneticlenseswhichcanonlyactasconverginglenses.
2)Advantages/Disadvantagesofelectronlenses:
Thefactthattherefractiveindexdoesnotchangeabruptlyinelectronlenseshasoneadvantageinthattherearenotroublesomereflectionsat
equipotentialsasatglassinterfaces.Thereisaseriousdisadvantageinthatequipotentialscannotbeshapedandcombinedinarbitraryfashionto
correctforchromaticaberrationandothererrors.
Althoughelectronmicroscopeswhichemployelectrostaticlenseshavebeenmade,mostmicroscopesuseelectromagneticlenses.Amajorreason
isthatelectrostaticlensesaremoresensitivetothequalityofthevacuumandcleanlinessofthecomponentsthanareelectromagneticlenses.
Somelensaberrationsaremoresevereforelectrostaticlensescomparedtoelectromagneticlenses.Electrostaticlensesrequireverypowerful
electrostaticfieldswhichcanleadtoelectricalbreakdownor"arcingover"insidethecolumn,especiallyunderpoorvacuumconditions.Forthis
reason,electrostaticlensescannotbemadewithfocallengthsasshortasmagneticlenses.
b.Electrostaticlens
Abasicunderstandingofelectrostaticlensesisimportantfortwomainreasons:i)theelectrongunuseselectrostaticlensactiontoformthe
primarybeamsource,andii)itisquitecommonforachargetodeveloponthenonconductingcontaminationwhichmayaccumulateonphysical
apertures(suchastheobjectiveaperture)andtransformthemintoweakelectrostaticlenseswhichcandistorttheelectronimage.
3)Propertiesofelectrostaticlenses:
a)Anyaxiallysymmetricalelectrostaticfieldhasthepropertiesofalensforraysconfinedtotheparaxialregion.Alltheideallensformulasapply
toelectrostaticlenses.
b)Forelectronlenses,replaceÃ(f)forrefractiveindexinthelensequations(f=valueofthepotentialontheaxis).Intheimageformingsystem
ofmostTEMs,fisthesameonbothsidesofthelens(SeeSec.I.A.5.c).
c)Ifboundedbyregionswherefisconstant,anelectrostaticlensisalwaysconvergent.
c.Magneticfieldsandmagneticlenses
1)Magneticfield
Anelectriccurrentpassingthroughaconductorgivesrisetoamagneticfield.TheconventionisthatNisthedirectioninwhichthelinesofthe
magneticfieldpoint(Fig.I.40).Themagneticfluxisthetotalnumberoflinesandthefluxdensityisthenumberoflinesperunitareaofasurface.
UsetheRIGHThandruletodeterminethedirectionofthefield(thumbpointstowardcurrentdirectionandfingerscurlindirectionoffield.NOTE:
Byconvention,thedirectionofelectronflowisoppositetothatofcurrentflow.
Fluxdensitydependsonthepropertiesofthematerialsurroundingtheconductor.Ironinducesahigherfluxdensitythanairoravacuum.The
propertyofthematerialwhichaffectsthefluxdensityiscalledthepermeability,m,ofthematerial.Forairandvacuum,m=1.0.For
ferromagneticmaterialsitcanbeaslargeasseveralhundredthousand.
Iftheconductorhastheshapeofacircularloop,thelinesofforceformcirclesaroundtheloop.Thefluxdensityisgreatestatthecenterofthe
loop.Themagnetinthecenteroftheloopisorientedperpendiculartotheplaneoftheloopifthecurrentthroughtheloopissufficientlystrongto
eliminatetheinfluenceoftheearth'sfield.ThesideoftheloopatwhichthelinesofforceleavetheloopistheNorth(N)poleofthemagnet(Figs.
I.41,I.42).
Ifthewireiswoundinseveralturnsaroundacylindricalsurface(solenoid),eachturnwillcontributetotheinducedmagneticfield.Theflux
densityinthecenterofthecoilisgivenby:
Inthecaseofairandnonmagneticmaterials,µ=1.0andB=H.
Thepermeabilityofirondependsonthefieldstrength,H,anddecreasestounityathighfieldstrengthorwhenthefluxdensity,B=H(Fig.I.43).
Thehighpermeabilityofironisduetotheinducedmagneticfieldorientingmicroscopiccrystalregionsactingastinymagnetsintheiron.Allthese
tinymagnetsaddtheirmagneticfieldstotheinducedfield(Fig.I.44).Whenallmicromagnetsarenearlyoriented,theironwillaffecttheflux
densitytoadecreasingamountsincethereorientationofmicromagnetsisnearingcompletion.Thus,thepermeabilityofironathighfieldstrengths
approachesthatofemptyspace.Atthispointtheironreachesmagneticsaturation.
2)Hysteresis
Thestrengthofthelensdependstosomeextentonthepreviousmagnetichistoryof
thelens.Whenthecurrentinalensisreduced,thedecreaseinmagnetizationdoes
notretracethesamepathobtainedwhenthecurrentwasincreased(Fig.I.45).
Inductionofmagnetizationinvolvesaphysicalmovementwithinthemagnetized
material,requiringtheovercomeofacertaindegreeofinertia.Asaresult,
magnetizationtendstolagbehindthemagnetizingforceapplied.Inducedmagnetic
fluxcanonlybereturnedtozerobyapplicationofacurrentintheoppositedirection.
Aconsequenceofhysteresisisthatthelevelofcurrentusedtoenergizeamagnetic
lensDOESNOTpreciselyspecifythelensstrength(i.e.focallength).
NormalizationofTEMlensesisaccomplishedbyreducingthelenscurrenttozero
somepredeterminednumberoftimes.Hysteresismayalsobeminimizedbytakinga
lenstosaturationandthenreturningittotheworkingcurrentwithoutovershooting.
Whenthefieldstrengthisreducedtozero,somemagnetizationstillremainsintheiron
(residualmagnetizationorremanence).Anadvantageofsoftironisthefactthat,
whenusedinanelectromagnet,hysteresisislow.
Introductionofpiecesofironinamagneticfielddrasticallyaffectsthefluxdensity.
Magneticmaterialhasashieldingeffect,theeffectbeinggreaterthegreaterthe
permeability.Permalloy(mmetal)hasamaximumpermeabilityof80,000140,000
comparedtoironusedintransformers(~7000).mmetalpermeabilityislimitedtolower
fieldstrengthsthanthatatwhichironstillretainshighpermeability.Thismetalis
thereforeusefulforshieldingtheTEMfromexternalmagneticfields.
d.Theelectromagneticlens
1)Lensdesigndevelopment(Figs.I.46I.48)
Theefficiencyofthemagneticfieldproducedbyashortsolenoidwasfirstimproved
byencasingtheenergizingcoilinasheathofsoftironwhichhasthepropertyofconcentratingthelinesofforceinamagneticfieldandthus
becomingmagnetizedbyinduction.Inthiswayamuchmorepowerfulaxialmagneticfieldisobtainedforthesameamountofcurrentflowing
throughthesolenoid.Furtherdevelopmentinvolvedencasingtheentirecoilwithsoftironexceptatanarrowannulargapintheinsideofthecoil.
Thisproducesagreaterconcentrationofthemagneticfieldalongashortaxialdistance.Toachieveshorterfocallengthlenses(andobtaingreater
magnifications)asoftironpolepiecewithanopenaxialborewasintroducedatthepositionoftheannulargap.
MagneticlensesusedinTEMsarealwaysconstructedwithanironcircuittoproduceahighfieldstrengthacrossashortgap.Themagneticfields
forTEMlensesareintherangeof10,00020,000gauss.
2)Forcesactingonacurrentinamagneticfield
Theforceonanelectroninamagneticfieldisalwaysatrightanglestothevelocityandthedirectionofthefield(Figs.I.49,I.50,andI.52).The
fieldonlyactsonthevelocitycomponentwhichisdirectedperpendiculartothelinesofforce.Usethelefthandrule(Fig.I.51:firstfingerfor
fielddirection,middlefingerforcurrentdirection,andthumbfordirectionofforce).Rayspassingthroughthelensareturnedthroughanangle
whichdoesNOTdependonthedistanceoftheraysfromtheaxis.Allelectronscontainedinagivenmeridionalplanebeforeenteringthefieldare
containedinarotatingmeridionalplaneastheypassthroughthelens,andthentheyleavethelenscoplanar.
Whenelectronsenterthelenstheyencounterasidewaysforcewhichcausestheelectrontorotate
asitcontinuesthroughthelens(Figs.I.53I.57).Sincetheradialcomponentofthemagneticfield
reversesafterthecenterofthelens,therotationalvelocitysetupinthefirsthalfofthelensis
countered.Theelectronenteredthelenswithoutangularmomentumabouttheaxisandleaves
withoutangularmomentum.Theneteffectisadeflectiontowardtheaxis,whichitmustcrossatthe
focalpointf
2
.Theanglebetweentheobjectvectorandtheimagevectoris180°+q,whereas,for
glasslensesandelectrostaticlenses,theanglebetweenarealobjectandtheimageisexactly180°.
Sincetheradialforceisdirectedtowardtheaxis,thelensisconvergentnomatterwhatthedirection
ofthefield.
3)Propertiesofamagneticlens:
Anyaxiallysymmetricmagneticfieldhasthepropertiesofanideallens.Alltheformulasfortheideallensmaybeapplied.
Magneticlensesarealwaysconvergent.Theconventional,axiallysymmetriclensisalwaysboundedbyregionswhicharefieldfree,the
consequencebeingthatthenetactionofelectronlensesisinevitablyconvergent.Limitedregionsmaybedivergentbutnotthelensasawhole.
Theseriousconsequenceofthisisthatneithersphericalorchromaticaberrationscanbecorrectedasisdoneinlightopticsbytheusedoublets
ofpositiveandnegativelenses.
Intheabsenceofelectrostaticfields,therefractiveindexisthesameinobjectandimagespace,thereforef
1
=f
2
.
Electronstravelingthroughaxiallysymmetricfieldsexperienceaspiraltrajectoryofdiminishingradius.Theimagevectorisatanangle180°+qto
theobjectvector.
Thedeflectionoftheelectrontowardstheaxismeansthatanelectronenteringthelensparalleltoitsaxiswillcrosstheaxisafterhavingpassed
thelens.Thedeflectionwillincreasewiththedistancefromtheaxis.Thus,abeamofelectronsinparallelpathsparalleltotheaxisofthelenswill
befocusedtoanimagepointontheaxiswhichrepresentsthesecond(back)focalpointofthelens(f
2
).Notethatmagneticlensesarehighly
inefficientinthatonlyaminorportionofthetotalfieldstrengthisactuallyeffectiveinfocusingtheelectron.
4)Magneticlensfocallength
Inamagneticelectronlensthefocallengthisdeterminedbythefieldstrengthinthelensgapandbythespeedoftheelectrons(determinedby
theacceleratingvoltage).
Formagneticlenses,focusingisachievedbyvaryingthecurrentwhichpassesthroughtheelectromagnet.Thisinturnchangesthestrengthof
themagneticfieldandtherebyaltersthefocallengthofthelensandisequivalenttoacombinedchangeinboththe"refractiveindex"and
"curvatureofsurface".Forabeamofmoreenergeticelectrons,thelenscurrenthastobeincreasedinordertokeepthefocallengthconstant.
FocallengthandcurrentareNOTlinearlyrelated:strengthincreasesinasigmoidfashion(Fig.I.45)ascurrentincreasesuntilapointisreached
wherethelensissaturatedandnofurtherincreaseinlensstrengthcanbeachieved.
Sincethefocallengthofthelensisdirectlyproportionaltotheacceleratingvoltage,avariationinthevelocityoftheelectronsintheimaging
beamaffectsimagequalitybyeliminatingperfectfocus(chromaticaberration).
5)Magneticlensdesign:(Figs.I.46,I.47).
Condenserlensesusuallyhavearelativelylargeboreandspacingwhichresultsinalongfieldandlongfocallength.
Typicalconstructionoftheobjectivelensproducesastrongfieldofshortaxialextent(i.e.shortfocallengthbetween(1.53mm)necessaryfor
formationofimagesathighmagnification.Thespecimenisplacedwithinthemagneticfieldoftheobjectivelens.Thus,anyfieldintroducedby
contaminantsinthespecimencandistortthefieldofthelens.Notethatthisalsomeansthatpartofthelensfield("prefield")isonthefrontside
oftheobjectandaffectstheelectronbeambeforeitpassesthroughtheobject.
Mostofatypicalmagneticlensliesoutsidethevacuumofthemicroscope.Onlythoseregionsthroughwhichtheelectronbeampassesareinhigh
vacuum.Magneticlensesmustbewatercooledtodissipatethelargeamountsofheatproducedbythecurrentsintheelectromagnetcoils.
DATE NAME EVENT
1897 J.J.Thompson Discoverstheelectron
1924 LouisdeBroglie Identifiesawavelengthtomovingelectrons
l =h/mv
where
l =wavelength
h=Planck'sconstant
m=mass
v=velocity
(Foranelectronat60kVl=0.005nm)
1926 H.Busch Magneticorelectricfieldsactaslensesforelectrons
1929 E.Ruska Ph.Dthesisonmagneticlenses
1931 Knoll&Ruska Firstelectronmicroscopebuilt
1931 Davisson&Calbrick Propertiesofelectrostaticlenses
1934 Driest&Muller SurpassresolutionoftheLM
1938 vonBorries&Ruska FirstpracticalEM(Siemens)10nmresolution
1940 RCA CommercialEMwith2.4nmresolution
1945 1.0nmresolution
Fig.I.1Comparisonoflightandelectronmicroscopes.Ineach
instrument,illuminationfromthesource(lamp,filamentinthe
electrongun)isfocusedbythecondenserlensontothespecimen.
Afirstmagnifiedimageisformedbytheobjectivelens.Thisimage
isfurthermagnifiedbytheprojectorlensontoagroundglass
screen(light)orfluorescentscreen(electrons).(FromAgar,p.8)
Fig.I.2CrosssectionalviewofthePhilipsEM300.(FromAgar,p.40)
Toviewtheanimatedmicroscope,clickhere.
Note:QuickTimePlugInrequired
(Thiscanbedownloadedathttp://apple.com/quicktime/download)
Fig.I.3Sectionthroughacomplex
doublecondenser6lensPhilips
EM200electronmicroscope.(From
Meek,p.99)
Fig.I.4Thestatisticalnatureofdiffraction
patterns.(FromHall,p.13)
"Theprecisenatureof'electronwaves'or'matterwaves'isverydifficulttounderstandordescribeinmaterialterms.Electronwavesarenot
electromagneticradiationofthekindtowhichlight,Xraysandradiowavesbelong.Theyconstituteasortofquantumor'packet'ofradiationwhich
accompanieseachindividualelectron,followingitspathandnotradiatingoutwardsfromit."(Meek,1976,pp.4849).
V l (nm)
v(
•
10
10
cm/sec)
v/c
10,000 0.0123 0.593 0.198
50,000 0.0055 1.326 0.442
100,000 0.0039 1.875 0.625
1,000,000 0.0012 5.930 1.977!
V l (nm)
v(
•
10
10
cm/sec)
v/c
10,000 0.0123 0.593 0.195
50,000 0.0055 1.326 0.414
100,000 0.0039 1.875 0.548
1,000,000 0.0012 5.930 0.941
FigI.5Aperfectpointsourcecannotbe
imagedbyalensasaperfectpointimagedue
tothepresenceoftheapertureAB(which
maybetheedgeofthelens).Diffractionat
thisaperturegivesrisetoaseriesoffringes,
whichsurroundtheimageformedofthepoint
source.Thepatternproducediscalledan'Airy'
disk.(FromMeek1sted.,p.35)
Fig.I.6Wheneverawavefrontstrikesa
barrier,itcanbendaroundthecorner'by
givingrisetoasecondarywavefrontatthe
edge,sinceeachpointonthewavefrontcan
giverisetoanewsourceofwaves.This
phenomenoniscalled'diffraction'.(FromMeek
1sted.,p.22)
Fig.I.7Diffractionpattern(right)formedbyanirregularlyshapedaperture
(left).(FromYoung,p.95)
Fig.I.8(a)
Photographof
theedgeofa
razorblade
illuminatedby
monochromatic
(blue)light
rendered
coherentby
passing
througha
narrowslit.(b)
Microdensitometer
tracingofthe
negativefrom
whichthe
photograph
wasmade.
FourFresnel
fringescanbe
distinguished.
(FromMeek1st
ed.,p.27)
(a)
(b)
(a) (c)
(b)
Fig.I.9(a)Fresnelfringesformed
byelectrons.Thesefringesare
formedoutsidetheedgeofahole
(white)inacarbonfilm(black).(b)
Amicrodensitometertracingofthe
fringesystem;thepatternis
identicalwiththeFresnelfringe
systemformedbyvisiblelight(see
Fig.I.8).(c)Anunderfocusedimage
ofaholeinafilm,showinga
completesystemofabout40
Fresnelfringesinsidethehole.
(FromMeek1sted.,pp.2930)
Fig.I.10Diffractionimagesoftwo
easilyresolvedpoints.(From
Slayter,p.243)
Fig.I.11Imagesoftwo
incoherentlyilluminatedpointsat
thelimitofresolution.(a)individual
intensities;(b)summedintensities.
(FromSlayter,p.244)
Fig.I.12Examplesofwhatoccurswhentwo
wavesofthesamewavelengthandequal
amplitudeadd.Ineachexample,thetwo
separatewavesareshownontheleftand
theirsumorresultantwaveontheright.The
differentexamplesarecharacterizedbyvarying
phasedifferences.Thephaseofawave
(usuallyexpressedasafractionofthe
wavelengthorindegrees)isthepositionofa
crestrelativetosomearbitrarypoint.Although
thephaseofagivenwavevarieswithtimeas
thewavetravels,thedifferenceinphaseofthe
twowavesofthesamewavelengthwiththe
samevelocity,isindependentoftime.Such
wavescaninterferewithoneanother.The
resultantwavehasthesamewavelength,l .
(a)Phasedifferencezero.Thewavestotally
reinforceandaresaidtobe"inphase"orto
showconstructiveinterference.
(b)Phasedifferencel /4.Partialreinforcement,
givingawaveofamplitude1.4(intensity2.0).
(c)Phasedifferencel /2.Thewavesare"outof
phase"andthereistotaldestructive
interferencetogivenoresultantwaveora
wavewithamplitude0(intensity0).(From
GluskerandTrueblood,p.19)
Fig.I.13Photographofan
interferencepatterninwater
wavesformedbythe
superpositionofwavesfromtwo
sourcesoscillatinginphasewith
thesamefrequency.(FromYoung,
p.22)
Fig.I.14Theangularapertureofthe
eyeisrelativelysmall.(FromMeek,
1sted.,p.13)
Fig.I.15Increasingtheangular
apertureoftheeyewithalens.The
lensallowstheobjecttobeheld
closertotheeye,whichisthereby
enabledtogathermoreinformation.
(FromMeek1sted.,p.14)
Fig.I.16Theinteractionofwaves
withanobstacle.Theboatridesthe
longwavelengthoceanwave,but
reflectsthesmallwavelength
surfaceripple.Anobserverwho
wishestodetectthepresenceof
theboatcandosoonlyby
observingwaveswhichhave
wavelengthssmallerthan,or
comparableto,thelengthofthe
boat.(FromSherwood,p.19)
Maximummagnification=
resolvingpoweroftheeye
resolvingpowerofthemicroscope
(a)
Fig.I.17(a)TwoAiry
disksrepresenting
twoimagepoints
shownatincreasing
separationfromleft
toright.Inthe
pictureatthe
extremerightthe
twodiskscanbe
distinguishedas
separatedisks.
(b)Theintensity
distributionatanAiry
disk.R,halfwidthof
thecentralmaximum
representedbya
bellshapedcurve.
(c)TheRayleigh
criteriaforresolution.
(FromSjostrand,
p.115)
i=r
Fig.I.18Reflection.(FromSlayter,
p.4)
Fig.I.19Refraction.(FromSlayter,
p.6)
Fig.I.20Principalraydiagramsshowing
imageformationbyaconvexlens.
(a)Whentheobjectdistanceisgreater
thanthefocallength,areal,inverted
imageisformed.
(b)Whentheobjectdistanceisless
thanthefocallength,avirtual,erect
imageisformed;itspositionis
obtainedbyprojectingtheprincipal
raysbackward.Theraysappearto
comefrompointQ.(FromYoung,
p.127)
Fig.I.21Definitionof
principalfocus,F,inimage
spaceofalens.(From
Sjostrand,p.20)
Fig.I.22Focusingeffectoflenson
raysoriginatingfrompointson
principalaxislocatedatdifferent
distancesfromthelens.(From
Sjostrand,p.21)
Fig.I.23Definitionofprincipal
focusinobjectspaceF1ofa
lens.(FromSjostrand,p.21)
Fig.I.24VirtualimageQof
objectpointlocatedbetween
principalfocusinobjectspace
andthelens.(FromSjostrand,
p.21)
Fig.I.25Constructionoftheimage
ofanobjectbymeansofray
tracing.(FromSjostrand,p.22)
Fig.I.26Magnifyingeffectof
apositivelens.(From
Sjostrand,p.22)
Fig.I.27Virtualmagnified
imageofobjectlocated
betweenprincipalfocusin
objectspaceandthelens.
(FromSjostrand,p.22)
Fig.I.28Amagnifyingglassformsan
enlarged,erectvirtualimage.The
angularsizeofthisimageis
approximately4"/15"or4/15.The
angularsizeoftheobjectatthe
closestdistanceforcomfortable
viewingis1"/10"or1/10.The
magnificationinthissituationis(4/15)/
(1/10),or22/3.(FromYoung,p.130)
Fig.I.29Theangularapertureofa
lens.Theangle2a isthe
acceptanceangleofthelens,and
thelargeritcanbemade,themore
informationcanthelenstransmit.A
largelensofhighaperturecan
thereforetellusmoreaboutan
objectthanasmalllensoflow
power.(FromMeek1sted.,p.12)
Fig.I.30Raydiagramforhighmagnification
modeofoperation.Notethateachlens
formsarealimage,withimageinversion.
I0istheimageformedbytheobjective
lensO,I1isformedbythefirstprojector
lensP1andI2bythesecondprojectorP2,
onthescreen.(FromAgar,p.30)
Fig.I.31Left:raydiagramofthe3realimagemediumandhighmagnificationimagingsystemofa3lens
microscope.Center:2realimageverylowor'scan'magnificationrangeofa3lensmicroscope.Right:2real
imagelowmagnificationsystemofa3lensmicroscope.(FromMeek1sted.,pp.118,120121)
Fig.I.32Raydiagramforacompleteelectron
microscope.FilamentF,condenser1lensC1,
condenser2lensC2,condenserapertureCA,
specimenS,objectivelensO,objectiveaperture
OA(inbackfocalplane).1stintermediateimage
andselectorapertureSA.IntermediatelensP1,
secondintermediateimageI2,projectorlensP2
andfinalimageonthefluorescentscreenFC.
(FromAgar,p.35)
a)f=2.0
x
o
=5.0
e)f=4.0
x
o
=3.0
b)f=10.5
x
o
=21.0
f)f=13.3
x
o
=13.3
c)f=3.5
x
o
=3.0
g)f=3.142
x
o
=0.0
d)f=5.0
x
o
=2.5
a)D=8.0
L1:f=2.0
x
o
=4.0
L2:f=3.0
b)D=8.0
L1:f=2.0
x
o
=6.0
L2:f=3.0
c)D=4.0
L1:f=2.0
x
o
=3.0
L2:f=2.0
FigI.33Accelerationofelectronin
electricfield.(FromSjostrand,p.26)
Fig.I.34Linesofforceatapositively
chargedsphericalbody.(FromSjostrand,
p.32)
Fig.I.35Linesofforceandequipotential
surfaces(stippledlines)associatedwith
twoequalchargesofoppositesign.
(FromSjostrand,p.32)
Fig.I.36Equipotentialsurfacesattwoparallel
platesofoppositechargeswiththepathofan
electronindicatedwithinthehomogeneous
partofthefield.(FromSjostrand,p.33)
Fig.I.37Refractionofelectronatan
equipotentialsurface.(FromSjostrand,p.33)
Fig.I.38.Negativelensactionof
electrostaticfieldatanaperturewhen
V2V1>V3V2.(FromSjostrand,
p.34)
Fig.I.39.Positivelensactionatan
aperturewhenV2V1<V3V2.
(FromSjostrand,p.34)
Fig.I.40Magneticfieldinducedbycurrent
passingthroughaconductor.(From
Sjostrand,p.35)
Fig.I.41Magneticfieldinducedbycurrent
passingthroughasolenoid.(From
Sjostrand,p.37)
Fig.I.42Solenoidwithironcore.(From
Sjostrand,p.40)
Fig.I.43a.Dependenceofpermeabilityonfluxdensity,B.
b.RelationshipbetweenfluxdensityBandfieldstrength.
(FromSjostrand,p.38).
Fig.I.44Magnetization.(FromSlayter,
p.361)
Fig.I.45Curves
showinghowthe
magnetizationof
softiron(lens
strength)is
relatedtothe
magnetizing
force(lens
current).An
unmagnetized
lensstartsfrom
thepointOand
followsthepath
OAaslens
current
increases.Atthe
pointA,further
increaseinlens
currentproduces
nofurther
increaseinlens
strength;thelensissaidtobe'saturated'.Whenlenscurrent
isreduced,thepathOAisnotretraced;adifferentpathABis
followed.Thisdisplacementiscalled'hysteresis'.Atzero
current(pointB),someresiduallensstrengthremains;thisis
called'remanence'.Tobringthelensbacktozerostrength,a
reversecurrentOCmustbeapplied.Lensstrengththen
increaseswithincreasingreversecurrent,followingthepath
CD.Thepolarityofthelenschanges,butthisdoesnotaffect
itsfocusingpower;onlythespiralelectronpathisreversed.
Becauseofhysteresis,itisnotpossibletocalibratealens
currentmeteraccuratelyintermsoflensstrengthor
magnification.
Fig.I.46Evolutionofmagneticelectron
lenses.(A)Shortsolenoidusedasa
magneticlens.(B)Softironcasing
enclosingoutersurfaceofthesolenoid,
thusconcentratingthefield.(C)Soft
ironencasingthesolenoidexceptata
narrowannulargaptherebyreducing
themagneticfieldtoaveryshortregion
alongthelensaxis.(D)Modern
objectivelensconsistingofasoftiron
encasedsolenoidandsoftironpole
piecessoastohaveanenormously
concentratedfieldatthelevelofthe
annulargap.(FromWischnizter2nded.,
p.33)
Fig.I.47(a)Amagneticlensconsisting
ofatightlywoundcoilandasoftiron
shroudsurroundingthecoilexceptfor
asmallgap.Thefieldisconcentratedin
thatgap.(b)Shortfocallength
electromagneticlenswithpolepieces.
(FromSjostrand,p.50)
Fig.I.48Fieldstrengthdistribution
curves.ThecurvesADcorrespondto
therespectivelensesillustratedinFig.
I.46.Eachrepresentsthefieldstrength
alongthelongaxisofthelens.The
changesintheshapeofthecurves
representtheshorteningor
concentrationofthefieldovera
shorteraxialdistance.Hz=
longitudinalmagneticfield.Z=
distancealongtheaxisofsymmetry.
(FromWischnizter2nded.,p.33)
Fig.I.49TheforceFactingon
astraightconductorina
homogeneousmagneticfield
offluxdensityBwhencurrent
Iispassedthroughthe
conductor.(FromSjostrand,
p.43)
Fig.I.50Pathofanelectronina
magneticfield.(A)Inalarge,uniform
magneticfield.(B)Inasmall,uniform
magneticfield.(FromWischnitzer2nd
ed.,p.25)
Fig.I.51Lefthandthumbrule.
(FromSjostrand,p.43)
Fig.I.52Thompson'sexperiment.A
streamofelectronsoriginatingfroma
sourceandpassing,invacuo,through
amagneticfieldproducedbyapairof
magnetswillbedeflected.The
directionofdeflectiondemonstrates
thatelectronsarenegativelycharged
particlesofmatter.(FromWischnitzer
2nded.,p.25)
Fig.I.53Actionofasolenoidonan
electronbeam.Anelectriccurrent
passingthroughthecoilproducesan
axialmagneticfield.Thisisthe
refractingmediumfortheelectrons.An
electronstartingatapointontheaxisA
andatanangletoitfollowsaspiral
path,returningtotheaxisatthepoint
B.Theactionisbasicallysimilartothat
oftheconverginglightlensshownin
Fig.I.20.(FromMeek1sted.,p.8)
Fig.I.54Actionofthemagnetic
lens.(a)Inperspective.(b)
Electrontrajectoryin
projection,alongdirectionof
propagation.(c)Electron
trajectoryinprojection,side
view.(FromSlayter,p.358)
Fig.I.55Componentsofthe
vectorHneartheaxisoffields
withaxialsymmetry.His
representedbytwo
components,Hz,the
componentinthez(axial)
direction,andHr,the
compnentinther(radial)
direction.(FromHall,p.85)
Fig.I.56Theycomponentof
themagneticfieldina
magneticlensisoriented
perpendiculartothedirection
ofanelectronenteringthe
lensalongapathparallelto
thelensaxis.Thisy
componentwillaffectthe
electron,deflectingitinthex
directionasindicatedbythe
arrowmarkedvx.(From
Sjostrand,p.48)
Fig.I.57Thezcomponentofthemagneticfield
andthexvelocitycomponentoftheelectron
inamagneticlensinteract,deflectingthe
electronintheydirectiontowardthelens
axis.(FromSjostrand,p.49)
CuuDuongThanCong.com https://fb.com/tailieudientucntt
cuu duong than cong . com

I.THEMICROSCOPE
I.A.PRINCIPLESOFTHETRANSMISSIONELECTRONMICROSCOPE(TEM)
I.A.1.OriginoftheTransmissionElectronMicroscope
I.A.2.ComparisonofLight(LM)andElectronMicroscopes(Fig.I.1)
a.Similarities(Arrangementandfunctionofcomponentsaresimilar)
1)Illuminationsystem:producesrequiredradiationanddirectsitontothespecimen.Consistsofasource,whichemitstheradiation,anda
condenserlens,whichfocusestheilluminatingbeam(allowingvariationsofintensitytobemade)onthespecimen.
2)Specimenstage:situatedbetweentheilluminationandimagingsystems.
3)Imagingsystem:Lenseswhichtogetherproducethefinalmagnifiedimageofthespecimen.Consistsofi)anobjectivelenswhichfocusesthe
beamafteritpassesthroughthespecimenandformsanintermediateimageofthespecimenandii)theprojectorlens(es)whichmagnifiesa
portionoftheintermediateimagetoformthefinalimage.
4)Imagerecordingsystem:Convertstheradiationintoapermanentimage(typicallyonaphotographicemulsion)thatcanbeviewed.
b.Differences
1)Opticallensesaregenerallymadeofglasswithfixedfocallengthswhereasmagneticlensesareconstructedwithferromagneticmaterialsand
windingsofcopperwireproducingafocallengthwhichcanbechangedbyvaryingthecurrentthroughthecoil.
2)MagnificationintheLMisgenerallychangedbyswitchingbetweendifferentpowerobjectivelensesmountedonarotatingturretabovethe
specimen.Itcanalsobechangedifoculars(eyepieces)ofdifferentpowerareused.IntheTEMthemagnification(focallength)oftheobjective
remainsfixedwhilethefocallengthoftheprojectorlensischangedtovarymagnification.
3)TheLMhasasmalldepthoffield,thusdifferentfocallevelscanbeseeninthespecimen.Thelarge(relative)depthoffieldintheTEMmeans
thattheentire(thin)specimenisinfocussimultaneously.
4)Mechanismsofimageformationvary(phaseandamplitudecontrast).
5)TEMsaregenerallyconstructedwiththeradiationsourceatthetopoftheinstrument:thesourceisgenerallysituatedatthebottomofLMs.
6)TEMisoperatedathighvacuum(sincethemeanfreepathofelectronsinairisverysmall)somostspecimens(biological)mustbedehydrated
(i.e.dead!!).
7)TEMspecimens(biological)arerapidlydamagedbytheelectronbeam.
8)TEMscanachievehighermagnificationandbetterresolutionthanLMs.
9)Pricetag!!!(100xmorethanLM)
I.A.3.Photons/Electrons
a.Dualconceptofwaveandparticle(Fig.I.4)
Lighthaspropertiesbothofaparticleandawave.Thisdualnatureisrequiredtosatisfactorilyexplaintheresultsofvariousphysicalexperiments.
Thediffractionoflight(bendingaroundcorners)illustratesthewavenature.TheWAVETHEORYisbasedonthestatisticalnatureofeventsand
haslittlemeaningwithrespecttothebehaviorofsingleparticles.ThewavetheorywasdevelopedandexpoundedbyHuygens(16291695)and
Hooke(16381703).TheCORPUSCULARTHEORYwasproposedbyNewton(16421727)andbecamethemoreacceptedtheoryevenafter
demonstrationofdiffractionbyYoung(17731829)andinterferencebyFresnel(17881827).Atabout1850,thewavetheorycamebackinto
favoruntilabout1900whenmoreevidenceforthecorpusculartheorywasdiscovered.
QUANTUMTHEORY(PlanckandEinstein)providesthebasisforexplainingthephenomenaofINTERFERENCE,DIFFRACTIONandthe
PHOTOELECTRICeffect(lightfallingoncertainmetalscausethemtoemitelectrons)andthusformsacommonbasisforexplainingthenatureof
actionoflight.Thetransferofenergybetweenlightandmatteroccursonlyindiscretequantitiesproportionaltothefrequencyofthe
lightwave.
E=hJ
where
E=energyofphoton(joules)
h=Planck'sconstant(6.624
•
10
34
joulesec)
J=frequency(cycles/sec)
b.Electronvelocityandwavelength
Therelationbetweenthewavelength(l )ofaparticleofmass,m,movingatavelocity,v,isgivenbytheDeBrogliewaveequation:
(1)
Anelectronofchargee(1.6
•
10
19
coulomb),andmassm(9.11
•
10
28
gm),whenpassingthroughapotentialdifferenceofVvolts(expressedin
joules/coulomb),hasakineticenergy:
(2)
Solvingforvelocity:
(3)
substitutingintotheDeBroglieequation(1):
(4)
Since1joule=10
7
dyne
•
cm=10
7
cm
2
•
gm/sec
2
(5)
Thus,forexample,ifV=60,000volts,l =0.005nm.
Fromequation(3)theelectronvelocitycanbecalculatedifVisknown:
(6)
Thefollowingtableillustratesthat,athighvoltage,electronvelocityiscomparabletothespeedoflightinavacuum(c=3
•
10
10
cm/sec).
Theequationbreaksdownwhenthevelocityoftheelectronapproachesthespeedoflightbecausearelativisticcorrectionmustbemadeforthe
valueofthemasswhere:
(7)
Therelationbetweenl andVismorecorrectlygivenby:(seeHall(1966)pp.3334)
(8)
Thefollowingtableisobtainedwhenrelativityeffectsareincluded:
c.Interference/diffraction/coherence
Anideallenssystemobtainsanexactimageoftheobject(eachpointfaithfullyreproduced).Thephenomenaofdiffractionmakesthis
unattainable(Figs.I.5,I.6).
Diffractionphenomenainvolvesthebendingofthepathofradiationpassingclosetoanobstacle(Fig.I.6).Thisresultsinaspreadingofthe
radiationintotheregionbehindtheobstructionthatthewavespassed.Thediffractionatedgescontributestothecontrastatwhichanedgecan
beobserved.Diffractionalsolimitstheresolvingpowerofthemicroscopesincetheimagepointproducedbyalensisadiffractionimageofthe
openingofthelensortheaperturerestrictingtheeffectiveopeningofthelens(Fig.I.5).
Ifthelightsourceandtheplaneatwhichthediffractionpatternisobservedareatfinitedistancesfromtheedge,thephenomenoniscalled
Fresneldiffraction.Thepatternisdescribedasduetointerferencebetweenthenondiffractedlightandawaveoflightdiffractedattheedge.
Theresultingsuperpositiongivesrisetoaseriesofdiffractionfringesorientedparalleltotheedgeandrepresentingperiodicallyvaryingbrightness,
maximaandminima.(Figs.I.7,1.8,I.9).
Coherence:Aprerequisiteforinterferenceisasuperpositionofwavesystemswhosephasedifferenceremainsconstantintime.Twobeams
arecoherentif,whencombined,theyproduceaninterferencepattern.Thebeamsareincoherentwhentheyareincapableofproducingan
interferencepattern.Twobeamsoflightfromselfluminoussourcesareincoherent.Iflightfromthetwosourcesfallsonascreen,theresultant
intensityissimplythesumofthetwointensitieswhichwouldoccurfromeachsourceseparately(Figs.I.10,I.11).Inpracticeanemittingsource
hasfiniteextentandeachpointofthesourcecanbeconsideredtogeneratelight.EachsourcegivesrisetoasystemofFresnelfringesatthe
edge.Thesuperpositionofthesefringesystemsisfairlygoodforthefirstmaximaandminimabutfartherawayfromtheedgeshadowtheoverlap
ofthefringepatternsbecomessufficientlyrandomtomakethefringesdisappear.Thenatureofwaves,phase,amplitude,andinterferenceare
illustratedinFigs.I.12andI.13.
d.Resolution
1)Definitions:
RESOLUTION:abilitytodistinguishcloselyspacedpointsasseparatepoints.
RESOLUTIONLIMIT:smallestseparationofpointswhichcanberecognizedasdistinct.
RESOLVINGPOWER:resolutionachievedbyaparticularinstrumentunderoptimumviewingconditions.
2)Distinctionbetweenresolutionandresolvingpower:
Notethedistinctionbetweenresolutionandresolvingpower.Resolvingpowerisapropertyoftheinstrumentandisaquantitythatmaybe
estimatedontheoreticalgrounds.Resolutionisequaltoorpoorerthantheresolvingpowerandisthequantityobservedunderanygivenset
ofexperimentalconditions.IntheTEM,especiallywithbiologicalsamples,theresolutionachievedmaybeconsiderablyinferiortothetheoretical
resolvingpoweroftheinstrument.
Microscopyisthescienceofseeingtheverysmall.Underidealconditions,theeyeresolvesabout1minuteofarc(=1/60degree=2.9x10
4
radian;recallthereare2p radiansin360°)andsinceitcanfocusdowntoabout250mm,thesmallestobjectwecanresolveisabout0.07mm
(70mm)(Fig.I.14).Thislimitisrelatedtothesizeofthereceptorsintheretinaoftheeye.Thefunctionofamicroscopeistomagnifytheimage
fallingontheretina(Fig.I.15).Theadvantageoflightandelectronmicroscopesisthattheyeffectivelygettheobjectclosertotheeyesoa
magnifiedimageisobtainedandmoredetailcanbediscerned.
TENNISBALLANALOGY:Eyecanresolve3cmat100meters,thusatennisballisclearlyvisible.Butifthetennisballisheldupagainstawhite
background,thevisibilitydecreases(becauseofthedecreaseincontrast).
3)Abbecriteriaofresolution:
Thefundamentalnatureoflightposeslimitsonthedetailthatcanberesolved(Fig.I.16).Abbe(1893)showedthatthesmallestresolvable
distanceisabout1/2thewavelengthoflightused.Thus,1/2thewavelengthoftheradiationusedistheultimateresolvingpowerofany
instrument.Thislimitstheusablemagnificationofopticalmicroscopesto<1000X.Atfirstitwasthoughtthatxraymicroscopeswouldbeuseful
buttherefractiveindexofsubstancesforxraysisnearly=1,thusrefractinglensescannotbemadeforxrays,andconsequently,xrayscannot
beeasilyfocusedtoformimages.
4)Magnificationlimits:
Themaximummagnificationofaninstrumentislimitedaccordingtothefollowingrelationship:
Thus,fortheLM,witharesolvingpowerofapproximately0.25µm,themaximum(useful)magnificationisabout250µm/0.25µm=1000X.Thevalue
usedfortheresolvingpoweroftheeyeinthisexample(250µm)representsamorerealisticviewingcondition.Anymagnificationabovethevalue
givenbytheaboveformularepresentsemptymagnification,sincesuchmagnificationleadstonomoreusefulinformationbutratheramagnified
blur.
AccordingtotheAbbecriteria,at60,000volts,theTEMshouldhavearesolvingpowerofabout0.0025nm.Thisshouldallowamaximumuseful
magnificationofabout100milliontimes!!!Inpractice,themaximumusefulmagnificationoftheTEMoperatedat60kVislimitedtomuchlessthan
1,000,000X.Thus,althoughtheLMnearlyobeystheAbbecriteria,theTEMfallsshortbyaconsiderableamount.Themainlimitingfactorinthe
TEM,withrespecttoachievingthetheoreticalresolvingpoweroftheinstrument,concernsthenatureoftheimaginglensesandtheprocessof
imageformation.
5)Rayleighcriteria(practicalbutarbitrary):(Fig.I.17).
Itistheabilityofmicroscopestomakeobjectpointswhichareclosetogetherappearintheimageasseparatepoints.Anideallenstakeseach
objectpointandrepresentsitexactlyasapointintheimage.Areallenstakeseachobjectpointandspreadsitoutintoacirculardisk(Airy
disk)intheimageplanewhosediameterdependsontheangularapertureofthelens.
Theshortestdistancebetween2disksatwhichthetwodisksappearpartiallyseparatedcorrespondstoabout1/2thewidthofthedisks.The
distance,d,inobjectspaceisgivenby:
d=0.61l /n
•
sina
where
l =wavelenghtoftheradiation
n=refractiveindexofthemedia
a=semiangularapertureofthelens
NOTE:n
•
sina=thenumericalaperture(N.A.)ofthelens.
Thus,tomaximizeresolvingpower,l mustbedecreased,nincreased,oraincreased.Recallthatweareconcernedatthemomentwithan
aberrationfreeopticalsystem.Thevaluefortheconstant(0.61)iscontroversialbecauseitdependsonthecoherenceoftheradiationanda
criteriaofvisibility.
FortheLM,usingoilimmersionoptics(n=1.5),sina=0.87,andvioletlight(l =400nm),d=0.2µm.Theonlywaytoimprovetheresolutionisto
uselightofshorterwavelengthsinceN.A.cannotbeincreasedbeyond~1.5.FortheTEM,n=1(vacuum),sina=10
2
andl =0.005nmfor60kV
electrons,thusd=0.3nm.
I.A.4.Optics(LensTheory)
a.Basiclawsofclassicalgeometricaloptics
1)Rectilinearpropagationoflightwhenn(refractiveindex)isconstant.
2)Lawofreflection:
3)Lawofrefraction(Snell'sLaw):
4)Independenceofrays.Theassumptionismadethatlightraystravelindependentlythroughspace.
Theselawsholdforelectrons,except#4,ifthecurrentdensityistoohighwhennegativechargedelectronscaninterfere.
b.Classicalvs.electronoptics
1)Classicaloptics:Therefractiveindexchangesabruptlyatasurfaceandisconstantbetweenthesurfaces.Therefractionoflightatsurfaces
separatingmediaofdifferentrefractiveindicesmakesitpossibletoconstructimaginglenses.Glasssurfacescanbeshaped.
2)Electronoptics:Here,changesintherefractiveindexaregradualsoraysarecontinuouscurvesratherthanbrokenstraightlines.Refraction
ofelectronsmustbeaccomplishedbyfieldsinspacearoundchargedelectrodesorsolenoids,andthesefieldscanassumeonlycertaindistributions
consistentwithfieldtheory.
c.Geometricalandphysicaloptics
Thefundamentalprinciplesofopticsgovernthedesignandoperationofboththelightandelectronmicroscopes.Thebasicopticalprinciples
involvingtheuseofrefractileelementsorlensesinordertoformmagnifiedimagesareidenticalinboththeLMandTEM.TheTEMdiffersfromthe
LMonlyintheradiationitusesandinthewayinwhichtheradiationisbentorrefracted.
Geometricalopticsdealswiththestudyofthepathsfollowedby'rays'oflightorelectronsthroughlensesandapertures,andthegeometrical
constructionsusedtofindtherelativepositionsandsizesofobjectsandtheirimages.Arayoflightorelectronsisdefinedasaninfinitelythin
pencilorbeam.Physicalopticsshowsthatthisanabstractionandcannotphysicallyexistbecauseof'diffraction'whichdealswiththewave
natureoflightandelectrons.Allresultsobtainedingeometricalopticscanbederivedfromtheprinciplesofphysicaloptics,alongwithother
phenomenasuchasinterferenceanddiffractionwhicharenotexplicableinsimplegeometricalterms.
d.Idealversesreallenses:
Lensesareusedtobendraysoflightorelectronssotheyaredeflectedinapredictablewayfromtheiroriginalpaths.Thepropertiesofanideal
lens,possessinganaxisofrotationalsymmetryare:
1)Eachrayofthebundleofrayswhichpassesfromanobjectpointwillberefractedbytheideallenstomeetinoneimagepoint.
2)Raysoriginatingfrompointswhichlieonaplaneperpendiculartotheaxis,mustbeimagedinaplanewhichisalsoperpendiculartotheaxis.
3)Theimageappearsliketheobjectirrespectiveofthemagnification,sotherelativelineardimensionsoftheobjectarepreservedintheimage.
Inpractice,theimagingbyanyreallensdoesnotcorrespondtothatoftheideallensowingtothefactthatanobjectpointisrepresentedbya
diffractionimage(Airydisc)ofthelensopeningortheapertureusedforrestrictingtheeffectiveopeningofthelens.Thisisaresultofthewave
likepropertiesoflight.Lensaberrationsalsocontributetomoreorlesspronounceddeviationsfromthepropertiesoftheideallens.
Thesinglerefractingsurfaceofsphericalcurvatureisthefundamentalunitoffocusingactionbyglasslenses.Sphericalrefractingsurfacesactas
lensesforparaxialrayswhicharethoseraysthatpassclosetotheprincipalaxisofthelens.RayswithlargeangleswillNOTobeyideallens
action.
Afundamentaldifferencebetweenlightandmagneticlensesisthattheelectronbeamdoesnotchangeinforwardvelocityasitpassesthrough
themagneticfield(lightraysslowdownwhenpassingintoamediumofhigherrefractiveindex).Refractioniscontinuouswithelectronswhenthey
areinthemagneticfield:lightisrefractedonlyattheinterfacebetweenmediaofdifferingrefractiveindex.Theelectronsalsofollowspiral
trajectoriesthroughthemagneticfield(seealsoSec.I.A.5.c(Magneticfieldsandmagneticlenses)
e.Raydiagrams:(Figs.I.20I.28)
Themethodofconstructionofraydiagramsisbasedonthreesimpleprinciples:
1)Allraysenteringthelensparalleltotheaxisarebroughttoacommonpointontheaxis,thefocalpoint.
2)Allrayspassingthroughthegeometricalcenterofthelensareundeviatedandpassstraighton,nomatterfromwhichdirectiontheycome.
3)Principleofreversibility:ifthedirectionofarayisreversedinanysystemtherayexactlyretracesitspaththroughthesystem.Thisapplies
onlytothelocationoflightpathsandnottotheintensityofthelight.
Theaboveprinciplesarebasedontheassumptionsthatwearedealingwithathinlensandconcernedwiththepathsofparaxialrays.The
standardconventionistodrawdiagramswithraysthattravelfromlefttoright.Theobjectistotheleft(infront)ofthelensandtheimageisto
theright(behind)ofthelens.
f.Definitions:
Realimage:oneatwhichlightraysphysicallyreunite,sothataphotographicplateplacedatthepositionofarealimageisexposed.
VirtualImage:onefromwhichlightraysappeartodiverge;raysarenotinfactconcentratedatthepositionofavirtualimage,sothata
photographicplateplacedatthepositionoftheimageisnotexposed(byfocusedrays).Placinganopticalsystemsuchastheeyebehindthe
lens,willenablethedivergentraystobefocusedtoformarealimage.TheintermediatelensofanTEMissometimesusedthiswayinorderto
reducethefinalsizeoftherealimageformedbytheprojectorlens(es).
Converging(positive)lens:bendsraystowardtheaxis.Ithasapositivefocallength.Formsarealinvertedimageofanobjectplacedtothe
leftofthefirstfocalpointandanerectvirtualimageofanobjectplacedbetweenthefirstfocalpointandthelens.
Diverging(negative)lens:bendsthelightraysawayfromtheaxis.Ithasanegativefocallength.Anobjectplacedanywheretotheleftofa
diverginglensresultsinanerectvirtualimage.Itisnotpossibletoconstructanegativemagneticlensalthoughnegativeelectrostaticlensescan
bemade.
g.Lensformula(thinlensequation):
where
f=focallengthofthethinlens(sameradiusofcurvatureforboth
sphericalsurfaces)
o=distanceofobjectfromlens(positivetotheleft)
i=distanceofimagefromthelens(positivetotheright)
NOTE:Foravirtualimage,ihasanegativevalue.
h.Magnification:
Foraconverginglens,iftheobjectismorethantwicethefocallengthfromthelens,thentheimageformedisreal,inverted,andsmallerinsize
thantheobject(M<1).Whentheobjectisatadistance=2f,theimageandobjectarethesamesize(M=1);whenitisbetweenfand2f,
theimageislargerthantheobject(M>1),andwhenitis<f,theimageisvirtual,erect,andlargerthantheobject(M>1).
i.Angularapertureofthelens(2a)(Fig.I.29)
Theaperturedeterminesthetotalamountofradiationarrivingfromtheobjectwhichcanbefocusedto
formanimage.Theaperturethuscontrolstheabilityofthelenstogatherinformationabouttheobject.
Thisdependsontheangleoftheconeofraysitisabletoacceptfromtheobject.Bringinganobject
closertotheeyeincreasestheangularaperture,butthereisalimittotheclosenessthattheobjectcan
bebroughttotheeye(~25cmcorrespondingtoanangleofabout0.9°fora4mmexitpupildiameterof
theeyelens;atypicalLMwithanoilimmersionobjectivelenshas2aof~175°).
j.Simplevs.compoundmicroscope(Figs.I.30I.32)
Inprinciple,arealimageofanydesiredmagnificationcanbeobtainedfromasinglepositivelens,butin
practicethisiscumbersomebecauseofthelonglensimagedistance.Oneormorelensescanbeusedto
magnifytheimageinstages(totalmagnificationequalingtheproductofthemagnificationsofeachlens).
Theimageformedbyonelensconstitutestheobjectforthesubsequentlens,whetherornotareal
intermediateimageisformed.
Comparisonofoneversestwostagemagnification:
Thefollowingdescriptionillustrateshowdifferentpathlengthsarerequiredtoachieveamagnificationof10,000Xusingeitheroneortwolenses
withf=2.0cm.
OneStageSystem:
TwoStageSystem:
Assumebothlenseshavef=2.0cmandarearrangedsoeachgives100Xmagnification.
Thus,M=100=x
i
/x
o
foreachstage.
FirstStage:
x
o
=2.02cm
x
i
=202.00cm
Therealimageformedinthefirststagebecomestheobjectforthesecondlens.
SecondStage:x
o
,x
i
sameasinthefirststage.
Totallengthofsystem
=lengthoffirststage+lengthofsecondstage
=(x
o
+x
i
)+(x
o
+x
i
)
=2(x
o
+x
i
)
=2(2.02+202.00)=408.04cm(4.08meters)
k.Problemset
Thefollowingproblemsareforyourownedificationtotesthowwellyouunderstandthebasicsoflensoptics.
1.Foreachsituationbelow,drawanaccurate(usegraphpaper)raydiagramshowingthepathof(atleasttwo)raysfromtheobjecttoimage.
Indicatewhethertheimageisrealorvirtualandspecifythedistanceoftheimagefromthelensandthemagnificationoftheimagewithrespect
totheobject.Ineachexample,thelensisconverging,withidenticalfrontandbackfocalpoints.Distancesareinarbitraryunits.Letf=lens
focallength,x
o
=distanceofobjectinfrontofthelens,andx
i
=distanceofimagebehindthelens.Theobjectmaybeanysize.
2.Inthefollowingexamples,therearetwoconverginglensesinsuccession.Drawraydiagramsshowingtheformationofboththeintermediate
andfinalimagesandgiveappropriateinformationaboutthenature(real/virtual),positions,andsizesoftheintermediateandfinalimages.What
isthemagnificationateachstageofimageformationandwhatisthemagnificationofthefinalimage?Thedistancefromthecenteroflens1(L1)
tothecenteroflens2(L2)equalsD.
I.A.5.ElectronOptics/ElectronLenses
a.Electronemission
Innershellelectronsinmetalatomsshieldtheelectricfieldofthenucleusthroughtherepulsiveforcestheyexertontheoutershell(valence)
electrons.Thustheattractionbetweenthevalenceelectronsandthenucleusisreduced.Metalatomsarecharacterizedashavingtwoloosely
boundvalenceelectronswhichmigratefreely(thisiswhymetalsaregoodelectricalconductors)andcanescapefromthemetalcompletelyif
sufficientadditionalenergyisimpartedtothem.Asthetemperatureofametalisincreased,thekineticenergyoftheelectronsincreasesbecause
ofincreasedthermalvibrationsofthemetalions,whichcollidemorefrequentlywiththeelectrons.Thermionicemissionisthetermusedto
describetheprocessbywhichthermalenergyissuppliedtolooselyboundelectronsinordertoformasourceofelectrons.
Atroomtemperatureelectronsareeffectivelypreventedfromescapingthesurfaceofthemetalowingtotheattractiveforceofthepositively
chargedions.Asthetemperatureisincreasedsomeelectronsacquiresufficientenergytoovercometheattractionandleavethemetal
temporarily.Metal,shapedasathinwire,caneasilybeheatedbypassinganelectriccurrentthroughit.Sincethemetalsurfacebecomes
positivelycharged,acertainlevelofenergy(workfunction)mustbesuppliedtoallowelectronstoescapefromthesurface.Eachmetalhasa
characteristicworkfunction.Tungsten,withalowworkfunction,emitsmoreelectronsthanmetalswithhigherworkfunctions(seealsopp.2930
andFig.I.59).
Ifastrongelectrostaticfieldisappliedinavacuumbetweenthewire(givenanegative,cathode,potential)andananode,theelectricfieldwill
causeelectronstoaccelerateawayfromthewiretowardstheanodesurface(Fig.I.33).Thespeedoftheelectronsdependsonthestrengthof
theelectrostaticfield(voltage)betweenthecathodeandanode(equation(3),Sec.I.A.3.b)Thenumberofelectronswhichleavethewire
dependsonthetemperaturetowhichthewireisheated,whichdependsonhowmuchfilamentcurrentpassesthroughthewire.
A"V"shapedwirewillhavethehighesttemperatureatthetip.Electronswithdrawnfromthefilamenttipcarryelectricchargestotheanode.This
electriccurrent,whichflowsbetweenthefilamentandtheanode,iscalledthebeamcurrent.
1)Electricfield/Equipotentials
Anelectricallychargedobjecthasassociatedwithitanelectricfield.Thus,anelectricallychargedparticle,whenbroughtnearachargedobject,
isinfluencedbyanelectricalforceinthevicinityoftheobject.Theforceisdirectedtowardthechargedobjectifthechargesareofopposite
signsandawayfromtheobjectiftheyareofsimilarsign.DEFINITION:Thedirectionofanelectricfieldisdefinedasthedirectionoftheforce
actingonapositivecharge.(Figs.I.3435)
Alongthelinesofforceconnectingthetwocharges,theelectricpotentialwillchangegraduallybetweentheextremevaluesrepresentedbythe
twocharges.DEFINITION:Equipotentiallinesdefinethepointsalongthelinesofforcewithidenticalelectricalpotential.Theseequipotential
surfacesarealwaysorientedperpendiculartothelinesofforce.Thechangesintheelectricpotentialaregradualinspace.
Electronswhichenterafieldbetweentwoparallelplatesinadirectionparalleltotheplatesareaffectedbytheforcedirectedperpendicularto
theplates(FigI.36).Theelectronswillbeattractedtowardthepositiveplate.Thepathchangesinaseriesofgradualstepsattheequipotential
surfaces.
FigureI.37showshowtheelectronpathis"refracted"attheequipotentialsurface.TheresultisfundamentallythesameasthatgivenbySnell's
Lawofrefractioninlightoptics.Aconsequenceofthisisthatasphericallycurvedequipotentialsurfaceexhibitsthepropertiesofalens.
FiguresI.38andI.39showhowbothpositive(converging)andnegative(diverging)electrostaticlensescanbeformed.Thisfeatureof
electrostaticlensesdiffersfromelectromagneticlenseswhichcanonlyactasconverginglenses.
2)Advantages/Disadvantagesofelectronlenses:
Thefactthattherefractiveindexdoesnotchangeabruptlyinelectronlenseshasoneadvantageinthattherearenotroublesomereflectionsat
equipotentialsasatglassinterfaces.Thereisaseriousdisadvantageinthatequipotentialscannotbeshapedandcombinedinarbitraryfashionto
correctforchromaticaberrationandothererrors.
Althoughelectronmicroscopeswhichemployelectrostaticlenseshavebeenmade,mostmicroscopesuseelectromagneticlenses.Amajorreason
isthatelectrostaticlensesaremoresensitivetothequalityofthevacuumandcleanlinessofthecomponentsthanareelectromagneticlenses.
Somelensaberrationsaremoresevereforelectrostaticlensescomparedtoelectromagneticlenses.Electrostaticlensesrequireverypowerful
electrostaticfieldswhichcanleadtoelectricalbreakdownor"arcingover"insidethecolumn,especiallyunderpoorvacuumconditions.Forthis
reason,electrostaticlensescannotbemadewithfocallengthsasshortasmagneticlenses.
b.Electrostaticlens
Abasicunderstandingofelectrostaticlensesisimportantfortwomainreasons:i)theelectrongunuseselectrostaticlensactiontoformthe
primarybeamsource,andii)itisquitecommonforachargetodeveloponthenonconductingcontaminationwhichmayaccumulateonphysical
apertures(suchastheobjectiveaperture)andtransformthemintoweakelectrostaticlenseswhichcandistorttheelectronimage.
3)Propertiesofelectrostaticlenses:
a)Anyaxiallysymmetricalelectrostaticfieldhasthepropertiesofalensforraysconfinedtotheparaxialregion.Alltheideallensformulasapply
toelectrostaticlenses.
b)Forelectronlenses,replaceÃ(f)forrefractiveindexinthelensequations(f=valueofthepotentialontheaxis).Intheimageformingsystem
ofmostTEMs,fisthesameonbothsidesofthelens(SeeSec.I.A.5.c).
c)Ifboundedbyregionswherefisconstant,anelectrostaticlensisalwaysconvergent.
c.Magneticfieldsandmagneticlenses
1)Magneticfield
Anelectriccurrentpassingthroughaconductorgivesrisetoamagneticfield.TheconventionisthatNisthedirectioninwhichthelinesofthe
magneticfieldpoint(Fig.I.40).Themagneticfluxisthetotalnumberoflinesandthefluxdensityisthenumberoflinesperunitareaofasurface.
UsetheRIGHThandruletodeterminethedirectionofthefield(thumbpointstowardcurrentdirectionandfingerscurlindirectionoffield.NOTE:
Byconvention,thedirectionofelectronflowisoppositetothatofcurrentflow.
Fluxdensitydependsonthepropertiesofthematerialsurroundingtheconductor.Ironinducesahigherfluxdensitythanairoravacuum.The
propertyofthematerialwhichaffectsthefluxdensityiscalledthepermeability,m,ofthematerial.Forairandvacuum,m=1.0.For
ferromagneticmaterialsitcanbeaslargeasseveralhundredthousand.
Iftheconductorhastheshapeofacircularloop,thelinesofforceformcirclesaroundtheloop.Thefluxdensityisgreatestatthecenterofthe
loop.Themagnetinthecenteroftheloopisorientedperpendiculartotheplaneoftheloopifthecurrentthroughtheloopissufficientlystrongto
eliminatetheinfluenceoftheearth'sfield.ThesideoftheloopatwhichthelinesofforceleavetheloopistheNorth(N)poleofthemagnet(Figs.
I.41,I.42).
Ifthewireiswoundinseveralturnsaroundacylindricalsurface(solenoid),eachturnwillcontributetotheinducedmagneticfield.Theflux
densityinthecenterofthecoilisgivenby:
Inthecaseofairandnonmagneticmaterials,µ=1.0andB=H.
Thepermeabilityofirondependsonthefieldstrength,H,anddecreasestounityathighfieldstrengthorwhenthefluxdensity,B=H(Fig.I.43).
Thehighpermeabilityofironisduetotheinducedmagneticfieldorientingmicroscopiccrystalregionsactingastinymagnetsintheiron.Allthese
tinymagnetsaddtheirmagneticfieldstotheinducedfield(Fig.I.44).Whenallmicromagnetsarenearlyoriented,theironwillaffecttheflux
densitytoadecreasingamountsincethereorientationofmicromagnetsisnearingcompletion.Thus,thepermeabilityofironathighfieldstrengths
approachesthatofemptyspace.Atthispointtheironreachesmagneticsaturation.
2)Hysteresis
Thestrengthofthelensdependstosomeextentonthepreviousmagnetichistoryof
thelens.Whenthecurrentinalensisreduced,thedecreaseinmagnetizationdoes
notretracethesamepathobtainedwhenthecurrentwasincreased(Fig.I.45).
Inductionofmagnetizationinvolvesaphysicalmovementwithinthemagnetized
material,requiringtheovercomeofacertaindegreeofinertia.Asaresult,
magnetizationtendstolagbehindthemagnetizingforceapplied.Inducedmagnetic
fluxcanonlybereturnedtozerobyapplicationofacurrentintheoppositedirection.
Aconsequenceofhysteresisisthatthelevelofcurrentusedtoenergizeamagnetic
lensDOESNOTpreciselyspecifythelensstrength(i.e.focallength).
NormalizationofTEMlensesisaccomplishedbyreducingthelenscurrenttozero
somepredeterminednumberoftimes.Hysteresismayalsobeminimizedbytakinga
lenstosaturationandthenreturningittotheworkingcurrentwithoutovershooting.
Whenthefieldstrengthisreducedtozero,somemagnetizationstillremainsintheiron
(residualmagnetizationorremanence).Anadvantageofsoftironisthefactthat,
whenusedinanelectromagnet,hysteresisislow.
Introductionofpiecesofironinamagneticfielddrasticallyaffectsthefluxdensity.
Magneticmaterialhasashieldingeffect,theeffectbeinggreaterthegreaterthe
permeability.Permalloy(mmetal)hasamaximumpermeabilityof80,000140,000
comparedtoironusedintransformers(~7000).mmetalpermeabilityislimitedtolower
fieldstrengthsthanthatatwhichironstillretainshighpermeability.Thismetalis
thereforeusefulforshieldingtheTEMfromexternalmagneticfields.
d.Theelectromagneticlens
1)Lensdesigndevelopment(Figs.I.46I.48)
Theefficiencyofthemagneticfieldproducedbyashortsolenoidwasfirstimproved
byencasingtheenergizingcoilinasheathofsoftironwhichhasthepropertyofconcentratingthelinesofforceinamagneticfieldandthus
becomingmagnetizedbyinduction.Inthiswayamuchmorepowerfulaxialmagneticfieldisobtainedforthesameamountofcurrentflowing
throughthesolenoid.Furtherdevelopmentinvolvedencasingtheentirecoilwithsoftironexceptatanarrowannulargapintheinsideofthecoil.
Thisproducesagreaterconcentrationofthemagneticfieldalongashortaxialdistance.Toachieveshorterfocallengthlenses(andobtaingreater
magnifications)asoftironpolepiecewithanopenaxialborewasintroducedatthepositionoftheannulargap.
MagneticlensesusedinTEMsarealwaysconstructedwithanironcircuittoproduceahighfieldstrengthacrossashortgap.Themagneticfields
forTEMlensesareintherangeof10,00020,000gauss.
2)Forcesactingonacurrentinamagneticfield
Theforceonanelectroninamagneticfieldisalwaysatrightanglestothevelocityandthedirectionofthefield(Figs.I.49,I.50,andI.52).The
fieldonlyactsonthevelocitycomponentwhichisdirectedperpendiculartothelinesofforce.Usethelefthandrule(Fig.I.51:firstfingerfor
fielddirection,middlefingerforcurrentdirection,andthumbfordirectionofforce).Rayspassingthroughthelensareturnedthroughanangle
whichdoesNOTdependonthedistanceoftheraysfromtheaxis.Allelectronscontainedinagivenmeridionalplanebeforeenteringthefieldare
containedinarotatingmeridionalplaneastheypassthroughthelens,andthentheyleavethelenscoplanar.
Whenelectronsenterthelenstheyencounterasidewaysforcewhichcausestheelectrontorotate
asitcontinuesthroughthelens(Figs.I.53I.57).Sincetheradialcomponentofthemagneticfield
reversesafterthecenterofthelens,therotationalvelocitysetupinthefirsthalfofthelensis
countered.Theelectronenteredthelenswithoutangularmomentumabouttheaxisandleaves
withoutangularmomentum.Theneteffectisadeflectiontowardtheaxis,whichitmustcrossatthe
focalpointf
2
.Theanglebetweentheobjectvectorandtheimagevectoris180°+q,whereas,for
glasslensesandelectrostaticlenses,theanglebetweenarealobjectandtheimageisexactly180°.
Sincetheradialforceisdirectedtowardtheaxis,thelensisconvergentnomatterwhatthedirection
ofthefield.
3)Propertiesofamagneticlens:
Anyaxiallysymmetricmagneticfieldhasthepropertiesofanideallens.Alltheformulasfortheideallensmaybeapplied.
Magneticlensesarealwaysconvergent.Theconventional,axiallysymmetriclensisalwaysboundedbyregionswhicharefieldfree,the
consequencebeingthatthenetactionofelectronlensesisinevitablyconvergent.Limitedregionsmaybedivergentbutnotthelensasawhole.
Theseriousconsequenceofthisisthatneithersphericalorchromaticaberrationscanbecorrectedasisdoneinlightopticsbytheusedoublets
ofpositiveandnegativelenses.
Intheabsenceofelectrostaticfields,therefractiveindexisthesameinobjectandimagespace,thereforef
1
=f
2
.
Electronstravelingthroughaxiallysymmetricfieldsexperienceaspiraltrajectoryofdiminishingradius.Theimagevectorisatanangle180°+qto
theobjectvector.
Thedeflectionoftheelectrontowardstheaxismeansthatanelectronenteringthelensparalleltoitsaxiswillcrosstheaxisafterhavingpassed
thelens.Thedeflectionwillincreasewiththedistancefromtheaxis.Thus,abeamofelectronsinparallelpathsparalleltotheaxisofthelenswill
befocusedtoanimagepointontheaxiswhichrepresentsthesecond(back)focalpointofthelens(f
2
).Notethatmagneticlensesarehighly
inefficientinthatonlyaminorportionofthetotalfieldstrengthisactuallyeffectiveinfocusingtheelectron.
4)Magneticlensfocallength
Inamagneticelectronlensthefocallengthisdeterminedbythefieldstrengthinthelensgapandbythespeedoftheelectrons(determinedby
theacceleratingvoltage).
Formagneticlenses,focusingisachievedbyvaryingthecurrentwhichpassesthroughtheelectromagnet.Thisinturnchangesthestrengthof
themagneticfieldandtherebyaltersthefocallengthofthelensandisequivalenttoacombinedchangeinboththe"refractiveindex"and
"curvatureofsurface".Forabeamofmoreenergeticelectrons,thelenscurrenthastobeincreasedinordertokeepthefocallengthconstant.
FocallengthandcurrentareNOTlinearlyrelated:strengthincreasesinasigmoidfashion(Fig.I.45)ascurrentincreasesuntilapointisreached
wherethelensissaturatedandnofurtherincreaseinlensstrengthcanbeachieved.
Sincethefocallengthofthelensisdirectlyproportionaltotheacceleratingvoltage,avariationinthevelocityoftheelectronsintheimaging
beamaffectsimagequalitybyeliminatingperfectfocus(chromaticaberration).
5)Magneticlensdesign:(Figs.I.46,I.47).
Condenserlensesusuallyhavearelativelylargeboreandspacingwhichresultsinalongfieldandlongfocallength.
Typicalconstructionoftheobjectivelensproducesastrongfieldofshortaxialextent(i.e.shortfocallengthbetween(1.53mm)necessaryfor
formationofimagesathighmagnification.Thespecimenisplacedwithinthemagneticfieldoftheobjectivelens.Thus,anyfieldintroducedby
contaminantsinthespecimencandistortthefieldofthelens.Notethatthisalsomeansthatpartofthelensfield("prefield")isonthefrontside
oftheobjectandaffectstheelectronbeambeforeitpassesthroughtheobject.
Mostofatypicalmagneticlensliesoutsidethevacuumofthemicroscope.Onlythoseregionsthroughwhichtheelectronbeampassesareinhigh
vacuum.Magneticlensesmustbewatercooledtodissipatethelargeamountsofheatproducedbythecurrentsintheelectromagnetcoils.
DATE NAME EVENT
1897 J.J.Thompson Discoverstheelectron
1924 LouisdeBroglie Identifiesawavelengthtomovingelectrons
l =h/mv
where
l =wavelength
h=Planck'sconstant
m=mass
v=velocity
(Foranelectronat60kVl=0.005nm)
1926 H.Busch Magneticorelectricfieldsactaslensesforelectrons
1929 E.Ruska Ph.Dthesisonmagneticlenses
1931 Knoll&Ruska Firstelectronmicroscopebuilt
1931 Davisson&Calbrick Propertiesofelectrostaticlenses
1934 Driest&Muller SurpassresolutionoftheLM
1938 vonBorries&Ruska FirstpracticalEM(Siemens)10nmresolution
1940 RCA CommercialEMwith2.4nmresolution
1945 1.0nmresolution
Fig.I.1Comparisonoflightandelectronmicroscopes.Ineach
instrument,illuminationfromthesource(lamp,filamentinthe
electrongun)isfocusedbythecondenserlensontothespecimen.
Afirstmagnifiedimageisformedbytheobjectivelens.Thisimage
isfurthermagnifiedbytheprojectorlensontoagroundglass
screen(light)orfluorescentscreen(electrons).(FromAgar,p.8)
Fig.I.2CrosssectionalviewofthePhilipsEM300.(FromAgar,p.40)
Toviewtheanimatedmicroscope,clickhere.
Note:QuickTimePlugInrequired
(Thiscanbedownloadedathttp://apple.com/quicktime/download)
Fig.I.3Sectionthroughacomplex
doublecondenser6lensPhilips
EM200electronmicroscope.(From
Meek,p.99)
Fig.I.4Thestatisticalnatureofdiffraction
patterns.(FromHall,p.13)
"Theprecisenatureof'electronwaves'or'matterwaves'isverydifficulttounderstandordescribeinmaterialterms.Electronwavesarenot
electromagneticradiationofthekindtowhichlight,Xraysandradiowavesbelong.Theyconstituteasortofquantumor'packet'ofradiationwhich
accompanieseachindividualelectron,followingitspathandnotradiatingoutwardsfromit."(Meek,1976,pp.4849).
V l (nm)
v(
•
10
10
cm/sec)
v/c
10,000 0.0123 0.593 0.198
50,000 0.0055 1.326 0.442
100,000 0.0039 1.875 0.625
1,000,000 0.0012 5.930 1.977!
V l (nm)
v(
•
10
10
cm/sec)
v/c
10,000 0.0123 0.593 0.195
50,000 0.0055 1.326 0.414
100,000 0.0039 1.875 0.548
1,000,000 0.0012 5.930 0.941
FigI.5Aperfectpointsourcecannotbe
imagedbyalensasaperfectpointimagedue
tothepresenceoftheapertureAB(which
maybetheedgeofthelens).Diffractionat
thisaperturegivesrisetoaseriesoffringes,
whichsurroundtheimageformedofthepoint
source.Thepatternproducediscalledan'Airy'
disk.(FromMeek1sted.,p.35)
Fig.I.6Wheneverawavefrontstrikesa
barrier,itcanbendaroundthecorner'by
givingrisetoasecondarywavefrontatthe
edge,sinceeachpointonthewavefrontcan
giverisetoanewsourceofwaves.This
phenomenoniscalled'diffraction'.(FromMeek
1sted.,p.22)
Fig.I.7Diffractionpattern(right)formedbyanirregularlyshapedaperture
(left).(FromYoung,p.95)
Fig.I.8(a)
Photographof
theedgeofa
razorblade
illuminatedby
monochromatic
(blue)light
rendered
coherentby
passing
througha
narrowslit.(b)
Microdensitometer
tracingofthe
negativefrom
whichthe
photograph
wasmade.
FourFresnel
fringescanbe
distinguished.
(FromMeek1st
ed.,p.27)
(a)
(b)
(a) (c)
(b)
Fig.I.9(a)Fresnelfringesformed
byelectrons.Thesefringesare
formedoutsidetheedgeofahole
(white)inacarbonfilm(black).(b)
Amicrodensitometertracingofthe
fringesystem;thepatternis
identicalwiththeFresnelfringe
systemformedbyvisiblelight(see
Fig.I.8).(c)Anunderfocusedimage
ofaholeinafilm,showinga
completesystemofabout40
Fresnelfringesinsidethehole.
(FromMeek1sted.,pp.2930)
Fig.I.10Diffractionimagesoftwo
easilyresolvedpoints.(From
Slayter,p.243)
Fig.I.11Imagesoftwo
incoherentlyilluminatedpointsat
thelimitofresolution.(a)individual
intensities;(b)summedintensities.
(FromSlayter,p.244)
Fig.I.12Examplesofwhatoccurswhentwo
wavesofthesamewavelengthandequal
amplitudeadd.Ineachexample,thetwo
separatewavesareshownontheleftand
theirsumorresultantwaveontheright.The
differentexamplesarecharacterizedbyvarying
phasedifferences.Thephaseofawave
(usuallyexpressedasafractionofthe
wavelengthorindegrees)isthepositionofa
crestrelativetosomearbitrarypoint.Although
thephaseofagivenwavevarieswithtimeas
thewavetravels,thedifferenceinphaseofthe
twowavesofthesamewavelengthwiththe
samevelocity,isindependentoftime.Such
wavescaninterferewithoneanother.The
resultantwavehasthesamewavelength,l .
(a)Phasedifferencezero.Thewavestotally
reinforceandaresaidtobe"inphase"orto
showconstructiveinterference.
(b)Phasedifferencel /4.Partialreinforcement,
givingawaveofamplitude1.4(intensity2.0).
(c)Phasedifferencel /2.Thewavesare"outof
phase"andthereistotaldestructive
interferencetogivenoresultantwaveora
wavewithamplitude0(intensity0).(From
GluskerandTrueblood,p.19)
Fig.I.13Photographofan
interferencepatterninwater
wavesformedbythe
superpositionofwavesfromtwo
sourcesoscillatinginphasewith
thesamefrequency.(FromYoung,
p.22)
Fig.I.14Theangularapertureofthe
eyeisrelativelysmall.(FromMeek,
1sted.,p.13)
Fig.I.15Increasingtheangular
apertureoftheeyewithalens.The
lensallowstheobjecttobeheld
closertotheeye,whichisthereby
enabledtogathermoreinformation.
(FromMeek1sted.,p.14)
Fig.I.16Theinteractionofwaves
withanobstacle.Theboatridesthe
longwavelengthoceanwave,but
reflectsthesmallwavelength
surfaceripple.Anobserverwho
wishestodetectthepresenceof
theboatcandosoonlyby
observingwaveswhichhave
wavelengthssmallerthan,or
comparableto,thelengthofthe
boat.(FromSherwood,p.19)
Maximummagnification=
resolvingpoweroftheeye
resolvingpowerofthemicroscope
(a)
Fig.I.17(a)TwoAiry
disksrepresenting
twoimagepoints
shownatincreasing
separationfromleft
toright.Inthe
pictureatthe
extremerightthe
twodiskscanbe
distinguishedas
separatedisks.
(b)Theintensity
distributionatanAiry
disk.R,halfwidthof
thecentralmaximum
representedbya
bellshapedcurve.
(c)TheRayleigh
criteriaforresolution.
(FromSjostrand,
p.115)
i=r
Fig.I.18Reflection.(FromSlayter,
p.4)
Fig.I.19Refraction.(FromSlayter,
p.6)
Fig.I.20Principalraydiagramsshowing
imageformationbyaconvexlens.
(a)Whentheobjectdistanceisgreater
thanthefocallength,areal,inverted
imageisformed.
(b)Whentheobjectdistanceisless
thanthefocallength,avirtual,erect
imageisformed;itspositionis
obtainedbyprojectingtheprincipal
raysbackward.Theraysappearto
comefrompointQ.(FromYoung,
p.127)
Fig.I.21Definitionof
principalfocus,F,inimage
spaceofalens.(From
Sjostrand,p.20)
Fig.I.22Focusingeffectoflenson
raysoriginatingfrompointson
principalaxislocatedatdifferent
distancesfromthelens.(From
Sjostrand,p.21)
Fig.I.23Definitionofprincipal
focusinobjectspaceF1ofa
lens.(FromSjostrand,p.21)
Fig.I.24VirtualimageQof
objectpointlocatedbetween
principalfocusinobjectspace
andthelens.(FromSjostrand,
p.21)
Fig.I.25Constructionoftheimage
ofanobjectbymeansofray
tracing.(FromSjostrand,p.22)
Fig.I.26Magnifyingeffectof
apositivelens.(From
Sjostrand,p.22)
Fig.I.27Virtualmagnified
imageofobjectlocated
betweenprincipalfocusin
objectspaceandthelens.
(FromSjostrand,p.22)
Fig.I.28Amagnifyingglassformsan
enlarged,erectvirtualimage.The
angularsizeofthisimageis
approximately4"/15"or4/15.The
angularsizeoftheobjectatthe
closestdistanceforcomfortable
viewingis1"/10"or1/10.The
magnificationinthissituationis(4/15)/
(1/10),or22/3.(FromYoung,p.130)
Fig.I.29Theangularapertureofa
lens.Theangle2a isthe
acceptanceangleofthelens,and
thelargeritcanbemade,themore
informationcanthelenstransmit.A
largelensofhighaperturecan
thereforetellusmoreaboutan
objectthanasmalllensoflow
power.(FromMeek1sted.,p.12)
Fig.I.30Raydiagramforhighmagnification
modeofoperation.Notethateachlens
formsarealimage,withimageinversion.
I0istheimageformedbytheobjective
lensO,I1isformedbythefirstprojector
lensP1andI2bythesecondprojectorP2,
onthescreen.(FromAgar,p.30)
Fig.I.31Left:raydiagramofthe3realimagemediumandhighmagnificationimagingsystemofa3lens
microscope.Center:2realimageverylowor'scan'magnificationrangeofa3lensmicroscope.Right:2real
imagelowmagnificationsystemofa3lensmicroscope.(FromMeek1sted.,pp.118,120121)
Fig.I.32Raydiagramforacompleteelectron
microscope.FilamentF,condenser1lensC1,
condenser2lensC2,condenserapertureCA,
specimenS,objectivelensO,objectiveaperture
OA(inbackfocalplane).1stintermediateimage
andselectorapertureSA.IntermediatelensP1,
secondintermediateimageI2,projectorlensP2
andfinalimageonthefluorescentscreenFC.
(FromAgar,p.35)
a)f=2.0
x
o
=5.0
e)f=4.0
x
o
=3.0
b)f=10.5
x
o
=21.0
f)f=13.3
x
o
=13.3
c)f=3.5
x
o
=3.0
g)f=3.142
x
o
=0.0
d)f=5.0
x
o
=2.5
a)D=8.0
L1:f=2.0
x
o
=4.0
L2:f=3.0
b)D=8.0
L1:f=2.0
x
o
=6.0
L2:f=3.0
c)D=4.0
L1:f=2.0
x
o
=3.0
L2:f=2.0
FigI.33Accelerationofelectronin
electricfield.(FromSjostrand,p.26)
Fig.I.34Linesofforceatapositively
chargedsphericalbody.(FromSjostrand,
p.32)
Fig.I.35Linesofforceandequipotential
surfaces(stippledlines)associatedwith
twoequalchargesofoppositesign.
(FromSjostrand,p.32)
Fig.I.36Equipotentialsurfacesattwoparallel
platesofoppositechargeswiththepathofan
electronindicatedwithinthehomogeneous
partofthefield.(FromSjostrand,p.33)
Fig.I.37Refractionofelectronatan
equipotentialsurface.(FromSjostrand,p.33)
Fig.I.38.Negativelensactionof
electrostaticfieldatanaperturewhen
V2V1>V3V2.(FromSjostrand,
p.34)
Fig.I.39.Positivelensactionatan
aperturewhenV2V1<V3V2.
(FromSjostrand,p.34)
Fig.I.40Magneticfieldinducedbycurrent
passingthroughaconductor.(From
Sjostrand,p.35)
Fig.I.41Magneticfieldinducedbycurrent
passingthroughasolenoid.(From
Sjostrand,p.37)
Fig.I.42Solenoidwithironcore.(From
Sjostrand,p.40)
Fig.I.43a.Dependenceofpermeabilityonfluxdensity,B.
b.RelationshipbetweenfluxdensityBandfieldstrength.
(FromSjostrand,p.38).
Fig.I.44Magnetization.(FromSlayter,
p.361)
Fig.I.45Curves
showinghowthe
magnetizationof
softiron(lens
strength)is
relatedtothe
magnetizing
force(lens
current).An
unmagnetized
lensstartsfrom
thepointOand
followsthepath
OAaslens
current
increases.Atthe
pointA,further
increaseinlens
currentproduces
nofurther
increaseinlens
strength;thelensissaidtobe'saturated'.Whenlenscurrent
isreduced,thepathOAisnotretraced;adifferentpathABis
followed.Thisdisplacementiscalled'hysteresis'.Atzero
current(pointB),someresiduallensstrengthremains;thisis
called'remanence'.Tobringthelensbacktozerostrength,a
reversecurrentOCmustbeapplied.Lensstrengththen
increaseswithincreasingreversecurrent,followingthepath
CD.Thepolarityofthelenschanges,butthisdoesnotaffect
itsfocusingpower;onlythespiralelectronpathisreversed.
Becauseofhysteresis,itisnotpossibletocalibratealens
currentmeteraccuratelyintermsoflensstrengthor
magnification.
Fig.I.46Evolutionofmagneticelectron
lenses.(A)Shortsolenoidusedasa
magneticlens.(B)Softironcasing
enclosingoutersurfaceofthesolenoid,
thusconcentratingthefield.(C)Soft
ironencasingthesolenoidexceptata
narrowannulargaptherebyreducing
themagneticfieldtoaveryshortregion
alongthelensaxis.(D)Modern
objectivelensconsistingofasoftiron
encasedsolenoidandsoftironpole
piecessoastohaveanenormously
concentratedfieldatthelevelofthe
annulargap.(FromWischnizter2nded.,
p.33)
Fig.I.47(a)Amagneticlensconsisting
ofatightlywoundcoilandasoftiron
shroudsurroundingthecoilexceptfor
asmallgap.Thefieldisconcentratedin
thatgap.(b)Shortfocallength
electromagneticlenswithpolepieces.
(FromSjostrand,p.50)
Fig.I.48Fieldstrengthdistribution
curves.ThecurvesADcorrespondto
therespectivelensesillustratedinFig.
I.46.Eachrepresentsthefieldstrength
alongthelongaxisofthelens.The
changesintheshapeofthecurves
representtheshorteningor
concentrationofthefieldovera
shorteraxialdistance.Hz=
longitudinalmagneticfield.Z=
distancealongtheaxisofsymmetry.
(FromWischnizter2nded.,p.33)
Fig.I.49TheforceFactingon
astraightconductorina
homogeneousmagneticfield
offluxdensityBwhencurrent
Iispassedthroughthe
conductor.(FromSjostrand,
p.43)
Fig.I.50Pathofanelectronina
magneticfield.(A)Inalarge,uniform
magneticfield.(B)Inasmall,uniform
magneticfield.(FromWischnitzer2nd
ed.,p.25)
Fig.I.51Lefthandthumbrule.
(FromSjostrand,p.43)
Fig.I.52Thompson'sexperiment.A
streamofelectronsoriginatingfroma
sourceandpassing,invacuo,through
amagneticfieldproducedbyapairof
magnetswillbedeflected.The
directionofdeflectiondemonstrates
thatelectronsarenegativelycharged
particlesofmatter.(FromWischnitzer
2nded.,p.25)
Fig.I.53Actionofasolenoidonan
electronbeam.Anelectriccurrent
passingthroughthecoilproducesan
axialmagneticfield.Thisisthe
refractingmediumfortheelectrons.An
electronstartingatapointontheaxisA
andatanangletoitfollowsaspiral
path,returningtotheaxisatthepoint
B.Theactionisbasicallysimilartothat
oftheconverginglightlensshownin
Fig.I.20.(FromMeek1sted.,p.8)
Fig.I.54Actionofthemagnetic
lens.(a)Inperspective.(b)
Electrontrajectoryin
projection,alongdirectionof
propagation.(c)Electron
trajectoryinprojection,side
view.(FromSlayter,p.358)
Fig.I.55Componentsofthe
vectorHneartheaxisoffields
withaxialsymmetry.His
representedbytwo
components,Hz,the
componentinthez(axial)
direction,andHr,the
compnentinther(radial)
direction.(FromHall,p.85)
Fig.I.56Theycomponentof
themagneticfieldina
magneticlensisoriented
perpendiculartothedirection
ofanelectronenteringthe
lensalongapathparallelto
thelensaxis.Thisy
componentwillaffectthe
electron,deflectingitinthex
directionasindicatedbythe
arrowmarkedvx.(From
Sjostrand,p.48)
Fig.I.57Thezcomponentofthemagneticfield
andthexvelocitycomponentoftheelectron
inamagneticlensinteract,deflectingthe
electronintheydirectiontowardthelens
axis.(FromSjostrand,p.49)
CuuDuongThanCong.com https://fb.com/tailieudientucntt
cuu duong than cong . com

I.THEMICROSCOPE
I.A.PRINCIPLESOFTHETRANSMISSIONELECTRONMICROSCOPE(TEM)
I.A.1.OriginoftheTransmissionElectronMicroscope
I.A.2.ComparisonofLight(LM)andElectronMicroscopes(Fig.I.1)
a.Similarities(Arrangementandfunctionofcomponentsaresimilar)
1)Illuminationsystem:producesrequiredradiationanddirectsitontothespecimen.Consistsofasource,whichemitstheradiation,anda
condenserlens,whichfocusestheilluminatingbeam(allowingvariationsofintensitytobemade)onthespecimen.
2)Specimenstage:situatedbetweentheilluminationandimagingsystems.
3)Imagingsystem:Lenseswhichtogetherproducethefinalmagnifiedimageofthespecimen.Consistsofi)anobjectivelenswhichfocusesthe
beamafteritpassesthroughthespecimenandformsanintermediateimageofthespecimenandii)theprojectorlens(es)whichmagnifiesa
portionoftheintermediateimagetoformthefinalimage.
4)Imagerecordingsystem:Convertstheradiationintoapermanentimage(typicallyonaphotographicemulsion)thatcanbeviewed.
b.Differences
1)Opticallensesaregenerallymadeofglasswithfixedfocallengthswhereasmagneticlensesareconstructedwithferromagneticmaterialsand
windingsofcopperwireproducingafocallengthwhichcanbechangedbyvaryingthecurrentthroughthecoil.
2)MagnificationintheLMisgenerallychangedbyswitchingbetweendifferentpowerobjectivelensesmountedonarotatingturretabovethe
specimen.Itcanalsobechangedifoculars(eyepieces)ofdifferentpowerareused.IntheTEMthemagnification(focallength)oftheobjective
remainsfixedwhilethefocallengthoftheprojectorlensischangedtovarymagnification.
3)TheLMhasasmalldepthoffield,thusdifferentfocallevelscanbeseeninthespecimen.Thelarge(relative)depthoffieldintheTEMmeans
thattheentire(thin)specimenisinfocussimultaneously.
4)Mechanismsofimageformationvary(phaseandamplitudecontrast).
5)TEMsaregenerallyconstructedwiththeradiationsourceatthetopoftheinstrument:thesourceisgenerallysituatedatthebottomofLMs.
6)TEMisoperatedathighvacuum(sincethemeanfreepathofelectronsinairisverysmall)somostspecimens(biological)mustbedehydrated
(i.e.dead!!).
7)TEMspecimens(biological)arerapidlydamagedbytheelectronbeam.
8)TEMscanachievehighermagnificationandbetterresolutionthanLMs.
9)Pricetag!!!(100xmorethanLM)
I.A.3.Photons/Electrons
a.Dualconceptofwaveandparticle(Fig.I.4)
Lighthaspropertiesbothofaparticleandawave.Thisdualnatureisrequiredtosatisfactorilyexplaintheresultsofvariousphysicalexperiments.
Thediffractionoflight(bendingaroundcorners)illustratesthewavenature.TheWAVETHEORYisbasedonthestatisticalnatureofeventsand
haslittlemeaningwithrespecttothebehaviorofsingleparticles.ThewavetheorywasdevelopedandexpoundedbyHuygens(16291695)and
Hooke(16381703).TheCORPUSCULARTHEORYwasproposedbyNewton(16421727)andbecamethemoreacceptedtheoryevenafter
demonstrationofdiffractionbyYoung(17731829)andinterferencebyFresnel(17881827).Atabout1850,thewavetheorycamebackinto
favoruntilabout1900whenmoreevidenceforthecorpusculartheorywasdiscovered.
QUANTUMTHEORY(PlanckandEinstein)providesthebasisforexplainingthephenomenaofINTERFERENCE,DIFFRACTIONandthe
PHOTOELECTRICeffect(lightfallingoncertainmetalscausethemtoemitelectrons)andthusformsacommonbasisforexplainingthenatureof
actionoflight.Thetransferofenergybetweenlightandmatteroccursonlyindiscretequantitiesproportionaltothefrequencyofthe
lightwave.
E=hJ
where
E=energyofphoton(joules)
h=Planck'sconstant(6.624
•
10
34
joulesec)
J=frequency(cycles/sec)
b.Electronvelocityandwavelength
Therelationbetweenthewavelength(l )ofaparticleofmass,m,movingatavelocity,v,isgivenbytheDeBrogliewaveequation:
(1)
Anelectronofchargee(1.6
•
10
19
coulomb),andmassm(9.11
•
10
28
gm),whenpassingthroughapotentialdifferenceofVvolts(expressedin
joules/coulomb),hasakineticenergy:
(2)
Solvingforvelocity:
(3)
substitutingintotheDeBroglieequation(1):
(4)
Since1joule=10
7
dyne
•
cm=10
7
cm
2
•
gm/sec
2
(5)
Thus,forexample,ifV=60,000volts,l =0.005nm.
Fromequation(3)theelectronvelocitycanbecalculatedifVisknown:
(6)
Thefollowingtableillustratesthat,athighvoltage,electronvelocityiscomparabletothespeedoflightinavacuum(c=3
•
10
10
cm/sec).
Theequationbreaksdownwhenthevelocityoftheelectronapproachesthespeedoflightbecausearelativisticcorrectionmustbemadeforthe
valueofthemasswhere:
(7)
Therelationbetweenl andVismorecorrectlygivenby:(seeHall(1966)pp.3334)
(8)
Thefollowingtableisobtainedwhenrelativityeffectsareincluded:
c.Interference/diffraction/coherence
Anideallenssystemobtainsanexactimageoftheobject(eachpointfaithfullyreproduced).Thephenomenaofdiffractionmakesthis
unattainable(Figs.I.5,I.6).
Diffractionphenomenainvolvesthebendingofthepathofradiationpassingclosetoanobstacle(Fig.I.6).Thisresultsinaspreadingofthe
radiationintotheregionbehindtheobstructionthatthewavespassed.Thediffractionatedgescontributestothecontrastatwhichanedgecan
beobserved.Diffractionalsolimitstheresolvingpowerofthemicroscopesincetheimagepointproducedbyalensisadiffractionimageofthe
openingofthelensortheaperturerestrictingtheeffectiveopeningofthelens(Fig.I.5).
Ifthelightsourceandtheplaneatwhichthediffractionpatternisobservedareatfinitedistancesfromtheedge,thephenomenoniscalled
Fresneldiffraction.Thepatternisdescribedasduetointerferencebetweenthenondiffractedlightandawaveoflightdiffractedattheedge.
Theresultingsuperpositiongivesrisetoaseriesofdiffractionfringesorientedparalleltotheedgeandrepresentingperiodicallyvaryingbrightness,
maximaandminima.(Figs.I.7,1.8,I.9).
Coherence:Aprerequisiteforinterferenceisasuperpositionofwavesystemswhosephasedifferenceremainsconstantintime.Twobeams
arecoherentif,whencombined,theyproduceaninterferencepattern.Thebeamsareincoherentwhentheyareincapableofproducingan
interferencepattern.Twobeamsoflightfromselfluminoussourcesareincoherent.Iflightfromthetwosourcesfallsonascreen,theresultant
intensityissimplythesumofthetwointensitieswhichwouldoccurfromeachsourceseparately(Figs.I.10,I.11).Inpracticeanemittingsource
hasfiniteextentandeachpointofthesourcecanbeconsideredtogeneratelight.EachsourcegivesrisetoasystemofFresnelfringesatthe
edge.Thesuperpositionofthesefringesystemsisfairlygoodforthefirstmaximaandminimabutfartherawayfromtheedgeshadowtheoverlap
ofthefringepatternsbecomessufficientlyrandomtomakethefringesdisappear.Thenatureofwaves,phase,amplitude,andinterferenceare
illustratedinFigs.I.12andI.13.
d.Resolution
1)Definitions:
RESOLUTION:abilitytodistinguishcloselyspacedpointsasseparatepoints.
RESOLUTIONLIMIT:smallestseparationofpointswhichcanberecognizedasdistinct.
RESOLVINGPOWER:resolutionachievedbyaparticularinstrumentunderoptimumviewingconditions.
2)Distinctionbetweenresolutionandresolvingpower:
Notethedistinctionbetweenresolutionandresolvingpower.Resolvingpowerisapropertyoftheinstrumentandisaquantitythatmaybe
estimatedontheoreticalgrounds.Resolutionisequaltoorpoorerthantheresolvingpowerandisthequantityobservedunderanygivenset
ofexperimentalconditions.IntheTEM,especiallywithbiologicalsamples,theresolutionachievedmaybeconsiderablyinferiortothetheoretical
resolvingpoweroftheinstrument.
Microscopyisthescienceofseeingtheverysmall.Underidealconditions,theeyeresolvesabout1minuteofarc(=1/60degree=2.9x10
4
radian;recallthereare2p radiansin360°)andsinceitcanfocusdowntoabout250mm,thesmallestobjectwecanresolveisabout0.07mm
(70mm)(Fig.I.14).Thislimitisrelatedtothesizeofthereceptorsintheretinaoftheeye.Thefunctionofamicroscopeistomagnifytheimage
fallingontheretina(Fig.I.15).Theadvantageoflightandelectronmicroscopesisthattheyeffectivelygettheobjectclosertotheeyesoa
magnifiedimageisobtainedandmoredetailcanbediscerned.
TENNISBALLANALOGY:Eyecanresolve3cmat100meters,thusatennisballisclearlyvisible.Butifthetennisballisheldupagainstawhite
background,thevisibilitydecreases(becauseofthedecreaseincontrast).
3)Abbecriteriaofresolution:
Thefundamentalnatureoflightposeslimitsonthedetailthatcanberesolved(Fig.I.16).Abbe(1893)showedthatthesmallestresolvable
distanceisabout1/2thewavelengthoflightused.Thus,1/2thewavelengthoftheradiationusedistheultimateresolvingpowerofany
instrument.Thislimitstheusablemagnificationofopticalmicroscopesto<1000X.Atfirstitwasthoughtthatxraymicroscopeswouldbeuseful
buttherefractiveindexofsubstancesforxraysisnearly=1,thusrefractinglensescannotbemadeforxrays,andconsequently,xrayscannot
beeasilyfocusedtoformimages.
4)Magnificationlimits:
Themaximummagnificationofaninstrumentislimitedaccordingtothefollowingrelationship:
Thus,fortheLM,witharesolvingpowerofapproximately0.25µm,themaximum(useful)magnificationisabout250µm/0.25µm=1000X.Thevalue
usedfortheresolvingpoweroftheeyeinthisexample(250µm)representsamorerealisticviewingcondition.Anymagnificationabovethevalue
givenbytheaboveformularepresentsemptymagnification,sincesuchmagnificationleadstonomoreusefulinformationbutratheramagnified
blur.
AccordingtotheAbbecriteria,at60,000volts,theTEMshouldhavearesolvingpowerofabout0.0025nm.Thisshouldallowamaximumuseful
magnificationofabout100milliontimes!!!Inpractice,themaximumusefulmagnificationoftheTEMoperatedat60kVislimitedtomuchlessthan
1,000,000X.Thus,althoughtheLMnearlyobeystheAbbecriteria,theTEMfallsshortbyaconsiderableamount.Themainlimitingfactorinthe
TEM,withrespecttoachievingthetheoreticalresolvingpoweroftheinstrument,concernsthenatureoftheimaginglensesandtheprocessof
imageformation.
5)Rayleighcriteria(practicalbutarbitrary):(Fig.I.17).
Itistheabilityofmicroscopestomakeobjectpointswhichareclosetogetherappearintheimageasseparatepoints.Anideallenstakeseach
objectpointandrepresentsitexactlyasapointintheimage.Areallenstakeseachobjectpointandspreadsitoutintoacirculardisk(Airy
disk)intheimageplanewhosediameterdependsontheangularapertureofthelens.
Theshortestdistancebetween2disksatwhichthetwodisksappearpartiallyseparatedcorrespondstoabout1/2thewidthofthedisks.The
distance,d,inobjectspaceisgivenby:
d=0.61l /n
•
sina
where
l =wavelenghtoftheradiation
n=refractiveindexofthemedia
a=semiangularapertureofthelens
NOTE:n
•
sina=thenumericalaperture(N.A.)ofthelens.
Thus,tomaximizeresolvingpower,l mustbedecreased,nincreased,oraincreased.Recallthatweareconcernedatthemomentwithan
aberrationfreeopticalsystem.Thevaluefortheconstant(0.61)iscontroversialbecauseitdependsonthecoherenceoftheradiationanda
criteriaofvisibility.
FortheLM,usingoilimmersionoptics(n=1.5),sina=0.87,andvioletlight(l =400nm),d=0.2µm.Theonlywaytoimprovetheresolutionisto
uselightofshorterwavelengthsinceN.A.cannotbeincreasedbeyond~1.5.FortheTEM,n=1(vacuum),sina=10
2
andl =0.005nmfor60kV
electrons,thusd=0.3nm.
I.A.4.Optics(LensTheory)
a.Basiclawsofclassicalgeometricaloptics
1)Rectilinearpropagationoflightwhenn(refractiveindex)isconstant.
2)Lawofreflection:
3)Lawofrefraction(Snell'sLaw):
4)Independenceofrays.Theassumptionismadethatlightraystravelindependentlythroughspace.
Theselawsholdforelectrons,except#4,ifthecurrentdensityistoohighwhennegativechargedelectronscaninterfere.
b.Classicalvs.electronoptics
1)Classicaloptics:Therefractiveindexchangesabruptlyatasurfaceandisconstantbetweenthesurfaces.Therefractionoflightatsurfaces
separatingmediaofdifferentrefractiveindicesmakesitpossibletoconstructimaginglenses.Glasssurfacescanbeshaped.
2)Electronoptics:Here,changesintherefractiveindexaregradualsoraysarecontinuouscurvesratherthanbrokenstraightlines.Refraction
ofelectronsmustbeaccomplishedbyfieldsinspacearoundchargedelectrodesorsolenoids,andthesefieldscanassumeonlycertaindistributions
consistentwithfieldtheory.
c.Geometricalandphysicaloptics
Thefundamentalprinciplesofopticsgovernthedesignandoperationofboththelightandelectronmicroscopes.Thebasicopticalprinciples
involvingtheuseofrefractileelementsorlensesinordertoformmagnifiedimagesareidenticalinboththeLMandTEM.TheTEMdiffersfromthe
LMonlyintheradiationitusesandinthewayinwhichtheradiationisbentorrefracted.
Geometricalopticsdealswiththestudyofthepathsfollowedby'rays'oflightorelectronsthroughlensesandapertures,andthegeometrical
constructionsusedtofindtherelativepositionsandsizesofobjectsandtheirimages.Arayoflightorelectronsisdefinedasaninfinitelythin
pencilorbeam.Physicalopticsshowsthatthisanabstractionandcannotphysicallyexistbecauseof'diffraction'whichdealswiththewave
natureoflightandelectrons.Allresultsobtainedingeometricalopticscanbederivedfromtheprinciplesofphysicaloptics,alongwithother
phenomenasuchasinterferenceanddiffractionwhicharenotexplicableinsimplegeometricalterms.
d.Idealversesreallenses:
Lensesareusedtobendraysoflightorelectronssotheyaredeflectedinapredictablewayfromtheiroriginalpaths.Thepropertiesofanideal
lens,possessinganaxisofrotationalsymmetryare:
1)Eachrayofthebundleofrayswhichpassesfromanobjectpointwillberefractedbytheideallenstomeetinoneimagepoint.
2)Raysoriginatingfrompointswhichlieonaplaneperpendiculartotheaxis,mustbeimagedinaplanewhichisalsoperpendiculartotheaxis.
3)Theimageappearsliketheobjectirrespectiveofthemagnification,sotherelativelineardimensionsoftheobjectarepreservedintheimage.
Inpractice,theimagingbyanyreallensdoesnotcorrespondtothatoftheideallensowingtothefactthatanobjectpointisrepresentedbya
diffractionimage(Airydisc)ofthelensopeningortheapertureusedforrestrictingtheeffectiveopeningofthelens.Thisisaresultofthewave
likepropertiesoflight.Lensaberrationsalsocontributetomoreorlesspronounceddeviationsfromthepropertiesoftheideallens.
Thesinglerefractingsurfaceofsphericalcurvatureisthefundamentalunitoffocusingactionbyglasslenses.Sphericalrefractingsurfacesactas
lensesforparaxialrayswhicharethoseraysthatpassclosetotheprincipalaxisofthelens.RayswithlargeangleswillNOTobeyideallens
action.
Afundamentaldifferencebetweenlightandmagneticlensesisthattheelectronbeamdoesnotchangeinforwardvelocityasitpassesthrough
themagneticfield(lightraysslowdownwhenpassingintoamediumofhigherrefractiveindex).Refractioniscontinuouswithelectronswhenthey
areinthemagneticfield:lightisrefractedonlyattheinterfacebetweenmediaofdifferingrefractiveindex.Theelectronsalsofollowspiral
trajectoriesthroughthemagneticfield(seealsoSec.I.A.5.c(Magneticfieldsandmagneticlenses)
e.Raydiagrams:(Figs.I.20I.28)
Themethodofconstructionofraydiagramsisbasedonthreesimpleprinciples:
1)Allraysenteringthelensparalleltotheaxisarebroughttoacommonpointontheaxis,thefocalpoint.
2)Allrayspassingthroughthegeometricalcenterofthelensareundeviatedandpassstraighton,nomatterfromwhichdirectiontheycome.
3)Principleofreversibility:ifthedirectionofarayisreversedinanysystemtherayexactlyretracesitspaththroughthesystem.Thisapplies
onlytothelocationoflightpathsandnottotheintensityofthelight.
Theaboveprinciplesarebasedontheassumptionsthatwearedealingwithathinlensandconcernedwiththepathsofparaxialrays.The
standardconventionistodrawdiagramswithraysthattravelfromlefttoright.Theobjectistotheleft(infront)ofthelensandtheimageisto
theright(behind)ofthelens.
f.Definitions:
Realimage:oneatwhichlightraysphysicallyreunite,sothataphotographicplateplacedatthepositionofarealimageisexposed.
VirtualImage:onefromwhichlightraysappeartodiverge;raysarenotinfactconcentratedatthepositionofavirtualimage,sothata
photographicplateplacedatthepositionoftheimageisnotexposed(byfocusedrays).Placinganopticalsystemsuchastheeyebehindthe
lens,willenablethedivergentraystobefocusedtoformarealimage.TheintermediatelensofanTEMissometimesusedthiswayinorderto
reducethefinalsizeoftherealimageformedbytheprojectorlens(es).
Converging(positive)lens:bendsraystowardtheaxis.Ithasapositivefocallength.Formsarealinvertedimageofanobjectplacedtothe
leftofthefirstfocalpointandanerectvirtualimageofanobjectplacedbetweenthefirstfocalpointandthelens.
Diverging(negative)lens:bendsthelightraysawayfromtheaxis.Ithasanegativefocallength.Anobjectplacedanywheretotheleftofa
diverginglensresultsinanerectvirtualimage.Itisnotpossibletoconstructanegativemagneticlensalthoughnegativeelectrostaticlensescan
bemade.
g.Lensformula(thinlensequation):
where
f=focallengthofthethinlens(sameradiusofcurvatureforboth
sphericalsurfaces)
o=distanceofobjectfromlens(positivetotheleft)
i=distanceofimagefromthelens(positivetotheright)
NOTE:Foravirtualimage,ihasanegativevalue.
h.Magnification:
Foraconverginglens,iftheobjectismorethantwicethefocallengthfromthelens,thentheimageformedisreal,inverted,andsmallerinsize
thantheobject(M<1).Whentheobjectisatadistance=2f,theimageandobjectarethesamesize(M=1);whenitisbetweenfand2f,
theimageislargerthantheobject(M>1),andwhenitis<f,theimageisvirtual,erect,andlargerthantheobject(M>1).
i.Angularapertureofthelens(2a)(Fig.I.29)
Theaperturedeterminesthetotalamountofradiationarrivingfromtheobjectwhichcanbefocusedto
formanimage.Theaperturethuscontrolstheabilityofthelenstogatherinformationabouttheobject.
Thisdependsontheangleoftheconeofraysitisabletoacceptfromtheobject.Bringinganobject
closertotheeyeincreasestheangularaperture,butthereisalimittotheclosenessthattheobjectcan
bebroughttotheeye(~25cmcorrespondingtoanangleofabout0.9°fora4mmexitpupildiameterof
theeyelens;atypicalLMwithanoilimmersionobjectivelenshas2aof~175°).
j.Simplevs.compoundmicroscope(Figs.I.30I.32)
Inprinciple,arealimageofanydesiredmagnificationcanbeobtainedfromasinglepositivelens,butin
practicethisiscumbersomebecauseofthelonglensimagedistance.Oneormorelensescanbeusedto
magnifytheimageinstages(totalmagnificationequalingtheproductofthemagnificationsofeachlens).
Theimageformedbyonelensconstitutestheobjectforthesubsequentlens,whetherornotareal
intermediateimageisformed.
Comparisonofoneversestwostagemagnification:
Thefollowingdescriptionillustrateshowdifferentpathlengthsarerequiredtoachieveamagnificationof10,000Xusingeitheroneortwolenses
withf=2.0cm.
OneStageSystem:
TwoStageSystem:
Assumebothlenseshavef=2.0cmandarearrangedsoeachgives100Xmagnification.
Thus,M=100=x
i
/x
o
foreachstage.
FirstStage:
x
o
=2.02cm
x
i
=202.00cm
Therealimageformedinthefirststagebecomestheobjectforthesecondlens.
SecondStage:x
o
,x
i
sameasinthefirststage.
Totallengthofsystem
=lengthoffirststage+lengthofsecondstage
=(x
o
+x
i
)+(x
o
+x
i
)
=2(x
o
+x
i
)
=2(2.02+202.00)=408.04cm(4.08meters)
k.Problemset
Thefollowingproblemsareforyourownedificationtotesthowwellyouunderstandthebasicsoflensoptics.
1.Foreachsituationbelow,drawanaccurate(usegraphpaper)raydiagramshowingthepathof(atleasttwo)raysfromtheobjecttoimage.
Indicatewhethertheimageisrealorvirtualandspecifythedistanceoftheimagefromthelensandthemagnificationoftheimagewithrespect
totheobject.Ineachexample,thelensisconverging,withidenticalfrontandbackfocalpoints.Distancesareinarbitraryunits.Letf=lens
focallength,x
o
=distanceofobjectinfrontofthelens,andx
i
=distanceofimagebehindthelens.Theobjectmaybeanysize.
2.Inthefollowingexamples,therearetwoconverginglensesinsuccession.Drawraydiagramsshowingtheformationofboththeintermediate
andfinalimagesandgiveappropriateinformationaboutthenature(real/virtual),positions,andsizesoftheintermediateandfinalimages.What
isthemagnificationateachstageofimageformationandwhatisthemagnificationofthefinalimage?Thedistancefromthecenteroflens1(L1)
tothecenteroflens2(L2)equalsD.
I.A.5.ElectronOptics/ElectronLenses
a.Electronemission
Innershellelectronsinmetalatomsshieldtheelectricfieldofthenucleusthroughtherepulsiveforcestheyexertontheoutershell(valence)
electrons.Thustheattractionbetweenthevalenceelectronsandthenucleusisreduced.Metalatomsarecharacterizedashavingtwoloosely
boundvalenceelectronswhichmigratefreely(thisiswhymetalsaregoodelectricalconductors)andcanescapefromthemetalcompletelyif
sufficientadditionalenergyisimpartedtothem.Asthetemperatureofametalisincreased,thekineticenergyoftheelectronsincreasesbecause
ofincreasedthermalvibrationsofthemetalions,whichcollidemorefrequentlywiththeelectrons.Thermionicemissionisthetermusedto
describetheprocessbywhichthermalenergyissuppliedtolooselyboundelectronsinordertoformasourceofelectrons.
Atroomtemperatureelectronsareeffectivelypreventedfromescapingthesurfaceofthemetalowingtotheattractiveforceofthepositively
chargedions.Asthetemperatureisincreasedsomeelectronsacquiresufficientenergytoovercometheattractionandleavethemetal
temporarily.Metal,shapedasathinwire,caneasilybeheatedbypassinganelectriccurrentthroughit.Sincethemetalsurfacebecomes
positivelycharged,acertainlevelofenergy(workfunction)mustbesuppliedtoallowelectronstoescapefromthesurface.Eachmetalhasa
characteristicworkfunction.Tungsten,withalowworkfunction,emitsmoreelectronsthanmetalswithhigherworkfunctions(seealsopp.2930
andFig.I.59).
Ifastrongelectrostaticfieldisappliedinavacuumbetweenthewire(givenanegative,cathode,potential)andananode,theelectricfieldwill
causeelectronstoaccelerateawayfromthewiretowardstheanodesurface(Fig.I.33).Thespeedoftheelectronsdependsonthestrengthof
theelectrostaticfield(voltage)betweenthecathodeandanode(equation(3),Sec.I.A.3.b)Thenumberofelectronswhichleavethewire
dependsonthetemperaturetowhichthewireisheated,whichdependsonhowmuchfilamentcurrentpassesthroughthewire.
A"V"shapedwirewillhavethehighesttemperatureatthetip.Electronswithdrawnfromthefilamenttipcarryelectricchargestotheanode.This
electriccurrent,whichflowsbetweenthefilamentandtheanode,iscalledthebeamcurrent.
1)Electricfield/Equipotentials
Anelectricallychargedobjecthasassociatedwithitanelectricfield.Thus,anelectricallychargedparticle,whenbroughtnearachargedobject,
isinfluencedbyanelectricalforceinthevicinityoftheobject.Theforceisdirectedtowardthechargedobjectifthechargesareofopposite
signsandawayfromtheobjectiftheyareofsimilarsign.DEFINITION:Thedirectionofanelectricfieldisdefinedasthedirectionoftheforce
actingonapositivecharge.(Figs.I.3435)
Alongthelinesofforceconnectingthetwocharges,theelectricpotentialwillchangegraduallybetweentheextremevaluesrepresentedbythe
twocharges.DEFINITION:Equipotentiallinesdefinethepointsalongthelinesofforcewithidenticalelectricalpotential.Theseequipotential
surfacesarealwaysorientedperpendiculartothelinesofforce.Thechangesintheelectricpotentialaregradualinspace.
Electronswhichenterafieldbetweentwoparallelplatesinadirectionparalleltotheplatesareaffectedbytheforcedirectedperpendicularto
theplates(FigI.36).Theelectronswillbeattractedtowardthepositiveplate.Thepathchangesinaseriesofgradualstepsattheequipotential
surfaces.
FigureI.37showshowtheelectronpathis"refracted"attheequipotentialsurface.TheresultisfundamentallythesameasthatgivenbySnell's
Lawofrefractioninlightoptics.Aconsequenceofthisisthatasphericallycurvedequipotentialsurfaceexhibitsthepropertiesofalens.
FiguresI.38andI.39showhowbothpositive(converging)andnegative(diverging)electrostaticlensescanbeformed.Thisfeatureof
electrostaticlensesdiffersfromelectromagneticlenseswhichcanonlyactasconverginglenses.
2)Advantages/Disadvantagesofelectronlenses:
Thefactthattherefractiveindexdoesnotchangeabruptlyinelectronlenseshasoneadvantageinthattherearenotroublesomereflectionsat
equipotentialsasatglassinterfaces.Thereisaseriousdisadvantageinthatequipotentialscannotbeshapedandcombinedinarbitraryfashionto
correctforchromaticaberrationandothererrors.
Althoughelectronmicroscopeswhichemployelectrostaticlenseshavebeenmade,mostmicroscopesuseelectromagneticlenses.Amajorreason
isthatelectrostaticlensesaremoresensitivetothequalityofthevacuumandcleanlinessofthecomponentsthanareelectromagneticlenses.
Somelensaberrationsaremoresevereforelectrostaticlensescomparedtoelectromagneticlenses.Electrostaticlensesrequireverypowerful
electrostaticfieldswhichcanleadtoelectricalbreakdownor"arcingover"insidethecolumn,especiallyunderpoorvacuumconditions.Forthis
reason,electrostaticlensescannotbemadewithfocallengthsasshortasmagneticlenses.
b.Electrostaticlens
Abasicunderstandingofelectrostaticlensesisimportantfortwomainreasons:i)theelectrongunuseselectrostaticlensactiontoformthe
primarybeamsource,andii)itisquitecommonforachargetodeveloponthenonconductingcontaminationwhichmayaccumulateonphysical
apertures(suchastheobjectiveaperture)andtransformthemintoweakelectrostaticlenseswhichcandistorttheelectronimage.
3)Propertiesofelectrostaticlenses:
a)Anyaxiallysymmetricalelectrostaticfieldhasthepropertiesofalensforraysconfinedtotheparaxialregion.Alltheideallensformulasapply
toelectrostaticlenses.
b)Forelectronlenses,replaceÃ(f)forrefractiveindexinthelensequations(f=valueofthepotentialontheaxis).Intheimageformingsystem
ofmostTEMs,fisthesameonbothsidesofthelens(SeeSec.I.A.5.c).
c)Ifboundedbyregionswherefisconstant,anelectrostaticlensisalwaysconvergent.
c.Magneticfieldsandmagneticlenses
1)Magneticfield
Anelectriccurrentpassingthroughaconductorgivesrisetoamagneticfield.TheconventionisthatNisthedirectioninwhichthelinesofthe
magneticfieldpoint(Fig.I.40).Themagneticfluxisthetotalnumberoflinesandthefluxdensityisthenumberoflinesperunitareaofasurface.
UsetheRIGHThandruletodeterminethedirectionofthefield(thumbpointstowardcurrentdirectionandfingerscurlindirectionoffield.NOTE:
Byconvention,thedirectionofelectronflowisoppositetothatofcurrentflow.
Fluxdensitydependsonthepropertiesofthematerialsurroundingtheconductor.Ironinducesahigherfluxdensitythanairoravacuum.The
propertyofthematerialwhichaffectsthefluxdensityiscalledthepermeability,m,ofthematerial.Forairandvacuum,m=1.0.For
ferromagneticmaterialsitcanbeaslargeasseveralhundredthousand.
Iftheconductorhastheshapeofacircularloop,thelinesofforceformcirclesaroundtheloop.Thefluxdensityisgreatestatthecenterofthe
loop.Themagnetinthecenteroftheloopisorientedperpendiculartotheplaneoftheloopifthecurrentthroughtheloopissufficientlystrongto
eliminatetheinfluenceoftheearth'sfield.ThesideoftheloopatwhichthelinesofforceleavetheloopistheNorth(N)poleofthemagnet(Figs.
I.41,I.42).
Ifthewireiswoundinseveralturnsaroundacylindricalsurface(solenoid),eachturnwillcontributetotheinducedmagneticfield.Theflux
densityinthecenterofthecoilisgivenby:
Inthecaseofairandnonmagneticmaterials,µ=1.0andB=H.
Thepermeabilityofirondependsonthefieldstrength,H,anddecreasestounityathighfieldstrengthorwhenthefluxdensity,B=H(Fig.I.43).
Thehighpermeabilityofironisduetotheinducedmagneticfieldorientingmicroscopiccrystalregionsactingastinymagnetsintheiron.Allthese
tinymagnetsaddtheirmagneticfieldstotheinducedfield(Fig.I.44).Whenallmicromagnetsarenearlyoriented,theironwillaffecttheflux
densitytoadecreasingamountsincethereorientationofmicromagnetsisnearingcompletion.Thus,thepermeabilityofironathighfieldstrengths
approachesthatofemptyspace.Atthispointtheironreachesmagneticsaturation.
2)Hysteresis
Thestrengthofthelensdependstosomeextentonthepreviousmagnetichistoryof
thelens.Whenthecurrentinalensisreduced,thedecreaseinmagnetizationdoes
notretracethesamepathobtainedwhenthecurrentwasincreased(Fig.I.45).
Inductionofmagnetizationinvolvesaphysicalmovementwithinthemagnetized
material,requiringtheovercomeofacertaindegreeofinertia.Asaresult,
magnetizationtendstolagbehindthemagnetizingforceapplied.Inducedmagnetic
fluxcanonlybereturnedtozerobyapplicationofacurrentintheoppositedirection.
Aconsequenceofhysteresisisthatthelevelofcurrentusedtoenergizeamagnetic
lensDOESNOTpreciselyspecifythelensstrength(i.e.focallength).
NormalizationofTEMlensesisaccomplishedbyreducingthelenscurrenttozero
somepredeterminednumberoftimes.Hysteresismayalsobeminimizedbytakinga
lenstosaturationandthenreturningittotheworkingcurrentwithoutovershooting.
Whenthefieldstrengthisreducedtozero,somemagnetizationstillremainsintheiron
(residualmagnetizationorremanence).Anadvantageofsoftironisthefactthat,
whenusedinanelectromagnet,hysteresisislow.
Introductionofpiecesofironinamagneticfielddrasticallyaffectsthefluxdensity.
Magneticmaterialhasashieldingeffect,theeffectbeinggreaterthegreaterthe
permeability.Permalloy(mmetal)hasamaximumpermeabilityof80,000140,000
comparedtoironusedintransformers(~7000).mmetalpermeabilityislimitedtolower
fieldstrengthsthanthatatwhichironstillretainshighpermeability.Thismetalis
thereforeusefulforshieldingtheTEMfromexternalmagneticfields.
d.Theelectromagneticlens
1)Lensdesigndevelopment(Figs.I.46I.48)
Theefficiencyofthemagneticfieldproducedbyashortsolenoidwasfirstimproved
byencasingtheenergizingcoilinasheathofsoftironwhichhasthepropertyofconcentratingthelinesofforceinamagneticfieldandthus
becomingmagnetizedbyinduction.Inthiswayamuchmorepowerfulaxialmagneticfieldisobtainedforthesameamountofcurrentflowing
throughthesolenoid.Furtherdevelopmentinvolvedencasingtheentirecoilwithsoftironexceptatanarrowannulargapintheinsideofthecoil.
Thisproducesagreaterconcentrationofthemagneticfieldalongashortaxialdistance.Toachieveshorterfocallengthlenses(andobtaingreater
magnifications)asoftironpolepiecewithanopenaxialborewasintroducedatthepositionoftheannulargap.
MagneticlensesusedinTEMsarealwaysconstructedwithanironcircuittoproduceahighfieldstrengthacrossashortgap.Themagneticfields
forTEMlensesareintherangeof10,00020,000gauss.
2)Forcesactingonacurrentinamagneticfield
Theforceonanelectroninamagneticfieldisalwaysatrightanglestothevelocityandthedirectionofthefield(Figs.I.49,I.50,andI.52).The
fieldonlyactsonthevelocitycomponentwhichisdirectedperpendiculartothelinesofforce.Usethelefthandrule(Fig.I.51:firstfingerfor
fielddirection,middlefingerforcurrentdirection,andthumbfordirectionofforce).Rayspassingthroughthelensareturnedthroughanangle
whichdoesNOTdependonthedistanceoftheraysfromtheaxis.Allelectronscontainedinagivenmeridionalplanebeforeenteringthefieldare
containedinarotatingmeridionalplaneastheypassthroughthelens,andthentheyleavethelenscoplanar.
Whenelectronsenterthelenstheyencounterasidewaysforcewhichcausestheelectrontorotate
asitcontinuesthroughthelens(Figs.I.53I.57).Sincetheradialcomponentofthemagneticfield
reversesafterthecenterofthelens,therotationalvelocitysetupinthefirsthalfofthelensis
countered.Theelectronenteredthelenswithoutangularmomentumabouttheaxisandleaves
withoutangularmomentum.Theneteffectisadeflectiontowardtheaxis,whichitmustcrossatthe
focalpointf
2
.Theanglebetweentheobjectvectorandtheimagevectoris180°+q,whereas,for
glasslensesandelectrostaticlenses,theanglebetweenarealobjectandtheimageisexactly180°.
Sincetheradialforceisdirectedtowardtheaxis,thelensisconvergentnomatterwhatthedirection
ofthefield.
3)Propertiesofamagneticlens:
Anyaxiallysymmetricmagneticfieldhasthepropertiesofanideallens.Alltheformulasfortheideallensmaybeapplied.
Magneticlensesarealwaysconvergent.Theconventional,axiallysymmetriclensisalwaysboundedbyregionswhicharefieldfree,the
consequencebeingthatthenetactionofelectronlensesisinevitablyconvergent.Limitedregionsmaybedivergentbutnotthelensasawhole.
Theseriousconsequenceofthisisthatneithersphericalorchromaticaberrationscanbecorrectedasisdoneinlightopticsbytheusedoublets
ofpositiveandnegativelenses.
Intheabsenceofelectrostaticfields,therefractiveindexisthesameinobjectandimagespace,thereforef
1
=f
2
.
Electronstravelingthroughaxiallysymmetricfieldsexperienceaspiraltrajectoryofdiminishingradius.Theimagevectorisatanangle180°+qto
theobjectvector.
Thedeflectionoftheelectrontowardstheaxismeansthatanelectronenteringthelensparalleltoitsaxiswillcrosstheaxisafterhavingpassed
thelens.Thedeflectionwillincreasewiththedistancefromtheaxis.Thus,abeamofelectronsinparallelpathsparalleltotheaxisofthelenswill
befocusedtoanimagepointontheaxiswhichrepresentsthesecond(back)focalpointofthelens(f
2
).Notethatmagneticlensesarehighly
inefficientinthatonlyaminorportionofthetotalfieldstrengthisactuallyeffectiveinfocusingtheelectron.
4)Magneticlensfocallength
Inamagneticelectronlensthefocallengthisdeterminedbythefieldstrengthinthelensgapandbythespeedoftheelectrons(determinedby
theacceleratingvoltage).
Formagneticlenses,focusingisachievedbyvaryingthecurrentwhichpassesthroughtheelectromagnet.Thisinturnchangesthestrengthof
themagneticfieldandtherebyaltersthefocallengthofthelensandisequivalenttoacombinedchangeinboththe"refractiveindex"and
"curvatureofsurface".Forabeamofmoreenergeticelectrons,thelenscurrenthastobeincreasedinordertokeepthefocallengthconstant.
FocallengthandcurrentareNOTlinearlyrelated:strengthincreasesinasigmoidfashion(Fig.I.45)ascurrentincreasesuntilapointisreached
wherethelensissaturatedandnofurtherincreaseinlensstrengthcanbeachieved.
Sincethefocallengthofthelensisdirectlyproportionaltotheacceleratingvoltage,avariationinthevelocityoftheelectronsintheimaging
beamaffectsimagequalitybyeliminatingperfectfocus(chromaticaberration).
5)Magneticlensdesign:(Figs.I.46,I.47).
Condenserlensesusuallyhavearelativelylargeboreandspacingwhichresultsinalongfieldandlongfocallength.
Typicalconstructionoftheobjectivelensproducesastrongfieldofshortaxialextent(i.e.shortfocallengthbetween(1.53mm)necessaryfor
formationofimagesathighmagnification.Thespecimenisplacedwithinthemagneticfieldoftheobjectivelens.Thus,anyfieldintroducedby
contaminantsinthespecimencandistortthefieldofthelens.Notethatthisalsomeansthatpartofthelensfield("prefield")isonthefrontside
oftheobjectandaffectstheelectronbeambeforeitpassesthroughtheobject.
Mostofatypicalmagneticlensliesoutsidethevacuumofthemicroscope.Onlythoseregionsthroughwhichtheelectronbeampassesareinhigh
vacuum.Magneticlensesmustbewatercooledtodissipatethelargeamountsofheatproducedbythecurrentsintheelectromagnetcoils.
DATE NAME EVENT
1897 J.J.Thompson Discoverstheelectron
1924 LouisdeBroglie Identifiesawavelengthtomovingelectrons
l =h/mv
where
l =wavelength
h=Planck'sconstant
m=mass
v=velocity
(Foranelectronat60kVl=0.005nm)
1926 H.Busch Magneticorelectricfieldsactaslensesforelectrons
1929 E.Ruska Ph.Dthesisonmagneticlenses
1931 Knoll&Ruska Firstelectronmicroscopebuilt
1931 Davisson&Calbrick Propertiesofelectrostaticlenses
1934 Driest&Muller SurpassresolutionoftheLM
1938 vonBorries&Ruska FirstpracticalEM(Siemens)10nmresolution
1940 RCA CommercialEMwith2.4nmresolution
1945 1.0nmresolution
Fig.I.1Comparisonoflightandelectronmicroscopes.Ineach
instrument,illuminationfromthesource(lamp,filamentinthe
electrongun)isfocusedbythecondenserlensontothespecimen.
Afirstmagnifiedimageisformedbytheobjectivelens.Thisimage
isfurthermagnifiedbytheprojectorlensontoagroundglass
screen(light)orfluorescentscreen(electrons).(FromAgar,p.8)
Fig.I.2CrosssectionalviewofthePhilipsEM300.(FromAgar,p.40)
Toviewtheanimatedmicroscope,clickhere.
Note:QuickTimePlugInrequired
(Thiscanbedownloadedathttp://apple.com/quicktime/download)
Fig.I.3Sectionthroughacomplex
doublecondenser6lensPhilips
EM200electronmicroscope.(From
Meek,p.99)
Fig.I.4Thestatisticalnatureofdiffraction
patterns.(FromHall,p.13)
"Theprecisenatureof'electronwaves'or'matterwaves'isverydifficulttounderstandordescribeinmaterialterms.Electronwavesarenot
electromagneticradiationofthekindtowhichlight,Xraysandradiowavesbelong.Theyconstituteasortofquantumor'packet'ofradiationwhich
accompanieseachindividualelectron,followingitspathandnotradiatingoutwardsfromit."(Meek,1976,pp.4849).
V l (nm)
v(
•
10
10
cm/sec)
v/c
10,000 0.0123 0.593 0.198
50,000 0.0055 1.326 0.442
100,000 0.0039 1.875 0.625
1,000,000 0.0012 5.930 1.977!
V l (nm)
v(
•
10
10
cm/sec)
v/c
10,000 0.0123 0.593 0.195
50,000 0.0055 1.326 0.414
100,000 0.0039 1.875 0.548
1,000,000 0.0012 5.930 0.941
FigI.5Aperfectpointsourcecannotbe
imagedbyalensasaperfectpointimagedue
tothepresenceoftheapertureAB(which
maybetheedgeofthelens).Diffractionat
thisaperturegivesrisetoaseriesoffringes,
whichsurroundtheimageformedofthepoint
source.Thepatternproducediscalledan'Airy'
disk.(FromMeek1sted.,p.35)
Fig.I.6Wheneverawavefrontstrikesa
barrier,itcanbendaroundthecorner'by
givingrisetoasecondarywavefrontatthe
edge,sinceeachpointonthewavefrontcan
giverisetoanewsourceofwaves.This
phenomenoniscalled'diffraction'.(FromMeek
1sted.,p.22)
Fig.I.7Diffractionpattern(right)formedbyanirregularlyshapedaperture
(left).(FromYoung,p.95)
Fig.I.8(a)
Photographof
theedgeofa
razorblade
illuminatedby
monochromatic
(blue)light
rendered
coherentby
passing
througha
narrowslit.(b)
Microdensitometer
tracingofthe
negativefrom
whichthe
photograph
wasmade.
FourFresnel
fringescanbe
distinguished.
(FromMeek1st
ed.,p.27)
(a)
(b)
(a) (c)
(b)
Fig.I.9(a)Fresnelfringesformed
byelectrons.Thesefringesare
formedoutsidetheedgeofahole
(white)inacarbonfilm(black).(b)
Amicrodensitometertracingofthe
fringesystem;thepatternis
identicalwiththeFresnelfringe
systemformedbyvisiblelight(see
Fig.I.8).(c)Anunderfocusedimage
ofaholeinafilm,showinga
completesystemofabout40
Fresnelfringesinsidethehole.
(FromMeek1sted.,pp.2930)
Fig.I.10Diffractionimagesoftwo
easilyresolvedpoints.(From
Slayter,p.243)
Fig.I.11Imagesoftwo
incoherentlyilluminatedpointsat
thelimitofresolution.(a)individual
intensities;(b)summedintensities.
(FromSlayter,p.244)
Fig.I.12Examplesofwhatoccurswhentwo
wavesofthesamewavelengthandequal
amplitudeadd.Ineachexample,thetwo
separatewavesareshownontheleftand
theirsumorresultantwaveontheright.The
differentexamplesarecharacterizedbyvarying
phasedifferences.Thephaseofawave
(usuallyexpressedasafractionofthe
wavelengthorindegrees)isthepositionofa
crestrelativetosomearbitrarypoint.Although
thephaseofagivenwavevarieswithtimeas
thewavetravels,thedifferenceinphaseofthe
twowavesofthesamewavelengthwiththe
samevelocity,isindependentoftime.Such
wavescaninterferewithoneanother.The
resultantwavehasthesamewavelength,l .
(a)Phasedifferencezero.Thewavestotally
reinforceandaresaidtobe"inphase"orto
showconstructiveinterference.
(b)Phasedifferencel /4.Partialreinforcement,
givingawaveofamplitude1.4(intensity2.0).
(c)Phasedifferencel /2.Thewavesare"outof
phase"andthereistotaldestructive
interferencetogivenoresultantwaveora
wavewithamplitude0(intensity0).(From
GluskerandTrueblood,p.19)
Fig.I.13Photographofan
interferencepatterninwater
wavesformedbythe
superpositionofwavesfromtwo
sourcesoscillatinginphasewith
thesamefrequency.(FromYoung,
p.22)
Fig.I.14Theangularapertureofthe
eyeisrelativelysmall.(FromMeek,
1sted.,p.13)
Fig.I.15Increasingtheangular
apertureoftheeyewithalens.The
lensallowstheobjecttobeheld
closertotheeye,whichisthereby
enabledtogathermoreinformation.
(FromMeek1sted.,p.14)
Fig.I.16Theinteractionofwaves
withanobstacle.Theboatridesthe
longwavelengthoceanwave,but
reflectsthesmallwavelength
surfaceripple.Anobserverwho
wishestodetectthepresenceof
theboatcandosoonlyby
observingwaveswhichhave
wavelengthssmallerthan,or
comparableto,thelengthofthe
boat.(FromSherwood,p.19)
Maximummagnification=
resolvingpoweroftheeye
resolvingpowerofthemicroscope
(a)
Fig.I.17(a)TwoAiry
disksrepresenting
twoimagepoints
shownatincreasing
separationfromleft
toright.Inthe
pictureatthe
extremerightthe
twodiskscanbe
distinguishedas
separatedisks.
(b)Theintensity
distributionatanAiry
disk.R,halfwidthof
thecentralmaximum
representedbya
bellshapedcurve.
(c)TheRayleigh
criteriaforresolution.
(FromSjostrand,
p.115)
i=r
Fig.I.18Reflection.(FromSlayter,
p.4)
Fig.I.19Refraction.(FromSlayter,
p.6)
Fig.I.20Principalraydiagramsshowing
imageformationbyaconvexlens.
(a)Whentheobjectdistanceisgreater
thanthefocallength,areal,inverted
imageisformed.
(b)Whentheobjectdistanceisless
thanthefocallength,avirtual,erect
imageisformed;itspositionis
obtainedbyprojectingtheprincipal
raysbackward.Theraysappearto
comefrompointQ.(FromYoung,
p.127)
Fig.I.21Definitionof
principalfocus,F,inimage
spaceofalens.(From
Sjostrand,p.20)
Fig.I.22Focusingeffectoflenson
raysoriginatingfrompointson
principalaxislocatedatdifferent
distancesfromthelens.(From
Sjostrand,p.21)
Fig.I.23Definitionofprincipal
focusinobjectspaceF1ofa
lens.(FromSjostrand,p.21)
Fig.I.24VirtualimageQof
objectpointlocatedbetween
principalfocusinobjectspace
andthelens.(FromSjostrand,
p.21)
Fig.I.25Constructionoftheimage
ofanobjectbymeansofray
tracing.(FromSjostrand,p.22)
Fig.I.26Magnifyingeffectof
apositivelens.(From
Sjostrand,p.22)
Fig.I.27Virtualmagnified
imageofobjectlocated
betweenprincipalfocusin
objectspaceandthelens.
(FromSjostrand,p.22)
Fig.I.28Amagnifyingglassformsan
enlarged,erectvirtualimage.The
angularsizeofthisimageis
approximately4"/15"or4/15.The
angularsizeoftheobjectatthe
closestdistanceforcomfortable
viewingis1"/10"or1/10.The
magnificationinthissituationis(4/15)/
(1/10),or22/3.(FromYoung,p.130)
Fig.I.29Theangularapertureofa
lens.Theangle2a isthe
acceptanceangleofthelens,and
thelargeritcanbemade,themore
informationcanthelenstransmit.A
largelensofhighaperturecan
thereforetellusmoreaboutan
objectthanasmalllensoflow
power.(FromMeek1sted.,p.12)
Fig.I.30Raydiagramforhighmagnification
modeofoperation.Notethateachlens
formsarealimage,withimageinversion.
I0istheimageformedbytheobjective
lensO,I1isformedbythefirstprojector
lensP1andI2bythesecondprojectorP2,
onthescreen.(FromAgar,p.30)
Fig.I.31Left:raydiagramofthe3realimagemediumandhighmagnificationimagingsystemofa3lens
microscope.Center:2realimageverylowor'scan'magnificationrangeofa3lensmicroscope.Right:2real
imagelowmagnificationsystemofa3lensmicroscope.(FromMeek1sted.,pp.118,120121)
Fig.I.32Raydiagramforacompleteelectron
microscope.FilamentF,condenser1lensC1,
condenser2lensC2,condenserapertureCA,
specimenS,objectivelensO,objectiveaperture
OA(inbackfocalplane).1stintermediateimage
andselectorapertureSA.IntermediatelensP1,
secondintermediateimageI2,projectorlensP2
andfinalimageonthefluorescentscreenFC.
(FromAgar,p.35)
a)f=2.0
x
o
=5.0
e)f=4.0
x
o
=3.0
b)f=10.5
x
o
=21.0
f)f=13.3
x
o
=13.3
c)f=3.5
x
o
=3.0
g)f=3.142
x
o
=0.0
d)f=5.0
x
o
=2.5
a)D=8.0
L1:f=2.0
x
o
=4.0
L2:f=3.0
b)D=8.0
L1:f=2.0
x
o
=6.0
L2:f=3.0
c)D=4.0
L1:f=2.0
x
o
=3.0
L2:f=2.0
FigI.33Accelerationofelectronin
electricfield.(FromSjostrand,p.26)
Fig.I.34Linesofforceatapositively
chargedsphericalbody.(FromSjostrand,
p.32)
Fig.I.35Linesofforceandequipotential
surfaces(stippledlines)associatedwith
twoequalchargesofoppositesign.
(FromSjostrand,p.32)
Fig.I.36Equipotentialsurfacesattwoparallel
platesofoppositechargeswiththepathofan
electronindicatedwithinthehomogeneous
partofthefield.(FromSjostrand,p.33)
Fig.I.37Refractionofelectronatan
equipotentialsurface.(FromSjostrand,p.33)
Fig.I.38.Negativelensactionof
electrostaticfieldatanaperturewhen
V2V1>V3V2.(FromSjostrand,
p.34)
Fig.I.39.Positivelensactionatan
aperturewhenV2V1<V3V2.
(FromSjostrand,p.34)
Fig.I.40Magneticfieldinducedbycurrent
passingthroughaconductor.(From
Sjostrand,p.35)
Fig.I.41Magneticfieldinducedbycurrent
passingthroughasolenoid.(From
Sjostrand,p.37)
Fig.I.42Solenoidwithironcore.(From
Sjostrand,p.40)
Fig.I.43a.Dependenceofpermeabilityonfluxdensity,B.
b.RelationshipbetweenfluxdensityBandfieldstrength.
(FromSjostrand,p.38).
Fig.I.44Magnetization.(FromSlayter,
p.361)
Fig.I.45Curves
showinghowthe
magnetizationof
softiron(lens
strength)is
relatedtothe
magnetizing
force(lens
current).An
unmagnetized
lensstartsfrom
thepointOand
followsthepath
OAaslens
current
increases.Atthe
pointA,further
increaseinlens
currentproduces
nofurther
increaseinlens
strength;thelensissaidtobe'saturated'.Whenlenscurrent
isreduced,thepathOAisnotretraced;adifferentpathABis
followed.Thisdisplacementiscalled'hysteresis'.Atzero
current(pointB),someresiduallensstrengthremains;thisis
called'remanence'.Tobringthelensbacktozerostrength,a
reversecurrentOCmustbeapplied.Lensstrengththen
increaseswithincreasingreversecurrent,followingthepath
CD.Thepolarityofthelenschanges,butthisdoesnotaffect
itsfocusingpower;onlythespiralelectronpathisreversed.
Becauseofhysteresis,itisnotpossibletocalibratealens
currentmeteraccuratelyintermsoflensstrengthor
magnification.
Fig.I.46Evolutionofmagneticelectron
lenses.(A)Shortsolenoidusedasa
magneticlens.(B)Softironcasing
enclosingoutersurfaceofthesolenoid,
thusconcentratingthefield.(C)Soft
ironencasingthesolenoidexceptata
narrowannulargaptherebyreducing
themagneticfieldtoaveryshortregion
alongthelensaxis.(D)Modern
objectivelensconsistingofasoftiron
encasedsolenoidandsoftironpole
piecessoastohaveanenormously
concentratedfieldatthelevelofthe
annulargap.(FromWischnizter2nded.,
p.33)
Fig.I.47(a)Amagneticlensconsisting
ofatightlywoundcoilandasoftiron
shroudsurroundingthecoilexceptfor
asmallgap.Thefieldisconcentratedin
thatgap.(b)Shortfocallength
electromagneticlenswithpolepieces.
(FromSjostrand,p.50)
Fig.I.48Fieldstrengthdistribution
curves.ThecurvesADcorrespondto
therespectivelensesillustratedinFig.
I.46.Eachrepresentsthefieldstrength
alongthelongaxisofthelens.The
changesintheshapeofthecurves
representtheshorteningor
concentrationofthefieldovera
shorteraxialdistance.Hz=
longitudinalmagneticfield.Z=
distancealongtheaxisofsymmetry.
(FromWischnizter2nded.,p.33)
Fig.I.49TheforceFactingon
astraightconductorina
homogeneousmagneticfield
offluxdensityBwhencurrent
Iispassedthroughthe
conductor.(FromSjostrand,
p.43)
Fig.I.50Pathofanelectronina
magneticfield.(A)Inalarge,uniform
magneticfield.(B)Inasmall,uniform
magneticfield.(FromWischnitzer2nd
ed.,p.25)
Fig.I.51Lefthandthumbrule.
(FromSjostrand,p.43)
Fig.I.52Thompson'sexperiment.A
streamofelectronsoriginatingfroma
sourceandpassing,invacuo,through
amagneticfieldproducedbyapairof
magnetswillbedeflected.The
directionofdeflectiondemonstrates
thatelectronsarenegativelycharged
particlesofmatter.(FromWischnitzer
2nded.,p.25)
Fig.I.53Actionofasolenoidonan
electronbeam.Anelectriccurrent
passingthroughthecoilproducesan
axialmagneticfield.Thisisthe
refractingmediumfortheelectrons.An
electronstartingatapointontheaxisA
andatanangletoitfollowsaspiral
path,returningtotheaxisatthepoint
B.Theactionisbasicallysimilartothat
oftheconverginglightlensshownin
Fig.I.20.(FromMeek1sted.,p.8)
Fig.I.54Actionofthemagnetic
lens.(a)Inperspective.(b)
Electrontrajectoryin
projection,alongdirectionof
propagation.(c)Electron
trajectoryinprojection,side
view.(FromSlayter,p.358)
Fig.I.55Componentsofthe
vectorHneartheaxisoffields
withaxialsymmetry.His
representedbytwo
components,Hz,the
componentinthez(axial)
direction,andHr,the
compnentinther(radial)
direction.(FromHall,p.85)
Fig.I.56Theycomponentof
themagneticfieldina
magneticlensisoriented
perpendiculartothedirection
ofanelectronenteringthe
lensalongapathparallelto
thelensaxis.Thisy
componentwillaffectthe
electron,deflectingitinthex
directionasindicatedbythe
arrowmarkedvx.(From
Sjostrand,p.48)
Fig.I.57Thezcomponentofthemagneticfield
andthexvelocitycomponentoftheelectron
inamagneticlensinteract,deflectingthe
electronintheydirectiontowardthelens
axis.(FromSjostrand,p.49)
CuuDuongThanCong.com https://fb.com/tailieudientucntt
cuu duong than cong . com

I.THEMICROSCOPE
I.A.PRINCIPLESOFTHETRANSMISSIONELECTRONMICROSCOPE(TEM)
I.A.1.OriginoftheTransmissionElectronMicroscope
I.A.2.ComparisonofLight(LM)andElectronMicroscopes(Fig.I.1)
a.Similarities(Arrangementandfunctionofcomponentsaresimilar)
1)Illuminationsystem:producesrequiredradiationanddirectsitontothespecimen.Consistsofasource,whichemitstheradiation,anda
condenserlens,whichfocusestheilluminatingbeam(allowingvariationsofintensitytobemade)onthespecimen.
2)Specimenstage:situatedbetweentheilluminationandimagingsystems.
3)Imagingsystem:Lenseswhichtogetherproducethefinalmagnifiedimageofthespecimen.Consistsofi)anobjectivelenswhichfocusesthe
beamafteritpassesthroughthespecimenandformsanintermediateimageofthespecimenandii)theprojectorlens(es)whichmagnifiesa
portionoftheintermediateimagetoformthefinalimage.
4)Imagerecordingsystem:Convertstheradiationintoapermanentimage(typicallyonaphotographicemulsion)thatcanbeviewed.
b.Differences
1)Opticallensesaregenerallymadeofglasswithfixedfocallengthswhereasmagneticlensesareconstructedwithferromagneticmaterialsand
windingsofcopperwireproducingafocallengthwhichcanbechangedbyvaryingthecurrentthroughthecoil.
2)MagnificationintheLMisgenerallychangedbyswitchingbetweendifferentpowerobjectivelensesmountedonarotatingturretabovethe
specimen.Itcanalsobechangedifoculars(eyepieces)ofdifferentpowerareused.IntheTEMthemagnification(focallength)oftheobjective
remainsfixedwhilethefocallengthoftheprojectorlensischangedtovarymagnification.
3)TheLMhasasmalldepthoffield,thusdifferentfocallevelscanbeseeninthespecimen.Thelarge(relative)depthoffieldintheTEMmeans
thattheentire(thin)specimenisinfocussimultaneously.
4)Mechanismsofimageformationvary(phaseandamplitudecontrast).
5)TEMsaregenerallyconstructedwiththeradiationsourceatthetopoftheinstrument:thesourceisgenerallysituatedatthebottomofLMs.
6)TEMisoperatedathighvacuum(sincethemeanfreepathofelectronsinairisverysmall)somostspecimens(biological)mustbedehydrated
(i.e.dead!!).
7)TEMspecimens(biological)arerapidlydamagedbytheelectronbeam.
8)TEMscanachievehighermagnificationandbetterresolutionthanLMs.
9)Pricetag!!!(100xmorethanLM)
I.A.3.Photons/Electrons
a.Dualconceptofwaveandparticle(Fig.I.4)
Lighthaspropertiesbothofaparticleandawave.Thisdualnatureisrequiredtosatisfactorilyexplaintheresultsofvariousphysicalexperiments.
Thediffractionoflight(bendingaroundcorners)illustratesthewavenature.TheWAVETHEORYisbasedonthestatisticalnatureofeventsand
haslittlemeaningwithrespecttothebehaviorofsingleparticles.ThewavetheorywasdevelopedandexpoundedbyHuygens(16291695)and
Hooke(16381703).TheCORPUSCULARTHEORYwasproposedbyNewton(16421727)andbecamethemoreacceptedtheoryevenafter
demonstrationofdiffractionbyYoung(17731829)andinterferencebyFresnel(17881827).Atabout1850,thewavetheorycamebackinto
favoruntilabout1900whenmoreevidenceforthecorpusculartheorywasdiscovered.
QUANTUMTHEORY(PlanckandEinstein)providesthebasisforexplainingthephenomenaofINTERFERENCE,DIFFRACTIONandthe
PHOTOELECTRICeffect(lightfallingoncertainmetalscausethemtoemitelectrons)andthusformsacommonbasisforexplainingthenatureof
actionoflight.Thetransferofenergybetweenlightandmatteroccursonlyindiscretequantitiesproportionaltothefrequencyofthe
lightwave.
E=hJ
where
E=energyofphoton(joules)
h=Planck'sconstant(6.624
•
10
34
joulesec)
J=frequency(cycles/sec)
b.Electronvelocityandwavelength
Therelationbetweenthewavelength(l )ofaparticleofmass,m,movingatavelocity,v,isgivenbytheDeBrogliewaveequation:
(1)
Anelectronofchargee(1.6
•
10
19
coulomb),andmassm(9.11
•
10
28
gm),whenpassingthroughapotentialdifferenceofVvolts(expressedin
joules/coulomb),hasakineticenergy:
(2)
Solvingforvelocity:
(3)
substitutingintotheDeBroglieequation(1):
(4)
Since1joule=10
7
dyne
•
cm=10
7
cm
2
•
gm/sec
2
(5)
Thus,forexample,ifV=60,000volts,l =0.005nm.
Fromequation(3)theelectronvelocitycanbecalculatedifVisknown:
(6)
Thefollowingtableillustratesthat,athighvoltage,electronvelocityiscomparabletothespeedoflightinavacuum(c=3
•
10
10
cm/sec).
Theequationbreaksdownwhenthevelocityoftheelectronapproachesthespeedoflightbecausearelativisticcorrectionmustbemadeforthe
valueofthemasswhere:
(7)
Therelationbetweenl andVismorecorrectlygivenby:(seeHall(1966)pp.3334)
(8)
Thefollowingtableisobtainedwhenrelativityeffectsareincluded:
c.Interference/diffraction/coherence
Anideallenssystemobtainsanexactimageoftheobject(eachpointfaithfullyreproduced).Thephenomenaofdiffractionmakesthis
unattainable(Figs.I.5,I.6).
Diffractionphenomenainvolvesthebendingofthepathofradiationpassingclosetoanobstacle(Fig.I.6).Thisresultsinaspreadingofthe
radiationintotheregionbehindtheobstructionthatthewavespassed.Thediffractionatedgescontributestothecontrastatwhichanedgecan
beobserved.Diffractionalsolimitstheresolvingpowerofthemicroscopesincetheimagepointproducedbyalensisadiffractionimageofthe
openingofthelensortheaperturerestrictingtheeffectiveopeningofthelens(Fig.I.5).
Ifthelightsourceandtheplaneatwhichthediffractionpatternisobservedareatfinitedistancesfromtheedge,thephenomenoniscalled
Fresneldiffraction.Thepatternisdescribedasduetointerferencebetweenthenondiffractedlightandawaveoflightdiffractedattheedge.
Theresultingsuperpositiongivesrisetoaseriesofdiffractionfringesorientedparalleltotheedgeandrepresentingperiodicallyvaryingbrightness,
maximaandminima.(Figs.I.7,1.8,I.9).
Coherence:Aprerequisiteforinterferenceisasuperpositionofwavesystemswhosephasedifferenceremainsconstantintime.Twobeams
arecoherentif,whencombined,theyproduceaninterferencepattern.Thebeamsareincoherentwhentheyareincapableofproducingan
interferencepattern.Twobeamsoflightfromselfluminoussourcesareincoherent.Iflightfromthetwosourcesfallsonascreen,theresultant
intensityissimplythesumofthetwointensitieswhichwouldoccurfromeachsourceseparately(Figs.I.10,I.11).Inpracticeanemittingsource
hasfiniteextentandeachpointofthesourcecanbeconsideredtogeneratelight.EachsourcegivesrisetoasystemofFresnelfringesatthe
edge.Thesuperpositionofthesefringesystemsisfairlygoodforthefirstmaximaandminimabutfartherawayfromtheedgeshadowtheoverlap
ofthefringepatternsbecomessufficientlyrandomtomakethefringesdisappear.Thenatureofwaves,phase,amplitude,andinterferenceare
illustratedinFigs.I.12andI.13.
d.Resolution
1)Definitions:
RESOLUTION:abilitytodistinguishcloselyspacedpointsasseparatepoints.
RESOLUTIONLIMIT:smallestseparationofpointswhichcanberecognizedasdistinct.
RESOLVINGPOWER:resolutionachievedbyaparticularinstrumentunderoptimumviewingconditions.
2)Distinctionbetweenresolutionandresolvingpower:
Notethedistinctionbetweenresolutionandresolvingpower.Resolvingpowerisapropertyoftheinstrumentandisaquantitythatmaybe
estimatedontheoreticalgrounds.Resolutionisequaltoorpoorerthantheresolvingpowerandisthequantityobservedunderanygivenset
ofexperimentalconditions.IntheTEM,especiallywithbiologicalsamples,theresolutionachievedmaybeconsiderablyinferiortothetheoretical
resolvingpoweroftheinstrument.
Microscopyisthescienceofseeingtheverysmall.Underidealconditions,theeyeresolvesabout1minuteofarc(=1/60degree=2.9x10
4
radian;recallthereare2p radiansin360°)andsinceitcanfocusdowntoabout250mm,thesmallestobjectwecanresolveisabout0.07mm
(70mm)(Fig.I.14).Thislimitisrelatedtothesizeofthereceptorsintheretinaoftheeye.Thefunctionofamicroscopeistomagnifytheimage
fallingontheretina(Fig.I.15).Theadvantageoflightandelectronmicroscopesisthattheyeffectivelygettheobjectclosertotheeyesoa
magnifiedimageisobtainedandmoredetailcanbediscerned.
TENNISBALLANALOGY:Eyecanresolve3cmat100meters,thusatennisballisclearlyvisible.Butifthetennisballisheldupagainstawhite
background,thevisibilitydecreases(becauseofthedecreaseincontrast).
3)Abbecriteriaofresolution:
Thefundamentalnatureoflightposeslimitsonthedetailthatcanberesolved(Fig.I.16).Abbe(1893)showedthatthesmallestresolvable
distanceisabout1/2thewavelengthoflightused.Thus,1/2thewavelengthoftheradiationusedistheultimateresolvingpowerofany
instrument.Thislimitstheusablemagnificationofopticalmicroscopesto<1000X.Atfirstitwasthoughtthatxraymicroscopeswouldbeuseful
buttherefractiveindexofsubstancesforxraysisnearly=1,thusrefractinglensescannotbemadeforxrays,andconsequently,xrayscannot
beeasilyfocusedtoformimages.
4)Magnificationlimits:
Themaximummagnificationofaninstrumentislimitedaccordingtothefollowingrelationship:
Thus,fortheLM,witharesolvingpowerofapproximately0.25µm,themaximum(useful)magnificationisabout250µm/0.25µm=1000X.Thevalue
usedfortheresolvingpoweroftheeyeinthisexample(250µm)representsamorerealisticviewingcondition.Anymagnificationabovethevalue
givenbytheaboveformularepresentsemptymagnification,sincesuchmagnificationleadstonomoreusefulinformationbutratheramagnified
blur.
AccordingtotheAbbecriteria,at60,000volts,theTEMshouldhavearesolvingpowerofabout0.0025nm.Thisshouldallowamaximumuseful
magnificationofabout100milliontimes!!!Inpractice,themaximumusefulmagnificationoftheTEMoperatedat60kVislimitedtomuchlessthan
1,000,000X.Thus,althoughtheLMnearlyobeystheAbbecriteria,theTEMfallsshortbyaconsiderableamount.Themainlimitingfactorinthe
TEM,withrespecttoachievingthetheoreticalresolvingpoweroftheinstrument,concernsthenatureoftheimaginglensesandtheprocessof
imageformation.
5)Rayleighcriteria(practicalbutarbitrary):(Fig.I.17).
Itistheabilityofmicroscopestomakeobjectpointswhichareclosetogetherappearintheimageasseparatepoints.Anideallenstakeseach
objectpointandrepresentsitexactlyasapointintheimage.Areallenstakeseachobjectpointandspreadsitoutintoacirculardisk(Airy
disk)intheimageplanewhosediameterdependsontheangularapertureofthelens.
Theshortestdistancebetween2disksatwhichthetwodisksappearpartiallyseparatedcorrespondstoabout1/2thewidthofthedisks.The
distance,d,inobjectspaceisgivenby:
d=0.61l /n
•
sina
where
l =wavelenghtoftheradiation
n=refractiveindexofthemedia
a=semiangularapertureofthelens
NOTE:n
•
sina=thenumericalaperture(N.A.)ofthelens.
Thus,tomaximizeresolvingpower,l mustbedecreased,nincreased,oraincreased.Recallthatweareconcernedatthemomentwithan
aberrationfreeopticalsystem.Thevaluefortheconstant(0.61)iscontroversialbecauseitdependsonthecoherenceoftheradiationanda
criteriaofvisibility.
FortheLM,usingoilimmersionoptics(n=1.5),sina=0.87,andvioletlight(l =400nm),d=0.2µm.Theonlywaytoimprovetheresolutionisto
uselightofshorterwavelengthsinceN.A.cannotbeincreasedbeyond~1.5.FortheTEM,n=1(vacuum),sina=10
2
andl =0.005nmfor60kV
electrons,thusd=0.3nm.
I.A.4.Optics(LensTheory)
a.Basiclawsofclassicalgeometricaloptics
1)Rectilinearpropagationoflightwhenn(refractiveindex)isconstant.
2)Lawofreflection:
3)Lawofrefraction(Snell'sLaw):
4)Independenceofrays.Theassumptionismadethatlightraystravelindependentlythroughspace.
Theselawsholdforelectrons,except#4,ifthecurrentdensityistoohighwhennegativechargedelectronscaninterfere.
b.Classicalvs.electronoptics
1)Classicaloptics:Therefractiveindexchangesabruptlyatasurfaceandisconstantbetweenthesurfaces.Therefractionoflightatsurfaces
separatingmediaofdifferentrefractiveindicesmakesitpossibletoconstructimaginglenses.Glasssurfacescanbeshaped.
2)Electronoptics:Here,changesintherefractiveindexaregradualsoraysarecontinuouscurvesratherthanbrokenstraightlines.Refraction
ofelectronsmustbeaccomplishedbyfieldsinspacearoundchargedelectrodesorsolenoids,andthesefieldscanassumeonlycertaindistributions
consistentwithfieldtheory.
c.Geometricalandphysicaloptics
Thefundamentalprinciplesofopticsgovernthedesignandoperationofboththelightandelectronmicroscopes.Thebasicopticalprinciples
involvingtheuseofrefractileelementsorlensesinordertoformmagnifiedimagesareidenticalinboththeLMandTEM.TheTEMdiffersfromthe
LMonlyintheradiationitusesandinthewayinwhichtheradiationisbentorrefracted.
Geometricalopticsdealswiththestudyofthepathsfollowedby'rays'oflightorelectronsthroughlensesandapertures,andthegeometrical
constructionsusedtofindtherelativepositionsandsizesofobjectsandtheirimages.Arayoflightorelectronsisdefinedasaninfinitelythin
pencilorbeam.Physicalopticsshowsthatthisanabstractionandcannotphysicallyexistbecauseof'diffraction'whichdealswiththewave
natureoflightandelectrons.Allresultsobtainedingeometricalopticscanbederivedfromtheprinciplesofphysicaloptics,alongwithother
phenomenasuchasinterferenceanddiffractionwhicharenotexplicableinsimplegeometricalterms.
d.Idealversesreallenses:
Lensesareusedtobendraysoflightorelectronssotheyaredeflectedinapredictablewayfromtheiroriginalpaths.Thepropertiesofanideal
lens,possessinganaxisofrotationalsymmetryare:
1)Eachrayofthebundleofrayswhichpassesfromanobjectpointwillberefractedbytheideallenstomeetinoneimagepoint.
2)Raysoriginatingfrompointswhichlieonaplaneperpendiculartotheaxis,mustbeimagedinaplanewhichisalsoperpendiculartotheaxis.
3)Theimageappearsliketheobjectirrespectiveofthemagnification,sotherelativelineardimensionsoftheobjectarepreservedintheimage.
Inpractice,theimagingbyanyreallensdoesnotcorrespondtothatoftheideallensowingtothefactthatanobjectpointisrepresentedbya
diffractionimage(Airydisc)ofthelensopeningortheapertureusedforrestrictingtheeffectiveopeningofthelens.Thisisaresultofthewave
likepropertiesoflight.Lensaberrationsalsocontributetomoreorlesspronounceddeviationsfromthepropertiesoftheideallens.
Thesinglerefractingsurfaceofsphericalcurvatureisthefundamentalunitoffocusingactionbyglasslenses.Sphericalrefractingsurfacesactas
lensesforparaxialrayswhicharethoseraysthatpassclosetotheprincipalaxisofthelens.RayswithlargeangleswillNOTobeyideallens
action.
Afundamentaldifferencebetweenlightandmagneticlensesisthattheelectronbeamdoesnotchangeinforwardvelocityasitpassesthrough
themagneticfield(lightraysslowdownwhenpassingintoamediumofhigherrefractiveindex).Refractioniscontinuouswithelectronswhenthey
areinthemagneticfield:lightisrefractedonlyattheinterfacebetweenmediaofdifferingrefractiveindex.Theelectronsalsofollowspiral
trajectoriesthroughthemagneticfield(seealsoSec.I.A.5.c(Magneticfieldsandmagneticlenses)
e.Raydiagrams:(Figs.I.20I.28)
Themethodofconstructionofraydiagramsisbasedonthreesimpleprinciples:
1)Allraysenteringthelensparalleltotheaxisarebroughttoacommonpointontheaxis,thefocalpoint.
2)Allrayspassingthroughthegeometricalcenterofthelensareundeviatedandpassstraighton,nomatterfromwhichdirectiontheycome.
3)Principleofreversibility:ifthedirectionofarayisreversedinanysystemtherayexactlyretracesitspaththroughthesystem.Thisapplies
onlytothelocationoflightpathsandnottotheintensityofthelight.
Theaboveprinciplesarebasedontheassumptionsthatwearedealingwithathinlensandconcernedwiththepathsofparaxialrays.The
standardconventionistodrawdiagramswithraysthattravelfromlefttoright.Theobjectistotheleft(infront)ofthelensandtheimageisto
theright(behind)ofthelens.
f.Definitions:
Realimage:oneatwhichlightraysphysicallyreunite,sothataphotographicplateplacedatthepositionofarealimageisexposed.
VirtualImage:onefromwhichlightraysappeartodiverge;raysarenotinfactconcentratedatthepositionofavirtualimage,sothata
photographicplateplacedatthepositionoftheimageisnotexposed(byfocusedrays).Placinganopticalsystemsuchastheeyebehindthe
lens,willenablethedivergentraystobefocusedtoformarealimage.TheintermediatelensofanTEMissometimesusedthiswayinorderto
reducethefinalsizeoftherealimageformedbytheprojectorlens(es).
Converging(positive)lens:bendsraystowardtheaxis.Ithasapositivefocallength.Formsarealinvertedimageofanobjectplacedtothe
leftofthefirstfocalpointandanerectvirtualimageofanobjectplacedbetweenthefirstfocalpointandthelens.
Diverging(negative)lens:bendsthelightraysawayfromtheaxis.Ithasanegativefocallength.Anobjectplacedanywheretotheleftofa
diverginglensresultsinanerectvirtualimage.Itisnotpossibletoconstructanegativemagneticlensalthoughnegativeelectrostaticlensescan
bemade.
g.Lensformula(thinlensequation):
where
f=focallengthofthethinlens(sameradiusofcurvatureforboth
sphericalsurfaces)
o=distanceofobjectfromlens(positivetotheleft)
i=distanceofimagefromthelens(positivetotheright)
NOTE:Foravirtualimage,ihasanegativevalue.
h.Magnification:
Foraconverginglens,iftheobjectismorethantwicethefocallengthfromthelens,thentheimageformedisreal,inverted,andsmallerinsize
thantheobject(M<1).Whentheobjectisatadistance=2f,theimageandobjectarethesamesize(M=1);whenitisbetweenfand2f,
theimageislargerthantheobject(M>1),andwhenitis<f,theimageisvirtual,erect,andlargerthantheobject(M>1).
i.Angularapertureofthelens(2a)(Fig.I.29)
Theaperturedeterminesthetotalamountofradiationarrivingfromtheobjectwhichcanbefocusedto
formanimage.Theaperturethuscontrolstheabilityofthelenstogatherinformationabouttheobject.
Thisdependsontheangleoftheconeofraysitisabletoacceptfromtheobject.Bringinganobject
closertotheeyeincreasestheangularaperture,butthereisalimittotheclosenessthattheobjectcan
bebroughttotheeye(~25cmcorrespondingtoanangleofabout0.9°fora4mmexitpupildiameterof
theeyelens;atypicalLMwithanoilimmersionobjectivelenshas2aof~175°).
j.Simplevs.compoundmicroscope(Figs.I.30I.32)
Inprinciple,arealimageofanydesiredmagnificationcanbeobtainedfromasinglepositivelens,butin
practicethisiscumbersomebecauseofthelonglensimagedistance.Oneormorelensescanbeusedto
magnifytheimageinstages(totalmagnificationequalingtheproductofthemagnificationsofeachlens).
Theimageformedbyonelensconstitutestheobjectforthesubsequentlens,whetherornotareal
intermediateimageisformed.
Comparisonofoneversestwostagemagnification:
Thefollowingdescriptionillustrateshowdifferentpathlengthsarerequiredtoachieveamagnificationof10,000Xusingeitheroneortwolenses
withf=2.0cm.
OneStageSystem:
TwoStageSystem:
Assumebothlenseshavef=2.0cmandarearrangedsoeachgives100Xmagnification.
Thus,M=100=x
i
/x
o
foreachstage.
FirstStage:
x
o
=2.02cm
x
i
=202.00cm
Therealimageformedinthefirststagebecomestheobjectforthesecondlens.
SecondStage:x
o
,x
i
sameasinthefirststage.
Totallengthofsystem
=lengthoffirststage+lengthofsecondstage
=(x
o
+x
i
)+(x
o
+x
i
)
=2(x
o
+x
i
)
=2(2.02+202.00)=408.04cm(4.08meters)
k.Problemset
Thefollowingproblemsareforyourownedificationtotesthowwellyouunderstandthebasicsoflensoptics.
1.Foreachsituationbelow,drawanaccurate(usegraphpaper)raydiagramshowingthepathof(atleasttwo)raysfromtheobjecttoimage.
Indicatewhethertheimageisrealorvirtualandspecifythedistanceoftheimagefromthelensandthemagnificationoftheimagewithrespect
totheobject.Ineachexample,thelensisconverging,withidenticalfrontandbackfocalpoints.Distancesareinarbitraryunits.Letf=lens
focallength,x
o
=distanceofobjectinfrontofthelens,andx
i
=distanceofimagebehindthelens.Theobjectmaybeanysize.
2.Inthefollowingexamples,therearetwoconverginglensesinsuccession.Drawraydiagramsshowingtheformationofboththeintermediate
andfinalimagesandgiveappropriateinformationaboutthenature(real/virtual),positions,andsizesoftheintermediateandfinalimages.What
isthemagnificationateachstageofimageformationandwhatisthemagnificationofthefinalimage?Thedistancefromthecenteroflens1(L1)
tothecenteroflens2(L2)equalsD.
I.A.5.ElectronOptics/ElectronLenses
a.Electronemission
Innershellelectronsinmetalatomsshieldtheelectricfieldofthenucleusthroughtherepulsiveforcestheyexertontheoutershell(valence)
electrons.Thustheattractionbetweenthevalenceelectronsandthenucleusisreduced.Metalatomsarecharacterizedashavingtwoloosely
boundvalenceelectronswhichmigratefreely(thisiswhymetalsaregoodelectricalconductors)andcanescapefromthemetalcompletelyif
sufficientadditionalenergyisimpartedtothem.Asthetemperatureofametalisincreased,thekineticenergyoftheelectronsincreasesbecause
ofincreasedthermalvibrationsofthemetalions,whichcollidemorefrequentlywiththeelectrons.Thermionicemissionisthetermusedto
describetheprocessbywhichthermalenergyissuppliedtolooselyboundelectronsinordertoformasourceofelectrons.
Atroomtemperatureelectronsareeffectivelypreventedfromescapingthesurfaceofthemetalowingtotheattractiveforceofthepositively
chargedions.Asthetemperatureisincreasedsomeelectronsacquiresufficientenergytoovercometheattractionandleavethemetal
temporarily.Metal,shapedasathinwire,caneasilybeheatedbypassinganelectriccurrentthroughit.Sincethemetalsurfacebecomes
positivelycharged,acertainlevelofenergy(workfunction)mustbesuppliedtoallowelectronstoescapefromthesurface.Eachmetalhasa
characteristicworkfunction.Tungsten,withalowworkfunction,emitsmoreelectronsthanmetalswithhigherworkfunctions(seealsopp.2930
andFig.I.59).
Ifastrongelectrostaticfieldisappliedinavacuumbetweenthewire(givenanegative,cathode,potential)andananode,theelectricfieldwill
causeelectronstoaccelerateawayfromthewiretowardstheanodesurface(Fig.I.33).Thespeedoftheelectronsdependsonthestrengthof
theelectrostaticfield(voltage)betweenthecathodeandanode(equation(3),Sec.I.A.3.b)Thenumberofelectronswhichleavethewire
dependsonthetemperaturetowhichthewireisheated,whichdependsonhowmuchfilamentcurrentpassesthroughthewire.
A"V"shapedwirewillhavethehighesttemperatureatthetip.Electronswithdrawnfromthefilamenttipcarryelectricchargestotheanode.This
electriccurrent,whichflowsbetweenthefilamentandtheanode,iscalledthebeamcurrent.
1)Electricfield/Equipotentials
Anelectricallychargedobjecthasassociatedwithitanelectricfield.Thus,anelectricallychargedparticle,whenbroughtnearachargedobject,
isinfluencedbyanelectricalforceinthevicinityoftheobject.Theforceisdirectedtowardthechargedobjectifthechargesareofopposite
signsandawayfromtheobjectiftheyareofsimilarsign.DEFINITION:Thedirectionofanelectricfieldisdefinedasthedirectionoftheforce
actingonapositivecharge.(Figs.I.3435)
Alongthelinesofforceconnectingthetwocharges,theelectricpotentialwillchangegraduallybetweentheextremevaluesrepresentedbythe
twocharges.DEFINITION:Equipotentiallinesdefinethepointsalongthelinesofforcewithidenticalelectricalpotential.Theseequipotential
surfacesarealwaysorientedperpendiculartothelinesofforce.Thechangesintheelectricpotentialaregradualinspace.
Electronswhichenterafieldbetweentwoparallelplatesinadirectionparalleltotheplatesareaffectedbytheforcedirectedperpendicularto
theplates(FigI.36).Theelectronswillbeattractedtowardthepositiveplate.Thepathchangesinaseriesofgradualstepsattheequipotential
surfaces.
FigureI.37showshowtheelectronpathis"refracted"attheequipotentialsurface.TheresultisfundamentallythesameasthatgivenbySnell's
Lawofrefractioninlightoptics.Aconsequenceofthisisthatasphericallycurvedequipotentialsurfaceexhibitsthepropertiesofalens.
FiguresI.38andI.39showhowbothpositive(converging)andnegative(diverging)electrostaticlensescanbeformed.Thisfeatureof
electrostaticlensesdiffersfromelectromagneticlenseswhichcanonlyactasconverginglenses.
2)Advantages/Disadvantagesofelectronlenses:
Thefactthattherefractiveindexdoesnotchangeabruptlyinelectronlenseshasoneadvantageinthattherearenotroublesomereflectionsat
equipotentialsasatglassinterfaces.Thereisaseriousdisadvantageinthatequipotentialscannotbeshapedandcombinedinarbitraryfashionto
correctforchromaticaberrationandothererrors.
Althoughelectronmicroscopeswhichemployelectrostaticlenseshavebeenmade,mostmicroscopesuseelectromagneticlenses.Amajorreason
isthatelectrostaticlensesaremoresensitivetothequalityofthevacuumandcleanlinessofthecomponentsthanareelectromagneticlenses.
Somelensaberrationsaremoresevereforelectrostaticlensescomparedtoelectromagneticlenses.Electrostaticlensesrequireverypowerful
electrostaticfieldswhichcanleadtoelectricalbreakdownor"arcingover"insidethecolumn,especiallyunderpoorvacuumconditions.Forthis
reason,electrostaticlensescannotbemadewithfocallengthsasshortasmagneticlenses.
b.Electrostaticlens
Abasicunderstandingofelectrostaticlensesisimportantfortwomainreasons:i)theelectrongunuseselectrostaticlensactiontoformthe
primarybeamsource,andii)itisquitecommonforachargetodeveloponthenonconductingcontaminationwhichmayaccumulateonphysical
apertures(suchastheobjectiveaperture)andtransformthemintoweakelectrostaticlenseswhichcandistorttheelectronimage.
3)Propertiesofelectrostaticlenses:
a)Anyaxiallysymmetricalelectrostaticfieldhasthepropertiesofalensforraysconfinedtotheparaxialregion.Alltheideallensformulasapply
toelectrostaticlenses.
b)Forelectronlenses,replaceÃ(f)forrefractiveindexinthelensequations(f=valueofthepotentialontheaxis).Intheimageformingsystem
ofmostTEMs,fisthesameonbothsidesofthelens(SeeSec.I.A.5.c).
c)Ifboundedbyregionswherefisconstant,anelectrostaticlensisalwaysconvergent.
c.Magneticfieldsandmagneticlenses
1)Magneticfield
Anelectriccurrentpassingthroughaconductorgivesrisetoamagneticfield.TheconventionisthatNisthedirectioninwhichthelinesofthe
magneticfieldpoint(Fig.I.40).Themagneticfluxisthetotalnumberoflinesandthefluxdensityisthenumberoflinesperunitareaofasurface.
UsetheRIGHThandruletodeterminethedirectionofthefield(thumbpointstowardcurrentdirectionandfingerscurlindirectionoffield.NOTE:
Byconvention,thedirectionofelectronflowisoppositetothatofcurrentflow.
Fluxdensitydependsonthepropertiesofthematerialsurroundingtheconductor.Ironinducesahigherfluxdensitythanairoravacuum.The
propertyofthematerialwhichaffectsthefluxdensityiscalledthepermeability,m,ofthematerial.Forairandvacuum,m=1.0.For
ferromagneticmaterialsitcanbeaslargeasseveralhundredthousand.
Iftheconductorhastheshapeofacircularloop,thelinesofforceformcirclesaroundtheloop.Thefluxdensityisgreatestatthecenterofthe
loop.Themagnetinthecenteroftheloopisorientedperpendiculartotheplaneoftheloopifthecurrentthroughtheloopissufficientlystrongto
eliminatetheinfluenceoftheearth'sfield.ThesideoftheloopatwhichthelinesofforceleavetheloopistheNorth(N)poleofthemagnet(Figs.
I.41,I.42).
Ifthewireiswoundinseveralturnsaroundacylindricalsurface(solenoid),eachturnwillcontributetotheinducedmagneticfield.Theflux
densityinthecenterofthecoilisgivenby:
Inthecaseofairandnonmagneticmaterials,µ=1.0andB=H.
Thepermeabilityofirondependsonthefieldstrength,H,anddecreasestounityathighfieldstrengthorwhenthefluxdensity,B=H(Fig.I.43).
Thehighpermeabilityofironisduetotheinducedmagneticfieldorientingmicroscopiccrystalregionsactingastinymagnetsintheiron.Allthese
tinymagnetsaddtheirmagneticfieldstotheinducedfield(Fig.I.44).Whenallmicromagnetsarenearlyoriented,theironwillaffecttheflux
densitytoadecreasingamountsincethereorientationofmicromagnetsisnearingcompletion.Thus,thepermeabilityofironathighfieldstrengths
approachesthatofemptyspace.Atthispointtheironreachesmagneticsaturation.
2)Hysteresis
Thestrengthofthelensdependstosomeextentonthepreviousmagnetichistoryof
thelens.Whenthecurrentinalensisreduced,thedecreaseinmagnetizationdoes
notretracethesamepathobtainedwhenthecurrentwasincreased(Fig.I.45).
Inductionofmagnetizationinvolvesaphysicalmovementwithinthemagnetized
material,requiringtheovercomeofacertaindegreeofinertia.Asaresult,
magnetizationtendstolagbehindthemagnetizingforceapplied.Inducedmagnetic
fluxcanonlybereturnedtozerobyapplicationofacurrentintheoppositedirection.
Aconsequenceofhysteresisisthatthelevelofcurrentusedtoenergizeamagnetic
lensDOESNOTpreciselyspecifythelensstrength(i.e.focallength).
NormalizationofTEMlensesisaccomplishedbyreducingthelenscurrenttozero
somepredeterminednumberoftimes.Hysteresismayalsobeminimizedbytakinga
lenstosaturationandthenreturningittotheworkingcurrentwithoutovershooting.
Whenthefieldstrengthisreducedtozero,somemagnetizationstillremainsintheiron
(residualmagnetizationorremanence).Anadvantageofsoftironisthefactthat,
whenusedinanelectromagnet,hysteresisislow.
Introductionofpiecesofironinamagneticfielddrasticallyaffectsthefluxdensity.
Magneticmaterialhasashieldingeffect,theeffectbeinggreaterthegreaterthe
permeability.Permalloy(mmetal)hasamaximumpermeabilityof80,000140,000
comparedtoironusedintransformers(~7000).mmetalpermeabilityislimitedtolower
fieldstrengthsthanthatatwhichironstillretainshighpermeability.Thismetalis
thereforeusefulforshieldingtheTEMfromexternalmagneticfields.
d.Theelectromagneticlens
1)Lensdesigndevelopment(Figs.I.46I.48)
Theefficiencyofthemagneticfieldproducedbyashortsolenoidwasfirstimproved
byencasingtheenergizingcoilinasheathofsoftironwhichhasthepropertyofconcentratingthelinesofforceinamagneticfieldandthus
becomingmagnetizedbyinduction.Inthiswayamuchmorepowerfulaxialmagneticfieldisobtainedforthesameamountofcurrentflowing
throughthesolenoid.Furtherdevelopmentinvolvedencasingtheentirecoilwithsoftironexceptatanarrowannulargapintheinsideofthecoil.
Thisproducesagreaterconcentrationofthemagneticfieldalongashortaxialdistance.Toachieveshorterfocallengthlenses(andobtaingreater
magnifications)asoftironpolepiecewithanopenaxialborewasintroducedatthepositionoftheannulargap.
MagneticlensesusedinTEMsarealwaysconstructedwithanironcircuittoproduceahighfieldstrengthacrossashortgap.Themagneticfields
forTEMlensesareintherangeof10,00020,000gauss.
2)Forcesactingonacurrentinamagneticfield
Theforceonanelectroninamagneticfieldisalwaysatrightanglestothevelocityandthedirectionofthefield(Figs.I.49,I.50,andI.52).The
fieldonlyactsonthevelocitycomponentwhichisdirectedperpendiculartothelinesofforce.Usethelefthandrule(Fig.I.51:firstfingerfor
fielddirection,middlefingerforcurrentdirection,andthumbfordirectionofforce).Rayspassingthroughthelensareturnedthroughanangle
whichdoesNOTdependonthedistanceoftheraysfromtheaxis.Allelectronscontainedinagivenmeridionalplanebeforeenteringthefieldare
containedinarotatingmeridionalplaneastheypassthroughthelens,andthentheyleavethelenscoplanar.
Whenelectronsenterthelenstheyencounterasidewaysforcewhichcausestheelectrontorotate
asitcontinuesthroughthelens(Figs.I.53I.57).Sincetheradialcomponentofthemagneticfield
reversesafterthecenterofthelens,therotationalvelocitysetupinthefirsthalfofthelensis
countered.Theelectronenteredthelenswithoutangularmomentumabouttheaxisandleaves
withoutangularmomentum.Theneteffectisadeflectiontowardtheaxis,whichitmustcrossatthe
focalpointf
2
.Theanglebetweentheobjectvectorandtheimagevectoris180°+q,whereas,for
glasslensesandelectrostaticlenses,theanglebetweenarealobjectandtheimageisexactly180°.
Sincetheradialforceisdirectedtowardtheaxis,thelensisconvergentnomatterwhatthedirection
ofthefield.
3)Propertiesofamagneticlens:
Anyaxiallysymmetricmagneticfieldhasthepropertiesofanideallens.Alltheformulasfortheideallensmaybeapplied.
Magneticlensesarealwaysconvergent.Theconventional,axiallysymmetriclensisalwaysboundedbyregionswhicharefieldfree,the
consequencebeingthatthenetactionofelectronlensesisinevitablyconvergent.Limitedregionsmaybedivergentbutnotthelensasawhole.
Theseriousconsequenceofthisisthatneithersphericalorchromaticaberrationscanbecorrectedasisdoneinlightopticsbytheusedoublets
ofpositiveandnegativelenses.
Intheabsenceofelectrostaticfields,therefractiveindexisthesameinobjectandimagespace,thereforef
1
=f
2
.
Electronstravelingthroughaxiallysymmetricfieldsexperienceaspiraltrajectoryofdiminishingradius.Theimagevectorisatanangle180°+qto
theobjectvector.
Thedeflectionoftheelectrontowardstheaxismeansthatanelectronenteringthelensparalleltoitsaxiswillcrosstheaxisafterhavingpassed
thelens.Thedeflectionwillincreasewiththedistancefromtheaxis.Thus,abeamofelectronsinparallelpathsparalleltotheaxisofthelenswill
befocusedtoanimagepointontheaxiswhichrepresentsthesecond(back)focalpointofthelens(f
2
).Notethatmagneticlensesarehighly
inefficientinthatonlyaminorportionofthetotalfieldstrengthisactuallyeffectiveinfocusingtheelectron.
4)Magneticlensfocallength
Inamagneticelectronlensthefocallengthisdeterminedbythefieldstrengthinthelensgapandbythespeedoftheelectrons(determinedby
theacceleratingvoltage).
Formagneticlenses,focusingisachievedbyvaryingthecurrentwhichpassesthroughtheelectromagnet.Thisinturnchangesthestrengthof
themagneticfieldandtherebyaltersthefocallengthofthelensandisequivalenttoacombinedchangeinboththe"refractiveindex"and
"curvatureofsurface".Forabeamofmoreenergeticelectrons,thelenscurrenthastobeincreasedinordertokeepthefocallengthconstant.
FocallengthandcurrentareNOTlinearlyrelated:strengthincreasesinasigmoidfashion(Fig.I.45)ascurrentincreasesuntilapointisreached
wherethelensissaturatedandnofurtherincreaseinlensstrengthcanbeachieved.
Sincethefocallengthofthelensisdirectlyproportionaltotheacceleratingvoltage,avariationinthevelocityoftheelectronsintheimaging
beamaffectsimagequalitybyeliminatingperfectfocus(chromaticaberration).
5)Magneticlensdesign:(Figs.I.46,I.47).
Condenserlensesusuallyhavearelativelylargeboreandspacingwhichresultsinalongfieldandlongfocallength.
Typicalconstructionoftheobjectivelensproducesastrongfieldofshortaxialextent(i.e.shortfocallengthbetween(1.53mm)necessaryfor
formationofimagesathighmagnification.Thespecimenisplacedwithinthemagneticfieldoftheobjectivelens.Thus,anyfieldintroducedby
contaminantsinthespecimencandistortthefieldofthelens.Notethatthisalsomeansthatpartofthelensfield("prefield")isonthefrontside
oftheobjectandaffectstheelectronbeambeforeitpassesthroughtheobject.
Mostofatypicalmagneticlensliesoutsidethevacuumofthemicroscope.Onlythoseregionsthroughwhichtheelectronbeampassesareinhigh
vacuum.Magneticlensesmustbewatercooledtodissipatethelargeamountsofheatproducedbythecurrentsintheelectromagnetcoils.
DATE NAME EVENT
1897 J.J.Thompson Discoverstheelectron
1924 LouisdeBroglie Identifiesawavelengthtomovingelectrons
l =h/mv
where
l =wavelength
h=Planck'sconstant
m=mass
v=velocity
(Foranelectronat60kVl=0.005nm)
1926 H.Busch Magneticorelectricfieldsactaslensesforelectrons
1929 E.Ruska Ph.Dthesisonmagneticlenses
1931 Knoll&Ruska Firstelectronmicroscopebuilt
1931 Davisson&Calbrick Propertiesofelectrostaticlenses
1934 Driest&Muller SurpassresolutionoftheLM
1938 vonBorries&Ruska FirstpracticalEM(Siemens)10nmresolution
1940 RCA CommercialEMwith2.4nmresolution
1945 1.0nmresolution
Fig.I.1Comparisonoflightandelectronmicroscopes.Ineach
instrument,illuminationfromthesource(lamp,filamentinthe
electrongun)isfocusedbythecondenserlensontothespecimen.
Afirstmagnifiedimageisformedbytheobjectivelens.Thisimage
isfurthermagnifiedbytheprojectorlensontoagroundglass
screen(light)orfluorescentscreen(electrons).(FromAgar,p.8)
Fig.I.2CrosssectionalviewofthePhilipsEM300.(FromAgar,p.40)
Toviewtheanimatedmicroscope,clickhere.
Note:QuickTimePlugInrequired
(Thiscanbedownloadedathttp://apple.com/quicktime/download)
Fig.I.3Sectionthroughacomplex
doublecondenser6lensPhilips
EM200electronmicroscope.(From
Meek,p.99)
Fig.I.4Thestatisticalnatureofdiffraction
patterns.(FromHall,p.13)
"Theprecisenatureof'electronwaves'or'matterwaves'isverydifficulttounderstandordescribeinmaterialterms.Electronwavesarenot
electromagneticradiationofthekindtowhichlight,Xraysandradiowavesbelong.Theyconstituteasortofquantumor'packet'ofradiationwhich
accompanieseachindividualelectron,followingitspathandnotradiatingoutwardsfromit."(Meek,1976,pp.4849).
V l (nm)
v(
•
10
10
cm/sec)
v/c
10,000 0.0123 0.593 0.198
50,000 0.0055 1.326 0.442
100,000 0.0039 1.875 0.625
1,000,000 0.0012 5.930 1.977!
V l (nm)
v(
•
10
10
cm/sec)
v/c
10,000 0.0123 0.593 0.195
50,000 0.0055 1.326 0.414
100,000 0.0039 1.875 0.548
1,000,000 0.0012 5.930 0.941
FigI.5Aperfectpointsourcecannotbe
imagedbyalensasaperfectpointimagedue
tothepresenceoftheapertureAB(which
maybetheedgeofthelens).Diffractionat
thisaperturegivesrisetoaseriesoffringes,
whichsurroundtheimageformedofthepoint
source.Thepatternproducediscalledan'Airy'
disk.(FromMeek1sted.,p.35)
Fig.I.6Wheneverawavefrontstrikesa
barrier,itcanbendaroundthecorner'by
givingrisetoasecondarywavefrontatthe
edge,sinceeachpointonthewavefrontcan
giverisetoanewsourceofwaves.This
phenomenoniscalled'diffraction'.(FromMeek
1sted.,p.22)
Fig.I.7Diffractionpattern(right)formedbyanirregularlyshapedaperture
(left).(FromYoung,p.95)
Fig.I.8(a)
Photographof
theedgeofa
razorblade
illuminatedby
monochromatic
(blue)light
rendered
coherentby
passing
througha
narrowslit.(b)
Microdensitometer
tracingofthe
negativefrom
whichthe
photograph
wasmade.
FourFresnel
fringescanbe
distinguished.
(FromMeek1st
ed.,p.27)
(a)
(b)
(a) (c)
(b)
Fig.I.9(a)Fresnelfringesformed
byelectrons.Thesefringesare
formedoutsidetheedgeofahole
(white)inacarbonfilm(black).(b)
Amicrodensitometertracingofthe
fringesystem;thepatternis
identicalwiththeFresnelfringe
systemformedbyvisiblelight(see
Fig.I.8).(c)Anunderfocusedimage
ofaholeinafilm,showinga
completesystemofabout40
Fresnelfringesinsidethehole.
(FromMeek1sted.,pp.2930)
Fig.I.10Diffractionimagesoftwo
easilyresolvedpoints.(From
Slayter,p.243)
Fig.I.11Imagesoftwo
incoherentlyilluminatedpointsat
thelimitofresolution.(a)individual
intensities;(b)summedintensities.
(FromSlayter,p.244)
Fig.I.12Examplesofwhatoccurswhentwo
wavesofthesamewavelengthandequal
amplitudeadd.Ineachexample,thetwo
separatewavesareshownontheleftand
theirsumorresultantwaveontheright.The
differentexamplesarecharacterizedbyvarying
phasedifferences.Thephaseofawave
(usuallyexpressedasafractionofthe
wavelengthorindegrees)isthepositionofa
crestrelativetosomearbitrarypoint.Although
thephaseofagivenwavevarieswithtimeas
thewavetravels,thedifferenceinphaseofthe
twowavesofthesamewavelengthwiththe
samevelocity,isindependentoftime.Such
wavescaninterferewithoneanother.The
resultantwavehasthesamewavelength,l .
(a)Phasedifferencezero.Thewavestotally
reinforceandaresaidtobe"inphase"orto
showconstructiveinterference.
(b)Phasedifferencel /4.Partialreinforcement,
givingawaveofamplitude1.4(intensity2.0).
(c)Phasedifferencel /2.Thewavesare"outof
phase"andthereistotaldestructive
interferencetogivenoresultantwaveora
wavewithamplitude0(intensity0).(From
GluskerandTrueblood,p.19)
Fig.I.13Photographofan
interferencepatterninwater
wavesformedbythe
superpositionofwavesfromtwo
sourcesoscillatinginphasewith
thesamefrequency.(FromYoung,
p.22)
Fig.I.14Theangularapertureofthe
eyeisrelativelysmall.(FromMeek,
1sted.,p.13)
Fig.I.15Increasingtheangular
apertureoftheeyewithalens.The
lensallowstheobjecttobeheld
closertotheeye,whichisthereby
enabledtogathermoreinformation.
(FromMeek1sted.,p.14)
Fig.I.16Theinteractionofwaves
withanobstacle.Theboatridesthe
longwavelengthoceanwave,but
reflectsthesmallwavelength
surfaceripple.Anobserverwho
wishestodetectthepresenceof
theboatcandosoonlyby
observingwaveswhichhave
wavelengthssmallerthan,or
comparableto,thelengthofthe
boat.(FromSherwood,p.19)
Maximummagnification=
resolvingpoweroftheeye
resolvingpowerofthemicroscope
(a)
Fig.I.17(a)TwoAiry
disksrepresenting
twoimagepoints
shownatincreasing
separationfromleft
toright.Inthe
pictureatthe
extremerightthe
twodiskscanbe
distinguishedas
separatedisks.
(b)Theintensity
distributionatanAiry
disk.R,halfwidthof
thecentralmaximum
representedbya
bellshapedcurve.
(c)TheRayleigh
criteriaforresolution.
(FromSjostrand,
p.115)
i=r
Fig.I.18Reflection.(FromSlayter,
p.4)
Fig.I.19Refraction.(FromSlayter,
p.6)
Fig.I.20Principalraydiagramsshowing
imageformationbyaconvexlens.
(a)Whentheobjectdistanceisgreater
thanthefocallength,areal,inverted
imageisformed.
(b)Whentheobjectdistanceisless
thanthefocallength,avirtual,erect
imageisformed;itspositionis
obtainedbyprojectingtheprincipal
raysbackward.Theraysappearto
comefrompointQ.(FromYoung,
p.127)
Fig.I.21Definitionof
principalfocus,F,inimage
spaceofalens.(From
Sjostrand,p.20)
Fig.I.22Focusingeffectoflenson
raysoriginatingfrompointson
principalaxislocatedatdifferent
distancesfromthelens.(From
Sjostrand,p.21)
Fig.I.23Definitionofprincipal
focusinobjectspaceF1ofa
lens.(FromSjostrand,p.21)
Fig.I.24VirtualimageQof
objectpointlocatedbetween
principalfocusinobjectspace
andthelens.(FromSjostrand,
p.21)
Fig.I.25Constructionoftheimage
ofanobjectbymeansofray
tracing.(FromSjostrand,p.22)
Fig.I.26Magnifyingeffectof
apositivelens.(From
Sjostrand,p.22)
Fig.I.27Virtualmagnified
imageofobjectlocated
betweenprincipalfocusin
objectspaceandthelens.
(FromSjostrand,p.22)
Fig.I.28Amagnifyingglassformsan
enlarged,erectvirtualimage.The
angularsizeofthisimageis
approximately4"/15"or4/15.The
angularsizeoftheobjectatthe
closestdistanceforcomfortable
viewingis1"/10"or1/10.The
magnificationinthissituationis(4/15)/
(1/10),or22/3.(FromYoung,p.130)
Fig.I.29Theangularapertureofa
lens.Theangle2a isthe
acceptanceangleofthelens,and
thelargeritcanbemade,themore
informationcanthelenstransmit.A
largelensofhighaperturecan
thereforetellusmoreaboutan
objectthanasmalllensoflow
power.(FromMeek1sted.,p.12)
Fig.I.30Raydiagramforhighmagnification
modeofoperation.Notethateachlens
formsarealimage,withimageinversion.
I0istheimageformedbytheobjective
lensO,I1isformedbythefirstprojector
lensP1andI2bythesecondprojectorP2,
onthescreen.(FromAgar,p.30)
Fig.I.31Left:raydiagramofthe3realimagemediumandhighmagnificationimagingsystemofa3lens
microscope.Center:2realimageverylowor'scan'magnificationrangeofa3lensmicroscope.Right:2real
imagelowmagnificationsystemofa3lensmicroscope.(FromMeek1sted.,pp.118,120121)
Fig.I.32Raydiagramforacompleteelectron
microscope.FilamentF,condenser1lensC1,
condenser2lensC2,condenserapertureCA,
specimenS,objectivelensO,objectiveaperture
OA(inbackfocalplane).1stintermediateimage
andselectorapertureSA.IntermediatelensP1,
secondintermediateimageI2,projectorlensP2
andfinalimageonthefluorescentscreenFC.
(FromAgar,p.35)
a)f=2.0
x
o
=5.0
e)f=4.0
x
o
=3.0
b)f=10.5
x
o
=21.0
f)f=13.3
x
o
=13.3
c)f=3.5
x
o
=3.0
g)f=3.142
x
o
=0.0
d)f=5.0
x
o
=2.5
a)D=8.0
L1:f=2.0
x
o
=4.0
L2:f=3.0
b)D=8.0
L1:f=2.0
x
o
=6.0
L2:f=3.0
c)D=4.0
L1:f=2.0
x
o
=3.0
L2:f=2.0
FigI.33Accelerationofelectronin
electricfield.(FromSjostrand,p.26)
Fig.I.34Linesofforceatapositively
chargedsphericalbody.(FromSjostrand,
p.32)
Fig.I.35Linesofforceandequipotential
surfaces(stippledlines)associatedwith
twoequalchargesofoppositesign.
(FromSjostrand,p.32)
Fig.I.36Equipotentialsurfacesattwoparallel
platesofoppositechargeswiththepathofan
electronindicatedwithinthehomogeneous
partofthefield.(FromSjostrand,p.33)
Fig.I.37Refractionofelectronatan
equipotentialsurface.(FromSjostrand,p.33)
Fig.I.38.Negativelensactionof
electrostaticfieldatanaperturewhen
V2V1>V3V2.(FromSjostrand,
p.34)
Fig.I.39.Positivelensactionatan
aperturewhenV2V1<V3V2.
(FromSjostrand,p.34)
Fig.I.40Magneticfieldinducedbycurrent
passingthroughaconductor.(From
Sjostrand,p.35)
Fig.I.41Magneticfieldinducedbycurrent
passingthroughasolenoid.(From
Sjostrand,p.37)
Fig.I.42Solenoidwithironcore.(From
Sjostrand,p.40)
Fig.I.43a.Dependenceofpermeabilityonfluxdensity,B.
b.RelationshipbetweenfluxdensityBandfieldstrength.
(FromSjostrand,p.38).
Fig.I.44Magnetization.(FromSlayter,
p.361)
Fig.I.45Curves
showinghowthe
magnetizationof
softiron(lens
strength)is
relatedtothe
magnetizing
force(lens
current).An
unmagnetized
lensstartsfrom
thepointOand
followsthepath
OAaslens
current
increases.Atthe
pointA,further
increaseinlens
currentproduces
nofurther
increaseinlens
strength;thelensissaidtobe'saturated'.Whenlenscurrent
isreduced,thepathOAisnotretraced;adifferentpathABis
followed.Thisdisplacementiscalled'hysteresis'.Atzero
current(pointB),someresiduallensstrengthremains;thisis
called'remanence'.Tobringthelensbacktozerostrength,a
reversecurrentOCmustbeapplied.Lensstrengththen
increaseswithincreasingreversecurrent,followingthepath
CD.Thepolarityofthelenschanges,butthisdoesnotaffect
itsfocusingpower;onlythespiralelectronpathisreversed.
Becauseofhysteresis,itisnotpossibletocalibratealens
currentmeteraccuratelyintermsoflensstrengthor
magnification.
Fig.I.46Evolutionofmagneticelectron
lenses.(A)Shortsolenoidusedasa
magneticlens.(B)Softironcasing
enclosingoutersurfaceofthesolenoid,
thusconcentratingthefield.(C)Soft
ironencasingthesolenoidexceptata
narrowannulargaptherebyreducing
themagneticfieldtoaveryshortregion
alongthelensaxis.(D)Modern
objectivelensconsistingofasoftiron
encasedsolenoidandsoftironpole
piecessoastohaveanenormously
concentratedfieldatthelevelofthe
annulargap.(FromWischnizter2nded.,
p.33)
Fig.I.47(a)Amagneticlensconsisting
ofatightlywoundcoilandasoftiron
shroudsurroundingthecoilexceptfor
asmallgap.Thefieldisconcentratedin
thatgap.(b)Shortfocallength
electromagneticlenswithpolepieces.
(FromSjostrand,p.50)
Fig.I.48Fieldstrengthdistribution
curves.ThecurvesADcorrespondto
therespectivelensesillustratedinFig.
I.46.Eachrepresentsthefieldstrength
alongthelongaxisofthelens.The
changesintheshapeofthecurves
representtheshorteningor
concentrationofthefieldovera
shorteraxialdistance.Hz=
longitudinalmagneticfield.Z=
distancealongtheaxisofsymmetry.
(FromWischnizter2nded.,p.33)
Fig.I.49TheforceFactingon
astraightconductorina
homogeneousmagneticfield
offluxdensityBwhencurrent
Iispassedthroughthe
conductor.(FromSjostrand,
p.43)
Fig.I.50Pathofanelectronina
magneticfield.(A)Inalarge,uniform
magneticfield.(B)Inasmall,uniform
magneticfield.(FromWischnitzer2nd
ed.,p.25)
Fig.I.51Lefthandthumbrule.
(FromSjostrand,p.43)
Fig.I.52Thompson'sexperiment.A
streamofelectronsoriginatingfroma
sourceandpassing,invacuo,through
amagneticfieldproducedbyapairof
magnetswillbedeflected.The
directionofdeflectiondemonstrates
thatelectronsarenegativelycharged
particlesofmatter.(FromWischnitzer
2nded.,p.25)
Fig.I.53Actionofasolenoidonan
electronbeam.Anelectriccurrent
passingthroughthecoilproducesan
axialmagneticfield.Thisisthe
refractingmediumfortheelectrons.An
electronstartingatapointontheaxisA
andatanangletoitfollowsaspiral
path,returningtotheaxisatthepoint
B.Theactionisbasicallysimilartothat
oftheconverginglightlensshownin
Fig.I.20.(FromMeek1sted.,p.8)
Fig.I.54Actionofthemagnetic
lens.(a)Inperspective.(b)
Electrontrajectoryin
projection,alongdirectionof
propagation.(c)Electron
trajectoryinprojection,side
view.(FromSlayter,p.358)
Fig.I.55Componentsofthe
vectorHneartheaxisoffields
withaxialsymmetry.His
representedbytwo
components,Hz,the
componentinthez(axial)
direction,andHr,the
compnentinther(radial)
direction.(FromHall,p.85)
Fig.I.56Theycomponentof
themagneticfieldina
magneticlensisoriented
perpendiculartothedirection
ofanelectronenteringthe
lensalongapathparallelto
thelensaxis.Thisy
componentwillaffectthe
electron,deflectingitinthex
directionasindicatedbythe
arrowmarkedvx.(From
Sjostrand,p.48)
Fig.I.57Thezcomponentofthemagneticfield
andthexvelocitycomponentoftheelectron
inamagneticlensinteract,deflectingthe
electronintheydirectiontowardthelens
axis.(FromSjostrand,p.49)
CuuDuongThanCong.com https://fb.com/tailieudientucntt
cuu duong than cong . com
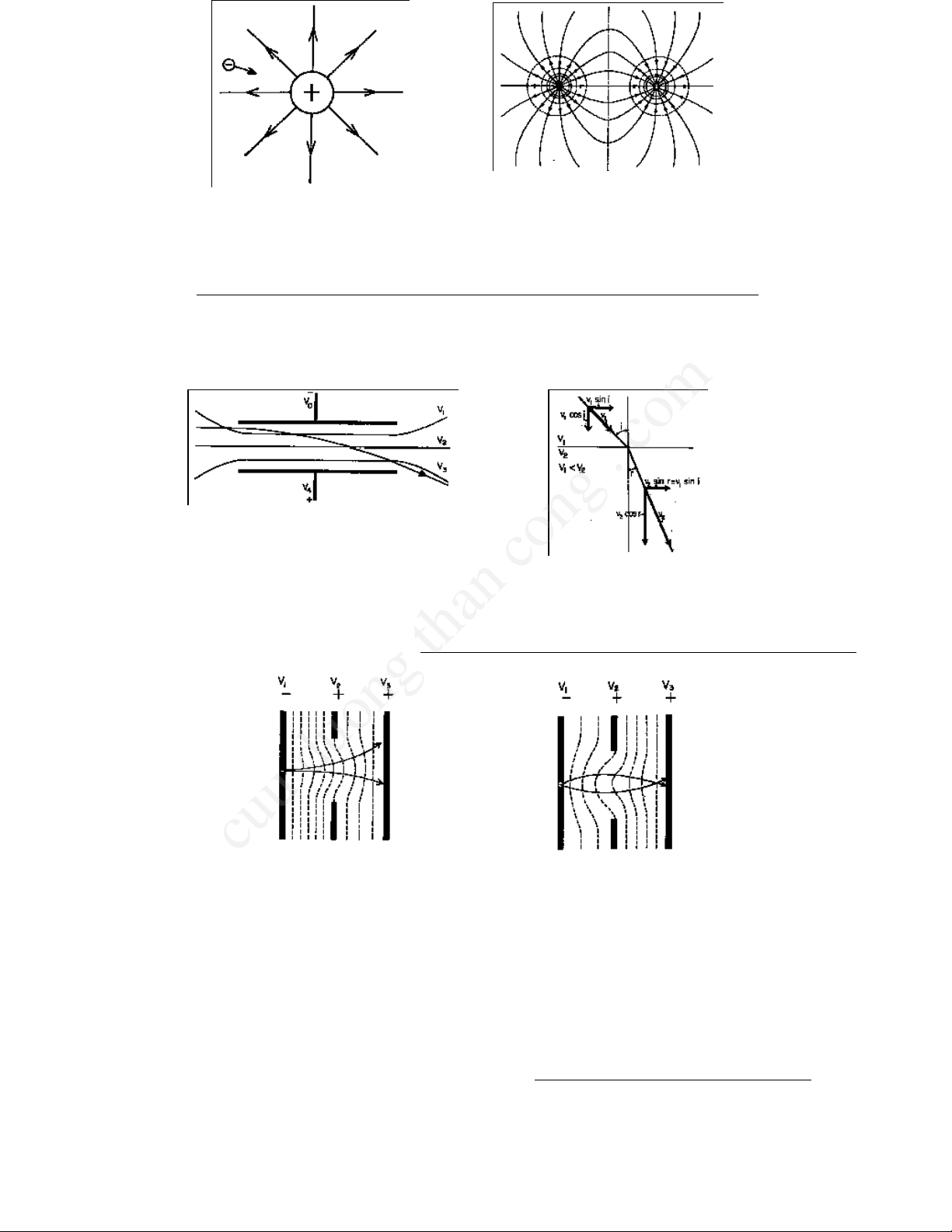
I.THEMICROSCOPE
I.A.PRINCIPLESOFTHETRANSMISSIONELECTRONMICROSCOPE(TEM)
I.A.1.OriginoftheTransmissionElectronMicroscope
I.A.2.ComparisonofLight(LM)andElectronMicroscopes(Fig.I.1)
a.Similarities(Arrangementandfunctionofcomponentsaresimilar)
1)Illuminationsystem:producesrequiredradiationanddirectsitontothespecimen.Consistsofasource,whichemitstheradiation,anda
condenserlens,whichfocusestheilluminatingbeam(allowingvariationsofintensitytobemade)onthespecimen.
2)Specimenstage:situatedbetweentheilluminationandimagingsystems.
3)Imagingsystem:Lenseswhichtogetherproducethefinalmagnifiedimageofthespecimen.Consistsofi)anobjectivelenswhichfocusesthe
beamafteritpassesthroughthespecimenandformsanintermediateimageofthespecimenandii)theprojectorlens(es)whichmagnifiesa
portionoftheintermediateimagetoformthefinalimage.
4)Imagerecordingsystem:Convertstheradiationintoapermanentimage(typicallyonaphotographicemulsion)thatcanbeviewed.
b.Differences
1)Opticallensesaregenerallymadeofglasswithfixedfocallengthswhereasmagneticlensesareconstructedwithferromagneticmaterialsand
windingsofcopperwireproducingafocallengthwhichcanbechangedbyvaryingthecurrentthroughthecoil.
2)MagnificationintheLMisgenerallychangedbyswitchingbetweendifferentpowerobjectivelensesmountedonarotatingturretabovethe
specimen.Itcanalsobechangedifoculars(eyepieces)ofdifferentpowerareused.IntheTEMthemagnification(focallength)oftheobjective
remainsfixedwhilethefocallengthoftheprojectorlensischangedtovarymagnification.
3)TheLMhasasmalldepthoffield,thusdifferentfocallevelscanbeseeninthespecimen.Thelarge(relative)depthoffieldintheTEMmeans
thattheentire(thin)specimenisinfocussimultaneously.
4)Mechanismsofimageformationvary(phaseandamplitudecontrast).
5)TEMsaregenerallyconstructedwiththeradiationsourceatthetopoftheinstrument:thesourceisgenerallysituatedatthebottomofLMs.
6)TEMisoperatedathighvacuum(sincethemeanfreepathofelectronsinairisverysmall)somostspecimens(biological)mustbedehydrated
(i.e.dead!!).
7)TEMspecimens(biological)arerapidlydamagedbytheelectronbeam.
8)TEMscanachievehighermagnificationandbetterresolutionthanLMs.
9)Pricetag!!!(100xmorethanLM)
I.A.3.Photons/Electrons
a.Dualconceptofwaveandparticle(Fig.I.4)
Lighthaspropertiesbothofaparticleandawave.Thisdualnatureisrequiredtosatisfactorilyexplaintheresultsofvariousphysicalexperiments.
Thediffractionoflight(bendingaroundcorners)illustratesthewavenature.TheWAVETHEORYisbasedonthestatisticalnatureofeventsand
haslittlemeaningwithrespecttothebehaviorofsingleparticles.ThewavetheorywasdevelopedandexpoundedbyHuygens(16291695)and
Hooke(16381703).TheCORPUSCULARTHEORYwasproposedbyNewton(16421727)andbecamethemoreacceptedtheoryevenafter
demonstrationofdiffractionbyYoung(17731829)andinterferencebyFresnel(17881827).Atabout1850,thewavetheorycamebackinto
favoruntilabout1900whenmoreevidenceforthecorpusculartheorywasdiscovered.
QUANTUMTHEORY(PlanckandEinstein)providesthebasisforexplainingthephenomenaofINTERFERENCE,DIFFRACTIONandthe
PHOTOELECTRICeffect(lightfallingoncertainmetalscausethemtoemitelectrons)andthusformsacommonbasisforexplainingthenatureof
actionoflight.Thetransferofenergybetweenlightandmatteroccursonlyindiscretequantitiesproportionaltothefrequencyofthe
lightwave.
E=hJ
where
E=energyofphoton(joules)
h=Planck'sconstant(6.624
•
10
34
joulesec)
J=frequency(cycles/sec)
b.Electronvelocityandwavelength
Therelationbetweenthewavelength(l )ofaparticleofmass,m,movingatavelocity,v,isgivenbytheDeBrogliewaveequation:
(1)
Anelectronofchargee(1.6
•
10
19
coulomb),andmassm(9.11
•
10
28
gm),whenpassingthroughapotentialdifferenceofVvolts(expressedin
joules/coulomb),hasakineticenergy:
(2)
Solvingforvelocity:
(3)
substitutingintotheDeBroglieequation(1):
(4)
Since1joule=10
7
dyne
•
cm=10
7
cm
2
•
gm/sec
2
(5)
Thus,forexample,ifV=60,000volts,l =0.005nm.
Fromequation(3)theelectronvelocitycanbecalculatedifVisknown:
(6)
Thefollowingtableillustratesthat,athighvoltage,electronvelocityiscomparabletothespeedoflightinavacuum(c=3
•
10
10
cm/sec).
Theequationbreaksdownwhenthevelocityoftheelectronapproachesthespeedoflightbecausearelativisticcorrectionmustbemadeforthe
valueofthemasswhere:
(7)
Therelationbetweenl andVismorecorrectlygivenby:(seeHall(1966)pp.3334)
(8)
Thefollowingtableisobtainedwhenrelativityeffectsareincluded:
c.Interference/diffraction/coherence
Anideallenssystemobtainsanexactimageoftheobject(eachpointfaithfullyreproduced).Thephenomenaofdiffractionmakesthis
unattainable(Figs.I.5,I.6).
Diffractionphenomenainvolvesthebendingofthepathofradiationpassingclosetoanobstacle(Fig.I.6).Thisresultsinaspreadingofthe
radiationintotheregionbehindtheobstructionthatthewavespassed.Thediffractionatedgescontributestothecontrastatwhichanedgecan
beobserved.Diffractionalsolimitstheresolvingpowerofthemicroscopesincetheimagepointproducedbyalensisadiffractionimageofthe
openingofthelensortheaperturerestrictingtheeffectiveopeningofthelens(Fig.I.5).
Ifthelightsourceandtheplaneatwhichthediffractionpatternisobservedareatfinitedistancesfromtheedge,thephenomenoniscalled
Fresneldiffraction.Thepatternisdescribedasduetointerferencebetweenthenondiffractedlightandawaveoflightdiffractedattheedge.
Theresultingsuperpositiongivesrisetoaseriesofdiffractionfringesorientedparalleltotheedgeandrepresentingperiodicallyvaryingbrightness,
maximaandminima.(Figs.I.7,1.8,I.9).
Coherence:Aprerequisiteforinterferenceisasuperpositionofwavesystemswhosephasedifferenceremainsconstantintime.Twobeams
arecoherentif,whencombined,theyproduceaninterferencepattern.Thebeamsareincoherentwhentheyareincapableofproducingan
interferencepattern.Twobeamsoflightfromselfluminoussourcesareincoherent.Iflightfromthetwosourcesfallsonascreen,theresultant
intensityissimplythesumofthetwointensitieswhichwouldoccurfromeachsourceseparately(Figs.I.10,I.11).Inpracticeanemittingsource
hasfiniteextentandeachpointofthesourcecanbeconsideredtogeneratelight.EachsourcegivesrisetoasystemofFresnelfringesatthe
edge.Thesuperpositionofthesefringesystemsisfairlygoodforthefirstmaximaandminimabutfartherawayfromtheedgeshadowtheoverlap
ofthefringepatternsbecomessufficientlyrandomtomakethefringesdisappear.Thenatureofwaves,phase,amplitude,andinterferenceare
illustratedinFigs.I.12andI.13.
d.Resolution
1)Definitions:
RESOLUTION:abilitytodistinguishcloselyspacedpointsasseparatepoints.
RESOLUTIONLIMIT:smallestseparationofpointswhichcanberecognizedasdistinct.
RESOLVINGPOWER:resolutionachievedbyaparticularinstrumentunderoptimumviewingconditions.
2)Distinctionbetweenresolutionandresolvingpower:
Notethedistinctionbetweenresolutionandresolvingpower.Resolvingpowerisapropertyoftheinstrumentandisaquantitythatmaybe
estimatedontheoreticalgrounds.Resolutionisequaltoorpoorerthantheresolvingpowerandisthequantityobservedunderanygivenset
ofexperimentalconditions.IntheTEM,especiallywithbiologicalsamples,theresolutionachievedmaybeconsiderablyinferiortothetheoretical
resolvingpoweroftheinstrument.
Microscopyisthescienceofseeingtheverysmall.Underidealconditions,theeyeresolvesabout1minuteofarc(=1/60degree=2.9x10
4
radian;recallthereare2p radiansin360°)andsinceitcanfocusdowntoabout250mm,thesmallestobjectwecanresolveisabout0.07mm
(70mm)(Fig.I.14).Thislimitisrelatedtothesizeofthereceptorsintheretinaoftheeye.Thefunctionofamicroscopeistomagnifytheimage
fallingontheretina(Fig.I.15).Theadvantageoflightandelectronmicroscopesisthattheyeffectivelygettheobjectclosertotheeyesoa
magnifiedimageisobtainedandmoredetailcanbediscerned.
TENNISBALLANALOGY:Eyecanresolve3cmat100meters,thusatennisballisclearlyvisible.Butifthetennisballisheldupagainstawhite
background,thevisibilitydecreases(becauseofthedecreaseincontrast).
3)Abbecriteriaofresolution:
Thefundamentalnatureoflightposeslimitsonthedetailthatcanberesolved(Fig.I.16).Abbe(1893)showedthatthesmallestresolvable
distanceisabout1/2thewavelengthoflightused.Thus,1/2thewavelengthoftheradiationusedistheultimateresolvingpowerofany
instrument.Thislimitstheusablemagnificationofopticalmicroscopesto<1000X.Atfirstitwasthoughtthatxraymicroscopeswouldbeuseful
buttherefractiveindexofsubstancesforxraysisnearly=1,thusrefractinglensescannotbemadeforxrays,andconsequently,xrayscannot
beeasilyfocusedtoformimages.
4)Magnificationlimits:
Themaximummagnificationofaninstrumentislimitedaccordingtothefollowingrelationship:
Thus,fortheLM,witharesolvingpowerofapproximately0.25µm,themaximum(useful)magnificationisabout250µm/0.25µm=1000X.Thevalue
usedfortheresolvingpoweroftheeyeinthisexample(250µm)representsamorerealisticviewingcondition.Anymagnificationabovethevalue
givenbytheaboveformularepresentsemptymagnification,sincesuchmagnificationleadstonomoreusefulinformationbutratheramagnified
blur.
AccordingtotheAbbecriteria,at60,000volts,theTEMshouldhavearesolvingpowerofabout0.0025nm.Thisshouldallowamaximumuseful
magnificationofabout100milliontimes!!!Inpractice,themaximumusefulmagnificationoftheTEMoperatedat60kVislimitedtomuchlessthan
1,000,000X.Thus,althoughtheLMnearlyobeystheAbbecriteria,theTEMfallsshortbyaconsiderableamount.Themainlimitingfactorinthe
TEM,withrespecttoachievingthetheoreticalresolvingpoweroftheinstrument,concernsthenatureoftheimaginglensesandtheprocessof
imageformation.
5)Rayleighcriteria(practicalbutarbitrary):(Fig.I.17).
Itistheabilityofmicroscopestomakeobjectpointswhichareclosetogetherappearintheimageasseparatepoints.Anideallenstakeseach
objectpointandrepresentsitexactlyasapointintheimage.Areallenstakeseachobjectpointandspreadsitoutintoacirculardisk(Airy
disk)intheimageplanewhosediameterdependsontheangularapertureofthelens.
Theshortestdistancebetween2disksatwhichthetwodisksappearpartiallyseparatedcorrespondstoabout1/2thewidthofthedisks.The
distance,d,inobjectspaceisgivenby:
d=0.61l /n
•
sina
where
l =wavelenghtoftheradiation
n=refractiveindexofthemedia
a=semiangularapertureofthelens
NOTE:n
•
sina=thenumericalaperture(N.A.)ofthelens.
Thus,tomaximizeresolvingpower,l mustbedecreased,nincreased,oraincreased.Recallthatweareconcernedatthemomentwithan
aberrationfreeopticalsystem.Thevaluefortheconstant(0.61)iscontroversialbecauseitdependsonthecoherenceoftheradiationanda
criteriaofvisibility.
FortheLM,usingoilimmersionoptics(n=1.5),sina=0.87,andvioletlight(l =400nm),d=0.2µm.Theonlywaytoimprovetheresolutionisto
uselightofshorterwavelengthsinceN.A.cannotbeincreasedbeyond~1.5.FortheTEM,n=1(vacuum),sina=10
2
andl =0.005nmfor60kV
electrons,thusd=0.3nm.
I.A.4.Optics(LensTheory)
a.Basiclawsofclassicalgeometricaloptics
1)Rectilinearpropagationoflightwhenn(refractiveindex)isconstant.
2)Lawofreflection:
3)Lawofrefraction(Snell'sLaw):
4)Independenceofrays.Theassumptionismadethatlightraystravelindependentlythroughspace.
Theselawsholdforelectrons,except#4,ifthecurrentdensityistoohighwhennegativechargedelectronscaninterfere.
b.Classicalvs.electronoptics
1)Classicaloptics:Therefractiveindexchangesabruptlyatasurfaceandisconstantbetweenthesurfaces.Therefractionoflightatsurfaces
separatingmediaofdifferentrefractiveindicesmakesitpossibletoconstructimaginglenses.Glasssurfacescanbeshaped.
2)Electronoptics:Here,changesintherefractiveindexaregradualsoraysarecontinuouscurvesratherthanbrokenstraightlines.Refraction
ofelectronsmustbeaccomplishedbyfieldsinspacearoundchargedelectrodesorsolenoids,andthesefieldscanassumeonlycertaindistributions
consistentwithfieldtheory.
c.Geometricalandphysicaloptics
Thefundamentalprinciplesofopticsgovernthedesignandoperationofboththelightandelectronmicroscopes.Thebasicopticalprinciples
involvingtheuseofrefractileelementsorlensesinordertoformmagnifiedimagesareidenticalinboththeLMandTEM.TheTEMdiffersfromthe
LMonlyintheradiationitusesandinthewayinwhichtheradiationisbentorrefracted.
Geometricalopticsdealswiththestudyofthepathsfollowedby'rays'oflightorelectronsthroughlensesandapertures,andthegeometrical
constructionsusedtofindtherelativepositionsandsizesofobjectsandtheirimages.Arayoflightorelectronsisdefinedasaninfinitelythin
pencilorbeam.Physicalopticsshowsthatthisanabstractionandcannotphysicallyexistbecauseof'diffraction'whichdealswiththewave
natureoflightandelectrons.Allresultsobtainedingeometricalopticscanbederivedfromtheprinciplesofphysicaloptics,alongwithother
phenomenasuchasinterferenceanddiffractionwhicharenotexplicableinsimplegeometricalterms.
d.Idealversesreallenses:
Lensesareusedtobendraysoflightorelectronssotheyaredeflectedinapredictablewayfromtheiroriginalpaths.Thepropertiesofanideal
lens,possessinganaxisofrotationalsymmetryare:
1)Eachrayofthebundleofrayswhichpassesfromanobjectpointwillberefractedbytheideallenstomeetinoneimagepoint.
2)Raysoriginatingfrompointswhichlieonaplaneperpendiculartotheaxis,mustbeimagedinaplanewhichisalsoperpendiculartotheaxis.
3)Theimageappearsliketheobjectirrespectiveofthemagnification,sotherelativelineardimensionsoftheobjectarepreservedintheimage.
Inpractice,theimagingbyanyreallensdoesnotcorrespondtothatoftheideallensowingtothefactthatanobjectpointisrepresentedbya
diffractionimage(Airydisc)ofthelensopeningortheapertureusedforrestrictingtheeffectiveopeningofthelens.Thisisaresultofthewave
likepropertiesoflight.Lensaberrationsalsocontributetomoreorlesspronounceddeviationsfromthepropertiesoftheideallens.
Thesinglerefractingsurfaceofsphericalcurvatureisthefundamentalunitoffocusingactionbyglasslenses.Sphericalrefractingsurfacesactas
lensesforparaxialrayswhicharethoseraysthatpassclosetotheprincipalaxisofthelens.RayswithlargeangleswillNOTobeyideallens
action.
Afundamentaldifferencebetweenlightandmagneticlensesisthattheelectronbeamdoesnotchangeinforwardvelocityasitpassesthrough
themagneticfield(lightraysslowdownwhenpassingintoamediumofhigherrefractiveindex).Refractioniscontinuouswithelectronswhenthey
areinthemagneticfield:lightisrefractedonlyattheinterfacebetweenmediaofdifferingrefractiveindex.Theelectronsalsofollowspiral
trajectoriesthroughthemagneticfield(seealsoSec.I.A.5.c(Magneticfieldsandmagneticlenses)
e.Raydiagrams:(Figs.I.20I.28)
Themethodofconstructionofraydiagramsisbasedonthreesimpleprinciples:
1)Allraysenteringthelensparalleltotheaxisarebroughttoacommonpointontheaxis,thefocalpoint.
2)Allrayspassingthroughthegeometricalcenterofthelensareundeviatedandpassstraighton,nomatterfromwhichdirectiontheycome.
3)Principleofreversibility:ifthedirectionofarayisreversedinanysystemtherayexactlyretracesitspaththroughthesystem.Thisapplies
onlytothelocationoflightpathsandnottotheintensityofthelight.
Theaboveprinciplesarebasedontheassumptionsthatwearedealingwithathinlensandconcernedwiththepathsofparaxialrays.The
standardconventionistodrawdiagramswithraysthattravelfromlefttoright.Theobjectistotheleft(infront)ofthelensandtheimageisto
theright(behind)ofthelens.
f.Definitions:
Realimage:oneatwhichlightraysphysicallyreunite,sothataphotographicplateplacedatthepositionofarealimageisexposed.
VirtualImage:onefromwhichlightraysappeartodiverge;raysarenotinfactconcentratedatthepositionofavirtualimage,sothata
photographicplateplacedatthepositionoftheimageisnotexposed(byfocusedrays).Placinganopticalsystemsuchastheeyebehindthe
lens,willenablethedivergentraystobefocusedtoformarealimage.TheintermediatelensofanTEMissometimesusedthiswayinorderto
reducethefinalsizeoftherealimageformedbytheprojectorlens(es).
Converging(positive)lens:bendsraystowardtheaxis.Ithasapositivefocallength.Formsarealinvertedimageofanobjectplacedtothe
leftofthefirstfocalpointandanerectvirtualimageofanobjectplacedbetweenthefirstfocalpointandthelens.
Diverging(negative)lens:bendsthelightraysawayfromtheaxis.Ithasanegativefocallength.Anobjectplacedanywheretotheleftofa
diverginglensresultsinanerectvirtualimage.Itisnotpossibletoconstructanegativemagneticlensalthoughnegativeelectrostaticlensescan
bemade.
g.Lensformula(thinlensequation):
where
f=focallengthofthethinlens(sameradiusofcurvatureforboth
sphericalsurfaces)
o=distanceofobjectfromlens(positivetotheleft)
i=distanceofimagefromthelens(positivetotheright)
NOTE:Foravirtualimage,ihasanegativevalue.
h.Magnification:
Foraconverginglens,iftheobjectismorethantwicethefocallengthfromthelens,thentheimageformedisreal,inverted,andsmallerinsize
thantheobject(M<1).Whentheobjectisatadistance=2f,theimageandobjectarethesamesize(M=1);whenitisbetweenfand2f,
theimageislargerthantheobject(M>1),andwhenitis<f,theimageisvirtual,erect,andlargerthantheobject(M>1).
i.Angularapertureofthelens(2a)(Fig.I.29)
Theaperturedeterminesthetotalamountofradiationarrivingfromtheobjectwhichcanbefocusedto
formanimage.Theaperturethuscontrolstheabilityofthelenstogatherinformationabouttheobject.
Thisdependsontheangleoftheconeofraysitisabletoacceptfromtheobject.Bringinganobject
closertotheeyeincreasestheangularaperture,butthereisalimittotheclosenessthattheobjectcan
bebroughttotheeye(~25cmcorrespondingtoanangleofabout0.9°fora4mmexitpupildiameterof
theeyelens;atypicalLMwithanoilimmersionobjectivelenshas2aof~175°).
j.Simplevs.compoundmicroscope(Figs.I.30I.32)
Inprinciple,arealimageofanydesiredmagnificationcanbeobtainedfromasinglepositivelens,butin
practicethisiscumbersomebecauseofthelonglensimagedistance.Oneormorelensescanbeusedto
magnifytheimageinstages(totalmagnificationequalingtheproductofthemagnificationsofeachlens).
Theimageformedbyonelensconstitutestheobjectforthesubsequentlens,whetherornotareal
intermediateimageisformed.
Comparisonofoneversestwostagemagnification:
Thefollowingdescriptionillustrateshowdifferentpathlengthsarerequiredtoachieveamagnificationof10,000Xusingeitheroneortwolenses
withf=2.0cm.
OneStageSystem:
TwoStageSystem:
Assumebothlenseshavef=2.0cmandarearrangedsoeachgives100Xmagnification.
Thus,M=100=x
i
/x
o
foreachstage.
FirstStage:
x
o
=2.02cm
x
i
=202.00cm
Therealimageformedinthefirststagebecomestheobjectforthesecondlens.
SecondStage:x
o
,x
i
sameasinthefirststage.
Totallengthofsystem
=lengthoffirststage+lengthofsecondstage
=(x
o
+x
i
)+(x
o
+x
i
)
=2(x
o
+x
i
)
=2(2.02+202.00)=408.04cm(4.08meters)
k.Problemset
Thefollowingproblemsareforyourownedificationtotesthowwellyouunderstandthebasicsoflensoptics.
1.Foreachsituationbelow,drawanaccurate(usegraphpaper)raydiagramshowingthepathof(atleasttwo)raysfromtheobjecttoimage.
Indicatewhethertheimageisrealorvirtualandspecifythedistanceoftheimagefromthelensandthemagnificationoftheimagewithrespect
totheobject.Ineachexample,thelensisconverging,withidenticalfrontandbackfocalpoints.Distancesareinarbitraryunits.Letf=lens
focallength,x
o
=distanceofobjectinfrontofthelens,andx
i
=distanceofimagebehindthelens.Theobjectmaybeanysize.
2.Inthefollowingexamples,therearetwoconverginglensesinsuccession.Drawraydiagramsshowingtheformationofboththeintermediate
andfinalimagesandgiveappropriateinformationaboutthenature(real/virtual),positions,andsizesoftheintermediateandfinalimages.What
isthemagnificationateachstageofimageformationandwhatisthemagnificationofthefinalimage?Thedistancefromthecenteroflens1(L1)
tothecenteroflens2(L2)equalsD.
I.A.5.ElectronOptics/ElectronLenses
a.Electronemission
Innershellelectronsinmetalatomsshieldtheelectricfieldofthenucleusthroughtherepulsiveforcestheyexertontheoutershell(valence)
electrons.Thustheattractionbetweenthevalenceelectronsandthenucleusisreduced.Metalatomsarecharacterizedashavingtwoloosely
boundvalenceelectronswhichmigratefreely(thisiswhymetalsaregoodelectricalconductors)andcanescapefromthemetalcompletelyif
sufficientadditionalenergyisimpartedtothem.Asthetemperatureofametalisincreased,thekineticenergyoftheelectronsincreasesbecause
ofincreasedthermalvibrationsofthemetalions,whichcollidemorefrequentlywiththeelectrons.Thermionicemissionisthetermusedto
describetheprocessbywhichthermalenergyissuppliedtolooselyboundelectronsinordertoformasourceofelectrons.
Atroomtemperatureelectronsareeffectivelypreventedfromescapingthesurfaceofthemetalowingtotheattractiveforceofthepositively
chargedions.Asthetemperatureisincreasedsomeelectronsacquiresufficientenergytoovercometheattractionandleavethemetal
temporarily.Metal,shapedasathinwire,caneasilybeheatedbypassinganelectriccurrentthroughit.Sincethemetalsurfacebecomes
positivelycharged,acertainlevelofenergy(workfunction)mustbesuppliedtoallowelectronstoescapefromthesurface.Eachmetalhasa
characteristicworkfunction.Tungsten,withalowworkfunction,emitsmoreelectronsthanmetalswithhigherworkfunctions(seealsopp.2930
andFig.I.59).
Ifastrongelectrostaticfieldisappliedinavacuumbetweenthewire(givenanegative,cathode,potential)andananode,theelectricfieldwill
causeelectronstoaccelerateawayfromthewiretowardstheanodesurface(Fig.I.33).Thespeedoftheelectronsdependsonthestrengthof
theelectrostaticfield(voltage)betweenthecathodeandanode(equation(3),Sec.I.A.3.b)Thenumberofelectronswhichleavethewire
dependsonthetemperaturetowhichthewireisheated,whichdependsonhowmuchfilamentcurrentpassesthroughthewire.
A"V"shapedwirewillhavethehighesttemperatureatthetip.Electronswithdrawnfromthefilamenttipcarryelectricchargestotheanode.This
electriccurrent,whichflowsbetweenthefilamentandtheanode,iscalledthebeamcurrent.
1)Electricfield/Equipotentials
Anelectricallychargedobjecthasassociatedwithitanelectricfield.Thus,anelectricallychargedparticle,whenbroughtnearachargedobject,
isinfluencedbyanelectricalforceinthevicinityoftheobject.Theforceisdirectedtowardthechargedobjectifthechargesareofopposite
signsandawayfromtheobjectiftheyareofsimilarsign.DEFINITION:Thedirectionofanelectricfieldisdefinedasthedirectionoftheforce
actingonapositivecharge.(Figs.I.3435)
Alongthelinesofforceconnectingthetwocharges,theelectricpotentialwillchangegraduallybetweentheextremevaluesrepresentedbythe
twocharges.DEFINITION:Equipotentiallinesdefinethepointsalongthelinesofforcewithidenticalelectricalpotential.Theseequipotential
surfacesarealwaysorientedperpendiculartothelinesofforce.Thechangesintheelectricpotentialaregradualinspace.
Electronswhichenterafieldbetweentwoparallelplatesinadirectionparalleltotheplatesareaffectedbytheforcedirectedperpendicularto
theplates(FigI.36).Theelectronswillbeattractedtowardthepositiveplate.Thepathchangesinaseriesofgradualstepsattheequipotential
surfaces.
FigureI.37showshowtheelectronpathis"refracted"attheequipotentialsurface.TheresultisfundamentallythesameasthatgivenbySnell's
Lawofrefractioninlightoptics.Aconsequenceofthisisthatasphericallycurvedequipotentialsurfaceexhibitsthepropertiesofalens.
FiguresI.38andI.39showhowbothpositive(converging)andnegative(diverging)electrostaticlensescanbeformed.Thisfeatureof
electrostaticlensesdiffersfromelectromagneticlenseswhichcanonlyactasconverginglenses.
2)Advantages/Disadvantagesofelectronlenses:
Thefactthattherefractiveindexdoesnotchangeabruptlyinelectronlenseshasoneadvantageinthattherearenotroublesomereflectionsat
equipotentialsasatglassinterfaces.Thereisaseriousdisadvantageinthatequipotentialscannotbeshapedandcombinedinarbitraryfashionto
correctforchromaticaberrationandothererrors.
Althoughelectronmicroscopeswhichemployelectrostaticlenseshavebeenmade,mostmicroscopesuseelectromagneticlenses.Amajorreason
isthatelectrostaticlensesaremoresensitivetothequalityofthevacuumandcleanlinessofthecomponentsthanareelectromagneticlenses.
Somelensaberrationsaremoresevereforelectrostaticlensescomparedtoelectromagneticlenses.Electrostaticlensesrequireverypowerful
electrostaticfieldswhichcanleadtoelectricalbreakdownor"arcingover"insidethecolumn,especiallyunderpoorvacuumconditions.Forthis
reason,electrostaticlensescannotbemadewithfocallengthsasshortasmagneticlenses.
b.Electrostaticlens
Abasicunderstandingofelectrostaticlensesisimportantfortwomainreasons:i)theelectrongunuseselectrostaticlensactiontoformthe
primarybeamsource,andii)itisquitecommonforachargetodeveloponthenonconductingcontaminationwhichmayaccumulateonphysical
apertures(suchastheobjectiveaperture)andtransformthemintoweakelectrostaticlenseswhichcandistorttheelectronimage.
3)Propertiesofelectrostaticlenses:
a)Anyaxiallysymmetricalelectrostaticfieldhasthepropertiesofalensforraysconfinedtotheparaxialregion.Alltheideallensformulasapply
toelectrostaticlenses.
b)Forelectronlenses,replaceÃ(f)forrefractiveindexinthelensequations(f=valueofthepotentialontheaxis).Intheimageformingsystem
ofmostTEMs,fisthesameonbothsidesofthelens(SeeSec.I.A.5.c).
c)Ifboundedbyregionswherefisconstant,anelectrostaticlensisalwaysconvergent.
c.Magneticfieldsandmagneticlenses
1)Magneticfield
Anelectriccurrentpassingthroughaconductorgivesrisetoamagneticfield.TheconventionisthatNisthedirectioninwhichthelinesofthe
magneticfieldpoint(Fig.I.40).Themagneticfluxisthetotalnumberoflinesandthefluxdensityisthenumberoflinesperunitareaofasurface.
UsetheRIGHThandruletodeterminethedirectionofthefield(thumbpointstowardcurrentdirectionandfingerscurlindirectionoffield.NOTE:
Byconvention,thedirectionofelectronflowisoppositetothatofcurrentflow.
Fluxdensitydependsonthepropertiesofthematerialsurroundingtheconductor.Ironinducesahigherfluxdensitythanairoravacuum.The
propertyofthematerialwhichaffectsthefluxdensityiscalledthepermeability,m,ofthematerial.Forairandvacuum,m=1.0.For
ferromagneticmaterialsitcanbeaslargeasseveralhundredthousand.
Iftheconductorhastheshapeofacircularloop,thelinesofforceformcirclesaroundtheloop.Thefluxdensityisgreatestatthecenterofthe
loop.Themagnetinthecenteroftheloopisorientedperpendiculartotheplaneoftheloopifthecurrentthroughtheloopissufficientlystrongto
eliminatetheinfluenceoftheearth'sfield.ThesideoftheloopatwhichthelinesofforceleavetheloopistheNorth(N)poleofthemagnet(Figs.
I.41,I.42).
Ifthewireiswoundinseveralturnsaroundacylindricalsurface(solenoid),eachturnwillcontributetotheinducedmagneticfield.Theflux
densityinthecenterofthecoilisgivenby:
Inthecaseofairandnonmagneticmaterials,µ=1.0andB=H.
Thepermeabilityofirondependsonthefieldstrength,H,anddecreasestounityathighfieldstrengthorwhenthefluxdensity,B=H(Fig.I.43).
Thehighpermeabilityofironisduetotheinducedmagneticfieldorientingmicroscopiccrystalregionsactingastinymagnetsintheiron.Allthese
tinymagnetsaddtheirmagneticfieldstotheinducedfield(Fig.I.44).Whenallmicromagnetsarenearlyoriented,theironwillaffecttheflux
densitytoadecreasingamountsincethereorientationofmicromagnetsisnearingcompletion.Thus,thepermeabilityofironathighfieldstrengths
approachesthatofemptyspace.Atthispointtheironreachesmagneticsaturation.
2)Hysteresis
Thestrengthofthelensdependstosomeextentonthepreviousmagnetichistoryof
thelens.Whenthecurrentinalensisreduced,thedecreaseinmagnetizationdoes
notretracethesamepathobtainedwhenthecurrentwasincreased(Fig.I.45).
Inductionofmagnetizationinvolvesaphysicalmovementwithinthemagnetized
material,requiringtheovercomeofacertaindegreeofinertia.Asaresult,
magnetizationtendstolagbehindthemagnetizingforceapplied.Inducedmagnetic
fluxcanonlybereturnedtozerobyapplicationofacurrentintheoppositedirection.
Aconsequenceofhysteresisisthatthelevelofcurrentusedtoenergizeamagnetic
lensDOESNOTpreciselyspecifythelensstrength(i.e.focallength).
NormalizationofTEMlensesisaccomplishedbyreducingthelenscurrenttozero
somepredeterminednumberoftimes.Hysteresismayalsobeminimizedbytakinga
lenstosaturationandthenreturningittotheworkingcurrentwithoutovershooting.
Whenthefieldstrengthisreducedtozero,somemagnetizationstillremainsintheiron
(residualmagnetizationorremanence).Anadvantageofsoftironisthefactthat,
whenusedinanelectromagnet,hysteresisislow.
Introductionofpiecesofironinamagneticfielddrasticallyaffectsthefluxdensity.
Magneticmaterialhasashieldingeffect,theeffectbeinggreaterthegreaterthe
permeability.Permalloy(mmetal)hasamaximumpermeabilityof80,000140,000
comparedtoironusedintransformers(~7000).mmetalpermeabilityislimitedtolower
fieldstrengthsthanthatatwhichironstillretainshighpermeability.Thismetalis
thereforeusefulforshieldingtheTEMfromexternalmagneticfields.
d.Theelectromagneticlens
1)Lensdesigndevelopment(Figs.I.46I.48)
Theefficiencyofthemagneticfieldproducedbyashortsolenoidwasfirstimproved
byencasingtheenergizingcoilinasheathofsoftironwhichhasthepropertyofconcentratingthelinesofforceinamagneticfieldandthus
becomingmagnetizedbyinduction.Inthiswayamuchmorepowerfulaxialmagneticfieldisobtainedforthesameamountofcurrentflowing
throughthesolenoid.Furtherdevelopmentinvolvedencasingtheentirecoilwithsoftironexceptatanarrowannulargapintheinsideofthecoil.
Thisproducesagreaterconcentrationofthemagneticfieldalongashortaxialdistance.Toachieveshorterfocallengthlenses(andobtaingreater
magnifications)asoftironpolepiecewithanopenaxialborewasintroducedatthepositionoftheannulargap.
MagneticlensesusedinTEMsarealwaysconstructedwithanironcircuittoproduceahighfieldstrengthacrossashortgap.Themagneticfields
forTEMlensesareintherangeof10,00020,000gauss.
2)Forcesactingonacurrentinamagneticfield
Theforceonanelectroninamagneticfieldisalwaysatrightanglestothevelocityandthedirectionofthefield(Figs.I.49,I.50,andI.52).The
fieldonlyactsonthevelocitycomponentwhichisdirectedperpendiculartothelinesofforce.Usethelefthandrule(Fig.I.51:firstfingerfor
fielddirection,middlefingerforcurrentdirection,andthumbfordirectionofforce).Rayspassingthroughthelensareturnedthroughanangle
whichdoesNOTdependonthedistanceoftheraysfromtheaxis.Allelectronscontainedinagivenmeridionalplanebeforeenteringthefieldare
containedinarotatingmeridionalplaneastheypassthroughthelens,andthentheyleavethelenscoplanar.
Whenelectronsenterthelenstheyencounterasidewaysforcewhichcausestheelectrontorotate
asitcontinuesthroughthelens(Figs.I.53I.57).Sincetheradialcomponentofthemagneticfield
reversesafterthecenterofthelens,therotationalvelocitysetupinthefirsthalfofthelensis
countered.Theelectronenteredthelenswithoutangularmomentumabouttheaxisandleaves
withoutangularmomentum.Theneteffectisadeflectiontowardtheaxis,whichitmustcrossatthe
focalpointf
2
.Theanglebetweentheobjectvectorandtheimagevectoris180°+q,whereas,for
glasslensesandelectrostaticlenses,theanglebetweenarealobjectandtheimageisexactly180°.
Sincetheradialforceisdirectedtowardtheaxis,thelensisconvergentnomatterwhatthedirection
ofthefield.
3)Propertiesofamagneticlens:
Anyaxiallysymmetricmagneticfieldhasthepropertiesofanideallens.Alltheformulasfortheideallensmaybeapplied.
Magneticlensesarealwaysconvergent.Theconventional,axiallysymmetriclensisalwaysboundedbyregionswhicharefieldfree,the
consequencebeingthatthenetactionofelectronlensesisinevitablyconvergent.Limitedregionsmaybedivergentbutnotthelensasawhole.
Theseriousconsequenceofthisisthatneithersphericalorchromaticaberrationscanbecorrectedasisdoneinlightopticsbytheusedoublets
ofpositiveandnegativelenses.
Intheabsenceofelectrostaticfields,therefractiveindexisthesameinobjectandimagespace,thereforef
1
=f
2
.
Electronstravelingthroughaxiallysymmetricfieldsexperienceaspiraltrajectoryofdiminishingradius.Theimagevectorisatanangle180°+qto
theobjectvector.
Thedeflectionoftheelectrontowardstheaxismeansthatanelectronenteringthelensparalleltoitsaxiswillcrosstheaxisafterhavingpassed
thelens.Thedeflectionwillincreasewiththedistancefromtheaxis.Thus,abeamofelectronsinparallelpathsparalleltotheaxisofthelenswill
befocusedtoanimagepointontheaxiswhichrepresentsthesecond(back)focalpointofthelens(f
2
).Notethatmagneticlensesarehighly
inefficientinthatonlyaminorportionofthetotalfieldstrengthisactuallyeffectiveinfocusingtheelectron.
4)Magneticlensfocallength
Inamagneticelectronlensthefocallengthisdeterminedbythefieldstrengthinthelensgapandbythespeedoftheelectrons(determinedby
theacceleratingvoltage).
Formagneticlenses,focusingisachievedbyvaryingthecurrentwhichpassesthroughtheelectromagnet.Thisinturnchangesthestrengthof
themagneticfieldandtherebyaltersthefocallengthofthelensandisequivalenttoacombinedchangeinboththe"refractiveindex"and
"curvatureofsurface".Forabeamofmoreenergeticelectrons,thelenscurrenthastobeincreasedinordertokeepthefocallengthconstant.
FocallengthandcurrentareNOTlinearlyrelated:strengthincreasesinasigmoidfashion(Fig.I.45)ascurrentincreasesuntilapointisreached
wherethelensissaturatedandnofurtherincreaseinlensstrengthcanbeachieved.
Sincethefocallengthofthelensisdirectlyproportionaltotheacceleratingvoltage,avariationinthevelocityoftheelectronsintheimaging
beamaffectsimagequalitybyeliminatingperfectfocus(chromaticaberration).
5)Magneticlensdesign:(Figs.I.46,I.47).
Condenserlensesusuallyhavearelativelylargeboreandspacingwhichresultsinalongfieldandlongfocallength.
Typicalconstructionoftheobjectivelensproducesastrongfieldofshortaxialextent(i.e.shortfocallengthbetween(1.53mm)necessaryfor
formationofimagesathighmagnification.Thespecimenisplacedwithinthemagneticfieldoftheobjectivelens.Thus,anyfieldintroducedby
contaminantsinthespecimencandistortthefieldofthelens.Notethatthisalsomeansthatpartofthelensfield("prefield")isonthefrontside
oftheobjectandaffectstheelectronbeambeforeitpassesthroughtheobject.
Mostofatypicalmagneticlensliesoutsidethevacuumofthemicroscope.Onlythoseregionsthroughwhichtheelectronbeampassesareinhigh
vacuum.Magneticlensesmustbewatercooledtodissipatethelargeamountsofheatproducedbythecurrentsintheelectromagnetcoils.
DATE NAME EVENT
1897 J.J.Thompson Discoverstheelectron
1924 LouisdeBroglie Identifiesawavelengthtomovingelectrons
l =h/mv
where
l =wavelength
h=Planck'sconstant
m=mass
v=velocity
(Foranelectronat60kVl=0.005nm)
1926 H.Busch Magneticorelectricfieldsactaslensesforelectrons
1929 E.Ruska Ph.Dthesisonmagneticlenses
1931 Knoll&Ruska Firstelectronmicroscopebuilt
1931 Davisson&Calbrick Propertiesofelectrostaticlenses
1934 Driest&Muller SurpassresolutionoftheLM
1938 vonBorries&Ruska FirstpracticalEM(Siemens)10nmresolution
1940 RCA CommercialEMwith2.4nmresolution
1945 1.0nmresolution
Fig.I.1Comparisonoflightandelectronmicroscopes.Ineach
instrument,illuminationfromthesource(lamp,filamentinthe
electrongun)isfocusedbythecondenserlensontothespecimen.
Afirstmagnifiedimageisformedbytheobjectivelens.Thisimage
isfurthermagnifiedbytheprojectorlensontoagroundglass
screen(light)orfluorescentscreen(electrons).(FromAgar,p.8)
Fig.I.2CrosssectionalviewofthePhilipsEM300.(FromAgar,p.40)
Toviewtheanimatedmicroscope,clickhere.
Note:QuickTimePlugInrequired
(Thiscanbedownloadedathttp://apple.com/quicktime/download)
Fig.I.3Sectionthroughacomplex
doublecondenser6lensPhilips
EM200electronmicroscope.(From
Meek,p.99)
Fig.I.4Thestatisticalnatureofdiffraction
patterns.(FromHall,p.13)
"Theprecisenatureof'electronwaves'or'matterwaves'isverydifficulttounderstandordescribeinmaterialterms.Electronwavesarenot
electromagneticradiationofthekindtowhichlight,Xraysandradiowavesbelong.Theyconstituteasortofquantumor'packet'ofradiationwhich
accompanieseachindividualelectron,followingitspathandnotradiatingoutwardsfromit."(Meek,1976,pp.4849).
V l (nm)
v(
•
10
10
cm/sec)
v/c
10,000 0.0123 0.593 0.198
50,000 0.0055 1.326 0.442
100,000 0.0039 1.875 0.625
1,000,000 0.0012 5.930 1.977!
V l (nm)
v(
•
10
10
cm/sec)
v/c
10,000 0.0123 0.593 0.195
50,000 0.0055 1.326 0.414
100,000 0.0039 1.875 0.548
1,000,000 0.0012 5.930 0.941
FigI.5Aperfectpointsourcecannotbe
imagedbyalensasaperfectpointimagedue
tothepresenceoftheapertureAB(which
maybetheedgeofthelens).Diffractionat
thisaperturegivesrisetoaseriesoffringes,
whichsurroundtheimageformedofthepoint
source.Thepatternproducediscalledan'Airy'
disk.(FromMeek1sted.,p.35)
Fig.I.6Wheneverawavefrontstrikesa
barrier,itcanbendaroundthecorner'by
givingrisetoasecondarywavefrontatthe
edge,sinceeachpointonthewavefrontcan
giverisetoanewsourceofwaves.This
phenomenoniscalled'diffraction'.(FromMeek
1sted.,p.22)
Fig.I.7Diffractionpattern(right)formedbyanirregularlyshapedaperture
(left).(FromYoung,p.95)
Fig.I.8(a)
Photographof
theedgeofa
razorblade
illuminatedby
monochromatic
(blue)light
rendered
coherentby
passing
througha
narrowslit.(b)
Microdensitometer
tracingofthe
negativefrom
whichthe
photograph
wasmade.
FourFresnel
fringescanbe
distinguished.
(FromMeek1st
ed.,p.27)
(a)
(b)
(a) (c)
(b)
Fig.I.9(a)Fresnelfringesformed
byelectrons.Thesefringesare
formedoutsidetheedgeofahole
(white)inacarbonfilm(black).(b)
Amicrodensitometertracingofthe
fringesystem;thepatternis
identicalwiththeFresnelfringe
systemformedbyvisiblelight(see
Fig.I.8).(c)Anunderfocusedimage
ofaholeinafilm,showinga
completesystemofabout40
Fresnelfringesinsidethehole.
(FromMeek1sted.,pp.2930)
Fig.I.10Diffractionimagesoftwo
easilyresolvedpoints.(From
Slayter,p.243)
Fig.I.11Imagesoftwo
incoherentlyilluminatedpointsat
thelimitofresolution.(a)individual
intensities;(b)summedintensities.
(FromSlayter,p.244)
Fig.I.12Examplesofwhatoccurswhentwo
wavesofthesamewavelengthandequal
amplitudeadd.Ineachexample,thetwo
separatewavesareshownontheleftand
theirsumorresultantwaveontheright.The
differentexamplesarecharacterizedbyvarying
phasedifferences.Thephaseofawave
(usuallyexpressedasafractionofthe
wavelengthorindegrees)isthepositionofa
crestrelativetosomearbitrarypoint.Although
thephaseofagivenwavevarieswithtimeas
thewavetravels,thedifferenceinphaseofthe
twowavesofthesamewavelengthwiththe
samevelocity,isindependentoftime.Such
wavescaninterferewithoneanother.The
resultantwavehasthesamewavelength,l .
(a)Phasedifferencezero.Thewavestotally
reinforceandaresaidtobe"inphase"orto
showconstructiveinterference.
(b)Phasedifferencel /4.Partialreinforcement,
givingawaveofamplitude1.4(intensity2.0).
(c)Phasedifferencel /2.Thewavesare"outof
phase"andthereistotaldestructive
interferencetogivenoresultantwaveora
wavewithamplitude0(intensity0).(From
GluskerandTrueblood,p.19)
Fig.I.13Photographofan
interferencepatterninwater
wavesformedbythe
superpositionofwavesfromtwo
sourcesoscillatinginphasewith
thesamefrequency.(FromYoung,
p.22)
Fig.I.14Theangularapertureofthe
eyeisrelativelysmall.(FromMeek,
1sted.,p.13)
Fig.I.15Increasingtheangular
apertureoftheeyewithalens.The
lensallowstheobjecttobeheld
closertotheeye,whichisthereby
enabledtogathermoreinformation.
(FromMeek1sted.,p.14)
Fig.I.16Theinteractionofwaves
withanobstacle.Theboatridesthe
longwavelengthoceanwave,but
reflectsthesmallwavelength
surfaceripple.Anobserverwho
wishestodetectthepresenceof
theboatcandosoonlyby
observingwaveswhichhave
wavelengthssmallerthan,or
comparableto,thelengthofthe
boat.(FromSherwood,p.19)
Maximummagnification=
resolvingpoweroftheeye
resolvingpowerofthemicroscope
(a)
Fig.I.17(a)TwoAiry
disksrepresenting
twoimagepoints
shownatincreasing
separationfromleft
toright.Inthe
pictureatthe
extremerightthe
twodiskscanbe
distinguishedas
separatedisks.
(b)Theintensity
distributionatanAiry
disk.R,halfwidthof
thecentralmaximum
representedbya
bellshapedcurve.
(c)TheRayleigh
criteriaforresolution.
(FromSjostrand,
p.115)
i=r
Fig.I.18Reflection.(FromSlayter,
p.4)
Fig.I.19Refraction.(FromSlayter,
p.6)
Fig.I.20Principalraydiagramsshowing
imageformationbyaconvexlens.
(a)Whentheobjectdistanceisgreater
thanthefocallength,areal,inverted
imageisformed.
(b)Whentheobjectdistanceisless
thanthefocallength,avirtual,erect
imageisformed;itspositionis
obtainedbyprojectingtheprincipal
raysbackward.Theraysappearto
comefrompointQ.(FromYoung,
p.127)
Fig.I.21Definitionof
principalfocus,F,inimage
spaceofalens.(From
Sjostrand,p.20)
Fig.I.22Focusingeffectoflenson
raysoriginatingfrompointson
principalaxislocatedatdifferent
distancesfromthelens.(From
Sjostrand,p.21)
Fig.I.23Definitionofprincipal
focusinobjectspaceF1ofa
lens.(FromSjostrand,p.21)
Fig.I.24VirtualimageQof
objectpointlocatedbetween
principalfocusinobjectspace
andthelens.(FromSjostrand,
p.21)
Fig.I.25Constructionoftheimage
ofanobjectbymeansofray
tracing.(FromSjostrand,p.22)
Fig.I.26Magnifyingeffectof
apositivelens.(From
Sjostrand,p.22)
Fig.I.27Virtualmagnified
imageofobjectlocated
betweenprincipalfocusin
objectspaceandthelens.
(FromSjostrand,p.22)
Fig.I.28Amagnifyingglassformsan
enlarged,erectvirtualimage.The
angularsizeofthisimageis
approximately4"/15"or4/15.The
angularsizeoftheobjectatthe
closestdistanceforcomfortable
viewingis1"/10"or1/10.The
magnificationinthissituationis(4/15)/
(1/10),or22/3.(FromYoung,p.130)
Fig.I.29Theangularapertureofa
lens.Theangle2a isthe
acceptanceangleofthelens,and
thelargeritcanbemade,themore
informationcanthelenstransmit.A
largelensofhighaperturecan
thereforetellusmoreaboutan
objectthanasmalllensoflow
power.(FromMeek1sted.,p.12)
Fig.I.30Raydiagramforhighmagnification
modeofoperation.Notethateachlens
formsarealimage,withimageinversion.
I0istheimageformedbytheobjective
lensO,I1isformedbythefirstprojector
lensP1andI2bythesecondprojectorP2,
onthescreen.(FromAgar,p.30)
Fig.I.31Left:raydiagramofthe3realimagemediumandhighmagnificationimagingsystemofa3lens
microscope.Center:2realimageverylowor'scan'magnificationrangeofa3lensmicroscope.Right:2real
imagelowmagnificationsystemofa3lensmicroscope.(FromMeek1sted.,pp.118,120121)
Fig.I.32Raydiagramforacompleteelectron
microscope.FilamentF,condenser1lensC1,
condenser2lensC2,condenserapertureCA,
specimenS,objectivelensO,objectiveaperture
OA(inbackfocalplane).1stintermediateimage
andselectorapertureSA.IntermediatelensP1,
secondintermediateimageI2,projectorlensP2
andfinalimageonthefluorescentscreenFC.
(FromAgar,p.35)
a)f=2.0
x
o
=5.0
e)f=4.0
x
o
=3.0
b)f=10.5
x
o
=21.0
f)f=13.3
x
o
=13.3
c)f=3.5
x
o
=3.0
g)f=3.142
x
o
=0.0
d)f=5.0
x
o
=2.5
a)D=8.0
L1:f=2.0
x
o
=4.0
L2:f=3.0
b)D=8.0
L1:f=2.0
x
o
=6.0
L2:f=3.0
c)D=4.0
L1:f=2.0
x
o
=3.0
L2:f=2.0
FigI.33Accelerationofelectronin
electricfield.(FromSjostrand,p.26)
Fig.I.34Linesofforceatapositively
chargedsphericalbody.(FromSjostrand,
p.32)
Fig.I.35Linesofforceandequipotential
surfaces(stippledlines)associatedwith
twoequalchargesofoppositesign.
(FromSjostrand,p.32)
Fig.I.36Equipotentialsurfacesattwoparallel
platesofoppositechargeswiththepathofan
electronindicatedwithinthehomogeneous
partofthefield.(FromSjostrand,p.33)
Fig.I.37Refractionofelectronatan
equipotentialsurface.(FromSjostrand,p.33)
Fig.I.38.Negativelensactionof
electrostaticfieldatanaperturewhen
V2V1>V3V2.(FromSjostrand,
p.34)
Fig.I.39.Positivelensactionatan
aperturewhenV2V1<V3V2.
(FromSjostrand,p.34)
Fig.I.40Magneticfieldinducedbycurrent
passingthroughaconductor.(From
Sjostrand,p.35)
Fig.I.41Magneticfieldinducedbycurrent
passingthroughasolenoid.(From
Sjostrand,p.37)
Fig.I.42Solenoidwithironcore.(From
Sjostrand,p.40)
Fig.I.43a.Dependenceofpermeabilityonfluxdensity,B.
b.RelationshipbetweenfluxdensityBandfieldstrength.
(FromSjostrand,p.38).
Fig.I.44Magnetization.(FromSlayter,
p.361)
Fig.I.45Curves
showinghowthe
magnetizationof
softiron(lens
strength)is
relatedtothe
magnetizing
force(lens
current).An
unmagnetized
lensstartsfrom
thepointOand
followsthepath
OAaslens
current
increases.Atthe
pointA,further
increaseinlens
currentproduces
nofurther
increaseinlens
strength;thelensissaidtobe'saturated'.Whenlenscurrent
isreduced,thepathOAisnotretraced;adifferentpathABis
followed.Thisdisplacementiscalled'hysteresis'.Atzero
current(pointB),someresiduallensstrengthremains;thisis
called'remanence'.Tobringthelensbacktozerostrength,a
reversecurrentOCmustbeapplied.Lensstrengththen
increaseswithincreasingreversecurrent,followingthepath
CD.Thepolarityofthelenschanges,butthisdoesnotaffect
itsfocusingpower;onlythespiralelectronpathisreversed.
Becauseofhysteresis,itisnotpossibletocalibratealens
currentmeteraccuratelyintermsoflensstrengthor
magnification.
Fig.I.46Evolutionofmagneticelectron
lenses.(A)Shortsolenoidusedasa
magneticlens.(B)Softironcasing
enclosingoutersurfaceofthesolenoid,
thusconcentratingthefield.(C)Soft
ironencasingthesolenoidexceptata
narrowannulargaptherebyreducing
themagneticfieldtoaveryshortregion
alongthelensaxis.(D)Modern
objectivelensconsistingofasoftiron
encasedsolenoidandsoftironpole
piecessoastohaveanenormously
concentratedfieldatthelevelofthe
annulargap.(FromWischnizter2nded.,
p.33)
Fig.I.47(a)Amagneticlensconsisting
ofatightlywoundcoilandasoftiron
shroudsurroundingthecoilexceptfor
asmallgap.Thefieldisconcentratedin
thatgap.(b)Shortfocallength
electromagneticlenswithpolepieces.
(FromSjostrand,p.50)
Fig.I.48Fieldstrengthdistribution
curves.ThecurvesADcorrespondto
therespectivelensesillustratedinFig.
I.46.Eachrepresentsthefieldstrength
alongthelongaxisofthelens.The
changesintheshapeofthecurves
representtheshorteningor
concentrationofthefieldovera
shorteraxialdistance.Hz=
longitudinalmagneticfield.Z=
distancealongtheaxisofsymmetry.
(FromWischnizter2nded.,p.33)
Fig.I.49TheforceFactingon
astraightconductorina
homogeneousmagneticfield
offluxdensityBwhencurrent
Iispassedthroughthe
conductor.(FromSjostrand,
p.43)
Fig.I.50Pathofanelectronina
magneticfield.(A)Inalarge,uniform
magneticfield.(B)Inasmall,uniform
magneticfield.(FromWischnitzer2nd
ed.,p.25)
Fig.I.51Lefthandthumbrule.
(FromSjostrand,p.43)
Fig.I.52Thompson'sexperiment.A
streamofelectronsoriginatingfroma
sourceandpassing,invacuo,through
amagneticfieldproducedbyapairof
magnetswillbedeflected.The
directionofdeflectiondemonstrates
thatelectronsarenegativelycharged
particlesofmatter.(FromWischnitzer
2nded.,p.25)
Fig.I.53Actionofasolenoidonan
electronbeam.Anelectriccurrent
passingthroughthecoilproducesan
axialmagneticfield.Thisisthe
refractingmediumfortheelectrons.An
electronstartingatapointontheaxisA
andatanangletoitfollowsaspiral
path,returningtotheaxisatthepoint
B.Theactionisbasicallysimilartothat
oftheconverginglightlensshownin
Fig.I.20.(FromMeek1sted.,p.8)
Fig.I.54Actionofthemagnetic
lens.(a)Inperspective.(b)
Electrontrajectoryin
projection,alongdirectionof
propagation.(c)Electron
trajectoryinprojection,side
view.(FromSlayter,p.358)
Fig.I.55Componentsofthe
vectorHneartheaxisoffields
withaxialsymmetry.His
representedbytwo
components,Hz,the
componentinthez(axial)
direction,andHr,the
compnentinther(radial)
direction.(FromHall,p.85)
Fig.I.56Theycomponentof
themagneticfieldina
magneticlensisoriented
perpendiculartothedirection
ofanelectronenteringthe
lensalongapathparallelto
thelensaxis.Thisy
componentwillaffectthe
electron,deflectingitinthex
directionasindicatedbythe
arrowmarkedvx.(From
Sjostrand,p.48)
Fig.I.57Thezcomponentofthemagneticfield
andthexvelocitycomponentoftheelectron
inamagneticlensinteract,deflectingthe
electronintheydirectiontowardthelens
axis.(FromSjostrand,p.49)
CuuDuongThanCong.com https://fb.com/tailieudientucntt
cuu duong than cong . com
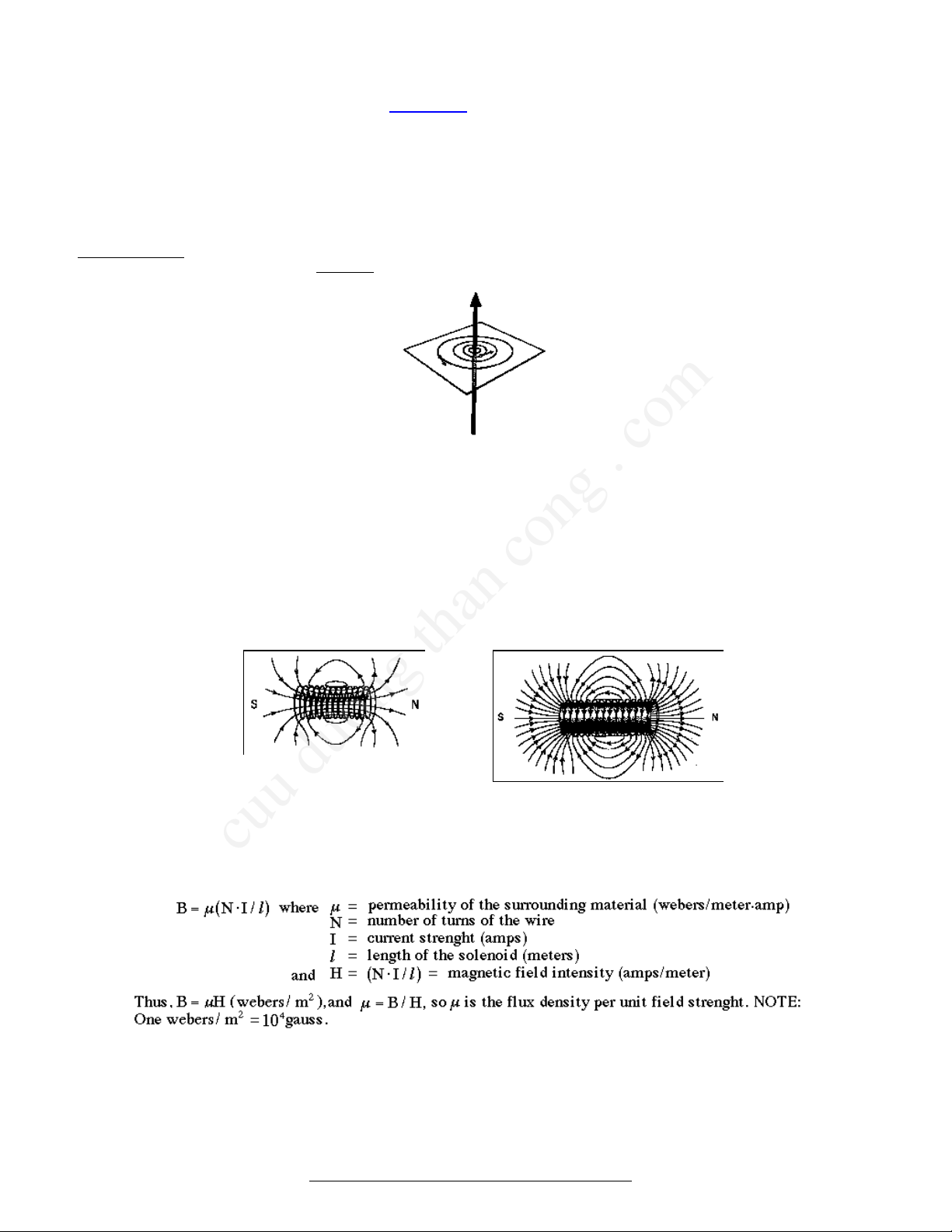
I.THEMICROSCOPE
I.A.PRINCIPLESOFTHETRANSMISSIONELECTRONMICROSCOPE(TEM)
I.A.1.OriginoftheTransmissionElectronMicroscope
I.A.2.ComparisonofLight(LM)andElectronMicroscopes(Fig.I.1)
a.Similarities(Arrangementandfunctionofcomponentsaresimilar)
1)Illuminationsystem:producesrequiredradiationanddirectsitontothespecimen.Consistsofasource,whichemitstheradiation,anda
condenserlens,whichfocusestheilluminatingbeam(allowingvariationsofintensitytobemade)onthespecimen.
2)Specimenstage:situatedbetweentheilluminationandimagingsystems.
3)Imagingsystem:Lenseswhichtogetherproducethefinalmagnifiedimageofthespecimen.Consistsofi)anobjectivelenswhichfocusesthe
beamafteritpassesthroughthespecimenandformsanintermediateimageofthespecimenandii)theprojectorlens(es)whichmagnifiesa
portionoftheintermediateimagetoformthefinalimage.
4)Imagerecordingsystem:Convertstheradiationintoapermanentimage(typicallyonaphotographicemulsion)thatcanbeviewed.
b.Differences
1)Opticallensesaregenerallymadeofglasswithfixedfocallengthswhereasmagneticlensesareconstructedwithferromagneticmaterialsand
windingsofcopperwireproducingafocallengthwhichcanbechangedbyvaryingthecurrentthroughthecoil.
2)MagnificationintheLMisgenerallychangedbyswitchingbetweendifferentpowerobjectivelensesmountedonarotatingturretabovethe
specimen.Itcanalsobechangedifoculars(eyepieces)ofdifferentpowerareused.IntheTEMthemagnification(focallength)oftheobjective
remainsfixedwhilethefocallengthoftheprojectorlensischangedtovarymagnification.
3)TheLMhasasmalldepthoffield,thusdifferentfocallevelscanbeseeninthespecimen.Thelarge(relative)depthoffieldintheTEMmeans
thattheentire(thin)specimenisinfocussimultaneously.
4)Mechanismsofimageformationvary(phaseandamplitudecontrast).
5)TEMsaregenerallyconstructedwiththeradiationsourceatthetopoftheinstrument:thesourceisgenerallysituatedatthebottomofLMs.
6)TEMisoperatedathighvacuum(sincethemeanfreepathofelectronsinairisverysmall)somostspecimens(biological)mustbedehydrated
(i.e.dead!!).
7)TEMspecimens(biological)arerapidlydamagedbytheelectronbeam.
8)TEMscanachievehighermagnificationandbetterresolutionthanLMs.
9)Pricetag!!!(100xmorethanLM)
I.A.3.Photons/Electrons
a.Dualconceptofwaveandparticle(Fig.I.4)
Lighthaspropertiesbothofaparticleandawave.Thisdualnatureisrequiredtosatisfactorilyexplaintheresultsofvariousphysicalexperiments.
Thediffractionoflight(bendingaroundcorners)illustratesthewavenature.TheWAVETHEORYisbasedonthestatisticalnatureofeventsand
haslittlemeaningwithrespecttothebehaviorofsingleparticles.ThewavetheorywasdevelopedandexpoundedbyHuygens(16291695)and
Hooke(16381703).TheCORPUSCULARTHEORYwasproposedbyNewton(16421727)andbecamethemoreacceptedtheoryevenafter
demonstrationofdiffractionbyYoung(17731829)andinterferencebyFresnel(17881827).Atabout1850,thewavetheorycamebackinto
favoruntilabout1900whenmoreevidenceforthecorpusculartheorywasdiscovered.
QUANTUMTHEORY(PlanckandEinstein)providesthebasisforexplainingthephenomenaofINTERFERENCE,DIFFRACTIONandthe
PHOTOELECTRICeffect(lightfallingoncertainmetalscausethemtoemitelectrons)andthusformsacommonbasisforexplainingthenatureof
actionoflight.Thetransferofenergybetweenlightandmatteroccursonlyindiscretequantitiesproportionaltothefrequencyofthe
lightwave.
E=hJ
where
E=energyofphoton(joules)
h=Planck'sconstant(6.624
•
10
34
joulesec)
J=frequency(cycles/sec)
b.Electronvelocityandwavelength
Therelationbetweenthewavelength(l )ofaparticleofmass,m,movingatavelocity,v,isgivenbytheDeBrogliewaveequation:
(1)
Anelectronofchargee(1.6
•
10
19
coulomb),andmassm(9.11
•
10
28
gm),whenpassingthroughapotentialdifferenceofVvolts(expressedin
joules/coulomb),hasakineticenergy:
(2)
Solvingforvelocity:
(3)
substitutingintotheDeBroglieequation(1):
(4)
Since1joule=10
7
dyne
•
cm=10
7
cm
2
•
gm/sec
2
(5)
Thus,forexample,ifV=60,000volts,l =0.005nm.
Fromequation(3)theelectronvelocitycanbecalculatedifVisknown:
(6)
Thefollowingtableillustratesthat,athighvoltage,electronvelocityiscomparabletothespeedoflightinavacuum(c=3
•
10
10
cm/sec).
Theequationbreaksdownwhenthevelocityoftheelectronapproachesthespeedoflightbecausearelativisticcorrectionmustbemadeforthe
valueofthemasswhere:
(7)
Therelationbetweenl andVismorecorrectlygivenby:(seeHall(1966)pp.3334)
(8)
Thefollowingtableisobtainedwhenrelativityeffectsareincluded:
c.Interference/diffraction/coherence
Anideallenssystemobtainsanexactimageoftheobject(eachpointfaithfullyreproduced).Thephenomenaofdiffractionmakesthis
unattainable(Figs.I.5,I.6).
Diffractionphenomenainvolvesthebendingofthepathofradiationpassingclosetoanobstacle(Fig.I.6).Thisresultsinaspreadingofthe
radiationintotheregionbehindtheobstructionthatthewavespassed.Thediffractionatedgescontributestothecontrastatwhichanedgecan
beobserved.Diffractionalsolimitstheresolvingpowerofthemicroscopesincetheimagepointproducedbyalensisadiffractionimageofthe
openingofthelensortheaperturerestrictingtheeffectiveopeningofthelens(Fig.I.5).
Ifthelightsourceandtheplaneatwhichthediffractionpatternisobservedareatfinitedistancesfromtheedge,thephenomenoniscalled
Fresneldiffraction.Thepatternisdescribedasduetointerferencebetweenthenondiffractedlightandawaveoflightdiffractedattheedge.
Theresultingsuperpositiongivesrisetoaseriesofdiffractionfringesorientedparalleltotheedgeandrepresentingperiodicallyvaryingbrightness,
maximaandminima.(Figs.I.7,1.8,I.9).
Coherence:Aprerequisiteforinterferenceisasuperpositionofwavesystemswhosephasedifferenceremainsconstantintime.Twobeams
arecoherentif,whencombined,theyproduceaninterferencepattern.Thebeamsareincoherentwhentheyareincapableofproducingan
interferencepattern.Twobeamsoflightfromselfluminoussourcesareincoherent.Iflightfromthetwosourcesfallsonascreen,theresultant
intensityissimplythesumofthetwointensitieswhichwouldoccurfromeachsourceseparately(Figs.I.10,I.11).Inpracticeanemittingsource
hasfiniteextentandeachpointofthesourcecanbeconsideredtogeneratelight.EachsourcegivesrisetoasystemofFresnelfringesatthe
edge.Thesuperpositionofthesefringesystemsisfairlygoodforthefirstmaximaandminimabutfartherawayfromtheedgeshadowtheoverlap
ofthefringepatternsbecomessufficientlyrandomtomakethefringesdisappear.Thenatureofwaves,phase,amplitude,andinterferenceare
illustratedinFigs.I.12andI.13.
d.Resolution
1)Definitions:
RESOLUTION:abilitytodistinguishcloselyspacedpointsasseparatepoints.
RESOLUTIONLIMIT:smallestseparationofpointswhichcanberecognizedasdistinct.
RESOLVINGPOWER:resolutionachievedbyaparticularinstrumentunderoptimumviewingconditions.
2)Distinctionbetweenresolutionandresolvingpower:
Notethedistinctionbetweenresolutionandresolvingpower.Resolvingpowerisapropertyoftheinstrumentandisaquantitythatmaybe
estimatedontheoreticalgrounds.Resolutionisequaltoorpoorerthantheresolvingpowerandisthequantityobservedunderanygivenset
ofexperimentalconditions.IntheTEM,especiallywithbiologicalsamples,theresolutionachievedmaybeconsiderablyinferiortothetheoretical
resolvingpoweroftheinstrument.
Microscopyisthescienceofseeingtheverysmall.Underidealconditions,theeyeresolvesabout1minuteofarc(=1/60degree=2.9x10
4
radian;recallthereare2p radiansin360°)andsinceitcanfocusdowntoabout250mm,thesmallestobjectwecanresolveisabout0.07mm
(70mm)(Fig.I.14).Thislimitisrelatedtothesizeofthereceptorsintheretinaoftheeye.Thefunctionofamicroscopeistomagnifytheimage
fallingontheretina(Fig.I.15).Theadvantageoflightandelectronmicroscopesisthattheyeffectivelygettheobjectclosertotheeyesoa
magnifiedimageisobtainedandmoredetailcanbediscerned.
TENNISBALLANALOGY:Eyecanresolve3cmat100meters,thusatennisballisclearlyvisible.Butifthetennisballisheldupagainstawhite
background,thevisibilitydecreases(becauseofthedecreaseincontrast).
3)Abbecriteriaofresolution:
Thefundamentalnatureoflightposeslimitsonthedetailthatcanberesolved(Fig.I.16).Abbe(1893)showedthatthesmallestresolvable
distanceisabout1/2thewavelengthoflightused.Thus,1/2thewavelengthoftheradiationusedistheultimateresolvingpowerofany
instrument.Thislimitstheusablemagnificationofopticalmicroscopesto<1000X.Atfirstitwasthoughtthatxraymicroscopeswouldbeuseful
buttherefractiveindexofsubstancesforxraysisnearly=1,thusrefractinglensescannotbemadeforxrays,andconsequently,xrayscannot
beeasilyfocusedtoformimages.
4)Magnificationlimits:
Themaximummagnificationofaninstrumentislimitedaccordingtothefollowingrelationship:
Thus,fortheLM,witharesolvingpowerofapproximately0.25µm,themaximum(useful)magnificationisabout250µm/0.25µm=1000X.Thevalue
usedfortheresolvingpoweroftheeyeinthisexample(250µm)representsamorerealisticviewingcondition.Anymagnificationabovethevalue
givenbytheaboveformularepresentsemptymagnification,sincesuchmagnificationleadstonomoreusefulinformationbutratheramagnified
blur.
AccordingtotheAbbecriteria,at60,000volts,theTEMshouldhavearesolvingpowerofabout0.0025nm.Thisshouldallowamaximumuseful
magnificationofabout100milliontimes!!!Inpractice,themaximumusefulmagnificationoftheTEMoperatedat60kVislimitedtomuchlessthan
1,000,000X.Thus,althoughtheLMnearlyobeystheAbbecriteria,theTEMfallsshortbyaconsiderableamount.Themainlimitingfactorinthe
TEM,withrespecttoachievingthetheoreticalresolvingpoweroftheinstrument,concernsthenatureoftheimaginglensesandtheprocessof
imageformation.
5)Rayleighcriteria(practicalbutarbitrary):(Fig.I.17).
Itistheabilityofmicroscopestomakeobjectpointswhichareclosetogetherappearintheimageasseparatepoints.Anideallenstakeseach
objectpointandrepresentsitexactlyasapointintheimage.Areallenstakeseachobjectpointandspreadsitoutintoacirculardisk(Airy
disk)intheimageplanewhosediameterdependsontheangularapertureofthelens.
Theshortestdistancebetween2disksatwhichthetwodisksappearpartiallyseparatedcorrespondstoabout1/2thewidthofthedisks.The
distance,d,inobjectspaceisgivenby:
d=0.61l /n
•
sina
where
l =wavelenghtoftheradiation
n=refractiveindexofthemedia
a=semiangularapertureofthelens
NOTE:n
•
sina=thenumericalaperture(N.A.)ofthelens.
Thus,tomaximizeresolvingpower,l mustbedecreased,nincreased,oraincreased.Recallthatweareconcernedatthemomentwithan
aberrationfreeopticalsystem.Thevaluefortheconstant(0.61)iscontroversialbecauseitdependsonthecoherenceoftheradiationanda
criteriaofvisibility.
FortheLM,usingoilimmersionoptics(n=1.5),sina=0.87,andvioletlight(l =400nm),d=0.2µm.Theonlywaytoimprovetheresolutionisto
uselightofshorterwavelengthsinceN.A.cannotbeincreasedbeyond~1.5.FortheTEM,n=1(vacuum),sina=10
2
andl =0.005nmfor60kV
electrons,thusd=0.3nm.
I.A.4.Optics(LensTheory)
a.Basiclawsofclassicalgeometricaloptics
1)Rectilinearpropagationoflightwhenn(refractiveindex)isconstant.
2)Lawofreflection:
3)Lawofrefraction(Snell'sLaw):
4)Independenceofrays.Theassumptionismadethatlightraystravelindependentlythroughspace.
Theselawsholdforelectrons,except#4,ifthecurrentdensityistoohighwhennegativechargedelectronscaninterfere.
b.Classicalvs.electronoptics
1)Classicaloptics:Therefractiveindexchangesabruptlyatasurfaceandisconstantbetweenthesurfaces.Therefractionoflightatsurfaces
separatingmediaofdifferentrefractiveindicesmakesitpossibletoconstructimaginglenses.Glasssurfacescanbeshaped.
2)Electronoptics:Here,changesintherefractiveindexaregradualsoraysarecontinuouscurvesratherthanbrokenstraightlines.Refraction
ofelectronsmustbeaccomplishedbyfieldsinspacearoundchargedelectrodesorsolenoids,andthesefieldscanassumeonlycertaindistributions
consistentwithfieldtheory.
c.Geometricalandphysicaloptics
Thefundamentalprinciplesofopticsgovernthedesignandoperationofboththelightandelectronmicroscopes.Thebasicopticalprinciples
involvingtheuseofrefractileelementsorlensesinordertoformmagnifiedimagesareidenticalinboththeLMandTEM.TheTEMdiffersfromthe
LMonlyintheradiationitusesandinthewayinwhichtheradiationisbentorrefracted.
Geometricalopticsdealswiththestudyofthepathsfollowedby'rays'oflightorelectronsthroughlensesandapertures,andthegeometrical
constructionsusedtofindtherelativepositionsandsizesofobjectsandtheirimages.Arayoflightorelectronsisdefinedasaninfinitelythin
pencilorbeam.Physicalopticsshowsthatthisanabstractionandcannotphysicallyexistbecauseof'diffraction'whichdealswiththewave
natureoflightandelectrons.Allresultsobtainedingeometricalopticscanbederivedfromtheprinciplesofphysicaloptics,alongwithother
phenomenasuchasinterferenceanddiffractionwhicharenotexplicableinsimplegeometricalterms.
d.Idealversesreallenses:
Lensesareusedtobendraysoflightorelectronssotheyaredeflectedinapredictablewayfromtheiroriginalpaths.Thepropertiesofanideal
lens,possessinganaxisofrotationalsymmetryare:
1)Eachrayofthebundleofrayswhichpassesfromanobjectpointwillberefractedbytheideallenstomeetinoneimagepoint.
2)Raysoriginatingfrompointswhichlieonaplaneperpendiculartotheaxis,mustbeimagedinaplanewhichisalsoperpendiculartotheaxis.
3)Theimageappearsliketheobjectirrespectiveofthemagnification,sotherelativelineardimensionsoftheobjectarepreservedintheimage.
Inpractice,theimagingbyanyreallensdoesnotcorrespondtothatoftheideallensowingtothefactthatanobjectpointisrepresentedbya
diffractionimage(Airydisc)ofthelensopeningortheapertureusedforrestrictingtheeffectiveopeningofthelens.Thisisaresultofthewave
likepropertiesoflight.Lensaberrationsalsocontributetomoreorlesspronounceddeviationsfromthepropertiesoftheideallens.
Thesinglerefractingsurfaceofsphericalcurvatureisthefundamentalunitoffocusingactionbyglasslenses.Sphericalrefractingsurfacesactas
lensesforparaxialrayswhicharethoseraysthatpassclosetotheprincipalaxisofthelens.RayswithlargeangleswillNOTobeyideallens
action.
Afundamentaldifferencebetweenlightandmagneticlensesisthattheelectronbeamdoesnotchangeinforwardvelocityasitpassesthrough
themagneticfield(lightraysslowdownwhenpassingintoamediumofhigherrefractiveindex).Refractioniscontinuouswithelectronswhenthey
areinthemagneticfield:lightisrefractedonlyattheinterfacebetweenmediaofdifferingrefractiveindex.Theelectronsalsofollowspiral
trajectoriesthroughthemagneticfield(seealsoSec.I.A.5.c(Magneticfieldsandmagneticlenses)
e.Raydiagrams:(Figs.I.20I.28)
Themethodofconstructionofraydiagramsisbasedonthreesimpleprinciples:
1)Allraysenteringthelensparalleltotheaxisarebroughttoacommonpointontheaxis,thefocalpoint.
2)Allrayspassingthroughthegeometricalcenterofthelensareundeviatedandpassstraighton,nomatterfromwhichdirectiontheycome.
3)Principleofreversibility:ifthedirectionofarayisreversedinanysystemtherayexactlyretracesitspaththroughthesystem.Thisapplies
onlytothelocationoflightpathsandnottotheintensityofthelight.
Theaboveprinciplesarebasedontheassumptionsthatwearedealingwithathinlensandconcernedwiththepathsofparaxialrays.The
standardconventionistodrawdiagramswithraysthattravelfromlefttoright.Theobjectistotheleft(infront)ofthelensandtheimageisto
theright(behind)ofthelens.
f.Definitions:
Realimage:oneatwhichlightraysphysicallyreunite,sothataphotographicplateplacedatthepositionofarealimageisexposed.
VirtualImage:onefromwhichlightraysappeartodiverge;raysarenotinfactconcentratedatthepositionofavirtualimage,sothata
photographicplateplacedatthepositionoftheimageisnotexposed(byfocusedrays).Placinganopticalsystemsuchastheeyebehindthe
lens,willenablethedivergentraystobefocusedtoformarealimage.TheintermediatelensofanTEMissometimesusedthiswayinorderto
reducethefinalsizeoftherealimageformedbytheprojectorlens(es).
Converging(positive)lens:bendsraystowardtheaxis.Ithasapositivefocallength.Formsarealinvertedimageofanobjectplacedtothe
leftofthefirstfocalpointandanerectvirtualimageofanobjectplacedbetweenthefirstfocalpointandthelens.
Diverging(negative)lens:bendsthelightraysawayfromtheaxis.Ithasanegativefocallength.Anobjectplacedanywheretotheleftofa
diverginglensresultsinanerectvirtualimage.Itisnotpossibletoconstructanegativemagneticlensalthoughnegativeelectrostaticlensescan
bemade.
g.Lensformula(thinlensequation):
where
f=focallengthofthethinlens(sameradiusofcurvatureforboth
sphericalsurfaces)
o=distanceofobjectfromlens(positivetotheleft)
i=distanceofimagefromthelens(positivetotheright)
NOTE:Foravirtualimage,ihasanegativevalue.
h.Magnification:
Foraconverginglens,iftheobjectismorethantwicethefocallengthfromthelens,thentheimageformedisreal,inverted,andsmallerinsize
thantheobject(M<1).Whentheobjectisatadistance=2f,theimageandobjectarethesamesize(M=1);whenitisbetweenfand2f,
theimageislargerthantheobject(M>1),andwhenitis<f,theimageisvirtual,erect,andlargerthantheobject(M>1).
i.Angularapertureofthelens(2a)(Fig.I.29)
Theaperturedeterminesthetotalamountofradiationarrivingfromtheobjectwhichcanbefocusedto
formanimage.Theaperturethuscontrolstheabilityofthelenstogatherinformationabouttheobject.
Thisdependsontheangleoftheconeofraysitisabletoacceptfromtheobject.Bringinganobject
closertotheeyeincreasestheangularaperture,butthereisalimittotheclosenessthattheobjectcan
bebroughttotheeye(~25cmcorrespondingtoanangleofabout0.9°fora4mmexitpupildiameterof
theeyelens;atypicalLMwithanoilimmersionobjectivelenshas2aof~175°).
j.Simplevs.compoundmicroscope(Figs.I.30I.32)
Inprinciple,arealimageofanydesiredmagnificationcanbeobtainedfromasinglepositivelens,butin
practicethisiscumbersomebecauseofthelonglensimagedistance.Oneormorelensescanbeusedto
magnifytheimageinstages(totalmagnificationequalingtheproductofthemagnificationsofeachlens).
Theimageformedbyonelensconstitutestheobjectforthesubsequentlens,whetherornotareal
intermediateimageisformed.
Comparisonofoneversestwostagemagnification:
Thefollowingdescriptionillustrateshowdifferentpathlengthsarerequiredtoachieveamagnificationof10,000Xusingeitheroneortwolenses
withf=2.0cm.
OneStageSystem:
TwoStageSystem:
Assumebothlenseshavef=2.0cmandarearrangedsoeachgives100Xmagnification.
Thus,M=100=x
i
/x
o
foreachstage.
FirstStage:
x
o
=2.02cm
x
i
=202.00cm
Therealimageformedinthefirststagebecomestheobjectforthesecondlens.
SecondStage:x
o
,x
i
sameasinthefirststage.
Totallengthofsystem
=lengthoffirststage+lengthofsecondstage
=(x
o
+x
i
)+(x
o
+x
i
)
=2(x
o
+x
i
)
=2(2.02+202.00)=408.04cm(4.08meters)
k.Problemset
Thefollowingproblemsareforyourownedificationtotesthowwellyouunderstandthebasicsoflensoptics.
1.Foreachsituationbelow,drawanaccurate(usegraphpaper)raydiagramshowingthepathof(atleasttwo)raysfromtheobjecttoimage.
Indicatewhethertheimageisrealorvirtualandspecifythedistanceoftheimagefromthelensandthemagnificationoftheimagewithrespect
totheobject.Ineachexample,thelensisconverging,withidenticalfrontandbackfocalpoints.Distancesareinarbitraryunits.Letf=lens
focallength,x
o
=distanceofobjectinfrontofthelens,andx
i
=distanceofimagebehindthelens.Theobjectmaybeanysize.
2.Inthefollowingexamples,therearetwoconverginglensesinsuccession.Drawraydiagramsshowingtheformationofboththeintermediate
andfinalimagesandgiveappropriateinformationaboutthenature(real/virtual),positions,andsizesoftheintermediateandfinalimages.What
isthemagnificationateachstageofimageformationandwhatisthemagnificationofthefinalimage?Thedistancefromthecenteroflens1(L1)
tothecenteroflens2(L2)equalsD.
I.A.5.ElectronOptics/ElectronLenses
a.Electronemission
Innershellelectronsinmetalatomsshieldtheelectricfieldofthenucleusthroughtherepulsiveforcestheyexertontheoutershell(valence)
electrons.Thustheattractionbetweenthevalenceelectronsandthenucleusisreduced.Metalatomsarecharacterizedashavingtwoloosely
boundvalenceelectronswhichmigratefreely(thisiswhymetalsaregoodelectricalconductors)andcanescapefromthemetalcompletelyif
sufficientadditionalenergyisimpartedtothem.Asthetemperatureofametalisincreased,thekineticenergyoftheelectronsincreasesbecause
ofincreasedthermalvibrationsofthemetalions,whichcollidemorefrequentlywiththeelectrons.Thermionicemissionisthetermusedto
describetheprocessbywhichthermalenergyissuppliedtolooselyboundelectronsinordertoformasourceofelectrons.
Atroomtemperatureelectronsareeffectivelypreventedfromescapingthesurfaceofthemetalowingtotheattractiveforceofthepositively
chargedions.Asthetemperatureisincreasedsomeelectronsacquiresufficientenergytoovercometheattractionandleavethemetal
temporarily.Metal,shapedasathinwire,caneasilybeheatedbypassinganelectriccurrentthroughit.Sincethemetalsurfacebecomes
positivelycharged,acertainlevelofenergy(workfunction)mustbesuppliedtoallowelectronstoescapefromthesurface.Eachmetalhasa
characteristicworkfunction.Tungsten,withalowworkfunction,emitsmoreelectronsthanmetalswithhigherworkfunctions(seealsopp.2930
andFig.I.59).
Ifastrongelectrostaticfieldisappliedinavacuumbetweenthewire(givenanegative,cathode,potential)andananode,theelectricfieldwill
causeelectronstoaccelerateawayfromthewiretowardstheanodesurface(Fig.I.33).Thespeedoftheelectronsdependsonthestrengthof
theelectrostaticfield(voltage)betweenthecathodeandanode(equation(3),Sec.I.A.3.b)Thenumberofelectronswhichleavethewire
dependsonthetemperaturetowhichthewireisheated,whichdependsonhowmuchfilamentcurrentpassesthroughthewire.
A"V"shapedwirewillhavethehighesttemperatureatthetip.Electronswithdrawnfromthefilamenttipcarryelectricchargestotheanode.This
electriccurrent,whichflowsbetweenthefilamentandtheanode,iscalledthebeamcurrent.
1)Electricfield/Equipotentials
Anelectricallychargedobjecthasassociatedwithitanelectricfield.Thus,anelectricallychargedparticle,whenbroughtnearachargedobject,
isinfluencedbyanelectricalforceinthevicinityoftheobject.Theforceisdirectedtowardthechargedobjectifthechargesareofopposite
signsandawayfromtheobjectiftheyareofsimilarsign.DEFINITION:Thedirectionofanelectricfieldisdefinedasthedirectionoftheforce
actingonapositivecharge.(Figs.I.3435)
Alongthelinesofforceconnectingthetwocharges,theelectricpotentialwillchangegraduallybetweentheextremevaluesrepresentedbythe
twocharges.DEFINITION:Equipotentiallinesdefinethepointsalongthelinesofforcewithidenticalelectricalpotential.Theseequipotential
surfacesarealwaysorientedperpendiculartothelinesofforce.Thechangesintheelectricpotentialaregradualinspace.
Electronswhichenterafieldbetweentwoparallelplatesinadirectionparalleltotheplatesareaffectedbytheforcedirectedperpendicularto
theplates(FigI.36).Theelectronswillbeattractedtowardthepositiveplate.Thepathchangesinaseriesofgradualstepsattheequipotential
surfaces.
FigureI.37showshowtheelectronpathis"refracted"attheequipotentialsurface.TheresultisfundamentallythesameasthatgivenbySnell's
Lawofrefractioninlightoptics.Aconsequenceofthisisthatasphericallycurvedequipotentialsurfaceexhibitsthepropertiesofalens.
FiguresI.38andI.39showhowbothpositive(converging)andnegative(diverging)electrostaticlensescanbeformed.Thisfeatureof
electrostaticlensesdiffersfromelectromagneticlenseswhichcanonlyactasconverginglenses.
2)Advantages/Disadvantagesofelectronlenses:
Thefactthattherefractiveindexdoesnotchangeabruptlyinelectronlenseshasoneadvantageinthattherearenotroublesomereflectionsat
equipotentialsasatglassinterfaces.Thereisaseriousdisadvantageinthatequipotentialscannotbeshapedandcombinedinarbitraryfashionto
correctforchromaticaberrationandothererrors.
Althoughelectronmicroscopeswhichemployelectrostaticlenseshavebeenmade,mostmicroscopesuseelectromagneticlenses.Amajorreason
isthatelectrostaticlensesaremoresensitivetothequalityofthevacuumandcleanlinessofthecomponentsthanareelectromagneticlenses.
Somelensaberrationsaremoresevereforelectrostaticlensescomparedtoelectromagneticlenses.Electrostaticlensesrequireverypowerful
electrostaticfieldswhichcanleadtoelectricalbreakdownor"arcingover"insidethecolumn,especiallyunderpoorvacuumconditions.Forthis
reason,electrostaticlensescannotbemadewithfocallengthsasshortasmagneticlenses.
b.Electrostaticlens
Abasicunderstandingofelectrostaticlensesisimportantfortwomainreasons:i)theelectrongunuseselectrostaticlensactiontoformthe
primarybeamsource,andii)itisquitecommonforachargetodeveloponthenonconductingcontaminationwhichmayaccumulateonphysical
apertures(suchastheobjectiveaperture)andtransformthemintoweakelectrostaticlenseswhichcandistorttheelectronimage.
3)Propertiesofelectrostaticlenses:
a)Anyaxiallysymmetricalelectrostaticfieldhasthepropertiesofalensforraysconfinedtotheparaxialregion.Alltheideallensformulasapply
toelectrostaticlenses.
b)Forelectronlenses,replaceÃ(f)forrefractiveindexinthelensequations(f=valueofthepotentialontheaxis).Intheimageformingsystem
ofmostTEMs,fisthesameonbothsidesofthelens(SeeSec.I.A.5.c).
c)Ifboundedbyregionswherefisconstant,anelectrostaticlensisalwaysconvergent.
c.Magneticfieldsandmagneticlenses
1)Magneticfield
Anelectriccurrentpassingthroughaconductorgivesrisetoamagneticfield.TheconventionisthatNisthedirectioninwhichthelinesofthe
magneticfieldpoint(Fig.I.40).Themagneticfluxisthetotalnumberoflinesandthefluxdensityisthenumberoflinesperunitareaofasurface.
UsetheRIGHThandruletodeterminethedirectionofthefield(thumbpointstowardcurrentdirectionandfingerscurlindirectionoffield.NOTE:
Byconvention,thedirectionofelectronflowisoppositetothatofcurrentflow.
Fluxdensitydependsonthepropertiesofthematerialsurroundingtheconductor.Ironinducesahigherfluxdensitythanairoravacuum.The
propertyofthematerialwhichaffectsthefluxdensityiscalledthepermeability,m,ofthematerial.Forairandvacuum,m=1.0.For
ferromagneticmaterialsitcanbeaslargeasseveralhundredthousand.
Iftheconductorhastheshapeofacircularloop,thelinesofforceformcirclesaroundtheloop.Thefluxdensityisgreatestatthecenterofthe
loop.Themagnetinthecenteroftheloopisorientedperpendiculartotheplaneoftheloopifthecurrentthroughtheloopissufficientlystrongto
eliminatetheinfluenceoftheearth'sfield.ThesideoftheloopatwhichthelinesofforceleavetheloopistheNorth(N)poleofthemagnet(Figs.
I.41,I.42).
Ifthewireiswoundinseveralturnsaroundacylindricalsurface(solenoid),eachturnwillcontributetotheinducedmagneticfield.Theflux
densityinthecenterofthecoilisgivenby:
Inthecaseofairandnonmagneticmaterials,µ=1.0andB=H.
Thepermeabilityofirondependsonthefieldstrength,H,anddecreasestounityathighfieldstrengthorwhenthefluxdensity,B=H(Fig.I.43).
Thehighpermeabilityofironisduetotheinducedmagneticfieldorientingmicroscopiccrystalregionsactingastinymagnetsintheiron.Allthese
tinymagnetsaddtheirmagneticfieldstotheinducedfield(Fig.I.44).Whenallmicromagnetsarenearlyoriented,theironwillaffecttheflux
densitytoadecreasingamountsincethereorientationofmicromagnetsisnearingcompletion.Thus,thepermeabilityofironathighfieldstrengths
approachesthatofemptyspace.Atthispointtheironreachesmagneticsaturation.
2)Hysteresis
Thestrengthofthelensdependstosomeextentonthepreviousmagnetichistoryof
thelens.Whenthecurrentinalensisreduced,thedecreaseinmagnetizationdoes
notretracethesamepathobtainedwhenthecurrentwasincreased(Fig.I.45).
Inductionofmagnetizationinvolvesaphysicalmovementwithinthemagnetized
material,requiringtheovercomeofacertaindegreeofinertia.Asaresult,
magnetizationtendstolagbehindthemagnetizingforceapplied.Inducedmagnetic
fluxcanonlybereturnedtozerobyapplicationofacurrentintheoppositedirection.
Aconsequenceofhysteresisisthatthelevelofcurrentusedtoenergizeamagnetic
lensDOESNOTpreciselyspecifythelensstrength(i.e.focallength).
NormalizationofTEMlensesisaccomplishedbyreducingthelenscurrenttozero
somepredeterminednumberoftimes.Hysteresismayalsobeminimizedbytakinga
lenstosaturationandthenreturningittotheworkingcurrentwithoutovershooting.
Whenthefieldstrengthisreducedtozero,somemagnetizationstillremainsintheiron
(residualmagnetizationorremanence).Anadvantageofsoftironisthefactthat,
whenusedinanelectromagnet,hysteresisislow.
Introductionofpiecesofironinamagneticfielddrasticallyaffectsthefluxdensity.
Magneticmaterialhasashieldingeffect,theeffectbeinggreaterthegreaterthe
permeability.Permalloy(mmetal)hasamaximumpermeabilityof80,000140,000
comparedtoironusedintransformers(~7000).mmetalpermeabilityislimitedtolower
fieldstrengthsthanthatatwhichironstillretainshighpermeability.Thismetalis
thereforeusefulforshieldingtheTEMfromexternalmagneticfields.
d.Theelectromagneticlens
1)Lensdesigndevelopment(Figs.I.46I.48)
Theefficiencyofthemagneticfieldproducedbyashortsolenoidwasfirstimproved
byencasingtheenergizingcoilinasheathofsoftironwhichhasthepropertyofconcentratingthelinesofforceinamagneticfieldandthus
becomingmagnetizedbyinduction.Inthiswayamuchmorepowerfulaxialmagneticfieldisobtainedforthesameamountofcurrentflowing
throughthesolenoid.Furtherdevelopmentinvolvedencasingtheentirecoilwithsoftironexceptatanarrowannulargapintheinsideofthecoil.
Thisproducesagreaterconcentrationofthemagneticfieldalongashortaxialdistance.Toachieveshorterfocallengthlenses(andobtaingreater
magnifications)asoftironpolepiecewithanopenaxialborewasintroducedatthepositionoftheannulargap.
MagneticlensesusedinTEMsarealwaysconstructedwithanironcircuittoproduceahighfieldstrengthacrossashortgap.Themagneticfields
forTEMlensesareintherangeof10,00020,000gauss.
2)Forcesactingonacurrentinamagneticfield
Theforceonanelectroninamagneticfieldisalwaysatrightanglestothevelocityandthedirectionofthefield(Figs.I.49,I.50,andI.52).The
fieldonlyactsonthevelocitycomponentwhichisdirectedperpendiculartothelinesofforce.Usethelefthandrule(Fig.I.51:firstfingerfor
fielddirection,middlefingerforcurrentdirection,andthumbfordirectionofforce).Rayspassingthroughthelensareturnedthroughanangle
whichdoesNOTdependonthedistanceoftheraysfromtheaxis.Allelectronscontainedinagivenmeridionalplanebeforeenteringthefieldare
containedinarotatingmeridionalplaneastheypassthroughthelens,andthentheyleavethelenscoplanar.
Whenelectronsenterthelenstheyencounterasidewaysforcewhichcausestheelectrontorotate
asitcontinuesthroughthelens(Figs.I.53I.57).Sincetheradialcomponentofthemagneticfield
reversesafterthecenterofthelens,therotationalvelocitysetupinthefirsthalfofthelensis
countered.Theelectronenteredthelenswithoutangularmomentumabouttheaxisandleaves
withoutangularmomentum.Theneteffectisadeflectiontowardtheaxis,whichitmustcrossatthe
focalpointf
2
.Theanglebetweentheobjectvectorandtheimagevectoris180°+q,whereas,for
glasslensesandelectrostaticlenses,theanglebetweenarealobjectandtheimageisexactly180°.
Sincetheradialforceisdirectedtowardtheaxis,thelensisconvergentnomatterwhatthedirection
ofthefield.
3)Propertiesofamagneticlens:
Anyaxiallysymmetricmagneticfieldhasthepropertiesofanideallens.Alltheformulasfortheideallensmaybeapplied.
Magneticlensesarealwaysconvergent.Theconventional,axiallysymmetriclensisalwaysboundedbyregionswhicharefieldfree,the
consequencebeingthatthenetactionofelectronlensesisinevitablyconvergent.Limitedregionsmaybedivergentbutnotthelensasawhole.
Theseriousconsequenceofthisisthatneithersphericalorchromaticaberrationscanbecorrectedasisdoneinlightopticsbytheusedoublets
ofpositiveandnegativelenses.
Intheabsenceofelectrostaticfields,therefractiveindexisthesameinobjectandimagespace,thereforef
1
=f
2
.
Electronstravelingthroughaxiallysymmetricfieldsexperienceaspiraltrajectoryofdiminishingradius.Theimagevectorisatanangle180°+qto
theobjectvector.
Thedeflectionoftheelectrontowardstheaxismeansthatanelectronenteringthelensparalleltoitsaxiswillcrosstheaxisafterhavingpassed
thelens.Thedeflectionwillincreasewiththedistancefromtheaxis.Thus,abeamofelectronsinparallelpathsparalleltotheaxisofthelenswill
befocusedtoanimagepointontheaxiswhichrepresentsthesecond(back)focalpointofthelens(f
2
).Notethatmagneticlensesarehighly
inefficientinthatonlyaminorportionofthetotalfieldstrengthisactuallyeffectiveinfocusingtheelectron.
4)Magneticlensfocallength
Inamagneticelectronlensthefocallengthisdeterminedbythefieldstrengthinthelensgapandbythespeedoftheelectrons(determinedby
theacceleratingvoltage).
Formagneticlenses,focusingisachievedbyvaryingthecurrentwhichpassesthroughtheelectromagnet.Thisinturnchangesthestrengthof
themagneticfieldandtherebyaltersthefocallengthofthelensandisequivalenttoacombinedchangeinboththe"refractiveindex"and
"curvatureofsurface".Forabeamofmoreenergeticelectrons,thelenscurrenthastobeincreasedinordertokeepthefocallengthconstant.
FocallengthandcurrentareNOTlinearlyrelated:strengthincreasesinasigmoidfashion(Fig.I.45)ascurrentincreasesuntilapointisreached
wherethelensissaturatedandnofurtherincreaseinlensstrengthcanbeachieved.
Sincethefocallengthofthelensisdirectlyproportionaltotheacceleratingvoltage,avariationinthevelocityoftheelectronsintheimaging
beamaffectsimagequalitybyeliminatingperfectfocus(chromaticaberration).
5)Magneticlensdesign:(Figs.I.46,I.47).
Condenserlensesusuallyhavearelativelylargeboreandspacingwhichresultsinalongfieldandlongfocallength.
Typicalconstructionoftheobjectivelensproducesastrongfieldofshortaxialextent(i.e.shortfocallengthbetween(1.53mm)necessaryfor
formationofimagesathighmagnification.Thespecimenisplacedwithinthemagneticfieldoftheobjectivelens.Thus,anyfieldintroducedby
contaminantsinthespecimencandistortthefieldofthelens.Notethatthisalsomeansthatpartofthelensfield("prefield")isonthefrontside
oftheobjectandaffectstheelectronbeambeforeitpassesthroughtheobject.
Mostofatypicalmagneticlensliesoutsidethevacuumofthemicroscope.Onlythoseregionsthroughwhichtheelectronbeampassesareinhigh
vacuum.Magneticlensesmustbewatercooledtodissipatethelargeamountsofheatproducedbythecurrentsintheelectromagnetcoils.
DATE NAME EVENT
1897 J.J.Thompson Discoverstheelectron
1924 LouisdeBroglie Identifiesawavelengthtomovingelectrons
l =h/mv
where
l =wavelength
h=Planck'sconstant
m=mass
v=velocity
(Foranelectronat60kVl=0.005nm)
1926 H.Busch Magneticorelectricfieldsactaslensesforelectrons
1929 E.Ruska Ph.Dthesisonmagneticlenses
1931 Knoll&Ruska Firstelectronmicroscopebuilt
1931 Davisson&Calbrick Propertiesofelectrostaticlenses
1934 Driest&Muller SurpassresolutionoftheLM
1938 vonBorries&Ruska FirstpracticalEM(Siemens)10nmresolution
1940 RCA CommercialEMwith2.4nmresolution
1945 1.0nmresolution
Fig.I.1Comparisonoflightandelectronmicroscopes.Ineach
instrument,illuminationfromthesource(lamp,filamentinthe
electrongun)isfocusedbythecondenserlensontothespecimen.
Afirstmagnifiedimageisformedbytheobjectivelens.Thisimage
isfurthermagnifiedbytheprojectorlensontoagroundglass
screen(light)orfluorescentscreen(electrons).(FromAgar,p.8)
Fig.I.2CrosssectionalviewofthePhilipsEM300.(FromAgar,p.40)
Toviewtheanimatedmicroscope,clickhere.
Note:QuickTimePlugInrequired
(Thiscanbedownloadedathttp://apple.com/quicktime/download)
Fig.I.3Sectionthroughacomplex
doublecondenser6lensPhilips
EM200electronmicroscope.(From
Meek,p.99)
Fig.I.4Thestatisticalnatureofdiffraction
patterns.(FromHall,p.13)
"Theprecisenatureof'electronwaves'or'matterwaves'isverydifficulttounderstandordescribeinmaterialterms.Electronwavesarenot
electromagneticradiationofthekindtowhichlight,Xraysandradiowavesbelong.Theyconstituteasortofquantumor'packet'ofradiationwhich
accompanieseachindividualelectron,followingitspathandnotradiatingoutwardsfromit."(Meek,1976,pp.4849).
V l (nm)
v(
•
10
10
cm/sec)
v/c
10,000 0.0123 0.593 0.198
50,000 0.0055 1.326 0.442
100,000 0.0039 1.875 0.625
1,000,000 0.0012 5.930 1.977!
V l (nm)
v(
•
10
10
cm/sec)
v/c
10,000 0.0123 0.593 0.195
50,000 0.0055 1.326 0.414
100,000 0.0039 1.875 0.548
1,000,000 0.0012 5.930 0.941
FigI.5Aperfectpointsourcecannotbe
imagedbyalensasaperfectpointimagedue
tothepresenceoftheapertureAB(which
maybetheedgeofthelens).Diffractionat
thisaperturegivesrisetoaseriesoffringes,
whichsurroundtheimageformedofthepoint
source.Thepatternproducediscalledan'Airy'
disk.(FromMeek1sted.,p.35)
Fig.I.6Wheneverawavefrontstrikesa
barrier,itcanbendaroundthecorner'by
givingrisetoasecondarywavefrontatthe
edge,sinceeachpointonthewavefrontcan
giverisetoanewsourceofwaves.This
phenomenoniscalled'diffraction'.(FromMeek
1sted.,p.22)
Fig.I.7Diffractionpattern(right)formedbyanirregularlyshapedaperture
(left).(FromYoung,p.95)
Fig.I.8(a)
Photographof
theedgeofa
razorblade
illuminatedby
monochromatic
(blue)light
rendered
coherentby
passing
througha
narrowslit.(b)
Microdensitometer
tracingofthe
negativefrom
whichthe
photograph
wasmade.
FourFresnel
fringescanbe
distinguished.
(FromMeek1st
ed.,p.27)
(a)
(b)
(a) (c)
(b)
Fig.I.9(a)Fresnelfringesformed
byelectrons.Thesefringesare
formedoutsidetheedgeofahole
(white)inacarbonfilm(black).(b)
Amicrodensitometertracingofthe
fringesystem;thepatternis
identicalwiththeFresnelfringe
systemformedbyvisiblelight(see
Fig.I.8).(c)Anunderfocusedimage
ofaholeinafilm,showinga
completesystemofabout40
Fresnelfringesinsidethehole.
(FromMeek1sted.,pp.2930)
Fig.I.10Diffractionimagesoftwo
easilyresolvedpoints.(From
Slayter,p.243)
Fig.I.11Imagesoftwo
incoherentlyilluminatedpointsat
thelimitofresolution.(a)individual
intensities;(b)summedintensities.
(FromSlayter,p.244)
Fig.I.12Examplesofwhatoccurswhentwo
wavesofthesamewavelengthandequal
amplitudeadd.Ineachexample,thetwo
separatewavesareshownontheleftand
theirsumorresultantwaveontheright.The
differentexamplesarecharacterizedbyvarying
phasedifferences.Thephaseofawave
(usuallyexpressedasafractionofthe
wavelengthorindegrees)isthepositionofa
crestrelativetosomearbitrarypoint.Although
thephaseofagivenwavevarieswithtimeas
thewavetravels,thedifferenceinphaseofthe
twowavesofthesamewavelengthwiththe
samevelocity,isindependentoftime.Such
wavescaninterferewithoneanother.The
resultantwavehasthesamewavelength,l .
(a)Phasedifferencezero.Thewavestotally
reinforceandaresaidtobe"inphase"orto
showconstructiveinterference.
(b)Phasedifferencel /4.Partialreinforcement,
givingawaveofamplitude1.4(intensity2.0).
(c)Phasedifferencel /2.Thewavesare"outof
phase"andthereistotaldestructive
interferencetogivenoresultantwaveora
wavewithamplitude0(intensity0).(From
GluskerandTrueblood,p.19)
Fig.I.13Photographofan
interferencepatterninwater
wavesformedbythe
superpositionofwavesfromtwo
sourcesoscillatinginphasewith
thesamefrequency.(FromYoung,
p.22)
Fig.I.14Theangularapertureofthe
eyeisrelativelysmall.(FromMeek,
1sted.,p.13)
Fig.I.15Increasingtheangular
apertureoftheeyewithalens.The
lensallowstheobjecttobeheld
closertotheeye,whichisthereby
enabledtogathermoreinformation.
(FromMeek1sted.,p.14)
Fig.I.16Theinteractionofwaves
withanobstacle.Theboatridesthe
longwavelengthoceanwave,but
reflectsthesmallwavelength
surfaceripple.Anobserverwho
wishestodetectthepresenceof
theboatcandosoonlyby
observingwaveswhichhave
wavelengthssmallerthan,or
comparableto,thelengthofthe
boat.(FromSherwood,p.19)
Maximummagnification=
resolvingpoweroftheeye
resolvingpowerofthemicroscope
(a)
Fig.I.17(a)TwoAiry
disksrepresenting
twoimagepoints
shownatincreasing
separationfromleft
toright.Inthe
pictureatthe
extremerightthe
twodiskscanbe
distinguishedas
separatedisks.
(b)Theintensity
distributionatanAiry
disk.R,halfwidthof
thecentralmaximum
representedbya
bellshapedcurve.
(c)TheRayleigh
criteriaforresolution.
(FromSjostrand,
p.115)
i=r
Fig.I.18Reflection.(FromSlayter,
p.4)
Fig.I.19Refraction.(FromSlayter,
p.6)
Fig.I.20Principalraydiagramsshowing
imageformationbyaconvexlens.
(a)Whentheobjectdistanceisgreater
thanthefocallength,areal,inverted
imageisformed.
(b)Whentheobjectdistanceisless
thanthefocallength,avirtual,erect
imageisformed;itspositionis
obtainedbyprojectingtheprincipal
raysbackward.Theraysappearto
comefrompointQ.(FromYoung,
p.127)
Fig.I.21Definitionof
principalfocus,F,inimage
spaceofalens.(From
Sjostrand,p.20)
Fig.I.22Focusingeffectoflenson
raysoriginatingfrompointson
principalaxislocatedatdifferent
distancesfromthelens.(From
Sjostrand,p.21)
Fig.I.23Definitionofprincipal
focusinobjectspaceF1ofa
lens.(FromSjostrand,p.21)
Fig.I.24VirtualimageQof
objectpointlocatedbetween
principalfocusinobjectspace
andthelens.(FromSjostrand,
p.21)
Fig.I.25Constructionoftheimage
ofanobjectbymeansofray
tracing.(FromSjostrand,p.22)
Fig.I.26Magnifyingeffectof
apositivelens.(From
Sjostrand,p.22)
Fig.I.27Virtualmagnified
imageofobjectlocated
betweenprincipalfocusin
objectspaceandthelens.
(FromSjostrand,p.22)
Fig.I.28Amagnifyingglassformsan
enlarged,erectvirtualimage.The
angularsizeofthisimageis
approximately4"/15"or4/15.The
angularsizeoftheobjectatthe
closestdistanceforcomfortable
viewingis1"/10"or1/10.The
magnificationinthissituationis(4/15)/
(1/10),or22/3.(FromYoung,p.130)
Fig.I.29Theangularapertureofa
lens.Theangle2a isthe
acceptanceangleofthelens,and
thelargeritcanbemade,themore
informationcanthelenstransmit.A
largelensofhighaperturecan
thereforetellusmoreaboutan
objectthanasmalllensoflow
power.(FromMeek1sted.,p.12)
Fig.I.30Raydiagramforhighmagnification
modeofoperation.Notethateachlens
formsarealimage,withimageinversion.
I0istheimageformedbytheobjective
lensO,I1isformedbythefirstprojector
lensP1andI2bythesecondprojectorP2,
onthescreen.(FromAgar,p.30)
Fig.I.31Left:raydiagramofthe3realimagemediumandhighmagnificationimagingsystemofa3lens
microscope.Center:2realimageverylowor'scan'magnificationrangeofa3lensmicroscope.Right:2real
imagelowmagnificationsystemofa3lensmicroscope.(FromMeek1sted.,pp.118,120121)
Fig.I.32Raydiagramforacompleteelectron
microscope.FilamentF,condenser1lensC1,
condenser2lensC2,condenserapertureCA,
specimenS,objectivelensO,objectiveaperture
OA(inbackfocalplane).1stintermediateimage
andselectorapertureSA.IntermediatelensP1,
secondintermediateimageI2,projectorlensP2
andfinalimageonthefluorescentscreenFC.
(FromAgar,p.35)
a)f=2.0
x
o
=5.0
e)f=4.0
x
o
=3.0
b)f=10.5
x
o
=21.0
f)f=13.3
x
o
=13.3
c)f=3.5
x
o
=3.0
g)f=3.142
x
o
=0.0
d)f=5.0
x
o
=2.5
a)D=8.0
L1:f=2.0
x
o
=4.0
L2:f=3.0
b)D=8.0
L1:f=2.0
x
o
=6.0
L2:f=3.0
c)D=4.0
L1:f=2.0
x
o
=3.0
L2:f=2.0
FigI.33Accelerationofelectronin
electricfield.(FromSjostrand,p.26)
Fig.I.34Linesofforceatapositively
chargedsphericalbody.(FromSjostrand,
p.32)
Fig.I.35Linesofforceandequipotential
surfaces(stippledlines)associatedwith
twoequalchargesofoppositesign.
(FromSjostrand,p.32)
Fig.I.36Equipotentialsurfacesattwoparallel
platesofoppositechargeswiththepathofan
electronindicatedwithinthehomogeneous
partofthefield.(FromSjostrand,p.33)
Fig.I.37Refractionofelectronatan
equipotentialsurface.(FromSjostrand,p.33)
Fig.I.38.Negativelensactionof
electrostaticfieldatanaperturewhen
V2V1>V3V2.(FromSjostrand,
p.34)
Fig.I.39.Positivelensactionatan
aperturewhenV2V1<V3V2.
(FromSjostrand,p.34)
Fig.I.40Magneticfieldinducedbycurrent
passingthroughaconductor.(From
Sjostrand,p.35)
Fig.I.41Magneticfieldinducedbycurrent
passingthroughasolenoid.(From
Sjostrand,p.37)
Fig.I.42Solenoidwithironcore.(From
Sjostrand,p.40)
Fig.I.43a.Dependenceofpermeabilityonfluxdensity,B.
b.RelationshipbetweenfluxdensityBandfieldstrength.
(FromSjostrand,p.38).
Fig.I.44Magnetization.(FromSlayter,
p.361)
Fig.I.45Curves
showinghowthe
magnetizationof
softiron(lens
strength)is
relatedtothe
magnetizing
force(lens
current).An
unmagnetized
lensstartsfrom
thepointOand
followsthepath
OAaslens
current
increases.Atthe
pointA,further
increaseinlens
currentproduces
nofurther
increaseinlens
strength;thelensissaidtobe'saturated'.Whenlenscurrent
isreduced,thepathOAisnotretraced;adifferentpathABis
followed.Thisdisplacementiscalled'hysteresis'.Atzero
current(pointB),someresiduallensstrengthremains;thisis
called'remanence'.Tobringthelensbacktozerostrength,a
reversecurrentOCmustbeapplied.Lensstrengththen
increaseswithincreasingreversecurrent,followingthepath
CD.Thepolarityofthelenschanges,butthisdoesnotaffect
itsfocusingpower;onlythespiralelectronpathisreversed.
Becauseofhysteresis,itisnotpossibletocalibratealens
currentmeteraccuratelyintermsoflensstrengthor
magnification.
Fig.I.46Evolutionofmagneticelectron
lenses.(A)Shortsolenoidusedasa
magneticlens.(B)Softironcasing
enclosingoutersurfaceofthesolenoid,
thusconcentratingthefield.(C)Soft
ironencasingthesolenoidexceptata
narrowannulargaptherebyreducing
themagneticfieldtoaveryshortregion
alongthelensaxis.(D)Modern
objectivelensconsistingofasoftiron
encasedsolenoidandsoftironpole
piecessoastohaveanenormously
concentratedfieldatthelevelofthe
annulargap.(FromWischnizter2nded.,
p.33)
Fig.I.47(a)Amagneticlensconsisting
ofatightlywoundcoilandasoftiron
shroudsurroundingthecoilexceptfor
asmallgap.Thefieldisconcentratedin
thatgap.(b)Shortfocallength
electromagneticlenswithpolepieces.
(FromSjostrand,p.50)
Fig.I.48Fieldstrengthdistribution
curves.ThecurvesADcorrespondto
therespectivelensesillustratedinFig.
I.46.Eachrepresentsthefieldstrength
alongthelongaxisofthelens.The
changesintheshapeofthecurves
representtheshorteningor
concentrationofthefieldovera
shorteraxialdistance.Hz=
longitudinalmagneticfield.Z=
distancealongtheaxisofsymmetry.
(FromWischnizter2nded.,p.33)
Fig.I.49TheforceFactingon
astraightconductorina
homogeneousmagneticfield
offluxdensityBwhencurrent
Iispassedthroughthe
conductor.(FromSjostrand,
p.43)
Fig.I.50Pathofanelectronina
magneticfield.(A)Inalarge,uniform
magneticfield.(B)Inasmall,uniform
magneticfield.(FromWischnitzer2nd
ed.,p.25)
Fig.I.51Lefthandthumbrule.
(FromSjostrand,p.43)
Fig.I.52Thompson'sexperiment.A
streamofelectronsoriginatingfroma
sourceandpassing,invacuo,through
amagneticfieldproducedbyapairof
magnetswillbedeflected.The
directionofdeflectiondemonstrates
thatelectronsarenegativelycharged
particlesofmatter.(FromWischnitzer
2nded.,p.25)
Fig.I.53Actionofasolenoidonan
electronbeam.Anelectriccurrent
passingthroughthecoilproducesan
axialmagneticfield.Thisisthe
refractingmediumfortheelectrons.An
electronstartingatapointontheaxisA
andatanangletoitfollowsaspiral
path,returningtotheaxisatthepoint
B.Theactionisbasicallysimilartothat
oftheconverginglightlensshownin
Fig.I.20.(FromMeek1sted.,p.8)
Fig.I.54Actionofthemagnetic
lens.(a)Inperspective.(b)
Electrontrajectoryin
projection,alongdirectionof
propagation.(c)Electron
trajectoryinprojection,side
view.(FromSlayter,p.358)
Fig.I.55Componentsofthe
vectorHneartheaxisoffields
withaxialsymmetry.His
representedbytwo
components,Hz,the
componentinthez(axial)
direction,andHr,the
compnentinther(radial)
direction.(FromHall,p.85)
Fig.I.56Theycomponentof
themagneticfieldina
magneticlensisoriented
perpendiculartothedirection
ofanelectronenteringthe
lensalongapathparallelto
thelensaxis.Thisy
componentwillaffectthe
electron,deflectingitinthex
directionasindicatedbythe
arrowmarkedvx.(From
Sjostrand,p.48)
Fig.I.57Thezcomponentofthemagneticfield
andthexvelocitycomponentoftheelectron
inamagneticlensinteract,deflectingthe
electronintheydirectiontowardthelens
axis.(FromSjostrand,p.49)
CuuDuongThanCong.com https://fb.com/tailieudientucntt
cuu duong than cong . com
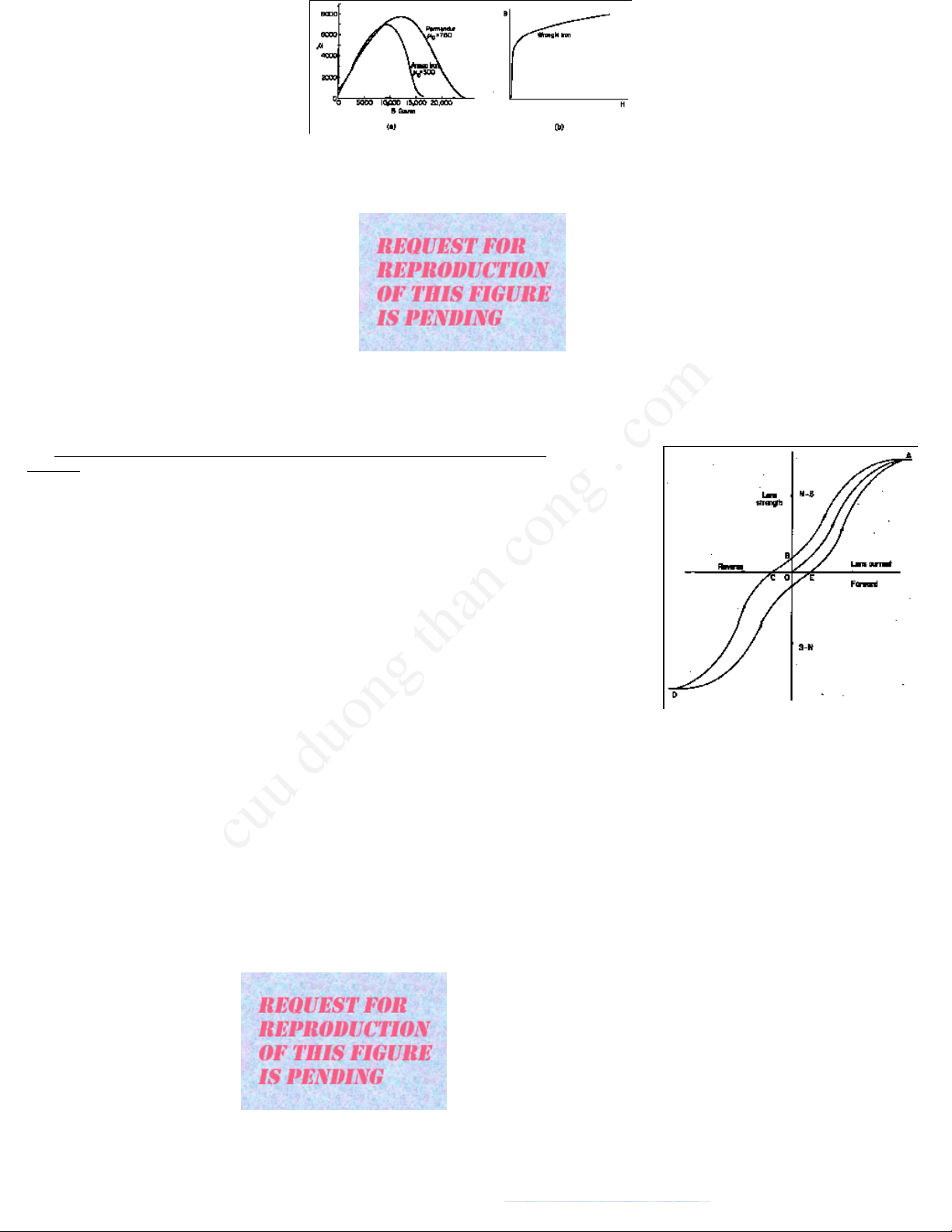
I.THEMICROSCOPE
I.A.PRINCIPLESOFTHETRANSMISSIONELECTRONMICROSCOPE(TEM)
I.A.1.OriginoftheTransmissionElectronMicroscope
I.A.2.ComparisonofLight(LM)andElectronMicroscopes(Fig.I.1)
a.Similarities(Arrangementandfunctionofcomponentsaresimilar)
1)Illuminationsystem:producesrequiredradiationanddirectsitontothespecimen.Consistsofasource,whichemitstheradiation,anda
condenserlens,whichfocusestheilluminatingbeam(allowingvariationsofintensitytobemade)onthespecimen.
2)Specimenstage:situatedbetweentheilluminationandimagingsystems.
3)Imagingsystem:Lenseswhichtogetherproducethefinalmagnifiedimageofthespecimen.Consistsofi)anobjectivelenswhichfocusesthe
beamafteritpassesthroughthespecimenandformsanintermediateimageofthespecimenandii)theprojectorlens(es)whichmagnifiesa
portionoftheintermediateimagetoformthefinalimage.
4)Imagerecordingsystem:Convertstheradiationintoapermanentimage(typicallyonaphotographicemulsion)thatcanbeviewed.
b.Differences
1)Opticallensesaregenerallymadeofglasswithfixedfocallengthswhereasmagneticlensesareconstructedwithferromagneticmaterialsand
windingsofcopperwireproducingafocallengthwhichcanbechangedbyvaryingthecurrentthroughthecoil.
2)MagnificationintheLMisgenerallychangedbyswitchingbetweendifferentpowerobjectivelensesmountedonarotatingturretabovethe
specimen.Itcanalsobechangedifoculars(eyepieces)ofdifferentpowerareused.IntheTEMthemagnification(focallength)oftheobjective
remainsfixedwhilethefocallengthoftheprojectorlensischangedtovarymagnification.
3)TheLMhasasmalldepthoffield,thusdifferentfocallevelscanbeseeninthespecimen.Thelarge(relative)depthoffieldintheTEMmeans
thattheentire(thin)specimenisinfocussimultaneously.
4)Mechanismsofimageformationvary(phaseandamplitudecontrast).
5)TEMsaregenerallyconstructedwiththeradiationsourceatthetopoftheinstrument:thesourceisgenerallysituatedatthebottomofLMs.
6)TEMisoperatedathighvacuum(sincethemeanfreepathofelectronsinairisverysmall)somostspecimens(biological)mustbedehydrated
(i.e.dead!!).
7)TEMspecimens(biological)arerapidlydamagedbytheelectronbeam.
8)TEMscanachievehighermagnificationandbetterresolutionthanLMs.
9)Pricetag!!!(100xmorethanLM)
I.A.3.Photons/Electrons
a.Dualconceptofwaveandparticle(Fig.I.4)
Lighthaspropertiesbothofaparticleandawave.Thisdualnatureisrequiredtosatisfactorilyexplaintheresultsofvariousphysicalexperiments.
Thediffractionoflight(bendingaroundcorners)illustratesthewavenature.TheWAVETHEORYisbasedonthestatisticalnatureofeventsand
haslittlemeaningwithrespecttothebehaviorofsingleparticles.ThewavetheorywasdevelopedandexpoundedbyHuygens(16291695)and
Hooke(16381703).TheCORPUSCULARTHEORYwasproposedbyNewton(16421727)andbecamethemoreacceptedtheoryevenafter
demonstrationofdiffractionbyYoung(17731829)andinterferencebyFresnel(17881827).Atabout1850,thewavetheorycamebackinto
favoruntilabout1900whenmoreevidenceforthecorpusculartheorywasdiscovered.
QUANTUMTHEORY(PlanckandEinstein)providesthebasisforexplainingthephenomenaofINTERFERENCE,DIFFRACTIONandthe
PHOTOELECTRICeffect(lightfallingoncertainmetalscausethemtoemitelectrons)andthusformsacommonbasisforexplainingthenatureof
actionoflight.Thetransferofenergybetweenlightandmatteroccursonlyindiscretequantitiesproportionaltothefrequencyofthe
lightwave.
E=hJ
where
E=energyofphoton(joules)
h=Planck'sconstant(6.624
•
10
34
joulesec)
J=frequency(cycles/sec)
b.Electronvelocityandwavelength
Therelationbetweenthewavelength(l )ofaparticleofmass,m,movingatavelocity,v,isgivenbytheDeBrogliewaveequation:
(1)
Anelectronofchargee(1.6
•
10
19
coulomb),andmassm(9.11
•
10
28
gm),whenpassingthroughapotentialdifferenceofVvolts(expressedin
joules/coulomb),hasakineticenergy:
(2)
Solvingforvelocity:
(3)
substitutingintotheDeBroglieequation(1):
(4)
Since1joule=10
7
dyne
•
cm=10
7
cm
2
•
gm/sec
2
(5)
Thus,forexample,ifV=60,000volts,l =0.005nm.
Fromequation(3)theelectronvelocitycanbecalculatedifVisknown:
(6)
Thefollowingtableillustratesthat,athighvoltage,electronvelocityiscomparabletothespeedoflightinavacuum(c=3
•
10
10
cm/sec).
Theequationbreaksdownwhenthevelocityoftheelectronapproachesthespeedoflightbecausearelativisticcorrectionmustbemadeforthe
valueofthemasswhere:
(7)
Therelationbetweenl andVismorecorrectlygivenby:(seeHall(1966)pp.3334)
(8)
Thefollowingtableisobtainedwhenrelativityeffectsareincluded:
c.Interference/diffraction/coherence
Anideallenssystemobtainsanexactimageoftheobject(eachpointfaithfullyreproduced).Thephenomenaofdiffractionmakesthis
unattainable(Figs.I.5,I.6).
Diffractionphenomenainvolvesthebendingofthepathofradiationpassingclosetoanobstacle(Fig.I.6).Thisresultsinaspreadingofthe
radiationintotheregionbehindtheobstructionthatthewavespassed.Thediffractionatedgescontributestothecontrastatwhichanedgecan
beobserved.Diffractionalsolimitstheresolvingpowerofthemicroscopesincetheimagepointproducedbyalensisadiffractionimageofthe
openingofthelensortheaperturerestrictingtheeffectiveopeningofthelens(Fig.I.5).
Ifthelightsourceandtheplaneatwhichthediffractionpatternisobservedareatfinitedistancesfromtheedge,thephenomenoniscalled
Fresneldiffraction.Thepatternisdescribedasduetointerferencebetweenthenondiffractedlightandawaveoflightdiffractedattheedge.
Theresultingsuperpositiongivesrisetoaseriesofdiffractionfringesorientedparalleltotheedgeandrepresentingperiodicallyvaryingbrightness,
maximaandminima.(Figs.I.7,1.8,I.9).
Coherence:Aprerequisiteforinterferenceisasuperpositionofwavesystemswhosephasedifferenceremainsconstantintime.Twobeams
arecoherentif,whencombined,theyproduceaninterferencepattern.Thebeamsareincoherentwhentheyareincapableofproducingan
interferencepattern.Twobeamsoflightfromselfluminoussourcesareincoherent.Iflightfromthetwosourcesfallsonascreen,theresultant
intensityissimplythesumofthetwointensitieswhichwouldoccurfromeachsourceseparately(Figs.I.10,I.11).Inpracticeanemittingsource
hasfiniteextentandeachpointofthesourcecanbeconsideredtogeneratelight.EachsourcegivesrisetoasystemofFresnelfringesatthe
edge.Thesuperpositionofthesefringesystemsisfairlygoodforthefirstmaximaandminimabutfartherawayfromtheedgeshadowtheoverlap
ofthefringepatternsbecomessufficientlyrandomtomakethefringesdisappear.Thenatureofwaves,phase,amplitude,andinterferenceare
illustratedinFigs.I.12andI.13.
d.Resolution
1)Definitions:
RESOLUTION:abilitytodistinguishcloselyspacedpointsasseparatepoints.
RESOLUTIONLIMIT:smallestseparationofpointswhichcanberecognizedasdistinct.
RESOLVINGPOWER:resolutionachievedbyaparticularinstrumentunderoptimumviewingconditions.
2)Distinctionbetweenresolutionandresolvingpower:
Notethedistinctionbetweenresolutionandresolvingpower.Resolvingpowerisapropertyoftheinstrumentandisaquantitythatmaybe
estimatedontheoreticalgrounds.Resolutionisequaltoorpoorerthantheresolvingpowerandisthequantityobservedunderanygivenset
ofexperimentalconditions.IntheTEM,especiallywithbiologicalsamples,theresolutionachievedmaybeconsiderablyinferiortothetheoretical
resolvingpoweroftheinstrument.
Microscopyisthescienceofseeingtheverysmall.Underidealconditions,theeyeresolvesabout1minuteofarc(=1/60degree=2.9x10
4
radian;recallthereare2p radiansin360°)andsinceitcanfocusdowntoabout250mm,thesmallestobjectwecanresolveisabout0.07mm
(70mm)(Fig.I.14).Thislimitisrelatedtothesizeofthereceptorsintheretinaoftheeye.Thefunctionofamicroscopeistomagnifytheimage
fallingontheretina(Fig.I.15).Theadvantageoflightandelectronmicroscopesisthattheyeffectivelygettheobjectclosertotheeyesoa
magnifiedimageisobtainedandmoredetailcanbediscerned.
TENNISBALLANALOGY:Eyecanresolve3cmat100meters,thusatennisballisclearlyvisible.Butifthetennisballisheldupagainstawhite
background,thevisibilitydecreases(becauseofthedecreaseincontrast).
3)Abbecriteriaofresolution:
Thefundamentalnatureoflightposeslimitsonthedetailthatcanberesolved(Fig.I.16).Abbe(1893)showedthatthesmallestresolvable
distanceisabout1/2thewavelengthoflightused.Thus,1/2thewavelengthoftheradiationusedistheultimateresolvingpowerofany
instrument.Thislimitstheusablemagnificationofopticalmicroscopesto<1000X.Atfirstitwasthoughtthatxraymicroscopeswouldbeuseful
buttherefractiveindexofsubstancesforxraysisnearly=1,thusrefractinglensescannotbemadeforxrays,andconsequently,xrayscannot
beeasilyfocusedtoformimages.
4)Magnificationlimits:
Themaximummagnificationofaninstrumentislimitedaccordingtothefollowingrelationship:
Thus,fortheLM,witharesolvingpowerofapproximately0.25µm,themaximum(useful)magnificationisabout250µm/0.25µm=1000X.Thevalue
usedfortheresolvingpoweroftheeyeinthisexample(250µm)representsamorerealisticviewingcondition.Anymagnificationabovethevalue
givenbytheaboveformularepresentsemptymagnification,sincesuchmagnificationleadstonomoreusefulinformationbutratheramagnified
blur.
AccordingtotheAbbecriteria,at60,000volts,theTEMshouldhavearesolvingpowerofabout0.0025nm.Thisshouldallowamaximumuseful
magnificationofabout100milliontimes!!!Inpractice,themaximumusefulmagnificationoftheTEMoperatedat60kVislimitedtomuchlessthan
1,000,000X.Thus,althoughtheLMnearlyobeystheAbbecriteria,theTEMfallsshortbyaconsiderableamount.Themainlimitingfactorinthe
TEM,withrespecttoachievingthetheoreticalresolvingpoweroftheinstrument,concernsthenatureoftheimaginglensesandtheprocessof
imageformation.
5)Rayleighcriteria(practicalbutarbitrary):(Fig.I.17).
Itistheabilityofmicroscopestomakeobjectpointswhichareclosetogetherappearintheimageasseparatepoints.Anideallenstakeseach
objectpointandrepresentsitexactlyasapointintheimage.Areallenstakeseachobjectpointandspreadsitoutintoacirculardisk(Airy
disk)intheimageplanewhosediameterdependsontheangularapertureofthelens.
Theshortestdistancebetween2disksatwhichthetwodisksappearpartiallyseparatedcorrespondstoabout1/2thewidthofthedisks.The
distance,d,inobjectspaceisgivenby:
d=0.61l /n
•
sina
where
l =wavelenghtoftheradiation
n=refractiveindexofthemedia
a=semiangularapertureofthelens
NOTE:n
•
sina=thenumericalaperture(N.A.)ofthelens.
Thus,tomaximizeresolvingpower,l mustbedecreased,nincreased,oraincreased.Recallthatweareconcernedatthemomentwithan
aberrationfreeopticalsystem.Thevaluefortheconstant(0.61)iscontroversialbecauseitdependsonthecoherenceoftheradiationanda
criteriaofvisibility.
FortheLM,usingoilimmersionoptics(n=1.5),sina=0.87,andvioletlight(l =400nm),d=0.2µm.Theonlywaytoimprovetheresolutionisto
uselightofshorterwavelengthsinceN.A.cannotbeincreasedbeyond~1.5.FortheTEM,n=1(vacuum),sina=10
2
andl =0.005nmfor60kV
electrons,thusd=0.3nm.
I.A.4.Optics(LensTheory)
a.Basiclawsofclassicalgeometricaloptics
1)Rectilinearpropagationoflightwhenn(refractiveindex)isconstant.
2)Lawofreflection:
3)Lawofrefraction(Snell'sLaw):
4)Independenceofrays.Theassumptionismadethatlightraystravelindependentlythroughspace.
Theselawsholdforelectrons,except#4,ifthecurrentdensityistoohighwhennegativechargedelectronscaninterfere.
b.Classicalvs.electronoptics
1)Classicaloptics:Therefractiveindexchangesabruptlyatasurfaceandisconstantbetweenthesurfaces.Therefractionoflightatsurfaces
separatingmediaofdifferentrefractiveindicesmakesitpossibletoconstructimaginglenses.Glasssurfacescanbeshaped.
2)Electronoptics:Here,changesintherefractiveindexaregradualsoraysarecontinuouscurvesratherthanbrokenstraightlines.Refraction
ofelectronsmustbeaccomplishedbyfieldsinspacearoundchargedelectrodesorsolenoids,andthesefieldscanassumeonlycertaindistributions
consistentwithfieldtheory.
c.Geometricalandphysicaloptics
Thefundamentalprinciplesofopticsgovernthedesignandoperationofboththelightandelectronmicroscopes.Thebasicopticalprinciples
involvingtheuseofrefractileelementsorlensesinordertoformmagnifiedimagesareidenticalinboththeLMandTEM.TheTEMdiffersfromthe
LMonlyintheradiationitusesandinthewayinwhichtheradiationisbentorrefracted.
Geometricalopticsdealswiththestudyofthepathsfollowedby'rays'oflightorelectronsthroughlensesandapertures,andthegeometrical
constructionsusedtofindtherelativepositionsandsizesofobjectsandtheirimages.Arayoflightorelectronsisdefinedasaninfinitelythin
pencilorbeam.Physicalopticsshowsthatthisanabstractionandcannotphysicallyexistbecauseof'diffraction'whichdealswiththewave
natureoflightandelectrons.Allresultsobtainedingeometricalopticscanbederivedfromtheprinciplesofphysicaloptics,alongwithother
phenomenasuchasinterferenceanddiffractionwhicharenotexplicableinsimplegeometricalterms.
d.Idealversesreallenses:
Lensesareusedtobendraysoflightorelectronssotheyaredeflectedinapredictablewayfromtheiroriginalpaths.Thepropertiesofanideal
lens,possessinganaxisofrotationalsymmetryare:
1)Eachrayofthebundleofrayswhichpassesfromanobjectpointwillberefractedbytheideallenstomeetinoneimagepoint.
2)Raysoriginatingfrompointswhichlieonaplaneperpendiculartotheaxis,mustbeimagedinaplanewhichisalsoperpendiculartotheaxis.
3)Theimageappearsliketheobjectirrespectiveofthemagnification,sotherelativelineardimensionsoftheobjectarepreservedintheimage.
Inpractice,theimagingbyanyreallensdoesnotcorrespondtothatoftheideallensowingtothefactthatanobjectpointisrepresentedbya
diffractionimage(Airydisc)ofthelensopeningortheapertureusedforrestrictingtheeffectiveopeningofthelens.Thisisaresultofthewave
likepropertiesoflight.Lensaberrationsalsocontributetomoreorlesspronounceddeviationsfromthepropertiesoftheideallens.
Thesinglerefractingsurfaceofsphericalcurvatureisthefundamentalunitoffocusingactionbyglasslenses.Sphericalrefractingsurfacesactas
lensesforparaxialrayswhicharethoseraysthatpassclosetotheprincipalaxisofthelens.RayswithlargeangleswillNOTobeyideallens
action.
Afundamentaldifferencebetweenlightandmagneticlensesisthattheelectronbeamdoesnotchangeinforwardvelocityasitpassesthrough
themagneticfield(lightraysslowdownwhenpassingintoamediumofhigherrefractiveindex).Refractioniscontinuouswithelectronswhenthey
areinthemagneticfield:lightisrefractedonlyattheinterfacebetweenmediaofdifferingrefractiveindex.Theelectronsalsofollowspiral
trajectoriesthroughthemagneticfield(seealsoSec.I.A.5.c(Magneticfieldsandmagneticlenses)
e.Raydiagrams:(Figs.I.20I.28)
Themethodofconstructionofraydiagramsisbasedonthreesimpleprinciples:
1)Allraysenteringthelensparalleltotheaxisarebroughttoacommonpointontheaxis,thefocalpoint.
2)Allrayspassingthroughthegeometricalcenterofthelensareundeviatedandpassstraighton,nomatterfromwhichdirectiontheycome.
3)Principleofreversibility:ifthedirectionofarayisreversedinanysystemtherayexactlyretracesitspaththroughthesystem.Thisapplies
onlytothelocationoflightpathsandnottotheintensityofthelight.
Theaboveprinciplesarebasedontheassumptionsthatwearedealingwithathinlensandconcernedwiththepathsofparaxialrays.The
standardconventionistodrawdiagramswithraysthattravelfromlefttoright.Theobjectistotheleft(infront)ofthelensandtheimageisto
theright(behind)ofthelens.
f.Definitions:
Realimage:oneatwhichlightraysphysicallyreunite,sothataphotographicplateplacedatthepositionofarealimageisexposed.
VirtualImage:onefromwhichlightraysappeartodiverge;raysarenotinfactconcentratedatthepositionofavirtualimage,sothata
photographicplateplacedatthepositionoftheimageisnotexposed(byfocusedrays).Placinganopticalsystemsuchastheeyebehindthe
lens,willenablethedivergentraystobefocusedtoformarealimage.TheintermediatelensofanTEMissometimesusedthiswayinorderto
reducethefinalsizeoftherealimageformedbytheprojectorlens(es).
Converging(positive)lens:bendsraystowardtheaxis.Ithasapositivefocallength.Formsarealinvertedimageofanobjectplacedtothe
leftofthefirstfocalpointandanerectvirtualimageofanobjectplacedbetweenthefirstfocalpointandthelens.
Diverging(negative)lens:bendsthelightraysawayfromtheaxis.Ithasanegativefocallength.Anobjectplacedanywheretotheleftofa
diverginglensresultsinanerectvirtualimage.Itisnotpossibletoconstructanegativemagneticlensalthoughnegativeelectrostaticlensescan
bemade.
g.Lensformula(thinlensequation):
where
f=focallengthofthethinlens(sameradiusofcurvatureforboth
sphericalsurfaces)
o=distanceofobjectfromlens(positivetotheleft)
i=distanceofimagefromthelens(positivetotheright)
NOTE:Foravirtualimage,ihasanegativevalue.
h.Magnification:
Foraconverginglens,iftheobjectismorethantwicethefocallengthfromthelens,thentheimageformedisreal,inverted,andsmallerinsize
thantheobject(M<1).Whentheobjectisatadistance=2f,theimageandobjectarethesamesize(M=1);whenitisbetweenfand2f,
theimageislargerthantheobject(M>1),andwhenitis<f,theimageisvirtual,erect,andlargerthantheobject(M>1).
i.Angularapertureofthelens(2a)(Fig.I.29)
Theaperturedeterminesthetotalamountofradiationarrivingfromtheobjectwhichcanbefocusedto
formanimage.Theaperturethuscontrolstheabilityofthelenstogatherinformationabouttheobject.
Thisdependsontheangleoftheconeofraysitisabletoacceptfromtheobject.Bringinganobject
closertotheeyeincreasestheangularaperture,butthereisalimittotheclosenessthattheobjectcan
bebroughttotheeye(~25cmcorrespondingtoanangleofabout0.9°fora4mmexitpupildiameterof
theeyelens;atypicalLMwithanoilimmersionobjectivelenshas2aof~175°).
j.Simplevs.compoundmicroscope(Figs.I.30I.32)
Inprinciple,arealimageofanydesiredmagnificationcanbeobtainedfromasinglepositivelens,butin
practicethisiscumbersomebecauseofthelonglensimagedistance.Oneormorelensescanbeusedto
magnifytheimageinstages(totalmagnificationequalingtheproductofthemagnificationsofeachlens).
Theimageformedbyonelensconstitutestheobjectforthesubsequentlens,whetherornotareal
intermediateimageisformed.
Comparisonofoneversestwostagemagnification:
Thefollowingdescriptionillustrateshowdifferentpathlengthsarerequiredtoachieveamagnificationof10,000Xusingeitheroneortwolenses
withf=2.0cm.
OneStageSystem:
TwoStageSystem:
Assumebothlenseshavef=2.0cmandarearrangedsoeachgives100Xmagnification.
Thus,M=100=x
i
/x
o
foreachstage.
FirstStage:
x
o
=2.02cm
x
i
=202.00cm
Therealimageformedinthefirststagebecomestheobjectforthesecondlens.
SecondStage:x
o
,x
i
sameasinthefirststage.
Totallengthofsystem
=lengthoffirststage+lengthofsecondstage
=(x
o
+x
i
)+(x
o
+x
i
)
=2(x
o
+x
i
)
=2(2.02+202.00)=408.04cm(4.08meters)
k.Problemset
Thefollowingproblemsareforyourownedificationtotesthowwellyouunderstandthebasicsoflensoptics.
1.Foreachsituationbelow,drawanaccurate(usegraphpaper)raydiagramshowingthepathof(atleasttwo)raysfromtheobjecttoimage.
Indicatewhethertheimageisrealorvirtualandspecifythedistanceoftheimagefromthelensandthemagnificationoftheimagewithrespect
totheobject.Ineachexample,thelensisconverging,withidenticalfrontandbackfocalpoints.Distancesareinarbitraryunits.Letf=lens
focallength,x
o
=distanceofobjectinfrontofthelens,andx
i
=distanceofimagebehindthelens.Theobjectmaybeanysize.
2.Inthefollowingexamples,therearetwoconverginglensesinsuccession.Drawraydiagramsshowingtheformationofboththeintermediate
andfinalimagesandgiveappropriateinformationaboutthenature(real/virtual),positions,andsizesoftheintermediateandfinalimages.What
isthemagnificationateachstageofimageformationandwhatisthemagnificationofthefinalimage?Thedistancefromthecenteroflens1(L1)
tothecenteroflens2(L2)equalsD.
I.A.5.ElectronOptics/ElectronLenses
a.Electronemission
Innershellelectronsinmetalatomsshieldtheelectricfieldofthenucleusthroughtherepulsiveforcestheyexertontheoutershell(valence)
electrons.Thustheattractionbetweenthevalenceelectronsandthenucleusisreduced.Metalatomsarecharacterizedashavingtwoloosely
boundvalenceelectronswhichmigratefreely(thisiswhymetalsaregoodelectricalconductors)andcanescapefromthemetalcompletelyif
sufficientadditionalenergyisimpartedtothem.Asthetemperatureofametalisincreased,thekineticenergyoftheelectronsincreasesbecause
ofincreasedthermalvibrationsofthemetalions,whichcollidemorefrequentlywiththeelectrons.Thermionicemissionisthetermusedto
describetheprocessbywhichthermalenergyissuppliedtolooselyboundelectronsinordertoformasourceofelectrons.
Atroomtemperatureelectronsareeffectivelypreventedfromescapingthesurfaceofthemetalowingtotheattractiveforceofthepositively
chargedions.Asthetemperatureisincreasedsomeelectronsacquiresufficientenergytoovercometheattractionandleavethemetal
temporarily.Metal,shapedasathinwire,caneasilybeheatedbypassinganelectriccurrentthroughit.Sincethemetalsurfacebecomes
positivelycharged,acertainlevelofenergy(workfunction)mustbesuppliedtoallowelectronstoescapefromthesurface.Eachmetalhasa
characteristicworkfunction.Tungsten,withalowworkfunction,emitsmoreelectronsthanmetalswithhigherworkfunctions(seealsopp.2930
andFig.I.59).
Ifastrongelectrostaticfieldisappliedinavacuumbetweenthewire(givenanegative,cathode,potential)andananode,theelectricfieldwill
causeelectronstoaccelerateawayfromthewiretowardstheanodesurface(Fig.I.33).Thespeedoftheelectronsdependsonthestrengthof
theelectrostaticfield(voltage)betweenthecathodeandanode(equation(3),Sec.I.A.3.b)Thenumberofelectronswhichleavethewire
dependsonthetemperaturetowhichthewireisheated,whichdependsonhowmuchfilamentcurrentpassesthroughthewire.
A"V"shapedwirewillhavethehighesttemperatureatthetip.Electronswithdrawnfromthefilamenttipcarryelectricchargestotheanode.This
electriccurrent,whichflowsbetweenthefilamentandtheanode,iscalledthebeamcurrent.
1)Electricfield/Equipotentials
Anelectricallychargedobjecthasassociatedwithitanelectricfield.Thus,anelectricallychargedparticle,whenbroughtnearachargedobject,
isinfluencedbyanelectricalforceinthevicinityoftheobject.Theforceisdirectedtowardthechargedobjectifthechargesareofopposite
signsandawayfromtheobjectiftheyareofsimilarsign.DEFINITION:Thedirectionofanelectricfieldisdefinedasthedirectionoftheforce
actingonapositivecharge.(Figs.I.3435)
Alongthelinesofforceconnectingthetwocharges,theelectricpotentialwillchangegraduallybetweentheextremevaluesrepresentedbythe
twocharges.DEFINITION:Equipotentiallinesdefinethepointsalongthelinesofforcewithidenticalelectricalpotential.Theseequipotential
surfacesarealwaysorientedperpendiculartothelinesofforce.Thechangesintheelectricpotentialaregradualinspace.
Electronswhichenterafieldbetweentwoparallelplatesinadirectionparalleltotheplatesareaffectedbytheforcedirectedperpendicularto
theplates(FigI.36).Theelectronswillbeattractedtowardthepositiveplate.Thepathchangesinaseriesofgradualstepsattheequipotential
surfaces.
FigureI.37showshowtheelectronpathis"refracted"attheequipotentialsurface.TheresultisfundamentallythesameasthatgivenbySnell's
Lawofrefractioninlightoptics.Aconsequenceofthisisthatasphericallycurvedequipotentialsurfaceexhibitsthepropertiesofalens.
FiguresI.38andI.39showhowbothpositive(converging)andnegative(diverging)electrostaticlensescanbeformed.Thisfeatureof
electrostaticlensesdiffersfromelectromagneticlenseswhichcanonlyactasconverginglenses.
2)Advantages/Disadvantagesofelectronlenses:
Thefactthattherefractiveindexdoesnotchangeabruptlyinelectronlenseshasoneadvantageinthattherearenotroublesomereflectionsat
equipotentialsasatglassinterfaces.Thereisaseriousdisadvantageinthatequipotentialscannotbeshapedandcombinedinarbitraryfashionto
correctforchromaticaberrationandothererrors.
Althoughelectronmicroscopeswhichemployelectrostaticlenseshavebeenmade,mostmicroscopesuseelectromagneticlenses.Amajorreason
isthatelectrostaticlensesaremoresensitivetothequalityofthevacuumandcleanlinessofthecomponentsthanareelectromagneticlenses.
Somelensaberrationsaremoresevereforelectrostaticlensescomparedtoelectromagneticlenses.Electrostaticlensesrequireverypowerful
electrostaticfieldswhichcanleadtoelectricalbreakdownor"arcingover"insidethecolumn,especiallyunderpoorvacuumconditions.Forthis
reason,electrostaticlensescannotbemadewithfocallengthsasshortasmagneticlenses.
b.Electrostaticlens
Abasicunderstandingofelectrostaticlensesisimportantfortwomainreasons:i)theelectrongunuseselectrostaticlensactiontoformthe
primarybeamsource,andii)itisquitecommonforachargetodeveloponthenonconductingcontaminationwhichmayaccumulateonphysical
apertures(suchastheobjectiveaperture)andtransformthemintoweakelectrostaticlenseswhichcandistorttheelectronimage.
3)Propertiesofelectrostaticlenses:
a)Anyaxiallysymmetricalelectrostaticfieldhasthepropertiesofalensforraysconfinedtotheparaxialregion.Alltheideallensformulasapply
toelectrostaticlenses.
b)Forelectronlenses,replaceÃ(f)forrefractiveindexinthelensequations(f=valueofthepotentialontheaxis).Intheimageformingsystem
ofmostTEMs,fisthesameonbothsidesofthelens(SeeSec.I.A.5.c).
c)Ifboundedbyregionswherefisconstant,anelectrostaticlensisalwaysconvergent.
c.Magneticfieldsandmagneticlenses
1)Magneticfield
Anelectriccurrentpassingthroughaconductorgivesrisetoamagneticfield.TheconventionisthatNisthedirectioninwhichthelinesofthe
magneticfieldpoint(Fig.I.40).Themagneticfluxisthetotalnumberoflinesandthefluxdensityisthenumberoflinesperunitareaofasurface.
UsetheRIGHThandruletodeterminethedirectionofthefield(thumbpointstowardcurrentdirectionandfingerscurlindirectionoffield.NOTE:
Byconvention,thedirectionofelectronflowisoppositetothatofcurrentflow.
Fluxdensitydependsonthepropertiesofthematerialsurroundingtheconductor.Ironinducesahigherfluxdensitythanairoravacuum.The
propertyofthematerialwhichaffectsthefluxdensityiscalledthepermeability,m,ofthematerial.Forairandvacuum,m=1.0.For
ferromagneticmaterialsitcanbeaslargeasseveralhundredthousand.
Iftheconductorhastheshapeofacircularloop,thelinesofforceformcirclesaroundtheloop.Thefluxdensityisgreatestatthecenterofthe
loop.Themagnetinthecenteroftheloopisorientedperpendiculartotheplaneoftheloopifthecurrentthroughtheloopissufficientlystrongto
eliminatetheinfluenceoftheearth'sfield.ThesideoftheloopatwhichthelinesofforceleavetheloopistheNorth(N)poleofthemagnet(Figs.
I.41,I.42).
Ifthewireiswoundinseveralturnsaroundacylindricalsurface(solenoid),eachturnwillcontributetotheinducedmagneticfield.Theflux
densityinthecenterofthecoilisgivenby:
Inthecaseofairandnonmagneticmaterials,µ=1.0andB=H.
Thepermeabilityofirondependsonthefieldstrength,H,anddecreasestounityathighfieldstrengthorwhenthefluxdensity,B=H(Fig.I.43).
Thehighpermeabilityofironisduetotheinducedmagneticfieldorientingmicroscopiccrystalregionsactingastinymagnetsintheiron.Allthese
tinymagnetsaddtheirmagneticfieldstotheinducedfield(Fig.I.44).Whenallmicromagnetsarenearlyoriented,theironwillaffecttheflux
densitytoadecreasingamountsincethereorientationofmicromagnetsisnearingcompletion.Thus,thepermeabilityofironathighfieldstrengths
approachesthatofemptyspace.Atthispointtheironreachesmagneticsaturation.
2)Hysteresis
Thestrengthofthelensdependstosomeextentonthepreviousmagnetichistoryof
thelens.Whenthecurrentinalensisreduced,thedecreaseinmagnetizationdoes
notretracethesamepathobtainedwhenthecurrentwasincreased(Fig.I.45).
Inductionofmagnetizationinvolvesaphysicalmovementwithinthemagnetized
material,requiringtheovercomeofacertaindegreeofinertia.Asaresult,
magnetizationtendstolagbehindthemagnetizingforceapplied.Inducedmagnetic
fluxcanonlybereturnedtozerobyapplicationofacurrentintheoppositedirection.
Aconsequenceofhysteresisisthatthelevelofcurrentusedtoenergizeamagnetic
lensDOESNOTpreciselyspecifythelensstrength(i.e.focallength).
NormalizationofTEMlensesisaccomplishedbyreducingthelenscurrenttozero
somepredeterminednumberoftimes.Hysteresismayalsobeminimizedbytakinga
lenstosaturationandthenreturningittotheworkingcurrentwithoutovershooting.
Whenthefieldstrengthisreducedtozero,somemagnetizationstillremainsintheiron
(residualmagnetizationorremanence).Anadvantageofsoftironisthefactthat,
whenusedinanelectromagnet,hysteresisislow.
Introductionofpiecesofironinamagneticfielddrasticallyaffectsthefluxdensity.
Magneticmaterialhasashieldingeffect,theeffectbeinggreaterthegreaterthe
permeability.Permalloy(mmetal)hasamaximumpermeabilityof80,000140,000
comparedtoironusedintransformers(~7000).mmetalpermeabilityislimitedtolower
fieldstrengthsthanthatatwhichironstillretainshighpermeability.Thismetalis
thereforeusefulforshieldingtheTEMfromexternalmagneticfields.
d.Theelectromagneticlens
1)Lensdesigndevelopment(Figs.I.46I.48)
Theefficiencyofthemagneticfieldproducedbyashortsolenoidwasfirstimproved
byencasingtheenergizingcoilinasheathofsoftironwhichhasthepropertyofconcentratingthelinesofforceinamagneticfieldandthus
becomingmagnetizedbyinduction.Inthiswayamuchmorepowerfulaxialmagneticfieldisobtainedforthesameamountofcurrentflowing
throughthesolenoid.Furtherdevelopmentinvolvedencasingtheentirecoilwithsoftironexceptatanarrowannulargapintheinsideofthecoil.
Thisproducesagreaterconcentrationofthemagneticfieldalongashortaxialdistance.Toachieveshorterfocallengthlenses(andobtaingreater
magnifications)asoftironpolepiecewithanopenaxialborewasintroducedatthepositionoftheannulargap.
MagneticlensesusedinTEMsarealwaysconstructedwithanironcircuittoproduceahighfieldstrengthacrossashortgap.Themagneticfields
forTEMlensesareintherangeof10,00020,000gauss.
2)Forcesactingonacurrentinamagneticfield
Theforceonanelectroninamagneticfieldisalwaysatrightanglestothevelocityandthedirectionofthefield(Figs.I.49,I.50,andI.52).The
fieldonlyactsonthevelocitycomponentwhichisdirectedperpendiculartothelinesofforce.Usethelefthandrule(Fig.I.51:firstfingerfor
fielddirection,middlefingerforcurrentdirection,andthumbfordirectionofforce).Rayspassingthroughthelensareturnedthroughanangle
whichdoesNOTdependonthedistanceoftheraysfromtheaxis.Allelectronscontainedinagivenmeridionalplanebeforeenteringthefieldare
containedinarotatingmeridionalplaneastheypassthroughthelens,andthentheyleavethelenscoplanar.
Whenelectronsenterthelenstheyencounterasidewaysforcewhichcausestheelectrontorotate
asitcontinuesthroughthelens(Figs.I.53I.57).Sincetheradialcomponentofthemagneticfield
reversesafterthecenterofthelens,therotationalvelocitysetupinthefirsthalfofthelensis
countered.Theelectronenteredthelenswithoutangularmomentumabouttheaxisandleaves
withoutangularmomentum.Theneteffectisadeflectiontowardtheaxis,whichitmustcrossatthe
focalpointf
2
.Theanglebetweentheobjectvectorandtheimagevectoris180°+q,whereas,for
glasslensesandelectrostaticlenses,theanglebetweenarealobjectandtheimageisexactly180°.
Sincetheradialforceisdirectedtowardtheaxis,thelensisconvergentnomatterwhatthedirection
ofthefield.
3)Propertiesofamagneticlens:
Anyaxiallysymmetricmagneticfieldhasthepropertiesofanideallens.Alltheformulasfortheideallensmaybeapplied.
Magneticlensesarealwaysconvergent.Theconventional,axiallysymmetriclensisalwaysboundedbyregionswhicharefieldfree,the
consequencebeingthatthenetactionofelectronlensesisinevitablyconvergent.Limitedregionsmaybedivergentbutnotthelensasawhole.
Theseriousconsequenceofthisisthatneithersphericalorchromaticaberrationscanbecorrectedasisdoneinlightopticsbytheusedoublets
ofpositiveandnegativelenses.
Intheabsenceofelectrostaticfields,therefractiveindexisthesameinobjectandimagespace,thereforef
1
=f
2
.
Electronstravelingthroughaxiallysymmetricfieldsexperienceaspiraltrajectoryofdiminishingradius.Theimagevectorisatanangle180°+qto
theobjectvector.
Thedeflectionoftheelectrontowardstheaxismeansthatanelectronenteringthelensparalleltoitsaxiswillcrosstheaxisafterhavingpassed
thelens.Thedeflectionwillincreasewiththedistancefromtheaxis.Thus,abeamofelectronsinparallelpathsparalleltotheaxisofthelenswill
befocusedtoanimagepointontheaxiswhichrepresentsthesecond(back)focalpointofthelens(f
2
).Notethatmagneticlensesarehighly
inefficientinthatonlyaminorportionofthetotalfieldstrengthisactuallyeffectiveinfocusingtheelectron.
4)Magneticlensfocallength
Inamagneticelectronlensthefocallengthisdeterminedbythefieldstrengthinthelensgapandbythespeedoftheelectrons(determinedby
theacceleratingvoltage).
Formagneticlenses,focusingisachievedbyvaryingthecurrentwhichpassesthroughtheelectromagnet.Thisinturnchangesthestrengthof
themagneticfieldandtherebyaltersthefocallengthofthelensandisequivalenttoacombinedchangeinboththe"refractiveindex"and
"curvatureofsurface".Forabeamofmoreenergeticelectrons,thelenscurrenthastobeincreasedinordertokeepthefocallengthconstant.
FocallengthandcurrentareNOTlinearlyrelated:strengthincreasesinasigmoidfashion(Fig.I.45)ascurrentincreasesuntilapointisreached
wherethelensissaturatedandnofurtherincreaseinlensstrengthcanbeachieved.
Sincethefocallengthofthelensisdirectlyproportionaltotheacceleratingvoltage,avariationinthevelocityoftheelectronsintheimaging
beamaffectsimagequalitybyeliminatingperfectfocus(chromaticaberration).
5)Magneticlensdesign:(Figs.I.46,I.47).
Condenserlensesusuallyhavearelativelylargeboreandspacingwhichresultsinalongfieldandlongfocallength.
Typicalconstructionoftheobjectivelensproducesastrongfieldofshortaxialextent(i.e.shortfocallengthbetween(1.53mm)necessaryfor
formationofimagesathighmagnification.Thespecimenisplacedwithinthemagneticfieldoftheobjectivelens.Thus,anyfieldintroducedby
contaminantsinthespecimencandistortthefieldofthelens.Notethatthisalsomeansthatpartofthelensfield("prefield")isonthefrontside
oftheobjectandaffectstheelectronbeambeforeitpassesthroughtheobject.
Mostofatypicalmagneticlensliesoutsidethevacuumofthemicroscope.Onlythoseregionsthroughwhichtheelectronbeampassesareinhigh
vacuum.Magneticlensesmustbewatercooledtodissipatethelargeamountsofheatproducedbythecurrentsintheelectromagnetcoils.
DATE NAME EVENT
1897 J.J.Thompson Discoverstheelectron
1924 LouisdeBroglie Identifiesawavelengthtomovingelectrons
l =h/mv
where
l =wavelength
h=Planck'sconstant
m=mass
v=velocity
(Foranelectronat60kVl=0.005nm)
1926 H.Busch Magneticorelectricfieldsactaslensesforelectrons
1929 E.Ruska Ph.Dthesisonmagneticlenses
1931 Knoll&Ruska Firstelectronmicroscopebuilt
1931 Davisson&Calbrick Propertiesofelectrostaticlenses
1934 Driest&Muller SurpassresolutionoftheLM
1938 vonBorries&Ruska FirstpracticalEM(Siemens)10nmresolution
1940 RCA CommercialEMwith2.4nmresolution
1945 1.0nmresolution
Fig.I.1Comparisonoflightandelectronmicroscopes.Ineach
instrument,illuminationfromthesource(lamp,filamentinthe
electrongun)isfocusedbythecondenserlensontothespecimen.
Afirstmagnifiedimageisformedbytheobjectivelens.Thisimage
isfurthermagnifiedbytheprojectorlensontoagroundglass
screen(light)orfluorescentscreen(electrons).(FromAgar,p.8)
Fig.I.2CrosssectionalviewofthePhilipsEM300.(FromAgar,p.40)
Toviewtheanimatedmicroscope,clickhere.
Note:QuickTimePlugInrequired
(Thiscanbedownloadedathttp://apple.com/quicktime/download)
Fig.I.3Sectionthroughacomplex
doublecondenser6lensPhilips
EM200electronmicroscope.(From
Meek,p.99)
Fig.I.4Thestatisticalnatureofdiffraction
patterns.(FromHall,p.13)
"Theprecisenatureof'electronwaves'or'matterwaves'isverydifficulttounderstandordescribeinmaterialterms.Electronwavesarenot
electromagneticradiationofthekindtowhichlight,Xraysandradiowavesbelong.Theyconstituteasortofquantumor'packet'ofradiationwhich
accompanieseachindividualelectron,followingitspathandnotradiatingoutwardsfromit."(Meek,1976,pp.4849).
V l (nm)
v(
•
10
10
cm/sec)
v/c
10,000 0.0123 0.593 0.198
50,000 0.0055 1.326 0.442
100,000 0.0039 1.875 0.625
1,000,000 0.0012 5.930 1.977!
V l (nm)
v(
•
10
10
cm/sec)
v/c
10,000 0.0123 0.593 0.195
50,000 0.0055 1.326 0.414
100,000 0.0039 1.875 0.548
1,000,000 0.0012 5.930 0.941
FigI.5Aperfectpointsourcecannotbe
imagedbyalensasaperfectpointimagedue
tothepresenceoftheapertureAB(which
maybetheedgeofthelens).Diffractionat
thisaperturegivesrisetoaseriesoffringes,
whichsurroundtheimageformedofthepoint
source.Thepatternproducediscalledan'Airy'
disk.(FromMeek1sted.,p.35)
Fig.I.6Wheneverawavefrontstrikesa
barrier,itcanbendaroundthecorner'by
givingrisetoasecondarywavefrontatthe
edge,sinceeachpointonthewavefrontcan
giverisetoanewsourceofwaves.This
phenomenoniscalled'diffraction'.(FromMeek
1sted.,p.22)
Fig.I.7Diffractionpattern(right)formedbyanirregularlyshapedaperture
(left).(FromYoung,p.95)
Fig.I.8(a)
Photographof
theedgeofa
razorblade
illuminatedby
monochromatic
(blue)light
rendered
coherentby
passing
througha
narrowslit.(b)
Microdensitometer
tracingofthe
negativefrom
whichthe
photograph
wasmade.
FourFresnel
fringescanbe
distinguished.
(FromMeek1st
ed.,p.27)
(a)
(b)
(a) (c)
(b)
Fig.I.9(a)Fresnelfringesformed
byelectrons.Thesefringesare
formedoutsidetheedgeofahole
(white)inacarbonfilm(black).(b)
Amicrodensitometertracingofthe
fringesystem;thepatternis
identicalwiththeFresnelfringe
systemformedbyvisiblelight(see
Fig.I.8).(c)Anunderfocusedimage
ofaholeinafilm,showinga
completesystemofabout40
Fresnelfringesinsidethehole.
(FromMeek1sted.,pp.2930)
Fig.I.10Diffractionimagesoftwo
easilyresolvedpoints.(From
Slayter,p.243)
Fig.I.11Imagesoftwo
incoherentlyilluminatedpointsat
thelimitofresolution.(a)individual
intensities;(b)summedintensities.
(FromSlayter,p.244)
Fig.I.12Examplesofwhatoccurswhentwo
wavesofthesamewavelengthandequal
amplitudeadd.Ineachexample,thetwo
separatewavesareshownontheleftand
theirsumorresultantwaveontheright.The
differentexamplesarecharacterizedbyvarying
phasedifferences.Thephaseofawave
(usuallyexpressedasafractionofthe
wavelengthorindegrees)isthepositionofa
crestrelativetosomearbitrarypoint.Although
thephaseofagivenwavevarieswithtimeas
thewavetravels,thedifferenceinphaseofthe
twowavesofthesamewavelengthwiththe
samevelocity,isindependentoftime.Such
wavescaninterferewithoneanother.The
resultantwavehasthesamewavelength,l .
(a)Phasedifferencezero.Thewavestotally
reinforceandaresaidtobe"inphase"orto
showconstructiveinterference.
(b)Phasedifferencel /4.Partialreinforcement,
givingawaveofamplitude1.4(intensity2.0).
(c)Phasedifferencel /2.Thewavesare"outof
phase"andthereistotaldestructive
interferencetogivenoresultantwaveora
wavewithamplitude0(intensity0).(From
GluskerandTrueblood,p.19)
Fig.I.13Photographofan
interferencepatterninwater
wavesformedbythe
superpositionofwavesfromtwo
sourcesoscillatinginphasewith
thesamefrequency.(FromYoung,
p.22)
Fig.I.14Theangularapertureofthe
eyeisrelativelysmall.(FromMeek,
1sted.,p.13)
Fig.I.15Increasingtheangular
apertureoftheeyewithalens.The
lensallowstheobjecttobeheld
closertotheeye,whichisthereby
enabledtogathermoreinformation.
(FromMeek1sted.,p.14)
Fig.I.16Theinteractionofwaves
withanobstacle.Theboatridesthe
longwavelengthoceanwave,but
reflectsthesmallwavelength
surfaceripple.Anobserverwho
wishestodetectthepresenceof
theboatcandosoonlyby
observingwaveswhichhave
wavelengthssmallerthan,or
comparableto,thelengthofthe
boat.(FromSherwood,p.19)
Maximummagnification=
resolvingpoweroftheeye
resolvingpowerofthemicroscope
(a)
Fig.I.17(a)TwoAiry
disksrepresenting
twoimagepoints
shownatincreasing
separationfromleft
toright.Inthe
pictureatthe
extremerightthe
twodiskscanbe
distinguishedas
separatedisks.
(b)Theintensity
distributionatanAiry
disk.R,halfwidthof
thecentralmaximum
representedbya
bellshapedcurve.
(c)TheRayleigh
criteriaforresolution.
(FromSjostrand,
p.115)
i=r
Fig.I.18Reflection.(FromSlayter,
p.4)
Fig.I.19Refraction.(FromSlayter,
p.6)
Fig.I.20Principalraydiagramsshowing
imageformationbyaconvexlens.
(a)Whentheobjectdistanceisgreater
thanthefocallength,areal,inverted
imageisformed.
(b)Whentheobjectdistanceisless
thanthefocallength,avirtual,erect
imageisformed;itspositionis
obtainedbyprojectingtheprincipal
raysbackward.Theraysappearto
comefrompointQ.(FromYoung,
p.127)
Fig.I.21Definitionof
principalfocus,F,inimage
spaceofalens.(From
Sjostrand,p.20)
Fig.I.22Focusingeffectoflenson
raysoriginatingfrompointson
principalaxislocatedatdifferent
distancesfromthelens.(From
Sjostrand,p.21)
Fig.I.23Definitionofprincipal
focusinobjectspaceF1ofa
lens.(FromSjostrand,p.21)
Fig.I.24VirtualimageQof
objectpointlocatedbetween
principalfocusinobjectspace
andthelens.(FromSjostrand,
p.21)
Fig.I.25Constructionoftheimage
ofanobjectbymeansofray
tracing.(FromSjostrand,p.22)
Fig.I.26Magnifyingeffectof
apositivelens.(From
Sjostrand,p.22)
Fig.I.27Virtualmagnified
imageofobjectlocated
betweenprincipalfocusin
objectspaceandthelens.
(FromSjostrand,p.22)
Fig.I.28Amagnifyingglassformsan
enlarged,erectvirtualimage.The
angularsizeofthisimageis
approximately4"/15"or4/15.The
angularsizeoftheobjectatthe
closestdistanceforcomfortable
viewingis1"/10"or1/10.The
magnificationinthissituationis(4/15)/
(1/10),or22/3.(FromYoung,p.130)
Fig.I.29Theangularapertureofa
lens.Theangle2a isthe
acceptanceangleofthelens,and
thelargeritcanbemade,themore
informationcanthelenstransmit.A
largelensofhighaperturecan
thereforetellusmoreaboutan
objectthanasmalllensoflow
power.(FromMeek1sted.,p.12)
Fig.I.30Raydiagramforhighmagnification
modeofoperation.Notethateachlens
formsarealimage,withimageinversion.
I0istheimageformedbytheobjective
lensO,I1isformedbythefirstprojector
lensP1andI2bythesecondprojectorP2,
onthescreen.(FromAgar,p.30)
Fig.I.31Left:raydiagramofthe3realimagemediumandhighmagnificationimagingsystemofa3lens
microscope.Center:2realimageverylowor'scan'magnificationrangeofa3lensmicroscope.Right:2real
imagelowmagnificationsystemofa3lensmicroscope.(FromMeek1sted.,pp.118,120121)
Fig.I.32Raydiagramforacompleteelectron
microscope.FilamentF,condenser1lensC1,
condenser2lensC2,condenserapertureCA,
specimenS,objectivelensO,objectiveaperture
OA(inbackfocalplane).1stintermediateimage
andselectorapertureSA.IntermediatelensP1,
secondintermediateimageI2,projectorlensP2
andfinalimageonthefluorescentscreenFC.
(FromAgar,p.35)
a)f=2.0
x
o
=5.0
e)f=4.0
x
o
=3.0
b)f=10.5
x
o
=21.0
f)f=13.3
x
o
=13.3
c)f=3.5
x
o
=3.0
g)f=3.142
x
o
=0.0
d)f=5.0
x
o
=2.5
a)D=8.0
L1:f=2.0
x
o
=4.0
L2:f=3.0
b)D=8.0
L1:f=2.0
x
o
=6.0
L2:f=3.0
c)D=4.0
L1:f=2.0
x
o
=3.0
L2:f=2.0
FigI.33Accelerationofelectronin
electricfield.(FromSjostrand,p.26)
Fig.I.34Linesofforceatapositively
chargedsphericalbody.(FromSjostrand,
p.32)
Fig.I.35Linesofforceandequipotential
surfaces(stippledlines)associatedwith
twoequalchargesofoppositesign.
(FromSjostrand,p.32)
Fig.I.36Equipotentialsurfacesattwoparallel
platesofoppositechargeswiththepathofan
electronindicatedwithinthehomogeneous
partofthefield.(FromSjostrand,p.33)
Fig.I.37Refractionofelectronatan
equipotentialsurface.(FromSjostrand,p.33)
Fig.I.38.Negativelensactionof
electrostaticfieldatanaperturewhen
V2V1>V3V2.(FromSjostrand,
p.34)
Fig.I.39.Positivelensactionatan
aperturewhenV2V1<V3V2.
(FromSjostrand,p.34)
Fig.I.40Magneticfieldinducedbycurrent
passingthroughaconductor.(From
Sjostrand,p.35)
Fig.I.41Magneticfieldinducedbycurrent
passingthroughasolenoid.(From
Sjostrand,p.37)
Fig.I.42Solenoidwithironcore.(From
Sjostrand,p.40)
Fig.I.43a.Dependenceofpermeabilityonfluxdensity,B.
b.RelationshipbetweenfluxdensityBandfieldstrength.
(FromSjostrand,p.38).
Fig.I.44Magnetization.(FromSlayter,
p.361)
Fig.I.45Curves
showinghowthe
magnetizationof
softiron(lens
strength)is
relatedtothe
magnetizing
force(lens
current).An
unmagnetized
lensstartsfrom
thepointOand
followsthepath
OAaslens
current
increases.Atthe
pointA,further
increaseinlens
currentproduces
nofurther
increaseinlens
strength;thelensissaidtobe'saturated'.Whenlenscurrent
isreduced,thepathOAisnotretraced;adifferentpathABis
followed.Thisdisplacementiscalled'hysteresis'.Atzero
current(pointB),someresiduallensstrengthremains;thisis
called'remanence'.Tobringthelensbacktozerostrength,a
reversecurrentOCmustbeapplied.Lensstrengththen
increaseswithincreasingreversecurrent,followingthepath
CD.Thepolarityofthelenschanges,butthisdoesnotaffect
itsfocusingpower;onlythespiralelectronpathisreversed.
Becauseofhysteresis,itisnotpossibletocalibratealens
currentmeteraccuratelyintermsoflensstrengthor
magnification.
Fig.I.46Evolutionofmagneticelectron
lenses.(A)Shortsolenoidusedasa
magneticlens.(B)Softironcasing
enclosingoutersurfaceofthesolenoid,
thusconcentratingthefield.(C)Soft
ironencasingthesolenoidexceptata
narrowannulargaptherebyreducing
themagneticfieldtoaveryshortregion
alongthelensaxis.(D)Modern
objectivelensconsistingofasoftiron
encasedsolenoidandsoftironpole
piecessoastohaveanenormously
concentratedfieldatthelevelofthe
annulargap.(FromWischnizter2nded.,
p.33)
Fig.I.47(a)Amagneticlensconsisting
ofatightlywoundcoilandasoftiron
shroudsurroundingthecoilexceptfor
asmallgap.Thefieldisconcentratedin
thatgap.(b)Shortfocallength
electromagneticlenswithpolepieces.
(FromSjostrand,p.50)
Fig.I.48Fieldstrengthdistribution
curves.ThecurvesADcorrespondto
therespectivelensesillustratedinFig.
I.46.Eachrepresentsthefieldstrength
alongthelongaxisofthelens.The
changesintheshapeofthecurves
representtheshorteningor
concentrationofthefieldovera
shorteraxialdistance.Hz=
longitudinalmagneticfield.Z=
distancealongtheaxisofsymmetry.
(FromWischnizter2nded.,p.33)
Fig.I.49TheforceFactingon
astraightconductorina
homogeneousmagneticfield
offluxdensityBwhencurrent
Iispassedthroughthe
conductor.(FromSjostrand,
p.43)
Fig.I.50Pathofanelectronina
magneticfield.(A)Inalarge,uniform
magneticfield.(B)Inasmall,uniform
magneticfield.(FromWischnitzer2nd
ed.,p.25)
Fig.I.51Lefthandthumbrule.
(FromSjostrand,p.43)
Fig.I.52Thompson'sexperiment.A
streamofelectronsoriginatingfroma
sourceandpassing,invacuo,through
amagneticfieldproducedbyapairof
magnetswillbedeflected.The
directionofdeflectiondemonstrates
thatelectronsarenegativelycharged
particlesofmatter.(FromWischnitzer
2nded.,p.25)
Fig.I.53Actionofasolenoidonan
electronbeam.Anelectriccurrent
passingthroughthecoilproducesan
axialmagneticfield.Thisisthe
refractingmediumfortheelectrons.An
electronstartingatapointontheaxisA
andatanangletoitfollowsaspiral
path,returningtotheaxisatthepoint
B.Theactionisbasicallysimilartothat
oftheconverginglightlensshownin
Fig.I.20.(FromMeek1sted.,p.8)
Fig.I.54Actionofthemagnetic
lens.(a)Inperspective.(b)
Electrontrajectoryin
projection,alongdirectionof
propagation.(c)Electron
trajectoryinprojection,side
view.(FromSlayter,p.358)
Fig.I.55Componentsofthe
vectorHneartheaxisoffields
withaxialsymmetry.His
representedbytwo
components,Hz,the
componentinthez(axial)
direction,andHr,the
compnentinther(radial)
direction.(FromHall,p.85)
Fig.I.56Theycomponentof
themagneticfieldina
magneticlensisoriented
perpendiculartothedirection
ofanelectronenteringthe
lensalongapathparallelto
thelensaxis.Thisy
componentwillaffectthe
electron,deflectingitinthex
directionasindicatedbythe
arrowmarkedvx.(From
Sjostrand,p.48)
Fig.I.57Thezcomponentofthemagneticfield
andthexvelocitycomponentoftheelectron
inamagneticlensinteract,deflectingthe
electronintheydirectiontowardthelens
axis.(FromSjostrand,p.49)
CuuDuongThanCong.com https://fb.com/tailieudientucntt
cuu duong than cong . com
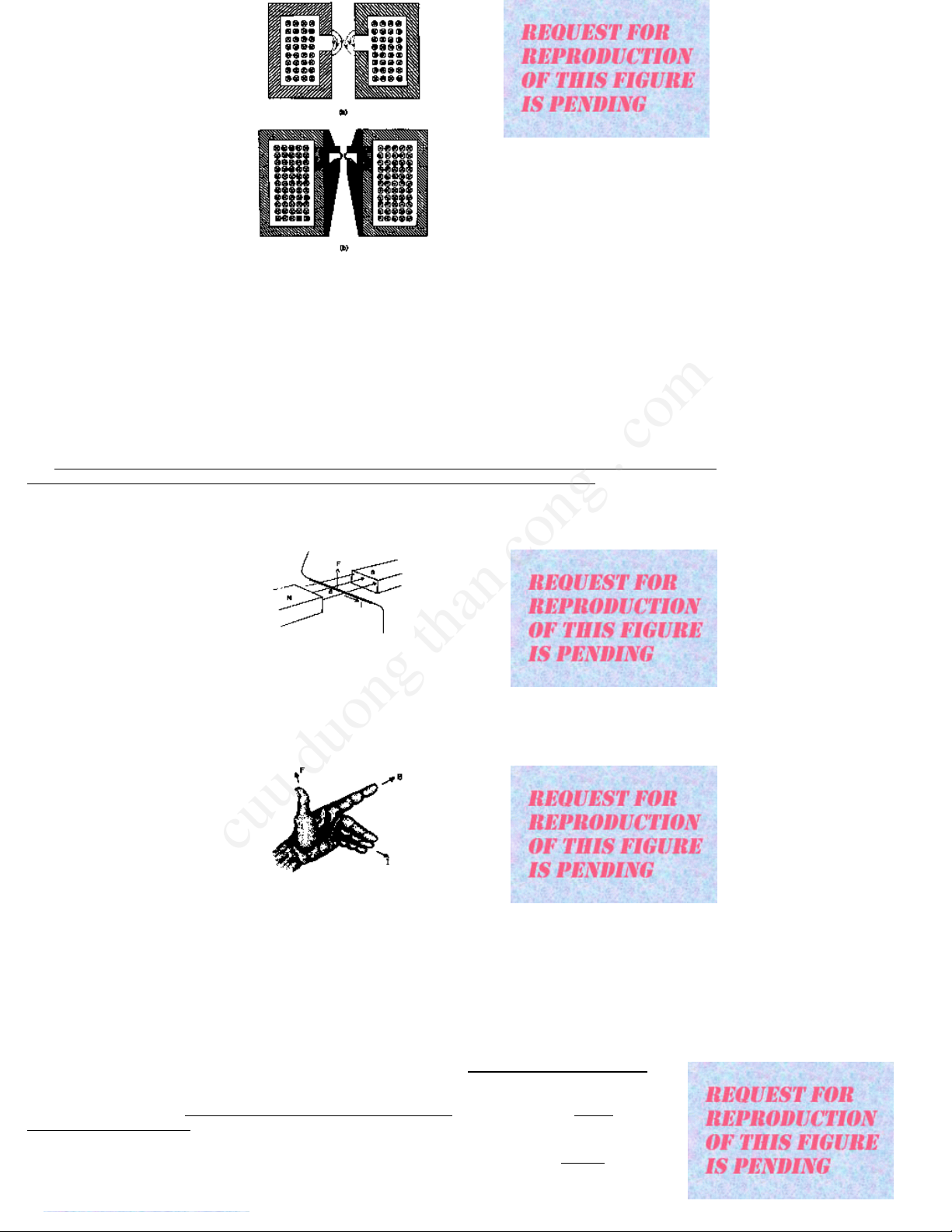
I.THEMICROSCOPE
I.A.PRINCIPLESOFTHETRANSMISSIONELECTRONMICROSCOPE(TEM)
I.A.1.OriginoftheTransmissionElectronMicroscope
I.A.2.ComparisonofLight(LM)andElectronMicroscopes(Fig.I.1)
a.Similarities(Arrangementandfunctionofcomponentsaresimilar)
1)Illuminationsystem:producesrequiredradiationanddirectsitontothespecimen.Consistsofasource,whichemitstheradiation,anda
condenserlens,whichfocusestheilluminatingbeam(allowingvariationsofintensitytobemade)onthespecimen.
2)Specimenstage:situatedbetweentheilluminationandimagingsystems.
3)Imagingsystem:Lenseswhichtogetherproducethefinalmagnifiedimageofthespecimen.Consistsofi)anobjectivelenswhichfocusesthe
beamafteritpassesthroughthespecimenandformsanintermediateimageofthespecimenandii)theprojectorlens(es)whichmagnifiesa
portionoftheintermediateimagetoformthefinalimage.
4)Imagerecordingsystem:Convertstheradiationintoapermanentimage(typicallyonaphotographicemulsion)thatcanbeviewed.
b.Differences
1)Opticallensesaregenerallymadeofglasswithfixedfocallengthswhereasmagneticlensesareconstructedwithferromagneticmaterialsand
windingsofcopperwireproducingafocallengthwhichcanbechangedbyvaryingthecurrentthroughthecoil.
2)MagnificationintheLMisgenerallychangedbyswitchingbetweendifferentpowerobjectivelensesmountedonarotatingturretabovethe
specimen.Itcanalsobechangedifoculars(eyepieces)ofdifferentpowerareused.IntheTEMthemagnification(focallength)oftheobjective
remainsfixedwhilethefocallengthoftheprojectorlensischangedtovarymagnification.
3)TheLMhasasmalldepthoffield,thusdifferentfocallevelscanbeseeninthespecimen.Thelarge(relative)depthoffieldintheTEMmeans
thattheentire(thin)specimenisinfocussimultaneously.
4)Mechanismsofimageformationvary(phaseandamplitudecontrast).
5)TEMsaregenerallyconstructedwiththeradiationsourceatthetopoftheinstrument:thesourceisgenerallysituatedatthebottomofLMs.
6)TEMisoperatedathighvacuum(sincethemeanfreepathofelectronsinairisverysmall)somostspecimens(biological)mustbedehydrated
(i.e.dead!!).
7)TEMspecimens(biological)arerapidlydamagedbytheelectronbeam.
8)TEMscanachievehighermagnificationandbetterresolutionthanLMs.
9)Pricetag!!!(100xmorethanLM)
I.A.3.Photons/Electrons
a.Dualconceptofwaveandparticle(Fig.I.4)
Lighthaspropertiesbothofaparticleandawave.Thisdualnatureisrequiredtosatisfactorilyexplaintheresultsofvariousphysicalexperiments.
Thediffractionoflight(bendingaroundcorners)illustratesthewavenature.TheWAVETHEORYisbasedonthestatisticalnatureofeventsand
haslittlemeaningwithrespecttothebehaviorofsingleparticles.ThewavetheorywasdevelopedandexpoundedbyHuygens(16291695)and
Hooke(16381703).TheCORPUSCULARTHEORYwasproposedbyNewton(16421727)andbecamethemoreacceptedtheoryevenafter
demonstrationofdiffractionbyYoung(17731829)andinterferencebyFresnel(17881827).Atabout1850,thewavetheorycamebackinto
favoruntilabout1900whenmoreevidenceforthecorpusculartheorywasdiscovered.
QUANTUMTHEORY(PlanckandEinstein)providesthebasisforexplainingthephenomenaofINTERFERENCE,DIFFRACTIONandthe
PHOTOELECTRICeffect(lightfallingoncertainmetalscausethemtoemitelectrons)andthusformsacommonbasisforexplainingthenatureof
actionoflight.Thetransferofenergybetweenlightandmatteroccursonlyindiscretequantitiesproportionaltothefrequencyofthe
lightwave.
E=hJ
where
E=energyofphoton(joules)
h=Planck'sconstant(6.624
•
10
34
joulesec)
J=frequency(cycles/sec)
b.Electronvelocityandwavelength
Therelationbetweenthewavelength(l )ofaparticleofmass,m,movingatavelocity,v,isgivenbytheDeBrogliewaveequation:
(1)
Anelectronofchargee(1.6
•
10
19
coulomb),andmassm(9.11
•
10
28
gm),whenpassingthroughapotentialdifferenceofVvolts(expressedin
joules/coulomb),hasakineticenergy:
(2)
Solvingforvelocity:
(3)
substitutingintotheDeBroglieequation(1):
(4)
Since1joule=10
7
dyne
•
cm=10
7
cm
2
•
gm/sec
2
(5)
Thus,forexample,ifV=60,000volts,l =0.005nm.
Fromequation(3)theelectronvelocitycanbecalculatedifVisknown:
(6)
Thefollowingtableillustratesthat,athighvoltage,electronvelocityiscomparabletothespeedoflightinavacuum(c=3
•
10
10
cm/sec).
Theequationbreaksdownwhenthevelocityoftheelectronapproachesthespeedoflightbecausearelativisticcorrectionmustbemadeforthe
valueofthemasswhere:
(7)
Therelationbetweenl andVismorecorrectlygivenby:(seeHall(1966)pp.3334)
(8)
Thefollowingtableisobtainedwhenrelativityeffectsareincluded:
c.Interference/diffraction/coherence
Anideallenssystemobtainsanexactimageoftheobject(eachpointfaithfullyreproduced).Thephenomenaofdiffractionmakesthis
unattainable(Figs.I.5,I.6).
Diffractionphenomenainvolvesthebendingofthepathofradiationpassingclosetoanobstacle(Fig.I.6).Thisresultsinaspreadingofthe
radiationintotheregionbehindtheobstructionthatthewavespassed.Thediffractionatedgescontributestothecontrastatwhichanedgecan
beobserved.Diffractionalsolimitstheresolvingpowerofthemicroscopesincetheimagepointproducedbyalensisadiffractionimageofthe
openingofthelensortheaperturerestrictingtheeffectiveopeningofthelens(Fig.I.5).
Ifthelightsourceandtheplaneatwhichthediffractionpatternisobservedareatfinitedistancesfromtheedge,thephenomenoniscalled
Fresneldiffraction.Thepatternisdescribedasduetointerferencebetweenthenondiffractedlightandawaveoflightdiffractedattheedge.
Theresultingsuperpositiongivesrisetoaseriesofdiffractionfringesorientedparalleltotheedgeandrepresentingperiodicallyvaryingbrightness,
maximaandminima.(Figs.I.7,1.8,I.9).
Coherence:Aprerequisiteforinterferenceisasuperpositionofwavesystemswhosephasedifferenceremainsconstantintime.Twobeams
arecoherentif,whencombined,theyproduceaninterferencepattern.Thebeamsareincoherentwhentheyareincapableofproducingan
interferencepattern.Twobeamsoflightfromselfluminoussourcesareincoherent.Iflightfromthetwosourcesfallsonascreen,theresultant
intensityissimplythesumofthetwointensitieswhichwouldoccurfromeachsourceseparately(Figs.I.10,I.11).Inpracticeanemittingsource
hasfiniteextentandeachpointofthesourcecanbeconsideredtogeneratelight.EachsourcegivesrisetoasystemofFresnelfringesatthe
edge.Thesuperpositionofthesefringesystemsisfairlygoodforthefirstmaximaandminimabutfartherawayfromtheedgeshadowtheoverlap
ofthefringepatternsbecomessufficientlyrandomtomakethefringesdisappear.Thenatureofwaves,phase,amplitude,andinterferenceare
illustratedinFigs.I.12andI.13.
d.Resolution
1)Definitions:
RESOLUTION:abilitytodistinguishcloselyspacedpointsasseparatepoints.
RESOLUTIONLIMIT:smallestseparationofpointswhichcanberecognizedasdistinct.
RESOLVINGPOWER:resolutionachievedbyaparticularinstrumentunderoptimumviewingconditions.
2)Distinctionbetweenresolutionandresolvingpower:
Notethedistinctionbetweenresolutionandresolvingpower.Resolvingpowerisapropertyoftheinstrumentandisaquantitythatmaybe
estimatedontheoreticalgrounds.Resolutionisequaltoorpoorerthantheresolvingpowerandisthequantityobservedunderanygivenset
ofexperimentalconditions.IntheTEM,especiallywithbiologicalsamples,theresolutionachievedmaybeconsiderablyinferiortothetheoretical
resolvingpoweroftheinstrument.
Microscopyisthescienceofseeingtheverysmall.Underidealconditions,theeyeresolvesabout1minuteofarc(=1/60degree=2.9x10
4
radian;recallthereare2p radiansin360°)andsinceitcanfocusdowntoabout250mm,thesmallestobjectwecanresolveisabout0.07mm
(70mm)(Fig.I.14).Thislimitisrelatedtothesizeofthereceptorsintheretinaoftheeye.Thefunctionofamicroscopeistomagnifytheimage
fallingontheretina(Fig.I.15).Theadvantageoflightandelectronmicroscopesisthattheyeffectivelygettheobjectclosertotheeyesoa
magnifiedimageisobtainedandmoredetailcanbediscerned.
TENNISBALLANALOGY:Eyecanresolve3cmat100meters,thusatennisballisclearlyvisible.Butifthetennisballisheldupagainstawhite
background,thevisibilitydecreases(becauseofthedecreaseincontrast).
3)Abbecriteriaofresolution:
Thefundamentalnatureoflightposeslimitsonthedetailthatcanberesolved(Fig.I.16).Abbe(1893)showedthatthesmallestresolvable
distanceisabout1/2thewavelengthoflightused.Thus,1/2thewavelengthoftheradiationusedistheultimateresolvingpowerofany
instrument.Thislimitstheusablemagnificationofopticalmicroscopesto<1000X.Atfirstitwasthoughtthatxraymicroscopeswouldbeuseful
buttherefractiveindexofsubstancesforxraysisnearly=1,thusrefractinglensescannotbemadeforxrays,andconsequently,xrayscannot
beeasilyfocusedtoformimages.
4)Magnificationlimits:
Themaximummagnificationofaninstrumentislimitedaccordingtothefollowingrelationship:
Thus,fortheLM,witharesolvingpowerofapproximately0.25µm,themaximum(useful)magnificationisabout250µm/0.25µm=1000X.Thevalue
usedfortheresolvingpoweroftheeyeinthisexample(250µm)representsamorerealisticviewingcondition.Anymagnificationabovethevalue
givenbytheaboveformularepresentsemptymagnification,sincesuchmagnificationleadstonomoreusefulinformationbutratheramagnified
blur.
AccordingtotheAbbecriteria,at60,000volts,theTEMshouldhavearesolvingpowerofabout0.0025nm.Thisshouldallowamaximumuseful
magnificationofabout100milliontimes!!!Inpractice,themaximumusefulmagnificationoftheTEMoperatedat60kVislimitedtomuchlessthan
1,000,000X.Thus,althoughtheLMnearlyobeystheAbbecriteria,theTEMfallsshortbyaconsiderableamount.Themainlimitingfactorinthe
TEM,withrespecttoachievingthetheoreticalresolvingpoweroftheinstrument,concernsthenatureoftheimaginglensesandtheprocessof
imageformation.
5)Rayleighcriteria(practicalbutarbitrary):(Fig.I.17).
Itistheabilityofmicroscopestomakeobjectpointswhichareclosetogetherappearintheimageasseparatepoints.Anideallenstakeseach
objectpointandrepresentsitexactlyasapointintheimage.Areallenstakeseachobjectpointandspreadsitoutintoacirculardisk(Airy
disk)intheimageplanewhosediameterdependsontheangularapertureofthelens.
Theshortestdistancebetween2disksatwhichthetwodisksappearpartiallyseparatedcorrespondstoabout1/2thewidthofthedisks.The
distance,d,inobjectspaceisgivenby:
d=0.61l /n
•
sina
where
l =wavelenghtoftheradiation
n=refractiveindexofthemedia
a=semiangularapertureofthelens
NOTE:n
•
sina=thenumericalaperture(N.A.)ofthelens.
Thus,tomaximizeresolvingpower,l mustbedecreased,nincreased,oraincreased.Recallthatweareconcernedatthemomentwithan
aberrationfreeopticalsystem.Thevaluefortheconstant(0.61)iscontroversialbecauseitdependsonthecoherenceoftheradiationanda
criteriaofvisibility.
FortheLM,usingoilimmersionoptics(n=1.5),sina=0.87,andvioletlight(l =400nm),d=0.2µm.Theonlywaytoimprovetheresolutionisto
uselightofshorterwavelengthsinceN.A.cannotbeincreasedbeyond~1.5.FortheTEM,n=1(vacuum),sina=10
2
andl =0.005nmfor60kV
electrons,thusd=0.3nm.
I.A.4.Optics(LensTheory)
a.Basiclawsofclassicalgeometricaloptics
1)Rectilinearpropagationoflightwhenn(refractiveindex)isconstant.
2)Lawofreflection:
3)Lawofrefraction(Snell'sLaw):
4)Independenceofrays.Theassumptionismadethatlightraystravelindependentlythroughspace.
Theselawsholdforelectrons,except#4,ifthecurrentdensityistoohighwhennegativechargedelectronscaninterfere.
b.Classicalvs.electronoptics
1)Classicaloptics:Therefractiveindexchangesabruptlyatasurfaceandisconstantbetweenthesurfaces.Therefractionoflightatsurfaces
separatingmediaofdifferentrefractiveindicesmakesitpossibletoconstructimaginglenses.Glasssurfacescanbeshaped.
2)Electronoptics:Here,changesintherefractiveindexaregradualsoraysarecontinuouscurvesratherthanbrokenstraightlines.Refraction
ofelectronsmustbeaccomplishedbyfieldsinspacearoundchargedelectrodesorsolenoids,andthesefieldscanassumeonlycertaindistributions
consistentwithfieldtheory.
c.Geometricalandphysicaloptics
Thefundamentalprinciplesofopticsgovernthedesignandoperationofboththelightandelectronmicroscopes.Thebasicopticalprinciples
involvingtheuseofrefractileelementsorlensesinordertoformmagnifiedimagesareidenticalinboththeLMandTEM.TheTEMdiffersfromthe
LMonlyintheradiationitusesandinthewayinwhichtheradiationisbentorrefracted.
Geometricalopticsdealswiththestudyofthepathsfollowedby'rays'oflightorelectronsthroughlensesandapertures,andthegeometrical
constructionsusedtofindtherelativepositionsandsizesofobjectsandtheirimages.Arayoflightorelectronsisdefinedasaninfinitelythin
pencilorbeam.Physicalopticsshowsthatthisanabstractionandcannotphysicallyexistbecauseof'diffraction'whichdealswiththewave
natureoflightandelectrons.Allresultsobtainedingeometricalopticscanbederivedfromtheprinciplesofphysicaloptics,alongwithother
phenomenasuchasinterferenceanddiffractionwhicharenotexplicableinsimplegeometricalterms.
d.Idealversesreallenses:
Lensesareusedtobendraysoflightorelectronssotheyaredeflectedinapredictablewayfromtheiroriginalpaths.Thepropertiesofanideal
lens,possessinganaxisofrotationalsymmetryare:
1)Eachrayofthebundleofrayswhichpassesfromanobjectpointwillberefractedbytheideallenstomeetinoneimagepoint.
2)Raysoriginatingfrompointswhichlieonaplaneperpendiculartotheaxis,mustbeimagedinaplanewhichisalsoperpendiculartotheaxis.
3)Theimageappearsliketheobjectirrespectiveofthemagnification,sotherelativelineardimensionsoftheobjectarepreservedintheimage.
Inpractice,theimagingbyanyreallensdoesnotcorrespondtothatoftheideallensowingtothefactthatanobjectpointisrepresentedbya
diffractionimage(Airydisc)ofthelensopeningortheapertureusedforrestrictingtheeffectiveopeningofthelens.Thisisaresultofthewave
likepropertiesoflight.Lensaberrationsalsocontributetomoreorlesspronounceddeviationsfromthepropertiesoftheideallens.
Thesinglerefractingsurfaceofsphericalcurvatureisthefundamentalunitoffocusingactionbyglasslenses.Sphericalrefractingsurfacesactas
lensesforparaxialrayswhicharethoseraysthatpassclosetotheprincipalaxisofthelens.RayswithlargeangleswillNOTobeyideallens
action.
Afundamentaldifferencebetweenlightandmagneticlensesisthattheelectronbeamdoesnotchangeinforwardvelocityasitpassesthrough
themagneticfield(lightraysslowdownwhenpassingintoamediumofhigherrefractiveindex).Refractioniscontinuouswithelectronswhenthey
areinthemagneticfield:lightisrefractedonlyattheinterfacebetweenmediaofdifferingrefractiveindex.Theelectronsalsofollowspiral
trajectoriesthroughthemagneticfield(seealsoSec.I.A.5.c(Magneticfieldsandmagneticlenses)
e.Raydiagrams:(Figs.I.20I.28)
Themethodofconstructionofraydiagramsisbasedonthreesimpleprinciples:
1)Allraysenteringthelensparalleltotheaxisarebroughttoacommonpointontheaxis,thefocalpoint.
2)Allrayspassingthroughthegeometricalcenterofthelensareundeviatedandpassstraighton,nomatterfromwhichdirectiontheycome.
3)Principleofreversibility:ifthedirectionofarayisreversedinanysystemtherayexactlyretracesitspaththroughthesystem.Thisapplies
onlytothelocationoflightpathsandnottotheintensityofthelight.
Theaboveprinciplesarebasedontheassumptionsthatwearedealingwithathinlensandconcernedwiththepathsofparaxialrays.The
standardconventionistodrawdiagramswithraysthattravelfromlefttoright.Theobjectistotheleft(infront)ofthelensandtheimageisto
theright(behind)ofthelens.
f.Definitions:
Realimage:oneatwhichlightraysphysicallyreunite,sothataphotographicplateplacedatthepositionofarealimageisexposed.
VirtualImage:onefromwhichlightraysappeartodiverge;raysarenotinfactconcentratedatthepositionofavirtualimage,sothata
photographicplateplacedatthepositionoftheimageisnotexposed(byfocusedrays).Placinganopticalsystemsuchastheeyebehindthe
lens,willenablethedivergentraystobefocusedtoformarealimage.TheintermediatelensofanTEMissometimesusedthiswayinorderto
reducethefinalsizeoftherealimageformedbytheprojectorlens(es).
Converging(positive)lens:bendsraystowardtheaxis.Ithasapositivefocallength.Formsarealinvertedimageofanobjectplacedtothe
leftofthefirstfocalpointandanerectvirtualimageofanobjectplacedbetweenthefirstfocalpointandthelens.
Diverging(negative)lens:bendsthelightraysawayfromtheaxis.Ithasanegativefocallength.Anobjectplacedanywheretotheleftofa
diverginglensresultsinanerectvirtualimage.Itisnotpossibletoconstructanegativemagneticlensalthoughnegativeelectrostaticlensescan
bemade.
g.Lensformula(thinlensequation):
where
f=focallengthofthethinlens(sameradiusofcurvatureforboth
sphericalsurfaces)
o=distanceofobjectfromlens(positivetotheleft)
i=distanceofimagefromthelens(positivetotheright)
NOTE:Foravirtualimage,ihasanegativevalue.
h.Magnification:
Foraconverginglens,iftheobjectismorethantwicethefocallengthfromthelens,thentheimageformedisreal,inverted,andsmallerinsize
thantheobject(M<1).Whentheobjectisatadistance=2f,theimageandobjectarethesamesize(M=1);whenitisbetweenfand2f,
theimageislargerthantheobject(M>1),andwhenitis<f,theimageisvirtual,erect,andlargerthantheobject(M>1).
i.Angularapertureofthelens(2a)(Fig.I.29)
Theaperturedeterminesthetotalamountofradiationarrivingfromtheobjectwhichcanbefocusedto
formanimage.Theaperturethuscontrolstheabilityofthelenstogatherinformationabouttheobject.
Thisdependsontheangleoftheconeofraysitisabletoacceptfromtheobject.Bringinganobject
closertotheeyeincreasestheangularaperture,butthereisalimittotheclosenessthattheobjectcan
bebroughttotheeye(~25cmcorrespondingtoanangleofabout0.9°fora4mmexitpupildiameterof
theeyelens;atypicalLMwithanoilimmersionobjectivelenshas2aof~175°).
j.Simplevs.compoundmicroscope(Figs.I.30I.32)
Inprinciple,arealimageofanydesiredmagnificationcanbeobtainedfromasinglepositivelens,butin
practicethisiscumbersomebecauseofthelonglensimagedistance.Oneormorelensescanbeusedto
magnifytheimageinstages(totalmagnificationequalingtheproductofthemagnificationsofeachlens).
Theimageformedbyonelensconstitutestheobjectforthesubsequentlens,whetherornotareal
intermediateimageisformed.
Comparisonofoneversestwostagemagnification:
Thefollowingdescriptionillustrateshowdifferentpathlengthsarerequiredtoachieveamagnificationof10,000Xusingeitheroneortwolenses
withf=2.0cm.
OneStageSystem:
TwoStageSystem:
Assumebothlenseshavef=2.0cmandarearrangedsoeachgives100Xmagnification.
Thus,M=100=x
i
/x
o
foreachstage.
FirstStage:
x
o
=2.02cm
x
i
=202.00cm
Therealimageformedinthefirststagebecomestheobjectforthesecondlens.
SecondStage:x
o
,x
i
sameasinthefirststage.
Totallengthofsystem
=lengthoffirststage+lengthofsecondstage
=(x
o
+x
i
)+(x
o
+x
i
)
=2(x
o
+x
i
)
=2(2.02+202.00)=408.04cm(4.08meters)
k.Problemset
Thefollowingproblemsareforyourownedificationtotesthowwellyouunderstandthebasicsoflensoptics.
1.Foreachsituationbelow,drawanaccurate(usegraphpaper)raydiagramshowingthepathof(atleasttwo)raysfromtheobjecttoimage.
Indicatewhethertheimageisrealorvirtualandspecifythedistanceoftheimagefromthelensandthemagnificationoftheimagewithrespect
totheobject.Ineachexample,thelensisconverging,withidenticalfrontandbackfocalpoints.Distancesareinarbitraryunits.Letf=lens
focallength,x
o
=distanceofobjectinfrontofthelens,andx
i
=distanceofimagebehindthelens.Theobjectmaybeanysize.
2.Inthefollowingexamples,therearetwoconverginglensesinsuccession.Drawraydiagramsshowingtheformationofboththeintermediate
andfinalimagesandgiveappropriateinformationaboutthenature(real/virtual),positions,andsizesoftheintermediateandfinalimages.What
isthemagnificationateachstageofimageformationandwhatisthemagnificationofthefinalimage?Thedistancefromthecenteroflens1(L1)
tothecenteroflens2(L2)equalsD.
I.A.5.ElectronOptics/ElectronLenses
a.Electronemission
Innershellelectronsinmetalatomsshieldtheelectricfieldofthenucleusthroughtherepulsiveforcestheyexertontheoutershell(valence)
electrons.Thustheattractionbetweenthevalenceelectronsandthenucleusisreduced.Metalatomsarecharacterizedashavingtwoloosely
boundvalenceelectronswhichmigratefreely(thisiswhymetalsaregoodelectricalconductors)andcanescapefromthemetalcompletelyif
sufficientadditionalenergyisimpartedtothem.Asthetemperatureofametalisincreased,thekineticenergyoftheelectronsincreasesbecause
ofincreasedthermalvibrationsofthemetalions,whichcollidemorefrequentlywiththeelectrons.Thermionicemissionisthetermusedto
describetheprocessbywhichthermalenergyissuppliedtolooselyboundelectronsinordertoformasourceofelectrons.
Atroomtemperatureelectronsareeffectivelypreventedfromescapingthesurfaceofthemetalowingtotheattractiveforceofthepositively
chargedions.Asthetemperatureisincreasedsomeelectronsacquiresufficientenergytoovercometheattractionandleavethemetal
temporarily.Metal,shapedasathinwire,caneasilybeheatedbypassinganelectriccurrentthroughit.Sincethemetalsurfacebecomes
positivelycharged,acertainlevelofenergy(workfunction)mustbesuppliedtoallowelectronstoescapefromthesurface.Eachmetalhasa
characteristicworkfunction.Tungsten,withalowworkfunction,emitsmoreelectronsthanmetalswithhigherworkfunctions(seealsopp.2930
andFig.I.59).
Ifastrongelectrostaticfieldisappliedinavacuumbetweenthewire(givenanegative,cathode,potential)andananode,theelectricfieldwill
causeelectronstoaccelerateawayfromthewiretowardstheanodesurface(Fig.I.33).Thespeedoftheelectronsdependsonthestrengthof
theelectrostaticfield(voltage)betweenthecathodeandanode(equation(3),Sec.I.A.3.b)Thenumberofelectronswhichleavethewire
dependsonthetemperaturetowhichthewireisheated,whichdependsonhowmuchfilamentcurrentpassesthroughthewire.
A"V"shapedwirewillhavethehighesttemperatureatthetip.Electronswithdrawnfromthefilamenttipcarryelectricchargestotheanode.This
electriccurrent,whichflowsbetweenthefilamentandtheanode,iscalledthebeamcurrent.
1)Electricfield/Equipotentials
Anelectricallychargedobjecthasassociatedwithitanelectricfield.Thus,anelectricallychargedparticle,whenbroughtnearachargedobject,
isinfluencedbyanelectricalforceinthevicinityoftheobject.Theforceisdirectedtowardthechargedobjectifthechargesareofopposite
signsandawayfromtheobjectiftheyareofsimilarsign.DEFINITION:Thedirectionofanelectricfieldisdefinedasthedirectionoftheforce
actingonapositivecharge.(Figs.I.3435)
Alongthelinesofforceconnectingthetwocharges,theelectricpotentialwillchangegraduallybetweentheextremevaluesrepresentedbythe
twocharges.DEFINITION:Equipotentiallinesdefinethepointsalongthelinesofforcewithidenticalelectricalpotential.Theseequipotential
surfacesarealwaysorientedperpendiculartothelinesofforce.Thechangesintheelectricpotentialaregradualinspace.
Electronswhichenterafieldbetweentwoparallelplatesinadirectionparalleltotheplatesareaffectedbytheforcedirectedperpendicularto
theplates(FigI.36).Theelectronswillbeattractedtowardthepositiveplate.Thepathchangesinaseriesofgradualstepsattheequipotential
surfaces.
FigureI.37showshowtheelectronpathis"refracted"attheequipotentialsurface.TheresultisfundamentallythesameasthatgivenbySnell's
Lawofrefractioninlightoptics.Aconsequenceofthisisthatasphericallycurvedequipotentialsurfaceexhibitsthepropertiesofalens.
FiguresI.38andI.39showhowbothpositive(converging)andnegative(diverging)electrostaticlensescanbeformed.Thisfeatureof
electrostaticlensesdiffersfromelectromagneticlenseswhichcanonlyactasconverginglenses.
2)Advantages/Disadvantagesofelectronlenses:
Thefactthattherefractiveindexdoesnotchangeabruptlyinelectronlenseshasoneadvantageinthattherearenotroublesomereflectionsat
equipotentialsasatglassinterfaces.Thereisaseriousdisadvantageinthatequipotentialscannotbeshapedandcombinedinarbitraryfashionto
correctforchromaticaberrationandothererrors.
Althoughelectronmicroscopeswhichemployelectrostaticlenseshavebeenmade,mostmicroscopesuseelectromagneticlenses.Amajorreason
isthatelectrostaticlensesaremoresensitivetothequalityofthevacuumandcleanlinessofthecomponentsthanareelectromagneticlenses.
Somelensaberrationsaremoresevereforelectrostaticlensescomparedtoelectromagneticlenses.Electrostaticlensesrequireverypowerful
electrostaticfieldswhichcanleadtoelectricalbreakdownor"arcingover"insidethecolumn,especiallyunderpoorvacuumconditions.Forthis
reason,electrostaticlensescannotbemadewithfocallengthsasshortasmagneticlenses.
b.Electrostaticlens
Abasicunderstandingofelectrostaticlensesisimportantfortwomainreasons:i)theelectrongunuseselectrostaticlensactiontoformthe
primarybeamsource,andii)itisquitecommonforachargetodeveloponthenonconductingcontaminationwhichmayaccumulateonphysical
apertures(suchastheobjectiveaperture)andtransformthemintoweakelectrostaticlenseswhichcandistorttheelectronimage.
3)Propertiesofelectrostaticlenses:
a)Anyaxiallysymmetricalelectrostaticfieldhasthepropertiesofalensforraysconfinedtotheparaxialregion.Alltheideallensformulasapply
toelectrostaticlenses.
b)Forelectronlenses,replaceÃ(f)forrefractiveindexinthelensequations(f=valueofthepotentialontheaxis).Intheimageformingsystem
ofmostTEMs,fisthesameonbothsidesofthelens(SeeSec.I.A.5.c).
c)Ifboundedbyregionswherefisconstant,anelectrostaticlensisalwaysconvergent.
c.Magneticfieldsandmagneticlenses
1)Magneticfield
Anelectriccurrentpassingthroughaconductorgivesrisetoamagneticfield.TheconventionisthatNisthedirectioninwhichthelinesofthe
magneticfieldpoint(Fig.I.40).Themagneticfluxisthetotalnumberoflinesandthefluxdensityisthenumberoflinesperunitareaofasurface.
UsetheRIGHThandruletodeterminethedirectionofthefield(thumbpointstowardcurrentdirectionandfingerscurlindirectionoffield.NOTE:
Byconvention,thedirectionofelectronflowisoppositetothatofcurrentflow.
Fluxdensitydependsonthepropertiesofthematerialsurroundingtheconductor.Ironinducesahigherfluxdensitythanairoravacuum.The
propertyofthematerialwhichaffectsthefluxdensityiscalledthepermeability,m,ofthematerial.Forairandvacuum,m=1.0.For
ferromagneticmaterialsitcanbeaslargeasseveralhundredthousand.
Iftheconductorhastheshapeofacircularloop,thelinesofforceformcirclesaroundtheloop.Thefluxdensityisgreatestatthecenterofthe
loop.Themagnetinthecenteroftheloopisorientedperpendiculartotheplaneoftheloopifthecurrentthroughtheloopissufficientlystrongto
eliminatetheinfluenceoftheearth'sfield.ThesideoftheloopatwhichthelinesofforceleavetheloopistheNorth(N)poleofthemagnet(Figs.
I.41,I.42).
Ifthewireiswoundinseveralturnsaroundacylindricalsurface(solenoid),eachturnwillcontributetotheinducedmagneticfield.Theflux
densityinthecenterofthecoilisgivenby:
Inthecaseofairandnonmagneticmaterials,µ=1.0andB=H.
Thepermeabilityofirondependsonthefieldstrength,H,anddecreasestounityathighfieldstrengthorwhenthefluxdensity,B=H(Fig.I.43).
Thehighpermeabilityofironisduetotheinducedmagneticfieldorientingmicroscopiccrystalregionsactingastinymagnetsintheiron.Allthese
tinymagnetsaddtheirmagneticfieldstotheinducedfield(Fig.I.44).Whenallmicromagnetsarenearlyoriented,theironwillaffecttheflux
densitytoadecreasingamountsincethereorientationofmicromagnetsisnearingcompletion.Thus,thepermeabilityofironathighfieldstrengths
approachesthatofemptyspace.Atthispointtheironreachesmagneticsaturation.
2)Hysteresis
Thestrengthofthelensdependstosomeextentonthepreviousmagnetichistoryof
thelens.Whenthecurrentinalensisreduced,thedecreaseinmagnetizationdoes
notretracethesamepathobtainedwhenthecurrentwasincreased(Fig.I.45).
Inductionofmagnetizationinvolvesaphysicalmovementwithinthemagnetized
material,requiringtheovercomeofacertaindegreeofinertia.Asaresult,
magnetizationtendstolagbehindthemagnetizingforceapplied.Inducedmagnetic
fluxcanonlybereturnedtozerobyapplicationofacurrentintheoppositedirection.
Aconsequenceofhysteresisisthatthelevelofcurrentusedtoenergizeamagnetic
lensDOESNOTpreciselyspecifythelensstrength(i.e.focallength).
NormalizationofTEMlensesisaccomplishedbyreducingthelenscurrenttozero
somepredeterminednumberoftimes.Hysteresismayalsobeminimizedbytakinga
lenstosaturationandthenreturningittotheworkingcurrentwithoutovershooting.
Whenthefieldstrengthisreducedtozero,somemagnetizationstillremainsintheiron
(residualmagnetizationorremanence).Anadvantageofsoftironisthefactthat,
whenusedinanelectromagnet,hysteresisislow.
Introductionofpiecesofironinamagneticfielddrasticallyaffectsthefluxdensity.
Magneticmaterialhasashieldingeffect,theeffectbeinggreaterthegreaterthe
permeability.Permalloy(mmetal)hasamaximumpermeabilityof80,000140,000
comparedtoironusedintransformers(~7000).mmetalpermeabilityislimitedtolower
fieldstrengthsthanthatatwhichironstillretainshighpermeability.Thismetalis
thereforeusefulforshieldingtheTEMfromexternalmagneticfields.
d.Theelectromagneticlens
1)Lensdesigndevelopment(Figs.I.46I.48)
Theefficiencyofthemagneticfieldproducedbyashortsolenoidwasfirstimproved
byencasingtheenergizingcoilinasheathofsoftironwhichhasthepropertyofconcentratingthelinesofforceinamagneticfieldandthus
becomingmagnetizedbyinduction.Inthiswayamuchmorepowerfulaxialmagneticfieldisobtainedforthesameamountofcurrentflowing
throughthesolenoid.Furtherdevelopmentinvolvedencasingtheentirecoilwithsoftironexceptatanarrowannulargapintheinsideofthecoil.
Thisproducesagreaterconcentrationofthemagneticfieldalongashortaxialdistance.Toachieveshorterfocallengthlenses(andobtaingreater
magnifications)asoftironpolepiecewithanopenaxialborewasintroducedatthepositionoftheannulargap.
MagneticlensesusedinTEMsarealwaysconstructedwithanironcircuittoproduceahighfieldstrengthacrossashortgap.Themagneticfields
forTEMlensesareintherangeof10,00020,000gauss.
2)Forcesactingonacurrentinamagneticfield
Theforceonanelectroninamagneticfieldisalwaysatrightanglestothevelocityandthedirectionofthefield(Figs.I.49,I.50,andI.52).The
fieldonlyactsonthevelocitycomponentwhichisdirectedperpendiculartothelinesofforce.Usethelefthandrule(Fig.I.51:firstfingerfor
fielddirection,middlefingerforcurrentdirection,andthumbfordirectionofforce).Rayspassingthroughthelensareturnedthroughanangle
whichdoesNOTdependonthedistanceoftheraysfromtheaxis.Allelectronscontainedinagivenmeridionalplanebeforeenteringthefieldare
containedinarotatingmeridionalplaneastheypassthroughthelens,andthentheyleavethelenscoplanar.
Whenelectronsenterthelenstheyencounterasidewaysforcewhichcausestheelectrontorotate
asitcontinuesthroughthelens(Figs.I.53I.57).Sincetheradialcomponentofthemagneticfield
reversesafterthecenterofthelens,therotationalvelocitysetupinthefirsthalfofthelensis
countered.Theelectronenteredthelenswithoutangularmomentumabouttheaxisandleaves
withoutangularmomentum.Theneteffectisadeflectiontowardtheaxis,whichitmustcrossatthe
focalpointf
2
.Theanglebetweentheobjectvectorandtheimagevectoris180°+q,whereas,for
glasslensesandelectrostaticlenses,theanglebetweenarealobjectandtheimageisexactly180°.
Sincetheradialforceisdirectedtowardtheaxis,thelensisconvergentnomatterwhatthedirection
ofthefield.
3)Propertiesofamagneticlens:
Anyaxiallysymmetricmagneticfieldhasthepropertiesofanideallens.Alltheformulasfortheideallensmaybeapplied.
Magneticlensesarealwaysconvergent.Theconventional,axiallysymmetriclensisalwaysboundedbyregionswhicharefieldfree,the
consequencebeingthatthenetactionofelectronlensesisinevitablyconvergent.Limitedregionsmaybedivergentbutnotthelensasawhole.
Theseriousconsequenceofthisisthatneithersphericalorchromaticaberrationscanbecorrectedasisdoneinlightopticsbytheusedoublets
ofpositiveandnegativelenses.
Intheabsenceofelectrostaticfields,therefractiveindexisthesameinobjectandimagespace,thereforef
1
=f
2
.
Electronstravelingthroughaxiallysymmetricfieldsexperienceaspiraltrajectoryofdiminishingradius.Theimagevectorisatanangle180°+qto
theobjectvector.
Thedeflectionoftheelectrontowardstheaxismeansthatanelectronenteringthelensparalleltoitsaxiswillcrosstheaxisafterhavingpassed
thelens.Thedeflectionwillincreasewiththedistancefromtheaxis.Thus,abeamofelectronsinparallelpathsparalleltotheaxisofthelenswill
befocusedtoanimagepointontheaxiswhichrepresentsthesecond(back)focalpointofthelens(f
2
).Notethatmagneticlensesarehighly
inefficientinthatonlyaminorportionofthetotalfieldstrengthisactuallyeffectiveinfocusingtheelectron.
4)Magneticlensfocallength
Inamagneticelectronlensthefocallengthisdeterminedbythefieldstrengthinthelensgapandbythespeedoftheelectrons(determinedby
theacceleratingvoltage).
Formagneticlenses,focusingisachievedbyvaryingthecurrentwhichpassesthroughtheelectromagnet.Thisinturnchangesthestrengthof
themagneticfieldandtherebyaltersthefocallengthofthelensandisequivalenttoacombinedchangeinboththe"refractiveindex"and
"curvatureofsurface".Forabeamofmoreenergeticelectrons,thelenscurrenthastobeincreasedinordertokeepthefocallengthconstant.
FocallengthandcurrentareNOTlinearlyrelated:strengthincreasesinasigmoidfashion(Fig.I.45)ascurrentincreasesuntilapointisreached
wherethelensissaturatedandnofurtherincreaseinlensstrengthcanbeachieved.
Sincethefocallengthofthelensisdirectlyproportionaltotheacceleratingvoltage,avariationinthevelocityoftheelectronsintheimaging
beamaffectsimagequalitybyeliminatingperfectfocus(chromaticaberration).
5)Magneticlensdesign:(Figs.I.46,I.47).
Condenserlensesusuallyhavearelativelylargeboreandspacingwhichresultsinalongfieldandlongfocallength.
Typicalconstructionoftheobjectivelensproducesastrongfieldofshortaxialextent(i.e.shortfocallengthbetween(1.53mm)necessaryfor
formationofimagesathighmagnification.Thespecimenisplacedwithinthemagneticfieldoftheobjectivelens.Thus,anyfieldintroducedby
contaminantsinthespecimencandistortthefieldofthelens.Notethatthisalsomeansthatpartofthelensfield("prefield")isonthefrontside
oftheobjectandaffectstheelectronbeambeforeitpassesthroughtheobject.
Mostofatypicalmagneticlensliesoutsidethevacuumofthemicroscope.Onlythoseregionsthroughwhichtheelectronbeampassesareinhigh
vacuum.Magneticlensesmustbewatercooledtodissipatethelargeamountsofheatproducedbythecurrentsintheelectromagnetcoils.
DATE NAME EVENT
1897 J.J.Thompson Discoverstheelectron
1924 LouisdeBroglie Identifiesawavelengthtomovingelectrons
l =h/mv
where
l =wavelength
h=Planck'sconstant
m=mass
v=velocity
(Foranelectronat60kVl=0.005nm)
1926 H.Busch Magneticorelectricfieldsactaslensesforelectrons
1929 E.Ruska Ph.Dthesisonmagneticlenses
1931 Knoll&Ruska Firstelectronmicroscopebuilt
1931 Davisson&Calbrick Propertiesofelectrostaticlenses
1934 Driest&Muller SurpassresolutionoftheLM
1938 vonBorries&Ruska FirstpracticalEM(Siemens)10nmresolution
1940 RCA CommercialEMwith2.4nmresolution
1945 1.0nmresolution
Fig.I.1Comparisonoflightandelectronmicroscopes.Ineach
instrument,illuminationfromthesource(lamp,filamentinthe
electrongun)isfocusedbythecondenserlensontothespecimen.
Afirstmagnifiedimageisformedbytheobjectivelens.Thisimage
isfurthermagnifiedbytheprojectorlensontoagroundglass
screen(light)orfluorescentscreen(electrons).(FromAgar,p.8)
Fig.I.2CrosssectionalviewofthePhilipsEM300.(FromAgar,p.40)
Toviewtheanimatedmicroscope,clickhere.
Note:QuickTimePlugInrequired
(Thiscanbedownloadedathttp://apple.com/quicktime/download)
Fig.I.3Sectionthroughacomplex
doublecondenser6lensPhilips
EM200electronmicroscope.(From
Meek,p.99)
Fig.I.4Thestatisticalnatureofdiffraction
patterns.(FromHall,p.13)
"Theprecisenatureof'electronwaves'or'matterwaves'isverydifficulttounderstandordescribeinmaterialterms.Electronwavesarenot
electromagneticradiationofthekindtowhichlight,Xraysandradiowavesbelong.Theyconstituteasortofquantumor'packet'ofradiationwhich
accompanieseachindividualelectron,followingitspathandnotradiatingoutwardsfromit."(Meek,1976,pp.4849).
V l (nm)
v(
•
10
10
cm/sec)
v/c
10,000 0.0123 0.593 0.198
50,000 0.0055 1.326 0.442
100,000 0.0039 1.875 0.625
1,000,000 0.0012 5.930 1.977!
V l (nm)
v(
•
10
10
cm/sec)
v/c
10,000 0.0123 0.593 0.195
50,000 0.0055 1.326 0.414
100,000 0.0039 1.875 0.548
1,000,000 0.0012 5.930 0.941
FigI.5Aperfectpointsourcecannotbe
imagedbyalensasaperfectpointimagedue
tothepresenceoftheapertureAB(which
maybetheedgeofthelens).Diffractionat
thisaperturegivesrisetoaseriesoffringes,
whichsurroundtheimageformedofthepoint
source.Thepatternproducediscalledan'Airy'
disk.(FromMeek1sted.,p.35)
Fig.I.6Wheneverawavefrontstrikesa
barrier,itcanbendaroundthecorner'by
givingrisetoasecondarywavefrontatthe
edge,sinceeachpointonthewavefrontcan
giverisetoanewsourceofwaves.This
phenomenoniscalled'diffraction'.(FromMeek
1sted.,p.22)
Fig.I.7Diffractionpattern(right)formedbyanirregularlyshapedaperture
(left).(FromYoung,p.95)
Fig.I.8(a)
Photographof
theedgeofa
razorblade
illuminatedby
monochromatic
(blue)light
rendered
coherentby
passing
througha
narrowslit.(b)
Microdensitometer
tracingofthe
negativefrom
whichthe
photograph
wasmade.
FourFresnel
fringescanbe
distinguished.
(FromMeek1st
ed.,p.27)
(a)
(b)
(a) (c)
(b)
Fig.I.9(a)Fresnelfringesformed
byelectrons.Thesefringesare
formedoutsidetheedgeofahole
(white)inacarbonfilm(black).(b)
Amicrodensitometertracingofthe
fringesystem;thepatternis
identicalwiththeFresnelfringe
systemformedbyvisiblelight(see
Fig.I.8).(c)Anunderfocusedimage
ofaholeinafilm,showinga
completesystemofabout40
Fresnelfringesinsidethehole.
(FromMeek1sted.,pp.2930)
Fig.I.10Diffractionimagesoftwo
easilyresolvedpoints.(From
Slayter,p.243)
Fig.I.11Imagesoftwo
incoherentlyilluminatedpointsat
thelimitofresolution.(a)individual
intensities;(b)summedintensities.
(FromSlayter,p.244)
Fig.I.12Examplesofwhatoccurswhentwo
wavesofthesamewavelengthandequal
amplitudeadd.Ineachexample,thetwo
separatewavesareshownontheleftand
theirsumorresultantwaveontheright.The
differentexamplesarecharacterizedbyvarying
phasedifferences.Thephaseofawave
(usuallyexpressedasafractionofthe
wavelengthorindegrees)isthepositionofa
crestrelativetosomearbitrarypoint.Although
thephaseofagivenwavevarieswithtimeas
thewavetravels,thedifferenceinphaseofthe
twowavesofthesamewavelengthwiththe
samevelocity,isindependentoftime.Such
wavescaninterferewithoneanother.The
resultantwavehasthesamewavelength,l .
(a)Phasedifferencezero.Thewavestotally
reinforceandaresaidtobe"inphase"orto
showconstructiveinterference.
(b)Phasedifferencel /4.Partialreinforcement,
givingawaveofamplitude1.4(intensity2.0).
(c)Phasedifferencel /2.Thewavesare"outof
phase"andthereistotaldestructive
interferencetogivenoresultantwaveora
wavewithamplitude0(intensity0).(From
GluskerandTrueblood,p.19)
Fig.I.13Photographofan
interferencepatterninwater
wavesformedbythe
superpositionofwavesfromtwo
sourcesoscillatinginphasewith
thesamefrequency.(FromYoung,
p.22)
Fig.I.14Theangularapertureofthe
eyeisrelativelysmall.(FromMeek,
1sted.,p.13)
Fig.I.15Increasingtheangular
apertureoftheeyewithalens.The
lensallowstheobjecttobeheld
closertotheeye,whichisthereby
enabledtogathermoreinformation.
(FromMeek1sted.,p.14)
Fig.I.16Theinteractionofwaves
withanobstacle.Theboatridesthe
longwavelengthoceanwave,but
reflectsthesmallwavelength
surfaceripple.Anobserverwho
wishestodetectthepresenceof
theboatcandosoonlyby
observingwaveswhichhave
wavelengthssmallerthan,or
comparableto,thelengthofthe
boat.(FromSherwood,p.19)
Maximummagnification=
resolvingpoweroftheeye
resolvingpowerofthemicroscope
(a)
Fig.I.17(a)TwoAiry
disksrepresenting
twoimagepoints
shownatincreasing
separationfromleft
toright.Inthe
pictureatthe
extremerightthe
twodiskscanbe
distinguishedas
separatedisks.
(b)Theintensity
distributionatanAiry
disk.R,halfwidthof
thecentralmaximum
representedbya
bellshapedcurve.
(c)TheRayleigh
criteriaforresolution.
(FromSjostrand,
p.115)
i=r
Fig.I.18Reflection.(FromSlayter,
p.4)
Fig.I.19Refraction.(FromSlayter,
p.6)
Fig.I.20Principalraydiagramsshowing
imageformationbyaconvexlens.
(a)Whentheobjectdistanceisgreater
thanthefocallength,areal,inverted
imageisformed.
(b)Whentheobjectdistanceisless
thanthefocallength,avirtual,erect
imageisformed;itspositionis
obtainedbyprojectingtheprincipal
raysbackward.Theraysappearto
comefrompointQ.(FromYoung,
p.127)
Fig.I.21Definitionof
principalfocus,F,inimage
spaceofalens.(From
Sjostrand,p.20)
Fig.I.22Focusingeffectoflenson
raysoriginatingfrompointson
principalaxislocatedatdifferent
distancesfromthelens.(From
Sjostrand,p.21)
Fig.I.23Definitionofprincipal
focusinobjectspaceF1ofa
lens.(FromSjostrand,p.21)
Fig.I.24VirtualimageQof
objectpointlocatedbetween
principalfocusinobjectspace
andthelens.(FromSjostrand,
p.21)
Fig.I.25Constructionoftheimage
ofanobjectbymeansofray
tracing.(FromSjostrand,p.22)
Fig.I.26Magnifyingeffectof
apositivelens.(From
Sjostrand,p.22)
Fig.I.27Virtualmagnified
imageofobjectlocated
betweenprincipalfocusin
objectspaceandthelens.
(FromSjostrand,p.22)
Fig.I.28Amagnifyingglassformsan
enlarged,erectvirtualimage.The
angularsizeofthisimageis
approximately4"/15"or4/15.The
angularsizeoftheobjectatthe
closestdistanceforcomfortable
viewingis1"/10"or1/10.The
magnificationinthissituationis(4/15)/
(1/10),or22/3.(FromYoung,p.130)
Fig.I.29Theangularapertureofa
lens.Theangle2a isthe
acceptanceangleofthelens,and
thelargeritcanbemade,themore
informationcanthelenstransmit.A
largelensofhighaperturecan
thereforetellusmoreaboutan
objectthanasmalllensoflow
power.(FromMeek1sted.,p.12)
Fig.I.30Raydiagramforhighmagnification
modeofoperation.Notethateachlens
formsarealimage,withimageinversion.
I0istheimageformedbytheobjective
lensO,I1isformedbythefirstprojector
lensP1andI2bythesecondprojectorP2,
onthescreen.(FromAgar,p.30)
Fig.I.31Left:raydiagramofthe3realimagemediumandhighmagnificationimagingsystemofa3lens
microscope.Center:2realimageverylowor'scan'magnificationrangeofa3lensmicroscope.Right:2real
imagelowmagnificationsystemofa3lensmicroscope.(FromMeek1sted.,pp.118,120121)
Fig.I.32Raydiagramforacompleteelectron
microscope.FilamentF,condenser1lensC1,
condenser2lensC2,condenserapertureCA,
specimenS,objectivelensO,objectiveaperture
OA(inbackfocalplane).1stintermediateimage
andselectorapertureSA.IntermediatelensP1,
secondintermediateimageI2,projectorlensP2
andfinalimageonthefluorescentscreenFC.
(FromAgar,p.35)
a)f=2.0
x
o
=5.0
e)f=4.0
x
o
=3.0
b)f=10.5
x
o
=21.0
f)f=13.3
x
o
=13.3
c)f=3.5
x
o
=3.0
g)f=3.142
x
o
=0.0
d)f=5.0
x
o
=2.5
a)D=8.0
L1:f=2.0
x
o
=4.0
L2:f=3.0
b)D=8.0
L1:f=2.0
x
o
=6.0
L2:f=3.0
c)D=4.0
L1:f=2.0
x
o
=3.0
L2:f=2.0
FigI.33Accelerationofelectronin
electricfield.(FromSjostrand,p.26)
Fig.I.34Linesofforceatapositively
chargedsphericalbody.(FromSjostrand,
p.32)
Fig.I.35Linesofforceandequipotential
surfaces(stippledlines)associatedwith
twoequalchargesofoppositesign.
(FromSjostrand,p.32)
Fig.I.36Equipotentialsurfacesattwoparallel
platesofoppositechargeswiththepathofan
electronindicatedwithinthehomogeneous
partofthefield.(FromSjostrand,p.33)
Fig.I.37Refractionofelectronatan
equipotentialsurface.(FromSjostrand,p.33)
Fig.I.38.Negativelensactionof
electrostaticfieldatanaperturewhen
V2V1>V3V2.(FromSjostrand,
p.34)
Fig.I.39.Positivelensactionatan
aperturewhenV2V1<V3V2.
(FromSjostrand,p.34)
Fig.I.40Magneticfieldinducedbycurrent
passingthroughaconductor.(From
Sjostrand,p.35)
Fig.I.41Magneticfieldinducedbycurrent
passingthroughasolenoid.(From
Sjostrand,p.37)
Fig.I.42Solenoidwithironcore.(From
Sjostrand,p.40)
Fig.I.43a.Dependenceofpermeabilityonfluxdensity,B.
b.RelationshipbetweenfluxdensityBandfieldstrength.
(FromSjostrand,p.38).
Fig.I.44Magnetization.(FromSlayter,
p.361)
Fig.I.45Curves
showinghowthe
magnetizationof
softiron(lens
strength)is
relatedtothe
magnetizing
force(lens
current).An
unmagnetized
lensstartsfrom
thepointOand
followsthepath
OAaslens
current
increases.Atthe
pointA,further
increaseinlens
currentproduces
nofurther
increaseinlens
strength;thelensissaidtobe'saturated'.Whenlenscurrent
isreduced,thepathOAisnotretraced;adifferentpathABis
followed.Thisdisplacementiscalled'hysteresis'.Atzero
current(pointB),someresiduallensstrengthremains;thisis
called'remanence'.Tobringthelensbacktozerostrength,a
reversecurrentOCmustbeapplied.Lensstrengththen
increaseswithincreasingreversecurrent,followingthepath
CD.Thepolarityofthelenschanges,butthisdoesnotaffect
itsfocusingpower;onlythespiralelectronpathisreversed.
Becauseofhysteresis,itisnotpossibletocalibratealens
currentmeteraccuratelyintermsoflensstrengthor
magnification.
Fig.I.46Evolutionofmagneticelectron
lenses.(A)Shortsolenoidusedasa
magneticlens.(B)Softironcasing
enclosingoutersurfaceofthesolenoid,
thusconcentratingthefield.(C)Soft
ironencasingthesolenoidexceptata
narrowannulargaptherebyreducing
themagneticfieldtoaveryshortregion
alongthelensaxis.(D)Modern
objectivelensconsistingofasoftiron
encasedsolenoidandsoftironpole
piecessoastohaveanenormously
concentratedfieldatthelevelofthe
annulargap.(FromWischnizter2nded.,
p.33)
Fig.I.47(a)Amagneticlensconsisting
ofatightlywoundcoilandasoftiron
shroudsurroundingthecoilexceptfor
asmallgap.Thefieldisconcentratedin
thatgap.(b)Shortfocallength
electromagneticlenswithpolepieces.
(FromSjostrand,p.50)
Fig.I.48Fieldstrengthdistribution
curves.ThecurvesADcorrespondto
therespectivelensesillustratedinFig.
I.46.Eachrepresentsthefieldstrength
alongthelongaxisofthelens.The
changesintheshapeofthecurves
representtheshorteningor
concentrationofthefieldovera
shorteraxialdistance.Hz=
longitudinalmagneticfield.Z=
distancealongtheaxisofsymmetry.
(FromWischnizter2nded.,p.33)
Fig.I.49TheforceFactingon
astraightconductorina
homogeneousmagneticfield
offluxdensityBwhencurrent
Iispassedthroughthe
conductor.(FromSjostrand,
p.43)
Fig.I.50Pathofanelectronina
magneticfield.(A)Inalarge,uniform
magneticfield.(B)Inasmall,uniform
magneticfield.(FromWischnitzer2nd
ed.,p.25)
Fig.I.51Lefthandthumbrule.
(FromSjostrand,p.43)
Fig.I.52Thompson'sexperiment.A
streamofelectronsoriginatingfroma
sourceandpassing,invacuo,through
amagneticfieldproducedbyapairof
magnetswillbedeflected.The
directionofdeflectiondemonstrates
thatelectronsarenegativelycharged
particlesofmatter.(FromWischnitzer
2nded.,p.25)
Fig.I.53Actionofasolenoidonan
electronbeam.Anelectriccurrent
passingthroughthecoilproducesan
axialmagneticfield.Thisisthe
refractingmediumfortheelectrons.An
electronstartingatapointontheaxisA
andatanangletoitfollowsaspiral
path,returningtotheaxisatthepoint
B.Theactionisbasicallysimilartothat
oftheconverginglightlensshownin
Fig.I.20.(FromMeek1sted.,p.8)
Fig.I.54Actionofthemagnetic
lens.(a)Inperspective.(b)
Electrontrajectoryin
projection,alongdirectionof
propagation.(c)Electron
trajectoryinprojection,side
view.(FromSlayter,p.358)
Fig.I.55Componentsofthe
vectorHneartheaxisoffields
withaxialsymmetry.His
representedbytwo
components,Hz,the
componentinthez(axial)
direction,andHr,the
compnentinther(radial)
direction.(FromHall,p.85)
Fig.I.56Theycomponentof
themagneticfieldina
magneticlensisoriented
perpendiculartothedirection
ofanelectronenteringthe
lensalongapathparallelto
thelensaxis.Thisy
componentwillaffectthe
electron,deflectingitinthex
directionasindicatedbythe
arrowmarkedvx.(From
Sjostrand,p.48)
Fig.I.57Thezcomponentofthemagneticfield
andthexvelocitycomponentoftheelectron
inamagneticlensinteract,deflectingthe
electronintheydirectiontowardthelens
axis.(FromSjostrand,p.49)
CuuDuongThanCong.com https://fb.com/tailieudientucntt
cuu duong than cong . com
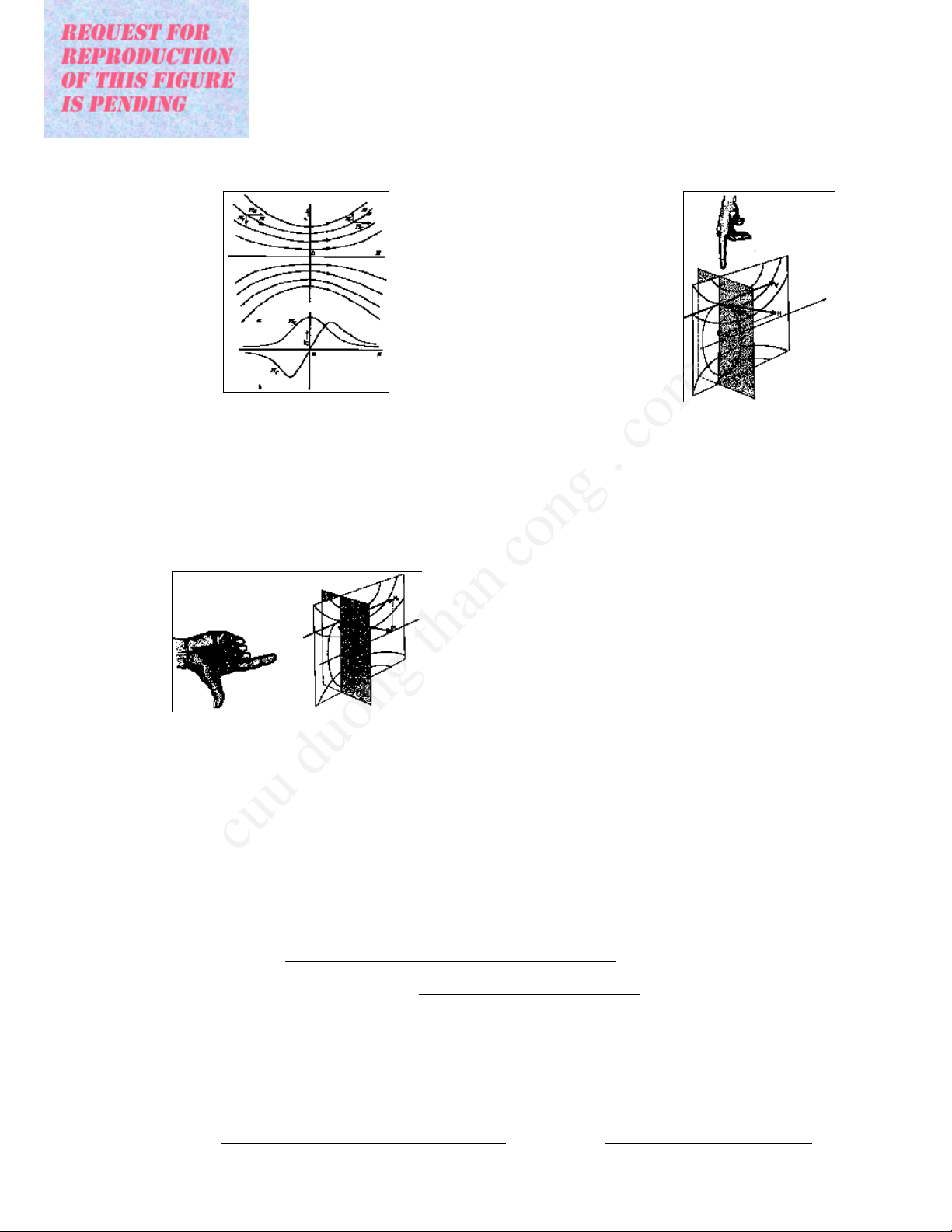
I.THEMICROSCOPE
I.A.PRINCIPLESOFTHETRANSMISSIONELECTRONMICROSCOPE(TEM)
I.A.1.OriginoftheTransmissionElectronMicroscope
I.A.2.ComparisonofLight(LM)andElectronMicroscopes(Fig.I.1)
a.Similarities(Arrangementandfunctionofcomponentsaresimilar)
1)Illuminationsystem:producesrequiredradiationanddirectsitontothespecimen.Consistsofasource,whichemitstheradiation,anda
condenserlens,whichfocusestheilluminatingbeam(allowingvariationsofintensitytobemade)onthespecimen.
2)Specimenstage:situatedbetweentheilluminationandimagingsystems.
3)Imagingsystem:Lenseswhichtogetherproducethefinalmagnifiedimageofthespecimen.Consistsofi)anobjectivelenswhichfocusesthe
beamafteritpassesthroughthespecimenandformsanintermediateimageofthespecimenandii)theprojectorlens(es)whichmagnifiesa
portionoftheintermediateimagetoformthefinalimage.
4)Imagerecordingsystem:Convertstheradiationintoapermanentimage(typicallyonaphotographicemulsion)thatcanbeviewed.
b.Differences
1)Opticallensesaregenerallymadeofglasswithfixedfocallengthswhereasmagneticlensesareconstructedwithferromagneticmaterialsand
windingsofcopperwireproducingafocallengthwhichcanbechangedbyvaryingthecurrentthroughthecoil.
2)MagnificationintheLMisgenerallychangedbyswitchingbetweendifferentpowerobjectivelensesmountedonarotatingturretabovethe
specimen.Itcanalsobechangedifoculars(eyepieces)ofdifferentpowerareused.IntheTEMthemagnification(focallength)oftheobjective
remainsfixedwhilethefocallengthoftheprojectorlensischangedtovarymagnification.
3)TheLMhasasmalldepthoffield,thusdifferentfocallevelscanbeseeninthespecimen.Thelarge(relative)depthoffieldintheTEMmeans
thattheentire(thin)specimenisinfocussimultaneously.
4)Mechanismsofimageformationvary(phaseandamplitudecontrast).
5)TEMsaregenerallyconstructedwiththeradiationsourceatthetopoftheinstrument:thesourceisgenerallysituatedatthebottomofLMs.
6)TEMisoperatedathighvacuum(sincethemeanfreepathofelectronsinairisverysmall)somostspecimens(biological)mustbedehydrated
(i.e.dead!!).
7)TEMspecimens(biological)arerapidlydamagedbytheelectronbeam.
8)TEMscanachievehighermagnificationandbetterresolutionthanLMs.
9)Pricetag!!!(100xmorethanLM)
I.A.3.Photons/Electrons
a.Dualconceptofwaveandparticle(Fig.I.4)
Lighthaspropertiesbothofaparticleandawave.Thisdualnatureisrequiredtosatisfactorilyexplaintheresultsofvariousphysicalexperiments.
Thediffractionoflight(bendingaroundcorners)illustratesthewavenature.TheWAVETHEORYisbasedonthestatisticalnatureofeventsand
haslittlemeaningwithrespecttothebehaviorofsingleparticles.ThewavetheorywasdevelopedandexpoundedbyHuygens(16291695)and
Hooke(16381703).TheCORPUSCULARTHEORYwasproposedbyNewton(16421727)andbecamethemoreacceptedtheoryevenafter
demonstrationofdiffractionbyYoung(17731829)andinterferencebyFresnel(17881827).Atabout1850,thewavetheorycamebackinto
favoruntilabout1900whenmoreevidenceforthecorpusculartheorywasdiscovered.
QUANTUMTHEORY(PlanckandEinstein)providesthebasisforexplainingthephenomenaofINTERFERENCE,DIFFRACTIONandthe
PHOTOELECTRICeffect(lightfallingoncertainmetalscausethemtoemitelectrons)andthusformsacommonbasisforexplainingthenatureof
actionoflight.Thetransferofenergybetweenlightandmatteroccursonlyindiscretequantitiesproportionaltothefrequencyofthe
lightwave.
E=hJ
where
E=energyofphoton(joules)
h=Planck'sconstant(6.624
•
10
34
joulesec)
J=frequency(cycles/sec)
b.Electronvelocityandwavelength
Therelationbetweenthewavelength(l )ofaparticleofmass,m,movingatavelocity,v,isgivenbytheDeBrogliewaveequation:
(1)
Anelectronofchargee(1.6
•
10
19
coulomb),andmassm(9.11
•
10
28
gm),whenpassingthroughapotentialdifferenceofVvolts(expressedin
joules/coulomb),hasakineticenergy:
(2)
Solvingforvelocity:
(3)
substitutingintotheDeBroglieequation(1):
(4)
Since1joule=10
7
dyne
•
cm=10
7
cm
2
•
gm/sec
2
(5)
Thus,forexample,ifV=60,000volts,l =0.005nm.
Fromequation(3)theelectronvelocitycanbecalculatedifVisknown:
(6)
Thefollowingtableillustratesthat,athighvoltage,electronvelocityiscomparabletothespeedoflightinavacuum(c=3
•
10
10
cm/sec).
Theequationbreaksdownwhenthevelocityoftheelectronapproachesthespeedoflightbecausearelativisticcorrectionmustbemadeforthe
valueofthemasswhere:
(7)
Therelationbetweenl andVismorecorrectlygivenby:(seeHall(1966)pp.3334)
(8)
Thefollowingtableisobtainedwhenrelativityeffectsareincluded:
c.Interference/diffraction/coherence
Anideallenssystemobtainsanexactimageoftheobject(eachpointfaithfullyreproduced).Thephenomenaofdiffractionmakesthis
unattainable(Figs.I.5,I.6).
Diffractionphenomenainvolvesthebendingofthepathofradiationpassingclosetoanobstacle(Fig.I.6).Thisresultsinaspreadingofthe
radiationintotheregionbehindtheobstructionthatthewavespassed.Thediffractionatedgescontributestothecontrastatwhichanedgecan
beobserved.Diffractionalsolimitstheresolvingpowerofthemicroscopesincetheimagepointproducedbyalensisadiffractionimageofthe
openingofthelensortheaperturerestrictingtheeffectiveopeningofthelens(Fig.I.5).
Ifthelightsourceandtheplaneatwhichthediffractionpatternisobservedareatfinitedistancesfromtheedge,thephenomenoniscalled
Fresneldiffraction.Thepatternisdescribedasduetointerferencebetweenthenondiffractedlightandawaveoflightdiffractedattheedge.
Theresultingsuperpositiongivesrisetoaseriesofdiffractionfringesorientedparalleltotheedgeandrepresentingperiodicallyvaryingbrightness,
maximaandminima.(Figs.I.7,1.8,I.9).
Coherence:Aprerequisiteforinterferenceisasuperpositionofwavesystemswhosephasedifferenceremainsconstantintime.Twobeams
arecoherentif,whencombined,theyproduceaninterferencepattern.Thebeamsareincoherentwhentheyareincapableofproducingan
interferencepattern.Twobeamsoflightfromselfluminoussourcesareincoherent.Iflightfromthetwosourcesfallsonascreen,theresultant
intensityissimplythesumofthetwointensitieswhichwouldoccurfromeachsourceseparately(Figs.I.10,I.11).Inpracticeanemittingsource
hasfiniteextentandeachpointofthesourcecanbeconsideredtogeneratelight.EachsourcegivesrisetoasystemofFresnelfringesatthe
edge.Thesuperpositionofthesefringesystemsisfairlygoodforthefirstmaximaandminimabutfartherawayfromtheedgeshadowtheoverlap
ofthefringepatternsbecomessufficientlyrandomtomakethefringesdisappear.Thenatureofwaves,phase,amplitude,andinterferenceare
illustratedinFigs.I.12andI.13.
d.Resolution
1)Definitions:
RESOLUTION:abilitytodistinguishcloselyspacedpointsasseparatepoints.
RESOLUTIONLIMIT:smallestseparationofpointswhichcanberecognizedasdistinct.
RESOLVINGPOWER:resolutionachievedbyaparticularinstrumentunderoptimumviewingconditions.
2)Distinctionbetweenresolutionandresolvingpower:
Notethedistinctionbetweenresolutionandresolvingpower.Resolvingpowerisapropertyoftheinstrumentandisaquantitythatmaybe
estimatedontheoreticalgrounds.Resolutionisequaltoorpoorerthantheresolvingpowerandisthequantityobservedunderanygivenset
ofexperimentalconditions.IntheTEM,especiallywithbiologicalsamples,theresolutionachievedmaybeconsiderablyinferiortothetheoretical
resolvingpoweroftheinstrument.
Microscopyisthescienceofseeingtheverysmall.Underidealconditions,theeyeresolvesabout1minuteofarc(=1/60degree=2.9x10
4
radian;recallthereare2p radiansin360°)andsinceitcanfocusdowntoabout250mm,thesmallestobjectwecanresolveisabout0.07mm
(70mm)(Fig.I.14).Thislimitisrelatedtothesizeofthereceptorsintheretinaoftheeye.Thefunctionofamicroscopeistomagnifytheimage
fallingontheretina(Fig.I.15).Theadvantageoflightandelectronmicroscopesisthattheyeffectivelygettheobjectclosertotheeyesoa
magnifiedimageisobtainedandmoredetailcanbediscerned.
TENNISBALLANALOGY:Eyecanresolve3cmat100meters,thusatennisballisclearlyvisible.Butifthetennisballisheldupagainstawhite
background,thevisibilitydecreases(becauseofthedecreaseincontrast).
3)Abbecriteriaofresolution:
Thefundamentalnatureoflightposeslimitsonthedetailthatcanberesolved(Fig.I.16).Abbe(1893)showedthatthesmallestresolvable
distanceisabout1/2thewavelengthoflightused.Thus,1/2thewavelengthoftheradiationusedistheultimateresolvingpowerofany
instrument.Thislimitstheusablemagnificationofopticalmicroscopesto<1000X.Atfirstitwasthoughtthatxraymicroscopeswouldbeuseful
buttherefractiveindexofsubstancesforxraysisnearly=1,thusrefractinglensescannotbemadeforxrays,andconsequently,xrayscannot
beeasilyfocusedtoformimages.
4)Magnificationlimits:
Themaximummagnificationofaninstrumentislimitedaccordingtothefollowingrelationship:
Thus,fortheLM,witharesolvingpowerofapproximately0.25µm,themaximum(useful)magnificationisabout250µm/0.25µm=1000X.Thevalue
usedfortheresolvingpoweroftheeyeinthisexample(250µm)representsamorerealisticviewingcondition.Anymagnificationabovethevalue
givenbytheaboveformularepresentsemptymagnification,sincesuchmagnificationleadstonomoreusefulinformationbutratheramagnified
blur.
AccordingtotheAbbecriteria,at60,000volts,theTEMshouldhavearesolvingpowerofabout0.0025nm.Thisshouldallowamaximumuseful
magnificationofabout100milliontimes!!!Inpractice,themaximumusefulmagnificationoftheTEMoperatedat60kVislimitedtomuchlessthan
1,000,000X.Thus,althoughtheLMnearlyobeystheAbbecriteria,theTEMfallsshortbyaconsiderableamount.Themainlimitingfactorinthe
TEM,withrespecttoachievingthetheoreticalresolvingpoweroftheinstrument,concernsthenatureoftheimaginglensesandtheprocessof
imageformation.
5)Rayleighcriteria(practicalbutarbitrary):(Fig.I.17).
Itistheabilityofmicroscopestomakeobjectpointswhichareclosetogetherappearintheimageasseparatepoints.Anideallenstakeseach
objectpointandrepresentsitexactlyasapointintheimage.Areallenstakeseachobjectpointandspreadsitoutintoacirculardisk(Airy
disk)intheimageplanewhosediameterdependsontheangularapertureofthelens.
Theshortestdistancebetween2disksatwhichthetwodisksappearpartiallyseparatedcorrespondstoabout1/2thewidthofthedisks.The
distance,d,inobjectspaceisgivenby:
d=0.61l /n
•
sina
where
l =wavelenghtoftheradiation
n=refractiveindexofthemedia
a=semiangularapertureofthelens
NOTE:n
•
sina=thenumericalaperture(N.A.)ofthelens.
Thus,tomaximizeresolvingpower,l mustbedecreased,nincreased,oraincreased.Recallthatweareconcernedatthemomentwithan
aberrationfreeopticalsystem.Thevaluefortheconstant(0.61)iscontroversialbecauseitdependsonthecoherenceoftheradiationanda
criteriaofvisibility.
FortheLM,usingoilimmersionoptics(n=1.5),sina=0.87,andvioletlight(l =400nm),d=0.2µm.Theonlywaytoimprovetheresolutionisto
uselightofshorterwavelengthsinceN.A.cannotbeincreasedbeyond~1.5.FortheTEM,n=1(vacuum),sina=10
2
andl =0.005nmfor60kV
electrons,thusd=0.3nm.
I.A.4.Optics(LensTheory)
a.Basiclawsofclassicalgeometricaloptics
1)Rectilinearpropagationoflightwhenn(refractiveindex)isconstant.
2)Lawofreflection:
3)Lawofrefraction(Snell'sLaw):
4)Independenceofrays.Theassumptionismadethatlightraystravelindependentlythroughspace.
Theselawsholdforelectrons,except#4,ifthecurrentdensityistoohighwhennegativechargedelectronscaninterfere.
b.Classicalvs.electronoptics
1)Classicaloptics:Therefractiveindexchangesabruptlyatasurfaceandisconstantbetweenthesurfaces.Therefractionoflightatsurfaces
separatingmediaofdifferentrefractiveindicesmakesitpossibletoconstructimaginglenses.Glasssurfacescanbeshaped.
2)Electronoptics:Here,changesintherefractiveindexaregradualsoraysarecontinuouscurvesratherthanbrokenstraightlines.Refraction
ofelectronsmustbeaccomplishedbyfieldsinspacearoundchargedelectrodesorsolenoids,andthesefieldscanassumeonlycertaindistributions
consistentwithfieldtheory.
c.Geometricalandphysicaloptics
Thefundamentalprinciplesofopticsgovernthedesignandoperationofboththelightandelectronmicroscopes.Thebasicopticalprinciples
involvingtheuseofrefractileelementsorlensesinordertoformmagnifiedimagesareidenticalinboththeLMandTEM.TheTEMdiffersfromthe
LMonlyintheradiationitusesandinthewayinwhichtheradiationisbentorrefracted.
Geometricalopticsdealswiththestudyofthepathsfollowedby'rays'oflightorelectronsthroughlensesandapertures,andthegeometrical
constructionsusedtofindtherelativepositionsandsizesofobjectsandtheirimages.Arayoflightorelectronsisdefinedasaninfinitelythin
pencilorbeam.Physicalopticsshowsthatthisanabstractionandcannotphysicallyexistbecauseof'diffraction'whichdealswiththewave
natureoflightandelectrons.Allresultsobtainedingeometricalopticscanbederivedfromtheprinciplesofphysicaloptics,alongwithother
phenomenasuchasinterferenceanddiffractionwhicharenotexplicableinsimplegeometricalterms.
d.Idealversesreallenses:
Lensesareusedtobendraysoflightorelectronssotheyaredeflectedinapredictablewayfromtheiroriginalpaths.Thepropertiesofanideal
lens,possessinganaxisofrotationalsymmetryare:
1)Eachrayofthebundleofrayswhichpassesfromanobjectpointwillberefractedbytheideallenstomeetinoneimagepoint.
2)Raysoriginatingfrompointswhichlieonaplaneperpendiculartotheaxis,mustbeimagedinaplanewhichisalsoperpendiculartotheaxis.
3)Theimageappearsliketheobjectirrespectiveofthemagnification,sotherelativelineardimensionsoftheobjectarepreservedintheimage.
Inpractice,theimagingbyanyreallensdoesnotcorrespondtothatoftheideallensowingtothefactthatanobjectpointisrepresentedbya
diffractionimage(Airydisc)ofthelensopeningortheapertureusedforrestrictingtheeffectiveopeningofthelens.Thisisaresultofthewave
likepropertiesoflight.Lensaberrationsalsocontributetomoreorlesspronounceddeviationsfromthepropertiesoftheideallens.
Thesinglerefractingsurfaceofsphericalcurvatureisthefundamentalunitoffocusingactionbyglasslenses.Sphericalrefractingsurfacesactas
lensesforparaxialrayswhicharethoseraysthatpassclosetotheprincipalaxisofthelens.RayswithlargeangleswillNOTobeyideallens
action.
Afundamentaldifferencebetweenlightandmagneticlensesisthattheelectronbeamdoesnotchangeinforwardvelocityasitpassesthrough
themagneticfield(lightraysslowdownwhenpassingintoamediumofhigherrefractiveindex).Refractioniscontinuouswithelectronswhenthey
areinthemagneticfield:lightisrefractedonlyattheinterfacebetweenmediaofdifferingrefractiveindex.Theelectronsalsofollowspiral
trajectoriesthroughthemagneticfield(seealsoSec.I.A.5.c(Magneticfieldsandmagneticlenses)
e.Raydiagrams:(Figs.I.20I.28)
Themethodofconstructionofraydiagramsisbasedonthreesimpleprinciples:
1)Allraysenteringthelensparalleltotheaxisarebroughttoacommonpointontheaxis,thefocalpoint.
2)Allrayspassingthroughthegeometricalcenterofthelensareundeviatedandpassstraighton,nomatterfromwhichdirectiontheycome.
3)Principleofreversibility:ifthedirectionofarayisreversedinanysystemtherayexactlyretracesitspaththroughthesystem.Thisapplies
onlytothelocationoflightpathsandnottotheintensityofthelight.
Theaboveprinciplesarebasedontheassumptionsthatwearedealingwithathinlensandconcernedwiththepathsofparaxialrays.The
standardconventionistodrawdiagramswithraysthattravelfromlefttoright.Theobjectistotheleft(infront)ofthelensandtheimageisto
theright(behind)ofthelens.
f.Definitions:
Realimage:oneatwhichlightraysphysicallyreunite,sothataphotographicplateplacedatthepositionofarealimageisexposed.
VirtualImage:onefromwhichlightraysappeartodiverge;raysarenotinfactconcentratedatthepositionofavirtualimage,sothata
photographicplateplacedatthepositionoftheimageisnotexposed(byfocusedrays).Placinganopticalsystemsuchastheeyebehindthe
lens,willenablethedivergentraystobefocusedtoformarealimage.TheintermediatelensofanTEMissometimesusedthiswayinorderto
reducethefinalsizeoftherealimageformedbytheprojectorlens(es).
Converging(positive)lens:bendsraystowardtheaxis.Ithasapositivefocallength.Formsarealinvertedimageofanobjectplacedtothe
leftofthefirstfocalpointandanerectvirtualimageofanobjectplacedbetweenthefirstfocalpointandthelens.
Diverging(negative)lens:bendsthelightraysawayfromtheaxis.Ithasanegativefocallength.Anobjectplacedanywheretotheleftofa
diverginglensresultsinanerectvirtualimage.Itisnotpossibletoconstructanegativemagneticlensalthoughnegativeelectrostaticlensescan
bemade.
g.Lensformula(thinlensequation):
where
f=focallengthofthethinlens(sameradiusofcurvatureforboth
sphericalsurfaces)
o=distanceofobjectfromlens(positivetotheleft)
i=distanceofimagefromthelens(positivetotheright)
NOTE:Foravirtualimage,ihasanegativevalue.
h.Magnification:
Foraconverginglens,iftheobjectismorethantwicethefocallengthfromthelens,thentheimageformedisreal,inverted,andsmallerinsize
thantheobject(M<1).Whentheobjectisatadistance=2f,theimageandobjectarethesamesize(M=1);whenitisbetweenfand2f,
theimageislargerthantheobject(M>1),andwhenitis<f,theimageisvirtual,erect,andlargerthantheobject(M>1).
i.Angularapertureofthelens(2a)(Fig.I.29)
Theaperturedeterminesthetotalamountofradiationarrivingfromtheobjectwhichcanbefocusedto
formanimage.Theaperturethuscontrolstheabilityofthelenstogatherinformationabouttheobject.
Thisdependsontheangleoftheconeofraysitisabletoacceptfromtheobject.Bringinganobject
closertotheeyeincreasestheangularaperture,butthereisalimittotheclosenessthattheobjectcan
bebroughttotheeye(~25cmcorrespondingtoanangleofabout0.9°fora4mmexitpupildiameterof
theeyelens;atypicalLMwithanoilimmersionobjectivelenshas2aof~175°).
j.Simplevs.compoundmicroscope(Figs.I.30I.32)
Inprinciple,arealimageofanydesiredmagnificationcanbeobtainedfromasinglepositivelens,butin
practicethisiscumbersomebecauseofthelonglensimagedistance.Oneormorelensescanbeusedto
magnifytheimageinstages(totalmagnificationequalingtheproductofthemagnificationsofeachlens).
Theimageformedbyonelensconstitutestheobjectforthesubsequentlens,whetherornotareal
intermediateimageisformed.
Comparisonofoneversestwostagemagnification:
Thefollowingdescriptionillustrateshowdifferentpathlengthsarerequiredtoachieveamagnificationof10,000Xusingeitheroneortwolenses
withf=2.0cm.
OneStageSystem:
TwoStageSystem:
Assumebothlenseshavef=2.0cmandarearrangedsoeachgives100Xmagnification.
Thus,M=100=x
i
/x
o
foreachstage.
FirstStage:
x
o
=2.02cm
x
i
=202.00cm
Therealimageformedinthefirststagebecomestheobjectforthesecondlens.
SecondStage:x
o
,x
i
sameasinthefirststage.
Totallengthofsystem
=lengthoffirststage+lengthofsecondstage
=(x
o
+x
i
)+(x
o
+x
i
)
=2(x
o
+x
i
)
=2(2.02+202.00)=408.04cm(4.08meters)
k.Problemset
Thefollowingproblemsareforyourownedificationtotesthowwellyouunderstandthebasicsoflensoptics.
1.Foreachsituationbelow,drawanaccurate(usegraphpaper)raydiagramshowingthepathof(atleasttwo)raysfromtheobjecttoimage.
Indicatewhethertheimageisrealorvirtualandspecifythedistanceoftheimagefromthelensandthemagnificationoftheimagewithrespect
totheobject.Ineachexample,thelensisconverging,withidenticalfrontandbackfocalpoints.Distancesareinarbitraryunits.Letf=lens
focallength,x
o
=distanceofobjectinfrontofthelens,andx
i
=distanceofimagebehindthelens.Theobjectmaybeanysize.
2.Inthefollowingexamples,therearetwoconverginglensesinsuccession.Drawraydiagramsshowingtheformationofboththeintermediate
andfinalimagesandgiveappropriateinformationaboutthenature(real/virtual),positions,andsizesoftheintermediateandfinalimages.What
isthemagnificationateachstageofimageformationandwhatisthemagnificationofthefinalimage?Thedistancefromthecenteroflens1(L1)
tothecenteroflens2(L2)equalsD.
I.A.5.ElectronOptics/ElectronLenses
a.Electronemission
Innershellelectronsinmetalatomsshieldtheelectricfieldofthenucleusthroughtherepulsiveforcestheyexertontheoutershell(valence)
electrons.Thustheattractionbetweenthevalenceelectronsandthenucleusisreduced.Metalatomsarecharacterizedashavingtwoloosely
boundvalenceelectronswhichmigratefreely(thisiswhymetalsaregoodelectricalconductors)andcanescapefromthemetalcompletelyif
sufficientadditionalenergyisimpartedtothem.Asthetemperatureofametalisincreased,thekineticenergyoftheelectronsincreasesbecause
ofincreasedthermalvibrationsofthemetalions,whichcollidemorefrequentlywiththeelectrons.Thermionicemissionisthetermusedto
describetheprocessbywhichthermalenergyissuppliedtolooselyboundelectronsinordertoformasourceofelectrons.
Atroomtemperatureelectronsareeffectivelypreventedfromescapingthesurfaceofthemetalowingtotheattractiveforceofthepositively
chargedions.Asthetemperatureisincreasedsomeelectronsacquiresufficientenergytoovercometheattractionandleavethemetal
temporarily.Metal,shapedasathinwire,caneasilybeheatedbypassinganelectriccurrentthroughit.Sincethemetalsurfacebecomes
positivelycharged,acertainlevelofenergy(workfunction)mustbesuppliedtoallowelectronstoescapefromthesurface.Eachmetalhasa
characteristicworkfunction.Tungsten,withalowworkfunction,emitsmoreelectronsthanmetalswithhigherworkfunctions(seealsopp.2930
andFig.I.59).
Ifastrongelectrostaticfieldisappliedinavacuumbetweenthewire(givenanegative,cathode,potential)andananode,theelectricfieldwill
causeelectronstoaccelerateawayfromthewiretowardstheanodesurface(Fig.I.33).Thespeedoftheelectronsdependsonthestrengthof
theelectrostaticfield(voltage)betweenthecathodeandanode(equation(3),Sec.I.A.3.b)Thenumberofelectronswhichleavethewire
dependsonthetemperaturetowhichthewireisheated,whichdependsonhowmuchfilamentcurrentpassesthroughthewire.
A"V"shapedwirewillhavethehighesttemperatureatthetip.Electronswithdrawnfromthefilamenttipcarryelectricchargestotheanode.This
electriccurrent,whichflowsbetweenthefilamentandtheanode,iscalledthebeamcurrent.
1)Electricfield/Equipotentials
Anelectricallychargedobjecthasassociatedwithitanelectricfield.Thus,anelectricallychargedparticle,whenbroughtnearachargedobject,
isinfluencedbyanelectricalforceinthevicinityoftheobject.Theforceisdirectedtowardthechargedobjectifthechargesareofopposite
signsandawayfromtheobjectiftheyareofsimilarsign.DEFINITION:Thedirectionofanelectricfieldisdefinedasthedirectionoftheforce
actingonapositivecharge.(Figs.I.3435)
Alongthelinesofforceconnectingthetwocharges,theelectricpotentialwillchangegraduallybetweentheextremevaluesrepresentedbythe
twocharges.DEFINITION:Equipotentiallinesdefinethepointsalongthelinesofforcewithidenticalelectricalpotential.Theseequipotential
surfacesarealwaysorientedperpendiculartothelinesofforce.Thechangesintheelectricpotentialaregradualinspace.
Electronswhichenterafieldbetweentwoparallelplatesinadirectionparalleltotheplatesareaffectedbytheforcedirectedperpendicularto
theplates(FigI.36).Theelectronswillbeattractedtowardthepositiveplate.Thepathchangesinaseriesofgradualstepsattheequipotential
surfaces.
FigureI.37showshowtheelectronpathis"refracted"attheequipotentialsurface.TheresultisfundamentallythesameasthatgivenbySnell's
Lawofrefractioninlightoptics.Aconsequenceofthisisthatasphericallycurvedequipotentialsurfaceexhibitsthepropertiesofalens.
FiguresI.38andI.39showhowbothpositive(converging)andnegative(diverging)electrostaticlensescanbeformed.Thisfeatureof
electrostaticlensesdiffersfromelectromagneticlenseswhichcanonlyactasconverginglenses.
2)Advantages/Disadvantagesofelectronlenses:
Thefactthattherefractiveindexdoesnotchangeabruptlyinelectronlenseshasoneadvantageinthattherearenotroublesomereflectionsat
equipotentialsasatglassinterfaces.Thereisaseriousdisadvantageinthatequipotentialscannotbeshapedandcombinedinarbitraryfashionto
correctforchromaticaberrationandothererrors.
Althoughelectronmicroscopeswhichemployelectrostaticlenseshavebeenmade,mostmicroscopesuseelectromagneticlenses.Amajorreason
isthatelectrostaticlensesaremoresensitivetothequalityofthevacuumandcleanlinessofthecomponentsthanareelectromagneticlenses.
Somelensaberrationsaremoresevereforelectrostaticlensescomparedtoelectromagneticlenses.Electrostaticlensesrequireverypowerful
electrostaticfieldswhichcanleadtoelectricalbreakdownor"arcingover"insidethecolumn,especiallyunderpoorvacuumconditions.Forthis
reason,electrostaticlensescannotbemadewithfocallengthsasshortasmagneticlenses.
b.Electrostaticlens
Abasicunderstandingofelectrostaticlensesisimportantfortwomainreasons:i)theelectrongunuseselectrostaticlensactiontoformthe
primarybeamsource,andii)itisquitecommonforachargetodeveloponthenonconductingcontaminationwhichmayaccumulateonphysical
apertures(suchastheobjectiveaperture)andtransformthemintoweakelectrostaticlenseswhichcandistorttheelectronimage.
3)Propertiesofelectrostaticlenses:
a)Anyaxiallysymmetricalelectrostaticfieldhasthepropertiesofalensforraysconfinedtotheparaxialregion.Alltheideallensformulasapply
toelectrostaticlenses.
b)Forelectronlenses,replaceÃ(f)forrefractiveindexinthelensequations(f=valueofthepotentialontheaxis).Intheimageformingsystem
ofmostTEMs,fisthesameonbothsidesofthelens(SeeSec.I.A.5.c).
c)Ifboundedbyregionswherefisconstant,anelectrostaticlensisalwaysconvergent.
c.Magneticfieldsandmagneticlenses
1)Magneticfield
Anelectriccurrentpassingthroughaconductorgivesrisetoamagneticfield.TheconventionisthatNisthedirectioninwhichthelinesofthe
magneticfieldpoint(Fig.I.40).Themagneticfluxisthetotalnumberoflinesandthefluxdensityisthenumberoflinesperunitareaofasurface.
UsetheRIGHThandruletodeterminethedirectionofthefield(thumbpointstowardcurrentdirectionandfingerscurlindirectionoffield.NOTE:
Byconvention,thedirectionofelectronflowisoppositetothatofcurrentflow.
Fluxdensitydependsonthepropertiesofthematerialsurroundingtheconductor.Ironinducesahigherfluxdensitythanairoravacuum.The
propertyofthematerialwhichaffectsthefluxdensityiscalledthepermeability,m,ofthematerial.Forairandvacuum,m=1.0.For
ferromagneticmaterialsitcanbeaslargeasseveralhundredthousand.
Iftheconductorhastheshapeofacircularloop,thelinesofforceformcirclesaroundtheloop.Thefluxdensityisgreatestatthecenterofthe
loop.Themagnetinthecenteroftheloopisorientedperpendiculartotheplaneoftheloopifthecurrentthroughtheloopissufficientlystrongto
eliminatetheinfluenceoftheearth'sfield.ThesideoftheloopatwhichthelinesofforceleavetheloopistheNorth(N)poleofthemagnet(Figs.
I.41,I.42).
Ifthewireiswoundinseveralturnsaroundacylindricalsurface(solenoid),eachturnwillcontributetotheinducedmagneticfield.Theflux
densityinthecenterofthecoilisgivenby:
Inthecaseofairandnonmagneticmaterials,µ=1.0andB=H.
Thepermeabilityofirondependsonthefieldstrength,H,anddecreasestounityathighfieldstrengthorwhenthefluxdensity,B=H(Fig.I.43).
Thehighpermeabilityofironisduetotheinducedmagneticfieldorientingmicroscopiccrystalregionsactingastinymagnetsintheiron.Allthese
tinymagnetsaddtheirmagneticfieldstotheinducedfield(Fig.I.44).Whenallmicromagnetsarenearlyoriented,theironwillaffecttheflux
densitytoadecreasingamountsincethereorientationofmicromagnetsisnearingcompletion.Thus,thepermeabilityofironathighfieldstrengths
approachesthatofemptyspace.Atthispointtheironreachesmagneticsaturation.
2)Hysteresis
Thestrengthofthelensdependstosomeextentonthepreviousmagnetichistoryof
thelens.Whenthecurrentinalensisreduced,thedecreaseinmagnetizationdoes
notretracethesamepathobtainedwhenthecurrentwasincreased(Fig.I.45).
Inductionofmagnetizationinvolvesaphysicalmovementwithinthemagnetized
material,requiringtheovercomeofacertaindegreeofinertia.Asaresult,
magnetizationtendstolagbehindthemagnetizingforceapplied.Inducedmagnetic
fluxcanonlybereturnedtozerobyapplicationofacurrentintheoppositedirection.
Aconsequenceofhysteresisisthatthelevelofcurrentusedtoenergizeamagnetic
lensDOESNOTpreciselyspecifythelensstrength(i.e.focallength).
NormalizationofTEMlensesisaccomplishedbyreducingthelenscurrenttozero
somepredeterminednumberoftimes.Hysteresismayalsobeminimizedbytakinga
lenstosaturationandthenreturningittotheworkingcurrentwithoutovershooting.
Whenthefieldstrengthisreducedtozero,somemagnetizationstillremainsintheiron
(residualmagnetizationorremanence).Anadvantageofsoftironisthefactthat,
whenusedinanelectromagnet,hysteresisislow.
Introductionofpiecesofironinamagneticfielddrasticallyaffectsthefluxdensity.
Magneticmaterialhasashieldingeffect,theeffectbeinggreaterthegreaterthe
permeability.Permalloy(mmetal)hasamaximumpermeabilityof80,000140,000
comparedtoironusedintransformers(~7000).mmetalpermeabilityislimitedtolower
fieldstrengthsthanthatatwhichironstillretainshighpermeability.Thismetalis
thereforeusefulforshieldingtheTEMfromexternalmagneticfields.
d.Theelectromagneticlens
1)Lensdesigndevelopment(Figs.I.46I.48)
Theefficiencyofthemagneticfieldproducedbyashortsolenoidwasfirstimproved
byencasingtheenergizingcoilinasheathofsoftironwhichhasthepropertyofconcentratingthelinesofforceinamagneticfieldandthus
becomingmagnetizedbyinduction.Inthiswayamuchmorepowerfulaxialmagneticfieldisobtainedforthesameamountofcurrentflowing
throughthesolenoid.Furtherdevelopmentinvolvedencasingtheentirecoilwithsoftironexceptatanarrowannulargapintheinsideofthecoil.
Thisproducesagreaterconcentrationofthemagneticfieldalongashortaxialdistance.Toachieveshorterfocallengthlenses(andobtaingreater
magnifications)asoftironpolepiecewithanopenaxialborewasintroducedatthepositionoftheannulargap.
MagneticlensesusedinTEMsarealwaysconstructedwithanironcircuittoproduceahighfieldstrengthacrossashortgap.Themagneticfields
forTEMlensesareintherangeof10,00020,000gauss.
2)Forcesactingonacurrentinamagneticfield
Theforceonanelectroninamagneticfieldisalwaysatrightanglestothevelocityandthedirectionofthefield(Figs.I.49,I.50,andI.52).The
fieldonlyactsonthevelocitycomponentwhichisdirectedperpendiculartothelinesofforce.Usethelefthandrule(Fig.I.51:firstfingerfor
fielddirection,middlefingerforcurrentdirection,andthumbfordirectionofforce).Rayspassingthroughthelensareturnedthroughanangle
whichdoesNOTdependonthedistanceoftheraysfromtheaxis.Allelectronscontainedinagivenmeridionalplanebeforeenteringthefieldare
containedinarotatingmeridionalplaneastheypassthroughthelens,andthentheyleavethelenscoplanar.
Whenelectronsenterthelenstheyencounterasidewaysforcewhichcausestheelectrontorotate
asitcontinuesthroughthelens(Figs.I.53I.57).Sincetheradialcomponentofthemagneticfield
reversesafterthecenterofthelens,therotationalvelocitysetupinthefirsthalfofthelensis
countered.Theelectronenteredthelenswithoutangularmomentumabouttheaxisandleaves
withoutangularmomentum.Theneteffectisadeflectiontowardtheaxis,whichitmustcrossatthe
focalpointf
2
.Theanglebetweentheobjectvectorandtheimagevectoris180°+q,whereas,for
glasslensesandelectrostaticlenses,theanglebetweenarealobjectandtheimageisexactly180°.
Sincetheradialforceisdirectedtowardtheaxis,thelensisconvergentnomatterwhatthedirection
ofthefield.
3)Propertiesofamagneticlens:
Anyaxiallysymmetricmagneticfieldhasthepropertiesofanideallens.Alltheformulasfortheideallensmaybeapplied.
Magneticlensesarealwaysconvergent.Theconventional,axiallysymmetriclensisalwaysboundedbyregionswhicharefieldfree,the
consequencebeingthatthenetactionofelectronlensesisinevitablyconvergent.Limitedregionsmaybedivergentbutnotthelensasawhole.
Theseriousconsequenceofthisisthatneithersphericalorchromaticaberrationscanbecorrectedasisdoneinlightopticsbytheusedoublets
ofpositiveandnegativelenses.
Intheabsenceofelectrostaticfields,therefractiveindexisthesameinobjectandimagespace,thereforef
1
=f
2
.
Electronstravelingthroughaxiallysymmetricfieldsexperienceaspiraltrajectoryofdiminishingradius.Theimagevectorisatanangle180°+qto
theobjectvector.
Thedeflectionoftheelectrontowardstheaxismeansthatanelectronenteringthelensparalleltoitsaxiswillcrosstheaxisafterhavingpassed
thelens.Thedeflectionwillincreasewiththedistancefromtheaxis.Thus,abeamofelectronsinparallelpathsparalleltotheaxisofthelenswill
befocusedtoanimagepointontheaxiswhichrepresentsthesecond(back)focalpointofthelens(f
2
).Notethatmagneticlensesarehighly
inefficientinthatonlyaminorportionofthetotalfieldstrengthisactuallyeffectiveinfocusingtheelectron.
4)Magneticlensfocallength
Inamagneticelectronlensthefocallengthisdeterminedbythefieldstrengthinthelensgapandbythespeedoftheelectrons(determinedby
theacceleratingvoltage).
Formagneticlenses,focusingisachievedbyvaryingthecurrentwhichpassesthroughtheelectromagnet.Thisinturnchangesthestrengthof
themagneticfieldandtherebyaltersthefocallengthofthelensandisequivalenttoacombinedchangeinboththe"refractiveindex"and
"curvatureofsurface".Forabeamofmoreenergeticelectrons,thelenscurrenthastobeincreasedinordertokeepthefocallengthconstant.
FocallengthandcurrentareNOTlinearlyrelated:strengthincreasesinasigmoidfashion(Fig.I.45)ascurrentincreasesuntilapointisreached
wherethelensissaturatedandnofurtherincreaseinlensstrengthcanbeachieved.
Sincethefocallengthofthelensisdirectlyproportionaltotheacceleratingvoltage,avariationinthevelocityoftheelectronsintheimaging
beamaffectsimagequalitybyeliminatingperfectfocus(chromaticaberration).
5)Magneticlensdesign:(Figs.I.46,I.47).
Condenserlensesusuallyhavearelativelylargeboreandspacingwhichresultsinalongfieldandlongfocallength.
Typicalconstructionoftheobjectivelensproducesastrongfieldofshortaxialextent(i.e.shortfocallengthbetween(1.53mm)necessaryfor
formationofimagesathighmagnification.Thespecimenisplacedwithinthemagneticfieldoftheobjectivelens.Thus,anyfieldintroducedby
contaminantsinthespecimencandistortthefieldofthelens.Notethatthisalsomeansthatpartofthelensfield("prefield")isonthefrontside
oftheobjectandaffectstheelectronbeambeforeitpassesthroughtheobject.
Mostofatypicalmagneticlensliesoutsidethevacuumofthemicroscope.Onlythoseregionsthroughwhichtheelectronbeampassesareinhigh
vacuum.Magneticlensesmustbewatercooledtodissipatethelargeamountsofheatproducedbythecurrentsintheelectromagnetcoils.
DATE NAME EVENT
1897 J.J.Thompson Discoverstheelectron
1924 LouisdeBroglie Identifiesawavelengthtomovingelectrons
l =h/mv
where
l =wavelength
h=Planck'sconstant
m=mass
v=velocity
(Foranelectronat60kVl=0.005nm)
1926 H.Busch Magneticorelectricfieldsactaslensesforelectrons
1929 E.Ruska Ph.Dthesisonmagneticlenses
1931 Knoll&Ruska Firstelectronmicroscopebuilt
1931 Davisson&Calbrick Propertiesofelectrostaticlenses
1934 Driest&Muller SurpassresolutionoftheLM
1938 vonBorries&Ruska FirstpracticalEM(Siemens)10nmresolution
1940 RCA CommercialEMwith2.4nmresolution
1945 1.0nmresolution
Fig.I.1Comparisonoflightandelectronmicroscopes.Ineach
instrument,illuminationfromthesource(lamp,filamentinthe
electrongun)isfocusedbythecondenserlensontothespecimen.
Afirstmagnifiedimageisformedbytheobjectivelens.Thisimage
isfurthermagnifiedbytheprojectorlensontoagroundglass
screen(light)orfluorescentscreen(electrons).(FromAgar,p.8)
Fig.I.2CrosssectionalviewofthePhilipsEM300.(FromAgar,p.40)
Toviewtheanimatedmicroscope,clickhere.
Note:QuickTimePlugInrequired
(Thiscanbedownloadedathttp://apple.com/quicktime/download)
Fig.I.3Sectionthroughacomplex
doublecondenser6lensPhilips
EM200electronmicroscope.(From
Meek,p.99)
Fig.I.4Thestatisticalnatureofdiffraction
patterns.(FromHall,p.13)
"Theprecisenatureof'electronwaves'or'matterwaves'isverydifficulttounderstandordescribeinmaterialterms.Electronwavesarenot
electromagneticradiationofthekindtowhichlight,Xraysandradiowavesbelong.Theyconstituteasortofquantumor'packet'ofradiationwhich
accompanieseachindividualelectron,followingitspathandnotradiatingoutwardsfromit."(Meek,1976,pp.4849).
V l (nm)
v(
•
10
10
cm/sec)
v/c
10,000 0.0123 0.593 0.198
50,000 0.0055 1.326 0.442
100,000 0.0039 1.875 0.625
1,000,000 0.0012 5.930 1.977!
V l (nm)
v(
•
10
10
cm/sec)
v/c
10,000 0.0123 0.593 0.195
50,000 0.0055 1.326 0.414
100,000 0.0039 1.875 0.548
1,000,000 0.0012 5.930 0.941
FigI.5Aperfectpointsourcecannotbe
imagedbyalensasaperfectpointimagedue
tothepresenceoftheapertureAB(which
maybetheedgeofthelens).Diffractionat
thisaperturegivesrisetoaseriesoffringes,
whichsurroundtheimageformedofthepoint
source.Thepatternproducediscalledan'Airy'
disk.(FromMeek1sted.,p.35)
Fig.I.6Wheneverawavefrontstrikesa
barrier,itcanbendaroundthecorner'by
givingrisetoasecondarywavefrontatthe
edge,sinceeachpointonthewavefrontcan
giverisetoanewsourceofwaves.This
phenomenoniscalled'diffraction'.(FromMeek
1sted.,p.22)
Fig.I.7Diffractionpattern(right)formedbyanirregularlyshapedaperture
(left).(FromYoung,p.95)
Fig.I.8(a)
Photographof
theedgeofa
razorblade
illuminatedby
monochromatic
(blue)light
rendered
coherentby
passing
througha
narrowslit.(b)
Microdensitometer
tracingofthe
negativefrom
whichthe
photograph
wasmade.
FourFresnel
fringescanbe
distinguished.
(FromMeek1st
ed.,p.27)
(a)
(b)
(a) (c)
(b)
Fig.I.9(a)Fresnelfringesformed
byelectrons.Thesefringesare
formedoutsidetheedgeofahole
(white)inacarbonfilm(black).(b)
Amicrodensitometertracingofthe
fringesystem;thepatternis
identicalwiththeFresnelfringe
systemformedbyvisiblelight(see
Fig.I.8).(c)Anunderfocusedimage
ofaholeinafilm,showinga
completesystemofabout40
Fresnelfringesinsidethehole.
(FromMeek1sted.,pp.2930)
Fig.I.10Diffractionimagesoftwo
easilyresolvedpoints.(From
Slayter,p.243)
Fig.I.11Imagesoftwo
incoherentlyilluminatedpointsat
thelimitofresolution.(a)individual
intensities;(b)summedintensities.
(FromSlayter,p.244)
Fig.I.12Examplesofwhatoccurswhentwo
wavesofthesamewavelengthandequal
amplitudeadd.Ineachexample,thetwo
separatewavesareshownontheleftand
theirsumorresultantwaveontheright.The
differentexamplesarecharacterizedbyvarying
phasedifferences.Thephaseofawave
(usuallyexpressedasafractionofthe
wavelengthorindegrees)isthepositionofa
crestrelativetosomearbitrarypoint.Although
thephaseofagivenwavevarieswithtimeas
thewavetravels,thedifferenceinphaseofthe
twowavesofthesamewavelengthwiththe
samevelocity,isindependentoftime.Such
wavescaninterferewithoneanother.The
resultantwavehasthesamewavelength,l .
(a)Phasedifferencezero.Thewavestotally
reinforceandaresaidtobe"inphase"orto
showconstructiveinterference.
(b)Phasedifferencel /4.Partialreinforcement,
givingawaveofamplitude1.4(intensity2.0).
(c)Phasedifferencel /2.Thewavesare"outof
phase"andthereistotaldestructive
interferencetogivenoresultantwaveora
wavewithamplitude0(intensity0).(From
GluskerandTrueblood,p.19)
Fig.I.13Photographofan
interferencepatterninwater
wavesformedbythe
superpositionofwavesfromtwo
sourcesoscillatinginphasewith
thesamefrequency.(FromYoung,
p.22)
Fig.I.14Theangularapertureofthe
eyeisrelativelysmall.(FromMeek,
1sted.,p.13)
Fig.I.15Increasingtheangular
apertureoftheeyewithalens.The
lensallowstheobjecttobeheld
closertotheeye,whichisthereby
enabledtogathermoreinformation.
(FromMeek1sted.,p.14)
Fig.I.16Theinteractionofwaves
withanobstacle.Theboatridesthe
longwavelengthoceanwave,but
reflectsthesmallwavelength
surfaceripple.Anobserverwho
wishestodetectthepresenceof
theboatcandosoonlyby
observingwaveswhichhave
wavelengthssmallerthan,or
comparableto,thelengthofthe
boat.(FromSherwood,p.19)
Maximummagnification=
resolvingpoweroftheeye
resolvingpowerofthemicroscope
(a)
Fig.I.17(a)TwoAiry
disksrepresenting
twoimagepoints
shownatincreasing
separationfromleft
toright.Inthe
pictureatthe
extremerightthe
twodiskscanbe
distinguishedas
separatedisks.
(b)Theintensity
distributionatanAiry
disk.R,halfwidthof
thecentralmaximum
representedbya
bellshapedcurve.
(c)TheRayleigh
criteriaforresolution.
(FromSjostrand,
p.115)
i=r
Fig.I.18Reflection.(FromSlayter,
p.4)
Fig.I.19Refraction.(FromSlayter,
p.6)
Fig.I.20Principalraydiagramsshowing
imageformationbyaconvexlens.
(a)Whentheobjectdistanceisgreater
thanthefocallength,areal,inverted
imageisformed.
(b)Whentheobjectdistanceisless
thanthefocallength,avirtual,erect
imageisformed;itspositionis
obtainedbyprojectingtheprincipal
raysbackward.Theraysappearto
comefrompointQ.(FromYoung,
p.127)
Fig.I.21Definitionof
principalfocus,F,inimage
spaceofalens.(From
Sjostrand,p.20)
Fig.I.22Focusingeffectoflenson
raysoriginatingfrompointson
principalaxislocatedatdifferent
distancesfromthelens.(From
Sjostrand,p.21)
Fig.I.23Definitionofprincipal
focusinobjectspaceF1ofa
lens.(FromSjostrand,p.21)
Fig.I.24VirtualimageQof
objectpointlocatedbetween
principalfocusinobjectspace
andthelens.(FromSjostrand,
p.21)
Fig.I.25Constructionoftheimage
ofanobjectbymeansofray
tracing.(FromSjostrand,p.22)
Fig.I.26Magnifyingeffectof
apositivelens.(From
Sjostrand,p.22)
Fig.I.27Virtualmagnified
imageofobjectlocated
betweenprincipalfocusin
objectspaceandthelens.
(FromSjostrand,p.22)
Fig.I.28Amagnifyingglassformsan
enlarged,erectvirtualimage.The
angularsizeofthisimageis
approximately4"/15"or4/15.The
angularsizeoftheobjectatthe
closestdistanceforcomfortable
viewingis1"/10"or1/10.The
magnificationinthissituationis(4/15)/
(1/10),or22/3.(FromYoung,p.130)
Fig.I.29Theangularapertureofa
lens.Theangle2a isthe
acceptanceangleofthelens,and
thelargeritcanbemade,themore
informationcanthelenstransmit.A
largelensofhighaperturecan
thereforetellusmoreaboutan
objectthanasmalllensoflow
power.(FromMeek1sted.,p.12)
Fig.I.30Raydiagramforhighmagnification
modeofoperation.Notethateachlens
formsarealimage,withimageinversion.
I0istheimageformedbytheobjective
lensO,I1isformedbythefirstprojector
lensP1andI2bythesecondprojectorP2,
onthescreen.(FromAgar,p.30)
Fig.I.31Left:raydiagramofthe3realimagemediumandhighmagnificationimagingsystemofa3lens
microscope.Center:2realimageverylowor'scan'magnificationrangeofa3lensmicroscope.Right:2real
imagelowmagnificationsystemofa3lensmicroscope.(FromMeek1sted.,pp.118,120121)
Fig.I.32Raydiagramforacompleteelectron
microscope.FilamentF,condenser1lensC1,
condenser2lensC2,condenserapertureCA,
specimenS,objectivelensO,objectiveaperture
OA(inbackfocalplane).1stintermediateimage
andselectorapertureSA.IntermediatelensP1,
secondintermediateimageI2,projectorlensP2
andfinalimageonthefluorescentscreenFC.
(FromAgar,p.35)
a)f=2.0
x
o
=5.0
e)f=4.0
x
o
=3.0
b)f=10.5
x
o
=21.0
f)f=13.3
x
o
=13.3
c)f=3.5
x
o
=3.0
g)f=3.142
x
o
=0.0
d)f=5.0
x
o
=2.5
a)D=8.0
L1:f=2.0
x
o
=4.0
L2:f=3.0
b)D=8.0
L1:f=2.0
x
o
=6.0
L2:f=3.0
c)D=4.0
L1:f=2.0
x
o
=3.0
L2:f=2.0
FigI.33Accelerationofelectronin
electricfield.(FromSjostrand,p.26)
Fig.I.34Linesofforceatapositively
chargedsphericalbody.(FromSjostrand,
p.32)
Fig.I.35Linesofforceandequipotential
surfaces(stippledlines)associatedwith
twoequalchargesofoppositesign.
(FromSjostrand,p.32)
Fig.I.36Equipotentialsurfacesattwoparallel
platesofoppositechargeswiththepathofan
electronindicatedwithinthehomogeneous
partofthefield.(FromSjostrand,p.33)
Fig.I.37Refractionofelectronatan
equipotentialsurface.(FromSjostrand,p.33)
Fig.I.38.Negativelensactionof
electrostaticfieldatanaperturewhen
V2V1>V3V2.(FromSjostrand,
p.34)
Fig.I.39.Positivelensactionatan
aperturewhenV2V1<V3V2.
(FromSjostrand,p.34)
Fig.I.40Magneticfieldinducedbycurrent
passingthroughaconductor.(From
Sjostrand,p.35)
Fig.I.41Magneticfieldinducedbycurrent
passingthroughasolenoid.(From
Sjostrand,p.37)
Fig.I.42Solenoidwithironcore.(From
Sjostrand,p.40)
Fig.I.43a.Dependenceofpermeabilityonfluxdensity,B.
b.RelationshipbetweenfluxdensityBandfieldstrength.
(FromSjostrand,p.38).
Fig.I.44Magnetization.(FromSlayter,
p.361)
Fig.I.45Curves
showinghowthe
magnetizationof
softiron(lens
strength)is
relatedtothe
magnetizing
force(lens
current).An
unmagnetized
lensstartsfrom
thepointOand
followsthepath
OAaslens
current
increases.Atthe
pointA,further
increaseinlens
currentproduces
nofurther
increaseinlens
strength;thelensissaidtobe'saturated'.Whenlenscurrent
isreduced,thepathOAisnotretraced;adifferentpathABis
followed.Thisdisplacementiscalled'hysteresis'.Atzero
current(pointB),someresiduallensstrengthremains;thisis
called'remanence'.Tobringthelensbacktozerostrength,a
reversecurrentOCmustbeapplied.Lensstrengththen
increaseswithincreasingreversecurrent,followingthepath
CD.Thepolarityofthelenschanges,butthisdoesnotaffect
itsfocusingpower;onlythespiralelectronpathisreversed.
Becauseofhysteresis,itisnotpossibletocalibratealens
currentmeteraccuratelyintermsoflensstrengthor
magnification.
Fig.I.46Evolutionofmagneticelectron
lenses.(A)Shortsolenoidusedasa
magneticlens.(B)Softironcasing
enclosingoutersurfaceofthesolenoid,
thusconcentratingthefield.(C)Soft
ironencasingthesolenoidexceptata
narrowannulargaptherebyreducing
themagneticfieldtoaveryshortregion
alongthelensaxis.(D)Modern
objectivelensconsistingofasoftiron
encasedsolenoidandsoftironpole
piecessoastohaveanenormously
concentratedfieldatthelevelofthe
annulargap.(FromWischnizter2nded.,
p.33)
Fig.I.47(a)Amagneticlensconsisting
ofatightlywoundcoilandasoftiron
shroudsurroundingthecoilexceptfor
asmallgap.Thefieldisconcentratedin
thatgap.(b)Shortfocallength
electromagneticlenswithpolepieces.
(FromSjostrand,p.50)
Fig.I.48Fieldstrengthdistribution
curves.ThecurvesADcorrespondto
therespectivelensesillustratedinFig.
I.46.Eachrepresentsthefieldstrength
alongthelongaxisofthelens.The
changesintheshapeofthecurves
representtheshorteningor
concentrationofthefieldovera
shorteraxialdistance.Hz=
longitudinalmagneticfield.Z=
distancealongtheaxisofsymmetry.
(FromWischnizter2nded.,p.33)
Fig.I.49TheforceFactingon
astraightconductorina
homogeneousmagneticfield
offluxdensityBwhencurrent
Iispassedthroughthe
conductor.(FromSjostrand,
p.43)
Fig.I.50Pathofanelectronina
magneticfield.(A)Inalarge,uniform
magneticfield.(B)Inasmall,uniform
magneticfield.(FromWischnitzer2nd
ed.,p.25)
Fig.I.51Lefthandthumbrule.
(FromSjostrand,p.43)
Fig.I.52Thompson'sexperiment.A
streamofelectronsoriginatingfroma
sourceandpassing,invacuo,through
amagneticfieldproducedbyapairof
magnetswillbedeflected.The
directionofdeflectiondemonstrates
thatelectronsarenegativelycharged
particlesofmatter.(FromWischnitzer
2nded.,p.25)
Fig.I.53Actionofasolenoidonan
electronbeam.Anelectriccurrent
passingthroughthecoilproducesan
axialmagneticfield.Thisisthe
refractingmediumfortheelectrons.An
electronstartingatapointontheaxisA
andatanangletoitfollowsaspiral
path,returningtotheaxisatthepoint
B.Theactionisbasicallysimilartothat
oftheconverginglightlensshownin
Fig.I.20.(FromMeek1sted.,p.8)
Fig.I.54Actionofthemagnetic
lens.(a)Inperspective.(b)
Electrontrajectoryin
projection,alongdirectionof
propagation.(c)Electron
trajectoryinprojection,side
view.(FromSlayter,p.358)
Fig.I.55Componentsofthe
vectorHneartheaxisoffields
withaxialsymmetry.His
representedbytwo
components,Hz,the
componentinthez(axial)
direction,andHr,the
compnentinther(radial)
direction.(FromHall,p.85)
Fig.I.56Theycomponentof
themagneticfieldina
magneticlensisoriented
perpendiculartothedirection
ofanelectronenteringthe
lensalongapathparallelto
thelensaxis.Thisy
componentwillaffectthe
electron,deflectingitinthex
directionasindicatedbythe
arrowmarkedvx.(From
Sjostrand,p.48)
Fig.I.57Thezcomponentofthemagneticfield
andthexvelocitycomponentoftheelectron
inamagneticlensinteract,deflectingthe
electronintheydirectiontowardthelens
axis.(FromSjostrand,p.49)
CuuDuongThanCong.com https://fb.com/tailieudientucntt
cuu duong than cong . com

I.THEMICROSCOPE
I.A.PRINCIPLESOFTHETRANSMISSIONELECTRONMICROSCOPE(TEM)
I.A.1.OriginoftheTransmissionElectronMicroscope
I.A.2.ComparisonofLight(LM)andElectronMicroscopes(Fig.I.1)
a.Similarities(Arrangementandfunctionofcomponentsaresimilar)
1)Illuminationsystem:producesrequiredradiationanddirectsitontothespecimen.Consistsofasource,whichemitstheradiation,anda
condenserlens,whichfocusestheilluminatingbeam(allowingvariationsofintensitytobemade)onthespecimen.
2)Specimenstage:situatedbetweentheilluminationandimagingsystems.
3)Imagingsystem:Lenseswhichtogetherproducethefinalmagnifiedimageofthespecimen.Consistsofi)anobjectivelenswhichfocusesthe
beamafteritpassesthroughthespecimenandformsanintermediateimageofthespecimenandii)theprojectorlens(es)whichmagnifiesa
portionoftheintermediateimagetoformthefinalimage.
4)Imagerecordingsystem:Convertstheradiationintoapermanentimage(typicallyonaphotographicemulsion)thatcanbeviewed.
b.Differences
1)Opticallensesaregenerallymadeofglasswithfixedfocallengthswhereasmagneticlensesareconstructedwithferromagneticmaterialsand
windingsofcopperwireproducingafocallengthwhichcanbechangedbyvaryingthecurrentthroughthecoil.
2)MagnificationintheLMisgenerallychangedbyswitchingbetweendifferentpowerobjectivelensesmountedonarotatingturretabovethe
specimen.Itcanalsobechangedifoculars(eyepieces)ofdifferentpowerareused.IntheTEMthemagnification(focallength)oftheobjective
remainsfixedwhilethefocallengthoftheprojectorlensischangedtovarymagnification.
3)TheLMhasasmalldepthoffield,thusdifferentfocallevelscanbeseeninthespecimen.Thelarge(relative)depthoffieldintheTEMmeans
thattheentire(thin)specimenisinfocussimultaneously.
4)Mechanismsofimageformationvary(phaseandamplitudecontrast).
5)TEMsaregenerallyconstructedwiththeradiationsourceatthetopoftheinstrument:thesourceisgenerallysituatedatthebottomofLMs.
6)TEMisoperatedathighvacuum(sincethemeanfreepathofelectronsinairisverysmall)somostspecimens(biological)mustbedehydrated
(i.e.dead!!).
7)TEMspecimens(biological)arerapidlydamagedbytheelectronbeam.
8)TEMscanachievehighermagnificationandbetterresolutionthanLMs.
9)Pricetag!!!(100xmorethanLM)
I.A.3.Photons/Electrons
a.Dualconceptofwaveandparticle(Fig.I.4)
Lighthaspropertiesbothofaparticleandawave.Thisdualnatureisrequiredtosatisfactorilyexplaintheresultsofvariousphysicalexperiments.
Thediffractionoflight(bendingaroundcorners)illustratesthewavenature.TheWAVETHEORYisbasedonthestatisticalnatureofeventsand
haslittlemeaningwithrespecttothebehaviorofsingleparticles.ThewavetheorywasdevelopedandexpoundedbyHuygens(16291695)and
Hooke(16381703).TheCORPUSCULARTHEORYwasproposedbyNewton(16421727)andbecamethemoreacceptedtheoryevenafter
demonstrationofdiffractionbyYoung(17731829)andinterferencebyFresnel(17881827).Atabout1850,thewavetheorycamebackinto
favoruntilabout1900whenmoreevidenceforthecorpusculartheorywasdiscovered.
QUANTUMTHEORY(PlanckandEinstein)providesthebasisforexplainingthephenomenaofINTERFERENCE,DIFFRACTIONandthe
PHOTOELECTRICeffect(lightfallingoncertainmetalscausethemtoemitelectrons)andthusformsacommonbasisforexplainingthenatureof
actionoflight.Thetransferofenergybetweenlightandmatteroccursonlyindiscretequantitiesproportionaltothefrequencyofthe
lightwave.
E=hJ
where
E=energyofphoton(joules)
h=Planck'sconstant(6.624
•
10
34
joulesec)
J=frequency(cycles/sec)
b.Electronvelocityandwavelength
Therelationbetweenthewavelength(l )ofaparticleofmass,m,movingatavelocity,v,isgivenbytheDeBrogliewaveequation:
(1)
Anelectronofchargee(1.6
•
10
19
coulomb),andmassm(9.11
•
10
28
gm),whenpassingthroughapotentialdifferenceofVvolts(expressedin
joules/coulomb),hasakineticenergy:
(2)
Solvingforvelocity:
(3)
substitutingintotheDeBroglieequation(1):
(4)
Since1joule=10
7
dyne
•
cm=10
7
cm
2
•
gm/sec
2
(5)
Thus,forexample,ifV=60,000volts,l =0.005nm.
Fromequation(3)theelectronvelocitycanbecalculatedifVisknown:
(6)
Thefollowingtableillustratesthat,athighvoltage,electronvelocityiscomparabletothespeedoflightinavacuum(c=3
•
10
10
cm/sec).
Theequationbreaksdownwhenthevelocityoftheelectronapproachesthespeedoflightbecausearelativisticcorrectionmustbemadeforthe
valueofthemasswhere:
(7)
Therelationbetweenl andVismorecorrectlygivenby:(seeHall(1966)pp.3334)
(8)
Thefollowingtableisobtainedwhenrelativityeffectsareincluded:
c.Interference/diffraction/coherence
Anideallenssystemobtainsanexactimageoftheobject(eachpointfaithfullyreproduced).Thephenomenaofdiffractionmakesthis
unattainable(Figs.I.5,I.6).
Diffractionphenomenainvolvesthebendingofthepathofradiationpassingclosetoanobstacle(Fig.I.6).Thisresultsinaspreadingofthe
radiationintotheregionbehindtheobstructionthatthewavespassed.Thediffractionatedgescontributestothecontrastatwhichanedgecan
beobserved.Diffractionalsolimitstheresolvingpowerofthemicroscopesincetheimagepointproducedbyalensisadiffractionimageofthe
openingofthelensortheaperturerestrictingtheeffectiveopeningofthelens(Fig.I.5).
Ifthelightsourceandtheplaneatwhichthediffractionpatternisobservedareatfinitedistancesfromtheedge,thephenomenoniscalled
Fresneldiffraction.Thepatternisdescribedasduetointerferencebetweenthenondiffractedlightandawaveoflightdiffractedattheedge.
Theresultingsuperpositiongivesrisetoaseriesofdiffractionfringesorientedparalleltotheedgeandrepresentingperiodicallyvaryingbrightness,
maximaandminima.(Figs.I.7,1.8,I.9).
Coherence:Aprerequisiteforinterferenceisasuperpositionofwavesystemswhosephasedifferenceremainsconstantintime.Twobeams
arecoherentif,whencombined,theyproduceaninterferencepattern.Thebeamsareincoherentwhentheyareincapableofproducingan
interferencepattern.Twobeamsoflightfromselfluminoussourcesareincoherent.Iflightfromthetwosourcesfallsonascreen,theresultant
intensityissimplythesumofthetwointensitieswhichwouldoccurfromeachsourceseparately(Figs.I.10,I.11).Inpracticeanemittingsource
hasfiniteextentandeachpointofthesourcecanbeconsideredtogeneratelight.EachsourcegivesrisetoasystemofFresnelfringesatthe
edge.Thesuperpositionofthesefringesystemsisfairlygoodforthefirstmaximaandminimabutfartherawayfromtheedgeshadowtheoverlap
ofthefringepatternsbecomessufficientlyrandomtomakethefringesdisappear.Thenatureofwaves,phase,amplitude,andinterferenceare
illustratedinFigs.I.12andI.13.
d.Resolution
1)Definitions:
RESOLUTION:abilitytodistinguishcloselyspacedpointsasseparatepoints.
RESOLUTIONLIMIT:smallestseparationofpointswhichcanberecognizedasdistinct.
RESOLVINGPOWER:resolutionachievedbyaparticularinstrumentunderoptimumviewingconditions.
2)Distinctionbetweenresolutionandresolvingpower:
Notethedistinctionbetweenresolutionandresolvingpower.Resolvingpowerisapropertyoftheinstrumentandisaquantitythatmaybe
estimatedontheoreticalgrounds.Resolutionisequaltoorpoorerthantheresolvingpowerandisthequantityobservedunderanygivenset
ofexperimentalconditions.IntheTEM,especiallywithbiologicalsamples,theresolutionachievedmaybeconsiderablyinferiortothetheoretical
resolvingpoweroftheinstrument.
Microscopyisthescienceofseeingtheverysmall.Underidealconditions,theeyeresolvesabout1minuteofarc(=1/60degree=2.9x10
4
radian;recallthereare2p radiansin360°)andsinceitcanfocusdowntoabout250mm,thesmallestobjectwecanresolveisabout0.07mm
(70mm)(Fig.I.14).Thislimitisrelatedtothesizeofthereceptorsintheretinaoftheeye.Thefunctionofamicroscopeistomagnifytheimage
fallingontheretina(Fig.I.15).Theadvantageoflightandelectronmicroscopesisthattheyeffectivelygettheobjectclosertotheeyesoa
magnifiedimageisobtainedandmoredetailcanbediscerned.
TENNISBALLANALOGY:Eyecanresolve3cmat100meters,thusatennisballisclearlyvisible.Butifthetennisballisheldupagainstawhite
background,thevisibilitydecreases(becauseofthedecreaseincontrast).
3)Abbecriteriaofresolution:
Thefundamentalnatureoflightposeslimitsonthedetailthatcanberesolved(Fig.I.16).Abbe(1893)showedthatthesmallestresolvable
distanceisabout1/2thewavelengthoflightused.Thus,1/2thewavelengthoftheradiationusedistheultimateresolvingpowerofany
instrument.Thislimitstheusablemagnificationofopticalmicroscopesto<1000X.Atfirstitwasthoughtthatxraymicroscopeswouldbeuseful
buttherefractiveindexofsubstancesforxraysisnearly=1,thusrefractinglensescannotbemadeforxrays,andconsequently,xrayscannot
beeasilyfocusedtoformimages.
4)Magnificationlimits:
Themaximummagnificationofaninstrumentislimitedaccordingtothefollowingrelationship:
Thus,fortheLM,witharesolvingpowerofapproximately0.25µm,themaximum(useful)magnificationisabout250µm/0.25µm=1000X.Thevalue
usedfortheresolvingpoweroftheeyeinthisexample(250µm)representsamorerealisticviewingcondition.Anymagnificationabovethevalue
givenbytheaboveformularepresentsemptymagnification,sincesuchmagnificationleadstonomoreusefulinformationbutratheramagnified
blur.
AccordingtotheAbbecriteria,at60,000volts,theTEMshouldhavearesolvingpowerofabout0.0025nm.Thisshouldallowamaximumuseful
magnificationofabout100milliontimes!!!Inpractice,themaximumusefulmagnificationoftheTEMoperatedat60kVislimitedtomuchlessthan
1,000,000X.Thus,althoughtheLMnearlyobeystheAbbecriteria,theTEMfallsshortbyaconsiderableamount.Themainlimitingfactorinthe
TEM,withrespecttoachievingthetheoreticalresolvingpoweroftheinstrument,concernsthenatureoftheimaginglensesandtheprocessof
imageformation.
5)Rayleighcriteria(practicalbutarbitrary):(Fig.I.17).
Itistheabilityofmicroscopestomakeobjectpointswhichareclosetogetherappearintheimageasseparatepoints.Anideallenstakeseach
objectpointandrepresentsitexactlyasapointintheimage.Areallenstakeseachobjectpointandspreadsitoutintoacirculardisk(Airy
disk)intheimageplanewhosediameterdependsontheangularapertureofthelens.
Theshortestdistancebetween2disksatwhichthetwodisksappearpartiallyseparatedcorrespondstoabout1/2thewidthofthedisks.The
distance,d,inobjectspaceisgivenby:
d=0.61l /n
•
sina
where
l =wavelenghtoftheradiation
n=refractiveindexofthemedia
a=semiangularapertureofthelens
NOTE:n
•
sina=thenumericalaperture(N.A.)ofthelens.
Thus,tomaximizeresolvingpower,l mustbedecreased,nincreased,oraincreased.Recallthatweareconcernedatthemomentwithan
aberrationfreeopticalsystem.Thevaluefortheconstant(0.61)iscontroversialbecauseitdependsonthecoherenceoftheradiationanda
criteriaofvisibility.
FortheLM,usingoilimmersionoptics(n=1.5),sina=0.87,andvioletlight(l =400nm),d=0.2µm.Theonlywaytoimprovetheresolutionisto
uselightofshorterwavelengthsinceN.A.cannotbeincreasedbeyond~1.5.FortheTEM,n=1(vacuum),sina=10
2
andl =0.005nmfor60kV
electrons,thusd=0.3nm.
I.A.4.Optics(LensTheory)
a.Basiclawsofclassicalgeometricaloptics
1)Rectilinearpropagationoflightwhenn(refractiveindex)isconstant.
2)Lawofreflection:
3)Lawofrefraction(Snell'sLaw):
4)Independenceofrays.Theassumptionismadethatlightraystravelindependentlythroughspace.
Theselawsholdforelectrons,except#4,ifthecurrentdensityistoohighwhennegativechargedelectronscaninterfere.
b.Classicalvs.electronoptics
1)Classicaloptics:Therefractiveindexchangesabruptlyatasurfaceandisconstantbetweenthesurfaces.Therefractionoflightatsurfaces
separatingmediaofdifferentrefractiveindicesmakesitpossibletoconstructimaginglenses.Glasssurfacescanbeshaped.
2)Electronoptics:Here,changesintherefractiveindexaregradualsoraysarecontinuouscurvesratherthanbrokenstraightlines.Refraction
ofelectronsmustbeaccomplishedbyfieldsinspacearoundchargedelectrodesorsolenoids,andthesefieldscanassumeonlycertaindistributions
consistentwithfieldtheory.
c.Geometricalandphysicaloptics
Thefundamentalprinciplesofopticsgovernthedesignandoperationofboththelightandelectronmicroscopes.Thebasicopticalprinciples
involvingtheuseofrefractileelementsorlensesinordertoformmagnifiedimagesareidenticalinboththeLMandTEM.TheTEMdiffersfromthe
LMonlyintheradiationitusesandinthewayinwhichtheradiationisbentorrefracted.
Geometricalopticsdealswiththestudyofthepathsfollowedby'rays'oflightorelectronsthroughlensesandapertures,andthegeometrical
constructionsusedtofindtherelativepositionsandsizesofobjectsandtheirimages.Arayoflightorelectronsisdefinedasaninfinitelythin
pencilorbeam.Physicalopticsshowsthatthisanabstractionandcannotphysicallyexistbecauseof'diffraction'whichdealswiththewave
natureoflightandelectrons.Allresultsobtainedingeometricalopticscanbederivedfromtheprinciplesofphysicaloptics,alongwithother
phenomenasuchasinterferenceanddiffractionwhicharenotexplicableinsimplegeometricalterms.
d.Idealversesreallenses:
Lensesareusedtobendraysoflightorelectronssotheyaredeflectedinapredictablewayfromtheiroriginalpaths.Thepropertiesofanideal
lens,possessinganaxisofrotationalsymmetryare:
1)Eachrayofthebundleofrayswhichpassesfromanobjectpointwillberefractedbytheideallenstomeetinoneimagepoint.
2)Raysoriginatingfrompointswhichlieonaplaneperpendiculartotheaxis,mustbeimagedinaplanewhichisalsoperpendiculartotheaxis.
3)Theimageappearsliketheobjectirrespectiveofthemagnification,sotherelativelineardimensionsoftheobjectarepreservedintheimage.
Inpractice,theimagingbyanyreallensdoesnotcorrespondtothatoftheideallensowingtothefactthatanobjectpointisrepresentedbya
diffractionimage(Airydisc)ofthelensopeningortheapertureusedforrestrictingtheeffectiveopeningofthelens.Thisisaresultofthewave
likepropertiesoflight.Lensaberrationsalsocontributetomoreorlesspronounceddeviationsfromthepropertiesoftheideallens.
Thesinglerefractingsurfaceofsphericalcurvatureisthefundamentalunitoffocusingactionbyglasslenses.Sphericalrefractingsurfacesactas
lensesforparaxialrayswhicharethoseraysthatpassclosetotheprincipalaxisofthelens.RayswithlargeangleswillNOTobeyideallens
action.
Afundamentaldifferencebetweenlightandmagneticlensesisthattheelectronbeamdoesnotchangeinforwardvelocityasitpassesthrough
themagneticfield(lightraysslowdownwhenpassingintoamediumofhigherrefractiveindex).Refractioniscontinuouswithelectronswhenthey
areinthemagneticfield:lightisrefractedonlyattheinterfacebetweenmediaofdifferingrefractiveindex.Theelectronsalsofollowspiral
trajectoriesthroughthemagneticfield(seealsoSec.I.A.5.c(Magneticfieldsandmagneticlenses)
e.Raydiagrams:(Figs.I.20I.28)
Themethodofconstructionofraydiagramsisbasedonthreesimpleprinciples:
1)Allraysenteringthelensparalleltotheaxisarebroughttoacommonpointontheaxis,thefocalpoint.
2)Allrayspassingthroughthegeometricalcenterofthelensareundeviatedandpassstraighton,nomatterfromwhichdirectiontheycome.
3)Principleofreversibility:ifthedirectionofarayisreversedinanysystemtherayexactlyretracesitspaththroughthesystem.Thisapplies
onlytothelocationoflightpathsandnottotheintensityofthelight.
Theaboveprinciplesarebasedontheassumptionsthatwearedealingwithathinlensandconcernedwiththepathsofparaxialrays.The
standardconventionistodrawdiagramswithraysthattravelfromlefttoright.Theobjectistotheleft(infront)ofthelensandtheimageisto
theright(behind)ofthelens.
f.Definitions:
Realimage:oneatwhichlightraysphysicallyreunite,sothataphotographicplateplacedatthepositionofarealimageisexposed.
VirtualImage:onefromwhichlightraysappeartodiverge;raysarenotinfactconcentratedatthepositionofavirtualimage,sothata
photographicplateplacedatthepositionoftheimageisnotexposed(byfocusedrays).Placinganopticalsystemsuchastheeyebehindthe
lens,willenablethedivergentraystobefocusedtoformarealimage.TheintermediatelensofanTEMissometimesusedthiswayinorderto
reducethefinalsizeoftherealimageformedbytheprojectorlens(es).
Converging(positive)lens:bendsraystowardtheaxis.Ithasapositivefocallength.Formsarealinvertedimageofanobjectplacedtothe
leftofthefirstfocalpointandanerectvirtualimageofanobjectplacedbetweenthefirstfocalpointandthelens.
Diverging(negative)lens:bendsthelightraysawayfromtheaxis.Ithasanegativefocallength.Anobjectplacedanywheretotheleftofa
diverginglensresultsinanerectvirtualimage.Itisnotpossibletoconstructanegativemagneticlensalthoughnegativeelectrostaticlensescan
bemade.
g.Lensformula(thinlensequation):
where
f=focallengthofthethinlens(sameradiusofcurvatureforboth
sphericalsurfaces)
o=distanceofobjectfromlens(positivetotheleft)
i=distanceofimagefromthelens(positivetotheright)
NOTE:Foravirtualimage,ihasanegativevalue.
h.Magnification:
Foraconverginglens,iftheobjectismorethantwicethefocallengthfromthelens,thentheimageformedisreal,inverted,andsmallerinsize
thantheobject(M<1).Whentheobjectisatadistance=2f,theimageandobjectarethesamesize(M=1);whenitisbetweenfand2f,
theimageislargerthantheobject(M>1),andwhenitis<f,theimageisvirtual,erect,andlargerthantheobject(M>1).
i.Angularapertureofthelens(2a)(Fig.I.29)
Theaperturedeterminesthetotalamountofradiationarrivingfromtheobjectwhichcanbefocusedto
formanimage.Theaperturethuscontrolstheabilityofthelenstogatherinformationabouttheobject.
Thisdependsontheangleoftheconeofraysitisabletoacceptfromtheobject.Bringinganobject
closertotheeyeincreasestheangularaperture,butthereisalimittotheclosenessthattheobjectcan
bebroughttotheeye(~25cmcorrespondingtoanangleofabout0.9°fora4mmexitpupildiameterof
theeyelens;atypicalLMwithanoilimmersionobjectivelenshas2aof~175°).
j.Simplevs.compoundmicroscope(Figs.I.30I.32)
Inprinciple,arealimageofanydesiredmagnificationcanbeobtainedfromasinglepositivelens,butin
practicethisiscumbersomebecauseofthelonglensimagedistance.Oneormorelensescanbeusedto
magnifytheimageinstages(totalmagnificationequalingtheproductofthemagnificationsofeachlens).
Theimageformedbyonelensconstitutestheobjectforthesubsequentlens,whetherornotareal
intermediateimageisformed.
Comparisonofoneversestwostagemagnification:
Thefollowingdescriptionillustrateshowdifferentpathlengthsarerequiredtoachieveamagnificationof10,000Xusingeitheroneortwolenses
withf=2.0cm.
OneStageSystem:
TwoStageSystem:
Assumebothlenseshavef=2.0cmandarearrangedsoeachgives100Xmagnification.
Thus,M=100=x
i
/x
o
foreachstage.
FirstStage:
x
o
=2.02cm
x
i
=202.00cm
Therealimageformedinthefirststagebecomestheobjectforthesecondlens.
SecondStage:x
o
,x
i
sameasinthefirststage.
Totallengthofsystem
=lengthoffirststage+lengthofsecondstage
=(x
o
+x
i
)+(x
o
+x
i
)
=2(x
o
+x
i
)
=2(2.02+202.00)=408.04cm(4.08meters)
k.Problemset
Thefollowingproblemsareforyourownedificationtotesthowwellyouunderstandthebasicsoflensoptics.
1.Foreachsituationbelow,drawanaccurate(usegraphpaper)raydiagramshowingthepathof(atleasttwo)raysfromtheobjecttoimage.
Indicatewhethertheimageisrealorvirtualandspecifythedistanceoftheimagefromthelensandthemagnificationoftheimagewithrespect
totheobject.Ineachexample,thelensisconverging,withidenticalfrontandbackfocalpoints.Distancesareinarbitraryunits.Letf=lens
focallength,x
o
=distanceofobjectinfrontofthelens,andx
i
=distanceofimagebehindthelens.Theobjectmaybeanysize.
2.Inthefollowingexamples,therearetwoconverginglensesinsuccession.Drawraydiagramsshowingtheformationofboththeintermediate
andfinalimagesandgiveappropriateinformationaboutthenature(real/virtual),positions,andsizesoftheintermediateandfinalimages.What
isthemagnificationateachstageofimageformationandwhatisthemagnificationofthefinalimage?Thedistancefromthecenteroflens1(L1)
tothecenteroflens2(L2)equalsD.
I.A.5.ElectronOptics/ElectronLenses
a.Electronemission
Innershellelectronsinmetalatomsshieldtheelectricfieldofthenucleusthroughtherepulsiveforcestheyexertontheoutershell(valence)
electrons.Thustheattractionbetweenthevalenceelectronsandthenucleusisreduced.Metalatomsarecharacterizedashavingtwoloosely
boundvalenceelectronswhichmigratefreely(thisiswhymetalsaregoodelectricalconductors)andcanescapefromthemetalcompletelyif
sufficientadditionalenergyisimpartedtothem.Asthetemperatureofametalisincreased,thekineticenergyoftheelectronsincreasesbecause
ofincreasedthermalvibrationsofthemetalions,whichcollidemorefrequentlywiththeelectrons.Thermionicemissionisthetermusedto
describetheprocessbywhichthermalenergyissuppliedtolooselyboundelectronsinordertoformasourceofelectrons.
Atroomtemperatureelectronsareeffectivelypreventedfromescapingthesurfaceofthemetalowingtotheattractiveforceofthepositively
chargedions.Asthetemperatureisincreasedsomeelectronsacquiresufficientenergytoovercometheattractionandleavethemetal
temporarily.Metal,shapedasathinwire,caneasilybeheatedbypassinganelectriccurrentthroughit.Sincethemetalsurfacebecomes
positivelycharged,acertainlevelofenergy(workfunction)mustbesuppliedtoallowelectronstoescapefromthesurface.Eachmetalhasa
characteristicworkfunction.Tungsten,withalowworkfunction,emitsmoreelectronsthanmetalswithhigherworkfunctions(seealsopp.2930
andFig.I.59).
Ifastrongelectrostaticfieldisappliedinavacuumbetweenthewire(givenanegative,cathode,potential)andananode,theelectricfieldwill
causeelectronstoaccelerateawayfromthewiretowardstheanodesurface(Fig.I.33).Thespeedoftheelectronsdependsonthestrengthof
theelectrostaticfield(voltage)betweenthecathodeandanode(equation(3),Sec.I.A.3.b)Thenumberofelectronswhichleavethewire
dependsonthetemperaturetowhichthewireisheated,whichdependsonhowmuchfilamentcurrentpassesthroughthewire.
A"V"shapedwirewillhavethehighesttemperatureatthetip.Electronswithdrawnfromthefilamenttipcarryelectricchargestotheanode.This
electriccurrent,whichflowsbetweenthefilamentandtheanode,iscalledthebeamcurrent.
1)Electricfield/Equipotentials
Anelectricallychargedobjecthasassociatedwithitanelectricfield.Thus,anelectricallychargedparticle,whenbroughtnearachargedobject,
isinfluencedbyanelectricalforceinthevicinityoftheobject.Theforceisdirectedtowardthechargedobjectifthechargesareofopposite
signsandawayfromtheobjectiftheyareofsimilarsign.DEFINITION:Thedirectionofanelectricfieldisdefinedasthedirectionoftheforce
actingonapositivecharge.(Figs.I.3435)
Alongthelinesofforceconnectingthetwocharges,theelectricpotentialwillchangegraduallybetweentheextremevaluesrepresentedbythe
twocharges.DEFINITION:Equipotentiallinesdefinethepointsalongthelinesofforcewithidenticalelectricalpotential.Theseequipotential
surfacesarealwaysorientedperpendiculartothelinesofforce.Thechangesintheelectricpotentialaregradualinspace.
Electronswhichenterafieldbetweentwoparallelplatesinadirectionparalleltotheplatesareaffectedbytheforcedirectedperpendicularto
theplates(FigI.36).Theelectronswillbeattractedtowardthepositiveplate.Thepathchangesinaseriesofgradualstepsattheequipotential
surfaces.
FigureI.37showshowtheelectronpathis"refracted"attheequipotentialsurface.TheresultisfundamentallythesameasthatgivenbySnell's
Lawofrefractioninlightoptics.Aconsequenceofthisisthatasphericallycurvedequipotentialsurfaceexhibitsthepropertiesofalens.
FiguresI.38andI.39showhowbothpositive(converging)andnegative(diverging)electrostaticlensescanbeformed.Thisfeatureof
electrostaticlensesdiffersfromelectromagneticlenseswhichcanonlyactasconverginglenses.
2)Advantages/Disadvantagesofelectronlenses:
Thefactthattherefractiveindexdoesnotchangeabruptlyinelectronlenseshasoneadvantageinthattherearenotroublesomereflectionsat
equipotentialsasatglassinterfaces.Thereisaseriousdisadvantageinthatequipotentialscannotbeshapedandcombinedinarbitraryfashionto
correctforchromaticaberrationandothererrors.
Althoughelectronmicroscopeswhichemployelectrostaticlenseshavebeenmade,mostmicroscopesuseelectromagneticlenses.Amajorreason
isthatelectrostaticlensesaremoresensitivetothequalityofthevacuumandcleanlinessofthecomponentsthanareelectromagneticlenses.
Somelensaberrationsaremoresevereforelectrostaticlensescomparedtoelectromagneticlenses.Electrostaticlensesrequireverypowerful
electrostaticfieldswhichcanleadtoelectricalbreakdownor"arcingover"insidethecolumn,especiallyunderpoorvacuumconditions.Forthis
reason,electrostaticlensescannotbemadewithfocallengthsasshortasmagneticlenses.
b.Electrostaticlens
Abasicunderstandingofelectrostaticlensesisimportantfortwomainreasons:i)theelectrongunuseselectrostaticlensactiontoformthe
primarybeamsource,andii)itisquitecommonforachargetodeveloponthenonconductingcontaminationwhichmayaccumulateonphysical
apertures(suchastheobjectiveaperture)andtransformthemintoweakelectrostaticlenseswhichcandistorttheelectronimage.
3)Propertiesofelectrostaticlenses:
a)Anyaxiallysymmetricalelectrostaticfieldhasthepropertiesofalensforraysconfinedtotheparaxialregion.Alltheideallensformulasapply
toelectrostaticlenses.
b)Forelectronlenses,replaceÃ(f)forrefractiveindexinthelensequations(f=valueofthepotentialontheaxis).Intheimageformingsystem
ofmostTEMs,fisthesameonbothsidesofthelens(SeeSec.I.A.5.c).
c)Ifboundedbyregionswherefisconstant,anelectrostaticlensisalwaysconvergent.
c.Magneticfieldsandmagneticlenses
1)Magneticfield
Anelectriccurrentpassingthroughaconductorgivesrisetoamagneticfield.TheconventionisthatNisthedirectioninwhichthelinesofthe
magneticfieldpoint(Fig.I.40).Themagneticfluxisthetotalnumberoflinesandthefluxdensityisthenumberoflinesperunitareaofasurface.
UsetheRIGHThandruletodeterminethedirectionofthefield(thumbpointstowardcurrentdirectionandfingerscurlindirectionoffield.NOTE:
Byconvention,thedirectionofelectronflowisoppositetothatofcurrentflow.
Fluxdensitydependsonthepropertiesofthematerialsurroundingtheconductor.Ironinducesahigherfluxdensitythanairoravacuum.The
propertyofthematerialwhichaffectsthefluxdensityiscalledthepermeability,m,ofthematerial.Forairandvacuum,m=1.0.For
ferromagneticmaterialsitcanbeaslargeasseveralhundredthousand.
Iftheconductorhastheshapeofacircularloop,thelinesofforceformcirclesaroundtheloop.Thefluxdensityisgreatestatthecenterofthe
loop.Themagnetinthecenteroftheloopisorientedperpendiculartotheplaneoftheloopifthecurrentthroughtheloopissufficientlystrongto
eliminatetheinfluenceoftheearth'sfield.ThesideoftheloopatwhichthelinesofforceleavetheloopistheNorth(N)poleofthemagnet(Figs.
I.41,I.42).
Ifthewireiswoundinseveralturnsaroundacylindricalsurface(solenoid),eachturnwillcontributetotheinducedmagneticfield.Theflux
densityinthecenterofthecoilisgivenby:
Inthecaseofairandnonmagneticmaterials,µ=1.0andB=H.
Thepermeabilityofirondependsonthefieldstrength,H,anddecreasestounityathighfieldstrengthorwhenthefluxdensity,B=H(Fig.I.43).
Thehighpermeabilityofironisduetotheinducedmagneticfieldorientingmicroscopiccrystalregionsactingastinymagnetsintheiron.Allthese
tinymagnetsaddtheirmagneticfieldstotheinducedfield(Fig.I.44).Whenallmicromagnetsarenearlyoriented,theironwillaffecttheflux
densitytoadecreasingamountsincethereorientationofmicromagnetsisnearingcompletion.Thus,thepermeabilityofironathighfieldstrengths
approachesthatofemptyspace.Atthispointtheironreachesmagneticsaturation.
2)Hysteresis
Thestrengthofthelensdependstosomeextentonthepreviousmagnetichistoryof
thelens.Whenthecurrentinalensisreduced,thedecreaseinmagnetizationdoes
notretracethesamepathobtainedwhenthecurrentwasincreased(Fig.I.45).
Inductionofmagnetizationinvolvesaphysicalmovementwithinthemagnetized
material,requiringtheovercomeofacertaindegreeofinertia.Asaresult,
magnetizationtendstolagbehindthemagnetizingforceapplied.Inducedmagnetic
fluxcanonlybereturnedtozerobyapplicationofacurrentintheoppositedirection.
Aconsequenceofhysteresisisthatthelevelofcurrentusedtoenergizeamagnetic
lensDOESNOTpreciselyspecifythelensstrength(i.e.focallength).
NormalizationofTEMlensesisaccomplishedbyreducingthelenscurrenttozero
somepredeterminednumberoftimes.Hysteresismayalsobeminimizedbytakinga
lenstosaturationandthenreturningittotheworkingcurrentwithoutovershooting.
Whenthefieldstrengthisreducedtozero,somemagnetizationstillremainsintheiron
(residualmagnetizationorremanence).Anadvantageofsoftironisthefactthat,
whenusedinanelectromagnet,hysteresisislow.
Introductionofpiecesofironinamagneticfielddrasticallyaffectsthefluxdensity.
Magneticmaterialhasashieldingeffect,theeffectbeinggreaterthegreaterthe
permeability.Permalloy(mmetal)hasamaximumpermeabilityof80,000140,000
comparedtoironusedintransformers(~7000).mmetalpermeabilityislimitedtolower
fieldstrengthsthanthatatwhichironstillretainshighpermeability.Thismetalis
thereforeusefulforshieldingtheTEMfromexternalmagneticfields.
d.Theelectromagneticlens
1)Lensdesigndevelopment(Figs.I.46I.48)
Theefficiencyofthemagneticfieldproducedbyashortsolenoidwasfirstimproved
byencasingtheenergizingcoilinasheathofsoftironwhichhasthepropertyofconcentratingthelinesofforceinamagneticfieldandthus
becomingmagnetizedbyinduction.Inthiswayamuchmorepowerfulaxialmagneticfieldisobtainedforthesameamountofcurrentflowing
throughthesolenoid.Furtherdevelopmentinvolvedencasingtheentirecoilwithsoftironexceptatanarrowannulargapintheinsideofthecoil.
Thisproducesagreaterconcentrationofthemagneticfieldalongashortaxialdistance.Toachieveshorterfocallengthlenses(andobtaingreater
magnifications)asoftironpolepiecewithanopenaxialborewasintroducedatthepositionoftheannulargap.
MagneticlensesusedinTEMsarealwaysconstructedwithanironcircuittoproduceahighfieldstrengthacrossashortgap.Themagneticfields
forTEMlensesareintherangeof10,00020,000gauss.
2)Forcesactingonacurrentinamagneticfield
Theforceonanelectroninamagneticfieldisalwaysatrightanglestothevelocityandthedirectionofthefield(Figs.I.49,I.50,andI.52).The
fieldonlyactsonthevelocitycomponentwhichisdirectedperpendiculartothelinesofforce.Usethelefthandrule(Fig.I.51:firstfingerfor
fielddirection,middlefingerforcurrentdirection,andthumbfordirectionofforce).Rayspassingthroughthelensareturnedthroughanangle
whichdoesNOTdependonthedistanceoftheraysfromtheaxis.Allelectronscontainedinagivenmeridionalplanebeforeenteringthefieldare
containedinarotatingmeridionalplaneastheypassthroughthelens,andthentheyleavethelenscoplanar.
Whenelectronsenterthelenstheyencounterasidewaysforcewhichcausestheelectrontorotate
asitcontinuesthroughthelens(Figs.I.53I.57).Sincetheradialcomponentofthemagneticfield
reversesafterthecenterofthelens,therotationalvelocitysetupinthefirsthalfofthelensis
countered.Theelectronenteredthelenswithoutangularmomentumabouttheaxisandleaves
withoutangularmomentum.Theneteffectisadeflectiontowardtheaxis,whichitmustcrossatthe
focalpointf
2
.Theanglebetweentheobjectvectorandtheimagevectoris180°+q,whereas,for
glasslensesandelectrostaticlenses,theanglebetweenarealobjectandtheimageisexactly180°.
Sincetheradialforceisdirectedtowardtheaxis,thelensisconvergentnomatterwhatthedirection
ofthefield.
3)Propertiesofamagneticlens:
Anyaxiallysymmetricmagneticfieldhasthepropertiesofanideallens.Alltheformulasfortheideallensmaybeapplied.
Magneticlensesarealwaysconvergent.Theconventional,axiallysymmetriclensisalwaysboundedbyregionswhicharefieldfree,the
consequencebeingthatthenetactionofelectronlensesisinevitablyconvergent.Limitedregionsmaybedivergentbutnotthelensasawhole.
Theseriousconsequenceofthisisthatneithersphericalorchromaticaberrationscanbecorrectedasisdoneinlightopticsbytheusedoublets
ofpositiveandnegativelenses.
Intheabsenceofelectrostaticfields,therefractiveindexisthesameinobjectandimagespace,thereforef
1
=f
2
.
Electronstravelingthroughaxiallysymmetricfieldsexperienceaspiraltrajectoryofdiminishingradius.Theimagevectorisatanangle180°+qto
theobjectvector.
Thedeflectionoftheelectrontowardstheaxismeansthatanelectronenteringthelensparalleltoitsaxiswillcrosstheaxisafterhavingpassed
thelens.Thedeflectionwillincreasewiththedistancefromtheaxis.Thus,abeamofelectronsinparallelpathsparalleltotheaxisofthelenswill
befocusedtoanimagepointontheaxiswhichrepresentsthesecond(back)focalpointofthelens(f
2
).Notethatmagneticlensesarehighly
inefficientinthatonlyaminorportionofthetotalfieldstrengthisactuallyeffectiveinfocusingtheelectron.
4)Magneticlensfocallength
Inamagneticelectronlensthefocallengthisdeterminedbythefieldstrengthinthelensgapandbythespeedoftheelectrons(determinedby
theacceleratingvoltage).
Formagneticlenses,focusingisachievedbyvaryingthecurrentwhichpassesthroughtheelectromagnet.Thisinturnchangesthestrengthof
themagneticfieldandtherebyaltersthefocallengthofthelensandisequivalenttoacombinedchangeinboththe"refractiveindex"and
"curvatureofsurface".Forabeamofmoreenergeticelectrons,thelenscurrenthastobeincreasedinordertokeepthefocallengthconstant.
FocallengthandcurrentareNOTlinearlyrelated:strengthincreasesinasigmoidfashion(Fig.I.45)ascurrentincreasesuntilapointisreached
wherethelensissaturatedandnofurtherincreaseinlensstrengthcanbeachieved.
Sincethefocallengthofthelensisdirectlyproportionaltotheacceleratingvoltage,avariationinthevelocityoftheelectronsintheimaging
beamaffectsimagequalitybyeliminatingperfectfocus(chromaticaberration).
5)Magneticlensdesign:(Figs.I.46,I.47).
Condenserlensesusuallyhavearelativelylargeboreandspacingwhichresultsinalongfieldandlongfocallength.
Typicalconstructionoftheobjectivelensproducesastrongfieldofshortaxialextent(i.e.shortfocallengthbetween(1.53mm)necessaryfor
formationofimagesathighmagnification.Thespecimenisplacedwithinthemagneticfieldoftheobjectivelens.Thus,anyfieldintroducedby
contaminantsinthespecimencandistortthefieldofthelens.Notethatthisalsomeansthatpartofthelensfield("prefield")isonthefrontside
oftheobjectandaffectstheelectronbeambeforeitpassesthroughtheobject.
Mostofatypicalmagneticlensliesoutsidethevacuumofthemicroscope.Onlythoseregionsthroughwhichtheelectronbeampassesareinhigh
vacuum.Magneticlensesmustbewatercooledtodissipatethelargeamountsofheatproducedbythecurrentsintheelectromagnetcoils.
DATE NAME EVENT
1897 J.J.Thompson Discoverstheelectron
1924 LouisdeBroglie Identifiesawavelengthtomovingelectrons
l =h/mv
where
l =wavelength
h=Planck'sconstant
m=mass
v=velocity
(Foranelectronat60kVl=0.005nm)
1926 H.Busch Magneticorelectricfieldsactaslensesforelectrons
1929 E.Ruska Ph.Dthesisonmagneticlenses
1931 Knoll&Ruska Firstelectronmicroscopebuilt
1931 Davisson&Calbrick Propertiesofelectrostaticlenses
1934 Driest&Muller SurpassresolutionoftheLM
1938 vonBorries&Ruska FirstpracticalEM(Siemens)10nmresolution
1940 RCA CommercialEMwith2.4nmresolution
1945 1.0nmresolution
Fig.I.1Comparisonoflightandelectronmicroscopes.Ineach
instrument,illuminationfromthesource(lamp,filamentinthe
electrongun)isfocusedbythecondenserlensontothespecimen.
Afirstmagnifiedimageisformedbytheobjectivelens.Thisimage
isfurthermagnifiedbytheprojectorlensontoagroundglass
screen(light)orfluorescentscreen(electrons).(FromAgar,p.8)
Fig.I.2CrosssectionalviewofthePhilipsEM300.(FromAgar,p.40)
Toviewtheanimatedmicroscope,clickhere.
Note:QuickTimePlugInrequired
(Thiscanbedownloadedathttp://apple.com/quicktime/download)
Fig.I.3Sectionthroughacomplex
doublecondenser6lensPhilips
EM200electronmicroscope.(From
Meek,p.99)
Fig.I.4Thestatisticalnatureofdiffraction
patterns.(FromHall,p.13)
"Theprecisenatureof'electronwaves'or'matterwaves'isverydifficulttounderstandordescribeinmaterialterms.Electronwavesarenot
electromagneticradiationofthekindtowhichlight,Xraysandradiowavesbelong.Theyconstituteasortofquantumor'packet'ofradiationwhich
accompanieseachindividualelectron,followingitspathandnotradiatingoutwardsfromit."(Meek,1976,pp.4849).
V l (nm)
v(
•
10
10
cm/sec)
v/c
10,000 0.0123 0.593 0.198
50,000 0.0055 1.326 0.442
100,000 0.0039 1.875 0.625
1,000,000 0.0012 5.930 1.977!
V l (nm)
v(
•
10
10
cm/sec)
v/c
10,000 0.0123 0.593 0.195
50,000 0.0055 1.326 0.414
100,000 0.0039 1.875 0.548
1,000,000 0.0012 5.930 0.941
FigI.5Aperfectpointsourcecannotbe
imagedbyalensasaperfectpointimagedue
tothepresenceoftheapertureAB(which
maybetheedgeofthelens).Diffractionat
thisaperturegivesrisetoaseriesoffringes,
whichsurroundtheimageformedofthepoint
source.Thepatternproducediscalledan'Airy'
disk.(FromMeek1sted.,p.35)
Fig.I.6Wheneverawavefrontstrikesa
barrier,itcanbendaroundthecorner'by
givingrisetoasecondarywavefrontatthe
edge,sinceeachpointonthewavefrontcan
giverisetoanewsourceofwaves.This
phenomenoniscalled'diffraction'.(FromMeek
1sted.,p.22)
Fig.I.7Diffractionpattern(right)formedbyanirregularlyshapedaperture
(left).(FromYoung,p.95)
Fig.I.8(a)
Photographof
theedgeofa
razorblade
illuminatedby
monochromatic
(blue)light
rendered
coherentby
passing
througha
narrowslit.(b)
Microdensitometer
tracingofthe
negativefrom
whichthe
photograph
wasmade.
FourFresnel
fringescanbe
distinguished.
(FromMeek1st
ed.,p.27)
(a)
(b)
(a) (c)
(b)
Fig.I.9(a)Fresnelfringesformed
byelectrons.Thesefringesare
formedoutsidetheedgeofahole
(white)inacarbonfilm(black).(b)
Amicrodensitometertracingofthe
fringesystem;thepatternis
identicalwiththeFresnelfringe
systemformedbyvisiblelight(see
Fig.I.8).(c)Anunderfocusedimage
ofaholeinafilm,showinga
completesystemofabout40
Fresnelfringesinsidethehole.
(FromMeek1sted.,pp.2930)
Fig.I.10Diffractionimagesoftwo
easilyresolvedpoints.(From
Slayter,p.243)
Fig.I.11Imagesoftwo
incoherentlyilluminatedpointsat
thelimitofresolution.(a)individual
intensities;(b)summedintensities.
(FromSlayter,p.244)
Fig.I.12Examplesofwhatoccurswhentwo
wavesofthesamewavelengthandequal
amplitudeadd.Ineachexample,thetwo
separatewavesareshownontheleftand
theirsumorresultantwaveontheright.The
differentexamplesarecharacterizedbyvarying
phasedifferences.Thephaseofawave
(usuallyexpressedasafractionofthe
wavelengthorindegrees)isthepositionofa
crestrelativetosomearbitrarypoint.Although
thephaseofagivenwavevarieswithtimeas
thewavetravels,thedifferenceinphaseofthe
twowavesofthesamewavelengthwiththe
samevelocity,isindependentoftime.Such
wavescaninterferewithoneanother.The
resultantwavehasthesamewavelength,l .
(a)Phasedifferencezero.Thewavestotally
reinforceandaresaidtobe"inphase"orto
showconstructiveinterference.
(b)Phasedifferencel /4.Partialreinforcement,
givingawaveofamplitude1.4(intensity2.0).
(c)Phasedifferencel /2.Thewavesare"outof
phase"andthereistotaldestructive
interferencetogivenoresultantwaveora
wavewithamplitude0(intensity0).(From
GluskerandTrueblood,p.19)
Fig.I.13Photographofan
interferencepatterninwater
wavesformedbythe
superpositionofwavesfromtwo
sourcesoscillatinginphasewith
thesamefrequency.(FromYoung,
p.22)
Fig.I.14Theangularapertureofthe
eyeisrelativelysmall.(FromMeek,
1sted.,p.13)
Fig.I.15Increasingtheangular
apertureoftheeyewithalens.The
lensallowstheobjecttobeheld
closertotheeye,whichisthereby
enabledtogathermoreinformation.
(FromMeek1sted.,p.14)
Fig.I.16Theinteractionofwaves
withanobstacle.Theboatridesthe
longwavelengthoceanwave,but
reflectsthesmallwavelength
surfaceripple.Anobserverwho
wishestodetectthepresenceof
theboatcandosoonlyby
observingwaveswhichhave
wavelengthssmallerthan,or
comparableto,thelengthofthe
boat.(FromSherwood,p.19)
Maximummagnification=
resolvingpoweroftheeye
resolvingpowerofthemicroscope
(a)
Fig.I.17(a)TwoAiry
disksrepresenting
twoimagepoints
shownatincreasing
separationfromleft
toright.Inthe
pictureatthe
extremerightthe
twodiskscanbe
distinguishedas
separatedisks.
(b)Theintensity
distributionatanAiry
disk.R,halfwidthof
thecentralmaximum
representedbya
bellshapedcurve.
(c)TheRayleigh
criteriaforresolution.
(FromSjostrand,
p.115)
i=r
Fig.I.18Reflection.(FromSlayter,
p.4)
Fig.I.19Refraction.(FromSlayter,
p.6)
Fig.I.20Principalraydiagramsshowing
imageformationbyaconvexlens.
(a)Whentheobjectdistanceisgreater
thanthefocallength,areal,inverted
imageisformed.
(b)Whentheobjectdistanceisless
thanthefocallength,avirtual,erect
imageisformed;itspositionis
obtainedbyprojectingtheprincipal
raysbackward.Theraysappearto
comefrompointQ.(FromYoung,
p.127)
Fig.I.21Definitionof
principalfocus,F,inimage
spaceofalens.(From
Sjostrand,p.20)
Fig.I.22Focusingeffectoflenson
raysoriginatingfrompointson
principalaxislocatedatdifferent
distancesfromthelens.(From
Sjostrand,p.21)
Fig.I.23Definitionofprincipal
focusinobjectspaceF1ofa
lens.(FromSjostrand,p.21)
Fig.I.24VirtualimageQof
objectpointlocatedbetween
principalfocusinobjectspace
andthelens.(FromSjostrand,
p.21)
Fig.I.25Constructionoftheimage
ofanobjectbymeansofray
tracing.(FromSjostrand,p.22)
Fig.I.26Magnifyingeffectof
apositivelens.(From
Sjostrand,p.22)
Fig.I.27Virtualmagnified
imageofobjectlocated
betweenprincipalfocusin
objectspaceandthelens.
(FromSjostrand,p.22)
Fig.I.28Amagnifyingglassformsan
enlarged,erectvirtualimage.The
angularsizeofthisimageis
approximately4"/15"or4/15.The
angularsizeoftheobjectatthe
closestdistanceforcomfortable
viewingis1"/10"or1/10.The
magnificationinthissituationis(4/15)/
(1/10),or22/3.(FromYoung,p.130)
Fig.I.29Theangularapertureofa
lens.Theangle2a isthe
acceptanceangleofthelens,and
thelargeritcanbemade,themore
informationcanthelenstransmit.A
largelensofhighaperturecan
thereforetellusmoreaboutan
objectthanasmalllensoflow
power.(FromMeek1sted.,p.12)
Fig.I.30Raydiagramforhighmagnification
modeofoperation.Notethateachlens
formsarealimage,withimageinversion.
I0istheimageformedbytheobjective
lensO,I1isformedbythefirstprojector
lensP1andI2bythesecondprojectorP2,
onthescreen.(FromAgar,p.30)
Fig.I.31Left:raydiagramofthe3realimagemediumandhighmagnificationimagingsystemofa3lens
microscope.Center:2realimageverylowor'scan'magnificationrangeofa3lensmicroscope.Right:2real
imagelowmagnificationsystemofa3lensmicroscope.(FromMeek1sted.,pp.118,120121)
Fig.I.32Raydiagramforacompleteelectron
microscope.FilamentF,condenser1lensC1,
condenser2lensC2,condenserapertureCA,
specimenS,objectivelensO,objectiveaperture
OA(inbackfocalplane).1stintermediateimage
andselectorapertureSA.IntermediatelensP1,
secondintermediateimageI2,projectorlensP2
andfinalimageonthefluorescentscreenFC.
(FromAgar,p.35)
a)f=2.0
x
o
=5.0
e)f=4.0
x
o
=3.0
b)f=10.5
x
o
=21.0
f)f=13.3
x
o
=13.3
c)f=3.5
x
o
=3.0
g)f=3.142
x
o
=0.0
d)f=5.0
x
o
=2.5
a)D=8.0
L1:f=2.0
x
o
=4.0
L2:f=3.0
b)D=8.0
L1:f=2.0
x
o
=6.0
L2:f=3.0
c)D=4.0
L1:f=2.0
x
o
=3.0
L2:f=2.0
FigI.33Accelerationofelectronin
electricfield.(FromSjostrand,p.26)
Fig.I.34Linesofforceatapositively
chargedsphericalbody.(FromSjostrand,
p.32)
Fig.I.35Linesofforceandequipotential
surfaces(stippledlines)associatedwith
twoequalchargesofoppositesign.
(FromSjostrand,p.32)
Fig.I.36Equipotentialsurfacesattwoparallel
platesofoppositechargeswiththepathofan
electronindicatedwithinthehomogeneous
partofthefield.(FromSjostrand,p.33)
Fig.I.37Refractionofelectronatan
equipotentialsurface.(FromSjostrand,p.33)
Fig.I.38.Negativelensactionof
electrostaticfieldatanaperturewhen
V2V1>V3V2.(FromSjostrand,
p.34)
Fig.I.39.Positivelensactionatan
aperturewhenV2V1<V3V2.
(FromSjostrand,p.34)
Fig.I.40Magneticfieldinducedbycurrent
passingthroughaconductor.(From
Sjostrand,p.35)
Fig.I.41Magneticfieldinducedbycurrent
passingthroughasolenoid.(From
Sjostrand,p.37)
Fig.I.42Solenoidwithironcore.(From
Sjostrand,p.40)
Fig.I.43a.Dependenceofpermeabilityonfluxdensity,B.
b.RelationshipbetweenfluxdensityBandfieldstrength.
(FromSjostrand,p.38).
Fig.I.44Magnetization.(FromSlayter,
p.361)
Fig.I.45Curves
showinghowthe
magnetizationof
softiron(lens
strength)is
relatedtothe
magnetizing
force(lens
current).An
unmagnetized
lensstartsfrom
thepointOand
followsthepath
OAaslens
current
increases.Atthe
pointA,further
increaseinlens
currentproduces
nofurther
increaseinlens
strength;thelensissaidtobe'saturated'.Whenlenscurrent
isreduced,thepathOAisnotretraced;adifferentpathABis
followed.Thisdisplacementiscalled'hysteresis'.Atzero
current(pointB),someresiduallensstrengthremains;thisis
called'remanence'.Tobringthelensbacktozerostrength,a
reversecurrentOCmustbeapplied.Lensstrengththen
increaseswithincreasingreversecurrent,followingthepath
CD.Thepolarityofthelenschanges,butthisdoesnotaffect
itsfocusingpower;onlythespiralelectronpathisreversed.
Becauseofhysteresis,itisnotpossibletocalibratealens
currentmeteraccuratelyintermsoflensstrengthor
magnification.
Fig.I.46Evolutionofmagneticelectron
lenses.(A)Shortsolenoidusedasa
magneticlens.(B)Softironcasing
enclosingoutersurfaceofthesolenoid,
thusconcentratingthefield.(C)Soft
ironencasingthesolenoidexceptata
narrowannulargaptherebyreducing
themagneticfieldtoaveryshortregion
alongthelensaxis.(D)Modern
objectivelensconsistingofasoftiron
encasedsolenoidandsoftironpole
piecessoastohaveanenormously
concentratedfieldatthelevelofthe
annulargap.(FromWischnizter2nded.,
p.33)
Fig.I.47(a)Amagneticlensconsisting
ofatightlywoundcoilandasoftiron
shroudsurroundingthecoilexceptfor
asmallgap.Thefieldisconcentratedin
thatgap.(b)Shortfocallength
electromagneticlenswithpolepieces.
(FromSjostrand,p.50)
Fig.I.48Fieldstrengthdistribution
curves.ThecurvesADcorrespondto
therespectivelensesillustratedinFig.
I.46.Eachrepresentsthefieldstrength
alongthelongaxisofthelens.The
changesintheshapeofthecurves
representtheshorteningor
concentrationofthefieldovera
shorteraxialdistance.Hz=
longitudinalmagneticfield.Z=
distancealongtheaxisofsymmetry.
(FromWischnizter2nded.,p.33)
Fig.I.49TheforceFactingon
astraightconductorina
homogeneousmagneticfield
offluxdensityBwhencurrent
Iispassedthroughthe
conductor.(FromSjostrand,
p.43)
Fig.I.50Pathofanelectronina
magneticfield.(A)Inalarge,uniform
magneticfield.(B)Inasmall,uniform
magneticfield.(FromWischnitzer2nd
ed.,p.25)
Fig.I.51Lefthandthumbrule.
(FromSjostrand,p.43)
Fig.I.52Thompson'sexperiment.A
streamofelectronsoriginatingfroma
sourceandpassing,invacuo,through
amagneticfieldproducedbyapairof
magnetswillbedeflected.The
directionofdeflectiondemonstrates
thatelectronsarenegativelycharged
particlesofmatter.(FromWischnitzer
2nded.,p.25)
Fig.I.53Actionofasolenoidonan
electronbeam.Anelectriccurrent
passingthroughthecoilproducesan
axialmagneticfield.Thisisthe
refractingmediumfortheelectrons.An
electronstartingatapointontheaxisA
andatanangletoitfollowsaspiral
path,returningtotheaxisatthepoint
B.Theactionisbasicallysimilartothat
oftheconverginglightlensshownin
Fig.I.20.(FromMeek1sted.,p.8)
Fig.I.54Actionofthemagnetic
lens.(a)Inperspective.(b)
Electrontrajectoryin
projection,alongdirectionof
propagation.(c)Electron
trajectoryinprojection,side
view.(FromSlayter,p.358)
Fig.I.55Componentsofthe
vectorHneartheaxisoffields
withaxialsymmetry.His
representedbytwo
components,Hz,the
componentinthez(axial)
direction,andHr,the
compnentinther(radial)
direction.(FromHall,p.85)
Fig.I.56Theycomponentof
themagneticfieldina
magneticlensisoriented
perpendiculartothedirection
ofanelectronenteringthe
lensalongapathparallelto
thelensaxis.Thisy
componentwillaffectthe
electron,deflectingitinthex
directionasindicatedbythe
arrowmarkedvx.(From
Sjostrand,p.48)
Fig.I.57Thezcomponentofthemagneticfield
andthexvelocitycomponentoftheelectron
inamagneticlensinteract,deflectingthe
electronintheydirectiontowardthelens
axis.(FromSjostrand,p.49)
CuuDuongThanCong.com https://fb.com/tailieudientucntt
cuu duong than cong . com
Bấm Tải xuống để xem toàn bộ.



