Bài giảng về Phương pháp bình phương tối thiểu | Xác suất thống kê

PHƯƠNG PHÁP BÌNH PHƯƠNG TỐI THIỂU XẤP XỈ HÀM SỐ Gv: Ts Đỗ Đức Tâm. Ngày 11 tháng 11 năm 2019 1 / 19 Sai số trung bình phương
Xét một phân hoạch xi , (i = 1, n) của đoạn [a, b].
Định nghĩa sai số trung bình phương
Cho hai hàm số f (x ) và ϕ(x ) xác định trên đoạn [a, b]. Đại lượng n !1/2 1 X σm = (f (xi ) − g (xi ))2 (1) n i=0
gọi là sai số (độ lệch) trung bình phương của hai hàm f (x ) và ϕ(x ) trên
tập hợp điểm xi ∈ [a, b] (i = 1, n). Ngày 11 tháng 11 năm 2019 2 / 19 Sai số trung bình phương
Giả sử các giá trị của hàm số f (x )
tại các điểm xi ∈ [a, b] đo được
trong thực nghiệm với sai số ξi
tương ứng là yi = f (xi ) với i = 0, n.
Phương pháp trung bình phương tối
thiểu là phương pháp tìm hàm ϕ(x )
xấp xỉ hàm số f (x ) sao cho sai số n !1/2 1 X σm = (yi − g (xi ))2 n i=0
đạt giá trị nhỏ nhất. Ngày 11 tháng 11 năm 2019 3 / 19 Nội dung phương pháp Đa thức suy rộng Cho các hàm số ϕk (x), k = 0, m (2)
là các hàm số 1 biến số phụ thuộc vào x . Hàm số dạng m X ϕ(x ) = ak ϕk (x) (3) k=0
gọi là đa thức suy rộng của hệ hàm (2). Hệ (2) gọi là hệ cơ bản. Ví dụ:
ϕk (x) = xk , k = 0, m gọi là hệ đại số;
1; cosx ; sinx ; cos2x ; sin2x ; · · · gọi là hệ lượng giác;
1; eα1x ; eα2x ; eα2x ; · · · trong đó {αi } − là dãy số nào đó, gọi là hệ hàm số mũ. Ngày 11 tháng 11 năm 2019 4 / 19 Nội dung phương pháp Xét hàm số m X ϕ(x ) = ak ϕk (x) k=0
là đa thức mở rộng của một hệ hàm nào đó.
Xấp xỉ hàm số f (x ) bởi hàm số ϕ(x ) bằng phương pháp bình phương tối
thiểu là đi tìm các hệ số a0, a1, · · · , am sao cho đại lượng n m !2 X X
σm = Φ(a0, a1, · · · , am) = yi − ak ϕk (xi ) i =0 k=0
đạt min trên phân hoạch ∆ = {a = x1 < x2 < · · · < xn = b} . Khi đó
a0, a1, · · · , am là nghiệm của hệ ∂Φ = 0 ∀i = 0, m. ∂ai Ngày 11 tháng 11 năm 2019 5 / 19
Phương pháp tìm a0, a1, · · · , am.
Do đó, để hàm số ϕ(x ) xấp xỉ tốt nhất hàm số f (x ) theo nghĩa bình
phương tối thiểu thì các hệ số a0, a1, · · · , am phải là nghiệm của hệ phương trình [ϕ 
0, ϕ0] a0 + [ϕ0, ϕ1] a1 + · · · + [ϕ0, ϕm] am = [y , ϕ0]   
[ϕ1, ϕ0] a0 + [ϕ1, ϕ1] a1 + · · · + [ϕ1, ϕm] am = [y , ϕ1] (4) · · ·    
[ϕm, ϕ0] a0 + [ϕm, ϕ1] a1 + · · · + [ϕm, ϕm] am = [y , ϕm]
trong đó tích vô hướng được định nghĩa như sau n X [ϕr , ϕk ] = ϕr (xi )ϕk (xi ) i =1 và vector y = (y1, y2, · · · , ym). Ngày 11 tháng 11 năm 2019 6 / 19
Phương pháp tìm a0, a1, · · · , am.
Định nghĩa hệ phương trình chuẩn
Hệ (4) là hệ phương trình tuyến tính m + 1 phương trình m + 1 ẩn được
gọi là hệ phương trình chuẩn.
Định thức của ma trận hệ số của hệ (4) được gọi là định thức Gram của
hệ hàm ϕ0, ϕ1, · · · , ϕm.
Nếu hệ hàm ϕ0, ϕ1, · · · , ϕm độc lập tuyến tính trên phân hoạch
∆ = {a = x1 < x2 < · · · < xn = b}
thì định thức Gram khác 0 và hệ (4) có nghiệm duy nhất (a0, a1, · · · , am). Hàm số m X ϕ(x ) = aj ϕj (x) j =0
xấp xỉ hàm f (x ) tốt nhất theo nghĩa trung bình phương. Ngày 11 tháng 11 năm 2019 7 / 19 Sai số của phương pháp
Sai số của phương pháp được cho bởi công thức n !1/2 1 X σm = (yi − ϕ(xi ))2 (5) n i=0
Do (a0, a1, · · · , am) là nghiệm của hệ (4) nên n
X (yi − ϕ(xi))2 = [y − ϕ, y − ϕ] = [y − ϕ, y]−[y − ϕ; ϕ] = [y, y]−[y, ϕ] . i =0
Thay vào biểu thức phía trên ta nhận được biểu thức tính sai số của phương pháp   1/2 m 1 X σm =  [y , y ] − aj [y , ϕj ] . (6) n j =0 Ngày 11 tháng 11 năm 2019 8 / 19
Hệ hàm là hệ trực chuẩn
Định nghĩa hệ trực giao Hệ hàm ϕk (x)
được gọi là hệ trực giao trên phân hoach ∆ của đoạn k=0,m [a, b] nếu n ( X = 0 nếu r 6= s [ϕr , ϕs ] =
ϕr (xi )ϕs (xi ) 6= 0 nếu r = s i =1
Định nghĩa hệ trực chuẩn Hệ hàm ϕk (x)
được gọi là hệ trực chuẩn nếu nó là hệ trực giao và k=0,m
các vector đều có chuẩn bằng 1. Nếu chọn hệ ϕk (x)
là hệ trực giao thì từ hệ phương trình chuẩn ta có k=0,m [y , ϕk ] ak = , k = 0, m. [ϕk , ϕk ] Ngày 11 tháng 11 năm 2019 9 / 19
Sai số của phương pháp khi hệ hàm là hệ trực chuẩn Thay [y , ϕk ] ak = , k = 0, m [ϕk , ϕk ]
vào công thức tính sai số (5) ta nhận được m !!1/2 1 X [y , ϕk ]2 σm = ky k2 − . n kϕk k2 k=0
Nhận xét: Ta thấy khi số chiều của hệ cơ bản tăng (m tăng) thì sai số σm giảm. Ngày 11 tháng 11 năm 2019 10 / 19
Hệ cơ bản là hệ đại số Xét hệ cơ bản là hệ ϕj (x) = xj , j = 0, m, (m ≤ n − 1).
Bài toán trở thành tìm aj , j = 0, m sao cho m X ϕ(x ) = Pm(x) = aj xj j =0 là đa thức bậc m.
Do hệ ϕj (x) = xj , j = 0, m là hệ độc lập tuyến tính nên hệ phương trình
chuẩn có nghiệm duy nhất. Ngày 11 tháng 11 năm 2019 11 / 19
Hệ cơ bản là hệ đại số Trong trường hợp này n n X X [y , ϕs ] = yi ϕs (xi ) = yi xsi; i =1 i =1 n n X X [ϕr , ϕs ] = ϕr (xi )ϕs (xi ) = x r+s . i i =1 i =1
Hệ phương trình chuẩn khi hệ cơ bản là hệ đại số có dạng na x x 2a x ma y  0 + Pn i a1 + Pn 2 + · · · + Pn m = Pn i  i =1 i =1 i i =1 i i =1  Pn  x x 2a x 3a x ma x i =1 i a0 + Pn i =1 i 1 + Pn i =1 i 2 + · · · + Pn i =1 i m = Pn i =1 i yi · · ·    Pn  x ma x m+1a x 2ma x my i =1 i 0 + Pn i =1 i 1 + · · · + Pn i =1 i m = Pn i =1 i i Ngày 11 tháng 11 năm 2019 12 / 19
Hệ cơ bản là hệ lượng giác Xét hệ cơ bản có dạng
ϕ0 = 1; ϕ1(x) = cos(x); ϕ2(x) = sin(x), · · ·
ϕ2r−1 = cos(rx); ϕ2r = sin(rx), (r = 1, k)
Khi đó bài toán quy về tìm đa thức xấp xỉ có dạng k X Tk (x) = α0 + αr cos(rx) + βr sin(rx) r =1
trong đó α0, αr , βr , r = 1, k được xác định từ hệ phương trình chuẩn. Ngày 11 tháng 11 năm 2019 13 / 19
Hệ cơ bản là hệ lượng giác
Trong trường hợp này các tính vô hướng được tính như sau: n n X X [ϕ0, ϕ0] = 12 = 1; [y , ϕ0] = yi ; i =1 i =1 (Pn cos(rxi ) nếu j = 2r − 1, [ϕ i =1 0, ϕj ] = Pn sin(rx i =1 i ) nếu j = 2r , Pn cos(rx  i =1
i )cos (sxi ) nếu l = 2r − 1, j = 2s − 1,  [ϕ Pn l , ϕj ] = sin(rx i =1
i )cos (sxi ) nếu l = 2r , j = 2s − 1,  Pn sin(rx i =1
i )sin(sxi ) nếu l = 2r , j = 2s , (Pn
yi cos(rxi ) nếu j = 2r − 1, [y , ϕ i =1 j ] = Pn y i =1 i sin(rxi ) nếu j = 2r . Ngày 11 tháng 11 năm 2019 14 / 19
Hệ cơ bản là hệ lượng giác
Hệ phương trình chuẩn khi hệ cơ bản là hệ đại số có dạng nα (α Pn cos(rx Pn sin(rx y  0 + Pk r =1 r i =1 i ) + βr i =1 i ) = Pn i =1 i )         Pn Pn α cos(px {α cos(rx  0 i =1 i ) + Pk r =1 r i =1 i ) cos(pxi )    Pn  +β sin(rx y  r i =1 i ) cos(pxi )} = Pn i =1 i cos(pxi )    Pn Pn α0 sin(px {αr cos(rx  i =1 i ) + Pk r =1 i =1 i )sin(pxi )    Pn  +βr sin(rxi )sin(pxi )} = Pn yi sin(pxi )  i =1 i =1        p = 1, 2, · · · , k .
Giải hệ trên ta tìm được α0, αr , βr , r = 1, k. Khi đó ta tìm được hàm xấp xỉ của f (x ) là k X T k (x) = α0 + αr cos(rx) + βr sin(rx) r =1 Ngày 11 tháng 11 năm 2019 15 / 19
Tìm hàm thực nghiệm theo phương pháp bình phương tối thiểu
Trong thực tế quan hệ giữa 2 đại lượng x và y thường được biểu diễn dưới
dạng bảng số là kết quả của việc đo đạc thực nghiệm chứ không có biểu
thức giải tích cụ thể. Việc từ bảng số này tìm ra quan hệ dạng y = f (x )
cụ thể gọi là lập công thức thực nghiệm. Dạng của hàm số f (x ) thường
được xác định bởi các định lý vật lý, hóa học,· · · . Một số các dạng hàm
thực nghiệm thường gặp: y = ax + b; y = a + bx + cx 2; y = a + bx + cx 2 + dx 3; y = a + bcosx + csinx ; y = aebx ; y = ax b. Ngày 11 tháng 11 năm 2019 16 / 19
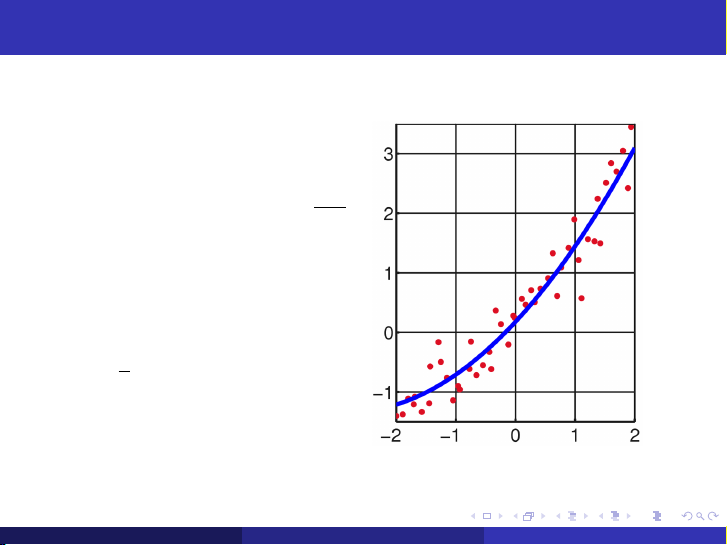
Một số trường hợp cụ thể của hàm thực nghiệm a) Trường hợp y = ax + b (na + b Pn x y i =0 i = Pn i =0 i a Pn x x 2 = Pn y i =0 i + b Pn i =0 i i =0 i xi
b) Trường hợp y = ax 2 + bx + c na + b Pn x x 2 = Pn y  i =0 i + c Pn i =0 i i =0 i  a Pn x x 2 + c Pn x 3 = Pn y i =0 i + b Pn i =0 i i =0 i i =0 i xi  a Pn x 2 + b Pn x 3 + c Pn x 4 = Pn y i =0 i i =0 i i =0 i i =0 i x 2 i Ngày 11 tháng 11 năm 2019 17 / 19
Một số trường hợp cụ thể của hàm thực nghiệm c)Trường hợp y = aebx .
Bằng cách lấy logarit hai vế ta đưa bài toán trên về dạng: Từ bảng số dạng Yi ≈ lg(f (xi )) i = 1, n
cần tìm hàm xấp xỉ trong dạng tuyến tính Y = A + BX trong đó Yi ≈ lg yi và Xi = xi .
Nhận xét: Khi bảng số đo được bằng thực nghiệm có các điểm (xi , lgyi )
gần như nằm trên 1 đường thẳng thì chúng ta dùng các hàm thực nghiệm dạng y = aebx .. Ngày 11 tháng 11 năm 2019 18 / 19
Một số trường hợp cụ thể của hàm thực nghiệm d) Trường hợp y = ax b.
Việc tìm hàm thực nghiệm dạng y = ax b
hoàn toàn tương tự như trong trường hợp dạng y = aebx
bằng cách quy về dạng tìm hàm xấp xỉ Y = A + bX trong đó Yi ≈ lgyi và Xi ≈ lgxi .
Nhận xét: Khi bảng số đo được bằng thực nghiệm có các điểm (lgxi , lgyi )
gần như nằm trên 1 đường thẳng thì chúng ta dùng các hàm thực nghiệm dạng y = ax b. Ngày 11 tháng 11 năm 2019 19 / 19
Document Outline

• Ngày 11 th¡ng 11 n«m 2019 4 / 1