Bài giảng về Thuật toán đệ quy | Cấu trúc dữ liệu và giải thuật | Đại học Bách Khoa Hà Nội

Bài giảng về Thuật toán đệ quy | Cấu trúc dữ liệu và giải thuật | Đại học Bách Khoa Hà Nội. Tài liệu được biên soạn giúp các bạn tham khảo, củng cố kiến thức, ôn tập và đạt kết quả cao kết thúc học phần. Mời các bạn đọc đón xem!

62 31 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Môn: Cấu trúc dữ liệu và giải thuật (ET2100)

Trường: Đại học Bách Khoa Hà Nội

Thông tin:

24 trang 6 tháng trước

Tác giả:

Profile Thùy Dương
1/10/2011
REVIEW
Xácđịnh m gi các c ốiquanhệ ữa ặphàm󰇛󰇜và󰇛󰇜sau
đây
a󰇜
.
3󰇛1󰇜, 6
b󰇜
3 1󰇜,
c󰇜
2
.
,
THUẬTTOÁN QUYĐÊ
Nộidung
Địnhnghĩađệquy
Thu toán quyật đệ
Phân thu toán quytích ật đệ
Đệquy có nhớ
Thu toán quay luiật (backtrackingalgorithm)
Địnhnghĩađệquy
Đối tượngbaogồm chínhnó
hoặcđượcđịnhngh a d iĩ ướ
d ng chính nóạ .
VD. nh ngh a m tĐị ĩ ộ công th c ứ hợp
toánphép
là công th c l ứ h pợ ệnếu là
bi ho c sến ặ ố
Nếu,là công th c l ứ hợp ệthì
󰇛󰇜 󰇛󰇜, ,󰇛∗󰇜,󰇛/󰇜,
󰇛^󰇜c ng là công th cũ ứ h pợ lệ
1
CuuDuongThanCong.com https://fb.com/tailieudientucntt
1/10/2011
Hàmđược nh nghđị ĩađệquy
!
1ế0
1!ế0

1ế1,2
1 2ế2
ð
0ế0
1ế1
21 2ế1
Địnhnghĩađệquy
M i nh nghọ đị ĩađệquy g m ph nđều ồ 2 ầ
Một tr ường chợp ơsở(nhỏnh t) có th x lý tr c ti màấ ể ử ự ếp không
c quy, vàầnđệ
Một ph ương th c t ng quát mà bi ứ ổ ếnđổi m t tr ng c th v ộ ườ h pợ ụ ể ề
các tr ng nh n. Do bi i các tr ng ườ h pợ ỏhơ đó ếnđổ ườ h pợ chođến
khiv tr ng cề ườ h pợ ơsở.
Thu t toán quyậ đệ
Thu t toánậ cóch aứ l iờ gọiđệquyđếnchínhnóv iớ đầu
vào kích th nh h n ước ỏ ơ .
VD. S x ắp ế ộp tr n– MergeSort
MergeSort(intA[], int start, int end)
{
if(start<end)
{
int mid = (start+end)/2;
MergeSort(A, start, mid);
MergeSort(A, mid+1, end);
Merge(A,start,mid,end);
}
}
khi chia
Trộn l n 1ầ
Trộn l n 2ầ
Trộn l n 3ầ
Danh sách ban uđầ
Chia lần 1
Chia lần 2
Chia lần 3
2
CuuDuongThanCong.com https://fb.com/tailieudientucntt
1/10/2011
Thu t toán quyậ đệ
Mô t th i gian th hi thu ả ờ ực ệncủa ậttoánđệquybằng
công th quy ứcđệ
VD. MergeSort có
Ο1ế1
2
2
Οế1
B qua v iỏ 󰇛󰇜 ớ cácgiátrịnnhỏ(coilà ng). Ta có th vi t l ihằ ể ế ạ
󰇛󰇜là
2
2
Ο
Phân tích thu t toán quy ậ đệ
Gi i công thả ứcđệquyđểtìmΘhoặcΟb ng:ằ
Ph ng pháp thay thươ ế
Ph ng pháp câyươ đệquy
Dùng nhđị lýthợ
Ph ng pháp thay thươ ế
Ph ng pháp thay thươ ế
Gồm2bước:
Đ ạ ảoánd ng củalờigi i
Sửd n hụng quy ạptoán ọcđểtìm ra các ng và hằ ch ng minhứ
l i gi iờ ả
công thứcđệquy
2
2
Đoán Ο󰇛log󰇜
Cầnch ng minhứ 󰇛󰇜logv i ng sớ hằ ố0đượcchọn
phù phợ
3
CuuDuongThanCong.com https://fb.com/tailieudientucntt
1/10/2011
Ph ng pháp thay thươ ế
Gi úng vảsử󰇛󰇜logđ ới
⁄ tứclà
󰇛
⁄ 󰇜
⁄ log
⁄ . Thay vào
2
⁄ log
⁄
log
⁄ loglog2
log
Đúngvới1
Ta c ch ra k ần ỉ ếtquảquy nạp nàyđúngtrong m i tr ng ọ ườ
hợp( úng cđ ảtrong tr ng c ườ hợp ơsở).
Ph ng pháp thay thươ ế
Gi tr ng cảsử ườ hợp ơsở1 1nh ng .ư 1log10
Kếtqu quy trongả n pạ sai trườnghợ ở pcơs .
Ta có th gi i quy ể ả ếtvấnđềnàykhisửd uụng các ký hi ệ
ti m c ( )ệ ận Ο,Ω,Θ
logv iớ
Ch v mọn
saocho ới ọi
thì k ếtquảluônđúng
VD v i ớ 2thì 2 21 242log2với
h nằngsốta ch ọ đủlớn(VD5).
Vậ y Ο󰇛log󰇜v iớ 5và2
Ph ng pháp thay thươ ế
Đ ạ ờ ảoánd ngl igi itốt:
Thêm ng không thaybớt1hằ số làm đổidạng k ế ảtqu
2
12 3v có ngẫn dạ Ο󰇛log󰇜
Ban i ng c trên,đầunớ lỏ ận dướiđể
gi m n.ả dầ
VD. V ới󰇛󰇜trong ví ta có th ch và dụbanđầu ể ọnΩ󰇛󰇜
Ο󰇛
󰇜r i ó gi m gi trên, t ng gi i iồ sauđ ả ớihạn ă ớ h nạ dướ cho
t i khi vớ hộitụ ề ịgiátr chínhxác
Ph ng pháp thay thươ ế
Tránh i hay m clỗ ắ
2
2
Ο󰇛󰇜
Sai do ta không ch ng minh ứ 󰇛󰇜
Thay biđổi ến
2 log
đặtlogta có 2
22
"
⁄
đặt 󰇛2
󰇜ta có 2
⁄
Οlog Ο󰇛logloglog󰇜
4
CuuDuongThanCong.com https://fb.com/tailieudientucntt
1/10/2011
Ví . Ch ng minh rdụ ứ ằng
2
1làΟ󰇛log󰇜
M s tính ch cột ố ất ủa hàm mũ, loga, giai th a ừ
Ta có các công thức:
a
= b
log
b
a
; log
b
a = 1/(log
a
b)
Do đó, trong ký hiệu tiệm cận cơ s c ng:ố ủa log là không quan trọ
O(lg n n) = O(ln ) = O(log )n
Công thức Stirling:
Giai th :ừa và hàm mũ
2
n
< n! < n
n
với n > 5 ;
log log n! = (n n).
ö ö
ö ö ö ö
÷ ÷÷ ÷ ÷ ÷
ø ø ø ø
ø ø
1
! 2 1
n
n
n n
e n
Vấnđềvớiphươngphápthay th ế
T(n) = T(n/2) + n 4ô
4ô ôc (n/2)
2
+ n
= c ôn
2
+ n
T(n) = 1 n=1
T(n) = 4ôT(n/2) + n n>1
Dự đoán (chặt hơn!):
T(n) côn
2
n>n
0
Giả s , ử T(k) côk
2
k<n. Chứng minh T(n) . côn
Chuy p:ển qui nạ
Không c n !ô
2
Ví d 2 (ti p) ụ ế
T(n) = 1 n=1
T(n) = 4ôT(n/2) + n n>1
Dự đoán:
T(n) côn
2
- dôn n>n
0
Gi n.ả s n, ử T(k) côk
2
- dô k<n. Cần CM T(n) côn
2
- dô
Sử d ụng dự đoán chính xác hơn.
tăng chậ ậm (là một kỹ thu t hay dùng).
5
CuuDuongThanCong.com https://fb.com/tailieudientucntt
1/10/2011
Ví d 2 (ti p) ụ ế
Khi n=1:
T(n) nh ngh a.=1 Theođị ĩ
1 c th ch n ‐d Có ể ọ c, d thích h p ợ để đẳcó b ất ng th c ứ này
T(n) = 1 n=1
T(n) = 4ôT(n/2) + n n>1
Dự đoán:
T(n) côn
2
- dôn n>n
0
Gi n.ả s n, ử T(k) côk
2
- dô k<n. CM T(n) côn
2
- dô
Ví d 2 (ti p) ụ ế
Chuy qui p,ển nạ n>1:
T(n) 4 T(n/2) nh a)= ô +n (đị nghĩ
4ô ô ô(c (n/2)
2
‐ d (n/2))+n (qui p)nạ
= +c 2ôn
2
‐ ôd nô n (biếnđổi)
=côn d
2
‐ ôn‐ (dôn‐ n) (biếnđổi)
côn
2
‐ d*n (Chọ n dó1)
T(n) = 1 n=1
T(n) = 4ôT(n/2) + n n>1
Dự đoán:
T(n) n côn
2
- dô n>n
0
Gi n.ả sử T(k) côk
2
- dôn, k<n. CM T(n) côn
2
- dô
Ví d 2 (ti p) ụ ế
T(n) = 1 n=1
T(n) = 4ôT(n/2) + n n>1
Đã chứng min
T(n) 2ôn
2
– 1ôn n>0
Vậy, T(n) = O(n
2
).
Ph ng pháp cây quyươ đệ
6
CuuDuongThanCong.com https://fb.com/tailieudientucntt
1/10/2011
Ph ng pháp cây quyươ đệ
Cây quy mergeSortđệ cho 
1ế1
2
ế1
Ph ng pháp cây quyươ đệ
Xét công th quy ứcđệ

Ο󰇛󰇜
Ph ng pháp cây quyươ đệ
Dùng ph ng thay th ch ng minh l i gi công ươ pháp ếđể ứ ờ ải
th quy tìmứcđệ được.
VD.

Ο Ο󰇛log󰇜


log

log



3
log

3
log3
2
3
log2
2
3
log3
loglog3
2
3
log2
log
V
ới
"""
"
Ph ng pháp cây quyươ đệ
Bài t p ậ :Xác nh m cđị ột ậntrêntốtchocôngthứcđệquy
3
dùng ph ng pháp th xác nh k ươ ếđể ậnl iạ ếtquả.
7
(chú ý ) log21
CuuDuongThanCong.com https://fb.com/tailieudientucntt
1/10/2011
Định lý th ợ
Mastertheorem
Dùng nh lý thđị ợ
Dùngđểgi các công th quy ngải ứcđệ dạ

,
đó1,1,ààệậươ
m cách hi qu .ột ệu ả
Bài toán toán con có kích ban bàiđầuđượcchiathành
th m là
ước ỗibài
⁄
,chiphí t ng các toán conđể ổ hợp bài
là󰇛󰇜
VD. Thu ật toán s p x ắ ếptrộn
chia toán con, kích th cthành2bài ướ /2. phí t ngChi ổ h pợ 2bài
toán con là Ο󰇛󰇜
Dùng nh lý thđị ợ
Định lý th ợ(Master Theorem)
1,1là các h ng ằ số , 󰇛󰇜làmộthàm.󰇛󰇜định ngh ĩađệ
quy trên các thamsốkhôngâm

⁄
󰇛󰇜, trong đó
⁄
có th ểhi u làể
⁄
ho cặ
⁄
. Thì 󰇛󰇜cóth b gi i h nể ị ớ ạ một cách ti ệmc n nh sau:ậ ư
N uế Ο󰇛
""" 
󰇜, v i h ng ớ ằ 0thì Θ󰇛 󰇜
N uế Ο󰇛
"""
󰇜thì Θ󰇛
"""
log󰇜
N uế Ω󰇛
""" 
󰇜, v i h ng ớ ằ 0, và n uế

⁄
󰇛󰇜v i h ngớ ằ 1và v i ớ mọi n l n đủ ớ thì
Θ󰇛󰇛󰇜󰇜
Dùng nh lý thđị ợ
Áp d ng ụ định lý th ợ:
9
.
9,3à ta có
"""
≡
"""
. âyĐ
là tr ng (v ườ hợp1 ới1) do ó đ Θ󰇛
󰇜

1.
1ta có
"""
/"
1. ây làĐ
tr ng 2, do óườ hợp đ Θ󰇛log󰇜
3
log
3,4và logta có
"""
≡
"""
Ο󰇛
.
󰇜, Ω󰇛
"""

󰇜với0.2,
⁄

≡3
󰇛log󰇜với
do v ậy
Θ󰇛log󰇜(TH3)
8
󰇛 g 󰇜
CuuDuongThanCong.com https://fb.com/tailieudientucntt
1/10/2011
Dùng nh lý thđị ợ
Chúý:Không ph i tr ng ả ườ hợpnàoc cũng áp ng dụ đượ
định lý thợ!
VD. 2
log
2,2và log
"""
≡
"""
"
do ó có v áp ng tr ngđ ẻ dụ ườ hợ p3.
Tuy nhiên
logti m cệ ậnlớnhơn2
v iớ
m i ng do ó không th áp ng c.ọ hằ số đ ể dụ đượ
Đệquycónhớ
Đệquycónhớ
Trong thu ậttoánđệquy, nh ng toán con có th ữ bài ểđược
gi i gi i nhi n!ả đi ảilạ ềulầ
VD. Tính sốFibonacci
1ế0,1
1 2ế2
Tính󰇛5󰇜
Ghi nh n l i gi i: dùng ng ậ ờ ả mả
Khi g toán con c gi i: Ki m tra xem toán con ặpbài ần ả ể bài
đãđượcgiảichưa:
Nếuđã gi i: l ả ấy k ế ảtqu
Ng c l i, gi i toán con và cượ ạ ả bài ậ ậ ảpnh tlờigi ivào ngbả
Thu toán quay luiật
Back tracking‐ algorithm
9
CuuDuongThanCong.com https://fb.com/tailieudientucntt
1/10/2011
Thu t toán quay luiậ
Bài toán con u: “Hãy x 8 hậ ế p8 conhậutrên c 8x8bàn ờ
sao cho chúngkhông th l ểăn ẫnnhau”
Thu t toán quay luiậ
Thuậttoán x ế ậph u:đặt tlầnlượ các quân lên c hậu bàn ờ
(theo cách ó) quân1 nàođ sao cho hậuđặtsaukhôngăn
đượcquânđãđặttrướcđó.
Thu t toán quay luiậ
solve_from (Current_config)
if Current_config đã achứ đủ8hậu
printCurrent_config
else
Với t ập p các trên bàn c ô ờmà ch b nh ưa ịả h ng b iưở ở Current_config
{
Thêm 1 quân hậu vào p;
Cập nh ậtl iạ Current_config
solve_from(Current_config);
Lo i b quân h u kh i p cạ ỏ ậ ỏ ủaCurrent_config;
}
Thu t toán quay luiậ
Deadend: tr ạngtháichưakế tthúc, nh ng ta không thư ể
đặt thêmđược 1quân hậu nào nữa.
Khi r vào tr ơi ạngtháideadendta ph i ti quay lui ả ếnhành
(backtrack) l i ch g ạ lựa ọn ầnnhấtđểthửmột khảnăng có
thểkhác.
10
CuuDuongThanCong.com https://fb.com/tailieudientucntt
1/10/2011
Thu t toán quay luiậ
Thuậttoán quay lui – backtrackingalgorithm:
Th tìm ki m giử ế lời ảiđầy toán vi xây ngđủchobài từ ệc dự
l i gi ph n, trongờ ảibộ ậ đó l gi ph ph i luôn phù ời ảibộ ận ả
hợpv i yêu c toán.ớ ầubài
Trong quá trình th ựchi n, thu toán m rệ ật ở ộ ờ ngdầnl igiải
b u nộph n.ậ Nế vi mệc ởr ng khi i gi iộ ếnlờ ả bộphậ vi ph m ạ
yêu c toán thì ti quay lui, lo i i ầubài ếnhành ạ bỏsửađổ
g nhần ất tvà th m ử ộ kh ng xây ngảnă dự lời giả ậibộph n
có th (h ) ể ợplệ khác.
Bài toán 8 con h u ậ
Nh n xét:ậ
Mỗi c ộtph i cóả 1 con h u ậ
Con h u 1 n ậ ằmtrên c ột1
…
Con h u n ậ j ằmtrên c ộtj
…
Con h u 8 n ậ ằmtrên c ột8
Cáccon ph ihậu ả khôngcùnghàng
Cáccon ph i m trên ng chéo c a nhauhậu ả khôngnằ đườ ủ
Gi thu tải ậ
function Try (column) {
for (row = 1; row <= 8; row++) {
if ([row, column] là an toàn ){
Đặtcon h u vào v trí [row, column]; ậ ị
mn == 8)
In k ế ảt qu ;
else
Try (column + 1);
Xóa con h u kh i v trí [row, column]; ậ ỏ ị
}
}
}
Con hậu thứ 8 là an toàn
Xóa vđể tiếp tục thử ị trí
[row+1, column]
Thử lần lượt từng vị trí hàng
Nếu vị trí thử không bị
con hậ ấu nào t n công
Đ
Ki tra An toànểm
11
CuuDuongThanCong.com https://fb.com/tailieudientucntt
1/10/2011
12
CuuDuongThanCong.com https://fb.com/tailieudientucntt
| 1/24
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

1/10/2011 REVIEW
 Xácđịnhmốiquanhệ g
 iữacáccặphàm󰇛󰇜 và󰇛󰇜 sau đây
a󰇜    .  3󰇛  1󰇜,   6
b󰇜      3   1󰇜,   
c󰇜    2.  ,    THUẬTTOÁNĐÊQUY Nộidung Địnhnghĩađệquy
 Đốitượngbaogồmchínhnó
 Địnhnghĩađệquy
hoặcđượcđịnhnghĩadư i ớ 
dạngchínhnó.
 Thuậttoánđệquy VD.Đ nh ị
nghĩamộtcôngthứchợp
 Phântíchthuậttoánđệquy phéptoán  Đệquycónhớ
  làcôngthứchợplệnếu là biếnhoặcsố
 Thuậttoánquaylui(backtrackingalgorithm)
 Nếu,  làcôngthứchợplệthì
󰇛  󰇜,󰇛  󰇜,󰇛 ∗ 󰇜,󰇛/󰇜,
󰇛^󰇜 cũnglàcôngthứchợplệ CuuDuongThanCong.com
https://fb.com/tailieudientucntt 1 1/10/2011
Hàmđượcđịnhnghĩađệquy Địnhnghĩađệquy
 Mọiđịnhnghĩađệquyđềugồm2phần
 !  1               ế  0
 ườnghợpcơsở(nhỏnhất)cóthể x
 ửlýtrựctiếpmàkhông
    1 !     ế  0  Một tr cầnđệquy,và
 Mộtphươngthứctổngquátmàbiếnđổimộttrườnghợpcụthể v  ề
cáctrườnghợpnhỏhơn.Dođóbiếnđổicáctrườnghợpchođến     
1          ế  1, 2
   1     2      ế  2 khivề t
 rườnghợpcơsở.
0          ế  0     ð
1          ế  1
2   1     2  ế  1
Danh sách banđầu Thuậttoánđệquy Chia lần 1
Thuậttoáncóchứalờigọiđệquyđếnchínhnóvớiđầu
vàokíchthướcnhỏ h  ơn. Chia lần 2
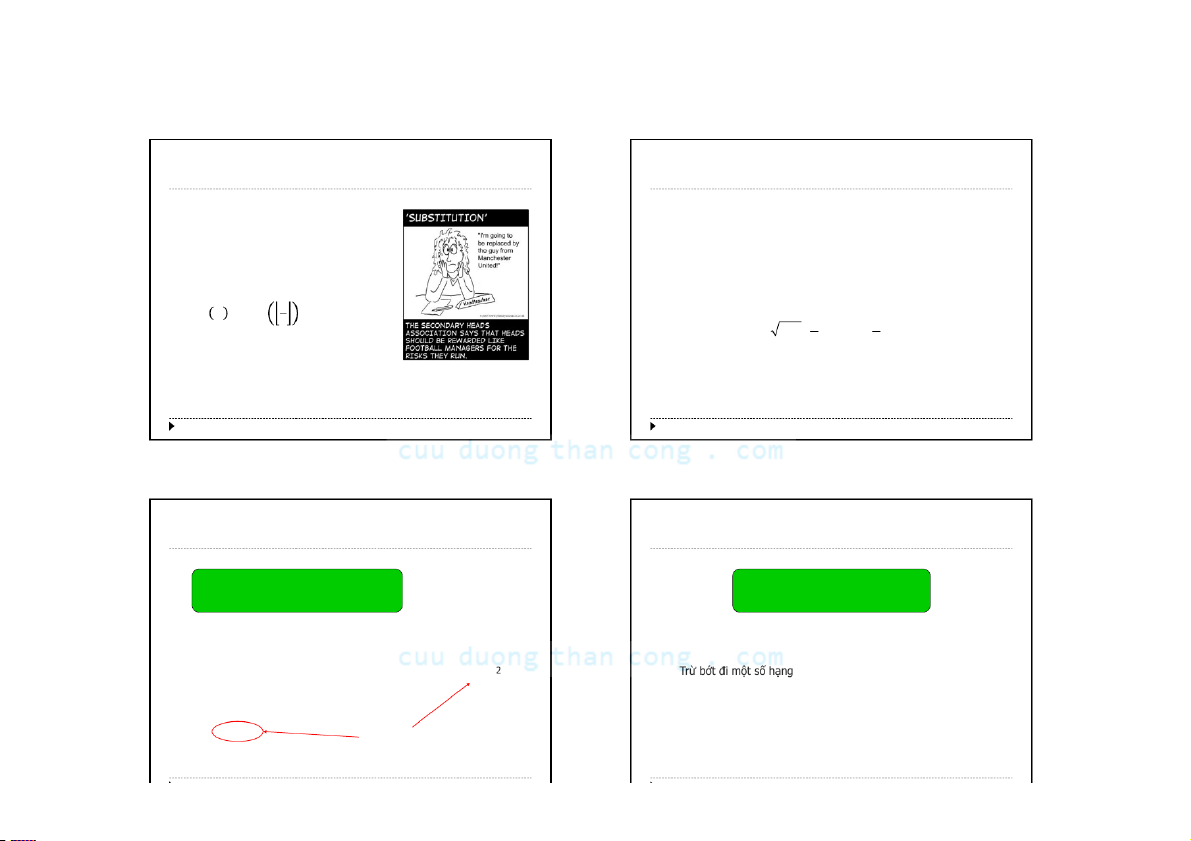
 VD.Sắpxếptrộn– MergeSort
MergeSort(intA[],intstart,intend) { Chia lần 3 if(start{ intmid=(start+end)/2; khi chia MergeSort(A,start,mid);
Trộn lần 1 MergeSort(A,mid+1,end); Merge(A,start,mid,end);
Trộn lần 2 } }
Trộn lần 3 CuuDuongThanCong.com
https://fb.com/tailieudientucntt 2 1/10/2011 Thuậttoánđệquy
Phântíchthuậttoánđệquy
 Môtảthờigianthựchiệncủathuậttoánđệquybằng côngthứcđệ quy 
 GiảicôngthứcđệquyđểtìmΘ hoặcΟ bằng:  VD.MergeSortcó
Ο 1     ế  1  Phư ng ơ phápthaythế      2 ươ   đệ
2  Ο     ế  1  Ph ng pháp cây quy
 Dùngđịnhlýthợ
Bỏqua󰇛󰇜 vớicácgiátrịnnhỏ(coilàhằng).Tacóthể v  iếtlại 󰇛󰇜 là     2 2  Ο  Phư ng ơ phápthaythế  Gồm2bước:
 Đoándạngcủalờigiải
 Sửdụngquynạptoánhọcđểtìmracáchằngvàchứngminh lờigiải
côngthứcđệquy Phư ng ơ phápthaythế    2  2   
Đoán   Ο󰇛log󰇜
Cầnchứngminh󰇛󰇜  log vớihằngsố  0 đượcchọn phùhợp CuuDuongThanCong.com
https://fb.com/tailieudientucntt 3 1/10/2011 Phư ng ơ phápthaythế Phư ng ơ phápthaythế
 Giảsử󰇛󰇜  log đúngvới   ⁄ tứclà
 Giảsửtrườnghợpcơsở 1  1 nhưng1log1  . 0  󰇛   ⁄ 󰇜     ⁄ log   ⁄ .Thayvào 
Kếtquảquynạpsaitrongtrườnghợpcơsở.  Tacóthể g
 iảiquyếtvấnđềnàykhisửdụngcáckýhiệu    2   ệ  ậ  ⁄ log   ⁄   ti m c n(Ο, Ω, Θ)  log 
   log với   
⁄    log  log2     log  Chọn v m
 saocho ới ọi   thìkếtquảluônđúng
VDvới  2 thì 2  2 1  2  4  2log2 với
hằngsố tachọnđủlớn(VD  5). Đúngvới  1
 Vậy   Ο󰇛log󰇜 với  5 và  2 Tacầnchỉ r
 akếtquảquynạpnàyđúngtrongmọitrường
hợp(đúngcảtrongtrườnghợpcơsở). Phư ng ơ phápthaythế Phư ng ơ phápthaythế
Đoándạnglờigiảitốt:
 Tránhlỗihaymắc
 Thêmbớt1hằngsố k
 hônglàmthayđổidạngkếtquả
   2   2        Ο󰇛󰇜
   2   12  3 vẫncódạngΟ󰇛log󰇜
Saidotakhôngchứngminh󰇛󰇜    Thayđổibiến
 Banđầunớilỏngcậntrên,dướiđể giảmdần.  2   log
đặt  log tacó 2  2 2 " ⁄  
VD.Với󰇛󰇜 trongvídụbanđầutacóthể c
 họnΩ󰇛󰇜 và
đặt   󰇛2󰇜 tacó   2   ⁄   
Ο󰇛󰇜 rồisau ó
đ giảmgiớihạntrên,tănggiớihạndướicho
Ο log  Ο󰇛logloglog󰇜 tớikhihộitụ v
 ềgiátrịchínhxác CuuDuongThanCong.com
https://fb.com/tailieudientucntt 4 1/10/2011
Mộtsốtínhchấtcủahàmmũ,loga,giaithừa  Ta có các công thức:
a = blogb a ; log a = 1/(log b) b a
 Do đó, trong ký hiệu tiệm cận cơ số của log là không quan trọng: O(lg n n
) = O(ln ) = O(log n)
 Vídụ.Chứngminhrằng  Công thức Stirling:
   2   1 làΟ󰇛log󰇜  ö ön n ö ö 1 ö ö n !   2 n 1   ÷ ÷ ÷ ÷ ÷ ÷ ø e ø ø ø n ø ø  Giai thừa và hàm mũ:
2n < n! < nn với n > 5 ;
log n! = (n log n).
Vấnđềvớiphươngphápthaythế Vídụ 2  (tiếp) T(n) = 1 n=1 Dự đoán (chặt hơn!): T(n) = 1 n=1 T(n) = 4ôT(n/2) + n n>1 T(n)  côn2 n>n0 T(n) = 4ôT(n/2) + n n>1 ụ đ Chuyển qui nạp:
Sử d ng dự oán chính xác hơn.
Giả sử T(k)  côk2, k tăng chậm (là một kỹ thuật hay dùng). T(n)=4ôT(n/2)+n  Dự đoán: 4ôcô(n/2)2 +n
T(n)  côn2 - dôn n>n =côn2 +n 0 Không  côn2 !
Giả sử T(k)  côk2 - dôn, kCuuDuongThanCong.com
https://fb.com/tailieudientucntt 5 1/10/2011 Vídụ 2  (tiếp) Vídụ 2  (tiếp) T(n) = 1 n=1 Dự đoán: T(n) = 1 n=1 Dự đoán: T(n) = 4ôT(n/2) + n
n>1 T(n)  côn2 - dôn n>n   0 T(n) = 4ôT(n/2) + n
n>1 T(n) côn2 - dôn n>n0
Giả sử T(k)  côk2 - dôn, kGiả sử T(k)  côk2 - dôn, kKhin=1:
Chuyểnquinạp,n>1: ô T(n)=1 Theođ nh ị nghĩa. T(n)=4 T(n/2)+n (địnhnghĩa)
 4ô(cô(n/2)2 ‐ dô(n/2))+n (quinạp) 1 c‐d
Cóthểchọnc,dthíchhợpđểcóbấtđẳngthứcnày =côn2 ‐ 2ôdôn+n (biếnđổi)
=côn2 ‐ dôn‐ (dôn‐ n) (biếnđổi)  côn2 ‐ d*n (Chọndó1) Vídụ 2  (tiếp) T(n) = 1 n=1 T(n) = 4ôT(n/2) + n n>1 Đã chứng min
T(n)  2ôn2 – 1ôn n>0 Phư ng ơ phápcâyđệquy Vậy, T(n) = O(n2). CuuDuongThanCong.com
https://fb.com/tailieudientucntt 6 1/10/2011 Phư ng ơ phápcâyđệquy Phư ng ơ phápcâyđệquy
 Xétcôngthứcđệquy         Ο󰇛󰇜  
 CâyđệquychomergeSort
 1     ế  1
   2        ế   1  Phư ng ơ phápcâyđệquy Phư ng ơ phápcâyđệquy
 Dùngphươngphápthaythếđểchứngminhlờigiảicông
thứcđệquytìmđược.
VD.         Ο   Ο󰇛log󰇜  
Bàitập:Xácđịnhmộtcậntrêntốtchocôngthứcđệquy
            
  log    log      3         
dùngphươngphápthếđểxácnhậnlạikếtquả.   2 2
3 log   3 log 3  3 log 2  3 log 3   2
  log    log 3  3 log2    log  Với   """ " (chúýlog 2  1)  CuuDuongThanCong.com
https://fb.com/tailieudientucntt 7 1/10/2011 Dùngđịnhlýthợ
 Dùngđểgiảicáccôngthứcđệquydạng 
        ,
đó  1,   1,   ààệậươ
mộtcáchhiệuquả.
 Bàitoánbanđầuđượcchiathành bàitoánconcókích
thướcmỗibàilà để ổ hợp bài   Địnhlýthợ  ⁄ ,chiphí t ng các toán con là󰇛󰇜 Mastertheorem
VD.Thuậttoánsắpxếptrộn
chiathành2bàitoáncon,kíchthước/2.Chiphítổnghợp2bài
toánconlàΟ󰇛󰇜 Dùngđịnhlýthợ Dùngđịnhlýthợ
Ápdụngđịnhlýthợ:
Địnhlýthợ(MasterTheorem)
  1,   1 làcáchằngsố,󰇛󰇜 làmộthàm.󰇛󰇜 địnhnghĩađệ
    9   . 
quytrêncácthamsốkhôngâm
  9,   3à    tacó""" 
 ≡ """   .Đây      
⁄  󰇛󰇜,trongđó 
⁄ cóthểhiểulà   ⁄ hoặc
làtrườnghợp1(với  1)dođó   Θ󰇛󰇜  
⁄ .Thì󰇛󰇜 cóthểbị gi
 ớihạnmộtcáchtiệmcậnnhư s  au:
       1.   1 tacó"""/"    1.Đâylà
 Nếu   Ο󰇛"""  
󰇜,vớihằng  0 thì    Θ󰇛 󰇜
trườnghợp2,dođó   Θ󰇛log 󰇜
 Nếu   Ο󰇛""" 󰇜 thì   Θ󰇛""" log 󰇜
    3    log  
 Nếu   Ω󰇛"""  
󰇜,vớihằng  0,vànếu   
  3,   4 và    log  tacó"""   ≡ """   
⁄  󰇛󰇜 vớihằng  1 vàvớimọinđủ lớnthì  
   Θ󰇛󰇛󰇜󰇜
Ο󰇛.󰇜,   Ω󰇛"""  󰇜 với  0.2,   ⁄ 
  ≡ 3   󰇛 log 󰇜 với   dovậy     Θ󰇛 log󰇜 (TH3) 󰇛 g 󰇜 CuuDuongThanCong.com
https://fb.com/tailieudientucntt 8 1/10/2011 Dùngđịnhlýthợ
Chúý:Khôngphảitrườnghợpnàocũngápdụngđược địnhlýthợ!
 VD.   2    log  
  2,   2 và    log """ 
 ≡ """ "   dođócóvẻ á
 pdụngtrườnghợp3.
Tuynhiên    log  tiệmcậnlớnhơn2  với Đệquycónhớ 
mọihằngsố dođókhôngthể á  pdụngđược. Đệquycónhớ
 Trongthuậttoánđệquy,nhữngbàitoánconcóthểđược
giảiđigiảilạinhiềulần!
 VD.TínhsốFibonacci    
1           ế  0,1
   1     2  ế  2 Tính󰇛5󰇜
Ghinhậnlờigiải:dùngmảng Thuậttoánquaylui
 Khigặpbàitoánconcầngiải:Kiểmtraxembàitoáncon Back‐trackingalgorithm
đãđượcgiảichưa:
 Nếuđãgiải:lấykếtquả
 Ngượclại,giảibàitoánconvàcậpnhậtlờigiảivàobảng CuuDuongThanCong.com
https://fb.com/tailieudientucntt 9 1/10/2011 Thuậttoánquaylui Thuậttoánquaylui
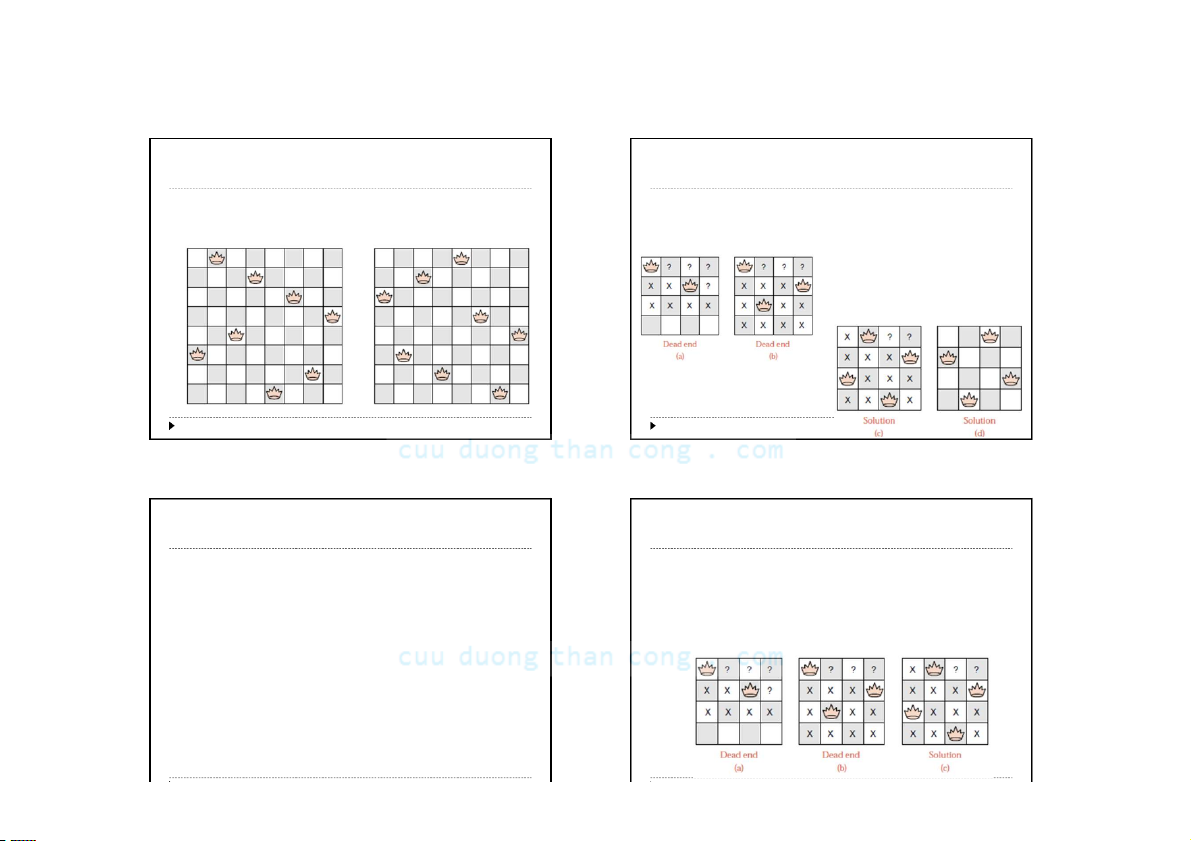
 Bàitoán8conhậu:“Hãyxếp8conhậutrênbàncờ 8  x8
Thuậttoánxếphậu:đặtlầnlượtcácquânhậulênbàncờ
saochochúngkhôngthểănlẫnnhau”
(theo1cáchnàođó)saochoquânhậuđặtsaukhôngăn
đượcquânđãđặttrướcđó.  Thuậttoánquaylui Thuậttoánquaylui
solve_from (Current_config)
 Deadend:trạngtháichưakếtthúc,nhưngtakhôngthể
ifCurrent_configđãchứađủ8hậu
đặtthêmđược1quânhậunàonữa. printCurrent_config
 Khirơivàotrạngtháideadendtaphảitiếnhànhquaylui else
(backtrack)lạilựachọngầnnhấtđểthửmộtkhảnăngcó
VớitậppcácôtrênbàncờmàchưabịảnhhưởngbởiCurrent_config thểkhác. {
Thêm1quânhậuvàop;
CậpnhậtlạiCurrent_config
solve_from(Current_config);
LoạibỏquânhậukhỏipcủaCurrent_config; } CuuDuongThanCong.com
https://fb.com/tailieudientucntt 10 1/10/2011 Thuậttoánquaylui Bàitoán8conhậu
Thuậttoánquaylui– backtrackingalgorithm:
 Thửtìmkiếmlờigiảiđầyđủchobàitoántừviệcxâydựng  Nhậnxét: lờigiảibộ ph 
ận,trongđólờigiảibộ ph 
ậnphảiluônphù
 ộtphảicó1conhậu
hợpvớiyêucầubàitoán.  Mỗi c
 Conhậu1nằmtrêncột1
 Trongquátrìnhthựchiện,thuậttoánmở r
 ộngdầnlờigiải  …
bộphận.Nếuviệcmởrộngkhiếnlờigiảibộphậnviphạm
yêucầubàitoánthìtiếnhànhquaylui,loạibỏsửađổi
 Conhậujnằmtrêncộtj
gầnnhấtvàthửmộtkhảnăngxâydựnglờigiảibộphận  … cóthể (  hợplệ)khác.
 Conhậu8nằmtrêncột8
 Cácconhậuphảikhôngcùnghàng
 Cácconhậuphảikhôngnằmtrênđườngchéocủanhau Giảithuật ể   function Try(column){
Thử lần lượt từng vị trí hàng Ki mtra An toàn
for (row=1;row<=8;row++){
if ([row,column]làantoàn){
Đặtconhậuvàovị t  rí[row,column];
Nếu vị trí thử không bị mn==8) Con hậu thứ 8 là an toàn
con hậu nào tấn công Inkếtquả; else Đ Try(column+1);
Xóaconhậukhỏivị t  rí[row,column]; } }
Xóa để tiếp tục thử vị trí } [row+1, column] CuuDuongThanCong.com
https://fb.com/tailieudientucntt 11 1/10/2011 CuuDuongThanCong.com
https://fb.com/tailieudientucntt 12