Bài giảng vectơ trong không gian, hai đường thẳng vuông góc

Tài liệu gồm 37 trang, tóm tắt lý thuyết trọng tâm, các dạng toán và bài tập chủ đề vectơ trong không gian, hai đường thẳng vuông góc, có đáp án

115 58 lượt tải Tải xuống

Chia sẻ Báo cáo tài liệu



Trang 1

CHUYÊN ĐỀ VECTƠ TRONG KHÔNG GIAN

QUAN HỆ VUÔNG GÓC TRONG KHÔNG GIAN

BÀI GIẢNG VECTƠ TRONG KHÔNG GIAN

HAI ĐƯỜNG THẲNG VUÔNG GÓC

Mục tiêu

 Kiến thức

+ Trình bày được các tính chất, quy tắc biểu diễn vectơ.

+ Phát biểu được tích vô hướng của hai vectơ, góc giữa hai đường thẳng.

 Kĩ năng

+ Chứng minh được các đẳng thức vectơ, biểu diễn được vectơ theo các vectơ không trùng

phương với nó.

+ Nắm được phương pháp chứng minh sự cùng phươ

ng của hai vectơ, tìm được điều kiện của ba

vectơ đồng phẳng.

+ Tính được góc giữa hai đường thẳng. Vận dụng được tích vô hướng của hai vectơ để giải các

bài toán.



TOANMATH.co

Trang 2

I. LÍ THUYẾT TRỌNG TÂM

A. VECTƠ TRONG KHÔNG GIAN

Các định nghĩa

a) Vectơ là một đoạn thẳng có hướng (có phân biệt

điểm đầu và điểm cuối).

+) Ký hiệu vectơ:



(điểm đầu là A, điểm cuối là B) hay

, , ,...axy



+) Độ dài của vectơ là khoảng cách giữa điểm đầu và điểm

cuối của vectơ đó.

+) Giá của vectơ là đường thẳng đi qua điểm đầu và điểm

cuối của vectơ đó.

Vectơ – không là vectơ có điểm đầu và điểm cuối

trùng nhau.

Hai vectơ được gọi là cùng phương nếu giá của

chúng song song hoặc trùng nhau.

Hai vectơ cùng phương thì cùng hướng hoặc ngược

hướng.

Hai vectơ bằng nhau là hai vectơ cùng hướng và có

cùng độ dài.

Hai vectơ đối nhau là hai vectơ ngược hướng

nhưng có cùng độ dài.

Các quy tắc tính toán với vectơ

g) Quy tắc ba điểm (với phép cộng)

BBC AC

  

Quy tắc ba điểm (với phép trừ)

OB OA AB

 

Quy tắc hình bình hành

Nếu tứ giác ABCD là hình bình hành thì

BADAC

 

Quy tắc hình hộp. Nếu .

BCDABCD



là hình

hộp thì

CABADAA





  

Phép nhân một số k với một vectơ a



Ta có



là một vectơ được xác định như sau.

+ cùng hướng với



nếu 0k  .

Sự cùng phương của hai vectơ





và

0b 



cùng phương

:.kakb  









và

0b 



cùng hướng

:.kakb



  









và 0b 



ngược hướng

:.kakb



  







Ba điểm A, B, C thẳng hàng

:.kABkAC  





Quy tắc ba điểm (mở rộng).

112 23 1

...

nn n

XXX XX XXXBAB



  

     



TOANMATH.co

Trang 3

+ ngược hướng với



nếu

0k 

+ có độ dài

.ka k a



Một số hệ thức vectơ hay dùng

l) Hệ thức về trung điểm của đoạn thẳng

I là trung điểm của đoạn thẳng

0AB IA IB

 

2OA OB OI



(với O là một điểm bất kỳ).

Hệ thức về trọng tâm của tam giác

G là trọng tâm của tam giác

0ABC GA GB GC

 

3OA OB OC OG

  

(với O là một điểm bất kỳ)

GAM

 

(với M là trung điểm cạnh BC).

Hệ thức về trọng tâm của tứ diện

G là trọng tâm của tứ diện ABCD

0GA GB GC GD 

 

4OA OB OC OD OG 

 

(với điểm O bất kỳ)

GAA





 

(với



là trọng tâm của

CD )

0GM GN

 

(với M, N là trung điểm một cặp cạnh

đối diện).

Sự đồng phẳng của ba vectơ

o) Định nghĩa

Trong không gian, ba vectơ được gọi là đồng phẳng nếu

giá của chúng cùng song song với một mặt phẳng nào đó.

Điều kiện để ba vectơ đồng phẳng

Trong không gian cho hai vectơ ,ab



không cùng phương

và vectơ



Khi đó, ,ab



và



đồng phẳng khi và chỉ khi tồn tại cặp số



;mn sao cho cmanb



(cặp số





;mn nêu trên là duy

nhất)

Phân tích một vectơ theo ba vectơ không đồng

phẳng

Cho ba vectơ

,ab



và c



không đồng phẳng.

Với mọi vectơ



, ta đều tìm được duy nhất một bộ số

Hệ quả

Nếu có một mặt phẳng chứa vectơ này đồng

thời song song với giá của hai vectơ kia thì

ba vectơ đó đồng phẳng.

Ứng dụng:

Bốn điểm phân biệt A, B, C, D đồng phẳng

BACAD



đồng phẳng

BmACnAD 



Chú ý:



TOANMATH.co

Trang 4



;;mnp

sao cho . . .

ma nb pc



Tích vô hướng của hai vectơ

a) Nếu

0a 



và

0b 



thì

...os(,)ab a b c a b

    

Nếu 0a 



và 0b 



thì .0ab



Một số ứng dụng của tích vô hướng

a) Nếu 0a 



và 0b 



ta có .0ab ab 

 

Công thức tính côsin của góc hợp bởi hai

vectơ khác





cos ,





Công thức tính độ dài của một đoạn thẳng

BAB AB



B. HAI ĐƯỜNG THẲNG VUÔNG GÓC

Góc giữa hai vectơ trong không gian

Định nghĩa:

Trong không gian, cho u



và v



là hai vectơ

khác



. Lấy một điểm A bất kì, gọi B và C là hai điểm sao

cho ,

BuACv



. Khi đó ta gọi







0 180BAC BAC   là góc giữa hai vectơ



và



trong không gian, kí hiệu là



,uv



Vectơ chỉ phương của đường thẳng

Vectơ a



khác 0



được gọi là vectơ chỉ phương của đường

thẳng

d nếu giá của vectơ a



song song hoặc trùng với

đường thẳng

Góc giữa hai đường thẳng

Bình phương vô hướng của một vectơ:

aa



Nhận xét:

a) Nếu a



là vectơ chỉ phương của đường

thẳng d thì vectơ



với 0k  cũng là

vectơ chỉ phương của d.

Một đường thẳng trong không gian hoàn

toàn xác định nếu biết một điểm A thuộc d

và một vectơ chỉ phương



của nó.

Hai đường thẳng song song với nhau khi

và chỉ khi chúng là hai đường thẳng phân

biệt và có hai vectơ chỉ phương cùng

phương.

Chú ý. Giả sử ,uv



lần lượt là vectơ chỉ

hương của đường thẳng a và b.

Đặt





,uv







Khi đó





090

180 90 180

khi



  







   



+) Nếu a//b hoặc ab thì





,0ab .





0,90ab  .



TOANMATH.co

Trang 5

Góc giữa hai đường thẳng a và b trong không gian là góc

giữa hai đường thẳng



và b



cùng đi qua một điểm và

lần lượt song song với

a và b.

Hai đường thẳng vuông góc

Định nghĩa:

Hai đường thẳng được gọi là vuông góc với

nhau nếu góc giữa chúng bằng

90

Kí hiệu: Đường thẳng a và b vuông góc với nhau kí hiệu

là

ab .

Nhận xét

a) Nếu hai đường thẳng a, b lần lượt có các

vectơ chỉ phương

,uv



thì

.0ab uv 



//ab











SƠ ĐỒ HỆ THỐNG HÓA

VECTƠ

TRONG

KHÔNG

,ab



cùng hướng

Định nghĩa

ab



Hai vectơ được gọi là

cùng phương nếu giá

của chúng song song

hoặc trùng nhau.

ab



Độ dài của vectơ là

khoảng cách giữa

điểm đầu và điểm

cuối của vectơ đó

Vectơ – không là vectơ có điểm

đầu và điểm cuối trùng nhau.

Vectơ là một đoạn

thẳng có hướng

Một số hệ thức vectơ

trọng tâm

Các phép toán

vectơ

,ab



ngược hướng

là trọng tâm của hệ n điểm

; ;...;

... 0

IA IA IA

 

,ab



đối nhau

ab



BAB



Quy tắc 3 điểm:

BBC AC

  

,ab



không cùng phương thì



và



đồng phẳng khi và chỉ khi tồn tại

cặp số



;mn sao cho cmanb



Phép trừ:

OB OA AB



ếu ABCD là hình bình hành thì

BAD AC

 

Nếu .

BCDABCD



là hình hộp thì

CABADAA





 

Sự đồng đẳng

của ba vectơ



TOANMATH.co

Trang 6

II. CÁC DẠNG BÀI TẬP

Dạng 1: Vectơ trong không gian

Bài toán 1. Xác định vectơ và chứng minh đẳng thức vectơ

Phương pháp giải

Vận dụng các kiến thức sau.

 Định nghĩa các khái niệm liên quan đến vectơ;

 Tính chất hình học của các đa giác đã học;

 Các quy tắc tính toán với vectơ;

 Một số hệ thức vectơ hay dùng;

 Các tính chất của các hình hình học cụ thể.

Ví dụ. Cho tứ diện ABCD. Gọi M, N lần lượt là trung điểm của AB và CD. Chứng minh rằng

CBD ADBC MN

    

Hướng dẫn giải

Ta có

CBD ADBC

   

CADBCBD

   

DC DC

 

(đẳng thức này đúng).

M, N lần lượt là trung điểm các cạnh AB và CD

nên

AM BM

NC ND















 

 

Do đó









DBC AM MN NB BM MN ND     

   









MBM NBND MN MN

   

Vậy

CBD ADBC MN

    

Ví dụ mẫu



TOANMATH.co

Trang 7

Ví dụ 1. Cho hình hộp

BCDABCD



. Sử dụng các đỉnh của hình hộp làm điểm đầu và điểm cuối của

vectơ.

Hãy kể tên các vectơ bằng nhau lần lượt bằng các vectơ ,,,

BACADAA





Hãy kể tên các vectơ luôn có độ dài bằng nhau và bằng độ dài của vectơ



Hướng dẫn giải

a) Ta có

BDCAB DC

 

 



CAC





 

DBCAD BC

 

 

   

ABBCCDD

 



  

Từ tính chất của hình bình hành, ta suy ra các

vectơ luôn có độ dài bằng độ dài của vectơ



là

,, ,, , , ,

BC CB AD DA A D D A B C C B

   

       

Ví dụ 2. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành.

Chứng minh SA SC SB SD

 

Nếu ABCD là hình chữ nhật thì

2222

SA SC SB SD

 

Hướng dẫn giải

a) Gọi O là tâm của hình bình hành ABCD thì O là

trung điểm của mỗi đường chéo

AC và BD.

Do đó

2SA SC SO

 

và 2SB SD SO

 

Vậy

SA SC SB SD

 

Ta có





222

2.SA SO OA SO OA SO OA 

 





222

2.SC SO OC SO OC SO OC  

  

Suy ra





22 22 2

22SA SC SO OA OC SO OA OC  

   





2 SO OA



(vì



và OC



là hai vectơ đối nhau nên 0OA OC

 

)





2 SO OA

Tương tự.





2SB SD SO OB 

 

Mà ABCD là hình chữ nhật nên

OA OB

Suy ra

2222

SA SC SB SD

 

Bài toán 2. Chứng minh ba vectơ đồng phẳng, ba điểm thẳng hàng



TOANMATH.co

Trang 8

Phương pháp giải

 Chứng minh ba vectơ đồng phẳng, sử dụng một trong các cách sau.

+ Chứng minh ba vectơ có giá cùng song song với một mặt phẳng.

+ Chứng minh hai vectơ có giá cùng song song với mặt phẳng chứa giá của vectơ còn lại.

+ Biến đổi vectơ để được đẳng thức dạng

..cmanb





Chứng minh ba điểm ,,

BC thẳng hàng

:.kABkAC  









:. 1 .kkMAkMBMC    

  



Ví dụ. Cho tứ diện ABCD. Gọi M và N lần lượt là các điểm trên các cạnh AD và BC sao cho

2, 3

MMDBCNC. Chứng minh ba vectơ ,,

BCDMN



đồng phẳng.

Hướng dẫn giải

Ta có



MN MA AB BN

NMDDCCN



















Cộng vế theo vế của hai đẳng thức này ta được













32 22

NMAMD BNCN ABDC  

   

Do 2 0, 2 0MA MD BN CN

 

     

nên

NABCD

 

Vậy , ,

BCDMN

  

đồng phẳng.

Ví dụ mẫu

Ví dụ 1. Cho hình lăng trụ tam giác .

BC A B C



có , ,

AaABbACc





  

. Hãy phân tích các vectơ

,BC BC





qua các vectơ

,,abc



Hướng dẫn giải

Ta có

CBBBC AAACAB abc

 

       

     

CBCCCACABAAabc

 

 

   



TOANMATH.co

Trang 9

Ví dụ 2. Cho hình chóp S.ABC. Lấy điểm M và N sao cho

SMA

 

và 2NC NB

 

. Chứng minh rằng ba vectơ

BMNSC



đồng phẳng.

Hướng dẫn giải

Từ giả thiết ta có 2 0; 2 0MS MA CN BN 

     

Lại có



MN MS SC CN

N MAABBN

















  

Cộng vế theo vế ta được









32222

NMSMACNBNSCABSCAB  

     

Vậy

BMNSC



đồng phẳng.

Ví dụ 3. Cho hình chóp S.ABC. Lấy các điểm ,,



lần lượt thuộc các tia ,,SA SB SC sao cho

., ., .SA a SA SB b SB SC c SC

 

, trong đó ,,abc là các số thay đổi. Chứng minh rằng mặt phẳng





đi qua trọng tâm của tam giác ABC khi và chỉ khi

3abc

Hướng dẫn giải

Từ giả thiết ta suy ra ., ., .SA a SA S B b SB SC c SC





  

Gọi G là trọng tâm của tam giác

BC . Ta có 3SA SB SC SG 

  





...G A B C SG x SA y SB z SC

   



  

với 1

yz

33.3.3.SG x SA y SB z SC



  

   

với

yz

...3.3.3.a SA b SB c SC x SA y SB z SC



  

     













3. 3. 3. 0a x SA b y SB c z SC



   



3330axbycz    (do , ,SA SB SC





không đồng phẳng)

+) Nếu





GABC



 ta có 3 3 3 0axbycz (với 1

yz).

Do đó

3abc

+) Nếu

3abc, ta đặt ,,

333

abc

xyz thì

abc

xyz



  và

3330axbycz

Do đó





GABC







TOANMATH.co

Trang 10

Ví dụ 4. Cho tứ diện ABCD, M và N là các điểm lần lượt thuộc AB và CD sao cho

2, 2

AMBNDNC 

   

; các điểm , ,IJK lần lượt thuộc , ,

DMN BC sao cho

., . , .IA kID JM kJN KB kKC



. Chứng minh rằng các điểm

,,IJK

thẳng hàng.

Hướng dẫn giải

Ta có

AMB

 

nên với điểm O bất kỳ thì

OA OB









Tương tự, ta chỉ ra được

2. . . .

,, ,

31 1 1

OD OC OA k OD OB k OC OM k ON

ON OI OK OJ

kkk

  

 



     

   

Ta có





.2.2.

OJ OA OB k OD k OC





  

 

.1 21

kOI kOK









 





112

333

OI OK OI OK

   

Suy ra









12 12

002

33 33

OI OJ OK OJ JI JK IJ JK  

 

Suy ra , ,IJK thẳng hàng.

Ví dụ 5. Cho hình hộp .

BCDABCD



. Gọi ,GG



lần lượt là trọng tâm của các tam giác ,

DA CB D



Chứng minh các điểm , , ,

GG C



thẳng hàng.

Hướng dẫn giải

Đặt

BaADbAA c





     

Ta có

C abc







(quy tắc hình hộp).

Theo quy tắc trọng tâm, ta có









GABADAA abc





  



TOANMATH.co

Trang 11













11 2

33 3

G AC AB AD abacbc abc



      

   

Vậy

CAGAG





  

nên các điểm , , ,

GG C



thẳng hàng.

Bài tập tự luyện dạng 1

Câu 1:

Cho bốn vectơ

,,,abcd



bất kỳ. Khẳng định nào sau đây sai?

A. ab



và cd acbd



B. ab a b

  

ac bd ad bc  



ab



và

cdadcb    



Câu 2: Trong không gian cho ba vectơ ,,abc



. Cho các khẳng định sau.

(1)

Nếu các vectơ

,,abc



đồng phẳng thì các vectơ

,,abc



thuộc một mặt phẳng nào đó.

(2)

Nếu các vectơ ,,abc



đồng phẳng thì ba vectơ ,,abc



cùng phương.

(3)

Nếu tồn tại hai số thực ,mn sao cho

cmanb



thì các vectơ ,,abc



đồng phẳng.

(4)

Nếu các vectơ ,,abc



đồng phẳng thì giá của chúng song song với mặt phẳng nào đó.

Có bao nhiêu khẳng định đúng?

A. 4 B. 3 C. 2 D. 1

Câu 3: Cho tam giác ABC có diện tích S. Giá trị nào của k thích hợp thỏa mãn



.2.

S AB AC k AB AC

  

k 

D. 1k 

Câu 4: Cho tứ diện ABCD. Hãy chọn khẳng định đúng?

BCD ACDB

   

CBD ABCD

  

DBC ABDC

  

ACD BDCA

   

Câu 5: Trong các mệnh đề sau đây, mệnh đề nào là đúng?

A. Từ 3

BAC



ta suy ra 3

ACA



Từ 3

BAC



ta suy ra 2CB AC



Nếu

BACAD 

  

thì bốn điểm

,,,

BCD

cùng thuộc một mặt phẳng.

Nếu

BBC



thì B là trung điểm của đoạn AC.

Câu 6: Hãy chọn mệnh đề đúng trong các mệnh đề sau đây.

A. Cho hình chóp S.ABCD. Nếu có SB SD SA SC

 

thì tứ giác ABCD là hình bình hành.

Tứ giác ABCD là hình bình hành nếu

BCD



Tứ giác ABCD là hình bình hành nếu 0AB BC CD DA



Tứ giác ABCD là hình bình hành nếu

BAC AD

 

Câu 7: Cho 3, 5ab



, góc giữa a



và b



bằng 120 . Khẳng định nào sai trong các khẳng định sau?



TOANMATH.co

Trang 12

7ab



19ab



29ab



2 139ab



Câu 8: Cho tứ diện ABCD, O là trọng tâm tam giác BCD, M là trung điểm của AD. Khẳng định nào dưới

đây đúng?

11 1

336

OM AB AC AD

  

211

336

OM AB AC AD  

  

11 1

336

OM AB AC AD  



111

336

OM AB AC AD

  

Câu 9: Khẳng định nào sau đây sai?

A. Cho hai vectơ không cùng phương a



và b



. Khi đó ba vectơ

,,abc



đồng phẳng khi và chỉ khi có

cặp số ,mn là duy nhất.

Nếu có 0ma nb pc 

 

và một trong ba số ,,mn p khác 0 thì ba vectơ ,,abc



đồng phẳng.

Ba vectơ ,,abc



đồng phẳng khi và chỉ khi ba vectơ đó cùng có giá thuộc một mặt phẳng.

Ba tia , ,Ox Oy Oz vuông góc với nhau từng đôi một thì ba tia đó không đồng phẳng.

Câu 10: Cho 2 điểm phân biệt A, B và một điểm O bất kì. Mệnh đề nào sau đây đúng?

A. Điểm M thuộc đường thẳng AB khi và chỉ khi

OM OB k BA



Điểm M thuộc đường thẳng AB khi và chỉ khi





OM OB k OB OA 

 

Điểm M thuộc đường thẳng AB khi và chỉ khi





1OM kOA k OB



Điểm M thuộc đường thẳng AB khi và chỉ khi OM OA OB



Câu 11: Cho hình lập phương .

BCDABCD



có cạnh bằng a. Giá trị .

BCA





bằng

a

2a C.

2a D.

Câu 12: Khẳng định nào sau đây đúng?

A. Ba vectơ đồng phẳng là ba vectơ cùng nằm trong một mặt phẳng.

Ba vectơ ,,abc



đồng phẳng thì có cmanb



với ,mn là các số duy nhất.

Ba vectơ ,,abc



không đồng phẳng khi có dmanbpc



với d



là vectơ bất kì.

Cả ba mệnh đề trên đều sai.

Câu 13: Khẳng định nào sau đây sai?

A. Vì 0NM NP

 

nên N là trung điểm của đoạn MP.

Vì I là trung điểm của đoạn AB nên từ một điểm O bất kì ta có





OI OA OB



Từ hệ thức 2 8

BACAD

  

ta suy ra ba vectơ ,,

BACAD



đồng phẳng.

Vì 0AB BC CD DA



nên bốn điểm

,,,

BCD

cùng thuộc một mặt phẳng.

Câu 14: Trong không gian cho ba điểm

bất kì. Khẳng định nào sau đây đúng?



22 2

BA BC BA BC AC





222

BA BC BA BC AC



222

ABC BA BC AC



22 2

ABC BA BC AC





TOANMATH.co

Trang 13

Câu 15: Cho tứ diện SABC. Đặt

,,SA a SB b SC c

    

. Gọi M là trung điểm của SA, N là điểm trên cạnh

BC sao cho

3NC NB . Phân tích vectơ



theo ba vectơ ,ab



và c



ta được

131

244

N abc  



131

244

Nabc



131

244

Nabc  



131

244

Nabc



Câu 16: Cho tứ diện ABCD. Đặt , ,

BaACbADc

     

. Gọi M là trung điểm của AB, N là điểm trên

cạnh CD sao cho

2ND NC

. Gọi O là trung điểm của đoạn thẳng MN. Biểu diễn vectơ



theo ba

vectơ ,ab



và



ta có

111

433

O abc

   

111

436

Oabc

   

111

444

Oabc

   

111

463

Oabc

   

Câu 17: Trong không gian cho tam giác ABC. Tìm M sao cho giá trị của biểu thức

22 2

MA MB MC

đạt giá trị nhỏ nhất.

A. M là trọng tâm tam giác ABC. B. M là tâm đường tròn ngoại tiếp tam giác ABC.

M là trực tâm tam giác ABC. D. M là tâm đường tròn nội tiếp tam giác ABC.

Câu 18: Cho tứ diện ABCD có trọng tâm G. Chọn khẳng định đúng?





222222 2222

BACADBCBDCD GAGBGCGD 





222222 2222

BACADBCBDCD GAGBGCGD 





222222 2222

BACADBCBDCD GAGBGCGD 





222222 2222

BACADBCBDCD GAGBGCGD 

Câu 19: Cho lăng trụ .

BC A B C



. Đặt , ,aAAbABcAC





    

Xét hai mệnh đề

(I)

Cabc



  



(II)

Cabc







Mệnh đề nào đúng?

A. Chỉ (I). B. Chỉ (II). C. Không có. D. Cả (I) và (II).

Câu 20: Cho lăng trụ

BC A B C



. Đặt

,,aAAbABcAC





    

. Gọi



là trọng tâm của tam giác



. Vectơ



bằng





abc







abc







ab c

 





abc



Câu 21: Cho hình hộp .

BCDABCD



. Biết . , .

AkMCNClND





 

. Khi MN song song với BD



thì

khẳng định nào sau đây đúng?

kl

B. 3kl C. 4kl D. 2kl



TOANMATH.co

Trang 14

Câu 22: Cho hình chóp S.ABCD có tất cả các cạnh bên và đáy đều bằng a và ABCD là hình vuông. Gọi M

là trung điểm của CD. Giá trị

SCB

 

bằng



Câu 23: Cho hình chóp S.ABC có

,,SA a SB b SC c

    

và các điểm M, N lần lượt là trung điểm của các

cạnh AB, SC. Các điểm P, Q trên các đường thẳng SA, BN sao cho / /

QCM. Biểu diễn vectơ



theo

ba vectơ

,,abc



được kết quả

224

333

Qabc  

   

112

333

Qabc

   

224

333

Qabc

   

112

333

Qabc  

   

Câu 24: Khẳng định nào sau đây sai?

A. Ba vectơ ,,

BACAD



đồng phẳng  bốn điểm ,,,

BCD cùng nằm trong một mặt phẳng.

B. ABCD là một tứ diện , ,

CCDAC

  

không đồng phẳng.

Ba vectơ ,,abc



đồng phẳng chỉ khi giá của chúng cùng nằm trong một mặt phẳng.

Ba vectơ ,,abc



không đồng phẳng khi và chỉ khi trong ba vectơ đó, vectơ này không thể biểu diễn

được theo hai vectơ kia.

Câu 25: Cho hình lập phương .

BCDABCD



cạnh bằng a. Gọi G là trọng tâm tam giác



. Giá trị

bằng

Câu 26: Cho hình chóp S.ABCD. Gọi O là giao điểm của AC và BD. Xét hai mệnh đề

(I). Nếu ABCD là hình bình hành thì

4SA SB SC SD SO 

  

(II). Nếu

4SA SB SC SD SO 

  

thì ABCD là hình bình hành.

Mệnh đề nào đúng?

A. Chỉ (I). B. Chỉ (II). C. Không có. D. Cả (I) và (II).

Câu 27: Cho tứ diện S.ABC có ,2SA SB SC AB AC a BC a    . Tích vô hướng giữa .SC AB

 

bằng



a D.

a

Câu 28: Cho hình chóp S.ABCD. Xét hai mệnh đề

(I)

Nếu ABCD là hình bình hành thì SA SC SB SD

 

(II)

Nếu SA SC SB SD

 

thì ABCD là hình bình hành.

Mệnh đề nào đúng?

A. Chỉ (I). B. Chỉ (II). C. Không có. D. Cả (I) và (II).

Câu 29: Cho ba vectơ ,,abc



không đồng phẳng. xét các vectơ 2, , 32

aby abcz b c  

  

Chọn khẳng định đúng?



TOANMATH.co

Trang 15

A. Ba vectơ



đồng phẳng. B. Hai vectơ



cùng phương.

Hai vectơ



cùng phương. D. Ba vectơ



đôi một cùng phương.

Câu 30: Cho ba vectơ ,,abc



không đồng phẳng. Khẳng định nào sau đây sai?

A. Các vectơ 2, 2 3 6, 3 6

ab cy a b cz a b c     

 

đồng phẳng.

Các vectơ 24, 332, 233

abcy abcz abc       

  

đồng phẳng.

Các vectơ ,23, 4

abcy a bcz a b    



đồng phẳng.

Các vectơ

,2 3, 24

abcy ab cz a b c    



đồng phẳng.

Câu 31:

Trong các kết quả sau đây, kết quả nào đúng?

Cho hình lập phương ABCD.EFGH có cạnh bằng a. Giá trị của

BEG



bằng

a B.

2a C.

3a D.

Câu 32: Cho hình lập phương

BCDABCD



có cạnh bằng a. Khẳng định nào sau đây sai?







DAB a







.0AB CD





 

20AB B C CD D A

 



    

Câu 33: Cho lăng trụ tam giác

BC A B C



. Gọi I, K lần lượt là trung điểm của

,BB A C



. Điểm M thuộc

cạnh



sao cho

BkMC







. Tìm k để bốn điểm , , ,

IMK đồng phẳng.

A. 1k  B.

k 

D. 3k 

Câu 34: Cho hình chóp S.ABCD có đáy là hình bình hành tâm O, M là điểm thay đổi trên SO. Tỉ số

sao cho biểu thức

222 2 2

MS MA MB MC MD nhỏ nhất bằng

Câu 35: Cho tứ diện ABCD. Gọi E, F lần lượt là trung điểm của AB, CD. Cho

2, 2, 2

BaCDbEFc. Với M là một điểm tùy ý, tổng

AMB bằng

Fb B.

Ea C.

Fa D.

Eb

Câu 36: Cho hình chóp S.ABC có M, N là các điểm thỏa mãn

SMANBkNC 

   

. Tìm k để ba

vectơ ,,

BMNSC



đồng phẳng.

2k 

k 

2k 

k 

Câu 37: Cho tứ diện ABCD có các điểm M, N, P lần lượt thuộc các cạnh BC, BD và AC sao cho

4, 3, 2BC BM AC AP BD BN. Mặt phẳng



NP cắt đường thẳng AD tại điểm Q. Tính tỉ số





TOANMATH.co

Trang 16

Câu 38: Trong không gian xét

,, ,mnpq

   

là các vectơ có độ dài bằng 1. Giá trị lớn nhát của biểu thức

222222

Smnmpmqnpnq pq     



là

A. 16. B. 6. C. 25. D. 8.

Dạng 2. Hai đường thẳng vuông góc

Bài toán 1. Tính góc giữa hai đường thẳng (chứng minh hai đường thẳng vuông góc trong hình lăng

trụ và hình hộp)

Phương pháp giải

 Để tính số đo của góc giữa hai đường thẳng





và



ta có thể thực hiện tính thông qua góc

giữa hai vectơ chỉ phương của đường thẳng đó.



cos , cos ,

dd uv





+) Định lí côsin trong tam giác



Để chứng minh hai đường thẳng AB và CD vuông

góc với nhau, ta thường chứng minh

.0AB CD 



Bước 1.

Sử dụng tính chất sau:







12 13

dd dd

















Bước 2. Áp dụng định lí côsin trong tam giác để

xác định góc.

Ví dụ. Cho hình lăng trụ đứng tam giác

BC A B C



có đáy ABC là tam giác cân,



, 120AB AC a BAC 

và cạnh bên





. Tính góc giữa hai đường thẳng



và

BC.

Hướng dẫn giải

Ta có









// , ,

C BC ABBC ABBC

   



Xét



 có

BAC ABBB a

 

  

Áp dụng định lý cosin cho

BC

, ta có



222

2. . .cos

C AB AC AB AC BAC

22 2

2...cos120 3aa aa a 

CBC a



 

Suy ra



 đều, do đó









,, 60AB BC AB B C AB C

   



Ví dụ mẫu

Ví dụ 1.

Cho hình lập phương

BCDABCD



. Tính góc giữa 2 đường thẳng

AB và



AC và



và





TOANMATH.co

Trang 17

Hướng dẫn giải

a) Ta có //

BAB



mà





,90AB BC

 

 nên





,90AB B C





Vì tứ giác ABCD là hình vuông nên





,45AC BC .

Ta có

CBC



nên





,45AC B C





Ta có //

CAC



và



 là tam giác đều vì có các cạnh đều bằng đường chéo của các hình

vuông bằng nhau. Do đó









,,60AC BC AC BC

  



Ví dụ 2. Cho hình hộp thoi .

BCDABCD



có tất cả các cạnh bằng a và



60ABC B BA B BC



 .

Chứng minh tứ giác

BCD



là hình vuông.

Hướng dẫn giải

Ta có tứ giác

BCD



là hình bình hành (tính chất hình hộp).



60BBC



 nên



 đều. Suy ra



 .

Do đó

CD B C a



 nên

BCD



là hình thoi.

Ta có



....0

CB CD CB BB BA CB BA BB BA

 

   

  

Suy ra

CB CD



 . Vậy tứ giác

BCD



là hình vuông.

Ví dụ 3. Cho hình hộp .

BCDABCD



có độ dài tất cả các cạnh bằng a và các góc

,,BAD DAA A AB



đều bằng

60. Gọi M, N lần lượt là trung điểm của ,

ACD



. Gọi



là góc tạo bởi hai đường thẳng MN

và



, tính giá trị của cos



Hướng dẫn giải



TOANMATH.co

Trang 18

Ta có

DBC

NAP











với P là trung điểm của



Suy ra









NBC APAD DAP

 



Vì



D60BA DAA A AB





và các cạnh của hình hộp bằng a.

Do đó

DaCDCA a



.

Suy ra

222

24 2

DAC DC a

AP AP

 





.

Áp dụng định lý cosin cho tam giác



, ta có

222

cos

2. 10

AD AP DP

ADAP











Ví dụ 4. Cho hình lập phương .

BCDABCD



có cạnh bằng a. Trên các cạnh CD và BB



ta lần lượt lấy

các điểm M và N sao cho

DM BN x với 0

a. Chứng minh rằng

CMN



 .

Hướng dẫn giải

Ta đặt , ,

AaABbADc





     

. Ta có abca



CAAABAD







hay

C abc







Mặt khác









NANAM ABBN ADDM    

     

với .

BN a



 

và .

DM b



 

Do đó

xxxx

Nb a c b aa bc

aaaa

 

    

 

 

     

Ta có



CMN a b c a a b c







  









   

Vì

.0,.0,.0ab ac bc

  

nên ta có



TOANMATH.co

Trang 19

222

.1 .1 0

xx x

AC MN a b c x a a a

aa a

 



  

 

 

  

Vậy

CMN





Bài toán 2. Tính góc giữa hai đường thẳng (hai đường thẳng vuông góc) trong hình chóp

Ví dụ mẫu

Ví dụ 1.

Cho hình chóp S.ABC có

SA SB SC AB AC a  

và

Ca

Tính góc giữa hai đường thẳng AB và SC.

Hướng dẫn giải

Ta có



cos ;

SC AB





 







SA AC AB

SA AB AC AB

SC AB





  

 



Vì

2222 2 2

2BC a a a AC AB 

Nên

BC vuông tại A.

Do đó

.0AB AC 



Mặt khác tam giác SAB đều nên





; 120SA AB 

 

Do đó ta có

. . .cos120

SA AB SA AB

 

Vậy



cos ;

SC AB







Do đó







; 120SC AB 



Suy ra góc





; 180 120 60SC AB 

Ví dụ 2. Cho tứ diện đều ABCD cạnh a. Tính góc giữa hai đường thẳng AB và CD.

Hướng dẫn giải

Đặt

BaACbADc

     

Ta có

CD AD AC c b

    







cos ,

ac b

AB CD

BCD ac b







 

 



    

.. ..

aa aa

ac ab

aa a



 

 

Vậy







,90AB CD 

 



TOANMATH.co

Trang 20

Ví dụ 3. Cho tứ diện ABCD có

BAC

và

BBD . Gọi P và Q lần lượt là trung điểm của AB và

CD. Chứng minh rằng

BPQ

Hướng dẫn giải

Vì

BAC và

BBD

nên

.0;.0AC AB BD AB

   

Ta có

QPAACCQ

 

và

QPBBDDQ

   

Do đó





22....0PQ AC BD PQ AB AC BD AB AC AB BD AB     

           

Hay . 0PQ AB 

 

Vậy

BPQ .

Ví dụ 4. Cho tứ diện đều ABCD cạnh a, M là trung điểm của cạnh BC. Tính góc giữa hai đường thẳng AB

và DM.

Hướng dẫn giải

Gọi N là trung điểm AC thì //

NAB.

Suy ra









BDM MNDM .

Ta có



222

cos

2. .

NDMDN

DMN

MN DM





22 2

2. .

aa a

















Suy ra



arccos

DMN  .

Vậy





,arccos

AB DM 

Ví dụ 5. Cho tứ diện ABCD có các cạnh đối bằng nhau từng đôi một,

,2, 6

CBDaABCD aADBCa  

Tính góc giữa hai đường thẳng AD và BC.

Hướng dẫn giải



TOANMATH.co

Trang 21







.. ....cos ..cos

D BC AD AC AB AD AC AD AB AD AC CAD AD AB BAD 

        

222 222

.. ..

2. . 2. .

CADCD ABADBD

AD AC AD AB

AC AD AB AD

 







 





2 2

62 2 6

6. . 6.2 .

2. . 6 2.2 . 6

aa a a a a

aa a a

aa aa

 



3a

Suy ra

 



.31

cos , , 120

6. 6

AD BC a

AD BC AD BC

AD BC



  

 

   

Vậy





;60AD BC .

Ví dụ 6. Cho hình chóp S.ABCD, có đáy ABCD là hình thang vuông tại A và D, cạnh

2, ; ,

B aADDCaSAABSAAD và

SA  .

Tính góc giữa đường thẳng SB và DC.

Gọi



là góc giữa SD và BC. Tính cos



Hướng dẫn giải

a) Vì









// , ,DC AB SB DC SB AB SBA

(vì

SAB vuông tại A nên



90SBA ).

Xét

SAB vuông tại A, ta có

 

tan 30

SBA SBA

AB a

  

Vậy





,30SB DC SBA.

Gọi E là trung điểm của AB.

Khi đó, BCDE là hình bình hành nên









// , ,DE BC SD BC SD DE





Ta có

222 2 2

33 3

SE SD a

SE SD SA AD a

DE a





 













Áp dụng định lí cosin trong tam giác SDE, ta được



TOANMATH.co

Trang 22

 

222 2

242

cos 0 90

2. 14

2. . 2

SD DE SE a

SDE SDE

SD DE





Vậy











,, coscos

SD BC SD DE SDE SDE





Ví dụ 7. Cho tứ diện ABCD có

CD AB

. Gọi

,,GEF

lần lượt là trung điểm của

CACDB

, biết

EF AB

. Tính góc giữa CD và AB.

Hướng dẫn giải

Gọi G là trung điểm của BC.

Đặt

Ba . Ta có

GE .

22 55

;

23 3 6 6

CD a a

GF AB EF AB   

Từ đó

22 2

425

49 36

aa a

GE GF EF 

GEF vuông tại G.

Vì / / , / /GE AB GF CD nên









,, 90AB CD GE GF EGF

Ví dụ 8. Cho hình chóp S.ABCD, có đáy ABCD là hình vuông tâm O, cạnh bằng a; SA vuông góc với đáy

và

3SA a . Tính côsin góc giữa SB và AC.

Hướng dẫn giải

Gọi I là trung điểm của SD

OI là đường trung bình của SBD . Suy ra

22 22

22 2

OI SB

SB SA AB a a

OI a









  





Vì









// , ,OI SB SB AC OI AC AOI

Ta có

22 22

22 2

SD SA AD a a



  

IOI AOI cân tại I.

Gọi H là trung điểm của

OA IH OA và

24 4

OA AC a

OH 

Xét

OHI có



cos

HOI

OI a

 

Vậy





cos , cos

SB AC HOI.



TOANMATH.co

Trang 23

Ví dụ 9. Cho hình chóp tứ diện OABC có

,,OA OB OC

đôi một vuông góc và

,2OA OB a OC a 

. Gọi

M là trung điểm của BC. Tính côsin góc giữa hai đường thẳng AB và OM.

Hướng dẫn giải

Ta có

2, 5

Ba BCa

BC a



























.. ...

BOM OB OA OB OC OB OBOC OAOB OAOC    

   



000

a

Vậy









cos , cos ,

.10

AB OM

AB OM AB OM

AB OM





 

Ví dụ 10. Cho tứ diện ABCD có

BADa

và



60 , 90BAC BAD CAD

. Gọi M là trung điểm

của cạnh CD. Tính độ dài cạnh AC để côsin góc giữa hai đường thẳng AC và BM bằng

Hướng dẫn giải

Gọi N là trung điểm của AD. Ta có









,,BM AC BM MN





Đặt

20AC x MN x 



TOANMATH.co

Trang 24

Theo bài ra ta có tam giác ABD đều cạnh a nên

BD a BN

Tam giác ACD vuông tại A nên

22222

4DC AD AC a x

Xét tam giác ABC ta có

22 2

Ca x ax 

Do đó

22 2 2 2 2 2

42 4 344

244

aa x axa x a x ax

    



Ta tính



22 2

222

344 3

cos

344

2. .

axax a

BM MN BN

BMN

BM MN

axax







22 22

84 2

4.344 344

xax xa

axax axax





 

Theo giả thiết ta có

cos 8 8 0

344

xax

axax



















0x  nên 22

aAC xa  

Bài tập tự luyện dạng 2

Câu 1: Mệnh đề nào sau đây đúng?

A. Hai đường thẳng cùng vuông góc với một đường thẳng thì song song với nhau.

Hai đường thẳng cùng vuông góc với một đường thẳng thì vuông góc với nhau.

Một đường thẳng vuông góc với một trong hai đường thẳng vuông góc với nhau thì song song với

đường thẳng còn lại.

Một đường thẳng vuông góc với một trong hai đường thẳng song song thì vuông góc với đường

thẳng còn lại.

Câu 2: Cho hai đường thẳng ,ab lần lượt có vectơ chỉ phương ,uv



. Mệnh đề nào sau đây sai?

A. Nếu ab thì . 0uv



B. Nếu . 0uv



thì ab



cos ,







cos ,





Câu 3: Cho ba đường thẳng ,,abc. Mệnh đề nào sau đây sai?

A. Nếu //ab thì









,,ac cb B. Nếu //cb thì









,,ab ac

Nếu

//ac

thì





,0ac  D. Nếu

ab

thì









,,ac cb

Câu 4: Cho ba đường thẳng ,,abc. Khẳng định nào sau đây đúng?

A. Nếu ab và bc thì //ab B. Nếu ab và bc thì ac

Nếu ac và bc thì ab D. Nếu //ab và cb thì ca

Câu 5: Cho hình lập phương ABCD.EFGH. Góc giữa cặp vectơ



và DH



là

A. 45 B. 90 C. 120 D. 60



TOANMATH.co

Trang 25

Câu 6: Cho hình lập phương

BCDABCD



. Chọn khẳng định

sai?

A. Góc giữa AC và



bằng 90 B. Góc giữa



và



bằng 60

Góc giữa AD và



bằng 45 D. Góc giữa BD và



bằng 90

Câu 7: Cho hình lập phương ABCD.EFGH. Góc giữa cặp vectơ



và EG



bằng

A. 90 B. 60 C. 45 D. 120

Câu 8: Cho tứ diện ABCD đều cạnh bằng a. Gọi O là tâm đường tròn ngoại tiếp tam giác BCD. Góc giữa

AO và CD bằng bao nhiêu?

0

30

90

60

Câu 9: Cho tứ diện đều ABCD, M là trung điểm của cạnh BC. Khi đó





cos ,

BDM bằng.

Câu 10: Cho hình hộp .

BCDABCD



có tất cả các mặt là hình thoi và các góc đỉnh A bằng 60. Góc

giữa hai đường thẳng BD và



bằng

90

30

45

60

Câu 11: Cho tứ diện ABCD có



,60,

CADCABDAB CDAD. Gọi



là góc giữa AB và CD.

Chọn khẳng định đúng.

cos



 B. 60



 C. 30



 D.

cos





Câu 12: Cho hình chóp tứ giác đều S.ABCD có tất cả các cạnh bằng a. Khẳng định nào sau đây đúng?

A. SA SC B. SA SB C. SA SD D. SA CD

Câu 13: Cho tứ diện ABCD có

BACAD và



60BAC BAD. Góc giữa cặp vectơ



vàCD



bằng

60

45

120

90

Câu 14: Cho hình chóp tứ giác đều S.ABCD có tất cả các cạnh đều bằng a. Gọi M là điểm bất kỳ trên

đường thẳng AC. Số đo góc giữa hai đường thẳng BD, SM bằng

90

120

60

45

Câu 15: Cho tứ diện ABCD có

BACAD và



60 , 90BAC BAD CAD. Gọi I và J lần lượt là

trung điểm của AB và CD. Góc giữa cặp vectơ



và IJ



bằng

A. 120 B. 90 C. 60 D. 45

Câu 16: Cho hình chóp tứ giác đều S.ABCD có tất cả các cạnh đều bằng a. Số đo giữa hai đường thẳng

BC và SA bằng

A. 45 B. 120 C. 90 D. 60

Câu 17: Cho hình chóp S.ABC có đáy là tam giác đều cạnh ,3aSA a và vuông góc với mặt đáy. Gọi

M là trung điểm cạnh SB. Côsin góc giữa hai đường thẳng AM và SC bằng

Câu 18: Cho hình chóp S.ABC có

BAC và



SAC SAB . Khi đó góc





,SA BC

 

bằng



TOANMATH.co

Trang 26

30

45

60



Câu 19: Cho hình chóp S.ABC có

SA SB SC

và



SB BSC CSA

. Góc





,SC AB



bằng

120

45

60



Câu 20: Cho hình chóp S.ABCD có đáy là hình vuông ABCD cạnh bằng a và các cạnh bên đều bằng a.

Gọi

M và N lần lượt là trung điểm của AD và SD. Số đo của góc





NSC bằng

45

30

90

60

Câu 21: Cho hình chóp S.ABCD có tất cả các cạnh đều bằng a. Gọi I và J lần lượt là trung điểm của SC

và BC. Số đo của góc





,IJ CD bằng

A. 90 B. 45 C. 30 D. 60

Câu 22: Cho hình lập phương .

BCDABCD



cạnh a. Gọi M, N lần lượt là trung điểm của AC và



Côsin góc giữa hai đường thẳng MN và



bằng

Câu 23: Cho hình lăng trụ đứng tam giác .

BC A B C



có đáy ABC là tam giác cân



, 120AB AC a BAC 

, cạnh bên 2



 . Góc giữa hai đường thẳng



và BC bằng

A. 90 B. 30 C. 45 D. 60

Câu 24: Cho hình lăng trụ tam giác đều .

BC A B C



có tất cả các cạnh bằng a. Gọi M, N lần lượt là

trung điểm các cạnh

BBC



. Côsin góc giữa hai đường thẳng MN và AC bằng

Câu 25: Cho hình chóp S.ABCD có ,,SA SB SC đôi một vuông góc với nhau và SA SB SC a. Gọi M

là trung điểm của

AB. Góc giữa hai đường thẳng SM và BC bằng

A. 30 B. 60 C. 90 D. 120

Câu 26: Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật. Các tam giác ,,SAB SAD SAC là các tam

giác vuông tại

A. Côsin góc giữa hai đường thẳng SC và BD bằng bao nhiêu, biết

3, , 3SA a AB a AD a?

2 130

4 130

Câu 27: Cho hình lăng trụ tam giác đều

BC A B C



có tất cả các cạnh đều bằng a. Côsin giữa hai đường

thẳng



và



bằng

Câu 28: Cho hình lăng trụ tam giác .

BC A B C



có đáy ABC là tam giác vuông tại

,, 3

AB a AC a. Hình chiếu vuông góc của



lên mặt phẳng





là trung điểm H của

,3BC A H a





. Gọi



là góc giữa hai đường thẳng



và



. Tính

cos



cos



 B.

cos



 C.

cos



 D.

cos







TOANMATH.co

Trang 27

Câu 29: Cho hình lập phương ABCD.EFGH. Góc giữa cặp vectơ



và



bằng



120



Câu 30: Cho tứ diện ABCD, gọi M, N lần lượt là trung điểm của BC, AD biết

AB CD a MN 

Côsin góc giữa hai đường thẳng

AB và CD bằng

Câu 31: Cho hình chóp S.ABC có tam giác SAB vuông cân tại S, có SA a , tam giác ABC vuông cân tại

C và



60BSC . Gọi M là trung điểm của SB. Côsin góc giữa hai đường thẳng AB và CM bằng

Câu 32: Cho hai vecto ,ab



thoả mãn, 4, 3, . 10abab 



.Xét hai vecto , 2yabxa b 

 

. Gọi



là góc giữa hai vecto ,



. Tính cos



A. cos





B. cos



C. cos



D. cos



Câu 33: Cho hình hộp chữ nhật .,6, 2

BCDABCD AB cm BC BB cm

 



. Điểm E là trung điểm cạnh

BC. Một tứ diện đều MNPQ có hai đỉnh M và N nằm trên đường thẳng CE



, hai đỉnh P, Q nằm trên

đường thẳng đi qua điểm



và cắt đường thẳng AD tại điểm F. Độ lớn DF bằng

A. 1cm B. 2cm C. 3cm D. 6cm



TOANMATH.co

Trang 28

ĐÁP ÁN

Dạng 1. Vecto trong không gian

1 - B 2 - C 3 - C 4 - D 5 – C 6 – A 7 – B 8 – C 9 – C 10 - C

11 – A 12 – D 13 – D 14 - B 15 – A 16 – B 17 – A 18 – B 19 – A 20 – B

21 – C 22 – A 23 – D 24 – C 25 – B 26 – D 27 – A 28 – D 29 - A 30 – B

31 - A 32 - D 33 - C 34 - D 35 - B 36 - D 37 - B 38 - A

HƯỚNG DẪN GIẢI CHI TIẾT

Câu 1.

Với ABC là tam giác đều ta có

BAC



nhưng

BAC

 

và

BAC



nên B sai.

Câu 2.

Khẳng định (1) sai vì khi , ,abc



đồng phẳng thì giá của chúng luôn song song với mặt mặt phẳng.

Khẳng định (2) sai vì các vectơ đồng phẳng không yêu cầu là phải cùng phương.

Khẳng định (3) và (4) đúng theo điều kiện và định nghĩa ba vectơ đồng phẳng.

Câu 3.



222 22 2

11 1

..sin . . sin . 1cos

22 2

S AB AC A AB AC A AB AC A 



22 22

222

..cos ..

B AC AB AC A AB AC AB AC 

  

Vậy

k 

Câu 4.

sai vì (sai)AB CD AC DB CA AB BD DC CD DC 

         

B sai vì (sai)AB BD AB CD AC AB CD DB BC CB

        

C sai vì (sai)AD BC AB DC AD AB DC CB BD DB

       

D đúng vì

ACDBDCA BABDDCCA DADA

  

(đúng)

Câu 5.

Ta có 3333

BAC BA CABACA CA

 

. Từ đó phương án A sai.

Ta có

3342

BACCBCACACBCAAC      

  

. Từ đó phương án B sai.

Ta có

25 ,,

BACADABACAD  

   

đồng phẳng

,,,

BCD

đồng phẳng (C đúng).

Phương án

D sai vì nếu B là trung điểm của đoạn thẳng AC thì

BBC



mà

CBC

 

Câu 6.

+) SB SD SA SC SB SA SC SD AB DC ABCD  

 

là hình bình hành (A đúng).

BCD



ta phải suy ra tứ giác ABDC là hình bình hành chứ không phải ABCD (B sai).

C sai vì 0AB BC CD DA



đúng với mọi vị trí của

,,,

BCD

D sai vì với

BAC AD

 

thì AD là đường chéo của hình bình hành ABCD.



TOANMATH.co

Trang 29

Câu 7.

Ta có:





2 . .cos , 3 5 2.3.5.cos120 19ab a b ab ab   

    

Suy ra

19ab



Câu 8.

Ta có O là trọng tâm tam giác

CD

nên

0BO CO DO 

   

(1)

Ta có: ; ;

OABBOAOACCOAOADDO  

        

Từ (1) suy ra





1111

3333

OABACAD AO ABACAD AB AC AD     

      

Suy ra

111

333

OA AB AC AD  

   

(2)

Mà

MAD



(3)

Từ (2) và (3) suy ra

111 1 111

333 2 336

OM OA AM AB AC AD AD AB AC AD       

     

Câu 9.

sai vì chỉ cần ba vectơ có giá cùng song song với một mặt phẳng thì ba vectơ đó đồng phẳng.

Câu 10.

, B sai vì OM OB M B



và ,,,OM BA thẳng hàng mà O là điểm bất kì.

C đúng vì







1.OM kOA k OB OM OB k OA OB BM k BA  

  

D sai vì

OM OA OB OAMB

 

là hình bình hành. Khi đó

AB

Câu 11.

Ta có:

.. 2cos

BAB ABCA ABAC a a





   

    





    

Câu 12.

sai khi ,ab



có giá cùng nằm trong





, còn



có giá song song với





B sai với ba vectơ ,0,ac



ta có 00. 0.ac



thì ,0,ac



đồng phẳng nhưng ..0cman



chỉ đúng khi a



và



cùng phương với nhau.

C sai vì với 3 vectơ ,,dab



khác



đồng phẳng với nhau ta có

dmanb



Khi đó (m 1)

danba 



Đặt

ca



thì

(m 1)

danbc 



nhưng

abc



lại đồng phẳng với nhau.

Vậy cả ba khẳng định trên đều sai.

Câu 13.

Phương án D sai do đẳng thức 0AB BC CD DA



luôn đúng với vị trí bất kì trong không gian của

bốn điểm , , ,

BCD nên không đủ điều kiện để khẳng định , , ,

BCD đồng phẳng.

Câu 14.



TOANMATH.co

Trang 30

Ta có:







222222

2. .

C AC BC BA BC BABC BA BABC BA BC AC    

    

Câu 15.

111

224

NMSSNSASBBNSASBBC       

  





11 131

24 244

SA SB SC SB a b c      

     

Câu 16.

Ta có





OAMAN

 

, trong đó

Ma



;





11 21

33 33

NACCNAC CDAC ADAC b c   

         

Vậy

11 2 1 1 1 1

22 3 3 4 3 6

O abc abc









      

Câu 17.

Gọi G là trọng tâm

BC thì G cố định và 0GA GB GC 

   

Ta cos:













22 2

MG GA MG GB MG GC

 





2222

32.

GMGGAGBGCGAGBGC 



222 2 22 2

GGAGBGC GAGBGC  

Dấu “=” xảy ra

G

Vậy

22 2

min

GA GB GC

với

G là trọng tâm tam giác ABC.

Câu 18.

Ta có

222222

BACADBCBDCD

























222222

GGB AGGC AGGD BGGC BGGD CGGD     

           





222 2

33332......(1)AG BG CG DG AG GB AG GC AG GD BG GD BG GD CG GD 

           

Mà





00GA GB GC GD GA GB GC GD   

     

22 2 2

GA GB GC GD





2......(2)AG GB AG GC AG GD BG GD BG GD CG GD 

           

Từ (1) và (2) ta có





222222 2222

BAC ADBCBDCD GAGBGCGD 



TOANMATH.co

Trang 31

Câu 19.

(I) Đúng vì





CBBBC AA ACAB

 

 

     

AABAC abc



     

  

(II)

Sai vì





CBBBCAABCAA ACAB

 

  

       

AABACabc





  

Câu 20.

Ta có:

GAAAGAA AI

  

 

   





AABAC



 

  









G AA ABAC AA ABAC



   

   





abc



Câu 21.

Đặt , ,

BaADbAA c





     

Từ

AkMC







, ta có





A AM k AC AM



 

   





ka b c

AA k AC







 



 

 



Từ

.NC l ND







, ta có





C AN l AD AN



 

   

ClADabclb





 







Suy ra

NAMAN

 





111

1111111

ka b c

abclb k k

ab c

klklkkl















 

 

 

Mặt khác

DADAB abc





 

Để

NBD



thì //

NBD





nên

121

11 1 11

11 11

11111

kkk

kl k kl

kklkl



 







  











 







Từ đó ta có:





. Vậy 4kl



TOANMATH.co

Trang 32

Câu 22.

Do tất cả các cạnh của hình chóp bằng nhau nên hình chóp

S.ABCD là hình chóp đều.

Suy ra

;;OC OS OD

 

đôi một vuông góc.

M là trung điểm của CD nên ta có:

SOSOM OC ODOS   

    

CB OB OC OD OC

  

;;OC OS OD

 

đôi một vuông góc với nhau nên

222

22 2

MS CB OC OD OC

 

Câu 23.

Đặt

;

AxSABQyBN



Suy ra:

QPAABBQ

 

SA SB SA yBN

   







SA SB y SN SB   

  

 

SA y SB SC  

  



aybc  



(*)

Lại có





111

222

CM SM SC SA SB SC a b c 



Để //

QCM thì

QkCM

 

hay















 

















Thay vào (*) ta được

112

333

Qabc  

   

Câu 24.

sai vì khi





BMNP ta vẫn có

BMN NP



đồng phẳng nhưng





BMNP



hay giá của



không nằm trong



Câu 25.









G AAABAC AAABABAD





   

Suy ra



2222

GAG AA ABAD



  





TOANMATH.co

Trang 33



222 2

aaa a

Câu 26.

Gọi ,

N lần lượt là trung điểm của AC và BD. Do O là giao điểm của AC và BD nên

4SA SB SC SD SO 

  

















0OS SA OS SC OS SB OS SD

  









0OA OC OB OD 

   

220OM ON OM ON O M N

   

BCD

là hình bình hành.

Vậy mệnh đề (I) và (II) đều đúng.

Bình luận: Để chứng minh mệnh đề (I) và (II) đúng, ta áp dụng: Cho ,

aB b và





Oab

Khi đó

OA OB O A B



Chứng minh: Nếu A không trùng O thì B không trùng O (do

OA OB



)

OA a

và

OB b

Nhưng , ,

OA OB O A B



thẳng hàng

ab aba

(trái với giả thiết

Oab

)

Câu 27.

Từ giả thiết suy ra SBC vuông cân tại

;SSAC

là tam giác đều.

Có





.. ..SC AB SC SB SA SC SB SC SA

   



. .cos . .cos60

SC SA ASC a a  

Vậy

SC AB a







Câu 28.

Gọi M, N lần lượt là trung điểm của AC và BD.

Ta có:

22SA SC SB SD SM SN SM SN M N ABCD   

     

là hình bình hành.

Câu 29.

Ta có





yxz



nên ba vectơ ,,



đồng phẳng.

Câu 30.

Khẳng định B sai.

Các vectơ ,,



đồng phẳng , :mn x my nz  



Ta có

my nz





321

24 332 233 3 3 2

234

abcmabcnabc mn







          









  

(hệ vô nghiệm).



TOANMATH.co

Trang 34

Vậy không tồn tại hai số

mn x my nz



Câu 31.

Ta có





...

BEG AB EF EH ABEF ABEH

       

BEH

nên .0AB EH 



Suy ra

BEG ABEF AB a

   

Câu 32.

+) A đúng vì





CABADAA





 





222

...0AB AD AA do AB AD AD AA AA AB



   

        

3a

Suy ra







B đúng vì









DAB AAADAAAB AA a

   

  

      





'. . . 0do AA AD AA AB AB AD

  

 

     

C đúng vì



..0

BCD DCCD do DC CD

   

 

 

D sai vì

220AB B C CD D A AB BC CD DA

 



       

Câu 33.

Đặt , ,

AaABbACc





  

Ta có









11 1

22 2

I ABAB ABABAA ab





      









11 1

22 2

K AAAC AAAAAC a c

 



     

BkMC







nên





BAMkACAM



 

  













11k AM k AC AB k a c a b k a b kc



     

    

Vì bốn điểm , , ,

MIK đồng phẳng nên , ,

MAIAK



đồng phẳng, do đó





1kAMxAIyAK

  



kabkcxabyac



   





    



TOANMATH.co

Trang 35



kxy



 







  









. Vậy

k 

Câu 34.

Gọi I là điểm thỏa mãn 4SI IO























222 2 2

MI IS MI IA MI IB MI IC MI ID         

   





2222 2 2

IISIAIBICID MIISIAIBICID 







2222 2 2

524

I IS IA IB IC ID MIIS IOOAOBOCOD 







2222 2 2

54;0MI IS IA IB IC ID do SI IO OA OB OC OD  

 

Vậy

min

PMI

 

Câu 35.

Áp dụng công thức độ dài đường trung tuyến, ta có:

222 2

2222

24 2

AMB AB AB

ME MA MB ME





Ea

Câu 36.

Đặt , ,SA a SB b SC c

    

, ta có:

BSBSAba



;





SMASM SASMSMSAa      

       

;





NB k NC SB SN k SC SN 





1k SN k SC SB kc b   

 

;

 







k MN k SN SM kc b a





    

Để ba vectơ

BMNSC



đồng phẳng ta có





1kMNxABySC









kc b a x b a yc



  

   



TOANMATH.co

Trang 36



xkk















 















Vậy

k 

Câu 37.

Đặt , ,

BaACbADc

     

Theo bài ra ta có





31 1 1

;;

44 2 3

MabAN acAPb   

 

Đặt

QkADkc

  

Ta có

111

442

412

NANAM a b c

MP AP AM a b

QAQAM a bkc



 



 





 





  

 

  

Vì , , ,

NPQ đồng phẳng nên

MN yMP MQ



111 3 1 31

442 412 44

abcy a b abkc



       





   

13 1 1 1 31

44 412 2 44

ya x yb xc a b kc

 

  

 

 



13 3

44 4

11 1 3

412 4 5

xy y























Vậy

AQ AD



 

Câu 38.

Ta có





042......m n p q mn m p mq n p nq pq      

   

Suy ra . . . . . . 2mn m p mq n p nq pq

           

222222

Smnmpmqnpnq pq     

 









12 2 . . . . . . 1mn m p mq n p nq pq do m n p q       

    

Vậy



222222

12 2. 2 16mn m p mq n p nq pq 





TOANMATH.co

Trang 37

Dấu “=” xảy ra chẳng hạn khi





1; 0; 0mn

 

và



1; 0; 0pq

 

Bấm Tải xuống để xem toàn bộ.

| 1/37

| | Tải xuống

Preview text:

CHUYÊN ĐỀ VECTƠ TRONG KHÔNG GIAN
QUAN HỆ VUÔNG GÓC TRONG KHÔNG GIAN
BÀI GIẢNG VECTƠ TRONG KHÔNG GIAN
HAI ĐƯỜNG THẲNG VUÔNG GÓC Mục tiêu  Kiến thức
+ Trình bày được các tính chất, quy tắc biểu diễn vectơ.
+ Phát biểu được tích vô hướng của hai vectơ, góc giữa hai đường thẳng.  Kĩ năng
+ Chứng minh được các đẳng thức vectơ, biểu diễn được vectơ theo các vectơ không trùng phương với nó.
+ Nắm được phương pháp chứng minh sự cùng phương của hai vectơ, tìm được điều kiện của ba
vectơ đồng phẳng.
+ Tính được góc giữa hai đường thẳng. Vận dụng được tích vô hướng của hai vectơ để giải các bài toán. Trang 1
I. LÍ THUYẾT TRỌNG TÂM
A. VECTƠ TRONG KHÔNG GIAN Các định nghĩa
a) Vectơ là một đoạn thẳng có hướng (có phân biệt
điểm đầu và điểm cuối). 
+) Ký hiệu vectơ: AB (điểm đầu là A, điểm cuối là B) hay   
a, x, y,...
+) Độ dài của vectơ là khoảng cách giữa điểm đầu và điểm cuối của vectơ đó.
+) Giá của vectơ là đường thẳng đi qua điểm đầu và điểm cuối của vectơ đó.
Sự cùng phương của hai vectơ
b) Vectơ – không là vectơ có điểm đầu và điểm cuối    trùng nhau.
 a và b  0 cùng phương  
c) Hai vectơ được gọi là cùng phương nếu giá của  k
   : a  k.b   
chúng song song hoặc trùng nhau.
 a và b  0 cùng hướng
d) Hai vectơ cùng phương thì cùng hướng hoặc ngược   k 
    : a  k.b hướng.   
 a và b  0 ngược hướng
e) Hai vectơ bằng nhau là hai vectơ cùng hướng và có   k 
    : a  k.b cùng độ dài.
 Ba điểm A, B, C thẳng hàng
f) Hai vectơ đối nhau là hai vectơ ngược hướng  
nhưng có cùng độ dài.  k
   : AB  k.AC
Các quy tắc tính toán với vectơ
g) Quy tắc ba điểm (với phép cộng)
Quy tắc ba điểm (mở rộng).
  
  
  
AB  BC  AC
AX  X X  X X ...  X X  X B  AB . 1 1 2 2 3 n 1  n n
h) Quy tắc ba điểm (với phép trừ)
  
OB  OA  AB
i) Quy tắc hình bình hành
  
Nếu tứ giác ABCD là hình bình hành thì AB  AD  AC .
j) Quy tắc hình hộp. Nếu ABC . D AB C  D   là hình hộp thì
   
AC  AB  AD  AA 
k) Phép nhân một số k với một vectơ a . 
Ta có ka là một vectơ được xác định như sau. 
+ cùng hướng với a nếu k  0 . TOANMATH.com Trang 2 
+ ngược hướng với a nếu k  0 .  
+ có độ dài ka  k . a
Một số hệ thức vectơ hay dùng
l) Hệ thức về trung điểm của đoạn thẳng   
I là trung điểm của đoạn thẳng AB  IA  IB  0   
OA  OB  2OI (với O là một điểm bất kỳ).
m) Hệ thức về trọng tâm của tam giác
   
G là trọng tâm của tam giác ABC  GA  GB  GC  0
   
 OA  OB  OC  3OG (với O là một điểm bất kỳ)  2 
 AG  AM (với M là trung điểm cạnh BC). 3
n) Hệ thức về trọng tâm của tứ diện
G là trọng tâm của tứ diện ABCD
    
 GA  GB  GC  GD  0
     
OA  OB  OC  OD  4OG (với điểm O bất kỳ)  3 
 AG  AA (với A là trọng tâm của BCD ) 4
   
GM  GN  0 (với M, N là trung điểm một cặp cạnh đối diện). Hệ quả
Sự đồng phẳng của ba vectơ
Nếu có một mặt phẳng chứa vectơ này đồng o) Định nghĩa
thời song song với giá của hai vectơ kia thì
Trong không gian, ba vectơ được gọi là đồng phẳng nếu ba vectơ đó đồng phẳng.
giá của chúng cùng song song với một mặt phẳng nào đó. Ứng dụng:
p) Điều kiện để ba vectơ đồng phẳng  
Bốn điểm phân biệt A, B, C, D đồng phẳng
Trong không gian cho hai vectơ a,b không cùng phương
   
 AB, AC, AD và vectơ c .      
đồng phẳng  AB  . m AC  . n AD Khi đó, ,
a b và c đồng phẳng khi và chỉ khi tồn tại cặp số     ;
m n sao cho c  ma  nb (cặp số  ;
m n nêu trên là duy nhất)
q) Phân tích một vectơ theo ba vectơ không đồng phẳng   
Cho ba vectơ a,b và c không đồng phẳng. 
Với mọi vectơ x , ta đều tìm được duy nhất một bộ số Chú ý: TOANMATH.com Trang 3      ; m ;
n p sao cho x  . m a  . n b  . p c
Bình phương vô hướng của một vectơ: 2  2
Tích vô hướng của hai vectơ a  a          
a) Nếu a  0 và b  0 thì .
a b  a . b . o c s(a,b)      
b) Nếu a  0 và b  0 thì . a b  0
Một số ứng dụng của tích vô hướng        
a) Nếu a  0 và b  0 ta có a  b  . a b  0
b) Công thức tính côsin của góc hợp bởi hai  vectơ khác 0 .     a b . a b cos ,    a . b
c) Công thức tính độ dài của một đoạn thẳng  2
AB  AB  AB
B. HAI ĐƯỜNG THẲNG VUÔNG GÓC Nhận xét:
Góc giữa hai vectơ trong không gian   
a) Nếu a là vectơ chỉ phương của đường
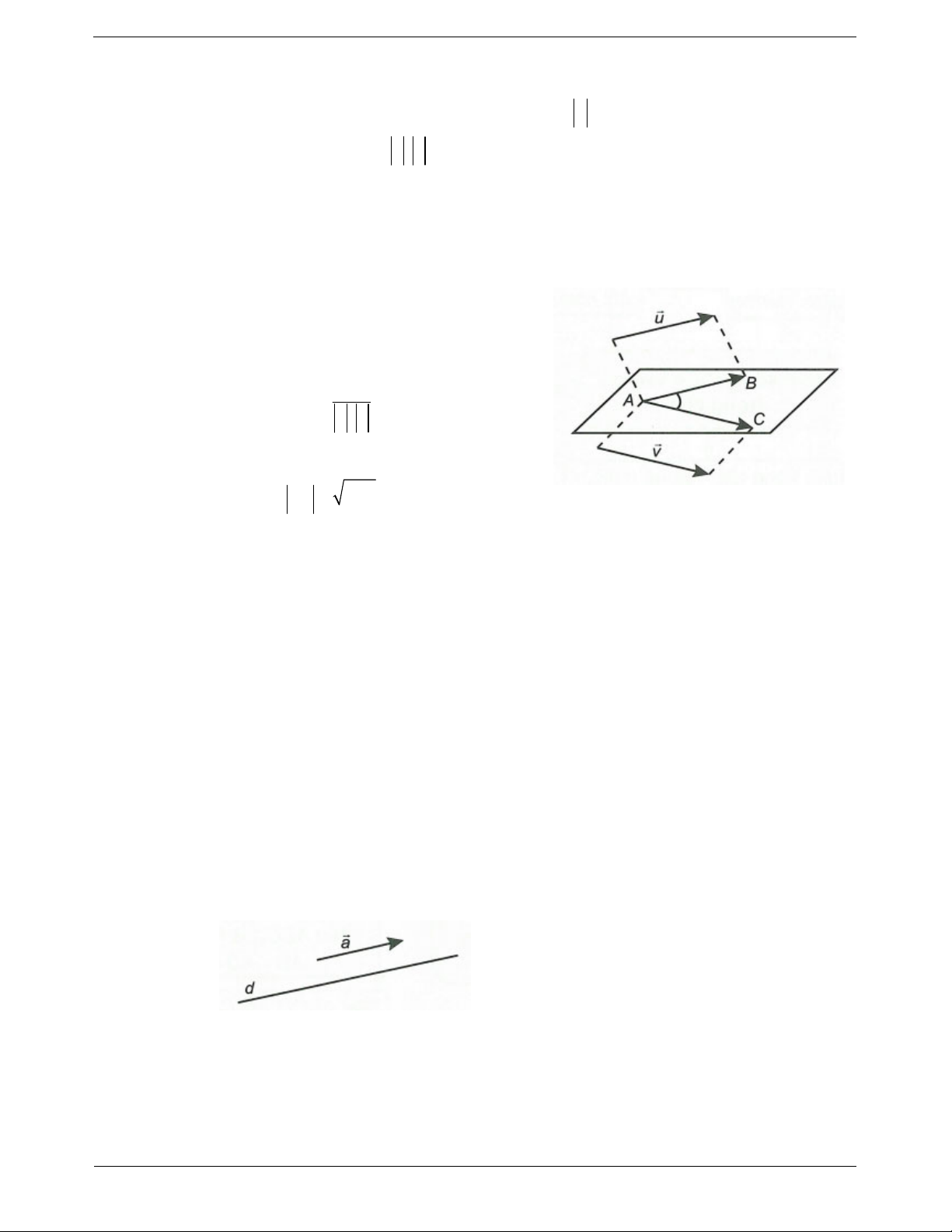
Định nghĩa: Trong không gian, cho u và v là hai vectơ  
thẳng d thì vectơ ka với k  0 cũng là
khác 0 . Lấy một điểm A bất kì, gọi B và C là hai điểm sao
vectơ chỉ phương của d.
    cho ,
AB  u AC  v . Khi đó ta gọi b) Một đường thẳng trong không gian hoàn    
BAC 0  BAC 180 là góc giữa hai vectơ u và v toàn xác định nếu biết một điểm A thuộc d   
và một vectơ chỉ phương a của nó.
trong không gian, kí hiệu là  u,v
c) Hai đường thẳng song song với nhau khi
Vectơ chỉ phương của đường thẳng
và chỉ khi chúng là hai đường thẳng phân  
Vectơ a khác 0 được gọi là vectơ chỉ phương của đường
biệt và có hai vectơ chỉ phương cùng 
thẳng d nếu giá của vectơ a song song hoặc trùng với phương.   đường thẳng d.
Chú ý. Giả sử u, v lần lượt là vectơ chỉ
phương của đường thẳng a và b.  
Đặt u,v   .   khi     
Khi đó a b  0 90 ,   180 
  khi 90   180
+) Nếu a//b hoặc a  b thì a b  ,  0 .
+)   a b  0 ,  90 .
Góc giữa hai đường thẳng TOANMATH.com Trang 4
Góc giữa hai đường thẳng a và b trong không gian là góc
giữa hai đường thẳng a và b cùng đi qua một điểm và Nhận xét
lần lượt song song với a và b.
a) Nếu hai đường thẳng a, b lần lượt có các   vectơ chỉ phương u,v thì  
a  b  u.v  0 . a / /b b)   c  b c  a
Hai đường thẳng vuông góc
Định nghĩa: Hai đường thẳng được gọi là vuông góc với
nhau nếu góc giữa chúng bằng 90 .
Kí hiệu: Đường thẳng a và b vuông góc với nhau kí hiệu là a  b .
SƠ ĐỒ HỆ THỐNG HÓA Vectơ là một đoạn     thẳng có hướng a,b a  b    cùng hướng a b Định nghĩa Độ dài của vectơ là  khoảng cách giữa Hai vectơ được gọi là AB  AB điểm đầu và điểm cùng phương nếu giá cuối của vectơ đó của chúng song song hoặc trùng nhau.
Vectơ – không là vectơ có điểm
đầu và điểm cuối trùng nhau.       a,b a  b a,b ngược hướng đối nhau VECTƠ TRONG
Một số hệ thức vectơ Các phép toán trọng tâm KHÔNG vectơ GIAN Quy tắc 3 điểm:
I là trọng tâm của hệ n điểm
  
A ; A ;...; A
AB  BC  AC 1 2 n    
 IA  IA  ... IA  0 1 2 n Phép trừ:
  
OB  OA  AB    
a,b không cùng phương thì a,b và  Sự đồng đẳng
c đồng phẳng khi và chỉ khi tồn tại
Nếu ABCD là hình bình hành thì của ba vectơ
      cặp số  ;
m n sao cho c  ma  nb
AB  AD  AC Nếu ABC . D AB C  D   là hình hộp thì
   
AC  AB  AD  AA TOANMATH.com Trang 5
II. CÁC DẠNG BÀI TẬP
Dạng 1: Vectơ trong không gian
Bài toán 1. Xác định vectơ và chứng minh đẳng thức vectơ Phương pháp giải
Vận dụng các kiến thức sau.
 Định nghĩa các khái niệm liên quan đến vectơ;
 Tính chất hình học của các đa giác đã học;
 Các quy tắc tính toán với vectơ;
 Một số hệ thức vectơ hay dùng;
 Các tính chất của các hình hình học cụ thể.
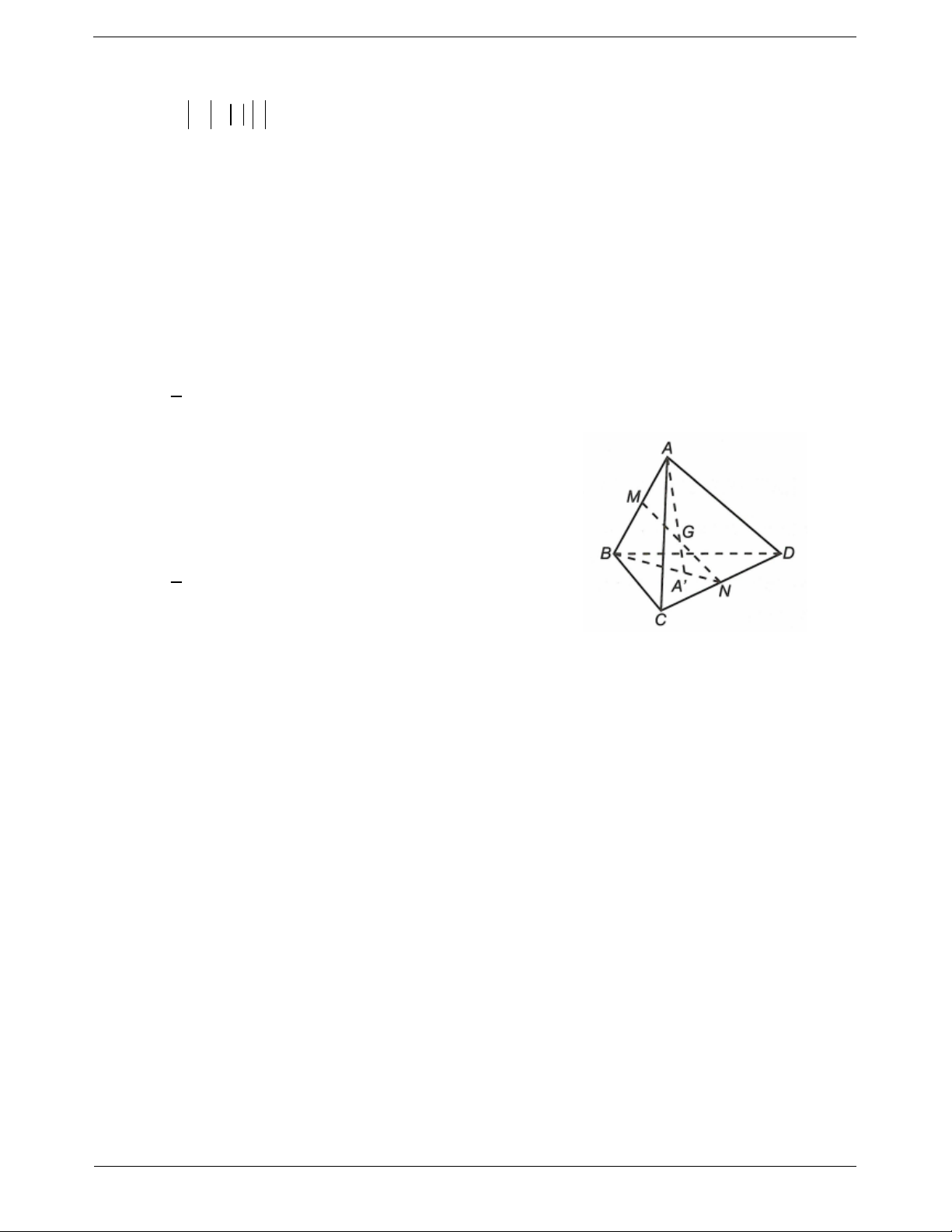
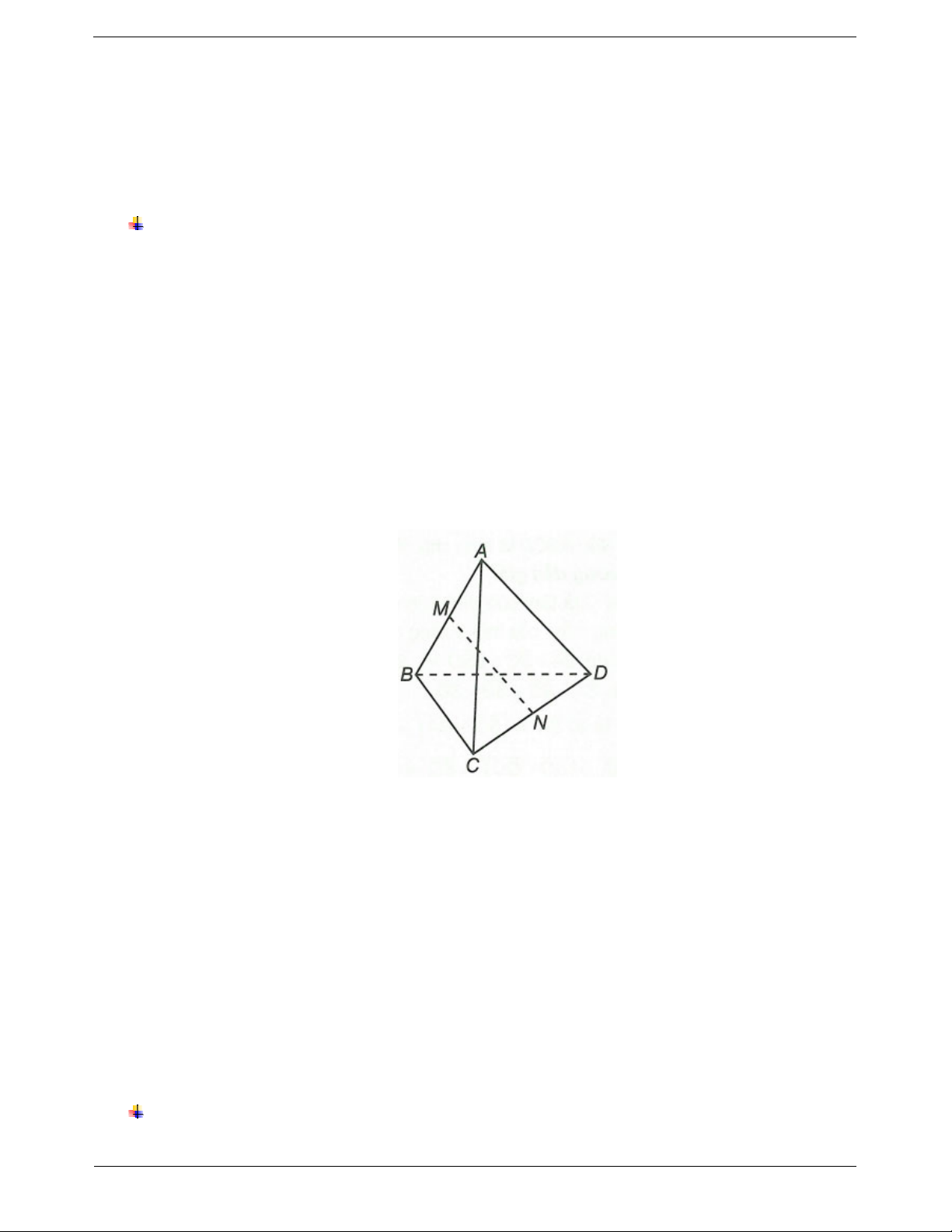
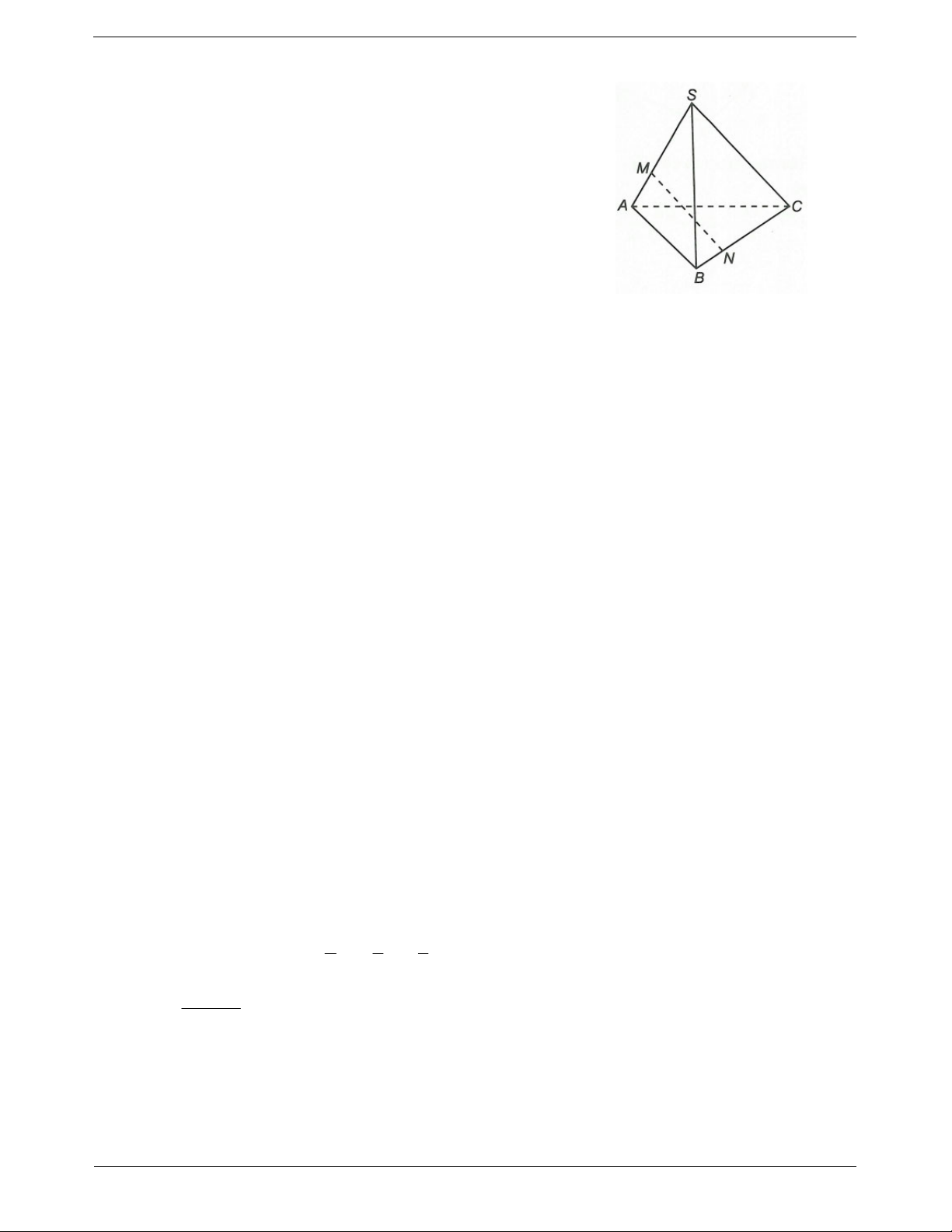
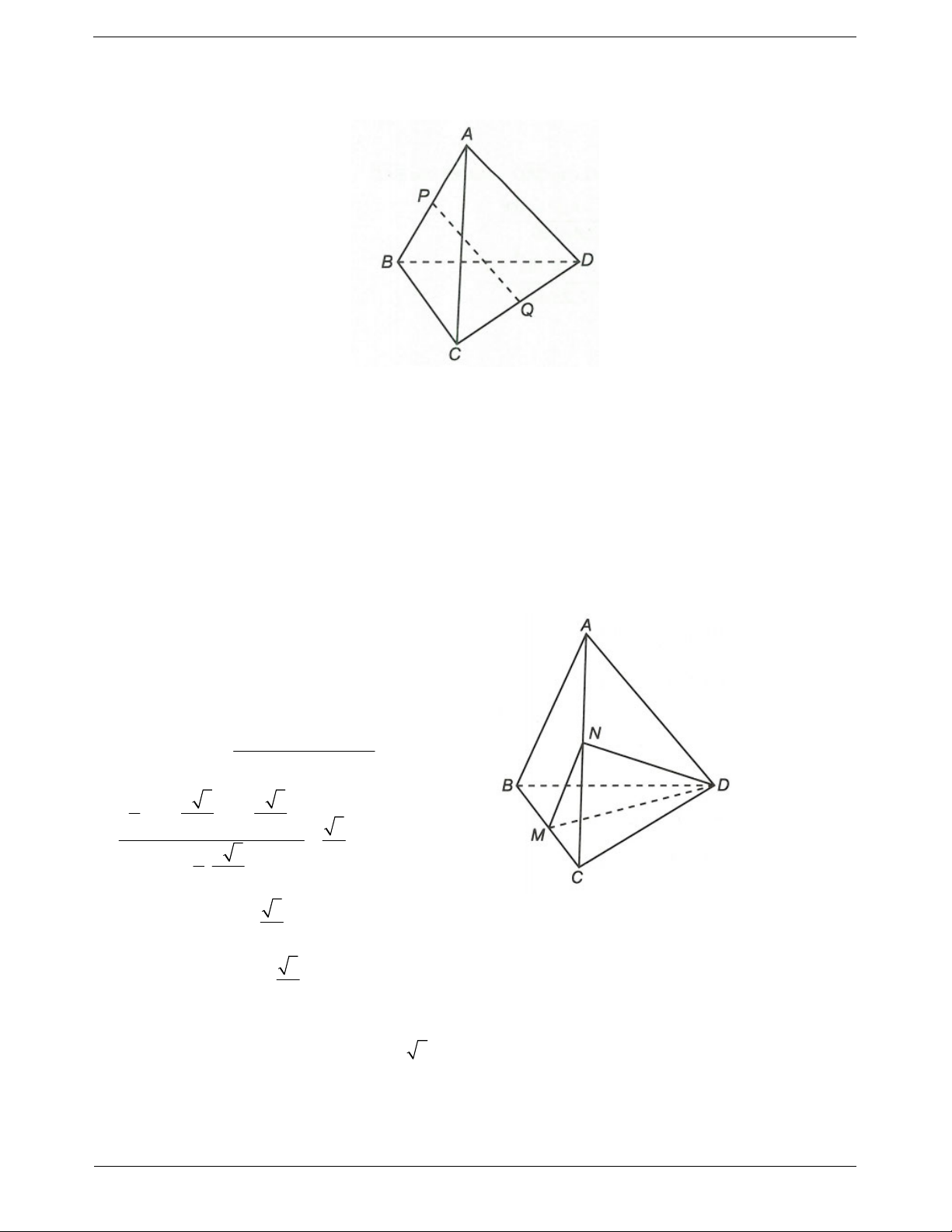
Ví dụ. Cho tứ diện ABCD. Gọi M, N lần lượt là trung điểm của AB và CD. Chứng minh rằng
    
AC  BD  AD  BC  2MN
Hướng dẫn giải
   
Ta có AC  BD  AD  BC
   
 AC  AD  BC  BD  
 DC  DC (đẳng thức này đúng).
Do M, N lần lượt là trung điểm các cạnh AB và CD
 
AM  BM  0
nên  
NC  ND  0  
  
  
Do đó AD  BC   AM  MN  NB  BM  MN  ND
     
  AM  BM  NB  ND 2MN  2MN
    
Vậy AC  BD  AD  BC  2MN Ví dụ mẫu TOANMATH.com Trang 6
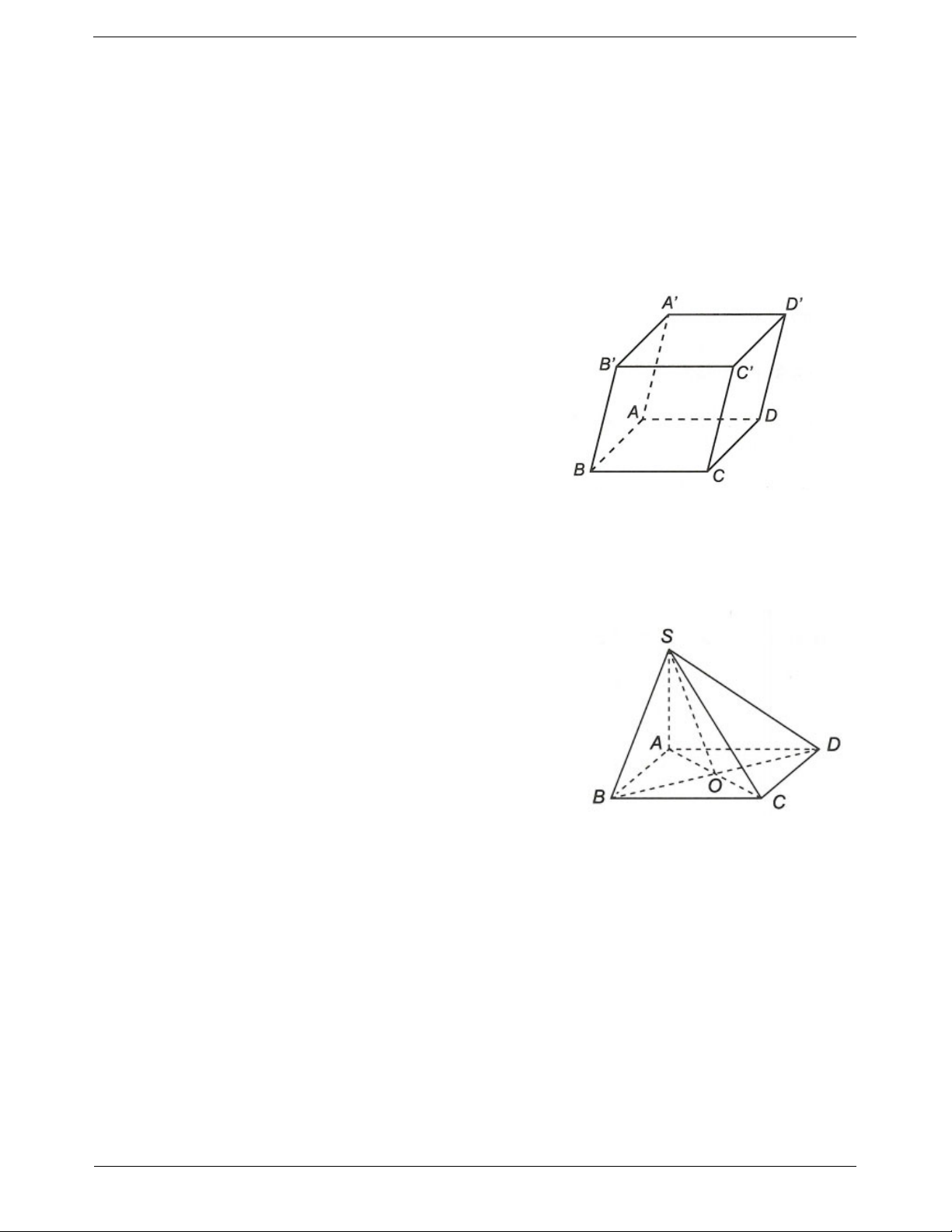
Ví dụ 1. Cho hình hộp ABC . D AB C  D
  . Sử dụng các đỉnh của hình hộp làm điểm đầu và điểm cuối của vectơ.
   
a) Hãy kể tên các vectơ bằng nhau lần lượt bằng các vectơ AB, AC, AD, AA . 
b) Hãy kể tên các vectơ luôn có độ dài bằng nhau và bằng độ dài của vectơ BC .
Hướng dẫn giải a) Ta có
   
+) AB  DC  AB  D C   .  
+) AC  AC .
   
+) AD  BC  AD  B C  
   
+) AA  BB  CC  DD
b) Từ tính chất của hình bình hành, ta suy ra các 
vectơ luôn có độ dài bằng độ dài của vectơ BC là
       
BC,CB, AD, D ,
A AD , D A  , B C  ,C B  .
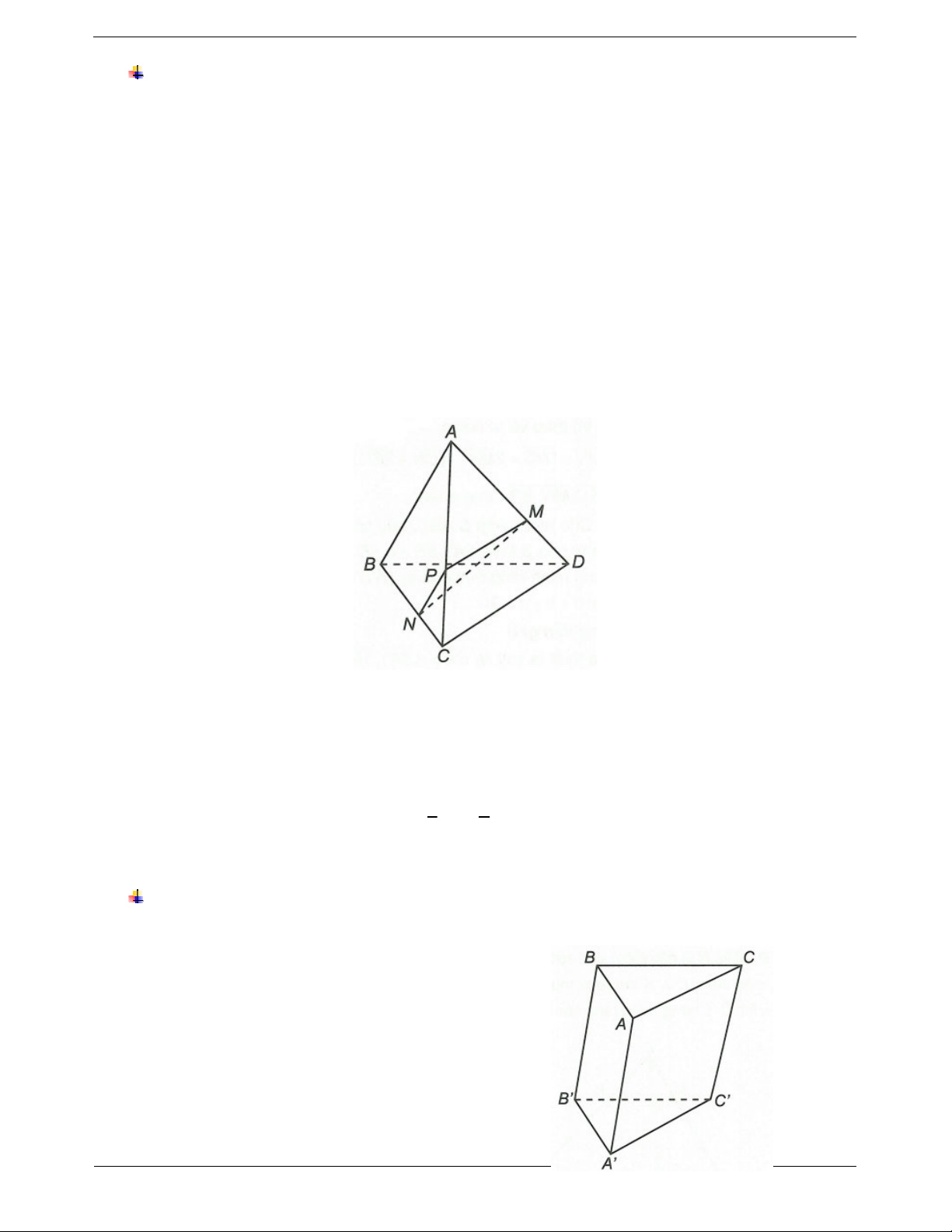
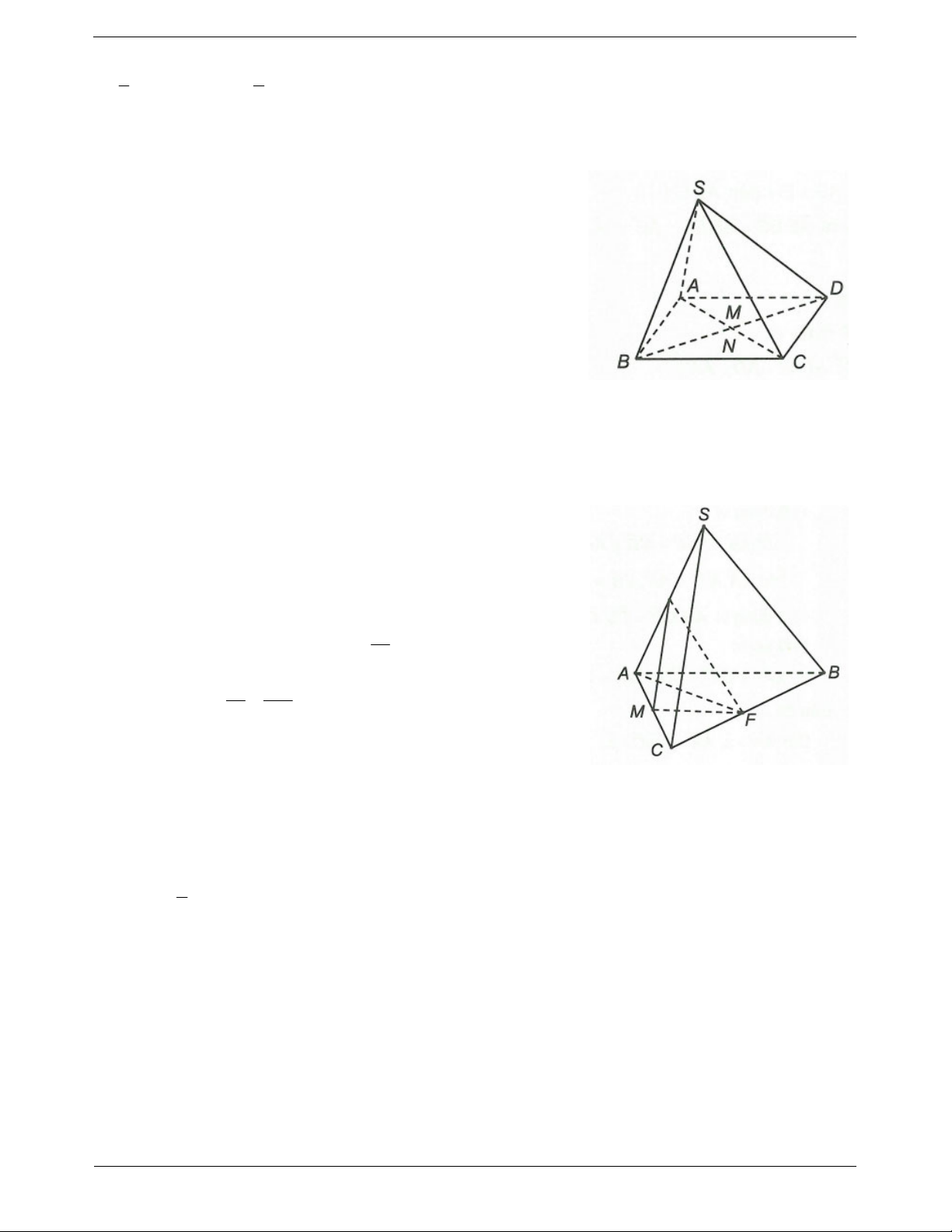
Ví dụ 2. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành.
   
a) Chứng minh SA  SC  SB  SD
2 2 2 2
b) Nếu ABCD là hình chữ nhật thì SA  SC  SB  SD
Hướng dẫn giải
a) Gọi O là tâm của hình bình hành ABCD thì O là
trung điểm của mỗi đường chéo AC và BD.      
Do đó SA  SC  2SO và SB  SD  2SO
   
Vậy SA  SC  SB  SD 2   2 2  
b) Ta có SA  SO  OA2  SO  OA  2 . SO OA , 2      
SC  SO  OC2 2 2
 SO  OC  2 . SO OC . 2 2
2 2 2
  
Suy ra SA  SC  2SO  OA  OC  2SO OA OC          2 2
2 SO  OA  (vì OA và OC là hai vectơ đối nhau nên OAOC  0 )   2 2 2 SO  OA  2 2
Tương tự. SB  SD   2 2 2 SO  OB 
Mà ABCD là hình chữ nhật nên OA  OB
2 2 2 2
Suy ra SA  SC  SB  SD
Bài toán 2. Chứng minh ba vectơ đồng phẳng, ba điểm thẳng hàng TOANMATH.com Trang 7 Phương pháp giải
 Chứng minh ba vectơ đồng phẳng, sử dụng một trong các cách sau.
+ Chứng minh ba vectơ có giá cùng song song với một mặt phẳng.
+ Chứng minh hai vectơ có giá cùng song song với mặt phẳng chứa giá của vectơ còn lại.   
+ Biến đổi vectơ để được đẳng thức dạng c  . m a  . n b  Chứng minh ba điểm ,
A B,C thẳng hàng    k
   : AB  k.AC     k
   : k.MA  1 k .MB  MC
Ví dụ. Cho tứ diện ABCD. Gọi M và N lần lượt là các điểm trên các cạnh AD và BC sao cho
  
AM  2MD, BC  3NC . Chứng minh ba vectơ AB,CD, MN đồng phẳng.
Hướng dẫn giải
   
MN  MA  AB  BN  Ta có  
   2MN  2 
MD DC CN       
Cộng vế theo vế của hai đẳng thức này ta được 3MN  MA 2MD  BN  2CN    AB  2DC 
    
 1  2  Do 2
MA  MD  0, BN  2CN  0 nên MN  AB  CD 3 3
   Vậy ,
AB CD, MN đồng phẳng. Ví dụ mẫu
     
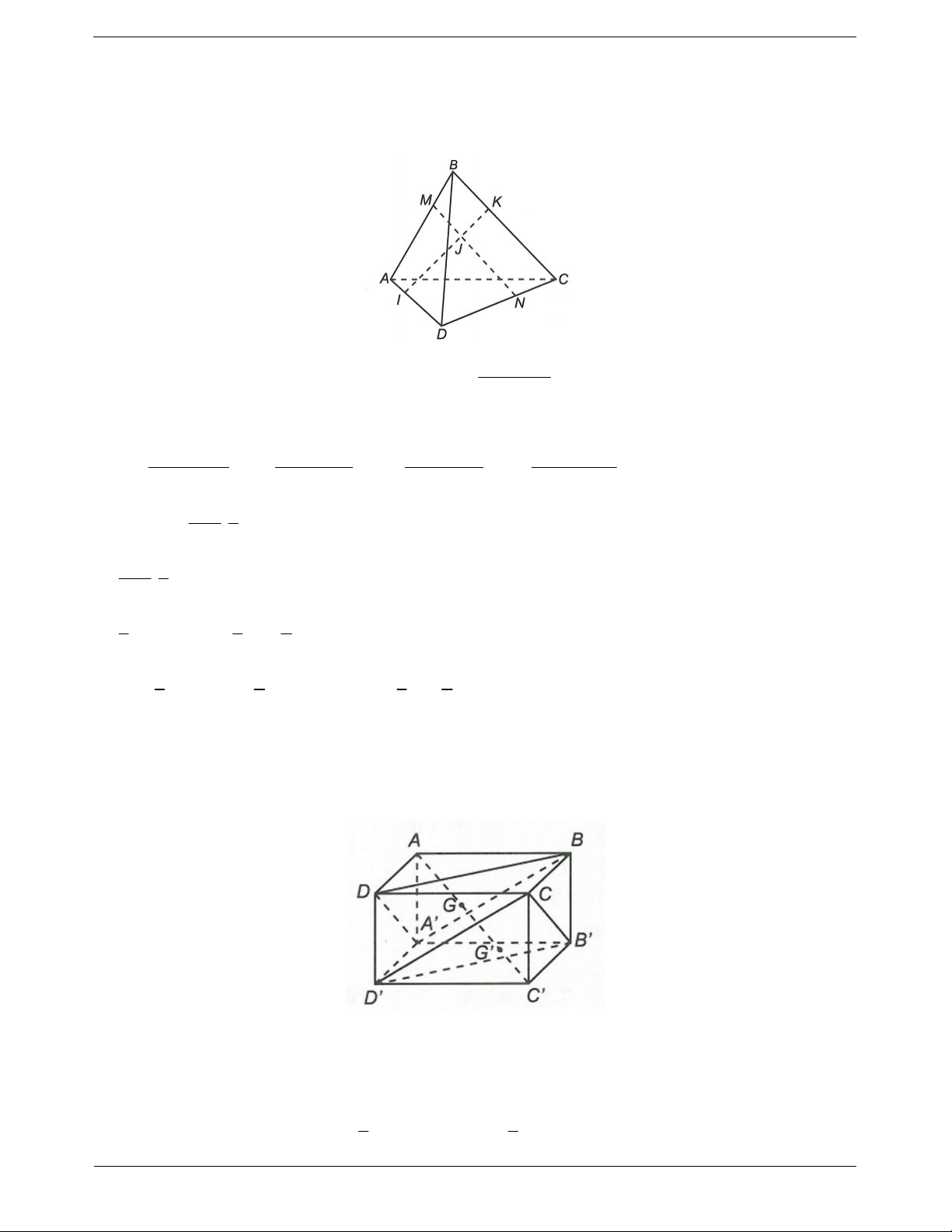
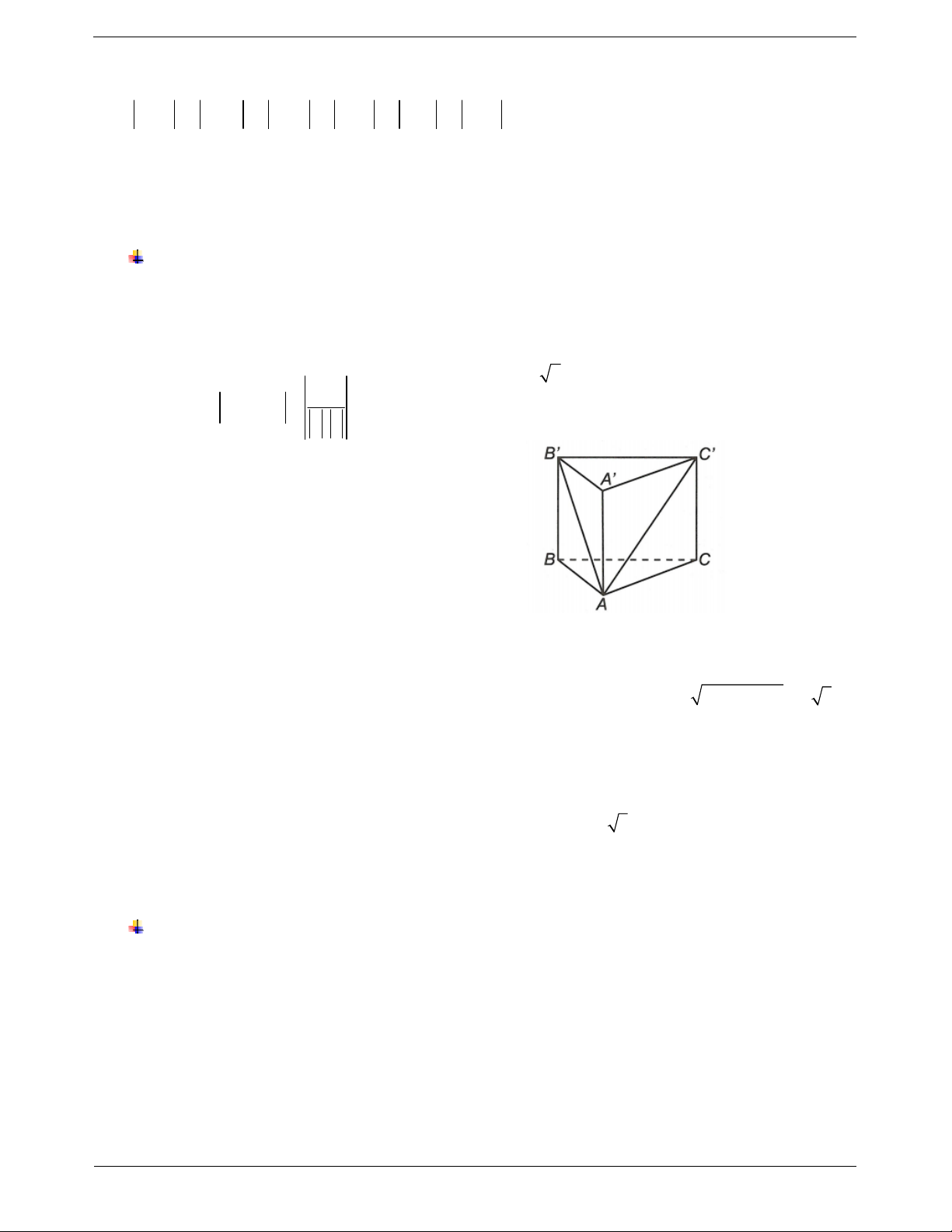
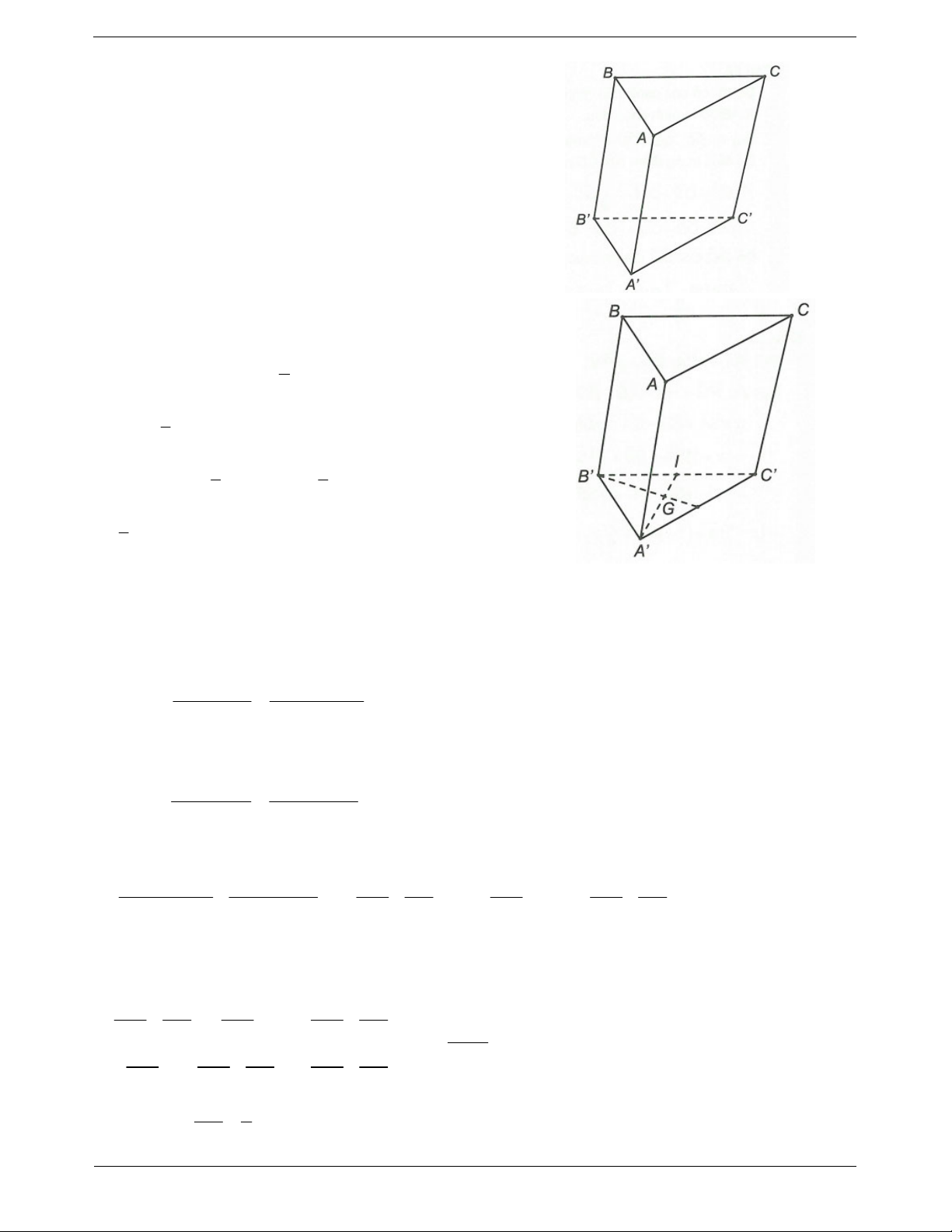
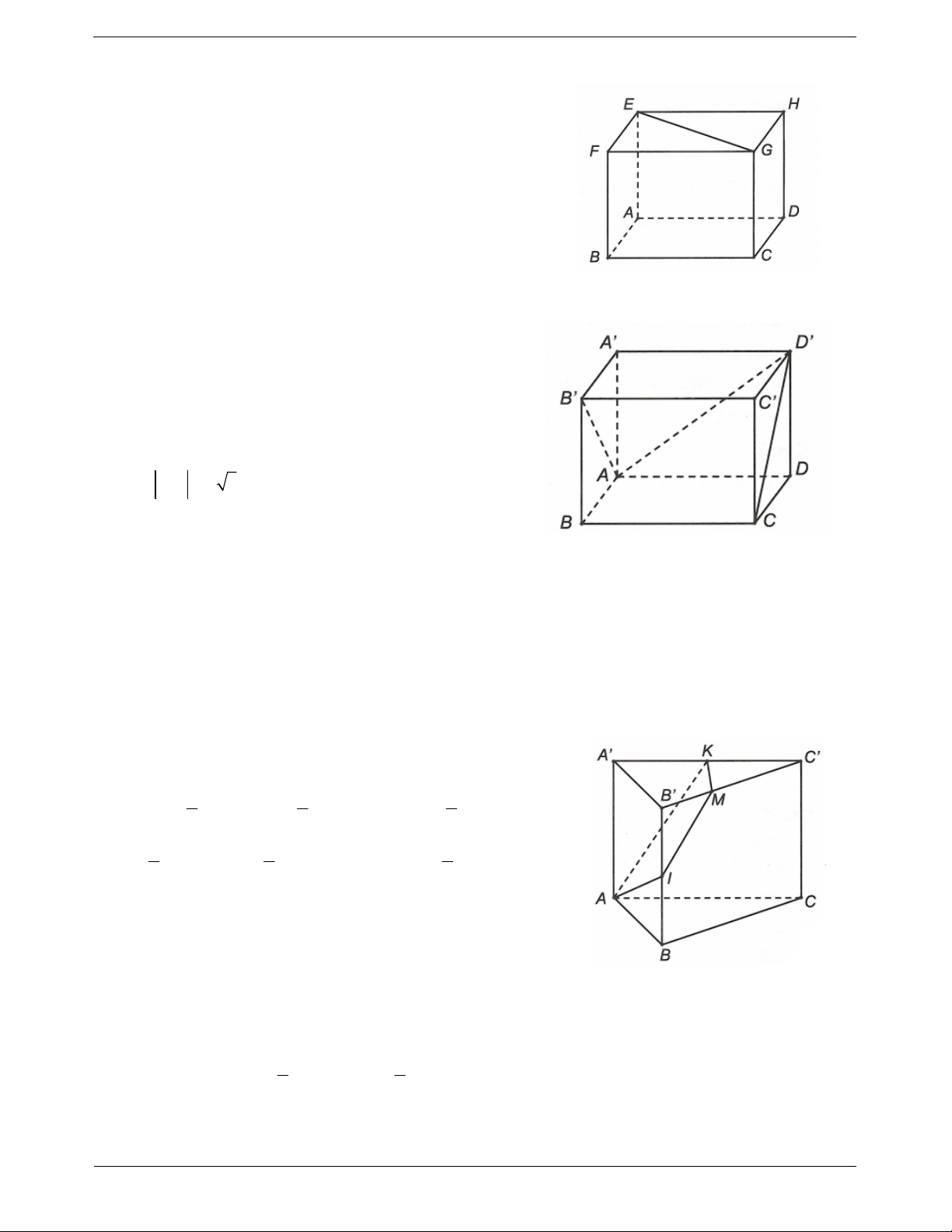
Ví dụ 1. Cho hình lăng trụ tam giác ABC.AB C
  có AA  a, AB  ,
b AC  c . Hãy phân tích các vectơ
     B C
 , BC qua các vectơ a,b,c .
Hướng dẫn giải
  
      Ta có B C   B B
  BC  AA  AC  AB  a  b  c
        
BC  BC  CC  AC  AB  AA  a  b  c TOANMATH.com Trang 8
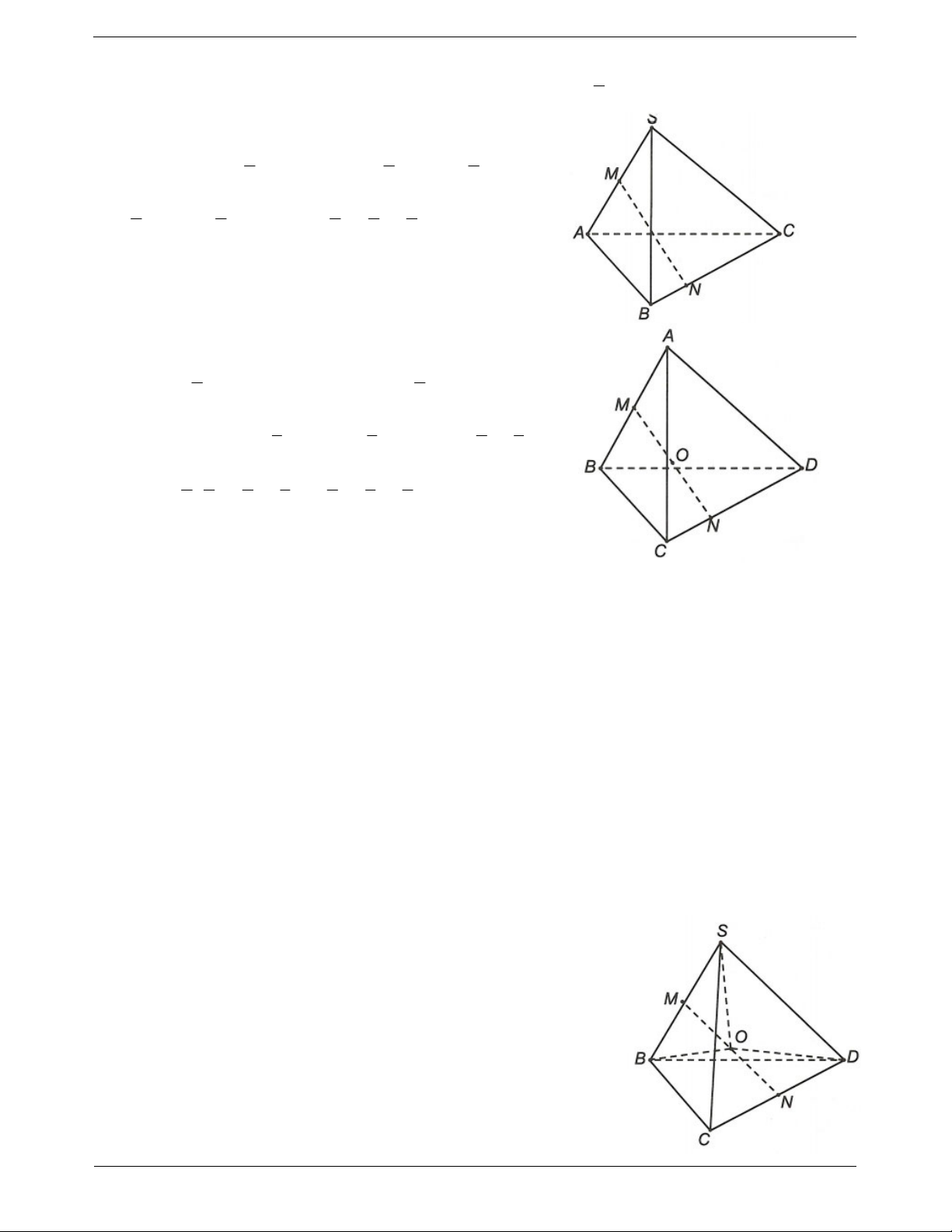
Ví dụ 2. Cho hình chóp S.ABC. Lấy điểm M và N sao cho     MS  2
 MA và NC  2
 NB . Chứng minh rằng ba vectơ
  
AB, MN, SC đồng phẳng.
Hướng dẫn giải      
Từ giả thiết ta có MS  2MA  0;CN  2BN  0
   
MN  MS  SC  CN  Lại có  
   2MN  2 
MA ABBN
Cộng vế theo vế ta được         
3MN  MS  2MA  CN  2BN   SC  2AB  SC  2AB
  
Vậy AB, MN, SC đồng phẳng.
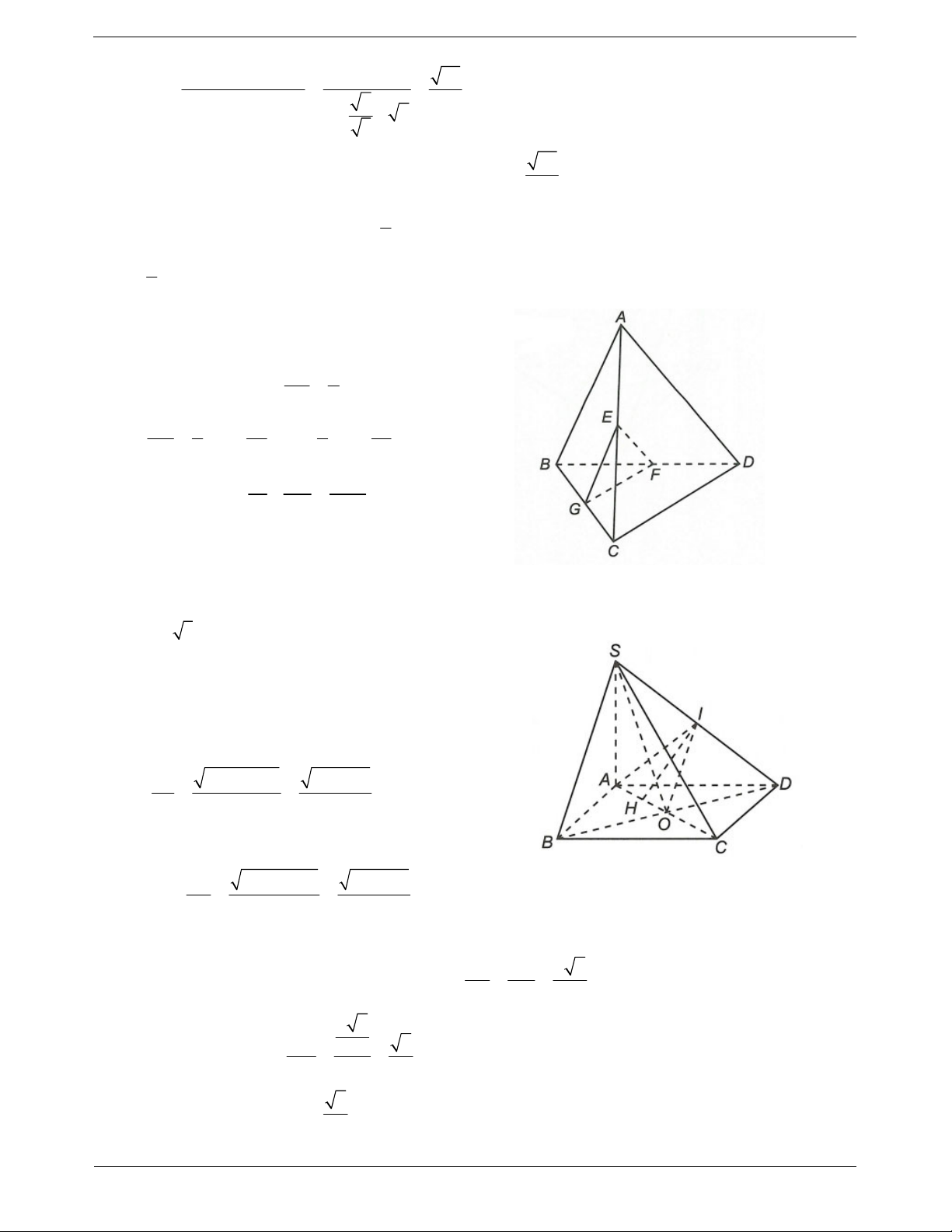
Ví dụ 3. Cho hình chóp S.ABC. Lấy các điểm A , B ,C lần lượt thuộc các tia S ,
A SB, SC sao cho SA  .
a SA , SB  .
b SB , SC  .
c SC, trong đó a, ,
b c là các số thay đổi. Chứng minh rằng mặt phẳng  AB C
  đi qua trọng tâm của tam giác ABC khi và chỉ khi a  b  c  3.
Hướng dẫn giải      
Từ giả thiết ta suy ra SA  .
a SA , S B  .
b SB , SC  . c SC
   
Gọi G là trọng tâm của tam giác ABC . Ta có SA  SB  SC  3SG    
G  AB C
   SG  .xSA .ySB  .zSC với x  y  z 1      3SG  3 . x SA  3 . y SB  3 .
z SC với x  y  z  1        . a SA  . b SB  . c SC  3 . x SA  3 . y SB  3 . z SC    
 a 3x.SA  b  3y.SB  c 3z.SC  0
  
 a  3x  b  3y  c  3z  0 (do SA , SB , SC không đồng phẳng)
+) Nếu G  AB C
  ta có a 3x  b 3y  c 3z  0 (với 1
x  y  z  ).
Do đó a  b  c  3 a b c
+) Nếu a  b  c  3 , ta đặt x  , y  , z  thì 3 3 3
a  b  c
x  y  z 
1 và a  3x  b  3y  c  3z  0 3
Do đó G  AB C  . TOANMATH.com Trang 9
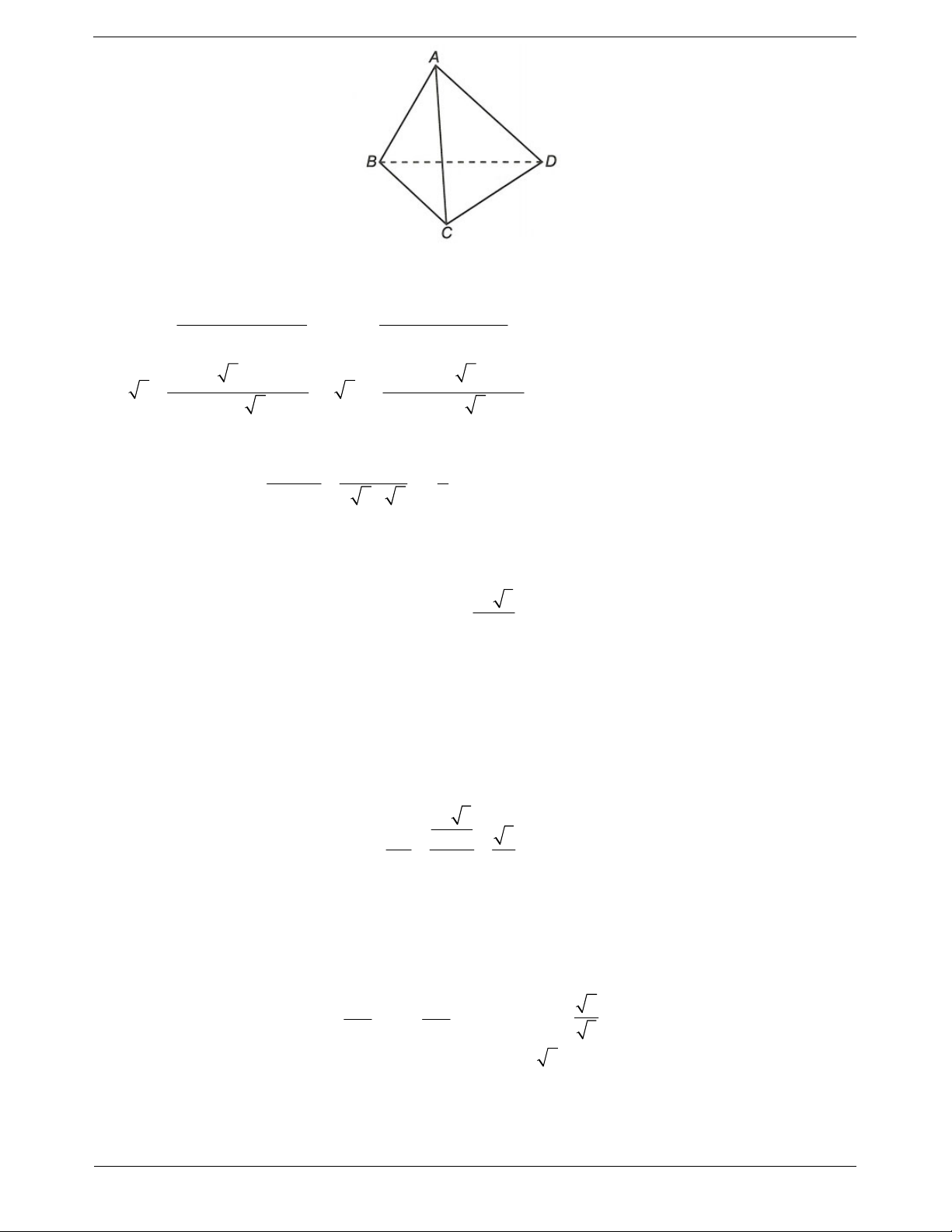
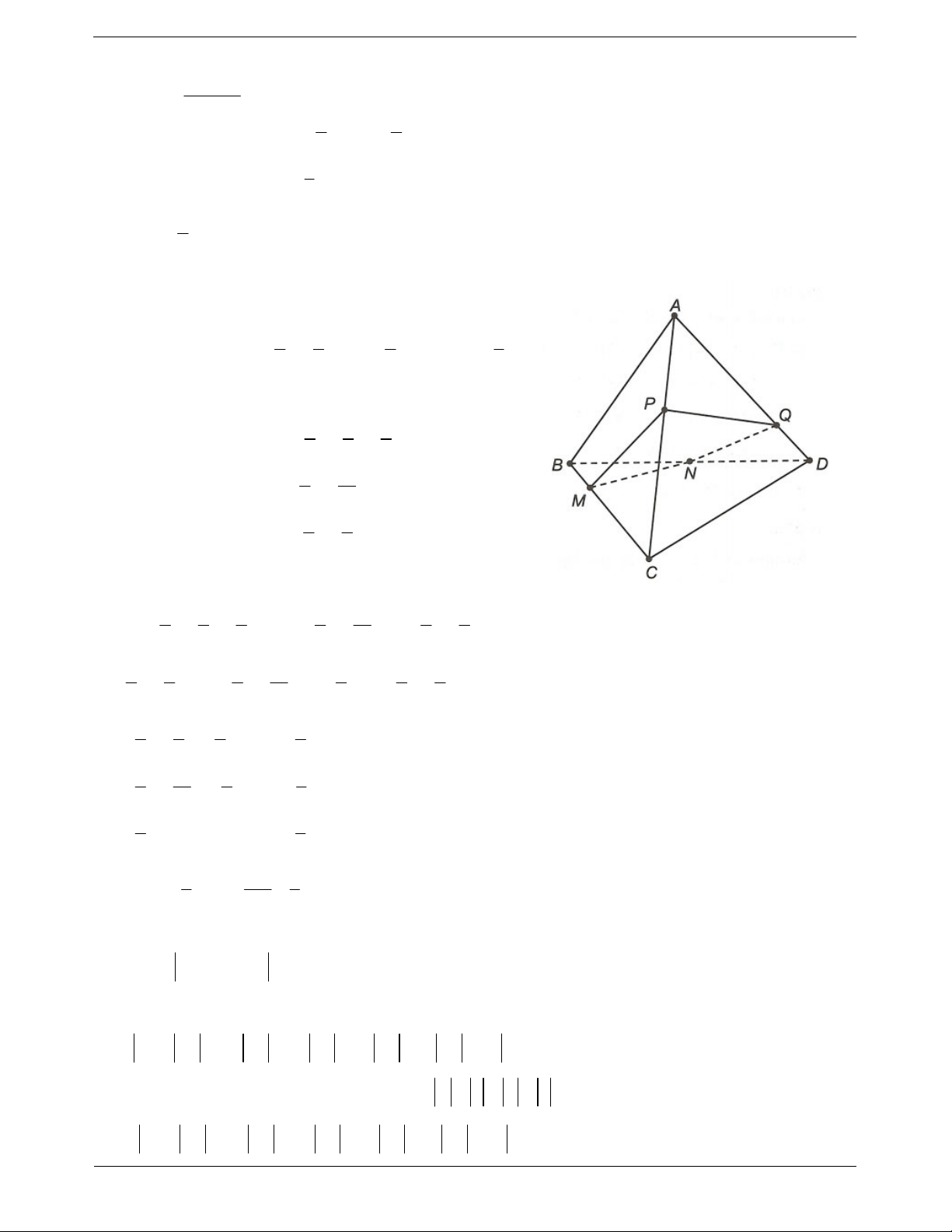
Ví dụ 4. Cho tứ diện ABCD, M và N là các điểm lần lượt thuộc AB và CD sao cho     MA  2  MB, ND  2  NC ; các điểm ,
I J , K lần lượt thuộc ,
AD MN, BC sao cho      
IA  k.ID, JM  k.JN, KB  k.KC . Chứng minh rằng các điểm I, J , K thẳng hàng.
Hướng dẫn giải    
 OA 2OB Ta có MA  2
 MB nên với điểm O bất kỳ thì OM  3
Tương tự, ta chỉ ra được        
 OD  2.OC  OA  k.OD  OB  k.OC  OM  k.ON ON  ,OI  ,OK  ,OJ  3 1 k 1 k 1 k  1 1     Ta có OJ 
. OA 2OB  k.OD  2k.OC 1 k 3 1 1   
. 1 k OI  21 k OK  1 k 3    1    
 OI  OK  1 2 2  OI  OK 3 3 3 1   2   1  2   
Suy ra OI OJ   OK OJ   0  JI  JK  0  IJ  2JK 3 3 3 3
Suy ra I, J , K thẳng hàng.
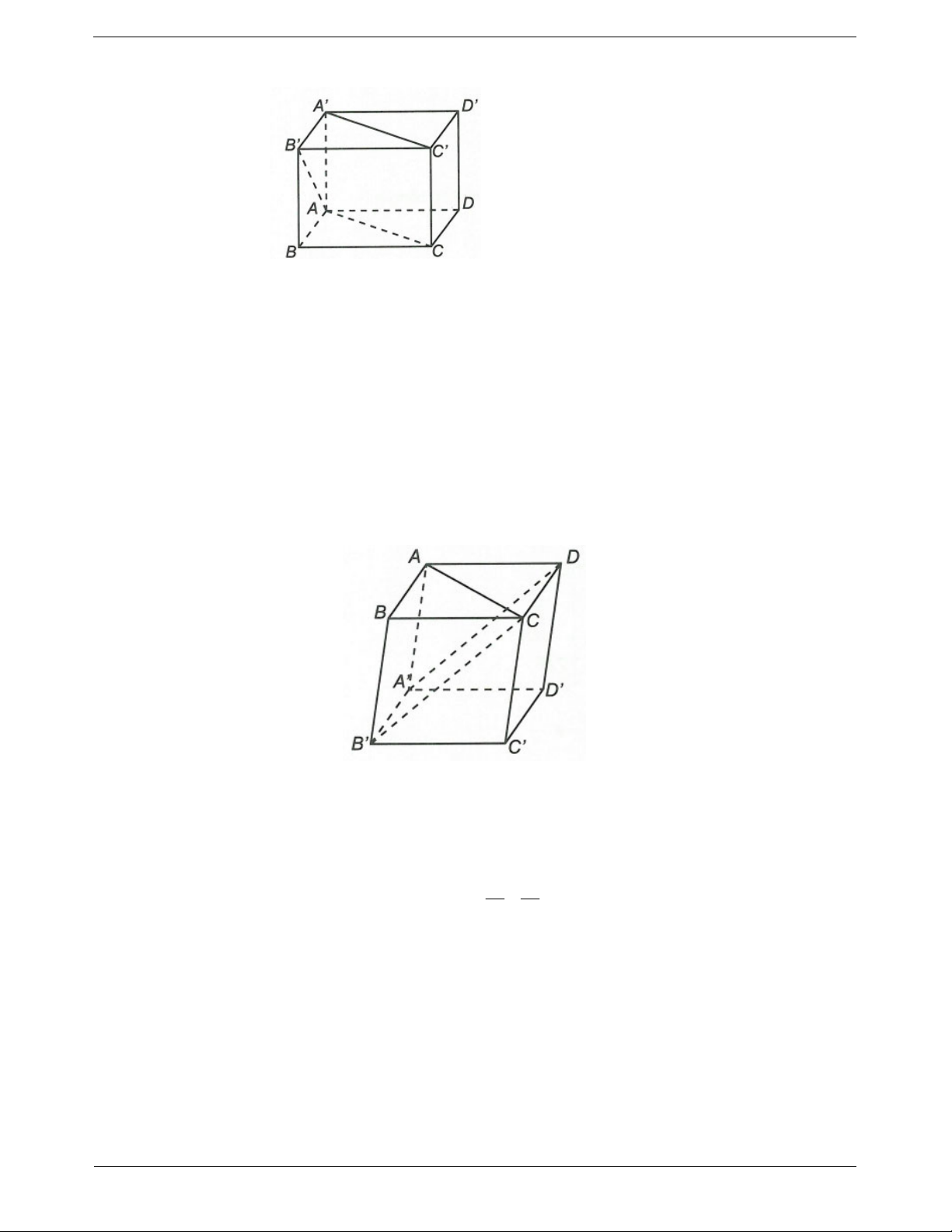
Ví dụ 5. Cho hình hộp ABC . D AB C  D   . Gọi ,
G G lần lượt là trọng tâm của các tam giác BDA ,CB D  . Chứng minh các điểm ,
A G,G ,C thẳng hàng.
Hướng dẫn giải
     
Đặt AB  a, AD  , b AA  c    
Ta có AC  a  b  c (quy tắc hình hộp).
 1    1   
Theo quy tắc trọng tâm, ta có AG   AB  AD  AA  a  b  c 3 3 TOANMATH.com Trang 10
 1            
AG   AC  AB AD 1
 a b  a  c b  c 2
 a b  c 3 3 3   3 
Vậy AC  3AG  AG nên các điểm ,
A G,G ,C thẳng hàng. 2
Bài tập tự luyện dạng 1    
Câu 1: Cho bốn vectơ a, ,
b c, d bất kỳ. Khẳng định nào sau đây sai?            
A. a  b và c  d  a  c  b  d B. a  b  a  b                
C. a  c  b  d  a  d  b  c D. a  b
 và c  d  a  d  c  b   
Câu 2: Trong không gian cho ba vectơ a, ,
b c . Cho các khẳng định sau.      
(1) Nếu các vectơ a, ,
b c đồng phẳng thì các vectơ a,b,c thuộc một mặt phẳng nào đó.      
(2) Nếu các vectơ a, ,
b c đồng phẳng thì ba vectơ a, , b c cùng phương.      
(3) Nếu tồn tại hai số thực ,
m n sao cho c  ma  nb thì các vectơ a, , b c đồng phẳng.   
(4) Nếu các vectơ a, ,
b c đồng phẳng thì giá của chúng song song với mặt phẳng nào đó.
Có bao nhiêu khẳng định đúng?
A. 4 B. 3 C. 2 D. 1
Câu 3: Cho tam giác ABC có diện tích S. Giá trị nào của k thích hợp thỏa mãn 1 2 2   S 
AB .AC  2k  . AB AC 2 ? 2 1 1 1
A. k  B. k  C. k  D. k  1 4 2 2
Câu 4: Cho tứ diện ABCD. Hãy chọn khẳng định đúng?
   
   
A. AB  CD  AC  DB B. AC  BD  AB  CD
   
   
C. AD  BC  AB  DC D. BA  CD  BD  CA
Câu 5: Trong các mệnh đề sau đây, mệnh đề nào là đúng?    
A. Từ AB  3AC ta suy ra BA  3  CA .     B. Từ AB  3
 AC ta suy ra CB  2AC .   
C. Nếu AB  2
 AC  5AD thì bốn điểm ,
A B,C, D cùng thuộc một mặt phẳng.  1 
D. Nếu AB   BC thì B là trung điểm của đoạn AC. 2
Câu 6: Hãy chọn mệnh đề đúng trong các mệnh đề sau đây.
   
A. Cho hình chóp S.ABCD. Nếu có SB  SD  SA  SC thì tứ giác ABCD là hình bình hành.  
B. Tứ giác ABCD là hình bình hành nếu AB  CD .
    
C. Tứ giác ABCD là hình bình hành nếu 0
AB  BC  CD  DA  .
  
D. Tứ giác ABCD là hình bình hành nếu AB  AC  AD .    
Câu 7: Cho a  3, b  5 , góc giữa a và b bằng 120 . Khẳng định nào sai trong các khẳng định sau? TOANMATH.com Trang 11        
A. a  b  7 B. a  b  19 C. a  2b  9 D. a  2b  139
Câu 8: Cho tứ diện ABCD, O là trọng tâm tam giác BCD, M là trung điểm của AD. Khẳng định nào dưới đây đúng?
 1  1  1  
2  1  1 
A. OM  AB  AC  AD B. OM   AB  AC  AD 3 3 6 3 3 6 
1  1  1 
 1  1  1 
C. OM   AB  AC  AD D. OM  AB  AC  AD 3 3 6 3 3 6
Câu 9: Khẳng định nào sau đây sai?     
A. Cho hai vectơ không cùng phương a và b . Khi đó ba vectơ a,b,c đồng phẳng khi và chỉ khi có cặp số ,
m n là duy nhất.       
B. Nếu có ma  nb  pc  0 và một trong ba số , m ,
n p khác 0 thì ba vectơ a, ,
b c đồng phẳng.   
C. Ba vectơ a, ,
b c đồng phẳng khi và chỉ khi ba vectơ đó cùng có giá thuộc một mặt phẳng.
D. Ba tia Ox,Oy,Oz vuông góc với nhau từng đôi một thì ba tia đó không đồng phẳng.
Câu 10: Cho 2 điểm phân biệt A, B và một điểm O bất kì. Mệnh đề nào sau đây đúng?   
A. Điểm M thuộc đường thẳng AB khi và chỉ khi OM  OB  k BA .    
B. Điểm M thuộc đường thẳng AB khi và chỉ khi OM  OB  k OB OA .   
C. Điểm M thuộc đường thẳng AB khi và chỉ khi OM  kOA  1 k OB .
  
D. Điểm M thuộc đường thẳng AB khi và chỉ khi OM  OA  OB .  
Câu 11: Cho hình lập phương ABC . D AB C  D
  có cạnh bằng a. Giá trị A . B C A   bằng A. 2 a B. 2 a 2 C. 2 a 2 D. 2 a
Câu 12: Khẳng định nào sau đây đúng?
A. Ba vectơ đồng phẳng là ba vectơ cùng nằm trong một mặt phẳng.      
B. Ba vectơ a, ,
b c đồng phẳng thì có c  ma  nb với ,
m n là các số duy nhất.        
C. Ba vectơ a, ,
b c không đồng phẳng khi có d  ma  nb  pc với d là vectơ bất kì.
D. Cả ba mệnh đề trên đều sai.
Câu 13: Khẳng định nào sau đây sai?
  
A. Vì NM  NP  0 nên N là trung điểm của đoạn MP. 1  
B. Vì I là trung điểm của đoạn AB nên từ một điểm O bất kì ta có OI  OA OB . 2   
   C. Từ hệ thức 2
AB  AC  8AD ta suy ra ba vectơ AB, AC, AD đồng phẳng.
    
D. Vì AB  BC  CD  DA  0 nên bốn điểm ,
A B,C, D cùng thuộc một mặt phẳng.
Câu 14: Trong không gian cho ba điểm ,
A B,C bất kì. Khẳng định nào sau đây đúng?   1   1 A. . BA BC   2 2 2
BA  BC  2AC  B. . BA BC   2 2 2
BA  BC  AC  2 2     C. 2 2 2 B .
A BC  BA  BC  AC D. 2 2 2 B .
A BC  BA  BC  2AC TOANMATH.com Trang 12
     
Câu 15: Cho tứ diện SABC. Đặt SA  a, SB  ,
b SC  c . Gọi M là trung điểm của SA, N là điểm trên cạnh    
BC sao cho NC  3NB . Phân tích vectơ MN theo ba vectơ a,b và c ta được  1  3  1   1  3  1 
A. MN   a  b  c . B. MN  a  b  c 2 4 4 2 4 4  1  3  1   1  3  1 
C. MN   a  b  c D. MN  a  b  c 2 4 4 2 4 4
     
Câu 16: Cho tứ diện ABCD. Đặt ,
AB  a AC  ,
b AD  c . Gọi M là trung điểm của AB, N là điểm trên 
cạnh CD sao cho ND  2NC . Gọi O là trung điểm của đoạn thẳng MN. Biểu diễn vectơ AO theo ba   
vectơ a,b và c ta có  1  1  1   1  1  1 
A. AO  a  b  c B. AO  a  b  c 4 3 3 4 3 6  1  1  1   1  1  1 
C. AO  a  b  c D. AO  a  b  c 4 4 4 4 6 3
Câu 17: Trong không gian cho tam giác ABC. Tìm M sao cho giá trị của biểu thức 2 2 2
P  MA  MB  MC đạt giá trị nhỏ nhất.
A. M là trọng tâm tam giác ABC. B. M là tâm đường tròn ngoại tiếp tam giác ABC.
C. M là trực tâm tam giác ABC. D. M là tâm đường tròn nội tiếp tam giác ABC.
Câu 18: Cho tứ diện ABCD có trọng tâm G. Chọn khẳng định đúng? A. 2 2 2 2 2 2
AB  AC  AD  BC  BD  CD   2 2 2 2
3 GA  GB  GC  GD  B. 2 2 2 2 2 2
AB  AC  AD  BC  BD  CD   2 2 2 2
4 GA  GB  GC  GD  C. 2 2 2 2 2 2
AB  AC  AD  BC  BD  CD   2 2 2 2
6 GA  GB  GC  GD  D. 2 2 2 2 2 2
AB  AC  AD  BC  BD  CD   2 2 2 2
2 GA  GB  GC  GD 
     
Câu 19: Cho lăng trụ ABC.AB C  . Đặt ,
a  AA b  AB,c  AC . Xét hai mệnh đề         (I) B C
  a  b  c (II)
BC  a  b  c Mệnh đề nào đúng?
A. Chỉ (I). B. Chỉ (II). C. Không có. D. Cả (I) và (II).
     
Câu 20: Cho lăng trụ ABC.AB C
 . Đặt a  AA ,b  AB,c  AC . Gọi G là trọng tâm của tam giác  AB C
  . Vectơ AG bằng 1    1    1    1   
A. a  3b  c B. 3a  b  c C. a  b  3c D. a  b  c 3 3 3 3 
  
Câu 21: Cho hình hộp ABC . D AB C  D   . Biết .
MA  k MC, NC  l.ND . Khi MN song song với BD thì
khẳng định nào sau đây đúng? 3
A. k  l   B. k  l  3 C. k  l  4 D. k  l  2 2 TOANMATH.com Trang 13
Câu 22: Cho hình chóp S.ABCD có tất cả các cạnh bên và đáy đều bằng a và ABCD là hình vuông. Gọi M  
là trung điểm của CD. Giá trị MS.CB bằng 2 a 2 a 2 a 2 2a A. B.  C. D. 2 2 3 2
     
Câu 23: Cho hình chóp S.ABC có SA  a, SB  ,
b SC  c và các điểm M, N lần lượt là trung điểm của các 
cạnh AB, SC. Các điểm P, Q trên các đường thẳng SA, BN sao cho PQ / /CM . Biểu diễn vectơ PQ theo   
ba vectơ a,b,c được kết quả  2  2  4   1  1  2 
A. PQ   a  b  c B. PQ  a  b  c 3 3 3 3 3 3  2  2  4   1  1  2 
C. PQ  a  b  c D. PQ   a  b  c 3 3 3 3 3 3
Câu 24: Khẳng định nào sau đây sai?
  
A. Ba vectơ AB, AC, AD đồng phẳng  bốn điểm ,
A B,C, D cùng nằm trong một mặt phẳng.
  
B. ABCD là một tứ diện ,
 BC CD, AC không đồng phẳng.   
C. Ba vectơ a, ,
b c đồng phẳng chỉ khi giá của chúng cùng nằm trong một mặt phẳng.   
D. Ba vectơ a, ,
b c không đồng phẳng khi và chỉ khi trong ba vectơ đó, vectơ này không thể biểu diễn được theo hai vectơ kia.
Câu 25: Cho hình lập phương ABC . D AB C  D
  cạnh bằng a. Gọi G là trọng tâm tam giác ABC . Giá trị 2 AG bằng 2 2a 2 a A. 2 a B. C. 2 3a D. 3 3
Câu 26: Cho hình chóp S.ABCD. Gọi O là giao điểm của AC và BD. Xét hai mệnh đề
    
(I). Nếu ABCD là hình bình hành thì SA  SB  SC  SD  4SO .
    
(II). Nếu SA  SB  SC  SD  4SO thì ABCD là hình bình hành. Mệnh đề nào đúng?
A. Chỉ (I). B. Chỉ (II). C. Không có. D. Cả (I) và (II).  
Câu 27: Cho tứ diện S.ABC có SA  SB  SC  AB  AC  a, BC  a 2 . Tích vô hướng giữa SC.AB bằng 2 a 2 a A.  B. C. 2 a D. 2 a 2 2
Câu 28: Cho hình chóp S.ABCD. Xét hai mệnh đề
   
(I) Nếu ABCD là hình bình hành thì SA  SC  SB  SD .
   
(II) Nếu SA  SC  SB  SD thì ABCD là hình bình hành. Mệnh đề nào đúng?
A. Chỉ (I). B. Chỉ (II). C. Không có. D. Cả (I) và (II).             
Câu 29: Cho ba vectơ a,b,c không đồng phẳng. xét các vectơ x  2a  ,
b y  a  b  c, z  3  b  2c .
Chọn khẳng định đúng? TOANMATH.com Trang 14     
A. Ba vectơ x, y, z đồng phẳng. B. Hai vectơ x, a cùng phương.     
C. Hai vectơ x,b cùng phương. D. Ba vectơ x, y, z đôi một cùng phương.   
Câu 30: Cho ba vectơ a, ,
b c không đồng phẳng. Khẳng định nào sau đây sai?             A. Các vectơ
x  a  b  2c, y  2a  3b  6c, z  a  3b  6c đồng phẳng.             B. Các vectơ
x  a  2b  4c, y  3a  3b  2c, z  2a  3b  3c đồng phẳng.           
C. Các vectơ x  a  b  c, y  2a  3b  c, z  a  4b đồng phẳng.            
D. Các vectơ x  a  b  c, y  2a  b  3c, z  a  2b  4c đồng phẳng.
Câu 31: Trong các kết quả sau đây, kết quả nào đúng?  
Cho hình lập phương ABCD.EFGH có cạnh bằng a. Giá trị của A . B EG bằng 2 a 2 A. 2 a B. 2 a 2 C. 2 a 3 D. 2
Câu 32: Cho hình lập phương ABC . D AB C  D
  có cạnh bằng a. Khẳng định nào sau đây sai?   
A. AC  a 3 B. 2
AD .AB  a  
    
C. AB .CD  0
D. 2AB  B C
   CD  D A    0
Câu 33: Cho lăng trụ tam giác ABC.AB C
 . Gọi I, K lần lượt là trung điểm của BB , AC. Điểm M thuộc   cạnh B C
  sao cho MB  kMC. Tìm k để bốn điểm ,
A I, M , K đồng phẳng. 3 1 A. k  1
 B. k   C. k   D. k  3  2 2 SM
Câu 34: Cho hình chóp S.ABCD có đáy là hình bình hành tâm O, M là điểm thay đổi trên SO. Tỉ số SO sao cho biểu thức 2 2 2 2 2
P  MS  MA  MB  MC  MD nhỏ nhất bằng 1 2 3 4
A. B. C. D. 2 3 4 5
Câu 35: Cho tứ diện ABCD. Gọi E, F lần lượt là trung điểm của AB, CD. Cho
AB  2a,CD  2 ,
b EF  2c . Với M là một điểm tùy ý, tổng 2 2
MA  MB bằng A. 2 2
2MF  2b B. 2 2
2ME  2a C. 2 2
2MF  2a D. 2 2 2ME  2b    
Câu 36: Cho hình chóp S.ABC có M, N là các điểm thỏa mãn MS  2  M ;
A NB  k NC . Tìm k để ba
  
vectơ AB, MN, SC đồng phẳng. 1 1 A. k  2
 B. k  C. k  2 D. k   2 2
Câu 37: Cho tứ diện ABCD có các điểm M, N, P lần lượt thuộc các cạnh BC, BD và AC sao cho AQ
BC  4BM , AC  3AP, BD  2BN . Mặt phẳng MNP cắt đường thẳng AD tại điểm Q. Tính tỉ số . AD AQ 5 AQ 3 AQ 2 AQ 5 A.  B.  C.  D.  AD 2 AD 5 AD 5 AD 3 TOANMATH.com Trang 15    
Câu 38: Trong không gian xét ,
m n, p, q là các vectơ có độ dài bằng 1. Giá trị lớn nhát của biểu thức   2   2   2   2   2   2
S  m  n  m  p  m  q  n  p  n  q  p  q là
A. 16. B. 6. C. 25. D. 8.
Dạng 2. Hai đường thẳng vuông góc
Bài toán 1. Tính góc giữa hai đường thẳng (chứng minh hai đường thẳng vuông góc trong hình lăng trụ và hình hộp) Phương pháp giải
 Để tính số đo của góc giữa hai đường thẳng d Ví dụ. Cho hình lăng trụ đứng tam giác 1 
ABC.AB C
  có đáy ABC là tam giác cân,
và d ta có thể thực hiện tính thông qua góc 2  
AB  AC  a, BAC  120 và cạnh bên
giữa hai vectơ chỉ phương của đường thẳng đó.  
AA  a 2 . Tính góc giữa hai đường thẳng AB và   . u v
+) cosd ,d  cos u,v    BC. 1 2    u.v
Hướng dẫn giải
+) Định lí côsin trong tam giác
 Để chứng minh hai đường thẳng AB và CD vuông  
góc với nhau, ta thường chứng minh . AB CD  0 .
Bước 1. Sử dụng tính chất sau:  
 d , d   1 2  
 d ,d  d ,d   1 2   1 3 d / /d  2 3
Bước 2. Áp dụng định lí côsin trong tam giác để         xác định góc. Ta có BC B C  AB BC  AB B C   / / , , Xét AB C   có 2 2
AB  AC  AB  BB  a 3
Áp dụng định lý cosin cho ABC , ta có 2 2 2 
BC  AB  AC  2.A . B AC.cos BAC 2 2 2
 a  a  2. . a .
a cos120  3a  BC  B C    a 3 Suy ra AB C   đều, do đó  AB BC
  AB B C     , ,  AB C    60 Ví dụ mẫu
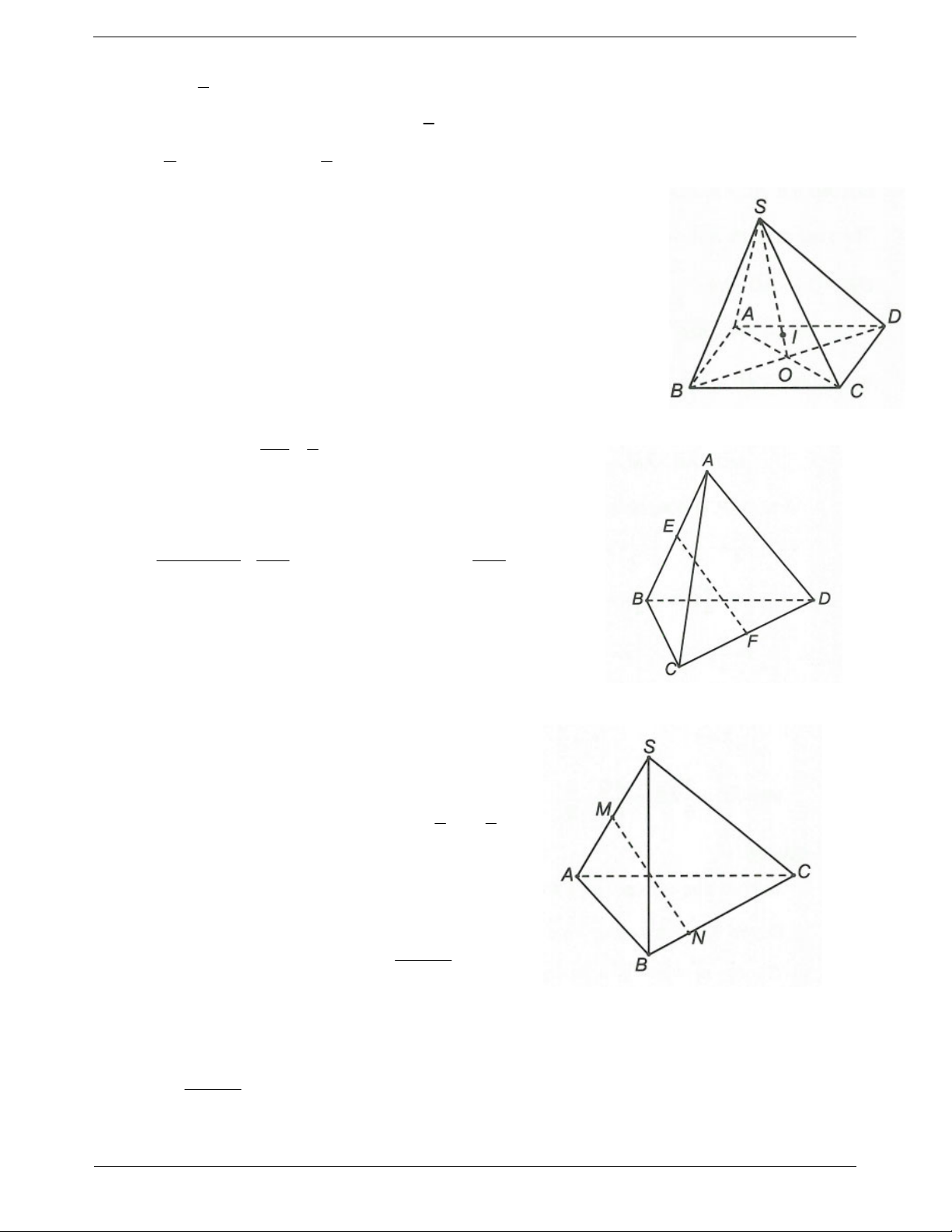
Ví dụ 1. Cho hình lập phương ABC . D AB C  D
  . Tính góc giữa 2 đường thẳng a) AB và B C   b) AC và B C  
c) AC và B C  TOANMATH.com Trang 16 Hướng dẫn giải
a) Ta có AB / / AB mà  AB B C    ,
 90 nên  AB B C    ,  90
b) Vì tứ giác ABCD là hình vuông nên  AC BC  ,  45. Ta có BC / /B C   nên  AC B C    ,  45
c) Ta có AC / / AC và ACB là tam giác đều vì có các cạnh đều bằng đường chéo của các hình
vuông bằng nhau. Do đó  AC B C     AC B C    , ,  60 .
Ví dụ 2. Cho hình hộp thoi ABC . D AB C  D
  có tất cả các cạnh bằng a và    ABC  B B  A  B BC   60 .
Chứng minh tứ giác AB C
 D là hình vuông. Hướng dẫn giải
Ta có tứ giác AB C
 D là hình bình hành (tính chất hình hộp). Do  B B
 C  60 nên BB C  đều. Suy ra B C   a .
Do đó CD  B C
  a nên AB C  D là hình thoi.  
       a a
Ta có CB CD  CB  BB 2 2 . .BA  .
CB BA  BB .BA     0 . 2 2
Suy ra CB  CD . Vậy tứ giác AB C
 D là hình vuông.
Ví dụ 3. Cho hình hộp ABC . D AB C  D
  có độ dài tất cả các cạnh bằng a và các góc BAD, DAA , AAB
đều bằng 60 . Gọi M, N lần lượt là trung điểm của AA ,CD . Gọi  là góc tạo bởi hai đường thẳng MN và B C
 , tính giá trị của cos . Hướng dẫn giải TOANMATH.com Trang 17
AD / /B C  Ta có 
với P là trung điểm của DC . MN / / A  P Suy ra MN B C  
  AP AD   , ,  DAP Vì    D
BA  DAA  AAB  60 và các cạnh của hình hộp bằng a.
Do đó AD  a,C D   C A    a 3 . 2 2 2
AD  AC DC 5a Suy ra AP    AP  . 2 4 2
Áp dụng định lý cosin cho tam giác ADP , ta có 2 2 2
AD  AP  DP 3 5 cos   2A . D AP 10
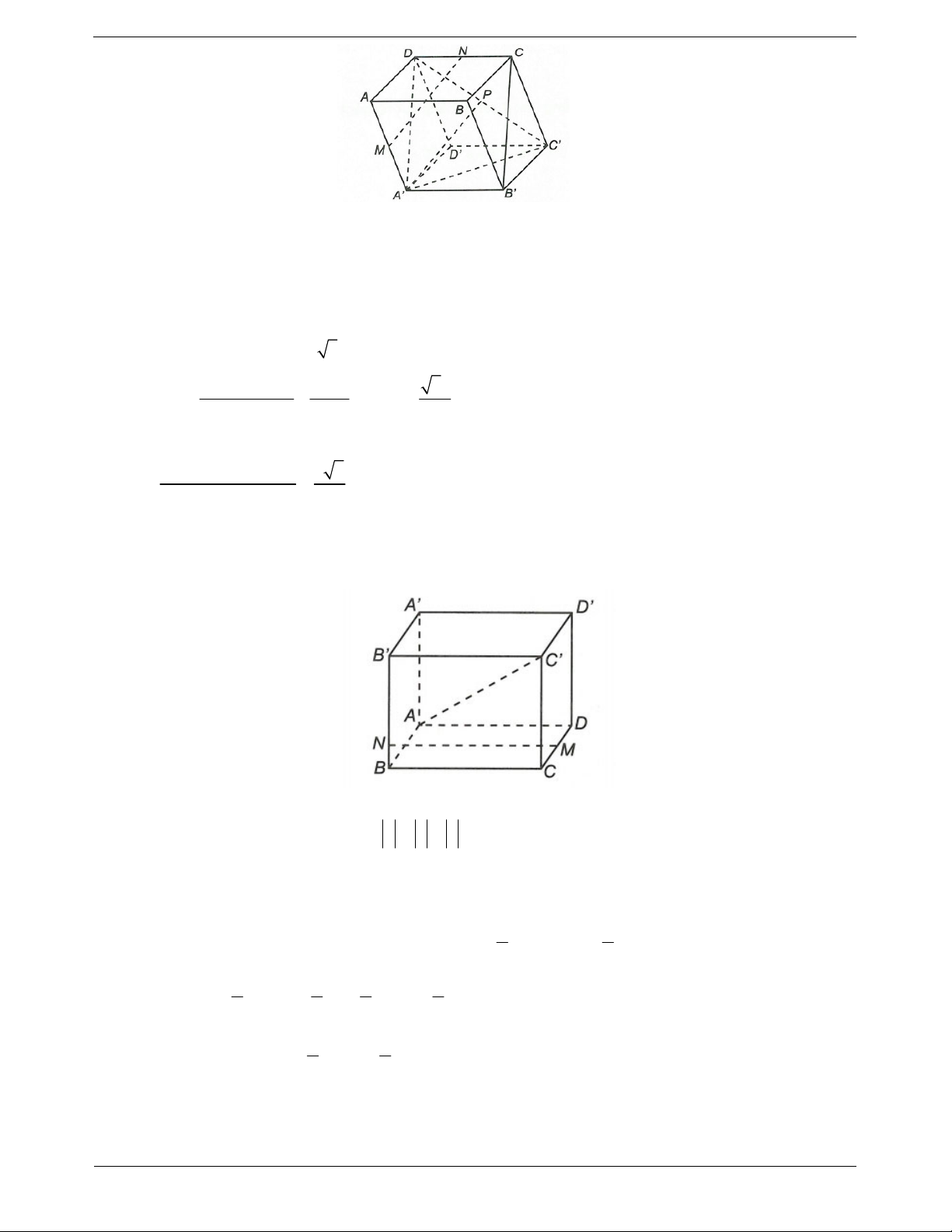
Ví dụ 4. Cho hình lập phương ABC . D AB C  D
  có cạnh bằng a. Trên các cạnh CD và BB ta lần lượt lấy
các điểm M và N sao cho DM  BN  x với 0  x  a . Chứng minh rằng AC  MN . Hướng dẫn giải
         Ta đặt ,
AA  a AB  ,
b AD  c . Ta có a  b  c  a
       
AC  AA  AB  AD hay AC  a  b  c Mặt khác
        x   x 
MN  AN  AM   AB  BN   AD  DM  với BN  .a và DM  .b a a
   x    x   x   x   
Do đó MN  b  a  c  b  a  a  b  c        a   a  a  a 
 
    x   x   
Ta có AC .MN  a  b  c a  a  b  c    a a           Vì . a b  0, . a c  0, . b c  0 nên ta có TOANMATH.com Trang 18
  x 2  x 2 2   x  2 2
AC .MN  a  1 b  c  . x a  1 a  a  0     a  a   a 
Vậy AC  MN .
Bài toán 2. Tính góc giữa hai đường thẳng (hai đường thẳng vuông góc) trong hình chóp Ví dụ mẫu
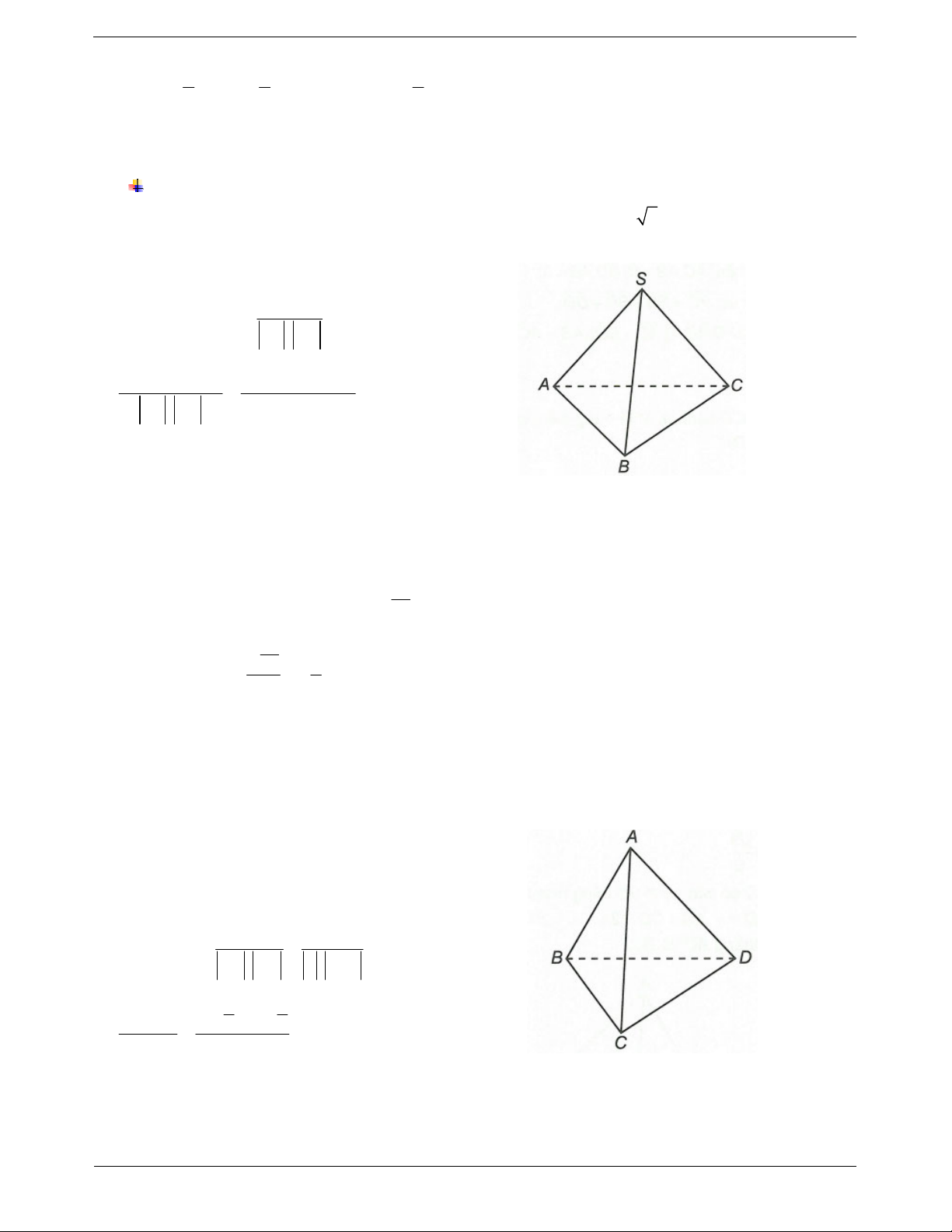
Ví dụ 1. Cho hình chóp S.ABC có SA  SB  SC  AB  AC  a và BC  a 2 .
Tính góc giữa hai đường thẳng AB và SC.
Hướng dẫn giải     SC AB Ta có SC AB . cos ;
   SC . AB
      
SA  AC .AB .
SA AB  AC.AB     SC . AB . a a Vì 2 2 2 2 2 2
BC  2a  a  a  AC  AB
Nên ABC vuông tại A.   Do đó . AB AC  0  
Mặt khác tam giác SAB đều nên SA AB  ; 120 . 2   a Do đó ta có . SA AB  . SA . AB cos120   . 2 2 a    1 Vậy SC AB 2 cos ;    . 2 a 2   Do đó SC AB  ;  120 Suy ra góc SC AB  ;
 180 120  60
Ví dụ 2. Cho tứ diện đều ABCD cạnh a. Tính góc giữa hai đường thẳng AB và CD.
Hướng dẫn giải
     
Đặt AB  a, AC  , b AD  c .
    
Ta có CD  AD  AC  c  b        a c  b AB CD cos AB,CD . .  
       AB . CD
a . c  b     1 1 . a . a  . a . .  . a a c a b 2 2    0 2 . a a a   Vậy  AB CD  ,  90 TOANMATH.com Trang 19
Ví dụ 3. Cho tứ diện ABCD có AB  AC và AB  BD . Gọi P và Q lần lượt là trung điểm của AB và
CD. Chứng minh rằng AB  PQ . Hướng dẫn giải    
Vì AB  AC và AB  BD nên AC.AB  0; . BD AB  0 .
   
   
Ta có PQ  PA  AC  CQ và PQ  PB  BD  DQ
    
      
Do đó 2PQ  AC  BD  2 .
PQ AB   AC  BD.AB  AC.AB  B . D AB  0   Hay . PQ AB  0 .
Vậy AB  PQ .
Ví dụ 4. Cho tứ diện đều ABCD cạnh a, M là trung điểm của cạnh BC. Tính góc giữa hai đường thẳng AB và DM. Hướng dẫn giải
Gọi N là trung điểm AC thì MN / / AB . Suy ra  AB DM    MN DM   , , . 2 2 2
MN  DM  DN Ta có  cos DMN  2.MN.DM 2 2 2  a 
 a 3   a 3           2  2 2     3   a a 3 6 2. . 2 2 Suy ra  3 DMN  arccos . 6 Vậy  AB DM   3 ,  arccos . 6
Ví dụ 5. Cho tứ diện ABCD có các cạnh đối bằng nhau từng đôi một,
AC  BD  a, AB  CD  2a, AD  BC  a 6 .
Tính góc giữa hai đường thẳng AD và BC. Hướng dẫn giải TOANMATH.com Trang 20
        
AD BC  AD  AC  AB   . .  A . D AC  A . D AB  A . D AC.cos CAD  . AD . AB cos BAD 2 2 2 2 2 2
AC  AD  CD
AB  AD  BD  A . D AC.  . AD . AB 2.AC.AD 2. . AB AD
a  a 2  a
 a a 2 2 2 2 2 6 2 2 6  a  a 6. . a  a 6.2 . a 2. . a a 6 2.2 . a a 6 2  3  a   2   . AD BC 3  a 1  
Suy ra cos AD, BC  
    AD, BC  120 . AD BC a 6.a 6 2 Vậy  AD BC  ;  60.
Ví dụ 6. Cho hình chóp S.ABCD, có đáy ABCD là hình thang vuông tại A và D, cạnh 2a 3
AB  2a, AD  DC  ;
a SA  AB, SA  AD và SA  . 3
a) Tính góc giữa đường thẳng SB và DC.
b) Gọi  là góc giữa SD và BC. Tính cos .
Hướng dẫn giải a) Vì DC
AB  SB DC   SB AB   / / , ,  SBA
(vì SAB vuông tại A nên  SBA  90). 2a 3 SA 3
Xét SAB vuông tại A, ta có  3  tan SBA     SBA  30 AB 2a 3 Vậy SB DC   ,  SBA  30 .
b) Gọi E là trung điểm của AB.
Khi đó, BCDE là hình bình hành nên DE BC  SD BC   SD DE  / / , ,   2 2  4a 7a  7 2 2 2 2 2
SE  SD  SA  AD   a 
SE  SD  a Ta có  3 3   3  2 2 DE 2a   DE  a 2
Áp dụng định lí cosin trong tam giác SDE, ta được TOANMATH.com Trang 21 2 2 2 2 
SD  DE  SE 2a 42  cos SDE   
 0  SDE  90 2 . SD DE 7 14 2.a .a 2 3 Vậy SD BC   SD DE    42 , ,
 SDE    cos  cos SDE  . 14 4
Ví dụ 7. Cho tứ diện ABCD có CD  AB . Gọi G, E, F lần lượt là trung điểm của BC, AC, DB , biết 3 5
EF  AB . Tính góc giữa CD và AB. 6 Hướng dẫn giải
Gọi G là trung điểm của BC. AB a
Đặt AB  a . Ta có GE   . 2 2 CD 2 2a 5 5a GF   AB  ; EF  AB  . 2 3 3 6 6 2 2 2 a 4a 25a Từ đó 2 2 2 GE  GF     EF 4 9 36  GEF  vuông tại G. Vì /
GE / AB,GF / /CD nên  AB CD   GE GF   , ,  EGF  90 .
Ví dụ 8. Cho hình chóp S.ABCD, có đáy ABCD là hình vuông tâm O, cạnh bằng a; SA vuông góc với đáy
và SA  a 3 . Tính côsin góc giữa SB và AC. Hướng dẫn giải
Gọi I là trung điểm của SD
 OI là đường trung bình của SBD  . Suy ra OI / /SB  2 2 2 2  SB SA  AB 3a  a OI     a  2 2 2 Vì OI
SB  SB AC    OI AC   / / , ,  AOI 2 2 2 2 SD SA  AD 3a  a Ta có AI     a 2 2 2
 AI  OI  A
 OI cân tại I. OA AC a 2
Gọi H là trung điểm của OA  IH  OA và OH    2 4 4 a 2 OH 2 Xét OH  I có  4 cos HOI    OI a 4 Vậy SB AC   2 cos ,  cos HOI  . 4 TOANMATH.com Trang 22
Ví dụ 9. Cho hình chóp tứ diện OABC có ,
OA OB,OC đôi một vuông góc và OA  OB  a,OC  2a . Gọi
M là trung điểm của BC. Tính côsin góc giữa hai đường thẳng AB và OM. Hướng dẫn giải
AB  a 2, BC  a 5  Ta có  BC a 5 OM     2 2      
     
AB OM  OB OA 1 OB  OC 1 . .   2 OB  O . B OC  O . A OB  O . A OC  2 2 1   a a  0  0  0 2 2  . 2 2 2   a   . AB OM 10 Vậy  AB OM    AB OM   2 cos , cos ,    . . AB OM a 5 10 a 2. 2
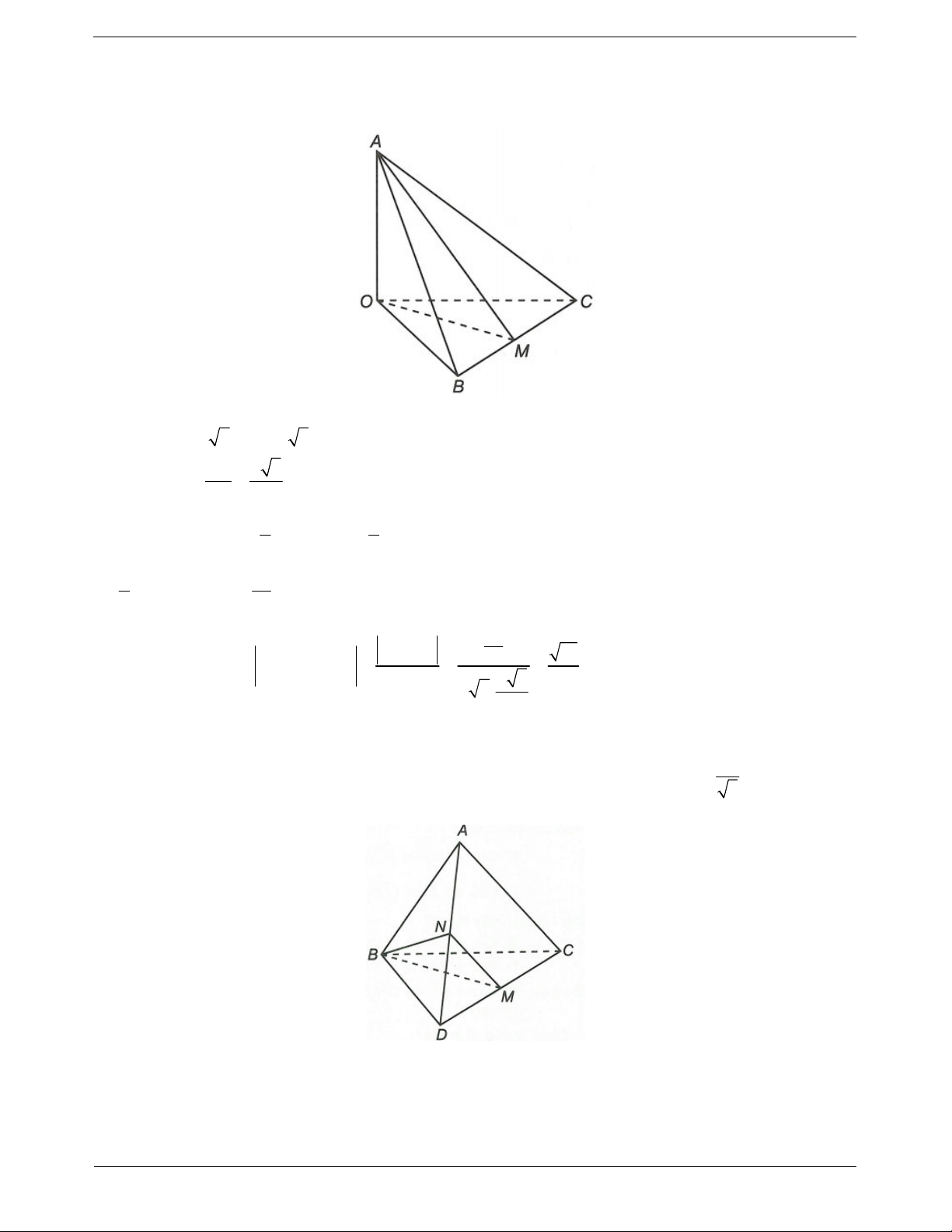
Ví dụ 10. Cho tứ diện ABCD có AB  AD  a và   
BAC  BAD  60 ,
 CAD  90 . Gọi M là trung điểm 1
của cạnh CD. Tính độ dài cạnh AC để côsin góc giữa hai đường thẳng AC và BM bằng . 3 Hướng dẫn giải
Gọi N là trung điểm của AD. Ta có BM AC   BM MN   , ,  
Đặt AC  2x  MN  x  0 TOANMATH.com Trang 23 a 3
Theo bài ra ta có tam giác ABD đều cạnh a nên BD  a, BN  . 2
Tam giác ACD vuông tại A nên 2 2 2 2 2
DC  AD  AC  a  4x Xét tam giác ABC ta có 2 2 2
BC  a  4x  2ax 2 2 2 2 2 2 2
a  a  4x  2ax a  4x
3a  4x  4ax Do đó 2 BM    2 4 4 2 2 2
3a  4x  4ax 2 3a 2 2 2  x 
BM  MN  BN Ta tính  4 4 cos BMN   2 2 2BM .MN
3a  4x  4ax 2. .x 2 2 8x  4ax 2x  a   2 2 2 2 4 .
x 3a  4x  4ax
3a  4x  4ax Theo giả thiết ta có 2x  a 1 x  0 2 cos  
 8x 8ax  0   2 2
3a  4x  4ax 3 x  a
Do x  0 nên x  a  AC  2x  2a
Bài tập tự luyện dạng 2
Câu 1: Mệnh đề nào sau đây đúng?
A. Hai đường thẳng cùng vuông góc với một đường thẳng thì song song với nhau.
B. Hai đường thẳng cùng vuông góc với một đường thẳng thì vuông góc với nhau.
C. Một đường thẳng vuông góc với một trong hai đường thẳng vuông góc với nhau thì song song với
đường thẳng còn lại.
D. Một đường thẳng vuông góc với một trong hai đường thẳng song song thì vuông góc với đường thẳng còn lại.  
Câu 2: Cho hai đường thẳng a,b lần lượt có vectơ chỉ phương ,
u v . Mệnh đề nào sau đây sai?    
A. Nếu a  b thì u.v  0 B. Nếu .
u v  0 thì a  b     . u v u v
C. cosa,b    D. a b . cos ,    u . v u . v
Câu 3: Cho ba đường thẳng a,b,c . Mệnh đề nào sau đây sai?
A. Nếu a / /b thì a c   c b  , ,
B. Nếu c / /b thì a b   a c  , ,
C. Nếu a / /c thì a c  ,
 0 D. Nếu a  b thì a c   c b  , ,
Câu 4: Cho ba đường thẳng a,b,c . Khẳng định nào sau đây đúng?
A. Nếu a  b và b  c thì a / /b B. Nếu a  b và b  c thì a  c
C. Nếu a  c và b  c thì a  b D. Nếu a / /b và c  b thì c  a  
Câu 5: Cho hình lập phương ABCD.EFGH. Góc giữa cặp vectơ AB và DH là
A. 45 B. 90 C. 120 D. 60 TOANMATH.com Trang 24
Câu 6: Cho hình lập phương ABC . D AB C  D
  . Chọn khẳng định sai?
A. Góc giữa AC và B D
  bằng 90 B. Góc giữa B D
  và AA bằng 60
C. Góc giữa AD và B C
 bằng 45 D. Góc giữa BD và AC bằng 90  
Câu 7: Cho hình lập phương ABCD.EFGH. Góc giữa cặp vectơ AB và EG bằng
A. 90 B. 60 C. 45 D. 120
Câu 8: Cho tứ diện ABCD đều cạnh bằng a. Gọi O là tâm đường tròn ngoại tiếp tam giác BCD. Góc giữa
AO và CD bằng bao nhiêu?
A. 0 B. 30 C. 90 D. 60
Câu 9: Cho tứ diện đều ABCD, M là trung điểm của cạnh BC. Khi đó cos  AB, DM  bằng. 2 3 1 3 A. B. C. D. 2 6 2 2
Câu 10: Cho hình hộp ABC . D AB C  D
  có tất cả các mặt là hình thoi và các góc đỉnh A bằng 60 . Góc
giữa hai đường thẳng BD và AC bằng
A. 90 B. 30 C. 45 D. 60 3
Câu 11: Cho tứ diện ABCD có  
AC  AD,CAB  DAB  60 ,
 CD  AD . Gọi  là góc giữa AB và CD. 2
Chọn khẳng định đúng. 3 1
A. cos  B. 60    C. 30
   D. cos  4 4
Câu 12: Cho hình chóp tứ giác đều S.ABCD có tất cả các cạnh bằng a. Khẳng định nào sau đây đúng?
A. SA  SC B. SA  SB C. SA  SD D. SA  CD  
Câu 13: Cho tứ diện ABCD có AB  AC  AD và  
BAC  BAD  60 . Góc giữa cặp vectơ AB và CD bằng
A. 60 B. 45 C. 120 D. 90
Câu 14: Cho hình chóp tứ giác đều S.ABCD có tất cả các cạnh đều bằng a. Gọi M là điểm bất kỳ trên
đường thẳng AC. Số đo góc giữa hai đường thẳng BD, SM bằng A. 90 B. 120 C. 60 D. 45
Câu 15: Cho tứ diện ABCD có AB  AC  AD và   
BAC  BAD  60 ,
 CAD  90 . Gọi I và J lần lượt là  
trung điểm của AB và CD. Góc giữa cặp vectơ AB và IJ bằng A. 120 B. 90 C. 60 D. 45
Câu 16: Cho hình chóp tứ giác đều S.ABCD có tất cả các cạnh đều bằng a. Số đo giữa hai đường thẳng
BC và SA bằng A. 45 B. 120 C. 90 D. 60
Câu 17: Cho hình chóp S.ABC có đáy là tam giác đều cạnh a, SA  3a và vuông góc với mặt đáy. Gọi
M là trung điểm cạnh SB. Côsin góc giữa hai đường thẳng AM và SC bằng 5 11 5 3 A. B. C. D. 16 16 8 8  
Câu 18: Cho hình chóp S.ABC có AB  AC và  
SAC  SAB . Khi đó góc    , SA BC bằng TOANMATH.com Trang 25 A. 30 B. 45 C. 60 D. 90  
Câu 19: Cho hình chóp S.ABC có SA  SB  SC và   
ASB  BSC  CSA . Góc SC, AB bằng A. 120 B. 45 C. 60 D. 90
Câu 20: Cho hình chóp S.ABCD có đáy là hình vuông ABCD cạnh bằng a và các cạnh bên đều bằng a.
Gọi M và N lần lượt là trung điểm của AD và SD. Số đo của góc MN SC  , bằng A. 45 B. 30 C. 90 D. 60
Câu 21: Cho hình chóp S.ABCD có tất cả các cạnh đều bằng a. Gọi I và J lần lượt là trung điểm của SC
và BC. Số đo của góc IJ CD  , bằng A. 90 B. 45 C. 30 D. 60
Câu 22: Cho hình lập phương ABC . D AB C  D
  cạnh a. Gọi M, N lần lượt là trung điểm của AC và B C  .
Côsin góc giữa hai đường thẳng MN và B D   bằng 10 4 3 10 A. B. C. D. 10 5 5 5
Câu 23: Cho hình lăng trụ đứng tam giác ABC.AB C
  có đáy ABC là tam giác cân 
AB  AC  a, BAC  120 , cạnh bên AA  a 2 . Góc giữa hai đường thẳng AB và BC bằng A. 90 B. 30 C. 45 D. 60
Câu 24: Cho hình lăng trụ tam giác đều ABC.AB C
  có tất cả các cạnh bằng a. Gọi M, N lần lượt là
trung điểm các cạnh AB, B C
  . Côsin góc giữa hai đường thẳng MN và AC bằng 1 5 2 5 A. B. C. D. 3 3 3 5
Câu 25: Cho hình chóp S.ABCD có S ,
A SB, SC đôi một vuông góc với nhau và SA  SB  SC  a . Gọi M
là trung điểm của AB. Góc giữa hai đường thẳng SM và BC bằng A. 30 B. 60 C. 90 D. 120
Câu 26: Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật. Các tam giác SAB, SAD, SAC là các tam
giác vuông tại A. Côsin góc giữa hai đường thẳng SC và BD bằng bao nhiêu, biết
SA  a 3, AB  a, AD  3a ? 1 3 2 130 4 130 A. B. C. D. 2 2 65 65
Câu 27: Cho hình lăng trụ tam giác đều ABC.AB C
  có tất cả các cạnh đều bằng a. Côsin giữa hai đường
thẳng AC và B C   bằng 2 1 3 2 A. B. C. D. 2 4 4 4
Câu 28: Cho hình lăng trụ tam giác ABC.AB C
  có đáy ABC là tam giác vuông tại ,
A AB  a, AC  a 3 . Hình chiếu vuông góc của A lên mặt phẳng  ABC là trung điểm H của
BC, AH  a 3 . Gọi  là góc giữa hai đường thẳng AB và B C  . Tính cos . 1 6 6 3
A. cos  B. cos  C. cos  D. cos  2 4 8 2 TOANMATH.com Trang 26  
Câu 29: Cho hình lập phương ABCD.EFGH. Góc giữa cặp vectơ AF và EG bằng
A. 90 B. 60 C. 45 D. 120 a 3
Câu 30: Cho tứ diện ABCD, gọi M, N lần lượt là trung điểm của BC, AD biết AB  CD  a, MN  . 2
Côsin góc giữa hai đường thẳng AB và CD bằng 3 2 1 1 A. B. C. D. 2 2 4 2
Câu 31: Cho hình chóp S.ABC có tam giác SAB vuông cân tại S, có SA  a , tam giác ABC vuông cân tại C và 
BSC  60 . Gọi M là trung điểm của SB. Côsin góc giữa hai đường thẳng AB và CM bằng 6 30 6 3 A. B. C. D. 6 6 3 3            
Câu 32: Cho hai vecto a,b thoả mãn, a  4, b  3, .
a b  10 .Xét hai vecto y  a  ,
b x  a  2b . Gọi   
là góc giữa hai vecto y, x . Tính cos 2  1 3 2 A. cos = B. cos = C. cos = D. cos = 15 15 15 15
Câu 33: Cho hình hộp chữ nhật ABC . D AB C  D
 , AB  6c ,
m BC  BB  2cm . Điểm E là trung điểm cạnh
BC. Một tứ diện đều MNPQ có hai đỉnh M và N nằm trên đường thẳng C E
 , hai đỉnh P, Q nằm trên
đường thẳng đi qua điểm B và cắt đường thẳng AD tại điểm F. Độ lớn DF bằng
A. 1cm B. 2cm C. 3cm D. 6cm TOANMATH.com Trang 27 ĐÁP ÁN
Dạng 1. Vecto trong không gian 1 - B 2 - C 3 - C 4 - D 5 – C 6 – A 7 – B 8 – C 9 – C 10 - C 11 – A 12 – D 13 – D 14 - B 15 – A 16 – B 17 – A 18 – B 19 – A 20 – B 21 – C 22 – A 23 – D 24 – C 25 – B 26 – D 27 – A 28 – D 29 - A 30 – B 31 - A 32 - D 33 - C 34 - D 35 - B 36 - D 37 - B 38 - A
HƯỚNG DẪN GIẢI CHI TIẾT Câu 1.      
Với ABC là tam giác đều ta có AB  AC nhưng AB  AC và AB  AC nên B sai. Câu 2.   
Khẳng định (1) sai vì khi a, ,
b c đồng phẳng thì giá của chúng luôn song song với mặt mặt phẳng.
Khẳng định (2) sai vì các vectơ đồng phẳng không yêu cầu là phải cùng phương.
Khẳng định (3) và (4) đúng theo điều kiện và định nghĩa ba vectơ đồng phẳng. Câu 3. 1 1 1 2 2 2 2 2 S  A .
B AC.sin A  . AB .AC sin A  AB .AC  2 1 cos A 2 2 2 1 2 2 1 2 2   2 2 2 
AB .AC  AB .AC cos A 
AB .AC   A . B AC 2 2 2 1 Vậy k  2
Câu 4.          
A sai vì AB  CD  AC  DB  CA  AB  BD  DC  CD  DC(sai)
   
     
B sai vì AB  BD  AB  CD  AC  AB  CD  DB  BC  CB(sai)
   
     
C sai vì AD  BC  AB  DC  AD  AB  DC  CB  BD  DB(sai)
   
     
D đúng vì BA  CD  BD  CA  BA  BD  DC  CA  DA  DA (đúng)
Câu 5.       
Ta có AB  3AC  BA  3
 CA  BA  3CA  3
 CA. Từ đó phương án A sai.         Ta có AB  3
 AC  CB  CA  3CA  CB  4CA  2AC . Từ đó phương án B sai.   
   Ta có AB  2
 AC  5AD  AB, AC, AD đồng phẳng  ,
A B,C, D đồng phẳng (C đúng).    1 
Phương án D sai vì nếu B là trung điểm của đoạn thẳng AC thì AB  BC mà BC   BC . 2 Câu 6.
   
     
+) SB  SD  SA  SC  SB  SA  SC  SD  AB  DC  ABCD là hình bình hành (A đúng).  
+) AB  CD ta phải suy ra tứ giác ABDC là hình bình hành chứ không phải ABCD (B sai).
    
+) C sai vì AB  BC  CD  DA  0 đúng với mọi vị trí của ,
A B,C, D .
  
+) D sai vì với AB  AC  AD thì AD là đường chéo của hình bình hành ABCD. TOANMATH.com Trang 28 Câu 7.   2 2 2    
Ta có: a  b  a  b  a b a b 2 2 2 . .cos ,
 3  5  2.3.5.cos120 19  
Suy ra a  b  19 Câu 8.
   
Ta có O là trọng tâm tam giác BCD nên BO  CO  DO  0 (1)
        
Ta có: AO  AB  B ;
O AO  AC  C ;
O AO  AD  DO
   
 1   
1  1  1 
Từ (1) suy ra 3AO  AB  AC  AD  AO   AB  AC  AD  AB  AC  AD 3 3 3 3 
1  1  1 
Suy ra OA   AB  AC  AD (2) 3 3 3  1 
Mà AM  AD (3) 2
  
1  1  1  1 
1  1  1 
Từ (2) và (3) suy ra OM  OA  AM   AB  AC  AD  AD   AB  AC  AD 3 3 3 2 3 3 6 Câu 9.
C sai vì chỉ cần ba vectơ có giá cùng song song với một mặt phẳng thì ba vectơ đó đồng phẳng. Câu 10.  
A, B sai vì OM  OB  M  B và O, M , B, A thẳng hàng mà O là điểm bất kì.         
C đúng vì OM  kOA  1 k OB  OM  OB  k OAOB  BM  k.BA
  
D sai vì OM  OA  OB  OAMB là hình bình hành. Khi đó M  AB . Câu 11.    
     Ta có: 2 2
AB  AB  A . B C A
   AB .AC   a 2 cos  a    4  Câu 12.   
A sai khi a,b có giá cùng nằm trong P , còn c có giá song song với P .               
B sai với ba vectơ a, 0, c ta có 0  0.a  0.c thì a,0,c đồng phẳng nhưng c  . m a  .
n 0 chỉ đúng khi a và 
c cùng phương với nhau.       
C sai vì với 3 vectơ d, a,b khác 0 đồng phẳng với nhau ta có d  ma  nb .     Khi đó (m d 
1)a  nb  a         
Đặt c  a thì d  (m1)a  nb  c nhưng a, ,
b c lại đồng phẳng với nhau.
Vậy cả ba khẳng định trên đều sai. Câu 13.
    
Phương án D sai do đẳng thức 0
AB  BC  CD  DA  luôn đúng với vị trí bất kì trong không gian của bốn điểm ,
A B,C, D nên không đủ điều kiện để khẳng định ,
A B,C, D đồng phẳng. Câu 14. TOANMATH.com Trang 29 2   2     1 Ta có: 2
AC  AC  BC  BA 2 2  BC  2B .
A BC  BA  B . A BC   2 2 2
BA  BC  AC  2 Câu 15.
  
1   
1   1 
MN  MS  SN   SA  SB  BN   SA  SB  BC 2 2 4
1   1     
  SA  SB  SC  SB 1 3 1
  a  b  c 2 4 2 4 4 Câu 16.  1    1 
Ta có AO   AM  AN  , trong đó AM  a ; 2 2
    1   1    
AN  AC  CN  AC  CD  AC   AD  AC 2 1  b  c 3 3 3 3 
1  1  2  1   1  1  1  Vậy AO 
a  b  c  a  b  c   2  2 3 3  4 3 6 Câu 17.
   
Gọi G là trọng tâm ABC thì G cố định và GA  GB  GC  0   2   2   2
Ta cos: P  MG  GA  MG  GB  MG  GC
    2
 MG  MG GAGB GC 2 2 2 3 2 .
 GA  GB  GC 2 2 2 2 2 2 2
 3MG  GA  GB  GC  GA  GB  GC
Dấu “=” xảy ra  M  G Vậy 2 2 2
P  GA  GB  GC với M  G là trọng tâm tam giác ABC. min Câu 18. Ta có 2 2 2 2 2 2
AB  AC  AD  BC  BD  CD               
2   2   2   2   2   2 AG GB AG GC AG GD BG GC BG GD CG GD
            2 2 2 2
 3AG  3BG  3CG  3DG  2 . AG GB  . AG GC  . AG GD  . BG GD  . BG GD  C . G GD(1)
    
   
Mà GA  GB  GC  GD   GA GB  GC  GD2 0  0 2 2 2 2
 GA  GB  GC  GD
             2 A . G GB  . AG GC  A . G GD  B . G GD  B . G GD  C . G GD(2) Từ (1) và (2) ta có 2 2 2 2 2 2
AB  AC  AD  BC  BD  CD   2 2 2 2
4 GA  GB  GC  GD  TOANMATH.com Trang 30 Câu 19. (I) Đúng vì
      B C   B B
  BC  AA  AC  AB
     
 AA  AB  AC  a  b  c (II) Sai vì
       
BC  BB  B C
   AA  BC  AA  AC  AB
     
 AA  AB  AC  a  b  c Câu 20. Ta có:
    2 
AG  AA  AG  AA  AI 3
 1  
 AA   AB AC 3
  1  
  
 AG  AA   AB  AC 1
 3AA AB  AC 3 3 1   
 3a b  c 3 Câu 21.
      Đặt ,
AB  a AD  , b AA  c      
Từ MA  k.MC , ta có AA  AM  k  AC  AM         k 
abc AA k AC  AM   1 k 1 k      
Từ NC  l.ND , ta có AC  AN  l. AD  AN        
AC  l.AD
a  b  c  lb  AN   1 l 1 l
  
Suy ra MN  AM  AN        
k a  b  c a  b  c lb  k 1    k    1 1        a   1 .b   c       1 k 1 l
 1 k 1 l   1 k 
1 k 1 l 
     
Mặt khác BD  AD  AB  a  b  c
 
Để MN / /BD thì MN / /BD nên  k 1 k  2k 1    1   1  1
  k 1l 1 k 1
  k 1l 3k 1      2   k  3  k 1 1 k 1 1 1 k  1        1   1 k 1 k 1 l
1 k 1 l 1 1 Từ đó ta có:   l  1
 . Vậy k  l  4  1 l 2 TOANMATH.com Trang 31 Câu 22.
Do tất cả các cạnh của hình chóp bằng nhau nên hình chóp
S.ABCD là hình chóp đều.
  
Suy ra OC;OS;OD đôi một vuông góc.
Do M là trung điểm của CD nên ta có:
  
1  1  
MS  OS  OM   OC  OD  OS 2 2
    
CB  OB  OC  OD   OC
  
Do OC;OS;OD đôi một vuông góc với nhau nên 2   1 1 a 2 2 2
MS.CB  OC  OD  OC  2 2 2 Câu 23.    
Đặt PA  xS ; A BQ  yBN
   
Suy ra: PQ  PA  AB  BQ    
 xSA  SB  SA  yBN      x  
1 SA  SB  y SN  SB        y
x 1 SA  1 y SB  SC 2        y
x 1 a  1 yb  c (*) 2
   1    1  1  
Lại có CM  SM  SC  SA SB  SC  a  b  c 2 2 2   Để
PQ / /CM thì PQ  kCM hay y  2 x  2  y x  x 1 1 y    2   3      1 1 y  1  1 y   4  4 y  2 2  3  1  1  2 
Thay vào (*) ta được PQ   a  b  c 3 3 3 Câu 24.
    
C sai vì khi AB / / MNP ta vẫn có AB, MN, NP đồng phẳng nhưng AB  MNP hay giá của AB
không nằm trong MNP . Câu 25.
 1   
   
AG   AA AB  AC 1
  AA AB  AB  AD 3 3 2 1 Suy ra 2
AG  AG   2 2 2
AA  4AB  AD  9 TOANMATH.com Trang 32 1   2 2 2 2
a  4a  a  2  a 9 3 Câu 26. Gọi ,
M N lần lượt là trung điểm của AC và BD. Do O là giao điểm của AC và BD nên
    
SA  SB  SC  SD  4SO         
 OS  SAOS  SC OS  SBOS  SD  0     
 OAOCOB OD  0     
 2OM  2ON  0  OM  ON  O  M  N
 ABCD là hình bình hành.
Vậy mệnh đề (I) và (II) đều đúng.
Bình luận: Để chứng minh mệnh đề (I) và (II) đúng, ta áp dụng: Cho A a, B b và  
O  a  b .  
Khi đó OA  OB  O  A  B .  
Chứng minh: Nếu A không trùng O thì B không trùng O (do OA  OB )  OA  a và OB  b   Nhưng ,
OA  OB  O ,
A B thẳng hàng  a  b  a  b  a (trái với giả thiết O  a  b ) Câu 27.
Từ giả thiết suy ra SBC vuông cân tại S; S
 AC là tam giác đều.
    
   
Có SC.AB  SC.SB  SA  SC.SB  SC.SA 2  a  SC. .
SA cos ASC   . a . a cos 60   2 2   1  a Vậy 2
SC.AB  a .  2 2 Câu 28.
Gọi M, N lần lượt là trung điểm của AC và BD.
       
Ta có: SA  SC  SB  SD  2SM  2SN  SM  SN  M  N  ABCD là hình bình hành. Câu 29.  1     
Ta có y  x  z nên ba vectơ x, y, z đồng phẳng. 2 Câu 30.
Khẳng định B sai.      
Các vectơ x, y, z đồng phẳng ,  m
 n : x  my  nz   
Ta có x  m y  nz 3
 m  2n 1          
 a  2b  4c  m3a 3b  2c n2a 3b 3c   3
 m  3n  2  (hệ vô nghiệm).
2m 3n  4  TOANMATH.com Trang 33   
Vậy không tồn tại hai số ,
m n : x  m y  nz Câu 31.
    
    Ta có A .
B EG  AB EF  EH   A . B EF  A . B EH  
Do AB  EH nên . AB EH  0
    2 Suy ra 2 A . B EG  A .
B EF  AB  a Câu 32. +) A đúng vì 2
  
AC   AB  AD  AA2
2 2 2
      
 AB  AD  AA do . AB AD  A .
D AA  AA .AB  0 2  3a 
Suy ra AC  a 3 +) B đúng vì  
    
AD AB   AA  AD AA  AB 2 2 .
 AA  a
      
do AA'.AD  AA .AB  AB .AD  0
   
+) C đúng vì AB .CD  DC .CD  0do DC  CD +) D sai vì
   
     2AB  B C
   CD  D A
   2AB  BC  CD  DA  0 Câu 33.
      Đặt ,
AA  a AB  , b AC  c  1  
1    1  
Ta có AI   AB  AB   AB  AB  AA  a  b 2 2 2  1  
    
AK   AA AC 1
  AA AA AC 1  a  c 2 2 2    
 
Do MB  k MC nên AB  AM  k  AC AM             k  
1 AM  k AC  AB  k a  c a  b  k  
1 a  b  kc
   Vì bốn điểm ,
A M , I, K đồng phẳng nên AM , AI, AK đồng phẳng, do đó     k  
1 AM  x AI  y AK              k   1 1
1 a  b  kc  x
a  b  y a  c      2   2  TOANMATH.com Trang 34    k   1 1  x  y  x  1 2     1  1   x  y  1  . Vậy k    2 y  1 k  k    2  2 Câu 34.  
Gọi I là điểm thỏa mãn SI  4IO          
    2   2   2    2    2 P MI IS MI IA MI IB MI IC MI ID
      2 2 2 2 2 2
 5MI  IS  IA  IB  IC  ID  2MI IS  IA IB  IC  ID  
     2 2 2 2 2 2
 5MI  IS  IA  IB  IC  ID  2MI IS  4IO OAOB OC OD 
      2 2 2 2 2 2
 5MI  IS  IA  IB  IC  ID do SI  4 ;
IO OA  OB  OC  OD  0 SM 4
Vậy P  M  I   . min SO 5 Câu 35.
Áp dụng công thức độ dài đường trung tuyến, ta có: 2 2 2 2 MA  MB AB AB 2 2 2 2 ME  
 MA  MB  2ME  2 4 2 2 2  2ME  2a Câu 36.
      Đặt ,
SA  a SB  ,
b SC  c , ta có:
    
AB  SB  SA  b  a ;        
MS   MA  SM   SA SM  2 2 2 2
 SM  SA  a ; 3 3      
NB  k NC  SB  SN  k SC  SN        k  
1 SN  k SC  SB  kc  b ;        
k   MN  k  SN  SM  2k 1 1 1  kc  b  a 3
  
Để ba vectơ AB, MN, SC đồng phẳng ta có     k  
1 MN  x AB  ySC   2k   1      kc  b 
a  x b  a  yc 3 TOANMATH.com Trang 35  2k 1   x   x  1  3    1 1  x  1 
 k    k   2 2 y k     1 y    3 1 Vậy k   2 Câu 37.
      Đặt ,
AB  a AC  , b AD  c 
3  1   1    1 
Theo bài ra ta có AM  a  ;
b AN  a  c; AP  b . 4 4 2 3   
Đặt AQ  k AD  kc .
   1  1  1 
MN  AN  AM   a  b  c  4 4 2 
   3  1 
Ta có MP  AP  AM   a  b 4 12 
   3  1  
MQ  AQ  AM   a  b  kc  4 4    Vì ,
M N, P,Q đồng phẳng nên xMN  yMP  MQ  1  1  1    3  1   3  1  
 x  a  b  c  y  a 
b   a  b  kc      4 4 2   4 12  4 4  1 3    1 1   1  3  1    x  y a  x 
y b  xc   a  b  kc      4 4   4 12  2 4 4 1 3 3  6 x  y  x  4 4 4  5   1 1 1  3   x 
y   y  4 12 4 5   1  3 x  k k  2    5  3  AQ 3
Vậy AQ  AD   . 5 AD 5 Câu 38.     2
         
Ta có 0  m  n  p  q  4  2 . m n  . m p  . m q  . n p  . n q  . p q
            Suy ra . m n  . m p  . m q  . n p  . n q  . p q  2    2  2   2   2   2   2
S  m  n  m  p  m  q  n  p  n  q  p  q
                 12  2 . m n  . m p  . m q  . n p  . n q  .
p qdo m  n  p  q   1   2   2   2   2   2   2
Vậy m  n  m  p  m  q  n  p  n  q  p  q  12  2. 2   16 TOANMATH.com Trang 36    
Dấu “=” xảy ra chẳng hạn khi m  n  1;0;0 và p  q   1;  0;0 . TOANMATH.com Trang 37

Bài giảng vectơ trong không gian, hai đường thẳng vuông góc

Thông tin :

Tài liệu liên quan:

Toán 11 Bài 25: Hai mặt phẳng vuông góc -

Toán 11 Bài 22: Hai đường thẳng vuông góc - Sách Kết Nối Tri Thức

Toán 11 Bài 23: Đường thẳng vuông góc với mặt phẳng - sách Kết Nối Tri Thức

Toán 11 Bài 27: Thể tích - sách Kết Nối Tri Thức

Toán 11 Bài 24: Phép chiếu vuông góc. Góc giữa đường thẳng và mặt phẳng - sách Kết Nối Tri Thức