Bài giảng Xác suất thống kê chương 4 | Trường đại học Công Nghệ Sài Gòn

Chương 4 CÁC PHÂN PHỐI XÁC SUẤT THÔNG DỤNG
Đừng đặt niềm tin của bạn vào những gì số liệu
thống kê nói cho đến khi bạn đã xem xét cẩn thận
những gì chúng không nói.
William Whyte Watt (1912-1996) 1.1 Biến ngẫu nhiên
Biến ngẫu nhiên (random variable) là biến nhận giá trị này hay giá
trị khác trong các giá trị có thể có ở những lần thử khác nhau mà ta
không dự đoán được trước khi thực hiện phép thử.
Biến ngẫu nhiên được chia thành 2 loại:
• Biến ngẫu nhiên rời rạc (discrete random variable). Tập hợp trị số mà nó có
thể lấy là hữu hạn hoặc liệt kê được.
o Ví dụ: số sản phẩm không đạt tiêu chuẩn kỹ thuật trong một đợt sản xuất, số chấm xuất
hiện khi gieo con xúc xắc, …
• Biến ngẫu nhiên liên tục (continuos random variable). Tập hợp trị số mà
nó có thể lấy thì lấp đầy một khoảng trên trục số.
o Ví dụ: trọng lượng của một sản phẩm, năng suất của một loại cây trồng, …
Đại học Công nghệ Sài Gòn Xác suất – Thống kê 3
1.3 Phân phối xác suất rời rạc
Phân phối xác suất của biến ngẫu nhiên rời rạc X có thể
được trình bày ở dạng bảng như sau: X x x x ... x TỔNG 1 2 3 k p p p p ... p 1 X 1 2 3 k
Ta có xác suất tại X = x : P(X=x ) = P(x ) = p i i i i
Ta cũng có thể trình bày phân phối xác suất của biến ngẫu
nhiên rời rạc X dưới dạng hàm số f(x) : f(x ) = p i i X f p ~ f/ X Σf 0 80 Ví dụ 4.1: 1 50 Cửa hàng 2 40 KZE bán tivi 3 10 Mô tả bằng bảng phân 4 20 phối xác suất. TỔNG 200 1
Đại học Công nghệ Sài Gòn Xác suất – Thống kê 7
1.4 Phân phối xác suất liên tục
Ta thường trình bày phân phối xác suất của biến ngẫu nhiên
liên tục X dưới dạng hàm số theo biến ngẫu nhiên f(x).
Vì giá trị của biến ngẫu nhiên liên tục lấp đầy một khoảng
trên trục số nên xác suất khi X nhận một giá trị bất kỳ luôn
bằng 0. Do đó ta chỉ tính xác suất khi X nhận giá trị trong
một khoảng (a;b) nào đó: 𝒃
𝑃 𝒂 ≤ 𝑋 ≤ 𝒃 = න 𝑓 𝑥 𝑑𝑥 𝒂
Ví dụ 4.2 Quy luật “số tiền chi tiêu”?? (1) 10000 9000 8000 7000 tiêu 6000 chi 5000 4000 3000 Số tiền 2000 1000 0 0 5 10 15 20 25 30 35 40 45 50 Số khách hàng
Đại học Công nghệ Sài Gòn Xác suất – Thống kê 11
Biến ngẫu nhiên rời rạc
Giá trị kỳ vọng của một biến ngẫu nhiên rời rạc:
E(X) = μ = Σ(x p ) i i
Phương sai của một biến ngẫu nhiên rời rạc:
Var(X) = σ2 = Σ[(x – μ)2p ] i i
Đại học Công nghệ Sài Gòn Xác suất – Thống kê 13
Biến ngẫu nhiên liên tục
Giá trị kỳ vọng của một biến ngẫu nhiên liên tục:
E(X) = μ = ∫[xf(x)]dx
Phương sai của một biến ngẫu nhiên liên tục:
Var(X) = σ2 = ∫[(x – μ)2f(x)]dx
Đại học Công nghệ Sài Gòn Xác suất – Thống kê 15
3.1 Phân phối nhị thức – ví dụ minh họa
• Thử nghiệm tung một đồng xu hay một xúc xắc.
• Kiểm tra chất lượng của một mẫu sản phẩm từ một lô hàng được sản xuất theo dây chuyền.
• Khảo sát sự yêu thích đối với một hương vị trà sữa mới.
• Mua một tờ vé số và hi vọng trúng giải độc đắc :)
Đại học Công nghệ Sài Gòn Xác suất – Thống kê 17
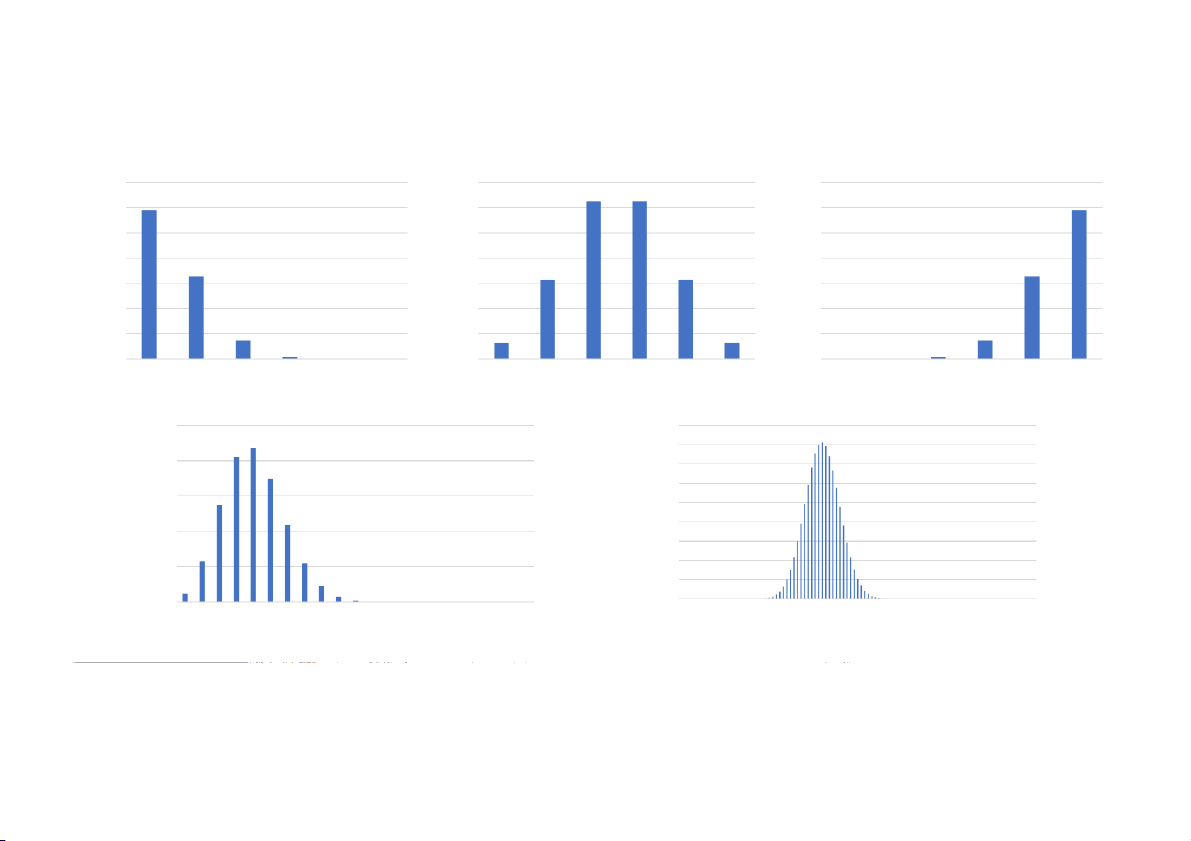
3.1 Một số phân phối nhị thức n = 5; p = 0,1 n = 5; p = 0,5 n = 5; p = 0,9 0.7 0.35 0.7 0.6 0.3 0.6 0.5 0.25 0.5 0.4 0.2 0.4 0.3 0.15 0.3 0.2 0.1 0.2 0.1 0.05 0.1 0 0 0 0 1 2 3 4 5 0 1 2 3 4 5 0 1 2 3 4 5 n = 20; p = 0,2 n = 100; p = 0,4 0.25 0.09 0.08 0.2 0.07 0.06 0.15 0.05 0.04 0.1 0.03 0.02 0.05 0.01 0 0 0 4 8 2 6 0 4 8 2 6 0 4 8 2 6 0 4 8 2 6 0 4 8 2 6 0 0 1 2 3 4 5 6 7 8 9
10 11 12 13 14 15 16 17 18 19 20 1 1 2 2 2 3 3 4 4 4 5 5 6 6 6 7 7 8 8 8 9 9 0 1
Đại học Công nghệ Sài Gòn Xác suất – Thống kê 19
Cửa hàng thiết bị KZE nhập một lô
hàng gồm 200 đèn bàn nhãn hiệu Ví dụ 4.3: Cửa
Green Latern về để bán. Theo thống hàng KZE
kê từ nhà sản xuất thì đèn bàn này có bán đèn bàn
một lỗi kỹ thuật khiến đèn không
hoạt động với tỉ lệ 1/10.
Lấy ngẫu nhiên 5 đèn bàn kiểm tra,
hãy tính khả năng có nhiều nhất 1 đèn bàn bị lỗi trên.
Đại học Công nghệ Sài Gòn Xác suất – Thống kê 21 3.2 Phân phối Poisson
Phân phối Poisson (Poisson distribution) được sử dụng để
mô tả số sự kiện xuất hiện trong một đơn vị thời gian hay
trong một không gian xác định.
Các thuộc tính của một thử nghiệm Poisson:
• Xác suất xuất hiện một sự kiện là như nhau với bất kỳ hai khoảng
thời gian (hay vùng không gian) bằng nhau nào.
• Số sự kiện xuất hiện [hoặc không xuất hiện] trong bất cứ khoảng
thời gian (hay vùng không gian) nào là độc lập với số sự kiện xuất
hiện [hoặc không xuất hiện] trong bất cứ khoảng thời gian (hay vùng không gian )nào khác.
Đại học Công nghệ Sài Gòn Xác suất – Thống kê 23
3.2 Hàm xác suất phân phối Poisson 𝝁𝒙𝒆−𝝁 𝑷 𝒙 = 𝒙! trong đó:
P(x) : xác suất có x sự kiện xuất hiện trong một đơn vị thời gian/không gian
µ : giá trị trung bình của số sự kiện xuất hiện trong một đơn vị thời
gian/không gian. Lưu ý: µ và x phải cùng đơn vị thời gian/không gian.
e = 2,71828. . (hằng số)
Phân phối Poisson được ký hiệu là P(μ)
Đại học Công nghệ Sài Gòn Xác suất – Thống kê 25
3.2 Trung bình và phương sai
Cho X là một biến ngẫu nhiên có phân phối
Poisson với tham số trung bình μ, ta có: Trung bình của X: E(X) = μ Phương sai của X:
Var(X) = σ2 = μ
Đại học Công nghệ Sài Gòn Xác suất – Thống kê 27
• Gọi X là biến ngẫu nhiên thể hiện số đèn
bàn Green Latern bị lỗi trả về – X có phân phối gì? Ví dụ 4.4:
• Gọi μ là số đèn bàn bị lỗi trả về trung Công ty DC-
bình – μ =? Đơn vị tính của μ là gì? Latern nhận
• “Trong một tuần công ty có thể nhận
nhiều nhất 5 đèn bàn bị lỗi trên trả về” đèn bàn lỗi
nghĩa là có bao nhiêu trường hợp có thể xảy ra?
• Công thức tính xác suất khi công ty nhận
x đèn bàn bị lỗi trả về là gì?
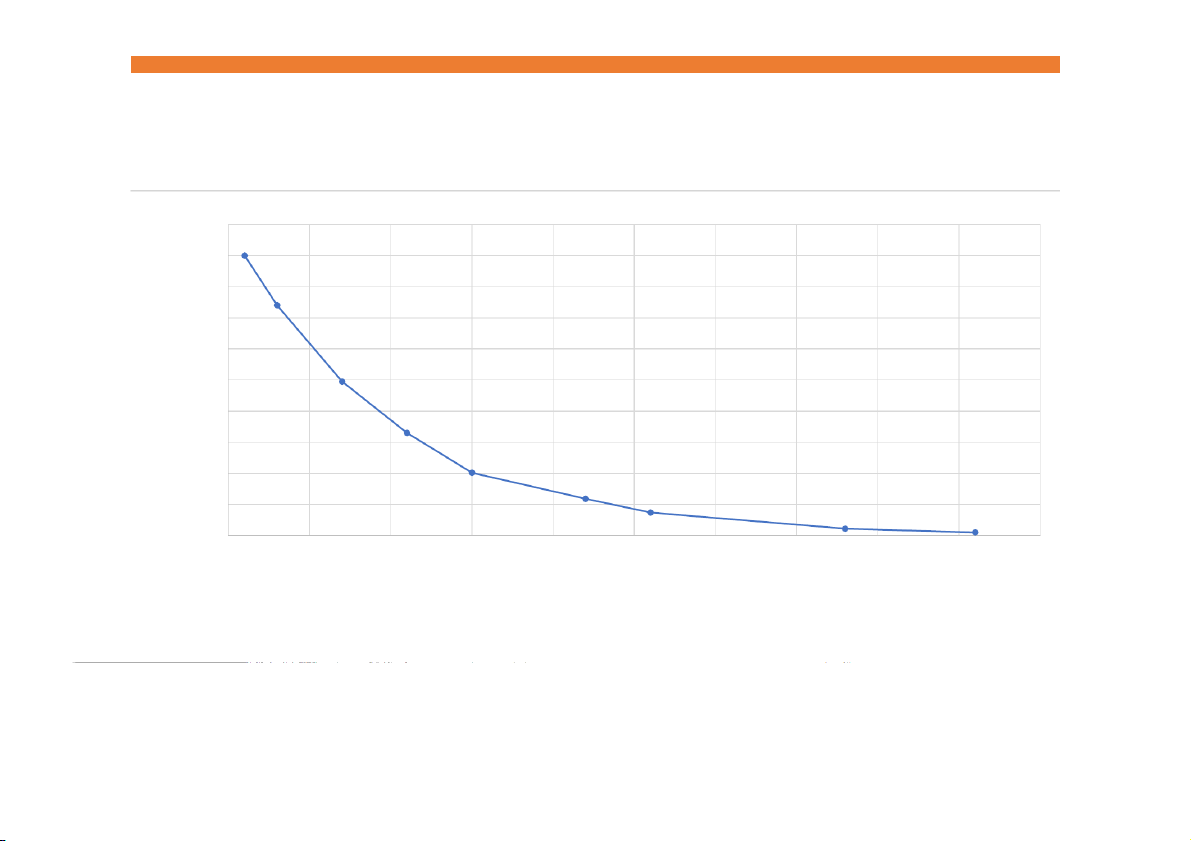
Đại học Công nghệ Sài Gòn Xác suất – Thống kê 29 4.1 Phân phối mũ
Giả sử một sự kiện nào đó xảy ra như là một quá trình Poisson,
nghĩa là số lần sự kiện đó xảy ra là một biến ngẫu nhiên có phân phối Poisson.
Gọi X là biến ngẫu nhiên về khoảng thời gian hoặc không gian
giữa các lần xảy ra liên tiếp của sự kiện trên thì X được mô tả
bằng phân phối mũ (exponential distribution).
Đại học Công nghệ Sài Gòn Xác suất – Thống kê 31
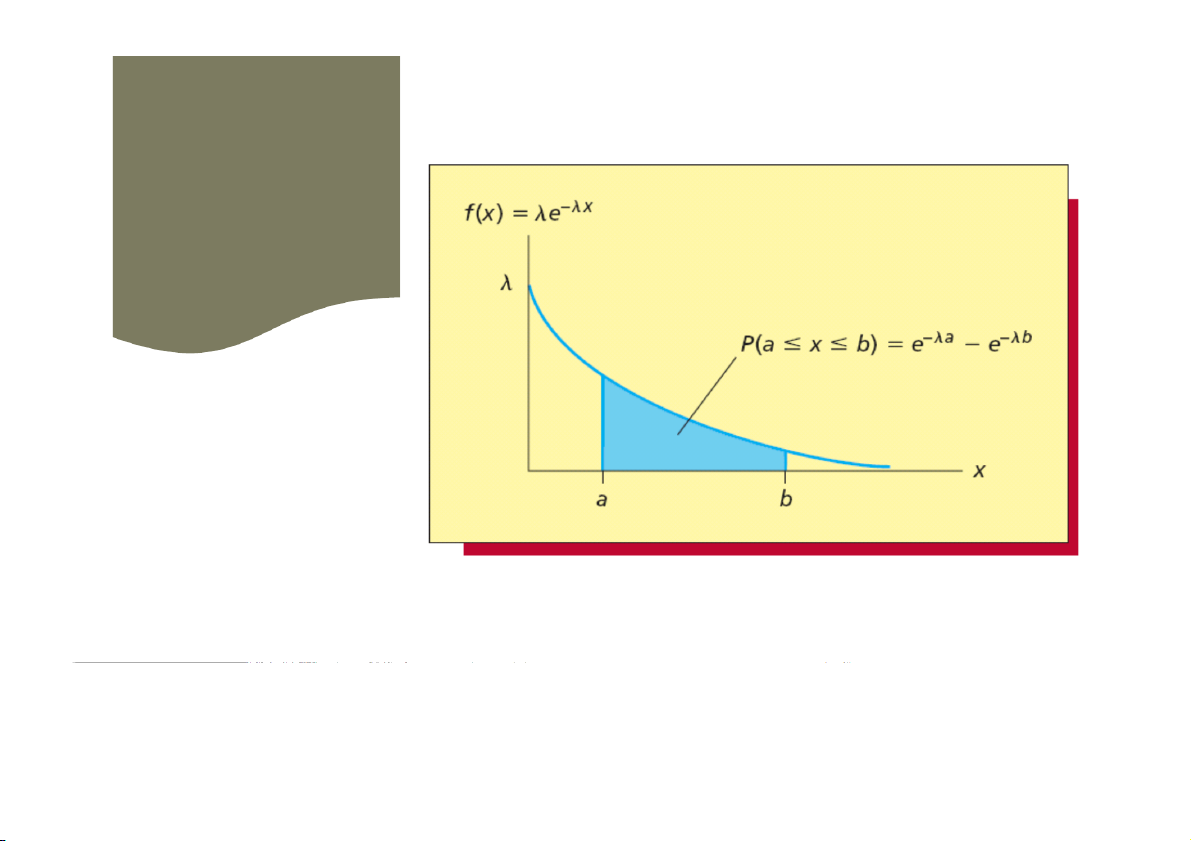
4.1 Hàm xác suất phân phối mũ
𝑓 𝑥 = ቊ𝜆𝑒−𝜆𝑥 ∀𝑥 ≥ 0 0 ∀𝑥 < 0 trong đó:
λ: là số sự kiện trung bình có thể xảy ra trong một khoảng thời
gian/không gian xác định. Vậy 1/λ là thời gian/không gian trung bình giữa
những sự kiện (λ > 0). λ đượ
c gọi là tham số tỉ lệ (rate parameter).
e = 2,71828 (e là hằng số)
Phân phối mũ được ký hiệu là E(λ)
Đại học Công nghệ Sài Gòn Xác suất – Thống kê 33 4.1 Minh họa xác suất phân phối mũ Xác suất – Thống kê
Đại học Công nghệ Sài Gòn 35
4.1 Trung bình và phương sai
Cho X là một biến ngẫu nhiên có phân phối mũ
với tham số tỉ lệ λ, ta có: Trung bình của X: E(X) = μ = Τ 1 𝜆 Phương sai của X:
Var(X) = σ2 = Τ 1 𝜆2
Đại học Công nghệ Sài Gòn Xác suất – Thống kê 37
Ví dụ 4.5: Cửa hàng KZE cải thiện dịch vụ
• Gọi X là biến ngẫu nhiên thể hiện thời gian giữa 2 khách hàng
ghé cửa hàng KZE liên tiếp – X có phân phối gì?
• Gọi λ là số khách hàng ghé cửa hàng trung bình – 1/λ là gì?
• 1/λ = ? Và đơn vị tính của 1/ λ là gì?
• Hãy viết công thức tính xác suất “để thời gian giữa hai khách
hàng ghé vào liên tiếp không quá 2 phút”.
Đại học Công nghệ Sài Gòn Xác suất – Thống kê 39 4.2 Đặc điểm của phân phối chuẩn
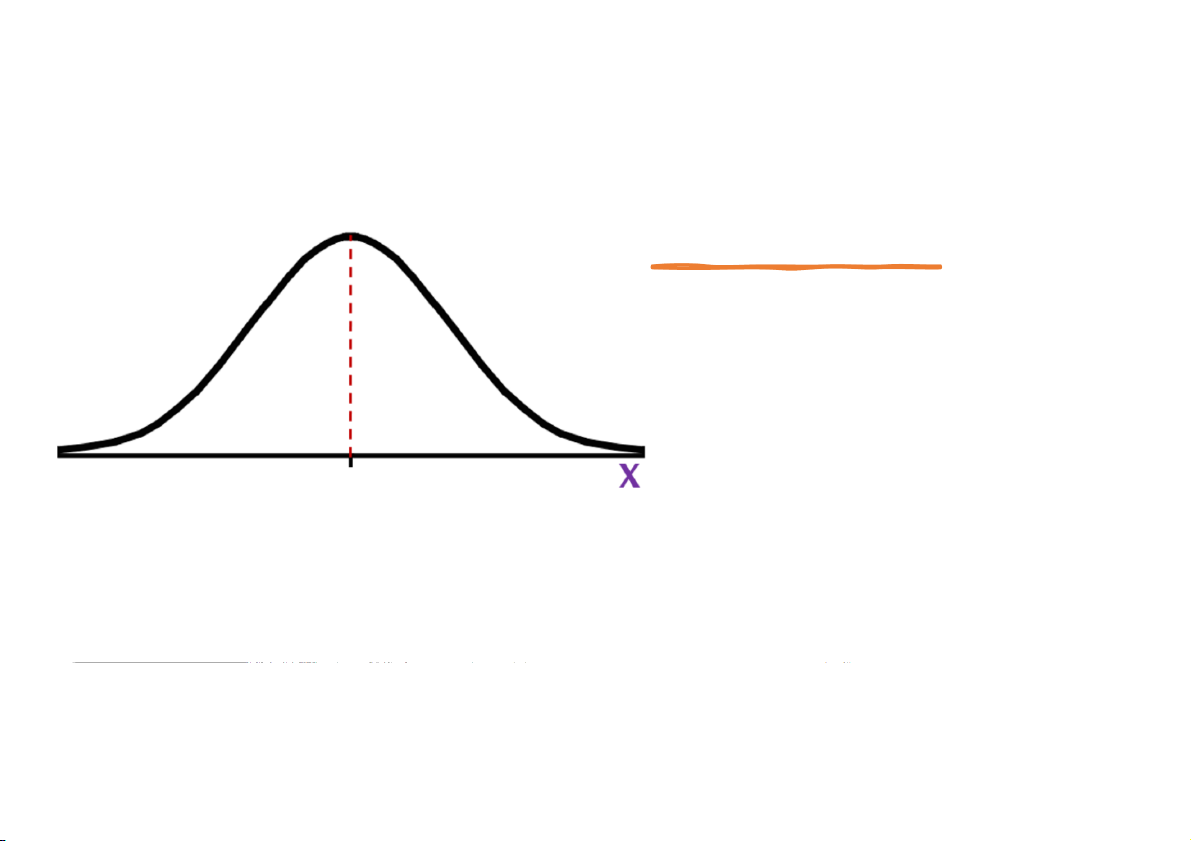
Phân phối có dạng đối xứng trục (dạng hình chuông): đặc trưng đo
lường độ lệch bằng 0.
Source: value-at-risk.net
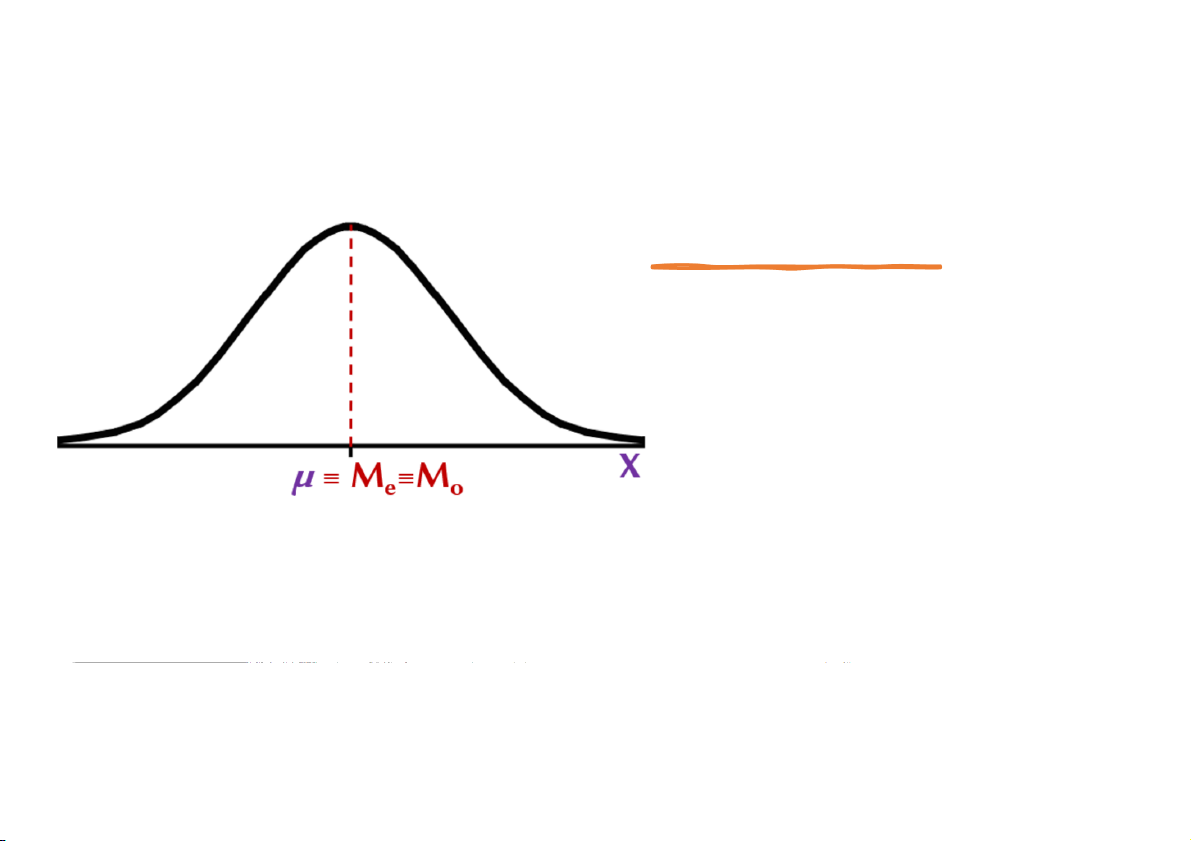
Đại học Công nghệ Sài Gòn Xác suất – Thống kê 41 4.2 Đặc điểm của phân phối chuẩn Điểm cao nhất trên đường cong chuẩn nằm ở trung bình, cũng là trung vị và yếu vị.
Source: value-at-risk.net
Đại học Công nghệ Sài Gòn Xác suất – Thống kê 43 4.2 Đặc điểm của phân phối chuẩn
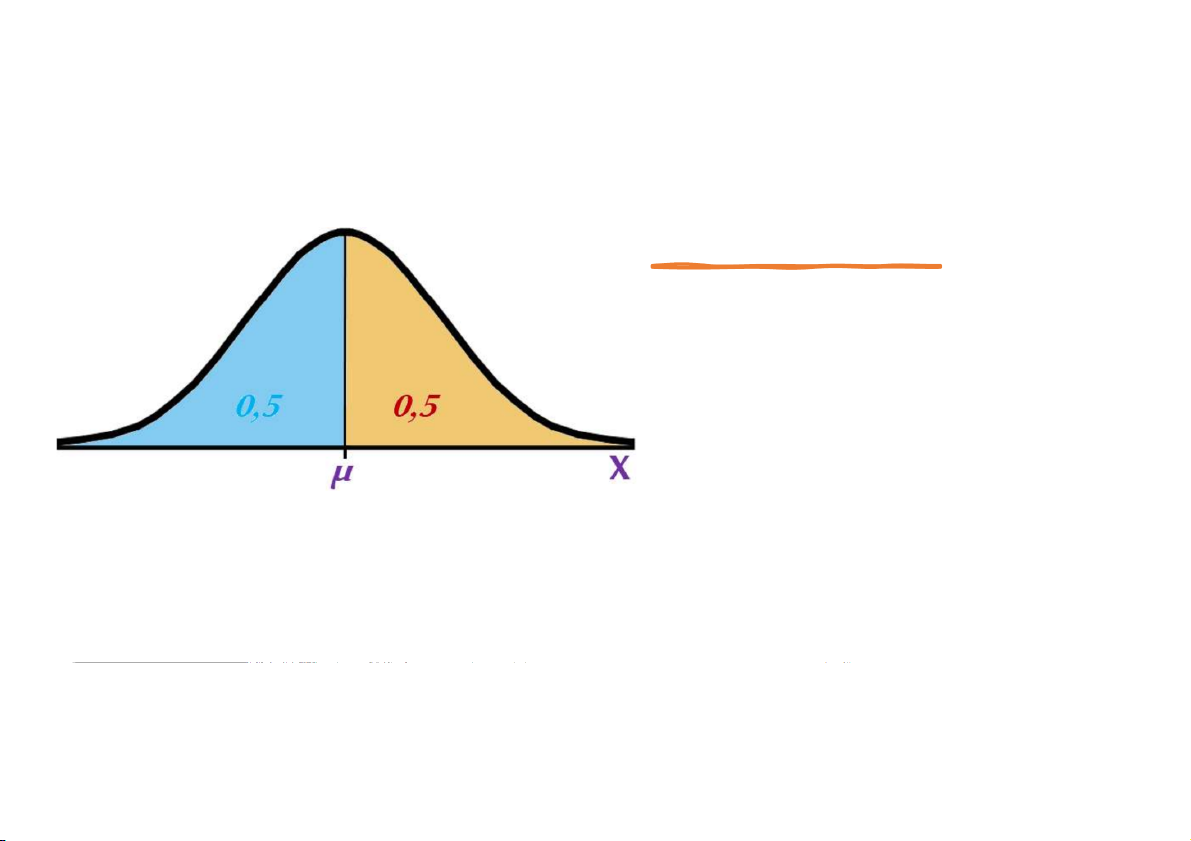
Xác suất của biến ngẫu
nhiên chuẩn được cho bởi
diện tích dưới đường cong này.
• Toàn bộ diện tích dưới đường cong này bằng 1
Source: value-at-risk.net
(0,5 ở về bên trái của trung
bình và 0,5 ở về bên phải).
Đại học Công nghệ Sài Gòn Xác suất – Thống kê 45
4.2 Phân phối chuẩn chuẩn hóa
Để tiện lợi, người ta đưa phân phối chuẩn dạng tổng
quát về phân phối chuẩn chuẩn hoá (standardized
normal distribution) với μ = 0 và σ2 = 1.
Một biến ngẫu nhiên có phân phối chuẩn chuẩn hóa, ký hiệu là Z.
Để chuyển từ biến ngẫu nhiên X ~ N(μ, σ2) sang biến
ngẫu nhiên Z ~ N(0,1), ta dùng phép biến đổi quy chuẩn như sau: 𝒙 − 𝝁 𝒛 = 𝝈 Đại học Công ngh Xệ á S c àsi Gò uất n – Thống kê 47
Sau khi nhận quá nhiều phàn nàn của khách
hàng về lỗi kỹ thuật trên đèn bàn Green Latern,
công ty DC-Latern quyết định yêu cầu quản lý Ví dụ 4.
xưởng sản xuất đèn bàn Green Latern tìm hiểu
6: Công nguyên nhân gây ra lỗi trên. ty DC-Latern
Qua một thời gian xem xét dữ liệu thu thập
khắc phục lỗi được từ quá trình sản xuất, vị quản lý này nghi
ngờ việc thiết lập thông số ban đầu cho dây đèn bàn (1)
chuyền lắp ráp mạch điện có thể là nguyên
nhân. Cụ thể là thời gian gắn cảm biến ánh sáng
(quang trở) quá ngắn khiến cho có khả năng cao là mạch điện bị hở.
Đồ thị sau đây thể hiện thời gian gắn cảm biến
ánh sáng trên mạch điện.
Đại học Công nghệ Sài Gòn Xác suất – Thống kê 49
Ví dụ 4.6: Công ty DC-Latern khắc phục lỗi đèn bàn (1)
• Gọi X là biến ngẫu nhiên thể hiện thời gian gắn cảm biến ánh sáng
vào mạch điện – X có phân phối gì?
• Hãy viết ký hiệu xác suất mà thời gian gắn cảm biến vào mạch
điện là “từ 400ms đến 600ms”.
• Hãy trình bày cách tính xác suất.
Đại học Công nghệ Sài Gòn Xác suất – Thống kê 51
Xấp xỉ chuẩn cho phân phối Poisson
Tương tự như phân phối nhị thức, khi xem xét một số phân phối
Poisson ta thấy rằng khi số sự kiện trung bình xảy ra tăng lên thì đồ
thị của phân phối Poisson có xu hướng tiến tới dạng hình quả chuông,
đối xứng của đường cong chuẩn.
Xấp xỉ chuẩn cho phân phối Poisson cần thiết và tốt nhất khi μ lớn, ví
dụ như khi μ vượt qua các giá trị trong bảng tra phân phối Poisson. Ta
chuyển các tham số của phân phối Poisson về tham số của phân phối chuẩn như sau: μ = μ σ2 = μ
Đại học Công nghệ Sài Gòn Xác suất – Thống kê 53