






















Preview text:
Bài tập chương 1
TẠI SAO CẦN NGHIÊN CỨU THỐNG KÊ?
1.1 Phân loại mỗi loại dữ liệu sau thành dữ liệu thang đo định danh, thứ bậc, khoảng và tỷ lệ:
a) Thời gian cần thiết để sản xuất mỗi lốp xe trên một dây chuyền lắp ráp
b) Số lít sữa mà một gia đình uống trong một tháng
c) Tuổi của từng người lao động trong công ty của bạn
d) Xếp hạng 4 máy trong nhà máy của bạn sau khi chúng đã được định rõ là tuyệt vời
(excellent), tốt (best), vừa ý (satisfactory), tồi (worst)
e) Mã điện thoại tỉnh của các khách hàng ở Việt Nam f) Doanh thu h
àng tháng của một tiệm bánh g) Các cỡ giày nam
h) Thể tích tối đa trong các chai đựng đồ uống nhẹ bằng Aoxơ
i) Xếp hạng của một công ty theo tạp chí Fortune 500
j) Số vé bán được tại một rạp chiếu bóng vào bất kỳ một buổi tối nào
k) Số chứng minh thư của người lao động
l) Số nhận diện (identification number) trên một bản câu hỏi (để điều tra)
m) Quy mô của một công ty được đo bằng số người lao động
1.2 Tập dữ liệu sau cung cấp một ảnh chụp nhanh về kết quả tài chính của Công ty Ameritech (Barrons, 29-12-1997). 1993 1994 1995 1996
Thu nhập trên mỗi cổ phần 2,78$ 2,13$ 3,41$ 3,83$ Tổng thu nhập (tỷ) 11,87$ 12,57$ 13,43$ 14,92$ Thu nhập ròng (tỷ) 1,51$ 1,17$ 1,89$ 2,12$
Thư giá của một cổ phần 14,35$ 10,98$ 12,67$ 13,98$ a) Có bao nhiêu biến?
b) Dữ liệu là định tính hay định lượng?
c) Dữ liệu là dữ liệu chéo hay dữ liệu chuỗi thời gian? Tại sao?
1.3 Hãy xác định mỗi một biến sau đây là định tính hay định lượng và cho biết thang đo thích hợp với mỗi biến. a) Tuổi b) Giới tính c) Xếp hạng trong lớp
d) Nhãn hiệu của chiếc xe ô tô
e) Số lượng sinh viên thích môn Thống kê trong kinh doanh
1.4 Hãy xác định mỗi một biến sau đây là định tính hay định lượng và cho biết thang đo được sử dụng. a) Doanh số hàng năm
b) Cỡ chai nước ngọt không có cồn (nhỏ, trung, lớn)
c) Thu nhập trên mỗi cổ phần
d) Phương thức thanh toán (tiền mặt, séc, thẻ tín dụng) 1
1.5 Tạp chí Fortune (Vận hội) cung cấp dữ liệu về 500 công ty công nghiệp lớn nhất của Mỹ
(FORTUNE 500) được xếp thứ hạng theo tổng thu nhập và lợi nhuận. Dữ liệu mẫu gồm 10 công
ty FORTUNE 500 được cho trong Bảng 1.1.
a) Có bao nhiêu phần tử trong tập dữ liệu này? b) Tổng thể là gì?
c) Tính tổng thu nhập trung bình cho mẫu.
d) Sử dụng kết quả ở câu (c), ước lượng tổng thu nhập trung bình cho tổng thể là bao nhiêu?
e) Có bao nhiêu biến trong tập dữ liệu?
f) (Những) biến nào là định tính và biến nào là định lượng?
g) Tính lợi nhuận trung bình cho mẫu.
h) Tỷ lệ phần trăm công ty kiếm được lợi nhuận trên 100 triệu đô la là bao nhiêu?
i) Tỷ lệ phần trăm công ty có mã ngành 3 là bao nhiêu?
j) dữ liệu ở Bảng 1.1 về các công ty FORTUNE 500, chúng là dữ liệu chéo hay dữ liệu
chuỗi thời gian? Tại sao? BẢNG 1.1
MỘT MẪU GỒM 10 CÔNG TY FORTUNE 500 Tổng thu nhập Lợi nhuận Công ty (triệu đô la) (triệu đô la) Mã ngành US Airways Group 8688,0 538,0 3 International Paper 19500,0 213,0 23 Tyson Foods 7414,1 25,1 20 Hewlett-Packard 47061,0 2945,0 13 Intel 26273,0 6068,0 49 Northup Grumman 8902,0 214,0 2 Seagate Technology 6819,0 -530,0 11 Unisys 7208,4 387,0 10 Westvaco 2904,7 132,0 23 Campbell Soup 7505,0 660,0 20 Nguồn: Fortune, 26-04-1999 2 Bài tập chương 2
THU THẬP VÀ MÔ TẢ DỮ LIỆU
2.1 Diễn giải bảng tần số dưới đây: Giá bán Tần số (Ngàn đô-la) 12 15 – 8 15 18 – 23 18 21 – 17 21 24 – 18 24 27 – 8 27 30 – 4 30 33 – 1 33 36 – 1 U U Tổng 80
2.2 Số liệu dưới đây là tuổi của một mẫu gồm 50 người quản lý các trung tâm chăm sóc trẻ ở thành phố Hồ Chí Minh: 42 30 53 50 52 30 55 49 61 74 57 30 49 26 58 40 40 28 36 30 33 31 37 40 25 50 32 37 30 32 23 32 58 43 30 29 52 32 34 50 47 31 35 26 64 46 40 43 60 54
a) Hãy lập bảng tần số cho tập dữ liệu này.
b) Bảng tần số cho ta biết gì về tuổi của các nhà quản lý. c) Tính tuổi trung bình.
d) Tính phương sai mẫu hiệu chỉnh và độ lệch chuẩn.
e) Theo định lý Chebyshev, có ít nhất bao nhiêu quan sát của tập dữ liệu tuổi rơi vào khoảng
từ 19,11 đến 63,37 tuổi? Thực tế thì có bao nhiêu?
2.3 Số con trong 30 gia đình ở một xóm được thống kê (tính đến ngày 30/12/1981) như sau: 0 2 2 3 4 5 3 5 4 4 1 1 5 4 3 6 4 1 2 5 2 2 4 2 3 4 1 6 4 2 Hãy lập bảng tần số.
2.4 Năng suất một vụ lúa năm 1990 của các hợp tác xã nông nghiệp thuộc huyện A được ghi
trong bảng dưới đây (tính theo tạ/ha): 28,7 31,0 33,0 35,0 29,0 33,9 31,2 33,7 34,9 31,8 33,7 29,4 31,8 36,9 28,3 34,3 36,6 32,0 34,6 39,0 29,8 32,1 33,8 35,2 34,9 34,3 30,0 38,9 32,2 35,7 30,2 32,4 34,8 28,9 33,1 38,0 34,4 32,6 35,8 36,4 37,2 36,7 30,4 32,9 34,6 36,8 42,7 30,9 35,2 34,7
a) Hãy lập bảng tần số 3
b) Dựng biểu đồ tần số
2.5 Các sinh viên Trường Cao đẳng Kỹ nghệ được yêu cầu điền vào bảng câu hỏi đánh giá môn
học lúc học xong các môn học của họ. Bảng câu hỏi gồm có nhiều câu hỏi có thang điểm trả lời 5
hạng mục. Một trong số các câu hỏi này như sau:
So với những môn học khác bạn đã học qua, chất lượng của môn học mà bạn bây giờ bạn sắp học xong là thế nào? Keù m Trung bình Toá t Raá t toá t Tuyeä t vôø i
Một mẫu gồm 60 sinh viên đã học môn Thống kê trong kinh doanh ở học kỳ II năm học 2002-
2003 đã đưa ra các câu trả lời sau đây. Để giúp xử lý kết quả điều tra bằng máy vi tính, các câu
trả lời mã hoá như sau: 1 = kém, 2 = trung bình, 3 = tốt, 4 = rất tốt và 5 = tuyệt vời. 3 4 4 5 1 5 3 4 5 2 4 5 3 4 4 4 5 5 4 1 4 5 4 2 5 4 2 4 4 4 5 5 3 4 5 5 2 4 3 4 5 4 3 5 4 4 3 5 4 5 4 3 5 3 4 4 3 5 3 3
a) Hãy bình luận tại sao dữ liệu này là định tính.
b) Hãy tóm tắt dữ liệu dưới dạng phân phối tần số và phân phối tần số tương đối.
c) Vẽ biểu đồ thanh và biểu đồ tròn.
d) Trên cơ sở các tóm tắt của bạn, hãy bình luận đánh giá chung của sinh viên về môn học.
2.6 Điều tra năng suất lúa của 40 hợp tác xã trong một khu vực ở địa phương, người ta thu được các số liệu sau: 31,8 28,7 31,2 33,1 35,1 29,1 33,9 31,2 33,7 34,9 39,5 33,7 29,4 31,8 26,9 28,3 34,3 36,6 23,2 34,6 35,7 29,8 32,1 33,8 35,2 34,9 34,3 30,6 38,9 32,2 38,4 30,2 32,4 34,8 28,9 33,1 34,1 34,4 32,6 35,8
Hãy lập bảng tần số (phân theo các tổ sau: từ 29 tạ trở xuống, (29 tạ – 31 tạ), (31 tạ – 33 tạ), …
2.7 Công ty Olson chế tạo vòng kim loại cho các động cơ công nghiệp. Vòng này cân nặng
khoảng 50 aoxơ. Một mẫu ngẫu nhiên 50 chiếc vòng kim loại này cho các trọng lượng (bằng aoxơ) sau: 51 53 56 50 44 47 53 53 42 57 46 55 41 44 52 56 50 57 44 46 41 52 69 53 57 51 54 63 42 47 47 52 53 46 36 58 51 38 49 50 62 39 44 55 43 52 43 42 57 49
Xây dựng phân phối tần số cho dữ liệu này sử dụng 8 tổ.
2.8 Số liệu sau đây là tuổi của một mẫu gồm 50 nhà quản lý từ các trung tâm chăm sóc trẻ ở các thành phố của Việt Nam 42 30 53 50 52 30 55 49 61 74 26 58 40 40 28 36 30 33 31 37 32 37 30 32 23 32 58 43 30 29 34 50 47 31 35 26 64 46 40 43 4 57 30 49 40 25 50 52 32 60 54
a) Xây dựng phân phối tần số cho dữ liệu này dùng khoảng cách tổ là 10.
b) Tính và trình bày các trị số giữa tổ, tần số tương đối, và tần số tích luỹ cho phân phối này.
c) Dựng biểu đồ tần số, đa giác tần số, và hình cung nhọn.
2.9 Khi hai công ty thông báo kế hoạch sát nhập, điều thường xảy ra là trong vòng vài tuần một
trong hai công ty trở nên bất mãn với hậu quả của việc sát nhập và vụ sát nhập bị hủy bỏ. Dodd
(1980) cho biết trong số 151 thông báo sát nhập ông nhận ra, 80 vụ bị hủy bỏ. Do đó, vào thời
điểm vụ sát nhập dự kiến được công bố có một số lượng không chắc chắn rất lớn về vụ sát nhập
đó sẽ xảy ra hay không. Sự không chắc chắn này có thể kéo dài trong một khoảng thời gian đáng
kể và nó có thể là nhiều tháng sau khi thông báo vụ sát nhập mới thực sự xảy ra. Trong nghiên
cứu của mình về 38 vụ sát nhập đã hoàn thành, Eger (1982) báo cáo số ngày giao dịch (số ngày
Sở giao dịch chứng khoán New York mở cửa hoạt động) từ khi thông báo sát nhập (được xác
định là lần đầu tiên đề cập đến vụ sát nhập có khả năng trên Tạp chí Wall Street) đến ngày có
hiệu lực của vụ sát nhập. Dữ liệu này được liệt kê dưới đây: 74 45 55 74 64 97 65 82 92 116 140 62 92 78 45 93 94 57 123 128 92 73 173 116 35 124 64 84 255 277 123 80 143 112 76 214 64 86
a) Hãy xây dựng bảng tần số (với khoảng cách đều nhau) để tóm tắt dữ liệu này.
b) Tính tần số tương đối, và tần số tương đối tích luỹ.
c) Vẽ biểu đồ tần số.
2.10 Dữ liệu sau đây là về số tiền chi tiêu cho hàng tạp phẩm của một mẫu ngẫu nhiên khách hàng ở một chợ: 10 13 15 21 23 24 25 25 30 32 34 35 37 38 39 39 41 48 53 58 58 58 70 70 74 80 82 88 250 254 58 63 64 40 15 20
a) Tập dữ liệu này có (các) quan sát bất thường (outlier) không?
b) Hãy xây dựng bảng tần số (với khoảng cách đều nhau) để tóm tắt dữ liệu này.
c) Tính tần số tương đối, và tần số tích luỹ.
d) Vẽ biểu đồ đa giác tần số.
2.11 Dữ liệu sau đây là cho 30 quan sát trên hai biến định tính, x và y. Các hạng mục cho x là
A, B và C; các hạng mục cho y là 1 và 2. Quan sát x y Quan sát x y 1 A 1 16 B 2 2 B 1 17 C 1 3 B 1 18 B 1 4 C 2 19 C 1 5 B 1 20 B 1 6 C 2 21 C 2 7 B 1 22 B 1 8 C 2 23 C 2 9 A 1 24 A 1 5 10 B 1 25 B 1 11 A 1 26 C 2 12 B 1 27 C 2 13 C 2 28 A 1 14 C 2 29 B 1 15 C 2 30 B 2
a) Lập bảng chéo cho dữ liệu, với x ở các dòng và y ở các cột.
b) Tính các tỷ lệ phần trăm theo dòng.
c) Tính các tỷ lệ phần trăm theo cột.
d) Mối quan hệ giữa x và y, nếu có, là gì?
2.12 Công ty phát triển nhà ở Gia Lai xây dựng bốn kiểu nhà làm bằng gỗ súc (log houses) và
bán nguyên căn (that are sold in kits). Giá (tính theo 1.000$) và kiểu nhà công ty đã bán trong
năm qua được cho dưới đây. Giá Kiểu Giá Kiểu Giá Kiểu <99 Colonial >100 A-Frame >100 Colonial <99 Ranch >100 Split-Level <99 Colonial >100 Split-Level <99 Colonial <99 A-Frame >100 Split-Level >100 Ranch >100 Split-Level <99 Colonial >100 Colonial >100 Ranch <99 A-Frame <99 A-Frame <99 Split-Level <99 Split-Level <99 Split-Level >100 Split-Level <99 A-Frame <99 Split-Level >100 Colonial >100 Ranch <99 Colonial >100 Ranch >100 Split-Level <99 Ranch >100 Split-Level <99 A-Frame >100 Split-Level <99 Colonial <99 Colonial >100 Colonial >100 Colonial >100 Ranch <99 Split-Level <99 Split-Level <99 Colonial
Hãy lập bảng chéo với các biến là giá và kiểu nhà.
2.13 Có tài liệu về một mẫu gồm 20 sinh viên tham dự một hội nghị như sau: Sinh viên năm 3 Sinh viên năm 4 Sinh viên năm 4 Sinh viên năm 2 Sinh viên năm 1 Sinh viên năm 1 Sinh viên năm 3 Sinh viên năm 2 Sinh viên năm 4 Sinh viên năm 4 Sinh viên năm 2 Sinh viên năm 3 Sinh viên năm 1 Sinh viên năm 1 Sinh viên năm 2 Sinh viên năm 3 Sinh viên năm 2 Sinh viên năm 2 Sinh viên năm 1 Sinh viên năm 2 a) Lập bảng tần số
b) Dựng biểu đồ thanh và biểu đồ hình tròn
2.14 Theo tạp chí Người tiêu dùng, Coca-Cola, Pepsi-Cola, Sprite, Seven Up, và Xá xị
Chương Dương là năm loại nước ngọt bán chạy nhất. Giả sử dữ liệu trong bảng sau trình bày loại
nước ngọt được chọn cho một mẫu gồm 50 lần mua nước ngọt. Coca-Cola Sprite Pepsi-Cola 6 Seven Up Coca-Cola Coca-Cola Pepsi-Cola Seven Up Coca-Cola Seven Up Coca-Cola Coca-Cola Coca-Cola Seven Up Pepsi-Cola Coca-Cola Coca-Cola Xá xị Chương Dương Xá x ị Chương Dương Sprite Coca-Cola Seven Up Pepsi-Cola Seven Up Pepsi-Cola Coca-Cola Pepsi-Cola Pepsi-Cola Coca-Cola Pepsi-Cola Coca-Cola Coca-Cola Pepsi-Cola Xá xị Chương Dương Pepsi-Cola Pepsi-Cola Sprite Coca-Cola Coca-Cola Coca-Cola Sprite Xá xị Chương Dương Seven Up Xá xị Chương Dương Pepsi-Cola Coca-Cola Pepsi-Cola Sprite Coca-Cola Seven Up a) Lập bảng tần số
b) Dựng biểu đồ thanh và biểu đồ hình tròn
2.15 Có tài liệu về tiền lương của một tổng thể bao gồm 7 nhân viên quản lý thuộc một công
ty xăng dầu trong tháng 3/2004 như sau:
5,5 ; 6,5 ; 6,8 ; 7,6 ; 7,8 ; 8,2 ; 8,5 (triệu đồng)
Một mẫu bao gồm 4 nhân viên được chọn ngẫu nhiên từ 7 nhân viên trên, số liệu về tiền lương như sau:
5,5 ; 7,6 ; 7,8 ; 8,2 (triệu đồng)
a) Tính tiền lương trung bình, phương sai về tiền lương của tổng thể.
b) Tính tiền lương trung bình, phương sai (không hiệu chỉnh) về tiền lương của mẫu.
2.16 Số liệu về năng suất lao động (số sản phẩm / ca sản xuất) của công nhân ở hai phân xưởng như sau:
Số sản phẩm / ca sản xuất
Số công nhân (người) Phân xưởng A Phân xưởng B 30 2 0 40 – 42 0 9 43 – 45 25 14 46 – 48 13 25 49 – 51 5 2 58 3 0 65 2 0
a) Xác định năng suất lao động trung bình của công nhân ở từng phân xưởng và chung cho cả hai phân xưởng.
b) Bằng các chỉ tiêu thống kê, hãy đánh giá sự đồng đều về năng suất lao động cho từng
phân xưởng. Nhận xét một cách ngắn gọn.
c) Hãy thảo luận ngắn gọn về sự khác biệt giữa độ lệch tuyệt đối trung bình và phương sai.
2.17 Có tài liệu về tiền lương tháng của 12 công nhân ở một tổ sản xuất như sau (ngàn đồng): 7
1600, 1800, 2600, 2500, 2000, 1800, 1700, 1500, 1800, 2000, 1900, 2500.
Căn cứ số liệu trên hãy tính:
a) Tiền lương trung bình, trung vị và mốt.
b) Phương sai (không hiệu chỉnh) và độ lệch chuẩn.
2.18 Dựa vào tiền lương hàng năm sau đây của một mẫu 5 nhà báo hành nghề tự do, hãy tính
trung bình, trung vị và mốt. Đặc trưng đo lường khuynh hướng tập trung nào là số tóm tắt thích hợp nhất? 17.000£ 18.000£ 20.000£ 23.000£ 65.000£
2.19 Bảng dưới trình bày thời gian ôn tập của những sinh viên thi môn thống kê ứng dụng trong kinh doanh.
a) Sử dụng bảng này để tính số giờ trung bình sử dụng để ôn thi của một mẫu 30 sinh viên. Thời gian (giờ) < 5 5 - 10 10 - 15 15 - 20 20 - 25 Tần số1 1 4 13 10 2
b) Dữ liệu gốc trước khi xây dựng bảng tần số như sau: 15 12 13 21 18 11 4 16 12 15 9 15 18 14 15 9 6 12 11 12 19 13 13 11 16 13 10 9 20 18
Sử dụng dữ liệu này, hãy tính trung bình, trung vị và mốt.
So sánh hai đáp số cho trung bình, chúng có khác nhau không? Nếu có, hãy giải thích tại sao như vậy.
c) Đặc trưng đo lường nào bạn cảm thấy thích hợp nhất? Tại sao?
2.20 Tìm tốc độ tăng trưởng trung bình hàng năm nếu doanh thu tăng 25% trong 5 năm qua.
2.21 Một người tư vấn đầu tư cho biết tốc độ tăng giá hàng năm của một loại cổ phiếu như sau: 4,3% 6,0% 3,5% 8,2% và 7,0%
a) Tính tốc độ tăng giá trung bình trong giai đoạn 5 năm nói trên.
b) Nếu tốc độ tăng này được duy trì thì mất bao nhiêu năm để giá tăng gấp hai lần?
2.22 Lạm phát ở một quốc gi năm vừa qua là a trong 5 10% 7% 13% 9% và 12%
a) Tỷ lệ lạm phát trung bình hàng ăm là bao nhiêu? n
b) Nếu tỷ lệ lạm phát này được duy trì thì mất bao nhiêu năm để giá tăng gấp hai lần?
2.23 Có hai tổ công nhân cùng sản xuất một loại sản phẩm trong 8 giờ. Tổ 1 có 15 công nhân.
Tổ 2 có 18 công nhân. Thời gian hao phí trung bình để mỗi công nhân hoàn thành một sản phẩm
của tổ 1, tổ 2 lần lượt là 15 phút, 2 phút. Hãy tính thời gian hao phí trung bình để hoàn thành 1
một sản phẩm của công nhân cả hai tổ?
2.24 Điểm tổng kết toán của từng em trong hai tổ học sinh được ghi lại trong bảng dưới đây (mỗi tổ có 12 em): 8 Tổ 1 1,7 2,4 3,5 4,6 5,2 5,3 5,4 6,1 6,3 7,6 8,8 9,1 Tổ 2 3,4 3,6 4,5 4,8 5,1 5,2 5,7 6,0 6,3 6,4 7,2 7,8
a) Tính số trung bình điểm tổng kết toán ở từng tổ;
b) Hãy tính phương sai và độ lệch chuẩn đối với từng tổ;
c) Hãy nhận xét về trình độ học toán của hai tổ trên.
2.25 Có số liệu về tỷ lệ thu hồi vốn đầu tư của 30 công ty thuộc một ngành kinh doanh như sau: Tỷ lệ thu hồi Hãy xác định:
vốn đầu tư (%) Số công ty
a) Tỷ lệ thu hồi vốn đầu tư trung bình 6,00 – 6,50 5
b) Phương sai và độ lệch chuẩn 6,50 – 7,00 8 c) Hệ số biến thiên 7,00 – 7,50 10 7,50 – 8,00 7
d) Mốt và số trung vị về tỷ lệ thu hồi vốn đầu tư Tổng cộng 30
2.26 Một xạ thủ bắn 60 phát súng, kết quả được ghi lại trong bảng dưới đây (số điểm của từng phát) 8 9 10 9 9 10 8 9 6 8 10 10 10 9 8 10 8 9 6 8 10 9 7 9 9 6 9 8 10 8 9 9 10 6 9 5 9 8 10 9 9 10 6 10 7 9 10 9 10 9 6 10 7 7 5 9 5 7 7 9
a) Gọi X là số điểm đạt được sau mỗi lần bắn. Lập bảng tần số, từ đó tính số trung bình,
phương sai và độ lệch chuẩn.
b) Ý nghĩa của độ lệch chuẩn trong trường hợp này là gì?
2.27 Giả định là điểm kiểm tra giữa kỳ môn thống kê trong kinh doanh của 130 sinh viên có
trung bình là 7 và độ lệch chuẩn là 0,5. Bao nhiêu sinh viên có điểm kiểm tra trong khoảng từ 6
đến 8? Bao nhiêu sinh viên có điểm kiểm tra trong khoảng từ 5,8 đến 8,2?
2.28 Một mẫu gồm số tiền chi tiêu hàng tháng cho thực phẩm của một người già sống một
mình có phân phối xấp xỉ chuẩn. Trung bình mẫu là 150$; độ lệch chuẩn là 20$. Dùng quy tắc thực nghiệm:
a) khoảng 68% chi tiêu hàng tháng cho thực phẩm rơi vào khoảng nào?
b) khoảng 95% chi tiêu hàng tháng cho thực phẩm rơi vào khoảng nào?
c) hầu như toàn bộ (khoảng 99,7%) chi tiêu hàng tháng cho thực phẩm rơi vào khoảng nào?
2.29 Số liệu sau đây về bưu phí của một mẫu 30 gồm bưu kiện của một công ty: 3,67$ 10,94$ 3,20$ 8,64$ 2,84$ 1,83 7,80 5,42 1,97 2,09 3,34 4,95 5,11 3,32 2,78 3,64 3,45 4,65 7,20 3,53 9,15 5,47 3,89 3,55 4,10 2,75 1,93 3,21 4,84 4,15
Hãy lập biểu đồ thân và lá. 9
2.30 Hai sinh viên A và B, khoa Lý, trong một kỳ thi tuyển sinh ở TP. HCM có cùng tổng
điểm là 16,5, nhưng khác nhau về điểm ba môn thi Toán, Lý, Hóa: sinh viên A có 5,5 về Toán,
5,5 về Lý và 5,5 về Hóa; sinh viên B có 6 về Toán, 6,5 về Lý và 4 về Hóa. Tuy tổng điểm bằng
nhau, nhưng hai thí sinh ấy không giống nhau về khả năng Toán, Lý và Hóa. Điểm trung bình và
độ lệch chuẩn về điểm của ba môn thi trong kỳ thi tuyển sinh mà A và B đã tham dự như sau: Toán Lý Hóa Điểm trung bình 4,447 6,015 3,682 Độ lệch chuẩn 1,779 1,776 1,644
Bằng cách chuẩn hóa các điểm số của hai thí sinh A và B (tính điểm z) để thấy rõ khả năng
Toán, Lý, Hóa của hai thí sinh này và nhận xét.1
2.31 Có bảng ma trận tương quan về môn Toán của 1280 sinh viên tại một trường đại học ở
TP.HCM, căn cứ trên điểm toán trung bình ở lớp 12 (TOÁN 12), điểm toán tuyển sinh (TOÁN
TS) và điểm toán trung bình vào cuối giai đoạn I ở đại học (TOÁN GĐ1). TOÁN 12 TOÁN TS TOÁN GĐ1 TOÁN 12 1,000 TOÁN TS 0,168 1,000 TOÁN GĐ1 0,094 0,194 1,000
Hãy nhận xét kết quả trên.2
2.32 Giá thuê xe mỗi ngày ở 7 thành phố miền Nam (mẫu) như sau: Thành phố B A M N O P W Giá hàng ngày (10.000đ) 43 35 34 58 30 30 36
a) Tính trung bình, trung vị, mốt, phương sai, độ lệch chuẩn và hệ số biến thiên cho mẫu trên.
b) Một mẫu tương tự gồm 7 thành phố ở miền Bắc cho biết giá thuê xe trung bình của mẫu
bằng 380.000đ mỗi ngày. Phương sai và độ lệch chuẩn tương ứng là 120.300 và 30.500.
Hãy thảo luận bất kỳ sự khác biệt nào giữa giá thuê xe ở các thành phố ở miền Nam và miền Bắc.
2.33 Nielson Media Research (một công ty cung cấp tỷ lệ phần trăm người xem của các
chương trình TV) cung cấp hai thước đo khán giả xem truyền hình: đánh giá chương trình truyền
hình, đó là tỷ lệ phần trăm hộ gia đình có ti vi xem một chương trình, và - đóng góp cho chương
trình truyền hình, đó là tỷ lệ phần trăm hộ gia đình xem một chương trình trong số những hộ gia
đình có ti-vi đang dùng. Dữ liệu sau đây cho thấy dữ liệu về đánh giá và đóng góp cho chương
trình truyền hình của Nielson cho Major League Baseball World Series qua một thời kỳ 9 năm. Mức đánh giá (Ratings) 19 17 17 14 16 12 15 12 13 Mức đóng góp (Share) 32 28 29 24 26 20 24 20 22
1 Theo Dương Thiện Tống, Suy nghĩ về giáo dục truyền thống và hiện đại, NXB. Trẻ, tr. 302-303
2 Theo Dương Thiện Tống, Suy nghĩ về giáo dục truyền thống và hiện đại, NXB. Trẻ, tr. 300-301 10
a) Vẽ biểu đồ phân tán với ratings đặt trên trục hoành.
b) Mối liên hệ giữa ratings và share là gì? Hãy giải thích.
c) Tính và diễn giải hiệp phương sai mẫu.
d) Tính và diễn giải hệ số tương quan mẫu.
2.34 Một đại lý lấy mẫu ngẫu nhiên sổ sách công ty để
tìm số bản phắc (fax) hàng tuần nhận
được thông báo các chuyến dạo chơi trên biển đặc biệt đế ế
n châu Âu. K t quả là: 20; 73; 75; 80
và 82 bản phắc. Bạn có để ý thấy điều gì về d ữ liệu này? 2.35 Một tậ ữ
p d liệu có tứ phân vị thứ ấ nh t bằ ứ
ng 42 và t phân vị thứ ba bằng 50. Hãy tính các
giới hạn dưới và trên của biểu đồ hình hộp tương ứng. Một trị số dữ liệ ằ
u b ng 65 có được xem là quan sát b ng hay không? ất thườ
2.36 Giả sử trung tâm tìm việc làm của một trường đại học gửi bảng câu h n m ỏi đế ộ ẫ t m u các cử ngh nhân QTKD đề
ị cung cấp thông tin về lương tháng khởi điểm. Bảng dưới đây trình bày
dữ liệu thu thập được : Cử nhân 1 2 3 4 5 6 7 8 9 10 11 12
Lương khởi điểm 2850 2950 3050 2880 2755 2710 2890 3130 2940 3325 2920 2880
Hãy vẽ biểu đồ hình h p. D ộ
ữ liệu này có quan sát b ng hay không? ất thườ
2.37 Báo Mua & Bán nhận đăng quảng cáo về b ng s ất độ ả ằ
n n m ở khắp vùng Đông Nam Bộ. Giá công b c
ố ủa 22 bất động sản được trình bày dưới đây. Giá tính bằng triệu đồng. 1500 895 719 619 625 4450 2200 1280 700 619 725 739 799 2495 1395 2995 880 3100 1699 1120 1250 912
a) Tìm năm con số tóm tắt.
b) Tính các giới hạn dưới và trên.3
c) Bất động sản có giá cao nhất, 4.450 triệu đồng, có được xem là quan sát bất thường hay không? Hãy giải thích.
d) Bất động sản có giá cao nhất thứ hai đượ
c công bố là 3.100 triệu đồng, có được xem là
quan sát bất thường hay không? Hãy giải thích.
e) Hãy vẽ biểu đồ hình hộp.
2.38 Doanh thu hàng năm, bằng triệu đô-la, của 21 công ty dược như sau: 8404 1374 1872 8879 2459 11413 608 14138 6452 1850 2818 1356 10498 7478 4019 4341 739 2127 3653 5794 8305
a) Tìm năm con số tóm tắt.
b) Tính các giới hạn dưới và trên.
3 Hàng rào chắn trong dưới và trên 11
c) Dữ liệu này có quan sát b ng hay không? ất thườ
d) Doanh thu của Johnson & Johnson là lớn nhất trên danh sách ở mức 14.138 triệu đô-la. Giả sử mộ ỗ t l ữ
i ghi chép d liệu (hoán vị) đã xảy ra và doanh thu được đưa vào là 41.138
triệu đô-la. Phương pháp phát hiệ ất thườ n quan sát b
ng ở câu c) có nhận ra vấn đề này và
cho phép hiệu chỉnh l i ghi chép d ỗ ữ liệu này hay không?
e) Hãy vẽ biểu đồ hình hộp.
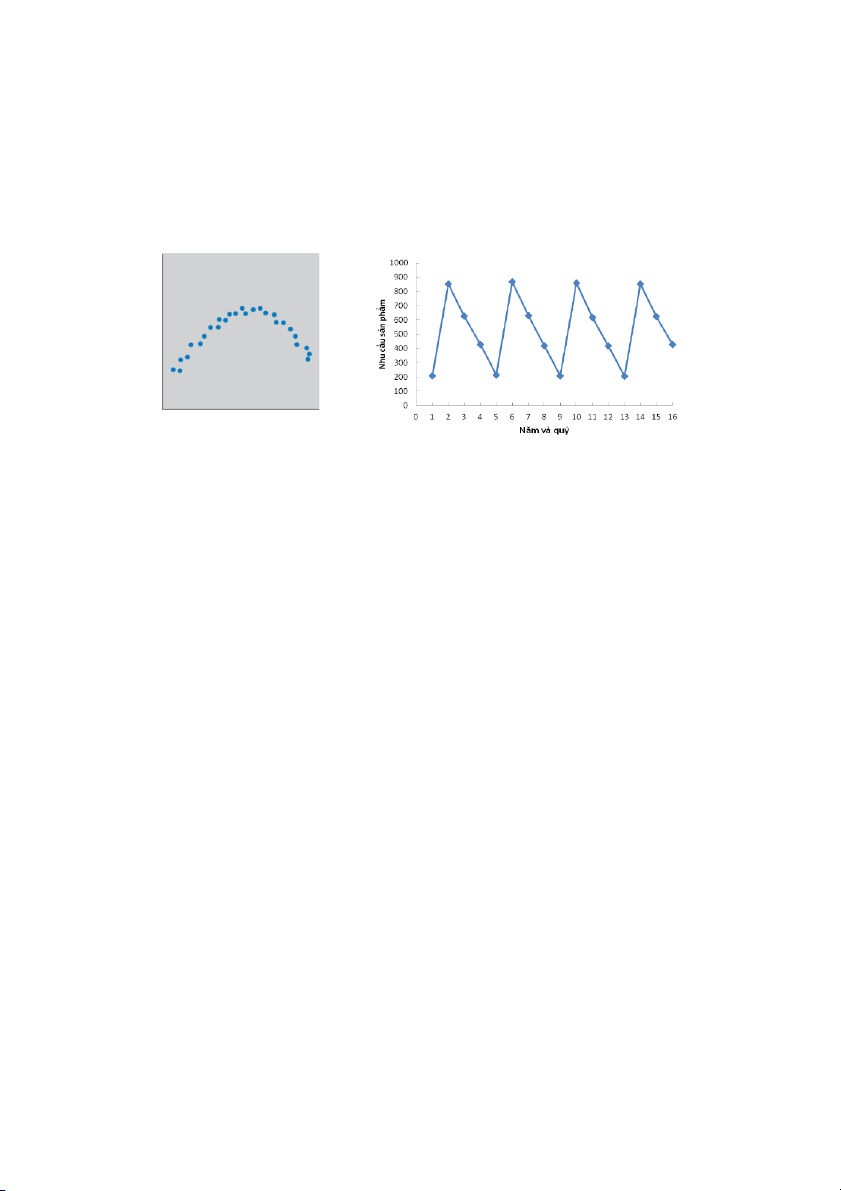
2.39 Hệ số tương quan ở
2 hình dưới đây là bao nhiêu?
2.40 Công ty RHM muốn nghiên cứu mối quan hệ giữ ố
a s công nhân, X, và số bàn, Y, được
sản xuất ở nhà máy của mình. Công ty lấy m t m ộ
ẫu ngẫu nhiên 10 ngày sản xuất. Các kết hợp
điểm (X; Y) sau đây thu được:
(12; 200) (30; 600) (15; 270) (24; 500) (14; 210)
(18; 300) (28; 610) (26; 540) (19; 320) (27; 570) a) Tính hiệp phương sai
b) Tính hệ số tương quan c) Bàn vắn tắt m i quan h ố ệ giữa s công nhân và s ố bàn s ố ản xuất m i ngày ỗ 12 Bài tập chương 3 XÁC SUẤT CĂN BẢN
3.1 Lấy ngẫu nhiên từ một lô hàng ra bốn sản phẩm và ta quan tâm đến số phế phẩm trong 4 sản phẩm đó.
a) Xác định các biến cố sơ cấp.
b) Biểu diễn các biến cố sau theo các biến cố sơ cấp: có nhiều nhất 1 phế phẩm, có ít nhất 1
phế phẩm, có ít nhất 2 phế phẩm.
c) Chỉ rõ các biến cố xung khắc và các biến cố đối lập trong các biến cố thu được.
3.2 Một tập hợp chứng khoán (cổ phiếu, trái phiếu, …) do một cá nhân hay một tổ chức nắm giữ được gọi là
. Một nhà đầu tư muốn đầu tư 2.000$ vào mỗi cổ phiếu trong năm loại cổ danh mục
phiếu khác nhau và đã xác định mười loại cổ phiếu khác nhau mà bà tin tưởng sẽ là những loại
đầu tư vững chắc. Bà có thể thiết lập được bao nhiêu danh mục khác nhau gồm năm loại cổ
phiếu từ danh sách gồm mười loại cổ phiếu của mình?
3.3 Xét tổng thể gồm các tài khoản tiết kiệm tại một ngân hàng mới sau đây: Số tài khoản 0001 0002 0003 0004 0005 Số dư tài khoản 1.000$ 12.500$ 850$ 1.000$ 3.450$
Giả sử bạn muốn lấy một mẫu ngẫu nhiên gồm hai tài khoản từ tổng thể này.
a) Liệt kê tất cả các cặp tài khoản khác nhau có thể có được
b) Xác suất chọn được các tài khoản 0001 và 0004 là bao nhiêu?
c) Xác suất chọn được hai tài khoản, mỗi tài khoản có số dư bằng 1.000$ là bao nhiêu? Mỗi
tài khoản có số dư khác 1.000$ là bao nhiêu?
3.4 Mỗi vé số có 5 chữ số. Tìm xác suất để một người mua một vé được vé:
a) có 5 chữ số khác nhau.
b) có 5 chữ số đều là lẻ.
3.5 Một phòng máy có 3 máy tính, người ta quan tâm đến số máy hỏng trong mỗi ngày.
a) Xác định tập các biến cố sơ cấp.
b) Biểu diễn các biến cố sau theo các biến cố sơ cấp: - có 1 máy hỏng. - cả 3 máy đều hỏng.
3.6 Từ một tổ gồm 9 nam và 6 nữ, ta chọn ngẫu nhiên ra 5 người. Tìm xác suất: a) chọn được 3 nam. b) chọn được 3 nữ. c) chọn được 1 nam d) chọn được 5 nữ. e) chọn được 5 nam.
3.7 Công ty sử dụng hai hình thức quảng cáo là đài phát thanh và vô tuyến truyền hình. Giả sử
25% khách hàng nắm được thông tin này qua vô tuyến truyền hình, 34% khách hàng nắm được
thông tin qua đài phát thanh và 10% khách hàng nắm được thông tin qua cả hai hình thức quảng
cáo. Tìm xác xuất để chọn ngẫu nhiên 1 khách hàng thì người đó nắm được thông tin về sản phẩm của công ty. 13
3.8 Đoàn thanh nhiên tổ chức vui chơi, kết hợp quay số có thưởng. Ban tổ chức đã phát ra 1000
vé (được đánh số từ 000 đến 999). Tìm xác suất để khi quay giải nhất ta nhận được:
a) vé có chữ số hàng đơn vị chẵn.
b) vé có 3 chữ số khác nhau.
c) vé có chữ số đầu tiên là 8 và 2 chữ số còn lại khác nhau.
d) vé có 3 chữ số trùng nhau.
3.9 Bảng số xe tại TP. HCM có 4 chữ số. Chọn ngẫu nhiên một bảng số xe. Tính xác suất chọn được bảng số xe:
a) có 4 chữ số khác nhau.
b) có 2 chữ số trùng nhau (giống nhau).
c) có 2 cặp chữ số trùng nhau (2233; 4114; …).
d) có 3 chữ số trùng nhau.
e) có 4 chữ số trùng nhau.
3.10 Có 8 người lên 3 toa tàu. Tìm xác suất để:
a) Cả 8 người lên cùng một toa.
b) Mỗi toa có ít nhất một người.
3.11 Có 30 sản phẩm trong đó có 3 phế phẩm được bỏ ngẫu nhiên vào 3 hộp, mỗi hộp 10 sản
phẩm. Tìm xác xuất để:
a) Có một hộp chứa một phế phẩm.
b) Mỗi hộp chứa một phế phẩm.
3.12 Một chuỗi nhà hàng hamburger nhận thấy rằng 75% khách hàng sử dụng tương mù tạc,
80% sử dụng nước xốt cà chua nấm, và 65% sử dụng được cả hai loại.
a) Xác suất để một khách hàng sẽ sử dụng ít nhất một loại là bao nhiêu?
b) Xác suất để một người sử dụng nước xốt cà chua nấm sử dụng tương mù tạc và một
người sử dụng tương mù tạc sử dụng nước xốt cà chua nấm là bao nhiêu?
3.13 Để kiểm tra chất lượng sản phẩm người ta lấy ra một lô 50 sản phẩm, rồi từ lô đó lấy
ngẫu nhiên 10 sản phẩm. Biết trong lô có 5 phế phẩm. Nếu trong 10 sản phẩm lấy ra có nhiều
nhất 1 phế phẩm thì lô được xếp đạt chất lượng, ngược lại nếu có nhiều hơn 1 phế phẩm lô phải
xếp không đạt chất lượng. Tìm xác xuất để lô đạt chất lượng và xác xuất để lô không đạt chất lượng.
3.14 Hai vận động viên A và B của địa phương Z tham gia giải bóng bàn đơn nữ toàn quốc.
Khả năng lọt qua vòng loại để vào vòng chung kết của từng người tương ứng là 80% và 60%
(mỗi bảng chỉ chọn một người vào vòng chung kết và hai vận động viên A, B không cùng trong
một bảng đấu loại). Tìm khả năng xảy ra các tình huống sau:
a) Cả hai lọt vào vòng chung kết.
b) Có ít nhất một người lọt vào vòng chung kết.
c) Chỉ có vận động viên A lọt vào vòng chung kết.
3.15 Ba công nhân cùng sản xuất một loại sản phẩm, xác suất để người thứ nhất và người thứ
hai làm ra chính phẩm bằng 0,9. Còn xác suất để người thứ 3 làm ra chính phẩm bằng 0,8. Một
người trong số đó làm ra 8 sản phẩm, thấy có 2 phế phẩm. Tìm xác suất để trong 8 sản phẩm tiếp
theo cũng do người đó sản xuất sẽ có 6 chính phẩm.
3.16 Lớp học của Nam có 80 sinh viên và sẽ được chia thành 20 nhóm thực tập. Trong lớp có
3 cô Liên, Hoa, Phượng khá xinh. Tìm xác suất để cho:
a) Nam cùng nhóm thực tập với Liên. 14
b) Nam cùng nhóm thực tập với Liên hay Hoa.
c) Nam cùng Liên, Hoa, Phượng hợp thành một nhóm.
3.17 Trong lô hàng 10 chiếc máy tính mới có 3 chiếc bị lỗi, lấy ngẫu nhiên ra 4 chiếc. Gọi Y là
số máy tính bị lỗi trong 4 chiếc lấy ra. Hãy:
a) Lập bảng phân phối xác suất của Y.
b) Khi lấy ra 4 chiếc thì có mấy chiếc bị lỗi là có khả năng xảy ra cao nhất?
c) Tìm xác suất khi lấy ra 4 chiếc sẽ bị ít nhất 1 chiếc lỗi.
d) Nếu người mua lấy ngẫu nhiên ra 3 chiếc để kiểm tra, thấy không có chiếc nào bị lỗi thì
sẽ chấp nhận cả lô hàng. Tìm xác suất người mua chấp nhận lô hàng; bác bỏ lô hàng.
3.18 Thống kê 2000 sinh viên một khoá của một trường ĐH theo giới tính và ngành học thu
được các số liệu sau: Nam Nữ Học kinh tế 400 500 Học quản trị kinh doanh 800 300
Lấy ngẫu nhiên một sinh viên khoá đó. Tìm xác suất để được a) nam sinh viên b) sinh viên học kinh tế
c) hoặc nam sinh viên hoặc học kinh tế
d) nam sinh viên và học kinh tế
e) Nếu đã chọn được một nam sinh viên thì xác suất để người đó học kinh tế bằng bao nhiêu?
3.19 Trong một cơ quan điều tra người ta dùng máy dò tìm tội phạm, kinh nghiệm cho biết cứ
10 người bị tình nghi thì 7 người là tội phạm.
− Máy báo đúng người có tội với xác suất 0,85.
− Máy báo sai người vô tội với xác suất 0,1.
Một người được máy phân tích. Hãy tính xác xuất:
a) Người này là tội phạm.
b) Máy báo người này là tội phạm.
c) Người này thực sự có tội, biết rằng máy đã báo có tội. d) Máy báo đúng.
3.20 Chọn ngẫu nhiên một gia đình có 3 con. Tính xác suất để gia đình này có 2 con trai nếu được thông báo rằng:
a) Gia đình này có ít nhất 1 con gái.
b) Đứa con cả là con gái.
3.21 Một thủ kho có một chùm chìa khóa gồm 9 chiếc bề ngoài giống hệt nhau, trong đó chỉ
có hai chiếc mở được cửa kho. Anh ta thử ngẫu nhiên từng chìa (chìa nào không trúng thì bỏ ra).
Tính xác suất để anh ta mở được cửa ở lần thử thứ ba.
3.22 Một người mua ba loại cổ phiếu khác nhau với xác suất để trong phiên giao dịch tới các
loại cổ phiếu này lên giá tương ứng là 1/3, 3/4 và 1/10. Tìm xác suất để trong phiên giao dịch tới
a) Tất cả các cổ phiếu đều lên giá.
b) Không có cổ phiếu nào lên giá.
c) Chỉ có một cổ phiếu lên giá.
d) Chỉ có hai cổ phiếu lên giá.
e) Có ít nhất một cổ phiếu lên giá. 15
f) Có ít nhất hai cổ phiếu lên giá.
3.23 Trước khi đưa sản phẩm ra thị trường người ta đã phỏng vấn ngẫu nhiên 200 khách hàng
về sản phẩm và thấy có 34 người trả lời “sẽ mua”, 96 người trả lời “có thể sẽ mua” và 70 người
trả lời “không mua”. Kinh nghiệm cho thấy tỷ lệ khách hàng thực sự sẽ mua sản phẩm tương ứng
với những cách trả lời trên là 40%, 20% và 1%
a) Hãy đánh giá thị trường tiềm năng của sản phẩm đó.
b) Trong số khách hàng thực sự mua sản phẩm thì có bao nhiêu phần trăm trả lời “sẽ mua”?
3.24 Tại công ty DuPond, một điều tra gần đây đã phát hiện 55% nam nhân viên của công ty
ủng hộ các khả năng lựa chọn công việc linh hoạt. Một người phân tích nhân sự chọn ngẫu nhiên 8 nam nhân viên
để phỏng vấn. Không người nào được phỏng vấn nhiều hơn một lần.
a) Xác suất để 5 trong số 8 nam nhân viên ủng hộ các khả năng lựa chọn công việc linh hoạt là bao nhiêu?
b) Xác suất để không ai trong số 8 nam nhân viên ủng hộ các khả năng lựa chọn công việc linh hoạt là bao nhiêu?
c) Xác suất để có ít nhất 6 nam nhân viên ủng hộ các khả năng lựa chọn công việc linh hoạt là bao nhiêu?
3.25 Một ngân hàng phân loại những người đi vay là rủi ro cao và rủi ro thấp. Chỉ có 15% các
khoản cho vay được cấp cho những người trong nhóm rủi ro cao. Trong số tất cả các khoản cho
vay, 5% không được hoàn trả (hay bị vỡ nợ), và 40% các khoản vay bị vỡ nợ là cấp cho những
người trong nhóm rủi ro cao. Xác suất để một người cho vay có rủi ro cao sẽ vỡ nợ là bao nhiêu?
3.26 Một ngân hàng địa phương đã xem xét lại chính sách thẻ tín dụng với mục đích thu hồi
một số thẻ tín dụng của mình. Trước đó khoảng 5% người có thẻ vỡ nợ, làm cho ngân hàng
không thể thu hồi số dư nợ. Do đó, ban giám đốc ấn định một xác suất tiên nghiệm bằng 0,05 để
người có thẻ cá biệt nào đó vỡ nợ. Ngân hàng này cũng nhận thấy xác suất không thanh toán
hàng tháng là 0,20 đối với những khách hàng không bị vỡ nợ. Dĩ nhiên, suất không thanh toán
hàng tháng đối với những khách hàng bị vỡ nợ là 1.
a) Căn cứ vào chỗ một khách hàng đã không thanh toán hàng tháng một hay nhiều lần, hãy
tính xác suất hậu nghiệm để khách hàng đó sẽ vỡ nợ.
b) Ngân hàng muốn thu hồi thẻ của mình nếu xác suất để một khách hàng sẽ vỡ nợ lớn hơn
0,20. Ngân hàng có nên thu hồi thẻ của mình nếu khách hàng không thanh toán hàng
tháng hay không? Tại sao và tại sao không?
3.27 Dữ liệu về 30 quỹ cân bằng lớn nhất cung cấp tỷ suất sinh lợi một năm và năm năm trong
giai đoạn kết thúc vào ngày 31/3/2000. Giả sử bạn xem xét tỷ suất sinh lợi một năm vượt quá
50% là cao và tỷ suất sinh lợi năm năm vượt quá 300% là cao. 9 quỹ có tỷ suất sinh lợi một năm
vượt quá 50%, 7 tỷ suất sinh lợi năm năm vượt quá 300%, và 5 quỹ vừa có tỷ suất sinh lợi một
năm vượt quá 50% vừa có tỷ suất sinh lợi năm năm vượt quá 300%.
a) Xác suất của tỷ suất sinh lợi một năm cao là bao nhiêu và xác suất của tỷ suất sinh lợi năm năm cao là bao nhiêu?
b) Xác suất của cả tỷ suất sinh lợi một năm cao lẫn tỷ suất sinh lợi năm năm cao là bao nhiêu?
c) Xác suất của tỷ suất sinh lợi một năm không cao mà tỷ suất sinh lợi năm năm cũng không cao là bao nhiêu?
d) Xác suất của tỷ suất sinh lợi năm năm cao khi biết biến cố tỷ suất sinh lợi một năm cao đã xảy ra là bao nhiêu?
e) Các biến cố tỷ suất sinh lợi năm năm cao và tỷ suất sinh lợi một năm cao có độc lập với nhau không? 16
3.28 Một công ty đầu tư tín thác có 6 quỹ đầu tư vào thị trường Việt Nam và 4 quỹ đầu tư vào
các thị trường tế. Một khách hàng muốn đầu tư vào 2 quỹ của Việt Nam và 2 quỹ quốc tế.
a) Công ty này có bao nhiêu tập hợp quỹ khác nhau để nhà đầu tư đó có thể lựa chọn?
b) Nhà đầu tư không biết là một trong các quỹ của Việt Nam và một quỹ quốc tế sẽ thực
hiện rất kém trong năm tới. Nếu nhà đầu tư đó chọn các quỹ để mua một cách ngẫu
nhiên, xác suất để có ít nhất một trong các quỹ được chọn sẽ thực hiện rất kém trong năm tới là bao nhiêu?
3.29 Các quảng cáo trên báo bất động sản cho biết 64% nhà biệt thự cần bán có ga ra ô tô,
21% có hồ bơi, và 17% có cả hai. Tính xác suất để một nhà biệt thự cần bán có:
a) một hồ bơi hoặc một ga ra ô tô
b) không hồ bơi mà cũng không ga ra ô tô
c) một hồ bơi nhưng không ga ra ô tô
3.30 Một hãng sản xuất vỏ xe gần đây thông báo thu hồi vì 2% vỏ xe của hãng bị hư hỏng.
Nếu bạn vừa mua một bộ 4 vỏ xe mới của hãng sản xuất này, xác suất để có ít nhất một trong số
4 vỏ xe mới bị hư hỏng là bao nhiêu?
3.31 Để xúc tiến bán
promotion), công ty Pepsi đặt biểu tượng trúng thưởng bên hàng (sales
dưới nắp chai cho 10% số chai Pepsi. Nếu bạn mua một túi 6 chai Pepsi, xác suất để bạn trúng thưởng là bao nhiêu?
3.32 Trong khi xây dựng chính sách bảo hàn của mình, một công ty ô tô ước h hời tính trong t
gian 1 năm 17% số xe mới của công ty cần sửa chữa một lần, 7% cần sửa chữa hai lần, và 4%
cần sử chữa ba lần hay nhiều hơn. Nếu bạn mua một chiếc xe mới của công ty này, hãy tính xác
suất để chiếc xe của bạn:
a) không cần phải sửa chữa
b) cần không nhiều hơn một lần sửa chữa c) cần sửa chữa
3.33 Nếu bạn mua hai chiếc xe mới, tính xác suất để
a) cả hai chiếc xe đều không cần sửa chữa
b) cả hai chiếc xe đều cần sửa chữa
c) có ít nhất một chiếc cần sửa chữa
3.34 Bạn đã dùng quy tắc nhân để tính các xác suất sửa chữa ch chiếc xe của bạn ở Bài tập o 3.32.
a) Điều gì phải đúng về các chiếc xe của bạn để làm cho phương pháp này có căn cứ vững chắc?
b) Bạn nghĩ giả định này có hợp lý không? Hãy giải thích.
3.35 Một công ty gần đây đã thay thế máy phục vụ thư điện tử (e-mail) vì trước đó các giao
dịch thư tử bị gián đoạn khoảng 15% trong những ngày thường. Để thấy tình hình xấu đến mức
nào, hãy tính xác suất để trong một tuần làm việc 5 ngày, hẳn sẽ có sự cố gián đoạn các giao dịch thư điện tử.
a) Vào thứ Hai và lần nữa vào thứ Ba?
b) Với lần đầu tiên vào thứ Năm? c) Hàng ngày?
d) Ít nhất là một lần trong tuần? 17
3.36 Một công ty xây dựng dự thầu hai hợp đồng. Xác suất trúng thầu hợp đồng hợp đồng A là
0,3. Nếu công ty trúng thầu hợp đồng A thì xác suất trúng thầu hợp đồng B là 0,4. Nếu công ty
không trúng thầu hợp đồng A, thì xác suất trúng thầu hợp đồng B giảm còn 0,2. Tìm xác suất của các biến cố sau:
a) Trúng thầu cả hai hợp đồng
b) Trúng thầu đúng một hợp đồng
c) Trúng thầu ít nhất một hợp đồng
3.37 Người giám sát dịch vụ khách hàng định kỳ tiến hành điều tra sự thỏa mãn của khách
hàng. Kết quả của điều tra mới nhất cho biết 8% khách hàng không thỏa mãn với dịch vụ họ
nhận được ở lần đến cửa hàng gần đây nhất của mình. Trong số những người không thỏa mãn,
chỉ 22% quay trở lại cửa hàng trong vòng một năm. Trong số những người thỏa mãn, 64% quay
trở lại cửa hàng trong vòng một năm. Một khách hàng vừa đi vào cửa hàng. Đáp lại câu hỏi của
bạn, người này nói cho bạn biết kể từ lần đến cửa hàng gần đây nhất của mình đến nay chưa
được một năm. Xác suất để người này thỏa mãn với dịch vụ nhận được là bao nhiêu?
3.38 Các nhà nghiên cứu đã phát triển các mô hình thống kê dựa trên các tỷ số tài chính để dự
đoán một công ty có bị phá sản trong vòng 12 tháng tới hay không. Trong một thử nghiệm một
mô hình như vậy, mô hình này đự đoán đúng sự phá sản của 85% số công ty mà trên thực tế phá
sản và nó đự đoán đúng sự không phá sản cho 74% số công ty mà trên thực tế không phá sản.
Giả sử là chúng ta kỳ vọng 8% số công ty ở một thành phố sẽ bị phá sản trong năm tới. Giả sử là mô h oán công ty ình này dự đ
của bạn sẽ bị phá sản. Xác suất để công ty của bạn sẽ bị phá sản
trong vòng 12 tháng tới là bao nhiêu? 18
Bài tập chương 4.1
BIẾN NGẪU NHIÊN VÀ CÁC PHÂN PHỐI XÁC SUẤT RỜI RẠC THÔNG DỤNG
4.1 Một công ty phần mềm máy tính phải quyết định lựa chọn mộ chiến lược quảng t trong hai
cáo: hoặc quảng cáo trên tivi hoặc quảng cáo trên báo. Phòng Marketing dự đoán về doanh thu
bán hàng và xác suất xảy ra chúng sau khi áp dụng mỗi hình thức quảng cáo như sau: Quảng cáo trên tivi Quảng cáo trên báo
Doanh thu bán (tỷ đồng) Xác suất (%) Doanh thu bán (tỷ đồng) Xác suất (%) 8 0,2 8 0,3 10 0,3 12 0,4 12 0,3 16 0,3 14 0,2
Biết tỷ suất lợi nhuận của công ty bằng 50% doanh thu bán hàng.
a. Tính lợi nhuận kỳ vọng của mỗi chiến dịch quảng cáo.
b. Tính độ lệch chuẩn phân bố lợi nhuận của mỗi chiến dịch quảng cáo.
c. Chiến lược quảng cáo nào có rủi ro cao hơn?
d. Hãng lựa chọn chiến lược nào?
4.2 Các công ty bảo hiểm sử dụng các bảng tỷ lệ tử vong để giúp họ xác định số phí bảo hiểm
tính cho một cá nhân cụ thể ứng với một chính
sách bảo hiểm nhân thọ cụ thể là bao nhiêu. Bảng
sau đây cho ta thấy xác suất xác suất sống đến tuổi 65 của những người có tuổi đã xác định. TUỔI XÁC SUẤT SỐNG TUỔI XÁC SUẤT SỐNG ĐẾN TUỔI 65 ĐẾN TUỔI 65 0 0,72 40 0,77 10 0,74 45 0,79 20 0,74 50 0,81 30 0,75 55 0,85 35 0,76 60 0,90
Nguồn: Bộ Y tế, Giáo dục và Anh sinh Hoa kỳ, Cục Y tế Công cộng, Trung tâm Thống kê Y tế
Quốc gia, United States Life Tables (các Bảng tính tuổi thọ Hoa Kỳ): 1969 -71 (1973)
a) Với một người 20 tuổi, xác suất để người này sẽ chết trước tuổi 65 là bao nhiêu?
b) Hãy mô tả bằng lời xu hướng được chỉ ra bởi xác suất ngày càng tăng ở các cột thứ hai và thứ tư.
4.3 Theo một điều tra về xã hội học cho thấy tỷ lệ sinh viên học tập không đúng với ngành nghề
mà họ yêu thích là 34%. Một lớp gồ
ên. Gọi X là số sinh viên không theo đúng ngành m 60 sinh vi
nghề yêu thích trong 60 sinh viên này. Hãy:
a) Mô tả quy luật phân phối của X.
b) Về trung bình thì trong 60 sinh viên sẽ có bao nhiêu sinh viên không thích ngành đang học.
c) Có bao nhiêu sinh viên không
thích ngành đang học là có khả năng nhất? 19
4.4 Một tổ gồm 12 người, trong đó có 5 nữ. Cần cử 4 người đi làm một việc. Để công bằng
người ta đã thực hiện chọn ngẫu nhiên. Gọi X là số nữ trong 4 người được chọn. Hãy:
a) Lập bảng phân phối xác suất của X.
b) Viết biể thức hàm phân phối của X. u
c) Tính EX, DX, ModX, E(3X 2), D(5 – 3X) –
4.5 Xác suất trúng số là 1%. Mỗi tuần mua một vé số. Hỏi phải mua vé số liên tiếp trong tối thiểu
bao nhiêu tuần để có không ít hơn 95% hy vọng trúng số ít nhất 1 lần?
4.6 Trong một nước có 50% y vọng trong h
năm sẽ không bị thiên tai. Tính xác suất trong năm nay sẽ có: a) đúng 1 thiên tai. b) ít nhất 2 thiên tai.
c) trung bình trong 10 năm có bao nhiêu thiên tai?
4.7 Một xe cam có 1000 trái, trong đó có 100 trái hư.
a) Một người chọn không hoàn lại 10 trái. Tính xác suất chọn được 10 trái tốt.
b) Nếu chọn có hoàn lại, tính xác suất trên.
4.8 Một nữ công nhân quản lý 12 máy dệt. Xác suất để mỗi máy trong khoảng thời gian t cần đến
sự chăm sóc của nữ công nhân là 1/3. Tính xác suất:
a) Trong khoảng thời gian t có 4 máy cần đến sự chăm sóc của nữ công nhân.
b) Trong khoảng thời gian t có từ 3 đến 6 máy cần đến sự chăm sóc của nữ công nhân.
4.9 Trong một lô hàng có 800 sản phẩm loại 1 và 200 sản phẩm loại 2. Lấy ngẫu nhiên ra 5 sản
phẩm theo phương thức có hoàn lại. Gọi X là số s ản phẩm loại 1 lấy được.
a) X tuân theo quy luật gì? Viết biểu thức tổng quát của quy luật. b) Tìm E(X) và Var(X)
c) Tìm số sản phẩm loại 1 trung bình được lấy ra và tính khả năng để xảy ra điều đó.
4.10 Một kho hàng chuyên cung cấp hàng cho 12 cửa hàng. Xác suất để mỗi cửa hàng đặt
hàng cho kho đó trong ngày là 0,3. Tìm số đơn đặt hàng có khả năng nhiều nhất cho một ngày và
xác suất tương ứng với nó.
4.11 Nhà máy sản xuất 100.000 sản phẩm, trong đó có 30.000 sản phẩm loại 2. KCS đến kiểm
tra và lấy ra 500 sản phẩm để thử.
a) Trong 2 trường hợp chọn lặp và không lặp, hãy tính xác suất để số sản phẩm loại 2 mà KCS phát hiện ra (i) từ 145 đến 155 (ii) ít hơn 150
b) Tính lại trong trường hợp KCS phát hiện đúng sản phẩm loại 2 với xác suất 0,95 còn
nhận lầm loại 1 thành loại 2 với xác suất 0,15 (xét phép chọn lặp).
4.12 Tổng đài điện thoại phục vụ 100 máy điện thoại. Xác suất để trong mỗi phút mỗi máy gọi
đến tổng đài là 0,02. Tìm số máy gọi đến tổng đài trung bình trong 1 phút.
4.13 Số khách hàng vào một cửa hàng bách hoá trong một giờ là biến ngẫu nhiên tuân theo
quy luật Poisson với mật độ (số khách trung bình) là 8 khách hàng trong 1 giờ. Tìm xác suất để
trong một giờ nào đó có hơn 4 khách vào.
4.14 Để thanh toán 1 triệu đồng tiền hàng, một khách hàng gian lận đã xếp lẫn 5 tờ 50 ngàn
đồng tiền giả với 15 tờ tiền thật. Chủ cửa hàng rút ngẫu nhiên 3 tờ giấy bạc đem đi kiểm tra và 20
giao hẹn nếu phát hiện có bạc giả thì cứ mỗi tờ giả khách hàng phải đền hai tờ thật. Tìm số tiền
phạt mà khách có thể phải trả.
4.15 Biết rằng tính trung bình có 3 khách hàng đến giao dịch với Ngân hàng mỗi phút trong
khoảng thời gian mở cửa thêm sau giờ làm việc từ 17g chiều đến 19g tối. Vậy thì xác suất để có
đúng 2 khách hàng đến giao dịch với Ngân hàng trong mỗi phút vào giờ làm việc thêm là bao
nhiêu? Khả năng sẽ có hơn một khách hàng đến trong khoảng thời gian 30 giây vào giờ này là bao nhiêu?
4.16 Hãng taxi M đã nghiên cứu nhu cầu gọi taxi tại một sân bay địa phương và nhận thấy
rằng trung bình mỗi giờ có 6 chiếc taxi được khách gọi. Nếu phòng điều độ của hãng quyết định
thường trực đặt 6 xe tại sân bay trong vòng mỗi giờ đồng hồ, hãy xác định khả năng thiếu xe để
phục vụ khiến cho có khách phải chờ xe tại sân bay là bao nhiêu?
4.17 Một công ty thuê một luật sư trong một vụ kiện với hai phương án trả công như sau:
- Phương án 1: 5 triệu đồng bất kể thắng hay thua kiện
- Phương án 2: 15 triệu đồng nếu thắng kiện và 100 ngàn đồng nếu thua kiện
Luật sư đã chọn phương án trả công thứ hai. Vậy theo đánh giá của luật sư xác suất thắng
kiện của công ty đó tối thiểu là bao nhiêu? 4.18 Phân ph c
ối xác suất ủa lương tháng Y (triệu đồng) và giới tính X của công nhân một công ty như sau: Y 0,5 1 1,5 X Nữ: 0 0,1 0,3 0,2 Nam: 1 0,06 0,18 0,16
a) Tìm phân phối xác suất của lương tháng của nữ công nhân.
b) Hãy cho biết lương tháng của công nhân có tương quan với giới công nhân ha tính của y
không và mức độ tương quan chặt chẽ đến đâu.
4.19 Thu nhập hàng năm của các cặp vợ chồng được lập bảng phân phối xác suất đồng thời (hay chung) như sau: Y X 10 20 30 40 10 0,2 0,04 0,01 0 20 0,1 0,36 0,09 0 30 0 0,05 0,1 0 40 0 0 0 0,05
trong đó: X là thu nhập của chồng (triệu đồng/năm)
Y là thu nhập của vợ (triệu đồng/năm)
Tìm phân phối biên của mỗi thành phần
4.20 Giá cổ phiếu A và B là các biến ngẫu nhiên XA và XB (Đơn vị: ngàn đồng) có bảng phâ n
phối xác suất đồng thời như sau: XA 15 16 17 21 XB 15 0,15 0,2 0,25 17 0,05 0,2 0,15
a) Tính giá trị trung bình của các cổ phiếu trên
b) XA và XB có độc lập với nhau hay không?
c) Khả năng để giá cổ phiếu B cao hơn giá trung bình của cổ phiếu A là bao nhiêu?
d) Cổ phiếu nào có mức độ rủi ro cao hơn.
4.21 Khi đầu tư vào hai thị trường A và B, lãi xuất XA và XB (Đơn vị: %) là các biến ngẫu
nhiên có bảng phân phối xác suất đồng thời như sau: XA -1 3 5 XB -2 0,05 0,1 0,15 3 0,1 0,2 0,15 6 0,1 0,1 0,05
a) Muốn có lãi suất hơn 3% thì ên lựa chọn n
phương án nào trong số các phương án sau:
+ Phương án 1: Đầu tư toàn bộ vào A
+ Phương án 2: Đầu tư toàn bộ vào B
+ Phương án 3: Chia đều vốn đầu tư vào A và B
b) Tìm lãi suất trung bình khi đầu tư vào thị trường B, biết năm đó lãi suất thị trường A là 3%.
c) Nếu muốn giảm rủi ro đầu tư xuống mức tối thiểu thì nên đầu tư như thế nào?
4.22 Lãi suất hàng năm của trái phiếu T và cổ phiếu S của một công ty có bảng phân phối xác suất như sau: S -10% 0 10% 20% P(T) T 6% 0 0 0,1 0,1 0,2 8% 0 0,1 0,3 0,2 0,6 10% 0,1 0,1 0 0 0,2 P(S) 0,1 0,2 0,4 0,3 1
Nếu muốn đầu tư tiền vào cả trái phiếu và cổ phiếu thì nên đầu tư theo tỷ lệ bao nhiêu để:
a) Lãi suất kỳ vọng thu được là lớn nhất
b) Độ rủi ro về lãi suất là nhỏ nhất
4.23 Lãi xuất đầu tư vào hai thị trườ
các biến ngẫu nhiên độc lập và cùng phân ng A và B là
phối với trung bình là 10% và 9%; độ lệch chuẩn là 4% và 3%.
a) muốn có lãi suất trên 8% thì nên chọn phương án nào trong các phương án sau:
+ Phương án 1: Đầu tư toàn bộ vào A
+ Phương án 2: Đầu tư toàn bộ vào B
+ Phương án 3: Chia đều vốn đầu tư vào hai thị trường
b) Nếu muốn rủi ro về lãi suất là nhỏ nhất thì nên đầu tư như thế nào?
4.24 Trong lô hàng có 6 chính phẩm và 4 phế phẩm. Lấy ngẫu nhiên ra 2 sản phẩm:
a) Phân phối xác suất của số chính phẩm có thể được lấy ra có dạn như thế nào g ?
b) Tìm kỳ vọng toán và phương sai của số chính phẩm có thể được lấy ra. 22
4.25 Ở một thành phố 65% gia đình có tivi màu. Chọn ngẫu nhiên 12 gia đình và gọi X là số gia đình có tivi màu.
a) Gọi tên phân phối xác suất của X.
b) Tìm giá trị trung bình và độ lệch chuẩn của X.
c) Tính xác suất để có đúng 5 gia đình có tivi màu.
4.26 Bạn đang nỗ lực xây dựng một chiến lược đầu tư vào hai cổ phiếu khác nhau. Mức sinh
lời hàng năm dự kiến với 1.000$ đầu tư vào mỗi cổ phiếu trong bốn tình trạng kinh tế khác nhau có phân p hối xác suất sau đây: Mức sinh lời Xác suất
Tình trạng kinh tế Cổ phiếu X Cổ phiếu Y 0,1 Suy thoái -100 50 0,3 Tăng trưởng chậm 0 150 0,3 Tăng trưởng vừa phải 80 -20 0,3 Tăng trưởng nhanh 150 -100 Hãy tính:
a) Mức sinh lời kỳ vọng của cổ phiếu X và cổ phiếu Y.
b) Độ lệch chuẩn về mức sinh lời của cổ phiếu X và cổ phiếu Y.
c) Hiệp phương sai của cổ phiếu X và cổ phiếu Y.
d) Bạn sẽ đầu tư vào cổ phiếu X hay cổ phiếu Y? Hãy giải thích.
e) Giả sử bạn muốn lập một danh mục bao gồm cổ phiếu X và cổ phiếu Y. Hãy tính mức sinh lời kỳ
vọng của danh mục và rủi ro của danh mục ứng với mỗi tỷ lệ % đầu tư vào cổ phiếu X sau: 30%;
50%; 70%. Bạn sẽ đề xuất chọn danh mục nào? Hãy giải thích.
4.27 Bạn dự định đầu tư 1.000$ vào quỹ trái phiếu công ty hay vào quỹ cổ phiếu thường. Thông tin
sau đây về mức sinh lời hàng năm (cho mỗi 1.000$) của mỗi loại đầu tư trong các tình trạng kinh tế khác
nhau, cùng với xác suất để mỗi tình trạng kinh tế này sẽ xảy ra: Mức sinh lời Xác suất
Tình trạng kinh tế Cổ phiếu X Cổ phiếu Y 0,01 Suy thoái mạnh -200 -999 0,09 Suy thoái -70 -300 0,15 Đình đốn 30 -100 0,35 Tăng trưởng chậm 80 100 0,30 Tăng trưởng vừa phải 100 150 0,10 Tăng trưởng nhanh 120 350 Hãy tính:
a) Mức sinh lời kỳ vọng của quỹ trái phiếu công ty và của quỹ cổ phiếu thường.
b) Độ lệch chuẩn về mức sinh lời của quỹ trái phiếu công ty và của quỹ cổ phiếu thường.
c) Hiệp phương sai của quỹ trái phiếu công ty và quỹ cổ phiếu thường.
d) Bạn sẽ đầu tư vào quỹ trái phiếu công ty hay quỹ cổ phiếu thường? Hãy giải thích.
e) Giả sử bạn muốn lập một danh mục bao gồm quỹ trái phiếu công ty và của quỹ cổ phiếu thường.
Hãy tính mức sinh lời kỳ vọng của danh mục và rủi ro của danh mục ứng trong mỗi tình huống sau đây:
i) Đầu tư 300$ vào quỹ trái phiếu công ty và 700$ vào quỹ cổ phiếu thường.
ii) Đầu tư 500$ vào mỗi quỹ.
iii) Đầu tư 700$ vào quỹ trái phiếu công ty và 300$ vào quỹ cổ phiếu thường.
iv) Bạn sẽ đề xuất chọn danh mục nào? Hãy giải thích.
Bài tập chương 4.2
CÁC PHÂN PHỐI XÁC SUẤT LIÊN TỤC THÔNG DỤNG 23
4.28 Sau một thời gian nghiên cứu, ban quản trị một công ty lắp ráp ôtô được biết thời gian
cần thiết của một công nhân lắp ráp bộ phận thân xe trung bình mất 75 giây, với độ lệch
chuẩn là 6 giây. Giả sử thời gian lắp ráp có phân phối chuẩn, tìm
a) Xác suất để một công nhân bất kỳ của nhà máy có thể lắp ráp bộ phận thân xe trong thời
gian ít hơn 75 giây hoặc nhiều hơn 81 giây.
b) Xác suất để một công nhân bất kỳ của nhà máy có thể lắp ráp bộ phận thân xe trong thời
gian từ 69 giây đến 81 giây.
c) Xác suất để một công nhân bất kỳ của nhà máy có thể lắp ráp bộ phận thân xe trong thời gian ít hơn 62 giây.
d) Xác suất để một công nhân bất kỳ của nhà máy có thể lắp ráp bộ phận thân xe trong thời
gian từ 62 giây đến 69 giây.
e) Thời gian mà 10% số công nhân có thể lắp ráp xong bộ phận thân xe.
f) Thời gian mà 50% số công nhân có thể lắp ráp xong bộ phận thân xe
4.29 Giả sử X là một biến ngẫu nhiên tuân theo phân phối chuẩn có giá trị trung bình là 15
và độ lệch chuẩn là 4, a) Tìm P(X < 19,8) b) Tìm P(X > 20,32) c) Tìm P(X < 9,2) d) Tìm P(X > 11)
e) Tìm P(19,8 < X < 20,32) f) Tìm P(9,2 < X < 11)
g) Nếu xác suất = 0,7 thì X sẽ nhỏ hơn số mấy?
h) Nếu xác suất = 0,25 thì X sẽ nhỏ hơn số mấy?
i) Nếu xác suất = 0,2 thì X sẽ lớn hơn số mấy?
j) Nếu xác suất = 0,6 thì X sẽ lớn hơn số mấy?
4.30 Theo Nielsen Media Research, trẻ em tuổi từ 12 đến 17 xem trung bình 3 giờ TV mỗi
ngày cho năm phát thanh kết thúc vào tháng Tám. Giả định là độ lệch chuẩn là 1 giờ và phân
phối của thời gian dùng để xem TV có phân phối dạng hình quả chuông.
a) Tỷ lệ phần trăm trẻ em tuổi từ 12 đến 17 xem TV trong khoảng từ 2 đến 3 giờ mỗi ngày là bao nhiêu?
b) Tỷ lệ phần trăm trẻ em tuổi từ 12 đến 17 xem TV trong khoảng từ 1 đến 4 giờ mỗi ngày là bao nhiêu?
c) Tỷ lệ phần trăm trẻ em tuổi từ 12 đến 17 xem TV nhiều hơn 4 giờ mỗi ngày là bao nhiêu?
4.31 Một nhà nghỉ có 1000 khách. Nhà ăn phục vụ bữa trưa làm hai đợt liên tiếp. Số chỗ
ngồi của nhà ăn phải ít nhất là bao nhiêu để xác suất của biến cố: “không đủ chỗ cho người đến ăn” nhỏ hơn 1%?
4.32 Thời gian làm việc của một linh kiện điện tử máy tính là một biến ngẫu nhiên có
trung bình là 250 giờ và độ lệch chuẩn là 250 giờ.
a) Giả sử ta dự trữ 30 linh kiện. Tính xác suất để 30 linh kiện này đủ dùng trong ít nhất 1 năm (8760 giờ).
b) Phải dự trữ ít nhất là bao nhiêu linh kiện để với xác suất 0,99 ta có thể đảm bảo cho máy
tính hoạt động ít nhất 1 năm?
4.33 Một người nuôi 50 con gà đẻ. Xác suất để 1 con đẻ trứng trong ngày là 70%.
a) Tính xác suất để trong ngày thu được ít nhất 40 trứng.
b) Theo anh/chị, làm thế nào để tính được xác suất 1 con gà đẻ trong ngày? 24
4.34 Một người nuôi 100 con gà đẻ. Xác suất để 1 con đẻ trứng trong ngày là 65%.
a) Tính xác suất để trong ngày thu được ít nhất 40 trứng.
b) Nếu muốn trung bình mỗi ngày thu được 120 trứng thì phải nuôi bao nhiêu con gà?
4.35 Có 5 máy sản xuất một loại sản phẩm, trong đó có 3 máy loại 1, 2 máy loại 2. Tỷ lệ
sản phẩm loại A do máy loại 1 sản xuất là 0,8; do máy loại 2 sản xuất là 0,6. Chọn ngẫu
nhiên 1 máy rồi từ máy đó sản xuất 100 sản phẩm.
a) Tính xác suất để để có ít nhất 70 sản phẩm sản xuất ra là sản phẩm loại A.
b) Giả sử được ít nhất 70 sản phẩm loại A, theo anh/chị các sản phẩm đó do máy nào sản xuất?
4.36 Trong một hội thi, công nhân dự thi sẽ chọn ngẫu nhiên 1 trong 2 máy, và với máy đã
chọn sản xuất 50 sản phẩm. Nếu số sản phẩm đạt yêu cầu loại A từ 40 trở lên thì đạt yêu cầu.
Giả sử với công nhân M, xác suất để sản xuất được sản phẩm loại A khi sử dụng máy thứ
nhất là 0,8; máy thứ 2 0,7.
a) Tìm xác suất để công nhân M đạt yêu cầu khi dự thi.
b) Nếu M dự thi 10 lần thì số lần đạt yêu cầu tin chắc nhất là bao nhiêu?
4.37 Nhà máy sản xuất 100.000 sản phẩm, trong đó có 30.000 sản phẩm loại 2. KCS đến
kiểm tra và lấy ra 500 sản phẩm để thử.
a) Trong hai trường hợp chọn lặp và không lặp, hãy tính xác suất để số sản phẩm loại 2 mà KCS phát hiện ra i. từ 145 đến 155 ii. ít hơn 150
b) Tính lại trong trường hợp KCS phát hiện đúng sản phẩm loại 2 với xác suất 0,95; còn
nhận lầm loại 1 thành loại 2 với xác suất 0,15 (xét phép chọn lặp).
4.38 Nhu cầu về một loại hàng hoá phân phối đều trong khoảng [30; 50] (tấn/tháng).
a) Xác định hàm mật độ xác suất.
b) Xác định hàm phân bố xác suất.
c) Tìm kỳ vọng toán và phương sai.
d) Vẽ đồ thị hàm mật độ xác suất và hàm phân bố xác suất.
e) Tìm xác suất để nhu cầu không vượt quá 45 tấn.
4.39 Thời gian phục vụ mỗi khách hàng tại một cửa hàng bách hoá là biến ngẫu nhiên X
tuân theo quy luật lũy thừa với hàm mật độ xác suất như sau: −5 5 x e vôùi x > 0 f ( ) x = 0 vôù i x < 0
Với x được tính bằng phút/khách hàng
a) Tìm xác suất để thời gian phục vụ một khách hàng nào đó sẽ nằm trong khoảng từ 0,4 đến 1 phút.
b) Tìm thời gian trung bình để phục vụ một khách hàng
4.40 Vòng đời của bóng đèn tuân theo phân phối mũ với giá trị trung bình bằng 1000 giờ.
Hãy tính xác suất để bóng đèn có vòng đời khoảng từ 600 đến 1500 giờ. 25
4.41 Một bệnh viện nhận thấy rằng trong ngày thứ 7 hàng tuần, số bệnh nhận đến ngẫu
nhiên và độc lập với số lượng trung bình khoảng 360 người mỗi giờ.
a) Hãy dùng phân phối mũ tính xác suất để bệnh nhân kế tiếp sẽ không đến trong vòng 30 giây.
b) Hãy dùng phân phối Poát-xông để tính xác suất yêu cầu ở câu a.
4.42 Trung tâm điều độ mạng lưới điện quốc gia phạm trung bình 20,8 lỗi trong vòng 1
năm và ta có thể coi số lỗi mắc phải trong một thời gian cho trước tuân theo phân phối Poát-
xông. Hãy tính xác suất để thời gian phạm lỗi giữa hai lần liên tiếp nằm trong khoảng từ 1 đến 2 tuần lễ.
4.43 Một tổ chức chuyên cung cấp dịch vụ cho hãng hàng không P quan tâm đến khoảng
thời gian cần thiết tính từ lúc một chiếc máy bay hạ cánh để bốc dỡ, vệ sinh và chuẩn bị cho
nó sẵn sàng cất cánh trở lại. Họ tìm hiểu thông tin từ nhà điều hành sân bay và biết rằng
khoảng thời gian này dao động trong khoảng từ 15 đến 45 phút. Không có thêm thông tin gì
khác nên nhà cung cấp dịch vụ này quyết định áp dụng phân phối đều cho khoảng thời gian
bốc dỡ, vệ sinh và chuẩn bị. Hãy
a) xác định thời gian trung bình để bốc dỡ, vệ sinh và chuẩn bị và độ lệch chuẩn.
b) tính xác suất để khoảng thời gian này không vượt quá 35 phút.
4.44 Các khách hàng đến máy ATM với cường độ 20 người mỗi giờ. Nếu một khách hàng
vừa đến, cho biết xác suất để khách hàng kế tiếp sẽ đến trong vòng 6 phút?
4.45 Một người cân nhắc giữa việc mua nhà ngay hay gửi tiền vào tiết kiệm với lãi suất
12% một năm và chờ một năm sau mới mua. Biết mức tăng giá nhà là biến ngẫu nhiên phân
phối chuẩn với trung bình là 8% và độ lệch chuẩn là 10%. Tìm khả năng rủi ro của người đó
nếu gửi tiền vào tiết kiệm và chờ 1 năm.
4.46 Xét 2 phương án đầu tư. Biết tỷ lệ lợi nhuận là biến ngẫu phân phối chuẩn với kỳ
vọng và độ lệch tiêu chuẩn được cho bởi bảng sau. Ta sẽ đầu tư nếu tỷ lệ lợi nhuận tối thiểu
10% và sẽ đầu tư vào phương án nào có khả năng đáp ứng yêu cầu này cao hơn. Vậy nên đầu
tư vào phương án nào? Để rủi ro (đo bằng phương sai) là nhỏ nhất nên đầu tư vào cả 2
phương án A và B theo tỷ lệ nào?
Kỳ vọng toán (%) Độ lệch chuẩn (%) Phương án A 10,5 1,5 Phương án B 11 2,5
4.47 Theo Cục Thống kê Lao động Mỹ, tiền lương trung bình hàng tuần của một công
nhân sản xuất Mỹ là 441,84$ năm 1998. Giả sử dữ liệu sẵn có cho biết tiền lương có phân
phối chuẩn với độ lệch chuẩn bằng 90$.
a) Xác suất để một công nhân kiếm được từ 400$ đến 500$ một tuần là bao nhiêu?
b) Với một công nhân được chọn ngẫu nhiên, xác suất để người công nhân ấy kiếm được ít
hơn 250$ một tuần là bao nhiêu?
c) Với một công nhân được chọn ngẫu nhiên, xác suất để người công nhân ấy kiếm được từ
480$ đến 600$ một tuần là bao nhiêu?
d) Một công nhân sản xuất phải kiếm được bao nhiêu tiền để lọt vào nhóm 20% số người
kiếm được nhiều tiền nhất? 26 Bài tập chương 5
LẤY MẪU VÀ PHÂN PHỐI MẪU
5.1 Bảng dưới đây là danh sách sinh viên lớp QTKD 03.1 học môn Thống kê ứng dụng trong
kinh doanh có mặt ở lớp vào ngày 10/10/2005. Với sự trợ giúp của danh sách số ngẫu nhiên dưới
đây anh/chị được yêu cầu chọn một mẫu có 5 sinh viên sẽ được gọi lên bảng làm bài tập, sử dụng:
a) lấy mẫu ngẫu nhiên đơn giản
b) lấy mẫu ngẫu nhiên phân tầng dựa vào giới tính
c) lấy mẫu ngẫu nhiên hệ thống Họ và tên Họ và tên Bùi Thị Kim Chi Nguyễn Thị Hồng Nguyễn Trần Ngọc Diễm Trần Viết Hùng Phan Vũ Dũng Nguyễn Thị Mỹ Hương Ngô Phương Em Huỳnh B Trang Thúy Linh Ngô Bích Hà Trần Hồng Lĩnh Phạm Thị Lệ Hằng Lữ Tấn Lợi Phạm Thị Mỹ Hằng Nguyễn Viên Nhật Minh
Nguyễn Nguyên Hồng Hạnh Nguyễn Quốc Nam Trần Thị Hảo Trần Mạnh Nam Võ Thị Bé Hoang Tăng Kim Ngân Các số ngẫu nhiên: 11 14 05 16 18 12 18 19 15 03 07 17 13 09 01 07 13 08 11 14 10 14 13 14 11 06 12 15 02 15 18 19 13
5.2 Xét một tổng thể hữu hạn với năm phần tử được đặt nhãn A, B, C, D và E. Mười mẫu ngẫu
nhiên đơn giản có cỡ là 2 có thể được chọn.
a) Hãy liệt kê 10 mẫu bắt đầu với AB, AC, và v.v…
b) Sử dụng lấy mẫu ngẫu nhiên đơn giản, xác suất để mỗi mẫu có cỡ là 2 được chọn là bao nhiêu?
c) Giả sử số ngẫu nhiên 1 tương ứng với A, số ngẫu nhiên 2 tương ứng với B, và v.v… Hãy
liệt mẫu ngẫu nhiên đơn giản có cỡ là 2 sẽ được chọn sử dụng các con số ngẫu nhiên 8 0 5 7 5 3 2.
5.3 Xét một tổng thể hữu hạn có 350 phần tử. Sử dụng ba con số sau cùng của từng số ngẫu
nhiên gồm năm con số sau đây (601, 022, 448, …), xác định bốn phần tử đầu tiên sẽ được chọn
cho một mẫu ngẫu nhiên đơn giản
5.4 Một tổng thể gồm năm giá trị sau đây: 12, 12, 14, 15 và 20
a) Hãy liệt kê tất cả các mẫu có cỡ bằng 3, và tính trung bình của từng mẫu. 27
b) Tính trung bình của phân phối của các trung bình mẫu và trung bình tổng thể. So sánh hai giá trị này.
c) So sánh sự phân tán trong tổng thể với sự phân tán của các trung bình mẫu.
5.5 Có năm đại điện bán hàng tại Ford. Năm đại diện bán hàng và số lượng xe họ bán được trong tuần qua là: Đại diện bán hàng A B C D E
Số lượng xe bán được 8 6 4 10 6
a) Có bao nhiêu mẫu khác nhau có cỡ bằng 2 có thể được chọn?
b) Hãy liệt kê tất cả các mẫu có cỡ bằng 2 có thể được chọn và tính trung bình của từng mẫu.
c) So sánh trung bình của phân phối mẫu của các trung bình mẫu với trung bình của tổng thể.
d) Vẽ biểu đồ hình gậy so sánh sự phân tán trong các trung bình mẫu với sự phân tán trong tổng thể.
5.6 Một tổng thể không có phân phối chuẩn với trung bình là 750, độ lệch chuẩn là 50. Với một
mẫu gồm 49 phần tử chọn từ tổng thể đó, hãy tính xác suất để trung bình mẫu: a) nhỏ hơn 740.
b) trong khoảng từ 740 đến 760.
c) trong khoảng từ 760 đến 770. d) lớn hơn 770.
5.7 Số liệu thống kê thu thập trong một tháng ở một nhà hàng cho thấy 80 trong số 120 khách
hàng nước ngoài thanh toán bằng thẻ tín dụng. Hãy tính sai số chuẩn của tỷ lệ mẫu.
5.8 Độ bền một loại vỏ xe của hãng Goodyear có phân phối chuẩn với độ bền trung bình là
38.000 km, độ lệch chuẩn bằng 3.000 km. Một doanh nghiệp sửa chữa ô tô mua 20 vỏ xe của
hãng Goodyear để lắp cho 5 chiếc ô tô của khách hàng. Yêu cầu: Hãy tính:
a) Xác suất để 20 vỏ xe nói trên bị hỏng trước 36.000 km.
b) Xác suất để độ bền của 20 vỏ xe nằm trong khoảng 1.000 km so với trung bình.
c) Xác suất để độ bền của 4 vỏ xe lắp cho một chiếc ô tô bất kỳ thấp hơn 35.000 km.
d) Xác suất để 4 vỏ xe lắp cho một chiếc ô tô bất kỳ có độ bền rơi vào khoảng 1.200 km so với trung bình.
5.9 Hãng Sony tung ra thị trường sản phẩm “AM/FM Walkman” sử dụng pin đôi có tuổi thọ
trung bình là 35 giờ. Được biết tuổi thọ của pin có phân phối chuẩn với độ lệch chuẩn bằng 5,5
giờ. Để kiểm tra chất lượng sản phẩm, chuyên viên kỹ thuật của hãng chọn ngẫu nhiên 25 bộ pin.
a) Có thể nói gì về hình dáng phân phối của trung bình mẫu?
b) Tính sai số chuẩn của trung bình mẫu.
c) Tính xác suất để tuổi thọ của trung bình mẫu trong khoảng từ 34,5 giờ đến 36 giờ. d) Tính xác
suất để tuổi thọ của trung bình mẫu ít hơn 33 giờ.
5.10 Một tổng thể có tỷ lệ tổng thể bằng 0,3. Một mẫu ngẫu nhiên với cỡ bằng 150 và tỷ lệ của
mẫu p sẽ được sử dụng để ước lượng tỷ lệ tổng thể. 28
a) Tính xác suất để tỷ lệ của mẫu nằm trong khoảng 0,03 so với tỷ lệ tổng thể.
b) Làm như câu a nhưng nằm trong khoảng 0,05.
5.11 Tỷ lệ học viên nữ tại một trung tâm ước lượng khoảng 40%. Một mẫu ngẫu nhiên 150
học viên được chọn để kiểm tra việc ước lượng này.
a) Nếu giả thuyết về tỷ lệ học viên nữ trên là đúng thì hãy tính xác suất để tỷ lệ của mẫu
p nằm trong khoảng 30% đến 50%.
b) Hãy tính xác suất để tỷ lệ của mẫu nằm trong khoảng 0,05 so với tỷ lệ tổng thể 0,4.
5.12 Giả sử rằng 20% sản phẩm bị khuyết tật. Ta chọn 100 sản phẩm để kiểm tra chất lượng.
a) Xác suất để tỷ lệ sản phẩm bị khuyết tật trong mẫu sẽ nằm trong khoảng 0,04 so với tỷ lệ tổng thể.
b) Nếu việc kiểm tra cho thấy p 0,15 thì dây chuyền sẽ được cho dừng lại để sửa chữa.
Tính xác suất để với mẫu 100 sản phẩm sẽ dẫn đến việc phải dừng dây chuyền sản xuất.
5.13 Theo thống kê của toàn ngành du lịch thì tỷ lệ người thích đi du lịch sinh thái là 30%
trong tổng số khách du lịch.
Giả sử ta chọn mẫu ngẫu nhiên gồm 1011 khách du lịch. Tính xác suất để tỷ lệ người thích đi du
lịch sinh thái trong mẫu ít nhất là 32%.
5.14 Một mẫu có cỡ bằng 10 cho dưới đây. Chúng ta sẽ chọn dùng ba số khác nhau mà từ đó
các độ lệch sẽ được tính. Số thứ nhất sẽ được sử dụng cho năm điểm dữ liệu mẫu đầu tiên; số
thứ hai sẽ được sử dụng ba điểm dữ liệu mẫu tiếp theo; và số thứ ba sẽ được sử dụng cho hai
điểm dữ liệu mẫu sau cùng. Mẫu # 1 2 3 4 5 6 7 8 9 10
Điểm mẫu 93 97 60 72 96 83 59 66 88 53
a) Ba con số nào ta sẽ chọn để tối thiểu hoá SSD (tổng bình phương các độ lệch so với trung bình)?
• Ghi chú: SSD = (x x) 2 −
b) Tính SSD với các số đã được chọn.
c) df ứng với SSD tính toán là bao nhiêu?
d) Hãy tính ước lượng không chệch của phương sai tổng thể. 29
Bài tập chương 6.1
ƯỚC LƯỢNG KHOẢNG CHO MỘT TỔNG THỂ
6.1 Hãy tìm khoảng tin cậy cho chiều cao trung bình của sinh viên dựa trên một mẫu kích thước
là 36 với trung bình mẫu là 66 insơ (1 insơ = 2,54 cm). Giả sử rằng độ lệch chuẩn của chiều cao
người lớn là 3 insơ. Cho độ tin cậy là 95%.
6.2 Một trường đại học tiến hành một nghiên cứu xem trung bình một sinh viên tiêu hết bao
nhiêu tiền gọi điện thoại trong một tháng. Một mẫu ngẫu nhiên gồm 59 sinh viên được chọn và kết quả như sau: 14 18 22 30 36 28 42 79 36 52 15 47 95 16 27 111 37 63 127 23 31 70 27 11 30 147 72 37 25 7 33 29 35 41 48 15 29 73 26 15 26 31 57 40 18 85 28 32 22 37 60 41 35 26 20 58 33 23 35
Hãy xây dựng khoảng tin cậy 95% cho số tiền gọi điện thoại trung bình hàng tháng của một sinh viên.
6.3 Một hãng hàng không thực hiện một nghiên cứu để ước lượng thời gian trung bình làm thủ
tục nhập cảnh cho một hành khách. Một mẫu gồm 16 hành khách được chọn ngẫu nhiên, kết quả ghi nhận như sau (phút):
14; 15; 14; 15; 12; 18; 12; 20; 22; 19; 18; 19; 20; 19; 18; 18.
Với độ tin cậy 95%, hãy ước lượng khoảng thời gian trung bình để hoàn thành thủ tục nhập cảnh
cho một hành khách (giả thiết thời gian làm thủ tục nhập cảnh có phân phối chuẩn). 6.4
Bưu điện Thành phố Hồ Chí Minh nghiên cứu việc sử dụng điện thoại cố định nhằm tính
toán giá cước hợp lý. Một mẫu ngẫu nhiên gồm 100 hộ gia đình được chọn từ các Quận, Huyện.
Số liệu cho trong bảng sau:
Cước trả hàng tháng Số hộ (ngàn đồng) < 60 10 60 – 80 15 80 – 100 22 100 – 120 27 120 – 140 12 140 – 160 9 ≥ 160 5
a) Giả sử tiền cước điện thoại hàng tháng có phân phối chuẩn, hãy ước lượng khoảng mức
cước trung bình của các hộ gia đình với độ tin cậy 95%.
b) Hãy ước lượng tỷ lệ hộ gia đình có mức cước điện thoại mỗi tháng lớn hơn hoặc bằng
100 ngàn đồng, với độ tin cậy 90%. 30
6.5 Biết rằng độ lệch chuẩn về chiều cao người lớn là 3 insơ, ta muốn xây dựng một khoảng tin
cậy 90% cho chiều cao trung bình với sai số không quá 0,5 insơ. Hãy xác định kích thước mẫu
n tối thiểu để đạt được yêu cầu trên.
6.6 Một nhà nông học muốn ước lượng tỉ lệ nảy mầm của một loại hạt giống A với độ tin cậy
90% với sai số không quá 0,02. Cần phải lấy mẫu với kích thước bao nhiêu?
6.7 Để xác định thu nhập trung bình trong năm của một công nhân ngành may, người ta tiến
hành điều tra chọn mẫu với yêu cầu là: phạm vi sai số
40 ngàn đồng; độ tin cậy 95%; độ lệch
chuẩn về thu nhập ước tính được là 220 ngàn đồng. Hãy xác định cỡ mẫu cần điều tra?
6.8 Tại một phân xưởng người ta muốn ước lượng thời gian trung bình để sản xuất một ram giấy.
Giả sử lượng thời gian đó tuân theo quy luật phân phối chuẩn với =0,3 phút. Trên một mẫu
gồm 36 ram thời gian trung bình tính được là 1,2 phút/ram.
a) Tính khoảng tin cậy 95% cho thời gian sản xuất trung bình trên.
b) Nếu muốn độ chính xác tăng gấp đôi nhưng độ tin cậy 95% không đổi thì cần nghiên cứu
mẫu có kích thước bằng bao nhiêu?
6.9 Trong một cuộc điều tra 150 nghiện thuốc lá được chọn ngẫu nhiên, người ta tính được số
điếu thuốc hút trong một tuần của họ có trung bình là 97 và độ lệch chuẩn là 36. Tìm khoảng tin
cậy 99% cho số điếu thuốc hút trung bình trong một tuần của người nghiện thuốc lá.
6.10 Từ một lớp học lớn, lấy ngẫu nhiên được 4 loại điểm 64, 66, 89 và 77. Tính khoảng tin
cậy 95% của điểm trung bình của cả lớp. Anh/Chị có nhận xét gì về khoảng tin cậy này?
6.11 Unilever là một trong những công ty hoá mỹ phẩm lớn nhất Việt Nam, ước tính thị
trường bột giặt chiếm khoảng 60%. Do đó, mức độ giao dịch hàng ngày rất lớn. Số tài liệu được
chuyển bằng fax thu thập được một điều tra trong 15 ngày cho thấy mỗi ngày có 267 trang với độ
lệch chuẩn là 32 trang. Nếu số trang tài liệu được chuyển bằng fax trong một ngày có phân phối
chuẩn thì ước lượng số tài liệu được chuyển bằng fax trong một ngày là bao nhiêu với độ tin cậy 95%.
6.12 Trở lại bài tập 7.11 gày
. Anh/Chị cảm thấy bất ổn với vì khoảng tin cậy 95% của 15 n
quan sát là khá rộng (từ 249 đến 285 trang). Anh/Chị cảm thấy muốn ước lượng số tài liệu được
chuyển bằng fax trong một ngày với độ tin cậy 99% và muốn thu hẹp khoảng cách xuống còn 10
trang mỗi bên. Rõ ràng, cần phải có sự đánh đổi giữa các điều kiện. Anh/Ch ị hãy xác định kích
thước mẫu là bao nhiêu hay nói cách khác, Anh/Chị cần thu thập số liệu trong ít nhất bao nhiêu ngày?
6.13 Trường Đại học Kinh tế TP. HCM thực hiện một số thí nghiệm về số giờ tự học của sinh
viên trong một tuần. Chọn ngẫu nhiên 200 sinh viên cho thấy trung bình số giờ tự học trong tuần
là 18,36 giờ và độ lệch chuẩn là 3,92 giờ. Như vậy, với độ tin cậy 95%, số giờ tự học trong tuần
tính trung bình ở trường này là như thế nào?
6.14 40 xe ôtô được chọn làm mẫu ngẫu nhiên trong một cuộc kiểm tra tốc độ trên xa lộ Hà
Nội (dùng máy bắn đo tốc độ), và vận tốc của các xe được đo có kết quả như sau (km/h): 49 83 58 65 68 60 76 86 74 53 71 74 65 72 64 42 62 62 58 82 78 64 55 87 56 50 71 58 57 75 58 86 64 56 45 73 54 86 70 73 31
Hãy tìm khoảng tin cậy 95% cho tốc độ trung bình của nhóm xe này khi bị bắn.
6.15 Ở một cửa hàng chế biến thủy sản, theo dõi nhu cầu của mặt hàng nước mắm trong một
số ngày, ta có kết quả sau:
a) Hãy ước lượng lượng nước mắm trung bình bán ra một ngày với độ tin cậy 99% trong hai trường hợp: Số bán ra (lít) Số ngày 20 - 30 3 30 - 40 8 40 - 50 30 50 - 60 45 60 - 70 20 70 - 80 25 80 - 90 17 90 - 100 9 > 100 3
- Biết phương sai 2 = 132,25 P P - Chưa biết 2 PP
b) Giả sử giá một lít nước mắm là 6 ngàn đồng. Cửa hàng này phải dự trù một món tiền
trung bình bằng bao nhiêu để cung cấp cho khách hàng.
c) Hãy ước lượng phương sai của lượng nước mắm bán trong ngày với độ tin cậy 95% (giả
thiết đại lượng này có phân phối chuẩn)
6.16 Giả sử trái cây của nông trường đã được đóng thành sọt, mỗi sọt 10 trái. Kiểm tra 50 sọt
được kết quả như sau:
Số trái hỏng trong sọt (k) 0 1 2 3 4 5 6 7 8 9 10
Số sọt có k trái hỏng 0 2 3 7 20 6 4 7 0 0 1
a) Tìm ước lượng cho tỷ lệ trái cây hỏng trong nông trường.
b) Tìm ước lượng cho tỷ lệ trái cây hỏng trung bình ở mỗi sọt
6.17 Điều tra mức doanh thu của 100 hộ kinh doanh về mặt hàng A, thu được bảng số liệu sau:
Mức doanh thu (triệu đồng) 20 22 24 26 28 Số hộ 10 16 22 28 12
a) Tìm ước lượng không chệch tốt nhất của doanh thu trung bình. Giả thiết mức doanh thu
của các hộ có phân phối chuẩn với độ lệch chuẩn là 0,1 triệu thì khả năng giá trị của ước
lượng trên sẽ sai lệch so với giá trị thực không vượt quá 20000 đồng là bao nhiêu?
b) Dựa vào số liệu thu được, hãy ước lượng mức
doanh thu trung bình của các hộ kinh
doanh mặt hàng A với độ tin cậy 95%. 32
6.18 Mẫu ngẫu nhiên của 15 nhà phân tích tài chính về số thu nhập của mỗi cổ phần trong một
công ty cho biết độ lệch chuẩn mẫu 0,88. Tìm khoảng tin cậy 90% cho phương sai của thu nhập
cho mỗi cổ phần. Biết rằng thu nhập của mỗi cổ phần tuân theo quy luật chuẩn.
6.19 Thế chấp là một loại vốn vay được bảo đảm bằng một món tài sản chỉ định. Nếu người đi
vay không trả được khoản vay, người cho vay có thể bán tài sản đó để thu lại món nợ chưa trả.
Vay thế chấp nhà là loại vốn vay cá nhân quan trọng nhất ở Mỹ. Trong một khoản vay thế chấp
nhà, người đi vay cầm cố ngôi nhà đang được nói đến làm vật bảo đảm cho vốn vay (Sharpe,
1985). Một thanh tra viên ngân hàng liên bang đang quan tâm đến việc ước tính số dư nợ gốc của
tất cả các khoản vay thế chấp nhà bị ngân hàng tịch thu do người đi vay không trả được nợ trong
3 năm qua. Một mẫu ngẫu nhiên gồm 12 khoản vay thế chấp bị tịch thu cho dữ liệu sau đây (tính bằng đô la): 95.982 81.422 39.888 46.836 66.899 69.110 59.200 62.331 105.812 55.545 56.635 72.123
a) Xây dựng khoảng tin cậy 95% cho trung bình của tổng thể quan tâm
b) Tổng thể này phải có đặc trưng gì mới cho phép ta xây dựng khoảng tin cậy cho số dư nợ gốc trung bình ở câu a.
c) Hãy cẩn thận giải thích khoảng tin cậy của bạn trong bối cảnh của bài toán này. 33
Bài tập chương 6.2
KIỂM ĐỊNH GIẢ THUYẾT CHO MỘT TỔNG THỂ
6.20 Lấy lại Bài tập 6.4
Một cán bộ kỹ thuật của Bưu điện Thành phố cho rằng tiền cước điện thoại trung bình của mỗi
hộ hàng tháng là 100 ngàn đồng. Với mức ý nghĩa 5%, hãy cho nhận xét về lời khẳng định trên.
6.21 Một máy tiện tự động quy định phương sai của đường kính trục máy không vượt quá 36.
Người ta tiến hành 25 quan sát về đường kính của trục máy và tính được 2 s = 35,266. Với mức ý
nghĩa = 5% ta có thể kết luận như thế nào về quá trình sản xuất
6.22 Một công ty sản xuất pin tuyên bố rằng pin của họ có tuổi thọ trung bình là 21,5 giờ. Một
cơ quan kiểm tra chất lượng kiểm tra 6 chiếc pin của công ty và thu được số liệu sau đây về tuổi
thọ của 6 chiếc pin này là 19, 18, 22, 20, 16, 25.
Kết quả này có xác nhận quảng cáo của công ty là đúng hay không? Mức ý nghĩa được chọn là = 0,05.
6.23 Một nhà máy sản xuất sản phẩm với tỷ lệ sản phẩm loại 1 lúc đầu là 0,20. Sau khi áp
dụng phương pháp sản xuất mới, kiểm tra 500 sản phẩm thấy số sản phẩm loại 1 là 150 sản
phẩm. Cho kết luận về phương pháp sản xuất mới với mức ý nghĩa = 1%.
6.24 Giả sử sản phẩm của một công ty sản xuất vỏ xe ô tô đã chiếm được 42% thị trường.
Hiện tại, trước sự cạnh tranh của đối thủ và những điều kiện thay đổi của môi trường kinh doanh,
ban lãnh đạo muốn kiểm tra lại xem thị phần công ty có còn là 42% hay không. Chọn ngẫu nhiên
550 ô tô trên đường, kết quả cho thấy có 219 xe sử dụng vỏ xe của công ty. Có thể kết luận gì, ở mức ý nghĩa = 0,1?
6.25 Một nghiên cứu được thực hiện để xác định mức độ hài lòng của khách hàng sau khi
công ty điện thoại thay đổi, cải tiến một số dịch vụ khách hàng. Trước khi thay đổi, mức độ hài
lòng của khách hàng tính trung bình là 77, theo thang điểm từ 0 đến 100. 350 khách hàng được
chọn ngẫu nhiên để gửi bảng điều tra xin ý kiến sau khi các thay đổi được thực hiện, mức độ hài
lòng trung bình tính được là 84, với độ lệch chuẩn là 28. Ở mức ý nghĩa = 0,01 có thể kết luận
khách hàng đã được làm hài lòng ở mức độ cao hơn được không?
6.26 Bộ phận giám sát chất lượng quan tâm đến đường kính một loại chi tiết sản phẩm. Quá
trình sản xuất còn được xem là tốt và chi tiết sản phẩm sản xuất ra được chấp nhận nếu phương
sai của đường kính tối đa bằng 1. Nếu phương sai vượt quá 1, phải xem xét lại máy móc và sửa
chữa. Với mẫu ngẫu nhiên 31 chi tiết, phương sai của đường kính tính được là 1,62. Ở mức ý
nghĩa = 0,05, ta có thể kết luận như thế nào về quá trình sản xuất?
6.27 Một hãng chế tạo thức ăn đóng hộp sử dụng máy để đổ trái cây vào hộp. Máy này được
thiết kế để đổ 16 aoxơ (1 aoxơ = 28,35g) trái cây vào hộp với độ lệch chuẩn 0,30 aoxơ. Định kỳ,
một mẫu ngẫu nhiên 100 hộp từ đầu ra của máy này được chọn và cân. Mẫu 100 hộp gần đây
nhất cho trung bình mẫu là 15,92 aoxơ. Hãy kiểm định giả thuyết H rằng máy này đang vận 0
hành như thiết kế ( = 16 aoxơ) ở mức ý nghĩa 5%.
6.28 Một trung tâm cai nghiện ma túy công bố rằng nhiều nhất là 22% số bệnh nhân của họ
mắc nghiện trở lại trong vòng hai năm. Một cuộc nghiên cứu theo dõi 35 bệnh nhân từ trung tâm 34
n ày trở về cho thấy có 10 người mắc nghiện trở lại. Với mức ý nghĩa 1% nhận định xem công bố
của trung tâm có cao hơn so với thực tế không.
6.29 Công ty mỹ phẩm P&G đã thành công trên thị trường Việt Nam với bột giặt “trắng sạch
như Tide”. Một nghiên cứu trước đây của công ty P&G cho biết họ đã chiếm được 42% thị
trường bột giặt dùng cho máy giặt. Đối thủ cạnh tranh của P&G không phải ai khác mà chính là
công ty Unilever với loại bột giặt OMO khử được “99 vết bẩn cứng đầu”. Sau cuộc chiến hạ giá
thành và đợt khuyến mãi của Unilever, ban lãnh đạo công ty P&G muốn kiểm tra về thị phần của
mình có còn đủ 42% hay không. P&G đã cử nhân viên xuống các siêu thị Cora, Citimart, Co-op
Saigon... điều tra khách hàng. Trong số 550 khách hàng được hỏi một cách ngẫu nhiên, kết quả
cho thấy có 219 khách hàng sử dụng Tide. Công ty có thể kết luận gì ở độ tin cậy 99%.
6.30 Theo thông báo của sở giao thông, hiện trên thị trường Hà Nội xe máy Trung Quốc đã
chiếm 60% thị phần. Kiểm tra ngẫu nhiên lượng xe máy đăng ký tại một trạm đăng ký xe máy
trong một tuần thấy trong 2000 xe máy được đăng ký có 950 xe Trung Quốc. Với mức ý nghĩa
= 0,05, hãy đánh giá thông báo của sở giao thông.
6.31 Một công ty A sản xuất bánh kẹo tuyên bố rằng 2/3 số trẻ em thích ăn bánh của công ty.
Trong một mẫu gồm 100 trẻ em được hỏi, có 55 em tỏ ra thích ăn bánh của công ty A. Với mức
ý nghĩa 5%, số liệu nói trên có chứng tỏ là tuyên bố của công ty là hơi quá đáng hay không?
6.32 Nếu máy móc hoạt động bình thường, thì độ dài của sản phẩm tuân theo luật phân phối
chuẩn N(100, 1). Qua một thời gian sản xuất người ta nghi ngờ độ dài sản phẩm có xu hướng
tăng lên. Đo thử 100 sản phẩm thì độ dài trung bình của sản phẩm là 100,3. Hãy kiểm tra nghi
ngờ trên với mức = 0,05.
6.33 Một bản nghiên cứu thông báo rằng mức tiêu dùng hàng tháng của một sinh viên là 420
nghìn đồng. Để kiểm tra người ta chọn ngẫu nhiên 16 sinh viên và tìm được trung bình mỗi
tháng họ tiêu 442 nghìn đồng với độ lệch chuẩn là 60 nghìn đồng. Với mức ý nghĩa 1% nhận
định xem kết luận của bản thông báo có thấp hơn sự thật hay không?
6.34 Trưởng phòng nhân sự một công ty muốn ước lượng số ngày nghỉ trung bình trong năm
do yếu tố con ốm của công nhân nữ. Chọn ngẫu nhiên 16 công nhân nữ, ghi nhận số ngày nghỉ
trong năm của họ do con ốm. Giả sử tổng thể phân phối chuẩn, độ lệch chuẩn là 4 ngày. Yêu cầu:
a) Số ngày nghỉ trung bình của công nhân nữ được ước lượng trong khoảng từ 13 đến 15
ngày, hãy xác định độ tin cậy.
b) Nếu muốn khoảng tin cậy 85% của trung bình tổng thể thay đổi trong khoảng ± 0,5 ngày
so với trung bình mẫu thì cần lấy mẫu bao nhiêu công nhân nữ?
c) Ở mức ý nghĩa 0,05, có thể kết luận rằng số ngày nghỉ trung bình trong năm do con ốm
của nữ công nhân ở công ty là 16 được không?
6.35 Một dây chuyền đóng gói, nếu hoạt động bình thường, sẽ cho ra sản phẩm với trọng
lượng trung bình là 550 gram. Chọn ngẫu nhiên 9 sản phẩm, trọng lượng (gram) được ghi nhận như sau: 606 545 545 584 592 569 542 595 589
a) Hãy ước lượng khoảng tin cậy 95% cho trọng lượng trung bình của sản phẩm.
b) Giả sử tổng thể phân phối chuẩn, ở mức ý nghĩa 0,05, có thể kết luận rằng dây chuyền
hoạt động bình thường được không? 35
6.36 Sau khi phân tích chi phí sản xuất, một công ty nhận định rằng để đạt được điểm hoà vốn
thì công ty phải chiếm được ít nhất 10% thị trường. Nếu công ty chiếm hơn 10% thị trường, thì
công ty sẽ có lãi. Công ty quyết định điều tra thăm dò. Sau khi phỏng vấn 400 khách hàng tiềm
năng xem khách hàng có quyết định mua sản phẩm sẽ sản xuất của mình hay không, có 52 khách
hàng trả lời sẽ mua sản phẩm này. Hãy quyết định giùm công ty xem có nên sản xuất loại sản
phẩm này hay không với độ tin cậy 95%?
6.37 Tỷ suất sinh lời của cổ phiếu của một công ty trong vòng 5 năm qua là 15%, 20%, 7%,
14% và 10%. Biết tỷ suất sinh lời của cổ phiếu là biến ngẫu nhiên phân phối chuẩn.
a) Với độ tin cậy 95% hãy ước lượng tỷ suất sinh lời trung bình của cổ phiếu công ty đó.
b) Với độ tin cậy 95% hãy ước lượng độ rủi ro của cổ phiếu công ty đó. Biết rằng độ rủi ro
của một loại cổ phiếu thường được đo bằng độ lệch chuẩn hay phương sai về tỷ suất sinh lời của cổ phiếu.
c) Một người phân tích chứng khoán cho rằng trong 5 năm qua loại cổ phiếu nào có tỷ suất
sinh lời trung bình cao hơn 15% là đáng đầu tư. Với mức ý nghĩa 5%, cổ phiếu của công
ty trên có đáng đầu tư hay không?
6.38 Có số liệu sau đây về tỷ lệ sinh lời trong năm qua của một mẫu 15 loại cổ phiếu trong một ngành: 12,5 13 14,8 11 16,7 9 8,3 -12 -3,9 15,5 16,2 18 11,6 10 9,5
a) Sử dụng dữ liệu này để xác định khoảng tin cậy 95% cho tỷ lệ sinh lời trung bình ngành năm qua.
b) Một công ty dịch vụ đầu tư quả quyết rằng tỷ lệ sinh lời trung bình ngành năm qua là
11,8%. Với mức ý nghĩa 0,05 hãy kết luận về điều quả quyết nêu trên.
6.39 Giả sử rằng Hiệp hội Ngân hàng Việt Nam muốn ước tính lãi suất thế chấp trung bình
hiện hành. Sử dụng một danh sách tổng thể, người phân tích của hiệp hội chọn ngẫu nhiên 12
nhà cho vay thế chấp trên cả nước và điều tra lãi suất của nhà cho vay bằng phỏng vấn qua điện
thoại. Điều tra này cho kết quả như sau:
9,45 9,73 9,84 9,30 9,59 9,49 9,25 10,09 9,40 9,35 9,53 9,29
a. Sử dụng dữ liệu này để xác định khoảng tin cậy 95% để ước lượng lãi suất thế chấp trung
bình hiện hành trên cả nước.
b. Một chuyên gia ngân hàng nhận định rằng mức lãi suất thế chấp trung bình hiện hành là
9,35%. Nhận định này có hợp lý hay không, sử dụng mức ý nghĩa 5%.
6.40 Thời gian trước số tiền gửi tiết kiệm bằng ngoại tệ trung bình của mỗi khách hàng là
1000 USD. Để đánh giá xem hiện nay xu hướng này còn giữ nguyên hay không người ta kiểm
tra ngẫu nhiên 64 sổ tiết kiệm và tìm được số tiền gửi tiết kiệm trung bình là 990 USD và độ lệch chuẩn là 100 USD.
a) Với mức ý nghĩa 0,05 hãy kiểm định xem số tiền gửi trung bình của khách hàng có thay đổi hay không?
b) Hãy kiểm định vấn đề trên bằng cách sử dụng giá trị p.
c) Tìm xác suất mắc sai lầm loại II nếu số tiền gửi tiết kiệm trung bình của khách hàng thực sự là 1050 USD.
d) Tìm lực kiểm định nếu nếu số tiền gửi tiết kiệm trung bình của khách hàng thực sự là 980 USD. 36
6.41 Trước đây định mức tiêu dùng điện cho 1 hộ gia đình trong một tháng là 140 kw. Do đời
sống nâng cao, người ta theo dõi 100 hộ gia đình và thu được các số liệu sau: Lượng tiêu dùng 100-120 120-140 140-160 160-180 180-200 Số hộ gia đình 14 25 30 20 11
a) Theo anh (chị) có cần nâng định mức tiêu dùng lên không? Cho = 0,05.
b) Nếu trước đây mức độ biến động của mức tiêu dùng điện cho 1 hộ gia đình là 2 = 400.
Vậy hiện nay mức độ biến động trên tăng hay giảm? Hãy cho kết luận với mức ý nghĩa 5%.
Giả thiết rằng lượng điện tiêu dùng của một hộ gia đình là biến ngẫu nhiên phân phối chuẩn 37