Bài giảng Xác suất thống kê chương 6 | Trường đại học Công Nghệ Sài Gòn

Chương 6 SUY DIỄN THỐNG KÊ CHO THAM SỐ MỘT TỔNG THỂ
Với một mẫu nhỏ, chúng ta có thể đánh giá
nguyên cả cái [bánh].
Don Quixote de la Mancha (1605–1615) Part I, Book I, Ch. 4. 3 Bài toán ước lượng tham số
Bài toán ước lượng tham số có thể phát biểu như sau: Cho biến
ngẫu nhiên (BNN) X với quy luật phân phối xác suất đã biết song
chưa biết tham số θ nào đó của nó. Phải ước lượng (xác định một
cách gần đúng) giá trị θ.
▪ Phương pháp mẫu cho phép giải quyết bài toán trên bằng quy nạp thống
kê như sau: từ tổng thể nghiên cứu rút ra một mẫu ngẫu nhiên kích
thước n và dựa vào đó mà xây dựng một thống kê መ𝜃 dùng để ước lượng θ
bằng cách này hay cách khác. Xác suất - Thống kê
Đại học Công nghệ Sài Gòn 1.2 Ước lượng khoảng
Phương pháp ước lượng điểm nói trên có một nhược điểm cơ bản là
khi kích thước mẫu nhỏ thì ước lượng điểm tìm được có thể sai lệch
rất nhiều so với giá trị của tham số cần ước lượng.
Mặt khác phương pháp ước lượng điểm còn không cung cấp thông
tin về mức độ gần đúng với tham số tổng thể của ước lượng.
Do đó khi kích thước mẫu nhỏ các nhà thống kê thường sử dụng
phương pháp ước lượng khoảng (interval estimation).
Đại học Công nghệ Sài Gòn Xác suất - Thống kê 5 1.2 Ước lượng khoảng
Cùng độ tin cậy có thể có nhiều khoảng tin cậy khác nhau,
khoảng nào càng hẹp càng tốt.
Nếu khoảng tin cậy có độ tin cậy (1 – α)100% thì khi lặp đi
lặp lại với các mẫu khác nhau sẽ có xấp xỉ (1 – α) 100% mẫu
mà ở đó khoảng tin cậy (θ ,θ ) sẽ bao gồm θ. Nói chung ta 1 2
không có cách gì để biết được một khoảng cụ thể nào đó có chứa θ hay không.
Đại học Công nghệ Sài Gòn Xác suất - Thống kê 7 1.3 Về sai số lấy mẫu
Một phát biểu xác suất về sai số lấy mẫu là một phát biểu về độ
chính xác (precision statement).
Giả sử với ε > 0 và q thỏa mãn điều kiện 𝑃( መ𝜃 − 𝜃 < 𝜀) ≥ (1 – α) thì khoảng ( ෠ 𝜃 − 𝜀; ෠
𝜃 + 𝜀) gọi là khoảng tin cậy đối xứng của θ với độ tin cậy (1 – α) với
sai số giới hạn ε (ε còn được gọi là độ chính xác, hay biên độ sai số). Lúc đó
độ dài khoảng tin cậy I sẽ bằng hai lần độ chính xác.
Với cùng độ tin cậy thì khoảng tin cậy đối xứng là khoảng tin cậy có độ dài
ngắn nhất. Vì thế những bài toán tìm khoảng tin cậy trong thực tế nếu không
có giả thiết nói rõ tìm khoảng tin cậy nào thì được xem như tìm khoảng tin cậy đối xứng.
Đại học Công nghệ Sài Gòn Xác suất - Thống kê 9
Bài toán ước lượng khoảng về trung bình của 1 tổng thể
Trường hợp cỡ mẫu lớn
• Đã biết phương sai tổng thể (σ2)
• Chưa biết phương sai tổng thể (σ2)
Trường hợp cỡ mẫu nhỏ • Đã biết σ2
• Chưa biết σ2 và tổng thể [giả định] có phân phối chuẩn.
• Chưa biết σ2 và tổng thể không [giả định] có phân phối chuẩn. Xác suất - Thống kê
Đại học Công nghệ Sài Gòn 11
2.1 Ước lượng khoảng về trung bình tổng thể
Trường hợp cỡ mẫu lớn và đã biết σ2
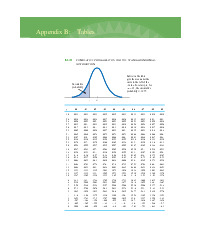
Khoảng ước lượng (1 – α)100% : 𝜎 𝐶𝐼(1 − 𝛼) ∈ ҧ 𝑥 ± 𝑧𝛼/2 𝑛 trong đó: ഥ 𝒙 là trung bình mẫu 𝒛
là trị số Z ứng với phần diện tích α/2 (bảng PP chuẩn 𝜶/𝟐 chuẩn hóa, xem Chương 4)
σ là độ lệch chuẩn của tổng thể n là cỡ mẫu
Đại học Công nghệ Sài Gòn Xác suất - Thống kê 13
2.2 Ước lượng khoảng về trung bình tổng thể
Trường hợp cỡ mẫu nhỏ, đã biết σ2, tổng thể có PP chuẩn
Sử dụng thủ tục ước lượng khoảng như của trường cỡ mẫu lớn.
Khoảng ước lượng (1 – α)100% : 𝜎 𝐶𝐼(1 − 𝛼) ∈ ҧ 𝑥 ± 𝑧𝛼/2 𝑛
Đại học Công nghệ Sài Gòn Xác suất - Thống kê 15
2.2 Ước lượng khoảng về trung bình tổng thể
Trường hợp chưa biết σ2 , cỡ mẫu nhỏ, tổng thể không có PP chuẩn
Trong trường hợp chưa biết phương sai tổng thể, cỡ mẫu
nhỏ và tổng thể không [được giả định] có phân phối
chuẩn thì tùy chọn duy nhất là tăng kích thước mẫu lên
n > 30 và sử dụng các thủ tục ước lượng khoảng với mẫu lớn.
Đại học Công nghệ Sài Gòn Xác suất - Thống kê 17
Ví dụ 6.1: Công ty DC-Latern khắc phục lỗi đèn bàn (3) 640 360 370 340 410 Dữ liệu về thời gian 400 670 790 740 660 gắn quang trở vào 870 800 570 550 590 mạch điện 780 840 790 700 650 của 25 quan sát. 870 650 890 500 770
Đại học Công nghệ Sài Gòn Xác suất – Thống kê 19
Ta có biên độ sai số ε là sai số lấy mẫu
tối đa được nói đến trong phát biểu độ
chính xác. Từ công thức tính: 𝜎 2.3 Xác định 𝜀 = 𝑧𝛼/2 kích thước mẫu 𝑛 Giải tìm n ta có: 𝑧 2 𝛼/2𝜎 𝑛 = 𝜀
Đại học Công nghệ Sài Gòn Xác suất - Thống kê 21
Ví dụ 6.3: Cửa hàng KZE giải quyết phàn nàn (1)
Tháng trước, KZE nhận được khá nhiều khiếu nại của các nhà bán lẻ về
việc TV Ant-Imonitor bị các hư hỏng vật lý (dù rằng đã được đóng gói rất
kỹ) trong quá trình vận chuyển trước khi đến cửa hàng. Thêm nữa, mỗi
TV bị hư hỏng theo một kiểu hoàn toàn độc lập với nhau.
Linda Danvers quyết định phải giải quyết tình trạng này. Theo thống kê
của KZE, trong 6 tháng gần đây, có 2000 TV Ant-Imonitor đã được vận
chuyển đến các nhà bán lẻ. Trong số đó, có 100 trường hợp bị các hư
hỏng vật lý trên. Hãy giúp Linda xây dựng một khoảng ước lượng 90% về
tỷ lệ tổng thể những hư hỏng này.
Đại học Công nghệ Sài Gòn Xác suất – Thống kê 23 4.1 Giả thuyết là gì?
Giả thuyết: Lý luận chưa được kiểm nghiệm, tạm thời đưa ra để
giải quyết một vấn đề khoa học, rồi dựa vào kết quả mà xác minh
những điều đã nhận định.
(Nguyễn Lân, Từ điển từ và ngữ Hán Việt, NXB Văn học, 2007)
Giả thuyết thống kê là giả thuyết về dạng phân phối xác suất
của BNN, về các tham số đặc trưng của BNN hoặc về tính độc lập của các BNN.
(Văn & Ninh, Giáo trình lý thuyết xác suất và thống kê toán, tr. 396)
Đại học Công nghệ Sài Gòn Xác suất - Thống kê 25
Đại học Công nghệ Sài Gòn 27
Kiểm định giả thuyết thống kê (statistical
hypothesis testing) là quá trình sử dụng
thống kê mẫu để kiểm định một lời tuyên bố
về giá trị của một tham số tổng thể. 4.1 Bài toán
Kiểm định giả thuyết có thể được dùng để kiểm định
quyết định có nên hoặc không nên bác bỏ một
phát biểu về trị số của một tham số tổng thể. giả thuyết Xác suất - Thống kê Đặt giả thuyết
Nói chung, một kiểm định giả thuyết về trị số của một tham số tổng
thể θ phải nhận một trong ba dạng sau đây (trong đó θ là trị số giả 0
thuyết của tham số tổng thể). H : θ = θ H : θ ≥ θ H : θ ≤ θ 0 0 0 0 0 0 H : θ ≠ θ H : θ < θ H : θ > θ a 0 a 0 a 0 Kiểm định 2 bên Kiểm định bên trái Kiểm định bên phải – kiểm tra sự bằng – kiểm tra sự kém – kiểm tra sự sự hơn nhau, khác nhau.
Đại học Công nghệ Sài Gòn Xác suất - Thống kê 29
4.2 Sai lầm loại I và loại II
Sai lầm loại I là bác bỏ H khi thực ra H đúng. 0 0
Người tiến hành kiểm định giả thuyết định rõ xác suất mắc sai lầm loại I
tối đa được phép, được ký hiệu là α và được gọi là mức ý nghĩa.
Sai lầm loại II là không bác bỏ H khi thực ra H sai. 0 0
Nói chung, các nhà thống kê không thể kiểm soát xác suất mắc sai lầm
loại II, được ký hiệu β. Chúng ta chỉ có thể giảm rủi ro mắc sai lầm loại
II bằng cách kết luận “chưa đủ bằng chứng thống kê để bác bỏ giả H ”. 0
Đại học Công nghệ Sài Gòn Xác suất - Thống kê 31
Kiểm định giả thuyết về μ – các bước
Trường hợp cỡ mẫu lớn
Bước 1: Xác định cụ thể dạng bài toán
• Phương sai (hay độ lệch chuẩn) tổng thể đã biết hay chưa? • Đặt giả thuyết:
o Diễn giải lại yêu cầu bài toán và sử dụng ký hiệu để mô tả.
o Xác định được giả thuyết H , H . 0 a H : μ = μ H : μ ≥ μ H : μ ≤ μ 0 0 0 0 0 0 H : μ ≠ μ H : μ < μ H : μ > μ a 0 a 0 a 0 Kiểm định 2 bên Kiểm định bên trái Kiểm định bên phải
Kiểm định giả thuyết về μ – các bước
Trường hợp cỡ mẫu lớn Bước 3: Kết luận
• Phát biểu quy tắc bác bỏ H : 0
• Sử dụng thống kê kiểm định Kiểm định 2 bên Kiểm định bên trái Kiểm định bên phải Bác bỏ H nếu |z| > z Bác bỏ H nếu z < – z Bác bỏ H nếu z > z 0 α/2 0 α 0 α
• Sử dụng giá trị p (p value): Bác bỏ H nếu p < α 0
• So sánh thống kê kiểm định và giá trị tới hạn (hay p và α) để kết
luận bác bỏ H hoặc không bác bỏ H với mức ý nghĩa đã cho. 0 0
• Kết luận theo yêu cầu của bài toán.
Kiểm định giả thuyết về μ – các bước
Trường hợp cỡ mẫu nhỏ
Bước 1: Xác định cụ thể dạng bài toán
• Phương sai (hay độ lệch chuẩn) tổng thể đã biết hay chưa? • Đặt giả thuyết:
o Diễn giải lại yêu cầu bài toán và sử dụng ký hiệu để mô tả.
o Xác định được giả thuyết H , H . 0 a H : μ = μ H : μ ≥ μ H : μ ≤ μ 0 0 0 0 0 0 H : μ ≠ μ H : μ < μ H : μ > μ a 0 a 0 a 0 Kiểm định 2 bên Kiểm định bên trái Kiểm định bên phải
Kiểm định giả thuyết về μ – các bước
Trường hợp cỡ mẫu nhỏ Bước 3: Kết luận
• Phát biểu quy tắc bác bỏ H : 0
• Sử dụng thống kê kiểm định Kiểm định 2 bên Kiểm định bên trái Kiểm định bên phải Bác bỏ H nếu |t| > t Bác bỏ H nếu t < – t Bác bỏ H nếu t > t 0 α/2 0 α 0 α
• Sử dụng giá trị p (p value): Bác bỏ H nếu p < α 0
• So sánh thống kê kiểm định và giá trị tới hạn (hay p và α) để kết
luận bác bỏ H hoặc không bác bỏ H với mức ý nghĩa đã cho. 0 0
• Kết luận theo yêu cầu của bài toán. (𝑧 2 𝛼 + 𝑧𝛽)𝜎 𝑛 = 𝜇0 − 𝜇𝑎 trong đó: 2.3 Xác định
𝑧 là trị số Z cho ở diện tích α ở đuôi 𝛼 kích thước mẫu
𝑧 là trị số Z cho ở diện tích β ở đuôi 𝛽
σ là độ lệch chuẩn tổng thể
μ là giá trị của trung bình tổng thể trong H 0 0
μ là giá trị của trung bình tổng thể được a dùng cho sai lầm loại II
Lưu ý: với kiểm định 2 bên thì ta dùng zα , z . /2 β/2
Đại học Công nghệ Sài Gòn Xác suất - Thống kê 41
Ví dụ 6.3: Cửa hàng KZE giải quyết phàn nàn (2)
Linda Danvers đang giải quyết vấn đề liên quan đến các khiếu nại của
các nhà bán lẻ về việc TV Ant-Imonitor bị các hư hỏng vật lý trong quá
trình vận chuyển trước khi đến cửa hàng. Theo thống kê mới của KZE,
trong 2 năm gần đây, có 414 trường hợp bị các hư hỏng trên. Một trong
các đối tác vận chuyển của KZE là công ty chuyển phát BHBA. Linda
cho rằng 50% các trường hợp bị hư hỏng là do BHBA vận chuyển.
Giả sử bạn kiểm tra một mẫu gồm 200 TV bị hư hỏng trên, trong đó có
103 TV được BHBA vận chuyển. Phát biểu trên của Linda có đúng hay
không? Hãy tự chọn mức ý nghĩa để kiểm định.
Đại học Công nghệ Sài Gòn Xác suất – Thống kê 43