XÁC SUẤT VS THỐNG KÊ PHẠM ĐĂNG QUYẾT phamdangquyet@gmail.com GIỚI THIỆU
Xác suất và thống kê (Probability and statistics) là hai ngành học liên quan nhưng riêng biệt XÁC SUẤT THỐNG KÊ ■ Từ xác suất (probability) bắt nguồn từ ■
Thuật ngữ “thống kê” của tiếng Anh “statistics” có gốc từ
chữ probare trong tiếng Latin và có nghĩa là "để chứng
“state” (nghĩa là quốc gia), nguồn gốc La tinh “statisticum minh,
để kiểm chứng". Nói một cách đơn
collegium” nghĩa là “hội đồng quốc gia”. Theo tiếng Đức,
giản, probable là một trong nhiều từ dùng để chỉ những
“statistik” có nghĩa gốc là “công tác dữ liệu của quốc gia”.
sự kiện hoặc kiến thức chưa chắc chắn, và thường đi ■
Ban đầu, thống kê dùng để diễn tả các hoạt động ghi
kèm với các từ như "có vẻ là", "mạo hiểm", "may rủi",
chép số liệu của một quốc gia như dân số, tài sản,
"không chắc chắn" hay "nghi ngờ", tùy vào ngữ cảnh.
thuế. Thống kê có thể được cho là đã bắt đầu trong nền
"Cơ hội" (chance), "cá cược" (odds, bet) là những từ cho
văn minh cổ xưa, ít nhất là từ cuối thế kỷ thứ 5 TCN, khái niệm tương tự.
nhưng cho đến thế kỷ 18 thì nó mới chịu ảnh hưởng ■
Xác suất chính là một khái niệm được nói đến khi tính
nhiều hơn từ số học và lý thuyết xác suất. Xác suất đã
khả năng xác suất xảy ra của các sự kiện, sự vật trong
trở thành một trong những công cụ thống kê cơ bản.
tương lai mà khả năng xảy ra những sự kiện này sẽ ■
Thống kê là một phần toán học của khoa học gắn liền với
không có bất kì điều gì có thể dự đoán chính xác được.
tập hợp dữ liệu, phân tích, giải thích hoặc thảo luận về ■
Lý thuyết xác suất là ngành toán học chuyên nghiên
một vấn đề nào đó, và trình bày dữ liệu. Có thể xem
cứu xác suất đã được phát triển vào thế kỷ 17. Lý thuyết
thống kê là một môn khoa học riêng biệt chứ không phải
xác suất biểu diễn các khái niệm xác suất bằng các thuật
là một nhánh của toán học, nó chính là một phần của
ngữ hình thức - nghĩa là các thuật ngữ mà có thể xác
khoa học dữ liệu. Mục tiêu cuối cùng của nó là chuyển
định một cách độc lập với ý nghĩa của nó. Các thuật ngữ
dữ liệu thành kiến thức và hiểu biết về thế giới xung
hình thức này được thao tác bởi các quy luật toán học và quanh chúng ta.
logic, và kết quả thu được sẽ được chuyển dịch trở lại
miền (domain) của bài toán. GIỚI THIỆU
Xác suất và thống kê (Probability and statistics) là hai ngành học liên quan nhưng riêng biệt XÁC SUẤT THỐNG KÊ
John Wilder Tukey (1915 – 2000) was an
American mathematician best known for development of
the Fast Fourier Transform (FFT) algorithm and box plot XÁC SUẤT VS THỐNG KÊ XÁC SUẤT THỐNG KÊ XÁC SUẤT VS THỐNG KÊ XÁC SUẤT THỐNG KÊ
■ Lý thuyết xác suất là ngành toán học chuyên
■ Lý thuyết thống kê liên quan tới những lập luận nghiên cứu xác suất
logic cơ bản giải thích của phương pháp tiếp cận
kết luận thống kê, cũng bao gồm toán thống kê. XÁC SUẤT VS THỐNG KÊ XÁC SUẤT THỐNG KÊ ■ Thuật ngữ ■ Thuật ngữ
■ NGẪU NHIÊN VÀ XÁC SUẤT ■ TỔNG THỂ VÀ MẪU
■ Một hiện tượng ngẫu nhiên có các kết cục
■ Toàn bộ nhóm các cá thể mà chúng ta muốn có
không thể dự đoán trước nhưng lại có quy luật
thông tin về nó được gọi là tổng thể.
phân bố nhất định sau nhiều lần lặp lại thử nghiệm.
■ Một mẫu là một phần của tổng thể mà thực tế
■ Xác suất của một biến cố là tỉ lệ số lần xuất
chúng ta khảo sát để thu thập thông tin.
hiện biến cố đó sau nhiều lần lặp đi lặp lại thử
nghiệm về một hiện tượng ngẫu nhiên ■ THAM SỐ VÀ THỐNG KÊ .
■ KHÔNG GIAN MẪU VÀ BIẾN CỐ
■ Tham số là một số diễn tả tổng thể. Một tham số
là một số cố định, nhưng trong thực tế chúng ta
■ Không gian mẫu S của một hiện tượng ngẫu
không biết giá trị của nó.
nhiên là tập hợp của tất cả các kết cục có thể xảy ra.
■ Thống kê là một số diễn tả mẫu. Giá trị của thống
kê được biết khi chúng ta lấy mẫu, nhưng nó có
■ Biến cố là một kết cục hoặc một tập hợp các
thể thay đổi theo từng mẫu. chúng ta thường sử
kết cục của một hiện tượng ngẫu nhiên. Một
dụng một thống kê để ước lượng một tham số
biến cố là tập con của không gian mẫu. chưa biết. XÁC SUẤT VS THỐNG KÊ XÁC SUẤT THỐNG KÊ ■ Thuật ngữ ■ Thuật ngữ ■ MÔ HÌNH XÁC SUẤT ■ THỐNG KÊ MÔ TẢ
■ Sự mô tả một hiện tượng ngẫu nhiên bằng
■ Dữ liệu: Dữ liệu là các con số trong một ngữ
ngôn ngữ toán học gọi là mô hình xác suất.
cảnh cụ thể, và chúng ta cần hiểu ngữ cảnh
■ Biến ngẫu nhiên là biến lấy các giá trị bằng
đó nếu chúng ta muốn làm các con số trở số nên có nghĩa.
xác định bởi kết cục của một hiện tượng ngẫu nhiên.
■ Các biến: Bất kỳ tệp dữ liệu nào cũng đều
■ Phân bố xác suất của một biến ngẫu nhiên X
chứa các thông tin về một nhóm nào đó của
các cá thể. Thông tin được tổ chức vào các
cho ta biết các giá trị có thể có của X là gì và biến.
xác suất được tìm cho các giá trị đó như thế nào.
■ Phân bố của một biến cho chúng ta biết nó
nhận những trị số nào và nhận những trị số đó bao nhiêu lần. XÁC SUẤT VS THỐNG KÊ XÁC SUẤT THỐNG KÊ ■ QUY LUẬT SỐ LỚN
■ THỐNG KÊ MÔ TẢ - CÁC PHÂN BỐ
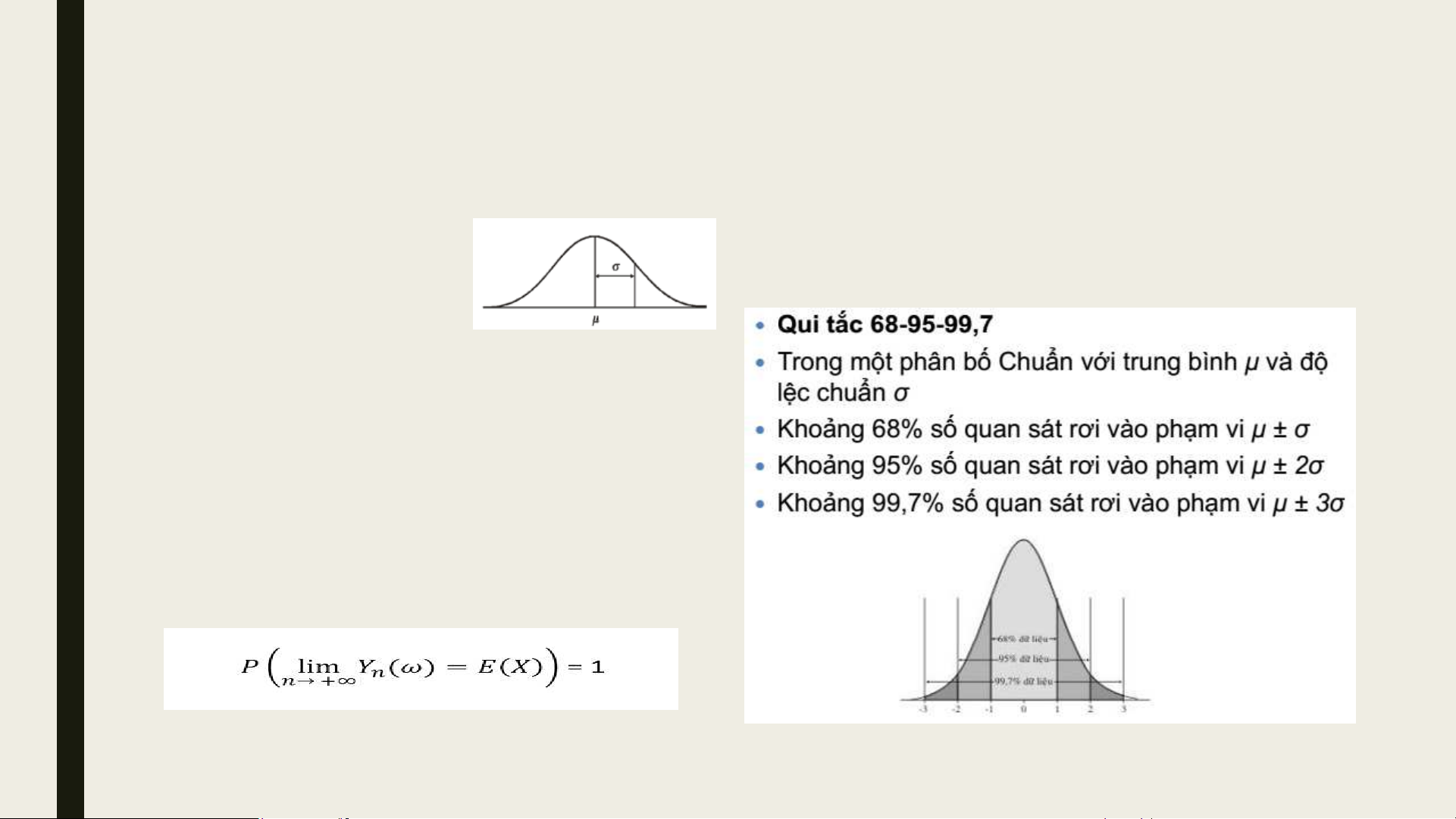
■ Phân bố xác suất chuẩn
■ Trung bình, phương sai và độ lệch
chuẩn của biến ngẫu nhiên
■ Quy luật số lớn chỉ ra rằng trung bình các
giá trị của X trong nhiều lần thử phải tiến gần đến µ.
■ Quy luật số lớn theo xác suất và thống kê
cho rằng khi kích thước mẫu tăng lên, giá trị
trung bình của nó sẽ gần với mức trung bình
của toàn bộ tổng thể. XÁC SUẤT VS THỐNG KÊ XÁC SUẤT THỐNG KÊ
■ ĐỊNH LÝ GIỚI HẠN TRUNG TÂM
■ THỐNG KÊ SUY LUẬN – KHOẢNG TIN CẬY
■ Định lý giới hạn trung tâm tuyên bố rằng
đối với n lớn, phân bố mẫu của 𝑥 gần đúng
phân bố Chuẩn N(μ, σ/ 𝑛 ) cho bất kỳ tổng
thể nào với trung bình μ và độ lệch chuẩn hữu hạn σ.
■ Khi cỡ mẫu được tăng lên, sự phân bố lấy mẫu của trung bình sẽ xấp xỉ phân phối chuẩn. Điều này là đúng
không phân biệt hình dạng phân bố của các giá trị cá thể trong tổng thể. XÁC SUẤT VS THỐNG KÊ XÁC SUẤT THỐNG KÊ Xác suất: Tại sao?
■ THỐNG KÊ SUY LUẬN – SAI SÔ CHUẨN
Thống kê không chứng minh bất cứ điều gì ...? Nó
chỉ hiển thị ngoài nghi ngờ hợp lý rằng một cái gì đó là sai
... Do đó, chúng ta sử dụng xác suất để nêu rõ mức
độ tự tin của mình trong việc chỉ ra một cái gì đó là sai lầm ■ XÁC SUẤT VS THỐNG KÊ XÁC SUẤT THỐNG KÊ Xác suất: Tại sao?
■ THỐNG KÊ SUY LUẬN – KIỂM ĐỊNH GIẢ THUYẾT
Trong thống kê, tôi không thể chứng minh bất
cứ điều gì là đúng, nhưng chỉ cho thấy ngoài
nghi ngờ hợp lý rằng một cái gì đó là sai
Vì vậy, với mỗi tuyên bố này tôi sẽ nói rằng
không có sự khác biệt giữa các trung bình
mẫu và trung bình tổng thể được giả thuyết ■ XÁC SUẤT VS THỐNG KÊ XÁC SUẤT THỐNG KÊ Xác suất: Tại sao?
■ SUY LUẬN THỐNG KÊ CHO HỒI QUI
Thống kê không chứng minh bất cứ điều gì ...? Nó
chỉ hiển thị ngoài nghi ngờ hợp lý rằng một cái gì đó là sai
... Do đó, chúng ta sử dụng xác suất để nêu rõ mức
độ tự tin của mình trong việc chỉ ra một cái gì đó là sai lầm ■ XÁC SUẤT VS THỐNG KÊ XÁC SUẤT THỐNG KÊ
Xác suất có điều kiện ■ SUY LUẬN BAYES
■ Xác suất mà biến cố A xảy ra, cho rằng biến cố B đã xảy ra ■
Định lý Bayes điều chỉnh các xác suất khi được cho
bằng chứng mới theo cách sau đây:
P( A and B)
P( A | B)  P(B) ■
H0 đại diện cho một giả thuyết, gọi là một giả thuyết
■ Xác suất tiên nghiệm (prior probability) hay xác không (null hypothesis)
suất vô điều kiện (unconditional probability): là
xác suất của một sự kiện trong điều kiện không ■
P(H0) được gọi là xác suất tiên nghiệm của H0
có tri thức bổ sung cho sự có mặt hay vắng mặt của nó. ■
P(E|H0) được gọi là xác suất có điều kiện của việc
quan sát thấy bằng chứng E nếu biết rằng giả thuyết
■ Xác suất hậu nghiệm (posterior probability ) H
hay xác suất có điều kiện (conditional 0 là đúng
probability): là xác suất của một sự kiện khi biết ■
P(E) được gọi là xác suất biên của E hay bằng chứng:
trước một hay nhiều sự kiện khác
xác suất của việc chứng kiến bằng chứng mới E dưới ■
tất cả các giả thuyết loại trừ nhau đôi một. ■
P(H0|E) được gọi là xác suất hậu nghiệm của H0 nếu biết E XÁC SUẤT VS THỐNG KÊ XÁC SUẤT THỐNG KÊ
Ý nghĩa của việc kiểm định - Frequentist vs Bayesian ■ Bayes Factor (BF) ■ p-value ■
Bayes Factor tương đương với giá trị p trong thống kê Bayesian. ■
Hãy hiểu nó một cách toàn diện.
Trong đó, tính t-score cho một mẫu cụ thể từ một phân bố mẫu
có cỡ mẫu cố định đã được tính. Sau đó, p-values được dự
đoán. Chúng ta có thể giải thích các p ■
Null hypothesis trong Bayesian giả định phân bố xác suất ∞ chỉ -values như (lấy ví dụ
trường hợp p-value = 0,02 cho một phân bố có mean = 100):
ở một giá trị cụ thể của một tham số (VD: θ = 0.5) và xác suất
Có 2% xác suất rằng mẫu sẽ có mean = 100.
bằng không ở những nơi khác. (M1) ■
Sự giải thích này có một khiếm khuyết là đối với phân phối mẫu ■
Giả thuyết thay thế (alternative hypothesis) là tất cả các giá trị
của các cỡ mẫu khác nhau, thì phải có t-scores khác nhau và từ
của θ đều có thể, do đó một đường cong dẹt đại diện cho sự
đó có p-values khác nhau. Nó hoàn toàn vô lý. Một p-value < phân bố này. (M2)
0.05 không đảm bảo rằng giả thuyết nul sai hoặc p-values lớn
hơn 5% cũng không đảm bảo là giả thuyết nul đúng. ■
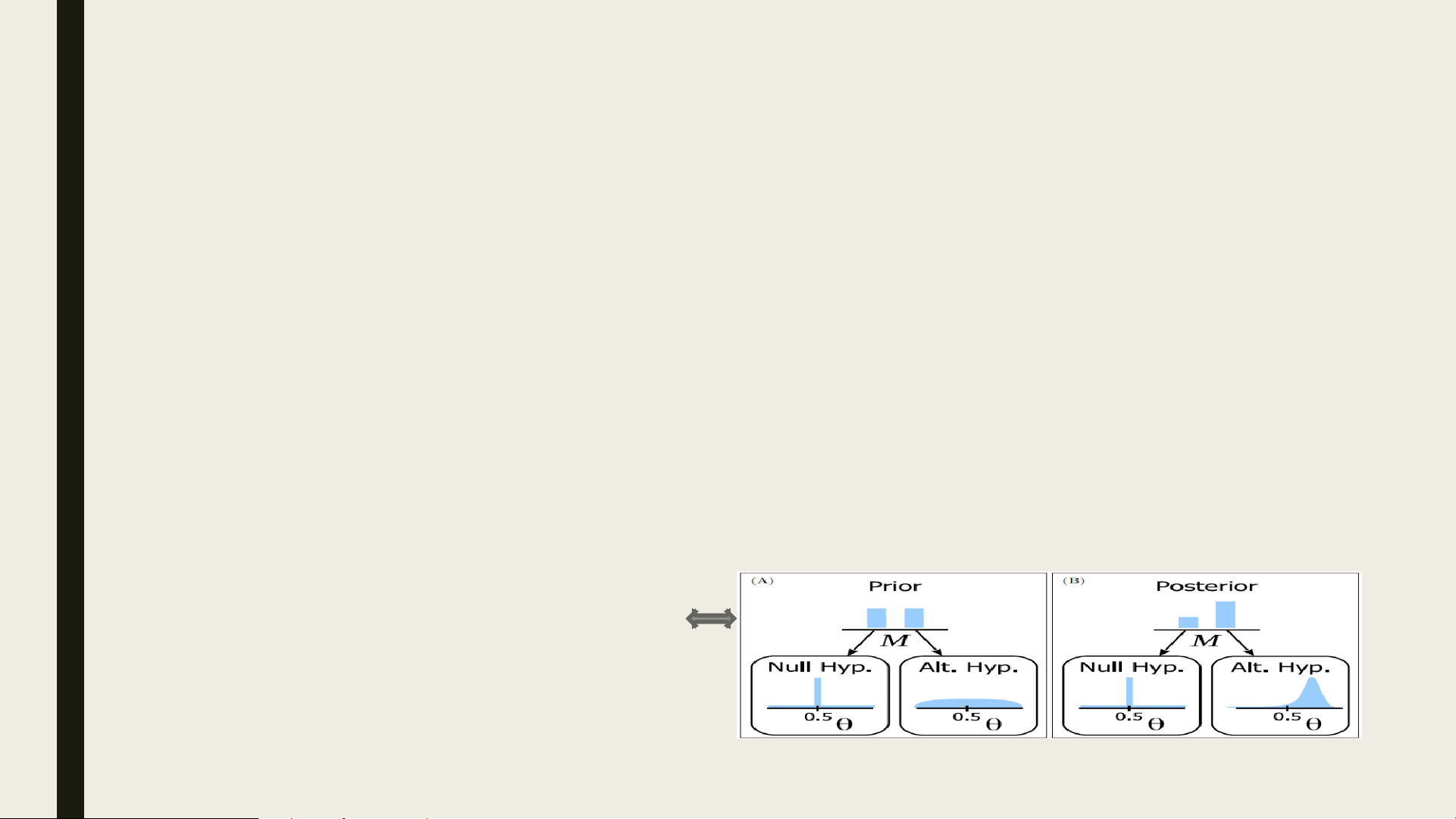
Bây giờ, phân phối hậu nghiệm của dữ liệu mới biểu diễn như hình dưới. ■
Trong bảng A (thể hiện ở bên): thanh trái (M1) là xác suất prior của nul hypothesis. ■
Trong bảng B (hiển thị), thanh bên trái là xác suất posterior của null hypothesis. ■
Bayes Factor được định nghĩa là tỷ lệ của các posterior
odds/prior odds. Để bác bỏ một giả thiết nul , ưu tiên BF <1/10. XÁC SUẤT VS THỐNG KÊ XÁC SUẤT THỐNG KÊ
Ý nghĩa của việc kiểm định - Frequentist vs Bayesian ■
Khoảng mật độ cao (HDI) ■ Khoảng tin cậy (CI) ■
HDI được hình thành từ phân phối hậu nghiệm sau
khi quan sát dữ liệu mới. Vì HDI là xác suất, HDI 95% ■
Khoảng tin cậy cũng bị khiếm khuyết tương tự. Hơn
cho 95% giá trị đáng tin cậy nhất. Nó cũng đảm bảo
nữa vì CI không phải là một sự phân bố xác suất, nên
rằng 95% giá trị sẽ nằm trong khoảng này không
không có cách nào để biết những giá trị nào có thể giống như CI. xảy ra nhất. ■
HDI 95% trong phân phối prior là rộng hơn so với
HDI 95% trong phân phối postorior. Điều này có được
là do độ tin cậy vào HDI tăng lên khi quan sát dữ liệu mới. XÁC SUẤT VS THỐNG KÊ XÁC SUẤT THỐNG KÊ Rủi ro Bayes ■ Quyết định Bayes ■
Định nghĩa : Rủi ro Bayes của hàm quyết định d được định nghĩa là ■
Định nghĩa: Nguyên tắc quyết định Bayes là một hàm
quyết định d* giảm tối thiểu rủi ro Bayes. ■ Đó là d* thỏa mãn ■
Trong đó kỳ vọng được thực hiện với đối θ. ■
Nếu xác suất phân bố π(θ) là rời rạc, hàm rủi ro có công ■ ở đây: thức như sau:
inf R( , d)  max(lowerR( , d)) d d R( , d )  R  ( d   i , ) ( i ) i ■
Khi phân bố hậu định π(θ|x) là có sẵn, rủi ro Bayes được viết là ■
Trong đó f(x) là hàm mật độ xác suất biên của X được tìm
thấy từ mật độ xác suất chung của X và θ. XÁC SUẤT VS THỐNG KÊ XÁC SUẤT THỐNG KÊ
Triết lý trong ứng dụng của xác suất ■
Ứng dụng thống kê ■
Một số nhà thống kê chỉ gán các xác suất cho các biến cố ngẫu ■
“Thống kê ứng dụng” bao gồm thống kê mô tả và các ứng
nhiên, ví dụ, các biến ngẫu nhiên, mà cho kết quả thử nghiệm
dụng của thống kê suy luận.
thực hay mang tính lý thuyết; đó là những nhà tần suất học (frequentist). ■
Thống kê được áp dụng cho một loạt các môn học, bao
gồm cả khoa học tự nhiên và xã hội, chính trị và kinh ■
Một số khác lại gán xác suất với những mệnh đề không chắc
chắn, tùy theo mức độ chủ quan (personal probability) tin vào doanh.
sự đúng đắn của nó. Những người như vậy là các nhà Bayes ■
Các công cụ thống kê cần thiết cho việc phân tích, dự báo (Bayesian).
và đưa ra quyết định dựa trên dữ liệu. ■
Ảnh hưởng chính của lý thuyết xác suất trong cuộc sống hằng ■
ngày đó là việc xác định rủi ro và trong buôn bán hàng hóa.
Suy luận có các ứng dụng trong trí tuệ nhân tạo và các hệ
chuyên gia. Các kỹ thuật suy luận Bayes đã là một phần căn ■
Chính phủ cũng áp dụng các phương pháp xác suất để điều tiết
bản của các kỹ thuật nhận dạng mẫu bằng máy tính kể từ
môi trường hay còn gọi là phân tích đường lối. cuối thập kỷ 1950. ■
Trong kinh tế, xác suất đóng góp rất nhiều cho việc tính toán và ■
Gần đây, suy luận Bayes đã trở nên thông dụng trong cộng
đưa ra các giải pháp nghiên cứu thị trường,...
đồng phylogenetics; các ứng dụng như BEAST và MrBayes
cho phép ước lượng đồng thời nhiều tham số nhân khẩu ■
Lý thuyết xác suất đóng một vai trò trung tâm trong các thuật học và tiến hóa.
toán machine learning để có thể đưa ra các dự đoán dễ xảy ra nhất. XÁC SUẤT VS THỐNG KÊ XÁC SUẤT THỐNG KÊ
Triết lý trong ứng dụng của xác suất ■
Ứng dụng thống kê XÁC SUẤT VS THỐNG KÊ
■ Phân tích quyết định trong điều kiện không chắc chắn, ví dụ:
■ Rất có thể hoàn cảnh kinh tế khó khăn hiện tại ở Mỹ và Anh sẽ ảnh hưởng đến số lượng các sinh viên đến
du học. Kết quả là lượng sách kỳ vọng bán cho sinh viên sẽ giảm và/hoặc thay đổi bất thường. Giả định bạn
thực hiện 1 vài nghiên cứu thị trường (ví dụ hỏi các đồng nghiệp của mình) về quan điểm của họ để thấy
được ảnh hưởng đó đến hoạt động của công ty bạn. Gợi ý rằng công ty có thể kỳ vọng khoản lợi nhuận
£1.5 triệu nếu số sinh viên đến học (đối với những người mới tham gia trong năm tới) giảm lượng nhỏ,
khoản lợi nhuận £0.5 triệu nếu số sinh viên giảm lượng vừa phải và mất £2 triệu nếu số sinh viên giảm lượng lớn.
■ Bạn ước tính rằng khả năng có thể xảy ra của các sự kiện này là P(nhỏ)=0.4, P(vừa phải)=0.3, P(lớn )=0.3. XÁC SUẤT VS THỐNG KÊ
■ Phân tích quyết định trong điều kiện không chắc chắn, ví dụ:
■ Do đó trong khi cây bộ giải pháp trên cho biết lợi nhuận có thể, quan tâm với xác suất thị trường ‘phỏng
đoán tốt nhất’ là quan tâm đối với công ty. Để có khả năng bù đắp này công ty của bạn đang xem xét việc
phân bổ lại năng lực sản xuất bằng việc cho thuê nó cho 1 tổ chức khác.
■ Nếu họ làm điều này, tổn thất tiềm năng của lợi nhuận sẽ không đáng kể như dự kiến ở trên (do thu nhập
cho thuê bổ sung), nhưng nó sẽ hạn chế năng lực sản xuất của công ty, nếu số sinh viên kỳ vọng giảm không xảy ra.
■ Trong kịch bản này, bạn có lợi nhuận dự kiến £1 triệu nếu số sinh viên giảm 1 lượng nhỏ, lợi nhuận £0.75
triệu nếu số sinh viên giảm lượng vừa phải và mất £0.5 nếu số sinh viên giảm nhiều.