





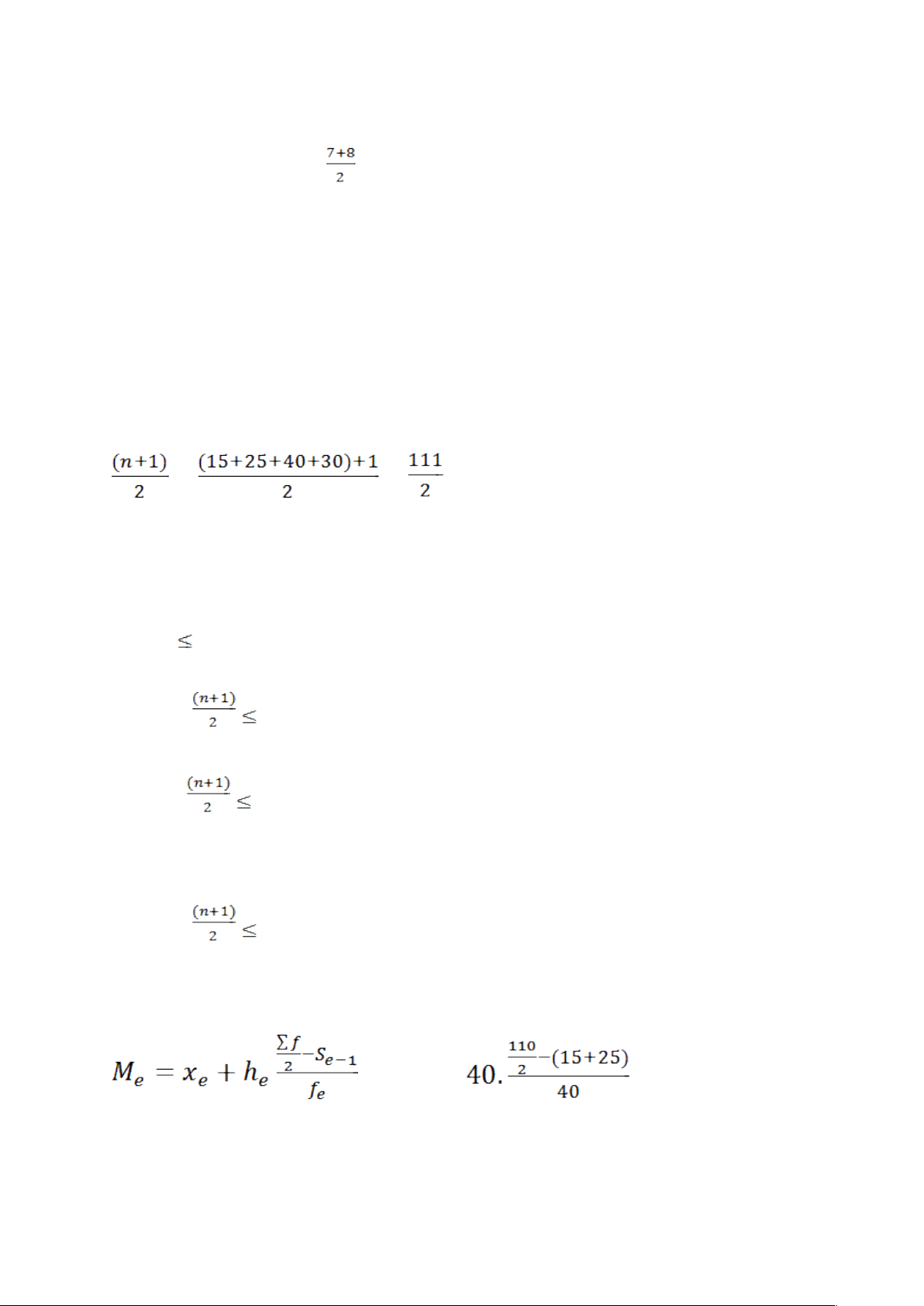






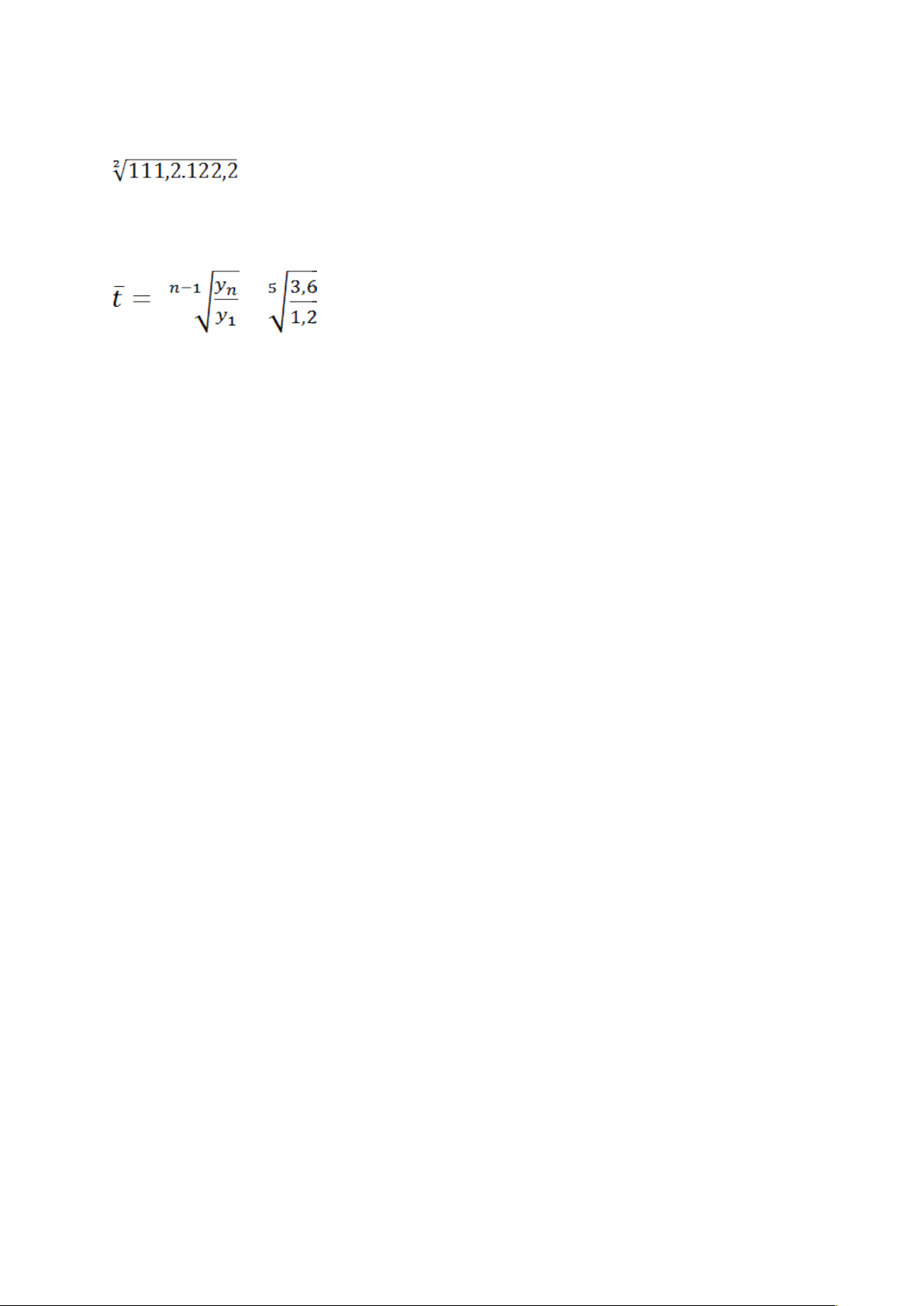




Preview text:
Cái này tớ làm theo dạng nên các bài tập không theo
thứ tự, muốn tìm dạng hoặc bài nào các bạn nhấn
Ctrl + F rồi nhập từ khóa cần tìm
Trung bình cộng....................................................................................................2
Số trung vị.............................................................................................................5
Mốt........................................................................................................................7
Các tham số đo độ phân tán và độ phân tán tương đối.........................................8
Mức độ trung bình theo thời gian.......................................................................10
Lượng tăng (hoặc giảm) tuyệt đối.......................................................................11
Tốc độ phát triển.................................................................................................11
Tốc độ tăng (hoặc giảm).....................................................................................12
Chỉ số giá cả........................................................................................................13
Chỉ số khối lượng................................................................................................15
Chỉ số giá cả không gian.....................................................................................16
Chỉ số tổng hợp về khối lượng theo không gian.................................................16
Hệ thống chỉ số trung bình..................................................................................17
Trung bình cộng
Trung bình cộng giản đơn
Trung bình cộng gia quyền
Trong trường hợp mỗi tổ có một phạm vi lượng biến ta lấy trị số giữa của khoảng
cách tổ làm lượng biến đại diện cho tổ đó Trung bình điều hòa: sử dụng khi biết
Trong trường hợp các quyền số bằng nhau, tức là = = thì = Trung bình nhân Bài 1: = = = 56 2A 3A 4A
Bài 5: Dãy số lượng biến có khoảng cách tổ mở
Khoảng cách tổ của các tổ ở giữa là 10, trị số giữa 35 45 55
Trị số giữa tổ dưới 25, tổ trên 65 = 47,7 16C 65A 66D 67C 68B 69B Bài 6: TBC gia quyền = 111,43
7A 8C 10D 11A 13A 14C 15D 20B 22C 34B 37A 59A 64A Bài 9: = = 717,778 12D 18A Bài 17:
Công nhân phân xưởng A chiếm 60% toàn xí nghiệp
=> công xưởng B chiếm 40% Lương TB 21D Bài 19: TBC điều hòa Quý 1
Doanh thu thực tế = Kế hoạch mức doanh thu x % hoàn thành kế hoạch =
Doanh thu thực tế Tivi: 200 . 105% = 210
Doanh thu thực tế Đầu Video: 200 . 103% = 206
Doanh thu thực tế Đầu VCD: 100 . 94,5 = 94,5 = = 102,1 (%) 55C 57A Bài 23: như nhau = = = 30 (phút) 27B Bài 24: =
= 10,81967… (phút) = 10 phút 49 giây
6 giờ phải nhân với 60 vì thời gian sản xuất 1 sản phẩm tính theo đơn vị phút Bài 26: = 3,33 25C 28C 29B 30C 31C 32A 33A Số trung vị
• Đối với dãy số lượng biến không có khoảng cách tổ, trung vị là giá trị của đơn vị đứng ở vị trí .
Nếu tổng số đơn vị trong dãy số là chẵn, trung vị sẽ là trung bình giữa hai lượng
biến của 2 đơn vị đứng giữa.
• Đối với dãy số lượng biến có khoảng cách tổ, xác định tổ chứa trung vị rồi
tính trị số gần đúng của trung vị theo công thức: : trung vị
: Giới hạn dưới của tổ chứa trung vị
: Khoảng cách tổ chứa trung vị : Tổng các tần số
: Tổng các tần số của các tổ đứng trên tổ chứa trung vị
: Tần số của tổ chứa trung vị
Bài 35: Dãy số lượng biến không có khoảng cách tổ, trung vị là vị trí = = 3 là 250
Bài 36: Tổng số đơn vị trong dãy số là chẵn (6 số), trung vị sẽ là trung bình của
2 số ở vị trí số 3 và 4 là = 7,5 Bài 39: = = = 55,5
Tổ thứ 3 (180 - 220) là tổ chứa trung vị vì NSLĐ 55 và 56 ở tổ này.
*) Nếu 15 thì tổ chứa trung vị là 100-140 Nếu 15<
(15+25) = 40 thì tổ chứa trung vị là 140-180 Nếu 40<
(15+25+40)= 80 thì tổ chứa trung vị là 180-220. Trong bài này là 55,5 Nếu 80<
(15+25+40+30)= 110 thì tổ chứa trung vị là 220-260. = 180 + = 195 40C 41D 42C 43A 44C Mốt
• Đối với dãy số lượng biến không có khoảng cách tổ, lượng biến nào có tần số cao nhất là mốt
• Đối với dãy số lượng biến có khoảng cách tổ, trước hết phải tìm tổ chứa mốt. Có 2 trường hợp
° Nếu các tổ có khoảng cách tổ bằng nhau thì tổ nào có tần số lớn nhất là tổ chứa mốt
° Nếu các tổ có khoảng cách tổ không bằng nhau thì phải tính mật độ phân
phối (bằng cách lấy tần số chia cho khoảng cách tổ . Tổ nào có mật độ
phân phối lớn nhất thì tổ đó chứa mốt
Sau khi tìm được tổ chứa mốt, ta tính mốt theo công thức : Mốt
: Giới hạn dưới của tổ chứa mốt
: Khoảng cách tổ chứa mốt = ( ) hoặc ( ) = ( ) hoặc ( )
: Tần số của tổ chứa mốt
: Tần số của tổ đứng liền trên tổ chứa mốt
: Tần số của tổ đứng liền dưới tổ chứa mốt
: Mật độ phân phối của tổ chứa mốt
: mật độ phân phối của tổ đứng liền trên tổ chứa mốt
: mật độ phân phối của tổ đứng liền dưới tổ chứa mốt Bài 38:
Dãy số lượng biến không có khoảng cách tổ, tần số lớn nhất là 30 => mốt =5 Bài 45:
Các tổ có khoảng cách tổ bằng nhau. Phân xương 4 có số công nhân nhiều nhất
(80) nên là tổ chứa mốt = 60 + 10. = 63,89 46B 47A 48B 49B 51C 52B Bài 50:
Dãy số lượng biến không có khoảng cách tổ, tần số f=22 lớn nhất =>
Các tham số đo độ phân tán và độ phân tán tương đối
• Khoảng biến thiên R =
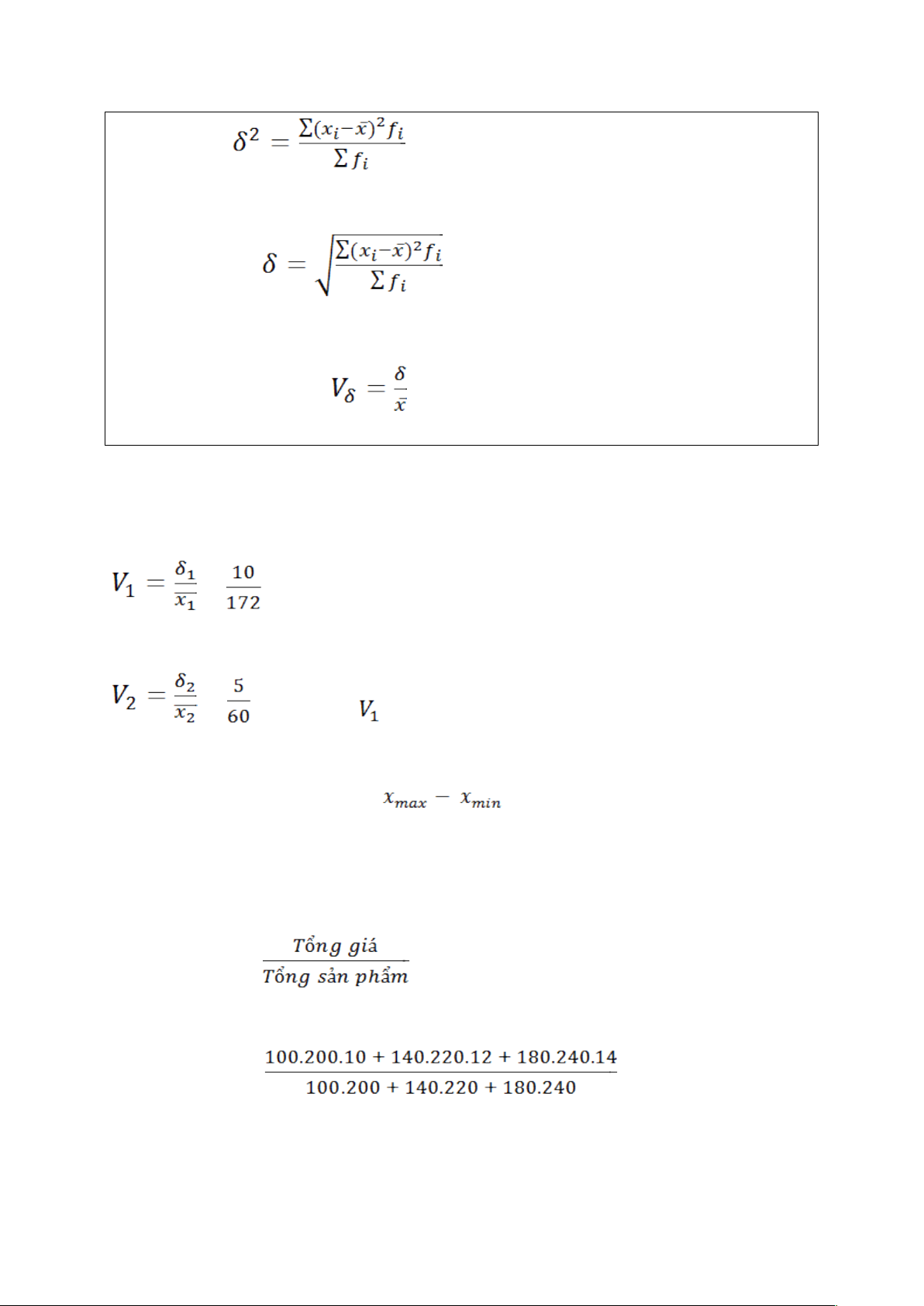
• Độ lệch trung bình = • Phương sai
• Độ lệch chuẩn
• Độ phân tán tương đối x 100 Bài 53:
Tính độ phân tán tương đối = = 0,058 = = 0,083 > => C
Bài 54: Khoảng biến thiên R = = 21 – 17 = 4 62B 63C Bài 56: Giá trung bình = = = 12 500 đ 58B 60B
Bài 61: Tính từng quý rồi lấy TBC => C
Mức độ trung bình theo thời gian
• Đối với dãy số thời kì
• Đối với dãy số thời điểm có khoảng cách thời gian bằng nhau
• Đối với dãy số thời điểm có khoảng cách thời gian không bằng nhau Bài 70:
Dãy số thời điểm có khoảng thời gian bằng nhau
Số công nhân ngày 1 tháng 4 là 325 người = = 315 71C 72A 73B 74A Bài 75:
Ngày 1 -> 17 có 16 ngày có 250 công nhân
17 ->21 có 5 ngày có 250-5 = 245 công nhân
22->25 có 4 ngày có 245 + 12 = 257 công nhân
26->30 có 5 ngày có 257 + 11 = 268 công nhân
Số công nhân trung bình trong tháng = 253 76A 77B 78D 79A
Lượng tăng (hoặc giảm) tuyệt đối Liên hoàn δ = - Định gốc Trung bình Bài 81: = = 300 82A
Tốc độ phát triển Liên hoàn Định gốc Trung bình Bài 83: = 116,5
Bài 84: Tốc độ phát triển bình quân = = 124,57% 85A 86B 87B 88D 90B Bài 89:
Năm 1996 tốc độ tăng là 11 => năm gốc là 1995 => có 6 năm
Tốc độ phát triển bình quân = = 113,58% Bài 91 = = 1,2 92A 93A 94A 95D 96A 97C 98
Tốc độ tăng (hoặc giảm) Liên hoàn Định gốc Trung bình Bài 99: = = 2 => = 1 100C 101B
Giá trị tuyệt đối của 1% tăng Bài 102: = = = 1,2 tỉ
103A 104C 105A 106C 107A (trang 28)
Chỉ số giá cả
• Chỉ số đơn về giá cả
• Chỉ số tổng hợp về giá cả
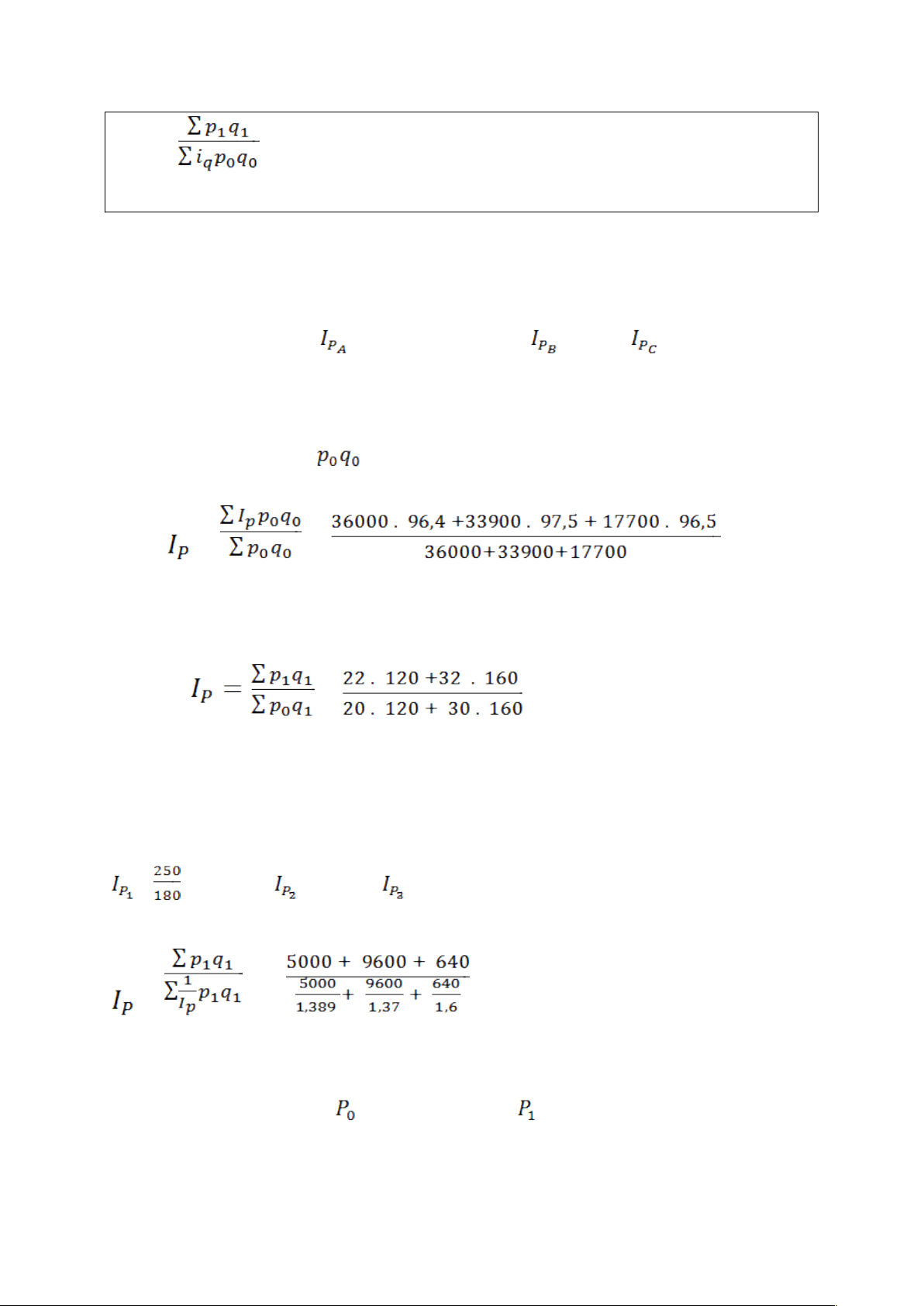
° Nếu chọn quyền số là khối lượng kì gốc = (với bài có ) =
(với bài có % lượng như 143,145)
° Nếu chọn quyền số là khối lượng kì nghiên cứu = (với bài có ) =
(với bài có % lượng như 144,146) Bài 108:
Tỷ lệ % giảm giá hàng năm 2002 so với 2001
Mặt hàng A là – 3,6 => = 100 – 3,6 = 96,4 ; = 97,5; = 96,5 Doanh thu = Giá x Lượng Doanh thu năm 2001 = = = = 0,9685
109A 106B 107C (trang 30) 108C 113B 114A Bài 110: = = 1,078
101B 102A 103A 104A 105B 109A 110A 115A 116A 117B 118C Bài 111: = = 1,389; = 1,37 ; = 1,6 = = = 138%
Bài 112: Giá 1kg tháng 5 , Giá 1 kg tháng 6
Số lượng đã bán trong tháng 6 => 106% Bài 143: = = = 98,33% Bài 144: = = = 99,4% 145B 146C



