Bài-tập-2 Bài để cương nghiên cứu mẫu ca nhan - Tài liệu tham khảo | Đại học Hoa Sen
Bài-tập-2 Bài để cương nghiên cứu mẫu ca nhan - Tài liệu tham khảo | Đại học Hoa Sen và thông tin bổ ích giúp sinh viên tham khảo, ôn luyện và phục vụ nhu cầu học tập của mình cụ thể là có định hướng, ôn tập, nắm vững kiến thức môn học và làm bài tốt trong những bài kiểm tra, bài tiểu luận, bài tập kết thúc học phần, từ đó học tập tốt và có kết q
Môn: Kinh tế quản trị, Quản trị kinh doanh (TV181)
Trường: Đại học Hoa Sen
Thông tin:
Tác giả:
Tài liệu liên quan:
Preview text:
Portfolio Management Homework Number 2
Submission deadline: Sunday 21/11/2021 1.
You have identified several different market conditions; Boom, Good, Average and Poor,
and the probabilities of these occurring. The following information relates to the return
on three shares under these conditions. Market Return Condition Probability Spec Stable Strange Boom 0.1 25% 12% -3% Good 0.3 7% 10% 1% Average 0.4 0% 9% 8% Poor 0.2 -8% -7% 12% Calculate (a)
the expected return on each share,
1. E(Spec) = �=1 � ∑ � � * � �=0.1 * 25%+0.3* 7%+0.4* 0%+0.2* (-8%)=3,2 2.
E(Stable) = �=1 � ∑ � � * � ��= 0.1*12%+0.3*10%+0.4*9%+0.2*(-7%)=6,2 3.
E(Strange) = �=1 � ∑ � � * � ��= 0.1*(-3%)+0.3*1%+0.4*8%+0.2*12%=5,6 (b)
the standard deviation of the return on each σSpec = =9% σStable= =6,75% σStrange= =4,93% (c)
the covariance of return between (i)
Spec and Stable=*+0,4*(0%-3)*(9%-6,2%)+0,2*(((-8)-3%)*((-7)-6,2)=0,43 (ii) Spec and Strange= -0,414 (iii)
Stable and Strange, and= - 0,2436 (d)
the correlation of return between (i)
Spec and Stable= 0,43/(9%*6,75%)=0,3225 (ii)
Spec and Strange= -0,414/(9%*4,93%)=-0.22678 (iii)
Stable and Strange, and=-0,2436/(6,75%*4,93%)=-0.1779182222
3.Barry Broadback has invested 10% of his available funds in Asset A, 50 % in Asset B, and the remainder in Asset
C. These assets have the following characteristics: Asset A Asset B Asset C Expected Return 10% 12% 15% Standard Deviation 2% 5% 4%
The correlation coefficient for Assets A, B and C are as follows: • AandB -0.8 • BandC 0.2 • AandC -0.3 Required: (i)
Calculate the expected return of Barry Broadback's portfolio.
� (� � ) = � � * �(� � ) = 10%* 10%+50%*12%+30%*15%=11.5% (ii)
Calculate the risk of the portfolio =70.42%
4 An investor invests 30 per cent of her funds in Company A's shares and the remainder in Company B's
shares. The standard deviation of the returns on A is 20 per cent and on B is 10 per cent. Calculate the
variance of return on the portfolio assuming the correlation between the returns on the two securities is: (a) +l .0
ρ � � = σ �� σ / � σ � => σ �� = ϱ �� * σ � σ � = 1 * 20% * 10% = 0. 02 (b) +0.5
ρ �� = σ �� σ / � σ � => σ �� = ϱ �� * σ � σ � = 0.5 * 20% * 10% = 0. 01 (c) 0
ρ �� = σ �� σ / � σ � => σ �� = ϱ �� * σ � σ � = 0 * 20% * 10% = 0 (d) -0.5
ρ �� = σ �� σ / � σ � => σ �� = ϱ �� * σ � σ � = -0.5 * 20% * 10% = -0.01 5
The following are the monthly rates of return for Madison Corp. and for
General Electric during a six-month period. Month Madison Corp. General Electric 1 -0.04 0.07 2 0.06 -0.02 3 -0.07 -0.10 4 0.12 0.15 5 -0.02 -0.06 6 0.05 0.02 Compute the following: a.
Average monthly rate of return for each stock
b. Standard deviation of returns for each stock
c. Covariance between the rates of return
d. the correlation coefficient between the rates of return a.
average return :E(R Madison Corp) =0.10/6=0.167; E(RGeneral Electric)=0,06/6=0,01 .b Month Madison Corp General Ri-E(Ri) Ri-E(Ri) (Ri-E(Ri))x(Ri- (Ri) Electric(Ri) E(Ri)) 1 -0.04 0.07 -0.057 0.06 -0.0034 2 0.043 -0.03 -0.0013 0.06 -0.02 3 -0.87 -0.11 0.0096 -0.07 -0.10 4 0.12 -0.037 0.14 0.0144 0.15 5 -0.037 -0.07 0.0026 -0.02 -0.06 6 0.033 0.01 0.0003 0.05 0.02 Sum 0.10 0.06 0.0222 . Madison Corp.= . General Electric.=
b. Covariance between the rates of return =1/5*(0.0222)=0.0044
d the correlation coefficient between the rates of return
r= 0.00444/0.0717*0.0908=0.0044/0.006510=0.6758
What level of correlation did you expect? How did your expectations
compare with the computed correlation? Would these two stocks offer a good
chance for diversification? Why or why not?
6.You are considering two assets with the following characteristics:
E(A1 ) = 0.15 .1= 0.10 W 1 = 0. 5
E(A ) = 0.20 .2 = 0.20 W = 0. 5 2 2
Compute the mean and standard deviation of two portfolio if
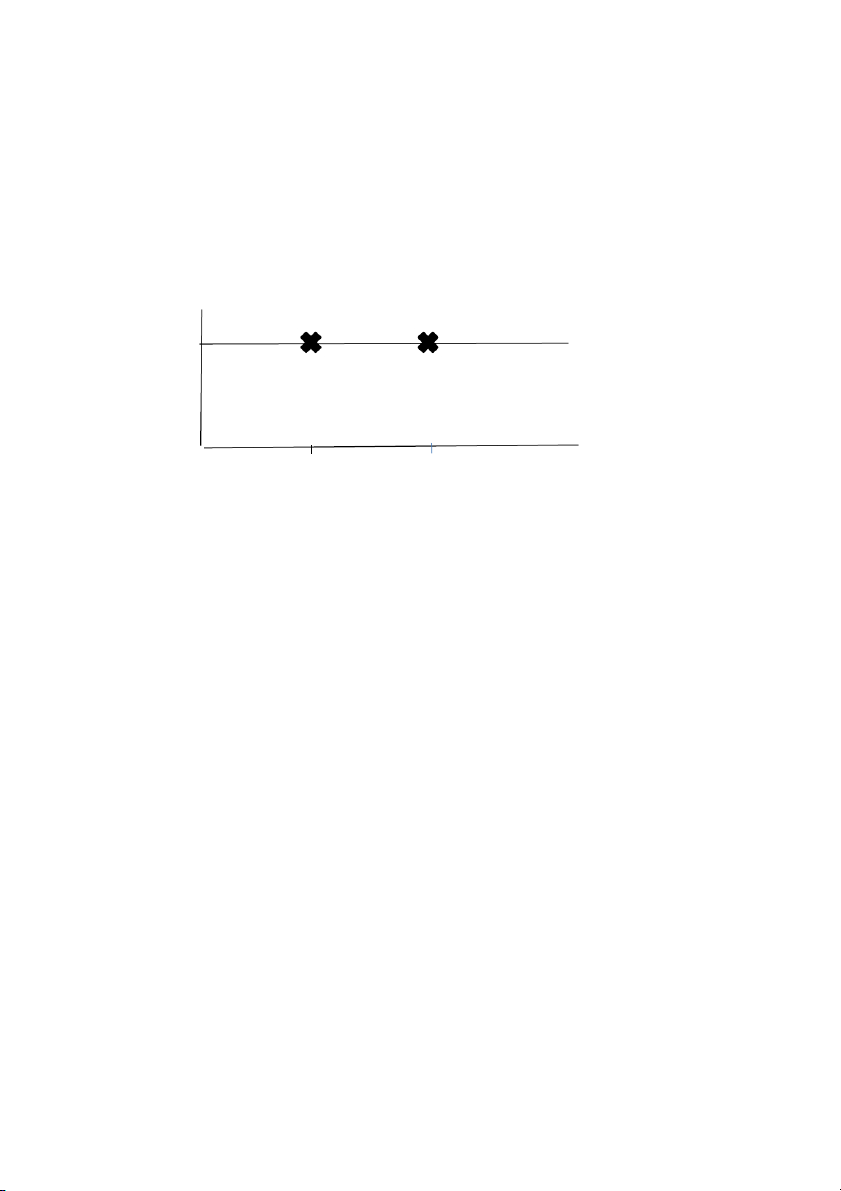
correlation between asset 1 and 2=0. 40 and — 0. 60, respectively. Plot the
two portfolios on a risk-return graph and briefly explain the results. E(A ) = 0.15 .1= 0.10 W 1 = 0. 5 E(A ) = 0.20 .2 = 0.20 W = 0. 5 2 2
E(R)= 0.5*(0.15)+0.5(0.20)=0.175 If r 1,2 = 0.40 r= = = = 0.012845 If r 1,2 = -0.60 2= = = = 0.08062 Expected return17.5% 8.06% 12.85% risk (standard deviation)
The negative correlation coeficient reduces risk without sacrificing return