











Preview text:
PHÂN TÍCH ĐỊNH LƯỢNG TRONG QUẢN TRỊ XÁC SUẤT
1. Một cuộc khảo sát khách hàng của Morgan Stanley lấy mẫu từ cả nam giới và
nữ giới để hỏi về việc liệu họ thích uống nước tinh khiết đóng chai hơn hay các
loại nước uống thể thao như Gatorade hoặc Propel Fitness hơn (Theo Tạp chí
Atlanta, ngày 28/12/2005). Giả sử có 200 khách hàng nam và 200 khách hàng nữ
tham gia trả lời trong vào cuộc khảo sát, và trong đó, 280 người trả lời rằng họ
thích nước tinh khiết đóng chai hơn. Trong nhóm trả lời rằng họ thích nước uống
thể thao hơn thì có 80 người là nam và 40 người là nữ. Gọi
M = Biến cố khách hàng là nam
W = Biến cố khách hàng là nữ
B = Biến cố khách hàng thích dùng nước tinh khiết đóng chai hơn
S = Biến cố khách hàng thích dùng nước uống thể thao hơn
a. Tính xác suất để một khách hàng thích dùng nước tinh khiết đóng chai hơn.
b. Tính xác suất để một khách hàng thích dùng nước uống thể thao hơn.
c. Tính các xác suất có điều kiện P(M | ) và S P(W | S)?
d. Tính các xác suất đồng thời P( ∩ M ) và S
P(W ∩ S)?
e. Nếu biết rằng một khách hàng là nam, tính xác suất để khách hàng này thích
các loại nước uống thể thao hơn.
f. Nếu biết rằng một khách hàng là nữ, tính xác suất để khách hàng này thích các
loại nước uống thể thao hơn.
g. Việc thích nước uống thể thao hơn có độc lập với việc khách hàng là nam giới
hay nữ giới hay không? Giải thích câu trả lời bằng các mức xác suất tính được.
2. Một giám đốc tài chính thực hiện hai quyết định đầu tư mới— một là đầu tư vào
công nghiệp dầu khí và một là đầu tư vào trái phiếu đô thị. Sau thời kỳ một năm,
mỗi quyết định đầu tư sẽ được đánh giá là thành công hay không thành công.
Nếu xem việc thực hiện hai quyết định đầu tư này là một phép thử.
a. Có bao nhiêu điểm mẫu trong phép thử này?
b. Vẽ biểu đồ cây và liệt kê các điểm mẫu.
c. Gọi O = biến cố quyết định đầu tư vào công nghiệp dầu khí là thành công và M
= biến cố quyết định đầu tư vào trái phiếu đô thị là thành công. Liệt kê các điểm
mẫu của O và của M.
d. Liệt kê các điểm mẫu của phần hợp (O ∪M).
e. Liệt kê các điểm mẫu của phần giao (O ∩ M).
f. Các biến cố O và có là biến cố xung khắc? Giải thích vì sao M .
3. Một công ty dầu khí mua một quyền chọn về đất đai ở Alaska. Một khảo sát địa
chất thu được các xác suất tiên nghiệm sau.
P(Có dầu chất lượng tốt) = 0,50
P(Có dầu chất lượng trung bình) = 0,20
P(Không có dầu) = 0,30
a. Xác suất để công ty tìm thấy dầu là bao nhiêu?
b. Sau khi khoan 200 feet của giếng khoan đầu tiên, một phân tích đất được thực
hiện. Xác suất để tìm thấy loại đất đặc thù xác định bởi phân tích đất này như sau.
P(đất ǀ Có dầu chất lượng tốt) = 0,20
P(đất ǀ Có dầu chất lượng trung bình) = 0,80
P(đất ǀ không tìm thấy dầu) = 0,20
Công ty nên diễn giải kết quả phân tích đất như thế nào? Tính lại các xác suất với
thông tin trên. Xác suất mới để tìm thấy dầu là bao nhiêu? BIẾN RỜI RẠC
1. Trung tâm dịch vụ cấp cứu nhận được từ 0 đến 5 cuộc gọi hàng ngày. Phân phối
xác suất của số cuộc gọi trong ngày như sau:
Số cuộc gọi Xác suất 0 0,10 1 0,15 2 0,30 3 0,20 4 0,15 5 0,10
a. Số cuộc gọi kỳ vọng trong ngày là bao nhiêu?
b. Phương sai của số cuộc gọi là bao nhiêu? Tính độ lệch chuẩn tương ứng.
2. Ở San Francisco, 30% công nhân đón xe công cộng để đi làm hàng ngày (USA Today, ngày 21/12/2005).
a. Với một mẫu gồm 10 công nhân, xác suất có đúng 3 công nhân đón xe công
cộng để đi làm hàng ngày là bao nhiêu?
b. Với một mẫu gồm 10 công nhân, xác suất có ít nhất 3 công nhân đón xe công
cộng để đi làm hàng ngày là bao nhiêu?
3. 9% sinh viên đại học có nợ thẻ tín dụng lớn hơn 7000 USD (Reader Digest, tháng 7, 2002).
Giả sử 10 sinh viên đại học được lựa chọn ngẫu nhiên để được phỏng vấn về việc sử dụng thẻ tín dụng.
a. Việc chọn 10 sinh viên có phải là dãy phép thử nhị thức? Giải thích.
b. Tính xác suất có 2 sinh viên có mức dư nợ thẻ tín dụng cao hơn 7000 USD.
c. Tính xác suất không có sinh viên có mức dư nợ thẻ tín dụng cao hơn 7000 USD.
d. Tính xác suất có ít nhất 3 sinh viên có mức dư nợ thẻ tín dụng cao hơn 7000 USD. BIẾN LIÊN TỤC
1. Giá cổ phiếu bình quân của các công ty trong danh sách S&P 500 là 30 USD, và
độ lệch chuẩn là 8,20 USD (BusinessWeek, Số đặc biệt của năm, Spring 2003).
Giả sử giá cổ phiếu có phân phối chuẩn.
a. Xác suất để một công ty sẽ có giá cổ phiếu ít nhất 40 USD là bao nhiêu?
b. Xác suất để một công ty sẽ có giá cổ phiếu không cao hơn 20 USD là bao nhiêu?
c. Giá cổ phiếu phải cao bao nhiêu để một công ty được đứng trong 10% cao nhất?
2. Thời gian cần thiết để hoàn thành bài thi cuối khóa đối với một khóa học cụ thể
ở một trường đại học có phân phối chuẩn với một trung bình là 80 phút và độ lệch
chuẩn là 10 phút. Hãy trả lời các câu hỏi sau.
a. Xác suất hoàn thành bài thi trong một giờ hoặc ít hơn là bao nhiêu?
b. Xác suất để một sinh viên hoàn thành bài thi trong thời gian hơn 60 phút
nhưng ít hơn 75 phút là bao nhiêu?
c. Giả sử rằng lớp học có 60 sinh viên và thời gian thi là 90 phút. Hỏi có bao nhiêu
sinh viên được dự tính sẽ không thể hoàn thành bài thi trong thời gian quy định?
3. Theo Advertising Age, mức lương cơ bản bình quân của nữ giới làm công việc
viết quảng cáo trong các công ty quảng cáo là cao hơn so với lương cơ bản trung
bình của nam giới. Mức lương cơ bản bình quân cho nữ là 67.000 USD và lương cơ
bản trung bình cho nam là 65.500 USD (Working Woman, tháng 7/tháng 8, 2000).
Giả sử tiền lương có phân phối chuẩn và độ lệch chuẩn là 7.000 USD cho cả nam và nữ.
a. Xác suất để một nhân viên nữ nhận được mức lương vượt quá 75.000 USD là bao nhiêu?
b. Xác suất để một nhân viên nam nhận được mức lương vượt quá 75.000 USD là bao nhiêu?
c. Xác suất để một nhân viên nữ nhận được mức lương dưới 50.000 USD là bao nhiêu?
d. Một nhân viên nữ phải có mức lương bao nhiêu để có thể cao hơn 99% đồng
nghiệp nam giới của mình? PHÂN TÍCH QUYẾT ĐỊNH
1. Chủ nhân một cửa hàng thể dục thể thao ghi nhận các số liệu về mức nhu cầu một loại dụng cụ thể dục thể thao như sau:
Nhu cầu trong năm (ngàn sản phẩm) Xác suất 100 0,15 200 0,20 300 0,30 400 0,15 500 0,20
Giá vốn và giá bán một sản phẩm lần lượt là 40 ngàn đồng và 50 ngàn đồng. Giả định rằng sản phẩm
sẽ không còn giá trị nếu không bán được. Yêu cầu:
1. Chủ nhân cửa hàng quyết định mức dự trữ tốt nhất là 300 ngàn sản phẩm vì ông cho rằng khả năng
có các mức cầu lớn hơn và ít hơn 300 ngàn sản phẩm là như nhau. Dựa vào tiêu chuẩn tổn thất cơ
hội kỳ vọng, bạn có đồng ý với ý kiến này không? Tại sao?
2. Chứng tỏ rằng lợi nhuận kỳ vọng cộng với thiệt hại kỳ vọng của từng phương án tồn trữ sẽ bằng
lợi nhuận kỳ vọng của tiên đoán hoàn hảo.
2. Để phân tích và dự đoán doanh thu vào tháng tới, một phân tích viên dựa vào số liệu được ghi nhận
trong thời gian qua như sau:
Nhu cầu trong ngày (sản phẩm) Xác suất 100 0,1 110 0,3 120 0,3 140 0,2 145 0,1
Lợi nhuận trên mỗi sản phẩm là 2000 đồng. Giá vốn mỗi sản phẩm là 10000 đồng. Nếu không bán
được trong ngày, mỗi sản phẩm chỉ còn bán được với giá 9200 đồng. Yêu cầu:
1. Hãy tính doanh thu trung bình trong ngày.
2. Lập bảng các mức lợi nhuận và bảng các mức tổn thất cơ hội. Hãy xác định mức tồn trữ tối ưu.
3. Xếp hạng các mức tồn trữ theo tổn thất. Tính các khác biệt giữa tổn thất kỳ vọng của từng mức tồn
trữ với mức tồn trữ tối ưu.
Tương tự như (3), nhưng dùng tiêu chuẩn lợi nhuận. So sánh các kết quả với (3).
3. Hàng ngày, chị Hương có thể đi đến nơi làm việc bằng ba lộ trình S , 1 S , 2 và S . 3 Theo kinh nghiệm,
Chị Hương ước lượng thời gian (phút) đi từ nhà đến nơi làm việc như sau: Tình trạng kẹt xe Lộ trình S1 S2 S3 Không kẹt xe 18 23 20 Kẹt xe ít 35 35 30 Kẹt xe nhiều 55 50 50
Trong 100 ngày qua, có 25 ngày chị Hương không bị kẹt xe, 42 ngày bị kẹt xe ít, còn lại là bị kẹt xe
nhiều. Giả sử rằng 100 ngày là đủ để cho thấy tình trạng kẹt xe chung cho cả 3 lộ trình và tình trạng có
thể bị kẹt xe mỗi ngày ở cả 3 lộ trình là như nhau. Yêu cầu :
1. Theo Anh (Chị), chị Hương nên chọn lộ trình nào để đến nơi làm việc nhanh nhất?
2. Giả sử rằng vào mỗi ngày, trước khi đi làm chị Hương đều có thể biết chắc chắn về tình trạng kẹt
xe từ bản tin của Trung tâm điều khiển giao thông thành phố. Tìm thời gian trung bình để chị
Hương đi từ nhà đến nơi làm việc trong trường hợp này.
4. Jim Sellers is thinking about producing a new type of electric razor for men. If
the market were favorable, he would get a return of $100,000, but if the market
for this new type of razor were unfavorable, he would lose $60,000. Since Ron
Bush is a good friend of Jim Sellers, Jim is considering the possibility of using Bush
Marketing Research to gather additional information about the market for the
razor. Ron has suggested that Jim either use a survey or a pilot study to test the
market. The survey would be a sophisticated questionnaire administered to a test
market. It will cost $5,000. Another alternative is to run a pilot study.
Jim đang xem xét việc sản xuất một loại dao cạo râu mới (sử dụng điện) dành cho
đàn ông. Nếu thị trường thuận lợi, lợi nhuận ước tính là $100,000, nhưng nếu thị
trường không thuận lợi, ước tính bị lỗ $60,000. Để có thêm thông tin về thị
trường, Jim có thể sử dụng dịch vụ khảo sát thị trường hoặc nghiên cứu thử. Chi
phí khảo sát thị trường là $5,000.
This would involve producing a limited number of the new razors and trying to
sell them in two cities that are typical of American cities. The pilot study is more
accurate but is also more expensive. It will cost $20,000. Ron Bush has suggested
that it would be a good idea for Jim to conduct either the survey or the pilot
before Jim makes the decision concerning whether to produce the new razor. But
Jim is not sure if the value of the survey or the pilot is worth the cost.
Chi phí thực hiện nghiên cứu thử là $20,000. Khi không thực hiện khảo sát hoặc
nghiên cứu thử, khả năng thị trường thuận lợi được ước tính là 0.5. Nếu khảo sát
thị trường, khả năng kết quả khảo sát thuận lợi với điều kiện thi trường thuận lợi
là 0.7, và nếu thị trường không thuận lợi thì khả năng kết quả khảo sát thuận lợi
là 0.2. Mặt khác, nếu nghiên cứu thử, khả năng kết quả nghiên cứu thử không
thành công với điều kiện thi trường không thuận lợi là 0.9, và nếu thị trường
thuận lợi thì khả năng nghiên cứu thử không thành công là 0.2.
Jim estimates that the probability of a successful market without performing a
survey or pilot study is 0.5. Furthermore, the probability of a favorable survey
result given a favorable market for razors is 0.7, and the probability of a favorable
survey result given an unsuccessful market for razors is 0.2. In addition, the
probability of an unfavorable pilot study given an unfavorable market is 0.9, and
the probability of an unsuccessful pilot study result given a favorable market for razors is 0.2.
(a) Draw the decision tree for this problem without the probability values.
(b) Compute the revised probabilities needed to complete the decision, and place
these values in the decision tree.
(c) What is the best decision for Jim? Use EMV as the decision criterion.
(Problem 3.44, Chap.3 – Render et al.)
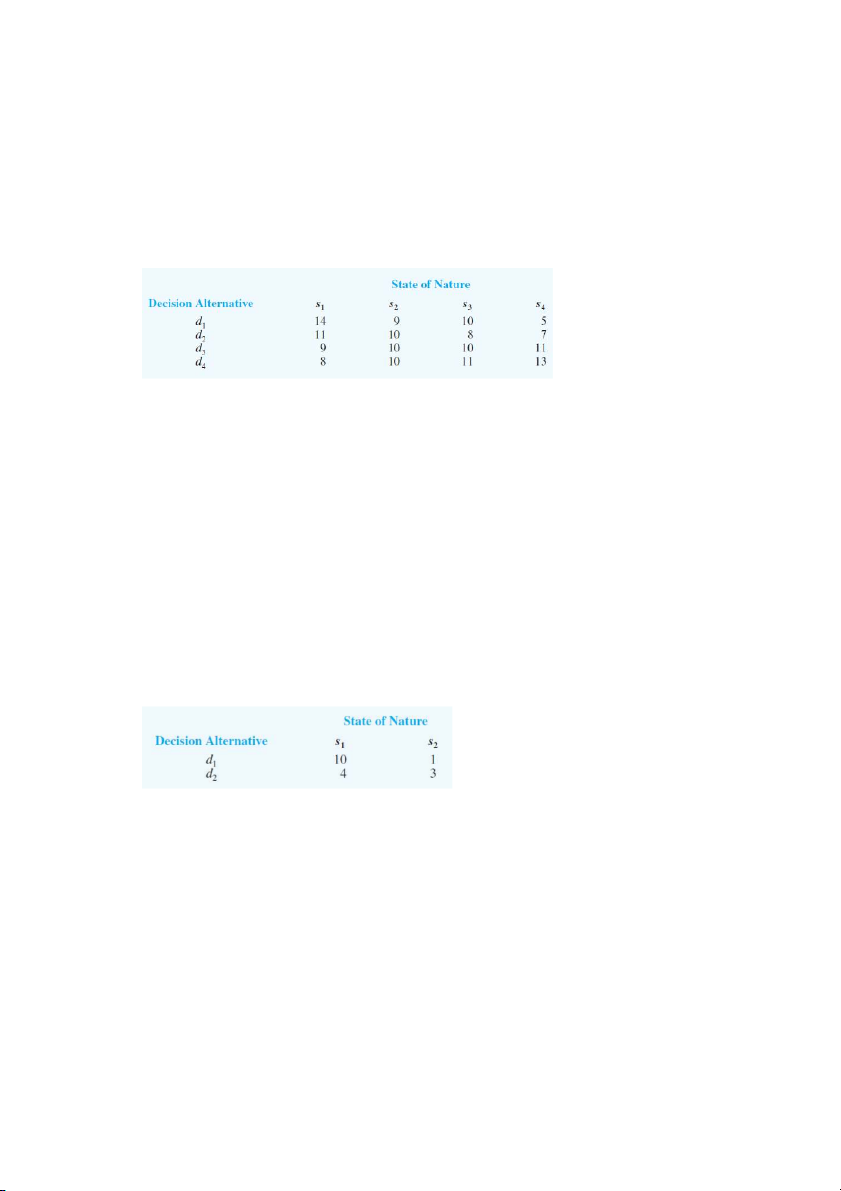
5. Suppose that a decision maker faced with four decision alternatives and four
states of nature develops the following profit payoff table:
a. If the decision maker knows nothing about the probabilities of the four states
of nature, what is the recommended decision using the optimistic, conservative, and minimax regret approaches?
b. Which approach do you prefer? Explain. Is establishing the most appropriate
approach before analyzing the problem important for the decision maker? Explain.
c. Assume that the payoff table provides cost rather than profit payoffs. What is
the recommended decision using the optimistic, conservative, and minimax regret approaches?
(Problem 2, Chap.4 – Anderson et al.)
6. The following payoff table shows the profit for a decision problem with two
states of nature and two decision alternatives:
a. Use graphical sensitivity analysis to determine the range of probabilities of
state of nature s1 for which each of the decision alternatives has the largest expected value.
Hãy sử dụng phương pháp phân tích độ nhạy (vẽ biểu đồ). (p: xác suất tình huống s1 xảy ra)
b. Suppose P(s1) = 0.2 and P(s2) = 0.8. What is the best decision using the expected value approach?
c. Perform sensitivity analysis on the payoffs for decision alternative d2. Assume
the probabilities are as given in part (b), and find the range of payoffs for d2 that
will keep the solution found in part (b) optimal.
Hãy phân tích độ nhạy đối với lợi nhuận của phương án d2. Giả định các xác suất
vẫn như ở câu (b) và giải pháp đã tìm thấy ở (b) được xem là tối ưu.
(Problem 8, Chap.4 – Anderson et al.)
7. Alexander Industries is considering purchasing an insurance policy for its new
office building in St. Louis, Missouri. The policy has an annual cost of $10,000. If
Alexander Industries doesn’t purchase the insurance and minor fire damage
occurs, a cost of $100,000 is anticipated; the cost if major or total destruction
occurs is $200,000. The costs, including the state-of-nature probabilities, are as follows:
a. Using the expected value approach, what decision do you recommend?
b. What lottery would you use to assess utilities? (Note: Because the data are costs, the best payoff is $0.)
c. Assume that you found the following indifference probabilities for the lottery
defined in part (b). What decision would you recommend?
d. Do you favor using expected value or expected utility for this decision problem? Why?
(Problem 2, Chap.5 – Anderson et al.)
8. Two different routes accommodate travel between two cities. Route A normally
takes 60 minutes and route B normally takes 45 minutes. If traffic problems are
encountered on route A, the travel time increases to 70 minutes; traffic problems
on route B increase travel time to 90 minutes. The probability of a delay is 0.20
for route A and 0.30 for route B.
a. Using the expected value approach, what is the recommended route?
b. If utilities are to be assigned to the travel times, what is the appropriate
lottery? (Note: The smaller times should reflect higher utilities.)
c. Use the lottery of part (b) and assume that the decision maker expresses indifference probabilities of: p = 0.80 for 60 minutes p = 0.60 for 70 minutes
What route should this decision maker select? Is the decision maker a risk taker or a risk avoider?
(Problem 4, Chap.5 – Anderson et al.)
9. A television network has been receiving low ratings for its programs. Currently,
management is considering two alternatives for the Monday night 8:00 P.M.–9:00
P.M. time slot: a western with a well-known star or a reality show. The
percentages of viewing audience estimates depend on the degree of program
acceptance. The relevant data are as follows: