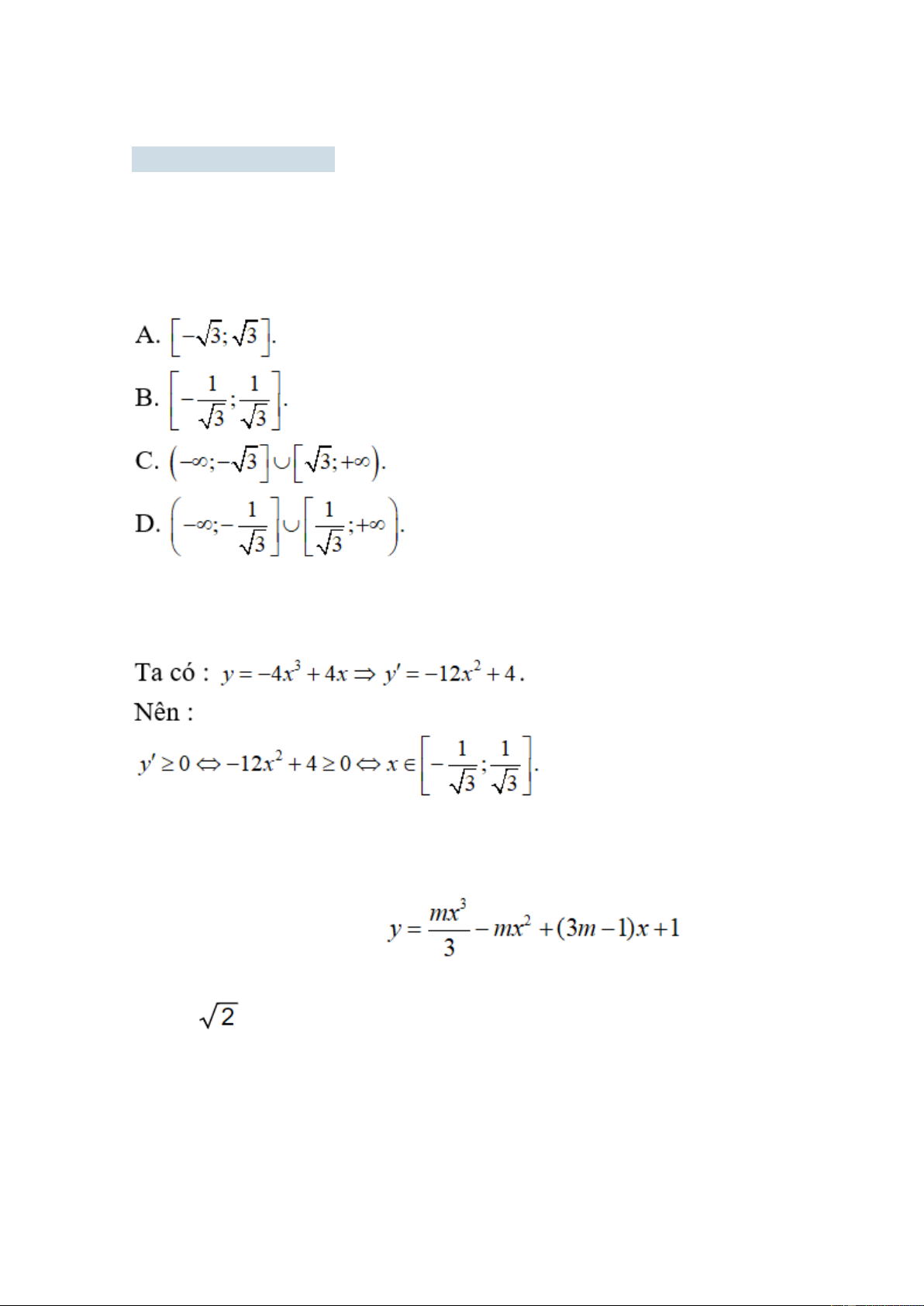

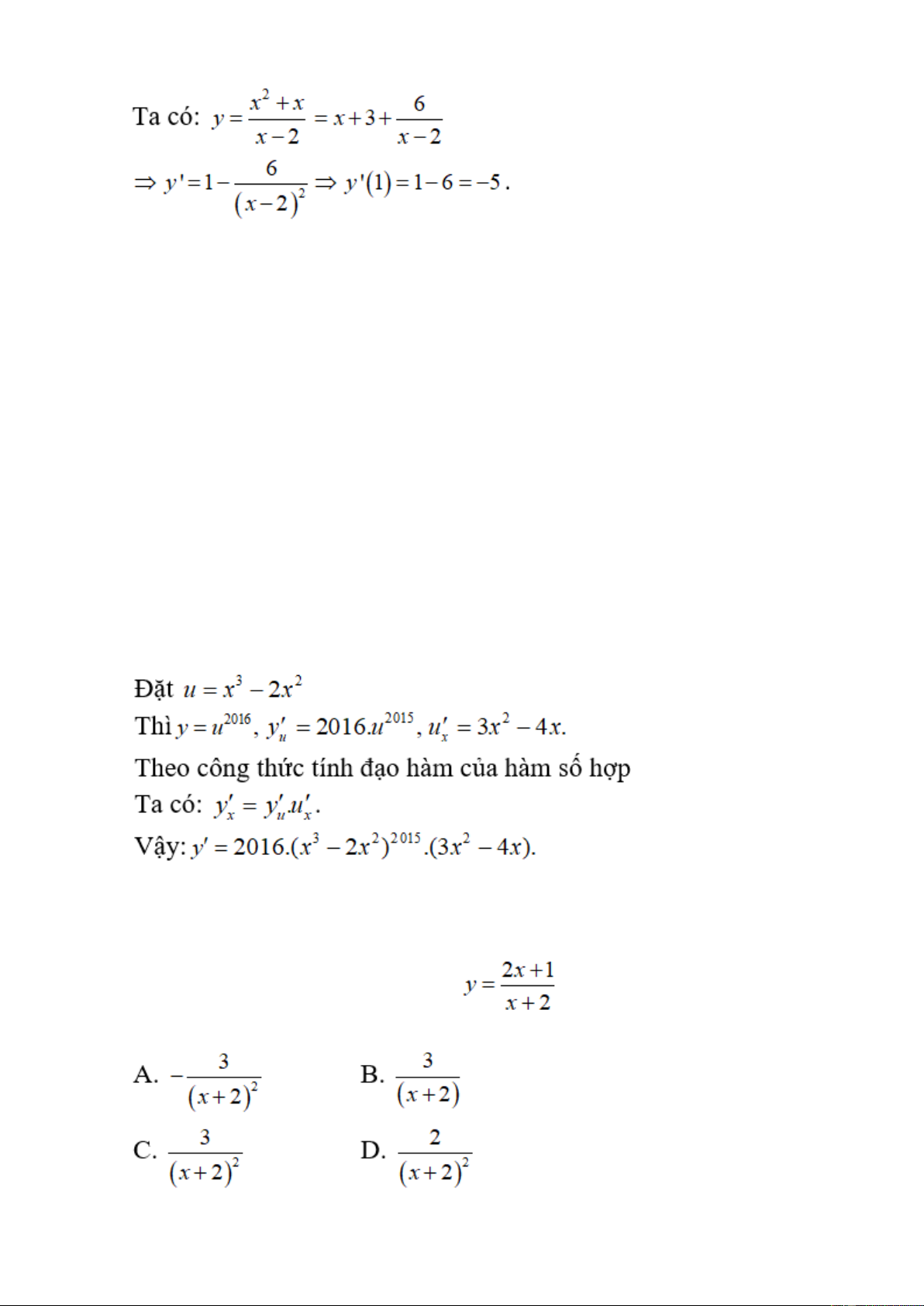
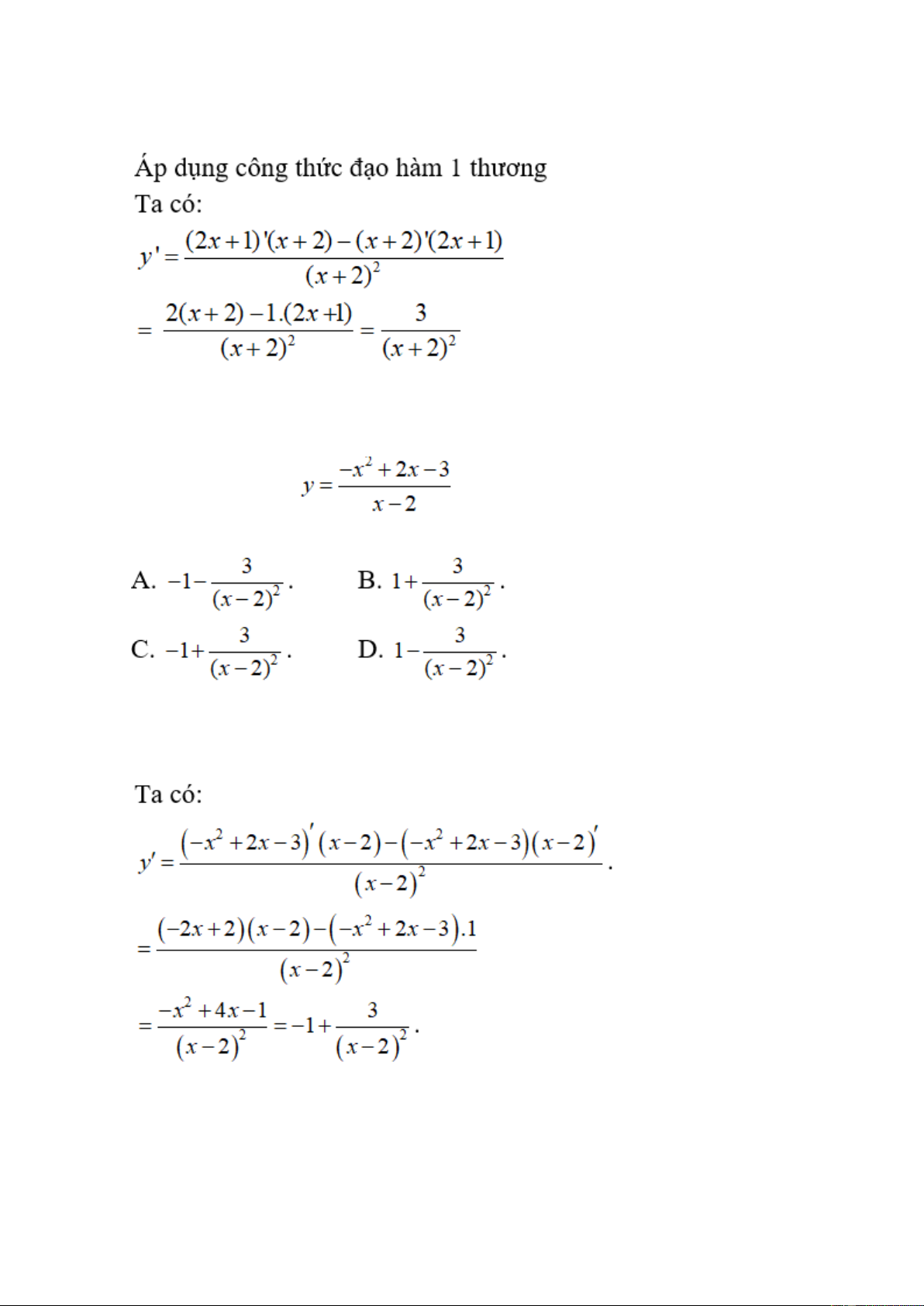



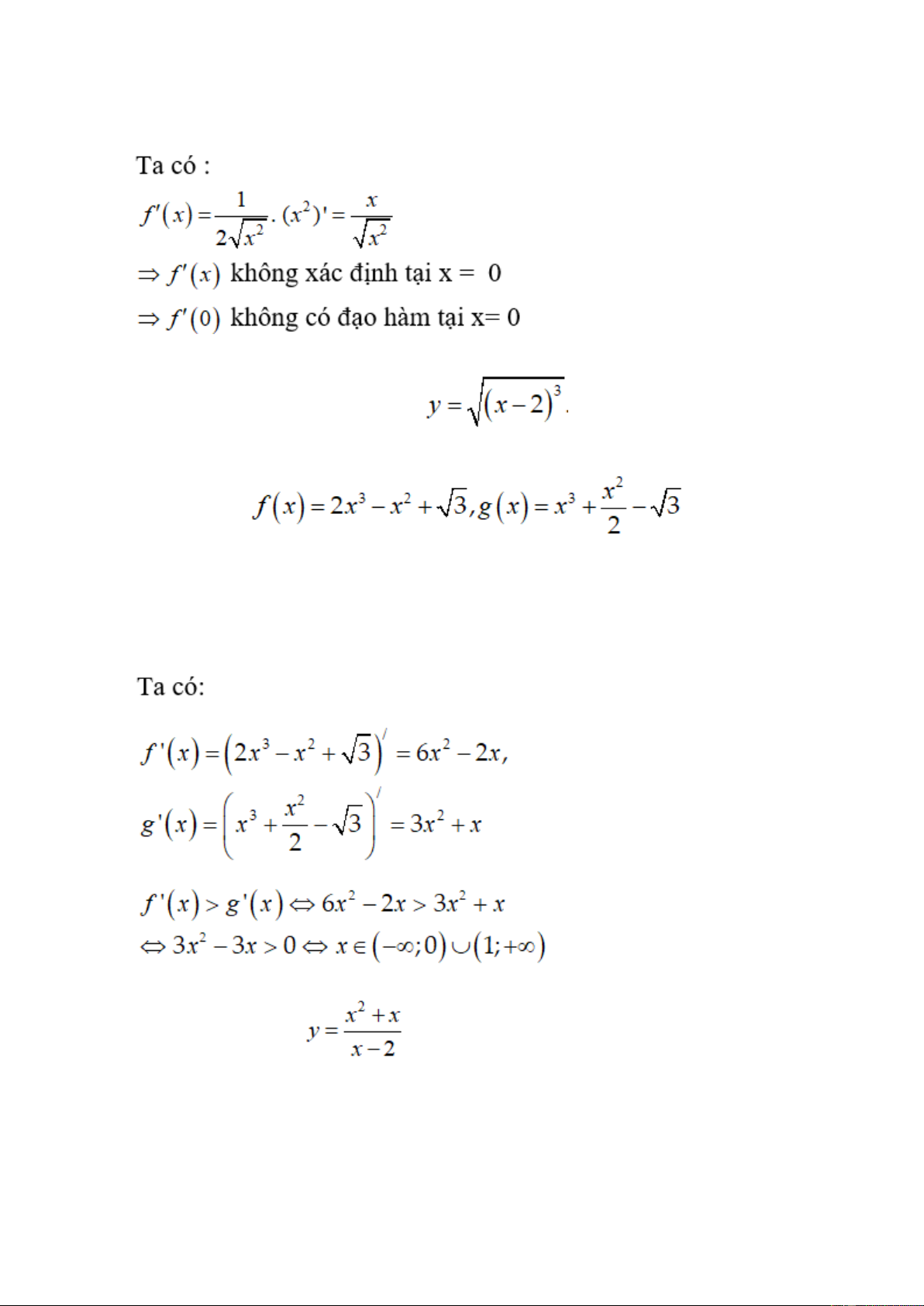

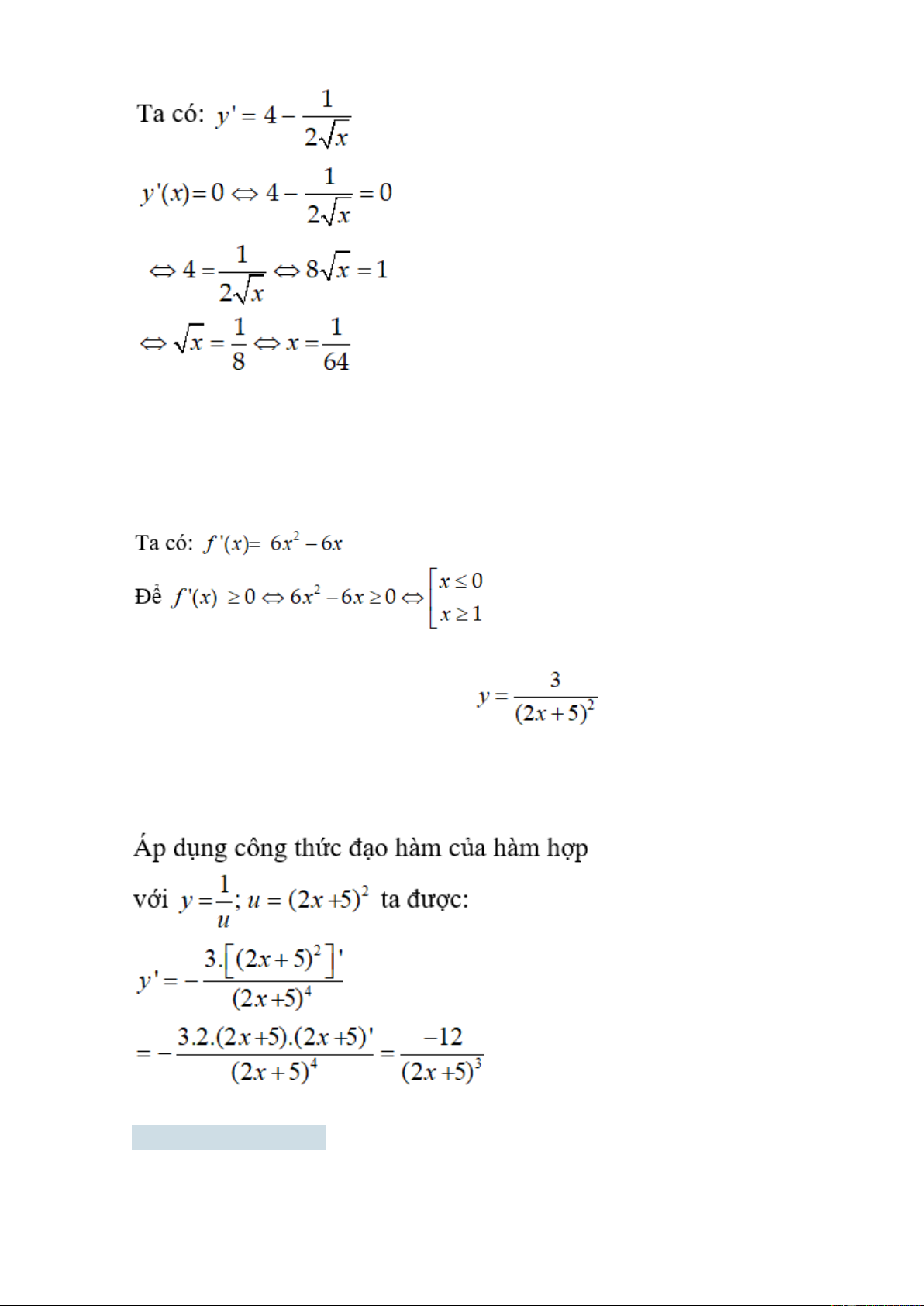
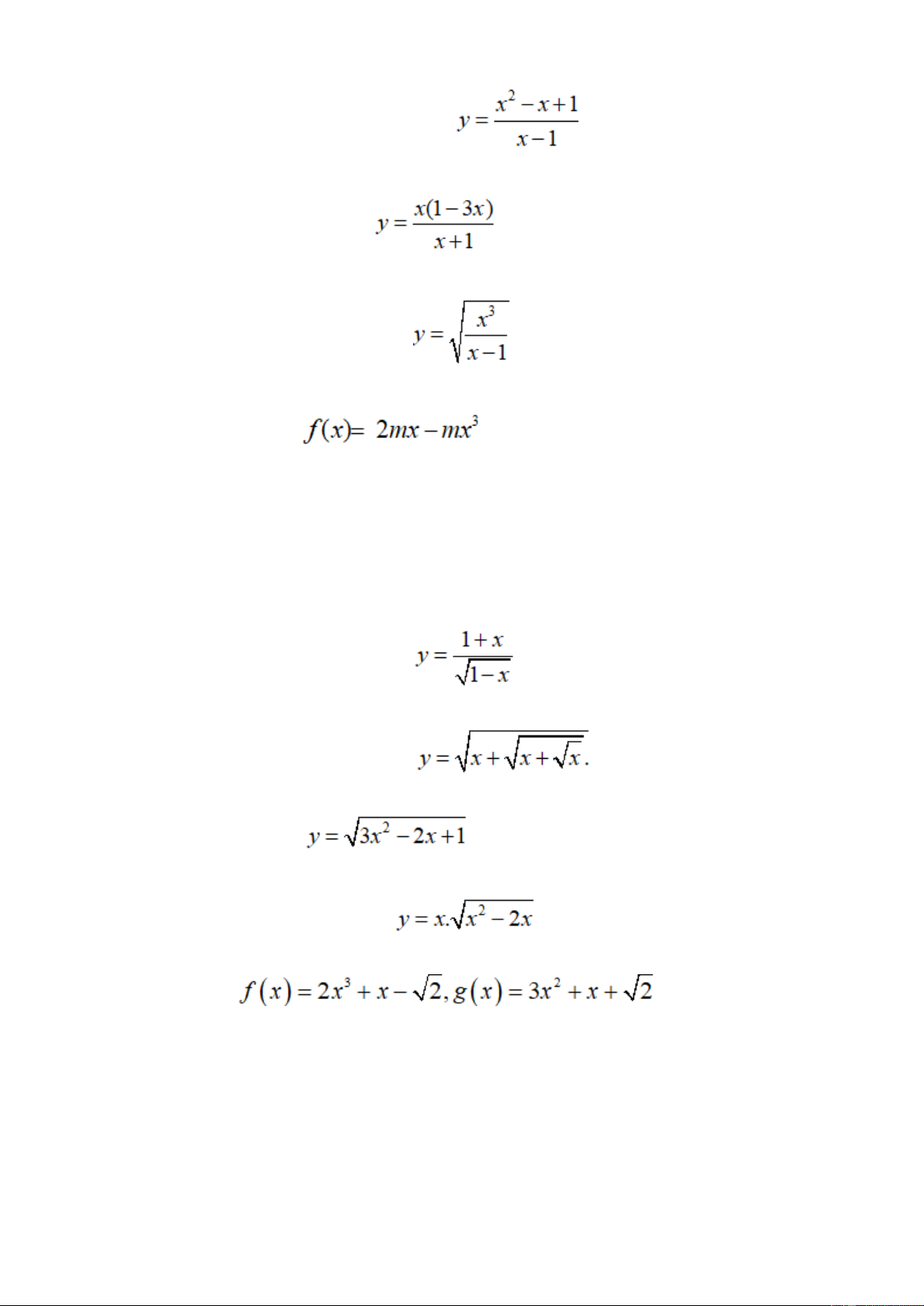
Preview text:
Bài tập Các quy tắc tính đạo hàm - Toán 11
I. Bài tập trắc nghiệm
Bài 1: Cho hàm số y = -4x3 + 4x. Để y' ≥ 0 thì x nhận các giá trị thuộc tập nào sau đây? Lời giải: Chọn đáp án B
Bài 2: Tìm m để các hàm số có y' ≤ 0 , ∀ x ∈ R. A. m ≤ B. m ≤ 2 C. m ≤ 0 D.m < 0 Lời giải: Chọn đáp án C Bài 3: Cho hàm số
, đạo hàm của hàm số tại x = 1 là: A. y'(1) = -4. B. y'(1) = -3. C. y'(1) = -2. D. y'(1) = -5. Lời giải: Chọn đáp án D
Bài 4: Đạo hàm của hàm số y = (x3 - 2x2)2016 là: A. y' = 2016(x3 - 2x2)
B. y' = 2016(x3 - 2x2)2015(3x2 - 4x).
C. y' = 2016(x3 - 2x2)(3x2 - 4x).
D. y' = 2016(x3 - 2x2)(3x2 - 2x). Lời giải: Chọn đáp án B
Bài 5: Tính đạo hàm của hàm số sau: Lời giải: Chọn đáp án C Bài 6: Cho hàm số
. Đạo hàm của hàm số là biểu thức nào sau đây? Lời giải: Chọn đáp án C Bài 7: Cho hàm số
. Đạo hàm của hàm số là: Lời giải: Chọn đáp án C
Bài 8: Cho hàm số f(x) xác định trên R bởi f(x) = 2x2 + 1. Giá trị f'(-1) bằng: A. 2 B. 6 C. - 4 D. 3 Lời giải:
Ta có : f'(x) = 4x ⇒ f'(-1) = -4. Chọn đáp án C
Bài 9: Cho hàm số f(x) = -x4 + 43 -32 + 2x + 1 xác định trên R. Giá trị f'(-1) bằng: A. 4 B. 14 C. 15 D. 24 Lời giải: Chọn đáp án D
Bài 10: Đạo hàm của hàm số f(x) = (x2 + 1)4 tại điểm x = -1 là: A. -32 B.30 C. - 64 D. 12 Lời giải: Chọn đáp án C
II. Bài tập tự luận có lời giải
Bài 1: Cho hàm số y = x3 - 3x2 - 9x - 5. Phương trình y' = 0 có nghiệm là? Lời giải: Bài 2: Với . Thì f'(-1) bằng? Lời giải:
Bài 3: Cho hàm số f(x) xác định trên R bởi . Giá trị f'(0) bằng? Lời giải:
Bài 4: Tính đạo hàm của hàm số Bài 5: Cho . Giải bất phương trình f'(x) > g'(x). Lời giải: Bài 6: Cho hàm số
đạo hàm của hàm số tại x = 1 là: Lời giải: Bài 7: Cho hàm số . Tính y'(0) bằng: Lời giải: Bài 8: Cho hàm số
. Nghiệm của phương trình y’ = 0 là Lời giải:
Bài 9: Giải bất phương trình f'(x) ≥ 0 với f(x)= 2x3 - 3x2 + 1 Lời giải:
Bài 10: Tính đạo hàm của hàm số sau: Lời giải:
III. Bài tập vận dụng
Bài 1 Tính đạo hàm của hàm số sau:
Bài 2 Đạo hàm của hàm số
bằng biểu thức nào sau đây?
Bài 3 Tính đạo hàm của hàm số Bài 4 Cho hàm số
.Để x = 1 là nghiệm của bất phương trình
f'(x) ≤ 1 khi và chỉ khi?
Bài 5 Tìm m để các hàm số y = (m - 1)x3 - 3(m + 2)x2 - 6(m + 2)x + 1 có y' ≥ 0, ∀ x ∈ R
Bài 6 Tính đạo hàm của hàm số
Bài 7 Tính đạo hàm của hàm số
Bài 8 Đạo hàm của bằng?
Bài 9 Đạo hàm của hàm số là Bài 10 Cho
. Giải bất phương trình f'(x) > g'(x)



