Bài tập chap 1 môn xác suất thống kê| Đại học Kinh tế Quốc Dân

1 Bài tập chương 1
A. Định nghĩa cổ điển về xác suất
1.1 Trong quyển sách "Phân tích kinh tế các dự án" của Herman gồm 200
trang. Tìm xác suất để khi mở hú họa ra một trang thì số trang là bội của 6.
1.2 Tại một công ty gồm 80 cán bộ công nhân viên, trong đó có 20 là nữ.
Ban giám đốc công ty quyết định giảm biên chế 5 người. Tìm xác suất để :
a. Không cán bộ nữ nào bị giảm biên chế.
b. Có hai cán bộ nữ bị giảm biên chế.
1.3 Một lô hàng gồm có 40 sản phẩm loại I, 60 sản phẩm loại II, 45 sản phẩm
loại III và 5 sản phẩm hỏng.
a. Lấy hú họa một sản phẩm. Tìm xác suất để sản phẩm đó thuộc loại I hoặc loại II.
b. Lấy ngẫu nhiên hai sản phẩm. Tìm xác suất để 2 sản phẩm đó cùng loại.
1.4 Một người viết 3 lá thư cho 3 người bạn khác nhau, sau khi dán lại cẩn
thận người đó mới đề địa chỉ ra ngoài. Tìm xác suất sao cho có ít nhất hai
người nhận nhầm thư của nhau.
1.5 Một em bé xếp chữ, em có 4 chữ cái A, N, O, H. Tìm xác suất để em đó
xếp ngẫu nhiên được chữ OANH.
1.6 Một người gọi điện thoại nhưng quên mất hai chữ số cuối, người đó chỉ
nhớ đó là hai chữ số khác nhau. Tìm xác suất để người đó quay ngẫu nhiên
một lần thì được luôn số cần gọi.
1.7 Một lô hàng gồm 10 sản phẩm loại I và 5 sản phẩm loại II. Lấy ngẫu
nhiên cùng lúc 3 sản phẩm. Tìm xác suất sao cho trong 3 sản phẩm lấy ra có cả hai loại sản phẩm.
1.8 Một cỗ bài tú lơ khơ gồm 52 quân. Lấy hú họa ra 3 quân bài. Tìm xác
suất sao cho trong 3 quân bài rút ra có:
a. Một quân át, một quân 10, một quân 9.
b. Cả 3 đều là quân át. 2 c. Ít nhất một quân át.
1.9 Một loại xổ số kiến thiết có cả thảy 15000 vé, trong đó có 1 vé trúng giải
500 nghìn đồng, 3 vé trúng giải 100 nghìn đồng, 6 vé trúng giải 50 nghìn đồng
và 200 vé trúng giải 2 nghìn đồng. Một người mua một vé xổ số loại trên. Tìm xác suất sao cho:
a. Người đó trúng không ít hơn 100 nghìn.
b. Người đó trúng ít nhất 2 nghìn đồng.
1.10 Một lô hàng gồm 10 sản phẩm loại I, 4 sản phẩm loại II và 3 phế phẩm.
Lấy ngẫu nhiên ra 3 sản phẩm. Tìm xác suất để có: a. Hai sản phẩm loại I.
b. Hai sản phẩm loại I và một sản phẩm loại II.
c. Cả 3 sản phẩm cùng loại.
1.11 Một lô hàng gồm n sản phẩm trong đó có m phế phẩm. Tìm xác suất
để khi chọn ngẫu nhiên k sản phẩm thì có đúng l phế phẩm
(1 ≤ k ≤ n; 0 ≤ l ≤ m; l ≤ k).
1.12 Có hai hộp đựng bút chì:
Hộp I có 6 bút xanh và 4 bút đỏ.
Hộp II có 4 bút xanh và 2 bút đỏ.
Lấy ngẫu nhiên 2 bút từ hộp I bỏ vào hộp II. Tìm xác suất để cả hai hộp
có số bút đỏ bằng nhau.
1.13 Một hộp có 9 quả cầu giống hệt nhau, trong đó có 2 quả ghi số 1, 3 quả
ghi số 2 và 4 quả ghi số 3. Lấy ngẫu nhiên ra 3 quả. Tìm xác suất để tổng các
số ghi trên 3 quả cầu bằng 5.
1.14 Bộ môn Toán trường ĐHTM cần tuyển 2 cán bộ. Có 8 người nộp đơn,
trong đó có 3 nữ và 5 nam. Khả năng để mỗi người được chọn là như nhau. Tìm xác suất để:
a. Hai người nữ được chọn.
b. Một người nam và một người nữ được chọn.
1.15 Trong một lô hàng gồm n sản phẩm tốt và k phế phẩm. Lấy ngẫu nhiên
ra l sản phẩm, kiểm tra thấy đều là phế phẩm (2 ≤ l ≤ k ≤ n). Tìm xác suất
sao cho lấy tiếp ngẫu nhiên 2 sản phẩm thì cả hai sản phẩm đều tốt.
1.16 Gieo đồng thời 2 đồng tiền xu. Tìm xác suất để được một mặt sấp một mặt ngửa. 3
1.17 Gieo đồng thời 2 con xúc xắc. Tìm xác suất để:
a. Tổng số chấm xuất hiện trên hai con là 11.
b. Hai mặt có số chấm khác nhau.
1.18 Một lớp học có 50 học sinh. Biết rằng trong đó có 15 học sinh giỏi toán,
12 học sinh giỏi văn, 10 học sinh giỏi ngoại ngữ, 8 học sinh giỏi cả toán và văn,
7 học sinh giỏi cả toán và ngoại ngữ, 5 học sinh giỏi cả văn và ngoại ngữ và 3 học sinh giỏi cả 3 môn.
a. Tìm tỉ lệ học sinh giỏi ít nhất 1 trong 3 môn toán, văn và ngoại ngữ.
b. Tìm tỉ lệ học sinh giỏi ít nhất một trong hai môn toán và văn.
c. Trong số học sinh giỏi toán lấy ngẫu nhiên ra 2 học sinh. Tìm xác suất
để 2 học sinh đó cùng học giỏi cả ba môn.
1.19 Có 3 đại biểu nam và 4 đại biểu nữ cùng ngồi ngẫu nhiên vào một dãy
ghế. Tìm xác suất để không có đại biểu nữ nào ngồi cạnh nhau.
1.20 Có 4 khách hàng vào ngẫu nhiên 3 quầy bán hàng. Tìm xác suất để cả
4 khách cùng vào một quầy.
1.21 Một phân xưởng có 10 máy. Trong tuần vừa qua có 4 lần phải sửa máy.
Tìm xác suất để không có máy nào phải sửa quá một lần, biết xác suất để mỗi
máy phải sửa ở mọi thời điểm là như nhau.
1.22 Có 5 sinh viên A, B, C, D và E ngồi vào một dãy bàn. Tìm xác suất để:
a. Hai sinh viên A và B ngồi hai đầu bàn.
b. Hai sinh viên A và B không ngồi cạnh nhau.
B. Các định lí về xác suất
1.23 Có hai hộp đựng bút chì:
Hộp I gồm 10 bút màu đỏ và 15 bút màu xanh.
Hộp II gồm 8 bút màu đỏ và 9 bút màu xanh.
Rút ngẫu nhiên từ mỗi hộp ra một bút. Tìm xác suất sao cho trong các bút lấy ra có:
a. Ít nhất một bút màu đỏ.
b. Chỉ một bút màu đỏ.
c. Hai bút có màu giống nhau. 4
1.24 Hai người ném bóng rổ, mỗi người ném 3 quả. Xác suất ném trúng rổ
của họ lần lượt là 0,7 và 0,8. Tìm xác suất sao cho:
a. Hai người bằng điểm nhau.
b. Người thứ nhất ít điểm hơn người thứ hai.
1.25 Một em bé có ở túi phải 5 viên bi trắng và 3 viên bi đỏ, ở túi trái có
6 viên bi trắng và 4 viên bi đỏ. Em đó lấy ngẫu nhiên ở mỗi túi ra 2 viên bi.
Tìm xác suất để 4 viên bi lấy ra: a. Cùng màu.
b. Có 3 viên bi màu trắng và một viên bi màu đỏ.
1.26 Một thùng đựng 24 chai bia trong đó có 4 chai bia giả.
a. Lấy ngẫu nhiên từ thùng ra 3 chai. Hãy chỉ ra một hệ đầy đủ các biến cố.
b. Lấy hú họa từng chai bia kiểm tra (lấy không hoàn lại) đến khi nào thấy
chai bia giả thì dừng. Tìm xác suất để quá trình kiểm tra kết thúc sau lần lấy thứ hai.
1.27 Một công nhân kỹ thuật đứng 3 máy tiện tự động hoạt động độc lập
với nhau. Xác suất để trong khoảng thời gian T các máy cần công nhân đến
chăm sóc lần lượt là 0,1; 0,2; 0,3. Tìm xác suất sao cho trong khoảng thời gian T :
a. Không máy nào cần công nhân đến chăm sóc.
b. Có 2 máy cần công nhân đến chăm sóc.
c. Ít nhất một máy cần công nhân đến chăm sóc.
d. Máy thứ nhất cần công nhân đến chăm sóc biết rằng có hai máy cần công nhân đến chăm sóc.
1.28 Có hai xe chở hàng độc lập về một xí nghiệp, xác suất để hai xe chở
hàng về tới xí nghiệp đúng giờ quy định lần lượt là 0,7 và 0,6. Tìm xác suất sao cho:
a. Chỉ có một xe chở hàng về tới xí nghiệp đúng giờ quy định.
b. Có xe chở hàng về tới xí nghiệp đúng giờ quy định.
1.29 Một lô hàng gồm 20 sản phẩm trong đó có 5 phế phẩm. Người ta kiểm
tra bằng phương pháp sau: kiểm tra lần lượt 4 sản phẩm (không hoàn lại).
Nếu có ít nhất 1 trong 4 sản phẩm đó là phế phẩm thì loại lô hàng đó. Tìm
xác suất để lô hàng đó được chấp nhận. 5
1.30 (Bài toán về 4 người nói dối) Người thứ nhất nhận một thông tin dưới
hai tín hiệu "có" hoặc "không" và thông báo cho người thứ hai biết, sau đó
người thứ hai thông báo cho người thứ ba và người thứ ba thông báo cho người
thứ tư. Bằng cách tương tự người thứ tư lại thông báo kết quả nhận được cho
người khác. Biết rằng mỗi một người trong 4 người đó chỉ nói đúng 1 lần trong
3 lần nói. Tìm xác suất để người nói dối thứ nhất nói đúng với điều kiện người thứ tư nói đúng.
1.31 (Bài toán về cách lựa chọn tối ưu) Một cửa hàng bán áo len gồm 1000
chiếc. Một người đi mua áo len và cần chọn áo tốt nhất có thể lựa chọn được.
Người đó lần lượt xem áo nếu ưng ý thì mua và việc lựa chọn kết thúc, nếu
không ưng thì trả lại áo đó để xem áo khác và chiếc áo đã trả thì không bao
giờ xem xét lại. Giả sử theo quy tắc trên người đó chọn áo ở lần thứ 100 (tức
là áo thứ 100 tốt hơn 99 áo đã xem). Tìm xác suất để áo đó là tốt nhất trong
toàn bộ 1000 áo của cửa hàng.
1.32 Một đợt thi tuyển viên chức có 3 vòng thi. Vòng 1 lấy 80% thí sinh dự
thi, vòng 2 lấy 70% thí sinh đã qua vòng 1 và vòng 3 lấy 90% thí sinh đã qua
vòng 2. Giả sử khả năng trúng tuyển của các thí sinh là như nhau.
a. Tìm xác suất để một thí sinh bất kì trúng tuyển.
b. Phỏng vấn ngẫu nhiên một thí sinh, biết thí sinh bị trượt. Tìm xác suất
để thí sinh bị trượt ở vòng 2.
1.33 Một hộp gồm 9 quả bóng, mỗi lần chơi người ta lấy ra 3 quả, chơi xong
lại bỏ vào hộp sau đó lại lấy tiếp 3 quả ra chơi. Tìm xác suất để sau 3 lần lấy
bóng ra chơi các bóng đều được sử dụng.
1.34 Một hộp gồm 24 sản phẩm trong đó có 2 sản phẩm loại II. Lấy ngẫu
nhiên từng sản phẩm ra kiểm tra (lấy không hoàn lại) đến khi nào được sản
phẩm loại II thì dừng lại. Tìm xác suất để quá trình kiểm tra kết thúc sau
không quá 3 lần kiểm tra.
1.35 Một hộp gồm 4 viên bi đỏ và 5 viên bi xanh. Hai người lần lượt lấy từng
viên theo phương thức không hoàn lại, người nào lấy được viên bi xanh trước
thì thắng cuộc. Tìm xác suất để người thứ hai thắng cuộc.
1.36 Một hộp đựng 9 quả bóng, mỗi lần chơi người ta lấy ra 3 quả, chơi xong
người ta trả hai quả vào hộp rồi lấy tiếp 3 quả ra chơi . . . Tìm xác suất để sau
3 lần lấy bóng ra chơi tất cả các quả bóng đều được sử dụng.
1.37 Hai xí nghiệp hoạt động độc lập với nhau, khả năng chỉ có một xí nghiệp
hoàn thành kế hoạch là 0,46. Tìm xác suất hoàn thành kế hoạch của xí nghiệp
thứ nhất, biết rằng xác suất để hoàn thành kế hoạch của xí nghiệp thứ hai là 0,6. 6
1.38 Một người say mê xổ số cào, người đó mua liên tiếp từng vé xổ số đến
khi nào được vé trúng thưởng thì dừng. Tìm xác suất sao cho người đó mua
đến vé thứ tư thì dừng biết rằng xác suất trúng thưởng của mỗi lần mua là như nhau và bằng 0,01.
1.39 Học kì này sinh viên được thi môn Lý thuyết xác suất và thống kê toán
3 lần. Xác suất để một sinh viên thi đỗ ở lần thứ nhất là 0,5. Nếu trượt ở lần
thi thứ nhất thì xác suất thi đỗ ở lần thứ hai là 0,7. Còn nếu trượt ở cả hai
lần đầu thì xác suất thi đỗ ở lần thứ 3 là 0,9. Tìm xác suất để sinh viên nói
trên thi đỗ trong học kì này.
1.40 Một người gọi điện thoại nhưng quên chữ số cuối cùng. Tìm xác suất
để người đó quay ngẫu nhiên không quá 3 lần thì được số cần gọi.
1.41 Phải gieo ít nhất bao nhiêu lần một con xúc xắc để với xác suất lớn hơn
hoặc bằng 0,9 có ít nhất 1 lần xuất hiện mặt 6 chấm.
1.42 Phải bắn ít nhất bao nhiêu viên đạn để xác suất không viên đạn nào bị
trượt nhỏ hơn 0,4? Biết rằng các lần bắn độc lập và xác suất bắn trúng của
mỗi viên đạn là như nhau và bằng 0,8.
C. Công thức xác suất đầy đủ và công thức Bayes
1.43 Có hai hộp đựng bút chì:
Hộp I có 10 bút đỏ và 5 bút xanh.
Hộp II có 8 bút đỏ và 2 bút xanh.
Lấy ngẫu nhiên 2 bút từ hộp I bỏ vào hộp II sau đó từ hộp II lấy ra 1 bút.
Tìm xác suất để bút lấy ra từ hộp II là đỏ.
1.44 Trong một kho hàng của công ty gồm sản phẩm của hai xí nghiệp, trong
đó sản phẩm của xí nghiệp I chiếm 70%. Biết tỉ lệ phế phẩm của xí nghiệp I
trong kho là 0,2 và xí nghiệp II là 0,1. Lấy ngẫu nhiên từ kho của công ty ra
1 sản phẩm để kiểm tra. Tìm xác suất để sản phẩm đó là phế phẩm.
1.45 Một lô hạt giống được phân làm ba loại, loại I chiếm 2/3 số hạt cả lô,
loại II chiếm 1/4 còn lại là loại III. Loại I có tỉ lệ nảy mầm là là 90%, loại II
có tỉ lệ nảy mầm là 70% và loại III có tỉ lệ nảy mầm là 35%. Lấy ngẫu nhiên
từ lô ra một hạt, tìm xác suất để hạt nảy mầm.
1.46 Bắn 3 viên đạn vào một máy bay, xác suất bắn trúng máy bay của các
viên đạn đều bằng 0,7. Nếu trúng 1 viên thì xác suất máy bay rơi là 0,3; nếu
trúng 2 viên đạn thì xác suất máy bay rơi là 0,8 còn nếu trúng cả 3 viên thì
xác suất máy bay rơi là 0,99. Tìm xác suất để máy bay rơi. 7
1.47 Một hộp gồm 12 quả bóng bàn trong đó có 8 quả mới và 4 quả đã sử
dụng. Lấy ngẫu nhiên ra 2 quả để chơi sau đó trả lại hộp, rồi lại lấy ngẫu nhiên
ra 2 quả nữa. Tìm xác suất để 2 quả lấy ra lần sau là mới.
1.48 Có 5 hộp đựng bóng đèn, trong đó có 3 hộp loại I, trong mỗi hộp loại
I có 9 bóng tốt và 1 bóng hỏng và có 2 hộp loại II, trong mỗi hộp loại II có
4 bóng tốt và 2 bóng hỏng. Lấy ngẫu nhiên ra một hộp, từ hộp này lấy ngẫu nhiên ra 1 bóng.
a. Tìm xác suất để bóng đó bị hỏng.
b. Biết bóng lấy ra là bóng tốt. Tìm xác suất để hộp lấy ra là loại I. 1.49 Có hai lô sản phẩm:
Lô I có 10 chính phẩm và 5 phế phẩm.
Lô II có 8 chính phẩm và 4 phế phẩm.
Từ lô I lấy ra 2 sản phẩm và từ lô II lấy ra 3 sản phẩm, rồi từ 5 sản phẩm
này lại lấy ngẫu nhiên ra 1 sản phẩm. Tìm xác suất để sản phẩm đó là chính phẩm.
1.50 Có 3 hộp đựng sản phẩm:
Hộp I có 10 chính phẩm và 5 phế phẩm.
Hộp II có 6 chính phẩm và 4 phế phẩm.
Hộp III có 7 chính phẩm và 3 phế phẩm.
Lấy ngẫu nhiên ra 1 hộp, từ hộp này lấy ngẫu nhiên ra 1 sản phẩm.
a. Tìm xác suất để sản phẩm đó là chính phẩm.
b. Biết sản phẩm lấy ra là phế phẩm, tìm xác suất để hộp lấy ra là hộp I. 1.51 Có hai hộp đựng bi:
Hộp I có 9 bi đỏ và 1 bi xanh.
Hộp II có 1 bi đỏ và 5 bi xanh.
Từ mỗi hộp lấy ngẫu nhiên ra 1 viên bi, số bi còn lại của hai hộp được dồn
vào hộp thứ III, từ hộp thứ III lấy ngẫu nhiên ra một viên. Tìm xác suất để viên bi lấy ra là bi xanh.
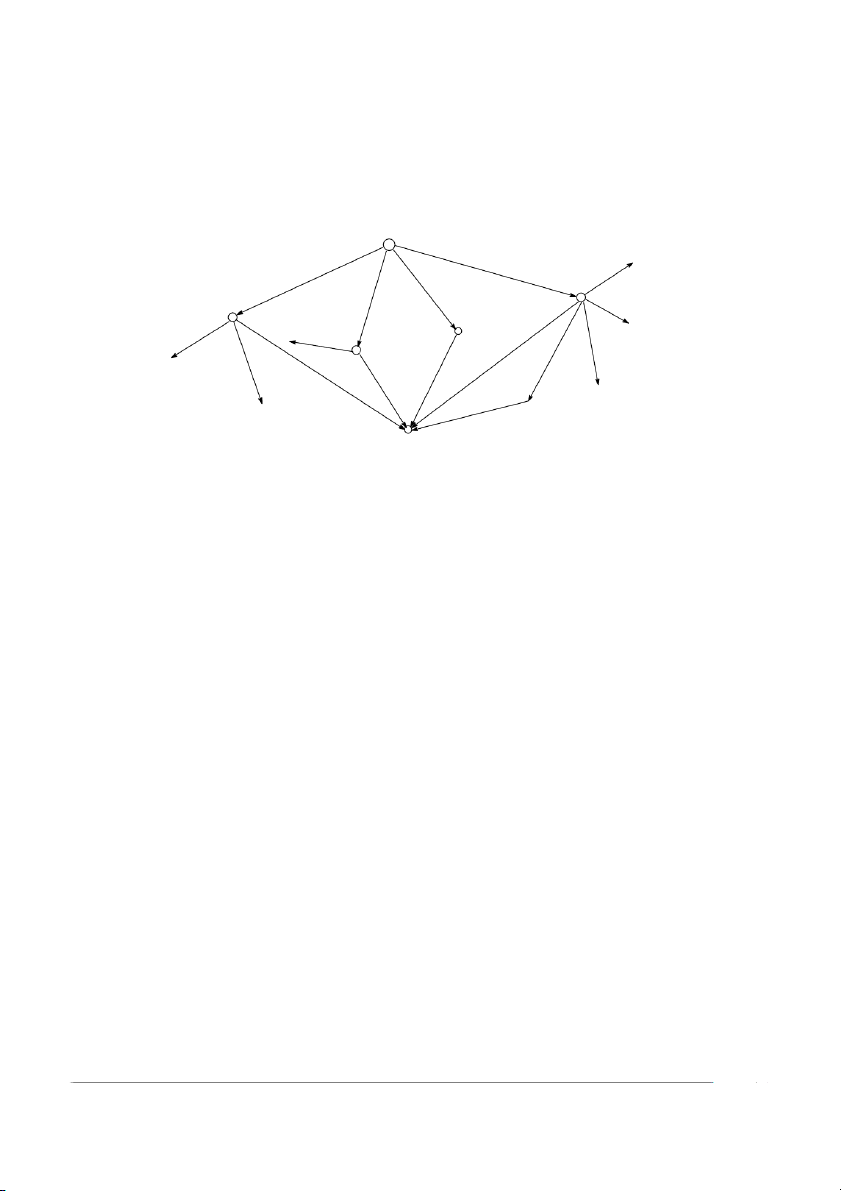
1.52 Có một du khách đi từ điểm O và cứ đến chỗ nào mà đường đi phân
nhánh thì chọn ngẫu nhiên một đường. Sơ đồ của đường đi ở hình 1. Trên
đường đó còn ghi cả điểm B và các đường dẫn đến B. Tìm xác suất để du
khách đó đi được đến B. 8 O B4 B1 B3 B2 B Hình 1
1.53 Một kho rượu, trong đó số chai rượu chanh và mơ bằng nhau (có cùng
kích thước và trọng lượng). Chọn ngẫu nhiên trong kho ra 1 chai và đưa cho
5 người sành rượu nếm thử để xác định xem loại rượu nào. Giả sử xác suất
đoán trúng của mỗi người là 75%. Có 4 người kết luận đó chai rượu đó là rượu
chanh còn 1 người kết luận là rượu mơ. Tìm xác suất để chai rượu được chọn là rượu chanh.
1.54 Hai xạ thủ bắn vào một mục tiêu, mỗi người bắn 1 viên. Xác suất bắn
trúng của mỗi người lần lượt là 0,6 và 0,7. Sau khi bắn chỉ thấy có 1 viên đạn
trúng mục tiêu. Tìm xác suất để viên đạn trúng đó là của người thứ hai bắn.
1.55 Một nhà máy sản xuất giầy, có 85% sản phẩm đạt tiêu chuẩn. Trong
quá trình kiểm nghiệm, xác suất để một đôi giầy đạt tiêu chuẩn kỹ thuật được
chấp nhận là 0,95 và xác suất để một đôi giầy không đạt tiêu chuẩn kỹ thuật
được chấp nhận là 0,09. Tìm xác suất để một đôi giầy được chấp nhận qua
kiểm nghiệm là đôi giầy đạt tiêu chuẩn kỹ thuật.
1.56 Trong kho của một công ty gồm sản phẩm của hai xí nghiệp, trong đó
số sản phẩm của xí nghiệp I gấp 3 lần số sản phẩm của xí nghiệp II. Tỉ lệ phế
phẩm tương ứng của hai xí nghiệp là 0,2 và 0,1. Lấy ngẫu nhiên từ kho của
công ty ra 1 sản phẩm để kiểm tra thấy nó là phế phẩm. Tìm xác suất để phế
phẩm đó là do xí nghiệp I sản xuất.
1.57 Có 3 em đồng thời ném bóng vào gôn cùng một lúc và chỉ có 1 em ném
trúng gôn. Tìm xác suất để quả bóng trúng gôn đó là do em thứ nhất ném.
Biết rằng các em ném độc lập với nhau và xác suất ném trúng gôn của các em
lần lượt là 0,4; 0,3; 0,6. 9
1.58 Khoa Thương mại quốc tế có 1000 sinh viên (SV). Trong đó năm thứ
nhất có 400 SV, năm thứ hai có 300 SV, năm thứ 3 có 180 SV, năm thứ tư có
120 SV. Lần lượt gọi ngẫu nhiên hai SV thì thấy SV gọi sau học ở khóa trên
so với SV được gọi trước. Tìm xác suất để SV gọi sau là SV năm thứ hai.
1.59 Hai máy cùng sản xuất một loại sản phẩm, tỉ lệ phế phẩm của máy thứ
nhất là 2%, của máy thứ hai là 1%. Từ lô sản phẩm chung của hai máy gồm
6 sản phẩm của máy thứ nhất và 4 sản phẩm của máy thứ hai.
a. Lấy ngẫu nhiên ra 1 sản phẩm thấy sản phẩm đó là phế phẩm. Hãy xác
định xem sản phẩm đó có khả năng là của máy nào nhiều hơn.
b. Lấy ngẫu nhiên 2 sản phẩm.
• Tìm xác suất để có ít nhất 1 sản phẩm là phế phẩm.
• Giả sử cả 2 sản phẩm lấy ra đều là phế phẩm thì xác suất lấy tiếp
được 2 phế phẩm nữa là bao nhiêu? 1.60 Có 3 hộp sản phẩm:
Hộp I đựng 7 sản phẩm loại I và 3 sản phẩm loại II.
Hộp II đựng 8 sản phẩm loại I và 2 sản phẩm loại II.
Hộp III đựng 6 sản phẩm loại I và 4 sản phẩm loại II.
Lấy ngẫu nhiên 1 sản phẩm từ hộp I bỏ sang hộp II sau đó từ hộp II lấy
ngẫu nhiên ra 1 sản phẩm bỏ sang hộp III. Cuối cùng từ hộp III lấy ngẫu
nhiên ra 1 sản phẩm. Tìm xác suất để sản phẩm lấy ra từ hộp III là sản phẩm loại I.
1.61 Có hai thùng sản phẩm:
Thùng I đựng 7 sản phẩm loại I và 5 sản phẩm loại II.
Thùng II đựng 8 sản phẩm loại I và 4 sản phẩm loại II.
Lấy ngẫu nhiên 1sản phẩm từ thùng I bỏ sang thùng II. Sau đó từ thùng
II lấy ngẫu nhiên ra 1 sản phẩm thấy đó là sản phẩm loại II. Tìm xác suất để
sản phẩm loại II này là của thùng I bỏ sang.
1.62 Một hộp đựng 4 sản phẩm. Lấy ngẫu nhiên ra 1 sản phẩm thấy nó là
chính phẩm. Tìm xác suất để cả 4 sản phẩm trong hộp đều là chính phẩm.
1.63 Một hộp đựng 3 sản phẩm. Lấy ngẫu nhiên ra 1 sản phẩm thấy sản
phẩm đó là chính phẩm. Không hoàn trả lại sản phẩm đã lấy, lấy tiếp sản phẩm thứ hai.
a. Tìm xác suất để sản phẩm thứ hai cũng là chính phẩm.
b. Biết sản phẩm thứ hai cũng là chính phẩm thì khả năng để cả 3 sản
phẩm trong hộp đều là chính phẩm bằng bao nhiêu? 10
1.64 Trong bài 1.13, nếu lấy ngẫu nhiên ra 3 quả thấy tổng các số ghi trên
3 quả bằng 5 thì xác suất để trong 3 quả đó có 1 quả ghi số 1 và hai quả ghi số 2 là bao nhiêu?
1.65 Trong bài 1.25, nếu lấy ngẫu nhiên từ mỗi túi ra 2 viên thấy cả 4 viên
cùng màu, tìm xác suất để 4 viên đó có cùng màu đỏ.
1.66 Nhà tài trợ gửi một hộp gồm 42 bộ quần áo thi đấu cho một đội tuyển
bóng đá. Các bộ được đóng gói riêng lẻ, trong đó có 20 bộ màu đỏ và 22 bộ
màu xanh. Nhưng khi nhận thì thấy bị thiếu 1 bộ và chỉ còn lại 41 bộ trong
hộp. Người ta lấy ngẫu nhiên từ hộp ra 1 bộ thấy là màu đỏ. Tìm xác suất để
bộ quần áo bị thiếu cũng là màu đỏ.