







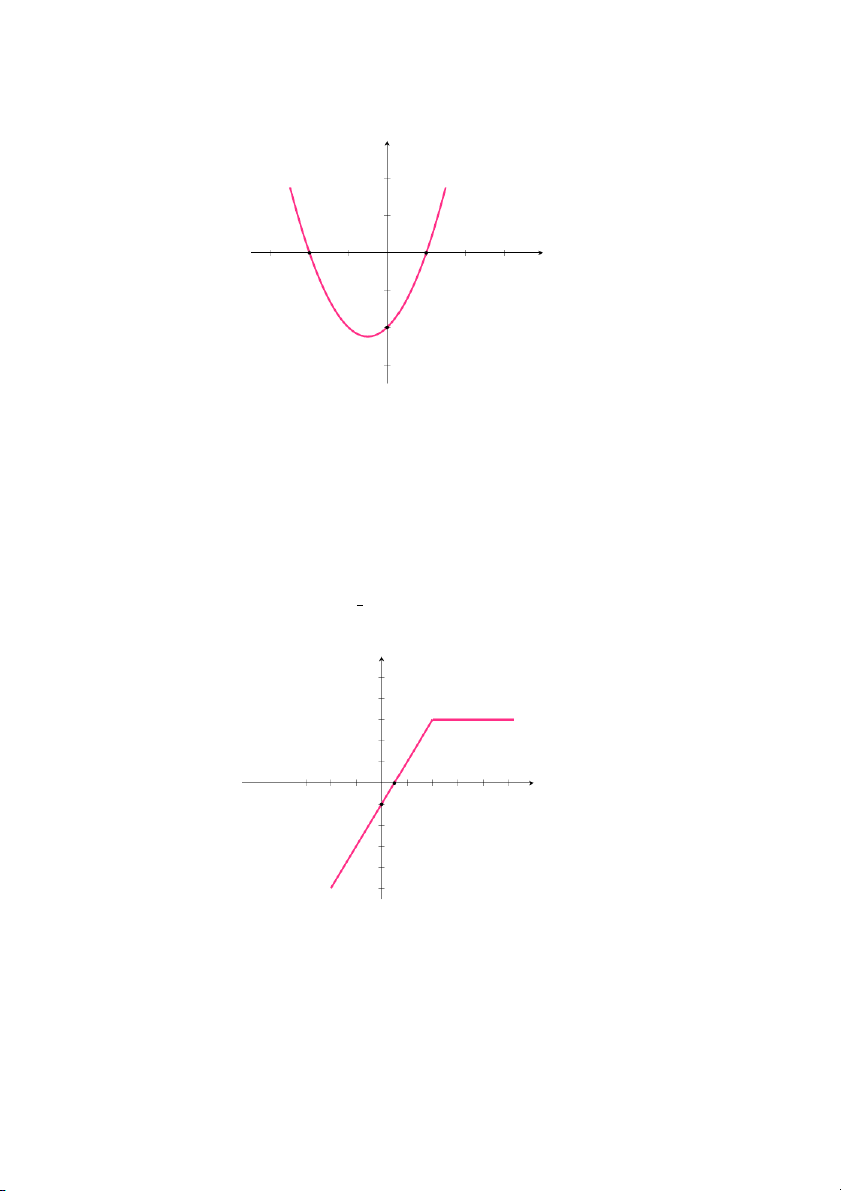

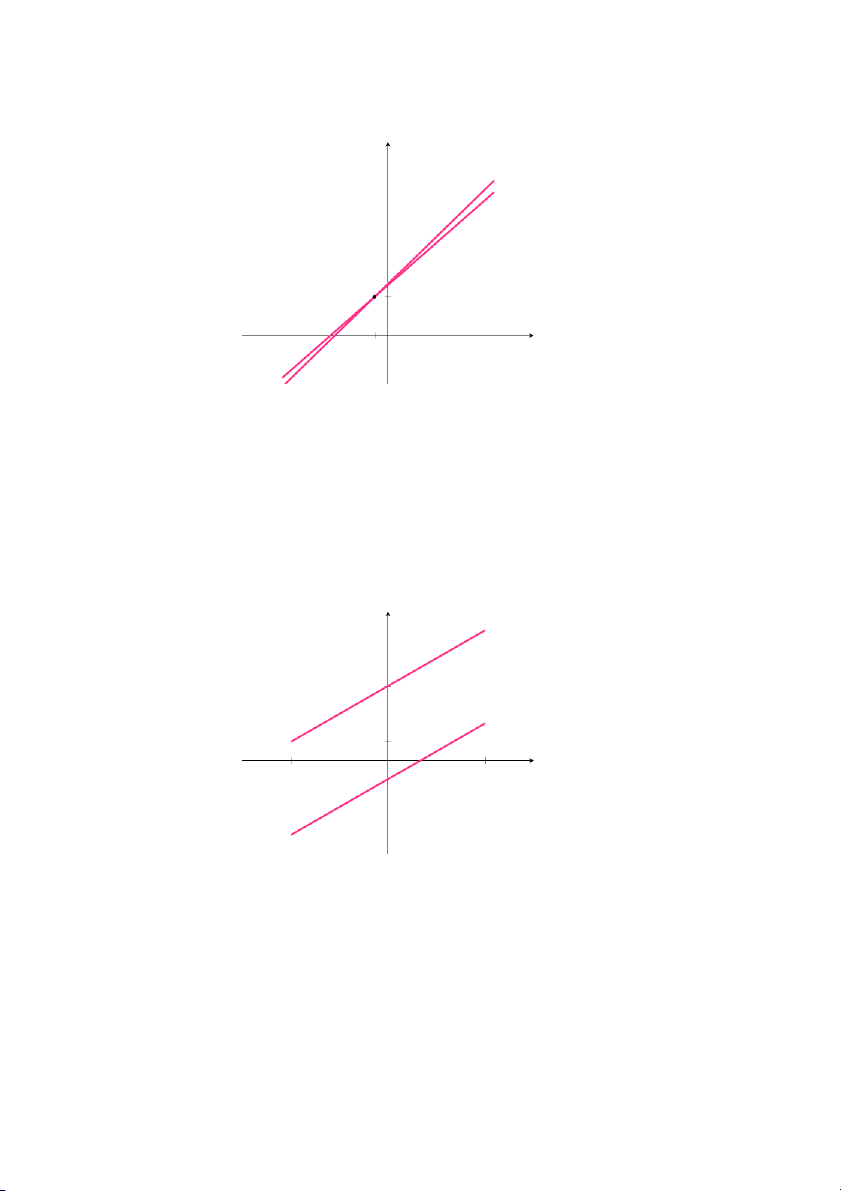
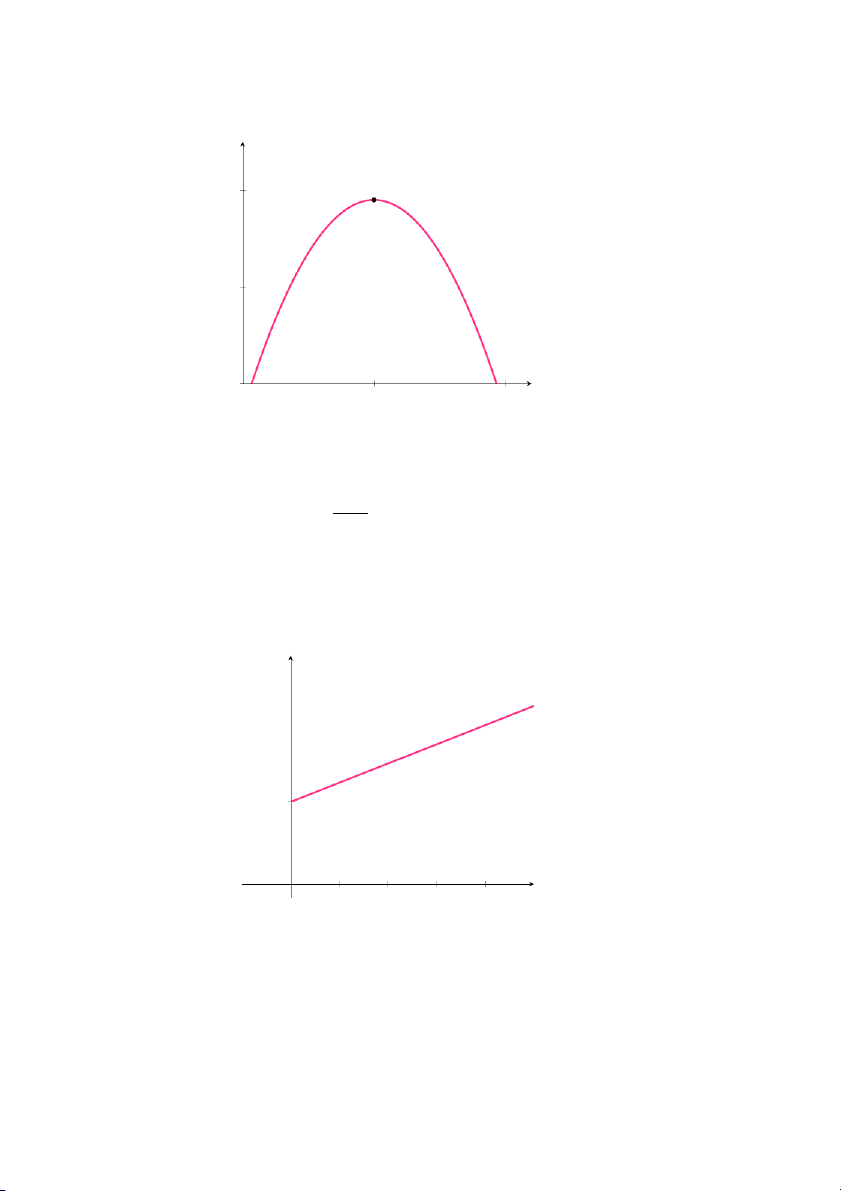






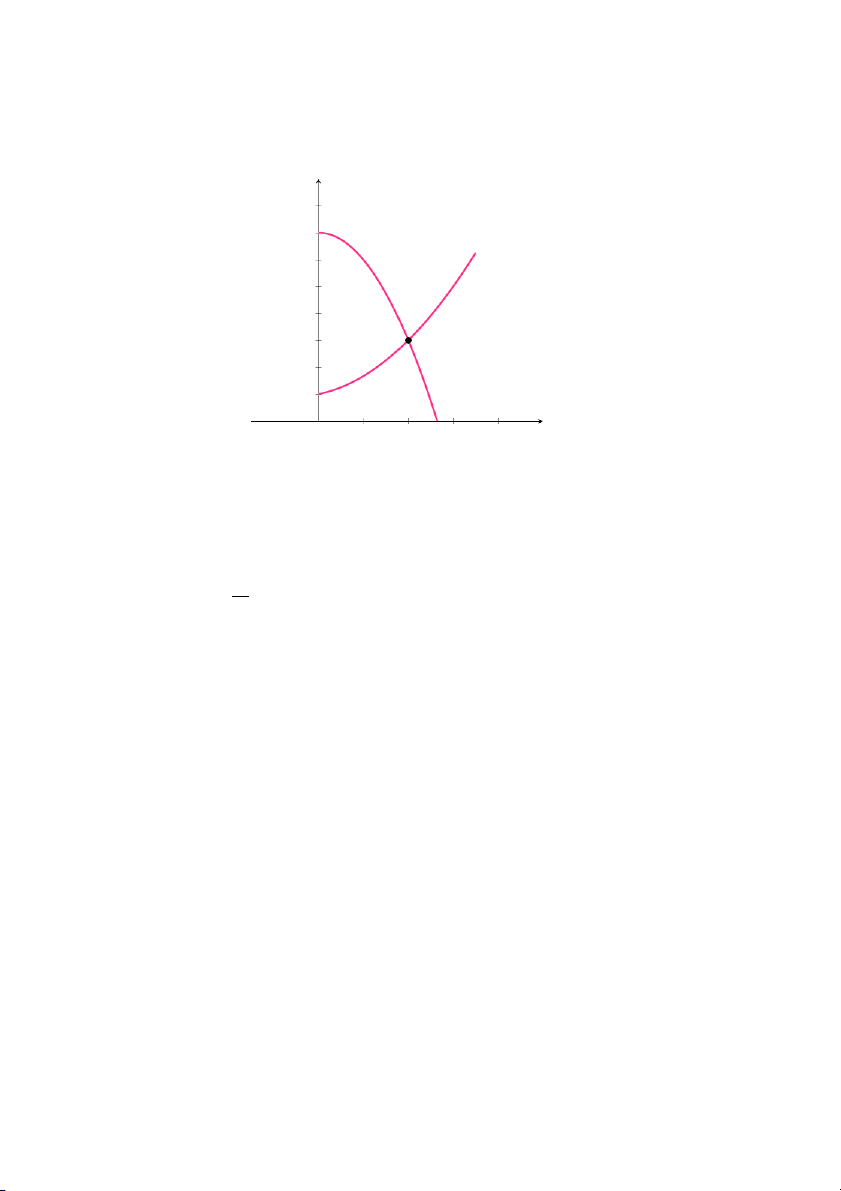











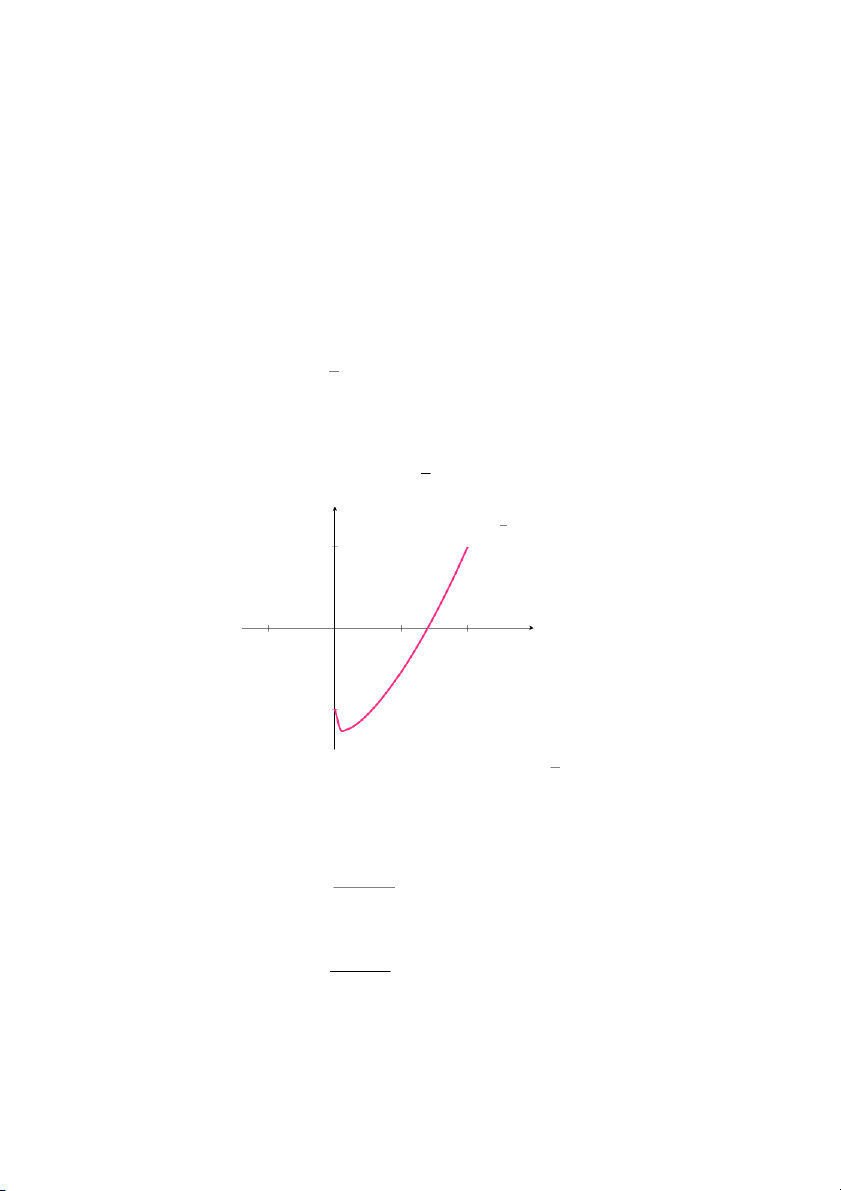

Preview text:
Chương 1
Hàm số, đồ thị và giới hạn 1.1 Hàm số KIẾN THỨC QUAN TRỌNG Định nghĩa
• Hàm là một quy tắc f cho tương ứng mỗi phần tử x thuộc tập A với
một và chỉ một phần tử y thuộc tập B.
Tập A được gọi là tập xác định của hàm số.
Tập B được gọi là tập giá trị của hàm số.
• Ký hiệu hàm số: y = f (x).
x được gọi là biến độc lập.
y được gọi là biến phụ thuộc.
• Quy ước tập xác định: Nếu tập A không được cho trước thì tập xác
định (hay tập xác định tự nhiên) của hàm số f(x) là tập tất cả những
số thực x sao cho f(x) là một số thực.
• Hàm xác định từng khúc là hàm được định nghĩa bởi nhiều hơn một
biểu thức, trong đó, mỗi biểu thức mô tả quy luật của hàm số trên
một tập con của tập xác định. 1
Các hàm số thường gặp trong kinh tế
• Hàm cầu D(x) đối với một loại hàng hoá là giá p = D(x) của mỗi đơn
vị hàng hoá đó nếu x đơn vị hàng hoá đó bán được.
• Hàm cung S(x) đối với một loại hàng hoá là giá p = S(x) mà các nhà
sản xuất sẵn sàng cung cấp x đơn vị hàng hoá đó ra thị trường.
• Doanh thu R(x) có được từ việc bán x đơn vị hàng hóa với đơn giá p: R(x) = xp(x).
• Chi phí C(x) là chi phí để sản xuất x đơn vị hàng hoá.
• Lợi nhuận P (x) là chênh lệch giữa doanh thu và chi phí: P (x) =
R(x) − C(x) = xp(x) − C(x).
• Các hàm chi phí bình quân AC(x) = C(x) ; doanh thu bình quân x
AR(x) = R(x) ; lợi nhuận bình quân AP (x) = P (x) . x x Hàm hợp
• Hàm hợp của các hàm số f (u) và g(x) là hàm f (g(x)) được tạo thành
bằng cách thay biểu thức u = g(x) vào biểu thức f(u). x+h)−f x)
• Tỷ số của các số gia đối với hàm f (x) là hàm hợp f ( ( , trong h
đó h là hằng số và h 6= 0.
HƯỚNG DẪN GIẢI CÁC BÀI TẬP CƠ BẢN
Bài 1 (Bài 20, 22 trang 12). Tìm tập xác định của hàm số
Lời giải: a. Do hàm số f(x) = x3 − 3x2 + 2x + 5 là đa thức nên tập xác
định của f(x) là toàn bộ tập số thực R.
b. Do hàm số f(t) = t+1 là phân thức nên tập xác định của f(t) là tập t2−t−2
tất cả các số thực t thỏa mãn:
t2 − t − 2 6= 0 ⇒ t 6= −1 và t 6= 2
Vậy tập xác định của f(t) là R \ {−1; 2}. 2
Bài 2 (Bài 4, 13 trang 12). Tính giá trị của hàm số
Lời giải: a. Xét hàm số h(t) = (2t + 1)3, ta có:
h(−1) = [(2)(−1) + 1]3 = −1; h(0) = [(2)(0) + 1]3 = 1; h(1) = [(2)(1) + 1]3 = 27. b. Xét hàm số −2x + 4 x ≤ 1 h(x) = , ta có: x2 + 1 x > 1
x = 3 > 1 nên h(3) = 32 + 1 = 10;
x = 1 nên h(1) = −2.1 + 4 = 2;
x = 0 < 1 nên h(0) = −2.0 + 4 = 4;
x = −3 < 1 nên h(−3) = −2.(−3) + 4 = 10.
Bài 3 (Bài 26 trang 12). Tìm hàm hợp của hàm số
Lời giải: Thay u bởi x − 1 vào biểu thức của f(u) ta được:
f (g(x)) = (x − 1)2 + 4 = x2 − 2x + 1 + 4 = x2 − 2x + 5
Vậy hàm hợp f(g(x)) = x2 − 2x + 5.
Bài 4 (Bài 35 trang 12). Tìm tỷ số của các số gia Lời giải: Ta có: f (x + h) − f(x)
[4(x + h) − (x + h)2] − (4x − x2) = h h 4h − 2xh − h2 = = 4 − 2x − h. h
Bài 5 (Bài 52 trang 13). Tìm các hàm thành phần
Lời giải: Có nhiều cách làm:
• Cách 1: Đặt h(x) = x5 − 3x2 + 12 và g(u) = u3, thay u = h(x) ta được
g(h(x)) = (x5 − 3x2 + 12)3 = f(x).
• Cách 2: Đặt h(x) = x5 − 3x2 và g(u) = (u + 12)3, thay u = h(x) ta được
g(h(x)) = (x5 − 3x2 + 12)3 = f(x). 3
Bài 6 (Bài 57 trang 13). Tìm chi phí sản xuất
Lời giải: a. Tổng chi phí để sản xuất 10 đơn vị sản phẩm là:
C(10) = (0.01)(102) + (0.9)(10) + 2 = 12 (nghìn đô-la)
Chi phí bình quân để sản xuất 10 đơn vị sản phẩm là: C(10) 12 AC(10) = = = 1.2 (nghìn đô-la) 10 10
b. Chi phí để sản xuất 9 đơn vị sản phẩm là:
C(9) = (0.01)(92) + (0.9)(9) + 2 = 10.91 (nghìn đô-la)
Chi phí để sản xuất đơn vị sản phẩm thứ 10 là:
C(10) − C(9) = 12 − 10.91 = 1.09 (nghìn đô-la)
Bài 7 (Bài 60 trang 13). Tìm doanh thu và lợi nhuận
Lời giải: a. Hàm doanh thu được xác định theo công thức:
P (x) = xp = xD(x) = x(−0.37x + 47) = −0.37x2 + 47x
Hàm lợi nhuận được xác định theo công thức:
P (x) = R(x) − C(x) = −0.37x2 + 47x − 1.38x2 − 15.15x − 115.5 = −1.75x2 + 31.85x − 115.5
b. Để việc sản xuất hàng hóa đó có lợi nhuận thì P (x) > 0, tức là:
−1.75x2 + 31.85x − 115.5 > 0 ⇒ 5 < x < 13.2
Vậy sản xuất thu được lợi nhuận khi mức sản xuất từ 5 đến 13.2 đơn vị sản phẩm.
Bài 8 (Bài 67 trang 14). Xác định cầu của người tiêu dùng
Lời giải: a. Để biểu diễn lượng cầu đối với cà phê theo thời gian, ta lập hàm hợp: 4, 374 Q(p(t)) = (t ≥ 0) (0.04t2 + 0.2t + 12)2 4
b. Lượng cà phê người tiêu dùng sẽ mua tại thời điểm t = 10 tuần sau kể
từ thời điểm hiện tại: 4, 374 Q(p(10)) = = 13.5 (kg)
[(0.04)(10)2 + (0.2)(10) + 12]2
c. Để xác định thời điểm lượng cà phê bán được bằng 30.375 kg, ta giải phương trình: 4, 374 Q(p(t)) = = 30.375 ⇒ t = 0 (0.04t2 + 0.2t + 12)2
Vậy ngay tuần đầu tiên (t = 0) khi nhà nhập khẩu cung cấp cà phê ra thị
trường với mức giá 12 đô-la/kg thì lượng cà phê bán được là 30.375 kg.
Bài 9 (Bài 76 trang 15). Xác định mức ô nhiễm không khí
Lời giải: a. Để biểu diễn mức carbon monoxide trong không khí theo thời gian, ta lập hàm hợp:
c(p(t)) = (0.4)(8 + 0.2t2) + 1 = 0.08t2 + 4.2 (t ≥ 0)
b. Mức khí carbon monoxide tại thời điểm t = 2 năm sau kể từ thời điểm hiện tại:
c(p(2)) = (0.08)(22) + 4.2 = 4.52 (ppm)
c. Để xác định thời điểm mức khí carbon monoxide đạt 6.2 ppm, ta giải phương trình:
c(p(t)) = 0.08t2 + 4.2 = 6.2 ⇒ t = 5
Vậy sau 5 năm thì mức carbon monoxide trung bình hàng ngày trong không
khí của khu vực đó đạt 6.2 ppm.
CÁC BÀI TẬP TỰ LUYỆN: HƯỚNG DẪN VÀ ĐÁP ÁN
Bài 10 (6, tr.12). Đáp án: f(2) = 2 f (0) = 0 f ( 5 −1) = −1 2
Bài 11 (8, tr.12). Đáp án: g(0) = 1 g(−1) = 0 g(8) = 27
Bài 12 (10, tr.12). Đáp án: f(1) = 1 f (−3) = 1 f (0) = 1 3 √3 5
Bài 13 (12, tr.12). Đáp án: g(−2) = 6 g(0) = 4 g(2) = 6
Bài 14 (16, tr.12). Không. Vì hàm số f(x) = x+1 có tập xác định là: x2−1 R \ {−1, 1}.
Bài 15 (18, tr.12). Đáp án: Có
Bài 16 (24, tr.12). Đáp án: (−∞; −2] ∪ [2; +∞)
Bài 17 (28, tr.12). Đáp án: f(g(x)) = 4x2
Bài 18 (30, tr.12). Trong biểu thức f(u), ta thay u bằng x2 + x − 2. 1
f (g(x)) = x4 + 2x3 − 3x2 − 4x + 4
Bài 19 (32, tr.12). Đáp án: f(g(x)) = 1 x2−2x+1
Bài 20 (34, tr.12). Đáp án: f(x+h)−f(x) = 2 h
Bài 21 (36, tr.12). Đáp án: f(x+h)−f(x) = 2x + h h
Bài 22 (38, tr.12). Đáp án: f(x+h)−f(x) = −1 h x(x+h)
Bài 23 (40, tr.12). Đáp án: f(g(x)) = x2 − 2x + 2 g(f(x)) = −x2.
Không tồn tại giá trị của x để f(g(x)) = g(f(x)).
Bài 24 (46, tr.12). Đáp án: f(x + 3) = 4x2
Bài 25 (50, tr.13). Đáp án: f(x2 − 2x + 9) = 2x2 − 4x − 2 Bài 26 √
(54, tr.13). Đáp án: h(x) = 3x − 5; g(u) = u. Bài 27 √
(56, tr.13). Đáp án: h(x) = x + 4 ; g(u) = u − 1u3
Bài 28 (58, tr.13). Tổng chi phí để sản xuất 10 đơn vị sản phẩm là:
C(10) = 2, 500 (nghìn đô-la)
Chi phí bình quân để sản xuất 10 đơn vị sản phẩm là: C(10) AC(10) = = 250 (nghìn đô-la) 10
Chi phí để sản xuất đơn vị sản phẩm thứ 10 là:
C(10) − C(9) = 101 (nghìn đô-la) 6
Bài 29 (62, tr.13). Đáp án: a. Hàm doanh thu: R(x) = −0.09x2 + 51x
Hàm lợi nhuận: P (x) = −1.41x2 + 39.3x − 101.4
b. Việc sản xuất có lợi nhuận khi và chỉ khi P (x) > 0 ⇐⇒ 2.87 < x < 24.99.
Bài 30 (66, tr.14). a. Đến 10 giờ sáng công nhân đó đã làm việc được 2
giờ, vậy x = 2. Số chiếc ti vi công nhân đó lắp ráp được là: f(2) = 46.
b. Số chiếc ti vi được lắp trong khoảng từ 9 đến 10 giờ sáng là f(2)−f(1) = 26.
Bài 31 (68, tr.14). a. Chi phí sản xuất: C(t) = 625t2 + 25t + 500
b. Với t = 3 , chi phí là C(3) = 6, 200 đô-la
c. Giải bất phương trình: 625t2 + 25t + 500 ≤ 11, 000 Suy ra 0 ≤ t < 4.08
Bài 32 (70, tr.14). a. Lúc 2 giờ sáng, t = 2, C(2) ≈ 17.3 độ C.
b. Thời điểm 6 giờ tối tương ứng với t = 18, 9 giờ tối tương ứng với t = 21.
Lượng tăng (giảm của nhiệt độ là: C(21) − C(18) = −7.5. Vậy nhiệt độ giảm 7.5 độ C. 1.2 Đồ thị hàm số KIẾN THỨC QUAN TRỌNG Định nghĩa
• Hệ tọa độ Đề-các vuông góc: Oxy
Ox được gọi là trục hoành; Oy được gọi là trục tung. • Điểm P (x, y)
x được gọi là hoành độ; y được gọi là tung độ.
• Công thức tính khoảng cách giữa hai điểm P (x1, y1) và Q(x2, y2): D = p(x 2 2 − x1)2 + (y2 − y1)
• Đồ thị của hàm số f gồm tất cả các điểm (x, y) trong đó x thuộc miền
xác định của f và y = f(x). 7 y P (x1, y1) y1 0.5 x −1 0 1 x1 −0.5
Hình 1.1: Hệ toạ độ Đề-các vuông góc và điểm P trong hệ toạ độ Các hệ số chặn
• Hệ số chặn x (nếu có) là các điểm tại đó đồ thị của hàm số f giao với trục hoành Ox.
Để tìm hệ số chặn x của hàm f, ta giải phương trình f(x) = 0.
• Hệ số chặn y (nếu có) là điểm tại đó đồ thị của hàm số f giao với trục tung Oy.
Để tìm hệ số chặn y của hàm f, ta tính giá trị f(0) (với điều kiện
x = 0 thuộc tập xác định của hàm f ).
Các hàm lũy thừa, đa thức và phân thức
• Hàm lũy thừa: f (x) = xn, với n là một số thực.
• Hàm đa thức: p(x) = a0 + a1x + a2x2 + ... + anxn, với n là một số nguyên không âm và a là các hằng số. 0, a1, ..., an
Nếu an 6= 0 thì số nguyên n được gọi là bậc của đa thức p(x).
• Hàm phân thức là thương p(x) của hai đa thức p(x) và q(x) (với điều q(x) kiện q(x) 6= 0). Hàm bậc hai
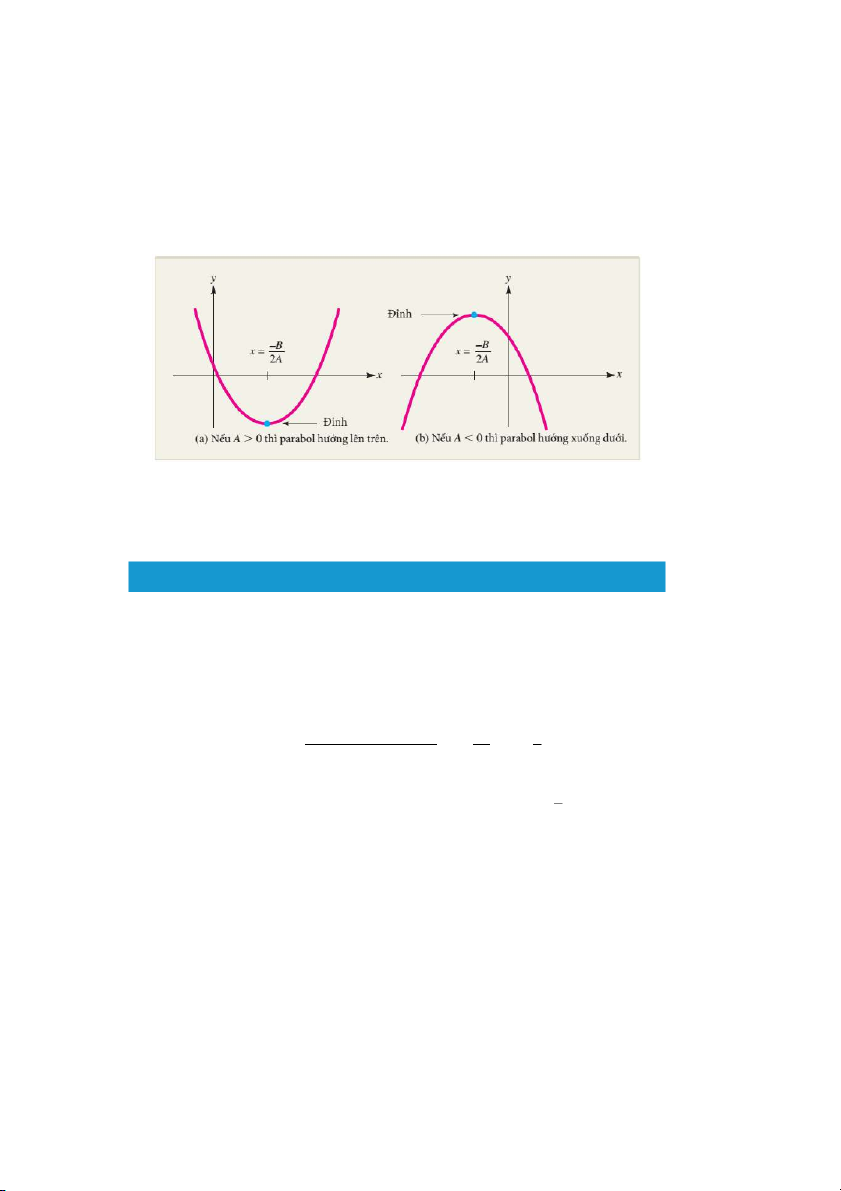
• Dạng tổng quát: f (x) = Ax2 + Bx + C, với A 6= 0.
• Đồ thị: là đường parabol có đỉnh đạt tại x = −B . 2A 8
Hai hệ số chặn x (nếu có) là hai nghiệm của phương trình bậc hai Ax2 + Bx + C = 0.
Hình 1.2: Hai dạng đồ thị của hàm bậc hai
HƯỚNG DẪN GIẢI CÁC BÀI TẬP CƠ BẢN
Bài 1 (Bài 8 trang 26). Tính khoảng cách giữa hai điểm
Lời giải: Ta áp dụng công thức khoảng cách: √ √ D = p(4 + 2)2 + (5 + 1)2 = 72 = 6 2
Vậy khoảng cách giữa hai điểm √
A(4, 5) và B(−2, −1) là 6 2.
Bài 2 (Bài 20, 26 trang 26). Phác họa đồ thị hàm số
Lời giải: a. Ta có: f(x) = (x − 1)(x + 2) = x2 + x − 2
Vậy đồ thị của hàm số f(x) là đường parabol hướng lên trên (do A =
1 > 0), các hệ số chặn x lần lượt là (−2, 0); (1, 0) và hệ số chặn y là (0, −2). 9 y y = x2 + x − 2 2 1 x −3 −2 −1 1 2 3 −1 −2 −3
Hình 1.3: Đồ thị của hàm số f(x)=x2 + x − 2 b. Xét hàm số 2x − 1 x < 2 f (x) = 3 x ≥ 2
Chú ý rằng hàm số f(x) là hàm xác định từng khúc nên trong khoảng
(−∞, 2) ta vẽ đường bậc nhất y = 2x − 1 và trong khoảng [2, ∞) ta vẽ
đường thẳng y = 3 song song với trục hoành.
Hàm số có hệ số chặn x là (1, 0) và hệ số chặn y là (0, −1). 2 y 5 4 y = 3 3 2 1 x −3 −2 −1 1 2 3 4 5 −1 −2 −3 −4 y = 2x − 1 −5
Hình 1.4: Đồ thị của hàm xác định từng khúc f(x)
Bài 3 (Bài 32 trang 26). Xác định giao điểm các đồ thị 10
Lời giải: Đồ thị hàm số y = x2 − x là đường parabol hướng lên trên (do
A = 1 > 0); đồ thị hàm số y = x − 1 là đường thẳng.
Để tìm giao điểm hai đồ thị bằng phương pháp đại số, ta giải phương trình:
x2 − x = x − 1 ⇒ (x − 1)2 = 0 ⇒ x = 1 ⇒ y = 0
Vậy giao điểm hai đồ thị là điểm P (1, 0). y y = x2 − x 4 3 y = x − 1 2 1 x −2 −1 1 2 3 −1 −2
Hình 1.5: Giao điểm của hai đồ thị y = x2 − x và y = x − 1
Bài 4 (Bài 36 trang 26). Xác định thông tin từ đồ thị
Lời giải: Nhìn đồ thị, ta thấy:
a. Đồ thị cắt trục hoành Ox tại các điểm (1, 0) và (3, 0) nên các hệ số chặn x là (1, 0) và (3, 0).
Đồ thị cắt trục tung Oy tại điểm (0, 2) nên hệ số chặn y là (0, 2).
b. Giá trị lớn nhất của f(x) bằng 3.5 đạt tại x = −1.
c. Giá trị nhỏ nhất của f(x) bằng −1 đạt tại x = 2.
Bài 5 (Bài 40 trang 27). Xác định mức giá tối ưu
Lời giải: a. Ta có thể lập hàm lợi nhuận theo công thức:
Tổng lợi nhuận = (lợi nhuận một sản phẩm)(số sản phẩm bán được)
trong đó lợi nhuận một sản phẩm là hiệu giữa giá bán mỗi sản phẩm p đô-la
và chi phí sản xuất một sản phẩm 20 đô-la. Vậy ta có hàm lợi nhuận theo 11 giá bán là:
f (p) = (p − 20)(1, 560 − 12p) = −12p2 + 1, 800p − 31, 200
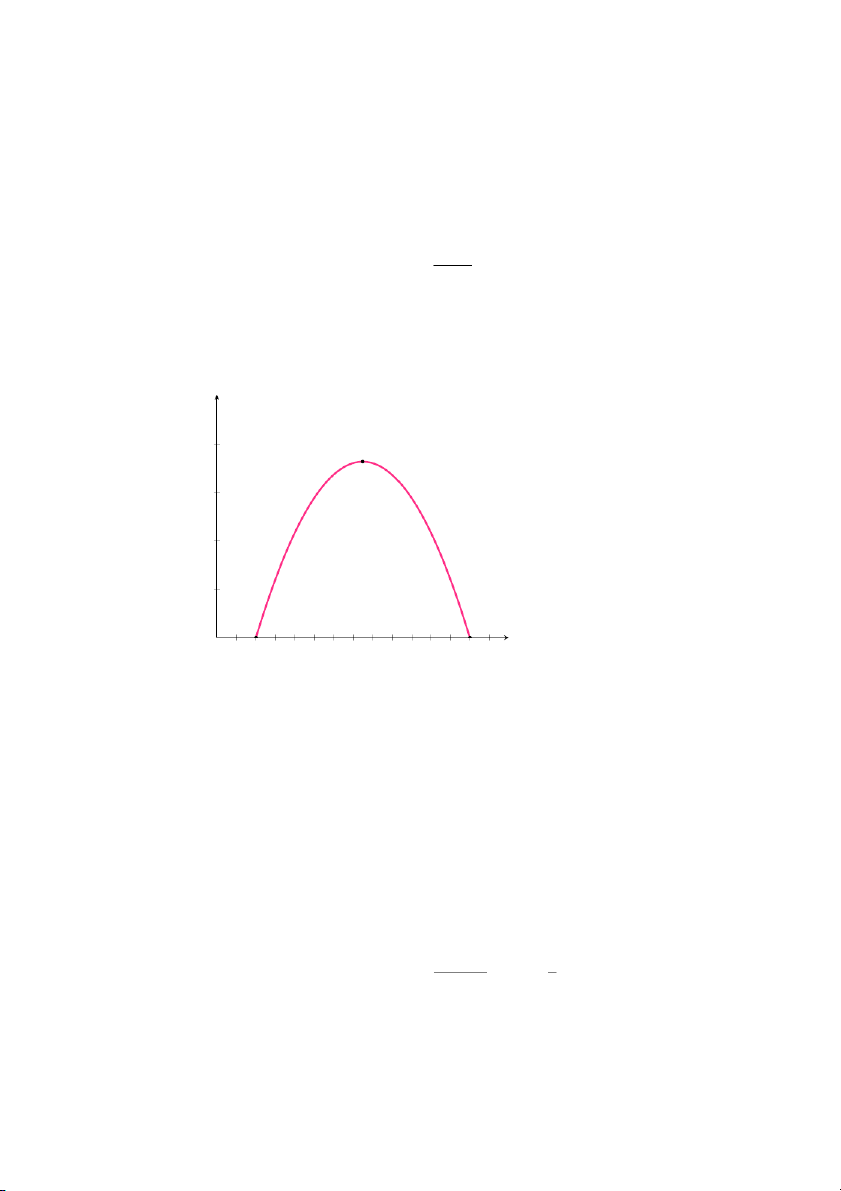
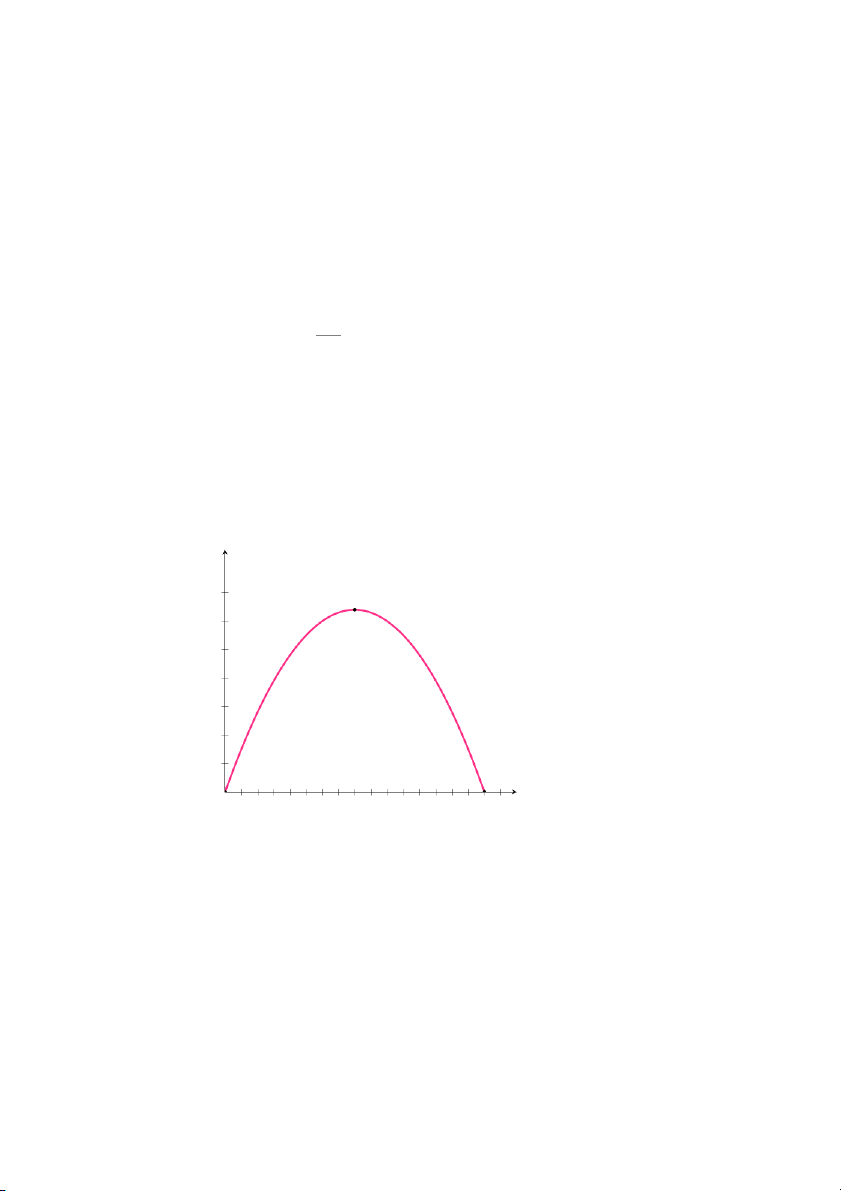
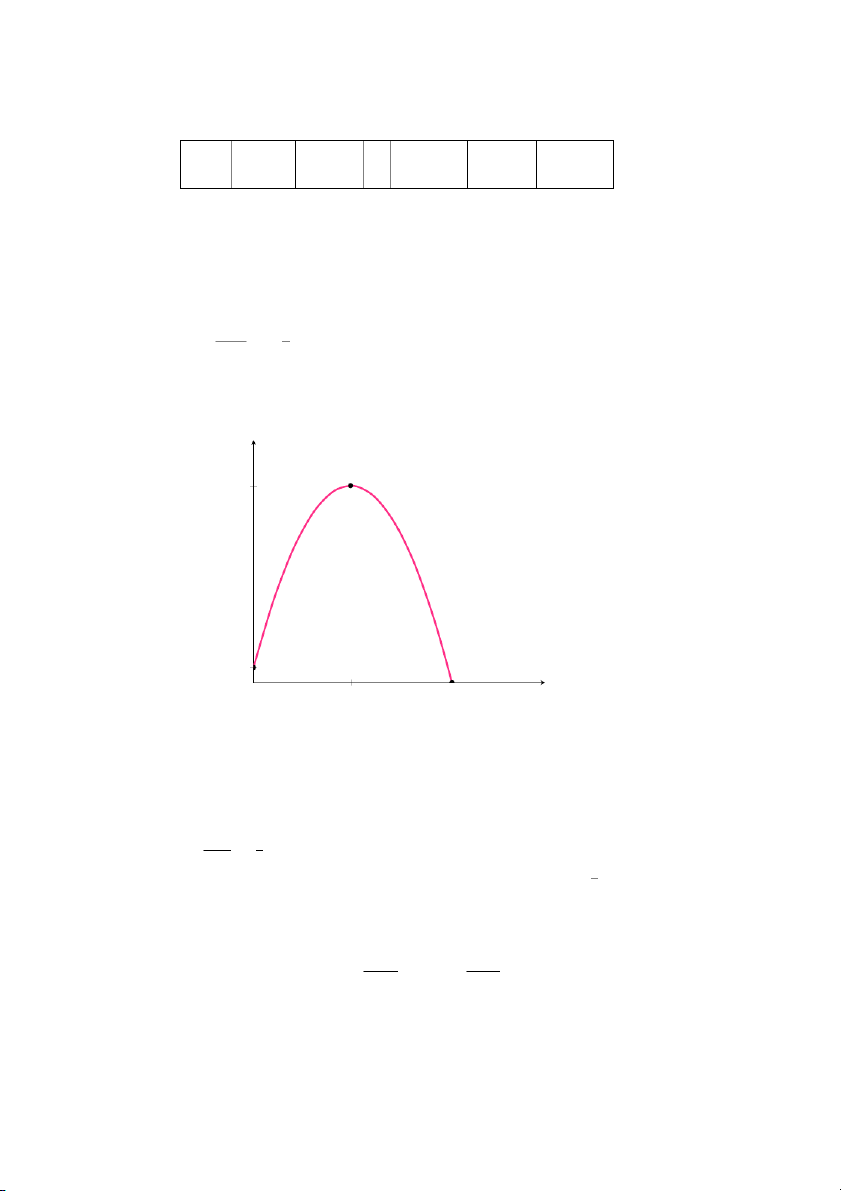
b. Đồ thị hàm lợi nhuận f(p) là đường parabol hướng xuống dưới (do
A = −12 < 0), đỉnh parabol đạt tại (p0 = −1,800 = 75; f(p0) = 36, 300), hai −24
hệ số chặn lần lượt là (20, 0) và (130, 0).
Chú ý rằng khi vẽ đồ thị hàm số thực tế, nếu các biến số chỉ có ý nghĩa
khi nhận giá trị không âm thì ta chỉ cần vẽ phần đồ thị nằm ở góc phần tư
thứ nhất (x ≥ 0; y ≥ 0).
f (p) (mười nghìn sản phẩm) 4 (75; 36,300) 3 2 1 p (chục đô-la) 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14
Hình 1.6: Đồ thị hàm số f(p)=−12p2 +1, 800p − 31, 200
Từ đồ thị hàm số f(p), ta thấy để thu được lợi nhuận tối đa thì nhà sản
xuất nên bán lốp xe ở mức giá p0 = 75 đô-la một sản phẩm. Khi đó số lốp
xe bán được hàng tháng là:
1, 560 − (12)(75) = 660 sản phẩm.
Bài 6 (Bài 44 trang 27). Xác định mức giá tối ưu
Lời giải: a. Để tính tổng chi tiêu hàng tháng của người tiêu dùng theo đơn
giá p, ta cần biến đổi x theo p: 120 − p p p(x) = 5(24 − x) ⇒ x(p) = = 24 − 5 5 12
Vậy ta có hàm tổng chi tiêu hàng tháng của người tiêu dùng (chú ý rằng
đơn vị của biến số x là nghìn đơn vị hàng hóa): p
E(p) = 1, 000px(p) = 1, 000p(24 − ) = −200p2 + 24, 000p 5
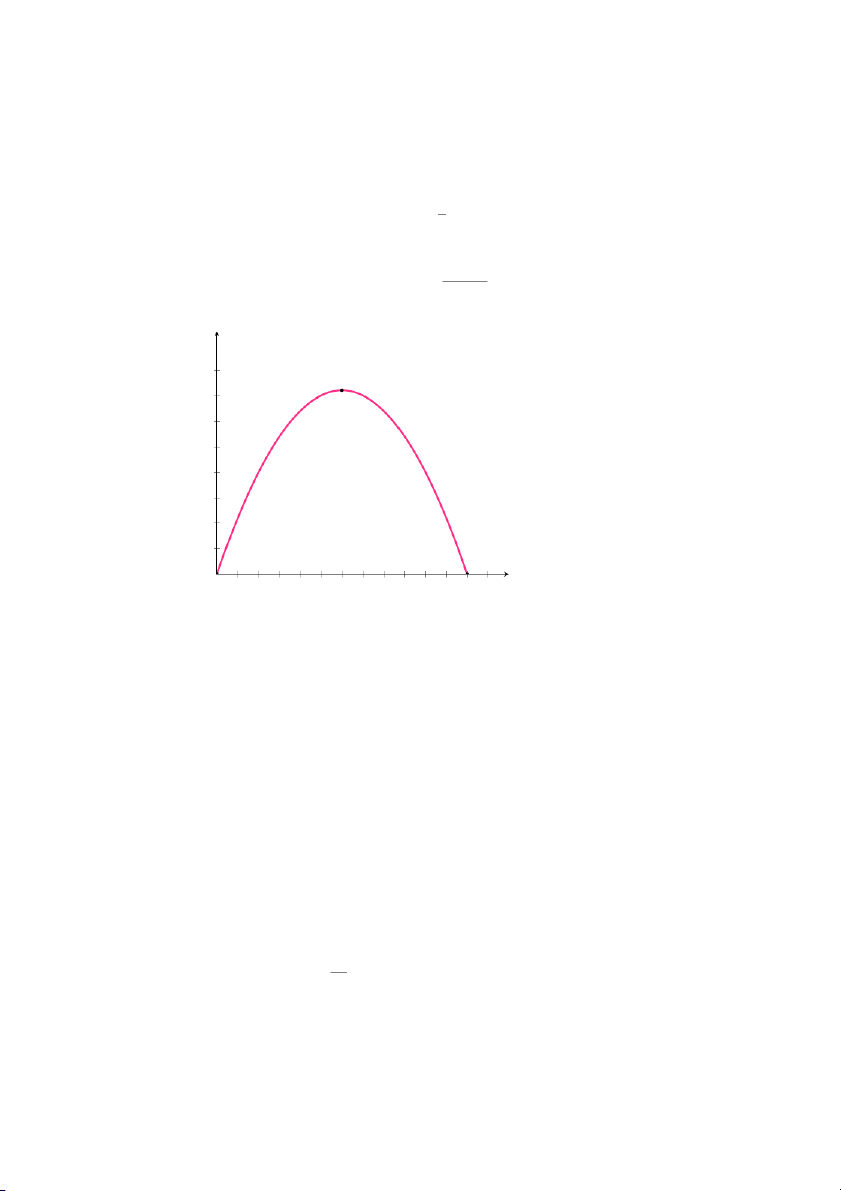
Đồ thị của hàm chi tiêu E(p) là đường parabol hướng xuống dưới (do
A = −200 < 0), đỉnh parabol đạt tại (p ,
0 = −24 000 = 60; E(p0) = 720, 000), −400
hai hệ số chặn lần lượt là (0, 0) và (120, 0). E(p) (trăm nghìn đô-la) 8 (60; 720,000) 7 6 5 4 3 2 1 p (chục đô-la) 0 1 2 3 4 5 6 7 8 9 10 11 12 13
Hình 1.7: Đồ thị hàm số E(p)=−200p2 +24, 000p
b. Ý nghĩa kinh tế của các hệ số chặn p:
Tại điểm (0, 0) ta có p1 = 0: Tại mức giá này (giá thấp nhất - "giá
sàn"), tuy nhu cầu của người tiêu dùng đối với loại hàng hóa đó là lớn nhất
(x = 24 nghìn đơn vị) nhưng nhà cung cấp không đồng ý bán nên tổng chi
tiêu của người tiêu dùng vẫn bằng 0.
Tại điểm (120, 0) ta có p2 = 120: Tại mức giá này (giá cao nhất - "giá
trần"), cầu của người tiêu dùng đối với loại hàng hóa đó bằng 0 nên tổng
chi tiêu của người tiêu dùng cũng bằng 0.
c. Từ đồ thị hàm số E(p), ta thấy p0 = 60 đô-la một đơn vị là mức giá thị
trường tạo ra tổng chi tiêu hàng tháng của người tiêu dùng lớn nhất. Khi
đó số lượng đơn vị hàng hóa bán được hàng tháng là: 60 x(60) = 24 −
= 12 nghìn đơn vị sản phẩm. 5 13
Bài 7 (Bài 51 trang 28). Xác định mức giá tối ưu
Lời giải: a. Nếu p là giá cho thuê mỗi căn hộ hàng tháng thì số lần tăng
giá (mỗi lần tăng 100 đô-la) là p−1,200. 100
Vì mỗi lần tăng giá sẽ có thêm 5 căn hộ không được thuê nên số căn hộ
được thuê ở mỗi mức giá p là: p − 1, 200 p 150 − 5. = 210 − 100 20
Vậy ta có hàm tổng doanh thu từ việc cho thuê căn hộ là: p p2 R(p) = p(210 − ) = − + 210p 20 20
b. Đồ thị của hàm doanh thu R(p) là đường parabol hướng xuống dưới (do
A = − 1 < 0), đỉnh parabol đạt tại (p 20
0 = 2, 100; R(p0) = 220, 500), hai hệ
số chặn lần lượt là (0, 0) và (4, 200; 0). R(p) (trăm nghìn đô-la) 3 (2,100; 220,500) 2 1 p (nghìn đô-la) 0 1 2 3 4 5
Hình 1.8: Đồ thị hàm số R(p)=− p2 +210p 20
c. Từ đồ thị hàm số R(p), ta thấy Yuri nên đặt mức giá cho thuê mỗi căn
hộ hàng tháng là p0 = 2, 100 đô-la để tối đa hóa doanh thu. Tại mức giá này:
Số căn hộ được thuê là: 2, 100 − 1, 200 150 − 5. = 105 căn hộ. 100 14
Doanh thu tối đa hàng tháng là: 2, 1002 R(2, 100) = −
+ (210)(2, 100) = 220, 500 đô-la. 20
CÁC BÀI TẬP TỰ LUYỆN: HƯỚNG DẪN VÀ ĐÁP ÁN Bài 8 √ (10, tr. 26). Đáp án: 89 . 40
Bài 9 (12, tr.26). Đáp án: a. Hàm đa thức b. Hàm khác c. Hàm phân thức d. Hàm phân thức
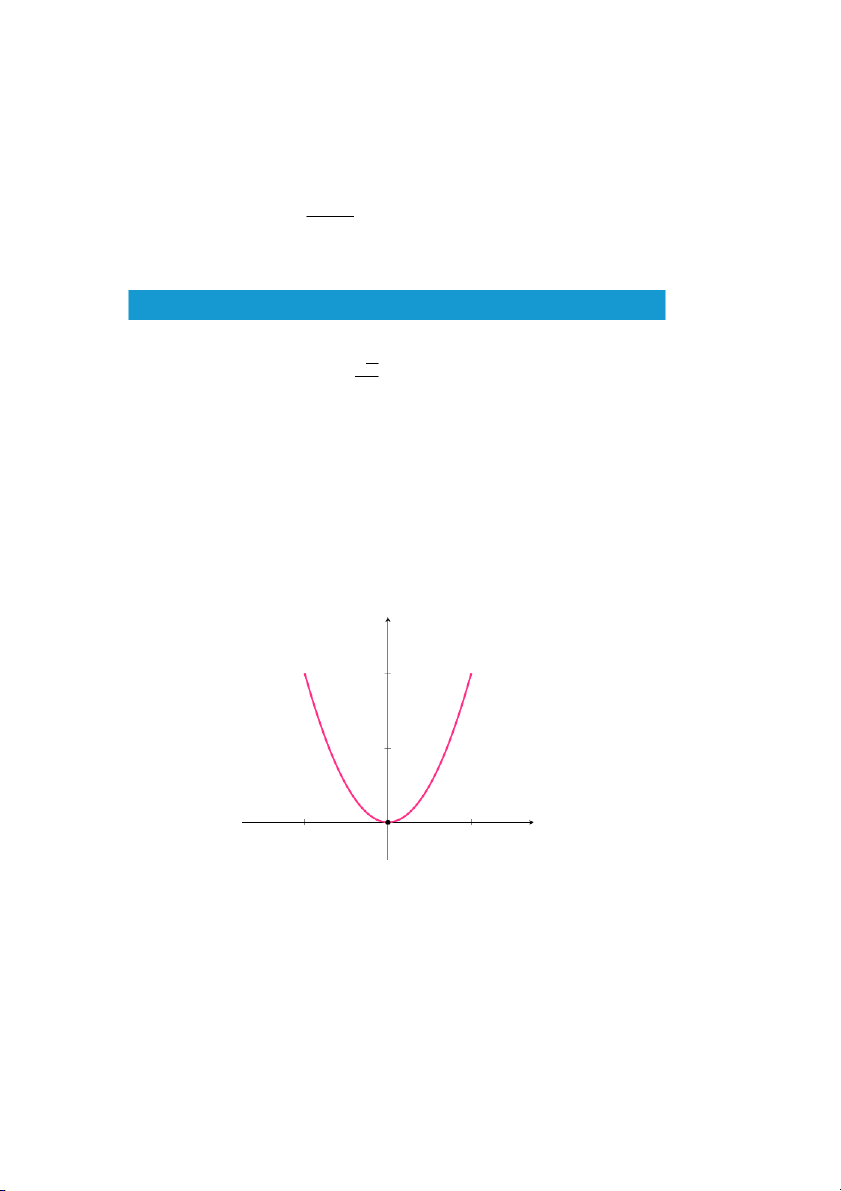
Bài 10 (14, tr. 26). Đáp án: Đồ thị hàm số có 1 hệ số chặn: O(0; 0). y 4 2 O x −2 2
Hình 1.9: Đồ thị hàm số f(x)=x2
Bài 11 (16, tr. 26). Đáp án: Hệ số chặn: A(1; 0) và B(0; 1) Đồ thị hàm số: 15 y 3 2 1 x −3 −1 0 1 2 3 √
Hình 1.10: Đồ thị hàm số f(x)= 1 − x
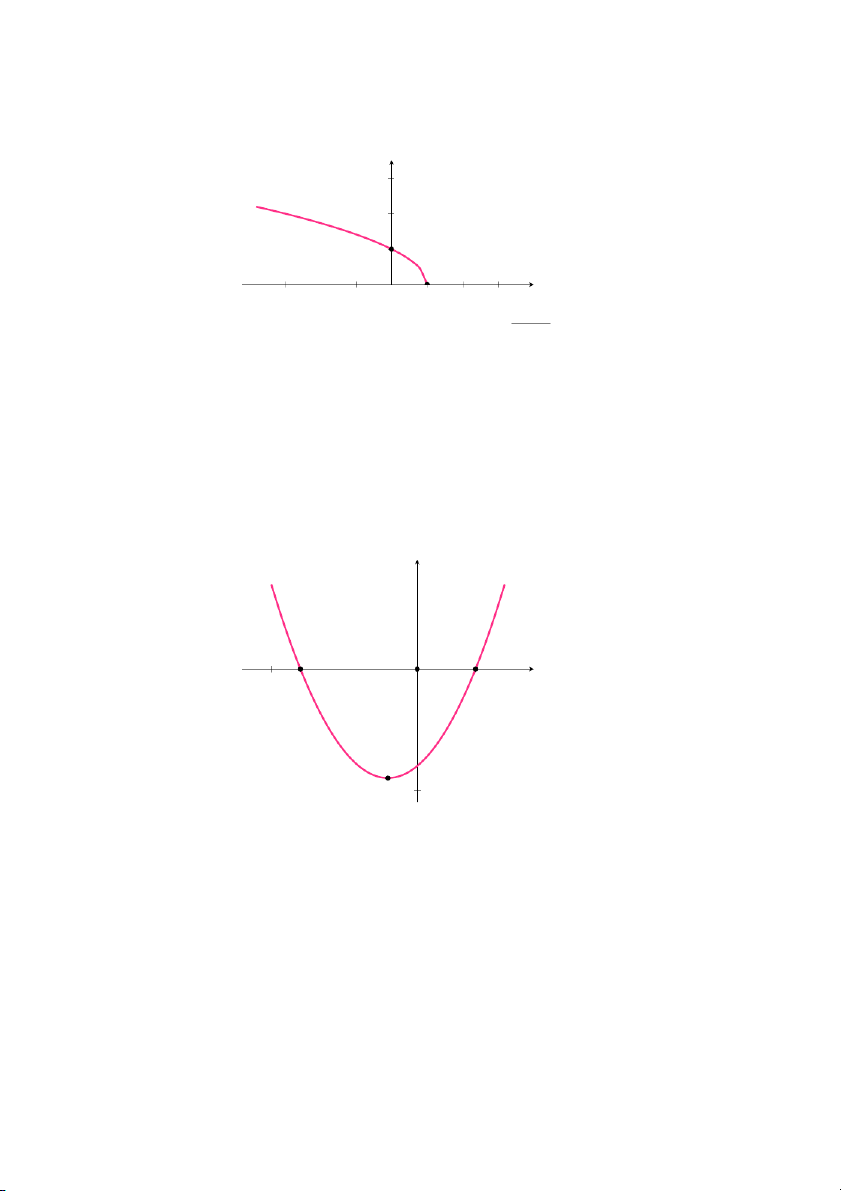
Bài 12 (22, tr. 26). Đáp án: Hệ số chặn: A(−4; 0) ; B(2; 0) và C(0; −8) y A(−4; 0) C(2; 0) O x −5 2 C(0; −8) −10
Hình 1.11: Đồ thị hàm số f(x)=x2 +2x − 8
Bài 13 (24, tr. 26). Cho y = 0, tìm được x = 1 suy ra hệ số chặn x là
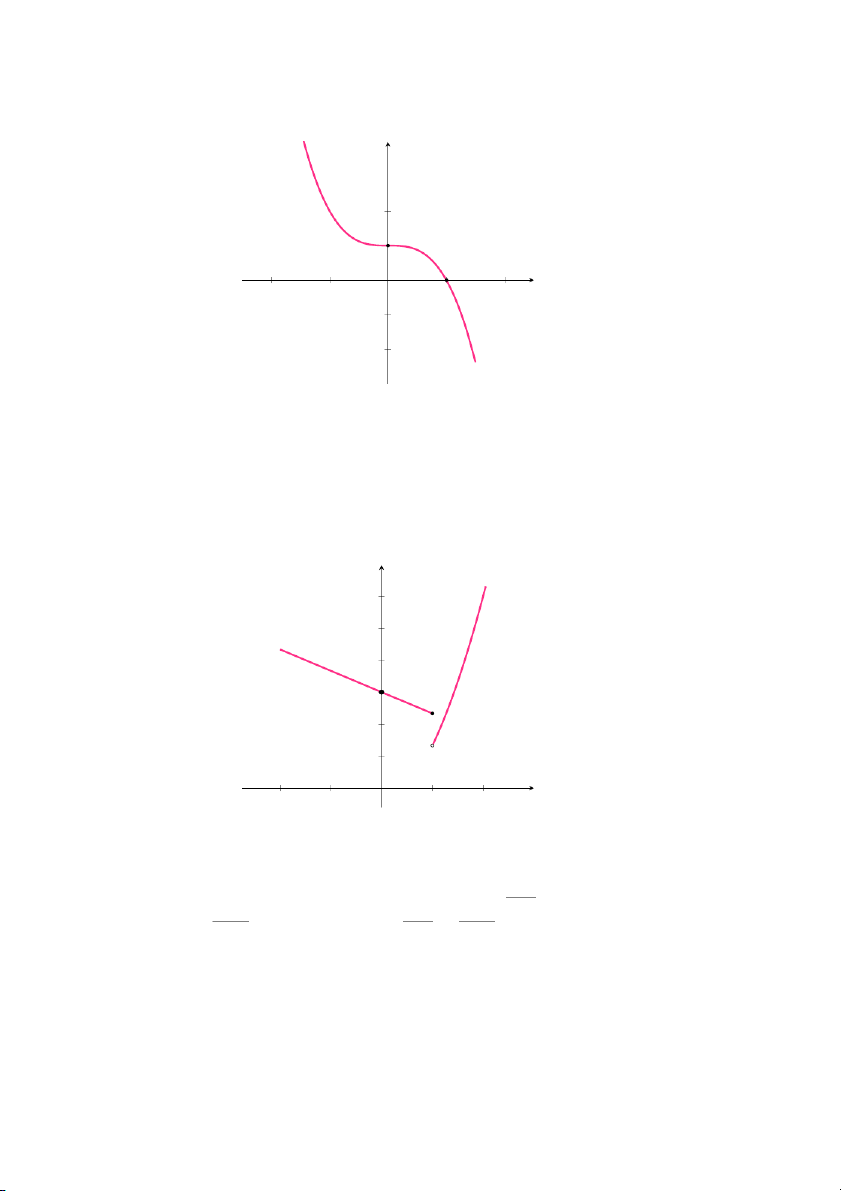
A(1, 0). Cho x = 0, tìm được y = 1 suy ra hệ số chặn y là: B(0, 1). 16 y 2 1 y = −x3 + 1 O x −2 −1 1 2 −1 −2
Hình 1.12: Đồ thị hàm số f(x)=−x3 +1
Bài 14 (28, tr. 26). Đáp án: Hàm số không có hệ số chặn x.
Hàm số có 1 hệ số chặn y là A(0; 9). y y = x2 + x − 2 18 15 y = 9 − x 12 9 6 3 x −4 −2 O 2 4
Hình 1.13: Đồ thị hàm xác định từng khúc g(x)
Bài 15 (34, tr. 26). Ta có: 2x−3y = −8 suy ra y = 2x+8. và 3x y = 3 −5 −13
suy ra y = 3x+13 . Giải phương trình: 2x+8 = 3x+13 , ta được x = 5 3 5 −1 từ đó
tính được y = 2. Vậy giao điểm của 2 đường thẳng đó là: A(−1, 2). Vẽ đồ thị 17 y 2x − 3y = −8 3x − 5y = −13 A( 2 −1; 2) x −1 O
Hình 1.14: Giao điểm của hai đồ thị 2x − 3y = −8 và 3x − 5y = −13
Nhìn vào đồ thị cũng thấy được: Giao điểm của 2 đường thẳng là: A(−1; 2)
Bài 16 (30, tr. 26). Giải phương trình: 3x + 8 = 3x − 2, ta thấy phương
trình vô nghiệm, từ đó suy ra 2 đường thẳng đó không cắt nhau. Vẽ đồ thị y y = 3x + 8 8 y = 3x − 2 2 x −2 O 2
Hình 1.15: Đồ thị hàm số y =3x +8 và y =3x − 2
Nhìn vào đồ thị ta cũng thấy 2 đường thẳng đó không cắt nhau.
Bài 17 (38, tr. 27). Đáp án: a. Hệ số chặn y : (0, 0) 18
b. Hệ số chặn x : (−2, 0); (0, 0) và (3.5, 0)
c. Giá trị lớn nhất của f(x) là: 2; đạt tại x = −1 hoặc x = 4
d. Giá trị nhỏ nhất của f(x) là: −4 ; đạt tại x = 2
Bài 18 (42, tr. 26). Hàm doanh thu là: R(x) = x.20(22−x) = 20x(22−x) (đô-la).
Hàm chi phí là: C(x) = 10.20(22 − x) (đô-la).
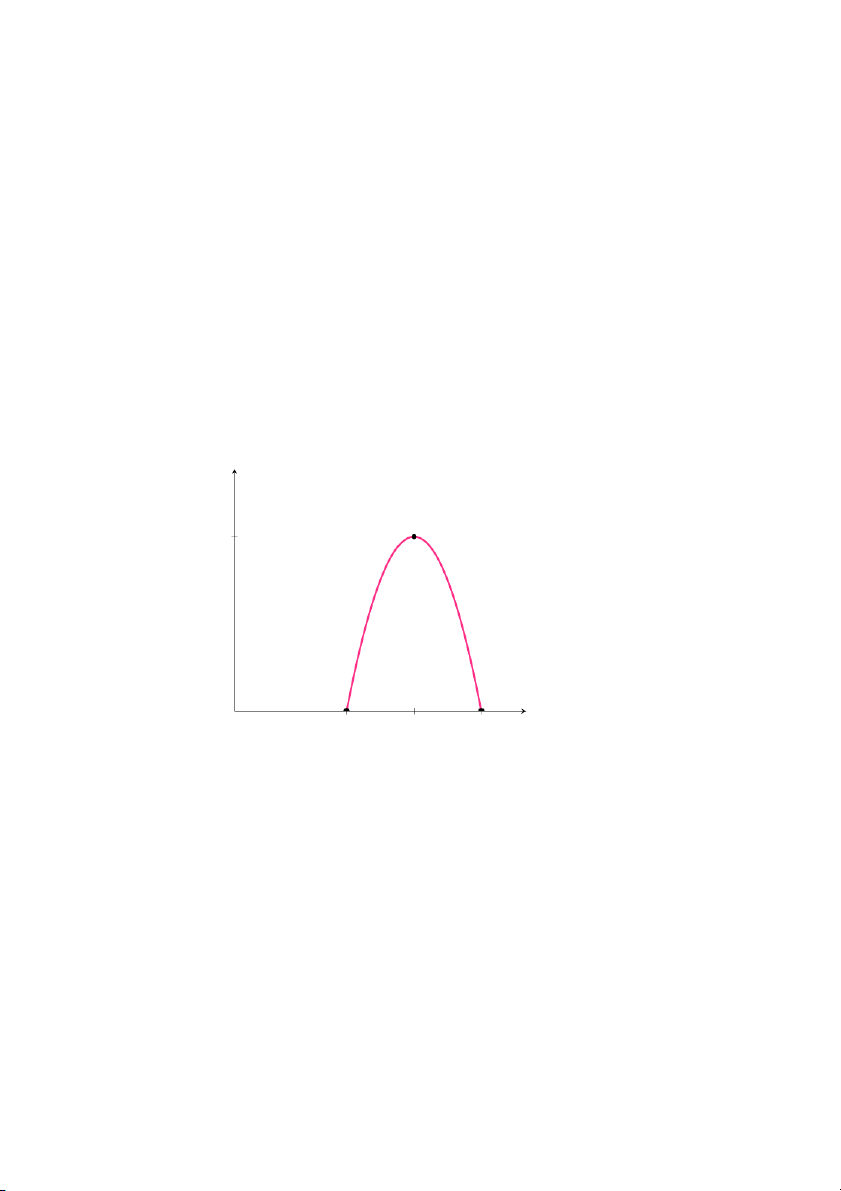
Hàm lợi nhuận là: P (x) = R(x) − C(x) = 20(x − 10)(22 − x) = −20x2 + 640x − 4400 (đô-la). p (đô-la) (16, 720) 720 x ( đô-la) 0 10 16 22
Hình 1.16: Đồ thị hàm lợi nhuận: P (x)=−20x2 +640x − 4400
Dựa vào đồ thị ta thấy: Hàm lợi nhuận đạt giá trị lớn nhất khi x = 16. Vậy
giá bán tối ưu là x = 16 đô-la.
Bài 19 (45, tr. 27). Đáp án: a. Hàm lợi nhuận là: P (x) = −0.07x2 + 35x − 574.77 19 P (trăm đô-la) (250; 3, 800.23) 4,000 2,000 x (trăm) 0 250 500
Hình 1.17: Đồ thị hàm lợi nhuận P (x)=−0.07x2 +35x − 574.77
b. Với p = 37 đô-la, giải phương trình: −0.05x + 38 = 37 suy ra x = 20
AP (x) = −0.07x + 35 − 574.77 ; AP (20) = 4.86 đô-la/1 đơn vị. x
c. Nhìn vào đồ thị, ta thấy: Mức sản xuất cho lợi nhuận tối đa là: x = 250
đơn vị. Khi đó lợi nhuận tối đa là: P = 3, 800.23 đô-la.
Bài 20 (46, tr. 28). Đáp án: b. Hàm chi phí: C(x) = 90 + 21x c. Vẽ đồ thị C C(x) = 90 + 21x 90 x O 1 2 3 4
Hình 1.18: Đồ thị hàm chi phí C(x) = 90+21x
Bài 21 (48, tr. 28). a. Hàm doanh thu là: R(x) = x(4.2 − 0.01x) = 20 4.2x − 0.01x2 (đô-la).
Hàm lợi nhuận là: P (x) = R(x) − C(x) = −0.012x2 + 4.2x − 30 (đô-la). b. p (chục đô-la) (17.5, 33.75) 35 30 25 20 15 10 5 x (chục chiếc xúc xích) 0 5 10 15 20
Hình 1.19: Đồ thị hàm lợi nhuận P (x)=−0.012x2 +4.2x − 30
Nhìn vào đồ thị ta thấy lợi nhuận đạt tối đa khi: x = 17.5 (chục) hay
175 chiếc xúc xích. Thay x = 175 vào biểu thức: p = 4.2˘0.01x ta được giá
mỗi chiếc xúc xích là: p = 2.45 đô-la.
Bài 22 (56, tr. 29). Đáp án: a. Hàm chi phí là: 44, 0 ≤ w ≤ 1 P (w) = 61, 1 < w ≤ 2 78, 2 < w ≤ 3
b. Đồ thị hàm chi phí P (w) 21 P (cents) 78 61 44 w (ounce) 0 1 2 3
Bài 23 (58, tr. 30). Đáp án: a. S(0) = −15 suy ra độ sâu của hầm chứa là 15 feet. b. Đồ thị: S (nghìn feet) (25, 9.985) 10 5 t (giây) O 25 50
Hình 1.20: Đồ thị hàm S(t)=−16t2 +800t − 15
c. Vật phóng đạt độ cao lớn nhất khi: t = 25 giây.
Độ cao lớn nhất đó là: 9985 feet 1.3 Các mô hình hàm số KIẾN THỨC QUAN TRỌNG 22
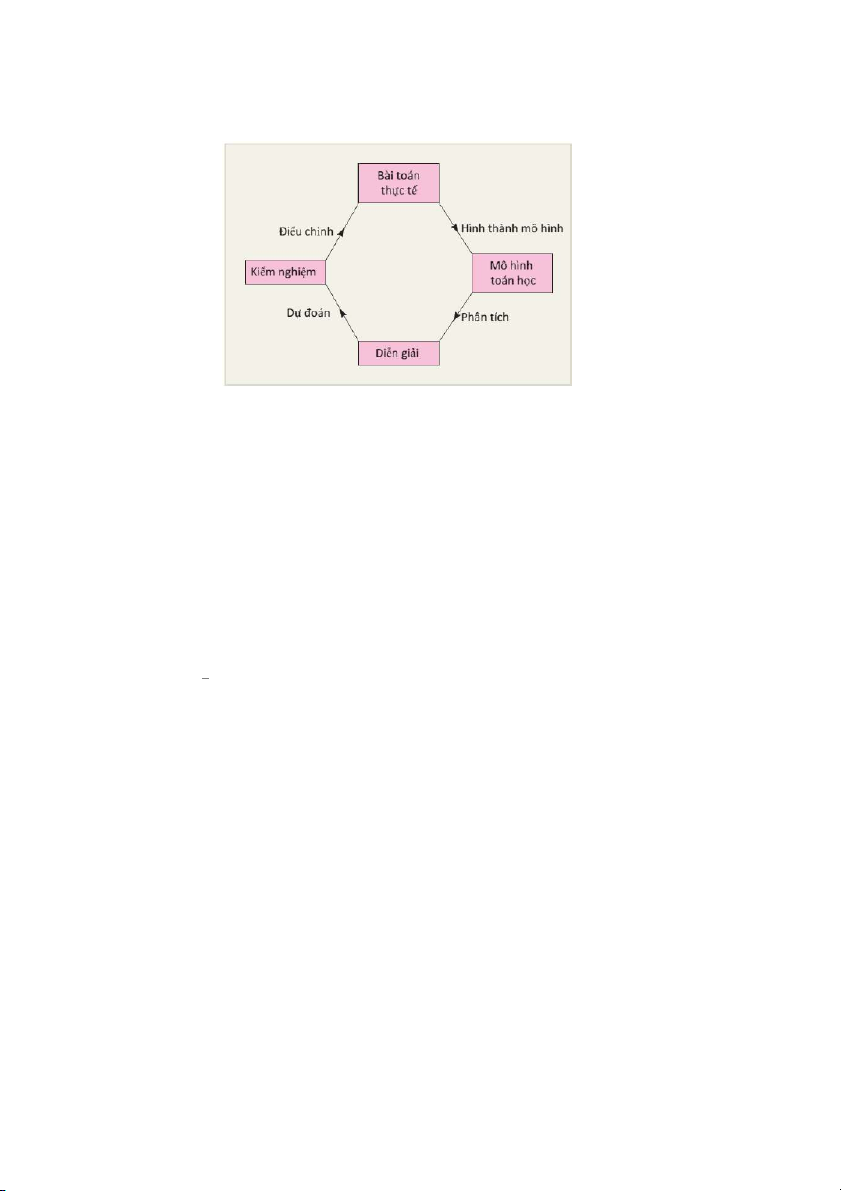
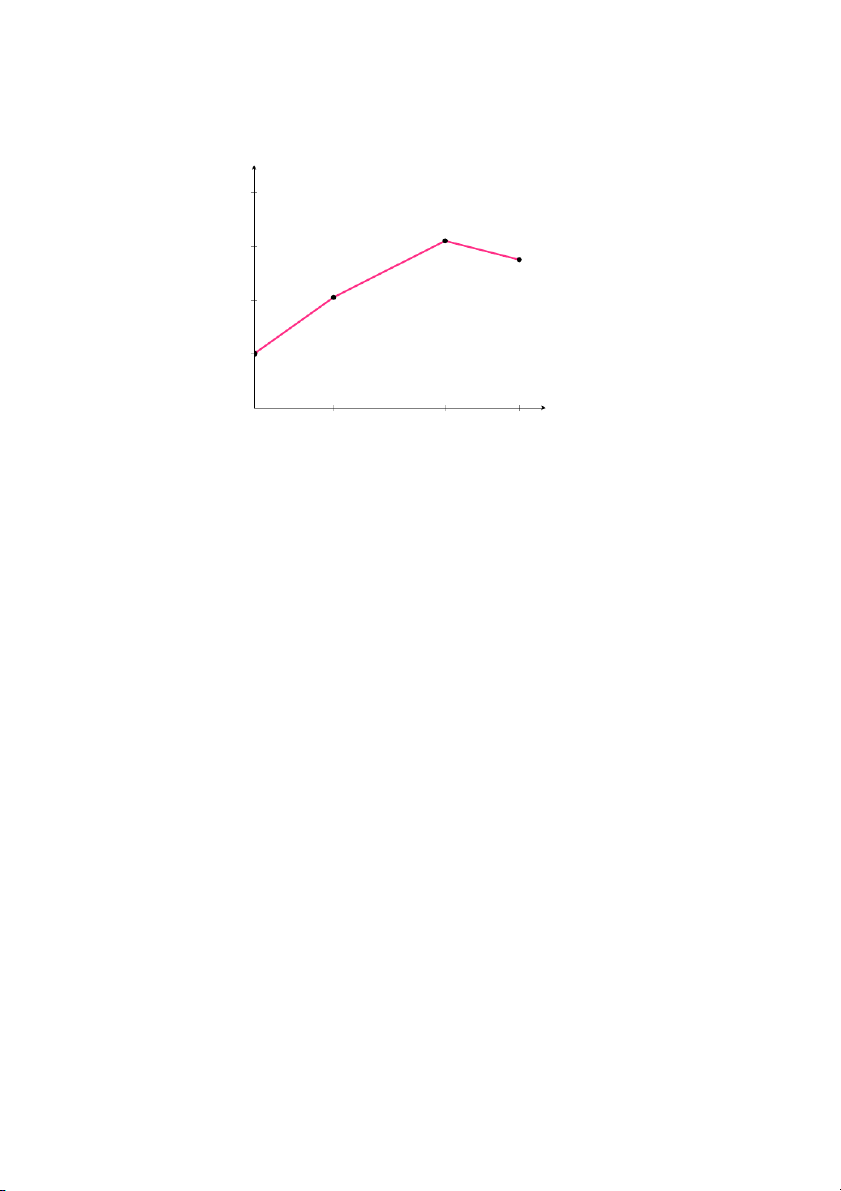
Quy trình lập mô hình toán học
Quy trình lập mô hình toán học được thực hiện theo bốn giai đoạn:
• Giai đoạn 1: Hình thành mô hình
Bắt nguồn từ một tình huống thực tế cần giải quyết và những dữ liệu
đã thu thập, ta đơn giản hóa các giả thiết ở mức độ cho phép để xác
định các biến số chính và thiết lập các phương trình liên quan đến các biến đó.
• Giai đoạn 2: Phân tích mô hình
Ta sử dụng các phương pháp toán học thích hợp để phân tích hoặc
giải mô hình toán học đã được lập ở giai đoạn 1, từ đó thu được các
kết luận.(Trong cuốn sách này, công cụ chính để phân tích mô hình
toán học là giải tích, nhưng trong thực tế có rất nhiều công cụ khác
như: đại số, thống kê,...)
• Giai đoạn 3: Diễn giải mô hình
Ta áp dụng các kết luận thu được ở giai đoạn 2 vào tình huống thực
tế ban đầu để đánh giá độ chính xác của mô hình và đưa ra các dự báo.
• Giai đoạn 4: Kiểm nghiệm và điều chỉnh mô hình
Ta kiểm tra tính chính xác của các dự báo được đưa ra ở giai đoạn 3
bằng cách thu thập các dữ liệu mới. Nếu các dự báo không được xác
nhận bởi dữ liệu mới thì các giả thiết của mô hình ở giai đoạn 1 cần
được điều chỉnh và quá trình lập mô hình được lặp lại. 23
Hình 1.21: Quy trình lập mô hình toán học
Biểu diễn quan hệ tỷ lệ • Tỷ lệ thuận
Nếu hai đại lượng x và y tỷ lệ thuận với nhau thì ta có thể biểu diễn
y = kx với k là một hằng số nào đó. • Tỷ lệ nghịch
Nếu hai đại lượng x và y tỷ lệ nghịch với nhau thì ta có thể biểu diễn
y = k với k là một hằng số nào đó. x • Tỷ lệ đồng thời
Nếu đại lượng Q tỷ lệ đồng thời với cả hai đại lượng x và y thì ta có
thể biểu diễn Q = kxy với k là một hằng số nào đó.
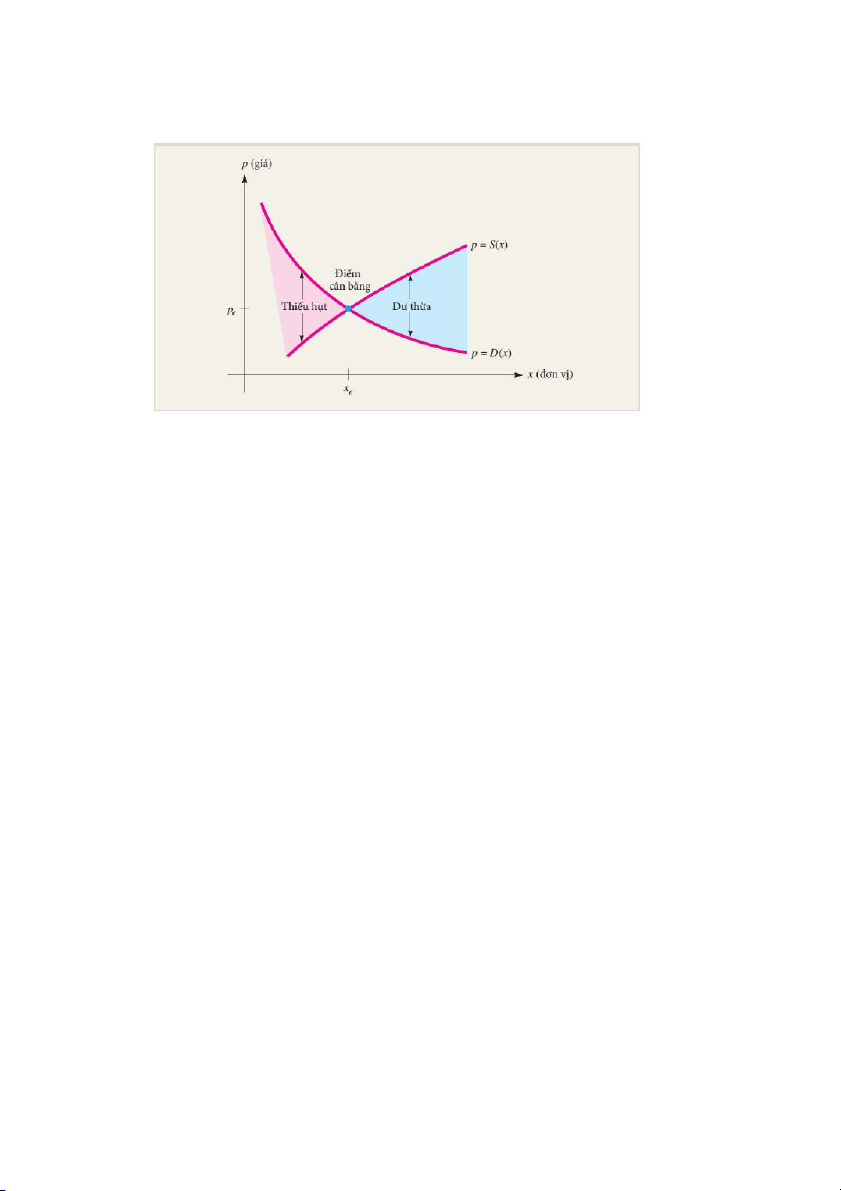
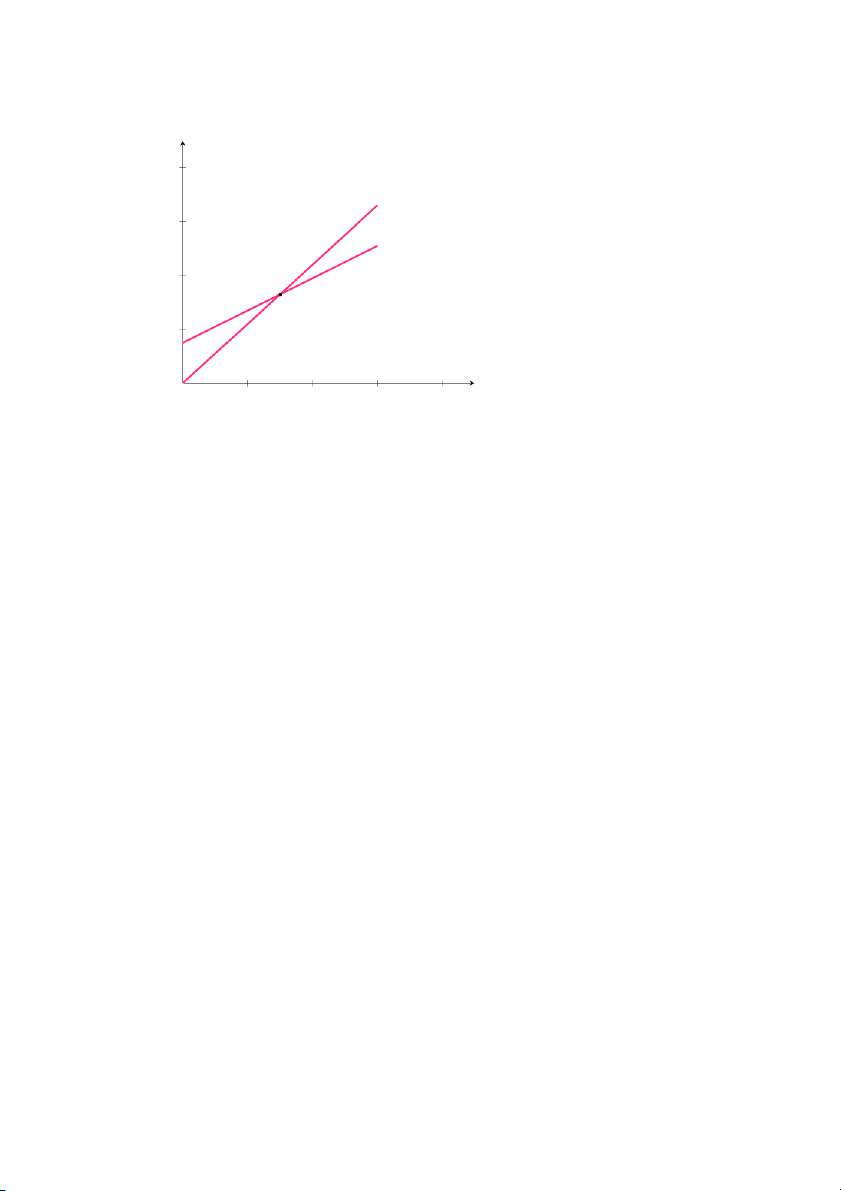
Mô hình cân bằng thị trường
Một loại hàng hóa được giới thiệu trên thị trường cạnh tranh với số
lượng là x. Cung và cầu của thị trường đối với loại hàng hóa đó được thể
hiện qua hàm cung p = S(x) và hàm cầu p = D(x). Trạng thái của thị
trường được xác định qua mối quan hệ giữa hàm cung và hàm cầu, được mô tả trong hình sau: 24
Hình 1.22: Mô hình cân bằng thị trường
• Để xác định lượng cân bằng x
bằng phương pháp đại số, ta giải e phương trình S(x) = D(x).
• Khi số lượng của loại hàng hóa đó trên thị trường đúng bằng lượng
cân bằng x thì thị trường ở trạng thái cân bằng. e
• Khi số lượng của loại hàng hóa đó trên thị trường thấp hơn lượng cân
bằng x thì thị trường ở trạng thái thiếu hụt (cầu vượt quá cung). e
• Khi số lượng của loại hàng hóa đó trên thị trường cao hơn lượng cân
bằng x thì thị trường ở trạng thái dư thừa (cung vượt quá cầu). e
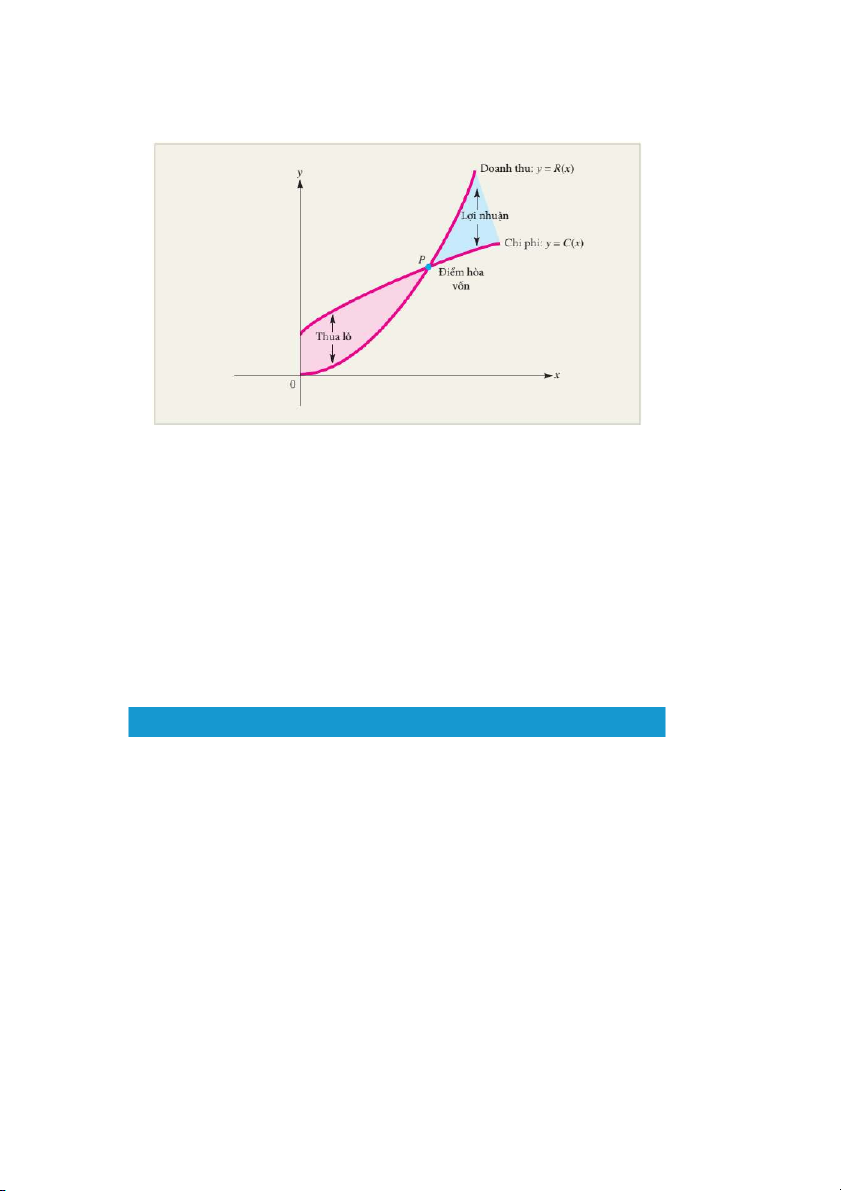
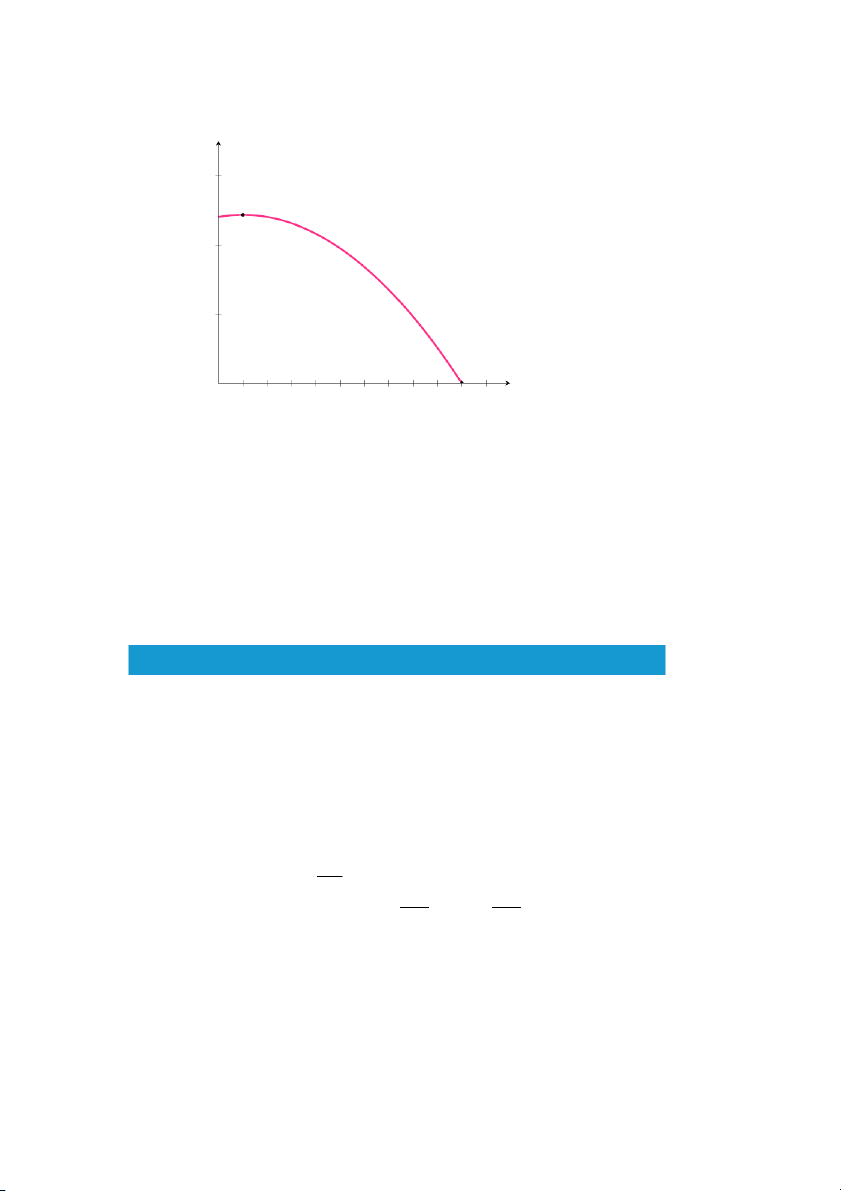
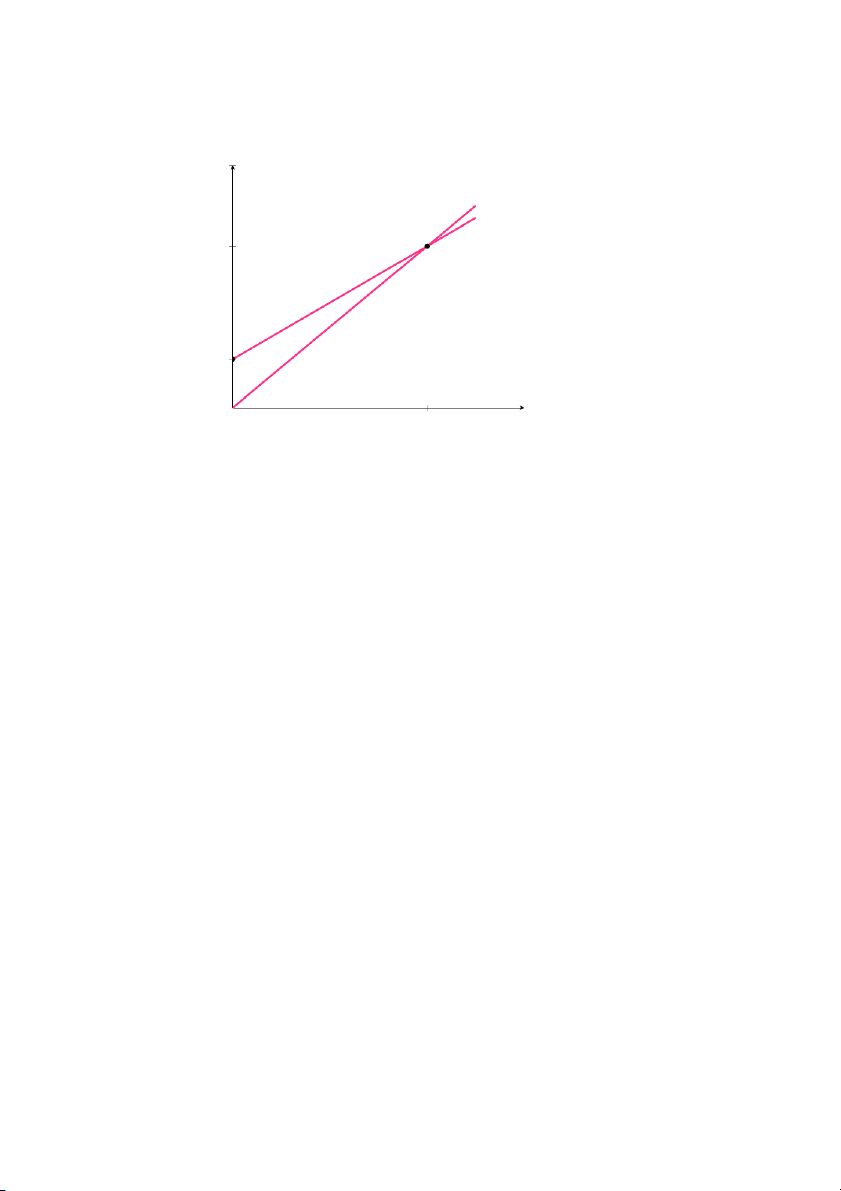
Mô hình phân tích hòa vốn
Một doanh nghiệp sản xuất và bán x đơn vị một loại sản phẩm với các
hàm chi phí C(x) và doanh thu R(x). Trạng thái kinh doanh của doanh
nghiệp được xác định qua mối quan hệ giữa chi phí và doanh thu, quan hệ
đó được mô tả trong hình sau: 25
Hình 1.23: Mô hình phân tích hòa vốn
• Để xác định lượng hàng hóa x mà tại đó doanh nghiệp đạt được trạng 0
thái hòa vốn, ta giải phương trình C(x) = R(x).
• Khi số lượng hàng hóa doanh nghiệp sản xuất và bán được thấp hơn
x thì doanh nghiệp ở trạng thái bị thua lỗ. 0
• Khi số lượng hàng hóa doanh nghiệp sản xuất và bán được cao hơn
x thì doanh nghiệp ở trạng thái có lợi nhuận. 0
HƯỚNG DẪN GIẢI BÀI TẬP CƠ BẢN MỘT SỐ LƯU Ý:
• Trong các bài tập dưới đây, tùy theo yêu cầu của từng đề bài, lời giải
sẽ được trình bày theo các phần tương ứng với bốn giai đoạn của Quy
trình lập mô hình toán học.
• Vì Giai đoạn 4 cần có sự thu thập dữ liệu thực tế nên tạm thời chỉ
được nêu nhưng chưa được trình bày chi tiết.
• Do các bài toán với dữ liệu thực tế khá lớn nên khi thể hiện đồ thị
của các hàm số đó chúng tôi buộc phải quy đổi về số liệu với giá trị 26
nhỏ hơn, vì vậy bạn đọc cần chú ý đến đơn vị của các vạch chia trên các trục số.
Bài 1 (Bài 14 trang 42). Xây dựng mô hình tính chi phí
Lời giải: Đề bài chỉ yêu cầu ta thực hiện Giai đoạn 1: Hình thành mô hình.
Gọi số lượng máy móc được sử dụng là x.
Chi phí thiết lập tỷ lệ thuận với x: C
là một hằng số nào đó. 1 = k1x, k1
Chi phí vận hành tỷ lệ nghịch với x: C2 = k2 , k x
2 là một hằng số nào đó.
Vậy tổng chi phí C(x) = C1(x) + C2(x) = k1x + k2 . x
Bài 2 (Bài 21 trang 42). Xây dựng mô hình tính thuế
Lời giải: a. Câu hỏi yêu cầu ta thực hiện giai đoạn 1 và 2.
• Giai đoạn 1: Hình thành mô hình
Theo bảng số liệu, ta thấy có bốn công thức tính thuế thu nhập T (x)
tương ứng với bốn mức thu nhập x của một cá nhân:
- Mức 1: 0 ≤ x ≤ 8, 375 đô-la: T (x) = 10%x = 0.1x (đô-la)
- Mức 2: 8, 375 < x ≤ 34, 000 đô-la:
T (x) = 10%(8, 375) + 15%(x − 8, 375) = 0.15x − 418.75 (đô-la)
- Mức 3: 34, 000 < x ≤ 82, 400 đô-la:
T (x) = 10%(8, 375) + 15%(34, 000 − 8, 375) + 25%(x − 34, 000)
= 0.25x − 3, 818.75 (đô-la)
- Mức 4: 82, 400 < x ≤ 171, 850 đô-la:
T (x) = 10%(8, 375) + 15%(34, 000 − 8, 375)
+ 25%(82, 400 − 34, 000) + 28%(x − 82, 400)
= 0.28x − 6, 290.75 (đô-la) 27
Vậy ta có thể biểu diễn thuế thu nhập dưới dạng hàm xác định từng khúc: 0.1x 0 ≤ x ≤ 8, 375 0.15x − 418.75 8, 375 < x ≤ 34, 000 T (x) = 0.25x − 3, 818.75 34, 000 < x ≤ 82, 400 0.28x − 6, 290.75 82, 400 < x ≤ 171, 850
• Giai đoạn 2: Phân tích mô hình
Ta vẽ đồ thị hàm T (x): y (mười nghìn đô-la) 5 (171, 850; 41, 827.25) 4 3 2 (82, 400; 16, 781.25) 1 (34, 000; 4681.25) (8, 375; 837.5) x (mười nghìn đô-la) 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18
Hình 1.24: Đồ thị hàm số T (x)
b. Câu hỏi yêu cầu ta thực hiện giai đoạn 3 và 4.
• Giai đoạn 3: Diễn giải mô hình.
Độ dốc của bốn đoạn thẳng trong đồ thị trên lần lượt là 0.1; 0.15; 0.25;
0.28 (hệ số của biến x trong các biểu thức T (x) tương ứng với từng khoảng
của x). Ta thấy các hệ số này tăng theo thu nhập chịu thuế, có nghĩa là khi
thu nhập chịu thuế càng lớn thì mức tăng của thuế càng nhanh (xem thêm Mục 2.1: Đạo hàm).
• Giai đoạn 4: Kiểm nghiệm và điều chỉnh mô hình.
Bài 3 (Bài 7 trang 41). Xác định kích thước tối ưu
Lời giải: Ta giải bài toán theo bốn giai đoạn. 28
• Giai đoạn 1: Hình thành mô hình
Ta đã biết các công thức tính chu vi C và diện tích S của một hình chữ
nhật có chiều dài hai cạnh lần lượt là a và b là: C = 2(a + b); S = ab
Gọi chiều dài một cạnh của sân bóng là x mét, biết chu vi sân bóng bằng
320 mét, ta có thể biểu diễn chiều dài cạnh còn lại của sân bóng theo x là: 320 − x = 160 − x (m) 2
Vậy diện tích của sân bóng được tính theo x bằng công thức:
S(x) = x(160 − x) = −x2 + 160x (m2)
• Giai đoạn 2: Phân tích mô hình
S(x) là hàm bậc hai có đồ thị là đường parabol hướng xuống dưới (do
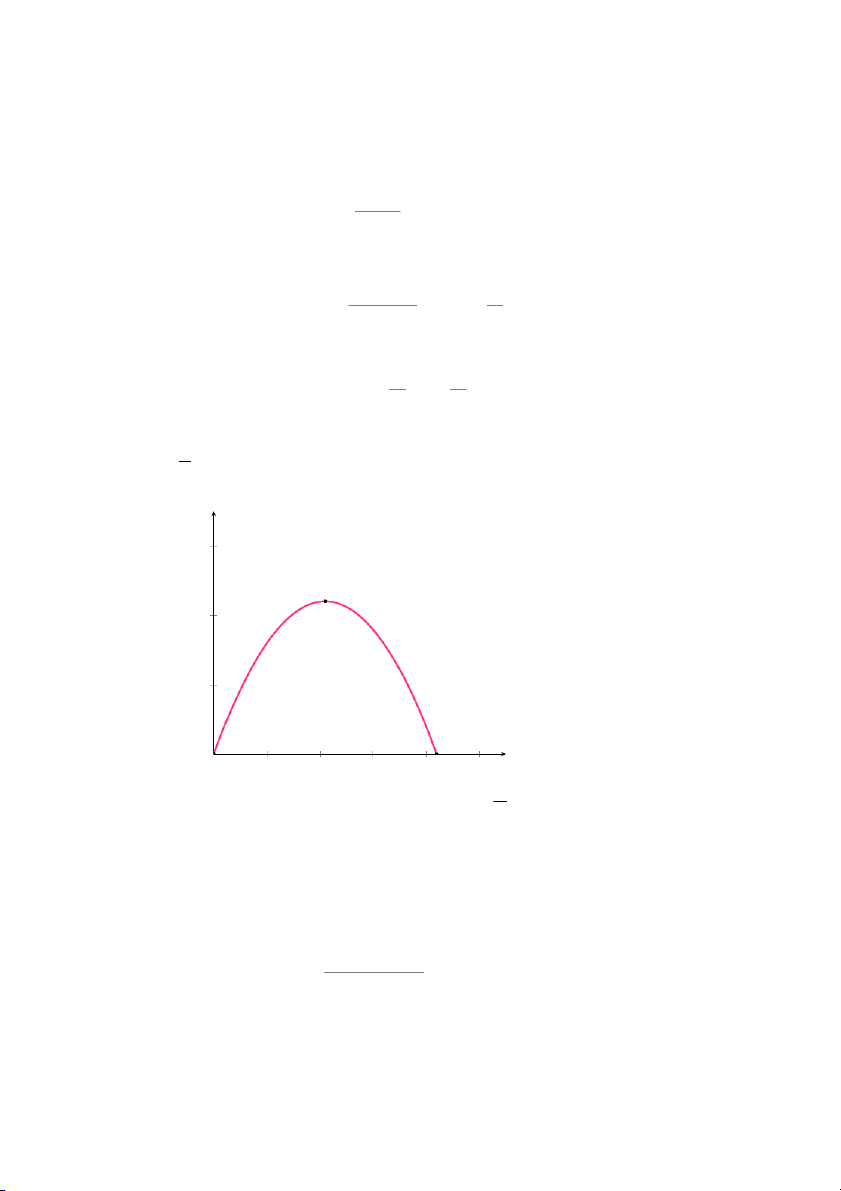
hệ số A = −1 < 0), đỉnh parabol đạt tại (x0 = 80; S(x0) = 6, 400), hai hệ
số chặn lần lượt là (0, 0) và (160, 0). y (nghìn m2) 7 (80; 6,400) 6 5 4 3 2 1 x (chục m) 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17
Hình 1.25: Đồ thị hàm số S(x)=−x2 +160x
• Giai đoạn 3: Diễn giải mô hình
Từ đồ thị, ta thấy nếu sân bóng có dạng hình vuông với độ dài cạnh là
80 mét thì sẽ có diện tích lớn nhất.
• Giai đoạn 4: Kiểm nghiệm và điều chỉnh mô hình. 29
Bài 4 (Bài 19 trang 42). Xác định giá bán tối ưu
Lời giải: Ta giải bài toán theo bốn giai đoạn.
• Giai đoạn 1: Hình thành mô hình
Gọi p là giá bán mỗi chiếc đèn, khi đó số lần giảm giá (mỗi lần giảm 1 đô-la) là 50 − p.
Vì mỗi lần giảm giá sẽ có thêm 1,000 chiếc đèn được bán nên số đèn bán
được hàng tháng ở mỗi mức giá p là:
3, 000 + 1, 000(50 − p) = −1, 000p + 53, 000 = 1, 000(53 − p)
Do chi phí sản xuất một chiếc đèn là 29 đô-la nên lợi nhuận thu được từ việc
bán mỗi chiếc đèn là (p − 29) đô-la. Vậy ta có hàm lợi nhuận hàng tháng
được tính theo công thức:
f (p) = 1, 000(p − 29)(53 − p) = 1, 000(−p2 + 82p − 1, 537) (đô-la)
• Giai đoạn 2: Phân tích mô hình
f (p) là hàm bậc hai có đồ thị là đường parabol hướng xuống dưới (do
hệ số A = −1, 000 < 0), đỉnh parabol đạt tại (p0 = 41; f(p0) = 144, 000),
hai hệ số chặn p lần lượt là (29, 0) và (53, 0). y (mười nghìn đô-la) 16 15 (41; 144,000) 14 13 12 11 10 9 8 7 6 5 4 3 2 1 p (chục đô-la) 0 1 2 3 4 5 6
Hình 1.26: Đồ thị hàm số f(p)=1, 000(−p2 +82p − 1, 537)
• Giai đoạn 3: Diễn giải mô hình 30
Từ đồ thị, ta thấy Sally nên bán đèn với mức giá 41 đô-la mỗi chiếc để
thu được lợi nhuận hàng tháng lớn nhất.
• Giai đoạn 4: Kiểm nghiệm và điều chỉnh mô hình.
Bài 5 (Bài 28 trang 43). Phân tích so sánh chi phí
Lời giải: Ta giải bài toán theo bốn giai đoạn.
• Giai đoạn 1: Hình thành mô hình
Gọi x là số lần thanh toán mỗi tháng của một khách hàng.
Nếu lựa chọn dịch vụ của ngân hàng thứ nhất thì chi phí mỗi tháng của
khách hàng đó là (chú ý cần đổi về cùng một đơn vị tiền tệ): C1(x) = 12 + 0.1x (đô-la)
Nếu lựa chọn dịch vụ của ngân hàng thứ hai thì chi phí mỗi tháng của khách hàng đó là: C2(x) = 10 + 0.14x (đô-la)
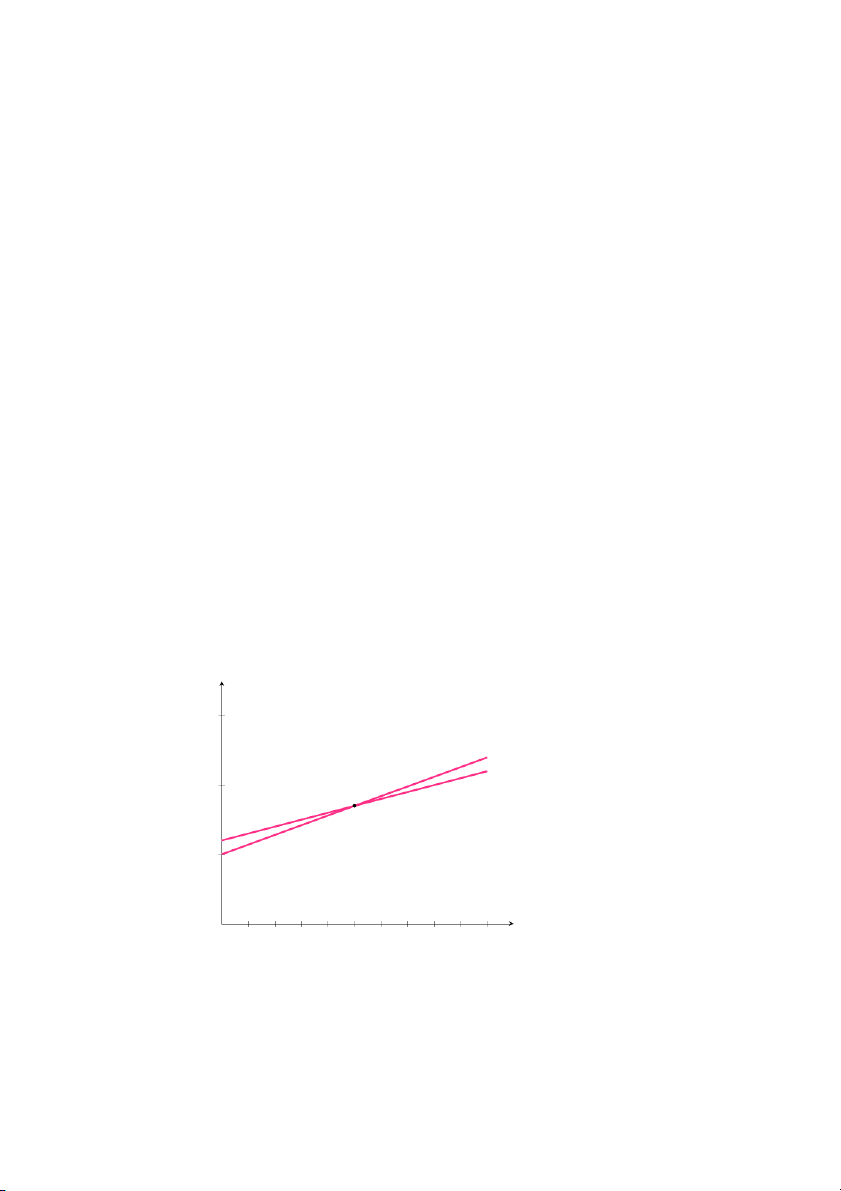
• Giai đoạn 2: Phân tích mô hình
Ta vẽ đồ thị của hai hàm số C1(x) và C2(x) trên cùng một hệ trục tọa độ. y (chục đô-la) 3 C2(x) 2 C1(x) 1 x (chục lần) 0 1 2 3 4 5 6 7 8 9 10
Hình 1.27: Đồ thị các hàm số C1(x) và C2(x) 31
Để xác định hoành độ giao điểm của hai đồ thị, ta giải phương trình:
C1(x) = C2(x) ⇒ 12 + 0.1x = 10 + 0.14x ⇒ x = 50
• Giai đoạn 3: Diễn giải mô hình Từ đồ thị, ta thấy:
- Nếu khách hàng thanh toán đúng 50 lần mỗi tháng thì có thể chọn
ngân hàng nào cũng được.
- Nếu khách hàng thanh toán dưới 50 lần mỗi tháng thì nên chọn ngân hàng thứ hai.
- Nếu khách hàng thanh toán trên 50 lần mỗi tháng thì nên chọn ngân hàng thứ nhất.
• Giai đoạn 4: Kiểm nghiệm và điều chỉnh mô hình.
Bài 6 (Bài 30 trang 44). Mô hình cân bằng thị trường
Lời giải: Đề bài đã cho các hàm số nên ta có thể bỏ qua Giai đoạn 1.
• Giai đoạn 2: Phân tích mô hình
a. Để tìm điểm cân bằng thị trường, ta giải phương trình:
S(x) = D(x) ⇒ 4x + 200 = −3x + 480 ⇒ x = 40 ⇒ p = S(40) = 360
Vậy lượng cân bằng xe = 40 và giá cân bằng pe = 360.
b. Ta vẽ đồ thị của hai hàm số S(x) và D(x) trên cùng một hệ trục tọa độ. 32
y (trăm đơn vị tiền tệ) 6 S(x) = 4x + 200 5 4 3 2 D(x) = −3x + 480 1
x (chục đơn vị hàng hóa) 0 1 2 3 4 5 6 7 8
Hình 1.28: Đồ thị các hàm số S(x) và D(x)
• Giai đoạn 3: Diễn giải mô hình
c. Từ đồ thị, ta thấy:
- Khi mức sản xuất x < 40 đơn vị hàng hóa thì thị trường ở trạng thái thiếu hụt.
- Khi mức sản xuất x > 40 đơn vị hàng hóa thì thị trường ở trạng thái dư thừa.
• Giai đoạn 4: Kiểm nghiệm và điều chỉnh mô hình.
Bài 7 (Bài 37 trang 44). Phân tích hòa vốn
Lời giải: Ta giải bài toán theo bốn giai đoạn. a. Ta có:
• Giai đoạn 1: Hình thành mô hình.
- Hàm tổng doanh thu: R(x) = 110x (đô-la)
- Hàm tổng chi phí: C(x) = 60x + 7, 500 (đô-la)
- Hàm tổng lợi nhuận: P (x) = R(x) − C(x) = 50x − 7, 500 (đô-la)
• Giai đoạn 2: Phân tích mô hình.
Ta vẽ đồ thị của hai hàm số R(x) và C(x) trên cùng một hệ trục tọa độ. 33 y (mười nghìn đô-la) 4 R(x) = 110x 3 C(x) = 60x + 7, 500 2 1
x (trăm đơn vị sản phẩm) 0 1 2 3 4
Hình 1.29: Đồ thị các hàm số R(x) và C(x)
• Giai đoạn 3: Diễn giải mô hình
b. Để xác định điểm hòa vốn, ta giải phương trình:
P (x) = 0 ⇒ 50x − 7, 500 = 0 ⇒ x = 150
Vậy Julia cần bán được 150 đơn vị sản phẩm để hòa vốn.
c. Từ đồ thị, ta thấy nếu Julia bán được 100 đơn vị sản phẩm (ít hơn 150)
thì cô ấy đang ở trạng thái bị thua lỗ. Cụ thể hơn:
P (100) = (50)(100) − 7, 500 = −2, 500
Vậy số tiền Julia bị thua lỗ là 2,500 đô-la.
d. Để xác định lượng hàng hóa cần bán sao cho Julia thu được lợi nhuận
1,250 đô-la, ta giải phương trình:
P (x) = 1, 250 ⇒ 50x − 7, 500 = 1, 250 ⇒ x = 175
Vậy số sản phẩm Julia cần bán được là 175 đơn vị.
• Giai đoạn 4: Kiểm nghiệm và điều chỉnh mô hình.
Bài 8 (Bài 44 trang 45). Xác định thời điểm kết thúc dự án
Lời giải: Ta giải bài toán theo bốn giai đoạn. 34
• Giai đoạn 1: Hình thành mô hình
Gọi t là số ngày dự án được câu lạc bộ thực hiện thêm.
Theo đề bài, trong 80 ngày câu lạc bộ thu gom được 24,000 pounds thủy
tinh, vậy tốc độ thu gom mỗi ngày là 300 pounds và tốc độ đó được giữ
không đổi trong t ngày tiếp theo. Vậy sau t ngày nữa thì câu lạc bộ thu
gom được lượng thủy tinh là (300t + 24, 000) pounds.
Hiện tại công ty tái chế trả 1 cent cho mỗi pound thủy tinh, vậy 100
pounds được trả 100 cents. Mặt khác, do mỗi ngày công ty lại giảm 1 cent
cho mỗi 100 pounds nên sau t ngày thì giá của 100 pounds thủy tinh là
(100 − t) cents, tức là khi đó giá của mỗi pound thủy tinh là 100−t cents. 100
Vậy tại thời điểm câu lạc bộ kết thúc dự án và giao một lần toàn bộ
số thủy tinh thu gom được cho công ty tái chế thì số tiền câu lạc bộ nhận được là: 100 − t f (t) = (300t + 24, 000) 100 = 3(t + 80)(100 − t)
= −3t2 + 60t + 24, 000 (cents)
= −0.03t2 + 0.6t + 240 (đô-la)
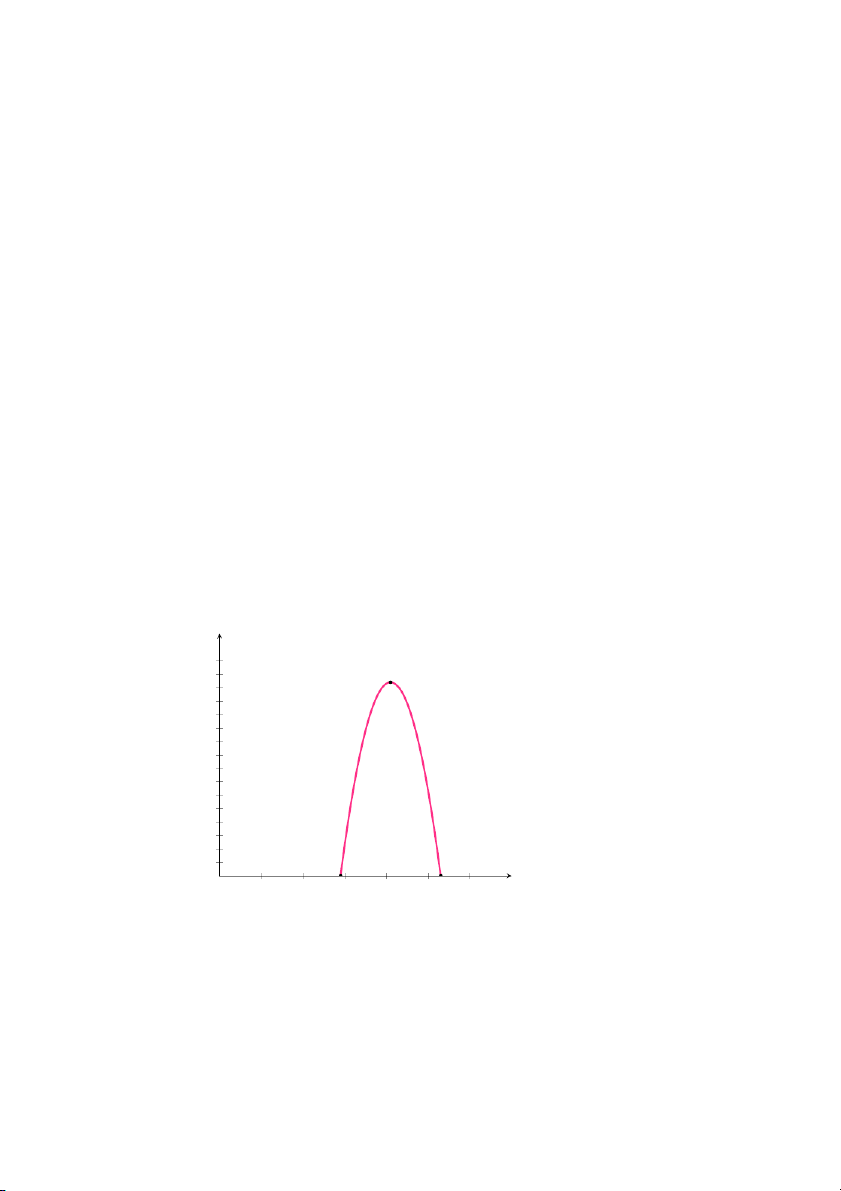
• Giai đoạn 2: Phân tích mô hình
f (t) là hàm bậc hai có đồ thị là đường parabol hướng xuống dưới (do
hệ số A = −0.03 < 0), đỉnh parabol đạt tại (t0 = 10; f(t0) = 243), hai hệ
số chặn t lần lượt là (−80, 0) và (100, 0).
Chú ý rằng hệ số chặn (−80, 0) có t = −80 < 0 không phù hợp với thực
tế nên trên đồ thị ta sẽ không thể hiện điểm này. 35 y (trăm đô-la) 3 (10; 243) 2 1 t (chục ngày) 0 1 2 3 4 5 6 7 8 9 10 11
Hình 1.30: Đồ thị hàm số f(t)=−0.03t2 +0.6t +240
• Giai đoạn 3: Diễn giải mô hình
Từ đồ thị, ta thấy câu lạc bộ nên kết thúc dự án sau 10 ngày thực hiện
thêm và giao thủy tinh cho công ty tái chế để tối đa hóa số tiền nhận được.
Khi đó số tiền câu lạc bộ sẽ nhận được là f(10) = 243 đô-la.
• Giai đoạn 4: Kiểm nghiệm và điều chỉnh mô hình.
CÁC BÀI TẬP TỰ LUYỆN: HƯỚNG DẪN VÀ ĐÁP ÁN
Bài 9 (2, tr.41). Gọi số nhỏ hơn là x.
Tích 2 số là: P (x) = x(18 − x) = −x2 + 18x.
Bài 10 (4, tr.41). Gọi chiều rộng vườn hoa là x.
Chiều dài vườn hoa là: 2x. Diện tích vườn hoa là: S(x) = 2x2.
Bài 11 (6, tr.41). Gọi chiều rộng sân chơi là x.
Chiều dài sân chơi là: 3600. x
Độ dài rào chắn là: C(x) = 2(x + 3,600 = 2x + 7,200) x x
Bài 12 (8, tr.41). Gọi độ dài cạnh đáy là x. Diện tích đáy là: x2 36 Chiều cao là: 1500 x2 Diện tích 2 đáy là: 2x2
Diện tích xung quanh là: 6000 x
Diện tích bề mặt là: 6000 + 2x2. x
Bài 13 (10, tr.41). Gọi lượng radium còn lại là x.
Tốc độ phân rã của mẫu radium đó là: P (x) = k.x trong đó k là hằng số.
Bài 14 (12, tr.41). Giả sử số dân của vùng đó là: b
Gọi số người đã mắc bệnh là: x
Số người chưa mắc bệnh là: b − x
Tốc độ lây lan dịch bệnh là: P (x) = kx(b − x) với k là hằng số
Bài 15 (14, tr.42). Gọi số lượng máy móc được sử dụng là x.
Tổng chi phí là: C(x) = kx + mx
Bài 16 (16, tr.42). a. Hàm chi phí: C(x) = 14x + 1, 200 Hàm doanh thu: : R(x) = 23x
Hàm lợi nhuận: P (x) = R(x) − C(x) = 9x − 1, 200
b. Với x = 2, 000, P (x) = 1680 Với x = 100, P (x) = −300
Công ty có lợi nhuận khi : P (x) > 0 ⇐⇒ x > 400 đơn vị 3 c. AP (x) = P(x) = 9 x − 1,200 x
Với x = 2, 500, AP (x) = 8.52 đô-la.
Bài 17 (18, tr. 42). a. Hàm doanh thu là:
R(x) = x(−6x + 100) = −6x2 + 100x (nghìn đô-la).
Thay x = 15, ta có doanh thu là: R(15) = 150 (nghìn đô- la).
b. Hàm doanh thu bình quân: AR(x) = R(x) = x −6x + 100 (nghìn đô- la).
Thay x = 10, ta có doanh thu bình quân là: AR(10) = 40 (nghìn đô- la).
Bài 18 (20, tr.42). Gọi giá bán cuốn sách là x đô–la ( x < 15)
Giá sách giảm là: 15 − x 37
Số sách bán được là: 200 + 20(15 − x) = 20(25 − x) Doanh thu là: 20x(25 − x)
Chi phí là: C(x) = 60(25 − x)
Lợi nhuận là: P (x) = 20(25 − x)(x − 3)
Đồ thị hàm lợi nhuận: P (đô-la) (14; 2, 420) 2,420 x (đô-la) 0 3 14 25
Hình 1.31: Đồ thị hàm lợi nhuận: P (x) = 20(25− x)(x − 3)
Từ đồ thị ta thấy giá bán tối ưu là 14 đô-la.
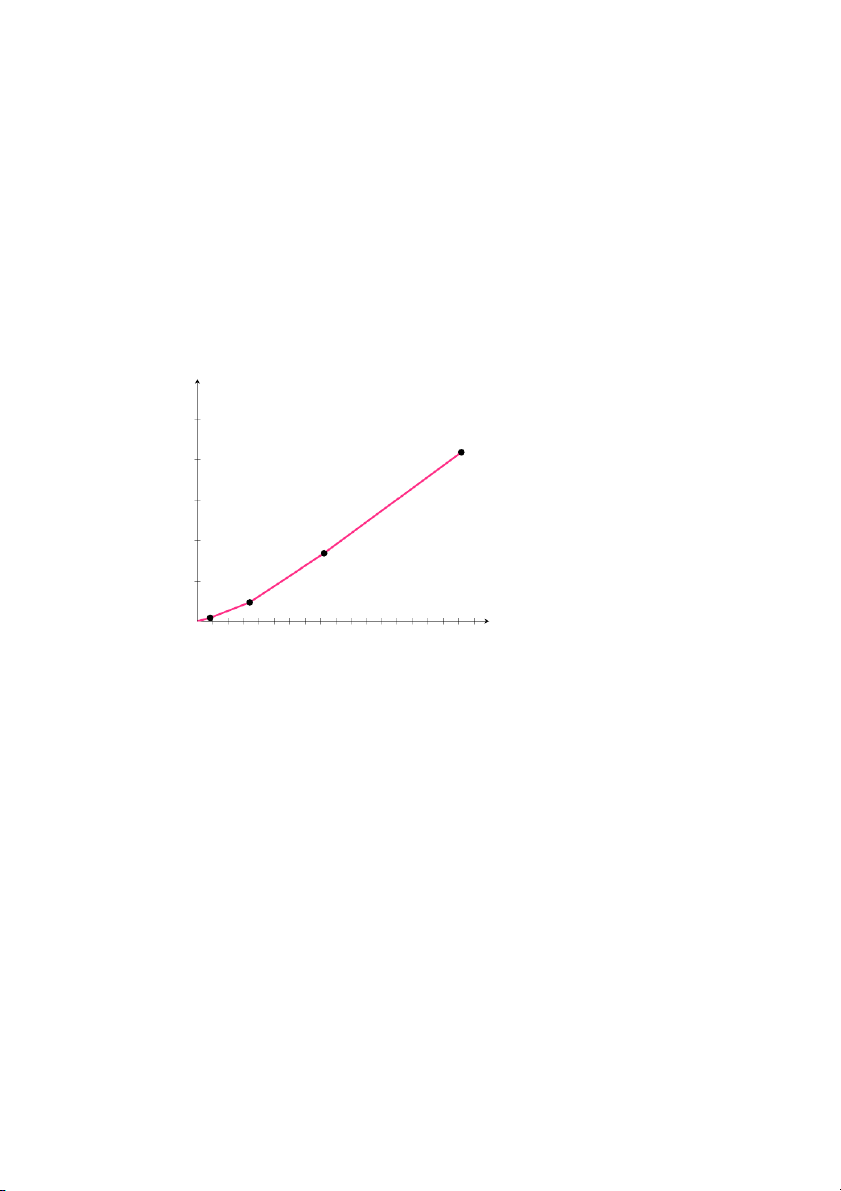
Bài 19 (22, tr. 42). a. Đồ thị hàm tổng lợi nhuận: 38 P (nghìn đô-la) 80 60 40 20 O x (%) 30 72 100
b. Ngân sách tiếp thị chia đều cho 2 sản phẩm nên: x = 50 Lợi nhuận là: P (50) = 51 (nghìn đô- la).
c. Phần trăm ngân sách chi tiêu cho việc tiếp thị sản phẩm A là: 100 – y. 55 + 0.25y, 0 ≤ y ≤ 28 Tổng lợi nhuận theo y: P (y) = 1 − 0.5y, 28 < y ≤ 70 90 − 0.7y, 70 < y ≤ 100
Bài 20 (24, tr.43). a. Với mức thắng thầu 1,000 đô-la: Chi phí dự thầu
là: 175 đô-la và tổng chi phí là: 1,175 đô-la
Với mức thắng thầu $ 25,000: Chi phí dự thầu là: $4,375 và tổng chi phí là: $29,375
Với mức thắng thầu 100,000 đô-la: Chi phí dự thầu là: 13,750 đô-la và
tổng chi phí là: 113,750 đô-la
b. Gọi giá thắng thầu là p, tổng số tiền phải trả để mua một lô đất là C Ta có hàm số: 1.175p, p ≤ 50, 000 C(p) = 1.1p + 3, 750, p > 50, 000
Bài 21 (32, tr. 42). Đáp án: a. Giải phương trình: S(x) = D(x), ta được
mức sản xuất cân bằng là: xe = 2, mức giá cân bằng là: Pe = 9 39 b. Phác họa đồ thị: p 24 D(x) = 21 2 − 3x 21 18 15 12 S(x) = x2) + x + 3 9 E(2; 9) 6 3 x 0 1 2 3 4
c. Thị trường thiếu hụt hàng hóa khi S(x) < D(x) ⇐⇒ 0 ≤ x < 2.
Thị trường dư thừa hàng hóa khi S(x) > D(x) ⇐⇒ x > 2.
Bài 22 (34, tr. 44). Lượng cung bằng lượng cầu khi và chỉ khi
p2 = 60 − p ⇐⇒ p = 20 ( điều kiện: p > 0). 10
Với p = 20, số đơn vị sẽ được bán là: 40 đơn vị.
Bài 23 (36, tr. 42). Gọi x là số chiếc bàn ăn được sản xuất. Doanh thu là: R(x) = 500x
Chi phí là: C(x) = 350x + 30, 000
Lợi nhuận là: P (x) = 150x − 30, 000
a. Hãng sản xuất hòa vốn khi P (x) = 0) suy ra x = 200.
b. Giải phương trình: P (x) = 6, 000, ta được: x = 240.
c. P (150) = −7, 500. Vậy khi sản xuất 150 chiếc bàn, hãng bị thua lỗ. d. Phác họa đồ thị:
Từ đồ thị của hàm chi phí thấy: Khi x = 0 thì C = 30, 000, tức là khi
không sản xuất, hãng vẫn phải chịu một mức chi phí là: 30,000 đô-la hay
chi phí cố định là 30,000 đô-la. 40 y (nghìn đô-la) 150 100 C(x) = 350x + 30, 000 30 R(x) = 500x x (chiếc bàn) 0 200
Hình 1.32: Đồ thị hàm chi phí C(x)=350x +30, 000và hàm doanh thu: R(x)=500x
Bài 24 (38, tr.44). a. Doanh thu là: R(x) = 2.75x
Chi phí là: C(x) = 0.35x + 12, 000
Lợi nhuận là: P (x) = 2.4x − 12, 000
b. Công ty hòa vốn khi và chỉ khi P (x) = 0 ⇐⇒ x = 5, 000.
c. x = 5, 000 suy ra P (x) = 0 nên công ty hòa vốn.
d. P (x) = 9, 000 ⇐⇒ 2.4x − 12, 000 = 9, 000 ⇐⇒ x = 8, 750.
e. Đồ thị của các hàm số: 41 y (nghìn) R = 2.75x 15 14 C = 0.35x + 12, 000 13 12 11 x (nghìn) 0 3 4 5 6
Hình 1.33: Đồ thị hàm chi phí C(x)=0.35x+12, 000và hàm doanh thu: R(x)=2.75x
Hàm chi phí cắt trục y tại điểm (0; 12, 000), điều đó cho ta biết khi
không sản xuất: x = 0 thì chi phí là: C(0) = 12, 000 hay chi phí cố định của công ty là 12,000 đô-la.
Bài 25 (42, tr. 45). Gọi số cây được trồng thêm vào là x. Sản lượng trung
bình khi đó là: 400 − 4x Tổng số cây trồng là: 60 + x. Tổng sản lượng là: −4x2 + 160x + 24, 000
Đồ thị hàm tổng sản lượng: y (nghìn quả) (20, 25.6) 25.6 x (cây) 0 20 100 42
Nhìn vào đồ thị ta thấy: Để tổng sản lượng tối đa, số cây trồng thêm vào là: x = 20 cây.
Bài 26 (46, tr.46). Theo quy tắc Cowling, khi N = 11 và A = 300 thì C = 150 (mg).
Theo quy tắc Friend, khi N = 11 và A = 300 thì C = 264 (mg).
Bài 27 (54, tr.47). a. Diện tích 2 đáy: 2πr2 Diện tích xung quanh 2πrh
Diện tích bề mặt: : 2πr2 + 2πrh = S
Từ đó suy ra: h = S−2πr2 . 2πr Thể tích là: 2 V = r.(S−2π.r ) . 2
b. Diện tích bề mặt: S = πr3+V . r
Bài 28 (56, tr.47). Gọi bán kính là: r (inches) Diện tích đáy: πr2 Diện tích xung quanh: 2πrh
Diện tích bề mặt không kể nắp: πr2 + 2πrh
Giải phương trình: πr2 + 2πrh = 27
Từ đó suy ra: h = 27−πr2 2πr Thể tích: V = r(27−πr2) 2
Bài 29 (60, tr.47). Độ dài cạnh hình vuông là: x Độ dài đáy: 18 − 2x.
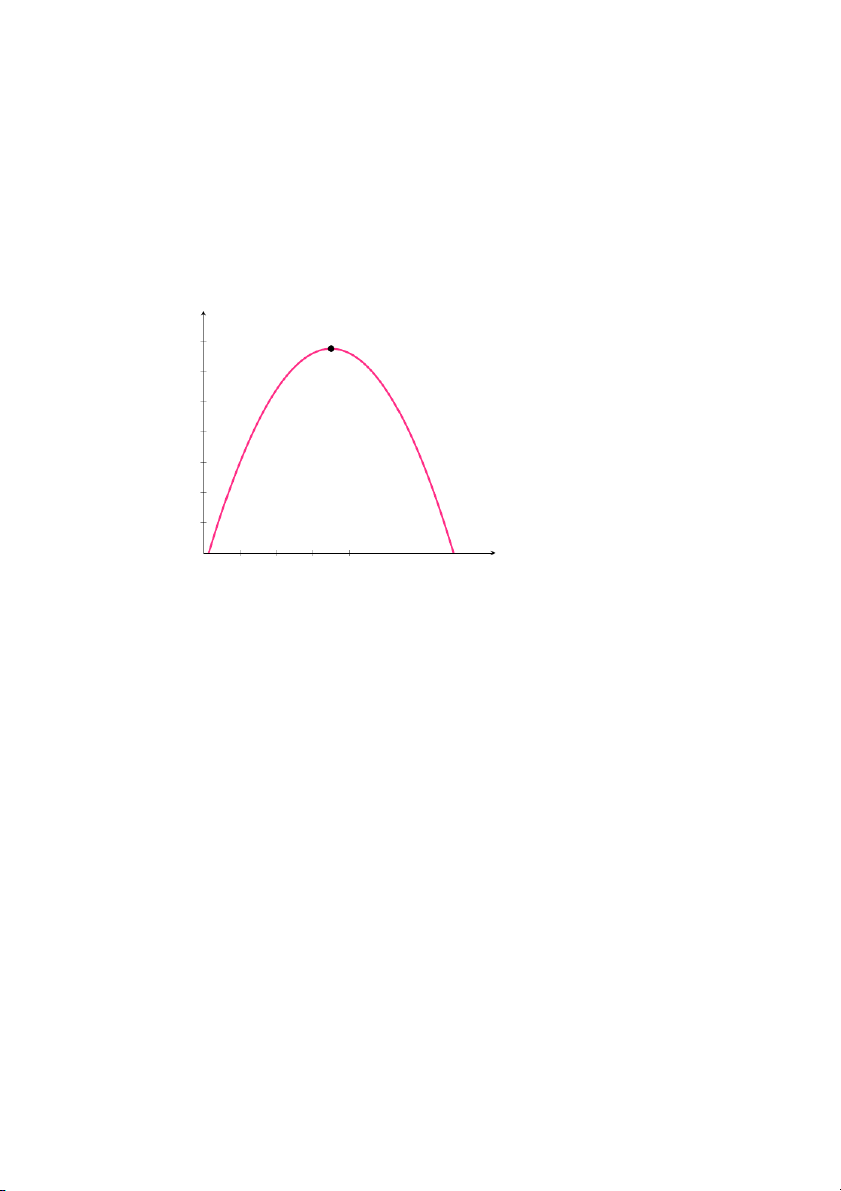
Thể tích chiếc hộp: V = x(18 − 2x)2 = 4x3 − 72x2 + 324x. 43 V (3; 432) 432 x 0 3
Hình 1.34: Đồ thị hàm số: V =4x3 − 72x2 +324x
Từ đồ thị suy ra thể tích chiếc hộp lớn nhất khi x = 3 1.4 Giới hạn KIẾN THỨC QUAN TRỌNG
Định nghĩa giới hạn của hàm số • Giới hạn hữu hạn
Nếu f(x) ngày càng gần tới số L khi x ngày càng gần tới c từ cả hai
phía thì số L được gọi là giới hạn của hàm f(x) khi x tiến gần đến c. lim f (x) = L x→c
• Giới hạn tại vô hạn
Nếu các giá trị của hàm f(x) tiến gần đến số L (hoặc M) khi x tăng
(hoặc giảm) không bị chặn thì ta viết lim f (x) = L (hoặc lim f (x) = M ) x→+∞ x→−∞ • Giới hạn vô hạn 44
Nếu hàm f(x) tăng (hoặc giảm) không bị chặn khi x → c thì ta nói
hàm f(x) có giới hạn vô hạn khi x → c và viết: lim f (x) = +∞ (hoặc lim f (x) = −∞) x→c x→c
Các tính chất đại số của giới hạn
Nếu lim f(x) và lim g(x) tồn tại thì: x→c x→c
• lim[f (x) + g(x)] = lim f (x) + lim g(x) x→c x→c x→c
• lim[f (x) − g(x)] = lim f (x) − lim g(x) x→c x→c x→c
• lim[kf (x)] = k lim f (x) với mọi hằng số k x→c x→c
• lim[f (x)g(x)] = [ lim f (x)][ lim g(x)] x→c x→c x→c lim f (x) f (x) x→c • lim = nếu lim g(x) 6= 0 x g(x) g(x) →c lim x→c x→c
• lim[f (x)]p = [ lim f (x)]p nếu [ lim f (x)]p tồn tại. x→c x→c x→c
Giới hạn của một số hàm số
• Hàm hằng: lim k = k với k là hằng số bất kì. x→c
• Hàm bậc nhất: lim x = c. x→c
• Hàm đa thức: lim p(x) = p(c) với p(x) là một đa thức. x→c p(x) • Hàm phân thức: lim
= p(c) với p(x), q(x) là các đa thức và q(c) 6= x q(x) q(c) →c 0.
Kỹ thuật tính giới hạn tại vô hạn của hàm phân thức
• Quy tắc giới hạn nghịch đảo: Nếu A và k là các hằng số với k > 0 và
xk xác định với mọi x thì A A lim = 0 và lim = 0 x→+∞ xk x→−∞ xk 45
• Các bước tính giới hạn tại vô hạn của hàm f (x) = p(x) : q(x)
- Bước 1: Chia mỗi số hạng của f(x) cho lũy thừa bậc cao nhất xk
xuất hiện trong đa thức mẫu q(x).
- Bước 2: Tính lim f(x) hoặc lim f(x) bằng cách sử dụng các x→+∞ x→−∞
tính chất của giới hạn và quy tắc tính giới hạn nghịch đảo.
HƯỚNG DẪN GIẢI CÁC BÀI TẬP CƠ BẢN
Bài 1 (Bài 8, 14 trang 60). Tính giới hạn tại điểm thuộc miền xác định
Lời giải: a. Đa thức x3 − 2x2 + x − 3 xác định tại x = −1 nên
lim x3 − 2x2 + x − 3 = (−1)3 − 2(−1)2 + (−1) − 3 = −7 x→−1
b. Phân thức 2x+3 xác định tại x = 1 nên x+1 2x + 3 2(1) + 3 5 lim = = x→1 x + 1 1 + 1 2
Bài 2 (Bài 16, 18 trang 60). Tính giới hạn tại điểm nằm ngoài miền xác định
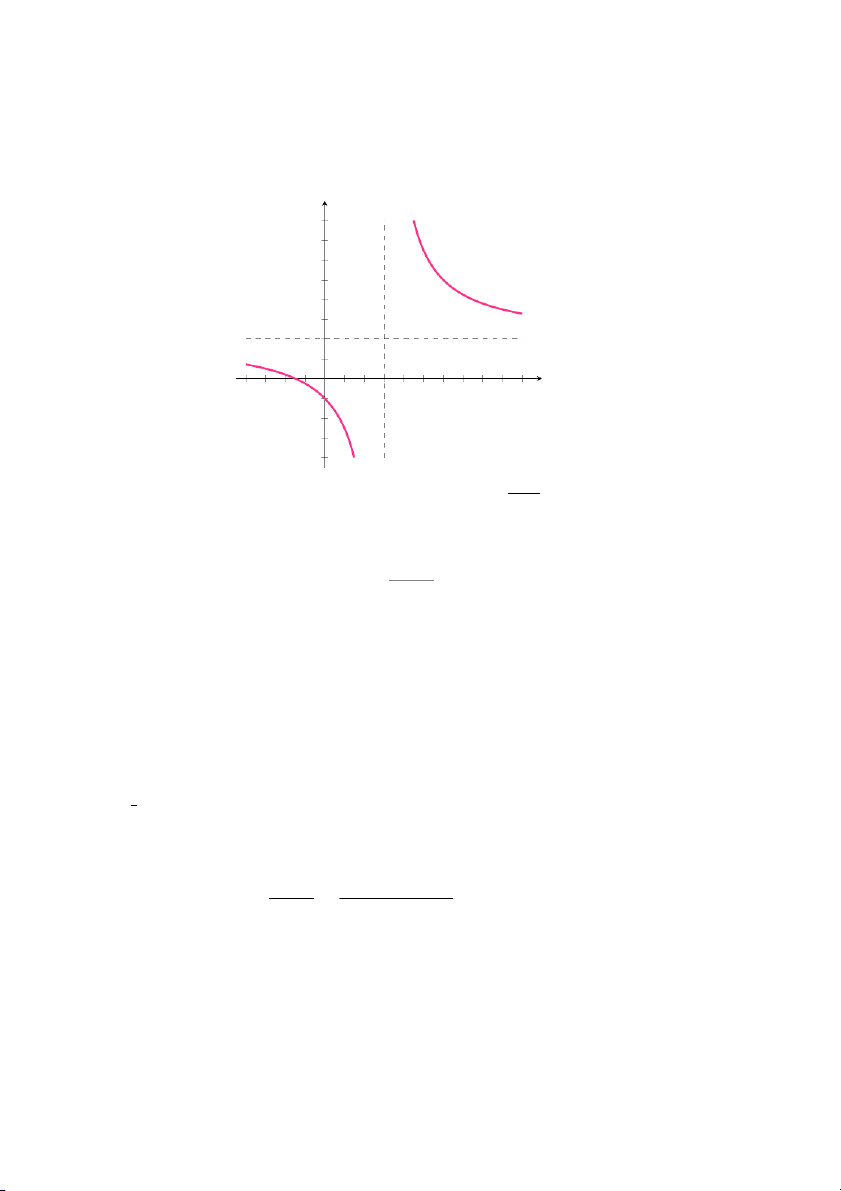
Lời giải: a. Xét giới hạn 2x + 3 lim x→3 x − 3
Ta xét riêng giới hạn của tử và mẫu
lim(2x + 3) = 2(3) + 3 = 9 6= 0 x→3 lim (x − 3) = 3 − 3 = 0 x→3
nên ta kết luận giới hạn trên không tồn tại (không tiến đến bất kì giá trị hữu hạn nào).
Đồ thị hàm số trong hình dưới giúp bạn đọc dễ hình dung hơn lý do vì
sao giới hạn trên không tồn tại. Ta thấy hàm f(x) tăng không bị chặn khi 46
x tiến đến gần 3 từ bên phải và giảm không bị chặn khi x tiến đến gần 3 từ bên trái. y 8 7 6 5 4 3 2 1 x −4 −3 −2 −1 10 2 3 4 5 6 7 8 9 10 −1 −2 −3 −4
Hình 1.35: Đồ thị hàm số f(x)= 2x+3x−3 b. Xét giới hạn 9 − x2 lim x→3 x − 3
Ta xét riêng giới hạn của tử và mẫu lim (9 − x2) = 9 − 9 = 0 x→3 lim (x − 3) = 3 − 3 = 0 x→3
Giới hạn này khác với giới hạn trong câu (a) vì cả tử và mẫu đều tiến
đến gần 0 khi x tiến gần đến 3 (trường hợp này được gọi là dạng vô định
0 ). Đối với dạng giới hạn này, ta có thể sử dụng phương pháp lập bảng tính 0
giá trị hoặc tối giản phân thức để tìm kết quả. Chúng tôi sẽ trình bày cách
giải dựa trên việc biến đổi đại số để tối giản phân thức. 9 − x2 −(x − 3)(x + 3) = = −x − 3 x − 3 x − 3
Chú ý rằng giới hạn mô tả hành vi của hàm số gần một điểm cụ thể,
không phải tại chính điểm đó. Vì vậy ta hiểu x tiến gần đến 3 tức là x ngày 47
càng gần tới 3 và x 6= 3, nên ta có thể rút gọn biểu thức (x − 3) ở cả tử và
mẫu của phân thức mà không cần lo lắng liệu biểu thức đó có khác 0 hay không. Khi đó ta có: 9 − x2 lim
= lim(−x − 3) = −3 − 3 = −6 x→3 x − 3 x→3
Bài 3 (Bài 20, 26 trang 60). Tính giới hạn bằng biến đổi đại số
Lời giải: a. Xét giới hạn x2 + x − 6 lim x→2 x − 2
Ta tối giản phân thức bằng cách phân tích đa thức tử thành tích của các nhân tử. x2 + x − 6 (x − 2)(x + 3) = = x + 3 x − 2 x − 2 vậy x2 + x − 6 lim = lim(x + 3) = 2 + 3 = 5 x→2 x − 2 x→2 b. Xét giới hạn √x − 3 lim x→9 x − 9
Ta tối giản phân thức bằng cách phân tích đa thức mẫu thành tích của các biểu thức. √ √ x − 3 x − 3 1 = √ √ = √ x − 9 ( x − 3)( x + 3) x + 3 Vậy √x − 3 1 1 1 lim = lim √ = √ = x→9 x − 9 x→9 x + 3 9 + 3 6
Bài 4 (Bài 32, 34, 36 trang 60). Tính giới hạn tại vô hạn của hàm phân thức
Lời giải: a. Xét hàm số 1 − 3x3 f (x) = 2x3 − 6x + 2 48
Ta chia mỗi số hạng của f(x) cho lũy thừa bậc cao nhất xuất hiện trong mẫu là x3: 1 − 3x3 1 f (x) = = x3 − 3 2x3 − 6x + 2 2 − 6 + 2 x2 x3
Áp dụng quy tắc giới hạn nghịch đảo, ta có −3 3 lim f (x) = lim f (x) = = − x→+∞ x→−∞ 2 2 b. Xét hàm số x2 + x − 5 f (x) = 1 − 2x − x3
Ta chia mỗi số hạng của f(x) cho lũy thừa bậc cao nhất xuất hiện trong mẫu là x3: x2 + x − 5 1 + 1 f (x) = = x x2 − 5 x3 1 − 2x − x3 1 x3 − 2 x2 − 1
Áp dụng quy tắc giới hạn nghịch đảo, ta có 0 lim f (x) = lim f (x) = = 0 x→+∞ x→−∞ 1 c. Xét hàm số 1 − 2x3 f (x) = x + 1
Ta chia mỗi số hạng của f(x) cho lũy thừa bậc cao nhất xuất hiện trong mẫu là x: 1 − 2x3 1 f (x) = = x − 2x2 x + 1 1 + 1x
Áp dụng quy tắc giới hạn nghịch đảo và chú ý rằng dù x → +∞ hay
x → −∞ thì x2 → +∞, ta có: lim f (x) = lim f (x) = −∞ x→+∞ x→−∞
Bài 5 (Bài 46, 48 trang 61). Sử dụng các tính chất đại số của giới hạn 49
Lời giải: a. Áp dụng các tính chất của giới hạn hữu hạn, ta có:
lim f (x)[g(x) − 3] = lim[f(x)g(x) − 3f(x)] x→c x→c
= lim[f (x)g(x)] − lim[3f(x)] x→c x→c
= [lim f (x)][lim g(x)] − 3[lim f(x)] x→c x→c x→c = (5)(−2) − 3(5) = −25 b. Xét giới hạn 2f (x) − g(x) lim x→c 5g(x) + 2f (x)
Ta xét riêng giới hạn của tử và mẫu
lim[2f (x) − g(x)] = 2(5) − (−2) = 12 6= 0 x→c
lim[5g(x) + 2f (x)] = 5(−2) + 2(5) = 0 x→c
nên ta kết luận giới hạn không tồn tại (không tiến đến bất kì giá trị hữu hạn nào).
Bài 6 (Bài 52 trang 61). Tính giới hạn tại vô hạn trong sản xuất
Lời giải: Sử dụng kỹ thuật tính giới hạn tại vô hạn của hàm phân thức, ta có: 6t2 + 5t 6 + 5 lim P (t) = lim = lim t = 6 t→∞ t→∞ (t + 1)2 t→∞ (1 + 1 )2 t
Vậy trong dài hạn, sản lượng của doanh nghiệp sẽ tiến tới mức 6,000 đơn
vị sản phẩm mỗi tháng.
Bài 7 (Bài 53 trang 61). Tính chi phí bình quân trong dài hạn
Lời giải: Ta tính giới hạn 7.5x + 120, 000 120, 000 lim A(x) = lim = lim 7.5 + = 7.5 x→+∞ x→+∞ x x→+∞ x
Vậy trong dài hạn, chi phí bình quân cho mỗi đơn vị hàng hóa của doanh
nghiệp sẽ tiến gần tới mức 7.5 đô-la. 50
CÁC BÀI TẬP TỰ LUYỆN: HƯỚNG DẪN VÀ ĐÁP ÁN
Bài 8 (2, tr.59). Đáp án: lim f(x) = b. x→a
Bài 9 (4, tr.59). Đáp án: Không tồn tại giới hạn của hàm số tại x = a.
Bài 10 (6, tr.59). Đáp án: lim f(x) = b. x→a
Bài 11 (10, tr.59). Đáp án: lim = 13. 8 x −1 → 2
Bài 12 (12, tr.59). Đáp án: lim (x2 + 1)(1 − 2x)2 = 2. x→−1
Bài 13 (22, tr.60). Đáp án: Ta có bảng liên hệ giữa giá trị của x và f(x) là: x −0.09 −0.009 0 0.0009 0.009 0.09 f (x) 11.21 111.1 k −1111.1 −111.1 −11.021
Nhìn vào bảng trên ta thấy không tồn tại lim x(x2−1). x x2 →0
Bài 14 (24, tr.60). Đáp án: 2
lim x +4x−5 = lim (x−1)(x+5) = lim x+5 = x x2 (x−1)(x+1) x+1 →1 −1 x→1 x→1 3.
Bài 15 (28, tr.60). Đáp án: lim 1 − x + 2x2 − 3x3 = +∞; x→−∞
lim 1 − x + 2x2 − 3x3 = −∞. x→+∞
Bài 16 (30, tr.60). Đáp án: lim (1+x2)3 = +∞; lim (1+x2)3 = +∞. x→−∞ x→+∞
Bài 17 (33, tr.60). Đáp án: lim 2x+1 = 0; lim 2x+1 = 0. x→−∞ 3x2+2x−7 x→+∞ 3x2+2x−7
Bài 18 (37, tr.60). Đáp án: Nhìn vào đồ thị, ta thấy:
lim f (x) = −1; lim f(x) = 1. x→−∞ x→+∞
Bài 19 (38, tr.60). Đáp án: Nhìn vào đồ thị, ta thấy: lim f (x) = −3; lim f (x) = 2. x→−∞ x→+∞
Bài 20 (40, tr.61). Ta có bảng liên hệ giữa giá trị của x và f(x) là: 51 x −0.09 −0.009 0 0.0009 0.009 0.09 f (x) 11.021 111.1 k −111.11 −111.1 −11.021
Nhìn vào bảng trên ta thấy không tồn tại lim f(x). x→0
Bài 21 (44, tr.61). Theo tính chất của giới hạn, ta có:
lim f (x)g(x) = 5.(−2) = −10. x→c
Bài 22 (50, tr.61). Theo tính chất của giới hạn, ta có: √ lim pg(x) = 4 = 2. x→+∞
Bài 23 (54, tr.61). a. Hàm lợi nhuận: P (x) = −3x2 + 120x + 100 y (mười nghìn đô-la) (20; 1, 300) 130 10 x (ngày) 20
Hình 1.36: Đồ thị hàm lợi nhuận: P (x)=−3x2 +120x +100
b. Nhìn vào đồ thị, ta thấy: Lợi nhuận đạt tối đa khi x = 20. Vậy: Nên
thông báo sự kiện trước 20 ngày.
c. lim R(x) = 4 cho ta biết nếu việc thông báo được tiến hành ngay sát x C(x) 3 →0
thời điểm diễn ra sự kiện thì tỷ lệ giữa doanh thu và chi phí là: 4. 3
Bài 24 (56, tr.61). a. Biểu thức của số tiền A(t) mà một công nhân có
kinh nghiệm làm việc t tuần kiếm được mỗi giờ là: 150 30 A(t) = 0.2(70 − ) = 14 − đô-la t + 4 t + 4 52
b. Để tính số tiền một công nhân dự kiến kiếm được trong một giờ khi có
kinh nghiệm làm việc dài hạn, ta tính: lim A(t) = 14Ø − la t→+∞
Bài 25 (58, tr.62). a. Thay t = 0 vào hàm P (t) được số dân hiện tại: P (0) = 20 (nghìn người).
b. Ta tính hiệu: P (3) − P(2) = 4.768 (nghìn người). Vậy dân số tăng lên
trong khoảng thời gian đó.
c. Tính giới hạn của hàm P (t) khi t → +∞: lim P(t) = 70 (nghìn người). t→+∞
Bài 26 (60, tr.61). lim 5n+17 = 5. n n →+∞
Nhận xét: Với số lần thử nghiệm đủ lớn thì thời gian con chuột ra được khỏi mê cung là 5 phút.
1.5 Các giới hạn một phía và sự liên tục KIẾN THỨC QUAN TRỌNG Các giới hạn một phía
• Định nghĩa giới hạn trái và giới hạn phải:
Nếu f(x) tiến gần tới số L khi x tiến gần tới c từ bên trái (x < c) thì
số L được gọi là giới hạn trái của hàm f(x) khi x tiến gần đến c. lim f (x) = L x→c−
Nếu f(x) tiến gần tới số M khi x tiến gần tới c từ bên phải (x > c)
thì số M được gọi là giới hạn phải của hàm f(x) khi x tiến gần đến c. lim f (x) = M x→c+
• Điều kiện tồn tại giới hạn: 53
Giới hạn (hai phía) của hàm f(x) tồn tại khi và chỉ khi cả hai giới
hạn một phía lim f(x) và lim f(x) đều tồn tại và bằng nhau. Khi x→c− x→c+ đó:
lim f (x) = lim f (x) = lim f (x) x→c x→c− x→c+
Tính liên tục của hàm số
• Khái niệm hàm liên tục hoặc gián đoạn tại một điểm:
Hàm số f(x) được gọi là liên tục tại x = c nếu thỏa mãn đồng thời ba điều kiện: a. f(c) xác định. b. lim f(x) tồn tại. x→c c. lim f(x) = f(c) x→c
Nếu f(x) không liên tục tại x = c (không thỏa mãn một trong ba điều
kiện trên) thì hàm số được gọi là gián đoạn tại c.
• Tính liên tục của hàm đa thức và phân thức:
Các hàm đa thức và phân thức liên tục tại tất cả các điểm mà nó xác định.
• Hàm số liên tục trên một khoảng hoặc một đoạn:
Hàm f(x) được gọi là liên tục trên khoảng mở a < x < b nếu nó liên
tục tại mọi điểm x = c trong khoảng đó.
Hàm f(x) được gọi là liên tục trên khoảng đóng a ≤ x ≤ b nếu nó liên
tục trên khoảng mở a < x < b và lim f (x) = f (a) và lim f (x) = f (b) x→a+ x→b−
Đồ thị hàm liên tục trên một khoảng là một đường liền nét trên khoảng đó.
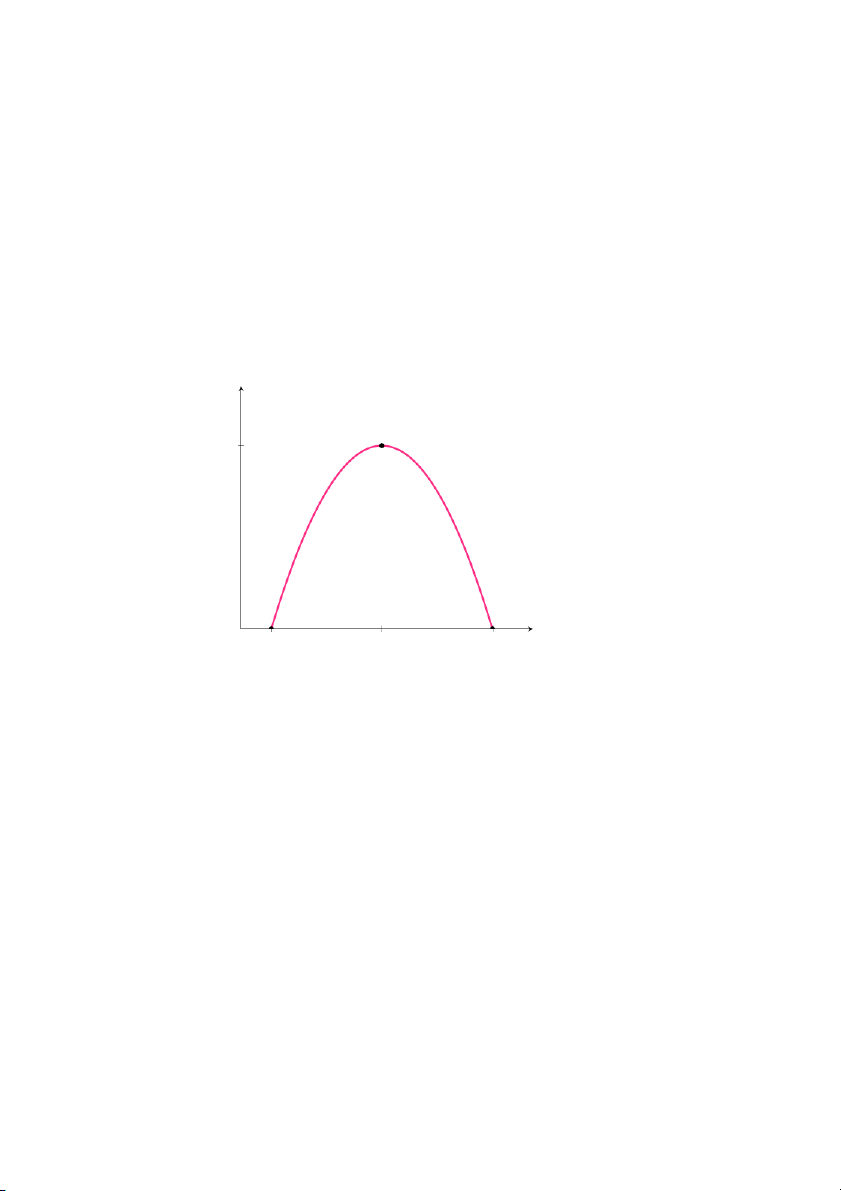
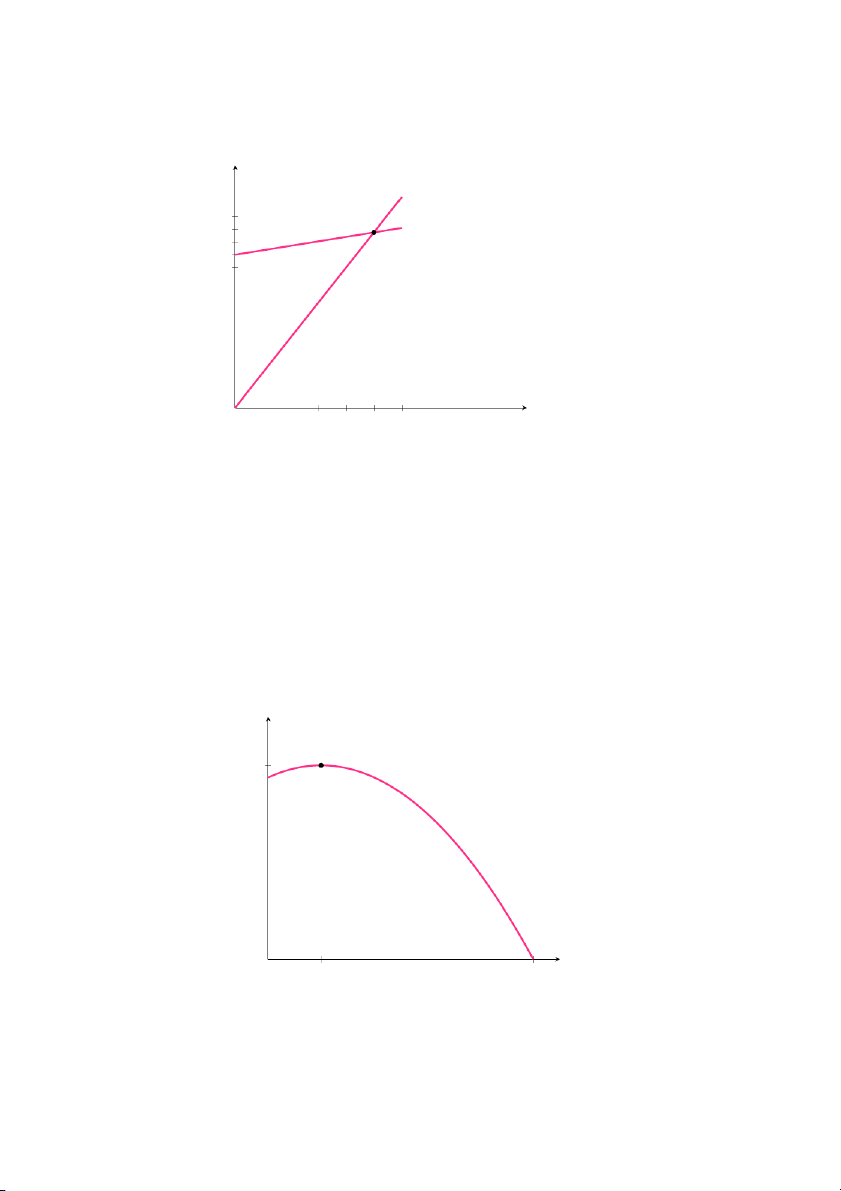
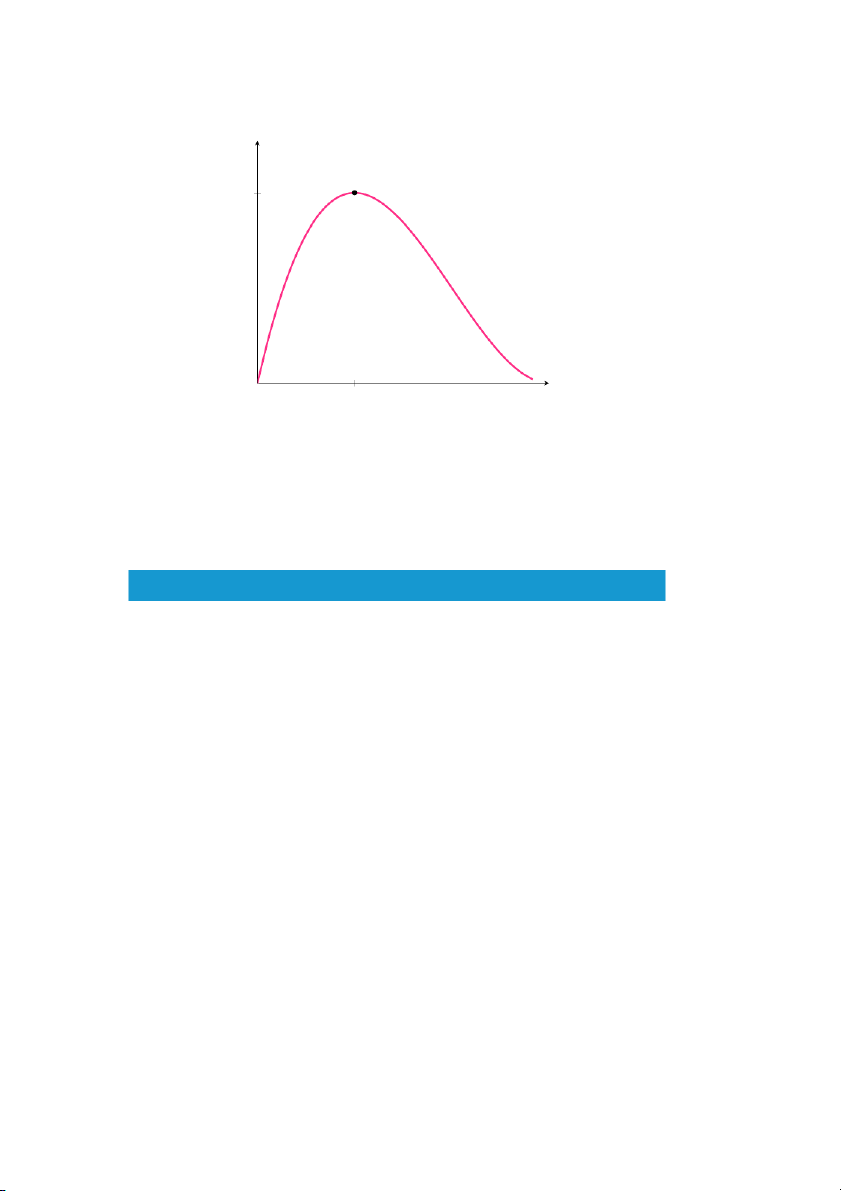
• Định lý giá trị trung gian:
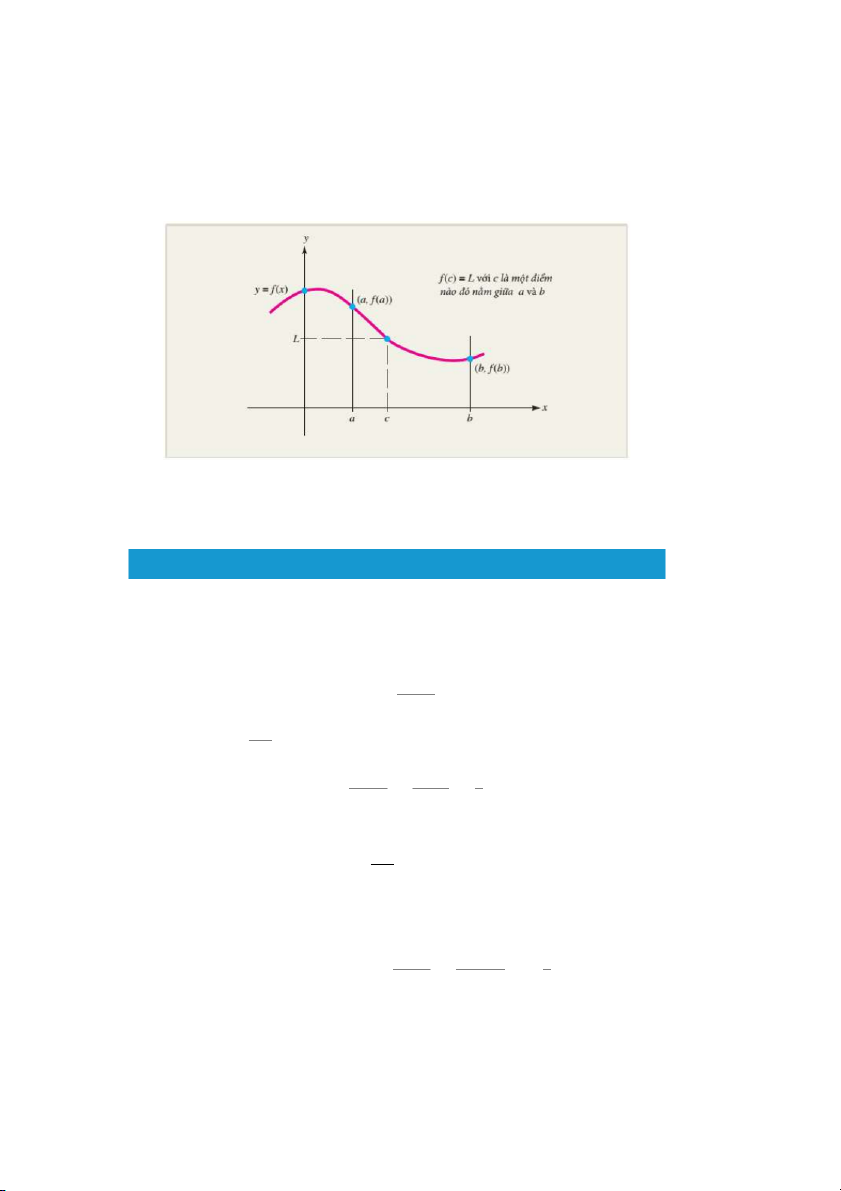
Nếu hàm f(x) liên tục trên khoảng đóng a ≤ x ≤ b và L là một số
nằm giữa f(a) và f(b) thì tồn tại số c nào đó nằm giữa a và b thỏa 54
mãn f(c) = L. Nói cách khác, một hàm liên tục nhận mọi giá trị nằm
giữa hai giá trị bất kì của nó.
Hình 1.37: Định lý giá trị trung gian
HƯỚNG DẪN GIẢI CÁC BÀI TẬP CƠ BẢN
Bài 1 (Bài 9, 16 trang 73). Tìm các giới hạn một phía
Lời giải: a. Xét giới hạn trái x + 3 lim x→2− x + 2
Hàm phân thức x+3 xác định tại x = 2 nên x+2 x + 3 2 + 3 5 lim = = x→2− x + 2 2 + 2 4 b. Xét hàm số 1 x < −1 f (x) = x−1 x2 + 2x x ≥ −1
Khi x → −1− thì x < −1 nên 1 1 1 lim f (x) = lim = = − x→−1− x→−1− x − 1 −1 − 1 2 55
Khi x → −1+ thì x > −1 nên
lim f (x) = lim (x2 + 2x) = (−1)2 + 2(−1) = −1 x→−1+ x→−1+
Bài 2 (Bài 18, 20, 25 trang 73). Xét tính liên tục tại một điểm
Lời giải: a. Hàm f(x) = x3 − 2x2 + x − 5 là đa thức và x = 0 thuộc miền
xác định nên f(x) liên tục tại x = 0.
b. Hàm f(x) = 2x−4 là phân thức và x = 2 thuộc miền xác định nên f(x) 3x−2 liên tục tại x = 2. c. Xét hàm số x + 1 x ≤ 2 f (x) = 2 x > 2
Ta tính các giới hạn một phía của hàm f(x) tại điểm x = 2:
lim f (x) = lim (x + 1) = 2 + 1 = 3 x→2− x→2− lim f (x) = lim (2) = 2 x→2+ x→2+
Vì lim f(x) 6= lim f(x) nên lim f(x) không tồn tại, do đó hàm f(x) x→2− x→2+ x→2
cũng không liên tục tại điểm x = 2.
Bài 3 (Bài 36, 37, 40, 42 trang 73). Xác định điểm gián đoạn của hàm số Lời giải: a. Vì hàm số x f (x) = (x + 5)(x − 1)
không xác định tại x = −5 và x = 1 nên −5 và 1 là hai điểm gián đoạn của hàm f(x). b. Vì hàm số x f (x) = x2 − x
không xác định tại x = 0 và x = 1 nên 0 và 1 là hai điểm gián đoạn của hàm f(x). 56 c. Xét hàm số x2 x ≤ 2 f (x) = 9 x > 2
Trong từng khoảng (−∞, 2) và (2, +∞) hàm f(x) đều có dạng đa thức
nên nó liên tục trên các khoảng đó. Ta cần xét riêng tại điểm x = 2: lim f (x) = lim x2 = 22 = 4 x→2− x→2− lim f (x) = lim 9 = 9 x→2+ x→2+
Vì lim f(x) 6= lim f(x) nên lim f(x) không tồn tại, do đó f(x) cũng x→2− x→2+ x→2
không liên tục tại điểm x = 2.
Vậy 2 là điểm gián đoạn của hàm f(x). d. Xét hàm số 2 − 3x x ≤ −1 f (x) = x2 − x + 3 x > −1
Trong từng khoảng (−∞, −1) và (−1, +∞) hàm f(x) đều có dạng đa
thức nên nó liên tục trên các khoảng đó. Ta cần xét riêng tại điểm x = −1:
lim f (x) = lim (2 − 3x) = 2 − 3(−1) = 5 x→−1− x→−1−
lim f (x) = lim (x2 − x + 3) = (−1)2 − (−1) + 3 = 5 x→−1+ x→−1+
Vì lim f(x) = lim f(x) = f(−1) = 5 nên f(x) liên tục tại điểm x→−1− x→−1+ x = −1.
Vậy hàm f(x) liên tục trên toàn bộ R.
Bài 4 (Bài 54 trang 75). Kiểm tra tính liên tục trên khoảng/đoạn
Lời giải: Trên khoảng mở (0, 2), hàm số có dạng một đa thức (duy nhất)
f (x) = x2 − 3x nên nó liên tục trên khoảng đó.
Trên khoảng đóng [0, 2], ta tính giới hạn trái
lim f (x) = lim (x2 − 3x) = −2 x→2− x→2− 57 Mặt khác, f (2) = 4 + 2(2) = 8
Vì lim f(x) 6= f(2) nên hàm số f(x) không liên tục trên khoảng đóng x→2− [0, 2].
Bài 5 (Bài 60 trang 75). Chứng minh sự tồn tại nghiệm của phương trình
Lời giải: Ta sử dụng định lý về giá trị trung gian của hàm số liên tục trên một đoạn. Đặt √ f (x) = x2 + 2x − 3 x − 1.
Hàm f(x) xác định và có một biểu thức (duy nhất) trên [0, 1] nên cũng
liên tục trên đoạn đó. Hơn nữa f(0) = −1 < 0 và f(1) = 1 > 0 nên tồn
tại số c nào đó nằm giữa 0 và 1 thỏa mãn f(c) = 0, tức là tồn tại điểm √
0 ≤ c ≤ 1 là nghiệm của phương trình 3 x = x2 + 2x − 1. y y = x2 + 2x 3 √ − x − 1 1 x −0.5 0 0.5 1 −1
Hình 1.38: Đồ thị hàm số f(x)=x2 +2x − 3 √x − 1
Bài 6 (Bài 45 trang 74). Phân tích lợi ích - chi phí
Lời giải: a. Chi phí để loại bỏ 25% chất gây ô nhiễm là: 12(25) C(25) = = 4 (nghìn đô-la) 100 − 25
Chi phí để loại bỏ 50% chất gây ô nhiễm là: 12(50) C(50) = = 12 (nghìn đô-la) 100 − 50 58
b. Phác họa đồ thị của hàm chi phí. y (nghìn đô-la) 16 C(x) = 12x 15 100−x 14 13 12 11 10 9 8 7 6 5 4 3 2 1 x (% ô nhiễm)
0 5 10 15 20 25 30 35 40 45 50 55 60 65 70 75 80 85 90 95100
Hình 1.39: Đồ thị hàm số C(x)= 12x100−x
c. Nhìn vào đồ thị, ta thấy hàm C(x) tăng không bị chặn khi x tiến gần
đến 100 từ phía bên trái, do đó: 12x lim C(x) = lim = +∞ x→100− x→100− 100 − x
Vậy thực tế là không thể loại bỏ được toàn bộ chất ô nhiễm, vì để làm
được điều đó thì chi phí là quá lớn.
Bài 7 (Bài 64 trang 75). Tính liên tục của sự phát triển chiều cao
Lời giải: Gọi t là tuổi của Juan và f(t) là hiệu chiều cao của Michaela và Juan.
Khi Juan 5 tuổi thì chiều cao của Michaela gấp đôi chiều cao của Juan, tức là f(5) > 0.
Khi Juan 21 tuổi thì chiều cao của Michaela kém chiều cao của Juan 6
inches, tức là f(21) < 0.
Ta biết rằng chiều cao (phụ thuộc vào tuổi) của trẻ em là một hàm liên
tục nên f(t) là hàm liên tục trên đoạn [5, 16]. Mặt khác f(5).f(16) < 0, do
đó theo định lý về giá trị trung gian, tồn tại thời điểm t0 (0 ≤ t0 ≤ 16) thỏa mãn f(t0) = 0.
Vậy khi Juan t tuổi thì chiều cao của hai chị em bằng nhau. 0 59
CÁC BÀI TẬP TỰ LUYỆN: HƯỚNG DẪN VÀ ĐÁP ÁN
Bài 8 (2, tr. 72). Dựa vào đồ thị hàm số ta có lim f(x) = 4 và x→2−
lim f (x) = 2. Như vậy hàm số không tồn tại giới hạn lim f (x). x→2+ x→2
Bài 9 (3, tr. 72). Dựa vào đồ thị hàm số ta có lim f(x) = lim f(x) = 2. x→2− x→2+
Như vậy hàm số tồn tại giới hạn lim f(x) = 2. x→2
Bài 10 (8, tr. 73). Ta thay x = 2 vào biểu thức và thu được kết quả là 0.
Bài 11 (10, tr. 73). Ta có lim x2 + 4 = 8 và lim x − 2 = 0 do đó giới x→2− x→2−
hạn đã cho là vô hạn, dựa vào dấu của tử số và mẫu số ta thu được kết quả là −∞.
Bài 12 (14, tr. 73). Ta thấy cả tử số và mẫu số đều có giới hạn bằng 0
khi x tiến gần đến 5. Do tử số là biểu thức chứa căn thức, bằng cách nhân
liên hợp cả tử và mẫu với √2x − 1 + 3 sau đó rút gọn và thay số vào ta thu được kết quả là 1 . 3
Bài 13 (15, tr. 73). lim f(x) = lim(2x2 − x) = 15 và lim f(x) = x→3− x→3− x→3+ lim (3 − x) = 0. x→3+
Bài 14 (22, tr. 73). Hàm số không liên tục tại x = 2 do x = 2 không
thuộc tập xác định của hàm số.
Bài 15 (26, tr. 73). Lần lượt kiểm tra 3 điều kiện liên tục của hàm số ta
thấy không đồng thời thỏa mãn, vậy hàm số không liên tục tại x = 0.
Thật vậy, do lim f(x) = lim (x+1) = 1 mà lim f(x) = lim (x−1) = −1 x→0− x→0− x→0+ x→0+
nên không tồn tại giới hạn lim f(x). x→0
Bài 16 (28, tr. 73). Tương tự bài 26, khi kiểm tra 3 điều kiện liên tục
của hàm số ta thấy thỏa mãn. Vậy hàm số liên tục tại x = −1.
Bài 17 (38, tr. 73). Đây là hàm phân thức, ta chú ý các điểm mà tại đó
mẫu số nhận giá trị bằng 0. Hàm số gián đoạn tại x = −1 và x = 2. 60 Bài 18 1 (43, tr. 73). a. C(0) =
= 0.333 trăm nghìn đô-la và C(100) = 3
201 = 7.179 trăm nghìn đô-la 28
b. Ta phải tìm x thỏa mãn C(x) = 7. Ta có C(0) < 7 < C(100) nhưng do
hàm số không liên tục trên 0 ≤ x ≤ 100 ( vì tại x = 80 mẫu số bằng 0, hàm
số không xác định) nên ta chưa thể áp dụng định lý giá trị trung gian với kết quả ở phần (a) .
Bài 19 (46, tr. 74). Đồ thị hàm số gián đoạn tại t = 6, t = 12. Đây là
các thời điểm hàng hóa được bổ sung vào trong kho. Bài 20 0.5 x2 + 3x (48, tr. 74). Tính lim . Đáp án là 0.375. x 3 2 →0+ x + x + 4x
Bài 21 (49, tr. 74). Ta tính lim p(t), sau đó tính giá trị của c(p) tại t→+∞
kết quả vừa tìm được. Kết quả là trong dài hạn mức độ ô nhiễm sẽ ở mức 8.4 (ppm).
Bài 22 (51, tr. 75). a. Tính I(30) = 80 và I(90) = 86. Vậy khi mức độ
ẩm tương đối bằng 30% và 90% thì chỉ số nhiệt độ tương ứng là 80oF và 86oF .
b. Ta tìm h để I(h) = 83. Dễ dàng thấy I(40) = 80, I(80) = 84 và hàm
số liên tục trên khoảng 40 ≤ h ≤ 80. Theo định lý giá trị trung gian ta
có thể tìm được h trong khoảng này sao cho I(h) = 83. Giải phương trình
80 + 0.1(h − 40) = 83 ta thu được h = 70.
c. Kiểm tra các điều kiện liên tục tại một điểm của hàm số đều thỏa mãn
với h = 40, h = 80 nên hàm số liên tục tại hai giá trị này.
Bài 23 (56, tr. 75). Đây là hàm xác định từng khúc với các hàm là đa thức
nên ta chỉ cần tìm giá trị của A để hàm số liên tục tại x = 4. Điều này chỉ xảy
ra khi lim f(x) = lim f(x) = f(4) hay lim (1−3x) = lim (Ax2+2x−3. x→4− x→4+ x→4− x→4+ Đáp án là A = −1. Bài 24 √
(59, tr. 75). Xét hàm số f(x) = 3 x − 8 + 9x2/3. Ta có f(0) =
−2; f(8) = 36 và hàm số liên tục trên khoảng 0 ≤ x ≤ 8. Theo định lý giá
trị trung gian ta có điều phải chứng minh. 61




