Bài tập Chương 1 môn Toán kinh tế | Học viện Công Nghệ Bưu Chính Viễn Thông

Mục lục
1 BÀI TẬP CHƯƠNG I .............................................................................................................. 1
1.1 ĐỀ BÀI.......................................................................................................................... 1
1.2 BÀI GIẢI ....................................................................................................................... 7 Chương 1 BÀI TẬP CHƯƠNG I 1.1 ĐỀ BÀI
1. Cho hàm doanh thu trung bình AR(Q) = 15 − Q.
a. Xác định mức doanh thu cận biên MR tại Q1 = 5,Q2 = 8.
b. Xác định mức chênh lệch của doanh thu cận biên và doanh thu trung bình nhưmột hàm của Q.
c. Nêu biểu thức tổng quát xác định mức chênh lệch của doanh thu cận biên và
doanhthu trung bình nếu hàm doanh thu trung bình có đạo hàm. 2. Cho hàm tổng chi phí
TC = Q3 − 5Q2 + 14Q + 144,(Q > 0)
a. Khảo sạt sự thay đổi tuyệt đối của TC theo Q.
b. Tính hệ số co giãn của TC theo Q tại Q = 2 3. Cho hàm tổng chi phí (Q là sản lượng).
a. Tìm hàm chi phí cận biên MC.
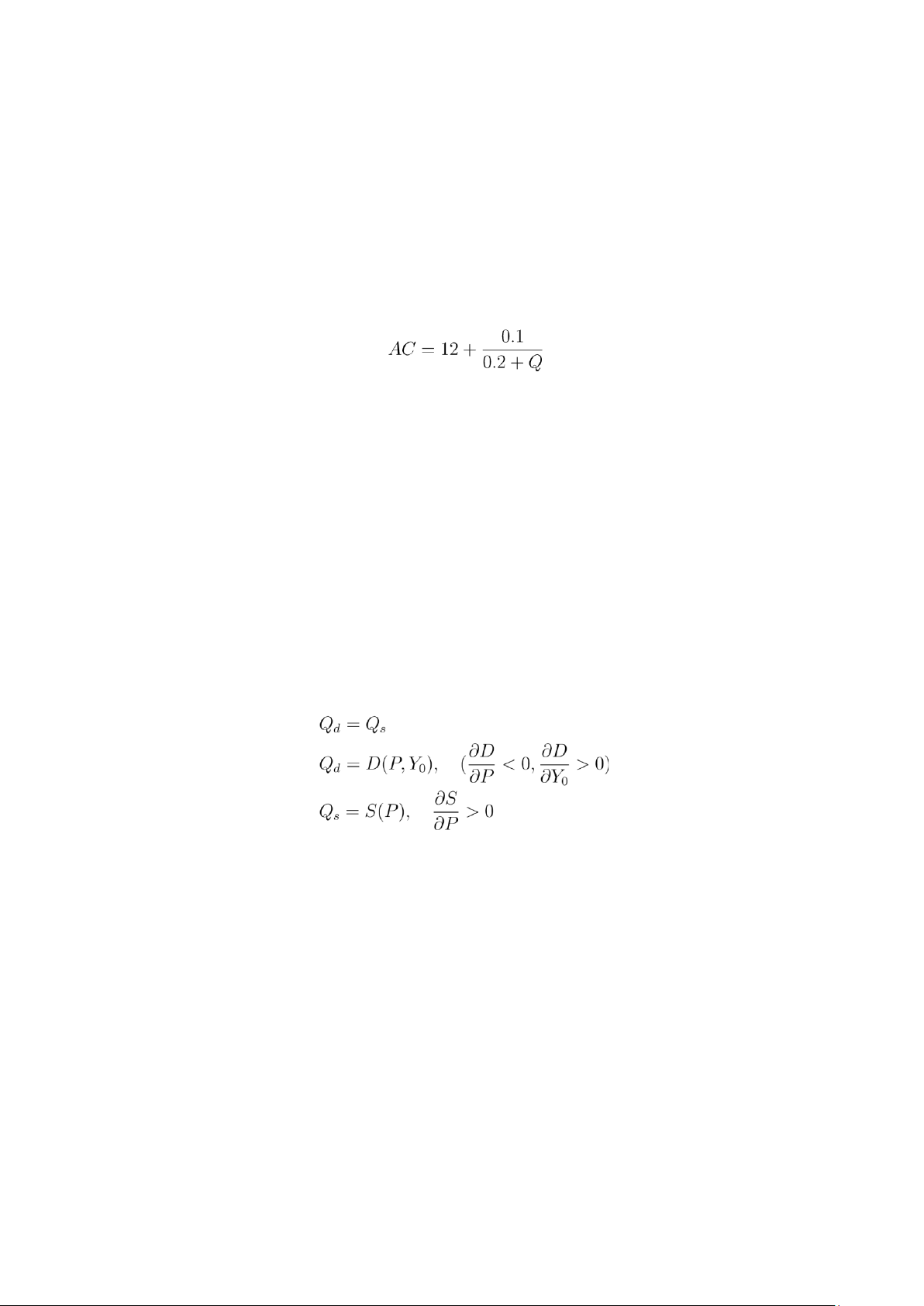
b. Tính chi phí trung bình AC tại Q = 100
c. Tính hệ số co giãn của TC theo Q tại Q = 17.
4. Cho hàm tổng chi phí TC = 4000+10Q+0.1Q2. Giá cả P được xác định bởi phương
trình: Q = 800 − 2.5P.
a. Tìm hàm chi phí cận biên MC.
b. Tìm hàm chi phí trung bình AC
5. Tìm hệ số co giãn của TC tại P = 80Chi phí trung bình khai thác một loại khoáng sản:
a. Tìm hàm chi phí cận biên MC tại Q = 10.
b. Tìm biểu thức tính chênh lệch của chi phí trung bình AC và chi phí cận biên MC.
c. Lập biểu thức tính hệ số co giãn của tổng chi phí TC
6. Cho hàm chi phí trung bình để sản xuất một loại sản phẩm:
AC = Q2 − 12Q + 60
a. Xác định hàm tổng chi phí TC, phần chi phí biến đổi VC và chi phí cố định FC.
b. Xác định biểu thức tính sự thay đổi tương đối của AC theo Q.
c. Xác định hàm chi phí cận biên MC.
7. Cho mô hình thị trường:
trong đó: Qd,Qs là mức cầu và mức cung một loại hàng, P là giá, Y0 là thu nhập.
a. Giải thích mô hình và các điều kiện.
b. Giả định tồn tại giá cân bằng P ∗; khi Y0 tăng thì giá cân bằng sẽ biến động như thế nào?
Giải thích ý nghĩa kinh tế.
c. Gọi Q∗ là lượng cung - cầu ở trạng thái cân bằng và hãy cho biết khi Y0 tăng thì lượng cân
bằng thay đổi như thế nào. Viết biểu thức mô tả sự thay đổi đó.
8. Cho mô hình cung - cầu:
Qd = 10 + 0.1Y0 − 0.2P
Qs = −14 + 0.6P
Trong đó, Qd,Qs là mức cầu và mức cung một loại hàng, P là giá, Y0 là thu nhập.
a. Tìm biểu thức tính giá cân bằng nếu điều kiện cân bằng là:
a1 : Qs = Qd
a2 : Qd = 0.9Qs
b. Tính hệ số co giãn của giá cân bằng theo Y0 tại Y0 = 80 trong cả hai trường hợp trên. 4 1.1. ĐỀ BÀI
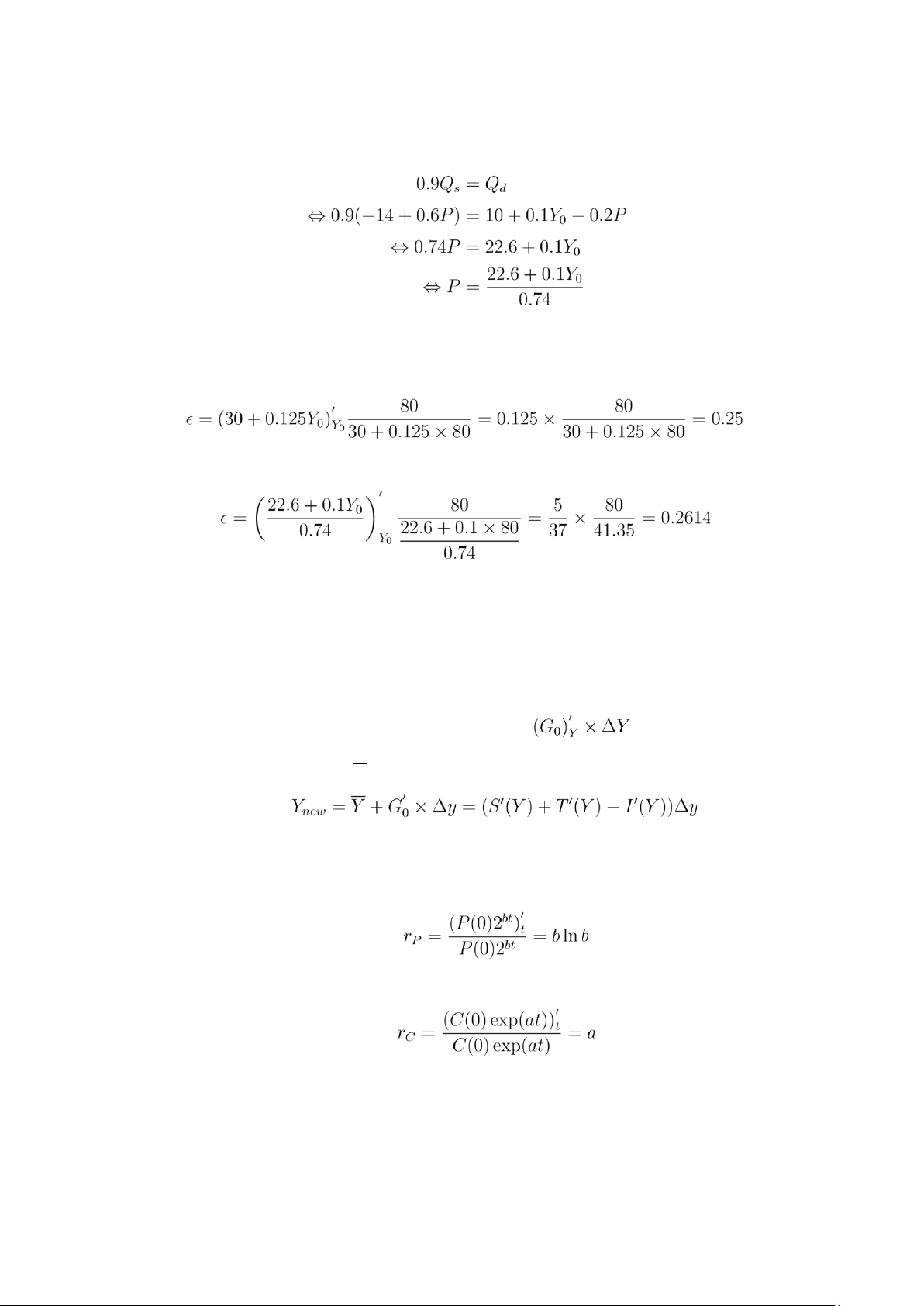
9. Cho mô hình cân bằng thu nhập quốc dân:
S(Y ) + T(Y ) = I(Y ) + G0
a, Giải thích ý nghĩa kinh tế của mô hình và ý nghĩa kinh tế của các mối quan hệ của các
đạo hàm bậc nhất S0,T 0,I0.
b. Xác định biểu thức mô tả sự thay đổi của thu nhập cân bằng Y theo G0
10. Giả sử dân số tăng theo mô hình P(t) = P(0)2bt và tiêu dùng dân cư tăng theo mô hình
C(t) = C(0)eat
a. Tính hệ số tăng trưởng của dân số và tiêu dùng dân cư.
b. Với điều kiện nào thì hệ số tăng trưởng của tiêu dùng cao hơn hệ số tăng trưởngcủa
dân số. Nêu ý nghĩa của quan hệ đó.
11. Cho hàm sản xuất Y (t) = 0.2K0.4L0.8, trong đó K = 120 + 0.1t,L = 200 + 0.3t.
a. Tính hệ số co giãn của Y theo K và L.
b. Tính hệ số tăng trưởng của vốn K, lao động L và Y.
12. Xét mô hình lợi nhuận π = TR(Q) − TC(Q) − aTR(Q)
Xác định biểu thức điều kiện của Q để lợi nhuận cực đại.
13. Một công ty có thể sản xuất và cung ứng cho thị trường hai mặt hàng với hàm tổng doanh
thu và tổng chi phí cho 2 mặt hàng:
TR = P1Q1 + P2Q2
Xác định công thức tính tổng lợi nhuận cực đại.
14. Chi phí cho tiêu dùng loại hàng A được ước lượng bởi hàm sau:
C = −12 + 0.1M − 0.05P
Trong đó: C là chi phí cho tiêu dùng hàng A của mỗi cá nhân, M là thu nhập cá nhân, P là giá hàng A.
a. Giải thích ý nghĩa kinh tế của các hệ số, có thể xem hàng A là thiết yếu không?
b. Hãy tính hệ số tăng trưởng của nhu cầu theo thời gian t nếu hệ số tăng của thunhập
theo thời gian là 12% và hệ số này của giá hàng A là 8%.
15. Tổng số vốn đầu tư nước ngoài I, phụ thuốc vào đơn giá tiền công W, và tốc độ tăng thu
nhập quốc dân p của một nước như sau:
I = −25 + 12p2 − 0.4W
a. Xác định biểu thức tính sự thay đổi của I khi các yếu tố đồng thời thay đổi.
b. Giả sử mức tăng thu nhập quốc dân ổn định là 6% xác định thời hạn tiền công cóthể thu
hút vốn đầu tư nước ngoài.
16. Giá của một loại hàng P và chênh lệch cung - cầu S liên hệ với nhau bởi phương trình: SP
− 0.1P2 lnS = c. Hãy tính tốc độ thay đổi của giá khi chênh lệch cung cầu thay đổi.
17. Cho hàm thu nhập tính trên đầu người: , trong đó:
• δ là hệ số giảm giá của vốn theo thời gian.
• β là hiệu ứng tiến bộ kỹ thuật đối với thu nhập.
• α là hệ số co giãn của vốn đối với thu nhập.
• n là tỉ lệ tăng dân số hằng năm.
Giả sử δ,α không đổi, để duy trì thu nhập đầu người ở mức y ∗ (t) cho trước cần có
chính sách đảm bảo tốc độ tăng của dân số theo sự biến đổi của hiệu ứng tiến bộ kỹ thuật như thế nào?
18. Giả sử lượng vốn (qui đổi thành tiền mặt) của một công ty hàng năm nhờ đầu tư là 12%.
Tỉ lệ mất giá của tiền mặt hàng năm là 4%. Hãy tính hệ số tăng trưởng của vốn mà công
ty đạt được sau 10 năm, biết rằng năm đầu tiên công ty có lượng vốn là K(0).
19. Thu nhập quốc dân của một quốc gia (Y ) phụ thuộc vào vốn (K), lao động được sử dụng
(L) và ngân sách đào tạo 5 năm trước đó (G) như sau:
Y = 0,24K0,3L0,8G0,05.
Trong đó các yếu tố biến đổi theo thời gian như sau: hàng năm vốn tăng 15%; công ăn việc
làm tăng 9%; chi phí cho đào tạo tăng 20%.
a. Tính hệ số tăng trưởng của thu nhập quốc dân. 6 1.1. ĐỀ BÀI
b. Trong điều kiện Y,K không đổi còn công ăn việc làm phụ thuộc vào ngân sách đào tạo
trước đó 5 năm, hãy viết biểu thức chỉ ra sự thay đổi của công ăn việc làm theo ngân
sách đào tạo 5 năm trước.
20. Giả sử trung bình tổng lượng lao động trong một thời kỳ tại một nước là Lo, khối lượng
lao động sẵn sàng làm việc (Y ) và tiền công (X), thỏa mãn phương trình sau:
Y − (a1X + a2X2 + a3X3)(Lo − Y ) = 0.
Hãy phân tích mô hình trên, trong các tình huống khác nhau về cung cầu lao động. Xác
định cách tính tiền công cận biên theo số giờ lao động sẵn sàng làm việc hoặc ngược lại.
21. Lượng lao động (việc làm) thu hút thêm vào các ngành sản xuất vật chất L và lượng vốn
đầu tư I có thể mô tả bởi mô hình
L2 + ao + a1I + a2I2 = 0, trong đó .
a. Giải thích sự vận động của các yếu tố lao động thu hút thêm vào vốn đầu tư. Tìm biểu
thức tính tốc độ cận biên của lượng việc làm tăng thêm theo vốn đầu tư.
b. Hãy chọn một bộ giá trị thích hợp của các tham số và tính lượng vốn đầu tư thu hút nhiều lao động nhất.
22. Quan hệ giữa tiền công của lao động có đào tạo (Y ) và tỉ lệ thất nghiệp của người lao
động trong một quốc gia (U), chi phí đào tạo (G) được mô tả bởi mô hình:
aY 2 − bG2 − clnU = 0,
trong đó Y = Y (t),G = G(t) và U = U(t).
a. Xác định hệ số co giãn của chi phí đào tạo theo các yếu tố khác.
b. Tính hệ số tăng trưởng của chi phí đào tạo như một hàm của các yếu tố khác.
23. Số lượng sinh viên của một quốc gia, S (người), phụ thuộc vào số dân, P (người) và thu
nhập bình quân đầu người, M (USD), như sau:
S = −5501688 + 378766,5lnP − 5716,6M + 6,9922M2.
a. Hãy xác định hệ số tăng trưởng của số lượng sinh viên hằng năm. Biết hệ số tăng
trưởng của thu nhập là 5% năm; tốc độ tăng dân số là 2,2%.
b. Tính hệ số co giãn toàn phần của lượng sinh viên theo thu nhập và dân số.
c. Trong trường hợp dân số, thu nhập liên hệ với nhau như sau:
P − 4,57 × 107 + 0,16583MP + 1050205t = 0.
Hãy viết biểu thức tính hệ số tăng trưởng của thu nhập và dân số, từ đó suy ra biểu thức
tính hệ số tăng trưởng của lượng sinh viên.
24. Xét mô hình thu nhập quốc dân: ,
trong đó: Y là thu nhập quốc dân; R là tỉ lệ lãi tiền gửi; Go là tiêu dùng của chính phủ; Mo là
tổng lượng cung tiền mặt.
a. Xác định trạng thái cân bằng trong đó tỉ lệ lãi và thu nhập như các hàm phụ thuộc vào Mo và Go.
b. Khi chính phủ tăng 1% tiêu dùng, muốn trạng thái cân bằng không thay đổi thì tổng lượng
cung tiền mặt bằng bao nhiêu %?
25. Cho mô hình thu nhập quốc dân:
S(Y ) + T(Y ) =
I(Y ) + Go, S(Y ) = 0,1lnY, T(Y ) =
0,04Y − 0,1Y 2, I(Y ) =
0,5Y + 0,02Y 2, Go = 1200;
với Y là thu nhập quốc dân, T là thuế, I là đầu tư và S là tiết kiệm.
a. Xác định thu nhập trong trạng thái cân bằng.
b. Trạng thái cân bằng thay đổi như thế nào khi Go giảm 5%?
c. Nếu nhà nước cần định một mức tổng thu thuế là To, không phụ thuộc thu nhập thì cần
đảm bảo mối quan hệ nào giữa To và Go để thu nhập quốc dân ở trạng thái cân bằng không đổi?
26. Với cuộc khủng hoảng tiền tệ trong một quốc gia vùng Đông Nam Á vào những năm cuối
thập kỷ 90. Giả sử tốc độ mất giá của đồng tiền quốc gia đó theo thời gian được biểu
diễn bởi hàm f(t) thỏa mãn các điều sau:
f(t) ≤ 0, f0(t) > 0
nếu t < t∗, f0(t) < 0
nếu t > t ∗ .
Hãy nêu một mô hình điều kiện thể hiện tình trạng thay đổi của lượng vốn đầu tư nước
ngoài vào quốc gia này theo thời gian t. Giải thích việc chọn mô hình đó.Với các dữ liệu của
mô hình dự trữ Wilson, hãy tìm biểu thức cho biết khi tăng qui mô đặt hàng mỗi lần 1% thì
tổng chi phí tăng bao nhiêu %? Nhận xét gì về giá trị của biểu này tại qui mô tối ưu, giải
thích. Điều đó có đúng với các mô hình tối ưu mà hàm mục tiêu đạt giá trị nhỏ nhất tại điểm cực trị không?
27. Với các quan hệ liên ngành hiện vật - giá trị trong mô hinhf I/O.
a. Hãy tìm biểu thức mô tả sự thay đổi lượng sản phẩm cuối cùng ngành i khi có sự thay
đổi định mức tiêu dùng sản phẩm của nó trong ngành j.
b. Phân tích tác động của sự thay đổi giá sản phẩm một ngành đến chi phí sản xuất. 1.2 BÀI GIẢI
1. a. Ta có, hàm doanh thu trung bình là AR(Q) = 15−Q, từ đó suy ra, tổng doanh thu là: TR
= AR×Q = 15Q−Q2. Do đó, doanh thu cận biên là: MR = TRQ = −2Q+15
Suy ra: MR(5) = 5,MR(8) = −1
b. Mức chênh lệch của doanh thu cận biên và doanh thu trung bình theo Q là: f(Q) = MR
− AR = −2Q + 15 − (15 − Q) = −Q
c. Biểu thức tổng quát xác định chênh lệch doanh thu cận biên và doanh thu trungbình là:
(AR × Q)0 − AR = AR0 × Q + 1 × AR − AR = AR0 × Q
2. a. Ta có hàm tổng chi phí là: TC = Q3 − 5Q2 + 14Q + 144 (Q > 0) Từ đây ta có, sự thay đổi
tuyệt đối của hàm chi phí là:
Do đó, vì 3Q2 − 10Q + 14 > 1 với mọi Q > 0 nên ta có, Q càng tăng thì chi phí tăng theo hàm bậc 2.
b. Hệ số co giãn của TC theo Q tại Q = 2 là: c. 3. a. Hàm tổng chi phí . Suy ra,
b. Chi phí trung bình AC tại Q = 100 là:
d. Hệ số co giãn của TC theo Q tại Q = 17 là:
4. a. Chi phí cận biên là:
b. Hàm chi phí trung bình AC là:
c. Hàm tổng chi phí TC theo P là:
TC = 4000 + 10(800 − 2.5P) + 0.1(800 − 2.5P)2
= 4000 + 8000 − 25P + 64000 − 400P + 0.625P2
= 0.625P2 − 425P + 76000 Từ
đây suy ra, hệ số co dãn của TC theo P là:
5. a. Hàm tổng chi phí TC là:
Từ đây suy ra, hàm chi phí cận biên MC là: Do đó:
MC(10) = 12.0002
b. Biểu thức tính chênh lệch của chi phí trung bình AC và chi phí cận biên MC là:
c. Biểu thức tính hệ số co giãn của tổng chi phí TC là:
6. a. Hàm tổng chi phí TC là:
TC = AC × Q = Q3 − 12Q2 + 60Q
Phần chi phí biến đổi VC là:
V C = Q3 − 12Q2 + 60Q
Phần chi phí cố định FC = 0
b. Sự thay đổi tuyệt đối của AC theo Q là:
Sự thay đổi tương đối của AC theo Q là:
c. Chi phí cận biên MC là:
7. a. Giải thích mô hình và các điều kiện:
Ta có, Qd = Qs tương ứng với mức cầu và mức cung của loại hàng đó bằng nhau. Qd =
D(P,Y0) cho thấy mức cầu phụ thuộc vào giá và thu nhập. Trong đó cho thấy khi
giá tăng, mức cầu cũng giảm xuống,
, cho thấy khi thu nhập tăng lên, mức cầu cũng tăng lên.
Tương tự, Qs = S(P), cho thấy hàm cung phụ thuộc vào giá, khi giá tăng thì mức cung cũng tăng theo.
b. Khi Y0 tăng, dẫn đến Qd tăng, do đó Qs cũng tăng theo. Điều này dẫn tới giá cân bằng P ∗ sẽ tăng theo.
c. Giả sử Y0 tăng một lượng ∆y, khi đó ta có Qd sẽ tăng một lượng . Do đó,
lượng cung - cầu mới là: 8. a.
Trường hợp 1: Qs = Qd Ta có:
Trường hợp 2: Qd = 0.9Qs
b. Hệ số co giãn tại Y0 = 80 là:
Trường hợp 1: Qs = Qd
Trường hợp 2: Qd = 0.9Qs
9. a. Ta có, mô hình cân bằng thu nhập quốc dân là:
S(Y ) + T(Y ) = I(Y ) + G0
Ý nghĩa kinh tế mô hình: Tổng thu nhập từ tiết kiệm và thuế bằng với tổng đầu tư và
tiêu dùng của chính phủ. Đồng thời, S0,T 0,I0 > 0 nên khi Y tăng, S,T,I cũng tăng.
b. Khi Y tăng một lượng ∆y thì G0 tăng một lượng . Do đó, sự thay đổi
của thu nhập cân bằng Y theo G0 là:
Từ đây ta thấy, khi thu nhập tăng thì thu nhập cân bằng cũng tăng theo.
10. a. Hệ số tăng trưởng của dân số là:
Hệ số tăng trưởng của tiêu dùng dân cư là:
b. Hệ số tăng trưởng của tiêu dùng cao hơn hệ số tăng trưởng của dân số khi: a > blnb
Ý nghĩa, khi hệ số tiêu dùng lớn hơn hệ số tăng trưởng của dân cư, tiêu dùng của dân
cư sẽ tăng nhanh hơn so với tốc độ tăng trưởng của dân cư đó.
11. a. Hệ số co giãn của Y theo K là:
Hệ số co giãn của Y theo L là:
b. Hệ số tăng trưởng của vốn K, lao động L và Y lần lượt là: 12. a. Ta xét mô hình
π = TR − TC − aTR ⇔ π = (1 − a)TR − TC
Để π đạt cực đại ta có, , tương đương với:
13. a. Điều kiện cần để có tổng lợi nhuận cực đại là:
MR = MC ⇔ P1 + P2 = 4Q1 + Q2 + 6Q2 + Q1 ⇔ P1 + P2 = 5Q1 + 7Q2
Khi đó, biểu thức tính tổng lợi nhuận là:
14. a. Giải thích ý nghĩa kinh tế của các hệ số:
• -12: Chi phí chi tiêu cố định
• 0.1: Hệ số của thu nhập cá nhân, hệ số dương chứng tỏ thu nhập càng tăng thì chi phí
mua hàng càng tăng (tăng chậm).
• -0.05: Hệ số chỉ mức độ phụ thuộc của giá mặt hàng A. Hệ số này âm chứng tỏ giá
càng tăng thì chi phí mua hàng càng giảm.
• Không thể xem A là mặt hàng thiết yếu.
b. Ta có, hàm cầu của mặt hàng A là:
Hệ số tăng của thu nhập theo thời gian là:
Hệ số tăng của giá hàng theo thời gian là:
Ta có hệ số tăng trưởng của nhu cầu theo thời gian là
15. a. Biểu thức tính sự thay đổi của I khi các yếu tố đồng thời thay đổi là:
b. Do mức tăng thu nhập quốc dân ổn định là 6% nên ta có
∆I = 24p × 0.06 − 0.4∆W
Từ đây ta thấy, để ∆I > 0 thì ∆W < 3.6p, suy ra W không được tăng quá 3.6p(%)
16. Đặt F(S,P) = SP −0.1P2 lnS −c, ta có Tồn tại S,P sao cho F(S,P) = 0. Từ công thức hàm ẩn ta có: ∂F
dP = − ∂S = −P2/(10S) + P dS
17. Bài tập này là một bài tập nhằm kiểm tra kiến thức người học về "Phân tích sự thay thế
giữa các biến số". Ở đây chúng ta cần xem xét sự thay thế giữa tốc độ tăng dân số và
hiệu ứng tiến bộ kỹ thuật, tức là n và β, trong điều kiện là các yếu tố khác không đổi.
18. Để giải bài toán này, sinh viên cần nắm rõ phân tích hệ số tăng trưởng của mô hình.
Nhắc lại rằng nếu y = F(x1,...,xn,t) với t là biến thời gian, thì hệ số tăng trưởng được định nghĩa bởi .
Sau năm đầu tiên, lượng vốn sẽ tăng nhờ đầu tư thành là Ko(1+0.12), Tuy nhiên, do
mất giá nên lúc này giá trị thực của vốn sẽ là Ko(1+0.12)(1−0.04) = Ko(1+0.0752). Suy
ra công thức tính lượng vốn hằng năm là
K(t) = Ko(1 + 0.0752)t.
Điều đó kéo theo hệ số tăng trưởng là ln(1 + 0.0752), và nó xấp xỉ bằng 0.0752.
19. Bài tập này nhằm kiểm tra kiến thức của sinh viên về hệ số tăng trưởng. Người học cần
hiểu cách tính hệ số tăng trưởng của một hàm khi ta biết hệ số tăng trưởng của các biến
trong hàm đó. Cụ thể thì người học chỉ cần tìm ra được cách tính hệ số tăng trưởng của Y = cKαLβGγ,
qua hệ số tăng trưởng của K,L,G (kí hiệu lần lượt là rK,rL,rG).
Qua sự tăng trưởng của K,L,G; hằng năm thu nhập quốc dân tăng theo công thức
Y (t) = c[K(1 + rK)]α [L(1 + rL)]β [G(1 + rG)]γ .
Nên, hệ số tăng trưởng của thu nhập quốc dân là rY = ln(1 + rK) · α + ln(1 + rL) ·
β + ln(1 + rG) · rG ≈ rKα + rLβ + rGγ.
Thế các con số vào, ta sẽ được đáp án của câu a là
rY ≈ 0.15 · 0.3 + 0.09 · 0.8 + 0.2 · 0.05 = 0.127.
Đối với câu b, khi Y,K không đổi, và công ăn việc làm (L) phụ thuộc vào ngân sách
(G), thì ta có thể xem L như một hàm ẩn theo G được cho bởi
Y − 0.24K0.3L0.8G0.05 = 0.
Theo yêu cầu đề bài, ta cần viết ra SỰ THAY ĐỔI của L theo G. Nghĩa là ta cần tính giá trị cận biên (ML)G. . Lưu ý rằng, từ
Y − 0.24K0.3L0.8G0.05 = 0,
ta cũng có thể biểu diễn L theo G như sau: .
Và từ đó tính được sự thay đổi của L theo G.
20. Trước tiên chúng ta cần phân tích mô hình theo các tình huống khác nhau của cung
(Y ) và cầu (Lo). Ta có thể xem cung và cầu các hàm ẩn theo X được xác định từ
F = Y − (a1X + a2X2 + a3X3)(Lo − Y ) = 0.
Do Y > 0, nên ta phải có .
Trường hợp 1. Nếu cung vượt quá cầu, tức là Y > Lo thì lúc đó tiền công sẽ thấp và bị
chặn trên bởi nghiệm dương bé nhất của phương trình a1 + a2X + a3X2 = 0. Trường hợp
2. Nếu cầu vượt quá cung, tức là Y < Lo thì lúc đó tiền công sẽ nằm giữa 2 nghiệm của
phương trình a1 + a2X + a3X2 = 0, tức là tiền công sẽ vượt qua mức thấp nhất, nhưng
không vượt quá ngưỡng lớn nhất.
Xác định cách tính tiền công cận biên theo số lao động sẵn sàng làm việc và ngược lại .
21. Từ các giả thiết của mô hình, ta có
L2 + a2(I − α)(I − β) = 0,
trong đó α,β > 0.
a. Như vậy, lượng vốn đầu tư I sẽ luôn nằm trong khoảng (α,β). Ngoài ra ta cũng có thể
viết lại mô hình như sau .
Như vậy, lao động tăng thêm và lượng vốn đầu tư sẽ nằm trên một phần của elip
tương ứng với phương trình trên. Bằng cách xem L như một hàm ẩn theo I, ta sẽ có Do đó, nếu
thì L sẽ đồng biến theo I và nếu thì
L sẽ nghịch biến theo I.
b. Chọn a1 = 8,a2 = 1 và a2 = −6. Ta dễ dàng tính được lượng vốn đầu tư thu hút nhiều
lao động nhất là I = −a1/2 = 3.
22. a. Bài tập này nhằm xác định hệ số co giãn của G theo các biến Y , U. Ta có thể sử dụng
công thức đạo hàm của hàm ẩn. Nhắc lại về đạo hàm của hàm ẩn như sau:
"Nếu G là hàm ẩn theo Y và U được xác định bởi ". Do đó ta có:
• Hệ số co giãn của G theo Y là
• Hệ số co giãn của G theo U là
• Hệ số co giãn của G đồng thời theo cả Y và U (hệ số co giãn toàn phần) là
b. Theo công thức tính hệ số tăng trưởng .
Nên ta cần tính G0(t). Hơn nữa G(t) lại là hàm ẩn theo Y (t) và U(t), nên .
Tương tự như bài tập trước, ta đã tính được , . Do đó,
23. Bài tập này nhằm giúp người học ôn tập lại kiến thức về hệ số tăng trưởng của biến nội
sinh khi ta đã biết hệ số tăng trưởng của các biến ngoại sinh trong mô hình. Khi ta có
hàm S = S(P,M), trong đó S là biến nội sinh còn P,M là các biến ngoại sinh, thì a. Do đó,
Lưu ý rằng ta cũng có thể áp dụng công thức tính trực tiếp .
b. Hệ số co giãn toàn phần . Vì và , nên
c. Đạo hàm theo t 2 vế của đẳng thức
P − 4.57 × 107 + 0.16583MP + 1050205t = 0, ta được , hay . Suy ra
(1 + 0.16583M)(rP · P) + (0.16583P)(rM · M) + 1050205 = 0, hay
(P + 0.16583MP)rP + (0.16583MP)rM + 1050205 = 0. Suy ra
24. Bài toán này giúp người học ôn tập lại kiến thức về mô hình thu nhập quốc dân. Giải
nghiệm ở trạng thái cân bằng (câu a) và đánh giá được sự thay thế tương đối của các
biến để trạng thái cân bằng không bị thay đổi.
a. Trạng thái cân bằng đạt được bằng cách giải hệ phương trình
Do (1), nên việc giải hệ phương trình trên tương đương với việc giải phương trình
(2) theo R. Với cách đặt hệ số thích hợp, phương trình (2) có dạng
Bằng phép đổi biến thích hợp, ta có thể đưa phương trình trên về dạng Lambert
(Lambert form) và từ đó giải được R (Do giới hạn của chương trình học nên chúng
tôi xin được dừng lại ở đây!).
b. Đạo hàm cả hai vế của cả hai phương trình trên theo Go, ta được . Do đó, ta có: . Suy ra . Tương tự, ta cũng có: .
Do R phụ thuộc vào Y , nên ta chỉ việc tính
là đủ. Khi chính phủ tăng 1% tiêu
dùng thì trạng thái cân bằng Yo thay đổi
%, còn khi tổng lượng cung tiền mặt tăng
β% thì Yo cân bằng thay đổi
%. Do đó, để trạng thái cân bằng không thay đổi
thì Mo phải tăng β % sao cho . Tức là .
Lưu ý rằng R trong công thức trên là R(Go,Mo) tại điểm cân bằng.
25. Cho mô hình thu nhập quốc dân:
S(Y ) + T(Y ) = I(Y ) + Go, S(Y ) = 0,1lnY, T(Y )
= 0,04Y − 0,1Y 2, I(Y )
= 0,5Y + 0,02Y 2, Go = 1200;
với Y là thu nhập quốc dân, T là thuế, I là đầu tư và S là tiết kiệm.
a. Thu nhập trong trạng thái cân bằng là nghiệm của phương trình
0,1lnY + 0.04Y − 0.1Y 2 = 0.5Y + 0.02Y 2 + 1200, hay
lnY − 4.6Y − 1.2Y 2 = 12000, Bài toán vô nghiệm!!!!
b. Để hiểu trạng thái cân bằng thay đổi thế nào khi Go giảm 5%, ta cần tính được hệ số
co giãn của Y theo Go. Do S(Y ) + T(Y ) = I(Y ) + Go, nên . Suy ra , hay . Do đó, ta có
Như vậy, khi Go giảm 5% thì Y thay đổi %.
c. Trong trường hợp To cố định thì ta có thể xem G như một hàm theo To. Như vậy
mô hình của chúng ta sẽ trở thành
= I(Y ) + G, S(Y ) + T o S(Y ) = 0,1lnY, I(Y )
= 0,5Y + 0,02Y 2, G = G(To).
Giải mô hình này, ta sẽ được trạng thái cân bằng, sau đó so sánh với trạng thái cân
bằng ở câu a thì ta có thể tính ra được mối quan hệ giữa G và To.