CHƯƠNG 2. BIẾN NGẪU NHIÊN & QUY LUẬT PHÂN PHỐI XÁC SUẤT September 7, 2016 BÀI TẬP CHƯƠNG 2
Bài 1 (bài 2.65/tr.136). Theo thống kê dân số thì một người ở độ tuổi 40 sẽ sống
thêm 1 năm nưa là 0,995. Một công ty bảo hiểm nhân thọ bán bảo hiểm một năm
cho những người ở độ tuổi đó với giá là 10 ngàn và trong trường hợp người mua
bảo hiểm bị chết thì số tiền bồi thường là 1 triệu. Hỏi lợi nhuận trung bình của công
ty khi bán mỗi thẻ bảo hiểm loại này là bao nhiêu? ĐS: 5 ngàn
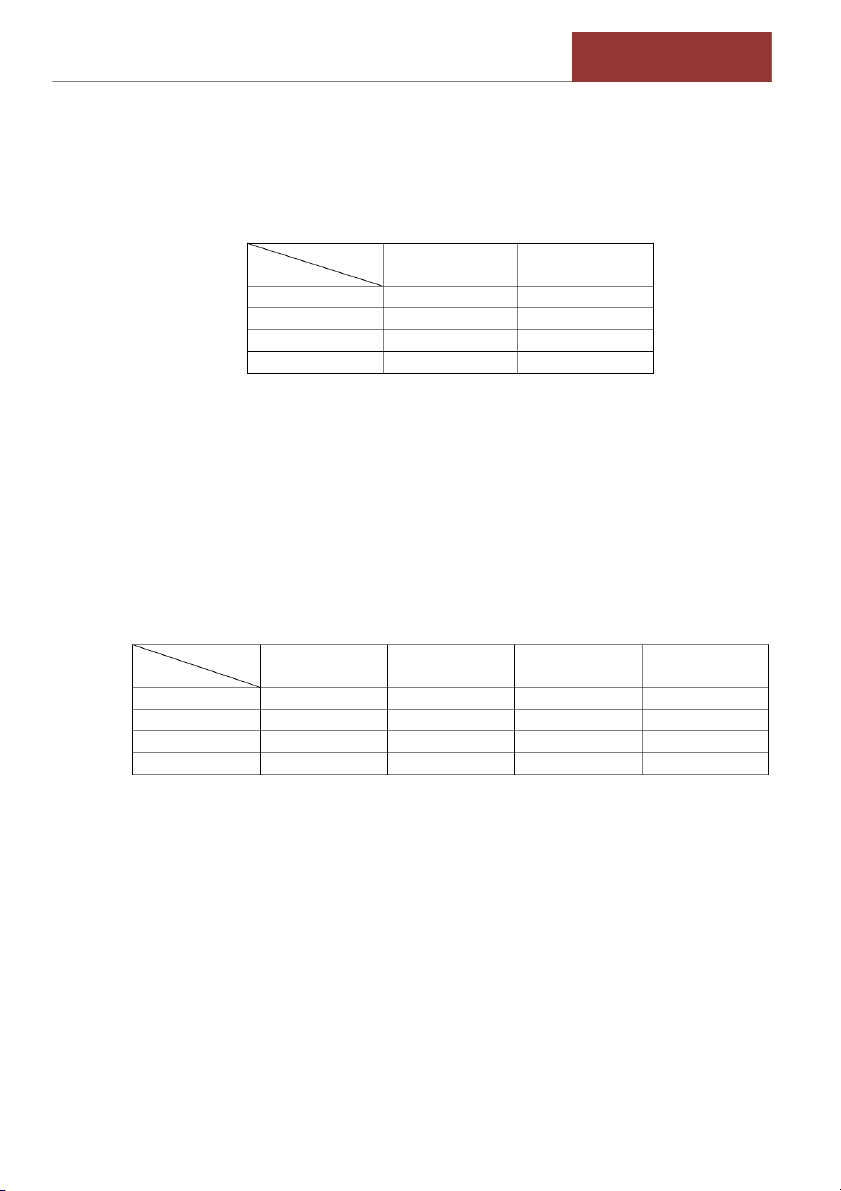
Bài 2 (bài 2.66/tr.136). Giá hàng ngày trên thị trường thế giới về đường (đơn vị:
USD/fao) có bảng phân phối xác suất như sau:
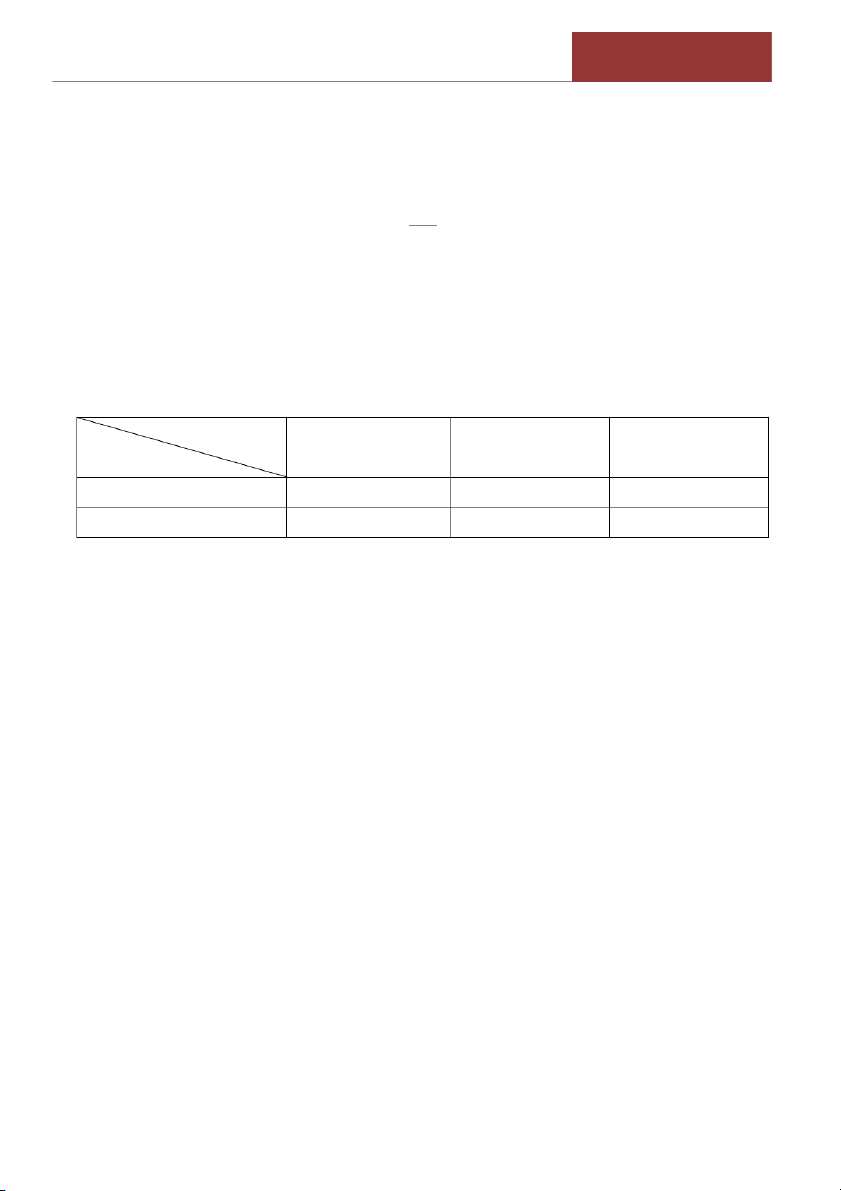
X 0,78 0,79 0,80 0,81 0,82 0,83
Px 0,05 0,10 0,25 0,40 0,15 0,05 a.
Tìm xác suất để giá đường vào một ngày
nào đó sẽ đạt ít nhất là 0,8 USD/fao.
b. Tìm xác suất để giá đường vào một ngày nào đó sẽ thấp hơn 0.82 USD/fao .
c. Giả sử giá hàng ngày của đường là độc lập nhau, tìm xác suất để trong hai ngày
liên tiếp giá đường đều cao hơn 0,8 USD/fao.
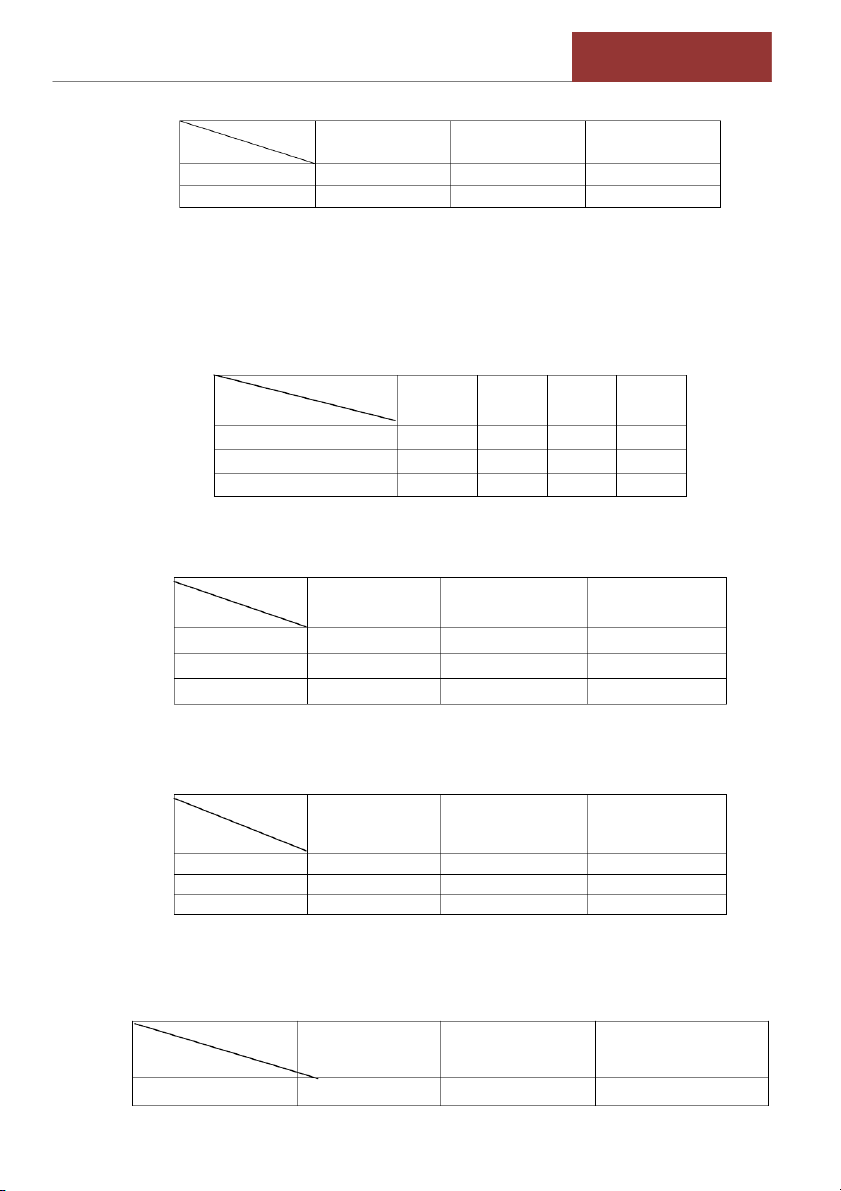
Bài 3 (bài 2.67/tr.136). Lợi nhuận X thu được khi đầu tư 50 triệu đồng vào một dự
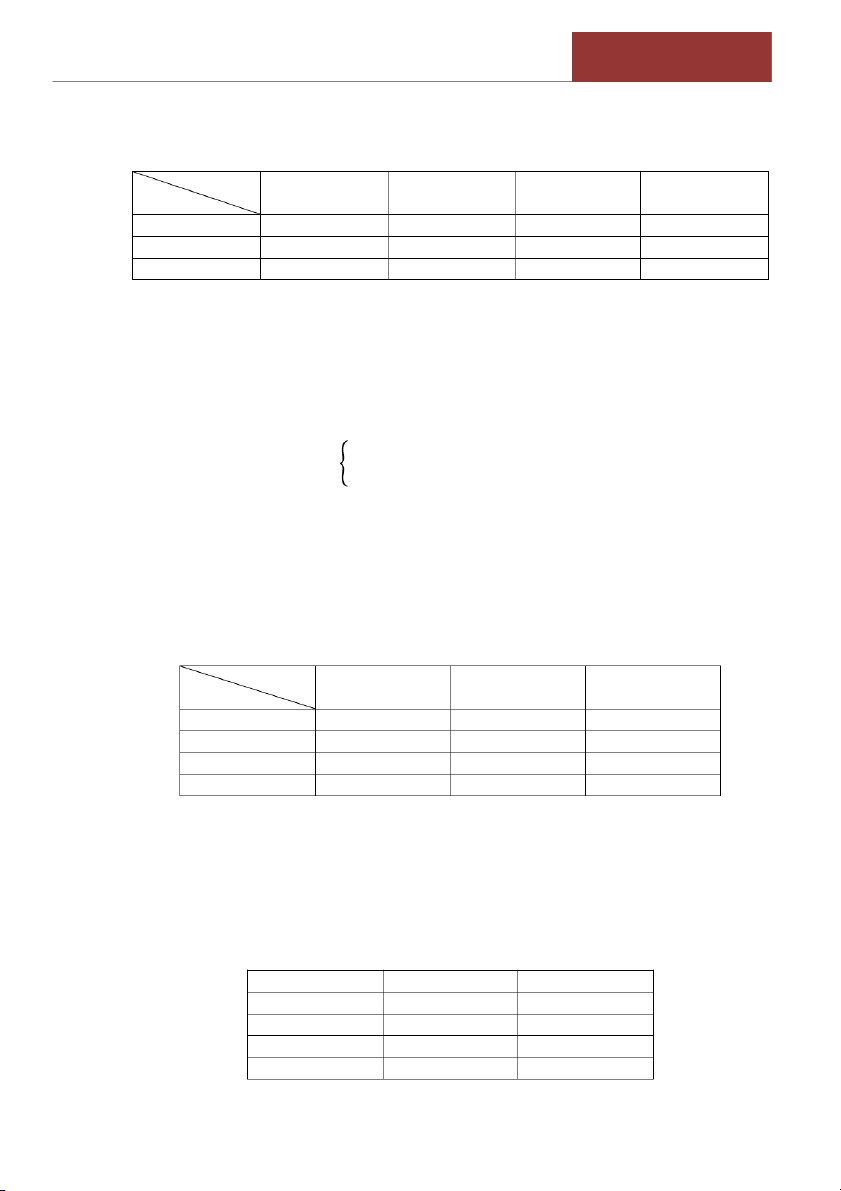
án có bảng phân phối xác suất như sau (đơn vị: triệu đồng). X -2 -1 0 1 2 3 Px 0,1 0,1 0,2 0,2 0,3 0,1
a. Tìm mức lợi nhuận có khả năng nhiều nhất khi đầu tư vào dự án đó.
b. Việc đầu tư vào dự án này có hiệu quả hay không? Tại sao?
c. Làm thế nào để đo được mức độ rủi ro của vụ đầu tư này? Hãy tìm mức độ rủi ro đó.
Bài 4 (bài2.68/tr.136). Lợi nhuận thu được từ 1 triệu đồng đầu tư vào công ty A(XA)
và công ty B(XB) có các bảng phân phối xác suất như sau: (đơn vị: ngàn đồng) XA -500 -100 100 500 700 PXA 0,2 0,3 0,2 0,2 0,1 XB -200 50 100 PXB 0,1 0, 0,3 1
CHƯƠNG 2. BIẾN NGẪU NHIÊN & QUY LUẬT PHÂN PHỐI XÁC SUẤT September 7, 2016
a. Nếu dự định đầu tư 10 triệu đồng thì lợi nhuận kỳ vọng khi đầu tư vào công ty A và B là bao nhiêu.
b. Nếu dùng hệ số biến thiên như độ đo mức độ rủi ro của đầu tư thì việc đầu tư
vào công ty nào rủi ro hơn?
Bài 5 (bài 2.69./tr.137). Một công ty thuê một luật sư trong một vụ kiện với hai
phương án trả công như sau:
Phương án 1: Trả 5 triệu đồng bất kể thắng hay thua kiện.
Phương án 2: Trả 100 ngàn đồng nếu thua kiện và 15 triệu đồng nếu thắng kiện.
Luật sư đã chọn phương án 2. Vậy theo đánh giá của luật sư thì khả năng thắng kiện
của công ty tối thiểu là bao nhiêu. ĐS: 0,329
Bài 6 (bài 2.70/tr.137). Trên một chuyến bay, người ta thống kê được rằng có 0,5%
hành khách bị mất hành lý và giá trị trung bình mà khách đòi bồi thường cho số
hành lý bị mất là 600 ngàn đồng. Công ty hàng không muốn tăng thêm giá vé để bù
đắp cho số tiền phải bồi thường cho hành lý bị mất. Vậy công ty nên tăng thêm giá vé là bao nhiêu? Tại sao?
Bài 7 (bài 2.71/tr.137). Số lượng thuyền gỗ X mà một xưởng đóng thuyền có thể
làm được trong một tháng có bảng phân phối xác suất như sau: X 2 3 4 5 6 7 8 Px 0,2 0,2 0,3 0,1 0,1 0,05 0,05 a.
Tìm xác suất để trong tháng tới xưởng đó sẽ đóng được từ 4 đến 7 con thuyền. b.
Tìm hàm phân phối xác suất của X. c.
Dùng hàm phân bố xác suất, hãy tính xác suất để trong tháng
tới xưởng đó sẽ đóng được không quá 6 con thuyền. d.
Số thuyền có khả năng nhiều nhất mà xưởng đó có thể đóng
được trong tháng tới là bao nhiêu? e.
Giả sử việc đóng thuyền có chi phí cố định hàng tháng là 25
triệu đồng và chi phí bổ sung cho mỗi con thuyền là 5 triệu đồng. Hãy tìm
chi phí bình quân hàng tháng của xưởng đó.
Bài 8 (bài 2.72/tr.138). Số lượng sản phẩm hỏng mà một công nhân có thể làm ra
trong một tháng có bảng phân phối xác suất như sau: Số SP hỏng 0 1 2 3 4 5 6 Xác suất tương 0,01 0,09 0,30 0,20 0,20 0,10 0,10 ứng
a. Tìm xác suất để trong một tháng người công nhân đó làm ra không quá 4 sản phẩm hỏng. 2
CHƯƠNG 2. BIẾN NGẪU NHIÊN & QUY LUẬT PHÂN PHỐI XÁC SUẤT September 7, 2016
b. Giả sử số sản phẩm mà người công nhân đó phải làm bù bình phương số sản
phẩm hỏng mà người đó đã làm trong tháng.Tìm số sản phẩm phải làm bù
bình quân mỗi tháng của người công nhân đó.
Bài 9 (bài 2.73/tr.138). Số lượng xe ô tô TOYOTA mà một đại lý bán được trong
một tuần có bảng phân phôi xác suất như sau: Số xe bán được 0 1 2 3 4 5 Xác suất tương ứng 0,1 0,1 0,2 0,2 0,3 0,1
a. Tìm xác suất để đại lý đó bán được ít nhất 4 xe trong một tuần.
b. Giả sử chi phí cho hoạt động của đại lý bằng căn bậc hai của số xe bán được
nhân với 3 triệu. Tìm chi phí trung bình cho hoạt động của đại lý mỗi tuần.
Bài 10 (bài 2.74/tr.138). Qua kinh nghiệm, một cửa hàng bán bánh trung thu biết
rằng dịp trung thu số bánh có thể bán được có phân phôi xác suất như sau Số bánh bán được (x) 400 500 600 700 800 900 Xác suất 0,05 0,15 0,41 0,34 0,04 0,01
a. Tìm trung bình và độ lệch chuẩn của số bánh bán được.
b. Nếu cửa hàng đặt mua 600 chiếc thì xác suất bán hết bánh là bao nhiêu xác
suất còn thừa lại là bao nhiêu.
c. Để có thể chắc chắn đến 95% là sẽ đủ bánh bán thì cửa hàng cần đặt mua bao nhiêu chiếc bánh.
Bài 11 (bài 2.75/tr.139). Trong 900000 vé số phát hành thì có 20 giải trị giá 50 triệu,
150 giải trị giá 5 triêu và 1600 giải trị giá 1 triệu. Tìm số tiền lãi kỳ vọng của một
người khi mua một vé, biết giá vé là 5 ngàn đồng.
Bài 12 (bài 2.76/tr.139). Một nhà kinh doanh muốn đầu tư 10 triệu đồng vào một
công ty mà nếu trong năm tới công ty làm ăn thuận lợi có thể sẽ mang lại lãi suất
đến 14% còn nếu gặp khó khăn thì lãi suất có thể giảm đến mức 4%. Trong khi đó
nếu gửi tiền vào ngân hàng thì lãi suất đảm bảo sau một năm là 8%. Vậy nếu dùng
tiền để đầu tư thì khả năng có lãi hơn gửi ngân hàng là bao nhiêu. ĐS: 0,6
Bài 13 (bài 2.77/tr.139). Nhu cầu hàng ngày về một loại thực phẩm tươi sống có
phân phối xác suất như sau: Nhu cầu (kg) 30 31 32 33 34 35 Xác suất 0,15 0,2 0,35 0,15 0,1 0,15
Mỗi kg thực phẩm mua vào với giá 2,5 ngàn và bán ra với giá 4 ngàn. Nếu bị ế đến
cuối ngày phải bán hạ giá còn 1,5 ngàn mới bán được hết. Vậy phải đặt mua hàng
bao nhiêu kg thực phẩm để có lãi nhất. ĐS: 32kg 3
CHƯƠNG 2. BIẾN NGẪU NHIÊN & QUY LUẬT PHÂN PHỐI XÁC SUẤT September 7, 2016
Bài 14 (bài 2.79/tr.140). Biến ngẫu nhiên liên tục X có hàm phân bố xác suất 3 1 x khi x x 3 0 F(x ) x x 0 0 0 0 khi x x0 Tìm E(X) và V(X)
Bài 15 (bài 2.80/tr.140). Biến ngẫu nhiên liên tục X có hàm mật độ xác suất si nx khi x 0, f(x) 2 0 khi x 0,
a. Tìm hàm phân bố xác suất F(x) b. Tìm P(0 < X < π/4) c. Tìm E(X) 0 khi x 0 1 cosx ĐS: a) F(x) khi 0 x 2 1 khi x
b) P(0 < X < �) = 1 − 2 4 2 4 c) E(X) = � 2
Bài 16 (bài 2.81/tr.140). Một công ty cung cấp nguyên vật liệu gửi 5 giấy đòi nợ tới
một xí nghiệp yêu cầu thanh toán tiền cho 5 đợt giao hàng vừa qua với số lượng
hàng của các đợt không khác nhau nhiều lắm. Trong số 5 giấy đòi nợ này (mỗi giấy
viết riêng cho từng đợt) có 2 giấy ghi sai số tiền phải thanh toán. Do đến hạn phải
trả nợ ngân hàng, công ty yêu cầu xí nghiệp thanh toán ngay cho ba đợt bất kỳ trong
5 đợt giao hàng ngày. Kế toán viên của xí nghiệp lấy ngẫu nhiên cùng một lúc ra 3
giấy để kiểm tra và làm phiếu chi.
Tính xác suất để trong số 3 giấy lấy ra đó có ít nhất một giấy ghi sai số tiền phải thanh toán.
Bài 17.(bài 2.82/tr.141). Xí nghiệp và công ty nói ở bài trên thoả thuận với nhau
rằng nếu kế toán viên của xí nghiệp phát hiện thấy có giấy đòi nợ nào trong số 3 tờ
giấy được lấy ra mà ghi sai số tiền thì xí nghiệp có quyền hoãn trả số nợ của đợt
giao hàng đó. Mỗi giấy bị hoãn trả sẽ làm thiệt cho công ty khoảng 5 triệu đồng do
phải trả lãi nợ quá hạn cho ngân hàng.
Hãy xác định số tiền thiệt hại trung bình có thể xảy ra đối với công ty do phải trả nợ quá hạn. 4
CHƯƠNG 2. BIẾN NGẪU NHIÊN & QUY LUẬT PHÂN PHỐI XÁC SUẤT September 7, 2016
Bài 18 (bài 2.83/tr.141). Tuổi thọ (tính theo giờ) của một loại van điện lắp trong
một thiết bị là biến ngẫu nhiên có hàm mật độ xác suất như sau: 0 khi x 0 f(x) 100 khi x 100 2 x
Tìm xác suất để có 2 trong số 5 van điện này bị thay thế trong 150 giờ hoạt động
đầu tiên biết rằng việc hỏng của các van điện là độc lập với nhau.
Bài 19 (bài 2.85/tr.141). Tuỳ theo tình hình kinh tế trong nước mà trong năm tới
một công ty thu được mức lãi (tính theo triệu đơn vị tiền tệ của nước này ) khi đầu
tư vào hai ngành A và B dẽ như nhau: Tình hình kinh tế Kém phát triển Ổn định Phát triển Mức lãi Ngành A 20 80 120 Ngành B -30 100 140
Theo dự báo thì xác suất để nền kinh tế của cả nước đang xét trong năm tới sẽ rơi
vào các tình trạng tương ứng nêu trên là 0,3; 0,5 và 0,2.
Vậy công ty nên đầu tư vào ngành nào để cho:
a. Mức lãi kỳ vọng là cao hơn.
b. Độ rủi ro ( phương sai của mức lãi) là ít hơn?
Bài 20 (bài 2.86/tr.142). Trong một cuộc thi, người ta có hai hình thức sau:
Hình thức thứ nhất là mỗi người phải trả lời hai câu hỏi, mỗi câu trả lời đúng được 5 điểm.
Hình thức thứ hai là nếu trả lời đúng câu thứ nhất mới được trả lời câu thứ
hai, nếu không thì dừng. Trả lời đúng câu thứ nhất được 5 điểm, trả lời đúng
câu thứ hai được 10 điểm.
Trong cả hai hình thức thi, các câu trả lời sai đều không được điểm. Giả sử xác
suất trả lời đúng mỗi câu đều là 0,75; việc trả lời đúng mỗi câu là độc lập với nhau.
Theo bạn, nên chọn hình thức nào để số điểm trung bình đạt được nhiều hơn.
Bài 21 (bài 2.87/tr.142). Chủ một cửa hàng sửa chữa điện dân dụng thuê 5 thợ sửa
chữa làm việc 40 giờ một tuần với lương là 800 ngàn/ tuần. Do nhu cầu sửa chữa
tăng lên nên nhiều hợp đồng phải từ chối. Để xét xem có cần thuê thêm một thợ nữa
không, ông chủ đã khảo sát nhu cầu X và thu được các số liệu sau: 5
CHƯƠNG 2. BIẾN NGẪU NHIÊN & QUY LUẬT PHÂN PHỐI XÁC SUẤT September 7, 2016 Nhu cầu X 180-190 190-200 200-210 210-220 220-230 230-240 240-250 250-260 Xác suất P(x) 0,03 0,09 0,12 0,15 0,22 0,21 0,13 0,05
Nếu mỗi giờ sửa chữa chủ cửa hàng thu được 30 ngàn thì có nên thuê thêm một
công nhân nữa không nếu:
a. Năm người công nhân cũ chỉ đồng ý làm đúng 40 giờ/ tuần.
b. Năm người công nhân cũ đồng ý làm thêm tối đa mỗi người 5 giờ mỗi tuần
với tiền công là 25 ngàn/ giờ làm thêm.
Bài 23 (bài 2.88/tr.143). Biến ngẫu nhiên X có hàm mật độ xác suất: 1 khi x ( , a a ) 2 2 f (x) a x 0 khi x ( , a a ) Tìm E(X) ĐS: E(X)=0
Bài 24 (bài 2.89/tr.143). Biến ngẫu nhiên X có hàm phân bố xác suất 0 khi x 2 1 1 f (x ) khi 2 x 2 2 1 khi x 2 a. Tìm P(-1< X< 1)
b. Tìm hàm mật độ xác suất f(x) ĐS: a. P = 1/3 b. 1 khi x ( 2,2) 2 f (x) 4 x 0 khi x ( 2,2) BÀI TẬP CHƯƠNG 3
Bài 1 (bài 3.77/tr.204). Xác suất để máy bị hỏng trong một ngày hoạt động là 0,01.
Mỗi lần máy hỏng chi phí sửa chữa hết khoảng 1 triệu đồng. Vậy có nên ký một
hợp đồng bảo dưỡng là 120 ngàn đồng một tháng để giảm xác suất hỏng của máy đi 6
CHƯƠNG 2. BIẾN NGẪU NHIÊN & QUY LUẬT PHÂN PHỐI XÁC SUẤT September 7, 2016
nửa hay không và nếu ký thì hiệu quả mang lại là bao nhiêu. Giả sử máy hoạt động liên tục cả năm.
ĐS: Nên ký vì sẽ tiết kiệm được khoảng 385 ngàn đồng một năm.
Bài 2 (bài 3.78/tr.204). Thời gian bảo hành sản phẩm được quy định là 3 năm. Nếu
bán được một sản phẩm thì cửa hàng lãi 150 ngàn song nếu sản phẩm bị hỏng trong
thời gian bảo hành thì cửa hàng phải chi phí 500 ngàn cho việc bảo hành. Biết rằng
tuổi thọ của sản phẩm là biến ngẫu nhiên phân phối chuẩn với tuổi thọ trung bình là
4,3 năm và độ lệch tiêu chuẩn là 1,8 năm.
a. Tìm số tiền lãi mà cửa hàng hy vọng thu được khi bán mỗi sản phẩm.
b. Nếu muốn số tiền lãi cho mỗi sản phẩm bán ra là 50 ngàn thì phải quy
định thời gian bảo hành là bao nhiêu.
ĐS: a. E(X)= 24,3 ngàn; b. Thời gian bảo hành 2,688 năm
Bài 3 (bài 3.79/tr.204). Ở một trạm bơm xăng bình quân mỗi giờ có 12 xe máy đến
tiếp xăng. Tìm xác suất để trong một giờ nào đó có.
a. Hơn 8 xe đến tiếp xăng.
b. Hơn 15 xe đến tiếp xăng.
c. Dưới 10 xe đến tiếp xăng.
ĐS: Pa=0,845; Pb=0,1556; Pc=0,2424
Bài 4 (bài 3.80/tr.204). Tuổi thọ của một số loại sản phẩm là biến ngẫu nhiên phân
phối chuẩn với trung bình là 11 năm và độ lệch chuẩn là 2 năm.
a. Nếu quy định thời gian bảo hành là 10 năm thì tỷ lệ sản phẩm phải bảo quản là bao nhiêu.
b. Nếu muốn tỷ lệ sản phẩm phải bảo hành là 10% thì phải quy định thời gian bảo hành là bao nhiêu.
Bài 5 (bài 3.81/tr.205). Độ dài chi tiết (tính bằng cm) do một máy tự động sản xuất
là biến ngẫu nhiên phân phối chuẩn với độ lệch chuẩn 9 cm.
Nếu được biết 84,13% chi tiết do máy sản xuất có độ dài không vượt quá 84cm thì
xác suất để lấy ngẫu nhiên 3 chi tiết được ít nhất 1 chi tiết có độ dài không dưới 80cm là bao nhiêu?
Bài 6 (bài 3.82/tr.205). Hàng sáng đi tàu đến nơi làm việc, một người mê trò chơi ô
chữ có đúng 30 phút để điền các ô chữ. Qua kinh nghiệm đối với ô chữ in trong báo
A thì trung bình phải mất 25,2 phút để điền xong với độ lệch chuẩn là 3,9 xong với
độ lệch chuẩn là 1,9 phút. Biết thời gian điền xong ô chữ là biến ngẫu nhiên phân
phối chuẩn. Vậy người này nên mua báo nào nhằm đảm bảo khả năng điền xong ô chữ cao hơn.
Bài 7 (bài 3.83/tr205). Cho Z là biến ngẫu nhiên tuân theo quy luật chuẩn hoá N(0,1)
và � = � +�2�+ ��2. Trong đó �,�,� là các hàng số. Hãy tính E(X) và V(X).
Bài 8 (bài 3.84/tr.205). Một người cân nhắc giữa việc mua nhà bây giờ hay gửi tiền
vào tiết kiệm với lãi suất 12% một năm để chờ một năm sau mới mua. Biết mức
tăng giá nhà là biến ngẫu nhiên phân phối chuẩn với kỳ vọng toán là 8% một năm 7
CHƯƠNG 2. BIẾN NGẪU NHIÊN & QUY LUẬT PHÂN PHỐI XÁC SUẤT September 7, 2016
và độ lệch chuẩn là 10% một năm. Tìm khả năng rủi ro của người đó nếu gửi tiền
vào tiết kiệm và chờ một năm.
Bài 9 (bài 3.85/tr.205). Thời gian cần thiết để hoàn thành một công việc là biến
ngẫu nhiên phân phối đều U [5; 9] (phút)
c. Viết biểu thức của hàm mật độ xác suất.
d. Tìm xác suất để công việc được hoàn thành dưới 8 phút.
e. Thời gian trung bình để công việc được hoàn thành công việc đó bằng bao nhiêu?
Bài 10 (bài 3.86/tr205). Một hãng quảng cáo tuyên bố rằng cứ 5 bác sĩ thì có hai
người chỉ định cho bệnh nhân dùng loại thuốc do hãng đó quảng cáo. Chọn ngẫu
nhiên 20 bác sĩ thì thấy chỉ có 2 người chỉ định cho bệnh nhân dùng loại thuốc đó.
a. Giả sử lời tuyên bố của hãng quảng cáo là đúng, tìm xác suất của biến cố trên.
b. Giả sử lời tuyên bố của hãng quảng cáo là đúng, tìm xác suất để có không
quá 2 người chỉ định dùng loại thuốc trên.
c. Với kết quả chọn ngẫu nhiên như trên, liệu có thể tin là lời tuyên bố đúng sự
thật được không? Tại sao?
Bài 11 (bài 3.87/tr206). Lãi suất đầu tư vào một công ty là biến ngẫu nhiên phân
phối chuẩn. Biết xác suất để đạt được lãi suất trên 20% một năm là 0,2 và dưới 10%
một năm là 0,1. Tìm xác suất để khi đầu tư vào công ty đó sẽ được lãi suất ít nhất là 14% năm.
Bài 12 (bài 3.88/tr206). Chiều dài X và chiều rộng Y của một chi tiết được gia công
một cách độc lập và là các biến ngẫu nhiên phân phối chuẩn với �� =8��; �� =
4��; �� = 0,3�à�� =0,2��. Chi tiết được coi là đạt tiêu chuân nếu các kích
thước trung bình không quá 0,1cm.
a. Tìm xác suất để chi tiết đạt tiêu chuẩn.
b. Tìm xác suất để khi gia công 3 chi tiết có ít nhất một chi tiết đạt tiêu chuẩn.
Bài 13 (bài 3.89/tr206). Thời gian hoạt động tốt (không phải sửa chữa) của một loại
tivi là biến ngẫu nhiên phân phối chuẩn với �=4300giờ và � = 250giờ. Giả thiết
mỗi ngày người ta dùng trung bình là 10 giờ và thời hạn bảo hành miễn phí là 1 năm (360 ngày).
a. Tìm tỉ lệ sản phẩm phải bảo hành.
b. Phải nâng chất lượng sản phẩm bằng cách tăng thời gian hoạt động tốt trung
bình của sản phẩm lên bao nhiêu để tỷ lệ bảo hành vẫn như trên song có thể
nâng thời gian bảo hành lên thành 2 năm?
Bài 14 (bài 3.90/tr206). Hội đồng quản trị doanh nghiệp có 7 thành viên và mọi vấn
đề đều được giải quyết theo đa số. Ông chủ tịch muốn thông qua một đề án kinh
doanh do ông soạn thảo. Giả sử khả năng ủng hộ hay phản đối của mỗi thành viên hội đồng là như nhau.
a. Tìm xác suất để đề án được thông qua.
b. Giả sử trong hội đồng quản trị ngoài ông chủ tịch ra còn có 2 thành viên khác
là đảng viên lập thành một chi bộ và chi bộ họp trù bị để thông qua đề án
cũng theo nguyên tắc đa số. Sau đó ra cuộc họp chung thì mọi đảng viên phải 8
CHƯƠNG 2. BIẾN NGẪU NHIÊN & QUY LUẬT PHÂN PHỐI XÁC SUẤT September 7, 2016
tuân theo quyết định của cuộc họp trù bị. Vậy lúc đó xác suất để đề án được thông qua là bao nhiêu.
c. Từ đó có thể rút ra kết luận gì về việc áp dụng nguyên tắc tập trung dân chủ.
Bài 15 (bài 3.91/tr207). Máy bay bay dọc theo cầu dài 8m, rộng 4m và ném hai quả
bom. Biết rằng khoảng cách từ điểm rơi của quả bom đến trục đối xứng theo chiều
dọc và ngang của cầu là các biến ngẫu nhiên độc lập, cùng phân phôi chuẩn với kì
vọng toán bằng 0 và các độ lệch tiêu chuẩn tương ứng là 4m và 6m. Tìm xác suất để cầu bị trúng bom.
Bài 16 (bài 3.92/tr207). Trên một tuyến bay người ta dùng loại máy bay ATR72 có
72 chỗ ngồi. Thực tế cho thấy đến giờ chót vẫn có khách bỏ chuyến bay. Để tận
dụng hết chỗ ngồi bằng cách bán thêm vé dự phòng người ta đã thống kê 20 chuyến
bay thu được các số liệu sau. Số khách bỏ chuyến bay 2 3 4 5 6 7 8 9 10 11 Số chuyến tương ứng 1 4 0 4 2 5 1 1 0 2
Hãy ước lượng xác suất để trong một chuyến bay nào đó có:
a. 1 khách bỏ chuyến bay đó.
b. 2 khách bỏ chuyến bay đó.
c. Tìm số khách bỏ chuyến trung bình và số khách bỏ chuyến có khả năng xảy
ra nhiều nhất ở mỗi chuyến bay.
Bài 17 (bài 3.93/tr207). Một người cân nhắc giữa việc mua cổ phiếu của công ty A
và công ty B hoạt động trong lĩnh vực độc lập nhau. Biết lãi suất cổ phiếu của hai
công ty là các biến ngẫu nhiên phân phối chuẩn với các tham số đặc trưng như sau Kỳ vọng toán (%) Độ lệch tiêu chuẩn (%) Công ty A 11 4 Công ty B 10,4 2,6
a. Vậy nếu người đó muốn đạt được lãi suất tối thiểu là 10% thì nên mua cổ phiếu của công ty nào.
b. Nếu người đó muốn hạn chế rủi ro bằng cách mua cổ phiếu của cả hai công
ty thì nên mua theo tỷ lệ bao nhiêu để mức độ rủi ro về lãi suất là nhỏ nhất.
BÀI TẬP TỔNG HỢP CHƯƠNG 4
Bài 1.(4.46/tr261). Một nhân viên bán hàng mỗi ngày đi chào hàng ở ba nơi với xác
suất bán được hàng mỗi nơi là 0,2. Nếu bán được hàng ở nơi thứ nhất và thứ hai thì
tiền lãi mỗi nơi là 100USD còn nếu bán được ở nơi thứ ba thì do hàng có chất lượng
cao hơn nên lãi được 200USD. a.
Thiết lập bảng phân phối xác suất đồng thời của số lần bán được hàng X và tổng số tiền lãi Y. b.
Tìm số lần bán được hàng trung bình và số tiền lãi trung bình của mỗi ngày bán hàng. 9
CHƯƠNG 2. BIẾN NGẪU NHIÊN & QUY LUẬT PHÂN PHỐI XÁC SUẤT September 7, 2016
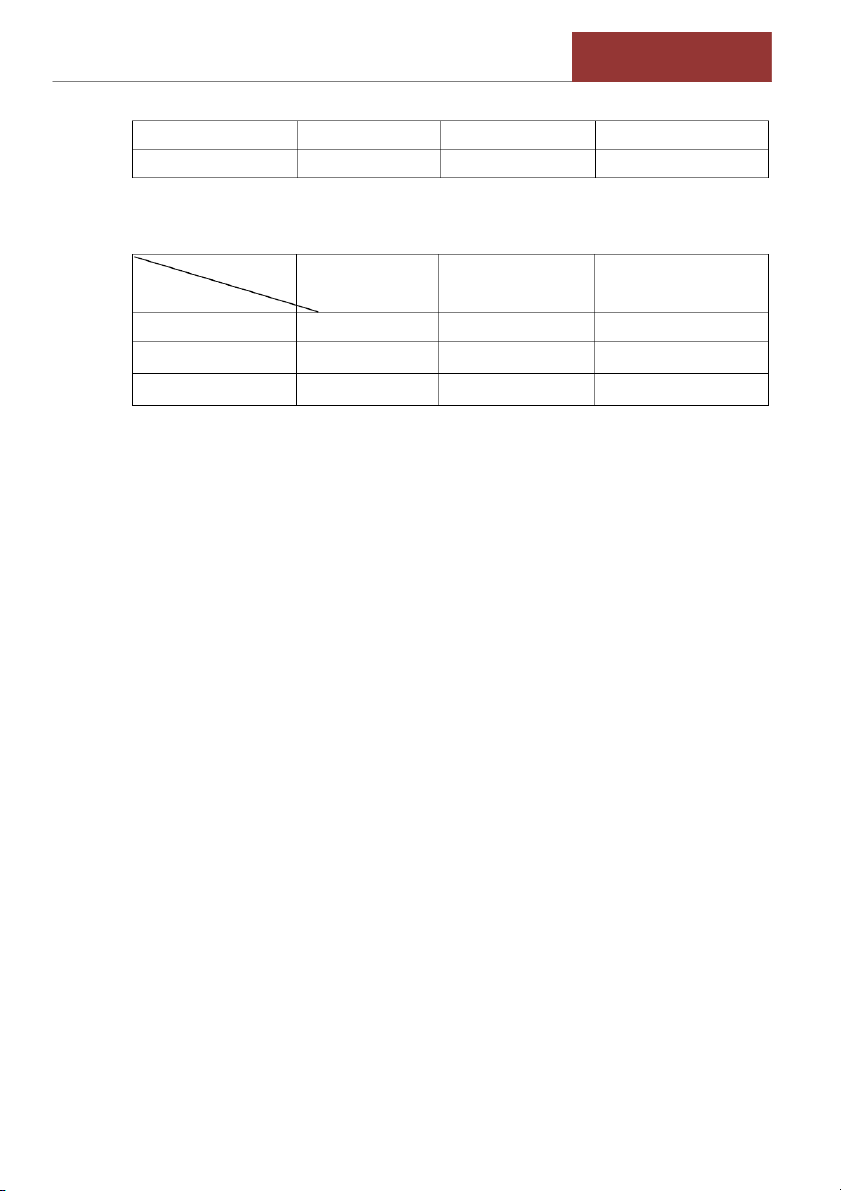
Bài 2. (4.47/tr261). Cho bảng phân phối xác suất đồng thời của biến ngẫu nhiên rời
rạc hai chiều (X, Y) như sau: Y 1 2 3 P(x) X -2 0,05 0,4 -1 0,2 P(y) 0,2 0,5
a. Hãy điền vào các giá trị còn thiếu của bảng. b. Tìm E(X + Y) c. Tìm V(X - Y)
Bài 3. (4.48/tr261).Cho biến ngẫu nhiên rời rạc hai chiều có xác suất đồng thời
được xác định bằng biểu thức sau: �(� ớ� � P(� �,2��)
�� = 1;2;3 �à �� = 0;1;2 �,��)= 0 �ớ��á��� ị á� �ℎ� á�� ủ���,��
Hãy thiết lập bảng phân phối xác suất đồng thời của (X, Y)
Bài 4. (4.49/tr262). Thống kê những người tuổi trưởng thành ở một nước theo hai chỉ tiêu sau:
X: thu nhập sau thuế (ngàn USD/ năm)
Y: mức độ hạnh phúc của người đó
Thu được bảng số liệu sau: Y Bất hạnh
Hạnh phúc vừa Rất hạnh phúc X phải 2,5 0,03 0,12 0,07 7,5 0,02 0,13 0,11 12,5 0,01 0,13 0,14 17,5 0,01 0,09 0,14 a.
Tìm mức độ hạnh phúc trung bình tương
ứng với mỗi mức thu nhập. Vẽ đồ thị và cho nhận xét. b.
Tìm hệ số tương quan và cho nhận xét.
Bài 5. (4.50/tr262). Một chủ cửa hàng điện tử dự kiến doanh thu của cửa hàn trong
tháng có phân phối xác suất như sau. Cột cuối cùng là mức thuế doanh thu tương ứng Doanh thu x Xác suất P(x) Thuế T(x) 20 0,10 4 30 0,30 6 40 0,40 9 50 0,20 13 10
CHƯƠNG 2. BIẾN NGẪU NHIÊN & QUY LUẬT PHÂN PHỐI XÁC SUẤT September 7, 2016 a. Tìm doanh thu kỳ vọng
b. Tìm mức thuế kỳ vọng
c. Tìm doanh thu sau thuế kỳ vọng
Bài 6. (4.51-4.54/tr263). Thống kê dân số của một nước theo hai chỉ tiêu học vấn X
và giới tính Z thu được kết quả sau: Z Nam 0 Nữ 1 X Thất học 0 0,04 0,05 Tiểu học 1 0,10 0,12 Trung học 2 0,23 0,29 Đại học 3 0,10 0,07
a. Lập bảng phân phối xác suất biên của học vấn.
b. Tìm xác suất để lấy ngẫu nhiên một người thì người đó tốt nghiệp từ trung học trở lên.
c. Tìm trình độ học vấn trung bình.
d. Lập bảng phân phối xác suất biên của Z và tính E(Z). Cho nhận xét.
e. Lập bảng phân phối xác suất về học vấn của nam.
f. Học vấn có độc lập với giới tính không.
g. Tìm trình độ học vấn trung bình của nam.
h. Tìm trình độ học vấn trung bình của nữ và so sánh với trình độ học vấn trung bình của nam.
Bài 7. (4.55/tr264). Cho bảng phân phối xác suất đồng thời của biến ngẫu nhiên rời
rạc hai chiều (X, Y) như sau: Y 0 1 2 3 X 1 0,08 0,12 0,16 0,4 2 0,06 0,09 0,12 0,3 3 0,06 0,09 0,12 0,3 Tổng số 0,2 0,3 0,4 1
a. X và Y có độc lập với nhau không? Tại sao? Tính Cov(X, Y), E(X), E(Y), V(X-Y)
b. Lập bảng phân phối xác suất của (X – Y). Tính xác suất để (X + Y) bé hơn 2.
Bài 8. (4.56/tr264). Một hộp đựng 5 sản phẩm, trong đó có 3 phế phẩm. Các sản
phẩm được lấy ra để kiểm tra cho tới khi phát hiện thấy phế phẩm.
Ký hiệu Xi là số lần kiểm tra tới khi phế phẩm đầu tiên bị phát hiện, X2 là số lần
kiểm tra thêm cho tới khi phế phẩm thứ hai bị phát hiện. a.
Lập bảng phân phối xác suất đồng thời của (X1, X2) b.
Tính hiệp phương sai giữa X1 và X2.
Bài 9. (4.57/tr265). Cho bảng phân phối xác suất đồng thời của biến ngẫu nhiên hai
chiều (X, Y) như sau: (trong đó y,a,b là các số chưa biết) 11
CHƯƠNG 2. BIẾN NGẪU NHIÊN & QUY LUẬT PHÂN PHỐI XÁC SUẤT September 7, 2016 Y y 0 1 X 0 1/4 a 1/8 1 1/5 b 1/10
a. Xác định a và b sao cho X và Y là độc lập với nhau
b. Quy luật phân bố xác suất có điều kiện của X đối với các giá trị khác nhau
của y trong trường hợp này như thế nào?
c. Giả thiết rằng a = 1/5, xác định giá trị y sao cho hiệp phương sai của (X, Y)
bằng không. X và Y trong trường hợp này có độc lập với nhau không?
Câu 1. Giả sử bạn đầu tư vào hai cổ phiếu A và B có lãi suất theo tháng (đơn vị: %)
được cho dưới dạng bảng phân phối xác suất đồng thời như sau: B -2 1 3 5 A -1 0,01 0,04 0,1 0,05 3 0,05 0,25 0,15 0,1 6 0,1 0,05 0,1 0
Tính lãi suất trung bình khi đầu tư vào cổ phiếu A nếu lãi suất cổ phiếu B bằng 3%.
Câu 2. Tỷ suất lợi nhuận (%/phiên giao dịch) của hai cổ phiếu A và B là hai
biến ngẫu nhiên X, Y có bảng phân phối như sau: X -4 1 2 Y -3 0,1 0,12 0,1 -1 0,06 0,18 0,14 3 0,15 0,1 0,05
Nếu tỷ suất lợi nhuận của cổ phiếu A là 1%/phiên thì tỷ suất lợi nhuận trung bình
của cổ phiếu B là bao nhiêu?
Câu 3. Tỷ suất lợi nhuận (%/ phiên giao dịch) của hai loại cổ phiếu A và B lần lượt là biến
ngẫu nhiên X, Y có bảng phân phối xác suất như sau: X -3 -1 5 Y -4 0,1 0,13 0,1 -1 0,15 0,2 0,12 6 0,02 0,12 0,06
Nếu tỷ suất lợi nhuận của cổ phiếu B là -1%/ phiên thì tỷ suất lợi nhuận trung bình của cổ phiếu A là bao nhiêu?
Câu 4 Khi đầu tư vào hai thị trường A và B lãi suất XA và XB (đơn vị: %/phiên) là các biến
ngẫu nhiên có bảng phân phối xác suất đồng thời như sau: XA -4 -1 6 XB -3 0,05 0,1 0,15 12
CHƯƠNG 2. BIẾN NGẪU NHIÊN & QUY LUẬT PHÂN PHỐI XÁC SUẤT September 7, 2016 -1 0,1 0,2 0,15 5 0,1 0,1 0,05
Tìm lãi suất trung bình khi đầu tư vào thị trường B biết năm đó lãi suất thị trường A là 6%.
Câu 5 Khi đầu tư vào thị trường Vàng và Ngoại tệ thì lãi suất X và Y (đơn vị: %) là các
biến ngẫu nhiên có bảng phân phối xác suất đồng thời như sau: X -3 2 3 Y -2 0,05 0,1 0,15 1 0,1 0,2 0,15 4 0,1 0,1 0,05
Tìm lãi suất trung bình khi đầu tư vào thị trường ngoại tệ biết năm đó lãi suất thị trường vàng là 2%. 13