









































Preview text:
Chương 2
Phép toán vi phân: Các khái niệm cơ bản 2.1 Đạo hàm KIẾN THỨC QUAN TRỌNG Định nghĩa
• Cho hàm số f (x) xác định trên tập D (D ⊂ R; D 6= ∅), đạo hàm của
hàm số f(x) theo x là hàm số f′(x) được xác định bởi df f (x + h) − f(x) = f ′(x) = lim dx h→0 h
Quá trình tính đạo hàm được gọi là phép toán vi phân, f(x) được gọi
là hàm khả vi tại x = c nếu f′(c) tồn tại.
• Liên hệ giữa độ dốc và đạo hàm: Độ dốc của tiếp tuyến với đồ thị
y = f (x) tại điểm (c, f (c) là mtt = f ′(c).
• Liên hệ giữa tốc độ thay đổi tức thời và đạo hàm: Tốc độ thay đổi của
f (x) theo x tại x = c là f ′(c).
Ý nghĩa dấu của đạo hàm
Nếu hàm số f khả vi tại x = c thì:
f tăng tại x = c nếu f ′(c) > 0
f giảm tại x = c nếu f ′(c) < 0 1
Tính liên tục của hàm số khả vi
Nếu hàm số f(x) khả vi tại x = c thì nó cũng liên tục tại x = c.
HƯỚNG DẪN GIẢI CÁC BÀI TẬP CƠ BẢN
Bài 1 (Bài 10 trang 95). Tìm đạo hàm và độ dốc của tiếp tuyến
Lời giải: Theo định nghĩa đạo hàm ta có: 1 1 − f (x + h) − f(x) (x + h)2 x2 f ′(x) = lim = lim h→0 h h→0 h x2 − (x + h)2 −2xh − h2 = lim = lim h→0 hx2(x + h)2 h→0 hx2(x + h)2 −2x − h 2 = lim = − h→0 x2(x + h)2 x3 Vậy 2 1 f ′(x) = − , do đó f′(2) = − . x3 4
Từ đó, độ dốc của tiếp tuyến với đồ thị của hàm số 1 y = tại điểm có x2 hoành độ 1 x = 2 là m = − . 4
Bài 2 (Bài 11 trang 95). Tìm đạo hàm và độ dốc của tiếp tuyến
Lời giải: Từ định nghĩa đạo hàm ta có: 1 1 √ − √ H(u + h) − H(u) u H′(u) = lim = lim u + h h→0 h h→0 h √ √ u − u + h u − (u + h) = lim √ √ = lim √ √ √ √ h→0 h u u + h h→0 h u u + h( u + u + h) −1 1 = lim √ √ √ √ = − √ h→0 u u + h( u + u + h) 2 u3 Vậy 1
H′(u) = − √ . Do đó tại điểm có hoành độ u = 4 độ dốc của 2 u3 tiếp tuyến là 1 m = H′(4) = − . 16
Bài 3 (Bài 21 trang 95). Tìm đạo hàm và viết phương trình tiếp tuyến 2
Lời giải: Theo định nghĩa ta có: √ √ f (x + h) − f(x) 2 x + h − 2 x f ′(x) = lim = lim h→0 h h→0 h 2[(x + h) − x] 2 = lim √ √ = lim √ √ h→0 h( x + h + x) h→0 x + h + x 1 = √x Vậy 1 √
f ′(x) = √ , từ đó độ dốc của tiếp tuyến với đường cong f(x) = 2 x x tại điểm có hoành độ 1 x = 4 là f ′(4) =
. Để tìm phương trình tiếp tuyến, 2 ta xác định tọa độ √
y của tiếp điểm là y = 2 4 = 4.
Do đó phương trình tiếp tuyến tại tiếp điểm (4, 4) là 1 1
y − 4 = (x − 4) hay y = x + 2 2 2
Bài 4 (Bài 30 trang 95). Tìm tốc độ thay đổi Lời giải: Ta có: f (x + h) − f(x)
[(x + h)2 − 2(x + h)] − (x2 − 2x) f ′(x) = lim = lim h→0 h h→0 h 2xh + h2 − 2h = lim = lim (2x + h − 2) h→0 h h→0 = 2x − 2
Do đó f′(1) = 0, nên tốc độ thay đổi dy của y = x2 − 2x khi x = 1 là 0. dx
Bài 5 (Bài 38 trang 95). Tìm tốc độ thay đổi
Lời giải: a. Tốc độ thay đổi trung bình của f (x) theo x khi x thay đổi từ 1 x = 0 đến x =
được tìm theo công thức: 2 Thay đổi của Tốc độ f (x) f (c + h) − f(c) f (c + h) − f(c) tb = = Thay đổi của = x (c + h) − c h Thay số vào ta có: 1 f ( ) − f(0) Tốc độ 2 0 − 0 tb = = 0 1 = 1 − 0 2 2 3
Vậy tốc độ thay đổi trung bình của f(x) theo x khi x thay đổi từ x = 0 đến 1 x = là 0. 2
b. Để tính tốc độ thay đổi tức thời của f(x) tại x = 0 cần tìm f′(0).
Theo định nghĩa đạo hàm ta có: f (x + h) − f(x)
[(x + h)[1 − 2(x + h)] − x(1 − 2x) f ′(x) = lim = lim h→0 h h→0 h −4xh + h − 2h2 = lim = lim (−4x + 1 − 2h) h→0 h h→0 = −4x + 1
Vậy f′(0) = 1, nên tốc độ thay đổi tức thời của f(x) tại x = 0 cần tìm
là 1 và lớn hơn tốc độ trung bình tìm được ở câu (a).
Bài 6 (Bài 43 trang 96). Lợi nhuận
Lời giải: a. Theo định nghĩa đạo hàm ta được: P (x + h) − P (x) P ′(x) = lim h→0 h
4, 000[15 − (x + h)][(x + h) − 2] − 4, 000(15 − x)(x − 2) = lim h→0 h
−8, 000xh − 4, 000h2 + 68, 000h = lim h→0 h
= lim (−8, 000x − 4, 000h + 68, 000) = −8, 000x + 68, 000 h→0
Vậy P ′(x) = −8, 000x + 68, 000 17
b. Giải phương trình P ′(x) = 0 ta được x trăm đơn vị hay m = 2
xm = 850 đơn vị. Tại mức sản xuất xm = 850 đơn vị do P ′(x) = 0 nên lợi
nhuận không tăng cũng không giảm.
Bài 7 (Bài 46 trang 97). Sản xuất
Lời giải: a. Theo công thức tính tốc độ thay đổi trung bình ta có: √ √ Tốc độ Q(3, 100) − Q(3, 025)
3, 100 3, 100 − 3, 100 3, 025 tb = = ≃ 28.009 3, 100 − 3, 025 75 4
Vậy tốc độ thay đổi trung bình của sản lượng khi số giờ lao động được
sử dụng L thay đổi từ L = 3, 025 giờ đến 3, 100 giờ xấp xỉ bằng 28.009 đơn vị mỗi giờ.
b. Để tìm tốc độ thay đổi tức thời của sản lượng theo số lao động khi
L = 3, 025 giờ ta cần tìm Q′(3, 025). Ta có: √ √ Q(L + h) − Q(L) 3, 100 L + h − 3, 100 L Q′(L) = lim = lim h→0 h h→0 h 3, 100[(L + h) − L] 3, 100h = lim √ √ = lim ( √ √ h→0 h[ L + h + L] h→0 h[ L + h + L] 1, 550 = √L Vậy 1, 550 Q′(3, 025) = √
≃ 28.182 hay tốc độ thay đổi tức thời của sản 3, 025
lượng theo số lao động khi L = 3, 025 giờ xấp xỉ bằng 28.182 đơn vị mỗi giờ.
Bài 8 (Bài 49 trang 97). Tài nguyên tái tạo
Lời giải: Giả sử V = V (t) là hàm số mô tả sự thay đổi của thể tích gỗ V
theo thời gian t. Để tính tốc độ thay đổi tức thời của V theo thời gian khi
t = 30 ta cần tìm V ′(30) hay độ dốc của tiếp tuyến tại điểm có hoành độ t = 30 trên đồ thị.
Từ đồ thị ta xác định được tiếp tuyến tại điểm có hoành độ t = 30 là
đường thẳng đi qua 2 điểm P (30, 50) và Q(50, 65). Do đó tiếp tuyến có độ dốc là 65 − 50 mtt = = 0.75 50 − 30
Vậy tốc độ thay đổi tức thời của V theo thời gian khi t = 30 bằng 0.75 đơn vị mỗi năm.
Khi t tăng (không bị chặn), theo đồ thị, ta thấy tiếp tuyến tại điểm
(t, V (t)) có xu hướng trở thành đường thẳng nằm ngang. Vì vậy độ dốc của
tiếp tuyến có xu hướng dần đến 0, hay tốc độ thay đổi của V khi t tăng
không bị chặn (nghĩa là, trong dài hạn) sẽ giảm dần về 0.
Bài 9 (Bài 52 trang 98). Tăng trưởng dân số 5
Lời giải: a. Tốc độ thay đổi trung bình của dân số từ năm 2010 (t = 0) đến năm 2012 (t = 2) là: Tốc độ P (2) − P (0) 151 − 151 tb = = = 0 2 − 0 2
Vậy tốc độ thay đổi trung bình của dân số theo thời gian từ năm 2010
đến năm 2012 bằng 0 nghìn người mỗi năm.
b. Tốc độ thay đổi tức thời của dân số theo thời gian vào năm 2012 (t = 2) chính là P ′(2).
Theo định nghĩa đạo hàm ta có: P (t + h) − P (t) P ′(t) = lim h→0 h
[−6(t + h)2 + 12(t + h) + 151] − [−6t2 + 12t + 151] = lim h→0 h −12th − 6h2 + 12h = lim = lim (−12t − 6h + 12) h→0 h h→0 = −12t + 12
Do đó P ′(2) = −12 hay tốc độ thay đổi tức thời của dân số theo thời
gian vào năm 2012 (t = 2) là −12 nghìn người mỗi năm.
Vì P ′(2) = −12 < 0 nên dân số đang có xu hướng giảm tại thời điểm này.
Bài 10 (Bài 53 trang 98). Hành vi của động vật Lời giải: a. Ta có: H(t + h) − H(t) H′(t) = lim h→0 h
[4.4(t + h) − 4.9(t + h)2] − [4.4t − 4.9t2] = lim h→0 h −9.8th − 4.9h2 + 4.4h = lim = lim (−9.8t − 4.9h + 4.4) h→0 h h→0 = −9.8t + 4.4. Vậy H′(t) = −9.8t + 4.4. 6
Tốc độ thay đổi của H(t) sau 1 giây là H′(1) = −5.4 (m/s). Do ở thời
điểm này H′(1) < 0 nên độ cao đang giảm với tốc độ 5.4(m/s).
b. Ta có H′(t) = 0 khi t = 0.449. Do H′(0.449) = 0 nên tiếp tuyến tại điểm
có hoành độ t = 0.449 nằm ngang. Vì vậy tại thời điểm này thì độ cao của
bước nhảy là lớn nhất.
c. Bọ chét rơi xuống mặt đất khi H(t) = 0 và đạt tại t = 0.898. Ở thời điểm
này tốc độ thay đổi của H(t) là H′(0.898) = −4.4(m/s).
CÁC BÀI TẬP TỰ LUYỆN: HƯỚNG DẪN VÀ ĐÁP ÁN
Bài 11 (8, tr. 95). Ta tính đạo hàm theo định nghĩa: f (x + h) − f(x) (−(x + h)3) − (−x3) f ′(x) = lim = lim h→0 h h→0 h
= lim (−3x2 − 3xh − h2) = −3x2 h→0
Độ dốc của tiếp tuyến với đồ thị hàm số tại x = 1 là f′(1) = −3.
Bài 12 (9, tr. 95). Ta tính đạo hàm theo định nghĩa: 2 2 g(t + h) − g(t) − g′(t) = lim = lim t + h t h→0 h h→0 h −2 −2 = lim = h→0 t2 + th t2
Độ dốc của tiếp tuyến với đồ thị hàm số tại 1 1 t = là f′( ) = −8. 2 2
Bài 13 (18, tr. 95). Ta tính đạo hàm theo định nghĩa: f (x + h) − f(x) f ′(x) = lim = lim h→0 h
h→0 2 − 3(x + h)2h − 2 − 3x2 −6xh − 3h2 = lim = lim (−6x − 3h) = −6x h→0 h h→0
Phương trình tiếp tuyến với đồ thị hàm số tại điểm có hoành độ x có dạng: 0
y = f ′(x0)(x − x0) + f(x0)
Tại x0 = 1 ta thu được y = −6x + 5. 7
Bài 14 (22, tr. 95). Tính đạo hàm theo định nghĩa ta thu được f′(x) = −1 1 3
√ . Phương trình tiếp tuyến với đồ thị hàm số tại c = 1 là y = − x + 2x x 2 2
Bài 15 (32, tr. 95). Tốc độ thay đổi dy khi x = −3 là f′(−3). Ta có, dx 1 1 − f (x + h) − f(x) 2 − (x + h) 2 − (−3) f ′(x) = lim = lim h→0 h h→0 h 1 1 = lim = h→0 (2 − x − h)(2 − x) (2 − x)2 Vậy, 1 f ′(−3) = . 25
Bài 16 (36, tr. 95). a. Độ dốc của cát tuyến đi qua hai điểm có hoành độ (x 1 x 2) − (x1) 1 và x2 là f f . Thay x ta thu được kết x 1 = −1 và x2 = − 2 − x1 2 quả 1 − . 3
b. Độ dốc của tiếp tuyến với đồ thị hàm số tại điểm có hoành độ x là 0 f ′(x0). Ta có: x + h x f (x + h) − f(x) − x + h f ′(x) = lim = lim − 1 x − 1 h→0 h h→0 h −h −1 = lim = lim h→0 h(x + h − 1)(x − 1) h→0 (x − 1)2
Thay x0 = −1 vào ta thu được kết quả là −1, lớn hơn kết quả trong câu 4 (a).
Bài 17 (40, tr. 96). a. Tốc độ thay đổi trung bình của s(t) theo t khi t thay đổi từ 1
t = t1 đến t = t2 là s(t2) − s(t1). Thay t ta thu t 1 = 1 và t2 = 2 − t1 4
được kết quả bằng 2 . 3 1
b. Tốc độ thay đổi tức thời của s(t) tại t = 1 là s′(1) = , nhỏ hơn vận tốc 2
trung bình tìm được trong câu (a).
Bài 18 (44, tr. 96). a. Lợi nhuận khi bán được một sản phẩm chính
bằng giá bán trừ đi chi phí sản xuất của sản phẩm đó hay: p − 50 = 8
120 − q − 50 = 70 − q. Như vậy hàm lợi nhuận khi bán được q sản phẩm sẽ
là P (q) = q(70 − q) = 70q − q2.
b. Tính P (20) − P (0) ta thu được kết quả là 50. 20 − 0
c. Tính đạo hàm theo định nghĩa, ta có P ′(20) = 30 > 0. Như vậy lợi nhuận đang tăng. C(11) Bài 19 − C(10) (45, tr. 96). a.
= 2.94 nghìn đô-la mỗi sản phẩm. 11 − 10
b. C′(10) = 2.9 nghìn đô-la mỗi sản phẩm, kết quả này xấp xỉ kết quả thu
được ở câu (a). Do C′(10) > 0, nên nếu tiếp tục tăng mức sản xuất chi phí sẽ tăng.
Bài 20 (48, tr. 97). a. Hàm chi tiêu E(x) = xD(x) = −35x2 + 200x. E(5) b.
− E(4) = −115 đô-la mỗi sản phẩm. 5 − 1
c. E′(4) = −80 đô-la mỗi sản phẩm. Chi tiêu có xu hướng giảm khi x = 4. D(61) Bài 21 − D(60) (55, tr. 98). a.
= 0.0211 mm mỗi mm thủy ngân. 61 − 60
b. D′(60) = 0.022 mm mỗi mm thủy ngân
c. Giải phương trình D′(p) = 0 ta tìm được p = 72.22 mm thủy ngân. Tại
mức áp suất này đường kính của động mạch chủ không tăng cũng không giảm.
Bài 22 (56, tr. 98). a. h(6) = 624 feet. h(6) b. − h(0) = 104 feet/giây. 6 − 0
c. h′(0) = 200 feet/giây và h′(40) = −1080 feet/giây. 2
Bài 23 (57, tr. 99). a. s′(t) = √ m/s. t + 1 b. s′(0) = 2 m/s.
c. s(3) = 4 m và s′(3) = 1 m/s.
Bài 24 (58, tr. 99). a. Đáp án: f′(x) = 3. b. Đáp án: y = 3x − 2. 9
c. Do đồ thị của hàm số là một đường thẳng nên tiếp tuyến với đồ thị hàm
số tại bất cứ điểm nào luôn là chính nó. Từ đó ta dễ dàng tìm được kết quả ở câu (a) và (b).
Bài 25 (66, tr. 171). Hai xe chạy theo hai hướng vuông góc với nhau nên
khoảng cách giữa hai xe sau t giờ là p D(t) = (60t)2 + (45t)2 = 75t
Như vậy tốc độ thay đổi khoảng cách giữa hai xe tại thời điểm 2 giờ sau là D′(2) = 75 miles/giờ.
2.2 Các kỹ thuật tính đạo hàm KIẾN THỨC QUAN TRỌNG Quy tắc tính đạo hàm
• Đạo hàm của hằng số:
d (c) = 0, với mọi hằng số c dx
• Đạo hàm của lũy thừa:
d (xn) = nxn−1, với mọi số thực n dx
• Đạo hàm của tích với hằng số: d d [cf (x)] = c
[f (x)], với c là hằng số dx dx
• Đạo hàm của tổng: Cho f (x); g(x) là các hàm số khả vi, khi đó: d d d [f (x) + g(x)] = [f (x)] + [g(x)] dx dx dx
Tốc độ thay đổi tương đối và tốc độ thay đổi phần trăm
• Tốc độ thay đổi tương đối của Q(x) theo x được tính bởi công thức: Q′(x) Q(x) 10
• Tốc độ thay đổi phần trăm của Q(x) theo x được tính bởi công thức: 100Q′(x) Q(x) Chuyển động thẳng
• Nếu vị trí tại thời điểm t của một vật di chuyển dọc theo một đường thẳng là s(t) thì Vật có vận tốc ds v(t) = s′(t) = dt Vật có gia tốc dv a(t) = v′(t) = dt
• Vật được gọi là đang tiến lên nếu v(t) > 0, đang lùi lại nếu v(t) < 0, đứng yên nếu v(t) = 0.
• Vật đang tăng tốc nếu a(t) > 0 và đang giảm tốc nếu a(t) < 0.
Chuyển động của vật phóng
Một vật được phóng lên theo phương thẳng đứng với gia tốc g ≃
32f t/s2 (tương đương 9.8m/s2). Tại thời điểm t sau khi phóng, độ
cao của vật được tính theo công thức 1 H(t) = − gt2 + V0t + H 2 0 với H và
lần lượt là độ cao và vận tốc ban đầu của vật. 0 V0
HƯỚNG DẪN GIẢI CÁC BÀI TẬP CƠ BẢN
Bài 1 (Bài 24 trang 109). Tính đạo hàm
Lời giải: Ta có thể viết lại hàm số như sau: 3 1 √ f (t) = 2t 2 + 4t− 2 − 2
Áp dụng quy tắc đạo hàm, ta có: df d 3 d 1 d √ d 3 d 1 = [2t 2 ] + [4t− 2 ] − [ 2] = 2 [t 2 ] + 4 [t−2 ] − 0 dt dt dt dt dt dt 3 1 1 3 √ 2
= 2( t 2 ) + 4(− t−2 ) = 3 t − √ 2 2 t3 11
Bài 2 (Bài 33 trang 109). Tìm phương trình tiếp tuyến
Lời giải: Ta có thể viết lại hàm số như sau: y = 2x3 + x2 − 3x
Áp dụng quy tắc đạo hàm, ta có: dy d d d = [2x3] + [x2] − [3x] dx dx dx dx d d d = 2 [x3] + [x2] − 3 [x] dx dx dx = 6x2 + 2x − 3
Từ đó, độ dốc của tiếp tuyến với đồ thị hàm số tại điểm (−1, 2) là
f ′(−1) = 6(−1)2 + 2(−1) − 3 = 1. Vậy phương trình tiếp tuyến cần tìm là:
y − 2 = 1[x − (−1)] hay y = x + 3
Bài 3 (Bài 45 trang 109). Tìm tốc độ thay đổi √ x + x
Lời giải: Tốc độ thay đổi của f (x) = √
theo x tại x = 1 là f′(1). x
Viết lại hàm số dạng tổng như sau: √ 1 f (x) = x + 1 = x2 + 1
Áp dụng quy tắc đạo, ta có: 1 −1 1 f ′(x) = x 2 + 0 = √ 2 2 x Vậy 1 f ′(1) =
hay tốc độ thay đổi của hàm số f(x) tại x = 1 là 1. 2 2
Bài 4 (Bài 47 trang 109). Tìm tốc độ thay đổi tương đối
Lời giải: Tốc độ thay đổi tương đối của hàmf (x) = 2x3 − 5x2 + 4 là f ′(x) 6x2 − 10x = f (x) 2x3 − 5x2 + 4
Vậy tốc độ thay đổi tương đối của f(x) = 2x3 − 5x2 + 4 theo x tại giá
trị x = 1 là 6(1)2 − 10(1) = −4. 2(1)3 − 5(1)2 + 4 12
Bài 5 (Bài 51 trang 110). Thu nhập hàng năm
Lời giải: a. Tốc độ tăng tổng thu nhập của công ty theo thời gian là đạo
hàm A′(t) = 0.2t + 10. Do đó, tốc độ tăng tổng thu nhập của công ty theo
thời gian vào năm 2012 (t = 4) là A′(4) = 0.2(4) + 10 = 10.8 nghìn đô-la mỗi năm.
b. Tốc độ tăng phần trăm của tổng thu nhập theo thời gian là 100A′(t) 20t + 1000 = A(t) 0.1t2 + 10t + 20
Từ đó, tốc độ tăng phần trăm của tổng thu nhập theo thời gian vào năm 2012 (t = 4) là 20(4) + 1000 ≃ 17.53(%). 0.1(4)2 + 10(4) + 20
Bài 6 (Bài 54 trang 110). Quảng cáo
Lời giải: Tốc độ thay đổi của doanh số theo chi phí quảng cáo là đạo hàm 125 1, 034 M ′(x) = − + . x2 x3
Vì vậy, khi chi phí quảng cáo là $9,000 (x = 9), tốc độ thay đổi của doanh số là 125 1, 034 M ′(9) = − +
≃ −0.125 (sản phẩm với mỗi nghìn 92 93 đô-la).
Do M′(9) < 0, nên doanh số đang giảm tại mức chi tiêu cho quảng cáo này.
Bài 7 (Bài 55 trang 110). Quản lý chi phí
Lời giải: a. Tổng chi phí cho chuyến đi là
C(x) = chi phí cho nhiên liệu + chi phí cho lái xe 1 9, 800 = (20) = 4x + 1, 200 25 x 0 x + x (250)(4) + 250 x 9, 800
b. Tốc độ thay đổi của chi phí C(x) theo x là đạo hàm C′(x) = 4− . x2
Vì vậy, khi xe tải chạy với tốc độ 40 miles mỗi giờ (x = 40) thì tốc độ thay đổi của chi phí là 9, 800 C′(40) = 4 −
= −2.125 (đô-la mỗi mile mỗi 402 giờ).
Do C′(40) < 0 nên tổng chi phí đang giảm tại thời điểm xe tải chạy với
tốc độ 40 miles mỗi giờ. 13
Bài 8 (Bài 58 trang 110). Tổng sản phẩm trong nước
Lời giải: Giả sử tổng sản phẩm trong nước của một quốc gia t năm sau kể
từ năm 2000 là N(t) tỷ đô-la. Theo giả thiết, tổng sản trong nước tăng với
tốc độ không đổi nên hàm N(t) là hàm tuyến tính có dạng N(t) = at + b
(a, b là hằng số). Vì năm 2000 (t = 0), GDP đạt 125 tỷ đô-la nên ta có: N (0) = a(0) + b = 125 (1)
Tương tự, năm 2008 (t = 8), GDP đạt 155 tỷ đô-la nên N (8) = a(8) + b = 155 (2)
Từ (1) và (2) ta tìm được a = 3.75, b = 125. Do đó, tổng sản phẩm trong
nước t năm sau kể từ năm 2000 là N(t) = 3.75t + 125 tỷ đô-la.
Tốc độ thay đổi phần trăm của GDP năm 2015 (t = 15) là 100N ′(15) 100(3.75) = = 2.07(%). N (15) 3.75(15) + 125
Bài 9 (Bài 62 trang 111). Tăng trưởng dân số
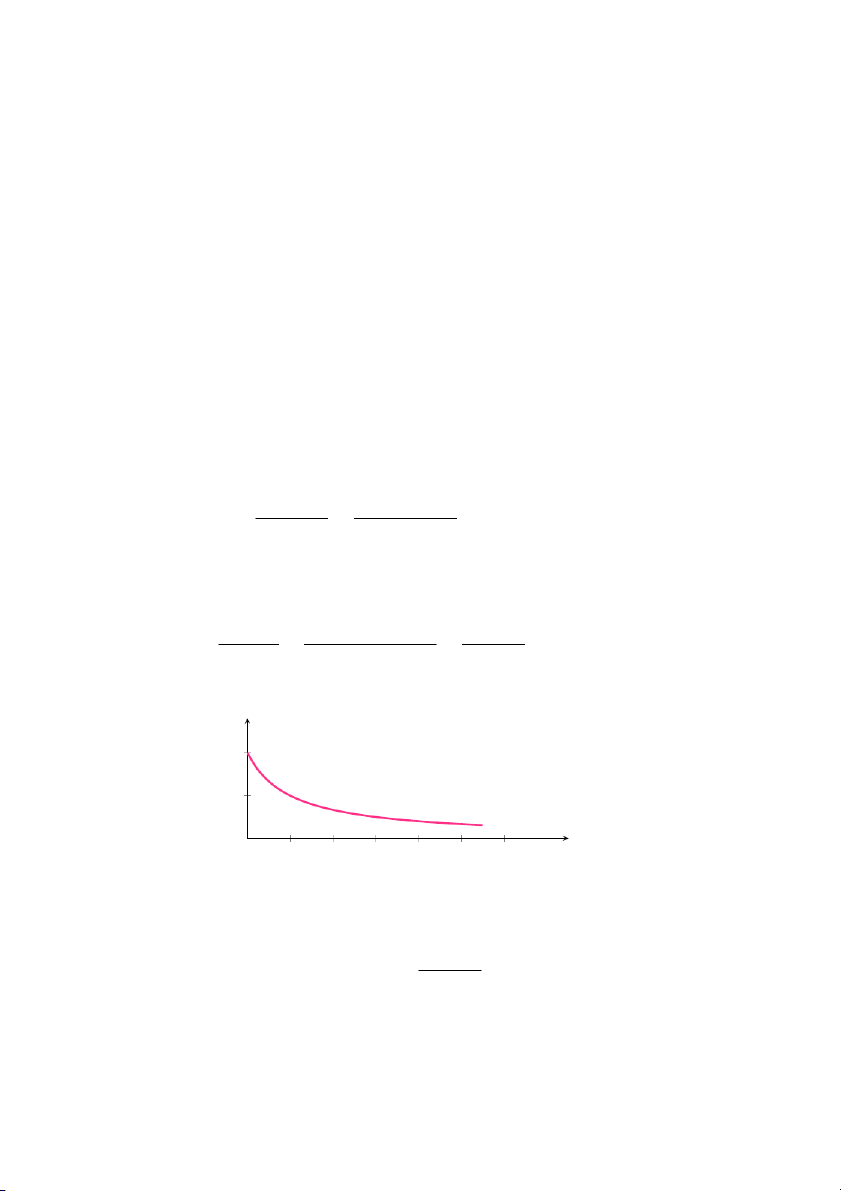
Lời giải: a. Tốc độ thay đổi phần trăm của dân số theo thời gian là 100P ′(t) 100(2t + 200) 2 = = = f (t) P (t) t2 + 200t + 10, 000 0.01t + 1
Đồ thị của hàm số f(t) được thể hiện trong hình sau. 2 1 f (t) t (trăm) 0 1 2 3 4 5 6
b. Trong dài hạn, tốc độ thay đổi phần trăm của dân số theo thời gian
là giới hạn của f(t) khi t tăng không bị chặn ( nghĩa là t → +∞) và bằng 2 lim f (t) = lim = 0 t→+∞ t→+∞ 0.01t + 1 14
Bài 10 (Bài 65 trang 111). Điểu học Lời giải: a. Ta có:
T ′(t) = −204.21t2 + 61.96t + 12.52
Đạo hàm T ′(t) cho biết tốc độ thay đổi nhiệt độ cơ thể của một loại chim theo thời gian t.
b. Tốc độ thay đổi của thân nhiệt của loài chim ở thời điểm đầu (t = 0)
là T ′(0) = 12.52 (0C/ngày). Do T ′(0) > 0 nên thân nhiệt của loài chim
đang tăng tại thời điểm này.
Tốc độ thay đổi của thân nhiệt của loài chim ở thời điểm cuối (t = 0.713)
là T ′(0.713) = −47.12(0C/ngày). Do T′(0.713) < 0 nên thân nhiệt của loài
chim đang giảm ở thời điểm này.
c. Thân nhiệt của loài chim không thay đổi tại thời điểm T ′(t) = 0.
Giải phương trình T ′(t) = 0 cho kết quả t = 0.442 ngày hay 10.61 giờ.
Khi đó nhiệt độ là T (0.442) = 42.80C, đây là nhiệt độ cao nhất trong một chu kì thời gian.
Bài 11 (Bài 69 trang 112). Truyện trinh thám
Lời giải: Chàng điệp viên ném hòn đá theo phương thẳng đứng từ mặt đất
(H0 = 0), nên độ cao của hòn đá so với mặt đất tại thời điểm t sau khi ném là 1 H(t) = − gt2 + v 2 0t.
Gọi t là thời điểm khi hòn đá ở độ cao tối đa, ta có: 0 gt2 . ( ( 2 0 + v0t0 = 37 5 ⇒ v20 = 75g (1) H(t −gt0 + v0 = 0 0) = 37.5 −1 ⇐⇒ H′(t0) = 0
Mặt khác, hòn đá chạm đất sau 5 giây khi nó rời khỏi tay anh ấy nên 1 H(5) = 0 ⇐⇒ − g(5)2 + v 2 0(5) = 0 ⇐⇒ v0 = 2.5g (2)
Từ (1) và (2) ta tìm được g = 12 (ft/s2). Do đó, chàng điệp viên đang ở trên Sao Hỏa. 15
Bài 12 (Bài 72 trang 112). Chuyển động thẳng ds
Lời giải: a. Vận tốc của vật là v(t) = = 3t2 − 18t + 15. dt Gia tốc của vật là dv a(t) = = 6t − 18. dt
b. Ta có v(t) = 3(t − 1)(t − 5).
Vật đứng yên khi v(t) = 0 (0 ≤ t ≤ 6) ⇐⇒ t = 1 hoặc t = 5.
Vậy vật đứng yên tại hai thời điểm là t = 1 và t = 5.
CÁC BÀI TẬP TỰ LUYỆN: HƯỚNG DẪN VÀ ĐÁP ÁN
Bài 13 (22, tr. 109). Ta biến đổi hàm số đã cho về dạng: 2 y = 3x−1 − 2x−2 + x−3 3
sau đó dễ dàng tính đạo hàm thu được kết quả là 3 4 2 − + − . x2 x3 x4
Bài 14 (27, tr. 109). Ta thực hiện phép chia, đưa hàm số về dạng: x5 − 4x2 y = = x2 − 4x−1 x3
sau đó tính đạo hàm ta thu được kết quả là 4 2x + . x2
Bài 15 (28, tr. 109). Ta nhân đa thức trước và đưa hàm số về dạng:
y = x2(x3 − 6x + 7) = x5 − 6x3 + 7x2
tính đạo hàm ta thu được kết quả là 5x4 − 18x2 + 14x. 9x Bài 16 − 1 (34, tr. 109). Đáp án: y = 2
Bài 17 (40, tr.109). Đáp án: y = 2x − 4
Bài 18 (46, tr. 109). Đáp án: f′(1) = −72 4
Bài 19 (50, tr. 109). Đáp án: f′(3) = − f (3) 3 16
Bài 20 (52, tr. 110). a. Tính f′(x) = −3x2 + 12x + 15.
b. Tính f′(1) = 24 và f(2) − f(1) = 26.
c. So sánh f′(1) và f′(4) ta có f′(4) = 15 < f′(1) = 24. Vậy Lupe đã đúng.
Bài 21 (56, tr. 110). a. C′(t) = 200t + 400.
b. C′(5) = 1, 400 tờ báo mỗi năm, lượng phát hành đang tăng tại thời điểm đó .
c. Tính C(6) − C(5) = 1, 500 tờ báo.
Bài 22 (57, tr. 110). a. Hàm số biểu diễn mức lương của Gary sau t năm
làm việc: S(t) = 45, 000+2, 000t. Tốc độ thay đổi phần trăm của mức lương của Gary sau S′(t 200 t năm là 100 ) = . S(t) 45 + 2t
b. Thay t = 1 vào công thức ở phần (a) ta thu được kết quả là 4.26%. 200 c. Ta xét lim
= 0. Như vậy trong dài hạn tốc độ thay đổi phần t→∞ 45 + 2t
trăm của mức lương gần tới 0.
Bài 23 (60, tr. 111). a. N′(8) = 1, 652 lượt mỗituần.
b. N(8) − N(7) = 1, 514 lượt.
Bài 24 (64a;b, tr.111). a. N′(3) = 108 người mỗi tuần .
b. Tính tốc dộ thay đổi phần trăm của N: 100N ′(t) 100(−4t3 + 24t2) = N (t) 5, 175 − t4 + 8t3
Ta chứng minh được tốc độ thay đổi phần trăm của N không khi nào vượt
quá 25%, vì vậy tổ chức y tế sẽ không phải ban bố trình trạng dịch bệnh.
Bài 25 (70, tr. 112). a. v(t) = s′(t) = 2t − 2 và a(t) = v′(t) = 2.
b. Vật đứng yên khi v(t) = 0. Ta tìm được t = 1.
Bài 26 (74, tr. 112). a. Độ cao của hòn đá tại thời điểm t là 1 H(t) = − gt2 + V0t + H 2 0 = −16t2 + 144
Hòn đá chạm đất khi H(t) = 0, suy ra t = 3. Vậy 3 giây sau khi thả hòn đá sẽ chạm đất.
b. Vận tốc hòn đá khi nó chạm đất v(3) = H′(3) = −96 feet/giây. 17
Bài 27 (76, tr. 112). Phương trình tiếp tuyến với đồ thị hàm số đã cho
tại điểm có hoành độ x có dạng: 0 y = f ′(x 2
0)(x − x0) + f (x0) = (2x0 − 4)(x − x0) + x0 − 4x0 + 25 = (2x 2 0 − 4)x − x0 + 25
nếu tiếp tuyến này đi qua gốc tọa độ (0, 0) thì phải thỏa mãn 0 = −x 2 0 + 25.
Ta tìm được hai giá trị x thỏa mãn là 0
x0 = −5 và x0 = 5, tương ứng là hai
đường tiếp tuyến với phương trình là y = −14x và y = 6x.
2.3 Quy tắc đạo hàm của tích và thương; Đạo hàm cấp cao KIẾN THỨC QUAN TRỌNG
Quy tắc đạo hàm của tích, thương
• Đạo hàm của tích: Nếu các hàm số f (x) và g(x) khả vi tại x thì tích
f (x)g(x) cũng khả vi tại x và d d d [f g] = g [f ] + f [g] dx dx dx
• Đạo hàm của thương: Nếu f (x) và g(x) khả vi tại x và g(x) 6= 0 thì
thương f(x) cũng khả vi tại x và g(x) d d d g [f ] − f [g] dx dx g2 f = dc g Đạo hàm cấp cao
• Đạo hàm cấp hai của một hàm số là đạo hàm của đạo hàm của hàm số đó.
Ký hiệu đạo hàm cấp hai của hàm số y = f(x) là f′′(x) hoặc d2y . dx2 Quy tắc tính: d2y d = dx2 dy . dx dx 18
Đạo hàm cấp hai của một hàm số biểu thị tốc độ thay đổi của tốc độ
thay đổi của hàm số đó.
Chú ý: Hàm gia tốc a(t) của một vật chuyển động thẳng là đạo hàm
của hàm vận tốc v(t), do đó là đạo hàm cấp hai của hàm quãng đường s(t). d2s a(t) = dt2
• Với n là số nguyên dương bất kỳ, đạo hàm cấp n của một hàm số được
xác định bằng cách lấy đạo hàm của hàm số đó liên tiếp n lần.
Đạo hàm cấp n của hàm số y = f(x) được ký hiệu là f (n)(x) hoặc dny dxn Quy tắc tính: dny d = dxn dn−1y dx dxn−1
HƯỚNG DẪN GIẢI CÁC BÀI TẬP CƠ BẢN
Bài 1 (Bài 3 trang 122). Tìm đạo hàm của hàm số
Lời giải: Áp dụng quy tắc đạo hàm của tích, ta có: dy d d = 10(1 − 5u) [3u + 1] + 10(3u + 1) [1 − 5u] du du du
= 10(1 − 5u)(3) + 10(3u + 1)(−5) = −300u − 20
Vậy đạo hàm cần tìm là dy = −300u − 20. du
Bài 2 (Bài 21 trang 123). Tìm phương trình tiếp tuyến
Lời giải: Áp dụng quy tắc đạo hàm của thương, ta có: d d dy (2x + 3) [x] − x [2x + 3] (2x + 3)(1) − x(2) 3 = dx dx = = dx (2x + 3)2 (2x + 3)2 (2x + 3)2
Từ đó, độ dốc của tiếp tuyến với đồ thị hàm số tại điểm có hoành độ x0 = −1 là 3
= 3. Để tìm phương trình đường tiếp tuyến, ta xác [2(−1) + 3]2 định tọa độ −1 y của tiếp điểm là y = = −1. 2(−1) + 3 19
Vậy phương trình tiếp tuyến cần tìm là
y − (−1) = 3[x − (−1)] hay y = 3x + 2
Bài 3 (Bài 29 trang 123). Tìm tốc độ thay đổi
Lời giải: Áp dụng quy tắc đạo hàm của tích, ta có: dy d d = (5 − 2x3) [x2 + 3] + (x2 + 3) [5 − 2x3] dx dx dx
= (5 − 2x3)(2x) + (x2 + 3)(−6x2) = −10x4 − 18x2 + 10x
Vậy tốc độ thay đổi dy tại x
−10(1)4 − 18(1)2 + 10(1) = −18 dx 0 = 1 là .
Bài 4 (Bài 36 trang 123). Tìm đạo hàm của hàm số
Lời giải: Áp dụng quy tắc đạo hàm của tích, ta có:
h′(x) = 2xg(x) + (x2 + 3)g′(x)
Vì vậy, tại x = 2 ta có đạo hàm là
h′(2) = 2(2)g(2) + [(2)2 + 3]g′(2) = 4(3) + 7(−2) = −2
(vì g(2) = 3 và g′(2) = −2).
Bài 5 (Bài 46 trang 124). Tìm đạo hàm cấp hai
Lời giải: Áp dụng quy tắc đạo hàm của tích, ta có: dy d [x2 − x] + (x2 − x) 1 d dx 1 = 2x − 2x − dx x dx x 1 1 = 2x − (2x − 1) + (x2 − x) 2 + = 6x2 − x 4 − 1 x2
Do đó, đạo hàm cấp hai của hàm số đã cho là d2y d = [6x2 − 4x − 1] = 12x − 4 dx2 dx
Bài 6 (Bài 48 trang 124). Cầu và doanh thu 20
Lời giải: a. Tốc độ thay đổi của p(x) theo x khi hãng sản xuất 3,000 chiếc
máy tính (x = 3) là p′(3).
Áp dụng quy tắc đạo hàm của thương, ta có: d d (0.3x2 + 8) [1, 000] − 1, 000 [0.3x2 + 8] −600x p′(x) = dx dx = (0.3x2 + 8)2 (0.3x2 + 8)2 Vậy −600(3) p′(3) =
= −15.72, hay tốc độ thay đổi của p(x) theo [0.3(3)2 + 8]2
x khi hãng sản xuất 3,000 chiếc máy tính là −15.72 đô-la/nghìn chiếc. 1, 000x
b. Doanh thu từ việc bán x nghìn chiếc máy tính là R(x) = . 0.3x2 + 8
Tốc độ thay đổi của doanh thu khi hãng sản xuất 3,000 chiếc máy tính (x = 3) là R′(3).
Áp dụng quy tắc lấy đạo hàm của thương, ta có: d d (0.3x2 + 8) [1, 000x] − 1, 000x [0.3x2 + 8] −300x2 + 8, 000 R′(x) = dx dx = (0.3x2 + 8)2 (0.3x2 + 8)2 Vậy −300(3)2 + 8, 000 R′(3) =
≃ 46.29, hay tốc độ thay đổi của doanh thu (0.3(3)2 + 8)2
khi hãng sản xuất 3,000 chiếc máy tính (x = 3) xấp xỉ bằng 46.29 nghìn đô-la/nghìn chiếc.
Do R′(3) > 0 nên doanh thu đang tăng ở mức sản xuất này.
Bài 7 (Bài 51 trang 124). Quảng cáo
Lời giải: a. Áp dụng quy tắc lấy đạo hàm của thương, ta có: d d (t2 + 10t + 30)
[t2 + 5t + 5] − (t2 + 5t + 5) [t2 + 10t + 30] P ′(t) = 100 dt dt (t2 + 10t + 30)2 500(t2 + 10t + 20) = (t2 + 10t + 30)2
Tốc độ thay đổi của phần trăm thị trường tiềm năng P (t) theo thời gian sau 5 tuần 500[(5)2 + 10(5) + 20] (t = 5) là P ′(5) = ≃ 4.31 (% mỗi tuần) [52 + 10(5) + 30]2 21
Thị trường tiềm năng ở thời điểm này đang tăng vì P ′(5) > 0. b. Ta có: 5 5 t2 + 5t + 5 1 + + lim P (t) = 100 lim = 100 lim t t2 = 100 t→+∞ t→+∞ t2 + 10t + 30 t→+∞ 10 30 1 + + t t2 và 500t2 + 5, 000t + 10, 000 lim P ′(t) = lim t 2 →+∞ t→+∞ (t2 + 10t + 30) 500 5, 000 10, 000 + + = lim t2 t3 t4 t→+∞ 30 + = 0 2 10 t 1 + t2
Vì vậy, trong dài hạn, P (t) tiến gần đến 100% và tốc độ thay đổi của
P (t) theo thời gian tiến gần đến 0.
Bài 8 (Bài 53 trang 124). Doanh thu
Lời giải: a. Giả sử p(t); x(t) là giá bán và mức sản xuất tại tuần thứ t kể
từ thời điểm hiện tại.
Theo giả thiết, giá đang tăng với tốc độ 5 cents mỗi tuần và tại thời
điểm hiện tại (t = 0) có p(0) = 5. Nên ta có hàm p(t) = 0.05t + 5 (1).
Mặt khác, cầu hàng hóa đang giảm với tốc độ 4 đơn vị mỗi tuần và tại
thời điểm hiện tại (t = 0) có p(0) = 1, 000. Nên ta có hàm x(t) = −4t+1, 000 (2).
Từ (2), ta có: t = 250−0.25x. Thay t vào (1), ta được: p = 17.5−0.0125x.
Vì vậy, doanh thu tại thời điểm thứ t là R(x) = px = 17.5x − 0.0125x2.
Tốc độ thay đổi của R(x) theo x là R′(x) = 17.5 − 0.025x đô-la mỗi đơn
vị. Vì vậy, tại thời điểm hiện tại (x = 1, 000), tốc độ thay đổi của R(x) theo
x là R′(1, 000) = 17.5 − 0.025(1, 000) = −7.5 đô-la mỗi đơn vị.
Do R′(1, 000) < 0, nên doanh thu tại thời điểm hiện tại đang giảm.
b. Doanh thu bình quân là R(x) = 17.5 − 0.0125x. x 22 ′ đô- T laốc m đ ỗ ộ i t đ h ơ a n yvịđ.ổi Vìcủ v a ậy do d a o n a h n th t u h bì b n ì h n qu q â u n â là R(x) dang giảm ở =t − hờ 0 i .0 đi125 ểm < hi 0 ện x tại.
Bài 9 (Bài 55 trang 125). Kiểm soát ô nhiễm
Lời giải: a. Tốc độ thay đổi của tỷ lệ ô nhiễm được kiểm soát khi dùng x
triệu đô-la cho chi phí của hoạt động này là P ′(x).
Áp dụng quy tắc đạo hàm của thương, ta có: d √ √ d (0.03x2 + 9) [100 x] − 100 x [0.03x2 + 9] P ′(x) = dx dx (0.03x2 + 9)2 −4.5x2 + 450 = √x(0.03x2 + 9)2
Vậy, tốc độ thay đổi của tỷ lệ ô nhiễm được kiểm soát nếu chi 16 triệu
đô-la cho hoạt động này là P ′(16) ≃ −0.631 % mỗi triệu đô-la.
Do P ′(16) < 0, nên tại mức chi phí này tỷ lệ ô nhiễm được kiểm soát đang giảm.
b. Tỷ lệ P (x) tăng khi P ′(x) > 0 ⇐⇒ −4.5x2 + 450 > 0 ⇐⇒ 0 < x < 10.
Tỷ lệ P (x) giảm khi P ′(x) < 0 ⇐⇒ −4, 5x2 + 450 < 0 ⇐⇒ x > 10.
Bài 10 (Bài 59 trang 125). Tăng trưởng dân số
Lời giải: a. Tốc độ thay đổi dân số theo thời gian sau t năm tính từ năm hiện tại là P ′(t). Ta có: d 6 6 P ′(t) = [20 − ] = dt t + 1 (t + 1)2
b. Sau 1 năm tính từ năm hiện tại, tốc độ thay đổi dân số là P ′(1) = 6
= 1.5 nghìn người mỗi năm. (1 + 1)2
c. Dân số thực tế tăng lên trong năm thứ hai là 6 6 P (2) − P (1) = (20 − ) − (20 − ) = 1 nghìn người. 2 + 1 1 + 1 23 6
d. Tốc độ tăng dân số sau 9 năm kể từ năm hiện tại là P ′(9) = = (9 + 1)2
0.06 nghìn người mỗi năm.
e. Trong dài hạn, tốc độ thay đổi dân số là giới hạn của P ′(t) khi t tăng
không bị chặn, nghĩa là t → +∞. Ta có: 6 lim P ′(t) = lim = 0 t→+∞ t→+∞ (t + 1)2
Vậy, trong dài hạn, tốc độ thay đổi dân số tiến gần đến 0. ‘
Bài 11 (Bài 60 trang 125). Sản xuất tế bào máu
Lời giải: a. Tốc độ sản sinh bạch cầu p′(x) là d d (B + xm) [Ax] − Ax [B + xm] AB + A(1 − m)xm p′(x) = dx dx = (B + xm)2 (B + xm)2
b. Đạo hàm cấp hai p′′(x) là
Amxm−1[−(1 + m)B + (m − 1)xm] p′′(x) = [p′(x)]′ = (B + xm)3 Ta có:
p′′(x) = 0 ⇐⇒ Amxm−1[−(1 + m)B + (m − 1)xm] = 0
Nếu 0 < m ≤ 1 thì p′′(x) = 0 ⇐⇒ x ∈ ∅. m 1. Nếu (1 + m)B
m > 1 thì p′′(x) = 0 ⇐⇒ x = m − 1
Bài 12 (Bài 65 trang 126). Tìm vận tốc
Lời giải: a. Vận tốc của vật là dD 5 v(t) = = 10 − dt (t + 1)2 24
Vậy vận tốc của vật sau 4 phút chuyển động là 5 v(4) = 10− = 9.8 (4 + 1)2 (mét/phút).
b. Quãng đường thực tế vật đi được trong phút thứ 5 là 5 5 D(5) − D(4) = (10(5) + − 5) − (10(4) − − 5) ≃ 9.83m. 5 + 1 4 + 1
CÁC BÀI TẬP TỰ LUYỆN: HƯỚNG DẪN VÀ ĐÁP ÁN Bài 13 (6, tr. 122). d √ √ d ( x + 2x) + ( x + 2x) dxd [f (x)] = −3 5x3 − 2x + 5 5x3 − 2x + 5 dx dx 1 √ = −3 5x3 − 10 2 5 x + 5 √ + 2 + ( x 1 + 5 2x) 15x2 √ − 2 = 2 x −120x3 −
x2√x + 24x + 9 x − √ − 30 2 2 x
Bài 14 (8, tr.122). Đáp án: 23 (5x + 4)2 Bài 15 (14, tr.123). d d (2x − 1) (2x − 1) dx d [f (x)] =
−x3 + 3x2 + 3x + 4 − 2−x3 + 3x2 + 3x + 4 dx dx (2x − 1) 2 (2x − 1) −3x2 + 6x + ( 3 2x −
− 1) −x3 + 3x2 + 3x + 4 (2)
= −6x3 + 12x2 + 6x + 3x2 − 6x − 3 + 2x3 − 6x2 − 6x − 8 = (2x − 1)2 −4x3 + 9x2 − 6x − 11 = (2x − 1)2
Bài 16 (16, tr.122). Ta khai triển về dạng tổng rồi tính đạo hàm. Đáp án là: 2 2x − . x3 x2 − 8x − 1
Bài 17 (18, tr. 123). Đáp án: (−x2 − 1) + (x2 − 1)2 (x2 + 1)2 19 7
Bài 18 (22, tr. 123). Đáp án: y = x + 25 5 25
Bài 19 (28, tr. 123). Đáp án: 141 2 Bài 20 (38, tr. 123). d h′(x) = 3x2 − 5g(x) dx g(x) + d 4 (g(x) + 4) (g(x) + 4) dx d =
3x2 − 5g(x) − 3x2 − 5g(x) dx (g(x) + 4)2 (6x − 5g′(x)) (g(x) (g+ (x4)) − + 4)23x2 − 5g(x) g′(x) =
Thay x = 0; g(0) = 2; g′(0) = −3 vào biểu thức trên ta thu được kết quả bằng 5. 3 8, 000
Bài 21 (49, tr. 124). a. Tính S′(t) = , sau đó thay t = 2 ta (4 + 0.3t)2
thu được kết quả xấp xỉ là 378.072. Vậy trong năm 2012, doanh số thay đổi
với tốc độ 378, 072 đô-la mỗi năm. , b. Ta tìm 20, 000 lim S(t) =
. Trong dài hạn doanh số sẽ đạt mức 20 000 t→+∞ 3 3 nghìn đô-la.
Bài 22 (50, tr. 124). a. Lập hàm lợi nhuận theo p: 500p P (p) = pB(p) − C(p) =
− (0.2p2 + 3p + 200) (đô-la) p + 3
b. Tìm P ′(p) và thay p = 12 ta thu được kết quả xấp xỉ bằng −1.133. Như
vậy lợi nhuận đang giảm tại mức giá này.
Bài 23 (52, tr. 124). a. Đáp án: R(t) = −3t2 + 16t + 15
b. Đáp án: R(1) = 28 sản phẩm mỗi giờ.
b. Hàm lợi nhuận bình quân: P (x) = 155 − 0.375x. Tính đạo hàm hàm số x
này và thay x = 400 ta thu được kết quả là −0.375. Lợi nhuận bình quân đang giảm.
Bài 24 (56, tr. 125). a. Ta có: −4(2t + 3)(3t − 2) P ′(t) = (t2 + 1)2 26
Tính P ′(1) = −5. Số lượng vi khuẩn đang giảm.
b. Số lượng vi khuẩn giảm nếu P ′(t) < 0, tức là khi t < −3 hoặc t > 2 . 2 3
Vậy sau 40 phút nữa, số lượng vi khuẩn bắt đầu giảm. 32 Bài 25 − 6t2 (58, tr. 125). a. R(t) = (3t2 + 16)3 và 36t t2 − 16 R′(t) = 26 (3t2 + 16)2 b. R(1) =
. Nồng độ thuốc đang tăng. 361 4 4
c. Ta có R(t) < 0 khi t < −√ hoặc t > √ . Vậy nồng độ thuốc bắt đầu 3 3 giảm tại thời điểm 4 t = √ = 2.3. 3
d. Nồng độ thuốc trong cơ thể thay đổi với tốc độ giảm dần khi R′(t) < 0 hay 0 < t < 4. 20 Bài 26 − 4t (66, tr. 126). a. D′′(t) = 3 4
b. D′′(6) = − km mỗi giờ, mỗi giờ. Vận tốc đang giảm. 3
c. D′(7) − D′(6) = −2 km.
2.4 Quy tắc đạo hàm của hàm hợp KIẾN THỨC QUAN TRỌNG
Quy tắc đạo hàm của hàm hợp
• Nếu y = f (u) là một hàm khả vi của u và u = g(x) là một hàm khả
vi của x thì hàm hợp y = f[g(x)] là một hàm khả vi của x và có đạo
hàm được tính theo công thức dy dy du = dx du dx Hoặc tương đương dy = f′[g(x)]g′(x) dx
• Quy tắc lũy thừa tổng quát 27
Với mọi số thực n và hàm khả vi h, ta có:
d [h(x)]n = n[h(x)]n−1 d [h(x)] dx dx
HƯỚNG DẪN GIẢI CÁC BÀI TẬP CƠ BẢN
Bài 1 (Bài 9 trang 136). Sử dụng quy tắc đạo hàm của hàm hợp
Lời giải: Áp dụng quy tắc đạo hàm của hàm hợp, ta có: dy dy du = dx du dx Trong đó dy d d √ 1 =
[u2 + 2u − 3] = 2u + 2 và du = [ x] = √ du du dx dx 2 x
Vậy đạo hàm của hàm hợp cần tìm là √ dy 1 x + 1 = (2u + 2) √ hay dy = √ dx 2 x dx x .
Bài 2 (Bài 25 trang 136). Sử dụng quy tắc lũy thừa tổng quát
Lời giải: Áp dụng quy tắc lũy thừa tổng quát, ta có: d f ′(x) =
[(x5 − 4x3 − 7)8] = 8(x5 − 4x3 − 7)7 d [x5 − 4x3 − 7] dx dx
= 8(x5 − 4x3 − 7)7(5x4 − 12x2)
= 8x2(x5 − 4x3 − 7)7(5x2 − 12).
Bài 3 (Bài 56 trang 137). Tìm đạo hàm cấp hai
Lời giải: Hàm số có thể viết lại dạng hàm lũy thừa f (t) = 2(5t + 1)−1.
Áp dụng quy tắc lũy thừa tổng quát, ta có:
f ′(t) = 2(−1)(5t + 1)−2 d [5t + 1] = −10(5t + 1)−2 dt
Đạo hàm cấp hai của hàm số là d 100 f ′′(t) =
[−10(5t + 1)−2] = −10(−2)(5t + 1)−3 d [5t + 1] = . dt dt (5t + 1)3 28
Bài 4 (Bài 61 trang 137). Tìm đạo hàm của hàm số 1
Lời giải: Ta có thể viết lại hàm số h(x) = [5x2 + g(x)] 2 .
Áp dụng quy tắc lũy thừa tổng quát, ta có: 1 1 d h′(x) = [5x2 + g(x)]− 2 [5x2 + g(x)] 2 dx 1 1 =
[5x2 + g(x)]− 2 [10x + g′(x)]. 2
Theo giả thiết, g(0) = 4 và g′(0) = 2, nên ta có: 1 1 1 1 1
h′(0) = [5(0)2 + g(0)]−2 [10(0) + g′(0)] = [0 + 4]−2 [0 + 2] = . 2 2 2
Bài 5 (Bài 65 trang 137). Thu nhập hàng năm
Lời giải: a. Tốc độ thay đổi của tổng thu nhập của công ty vào tháng 1 năm 2015 (t = 5) là f′(5) Ta có: 20t + 1 f ′(t) = √ 2 10t2 + t + 229 Vì vậy 20(5) + 1 f ′(5) = 101 p =
≃ 2.295 hay tốc độ thay đổi 44 2 10(5)2 + 5 + 229
của tổng thu nhập của công ty vào tháng 1 năm 2015 xấp xỉ 2.295 nghìn đô-la mỗi năm.
b. Tốc độ thay đổi phần trăm của tổng thu nhập của công ty đó vào tháng 1 năm 2015 (t = 5) là 100f ′(5) = 101 ≃ 10.43(% mỗi năm). f (5) 100 2244
Bài 6 (Bài 67 trang 137). Cầu tiêu dùng
Lời giải: a. Tốc độ thay đổi của cầu đối với cà phê theo giá là đạo hàm D′(p).
Áp dụng quy tắc lũy thừa tổng quát, ta có: d 8, 750 D′(p) =
[4, 375p−2] = 4, 375(−2)p−3 = − dp p3 29
Do đó, tốc độ thay đổi của cầu đối với cà phê theo giá khi giá $9 là 8, 750 D′(9) = −
≃ −12 pounds mỗi đô-la. 93
b. Tại thời điểm 10 tuần sau tính từ thời điểm hiện tại (t = 10), giá bán
mỗi pound cà phê là p(10) = 0.02(10)2 + 0.1(10) + 6 = 9($). Khi đó, tốc độ
thay đổi của cầu đối với cà phê theo thời gian là dD .
Áp dụng quy tắc đao hàm của hàm hợp, ta có d : t t=10 dD dD dp = dt dp dt t=10 p=9 t=10 trong đó dD = D′(9) = −12 và dp = (0.04t + 0.1)|t=10 = 0.5. dp dt p=9 t=10
Vậy, ở thời điểm 10 tuần sau tính từ thời điểm hiện tại (t = 10), tốc độ
thay đổi của cầu đối với cà phê thời gian là (−12)(0.5) = −6 pounds mỗi tuần. Do dD
< 0 nên cầu đối với cà phê đang giảm. dt Bài 7 t (Bài 71 tr = a 10 ng 138). Sản xuất
Lời giải: a. Chi tiêu cho vốn sau 3 tháng kể từ thời điểm hiện tại (t = 3) là 2(3)4 + 3(3) + 149 K(3) = = 64 nghìn đô-la. 3 + 2
Khi đó, số đơn vị hàng hóa được sản xuất là 2 Q(64) = 500(64) 3 = 8, 000 đơn vị.
b. Tại tháng thứ 5 kể từ thời điểm hiện tại (t = 5), chi tiêu cho vốn là 2(5)4 + 3(5) + 149 K(5) = = 202. 5 + 2
Tốc độ thay đổi của sản lượng theo thời gian ở tháng thứ 5 kể từ thời
điểm hiện tại (t = 5) là dQ . Áp dụng quy tắc đạo dt hàm t củ = a 5hàm hợp, ta có: dQ dQ dK = dt dK dt t=5 K=202 t=5 30 trong đó dQ 1, 000 1 1, 000 = K− = √ 3 3 3 202 3 và dK K=202 K=202 dK 6t4 + 16t3 − 143 801 = = . 7 dt (t + 2)2 t=5 t=5
Vậy, ở thời điểm 5 tháng sau tính từ thời điểm hiện tại (t = 5), tốc độ
thay đổi của sản lượng theo thời gian là 1, 000 801 √ ≃ 6, 501 đơn vị mỗi 3 3 202 7 tháng. Do dQ
> 0 nên sản lượng đang tăng. dt Bài 8 (Bài 73 tr t a=5 ng 138). Lãi gộp
Lời giải: a. Tốc độ thay đổi tức thời của A theo r là đạo hàm A′(r).
Áp dụng quy tắc lũy thừa tổng quát, ta có: 0.01r [1 + 119 119 0.01r d dr 0.01r A′(r) = 10, 000(120) 1 + 12 ] = 1, 000 1 + 12 12 119
Khi r = 5, ta có A′(5) = 1, 000 1 + 0.01(5) 12 ≃ 1, 640.18 đô-la mỗi %.
b. Nếu lãi suất hàng năm tăng từ 5% lên 6% thì tổng số tiền thay đổi
thực tế là bao nhiêu sau 10 năm là 120 120 0.01(6) 0.01(5) A(6) − A(5) = 10, 000 1 + ≃ 1, 723.87 đô-la. 12 − 10, 000 1 + 12
Bài 9 (Bài 84a trang 140). Sử dụng quy tắc hàm hợp
Lời giải: Ta coi hàm số f (x) = L(x2) là hàm hợp của hai hàm số f (u) = L(u); u = x2.
Áp dụng quy tắc đạo hàm của hàm hợp, ta có: dL du 1 1 2 1 f ′(x) = = (2x) = (2x) = vì L′(u) = (theo giả thiết) du dx u x2 x u
Vậy, đạo hàm cần tìm là 2 f ′(x) = . x 31
2.5 Phân tích cận biên và phép tính xấp xỉ sử dụng số gia KIẾN THỨC QUAN TRỌNG Phân tích cận biên
• Chi phí cận biên: Nếu C(x) là tổng chi phí sản xuất x đơn vị một
loại hàng hóa thì chi phí cận biên khi sản xuất x đơn vị là đạo hàm 0 C′(x0).
Nếu x đủ lớn thì chi phí cận biên 0
C′(x0) được dùng để ước lượng chi phí tăng thêm C(x lên
0 + 1) − C(x0) khi mức sản xuất tăng từ x0 x0 + 1.
• Doanh thu cận biên và lợi nhuận cận biên: Giả sử R(x) và P (x) lần
lượt là doanh thu và lợi nhuận thu được khi sản xuất và tiêu thụ x
đơn vị hàng hóa. Khi x0 đơn vị được sản xuất thì:
Doanh thu cận biên là R′(x0) và xấp xỉ với doanh thu tăng thêm R(x lên
0 + 1) − R(x0) khi mức sản xuất tăng từ x0 x0 + 1 đơn vị.
Lơi nhuận cận biên là P ′(x0) và xấp xỉ với lợi nhuận tăng thêm P(x0+ 1) − P (x lên
0) khi mức sản xuất tăng từ x0 x0 + 1 đơn vị.
Tính xấp xỉ bằng các số gia
• Nếu hàm f (x) khả vi tại x = x và 0
∆x là một lượng thay đổi nhỏ của x thì: f (x ′
0 + ∆x) ≃ f (x0) + f (x0)∆x
Hoặc tương đương, nếu ∆f = f(x0 + ∆x) − f(x0) thì ∆f ≃ f′(x0)∆x
• Thay đổi tương đối, thay đổi phần trăm: Trong ứng dụng, lượng thay
đổi thực tế ∆Q = Q(x0 +∆x)−Q(x0) của đại lượng Q thường ít được 32
quan tâm. Thay vào đó, ta thường quan tâm đến: Thay đổi tương đối: ∆Q Q′(x)∆x = Q Q(x) Thay đổi phần trăm: ∆Q Q′(x)∆x 100 = 100 . Q Q(x) Vi phân
Vi phân của x là dx = ∆x và nếu y = f(x) là một hàm khả vi của x
thì dy = f′(x)dx được gọi là vi phân của y.
HƯỚNG DẪN GIẢI CÁC BÀI TẬP CƠ BẢN
Bài 1 (Bài 1 trang 148). Tìm chi phí cận biên và doanh thu cận biên 2
Lời giải: a. Chi phí cận biên là C′(x) = x + 4. 5 Do 1
x đơn vị hàng hóa được bán với mức giá p(x) = (48 − x) đô-la mỗi 4
đơn vị nên tổng doanh thu là
R(x) = (Số đơn vị được bán)(Giá bán mỗi đơn vị) x2 1 1 4 = xp(x) = x (48 − x) = 12x − 4 Doanh thu cận biên là 1 R′(x) = 12 − x. 2
b. Chi phí sản xuất đơn vị thứ 21 là mức thay đổi của chi phí khi x tăng
từ 20 lên 21 đơn vị và được ước tính bằng chi phí cận biên khi sản xuất 20 đơn vị: 2 C′(20) = (20) + 4 = $12 5
Chi phí thực tế để sản xuất đơn vị thứ 21 là
C(21) − C(20) = 229.2 − 217 = $12.2 33
c. Doanh thu thu được từ việc bán đơn vị hàng hóa thứ 21 được ước
tính bằng doanh thu cận biên khi bán 20 đơn vị: 1 R′(20) = 12 − (20) = $2 2
Doanh thu thực tế khi bán đơn vị thứ 21 là
R(21) − R(20) = 141.75 − 140 = $1.75
Bài 2 (Bài 7 trang 148). Ước tính sự thay đổi giá trị của hàm số
Lời giải: Áp dụng công thức tính xấp xỉ, thay đổi tương ứng của giá trị
hàm f(x) khi x tăng từ 5 lên 5.3 (∆x = 0.3) là
∆f = f (5.3) − f(5) ≃ f′(5)∆x Do
f ′(x) = 2x − 3 và f′(5) = 2(5) − 3 = 7 nên ta có:
∆f ≃ [f′(5)](0.3) = 7(0.3) = 2.1
Vậy, khi x tăng từ 5 lên 5.3 thì giá trị của hàm f(x) tăng xấp xỉ 2.1 đơn vị.
Bài 3 (Bài 9 trang 148). Ước tính phần trăm thay đổi của hàm số
Lời giải: Thay đổi phần trăm của hàm f (x) khi tăng x từ 4 lên 4.3 (∆x = f ′(4)∆x 0.3) là 100 . f (4) Do
f ′(x) = 2x + 2 và f ′(4) = 2(4) + 2 = 10 nên ta có: f ′(4)∆x 10(0.3) 100 = 100 = 20 f (4) 42 + 2(4) − 9
Vậy, khi x tăng từ 4 lên 4.3 thì hàm f(x) tăng xấp xỉ 20%.
Bài 4 (Bài 11 trang 148). Quản trị kinh doanh 34
Lời giải: a. Doanh thu tăng thêm khi sản xuất đơn vị hàng hóa thứ 81
được ước lượng bằng doanh thu cận biên tại q = 80. Doanh thu cận biên là
R′(q) = 240 − 0.1q và R′(80) = 240 = 0.1(80) = 232
Vậy doanh thu tăng thêm xấp xỉ 232 đô-la khi xản xuất thêm đơn vị
hàng hóa thứ 81. Theo kết quả này, Leticia nên ra quyết định tăng mức sản xuất.
b. Doanh thu thực tế thu được từ việc sản xuất đơn vị hàng hóa thứ 81 là R(81) − R(80) = $231.95
Kết quả này phù hợp với phép tính xấp xỉ bởi doanh thu cận biên R′(80) = $232.
Bài 5 (Bài 14 trang 148). Sản xuất
Lời giải: Theo giả thiết, mức sản xuất hiện tại là q = 4 (4,000 đơn vị) và
thay đổi trong mức sản xuất là ∆q = 0.1 ( tăng thêm 100 đơn vị). Theo
công thức xấp xỉ, thay đổi tương ứng trong chi phí là
∆C = C(4.1) − C(4) ≃ C′(4) ∆q = [C′(4)](0.1) Do
C′(q) = 0.3q2 − q + 500 và C′(4) = 0.3(42) − 4 + 500 = 500.8 nên ta có:
∆C ≃ [C′(4)](0.1) = 500.8(0.1) = 50.08
Tức là chi phí sẽ tăng thêm xấp xỉ 50.08 đô-la khi mức sản xuất tăng
từ 4,000 đơn vị lên 4,100 đơn vị hàng hóa.
Bài 6 (Bài 19 trang 149). Quản trị kinh doanh
Lời giải: Theo công thức xấp xỉ, tại mức sử dụng hiện tại (K0 = 400; L0 =
1, 331), nếu tăng vốn đầu từ thêm $10,000 (∆K = 10) và giữ nguyên số giờ
lao động thì sản lượng sẽ thay đổi là dQ ∆Q ≃ ∆K dK (K0;L0) 35 với √ dQ 3 1 d 1 1 1 L = 3, 000L 3 [K 2 ] = 3, 000L K− √ dK dK 12 K 3 2 = 1500 Thay số vào ta có: √ 3 1, 331 ∆Q ≃ 1500 √ (10) = 8, 250 400
Vậy, tại thời điểm hiện tại, nếu giữ nguyên số giờ lao động và tăng mức
sử dụng vốn thêm $10,000 thì sản lượng tăng thêm xấp xỉ 8,250 đơn vị.
Tương tự, nếu tại thời điểm hiện tại, giữ nguyên mức sử dụng vốn và
tăng thêm 10 giờ lao động (∆L = 10) thì sản lượng thay đổi là dQ ∆Q ≃ ∆L dL (K0;L0) với dQ 1 d 1 1 2 = 3, 000K √ 2 [L 3 ] = 3, 000K L− √ dL dL 3 K 1 3 3 = 1000 L2 2 Thay số vào ta có: √400 ∆Q ≃ 1000 3p (10) ≃ 1, 652.9 (1, 331)2
Vậy, tại thời điểm hiện tại, nếu giữ nguyên mức sử dụng vốn và tăng sử
dụng lao động thêm 10 giờ mỗi ngày thì sản lượng tăng thêm xấp xỉ 1,652.9 đơn vị.
Do 8,250 > 1,652.9, nên để sản lượng hàng ngày tăng thêm nhiều hơn
thì Matthew nên tăng vốn đầu tư.
Bài 7 (Bài 20 trang 149). Quản trị kinh doanh
Lời giải: Giả sử số giờ lao động cần bổ sung là ∆L. Khi đó ∆L được xác
định từ công thức xấp xỉ ∆Q ≃ Q′(L) ∆L với 1
∆Q = 12.5; L = 512 và Q′(L) = 200L−3 . 36 Thay vào ta có: −1 12.5 1
12.5 ≃ 200(512) 3 ∆L → ∆L ≃
(512) 3 = 0.5 giờ làm việc 200
Vậy để sản lượng tăng thêm 12.5 đơn vị mỗi ngày thì Aurelia cần bổ
sung thêm khoảng 0.5 giờ làm việc tại mức sử dụng 512 giờ làm việc mỗi ngày.
Bài 8 (Bài 24 trang 149). Ô nhiễm không khí
Lời giải: Tính từ thời điểm hiện tại (t = 0), lượng carbon monoxide trong
không khí 6 tháng sau (∆t = 0.5) sẽ thay đổi là
∆Q ≃ Q′(0) ∆t = [Q′(0)](0.5) Do
Q′(t) = 0.1t + 0.1 và Q′(0) = 0.1 nên ta có:
∆Q ≃ [Q′(0)](0.5) = 0.1(0.5) = 0.05 ppm
Vậy, trong 6 tháng tới, lượng carbon monoxide trong không khí sẽ tăng
khoảng 0.05 ppm so với mức hiện tại.
Bài 9 (Bài 27 trang 150). Cung lượng tim
Lời giải: Sai số phần trăm của cung lượng tim theo công thức Fick là a −100 ∆x 100∆C 100C′(x)∆x (x − b)2 100∆x ≃ = = − C C(x) a x − b x − b
Do phép đo x tại x = c có sai số tối đa 3%, tương đương với ∆x ≃ ±0.03c, nên thay số vào ta có: 100∆C 100(±0.03c) 3c ≃ − = C c − b |c − b|
Vậy, sai số phần trăm tối đa của cung lượng tim theo công thức của Fick là 3c . |c − b| 37
CÁC BÀI TẬP TỰ LUYỆN: HƯỚNG DẪN VÀ ĐÁP ÁN
Bài 10 (2, tr. 148). a) Hàm chi phí cận biên C’(x) = 1x + 3 2
Hàm doanh thu cận biên: R’(x) = 9 − 2x 5
b) C′(20) = 13; C (21) - C(20) = 13.25
c) R′(20) = 1; R(21) − R(20) = 0.8
Bài 11 (3, tr. 148). a) Hàm chi phí cận biên C’(x) = 2x + 2 3
Hàm doanh thu cận biên: R’(x) = −3x2 − 20x + 4, 000
b) C′(20) = 15.33; C (21) - C(20) = 15.67
c) R′(20) = 2, 400; R(21) − R(20) = 2, 329
Bài 12 (4, tr. 148). a) Hàm chi phí cận biên C’(x) = 10x + 5 9
Hàm doanh thu cận biên: R’(x) = −6x2 − 30x + 6, 000 b)C′(20) = 27.22 c) R(21) − R(20) = 2, 863
Bài 13 (6, tr. 148). a) Hàm chi phí cận biên C’(x) = 4x 7
Hàm doanh thu cận biên: R’(x) = 2x2+12x+36 (x+3)2
b) C′ (20) = 80; C (21) - C(20) = 11.71 7
c) R′(20) = 2.03; R(21) − R(20) = 2.03
Bài 14 (8, tr. 148). f’(4) = 0.04
Lượng thay đổi giá trị của f(x) là ∆f = −0.008
Bài 15 (10, tr. 148). Đáp án: -7.58%
Bài 16 (12, tr. 148). C’(q) = 0.003q2 − 0.1q + 40 a) C’(250) = 202.5 b) C(251) - C (250) = 203.2
Bài 17 (13, tr. 148). a) C’(q ) = 6q+1 ; C’ (40) = 241
b) Chi phí thực tế để sản xuất đơn vị hàng hóa thứ 41 C(41) − C(40) = 244 38
Bài 18 (15, tr. 149). Đáp án: ∆R(q) = 150.8
Bài 19 (16, tr. 149). Đáp án: ∆f = 6
Bài 20 (17, tr. 149). Q’(L) = 300 √ ; Q′(900) = 10 K ∆Q = 8
Bài 21 (18, tr. 149). Đáp án: ∆Q = −12, 000
Bài 22 (21, tr. 149). C’(q) = 1q2 + 642; C′(4) = 650 2
Cầu cắt giảm 0.2 đơn vị
Bài 23 (22, tr. 149). Đáp án: 5.12 %
Bài 24 (25, tr. 149). a) P’(t) = −3t2 + 18t + 48 b) R’(t) = −6t + 18
c) Ước tính thay đổi của R(t) là 0; Thay đổi thực tế của R(t) là 0,021
Bài 25 (32, tr. 168). Đáp án: y” = −4y2−16x2 y3
Bài 26 (38, tr. 168). Đáp án: 1,652; 1,514
Bài 27 (39, tr. 169). a) Q’(x) = 100x + 9, 000 ∆Q = 12, 000
b) Mức thay đổi thực tế của Q(x) là 12,050
Bài 28 (40, tr. 169). Đáp án: 0.11 %;
Bài 29 (46, tr. 169). a. P’(t) = 3.105t2 + 207t + 6, 900
b. P’(1) = 7, 110.105; P ′(10) = 9, 280.5
Bài 30 (48, tr. 169). Đáp án: -0.172 %;
Bài 31 (50, tr. 169). Đáp án: 6 %;
Bài 32 (55, tr. 170). x’(t) = −17p 75x ∆x = 0.1542
Bài 33 (57, tr. 170). P’(t) = 6 (t+1)2
Dân số sẽ tăng là 10.7 %
Bài 34 (62, tr. 171). Đáp án: 1663.2; 39
2.6 Đạo hàm của hàm ẩn và các tốc độ liên quan KIẾN THỨC QUAN TRỌNG Đạo hàm của hàm ẩn
• Định nghĩa hàm ẩn: Trong thực tế, ta gặp một phương trình chứa x
và y, trong đó y là hàm số của x nhưng không giải được y theo x một
cách tường minh. Ta gọi hàm số này là một hàm ẩn.
• Tính đạo hàm của hàm ẩn: Giả sử một phương trình xác định y là
một hàm ẩn khả vi của x. Để tìm dy ta làm như sau: dx
1. Lấy đạo hàm hai vế của phương trình đó theo x. Lưu ý rằng y là
một hàm của x và sử dụng quy tắc lấy đạo hàm của hàm hợp khi tính
đạo hàm của các số hạng chứa y trong phương trình.
2. Biến đổi đại số phương trình sau khi lấy đạo hàm để tìm dy theo dx x và y. Các tốc độ liên quan
Giả sử x và y liên hệ với nhau bởi một phương trình, trong đó x và
y là các hàm số của biến thứ ba là t. Khi đó có thể sử dụng đạo hàm
của hàm ẩn để xác định mối liên hệ giữa dy và dx bằng quy trình: dt dt
1. Vẽ hình (nếu có thể) và đặt ký hiệu cho các biến số.
2. Tìm một công thức biểu diễn mối quan hệ giữa các biến số.
3. Sử dụng đạo hàm của hàm ẩn để xác định mối liên hệ giữa các tốc độ.
4. Thay các thông tin bằng số được cho vào phương trình tìm được
trong Bước 3 để tìm tốc độ thay đổi mong muốn.
HƯỚNG DẪN GIẢI CÁC BÀI TẬP CƠ BẢN
Bài 1 (Bài 12 trang 161). Tìm đạo hàm của hàm ẩn 40
Lời giải: Lấy đạo hàm hai vế của phương trình 5x − x2y3 = 2y theo x, ta có: dy 5 − 2xy3 − 3x2y2 dy = 2 dx dx dy (3x2y2 + 2) = 5 − 2xy3 dx dy 5 − 2xy3 = dx 3x2y2 + 2
Vậy đạo hàm cần tìm là dy 5 − 2xy3 = . dx 3x2y2 + 2
Bài 2 (Bài 29 trang 161). Tìm phương trình tiếp tuyến
Lời giải: Lấy đạo hàm hai vế của phương trình (1 − x + y)3 = x + 7 theo x, ta có:
3(1 − x + y)2 d [1 − x + y] = 1 dx dy 3(1 − x + y)2 −1 + dy = 1 1 dx = + 1 dx 3(1 − x + y)2
Độ dốc tại điểm (1, 2) là giá trị của đạo hàm tại x = 1 và y = 2: dy 13 = 1 12 = + 1 dx 3(1 ( − x + y)2 x=1,y=2) (x=1,y=2)
Phương trình tiếp tuyến với đồ thị hàm số tại điểm (1, 2) với hệ số góc 13 là 12 13 13 11 y − 2 = (x − 1) hay y = x + . 12 12 12
Bài 3 (Bài 31 trang 161). Tìm tiếp điểm
Lời giải: Lấy đạo hàm hai vế của phương trình x + y2 = 9 theo x, ta có: dy 1 + 2y = 0 dx dy 1 = − dx 2y 41
a. Đồ thị của hàm số có tiếp tuyến nằm ngang tại điểm có độ dốc bằng 0, nghĩa là dy = 0. dx Ta có: 1 − = 0 → vô nghiệm 2y
Vậy không có điểm nào nằm trên đồ thị của hàm số mà ở đó tiếp tuyến
là đường thẳng nằm ngang.
b. Do độ dốc của đường thẳng đứng là không xác định nên đồ thị của
hàm số có tiếp tuyến thẳng đứng khi mẫu thức 2y của dy bằng 0: dx 2y = 0 ⇐⇒ y = 0
Để tìm giá trị tương ứng của x, thay y = 0 vào phương trình ban đầu, ta được: x + 02 = 9 ⇐⇒ x = 9
Vậy, đồ thị của hàm số có tiếp tuyến thẳng đứng tại điểm (9, 0).
Bài 4 (Bài 37 trang 161). Tìm đạo hàm cấp hai
Lời giải: Lấy đạo hàm hai vế của phương trình x2 + 3y2 = 5 theo x, ta được: dy 2x + 6y = 0 dx dy x = − dx 3y
Đạo hàm cấp hai cần tìm là dy d2y 1 d 1(y) − x = − dx dx2 3 x 1 3 y2 = − dx y 1 x2 + 3y2 5 = − x = − = − . 3 y − x y − 2 3y 9y3 9y3
Bài 5 (Bài 39 trang 161). Sản xuất 42
Lời giải: Mức sản lượng hiện tại khi nhà máy sử dụng 80 giờ lao động có
kỹ năng (x = 80) và 200 giờ lao động giản đơn (y = 200) là
Q = Q(80, 200) = 0.08(80)2 + 0.12(80)(200) + 0.03(200)2 = 3, 632 đơn vị
Nếu duy trì mức sản lượng hiện tại thì mối liên hệ giữa số giờ lao động
có kỹ năng x và số giờ lao động giản đơn y được xác định bởi phương trình
3, 632 = 0.08x2 + 0.12xy + 0.03y2
và phương trình này xác định y là hàm dưới dạng ẩn của x.
Khi đó, lượng thay đổi của y gây ra bởi 1 đơn vị tăng thêm của x xấp xỉ bằng đạo hàm dy. dx
Áp dụng quy tắc tính đạo hàm của hàm ẩn, ta có: dy dy 0 = 0.16x + 0.12y + 0.12x + 0.06y dx dx dy
0 = 0.16x + 0.12y + (0.12x + 0.06y)dx dy −(0.12x + 0.06y) = 0.16x + 0.12y dx dy 8x + 6y = − . dx 6x + 3y
Do đó, giá trị của đạo hàm tại x = 80 và y = 200 là dy 8(80) + 6(200) = − ≃ −1.704 giờ 6(80) + 3(200) dx (x=80,y=200)
Vậy, lượng thay đổi của y xấp xỉ bằng −1.704 giờ. Hay, để duy trì mức
sản lượng hiện tại khi tăng 1 giờ lao động có kỹ năng thì nhà máy cần giảm
khoảng 1.704 giờ lao động giản đơn.
Bài 6 (Bài 41 trang 162). Tốc độ của cung
Lời giải: Khi giá bán hàng hóa là $4 mỗi đơn vị thì lượng cung x thỏa mãn
3(4)2 − x2 = 12 ⇐⇒ x = 36 → x = 6 (do x > 0) 43
Tốc độ thay đổi của cung x theo thời gian t là dx. Đạo hàm hai vế của dt
phương trình 3p2 − x2 = 12 theo thời gian t, ta có: dp dx 6p − 2x = 0 dt dt dx dp 2x = 6p dt dt dx 3p dp = dt x dt
Vậy, khi p = $4 và dp = 0.87 tốc độ thay đổi của lượng cung x theo dt thời gian t là dx 3(4) =
(0.87) = 1.74 trăm đơn vị mỗi tháng. 6 dt=0.87 dt Bài 7 p (Bài 45 = t 4 r ; dp ang 162). Sản xuất
Lời giải: Sản lượng của nhà máy tại thời điểm K = 8, L = 1000 là 1 2
Q = Q(8, 1000) = 60(8)3 (1000) 3 = 12, 000
Nếu giữ nguyên mức sản lượng này thì mối liên hệ giữa lượng vốn đầu tư
K và quy mô lao động L được xác định bởi phương trình 1 2 12, 000 = 60K 3 L 3
Khi đó, tốc độ thay đổi của vốn K theo thời gian t là dK với K = 8; L = dt
1, 000 và dL = 25 (giờ làm việc mỗi tuần). dt
Đạo hàm hai vế của phương trình 1 2
12, 000 = 60K 3 L 3 theo t, ta được: 2 dK 1 1 dL K− 3 3 + 60K L− 3 13 2 23 2 2 d 0 K = 60 1 1 dL L 3 3 3 3 3 dt dt 20K− L = −40K L− dt dt dK 2K dL = − dt L dt
Vậy, tốc độ thay đổi của vốn đầu tư K theo thời gian t là dK 2(8) = −
(25) = −0.4 nghìn đô-la mỗi tuần. 1, 000 dt =25 dt K=8,L=1,000, dL 44
Bài 8 (Bài 46 trang 162). Sản xuất
Lời giải: Mức sản lượng hiện tại của nhà máy khi x = 30, y = 20 là
Q = Q(30, 20) = 2(30)3 + 3(30)2(20)2 + (1 + 20)3 = 1, 143, 261 đơn vị.
Nếu giữ nguyên mức sản lượng hiện tại thì mối liên hệ giữa đầu vào x và y
được xác định bởi phương trình
1, 143, 261 = 2x3 + 3x2y2 + (1 + y)3
và phương trình này xác định y dưới dạng hàm ẩn theo x.
Khi đó, theo công thức xấp xỉ, mức thay đổi của y khi đầu vào x giảm
0.8 đơn vị (∆x = −0.8) là dy dy ∆y ≃ ∆x = (−0.8) dx dx (x=30,y=20) (x=30,y=20)
Đạo hàm hai vế của phương trình 1, 143, 261 = 2x3 + 3x2y2 + (1 + y)3 theo x, ta được: dy 0 = 6x2 + 6xy2 + 6x2y + 3(1 + y)2 dy dx dx dy
0 = 6x(x + y2) + 3[2x2y + (1 + y)2] dx dy 3[2x2y + (1 + y)2] = −6x(x + y2) dx dy 2x(x + y2) = − dx 2x2y + (1 + y)2
Vậy, mức thay đổi của y là 2x(x + y2) ∆y ≃ − (−0.8) ≃ 0, 566 đơn vị 2x2y + (1 + y)2 (x=30;y=20)
hay tại mức đầu vào hiện tại x = 30 và y = 20, nếu x giảm 0.8 đơn vị mà
không làm thay đổi mức sản lượng hiện tại thì y phải tăng xấp xỉ 0.566 đơn vị.
Bài 9 (Bài 55 trang 163). Lưu lượng máu 45
Lời giải: a. Nếu A và D không đổi, ta có: dF kD2 = − √ dC 2 A − C
Với k là hằng số dương, D > 0, và 0 < C < A ta có dF < 0, vì vậy, lưu dC
lượng máu F thay đổi ngược lại với áp suất C trong mao mạch. Tức là, khi
áp suất trong mao mạch tăng thì lưu lượng máu sẽ giảm.
b. Nếu C và D không đổi, ta có: dF kD2 = √ dA 2 A − C
Do đó, tốc độ thay đổi phần trăm của lưu lượng máu F theo A khi C và D không đổi là dF 100 dA 50 = (%). F A − C
Bài 10 (Bài 60 trang 164). Làm lạnh
Lời giải: a. Khi độ dài cạnh của khối lập phương là s, thì thể tích của khối lập phương là V = s3.
Do đó, độ dài hiện tại của mỗi cạnh hình lập phương là s = 50cm (vì s3 = 125, 000cm3).
Hiện tại, tốc độ thay đổi của s theo thời gian t (t = 0) là ds với
s = 50cm và dV = 1, 000cm3 mỗi giờ. dt t=0 dt
Đạo hàm hai vế của phương trình V = s3 theo t, ta có: dV = 3s2 ds dt dt ds 1 dV = dt 3s2 dt
Vì vậy,hiện tại, tốc độ thay đổi theo thời gian t của s là ds 1 =
(1, 000) ≃ 0.133cm mỗi giờ. dt 3(50)2
b. Diện tích bề mặt S của khối lập phương là S = 6s2cm2. 46
Tốc độ thay đổi của diện tích bề mặt S theo thời gian t khi t = 0 là dS
với s = 50cm và ds ≃ 0.133cm mỗi giờ. dt
dt Đạo hàm hai vế của phương trình S = 6s2 theo t, ta có: t=0 dS ds = 12s dt dt
Do vậy, tốc độ thay đổi của S theo thời gian t khi t = 0 là dS
≃ 12(50)(0.133) = 79.8cm2 mỗi giờ. dt t=0
CÁC BÀI TẬP TỰ LUYỆN: HƯỚNG DẪN VÀ ĐÁP ÁN
CÁC BÀI TẬP TỰ LUYỆN: HƯỚNG DẪN VÀ ĐÁP ÁN
Bài 11 (2, tr. 161). Đáp án: dy = 5 dx 7
Bài 12 (4, tr. 161). Đáp án: dy = −2x dx 3y2
Bài 13 (6, tr. 161). Đáp án: dy = y2 dx
Bài 14 (8, tr. 161). Đáp án: dy = 2x−y dx x+2
Bài 15 (10, tr. 161). Đạo hàm hai vế và sử dụng quy tắc đạo hàm hàm
hợp ta được: dy = −3x2+2x dx 2y−1
Bài 16 (13, tr. 161). Đạo hàm hai vế và sử dụng quy tắc đạo hàm hàm
hợp ta được: 2yy’ + 2y2 + 4xyy′ − 3 = 0 dy = 3−2y2 dx 2y(1+2x)
Bài 17 (14, tr. 161). Đạo hàm hai vế và sử dụng quy tắc đạo hàm hàm
hợp ta được: y′ = −y2 x2
Bài 18 (16, tr. 161). Đạo hàm hai vế và sử dụng quy tắc đạo hàm hàm hợp ta được: y′ = −1 √ 2y 2x
Bài 19 (18, tr. 161). Đạo hàm hai vế và sử dụng quy tắc đạo hàm hàm
hợp ta được: y′ = 8x−3y 3x+2y 47
Bài 20 (20, tr. 161). Đạo hàm hai vế và sử dụng quy tắc đạo hàm hàm
hợp ta được: y′ = 2x−4y 4x−8y+1
Bài 21 (21, tr. 161). Đạo hàm hai vế và sử dụng quy tắc đạo hàm hàm
hợp ta đưyợc: 5 x2 + 3y2 4 (2x + 6yy′) = 2xy′ + 2y y′ = −5x(x2+3y2)4 15y(x2+3y2)4−x h i 2 Bài 22 −4(3xy2+31)33y2
(22, tr. 161). Đáp án:y′ = 4(3xy2+1) .6xy+3
Bài 23 (24, tr. 161). Đáp án: Phương trình tiếp tuyến là: y = −1;
Bài 24 (26, tr. 161). Đáp án: Phương trình tiếp tuyến là: y = 4x − 1; 2
Bài 25 (27, tr. 161). Ta có: y2 + 2xyy′ − 2xy − x2y′ = 0
Phương trình tiếp tuyên là: y = 5 (x 8 − 2) − 1; y = 1 x + 2 12
Bài 26 (28, tr. 161). Đáp án: Phương trình tiếp tuyến là: y = −4x − 1;
Bài 27 (30, tr. 161). Đáp án: Phương trình tiếp tuyên là: y = 1 x + 2; 12
Bài 28 (32, tr. 161). Ta có: y′ = −y−2x x+1
a. Không có tiếp tuyến nằm ngang
b. Không có tiếp tuyến thẳng đứng
Bài 29 (33, tr. 161). Ta có: y′ = y−1 32y−x
a. Không có tiếp tuyến nằm ngang
b. Tiếp tuyến thẳng đứng tại các điểm (0,0); (64,2)
Bài 30 (34, tr. 161). Đáp án: Đồ thị hàm số không có tiếp tuyến nằm
ngang, không có tiếp tuyến thẳng đứng
Bài 31 (35, tr. 161). Ta có: y′ = −y−2x x+2y
a. Các điểm A(1;-2), B(-1;2) có tiếp tuyến nằm ngang
b. Các điểm (-2;1) và (2;-1) có tiếp tuyến là đường thẳng đứng
Bài 32 (36, tr. 161). Ta có: y′ = 2x−y x−2y
a. A(1;2), B(-1;-2) có tiếp tuyến nằm ngang
b. Các điểm (2;1) và (-2;-1) có tiếp tuyến là đường thẳng đứng 48
Bài 33 (38, tr. 161). Đáp án: y′′ = 2xy+2y2 (x+2y)3
Bài 34 (40, tr. 161). Đáp án: y′ = −1.24
Bài 35 (42, tr. 162). Đáp án: x′(p) = −0.27
Bài 36 (43, tr. 162). D’(t) = −65,340 √t (2p+1)2 0.06 D’(25) = −2 < 0
Bài 37 (48, tr. 162). Q′ (p) = 2p + 4 ∆Q = 156
Bài 38 (51, tr. 163). Ta có: M′ (w) = 52,5 4√w a. 14.04 (Kcal) b. -9.87 (Kcal)
Bài 39 (52, tr. 163). Đáp án: ∆S = 0.00065
Bài 40 (54, tr. 163). Đáp án: 16.3% 49




