Bai tap tong hop NLTK - bài tập NLTK khóa K18
BÀI TẬP ÁP DỤNG CHƯƠNG 3
Bài 1. Một cơ quan bảo vệ môi trường lấy các mẫu nước từ 12 sông và suối khác nhau, sau đó đưa vào
phòng thí nghiệm để xác định tỷ lệ ô nhiễm cho từng mẫu nước. Kết quả xét nghiệm như sau: Mẫu nước
Tỷ lệ ô nhiễm (%) Mẫu nước
Tỷ lệ ô nhiễm (%) 1 35,4 7 41,2 2 45,3 8 50,7 3 67,3 9 60,8 4 57,4 10 47,3 5 52,9 11 38,6 6 32,1 12 46,2 Yêu cầu:
1. Sắp xếp số liệu theo thứ tự giảm dần.
2. Xác định số mẫu nước có tỷ lệ ô nhiễm trong các khoảng 30 – 40; 40 – 50; 50 – 60; 60 – 70.
3. Nếu theo các nhà khoa học tỷ lệ ô nhiễm từ 45% trở lên là quá mức thì có bao nhiêu mẫu nước rơi vào trường hợp này?
Bài 2. Có số liệu về công nhân tại 20 xí nghiệp như sau: ST ST ST ST T Số công T Số công T Số công T Số công XN nhân (người) XN nhân (người) XN nhân (người) XN nhân (người) 1 1200 6 1430 11 1650 16 2883 2 1304 7 1350 12 2050 17 2540 3 1800 8 1240 13 2120 18 2760 4 1670 9 1700 14 1980 19 2300 5 1400 10 1800 15 2400 20 2130 Yêu cầu:
1. Phân tổ các Xí nghiệp trên căn cứ vào quy mô bao gồm loại nhỏ, trung bình, lớn và rất lớn.
2. Tính số công nhân trong mỗi tổ đã phân ở trên.
Bài 3. Có số liệu của các công nhân tại một doanh nghiệp như sau: Số CN Số lượng SP Số lượng SP Tổ Số CN (người) Tổ (kg) (người) (kg) 1 26 2405 11 25 2125 2 20 1866 12 14 1134 3 16 1448 13 18 1494 4 12 936 14 22 1980 5 17 1530 15 8 728 6 14 1261 16 15 1382 7 15 1365 17 6 488 8 10 845 18 7 527 9 20 1884 19 15 1365 10 9 675 20 10 920 Yêu cầu:
1. Căn cứ theo tiêu thức số công nhân, hãy phân tổ 20 tổ lao động trên thành 4 nhóm có khoảng cách tổ đều.
Trong mỗi nhóm hãy tính số tổ lao động, số sản phẩm sản xuất được.
2. Căn cứ vào năng suất lao động bình quân một công nhân, hãy phân tổ số công nhân trên thành 4 nhóm có
khoảng cách tổ đều. Trong mỗi nhóm, hãy tính số công nhân và số lượng sản phẩm.
Bài 4.Có số liệu về mức thu nhập và số công nhân của các nhóm trong một doanh nghiệp như sau: Số Thu nhập BQ Số CN Số Thu nhập BQ Số CN TT (nghìn đồng/CN) (người) TT (nghìn đồng/CN) (người) 1 1000 5 11 1430 14 2 1125 7 12 1500 13 3 1025 8 13 1480 15 4 1200 6 14 1520 16 5 1118 9 15 1600 17 6 1230 10 16 1400 18 7 1300 11 17 1550 17 8 1225 13 18 1580 19 9 1325 15 19 1620 20 10 1564 14 20 1420 18 Yêu cầu:
1. Căn cứ vào thu nhập bình quân một công nhân, hãy phân tổ các nhóm công nhân trên thành 3 tổ khoảng
cách đều ( với đơn vị tính tiền là 1.000 đồng), trong mỗi tổ hãy tính số nhóm, số lao động.
2. Tương tự như trên nhưng phân thành 4 tổ
CHƯƠNG 4: CÁC MỨC ĐỘ CỦA HIỆN TƯỢNG KINH TẾ XÃ HỘI
Bài 1. Có số liệu về doanh thu của các cửa hàng như sau: Doanh thu (triệu đồng) 200 300 350 420 600 Số cửa hàng 15 25 30 20 10
Câu 1: Doanh thu bình quân là:
Câu 2: Mốt về doanh thu là:
Câu 3: Trung vị về doanh thu là:
Câu 4: Khoảng biến thiên về doanh thu là:
Câu 5: Khoảng tam phân vị về doanh thu là:
Câu 6.Khoảng tứ phân vị về doanh thu là:
Bài 2. Có số liệu về năng suất lao động của các công nhân như sau: Năng suất lao động (SP) 400 500 600 700 800 Số công nhân 20 30 45 80 25
Câu 1: Năng suất lao động bình quân là:
Câu 2: Mốt về năng suất lao động là:
Câu 3: Trung vị về năng suất lao động là:
Câu 4: Khoảng biến thiên về năng suất lao động là:
Câu 5: Khoảng tam phân vị về năng suất lao động là:
Câu 6.Khoảng tứ phân vị về năng suất lao động là:
Có số liệu về năng suất lao động của công nhân trong một doanh nghiệp như sau: Năng suất lao động (sp) Số công nhân (người) 25 – 35 20 35 – 45 32 45 – 55 38 55 – 65 10
Câu 1: Năng suất lao động bình quân một công nhân là:
Câu 2: Mốt về năng suất lao động là:
Câu 3: Trung vị về năng suất lao động là:
Bài 3. Có số liệu như sau: Năng suất lao động (sp) Số công nhân (người) 400 – 500 20 500 – 600 30 600 – 700 35 700 – 800 80 800 – 900 25
Câu 1: Năng suất lao động bình quân một công nhân là:
Câu 2: Mốt về năng suất lao động là:
Câu 3: Trung vị về năng suất lao động là:
Bài 4. Có 3 công nhân cùng sản xuất một loại sản phẩm trong thời gian như nhau. Người thứ nhất làm ra
một sản phẩm hết 15 phút, người thứ hai hết 18 phút, người thứ ba hết 20 phút. Thời gian hao phí bình quân
để sản xuất ra một sản phẩm của cả ba công nhân nói trên là:
Bài 5. Hai tổ công nhân ( tổ 1 có 10 người, tổ 2 có 15 người) cùng sản xuất một loại sản phẩm trong 6 giờ.
Trong tổ một, mỗi công nhân sản xuất một sản phẩm hết 15 phút. Trong tổ hai, mỗi công nhân sản xuất một
sản phẩm hết 10 phút. Hãy tính thời gian hao phí bình quân để sản xuất một sản phẩm của 2 tổ công nhân.
Bài 6. Tốc độ phát triển về doanh thu của một cửa hàng như sau:
Năm 2005 so với 2004 là 105%
Năm 2006 so với 2005 là 118%
Năm 2007 so với 2006 là 115%
Năm 2008 so với 2007 là 85%
Tốc độ phát triển bình quân về doanh thu của cửa hàng giai đoạn 2004-2008 là:
Bài 7. Tốc độ phát triển về doanh thu của một cửa hàng trong 10 năm như sau:
Có 5 năm phát triển với tốc độ 110%/năm.
Có 2 năm phát triển với tốc độ 115%/năm.
Có 3 năm phát triển với tốc độ 125%/năm.
Tốc độ phát triển bình quân về doanh thu của cửa hàng nói trên là:
Bài 8. Doanh thu của một cửa hàng năm 2009 là 2,2 (tỷ đồng). Theo kế hoạch, năm 2010, cửa hàng phải đạt
mức doanh thu là 3,4 (tỷ đồng). Thực tế năm 2010, cửa hàng đạt mức doanh thu là 3,6 (tỷ đồng).
Câu 1: Số tương đối động thái về doanh thu là:
Câu 2: Số tương đối nhiệm vụ kế hoạch về doanh thu là:
Câu 3: Số tương đối hoàn thành kế hoạch về doanh thu là:
Bài 8 . Có số liệu về tiền lương của công nhân trong một doanh nghiệp như sau: Tiền lương (1.000đ) Số công nhân (người) 3.000 20 3.500 50 3.800 30
Biết thêm rằng tiền lương bình quân là: 3.490 (1.000đ)
Câu 1: Độ lệch tuyệt đối bình quân về tiền lương là:
Câu 2: Phương sai về tiền lương là:
Câu 3: Độ lệch chuẩn về tiền lương là:
Bài 9 . Cho bảng số liệu sau: Năng suất lao động (SP) Số công nhân (người) 400 – 500 20 500 - 600 30 600 – 700 45 700 – 800 80 800 - 900 25
Biết thêm rằng năng suất lao động bình quân là: 680 (SP)
Câu 1: Độ lệch tuyệt đối bình quân về năng suất lao động là:
Câu 2: Phương sai về năng suất lao động là:
Câu 3: Độ lệch chuẩn về năng suất lao động là:
BÀI TẬP VẬN DỤNG CHƯƠNG 5
- Ước lượng bình quân:
5.1. Trong một xí nghiệp có 2.000 công nhân, để điều tra về tiền lương, người ta chọn ra 100
người theo phương pháp chọn ngẫu nhiên đơn giản có hoàn lại. Kết quả điều tra cho thấy,
tiền lương bình quân là 4.800 (1.000đ), độ lệch chuẩn mẫu là 500 (1.000đ). Với xác suất
0,683; tiền lương bình quân chung của toàn xí nghiệp là?
5.2. Trong một xí nghiệp có 1.000 công nhân, để điều tra về tiền lương, người ta chọn ra 100
người theo phương pháp chọn ngẫu nhiên đơn giản không hoàn lại. Kết quả điều tra cho thấy,
tiền lương bình quân là 4.500 (1.000đ), độ lệch chuẩn mẫu là 600 (1.000đ). Với xác suất
0,954; tiền lương bình quân chung của toàn xí nghiệp là ?
5.3. Trong một xí nghiệp có 2.000 công nhân, để điều tra về năng suất lao động, người ta
chọn ra 100 người theo phương pháp chọn ngẫu nhiên đơn giản không hoàn lại. Kết quả điều
tra cho thấy, năng suất lao động bình quân là 39 (sp), độ lệch chuẩn mẫu là 7 (sp). Với xác
suất 0,683; năng suất lao động bình quân chung của toàn xí nghiệp là?
5.4. Một địa phương có 1.000 (ha) đất nông nghiệp, để điều tra về năng suất thu hoạch lúa,
người ta chọn ra 100 (ha) theo phương pháp chọn ngẫu nhiên đơn giản không hoàn lại. Kết
quả điều tra cho thấy, năng suất thu hoạch lúa bình quân là 57 (tạ/ha), phương sai mẫu là 40.
Với xác suất 0,997; năng suất thu hoạch lúa bình quân chung của toàn địa phương là ?
5.5. Trong một xí nghiệp có 1.000 công nhân, để điều tra về tiền lương, người ta chọn ra 100
người theo phương pháp chọn ngẫu nhiên đơn giản có hoàn lại. Kết quả điều tra cho thấy,
tiền lương bình quân là 4.500 (1.000đ), độ lệch chuẩn mẫu là 600 (1.000đ). Với xác suất
0,954; tiền lương bình quân chung của toàn xí nghiệp là ?
5.6 Trong một xí nghiệp có 2.000 công nhân, để điều tra về tiền lương, người ta chọn ra 100
người theo phương pháp chọn ngẫu nhiên đơn giản không hoàn lại. Kết quả điều tra cho thấy,
tiền lương bình quân là 4.500 (1.000đ), độ lệch chuẩn mẫu là 600 (1.000đ). Với xác suất
0,683; tiền lương bình quân chung của toàn xí nghiệp là ?
5.7. Một địa phương có 1.000 (ha) đất nông nghiệp, để điều tra về năng suất thu hoạch lúa,
người ta chọn ra 100 (ha) theo phương pháp chọn ngẫu nhiên đơn giản không hoàn lại. Kết
quả điều tra cho thấy, năng suất thu hoạch lúa bình quân là 35 (tạ/ha), phương sai mẫu là 41.
Với xác suất 0,954; năng suất thu hoạch lúa bình quân chung của toàn địa phương là ?
5.8. Một xí nghiệp trong kỳ sản xuất được 100 thùng chi tiết máy (mỗi thùng có 500 chi tiết).
Để điều tra về trọng lượng trung bình của một chi tiết, người ta chọn ra 5 thùng theo phương
pháp chọn cả khối. Kết quả điều tra cho thấy trọng lượng trung bình của một chi tiết là 40
(g), phương sai mẫu là 6,8. Với xác suất 0,954; trọng lượng trung bình của một chi tiết trong tất cả các thùng là ?
5.9. Một xí nghiệp trong kỳ sản xuất được 100 thùng chi tiết máy (mỗi thùng có 300 chi tiết).
Để điều tra về trọng lượng trung bình của một chi tiết, người ta chọn ra 5 thùng theo phương
pháp chọn cả khối. Kết quả điều tra cho thấy trọng lượng trung bình của một chi tiết là 50
(g), phương sai mẫu là 6,55. Với xác suất 0,954; trọng lượng trung bình của một chi tiết trong tất cả các thùng là?
5.10. Một xí nghiệp trong kỳ sản xuất được 80 thùng chi tiết máy (mỗi thùng có 500 chi tiết).
Để điều tra về trọng lượng trung bình của một chi tiết, người ta chọn ra 4 thùng theo phương
pháp chọn cả khối. Kết quả điều tra cho thấy trọng lượng trung bình của một chi tiết là 45
(g), phương sai mẫu là 2. Với xác suất 0,683; trọng lượng trung bình của một chi tiết trong tất cả các thùng là?
5.11. Một xí nghiệp trong kỳ sản xuất được 100 thùng chi tiết máy (mỗi thùng có 500 chi
tiết). Để điều tra về trọng lượng trung bình của một chi tiết, người ta chọn ra 5 thùng theo
phương pháp chọn cả khối. Kết quả điều tra cho thấy trọng lượng trung bình của một chi tiết
là 40 (g), phương sai mẫu là 6,5. Với xác suất 0,683; trọng lượng trung bình của một chi tiết
trong tất cả các thùng là ?
5.12. Một xí nghiệp trong kỳ sản xuất được 100 thùng chi tiết máy (mỗi thùng có 300 chi
tiết). Để điều tra về trọng lượng trung bình của một chi tiết, người ta chọn ra 6 thùng theo
phương pháp chọn cả khối. Kết quả điều tra cho thấy trọng lượng trung bình của một chi tiết
là 45 (g), phương sai mẫu là 5,68. Với xác suất 0,954; trọng lượng trung bình của một chi tiết
trong tất cả các thùng là ?
- Ước lượng tỷ lệ:
5.13. Trong một xí nghiệp có 1.000 công nhân, để điều tra về tiền lương, người ta chọn ra
100 người theo phương pháp chọn ngẫu nhiên đơn giản có hoàn lại. Kết quả điều tra cho
thấy, số công nhân có tiền lương từ 5.000 (1.000đ) trở lên là 50 (người). Với xác suất 0,683;
tỷ lệ công nhân trong toàn xí nghiệp có tiền lương bình quân từ 5.000 (1.000đ) trở lên là ?
5.14. Trong một xí nghiệp có 2.000 công nhân, để điều tra về năng suất lao động, người ta
chọn ra 100 người theo phương pháp chọn ngẫu nhiên đơn giản không hoàn lại. Kết quả điều
tra cho thấy, số công nhân có năng suất lao động từ 50 (sp) trở lên là 20 (người). Với xác suất
0,683; tỷ lệ công nhân trong toàn xí nghiệp có năng suất lao động từ 50 (sp) trở lên là?
5.15. Một địa phương có 1.000 (ha) đất nông nghiệp, để điều tra về năng suất thu hoạch lúa,
người ta chọn ra 100 (ha) theo phương pháp chọn ngẫu nhiên đơn giản không hoàn lại. Kết
quả điều tra cho thấy, số ha đất có năng suất thu hoạch lúa từ 50 (tạ/ha) là 10 (ha). Với xác
suất 0,954; tỷ lệ đất có năng suất thu hoạch lúa từ 50 (tạ/ha) chung của toàn địa phương là ?
5.16. Trong một xí nghiệp có 2.000 công nhân, để điều tra về năng suất lao động, người ta
chọn ra 100 người theo phương pháp chọn ngẫu nhiên đơn giản không hoàn lại. Kết quả điều
tra cho thấy, số công nhân có năng suất lao động từ 45 (sp) trở lên là 30 (người). Với xác suất
0,954; tỷ lệ công nhân trong toàn xí nghiệp có năng suất lao động từ 45 (sp) trở lên là ?
5.17. Trong một xí nghiệp có 2.000 công nhân, để điều tra về năng suất lao động, người ta
chọn ra 100 người theo phương pháp chọn ngẫu nhiên đơn giản có hoàn lại. Kết quả điều tra
cho thấy, số công nhân có năng suất lao động từ 45 (sp) trở lên là 20 (người). Với xác suất
0,683; tỷ lệ công nhân trong toàn xí nghiệp có năng suất lao động từ 45 (sp) trở lên là ?
5.18. Một địa phương có 1.000 (ha) đất nông nghiệp, để điều tra về năng suất thu hoạch lúa,
người ta chọn ra 100 (ha) theo phương pháp chọn ngẫu nhiên đơn giản không hoàn lại. Kết
quả điều tra cho thấy, số ha đất có năng suất thu hoạch lúa từ 50 (tạ/ha) là 10 (ha). Với xác
suất 0,683; tỷ lệ đất có năng suất thu hoạch lúa từ 50 (tạ/ha) chung của toàn địa phương là ?
5.19. Trong một doanh nghiệp có 2.000 công nhân, đề điều tra về năng suất lao động, người
ta chọ ra 100 người theo phương pháp chọn ngẫu nhiên đơn giản không hoàn lại. Kết quả điều tra như sau: Năng suất lao động (sp) Số công nhân (người) 50 – 60 20 60 – 70 70 – 80 38 80 – 90 25 17
Với xác suất 0,954; hãy tính:
1.Năng suất lao động bình quân của công nhân trong toàn doanh nghiệp.
2.Tỷ lệ công nhân trong toàn doanh nghiệp có năng suất lao động từ 80 (sp) trở lên.
5.20. Trong một xí nghiệp có 1.000 công nhân. Để điều tra năng suất lao động người ta đã
chọn ra 100 công nhân theo phương pháp chọn mẫu ngẫu nhiên đơn giản không hoàn lại. Kết
quả điều tra NSLĐ trên tổng thể mẫu như sau: NSLĐ (tấn) Số công nhân (người) 30-40 30 40-50 33 50-60 24 60-70 13 Hãy tính:
a. Năng suất lao động bình quân của số công nhân toàn doanh nghiệp với xác suất tin cậy là 0,683?
b. Xác suất để cho NSLĐ bình quân chung vừa tính ở câu a, không chênh lệch quá 1,94 tấn
với NSLĐ trung bình chung của số công nhân được điều tra?
c. Giả sử xí nghiệp tiến hành 1 cuộc điều tra mới. Hãy tính số công nhân cần chọn để điều tra
sao cho với xác suất 0,954 phạm vi sai số chọn mẫu khi suy rộng năng suất lao động bình
quân chung không vượt quá 2 tấn?
d. Tỷ lệ số công nhân trong xí nghiệp có mức NSLĐ trung bình từ 60 tấn trở lên với trình độ tin cậy là 0,683?
e. Xác suất để tỷ lệ chung về số công nhân trong cả xí nghiệp có năng suất lao động trung
bình từ 60 tấn trở lên ( vừa tính được ở câu d ) không chênh lệch quá 9,6% so với tỷ lệ đã điều tra được ?
5.20. Trong một nông trại chăn nuôi có 1.000 bò sữa. Người ta tiến hành điều tra chọn mẫu
để tính sản lượng sữa trung bình hàng ngày của mỗi con bò. Số bò được chọn ra là 200 con
theo phương pháp chọn mẫu ngẫu nhiên đơn giản không hoàn lại. Kết quả điều tra trên tổng thể mẫu như sau: Sản lượng sữa hàng Số con bò ngày của 1 con (con) (kg) 7-9 12 9-11 23 11-13 85 13-15 55 15-17 25 Hãy tính:
a. Sản lượng sữa trung bình hàng ngày của một con bò với trình độ tin cậy là 0,683?
b. Xác suất để cho sản lượng sữa bình quân chung vừa tính ở câu a, không chênh lệch quá
0,4kg so với sản lượng sữa trung bình chung điều tra được?
c. Tỷ lệ chung về số bò có sản lượng sữa trung bình từ 13kg trở lên với trình độ tin cậy là 0,954?
d. Xác suất để cho tỷ lệ chung về số bò có sản lượng sữa trung bình từ 13kg trở lên ( vừa tính
được ở câu c ) không chênh lệch quá 6,2% so với tỷ lệ mẫu điều tra được ?
e. Tính số bò cần chọn điều tra ở cuộc điều tra mới sao cho với xác suất 0,954 phạm vi sai số
về tỷ lệ không vượt quá 6% ?
5.21. Một xí nghiệp sản xuất trong tháng được 100 hòm chi tiết máy (mỗi hòm có 400 chi
tiết). Người ta tổ chức điều tra chọn mẫu theo phương pháp chọn cả khối và rút ngẫu nhiên
được 5 hòm. Tất cả các chi tiết trong 5 hòm đều được cân lại và có kết quả như sau: Trọng lượng trung Hòm bình 1 chi tiết (g) 1 50 2 49 3 53 4 53 5 55
Căn cứ vào các số liệu trên, hãy tính:
a. Trọng lượng bình quân của mỗi chi tiết máy nói trên trong tất cả các hòm, với xác suất 0,954?
b. Xác suất để cho trọng lượng bình quân của mỗi chi tiết máy nói trên trong tất cả các hòm
không chênh lệch quá 3g so với trọng lượng bình quân của mỗi chi tiết trong các hòm đã được điều tra?
c. Số hòm cần chọn ra để điều tra (chọn cả khối theo phương pháp chọn ngẫu nhiên đơn giản
không hoàn lại) sao cho với xác suất 0,683 phạm vi sai số chọn mẫu khi tính trọng lượng
bình quân một chi tiết máy không vượt quá 0,7g?
BÀI TẬP VẬN DỤNG CHƯƠNG 6
-Phương trình hồi quy tuyến tính:
6.1. Có số liệu về năng suất lao động và tuổi nghề của 5 công nhân trong một doanh nghiệp như sau: Tuổi nghề (năm) 2 5 8 10 11 NSLĐ (sp) 100 150 120 180 170
Biết thêm rằng: Σxy = 5.580 và Σx2 = 314
Phương trình hồi quy tuyến tính là ?
6.2. Có số liệu về thu nhập và chi tiêu của 5 công nhân trong một doanh nghiệp như sau: Thu nhập (1.000.000đ) 5 6 8 9 10 Chi tiêu (1.000.000đ) 3 5 5,5 7 6
Biết thêm rằng: Σxy = 212 và Σx2 = 306
Phương trình hồi quy tuyến tính là ?
6.3. Có số liệu về năng suất thu hoạch và lượng phân bón của một loại cây trồng trong 5 năm như sau: Lượng phân bón (tạ/ha) 6 10 12 14 16
Năng suất thu hoạch (tạ/ha) 40 44 46 48 52
Biết thêm rằng: Σxy = 2.736 và Σx2 = 732
Phương trình hồi quy tuyến tính là ?
6.4. Có số liệu về tiền lương và năng suất lao động của 5 công nhân trong một doanh nghiệp như sau: Năng suất lao động (sp) 5 6 8 9 10 Tiền lương (1.000.000đ) 10 12 14 15 17
Biết thêm rằng: Σxy = 539 và Σx2 = 306
Phương trình hồi quy tuyến tính là?
6.5. Có số liệu về tiền lương và tuổi nghề của 5 công nhân trong một doanh nghiệp như sau: Tuổi nghề (năm) 3 4 5 7 10 Tiền lương (1.000.000đ) 5 7 8 9 15
Biết thêm rằng: Σxy = 296 và Σx2 = 199
Phương trình hồi quy tuyến tính là ?
6.6. Có số liệu về tiền lương và bậc thợ của 5 công nhân trong một doanh nghiệp như sau: Bậc thợ 1 2 4 5 6 Tiền lương (1.000.000đ) 5 6 7 9 10
Biết thêm rằng: Σxy = 150 và Σx2 = 82
Phương trình hồi quy tuyến tính là ?
6.7. Có số liệu về thời hạn thu hoạch sau khi lúa chín và lượng lúa bị hao hụt của một hợp tác xã như sau:
Thời hạn thu hoạch sau khi 1 5 9 12 15 lúa chín (ngày)
Lượng lúa bị hao hụt (kg) 3 7 15 20 24
Biết thêm rằng: Σxy = 773 và Σx2 = 476
Phương trình hồi quy tuyến tính là ?
6.8. Có số liệu về năng suất lao động và bậc thợ của 5 công nhân trong một doanh nghiệp như sau: Bậc thợ 1 2 3 4 5 NSLĐ 90 140 120 170 160 (sp)
Biết thêm rằng: Σxy = 2.210 và Σx2 = 55
Phương trình hồi quy tuyến tính là ?
-Phương trình hồi quy parabol:
6.9. Có số liệu về tuổi và tỷ lệ sinh của một địa phương như sau: Tuổi (năm) 18 20 22 24 26 Tỷ lệ sinh (%) 8 12 25 18 15
Biết thêm rằng: Σxy = 1.756 Σx2y = 40.000 Σx2 = 2.460 Σx3 = 55.880 Σx4 = 1.287.984
Phương trình hồi quy parabol là ?
6.10. Có số liệu về năng suất thu hoạch và lượng phân bón của một loại cây trồng trong 5 năm như sau: Lượng phân bón (tạ/ha) 8 10 12 14 16
Năng suất thu hoạch (tạ/ha) 40 45 53 46 42
Biết thêm rằng: Σxy = 2.722 Σx2y = 34.460 Σx2 = 760 Σx = 10.080 Σx 3 4 = 138.784
Phương trình hồi quy parabol là ?
6.11. Có số liệu về thời hạn thu hoạch sau khi lúa chín và lượng lúa bị hao hụt của một hợp tác xã như sau:
Thời hạn thu hoạch sau khi lúa chín (ngày) 1 4 10 14 17
Lượng lúa bị hao hụt (kg) 2 6 12 15 20
Biết thêm rằng: Σxy = 696 Σx y = 10.018 Σx 2 = 602 Σx 2 3 = 8.722 Σx4 = 132.194
Phương trình hồi quy parabol là ?
6.12. Có số liệu về tuổi và tỷ lệ sinh của một địa phương như sau: Tuổi (năm) 18 20 22 24 26 Tỷ lệ sinh (%) 8 12 25 18 15
Biết thêm rằng: Σxy = 1.756 Σx2y = 40.000 Σx2 = 2.460 Σx3 = 55.880 Σx4 = 1.287.984
Phương trình hồi quy parabol là ?
-Phương trình hồi quy hyperbol:
6.13. Có số liệu về lượng cầu và giá bán của một loại máy tính như sau: Giá bán (triệu đồng) 4 5 6 7 8 Lượng cầu (chiếc) 210 180 170 150 130
Biết thêm rằng: Σ1/x = 0,885 Σ1/x2 = 0,166 Σy/x = 154,512
Phương trình hồi quy hyperbol là ?
6.14. Có số liệu về năng suất lao động và giá thành sản phẩm của 5 doanh nghiệp cùng sản
xuất một loại sản phẩm như sau: Năng suất lao động (sp) 4 6 8 10 12 Giá thành (1.000đ) 20 18 17 15 12
Biết thêm rằng: Σ1/x = 0,725 Σ1/x2 = 0,1228 Σy/x = 12,625
Phương trình hồi quy hyperbol là ?
6.15. Có số liệu về 5 xí nghiệp cùng ngành sản xuất như sau: Số lượng sản phẩm Mức nguyên vật liệu Doanh nghiệp sản xuất (1000 tấn) tiêu dùng (1000 tấn) A 220 30 B 60 10 C 150 22 D 120 16 E 200 28
a. Hãy trình bày bằng đồ thị mối liên hệ giữa số lượng sản phẩm và mức nguyên vật liệu tiêu thụ?
b. Hãy xác định phương trình hồi quy tuyến tính biểu hiện mối liên hệ trên. Giải thích các tham số đã tính được?
6.16. Có số liệu về 5 xí nghiệp cùng ngành sản xuất như sau: Sản lượng sản phẩm Lượng nhiên liệu tiêu Xí nghiệp sản xuất (1000 tấn) thụ (100 tấn) A 12 7 B 16 7,7 C 11 5,5 D 9 5,1 E 20 9
Hãy xác định phương trình hồi quy tuyến tính biểu hiện mối liên hệ trên?
6.17. Cho số liệu về 10 cửa hàng thuộc doanh nghiệp X như sau: Tên cửa hàng Doanh số (tr.đ) Chi phí lưu thông (tr.đ) A 200 20 B 300 27 C 400 38 D 500 48 E 600 57 G 700 60 H 800 68 I 900 72 K 1000 80 M 1100 82
Hãy xác định phương trình hồi quy biểu hiện mối liên hệ trên?
6.18. Kết quả điều tra chọn mẫu về một doanh nghiệp về mối liên hệ giữa chi phí lao động và
năng suất lao động của 5 công nhân: Chi phí lao động Năng suất lao động Tên công nhân (1000 đ) (1000đ) A 10 6 B 7 8 C 8.5 9 D 11 12 E 10 14
Hãy xác định phương trình Parabol bậc 2 phản ánh mối liên hệ giữa chi phí lao động và năng suất lao động?
6.19. Kết quả điều tra chọn mẫu tại một địa phương về mối liên hệ giữa lượng lúa hao hụt và
thời gian thu hoạch sau khi lúa đã chín như sau:
Thời gian thu hoạch sau khi lúa chín 0 5 10 15 20 (ngày)
Lượng lúa bị hao hụt (tạ/ha) 0 2 8 10 11
Hãy xác định phương trình Parabol bậc 2 phản ánh mối liên hệ giữa thời gian thu hoạch sau
khi lúa chín và lượng lúa bị hao hụt sau khi thu hoạch chậm?
6.20. Có tài liệu về sản lượng và giá thành ở 4 xí nghiệp cùng sản xuất một loại sản phẩm: Tên xí nghiệp
Sản lượng (1000 T) Giá thành 1 tấn (1000đ) A 1 21 B 5 19 C 10 14 D 15 9
Hãy xác định phương trình Hypecbol phản ánh mối liên hệ giữa sản lượng và giá thành?
CHƯƠNG 7: DÃY SỐ THỜI GIAN
Bài 1: Đề bài sau dùng cho 15 câu (từ câu 1 đến câu 15)
Có số liệu về doanh thu của một cửa hàng như sau: Năm 2005 2006 2007 2008 2009 Doanh thu (triệu đồng) 1.000 1.500 1.800 2.000 2.400
Câu 1: Tốc độ phát triển doanh thu năm 2006 so với 2005 là:
Câu 2: Tốc độ phát triển doanh thu năm 2007 so với 2006 là:
Câu 3: Tốc độ phát triển doanh thu năm 2008 so với 2005 là:
Câu 4: Tốc độ phát triển doanh thu năm 2009 so với 2005 là:
Câu 5: Tốc độ phát triển bình quân về doanh thu là:
Câu 6: Doanh thu năm 2006 so với 2005 tăng:
Câu 7: Doanh thu năm 2007 so với 2006 tăng:
Câu 8: Doanh thu năm 2008 so với 2005 tăng:
Câu 9: Doanh thu năm 2009 so với 2005 tăng:
Câu 10: Tốc độ tăng bình quân về doanh thu là:
Câu 11: Năm 2006 so với 2005, cứ 1% tăng lên của doanh thu tương ứng về số tuyệt đối tăng:
Câu 12: Năm 2007 so với 2006, cứ 1% tăng lên của doanh thu tương ứng về số tuyệt đối tăng:
Câu 13: Năm 2008 so với 2007, cứ 1% tăng lên của doanh thu tương ứng về số tuyệt đối tăng:
Câu 14: Năm 2009 so với 2008, cứ 1% tăng lên của doanh thu tương ứng về số tuyệt đối tăng:
Câu 15: Doanh thu bình quân của cửa hàng giai đoạn 2005 – 2009 là:
Bài 2: Có tài liệu về số công nhân của một doanh nghiệp như sau: Ngày 1/1 1/2 1/3 1/4 Số công nhân (người) 100 120 130 100
Số công nhân bình quân của doanh nghiệp trong quý I là ?
Bài 3: Có tài liệu về số công nhân của một doanh nghiệp trong tháng 6 năm 2016 như sau:
Từ ngày 1 đến ngày 8 có 90 công nhân
Từ ngày 9 đến ngày 15 có 96 công nhân
Từ ngày 16 đến ngày 27 có 105 công nhân
Từ ngày 28 đến ngày 30 có 112 công nhân
Số công nhân bình quân của doanh nghiệp trong tháng 4 năm 2010 là ?
CHƯƠNG 8: DỰ ĐOÁN THỐNG KÊ NGẮN HẠN
Bài 1:Đề bài sau dùng cho 4 câu (từ câu 1 đến câu 4)
Có số liệu về doanh thu của một cửa hàng như sau: Năm 2005 2006 2007 2008 2009 Doanh thu (triệu đồng) 1.000 1.500 1.800 2.000 2.400
Câu 1: Doanh thu dự đoán của cửa hàng năm 2010 dựa vào lượng tăng tuyệt đối bình quân là:
Câu 2: Doanh thu dự đoán của cửa hàng năm 2011 dựa vào lượng tăng tuyệt đối bình quân là:
Câu 3: Doanh thu dự đoán của cửa hàng năm 2011 dựa vào tốc độ phát triển bình quân là:
Câu 4: Doanh thu dự đoán của cửa hàng năm 2012 dựa vào tốc độ phát triển bình quân là:
Bài 2:Đề bài sau dùng cho 2 câu (từ câu 5 đến câu 6)
Có số liệu về doanh thu của một cửa hàng như sau: Năm 2005 2006 2007 2008 2009 Doanh thu (triệu đồng) 1.000 1.500 1.800 2000 2.400
Biết thêm rằng: Hàm xu thế tuyến tính theo thời gian có dạng: Ŷt = 750 + 330t
Câu 5: Doanh thu dự đoán của cửa hàng năm 2010 dựa vào việc ngoại suy hàm xu thế tuyến tính là:
Câu 6: Doanh thu dự đoán của cửa hàng năm 2011 dựa vào việc ngoại suy hàm xu thế tuyến tính là: CHƯƠNG 9: CHỈ SỐ
Đề bài sau dùng cho 4 câu (từ câu 1 đến câu 4)
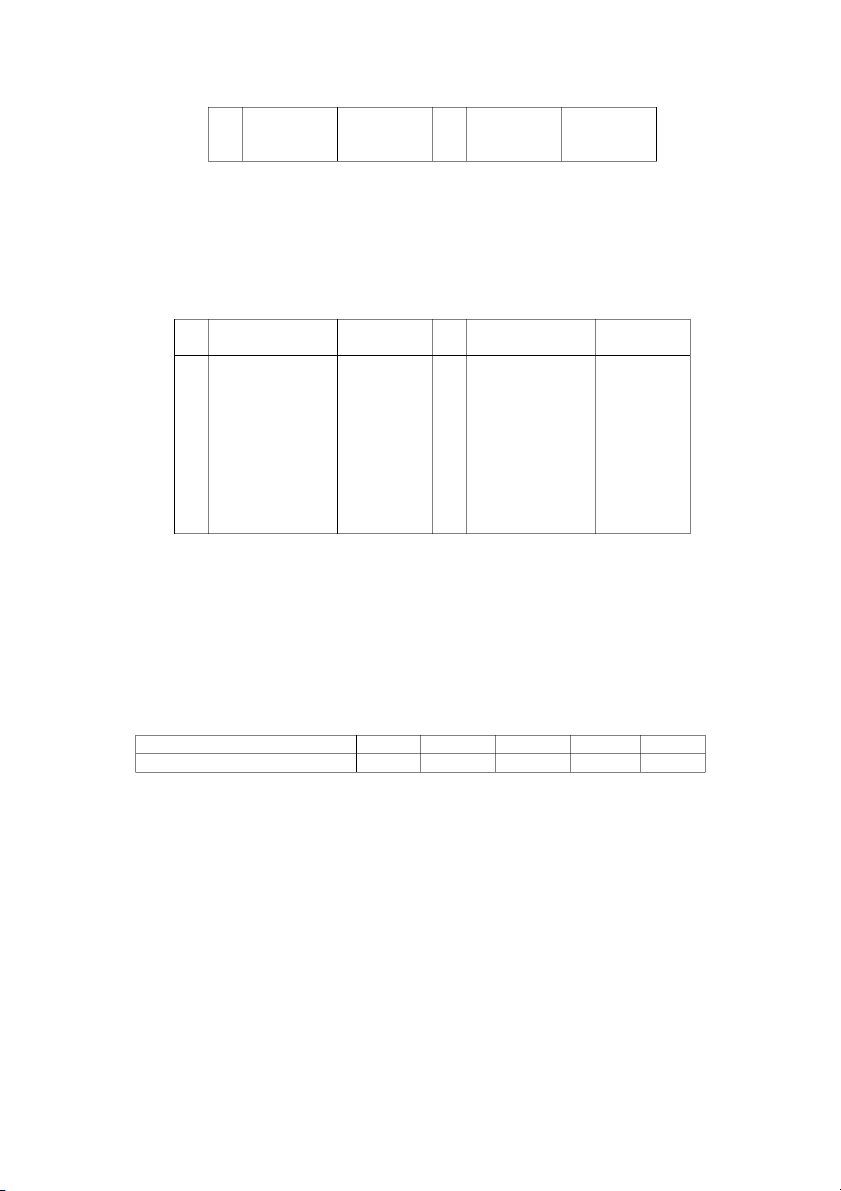
Có tài liệu của một thị trường như sau: Tên Doanh thu (1.000.000đ)
Tỷ lệ% tăng (giảm) giá bán kỳ báo hàng Kỳ gốc Kỳ báo cáo cáo so với kỳ gốc (p0q ) 0 (p1q ) 1 A 20 22 +5 B 30 38 -6
Câu 1: Chỉ số chung về giá bán với quyền số kỳ gốc ?
Câu 2: Chỉ số chung về giá bán với quyền số kỳ báo cáo ?
Câu 3: Chỉ số chung về lượng hàng tiêu thụ với quyền số kỳ gốc ?
Câu 4: Chỉ số chung về lượng hàng tiêu thụ với quyền số kỳ báo cáo ?
Đề bài sau dùng cho 4 câu (từ câu 5 đến câu 8)
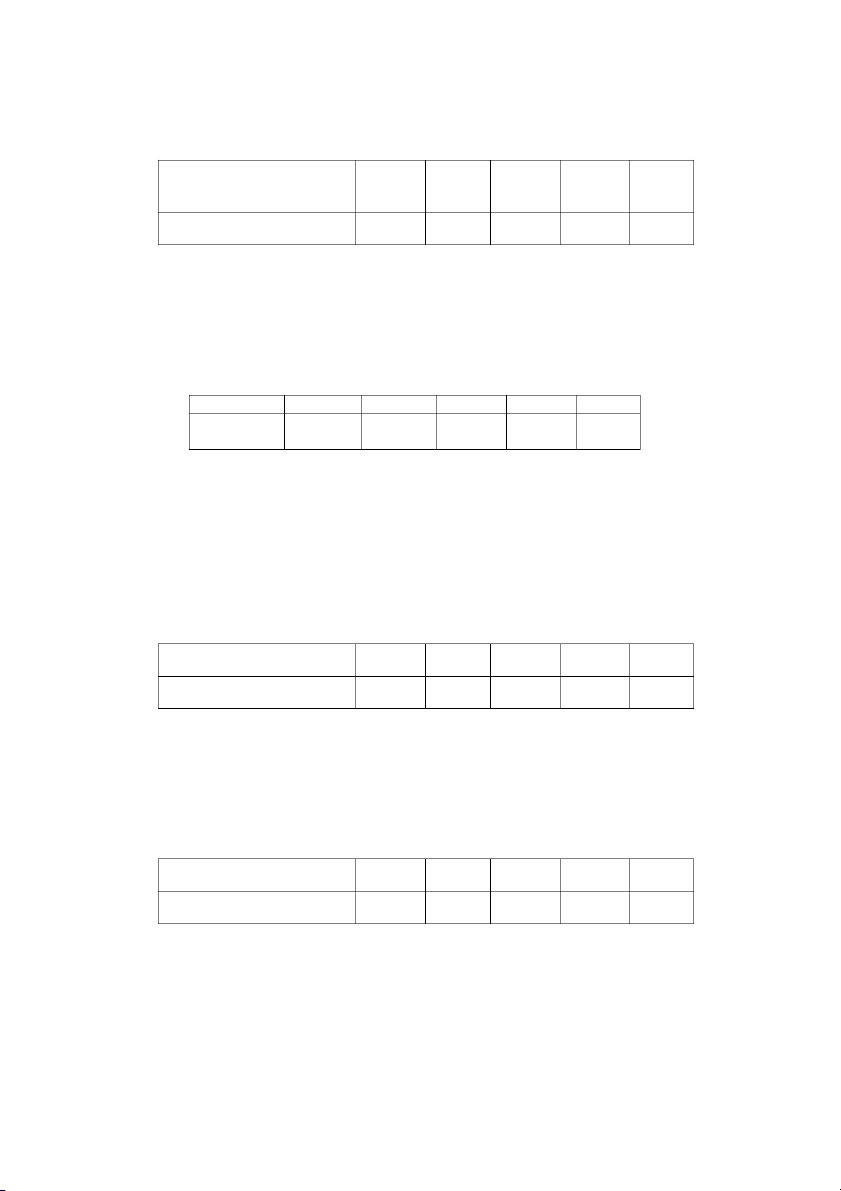
Có tài liệu của một doanh nghiệp như sau: Tên
Tổng giá thành (1.000.000đ)
Tỷ lệ% tăng (giảm) giá thành kỳ phân Kỳ gốc Kỳ báo cáo
báo cáo so với kỳ gốc (iz = z1/z0) xưởng (z0q ) 0 (z1q1) A 55 52 -3 B 65 48 +6
Câu 5: Chỉ số chung về giá thành với quyền số kỳ gốc ?
Câu 6: Chỉ số chung về giá thành với quyền số kỳ báo cáo ?
Câu 7: Chỉ số chung về sản lượng với quyền số kỳ gốc ?
Câu 8: Chỉ số chung về sản lượng với quyền số kỳ báo cáo ?
Đề bài sau dùng cho 4 câu (từ câu 9 đến câu 12)
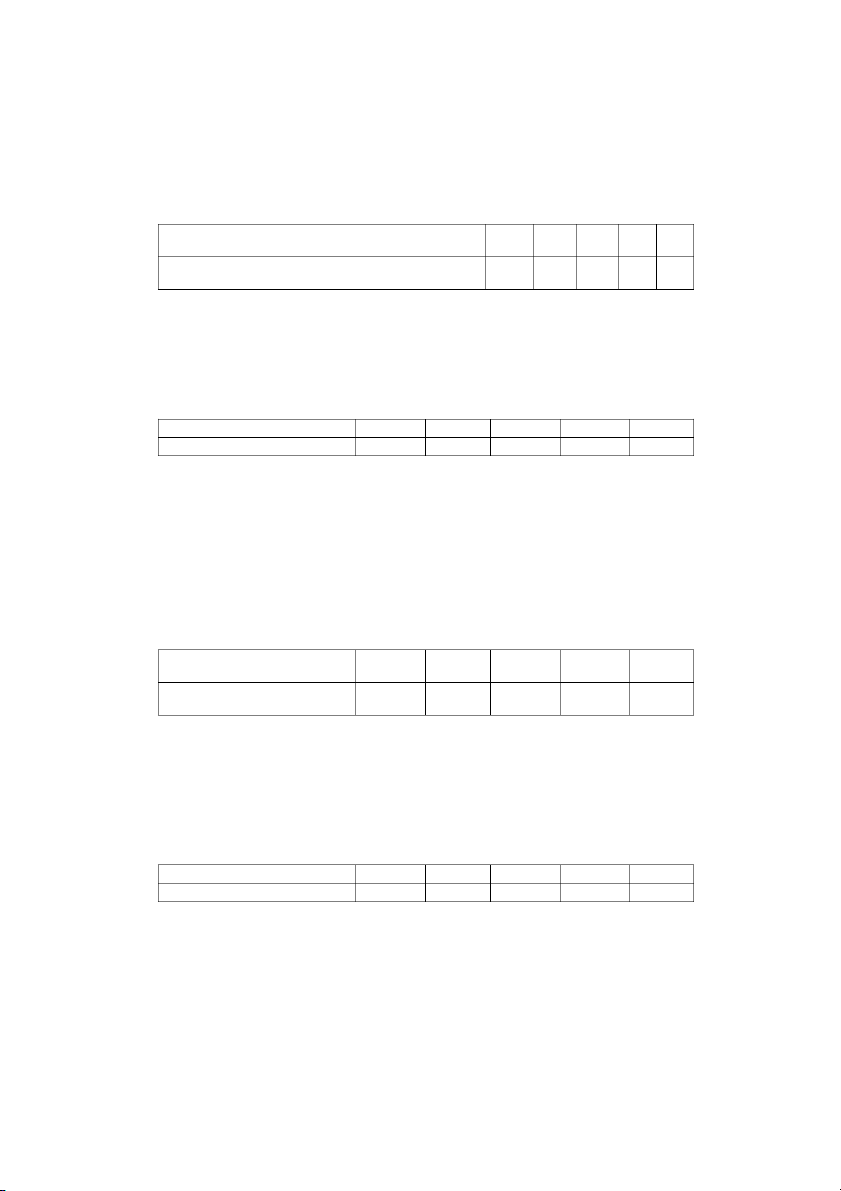
Có tài liệu của một doanh nghiệp như sau: Tên Tổng sản lượng (sp)
Tỷ lệ% tăng (giảm) năng suất lao phân Kỳ gốc Kỳ báo cáo
động kỳ báo cáo so với kỳ gốc xưởng A 60 67 -5 B 90 72 +2
Câu 9: Chỉ số chung về năng suất lao động với quyền số kỳ gốc ?
Câu 10: Chỉ số chung về năng suất lao động với quyền số kỳ báo cáo ?
Câu 11: Chỉ số chung về số công nhân với quyền số kỳ gốc ?
Câu 12: Chỉ số chung về số công nhân với quyền số kỳ báo cáo ?
Đề bài sau dùng cho 4 câu (từ câu 13 đến câu 16)
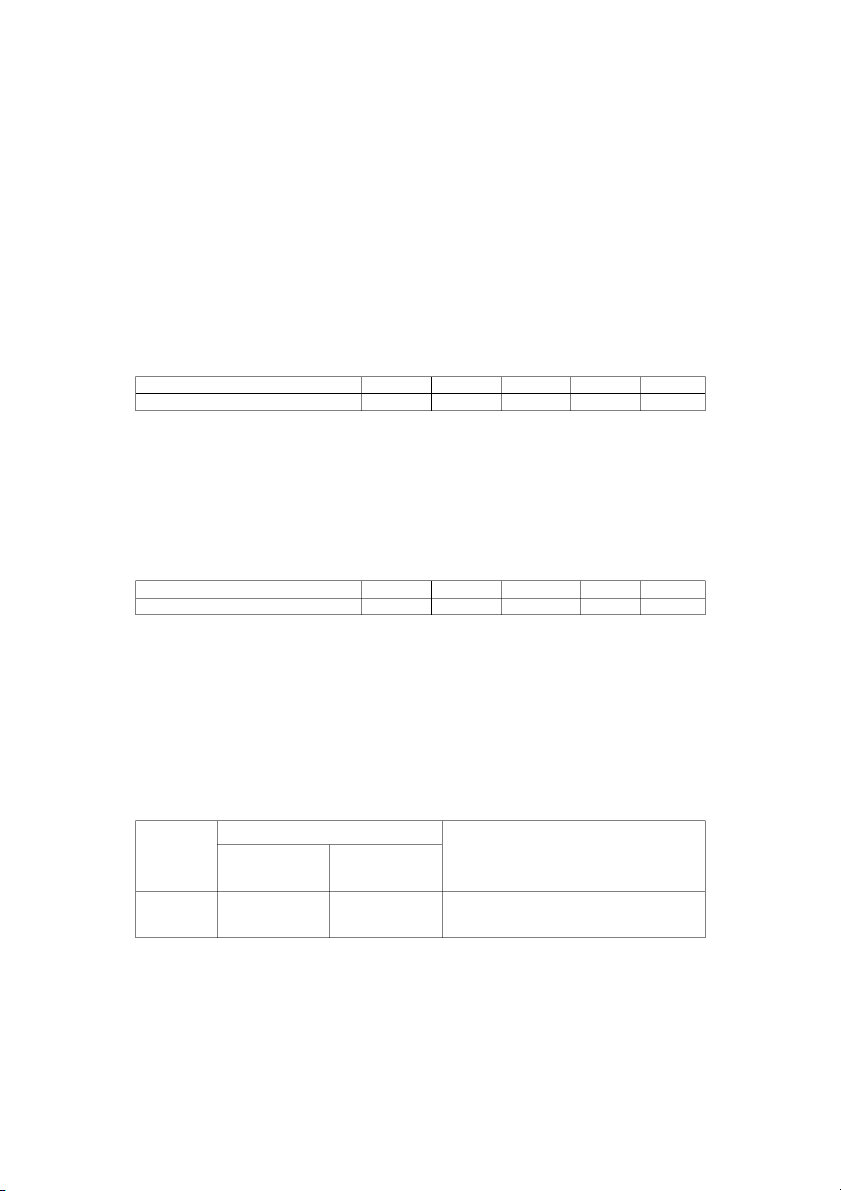
Có tài liệu của một doanh nghiệp như sau: Tên
Tổng quỹ lương (1.000.000đ)
Tỷ lệ% tăng (giảm) tiền lương kỳ phân Kỳ gốc Kỳ báo cáo báo cáo so với kỳ gốc xưởng A 120 100 +4 B 80 150 -8
Câu 13: Chỉ số chung về tiền lương với quyền số kỳ gốc ?
Câu 14: Chỉ số chung về tiền lương với quyền số kỳ báo cáo ?
Câu 15: Chỉ số chung về số công nhân với quyền số kỳ gốc ?
Câu 16: Chỉ số chung về số công nhân với quyền số kỳ báo cáo ?
Đề bài sau dùng cho 4 câu (từ câu 17 đến câu 20)
Có tài liệu của một thị trường như sau: Tên hàng Giá bán (1.000đ) Lượng tiêu thụ (sp) Kỳ gốc Kỳ báo cáo Kỳ gốc Kỳ báo cáo A 6 5 30 45 B 8 10 50 65
Câu 17: Chỉ số chung về giá với quyền số kỳ gốc ?
Câu 18: Chỉ số chung về giá với quyền số kỳ báo cáo ?
Câu 19: Chỉ số chung về lượng hàng tiêu thụ với quyền số kỳ gốc ?
Câu 20: Chỉ số chung về lượng hàng tiêu thụ với quyền số kỳ báo cáo ?
Đề bài sau dùng cho 4 câu (từ câu 21 đến câu 24)
Có tài liệu của một doanh nghiệp như sau: Tên hàng Giá thành (1.000đ) Sản lượng (sp) Kỳ gốc Kỳ báo cáo Kỳ gốc Kỳ báo cáo A 12 11 60 50 B 10 12 40 70
Câu 21: Chỉ số chung về giá thành với quyền số kỳ gốc ?
Câu 22: Chỉ số chung về giá thành với quyền số kỳ báo cáo ?
Câu 23: Chỉ số chung về sản lượng với quyền số kỳ gốc ?
Câu 24: Chỉ số chung về sản lượng với quyền số kỳ báo cáo ?
Đề bài sau dùng cho 4 câu (từ câu 25 đến câu 28)
Có tài liệu của một doanh nghiệp như sau: Tên phân Năng suất lao động (sp) Số công nhân (người) xưởng Kỳ gốc Kỳ báo cáo Kỳ gốc Kỳ báo cáo A 3 5 30 40 B 4 3 70 40
Câu 25: Chỉ số chung về năng suất lao động với quyền số kỳ gốc ?
Câu 26: Chỉ số chung về năng suất lao động với quyền số kỳ báo cáo ?
Câu 27: Chỉ số chung về số công nhân với quyền số kỳ gốc ?
Câu 28: Chỉ số chung về số công nhân với quyền số kỳ báo cáo ?
Đề bài sau dùng cho 4 câu (từ câu 29 đến câu 32)
Có tài liệu của một doanh nghiệp như sau: Tên phân Tiền lương (1.000.000đ) Số công nhân (người) xưởng Kỳ gốc Kỳ báo cáo Kỳ gốc Kỳ báo cáo A 20 25 30 45 B 22 21 40 32
Câu 29: Chỉ số chung về tiền lương với quyền số kỳ gốc ?
Câu 30: Chỉ số chung về tiền lương với quyền số kỳ báo cáo ?
Câu 31: Chỉ số chung về số công nhân với quyền số kỳ gốc ?
Câu 32: Chỉ số chung về số công nhân với quyền số kỳ báo cáo ?
Đề bài sau dùng cho 4 câu (từ câu 33 đến câu 36)
Có tài liệu của một thị trường như sau: Tên Doanh thu (1.000.000đ)
Tỷ lệ% tăng (giảm) lượng hàng tiêu hàng Kỳ gốc Kỳ báo cáo
thụ kỳ báo cáo so với kỳ gốc A 35 51 +8 B 42 40 -6
Câu 33: Chỉ số chung về giá bán với quyền số kỳ gốc ?
Câu 34: Chỉ số chung về giá bán với quyền số kỳ báo cáo ?
Câu 35: Chỉ số chung về lượng hàng tiêu thụ với quyền số kỳ gốc ?
Câu 36: Chỉ số chung về lượng hàng tiêu thụ với quyền số kỳ báo cáo ?
Đề bài sau dùng cho 4 câu (từ câu 37 đến câu 40)
Có tài liệu của một doanh nghiệp như sau: Tên
Tổng giá thành (1.000.000đ)
Tỷ lệ% tăng (giảm) sản lượng kỳ phân Kỳ gốc Kỳ báo cáo báo cáo so với kỳ gốc xưởng A 100 90 +5 B 120 100 -7
Câu 37: Chỉ số chung về giá thành với quyền số kỳ gốc ?
Câu 38: Chỉ số chung về giá thành với quyền số kỳ báo cáo ?
Câu 39: Chỉ số chung về sản lượng với quyền số kỳ gốc ?
Câu 40: Chỉ số chung về sản lượng với quyền số kỳ báo cáo ?