1 Bài tập  0 nếu 𝑥 ∉ (0; 4)
Bài 0.1. Cho hàm số 𝑓 (𝑥) = 1 1   𝑥 + nếu 𝑥 ∈ (0; 4)  16 8
a) Chứng minh 𝑓 (𝑥) là hàm mật độ xác suất của biến ngẫu nhiên liên tục 𝑋.
b) Tính xác suất để trong một phép thử 𝑋 nhận giá trị lớn hơn 2.
c) Tính xác suất để trong 3 phép thử độc lập có đúng 1 lần 𝑋 nhận giá trị nhỏ hơn 2.
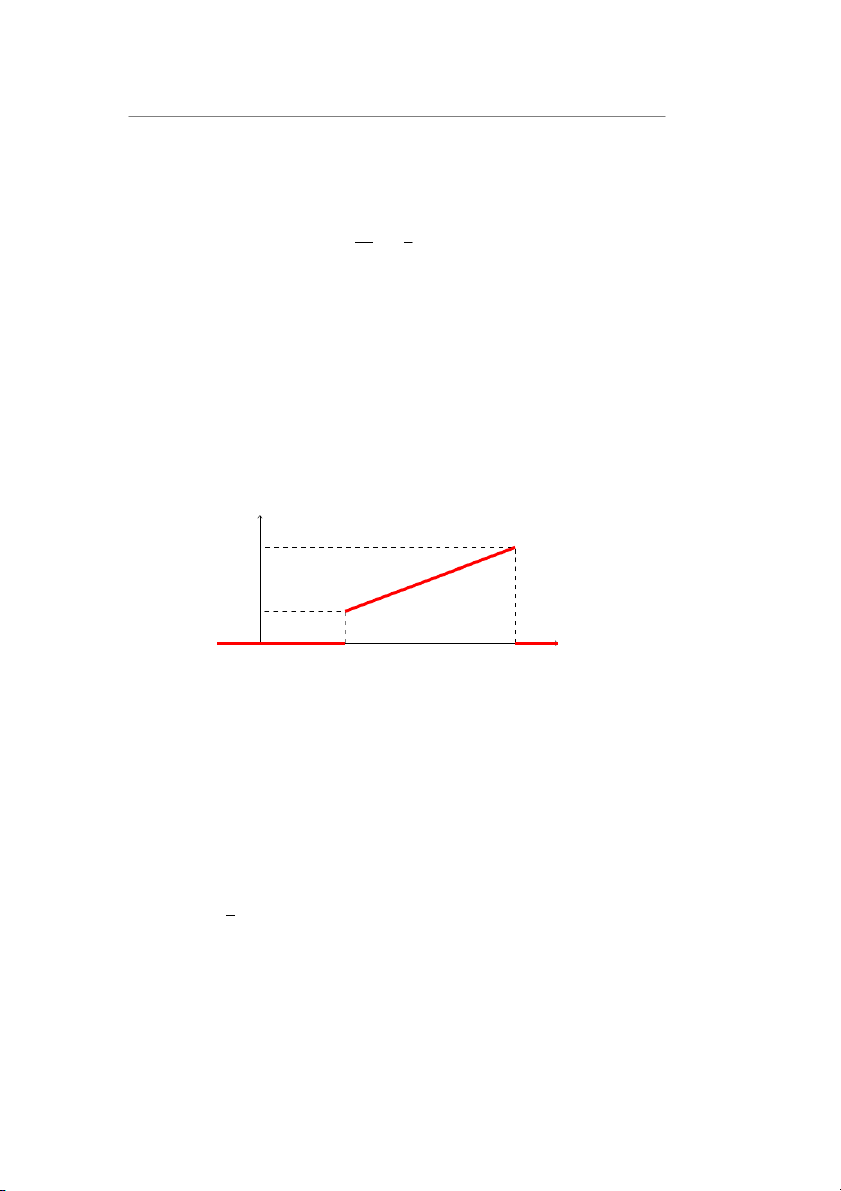
Bài 0.2. Cho biến ngẫu nhiên liên tục 𝑋 có đồ thị hàm mật độ xác suất 𝑓 (𝑥) như hình vẽ 𝑓 (𝑥) 0, 75 0, 25 𝑥 0 1 3
a) Tính xác suất để trong một phép thử 𝑋 nhận giá trị không quá 2.
b) Tính xác suất để trong 5 phép thử độc lập có không quá 1 lần X nhận giá trị lớn hơn 2.
Bài 0.3. Thời gian (đơn vị: phút) để thí sinh hoàn thành một câu hỏi trắc
nghiệm là biến ngẫu nhiên liên tục có hàm mật độ xác suất:     0 nếu 𝑥 ∉ (0; 3) 𝑓 (𝑥) = 2 
 𝑥(3 − 𝑥) nếu 𝑥 ∈ (0; 3)  9
a) Tìm tỷ lệ câu hỏi có thời gian hoàn thành nhiều hơn 2 phút. 2
b) Biết đề thi có 10 câu có nội dung độc lập nhau, tính xác suất để có ít
nhất 2 câu hỏi có thời gian hoàn thành nhiều hơn 2 phút.
Bài 0.4. Thời gian (đơn vị: phút) giữa hai khách hàng liên tiếp vào một cửa
hàng là biến ngẫu nhiên liên tục có hàm mật độ xác suất:     0 nếu 𝑥 < 0 𝑓 (𝑥) = 1 
 𝑒−1 𝑥 4 nếu 𝑥 ≥ 0  4
a) Tính thời gian trung bình giữa hai khách hàng liên tiếp vào cửa hàng.
b) Tính xác suất để khoảng thời gian giữa 2 khách hàng liên tiếp vào cửa hàng nhỏ hơn 3 phút.
Bài 0.5. Biến ngẫu nhiên liên tục 𝑋 có hàm mật độ xác suất:     0 nếu 𝑥 ∉ (0; 4) 𝑓 (𝑥) = 1 1   𝑥 + nếu 𝑥 ∈ (0; 4)  16 8
a) Tính kì vọng và phương sai của 𝑋.
b) Tìm giá trị trung vị của 𝑋.
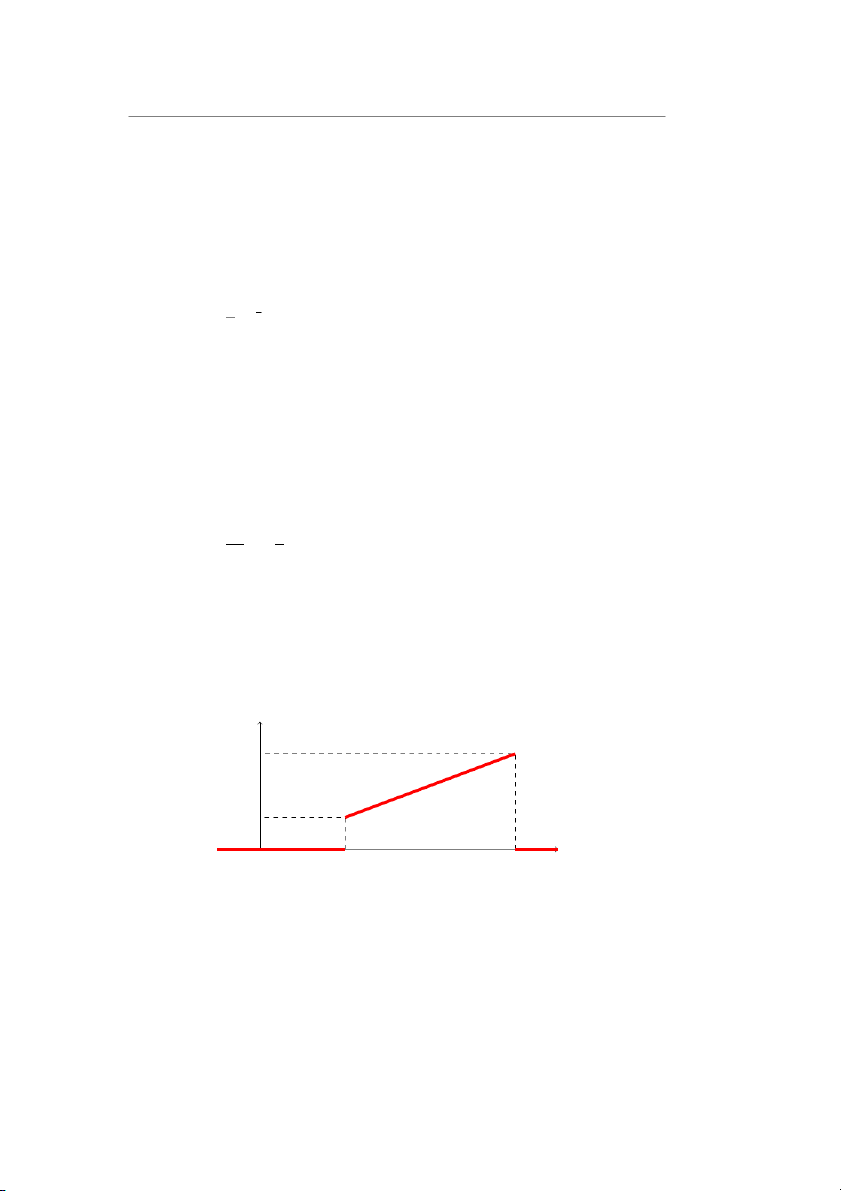
Bài 0.6. Cho biến ngẫu nhiên liên tục 𝑋 có đồ thị hàm mật độ xác suất 𝑓 (𝑥) như hình vẽ: 𝑓 (𝑥) 0, 75 0, 25 𝑥 0 1 3
a) Tính kì vọng và phương sai của 𝑋.
b) Tính xác suất để trong một phép thử 𝑋 nhận giá trị lớn hơn giá trị trung bình của nó. 3
Bài 0.7. Thời gian (đơn vị: phút) để thí sinh hoàn thành một câu hỏi trắc
nghiệm là biến ngẫu nhiên liên tục có hàm mật độ xác suất:     0 nếu 𝑥 ∉ (0; 3) 𝑓 (𝑥) = 2 
 𝑥(3 − 𝑥) nếu 𝑥 ∈ (0; 3)  9
a) Tính thời gian trung bình và độ lệch chuẩn để hoàn thành một câu hỏi trắc nghiệm.
b) Tính thời gian hoàn thành một câu có khả năng xuất hiện nhiều nhất.
Bài 0.8. Cho X là biến ngẫu nhiên có phân phối đều trên đoạn [2; 12].
a) Tìm hàm mật độ xác suất của X.
b) Tính xác suất để X nhận giá trị từ 4 đến 8.
c) Tính xác suất để trong 5 phép thử độc lập có đúng 2 lần X nhận giá trị nhỏ hơn 4.
Bài 0.9. Thời gian hoàn thành một sản phẩm của công nhân là biến ngẫu
nhiên có phân phối đều. Sản phẩm có thời gian hoàn thành ít nhất là 5 phút,
sản phẩm có thời gian hoàn thành nhiều nhất là 10 phút.
a) Tính thời gian hoàn thành sản phẩm trung bình của công nhân.
b) Tìm trung vị của thời gian hoàn thành sản phẩm của công nhân.
c) Tìm tỷ lệ sản phẩm có thời gian hoàn thành nhiều hơn 8 phút.
Bài 0.10. Biến ngẫu nhiên Z có phân phối chuẩn hóa. Tính xác suất:
a) 𝑃(𝑍 > −1,96)
b) 𝑃(𝑍 < 1,65)
c) 𝑃(1,28 < 𝑍 < 1,96)
Bài 0.11. Biến ngẫu nhiên 𝑋 ∼ 𝑁(10; 9). Tính xác suất:
a) 𝑋 nhận giá trị lớn hơn 17,5. 4
b) 𝑋 nhận giá trị không quá 7.
c) 𝑋 nhận giá trị trong khoảng từ 5,5 đến 16.
Bài 0.12. Biến ngẫu nhiên 𝑋 có phân phối Chuẩn, trung bình bằng 20,
phương sai bằng 4. Tính xác suất để:
a) 𝑋 nhận giá trị sai lệch so với giá trị trung bình của nó không quá 3 đơn vị.
b) Trong 3 phép thử độc lập, có đúng 1 lần 𝑋 nhận giá trị lớn hơn giá trị trung bình của nó.
Bài 0.13. Cho 𝑋, 𝑌 là các biến ngẫu nhiên độc lập, 𝑋 ∼ 𝑁(20; 9),𝑌 ∼
𝑁 (30; 25). Tính xác suất:
a) 𝑃(𝑋 < 𝑌)
b) 𝑃(3𝑋 ≥ 2𝑌 + 15)
Bài 0.14. Doanh thu trong một ngày tại một cửa hàng là biến ngẫu nhiên
có phân phối Chuẩn, doanh thu trung bình là 100 triệu, độ lệch chuẩn là 20
triệu. Tính xác suất để:
a) Doanh thu trong một ngày cao hơn 130 triệu.
b) Doanh thu trong một ngày không quá 80 triệu.
c) Doanh thu chênh lệch so với doanh thu trung bình nhiều hơn 10 triệu.
Bài 0.15. Tại một trang trại nuôi lợn, qua theo dõi người ta thấy số kg tăng
thêm trong một tháng của mỗi con lợn là biến ngẫu nhiên có phân phối
Chuẩn, trung bình là 20 kg. Tỷ lệ lợn có cân nặng tăng thêm nhiều hơn 24 kg là 2,28%.
a) Tìm tỷ lệ lợn có cân nặng tăng thêm trong một tháng ít hơn 18 kg.
b) Tính xác suất để trong 5 con lợn thì có đúng 1 con có cân nặng tăng
thêm trong tháng từ 19 kg đến 25 kg. 5
Bài 0.16. Một cửa hàng chuyên bán điện thoại xách tay với chế độ bảo hành
tại cửa hàng, thời gian quy định bảo hành là 12 tháng. Khi bán được một
chiếc điện thoại cửa hàng có lãi 2 triệu, song nếu điện thoại hỏng trong thời
gian bảo hành thì cửa hàng phải chi phí 1,5 triệu cho việc bảo hành. Tính
tiền lãi trung bình của mỗi chiếc điện thoại, biết thời gian không phải sửa
chữa là biến ngẫu nhiên có phân phối Chuẩn, trung bình là 24 tháng, độ lệch chuẩn là 6 tháng. 6 Bài tập tổng hợp Bài tập tự luận
Bài 0.17. Thời gian hoàn thành một sản phẩm (đơn vị: phút) là biến ngẫu
nhiên liên tục có hàm mật độ xác suất     0 nếu 𝑥 ∈ (1; 5) 𝑓 (𝑥) = 1   (5 − 𝑥) nếu 𝑥 ∉ (1; 5)  8
a) Tính xác suất để để một sản phẩm có thời gian hoàn thành nhiều hơn 4 phút.
b) Tính xác suất để trong 6 sản phẩm thì có không quá 2 sản phẩm có
thời gian hoàn thành ít hơn 3 phút.
c) Tính thời gian hoàn thành sản phẩm trung bình và phương sai thời
gian hoàn thành sản phẩm. 7 8
Đáp số: a) 0,0625 b) 0,0376 c) 𝐸 (𝑋) = , 𝑉 (𝑋) = 3 9
Bài 0.18. Thời gian chờ để thanh toán (đơn vị: phút) của khách hàng tại
một siêu thị là biến ngẫu nhiên liên tục X có hàm mật độ xác suất:     0 nếu 𝑥 ∉ (0; 30) 𝑓 (𝑥) = 30 − 𝑥   nếu 𝑥 ∈ (0; 30)  450
a) Nếu tỷ lệ khách hàng phải chờ từ 10 phút trở lên vượt quá 50% thì
siêu thị sẽ tăng thêm quầy thanh toán. Hỏi siêu thị có cần tăng thêm quầy thanh toán không?
b) Nếu xác suất trong 5 khách có từ 2 khách trở lên phải chờ quá 10
phút lớn hơn 50% phải thêm quầy thanh toán thì kết luận ở câu a có thay đổi không?
c) Tính trung bình và độ lệch chuẩn thời gian chờ để thanh toán của khách hàng.
Đáp số: a) 0,4444 b) 0,7354 c) 𝐸 (𝑋) = 10, 𝑉 50 (𝑋) =
Bài 0.19. Một nhà đầu tư dự định mua cổ phiếu A và nắm giữ trong vòng 7
1 tháng. Biết tỷ suất sinh lời của cổ phiếu A là biến ngẫu nhiên liên tục 𝑋.
Nếu thị trường thuận lợi thì X có thể lên đến 10%. Nếu thị trường khó khăn
thì X có thể xuống −6%. Vì không có thêm thông tin gì nên nhà đầu tư coi như X phân phối Đều.
a) Xác suất để tỷ suất sinh lời dương bằng bao nhiêu?
b) Biết lãi suất tiền gửi ngân hàng kì hạn 1 tháng là 0,375%. Nếu nhà
đầu tư quan tâm đến lãi trung bình thì nên dùng toàn bộ vốn để mua cổ
phiếu A hay gửi ngân hàng?
Đáp số: a) 𝑃(𝑋 > 0) = 0, 625 b) 𝐸 (𝑋) = 2%
Bài 0.20. Thời gian (đơn vị: giờ) từ lúc khách hàng đặt hàng thành công
trên mạng đến khi nhận được hàng là biến ngẫu nhiên liên tục có hàm mật độ xác suất:   1   𝑒−𝑥/48 nếu 𝑥 > 0 𝑓 (𝑥) = 48   0 nếu 𝑥 < 0 
a) Tính xác suất để khách hàng nhận được hàng trong vòng 24 giờ kể từ lúc đặt hàng.
b) Tính thời gian chờ trung bình của khách hàng cho mỗi đơn đặt hàng.
Đáp số: a) 𝑃(𝑋 ≤ 24) = 0,3935 , b) 𝐸 (𝑋) = 48
Bài 0.21. Một người cân nhắc giữa việc mua nhà bây giờ hay gửi tiền vào
tiết kiệm với lãi suất 9% một năm để chờ một năm sau mới mua. Biết mức
tăng giá nhà là biến ngẫu nhiên có phân phối Chuẩn, trung bình là 6%, độ
lệch chuẩn là 4%. Tìm khả năng rủi ro của người đó nếu gửi tiền vào tiết
kiệm để một năm sau mua nhà. Đáp số: 0,0668
Bài 0.22. Một người cân nhắc giữa việc mua cổ phiếu của hai công ty A và
B. Tỷ suất lợi nhuận (đơn vị: %) của cổ phiếu hai công ty là các biến ngẫu
nhiên độc lập 𝑋𝐴, 𝑋𝐵, biết 𝑋𝐴 ∼ 𝑁 (12; 16 10; 9
), 𝑋𝐵 ∼ 𝑁 ( ).
a) Người đó muốn tỷ suất lợi nhuận tối thiểu là 11% thì nên mua cổ phiếu của công ty nào? 8
b) Người đó muốn hạn chế rủi ro bằng cách mua cổ phiếu của cả hai
công ty thì nên mua theo tỷ lệ như thế nào?
Đáp số: a) 𝑃(𝑋𝐴 > 11 0 5987 11 3694 ) = ,
, 𝑃(𝑋𝐵 > ) = 0,
b) 36% công ty A và 84% công ty B.
Bài 0.23. Tuổi thọ của một loại sản phẩm là biến ngẫu nhiên phân phối
Chuẩn với trung bình là 4,5 năm và độ lệch chuẩn là 1,6 năm. Khi bán được
một sản phẩm thì hãng sản xuất lãi 300 nghìn đồng. Nếu sản phẩm bị hỏng
trong thời gian bảo hành miễn phí thì hãng phải chi trung bình 900 nghìn
đồng cho mỗi sản phẩm hỏng đó.
a) Tìm tỷ lệ sản phẩm có tuổi thọ dưới 18 tháng.
d) Nếu quy định thời gian bảo hành miễn phí là 18 tháng thì số tiền lãi
hãng thu được từ mỗi sản phẩm bán ra là bao nhiêu?
c) Muốn bảo hành miễn phí cho 2% số sản phẩm thì nên quy định thời
gian bảo hành miễn phí là bao nhiêu năm?
d) Nếu muốn tiền lãi trung bình trên nỗi sản phẩm bán ra là 273 nghìn
đồng thì nên quy định thời gian bảo hành miễn phí bao lâu? Đáp số:
a) 𝑃(𝑋 < 18) = 0,0304 b) 272,64 c) 1,214 năm d) 1,491 năm
Bài 0.24. Chiều cao của học sinh lớp 12 là biến ngẫu nhiên có phân phối
Chuẩn, chiều cao trung bình là 162 cm, độ lệch chuẩn là 5 cm. Một học
sinh lớp 12 được coi là có chiều cao bình thường nếu sai lệch so với chiều
cao trung bình không quá 10 cm.
a) Tìm tỷ lệ học sinh lớp 12 có chiều cao bình thường.
b) Chọn ngẫu nhiên 100 học sinh lớp 12 thì số học sinh có chiều cao
không bình thường xuất hiện nhiều nhất là bao nhiêu?
Đáp số: a) 95,45%; b) 5 học sinh
Bài 0.25. Chiều dài của một loại sản phẩm là biến ngẫu nhiên có phân phối
Chuẩn, độ lệch chuẩn là 4 cm. Tỷ lệ sản phẩm có chiều dài lớn hơn 20 cm là 10,56%. 9
a) Tìm chiều dài trung bình của sản phẩm.
b) Lấy ngẫu nhiên 10 sản phẩm thì xác suất để có nhiều nhất 2 sản phẩm
có chiều dài nhỏ hơn 12 cm là bao nhiêu? Đáp số: a) 15 b) 0,5967
Bài 0.26. Số tiền chi cho cước điện thoại di động hằng tháng của người dân
là biến ngẫu nhiên có phân phối Chuẩn. Theo khảo sát thì số người chi cho
cước điện thoại di động hằng tháng nhiều hơn 300 nghìn đồng là 2,28%, ít
hơn 250 nghìn đồng là 84,13%. Số tiền trung bình chi cho cước điện thoại
di động hằng tháng của người dân bằng bao nhiêu?
Đáp số: 200 nghìn đồng.
Bài 0.27. Thời gian sử dụng điện thoại trong một ngày của sinh viên là biến
ngẫu nhiên có phân phối Chuẩn, trung bình là 3 tiếng. Theo khảo sát thì có
15,87% sinh viên sử dụng điện thoại nhiều hơn 5 tiếng một ngày. Tìm tỷ lệ
sinh viên sử dụng điện thoại trong một ngày: a) Ít hơn 2 tiếng
b) Từ 1 tiếng đến 6 tiếng
Đáp số: a) 30,87% b) 77,45%
Bài 0.28. Tỷ lệ người sử dụng điện thoại thông minh có vào mạng xã hội ít
nhất một lần trong một ngày là 80%. Tính xác suất để trong 400 người sử
dụng điện thoại thông minh thì có:
a) Nhiều nhất 310 người vào mạng xã hội ít nhất một lần trong ngày.
b) Ít nhất 70 người không vào mạng xã hội trong một ngày.
Đáp số: a) 0,1056 b) 0,8944
Bài 0.29. Cho 𝑋, 𝑌 là các biến ngẫu nhiên độc lập. 𝑋 ∼ 𝑁(15; 4),𝑌 ∼ 𝑁 (20; 9)
a) Tìm phân phân phối xác suất của biến ngẫu nhiên 2𝑋 − 𝑌
b) Tính 𝑃(2𝑋 − 𝑌 > 6)
Đáp số a) 2𝑋 − 𝑌 ∼ 𝑁 (10; 25) b) 0,7881 10
Bài 0.30. Biết lợi suất trái phiếu hai công ty A, B là các biến ngẫu nhiên
độc lập 𝑋𝐴 ∼ (11; 4), 𝑋𝐵 ∼ 𝑁 (12; 9). Một người đầu tư 40% vốn vào trái
phiếu công ty A và 60% vốn vào trái phiếu công ty B. Tính xác suất để lợi
suất thu được cao hơn 13%. Đáp số: 0,2386 Câu hỏi đúng sai
Câu 0.1. Các khẳng định dưới đây đúng hay sai? Hãy giải thích vì sao.
a) Giá trị của hàm mật độ xác suất 𝑓 (𝑥) là xác suất để biến ngẫu nhiên
liên tục 𝑋 nhận giá trị bằng 𝑥.
b) Nếu tỷ suất lợi nhuận cổ phiếu công ty Hòa Phát (mã cổ phiếu HPG)
trong một phiên giao dịch là biến ngẫu nhiên liên tục 𝑋 ∈ (−7%; 7%) thì
𝑃(𝑋 = 5%) > 0.
c) Bài thi môn Xác suất thống kê toán có 40 câu hỏi trắc nghiệm, mỗi
câu có 4 phương án trả lời và chỉ có 1 đáp án đúng. Điểm thi của sinh viên
có thể đạt được là biến ngẫu nhiên liên tục.
d) Thời gian để vận động viên chạy về đích trên quãng đường 100 m là
biến ngẫu nhiên liên tục.
Câu 0.2. Các khẳng định dưới đây đúng hay sai? Hãy giải thích vì sao.
a) Nếu 𝑈 là biến ngẫu nhiên có phân phối Đều trên khoảng (𝑎; 𝑏) thì
xác suất để 𝑈 nhận giá trị trong mọi khoảng con của (𝑎; 𝑏) đều bằng nhau.
b) Khi tham gia thị trường một công ty có thể dự đoán được lợi nhuận
thấp nhất là 𝑎 và lợi nhuận cao nhất là 𝑏, mà không có thêm thông tin gì
khác thì có thể coi lợi nhuận có phân phối Đều trên khoảng (𝑎; 𝑏).
Câu 0.3. Các khẳng định dưới đây đúng hay sai? Hãy giải thích vì sao.
a) Nếu 𝑋 ∼ 𝑁 (𝜇; 𝜎2) thì 𝜇 là giá trị có khả năng xuất hiện nhiều nhất
b) Cho 𝑋 ∼ 𝑁 (𝜇; 𝜎2). Nếu 𝜎 giảm thì đồ thị hàm mật độ xác suất có
độ rộng giảm đi và độ cao tăng lên. 11
c) Cho 𝑍 ∼ 𝑁 (0; 1) và có hàm phân phối xác suất Φ(𝑧). Ta có: Φ(𝑧) + Φ(−𝑧) = 1
d) Nếu 𝑧𝛼 là giá trị tới hạn Chuẩn mức 𝛼 thì Φ(𝑧𝛼) = 1 − 𝛼
e) Cho 𝑋 ∼ 𝑁 (𝜇𝑋; 𝜎2𝑋),𝑌 ∼ 𝑁(𝜇𝑌; 𝜎2 +9𝜎2
𝑌 ). Ta có: 𝑉 (2𝑋 +3𝑌 ) = 4𝜎2 𝑋 𝑌
Câu hỏi trắc nghiệm
Câu 0.4. Trong các phát biểu sau, phát biểu nào được đại diện bởi biến ngẫu nhiên liên tục?
A. Số tín chỉ sinh viên đăng ký trong một học kỳ
B. Số khách vào một cửa hàng trong một giờ
C. Cân nặng của sinh viên
D. Nhiệt độ sôi của nước tinh khiết
Câu 0.5. Trong các biến ngẫu nhiên dưới đây, biến ngẫu nhiên nào không
phải là biến ngẫu nhiên liên tục?
A. Số trẻ em sinh ra trong một giờ tại một bệnh viện
B. Cân nặng của trẻ sơ sinh
C. Thời gian hoàn thành một bài thi của sinh viên
D. Lợi tức trong một tháng của một loại cổ phiếu
Câu 0.6. Trong các hàm số dưới đây, hàm số nào là hàm mật độ xác suất
của biến ngẫu nhiên liên tục?     0 nếu 𝑥 ∉ (2; 6)
A. 𝑓 (𝑥) = 1   𝑥 nếu 𝑥 ∈ (2; 6)  36  0 nếu 𝑥 ∉ (2; 6)
B. 𝑓 (𝑥) = 1   𝑥 nếu 𝑥 ∈ (2; 6)  4 12     0 nếu 𝑥 ∉ (2; 6)
C. 𝑓 (𝑥) = 1   𝑥 nếu 𝑥 ∈ (2; 6)  32     0 nếu 𝑥 ∉ (2; 6)
D. 𝑓 (𝑥) = 1   𝑥 nếu 𝑥 ∈ (2; 6)  16
Câu 0.7. Tuổi thọ của một loại sản phẩm (đơn vị: năm) là biến ngẫu nhiên
liên tục có hàm mật độ xác suất:     0 nếu 𝑥 ∉ (0; 4) 𝑓 (𝑥) = 3  
𝑥 (4 − 𝑥) nếu 𝑥 ∈ (0; 4)  32
Xác suất để sản phẩm có tuổi thọ nhiều hơn 3 năm là: A. 0,5234 C. 0,15625 B. 0,25 D. 0,5324
Câu 0.8. Tuổi thọ của một loại sản phẩm (đơn vị: năm) là biến ngẫu nhiên
liên tục có hàm mật độ xác suất:     0 nếu 𝑥 ∉ (0; 4) 𝑓 (𝑥) = 3  
𝑥 (4 − 𝑥) nếu 𝑥 ∈ (0; 4)  32
Tỷ lệ sản phẩm có tuổi thọ từ 2 đến 5 năm là: A. 50% C. 75% B. 28,125% D. 71,75%
Câu 0.9. Tuổi thọ của một loại sản phẩm (đơn vị: năm) là biến ngẫu nhiên
liên tục có hàm mật độ xác suất:     0 nếu 𝑥 ∉ (0; 4) 𝑓 (𝑥) = 3  
𝑥 (4 − 𝑥) nếu 𝑥 ∈ (0; 4)  32
Xác suất để trong 5 sản phẩm loại đó có đúng 1 sản phẩm có tuổi thọ nhiều hơn 2 năm là: A. 0,5 C. 0,3215 B. 0,15625 D. 0,0625 13
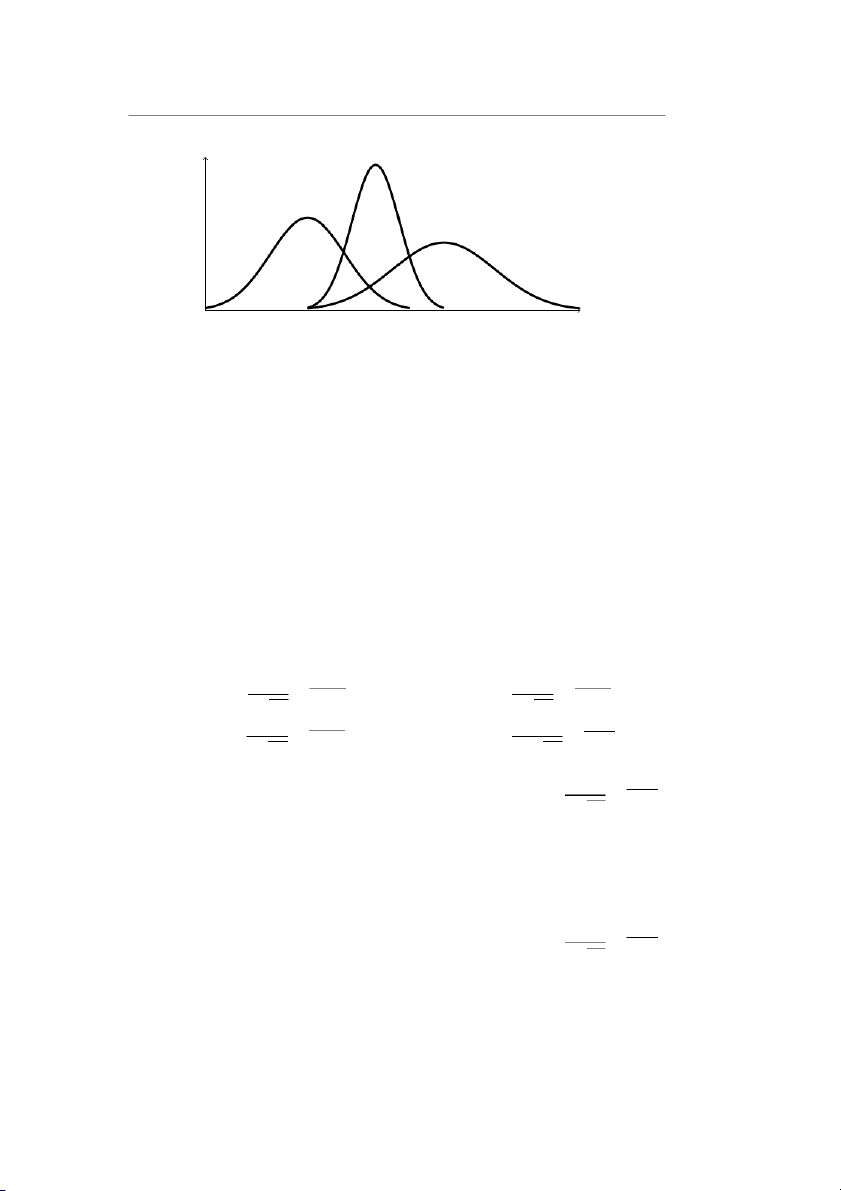
Câu 0.10. Lợi nhuận của ba công ty là ba biến ngẫu nhiên liên tục có đồ
thị hàm mật độ xác suất dưới đây:
Để xác suất có lợi nhuận dương là cao hơn thì nên chọn công ty nào? A. Công ty I. C. Công ty III. B. Công ty II.
D. Chọn công ty nào cũng được.
Câu 0.11. Biến ngẫu nhiên liên tục X có hàm mật độ xác suất:     0 nếu 𝑥 ∉ (0; 5) 𝑓 (𝑥) = 3   𝑥2 nếu 𝑥 ∈ (0; 5)  125
Giá trị kì vọng của X bằng: A. 3,75 C. 4,75 B. 2,5 D. 2,75
Câu 0.12. Mức tiêu thụ nhiên liệu (đơn vị: lít) của một loại xe máy trên
quãng đường 100 km là biến ngẫu nhiên liên tục có hàm mật độ xác suất:     0 nếu 𝑥 ∉ (2; 4) 𝑓 (𝑥) = 3 
 (𝑥 − 2)(4 − 𝑥) nếu 𝑥 ∈ (2; 4)  4
Mức tiêu thụ nhiên liệu trung bình trên quãng đường 100 km của loại xe máy đó là: A. 3,2 lít C. 3 lít B. 2,8 lít D. 2,5 lít
Câu 0.13. Biến ngẫu nhiên liên tục X có hàm mật độ xác suất: 14     0 nếu 𝑥 ∉ (0; 5) 𝑓 (𝑥) = 3   𝑥2 nếu 𝑥 ∈ (0; 5)  125 Phương sai của X bằng: A. 15 C. 11,25 B. 0,9375 D. 3,83
Câu 0.14. Mức tiêu thụ nhiên liệu của một loại xe máy trên quãng đường
100 km là biến ngẫu nhiên liên tục có hàm mật độ xác suất:     0 nếu 𝑥 ∉ (2; 4) 𝑓 (𝑥) = 3 
 (𝑥 − 2)(4 − 𝑥) nếu 𝑥 ∈ (2; 4)  4
Độ lệch chuẩn mức tiêu thụ nhiên liệu trên quãng đường 100 km của loại xe máy đó là: A. 0,2 C. 3,033 B. 2,49 D. 0,447
Câu 0.15. Biến ngẫu nhiên liên tục X có hàm mật độ xác suất:     0 nếu 𝑥 ∉ (1; 4) 𝑓 (𝑥) = 2 
 (𝑥 − 1)(4 − 𝑥) nếu 𝑥 ∈ (1; 4)  9
Giá trị mốt của biến ngẫu nhiên bằng: A. 2,8 C. 3 B. 2,5 D. 3,2
Câu 0.16. Lợi nhuận của ba công ty I, II, III là các biến ngẫu nhiên phân
phối Chuẩn, có đồ thị hàm mật độ xác suất như Hình 1. Nếu muốn chọn
công ty có lợi nhuận ổn định nhất thì chọn công ty nào? A. Công ty I C. Công ty III B. Công ty II
D. Không chọn được công ty nào
Câu 0.17. Cho lợi nhuận của ba công ty I, II, III là các biến ngẫu nhiên
phân phối Chuẩn, đồ thị hàm mật độ xác suất như trong Hình 1. Nếu muốn
chọn công ty có lợi nhuận trung bình cao nhất thì chọn công ty nào? 15 𝑓 (𝑥) Công ty II Công ty I Công ty III 𝑥
Hình 1 – Lợi nhuận 3 công ty A. công ty I C. công ty III B. công ty II
D. Không chọn được công ty nào
Câu 0.18. Cho 𝑋 ∼ 𝑁(𝜇; 𝜎2). Khi tăng 𝜇 và giảm 𝜎2 thì kết luận nào sau
đây đúng về đồ thị của hàm mật độ xác suất 𝑓 (𝑥)?
A. Đồ thị dịch chuyển sang phải và đỉnh của đồ thị cao lên.
B. Đồ thị dịch chuyển sang phải và đỉnh của đồ thị thấp xuống.
C. Đồ thị dịch chuyển sang trái và đỉnh của đồ thị cao lên.
D. Đồ thị dịch chuyển sang trái và đỉnh của đồ thị thấp xuống.
Câu 0.19. Cho 𝑋 ∼ 𝑁(12; 9), khi đó hàm mật độ xác suất của 𝑋 là: 1 A. 1
𝑓 (𝑥) = √ 𝑒− (𝑥−12)2 18
C. 𝑓 (𝑥) = √ 𝑒− (𝑥−12)2 6 9 2𝜋 3 2𝜋 1 B. 1
𝑓 (𝑥) = √ 𝑒− (𝑥−12)2 18
D. 𝑓 (𝑥) = √ 𝑒− (𝑥−9)2 24 3 2𝜋 12 2𝜋 1
Câu 0.20. Cho 𝑋 ∼ 𝑁(𝜇; 𝜎2) có hàm mật độ là: 𝑓 (𝑥) = √ 𝑒− (𝑥−5)2 8 . 2 2𝜋
Điều nào sau đây là đúng?
A. 𝜇 = 5; 𝜎 = 4
C. 𝜇 = 4; 𝜎 = 25
B. 𝜇 = 4; 𝜎 = 5
D. 𝜇 = 5; 𝜎 = 2 1
Câu 0.21. Cho 𝑋 ∼ 𝑁(𝜇; 𝜎2) có hàm mật độ là: 𝑓 (𝑥) = √ 𝑒− (𝑥−8)2 32 . 4 2𝜋 Điều nào sau đây đúng? 16 A. 𝑚0 = 32 C. 𝑚0 = 8 B. 𝑚0 = 16 D. 𝑚0 = 4
Câu 0.22. Cho 𝑋 ∼ 𝑁(16; 𝜎2) . Khẳng định nào sau đây đúng?
A. 𝑃(𝑋 < 16 0 ) = ,5
C. 𝑃(𝑋 > 4) = 0,5
B. 𝑃(𝑋 = 16) = 0,5
D. 𝑃(𝑋 = 4) = 0,5
Câu 0.23. Cho 𝑍 ∼ 𝑁(0; 1) có hàm mật độ xác suất 𝜑(𝑧) Khẳng định nào sau đây sai?
A. Giá trị lớn nhất của 𝜑(𝑧) bằng 1
B. Đồ thị hàm 𝜑(𝑧) nhận trục tung làm trục đối xứng
C. 𝑃(𝑍 > 0 0 ) = ,5
D. 𝑃(𝑍 > 1) = 𝑃(𝑍 < −1)
Câu 0.24. Nhiệt độ trong ngày là biến ngẫu nhiên có phân phối Chuẩn với
trung bình 25 độ C, phương sai là 6,25 độ2. Xác suất để vào một thời điểm
ngẫu nhiên nhiệt độ lớn hơn 30 độ C là: A. 0,9772 C. 0,2119 B. 0,7881 D. 0,0228
Câu 0.25. Cho 𝑋 ∼ 𝑁(30; 16). Giá trị 𝑃(𝑋 > 28) là: A. 0,3085 C. 0,5497 B. 0,6915 D. 0,4503
Câu 0.26. Thời gian chờ khám bệnh tại một bệnh viện là biến ngẫu nhiên
có phân phối Chuẩn, thời gian chờ trung bình là 20 phút, phương sai là 16.
Xác suất để một bệnh nhân phải chờ không quá 15 phút là: A. 0,6227 C. 0,8944 B. 0,3773 D. 0,1056 17
Câu 0.27. Thời gian chờ khám bệnh tại một bệnh viện là biến ngẫu nhiên
có phân phối Chuẩn, thời gian chờ trung bình là 20 phút, phương sai là 4.
Xác suất để trong 5 bệnh nhân đến khám có không quá 2 bệnh nhân phải
chờ nhiều hơn 22 phút là: A. 0,1587 C. 0,5475 B. 0,9689 D. 0,15
Câu 0.28. Thời gian chờ khám bệnh tại một bệnh viện là biến ngẫu nhiên
có phân phối Chuẩn, thời gian chờ trung bình là 20 phút. Tỷ lệ bệnh nhân
phải chờ nhiều hơn 25 phút là 15,87%. Tỷ lệ bệnh nhân phải chờ ít hơn 15 phút là: A. 15,87% C. 42,07% B. 84,13% D. 57,93%
Câu 0.29. Thời gian chờ khám bệnh tại một bệnh viện là biến ngẫu nhiên
có phân phối Chuẩn. Biết có 15,87% bệnh nhân phải chờ ít hơn 14 phút và
2,28% bệnh nhân phải chờ nhiều hơn 26 phút. Thời gian chờ khám trung bình tại bệnh viện là: A. 17% C. 15% B. 16% D. 14%
Câu 0.30. Thời gian hoạt động tốt không phải sửa chữa của một loại điện
thoại là biến ngẫu nhiên có phân phối Chuẩn, trung bình là 5 năm, độ lệch
chuẩn là 2 năm. Nhà sản xuất quy định thời gian bảo hành là 1 năm. Khi
bán được một chiếc điện thoại nhà sản xuất có lãi 400 nghìn đồng, nếu điện
thoại hỏng trong thời gian bảo hành thì nhà sản xuất phải chi phí 700 nghìn
đồng để sửa chữa. Tiền lãi trung bình của mỗi chiếc điện thoại là:
A. 393,16 nghìn đồng
C. 384,04 nghìn đồng
B. 390,88 nghìn đồng
D. 339,16 nghìn đồng
Câu 0.31. Thời gian hoạt động tốt không phải sửa chữa của một loại điện
thoại là biến ngẫu nhiên có phân phối Chuẩn, trung bình là 5 năm, độ lệch
chuẩn là 2 năm. Nhà sản xuất muốn bảo hành cho 4% sản phẩm bán được
thì cần quy định thời gian bảo hành là: 18 A. 1,5 năm C. 1,2 năm B. 1 năm D. 2 năm
Câu 0.32. Thời gian hoạt động tốt không phải sửa chữa của một loại điện
thoại là biến ngẫu nhiên có phân phối Chuẩn, trung bình là 5 năm, độ lệch
chuẩn là 2 năm. Khi bán được một chiếc điện thoại nhà sản xuất có lãi 400
nghìn đồng, nếu điện thoại hỏng trong thời gian bảo hành thì nhà sản xuất
phải chi 600 nghìn cho việc bảo hành. Để tiền lãi kì vọng của mỗi sản phẩm
là 376 nghìn đồng thì thời gian quy định bảo hành là bao lâu? A. 1,5 năm C. 1,2 năm B. 1 năm D. 2 năm
Câu 0.33. Cho X, Y là các biến ngẫu nhiên độc lập, 𝑋 ∼ 𝑁(40; 16);𝑌 ∼ 𝑁 (20; 4)
Tính 𝑃(2𝑋 − 3𝑌 > 15) A. 0,8276 C. 0,5709 B. 0,6915 D. 0,5199
Câu 0.34. Giá bán sản phẩm trên thị trường là biến ngẫu nhiên có phân
phối Chuẩn. Sản phẩm A có giá bán trung bình là 200 nghìn, độ lệch chuẩn
là 30 nghìn; sản phẩm B có giá bán trung bình là 250 nghìn, độ lệch chuẩn
là 40 nghìn, giá bán hai loại sản phẩm A, B độc lập nhau. Tỷ lệ sản phẩm
A có giá bán thấp hơn sản phẩm B là: A. 97,06% C. 84,13% B. 52,58% D. 15,87%
Câu 0.35. Tỷ lệ người có xem quảng cáo về sản phẩm của công ty A trên
mạng là 15%. Xác suất để trong 200 người vào mạng có nhiều hơn 35 người
xem quảng cáo về sản phẩm của công ty A là: A. 57,77% C. 16,11% B. 42,23% D. 83,89%
Câu 0.36. Thu nhập hằng tháng của người dân tỉnh A là biến ngẫu nhiên
có phân phối Chuẩn, trung bình là 15 triệu, độ lệch chuẩn là 4 triệu. Một 19
người có mức thu nhập bình thường nếu thu nhập hằng tháng chênh lệch so
với thu nhập trung bình không quá 5 triệu. Tỷ lệ người có thu nhập bình thường của tỉnh A là: A. 21,13% C. 24,53% B. 78,87% D. 75,47%
Câu 0.37. Cân nặng một loại sản phẩm là biến ngẫu nhiên có phân phối
Chuẩn. Sản phẩm đạt tiêu chuẩn nếu cân nặng chênh lệch so với trung bình
không quá hai lần độ lệch chuẩn. Trong 1000 sản phẩm thì số sản phẩm đạt tiêu chuẩn trung bình là: A. 683 sản phẩm. C. 954 sản phẩm. B. 997 sản phẩm. D. 865 sản phẩm.
Câu 0.38. Cho 𝑍 ∼ 𝑁(0; 1). Biết 𝑃(𝑍 < 1, 23) = 0, 8907, khẳng định nào dưới đây đúng?
A. 𝑧0,1093 = 1, 23
C. 𝑧1,23 = 0, 1093
B. 𝑧0,8907 = 1, 23
D. 𝑧1,23 = 0, 8907
Câu 0.39. Cho 𝑇 ∼ 𝑇 (20), 𝑡(20) = 1, 725. Khẳng định nào sau đây đúng? 0,05
A. 𝑃(𝑇 < −1,725) = 0,05
C. 𝑃(𝑇 > 1,725) = 0,95
B. 𝑃(𝑇 < 1,725) = 0, 05
D. 𝑃(𝑇 > −1,725 0 ) = ,05
Câu 0.40. Cho 𝑇 ∼ 𝑇 (10). Tính 𝑃(𝑇 < 2, 228) ta được:
A. 𝑃(𝑇 < 2,228 0 ) = ,025
C. 𝑃(𝑇 < 2,228) = 0,05
B. 𝑃(𝑇 < 2,228) = 0,975
D. 𝑃(𝑇 < 2,228) = 0,95 Câu 0.41. Cho 2
𝜒2 ∼ 𝜒2(10), 𝜒 (10) = 18,307. 0,05
Khẳng định nào sau đây đúng?
A. 𝑃(𝜒2 < 18,307 0 ) = ,05
C. 𝑃(𝜒2 < −18,307 05 ) = 0,
B. 𝑃(𝜒2 > 18,307) = 0,95
D. 𝑃(𝜒2 < 18,307 0 95 ) = ,
Câu 0.42. Cho 𝜒2 ∼ 𝜒2(6). Tính 𝑃(𝜒2 > 10, 64) ta được: 20
A. 𝑃(𝜒2 > 10,64) = 0,95
C. 𝑃(𝜒2 > 10,64 1 ) = 0,
B. 𝑃(𝜒2 > 10,64 0 ) = ,975
D. 𝑃(𝜒2 > 10,64 9 ) = 0,
Câu 0.43. Cho 𝐹 ∼ 𝐹(10; 8), 𝑓 (10,8) = 4,295. 0,025
Khẳng định nào sau đây đúng?
A. 𝑃(𝐹 < −4,295) = 0,025
C. 𝑃(𝐹 > 4,295) = 0,025
B. 𝑃(𝐹 > 4,295) = 0,975
D. 𝑃(𝐹 < 4,295) = 0,025
Câu 0.44. Cho 𝑍1 ∼ 𝑁(0; 1 0; 1
), 𝑍2 ∼ 𝑁 (
), 𝑍1, 𝑍2 là các biến ngẫu nhiên
độc lập. Đặt 𝑋 = 𝑍2 . Tính 𝑃 1 + 𝑍 2 2
(𝑋 > 0, 211) ta được:
A. 𝑃(𝑋 > 0,2107) = 0,95
C. 𝑃(𝑋 > 0,2107) = 0,975
B. 𝑃(𝑋 > 0,2107) = 0,9
D. 𝑃(𝑋 > 0,2107) = 0,1
Câu 0.45. Cho 𝜒2
, 𝜒2 là các biến ngẫu nhiên độc
1 ∼ 𝜒2(3) , 𝜒2
2 ∼ 𝜒2(3) , 𝜒2 1 2 𝜒2
lập. Đặt 𝑋 = 1 . Tính 𝑃(𝑋 > 15, 44) ta được: 𝜒2 2
A. 𝑃(𝑋 > 15,44) = 0,25
C. 𝑃(𝑋 > 15,44 0 ) = ,025
B. 𝑃(𝑋 > 15,44) = 0,01
D. 𝑃(𝑋 > 15,44 0 ) = ,05