Bài tập chương 4: Tính đơn ánh, toàn ánh và ánh xạ tuyến tính môn Toán cao cấp 2 | Học viện Công Nghệ Bưu Chính Viễn Thông

lOMoAR cPSD| 58800262 BÀI TẬP CHƯƠNG 4 Bài 1.
Xét tính đơn ánh, toàn ánh, song ánh của các ánh xạ dưới đây.
a) f : R→R,f(x) = x2 − 2x.
b) f : N→N,f(x) = x2 + x.
c) f : R2 →R2,f(x,y) = (2x + y,5x + 3y).
d) f : R2 →R2,f(x,y) = (2x + 4y,x + 2y). Bài 2.
Ánh xạ nào dưới đây là ánh xạ tuyến tính?
a) f : R2 →R2,f(x,y) = (2x,x + y).
b) f : R2 →R2,f(x,y) = (x2,y).
c) f : R3 →R2,f(x,y,z) = (2x + y − z,5x + 3y + z).
d) f : R3 →R3,f(x,y,z) = (2x + y − z,5x + 3y + z,y + z + 1).
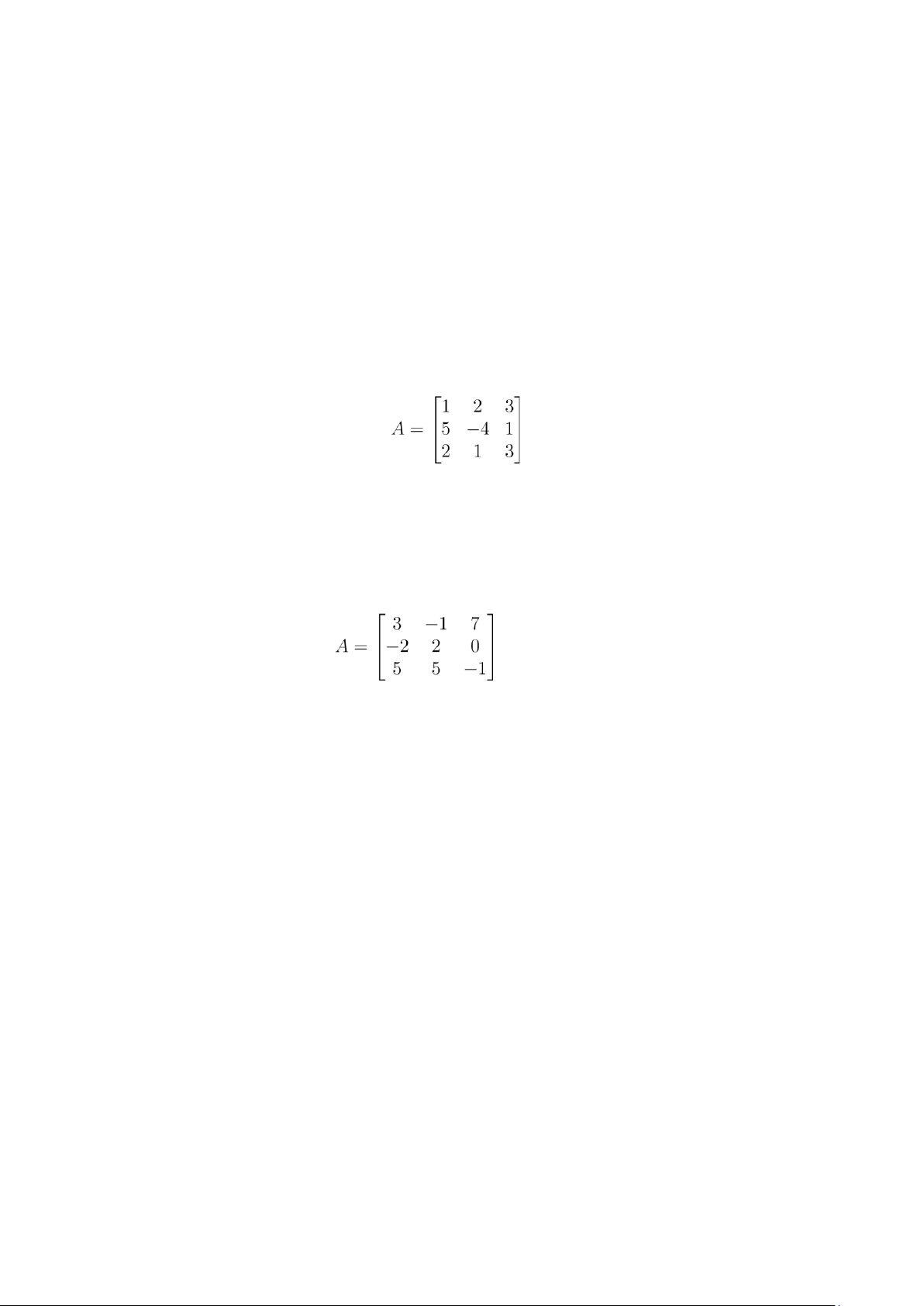
e) f : R3 →R2,f(x,y,z) = (2x + y − αz,3x + βyz). Bài 3. Cho ma trận
a) Viết đa thức đặc trưng của A.
b) Tìm một ma trận không suy biến P sao cho P −1AP là ma trận đường
chéo và xác định P −1AP.
Bài 4. Cho ánh xạ tuyến tính f : R3 →R3 có công thức xác định ảnh f(x,y,z) = (−x + y
− z,x + 2y − z,x + 5y − 3z).
a) Viết ma trận A của f trong cơ sở chính tắc của R3. lOMoAR cPSD| 58800262
b) Tìm ma trận chuyển từ cơ sở {v1 = (1,1,0),v2 = (0,1,1),v3 = (0,0,1)} sang cơ sở chính tắc của R3.
c) Viết ma trận A′ của f trong cơ sở {v1,v2,v3}. 1
Bài 5. Cho ánh xạ tuyến tính f : R3 →R3 có ma trận trong cơ sở chính tắc là
a) Viết công thức xác định ảnh của f.
b) Tìm một cơ sở của kerf, Imf và tính hạng của f.
c) f2 có phải là song ánh không? Vì sao? Bài 6. Cho ma trận .
a) Viết đa thức đặc trưng của A.
b) Viết công thức xác định ảnh của phép biến đổi tuyến tính f : R3 →R3 có ma
trận chính tắc là A.
c) Tìm λ để f2 − λf là một song ánh.
Bài 7. Cho phép biến đổi tuyến tính f : R3 →R3 được xác định bởi f(x,y,z) = (x + 2y +
z,2x − 2z,−x + 2y + 3z).
a) Viết ma trận A của f trong cơ sở chính tắc của R3.
b) f có chéo hóa được không? Nếu f chéo hóa được, tìm một cơ sở của R3 để
ma trận của f trong cơ sở này có dạng chéo.
c) Tìm ma trận chính tắc của f2. lOMoAR cPSD| 58800262 Bài 8. Cho ma trận .
a) Tìm các giá trị riêng của A.
b) Với mỗi giá trị riêng tìm được, hãy tìm một cơ sở của không gian riêng tương ứng.
c) Ma trận A có chéo hóa được không? Vì sao? 2
Bài 9. Cho ánh xạ tuyến tính f : R2 →R3 được xác định bởi f(x,y,z) = (−3x + y −
z,−7x + 5y − z,−6x + 6y − 2z).
a) Viết ma trận A của f trong cơ sở chính tắc của R3.
b) A có khả nghịch không? Nếu có, hãy tìm ma trận nghịch đảo A−1.
c) Tìm công thức xác định ảnh của ánh xạ ngược f−1(x,y,z) nếu có.
Bài 10. Cho phép biến đổi tuyến tính f : R3 →R3 được xác định bởi f(x,y,z) = (5x +
7y − 5z,4y − z,2x + 8y − 3z).
a) Viết ma trận A của f trong cơ sở chính tắc của R3.
b) Tìm một cơ sở gồm các véc tơ riêng của f. Viết ma trận của f trong cơ sở này.
c) Tìm số chiều của kerf, Imf.