Bài tập chương 5 môn Kinh tế học đại cương (có đáp án)
Bài tập chương 5 môn Kinh tế học đại cương (có đáp án)
Preview text:
CHƯƠNG 5.
BÀI 1. Có biểu cầu về một hàng hoá như sau:
P (nghìn đồng/tấn) 40 36 32 28 24 20 Lượng (tấn) 0,5 1 1,5 2 2,5 3
a. Xác định phương trình đường cầu?
b. Tại mọi mức giá, lượng cung là 2 tấn. Hãy xác định giá cân bằng và tổng doanh thu?
Tính PS và CS tại trạng thái cân bằng?
c. Khi giá bán trên thị trường là 25 nghìn đồng/tấn. Tính thặng CS và PS tại mức giá này? Hướng dẫn:
a. Phương trình đường cầu tuyến tính có dạng: QD = a – bP (a, b là hằng số và b ≥ 0)
Từ dữ liệu ở biểu cầu ta có thể lập được hệ phương trình: 0,5 = a – 40b (1) 1 = a – 36b (2)
Giải hệ phương trình (1) và (2) ta có: a = 5,5 và b = 1/8
Thay a và b vào phương trình tổng quát ở trên ta có hàm cầu: QD = 5,5 – 1/8P
b. Ta có hàm cung thị trường: QS = 2
Tại điểm cân bằng của thị trường QD = QS
5,5 – 1/8P = 2 => Pcân bằng = 28 (nghìn đồng/tấn)
Tổng doanh thu tại trạng thái cân bằng: TR = 28*2 = 56 (nghìn đồng)
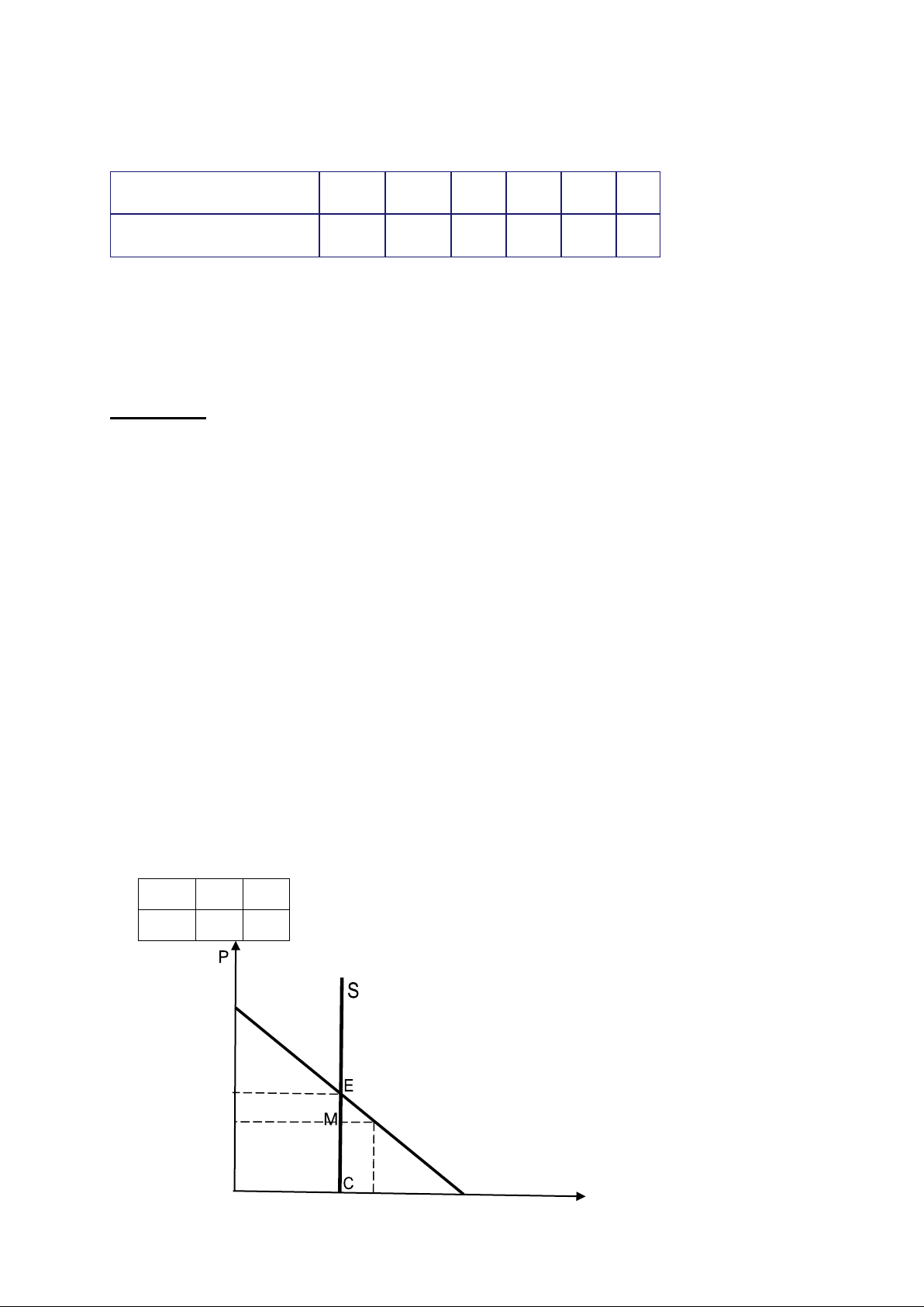
Để tính được CS và PS cần vẽ đồ thị cung cầu:
- Do lượng cung không đổi tại mọi mức giá nên đường cung sẽ có dạng thẳng đứng
song song với trục giá ở mức Q = 2.
- Từ phương trình đường cầu ta thấy đường cầu sẽ có dạng đường thẳng và dốc xuống từ trái qua phải: QD 0 5,5 P 44 0 44 A 28 B 25 H G D Q 0 2 5,5 1
- Tại mức giá cân bằng:
CS = Diện tích tam giác ABE = ½ (44 – 28)*2 = 16 (nghìn đồng)
PS = Diện tích hình chữ nhật BEC0 = 28*2 = 56 (nghìn đồng)
c. Khi giá bán trên thị trường là P = 25:
CS = diện tích hình thang AEMH = [(19 + 3)*2]/2 = 22 (nghìn đồng)
PS = diện tích hình chữ nhật HMC0 = 25*2 = 50 (nghìn đồng)
BÀI 2. Cung và cầu của hàng hóa X có phương trình như sau:
QD = 150 – 5P và QS = 5P - 10
a. Tính giá và lượng cân bằng trên thị trường.
b. Nếu giá bán trên thị trường là P = 18 thì điều gì xảy ra trên thị trường?
c. So sánh thặng dư sản xuất và thặng dư tiêu dùng tại trạng thái cân bằng và khi P = 18 Hướng dẫn:
a. Tại điểm cân bằng của thị trường: QD = QS 150 – 5P = 5P – 10 Pcân bằng = 16 và
Qcân bằng = 5*16 – 10 = 70 b. Khi P = 18 thì: QD = 150 – 5*18 = 60 QS = 5*18 – 10 = 80
Như vậy QS > QD nên thị trường xảy ra hiện tượng dư cung (hay dư thừa hàng hóa)
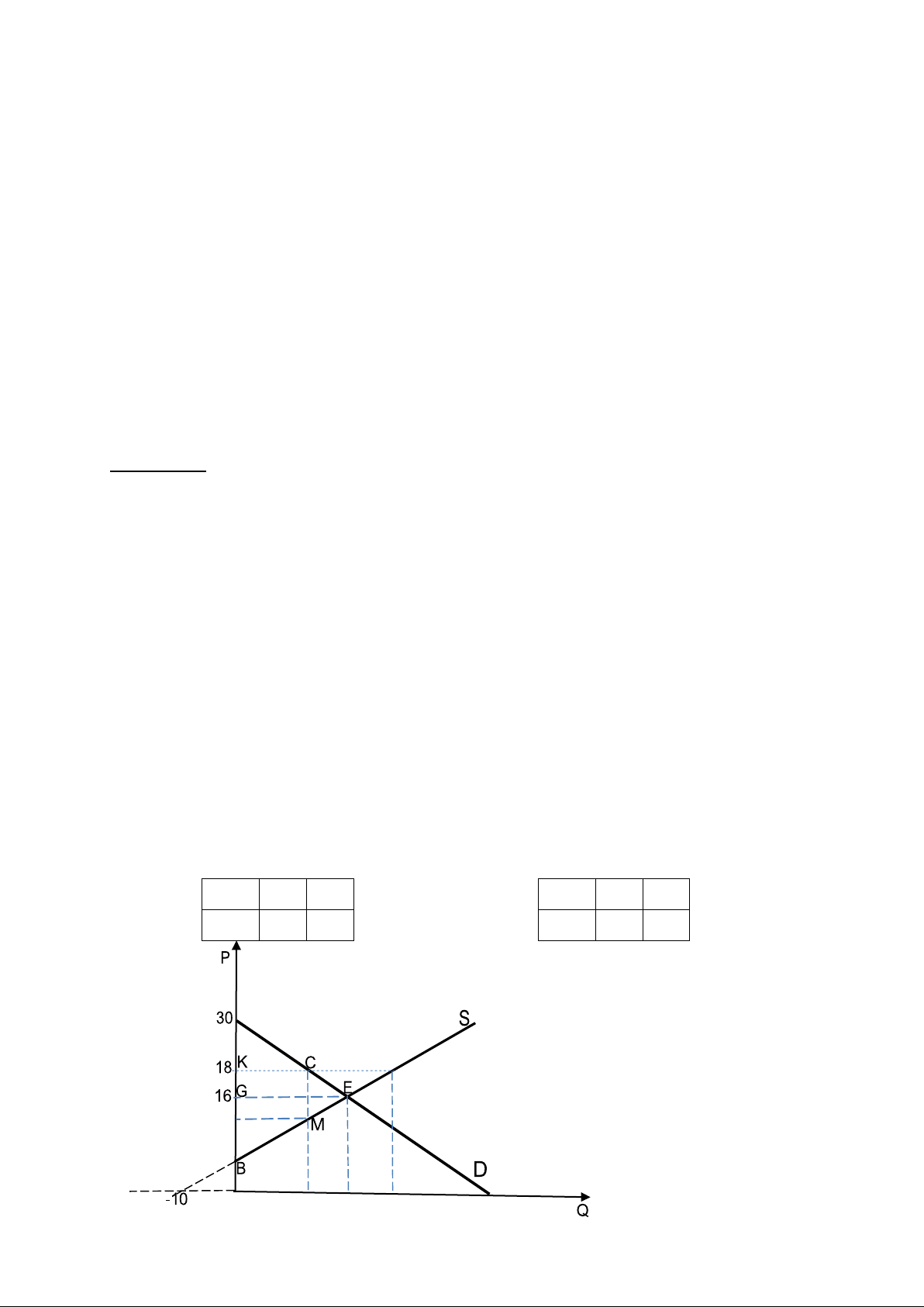
c. Để tính được CS và PS cần vẽ đồ thị cung cầu:
- Từ phương trình đường cầu ta thấy đường cầu sẽ có dạng đường thẳng và dốc xuống từ trái qua phải.
- Từ phương trình đường cung ta thấy đường cung có dạng đường thẳng và dốc lên từ trái qua phải. QD 0 150 QS 0 -10 P 30 0 P 2 0 A 14 2 0 60 70 80 150 2
- Tại trạng thái cân bằng:
CS= diện tích tam giác AGE = ½ (30 – 16)*70 = 490
PS = diện tích tam giác GEB = ½ (16 – 2)*70 = 490
- Tại mức giá P = 18:
CS = diện tích tam giác ACK = ½ (30 – 18)*60 = 360
PS = diện tích hình thang KCMB = [(KB + CM)*KC]/2
Để tính được CM cần biết mức giá ở điểm M.
Thay Q = 60 vào hàm cung ta có: 60 = 5P – 10 => P = 14
PS = diện tích hình thang KCMB = [(16 + 4)*60]/2 = 600
- Như vậy thặng dư tiêu dùng CS ở mức giá P = 18 thấp hơn ở mức giá cân bằng còn
thặng dư sản xuất PS ở mức giá P = 18 cao hơn mức giá cân bằng.
BÀI 3. Hàm cầu và hàm cung của trứng gà như sau:
PD = 10 – Q và PS = Q – 4
(P tình bằng nghìn đồng/1 quả, Q tính bằng triệu quả)
a. Tính giá và sản lượng cân bằng trên thị trường. Tính hệ số co giãn của cung và cầu tại mức giá cân bằng.
b. Tính thặng dư sản xuất và thặng dư tiêu dùng tại mức giá cân bằng.
c. Khi giá bán trên thị trường P= 2 nghìn đồng/quả. Thặng dư sản xuất và thặng dư tiêu
dùng thay đổi như thế nào so với trước? Hướng dẫn:
a. Tại trạng thái cân bằng thị trường: PD = PS
10 – Q = Q – 4 Qcân bằng = 7 (triệu quả)
Pcân bằng = 7 – 4 = 3 (nghìn đồng/1 quả)
- Tính hệ số co giãn của cung và cầu tại mức giá cân bằng:
Đổi lại hàm cung và hàm cầu thuận ta có: QD = 10 – P và QS = 4 + P
EDP = QD’(P) * P/Q = (-1) * 3/7 = - 3/7
ESP = QS’(P) * P/Q = 1 * 3/7 = 3/7
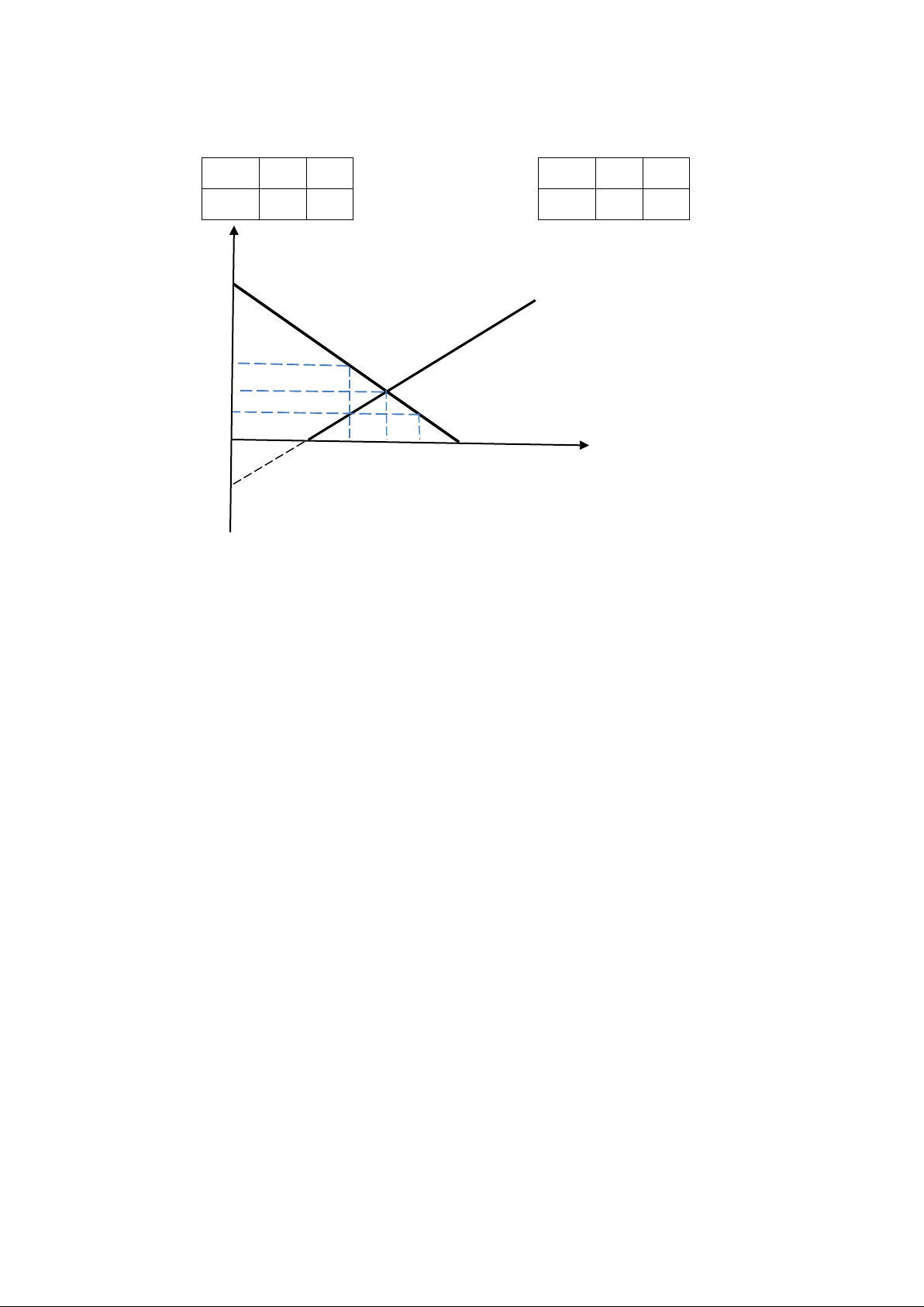
b. Để tính các khái niệm thặng dư cần vẽ đồ thị cung cầu:
- Từ phương trình hàm cầu ta thấy đường cầu có dạng đường thẳng và dốc xuống từ trái qua phải trên đồ thị. 3
- Từ phương trình hàm cung ta thấy đường cung có dạng đường thẳng và dốc lên từ trái qua phải trên đồ thị. QD 10 0 QS 4 0 P 0 10 P 0 - 4 P (nghìn đồng/1 quả) 10 A cung 4 H 3 B E 2 K C Cầu 0 G 4 6 7 8 10 Q (triệu quả) -4
- Tại mức giá cân bằng:
CS= diện tích tam giác ABE = ½ (10 – 3)*7*1.000.000 = 24.500.000 (nghìn đồng)
PS = diện tích hình thang BEG0 = [(4 + 7)*3*1.000.000]/2 = 16.500.000 (nghìn đồng)
c. Khi mức giá P = 2 (nghìn đồng/1 quả) thì:
QD = 10 – 2 = 8 (triệu quả)
QS = 4 + 2 = 6 (triệu quả)
PS = diện tích hình thang KCG0 = [(4 + 6)*2*1.000.000]/2 = 10.000.000 (nghìn đồng)
CS = diện tích hình thang AHCK
Để tính được HC cần biết mức giá ở điểm H. Thay Q = 6 vào hàm cầu ta có: P = 10 – 6 = 4
CS = [(8 + 2)*6*1.000.000]/2 = 30.000.000 (nghìn đồng)
- Như vậy tại mức giá P = 2 nghìn đồng/1 quả thì CS tăng còn PS giảm so với tại
mức giá cân bằng. ************************ 4