Bài tập củng cố 3 môn xác suất thống kê| Đại học Kinh tế Quốc Dân

BÀI T P LẬÝ THUYẾẾT XÁC SUẤẾT & THỐẾNG KẾ TOÁN Bài mẫu:
Ví dụ 1. Trong 1 phân xưởng có 3 máy hoạt động độc lập với nhau. Xác suất các máy bị hỏng
lần lượt tương ứng là 0,1-0,2-0,3. X= “số máy bị hỏng trong 1 ca sản xuất”
a. Xác định quy luật phân phối xác suất của X
b. Tìm xác suất trong 3 ca sản xuất liên tục có ít nhất 1 ca không có máy nào hỏng.
c. Số máy hỏng trong 1 ca sản xuất nằm trong khoảng nào?
Ví dụ 2. Theo tài liệu thống kê về tai nạn giao thông ở một khu vực người ta thấy tỷ lệ xe máy
bị tai nạn là 0,0055 vụ/tổng số xe/ năm. Một công ty bảo hiểm đề nghị tất cả các chủ xe phải mua
bảo hiểm xe máy với số tiền là 30k/ xe và số tiền bảo hiểm trung bình cho một vụ tai nạn là 3000k.
Hỏi lợi nhuận công ty kỳ vọng thu được đối với mỗi hợp đồng là bao nhiêu biết rằng chi phí quản
lý và các chi phí khác chiếm 30% số tiền bán bảo hiểm?
Ví dụ 3. Quy luật phân phối
A(p): Điều tra ý kiến của khách hàng đối với sản phẩm của doanh nghiệp thì thấy có 60% khách
hàng thích sản phẩm đó. Tìm quy luật phân phối xác suất và các tham số đặc trưng của thái độ ưa
thích của khách hàng với sản phẩm.
B(n;p): Một nữ công nhân quản lý 12 máy dệt. Xác suất trong một ngày làm việc 1 máy cần sửa
chữa là 1/3. Tìm xác suất:
- Trong 1 ngày làm việc có từ 3 đến 6 máy cần sửa chữa
- Trong 3 ngày làm việc liên tiếp có ít nhất 2 ngày có từ 3 đến 6 máy cần sửa chữa
P(λ):Tổng đài phục vụ điện thoại phục vụ 100 máy điện thoại. Xác suất trong mỗi phút mỗi máy
gọi đến là 0,02. Tìm số máy gọi đến tổng đài trung bình trong 1 phút. Xác suất để trong 1 phút nào
đó có hơn 5 số máy gọi đến tổng đài.
Ví dụ 4: Biến ngẫu nhiên 2 chiều
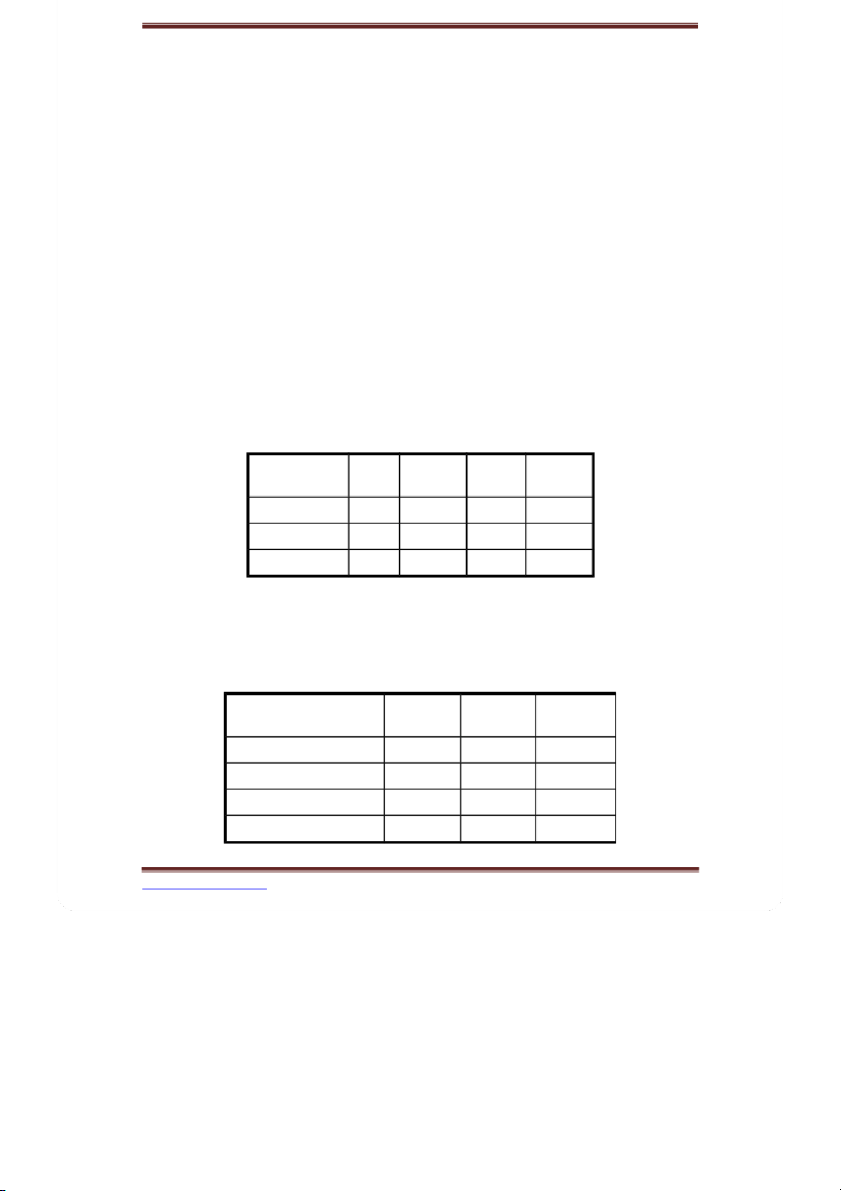
Cho bảng phân phối xác suất đồng thời về thu nhập của chồng (X) và vợ (Y) trong hộ gia đình như sau: Y 10 20 30 40 X 10 0,2 0,04 0,01 0 20 0,1 0,36 0,09 0 30 0 0,05 0,1 0 40 0 0 0 0,05
a. Lập bảng phân phối xác suất biên của thu nhập vợ/ chồng
b. Biết thu nhập của vợ là 20 triệu/ tháng, lập bảng phân phối xác suất phân phối thu nhập của chồng
c. Tính tỷ lệ các hộ gia đình có thu nhập vợ và chồng đều trên 30 triệu/ tháng. Tính tỷ lệ các
hộ gia đình có tổng thu nhập 2 vợ chồng dưới 30 triệu nếu giả sử thu nhập vợ và chồng độc lập.
d. Tính các tham số đặc trưng của thu nhập vợ/ chồng
e. Thu nhập của vợ tăng có làm thu nhập của chồng tăng lên không?
BÀI T P LẬÝ THUYẾẾT XÁC SUẤẾT & THỐẾNG KẾ TOÁN
b. Tìm phương sai và độ lệch chuẩn của số xe bán được mỗi tuần và giải thích ý nghĩa.
c. Nếu giá bình quân mỗi xe máy bán ra tại cửa hàng là 30 triệu đồng thì doanh thu bình
quân của cửa hàng trong một tuần là bao nhiêu. Giả sử 1 năm có 52 tuần thì doanh thu 1 năm của
cửa hàng kỳ vọng thu được là bao nhiêu?
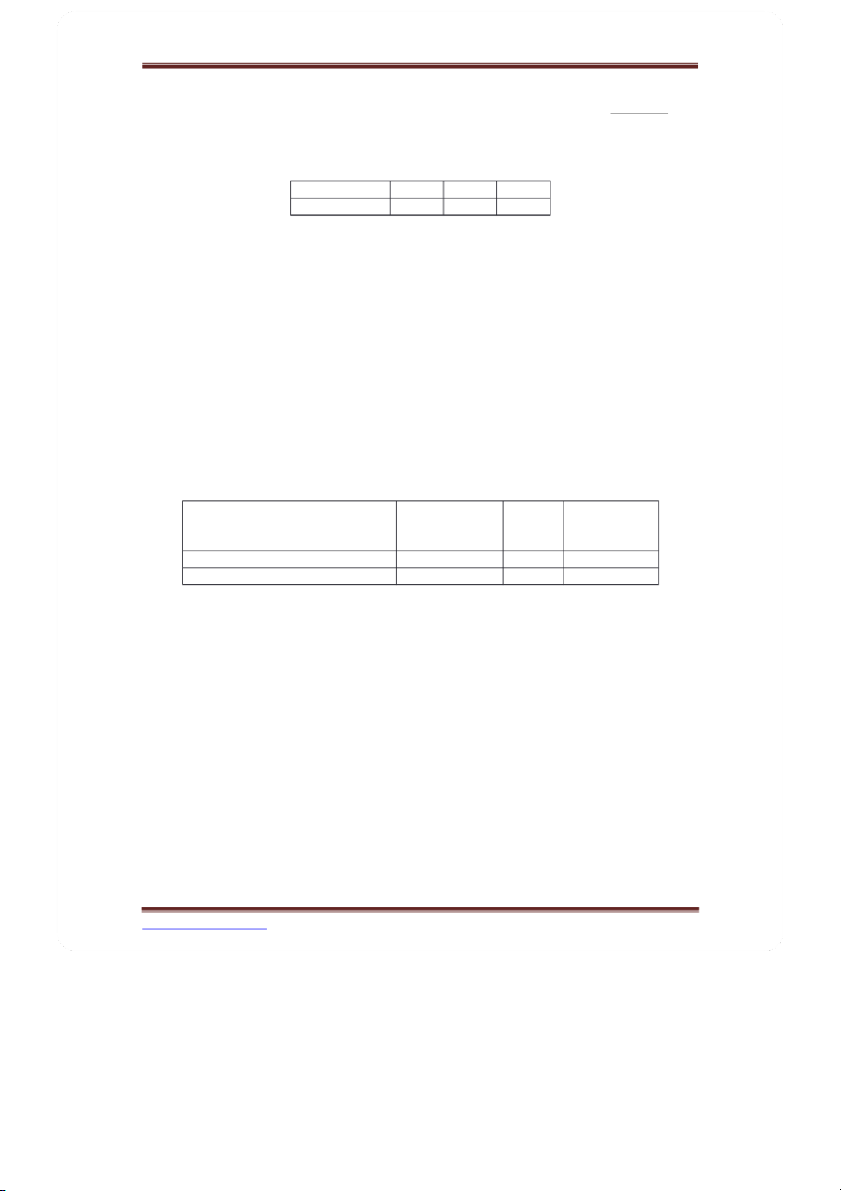
Bài 8. Số tiền lãi khi đầu tư 100 triệu đồng vào ngành A là biến ngẫu nhiên X có bảng phân phối xác suất như sau: X (triệu đồng) 1 3 5 P a b 0,2
Biết rằng E(X) = 2,8 (triệu đồng). Tìm a và b.
Bài 9. Xạ thủ dùng 4 viên đạn để tập bắn với quy định nếu bắn trúng hai viên liên tiếp hoặc hết
đạn thì dừng bắn. Các viên đạn được bắn độc lập với xác suất trúng đều là 0,8. Tính trung bình số
viên đạn xạ thủ sử dụng.
Bài 10. Một người dự định đầu tư vào một dự án. Nếu dự án thành công thì lãi là 7 (tỷ VND),
nếu không thành công thì lỗ 2 (tỷ VND). Biết xác suất thành công là 0,6. Tính kỳ vọng và độ rủi ro của lợi nhuận.
Bài 11. Công ty bán sản phẩm cho khách hàng với thời gian bảo hành miễn phí quy định là 1
năm. Tỷ lệ sản phẩm của công ty bị hỏng trong 1 năm đầu sử dụng là 10%. Khi bán 1 sản phẩm thì
công ty thu lãi 120 nghìn đồng. Nếu sản phẩm bị hỏng trong thời gian bảo hành miễn phí thì công
ty phải chi 100 nghìn đồng cho việc bảo hành. Tính tiền lãi trung bình trên mỗi sản phẩm bán được của công ty.
Bài 12: Tùy tình hình kinh tế trong nước mà năm sau công ty sẽ thu được mức lãi khi đầu tư
vào ngành bất động sản hoặc du lịch với bảng số liệu sau: Tình hình kinh tế Kém phát triển Ổn định Phát triển Mức lãi (%) Bất động sảnX -20 80 120 Du lịch Y -50 100 140
Theo dự báo của các chuyên gia kinh tế thì khả năng năm tới kinh tế trong nước sẽ kém phát
triển là 30%, ổn định là 50% và phát triển là 20%. Công ty nên đầu tư vào ngành nào để mức lãi là
cao nhất hoặc mức độ rủi ro là thấp nhất? Bài 13:
Hai kiện tướng bóng bàn ngang sức thi đấu với nhau. Hỏi thắng 2 trong 4 ván dễ hơn hay 3 trong 6 ván dễ hơn?
Một cầu thủ nổi tiếng về đá phạt đền với xác suất đã vào gôn là 4/5. Có người cho rằng vậy cứ
sút 5 quả thì chắc chắn có 4 quả vào gôn. Điều này có đúng không? Bài 14:
Ở một trạm xăng bình quân mỗi giờ có 12 xe máy đến tiếp xăng. Tình xác suất để trong một giờ
nào đó có: Hơn 8 xe đến tiếp xăng, Hơn 15 xe đến tiếp xăng, Dưới 10 xe đến tiếp xăng. Bài 15:
Hãng kem đánh răng P/S tuyên bố rằng cứ 5 nha sỹ thì có 2 người sử dụng kem đánh răng của
hãng mình. Chọn ngẫu nhiên 20 nha sỹ ở Viện Răng hàm mặt TW hỏi thì thấy có 2 người sử dụng kem đánh răng P/S.
- Giả sử lời tuyên bố của P/S là đúng, tìm xác suất của biến cố trên?
BÀI T P LẬÝ THUYẾẾT XÁC SUẤẾT & THỐẾNG KẾ TOÁN
- Giả sử lời tuyên bố của P/S là đúng, tìm xác suất để có không quá 2 nha sỹ dùng kem đánh răng P/S
- Với kết quả chọn ngẫu nhiên như trên, liệu lời tuyên bố đúng với sự thật không? Tại sao? Bài 16:
Hội đồng quản trị của doanh nghiệp có 7 thành viên và mọi vấn đề đều thực hiện theo nguyên
tắc đa số. Ông chủ tịch muốn thông qua một đề án mà ông soạn thảo. Giả sử khả năng ủng hộ hoặc
phản đối của mỗi thành viên hội đồng là như nhau.
- Tìm xác suất để đề án được thông qua
- Giả sử trong hội đồng có 1 ban lãnh đạo gồm ông chủ tịch, tổng giám đốc và phó tổng
giám đốc. Ban lãnh đạo sẽ họp trước trù bị và cũng thông qua đề án theo nguyên tắc đa số. Sau
đó ra cuộc họp thành viên thì cả ban lãnh đạo đều phải tuân theo quyết định của phiên họp trù
bị. Vậy lúc đó xác suất để đề án được thông qua là bao nhiêu?(bỏ) Bài 17:
Trong một phân xưởng dệt có 50 máy dệt hoạt động độc lập với nhau. Xác suất các máy bị hỏng
trong 1 ca sản xuất là như nhau và đều bằng 0,07.
- Tìm quy luật phân phối xác suất của số máy dệt bị hỏng trong 1 ca sản xuất - Trung
bình có bao nhiêu máy dệt bị hỏng trong 1 ca sản xuất.
- Xác suất để trong ca sản xuất có 48 máy hoạt động tốt.
- Nếu trong 1 ca sản xuất 1 kỹ sư của nhà máy chỉ có thể đảm bảo sửa chữa kịp thời tối
đa 2 máy thì cần bố trí bao nhiêu kỹ sư để sửa chữa kịp thời tất cả các máy hỏng trong ca là hợp lý nhất.
Bài 18. Xác suất để mỗi sản phẩm có lỗi là 0,05. Tính kì vọng và phương sai của số sản phẩm
không có lỗi trong lô hàng gồm 40 sản phẩm.
Bài 19. Gọi X và Y lần lượt là lãi suất của cổ phiếu A và B (đơn vị %). Giả sử biến ngẫu nhiên
rời rạc hai chiều (X, Y) có bảng phân phối xác suất đồng thời như sau X -2 0 5 10 Y 0 0 0,05 0,05 0,1 4 0,05 0,1 0,25 0,15 6 0,1 0,05 0,1 0
a) Nếu đầu tư toàn bộ vào cổ phiếu A thì lãi suất kỳ vọng và mức độ rủi ro là bao nhiêu ?
b) Nếu mục tiêu là đạt được lãi suất kỳ vọng lớn nhất thì nên đầu tư vào hai loại cổ phiếu trên theo tỉ lệ nào ?
c) Muốn hạn chế rủi ro về lãi suất đến mức thấp nhất thì nên đầu tư vào hai loại cổ phiếu trên theo tỉ lệ nào ?
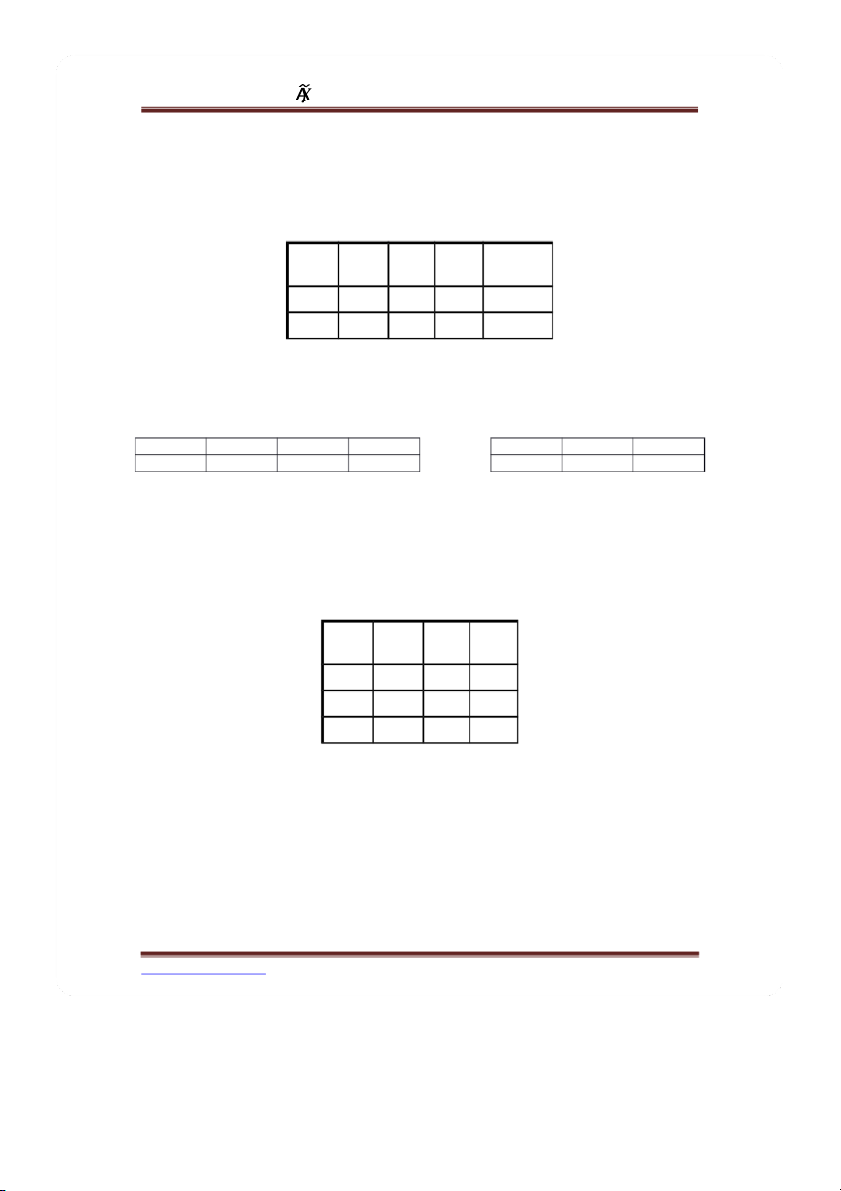
Bài 20: Thống kê dân số của một nước theo trình độ học vấn X và lứa tuổi Y cho kết quả sau: Lứa tuổi Y 25-35 35-55 55-100 Học vấn X Thất học 0 0,01 0,02 0,05 Tiểu học 1 0,03 0,06 0,1 Trung học 2 0,18 0,21 0,15 Đại học 3 0,07 0,08 0,04
BÀI T P L Ý THUYẾ ẾT XÁ C SUẤ ẾT & THỐẾNG KẾ TO ÁN
a. T ỷ lệ người thất học của nước đó
b. Tìm xác suất để lấy ngẫu nhiên một người thì người đó có độ tuổi trên 50 tuổi và chưa tốt nghiệp trung học.
c. Mức học vấn trung bình của các độ tuổi là bao nhiêu?
d. Độ tuổi có ảnh hưởng đến học vấn của dân số không?
Bài 21: Cho bảng phân phối xác suất đồng thời của biến ngẫu nhiên rời rạc (X,Y) như sau: Y -1 0 1 P(X) X 0 0 ,25 0 , 15 1 0 , 15 0 , 2 0 , 45
a. Hãy điền các giá trị còn thiếu vào bảng
b. Tì m các phân phối biên của X, Y
c. Lập bảng phân phối của X khi Y=1
d. Tí nh các tham số đặc trưng của X, Y
Bài 22. Cho hai biến ngẫu nhiên X, Y độc lập với nhau và có bảng phân phối xác suất: X 1 2 3 Y -2 -1 P 1 / 4 1 3 / 5 / 12 P 1 / 3 2 / 3
Lập bảng phân phối xác suất đồng thời của (X, Y)
Bài 23 . Một người tham gia đầu thầu 6 dự án với xác suất thắng thầu mỗi dự án là 0 , 4. Nếu
thắng mỗi dự án thu được 200 USD. Chi phí để chuẩn bị cho 6 dự án là 300 USD.
a. Số dự án người đó hy vọng thắng được.
b. Tì m xác suất để người đó có lãi khi có dự án.
c. Nếu thắng thầu nhiều lại phải thuê thêm công nhân. Lợi nhuận P phụ thuộc số dự án thắng
thầu X như sau: P=200X-300-20X 2. Lúc đó lợi nhuận kỳ vọng là bao nhiêu?
Bài 24. Lợi nhuận khi đầu tư của 2 công ty A, B có bảng phân phối xác suất như sau: X A -1 3 5 X B 2 0.05 0.1 0.15 3 0.1 0.2 0.1 6 0.15 0.1 0.05
a. Muốn có lãi trên 3% thì nên lựa chọn phương án nào: đầu tư toàn bộ vào A, đầu t ư toàn bộ
vào B hoặc chia đều vốn đầu tư vào A, B.
b. Lãi suất trung bình khi đầu tư vào công ty B biết năm đó lợi nhuận công t y A là 3%.
c. Nếu muốn giảm rủi ro đầu tư xuống mức thấp nhất thì nên đầu tư như t hế nào?