Bài tập đại số tuyến tính cấp cao 1 | Đại học Kiến trúc Thành phố Hồ Chí Minh

lOMoAR cPSD| 59256994
BÀI TẬP ĐẠI SỐ TUYẾN TÍNH 1. MA TRẬN.
1.1. Cho A là ma trận vuông cấp n thỏa mãn A2  A In . Chứng minh rằng A có ma trận
nghịch ảo và tìm ma trận nghịch ảo của A. 5 6 2  1.2. Cho M N,
là các ma trận vuông cấp 3 thỏa mãn MN 6 7 2  6 6 1 a. Tính (MN)2 .
b. Chứng minh NM khả nghịch. Tìm ma trận nghịch ảo của NM .
1.3. Cho A là ma trận cấp n thỏa mãn A2  A. Chứng minh rằng ma trận B 2A I có ma trận nghịch ảo. 1.4. Cho ma trận ( )
a. Chứng minh rằng nếu thì
b. Tìm sao cho tồn tại ể ( ) 1.5. Tính 1 0 1n 2 1 0n   
a. 0 1 0  b. 0 1 0  0 0 1 0 0 2 
1.6. Tính lũy thừa bậc n của A cosx sinx sinx cosx  . 2017 1 2017   1.7. Cho ma trận A 2016
2 2017  . Xác ịnh các phần tử nằm trên ường chéo chính lOMoAR cPSD| 59256994 2016 1 2016
của ma trận S  I  A A2  A2017.
1.8. Cho là ma trận vuông cấp ( )
Tính , với là số nguyên dương.
1.9. Cho thỏa mãn . Chứng minh rằng .
1.10. Cho thỏa mãn Chứng minh rằng tồn tại ma trận khác ma trận 0 thỏa mãn
1.11. Cho ma trận vuông A, B cấp n. Vết của ma trận A là tổng tất cả các phần tử trên ường
chéo chính của A, kí hiệu Tr A . Chứng minh rằng: a. Tr A B   Tr A Tr B   .
b. Tr kA kTr A k ,  .
c. Tr AB Tr BA 
1.12. Chứng minh rằng không tồn tại các ma trận A B C D, , , vuông cấp n sao cho AC BD I  và CA BD
 0, I là ma trận ơn vị, 0 là ma trận không. 1.13. (Đẳng thức Wagner)
a. Chứng minh rằng với mọi ma trận A B C, , vuông cấp 2 ta luôn có
ABBA C2 C AB BA2  0
b. Chứng minh rằng với mọi ma trận A B C, , vuông cấp 2 ta luôn có
ABBA2016CC AB BA2016  0 1 2 1 1 1  
1.14. Tùy theo giá trị của m , hãy tìm hạng của ma trận A m 1 1 1 1  1 m 0 1 1   1 2 2 1 1  lOMoAR cPSD| 59256994 3 1 4 1  
1.15. Tìm m ể hạng của ma trận sau nhỏ nhất A m 2 3 1 3 1 1 0   3 3 7 2 1 m 0 ... 0 0  1 m ... 0  0 ... ... ... ...  0
0 ... ... 1 .... Tìm m ể hạng của ma trận A 
1.16. Cho ma trận vuông cấp n: A... 0 0 ... 0 m   1 0 m nhỏ hơn n.
1.17. Chứng minh rằng mọi ma trận hạng r ều có thể phân tích ược thành tổng của r ma trận có hạng bằng 1.
1.18. Giả sử A, B là các ma trận vuông cấp n thỏa mãn AB BA A , 2016  0, B2017  0.
a. Chứng minh rằng tồn tại số tự nhiên k ể A Bk  0.
b. Chứng minh rằng r I   A B r I   A B n. 2. ĐỊNH THỨC 1 x x2 x3
2.1. Giải phương trình: 1 2 4 8 0 1 3 9 27 1 4 14 64 2.2. Tính ịnh thức : 1 1 1 1a b c d
a. x12 x22 x32 x42 b. bc ad da bc x1 x2 x3 x4 x13 x23 x33 x43d c b a lOMoAR cPSD| 59256994 a b c 2.3. Tính b c a
trong ó a b c,, là 3 nghiệm của phương trình bậc 3 : x3  px q  0. c a b
2.4. Cho m, n, p, q là các nghiệm của phương trình x4   x 1 0 và m1 1 1 1   1 n1 1 1  A   1 1 p 1 1   1  1 1 1 q Tính det A .
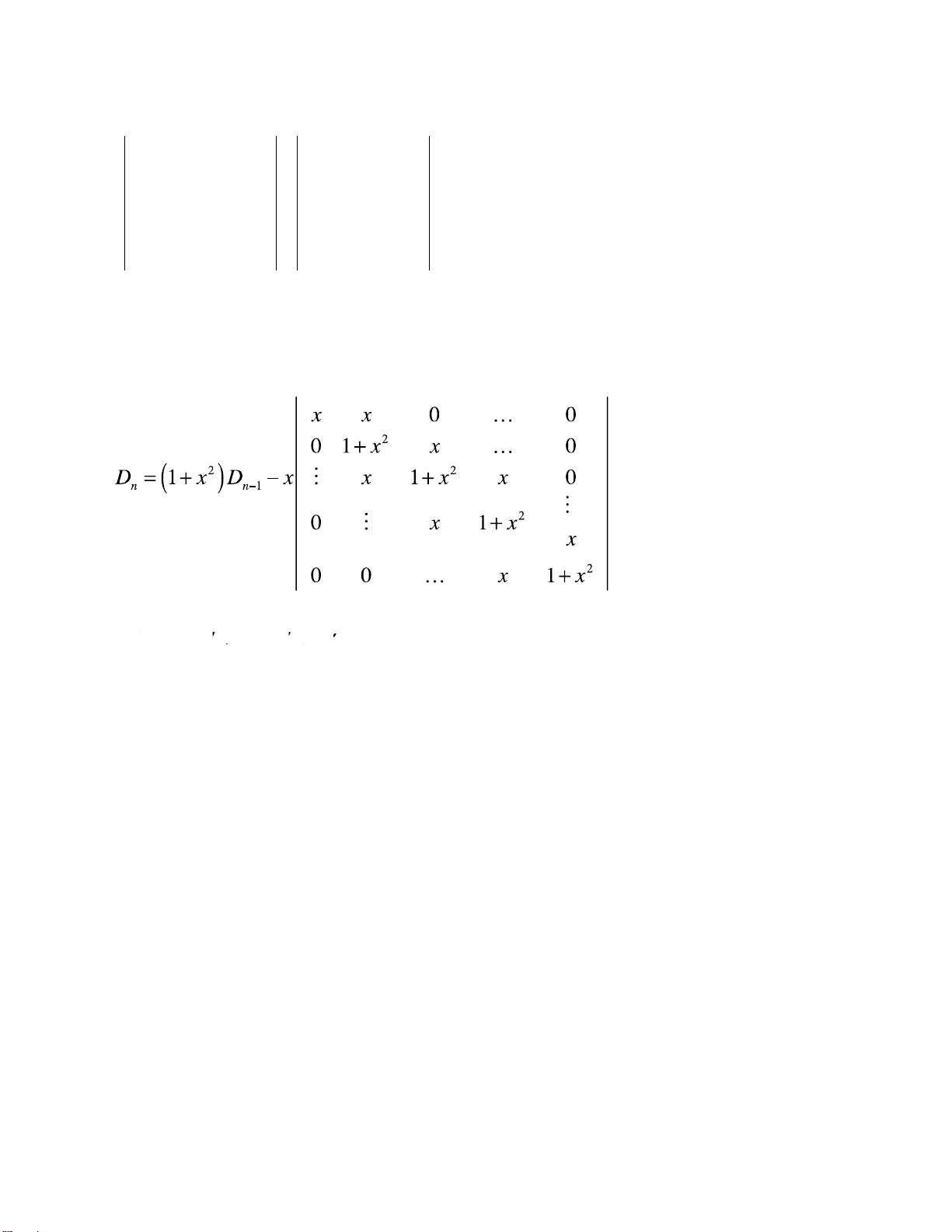
2.5. Tính các ịnh thức cấp n sau : 1 2 2 ... 21 2 3 ... n 2 2 2 ... 21 0 3 ... n a. 2 2 3 ... 2; b. 1 2 0 ... n . . . ... .. . . ... . 2 2 2 ... 21 2 3 ... 0 0 1 1 ... 1a b b ... b 1 0 x ... xb a b ... b c. 1 x 0 ... x ; d.b b a ... b . . . ... .. . . ... . 1 x x ... x b b b ... a 1 x2 x 0 x ... 0 x e. D 1 ... 0 n 1 x2 0 x x2 ... 0, ... . . . . ... 0 0 0 lOMoAR cPSD| 59256994 1 x2
Dn là ịnh thức cấp n mà các phần tử nằm trên ường chéo chính bằng 1+x2, các phần tử
thuộc hai ường chéo gần ường chéo chính bằng x và các phần tử còn lại bằng 0. 2.6. a.
A là một ma trận vuông cấp n thỏa mãn A1  A. Chứng minh det(A I ) 0 hoặc det(A I ) 2n. b.
A B, là hai ma trận vuông cùng cấp n thỏa mãn AB BA B  . Chứng minh det(B)  0.
2.7. Cho A B, là các ma trận thực vuông cấp n thỏa mãn AB A B  và A2016  0. Chứng minh rằng det( )B  0.
2.8. Cho các ma trận vuông A B, thỏa mãn A A I B B It  ; t  . Biết det A det B. Chứng
minh rằng det(A B)  0. 
2.9. Cho ma trận vuông cấp n A a  ij
;aij  mini j, . Tính det A .  2.10. Cho A a   ij
là một ma trận vuông cấp n2 và A11  A12  A1n  0,
trong ó A1j là phần bù ại số của a1j . Chứng minh rằng tồn tại số thực  ể a2n
a11  a12  ... a1n a  21 a22 ...  ... an1 2016 an2 ... ... ... ... ann
3. HỆ PHƯƠNG TRÌNH TUYẾN TÍNH
3.1. Giải hệ phương trình: lOMoAR cPSD| 59256994
 3x  y 2z   t u 1
 2x  y 7z  3t 5u  2  x 3y 2z  5t 7u  3
3x 2y 7z  5t 8u  3
3.2. Giải hệ phương trình thuần nhất sau:  x1  x2  x3  0  x2  x3  x4  0  x3  x4  x5  0   ........
 x8  x9  x10  0
x1  ... x9  x10  0 
x1  x2  ...x10  0
3.3. Giải và biện luận các hệ phương trình sau
mxxx    myy y  mzzz  ttt 111
b. 4xxx287xyy2   y4y4 zzzz16114tttt  1mm2 1 a.
3.4. Cho là các số nguyên. Giải hệ: lOMoAR cPSD| 59256994 {
3.5. Chứng minh rằng hệ phương trình sau có nghiệm khác nghiệm tầm thường: { trong ó và n lẻ.
3.6. Tìm m ể hệ sau có nghiệm duy nhất  mx 8z  7t  m1
3xmy  2z  4t  m   mz  5t  m2 1  5z mt  2m 2
3.7. Tùy theo giá trị của m, hãy biện luận số nghiệm của hệ :  mx   y z t m
 3y 2z (5m3)t  m 1  2x
(m1)x3y 2z (m2 m t)  4 
3.8. Tìm iều kiện của m ể hai hệ sau có nghiệm chung  2x   y z 2t 3u  3  x    y z t u 1  3x   y z 3t 4u  2m x y 2z 2mt  0  2x   y z t m lOMoAR cPSD| 59256994 3.9. Cho a b c d, , ,
 . Chứng minh rằng hệ phương trình sau chỉ có nghiệm tầm thường:
 1a2x   by cz dt 0 
  bx 1 a2 y   dz ct 0 
   cx dy 1 a2z  bt 0 
    dx cy bz 1 a2t  0 4. ĐA THỨC
4.1. (Xác ịnh a thức) Tìm tất cả các a thức P x( ) có hệ số nguyên sao cho
P P x('( ))  P P x'(( )), x
4.2. (Nghiệm của a thức) Cho P x( ) là a thức bậc n có n nghiệm phân biệt x x1 2, ,...,xn. Chứng minh rằng: a. 1  1  ... 1  0. P x'( 1) P x'( 2) P x'( n) b.
P x' ( 1) P x' ( 2)  ... P x' ( n)  0. P x'( 1) P x'( 2) P x'( n)
4.3. (Đa thức với yếu tố giải tích) Với mỗi số nguyên dương n2xét a thức P xn( ) nxn
xn1   ... x 1. Hỏi P xn( ) có bao nhiêu nghiệm thực: a. Khi n  2;n  3? b. Khi n  4?
4.4. (Tính chia hết của a thức) Cho m n, là các số nguyên dương. Chứng minh rằng iều kiện
cần và ủ ể a thức xm  xn 1chia hết cho x2  x 1 là mn2 chia hết cho 3.
4.5. Cho a thức P x( )  4x3 ax2 bx c trong ó a b c, , là các số thực. Hãy tìm a b c, , sao
cho P x( ) 1 với mọi x thoả mãn x 1.
HƯỚNG DẪN GIẢI BÀI TẬP ĐS OLIMPIC lOMoAR cPSD| 59256994 MA TRẬN
1.1 Có A A(  I) In  A có ma trận nghịch ảo là A – I 1.2 a) Có (MN)2  I3
b)Ta có det(MN)  1 detNM1  NM có ma trận nghịch ảo det(MN)  0
detM  0 và detN  0  N và M có ma trận nghịch ảo
(MN)2  I3 MNMN  I3
NM M N1 1  (NM)1. Vậy NM có ma trận nghịch ảo là NM.
1.3 Ta có (2A I )(2A I ) 4A2     4A I 4A 4A I I  B có ma trận nghịch ảo là chính nó. 1.4 a) tính suy ra
b) Sử dụng phân tích ý 1) rồi tìm ra a,b,c. 1.5 1 0 1n 1 0 n
0 1 0  0 1 0 
0 0 1 0 0 1 2 1 0n 2n n0   
0 1 0   0 1 0  
0 0 2  0 0 2n 
An  cosnx sinnx 1.6 sinnx cosnx  lOMoAR cPSD| 59256994 2017 1.7 Cho ma trận
chéo chính của 1 2016  A 2016
2016 1 Ta có A I B B, 2016 1 2016 1 2016 2017 1 2017  
2017  . Dễ dàng kiểm tra B2  0. Do ó, với mọi số tự nhiên k 
2 2017  . Xác ịnh các
ma trận S  I  A A2  A2017.
phần tử nằm trên ường 2017
ta có: Ak  I kB . Từ ó suy ra S  2018I 1009.2017.B.
Vậy các phần tử trên ường chéo chính của ma trận S là s11  2018
1009.2017.2016 ; s22  2018 1009.2017 ;s33  2018 1009.2017.2017 ; 1.8 HD : , với . 1.9 HD: suy ra . Suy ra .
ừ iều kiện suy ra không khả nghịch. Do ó tồn tại các ma trận 1.10 HD: T
khác ma trận 0, sao cho , ặt là ma trận cần tìm. 1.11 Dễ dàng chứng minh
1.12. Giả sử tồn tại các ma trận A B C D, , ,
vuông cấp n sao cho ACBD  I và CABD  0
CA BD 0 Tr CA BD  0
Tr AC BD   nTr ACTr BD nTr CA Tr BD   n Tr CA BD  n , vô lí . Suy ra pcm.
1.13. a. AB BA C C AB BA 2    2  0 lOMoAR cPSD| 59256994 Ta có Tr AB BA   0 AB BA
x yxAB BA 2 x2 0 yz
x2 0 yzx2  yz I z Ta có IC CI , suy ra pcm. b. cmtt
1.14 r A   3m 1; r A   4 m 1
3 1 4 1 3 1 4 1  3 1 4 1  2 3 1    
1.15 A  m31 10  m022 3311   m0 22
33 11. Ta thấy r A 2. Dấu “=”
3 3 7 2 0 2 3 1 0 0 0 0 xảy ra khi m  0
1.16 Khai triển ịnh thức theo cột 1, ta ược det A   1  1n1mn.
Hạng của ma trận A nhỏ hơn n khi và chỉ khi
det A    01  1n1mn   0 1n1mn 1
Nếu n lẻ thì m1. Nếu n chẵn thì m1. .
1.17 Giả sử ma trận A cấpm n có hạng bằng r. Bằng cách sử dụng các phép biến ổi sơ cấp Ir 0 
trên hàng hoặc cột của A có thể ưa A về dạng R 
 , tức là tồn tại các ma trận không 0 0m n
suy biến P Q, sao cho A  PRQ( các thầy cô xem chứng minh trong giáo trình ại số tuyến tính của thầy Vĩnh, nếu cần ).
Ta phân tích R R R 1  2 ... Rr , trong ó Ri là các ma trận có tất cả các phần tử ều bằng 0 trừ phần
tử ở hàng i, cột i bằng 1. lOMoAR cPSD| 59256994 Ta có r PRQ  i
r R i 1 (các phép biến ối sơ cấp không làm thay ổi hạng của ma trận). Vậy A P R   1  R2... R Q PRQr
 1  ... PRQr là cách phân tích thỏa mãn yêu cầu của bt.
1.18 a) Do AB BA nên A B k k CABki i k i . i0
Vì A2016  0, B2017  0 nên k2017thì A B k  0.
b) Vì A B k  0,k  2017 nên ta có
I  I A B k I  A B I 
 A B  ... A B k1  
 1det I  detI  A B.det I A B  ... A B k  1 
 detI  A B 0 r I  A Bn
Ta có: I  I A B 2 1k I  A B I A B  ... A B 2k . Tương
tự như trên suy ra r I   A B n. Suy ra pcm. ĐỊNH THỨC
2.1 Khi khai triển ịnh thức ở vế trái theo dòng ầu, ta sẽ có vế trái là a thức bậc 3 của x , ký hiệu
là f x( ) . Ta có f (2)  0 vì khi ó ịnh thức có 2 dòng ầu bằng nhau. Tương tự, có f (3)  0, f (4) 
0. Vì f x( ) là a thức bậc 3 nên có 3 nghiệm 2, 3, 4 nên pt có 3 nghiệm 2, 3, 4. 2.2 a) 1 1 1 1 0 x2 −x1 x3 −x1 x4 −x1 0 (x2 −x1)(x2 +x1) (x3 −x1)(x3 +x1) (x4 −x1)(x4 +x1) 0
(x2 −x1)(x22 +x2x1 +x12) (x3 −x1)(x32 +x3x1
+x12) (x4 −x1)(x42 +x4x1 +x12) lOMoAR cPSD| 59256994 1 1 1 =(x2 −x1)(x3 −x1)(x4 −x1)x2 +x1 x3 +x1 x4 +x1
x22 +x2x1 +x12 x32 +x3x1 +x12 x42 +x4x1 +x12 1 0 0 =(x2 −x1)(x3 −x1)(x4 −x1)x2 +x1 x3 −x2 x4 −x2 x22 +x2x1 +x12
(x3 −x2)(x3 +x2 −x1) (x4 −x2)(x4 +x2 −x1) 1 1
=(x2 −x1)(x3 −x1)(x4 −x1)(x3 −x2)(x4 −x2)x3 +x2 −x1 x4 +x2 −x1 =∏(x ) i −xj i>j b) Ta có: 2 a b c da b c da   b c d b a d cb a d c b a d c  .  c d a b c d a bc d a b d c b ad c b ad c b a 
a2   b2 c2 d2 0 0 0 0 a2   b2 c2 d2 0 0 0 0 a2   b2 c2 d2 0 0 0 0 a2   b2 c2 d2 a 4 2   b2 c2 d2 a b c d ba d ca  2   b2 c2 d2 2  c d a b d c b a lOMoAR cPSD| 59256994
2.3 Theo ịnh lý Viet, ta có a b c   0, nên a b ca b a b ca b 0 b c a  b c a  b cb c 0 0 c a bc a a b cc a 0
2.4. Ta có m, n, p, q là nghiệm của phương trình x x4   1 0 theo ịnh lý Viet
Nhân cột 4 với -1 rồi cộng vào các cột còn lại ta có m 0 0 1 0 n 0 1n 0 10 0 1 = m detA=0 0 p 10 p 1 +q n 0 1
−q −q −q q+1−q −q 1+q0 p 1 =mnp+mnq+mpq+npq+mnpq=1+1=2 2.5
a) Nhân dòng 2 với (-1) sau ó cộng vào các dòng (3), (4),…., (n). Ta có 1 2 2 ... 21 2 2 ... 21 2 2 ... 2 2 2 2 ... 22 2 2 ... 20  2 2 ... 2 (1) 2 2 3 ... 2  0 0 1 ... 0  0 0 1 ... 0 2(n 2)! . . . ... .. . . ... .. . . ... . 2 2 2 ... 22 2 2 ... n22 2 2 ... n2
(1) : Nhân dòng (1) với (-2) sau ó cộng vào dòng (2). lOMoAR cPSD| 59256994
b) Lần lượt cộng dòng (1) vào các dòng (2), (3), …., (n) 1 2 3 ... n1 2 3 ... n 1 0 3 ... n0 2 6 ... 2n  1 2 0 ... n  0 0 3 ... 2nn! . . . ... .. . . ... .   1 2 3 ... 00 0 0 ... n
Khai triển theo hàng 1 ta có: c) = 1
( + x 2 )D n − 1− x 2 D n − 2 ; D 1 = 1 + x 2 Mặt khác, D2 =(1+x2)2 −x2 =x4 +x2 +x
Dn −Dn−1 =x2(Dn−1 −Dn−2)....
Dn =Dn−1 +x2n ⇒Dn =1+x2 +x4 +....+x2n
d) Đầu tiên cộng các cột (2), (3), …, (n) vào cột (1). Sau ó nhân dòng (1) với (-1) cộng vào các
dòng (2), (3), …(n). Ta có lOMoAR cPSD| 59256994 a b b ... ba (n 1)b b b ... b a (n 1)b b b ... b b a b ... ba (n 1)b a b ... b 0 a b 0 ... 0 b     b b a ... b  a (n 1)b b a ...0 0 a b ... 0 a n 1b a b  n1 . . . ... .. . . ... .. . . ... . b b b ... aa (n 1)b b b ... a 0 0 0 ... a b 2.6 a)
Ta có A A 1       A2 I (A I)2 2(A I) detA I 2 2n detA I  . Suy ra iều phải cm. b) Ta có AB BA B
 . Nhân cả 2 vế với Bk1 vào bên phải các ma trận ta có :
AB. k B AB.. k1  Bk. Lấy det 2 vế : 0  det A. det Bk det Bk .det AdetBk . Suy ra iều phải chứng minh. 2.7
Ta có A2016  0 det(A2016) (det A)2016  0 det A0 AB    A B B AB  A B A B(  I) det B  det A.det(BI)  0 2.8
Ta có, det A1,det B 1. Do det A det Bdet Adet B 0. Xét
det B.det(A B )  det B.detA B t  det( .B At I)  det( .B At  AA. t )
 det A.det(A B ) det B.det(A B )
Mà det B  0 det(A B)  0. Điều phải cm.
2.9. Nhân hàng 1 với -2; -3; ...;-n rồi cộng tương ứng vào các hàng 2, 3,....n. lOMoAR cPSD| 59256994 1 1 1 ... 1
−1 0 0 ... 0 detA=−2 −1 0 0 ... ... ... ....
−(n−1) −(n− 2 −(n− 3) .... 0 −1 0 0 ... 0 −2 −1 0 0
Khai triển theo cột n detA= −( 1)n+1−2 −1 ... = ... ...
−(n−1) −(n− 2) −(n− 3) ... −1
= −( 1)n+1.(−1)n−1 = −( 1)2n =1  2.10 Cho A a  ij
là một ma trận vuông cấp n 2 và A A11  12  A1n  0, trong ó A1j là phần
bù ại số của a1j . Chứng minh rằng tồn tại số thực  ể a ... 11  a12  a1n  a ... 21 a22 ... ... a ... a2n 2016 n1 ... ... an2 ann Ta có lOMoAR cPSD| 59256994 a11  a12  ... a1n a11 a12 ... a   1n  ... a21 a22 ... a2na21 a22 ... a2na21 a22 ... a n 2
 A A  A ... A  ... ... ... ...... ... ... ...... ... ... ...11 12 1n an1 an2 ... annan1 an2 ... annan1 an2 ... ann 2016 A Suy ra  .
A11  A12  A1n
HỆ PHƯƠNG TRÌNH TUYẾN TÍNH 3.1 Gợi ý: Đổi
chỗ hai pt cuối lên trên rồi giải hệ bằng phương pháp khử Gauss: 1 3  2 5 73 1 3 2 5 73 3  2 7  5 83 0 11 7 5 83 ↔ 3 1  2 1 11 3 1
2 1 11 2 1 7  3 52 2 1 7 3 52 3.2
Tổng 10 phương trình ta ược 3(x1+…. + x9+ x10)=0 nhóm 3 số hạng lại thành một nhóm ược
x10=0 suy ra x1+x2=0 nên x3=0 suy ra x6= x9=0 nên x8=0 nên x7= x5= x2= x1=0… hệ chỉ có nghiệm tầm thường. 3.3
a) Lập ma trận hệ số mở rộng và dùng các phép biến ổi sơ cấp ưa ma trận về dạng bậc thang: lOMoAR cPSD| 59256994
Do . Ta có các khả năng sau:
Nếu . hệ có vô số nghiệm
Nếu . hệ có vô số nghiệm
Nếu . hệ có vô số nghiệm
b) Lập ma trận hệ số mở rộng và dùng các phép biến ổi sơ cấp ưa ma trận về dạng bậc thang: Nếu . Hệ vô nghiệm.
Nếu . Hệ có vô số nghiệm lOMoAR cPSD| 59256994
3.4 Hệ phương trình tương ương với:
Gọi là ma trận hệ số của phương trình trên. Ta có:
Do ó là một số chẵn. Suy ra và có cùng tính chẵn lẻ, với mọi n. Mà là số
lẻ nên cũng là số lẻ. do ó . Vậy hệ trên là hệ Cramer và có nghiệm duy nhất : .
3.5 Gọi A là ma trận các hệ số. Ta có do ó . Mà nên (do n lẻ)
Bởi vậy detA = 0 tức là r(A) < n. Theo ịnh lý Cronecker – Capelly hệ có vô số nghiệm phụ thuộc
vào (n – r ) tham số. Do ó hệ có nghiệm khác 0. m 0 8 7 3 m   2 4m 0m 52 2  3.6 detA= m m  25 0 0 m 53 m5 m 0 0 5 m
Hệ có nghiệm duy nhất ↔ detA≠0↔m≠0