BÀI TẬP ĐIỀU KIỂN TỰ ĐỘNG | Đại học Điện lực

lOMoARcPSD| 59149108
BÀI TẬP ĐIỀU KIỆN LÝ THUYẾT ĐIỀU KHIỂN TỰ ĐỘNG
1) Hãy xác định hàm trọng lượng g(t) và hàm quá độ h(t) của các hệ thống tuyến tính có
hàm truyền đạt như sau: a) G s( ) = b) G s( ) = 1+ 2s (1+3 )(1s +5 )s s+1 2s − 2 2s +3 c) G s( )= 2 d) G s( ) = 2 2s + +3s 4
s(2s − +4s 1) e) G s( ) = 3 + − + 2s3 3s22 4s 8 f ) G s( ) = 1 3
(s + 4)(s + +2s 2) s(1+ 2 )s
2) Hãy vẽ đường đặc tính tần số biên – pha, đặc tính tần số logarith (biểu đồ bode) của
các hệ thống có hàm truyền đạt như sau: a) G s( )= 1 b) G s( ) = 1 1+sT (1+sT1)(1+sT2) k ⎛ c) G s( ) = ⎞
d) G s( )=k⎜1+ 1 +sTD ⎟
s(1+sT1)(1+sT2) ⎝ sT ⎠ 1
3) Vẽ biểu đồ bode tiệm cận của hệ thống sau: G s( ) =
100(0,052 s+1) 2 ;0 <ξ<1
s(0,02s+1)(0,01s+1) (0,04s +0,4ξs+1)
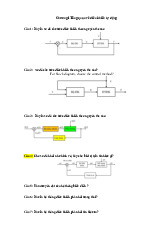
4) Xác định hàm truyền vòng kín cho sơ đồ khối hình B2.11. lOMoARcPSD| 59149108 + K 1 s+ ( 20) 1 1 R(s) C(s) s s s - - K 2 K 3 ( s+K 4 ) s + K 5
Hình B2.11: Sơ đồ khối của hệ thống vận chuyển băng tải.
5) Hãy xác định giá trị tới hạn của K để hệ thống luôn ổn định: a) s4 + 20s3 + 15s2 + 2s + K b) s4 + 20s3 + 2s2 + (K+1)s c) s3 + (K+1)s2 + Ks + 50 d) s3 + Ks2 + 5s + 10
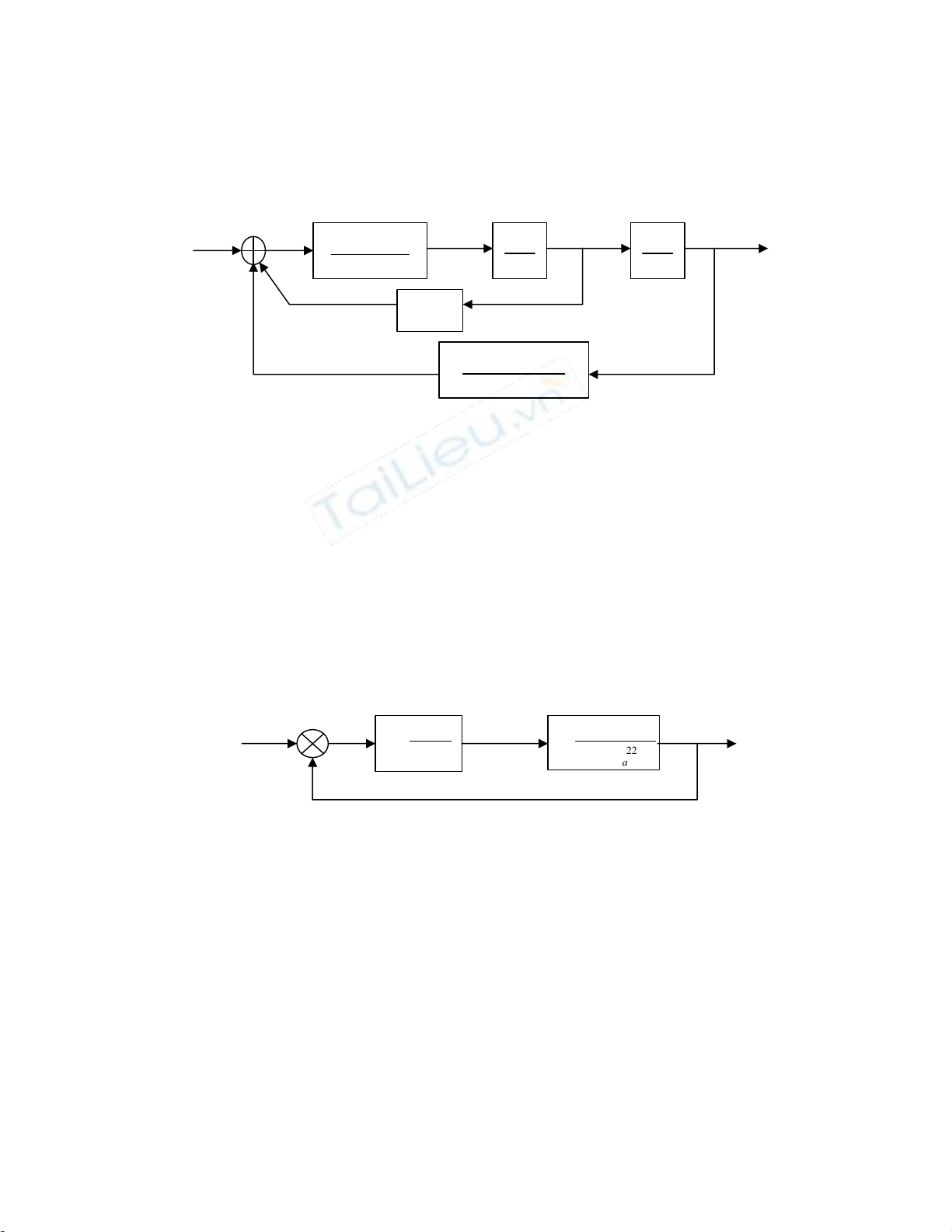
6) Cho hệ thống như hình vẽ B3.5 có K1 = 25; Ta = 0,01; K2 = 1. Hãy tìm giá trị của T
để hệ thống ổn định. 1 Ts − K K 1 K 2 2 1 Ts + 22 s(1 Ts + a ) Hình B3.5:
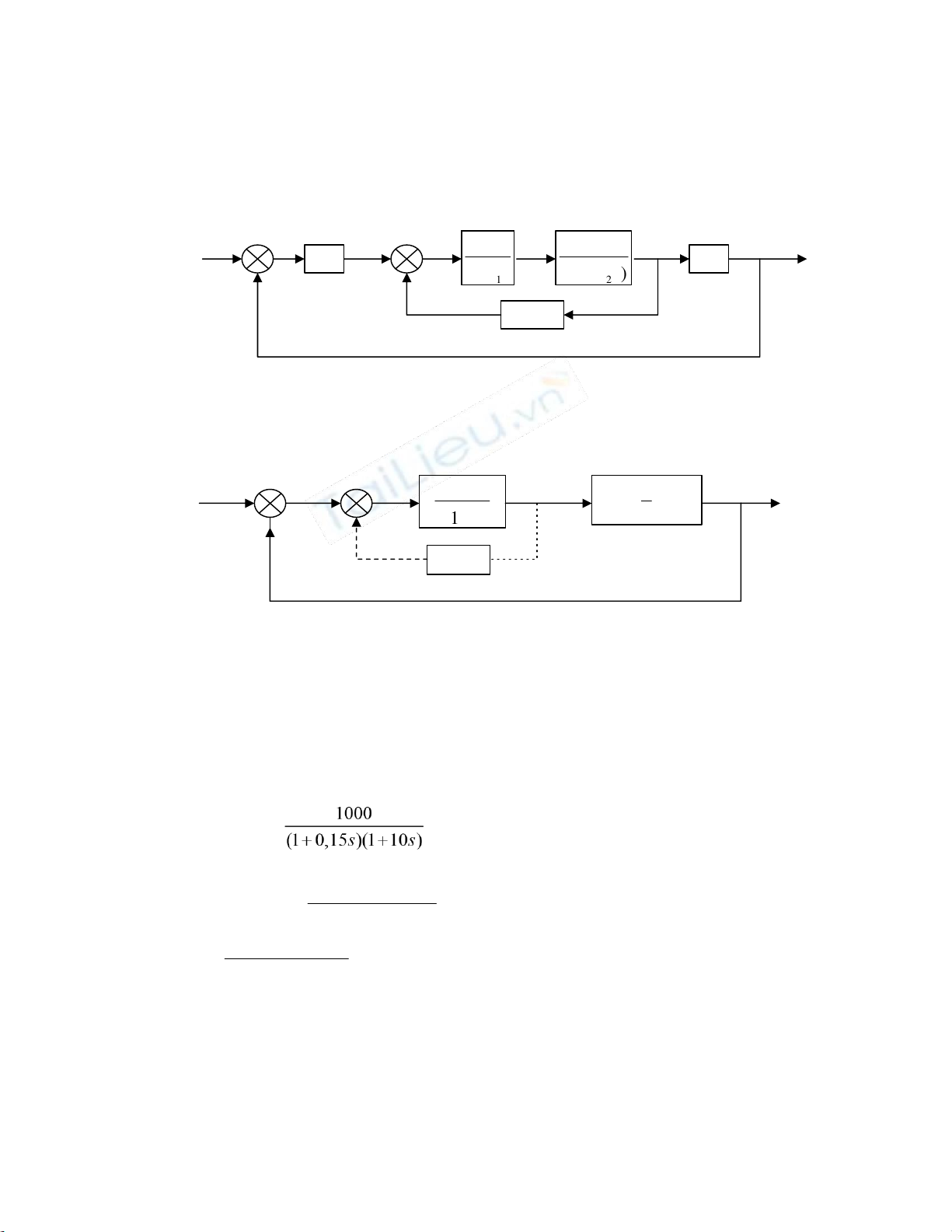
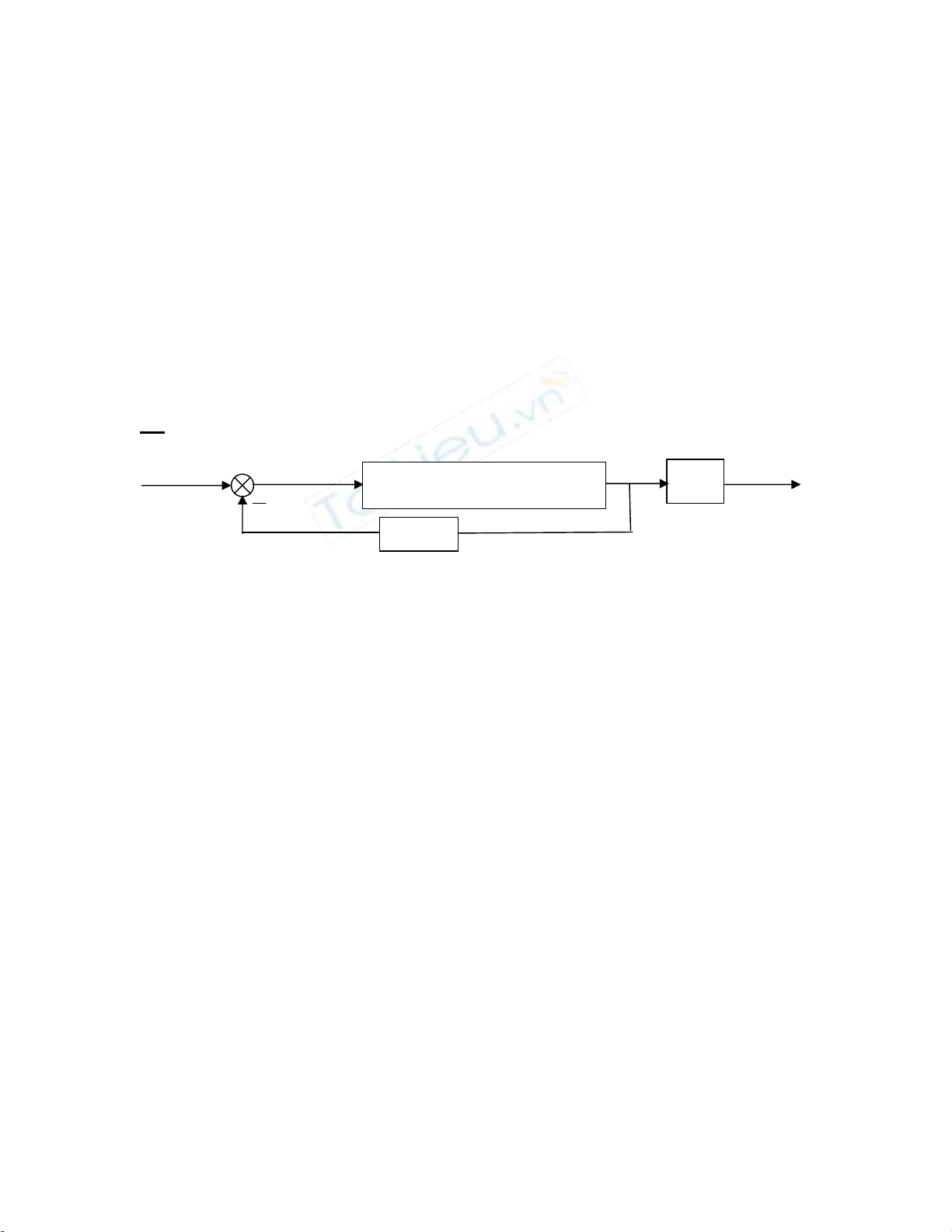
7) Cho hệ thống điều khiển động cơ như hình B3.2 có K1 = 57,3; K2= 103; K3 = 50; K4 =
10-3; T1 = 0,005 sec; T2 = 0,05 sec.
b. Xét ổn định của hệ thống khi không có máy phát tốc KFT = 0.
c. Xác định KFT để hệ thống ổn định. lOMoARcPSD| 59149108 K K 2 3 R(s) K 1 K 4 C(s) 1 Ts + s(1 Ts + ) 1 2 K FT s Hình B3.9:
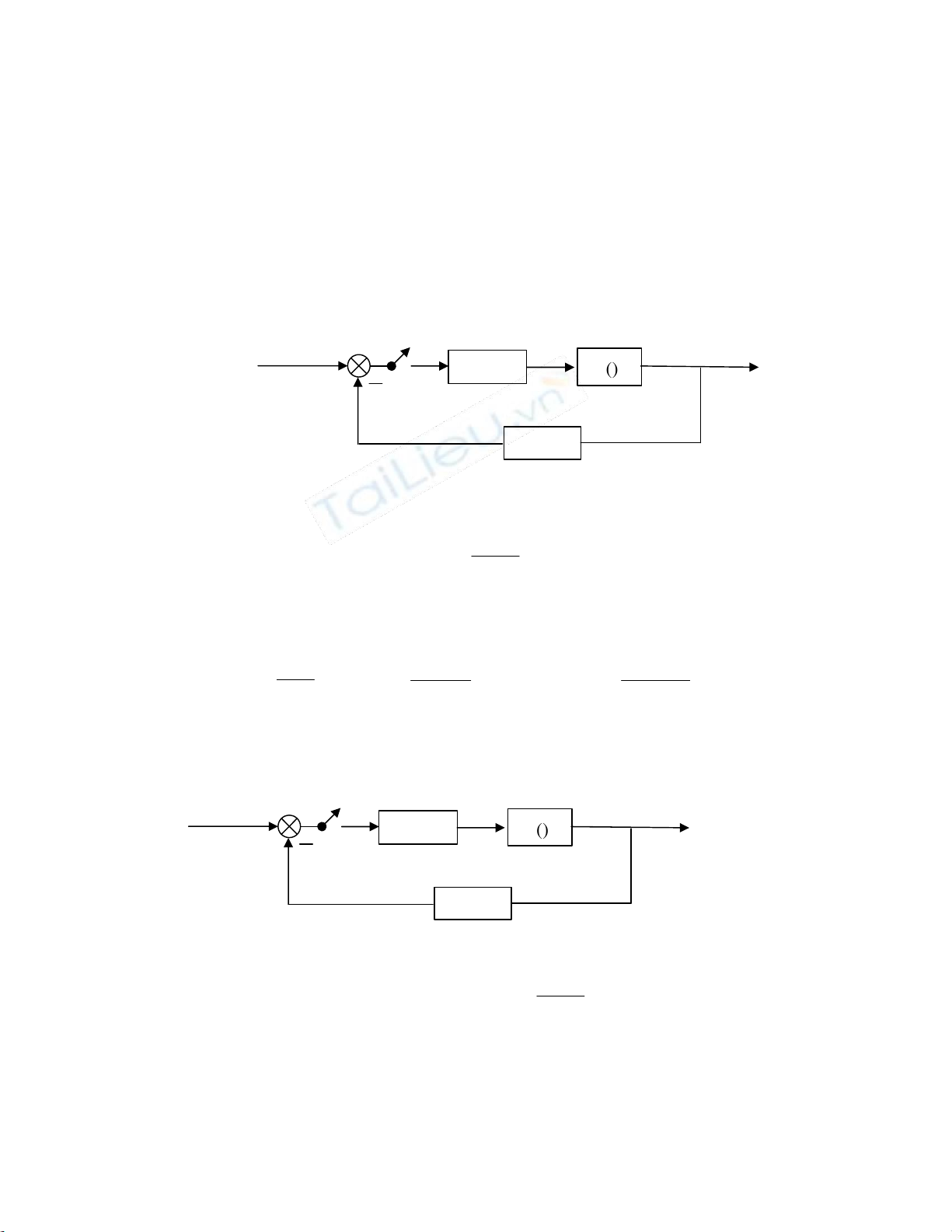
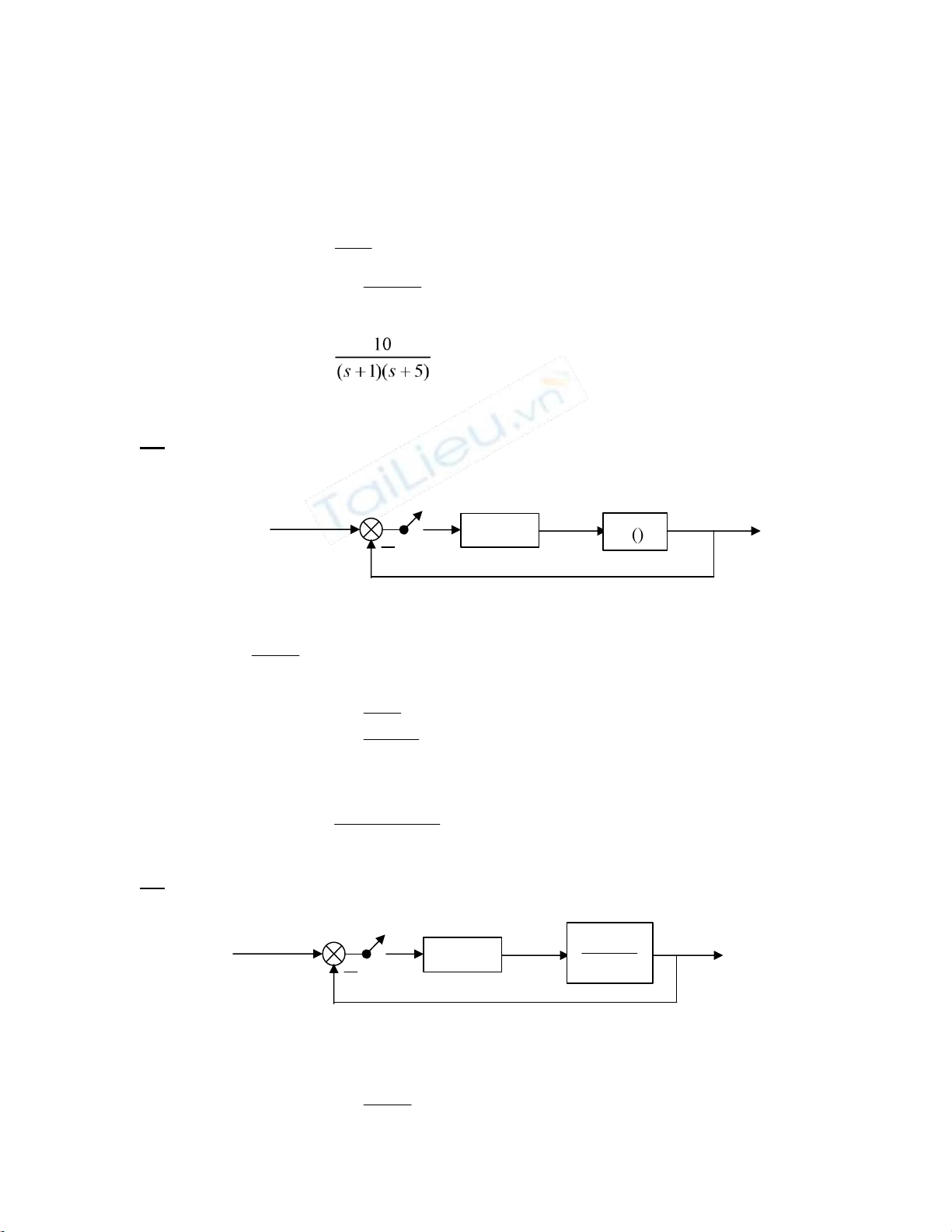
8) Cho hệ thống điều khiển như hình vẽ: 70 1 , 0 1 s 1 + s - - K h Hình B4.1:
a) Tìm thời gian xác lập và độ vọt lố khi không có khâu Kh.
b) Muốn độ vọt lố ≤ 20% thì Kh phải bằng bao nhiêu? Tính thời gian quá độ.
9) Hãy tìm sai số xác lập đồi với hàm bậc thang và hàm dốc của các hệ thống điều khiển
hồi tiếp đơn vị có hàm truyền hở hướng tới như sau: a) Go( )s = b) Go( )s = 1000
s s( +10)(s +100) c) G s + o( )= K(1 2 )(1 4 )2 2s + s s s( + +s 1)
10. Vẽ QĐNS của các hệ thống có các phương trình đặc trưng như sau:
a) s3 +3s2 +(K+2)s+5K =0
b) s3 +s2 +(K+2)s+3K =0 lOMoARcPSD| 59149108
c) s4 +8s3 +16s2 +K s( 2 +4s+5)s=0
11) Cho hệ thống rời rạc có sơ đồ khối như sau: T R(s) + C(s) ZOH () Gs H ( s ) 1− eTs
Cho T= 1 sec, H(s) = 1, GZOH ( )s = s
Hãy tìm hàm truyền đạt của hệ khi: a a.)G( )s = 1 b.)G( )s = 1 2 c.)G s( ) = 2
s a− (s a− ) s s a( + )
12. Cho hệ thống rời rạc có sơ đồ khối như sau: T R(s) + C(s) ZOH () Gs H ( s ) e Ts 1 −
Cho T= 1 sec, H(s) = 1; GZOH ( )s = s
Hãy tìm đáp ứng quá độ khi đầu vào là hàm bậc thang đơn vị và G(s) có các trường hợp sau: lOMoARcPSD| 59149108 a) G( )s = 10 s+5 b) G s( ) = 10 s s( + 5) c) G s( ) =
13) Tìm điều kiện của K để hệ thống ổn định T=0.1 C(s) R(s) + ZOH () Gs
1−eTs Biết T= 0.1 sec; GZOH ( )s =
; và G(s) có các trường hợp sau: s K a) G s( ) = s+2 K b) G s( ) = s s( +1) K c) G s( ) = (s+ 2)(s+10)
14) Cho hệ rời rạc có sơ đồ khối như sau: T C(s) R(s) + 5 ZOH s 2 s +2 1−eTs Biết
T= 1 sec; GZOH ( )s = ; s lOMoARcPSD| 59149108
a. Xác định hàm truyền của hệ
b. Xác định c(nT), khi tín hiệu vào là hàm bậc thang đơn vị.
c. Tính giá trị xác lập, sai số xác lập và độ vọt lố.
15) Cho h ệ th ố ng r ờ i r ạ c nh ư hình v ẽ : C(k) T u(k) x(k) R(k) + x(k+1)=A D d
d x(k)+B d u(k) H ( s )
Hệ phương trình biến trạng thái mô tả hệ là:
⎨⎧x k( + =1) A x kd ( ) +B u kd ( ) ⎩
c k( ) = D x kd ( ) ⎡0,4650 − 2,0989⎤ ⎡0,1499⎤ trong đó A = ⎢ = ⎢ =[ d ⎥ Bd ⎥ Dd 0 5] ⎣0,1499 0,7648 ⎦ ⎣0,0168⎦
hãy tính vector độ lợi hồi tiếp trạng thái sao cho hệ kín có cặp cực phức tại z =− ± 1,2 0,7 0,2 j