Đề cương môn Lí thuyết Điều khiển Tự động | Đại học Điện lực

lOMoARcPSD| 59149108
ĐỀ CƯƠNG MÔN LÍ THUYẾT ĐIỀU KHIỂN TỰ ĐỘNG
A.Câu hỏi loại 1 ( 15đ)
Câu 1 : Khái niệm hệ thống điều khiển và mô hình toán của nó ?
- Hệ thống tự động là một tập hợp các thiết bị được sắp xếp một cách khoa học nhằm thực
hiện mục đích nào đó của con người y(t)=f(u(t),x(t))
(Trong đó : y(t) : tín hiệu ra , u(t) : tín hiệu vào , x(t): trạng thái của hệ thống )
- Mô hình toán học của hệ thống là mối quan hệ giữa tín hiệu ra và các tín hiệu vào và trạng
thái của hệ thống .
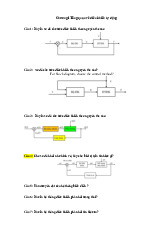
Câu 2 : Trình bày về cấu trúc đơn giản và cấu trúc mạch hở của hệ thống ?
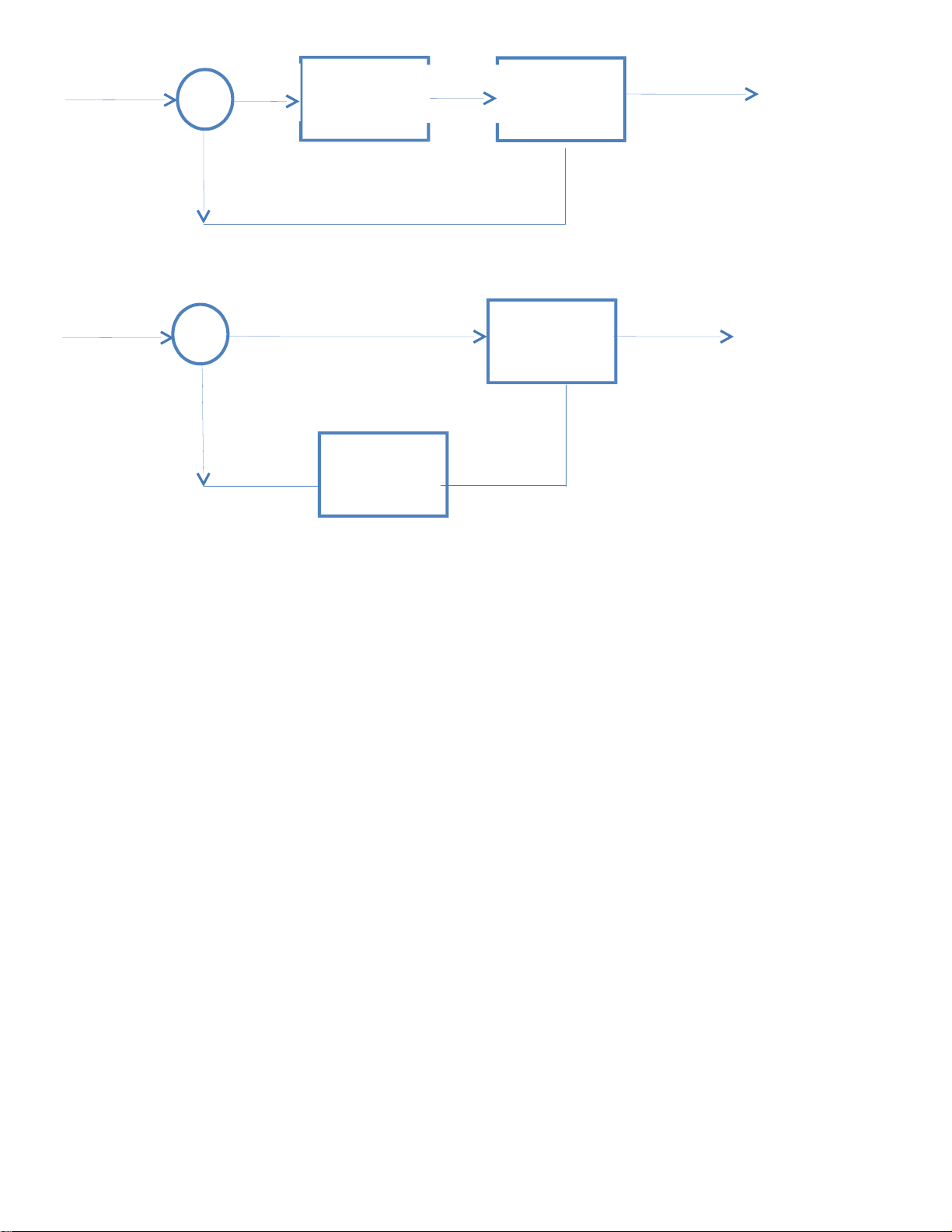
- Cấu trúc đơn giản của hệ DKTĐ R Controller(Bộ Plant( Đối e Y u điều khiển ) tượng điều khiển)
- Cấu trúc mạch hở của hệ ĐKTĐ R u Y Controller(Bộ Plant( Đối điều khiển ) tượng điều khiển)
Giải thích đại lượng : R là tín hiệu đặc ( tín hiệu vào ) , Y là tín hiệu ra , u là luật điều khiển ,
e là sai lệch điều khiển
VD : - Điều hòa có bộ phận cảm ứng nhiệt sao cho khi nó đủ nhiệt thì nó phản hồi để động cơ
tự động ngắt ( Cấu trúc đơn giản nhất )
- Nếu điều khiển tàu thủy theo 1 quỹ đạo y(t) tùy ý nào đó , thủy thủ luôn phải bẻ lái 1 góc
R(t) để tạo ra 1 góc bánh lái U(t) ( Cấu trúc mạch hở ) Câu 3 : Phương trình vi phân tổng
quát mô tả hệ thống ? lOMoARcPSD| 59149108
Dựa trên các định luật có sẵn về quan hệ vật lí bên trong và quan hệ giao tiếp với môi
trường bên ngoài của hệ thống . Các quan hệ này được mô tả theo qyu luật lí hóa , cân
bằng….rút ra được ptvp mô tả bản chất động học của các phần tử , hệ thống. Nó mô tả đúng
với bản chất thực của hệ thống : PT : =
Trong đó : ao…an và bo…bm : hệ số của mô hình ( phụ thuộc vào cấu trúc của hệ thống ),
Y : tín hiệu ra , u : tín hiệu vào , n : bậc vi phân tín hiệu ra , m : bậc vi phân tín hiệu vào,
và là các đạo hàm của tín hiệu vào , ra .
Câu 4 : Tính chất động học của khâu khuyếch đại ?
HTĐ : G(s) = k
-Nyquist : Là 1 điểm nằm trên trục thực
-Bode : Là đường thẳng nằm ngang
-Step : là đường thẳng nằm ngang
-Impulse : là đường thẳng trùng với trục thực ==> ko ảnh hưởng bởi nhiễu
Câu 5 :Tính chất động học của khâu quán tính bậc nhất ?
HTĐ : G(s) = .
Trong đó ( k : hệ số khuyếch đại , T hằng số thời gian quán tính, s : toán tử laplace
-Nyquist : Là đường tròn có bán kính r = k/2 và tâm là ( k/2,0)
-Bode : L(w) = -20db/dec ( Cứ tần số thay đổi 10 lần thì biên độ thay đổi -20db )
(w) =- ( Khi tần số thay đổi từ O đến thì chậm pha )
- Step : Là 1 đường cong xuất phát từ 0 và xác lập tại k và không có quá điều chỉnh
Thời gian quá độ phụ thuộc vào hằng số thời gian quán tính T
-Impulse : Ban đầu khi bị nhiễu tác động thì nó nhảy vọt lên , sau đó dần dần trở về trạng thái ban đầu
Thời gian trở về TT ban đầu phụ thuộc vào hằng số thời gian quán tính T
Câu 6 : Tính chất động học của khâu dao động bậc 2 ? lOMoARcPSD| 59149108 HTĐ : G(s) =
Trong đó : k là hệ số khuyếch đại , D: Hệ số suy giảm , T: hằng số thời gian quán tính
-Nyquist : Có HTĐ tần số : G(jw) =
Có vùng cộng hưởng trong đó k=const
- Bode : Có vùng cộng hưởng trong đó k=const L(w)= -40db/dec (w) =-
-Step : là một đường cong xuất phát từ 0 và xác lập tại k , có quá điều chỉnh ( dao động )
-Impulse : Là một đường cong xuất phát từ gốc tọa độ vọt lên rồi triệt tiêu theo trục hoành
( bị ảnh hưởng của nhiễu mạnh )
Câu 7 : Tính chất động học của khâu tích phân ? HTD: G(s) =
-Nyquist : Một nửa phần âm của trục ảo - Bode : L(w)= -20db/dec (w) =-
-Step : Là 1 đường thẳng có độ dốc là k
-Impulse : Là đường nằm ngang k
Câu 8 : Tính chất động học của khâu vi phân ? HTĐ: G(s)=k.s
-Nyquist : Một nửa phần dương của trục ảo - Bode : L(w)= 20db/dec (w) =
-Step : Là hàm xung dirac
-Impulse : Là hàm xung dirac
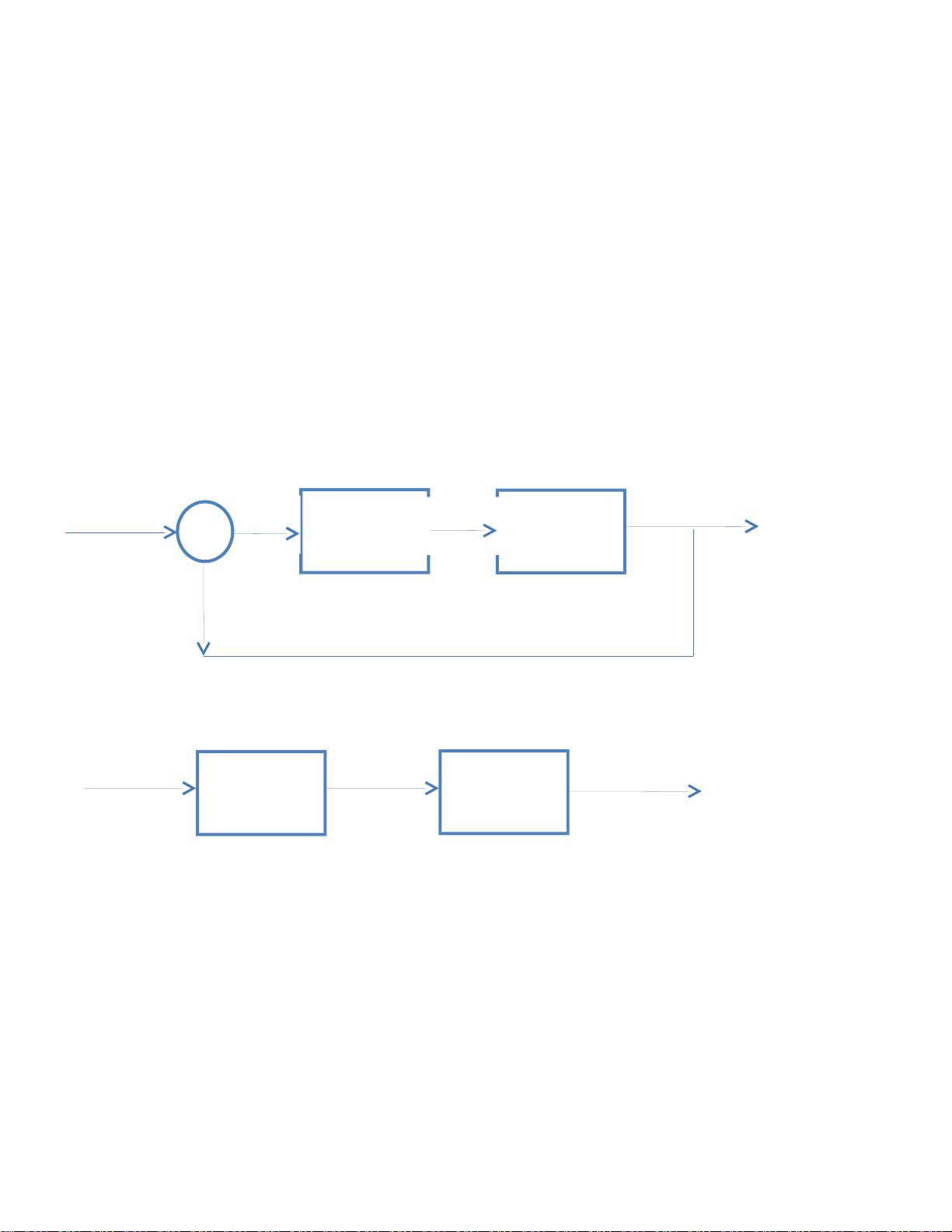
Câu 9 : Trình bày khái niệm về tính ổn định của hệ thống ? lOMoARcPSD| 59149108
K/n : Hệ đang ở trạng thái cân bằng , bị kích thích tác đông và văng ra khỏi vị trí cân bằng.
Sau đó nó tự trở về trạng thái cân bằng ban đầu khi mất kích thích. Ta nói hệ ổn định tại lân cân điểm cân bằng
Hay nói cách khác : Một hệ thống ổn định nếu quá trình quá độ (QTQĐ) tắt dần theo thời
gian, hệ k ổn định nếu QTQĐ tăng dần theo thời gian , biên giới ổn định nếu QTQĐ không đổi
hoặc dao động tăng dần
HT ổn HT biên giới ổn HT ko định định ổn định
Câu 10: Điều kiện ổn định của hệ liên tục tuyến tính trong miền phức ?
- Đa thức đặc tính : là đa thức dưới mẫu của HTĐ, đặc trưng tính chất động học của hệ
-Phương trình đặc trưng : Là đa thức đặc tính có vế phải bằng không
- Được thể hiện ở sự phân bố nghiệm của phương trình đặc trưng trên mặt phẳng nghiệm số
-ĐK : Nếu tất cả các nghiệm của pt đặc trưng đều nằm bên trái mặt phẳng phức thì hệ ổn
định. Tức là tất cả các nghiệm có phần thực phải âm. Nếu có ít nhất một nghiệm có phần
thực dương thì hệ không ổn định , nếu ít nhất có 1 nghiệm phần thực bằng 0 thì hệ ở bên giới ổn định
Câu 11 : Trình bày tiêu chuẩn ổn định Routh ?
Giả sử ta có HTĐ có dạng G(s)= A(s) =
-Phát biểu : Nếu cột một của bảng Routh dương cả thì hệ ổn định . Nếu có ít nhất 1 số âm thì
hệ không ổn định
-Cách lập bảng Routh : lOMoARcPSD| 59149108 Ta có A(s) = Với : , , a o a 2 a 4 …. a n 2
Nếu cột 1 , các hệ số đều dương thì hệ ổn a 1 a 3 a 5 … a 2 n +1 định. b o b 2 b 4 … b 2 n
Câu 12 : Trình bày tiêu chuẩn ổn định … … … … … Mikhailow ?
Xét đa thức đặc tính A(s) = =
==> A(jw) = =p(w)+ jQ(w)
Phát biểu : Hệ ổn định nếu đường cong A(jw) bao quanh gốc tọa độ một góc khi
tần số thay đổi từ 0 đến vô cùng, với n là bậc của hệ thống
Câu 13 : Trình bày tiêu chuẩn ổn định Nyquist ?
( là phương pháp xét tính ổn định của hệ kín dựa vào hàm truyền đạt hệ hở ) dựa vào đường cong nyquist
- Nếu hệ hở ổn định thì hệ kín ổn định . Khí đó đường cong Nyquist không bao điểm (-1 j0)
- Nếu hệ hở ko ổn định ( tức là có N nghiệm có phần thực dương ) . Khi đó hệ kín ổn định khi
đường cong Nyquist bao điểm (-1 j0) N/2 vòng kín
Câu 14 : Khái niệm về sai lệch tĩnh của hệ thống điều khiển ?
Sơ đồ cấu trúc hệ thống vòng kín : C(s) R(s) E(s) G(s) R(s) E(s) H(s) =
-Sai lệch tĩnh ( sai số ở trạng thái xác lập ) là sự
khác nhau ( sai khác ) giữa tín hiệu ra và tín hiệu vào của HT ở trạng thái ổn định khi thời
gian tiến tới vô cùng. H(s) G(s)
-Từ HTĐ trên ta có thể tính sai số E(s) =
-Sai số ảnh của Laplace : Ess=
- Ta có thể tính sai số ở trạng thái xác lập dựa vào định lí giá trị cuối lOMoARcPSD| 59149108
- Sai số ở trạng thái xác lập phụ thuộc vào dạng tín hiệu vào và cấu trúc của hệ thốngCâu
15 : Khái niệm về bộ điều khiển PID ?
- PID là bộ điều khiển bao gồm các khâu tỉ lệ ( Proportional) , khâu tích phân ( Intergral),
khâu vi phân ( Derivative )
- Bộ điều khiển PID được dùng trong kĩ thuật , giúp cho hệ thống Nhanh (do khâu vi phân ),
mạnh ( do khâu khuyếch đại ) , Chính xác ( do khâu tích phân ) R e Controller(Bộ u Plant( Đối Y điều khiển ) tượng điều khiển)
Mô hình toán mô tả bộ điều khiển :
Cấu trúc PID còn được
biểu diễn dưới dạng : K p e u R Y S(s) K D .s
Hàm truyền đạt của bộ
đk PID: R(s) = K p (1 + T /s + T D .s)
Câu 16 : Trình bày mô
hình KGTT dạng tổng quát
mô tả hệ thống ? B
- ất kì một hệ thống nào
cũng được mô tả theo
phương trình KGTT tổng quát như sau :
Với A : là Ma trận hệ
thống , B : ma trận điều
khiển , C : Ma trận đầu ra
, D : ma trận vào ra lOMoARcPSD| 59149108 U(t)= I -
Từ mô hình không gian trạng thái dạng tổng quát như trên , ta xây dựng được :
Câu 17 : Điều kiện ổn định BIBO của hệ thống ?
Từ mối quan hệ giữa mô hình trạng thái và mô hình HTĐ : G(s) = cT(sI-A)-1.b +d
ĐK Hệ ổn định BIBO khi và chỉ khi ma trận A có tất cả các giá trị riêng nằm bên trái trục ảo
Hay nghiệm của đa thức p(s) = det(sI-A) nằm bên trái trục ảo
Câu 18 : Khái niệm về tính điều khiển được của hệ thống điều khiển ? -
Một hệ thống tuyến tính liên tục được gọi là điều khiển được hoàn toàn nếu tồn
tại ít nhất một tín hiệu điều khiển đưa được hệ từ 1 điểm trạng thái ban đầu x.0 tùy ý đến
một trạng thái x tùy ý trong 1 khoảng thời gian hữu hạn -
Một hệ thống tuyến tính liên tục được gọi là điều khiển được nếu tồn tại ít nhất
một tín hiệu điều khiển đưa được hệ từ 1 điểm trạng thái ban đầu x.0 tùy ý đến trạng thái gốc
tọa độ 0 trong 1 khoảng thời gian hữu hạn lOMoARcPSD| 59149108
Câu 19 : Khái niệm về tính quan sát được của hệ thống điều khiển ? -
Một hệ thống quan sát được tại thời điểm t0 nếu tồn tại ít nhất một giá trị hữu
hạn T > t0 để điểm trạng thái x(t)= x0 tùy ý có thể xác định một cách chính xác thông qua việc
quan sát tín hiệu vào , ra trong khoảng thời gian (t0 - T ) -
Một hệ thống quan sát được hoàn toàn tại thời điểm t0 nếu tồn tại mọi giá trị
hữu hạn T > t0 để điểm trạng thái x(t) = x0 tùy ý có thể xác định một cách chính xác thông
qua việc quan sát tín hiệu vào , ra trong khoảng thời gian( t0 – T )
B. Câu hỏi loại 2 ( 20đ)
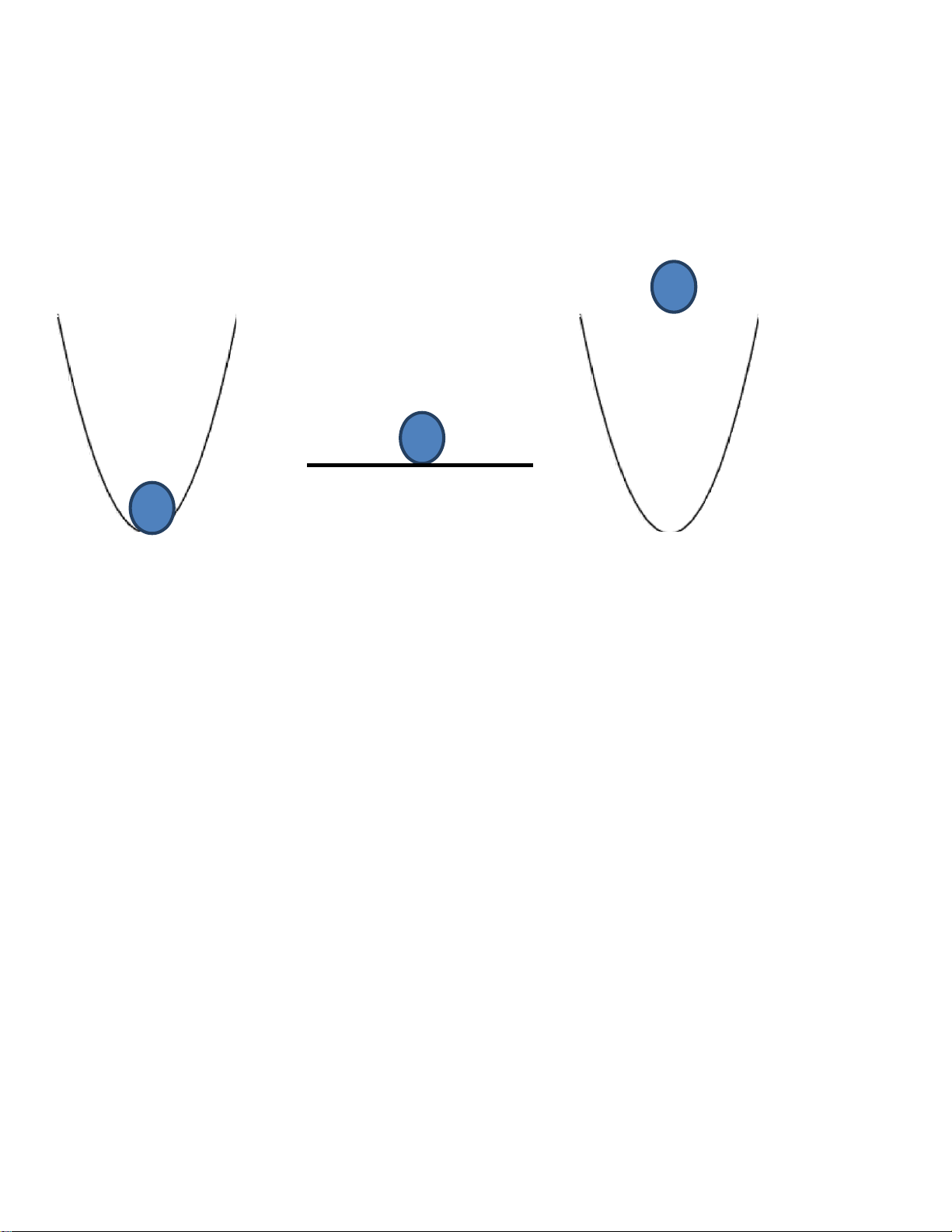
Câu 1 : TRình bày cấu trúc điều khiển phản hồi đầu ra ?
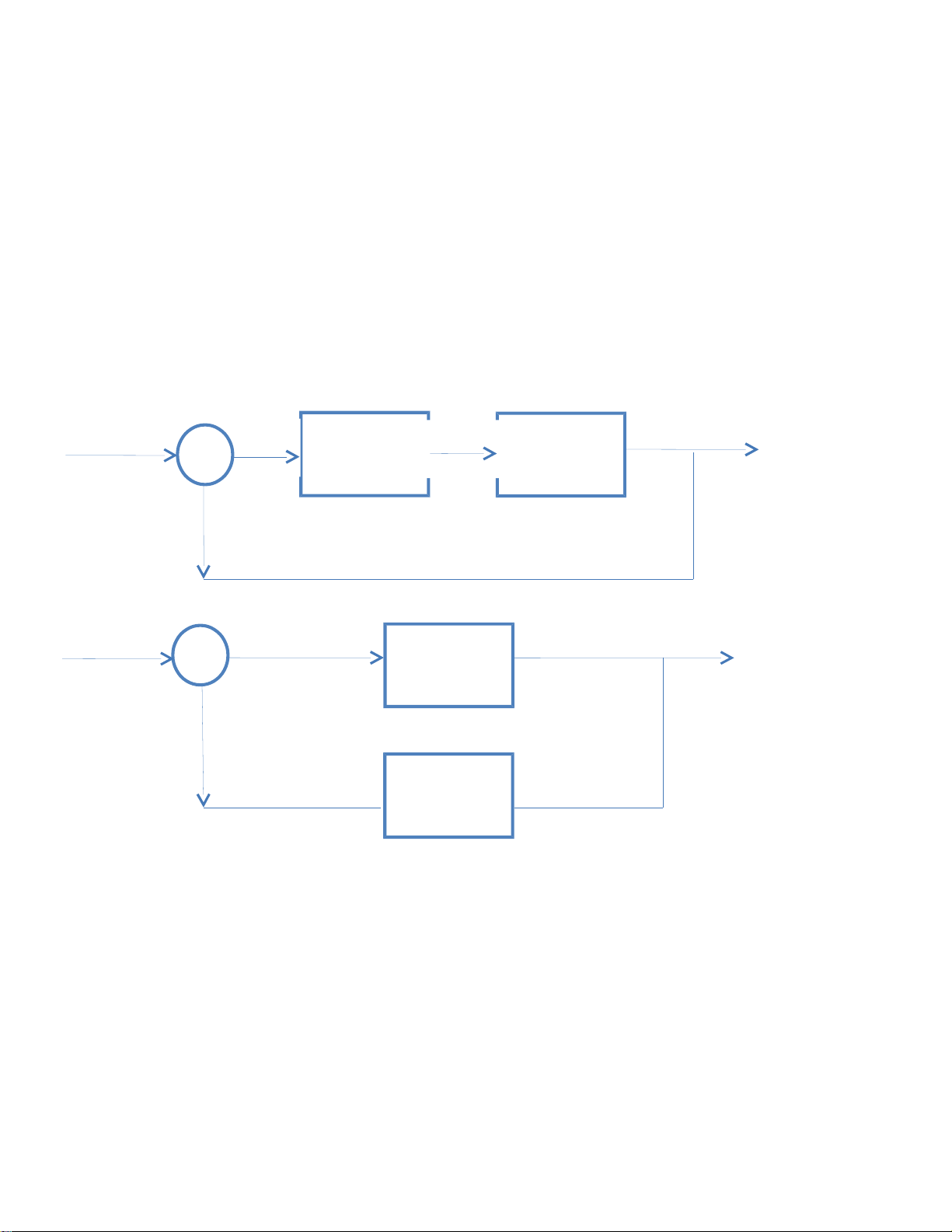
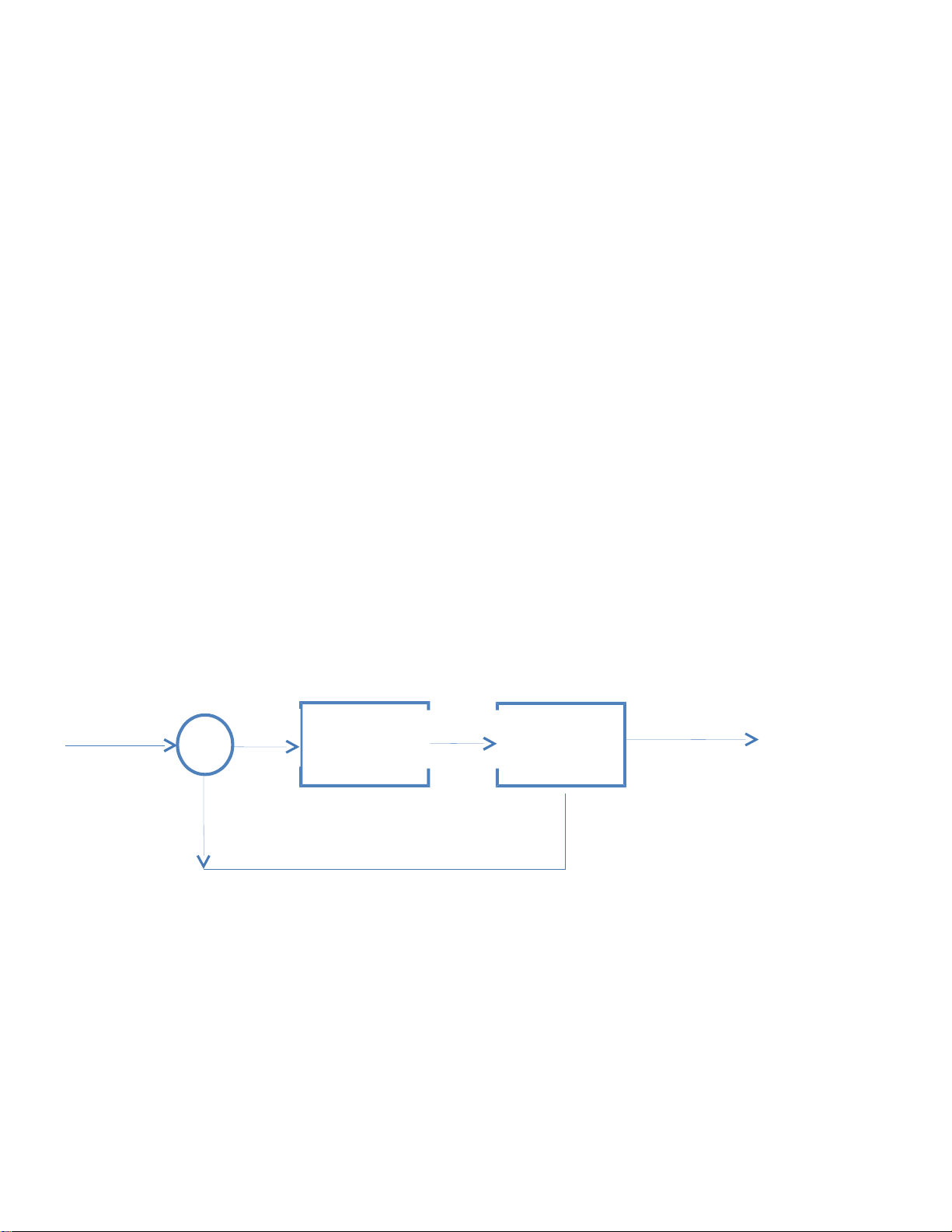
-CẤU TRÚC PHẢN HỒI TÍN HIỆU RA Ở MẠCH CHÍNH : R Controller(Bộ Y Plant( Đối e u điều khiển ) tượng điều khiển)
-CẤU TRÚC PHẢN HỒI TÍN HIỆU RA Ở MẠCH PHẢN HỒI : R e y Plant( Đối tượng điều khiển) Controller(Bộ điều khiển )
Như vậy, ta rút ra được cấu trúc phản hồi đầu ra như sau :
Ưu : Chính xác , ổn định , dễ thực hiện
Nhược : Chậm ( Chậm so với phương pháp phản hồi trạng thái )
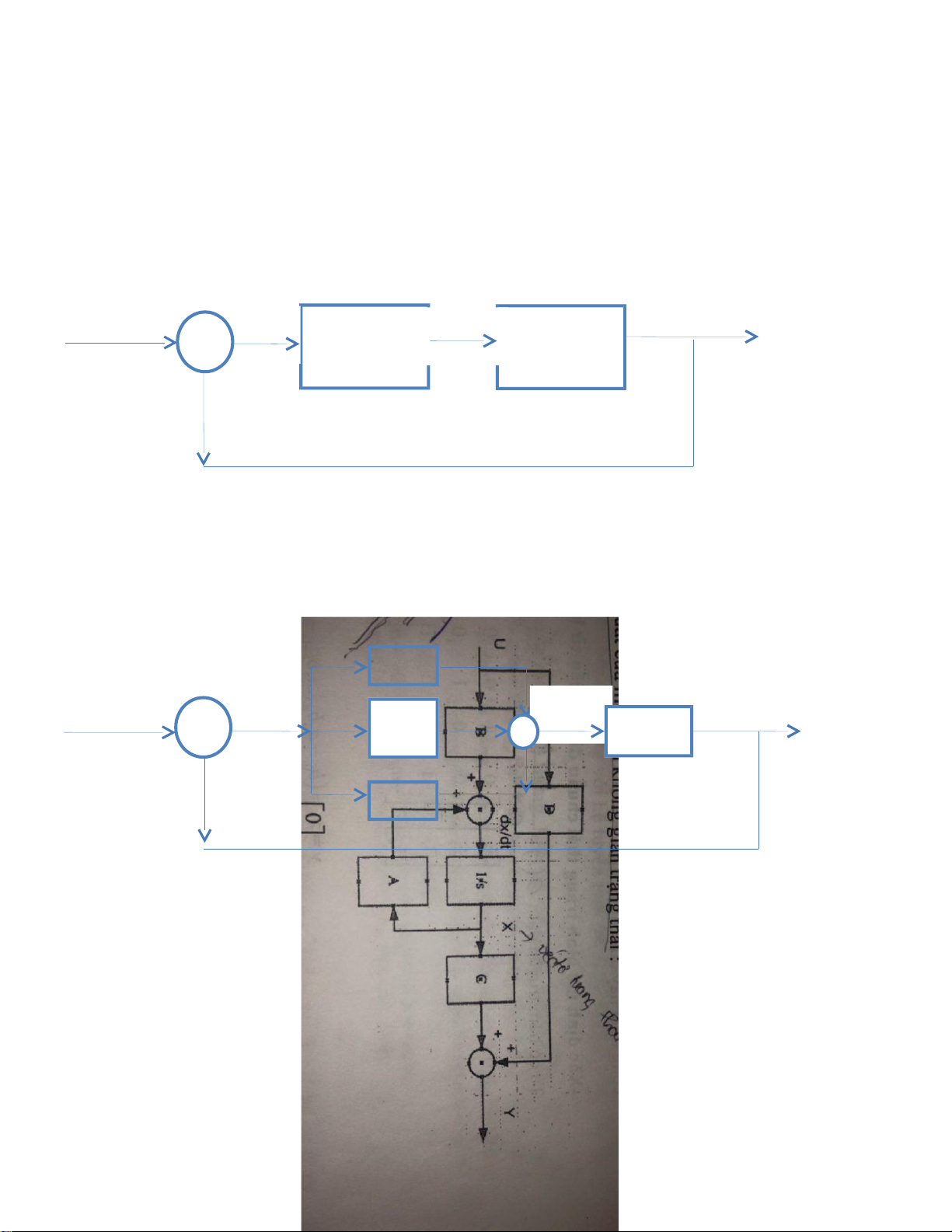
Câu 2 : Trình bày về cấu trúc điều khiển phản hồi trạng thái :
- CẤU TRÚC PHẢN HỒI TRẠNG THÁI CÓ BỘ ĐK NẰM Ở MẠCH CHÍNH : lOMoARcPSD| 59149108 R Controller(Bộ Plant( Đối e Y u điều khiển ) tượng điều khiển)
==> LUẬT ĐK THAY ĐỔI KẾT QUẢ ĐẦU RA
- CẤU TRÚC PHẢN HỒI TRẠNG THÁI CÓ BỘ ĐK NẰM Ở MẠCH PHẢN HỒI: R e Plant( Đối y tượng điều khiển) Controller(Bộ điều khiển )
Như vậy, ta rút ra được cấu trúc phản hồi trạng thái có đặc điểm như sau :
- Ưu điểm : Nhanh
- Nhược điểm : Khó thực hiện
Câu 4 : Trình bày đặc tính tần số biên pha ( Nyquist) và đặc tính tần số logarit ( Bode) ?
- Đặc tính tần số biên pha ( Đường cong Nyquist )
Đường cong Nyquist biểu diễn G(jw) trong hệ tọa độ cực khi w thay đổi từ 0 đến vô cùng. Cho
ta biết về sự sai khác về biên độ, pha của tín hiệu ra so với tín hiệu vào phụ thuộc vào tần số như thế nào . A =
Đồ thị Nyquist được ứng dụng việc đánh giá chất lượng hệ kín từ HTĐ hệ hở
- Đặc tính tần số logarit ( Đường cong Bode )
Đường cong Bode là đường biểu diễn mối quan hệ giữa biên độ và pha của tín hiệu ra so với
tín hiệu vào khi tần số làm việc thay đổi từ 0 đến vô cùng ở trục log ( tần số ) và trục
Đồ thị Bode gồm 2 phần : Đồ thị TSBĐ và TSPH ( L(w) và )
A = ==> L(w)= 20logA(w)
Câu 5 : Trình bày hàm quá độ , hàm trọng lượng ? lOMoARcPSD| 59149108
- Hàm quá độ ( Step respone ) :
Đáp ứng hệ thống khi hệ ở trạng thái O được kích thích đầu vào là hàm 1(t) hoặc h(t) .
Là đường cong mô tả quá trình hệ thống chuyển từ một trạng thái xác lập này sang trạng thái xác lập khác
Hàm quá độ được sử dụng để đánh giá chất lượng động học của HT ở quá trình quá độ
Các đại lượng đặc trưng :
Tr(Rise time ) = 10% - 90% : thời gian tăng đặc trưng cho khả năng cường kích của hệ thống ;
Td(delay time ) = 50% : Thời gian trễ ;
Ts(settling time ) : là thời điểm đạt trạng thái xác lập với sai số cho phép ,
(overshoot) : quá điều chỉnh , là tỉ lệ phần trăm của giá trị hàm h(t) đạt lớn nhất so với giá trị xác lập
- Hàm trọng lượng ( Impulse Respone )
Đáp ứng hệ thống khi hệ đang ở trạng thái O được kích đầu vào bởi xung dirac
Là đường cong mô tả sự phản ứng của Hệ thống đối với nhiễu. Đó là quá trình hệ quay trở về
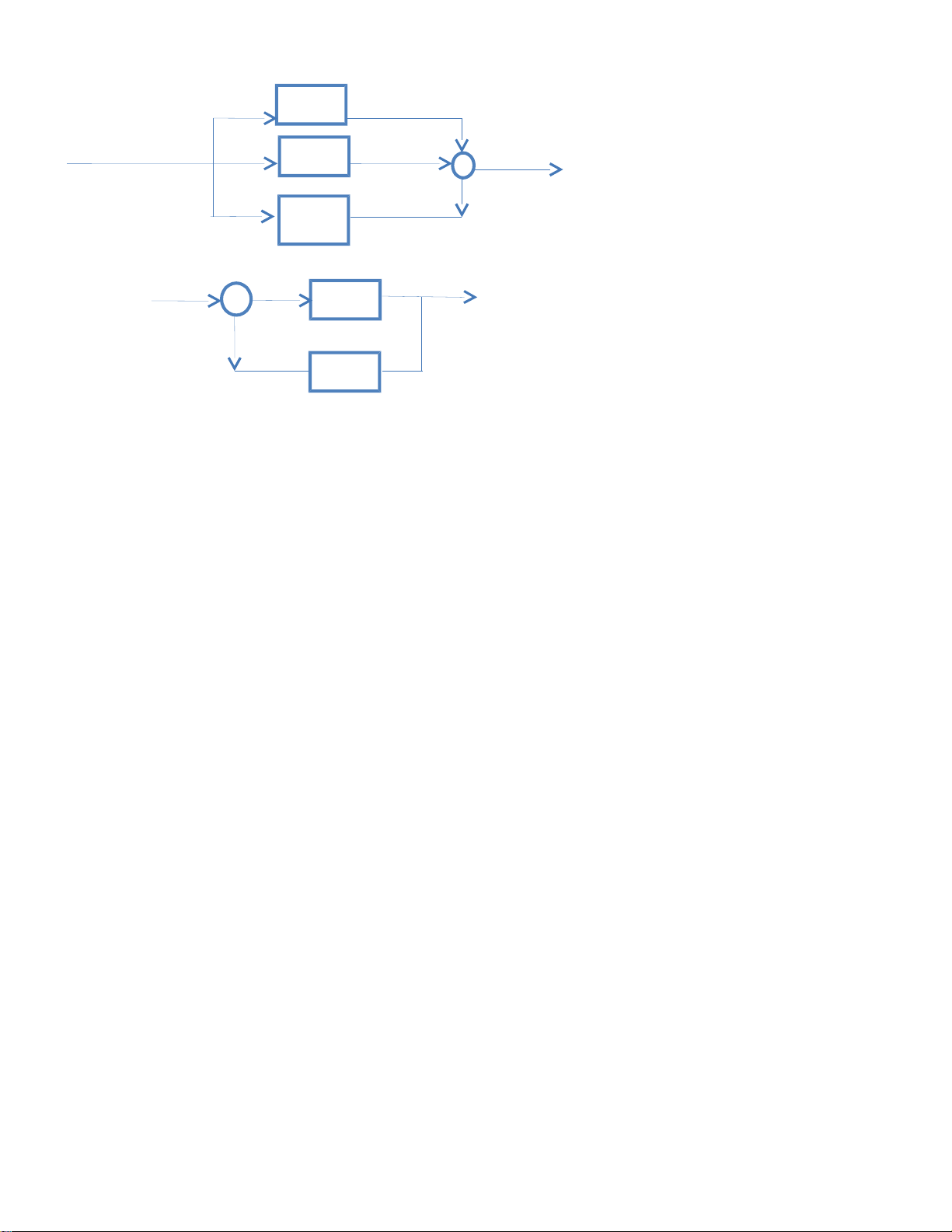
trạng thái ban đầu khi bị nhiễu đánh bật ra khỏi vị trí làm việc Câu 6 : Trình bày về các phép ghép nối cơ bản ? - Ghép nối tiếp Gnt = G1.G2….Gn R(s) C(s) G1(s) G2(s) …… Gn(s) lOMoARcPSD| 59149108
-Ghép song song : G song song = G1+ G2+..+Gn G1(s) C(s) R(s) G2(s) Gn(s)
Phản hồi âm, dương : G k s) = ( C(s) R(s) G(s) H(s)
Câu 7 : Trình bày về phép chuyển nút trong đại số sơ đồ khối ( Giáo trình / 13 )
Câu 8 : Khái niệm về độ dữ trữ biên độ, pha , dải thông của hệ thống
- Độ dữ trữ biên độ là sự thay đổi hệ số khuyếch đại hệ hở đến giá trị tới hạn làm hệ kín ko ổnđịnh
- HT có độ dự trữ càng lớn thì khả năng thay đổi các tham số càng lớn khi hệ kín mất ổn
- Độ dự trữ pha là sự thay đổi pha của hệ hở đến lúc hệ kín mất ổn định
- Đo được Td(t/g trễ ) . Nếu Td> 180 Wpc thì hệ k ổn định. Td= 1 =>=w.Td
-Giải thông : Là tần số mà tại đó biên độ đáp ứng ra của hệ kín bằng -3db ( Hay hệ số khuyết
đại suy giảm đi 3db)
Câu 9 : Trình bày phương pháp xác định sai lệch tĩnh của HT ? ( Giống phần 1 câu 14 )
Từ sơ đồ mạch kín ta suy ra được sơ đồ mạch hở . Sau đó tính được sai số E(s) và Ess
Suy ra exl và và dạng G(s) = k/sr .B(s)/A(s)
Câu 10 : Khái niệm hệ số sai số , hệ số sai số tốc độ , hệ số sai số gia tốc ?
- Hệ số sai số kp : xuất hiện trong trường hợp đầu vào là hàm step 1(t) và do các phần tử
trong hệ thống gây ra . với
- Hệ số sai số tốc độ : xuất hiện trong trường hợp đầu vào là hàm Ramp R(t)=t và do các
phần tử trong hệ thống gây ra với lOMoARcPSD| 59149108
- Hệ số sai số gia tốc: Xuất hiện trong trường hợp đầu vào là hàm Parabolic R(t)= t2/2 và do
các phần tử trong hệ thống gây ra với
Câu 11 : Phân tích chất lượng điều khiển của bộ điều khiển PID ?
- Có thể nói bộ điều khiển PID đem lại cho Hệ thống 3 tiêu chuẩn : Mạnh , nhanh và chính xác
-P : Phục tùng và thực hiện chính xác mệnh lệnh được giao ==> làm giảm thời gian tăng Tr
và sai số ở trạng thái xác lập
I : Làm việc và có tích lũy kinh nghiệm để thực hiện tốt nhiệm vụ ==> Khử đc sai số ở trạng
thái xác lập nhưng có thể làm xấu đường cong đáp ứng
D : Luôn có sáng kiến và phản ứng nhanh nhạy với sự thay đổi tình huống trong quá trình
thực hiện nhiệm vụ ==> Tăng tính ổn định của hệ thông , giảm quá điều chỉnh và cải tiến
dạng đường cong đáp ứng
===> Như vậy , bộ điều khiển PID đã giúp hệ thống trở lên hiệu quả : nhanh , mạnh , c-xác
Câu 12 :Trình bày phương pháp tối ưu độ lớn tổng hợp bộ điều khiển PID ?
- Mong muốn thiết kế có được 1 bộ điều khiển để đáp ứng đầu ra của hệ thống y(t) giống
đầuvào x(t) tại mọi điểm hoặc ít ra trong thời gian quá độ thì y càng bám x càng tốt .Hay
nếu bộ điều khiển R(s) mang lại cho hệ thống chất lượng |G(jw)|= 1 với mọi w thì gọi là bộ
điều khiển tối ưu độ lớn R(s) S(s) e Y x u
- Trong thực tế thì G(jw)1 trong 1 khoảng tần số đủ rộng - Đối với khâu quán tính bậc 1 : S(s) = => R(s) =
- Đối với khâu quán tính bậc 2
S(s) ===> R(s)=kp(1 + ) với kp = và TI= T1 -
Đối với khâu quán tính bậc 3 :
S(s) = ==> R(s)= kp(1 + +TD.s) với kp = , TI=T1 + T2 , TD = lOMoARcPSD| 59149108
Câu 13 : Trình bày phương pháp xây dựng mô hình không gian trạng thái ?
- Dựa trên các định luật có sẵn về quan hệ vật lí bên trong và quan hệ giao tiếp với mối quan
hệ môi trường bên ngoài của hệ thống. Các quan hệ này đc mô tả theo qui luật lí hóa , qui
luật cân bằng được rút ra từ hpt vi phân mô tả bản chất động học của các phần tử trong hệ thống =
- Từ pt vi phân bậc n ==> Ta rút ra được n hệ ptvp bậc nhất và 1 phương trình tín hiệu ra.
- Từ n hệ ptvp bậc nhất đó chính là mô hình KGTT
Câu 14 : Trình bày mối quan hệ giữa mô hình HTĐ và mô hình KGTT
- Xác định HTĐ từ Mô hình KGTTTa có mô hình KGTT là :
Từ đó ta tìm đc A, B, C,D
Sau đó ta xác định HTĐ như sau : G(s)= CT(sI-A)-1.B + D
-Xác định Mô hình KGTT từ HTĐ
Ta có HTĐ : G(s) = . Ta tìm được mô hình không gian trạng thái : = . + . u
y=(b0-aobn…..bn-1 –an-1bn). + bn.u
Câu 15 : Trình bày tiêu chuẩn Kalman về tính điều khiển được ?
- Trước tiên ta tính ma trận điều khiển CO CO = [B
AB A2B An-1B] với n là hạng của ma trận hệ thống ( Rank của ma trận A )
- Điều kiện cần và đủ theo tiêu chuẩn Kalman dể hệ có tính điều khiển được là : Rank(CO)=n
-Nếu hạng của CO bằng hạng của ma trận hệ thống ta nói hệ điều khiển được hoàn toàn
Câu 16 : Trình bày tiêu chuẩn Kalman về tính quan sát được ?
Trước tiên ta tính ma trận quan sát OB lOMoARcPSD| 59149108
OB= với n là hạng của ma trận hệ thống
- Điều kiện cần và đủ theo tiêu chuẩn Kalman để hệ có tính quan sát được là Rank(OB)=n-
Nếu hạng của OB bằng hạng của ma trận hệ thống ta nói hệ quan sát được hoàn toàn .