























































































Preview text:
BỘ MÔN GIẢI TÍCH
BÀI TẬP GIẢI TÍCH B2 Lê Văn Chánh, Ông Thanh Hải, Nguyễn Vũ Huy, Nguyễn Nhựt Hưng, Phan Thị Phương, Lê Thị Mai Thanh, Hồ Thị Kim Vân
Trích soạn từ: J. Stewart, CALCULUS, 6th. Edition.
KHOA TOÁN TIN HỌC, ĐH. KHTN TPHCM Mục lục
1 Sự liên tục của hàm số nhiều biến 4
1.1 Hàm số nhiều biến . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 4 1.1.1
Miền xác định và miền giá trị . . . . . . . . . . . . . . . . . . . . 4 1.1.2
Đồ thị của hàm số hai biến . . . . . . . . . . . . . . . . . . . . . . 5 1.1.3
Đường đồng mức và contourmap của hàm hai biến . . . . . . . . . 7 1.1.4
Hàm 3 biến; Hàm n biến . . . . . . . . . . . . . . . . . . . . . . . 13
1.2 Giới hạn của hàm nhiều biến . . . . . . . . . . . . . . . . . . . . . . . . . 13
1.3 Sự liên tục của hàm nhiều biến . . . . . . . . . . . . . . . . . . . . . . . . 16
2 Vi phân của hàm nhiều biến 19
2.1 Đạo hàm riêng . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 19 2.1.1
Định nghĩa đạo hàm riêng và ý nghĩa của nó . . . . . . . . . . . . . 19 2.1.2
Đạo hàm riêng cấp cao . . . . . . . . . . . . . . . . . . . . . . . . 21
2.2 Mặt phẳng tiếp xúc, xấp xỉ tuyến tính . . . . . . . . . . . . . . . . . . . . 24
2.3 Quy tắc móc xích và đạo hàm của hàm ẩn . . . . . . . . . . . . . . . . . . 27
2.4 Đạo hàm theo hướng . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 32 2.4.1
Định nghĩa và công thức tính đạo hàm theo hướng . . . . . . . . . 32 2.4.2
Cực trị hóa đạo hàm theo hướng . . . . . . . . . . . . . . . . . . . 36 2.4.3
Vectơ gradient là pháp vectơ của mặt tiếp xúc với mặt đồng mức . . 37
2.5 Cực trị của hàm hai biến . . . . . . . . . . . . . . . . . . . . . . . . . . . 40 2.5.1
Cực trị không điều kiện của hàm hai biến . . . . . . . . . . . . . . 40 2.5.2
Cực trị tuyệt đối của hàm hai biến . . . . . . . . . . . . . . . . . . 43 2.5.3
Cực trị có một điều kiện của hàm nhiều biến (Mục này để dành đọc
thêm) . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 45 3 Tích phân bội 49
3.1 Tích phân kép . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 49 3.1.1
Tích phân kép trên một hình chữ nhật . . . . . . . . . . . . . . . . 49 3.1.2
Giá trị trung bình của hàm hai biến trên hình chữ nhật . . . . . . . 53 3.1.3
Tích phân kép trên một miền phẳng tổng quát . . . . . . . . . . . . 53 MỤC LỤC 3 3.1.4
Đổi biến tích phân kép theo tọa độ cực . . . . . . . . . . . . . . . . 58
3.2 Tích phân bội ba . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 62 3.2.1
Tích phân bội ba trong một hình hộp . . . . . . . . . . . . . . . . . 63 3.2.2
Tích phân bội ba trong một khối tổng quát . . . . . . . . . . . . . . 63 3.2.3
Đổi biến tích phân bộ ba theo tọa độ trụ . . . . . . . . . . . . . . . 63 3.2.4
Đổi biến tích phân bộ ba theo tọa độ cầu . . . . . . . . . . . . . . . 63 4 Giải tích vectơ 64
4.1 Tích phân đường . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 64 4.1.1
Đường đi hay lộ trình (path) . . . . . . . . . . . . . . . . . . . . . 64 4.1.2
Tiếp tuyến và độ dài của đường cong . . . . . . . . . . . . . . . . . 67 4.1.3
Tích phân đường loại 1 . . . . . . . . . . . . . . . . . . . . . . . . 72 4.1.4
Tích phân đường loại 2 . . . . . . . . . . . . . . . . . . . . . . . . 74 4.1.5
Định lý Green (Định lý cơ bản của tích phân kép) . . . . . . . . . . 78 4.1.6
Đặc trưng của trường bảo toàn 2 chiều . . . . . . . . . . . . . . . . 80
4.2 Tích phân mặt . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 83 4.2.1
Mặt cong . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 83 4.2.2
Tích phân mặt loại 1 . . . . . . . . . . . . . . . . . . . . . . . . . 83 4.2.3
Tích phân mặt loại 2 . . . . . . . . . . . . . . . . . . . . . . . . . 83 4.2.4
Các định lý cơ bản của tích phân mặt . . . . . . . . . . . . . . . . 83
5 Làm quen vài mô hình phương trình vi phân 84
5.1 Phương trình vi phân cấp 1 . . . . . . . . . . . . . . . . . . . . . . . . . . 84 5.1.1
Phương trình vi phân tách biến . . . . . . . . . . . . . . . . . . . . 84 5.1.2
Phương trình vi phân đẳng cấp . . . . . . . . . . . . . . . . . . . . 86 5.1.3
Phương trình vi phân tuyến tính cấp 1 . . . . . . . . . . . . . . . . 86 5.1.4
Ứng dụng các mô hình phương trình vi phân cấp 1 trong các bài
toán thực tiễn . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 88
5.2 Phương trình vi phân tuyến tính cấp 2 với hệ số hằng . . . . . . . . . . . . 91 5.2.1
Phương trình thuần nhất . . . . . . . . . . . . . . . . . . . . . . . 91 5.2.2
Phương trình không thuần nhất . . . . . . . . . . . . . . . . . . . . 92
5.3 Phương trình vi phân toàn phần . . . . . . . . . . . . . . . . . . . . . . . . 95 Chương 1
Sự liên tục của hàm số nhiều biến
1.1 Hàm số nhiều biến
1.1.1 Miền xác định và miền giá trị
Nhắc lại kiến thức. Ta ký hiệu f .x; y/ là một biểu thức phụ thuộc vào cặp số thực x và y,
hoặc tổng quát hơn f .x; y/ là một giá trị thực tương ứng với mỗi cặp giá trị .x; y/ 2 D
R2. Khi đó f được gọi là hàm số hai biến xác định trên D. Nếu không chỉ rõ tập D thì ta
quy ước tập xác định của f là tập hợp ˚ D D .x; y/ 2 R
R=biểu thức f .x; y/ có nghĩa :
Còn tập giá trị của hàm số f là ˚
G D z 2 R=z D f .x; y/ với .x; y/ thuộc D :
Khi người ta viết z D f .x; y/ thì z được gọi là biến phụ thuộc vào hai biến độc lập x và y thông qua hàm số f . Bài tập
1. Cho f .x; y/ D ln.x C y 1/.
a) Tính f .2; 1/ và f .e; 1/. của f .
b) Tìm và phác họa miền xác định
c) Tìm miền giá trị của f
2. Cho f .x; y/ D x2e3xy. a) Tính f .2; 0/.
c) Tìm miền giá trị của f .
b) Tìm miền xác định của f . q 3. gì?
Tìm và phác họa miền xác định của f .x; y/ D 1 C x
y2. miền giá trị của f là p
4. Cho f .x; y; z/ D e z x2 y2.
Sự liên tục của hàm số nhiều biến 5 a) Tính f .2; 1; 6/.
c) Tìm miền giá trị của f .
b) Tìm miền xác định của f .
5. Cho g.x; y; z/ D ln.25 x2 y2 z2/. a) Tính g.2; 2; 4/.
c) Tìm miền giá trị của g.
b) Tìm miền xác định của g.
6-15 Tìm và phác họa miền xác định của hàm số cho bởi p p 6. f .x; y/ D px C y 7. f . y x2 1 x2 x; y/ D xy 12. f .x; y/ D 8. f .x; y/ D ln.9 x2 9y2/
13. f .x; y/ D arcsin.x2 C y2 2/ p 9. f .x; y/ D y x ln.y C x/ q p q 14. f . 10. x; y/ D 1 x2 y2 z2 f .x; y/ D 1 x2 1 y2 q 15. f .x; y/ D ln.16 4x2 4y2 z2/ p 11. f .x; y/ D y C 25 x2 y2
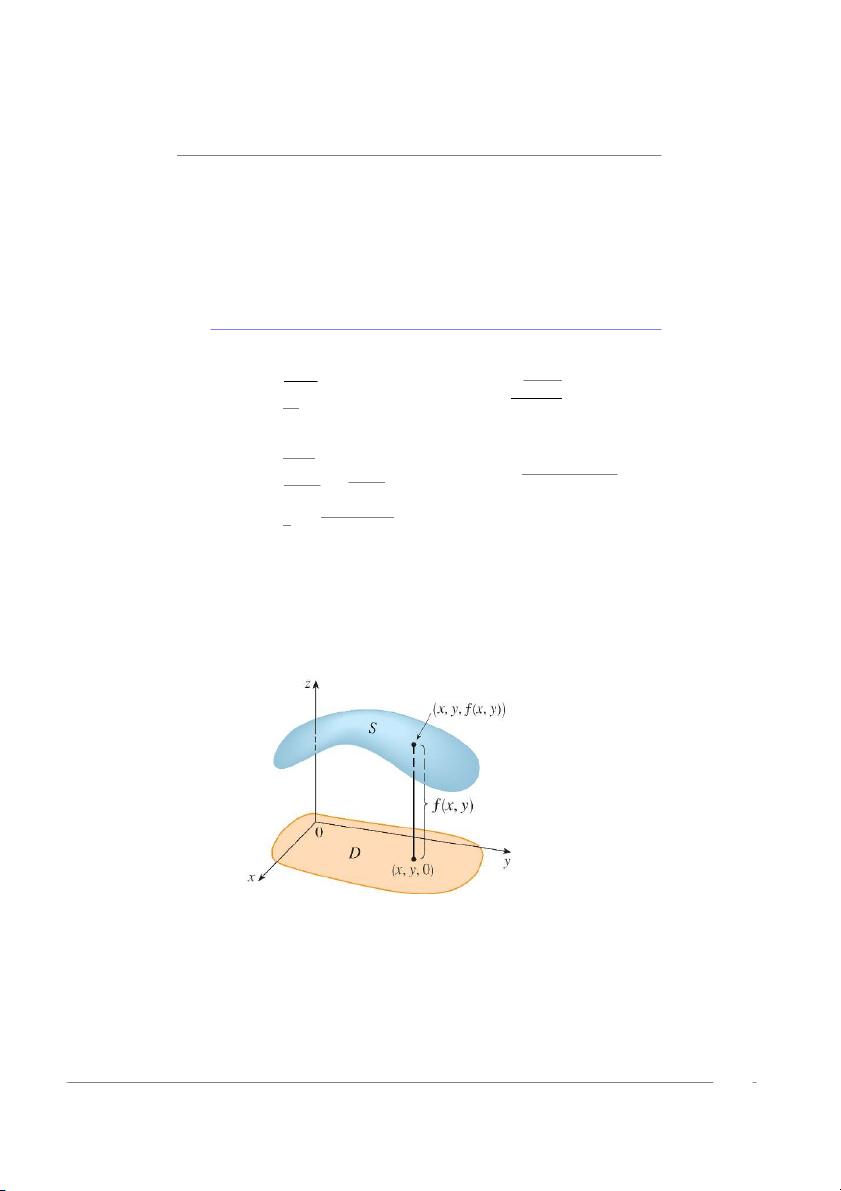
1.1.2 Đồ thị của hàm số hai biến
Nhắc lại kiến thức. Cho hàm số hai biến f có miền xác định D.
Đồ thị của f là tập hợp các điểm .x; y; z/ trong R3 sao cho z D f .x; y/ và .x; y/
thuộc D. Nói chung, khi biểu thị đồ thị trong không gian có ba trục tọa độ Oxyz, đồ
thị này có dạng mặt cong
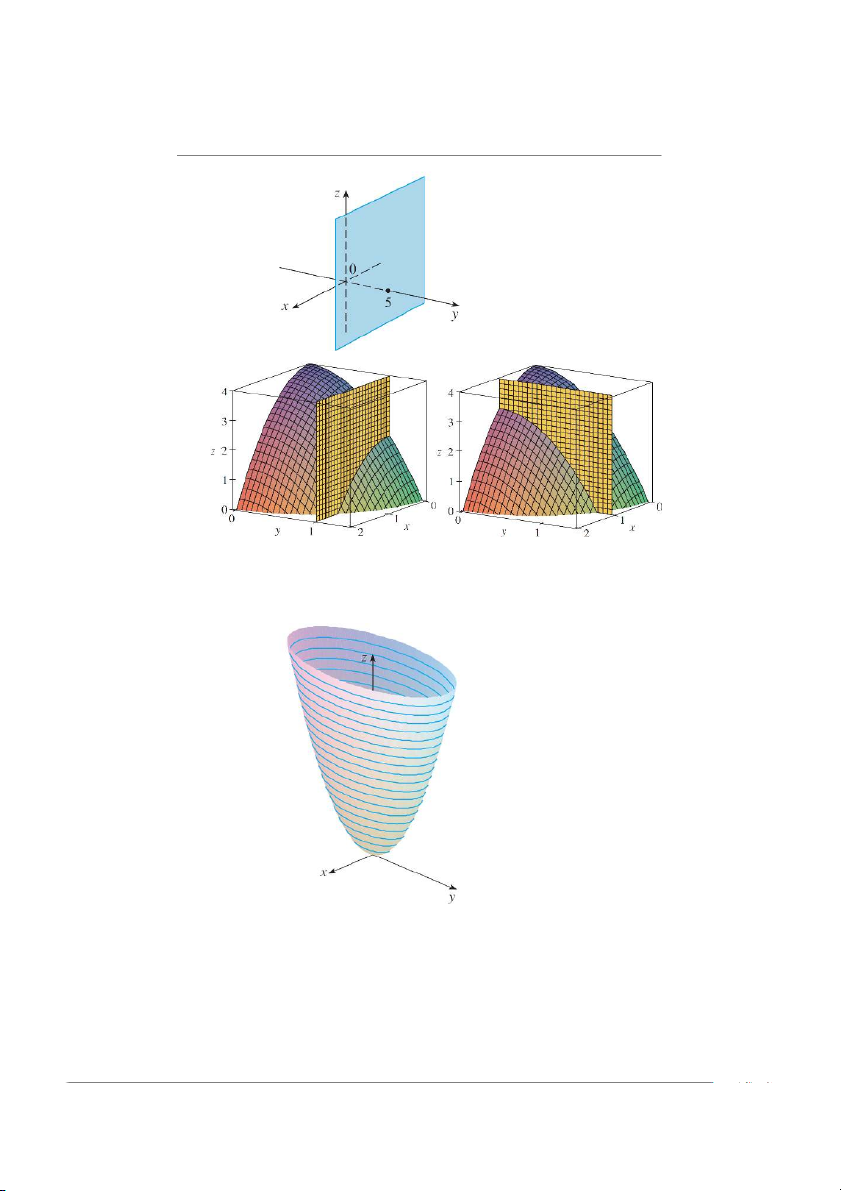
Khi phác họa đồ thị của f , người ta hình dung các vết của đồ thị, là các đường giao
nhau giữa đồ thị với các mặt phẳng đứng x D k hoặc y D k. Các vết tạo thành mặt
lưới. Hình sau là mặt phẳng đứng y D 5 6
Sự liên tục của hàm số nhiều biến
Mặt đứng y D k với các vết.
Mặt phẳng đứng x D k với các vết.
Hoặc người ta cũng phác họa đồ thị bằng cách hình dung các vết giao nhau giữa đồ
thị của f với các mặt phẳng ngang z D k (k là hằng số). Trong hình sau, vết trên các
mặt phẳng ngang z D k các đường cong ê-lip Bài tập
1-10 Phác họa đồ thị của hàm số.
Sự liên tục của hàm số nhiều biến 7 1. f .x; y/ D 3 6. f .x; y/ D 3 x2 y2 2. f .x; y/ D y 7. f .x; y/ D 3 x2 y2 2 3. f .
8. f .x; y/ D 4x C y2 C 1 x; y/ D 10 4x 5y 4. f .x; y/ D cos x q 9. f .x; y/ D 16 x2 16y2 5. f .x; y/ D y2 C 1 q 10. f .x; y/ D x2 C y2
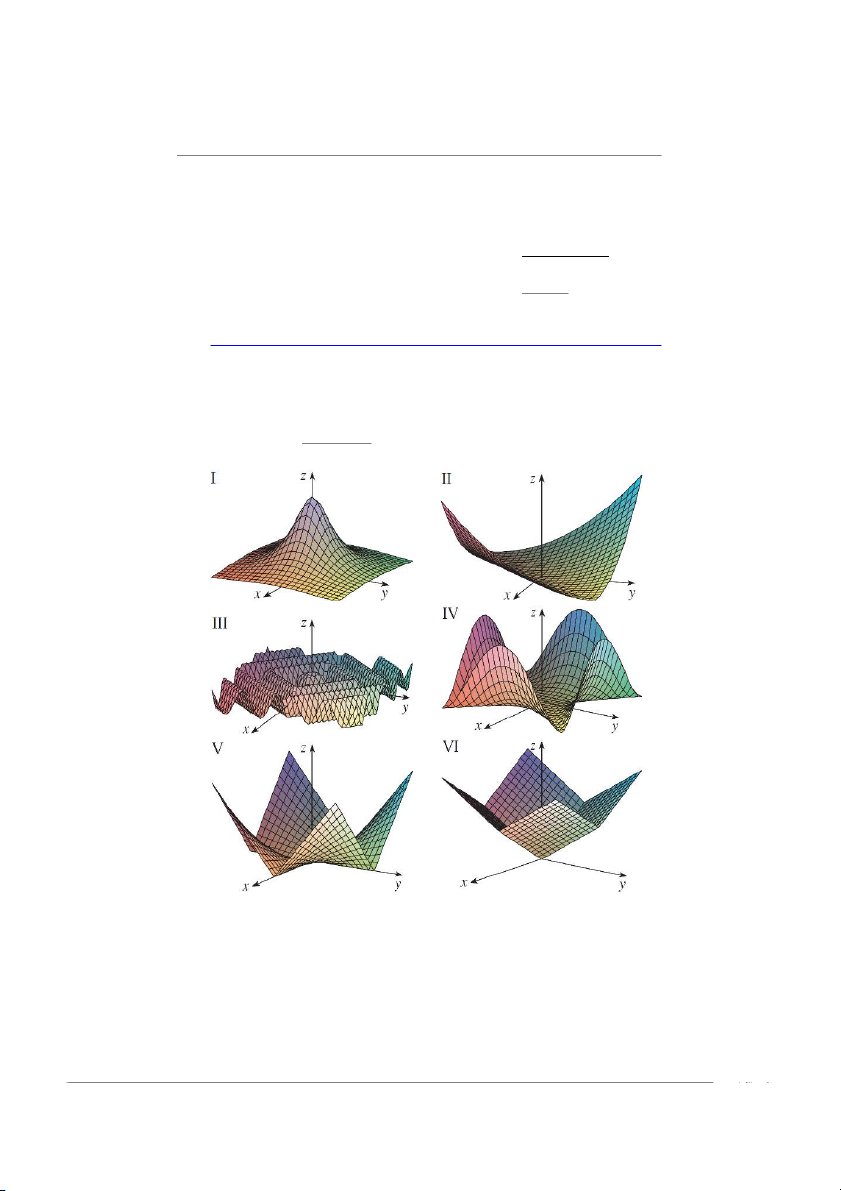
11. Trong mỗi câu, chỉ rõ hàm số nào có đồ thị trong số từ I đến VI. Hãy giải thích lý do. a) f .x; y/ D jxj C jyj d) f .x; y/ D .x2 y2/2 b) f .x; y/ D jxyj e) f .x; y/ D .x y/2 c) 1 f .x; y/ D 1 C x2 C y2
f) f .x; y/ D sin jxj C jyj
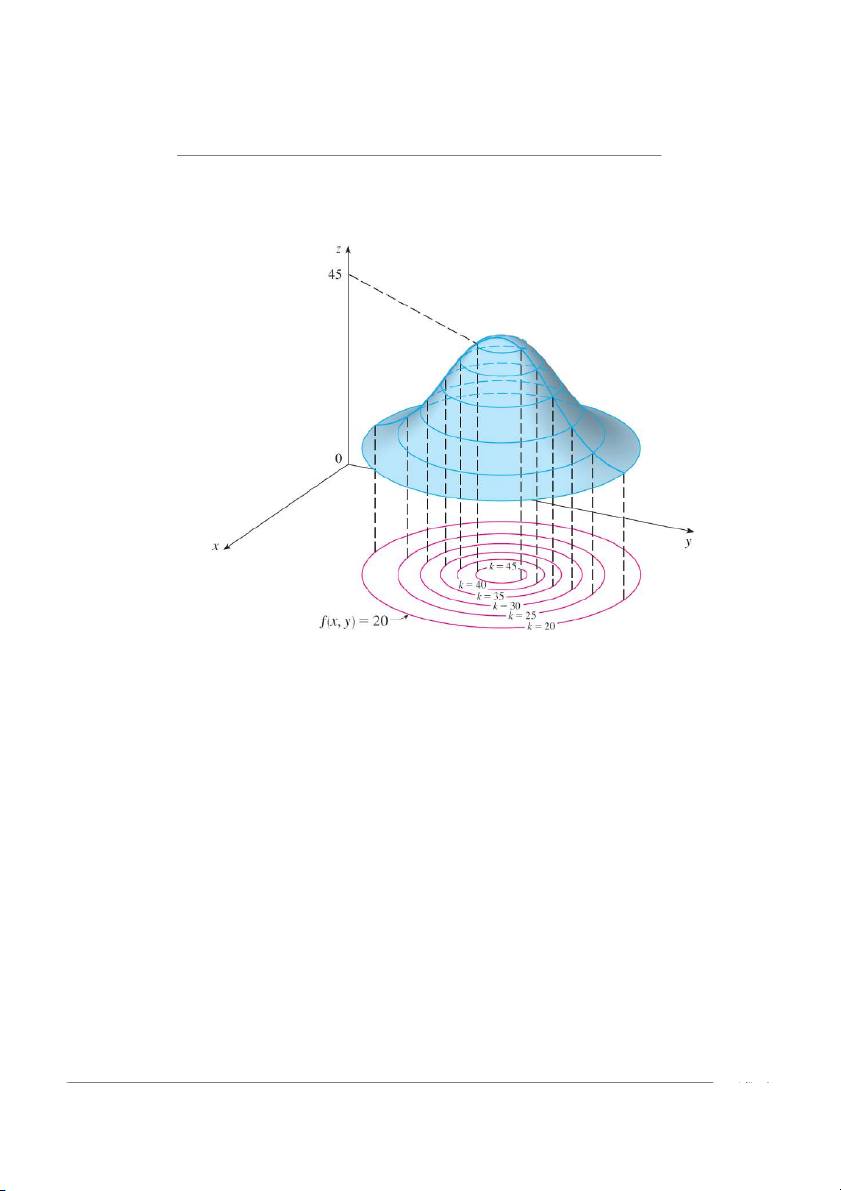
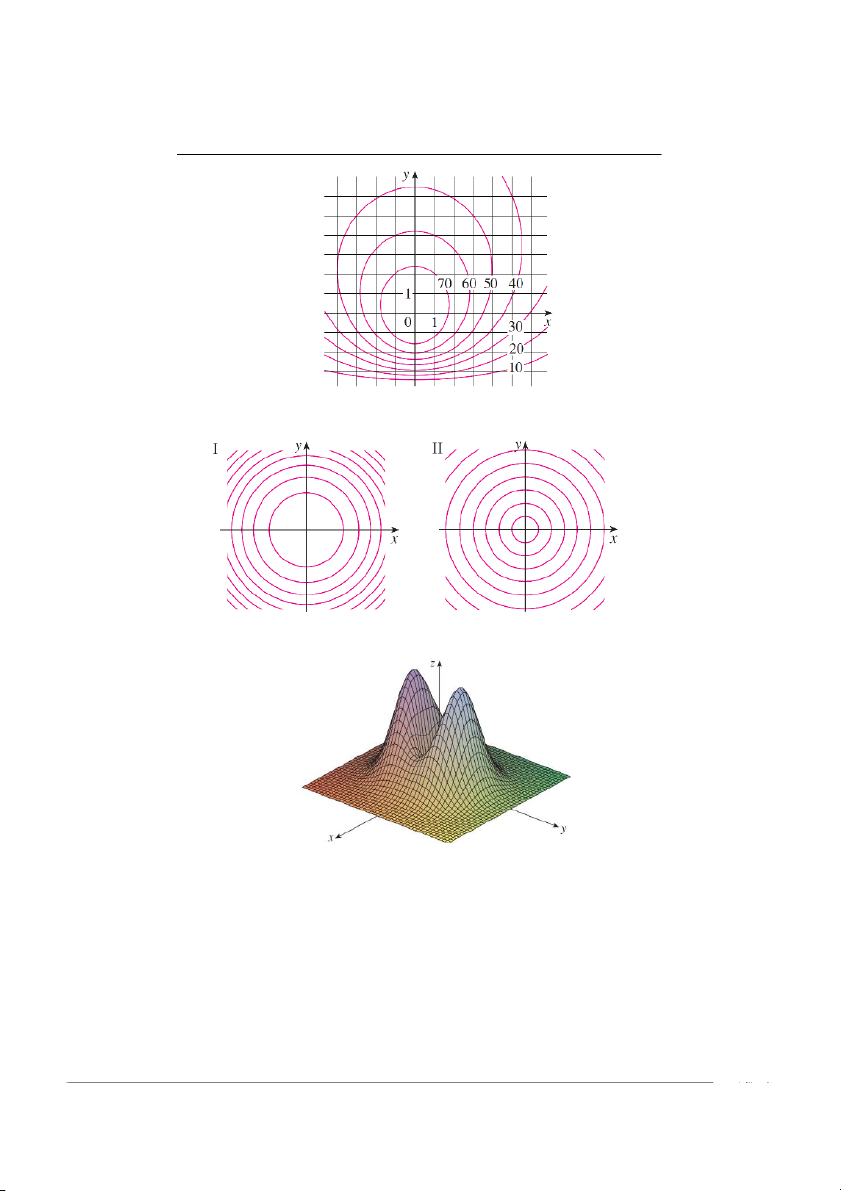
1.1.3 Đường đồng mức và contourmap của hàm hai biến
Nhắc lại kiến thức. 8
Sự liên tục của hàm số nhiều biến
Các đường đồng mức của một hàm số f , có hai biến, là những đường cong (trong mặt
phẳng Oxy) có phương trình f .x; y/ D k, với k là hằng số thuộc miền giá trị của f .
Nói cách khác, vết của đồ thị hàm f với mặt ngang z D k có hình chiếu lên mặt-xy là đường đồng mức.
Tập hợp các đường đồng mức trong mặt-xy được gọi là contour map, một thuật ngữ
của ngành địa lý, dùng để mô tả địa hình trên bản đồ. Bài tập
1. Dựa vào contour map của một hàm số dưới đây, hãy ước đoán giá trị của f . 3; 3/ và
f .3; 2/. Ta có thể nói gì về đồ thị của hàm số này?
Sự liên tục của hàm số nhiều biến 9
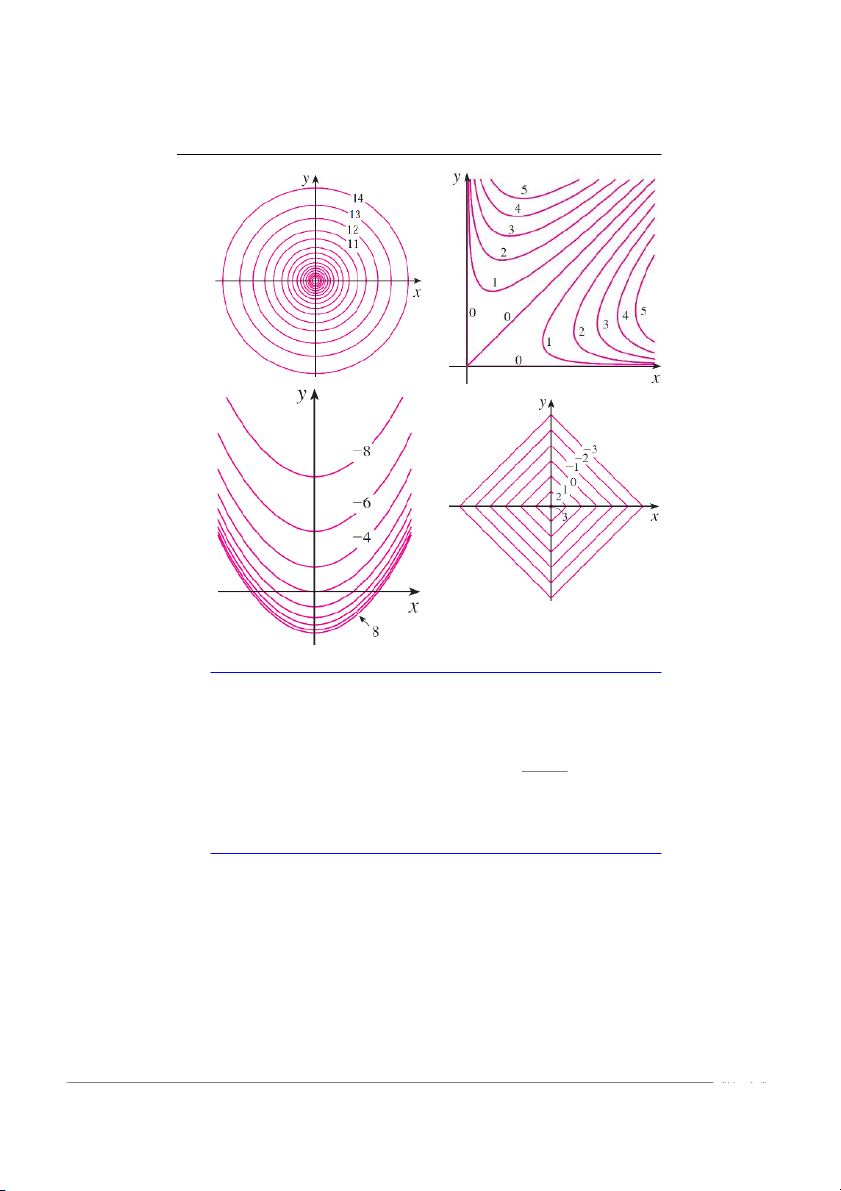
2. Đồ thị của hàm số f là hình nón, của hàm số g là hình paraboloid. Trong hai contour
map dưới đây, cái nào của f và của g, hãy giải thích.
3. Hãy phác họa sơ contour map của một hàm số có đồ thị như dưới đây
4-7 Cho trước contour map, dựa vào đó hãy phác họa đồ thị của f . 10
Sự liên tục của hàm số nhiều biến 4. 6. 7. 5.
8-15 Vẽ contour map của hàm số với vài đường đồng mức. 8. f .x; y/ D .y 2x/2 12. f .x; y/ D yex 9. f .x; y/ D x3 y 13. f .x; y/ D y= cos x 10. f .x; y/ D y ln x q 14. f .x; y/ D y2 x2 11. f .x; y/ D ey=x
15. f .x; y/ D y=.x2 C y2/
16. Một tấm kim loại mỏng, đặt trong mặt-phẳng-xy, có nhiệt độ T .x; y/ ở điểm .x; y/.
Các đường đồng mức của T đường gọi là các đường đẳng nhiệt (isothermals), vì tại
mọi điểm trên cùng một đường đẳng nhiệt có cùng nhiệt độ. Hãy phác họa vài đường
đẳng nhiệt với hàm nhiệt độ cho bởi T .x; y/ D 100=.1 C x2 C 2y2/
Sự liên tục của hàm số nhiều biến 11
17. Nếu V .x; y/ là điện thế tại điểm .x; y/ trong mặt-phẳng-xy, thì các đường đồng mức
của V được gọi là các đường thẳng thế (equipotential curves). Hãy phác họa vài q đsư ố ờn d g ươ đnẳn
g. g thế của hàm điện thế V.x; y/ D c= r2 x2 y2, trong đó c là hằng
18-23 Hãy chọn hàm số, có giải thích, khớp với:
a) đồ thị của nó trong nhóm được đánh số từ A-F
b) contour map trong nhóm được đánh số từ I-VI. 18. z D sin.xy/ 21. z D sin x sin y 19. z D ex cos y 22. z D .1 x2/.1 y2/ x y 20. z D sin.x y/ 23. z D 1 C x2 C y2 12
Sự liên tục của hàm số nhiều biến
24-27 Mô tả các mặt đồng mức của các hàm số sau
24. f .x; y; z/ D x C 3y C 5z 26. f .x; y; z/ D x2 y2 C z2
25. f .x; y; z/ D x2 C 3y2 C 5z2 27. f .x; y; z/ D x2 y2
Sự liên tục của hàm số nhiều biến 13
28-29 Từ đồ thị của hàm số f , đồ thị của hàm g được thành lập như thế nào? 28.
a) g.x; y/ D f .x; y/ C 2 c) g.x; y/ D f .x; y/ b) g.x; y/ D 2f .x; y/ d) g.x; y/ D 2 f .x; y/ 29. a) g.x; y/ D f .x 2; y/
c) g.x; y/ D f .x C 3; y 4/
b) g.x; y/ D f .x; y C 2/
1.1.4 Hàm 3 biến; Hàm n biến
Nhắc lại kiến thức.
Hàm số 3 biến f , xác định trên D
R3, là cách gán mỗi bộ ba giá trị thực .x; y; z/ 2
D với duy nhất một giá trị thực f .x; y; z/. Thông thường cách gán này cho bởi một
biểu thức f .x; y; z/ phụ thuộc theo x, y, z. Ví dụ, f .x; y; z/ D x2 C y2 C z2.
Ta không biểu diễn được đồ thị của hàm số 3 biến. Thay vào đó ta có thể biểu diễn các
mặt đồng mức cho bởi phương trình f .x; y; z/ D k, với k đại diện cho các hằng số.
Hình dưới biểu diễn ba mặt đồng mức của hàm số cho bởi f .x; y; z/ D x2 C y2 C z2
Khái niệm hàm số nhiều biến f và ký hiệu f .x1; x2; : : : ; xn/ được định nghĩa tương tự như trên.
1.2 Giới hạn của hàm nhiều biến
Nhắc lại kiến thức.
Cho f là hàm số hai biến xác định trên D và .a; b/ là điểm tụ của D, nghĩa là, D luôn
chứa những điểm có thể gần .a; b/ tùy ý. Ta nói rằng giới hạn của f .x; y/ khi .x; y/ 14
Sự liên tục của hàm số nhiều biến
tiến về .a; b/ bằng L, và ta viết lim f .x; y/ D L; (1.1) .x;y/!.a;b/
có nghĩa là với mọi số " > 0 cho trước, theo đó có một số ı > 0 sao cho q ˇ ˇ nếu .x; y/ 2 D và 0 < .x a/2 C .y b/2 < ı thì ˇf .x; y/ Lˇ < "
Những cách viết khác của (1.1) là
lim f .x; y/ D L hoặc f .x; y/ ! L khi .x; y/ ! .a; b/ x!a y!b ˇ ˇ q lLàưu kh ýo rằn ảng g ˇf cách. . ; . / x g;i y ữ /ah L ai ˇ đi là đ ểm ộxlớn y/ sai và sốa;gibữ.a f Do.xđ;óy,/đ vịà nhLn,gh.ĩxa tr a ên/2đ C ượ.y c hi b ểu /2đại
khái rằng sai số giữa f .x; y/ và L có thể nhỏ tùy ý, miễn là điểm .x; y/ đủ gần (và
không trùng) điểm .a; b/. Hình dưới minh họa ý đó
Với " > 0 cho trước, theo đó ta tìm được đĩa tròn Dı tâm .a; b/, bán kính ı sao cho
mọi điểm trong đĩa tròn được f ánh xạ vào khoảng .L "; L C "/.
Cách minh họa khác cho định nghĩa giới hạn như sau, với số " > 0 cho trước, theo đó
ta tìm được đĩa tròn Dı sao cho khi .x; y/ nằm trong đĩa Dı thì phần tương ứng của
đồ thị nằm giữa hai mặt phẳng ngang z D L " và z D L C ".
Trong giới hạn hàm số một biến, lim
f .x/, x tiến về a theo hai hướng trái và x!a
phải. Nhắc lại rằng giới hạn limf .x/ tồn tại khi và chỉ khi tồn tại lim x!a f .x/ D x!a
Sự liên tục của hàm số nhiều biến 15
limf .x/. Nhưng trong giới hạn hàm hai biến, lim f .x; y/, thì .x; y/ có x!aC .x;y/!.a;b/
thể tiến về .a; b/ theo vô số hướng, miễn là .x; y/ vẫn trong miền xác định của f . Do đó
Định lý 1.1: Hệ quả của định nghĩa giới hạn
Nếu f .x; y/ ! L1 khi .x; y/ ! .a; b/ dọc theo đường cong C1; f .x; y/ !
L2 khi .x; y/ ! .a; b/ dọc theo đường cong C2, trong đó L1 ¤ L2, thì không tồn tại lim f .x/. .x;y/!.a;b/
Để chứng tỏ f không có giới hạn tại
.a; b/, ta cũng có thể chỉ ra hai dãy n.x0n; y0 sao cho lim điểm M x0 n.xn; yn D / li v mà M 0 n!1 n D a và n/ n!1
limyn D lim y0 n D b, nhưng hai n!1 n!1 hai giá trị dãy số f . LM 1 và L2 khác nhau. n/ và f .M 0 n/ hội tụ về
Các tính chất bảo toàn phép tính của giới hạn (ví dụ như giới hạn của tổng bằng tổng
các giới hạn, nếu tồn tại, v.v. . . ) trong hàm số một biến cũng đúng cho hàm số hai
biến. Định lý giới hạn kẹp cũng vậy: Định lý 1.2 Giả sử
– tồn tại các giới hạn lim g.x; y/ D lim h.x; y/ D L .x;y/!.a;b/ .x;y/!.a;b/ – g.x; y/ f .x; y/
h.x; y/, đúng với mọi .x; y/ trong một đĩa tròn nào đó có tâm .a; b/. Khi đó, lim f .x; y/ D L. .x;y/!.a;b/ Bài tập
1-20 Tìm giới hạn, nếu tồn tại, hoặc chứng minh giới hạn không tồn tại. 1. lim.5x3 x2y2/ 5. lim x2 y2 .x;y/!.1;2/ .x;y/!.0;0/ x2 C y2 2. lim e xy cos.x C y/ 6. xy lim .x;y/!.1; 1/ .x;y/!.0;0/ x2 C y2 3. lim 4 xy 7. y4 lim .x;y/!.2;1/ x2 C 3y2 .x;y/!.0;0/ x4 C 3y4 4. lim 8. lim x2 C sin2 y .x;y/!.1;0/ 1 C y2 ln .x;y/!.0;0/ 2x2 C y2 x2 C xy 16
Sự liên tục của hàm số nhiều biến cos 9. xy y lim 15. lim x2 C y2 .x;y/!.0;0/ 3x2 C y2 .x;y/!.0;0/ 3 p 10. 6x y lim x2 C y2 1 1 xy4 .x;y/!.0;0/ 2x4 C y4 16. lim .x;y/!.0;0/ x2 C y8 11. x2y lim 17. lim e xy sin. z=2/ .x;y/!.0;0/ x2 C y2 .x;y;z/!.3;0;1/ 12. lim x4 y4 2 2 18. lim x2 C 2y C 3z .x;y/!.0;0/ x2 C y2 .x;y;z/!.0;0;0/ x2 C y2 C z2 13. x2yey lim 2 2 19. lim xy C yz C xz .x;y/!.0;0/ x4 C 4y2 .x;y;z/!.0;0;0/ x2 C y2 C z4 x2 sin2 y 14. yz lim 20. lim .x;y/!.0;0/ x2 C 2y2 .x;y;z/!.0;0;0/ x2 C 4y2 C 9z2 q 21-23 V Pớiđ mỗ ến ig đ ố icểm O, . / P đ .x ặt ; y/l tàro g n ó g c m quặt a - y pthừẳn ti g a -x O yx, tđa đ ến ặt tiar D OP . x2 Kh C i y đó2 là cặpkh s o ố ản r; g cách đư từ ợc gọi
là tọa độ cực của điểm P và ta có .x; y/ D .r cos ; r sin /. Sử dụng tọa độ cực, hãy tìm các giới hạn. 21. lim x3 C y3 23. lim e x2 y2 1 .x;y/!.0;0/ x2 C y2 .x;y/!.0;0/ x2 C y2 22. lim.x2 C y2/ ln.x2 C y2/ .x;y/!.0;0/
1.3 Sự liên tục của hàm nhiều biến
Nhắc lại kiến thức. Hàm số f hai biến, xác định trên D, được gọi là liên tục tại điểm .a; b/ có nghĩa là
lim f .x; y/ D f .a; b/ (đương nhiên .a; b/ 2 D) .x;y/!.a;b/
Ta nói f liên tục trên D (hoặc nói vắn tắt là liên tục) nghĩa là f liên tục tại mọi điểm thuộc D.
Định lý 1.3: Sự bảo toàn tính liên tục qua phép toán
1. Nếu các hàm số (hai biến) liên tục thì tổng, hiệu, tích và thương (nếu thương có
nghĩa) của chúng cũng là một hàm số liên tục.
2. Nếu f là hàm số hai biến liên tục (hoặc liên tục tại .a; b/) và g là số một biến
liên tục (hoặc liên tục tại f .a; b/) thì hàm hợp g B f là hàm hai biến liên tục
(hoặc liên tục tại .a; b/).
Ví dụ. Hàm sin là hàm số một biến liên tục, và hàm f định bởi f .x; y/ D x C y cũng liên
tục (sẽ nói sau). Khi đó hàm hợp sin Bf .x; y/ D sin.x C y/ cũng liên tục.
Sự liên tục của hàm số nhiều biến 17
Dựa vào định nghĩa giới hạn, sự liên tục và dựa vào hai bất đẳng thức sau q q jxj x2 C y2; jyj x2 C y2; ta có Định lý 1.4
Hàm hằng cùng với hai hàm hình chiếu p1 và p2 định bởi p1.x; y/ D xI p2.x; y/ D y; là các hàm liên tục.
Định lý 1.5: Sự liên tục của hàm sơ cấp
Các hàm sơ cấp một biến, các hàm trong định lý 1.4, kết hợp với định lý 1.3, sẽ tạo ra
các hàm hai biến mới liên tục tại mọi điểm thuộc miền xác định, mà ta tạm gọi là các hàm hai biến sơ cấp.
Ví dụ. Các hàm số f , g định bởi x y f .x; y/ D
; f liên tục tại .x; y/ ¤ .0; 0/ 2x2 C y2 x y g.x; y/ D ln
; liên tục tại .x; y/ ¤ .0; 0/ sao cho x > y; vì chúng là các hàm sơ 2x2 cấp. C y2 Bài tập 1. Giả sử
lim f .x; y/ D 6. Ta có thể nói gì về giá trị của f .3; 1/ không? Nếu f .x;y/!.3;1/ liên tục thì sao?
2. Giải thích vì sao mỗi hàm số sau đây là liên tục hay là không liên tục.
a) Nhiệt độ ngoài môi trường tự nhiên (không có biến cố bất thường xảy ra) như là
hàm số theo kinh độ, vĩ độ và thời gian
b) Độ cao so với mực nước biển như là hàm số theo kinh độ, vĩ độ và thời gian
c) Tiền trả của một khách hàng cho tài xế taxi như là hàm số theo quãng đường đi được và theo thời gian 3-4 Tìm h.x; y/ D
p g f .x; y/ và tìm tập hợp mà h liên tục trên đó.
3. g.t/ D t2 C t; f .x; y/ D 2x C 3y 6 4. 1 xy g.t / D t C ln t; f .x; y/ D 1 C x2y2 18
Sự liên tục của hàm số nhiều biến
5-9 Xác định tập hợp các điểm mà tại đó f liên tục 5. x y f .x; y/ D 1 C x2 C y2 p
6. f .x; y/ D arctan.x C y/ q
7. f .x; y/ D ex2y C x C y2 x2y3 8 nếu .x; y/ ¤ .0; 0/ ˆ< 2x2 C y2 8. f .x; y/ D 1 nếu .x; y/ D .0; 0/ ˆ: xy 8 nếu .x; y/ ¤ .0; 0/ < x2 C xy C y2 9. f .x; y/ D 0 nếu .x; y/ D .0; 0/ : Chương 2
Vi phân của hàm nhiều biến 2.1 Đạo hàm riêng
2.1.1 Định nghĩa đạo hàm riêng và ý nghĩa của nó
Nhắc lại kiến thức. Với hàm số hai biến cho bởi công thức z D f .x; y/,
nếu ta cố định giá trị của y, thì z chỉ còn phụ thuộc x như là hàm một biến. Lấy đạo
hàm của z theo biến x như định nghĩa của đạo hàm một biến, ta dùng các ký hiệu như sau @ @f lim f .x C h; y/ f .x; y/ z D .x; y/ D .x; y/ h!0 h @x @x D fx.x; y/ D Dxf .x; y/ (2.1) D f1.x; y/ D D1f .x; y/
Tương tự cho đạo hàm riêng theo biến y @ @f lim f .x; y C h/ f .x; y/ z D .x; y/ D .x; y/ h!0 h @y @y D fy.x; y/ D Dyf .x; y/ (2.2) D f2.x; y/ D D2f .x; y/
Ý nghĩa đạo hàm riêng: Nếu trong định nghĩa (2.1)-(2.2), tính tại x D a, x D b thì ta
được hai giá trị fx.a; b/ và fy.a; b/. Mặt cong đồ thị S của f chứa điểm P.a; b; c/
với c D f .a; b/. Mặt phẳng đứng x D a cắt S theo vết là đường cong C1; mặt phẳng
y D b cắt S theo vết là đường cong C2. Cả hai đường cong C1 và C2 đều đi qua P. 20
Vi phân của hàm nhiều biến
Tiếp tuyến T1 tại P của đường cong C1 có độ dốc bằng fx.a; b/, tương tự cho tiếp
tuyến T2 có độ dốc fy.a; b/ @z
Nếu viết z D f .x; y/ thì ngoài ý nghĩa nói trên, fx.a; b/ D .a; b/ là tỉ lệ biến @x
thiên tức thời của z theo x tại điểm .a; b/. Tương tự cho ý nghĩa của fy.a; b/ D @z .a;b/. @y Bài tập
1-24 Tìm các đạo hàm riêng bậc nhất của hàm số. 1. f .x; y/ D y5 3xy Z cos.t2/ y dt x
2. f .x; y/ D x4y3 C 8x2y 14. f .x; y/ D 15. f .x; y; z/ D xz 5x2y3z4 3. f .x; t/ D e t cos x p 16. f . 4. x; y; z/ D x sin.y z/ f .x; t/ D x ln t 5. z D .2x C 3y/10 17. w D ln.x C 2y C 3z/ 6. z D tan xy 18. w D zexyz 7. x y f .x; y/ D 19. u D xy arcsin.yz/ x C y 8. f . 20. x; t / D xy u D xy=z 9. w D sin ˛ cos ˛
21. f .x; y; z; t/ D xyz2 tan.yt/ 10. w D ev=.u C v2/ 22. xy2 f .x; y; z; t/ D
11. f .r; s/ D r ln.r2 C s2/ t C 2z p 12. f . C x; t / D arctan.x t / q C C 1 x22 x2 n 23. 13. u D x2 u D t ew=t 24. u D sin.x1 C 2x2 C C nxn/
25-28 Tính các đạo hàm riêng tại điểm được chỉ rõ. q
25. f .x; y/ D ln.x C x2 C y2/I f 26. f . I f x .3; 4/ x; y/ D arctan.y=x/ x .2; 3/ 27. y f .x; y; z/ D I fy.2; 1; 1/ x C y C z q
28. f .x; y; z/ D sin2 x C sin2 y C sin2 zI fz.0; 0; =4/
29-34 Sử dụng định nghĩa đạo hàm riêng như là giới hạn để tính fx và fy tại .x; y/ nói
chung; hoặc tại điểm được chỉ rõ.
Vi phân của hàm nhiều biến 21 29. f . p x; y/ D xy2 x3y
31. f .x; y/ D 3 xy ; tại .0; 0/ 30. x f .x; y/ D 32. f .x; y/ D 3 x C y2 q x3 C y3 ; tại .0; 0/ xy 8 p nếu .x; y/ ¤ .0; 0/ ; tại .0; 0/ < x2 C y2 33. f .x; y/ D 0 nếu .x; y/ D .0; 0/ : x2y 8 nếu .x; y/ ¤ .0; 0/ ˆ ; tại .0; 0/ < x2 C y2 34. f .x; y/ D 0 nếu .x; y/ D .0; 0/ ˆ:
35-38 Giả sử từ các phương trình sau, giá trị z phụ thuộc theo x và y như là một ẩn hàm, tìm @z=@x và @z=@y. 35. x2 C y2 C z2 D 3xyz 37. x z D arctan.yz/ 36. yz D ln.x C z/
38. sin.xyz/ D x C 2y C 3z
39. Nhiệt độ tại điểm .x; y/ trên một tấm kim loại phẳng được cho bởi T .x; y/ D
60=.1 C x2 C y2/, trong đó T là nhiệt đo theo 0C và x, y theo mét. Tìm tốc độ
biến thiên nhiệt độ theo khoảng cách tại điểm .2; 1/ theo hướng-x và theo hướng-y.
40. Tại nhiệt độ tuyệt đối T (oK), áp suất P và thể tích V , định luật chất khí áp dụng cho
một khối lượng m của khí lý tưởng là phương trình P V D mRT , trong đó R hằng
số phụ thuộc chất khí (the gas constant). Chứng minh rằng @P@V@T @P @ D V 1 và T @V@T@P @T D mR @T
41. Chỉ số lạnh cảm tính W (the wind-chill index) của gió phụ thuộc vào nhiệt độ T (0C)
và vận tốc gió v (km/h). W được lập mô hình bởi hàm số W D 13; 12 C 0; 6215T 11; 37v0;16 C 0; 3965T v0;16
Theo mô hình trên, ta thấy rằng nhiệt độ càng hạ hoặc vận tốc gió càng lớn thì W
càng hạ thấp, làm cho ta cảm thấy càng ớn lạnh. Tại T D
150C và v D 30 km/h, chỉ số lạnh W xuống khoảng bao nhiêu nếu giảm
nhiệt 10C? Nếu tăng tốc độ gió lên 1 km/h thì sao?
2.1.2 Đạo hàm riêng cấp cao
Nhắc lại kiến thức. Nếu f là hàm số hai biến thì fx và fy cũng là các hàm số hai biến.
Các đạo hàm riêng của fx và fy là .fx/x, .fx/y, .fy/x và .fy/y được gọi là các đạo hàm 22
Vi phân của hàm nhiều biến
riêng cấp hai. Nếu viết z D f .x; y/ thì ta có các ký hiệu sau @ .fx/x D fxx D f11 D @f @2 @x f 2 D @ @x @x .fx/y D fxy D f12 D @f @2 @y f @ D x @ @y @x .fy/x D fyx D f21 D @f @2 @ f D x@y @ @x @y .fy/y D fyy D f22 D @f @2 @y f 2 D @y @y
Định lý 2.1: Định lý Clairaut-Schwartz
Nếu f xác định trên một đĩa D tâm .a; b/ sao cho tồn tại hai đạo hàm fxy và fyx cùng liên tục trên D. Khi đó fxy.x; y/ D fyx.x; y/ 8.x; y/ 2 D;
nghĩa là đạo hàm riêng cấp hai hỗn hợp không phụ thuộc thứ tự lấy đạo hàm theo các
biến, miễn là chúng liên tục.
Ghi chú. Ta cũng có thể định nghĩa các đạo hàm riêng cấp 3 hoặc cao hơn, ví dụ @ fxyy D .fxy/y D @2f @3f : D @y2@x @y @y@x
Sử dụng định lý Clairaut, nếu các đạo hàm riêng fxyy, fyxy và fyyx cùng liên tục thì chúng
bằng nhau (định lý Clairaut mở rộng cho đạo hàm bậc cao hơn). Bài tập
1. Cho một hàm số hai biến có đồ thị như sau
Hãy xác định dấu (âm, dương) của
Vi phân của hàm nhiều biến 23 a) fx.1; 2/ c) f g) f x . 1; 2/ e) fxx. 1; 2/ xy.1; 2/ b) fy.1; 2/ d) fy. 1; 2/ f) fyy. 1; 2/ h) fxy. 1; 2/
2-7 Tìm tất cả các đạo hàm riêng cấp hai. xy
2. f .x; y/ D x3y5 C 2x4y 5. v D x y
3. f .x; y/ D sin2.mx C ny/ 6. x C y z D arctan 1 xy 7. v D exey p 4. w D u2 C v2
8-11 Kiểm tra kết luận của định lý Clairaut thỏa, nghĩa là uxy D uyx. 8. u D x sin.x C 2y/ q 9. x2 C y2 u D x4y2 2xy5 10. u D ln 11. u D xyey
12-19 Tìm các đạo hàm riêng được chỉ rõ.
12. f .x; y/ D 3xy4 C x3y2I fxxy; fyyy
13. f .x; t/ D x2e ctI fttt; ftxx
14. f .x; y; z/ D cos.4x C 3y C 2z/I fxyz; fyzz
15. f .r; s; t/ D r ln.rs2t3/I frss; frst @3 16. u D er sin I @r2@ p @3 17. z z D u v wI @u@v@w @3w 18. x @3w w D I ; y C 2z @z@y@x @x2@y @6 19. u u D xaybzcI @x@y2@z3
20. Nếu u D ea1x1Ca2x2C
Canxn , trong đó các hằng số ak thỏa a2 1 C a22 C C a2 n D 1, chứng minh rằng @2u @2u @2u C C C @x2 @x2 @x2D u 1 2 n 24
Vi phân của hàm nhiều biến
21. Chứng minh rằng hàm số z D ln.ex C ey/ là nghiệm của các phương trình sau @z @z @2z@2z C D 1 và @x @y @x2 @2z 2 D 0 @y2 @x@y
22. Cho hàm số f định bởi 8 x3y xy3 nếu .x; y/ ¤ .0; 0/ ˆ< x2 C y2 f .x; y/ D 0 nếu .x; y/ D .0; 0/ ˆ:
a) Tìm fx.x; y/ và fy.x; y/ khi .x; y/ ¤ .0; 0/.
b) Tìm fx.0; 0/ và fy.0; 0/.
c) Chứng minh fxy.0; 0/ D 1 và fyx.0; 0/ D 1.
d) Kết quả trong phần c) có mâu thuẫn với định lý Clairaut không? Vì sao?
23. Hỏi tương tự bài tập 22 với hàm số f cho bởi x2y xy2 8ˆ< p nếu .x; y/ ¤ .0; 0/ x2 C y2 f .x; y/ D 0 nếu .x; y/ D .0; 0/ ˆ:
2.2 Mặt phẳng tiếp xúc, xấp xỉ tuyến tính
Nhắc lại kiến thức.
Định nghĩa. Ta ký hiệu lớp-C 1 là lớp bao gồm các hàm nhiều biến mà các đạo hàm riêng
cấp 1 của chúng liên tục trên một tập xác định. Nếu tập xác định được chỉ rõ là D thì ta lớp
này được viết là C 1.D/. Ta có nghĩa tương tự cho lớp-C k.
Dưới đây, ta giả sử z D f .x; y/ với f là hàm số thuộc lớp-C 1.
Biểu thức L.x; y/ D f .a; b/ C fx.a; b/.x a/ C fy.a; b/.y b/ là tuyến tính hóa
của f tại .a; b/. Phép xấp xỉ f .x; y/ L.x; y/
với .x; y/ rất gần .a; b/ (2.3)
được gọi là phép xấp xỉ tuyến tính của f xung quanh điểm .a; b/.
Mặt phẳng có phương trình z D L.x; y/ (tức là đồ thị của hàm L) là mặt phẳng tiếp
xúc với đồ thị hàm số f tại điểm P a; b; f .a; b/ nằm trên đồ thị.
Nếu đã ngầm định giá trị .a; b/, người ta ký hiệu z D f .x; y/ f .a; b/, được gọi
là lượng biến thiên của z xung quanh điểm .a; b/. Lượng dz D L.x; y/ L.a; b/ D
fx.a; b/.x a/ C fy.a; b/.y b/ được gọi là vi phân của z tại .a; b/. Đôi khi người
ta cũng viết df thay cho dz. Khi đó, (2.3) được viết theo hình thức mới, gọi là phép xấp xỉ vi phân, như sau z dz khi .x; y/ rất gần .a; b/ (2.4)
Vi phân của hàm nhiều biến 25 Ký hiệu dx D x a, dy D y
b thì ta có thể viết lại dz D fx.a; b/dx C fy.a; b/dy và z dz khi dx và dy rất nhỏ (2.5)
Với lý do tương tự như trong lý thuyết vi phân hàm một biến, người ta đồng nhất ký hiệu dx x, dy y. Bài tập
1-6 Tìm phương trình mặt phẳng tiếp xúc với mặt cong tại điểm cho trước. 1. z D 4x2 y2 C 2y; . 1; 2; 4/ 4. z D y ln x; .1; 4; 0/ 2. z D 3.x 1/2 C 2.y C 3/2 C 5. z D y cos.x y/; .2; 2; 2/ 7; .2; 2; 12/ p 3. z D xy; .1; 1; 1/ 6. z D ex2 y2; .1; 1; 1/
7-12 Các hàm dưới đây thuộc lớp C 1. Tìm tuyến tính hóa L.x; y/ của hàm đó tại điểm cho trước. p 7. f .x; y/ D x y; .1; 4/ p 8. f . 10. f . x; y/ D x2y4; .1; 1/ x; y/ D x C e4y; .3; 0/
11. f .x; y/ D e xy cos y; . ; 0/ 9. x f .x; y/ D ; .2; 1/ x C y
12. f .x; y/ D sin.2x C 3y/, . 3; 2/
13-14 Kiểm tra dưới đây có đúng là phép xấp xỉ tuyến tính tại .0; 0/? 26
Vi phân của hàm nhiều biến C 13. 2x 3 q y 1 2 3 C 2x 12 14. y C cos2 x 1 C 4y C 1 q 15. T d ìm ùngph n ép ó đ x ể ấp tín x h ỉx tu ấpyến xỉ f tí.n1h:9 c5h;o1: h 0 àm 8/ số f .x; y/ D 20 x2 7y2 tại .2; 1/ và
16. Tìm phép xấp xỉ tuyến tính cho hàm số f .x; y/ D ln.x 3y/ tại .7; 2/ và dùng nó
để tính xấp xỉ f .6:9; 2:06/. q
17. Tìm phép xấp xỉ tuyến tính cho hàm số f .x; y; z/ D x2 C y2 C z2 tại .3; 2; 6/. q
Dựa vào đó tính xấp xỉ giá trị của .3:02/2 C .1:97/2 C .5:99/2
18-23 Tìm vi phân của hàm số. 18. v z D x3 ln.y2/ 21. T D 1 C uvw 19. v D y cos xy 22. R D ˛ˇ2 cos 20. m D p5q3 23. w D xyexz
24. Nếu z D 5x2 C y2 và .x; y/ biến thiên từ .1; 2/ đến .1:05; 2:1/, hãy so sánh giá trị của z và dz. 25. Nếu z D x2
xy C 3y2 và .x; y/ biến thiên từ .3; 1/ đến .2:96; 0:95/, hãy so
sánh giá trị của z và dz.
26. Chiều dài và rộng của một hình chữ nhật lần lượt là 30 cm và 24 cm, với sai số phép
đo không quá 0.1 cm cho mỗi cạnh. Sử dụng vi phân, hãy ước tính sai số tối đa khi
tính diện tích hình chữ nhật.
27. Kích thước của khối hộp chữ nhật là 80 cm, 60 cm, và 50 cm, với sai số có thể là
0.2 cm cho mỗi chiều kích thước. Dùng vi phân, hãy ước tính sai số tối đa khi tính thể tích hộp.
28. Dùng vi phân, hãy ước tính lượng thiếc của một hộp thiếc kín, dạng lon với đường
kính 8 cm và chiều cao 12 cm nếu thiếc có độ dày 0.04 cm.
29. Một ống trụ kín bằng nhôm có đường kính 4 cm, cao 10 cm, độ dày hai nắp đáy là
0,1 cm, độ dày thành ống là 0,05 cm. Sử dụng vi phân để ước tính lượng nhôm làm vỏ ống.
30. Áp suất, thể tích và nhiệt độ của một mol khí lý tưởng có quan hệ P V D 8:31T , trong
đó P đo theo đơn vị kilopascals, V đo theo đơn vị lít, và T theo đơn vị kelvins. Dùng
vi phân, hãy tính xấp xỉ độ biến thiên áp suất nếu thể tích tăng từ 12 L lên 12.3 L và
nhiệt độ giảm từ 310 K xuống 305 K.
Vi phân của hàm nhiều biến 27
31. Ba điện trở với trở kháng là R1, R2, R3 được mắc song song thì trở kháng toàn phần là R thỏa 1 1 1 1 D C C R R1 R2 R3
Nếu các trở kháng đo được là R1 D 25 , R2 D 40 và R3 D 50 , với sai số đo
trong phạm vi 0.5 %, hãy ước ước tính sai số tối đa khi tính giá trị của R.
32. Bốn số dương, mỗi số bé hơn 50, được làm tròn đến chữ số thập phân đầu tiên, sau đó
nhân với nhau. Dùng vi phân, hãy ước tính sai số lớn nhất có thể khi tính tích bốn số
từ việc làm tròn từng số nói trên.
33. Diện tích ngoài da toàn bộ cơ thể người được lập công thức mô hình là S D 0; 109w0;425h0;725
trong đó w là trọng lượng (tính theo pounds), h là chiều cao (tính theo inches), và S
được đo theo feet vuông. Nếu sai số của w khi cân và của h khi đo không quá 2 %,
dùng vi phân, hãy tính sai số phần trăm lớn nhất có thể khi tính S.
2.3 Quy tắc móc xích và đạo hàm của hàm ẩn
Nhắc lại kiến thức. Giả sử tất cả các hàm dưới đây đều thuộc lớp C 1. Khi đó
Nếu z D f .x1; : : : ; xn/ và mỗi biến cũ xi phụ thuộc một biến mới t, thông qua hàm
các hàm một biến xi D gi.t/, thì dz @z dx1 @z dx2 @zdxn D C C C (2.6) dt @x1 dt @x2 dt @xn dt @z @z @z D @xg01.t/ C g02.t / C C g0n.t/ 1 @x2 @xn
Nếu z D f .x1; : : : ; xn/ và mỗi biến cũ xi phụ thuộc m biến mới .t1; t2; : : : ; tm/,
thông qua các hàm nhiều biến xi D gi.t1; t2; : : : ; tm/, thì @z @z @x @z @x @z@x D 1 C 2 C C n (2.7) @tk @x1 @tk @x2 @tk @xn @tk @z @g @z @g @z@g D 1 C 2 C C n @x1 @tk @x2 @tk @xn @tk
Nếu một khoảng của đường cong, với phương trình F.x; y/ D 0, là đồ thị của một ẩn
hàm y có đạo hàm theo x thì @F dy @x D d @ x F @y
Nếu một mảnh của mặt cong, với phương trình F.x; y; z/ D 0, là đồ thị của một ẩn
hàm z thuộc lớp C 1 và phụ thuộc theo hai biến x và y, thì 28
Vi phân của hàm nhiều biến @F @F @z @x @z @y D ; D @ @ @ x F @y F @z @z
Các công thức (2.6)-(2.7) được gọi là quy tắc móc xích (chain rule) hay quy tắc đạo hàm hàm hợp. Bài tập
1-6 Dùng quy tắc móc xích (đạo hàm hàm hợp) để tìm dz=dt hoặc dw=dt.
1. z D x2 C y2 C xy; x D sin t; y D et 2. z D cos.x C 4y/; x D 5t 4; y D 1=t q
3. z D 1 C x2 C y2; x D ln t; y D cos t 4. z D arctan.y=x/; x D et ; y D 1 e 1t
5. w D xey=z; x D t2; y D 1 t; z D 1 C 2t q
6. w D ln x2 C y2 C z2; x D sin t; y D cos t; z D tan t
7-12 Dùng quy tắc móc xích, hãy tìm @z=@s và @z=@t
7. z D x2y3; x D s cos t; y D s sin t 8. z D arcsin.x y/; x D s2 C t 2; y D 1 2st 9. z D sin cos ; D st 2; D s2t
10. z D exC2y; x D s=t; y D t=s p 11. z D er cos ; r D st; D s2 C t2 12. z D tan.u=v/; u D 2s C 3t; v D 3s 2t
13. Nếu z D f .x; y/ với f thuộc lớp C 1, và x D g.t / y D h.t / g.3/ D 2 h.3/ D 7 g0.3/ D 5 h0.3/ D 4 fx.2; 7/ D 6 fy.2; 7/ D 8 tìm dz=dt tại t D 3.
14. Đặt W .w; t/ D F u.s; t/; v.s; t/ , trong đó F; u; v thuộc lớp C 1, và u.1; 0/ D 2 v.1; 0/ D 3 us.1; 0/ D 2 vs.1; 0/ D 5 ut .1; 0/ D 6 vt.1; 0/ D 4 Fu.2; 3/ D 1 Fv.2; 3/ D 10 Tìm Ws.1; 0/ và Wt.1; 0/.
Vi phân của hàm nhiều biến 29
15-18 Giả sử các hàm số đều thuộc lớp C 1, dùng quy tắc móc xích, hãy tính các đạo hàm
riêng cho tất cả trường hợp. 15. u D f .x; y/;
trong đó x D x.r; s; t/, y D y.r; s; t/ 16. R D f .x; y; z; t/;
trong đó x D x.u; v; w/, y D y.u; v; w/, z D z.u; v; w/, t D t .u; v; w/ 17. w D f .r; s; t/;
trong đó r D r.x; y/, s D s.x; y/, t D t.x; y/
18. t D f .u; v; w/; trong đó u D u.p; q; r; s/, v D v.p; q; r; s/, w D w.p; q; r; s/
19-24 Dùng quy tắc móc xích, hãy tính các đạo hàm riêng được chỉ rõ
19. z D x2 C xy3; x D uv2 C w3; y D u C vew; @z @z @z ; ; @ khi u D 2; v D 1; w D 0 u @v @w p @ @ @ 20. u u u u D ; r 2 C; s2; r D y C x cos t; s D x C y sin t ; @ khi x D 1; y D 2; t D 0 x @y @t
21. R D ln.u2 C v2 C w2/; u D x C 2y; v D 2x y; w D 2xy; @R @R ; @ khi x D y D 1 x @y
22. M D xey z2; x D 2uv; y D u v; z D u C v; @M @M ; @ khi u D 3; v D 1 u @v
23. u D x2 C yz; x D pr cos ; y D pr sin ; z D p C r ; @u @u @u ; ; @ khi p D 2; r D 3; D 0 p @r @ 24. Y D w arctan.uv/; u D r C s; v D s C t; w D t C r; @Y @Y @Y ; ; @ khi r D 1; s D 0; t D 1 r @s @t
25-28 Sử dụng công thức tính đạo hàm của hàm ẩn, tìm dy=dx. p 25. xy D 1 C x2y 27. cos.x y/ D xey
26. y5 C x2y3 D 1 C yex2
28. sin x C cos y D sin x cos y
29-32 Sử dụng công thức tính đạo hàm của hàm ẩn, tìm @z=@x và @z=@y. 29. x2 C y2 C z2 D 3xyz 31. x z D arctan.yz/
30. xyz D cos.x C y C z/ 32. yz D ln.x C z/ 30
Vi phân của hàm nhiều biến
33. Nhiệt độ tại điểm .x; y/ trên một tấm phẳng là T .x; y/, đo theo ıC. Đường đi của p 1
con bọ trên tấm phẳng có phương trình x D 1 C t, y D 2 C t , trong đó x và y 3
được đo theo cm, t đo theo giây. Hàm nhiệt độ thỏa Tx.2; 3/ D 4 và Ty.2; 3/ D 3.
Tốc độ tăng nhiệt là bao nhiêu trên đường đi của con bọ tại thời điểm t D 3?
34. Sản lượng lúa mì W trong năm phụ thuộc nhiệt độ trung bình T và lượng mưa R
của năm. Các nhà khoa học ước tính rằng nhiệt độ bình quân đang tăng với tốc độ
0; 15 ıC/năm và lượng mưa đang giảm với tốc độ 0; 1 cm/năm. Họ cũng ước tính rằng,
tại mức sản lượng hiện tại, @W =@T D 2 và @W =@R D 8.
a) Dấu của các đạo hàm riêng ở trên có ý nghĩa gì?
b) Hãy ước tính tốc độ biến thiên của sản lượng dW =dt ở mức sản lượng hiện tại.
35. Vận tốc truyền âm trong nước biển, với độ mặn 35 phần ngàn, được lập mô hình theo công thức C D 1449; 2 C 4; 6T
0:055T 2 C 0; 00029T 3 C 0; 016D
trong đó C là vận tốc âm thanh (mét/giây), T là nhiệt độ (ıC) và D là độ sâu cách
mặt nước biển (mét). Một thợ lặn từ từ lặn xuống biển, độ sâu lặn xuống và nhiệt độ
xung quanh trong suốt thời gian được ghi nhận bằng đồ thị dưới đây.
Hãy ước tính tốc độ biến thiên (theo thời gian) của vận tốc truyền âm trong nước biển
khi thợ lặn vừa trải qua 20 phút lặn. Đơn vị tính là gì?
36. Giả sử một hình nón tròn đang biến đổi kích thước. Bán kính đáy tăng với tốc độ
1,8 in/s, trong khi chiều cao giảm với tốc độ 2,5 in/s. Hỏi thể tích nón biến thiên theo
tốc độ nào khi bán kính đáy là 120 in và chiều cao là 140 in?
37. Giả sử chiều dài `, chiều rộng w và chiều cao h của một cái hộp đang biến đổi theo
thời gian. Tại một thời điểm nào đó, kích thước hộp là ` D 1 m và w D h D 2 m, và
` và w tăng với tốc độ 2 m/s trong khi h giảm với tốc độ 3 m/s. Ở thời điểm đó, hãy
tính tốc độ biến thiên của các đại lượng sau a) Thể tích
c) Độ dài đường chéo
b) Diện tích toàn phần
Vi phân của hàm nhiều biến 31
38. Hiệu điện thế V ở hai đầu một mạch điện sẽ giảm từ từ khi năng lượng pin hao hụt
dần. Trở kháng mạch R tăng dần khi điện trở mạch nóng lên. Dùng định luật Ohm,
V D IR, hãy cho biết dòng điện I biến thiên ra sao tại thời điểm mà R D 400 , I D 0:08 A, dV =dt D 0:01 V/s, và dR=dt D 0:03 /s.
39. Giả sử áp suất của một mol khi lý tưởng đang tăng với tốc độ 0.15 kPa/s (kilopas-
cal/giây). Dùng phương trình P V D 8:31T , hãy tìm tốc độ biến thiên của thể tích
khi áp suất là 20 kPa và nhiệt độ là 320 K.
40. Xe A chạy lên hướng Bắc trên xa lộ 16 và xe B chạy sang hướng Tây trên xa lộ 83.
Mỗi xe đang tiến đến giao lộ. Tại một thời điểm, xe A cách giao lộ 0.3 km và chạy với
vận tốc 90 km/h, trong khi xe B cách giao lộ 0.4 km và chạy với vận tốc 80 km/h. Tại
thời điểm đó, khoảng cách giữa hai xe biến thiên nhanh cỡ nào?
41. Giả sử một cạnh của tam giác đang tăng với tốc độ 3 cm/s, cạnh thứ hai đang giảm
với tốc độ 2 cm/s. Nếu diện tích tam giác duy trì một giá trị hằng số, thì góc giữa hai
cạnh nói trên có tốc độ biến thiên bao nhiêu khi cạnh thứ nhất dài 20 cm, cạnh thứ hai
dài 30 cm và số đo góc giữa chúng là =6?
42. Nếu một âm thanh với tần số fs được phát ra từ một nguồn âm đang di chuyển trên
đường thẳng với vận tốc vs, và một quan sát viên đang đi trên đường thẳng đó theo
hướng ngược lại với vận tốc v0, thì tần số âm thanh mà quan sát viên nghe được là c C v f 0 0 D fs
trong đó c là vận tốc truyền âm, khoảng c 332 vs
m/s. (Đây là hiệu ứng Doppler).) Giả sử
rằng tại một thời điểm, bạn trong một xe lửa đang chạy với vận tốc 34 m/s và tăng
tốc ở mức 1.2 m/s2. Một xe lửa khác đang tiến về phía bạn theo hướng ngược lại trên
đường ray khác với vận tốc 40 m/s, đang tăng tốc ở mức 1.4 m/s2, và phát ra tiếng còi
có tần số 460 Hz. Tại thời điểm đó, tần số cảm tính mà bạn nghe được là bao nhiêu
và tần số đó biến thiên nhanh như thế nào?
43-46 Giả sử rằng các hàm số cho trước là thuộc lớp C 1.
43. Nếu z D f .x; y/, trong đó x D r cos
và y D r sin , (a) tìm @z=@r và @z=@ và (b) chứng minh rằng 1 C @z 2 @z 2 @z 2 @z 2 C D @x @y @r r 2 @
44. Nếu u D f .x; y/, trong đó x D es cos t và y D es sin t, chứng minh rằng @u 2 @u 2 2 @u C C 2 @ D x @y e 2s @u @s @t @ @ 45. z z Nếu z D f .x y/, chứng minh rằng C @ D 0. x @y
46. Nếu z D f .x; y/, trong đó x D s C t và y D s t , chứng minh rằng @z@z D @z 2 @z 2 @s@t @x @y 32
Vi phân của hàm nhiều biến
2.4 Đạo hàm theo hướng
2.4.1 Định nghĩa và công thức tính đạo hàm theo hướng
Nhắc lại kiến thức.
Vectơ đơn vị !u D ha; bi là vectơ thỏa a2 C b2 D 1. Đôi khi vectơ ! u cũng được cho bởi góc chỉ hướng
và !u D hcos ; sin i như hình sau
Trong mặt phẳng Oxy, xét điểm !u một độ dời
P 0.x0; y0/. Đi từ P 0 theo hướng của
Vi phân của hàm nhiều biến 33 ! (displacement) !
h, ta đến điểm Q0.x; y/, nghĩa là P 0Q0 D h u hay x D x0 C ha,
y D y0 C hb (ở đây h có thể âm hoặc dương). Xét hàm hai biến z D f .x; y/. Điểm 0 P thị x
của hàm số. Hình chiếu của hai điểm này lên mặt phẳng Oxy là và . Tỉ lệ 0; y0; z0
, với z0 D f .x0; y0/, và điểm Q x; y; z , với z D f .x P 0; y/, th Q uộc đồ
biến thiên của z D f .x; y/ từ .x0; y0/ đến .x; y/, cũng gọi là độ dốc của đường thẳng PQ, là tỉ số z z z f .Q0/ f .P 0/ f .x ; / f .x D 0 D D 0 C ha y0 C hb 0; y0/ h h h h
Đạo hàm của f theo hướngu !tại .x0; y0/ là giới hạn (nếu tồn tại) cùng với ký hiệu sau đây z f . / f .x0; y0/ D x ! f . D lim 0 C ha; y0 C hb u x0; y0/ D lim h!0 h h!0 h ! !
Với hai hướng đặc biệt, i D h1; 0i và j D h0; 1i, thì D! f .x i 0; y0/ D fx .x0; y0/ và D! f .x j 0; y0/ D fy .x0; y0/. Ý nghĩa. D!f . u
x0; y0/ là độ dốc của tiếp tuyến của đồ thị tại P , theo hướng ! u .
Tưởng tượng rằng đồ thị là bề mặt địa hình. Nếu đứng tại P trên địa hình ấy, xoay
người nhìn về hướng !u thì độ dốc trước mặt là D! f . u x0; y0/. Nếu D! f . u x0; y0/ >
0 địa hình lên dốc, nếu D! f . u
x0; y0/ < 0 thì địa hình xuống dốc.
Vectơ rf .x; y/ D hfx.x; y/; fy.x; y/i được đọc là gradient của f tại .x; y/.
Định lý 2.2: Công thức tính đạo hàm theo hướng
Nếu f là hàm số thuộc lớp C 1 thì f có đạo hàm theo mọi hướng ! u D ha; bi (a2 C b2 D 1) và D! f .x; y/ D rf . u x; y/ !u D a fx.x;y/ C b fy.x;y/: Bài tập
1. Bản đồ các đường đẳng áp (đơn vị đo là milibars) dưới đây được ghi nhận lúc
6:00 AM, ngày 10, tháng 11, 1998. Khoảng cách từ điểm K (Kearney, Nebraska)
đến điểm S (Sioux City, Iowa) dọc theo đoạn thẳng KS là 300 km. Từ K đến S có hiện
tượng tụt áp theo hướng Đông Bắc. Hãy ước tính giá trị của đạo hàm của hàm khí áp
tại Kearney theo hướng tiến về Sioux City. Đơn vị của đạo hàm này là gì? 34
Vi phân của hàm nhiều biến
2. Contour map dưới đây cho biết nhiệt độ cao nhất trong tháng 11, 2004 (đơn vị ıC).
Hãy ước tính giá trị đạo hàm của hàm nhiệt độ tại Dubbo, New South Wales, theo
hướng tiến về Sydney. Đơn vị của đạo hàm này là gì?
3-5 Tìm đạo theo hướng của f tại một điểm cho trước với góc chỉ hướng là . 3. f .x; y/ D x2y3 y4; .0; 2/; D =4. 4. f .x; y/ D ye x; .0; 4/; D 2 =3.
5. f .x; y/ D x sin.xy/; .2; 0/; D =3. 6-9
a) Tìm vectơ gradient của f
b) Tính gradient của f tại điểm P .
c) Tìm tốc độ biến thiên của f tại P theo hướng của vectơ ! u
Vi phân của hàm nhiều biến 35 1 p ! ! 6. f . j /: x; y/ D sin.2x C 3y/; P . 6; 4/; ! u D . 3 i 2 1 ! p ! 7. f . j /. x; y/ D y2=2; P .1; 2/; !u D .2 i C 5 3 2 2 1 8. f . ; x; y/ D xe2yz; P .3; 0; 2/; ! u D h ; i. 3 3 3 2 3 6 u D h ; ; p 7 7 i. 9. f . 7 x; y/ D x C yz; P .1; 3; 1/; !
10-16 Tìm đạo hàm theo hướng của f tại điểm cho trước theo hướng của vectơ ! v . p
10. f .x; y/ D 1 C 2x y; .3; 4/; ! v D h4; 3i.
11. f .x; y/ D ln.x2 C y2/; .2; 1/; ! v D h 1; 2i. ! ! 12. f . j . x; y/ D p4 p2q3; .2; 1/; !v D i C 3 ! ! 13. j . g.r; s/ D arctan.r s/; .1; 2/; ! v D 5 i C 10
14. f .x; y; z/ D xey C yez C zex; .0; 0; 0/; ! v D h5; 1; 2i. p 15. f .x; y; z/ D xyz; .3; 2; 6/; ! v D h 1; 2; 2i. ! 16. ! k . g.x; y; z/ D .x C 2y C 3z/3=2; .1; 1; 2/; ! v D 2 j
17. Sử dụng hình để ước lượng D! f . u 2; 2/: p
18. Tìm đạo hàm của hàm số f .x; y/ D xy, tại P(2,8) theo hướng đến Q.5; 4/.
19. Tìm đạo hàm của hàm số f .x; y; z/ D xy C yz C zx, tại P.1; 1; 3/ theo hướng đến Q.2; 4; 5/.
20. Chứng minh rằng hàm số f . p
x; y/ D 3 xy có đạo hàm riêng fx và fy tại gốc tọa độ,
nhưng không tồn tại đạo hàm theo bất cứ hướng nào khác với các hướng trên hai trục Ox, Oy.
21. Cho hàm f hai biến thuộc lớp C 1. Giả sử biết trước đạo hàm của f theo 2 hướng của
2 vectơ đơn vị !u và !v khác phương cho trước, tại một điểm P cho trước. Hãy chỉ rõ cách tìm rf .P /. 36
Vi phân của hàm nhiều biến
22. Cho f là hàm 2 biến có các đạo hàm riêng liên tục và cho các điểm A.1; 3/, B.3; 3/, !
C .1; 7/ và D.6; 15/. Đạo hàm của f tại A theo hướng của vectơ AB là 3 và đạo hàm !
tại A theo hướng của vectơ AC là 26. Tìm đạo hàm của f tại A theo hướng của vectơ ! AD.
2.4.2 Cực trị hóa đạo hàm theo hướng
Định lý 2.3: Cực trị hóa đạo hàm theo hướng
Nếu f là hàm số thuộc lớp C 1 thì tại một điểm .x; y/ cố định,
giá trị lớn nhất của D! u cùng hướng với vectơ ˇ ˇ f . 1 ˇrf . ˇ, đạt được khi ! u x; y/ là x; y/ rf .x; y/, nghĩa là ! u D ˇ ˇ ˇrf .x; y/ˇrf .x; y/.
giá trị nhỏ nhất của D! u ngược hướng với ˇ ˇ f . ˇr1f . ˇ, đạt được khi ! u x; y/ là x; y/
vectơ rf .x; y/, nghĩa là ! u D ˇ ˇ ˇrf .x; y/ˇrf .x; y/. Bài tập
1-6 Tìm tốc độ biến thiên lớn nhất của f tại điểm cho trước, và tìm hướng mà theo đó tốc
độ biến thiên này đạt được. 1. f .x; y/ D y2=x; .2; 4/:
2. f .p; q/ D qe p C pe q; .0; 0/: 3. f .x; y/ D sin.xy/; .1; 0/:
4. f .x; y; z/ D .x C y/=z; .1; 1; 1/: q
5. f .x; y; z/ D x2 C y2 C z2; .3; 6; 2/:
6. f .x; y; z/ D tan.x C 2y C 3z/; . 5; 1; 1/:
7. Tìm hướng theo đó hàm số f .x; y/ D x4y x2y3 giảm nhanh nhất tại điểm .2; 3/.
8. Tìm hướng theo đó đạo hàm của f .x; y/ D ye xy tại điểm .0; 2/ có giá trị là 1.
9. Tìm tất cả các điểm mà tại đó hướng biến thiên nhanh nhất của hàm số f .x; y/ D ! ! x2 C y2 2x 4y là i C j :
10. Ở khu vực quanh một cái phao, độ sâu của một hồ nước tại điểm .x; y/ được cho bởi z D 200 C 0:02x2
0:001y3, với x; y; z đo theo đơn vị mét. Một ngư dân trên
một con thuyền nhỏ xuất phát tại điểm .80; 60/ và di chuyển về phía cái phao, đặt tại
.0; 0/. Khi anh ta di chuyển như vậy thì dưới thuyền trở nên sâu hơn hay nông hơn? Giải thích.
Vi phân của hàm nhiều biến 37
11. Nhiệt độ T tại một điểm bên trong một quả cầu kim loại, tỉ lệ nghịch với khoảng cách
từ điểm đó đến tâm của quả cầu, được lấy làm gốc tọa độ. Nhiệt độ tại điểm .1; 2; 2/ là 120ı.
a) Tìm tốc độ biến thiên của T tại .1; 2; 2/ theo hướng tiến đến điểm .2; 1; 3/.
b) Chứng minh rằng tại điểm bất kỳ bên trong quả cầu, hướng mà theo đó nhiệt độ
tăng nhanh nhất là hướng của vectơ từ điểm đang xét hướng đến tâm.
12. Nhiệt độ tại điểm .x; y; z/ được cho bởi công thức: 2 2 T .x; y; z/ D 2000e x2 3y 9z
với T được đo theo ıC và x; y; z đo theo mét.
a) Tìm tốc độ biến thiên của nhiệt độ tại điểm P .2; 1; 2/ theo hướng tiến đến điểm .2; 1; 3/:
b) Theo hướng nào thì nhiệt độ tăng nhanh nhất tại P?
c) Tìm tốc độ tăng lớn nhất của nhiệt độ tại P.
13. Giả sử điện thế V trong không gian được cho bởi công thức V .x; y; z/ D 5x2 3xy C xyz:
a) Tìm tốc độ biến thiên của điện thế tại điểm P .3; 4; 5/ theo hướng của vectơ ! ! ! ! v D i C j k .
b) Theo hướng nào V thay đổi nhanh nhất tại P?
c) Tốc độ biến thiên lớn nhất của V tại P là bao nhiêu?
14. Giả sử bạn đang trèo lên một ngọn đồi có địa hình được cho bởi phương trình z D 1000 0:005x2
0:01y2,ở đây x; y; z được đo bởi đơn vị mét, và bạn đang đứng
tại một điểm .60; 40; 966/. Hướng dương của trục 0x là hướng Đông và hướng dương trục Oy là hướng Bắc.
a) Nếu đi về hướng nam, bạn sẽ lên cao hay xuống thấp? Và độ dốc tại đó là bao nhiêu?
b) Nếu đi về hướng Tây Bắc, bạn lên cao hay xuống thấp? Và độ dốc tại đó là bao nhiêu?
c) Theo hướng nào thì độ dốc là lớn nhất, và độ dốc đó là bao nhiêu? Góc chỉ
hướng đó là bao nhiêu so với phương Đông?
2.4.3 Vectơ gradient là pháp vectơ của mặt tiếp xúc với mặt đồng mức
Nhắc lại kiến thức. Với hàm số F, 3 biến, thuộc lớp C 1 thì mặt cong có phương trình
F.x; y; z/ D k (k là hằng số) được gọi là mặt đồng mức của hàm số F . Dạng phương trình
F.x; y; z/ D k của mặt cong cũng được gọi là dạng chính tắc.
Đồ thị .S1/ của hàm số hai biến f cũng là mặt đồng mức .S1/ W F.x; y; z/ D 0 của
hàm số ba biến F định bởi F.x; y; z/ D f .x; y/ z. 38
Vi phân của hàm nhiều biến
Định nghĩa 2.1. Mặt phẳng qua điểm
n , được gọi là mặt phẳng
P , với vectơ pháp tuyến ! tiếp xúc với mặt cong . n vuông góc với
S / W F.x; y; z/ D F.P / tại điểm P có nghĩa là !
mọi tiếp tuyến tại P của mọi đường cong1 đi qua P và nằm trong .S/. Định lý 2.4
Cho hàm số 3 biến F.x; y; z/ thuộc lớp C 1. Với hằng số k D F.P /, trong đó
P .x0; y0; z0/ là điểm thuộc tập xác định của F , thì mặt đồng mức .S/ W F.x; y; z/ D ˝ ˛ 0 . Khi đó, mặt !
k sẽ chứa điểm P . Giả sử rF.P / D F
phẳng qua P với rF.P / là vectơ pháp tuyx.P /; F ến, có py.P /; F hương t z.P / ¤ rình Fx.P /.x x0/ C Fy.P /.y y0/ C Fz.P /.z z0/ D 0; (2.8)
là mặt phẳng tiếp xúc với (S) tại P , và người ta gọi đường thẳng qua P với rF.P / là
vectơ chỉ phương, có phương trình x x0 y y z z D 0 D 0 ; F F x .P / Fy.P / z .P /
là đường pháp tuyến của mặt (S) tại P (với giả thiết các mẫu số ở trên khác 0). !
Tương tự, cho hàm 2 biến f thuộc lớp 0 , C 1 và rf .P / ¤ P .x0; y0/ là điểm thuộc
miền xác định của f . Khi đó, đường đồng mức .C / W f .x; y/ D k, với k D f .P /, có tiếp
tuyến .t/ tại P được định nghĩa là đường thẳng qua P , nhận rf .P / làm vectơ pháp tuyến, và có phương trình .t/ W fx.P/.x x0/ C fy.P /.y y0/ D 0:
Đường thẳng .d/ qua P với vectơ chỉ phương rf .P / được gọi là đường pháp tuyến của
đường cong .C / tại P, và có phương trình x x y y . 0 0 d / W D : f f x .P / y .P / Bài tập
1Xem mục 4.1.1 cho khái niệm đường cong và tiếp tuyến của đường cong.
Vi phân của hàm nhiều biến 39
1-6 Tìm phương trình mặt phẳng tiếp xúc và phương trình đường thẳng vuông góc với các
mặt được cho dưới đây tại những điểm cụ thể. 1. 2.x 2/2 C .y 1/2 C .z 3/2 D 10; .3; 3; 5/ 2. y D x2 z2; .4; 7; 3/ 3. x2 2y2 C z2 C yz D 2; .2; 1; 1/ 4. x z D 4 arctan.yz/; .1 C ; 1; 1/ 5. z C 1 D xey cos z; .1; 0; 0/ 6. yz D ln.y C z/; .0; 0; 1/
7. Nếu f .x; y/ D xy tìm vectơ gradient rf .3; 2/ và sử dụng nó để tìm tiếp tuyến với
đường cong f .x; y/ D 6 tại điểm .3; 2/. Vẽ phác họa đường cong, tiếp tuyến và vectơ gradient.
8. Nếu g.x; y/ D x2 C y2
4x, tìm vectơ gradient rg.1; 2/ và sử dụng nó để tìm
tiếp tuyến với đường cong g.x; y/ D 1 tại điểm .1; 2/. Vẽ phác họa đường cong, tiếp tuyến và vectơ gradient.
9. Chứng minh rằng phương trình mặt phẳng tiếp xúc với ellipsoid x2=a2 C y2=b2 C
z2=c2 D 1 tại điểm .x0; y0; z0/ có thể viết là xx0 yy zz C 0 C 0 a2 b2 D 1 c2
10. Tìm phương trình mặt phẳng tiếp xúc với hyperboloid x2=a2 C y2=b2 z2=c2 D 1
tại điểm .x0; y0; z0/ và mô tả nó dưới một dạng tương tự như bài tập trên.
11. Chứng minh rằng phương trình mặt phẳng tiếp xúc với elliptic paraboloid z=c D
x2=a2 C y2=b2 tại điểm .x0; y0; z0/ có thể viết là 2xx0 2yy C 0 z C z0 a2 D b2 c
12. Điểm nào trên paraboloid y D x2 C z2 có mặt phẳng tiếp xúc song song với mặt phẳng x C 2y C 3z D 1?
13. Có bất kì điểm nào trên hyperboloid x2 y2
z2 D 1 mà mặt phẳng tiếp xúc tại
điểm đó song song với mặt phẳng z D x C y?
14. Chứng minh rằng ellipsoid 3x2 C 2y2 C z2 D 9 và mặt cầu x2 C y2 C z2 8x 6y
8z C 24 D 0 tiếp xúc với nhau tại điểm .1; 1; 2/(Nghĩa là chúng có một mặt
phẳng tiếp xúc chung tại điểm này.)
15. Chứng minh rằng bất kì mặt phẳng nào tiếp xúc với mặt nón x2 C y2 D z2 đều đi qua gốc tọa độ.
16. Chứng minh rằng mọi đường thẳng pháp tuyến của mặt cầu x2 C y2 C z2 D r2 đều
đi qua tâm của mặt cầu. 40
Vi phân của hàm nhiều biến
17. Chứng minh rằng tổng của hoành độ, tung độ và cao độ trên các trục Ox, Oy, Oz bị p p p p
chắn bởi bất kỳ mặt phẳng nào tiếp xúc với mặt x C y C z D c là một hằng số.
18. Chứng minh rằng những hình chóp được cắt từ khối tam diện vuông thứ nhất bằng
bất kì mặt phẳng tiếp xúc nào của mặt xyz D 1 tại những điểm nằm trong khối tam
diện vuông thứ nhất đều có cùng thể tích.
19. Viết phương trình tham số cho đường thẳng tiếp tuyến với đường cong giao tuyến giữa
paraboloid z D x2 C y2 và ellipsoid 4x2 C y2 C z2 D 9, tại điểm .0 1; 1; 2/.
20. Mặt phẳng y Cz D 3 cắt hình trụ x2 Cy2 D 5 tạo thành thiết diện là một ellipse. Tìm
phương trình tham số cho đường thẳng tiếp tuyến của ellipse này tại đểm .1; 2; 1/: 21.
a) Hai mặt phẳng được gọi là orthogonal (trực giao) tại một điểm chung nếu hai
đường thẳng pháp tuyến của chúng vuông góc với nhau tại điểm chung này.
Chứng minh rằng hai mặt phẳng F.x; y; z/ D 0 và G.x; y; z/ D 0 là trực giao ! ! tại điểm chung P, với r 0 , nếu và chỉ nếu F.P / ¤ 0 và rG.P / ¤ FxGx C FyGy C FzGz D 0 tại P
b) Sử dụng câu a) để chứng minh rằng mặt z2 D x2 C y2 và x2 C y2 C z2 D r2
là trực giao tại mọi điểm chung. Bạn có thể giải thích điều này tại sao đúng mà
không cần tính toán không?
2.5 Cực trị của hàm hai biến
2.5.1 Cực trị không điều kiện của hàm hai biến
Nhắc lại kiến thức. Trên đồ thị của một hàm số f như hình dưới, có hai đỉnh đồi và hai thung lũng. N t ếu hì f đ.iểm
a; b/ lớn hơn mọi giá trị f .x; y/ khi a; b; f .a; b/ là đỉnh ngọn đồi
.x; y/ gần .a; b/, và ta nói f có cực đại
địa phương tại .a; b/. Có một đỉnh đồi cao
nhất, tại đó f đạt cực đại tuyệt đối, hay giá
trị lớn nhất. Ta cũng có khái niệm tương tự cho điểm đáy thung lũng.
Một hàm số 2 biến f có cực đại địa phương (gọi tắt là cực đại) tại điểm .a; b/ có
nghĩa là tồn tại một đĩa tròn T tâm .a; b/ bên trong miền xác định sao cho: 8.x; y/ 2 T; f .a; b/
f .x; y/. Số f .a; b/ được gọi là giá trị cực đại (địa phương) của f . Nếu
bất đẳng thức đúng với mọi .x; y/ thuộc miền xác định của f thì ta nói f có cực đại
tuyệt đối (hay là giá trị lớn nhất) tại điểm .a; b/.
Nếu dấu bất đẳng thức ở trên đổi chiều, ta có khái niệm tương ứng là cực tiểu địa
phương, cực tiểu tuyệt đối.
Vi phân của hàm nhiều biến 41
Định lý 2.5: Điều kiện cần của cực trị
Nếu f đạt cực trị địa phương và có các đạo hàm riêng tại .a; b/, thì .a; b/ là điểm
dừng (statonary point) của f , nghĩa là fx.a; b/ D fy.a; b/ D 0.
Chú ý. Nếu .a; b/ là điểm dừng của f
thì chưa hẳn f đạt cực trị tại .a; b/. Trong
trường hợp .a; b/ là điểm dừng mà không là
điểm cực trị của f , thì ta nói .a; b/ là điểm
yên ngựa của f . Ví dụ, điểm .0; 0/ là điểm
yên ngựa của hàm số f .x; y/ D y2 x2
với đồ thị như hình bên.
Định lý 2.6: Điều kiện đủ của cực trị
Giả sử f thuộc lớp C 2 trên một đĩa tròn tâm .a; b/, đồng thời .a; b/ là điểm dừng của f . Đặt fxx.a; b/ fxy.a; b/ 2 D.a; b/ D det D f f xx.a; b/fyy.a; b/ fxy.a; b/ yx.a; b/ fyy.a; b/
(a) Nếu D.a; b/ > 0 và fxx.a; b/ > 0 thì f .a; b/ là cực tiểu địa phương.
(b) Nếu D.a; b/ > 0 và fxx.a; b/ < 0 thì f .a; b/ là cực đại địa phương.
(c) Nếu D.a; b/ < 0 thì .a; b/ là điểm yên ngựa, nghĩa là f không có cực trị tại .a; b/.
(d) Nếu D.a; b/ D 0 thì ta không có kết luận tổng quát, tùy bài toán cụ thể mà ta xét. Bài tập
1. Giả sử .1; 1/ là điểm tới hạn của một hàm f có đạo hàm cấp hai liên tục. Trong mỗi
trường hợp, ta có thể nói gì về f ? a) fxx.1; 1/ D 4; fxy.1; 1/ D 1; fyy.1; 1/ D 2 b) fxx.1; 1/ D 4; fxy.1; 1/ D 3; fyy.1; 1/ D 2
2. Giả sử .0; 2/ là điểm tới hạn của một hàm g có đạo hàm cấp hai liên tục. Trong mỗi
trường hợp, ta có thể nói gì về g a) gxx.0; 2/ D 1; gxy.0; 2/ D 6; gyy.0; 2/ D 1 b) gxx.0; 2/ D 1; gxy.0; 2/ D 2; gyy.0; 2/ D 8
c) gxx.0; 2/ D 4; gxy.0; 2/ D 6; gyy.0; 2/ D 9 42
Vi phân của hàm nhiều biến
3-4 Dựa vào các đường đồng mức trong hình, hãy đoán trước các điểm dừng của f , và f
có điểm yên ngựa, cực đại hay cực tiểu tại mỗi điểm dừng hay không. Giải thích. Sau
đó kiểm chứng bằng điều kiện đủ của cực trị.
3. f .x; y/ D 4 C x3 C y3 3xy. 4. f .x; y/ D 3x x3 2y2 C y4.
5-18 Tìm giá trị cực đại và cực tiểu địa phương và các điểm yên ngựa của hàm số. 5. f .x; y/ D 9 2x C 4y x2 4y2 8. f .x; y/ D e4y x2 y2
6. f .x; y/ D x3y C 12x2 8y
9. f .x; y/ D .1 C xy/.x C y/ 7. f .x; y/ D x4 C y4 4xy C 2
10. f .x; y/ D 2x3 C xy2 C 5x2 C y2
Vi phân của hàm nhiều biến 43 11. f .x; y/ D x3 12xy C 8y3
15. f .x; y/ D .x2 C y2/e.y2 x2/ 12. 1 1 f .x; y/ D xy C C 16. f .x; y/ D ey.y2 x2/ x y 17. f .x; y/ D y2 2y cos x; 1 x 7 13. f .x; y/ D ex cos y
18. f .x; y/ D sin x sin y; < x < 14. f .x; y/ D y cos x ; < x <
19. Chứng minh rằng f .x; y/ D x2 C 4y2
4xy C 2 có vô hạn điểm dừng và D D 0
tại mỗi điểm. Tiếp đó, chứng minh f đạt cực tiểu tại mỗi điểm dừng. p
20. Chứng minh f .x; y/ D x2ye x2 y2 có giá trị cực đại tại .˙1; 1= 2/ và giá trị cực p
tiểu tại .˙1; 1= 2/. Chứng minh f cũng có rất nhiều điểm dừng khác và D D 0
tại mỗi điểm đó. Hãy phân loại các điểm dừng này.
2.5.2 Cực trị tuyệt đối của hàm hai biến
Nhắc lại kiến thức. Đối với hàm số một biến f liên tục trên đoạn Œa; b , người ta tìm giá trị
lớn nhất và nhỏ nhất (cực trị tuyệt đối) của f trên Œa; b theo ba bước sau
Tìm các điểm tới hạn (điểm nghi ngờ) trong khoảng .a; b/, là các điểm tại đó không
có đạo hàm hoặc có đạo hàm bằng không.
Tính giá trị của hàm tại các điểm tới hạn nói trên và tại hai biên a và b.
So sánh các giá trị ở bước hai để xác định cực trị tuyệt đối.
Tương tự cho hàm hai biến liên tục trên một tập đóng và bị chặn, luôn có cực trị tuyệt đối
trên tập này, và ta cũng có ba bước tìm cực trị tuyệt đối. Trước tiên ta định nghĩa khái niệm
đóng và bị chặn của một tập hợp. Xét một tập hợp D
R2, điểm .x; y/ 2 R2 được gọi là điểm biên của tập D có nghĩa
là mọi hình tròn tâm .x; y/ luôn có điểm chung với D và với phần bù R2 n D.
Tập D được gọi là tập đóng có nghĩa là mọi điểm biên của D đều thuộc D.
Sau đây là minh họa cho hai tập đóng
Kế tiếp là minh họa của ba tập hợp không đóng
Biên của D, ký hiệu bởi @D, là tập hợp tất cả các điểm biên của D.
Tập D được gọi là bị chặn khi D bị bao vây trong một đường tròn. 44
Vi phân của hàm nhiều biến
Tìm cực trị tuyệt đối trên tập đóng bị chặn.
Để tìm cực trị tuyệt đối của một hàm số f liên tục trên một tập D đóng và bị chặn trong R2:
1. Tính giá trị của f tại các điểm dừng và tại các điểm không có đạo hàm riêng ở bên trong D.
2. Tìm cực trị tuyệt đối của f ở trên biên @D của D (quy về hàm một biến).
3. Giá trị lớn nhất và nhỏ nhất trong số các giá trị ở các bước 1 & 2 là cực đại tuyệt đối
và cực tiểu tuyệt đối của f trên toàn D. Bài tập
1-7 Tìm giá trị cực đại và cực tiểu tuyệt đối của f trên tập D. 1. f .x; y/ D 1 C 4x
5y, D là miền tam giác đóng với 3 đỉnh .0; 0/; .2; 0/; .0; 3/ 2. f .x; y/ D 3 C xy x 2y,
D là miền tam giác đóng với đỉnh .1; 0/, .5; 0/, .1; 4/ ˚ ˇ
3. f .x; y/ D x2 C y2 C x2y C 4, D D .x; y/ ˇ jxj 1; jyj 1 ˚ ˇ 4. f .x; y/ D x4 C y4 4xy C 2, D D .x; y/ ˇ 0 x 3; 0 y 2 ˚ ˇ
5. f .x; y/ D xy2, D D .x; y/ ˇ x; y 0; x2 C y2 3 ˚ ˇ
6. f .x; y/ D 2x3 C y4, D D .x; y/ ˇ x2 C y2 1 7. f .x; y/ D x3 3x
y3 C 12y; D là tứ giác có các đỉnh là . 2; 3/, .2; 3/, .2; 2/, . 2; 2/.
8. Một thùng các-tông không có nắp có thể tích 32000 cm3. Tìm kích thước của thùng
để làm tốn ít nhất lượng các-tông cần dùng.
9. Một tòa nhà hình hộp chữ nhật đang được thiết kế để làm giảm tối thiểu sự mất nhiệt.
Tường phía đông và phía tây làm thoát nhiệt với mức độ 10 đơn vị nhiệt/m2 mỗi ngày,
tường phía bắc và nam với mức thoát nhiệt 8 đơn vị nhiệt/m2 mỗi ngày, sàn nhà với
mức độ 1 đơn vị nhiệt/m2, mái nhà với mức độ 5 đơn vị nhiệt/m2. Mỗi bức tường phải
dài ít nhất 30 m và cao ít nhất 4 m và thể tích nhà phải đạt chính xác 4000 m3.
a) Tìm và phác họa miền xác định của lượng nhiệt thất thoát như là một hàm số
theo độ dài của các cạnh.
b) Tìm kích thước của tòa nhà làm giảm tối thiểu sự mất nhiệt (kiểm tra các điểm
dừng và những điểm trên biên của miền xác định).
c) Có thể thiết kế được một tòa nhà sao cho ít mất nhiệt mà không hạn chế chiều dài tường hay không?
Vi phân của hàm nhiều biến 45
10. Ba gien đẳng vị A, B và O xác định 4 nhóm máu A (AA hoặc AO), B (BB hoặc BO),
O (OO) và AB. Định luật Hardy-Weinberg phát biểu rằng tỉ lệ cá thể mang 2 gien
khác nhau trong quần thể là P D 2pq C 2pr C 2r q
với p; q; r là tỉ lệ của A, B, O trong quần thể. Dựa vào p C q C r D 1, chứng minh 2 P tối đa là . 3
11. Giả sử một nhà khoa học có cơ sở để tin rằng 2 đại lượng x và y có quan hệ tuyến
tính với nhau, nghĩa là là y D mx C b. Nhà khoa học thực hiện thí nghiệm đo đạc
và thu được dữ liệu dưới dạng những điểm .x1; y1/, .x2; y2/, . . . , .xn; yn/ và sau đó
vẽ những điểm này. Các điểm không nằm chính xác trên một đường thẳng, vì thế nhà
khoa học muốn tìm các hằng số m và b sao cho đường thẳng y D mx C b “khớp” với
các điểm đó tốt nhất có thể. (Xem hình vẽ) Đặt di D y
.mxi C b/ là độ lệch đứng của điểm .xi; yi/ so với đường thẳng.
Phương pháp bình phương cực tiểu (Least squares) xác định m; b để làm tối thiểu n d 2 X
j , tổng bình phương của các độ lệch này. Chứng minh rằng, theo phương pháp jD1
này, đường thẳng khớp tốt nhất tìm được với m, b thỏa n n m yi X xi C bn D X iD1 iD1 n n n m x2 xiyi X i C b X xi D X iD1 iD1 iD1
Nghĩa là, đường thẳng được tìm bằng việc giải 2 phương trình trên với 2 ẩn m và b.
(Xem mục 1.2, J. Stewart, Calculus, 6th, để biết thêm chi tiết, cũng như như các ứng
dụng của phương pháp “Least squares”.)
12. Tìm phương trình mặt phẳng đi qua điểm .1; 2; 3/ và cắt ra được phần thể tích nhỏ
nhất trong phần tám thứ nhất của không gian Oxyz.
2.5.3 Cực trị có một điều kiện của hàm nhiều biến (Mục này để dành đọc thêm)
Nhắc lại kiến thức. Cho hai hàm số f và g (2 hoặc 3 biến) thuộc lớp C 1 và hằng số k. Viết
gọn M thay cho .x; y/ hoặc .x; y; z/. Nếu giá trị f .M /, với M thỏa điều kiện g.M / D k, 46
Vi phân của hàm nhiều biến ! đạt cực trị tại 0 , thì có một số
(gọi là nhân tử Lagrange) sao cho M0 và rg.M0/ ¤ rf .M0/ D rg.M0/.
Tìm cực trị tuyệt đối có điều kiện (phương pháp nhân tử Lagrange). !
Cho f và g thuộc lớp C 1 và rg ¤
0 tại mọi điểm M thỏa điều kiện g.M / D k. Giả sử
biết trước f có cực trị tuyệt đối, với điều kiện g D k. Khi đó:
(a) Tìm tất cả các điểm M và số sao cho rf .M / D rg.M / và g.M / D k
(b) Tính các giá trị của f tại các điểm M tìm được ở bước (a). Giá trị lớn nhất (nhỏ nhất)
trong số các giá trị này cực trị tuyệt đối cần tìm. Bài tập
1-15 Sử dụng Phương Pháp Nhân Tử Lagrange để tìm những giá trị lớn nhất, nhỏ nhất của
những hàm số với những điều kiện ràng buộc cho trước sau đây.
1. f .x; y/ D x2 C y2I xy D 1
2. f .x; y/ D 4x C 6yI x2 C y2 D 13
3. f .x; y/ D x2yI x2 C 2y2 D 6
4. f .x; y/ D exyI x3 C y3 D 16
5. f .x; y; z/ D 2x C 6y C 10zI x2 C y2 C z2 D 35 6. f .x; y; z/ D 8x 4zI x2 C 10y2 C z2 D 5
7. f .x; y; z/ D xyzI x2 C 2y2 C 3z2 D 6
8. f .x; y; z/ D x2y2z2I x2 C y2 C z2 D 1
9. f .x; y; z/ D x2 C y2 C z2I x4 C y4 C z4 D 1
10. f .x; y; z/ D x4 C y4 C z4I x4 C y4 C z4 D 1
11. f .x; y; z; t/ D x C y C z C tI x2 C y2 C z2 C t2 D 1
12. f .x1; x2; : : : ; xn/ D x1 C x2 C C xnI x2 1 C x22 C C x2 n D 1
13. f .x; y; z/ D x C 2yI x C y C z D 1; y2 C z2 D 4 14. f .x; y; z/ D 3x y 3zI x C y z D 0; x2 C 2z2 D 1
15. f .x; y; z/ D yz C zxI xy D 1; y2 C z2 D 1
16-17 Tìm những cực trị tuyệt đối trên miền được cho bởi bất đẳng thức.
16. f .x; y/ D 2x2 C 3y2 4x 5; x2 C y2 16
Vi phân của hàm nhiều biến 47
17. f .x; y/ D e xy; x2 C 4y2 1
18. Xét bài toán giá trị lớn nhất của hàm số f .x; y/ D 2x C 3y với điều kiện ràng buộc p p x C y D 5
a) Thử sử dụng nhân tử Lagrange để giải bài toán này.
b) Giá trị f .25; 0/ có lớn hơn giá trị tìm được ở câu a?
c) Dùng máy tính, hãy vẽ đường cong có phương trình điều kiện và vẽ vài đường
đồng mức của hàm f , dựa vào đó, đoán xem f đạt cực đại ở đâu.
d) Giải thích tại sao phương pháp nhân tử Lagrange không giải được bài toán này.
e) Ý nghĩa của f .9; 4/ là gì?
19. Xét bài toán giá nhỏ nhất của hàm số f .x; y/ D x với điều kiện ràng buộc y2 C x4 x3 D 0 (hình trái lê)
a) Thử dùng nhân tử Lagrange để giải bài toán này.
b) Chứng minh rằng giá trị nhỏ nhất là f .0; 0/ D 0 nhưng điều kiện Lagrange
rf .0; 0/ D rg.0; 0/ không thõa mãn với bất kì giá trị nào của
c) Giải thích tại sao phương pháp nhân tử Lagrange không giải được giá trị nhỏ
nhất trong trường hợp này.
20. Sử dụng Nhân Tử Lagrange, chứng minh rằng: Trong các hình chữ nhật có cùng chu
vi p, hình vuông có diện tích lớn nhất.
21. Sử dụng Nhân Tử Lagrange, chứng minh rằng: Trong các hình tam giác có cùng chu
vi p, hình tam giác đều là hình tam giác có diện tích lớn nhất. p H v ướiớnpglà dẫ n n ử :acShửu d viụnvgà cô x; nyg; th z ứlc à d đ iộện dàitích ba Her cạnhotn: am giác. S D p.p x/.p y/.p z/
22. Tìm khoảng cách ngắn nhất từ điểm .2; 1; 1/ đến mặt phẳng x C y z D 1:
23. Tìm điểm trên mặt phẳng x
y C z D 4 gần nhất với điểm .1; 2; 3/:
24. Tìm điểm trên mặt nón z2 D x2 C y2 gần nhất với điểm .4; 2; 0/:
25. Tìm điểm trên mặt y2 D 9 C xz gần nhất với gốc tọa độ.
26. Tìm 3 số dương có tổng là 100 và tích đạt cực đại.
27. Tìm 3 số dương có tổng là 12 và tổng bình phương của chúng nhỏ nhất.
28. Tìm thể tích lớn nhất của hình hộp chữ nhật nội tiếp mặt cầu bán kính r.
29. Tìm kích thước của hộp chữ nhật có thể tích 1000 cm3 và có diện tích bề mặt nhỏ nhất.
30. Tìm thể tích của hình hộp chữ nhật lớn nhất trong tam diện vuông (octant) thứ nhất
với 3 mặt nằm trong mặt phẳng tọa độ và một đỉnh thuộc mặt x C 2y C 3z D 6. 48
Vi phân của hàm nhiều biến
31. Tìm kích thước của hình hộp chữ nhật có thể tích lớn nhất với tổng diện tích bề mặt là 64 cm2.
32. Tìm kích thước của hình hộp chữ nhật có thể tích lớn nhất sao cho tổng độ dài 12 cạnh
của nó là một hằng số c.
33. Đáy của một bể cá với thể tích V cho trước được làm bằng đá phiến và các mặt bên
làm bằng kính. Giả sử giá thành của đá gấp 5 lần (tính trên mỗi đơn vị diện tích) của
kính. Hãy tìm kích thước của bể cá để làm tối thiểu giá thành vật liệu.
34. Nếu chiều dài đường chéo hình hộp chữ nhật là L thì thể tích lớn nhất có thể là bao nhiêu?
35. Tìm thể tích lớn nhất và nhỏ nhất của một hình hộp chữ nhật có diện tích bề mặt
1500 cm2 và tổng độ dài các cạnh là 200 cm.
36. Mặt phẳng x C y C 2z D 2 cắt paraboloid z D x2 C y2 tạo thành thiết diện là một
ellipse. Tìm những điểm nằm trên ellipse có khoảng cách đến gốc tọa độ gần nhất, xa nhất. Chương 3 Tích phân bội 3.1 Tích phân kép
3.1.1 Tích phân kép trên một hình chữ nhật
Nhắc lại kiến thức.
Hình bên là đồ thị của một hàm số f
dương, xác định trên hình chữ nhật R R D Œa; b Œc; d ˚ ˇ D .x; y/ 2 R2 ˇ a x b và c y d
Gọi K là khối, hay “tòa nhà” tọa lạc trên
mảnh đất R, mái cong là đồ thị của f . ˚ ˇ K D .x; y; z/ 2 R3 ˇ 0 z f .x; y/; .x; y/ 2 R Chia đoạn Œa; b
thành m đoạn con Œxi 1; xi đều nhau với độ dài x D .b a/=m; chia đoạn Œc; d
thành n đoạn con Œyj 1; yj đều nhau với độ dài y D .d c/=n. Như vậy ta có m
n hình chữ nhật con có dạng ˚ ˇ R ˇ ij D Œxi 1; xi Œyj 1; yj D .x; y/ xi 1 x xi; yj 1 y yj với diện tích A D x y. 50 Tích phân bội
Trên mỗi ô con Rij, chọn một điểm mẫu .x ij; y ij/ ngẫu nhiên. Thể tích cột dạng hộp có
đáy Rij và chiều cao bằng f .x ij; y ij/ bằng f .x ij; y ij/ A.
Tổng thể tích các cột trên là m n X X f .x ij; y ij/ A iD1 jD1
và được gọi là tổng Riemann của f trên hình chữ nhật R. Tích phân bội 51
Nếu hàm số f liên tục, dương thì thể tích tích “tòa nhà”, hay khối K, được định nghĩa là m n V .K/ D lim f .x m;n!1 X X ij ; y ij / A iD1 jD1
Nếu hàm số f liên tục và không nhất thiết dương thì giới hạn trên được ký hiệu là m n “ f .x; y/dA D lim f .x m;n!1 X X ij ; y ij / A iD1 jD1 R
và được gọi là tích phân kép của f trên hình chữ nhật R.
Dựa trên ý tưởng của kỹ thuật cắt lát khi tính thể tích, ta có định lý sau đây
Định lý 3.1: định lý Fubini
Giả sử f là hàm số liên tục trên hình chữ nhật R D Œa; b Œc; d . Khi đó “ Z f .x; y/dydx (3.1) b Z d f . c x; y/dA D R a Z f .x; y/dxdy (3.2) d Z b D a c
Vế phải của (3.1) và (3.2) được gọi là các tích phân lặp, nghĩa là lấy tích phân theo từng 52 Tích phân bội biến Z Z bZ d b Z c d f . c x; y/dydx D f .x; y/dy dx a a Z d Z b Z Z d b a f . a x; y/dxdy D f .x; y/dx dy c c Bài tập Z f .x; y/dy 5 Z 1 1-2 Tính 0 f . 0 x; y/dx và 1. f .x; y/ D 12x2y3 2. f .x; y/ D y C ey
3-14 Tính các tích phân lặp sau: y Z Z Z C 3 1.1 C 4xy/dxdy Z 4 2 x y 3. 0 9. dydx 1 1 1 x Z 3 2 1 Z 2.4x 9x y2/dydx Z Z 1 3 exC3ydxdy 4. 1 10. 0 0 0 Z Z x sin ydydx 5 2 =2 Z Z 1 1 .u v/ dudv 5. 0 0 11. 0 0 Z cos ydxdy =2 Z 5 Z 1 Z 1 q 6. 1 12. 0 xy x2 C y2dydx =6 0 Z 8 r sin2 d dr 2 Z 1.2x C y/ dxdy Z 2 Z 7. 0 13. 0 0 xex 0 p Z Z dydx 1 2 Z Z y 1 1 s C t dsdt 8. 1 14. 0 0 0
15-22 Tính các tích phân tích phân kép sau: 2 4 “ .6x y3 5y /dA; R D f.x; y/ j 0 x 3; 0 y 1g 15. R “ cos.x C 2y/dA; R D f.x; y/ j 0 x ; 3 y =2g 16. R xy2 “ dA; R D f.x; y/ j 0 x 1; 3 y 3g x2 C 1 17. R 1 C x2 “ dA; R D f.x; y/ j 0 x 1; 0 y 1g 1 C y2 18. R Tích phân bội 53 “ x sin.x C y/dA; R D Œ0; =6 Œ0; =3 19. R x “ dA; R D Œ0; 1 Œ0; 1 1 C xy 20. R x2y “ xye dA; R D Œ1; 2 Œ0; 2 21. R x “ dA; R D Œ1; 2 Œ0; 1 x2 C y2 22. R
23-24 Phác họa thể tích khối rắn được cho bởi tích phân lặp sau: Z 1 Z 1 Z 1 Z 1.2 x2 y2/dydx 23. 0 . 0 4 x 2y/dxdy 24. 0 0
25. Tính thể tích khối rắn làm dưới măt phẳng 3x C 2y C z D 12 và trên hình chữ nhật R D f.x; y/j0 x 1; 2 y 3g
26. Tính thể tích khối rắn làm dưới mặt hyperbolic paraboloid z D 4 C x2 y2 và trên hình vuông R D Œ 1; 1 Œ0; 2 .
27. Tính thể tích khối rắn nằm dưới mặt eliptic paraloid x2=4 C y2=9 C z D 1 và trên miền R D Œ 1; 1 Œ 2; 2 .
28. Tính thể tích khối rắn được bao quanh bởi các mặt z D x sec2 y, z D 0; x D 0; x D 2; y D 0 và y D =4.
29. Tính thể tích khối rắn trong góc phần tám thứ nhất, được bao bởi hình trụ z D 16 x2 và mặt phẳng y D 5.
30. Tính thể tích khối rắn được bao bởi mặt paraboloid z D 2 C x2 C .y 2/2 và các
mặt phẳng z D 1; x D 1; x D 1; y D 0; y D 4.
3.1.2 Giá trị trung bình của hàm hai biến trên hình chữ nhật
Sinh viên tự đọc thêm kiến thức của mục này trong giáo trình.
3.1.3 Tích phân kép trên một miền phẳng tổng quát
Nhắc lại kiến thức. Tích phân kép của hàm số f dương, liên tục trên hình chữ nhật, như
định nghĩa mục trước, được xem là thể tích của “tòa nhà, mái cong” tọa lạc trên mảnh đất
hình chữ nhật. Nếu thay hình chữ nhật bởi miền phẳng D
R2 tổng quát thì ta cũng có
khái niệm tích phân kép như là thể tích “tòa nhà, mái cong” tọa lạc trên mảnh đất D như hình dưới đây. 54 Tích phân bội
Sau đây ta chỉ xét D có các dạng sau
Miền D được gọi là lồi theo phương Oy, hoặc là đơn giản theo phương Oy, nếu D
nằm giữa hai đồ thị của hai hàm số theo biến x, ˚ ˇ
D D .x; y/ ˇ x 2 Œa; b ; g1.x/ y g2.x/
Miền D được gọi là lồi theo phương Ox, hoặc là đơn giản theo phương Ox, nếu D
nằm giữa hai đồ thị của hai hàm số theo biến y, Tích phân bội 55 ˚ ˇ
D D .x; y/ ˇ y 2 Œc; d ; h1.y/ x h2.y/
Định lý 3.2: Định lý Fubini
Cho hàm số hai biến f liên tục (không nhất thiết dương) trên miền D; và các hàm số
một biến g1, g2, h1, h2 dưới đây cũng liên tục. ˚ ˇ 1. N thếu
ì D D .x; y/ ˇ x 2 Œa; b ; g1.x/ y g2.x/ (D lồi theo phương Oy), “ Z f .x; y/dy dx: b Z g2.x/ f . g x; y/dA D 1.x/ D a ˚ ˇ 2. thì
Nếu D D .x; y/ ˇ y 2 Œc; d ; h1.y/ x h2.y/ (D lồi theo phương Ox), “ Z f .x; y/dx dy: d Z h2.y/ f . h x; y/dA D 1.y/ D c
Chú ý. Nếu D D D1 [ D2 với D1 và D2 là các miền lồi theo một phương Ox hoặc Oy; và
chúng “không dẫm” lên nhau thì “ “ “ f .x; y/dA: f .x; y/dA D f .x; y/dA C D D1 D2 Bài tập
1-5 Tính các tích phân lặp: Z Z p 2 y xy dxdy Z esin drd 4 Z =2 cos 1. 0 4. 0 0 0 Z Z 1 2.x y/dydx Z 1Z vp 2. 2x 5. 1 v2dudv 0 0 Z 0 1 Z x.1 C 2y/dydx 3. x2 0
6-17 Tính các tích phân kép sau: 56 Tích phân bội “ y2dA; D D f.x; y/ j 1 y 1; y 2 x yg 6. D y “ dA; D D f.x; y/ j 0 x 1; 0 y x2g x5 C 1 7. D “ xdA; D D f.x; y/ j 0 x ; 0 y sin xg 8. D “ x3dA; D D f.x; y/ j 1 x e; 0 y ln xg 9. D “ y2exydA; D D f.x; y/ j 0 y 4; 0 x yg 10. D “ q 11. x y2 x2dA; D D f.x; y/ j 0 x 1; 0 x yg D “
x cos ydA, D là miền được bao bởi y D 0; y D x2; x D 1 12. D p “
.x C y/dA, D là miền được bao bởi y D x; y D x2 13. D “
y3dA, D là miền hình tam giác với các đỉnh .0; 2/; .1; 1/; .3; 2/ 14. D “ q 15.
xy2dA, D là miền bị chặn bởi mặt x D 0; x D 1 y2 D “ .2x
y/dA, D là miền được bao bởi hình tròn có tâm tại góc tọa độ và bán kính 16. bằng 2. D “
2xydA, D là miền hình tam giác với các đỉnh .0; 0/; .1; 2/; .0; 3/ 17. D
18-27 Tính thể tích các khối rắn được cho sau:
18. Dưới mặt phẳng x C 2y
z D 0 và trên miền bị chặn bởi y D x và y D x4
19. Dưới mặt z D 2x C y2 và trên miền bị chặn bởi x D y2 và x D y3
20. Dưới mặt z D xy và trên miền tam giác với các đỉnh .1; 1/; .4; 1/; .1; 2/
21. Được bao bởi paraboloid z D x2 C 3y3 và mặt x D 0; y D 1; y D x; z D 0
22. Được bao bởi các mặt phẳng tọa độ và mặt phẳng 3x C 2y C z D 6
23. Được bao bởi các mặt phẳng z D x; y D x; x C y D 2, và z D 0
24. Được bao bởi các hình trụ z D x2; y D x2 và các mặt z D 0; y D 4
25. Được bao bởi hình trụ y2 C x2 D 4 và các mặt x D 2y; x D 0; z D 0 trong góc phần
phần tám thứ nhất của hệ tọa độ. Tích phân bội 57
26. Được bao bởi hình trụ x2 C y2 D 1 và các mặt y D z; x D 0; z D 0 trong góc phần
phần tám thứ nhất của hệ tọa độ.
27. Được bao bởi hình trụ x2 C y2 D r2 và y2 C z2 D r2
28-29 Tìm thể tích của khối rắn bằng cách trừ hai khối thể tích:
28. Khối rắn được bao bởi mặt y D 1 x2; y D x2 1 và các mặt phẳng x C y C z D 2, 2x C 2y z C 10 D 0
29. Khối rắn được bao bởi mặt y D x2 và mặt z D 3y; z D 2 C y
30-31 Tính các tích phân lặp: Z 1 Z 1 x Z Z 1 1 x2 .1 x/dydx 30. 0 . 0 1 x y/dydx 31. 0 0
32-37 Phác họa miền lấy tích phân và đổi thứ tự của tích phân sau: Z Z px f .x; y/dydx Z p9 x2 f .x; y/dxdy 4 Z 3 32. 0 0 0 35. 0 Z f .x; y/dydx 1 Z 4 Z Z f .x; y/dydx 2 ln x 33. 4x 36. 0 0 Z p 1 Z 9 x2 f .x; y/dxdy f .x; y/dydx 3 p Z 1 Z =4 34. 9 x2 arctan x 0 37. 0
38-43 Tính tích phân bằng cách đổi thứ tự trong tích phân lặp: Z ex2dxdy ex=ydydx 1 Z 3 Z 1 Z 1 38. 3y 41. x 0 0 Z p Z p cos.x2/dxdy Z Z 1 =2 39. p 0 42. arcsin y cos x 0 1 C cos2 xdxdy 0 1 Z dydx Z ex4dxdy 4 Z 2 Z p y3 C 1 8 2 3p 40. x 43. y 0 0
44-45 Hãy biểu diễn D là hợp của các miền lồi theo phương Ox hoặc Oy rồi tính tích phân 58 Tích phân bội “ “ ydA 44. x2dA 45. D D
46. Khi tính tích phân kép trên miền D, ta được tổng tích phân lặp như sau “ Z f .x; y/dxdy 1 Z 2y Z 3 Z 3 y f . 0 0 x; y/dA D f .x; y/dxdy C Phác họ D 0 1
a miền D và biểu diễn tích phân kép theo dạng tích phân lặp với thứ tự ngược với thứ tự ở trên.
3.1.4 Đổi biến tích phân kép theo tọa độ cực Nhắc lại kiến thức.
Với mỗi điểm P .x; y/ trong mặt phẳng
tọa độ Descartes Oxy, ta đặt ! q i ! ; r D OP D x2 C y2I D ∡ OP thì x D r cos và y D r sin . Cặp số .r;
/ được gọi là tọa độ cực của điểm P.
Quy ước. Trong tọa độ cực, điểm . r; /
đối xứng với điểm .r; / qua gốc O.0; 0/
Vậy với một tập hợp D trong mặt phẳng Descartes có dạng ˚ ˇ
D D .x; y/ ˇ x và y thỏa tính chất (T) nào đó ;
nó có thể được mô tả dưới dạng tọa độ cực như sau ˚ ˇ D D .r; / ˇ r và
thỏa tính chất “tương đồng” với (T) Ví dụ.
Miền R trong hình (a) ở dưới có thể viết theo ba dạng sau ˚ ˇ R D .x; y/ ˇ x2 C y2 1 ˚ ˇ R D .x; y/ ˇ x D r cos ; y D r sin ; .r; / 2 Œ0; 1 Œ0; 2 ˚ ˇ R D .r; / ˇ 0 r 1; 0 2 Tích phân bội 59
Trong hình (b) thì miền R được viết dưới dạng ˚ ˇ R D .x; y/ ˇ 1 x2 C y2 4; y 0 ˚ ˇ R D .x; y/ ˇ x D r cos ; y D r sin ; .r; / 2 Œ1; 2 Œ0; ˚ ˇ R D .r; / ˇ 1 r 2; 0 Hình (a) Hình (b)
Định lý 3.3: Đổi biến tích phân theo tọa độ cực
Nếu hàm số hai biến f liên tục trên một
miền D được biểu diễn theo dạng tọa độ cực sau đây ˚ ˇ D D .r; / ˇ 2 Œ˛; ˇ ; h1. / r h2. /
với hình minh họa kế bên, thì “ Z ˇ Z h f .r cos ; r sin / r dr d 2. / f . h x; y/dA D 1. / D ˛ Bài tập
1-4 Cho miền R như sau. Hãy lựa chọn hệ tọa độ cực hay tọa độ Descartes để viết “
f .x; y/dA như là một tích phân lặp, với f là hàm liên tục tùy ý. 1. R 60 Tích phân bội 2. 4. 3.
5-6 Phác họa miền lấy tích phân và tính các tích phân sau: Z rdrd 2 Z 7 Z =2Z 4cos 5. 4 0 rdrd 6. 0
7-13 Tính các tích phân sau bằng cách đổi hệ tọa độ cực: “
xydA, với D là đĩa tròn tâm tại gốc tọa độ và bán kính bằng 3 7. D “
.x Cy/dA, với R là miền nằm bên trái trục Oy và giữa hai đường tròn x2 Cy2 D 8. 1 và x2 C y2 D 4 R “
cos.x2 C y2/dA, với R là miền nằm dưới trục Ox và bên trong đường tròn 9. x2 C y2 D 9 R “ q 10. 4 x2
y2dA, với R D f.x; y/ j x2 C y2 4; x 0g R “
yexdA, với R là góc phần tư thứ nhất bị chặn bởi đường tròn x2 C y2 D 25 11. R “
arctan.y=x/dA, với R D f.x; y/ j 1 x2 C y2 4; 0 y xg 12. R Tích phân bội 61 “
xdA, với D là miền trong góc phần tư thứ nhất nằm giữa đường tròn x2 Cy2 D 4 13. và x2 C y2 D 2x D
14-17 Dùng tích phân kép để tính diện tích các miền sau đây:
14. Một cánh hoa có r D cos 3
15. Miền được bao bởi đường cong r D 4 C 3 cos
16. Miền nằm trong cả hai đường tròn r D cos và r D sin
17. Miền nằm trong đường r D 1 C cos
và ngoài đường tròn r D 3 cos
18-26 Dùng tọa độ cực để tìm thể tích các khối rắn sau: q
18. Dưới hình nón z D x2 C y2 và trên đĩa tròn x2 C y2 4
19. Dưới miền paraboloid z D 18 2x2
2y2 và trên mặt phẳng Oxy
20. Miền được bao bởi hyperboloid x2
y2 C z2 D 1 và mặt phẳng z D 2
21. Miền nằm trong mặt cầu x2 C y2 C z2 D 16 và ngoài hình trụ x2 C y2 D 4
22. Một quả cầu bán kính a
23. Miền được bao bởi hyperboloid z D 1 C 2x2 C 2y2 và mặt z D 7 trong góc phần tám thứ nhất q
24. Trên hình nón z D x2 C y2 và dưới mặt cầu x2 C y2 C z2 D 1
25. Miền được bao bởi hyperboloid z D 1 C 3x2 C 3y2 và mặt z D 4 x2 y2
26. Miền nằm trong hình trụ x2 C y2 D 4 và elipsoid 4x2 C 4y2 C z2 D 64 27.
a) Dùng một mũi khoan hình trụ có bán kính r1 để khoan xuyên qua tâm quả cầu
bán kính r2. Tìm thể tích khối rắn có dạng chiếc nhẫn còn lại sau khi khoan.
b) Tính thể tích khối rắn đó theo chiều cao h của chiếc nhẫn. Chú ý rằng thể tích
chỉ phụ thuộc vào h không phụ thuộc vào r1 hay r2.
28-31 Dùng tích phân kép để tính diện tích các miền sau đây: Z p Z p Z 9 x2 2 y2 3 sin.x2 C y2/dydx Z 1 .x C y/dxdy 28. 0 y 3 30. 0 Z Z x2ydxdy Z p2x x2 a 0p Z 2 q 29. a2 y2 31. x2 C y2dydx 0 0 0 62 Tích phân bội
32. Một hồ bơi hình tròn đường kính 40-ft. Độ sâu từ Đông sang Tây là không đổi, nhưng
tăng từ 2-ft đến 7-ft theo một hướng thẳng từ Nam lên Bắc. Tìm thể tích nước trong hồ.
33. Dùng tọa độ cực để gộp tổng Z p Z p Z 2 4 x2 xydydx 1 Z x Z p x Z 2 1 x2 xydydx C 0 p 0 p xydydx C 2 1= 2 1
thành một tích phân kép. Tính tích phân đó. 34.
a) Tìm tích phân suy rộng (trong toàn miền R2 (the improper integral)) “ Z Z e .x2Cy2/dxdy 1 11 I D e .x2Cy2/dA D R2 1 D lim“ e .x2Cy2/dA a!1 Da
với Da là đĩa tròn với bán kính a và tâm tại gốc tọa độ. Chứng minh rằng Z 1 Z 1 e .x2Cy2/dA D 1 1
b) Một định nghĩa tương đương của tích phân trong câu (a) là “ e .x2Cy2/dA D lim “ e .x2Cy2/dA R2 a!1 Sa
với Sa là hình vuông với các đỉnh .˙a; ˙a/. Dùng điều này để chứng minh Z 1 Z e y2dy D 1 1 e x2 1 c) Suy ra rằng p Z 1 e x2 D 1 p
d) Bằng cách đổi biến t D 2x, chứng minh rằng p Z 1 e x2=2dx D 2 1
(Đây là kết quả cơ bản trong xác suất và thống kê.)
35. Dùng kết quả câu c bài trên để tính các tích phân sau: p Z 1 Z xe xdx 0 1 0 a) x2e x2dx b)
3.2 Tích phân bội ba
Sinh viên tự bổ sung kiến thức trong mục này bằng cách đọc thêm tài liệu. Tích phân bội 63
3.2.1 Tích phân bội ba trong một hình hộp
3.2.2 Tích phân bội ba trong một khối tổng quát
3.2.3 Đổi biến tích phân bộ ba theo tọa độ trụ
3.2.4 Đổi biến tích phân bộ ba theo tọa độ cầu Chương 4 Giải tích vectơ
4.1 Tích phân đường
4.1.1 Đường đi hay lộ trình (path)
Nhắc lại kiến thức. Cho n hàm số một biến f1; : : : ; fn. Với mỗi giá trị của biến t (thuộc
một khoảng-đoạn nào đó), ta xét vectơ trong Rn như sau ! ˝ ˛
r .t/ D f1.t/; f2.t/; : : : ; fn.t/
Vậy ta có hàm vectơ một biến !r . Nếu các hàm số fk có giới hạn tại a, ta định nghĩa lim! f1.t/; : : : ; lim t!a ˝ t!a ˛ r .t/ D lim fn.t/ t!a
Hàm vectơ !r D hf1; : : : ; fni liên tục tại a có nghĩa là lim! r .t/ D ! r .a/; t!a
cũng có nghĩa là các hàm thành phần fk liên tục tại a. Khi đó, nếu giá trị t tăng dần, điểm
Hướng của C là hướng di chuyển của P khi t tăng. P f .t /; g.t /; h.t /
di chuyển sẽ để lại dấu vết là một đường cong C liên tục (không bị đứt). !
Người ta cũng nói !r .t/ là vectơ vị trí của điểm P, là vì
OP D !r .t /, với O là điểm gốc tọa
độ. Tóm lại, ta có các định nghĩa Giải tích vectơ 65
Một đường đi hay một lộ trình (path) là một hàm vectơ
r !có 1 biến, xác định trên đoạn Œa; b .
Đường đi !r được gọi là liên tục có nghĩa là hàm !r liên tục.
Vết của đường đi !r là tập hợp C các giá trị của hàm vectơ !r , ˚! C D r .t/=t 2 Œa; b ;
cũng được xem là tập hợp các “dấu vết” mà điểm P , với vectơ vị trí !r .t/, đi qua khi
t tăng từ a đến b. Thông thường biểu diễn hình học của C là một đường cong.
Lưu ý rằng với cùng một đường cong C , có thể có nhiều đường đi hay lộ trình khác nhau trên đó.
Nếu f; g; h là ba hàm số một biến, xác định trên một đoạn-khoảng I nào đó, thì tập
hợp C gồm các điểm .x; y; z/ sao cho x D f .t /; y D g.t /; z D h.t /; (4.1)
với các giá trị của t trong khoảng-đoạn I, là một đường cong trong không gian. Phương
trình (4.1) được gọi là hệ phương trình tham số của C , và t là tham số. Hàm vectơ biểu
diễn đường đi (có hướng) trên đường cong đó định bởi !r .t/ D hf .t/; g.t/; h.t/i. Bài tập
1-8 Vẽ đường cong có phương trình vectơ cho trước. Dùng mũi tên chỉ rõ hướng của đường cong khi t tăng. 1. !r .t/ D hsin t; ti
5. !r .t/ D h1; cos t; 2 sin ti 2. !r .t/ D ht3; t2i 6. !r .t/ D ht2; t; 2i
3. !r .t/ D ht; cos 2t; sin 2ti
7. !r .t/ D t2! i C t4!j C t6! k ! ! !
4. !r .t/ D h1 C t; 3t; ti 8. !r . k t / D cos t i cos t j C sin t
9-14 Tìm phương trình tham số phù hợp với các đường cong được đánh số từ I-VI. Giải thích vì sao.
9. x D cos 4t, y D t, z D sin 4t
10. x D t, y D t2, z D e t
11. x D t, y D 1=.1 C t2/, z D t2
12. x D e t cos 10t, y D e t sin 10t, z D e t
13. x D cos t, y D sin t, z D sin 5t
14. x D cos t, y D sin t, z D ln t 66 Giải tích vectơ
15. Chứng minh đường cong với phương trình tham số x D t cos t, y D t sin t, z D t
nằm trên mặt nón z2 D x2 C y2. Dựa vào đó hãy phác họa đường cong.
16. Chứng minh đường cong với phương trình tham số x D sin t, y D cos t, z D sin2 t
là đường cong giao tuyến của hai mặt z D x2 và mặt x2 C y2 D 1. Dựa vào đó hãy phác họa đường cong. ! !
17. Đường cong !r .t/ D t i C .2t
t 2/ k cắt mặt paraboloid z D x2 C y2 tại những điểm nào?
18. Lò xo !r .t/ D hsin t; cos t; ti cắt mặt cầu x2 C y2 C z2 D 5 tại những điểm nào?
19. Tìm phương trình vectơ biểu diễn đường cong giao tuyến của hai mặt
a) Mặt x2 C y2 D 4 và mặt z D xy q
b) Mặt z D x2 C y2 và mặt z D 1 C y
c) Mặt z D 4x2 C y2 và mặt y D x2 Giải tích vectơ 67
20. Nếu hai vật bay trong không gian theo hai quỹ đạo khác nhau, điều quan trọng người
ta hay quan tâm là chúng có va chạm nhau không. (Tên lửa có bay trúng mục tiêu
di động của nó không? Hai máy bay có va chạm trên không hay không? v.v..). Các
đường cong quỹ đạo có thể cắt nhau, nhưng chúng ta cần biết liệu các vật thể có cùng
vị trí ở cùng thời điểm hay không. Giả sử đường bay của hai vật thể được cho bởi phương trình
!r1.t/ D ht2;7t 12;t2i !r2.t/ D h4t 3;t2;5t 6i
Các vật thể này có va chạm nhau không?
21. Hai vật bay theo quỹ đạo không gian cho bởi
!r1.t/ D ht;t2;t3i !r2.t/ D h1 C 2t;1 C 6t;1 C 14ti
Hai vật đó có va chạm nhau không? Hai quỹ đạo có cắt nhau không?
4.1.2 Tiếp tuyến và độ dài của đường cong
Với hàm vectơ !r , ta định nghĩa d!r !r .t C h/ ! r .t/ D !r 0.t/ D lim dt h!0 h
nếu giới hạn trên tồn tại. Nếu !r .t/ D hx.t/; y.t/i thì ! r 0.t/ D hx0.t/; y0.t/i.
Ý nghĩa của vectơ !r 0.t/ được minh họa trong hình dưới đây !
Nếu hai điểm P và Q có vectơ vị trí là !r . PQ là biểu
t / và ! r .t C h/ tương ứng thì
diễn hình học của !r .t C h/ ! r .t/, được gọi là vectơ cát tuyến của đường cong. Nếu
h > 0 thì Œ!r .t Ch/ ! r .t / = h có cùng hướng với !r .t Ch/ ! r .t /. Khi h ! 0, có vẻ
như PQ tiến dần đến một vị trí mà ta quen gọi là vị trí tiếp xúc. Vì lý do này mà !r 0.t/ !
được gọi vectơ tiếp tuyến với đường cong tại điểm 0 . P , miễn là tồn tại ! r 0.t/ ¤
Vậy ta định nghĩa tiếp tuyến với đường cong tại P là đường thẳng qua P có vectơ chỉ
phương là !r 0.t/. Hướng của !r 0.t/ thuận theo hướng của đường đi khi t tăng.
Trong Vật lý, nếu t là đại lượng thời gian thì !r 0.t/ là vectơ biểu diễn vận tốc của chất
điểm P tại thời điểm t. 68 Giải tích vectơ
Đôi khi, ta cũng xét vectơ tiếp tuyến đơn vị định bởi ! ! r 0.t/ T .t/ D : ˇ ˇ! ˇ r 0.t/ˇ
!r được gọi là đường đi trơn nghĩa là tồn tại đạo hàm vectơ !r0 liên tục trên Œa; b ,
trong đó !r 0.a/ và ! r 0.b/ được hiểu là đạo hàm bên phải tại a và đạo hàm bên trái tại b của !r . Định lý 4.1
Giả sử !r .t/ D hf .t/; g.t/; h.t/i, với f; g; h là các hàm số 1 biến có đạo hàm; ! u và
!v là hai hàm vectơ có đạo hàm; c là hằng số thực. Khi đó ! ! ! 1. !r 0. k
t / D hf 0.t /; g0.t /; h0.t /i D f 0.t / i C g0.t / j C h0.t / d 2. Œ! u .t/ C ! v .t/ D ! u 0.t/ C ! v 0.t/ dt d 3. Œ ! ! cu .t / D cu 0.t/ dt d 4. Œf .t/! u .t/ D f 0.t/!u .t/ C f .t/! u 0.t/ dt d 5. Œ! u .t/
!v .t/ D !u 0.t/ !v .t/ C ! u .t/ !v 0.t/. dt ˇ ˇ r 0.t/ là vectơ vuông
Hệ quả là nếu ˇ!r .t/ˇ D
t c (là hằng số độc lập với t ) thì !
góc với !r .t/, với mọi . d 6. Œ! u .t/
! v .t/ D !u 0.t/ !v .t/ C ! u .t/ !v 0.t/ dt d 7. Œ! u .f .t// D f 0.t/!u 0.f .t// dt
Định nghĩa 4.1 (Độ dài đường cong). Giả sử đường cong C (trong không gian hoặc trong
mặt phẳng) là vết của đường đ r it !rơn,
!r .t/ D hf .t/; g.t/; h.t/i hoặc !r .t/ D hf .t/; g.t/i; với a t b
(các đạo hàm f 0; g0; h0 liên tục trên Œa; b ). Hơn nữa, khi t tăng từ a đến b, điểm P f .t/; g.t/; h.t/
đó, độ dài của đường cong được định nghĩa bởi công thức sau
(hoặc là P f .t/; g.t/ ) không đi qua khoảng nào của đường cong nhiều hơn một lần. Khi Z bˇ ˇ Z b q L D ˇ! r 0.t/ˇdt D Œf 0.t/ 2 C Œg0.t/ 2dt (4.2) a hoặc là a Z bˇ ˇ Z b q L D ˇ! r 0.t/ˇdt D
Œf 0.t/ 2 C Œg0.t/ 2 C Œh0.t/ 2dt: (4.3) a a Giải tích vectơ 69 ˇ ˇ T r ro ằnnggđcô ộ n d g ài th q ứ u c ãn(4 g .2 đ )ư-ờ(4 n .g3)đ,i nbếu ằn tg lđàộ đlại ớn lưvợn ận gt t ố h c ờnihgian ân thth ờiì k giý h an. iệu Ý tˇ!
ưởng để lập công thức r 0.t/ˇdt cũng hàm ý
định nghĩa độ dài đường cong ở trên là lấy giới hạn tổng độ dài các đoạn thẳng gấp khúc nối
các điểm liên tiếp trên đường cong, xem hình dưới, khi số điểm dần đến vô hạn. Bài tập
1. Hình vẽ dưới trình bày đường cong C cho bởi hàm vectơ !r .t/
a) Xác định các vectơ !r .4; 5/
! r .4/ và ! r .4; 2/ ! r .4/. Sau đó vẽ các vectơ !r . ! 4; 5/ ! r .4/ r .4; 2/ ! r .4/ và 0; 5 0; 2 !
b) Viết biểu thức của !r 0. T .4/.
t / và của vectơ tiếp tuyến đơn vị ! c) Vẽ T .4/. 2.
a) Phác họa thật lớn đường cong cho bởi !r .t/ D ht2; ti, 0 t 2 và vẽ các vectơ !r . . 1/, ! r .1; 1/ và ! r .1; 1/ ! r .1/
b) Vẽ vectơ !r 0.1/ đặt tại điểm .1; 1/ và so sánh nó với vectơ !r .1; 1/ ! r .1/ 0; 1 70 Giải tích vectơ
Hãy giải thích vì sao hai vectơ này có vẻ gần trùng nhau. 3-8
a) Phác họa đường cong phẳng với phương trình vectơ cho trước. b) Tìm !r 0.t/.
c) Phác họa vectơ vị trí !r .t/ và vectơ tiếp tuyến ! r 0.t/ tại giá trị t cho trước. 3. !r .t/ D ht 2; t 2 C 1i, t D 1 p
4. !r .t/ D ht C 1; ti, t D 1
5. !r .t/ D hsin t; 2 cos ti, t D =4
6. !r .t/ D het; e ti, t D 0
7. !r .t/ D het; e3ti, t D 0
8. !r .t/ D h1 C cos t; 2 C sin ti, t D =6
9-16 Tìm đạo hàm của các hàm vectơ
9. !r .t/ D ht sin t; t2; t cos 2ti
10. !r .t/ D htan t; sec t; 1=t2i ! ! 11. !r .t/ D i j C e4t! k ! 12. ! ! r . k t / D arcsin t p ! j C i C 1 t 2 ! ! 13. !r . k t / D et2! i j C ln.1 C 3t/ ! ! ! 14. !r . k
t / D at cos 3t i C b sin3 t j C c cos3 t !
15. !r .t/ D ! a C t b C t2! c 16. ! ! r . ! ! t / D t a . b C t c / !
17-20 Tìm vectơ tiếp tuyến đơn vị T .t/ tại giá trị của tham số t cho trước.
17. !r .t/ D hte t; 2 arctan t; 2eti, t D 0 p ! ! 18. !r .t/ D 4 t i C t2! j C t k , t D 1 ! ! 19. ! !
r .t/ D cos t i C 3t j C 2 sin 2t k , t D 0 ! ! !
20. !r .t/ D 2 sin t i C 2 cos t j C tan t k , t D =4 !
21. Nếu !r .t/ D ht; t2; t3i, tìm ! r 0.t/, T .1/, ! r 00.t/ và !r 0.t/ !r 00.t/. !
22. Nếu !r .t/ D he2t; e 2t; t e2ti, tìm T .0/, ! r 00.0/ và !r 0.t/ !r 00.t/. Giải tích vectơ 71
23-26 Viết phương trình tham số của tiếp tuyến của đường cong với phương trình tham số
cho trước tại một điểm được chỉ rõ. p 23. x D 1 C 2 t; y D t3 t; z D t 3 C t I .3; 0; 2/
24. x D et; y D tet; z D tet2I .1; 0; 0/
25. x D e t cos t; y D e t sin t; z D e tI .1; 0; 1/ p
26. x D ln t; y D 2 t; z D t2I .0; 2; 1/
27. Tìm giao điểm của hai đường tiếp tuyến với đường cong 1
!r .t/ D hsin t; 2 sin t; cos ti tại các điểm t D 0 và t D . 2
28. Tại điểm nào thì các đường cong !r1.t/ D ht; 1 t; 3Ct2i và !r2.s/ D h3 s; s 2; s2i
giao nhau? Tính góc giao nhau giữa hai đường cong, chính xác đến 10. ! p ! ! ! 29. Tìm !r . j .
t / biết ! r 0.t / D 2t i C 3t 2! j C t k và !r .1/ D i C ! ! ! ! 30. Tìm !r . k .
t / biết ! r 0.t / D t i C et ! j C t et ! k và !r .0/ D i C j C
31. Cho !u .t/ D hsin t; cos t; ti và !v .t/ D ht; cos t; sin ti. Tính theo các quy tắc đã biết a) d Œ!u.t/ !v .t/ b) dŒ!u.t/ !v .t/ dt dt
32. Nếu !r là một hàm vectơ sao cho !r 00 tồn tại. Chứng minh d Œ! r .t/ ! r 0.t/ D !r.t/ ! r 00.t/ dt 33. d Tìm biểu thức cho u . ! t/ Œ! v .t/ ! w . dt t / . d
34. Nếu !r .t/ ¤ 0, chứng minh ! ˇ ˇ 1 r .t/ !r 0.t/. ˇ!r .t/ˇ D ˇ ˇ dt ˇ!r .t/ˇ
35. Nếu một đường cong có tính chất là vectơ vị trí !r .t/ luôn vuông góc với vectơ tiếp
tuyến !r 0.t/, chứng minh đường cong đó nằm trên một mặt cầu có tâm ở gốc tọa độ. 36. Nếu !u .t/ D ! r 0.t/ ! r .t/ ! r 00.t/ , chứng minh rằng
!u 0.t/ D !r .t/ !r0.t/ !r000.t/
37-42 Tính độ dài đường cong.
37. !r .t/ D h2 sin t; 5t; 2 cos ti, 10 t 10 1
38. !r .t/ D h2t; t2; t2i, 0 t 1. 3 72 Giải tích vectơ p 39. ! ! r .t/ D t 2 i C et! j C e t! k , 0 1 ! ! !
40. !r .t/ D cos t i C sin t j C ln cos t k , 0 =4 !
41. !r .t/ D i C t2! j C t3! k , 0 1 !
42. !r .t/ D 12t i C 8t 3=2! j C 3t2! k , 0 1
43. Gọi C là đường cong giao tuyến của mặt trụ parabolic x2 D 2y với mặt cong 3z D
xy. Tính độ dài đường cong từ gốc tọa độ đến điểm .6; 18; 36/.
44. Tham số hóa lại đường cong theo độ dài đường cong tính từ điểm ứng với t D 0 theo hướng tăng của t. ! ! ! a) !r . k t / D 2t i C .1 3t / j C .5 C 4t/ ! ! !
b) !r .t/ D e2t cos 2t i C 2 j C e2t sin 2t k
45. Giả sử ta bắt đầu từ điểm .0; 0; 3/ và di chuyển một quãng đường 5 đơn vị dọc theo
đường cong x D 3 sin t, y D 4t, z D 3 cos t theo hướng dương. Cuối cùng ta đứng ở đâu?
46. Hãy tham số hóa lại đường cong 2t ! i C ! j 2 ! r .t/ D 1 t 2 C 1
theo độ dài cung, được đo từ đi t2 ểm C .1 1
; 0/ theo hướng tăng của t. Biểu diễn tham số
hóa vừa thực hiện theo dạng rút gọn nhất. Ta có thể kết luận gì về đường cong này?
4.1.3 Tích phân đường loại 1
Nhắc lại kiến thức. Cho !r W Œa; b ! Rn (n D 2 hay n D 3) là một đường đi trơn, có vết
là C . Giả sử f là hàm số nhiều biến xác định và liên tục trên vết C của đường đi ! r . Khi đó
tích phân đường của f dọc theo đường đi !
Z f ds, và được định nghĩa r là r được ký hiệu bởi ! Z Z b ˇ r ˇ f d a s D f !r .t/ ˇ!r 0.t/ˇdt (4.4) Ghi chú. !
Nếu !r là đường đi trơn trên từng khúc Œti 1; ti , với a D t0 < t1 < : : : < tn D b, thì người ta định nghĩa n Z f ds D Z t ˇ r X i ti 1 f !r . ˇ t / ˇ!r 0.t/ˇdt ! iD1
Đường đi !r được gọi là đơn (simple) khi nó không đi qua một vị trí nào giữa điểm
đầu và cuối của đường đi hơn một lần, theo nghĩa sau
8t1; t2; nếu a < t1 < t2 < b thì ! r .t1/ ¤ ! r .t2/: !
Đường đi !r được gọi là chính quy (regular) khi 8 0 . t; !r .t / ¤ Giải tích vectơ 73 Định lý 4.2 Nếu !r C
1 và !r2 là hai đường đi trơn-đơn-chính quy và có chung một vết thì Z Z f ds: r1 r2 f ds D ! !
Định nghĩa 4.2 (Tích phân đường trên đường cong, thay vì đường đi). Cho đường Z
Z f ds, miễn là tồn tại một đường đi r c!o r ntgrơ C n, .đK ơ ý n, hciệ híunh f d q s uy đư v ợ à c đ ó ịn v h ết n l g à hĩa C . là C !
Nếu C là hợp của hữu hạn các đường cong rời nhau hoặc nối tiếp nhau: C1; C2; : : : ; Cn,
hơn nữa các đường cong này là vết của các đường đi trơn-đơn-chính quy, thì ta định nghĩa n Z f ds D f ds X Z C iD1 Ci
Quy ước. Trong chương giải tích vectơ này, khi nói đến đường cong thì ta mặc định
đó là hợp của hữu hạn các vết của các đường đi trơn-đơn-chính quy như vừa nói trên.
Z f ds chính là độ dài của đường cong C . Nếu f 1 thì C Nếu ! ˇ r ˇ 2 dy 2 ˇ ˇ r D h d C x; yi thì ˇ! x r 0. ˇ! t /ˇ D dt . Nếu !r D h ˇ d x; y; zi thì t r 0.t/ D r dy dz d 2 2 x C C 2 dt dt . dt ˇ
Để dễ nhớ đẳng thức (4.4), hình thức d ˇ
s xem như đồng nhất với ˇ! ˇ r 0.t/ˇdt. Ta có thể hiểu của d ˇ C s( h t a a yq ˇ
u !en gọi là vi phân của độ dài).
r 0.t/ˇdt như là độ dài của một khoảng cong vô cùng nhỏ trên các vị trí
Tùy theo việc ký hiệu độ dài đường cong là s hay là l v.v.., một số sách dùng ký hiệu dl v.v.. thay cho ds. Bài tập 74 Giải tích vectơ
1-1 Tính các tích phân sau với C là đường cong cho trước Z y3ds, C W x D t3; y D t; 0 t 2 1. C Z xyds, C W x D t2; y D 2t; 0 t 1 2. C
Z xy4ds, C là nửa bên phải của đường tròn x2 C y2 D 16 3. C
Z x sin yds, C là đoạn thẳng nối từ .0; 3/ đến .4; 6/ 4. C
Z xyzds, C W x D 2 sin t; y D t; z D 2 cos t 0 t 5. C
Z xyz2ds, C là đoạn thẳng nối từ . 1; 5; 0/ đến .1; 6; 4/ 6. C yz
Z xe ds, C là đoạn thẳng nối từ .0; 0; 0/ đến .1; 2; 3/ 7. C
Z .2x C 9z/ds, C W x D t; y D t2; z D t3 0 t 1 8. C
9. Chân của một hàng rào hình tròn với bán kính 10 m được biểu diễn bởi phương trình
tham số x D 10 cos t, y D 10 sin t. Độ cao hàng rào tại vị trí .x; y/ là h.x; y/ D 4 C 0; 01.x2
y2/. Giả sử phải dùng 1 L sơn để phủ 100 m2 hàng rào. Hãy phác họa
hình dạng hàng rào và tính lượng sơn để phủ hết hai mặt hàng rào.
4.1.4 Tích phân đường loại 2
Nhắc lại kiến thức. Cho tập hợp D
Rn, với n D 2 hay n D 3. Ta nói trường vectơ trên D là hàm vectơ ! ! xác định trên F trên D sẽ cho tại mỗi
D, F W D ! Rn. Nói cách khác, trường vectơ ! điểm
F .P /. Ví dụ, xét không gian tọa độ Oxyz, đồng
P 2 D một vectơ duy nhất là
nhất với R3, với O là tâm Trái Đất. Giả sử M là khối lượng Trái Đất. Theo Định Luật
Hấp Dẫn Newton, lực hút của Trái Đất tác dụng vào vật có khối lượng m đặt tại điểm
P .x; y; z/ trong không gian Oxyz là ! mM G F .P / D !
OP ; với G là hằng số hấp dẫn. ˇ 3 ˇ ! ˇ OP ˇ Viết cách khác là ! mM Gx mM Gy F .x; y; z/ D ! i ! j .x2 C y2 C z2/3=2 .x2 C y2 C z2/3=2 mM Gz ! k (4.5) .x2 C y2 C z2/3=2 !
Như vậy F định bởi (4.5) là trường (vectơ) lực hấp dẫn trên R3. Giải tích vectơ 75 !
Giả sửF là một trường vectơ liên tục xác định trên vết của một đường đi trơn !r W F ! Œ dọc a; b
! Rn, n D 2 hay n D 3. Khi đó, tích phân đường (loại 2) của trường ! theo đường đi ! Z F
dr! và được định nghĩa là r r được ký hiệu là ! ! ! Z F d! Z b r 0.t/dt r r D a F !r .t/ ! ! !
Nếu F D hP; Qi là trường vectơ hai chiều (nghĩa là P , Q là các hàm số hai biến) và
!r .t/ D hx.t/; y.t/i thì ! r 0.t/ D hx0.t/; y0.t/i và người ta cũng dùng ký hiệu khác
Z P dx C Qdy. Ký hiệu này dựa theo hình thức vi phân r
cho tích phân đường loại 2,
dx D x0.t/dt, dy D y0.t/dt, !dẫn đến Z Z b r h i P dx C Qdy D
P x.t /; y.t / x0.t / C Q x.t /; y.t / y0.t / dt ! a Z ! ! b Z F d! r D a F !r . r t / ! r 0.t/dt D ! !
Tương tự, ký hiệu tích phân đường loại 2 cho trường vectơ ba chiều F D hP; Q; Ri Z P dx C Qdy C Rdz. r là ! ! !
Trong Vật lý, nếu F là trường vectơ lực trên đường đi ! Z F d!r được xem là r ! r thì !
công của lực F tác dụng vào chất điểm P với vectơ vị trí !r .
Một đường cong C có thể là vết chung của nhiều đường đi khác nhau. Các đường
đi này có thể cùng hướng hoặc ngược hướng trên C . Ví dụ, nếu !r1 là đường đi đơn,
chính quy, xác định trên Œa; b với vết C , định hướng từ điểm A đến điểm B,
thì đường đi !r2, cũng xác định trên Œa; b , cho bởi !
r2.t/ D ! r1.a C b t/, cũng có vết
C nhưng định hướng từ B đến A khi t tăng từ a đến b. Ngoài ra, đường đi !r3 xác định trên Œ0; 1 , cho bởi ! r3.t/ D ! khi t tăng từ 0 đến 1. r1 ta C .1
t /b , cũng có vết C định hướng từ B đến A 76 Giải tích vectơ Định lý 4.3
Giả sử !r1 và !r2 là hai đường cong trơn-đơn-chính quy, có chung một vết C . Khi đó Nếu !r C
1 và !r2 có cùng định hướng trên thì ! ! Z F d! Z F d! r : r1 r2 r D ! ! Nếu !r C
1 và !r2 ngược hướng trên thì ! ! Z F d! Z F d! r (4.6) r1 r r D 2 ! !
Định nghĩa 4.3 (Tích phân đường trên đường loại 2 trên đường cong, thay vì đường !F Zd!r được hiểu
đi). Cho đường cong C đã xác định một hướng trên đó. Ký hiệu ! Z F d!
r , miễn là tồn tại đường đrit !rơn-đơn-chính quy, có vết C là C và thuận r là
theo hướng đã cho. Người ta cũng định nghĩa !
C là đường cong C được định ngược
hướng ngược lại, và từ (4.6) ta có thể viết ! ! Z F d! Z F d! r r D C C
Trường hợp C là hợp của hữu hạn các đường cong có hướng, rời nhau hoặc nối tiếp
nhau: C1; C2; : : : ; Cn, hơn nữa các đường cong này là vết của các đường đi trơn-
đơn-chính quy, thì ta định nghĩa n ! ! Z F d!r D X Z F d!r C iD1 Ci
Tích phân đường loại 1 và loại 2 có một sự liên hệ. Nếu !r là một đường đi trơn, chính ! ! r quy và T D
là vectơ tiếp tuyến đơn vị trên đường đi !r , thì ta dễ dàng kiểm ˇ chứng được ˇ! ˇ r ˇ ! ! ! Z F d! Z F T ds: r r r D ! ! !
Đẳng thức trên cũng hàm ý rằng công của trường lực F tác dụng lên chất điểm P !
dịch chuyển theo đường đi !r bằng tích phân đường loại 1 của thành phần củaF trên
phương tiếp tuyến đơn vị của đường đi (thuật ngữ thành phần được hiểu là độ dài đại ! !
số của F lên trục chứa vectơ đơn vị T ). Bài tập
1-8 Tính các tích phân đường loại 2 Giải tích vectơ 77 p p Z .x2y3
x/ dy với C là đoạn cong y D x từ .1; 1/ đến .4; 2/ 1. C
Z xey dx với C là đoạn cong x D ey từ .1; 0/ đến .e; 1/ 2. C Z xy dx C .x
y/ dy với C gồm các đoạn thẳng từ .0; 0/ đến .2; 0/ và từ .2; 0/ đến 3. .3; 2/ C
Z sin x dx C cos y dy với C gồm nửa trên của đường tròn x2 C y2 D 1 từ .1; 0/ đến
4. . 1; 0/ và đoạn thẳng từ . 1; 0/ đến . 2; 3/ C p
Z x2y z dz với C W x D t3; y D t; z D t2, 0 t 1 5. C
Z z dx C x dy C y dz với C W x D t2; y D t3; z D t2, 0 t 1 6. C
Z .x C yz/ dx C 2x dy C xyz dz với C gồm các đoạn thẳng từ .1; 0; 1/ đến .2; 3; 1/
7. và từ .2; 3; 1/ đến .2; 5; 2/ C
Z x2 dx C y2 dy C z2 dz với C gồm các đoạn thẳng từ .0; 0; 0/ đến .1; 2; 1/ và từ
8. .1; 2; 1/ đến .3; 2; 0/ C ! Z F d!
r với C là vết của đường đi ! r cho trước 9-13 Tính ! C !
9. F .x; y/ D xy i C 3y2! j , !r .t/ D 11t4! i C t3! j , 0 t 1 ! ! !
10. F .x; y; z/ D .x C y/ i C .y z/ j C z2! k , !r .t/ D t2! i C t3! j C t2! k , 0 t 1 ! ! ! ! !
11. F .x; y; z/ D sin x i C cos y j C xz k , !r .t/ D t3! i t 2!j C t k , 0 t 1 ! ! ! ! ! ! !
12. F .x; y; z/ D z i C y j x k , !r .t / D t i C sin t j C cos t k , 0 t ! !
13. F .x; y/ D ex 1! i C xy j , !r .t/ D t2! i C t3! j , 0 t 1 ! !
14. Tính công của trường lực F .
j tác động lên chất điểm di chuyển x; y/ D x2! i C xy
một vòng ngược chiều kim đồng hồ trên C W x2 C y2 D 4. ! ! !
15. Tính công của trường lực F .
j tác động lên chất điểm di x; y/ D x i C .y C 2/
chuyển trên đoạn cong cho bởi !r .t/ D ht sin t; 1 cos ti, 0 t 2 . ! ! !
16. Tính công thực hiện bởi trường lực F . j khi dịch chuyển chất x; y/ D x sin y i C y
điểm theo quỹ đạo parabola y D x2 từ . 1; 1/ đến .2; 4/. !
17. Tính công thực hiện bởi trường lực F .x; y; z/ D hy C z; x C z; x C yi khi dịch
chuyển chất điểm dọc theo đoạn thẳng từ .1; 0; 0/ đến .3; 4; 2/. 78 Giải tích vectơ
18. Một người nặng 160-lb mang thùng sơn nặng 25-lb lên cầu thang xoắn lò xo với bán
kính 20 ft. Độ cao thang xoắn là 90 ft và người đó đi đúng 3 vòng xoắn lên hết thang.
Hỏi người đó thực hiện công là bao nhiêu để chống lại trọng lực khi đi lên hết thang?
19. Giả sử thùng sơn trong bài tập 18 có lỗ thủng ở đáy và 9-lb sơn chảy ra ngoài một
cách liên tục, đều đặn khi người lên đến đỉnh thang. Công người đó thực hiện là bao nhiêu?
4.1.5 Định lý Green (Định lý cơ bản của tích phân kép)
Nhắc lại kiến thức. Xét D là miền phẳng bị giới hạn bởi đường biên @D là hữu hạn các
đường cong đơn kín. Hướng dương của đường cong @D được quy ước là hướng mà khi đi
theo hướng đó, miền trong của D luôn nằm bên tay trái.
Hình trên mô tả hướng dương của @D D C1 [ C2. !
Tích phân đường của trường F D hP; Qi dọc theo @D theo hướng dương được ký hiệu bởi ! I F d! I P dx C Q dy: r D @D @D
Định lý 4.4: Định lý Green, hay Định Lý Cơ Bản Của Tích Phân Kép
Giả sử D là miền phẳng bị giới hạn bởi biên @D là hữu hạn các đường cong đơn kín,
trơn từng khúc. Giả sử P; Q là các hàm số có các đạo hàm riêng cấp 1 liên tục trên
một tập mở chứa D, viết là P; Q 2 C 1.D [ @D/. Khi đó @P “ I P dx C Q dy: @Q @x dA D D @y @D Bài tập
1-4 Tính các tính phân đường theo hai cách: (a) Tính trực tiếp (b) Dùng định lý Green I .x
y/ dx C .x C y/ dy với C là đường tròn có tâm ở gốc tọa độ, bán kính 2 1. C
I xy dx C x2 dy với C là hình chữ nhật có các đỉnh .0; 0/, .3; 0/, .3; 1/ và .0; 1/ 2. C
I xy dx C x2y3 dy với C là tam giác .0; 0/, .1; 0/ và .1; 2/ 3. C Giải tích vectơ 79
I x dx C y dy với C bao gồm các đoạn thẳng từ .0; 1/ đến .0; 0/; từ .0; 0/ đến .1; 0/
4. và đoạn parabola y D 1 x2 từ .1; 0/ đến .0; 1/. C
5-10 Dùng định lý Green để tính tích phân dọc theo đường cong kín C định hướng dương cho trước
I xy2 dx C 2x2y dy với C là tam giác có đỉnh .0; 0/, .2; 2/ và .2; 4/ 5. C
I cos y dx C x2 sin y dy với C là hình chữ nhật có đỉnh .0; 0/, .5; 0/, .5; 2/ và .0; 2/ 6. C p
I .y C e x/ dx C .2x C cos y2/ dy với C là biên của miền bị bao bởi hai parabolas 7. y D x2 và x D y2 C
I xe 2x dx C .x4 C 2x2y2/ dy với C là biên của hình khuyên nằm giữa hai đường
8. tròn x2 C y2 D 1 và x2 C y2 D 4 C I y3 dx
x3 dy với C là đường tròn x2 C y2 D 4 9. C
I sin y dx C x cos y dy với C là ê lip x2 C xy C y2 D 1 10. C ! Z F
d!r (nhớ kiểm tra hướng của đường cong C trước 11-14 D k ù hing ápđịdnụhn l gýđG ịnreen h lý) để tính C ! 11. ˝p p ˛ F . .x ; ;0y / /v D à đo x ạn tC h y3 ẳng; x2 từ . C; y 0/ ,đ C ến g . ồ 0; m
0/ các đoạn cong y D sin x từ .0; 0/ đến ! 12. ˝ ˛ F
.0 .;x0;/ y/ D y2 cos x; x2 C 2y sin x , C là tam giác từ .0; 0/ đến .2; 6/ đến .2; 0/ đến ! 13. ˝ ˛ F .x; y/ D ex C x2y; ey
xy2 , C là đường tròn thuận chiều kim đồng hồ ! 14. D y E F . có x h;ưy ớ /n D g ng y ược ln. ch x2 iều C k y2 im /;đ 2 ồnar g chta ồ n .
, C là đường tròn .x 2/2 C .y 3/2 D 1 x !
15. Dùng định lý Green để tính công thực hiện bởi trường lực ˝ ˛
khi di chuyển chất điểm từ .0; 0/ dọc theo trục Ox đến .1; F0/.,xr;ồyi/d D ọc t xh.x eo Cđy o /; ạn x t y h 2 ẳng
.0; 1/, rồi trở về .0; 0/ theo trục Oy.
16. Một chất điểm di chuyển từ . 2; 0/ theo trục Ox đến .2; 0/, rồi dọc theo nửa đường p ! ! ! tr t ò r n ườ y ng Dlực4F . x2
j tác động lên chất điểm tại mỗi vị trí x; t y r/ở v D ề đ x iểm i k C h . ở x i 3 đ Cầu 3 . x D y ù
2/ng định lý Green tính công thực hiện bởi .x; y/ của chất điểm. 80 Giải tích vectơ 17. Giả sử miền D
R2 giống như mô tả trong định lý Green. Chứng minh rằng diện
tích của miền D có thể tính theo các công thức sau 1 I I y dx D I x dy y dx: A.D/ D x dy D @D @D 2 @D Z x dy 18. a) N y ếu dx CD là x đ 1yoạn th 2
x ẳng nối .x1; y1/ đến .x2; y2/, chứng minh rằng 2y1 C
b) Nếu theo thứ tự ngược chiều kim đồng hồ, .x1; y1/, .x2; y2/, . . . , .xn; yn/ là
các đỉnh của một đa giác, chứng minh rằng diện tích của đa giác đó là 1 A D .x1y2 x2y1/C.x2y3 x3y2/C C.xn 1yn xnyn 1/C.xny1 x1yn/
c) Tính 2diện tích của đa giác có các đỉnh là .0; 0/, .2; 1/, .1; 3/, .0; 2/ và . 1; 1/.
4.1.6 Đặc trưng của trường bảo toàn 2 chiều
Định lý 4.5: Định Lý Cơ Bản Của Tích Phân Đường hay định lý Newton-Leibnitz
Cho f là hàm số nhiều biến thuộc lớp C 1 trên một tập mở a D Rn (nghĩa là f có
các đạo hàm riêng cấp 1 liên tục trên tập D). Với đường đi trơn bất kỳ !r .t/, a t b, có vết trong D thì Z rf ! d r r D f !r .b/ f !r .a/ D f .B/ f .A/; !
trong đó điểm A và B là điểm đầu và điểm cuối của đường đi.
aNhắc lại: mục cực trị hàm nhiều biến có định nghĩa tập D trong R2 được gọi là mở khi mọi điểm của
D đều là tâm của một đĩa tròn nằm trong D. Tương tự cho khái niệm tập mở trong R3.
Sau đây là vài định nghĩa
Một đường cong C được gọi là đường cong kín (closed curve) khi nó là vết của một
đường đi !r xác định trên Œa; b thỏa !
r .a/ D ! r .b/. Đường cong C được gọi là
đường cong đơn (simple curve) khi nó là vết của một đường đi đơn. Từ trái sang phải
dưới đây là các đường cong: đơn và không kín; đơn và kín; kín và không đơn; không đơn và không kín !
Ta nói trường F có tích phân độc lập với đường đi trong D nghĩa là giá trị tích phân ! Z F
d!r là như nhau với mọi đường cong C nằm trong D và có cùng điểm đầu, ! C Z F
d!r D 0 với mọi đường cong cù kí ngCđiểm bên cu troốni.g Đi D ều .
này cũng đồng nghĩa với C Giải tích vectơ 81 ! !
Trường F được gọi là trường bảo toàn trong F có nguyên hàm D nghĩa là trường
hay hàm thế xác định trên D, tức là hàm số nhiều biến f thỏa !F .P/ D rf .P/; 8P 2 D:
Định Lý Cơ Bản Của Tích Phân Đường cho ta ! Z F ! dr D f .B/ f .A/ C !
nếu f là nguyên hàm của trường F bảo toàn, liên tục trên D; A và B là điểm đầu và
điểm cuối của đường cong C nằm trong D. Vậy
Trường bảo toàn liên tục trên D sẽ có tích phân độc lập với đường đi trong D.
Tập hợp D được gọi là tập liên thông có nghĩa là hai điểm bất kỳ thuộc D luôn là
điểm đầu và điểm cuối của một đường đi liên tục nằm trong D.
Tập hợp D trong R2 (D là miền phẳng) được gọi là tập đơn liên khi nó là tập hợp
liên thông sao cho mọi đường cong đơn-kín bên trong D sẽ bao quanh một miền hoàn toàn nằm trong D.
Định lý 4.6: Đặc trưng của trường bảo toàn 2 chiều !
Giả sử F D hP; Qi là trường vectơ 2 chiều thuộc lớp C 1.D/, D là tập mở trong R2. Khi đó !
1. Nếu F là trường bảo toàn trên D thì @P @Q D
trên tập D (suy từ định lý Clairaut). @y @x @ @ 2. P Q
Nếu D là tập đơn liên và D
!F là trường bảo toàn trên D @y trên tập D thì @x
(được suy từ định lý Green). Bài tập
1-4 Xác định các tập cho trước có tính chất sau hay không: (a) mở, (b) liên thông, (c) đơn liên 82 Giải tích vectơ ˚
1. .x; y/=x > 0; y > 0 ˚ 2. .x; y/=x ¤ 0 ˚
3. .x; y/=1 < x2 C y2 < 4 ˚ 4. .x; y/=x2 C y2 1 hoặc 4 x2 C y2 9 !
5-12 Xác định xem các trường 2 chiều F có bảo toàn không? Nếu có thì tìm hàm thế f của trường này. ! ! ! 5. F . j x; y/ D .2x 3y/ i C . 3x C 4y 8/ ! ! ! 6. F . j x; y/ D ex cos y i C ex sin y ! ! ! 7. F . j x; y/ D ex sin y i C ex cos y ! ! 8. F . j x; y/ D .3x2 2y2 ! / i C .4xy C 3/ ! ! !
9. F .x; y/ D .yex C sin y/ i C .ex C x cos y/ j ! ! !
10. F .x; y/ D .xy cos xy C sin xy/ i C x2 cos xy j ! !
11. F .x; y/ D .ln y C 2xy3 !/ i C .3x2y2 C x=y/ j ! ! !
12. F .x; y/ D .xy cosh xy C sinh xy/ i C .x2 cosh xy/ j , với cosh xy D 1 . 2 exy C e xy/ và sinh xy D 1 . 2 exy e xy/ ! ! !
13-15 Chứng minh F trường bảo toàn, sau đó dùng hàm thế của Z F d! r với C cho trước. F để tính C !
13. F .x; y/ D x2! i C y2! j , C là đoạn parabola y D 2x2 nối từ . 1; 2/ đến .2; 8/ ! !
14. F .x; y/ D xy2! i C x2y j , C W ! ˝ 2 t; t C 1 ˛ r .t/ D t C sin 1 cos , 2 t 0 t 1 ! y2 ! ! 15. F .x; y/ D
! i C 2y arctanx j , C W !r.t/ D t2! i C 2t j , 0 t 1 1 C x2
16-17 Chứng minh các tích phân sau độc lập với đường đi và tính tích phân đó. x Z tan y dx C
dy, C là bất kỳ đường đi nào nối từ .1; 0/ đến .2; / cos2 y 4 16. C Z .1
ye x/ dx C e x dy, C là bất kỳ đường đi nào nối từ .0; 1/ đến .1; 2/ 17. C
18-19 Tính công của trường lực khi dịch chuyển một chất điểm từ P đến Q. ! p ! 18. F . j , P .1; 1/, Q.2; 4/ x; y/ D 2y3=2! i C 3x y Giải tích vectơ 83 ! 19. F .x; y/ D e y! i xe y !j , P .0; 1/, Q.2; 0/ ! ! ! i C j 20. y x Cho F D
, với .x; y/ ¤ .0; 0/. Chứng minh @P=@y D @Q=@x nhưng x2 C y2 !
tích phân của F không độc lập với đường đi trong R2 n f.0; 0/g. Điều này có mâu
thuẫn với đặc trưng của trường bảo toàn không? 4.2 Tích phân mặt
Sinh viên có thể đọc thêm giáo trình để mở rộng kiến thức trong mục này. 4.2.1 Mặt cong
4.2.2 Tích phân mặt loại 1
4.2.3 Tích phân mặt loại 2
4.2.4 Các định lý cơ bản của tích phân mặt Chương 5
Làm quen vài mô hình phương trình vi phân
5.1 Phương trình vi phân cấp 1
5.1.1 Phương trình vi phân tách biến
Nhắc lại kiến thức. Phương trình vi phân dạng tách biến (seperable equation) là phương
trình vi phân cấp 1 có hình thức như sau
y0 D g.x/f .y/ (y là hàm số chưa biết, biến x)
Sở dĩ gọi là tách biến vì phương trình trên có thể đưa về dạng có x và y ở từng vế riêng biệt,
rồi lấy nguyên hàm hai vế
y0 D g.x/ (giả sử f .y/ ¤ 0) f .y/ Z d Z y suy ra D g.x/dx f .y/
Từ đó ta có phương trình để có thể tính y theo x một cách tường minh (explicit function);
hoặc phương trình xác định một ẩn hàm (implicit function) y theo x. Bài tập
1-21 Giải các phương trình vi phân p 1. du xy0 D y 6. 1 C r D p p dr 1 C u 2. y0ey D x dy t et 3. . 7. D x2 C 1/y0 D xy dt p 4. y0 D y2 sin x y 1 C y2 d 8. y ey sin2 D
5. .1 C tan y/y0 D x2 C 1 d y sec
Làm quen vài mô hình phương trình vi phân 85 9. dv u0.t / D 2 C 2u C t C t u 16. s C 1 D d ds sv C s 10. z C etCz D 0 dp dt 17. D t2p p C t 2 1 d dt 11. y D xy2 dx 18. dz C etCz D 0 d dt 12. y D xe y d dy x 19. .x2 C 4/ D xy 13. dx xy2y0 D x C 1 20. y0 D y2x3 14. .y2 C xy2/y0 D 1 d 21. x
15. .y C sin y/y0 D x C x3 D x2 2x C 2 dt
22-33 Tìm nghiệm của phương trình vi phân thỏa điều kiện đầu cho trước 22. y0y D x; y.0/ D 3
23. .1 C y2/y0 D y cos x; y.0/ D 1
24. x cos x D .2y C e3y/y0; y.0/ D 0 p
25. P 0.t/ D tP ; P .1/ D 2 d 26. y 2t C sec2 t D ; d u.0/ D 5 t 2u
27. xy0 C y D y2; y.1/ D 1
28. y0 tan x D a C y; y. / D a; 0 < x < 3 2 d
29. L D kL2 ln t; L.1/ D 1 dt d 30. y x D dx ; y.0/ D 3 y d ln 31. y x D dx ; y.1/ D 2 xy d 32. P p D P t; P .1/ D 2 dt d
33. L D kL2 ln t; L.1/ D 1 dt
34. Tìm một phương trình đường cong đi qua điểm .0; 1/ mà độ dốc của nó tại .x; y/ là xy. 35. 1
Tìm hàm số f sao cho f 0.x/ D f .x/Œ1 f .x/ và f .0/ D . 2
36. Giải phương trình y0 D x C y bằng cách đổi biến u D x C y. 86
Làm quen vài mô hình phương trình vi phân
5.1.2 Phương trình vi phân đẳng cấp
Nhắc lại kiến thức. Sau đây là phương trình vi phân cấp 1, có thể đưa về dạng tách biến được y y0 D f
(f là hàm số một biến, khác ánh xạ đồng nhất) (5.1) x
Đặt u D y=x thì y D xu và y0 D u C xu0, thay vào (5.1), ta được f .u/ u (5.2) u0 D x
Nếu có số thực a0 thỏa f .a0/ D a0 thì hàm số y D a0x là một nghiệm riêng của (5.2).
Nếu f .a/ ¤ a, 8a, thì (5.2) được đưa về dạng tách biến u0 1 D f . Z Z u/ u du dx ) D x f .u/ u Bài tập
1-18 Giải phương trình vi phân bằng cách đổi biến u D y=x d 1. y xy0 D y C xey=x 12. 4x 3y D d 2. y x x y xy0 D x sin C y x dy y 6x 8 D
3. x2y0 C y2 C xy C x2 D 0 < dx 2x y 13. y.0/ D 1 4. xy0 D x C 2y : x2 C y2 5. .x2 xy/y0 D y2 14. y0 D , y.1/ D 2 xy 6. xyy0 y2 D .x C y/2e y=x d 15. y .x2 C y2/ C 2x.y C 2x/ D 0
7. xy0 C y ln x D y ln y và y.1/ D 1 dx 8. y C x y0 D ( x 0/. 2 16. x2y x/ D D y xy C x2 y.1 2 9. y x y0 D x d 17. y y2 D .xy x2/ dx C 10. 2y x y0 D x dx x2 C t 2 8 x D dt t 11. x y < y0.x/ D x C y 18. x.2/ D 1 :
5.1.3 Phương trình vi phân tuyến tính cấp 1
Nhắc lại kiến thức. Phương trình vi phân tuyến tính cấp 1 có dạng y0 C q.x/y D p.x/ (5.3)
Làm quen vài mô hình phương trình vi phân 87
trong đó p.x/ và q.x/ là hai hàm số cho trước. Cách giải như sau Z
Tìm một nguyên hàm của q.x/ là Q.x/ D q.x/ dx.
Nhân cả hai vế của (5.3) với eQ.x/, đưa về dạng d
y0eQ.x/ C Q0.x/eQ.x/y D p.x/eQ.x/ , yeQ.x/ D p.x/eQ.x/ dx Z suy ra yeQ.x/ D
p.x/eQ.x/ dx. Từ đó tìm được y.
Phương trình vi phân Bernouli có dạng
y0 C q.x/y D p.x/yn, với n ¤ 0 và n ¤ 1 (5.4)
trong đó p.x/ và q.x/ là hai hàm số cho trước. Đặt u D y1 n, thay vào (5.4), ta đưa về
phương trình vi phân tuyến tính cấp 1 u0 C .1 n/q.x/u D .1 n/p.x/ Bài tập
1-4 Các phương trình vi phân có tuyến tính hay không? 1. y0 C cos x D y 3. yy0 C xy D x2 p 2. y0 C cos y D tan x 4. xy C x D exy0
5-25 Giải phương trình vi phân 5. y0 C 2y D 2ex 14. y0 C y D 1. 6. y0 D x C 5y 15. y0 y D ex. 7. 16. y0 D x y. xy0 2y D x2
17. 4x3y C x4y0 D sin3 x. 8. x2y0 C 2xy D cos2 x p p 18. xy0 C y D x. 9. xy0 C y D x 19. y0 C y D sin.ex/. 10. y0 C y D sin.ex/ d 20. y x 4y D x4ex.
11. y0 sin x C y cos x D sin.x2/ dx d 21. u 12. .1 C t/ xy0 4y D x4ex C u D 1 C t; t > 0. dt d d 13. u r .1 C t/ C 22. t ln t u D 1 C t; t > 0 C r D tet . dt dt 88
Làm quen vài mô hình phương trình vi phân d 23. dz r D 25. t ln t xz x: C r D tet dx dt 24. 2 z0 2z D x4. x 3
26-37 Giải bài toán giá trị đầu
26. y0 D x C y; y.0/ D 2 d 27. y t C 2y D t3; t > 0; y.1/ D 0 dt dv 28. 2t v D 3t 2et2; v.0/ D 5 dt
29. 2xy0 C y D 6x; x > 0; y.4/ D 20
30. xy0 D y C x2 sin x; y. / D 0 31. y0 C 3xy D 4x.
32. x2y0 C 2xy D ln x, y.1/ D 2 d 33. u t D t2 C 3u; t > 0; u.2/ D 4 dt
34. 2xy0 C y D 6x; x > 0; y.4/ D 20 d 35. y .x2 C 1/ C 3x.y 1/ D 0; y.0/ D 2 dx
36. y0 C y cos x D e sin x. 37. .x2 C 1/y0 C 3x.y 1/ D 0; y.0/ D 2
38-39 Giải các phương trình Bernoulli. 38. xy0 C y D xy2 y3 39. 2 y0 C y D x x2
40. Giải phương trình vi phân cấp 2 xy00 C y0 D 12x2 bằng cách thế u D y0.
5.1.4 Ứng dụng các mô hình phương trình vi phân cấp 1 trong các bài toán thực tiễn
1. Một quần thể vi khuẩn có tốc độ tăng trưởng số lượng tỉ lệ với số lượng hiện có. Sau
1 giờ có 1000 cá thể vi khuẩn, sau 4 giờ có 3000 cá thể. Hãy tìm số cá thể ở một thời
điểm bất kì và số cá thể ở thời điểm ban đầu.
2. Lượng muỗi trong môi trường đang tăng với tốc độ theo thời gian (tính bằng ngày)
tỉ lệ với số lượng hiện có, và gấp đôi sau mỗi tuần. Giả sử số lượng muỗi ban đầu là
100 000 con, hãy tìm công thức của số lượng muỗi tại thời điểm bất kì.
Làm quen vài mô hình phương trình vi phân 89
3. (Mô hình lãi nhập vốn liên tục) Một tài khoản có lượng tiền ban đầu là P (gốc). Lãi
suất theo thời gian là r/năm, thường được viết ở dạng phần trăm/năm. Chẳng hạn
r D 0;05 D 5% có nghĩa là sau 1 năm thì cứ 100 đơn vị tiền tài khoản sẽ nhận được
một khoản lãi là 5 đơn vị tiền. Nếu lãi được nhập vào vốn, thì r chính là tốc độ tăng
tương đối của lượng tiền trong tài khoản. Trong mô hình lãi nhập vốn liên tục thì
lượng tiền A ở thời điểm t (tính bằng năm) thỏa A0.t / D r: A.t /
a) Chứng tỏ lượng tiền trong tài khoản được cho bởi A.t / D P ert :
b) Chứng tỏ thời gian cần để lượng tiền trong tài khoản tăng gấp đôi không phụ
thuộc vào khoản đầu tư ban đầu.
c) Để lượng tiền tăng gấp đôi mỗi 10 năm thì lãi suất phải bằng bao nhiêu?
4. (Sự phân rã của đồng vị carbon C 14)
Carbon C 14 là một chất phóng xạ. Theo hóa học số lượng nguyên tử bị phân rã trong
một đơn vị thời gian trên một đơn vị số lượng nguyên tử là không đổi. Như vậy nếu
gọi C là số lượng nguyên tử ở thời điểm t thì C 0.t / D k C .t /
trong đó k là một số thực không thay đổi theo t. a) Chứng tỏ C .t / D C0ekt trong đó C0 D C.0/.
b) Người ta biết C 14 phân rã theo qui luật số lượng giảm đi phân nửa sau 5730
năm. Từ đó hãy kiểm rằng k D 0; 00012.
5. (Định tuổi bằng carbon)
Carbon C 14 được sinh ra trong khí quyển Quả Đất do tác động của tia vũ trụ. Tỉ lệ
giữa C 14 (phóng xạ) và C 12 (không phóng xạ) trong môi trường có thể coi là không
thay đổi theo thời gian. Các cơ thể sống trao đổi chất với môi trường nên tỉ lệ giữa
C 14 và C 12 trong cơ thể bằng với tỉ lệ trong môi trường. Khi một cơ thể chết đi, nó
không trao đổi chất nữa, lượng C 12 không đổi trong khi lượng C 14 giảm đi theo thời
gian do phóng xạ. Bằng cách đo tỉ lệ C 14 còn trong cơ thể người ta có thể suy ra thời
điểm mà cơ thể chết. Đây là nguyên lí của phương pháp định tuổi bằng Carbon. Về C .t /
mặt toán học, nếu biết giá trị của ta có thể tính được t. C .0/
Năm 1991 người ta phát hiện được một xác người đóng băng trên dãy núi Alps ở Châu
Âu, và đo được lượng C 14 trong xác ướp này bằng 53% lượng C 14 có trong một cơ
thể sống. Hãy tính xem xác ướp này bao nhiêu tuổi? 90
Làm quen vài mô hình phương trình vi phân
6. Năm 1950 người ta phát hiện ở gần Biển Chết những phần của những cuốn sách viết
trên giấy và da có nội dung liên quan tới kinh của người Do Thái cổ. Các nhà khảo
cổ xác định được hàm lượng Carbon-14 trong các cuốn sách chỉ còn là 78%. Hãy tính
tuổi của các cuốn sách này.
7. Người ta tìm thấy những bánh xe bằng gỗ của các chiến xa do ngựa kéo ở Kazakhstan.
Hàm lượng Carbon-14 trong gỗ chỉ còn bằng 62.5% so với hàm lượng trong cây sống.
Hãy tính tuổi của các bánh xe này.
8. Dân số loài người là 5; 28 tỉ người vào năm 1990 và 6; 07 tỉ người vào năm 2000.
Giả thiết rằng do các hạn chế về tài nguyên, Quả Đất không thể đủ chỗ cho quá 10 tỉ
người. Hãy dùng mô hình tăng trưởng dân số có kìm hãm để dự đoán dân số thế giới vào năm 2025.
9. Hình dưới đây là sơ đồ mạch điện đơn giản
trong đó gồm một nguồn phát điện, một tụ điện có điện dung C Farads (F), một điện
trở có trở kháng R Ohms ( ). Hiệu điện thế ở hai đầu tụ là Q=C , trong đó Q là Q
điện lượng (đơn vị Coulombs). Định luật Kirchhoff cho RI C D E.t/. Nhưng C I D dQ=dt, do đó ta có dQ 1 R C dt Q D E.t / C
Giả sử R D 5 , điện dung là C D 0:05 F và pin cấp điện năng 60 V, điện lượng lúc
đầu Q.0/ D 0 C. Tìm điện lượng trong tụ ở thời điểm t.
10. Trong Bài tập 9, R D 2 , C D 0:01 F, Q.0/ D 0 và E.t/ D 10 sin 60t. Tìm điện lượng ở thời điểm t.
11. Hàm số P .t/ là đại lượng đo mức độ thuần thục của một người đang thụ huấn một kỹ
năng nào đó, theo thời gian huấn luyện t. Đồ thị của P được gọi là đường cong rèn
luyện (learning curve). Người ta lập mô hình P .t/ như là nghiệm của phương trình vi phân dP D k M P .t /
trong đó k là hằng số dương, d
M tlà mức độ bão hòa của kỹ năng. Hãy giải phương
trình trên rồi vẽ đường cong rèn luyện.
12. Hai công nhân được nhận vào một dây chuyền lắp ráp. Jim gia công được 25 đơn vị
(trong 1 công đoạn của sản phẩm) trong giờ đầu và 45 đơn vị trong giờ tiếp theo.
Mark gia công được 35 đơn vị trong giờ đầu và 50 đơn vị trong giờ tiếp theo. Sử dụng
mô hình trong Bài tập 11, với giả thiết P .t/ D 0, hãy ước tính số đơn vị tối đa được
gia công trong một giờ mà mỗi công nhân có khả năng làm được.
Làm quen vài mô hình phương trình vi phân 91
5.2 Phương trình vi phân tuyến tính cấp 2 với hệ số hằng
5.2.1 Phương trình thuần nhất
Nhắc lại kiến thức. Phương trình vi phân tuyến tính cấp 2, thuần nhất, với hệ số hằng có dạng ay00 C by0 C cy D 0
trong đó a; b; c là các hằng số, a ¤ 0. Phương trình đặc trưng tương ứng là phương trình đại số ar2 C br C c D 0.
Cách tìm nghiệm tổng quát của phương trình thuần nhất như sau:
1. Nếu phương trình đặc trưng có nghiệm kép r0 thì phương trình thuần nhất có nghiệm tổng quát là yc D .c1 C c2x/er0x
với c1; c2 là hằng số tùy ý
2. Nếu phương trình đặc trưng có hai nghiệm thực phân biệt là r1 và r2 thì nghiệm tổng quát của là yc D c1er1x C c2er2x
3. Nếu phương trình đặc trưng có hai nghiệm phức liên hợp là r1 D ˛Ciˇ và r2 D ˛ iˇ
thì nghiệm tổng quát của là
yc D .c1 cos ˇx C c2 sin ˇx/e˛x Bài tập
1-13 Giải các phương trình vi phân sau 1. y00 y 6y D 0 9. y00 4y0 C 13y D 0 2. y00 C 4y0 C 4y D 0 10. y00 C 3y0 D 0 3. y00 C 16y D 0 d2y dy 4. y00 8y0 C 12y D 0 11. 2 C 2 dt2 y D 0 dt 5. 9y00 12y0 C 4y D 0 d2y dy 6. 12. 8 C 25y00 C 9y D 0 12 dt2 C 5y D 0 dt 7. y0 D 2y00 d2P dP 8. 13. 100 C 200 y00 4y0 C y D 0 dt2 C 101P D 0 dt
14-21 Giải bài toán điều kiện đầu (giá trị đầu)
14. 2y00 C 5y0 C 3y D 0; y.0/ D 3; y0.0/ D 4 92
Làm quen vài mô hình phương trình vi phân
15. y00 C 3y D 0; y.0/ D 1; y0.0/ D 3 16. 4y00 4y0 C y D 0; y.0/ D 1; y0.0/ D 1:5 17. 2y00 C 5y0 3y D 0; y.0/ D 1; y0.0/ D 4
18. y00 C 16y D 0; y. =4/ D 3; y0. =4/ D 4 19. y00 2y0 C 5y D 0; y. / D 0; y0. / D 2
20. y00 C 2y0 C 2y D 0; y.0/ D 2; y0.0/ D 1
21. y00 C 12y0 C 36 D 0; y.1/ D 0; y0.1/ D 1
22-29 Giải bài toán giá trị biên (the boundary-value problem), nếu được
22. 4y00 C y D 0; y.0/ D 3; y. / D 4
23. y00 C 2y0 D 0; y.0/ D 1; y.1/ D 2 24. y00 3y0 C 2y D 0; y.0/ D 1; y.3/ D 0
25. y00 C 100y D 0; y.0/ D 2; y. / D 5 26. y00 6y0 C 25y D 0; y.0/ D 1; y. / D 2 27. y00 6y0 C 9y D 0; y.0/ D 1; y.1/ D 0
28. y00 C 4y0 C 13y D 0; y.0/ D 2; y. =2/ D 1 29. 9y00 18y0 C 10y D 0; y.0/ D 0; y. / D 1
30. Cho L là số thực khác không.
a) Chứng minh rằng bài toán giá trị biên y00 C y D 0, y.0/ D 0, y.L/ D 0 chỉ
có nghiệm tầm thường (the trivial solution) khi 0. b) Khi
> 0, hãy tìm giá trị của
sao cho bài toán có một nghiệm không tầm
thường và tìm nghiệm đó.
31. Nếu a; b; c là ba hằng số dương và y.x/ là nghiệm của phương trình ay00Cby0Ccy D 0, chứng minh limy.x/ D 0. x!1
5.2.2 Phương trình không thuần nhất
Nhắc lại kiến thức. Phương trình vi phân tuyến tính cấp 2 không thuần nhất với hệ số hằng có dạng ay00 C by0 C cy D G.x/ (A)
Làm quen vài mô hình phương trình vi phân 93
trong đó a; b; c là các hằng số, a ¤ 0, G.x/ là hàm số cho trước. Phương trình (A) được
gọi là phương trình (vi phân tuyến cấp 2, hệ số hằng) không thuần nhất (nonhomogeneous
equation). Phương trình thuần nhất (complementary equation) tương ứng với (A) là ay00 C by0 C cy D 0 (C)
Nếu không xét điều kiện đầu (initial condition) thì cả phương trình (A) và (C) có một họ (vô
số) nghiệm có dạng tổng quát (general solution) lần lượt được ký hiệu là y và yc (chỉ số c
ám chỉ chữ complementary).
Cách tìm nghiệm tổng quát của phương trình (A) như sau:
1. Tìm nghiệm tổng quát yc của phương trình thuần nhất (C).
2. Tìm một nghiệm riêng yp của phương trình (A) theo trình tự sau
a) Nếu hàm G ở vế phải (A) có dạng đặc biệt thì sẽ có công thức đặc biệt cho yp (sẽ nói sau).
b) Nếu G D G1 C G2, trong đó G1 và G2 có dạng đặc biệt thì ta dùng nguyên lý
chồng chất nghiệm (sẽ nói sau) để tìm yp.
c) Nếu hàm G không có dạng đặc biệt thì dùng phương pháp biến thiên hằng số (sẽ nói sau) để tìm yp.
3. Nghiệm tổng quát của (A) là y D yp C yc.
Các dạng đặc biệt của hàm G ở vế phải phương trình (A) là
1. Nếu G.x/ D Pn.x/erx, trong đó Pn là đa thức bậc n thì ta có ba trường hợp phụ
a) Trường hợp r là nghiệm kép của phương trình đặc trưng thì yp D x2 Qn.x/erx,
Qn là đa thức bậc n được tìm theo phương pháp hệ số bất định (the method of
undetermined coefficients) khi thay y D yp vào (A).
b) Trường hợp r là một nghiệm đơn, thực, của phương trình đặc trưng thì yp D x Qn.x/erx.
c) Trường hợp r không phải là nghiệm của phương trình đặc trưng thì yp D Qn.x/erx. 2. N h ếu ai trường hợp phụ
G.x/ D e˛x Pn.x/ cos ˇx C Qm.x/ sin ˇx
thì ta đặt s D maxfm; ng và ta có
a) Trường hợp ˛ ˙ iˇ là nghiệm phức của phương trình đặc trưng thì yp D x s,e˛đxượ R
c tìm theo phương pháp hệ số bất định. s.x/ cos ˇx C Ts.x/ sin ˇx
, trong đó Rs và Ts là hai đa thức bậc
b) Trường hợp ˛ ˙ iˇ không là nghiệm phức của phương trình đặc trưng thì yp D
e˛x Rs.x/ cos ˇx C Ts.x/ sin ˇx . 94
Làm quen vài mô hình phương trình vi phân
Định lý 5.1: Nguyên lý chồng chất nghiệm-the principle of superposition
Giả sử yp và y lần lượt là nghiệm của hai phương trình 1 p2 ay00 C by0 C cy D G 00 0 1.x/ và ay C by C cy D G2.x/ thì y 00 0 p D yp C y
là nghiệm của phương trình ay C by C cy D G / C G /. 1 p2 1.x 2.x
Phương pháp biến thiên hằng số (the method of variation of parameters)
Giả sử nghiệm tổng quát của phương trình thuần nhất (C) có dạng yc.x/ D c1y1.x/ C
c2y2.x/, thì một nghiệm riêng của (A) là yp D u1.x/y1.x/ C u2.x/y2.x/, trong đó hai
hàm số u1 và u2 tìm được bằng cách giải hệ ( 1y1 C u02y2 D 0 u0
a.u01y01 C u02y02/ D G; (hệ số a trong phương trình (A)) Bài tập
1-10 Giải phương trình vi phân hoặc bài toán giá trị đầu với phương pháp hệ số bất định 1. y00 C 3y0 C 2y D x2 2. y00 C 9y D e3x 3. y00 2y0 D sin 4x
4. y00 C 6y0 C 9y D 1 C sin x 5. y00 4y0 C 5y D e x 6. y00 C 2y0 C y D xe x
7. y00 C y D ex C x3; y.0/ D 2; y0.0/ D 0 8. y00 4y D ex cos x; y.0/ D 1; y0.0/ D 2 9. y00 y0 D xex; y.0/ D 2; y0.0/ D 1 10. y00 C y0 2y D x C sin 2x; y.0/ D 1; y0.0/ D 0
11-16 Viết dạng nghiệm cho phương pháp hệ số bất định, không tính giá trị của hệ số
11. y00 C 9y D e2x C x2 sin x 14. y00 C 3y0 4y D .x3 C x/ex
12. y00 C 9y D xe x cos x
15. y00 C 2y0 C 10y D x2e x cos 3x 13. y00 C 9y D 1 C xe9x
16. y00 C 4y D e3x C x sin 2x
17-20 Giải phương trình vi phân bằng cách dùng (a) hệ số bất định và (b) biến thiên hằng số
Làm quen vài mô hình phương trình vi phân 95 17. y00 C y D cos x 19. y00 2y0 C y D e2x 18. y00 2y0 3y D x C 2 20. y00 y0 D ex
21-26 Giải phương trình bằng cách dùng phương pháp biến thiên hằng số 21. 1 y00 C y D ; 0 < x <
24. y00 C 3y0 C 2y D sin.ex/ cos2 x 2 ex 22. 1 25. y00 2y0 C y D y00 C y D ; 0 < x < cos3 x 2 1 C x2 23. 1 y00 3y0 C 2y D 26. e 2x y00 C 4y0 C 4y D 1 C e x x3
5.3 Phương trình vi phân toàn phần
Nhắc lại kiến thức. Phương trình vi phân toàn phần (hay phương trình vi phân khớp) là phương trình có dạng P .x; y/ y0 D
hoặc P .x; y/dx C Q.x; y/dy D 0 Q.x; y/ @P @Q
trong đó P và Q là các hàm số hai biến thuộc lớp C 1 và thỏa D . Cách giải là tìm @y @x một hàm hai biến f thỏa @f @f D P và @x D Q: @y
Khi đó phương trình f .x; y/ D C , với C là hằng số tùy ý, xác định nghiệm y như một ẩn hàm theo x. Bài tập 2 C yexy 1. 2xy y0 D . 3. y0 D . 1 C x2 2y xexy x2 C y C 1 2. y2 y0 D . 4. y0 D . 2xy C 1 x C y C y3
5. Một phương trình tích phân là một phương trình chứa một ẩn hàm y.x/ và một tích
phân chứa y.x/. Giải phương trình tích phân sau. (Hướng dẫn: Lấy đạo hàm và sử
dụng một điều kiện đầu thu được từ phương trình tích phân.) Z x Z x p a) 2 0 y.x/ D 2 C Œt ty.t / dt . b) y.x/ D 4 C 2t y.t /dt .




