Bài tập Giải tích 1 - Giới hạn, Liên tục và Đạo Hàm. Môn Giải tích 1 (GT01) | Trường Đại học Giao thông Vận tải.
Bài tập Giải tích 1 - Giới hạn, Liên tục và Đạo Hàm. Môn Giải tích 1 (GT01) | Trường Đại học Giao thông Vận tải.
Tài liệu gồm 12 trang giúp bạn tham khảo, củng cố kiến thức và ôn tập đạt kết quả cao trong kỳ thi sắp tới. Mời bạn đọc đón xem!
Môn: Giải tích 1 (GT01) 20 tài liệu
Trường: Đại học Giao thông vận tải 307 tài liệu
Tác giả:
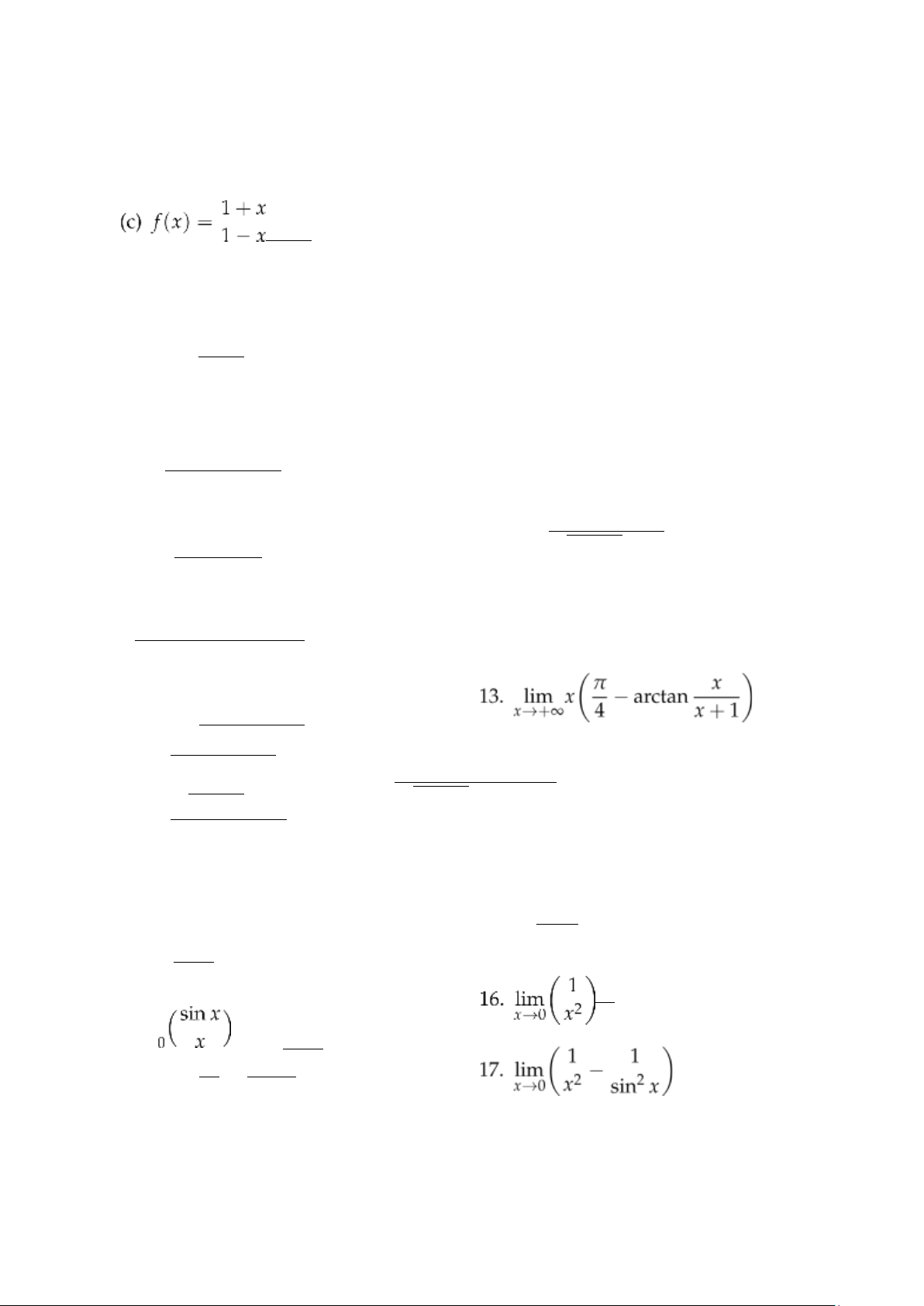
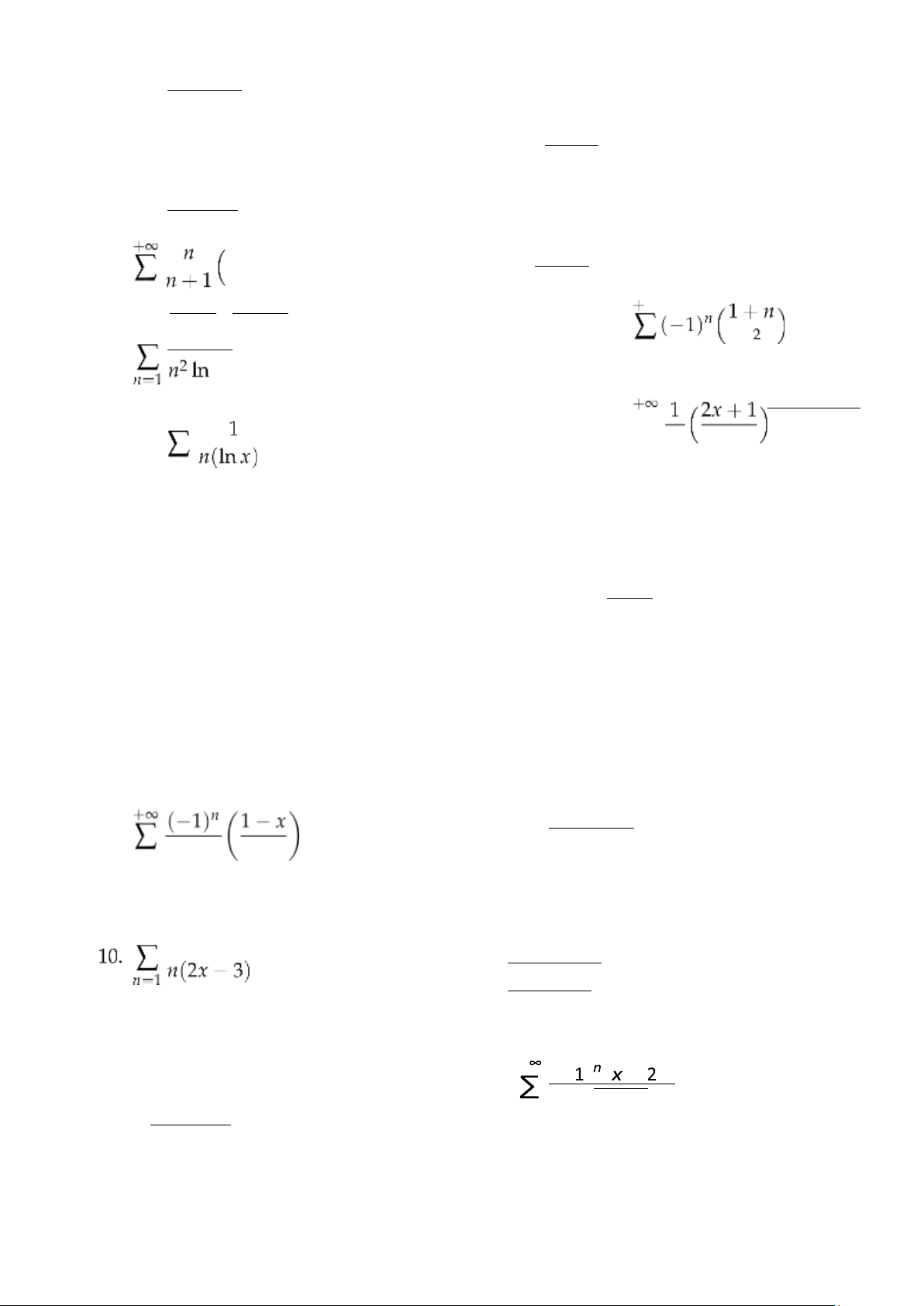
Preview text:
lOMoAR cPSD| 58833082
BÀI TẬP GIẢI TÍCH 1 Năm học 2021 - 2022
Chương 1. Giới hạn và liên tục
Bài 1. Tính giới hạn
1. lim (√x2 + 2x + 5 − x) 12. lim √ex − cos x . x→+∞ x→0 1 + 2x − 1 √ √
2. x→−lim∞√( x2 − 5√x − 1−
x2 + 3x + 3) 13. xlim→0 √4 11+−4cosx2 −x 1.
cos x − 3 cos x
3. xlim→0 sin2 x 14. I = lim 1 − cos5x .
x→0 ln(1 + x sin x) √ √ √ − √ 4. → 1 − − − cos x. cos2x
15. I = xlim→0 sin2 x . + 5. → − + 16. lim(1 − x) tan πx √ x→1 2 p + √ → + + x x 7. lim x x→∞ √x2
1 + 2x2 − cos x 8. xlim→0 x2 √ √x 5 − 4 + cos x 9. xlim→0 x2
21. lim(1 + sin πx)cotπx 2x − x2 x→1 1 lOMoAR cPSD| 58833082
10. xlim→2 x − 2 22. lim(1 − 2x2)cot2 x x→0 ex3 − 1 + x2 px √ 11. lim
23. lim cos x x→0 x tan x x→0+
Bài 2. Vô cùng bé, vô cùng lớn 1. So sánh các VCB sau:
(a) f(x) = 1 − cos2x và g(x) = x khi x → 0.
(b) f(x) = ln (1 + sin x) và g(x) = 2x khi x → 0. √ √
(c) f(x) = 1 + x −
1 − x và g(x) = x2 khi x → 0. πx
(d) f(x) = x − 1 và g(x) = cot khi x → 1. 2
(e) f(x) = 1 − cos2 x và g(x) = ln(1 + x2) khi x → 0. √ √
(f) f(x) = 1 + x −
1 − x và g(x) = sin x khi x → 0. 2 1 1 (g) f(x) = cos − cos và g(x) =
khi x → ∞. x x x 1
(h) f(x) = x.cos
và g(x) = x khi x → 0. x
2. So sánh các VCL f(x) = ex + e−x, g(x) = ex − e−x khi
(a) x → +∞. (b) x → −∞.
3. Tìm phần chính dạng Cxα khi x → 0 của VCB: √
(a) f(x) = 1 − 2x − 1 + x.
(b) f(x) = tan x − sin x..
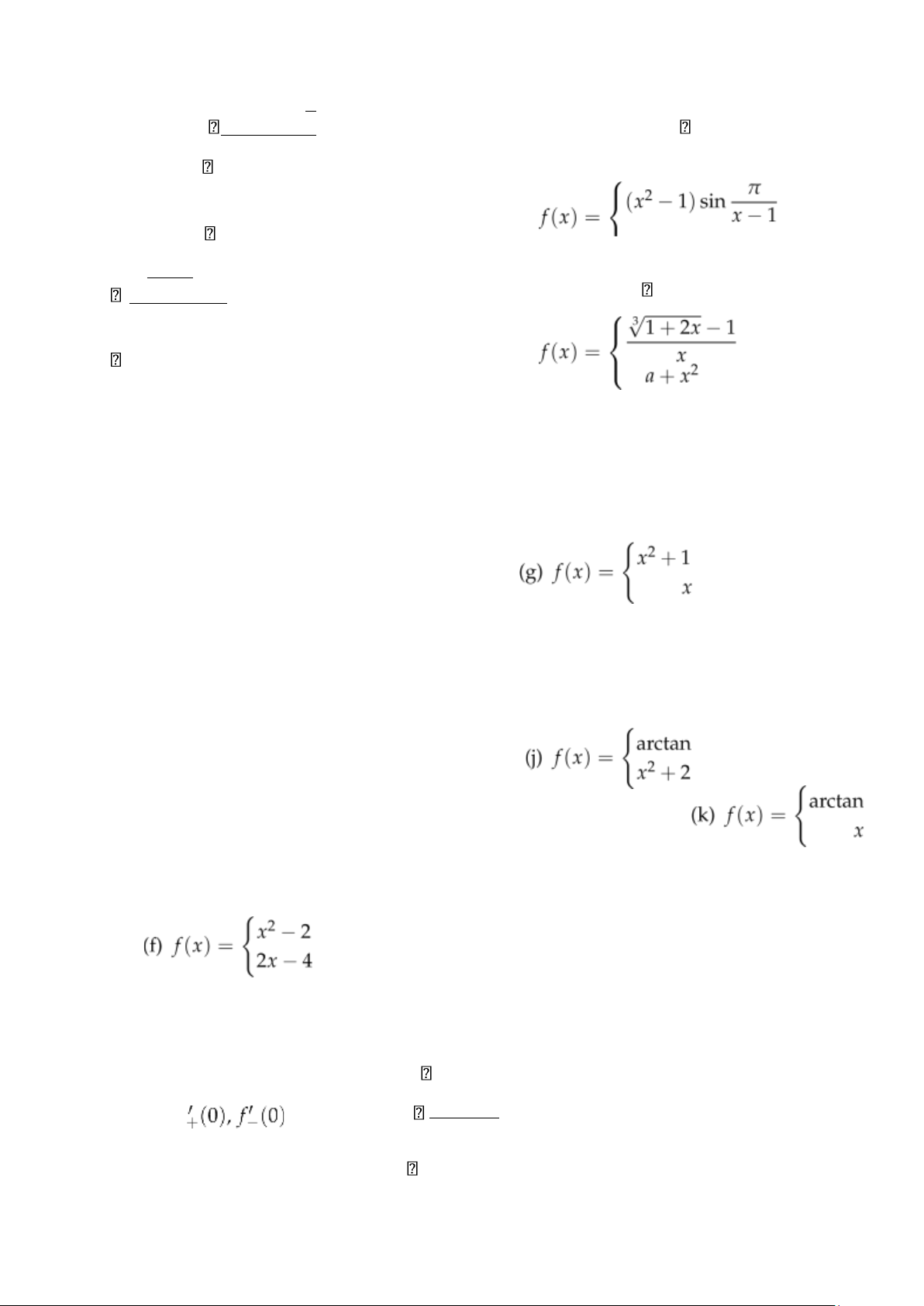
Bài 3. Xét tính liên tục 2x a với x 6= 0 với 4. f 1. f(x) =
e2x − e−x x = 0 nếu x 6= 1 2.5. a nếu x = 1 √ 2 lOMoAR cPSD| 58833082 1 − cos x > nếu x > 0 3. f(x) = x 6. nếu x 6= a nếu x ≤ 0 √ 1 a nếu x = 1 1 + x − 1 (x) = x nếu x 0 nếu x ≤ 0
nếu x > 0 nếu x a + 2cos x ≤ 0
Chương 2. Đạo hàm và vi phân với x ≤ 2, 9 − 2 với x > 2.
Bài 1. Tính đạo hàm 1. Tính đạo hàm ( 2x2 + 3x nếu x ≤ 0, của các hàm số sau:
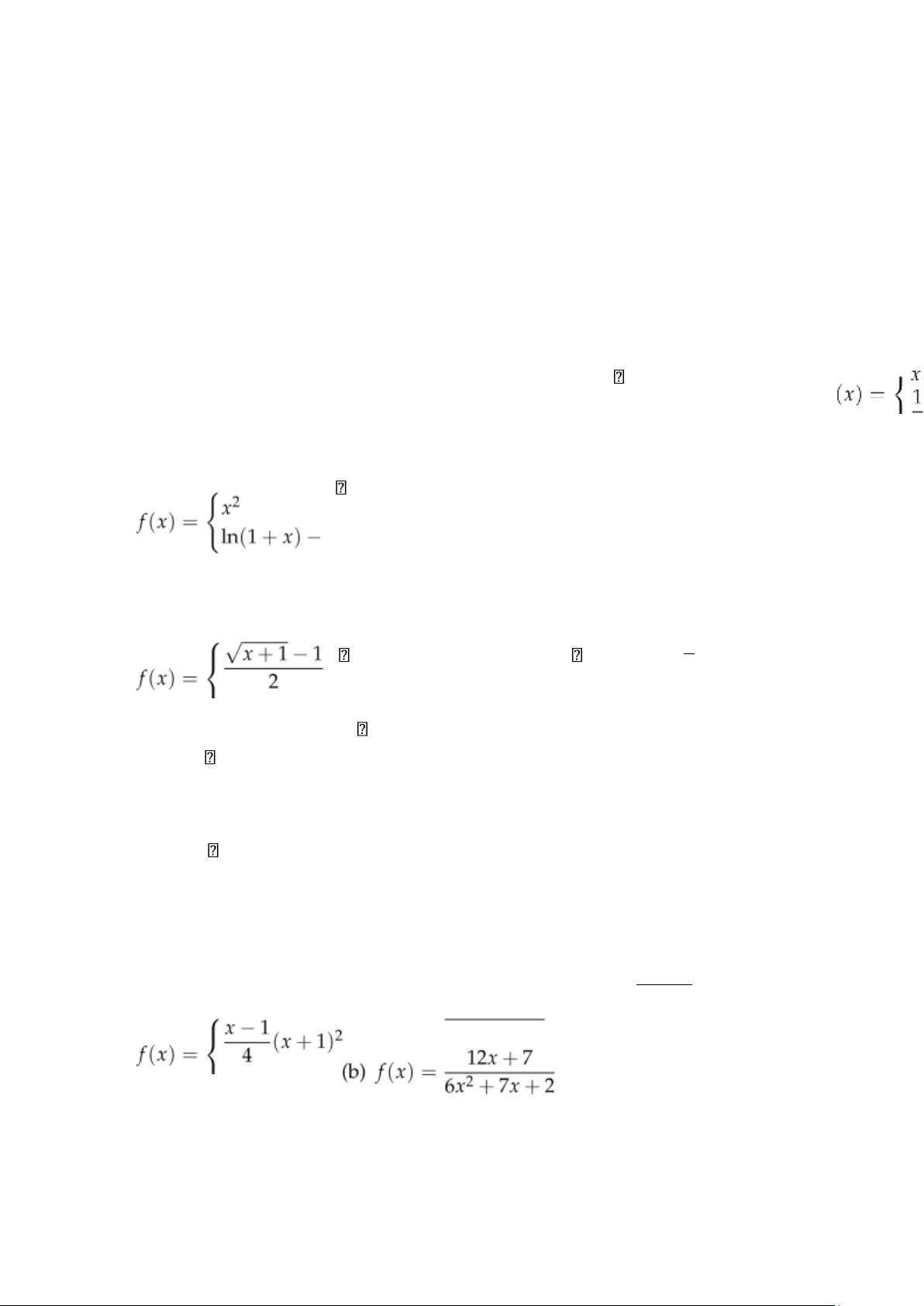
f(x) = ln(1 + x) −
(a) y(x) = x|x|.
x nếu x > 0.
(b) y(x) = |(x − 1)2(x + 1)|. ( x − 1 nếu x ≤ 0,
(c) y(x) = |(x + 1)2(x + 2)3|. (h) 2
f(x) = ln(1 + x) nếu x > 0. ( x(x + 1)2 với x ≥ 0,
x − x nếu x < 0, x
(d) f(x) = −x(x + 1)2 với x < 0. (i) nếu x ≥ 0. ( x với x ex với x < 0, ≥ 0 x2 (e) f(x) = + với x < 0 1 + x với x ≥ 0.
x nếu x < 2 nếu x ≥ 2 2.
Tính y0(0) bằng định nghĩa. Biết:
y = x(x − 1)(x − 2)...(x − 2020)(x − 2021) x
1/x nếu x 6= 0 3. Tính
fcủa: f(x) = 1 + e 0 nếu x = 0 3 lOMoAR cPSD| 58833082
4. Tính y0(x), y00(x) của hàm số cho dưới dạng tham số:
( t cos2t x = e ( (
t x = a(t − sin t)
x = t + e (a)
t sin2t y = e (c) (e)
2 + 2t3 y = a(1 − cos t) y = t ( 3 t x = a cos (b) 3 t y = a sin
( t cos t x = 2e (d)
t sin t y = 3e
Bài 2. Xét tính khả vi
1. y = (x + 2)|x − 1|.
6. Xét tính khả vi tại x = 1 của hàm số: ( 2 1 − cos x
nếu x ≤ 02e1−x nếu x ≤ 1 2. f(x) =
ln(1 + x) nếu x > 0 y
nếu x > 1 x nếu x ≤ 0 3. x nếu x > 0
7. Xét tính khả vi tại x = 0 của hàm số: 2 arctan 1
nếu x 6= 0 x nếu x > 0 f(x) = x 4. 0 nếu x = 0 0 nếu x ≤ 0
8. Tìm a, b để hàm số sau khả vi trên R x − 1 nếu x < 1 ax + b nếu x ≥ 2
Bài 3. Đạo hàm cấp cao
1. Tính đạo hàm cấp n của hàm số x − 1 √ ( ) =
(d) f(x) = ln 3 1 − 4x. ( nếu x ≥ 1 x2 − 3x + 4 nếu x < 2 5.f(x) = 4 lOMoAR cPSD| 58833082 (a) f x x2 + 5x + 6.
(e) f(x) = cos4 x + sin4 x. .
(f) f(x) = e2x(3x + 5). .
(g) f(x) = (2x + 1) sin x.
2. Cho hàm số f(x) = ln(1 − 3x). Tính f(n)(0). 3. Cho y = x4 . Tính d4y. 2 − x
Bài 4. Áp dụng quy tắc L’Hospital, tính giới hạn ln(1 + x) − x
10. lim x(π − 2arctan x) 1. lim x→+∞ 2 x→0 x x − sin x ex − 1 − x
11. lim √ x→0 1 + 2x − ex 2. lim x→0
12. lim x2 ln x x→0+ x.sin x
4arctan(1 + x) − π 3. lim x→0 x arctan x − x 4. xlim→0
x3 e2x − 1 − 2x 5. xlim→0 2x2 . 14. xlim→0
√5 1 + 5xx−2 (1 + x) √ 1 + 2x − ex 6. lim 2 . x2017 x→0 x 15. lim ln3 x x x→+∞ e 7. lim
x→+∞ xsinx 1/x2 8. lim x→ 9. lim (sin x)tan2x x→0+ 5 lOMoAR cPSD| 58833082
Chương 3. Tích phân
Bài 1. Ứng dụng của tích phân xác định 1.
Tính độ dài của các đường cong sau:
(a) y = ln x, với 1 ≤ x ≤ e.
(f) x2/3 + y2/3 = a2/3, a > 0.
(b) y = ex, 0 ≤ x ≤ 1.
(g) r = a(1 + cos ϕ), a > 0.
x; 1 ≤ x ≤ e.
(h) y = arcsin (e−x) ; 0 ≤ x ≤ 1 (i) r = 2 y, 1 ≤ y ≤ e. ϕ, 0 ≤ ϕ ≤ 2π. ≤ ≤ 1 (
x = a(t − sin t) (e)
; 0 y = a(1 − cos t).
2. Tính diện tích hình phẳng giới hạn bởi: x2
(a) y = x2 − 1 và y = 3 − x2.
(e) y = x2, y , y = 2x. x2 y2
(b) y = 1 + 2x − x2 và y = 3 − x.
(f) (E): a2 + b2 = 1.
(c) y = x3, y = 4x.
(g) r = a(1 + cos ϕ); 0 ≤ ϕ ≤
(d) x + y = 0; y = 3x − x2. 2π, a > 0. (l) Một cung (một nhịp) Xicloit (
(h) y = x2, y = 4x2, y = 4.
x = a(t − sin t)
(0 ≤ t ≤ 2π)
(i) (x2 + y2)2 = a2(x2 − y2). y = a(1 − cos t) √ (j) y = −
4 − x2 và x2 + 3y = 0. và trục Ox.
(k) y = 4 − x2 và y = 2x + 1. (m) y = x3 (x ≥ 0), y = x và y = 2x.
3. Tính thể tích của vật thể tạo thành khi quay hình phẳng giới hạn bởi:
(a) y = 2x − x2, y = 0 quanh trục Ox.
(b) y = 4x − x2 và y = x quay quanh trục Ox.
(c) y = x2 và x = y2 quanh trục Ox. 6 lOMoAR cPSD| 58833082
(d) x2/3 + y2/3 = a2/3, a > 0 quanh trục Ox.
(e) x2 +(y − 2)2 = 1 quanh Ox. √
(f) y = x, x = 0, y = 1 − x2 quanh trục Oy.
(g) y = ln x, y = 0, x = e, quay quanh trục Ox.
(h) x2 + y2 = 4x − 3 quanh trục Oy.
(i) x = y2 − 4 và x = 0 quanh trục Oy. (j) y2 + x = 9 và x = 0 quanh trục Oy. x2 x3 (k) y = và y quanh trục Ox. 2 x2 y2 +
(l) 2 b2 ≤ 1 quanh trục Oy. a
Bài 2. Tính các tích phân suy rộng +∞ +∞ Z dx dx Z √ x x2 1. 6. x2(x + 2) − 1 1 2 dx
2. 7.x√4 1 + x3 1 +∞ xdx Z ln x 3. 8. 2 dx x 1 +∞ Z dx 4. √ 9.. x x4 + 1 1 arctan x 5. (√x + 1)3 x2 dx 0 1 +∞ Z √ 11. e− xdx. 7 lOMoAR cPSD| 58833082 Z x3 12. x2dx 1 e 1 Z √ +∞ x ( − ) − Z 13.
x2e−xdx Z x 14. p 2)3dx . (1 + x 0 + Bài 3.
Xét sự hội tụ của tích phân suy rộng Z √ 1.dx + 6. √ dx x x 1 + √ Z xdx 7. 2. x2 + sin x 1 dx 3. dx 8.. 4. 2√ dx x 1 9. +∞ Z arctan x x 5. dx x p d Z x x 8 lOMoAR cPSD| 58833082 1 14. + tan x − sin x x 0 1 1 √ 1 Z Z dx 15. e 11. √ sin2x − 1dx 0 tan x 1 √ 0 Z sin x 1 √ 16. √3 2 dx Z 0 e x − 1 12.
esinx − 1dx 1 √ 0 Z ln(1 + x) 1 Z 17.
esinx − 1 dx dx 0 13. e√4 x − 1 1 √ 0 Z 1 − cos x 1 Z 18. √ dx x x xdx 0 1 √ 1 √ Z x Z e x − 1 19.dx 20.dx x 0 Chương 4. Chuỗi
Bài 1. Xét sự hội tụ của chuỗi số +∞ 1. + √ n = 2. +∞ 1)n2 9 lOMoAR cPSD| 58833082 n=1 n= nn 1n 1 n +∞ ln(n + 1) 3. n=1 3 + n2 + 2 12. ∑ 3 n n=1 n n ∞ n 4. n=2 2 − 1 n=1 n n 5. +∞ nn n 14. +∑∞ 1k
n=2 n.ln n 6. n n
n=1 2.5.8...(3n − 1) n=2 n2 − 1
+∞ 3n.n!n 7. n∑=1 nn n=1 2n + 7 n2n 8. n∑=1 2n 1 + n + 1 n3 n=1 +n 9. ∑
1 . n ln(n2 + 1)
6. n=1 ln(n + 1) n=1 10 lOMoAR cPSD| 58833082 nn=1 n + 1
Bài 2. Xét sự hội tụ tuyệt đối, hội tụ tương đối +∞ πn2 (n + 1)(n + 2)
n + 1 n=1 1. 4. ∑ n=1 sin n 2. n=1 n=1 5. n! n n n 7. n=1
Bài 3. Tìm miền hội tụ của chuỗi hàm
+∞ (−4)n arcsinn x +∞ (x + 1)2n 1. ∑ 12. ∑ n(n + n4 1) n n=0 π n=1 x n2n n 1 n 2n 2. = 1 n=1 +∞ n2n (− ln x)n x + 1 3. ∑
+∞ (x − 1)2n 13. 2n + 1 n=1 14. ∑ n9n n=1 +∞ n 2 ( − ) 11 lOMoAR cPSD| 58833082 4. (−1)n n enx +∑∞ (−2)n n 15. n x +∞ n=1 nπ x 16. ∑ n2 + 6. n 1xn n=1 2x + 1 n=1 7.n x +∞ (x + 1)n 5. n +∞ ln n n=1 n=1 ∞ +∞ 1 17. n xn ∑ n
18. n∑=1 n(2n + 1) 8. n=1 n x + 2 2 2
n +∞ (−1)nxn
9.19. n∑=1 n(2n + 1) n=1 2n + 1 1 + x +∞ (−1)n 20. ∑+n=∞1 2
(nx(n−+1)2n) n + +
∞ (x − 1)2nn ( − ) ( + ) 11. ∑ n 21. √ 2 + 1 n=1 n4 n=0 n 12