Ôn Tập Về Hàm Một Biến - Giới Hạn và Tính Liên Tục - Giải Tích 1. Môn Giải tích 1 (GT01) | Trường Đại học Giao thông Vận tải.

lOMoAR cPSD| 58833082
TRƯỜNG ĐẠI HỌC GIAO THÔNG VẬN TẢI THÀNH PHỐ HỒ CHÍ MINH
KHOA CƠ BẢN – BỘ MÔN TOÁN
BÀI GIẢNG GIẢI TÍCH 1
CHƯƠNG I. GIỚI HẠN VÀ SỰ LIÊN
TỤC CỦA HÀM MỘT BIẾN
§0. Ôn tập về hàm số một biến số thực
ThS. Đinh Tiến Dũng
Downloaded by Trang Lê (letrang23091909@gmail.com) lOMoAR cPSD| 58833082
Giới thiệu giảng viên
• ThS: Đinh Tiến Dũng
• SĐT: 0793112122 (Zalo)
• Mail: dung.dinh@ut.edu.vn lOMoAR cPSD| 58833082
Giới thiệu học phần
Học phần này cung cấp các kiến thức cơ bản về giới hạn và sự liên tục
của hàm một biến, phép tính vi phân hàm một biến (đạo hàm, vi phân,
ứng dụng), phép tính tích phân hàm một biến (tích phân bất định, tích
phân xác định, ứng dụng tích phân xác định, tích phân suy rộng), phép
Downloaded by Trang Lê (letrang23091909@gmail.com)
tính vi phân hàm nhiều biến (đạo hàm, vi phân hàm nhiều biến, cực trị hàm nhiều biến).
Đây là phần kiến thức cần thiết để sinh viên tiếp thu các học phần khác
trong tất cả các chuyên ngành kinh tế, kỹ thuật. lOMoAR cPSD| 58833082
TÀI LIỆU THAM KHẢO
• [1] Bộ môn Toán, Bài giảng giải tích 1 (lưu hành nội bộ), Trường
đại Học GTVT TP.HCM, 2019
• [2] Đỗ Công Khanh (chủ biên), Toán cao cấp – Giải tích hàm nhiều
biến và phương trình vi phân, NXB. ĐHQG. TPHCM, 2010.
• [3] Nguyễn Đình trí (chủ biên), Giáo trình Toán cao cấp, tập 1, tập
2 . NXB Giáo dục, Hà nội, 2005.
• [4] Jean – Marie Monier, Giáo trình Toán, Tập 1, 2, 5. NXB Giáo
dục, Hà nội, 2006 (dịch từ tiếng Pháp, DUNOD, Paris, 1996).
• [5] George B.Thomas,
Jr.Thomas’Calculus,twelfth edition, Pearson, 2010.
Downloaded by Trang Lê (letrang23091909@gmail.com) lOMoAR cPSD| 58833082 NỘI DUNG CHÍNH
Bài 1. Hàm số một biến số thực (hàm số và đồ thị hàm số, các
phép toán đối với hàm số, hàm hợp, hàm ngược, hàm số sơ cấp).
Bài 2. Giới hạn của hàm một biến (định nghĩa giới hạn hàm số,
các quy tắc, giới hạn một phía, tính chất của giới hạn.
Bài 3. Vô cùng bé và vô cùng lớn.
Bài 4. Tính liên tục của hàm một biến (các định nghĩa về hàm
liên tục; sự gián đoạn). lOMoAR cPSD| 58833082
CHƯƠNG I. GIỚI HẠN VÀ SỰ
LIÊN TỤC CỦA HÀM MỘT BIẾN
§1. Hàm số một biến số thực
1.1 Hàm số và đồ thị của hàm số
Định nghĩa và cách xác định hàm số •
Cho tập hợp khác rỗng ⊂
. Hàm số đi từ vào là một
quy tắc biến mỗi
thành một phần tử duy nhất ∈ .
• Cách xác định và ký hiệu hàm số: Cách 1:
Xác định hàm số bởi công thức .
Cách 2: Xác định hàm số kiểu ánh xạ (chỉ rõ tập xác định ) : . ⟼ =
Downloaded by Trang Lê (letrang23091909@gmail.com) lOMoAR cPSD| 58833082
Cách 3: Xác định hàm số bằng cách cho bảng giá trị. lOMoAR cPSD| 58833082
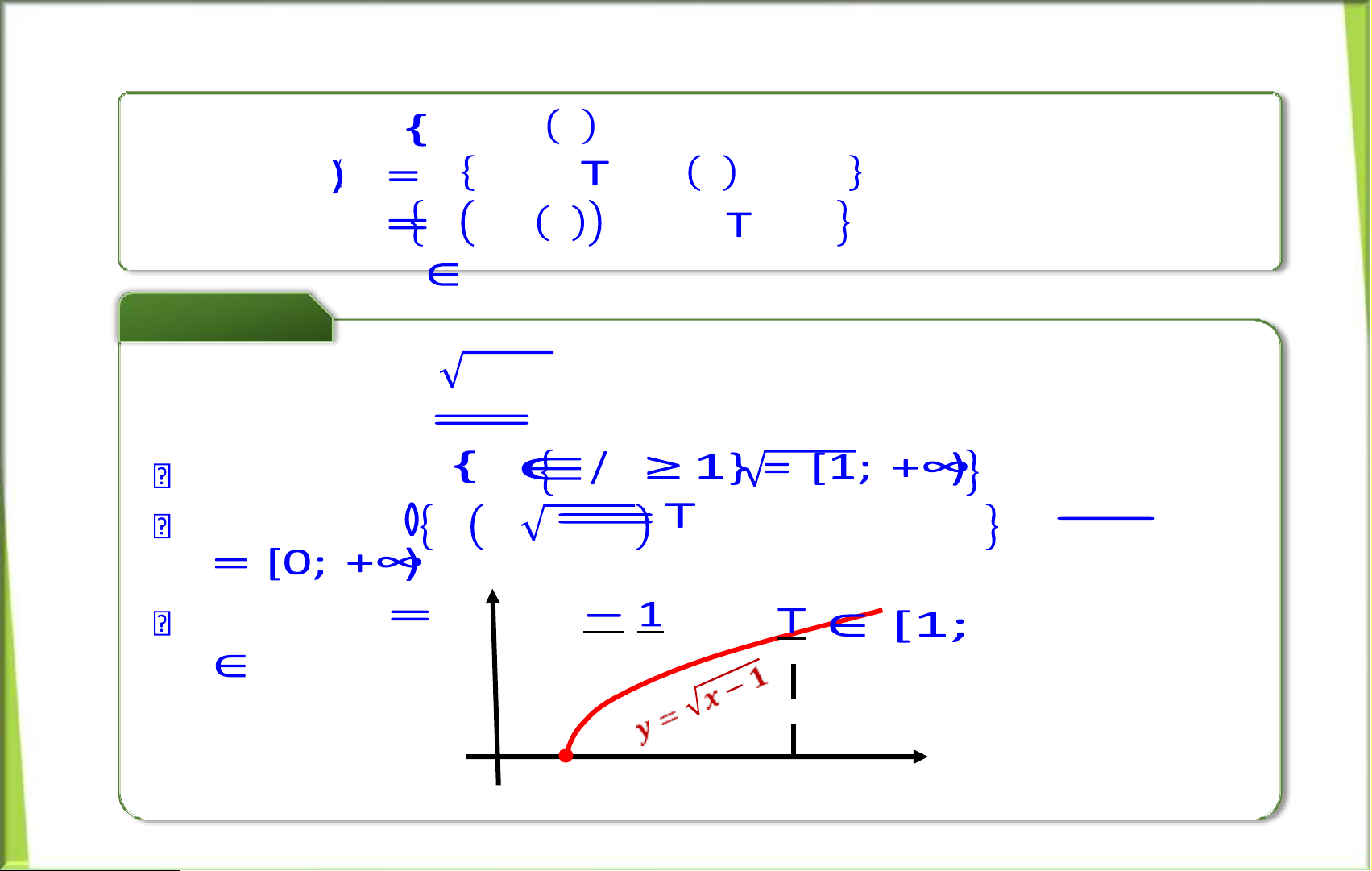
• Tập hợp =
xác định} gọi là tập xác định hàm số.
• Tập hợp ∈
gọi là tập giá trị hàm số. • Tập hợp , ∈
gọi là đồ thị hàm số. Ví dụ Cho hàm số . Ta có: Tập xđ: . = Tập giá trị = . Đồ thị ,
Downloaded by Trang Lê (letrang23091909@gmail.com) lOMoAR cPSD| 58833082 lOMoAR cPSD| 58833082
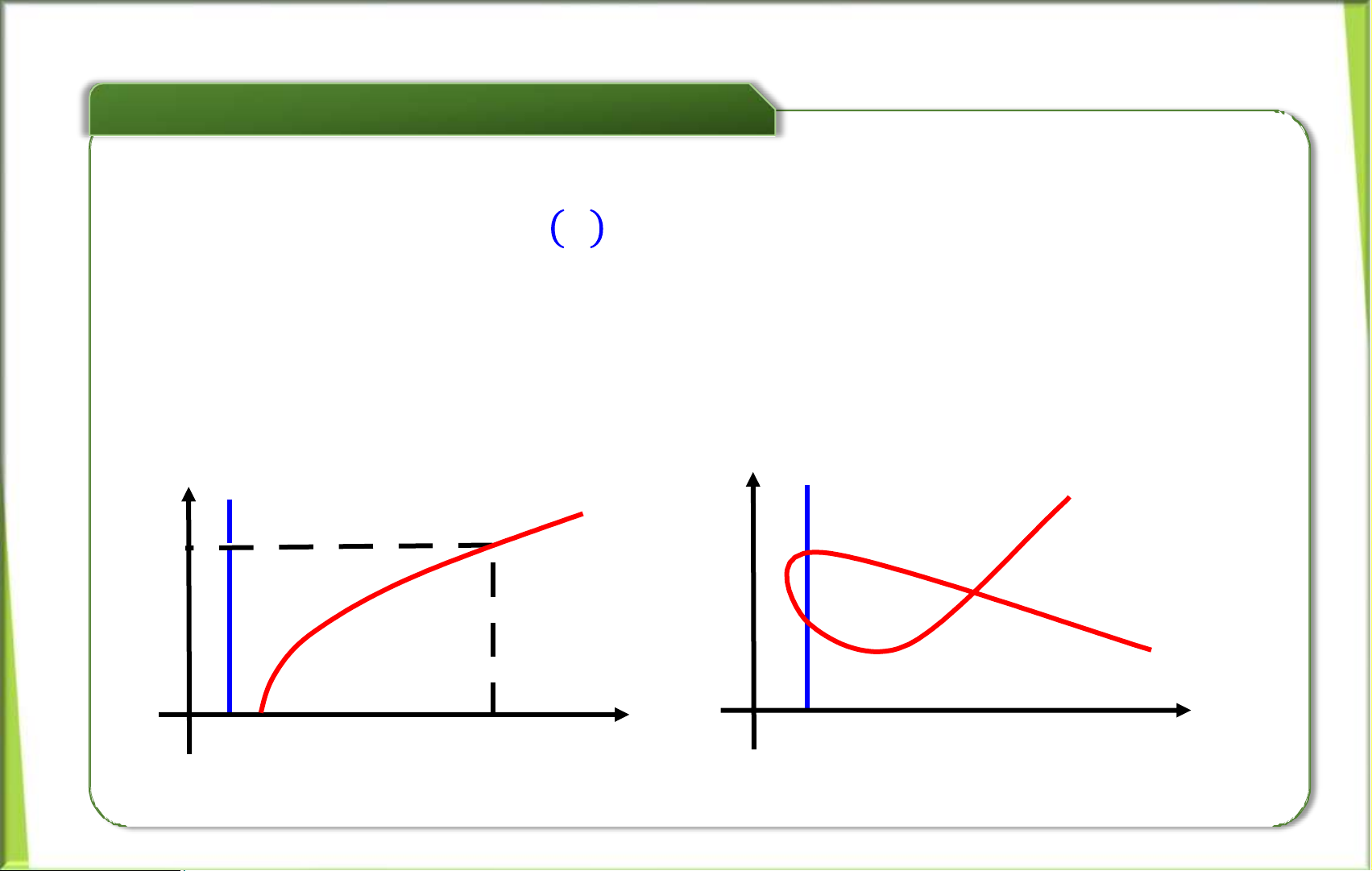
b) Tiêu chuẩn đường thẳng đứng
• Với mỗi giá trị = thuộc tập xác định ta chỉ xác định được duy nhất
một giá trị = , nên mỗi đường thẳng đứng = chỉ cắt đồ thị hàm số
= () một điểm duy nhất.
• Đây là tiêu chuẩn để nhận biết một đường cong có phải là đồ thị của
một hàm số hay không. = = lOMoAR cPSD| 58833082
Đường cong này là đồ thị hàm số
Đường cong này không phải là đồ thị hàm số nào lOMoAR cPSD| 58833082
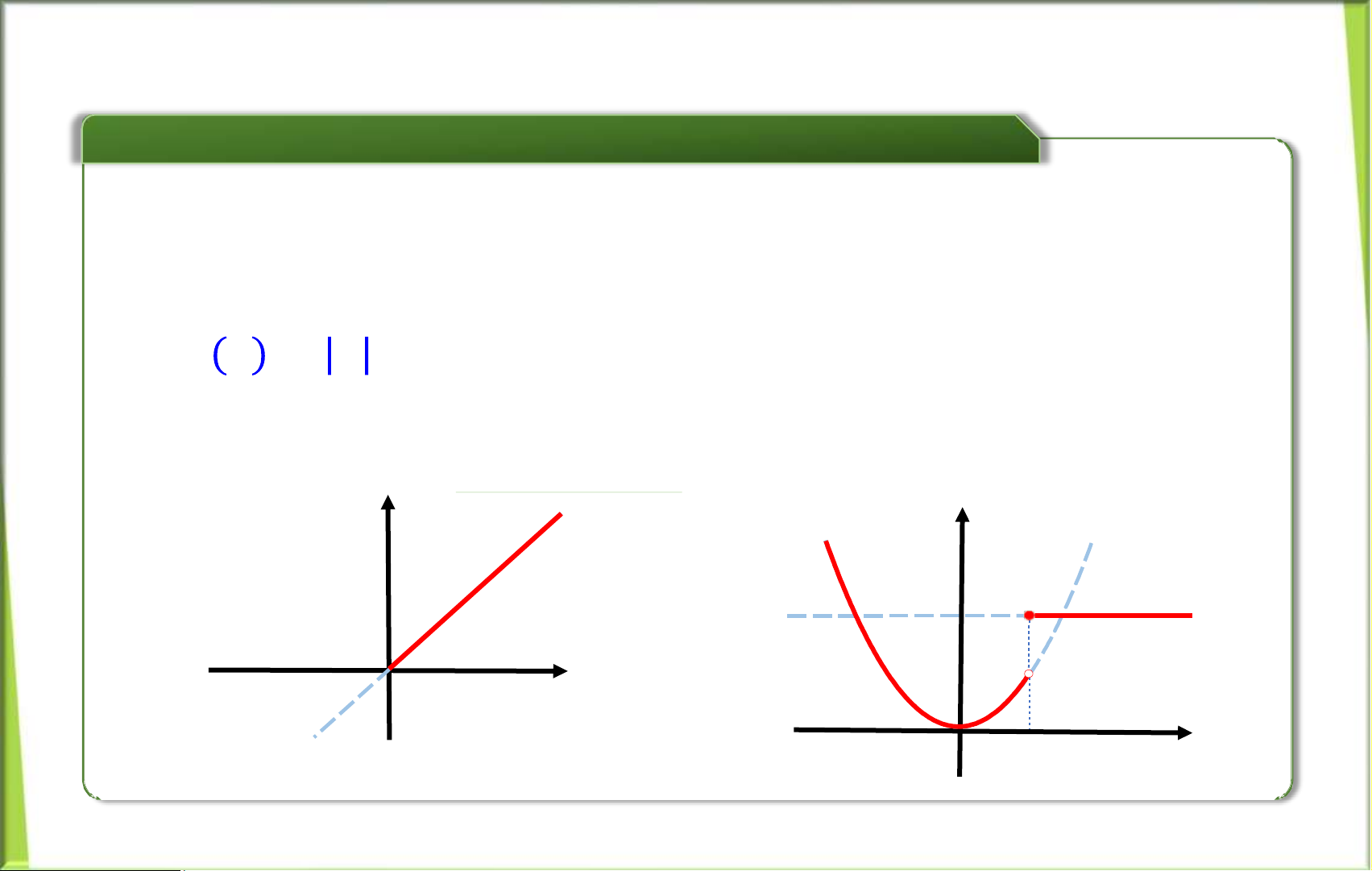
c) Hàm xác định từng khúc (Hàm nhiều công thức)
Đó là những hàm số được mô tả bằng nhiều công thức khác
nhau trên những miền khác nhau của đối số. a) ൜
Ví dụ: = = ế 0 , ; ≥
b) g൜ () = 2, ế < .1 − ế , < 0 2, ế ≥ 1
= − (Đồ thị hàm số , < )
= = ( |, | ≥ = Đồ thị hàm số , ( < )
= =( ) , ) lOMoAR cPSD| 58833082 lOMoAR cPSD| 58833082
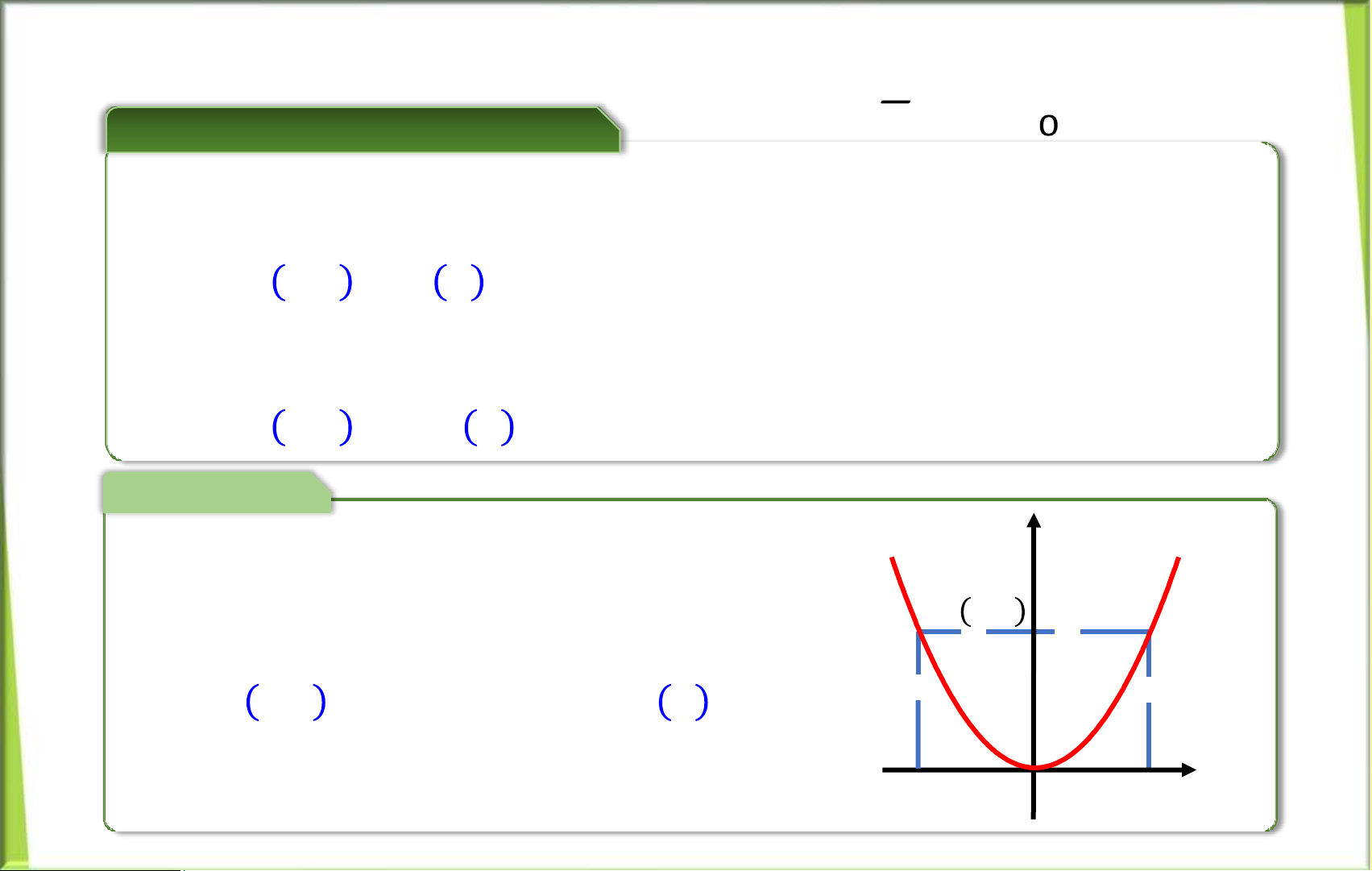
d) Hàm số chẵn, hàm số lẻ Hàm = ()
gọi là hàm chẵn theo nếu thoả 2 điều kiện:
• có txđ là tập đối xứng, tức là: ∀ ∈ ⇒ − ;
• − = , ∀ ∈ .
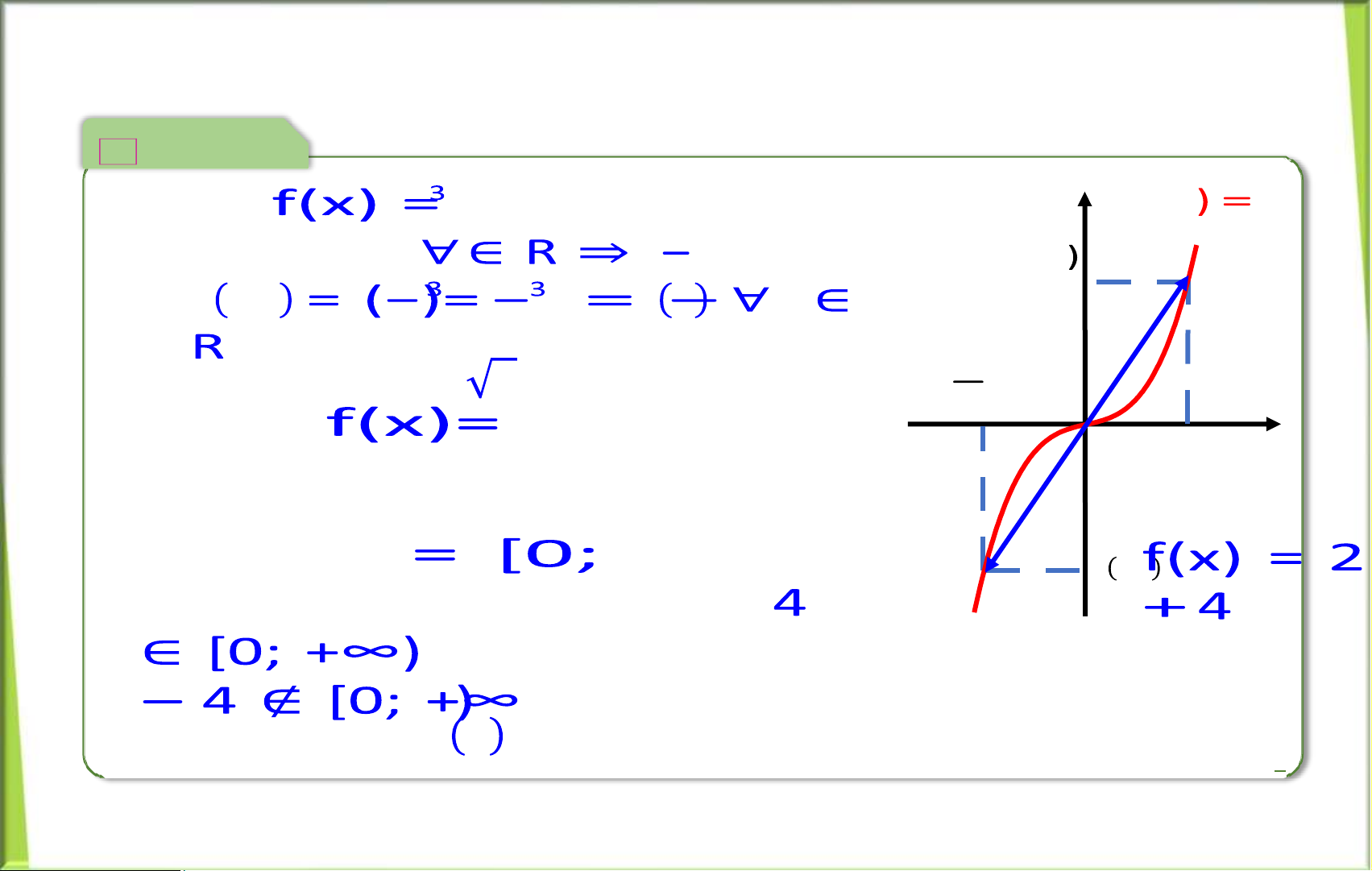
Hàm = () gọi là hàm lẻ theo nếu thoả 2 điều kiện:
• có txđ là tập đối xứng, tức là: ∀ ∈ ⇒ − ∈ ;
• − = − , ∀ ∈ . Ví dụ () = a) Hàm f(x) = 2 là hàm chẵn vì:
− = ()
• có txđ = và ∀ ∈ R ⇒ − ∈ ; • − = (−)2 =2 = , ∀ lOMoAR cPSD| 58833082 ∈ . lOMoAR cPSD| 58833082 lOMoAR cPSD| 58833082 Ví dụ b) ( Hàm là hàm lẻ vì: • có txđ và . ( • − , . c) Hàm khôngchẵn, không lẻvì: d) Hàm cóTXĐ không
đối xứng bởi tồn tại nhưng không . chẵn, không lẻ vì: lOMoAR cPSD| 58833082 (−1) = 2 ≠ 1 = 6 ≠ 0 −(1) = −6 −