CHƯƠNG 1: HÀM SỐ, GIỚI HẠN VÀ SỰ LIÊN TỤC - BÀI GIẢNG 2023. Môn Giải tích 1 (GT01) | Trường Đại học Giao thông Vận tải.
CHƯƠNG 1: HÀM SỐ, GIỚI HẠN VÀ SỰ LIÊN TỤC - BÀI GIẢNG 2023. Môn Giải tích 1 (GT01) | Trường Đại học Giao thông Vận tải.
Tài liệu gồm 56 trang giúp bạn tham khảo, củng cố kiến thức và ôn tập đạt kết quả cao trong kỳ thi sắp tới. Mời bạn đọc đón xem!
Môn: Giải tích 1 (GT01) 20 tài liệu
Trường: Đại học Giao thông vận tải 307 tài liệu
Tác giả:
Preview text:
lOMoAR cPSD| 58833082
H ỌC PH N TOÁN GT Ầ 1
CHƯƠNG 1: HÀM SỐ, GIỚI HẠN VÀ SỰ LIÊN TỤC
CHƯƠNG 2: PHÉP TÍNH VI PHÂN
CHƯƠNG 3: PHÉP TÍNH TÍCH PHÂN
CHƯƠNG 4: VI PHÂN HÀM NHIỀU BIẾN
CHƯƠNG 1: HÀM SỐ, GIỚI HẠN VÀ SỰ LIÊN TỤC
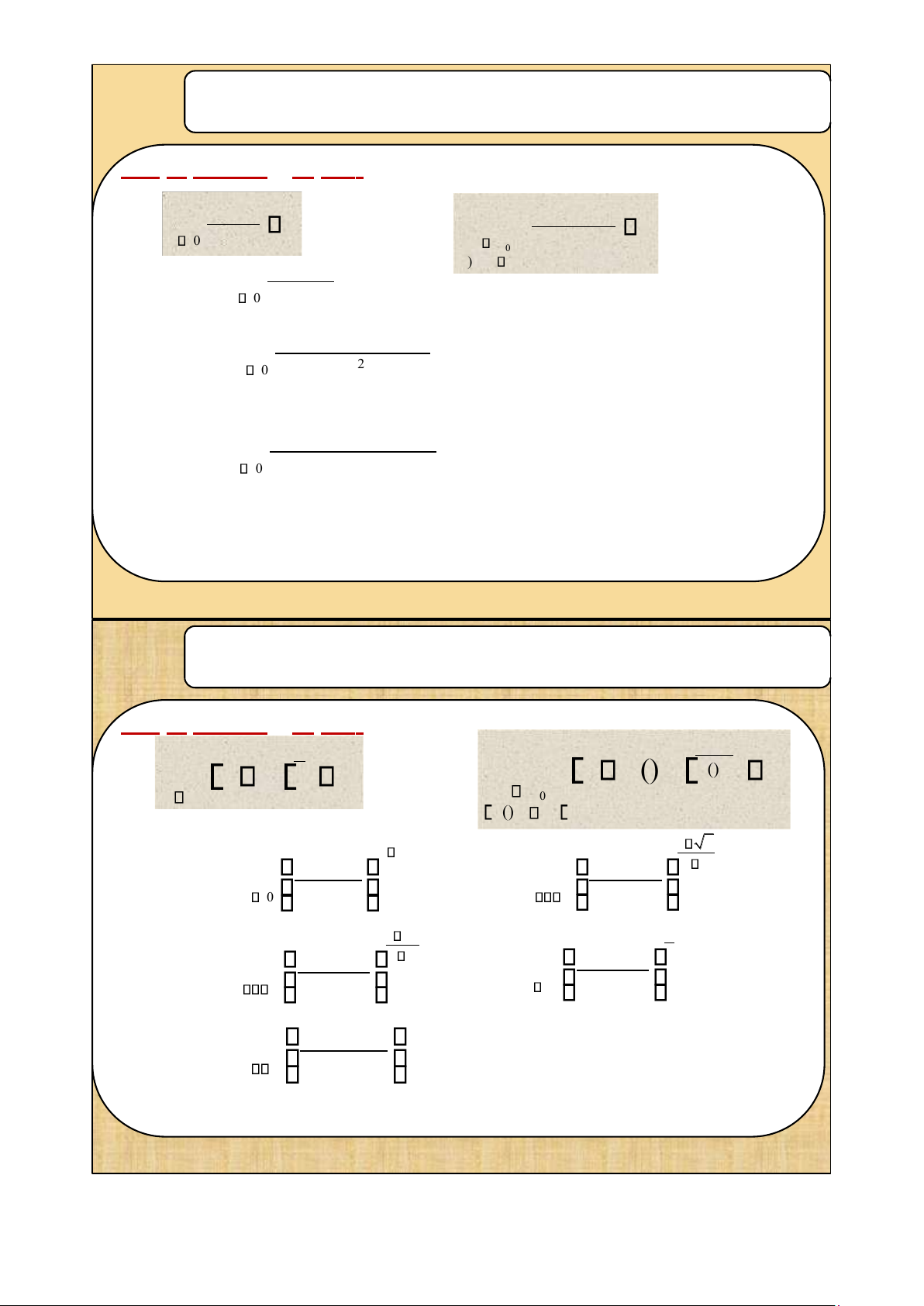
1.1. Khái niệm mở ầu 1.1.1.Tập hợp
- Tập hợp là một khái niệm cơ bản của toán học, khái niệm này không
ược ịnh nghƿa mà ta chỉ thừa nhận ngay từ ban ầu.
- Ví dụ:+ Tập hợp sinh viên 1 của lớp.
+ Tập hợp các số tự nhiên N.
+ Tập hợp các nghiệm của một phương trình: sinx = ½. - Mỗi
ối tượng trong một tập hợp gọi là phần tử của tập hợp ó.
+ Nếu a là một phần tử của tập hợp A, ta viết a A.
+ Nếu phần tử a không thuộc tập A, ta viết a A.
-Tập rỗng: là tập không có phần tử nào, kí hiệu:
-Tập con: Tập hợp A ược gọi là tập con của tập hợp B (A B) nếu
mỗi phần tử của A ều là phần tử của B.
A B x A => x B B A lOMoAR cPSD| 58833082
CHƯƠNG 1: HÀM SỐ, GIỚI HẠN VÀ SỰ LIÊN TỤC 1.1.2.C
ácphéptoán của tập hợp :
Tậphợpbằng nhau: A=B A BvàB A
- Giaohai tậphợp : A B={x/x Avàx B} A B
- Hợp hai tậphợp : A B={x/x A hoặc x B} A B
- Hiệu hai tậphợp : A\B={x/x
Avàx B}
- Tính chất : Sgk A\B B 1.1.3.C
ác tập số
CHƯƠNG 1: HÀM SỐ, GIỚI HẠN VÀ SỰ LIÊN TỤC
1.1.4. Tập tích Ěề các
- Cho hai tập hợp A, B , với mỗi a A và mỗi b B ta lập cặp
(a; b) a viết trước, b viết sau thì ta gọi là một cặp sắp thứ tự - Tích
Ěề các của hai tập hợp A và B, kí hiệu: AxB, là một tập hợp ược ịnh nghƿa bởi
AxB = {(a;b)/ a A ; b B } 1.1.5. Ánh xạ
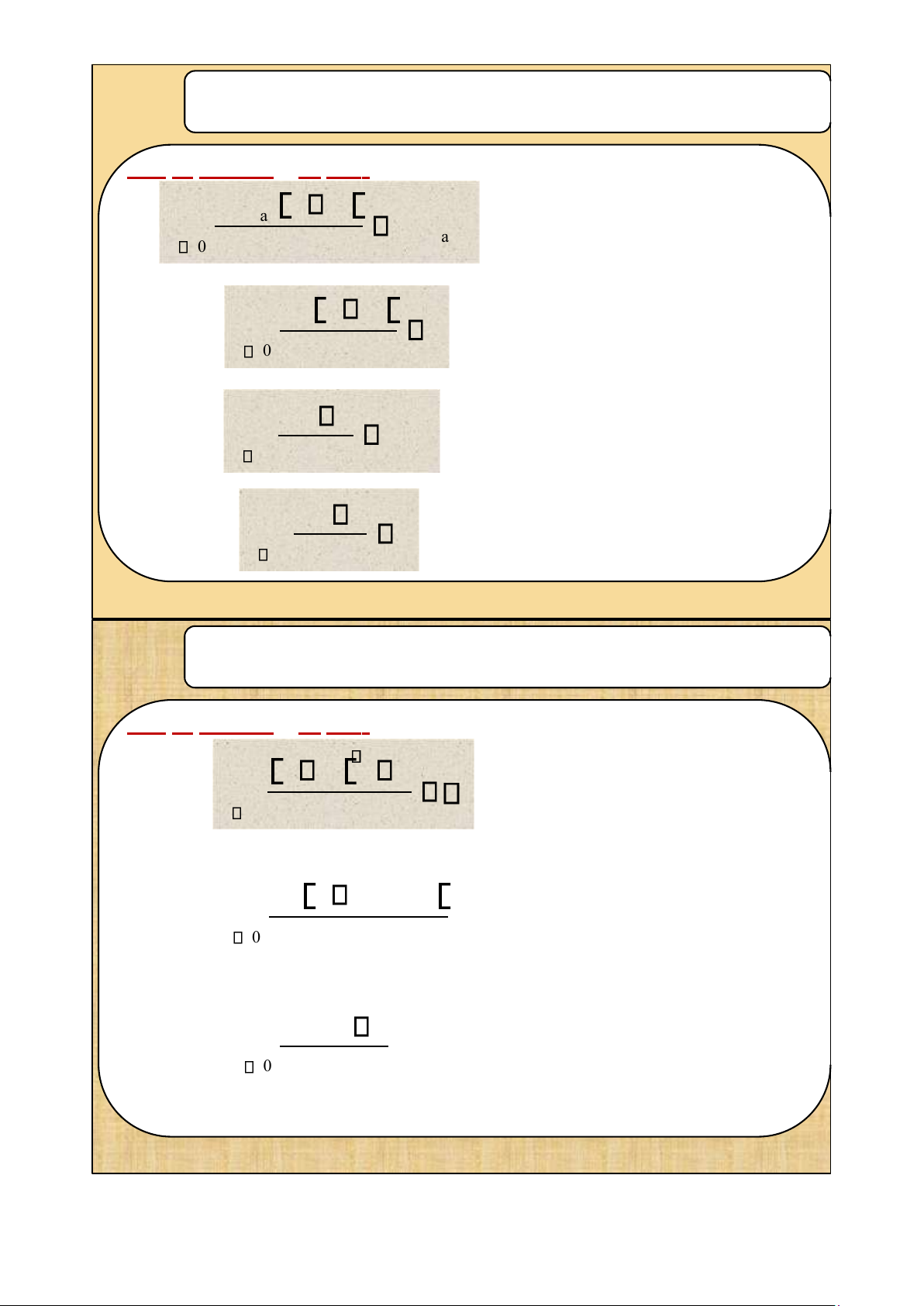
-Ěịnh nghƿa 1:Cho hai tập hợp X và Y, ta gọi f là một ánh xạ từ X
vào Y là một quy tắc cho tương ứng mỗi phần tử của tập X với
một và chỉ một phần tử của tập Y, kí hiệu: f: X Y x y = f(x) X Y
X : Tập gốc (tập nguồn) f
Y: Tập ảnh ( tập ích) x X gọi là tạo ảnh ,
y Y gọi là ảnh lOMoAR cPSD| 58833082
CHƯƠNG 1: HÀM SỐ, GIỚI HẠN VÀ SỰ LIÊN TỤC Ví dụ: 1/ f: R R 2/ f: R R x y = 2x + 3 x y = x2 3/ f: R R x y = sinx
Ěịnh nghƿa 2: Ánh xạ f ược gọi là một ơn ánh nếu phương trình y =
f(x) có nhiều nhất một nghiệm x X với y Y.
Ví dụ: Trong ví dụ 1 ở trên.
Ěịnh nghƿa 3: Ánh xạ f ược gọi là một toàn ánh nếu phương trình
f(x) = y có ít nhất một nghiệm x X với y Y.
Ví dụ: Trong ví dụ 1 ở trên.
Ěịnh nghƿa 3: Ánh xạ f ược gọi là một song ánh nếu nó vừa là ơn
ánh vừa là toàn ánh. Ví dụ1: Trong ví dụ 1 ở trên.
Ví dụ 2: Xác ịnh xem khi nào các ánh xạ trong ví dụ 2, 3 ở trên là song ánh
CHƯƠNG 1: HÀM SỐ, GIỚI HẠN VÀ SỰ LIÊN TỤC
1.2 .Hàm số
1 .2.1. Ěịnhnghƿa : Chohai tậphợp X,Y R,ánh xạ f:X Y
ược gọi làhàm số một biến số thực .
X: Miền xác ịnh ,kí hiệu : D f
Y: Miền giá trị ,kí hiệu : R f
x D f gọi
là ối số
y=f(x) R f gọi làhàm số
Ví dụ :1 /f:R R x y=2x+3 2/f :R R x y=x 2 3 /f:R R x y=sinx
1 .2.2 .Hàm số chẵn , lẻ ,hàm số tuần hoàn,hàm số ơniệu sgk lOMoAR cPSD| 58833082
CHƯƠNG 1: HÀM SỐ, GIỚI HẠN VÀ SỰ LIÊN TỤC
1 .2.3 .Hàm số hợp :
Ěịnhnghƿa : Chocác tập X,Y,Z R,vàcáchàm số g:X Y, f:Y
Z,xéthàm số h:X
Z ược ịnhnghƿabởi .
h(x) = f[g(x)] , x X
h ược gọi làhàm số hợpcủa haihàm số fvàhàm số g.
Ví dụ : f(x)=2x 2 +3 ; g(x)=sinx
Khi ó cócáchàm số hợp :
+ h(x)=f[g(x)]=2(sinx ) 2 +3 + 2 u(x)=g[f(x)]=sin(2x +3)
CHƯƠNG 1: HÀM SỐ, GIỚI HẠN VÀ SỰ LIÊN TỤC
1.2.4. Hàm số ngược
Ěịnh nghƿa: Cho hai tập X, Y R, và ánh xạ f: X Y x y = f(x)
là một song ánh, nghƿa là mỗi phần tử y Y ều là ảnh của úng một
phần tử x X nên có thể ặt tương ứng một phần tử y Y với một
phần tử x X; phép cho tương ứng ó ã xác ịnh một hàm số ánh xạ
từ Y sang X, hàm số này ược gọi là hàm số ngược
của song ánh f , kí hiệu là f -1 :Y X y x = f-1(y)
Từ ịnh nghƿa hàm ngược, ta có: y = f(x) x = f-1(y) Do vậy trong
cùng một hệ tọa ộ, ồ thị của hai hàm số là trùng nhau nhưng thông
thường người ta dùng chữ x ể kí hiệu là biến còn y kí hiệu là hàm, nghƿa là: y = f-1(x)
Do ó ồ thị của hai hàm số ngược nhau ối xứng nhau qua ường phân giác thứ nhất. lOMoAR cPSD| 58833082
CHƯƠNG 1: HÀM SỐ, GIỚI HẠN VÀ SỰ LIÊN TỤC
Ví dụ : Tìmhàm số ngượccủa cáchàm số sau: VD1.f:R R x y=2x+3 Làsongánhnêncóhàm
số ngược là
f -1 : R R y
x=(y – 3) / 2
Dokí hiệu xlà biến nên
f -1 : R R x
y=(x – 3) 2 / VD2.f:R R x y=x 2 VD3.f:R R x y=sinx,cosx,tanx,cotx
CHƯƠNG 1: HÀM SỐ, GIỚI HẠN VÀ SỰ LIÊN TỤC
1.2.5. Hàm số sơ cấp:
a.Hàm số sơ cấp cơ bản: Các hàm số sau
ây ược gọi là các hàm số sơ cấp cơ bản:
1/ y = x ; R
2/ y = ax ; a > 0; a 1 3/ y = log x
a ; a > 0; a 1
4/ y = sinx; cosx; tanx; cotx
5/ y = arcsinx; arccosx; arctanx; arccotx b.Hàm số sơ cấp:
Là những hàm số ược tạo thành bởi một số hữu hạn các phép toán
số học (cộng, trừ, nhân, chia), các phép lấy hàm số hợp ối với các
hàm số sơ cấp cơ bản và các hằng số. c. Ěa thức:
Trong các hàm số sơ cấp người ta ặc biệt chú ý ến hai loại hàm số:
các a thức, các phân thức vì khi tính giá trị của các hàm số này ta
chỉ cần thực hiện các phép toán số học ối với biến
CHƯƠNG 1: HÀM SỐ, GIỚI HẠN VÀ SỰ LIÊN TỤC lOMoAR cPSD| 58833082
1.3. Giới hạn và sự liên tục của hàm số 1.3.1.
Giới hạn của hàm số a. Ěịnh nghƿa
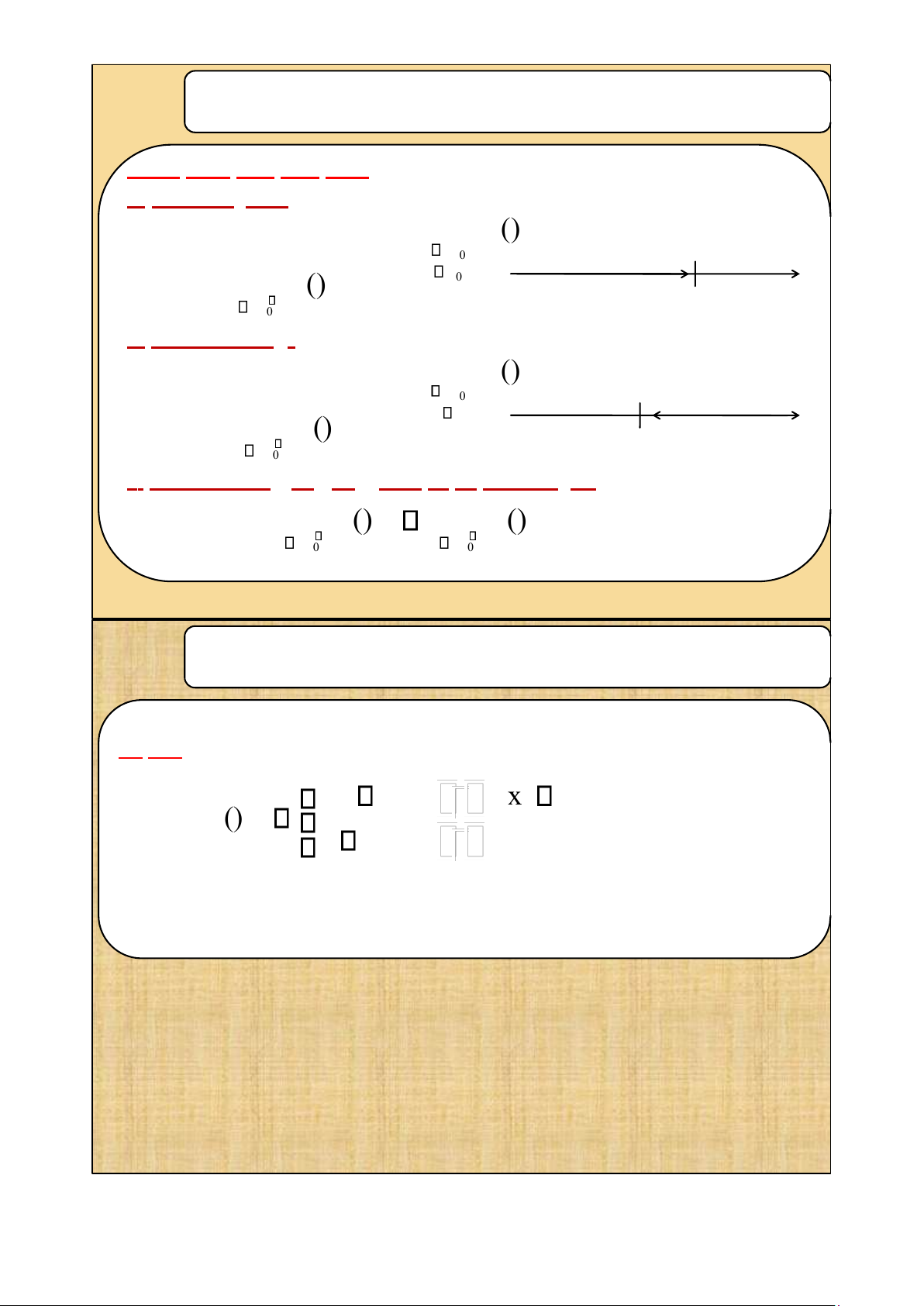
Ěịnh nghƿa 1: Hàm số f(x) xác ịnh trong khoảng (a;b), ta nói rằng
f(x) có giới hạn là k (hữu hạn) khi x dần ến x0, x0 [a;b] nếu với
> 0 , > 0 sao cho x – x0 < thì f(x) – k < , Kí hiệu là: lim f(x) = k x x 0
Ěịnh nghƿa 2: Hàm số f(x) ược gọi là có giới hạn là k (hữu hạn) khi x
dần ến + , nếu với > 0 , N > 0 sao cho x > N thì
f(x) – k < ,Kí hiệu là: lim f(x) = k x
CHƯƠNG 1: HÀM SỐ, GIỚI HẠN VÀ SỰ LIÊN TỤC
Ěịnh nghƿa 3: Hàm số f(x) ược gọi làcó giớihạn làk( hữuhạn )
khix dần ến - , nếuvới >0 , N<0saocho x limf(x) = k
f(x) – k < ,kí hiệu là: x
b .Tính chất
Ěịnh lí1: Cho
; l ,k –hữuhạn ,khi ó : limf(x) = ; limg(x l ) = k xa xa a. limf(x ) + g(x) = + k l xa b. limC.f(x) = C. l xa c. limf(x ).g(x) = . k l xa d. f(x) l lim = ; k 0 xa g(x) k
CHƯƠNG 1: HÀM SỐ, GIỚI HẠN VÀ SỰ LIÊN TỤC lOMoAR cPSD| 58833082
Nhận xét: (1) Từ các ví dụ ã nêu và từ ịnh lí 1 ta có thể suy ra: nếu
Pn(x) là một a thức bậc n ối với x, nghƿa là Pn(x) = a0 + a1x + … +
anxn Thì lim P (x) = P (x ) 0 n n 0 x x
(2) Hơn nữa, cǜng từ ví dụ và từ ịnh lí 1 suy ra: nếu R(x) là một phân
thức hữu tỷ, nghƿa là:
R(x) a + a x + ... + a x nm 0 1 n Q (x)P
(x)nm b + b x + ... + b x0 1 m Thì 0 x xlim R(x) 0
Q (x )P (x )nm 0 miễn là Qm(x0) 0
(3) Trong ịnh lí 1 chưa khảng ịnh ược khi l và k không là hữu hạn
hoặc bằng 0, các giới hạn trong ịnh lí có dạng 0/0; / ; - 0. , ó là
các dạng vô ịnh của giới hạn, khi gặp các dạng ó ta phải tìm cách khử dạng vô ịnh. lOMoAR cPSD| 58833082
CHƯƠNG 1: HÀM SỐ, GIỚI HẠN VÀ SỰ LIÊN TỤC
Ví dụ : Tìmcác giớihạn sau: n x 1 (1) lim 1 m x x 1 (2) 5 x 1 2 lim 2 x 1 x 1 3 (3)
5 x 1 x 7 lim 2 x 1 x 1 2 2 x 3 x 5 (4) lim 2 x 5 x 1 (5) 2 lim x 3 x 5 x x
CHƯƠNG 1: HÀM SỐ, GIỚI HẠN VÀ SỰ LIÊN TỤC
Ěịnh lí2: Giả sử bahàm số f(x),g(x)vàh(x) thỏa mãn:
f(x) g(x) h(x) với x ( a; b )
Khi ó , nếu limf(x) = limh(x) =
l thì limg(x) = l xx 0 xx 0 xx 0
Ěịnh lí3: Chof(x)là một hàm số xác ịnh , tĕng ( giảm ) trênR;khi
ó , nếu f(x) bị chặn trên( bị chặndưới ) thì tồntại giớihạn : limf(x) = l x ( x ) lOMoAR cPSD| 58833082
CHƯƠNG 1: HÀM SỐ, GIỚI HẠN VÀ SỰ LIÊN TỤC
Một số giớihạn ặc biệt : sinx (1) sinu(x) lim 1
=> mở rộng lim 1 x 0 x xx 0 u(x) (() ux 0) tan3x Ví
dụ :1 / lim x 0 sin2x cos3x - cos5x 2 lim / 2 x 0 sinx 1- 3 cos3x.cos5x / lim x 0 1- cosx
CHƯƠNG 1: HÀM SỐ, GIỚI HẠN VÀ SỰ LIÊN TỤC
Một số giớihạn ặc biệt : 1 1 (2) lim () 1 ux ux e () lim1 x x e
=> mở rộng x 0 xx 0 () ux 0
Ví dụ : 1 x 2 2+3 x x 1 1 + 2x x 1 / lim 2 / lim x 0 3 x - 4x 1 + x 2 1 x 1 1 1 + 2x x 1 + 2x x 3 / lim 4 / lim x x 0 1 + x 1 + x 3 3 + 2x x 5 / lim x 2x lOMoAR cPSD| 58833082
CHƯƠNG 1: HÀM SỐ, GIỚI HẠN VÀ SỰ LIÊN TỤC
Một số giớihạn ặc biệt : log 1 u a (3) lim log e a u 0 u Ěặcbiệt : ln 1 u lim 1 u 0 u u (4) a 1 lim lna u 0 u Ěặcbiệt : u e 1 lim 1 u 0 u
CHƯƠNG 1: HÀM SỐ, GIỚI HẠN VÀ SỰ LIÊN TỤC
Một số giớihạn ặc biệt : (5) 1 u 1 lim u 0 u
Ví dụ : ln1 sin2 x 1 / lim x 0 tanx sin2 x e 1 2 / lim x 0 3 x lOMoAR cPSD| 58833082
CHƯƠNG 1: HÀM SỐ, GIỚI HẠN VÀ SỰ LIÊN TỤC
1 .3.2. Giới hạn một phía
a . Giớihạn trái: là giớihạncủa hàm số f(x)khix dầntới x 0 ( hữu x 0
hạn) từ phíabêntrái, tức là: lim () fx xx 0 x x 0 Kí (xx hiệu : 0 ) lim () fx xx 0
b . Giớihạnphải : là giớihạncủa hàm số f(x)khix dầntới x 0 x ( hữu 0
hạn) từ phíabên phải,tức là: lim () fx xx 0 x 0 x Kí (x x) hiệu : 0 lim () fx xx 0
c . Ěiềukiệncần và ủể hàm số có giớihạn là: lim () fx lim () fx xx 0 xx 0
CHƯƠNG 1: HÀM SỐ, GIỚI HẠN VÀ SỰ LIÊN TỤC
Ví dụ : Chohàm số : 2 x 1 n u x 0 () fx ế x 1 n u x < 0 ế
Tìm giớihạn trái, phảicủa hàm số tại x=0,hàm số có giớihạn tại x=0không? lOMoAR cPSD| 58833082
CHƯƠNG 1: HÀM SỐ, GIỚI HẠN VÀ SỰ LIÊN TỤC
1.3.3. Vô cùng bé (VCB), vô cùng lớn(VCL):
a. Vô cùng bé (VCB): Hàm số f(x) ược gọi là một VCB khi x x0
nếu : lim f x( ) 0 x x 0
Ví dụ: f(x) = x – 2 là một VCB khi x 2 vì:
lim f x( ) lim(x 2) 0 x 2 x 2
b. Vô cùng lớn (VCL): Hàm số f(x) ược gọi là một VCL khi x x0
nếu : lim f x( ) x x 0
Ví dụ: f x( ) 1x 2 là một VCL khi x 2 vì: 1
lim f x( ) lim x2 x2 x 2
CHƯƠNG 1: HÀM SỐ, GIỚI HẠN VÀ SỰ LIÊN TỤC
c. Một số tính chất ơn giản:
(1) Nếu f(x) là một VCB khi x x0 thì 1/f(x) là một VCL khi x x0.
Ngược lại, nếu f(x) là một VCL khi x x0 thì 1/f(x) là một VCB khi x x0.
(2) Một số tính chất tổng, tích của các VCB và VCL cǜng ược suy ra
từ tổng, tích của các ại lượng có giới hạn.
d.Tốc ộ tiến tới VCB, VCL: Trong phần này ta xét tốc ộ tiến tới VCB
của các hàm số, tiến tới VCL ta làm tương tự. Cho các hàm số f(x),
g(x) là hai VCB khi x x0 , ta nói rằng: f x( ) + f(x) có bậc cao hơn
g(x) khi x x0 nếu : lim 0 x x 0 g x( )
ký hiệu là: f(x) = o(g(x)) khi x x0
Khi ó ta cǜng nói rằng g(x) có bậc thấp hơn f(x) khi x x0 lOMoAR cPSD| 58833082
CHƯƠNG 1: HÀM SỐ, GIỚI HẠN VÀ SỰ LIÊN TỤC
+ f(x) cùng bậc với g(x) khi x x0 nếu : lim f x( ) C 0 x x 0 g x( )
ký hiệu là: f(x) = O(g(x)) khi x x0 f x( )
Ěặc biệt là nếu: lim 1 x x 0 g x( )
thì ta nói f(x) và g(x) là hai VCB tương
ương khi x x0
Kí hiệu là: f(x) g(x) khi x x0
Chú ý: Nếu lim f x( ) l thì ta có f(x) = l + (x),
x x 0 trong ó (x) là một
VCB khi x x0 Một số VCB tương ương:
+/ tanx sinx arctanx arcsinx x khi x 0
+/ ln(1+x) x khi x 0; (1+x)a -1~ a.x khi x 0
+/ ex – 1 x khi x 0
CHƯƠNG 1: HÀM SỐ, GIỚI HẠN VÀ SỰ LIÊN TỤC
Ěịnh lí: Nếu trongquátrìnhx x 0,cóf(x)
( x)vàg(x ) (x ) f 1 g 1 f(x)=o(g(x)) thìtacó:
1) f(x).g(x)~f 1( (
x).g 1 x); f(x)+g(x)~g(x) () fx () fx1 2) lim lim xx 0 () xx gx 0 gx() 1
Ví dụ : Tìmcác giớihạn sau: 2 x e 1 2 / lim 2 x . sin 1 / lim x x 1 x 0 sin3 x arcsin x 1 3 / lim e 1. 3 x x 2 2 x ln cosx 3 x 1 5 / lim 4 / lim x 2 x 0 3 x x 2 x lOMoAR cPSD| 58833082
CHƯƠNG 1: HÀM SỐ, GIỚI HẠN VÀ SỰ LIÊN TỤC
1 .3.4. Sự liên tụccủa hàm số :
a . Ěịnhnghƿa :
(1) Hàm số f(x)xác ịnh trong(a;b),tanói
rằng f(x)liên tụctại
iểm x 0 ( a;b ) nếu lim () fx ( fx ) 0 xx 0
Trong trườnghợpngượclại tanói rằng hàm số f(x)gián oạntại x 0
Ví dụ: Xét sự liên tục của hàm số sau tại x = 0 ar ctan 2 x 2 x fx n u x 0 ế 3 x A
n u x 0 ế
CHƯƠNG 1: HÀM SỐ, GIỚI HẠN VÀ SỰ LIÊN TỤC
(2) Hàm số f(x) ược gọi làliên tục trên(a; b) nếu f(x) liên tục tại
x ( a; b ).
Ví dụ : Xét sự liên tụccủa hàm số sau: 2 arctan x 2 x fx n u x 0 ế 3 x A
n u x 0 ế
b. Tính chất : sgk lOMoAR cPSD| 58833082
CHƯƠNG 2: PHÉP TÍNH VI PHÂN
2.1. Ěạo hàm
2.1.1. Ěịnhnghƿa
- Chohàm số f(x)xác ịnh trong khoảng ( a;b)nói rằng f(x) khả vi
tại x 0 ( a;b ) nếu tồntại giớihạn : () fx - ( fx ) 0 lim = A , x x0 xx 0 x - x0
Số A ở trên ược gọi là ạo hàm của hàm số f(x) lấy tại x=x 0
Kí hiệu : f’(x 0)
- Nếu hàm số f(x) khả vi tại x ( a;b)thìtanói
rằng f(x) khả vi
trong khoảng (a ;b).
Kí hiệu ạo hàm tại x bất k : f’(x) Ƕ
CHƯƠNG 2: PHÉP TÍNH VI PHÂN
Nhận xét:
(1) Nếu ặt x – x 0 = của số
x,và gọi là số gia ối .
y=f(x) – f(x 0)= f(x + )
0 x) – f(x 0 , gọi là số gia của hàm số . Khi ó : y lim = '(f x ) 0 x 0 x
(2) Nếu hàm số f(x) khả vi tại x 0 thì:
f(x 0 + x) – f(x 0 )= f’(x 0 ) x+o( x)
Trong ó o( x)là một VCB bậc cao hơn xkhi x 0
(3) Nếu hàm số f(x) khả vi tại x 0 thìf(x)liên ,
tục tại x 0 iềungược
lại không úng .
(4) Nếu hàm số f(x) khả vi tại x 0 thì )
f’(x 0 chínhlà hệ số góc của
tiếptuyếncủa ồ thị hàm số f(x) tại x 0 lOMoAR cPSD| 58833082
CHƯƠNG 2: PHÉP TÍNH VI PHÂN
2.1.2 .Tính chất
Ěịnh lí1 Nếu cáchàm số f(x)vàg(x) khả vitrên khoảng ( a;b)thì
f(x)+g(x);cf(x);f(x).g(x) cǜng khả vitrên khoảng ( a;b)và (1)
( f(x )+ g(x))’ = f’(x) + g’(x)
(2) ( cf(x))’ = cf’(x) (3)
( f(x ). g(x))’ = f’(x)g(x) + f(x)g’(x)
CHƯƠNG 2: PHÉP TÍNH VI PHÂN
Ěịnh lí 2: (Về ạo hàm của hàm số hợp) Nếu các hàm số: -
u = g(x) xác ịnh trong khoảng (a;b) và lấy giá trị trong khoảng
(c;d), g(x) khả vi trên khoảng (a;b). -
y = f(u) xác ịnh trong khoảng (c;d) và khả vi trên khoảng (c;d).
Thì khi ó hàm số hợp y = f[g(x)] khả vi trên khoảng (a;b) và
y’ = {f[g(x)]}’ = f’u.u’x
Ěịnh lí 3: (Về
ạo hàm của hàm số ngược)
Cho hàm số f(x) có hàm số ngược là g(y) = f-1(y), nếu f(x) có ạo hàm
và f’(x) 0 thì : 1 g y'( )
2.1.3. Bảng ạo hàm: sgk f '(x) lOMoAR cPSD| 58833082
CHƯƠNG 2: PHÉP TÍNH VI PHÂN 2.2. Vi phân
2.2.1. Ěịnh nghƿa
Cho hàm số y = f(x) khả vi trên khoảng (a;b), khi ó tích f’(x) x gọi
là vi phân của hàm số f(x), lấy tại x. Kí hiệu:
df(x) = f’(x) x
2.2.2. Chú ý: (1)
dx = x ( vì xét f(x) = x) nên df(x) = f’(x)dx
(2) Từ (1) ta suy ra f '(x) df x( ) dx
2.2.3. Ěạo hàm theo tham số:
Cho hàm số y = f(x) xác ịnh bởi các hàm số x = x(t); y = y(t) với
t ( ; ) . Nếu x = x(t); y = y(t) khả vi trên ( ; ) thì y = f(x) cǜng
khả vi và y t'( ) f '(x) x t'( )
CHƯƠNG 2: PHÉP TÍNH VI PHÂN
2.3. Ěạo hàm một phía, ạo hàm vô cùng. sgk
2.4.Ěạo hàm và vi phân cấp cao
2.4.1. Ěạo hàm cấp cao
Ěịnh nghƿa: Cho hàm số f(x) khả vi trong khoảng (a;b), khi ó f’(x)
gọi là ạo hàm cấp 1 của hàm số f(x).
Nếu f’(x) khả vi trong khoảng (a;b) thì ạo hàm của f’(x) gọi là ạo
hàm cấp 2 của hàm số f(x), kí hiệu là: f’’(x)
f’’(x) = [f’(x)]’
Tương tự nếu f’’(x) khả vi trong khoảng (a;b) thì [f’’(x)]’ gọi là ạo
hàm cấp 3 của hàm số f(x), kí hiệu là: f’’’(x) hoặc f(3)(x) = [f’’(x)]’ ……….
Hàm số f(x) khả vi n – 1 lần trong (a;b) và ạo hàm cấp n – 1 của f(x)
cǜng khả vi. Khi ó ạo hàm cấp n của f(x), kí hiệu: f(n)(x), ược xác ịnh
như sau: f(n)(x) = [f(n - 1)(x)]’ lOMoAR cPSD| 58833082
CHƯƠNG 2: PHÉP TÍNH VI PHÂN
Ví dụ : Tìm ạo hàm cấp cao của cáchàm số sau: 1/y =2x
3 – 3 x 2 +5 ; tìmy (2)
2 /y=e 2 x +3 ;
tìmy ( n )
3 /y=sin (3x+4) ;
tìmy ( n ) 1 ( n ) 4 / y ; tìm y 2 x 3 5 (
/y=cos(2x – 3) ;
tìmy n )
6 /y=ln (3 – 4 x ) ;
tìmy ( n )
CHƯƠNG 2: PHÉP TÍNH VI PHÂN
Tính chất :
Chocáchàm số f(x),g(x) khả vi cấp ntrên khoảng ( a;b),khi ó :
f(x)+g(x);cf(x);f(x).g(x)
khả vi cấp nvà 1 /(f+g
) ( n ) = f (n ) + g ( n )
2 /(c.f ) (n ) = c.f ( n ) (n ) 0 (n ) 1 (n-1) n (n ) 3 / (f.g ) = C.f.g + C.f '.g + ... + C.f .g n n n n k ( k ) (n - k) = C.f .g n k = 0 Ví
dụ : Tìm ạo hàm cấp cao của cáchàm số sau: 3 4 x 16 x 18 1 / y tìmy (n ) ; 2 2 x x 6 2/y =(2x
2 +3) e (2x+3) tìmy (30)
3 /y =(3 – 4 x 2 )si
n(2x – 3) tìmy (30)