
































































Preview text:
CHUÛ ÑEÀ
HAØM SOÁ LUÕY THÖØA 2.
HAØM SOÁ MUÕ - HAØM SOÁ LOGARIT
TỔNG HỢP KIẾN THỨC Baøi 01
LUÕY THÖØA – HAØM SOÁ LUÕY THÖØA I. LŨY THỪA
1. Lũy thừa số mũ nguyên dương n a = . a . a ... ,
a ( n thừa số). Ở đây n +
∈ ℤ , n > 1 . Quy ước 1 a = a .
2. Lũy thừa số mũ 0 - Lũy thừa số mũ nguyên âm −n 1 0 a = ( 1 a ≠ 0) ; a =
(a ≠ 0) , với n + ∈ ℤ . n a
3. Lũy thừa số mũ hữu tỷ m n m n a = a ,(a > 0)
Lũy thừa số mũ hữu tỷ có tính chất như lũy thừa số mũ nguyên (xem mục 5).
4. Lũy thừa số thực aα = lim rn a
( α là số vô tỉ, r là số hữu tỉ và lim r α = ). n n n→+∞
Lũy thừa số mũ thực có tính chất như lũy thừa số mũ nguyên (xem mục 5).
5. Tính chất của lũy thừa số mũ nguyên
a) Với a, b ∈ ℝ; a ≠ 0, b ≠ 0; ,
m n ∈ ℤ , ta có m m a m n a a m . n m n a a a + = ; m−n = a ; ( m ) m.n a = a ; ( )m m m ab = a b ; = . a m b b n n n b) Nếu
a < b , ∀n > 0 0 a b < < ⇒ . n n a
> b , ∀n < 0 Nếu >1 m n a
⇒ a > a với m > n . Nếu 0 < <1 m n a
⇒ a < a với m > n .
6. Công thức lãi kép
a) Định nghĩa: Lãi kép là phần lãi của kì sau được tính trên số tiền gốc kì trước
cộng với phần lãi của kì trước.
b) Công thức: Giả sử số tiền gốc là A ; lãi suất r % /kì hạn gửi (có thể là tháng, quý hay năm). n
● Số tiền nhận được cả gốc và lãi sau n kì hạn gửi là A(1+ r ) n n
● Số tiền lãi nhận được sau n kì hạn gửi là A(1+ r ) − A = A (1+ r ) −1
c) Ví dụ: Bà Hoa gửi 100 triệu vào tài khoản định kỳ tính lãi kép với lãi suất là
8%/năm. Tính số tiền lãi thu được sau 10 năm. Lời giải
Áp dụng công thức tính lãi kép, sau 10 năm số tiền cả gốc và lãi bà Hoa thu về là: ( + )n A r = ( + )10 1 100tr. 1 0,08 ≈ 215,892tr .
Suy ra số tiền lãi bà Hoa thu về sau 10 năm là: A( + r)n 10 1
− A = 100tr(1+ 0,08) −100tr = 115,892tr . II. HCM SỐ LŨY THỪA 1. Định nghĩa: α ℝ y = x α , ∈
gọi là hàm số lũy thừa.
2. Tập xác định: y xα =
tùy thuộc giá trị α . Cụ thể:
● α nguyên dương thì hàm số có TXĐ là ℝ .
● α nguyên âm hoặc bằng 0 thì hàm số xác định khi cơ số khác 0 .
● α không nguyên thì hàm số xác định khi cơ số dương. 1
Chú ý: Theo định nghĩa, đẳng thức n n
x = x chỉ xảy ra nếu x > 0 . Do đó hàm số 1 n
y = x không đồng nhất với hàm số n y = x ( ℕ* n ∈
). Chẳng hạn: hàm số y = x có 1 D = [0;+ ) ∞ còn hàm số 2
y = x có D = (0;+∞) ; hàm số 3 y = x có ℝ D = còn hàm số 1 3
y = x có D = (0;+ ) ∞ . 3. Đạo hàm: α α− α ℝ y = x α , ∈
với ∀x > 0 . Đạo hàm y = (x ) 1 ' ' α = x .
4. Tính chất của hàm số lũy thừa: (Xét trên khoảng (0;+∞) )
● Đồ thị qua điểm (1; ) 1 .
● α > 0 hàm số đồng biến; α < 0 hàm số nghịch biến.
● Khi α > 0 đồ thị không có tiệm cận; khi α < 0 đồ thị có tiệm cận ngang y = 0 ,
tiệm cận đứng x = 0 .
CÂU HỎI VC BCI TẬP TRẮC NGHIỆM 12
NGUYỄN PHÚ KHÁNH HUỲNH ĐỨC KHÁNH –
Đăng ký mua trọn bộ trắc nghiệm 12 FILE WORD
Liên hệ tác giả HUỲNH ĐỨC KHÁNH 0975 120 189 –
https://web.facebook.com/duckhanh0205 Khi mua có sẵn File đề riêng;
File đáp án riêng để thuận tiện cho việc in ấn dạy học
CÂU HỎI TRẮC NGHIỆM π
Câu 1. Tìm tập xác định D của hàm số y = ( 3 x − )2 27 .
A. D = ℝ \{2} . B. D = ℝ . C. D = [3;+∞). D. D = (3;+∞).
Lời giải. Áp dụng lý thuyết ' Lũy thừa với số mũ không nguyên thì cơ số phải dương ' . π
Do đó hàm số y = ( 3 x − )2 27 xác định khi 3
x − 27 > 0 ⇔ x > 3 . Chọn D.
Câu 2. (ĐỀ CHÍNH THỨC 2016 2017) Tìm tập xác định – D của hàm số −
y = (x − x − ) 3 2 2 . A. D = . ℝ B. D = ℝ \{−1;2}. C. D = (− ; ∞ − ) 1 ∪(2;+∞). D. D = (0;+∞) .
Lời giải. Áp dụng lý thuyết ' Lũy thừa với số mũ nguyên âm thì cơ số phải khác 0 ' .
Do đó hàm số đã cho xác định khi x ≠ −1 2 x x 2 0 − − ≠ ⇔ . Chọn B. x ≠ 2
Câu 3. Tìm tập xác định D của hàm số y = (x − x − ) 2 4 2 3 4 . A. D = (− ; ∞ − ) 1 ∪(4;+∞). B. D = (− ; ∞ −2)∪(2;+∞). C. D = (− ; ∞ −2]∪[2;+∞). D. D = (− ; ∞ +∞).
Lời giải. Áp dụng lý thuyết ' Lũy thừa với số mũ không nguyên thì cơ số phải dương ' .
Do đó hàm số đã cho xác định khi 4 2
x −3x − 4 > 0 x > 2 ⇔ ( 2 x − 4)( 2 x + ) 2
1 > 0 ⇔ x − 4 > 0 ⇔ . Chọn B. x < −2
Câu 4. Tìm tập xác định π D của hàm số 2 y x (x ) 1 = + . A. D = (0;+∞).
B. D = (−1;+∞)\{0}. C. D = (− ; ∞ + ) ∞ .
D. D = (−1;+∞).
Lời giải. Hàm số xác định khi x > −1 2 x (x ) 1 0 + > ⇔ . Chọn B. x ≠ 0 4
Câu 5. Rút gọn biểu thức a + ab a − b P = −
với a > 0, b > 0. 4 4 4 4 a + b a − b A. 4 4
P = 2 a − b . B. 4 P = − b . C. 4 P = b . D. 4 P = a .
( a)2 + ab ( a)2 − + − ( b a ab a b )2 4 4 4 4 4
Lời giải. Ta có P = − = − 4 4 4 4 4 4 4 4 a + b a − b a + b a − b 4 a (4 4 a + b ) (4 4 a − b )(4 4 a + b ) 4 = − = a −(4 4 a + b ) 4
= − b . Chọn B. 4 4 4 4 a + b a − b 1
Câu 6. (ĐỀ CHÍNH THỨC 2016 2017) Rút gọn biểu thức 3 6 với – P = x . x x > 0. 1 1 A. 2 P = x .
B. P = x . C. 3 P = x . D. 9 P = x . 1 1 1 1 1 1 Lời giải. Ta có + 3 6 3 6 3 6 2
P = x . x = x .x = x = x . 1 Vì x > 0 nên 2
x = x . Chọn B.
Câu 7. Rút gọn biểu thức 3 5 4 P = x
x với x > 0. 20 21 20 12 A. 21 P = x . B. 12 P = x . C. 5 P = x . D. 5 P = x .
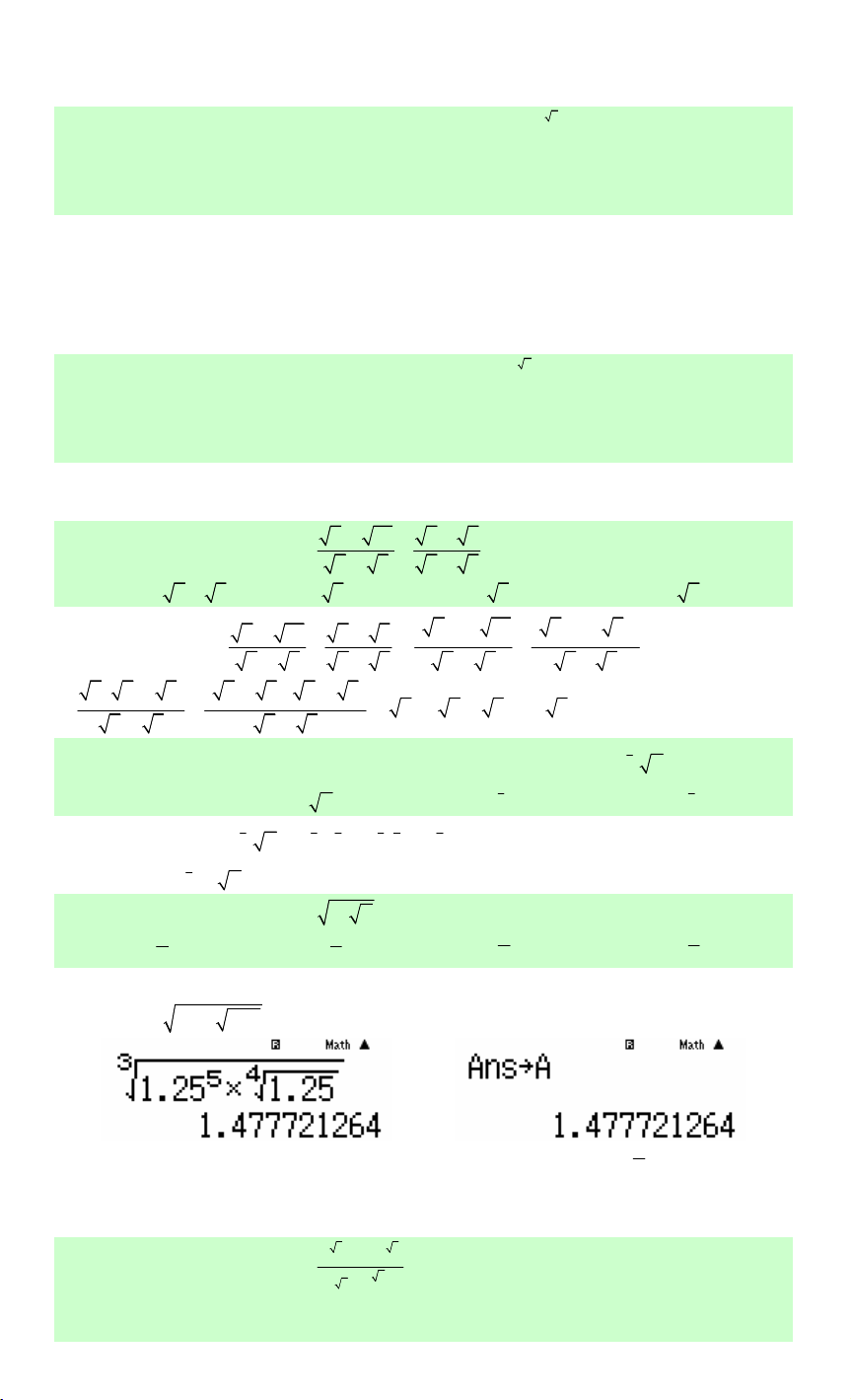
Lời giải. Cách CASIO. Chọn x > 0 ví dụ như x = 1,25 chẳng hạn. Tính giá trị 3 5 4 1, 25
1, 25 rồi lưu vào A 20
Tiếp theo ta tính hiệu, ví dụ như đáp án A ta cần tính A −( )21 1,25 . Nếu màn hình
máy tính xuất hiện kết quả bằng 0 thì chứng tỏ đáp án A đúng.
Đáp số chính là B. Chọn B. 3 1 + 2− 3
Câu 8. Rút gọn biểu thức a .a P = với a > 0 . ( + a − ) 2 2 2 2 A. 4 P = a . B. P = . a C. 5 P = a . D. 3 P = a . 3 1 + + − ( + 2− 3 3 1 2 3 ) 3 a .a = a = a 3
Lời giải. Ta có a 3 ( − 2 − ) 5 → P = = a = a . Chọn C. ( ) 2+2 ( − )( + − ) −2 2 2 2 2 2 2 2−4 2 − a a = a = a = a 2 1 − 1 1
Câu 9. Rút gọn biểu thức y y 2 2
K = x − y 1 − 2 + với .
x > 0, y > 0 x x
A. K = x.
B. K = 2x.
C. K = x +1.
D. K = x −1. 2 1 1
Lời giải. Rút gọn x − y = ( x − y)2 2 2 . 1 −1 2 − 2 − 2 Rút gọn y y y y − x x 1 −2 + = −1 = = . x x x x
y − x 2 Vậy = ( − )2 x K x y
= x. Chọn A. y − x
Câu 10. Với giá trị nào của 1 a thì đẳng thức 3 4 24 5 . a . a a = 2 . đúng? −1 2 A. a = 1. B. a = 2 . C. a = 0 . D. a = 3 . 1 1 2 1 17 3 3 4 4 24 . a . a a = . a . a a = a Lời giải. Ta có 1 3 4 24 5 → . a . a a = 2 . ⇔ a = 2. −1 2 5 1 17 1 24 5 24 2 24 2 . = 2 .2 = 2 1 2− Chọn B.
Câu 11. Cho số thực 1
a ≠ 0 . Với giá trị nào của x thì đẳng thức ( x x a a− + )=1 đúng? 2 A. x = 1. B. x = 0 .
C. x = a . D. 1 x = . a
Lời giải. Ta có 1 ( x −x a + a ) x 1 = 1 ⇔ a + = 2 ⇔ a − a + = x ( x )2 2 x 1 0 2 a ⇔ ( x − )2 1 = 0 x a
⇔ a = 1 ⇔ x = 0 . Chọn B.
Câu 12. Tìm tất cả các giá trị của a thỏa mãn 15 7 5 2 a > a . A. a = 0 . B. a < 0 . C. a >1 .
D. 0 < a <1 . 7 2 7 6
Lời giải. Ta có 15 7 5 2 15 5 15 15
a > a ⇔ a
> a ⇔ a > a
→a > 1. Chọn C. 2 1
Câu 13. Tìm tất cả các giá trị của − −
a thỏa mãn (a − ) 3 < (a − ) 3 1 1 . A. a > 2 . B. a >1 .
C. 1< a < 2 .
D. 0 < a <1 . 2 1 Lời giải. Ta có 2 1
− < − , kết hợp với ( − −
a − ) 3 < (a − ) 3 1 1
. Suy ra hàm số đặc trưng 3 3 = ( − )x y a 1 đồng biến
→ cơ số a −1 > 1 ⇔ a > 2 . Chọn A.
Câu 14. Một người lần đầu gửi vào ngân hàng 100 triệu đồng với kì hạn 3 tháng, lãi
suất 2% một quý. Biết rằng nếu không rút tiền ra khỏi ngân hàng thì cứ sau mỗi quý
số tiền lãi sẽ được nhập vào gốc để tính lãi cho quý tiếp theo. Sau đúng 6 tháng, người
đó gửi thêm 100 triệu đồng với kỳ hạn và lãi suất như trước đó. Tổng số tiền người đó
nhận được 1 năm sau khi gửi tiền (cả vốn lẫn lãi) gần nhất với kết quả nào sau đây? A. 210 triệu. B. 220 triệu. C. 212 triệu. D. 216 triệu.
Lời giải. Số tiền nhận về sau 1 năm của 100 triệu gửi trước là ( + )4 100 1 2% triệu.
Số tiền nhận về sau 6 tháng của 100 triệu gửi sau là ( + )2 100 1 2% triệu. Vậy tổng số tiền là ( + )4 + ( + )2 100 1 2% 100 1 2% = 212,283216(≈ 212,28 ) 3 triệu.Chọn C.
Câu 15. Bác An đem gửi tổng số tiền 320 triệu đồng ở hai loại kỳ hạn khác nhau. Bác
gửi 140 triệu đồng theo kỳ hạn ba tháng với lãi suất 2,1% một quý. Số tiền còn lại
bác An gửi theo kỳ hạn một tháng với lãi suất 0,73% một tháng. Biết rằng nếu không
rút tiền ra khỏi ngân hàng thì cứ sau mỗi kỳ hạn số tiền lãi sẽ được nhập vào gốc để
tính lãi cho kỳ hạn tiếp theo. Sau 15 tháng kể từ ngày gửi bác An đi rút tiền. Tính
gần đúng đến hàng đơn vị tổng số tiền lãi thu được của bác An. A. 36080251 đồng. B. 36080254 đồng. C. 36080255 đồng. D. 36080253 đồng.
Lời giải. Số tiền nhận về sau 15 tháng của 140 triệu gửi trước là ( + )5 140. 1 2,1% triệu.
Số tiền nhận về sau 15 tháng của 180 triệu gửi sau là ( + )15 180. 1 0,73% triệu.
Suy ra tổng số tiền cả vốn lẫn lãi mà bác An thu được là ( + )5 + ( + )15 140. 1 2,1% 180. 1 0,73% ≈ 356, 080253 triệu.
Suy ra số tiền lãi: 356,080253−320 = 360,80253 = 36080253 đồng. Chọn D. Baøi 02 LOGARIT 1. Định nghĩa
Cho hai số dương a, b và a ≠ 1. Số α
α thỏa mãn đẳng thức a
= b được gọi là
logarit cơ số a của b và kí hiệu là log b . a log b aα α = ⇔
= b (a, b > 0, a ≠ ) 1 a 2. Tính chất
Cho hai số dương a, b và a ≠ 1, ta có các tính chất sau: log 1 = 0 ; log a = 1 ; loga b a = b ; log aα α = . a a a
3. Các quy tắc tính lôgarit
Cho ba số dương a, b , b và a ≠ 1, ta có các quy tắc sau: 1 2 b
log (b b = log b + log b ; 1 log
= log b − log b ; a 1 2 ) a 1 a 2 a a 1 a 2 b2 1 log bα α = log b ; log n b = log b . a 1 a 1 a 1 a 1 n 4. Đổi cơ số Cho ba số dương b
a, b, c và a ≠ 1, c ≠ 1 , ta có log log c b = a log a c Đặc biệt: 1 log b = , với b ≠ 1 ; 1 log = , với α ≠ 0 . α b log b a log a a a α b
5. Logarit thập phân, logarit tự nhiên
Logarit thập phân: Logarit cơ số 10 gọi là logarit thập phân, log N N > 0 10 ( )
thường được viết là lg N hay log N .
Logarit tự nhiên: Logarit cơ số e gọi là logarit tự nhiên, log N (N > 0 , được viết là e ) ln N .
CÂU HỎI TRẮC NGHIỆM
Câu 1. Cho các mệnh đề sau:
(I). Cơ số của logarit phải là số nguyên dương.
(II). Chỉ số thực dương mới có logarit.
(III). ln(A + B)= ln A + ln B với mọi A > 0, B > 0 . (IV) log .
b log c.log a = 1 , với mọi a, b, c ∈ ℝ . a b c Số mệnh đề đúng là: A. 1. B. 2 . C. 3 . D. 4 .
Lời giải. Cơ số của lôgarit phải là số dương khác 1. Do đó (I) sai.
Rõ ràng (II) đúng theo lý thuyết SGK.
Ta có ln A + ln B = ln( .
A B) với mọi A > 0, B > 0 . Do đó (III) sai. Ta có log .
b log c.log a = 1 với mọi 0 < ,
a b, c ≠ 1 . Do đó (IV) sai. a b c
Vậy chỉ có mệnh đề (II) đúng. Chọn A. Câu 2. Cho a, ,
A B, M , N là các số thực với a, M , N dương và khác 1 . Có bao nhiêu
phát biểu đúng trong các phát biểu dưới đây?
(I). Nếu C = AB với AB > 0 thì 2 lnC = ln A + ln B . (II). (a − )
1 log x ≥ 0 ⇔ x ≥ 1 . a (III). log N log a = a M M N .
(IV). lim log x = −∞ . 1 x →+∞ 2 A. 1. B. 2 . C. 3 . D. 4 .
Lời giải. Nếu C = AB với AB > 0 thì 2 lnC = ln A + ln B . Do đó (I) sai.
● Với a > 1 thì (a − )
1 log x ≥ 0 ⇔ log x ≥ 0 ⇔ x ≥ 1 . a a
● Với 0 < a < 1 thì (a − )
1 log x ≥ 0 ⇔ log x ≤ 0 ⇔ x ≥ 1 . Do đó (II) đúng. a a
Lấy lôgarit cơ số a hai vế của log N log a = a M M N , ta có M N N M M N . a ( log N M a )= a ( log log log a ) ⇔ log .log = log . log a a a a Do đó (III) đúng.
Ta có lim log x = lim −log x = − lim log x = −∞ . Do đó (IV) đúng. 1 [ 2 ] ( 2 ) x →+∞ x →+∞ x →+∞ 2
Vậy ta có các mệnh đề (II), (III) và (IV) đúng. Chọn C.
Câu 3. Tính giá trị của biểu thức P = ( 3 log .
a a a với 0 < a ≠ 1. a ) A. 1 P = . B. 3 P = . C. 2 P = . D. P = 3 . 3 2 3 1 1 3 3 Lời giải. Ta có 3 3 2 2 P = log . a .
a a = log a = log a = . Chọn B. a a 2 a 2
Cách trắc nghiệm: Chọn a = 2 và bấm máy.
Câu 4. (ĐỀ CHÍNH THỨC 2016 2017) Cho –
a là số thực dương và khác 1. Tính
giá trị biểu thức P = log . a a A. P = −2 . B. P = 0 . C. 1 P = . D. P = 2 . 2
Lời giải. Với 0 < a ≠ 1 , ta có P = log a = log a = 2 log a = 2.1 = 2. Chọn D. 1 a a 2 a 1 1 1 2 1+ Câu 5.
Cho hàm số f (x) 3 log x 2 2 2 log 4 = x + 8 x +1 −1
với 0 < x ≠ 1 . Tính giá trị biểu
thức P = f ( f (2017)). A. P = 2016. B. P = 1009. C. P = 2017. D. P = 1008. 1 1 1+ 1+ 2 log x log x 1+ log 2 log x x x (2 ) 4 2 x = x = x = x = 2x
Lời giải. Ta có . 1 1 1 3. 3log 2 3. log 2 log 2 2 2 2 2 log x x x 2 x 2 8 = 2 = 2 = 2 = x 1 1
Khi đó f (x) = (x + x + ) − = (x + )2 2 2 2 2 1 1 1 −1 = x.
Suy ra f (2017)= 2017
→ f ( f (2017)) = f (2017) = 2017. Chọn C.
Câu 6. Cho a, b là các số thực dương khác 1 và thỏa mãn ab ≠1. Rút gọn biểu thức
P = (log b + log a + 2)(log b − log b)log a −1. a b a ab b A. P = log . a B. P = 1. C. P = 0. D. P = log . b b a
Lời giải. Từ giả thiết, ta có 1
P = (log b + log a + 2 b − a − a b ). log .log 1 a 1+ log b a b t + t = a 1 1 1 ( )2 1 log 1 t +1 1 b → t + + 2 − t −1 = . t −1 = −1 = = log . b Chọn D. t t t +1 t t (t + ) 1 a t t
Câu 7. Cho ba điểm A(b;log b), B(c;2 log c , C (b;3log b với 0 < a ≠1, b > 0 , c > 0 . a ) a a )
Biết B là trọng tâm của tam giác OAC với O là gốc tọa độ. Tính S = 2b + c. A. S = 9. B. S = 7. C. S = 11. D. S = 5. 0 + b + b = c Lời giải. Vì 3
B là trọng tâm của tam giác OAC nên
0 + log b + 3 log b a a = 2 log c 3 a b + b = 3c 2 b = 3c 2 b = 3c ⇔ ⇔ ⇔ 2 3 4
log b = 6 log c 2
log b = 3 log c b = c a a a a log log a a 27 b = 2 b = 3c c >0 8 ⇔ →
→S = 2b + c = 9. Chọn A. 2 3 b = c 9 c = 4
Câu 8. Cho a, b, c là các số thực dương thỏa mãn 2
a = bc. Tính S = 2 ln a − ln b − ln c . A. a a S 2 ln = . B. S = 1.
C. S = −2 ln . D. S = 0. bc bc
Lời giải. Ta có S = a −( b + c ) 2 2 ln ln ln
= ln a − ln(bc) = ln(bc )− ln(bc) = 0. Chọn D.
Câu 9. Cho M = log x = log y với x > 0, y > 0. Mệnh đề nào sau đây là đúng? 12 3 A. x x M = log
. B. M = log .
C. M = log x − y . D. M = log x + y . 15 ( ) 9 ( ) 4 y 36 y M = Lời giải. Từ x 12 x x
M = log x = log y → → = 4M → M = log . Chọn A. 12 3 4 y = 3M y y
Cách trắc nghiệm. ● Cho x = 12
→ y = 3 . Khi đó M = 1.
Thử x = 12; y = 3 vào các đáp án thì có các đáp án A, C, D đều thỏa. Ta chưa kết luận được. ● Cho 2 2 x = 12
→ y = 3 . Khi đó M = 2 .
Thử x = 144; y = 9 vào các đáp án thì có các đáp án A thỏa.
Câu 10. Cho a, b, c là các số thực dương khác 1 và thỏa 2 log b = x, log c = y . 2 a b
Tính giá trị của biểu thức P = log . a c A. 2 xy P = .
B. P = 2xy. C. 1 P = . D. P = . xy 2xy 2
Lời giải. Nhận thấy các đáp án đều có tích xy nên ta sẽ tính tích này. Ta có 1 1 1 2 xy = log b . log c = log c = log c = → log a = . Chọn C. 2 a a 2 a 2 log c b a 2xy c
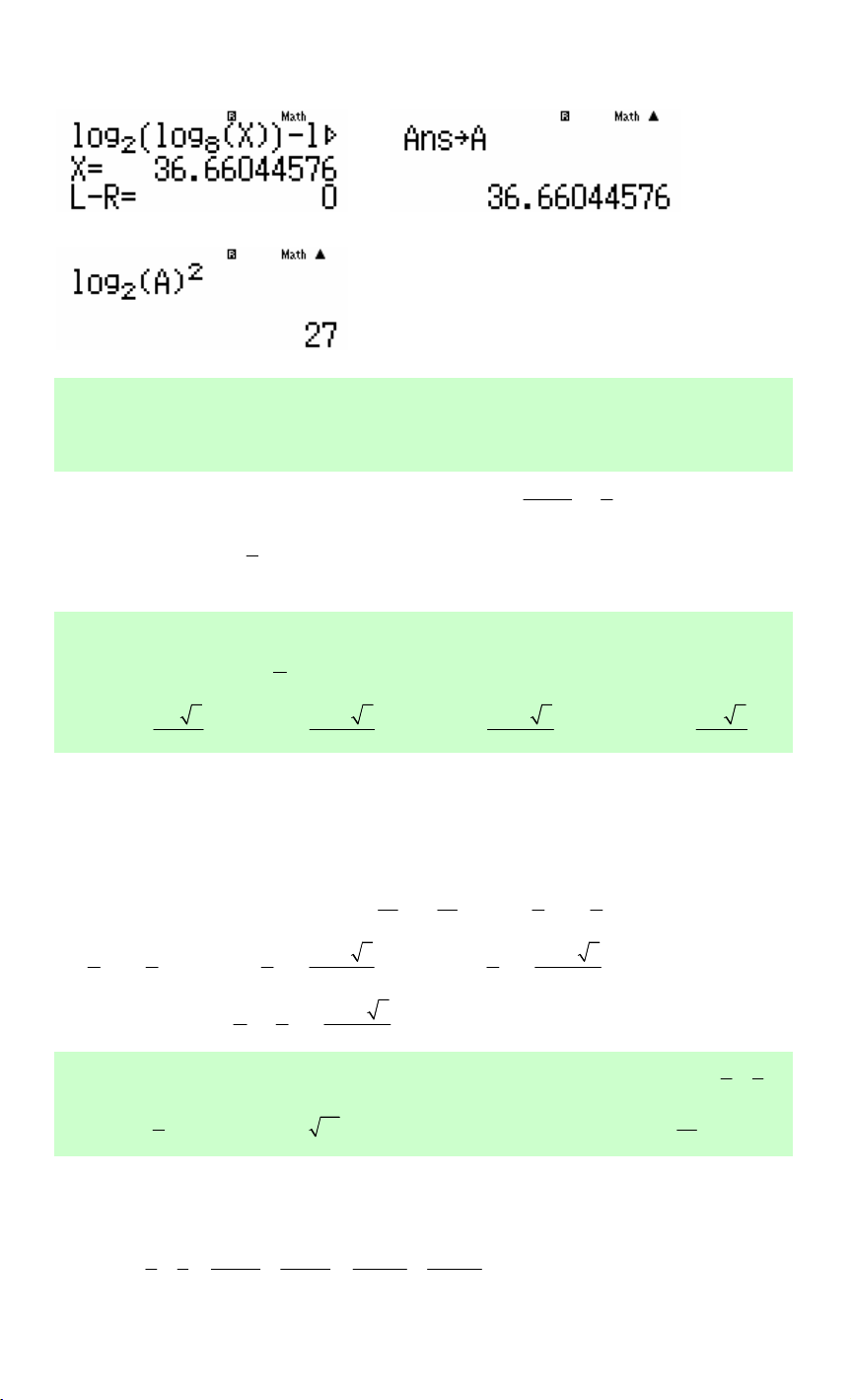
Câu 11. Cho x là số thực dương thỏa log log x = log log x . Tính P = (log x . 2 )2 2 ( 8 ) 8 ( 2 ) A. P = 3. B. P = 3 3. C. P = 27. D. 1 P = . 3
Lời giải. Ta có log x = P thay vào giả thiết, ta có 2 P 1 P 6 6 log = log P = log P ⇔
= P ⇔ P = 27. Chọn C. 2 2 2 3 3 3
Cách CASIO. Phương trình ⇔ log log x −log log x = 0. 2 ( 8 ) 8 ( 2 )
Dò nghiệm phương trình, lưu vào A
Thế x = A để tính (log x)2 2
Đáp số chính xác là C. Chọn C.
Câu 12. Cho x là số thực lớn hơn 1 và thỏa mãn log log x = log log x + a , với 2 ( 4 ) 4 ( 2 )
a ∈ ℝ . Tính giá trị của P = log x theo a . 2 A. a 1 P 4 + = . B. 2 P = a . C. 2a P = . D. a 1 P 2 + = . Lời giải. Ta có log x 1
log (log x) = log (log x ) 2 + a ← → log = log log x + a 2 4 4 2 2 2 ( 2 ) 2 2 1 ← → log log x −1 = log log x + a ←
→ log log x = 2a + 2 2 ( 2 ) 2 ( 2 ) 2 ( 2 ) 2 2a+2 a 1 log x 2 log x 4 + ← → = ← → = . Chọn A. 2 2
Câu 13. Cho p , q là các số thực dương thỏa mãn log p = log q = log p + q . Tính 9 12 16 ( )
giá trị của biểu thức p A = . q A. 1− 5 − − − + + A = . B. 1 5 A = . C. 1 5 A = . D. 1 5 A = . 2 2 2 2 p = 9t
Lời giải. Đặt t log p log q log p q q = = = + → = 12t 9 12 16 ( )
p+q =16t
→ 9t +12t = + = 16t p q . (*) t t 2t t Chia hai vế của 9 12 3 3
(*) cho 16t , ta được + = 1 ↔ + = 1 16 16 4 4 2t t t t 3 3 3 −1− 5 − + ↔ + −1 = 0 ↔ = (loại) hoặc 3 1 5 = . 4 4 4 2 4 2 t Giá trị cần tính p 3 −1+ 5 A = = = . Chọn C. q 4 2
Câu 14. Cho a, b, c là các số thực khác 0 thỏa mãn 4a 25b 10c = = . Tính c c T = + . a b A. 1 T = . B. T = 10. C. T = 2. D. 1 T = . 2 10 a = log t 4
Lời giải. Giả sử 4a 25b 10c t = = =
→ b = log t . 25
c = log t 10 Ta có c c log t log t log 4 log 25 10 10 t t T = + = + = + = log 4 + log 25 10 10 a b log t log t log 10 log 10 4 25 t t = log
4.25 = log 100 = 2. Chọn C. 10 ( ) 10
Câu 15. Cho a, b, c là các số thực dương thỏa mãn log3 7 log7 11 log 25 11 a = 27, b = 49, c = 11 .
Tính giá trị của biểu thức 2 2 2 log 7 log 11 3 7 log 25 11 T = a + b + c .
A. T = 76 + 11 . B. T = 31141. C. T = 2017 . D. T = 469 .
Lời giải. Ta có = ( )log37 +( )log711 +( log 25 T a b c )lo 1g125 log 7 log 11 3 7 11 log 25 = ( )log 7 +( )log 11 27 49 +( 11) 11 3 7 . log 7 3 (27 )log 7 = ( 3 3 ) 3 3 = ( log 7 3 3 ) 3 = 7 = 343 Áp dụng log 11 2 log b log 11 7 2 log 11 a a = b , ta được ( 49) 7 = (7 ) = ( 7 7 ) 2 = 11 = 121 . log 25 11 1 1 1 ( 11 )lo 1g125 = 1 1 = ( log 25 2 11 11 )2 2 = 25 = 25 = 5
Vậy T = 343 +121+5 = 469. Chọn D.
Câu 16. Cho a, b là các số thực dương khác 1 và n ∗ ∈ ℕ . Một học sinh tính 1 1 1 P = + +... + theo các bước sau: log b log b log b 2 n a a a I) 2
P = log a + log a + ... + log n a . b b b II) P = ( 1 2 3 log a a a ... n a . b ) III) 1 2 3 ... P log n a + + + + = . b
IV) P = n(n + ) 1 log a . b
Trong các bước trình bày, học sinh đã trình bày sai ở bước nào? A. I. B. II. C. III. D. IV.
Lời giải. Chọn D. Vì n n +1 1+2+3 . + ..+n ( ) P = log a = + + + + n a = a . b (1 2 3 ... ).log . log b 2 b Câu 17. Cho 1 1 1 M = + +... +
với 0 < a ≠ 1 và 0 < x ≠ 1 . Mệnh đề log x log x log x 2 k a a a nào sau đây là đúng? A. k (k + ) 1 4k k +1 k k + k k + M = . B. ( ) M = . C. ( ) 1 M = . D. ( ) 1 M = . log x log x 2 log x 3 log x a a a a Lời giải. Ta có 1 1 1 1 M = + + +... + log x 1 1 1 a log x log x log x 2 a 3 a a k 1 2 3 k 1 1 k (k + ) 1 = + + +... + = .(1+ 2 + 3 +...+ k) = . . log x log x log x log x log x log x 2 a a a a a a Chọn C Câu 18. Tính 1 1 1 1 P = + + +... + . log 2017! log 2017! log 2017! log 2017! 2 3 4 2017 A. P = 2017. B. P = 1. C. P = 0. D. P = 2017!.
Lời giải. Áp dụng công thức 1 log b = , ta được a log a b P = log 2 + log 3 +... + log 2017 = log 2.3.4....2017 = log 2017! = 1. 2017! 2017! 2017! 2017! ( ) 2017! Chọn B.
Câu 19. Đặt a = ln 3, b = ln 5. Tính 3 4 5 124 I = ln + ln + ln +... + ln theo a và . b 4 5 6 125
A. I = a −2 . b
B. I = a +3 . b
C. I = a + 2 . b
D. I = a −3 . b Lời giải. Ta có 3 4 5 124 3 I ln = . . ... = ln
= ln 3− ln125 = ln 3−3 ln 5 = a −3 . b 4 5 6 125 125 Chọn D.
Câu 20. Tính P = ( 0 ) ( 0 ) ( 0 ) ( 0
ln 2 cos1 .ln 2 cos 2 .ln 2 cos 3 ... ln 2 cos 89 ) , biết rằng trong tích
đã cho có 89 thừa số có dạng ( 0
ln 2 cos a ) với 1 ≤ a ≤ 89 và a ∈ ℤ . 89 A. 2 P = 1. B. P = −1 . C. P = . D. P = 0 . 89!
Lời giải. Trong tích trên có ln ( 1 0 2 cos 60 ) ln = 2.
= ln1 = 0 . Vậy P = 0 . Chọn D. 2 Câu 21. Cho hàm số 1 2x f (x) = log . Tính tổng 2 2 1− x 1 2 3 2015 2016 S f f f ... f f = + + + + + . 2017 2017 2017 2017 2017 A. S = 2016. B. S = 1008. C. S = 2017. D. S = 4032. Lời giải. Xét 1 2x 1 2(1− x)
f (x)+ f (1− x) = log + log 2 2 2 1− x 2 1− (1− x) 1 2x 1 2(1− x) 1
2x 2(1− x) 1 = log + log = log . = log 4 = 1 . 2 2 2 2 2 1− x 2 x 2 1− x x 2
Áp dụng tính chất trên, ta được 1 2016 2 2015 1008 1009 S = f + f + f + f +... + f + f 2017 2017 2017 2017 2017 2017
= 1+1+... +1 = 1008. Chọn B.
Câu 22. Cho log x = 2 . Tính giá trị biểu thức 2 3
P = log x + log x + log x. 2 2 1 4 2 A. 11 2 P = . B. P = 2 . C. 2 P = − . D. P = 3 2. 2 2 Lời giải. Ta có 1 1 1 2
P = 2 log x −3 log x + log x = − log x = − . 2 = − . Chọn C. 2 2 2 2 2 2 2 2
Câu 23. (ĐỀ CHÍNH THỨC 2016 2017) Với –
a, b là các số thực dương tùy ý và a khác 1, đặt 3 6
P = log b + log b . Mệnh đề nào dưới đây đúng ? 2 a a A. P = 27 log .
b B. P = 15 log b. C. P = 9 log . b D. P = 6 log . b a a a a Lời giải. Ta có 6 3 6
P = log b + log b = 3 log b + log b = 6 log b. Chọn D. 2 a a 2 a a a
Câu 24. Cho a = log m và A = log 8m , với 0 < m ≠ 1 . Mệnh đề nào sau đây đúng? 2 m A. − a + a A = (3− a) . a
B. A = (3+a) . a C. 3 A = . D. 3 A = . a a Lời giải. Ta có 3 3 3 + a
A = log 8m = log 8 + log m = 3 log 2 +1 = +1 = +1 = . m m m m log m a a 2 Chọn D.
Câu 25. (ĐỀ CHÍNH THỨC 2016 2017) Với các số thực dương –
x, y tùy ý, đặt
log x = a và log y = b . Mệnh đề nào sau đây là đúng ? 3 3 3 3 A. x a x a log = + . b B. log = − . b 27 y 2 27 y 2 3 3 C. x a x a log = 9 +b D. . log = 9 −b . 27 y 2 27 y 2 3 Lời giải. Ta có x 3 x 1 a log = log = log x − log y =
log x − log y = − . b 27 3 3 3 3 3 y 3 y 2 2 Chọn B. Câu 26. Cho log 120
log 5 = a, log 5 = b . Tính giá trị biểu thức 5 A =
theo a và b . 2 3 log4 2 2 A.
2b + ab + a + + A = . B. 3b ab a A = . 4 2ab ab C.
3b + ab + a
b + ab + 3a A = . D. A = . 4 2ab 4 2ab log ( 3 2 .5.3 log 120 5 ) Lời giải. Ta có 3 log 2 +1+ log 3 5 5 5 A = = = 1 log 2 4 4 2 2 4 2 3 1 +1+
3b + ab + a a b = = . Chọn C. 4 4 2 2ab
Cách 2. Dùng CASIO:
Bấm máy log 5 và lưu vào biến A; Bấm máy log 5 và lưu vào biến B. 2 3
Giả sử với đáp án A, nếu đúng thì hiệu log 120 2b + ab + a 5 − phải bằng 0. log4 2 4 2 2ab
Nhập vào màn hình log 120 2B+ AB + A 5 −
với A, B là các biến đã lưu và nhấn dấu =. log4 2 4 2 2AB
Màn hình xuất hiện số khác 0. Do đó đáp án A không thỏa mãn.
Thử lần lượt và ta chọn được đáp án đúng là C.
Câu 27. (ĐỀ MINH HỌA 2016 2017) Đặt và . Hãy biểu diễn – a = log 3 b = log 3 2 5
log 45 theo a và b . 6 2 A. a + 2ab 2a − 2ab log 45 = . B. log 45 = . 6 ab 6 ab 2 C. a + 2ab 2a − 2ab log 45 = . D. log 45 = . 6 ab + b 6 ab + b
Lời giải. Ta có log 45 = log 9 + log 5. 6 6 6 2 2 2 2a log 9 = 2 log 3 = = = = . 6 6 log 6 1+ log 2 1 a +1 3 3 1+ a 1 1 a b log 5 = = = vì log 2 = . 6 log 6 log 3 + log 2 b a +1 5 a 5 5 5 ( ) Vậy 2a a a + 2ab log 45 = + = . Chọn C. 6 a +1 b (a + ) 1 ab + b
Câu 28. (ĐỀ CHÍNH THỨC 2016 2017) Với mọi –
a, b, x là các số thực dương thoả
mãn log x = 5log a +3log b . Mệnh đề nào dưới đây là đúng? 2 2 2
A. x = 3a + 5b .
B. x = 5a + 3b . C. 5 3
x = a + b . D. 5 3 x = a b . Lời giải. Ta có 5 3 5 3 5 3
log x = 5 log a + 3 log b = log a + log b = log a b ⇔ x = a b . 2 2 2 2 2 2 Chọn D.
Câu 29. (ĐỀ CHÍNH THỨC 2016 2017) Cho và 1 – log a = 2 log b = . Tính giá trị 3 2 2
biểu thức I = 2 log log (3a) 2 + log b . 3 3 1 4 A. 5 I = . B. I = 4 . C. I = 0 . D. 3 I = . 4 2 1 Lời giải. Ta có 1 2 log a = 2 → a = 3 = 9 và 2 log b = →b = 2 = 2. 3 2 2 Vậy 2 1 3
I = 2 log log 3.9 + log 2 = 2 − = . Chọn D. 3 3 ( ) 1 ( ) CASIO 2 2 4
Câu 30. (ĐỀ CHÍNH THỨC 2016 2017) Cho –
a là số thực dương tùy ý khác 1.
Mệnh đề nào dưới đây đúng ? A. 1 1
log a = log 2. B. log a = . C. log a = .
D. log a = −log 2. 2 a 2 log a 2 log 2 2 a 2 a
Lời giải. Chọn C.
Câu 31. (ĐỀ CHÍNH THỨC 2016 2017) Với mọi số thực dương –
a và b thỏa mãn 2 2
a + b = 8ab , mệnh đề nào dưới đây đúng? A. 1
log(a + b) = (log a + log b).
B. log(a +b)=1+ log a + log . b 2 C. 1 1
log(a + b) = (1+ log a + log b).
D. log(a +b)= + log a + log . b 2 2
Lời giải. Ta có a +b = ab ⇔ (a +b)2 2 2 8 = 10ab ⇔ (a + b)2 log
= log (10ab) ⇔ 2 log(a + b) = log10 + log a + log b 1
⇔ log(a + b) = (1+ log a + log b). Chọn C. 2
Câu 32. (ĐỀ CHÍNH THỨC 2016 2017) Cho –
x, y là các số thực lớn hơn 1 thỏa mãn 1+ log x + log y 2 2
x + 9 y = 6xy . Tính 12 12 M = . 2 log x + 3y 12 ( ) A. 1 M = . B. 1 M = . C. 1 M = . D. M = 1. 2 3 4
Lời giải. Ta có x + y = xy ⇔ (x − y)2 2 2 9 6 3
= 0 ⇔ x = 3y . 1+ log x + log y 1+ log 3y + log y 1+ log ( 2 3y ) log ( 2 36 y 12 12 12 12 12 12 ) Suy ra ( ) M = = = = 2 log x + 3y 2 log 3y + 3y 2 log 6 y 2 log 6 y 12 ( ) 12 ( ) 12 ( ) 12 ( ) log ( 2 36 y 12 ) =1. Chọn D. log ( 2 36 y 12 )
Câu 33. (ĐỀ MINH HỌA 2016 2017) Cho các số thực dương . Khẳng – ,
a b với a ≠ 1
định nào sau đây là khẳng định đúng ? A. 1 log ab = log b .
B. log ab = 2 + 2 log b . 2 ( ) 2 ( ) 2 a a a a C. 1 1 1 log ab = log b .
D. log ab = + log b . 2 ( ) 2 ( ) 4 a a 2 2 a a Lời giải. Ta có 1 1 1 1 log ab = log ab = log a + log b =
+ log b . Chọn D. 2 ( ) ( a ) ( a a ) 2 2 2 2 a a
Câu 34. (ĐỀ CHÍNH THỨC 2016 2017) Cho –
a là số thực dương khác 1. Mệnh đề
nào dưới đây là đúng với mọi số thực dương x, y. A. x log x x log a = B. log = log x − y a a ( ) a y log y y a C. x x log
= log x + log y D. log
= log x − log y . a a a y a a a y
Lời giải. Chọn D.
Câu 35. Cho a, b, x, y là các số thực dương và khác 1. Mệnh đề nào dưới đây là đúng ?
A. log (x + y)= log x + log y . B. log .
a log x = log x . a a a b a b C. 1 1 x x log = . D. log log a = . a x log x a y log y a a
Lời giải. Ta có log x + log y = log xy → A sai. a a a x
log x − log y = log → D sai. a a a y 1 log = −log x → C sai. a a x log .
a log x = log x
→ B đúng. Chọn B. b a b
Câu 36. Cho a, b là các số thực dương và a ≠1. Khẳng định nào sau đây đúng? A. ( 2 log
a + ab) = 4 + 2 log . b B. a + ab = a + b a ( 2 log ) 4 loga ( ). a a C. ( 2 log
a + ab) = 2 + 2 log (a +b). D. ( 2 log
a + ab) = 1+ 4 log . b a a a a Lời giải. Ta có a + ab = a a +b =
a a +b = a + a + b a ( 2 log ) log 2 log 2 log log 1 ( ) a ( ) a a ( ) 2 a
= 2 log a + 2 log (a + b) = 2 + 2 log a + b . Chọn C. a a a ( )
Câu 37. Cho các số thực a < b < 0 . Mệnh đề nào sau đây là sai? A. 3
ln(ab) = ln a + ln . b B. ( 2 a −b) = ( 2 ln 3 ln a −b). 2 C. a a ln 2 2
= ln a − ln b . D. ln
= ln a − ln b . b b
Lời giải. Vì a < b < 0 nên ln a và ln b không có nghĩa. Chọn A.
Câu 38. Cho a, b là hai số số thực dương và a ≠1. Khẳng định nào sau đây đúng? A. a 1 1 a 1 log 1 = + log b B. log = 1− 2 log b . 3 ( ) . 3 b 3 2 a a b 3 a a C. a 1 1 a 1 log 1 = D. log 3 1 = − log b . − log b . 3 3 b 3 2 a a b 2 a a a 1 log a 1− log b a Lời giải. Ta có a b log a − log b a a 2 log = = = . Chọn C. 3 a 3 b log a 3 log a 3 a a
Câu 39. (ĐỀ MINH HỌA 2016 2017) Cho hai số thực . Khẳng –
a và b , với 1 < a < b
định nào dưới đây là khẳng định đúng ?
A. log b <1< log a .
B. 1< log b < log a . a b a b
C. log a < log b <1.
D. log a <1 < log b . b a b a Lời giải.
log b > log a ⇔ log b > 1 Ta có b a 1 a a a > > ⇔
⇔ log a < 1 < log . b Chọn D.
log b > log a ⇔ 1> log b a a b b b
Câu 40. Cho các số thực dương a, b với a ≠1 và log b > 0. Khẳng định nào sau đây a là đúng? a ∈(0; ) 1
A. a;b ∈(0; ) 1 hoặc .
B. a;b ∈(0; )
1 hoặc a;b ∈ (1;+∞). b ∈(1;+∞ ) a ∈(1;+∞) C.
hoặc a;b ∈(1;+∞). D. a;b ∈(0; )
1 hoặc b ∈ (1;+∞). b ∈ (0; ) 1
Lời giải. Với điều kiện a, b > 0 và a ≠ 1, ta xét các trường hợp sau:
TH1: 0 < a <1 , ta có 0<a 1 log b 0 log b log 1 < > ← → > → b < 1. a a a
TH2: a >1 , ta có a 1 log b 0 log b log 1 > > ← → > → b > 1. a a a
Từ hai trường hợp trên, ta được 0 < a, b <1 . Chọn B.
a > 1, b > 1
Câu 41. Cho bốn số thực dương a, b, x, y thỏa mãn a ≠ 1, b ≠ 1 và 2 2
x + y = 1 . Biết
rằng log (x + y)> 0 và log xy < . Mệnh đề nào sau đây là đúng? b ( ) 0 a A. a > 1 a > < a < < a < . B. 1 . C. 0 1 . D. 0 1 . 0 < b <1 b > 1 b > 1 0 < b <1 2 2 2 Lời giải.
1 = x + y = x + y − 2xy ● Ta có ( )
→(x + y)2 > 1
→ x + y > 1 .
x, y > 0
Kết hợp với log (x + y)> 0 → a > 1 . a
x, y > 0 ● Ta có
→ x, y ∈ (0; ) 1 → 0 < xy < 1 . 2 2 x + y = 1
Kết hợp với log (xy)< 0
→b > 1 . Chọn B. b
Cách giải trắc nghiệm: Chọn 1 3 x = → y = . 2 2 1+ 3 x + y = > 1 l
og x + y > a ( ) 0 Khi đó 2 a > , kết hợp với suy ra 1 . 3 l og xy < b > 1 b ( ) 0 0 < xy = <1 4
Câu 42. Cho a, b, c là các số thực dương khác 1 và thỏa mãn b = Khẳng a ( log log a c ) 1.
định nào sau đây là đúng? A. 2 a = bc. B. 2 a = log c.
C. b = c.
D. a = c. b
Lời giải. Áp dụng log n x = .
n log x với x > 0 , ta được m m b = a b = b a ( log log a c ) log .log log . c a c
Suy ra log b = 1 ⇔ b = c . Chọn C. c
Câu 43. Cho x, y là các số thực dương thỏa mãn x + ( y)2 2 9 log 4 log
= 12 log x. log y .
Mệnh đề nào sau đây là đúng? A. 3 2 x = y . B. 2 3 x = y .
C. 2x = 3y .
D. 3x = 2y . Lời giải. Ta có x + ( y)2 2 9 log 4 log
= 12 log x.log y ⇔ ( x )2 − x y +( y)2 3 log 2.3 log .2 log 2 log = 0 ⇔ ( x − y)2 3 2 3 2 3 log 2 log
= 0 ⇔ 3 log x = 2 log y ⇔ log x = log y ⇔ x = y . Chọn A.
Câu 44. Tìm x để ba số ln 2, ln(2x ) 1 , ln (2x − + )
3 theo thứ tự đó lập thành cấp số cộng. A. x = 1. B. x = 2. C. x = log 5. D. x = log 3. 2 2
Lời giải. Điều kiện: x > 0. Vì ln 2, ln(2x ) 1 , ln(2x −
+ 3) theo thứ tự đó lập thành CSC nên ta có ( x ) ( x ) ( x ) ( x )2 ( x ) ( x ⇔ + + = − ⇔ + = − ⇔ + = − )2 ln 2 ln 2 3 2 ln 2 1 ln 2 2 3 ln 2 1 2 2 3 2 1 2x = − ( 1 loaïi) 2 2 x 4.2x ⇔ − −5 = 0 ⇔
⇔ 2x = 5 ⇔ x = log 5. Chọn C. 2 2x = 5
Câu 45. Trong các giá trị của a được cho trong bốn phương án A, B, C, D dưới đây,
giá trị nào của a thỏa mãn 2 log a > log a ? 0,5 0,5 A. 5 a = − . B. 5 a = . C. 4 a = . D. 2 a = . 4 4 5 3
Lời giải. Điều kiện: a > 0 . Loại A. Vì cơ số a > 1 0,5 < 1 nên 2 2 log a > log
a ⇔ a < a ⇔ a a −1 > 0 ⇔ . 0,5 0,5 ( ) a < 0
Đối chiếu với điều kiện ta được: a >1 .
Do đó trong các số đã cho chỉ có 5 là thỏa mãn. Chọn B. 4
Cách trắc nghiệm: Thay lần lượt bốn đáp án và bấm máy tính. x Câu 46. Điểm
M (x ; y thuộc đồ thị hàm số 1 y
= và nằm hoàn toàn phía dưới 0 0 ) 3 đường thẳng 1 y =
. Mệnh đề nào sau đây là đúng? 9 A. x < 2 .
B. x < −2 .
C. x > −2 . D. x > 2 . 0 0 0 0 x
Lời giải. Hoành độ các điểm trên đồ thị hàm số 1 y
= và nằm hoàn toàn phía dưới 3 x x 2 đường thẳng 1 1 1 1 1 y = thỏa mãn <
↔ < ⇔ x > 2 . Chọn D. 9 3 9 3 3
Câu 47. (ĐỀ CHÍNH THỨC 2016 2017) Một người gửi 50 triệu đồng vào một ngân –
hàng với lãi suất 6% / năm. Biết rằng nếu không rút tiền ra khỏi ngân hàng thì cứ
sau mỗi năm số tiền lãi sẽ được nhập vào gốc để tính lãi cho năm tiếp theo. Hỏi sau ít
nhất bao nhiêu năm người đó nhận được số tiền nhiều hơn 100 triệu đồng bao gồm cả
gốc và lãi? Giả sử trong suốt thời gian gửi lãi suất không đổi và người đó không rút tiền ra A. 13 năm. B. 12 năm. C. 14 năm. D. 11 năm.
Lời giải. Gọi M là số tiền gửi ban đầu, r = 6% /năm là lãi suất, n là số năm gửi.
Ta có công thức lãi kép: = ( n T
M 1+ r ) là số tiền nhận được sau n năm. Theo đề bài, ta có n
> 100 ⇔ 50.(1+ 6%) > 100 ⇔ 1,06n T > 2 → n > 11.
Do kỳ hạn là 1 năm nên phải đúng hạn mới được nhận.
Vậy người này cần ít nhất 12 năm. Chọn B.
Câu 48. (ĐỀ CHÍNH THỨC 2016 2017) Đầu năm 2016, ông – A thành lập một
công ty. Tổng số tiền ông A dùng để trả lương cho nhân viên trong năm 2016 là 1 tỷ
đồng. Biết rằng cứ sau mỗi năm thì tổng số tiền dùng để trả lương cho nhân viên
trong cả năm đó tăng thêm 15% so với năm trước. Hỏi năm nào dưới đây là năm đầu
tiên mà tổng số tiền ông A dùng để trả lương cho nhân viên trong cả năm lớn hơn 2 tỷ đồng? A. Năm 2022. B. Năm 2021. C. Năm 2020. D. Năm 2023.
Lời giải. Ta xem đây như bài toán lãi suất gởi ngân hàng được phát biểu ngắn gọn như
sau: ' Đầu năm 2016, ông A gởi vào ngân hàng 1 tỷ đồng với lãi suất hàng năm là 15% .
Hỏi đến năm nào là năm đầu tiên ông A nhận được số tiền lớn hơn 2 tỷ đồng. Biết
rằng nếu không rút tiền ra khỏi ngân hàng thì cứ sau mỗi năm số tiền lãi sẽ được
nhập vào gốc để tính lãi cho năm tiếp theo ' .
Gọi M là số tiền gửi ban đầu, r = 15% /năm là lãi suất, n là số năm gửi.
Ta có công thức lãi kép: = ( n T
M 1+ r ) là số tiền nhận được sau n năm. Theo đề bài, ta có n
> 2 ⇔ 1.(1+15%) > 2 ⇔ 1,15n T > 2 → n > 4.
Do kỳ hạn là 1 năm nên phải đúng 5 năm sau mới nhận được. Lúc đấy là năm
2016 + 5 = 2021 . Chọn B.
Câu 49. Anh Nam mong muốn rằng sau 6 năm sẽ có 2 tỷ để mua nhà. Hỏi anh Nam
phải gửi vào ngân hàng một khoản tiền tiền tiết kiệm như nhau hàng năm gần nhất
với giá trị nào sau đây, biết rằng lãi suất của ngân hàng là 8% /năm và lãi hàng năm được nhập vào vốn.
A. 253,5 triệu. B. 251 triệu. C. 253 triệu. D. 252,5 triệu.
Lời giải. Giả sử anh Nam bắt đầu gửi M đồng từ đầu kì 1 với lãi suất là r . +
● Cuối kì 1 có số tiền là: T = M 1+ r . 1 ( )
● Đầu kì 2 có số tiền là: T = M 1+ r + M 2 ( ) M M
= M ( + r )+ = ( + r )2 − = ( + r )2 1 1 . 1 1 1 −1 . (1+ r )−1 r M 2 +
● Cuối kì 2 có số tiền là: T = 1+ r −1 1+ r . 2 ( ) ( ) r M 2
● Đầu kì 3 có số tiền là: T = 1+ r −1 1+ r + M 3 ( ) ( ) r M M ( r )3 ( r ) r ( r )3 1 1 1 1 = + − + + = + − . r r M 3 M 4 +
● Cuối kì 3 có số tiền là: T = 1+ r −1 1+ r = 1+ r − 1+ r . 3 ( ) ( ) ( ) ( ) r r ………….
Tổng quát, ta có cuối kì M n 1 + n có số tiền là: + T = + r − + r . n (1 ) (1 ) r + Suy ra T .r n M = . ( n+
1+ r ) 1 −(1+ r ) T + = 2000000000 n
Áp dụng công thức với n = 6
, ta được M = 252435900 . Chọn D. r = 8% = 0,08
Câu 50. Ông A muốn sau 5 năm có 1.000.000.000 đồng để mua ô tô Camry. Hỏi rằng
ông A phải gửi ngân hàng mỗi tháng (số tiền như nhau) là bao nhiêu? Biết lãi suất
hằng tháng là 0.5% và tiền lãi sinh ra hằng tháng được nhập vào tiền vốn.
A. a = 14.261.000 (đồng).
B. a = 14.260.000 (đồng).
C. a = 14.261.500 (đồng).
D. a = 14.260.500 (đồng).
Lời giải. Gọi r, T, a lần lượt là lãi suất hàng tháng, tổng số tiền sau mỗi tháng, số
tiền gởi đều đặn mỗi tháng .
● Cuối tháng thứ nhất, người đó có số tiền là: T = a + .
a r = a 1+ r . 1 ( )
● Đầu tháng thứ hai, người đó có số tiền là: a(1+ r )+ a = a (1+ r )+1 a a ( r )2 ( r )2 1 1 1 1 = + − = + − . ( 1+ r )−1 r a a
● Cuối tháng thứ hai, người đó có số tiền là: T (1 r )2 1 (1 r )2 1 = + − + + − .r 2 r r a ( r )2 1 1 = + − (1+ r ). r ⋮ a ● Cuối tháng thứ n
n , người đó có số tiền cả gốc lẫn lãi là: T r = + − + r . n (1 ) 1 (1 ) r Suy ra T .r n a = . ( n 1 r) 1 + − (1+ r ) Áp dụng, ta có 1.000.000.000×0,5% a = = 14.261.494, 06 . (1 0,5%) (1 0,5%)60 1 + + −
Vậy mỗi tháng ông A phải gửi tiết kiệm 14 triệu 261 ngàn 500 đồng vào ngân hàng,
liên tục trong 5 năm. Chọn C.
Câu 51. (ĐỀ MINH HỌA 2016 2017) Ông Việt vay ngắn hạn ngân hàng 100 triệu –
đồng, với lãi suất 12% /năm. Ông muốn hoàn nợ cho ngân hàng theo cách: Sau đúng
một tháng kể từ ngày vay, ông bắt đầu hoàn nợ; hai lần hoàn nợ liên tiếp cách nhau
đúng một tháng, số tiền hoàn nợ ở mỗi lần là như nhau và trả hết tiền nợ sau đúng 3
tháng kể từ ngày vay. Hỏi, theo cách đó, số tiền m mà ông Việt sẽ phải trả cho ngân
hàng trong mỗi lần hoàn nợ là bao nhiêu? Biết rằng, lãi suất ngân hàng không thay
đổi trong thời gian ông Việt hoàn nợ. 3 A. ( )3 100. 1,01 1,01 m = (triệu đồng). B. ( ) m = (triệu đồng). 3 (1,0 )3 1 −1 3 C. 100 1 × ,03 120. 1,12 m = (triệu đồng). D. ( ) m = (triệu đồng). 3 (1,12)3 −1
Lời giải. Ở đây, ta phải quy ước số tiền lãi thay đổi theo từng tháng. Nếu không, học
sinh sẽ tính tổng số tiền vay là 100 triệu đồng, lãi cần trả là 0,12×3 = 0,03 (do chỉ trả 12 trong 3 tháng).
Khi đó, số tiền cần trả là 100 ( × 1+ 0, 03) 100 1 × ,03 = , là đáp án C. 3 3
Tuy nhiên nếu lãi suất thay đổi theo tháng thì vấn đề phức tạp hơn (và có lẽ đây cũng
là cách hiểu mà đề đang hướng đến, vì cách hiểu này phù hợp với thực tế).
Lãi hàng tháng mà ông phải trả là 0,12 = 0,01 nhân với số tiền đang nợ, tức là tổng 12
số nợ tháng sau sẽ bằng số nợ tháng trước nhân với 1,01. Tiền Tháng Số tiền còn nợ Tiền lãi trong tháng trả 0 0 100 100×0,01 1 m 100 1 × ,01− m (100 1 × , 01− m)×0,01 2 m (100 1 × ,01− m) 1 × , 01− m (100 1 × ,01− m) 1 × , 01− m×0, 01 100 1 × ,01− m 1 × , 01− m 1
× ,01− m 0 (theo giả thiết thì đến đây hết 3 m ( ) nợ) Do ta có phương trình: ( × − m)× − m × − m = ← → × = m + +( )2 3 100 1,01 1, 01 1, 01 0 100 1, 01 1 1,01 1,01 100 ( × 1,0 )3 1 100 ( × 1,0 )3 1 ( × 1,01− ) 1 (1,0 )3 1 → m = = =
(triệu đồng).Chọn B. 1+1, 01+(1, 0 )2 1 (1,01− ) 1 ( 2 1+1,01+1,01 ) (1,0 )3 1 −1
Câu 52. Một người đàn ông vay vốn ngân hàng với số tiền 100000000 đồng. Người đó
dự định sau đúng 5 năm thì trả hết nợ; Sau đúng một tháng kể từ ngày vay, ông bắt
đầu hoàn nợ; hai lần hoàn nợ liên tiếp cách nhau đúng một tháng, số tiền hoàn nợ ở
mỗi lần là như nhau. Hỏi, theo cách đó, số tiền a mà ông sẽ phải trả cho ngân hàng
trong mỗi lần hoàn nợ là bao nhiêu? Biết lãi suất hàng tháng là 1,2% và không thay
đổi trong thời gian ông hoàn nợ. 59 60 1, 2 1,2 5 12.10 +1 5 12.10 +1 A. 100 100 a = (đồng). B. a = (đồng). 60 60 1,2 1,2 +1 −1 +1 −1 100 100 60 59 1,2 1,2 6 12.10 +1 6 12.10 +1 C. 100 100 a = (đồng). D. a = (đồng). 60 60 1,2 1,2 +1 −1 +1 −1 100 100 Lời giải. Gọi ,
m r, T , a lần lượt là số tiền vay ngân hàng, lãi suất hàng tháng, tổng
số tiền vay còn lại sau mỗi tháng, số tiền trả đều đặn mỗi tháng .
● Sau khi hết tháng thứ nhất (n = )
1 thì còn lại: T = m r +1 − . a 1 ( )
● Sau khi hết tháng thứ hai (n = 2) thì còn lại: T = m r +1 −a r +1 −a 2 ( ) ( ) a m(r )2 a(r ) a m(r )2 a(r ) m(r )2 (r )2 1 1 1 2 1 1 1 = + − + − = + − + = + − + − . r a
● Sau khi hết tháng thứ ba ( 2 2 n = )
3 thì còn: T = m r +1 − r +1 −1 r +1 − a 3 ( ) ( ) ( ) r a m(r )3 (r )3 1 1 1 = + − + − . r ⋮ a
● Sau khi hết tháng thứ n n
n thì còn lại: T m r r = + − + − n ( ) 1 ( ) 1 1 . r 60 1,2 5 n 12.10 +1 +
Áp dụng công thức trên, ta có m(r ) 1 r 100 T = 0 ⇔ a = = (đồng). n (r + )n 60 1 −1 1,2 +1 −1 100 Chọn B.
Câu 53. Biết rằng năm 2001, dân số Việt Nam là 78685800 người và tỉ lệ tăng dân số
năm đó là 1,7% . Cho biết sự tăng dân số được ước tính theo công thức . = . N r S A e
(trong đó A : là dân số của năm lấy làm mốc tính, S là dân số sau N năm, r là tỉ lệ
tăng dân số hàng năm). Cứ tăng dân số với tỉ lệ như vậy thì đến năm nào dân số nước
ta ở mức 120 triệu người? A. 2020. B. 2022. C. 2025. D. 2026. Lời giải. Ta có S N r 1 . S = . A e → N = .ln . r A 6
Để dân số nước ta ở mức 120 triệu người thì cần số năm 100 120.10 N = .ln ≈ 25. 1,7 78685800
Lúc đấy là năm 2001+ 25 = 2026. Chọn D.
Câu 54. Các khí thải gây hiệu ứng nhà kính là nguyên nhân chủ yếu làm trái đất
nóng lên. Theo OECD (Tổ chức hợp tác và phát triển kinh tế thế giới), khi nhiệt độ
trái đất tăng lên thì tổng giá trị kinh tế toàn cầu giảm. Người ta ước tính rằng khi
nhiệt độ trái đất tăng thêm 2 C
° thì tổng giá trị kinh tế toàn cầu giảm 3%, còn khi
nhiệt độ trái đất tăng thêm 5 C
° thì tổng giá trị kinh tế toàn cầu giảm 10% . Biết rằng
nếu nhiệt độ trái đất tăng thêm t C
° , tổng giá trị kinh tế toàn cầu giảm f (t) % thì ( ) = . t f t
k a (trong đó a, k là các hằng số dương). Nhiệt độ trái đất tăng thêm bao
nhiêu độ C thì tổng giá trị kinh tế toàn cầu giảm 20% ? A. 9,3 C ° . B. 7,6 C ° . C. 6,7 C ° . D. 8,4 C ° . 2 Lời giải.
Theo đề bài, ta có k.a = 3% ( )
1 . Cần tìm t thỏa mãn . t k a = 20% . 5 k .a = 10% Từ 3% 10 ( ) 1 ⇒ k = và 3 a = . 2 a 3 Khi đó t 3% t t 20 20 −2 k.a = 20% → .a = 20% ⇔ a = → t = 2 + log ≈ 6,7. Chọn C. 2 10 3 a 3 3 3
Câu 55. Một người đã thả một lượng bèo hoa dâu chiếm 4% diện tích mặt hồ. Biết
rằng cứ sau đúng một tuần bèo phát triển thành 3 lần lượng đã có và tốc độ phát
triển của bèo ở mọi thời điểm như nhau. Sau bao nhiêu ngày, lượng bèo sẽ vừa phủ kín mặt hồ? 25 A. 7×log 25. B. 7 3 . C. 24 7× . D. log 25. 3 3 3
Lời giải. Gọi A là lượng bèo ban đầu, để phủ kín mặt hồ thì lượng bèo là 100 . A 4
Sau một tuần số lượng bèo là 3A
→ sau n tuần lượng bèo là 3n . A
Để lượng bèo phủ kín mặt hồ thì n 100 3 .A = .A 4 100 → n = log = log 25
→ thời gian để bèo phủ kín mặt hồ là t = 7 log 25 . 3 3 4 3 Chọn A. Baøi 03
HAØM SOÁ MUÕ – HAØM SOÁ LOGARIT I. H M SỐ LOGARIT 1. Định nghĩa
Cho a là số thực dương và a ≠ 1. Hàm số y = log x gọi là hàm số logarit cơ số a . a
2. Đạo hàm hàm số logarit 1 y = log x → y ' = ; a x ln a 1 y = ln x → y ' = ; x u '(x)
y = log u x → y = a ( ) ' . u(x).ln a
3. Khảo sát hàm số logarit
Tập xác định: của hàm số logarit y = log x (a > 0, a ≠ ) 1 là (0;+∞) . a
Chiều biến thiên: a >1 : Hàm số đồng biến.
0 < a <1 : Hàm số nghịch biến.
Tiệm cận: Trục tung Oy là đường tiệm cận đứng.
Đồ thị: Đồ thị đi qua điểm M (1;0), N (a; )
1 và nằm phía bên phải trục tung. II. H M SỐ MŨ 1. Định nghĩa
Cho a là số thực dương và a ≠1. Hàm số x
y = a được gọi là hàm số mũ cơ số a .
2. Đạo hàm của hàm số mũ x = → ' x y a
y = a ln a ; x = → ' x y e y = e ; u(x ) y = a
→ y = u (x) u(x) ' ' . ln . a a .
3. Khảo sát hàm số mũ
Tập xác định: của hàm số mũ x
y = a (a > 0, a ≠ ) 1 là ℝ .
Chiều biến thiên: a >1 : Hàm số luôn đồng biến.
0 < a <1 : Hàm số luôn nghịch biến.
Tiệm cận: Trục hoành Ox là đường tiệm cận ngang.
Đồ thị: Đồ thị đi qua điểm (0; )
1 , (1;a) và nằm phía trên trục hoành.
Nhận xét. Đồ thị hàm số x
y = a và đồ thị hàm số y = log x đối xứng với nhau qua a
đường thẳng y = x .
CAÂU HOÛI TRAÉC NGHIEÄM
Vấn đề 1. TÌM TẬP XÁC ĐỊNH CỦA H M SỐ
Câu 1. (ĐỀ MINH HOẠ 2016 2017) Tìm tập xác định – D của hàm số y = log ( 2 x − 2x −3 . 2 ) A. D = (− ; ∞ − ] 1 ∪[3;+ ) ∞ . B. D =[−1;3]. C. D = (− ; ∞ − ) 1 ∪(3;+∞) . D. D = (−1; ) 3 .
Lời giải. Hàm số xác định x > 3 2
⇔ x − 2x −3 > 0 ⇔ . x < −1
Vậy tập xác định của hàm số là D = (− ; ∞ − )
1 ∪(3;+∞) . Chọn C.
Câu 2. Tìm tập xác định x −1
D của hàm số y = log . 2 x A. D = (0; ) 1 . B. D = (1;+∞). C. D = ℝ \{0} . D. (− ; ∞ 0)∪(1;+∞) . −
Lời giải. Hàm số xác định x 1 x > 1 ⇔ > 0 ⇔ . Chọn D. x x < 0
Câu 3. (ĐỀ CHÍNH THỨC 2016 2017) Tìm tập xác định – D của hàm số x −3 y = log . 5 x + 2 A. D = (−2; ) 3 . B. D = (− ; ∞ −2)∪[3;+∞). C. D = ℝ \{−2} . D. D = (− ; ∞ −2)∪(3;+∞) . −
Lời giải. Hàm số xác định x 3 x < −2 ⇔ > 0 ⇔ . Chọn D. x + 2 x > 3
Câu 4. Tìm tập xác định D của hàm số y = 2−ln(ex). A. D = (1;2) . B. D = (1;+∞). C. D = (0; ) 1 . D. D = (0;e]. e x > 0 >
Lời giải. Hàm số xác định x 0 x > 0 ⇔ ⇔ ⇔
⇔ 0 < x ≤ e. Chọn D. 2 − ln(ex) 2 ≥ 0 e x e x ≤ e ≤
Câu 5. Tìm tập xác định D của hàm số y = log x +1 −1. 2 ( ) A. D = (− ; ∞ ] 1 . B. D = (3;+∞) . C. D =[1;+∞). D. D = ℝ \{ } 3 . x +1> 0 x > −
Lời giải. Hàm số xác định 1 x > −1 ⇔ ⇔ ⇔
⇔ x ≥ 1 . Chọn C. log x +1 ≥1 x +1 ≥ 2 x ≥1 2 ( )
Câu 6. Tìm tập xác định D của hàm số y = ln( x −5 +5− x). A. D = ℝ \{ } 5 . B. D = ℝ . C. D = (− ; ∞ 5) . D. D = (5;+∞).
Lời giải. Hàm số xác định ⇔ x −5 +5− x > 0
⇔ x −5 > x −5 ⇔ x −5 < 0 ⇔ x < 5 . Chọn C. Chú ý: A > A ⇔ A < 0.
Câu 7. Tìm tập xác định D của hàm số y = log
x +1 − log (3− x)− log (x − )3 1 . 1 3 2 2 A. D = (1;3). B. D = (−1; ) 1 . C. D = (− ; ∞ 3) . D. D = (1;+∞). x +1> 0 x > −1
Lời giải. Hàm số xác định 3 x 0 ⇔
− > ⇔ x < 3 ⇔ 1 < x < 3 → D = (1; ) 3 . Chọn A. x −1> 0 x > 1
Câu 8. Tìm tất cả các giá trị thực của tham số m để hàm số y = ( 2
ln x − 2mx + m) có tập xác định là ℝ .
A. m < 0 ; m > 1 . B. 0 < m <1.
C. m ≤ 0 ; m ≥1 .
D. 0 ≤ m ≤1. Lời giải. Ycbt a > 0 2 x 2mx m 0, x ⇔ − + > ∀ ∈ ℝ ⇔
⇔ 0 < m < 1 . Chọn B. 2
∆' = m −m < 0
Câu 9. (ĐỀ CHÍNH THỨC 2016 2017) Tìm tất cả các giá trị thực của tham số – m để hàm số y = ( 2
log x − 2x − m + )
1 có tập xác định là ℝ . A. m ≥ 0 . B. m < 0 . C. m ≤ 2 . D. m > 2 . Lời giải. Ycbt a > 0 2 x 2x m 1 0, x ⇔ − − + > ∀ ∈ ℝ ⇔
⇔ m < 0 . Chọn B.
∆' = 1+ m −1 < 0
Câu 10. Tìm tập xác định D của hàm số y = ln(1−log x . 2 ) A. D = (2;+ ) ∞ . B. D = (− ; ∞ 2). C. D = (0;2). D. D = (−2;2) .
Lời giải. Hàm số xác định x > 0 ⇔ 1 − log x > 0 2 x > 0 x > 0 ⇔ ⇔
⇔ 0 < x < 2 . Chọn C. l og x <1 x < 2 2
Câu 11. Tìm tập xác định D của hàm số y = log log x −1 −1. 3 2 ( ) A. D = (− ;
∞ 3) . B. D = (3;+∞) . C. D =[3;+∞). D. D = ℝ \{ } 3 . x −1> 0 >
Lời giải. Hàm số xác định x 1 x > 1 ⇔ ⇔ ⇔
⇔ x > 3. Chọn B. log x −1 > 1 x −1> 2 x > 3 2 ( )
Câu 12. Tìm tập xác định 1 D của hàm số y = + ln (x − ) 1 . 2 − x A. D = ℝ \{2} . B. D = (1;2) . C. D = [0;+ ) ∞ . D. D = (− ; ∞ ) 1 ∪(2;+ ) ∞ . − >
Lời giải. Hàm số xác định x 1 0 x > 1 ⇔ ⇔
⇔ 1 < x < 2 . Chọn B. 2 − x > 0 x < 2
Câu 13. Tìm tập xác định D của hàm số y = ( 2 x + x + ) 1 .log x + 2 . 1 ( ) 2
A. D = (−2;+∞). B. D =[−2;− ] 1 . C. D = (−2;− ) 1 . D. D = (−2;− ] 1 . x + 2 > 0 x > −2
Lời giải. Hàm số xác định ⇔ ( 2 x + x + ) 1 . log x + 2 ≥ 0 ⇔ log x + 2 ≥ 0 1 ( ) 1 ( ) 2 2 x > −2 x > −2 ⇔ ⇔
⇔ −2 < x ≤ −1 . Chọn D. x + 2 ≤1 x ≤ −1
Câu 14. Tìm điều kiện của x để hàm số y = log ( 2 1− 2x + x có nghĩa. 1 ) x A. x > x > 0 . B. x ≥ 0 . C. 0 . D. x >1 . x ≠ 1 2 1
−2x + x > 0 x ≠ 1
Lời giải. Hàm số có nghĩa 1 x > 0 ⇔ > 0 ⇔ x > 0 ⇔ . Chọn C. x x ≠ 1 x ≠ 1 1 ≠1 x
Câu 15. Hàm số nào dưới đây có tập xác định là đoạn [−1;3]? A. 1 y = ( 2
ln 3 + 2x − x ) . B. y = . 2 3 + 2x − x C. 1 2
y = 3 + 2x − x . D. y = . 2 3 + 2x − x
Lời giải. Hàm số 1 y = ( 2
ln 3 + 2x − x ) và hàm số y = xác định khi 2 3 + 2x − x 2
3 + 2x − x > 0 ⇔ (x + )
1 (x − 3) < 0 ⇔ 1
− < x < 3 : không phù hợp. Hàm số 1 x ≠ −1 y = xác định khi 2 3 2x x 0 + − ≠ ⇔ . 2 3 + 2x − x x ≠ 3
Hàm số này có tập xác định là D = ℝ \{−1; } 3 : không phù hợp. Hàm số 2
y = 3 + 2x − x xác định khi 2
3 + 2x − x ≥ 0 ⇔ 1
− ≤ x ≤ 3 : thỏa mãn. Chọn C. x
Câu 16. Tìm tập xác định e D của hàm số y = . x e −1
A. D = ℝ \{0} . B. D = ℝ . C. D = ℝ \{ } 1 .
D. D = ℝ \{e} .
Lời giải. Hàm số xác định x ⇔ −1 ≠ 0 x e
⇔ e ≠ 1 ⇔ x ≠ 0 . Chọn A.
Câu 17. Tìm tập xác định D của hàm số 2 x 5 − x +6 y = 1−3 . A. D = [2;3] . B. D = (− ; ∞ 2]∪[3;+∞). C. D =[1;6] . D. D = (2;3) .
Lời giải. Hàm số xác định 2 2 x 5 − x +6 x 5 − x +6 ⇔ 1−3 ≥ 0 ⇔ 3 ≤ 1 2
⇔ x −5x + 6 ≤ 0 ⇔ 2 ≤ x ≤ 3 . Chọn A. 2 x 3 − x
Câu 18. Tìm tập xác định 2 9 D của hàm số y = − . 3 4 A. D = [0;3] . B. D = (− ; ∞ ] 1 ∪[2;+∞) . C. D =[1;2] . D. D =[−1;2] . 2 2 x 3 − x x 3 − x 2 −
Lời giải. Hàm số xác định 2 9 2 2 2 ⇔ ≥ ⇔
≥ ⇔ x −3x ≤ −2 3 4 3 3 2
⇔ x −3x + 2 ≤ 0 ⇔ 1 ≤ x ≤ 2 . Chọn C.
Câu 19. Đẳng thức log3 3 x x = có nghĩa khi: A. x > 0 .
B. Với mọi x . C. x ≥ 0 . D. x >1 .
Lời giải. Điều kiện: x > 0 .
Lôgarit cơ số 3 hai vế của log3 3 x x = , ta được log log 3 x x = 3 3 ( log3 )
⇔ log x = log x. log 3 ⇔ log x = log x : luôn đúng ∀x > 0 . Chọn A. 3 3 3 3 3
Câu 20. Cho a là số thực dương khác 1. Tìm điều kiện của x để x = log x a xảy ra. a
A. Với mọi x . B. x > 0 . C. x ≥ 0 . D. x >1 . Lời giải. Đặt x
N = a > 0
→ x = log N (với 0 < a ≠ 1 ). a
Khi đó x = log x
a ⇔ log N = log x x x x
a ⇔ N = a ⇔ a = a : luôn đúng ∀x ∈ ℝ . Chọn A. a a a
Vấn đề 2. TÍNH ĐẠO H M 2
Câu 21. Tính đạo hàm của hàm số y = ( 2 x + x − )3 2 1 . A. 2(4x + ) 1 2 4x +1 y ' = . B. ( ) y ' = . 3 2 3 2x + x −1 3 (2x + x − )2 2 3 1 C. 3(4x + ) 1 3 4x +1 y ' = . D. ( ) y ' = . 3 2 2 2x + x −1 2 (2x + x − )2 2 3 1 1
Lời giải. Áp dụng công thức ( 2 − / uα )/ α 1 − / = . α u .u , ta có / y = .( 2 2x + x − ) 1 .( 2 3 2x + x − ) 1 3 2 1 2(4x + ) 1 = . .(4x + ) 1 = . Chọn A. 3 2 3 2 3 2x + x −1 3 2x + x −1
Câu 22. (ĐỀ MINH HỌA 2016 2017) Tính đạo hàm của hàm số – 13x y = . x A. 1 ' .13x y x − =
. B. ' 13x y = .ln13 . C. ' 13x y = . D. 13 y ' = . ln13
Lời giải. Áp dụng công thức ( x )/ x a
= a .ln a , ta có ( x )/ ' 13 13x y = = . ln13 . Chọn B.
Câu 23. Tính đạo hàm của hàm số 2 2x y = . 2 1+x 1+x A. x.2 x.2 y ' = . B. 2 1 ' .2 x y x + = .ln 2 . C. ' 2x.ln 2x y = . D. y ' = . ln 2 ln 2
Lời giải. Áp dụng công thức ( / u )/ / = . u a
u a .ln a , ta có / = ( 2 ) 2 .2x y x .ln 2 2 2 x 1 2 .2 .ln 2 .2 x x x + = = .ln 2 . Chọn B.
Câu 24. Tính đạo hàm của hàm số 2 x y = e . 2 x x 2 x A. e e e y ′ = . B. y′ = . C. y′ = . D. 2 ′ = 2 . x y x e . 2 2x 2x 2x 2 x
Lời giải. Ta có ′ = ( ′ e y 2x ) x 2 2 2 .e = . x e = . Chọn C. 2 2x 2x
Câu 25. (ĐỀ MINH HỌA 2016 2017) Tính đạo hàm của hàm số x +1 – y = . 4x A. 1− 2(x + ) 1 ln 2 1+ 2 x +1 ln 2 y ' = . B. ( ) y ' = . 2 2 x 2 2 x C. 1− 2(x + ) 1 ln 2 1+ 2 x +1 ln 2 y ' = . D. ( ) y ' = . 2 2 4x 4x / + (x + )/ / 1 .4x −(x x + ) 1 .(4x 1 )
Lời giải. Ta có y ' = = 4x (4x )2 4x −(x + ) 1 .4x.ln 4 1−(x + ) 1 .ln 4 1− 2 x +1 ln 2 ln 4=2. ln 2 ( ) = =
→ y = . Chọn A. x ' ( )2 4x x ( 2 = ) 2 x 2 x x 4 2 =2 2 4
Câu 26. Tính đạo hàm của hàm số −x cos = 3 + 2017 x y e e . A. −x cos ' = −3 + 2017 sin x y e xe . B. −x cos ' = −3 − 2017 sin x y e xe . C. −x cos ' = 3 − 2017 sin x y e xe . D. −x cos ' = 3 + 2017 sin x y e xe . ( −x e )/ −x = e −
Lời giải. Ta có −x cos → y ' = −3e − 2017.sin x. x e . x e = (cos x)/ cos cos x cos e = −sin x. x e Chọn B.
Câu 27. Tính đạo hàm của hàm số x
y = x với x > 0. x A. x 1 ' . x y x x − = . B. ' = (ln + ) 1 x y x x . C. ' x
y = x ln x . D. y ' = . ln x
Lời giải. Viết lại x x ln x y = x = e . Suy ra = ( ) x lnx = ( + ) x ln ' ln ' ln 1 . x = (ln + ) 1 x y x x e x e x x . Chọn B.
Câu 28. Tính đạo hàm của hàm số = ( )= . x y f x
x π π tại điểm x = 1 . A. f '( ) 1 = . π B. f ( ) 2
' 1 = π + ln π . C. f ( ) 2
' 1 = π + π ln .
π D. f '( ) 1 = 1 .
Lời giải. Đạo hàm / / ( ) ( π ) x π ( x ) π 1 ' . . . − = + = . x π π π π π + . x f x x x x x π .ln π Suy ra f ( ) 2
' 1 = π + π ln π . Chọn C.
Câu 29. Cho hàm số = ( )= 2x.5x y f x . Tính / f (0). A. 1 / f (0) = 10. B. / f (0) = 1. C. / f (0) = . D. / f (0) = ln10. ln10
Lời giải. Viết lại ( ) 2x.5x 10x f x = = . Suy ra ( ) ( x )/ / 10 10x f x = = .ln10. Vậy f ( ) 0
' 0 = 10 .ln10 = 1.ln10 = ln10. Chọn D. Câu 30. Cho hàm số 1 ( ) 2 = 5 x f x
e . Tính P = f '(x)−2x. f (x)+
f (0)− f '(0) . 5 A. P =1.
B. P = 2 .
C. P = 3 . D. P = 4 .
Lời giải. Ta có ( ) 2 ' = 10 . x f x x e
. Do đó f '(0)= 0 và f (0)= 5 .
Vậy P = f (x)− xf (x)+ f ( )− f ( ) 2 2 1 x x 1 ' 2 0
' 0 = 10xe − 2x.5e
+ .5 − 0 = 1 . Chọn A. 5 5
Câu 31. Cho hàm số ( ) 2 1 2 2x f x + = Tính −x 1 T 2 − =
. f '(x)− 2x ln 2 + 2. A. T = −2. B. T = 2. C. T = 3. D. T = 1. Lời giải. Ta có / f (x ) ( 2 x ) 2 2 x 1 + x 1 ' 1 .2 . ln 2 2x.ln 2.2 + = + = . Vậy 2 2 −x 1 − x 1 T 2 .2x ln 2.2 + =
− 2x ln 2 + 2 = 2x ln 2 − 2x ln 2 + 2 = 2. Chọn B. Câu 32. Cho hàm số 1 1 f (x ) = +
. Trong các khẳng định sau, có bao nhiêu 3 + 2x 3 + 2−x khẳng định đúng?
1) f ′(x)≠ 0 với mọi x ∈ . ℝ 2) f ( )
1 + f (2)+...+ f (2017) = 2017. 3) f ( 1 1 2 x ) = + . 3 + 4x 3 + 4−x A. 0. B. 1. C. 2. D. 3. Lời giải. Ta có −2x ln 2 2−x ln 2 • f '(x) = +
. Tại x = 0 ta có f '(x)= 0 nên khẳng định 1 sai.
(3+2x )2 (3+2−x )2 2x + 2−x + 6 2x + 2−x + 6 • f (x ) = = < 1 → f ( )
1 + f (2)+...+ f (2017) < 2017
(3+2x )(3+2−x ) 3.(2x +2−x )+10 nên khẳng định 2 sai. • f ( 1 1 1 1 2 x ) = + ≠ +
với x = 1 chẳng hạn nên khẳng định 3 2 2 x −x 3 + 2x 3 + 2−x 3 + 4 3 + 4 sai.
Do đó không có khẳng định nào đúng. Chọn A. x −x x −x Câu 33. Cho a + a a − a
0 < a ≠ 1+ 2 và các hàm f (x ) = , g(x)= . Trong các 2 2
khẳng định sau, có bao nhiêu khẳng định đúng? 1) 2 f (x) 2 − g (x) = 1.
2) g(2x)= 2g(x) f (x).
3) f (g(0)) = g( f (0)).
4) g′(2x)= g′(x) f (x)− g(x) f ′(x). A. 0. B. 1. C. 2. D. 3. Lời giải. Ta có 2 2 x −x x −x a a a a + − 2 • f (x) 2 − g (x ) = − = 1
→ khẳng đinh 1 đúng. 2 2 2 2 − ( x −x − )( x −x x x + − ) x −x x −x a a a a a a a − a a + a • g (2x) = = = 2. .
= 2 g (x). f (x) → 2 2 2 2 khẳng đinh 2 đúng. f
( g (0)) = f (0) = 1. 1 • → f
khẳng định 3 sai. a
(g(0)) ≠ g( f (0)) → − 2 ( a −1 (0)) = ( ) 1 a g f g = = 2 2a
• Do g (2x) = 2 g (x ) f (x) , lấy đạo hàm hai vế (để ý là g (u) ′ = u g ′ ′(u)), ta có: g (2x) ′
= 2 g′(x) f (x)+ g(x) f ′(x) ⇔ 2g′(2x)= 2 g′(x) f (x)+ g(x) f ′(x)
⇔ g′(2x ) = g ′(x) f (x)+ g (x ) f ′(x ) → khẳng định 4 sai.
Vậy có 2 khẳng định đúng. Chọn C.
Câu 34. Tính đạo hàm của hàm số y = log x. 2017 A. ln 2017 log e y ' = . B. 2017 y ' = . C. 1 y ' = . D. 2017 y ' = . x x x.log 2017 x.ln 2017
Lời giải. Áp dụng 1 log e ( x = , ta được 2017 y ' = = . Chọn B. a )/ 1 log x. ln a x.ln 2017 x
Câu 35. (ĐỀ CHÍNH THỨC 2016 2017) Tính đạo hàm của hàm số y = log 2x +1 . – 2 ( ) A. 2 2 1 y ' = . B. 1 y ' = . C. y ' = . D. y ' = . 2x +1 2x +1 (2x + ) 1 ln 2 (2x + ) 1 ln 2 /
Lời giải. Áp dụng u 2x +1 2 ( u = , ta được ( ) y ' = = . Chọn C. a )/ ' log . u ln a (2x + ) 1 . ln 2 (2x + ) 1 .ln 2
Câu 36. Tính đạo hàm của hàm số y = log 2x. A. 1 1 1 ln10 / y = . B. / y = . C. / y = . D. / y = . x ln 2 x ln10 2x ln10 x
Lời giải. Viết lại ln 2x 1 y = log 2x = = .ln 2x . ln10 ln10 Suy ra 1 / 1 (2x)/ 1 2 1 y ' = .(ln 2x) = . = . = . Chọn B. ln10 ln10 2x ln10 2x x ln10
Câu 37. Tính đạo hàm của hàm số y = ln(1+ x +1) . A. 1 y ′ = . B. 1 y ′ = . 2 x +1(1+ x +1) 1+ x +1 C. 1 2 y ′ = . D. y′ = . x +1(1+ x +1) x +1(1+ x +1) ( ′ 1+ x +1)
Lời giải. Áp dụng công thức u′ (ln u)′ = , ta được y′ = . u 1+ x +1 Mà ( ′ + x + ) 1 1 1 1 = → y′ = . Chọn A. 2 x +1 2 x +1(1+ x +1)
Câu 38. Cho hàm số f (x)= ln x. Tính đạo hàm của hàm số g(x)= log ( 2 x f ′ x . 3 ( )) A. 1 1 ln 3 x g '(x ) = .
B. g '(x)= .
C. g '(x)=
. D. g '(x ) = . x x ln 3 x ln 3 Lời giải. Ta có 1 1 / f (x ) =
→ g (x) = log ( 2
x . f ′(x)) 2 = log x . = log x. 3 3 3 x x Suy ra 1 g '(x) = . Chọn B. x ln 3
Câu 39. Tính đạo hàm của hàm số ( 2 ln x + ) 1 y = 2 . ( 2 ln x + ) 1 A. 2 2 ln x 1 + y ′ = . B. ( ) y ′ = 2 . 2 x +1 ( 2 ln x + ) 1 ( 2 ln x + ) 1 C. 2x.2 .ln 2 x.2 y ′ = . D. y′ = . 2 x +1 ( 2 x + ) 1 ln 2 Lời giải. Ta có 2 2 x + x x + ′ y ln Chọn C. (x ) ln( )1 2 ln( )1 2 1 ′ = + .2 .ln 2 = .2 .ln 2. 2 x +1
Câu 40. Hàm số g(x) 2 x +x 1 8 + = .(6x + )
3 .ln 2 là đạo hàm của hàm số nào sau đây ?
A. f (x) 2 x +x 1 2 + =
. B. f (x ) 2 x +x 1 8 + = .
C. f (x) 2 3x +3x 1 2 + = . D. f (x) 2 3x +3x 1 8 + = .
Lời giải. Thử đạo hàm lần lượt từng hàm số ở các đáp án và được đáp án đúng là B.
Thật vây: Ta có ( 2x+x 1+)/ ( 2 x x )/ 2x+x 1 8 1 .8 + = + + . ln 8 ( x ) 2 2 x +x 1 + x +x 1 2 1 .8 .3 ln 2 8 + = + = .(6x + ) 3 .ln 2 .Chọn B.
Câu 41. Tính đạo hàm của hàm số 2
y = ln (ln x) tại điểm x = e . A. 2 /
y (e) = e . B. / y (e) = 1 . C. / y (e) = . D. / y (e) = 0 . e
Lời giải. Nhận thấy có dạng uα →(uα )/ α 1 − / = . α u
.u với u = ln(ln x ).
Áp dụng, ta được y = ( x) ( x) / / 2.ln ln . ln ln . ( ) 1
----------------------------------------------------------------------- / Tính u ( ) / /
ln ln x . Nhận thấy có dạng . (ln u) = với u = ln x u 1 Áp dụng, ta được / (ln x)/ 1 ln(ln ) x x = = = . (2) ln x ln x x ln x Từ 2 ln ln x 2 ln ln e 2. ln1 / / ( ) ( ) 1 và (2) , ta có ( ) y = → y (e) = = = 0. Chọn D. x ln x e. ln e e.ln e
Câu 42. Cho hàm số f (x)= ( x − + x ) 2 4 ln 4
+ x − 4x với x ≥ 4 . Tính giá trị của
biểu thức P = f ( )− f ( ) 2 4 ' 8 . ln 2. A. P = 2 ln 2 . B. P = 4 ln 2 . C. P = 6 ln 2 . D. P = 8ln 2 . ( x −4 + x )' Lời giải. Ta có x − 2 x f '(x ) = 4. + = . 2 2 x − 4 + x x − 4x x − 4x
Khi đó f '(8)= 2 và f (4)= 4 ln2 .
Vậy P = f ( )− f ( ) = − . Chọn A. ( )2 2 4 ' 8 .ln 2 4 ln 2 2 .ln 2 = 2.ln 2 Câu 43. Cho hàm số cos = x y e
. Mệnh đề nào sau đây đúng?
A. y '.cos x + .
y sin x + y ' = 0 .
B. y '.sin x + .
y cos x + y ' = 0 .
C. y '.sin x − y ' .cos x + y ' = 0 .
D. y '.cos x − y.sin x − y ' = 0 . cos x
Lời giải. Ta có y ' = −sin x.e
. Thay lần lượt vào các đáp án thì ta được 2 cos x cos y ' = sin x.e − cos x. x e
đáp án B đúng. Thật vậy: Ta có y '.sin x + y.cos x + y ' cos x cos x 2 cos x cos = −sin . .sin + .cos + sin . − cos . x x e x e x x e x e = 0 .Chọn B. Câu 44. Cho hàm số . − = x y x e
. Mệnh đề nào sau đây đúng?
A. (1− x) y ' = x.y .
B. x.y ' = (1+ x) y .
C. x.y ' = (1− x).y .
D. (1+ x).y ' = (x − ) 1 .y . Lời giải. Ta có ' −x =
− . −x = (1− ) −x y e x e x e
Nhân hai vế cho x , ta được . ' = .(1− ). −x x y x x e
= (1− x).y . Chọn C. Câu 45. Cho hàm số − = x y
e .sin x . Mệnh đề nào sau đây đúng?
A. y '+ 2y '−2y = 0 .
B. y ' + 2y '+ 2y = 0 .
C. y ' −2y '−2y = 0 .
D. y '−2y ' + 2y = 0 . Lời giải. Ta có ' −x = − .sin −x + .cos −x y e x e x = e
(cos x −sin x). Lại có ' −x (cos sin ) −x ( sin cos ) 2 − = − − + − − = − x y e x x e x x e .cos x Ta thấy ' 2 ' 2 2 −x .cos 2 −x (cos sin ) 2 − + + = − + − + x y y y e x e x x
e .sin x = 0 . Chọn B. 1 Câu 46. Cho hàm số x . ln 8 y = 2016.e
. Mệnh đề nào sau đây đúng?
A. y '+ 2y ln 2 = 0. B. y '+3y ln 2 = 0. C. y '−8y ln 2 = 0.
D. y '+8y ln 2 = 0. / 1 1 Lời giải. Ta có x. ln x. ln 1 1 1 8 8 y ' = 2016. x ln .e = 2016.ln .e
= ln .y = −3 ln 2.y. 8 8 8
Suy ra y '+3ln 2.y = 0. Chọn B. 2 x Câu 47. Cho hàm số − 2 y = x.e
. Mệnh đề nào sau đây đúng? A. xy = ( 2 1 + x ) y ' . B. x y = ( 2 . ' 1 + x ).y . C. xy = ( 2 1− x ).y ' . D. xy = ( 2 ' 1− x ).y . 2 2 2 2 2 x x x x x Lời giải. Ta có − − − − − 2 y = e + x −xe = e − x e = ( 2 2 2 2 2 − x ) 2 ' . 1 e . 2 x Nhân hai vế cho −
x , ta được x y = x ( 2 − x )e = ( 2 2 . ' 1
1− x ) y . Chọn D. Câu 48. Cho hàm số 1 y =
. Mệnh đề nào sau đây đúng? 1 + x + ln x
A. xy = y '(y ln x + ) 1 .
B. xy ' = y(y ln x − ) 1 .
C. xy = y(y ' ln x − ) 1 .
D. xy ' = y(y ln x + ) 1 . 1 1 + Lời giải. Ta có x +1 ' = − x y = − (1+ x + ln x)2
x (1+ x + ln x)2 Suy ra
(1+ x + ln x)− ln x 1 ln x 2 xy ' = − = − +
= −y + ln x.y (1+ x + ln x)2 1 + x + ln x (1+ x + ln x)2
⇔ xy ' = y (y ln x − ) 1 . Chọn B.
Câu 49. Tìm giá trị lớn nhất M của hàm số f (x) 3 x 3 x 3 e − + = trên đoạn [0;2].
A. M = e . B. 2 M = e . C. 3 M = e . D. 5 M = e .
Lời giải. Hàm số f (x) xác định và liên tục trên đoạn [0;2]. x =1 ∈ 0;2 3 [ ]
Đạo hàm f '(x) ( 2 3x ) x 3 − x 1 3 e + f '(x) 2 0 3x 3 0 = − → = ⇔ − = ⇔ . x = 1 − ∉ [0;2] f (0) 3 = e Ta có f ( ) 1 = e
→max f (x) = f (2) 5 = e . Chọn D. [0;2] f (2) 5 = e
Câu 50. Gọi m và M lần lượt là giá trị nhỏ nhất và lớn nhất của hàm số ( ) 2 3x f x e − =
trên đoạn [0;2]. Mệnh đề nào sau đây là đúng? A. 1 M m + M = 1 .
B. M −m = e. C. M.m = . D. 2 = e . 2 e m
Lời giải. Hàm số f (x) xác định và liên tục trên đoạn [0;2]. Đạo hàm ( ) 2 3 ' = 3 − x f x − e < 0, x
∀ ∈ ℝ . Do đó hàm số f (x) nghịch biến trên [0;2]. m
ax f (x)= f (0) 2 = e [0;2] Suy ra 1 1 2 → m = , M = e → M .m = . Chọn C. 4 2 1 m in ( ) = (2) e e f x f = [ ] 4 0;2 e
Câu 51. Tìm tập giá trị ln x
T của hàm số f (x ) = với 2 x 1 ;e ∈ . x A. T = [0;e] . B. 1 T = ;e . C. 1 T = 0; . D. 1 T = − ;e . e e e
Lời giải. Hàm số f (x) xác định và liên tục trên đoạn 2 1 ;e . Đạo hàm 1− ln x f '(x ) f '(x ) 2 0 1 ln x 0 x e 1 ;e = → = ⇔ − = ⇔ = ∈ . 2 x f ( )1=0 Ta có 1 1 1 f (e)=
→ min f (x) = 0, max f (x) =
→ T = 0; . Chọn C. 2 2 e x 1;e x 1 ;e ∈ ∈ e e f ( 2 2 e ) = 2 e
Câu 52. Biết rằng hàm số f (x)= x ln x đạt giá trị lớn nhất trên đoạn [1;e] tại x = x . 0
Mệnh đề nào sau đây là đúng? A. 3 3 x ∈ 1 ; . B. x ∈ ; e .
C. x ∈ e;2 .
D. x ∈ 2;e . 0 ( ] 0 e 0 0 e
Lời giải. Hàm số xác định và liên tục trên đoạn [1;e] . Đạo hàm / x x +
f (x ) = ( x )
x + x ( x)/ ln 1 ln 2 ' .ln . ln = + = . 2 x x 2 x Suy ra 1 f '(x ) −
= 0 ⇔ ln x + 2 = 0 ⇔ ln x = −2 ⇔ x = 2 e = ∉ [1;e]. 2 e f ( ) 1 = 0 Ta có
→ GTLN của hàm số bằng e , đạt tại x = e . Chọn D. f (e) = e Nhận xét. Ta có ln x + 2 f '(x ) = > 0, x ∀ ∈[1;e]
→ f (x) đồng biến trên [1;e] . 2 x
Câu 53. Tìm giá trị nhỏ nhất m của hàm số f (x)= ( 2 2
ln x + x + e ) trên đoạn [0;e]. A. 1 m = . B. m = 1 . 2
C. m = 1+ ln(1+ 2).
D. m = 1− ln(1+ 2) .
Lời giải. Hàm số xác định và liên tục trên đoạn [0;e]. x (x x e )/ 2 2 1+ + + 2 2 Đạo hàm x + e 1 f '(x ) = = =
> 0, ∀x ∈ [0;e] 2 2 2 2 2 2 x + x + e x + x + e x + e
Suy ra hàm số luôn đồng biến trên [0;e]
→ min f (x) = f (0) = 1. Chọn B. [0;e]
Câu 54. Tìm điểm cực trị x của hàm số . − = x y x e . 0
A. x = e . B. 2 x = e . C. x = 1 . D. x = 2 . 0 0 0 0
Lời giải. Hàm số xác định và liên tục trên . ℝ Ta có ' −x = + .( −x − ) −x y e x e = e (1− x)
→ y ' = 0 ⇔ 1− x = 0 ⇔ x = 1.
Vậy hàm số đạt cực trị tại x = 1 . Chọn C.
Câu 55. Tính giá trị cực tiểu y của hàm số x y = xe . CT A. 1 1 y = .
B. y = e . C. y = − . D. y = −1. CT e CT CT e CT
Lời giải. Hàm số xác định và liên tục trên . ℝ Ta có ' x x x
y = e + xe = e (1+ x)
→ y ' = 0 ⇔ 1+ x = 0 ⇔ x = 1 − . Bảng biến thiên x −∞ −1 +∞ y' − 0 + +∞ y 0
Từ bảng biến thiên, suy ra hàm số có giá trị cực tiểu 1 y = y 1 − = − . Chọn C. CT ( ) e
Vấn đề 3. TÍNH ĐƠN ĐIỆU CỦA H M SỐ
Câu 56. Hàm số nào sau đây đồng biến trên khoảng (0;+∞) ?
A. y = log x . B. y = log x .
C. y = log x .
D. y = log x . 2 e e π 2 3 2 4
Lời giải. Áp dụng lý thuyết
' Hàm số y = log x đồng biến khi a > 1 , nghịch biến khi 0 < a < 1 ' . a
Trong các hàm số đã cho chỉ có hàm số e
y = log x đồng biến vì cơ số a = > 1 . Chọn C. e 2 2
Câu 57. Hàm số nào sau đây đồng biến trên ℝ ? x x x x A. 3 + π y = . B. 2 3 y = . C. 3 y = . D. y . = π 3 2 2 + 3
Lời giải. Áp dụng lý thuyết ' Hàm số x
y = a đồng biến khi a > 1 , nghịch biến khi 0 < a < 1 ' . x
Trong các hàm số đã cho chỉ có hàm số 2 + 3 + y =
đồng biến vì cơ số 2 3 . a = > 1 3 3 Chọn B.
Câu 58. Hàm số nào sao đây nghịch biến trên ℝ . x A. π 2017x y = .
B. y = log x . C. y = log ( 2
x +1 . D. y = . 2 ) 1 4 2
Lời giải. Hàm số 2017x y =
có TXĐ: D = ℝ ; cơ số 2017 >1 nên đồng biến trên ℝ .
Hàm số y = log x có TXĐ: D = (0;+∞) → không thỏa mãn. 1 2 Hàm số 2x y = log ( 2
x +1 có TXĐ: D = ℝ . Ta có y ' = nên hàm số 2 ) ( 2 x + ) 1 ln 2 y = log ( 2
x +1 đồng biến khi x > 0 , nghịch biến khi x < 0. Do đó C sai. 2 ) x Hàm số π π y
= có TXĐ: D = ℝ ; cơ số <1 nên nghịch biến trên ℝ . Chọn D. 4 4
Câu 59. Tìm tất cả các giá trị thực của tham số a để hàm số y = log x với M 2
M = a − 4 nghịch biến trên tập xác định.
A. 2 < a < 5 . B. a = 5 .
C. − 5 < a < −2 ; 2 < a < 5 . D. a = 2 .
Lời giải. Hàm số đã cho nghịch biến khi cơ số 0 < M <1 hay 2 0 < a − 4 < 1 2 < a < 5 2 4 a 5 ⇔ < < ⇔ . Chọn C. − 5 < a < 2 −
Câu 60. Tìm tất cả các giá trị của tham số x
a để hàm số y = ( 2 a −3a + ) 3 đồng biến. A. a =1. B. a = 2 . C. a ∈(1;2). D. a ∈(− ; ∞ ) 1 ∪(2;+∞).
Lời giải. Hàm số đồng biến khi a <1 2 2
a −3a + 3 > 1 ⇔ a −3a + 2 > 0 ⇔ . Chọn D. a > 2 Câu 61. Cho hàm số log ( 3 2 3 2 3 − + = x x y
. Mệnh đề nào sau đây đúng? 1 ) 2
A. Hàm số đã cho đồng biến trên khoảng (2;+∞) .
B. Hàm số đã cho đồng biến trên các khoảng (− ; ∞ 2) và (2;+∞) .
C. Hàm số đã cho đồng biến trên khoảng (− ; ∞ 2).
D. Hàm số đã cho đồng biến trên khoảng (0;2).
Lời giải. Viết lại y log ( 3 2 x 3 − x 2 3 + = )=( 3 2
x − 3x + 2)log 3 = −( 3 2
x − 3x + 2 . log 3 . 1 1 ) 2 2 2
Nếu để ý thấy thì đây là hàm bậc ba thuần túy và có đạo hàm x = 0 y ' = ( 2
− 3x − 6x).log 3 = 3
− x x − 2 .log 3 → y ' = 0 ⇔ . 2 ( ) 2 x = 2
Lập bảng biến thiên, suy ra hàm số đồng biến trên khoảng (0;2). Chọn D. 3 2
Câu 62. Cho a, b là hai số thực thỏa mãn 3 2 a > a và 3 4 log < log . Mệnh đề nào b 4 b 5 sau đây là đúng?
A. 0 < a <1, 0 < b <1 .
B. 0 < a <1, b >1 .
C. a >1, 0 < b <1 .
D. a >1, b >1 . 3 2 Lời giải. Ta có 3 2 < , mà 3 2 a > a . 3 2 Suy ra hàm đặc trưng x
y = a nghịch biến nên 0 < a < 1 . Tượng tự có 3 4 < và 3 4 log < log . 4 5 b 4 b 5
Suy ra hàm đặc trưng y = log x đồng biến nên b >1 . b
Vậy 0 < a <1 và b >1 . Chọn B.
Câu 63. Cho hàm số y = x −ln(1+ x). Khẳng định nào sau đây đúng?
A. Hàm số giảm trên ( 1 − ;+ ) ∞ .
B. Hàm số tăng trên ( 1 − ;+ ) ∞
C. Hàm số giảm trên ( 1
− ;0) và tăng trên (0;+∞) .
D. Hàm số tăng trên ( 1
− ;0) và giảm trên (0;+∞) . Lời giải. TXĐ: x D = ( 1 − ;+∞) . Đạo hàm 1 y ' = 1− =
→ y ' = 0 ⇔ x = 0. 1+ x x +1 Bảng biến thiên x 1 − 0 +∞ y' − 0 + y 0
Từ bảng biến thiên, ta thấy hàm số giảm trên ( 1
− ;0) và tăng trên (0;+∞) . Chọn C.
Câu 64. Cho a là một số thực dương khác 1 và các mệnh đề sau:
1) Hàm số y = ln x là hàm số nghịch biến trên (0;+∞) . 2) Trên khoảng (1; )
3 hàm số y = log x nghịch biến. 1 2
3) Nếu M > N > 0 thì log M > log N . a a
4) Nếu log 3 < 0 thì 0 < a <1 . a
Hỏi có bao nhiêu mệnh đề đúng? A. 1. B. 2 . C. 3 . D. 4 .
Lời giải. Vì cơ số e >1
→ y = ln x đồng biến trên (0;+∞) . Do đó 1) sai. Hàm số 1
y = log x có cơ số a = ∈ (0; )
1 nên nghịch biến trên ℝ , suy ra nghịch 1 2 2 biến trên khoảng (1; ) 3 . Do đó 2) đúng.
Nếu cơ số a ∈(0; )
1 thì hàm số y = log x nghịch biến. Vì vậy với M > N > 0 , suy ra a
log M < log N . Do đó 3) sai. a a
Ta có log 3 < 0 ⇔ log 3 < log 1
→ 0 < a < 1 . Do đó 4) đúng. a a a
Vậy có 2) và 4) đúng. Chọn B.
Câu 65. Cho a là một số thực dương khác 1 và các mệnh đề sau:
1) Hàm số y = log x liên tục trên ℝ . a 2) Nếu 2 log < 0 thì a > 1 . a 3 3) 2
log x = 2 log x . a a
Hỏi có bao nhiêu mệnh đề đúng? A. 1. B. 2 . C. 3 . D. 0.
Lời giải. Hàm số y = log x xác định trên (0;+∞) . Do đó 1) sai. a Ta có 2 2 log < 0 ⇔ log < log 1
→ a > 1 . Do đó 2) đúng. a 3 a 3 a Ta có 2
log x = 2 log x . Do đó 3) sai. a a
Vậy chỉ có 2) đúng. Chọn A.
Câu 66. Mệnh đề nào sau đây là sai? A. Hàm số x
y = e không chẵn cũng không lẻ
B. Hàm số y = ( 2
ln x + x +1) là hàm số lẻ. C. Hàm số x
y = e có tập giá trị là (0;+∞) .
D. Hàm số y = ( 2
ln x + x +1) không chẵn cũng không lẻ. Lời giải. Ta có −x 1 f ( x − ) = e = . Do đó A đúng. x e f (x) x
= e > 0, ∀x ∈ ℝ; lim x
e = +∞ . Do đó C đúng. x →+∞ Xét hàm số y = ( 2 ln x + x +1) . Ta có 2 2
x + x +1 > x + x = x + x ≥ 0, ∀x ∈ . ℝ Do đó hàm số y = ( 2
ln x + x +1) có TXĐ: D = ℝ . Rõ ràng ∀x ∈ D ⇒ −x ∈ D . Ta có y( x − )+ y(x ) = x − + ( x − ) ( 2 + )+ ( 2 ln 1 ln x + x +1) ( 2 = x + − x )+ ( 2 x + x + )= ( 2x + − x )( 2 ln 1 ln 1 ln 1
x +1 + x ) = ln1= 0 hay y( x
− ) = −y(x) . Suy ra hàm số y = ( 2
ln x + x +1) là hàm số lẻ. Do đó đáp án D sai. Chọn D.
Câu 67. Cho hàm số y = x ( 2 x + + x ) 2 ln 1
− 1+ x . Mệnh đề nào sau đây sai?
A. Hàm số có đạo hàm y = ( 2 ' ln x + 1+ x ) .
B. Hàm số tăng trên khoảng (0;+∞) .
C. Tập xác định của hàm số là D = ℝ .
D. Hàm số giảm trên khoảng (0;+∞) . Lời giải. Ta có 2 2
x + x +1 > x + x = x + x ≥ 0, ∀x ∈ ℝ.
Do đó hàm số có tập xác định là D = ℝ . Suy ra C đúng. x 1+ 2 Đạo hàm + y = ( x x 2 x + + x ) 1 ' ln 1 + x. − = ln( 2 x + 1+ x . Do đó A đúng. 2 2 ) x + 1+ x 1+ x 2 Trên khoảng 1+ x > 1 (0;+∞) , ta có 2
⇒ 1+ x > 1− x hay 2
x + 1+ x > 1 . 1 − x <1 Suy ra y = ( 2 '
ln x + 1+ x )> 0, ∀x ∈(0;+∞). Do đó B đúng, D sai. Chọn D.
Câu 68. Cho a là một số thực dương khác 1 và các mệnh đề sau: 1) Hàm số = (− )x y 5 là hàm số mũ. 2) Nếu α 2α π < π thì α <1. 3) Hàm số x
y = a có tập xác định là ℝ . 4) Hàm số x
y = a có tập giá trị là (0;+∞) .
Hỏi có bao nhiêu mệnh đề đúng? A. 1. B. 2 . C. 3 . D. 4 .
Lời giải. Hàm số = (− x y
5) không phải là hàm số mũ vì cơ số 5 − < 0. Do đó 1) sai.
Vì cơ số π >1 nên từ α 2α π < π
⇒ α < 2α ⇔ 0 < α . Do đó 2) sai. Hàm số x
y = a xác định với mọi x . Do đó 3) đúng. Vì x
a > 0, ∀x ∈ ℝ và lim x a = +∞ nên hàm x
y = a có TGT là (0;+∞) . Do đó 4) đúng. x →+∞
Vậy có 3) và 4) đúng. Chọn B.
Câu 69. Cho a là một số thực dương khác 1 và các mệnh đề sau: 1) x
a > 0 với mọi x ∈ ℝ . 2) Hàm số = x y
a đồng biến trên ℝ . 3) Hàm số 2017 x y = e
là hàm số đồng biến trên ℝ . 4) Đồ thị hàm số x
y = a nhận trục Ox làm tiệm cận ngang.
Hỏi có bao nhiêu mệnh đề đúng? A. 1. B. 2 . C. 3 . D. 4 .
Lời giải. Rõ ràng 1) đúng theo định nghĩa. Hàm số = x y
a đồng biến khi a > 1 , nghịch biến khi 0 < a < 1 . Do đó 2) sai.
Vì cơ số e >1 nên hàm số 2017 x y = e
là hàm số đồng biến trên ℝ . Do đó 3) đúng.
Rõ ràng 4) đúng theo định nghĩa SGK.
Vậy có 1), 3) & 4) đúng. Chọn C. b a Câu 70. Cho a −b
a, b là hai số thực dương thỏa mãn .2 .2 a −b = . Tính giá trị biểu 2a + 2b thức 2017a 2017b P = − . A. P = 0. B. P = 2016. C. P = 2017. D. P = −1. b a
Lời giải. Từ giả thiết, ta có . a 2 − . b 2 a −b = ← →(a −b) + = a −b . a b (2a 2b ) .2b .2a 2 + 2 ←
→ .2a + .2b − .2a − .2b = .2b − .2a ⇔ .2a = .2b a a b b a b a b . ( ) ∗ Xét hàm số ( )= .2x f x x
với x > 0 , có ′( )= 2x + .2x.ln 2 = 2x f x x
(1+ x.ln 2)> 0; ∀x > 0 .
Suy ra hàm số f (x) là đồng biến trên khoảng (0;+∞). Nhận thấy ( )
∗ ⇔ f (a) = f (b) ⇒ a = . b
Khi a = b thì 2017a 2017b 2017a 2017a − = − = 0 . Chọn A.
Cách trắc nghiệm. Chọn a = b = 1 thỏa điều kiện. Khi đó 1 1 P = 2017 − 2017 = 0.
Vấn đề 4. ĐỒ THỊ
Câu 71. Đường cong trong hình bên là đồ thị của một y 3
hàm số trong bốn hàm số được liệt kê ở bốn phương án A,
B, C, D dưới đây. Hỏi hàm số đó là hàm số nào? x 1 A. ( x y = 3) . B. 1 y = . 2 x x -1 O C. x 5 y = 2 + . D. 1 y = . 2 3
Lời giải. Dựa vào hình dáng đồ thị từ trái sang phải ta thấy: x tăng nhưng y giảm.
Suy ra hàm số tương ứng của đồ thị là hàm nghịch biến. Loại A, C.
Đồ thị hàm số đi qua điểm có tọa độ ( 1 − ; )
3 nên chỉ có D thỏa mãn. Chọn D.
Câu 72. Đường cong trong hình bên là đồ thị của một y
hàm số trong bốn hàm số được liệt kê ở bốn phương án A,
B, C, D dưới đây. Hỏi hàm số đó là hàm số nào? x x O A. -1 2x y = − . B. 1 y = . 2 x C. 2x y = . D. 1 y = − . 2
Lời giải. Đồ thị nằm phía dưới trục hoành. Loại B, C.
Lấy đối xứng đồ thị qua trục hoành ta được đồ thị của một hàm số đồng biến. Chọn A.
Câu 73. Đường cong trong hình bên là đồ thị của một y
hàm số trong bốn hàm số được liệt kê ở bốn phương án A, 1
B, C, D dưới đây. Hỏi hàm số đó là hàm số nào? x O
A. y = log x .
B. y = log x +1 . -1 2 2 ( ) 2
C. y = log x +1 . D. y = log x +1 . 3 ( ) 3
Lời giải. Dựa vào đồ thị thấy có tiệm cận đứng x = −1. Loại đáp án A, C.
Đồ thị hàm số đi qua điểm có tọa độ (2; )
1 nên chỉ có D thỏa mãn. Chọn D. Câu 74. Cho hàm số ( x y =
2) có đồ thị Hình 1. Đồ thị Hình 2 là của hàm số nào dưới đây? y y 1 x 1 x O O Hình 1 Hình 2 A. ( x x x x y = 2) .
B. y = −( 2) . C. y = ( 2) .
D. y = − ( 2) .
Lời giải. Từ đồ thị ta thấy: Đồ thị Hình 2 có được là lấy đối xứng đồ thị Hình 1 (phần
x ≥ 0 ) qua trục Oy . Do đó hàm số của đồ thị Hình 2 là hàm số chẵn. Chọn C.
Câu 75. Cho hàm số y = ln x có đồ thị như Hình 1. Đồ thị Hình 2 là của hàm số nào dưới đây? y y 1 x 1 1 O e x 1 O e Hình 1 Hình 2
A. y = ln x .
B. y = ln x .
C. y = ln(x + ) 1 .
D. y = ln x +1 .
Lời giải. Đồ thị Hình 2 được suy ra từ đồ thị Hình 1 bằng cách:
● Giữ nguyên phần y ≥ 0.
● Lấy đối xứng qua Ox phần y < 0. Chọn B.
Câu 76. Cho a, b, c là các số thực dương khác 1. y x x y = b y = c
Hình vẽ bên là đồ thị của ba hàm số x y = a , x y = b , x
y = c . Khẳng định nào sau đây là đúng? x y = a
A. a > b > c.
B. a < b < c.
C. c > a > . b
D. a > c > . b 1 O x
Lời giải. Ta thấy hàm x
y = c có đồ thị từ trái sang phải theo hướng đi lên nên là hàm đồng biến
→ c > 1. Còn hàm số x y = a và x
y = b là những hàm nghịch biến
→ a, b <1. Từ đó loại được các đáp án A, D.
Từ đồ thị hàm số ta thấy tại cùng một giá trị x < 0 thì đồ thị hàm số x y = b nằm 0 x = −1 = − trên đồ thị hàm số x < x 1 x y = a hay 0
→b < a . Ví dụ ⇔ 1 1 → b < . a x x b > a 1 − 1 − b > a > b a
Vậy c > a > . b Chọn C.
Cách trắc nghiệm. Kẻ đường thẳng x = 1 cắt đồ y x x y = b y = c thị các hàm số x y = a , x y = b , x
y = c lần lượt tại
các điểm có tung độ y = a, y = b, y = c . Dựa vào x y = a c
đồ thị ta thấy ngay c > a > . b 1 a b O 1 x
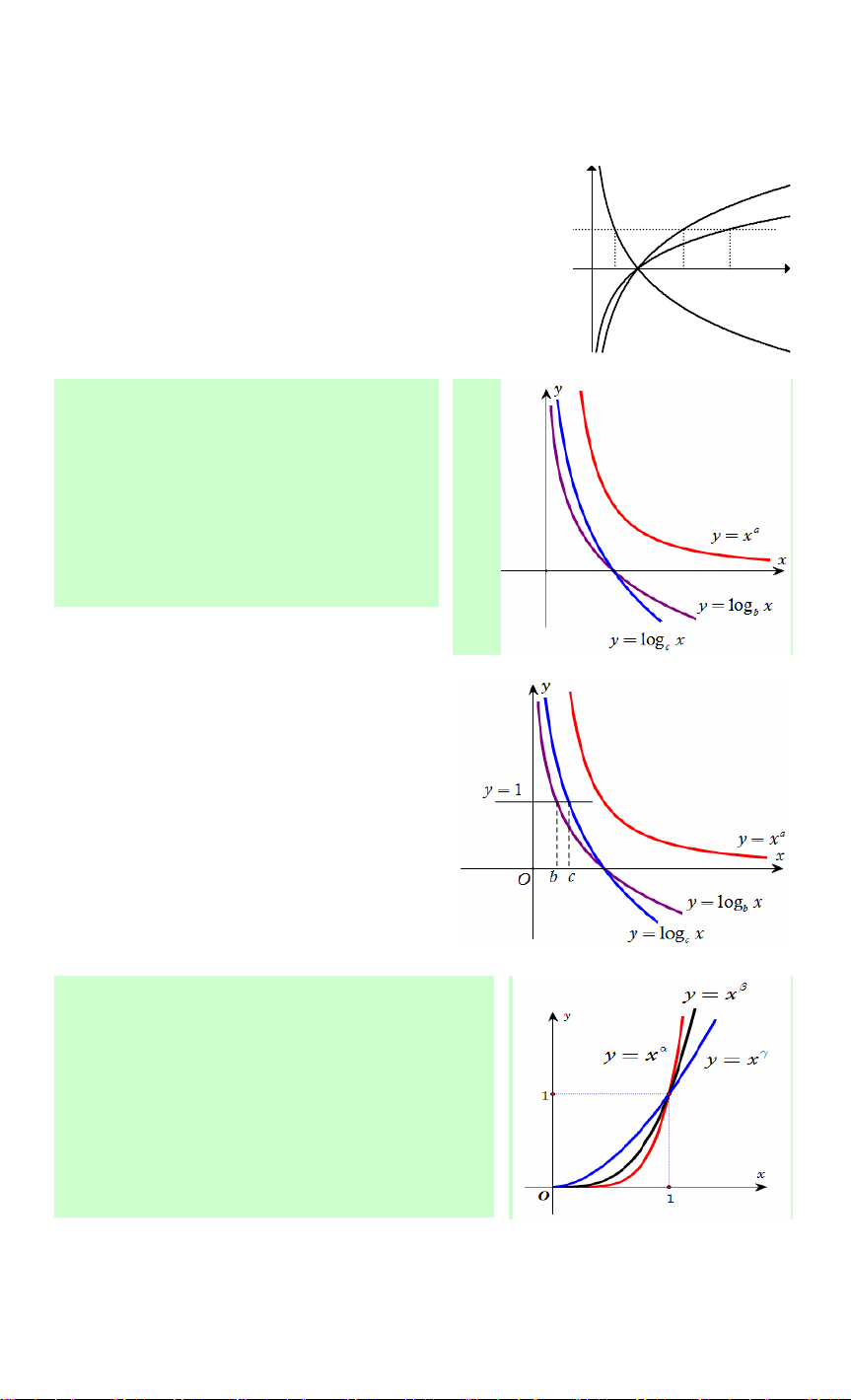
Câu 77. Cho a, b, c là các số thực dương khác 1. Hình y y = log x b
vẽ bên là đồ thị của ba hàm số y = log x , y = log x , a b
y = log x . Khẳng định nào sau đây là đúng? y = log x c c x O
A. a < c < . b
B. a < b < c. 1
C. b < a < c.
D. b > a > c. y = log x a
Lời giải. Ta thấy hàm y = log x có đồ thị từ trái sang phải theo hướng đi xuống nên a
là hàm nghịch biến
→ 0 < a < 1. Còn hàm số y = log x và y = log x là những hàm b c đồng biến
→ b, c > 1. Từ đó loại được các đáp án C, D.
Từ đồ thị hàm số ta thấy tại cùng một giá trị x >1 thì đồ thị hàm số y = log x nằm 0 b trên đồ thị hàm số x > y = log x hay 1 →b < c . c l
og x > log x b c
Vậy a < b < c. Chọn B.
Cách trắc nghiệm. Kẻ đường thẳng y = 1 cắt đồ thị các y y = log x b
hàm số y = log x , y = log x , y = log x lần lượt tại các a b c 1
điểm có hoành độ x = a, x = b, x = c . Dựa vào đồ thị ta y = log x c x O
thấy ngay a < b < c. a 1 b c y = log x a
Câu 78. Cho a là số thực tùy ý và b, c là
các số thực dương khác 1. Hình vẽ bên là đồ
thị của ba hàm số y = log x , y = log x và b c a
y = x , x > 0 . Khẳng định nào sau đây là đúng?
A. a < c < . b
B. a < b < c.
C. a > b > c.
D. a > c > . b
Lời giải. Nhận thấy hàm số a y = x nghịch biến
→ a < 0. Do đó ta loại ngay đáp án
C & D (vì b, c là các số thực dương khác 1).
Kẻ đường thẳng y = 1 cắt đồ thị của hai
hàm số y = log x , y = log x lần lượt tại b c
điểm có hoành độ là x = b và x = c như
hình vẽ. Dựa vào hình vẽ ta thấy 0 < b < c.
Vậy a < b < c. Chọn B.
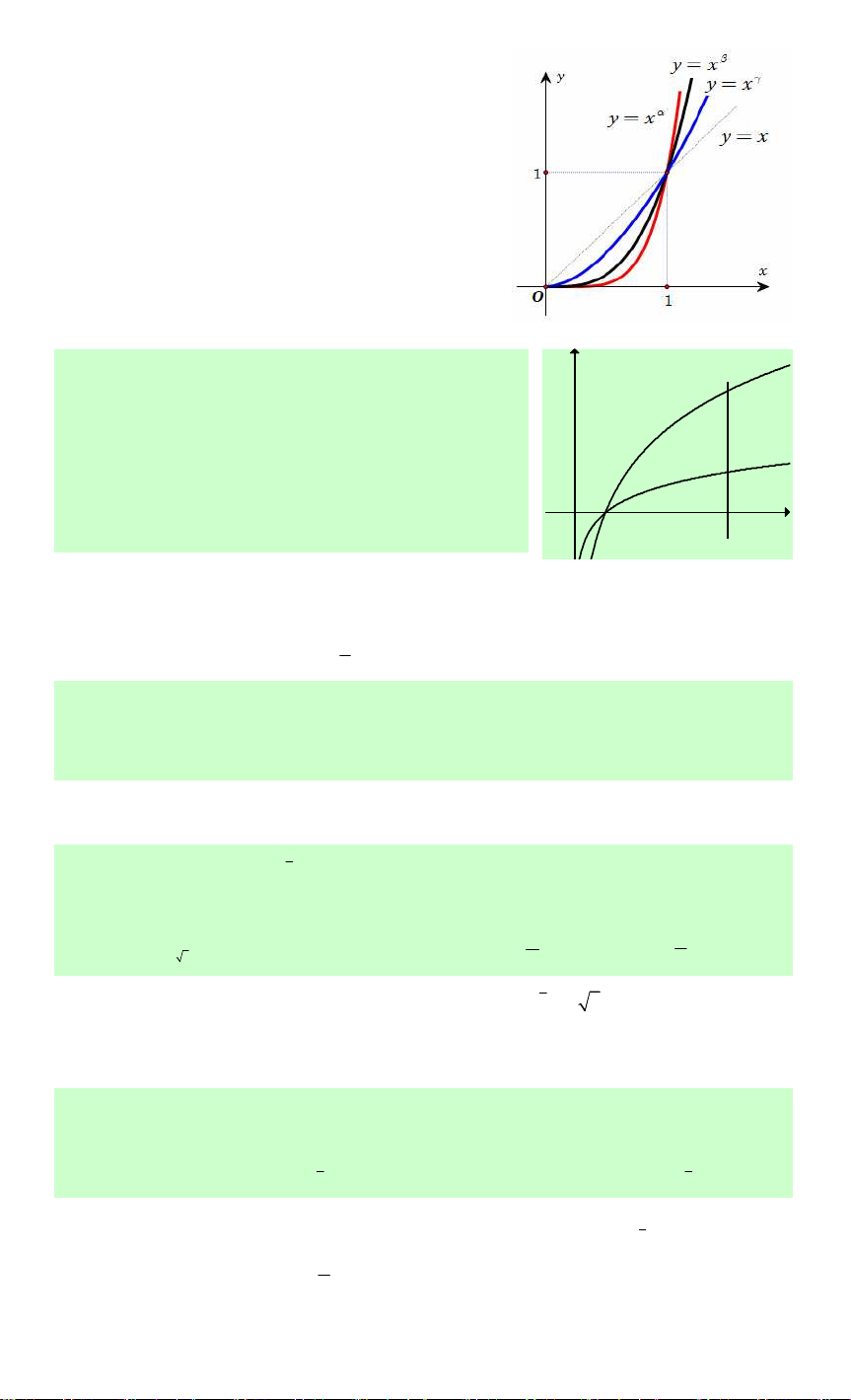
Câu 79. Cho đồ thị của ba hàm số y x α , y x β , y x γ = = =
trên khoảng (0;+∞) trên
cùng một hệ trục tọa độ như hình vẽ bên. Mệnh đề nào sau đây đúng ?
A. γ < β < α < 0.
B. 0 < γ < β < α <1.
C. 1< γ < β < . α
D. 0 < α < β < γ <1.
Lời giải. Dựa vào đồ thị, ta có
● Với 0 < x <1 thì α β γ 1
x < x < x < x
→ α > β > γ > 1 .
● Với x > 1 thì 1
x < x γ < x β < x α
→1 < γ < β < α .
Vậy với mọi x > 0 , ta có α > β > γ >1. Chọn C.
Nhận xét. Ở đây là so sánh thêm với đường 1
y = x = x .
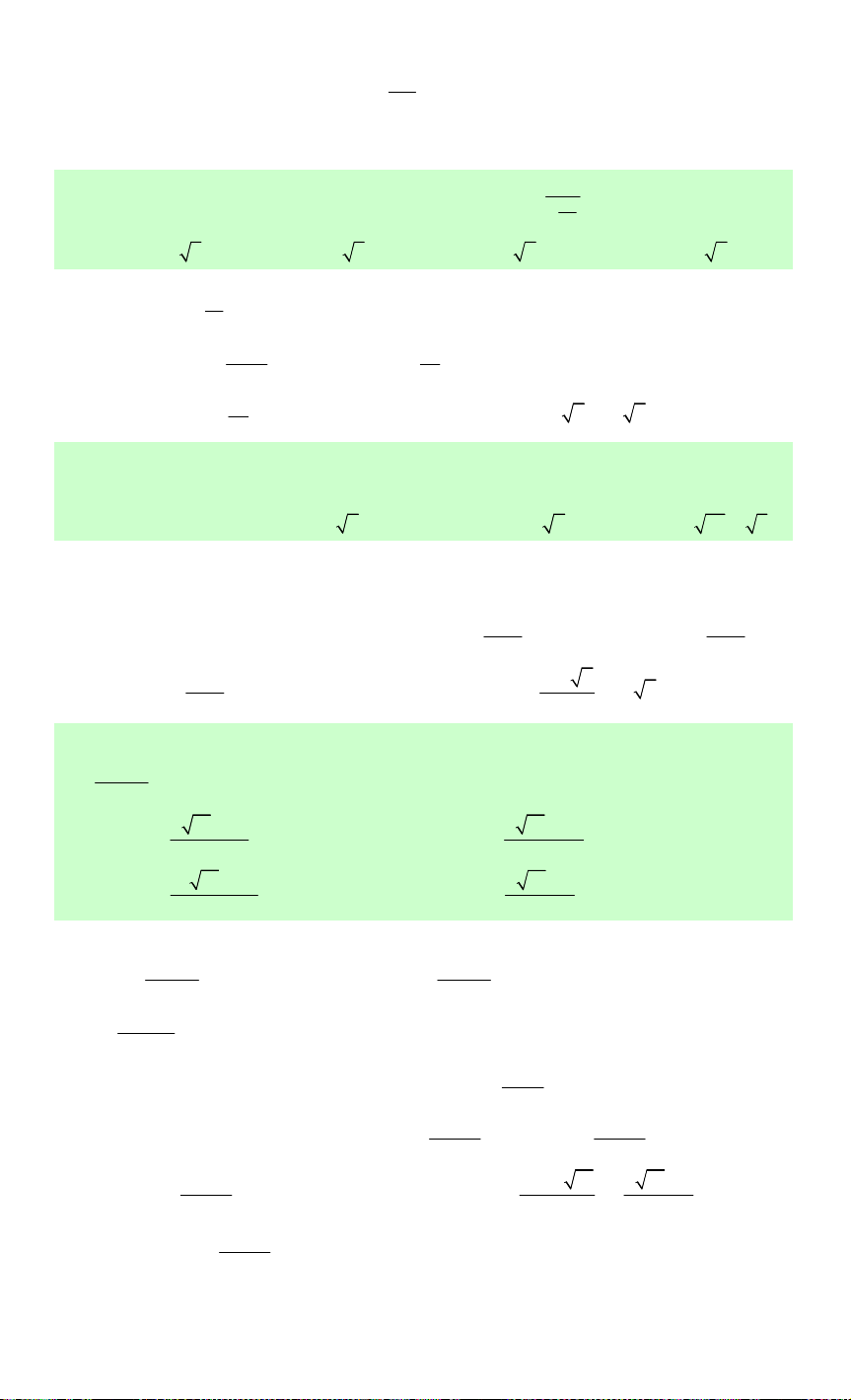
Câu 80. Cho các hàm số y = log x và y = log x có đồ y a b
thị như hình vẽ bên. Đường thẳng x = 5 cắt trục y = log x b C
hoành, đồ thị hàm số y = log x và y = log x lần lượt a b tại ,
A B và C . Biết rằng CB = 2AB. Mệnh đề nào sau y = log x B a đây là đúng? x A. 2 A a = b . B. 3 a = b . O C. 3 a = b
D. a = 5b . x = 5
Lời giải. Theo giả thiết, ta có A(5;0), B(5;log 5), C (5;log ) 5 . a b
Do CB = 2AB
→CB = 2BA ↔ log 5− log 5 = 2.(−log 5 a b a ) 1 3 ← →3 log 5 = log 5← → log 5 = log 5← → log 5 = log 5
→ a = b . Chọn C. 3 a b a 3 b a b Câu 81. Cho hàm số 5x y =
có đồ thị (C). Hàm số nào sau đây có đồ thị đối xứng với
(C ) qua đường thẳng y = x. A. 5 x y − = .
B. y = log x.
C. y = −log x. D. 5 x y − = − . 5 5
Lời giải. Dựa vào lý thuyết ' Đồ thị hàm số x
y = a và đồ thị hàm số y = log x đối a
xứng với nhau qua đường thẳng y = x ' . Chọn B. x Câu 82. Cho hàm số 2
y = 3 có đồ thị (C ). Hàm số nào sau đây có đồ thị đối xứng với
(C ) qua đường thẳng y = x. A. x 1 y = log x . B. 2 y = log x .
C. y = log .
D. y = log x . 3 3 3 2 3 2 x
Lời giải. Trước tiên ta đưa hàm số về dạng chuẩn: x 2 y = 3 = ( 3) .
Dựa vào lý thuyết ' Hai hàm số x
y = a và y = log x có đồ thị đối xứng nhau qua a
đường phân giác của góc phần tư thứ nhất y = x ' . Chọn A.
Câu 83. Cho hàm số y = −log x có đồ thị (C). Hàm số nào sau đây có đồ thị đối 2
xứng với (C) qua đường thẳng y = x. 1 x A. 2x y = . B. 2 x y = . C. 2 x y − = . D. 2 y = 2 .
Lời giải. Trước tiên ta đưa hàm số về dạng chuẩn: y = −log x = log x . 2 1 2 x
Suy ra hàm số cần tìm là 1 = = 2 x y − . Chọn C. 2
Câu 84. Biết hai hàm số x x
y = a và y = f (x) có đồ thị y = −x y = a y
như hình vẽ đồng thời đồ thị của hai hàm số này đối
xứng nhau qua đường thẳng d : y = −x . Tính f ( 3 a − ). A. ( 3) 3a f a a− − = − . 1 y = f (x) B. f ( 1 3 a − ) = − . 3 -1 O x C. f ( 3 a − ) = −3. D. ( 3 − ) 3a f a = a − .
Lời giải. Giả sử M (x ; y là điểm thuộc hàm số x
y = a ; N (x ; y là điểm đối xứng 0 0 ) M M )
của M qua đường thẳng y = −x . Gọi x + x y + y
I là trung điểm của M 0 M 0 MN I → ; . 2 2 y + y x + x M 0 M 0 I ∈ d = − Vì 2 2 x = −y
M , N đối xứng nhau qua 0 M d → ⇔ ⇔ . MN n x − x y − y y = −x M 0 M 0 0 M d = 1 1
Ta có M (x ; y ∈ đồ thị x y = a nên xM y = a . M M ) M Do đó x − y M 0 x = −y = a − = a −
→−y = log −x
⇔ y = −log −x . Điều này 0 M 0 a ( 0 ) 0 a ( 0 )
chứng tỏ điểm N thuộc đồ thị hàm số f (x)= −log (−x). a Khi đó f ( 3 a − ) 3
= −log a = −3. Chọn C. a
Cách 2. Lấy đối xứng đồ thị hàm số x
y = a qua Oy là được đồ thị hàm số x −x 1 y = a = . a
Lấy đối xứng đồ thị hàm số y = f (x) qua Oy là được đồ thị hàm số y = f (−x).
Theo giả thiết, ta có đồ thị hai hàm số x
y = a và y = f (x ) đối xứng nhau qua đường x thẳng
y = −x nên suy ra đồ thị của hai hàm số 1 y
= và y = f (−x) đối xứng nhau a
qua đường thẳng y = x . ( ) 1
Theo lý thuyết (SGK) thì đồ thị của hai hàm số x
y = a và y = log x đối xứng nhau a
qua đường thẳng y = x. (2) Từ ( ) 3
1 và (2) , suy ra f (−x) = log x =a x → f ( 3 a − ) 3 = log a = −3. 1 1 a a
Câu 85. Đối xứng qua trục hoành của đồ thị hàm số y = log x là đồ thị nào trong các 2
đồ thị có phương trình sau đây? x A. y = log x . B. 2x y = . C. y = log x . D. 1 y = . 1 2 2 2
Lời giải. Dựa vào lý thuyết ' Đồ thị hàm số y = f (x) đối xứng qua trục hoành ta
được đồ thị hàm số y = − f (x) ' . Do đó đồ thị hàm số y = log x đối xứng qua trục 2
hoành ta được đồ thị hàm số y = −log x. 2
Chưa thấy đáp án nên ta biến đổi: y = −log x = log x . Chọn A. 2 1 2 Câu 86. Cho hàm số x
y = a (0 < a ≠ )
1 có đồ thị (C ) . Mệnh đề nào sau đây là sai?
A. Đồ thị (C) luôn đi qua M (0; ) 1 và N (1;a)
B. Đồ thị (C) có tiệm cận y = 0 .
C. Đồ thị (C) luôn nằm phía trên trục hoành.
D. Hàm số luôn đồng biến. Lời giải. Với 0
x = 0 ⇒ y = a = 1 và 1
x = 1 ⇒ y = a = a . Do đó A đúng.
Ta có lim y = 0 nếu 0 < a <1 và lim y = 0 nếu a >1. Suy ra y = 0 là tiệm cận x →+∞ x →−∞ ngang. Do đó B đúng. Vì x
a > 0, ∀x ∈ ℝ . Do đó C đúng. Hàm số x
y = a đồng biến khi a > 1 , nghịch biến khi 0 < a < 1 . Do đó D sai. Chọn D.
Câu 87. Cho hàm số y = log x (x ≠ 0) có đồ thị (C). Mệnh đề nào sau đây là đúng? 4
A. Hàm số có tập xác định D = ℝ .
B. Hàm số nghịch biến trên từng khoảng tập xác định.
C. Đồ thị (C) nhận Oy làm trục đối xứng.
D. Đồ thị (C) không có đường tiệm cận.
Lời giải. Tập xác định: D = ℝ \{0} . Do đó A sai.
Với x > 0 , ta có y = log x → y đồng biến. 4 Với −1
x < 0 , ta có y = log −x → y ' =
< 0, ∀x < 0
→ y nghịch biến. 4 ( ) (−x)ln 4 Do đó B sai.
∀x ∈ D ⇒ (−x)∈ D Ta có
⇒ hàm số y = log x chẵn trên tập xác định 4 y
(−x ) = log −x = log x = y x 4 4 ( )
nên nhận Oy làm trục đối xứng. Do đó C đúng. Chọn C.
Đáp án D sai. Ta có lim log x = lim log x = −∞ . Suy ra x = 0 là tiệm cận đứng. 4 4 x 0+ x 0− → →
Câu 88. Cho a là số thực dương và khác 1. Mệnh đề nào sau đây là đúng? x
A. Đồ thị của hai hàm số x y = a và 1 y =
đối xứng nhau qua trục hoành. a
B. Đồ thị của hai hàm số y = log x và y = log x đối xứng nhau qua trục tung. a 1 a
C. Đồ thị của hai hàm số x
y = e và y = ln x đối xứng nhau qua đường phân giác
của góc phần tư thứ nhất.
D. Đồ thị của hai hàm số x
y = a và y = log x đối xứng nhau qua đường thẳng a y = −x x
Lời giải. Đồ thị của hai hàm số x y = a và 1 y =
đối xứng nhau qua trục tung. a Do đó A sai.
Đồ thị của hai hàm số y = log x và y = log x đối xứng nhau qua trục hoành. Do a 1 a đó B sai.
Dựa vào lý thuyết ' Đồ thị của hai hàm số x
y = a và y = log x đối xứng nhau qua a
đường y = x ' . Do đó C đúng. Chọn C.
Đồ thị của hai hàm số x
y = a và y = log x đối xứng nhau qua đường thẳng y = x . a Do đó D sai.
Câu 89. Cho hai hàm số y = f (x)= log x và = ( ) x y
g x = a (0 < a ≠ ) 1 . Xét các mệnh a đề sau:
1) Đồ thị của hai hàm số f (x) và g(x) luôn cắt nhau tại một điểm.
2) Hàm số f (x)+ g(x) đồng biến khi a >1 , nghịch biến khi 0 < a <1 .
3) Đồ thị hàm số f (x) nhận trục Oy làm tiệm cận.
4) Chỉ có đồ thị hàm số f (x) có tiệm cận.
Hỏi có tất cả bao nhiêu mệnh đề đúng? A. 1. B. 2 . C. 3 . D. 4 .
Lời giải. Chọn a = 2 chẳng hạn, khi đó f (x) và g(x) cùng đồng biến. Mà hai hàm
cùng đồng biến thì không kết luận được số nghiệm của phương trình f (x)= g(x) vì
nó có thể vô nghiệm, hoặc có một nghiệm, hoặc có hai nghiệm,….Do đó 1) sai.
Tổng của hai hàm đồng biến là hàm đồng biến, tổng của hai hàm nghịch biến là hàm
nghịch biến. Do đó 2) đúng.
Dựa vào lý thuyết, đồ thị hàm số y = log x nhận trục Oy làm tiệm cận đứng. Do đó a 3) đúng. Đồ thị hàm số x
y = a nhận trục Ox làm tiệm cận ngang. Do đó 4) sai.
Vậy có các mệnh đề 2) và 3) đúng. Chọn B.
Câu 90. Trong mặt phẳng với hệ tọa độ Oxy , cho hình vuông ABCD có diện tích bằng
36, đường thẳng chứa cạnh AB song song với trục Ox, các đỉnh ,
A B và C lần lượt
nằm trên đồ thị của các hàm số y = log x, y = log x và y = log x với a là số thực a a 3 a lớn hơn 1. Tìm a .
A. a = 3 . B. 3
a = 6 . C. a = 6 D. 6 a = 3 .
Lời giải. Do AB Ox → ,
A B nằm trên đường thẳng y = m (m ≠ 0). Lại có ,
A B lần lượt nằm trên đồ thị của các hàm số y = log x, y = log x . a a m Từ đó suy ra ( m A a ;m), 2
B a ;m . m
Vì ABCD là hình vuông nên suy ra 2
x = x = a . C B m Lại có 3m
C nằm trên đồ thị hàm số y = log x , suy ra 2 C a ; . 3 a 2 m m 2 a − a = 6 Theo đề bài AB = 6 S 36 = → → ABCD BC = 6 3m − m = 6 2 m = −12 m = 12 ← → 1 hoặc . Chọn D. 6 a = < 6 ( 1 loaïi) a = 3 3
Vấn đề 5. TÍNH GIÁ TRỊ BIỂU THỨC x −x Câu 91. Cho + +
9x + 9−x = 23 . Tính giá trị biểu thức 5 3 3 P = . 1−3x −3−x A. P = 2. B. 3 P = . C. 1 P = . D. 5 P = − . 2 2 2 Lời giải. Đặt x −x 2 = 3 + 3 → = 9x + 9−x t t + 2 = 25← → t = ±5 .
Vì 3x + 3−x > 0 nên t > 0 . Do đó ta chọn t = 5 hay 3x + 3−x = 5 . Thay +
3x + 3−x = 5 vào P , ta được 5 5 5 P = = − . Chọn D. 1−5 2
Câu 92. Cho số thực x thỏa mãn log 4 log 8log x = 8 . Tính ln x . 2 4 ( 2 ) A. 125
ln x = 2 . ln 2 . B. 126 ln x = 2 .ln 2 . C. 127 ln x = 2 .ln 2 . D. 128 ln 2 ln x = 2 .
Lời giải. Ta có log 4 log (8 log x) = 8 → 4 log (8 log x ) 8 = 2 2 4 2 4 2 → log (8 log x) 64 125 = 64 →8 log x = 4 → log x = 2 4 2 2 2 ( 125) ( 125 2 2 ) 125 → x = 2 → ln x = ln 2 = 2 ln 2 . Chọn A. x Câu 93. Cho hàm số 1 f (x )
= và biểu thức P = f (x − )
1 + f (x −2). Mệnh đề nào 2 sau đây là đúng? A. 3 P = f (x).
B. P = 6 f (x).
C. P = −3 f (x).
D. P = −8 f (x). 4 x 1 − x −2 Lời giải. Ta có 1 1
P = f (x − )
1 + f (x − 2) = + 2 2 x x x 1 1 1 = 2. + 4. = 6
= 6 f (x ). Chọn B. 2 2 2 Câu 94. Cho hàm số
f x f x +1 f x + 2 ( ) 2017x f x = . Tính ( ) ( ) ( ) P = . f (3x ) A. 2017x P = . B. P = 3.2017. C. P = 3. D. 3 P = 2017 . x x 1 + x +2 Lời giải. Ta có
f (x) f (x + ) 1 f (x + 2) 2017 .2017 .2017 P = = f (3x) 3 2017 x 3x +3 2017 3 = = 2017 . Chọn D. 3 2017 x x Câu 95. Cho hàm số 4 f (x) = . Tính tổng 1 2 2016 S = f + f +...+ f . 4x + 2 2017 2017 2017 A. S = 2016. B. S =1008. C. S =1007. D. S = 2017.
Lời giải. Sử dụng tính chất ' Nếu a +b =1 thì f (a)+ f (b)=1 ' . Thật vậy: 4a 2.4a ● f (a) = = . 4a + 2 2.4a + 4 4 1 4 a − a 4
● a + b = 1
→ b = 1− a . Do đó f (b) = f ( −a) 4 1 = = = . 1 4 −a + 2 4 4 + 2.4a + 2 4a a Suy ra 2.4 4
f (a)+ f (b) = + = 1 . 2.4a + 4 4 + 2.4a Áp dụng: Ta có 1 2016 + = 1 nên 1 2016 f + f = 1 . 2017 2017 2017 2017 Vậy 1 2016 2 2015 1008 1009 S = f + f + f + f +... + f + f 2017 2017 2017 2017 2017 2017
= 1+1+... +1 = 1008 . Chọn B. x
Bài toán tổng quát: Nếu M f (x ) =
(M > 0) thì f (x)+ f (1− x) = 1. x M + M x Câu 96. Cho hàm số 9 f (x) = . Tính tổng 1 2 2016 S = f + f +...+ f . 9x + 3 2017 2017 2017 A. S = 2016. B. S = 2017. C. S = 1008. D. S = 1007. Lời giải. Ta có 1 2016 2 2015 1008 1009 S = f + f + f + f +... + f + f 2017 2017 2017 2017 2017 2017
= 1+1+... +1 = 1008 . Chọn C. x Câu 97. Cho hàm số 4 f (x) =
và góc α tùy ý. Tính S = f ( 2 α)+ f ( 2 sin cos α). 4x + 2 A. S =1. B. S = 2. C. S = 3. D. sin 2 4 a S = . Lời giải. Do 2 2
sin α + cos α = 1 nên S = f ( 2 α)+ f ( 2 sin
cos α). = 1 . Chọn A. x Câu 98. Cho hàm số 9 f (x) =
. Biết a +b = 3 , tính S = f (a)+ f (b −2). 9x + 3 A. S = 1. B. S = 2. C. 1 S = . D. 3 S = . 4 4
Lời giải. Ta có a +(b −2)= a +b−2 = 3−2 =1
→ f (a)+ f (b −2) = 1. Chọn A. t
Câu 99. (ĐỀ CHÍNH THỨC 2016 2017) Xét hàm số 9 với – f (t) = m là tham t 2 9 + m
số thực. Gọi S là tập hợp tất cả các giá trị của m sao cho f (x)+ f (y)=1 với mọi
x, y thỏa mãn x+y e
≤ e (x + y). Tìm số phần tử của S . A. 0. B. 1. C. 2. D. Vô số.
Lời giải. Xét hàm số ( ) t
g t = e − et, ∀t ∈ . ℝ Ta có '( ) t
g t = e − e
→ g '(t) = 0 ⇔ t = 1.
Lập bảng biến thiên ta thấy g(t)≥ 0, ∀t ∈ ℝ và đẳng thức xảy ra ⇔ t =1. Ta có ( + ) x + y g x y = e
− e (x + y) ≥ 0 x + y ⇔ e
≥ e (x + y).
Kết hợp với giải thiết x+y e
≤ e (x + y), suy ra x+y e
= e (x + y) ⇔ x + y = 1. Chọn một bộ 1 1 1 3 x = y =
theo giả thiết, có f + f = 1 ⇔ 2. = 1 ⇔ m = ± 3. 2 2 2 2 3 + m
Vậy có hai giá trị m thỏa mãn yêu cầu. Chọn C.
Câu 100. Cho hàm số x +1
f (x ) = ln 2017 − ln
. Tính S = f '( )
1 + f '(2)+...+ f '(2017) . x A. 4035 S = . B. S = 2017. C. 2016 S = . D. 2017 S = . 2018 2017 2018 / x +1 −1 Lời giải. Ta có 2 x 1 1 1 '( ) x f x = − = − = = − . x +1 x +1 x (x + ) 1 x x +1 x x
Khi đó S = f '( )
1 + f '(2)+...+ f '(2017) 1 1 1 1 1 1 1 1 2017 = − + − +... + − = − = . Chọn D. 1 1+1 2 2 +1 2017 2017 +1 1 2017 +1 2018
Câu 101. (ĐỀ CHÍNH THỨC 2016 2017) Xét các số nguyên dương – a, b sao cho phương trình 2
a ln x + b ln x + 5 = 0 có hai nghiệm phân biệt x , x và phương trình 1 2 2
5 log x + b log x + a = 0 có hai nghiệm phân biệt x , x thỏa mãn x x > x x . Tính giá 3 4 1 2 3 4
trị nhỏ nhất S của S = 2a +3b . min A. S = 30 . B. S = 25 . C. S = 33 . D. S = 17 . min min min min
Lời giải. Điều kiện x > 0 . Phương trình 2
a ln x + b ln x + 5 = 0 có hai nghiệm phân biệt 2
⇔ b > 20a . Phương trình 2
5 log x + b log x + a = 0 có hai nghiệm phân biệt 2
⇔ b > 20a . Ta có 2 t =ln x 2
a ln x + b ln x + 5 = 0
→ at + bt + 5 = 0. ( ) 1 2 u=log x 2
5 log x + b log x + a = 0 →5u + bu + a = 0. (2)
Với mỗi một nghiệm t thì có một nghiệm x , một nghiệm u thì có một nghiệm x . b − t t t +t 1 2 1 2 a b b
Ta có x .x = e .e = e = e − − 1 2 , kết hợp giả thiết a 5
x x > x x → e > 10 b 1 2 3 4 − u +u 1 2 5 x .x = 10 = 10 3 4 b b 5 + ln10 a a ∈ →− > − ⇔ > ℤ → a ≥ 3 . a 5 ln10 Suy ra 2 + 20 60 b b a ∈ > ≥ ℤ → b ≥ 8 . Vậy a =
S = 2a + 3b ≥ 2.3 + 3.8 = 30 , suy ra S = 30 đạt được khi 3 . Chọn A. min b = 8
Câu 102. Cho a, b là các số thực thỏa mãn 2 2
a + b > 1 và log
a + b ≥ 1. Tìm giá trị 2 2 a +b
lớn nhất P của biểu thức P = 2a + 4b −3. max A. 1 10 P = 10. B. P = . C. P = . D. P = 2 10. max max max max 10 2 Lời giải. 2 2 Do 1 1 1 2 2
a + b > 1 nên 2 2 log
a + b ≥ 1 ⇔ a + b ≥ a + b ⇔ a − + b − ≤ . ( ) 1 2 2 ( ) a +b 2 2 2 Ta có 1 1 3 a + 2b = a − + 2 b −
+ . Áp dụng bất đẳng thức Bunhiacopxky ta có 2 2 2 2 2 2 1 1 a − + 2 b − ≤ ( 1 1 1 5 2 2 1 + 2 )a − + b − ≤ 5. = . 2 2 2 2 2 2 Do đó 1 1 10 10 3 a − + 2 b − ≤ → a + 2b ≤ +
→ P = 2a + 4b −3 ≤ 10. 2 2 2 2 2 Dấu + + " = " xảy ra 5 10 5 2 10 ⇔ a = ; b = . Chọn A. 10 10 Cách 2. Ta thấy ( ) 1 là hình tròn tâm 1 1 I ; , bán kính 2 R = . 2 2 2
Ta có P = 2a + 4b −3 ⇔ ∆ : 2a + 4b −3− P = 0. Xem đây là phương trình đường thẳng.
Để đường thẳng và hình tròn có điểm chung ⇔ d [I,∆]≤ R 1 1 2. + 4. −3− P 2 2 2 ⇔ ≤ ⇔ P ≤ 10 → P ≤ 10. 4 +16 2
Câu 103. Xét các số thực 1 a
a, b thỏa mãn a ≥b >1. Biết rằng P = + log đạt log a a b (ab) giá trị lớn nhất khi k
b = a . Khẳng định nào sau đây đúng? A. 3 k ∈ 0; .
B. k ∈(−1;0). C. 3 k ∈ ;2 . D. k ( ∈ 2; ) 3 . 2 2 Lời giải. Ta có 1 a P = + log
= log (ab)+ 1− log b = 1+ log b + 1− log b log a a a a a a b (ab) Khi k b = a
→ P = 1+ k + 1− k . 2 Đặt 1 9 9
t = 1− k (k ≤ ) 1 , ta được 2 P t t 2 = − + + = − t − + ≤ . 2 4 4 Dấu ' = ' xảy ra 1 3 3 t k ⇔ = → = ∈ 0; . Chọn A. 2 4 2
Cách trắc nghiệm. Ta chọn 1 2 = 2 ⇒ = 2k a b . Khi đó P = + log . 2 log k k 2 2 2.2 S tart = 1 −
Sử dụng MODE7 khảo sát hàm 1 2 f (X ) = + log với E nd = 3 . 2 log X X 2 2 2.2 S tep = 0,2
Dựa vào bảng giá trị dễ dàng thấy được 3 k ∈ 0;
thì f (X ) lớn nhất. 2
Câu 104. (ĐỀ THỬ NGHIỆM 2016 2017) Xét các số thực . –
a, b thỏa mãn a > b > 1
Tìm giá trị nhỏ nhất của biểu thức a 2 P = ( 2 log a )+3log . a b b b A. P = 19 . B. P = 13 . C. P = 14 . D. P = 15 . min min min min Lời giải. Ta có a a 2 P = (a ) 2 2 log + 3 log
= 2 log a + 3 log a b a b b b b b 2 a a 2 a = 4 log .b + 3 log . = 4 1
+ log b + 3 log a b a b b b b b b Đặt 3 3
t = log b > 0 (vì a > b > 1 ). Khi đó P = 4(1+ t)2 2
+ = 4t + 8t + + 4. a t t b Xét hàm 3 1 f (t) 2
= 4t + 8t + + 4 trên (0;+∞) , ta được P = f (t) ≥ f
= 15. Chọn D. t 2
Cách CASIO. Cho b = 1,1 và coi a là X . 2 S tart = 1,1 Dùng MODE 7 khảo sát X f (X ) = log X + với E nd = 3 X ( 2 ) 3 log1,1 1,1 1,1 S tep = 0,1
Quan sát bảng giá trị, ta thấy f (X ) nhỏ nhất bằng 15 khi X = 1,3 .
Câu 105. Xét các số thực a, b thỏa mãn 2
a ≥ b và b > 1 . Tìm giá trị nhỏ nhất của biểu thức a P = log a + log . a b b b A. 1 P = . B. P = 1. C. P = 3. D. P = 9. min 3 min min min −
Lời giải. Từ điều kiện, suy ra a > 1 1 b . Ta có 1 loga P = + . b > 1 1 − log b log b a a Đặt 1
t = log b > 0 . Do 2 2 a ≥ b
→ log a ≥ log b = 2
→ t = log b ≤ . a b b a 2 Khi đó 1 1 − t P = + = f (t) . 1 − t t Khảo sát hàm f (t ) trên 1
0; , ta được P = f (t ) 1
≥ f = 3 . Chọn C. 2 2 Cách 2. Cosi 1 1− t 1− t + t 1− t t 1− t P = + = + = 1+ + ≥ 1+ 2 = 3. 1− t t 1− t t 1− t t
Cách CASIO. Cho a = 4 khi đó 1< b ≤ 4. Dùng MODE 7 khảo sát 4
f (X ) = log 4 + log
với Start = 1,1, End = 2, Step = 0,1. 4
X X X
Quan sát bảng giá trị, ta thấy f (X ) nhỏ nhất bằng 3 khi X = 2 .
Câu 106. Xét các số thực a, b thỏa mãn điều kiện b >1 và a ≤ b < a . Biểu thức a
P = log a + 2 log
đạt giá trị khỏ nhất khi: a b b b A. 2 a = b . B. 2 3 a = b . C. 3 2 a = b . D. 2 a = . b
Lời giải. Từ điều kiện, suy ra a > 1 . b > 1 Ta có 1 1 4 P = + 4(log a − = + − . b ) 1 4 1− log b 1− log b log b a a a
Đặt t = log b > 0 . Do 1
a ≤ b < a → log
a ≤ log b < log a → ≤ t < 1. a a a a 2 Khi đó 1 4 P =
+ − 4 = f (t) . 1− t t Khảo sát
f (t) trên 1 ;1
, ta được f (t ) đạt giá trị nhỏ nhất bằng 5 khi 2 t = . 2 3 Với 2 2 2 3 t = → log b =
↔ a = b . Chọn B. 3 a 3 Cách 2. 1 4 1− t + t 4(1−t)+ 4t t 4(1−t) P = + − 4 = + − 4 = 1+ + ≥ 1+ 2.2 = 5. 1− t t 1− t t 1− t t
Cách trắc nghiệm. Dễ dàng nhận thấy đáp án C & D không thỏa mãn điều kiện. Thử đáp án A với 2
a = b , ta được 2
P = log b + 2 log b = 2 + 4 = 6. b b 2 Thử đáp án B với a a 2 3
a = b , ta được 2
P = log a + 2 log
= log a + log 2 a b a b 2 b b b 2 b 3 = log b + log b = 3 + 2 = 5. b b
So sánh hai đáp án, ta thấy ứng đáp án B thì P có giá trị nhỏ hơn.
Câu 107. Xét các số thực a, b thỏa mãn a >1> b > 0. Tìm giá trị lớn nhất của biểu thức 2 3 P = log a b + log a . 2 a ( ) b A. P = 1+ 2 3. B. P = −2 3. C. P = −2. D. P = 1− 2 3. max max max max 2 3 Lời giải. Ta có log a b log a log b + 2 6 2 3
P = log a b + log a a a a = + = + . 2 a b 2 log a b b a log 2 log a a
Đặt t = log b . Do a >1> b > 0
→ log b < log 1 = 0 → t < 0. a a a Cauchy Khi đó t + 2 6 t 6 t 6 P = + = + +1 = 1 − − −
≤ 1− 2 3. Chọn D. 2 t 2 t 2 t 2 Cách CASIO. Cho 1 a b = khi đó 3 P = log − log a . 2 4 2 a 4 S tart = 1,1 2 Dùng MODE 7 khảo sát X f (X ) 3 = log − log X với E nd = 5 . 2 2 X 4 S tep = 0,3
Quan sát bảng giá trị của f (X ) và so sánh với các đáp án ta chọn D.
Câu 108. Tìm giá trị nhỏ nhất của biểu thức y 12 3 logx P = e +
với 0 < x ≠1 và y > 0. 1 ln x y A. P = 8 3. B. 2 P = e 3. C. P = 8 2. D. P = 4 6. min min min min 1 Lời giải. Ta có log e log ln x x y x y = y = e
. (ở đây là sử dụng log c log b b a a = c ) Suy ta log y 12 y x t =e 12 3 log 3 x P = e + → P = t + , t > 0. logx y e t Xét hàm 12 f (t) 3 = t +
trên (0;+∞) , ta được P = f (t)≥ f ( 2)= 8 2. Chọn C. t
Câu 109. Cho x, y là số thực dương thỏa mãn x + y ≥ ( 2 ln ln
ln x + y) . Tìm giá trị nhỏ
nhất của P = x + y . A. P = 6 .
B. P = 2 2 +3 . C. P = 2 +3 2 . D. P = 17 + 3 . min min min min
Lời giải. Ta có ln x + ln y ≥ ( 2
x + y) ⇔ ln(xy)≥ ln( 2 x + y) 2 ln
⇔ xy ≥ x + y.
Nếu 0 < x ≤1 thì 2 2
y ≥ xy ≥ x + y ⇔ 0 ≥ x : mâu thuẫn. 2 2 Nếu x x x > 1 thì 2
xy ≥ x + y ⇔ y (x − ) 2
1 ≥ x ⇔ y ≥
. Vậy P = x + y ≥ x + . x −1 x −1 2 Xét x 2 + 2
f (x ) = x +
trên (1;+∞), ta được min f (x)= f
= 2 2 + 3. Chọn B. x −1 (1; ∞ + ) 2
Câu 110. (ĐỀ CHÍNH THỨC 2016 2017) Xét các số thực dương –
x, y thỏa mãn 1− xy log
= 3xy + x + 2 y − 4. Tìm giá trị nhỏ nhất P
của biểu thức P = x + y . 3 x + 2y min A. 9 11 −19 9 11 +19 P = . B. P = . min 9 min 9 C. 18 11 − 29 2 11 −3 P = . D. P = . min 21 min 3
Lời giải. Điều kiện: x > 0, y > 0, xy <1. Ta có 1− xy 1− xy log
= 3xy + x + 2 y − 4 ⇔ 1+ log
= 3xy + x + 2 y −3 3 3 x + 2 y x + 2 y 3−3xy ⇔ log
= 3xy −3 + x + 2 y ⇔ log 3−3xy + 3−3xy = log x + 2 y + x + 2 y. (*) 3 3 ( ) 3 ( ) x + 2 y Xét hàm 1
f (t) = log t + t trên (0;+∞) , ta có f '(t) =
+1 > 0, ∀t ∈ (0;+∞). 3 t.ln 3 Từ đó suy ra 3− x 3− x
(*) ⇔ 3−3xy = x + 2y → y = → P = x + . 3x + 2 3x + 2 Xét 3− x −2 + 11 2 11 −3
f (x ) = x + trên(0; )
3 , ta được min f (x ) = f = . Chọn D. 3x + 2 (0; ) 3 3 3 Nhận xét. Do 3− x y = , mà y > 0
→ x < 3 . Kết hợp giả thiết ta có x ∈ (0; ) 3 . 3x + 2 Baøi 04
PHÖÔNG TRÌNH MUÕ, PHÖÔNG TRÌNH LOGARIT
BAÁT PHÖÔNG TRÌNH MUÕ, BAÁT PHÖÔNG TRÌNH LOAGRIT
I. PHƯƠNG TRÌNH, BẤT PHƯƠNG TRÌNH MŨ
1. Phương trình mũ cơ bản x
a = b (a > 0, a ≠ ) 1 .
● Phương trình có một nghiệm duy nhất khi b > 0 .
● Phương trình vô nghiệm khi b ≤ 0 .
2. Biến đổi, quy về cùng cơ số 0 < a ≠ 1 f (x) g(x) a = a ⇔ a = 1 hoặc .
f (x) = g (x) 3. Đặt ẩn phụ g(x ) t = a > g(x) 0 f a = 0 (0 < a ≠ ) 1 ⇔ . f (t ) = 0
Ta thường gặp các dạng: ● 2 f (x) f (x ) . m a + . n a + p = 0 ● f (x ) f (x ) . m a + . n b + p = 0 , trong đó . a b = 1 . Đặt f (x ) t = a
( t > 0) , suy ra f (x) 1 b = . t f (x) f x f x a ● 2 ( ) . m a + . n ( . a b) ( ) 2 f (x ) + . p b
= 0 . Chia hai vế cho 2 f (x) b và đặt t = > 0 . b 4. Logarit hóa 0
< a ≠ 1, b > 0
● Phương trình f (x) a b = ⇔ .
f (x) = log b a
● Phương trình f (x) g(x ) f (x ) g(x ) a = b ⇔ log a = log b ⇔ f x = g x b a a ( ) ( ).loga hoặc f (x ) g(x ) log a = log b ⇔ f x a = g x b b ( ).logb ( ).
5. Giải bằng phương pháp đồ thị
Giải phương trình: x
a = f (x) (0 < a ≠ ) 1 . ( ) ∗ Xem phương trình ( )
∗ là phương trình hoành độ giao điểm của hai đồ thị x y = a (0 < a ≠ )
1 và y = f (x ) . Khi đó ta thực hiện hai bước:
Bước 1. Vẽ đồ thị các hàm số x
y = a (0 < a ≠ )
1 và y = f (x) .
Bước 2. Kết luận nghiệm của phương trình đã cho là số giao điểm của hai đồ thị.
6. Sử dụng tính đơn điệu của hàm số
Tính chất 1. Nếu hàm số y = f (x) luôn đồng biến (hoặc luôn nghịch biến) trên
(a;b) thì số nghiệm của phương trình f (x) = k trên (a;b) không nhiều hơn một và
f (u) = f (v) ⇔ u = v, ∀ ,
u v ∈ (a;b).
Tính chất 2. Nếu hàm số y = f (x) liên tục và luôn đồng biến (hoặc luôn nghịch
biến) trên D ; hàm số y = g(x) liên tục và luôn nghịch biến (hoặc luôn đồng biến)
trên D thì số nghiệm trên D của phương trình f (x)= g(x) không nhiều hơn một.
Tính chất 3. Nếu hàm số y = f (x) luôn đồng biến (hoặc luôn nghịch biến) trên
D thì bất phương trình f (u)> f (v) ⇔ u > v (hoặc u < v ) , ∀ , u v ∈ D.
7. Sử dụng đánh giá
Giải phương trình f (x)= g(x).
f (x)≥ m
f (x) = m
Nếu ta đánh giá được
thì f (x)= g(x) ⇔ . g (x ) ≤ m g (x ) = m
II. PHƯƠNG TRÌNH, BẤT PHƯƠNG TRÌNH LOGARIT
1. Biến đổi, quy về cùng cơ số 0 < a ≠ 1 log f x g x = ⇔ a ( ) loga ( ) .
f (x) = g (x)> 0 2. Đặt ẩn phụ t = log g x a ( ) f log g x a = < ≠ ⇔ a ( ) 0 (0 ) 1 . f (t ) = 0 3. Mũ hóa hai vế
g (x)> 0 log g (x) f (x) ( 0 a ) 1 = < ≠ ⇔ . a g (x ) f (x ) = a
4. Phương pháp đồ thị
5. Sử dụng tính đơn điệu của hàm số
CAÂU HOÛI TRAÉC NGHIEÄM
Vấn đề 1. PHƯƠNG TRÌNH, BẤT PHƯƠNG TRÌNH MŨ
Câu 1. Tìm tọa độ giao điểm của đồ thị hàm số 2 x y − =
+ 3 và đường thẳng y = 11. A. (3;1 ) 1 . B. (−3;1 ) 1 . C. (4;1 ) 1 . D. (−4;1 ) 1 .
Lời giải. Phương trình hoành độ giao điểm: 2−x +3 = 11 ⇔ 2−x = 8 −x 3 ⇔ 2
= 2 ⇔ −x = 3 ⇔ x = −3 .
Vậy tọa độ giao điểm cần tìm là (−3;1 ) 1 . Chọn B. 2
Câu 2. Tìm tập nghiệm x +2 x +3
S của phương trình 2 = 8x. A. S = {1; } 3 . B. S = {−1; } 3 . C. S = {−3; } 1 . D. S = {− } 3 . 1 2
Lời giải. Phương trình (x +2x+ ) 3 x 1 3 ⇔ 2 = 2 ⇔ ( 2 x + 2x + 3) 2 2
= 3x ⇔ x − 4x + 3 = 0 2
⇔ x = 1 hoặc x = 3. Chọn A.
Cách 2. CALC với các giá trị của đáp án xem giá trị nào là nghiệm. 2
Nhập vào máy tính phương trình: x +2 x +3 2 −8x CALC tại X=1ta được 0 CALC tại X=3ta được 0 4 x 2 x −6
Câu 3. Tìm tập nghiệm 2 3
S của phương trình = . 3 2 A. S = { } 1 . B. S = {− } 1 . C. S = {− } 3 . D. S = { } 3 . 4 x 2 x 6 − 4 x 6−2 x
Lời giải. Ta có 2 3 2 2 = ⇔ =
⇔ 4x = 6 − 2x ⇔ x = 1. Chọn A. 3 2 3 3 Câu 4. Tính tổng x − x 1
T tất cả các nghiệm của phương trình 2 3 e = . 2 e A. T = 3. B. T = 1. C. T = 2. D. T = 0. Lời giải. Ta có 2 2 x = x − x 1 1 3 x 3 − x 2 − 2 2 e = ⇔ e = e
⇔ x −3x = −2 ⇔ x −3x + 2 = 0 ⇔ . 2 e x = 2
→S = {1;2} T → = 1+ 2 = 3. Chọn A.
Câu 5. Biết rằng phương trình 2018 x log8 9 3 − 2
= 0 có nghiệm duy nhất x = x . Khẳng 0
định nào sau đây đúng?
A. x là số nguyên tố.
B. x là số chính phương. 0 0
C. x chia hết cho 3.
D. x là số chẵn. 0 0 2 x
Lời giải. Phương trình log 3 2 x log 9 8 2018 2018 3 ← → 2 = 3 ← → 2 = 3 2 x 2 x ← →( 2x log2 3 2 ) 2018 2018 3 3 = 3 ← →3 = 3 ← → = 2018←
→ x = 3027 . Chọn C. 3 1 3
Câu 6. Biết rằng phương trình x + x + x 2 x 1 2 2 9 2 2 3 − − = −
có nghiệm duy nhất x = x . Tính 0 giá trị biểu thức 1 P = x + log 2. 0 9 2 2 A. 1 1 P = 1.
B. P = 1− log 2 . C. P = 1− log 2 . D. P = log 2 . 9 2 9 9 2 2 2 2 1 3 3 1 Lời giải. Ta có x + x + x + x + x 2 x 1 − x 2 x 1 2 2 − 2 2 9 − 2 = 2 −3 ← → 9 + 3 = 2 + 2 x x 1 x x x 4 x x 9 9 9 ⇔ 9 + .9 = 2 2.2 + 2.2 ⇔ .9 = 3 2.2 ⇔ = ⇔ x = log = x . 9 0 3 3 2 2 2 2 2 2 CASIO Khi đó 1 9 1
P = x + log 2 = log + log 2 = 1. Chọn A. 0 9 9 9 2 2 2 2 2 2 2
Câu 7. (ĐỀ CHÍNH THỨC 2016 2017) Cho phương trình x x 1 + . Khi đặt – 4 + 2 −3 = 0 2x t = , ta được: A. 2
t + t −3 = 0. B. 2 2t −3 = 0. C. 2
t + 2t −3 = 0.
D. 4t −3 = 0.
Lời giải. Ta có x x + + − = ⇔ ( x )2 1 4 2 3 0 2
+ 2.2x −3 = 0. Khi đặt 2x t =
, thay vào phương trình ta được 2
t + 2t −3 = 0 . Chọn C.
Câu 8. Tính P là tích tất cả các nghiệm của phương trình 3.9x 10.3x − + 3 = 0. A. P =1. B. P = −1 . C. P = 0 . D. P = 9.
Lời giải. Phương trình 2 3.3 x 10.3x ⇔ − + 3 = 0 . Đặt 1 3x t =
> 0. Phương trình trở thành 2
3t −10t + 3 = 0 ⇔ t = hoặc t = 3 . 3 Với 1 x 1 t = → 3 =
⇔ x = −1 = x . 1 3 3 Với = 3 → 3x t
= 3 ⇔ x = 1 = x . 2
Vậy P = x x = −1. Chọn B. 1 2
Câu 9. Tìm tập S nghiệm của phương trình 6x 3 −3 x e e + 2 = 0. A. S = {0;ln 2} . B. ln 2 S 0; = . C. ln 2 S 1; = .
D. S = {1;ln 2} . 3 3 Lời giải. Đặt t = 1 3x e
= t > 0 . Phương trình trở thành 2
t −3t + 2 = 0 ⇔ . t = 2 3x x = 0 e = 1 3x = 0 ln 2 → ⇔ ⇔ ln 2 →S = 0 ; . Chọn B. 3x e = 2 3x = ln 2 x = 3 3
Câu 10. Phương trình 2 2 x +x x +x 1 4 2 + +
−3 = 0 có bao nhiêu nghiệm không âm? A. 0. B. 1. C. 2. D. 3.
Lời giải. Phương trình tương đương với 2 2
4x +x + 2.2x +x − 3 = 0 . t = 1 Đặt 2 2x x t + =
, t > 0 . Phương trình trở thành 2 t 2t 3 0 + − = ⇔ . t = −3 (loaïi) Với x = 0 t = 1 , ta được 2 x +x 2 2
= 1 ⇔ x + x = 0 ⇔ . x = −1
Vậy chỉ có duy nhất nghiệm x = 0 là nghiệm không âm. Chọn B. 1
Câu 11. Tính tổng T tất cả các nghiệm của phương trình 2 2 tan x cos 4 2 x + −3 = 0 trên
đoạn [0;3π]. A. π T . π = B. 3 T = . C. T 6 . π = D. T = 0. 2 c os x ≠ 0
Lời giải. Điều kiện: π 3π 5π x ; ; ⇔ ≠ . x ∈ [0;3π] 2 2 2 1 2 Ta có 2 tan x x ( 2 tan x ) 2 2 tan x 1 cos 4 2 3 0 2 2 + + − = ⇔ + −3 = 0 2 tan x ⇔ ( 2 2 = 1 2 tan 2 x ) 2 2 tan x tan x 2 + 2.2 −3 = 0 ⇔ ⇔ 2
= 1 ⇔ tan x = 0 ⇔ x = k , π k ∈ . ℤ 2 tan 2 x = −3 (loaïi) Vì 0 x 3 thoûa maõn π x
{0; π; 2π; 3π} ( ) T 6 . π ≤ ≤ → = → = Chọn C.
Câu 12. Tính P là tổng bình phương tất cả các nghiệm
của phương trình x 1 − 2 2 + 2 −x = 3. A. P = 1. B. P = 3. C. P = 5. D. P = 9.
Lời giải. Ta có x− −x 1 x 4 1 2 2 + 2 = 3 ⇔ .2 + = 3 . 2 2x Đặt 1 4 t = 2 = 2x t
, t > 0 . Phương trình trở thành 2 .t +
= 3 ⇔ t − 6t + 8 = 0 ⇔ 2 t t = 4 2x = 2 x = 1 = x1 2 2 → ⇔
→ P = x + x = 5. Chọn C. 1 2 2x = 4 x = 2 = x2
Câu 13. Gọi S là tập nghiệm của phương trình 2 2 1+x 1 5
−5 −x = 24 . Tập S có bao nhiêu phần tử? A. 0. B. 1. C. 2. D. 4.
Lời giải. Phương trình 2 x 5 ⇔ 5.5 − − 24 = 0. 2 5x Đặt 2 5 = 5x t
, t ≥1. Phương trình trở thành 2
⇔ 5.t − − 24 = 0 ⇔ 5t − 24t −5 = 0 t t = 5 2 x 2 ⇔ 1 ⇔ t = 5
→5 = 5 ⇔ x = 1 ⇔ x = ±1 →S = {−1; } 1 . Chọn C. t = − (loaïi) 5 2 x 2 x +
Câu 14. Phương trình 1 2 9 + 9.
− 4 = 0 có tất cả bao nhiêu nghiệm? 3 A. 0. B. 1. C. 2. D. 4. x 1 + x
Lời giải. Phương trình x 1 x 1 x 1 3 + 9. − 4 = 0 ⇔ 3 + 3. − 4 = 0 ⇔ 3 + 3. − 4 = 0. 3 3 3x Đặt 1 t = 1 3x t =
, t > 0 . Phương trình trở thành 2
t + 3. − 4 = 0 ⇔ t − 4t + 3 = 0 ⇔ t t = 3
3x = 1 ⇔ x = 0 → . Chọn C.
3x = 3 ⇔ x = 1
Câu 15. Tính tổng T tất cả các nghiệm của phương trình 2 2 sin x cos 5 5 x + = 2 5 trên
đoạn [0;2π]. A. π T . π = B. 3 T = . C. T 2 . π = D. T 4 . π = 4 Lời giải. Ta có 2 2 2 2 2 x x x − x x 5 sin cos sin 1 sin sin 5 + 5 = 2 5 ⇔ 5 + 5 = 2 5 ⇔ 5 + = 2 5 2 sin 5 x 1 ⇔ ( 2 sin x )2 2 sin x − + = ⇔ ( 2 sin x − )2 2 2 sin x sin x 2 5 2 5.5 5 0 5 5 = 0 ⇔ 5 − 5 = 0 ⇔ 5 = 5 2 sin x = 1 π k 2 2 π ⇔ sin x = ⇔ ⇔ x = + , k ∈ ℤ . 2 4 2 2 sin x = − 2 Do π
3π 5π 7π π 3π 5π 7π x ∈ [0;2 π ] → x = ; ; ; →T = + + + = 4 . π Chọn D. 4 4 4 4 4 4 4 4
Câu 16. Tổng lập phương các nghiệm của phương trình 2x 2.3x 6x + − = 2 bằng: A. 2 2 . B. 25. C. 7. D. 1.
Lời giải. Phương trình 2x 6x 2 2.3x
2x (1 3x ) 2(1 3x ⇔ − = − ⇔ − = − ) 3x = 1 x = 0
⇔ (1−3x )(2x −2) 3 3 = 0 ⇔ ⇔
→ 0 +1 = 1. Chọn D. 2x = 2 x = 1
Câu 17. Tính P là tích tất cả các nghiệm của phương trình 6x 2.2x 81.3x − − +162 = 0. A. P = 4. B. P = 6. C. P = 7. D. P = 10.
Lời giải. Phương trình
(6x 2.2x ) (81.3x 162) 0 2x (3x 2) 8 ( 1 3x ⇔ − − − = ⇔ − − − 2) = 0 3x −2 = 0 x = log 2 = x
⇔ (3x −2)(2x −8 ) 3 1 1 = 0 ⇔ ⇔
→ P = x .x = 4. Chọn A. 1 2 2x −81 = 0
x = log 81 = x 2 2
Câu 18. Gọi x , x lần lượt là nghiệm nhỏ nhất và nghiệm lớn nhất của phương trình 1 2 2 2 x +x 1 − x 1 − 2 2 − 2
= 2 x − 2x . Tính S = x + x . 1 2 A. S = 0. B. S = 1. C. 1 S = . D. 5 S = . 2 2
Lời giải. Phương trình 2 x − ( x ) x ( x ) ( x )( 2 1 x 1 2 2 1 2 2 1 2 1 2 − ⇔ − = − ⇔ − − 2x ) = 0 x = x x 0 2 −1 = 0 2 = 1 x = 0 x = 0 ⇔ ⇔ ⇔ ⇔ ⇔ . 2 2 2 2 1± 5 x 1 − x x 1 2 − 2 = 0 2 − = 2x x 1 x x x 1 0 − = − − = x = 2 Suy ra nghiệm nhỏ nhất 1− 5 + x = , nghiệm lớn nhất 1 5 x = . Chọn B. 2 2
Câu 19. Phương trình x +x 1−x (x + )2 2 2 1 4 + 2 = 2
+1 có tất cả bao nhiêu nghiệm? A. 1. B. 2. C. 3. D. 4.
Lời giải. Phương trình 2 2 2 2 x +2 x 1−x x +2 x 1 2 2 2 + ⇔ + = +1 . 2 2 x +2 x Đặt a = 2 > 0 , suy ra 2+2 1 2x x +
= ab . Khi đó phương trình trở thành a + b = ab +1 2 1 b = 2 −x > 0 a = 1
⇔ a − ab + b −1 = 0 ⇔ a(1−b)+(b − )
1 = 0 ⇔ (1−b)(a − ) 1 = 0 ⇔ . b = 1 x = 0
● Với a = 1 , ta được 2 2 x +2 x 2 2
= 1 ⇔ 2x + 2x = 0 ⇔ . x = −1
● Với b = 1 , ta được 2 1−x 2 2
= 1 ⇔ 1− x = 0 ⇔ x = ±1 .
Vậy phương trình đã cho có ba nghiệm x = 0 , x = ±1 . Chọn C.
Câu 20. Tính S là tổng tất cả các nghiệm của phương trình ( 2x 2 4. 2
+ 2− x )−4.(2x + 2−x )−7 = 0 A. S = 1. B. S = −1. C. S = 3. D. S = 0. Lời giải. Đặt 2x 2 x t − = + , suy ra 2 2 x 2 2 2 x t − = + + 2 . Cauchy Ta có 2x 2 x 2 2x.2 x t − − = + ≥ = 2 . 5 t = (thoûa maõn) Phương trình trở thành ( 2 t − ) 2 2 4
2 − 4t −7 = 0 ⇔ 4t − 4t −15 = 0 ⇔ 3 t = − (loaïi) 2 2x = 2 5 x = = x x −x 5 x 1 5 1 2 x x 1 ⇔ t = → 2 + 2 = ⇔ 2 + = ⇔ 2.2 −5.2 + 2 = 0 ⇔ ⇔ x x 1 2 2 2 2 2 = x = −1 = x2 2
→S = x + x = 0. Chọn D. 1 2
Câu 21. Phương trình log +3 5 ( ) 2 x
= x có tất cả bao nhiêu nghiệm? A. 1. B. 2 . C. 3 . D. 0 .
Lời giải. Điều kiện: x > −3. Do log x+3 5 ( ) 2
> 0 nên để phương trình có nghiệm thì x > 0.
Lấy logarit cơ số 2 của hai vế phương trình, ta được log x +3 = log x . 5 ( ) 2 t t + = Đặt x 3 5 x = 5 −3 t log x 3 log x = + = → ⇔
⇔ 5t −3 = 2t ⇔ 5t = 3.1t + 2t. 5 ( ) 2 x 2t = x = 2t t t
Chia hai vế phương trình cho 5t , ta được 1 2 1 = 3.
+ . Đây là phương trình hoành 5 5 t t
độ giao điểm của đường
y = 1 (hàm hằng) và đồ thị hàm số 1 2 y = 3. + (hàm số 5 5
này nghịch biến vì nó là tổng của hai hàm số nghịch biến). Do đó phương trình có
nghiệm duy nhất. Nhận thấy t = 1 thỏa mãn phương trình. Với = 1 → = 2t t x
= 2(thoûa maõn). Vậy phương trình có nghiệm duy nhất. Chọn A.
Câu 22. Biết rằng phương trình 2 log 2 x log 6 log 4 x 2 2 2 4 − x = 2.3
có nghiệm duy nhất x = x . 0
Mệnh đề nào sau đây là đúng? A. x ∈ − ;
∞ −1 . B. x ∈ −1;1 .
C. x ∈ 1; 15 . D. x ∈ 15;+∞ . 0 ) 0 ( ) 0 [ ] 0 ( )
Lời giải. Điều kiện: x > 0 . Phương trình 1+log x log 6 2. log 2 x log x log 6 1+log x 2 2 2 2 2 2 ⇔ 4 − x = 2.3 ⇔ 4.4 − x = 2.9 log x log 6 log x log x log x log x 2 2 2 2 2 2 ⇔ 4.4 − x = 18.9 ⇔ 4.4 − 6 = 18.9 . 2t t Đặt t t t 2 2
t = log x , phương trình trở thành 4.4 − 6 = 18.9 ⇔ 4. − −18 = 0 2 3 3 t 2 9 = 3 4 t 2 9 1 ⇔ ⇔ = ⇔ t = −2
→ log x = −2 ⇔ x = ∈ −1;1 . Chọn B. 2 [ ] t 3 4 4 2 = −2(loaïi) 3
Cách CASIO. Loại ngay đáp án A vì không thỏa mãn điều kiện.
Dùng CASIO với chức năng TABLE ta dò được nghiệm nằm trong khoảng (0,2;0,3). Câu 23. Tính tổng 2 2 x 5 − x
T tất cả các nghiệm của phương trình (x − ) 3 = 1 . A. T = 0. B. T = 4. C. 13 T = . D. 15 T = . 2 2
Lời giải. Ta xét các trường hợp sau:
TH1. x −3 = 1 ⇔ x = 4 thỏa mãn phương trình. x = 0 x −3 ≠ 0 TH2. ⇔ 5 . 2 2 x −5x = 0 x = 2
Vậy phương trình đã cho có ba nghiệm 5 13 x = 0; x = ; x = 4 T → = . Chọn C. 2 2
Câu 24. Cho phương trình 2 2016x .2017x 2016x =
. Mệnh đề nào sau đây là đúng?
A. Phương trình đã cho có hai nghiệm âm phân biệt.
B. Phương trình đã cho có một nghiệm bằng 0 và một nghiệm âm.
C. Phương trình đã cho có một nghiệm bằng 0 và một nghiệm dương.
D. Phương trình đã cho có hai nghiệm trái dấu và một nghiệm bằng 0.
Lời giải. Phương trình 2 − ( x x x x x 1 2016 .2017 1 2016 − ⇔ = ⇔ .2017) = 1 x = 0 x = 0 ⇔ ⇔ . Chọn B. x 1 2016 − .2017 =1 x = 1−log 2017 < 0 2016
Câu 25. Phương trình
x−2 +( x − ) x−2 3.25 3 10 5
+ 3− x = 0 có tất cả bao nhiêu nghiệm? A. 1. B. 2. C. 3. D. 4. Lời giải. Đặt x −2 t = 5
> 0 , phương trình trở thành 2
3t +(3x −10)t + 3− x = 0 . (*)
Ta coi đây là phương trình bậc hai ẩn 2 2
t và có ∆ = (3x −10) − 4.3(3− x ) = (3x −8) .
Suy ra phương trình (*) có hai nghiệm: 1 t =
hoặc t = 3− x . 3 Với 1 x 1 1 1 −2 t 5 x 2 log x 2 log = → = ⇔ − = ⇔ = + . 5 5 3 3 3 3 Với x −2
t = 3− x → 5
= 3− x . Dễ thấy x = 2 là nghiệm duy nhất (Vế trái là hàm
đồng biến, vế phải là hàm nghịch biến).
Vậy phương trình đã cho có hai nghiệm: 1
x = 2, x = 2 + log . Chọn B. 5 3
Câu 26. Gọi T là tổng tất cả các nghiệm của phương trình 2
3x .2x = 1 . Mệnh đề nào sau đây là đúng? A. T >1. B. T = 1. C. 1 − <T <1. D. 1 T < − . 2 2
Lời giải. Lấy logarit cơ số 3 hai vế của phương trình, ta được log ( 2 3x .2x = log 1 3 ) 3 x = 0 2 x x 2
⇔ log 3 + log 2 = 0 ⇔ x + x.log 2 = 0 ⇔ x x + log 2 ⇔ . 3 3 3 ( 3 ) x = −log 2 3 Suy ra 1
T = 0 +(−log 2 ≃ −0,63 < − . Chọn D. 3 ) 2
Câu 27. Cho hàm số ( ) 2 x 1 3 .5x f x + =
. Mệnh đề nào sau đây là sai?
A. f (x)=1 ⇔ (x + ) 2 1 log 3 + x = 0.
B. f (x)=1 ⇔ (x + ) 2 1 log 3− x = 0. 5 1 5 C. f (x) 2
= 1 ⇔ x +1− x log 5 = 0.
D. f (x)= ⇔ (x + ) 2 1 1 ln 3 + x ln 5 = 0. 3
Lời giải. Ta có ( ) 2 x 1 1 3 .5x f x + = ⇔ = 1. (*)
Lấy logarit cơ số 5 hai vế của ( 2
*) , ta được log ( x 1 3 + .5x = log 1 5 ) 5 2 x 1 log 3 + ⇔
+ log 5x = 0 ⇔ (x + ) 2
1 log 3 + x = 0 . Do đó A đúng. 5 5 5
Lấy logarit cơ số 1 hai vế của ( 2
*) , ta được log ( x 1 3 + .5x = log 1 1 ) 5 1 5 5 ⇔ (x + ) 2
1 log 3 + x log 5 = 0 ⇔ (x + ) 2
1 log 3− x = 0 .Do đó B đúng. 1 1 1 5 5 5
Lấy logarit cơ số 3 hai vế của ( 2
*) , ta được log ( x 1 3 + .5x = log 1 3 ) 3 2 x 1 + x 2 ⇔ log 3
+ log 5 = 0 ⇔ x +1+ x log 5 = 0 . Do đó C sai. Chọn C. 3 3 3 Lấy ln hai vế của ( 2 *) , ta được ( x 1 ln 3 + .5x ) = ln1 2 x 1 + x ⇔ + = ⇔ (x + ) 2 ln 3 ln 5 0
1 ln 3 + x ln 5 = 0. Do đó D đúng. x
Câu 28. Gọi x là nghiệm nguyên của phương trình x x 1
5 .8 + = 100 . Tính giá trị của 0
biểu thức P = x 5− x x + 8 . 0 ( 0 )( 0 ) A. P = 40. B. P = 50. C. P = 60. D. P = 80.
Lời giải. Điều kiện: x ≠ −1. 3x 2−x
Phương trình tương đương x x 1 2 2 x + −2 x 1 5 .2 2 .5 5 2 + = ⇔ = . (*) Lấy ln hai vế của 2 − x
(*), ta được (x −2)ln 5 = ln 2 x +1 ln 2 x = 2 ⇔ (x −2)ln 5 + = 0 ⇔ x +1 x = −log 2−1 5 Suy ra x = 2
→ P = x 5− x
x + 8 = 60. Chọn C. 0 0 ( 0 )( 0 ) 2 x 3 −
Câu 29. Phương trình 2x−2 3 .4 x
= 18 có tất cả bao nhiêu nghiệm? A. 0. B. 1. C. 2. D. 4.
Lời giải. Điều kiện: x ≠ 0. 2 x 3 − 4 x 6 − 6 3 − x Phương trình 2 2 2 x −2 x −2 2 x −4 3 .4 x = 18 ⇔ 3 .2 x = 2.3 ⇔ 3 = 2 x . (*)
Lấy logarit cơ số 3 hai vế của 6 −3x (*), ta được 2 ⇔ x − 4 = log 2 3 x x −2 = 0 x = 2 3
⇔ (x −2)x + 2 + log 2 = 0 ⇔ 3 ⇔ . 3 2 x x + 2 + log 2 = 0
x + 2x +3log 2 = 0 VN 3 3 ( ) x
Vậy phương trình đã cho có nghiệm duy nhất x = 2 . Chọn B. 2 x −2−m
Câu 30. Tìm tập nghiệm S của phương trình x 1 3 − .5 x−m
= 15 , m là tham số khác 2.
A. S = {2;m log 5 .
B. S = {2;m + log 5 . 3 } 3 } C. S = {2}.
D. S = {2;m −log 5 . 3 }
Lời giải. Điều kiện: x ≠ . m 2 x −2−m 2 x −2−m x −2 Phương trình 1 − x 1 − 1 ( − x − ) 1 2 3 .5 − 3.5 5 − 3 5 − ⇔ = ⇔ = ⇔ = 3 −x x m x m x m . (*)
Lấy logarit cơ số 5 hai vế của (*), ta được x − 2 1 (2 x)log 3 x 2 = − ⇔ − + log 3 = 0. 5 ( ) 5 x − m x −m
Với x −2 = 0 ⇔ x = 2(thoûa maõn). Với 1 1
+ log 3 = 0 ⇔ x − m = −
⇔ x = m − log 5 thoûa maõn . 5 3 ( ) x − m log 3 5
Vậy phương trình có tập nghiệm S = {2;m −log 5 . Chọn D. 3 }
Câu 31. Biết rằng phương trình 2x+ x 3 1 1 3 .25 − =
có đúng hai nghiệm x , x . Tính giá trị 25 1 2 của x x 1 2 P = 3 + 3 . A. 26 P = . B. P = 26. C. P = 26. D. 26 P = . 5 25 2 x 1 +
Lời giải. Phương trình 2 2 x + x 3 3 1 − x 1 1 1 3 .25 = ⇔ = ⇔ 3 = . (*) x 1 25 3 25 − .25 25x
Lấy logarit cơ số 3 hai vế của x 1 (*), ta được 2 ⇔ log 3 = log 3 3 25x x = 0 = x1 1 1 2 2 ⇔ x = x log ⇔ x − x log = 0 ⇔ 1 . 3 3 25 25 x = log = x 3 2 25 1 Suy ra log3 x x 26 1 2 0 25 P = 3 + 3 = 3 + 3 = . Chọn A. 5
Câu 32. Phương trình 2 x − x −x − = (x − )2 1 2 2
1 có tất cả bao nhiêu nghiệm? A. 1. B. 2. C. 3. D. 4.
Lời giải. Phương trình 2 x − x −x − = ( − ) x − ⇔ +( − ) 2 2 1 1 x −x x x = +( 2 2 2 1 2 1 2 x − x ). (*) Xét hàm số ( )= 2t f t + t trên , ℝ ta có '( ) = 2t f t
ln 2 +1 > 0, ∀t ∈ . ℝ
Suy ra hàm số f (t) đồng biến trên . ℝ
Nhận thấy (*) có dạng f (x − )= f (x − x) ⇔ x − = x − x ⇔ (x − )2 2 2 1 1 1 = 0 ⇔ x = 1.
Vậy phương trình có một nghiệm duy nhất x = 1. Chọn A.
Câu 33. Tính tổng T tất cả các nghiệm của phương trình 2 2 sin x cos 2017 − 2017 x = cos 2x trên đoạn [0;π]. A. π π π x . π = B. x = . C. x = . D. 3 x = . 4 2 4
Lời giải. Phương trình 2 2 sin x cos x 2 2 ⇔ 2017 − 2017
= cos x − sin x 2 2 sin x 2 cos x 2 ⇔ 2017 + sin x = 2017 + cos x. (*)
Xét hàm số ( ) = 2017t f t + t trên ℝ, ta có '( ) = 2017t f t
ln 2017 +1 > 0, ∀t ∈ . ℝ
Suy ra hàm số f (t) đồng biến trên . ℝ
Nhận thấy (*) có dạng f ( 2 x)= f ( 2 x) 2 2 sin cos
⇔ sin x = cos x 2 2 π π
⇔ cos x − sin x = 0 ⇔ cos 2x = 0 ⇔ x = + k , k ∈ . ℤ 4 2 Vì π 3π π 3π x ∈ [0; π ] → x = ; T → = + = . π Chọn A. 4 4 4 4
Câu 34. Biết rằng phương trình 2x 1 − ( 2 x ) x 1 3 1 3 + + −
= 1 có đúng hai nghiệm phân biệt.
Tổng lập phương hai nghiệm của phương trình bằng: A. 2. B. 0. C. 8. D. 8 − . Lời giải. Nếu 2 x ∈ (− ; ∞ − ) 1 ∪(1;+∞) thì 2 x −1 > 0 . Suy ra x 1 − ( 2 x ) x 1 3 1 3 + ⇒ + − > 1 .
Do đó phương trình đã cho vô nghiệm. Nếu 2 x ∈ ( 1 − ; ) 1 thì 2
x −1 < 0 . Suy ra x 1 − ( 2 x ) x 1 3 1 3 + + − < 1.
Do đó phương trình đã cho vô nghiệm.
Kiểm tra x = ±1 thỏa mãn phương trình đã cho.
Vậy phương trình đã cho có hai nghiệm x = 1
− = x , x = 1 = x . 1 2 Suy ra 3 3
x + x = 0. Chọn B. 1 2
Câu 35. Cho phương trình 2 x 1 − +( 2 2016 − ) 1 .2017x x
= 1. Mệnh đề nào sau đây là đúng?
A. Phương trình đã cho có tổng các nghiệm bằng 0
B. Phương trình đã cho có nghiệm duy nhất.
C. Phương trình đã cho có hai nghiệm dương phân biệt.
D. Phương trình đã cho có nhiều hơn hai nghiệm. 2 x 1 2 016 − >1 Lời giải. Nếu x ∈ (− ; ∞ − ) 1 ∪(1;+∞) thì 2
x −1 > 0 . Suy ra ( 2 − ) 1 .2017x x > 0 2 x 1 − ⇒ +( 2 2016 − ) 1 .2017x x
> 1 . Do đó phương trình đã cho vô nghiệm. 2 x 1 2 016 − <1 Nếu x ∈ ( 1 − ; ) 1 thì 2
x −1 < 0 . Suy ra ( 2 − ) 1 .2017x x < 0 2 x 1 − ⇒ +( 2 2016 − ) 1 .2017x x
<1. Do đó phương trình đã cho vô nghiệm. Kiểm tra x = 1
± thỏa mãn phương trình đã cho.
Vậy phương trình đã cho có hai nghiệm x = −1 = x , x = 1 = x . 1 2
Suy ra phương trình đã cho có tổng các nghiệm bằng 0 . Chọn A. 1 3 Câu 36. x Tìm tập nghiệm 2 2
S của bất phương trình ≤ . 5 5 A. 1 S = 0; . B. 1 S = 0; . 3 3 C. 1 1 S = − ; ∞ . D. S = − ; ∞ ∪(0;+∞) . 3 3 Lời giải. Vì 2 − x
< 1 nên bất phương trình 1 1 3 1 ⇔ ≥ 3 ⇔
≥ 0 ⇔ 0 < x ≤ . Chọn B. 5 x x 3 2 x −x −9 x 1 −
Câu 37. Tìm tất cả các giá trị của π π
x thỏa mãn tan ≤ tan . 7 7 A. x ≤ −2. B. x ≥ 4.
C. −2 ≤ x ≤ 4.
D. x ≤ −2 ; x ≥ 4. Lời giải. Do π tan
< 1 nên bất phương trình 2
⇔ x − x − 9 ≥ x −1 7 x ≥ 4 2
⇔ x − 2x −8 ≥ 0 ⇔ . Chọn D. x ≤ −2
Câu 38. Có bao nhiêu giá trị nguyên của x trong đoạn [ 2
− 017;2017] thỏa mãn bất phương trình x 3 x 3 4 .3 > 3 .4 ? A. 2013. B. 2017. C. 2014. D. 2021. x 3 x 3
Lời giải. Bất phương trình x x 4 4 4 4 3 3 4 .3 > 3 .4 ⇔ >
⇔ > ⇔ x > 3. x 3 3 3 3 3
Vì x nguyên và thuộc đoạn [ 2 − 017;2017]
→ x = {4;5;6;...2017} .
Vậy có tất cả 2014 giá trị thỏa mãn. Chọn C.
Câu 39. Có tất cả bao nhiêu giá trị nguyên dương của x thỏa mãn bất phương trình 2 −x > ( )2x x 1 8 .2 2 ? A. 2 . B. 3 . C. 4 . D. 5 .
Lời giải. Bất phương trình 2 x x 1−x > ( )2 2 2 3 x 1−x x 3 x 1 8 .2 2 ⇔ 2 .2
> 2 ⇔ 2 + −x > 2x 2 2
⇔ 3x +1− x > x ⇔ x − 2x −1 < 0 ⇔ 1− 2 < x < 1+ 2 .
Vậy tập nghiệm của bất phương trình là S = (1− 2;1+ 2).
Suy ra các giá trị nguyên dương thuộc S là {1;2}. Chọn A. Câu 40. Gọi x
S là tập nghiệm của bất phương trình −x + ( )2 1 3 2. 3
≤ 7 . Khi đó S có
dạng [a;b] với a < b . Tính P = b + . a log 3. 2 A. P = 2. B. P = 1. C. P = 0. D. P = 2 log 3. 2
Lời giải. Bất phương trình 3 x 2 ⇔
+ 2.3 ≤ 7 ⇔ 2.3 x −7.3x + 3 ≤ 0. 3x Đặt 1 3x t =
, t > 0 . Bất phương trình trở thành 2
2t −7t + 3 ≤ 0 ⇔ ≤ t ≤ 3 . 2 1 a = −log 2 x 3 3 3 log 2 x 1 → ≤ ≤ ⇔ − ≤ ≤ → → P = b + .
a log 3 = 0. Chọn C. 3 2 2 b = 1
Câu 41. Gọi a, b lần lượt là nghiệm nhỏ nhất và nghiệm lớn nhất của bất phương
trình 3.9x 10.3x −
+ 3 ≤ 0 . Tính P = b − . a A. P =1. B. 3 P = . C. P = 2 . D. 5 P = . 2 2
Lời giải. Bất phương trình tương đương với 2 3.3 x 10.3x − + 3 ≤ 0 . Đặt 1 3x t =
, t > 0 . Bất phương trình trở thành 2
3t −10t + 3 ≤ 0 ⇔ ≤ t ≤ 3 . 3 1 a = −1 3x 3 1 x 1 → ≤ ≤ ⇔ − ≤ ≤ →
→ P = b − a = 2. Chọn C. 3 b = 1
Câu 42. Tìm tập nghiệm x
S của bất phương trình ( 2 x + x + ) 1 < 1.
A. S = (0;+∞) . B. S = (− ; ∞ 0) . C. S = (− ; ∞ − ) 1 . D. S = (0; ) 1 . 2 Lời giải. Ta có 1 3 2 x x 1 + + = x + + > 0. 2 4
Bất phương trình tương đương với ( + + )x x x < (x + x + )0 2 2 1 1 . (*) Nếu 2 2
x + x +1 < 1 ⇔ x + x < 0 ⇔ −1 < x < 0 thì (*) ⇔ x > 0 : không thỏa mãn. Nếu x < −1 2 2
x + x +1 > 1 ⇔ x + x > 0 ⇔
thì (*) ⇔ x < 0 . x > 0
Kết hợp điều kiện x < −1
ta được x < −1 . x > 0
Vậy bất phương trình có tập nghiệm S = (− ; ∞ − ) 1 . Chọn C.
Câu 43. Cho bất phương trình log x 4 2 x +
≤ 32 . Mệnh đề nào sau đây đúng?
A. Tập nghiệm của bất phương trình là một khoảng.
B. Tập nghiệm của bất phương trình là một đoạn.
C. Tập nghiệm của bất phương trình là nửa khoảng.
D. Tập nghiệm của bất phương trình là hợp của hai đoạn mà hai đoạn này giao nhau bằng rỗng.
Lời giải. Điều kiện: x > 0 . Đặt log = → = 2t x t x . 2 Bất phương trình ⇔ ( + t )t 4 t(t +4) 5 2 2 ≤ 32 ⇔ 2
≤ 2 ⇔ t + 4t ≤ 5 ⇔ 5 − ≤ t ≤ 1 1 1 → 5 − ≤ log x ≤ 1 ⇔ ≤ x ≤ 2 →S = ;2 . Chọn B. 2 32 32
Câu 44. Gọi a, b là hai nghiệm của bất phương trình 2 ln x ln x 4 x + e
≤ 2e sao cho a −b
đạt giá trị lớn nhất. Tính P = ab.
A. P = e. B. P = 1. C. 3 P = e . D. 4 P = e .
Lời giải. Điều kiện: 2 ln x
x > 0. Ta có đẳng thức ln x = ( lnx ) ln x e e = x . Do đó bất phương trình 2 ln x 4 2 ⇔ 2.e
≤ 2.e ⇔ ln x ≤ 4 ⇔ ln x ≤ 2 1 = − 1 a 2 2 2 2 ⇔ 2
− ≤ ln x ≤ 2 ⇔ e ≤ x ≤ e ⇔
≤ x ≤ e → e
→ P = ab = 1. Chọn B. 2 e 2 b = e
Câu 45. (ĐỀ MINH HỌA 2016 2017) Cho hàm số x x . Khẳng định nào sau – f (x ) 2 = 2 .7 đây là sai ?
A. f (x) 2
< 1 ⇔ x + x log 7 < 0 . B. f (x) 2
< 1 ⇔ x ln 2 + x ln 7 < 0 . 2 C. f (x) 2
< 1 ⇔ x log 2 + x < 0 .
D. f (x)<1 ⇔ 1+ x log 7 < 0 . 7 2
Lời giải. Ta có ( ) 2 1 2x.7x f x < ⇔ < 1. (*)
Lấy logarit cơ số 2 hai vế của ( 2
*) , ta được log 2x.7x < log 1 2 ( ) 2 2 x x 2
⇔ log 2 + log 7 < 0 ⇔ x + x log 7 < 0 . Do đó A đúng. 2 2 2 Lấy ln hai vế của ( 2
*) , ta được ln(2x.7x )< ln1 2 x x 2
⇔ ln 2 + ln 7 < 0 ⇔ x ln 2 + x ln 7 < 0. Do đó B đúng.
Lấy logarit cơ số 7 hai vế của ( 2
*) , ta được log 2x.7x < log 1 7 ( ) 7 2 x x 2
⇔ log 2 + log 7 < 0 ⇔ x log 2 + x < 0 . Do đó C đúng. 7 7 7
Vì x ∈ ℝ nên từ kết quả của đáp án A, khẳng định 2
x + x log 7 < 0 2
⇔ x (1+ x log 7 < 0 ⇔ 1+ x log 7 < 0 là sai. Chọn D. 2 ) 2
Vấn đề 2. PHƯƠNG TRÌNH, BẤT PHƯƠNG TRÌNH LOGARIT
Câu 46. (ĐỀ MINH HỌA 2016 2017) Giải phương trình . – log x −1 = 3 4 ( ) A. x = 63 . B. x = 65 . C. x = 80 . D. x = 82 .
Lời giải. Phương trình 3
⇔ x −1 = 4 ⇔ x −1 = 64 ⇔ x = 65. Chọn B.
Câu 47. Tìm tập nghiệm S của phương trình log x 5− x = 1. 6 ( ) A. S = {2; } 3 . B. S = {4;6} . C. S = {1; 6 − } . D. S = { 1 − ;6} . Lời giải. x = 2
Phương trình ⇔ x (5− x) 2
= 6 ⇔ x −5x + 6 = 0 ⇔ . Chọn A. x = 3
Câu 48. Phương trình log x −3 x + 4 = 3 có tất cả bao nhiêu nghiệm? 2 ( ) A. 4. B. 1. C. 2. D. 0.
Lời giải. Phương trình ⇔ x −3 x + 4 = 8 ⇔ x −3 x −4 = 0 x = − ( 1 vo nghiem) ⇔ ⇔ x = 16. Chọn B. x = 4 2 Câu 49. Tính x − 3x + 2
P là tích tất cả các nghiệm của phương trình log = 0. 1 x 2 A. P = 4. B. P = 2 2. C. P = 2. D. P = 1. 2 Lời giải. x −3x + 2 x = 2 − 2 = x Phương trình 2 1 1 x 4x 2 0 ⇔ = ⇔ − + = ⇔ . x
x = 2 + 2 = x2
→ P = x x = 2 − 2 2 + 2 = 4 − 2 = 2. Chọn C. 1 2 ( )( ) Hoặc từ phương trình 2 Viet
x − 4x + 2 = 0 → x x = 2. 1 2
Câu 50. Phương trình log x −3 +2 log 3.log x = 2 có tất cả bao nhiêu nghiệm? 2 ( ) 4 3 A. 1. B. 2. C. 3. D. 0.
Lời giải. Điều kiện: x −3 > 0 ⇔ x > 3. x > 0
Phương trình ⇔ log x −3 +2 log x = 2 ⇔ log x −3 + log x = 2 2 ( ) 4 2 ( ) 2 x = 1 − (loaïi) ⇔ log (x − )
3 x = 2 ⇔ (x − ) 2 2
3 x = 2 ⇔ x −3x − 4 = 0 ⇔ . Chọn A. 2 x = 4 (thoaû maõn)
Câu 51. Biết rằng phương trình 2 log(x + 2)+ log 4 = log x + 4 log 3 có hai nghiệm phân biệt x x , x x < x . Tính 1 P = . 1 2 ( 1 2 ) x2 A. P = 4. B. 1 P = . C. P = 64. D. 1 P = . 4 64
Lời giải. Điều kiện: x > 0. Phương trình (x )2 x (x )2 log 2 log 4 log log 81 log 4 2 ⇔ + + = + ⇔ + = log(81x) 1 x = = x thoûa maõn 2 x 1 1 2 1 ( ) ⇔ 4(x + 2) 1
= 81x ⇔ 4x − 65x +16 = 0 ⇔ 4 → P = = = . x
x = 16 = x (thoûa maõn) 4.16 64 2 2 Chọn D. 2 2
Câu 52. Biết rằng phương trình x log 9x + log
−7 = 0 có hai nghiệm phân biệt 1 ( ) 3 81 3
x , x . Tính P = x x . 1 2 1 2 A. 1 P = . B. 6 P = 3 . C. 3 P = 9 . D. 8 P = 3 . 3 9
Lời giải. Điều kiện: x > 0 .
Phương trình ⇔ (−2 −log x)2 2
+ log x − log 81−7 = 0 3 3 3 log x = 1
x = 3 = x thoûa maõn 2 3 1 ( )
⇔ log x + 6 log x −7 = 0 ⇔ ⇔ 3 3 7 log x = 7 − − thoûa maõn 3 x = 3 = x2 ( ) 1 1 7 − 6 P x x 3.3 3− → = = = = = . Chọn A. 1 2 6 3 3 9
Câu 53. (ĐỀ CHÍNH THỨC 2016 2017) Tìm tập nghiệm –
S của phương trình log (x − ) 1 + log x +1 = 1. 1 ( ) 2 2 A. 3 + 13 S = . B. S = { } 3 . 2
C. S = {2− 5;2+ 5}.
D. S = {2+ 5}.
Lời giải. Điều kiện: x >1.
Phương trình ⇔ 2 log (x − ) 1 − log (x + ) 1 = 1 ⇔ log (x − )2 1 = 1+ log x +1 2 2 2 2 ( ) ⇔ log (x − )2 1 = log 2(x + ) 1 ⇔ (x − )2 1 = 2 x +1 2 2 ( )
x = 2 + 5(thoûa maõn) 2 x 4x 1 0 ⇔ − − = ⇔ →S = {2+ 5}. Chọn D. x = 2 − 5 (loaïi)
Câu 54. Cho phương trình log log ( 3 x log x x 1 +
+ + = 3. Mệnh đề nào sau đây là 2 1 ) 2 8 đúng?
A. Nghiệm của phương trình là số nguyên âm.
B. Nghiệm của phương trình là số chính phương.
C. Nghiệm của phương trình là số nguyên tố.
D. Nghiệm của phương trình là số vô tỉ.
Lời giải. Điều kiện: x > 0.
Phương trình ⇔ log −log x + log x + x +1 = 3 2 [ 2 2 ]
⇔ log x +1 = 3 ⇔ x +1 = 8 ⇔ x = 7 thoûa maõn . Chọn C. 2 ( ) ( )
Câu 55. Số nghiệm của phương trình log log x + log log x = 2 là: 4 ( 2 ) 2 ( 4 ) A. 0. B. 1. C. 2. D. Nhiều hơn 2 . x > 0
Lời giải. Điều kiện: l
og x > 0 ⇔ x >1 . 2 log x > 0 4 Phương trình 1 1 log log x log ⇔ + log x = 2 2 ( 2 ) 2 2 2 2 1 1 ⇔ log log x + log + log log x = 2 2 ( 2 ) 2 2 ( 2 ) 2 2 1 3 ⇔ log
log x −1+ log log x = 2 ⇔ log
log x = 3 ⇔ log log x = 2 2 ( 2 ) 2 ( 2 ) 2 ( 2 ) 2 ( 2 ) 2 2
⇔ log x = 4 ⇔ x = 16 thoûa maõn . Vậy phương trình có nghiệm duy nhất. Chọn B. 2 ( )
Câu 56. Tính P tích tất cả các nghiệm của phương trình log x −log 64 =1. 2 x A. P = 1. B. P = 2 . C. P = 4 . D. P = 8 .
Lời giải. Điều kiện: 0 < x ≠ 1 .
Phương trình ⇔ log x −6 log 2 = 1. 2 x 2 − − = Đặt 6 t t 6 0 t = 3
t = log x t ≠ 0 , phương trình trở thành t − = 1 ⇔ ⇔ 2 ( ) t t ≠ 0 t = −2 x = 8 = x1 log x = 3 2 → ⇔ → P = x x = 2. 1 Chọn B. 1 2 log x = −2 x = = x 2 2 4
Câu 57. Tìm tập nghiệm S của phương trình log 9−2x = 3− x. 2 ( )
A. S = {−3;0}. B. S = {0; } 3 . C. S = {1; } 3 . D. S = {−3; } 1 .
Lời giải. Phương trình x −x x 8 3 ⇔ 9 − 2 = 2 ⇔ 9 − 2 = 2x x = x = ⇔ ( x )2 2 1 0 2 − 9.2x + 8 = 0 ⇔ ⇔ . Chọn B. 2x = 8 x = 3
Câu 58. Biết rằng phương trình 1 x ( 2
log .log 100x ) = 4 có hai nghiệm có dạng x và 1 x2
trong đó x , x là những số nguyên. Mệnh đề nào sau đây là đúng? 1 2 A. 1 x = . B. 2 x = x .
C. x .x = 1.
D. x = 100x . 2 2 x 2 1 1 2 2 1 1
Lời giải. Điều kiện: x > 0 . Phương trình ⇔ x ( 2 log
log100 + log x ) = 4 ⇔ log x (2 + 2 log x) = 4 x = 10(thoûa maõn) log x = 1 2
⇔ 2 log x + 2 log x − 4 = 0 ⇔ ⇔ . 1 log x = −2 x = (thoûa maõn) 100
Suy ra x = 10 và x = 100 nên 2
x = x . Chọn B. 1 2 2 1
Câu 59. Phương trình log x + log
x = 0 có tất cả bao nhiêu nghiệm? 2017 2016 A. 0. B. 1. C. 2. D. 3.
Lời giải. Điều kiện: x > 0 . Phương trình ⇔ log x + log 2017. log x = 0 ⇔ log x. 1+ log 2017 = 0 2017 2016 2017 2017 ( 2016 ) ⇔ log x = 0←
→ x = 1. Chọn B. 2017 3
Câu 60. Cho phương trình x log x.log 4x + log
= 0 . Nếu đặt t = log x, ta được 4 2 ( ) 2 2 2
phương trình nào sau đây? A. 2
t +14t − 4 = 0. B. 2
t +11t − 3 = 0. C. 2
t +14t − 2 = 0. D. 2
t +11t − 2 = 0. Lời giải. Ta có 1 1 l
og x.log 4x = log x. 2 + log x = log x 2 + log x = t + t 4 2 ( ) 2 2 ( 2 ) 2 ( 2 ) 2 2 2 . 3 3 3 x x x 3 l og = log = 2 log
= 2 log x −1 = 6 log x −2 = 6t −2 1 2 ( 2 ) 2 2 2 2 2 2 2
Do đó phương trình đã cho trở thành 1 2 2
t + t + 6t − 2 = 0 ⇔ t +14t − 4 = 0 . Chọn A. 2
Câu 61. Tổng lập phương các nghiệm của phương trình log x.log 2x −1 = 2 log x 2 3 ( ) 2 bằng: A. 6 . B. 26 . C. 126 . D. 216 .
Lời giải. Điều kiện: 1 x > . 2 log x = 0 Phương trình x = 1
⇔ log x. log (2x − ) 2 1 − 2 = 0 ⇔ ⇔ 2 3 log 2x −1 = 2 2x −1 = 9 3 ( ) x = ( 1 thoûa maõn) 3 3 ⇔
→1 + 5 = 126. Chọn C. x = 5 (thoûa maõn)
Câu 62. Biết rằng phương trình log ( x 1
3 + −1 = 2x + log 2 có hai nghiệm x và x . 3 ) 1 1 2 3 Hãy tính tổng 1 x x2 S = 27 + 27 . A. S = 180. B. S = 45. C. S = 9. D. S = 252.
Lời giải. Điều kiện: x 1
3 + −1 > 0 ⇔ x > −1. Phương trình log ( x 1 3 + ) 1 2x log 2 log ( x 1 3 + ⇔ − = − ⇔ −1 + log 2 = 2x 3 3 3 ) 3 log ( x 1 3 + ) 1 .2 2 ( x 1 3 + ⇔ − = ⇔ − ) 2 x x 2 1 .2 = 3 ⇔ 6.3 − 2 = 3 x x 3 x x 1 2 3 + 3 = 6 2 x x Viet 3 6.3 2 0 ⇔ − + = → . x x 1 2 3 .3 = 2 Ta có 3 x x x x x x x x 1 2 S = + = ( 1 2 + ) 1 2 − ( 1 2 + ) 3 27 27 3 3 3.3 .3 3 3
= 6 −3.2.6 = 180. Chọn A. 3 2
Câu 63. Số nghiệm của phương trình x −5x + 6x = 0 là: ln (x − ) 1 A. 0. B. 1. C. 2. C. 3. x −1> 0
Lời giải. Điều kiện: x > 1 ⇔ . l n(x − ) 1 ≠ 0 x ≠ 2 x = 0 Phương trình 3 2 x 5x 6x 0 ⇔ − + = ⇔ x = 2. x = 3
Đối chiếu với điều kiện, phương trình có nghiệm duy nhất x = 3 . Chọn B.
Câu 64. Biết rằng phương trình 1
2 log x + log 1− x = log
x − 2 x + 2 có nghiệm 2 1 ( ) 2 ( ) 2 2
duy nhất có dạng a +b 3 với a, b ∈ ℤ . Tính tổng S = a + . b A. S = 6. B. S = 2. C. S = −2. D. S = −6.
Lời giải. Điều kiện: 0 < x <1. Phương trình 2
⇔ log x − log 1− x = log x − 2 x + 2 2 2 ( ) 2 ( ) 2 2 x x ⇔ log
= log x − 2 x + 2 ⇔ = x − 2 x + 2 2 2 ( ) 1− x 1− x 2 2 2 x x x x x ⇔
= x + 2(1− x ) ⇔ = + 2 ⇔ − − 2 = 0 1− x ( − )2 1− x 1− x 1 1 − x x x x ⇔ = −1 (vô nghiệm) hoặc = 2 1− x 1− x a = 4 x 2 x 2 0 x 1 3 x 4 2 3 ⇔ + − = → = − + → = − → . Chọn B. b = −2 2
Câu 65. Phương trình x − 2x +1 2 log
+ x +1 = 3x có tổng tất cả các nghiệm bằng: 3 x A. 3. B. 5. C. 5 . D. 2.
Lời giải. Điều kiện: x −2x +1 (x − )2 2 1 > 0 ⇔
> 0 ⇔ 0 < x ≠ 1. x x Phương trình (x − )2 1 2 ⇔ log
+ x − 2x +1 = x 3 x ⇔ log (x − )2
1 − log x +(x − )2 1
= x ⇔ log (x − )2 1 +(x − )2 1 = log x + x. (*) 3 3 3 3 Xét hàm số 1
f (t) = log t + t với t > 0 . Ta có f '(t) =
+1 > 0, ∀t > 0 . 3 t ln 3
Suy ra hàm số f (t) đồng biến trên (0;+ ) ∞ . Nhận thấy ( 2 2 *) có dạng f ( x ) 1 −
= f (x)⇔ (x − ) 1 = x 3 + 5 x = (thoûa maõn) 2 3 + 5 3− 5 2
⇔ x −3x +1 = 0 ⇔ → + = 3. Chọn A. 2 2 3− 5 x = (thoûa maõn) 2
Câu 66. (ĐỀ MINH HỌA 2016 2017) Giải bất phương trình . – log 3x −1 > 3 2 ( ) A. x > 3 .
B. 1 < x < 3 . C. x < 3 . D. 10 x > . 3 3
Lời giải. Bất phương trình 3
⇔ 3x −1 > 2 ⇔ 3x > 9 ⇔ x > 3. Chọn A.
Câu 67. Cho bất phương trình log ( 2
x − 2x + 6 ≤ −2 . Mệnh đề nào sau đây là đúng? 1 ) 3
A. Tập nghiệm của bất phương trình là nửa khoảng.
B. Tập nghiệm của bất phương trình là một đoạn.
C. Tập nghiệm của bất phương trình là hợp của hai nửa khoảng.
D. Tập nghiệm của bất phương trình là hợp của hai đoạn.
Lời giải. Bất phương trình ⇔ −log ( 2
x − 2x + 6) ≤ −2 ⇔ log ( 2
x − 2x + 6 ≥ 2 3 3 ) x ≥ 3 2 2
⇔ x − 2x + 6 ≥ 9 ⇔ x − 2x −3 ≥ 0 ⇔ . x ≤ −1
Vậy bất phương trình có tập nghiệm là S = (− ; ∞ − ]
1 ∪[3;+∞) . Chọn C.
Câu 68. Gọi M (x ; y là điểm thuộc đồ thị hàm số y = log x . Tìm điều kiện của x 0 0 ) 3 0
để điểm M nằm phía trên đường thẳng y = 2 . A. x > 0 . B. x > 9 . C. x > 2 . D. x < 2 . 0 0 0 0
Lời giải. Đồ thị y = log x nằm ở phía trên đường thẳng y = 2 khi log x > 2 ⇔ x > 9 . 3 3 Chọn B.
Câu 69. Tìm tập nghiệm S của bất phương trình log ( 2 x −1 < log 3x − 3 . 1 ) 1 ( ) 5 5
A. S = (2;+∞). B. S = (− ; ∞ ) 1 ∪(2;+ ) ∞ . C. S = (− ; ∞ − ) 1 ∪(2;+ ) ∞ . D. S = (1;2). 2
Lời giải. Điều kiện: x −1> 0 ⇔ x > 1. 3 x −3 > 0 Bất phương trình: log ( 2 x − ) 1 < log (3x −3) 2
⇔ x −1 > 3x − 3 (chú ý với cơ số 1 <1 ) 1 1 5 5 5 x > 2 2 dk:x 1
⇔ x −3x + 2 > 0 > ⇔
→ x > 2. Chọn A. x <1
Câu 70. Tìm tập nghiệm S của bất phương trình ( 2
x − x − )> ( 2 log 2
log −x + 2x + 3 , a a ) biết 9 thuộc S. 4 A. 5 S = 2; . B. 5 S = −1; . C. S = (− ; ∞ − ) 1 . D. 5 S = ; +∞ . 2 2 2 2
x − x −2 > 0
Lời giải. Điều kiện: 2 < x < 3 2 x 2x 3 0 − + + > ⇔ . 0 < a ≠ 1 0 a 1 < ≠ Do 9 x =
là nghiệm của bất phương trình đã cho nên 13 39 log > log →0 < a <1. 4 a 16 a 16
Vì 0 < a <1 nên bất phương trình 2 2
⇔ x − x − 2 < −x + 2x + 3 5 <x 5 2 dk: 2 3 2x 3x 5 0 1 x < ⇔ − − < ⇔ − < <
→ 2 < x < . Chọn A. 2 2
Câu 71. Tìm tập nghiệm S của bất phương trình 2
ln x > ln(4x − 4).
A. S = (2;+∞) . B. S = (1;+∞).
C. S = ℝ \{2} . D. S = (1;+ ) ∞ \ {2}.
Lời giải. Điều kiện: 4 x − 4 > 0 ⇔ x > 1. x ≠ 0
Bất phương trình ⇔ x > x − ⇔ x − x + > ⇔ (x − )2 2 2 4 4 4 4 0 2 > 0 ⇔ x ≠ 2 .
Đối chiếu điều kiện, ta được tập nghiệm của bpt là S = (1;+∞)\{2} . Chọn D.
Câu 72. Gọi S là tập nghiệm của bất phương trình log ( 2 4x ≥ log 12x −5 . Kí 0,3 ) 0,3 ( ) hiệu ,
m M lần lượt là giá trị nhỏ nhất và giá trị lớn nhất của tập S . Mệnh đề nào sau đây là đúng?
A. m + M = 3. B. m + M = 2 .
C. M −m = 3.
D. M −m = 1.
Lời giải. Điều kiện: 5 x ≥ . 12 Bất phương trình 1 5 2 2
⇔ 4x ≤ 12x −5 ⇔ 4x −12x + 5 ≤ 0 ⇔
≤ x ≤ (thoûa maõn). 2 2
Suy ra tập nghiệm của bất phương trình là 1 5 S = ; . 2 2 Suy ra 1 m = và 5 M =
nên m + M = 3. Chọn A. 2 2 Câu 73. 2 Tìm tập nghiệm log x +21
S của bất phương trình ( ) log10 < 1+ log x. A. S = (3;7). B. S = (− ; ∞ 3)∪(7;+∞). C. S = (− ; ∞ 3).
D. S = (7;+∞).
Lời giải. Điều kiện: x > 0. Bất phương trình ⇔ ( 2 x + ) < + x ⇔ ( 2 log 21 . log10 log10 log log x + 2 ) 1 < log(10x ) 2
⇔ x + 21 <10x ⇔ 3 < x < 7(thoûa maõn)
→S = (3;7). Chọn A.
Câu 74. Có bao nhiêu số nguyên dương x thỏa mãn bất phương trình
log(x − 40)+ log(60 − x) < 2 ? A. 20. B. 18. C. 21. D. 19.
Lời giải. Điều kiện: 40 < x < 60 .
Bất phương trình ⇔ log (x −40)(60− x) < 2 ⇔ (x − )( − x)< ⇔ x − x + > ⇔ (x − )2 2 2 40 60 10 100 2500 0 50 > 0 ⇔ x ≠ 50.
Kết hợp với điều kiện, ta được 4 0 < x < 60 x + ∈ ℤ
→ x ∈ {41;...;59}\{50} . Chọn B. x ≠ 50
Câu 75. Biết rằng tập nghiệm của bất phương trình log 1
+ log x − log x < 1 có dạng 2 1 9 9 1 S = ;b
với a, b là những số nguyên. Mệnh đề nào sau đây là đúng? a A. a = b − .
B. a +b = 1 .
C. a = b .
D. a = 2b . x > 0
Lời giải. Điều kiện: 1
+ log x −log x > 0 1 9 9 x > 0 x > 0 x > 0 ⇔ ⇔ 1 ⇔ ⇔ 0 < x < 3. 1 −2 log x > 0 log x < x < 3 9 9 2 Bất phương trình 1 1
⇔ 1− 2 log x < 2 ⇔ log x > − ⇔ x > . 9 9 2 3
Đối chiếu với điều kiện, ta được tập nghiệm của bất phương trình là 1 S = ;3 . 3
Suy ra a = 3, b = 3 . Chọn C.
Câu 76. Có bao nhiêu giá trị nguyên của x trong đoạn [−2018;2018] thỏa mãn bất phương trình log log + − < π ( 2 x 2x x 0 ? 2 ) 4 A. 4033. B. 4031. C. 4037. D. 2018. 2
x + 2x −x > 0 ( ) 1
Lời giải. Điều kiện: . l og ( 2
x + 2x − x > 0 2 2 ) ( ) Bất phương trình log log ( 2
x + 2x − x ) < log 1 ⇔ log + − > (thỏa (2) ) π π ( 2 x 2x x 1 2 2 ) 4 4 ⇔ log ( 2
x + 2x − x ) 2
> log 2 ⇔ x + 2x − x > 2 (thỏa ( ) 1 ) 2 2 2 − x < 0 2 2
x − x ≥ 0 x > 1 2
⇔ 2x − x > 2 − x ⇔ ⇔ 2 − x ≥ 0 x < −4 2 x − x > (2 − x)2 2 x [ ∈ 2 − 018;2018]
→ x ∈ − − − − → có 4031 giá trị x ℤ
{ 2018; 2017;...; 6; 5;2;3;...;2017;2018} ∈
nguyên của x thỏa mãn. Chọn B.
Câu 77. Tìm tập nghiệm S của bất phương trình log x + log x >1+ log x log x. 2 3 2 3 A. S = (3;+ ) ∞ .
B. S = (0;2)∪(3;+∞). C. S = (2;3). D. S = (− ; ∞ 2)∪(3;+∞).
Lời giải. Điều kiện: x > 0 .
Bất phương trình ⇔ (log x −log x log x + log x −1> 0 2 2 3 ) 3
⇔ log x 1− log x + log x −1 > 0 ⇔ 1− log x log x −1 > 0. (*) 2 ( 3 ) 3 ( 3 )( 2 ) l og x −1> 0 log x >1 TH1: x > 2 2 2 ⇔ ⇔
⇔ 2 < x < 3 (thoûa maõn). 1 − log x > 0 log x <1 x < 3 3 3 l og x −1< 0 log x <1 TH2: x < 2 2 2 ⇔ ⇔ : vô nghiệm. 1 − log x < 0 log x > 1 x > 3 3 3
Vậy tập nghiệm của bất phương trình là S = (2; ) 3 .Chọn C.
Câu 78. Có tất cả bao nhiêu số nguyên thỏa mãn bất phương trình log log ? ( 2 2 x − > 0 1 2 ) 2 A. 1. B. 2 . C. 3 . D. 0 . 2 2 2 − x > 0
Lời giải. Điều kiện: 2 − x > 0 2 ⇔
⇔ 2 − x > 1 ⇔ −1 < x < 1. log ( 2 2 − x ) 2 > 0 2 − x > 1 2 Bất phương trình log log ( 2 2 x ) ⇔ − > log 1 ⇔ log ( 2
2 − x ) <1 ⇔ log ( 2 2 − x < log 2 1 2 1 2 2 ) 2 2 2 2 2
⇔ 2 − x < 2 ⇔ x > 0 ⇔ x ≠ 0.
Đối chiếu điều kiện, bất phương trình có tập nghiệm S = ( 1 − ;0)∪(0; ) 1 .
Suy ra không có số nguyên nào thuộc tập S . Chọn D.
Câu 79. Tìm tập nghiệm 2x +1
S của bất phương trình log log > 0. 1 3 x −1 2 A. S = (− ; ∞ ) 1 ∪(4;+∞). B. S = (− ; ∞ 2 − )∪(1;+∞). C. S = ( 2 − ; ) 1 ∪(1;4). D. S = (− ; ∞ 2 − )∪(4;+∞). 2x +1 2x +1 > 0 > 0 − − +
Lời giải. Điều kiện: x 1 x 1 2x 1 x > 1 ⇔ ⇔ > 1 ⇔ . 2x +1 2x +1 x −1 x < −2 l og 0 1 > > 3 x 1 − x −1 + + − Bất phương trình 2x 1 2x 1 4 x x <1 ⇔ log <1 ⇔ < 3 ⇔ < 0 ⇔ . 3 x −1 x −1 x −1 x > 4
Đối chiếu điều kiện, ta được tập nghiệm S = (− ; ∝ 2 − )∪(4;+ ) ∝ . Chọn D.
Câu 80. Tìm tập nghiệm 1− log x 1
S của bất phương trình 4 ≤ . 1− log x 2 2 A. S = (0;2). B. S =[2;+∞). C. S = (− ; ∞ 2).
D. S = (2;+∞). > Lời giải. x 0 Điều kiện: x > 0 ⇔ . l og x ≠ 1 x ≠ 2 2 1 1− log x 2 Bất phương trình 1 2 − log x 1 2 − log 2 x 2 2 ⇔ ≤ ⇔ ≤ ⇔ ≤1 1− log x 2 2 1− log x 2 1− log x 2 ( 2 ) 2 2 − log x 1 2 ⇔ −1 ≤ 0 ⇔
≤ 0 ⇔ 1− log x < 0 ⇔ log x > 1 ⇔ x > 2 thoûa maõn . 2 2 ( ) 1− log x 1− log x 2 2
Vậy tập nghiệm của bất phương trình là S = (2;+∞) . Chọn D.
Vấn đề 3. PHƯƠNG TRÌNH, BẤT PHƯƠNG TRÌNH CHỨA THAM SỐ
Câu 81. Tìm tất cả các giá trị thực của tham số m để phương trình 2x 1 − 2 2 + m − m = 0 có nghiệm. A. m < 0 .
B. 0 < m <1.
C. m < 0 ; m >1 . D. m > 1 .
Lời giải. Ta có 2x 1 − 2 2 x 1 − 2 2
+ m − m = 0 ⇔ 2 = m − + . m
Vì 2x −1 có miền giá trị là ℝ nên 2 1
2 x− có miền giá trị là (0;+∞) , do đó phương trình có nghiệm 2 ⇔ m −
+ m > 0 ⇔ 0 < m < 1. Chọn B.
Chúy ý: Cần phải nói rõ 2x −1 có miền giá trị là ℝ thì mới kết luận được 2 1 2 x y − = có
miền giá trị là (0;+∞) . Sai lầm hay gặp là phương trình x
a = m có nghiệm ⇔ m > 0
thì đúng, còn phương trình u
a = m có nghiệm ⇔ m > 0 nói chung không đúng. Ví dụ như hàm số 2 1 2x y + =
có miền giá trị là [2;+∞).
Câu 82. Tìm tất cả các giá trị của tham số m để phương trình x 1 + x +2 4 − 2 + m = 0 có nghiệm. A. m ≤ 0 . B. m ≥ 0 . C. m ≤1 . D. m ≥1 .
Lời giải. Ta có x+ x + m ( x+ )2 1 2 1 x 1 4 2 0 2 2.2 + − + = ⇔ − + m = 0 . ( ) 1 Đặt x 1
2 + = t > 0 . Phương trình ( ) 1 trở thành 2 2
t − 2t + m = 0 ⇔ t − 2t = m − . (2) Để phương trình ( )
1 có nghiệm ⇔ phương trình (2) có nghiệm t > 0.
Cách 1. Xét hàm f (t) 2
= t −2t với t > 0 .
Đạo hàm và lập bảng biến thiên, ta kết luận được m
− ≥ −1 ⇔ m ≤ 1. Chọn C.
0 < t ≤ t
Cách 2. Ycbt ⇔ phương trình (2) có hai nghiệm t , t thỏa mãn 1 2 1 2
t ≤ 0 < t 1 2
∆' ≥ 0, P > 0,S > 0 0 < m ≤1 ⇔ ⇔ ⇔ m ≤1. P ≤ 0 m ≤ 0
Câu 83. Tìm tất cả các giá trị thực của tham số m để phương trình ( x x
2 + 3) +(2− 3) = m có nghiệm. A. m ∈(− ; ∞ )
5 . B. m ∈ (− ; ∞ 5] .
C. m ∈(2;+∞) . D. m ∈[2;+ ) ∞ . Lời giải. Đặt ( x x
2 + 3) = t > 0 , suy ra ( − ) 1 2 3 = . t
Phương trình đã cho trở thành 1 t + = . m t Xét hàm 1
f (t) = t + với t > 0 . t
Đạo hàm và lập bảng biến thiên, ta kết luận được m ≥ 2 . Chọn D.
Câu 84. Tìm tất cả các giá trị của tham số m để phương trình sinx 1+sin 4 + 2 x −m = 0 có nghiệm.
A. 5 ≤ m ≤ 8.
B. 5 ≤ m ≤ 9.
C. 5 ≤ m ≤ 7.
D. 5 ≤ m ≤ 8. 4 4 4 3 Lời giải. Đặt sin 2 x t =
, điều kiện 1 ≤ t ≤ 2. 2 Phương trình trở thanh 2 2
t + 2t − m = 0 ⇔ t + 2t = m . Xét hàm 1 f (t) 2
= t + 2t trên đoạn 1
;2 , ta có f '(t) 2t 2 0, t = + > ∀ ∈ ;2 . 2 2 Suy ra hàm số
f (t) đồng biến trên đoạn 1 ;2 . 2
Do đó phương trình có nghiệm khi và chỉ khi min f (t)≤ m ≤ max f (t) 1 1 ;2 ;2 2 2 1 5 ⇔ f
≤ m ≤ f (2) ⇔
≤ m ≤ 8. Chọn A. 2 4
Câu 85. Tìm tất cả các giá trị thực của tham số m để bất phương trình 2 x +2mx 1 + 2 x 3 − m 2 e ≤
nghiệm đúng với mọi x . e 2 A. m ∈( 5 − ;0) . B. m ∈[ 5 − ;0]. C. m ∈(− ; ∞ − ) 5 ∪(0;+∞). D. m ∈(− ; ∞ 5 − ]∪[0;+∞) . 2 −x −2mx 1 − 2 x 3 − m
Lời giải. Bất phương trình e e 2 ⇔ ≤ ⇔ x −
−2mx −1 ≤ 2x −3m 2 2 2 ⇔ x + 2(m + )
1 x −3m +1 ≥ 0. 1 > > 0 a 0 Ycbt 2 ⇔ x + 2(m + )
1 x −3m +1 ≥ 0, ∀x ∈ ℝ ⇔ ⇔ ∆' ≤ 0 ( m + )2 1 + 3m −1 ≤ 0 2
⇔ m + 5m ≤ 0 ⇔ −5 ≤ m ≤ 0. Chọn B.
Câu 86. (ĐỀ CHÍNH THỨC 2016 2017) Tìm giá trị thực của tham số – m để phương trình x x 1 9 2.3 + −
+ m = 0 có hai nghiệm thực x , x thỏa mãn x + x = 1. 1 2 1 2 A. m = 6. B. m = −3. C. m = 3. D. m = 1.
Lời giải. Ta có x x 1 + 2 9 − 2.3 +
= 0 ⇔ 3 x − 6.3x m + m = 0. Đặt 3x t =
> 0 , phương trình trở thành 2
t − 6t + m = 0 . (*)
Để phương trình đã cho có hai nghiệm ⇔ phương trình (*) có hai nghiệm dương ∆ ' ≥ 0 9 −m ≥ 0 S 0 6 ⇔ > ⇔ > 0 ⇔ 0 < m ≤ 9. P > 0 m > 0
Theo định lí Viet, ta có 1x x2 1 x +x2 3 .3 = m ⇔ 3 = m ⇔ 3 = .
m (thỏa). Chọn C.
Cách trắc nghiệm. Thử lần lượt 4 đáp án để chọn.
Câu 87. Tìm giá trị thực của tham số m để phương trình x x 1 4 . m 2 + − + 2m = 0 có hai
nghiệm thực x , x thỏa mãn x + x = 2. 1 2 1 2 A. m = 4. B. m = 3. C. m = 2. D. m =1.
Lời giải. Phương trình tương đương với ( x )2 2 − 2 .2x m + 2m = 0 . Đặt 2x t =
> 0 , phương trình trở thành 2
t − 2mt + 2m = 0 . (*)
Để phương trình đã cho có hai nghiệm ⇔ phương trình (*) có hai nghiệm dương 2 ∆ ' ≥ 0 m − 2m ≥ 0 S 0 2 ⇔ > ⇔ m > 0 ⇔ m ≥ 2. P > 0 2 m > 0
Theo định lí Viet, ta có 1x x2 1 x +x2 2 .2 = 2m ⇔ 2
= 2m ⇔ 4 = 2m ⇔ m = 2 (thỏa). Chọn C.
Câu 88. Tìm giá trị thực của tham số m để phương trình 2 x 1 2017 − − 2 .2017x m + m = 0
có hai nghiệm thực x , x thỏa mãn x + x = 1. 1 2 1 2 A. m = 0. B. m = 3. C. m = 2. D. m = 1.
Lời giải. Phương trình 1 ⇔
(2017x )2 −2 .2017x m + m = 0 2017 ⇔ ( x )2 2017 − 4034 .2017x m + 2017m = 0.
Giả sử phương trình có hai nghiệm x , x . 1 2 Theo Viet, ta có 1 x x2 1 x +x2 2017 .2017 = 2017m ⇔ 2017
= 2017m ⇔ 2017 = 2017m ⇔ m = 1.
Thử lại với m = 1 ta thấy thỏa mãn. Chọn D.
Câu 89. Cho phương trình ( + )
1 16x − 2(2 −3)4x m m
+ 6m + 5 = 0 với m là tham số
thực. Tập tất cả các giá trị của m để phương trình có hai nghiệm trái dấu có dạng
(a;b). Tính P = ab. A. P = 4 . B. P = −4 . C. 3 P = − . D. 5 P = . 2 6 Lời giải. Đặt 4x t = > 0 .
Phương trình trở thành (m + ) 2
1 t − 2(2m − )
3 t + 6m + 5 = 0. (*) f (t)
Phương trình đã cho có hai nghiệm x , x thỏa mãn x < 0 < x 1 2 1 2 x x 1 0 2 → 4 < 4 < 4
→ t < 1 < t . 1 2 m +1 ≠ 0
Ycbt ⇔ phương trình (*) có hai nghiệm t , t thỏa 0 t 1 t < < <
⇔ m +1 f 1 < 0 1 2 ( ) ( ) 1 2 (m+ ) 1 f (0)> 0 m +1≠ 0 a = −4 ( m ) 1 (3m 12) 0 4 m 1 ⇔ + + < ⇔ − < < − →
→ P = 4. Chọn A. b = −1 ( m + ) 1 (6m + 5)> 0
Câu 90. Tìm tất cả các giá trị của tham số m để phương trình 9x −( − ) 1 3x m + 2m = 0 có nghiệm duy nhất. A. m = 5+2 6 .
B. m = 0 ; m = 5+ 2 6 . C. m < 0 .
D. m < 0 ; m = 5+ 2 6 . Lời giải. Đặt 3x t =
> 0 , phương trình trở thành 2 t −(m − ) 1 t + 2m = 0 . (*)
Yêu cầu bài toán ←→ phương trình (*) có đúng một nghiệm dương. ∆ = ( m − )2 0 1 −8m = 0
● (*) có nghiệm kép dương ← → b ← → ← → m = 5 + 2 6. m −1 − > 0 > 0 2a 2
● (*) có hai nghiệm trái dấu ac <0 ← → 2m < 0 ← → m < 0 .
Vậy m < 0 hoặc m = 5+ 2 6 thỏa yêu cầu bài toán. Chọn D.
Câu 91. Cho phương trình 2 2 x −2 x 1 + x −2 x +2 4 − . m 2
+ 3m − 2 = 0 với m là tham số thực.
Tìm tất cả các giá trị của m để phương trình có bốn nghiệm phân biệt. A. m <1 .
B. m <1 ; m > 2. C. m ≥ 2. D. m > 2. Lời giải. Đặt ( )2 1 2 x t − =
, điều kiện t ≥1 . Phương trình trở thành 2
t − 2mt + 3m − 2 = 0. (*) f (t)
Ta thấy cứ một nghiệm t > 1 tương ứng cho hai nghiệm x .
Do đó phương trình đã cho có bốn nghiệm phân biệt ⇔ phương trình (*) có hai 2 ∆ ' > 0 m −3m + 2 > 0
nghiệm phân biệt t < t thỏa mãn 1 t t .a f 1 0 1 < < ⇔
> ⇔ . m −1 > 0 ⇔ m > 2. 1 2 ( ) ( ) 1 2 S m > 1 1 > 2 Chọn D.
Câu 92. Cho phương trình 2 2 x 5 − x +6 1−x 6 5 .2 + 2 = 2.2 − x m
+ m với m là tham số thực. Có
tất cả bao nhiêu giá trị của m để phương trình có đúng ba nghiệm phân biệt. A. 1. B. 2. C. 3. D. 4. Lời giải. Ta có 2 2 2 2 x 5 − x +6 1−x 6 5 − x x 5 − x +6 1−x 7 5 .2 + 2 = 2.2 + ⇔ .2 + 2 = 2 − x m m m + m ⇔ ( 2x− x+ − ) 2 −x + ( 2 x − x + −
)= ⇔ ( 2x− x+ − )( 2 5 6 1 5 6 5 6 1 2 1 2 1 2 0 2 1 − 2 −x m m )= 0. x = 2 2 x 5 − x +6 2 −1 = 0 ⇔ ⇔ x = 3 . 2 1 2 −x = m 2 1
2 −x = m (*)
Yêu cầu bài toán tương đương với
TH1: Phương trình (*) có nghiệm duy nhất (x = 0), suy ra m = 2.
TH2: Phương trình (*) có hai nghiệm phân biệt, trong đó có một nghiệm là 2 và nghiệm còn lại khác 3 −3 → m = 2 .
TH3: Phương trình (*) có hai nghiệm phân biệt, trong đó có một nghiệm là 3 và nghiệm còn lại khác 2 −8 → m = 2 .
Vậy có tất cả ba giá trị m thỏa mãn. Chọn C.
Câu 93. Cho phương trình 2 + −x −( + ) 2 1 1 1+ 1 25 2 5 −x m
+ 2m +1 = 0 với m là tham số
thực. Số nguyên dương m lớn nhất để phương trình có nghiệm là? A. m = 20. B. m = 35. C. m = 30. D. m = 25.
Lời giải. Điều kiện: −1≤ x ≤1 . m
ax u(x) = 2 Xét −x [ 1 − ; ] 1 u(x ) 2
= 1+ 1− x , có u '(x ) = ; u '(x) 0 x 0 [ 1; ] 1 = ⇔ = ∈ − → . 2 1− x m in u (x) = 1 [ 1 − ; ] 1 Đặt 2 1+ 1 = 5 −x t →5 ≤ t ≤ 25 . 2 Phương trình trở thành t − 2t +1 2
t −(m + 2)t + 2m +1 = 0← → m = = f (t) . t − 2
Do đó phương trình đã có nghiệm 16 576
⇔ min f (t) ≤ m ≤ max f (t)←→ ≤ m ≤ . [5;25] [5;25] 3 23
Suy ra số nguyên dương m lớn nhất là m = 25. Chọn D. 2 2 1+ 1−x 1+ 1−x Cách CASIO. Cô lập 25 − 2.5 +1
m ta được m = . 2 1+ 1 5 −x − 2 2 2 1+ 1−x 1+ 1−x Đặt 25 − 2.5 +1 f (x ) =
. Khi đó phương trình ⇔ f (x) = . m 2 1+ 1 5 −x − 2
Sử dụng MODE7 khảo sát hàm f (x) với thiết lập Start −1, End 1, Step 0,2. (Do điều kiện 2
1− x ≥ 0 ↔ −1 ≤ x ≤ 1 nên Start −1, End 1 )
Quan sát bảng giá trị ta thấy f (x)≤ f (0) = 25.043... hay m ≤ f (0).
Vậy m nguyên dương lớn nhất là 25.
Câu 94. Tìm tất cả các giá trị thực của tham số m để phương trình 2x 2
2 .5 x+m = 3 có hai nghiệm.
A. m < log 3+ log 5.
B. m > log 5+ log 2. 5 2 3 5
C. m < log 3 + log 2.
D. m > log 3 + log 5. 5 5 5 2
Lời giải. Lấy logarit cơ số 2 hai vế của phương trình, ta được log ( 2x 2
2 .5 x+m = log 3 2 ) 2 2
⇔ x +(2x + m) 2
log 5− log 3 = 0 ⇔ x + 2 log 5 x + m log 5 − log 3 = 0. 2 2 ( 2 ) 2 2
Để phương trình đã cho có hai nghiệm 2
∆' = log 5− m log 5 + log 3 > 0 2 2 2 2
⇔ m log 5 < log 5 + log 3 ⇔ m < log 5 + log 3. Chọn A. 2 2 2 2 5
Câu 95. Cho phương trình m.sinx c − os x 2(1−cos x) e − e = 2 − cos x − .
m sin x với m là tham số
thực. Tìm tất cả các giá trị của m để phương trình có nghiệm. A. m ∈(− ; ∞ − 3)∪( 3;+ ) ∞ . B. m 3; 3 ∈ − .
C. m ∈(− 3; 3). D. m ( ; 3 ∈ −∞ − ∪ 3; + ) ∞ .
Lời giải. Phương trình
m sin x −cos x 2−2 cos ⇔ + sin − cos x e m x x = e + 2 − 2 cos x. (*) Xét hàm số ( ) t
f t = e + t trên ℝ . Ta có '( ) t f
t = e +1 > 0, ∀t ∈ ℝ .
Suy ra hàm số f (t) đồng biến trên ℝ .
Nhận thấy (*) có dạng f (m sin x −cos x)= f (2−2 cos x)←→m sin x −cos x = 2−2cos x
⇔ m sin x + cos x = 2 . (Đây là phương trình lượng giác dạng a sin x + b cos x = c , điều kiện có nghiệm là 2 2 2
a + b ≥ c )
Để phương trình đã cho có nghiệm m ≥ 3 2 2 m 1 4 m 3 ⇔ + ≥ ⇔ ≥ ⇔ . Chọn D. m ≤ − 3
Câu 96. Tìm tất cả các giá trị của tham số m để phương trình 3
x −3x − log m = 0 có 2 đúng một nghiệm.
A. 1 < m < 4. B. 1 0 < m < ; m > 4. C. 1 m = . D. 1 m < ; m > 4 . 4 4 4 4
Lời giải. Điều kiện: m > 0. Phương trình 3
⇔ x −3x = log m . Đây là phương trình hoành độ giao điểm của đồ thị 2 hàm số 3
y = x −3x với đường thẳng y = log m (có phương song song trục hoành). 2 Xét hàm
x = 1 → y = −2 3
y = x −3x . Ta có 2
y ' = 3x −3; y ' = 0 ⇔ .
x = −1 → y = 2 1 log m < −2
Dựa vào dáng điệu của đồ thị hàm bậc ba, suy ra ycbt m < 2 ⇔ ⇔ 4 . log m > 2 2 m > 4
Đối chiếu điều kiện, ta được 1 0 < m <
hoặc m > 4. Chọn B. 4
Câu 97. Gọi S là tổng tất cả các giá trị nguyên của tham số m sao cho phương trình log ( 2x x +2 2 2 + 2 + 2
= log m − 2 vô nghiệm. Giá trị của S bằng: 4 ) 2 A. S = 6. B. S = 8. C. S = 10. D. S = 12.
Lời giải. Điều kiện:
m ≠ 2. Phương trình ⇔ log (2x + 2 )2 = log m−2 4 2 2x 2 m 2 + = − 2x = m − 4 log 2x 2 log m 2 2x 2 m 2 ⇔ + = − ⇔ + = − ⇔ ⇔ 2 ( ) 2 2x 2 2 m + = − 2x = m − − ≤
Để phương trình vô nghiệm m 4 0 m ≤ 4 ⇔ ⇔ ⇔ 0 ≤ m ≤ 4 m − ≤ 0 m ≥ 0 m∈
ℤ→ m ∈ {0;1;3;4}
→S = 0 +1+ 3 + 4 = 8. Chọn B. m≠2
Câu 98. Tìm tất cả các giá trị thực của tham số log mx − 2
m để phương trình ( ) = 1 có log(x + ) 1 nghiệm duy nhất.
A. 0 < m <100. B. m < 0 ; m >100 . C. m = 1. D. Không tồn tại . m m x > 0 m x > 0
Lời giải. Điều kiện: x 1 0 + > ⇔ x +1> 0. l og(x + ) 1 ≠ 0 x +1 ≠ 1 Phương trình mx mx
⇔ log(mx )−2 = log(x + ) 1 ⇔ log = log(x + ) 1 ⇔ = x +1 100 100 100
⇔ mx = 100x +100 ⇔ (m −100)x = 100 ⇔ x = . m −100 100 . m > 0 m−100
Thay vào điều kiện, ta có 100 m m > 100 +1 > 0 ⇔ > 0 ⇔ . Chọn B. m −100 m −100 m < 0 100 +1 ≠ 1 m −100
Câu 99. Tìm giá trị thực của tham số m để phương trình 2 log x − m log x +1 = 0 có 3 3
nghiệm duy nhất nhỏ hơn 1. A. m = 2 . B. m = −2 . C. m = 2 . D. m = 0 .
Lời giải. Điều kiện: x > 0 .Vì phương trình có nghiệm nhỏ hơn 1 nên suy ra 0 < x <1.
Đặt log x = t , với 0 < x <1 → t < 0 . 3
Phương trình đã cho trở thành 1 2
t − mt +1 = 0 ⇔ t + = . m t Xét hàm 1
f (t) = t + với t < 0 . t
Đạo hàm và lập bảng biến thiên ta được m = −2 thỏa mãn bài toán. Chọn B.
Câu 100. (ĐỀ CHÍNH THỨC 2016 2017) Tìm tất cả các giá trị thực của tham số –
m để bất phương trình 2
log x − 2 log x + 3m − 2 < 0 có nghiệm thực. 2 2
A. m <1.
B. m ≤1.
C. m < 0. D. 2 m < . 3
Lời giải. Điều kiện: x > 0 . Đặt t = log x , với x > 0 suy ra t ∈(− ; ∞ +∞) . 2
Bất phương trình đã cho trở thành 2 2
t − 2t + 3m − 2 < 0 ⇔ 3m < −t + 2t + 2 ( ) ∗ . Ycbt ⇔ phương trình ( )
∗ có nghiệm ⇔ 3m < max g (t) với g (t) 2
= −t + 2t + 2 . (−∞;+∞)
Ta có g(t) = −t + t + = −(t − )2 2 2 2 3 1
≤ 3, ∀t ∈ ℝ . Suy ra max g (t) = 3 . (−∞;+∞)
Từ đó suy ra 3m < 3 ⇔ m <1 thỏa mãn yêu cầu bài toán. Chọn A.
Câu 101. (ĐỀ CHÍNH THỨC 2016 2017) Tính giá trị thực của tham số – m để phương trình 2
log x − m log x + 2m −7 = 0 có hai nghiệm x , x thỏa mãn x x = 81. 3 3 1 2 1 2
A. m = 81.
B. m = 44.
C. m = −4.
D. m = 4.
Lời giải. Điều kiện: x > 0 . Giả sử phương trình có hai nghiệm x , x . 1 2
Theo Viet, ta có log x + log x = m ⇔ log x x = m ⇔ log 81 = m ⇔ 4 = . m 3 1 3 2 3 ( 1 2 ) 3
Thử lại với m = 4 ta thấy thỏa mãn. Chọn D.
Câu 102. Có bao nhiêu giá trị nguyên của tham số m để bất phương trình + ( 2 x + )≥ ( 2 log 5 log 1
log mx + 4 x + m) đúng với mọi x ? A. 0. B. 1. C. 2. D. 4.
Lời giải. Để bất phương trình đúng với mọi x khi và chỉ khi:
● Bất phương trình xác định với mọi 2
x ⇔ mx + 4 x + m > 0, ∀x ∈ ℝ m > 0 m > 0 ⇔ ⇔ ⇔ m > 2. ( ) 1 2 ∆' < 0 4 −m < 0
● Bất phương trình nghiệm đúng với mọi x ⇔ ( 2 x + ) ≥ ( 2 log 5 5
log mx + 4x + m), ∀x ∈ ℝ 2 2
⇔ 5x + 5 ≥ mx + 4x + , m ∀x ∈ ℝ ⇔ (5−m) 2
x − 4x + 5− m ≥ 0, ∀x ∈ ℝ 5 −m > 0 m < 5 ⇔ ⇔ ⇔ m ≤ 3. (2) 2 ∆' ≤ 0 m − +10m − 21 ≤ 0 Từ ( ) 1 và (2) , ta được 2 3 m m ∈ < ≤
ℤ→ m = 3. Chọn B.
Câu 103. Có bao nhiêu giá trị m nguyên thuộc đoạn [−2017;2017] để bất phương trình ( 2 log
x + 2x + m + )
1 > 0 đúng với mọi x ? m A. 2015 . B. 4030. C. 2016. D. 4032.
Lời giải. Để bất phương trình đúng với mọi x khi và chỉ khi: 2
x + 2x + m +1> 0, ∀x ∈ ℝ
● Bất phương trình xác định với mọi x ⇔ 0 < m ≠ 1 ( x + )2
1 + m > 0, ∀x ∈ ℝ ⇔ ⇔ 0 < m ≠ 1. 0 < m ≠1
● Bất phương trình nghiệm đúng với mọi x ⇔ ( 2 log
x + 2x + m + ) 1 > 0, ∀x ∈ . ℝ (*) m Nếu m > 1 thì ( ) 2
* ⇔ x + 2x + m > 0, ∀x ∈ ℝ ⇔ ∆ ' = 1− m < 0 ⇔ m > 1: (thỏa mãn). Nếu 1 < 0
0 < m < 1 thì (*) 2 x 2x m 0, x ⇔ + + < ∀ ∈ ℝ ⇔ : vô lí. ∆ = 1−m < 0
Vậy m >1 thỏa mãn yêu cầu bài toán m [∈−2017;2017]
→ m ∈ Chọn C. m ℤ {2;3;4;...;2017}. ∈
Câu 104. Gọi m là giá trị thực nhỏ nhất của tham số m sao cho phương trình 0 (m − ) 2 1 log
x − 2 − m −5 log
x − 2 + m −1 = 0 có nghiệm thuộc (2;4) . Mệnh đề nào 1 ( ) ( ) 1 ( ) 2 2 sau đây là đúng? A. 5 m ∈ −5; − . B. 4 m ∈ −1; . C. 10 m ∈ 2; D. Không tồn tại. 2 3 3
Lời giải. Đặt t = log x −2 , do 2 < x < 4 → 0 < x −2 < 2 → t > −1. 1 ( ) 2 2 Phương trình trở thành t −5t +1 (m − ) 2 1 t −(m − )
5 t + m −1 = 0 ⇔ m = . 2 t − t +1 2 Xét hàm số t −5t +1 f (t) = với t > −1 . 2 t − t +1
Đạo hàm và lập bảng biến thiên, ta được t −1 1 +∞ f '(t) − 0 + 7 3 f (t) 1 −3
Dựa vào bảng biến thiên, ta thấy phương trình có nghiệm 7 −3 ≤ m < . 3 Suy ra 5 m 3 = − ∈ −5; − . Chọn A. 0 2
Câu 105. Cho phương trình 2
log x − 2 log x −3 = m log x −3 với m là tham số 2 2 ( 2 )
thực. Tìm tất cả các giá trị của m để phương trình có nghiệm thuộc [16;+∞) .
A. 1< m ≤ 2 .
B. 1< m ≤ 5 .
C. 3 ≤ m ≤ 5 .
D. 1≤ m ≤ 5 . 4
Lời giải. Đặt t = log x , với x ≥16 → t ≥ 4 . 2 Phương trình trở thành 2
t − 2t −3 = m(t −3). (*) 2
t −2t −3 > 0
● Với m ≤ 0 thì phương trình vô nghiệm, do , ∀t ≥ 4. t −3 > 0
● Với m > 0 thì ( ) ⇔ t − t − = m (t − )2 2 2 * 2 3 3 ⇔ ( 2 − m ) 2 t + ( 2 m − )t − ( 2 1 2 3 1 3 1+ 3m ) = 0 . Nếu m = 1
→ t = 3 : không thỏa mãn.
Nếu m ≠ 1 , ta nhẩm được một nghiệm t = 3 (không thỏa mãn), suy ra nghiệm 2 còn lại −3m −1 t = . 2 1− m 2
Do đó để phương trình đã cho có nghiệm −3m −1 ⇔
≥ 4 ⇔ 1 < m ≤ 5 (thoû ) a . Chọn B. 2 1− m 2 Nhận xét. Phương trình t − 2t −3 (*) ⇔ m =
= f (t), ∀t ≥ 4 . Xét hàm f (t) với t ≥ 4. t −3 x
Câu 106. Tìm tất cả các giá trị thực của tham số m để phương trình 4 2 2 x m +e = e +1 có nghiệm thực.
A. 0 < m <1. B. 2 0 < m ≤ .
C. 1 ≤ m <1. D. −1< m < 0. e e Lời giải. Đặt 4 2 x t = e +1 , vì 2x e > 0 → t > 1 . 4 x x Suy ra 4 2 x 4 4 4 2 2 t = e
+1 ⇔ e = t −1 ⇔ e = t −1 .
Khi đó phương trình trở thành 4 4 4 4
m + t −1 = t ⇔ m = t − t −1. ( ) ∗ 3 Xét hàm t f (t) 4 4
= t − t −1 trên (1;+ )
∞ . Ta có f '(t) = 1− < 0, ∀t > 1 . (t − )3 4 4 1
Suy ra hàm số f (t) nghịch biến trên (1;+ ) ∞ . t 1 +∞ f '(t) − 1 f (t) 0
Dựa vào bảng biến thiên, ta thấy phương trình có nghiệm ⇔ 0 < m <1 . Chọn A.
Câu 107. (ĐỀ THAM KHẢO 2016 2017) Hỏi có bao nhiêu giá trị – m nguyên trong
[−2017;2017] để phương trình log(mx) = 2 log(x + ) 1 có nghiệm duy nhất?
A. 2017 . B. 4014. C. 2018. D. 4015.
Lời giải. Điều kiện: x > −1. Phương trình 2 (x + )2 1
log(mx ) = 2 log(x + )
1 ⇔ mx = (x + ) 1 ⇔ m = . x Xét hàm (x + )2 1 f (x ) = trên (−1;+∞). x
Đạo hàm và lập bảng biến thiên, ta được x −1 0 1 +∞ f '(x) − − 0 + +∞ +∞ f (x ) 4 0 −∞
Dựa vào bảng biến thiên, ta thấy phương trình có nghiệm duy nhất m = 4 ⇔ m < 0 m [ ∈ −2017;2017]
→ m ∈ − − −
→ có 2018 giá trị m nguyên. Chọn C. m ℤ { 2017; 2016;...; 1;4} ∈ x
Câu 108. Tìm tất cả các giá trị của tham số 4 −1
m để phương trình log − m = 0 có 2 4x +1 nghiệm. A. m < 0.
B. −1< m <1. C. m ≤ −1.
D. −1< m < 0.
Lời giải. Điều kiện: 4x −1> 0 ⇔ x > 0. Đặt t −1 4x t = , với x > 0
→ t > 1. Phương trình trở thành m = log . (*) 2 t +1 Xét hàm số t −1 2 f (t) = log
trên (1;+∞). Ta có f '(t)= > 0, ∀t > 1. 2 t +1 ( 2t − ) 1 ln 2
Suy ra hàm số f (t) đồng biến trên khoảng (1;+∞). t 1 +∞ f '(t) + 0 f (t) −∞
Dựa vào bảng biến thiên, ta thấy phương trình có nghiệm ⇔ m < 0. Chọn A.
Câu 109. Cho phương trình (x− )2 1 2
.log ( 2 −2 +3 = 4 x−m x x . log
2 x − m + 2 với m là 2 ) 2 ( )
tham số thực. Tìm tất cả các giá trị của m để phương trình có đúng hai nghiệm phân biệt. A. 1 3 m ; ∈ −∞ ∪ ;+∞ . B. 1 3 m ∈ − ; ∞ ∪ ;+∞ . 2 2 2 2 C. m ∈(− ; ∞ − ] 1 ∪[1;+∞).
D. m ∈(−∞ ) ;1 ∪(1;+ ) ∞ .
Lời giải. Phương trình 2 x −2 x +3 ⇔ 2 .log ( 2
x − 2x + 3 = 2 x−m + .log 2 x − m + 2 . ( ) ∗ 2 ) 2 2 2 ( ) t Xét hàm t 2 ( ) = 2t f t
.log t trên [2;+∞) . Ta có f ′(t) = 2 .ln 2.log t +
> 0, ∀t > 2. 2 2 t.ln 2
Suy ra hàm số f (t) là hàm số đồng biến trên [2;+∞). Nhận thấy ( ) ∗ có dạng f ( 2
x − x + ) = f ( x −m + ) 2 2 3 2
2 ⇔ x − 2x + 3 = 2 x − m + 2 (x )2 1 2(x m) 2 − = −
x − 4x + 2m +1 = 0 1 2 ( ) ( x ) 1 2 x m ⇔ − = − ⇔ ⇔ . (x − )2 1 = −2(x −m) 2 x = 2m −1 (2)
Phương trình đã cho có hai nghiệm phân biệt khi và chỉ khi
TH1. Phương trình ( )
1 và (2) đều có nghiệm kép và hai nghiệm này khác nhau ∆ ′ = 0 ( )1 ⇔ → m ∈ . ∅ 2
x = 2m−1= 0
TH2. Phương trình ( )
1 có hai nghiệm phân biệt, phương trình (2) vô nghiệm ∆ ′ > 0 ( )1 4 −(2m + ) 1 > 0 1 ⇔ ⇔ ⇔ m < . 2
x = 2m−1< 0 2 m −1 < 0 2
TH3. Phương trình ( )
1 vô nghiệm, phương trình (2) có hai nghiệm phân biệt ∆ ′ < 0 ( )1 4 −(2m + ) 1 < 0 3 ⇔ ⇔ ⇔ m > . 2
x = 2m−1> 0 2m −1> 0 2
TH4. Phương trình ( )
1 có hai nghiệm phân biệt, phương trình (2) cũng có hai
nghiệm phân biệt và hai nghiệm của ( )
1 giống hai nghiệm của (2) hay nói cách khác
hai phương trình tương đương → m ∈ . ∅ Vậy 1 3 m ; ∈ −∞ ∪ ; +∞
là giá trị cần tìm. Chọn A. 2 2
Câu 110. Cho phương trình log ( 2 x + 4mx + log
2x − 2m −1 = 0 với m là tham số 3 ) 1 ( ) 3
thực. Gọi S là tập tất cả các giá trị của m để phương trình có nghiệm duy nhất, khi
đó S có dạng [a;b]∪{c} với a < b < c . Tính P = 2a +10b + c . A. P = 0 . B. P = 15 . C. P = −2 . D. P = 13 .
Lời giải. Phương trình ⇔ log ( 2
x + 4mx = log 2x − 2m −1 3 ) 3 ( ) 2m +1 2
x −2m −1> 0 x > ( ) 1 ⇔ ⇔ 2 . 2
x + 4mx = 2x −2m −1 2 x + 2(2m − ) 1 x + 2m +1 0 (*) =
Yêu cầu bài toán ⇔ phương trình (*) có một nghiệm thỏa mãn ( ) 1 . ∆ = (2m − )2 / 1 − 2m +1 = 0 * ( )
● TH1: (*) có nghiệm kép thỏa ( ) 1 ← → 2m +1
x =1−2m > 2 2 4
m −6m = 0 ⇔ ⇔ m = 0. 6 m <1 ∆ = (2m − )2 / 1 − 2m +1 > 0 * ( ) 2m +1
● TH2: (*) có hai nghiệm x , x thỏa x x < < ⇔ 1 2 1 2 2m +1 2m +1 2 x − x − ≤ 0 1 2 2 2 2 4
m −6m > 0 1 1 ⇔ ⇔ − < m < − . 2 2 0m +12m +1 < 0 2 10 2m +1 2m +1 2m +1
● TH3: (*) có nghiệm x = và nghiệm x > . Thay x = vào 1 2 2 2 1 2
phương trình (*) ta nhận được 1 m = − hoặc 1 m = −
. Thử lại ta thấy thỏa mãn. 2 10
Kết hợp các trường hợp, ta được 1 1 − ≤ m ≤ −
hoặc m = 0 thỏa mãn yctb. 2 10 1 1
→ a = − ;b = −
;c = 0 . Chọn C. 2 10 Baøi 05
HEÄ PHÖÔNG TRÌNH MUÕ, HEÄ PHÖÔNG TRÌNH LOGARIT
Để giải hệ phương trình mũ, hệ phương trình logarit ta thường sửa dụng các
phương pháp quen thuộc như: phương pháp thế, biến đổi hệ về phương trình Đại số,
phương pháp hàm số,… Cuối cùng là tạo ra một hệ đơn giản và kết luận nghiệm.
CAÂU HOÛI TRAÉC NGHIEÄM
x + 2y = −1
Câu 1. Giải hệ phương trình . 2 4x+y = 16
A. (x; y)= (−1; )
1 , (x; y) = (3;−7) .
B. (x; y)= (1;− )
1 , (x; y) = (−7;3) .
C. (x; y)= (1; )
1 , (x; y) = (3;7) .
D. (x; y) = (−1; )
1 , (x; y) = (3;7).
x + 2y = −1
Lời giải. Hệ phương trình tương đương với 2 x + y 2 4 = 4
x = −2y −1
x + 2y = −1
x = −2y −1
x = −2y −1
y = −1; x = 1 ⇔ ⇔ ⇔ ⇔ y = −1 ⇔ . 2 2 2 x + y = 2
y −2y −1 = 2
y −2y −3 = 0
y = 3; x = −7 y = 3 Chọn B.
Cách trắc nghiệm: Thay ngược từng đáp án và bấm máy tính.
Câu 2. Giải hệ phương trình l
og x − log y = 2 .
x −10 y = 900 A. x = 100 x = x = x = . B. 1800 . C. 1000 . D. 10 . y = 10 y = 900 y = 10 y = 1000
Lời giải. Điều kiện: x, y > 0 . Hệ phương trình tương đương với x x l og = 2 = 100
x −100 y = 0 x = 1000 y y ⇔ ⇔ ⇔ . Chọn C.
x −10 y = 900 y = 10 x 10y 900 x 10y 900 − = − = x + y = 25
Câu 3. Gọi (x ; y là một nghiệm của hệ phương trình . Mệnh đề 0 0 )
log x − log y = 2 2 2 nào sau đây đúng?
A. x = 4 y .
B. x = 4 + y .
C. y = 4x .
D. y = 4 + x . 0 0 0 0 0 0 0 0
Lời giải. Điều kiện: x > 0
. Hệ phương trình tương đương với y > 0 x + y = 25 x + y = 25 x + y = 25
x = 20 = x0 x x ⇔ ⇔ ⇔
→ x = 4 y . Chọn A. 0 0 l og = 2 = 4 x − 4 y = 0 y = 5 = y 2 0 y y Câu 4. Cặp số
log x + log 2 y = 1 + log 9
(x; y) nào sau đây thỏa mãn hệ phương trình 4 4 4 ? x + 2 y = 20
A. (x; y)= (9;2). B. (x; y)= (18; ) 1 .
C. (x; y)= (1;18) .
D. (x; y) = (16;2).
Lời giải. Điều kiện: x > 0 l og 2xy = log 36
. Hệ phương trình tương đương với 4 ( ) 4 y > 0 x + 2y = 20 y = 1 2 2 xy = 36 xy = 18 2
y −20y +18 = 0
y = 1; x = 18 ⇔ ⇔ ⇔ ⇔ y = 9 ⇔ . x + 2 y = 20 x = 20 −2 y x = 20 −2y y = 9; x = 2 x = 20 −2 y Chọn B.
Cách 2. Dùng CASIO thử từng đáp án. x y
Câu 5. Hệ phương trình 2 .9 = 162
có tất cả bao nhiêu nghiệm (x; y) ? 3x .4y = 48 A. 0 . B. 1. C. 2 . D. 3 .
Lời giải. Nhân vế theo vế trong hệ phương trình, ta được 6x.36y = 162.48 x +2 y 5 ⇔ 6
= 6 ⇔ x + 2 y = 5 .
Thay x = 5− 2y và phương trình thứ hai của hệ, ta có 5−2 3 y.4 y = 48 2 y 4 5 3 y 2 2 4 ⇔ .4 = 2 .3
⇔ = ⇔ 2y = 4 ⇔ y = 2 → x = 1. 9 y 3 3
Vậy hệ phương trình có duy nhất nghiệm (x; y) = (1;2) . Chọn B. x y
Câu 6. Tìm tất cả các cặp số − =
(x; y) thỏa mãn hệ phương trình 6 2.3 2 . 6x .3y = 12
A. (x; y)= (1;log 4 .
B. (x; y)= (log 2;1 . 6 ) 3 )
C. (x; y) = (1;log 2 .
D. (x; y) = (1;log 2 , (x; y) = (log 2;1 . 6 ) 3 ) 3 ) x
Lời giải. Đặt 6 = a > 0 a − b =
. Hệ phương trình trở thành 2 2 3y = b > 0 ab = 12 a = 2b + 2 a = 2b + 2 a = 2b + 2 a = 6 ⇔ ⇔ ⇔ b = 3 − (loaïi) ⇔ . (2b + 2) 2 b = 12 b + b − 6 = 0 b = 2 b = 2 thoûa maõn ( ) 6x = 6 x = 1 Suy ra ⇔ . Chọn C. 3y = 2 y = log 2 3 l og y = 2 Câu 7. Gọi ( x x ; y
là một nghiệm của hệ phương trình . Mệnh đề 0 0 ) l og y + 23 = 3 x 1 + ( ) nào sau đây đúng?
A. x = y .
B. x > y .
C. x < y .
D. x = y + 2. 0 0 0 0 0 0 0 0 2 y = x
Lời giải. Điều kiện: 0 < x ≠ 1
. Hệ phương trình tương đương với y > 0 3 y + 23 = (x + ) 1 2 2 2 y = x y = x y = x x = 2 = x0 ⇔ ⇔ ⇔ ⇔ . 2 x + 23 = (x + )3 3 2 1 x
+ 2x + 3x − 22 = 0 ( x −2 )( 2 x + 4x +1 ) 1 = 0 y = 4 = y 0 Chọn C. 3x = 27.3y
Câu 8. Tìm tập nghiệm S của hệ phương trình . l og
(x + 2y) = log 5+ log 3 A. S = (
{ 7;4)}. B. S = ( { 4;7)}. C. S = ( { 6;3)}. D. S = ( { 9;6)}. x 3 3 = 3 .3y
Lời giải. Điều kiện: x + 2y > 0. Hệ phương trình ⇔ log (x + 2y) = log15 x = y +3 x = 7 ⇔ ⇔ . Chọn A. x + 2 y = 15 y = 4
Cách 2. Dùng CASIO thử từng đáp án. x
Câu 9. Tìm tất cả các cặp số (x; y) thỏa mãn 4 = 2 và log(2x + 2y) =1. 2y
A. (x; y) = (4; )
1 . B. (x; y) = (2;3).
C. (x; y)= (3;2).
D. (x; y) = (5;9).
Lời giải. Điều kiện: x + y > 0 . x 4 2
= 2 ⇔ 2 x−y = 2 ⇔ 2x − y = 1. ( ) 1 2y
log(2x +2y) =1 ⇔ 2x + 2y =10. (2) − = Từ x y x = ( ) 1 và (2) , ta có hệ 2 1 2 ⇔ . Chọn B. 2 x + 2 y = 10 y = 3 2 x − y 2 x −y 2 2 2
Câu 10. Cho hệ phương trình + 6 −7 = 0 3 3
. Chọn khẳng định đúng? log 9 (x − y) 3 = 1
A. Điều kiện xác định của hệ phương trình là x > y > 0 .
B. Hệ phương trình đã cho có hai nghiệm (x; y) .
C. Hệ phương trình đã cho có một nghiệm duy nhất (x; y) = (−1;−2) .
D. Hệ phương trình đã cho vô nghiệm.
Lời giải. Điều kiện: x − y > 0 ⇔ x > y . Do đó A sai. 2 x − y 2 x − y 2 x − y
Xét phương trình thứ nhất của hệ: 2 2 2 2 2 + 6 −7 = 0 . Đặt t = > 0 , 3 3 3 2 x −y t = ( 1 thoûa maõn) phương trình trở thành 2 2 2x − y 2 t + 6t −7 = 0 ⇔ → = 1 ⇔ = 0. t = −7 (loaïi) 3 2
Phương tình thứ hai của hệ: log9(x−y) log9 (x−y) 0 3 = 1 ⇔ 3
= 3 ⇔ log x − y = 0 ⇔ x − y = 1. 9 ( ) − = Từ đó ta có 2x y 0 x = −1 ⇔ ⇔ : thỏa mãn điều kiện. x − y = 1 y = −2
Vậy hệ phương trình đã cho có một nghiệm duy nhất (x; y) = (−1;−2) . Chọn C.




