Bài Tập Hình 8 Bài Các Trường Hợp Đồng Dạng Của Tam Giác Vuông Có Lời Giải

8. CÁC TRƯỜNG HỢP ĐỒNG DẠNG CỦA TAM GIÁC VUÔNG
I. KIẾN THỨC CƠ BẢN
 Áp dụng các trường hợp đồng dạng của tam giác vào tam giác vuông
Hai tam giác vuông đồng dạng với nhau nếu:
- Tam giác vuông này có một góc nhọn bằng góc nhọn của tam giác vuông kia.
- Tam giác vuông này có hai cạnh góc vuông tỉ lệ với hai cạnh góc vuông của tam giác vuông kia.
 Dấu hiệu đặc biệt nhận biết hai tam giác vuông đồng dạng
Nếu cạnh huyền và một cạnh góc vuông của tam giác vuông này tỉ lệ với cạnh huyền và
cạnh góc vuông của tam giác vuông kia thì hai tam giác vuông đó đồng dạng.
 Tỉ số hai đường cao, trung tuyến, phân giác của hai tam giác đồng dạng
- Tỉ số hai đường cao tương ứng của hai tam giác đồng dạng bằng tỉ số đồng dạng.
- Tỉ số hai đường trung tuyến tương ứng của hai tam giác đồng dạng bằng tỉ số đồng dạng.
- Tỉ số hai đường phân giác tương ứng của hai tam giác đồng dạng bằng tỉ số đồng dạng.
 Tỉ số diện tích của hai tam giác đồng dạng
Tỉ số diện tích của hai tam giác đồng dạng bằng bình phương tỉ số đồng dạng. III. BÀI TẬP
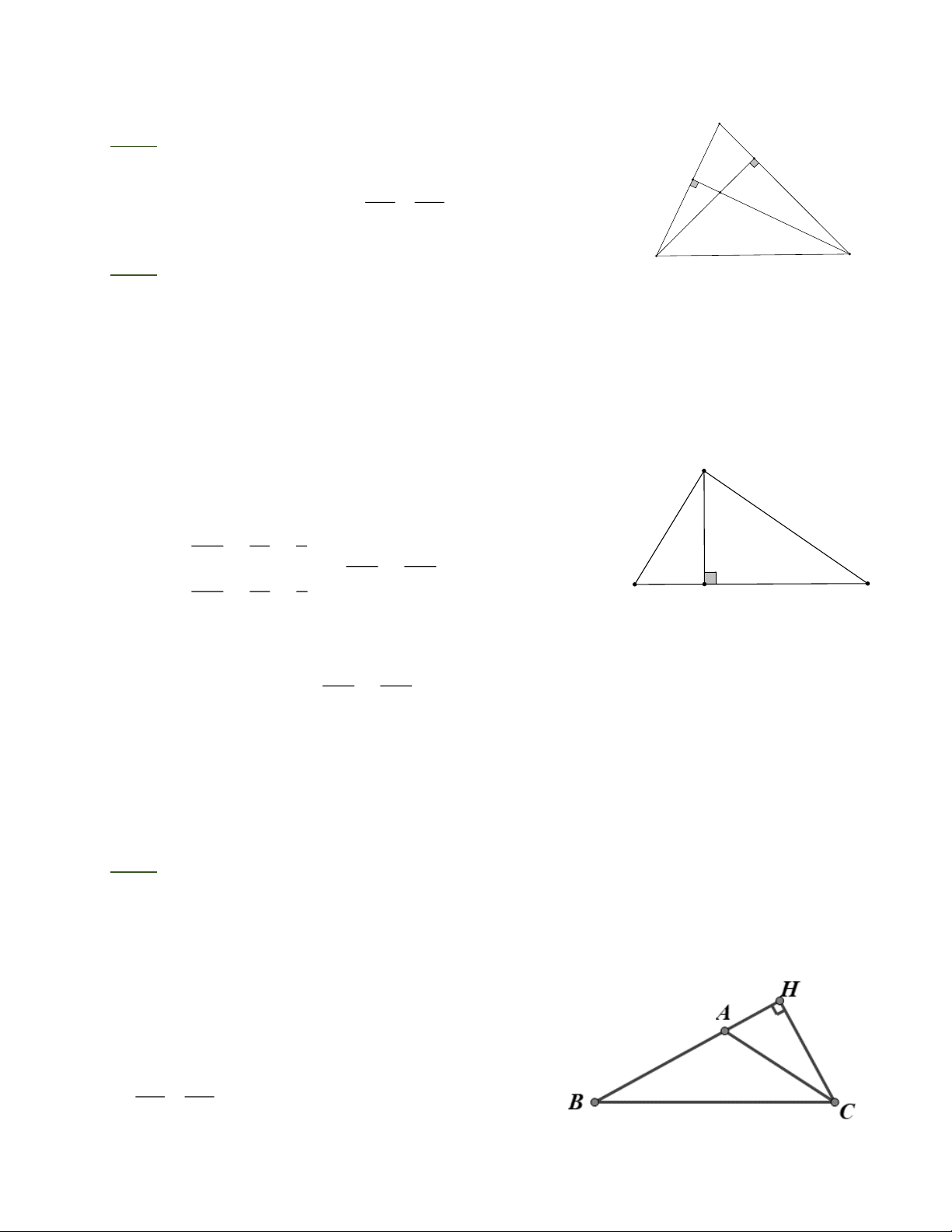
Bài 1: Cho tam giác ABC có các đường cao BD và CE cắt nhau tại H. Chứng minh: a) B  EH” C  DH; b) E  HD” B  HC. Bài 2:
Cho ABC có đường cao AH, biết A B = 30cm, BH = 18cm ; A C = 40cm
a) Tính độ dài AH và chứng minh: ABH ” CAH
b) Chứng minh ABH ” CBA µ µ
Bài 3: Cho tam giác ABC, có A = 90° + B , đường cao CH . Chứng minh: a) CBA = ACH b) 2
CH = BH .A H
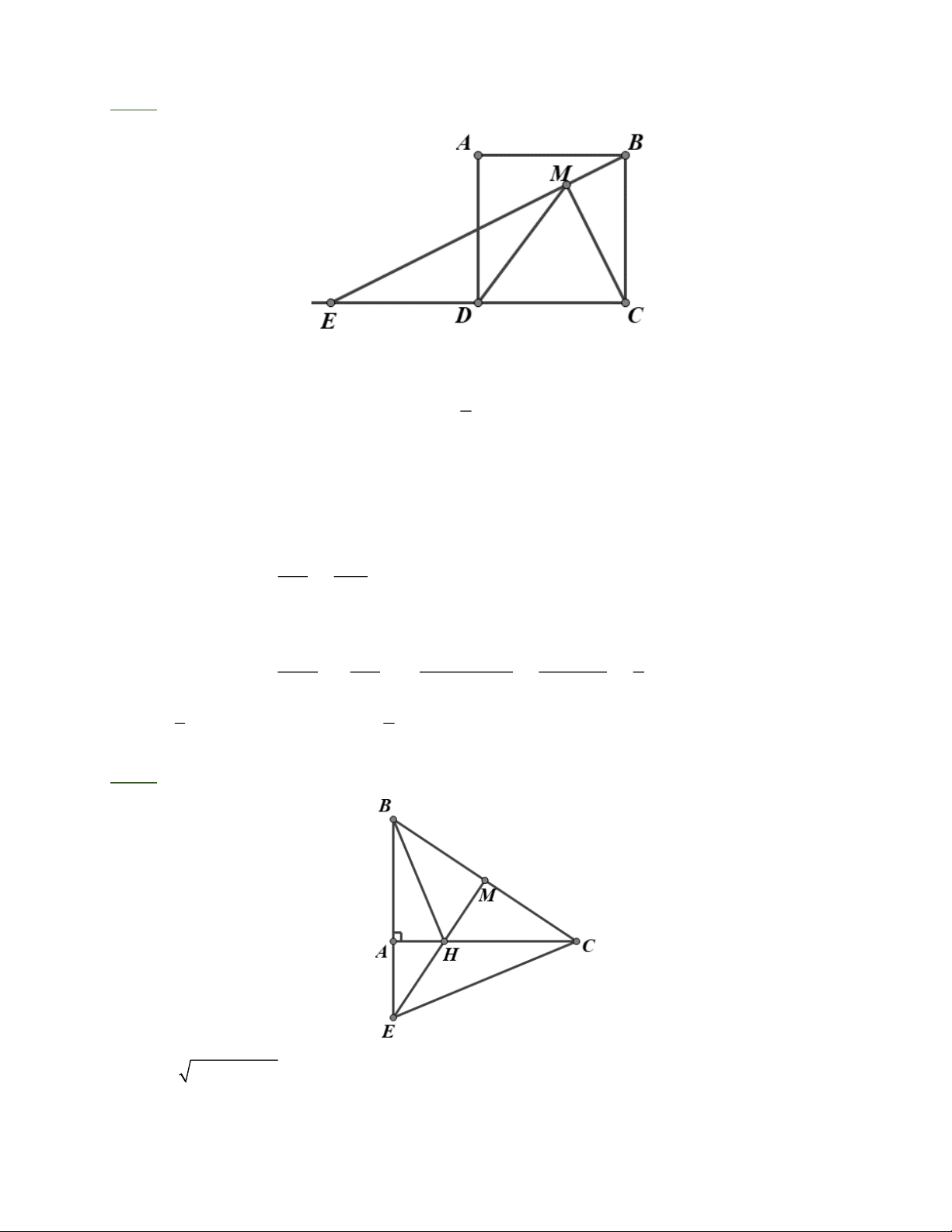
Bài 4: Cho hình vuông A B CD , cạnh a. Gọi E là điểm đối xứng với C qua D, EB cắt AD tại
I. Trên EB lấy điểm M sao cho DM = DA. a) Chứng minh D EMC ~ D ECB b) Chứng minh 2 EB .MC = a 2 .
c) Tính diện tích tam giác EMC theo a. Trang 1
Bài 5: Cho tam giác ABC vuông ở A, AB = 5,4cm, AC = 7,2cm. a) Tính BC.
b) Từ trung điểm M của BC, vẽ đường thẳng vuông góc với BC, cắt đường thẳng AC tại H
và cắt đường thẳng AB tại E. Chứng minh EMB ~ CAB. c) Tính EB và EM.
d) Chứng minh BH vuông góc với EC.
e) Chứng minh HA.HC = HM .HE .
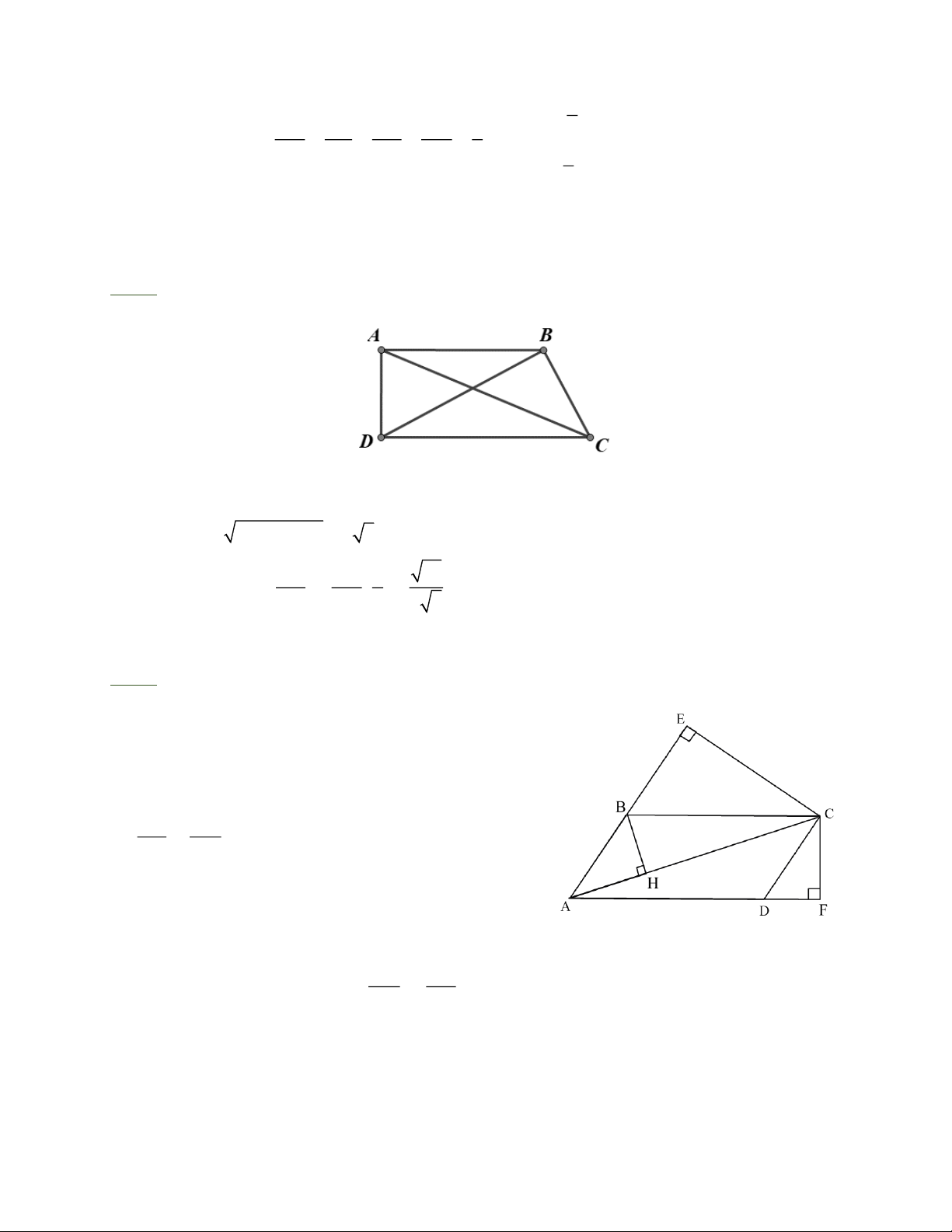
Bài 6: Cho tứ giác ABCD, có DBC 0 = 90 , AD = c
20 m, AB = c
4 m, DB = c
6 m , DC = c 9 m . a) Tính góc BAD b) Chứng minh B V A D ” DDBC
c) Chứng minh DC / / A B .
Bài 7: Cho hình bình hành ABCD ( AC > BD) vẽ CE vuông góc với AB tại E, vẽ CF vuông
góc với AD tại F.Chứng minh rằng 2
A B .A E + A D. A F = A C
BÀI TẬP TỰ LUYỆN
Bài 1: Cho hình thang vuông ABCD (AB // DC, A = D 0
= 90 ). Đường chéo BD vuông góc
với cạnh bên BC. Chứng minh BD2 = AB D . C .
Bài 2: Cho tam giác ABC. Một đường thẳng song song với BC cắt cạnh AB, AC theo thứ tự
ở D và E. Gọi G là một điểm trên cạnh BC. Tính diện tích tứ giác ADGE biết diện tích tam 2 2
giác ABC bằng 16cm , diện tích tam giác ADE bằng 9cm .
Bài 3: Cho tam giác ABC vuông tại A, đường cao AH, BC = 20cm,AH = 8cm. Gọi D là
hình chiếu của H trên AC, E là hình chiếu của H trên AB.
a) Chứng minh tam giác ADE đồng dạng với tam giác ABC.
b) Tính diện tích tam giác ADE. Trang 2
KẾT QUẢ - ĐÁP SỐ A Bài 1: D
a) BEH ” CDH (g − g) E HE HB
b) Có BEH ~ CDH ta suy ra = H HD HC
Từ đó chứng minh được EHD ” BHC( . c g c) Bài 2: B C
a) Vì AH ⊥ BC  AHB vuông tại H, theo định lý Pitago ta có: 2 2 2 2 2 2
AB = AH + BH  AH = AB − BH 2 2 2
 AH = 30 −18 = 900 − 324 = 576  AH = 24cm
Vì AH ⊥ BC → AHC vuông tại H, theo định lý Pitago ta có: 2 2 2
AC = AH + HC 2 2 2
 HC = AC − AH A 2 2 2
 HC = 40 − 24 = 1600 − 576 = 1024  HC = 32cm A H 24 4üïï = = ïï A H HC Ta lại có: BH 18 3ïý Þ = HC 32 4ï BH A H ï = = ï B H C A H 24 3ïïþ · · A HB CHA 90 üï = = °ïïï · ·
Xét AHB và CHA có:
ý Þ DA HB ” DCHA (c. .
g c) Þ A BH = CA H A H HC (cmt ) ï = ï BH A H ïïþ · · · ·
b) Ta có: HBA + BA H = 90° Þ CA H + HA B = 90°
AHB = CAB = 90
Xét ABH và CBA có:
  ABH ” CAB (g− g) (đpcm) B (chung)  Bài 3: a) CBA = ACH 0 0 0 0
ACH = 90 − CAH = 90 − (180 − BAC) = 90 + BAC = CBA
b) CH 2 = BH.AH ACH = CBH 
 HCA” HBC 0
CHA = BHC = 90 HC HA 2  =  HC = H . A HB HB HC Trang 3 Bài 4: a) Chứng minh D EMC ~ D ECB 1
Tam giác EMC có trung tuyến MD = DA =
EC nên là tam giác vuông tại M. 2 MEC = CEB 
 ECB ~ EMC 0
EMC = ECB = 90 b) Chứng minh 2 EB .MC = a 2 . EB BC 2 DECB ” DEMC Þ =
Þ EB.MC = EC .BC = 2a EC MC
c) Tính diện tích tam giác EMC theo a. 2 2 2 S E æ C ö ç ÷ EC 4a 4 EMC DECB ” DEMC Þ = ç ÷ = = = ç ÷ 2 2 2 2 S çèEB ÷ø EC + CB 4a + a 5 ECB 1 4 2 2 S =
EC .BC = a Þ S = a EBC 2 EMC 5 Bài 5: a) 2 2
BC = AB + AC = 9cm (Pitago) b) 0
EMB = CAB (= 90 ), EBM = CBA (góc chung)  EMB ~ CAB (g.g) Trang 4  5
ME = AC = 6cm ME BE MB 9 : 2 5  6
c) EMB ” CAB  = = = =   AC BC AB 5, 4 6 5 BE = BC = 7,5  cm  6
d) ΔBEC có 2 đường cao CA,EM cắt nhau tại H nên H là trực tâm ΔBEC, BH ⊥ EC
e) Chứng minh DA HE ” D MHC từ đó suy ra HA.HC = HM .HE . Bài 6: a) Ta có 2 2 2
BD = AB + AD , suy ra tam giác ABD vuông tại A (Pitago đảo) b) Ta có 2 2
BC = CD − BD = 3 5 (Pitago) æ ö · · A B A D ç4 20 ÷
BA D = CBD = 90 , ° = ç ÷ = ç
÷Þ DA BD ” DBDC (c. . g c) BD BC ç6 è 3 5 ÷÷ø
c) ABD ” BDC  ABD = BDC  AB / /CD
Bài 7: Vẽ BH ⊥ A C(H  A C) Xét  ABH và  ACE có = = 0 A HB A EC 90 ; BA C chung . Suy ra DABH ” A V CE (g g × )
 AB = AH  AB.AE = AC.AH (1) A C A E
Xét D CB H và D A CF có BCH = CAF (so le trong) = (= 0 CHB CFA 90 ) BC CH Suy ra D CBH ” D ACF(g.g) Þ =
Þ BC .AF = A C .CH (2) A C AF
Cộng vế theo vế (1) và (2) ta được:
A B A E + BC AF = A C A H + A C CH Þ A B A E + A D AF = A C (AH + CH ) 2 . . . . . . = A C . Trang 5