Bài Tập Hình 8 Bài Diện Tích Đa Giác Có Lời Giải

6. DIỆN TÍCH ĐA GIÁC
I. KIẾN THỨC CƠ BẢN
Để diện tích đa giác, ta thường chia đa giác đó thành các tam giác, các tứ giác tính được
diện tích rồi tính tổng các diện tích đó; hoặc tạo ra một đa giác nào đó chứa đa giác ấy rồi
tính hiệu các diện tích. II. BÀI TẬP
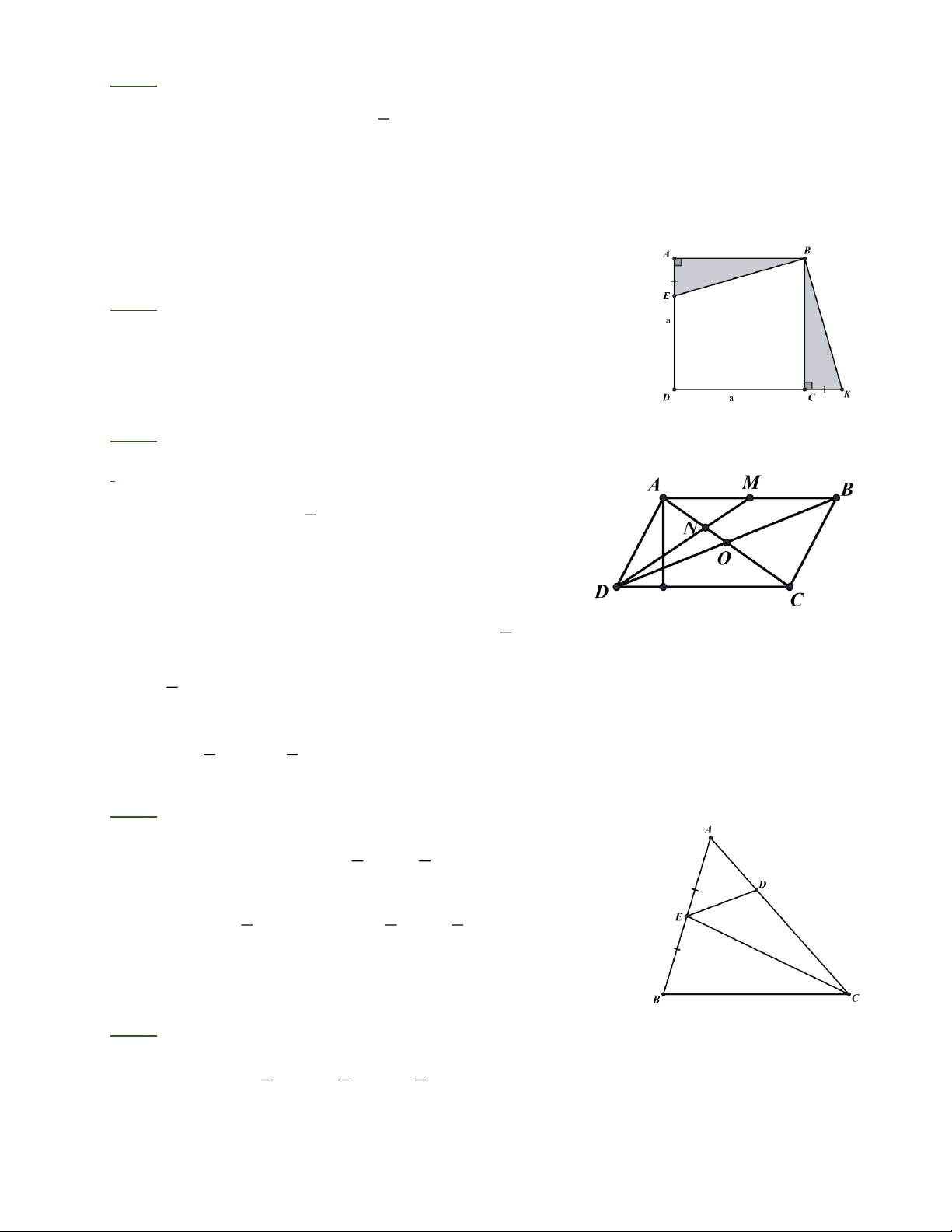
Bài 1: Cho hình vuông ABCD. Trên cạnh AD lấy điểm E, trên tia đối của tia CD lấy điểm
K sao cho CK = AE . Chứng minh rằng diện tích tứ giác BEDK bằng diện tích hình vuông?
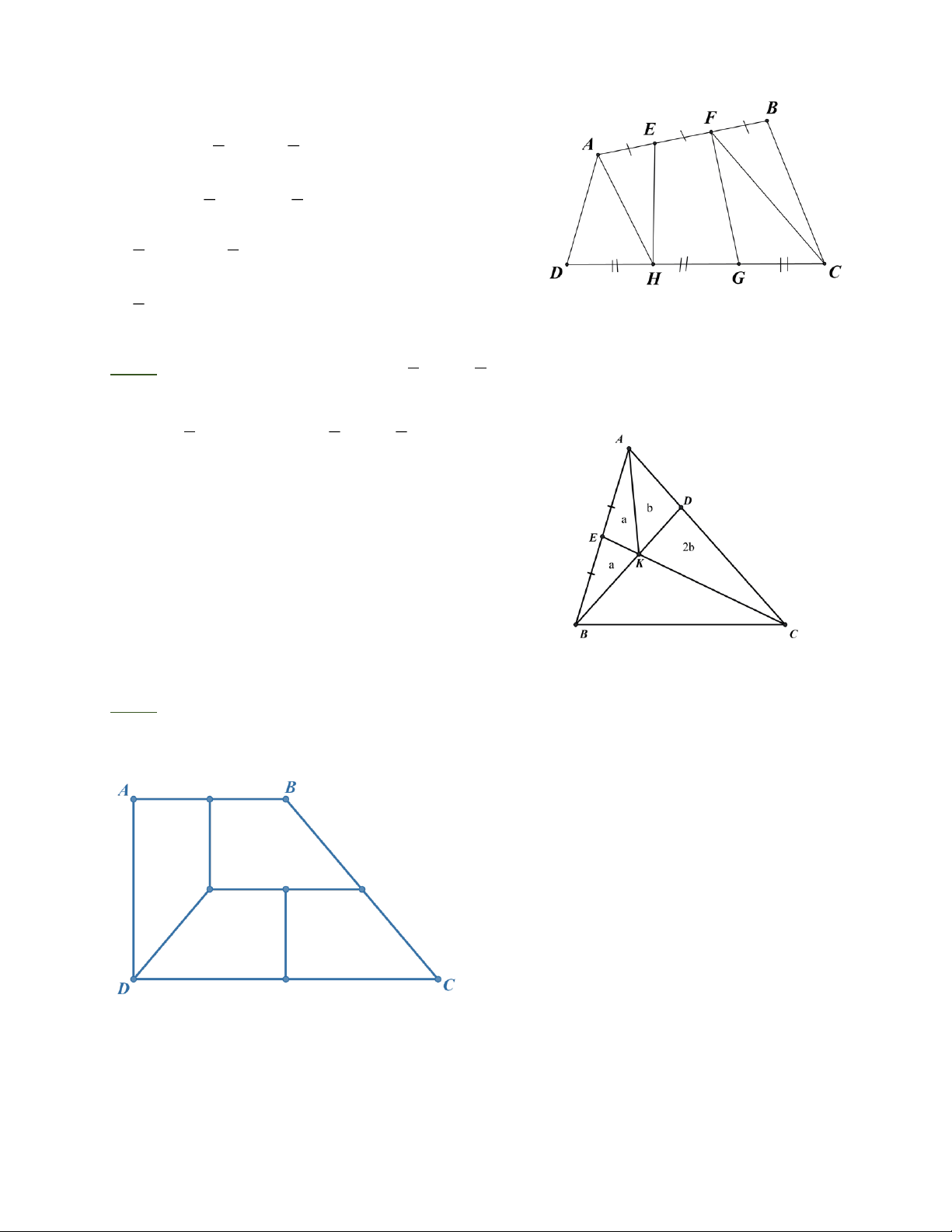
Bài 2: Cho hình bình hành ABCD có CD = 4 c ,
m đường cao vẽ từ A đến cạnh CD bằng 3 . cm
a) Tính diện tích hình bình hành ABCD;
b) Gọi M là trung điểm của .
AB Tính diện tích tam giác ADM ;
c) DM cắt AC tại N. Chứng minh DN = 2NM ;
d) Tính diện tích tam giác AMN. 1
Bài 3: Tam giác ABC có diện tích 2
30m . Điểm D trên cạnh AC sao cho D A = AC . Gọi E 3
là trung điểm của AB. Tính diện tích tứ giác BEDC?
Bài 4: Cho tứ giác ABCD có diện tích 2
60 cm . Trên cạnh AB lấy các điểm E, F sao cho AE = EF = .
FB Trên cạnh CD lấy các điểm G, H sao cho CG = GH = . HD
a) Tính tổng diện tích các tam giác ADH và CBF.
b) Tính diện tích tứ giác EFGH . 1
Bài 5: Tam giác ABC có diện tích 2
30m . Điểm D trên cạnh AC sao cho D A = AC , E là 3
trung điểm của AB. Gọi K là giao điểm của BD và CE. Tính diện tích tứ giác A DK E .
Bài 6: Cho hình thang vuông có đáy nhỏ và chiều cao bằng a , đáy lớn bằng 2a . Hãy chia
hình thang vuông đó thành bốn hình như nhau. Tự luyện
Bài 7: Cho tam giác ABC cân tại ,
A có diện tích S. Gọi O là trung điểm của đường cao
AH. Gọi D là giao điểm của BO với cạnh AC và E là giao điểm của CO với cạnh . AB
Tính diện tích tứ giác ADOE theo S. Trang 1
Bài 8: Cho tam giác ABC có diện tích 2
30 cm . Các điểm D, E theo thứ tự lấy trên các cạnh 1
AC, AB sao cho AD = DC; AE = E .
B Gọi K là giao điểm của BD và CE. Tính diện tích tứ 2 giác ADKE.
KẾT QUẢ - ĐÁP SỐ Bài 1: Vì B  CK = B  E A ( . c . g c) nên S = S BCK B E A Suy ra S + S = S + S BCK BCDE B E A BCDE Hay S = S B D E K ABCD Bài 2: a) S = 3.4 = 2 ABCD 12cm 1 b) AM = 2cm. S = 3.2 = 3( 2 ADM cm ). 2 c) Gọi   O = AC  BD. 2
Chứng minh N là trọng tâm của ADB : DN = DM  DN = 2MN hay 3 = 1 NM MD. 3 1 1 d) S = S = .3 = 2 ANM ADM 1cm . 3 3 Bài 3: 1 1
Vì AE = EB nên S = S = S = .30 = 15 m CA CB ABC ( 2 E E ) 2 2 2 2 2 Mặt khác DC = AC nên S = S = .15 = 10 m C E C E ( 2 D D ) 3 3 3 S = S + S = 15 + 10 = 25 m BE C CEB C E ( 2 D D ) Bài 4: 1 1 1 a) S + S = S + S = S = 2 ADH CBF ACD ABC ABCD 20cm 3 3 3 Trang 2 b) S = S − (S + EFGH AFCH AEH SCGF )  1 1  = S − S + AFCH  AHF SCFH   2 2  = − 1 S = 1 SAFCH AFCH SAFCH 2 2 1  1  = S −  ABCD SABCD  2  3  = 1 S = 20( 2 ABCD cm ) 3 1 1
Bài 5: Vì AE = EB nên S = S = S = .30 = 15 m CA CB ABC ( 2 E E ) 2 2 1 1 1 Vì D A = AC nên S = S = .30 = 10 m BA ABC ( 2 D ) 3 3 3 Đặt S = a,S = . b Ta có: E A K D A K 2a + b = S
= 10 nên 2a = 10 − b ; D AB
a + 3b = S
= 15 nên 2a = 30 − 6b ACE
Từ 10 − b = 30 − 6b suy ra 5b = 20 , vậy b = 4 do đó a = 3 S
= a + b = 3 + 4 = 7 m A KE ( 2 D ) Bài 6:
Tham khảo hình vẽ: Trang 3