Bài Tập Hình 8 Bài Diện Tích Hình Chữ Nhật Tam Giác Có Lời Giải

2+3. DIỆN TÍCH HÌNH CHỮ NHẬT – DIỆN TÍCH TAM GIÁC
I. KIẾN THỨC CƠ BẢN
Diện tích hình chữ nhật bằng tích hai kích thước của nó. Ta có: S = .
a b với a, b là độ dài hai cạnh của hình chữ nhật.
Diện tích hình vuông bằng bình phưong cạnh của nó. Ta có: 2
S = a với a là độ dài hai cạnh hình vuông.
Diện tích tam giác vuông bằng nửa tích hai cạnh góc vuông. 1 Ta có: S = .
a b với a, b là độ dài hai cạnh góc vuông của tam giác vuông. 2
Diện tích tam giác thường bằng nửa diện tích một cạnh và chiều cao hạ xuống cạnh đó:Ta 1 1 1 có: S = . a h = . b h = .
c h với a, b, c là độ dài các cạnh tam giác và h , h , h là độ dài 2 a 2 b 2 c a b c
đường cao tương ứng hạ xuống cạnh đó. II. BÀI TẬP
Bài 1: Một hình chữ nhật có các kích thước 6m và 2m. Một hình tam giác có các cạnh bằng
5m, 5m, 6m. Chứng minh rằng hai hình đó có chu vi bằng nhau và diện tích bằng nhau.
Bài 2: Tứ giác ABCD có hai đường chéo vuông góc, A C = 16cm, BD = 10cm . Gọi E, F, G, H
theo thứ tự là trung điểm của AB, BC, CD, DA. Tính diện tích tứ giác EFGH .
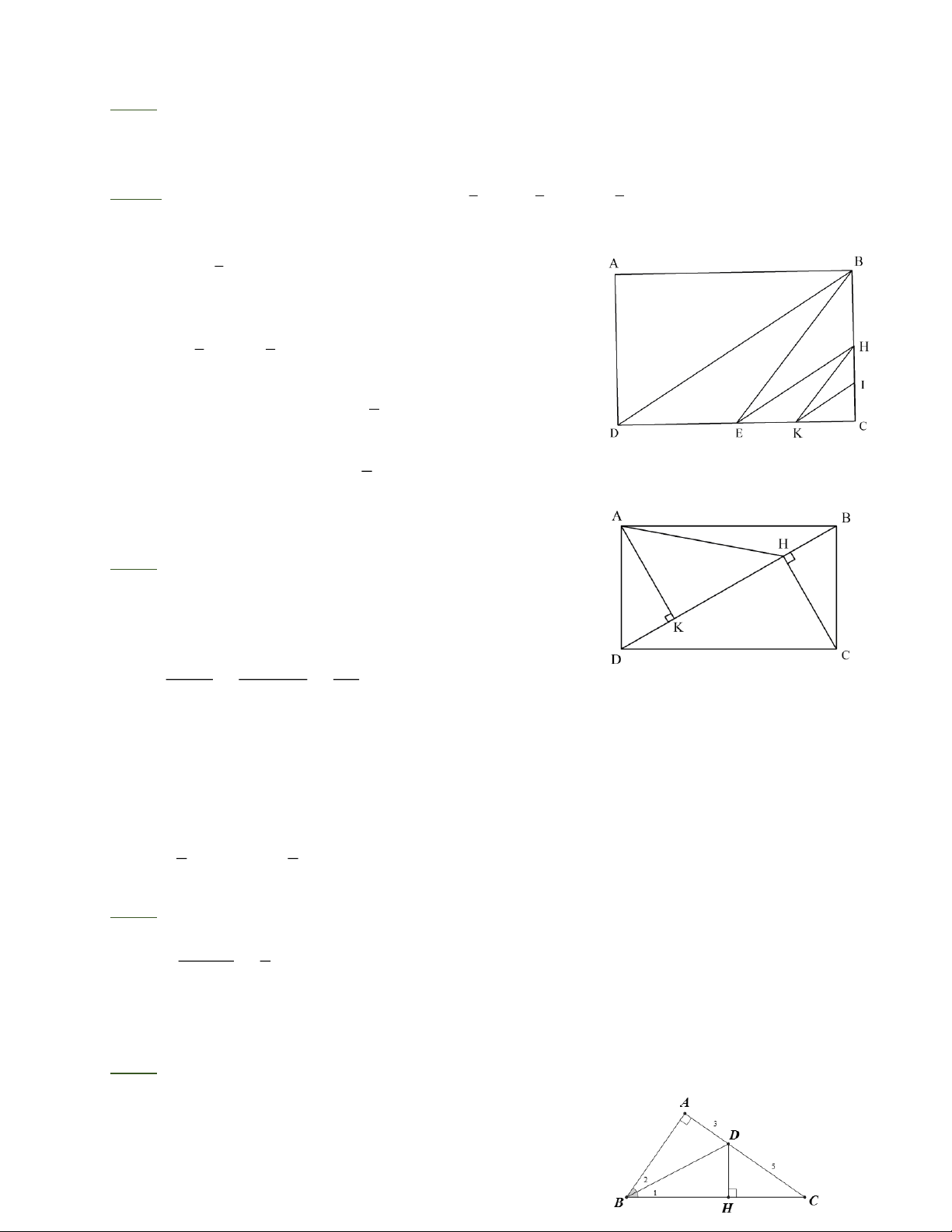
Bài 3: Cho hình chữ nhật ABCD có A B = 12 cm , A D = 6, 8 cm . Gọi H, I, E, K là các trung
điểm tương ứng của BC, HC, DC, EC.
a) Tính diện tích tam giác DB E .
b) Tính diện tích tứ giác EHIK .
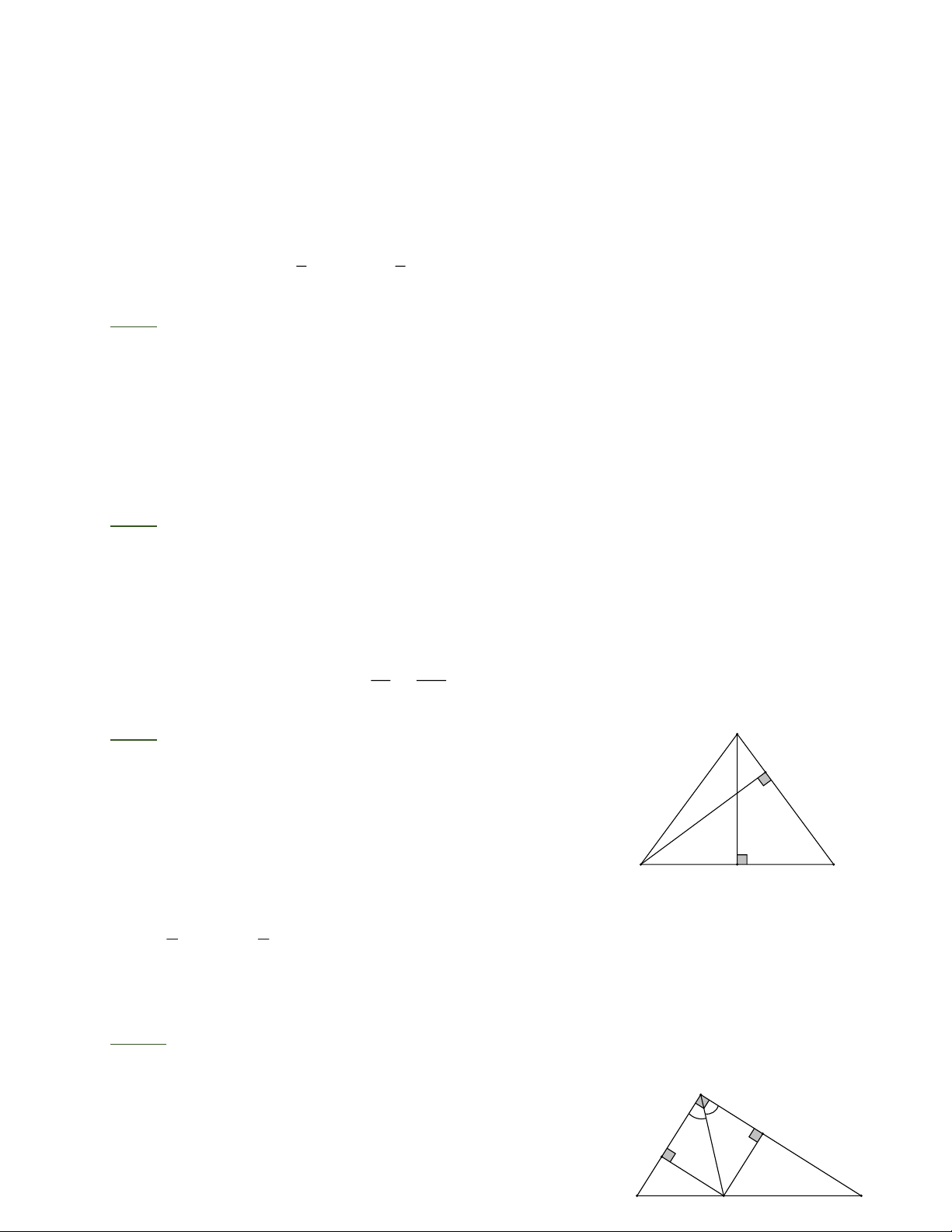
Bài 4: Cho hình chữ nhật ABCD có CD = 4cm, BC = 3cm. Gọi H là hình chiếu của C trên
BD. Tính diện tích tam giác ADH.
Bài 5: Hai hình vuông có hiệu hai cạnh bằng 3m và hiệu diện tích bằng 69m2. Tính cạnh của mỗi hình vuông.
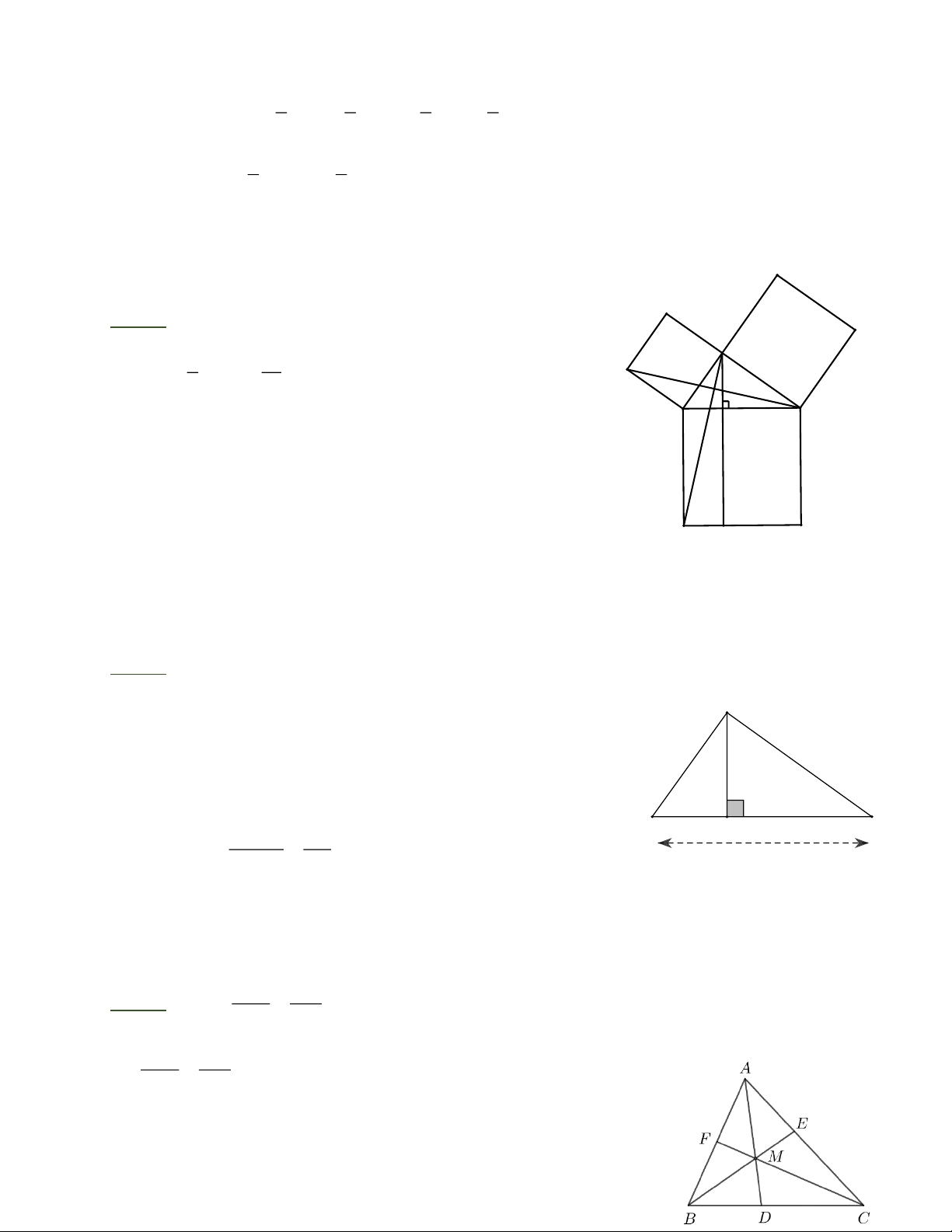
Bài 6: Cho tam giác ABC vuông ở A, đường phân giác BD. Biết AD = 3cm, DC = 5cm. Tính diện tích tam giác ABC.
Bài 7: Trong hình chữ nhật có chu vi 100m, hình nào có diện tích lớn nhất? Tính diện tích đó. Trang 1
Bài 8: Tính diện tích một tam giác vuông có cạnh huyền bằng 26m, hiệu hai cạnh góc vuông bằng 14m.
Bài 9: Cho tam giác ABC cân tại A, BC = 15c ,
m đường cao AH = 10 .
cm Tính đường cao ứng với cạnh bên.
Bài 10: Tam giác ABC vuông tại A, đường phân giác AD, AB = 10cm , AC = 15c . m Tính
diện tích hình vuông có đường chéo là AD.
Bài 11: Cho tam giác ABC vuông tại A, AB = a , AC = b , đường cao AH. Ở phía ngoài tam
giác vẽ các hình vuông ABDE, ACFG, BCIK.
a) Tính diện tích tam giác DBC.
b) Chứng minh rằng AK = DC .
c) Đường thẳng AH cắt KI ở M. Tính diện tích các tứ giác BHMK ,CHMI , BCIK .
Bài 12: Tam giác ABC có AB = 10c ,
m AC = 17 cm, BC = 21cm.
a) Gọi AH là đường vuông góc kẻ từ A đến DC. Tính 2 2
HC − HB và HC − HB .
b) Tính diện tích tam giác ABC.
Bài 13: Cho điểm M nằm trong ABC. Các tia AM , BM , CM lần lượt cắt cạnh đối diện tại MD ME MF
D, E, F. Chứng minh + + = 1 A D BE CF Tự luyện:
Bài 14: Một hình chữ nhật có diện tích 2
350 cm và hai cạnh tỉ lệ với các số 2 và 7. Tính
diện tích hình vuông có cùng chu vi với hình chữ nhật.
Bài 15: Tính diện tích một tam giác vuông có cạnh huyền bằng 13 cm và tổng hai cạnh góc vuông bằng 17 . cm
Bài 16: Cho tam giác nhọn ABC, các đường cao AD, BE, CF cắt nhau tại H. Chứng minh HD HE HF + + = 1. A D BE CF
KẾT QUẢ - ĐÁP SỐ
Bài 1: Chu vi hình chữ nhật và chu vi hình tam giác cùng bằng
16m. Diện tích hình chữ nhật và diện tích hình tam giác cùng bằng 2 12m Trang 2
Bài 2: EFGH là hình chữ nhật, có EF = 8cm, EH = 5cm.
Diện tích hình chữ nhật EFGH bằng 2 40cm .
Bài 3: a) ABCD là hình chữ nhật nên 1 1 1 2 S = .S
= .A B.A D= .12.6, 8 = 40, 8cm . BCD A BCD 2 2 2
E là trung điểm của CD, suy ra: 1 2 S = S = .S = 20, 4cm . BDE BCE BCD 2
b) H là trung điểm BC 1 1 2 Þ S = .S =
.20, 4 = 10, 2cm . CHE 2 BCE 2 1 K là trung điểm CE 2 Þ S = .S = 5,1cm . HKC 2 CHE 1 I là trung điểm CH 2 Þ S = .S = 2, 55cm . CKI 2 HKC Vậy 2 S = S - S
= 10, 2 - 2, 55 = 7, 65cm . EHIK CHE CIK
Bài 4: Áp dụng định lí Py-ta-go trong tam giác vuông BCD , ta có 2 2 2 2 2 2
BD = BC + CD = 3 + 4 = 25 = 5 nên BC = 5cm 2S BC C × D 3.4 BCD CH = = = = 2, 4cm BD BD 5
Xét tam giác vuông CDH, ta có 2 2 2 2 2 2
DH = CD - CH = 4 - 2, 4 = 10, 24 = 3.2
nên DH = 3, 2cm .
Kẻ A K ^ BD . Ta có S = S
nên A K = CH = 2, 4cm . Vậy A BD CBD 1 1 S = DH A × K = 3 × , 2.2, 4 = 3, 86 (cm2). A DH 2 2
Bài 5: Gọi a và b là cạnh của hình vuông. Ta có a - b = 3 và 2 2
a - b = 69, do đó 2 2 a - b 6 a + b = = = 23 a - b 9
Biết tổng a + b = 23 , a - b = 3 ta tính được a = 13;b = 10.
Bài 6: Kẻ DH ^ BC . Ta có D HBD = D A BD (cạnh huyền BD chung, góc nhọn 1 B = B2 )nên
DH = A D = 3cm và BH = A B. Trang 3
Áp dụng định lý Py-ta-go vào DHC vuông, ta có 2 2 2 2 2 2
HC = DC - DH = 5 - 3 = 4 , nên
HC = 4cm . Đặt A B = BH = x.
Áp dụng định lý Py –ta-go vào ABC vuông, ta có 2 2 2
BC = A B + A C nên 2 2 2
(x + 4) = x + 8 Þ x = 6. 1 1 Diện tích ABC bằng 2 A B.A C = 6.8 = 24cm . 2 2
Bài 7: Gọi một kích thước của hình chữ nhật là x(m), kích thước kia là 50 − x(m)
Diện tích hình chữ nhật bằng: 2 2
S = x(50 - x) = - x + 50x = - (x - 25) + 625 £ 625.
Giá trị lớn nhất của S bằng 625 tại x = 25.Vậy diện tích lớn nhất của hình chữ nhật bằng 625 2
m , khi đó hình chữ nhật là hình vuông có cạnh 25m.
Bài 8: Gọi a, b là cách cạnh góc vuông. Ta có a - b = 14 và 2 2 2
a + b = 26 = 676 ( ) 1 Từ a − b = 14 suy ra 2 2 (a - ) b = 14 , tức là 2 2
a + b - 2ab = 196 (2) Từ ( )
1 và (2)suy ra 2ab = 676 - 196 = 480. ab 480
Diện tích tam giác vuông bằng 2 = = 120m . 2 4
Bài 9: Tam giác ABC cân tại A. Đường cao AH nên A
BH = HC = BC : 2 = 15 : 2 = 7,5(cm) K
Áp dụng định lý Py-ta-go vào tam giác vuông AHC ta có 2 2 2 2 2
AC = AH + HC = 10 + 7,5 B C H 2
=156.25 =12,5 ; suy ra AC =12,5 cm. 1 1 S
= BC.AH = .15.10 = 75 cm ABC ( 2). 2 2
Kẻ BK ⊥ AC, ta có BK = 2S
: AC = 2.75 :12,5 = 12 cm ABC ( ).
Bài 10: Kẻ DH ⊥ AB, DK ⊥ AC . Điểm D thuộc tia phân
giác của góc A nên DH = DK . A
Đặt DH = DK = x , ta có 1 2 K H Trang 4 B D C 1 1 1 1 S = S + S = A .
B x + AC.x = .10.x + .15.x = 12,5 . x 1 ABC ADB ADC ( ) 2 2 2 2 1 1 Mặt khác S = A . B AC = .10.15 = 75. ABC (2) 2 2 Từ ( )
1 và (2) suy ra 12,5x = 75. Do đó x = 75:12,5 = 6. 2 S = = cm G AHDK ( 2 6 36 ). E Bài 11: F A 2 1 a a) S = S = D b DBC 2 ADBE 2 a B C
b) ABK = DBC ( .
c g.c)  AK = DC. H C) 2 S = 2S = 2S = a BHMK ABK DBC Chứng minh tương tự, 2 S = S = b . CHMI ACFG K M I Vậy 2 2 S = a + b BICK
Lưu ý. Bài toán trên cho ta một cách chứng minh định lý Py-ta-go: Nếu ABC vuông tại A thì 2 2 2
BC = AB + AC Bài 12:
a) Đặt HC = x, HB = y . Ta có: A 2 2 x y ( 2 2 AC AH ) ( 2 2 − = − − AB − AH ) 17 10 2 2 2 2
= AC − AB = 17 −10 = 189 y x C B 2 2 x − y 189 H 21
Do đó: x − y = = = 9 . x + y 21
b) Biết tổng ( x + y) và hiệu ( x − y) ta tính được y = 6 cm , từ đó AH = 8cm . Đáp số: 2 S = 84cm ABC . S MD
Bài 13: Ta có: BMD =
( BMD và BAD có chung đường cao kẻ từ B) S AD BAD S MD Và CMD =
( CMD và CAD có chung đường cao kẻ từ C) S AD CAD Trang 5 MD S S S + S S Suy ra: BMD CMD BMD CMD MBC = = = = AD S S S + S S BAD CAD BAD CAD ABC S ME S MF
Chứng minh tương tự: MAC = ; MAB = S BE S CF BAC CAB MD ME MF S + S + S S Suy ra: MBC MA C MA B A BC + + = = = 1 (đpcm) A D BE CF S S A BC A BC Trang 6