Bài Tập Hình 8 Bài Tính Chất Đường Phân Giác Của Tam Giác Có Lời Giải

3. TÍNH CHẤT ĐƯỜNG PHÂN GIÁC CỦA TAM GIÁC
I. KIẾN THỨC CƠ BẢN
 Định lý: Trong tam giác, đường phân giác của một góc chia cạnh đối diện thành hai đoạn thẳng tỉ
lệ với hai cạnh kề hai đoạn ấy. DB A B
 AD là phân giác trong của ABC Þ = DC A C
 Tính chất trên vẫn đúng với phân giác ngoài AE EB A B
( D ABC không cân ở A ) = EC A C II. BÀI TẬP
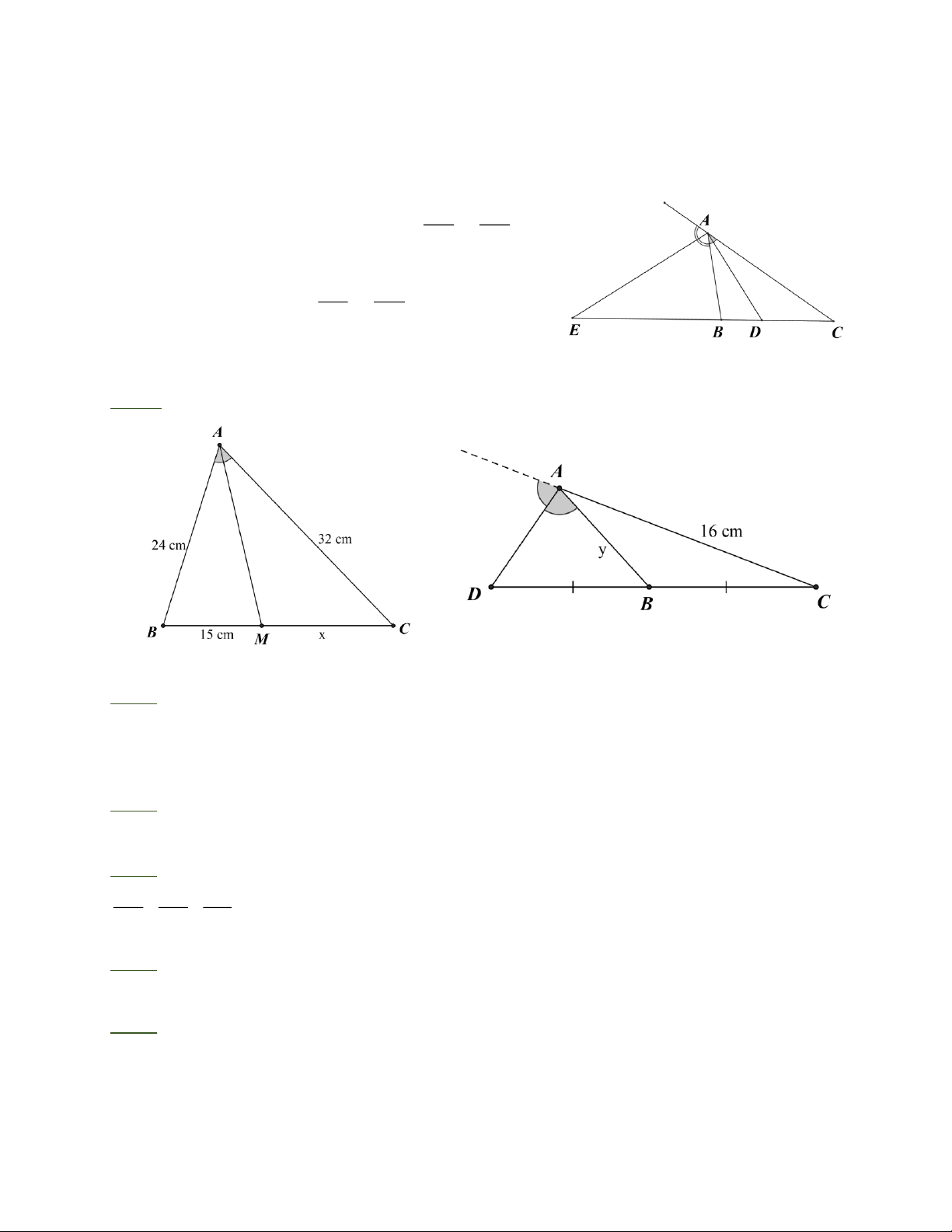
Bài 1: Tính độ dài x , y trong các hình vẽ sau: Hình 1 Hình 2
Bài 2: Cho tam giác A B C có A B = 4cm, A C = 5cm, BC = 6cm, các đường phân giác BD
và CE cắt nhau ở I .
a) Tính các độ dài A D, DC .
b) Tính các độ dài A E , B E .
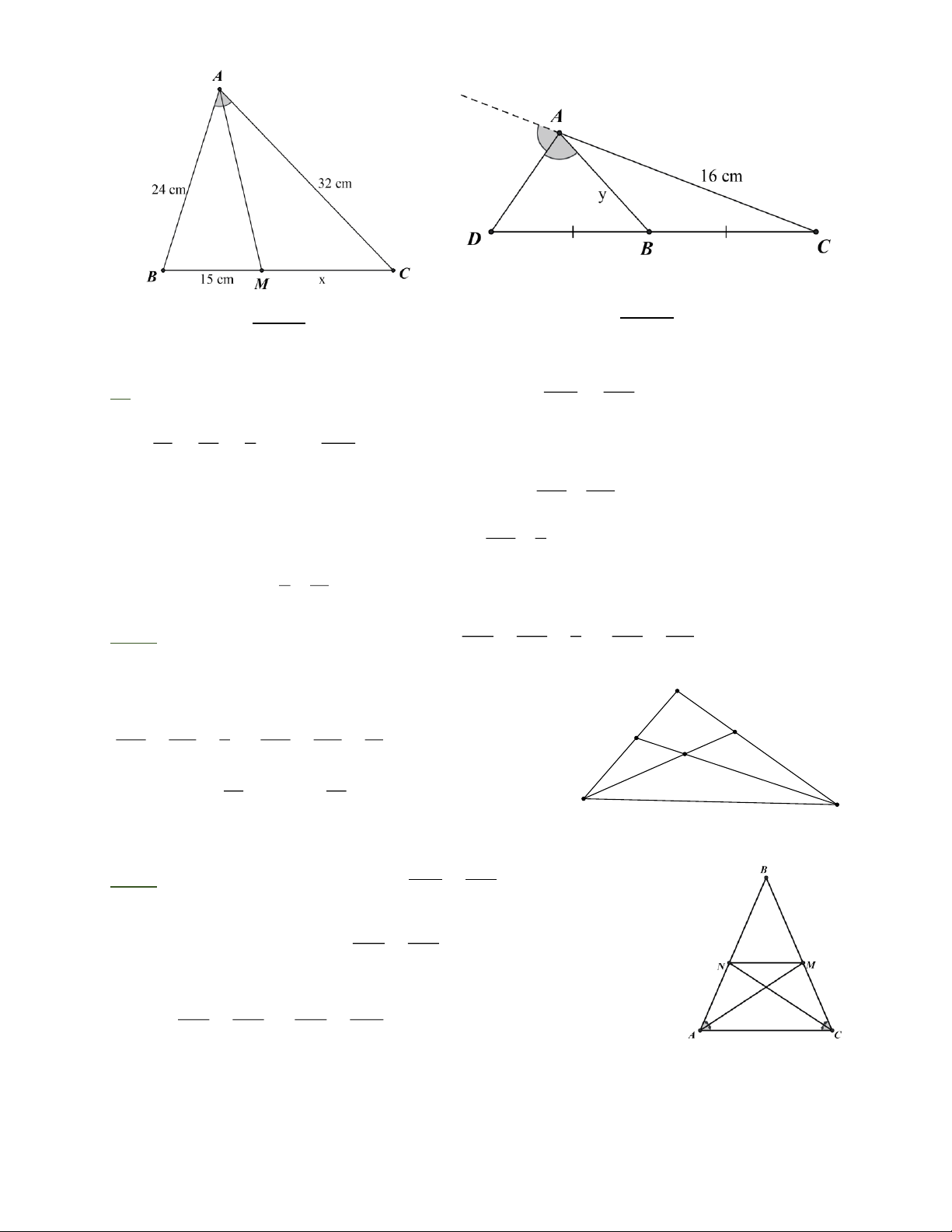
Bài 3: Cho tam giác cân A B C có A B = BC . Đường phân giác góc A cắt BC tại M ,
đường phân giác góc C cắt BA tại N . Chứng minh MN // A C .
Bài 4: Cho ΔABC có AD , BE , CF là các đường phân giác. Chứng minh rằng: A E CD BF . . = 1. EC DB FA
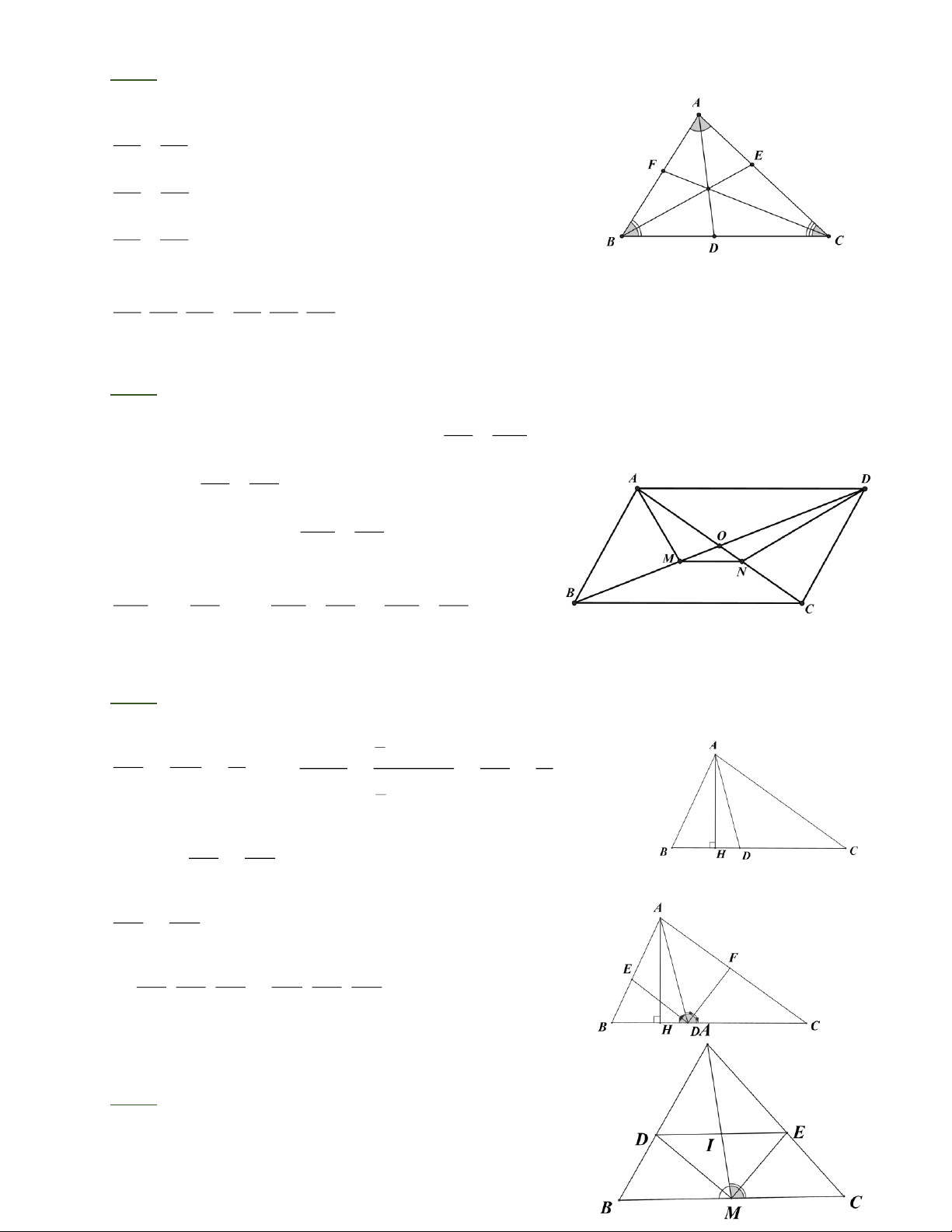
Bài 5: Cho hình bình hành ABCD. Phân giác của A và D cắt các đường chéo BD và AC
lần lượt tại M và N. Chứng minh: MN song song với AD.
Bài 6: Cho ΔABC có phân giác AD , biết A B = m, A C = n .
a) Tính tỉ số diện tích của ΔABD và ΔACD theo m và n .
b) Vẽ phân giác DE của ADB và vẽ phân giác DF của ADC . Chứng minh rằng:
A F .CD.BE = A E .BD.CF . Trang 1
Bài 7: Cho ΔABC , trung tuyến AM , đường phân giác của AMB cắt AB ở D , đường phân
giác của AMC cắt AC ở E .
a) Chứng minh rằng DE / /BC .
b) Gọi I là giao điểm của AM và DE . Chứng minh rằng DI = IE.
c) Tính DE , biết BC = 30cm,AM = 10cm.
d) ΔABC phải thêm điều kiện gì để ta có DE = AM ?
e) Chứng minh rằng ΔABC cân nếu biết MD = ME .
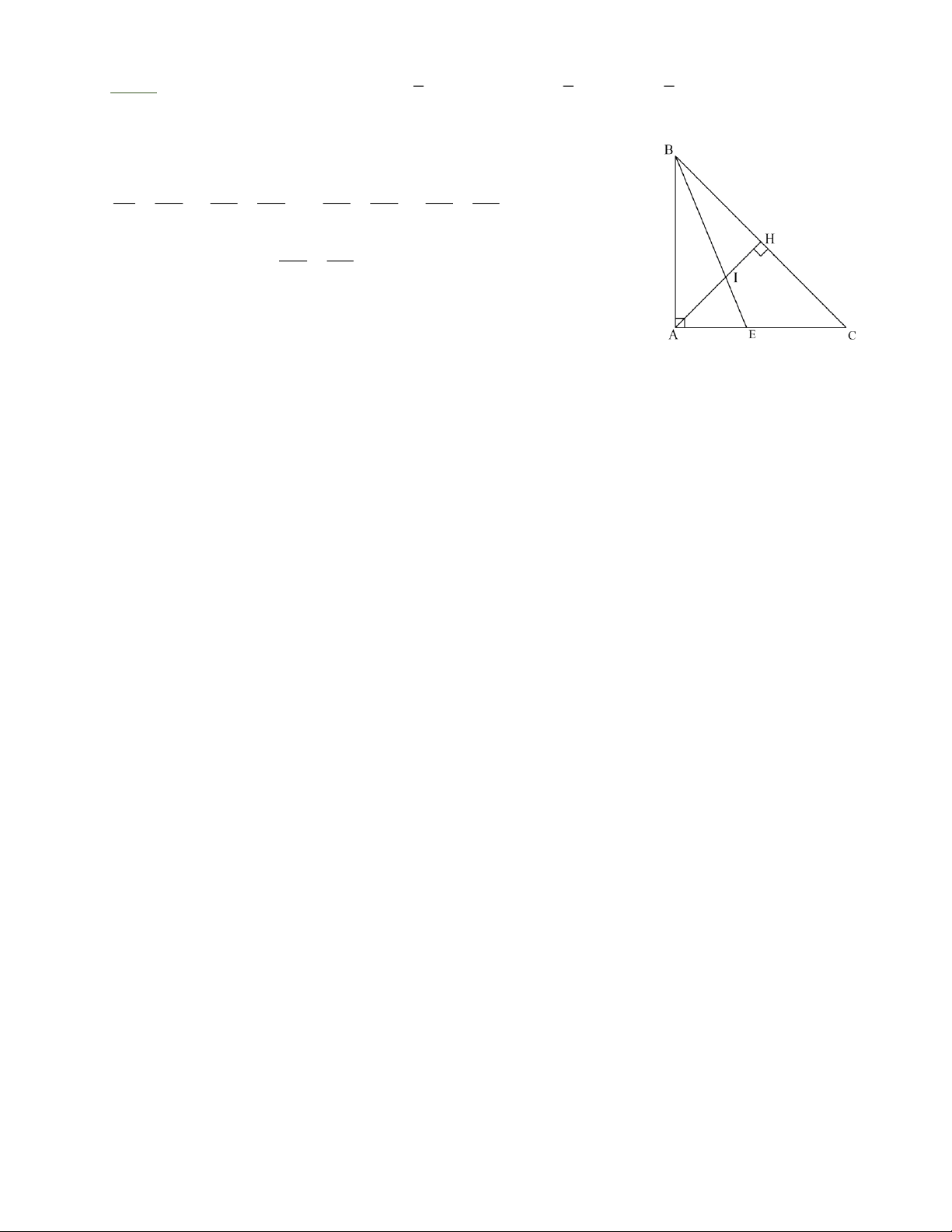
Bài 8: Cho ∆ABC vuông cân tại A. Đường cao AH và đường phân giác BE cắt nhau tại I.
Chứng minh rằng: CE = 2.HI . Tự luyện
Bài 1: Cho tam giác ABC , đường phân giác AD. Biết rằng BC = 10cm và 2AB = 3AC.
Tính độ dài đoạn thẳng BD và CD.
KQ: BD = 6 cm; CD = 4cm.
Bài 2: Gọi AI là đường phân giác của tam giác ABC; IM, IN thứ tự là các đường phân giác
của góc AIC và góc AIB. Chứng minh rằng: A N .BI .CM = BN . IC .A M .
Bài 3: Cho tam giác ABC có chu vi bằng 18cm. Đường phân giác của góc B cắt AC tại M , MA 1 NA 3
đường phân giác của góc C cắt AB tại N. Biết rằng = ; = , tính độ dài các MC 2 NC 4 cạnh của tam giác ABC.
KQ: AB = 4cm; AC = 6cm, BC = 8 cm.
Bài 4: Cho tam giác ABC vuông tại A, AB = 6cm,AC = 8cm, đường phân giác BD.
a) Tính các độ dài DA, DC. 0
b) Tia phân giác của C cắt BD ở I. Gọi M là trung điểm của BC. Chứng minh BIM = 90
KẾT QUẢ - ĐÁP SỐ Bài 1: Trang 2 Hình 1 Hình 2 MB A B
a) Xét ΔABC có AM là đường phân giác trong nên: = MC A C 15 24 3 15.4 Hay = = Þ x = = 20( cm ) x 32 4 3 DB AB
b) Xét ΔABC có AD là đường phân giác ngoài nên: = (1) DC AC DB 1
Mà 𝐵 là trung điểm của đoạn thẳng DC nên: = (2) DC 2 1 y Từ (1) và (2) suy ra: =  y = ( 8 cm) 2 16 A D BA 2 A D CD
Bài 2: a) Theo tính chất đường phân giác: = =  = = 1. DC BC 3 2 3
Do đó, A D = 2cm,CD = 3cm . A
b) Ta có: Theo tính chất đường phân giác: A E CA 5 A E EB 4 = =  = = . EB CB 6 5 6 11 E D I 20 24 Do đó, A E = cm, BE = cm. 11 11 B C BM A B
Bài 3: A M là phân giác của A nên = . CM A C BN BC
CN là phân giác của C nên = . A N A C
Lại có: A B = BC . A B BC BN BM Suy ra: =  =
 MN // A C . A C A C A N CM Trang 3
Bài 4: Xét ΔABC , áp dụng tính chất đường phân giác ta có: AE AB = (1) EC BC CD AC = (2) DB AB BF BC = (3) FA AC
Nhân (1), (2), (3) theo vế ta được: AE CD BF AB AC BC . . = . . =1. EC DB FA BC AB AC
Bài 5: Gọi O là giao điểm của BD và AC. AB BM
Xét tam giác ABD, phân giác AM, ta có: = AD DM CD CN Tương tự, = ; AD AN BM CN
Mà A B = CD , suy ra = DM AN Từ đó, ta có: BM + CN BD CA DO AO 1 = +1  =  = DM AN DM AN DM AN
Suy ra MN / / A D.
Bài 6: a) Vẽ đường cao AH của ABC .Vì ΔABC có phân giác AD nên: 1 BD A B m .A H .BD S BD m = = . Vậy DABD 2 = = = CD A C n S 1 CD n DA CD .A H .CD 2 A F A D b) Ta có: = (do DF là phân giác ADC ) CF CD BE BD = (do DE là phân giác ADB ) A E A D A F CD BE A D CD BD Þ . . = . . = 1 CF BD A E CD BD A D
Þ A F .CD.BE = A E .BD.CF Bài 7: a) Ta có Trang 4 BD MB =
(do MD là phân giác của AMB ) AD MA CE MC =
(do ME là phân giác của AMC ) AE MA
Mà MB = MC ( M là trung điểm của BC ) BD CE  =  DE / /BC AD AE
b) Xét ABM và ACM lần lượt có DI / /BM và EI / /CM . DI EI  AI  = =   Mà BM = CM  DI = EI BM CM  AM  BD MB BD IM BM IM c) Ta có: = . Mà = (do DI / /BM )  = AD MA AD AI AM AI BM AM Ta lại có: = ( do DI / /BM ) DI AI BM A I + IM IM BM A M + BM = = 1 + = 1 + = DI A I A I A M A M BM .A M 15.10 150 Þ DI = = = = 6 A M + BM 10 + 15 25 1
Þ ED = 2DI = 2.6 = 12 (do DI = IE = DE ) 2
d) Để DE = AM ta cần tứ giác ADME là hình chữ nhật Hay 0 DM / /AE,EM / /AD,BAC = 90 Khi 0
BAC = 90 thì AM = MB = MC (đường trung tuyến ứng với cạnh huyền BC )  A  BM, A  CM cân tại M
 MD ⊥ AB,ME ⊥ AC (đường phân giác của tam giác cân đồng thời là đường cao
Mà AB ⊥ AC . Suy ra DM / /AE, EM / /AD . Suy ra tứ giác ADME là hình chữ nhật
Vậy ABC vuông tại A thì DE = AM .
e) Khi DM = EM thì DME cân tại M có MI là trung tuyến ( DI = IE ) nên đồng thời là đường cao  MI ⊥ DE
Mà DE / /BC (cmt) nên MI ⊥ BC
ABC có AI vừa là đường trung tuyến vừa là đường cao nên là tam giác cân. Trang 5 · · · 1 µ µ 1 µ 1 µ ·
Bài 8: Ta có AIE = BAH + ABI = (A + B) = 45° + B = 45° + C = AEI . 2 2 2
Suy ra ∆AIE cân tại A  A I = A E (1).
Áp dụng tính chất đường phân giác của ∆ABH và ∆BAC ta có: IH BH AB BH =  = EC BC AB BC (2); =  = (3) IA BA AI IH EA BA AE EC BH BC Từ (2) và (3) suy ra: = (4) IH EC
Vì ∆ABC vuông cân tại A nên BC = 2.BH
Từ đó kết hợp với (4) suy ra EC = 2.IH . Trang 6