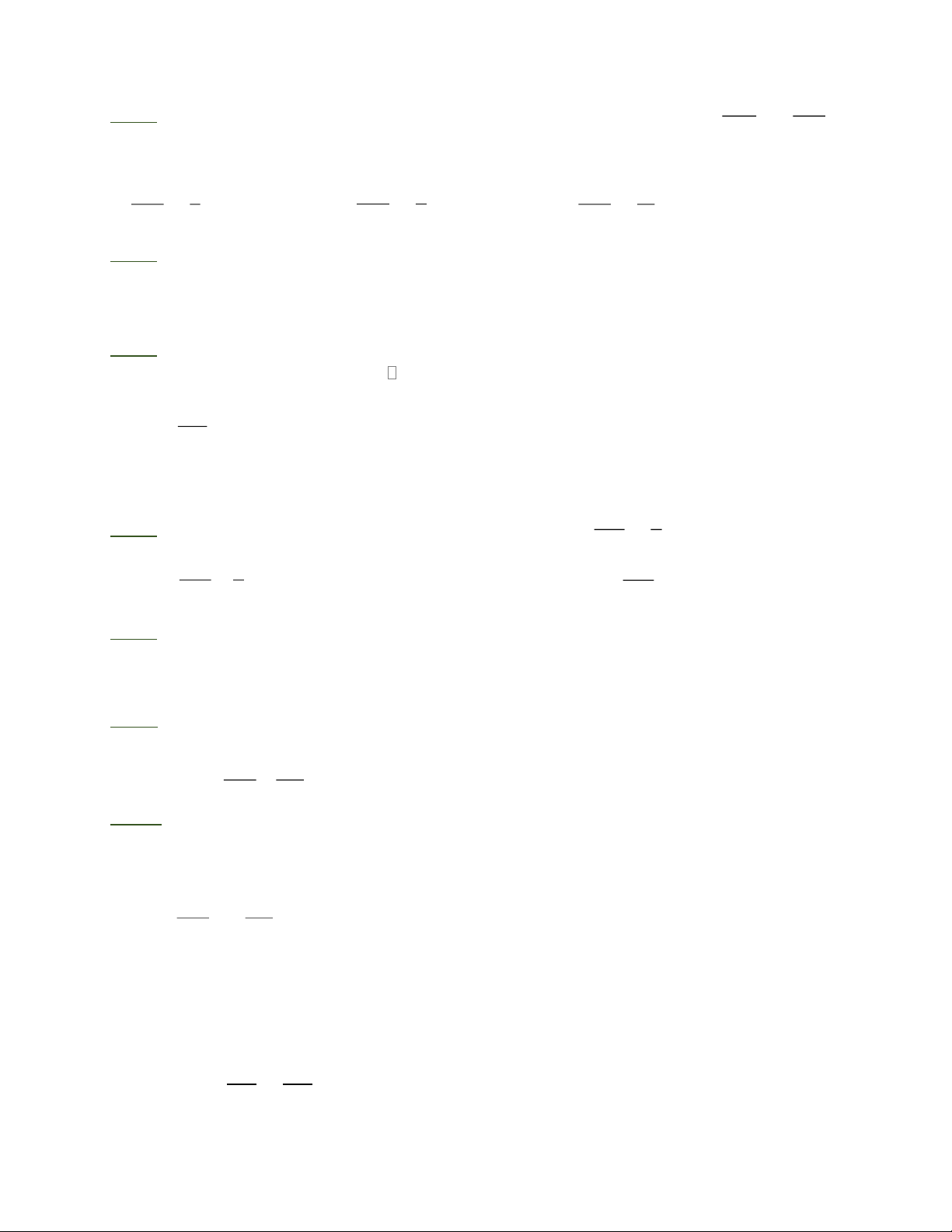

Preview text:
1. ĐỊNH LÍ TALET TRONG TAM GIÁC
I. KIẾN THỨC CƠ BẢN
1. Đoạn thẳng tỉ lệ A B A ' B '
Hai đoạn thẳng AB và CD gọi là tỉ lệ với hai đoạn thẳng A 'B' và C' D ' nếu = CD C ' D ' A B CD (hoặc = ). A ' B ' C ' D '
2. Định lý Ta – lét
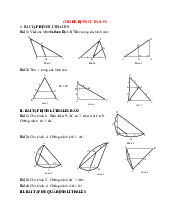
Nếu một đường thẳng song song với một cạnh của tam giác và cắt hai cạnh còn lại thì
đường thẳng định ra trên hai cạnh đó những đoạn thẳng tương ứng tỉ lệ.
D A B C : DE / / BC GT
(D Î AB,E Î AC) A D A E = A B A C A D A E KL = DB EC DB EC = A B A C
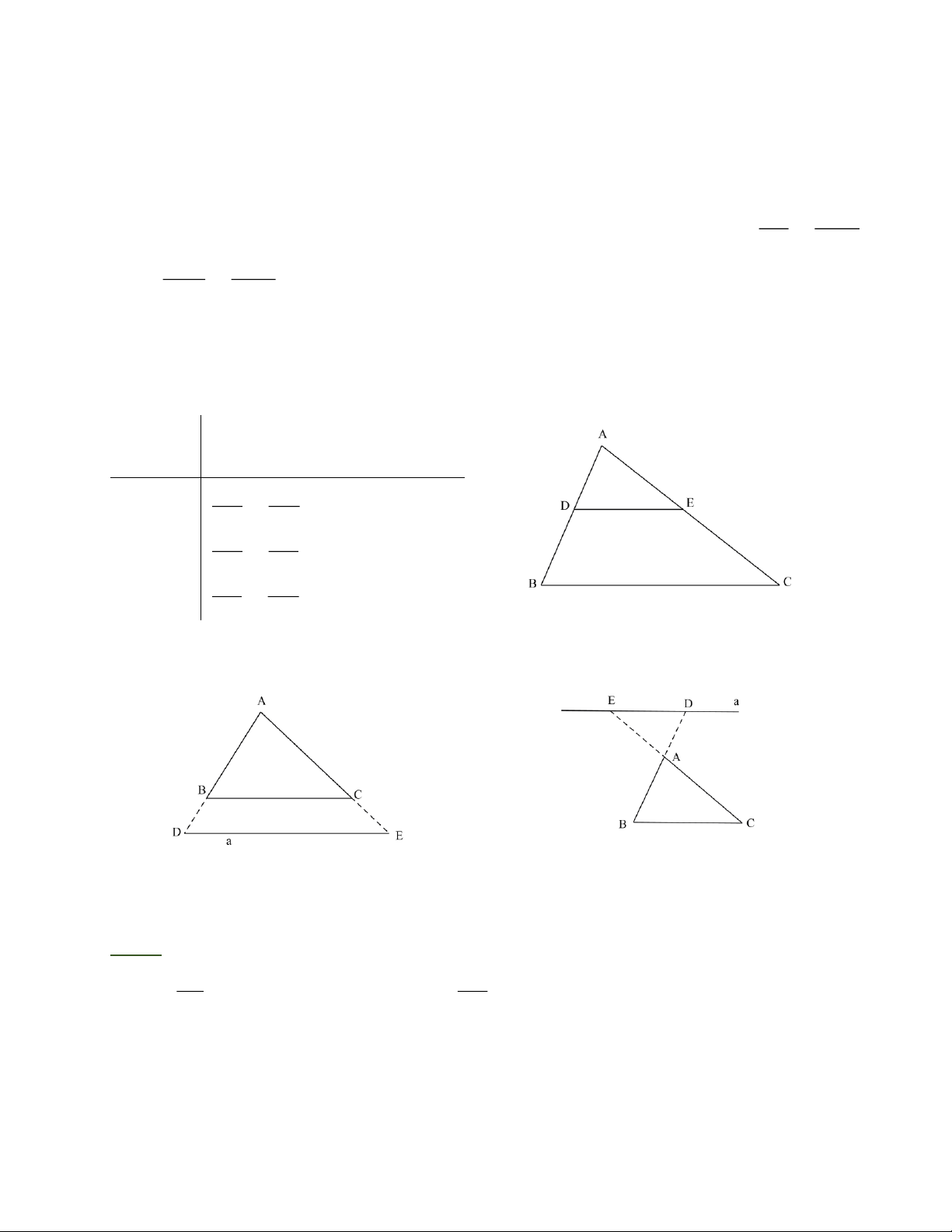
Chú ý: Định lý Ta – lét vẫn đúng trong trường hợp đường thẳng song song với một cạnh
của tam giác và cắt phần kéo dài của hai cạnh còn lại. III. BÀI TẬP
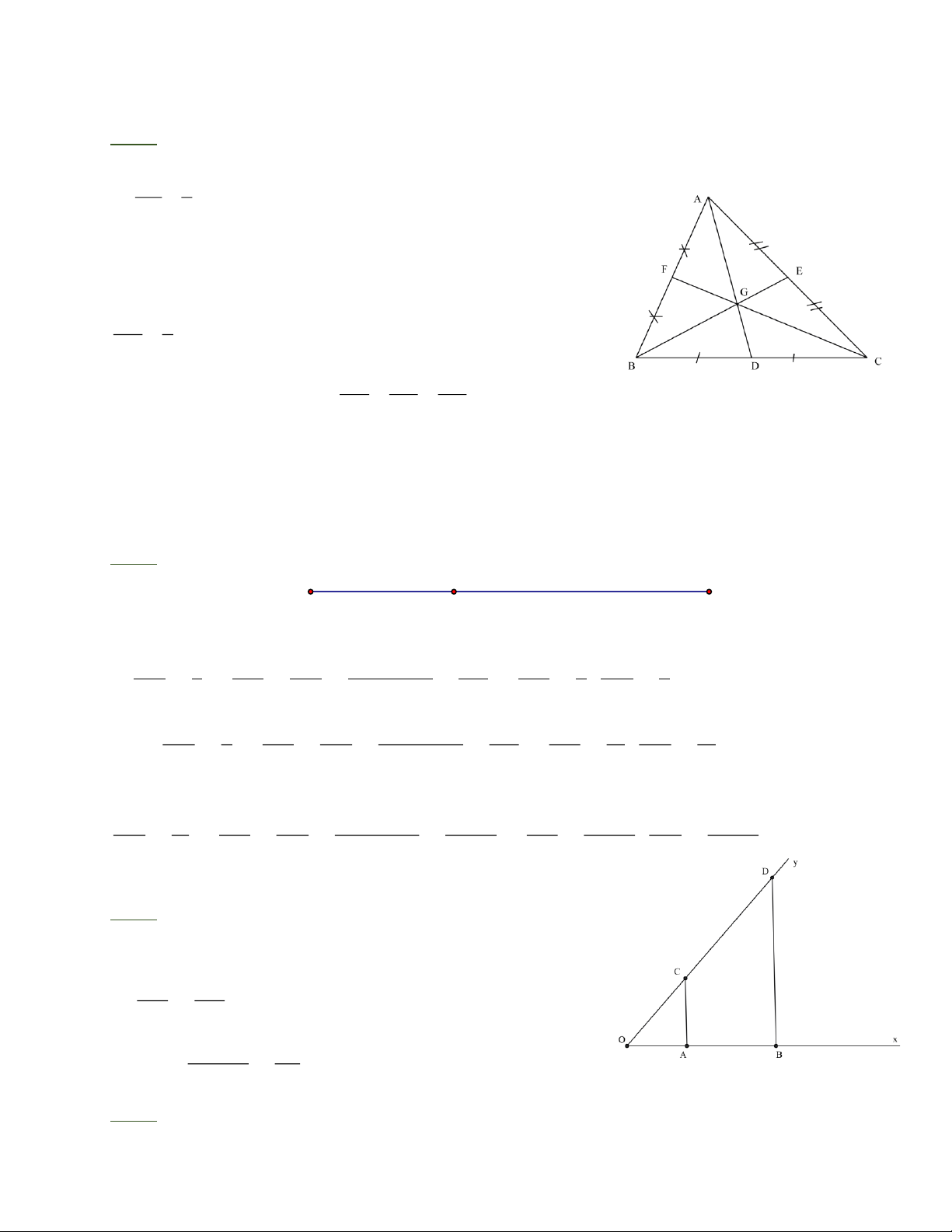
Bài 1: Cho tam giác ABC , các trung tuyến A D, BE ,CF cắt nhau tại G . AE AG a) Tính b) Tính AC GD
b) Kể hai cặp đoạn thẳng tỉ lệ với AG và GD . Trang 1 A M MB
Bài 2: Cho đoạn thẳng AM , M là một điểm trên đoạn AB . Tính các tỉ số và A B A B nếu: MA 1 MA 7 MA m a) = b) = c) = MB 2 MB 4 MB n
Bài 3: Cho góc xOy . Trên tia Ox , lấy theo thứ tự 2 điểm A, B sao cho
OA = 2cm, AB = 3cm. Trên tia Oy , lấy điểm C với OC = 3cm . Từ B , kẻ đường thẳng song
song với AC cắt Oy tại D . Tính độ dài CD .
Bài 4: Cho tam giác ACE có AC = 11cm. Lấy điểm B trên cạnh AC sao cho BC = 6cm . Lấy
điểm D trên cạnh AE sao cho DB EC . Giả sử AE + ED = 25,5cm . Hãy tính: DE a) Tỉ số ; AE
b) Độ dài các đoạn thẳng AE,DE và AD. BD 3
Bài 5: Cho tam giác ABC và điểm D trên cạnh BC sao cho = , điểm E trên đoạn AD BC 4 AE 1 A K sao cho
= . Gọi K là giao điểm của BE và AC. Tính tỉ số . AD 3 KC
Bài 6: Cho tam giác ABC có AM là trung tuyến và điểm E thuộc đoạn thẳng MC. Qua E kẻ
đường thẳng song song với AC, cắt AB ở D và cắt AM ở K. Qua E kẻ đường thẳng song
song với AB, cắt AC ở F. Chứng minh CF = DK.
Bài 7: Cho ABC . Từ D trên cạnh AB , kẻ đường thẳng song song với BC cắt AC tại E .
Trên tia đối của tia CA , lấy điểm F sao cho CF = DB. Gọi M là giao điểm của DF và BC . DM AC Chứng minh = MF AB
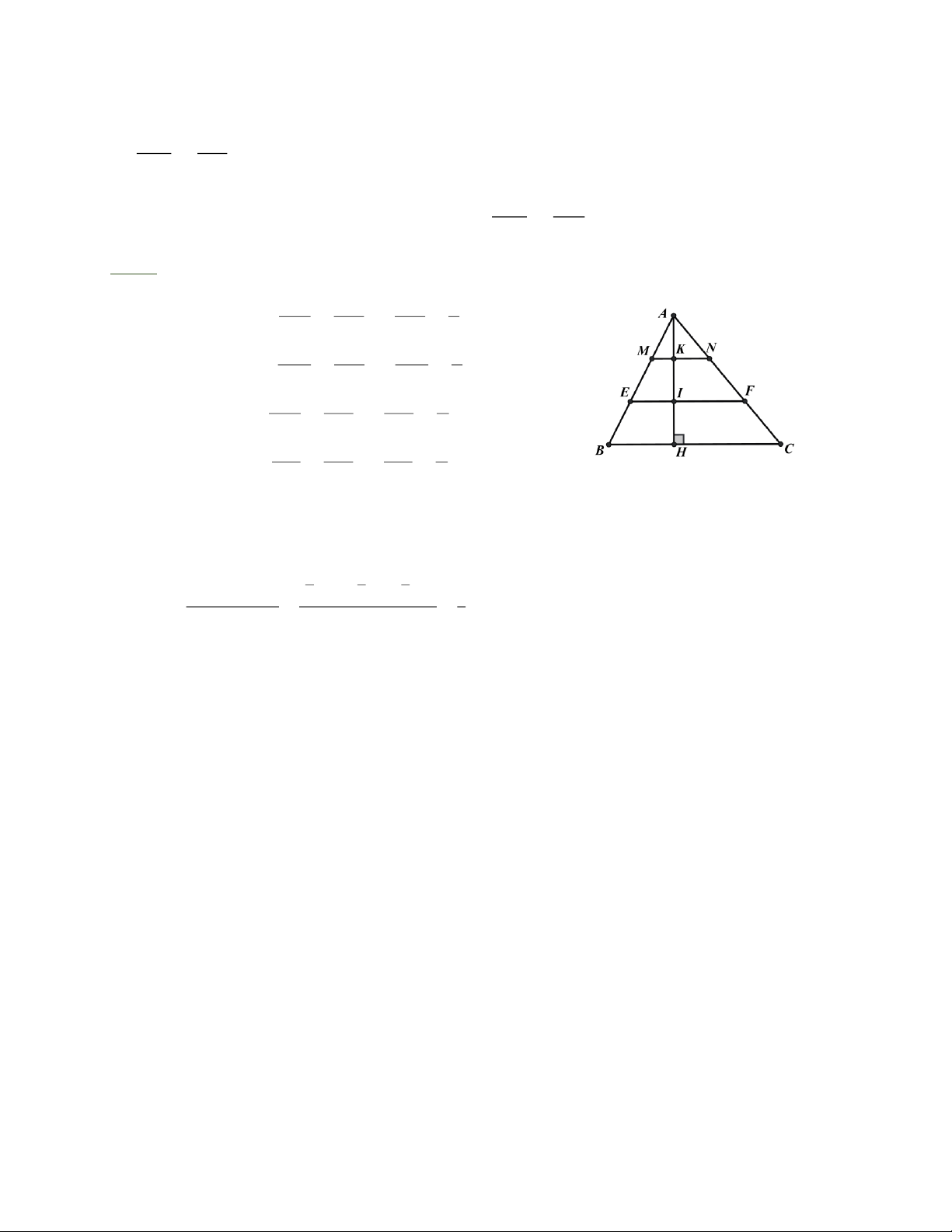
Bài 8: Cho tam giác ABC có đường cao AH. Trên AH, lấy các điểm K, I sao cho
A K = KI = IH . Qua I, K lần lượt vẽ các đường thẳng EF / / BC , MN / / BC ( E, M AB, F, N AC). MN EF a) Tính và . BC BC
b) Cho biết diện tích của tam giác ABC là 90 cm2. Tính diện tích tứ giác MNFE . Tự luyện:
Bài 1: Cho 5 điểm A, B, C, D, E theo thứ tự trên một đường thẳng. Biết AB = 6cm, BC = 9cm A B CD CD = 4cm và = . Tính AE. BC DE Trang 2 A B CB 2
Bài 2: Cho 4 điểm A, B, C, D theo thứ tự trên một đường thẳng và = = . A D CD 3
a) Nếu BD = 10cm , tính CB; DA. 3A B + 2A D
b) Chứng minh rằng A C = 5
c) Gọi O là trung điểm của BD . Chứng minh rằng 2
OB = OA.OC DB 1
Bài 3: Cho ABC có AB = 7,5cm . Trên AB lấy điểm D với = DA 2
a) Tính DA, DB . DH
b) Gọi DH, BK lần lượt là khoảng cách từ D, B đến cạnh AC . Tính . BK
c) Cho biết A K = 4, 5cm . Tính HK.
Bài 4: Cho hình bình hành ABCD. Gọi E là một điểm bất kỳ trên cạnh AB. Qua E kẻ đường
thẳng song song với AC cắt BC ở F và kẻ đường thẳng song song với BD cắt AD ở H.
Đường thẳng kẻ qua F song song với BD cắt CD ở G. Chứng minh AH.CD = AD.CG. AH AE CF CG HD: = = = AD AB CB CD
Bài 5: Cho ABC có AD là đường trung tuyến, G là trọng tâm. Qua G kẻ đường thẳng d
cắt AB, AC thứ tự tại M , N. Chứng minh: AB AC BM CN a) + = 3;; b) + = 1.; AM AN AM AN
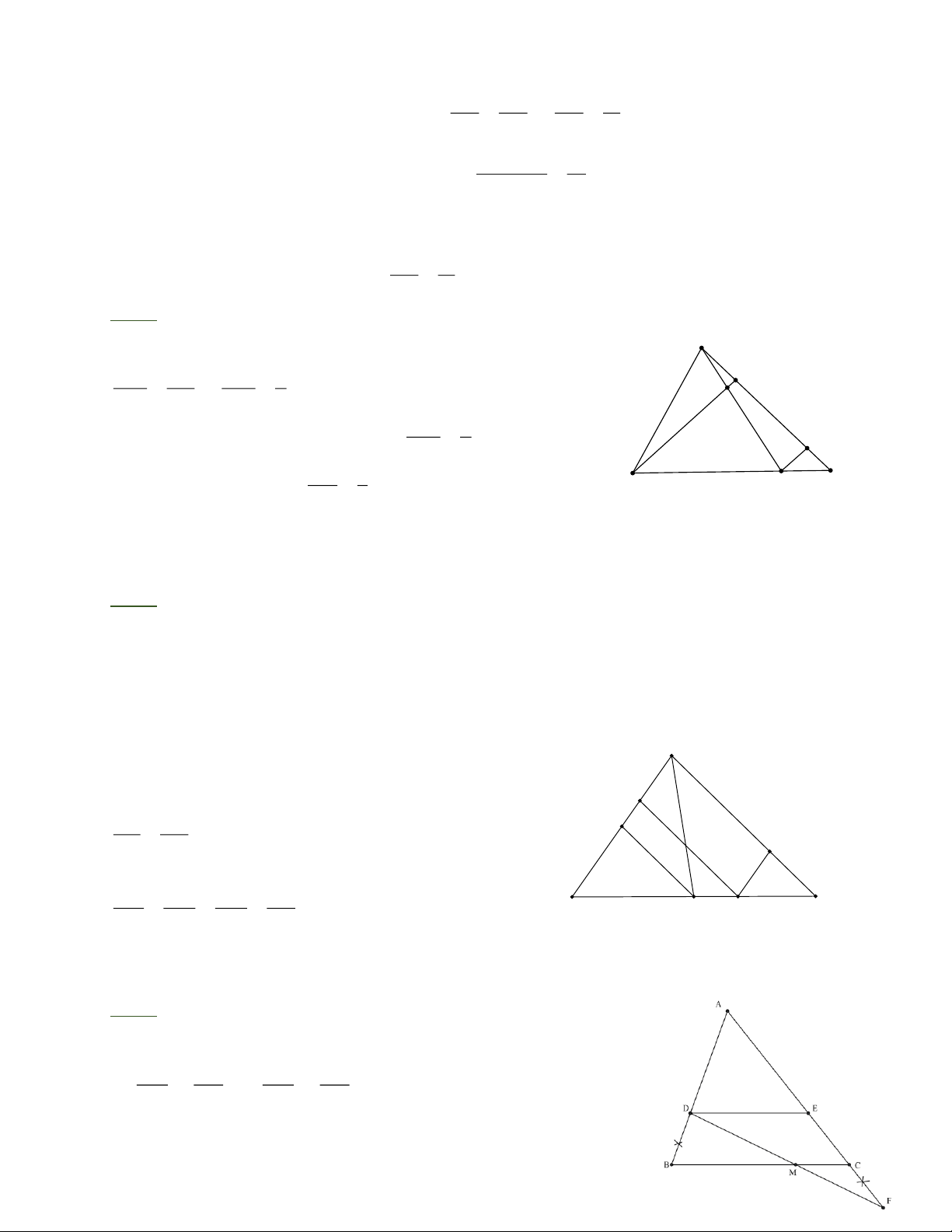
Bài 6: Cho tam giác ABC ( AB AC ) , đường phân giác AD . Qua điểm M là trung điểm
của BC kẻ đường thẳng song song với AD , cắt AB và AC lần lượt tại E và K . Chứng minh: a) AE = AK . b) BE = CK . Trang 3
KẾT QUẢ - ĐÁP SỐ Bài 1:
a) Có E là trung điểm của AC (vì BE là trung tuyến) AE 1
= (tính chất trung điểm của đoạn thẳng) AC 2
b) ABC có các trung tuyến AD, BE, CF cắt nhau tại G G là trọng tâm ABC AG 2
= = 2 ( G là trọng tâm ABC ) GD 1 AG BG CG
c) G là trọng tâm ABC = = GD GE GF
BG và GE là cặp đoạn thẳng tỉ lệ với AG và GD .
CG và GF là cặp đoạn thẳng tỉ lệ với AG và GD . Bài 2: B A M MA 1 MA MB MA + MB A B MA 1 MB 2 a) = Þ = = = Þ = ; = MB 2 1 2 1 + 2 3 A B 3 A B 3 MA 7 MA MB MA + MB A B MA 7 MB 4 b) Có = Þ = = = Þ = ; = MB 4 7 4 7 + 4 11 A B 11 A B 11 c) MA m MA MB MA + MB A B MA m MB n = Þ = = = Þ = ; = MB n m n m + n m + n A B m + n A B m + n Bài 3:
Xét OBD có: AC / /BD (gt) A O OC Þ =
(định lí Ta-let trong tam giác) A B CD A B.OC 3.3 Þ CD = = = 4, 5(cm ) OA 2 Bài 4: Trang 4 DE BC DE 6
a) Theo định lý Ta-lét trong ACE , ta có: = = . AE AC AE 11 DE + AE 17
b) Cách 1. Theo tính chất của tỉ lệ thức ta có: = AE 11
Từ đó tính được AE = 16,5cm; DE = 9cm và AD = 7,5cm .
Cách 2. Áp dụng tính chất của dãy tỉ số bằng nhau DE 6
Cách 3. Thay DE = 25,5 − AE vào = AE 11
Bài 5: Kẻ DM / /BK (M AC) A
Áp dụng định lý Ta-lét trong CBK , ta có: KM BD KM 3 K = = (1) E KC BC KC 4 AK 1
Tương tự với ADM ADM , ta có: = (2) M KM 2 AK 3 C
Từ (1) và (2), tìm được: = B D KC 8
Bài 6: Cho tam giác ABC có AM là trung tuyến và điểm E thuộc đoạn thẳng MC. Qua E kẻ
đường thẳng song song với AC, cắt AB ở D và cắt AM ở K. Qua E kẻ đường thẳng song
song với AB, cắt AC ở F. Chứng minh CF = DK. Hướng dẫn giải
Chứng minh được ADEF là hình bình hành, từ đó:
EF = A D (1) A
Kẻ MG / / A C (G AB), ta được G là trung điểm
của AB. Áp dụng định lý Ta-lét trong ABC , ta có: D CF G = AC (2) EF AB F
Tương tự với AGM và ABC , ta có:
DK = MG = MG = AC (3) B C M E AD AG BG AB
Từ (1), (2), (3) ta suy ra CF = DK Bài 7: Xét ABC có: DE / /BC A C A B A C EC Þ = hay =
(định lí Ta-let trong tam giác) ( ) 1 EC BD A B BD Trang 5
Xét DEF có: DE / /MC (vì DE / /BC ) DM EC Þ =
(định lí Ta-let trong tam giác) (2) MF CF DM A C
Mà CF = DB (gt) (3) nên từ ( ) 1 , (2) và (3) = MF A B Bài 8: AK AN AN 1
a) +) NK / / CH = = AH AC AC 3 MN AN MN 1 MN / / BC = = BC AC BC 3 AI AF AF 2
+) IF / / CH = = AH AC AC 3 EF AF EF 2 EF / / BC = = BC AC BC 3
b) MNFE có MN / / FE và KI ⊥ MN . Do đó MNEF là hình thang có 2 đáy MN, FE, chiều cao KI. 1 æ 2 ö ç ÷ 1 ç BC + BC . ÷ A H (MN+ FE). KI çè3 3 ÷÷ø 3 1 2 Þ S = = = .S = 30(cm ) MNEF 2 2 3 ABC Trang 6