Bài Tập Hình 8 Bài Đường Trung Bình Của Tam Giác Có Lời Giải

3. ĐƯỜNG TRUNG BÌNH CỦA TAM GIÁC
I. KIẾN THỨC CƠ BẢN
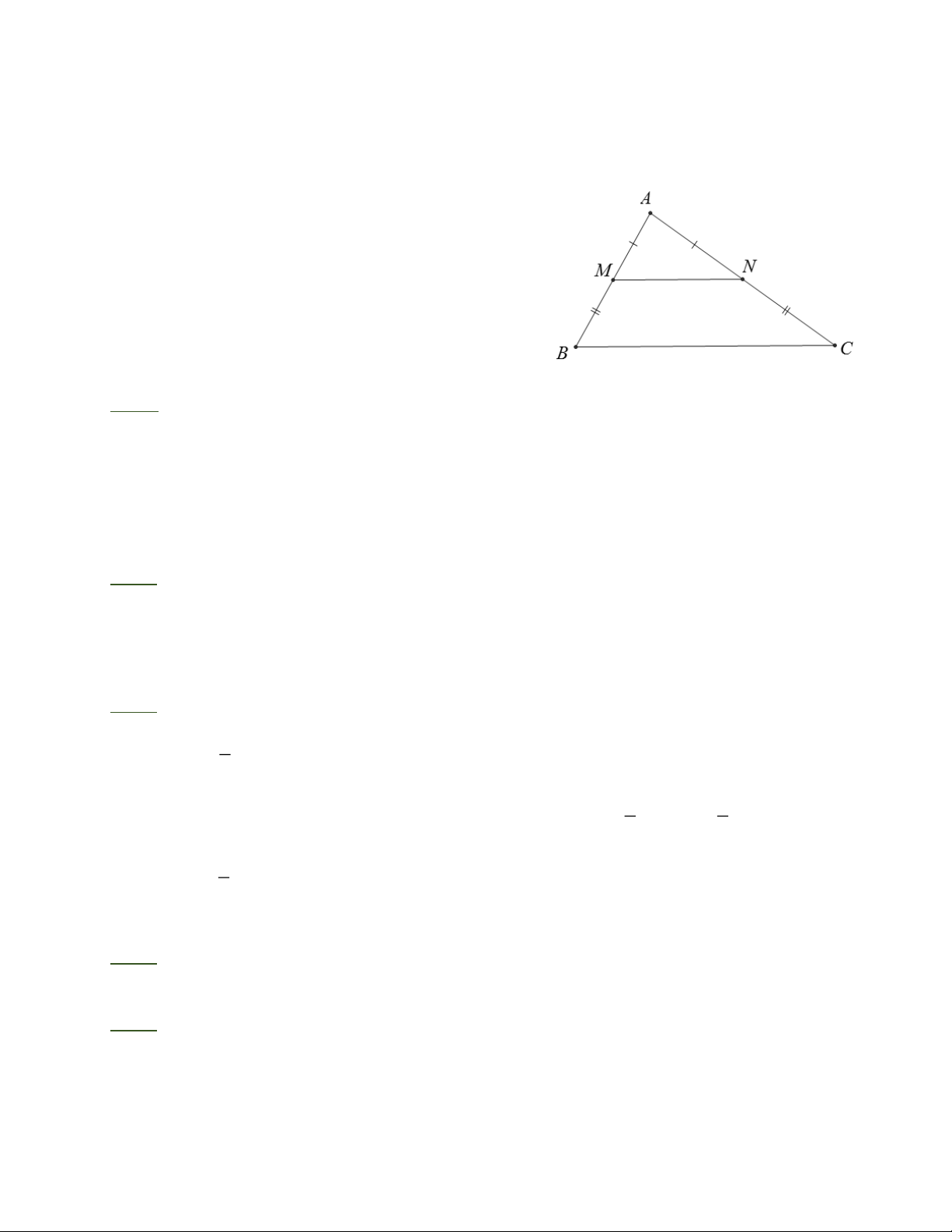
Định nghĩa: Đường trung bình của tam giác là đoạn thẳng nối trung điểm hai cạnh của tam giác.
Định lí 1: Đường thẳng đi qua trung điểm của một
cạnh của tam giác và song song với cạnh thứ hai thì
đi qua trung điểm của cạnh thứ ba.
Định lí 2: Đường trung bình của tam giác thì song
song với cạnh thứ ba và bằng nửa cạnh ấy. III. BÀI TẬP
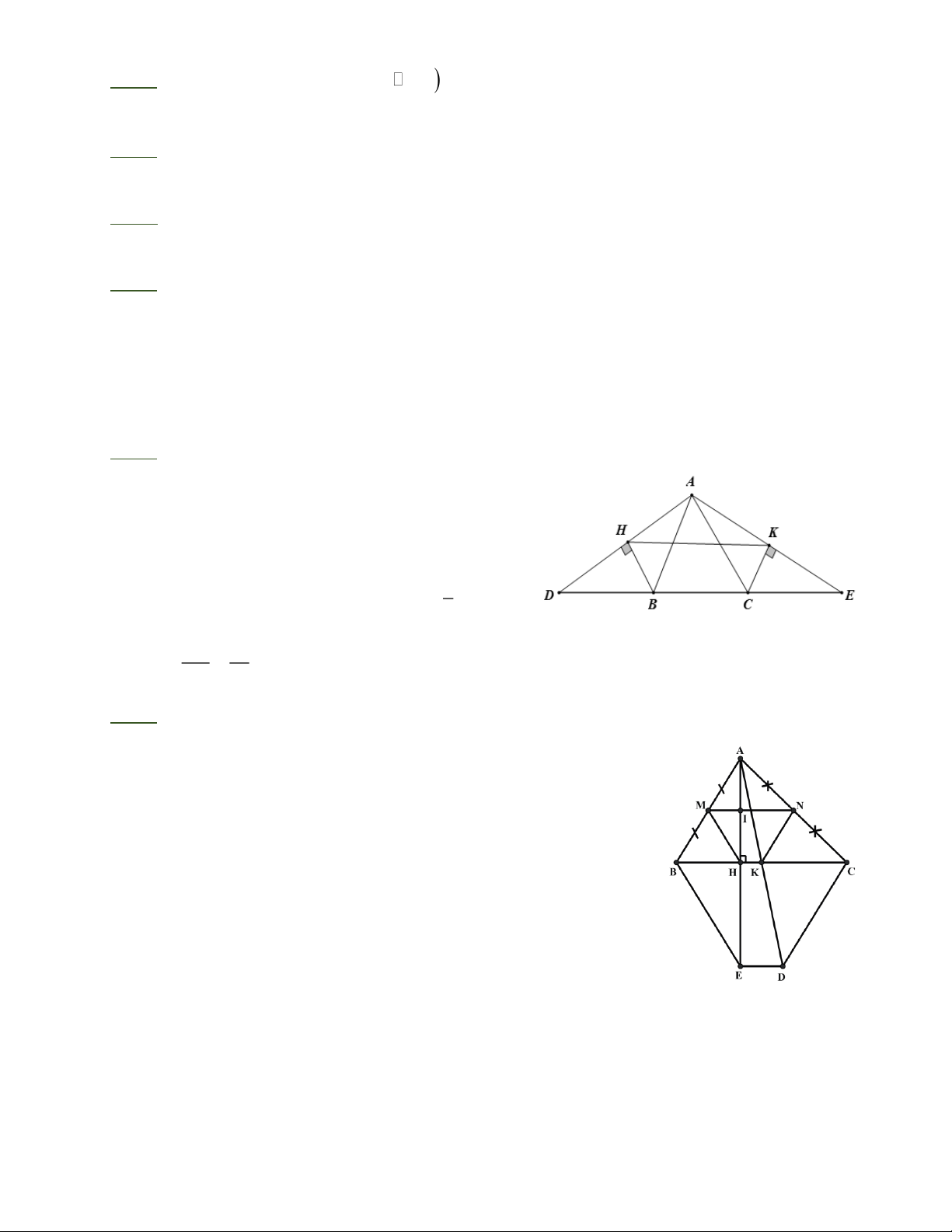
Bài 1: Cho tam giác ABC. Trên tia đối của tia BC lấy điểm D sao cho BD = AB . Trên tia
đối của tia CD lấy điểm E sao cho CE = AC . Gọi H là chân đường vuông góc kẻ từ D đến
AD, K là chân đường vuông góc kẻ từ C đến AE.
a) Chứng minh rằng HK song song với DE.
b) Tính HK, biết chu vi tam giác ABC bằng 10.
Bài 2: Cho ABC có AB  AC, AH là đường cao. Gọi M, N, K lần lượt là trung điểm của AB, AC, BC.
a) Chứng minh MNKH là hình thang cân.
b) Trên tia AH và AK lần lượt lấy điểm E và D sao cho H là trung điểm của AE và K là
trung điểm của AD. Chứng minh tứ giác BCDE là hình thang cân.
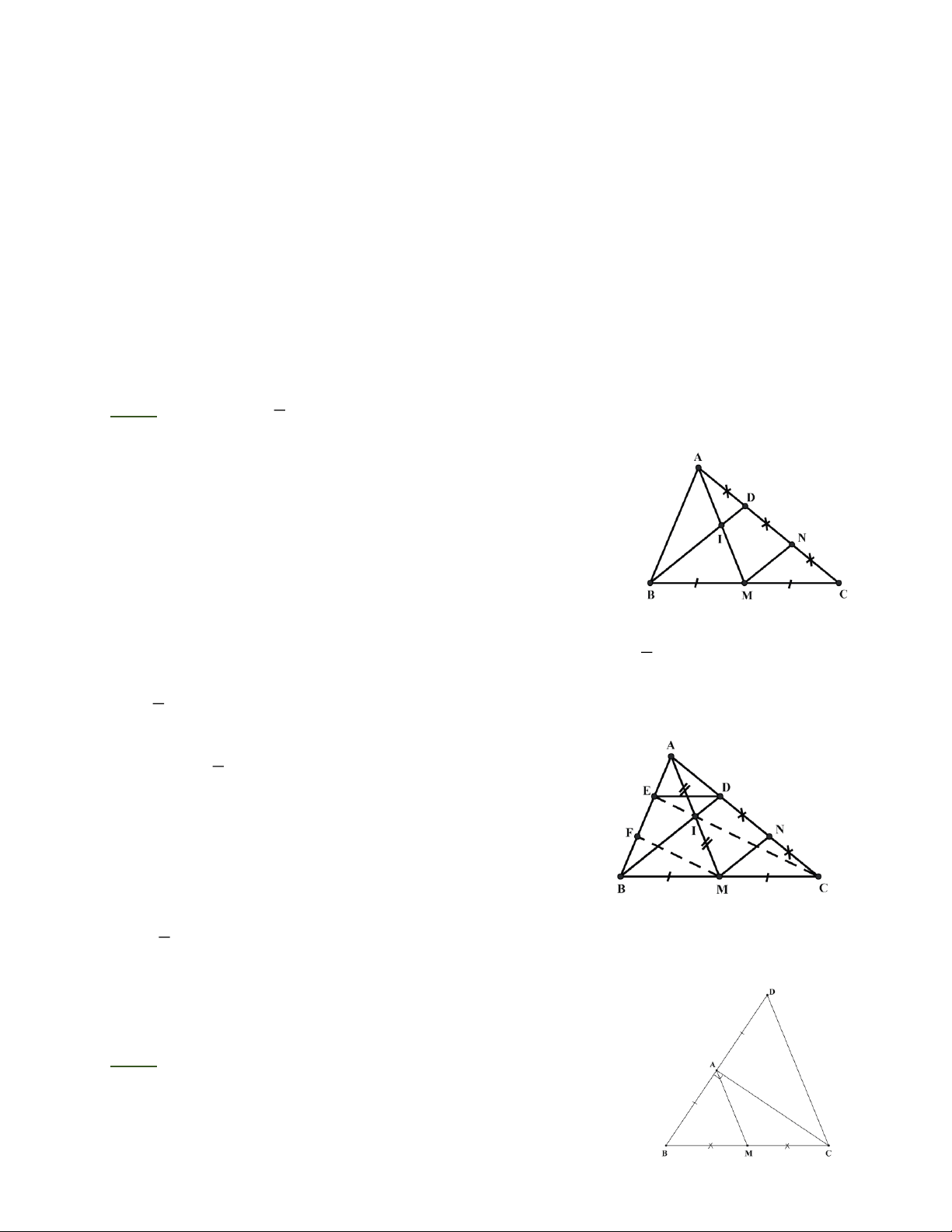
Bài 3: Cho ABC có trung tuyến AM, I là một điểm thuộc đoạn thẳng AM, BI cắt AC ở D. 1 a) Nếu AD =
DC. Khi đó hãy chứng minh I là trung điểm của AM. 2 1 1
b) Nếu I là trung điểm của AM. Khi đó hãy chứng minh AD =
DC, ID = B . D 2 4 1 c) Nếu AD =
DC. Khi đó trên cạnh AB lấy điểm E sao cho AB = 3AE. Chứng minh BD, 2 CE, AM đồng quy.
Bài 4: Dùng tính chất đường trung bình của tam giác chứng minh trong tam giác vuông
đường trung tuyến ứng với cạnh huyền bằng nửa cạnh huyền.
Bài 5: Cho tứ giác ABCD có AB = CD. Gọi E, F lần lượt là trung điểm của AC, DB. Đường
thẳng EF lần lượt cắt AB, CD tại H,K. Chứng minh rằng: KHB = HKC Trang 1
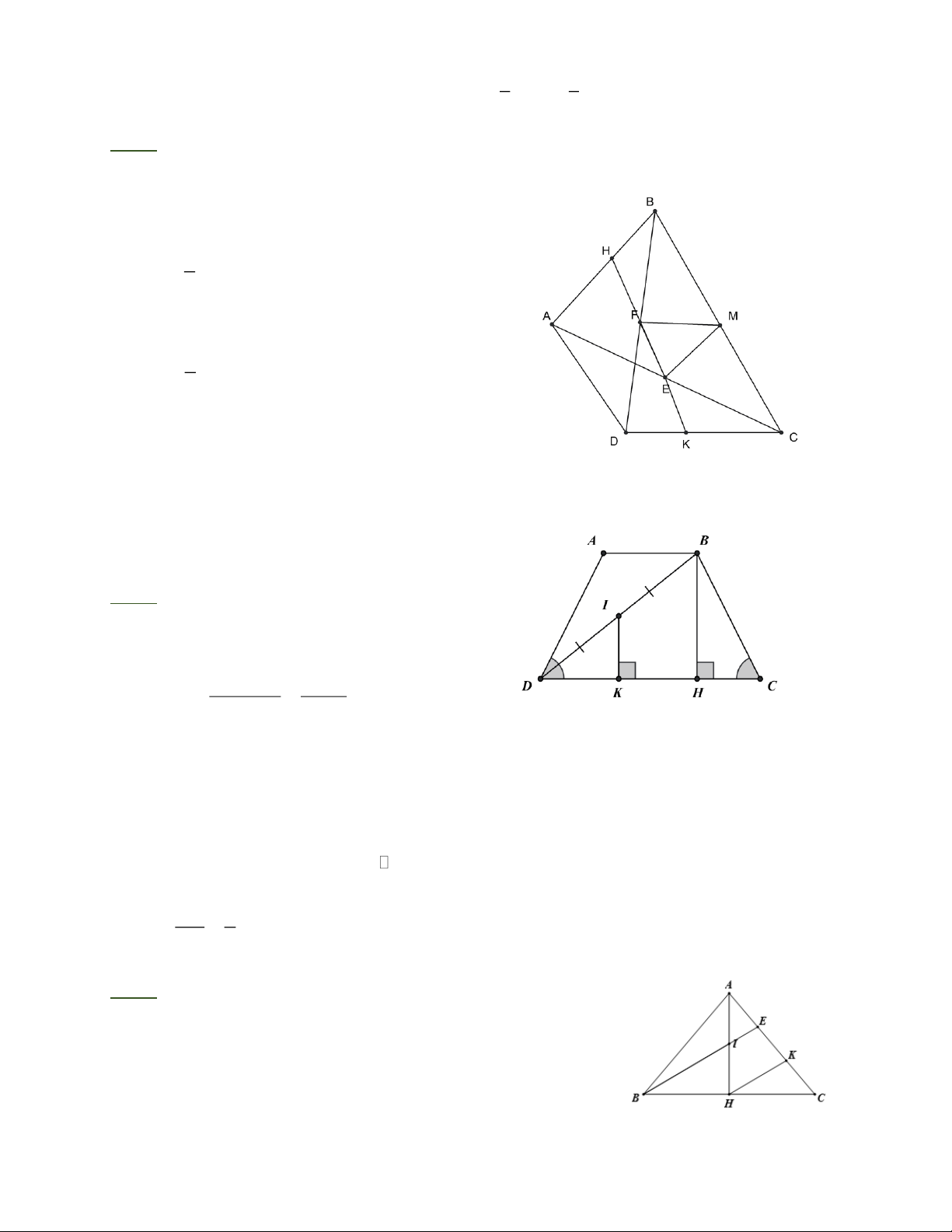
Bài 6: Hình thang cân ABCD(AB CD) có AB = 4 cm, CD = 10 cm, BD = 5 cm. Tính
khoảng cách từ trung điểm I của BD đến cạnh CD.
Bài 7: Cho tam giác ABC cân tại A, đường cao AH. Gọi I là trung điểm của AH, E là giao
điểm của BI và AC. Tính các độ dài AE và EC, biết AH = 12 cm, BC = 18 cm.
Bài 8: Cho tam giác ABC vuông tại A, đường cao AH. Gọi M là trung điểm của HC, K là
trung điểm của AH. Chứng minh rằng BK vuông góc với AM.
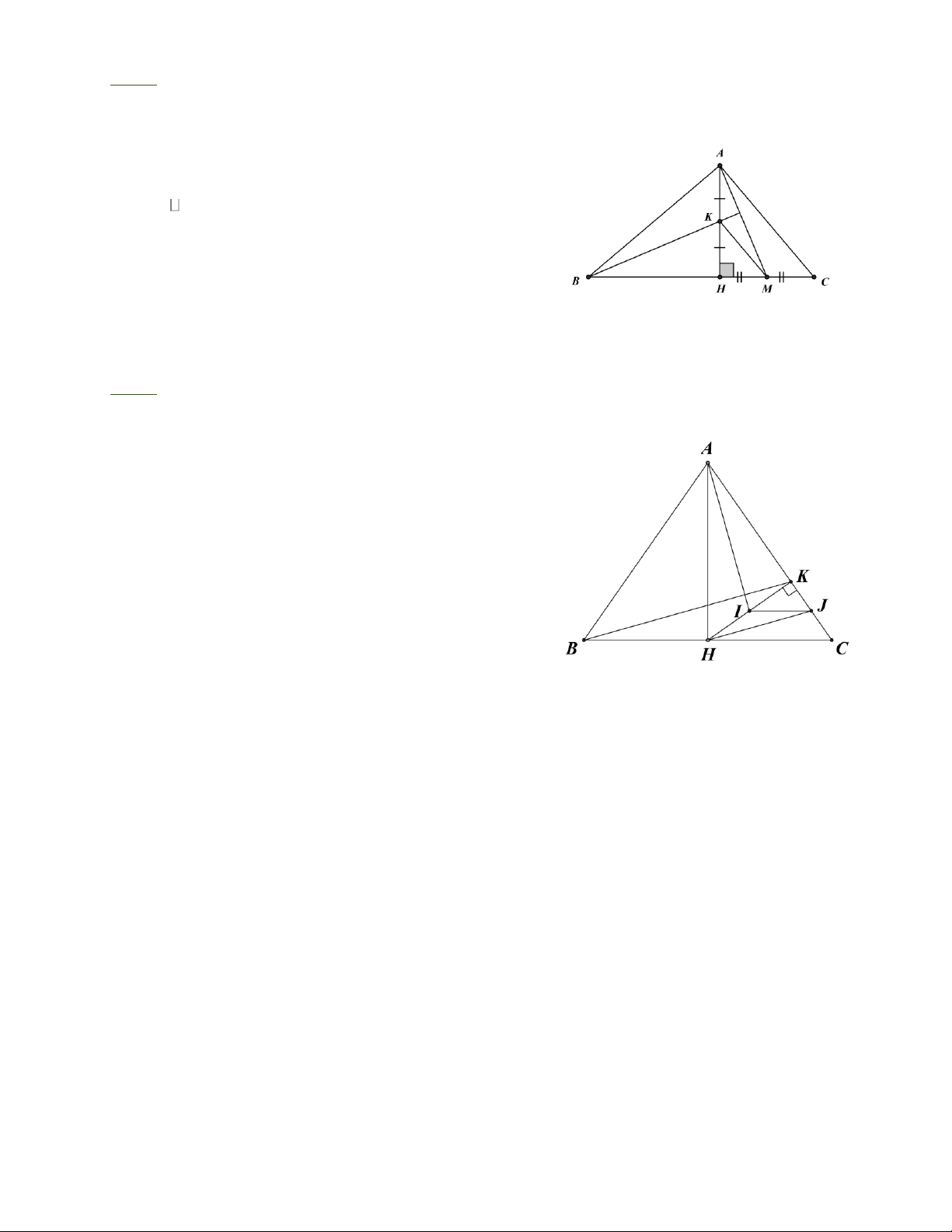
Bài 9: Cho tam giác ABC cân tại A, đường cao AH. Gọi K là hình chiếu vuông góc của H
lên AC. Gọi I là trung điểm HK. Chứng minh rằng: AI ^ BK
KẾT QUẢ - ĐÁP SỐ Bài 1:
a) D A B D cân tại B, đường cao BH nên BH đồng
thời là đường trung tuyến nên A H = HD
Tương tự A K = K E nên HK là đường trung 1
bình của D A DE nên HK / / DE ; HK = DE 2 DE 10 b) HK = =
= 5(cm) (vì DE = DB + BC + CF = AB + BC + CA = 10 cm ) 2 2 Bài 2:
a) MN là đường trung bình của D A B C Þ MN / / BC
Þ MN / / HK , hayMI / / BH
MI / / BH và MA = MB Þ IA = IH D MA H · ·
cân tại A nên HMI = IMA (1)
NK là đường trung bình của D A B C Þ NK / / AB · ·
Þ MNK = IMA (hai góc ở vị tri so le trong) (2) · ·
Từ (1) và (2) suy ra HMI = MNK (so le trong) hay · · HMN = MNK · ·
Tứ giác MNHK có MN / / HK nên tứ giác là hình thang, lại có HMN = MNK là hình thang cân. Trang 2
b) HK là đường trung bình của AED
 HK //ED hay BC//ED nên tứ giác BCDE là hình thang.
NK là đường trung bình của ACD  NK //CD mà NK / / AB nên A B / / CD
 ABH = BCD (so le trong) (3)
Dễ thấy ABE cân tại B vì BH vừa là đường cao vừa là trung tuyến
 BH là phân giác của ABE  ABH = HBE (4)
Từ (3), (4)  HBE = BCD hay  CBE = BCD
Hình thang B CDE có CBE = BCD tứ giác BCDE là hình thang cân. 1
Bài 3: a) Khi AD = DC. 2
Gọi N là trung điểm của DC, khi đó MN là đường trung bình
của D B CD Þ MN / / BD Þ MN / / ID
D A MN có MN / / ID và A D = DN Þ A I = IM
b) Khi A I = IM . Kẻ MN / / BD . Xét D A MN ta có ID/ / MN
và A I = IM nên A D = DN . 1
Xét D B CD có MN / / BD;MB = MC nên ND = NC . Vậy AD =
DC, và dễ dàng chỉ ra 2 1 ID = B . D 4 1 c) Khi AD =
DC. AB = 3AE. 2
Ta có I là giao điểm của BD và AM
Gọi F là trung điểm của BE. Ta có MF là đường trung
bình của D BEC Þ FM / / CE 1
AD = DC thì IA = IM (theo câu a) nên EI là đường trung bình của DA FM Þ EI / / FM 2
Có FM / / CE và EI / / FM nên E, I, C thẳng hàng hay EC đi qua điểm I
Bài 4: Trên tia đối của tia AB lấy điểm D sao cho A D = A B .
Khi đó D B CD cân tại C nên BC = CD Trang 3 1 1
AM là đường trung bình của DBCD Þ A M = DC = BC 2 2
Bài 5: E là trung điểm của AC, F là trung điểm của BD
Gọi M là trung điểm của BC
Nên EM là đường trung bình của ABC 1
 EM = AB và EM / / A B · · Þ MEF = A HK 2
Và FM là đường trung bình của BCD 1 · ·
 FM = CD và FM/ / CD Þ EFM = HKD 2
Mà A B = CD nên A B = CD Þ F V ME cân · · · ·
Þ MEF = A HK = EFM = HKD · · Þ A HK = HKD · ·
Þ KHB = HKC (kề bù) Bài 6: Kẻ BH ⊥ CD,IK ⊥ CD . CD − AB 10 − 4 Ta có: CH = = = 3 (cm). 2 2
Áp dụng định lí Py-ta-go vào ΔBHC , ta có: 2 = 2 − 2 = 2 − 2 = = 2 BH BC CH 5 3 16 4  BH = 4 cm.
Tam giác BDH có BI = ID và IK BH nên IK là đường trung bình.  = BH = 4 IK = 2 (cm). 2 2 Bài 7:
Kẻ HK // BE ta chứng minh được AE = EK = KC
Kết quả: AE = 5cm, EC = 10cm Trang 4 Bài 8:
Tam giác AHC có AK = KH và HM = MC  MK là
đường trung bình của ΔAHC .
 MK AC . Ta lại có AC ⊥ AB nên MK ⊥ AB
Tam giác ABM có: AH ⊥ BM và MK ⊥ AB
 K là trực tâm, suy ra BK ⊥ AM . Bài 9:
Gọi J là trung điểm của KC, ta có IJ là đường trung bình trong tam giác KHC. Do đó IJ / / HC Þ IJ ^ AH
Trong tam giác AHJ có IJ ^ AH, HI ^ AJ . Từ đó, I
là trực tâm tam giác AHJ.  AI ⊥ HJ (1).
Trong tam giác BKC, HJ là đường trung bình, suy ra HJ / / BK (2).
Từ (1) và (2) suy ra AI ^ BK Trang 5