Bài Tập Hình 8 Bài Khái Niệm Hai Tam Giác Đồng Dạng Có Lời Giải

4. KHÁI NIỆM HAI TAM GIÁC ĐỒNG DẠNG
I. KIẾN THỨC CƠ BẢN  Định nghĩa
- Hai tam giác gọi là đồng dạng với nhau nếu chúng có ba cặp góc bằng nhau đôi một và ba
cặp cạnh tương ứng tỉ lệ. ìï µ ¶ µ ¶ µ ¶
ï A = A ';B = B ';C = C ' ï - Ta có A BC ”
A ' B 'C ' ï D D Û í AB BC CA ïï = =
ïïî A 'B ' B 'C ' C 'A '  Tính chất
a) Mỗi tam giác đồng dạng với chính tam giác đó (hoặc nói: Hai tam giác bằng nhau thì đồng dạng với nhau). 1
b) Nếu D A BC ” D A ' B 'C ' theo tỉ số k thì D A ' B 'C ' ” D A BC theo tỉ số . k
c) Nếu D A BC ” D A ' B 'C ' và DA ' B 'C ' ” DA "B "C " thì ABC ∽ A " B" C".  Định lý
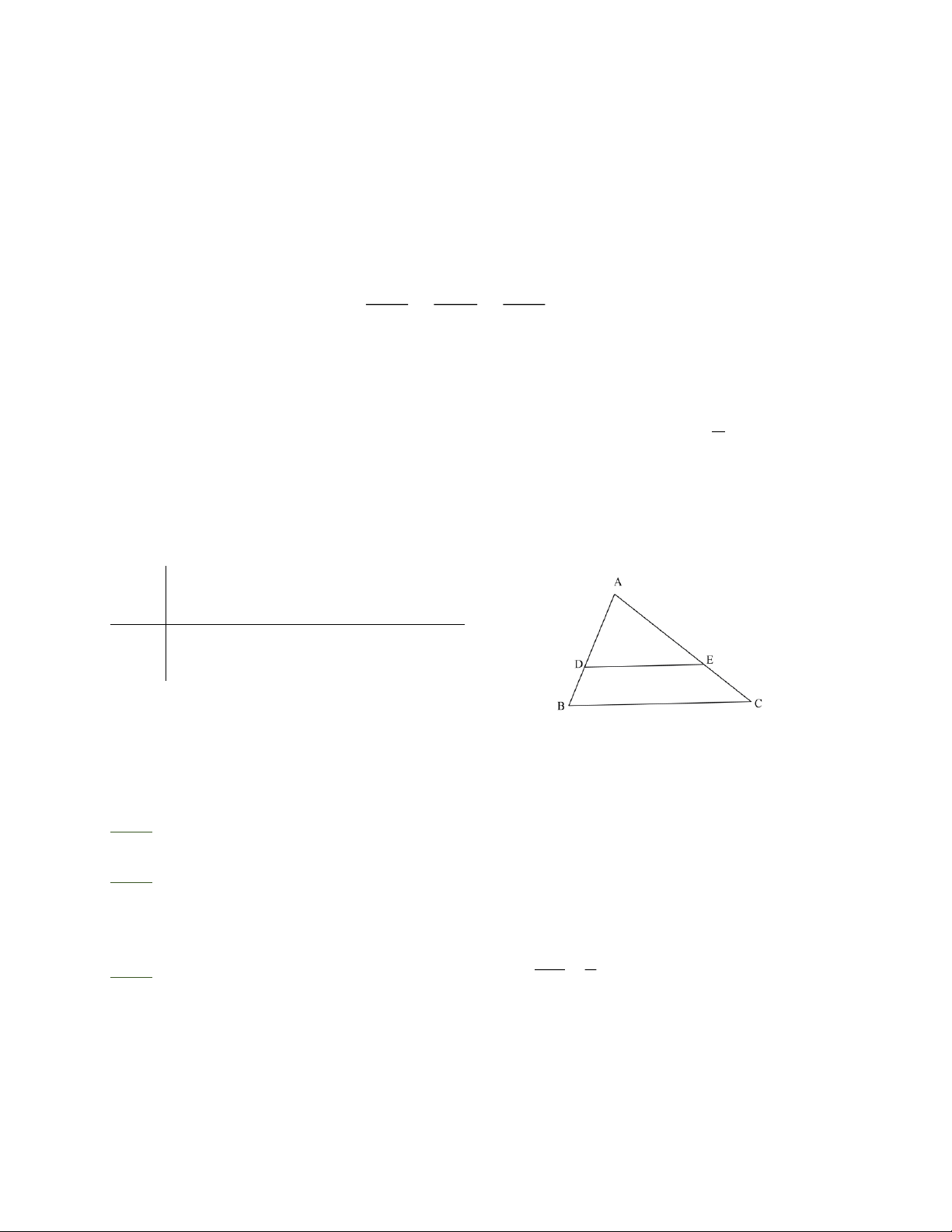
Nếu một đường thẳng cắt hai cạnh của tam giác và song song với cạnh còn lại thì nó tạo
thành một tam giác mới đồng dạng với tam giác đã cho. DA BC GT
DE / / BC (D Î AB,E Î AC ) KL
DA DE ” DA BC III. BÀI TẬP
Bài 1: Cho hai tam giác ABC và A 'B'C' đồng dạng với nhau theo tỉ số k, chứng minh rằng
tỉ số chu vi của hai tam giác ABC và A 'B'C' cũng bằng k.
Bài 2: Cho tam giác ABC có cạnh BC = 10cm,CA = 14cm, A B = 6cm . Tam giác ABC đồng
dạng với tam giác DEF có cạnh nhỏ nhất là 9cm. Tính các cạnh còn lại của tam giác DEF. DB 1
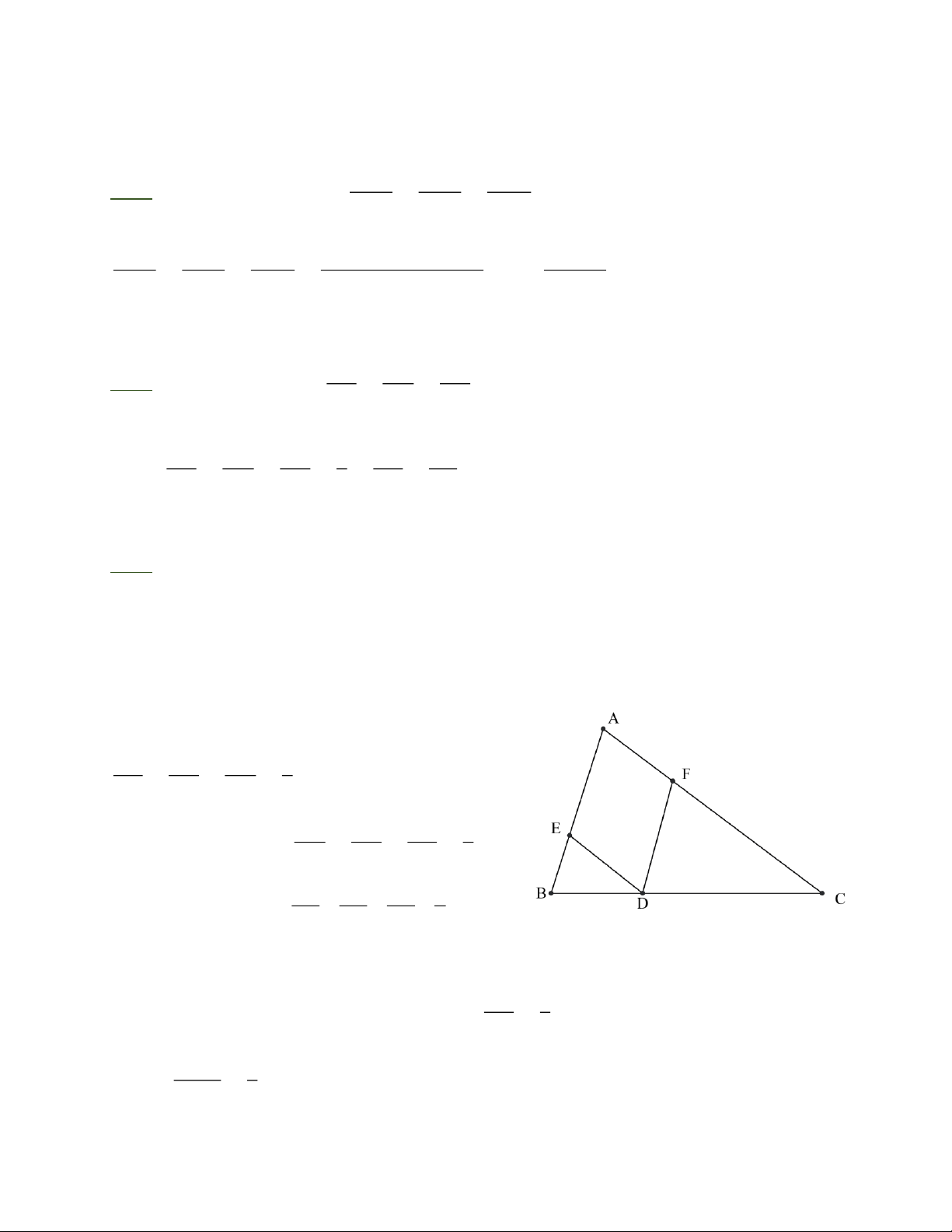
Bài 3: Cho  ABC, điểm D thuộc cạnh BC sao cho:
= . Kẻ DE / / A C ; DF / / A B DC 2 (E Î AB;F Î AC) .
a) Nêu tất cả các cặp tam giác đồng dạng. Đối với mỗi cặp, hãy viết các góc bằng nhau và các tỉ số tương ứng.
b) Hãy tính chu vi D B ED , biết hiệu chu vi của D DFC và D B ED là 30cm Trang 1
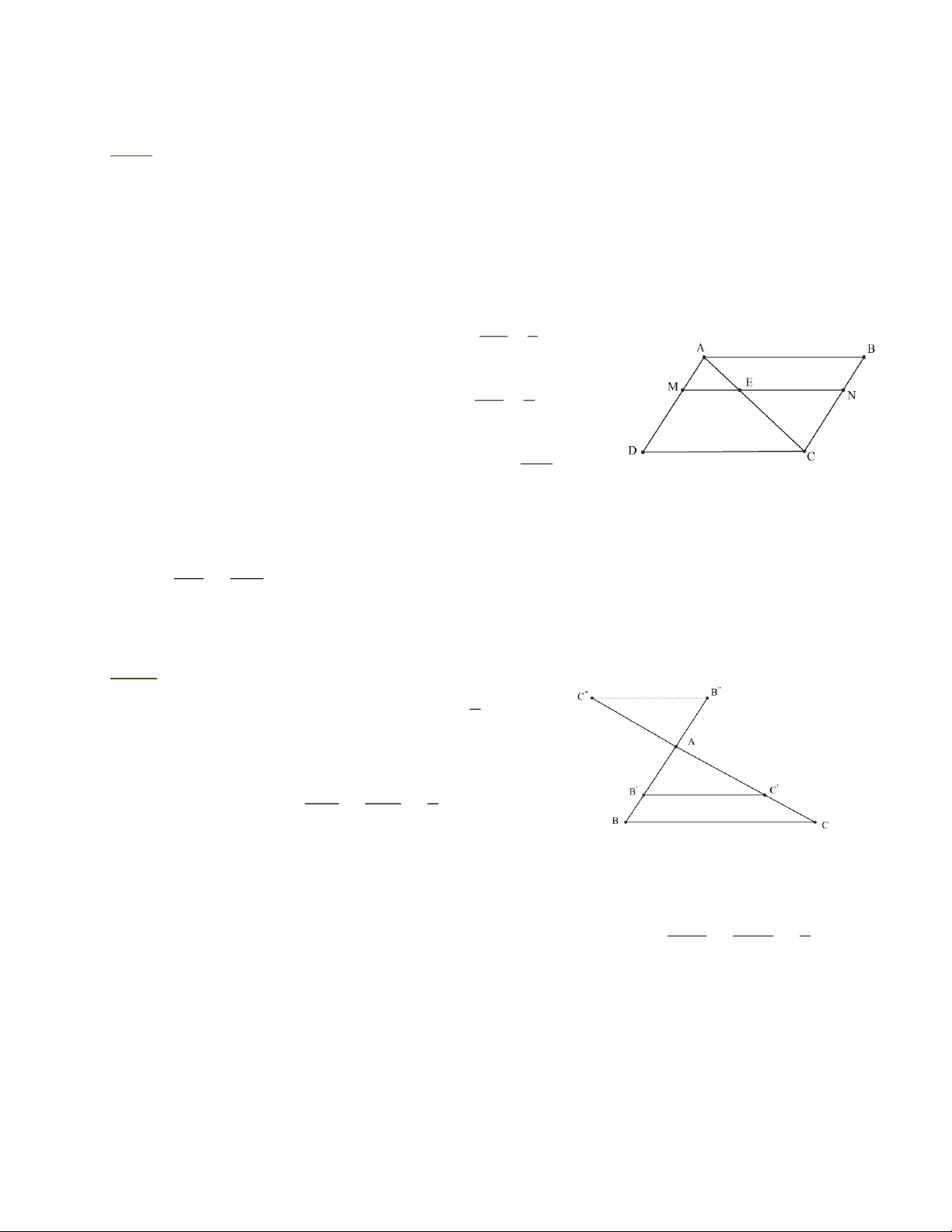
Bài 4: Cho hình bình hành ABCD. Trên đường chéo AC lấy điểm E sao cho A C = 3A E .
Qua E vẽ đường thẳng song song với CD, cắt AD và BC theo thứ tự ở M và N.
a)Tìm các tam giác đồng dạng với  ADC và tìm tỉ số đồng dạng.
b) Điểm E nằm ở vị trí nào trên AC thì E là trung điểm của MN? 2
Bài 5: Cho  ABC. Vẽ tam giác đồng dạng với tam giác đó, biết tỉ số đồng dạng k = . Có 3
thể dựng được bao nhiêu tam giác như thế? Tự luyện
Bài 1: Cho hình bình hành ABCD, có AB = 6cm,AD = 5cm. Lấy F trên cạnh BC sao cho
CF = 3cm. Tia DF cắt tia AB tại G.
a) Chứng minh D GBF ” D DCF và D GA D” D DCF .
b) Tính độ dài đoạn thẳng AG.
c) Chứng minh A G.CF = A D.A B .
Bài 2: Cho tam giác ABC, kẻ Ax song song với BC. Từ trung điểm M của cạnh BC, kẻ một PN QN
đường thẳng bất kỳ cắt Ax ở N, cắt AB ở P và cắt AC ở Q. Chứng minh = . PM QM
Bài 3: Hình thang ABCD (A B / / CD) có A B = 10cm,CD = 25cm và hai đường chéo cắt
nhau tại O. Chứng minhh rằng A  OB” C
 OD và tìm tỉ số đồng dạng. Trang 2
KẾT QUẢ - ĐÁP SỐ A B A C BC
Bài 1: DA BC ” DA ' B 'C ' Þ = = = k A ' B ' A 'C ' B 'C '
Áp dụng tính chất dãy tỉ số bằng nhau ta có : A B A C BC
A B + A C + BC C DABC = = = = k = A ' B ' A 'C ' B 'C '
A ' B '+ A 'C '+ B 'C '
C DA'B 'C ' Với C
là chu vi tam giác ABC và C
là chu vi tam giác A ' B 'C ' DA BC
D A ' B 'C ' A B A C BC
Bài 2: DA BC ” DDEF Þ = = . DE DF EF
D A BC cạnh nhỏ nhất là cạnh A B = 6cm . Nên cạnh nhỏ nhất của D DEF là DE = 9cm A B A C BC 6 14 10 Ta có: = = = = = DE DF EF 9 DF EF
Từ đó tính được DF = 21cm;EF = 15cm Bài 3:
a) Các cặp tam giác đồng dạng: DABC ” E
V BD ; DA BC ” DFDC ; DFDC ” DEBD ( vì cùng đồng dạng với D A BC ) * DABC ” E V BD Þ · · · · · ·
BA C = BED;A BC = EBD;A CB = EDB ; A B BC A C 3 = = = EB BD ED 1 A C BC A B 3
* DA BC ” DFDC có : = = = FC CD FD 2 FC CD FD 2
* D FDC ” D EBD có: = = = ED DB EB 1
c) Ta có tỉ số về chu vi bằng tỉ số đồng dạng CD 2
* DDFC ” D BED theo tỉ số đồng dạng k = = DB 1 P 2 Do đó: DDFC = Þ P = 2P P 1 DDFC DBED DBED Trang 3
Mà theo giả thiết: P - P = 30 Þ 2P - P = 30 Þ P = 30(cm ) DDFC DBED DBED DBED DBED Bài 4:
a) Tam giác đồng dạng với D A DC
* DA DC ” DA DC . Tỉ số đồng dạng: k = 1 1
* DA DC ” DCBA . Tỉ số đồng dạng: k = 1 (hai tam giác bằng nhau thì đồng dạng) 1 AE 1
DA DC ” DA ME theo tỉ số đồng dạng k = = 2 AC 3 AC 3
DA DC ” DCNE theo tỉ số đồng dạng k = = 3 CE 2 EM
b) E là trung điểm của MN thì EM = EN suy ra: =1 EN
Ta có: DA ME ” DCNE (cùng đồng dạng với D A DC ) A E EM suy ra: =
= 1 Þ A E = CE = 1 CE EN
Suy ra E là trung điểm của AE
Bài 5: Cách 1: - Tại đỉnh A dựng tam giác A B 'C ' 2
đồng dạng với tam giác ABC theo tỉ số k = bằng 3 cách ' ' A B A C 2
Kẻ B 'C ' / / BC sao cho = = A B A C 3
- Tam giác có 3 đỉnh, tại mỗi đỉnh ta dựng tương tự như trên, sẽ được ba tam giác đồng
dạng với tam giác A B C . A B ' A C ' 2
Cách 2: - Ta có cách dựng thứ 2 bằng cách vẽ B ' C ' / / BC sao cho: = = A B A C 3
- -Tam giác có 3 đỉnh, tại mỗi đỉnh ta dựng tương tự như trên, sẽ được ba tam giác đồng dạng với tam giác ABC
Kết luận: Ta có thể dựng được sáu tam giác đồng dạng với tam giác A B C ( trong đó tại
mỗi đỉnh có một cặp tam giác bằng nhau) Trang 4