Bài Tập Hình 8 Bài Trường Hợp Đồng Dạng Thứ Ba Có Lời Giải

7. TRƯỜNG HỢP ĐỒNG DẠNG THỨ BA
I. KIẾN THỨC CƠ BẢN
 Định lý: Nếu hai góc của tam giác này lần lượt bằng hai góc của tam giác kia thì hai tam giác đó đồng dạng. A
DA BC , DA ' B 'C ' GT µ µµ ¶
A = A', B = B ' A' KL
D A BC ” D A ' B 'C ' B C B' C' II. BÀI TẬP
Bài 1: Cho tam giác ABC có đường phân giác trong AD. Qua C kẻ đường thẳng song song
với AB, cắt tia AD tại E. Chứng minh:
a) DA BD ” DECD; b) ACE cân tại C. µ ·
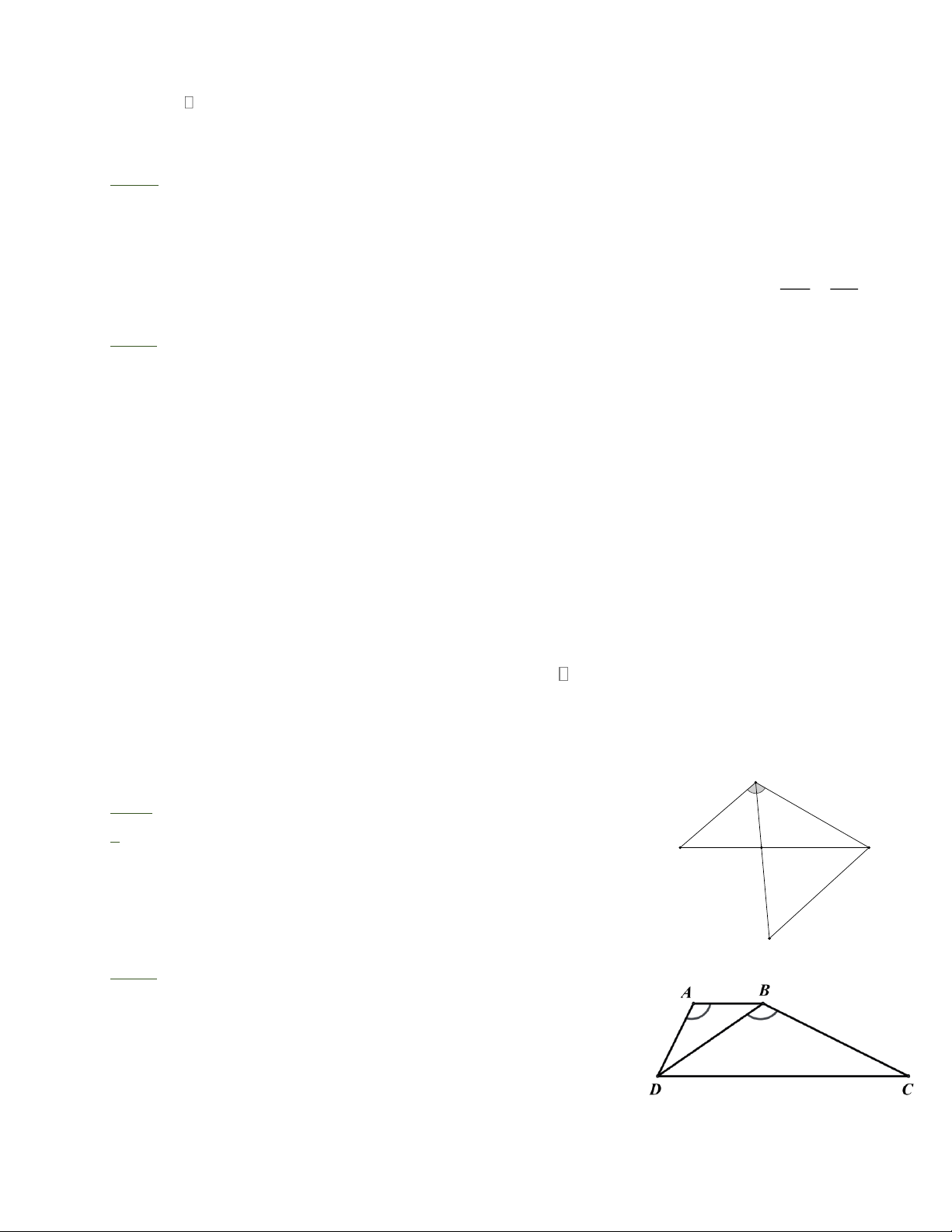
Bài 2: Cho hình thang ABCD có AB//CD, A B = 4cm , DB = 6cm và A = CBD . Tính độ dài CD.
Bài 3: Cho D ABC vuông tại A có AK là đường cao AB = 12cm, AC = 16cm.
a) Chứng minh: D ABK ∽ D CBA. Tính độ dài đoạn thẳng BC, AK.
b) Chứng minh: D A BK ” D CA K
c) Chứng minh: D CA K ” D CBA
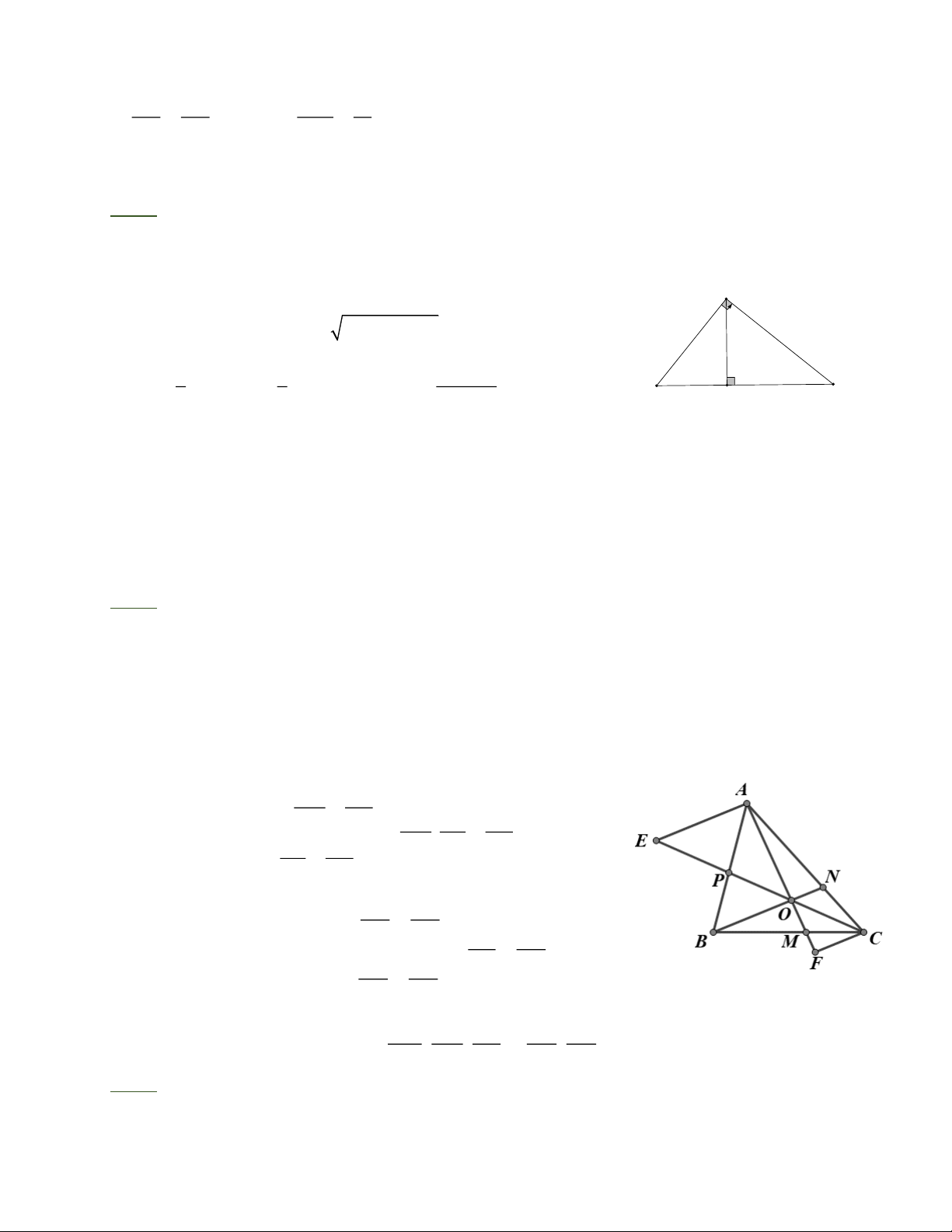
Bài 4: Cho tam giác ABC. Trên các cạnh BC, CA, AB lấy lần lượt các điểm M, N, P sao cho
AM, BN, CP đồng qui tại O. Qua A và C vẽ các đường thẳng song song với BO cắt CO, OA lần lượt ở E và F.
a) Chứng minh: D F CM” D OBM và DP AE ” DP BO MB NC PA b) Chứng minh: . . = 1 . MC NA PB
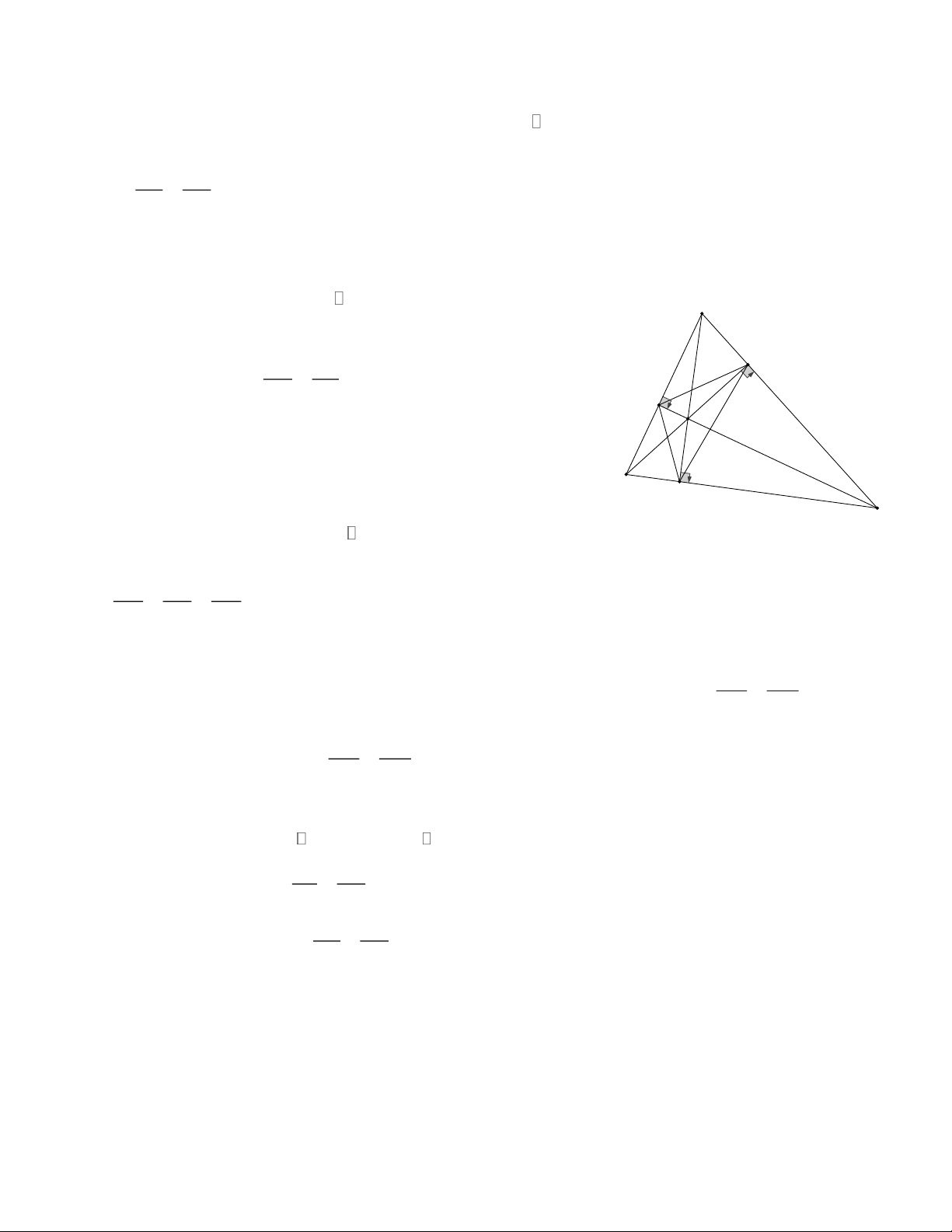
Bài 5: Cho ABC có 3 góc nhọn, các đường cao AD, BE, CF cắt nhau ở H . Chứng minh: a) .
AD BC = BE.AC = CF.AB b) . AD HD = .
DB DC và suy ra các hệ thức tương tự c) ABH  ” EDH 
và suy ra các kết quả tương tự d) AEF ABC và BDF  EDC  Trang 1 e) AHB  AFD 
và suy ra các kết quả tương tự.
f) Điểm H cách đều 3 cạnh của DEF
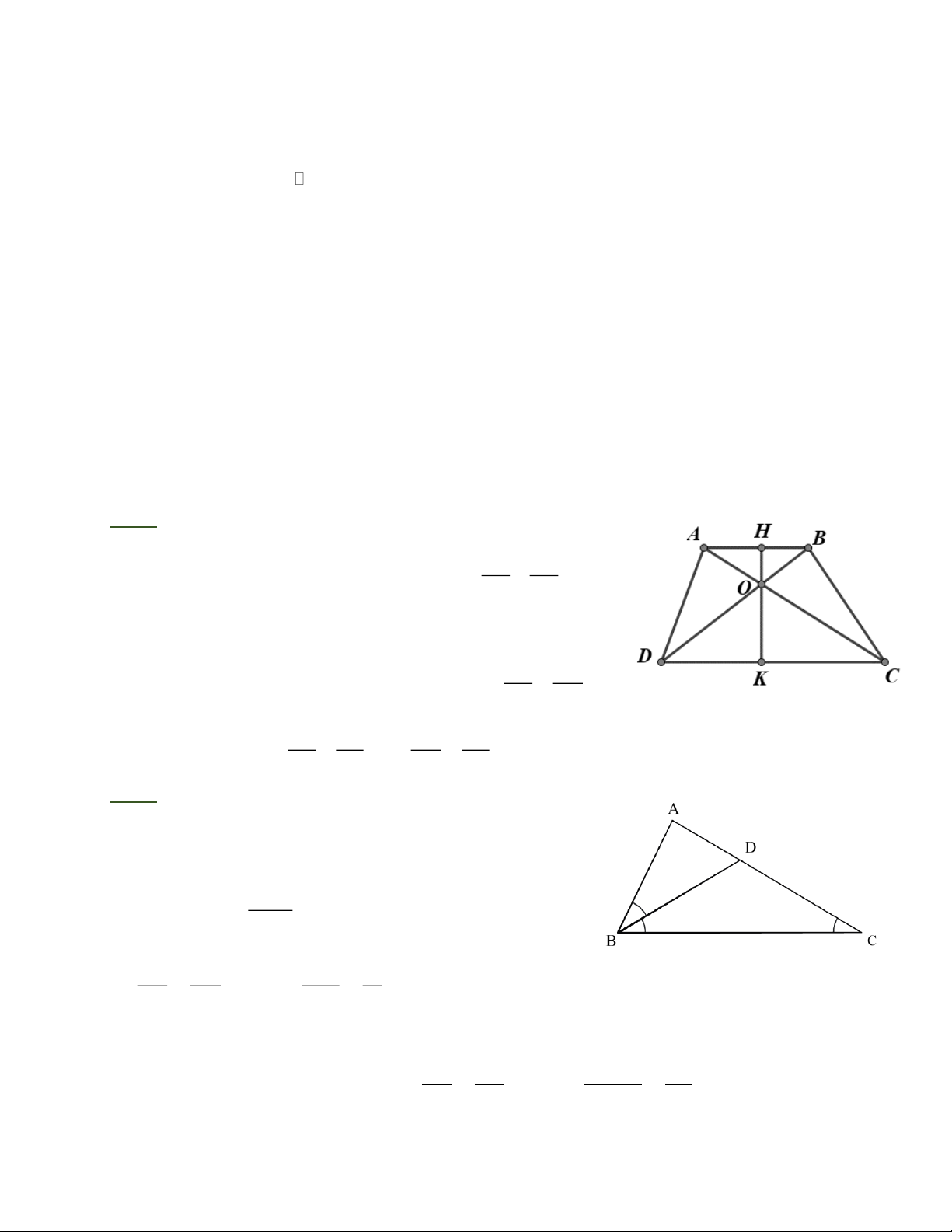
Bài 6: Cho hình thang ABCD (AB // CD). Gọi O là giao điểm của hai đường chéo AC và BD.
a) Chứng minh OA.OD = OB.OC. OH AB
b) Đường thẳng qua O, vuông góc với AB, CD theo thứ tự tại H, K. Chứng minh = OK CD
Bài 7: Cho tam giác ABC có B = 2.C , AB = 4 cm, AC = 8 cm, Tính độ dài cạnh BC ? BÀI TẬP TỰ LUYỆN
Bài 1: Cho D ABC nhọn có ba đường cao AD, BE, CF cắt nhau tại H.
a) Chứng minh: BH.BE= BD.BC .
b) Chứng minh: CH .CF = CD.CB . c) Chứng minh: 2
BH .BE + CH .CF = BC .
Bài 2: Cho tam giác ABC và d là đường thẳng tùy ý qua B. Qua E là điểm bất kì trên AC, vẽ
đường thẳng song song với AB và BC, lần lượt cắt d tại M và N. Gọi D là giao điểm của
ME và BC. Đường thẳng NE cắt AB và MC lần lượt tại F và K. Chứng minh: a) A  FN ∽ M  DC; b) AN MK.
KẾT QUẢ - ĐÁP SỐ A Bài 1:
a) Do A B / / CE nên BAD = DEC . Chứng minh được  C
ABD ~ ECD(g  g) B D
b) Chứng minh được CAD = CED(= BAD) nên ACE cân tại C. E
Bài 2: Xét ABD và BDC:
A = CBD ; ABD = BDC (so le trong)  Þ A V BD ” DBDC (g – g) Trang 2 2 2  AB BD BD 6 = Þ CD = = = 9 cm BD CD AB 4
Bài 3: a) Chứng minh: D ABK ∽ D CBA. Tính độ dài đoạn thẳng BC, AK. ìï · · 0 ·
ï A BK = CBA(= 90 - BA K ) A BK ,CBA : ï D í ” ï · · Þ DA BK DCBA 0
ï A KB = CA B (= 90 ) ïî A ΔABC vuông tại A: 2 2 BC =
A B + A C = 20cm 1 1 BA.A C S = A K .BC =
A B.A C Þ A K = = 8, 6cm C A BC B 2 2 BC K ìï · · 0 ·
ï A BK = KA C (= 90 - BA K )
b) A BK ,CA K : ï D í ” ï · · Þ DA BK DCA K 0
ï A KB = CKA(= 90 ) ïî
ìï DA BK ” DCA K ï c) í
Þ D CA K ” DCBA ï (cách khác g-g) DA BK ” DCBA ïî Bài 4:
FCM = OBM (OB / /CF)
a) FCM ,OBM :   FC  M ~ OBM  FMC = OMB ìï · ·
ï PA E = PBO (OB / / A E ) PA E, PBO : ï D í ” ï · · Þ DPA E DPBO ï EPA = OPB ïî  MB OB F  CM ” O  BM  =  MC FC MB PA AE b)   . = PA AE MC PB FC  P  AE” P  BO  =  PB BO  N  AC AE AC  AEC  : ON / / AE,   =  O   EC ON NC AE AN   = O    FA ON AN FC NC AFC  : ON / /CF,   =  O    AC FC AC MB NC PA A E FC
Từ các kết quả trên suy ra đpcm: . . = . = 1 MC NA PB FC A E
Bài 5: a) Vì AD, BE, CF là đường cao của ABC  AD ⊥ BC; CF ⊥ AB; BE ⊥ AC Trang 3
CFA = BEA = 90
Xét CFA và BEA có:   C  FA  ( BEA g − g) A chung  CF AC  =
 AC.BE = CF.AB (1) BE AB
Xét CFB và ADB có:
CFB = ADB = 90 C  FB ADB  (g − g) B chung  A  CF CB E FCB = DAB và =  A .
D BC = CF.AB (2) AD AB F Từ (1) và (2) suy ra: .
AD BC = BE.AC = CF.AB H B
b) Xét CDH và ADB có: D
CDH = ADB = 90 C   C  DH ADB  (g − g)
HCD = BAD(cmt)  HD CD CH = =  . AD HD = C . D ; BD . AB HD = CH. ; BD C .
D AB = CH.AD BD AD AB
AEH = BDH = 90 AH EH
c) Xét AEH và BDH có:
  AHE” BDH (g − g)  =
AHE = BHD(dd)  BH DH AH EH  = (cmt)
Xét AHB và EHD có: BH DH   A  HB” E
 DH (c − g − c) AHB E D H (dd) =  Tương tự ta có: AH  C FH  ; D BH  C FH  E FA AC d) Vì C  FA” B  EA  = EA AB FA AC  = (cmt)
Xét AEF và ABC có: AE AB   A  EF” A
 BC(c − g − c) ( A chung)  B  DF” B  AC
Chứng minh tương tự ta có   B  DF” E  DC (t/c..) B  AC” E  DC · ·
e) Vì D BDF ” D BA C Þ BDF = BA C  ADF = ABH (cùng phụ với BDF = BAC ) Trang 4 ABH = ADF 
Xét AHB và AFD có:   AHB  ” AFD  (g − g) ( A chung)  Tương tự ta có: AE  D AH  C f) · · A HB ” A FD A BH FDA üï D D ® = ïï · · · ·
ý Þ FDA = EDH  DH là tia phân giác FDE (3) A HB ” EHD A BH EDH ï D D ® = ïïþ
Lại có: FEB = FAD (cùng phụ với AEF = FDB )
Mà: HAB = HED(cmt)
 FEB = HED  EH là tia phân giác FED (4)
Từ (3) và (4) suy ra: H là giao điểm của 3 đường phân giác trong tam giác FED hay H cách
đều 3 cạnh của tam giác FED Bài 6: AOB = COD OA OB a)   OAB  ” OC  D  =  = ( // ) OC OD OAB OCD AB CD đpcm 0
AHO = CKO(= 90 ) OA OH b)   OAH  ” OC  K  = OAH  = OCK  (AB//CD) OC OK OA AB OH AB Mà O  AB” O  CD  = nên = OC CD OK CD Bài 7:
Kẻ đường phân giác BD của tam giác ABC.
Xét ∆ABC và ∆ADB có A chung, æ · ö · · ç A BC ÷ A CB = A BDç ÷ = ç ÷ ç
suy ra ∆ABC ∽ ∆ADB (g.g) ç 2 ÷÷ è ø 2 2 AB AC AB 4  =  AD = = = 2 (cm) AD AB AC 8  CD = 6 (cm). BC D C A . B D C 4.6
∆ABC có BD là đường phân giác nên =  BC = = = 12 (cm). AB AD AD 2 Trang 5 Trang 6