
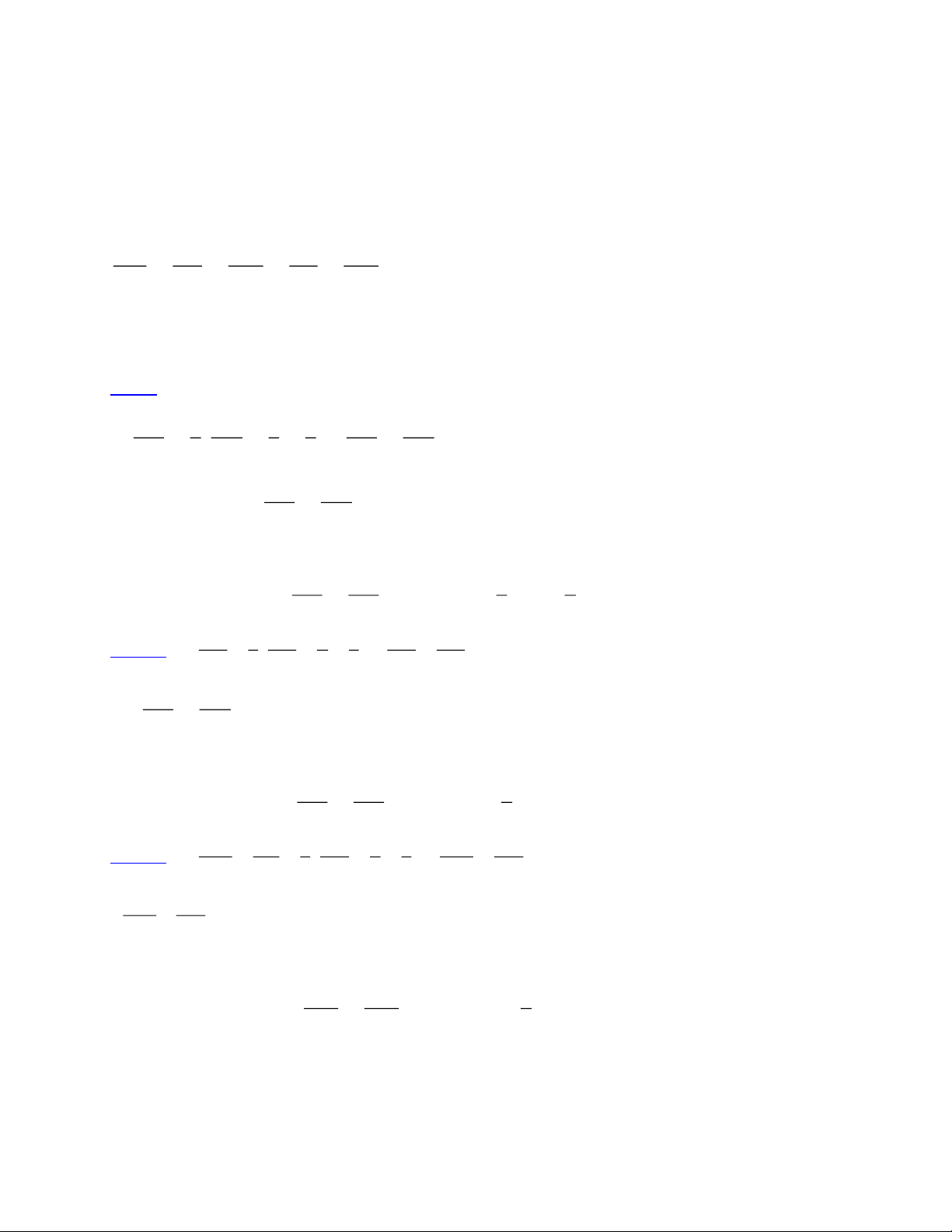
Preview text:
6. TRƯỜNG HỢP ĐỒNG DẠNG THỨ HAI
I. KIẾN THỨC CƠ BẢN
Định lý: Nếu hai cạnh của tam giác này tỉ lệ với hai cạnh của tam giác kia và hai góc tạo
bởi các cặp cạnh đó bằng nhau, thì hai tam giác đó đồng dạng.
DA BC , DA ' B 'C ' GT A B BC µ ¶ = , B = B ' A ' B ' B 'C '
DA BC ” DA ' B 'C ' KL III. BÀI TẬP
Bài 1: Cho hình thang ABCD (AB//CD) , biết A B = 9cm, BD = 12cm, DC = 16cm. Chứng minh A BD” B DC. ·
Bài 2: Cho xOy , phân giác Ot. Trên Ox lấy các điểm A và C ' sao cho
OA = 4cm,OC ' = 9cm , trên Oy lấy các điểm A ' và C sao cho OA ' = 12cm,OC = 3cm, trên
tia Ot lấy các điểm B và B' sao cho OB = 6cm,OB ' = 18cm . Chứng minh: A B A C BC
a) D OA B ” DOA ' B '; b) = = . A ' B ' A'C ' B 'C '
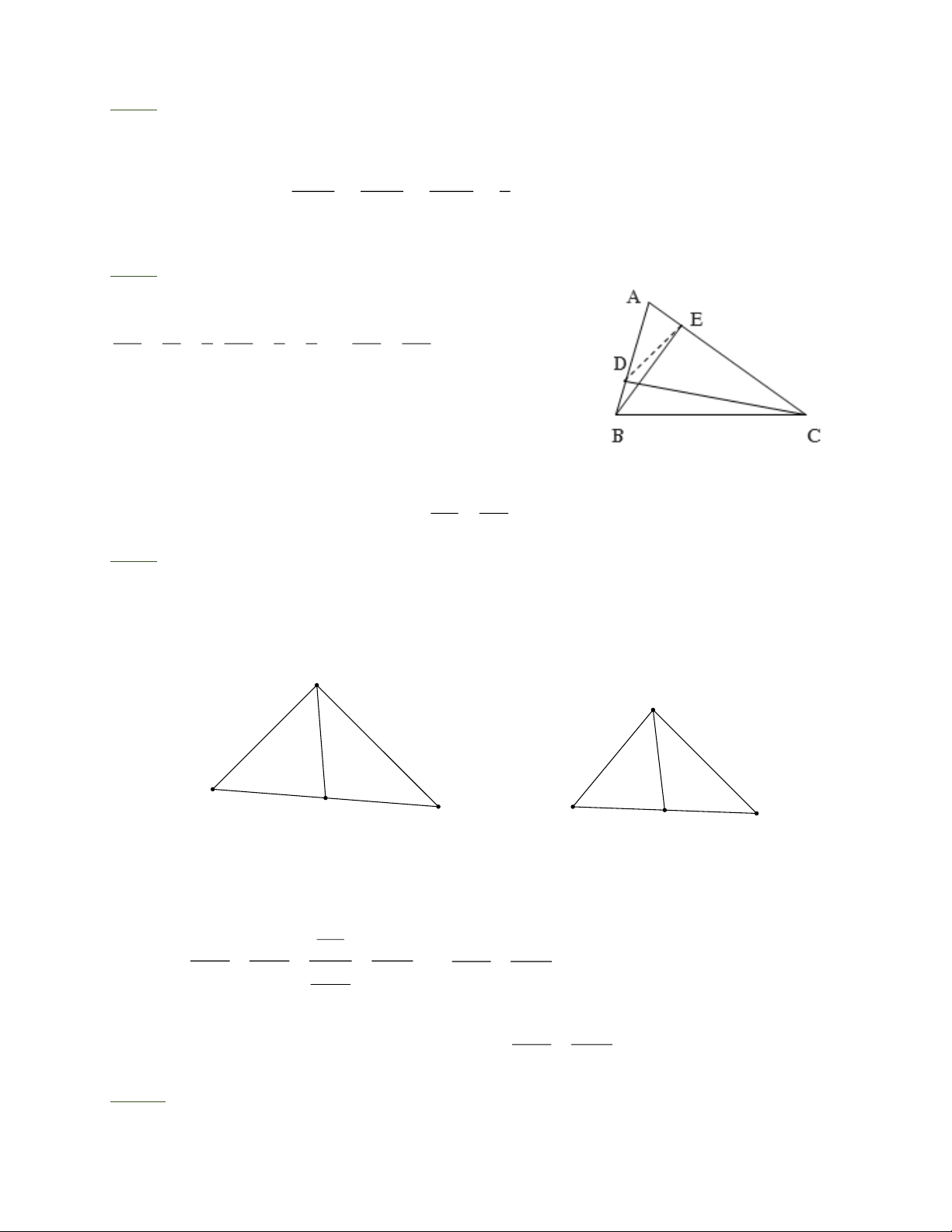
Bài 3: Cho ABC có A B = 8cm , A C = 16cm ,. Gọi D và E là hai điểm lần lượt trên các
cạnh AB, AC sao cho BD = 2cm , CE = 13cm . Chứng minh :
a) AEB ” ADC b) AED = ABC c) AE.AC = . AB AD
Bài 4: Chứng minh rằng nếu A’B’C’ đồng dạng với ABC theo tỉ số k thì tỉ số hai
đường trung tuyến tương ứng cũng bằng k. µ µ
Bài 5: Cho tam giác ABC có A B = 9cm, A C = 12cm, BC = 7cm . Chứng minh B = 2C . µ
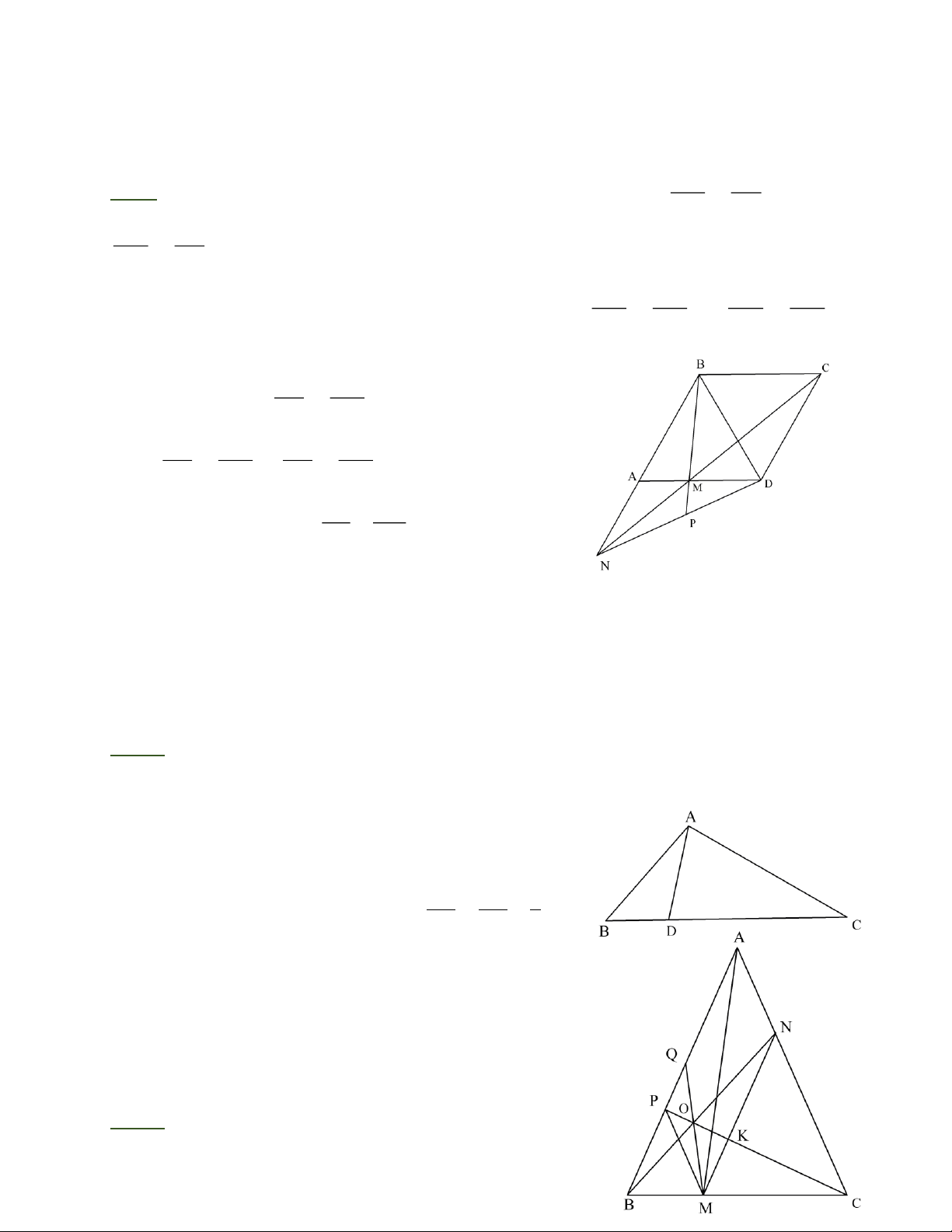
Bài 6: Cho hình thoi ABCD có 0
A = 60 . Gọi M là một cạnh thuộc cạnh AD. Đường thẳng
CM cắt đường thẳng AB tại N. a) Chứng minh 2
A B = DM .BN ; ·
b) BM cắt DN tại P. Tính góc BPD .
Bài 7*: Cho tam giác ABC có A B = 2cm ; A C = 3cm ; BC = 4cm . Chứng minh rằng: BA C = A BC + 2.A CB . Trang 1
Bài 8*: Cho D A B C cân tại A. Lấy M tùy ý thuộc BC, kẻ MN song song với AB (với N ∈
AC), kẻ MP song song với AC ( với P ∈ AB). Gọi O là giao điểm của BN và CP. Chứng minh rằng OM P = A M N .
Bài 9: Cho D ABC, biết AB = 3cm, AC = 6cm, BC = 4cm. Trên AB lấy điểm E sao cho AE =
2cm, trên AC lấy điểm D sao cho AD = 1cm. A D A E a) Chứng minh: = . A B A C b) Chứng minh: A V DE ” A V BC
c) Tính độ dài đoạn DE.
Bài 10: Cho D ABC, biết AB = 3cm, AC = 6cm, BC = 6cm. Trên AB lấy điểm E sao cho AE =
2cm, trên AC lấy điểm D sao cho AD = 1cm. AD AE a) Chứng minh: = . AB AC b) Chứng minh: A V DE ” A V BC
c) Tính độ dài đoạn DE.
Bài 11: Cho D ABC, biết AB = 7,5cm, AC = 9cm, BC = 12cm. Trên AB, AC theo thứ tự lấy
điểm M và N sao cho AN = 3cm, AM = 2,5cm. a) Chứng minh: A V MN” DABC
b) Tính độ dài đoạn MN. Tự luyện: 0
Bài 1: Cho hình thang ABCD biết A = D = 90 . Trên cạnh AD lấy điểm I sao cho AB.DC = AI.DI. Chứng minh: 0 a) A BI ∽ D IC; b) BIC = 90 . 0
Bài 2: Cho hình thoi ABCD, A = 60 . Qua C kẻ đường thẳng d bất kì cắt các tia đối của các
tia BA, DA theo thứ tự tại E và F. Gọi I là giao điểm của BF và ED. Chứng minh: EB AD a) = ; b) E BD ∽ B DF; BA DF c) 0 BID = 120 .
KẾT QUẢ - ĐÁP SỐ · · A B BD 3 A B
Bài 1: Ta chứng minh được A BD = BDC và = = . BD DC 4
Từ đó suy ra DA BD ” DBDC (c.gc) C D Trang 2 Bài 2:
a) Chứng minh được OA B ” OA B ¢ (¢ D D c. . g c) A B A C BC 1 b) Chứng minh được = = = A ' B ' A 'C ' B 'C ' 3 Bài 3:
a) Xét tam giác AEB và tam giác ADC có AB 8 1 = = AE 3 1 AB AE ; = = = AC 16 2 AD 6 2 AC AD
Mặt khác lai có góc A chung
AEB ” ADC (c-g-c)
b) Chứng minh tương tự câu a) ta có AED” ABC
AED = ABC (hai góc tương ứng) AE AD
c) Theo câu b) ta có AED ” ABC = AE.AC = . AB AD AB AC Bài 4: A A' B D C B' D' C'
HD: a) D A BC ” D A 'B'C' có AD và A ' D ' lần lượt là trung tuyến xuất phát từ đỉnh A và
A’ xuống cạnh BC và B’C’ của hai tam giác đó. BC AB BC BD AB BD Ta có 2 k = = = = . = Có B = B ' . A' B ' B 'C ' B 'C ' B ' D ' A' B ' B ' D ' 2 AB AD
Vậy D ABD ” D A ' B ' D ' (c-g-c) Từ đó suy ra k = = A' B ' A' D '
Bài 5: Trên tia đối của tia BA lấy điểm E sao cho BE = BC = 7cm . Chứng minh được
DA BC ” DA CE (c. . g c) Trang 3 · µ suy ra BCA = E · · µ µ ·
Từ đó ta có A BC = BCE + E = 2E = 2BCA NA NB
Bài 6: a) Ta có A M / / BC ( do AD // BC) suy ra DNA M ” DNBC Þ = hay A M BC NA NB = (1) (vì BC = AB). A M A B NA CD NA A B
Ta có NA // DC ( do AB // DC) suy ra DNA M ” DCDM Þ = hay = (2) A M DM A M DM
(vì CD = A B ). NA A B Từ (1) và (2) suy ra = hay 2
A B = DM .BN A B DM . NB A B NB BD b) Từ = Þ = A B DM BD DM NB BD Xét BND và DBM có = và BD DM · · 0
NBD = BDM = 60 .
Suy ra DBND” DDBM (c. . g c) · · · · · · 0
Þ MBD = BND Þ MBD + MBN = BND + MBN = 60 · · ·
Mà BPD = BND + MBN nên = 0 BPD 60 . Bài 7*:
Trên đoạn thẳng BC lấy điểm D sao cho BD = 1cm
CD = BC - BD = 3 cm CD = A C nên DA CD
cân tại C, do vậy DA C = A DC (1) BD A B 1
D A BD và D CBA có A BD chung và = = . BA CB 2
Suy ra DA BD ” DCBA (c.g.c) BA D = BCA (2) Từ (1) và (2) ta có :
BA C = BA D + DA C = A CB + A DC = A CB + A BC + BA D
Do đó BA C = A BC + 2.A CB . Bài 8*: Trang 4
Giả sử MB £ MC . Gọi Q là giao điểm MO và AB ; K là giao điểm CP và MN. · ·
Vì MNA P là hình bình hành nên QPM = A NM (1)
Vì ∆ABC cân tại A nên suy ra D PB M cân tại P và D NCM cân tại N.
Do đó PB = PM = A N và NC = NM = A P kết hợp với MN / / A P , suy ra PQ PQ KM PB NA = = = = (2) PM PB KN PA NM
Từ (1) và (2) suy ra D QPM ” D A NM (c.g.c) QM P = A M N hay OM P = A M N . Điều phải chứng minh. Bài 9: A D 1 A E 2 1 A D A E a) = ; = = Þ = A B 3 A C 6 3 A B A C ìï AB A C ïï = ï
b) D A BC , A DE : í A D A E Þ DA BC ~ DA DE ï · · ï BA C = DA E ïïî A B BC 1 4
c) DA BC ” DA DE Þ = = 3 Þ DE = BC = (cm ) A D DE 3 3 AD 1 AE 2 1 AD AE Bài 10: a) = ; = = = AB 3 AC 6 3 AB AC ìï AB A C ïï = ï b) í A D A E
Þ DA BC ” DA DE ï (c.g.c) · · ï BA C = DA E ïïî A B BC 1
c) DA BC ” DA DE Þ = = 3 Þ DE = BC = 2(cm ) A D DE 3 AM 2,5 1 AN 3 1 AM AN Bài 11: a) = = ; = = = AB 7,5 3 AC 9 3 AB AC AB AC = AM AN AB
C ” AMN (c.g.c) BAC = MAN A B BC 1
b) DA BC ” DA MN Þ = = 3 Þ MN = BC = 4(cm ) A M MN 3 Trang 5




