Bài Tập Hình 8 Bài Trường Hợp Đồng Dạng Thứ Nhất Có Lời Giải

5. TRƯỜNG HỢP ĐỒNG DẠNG THỨ NHẤT
I. KIẾN THỨC CƠ BẢN
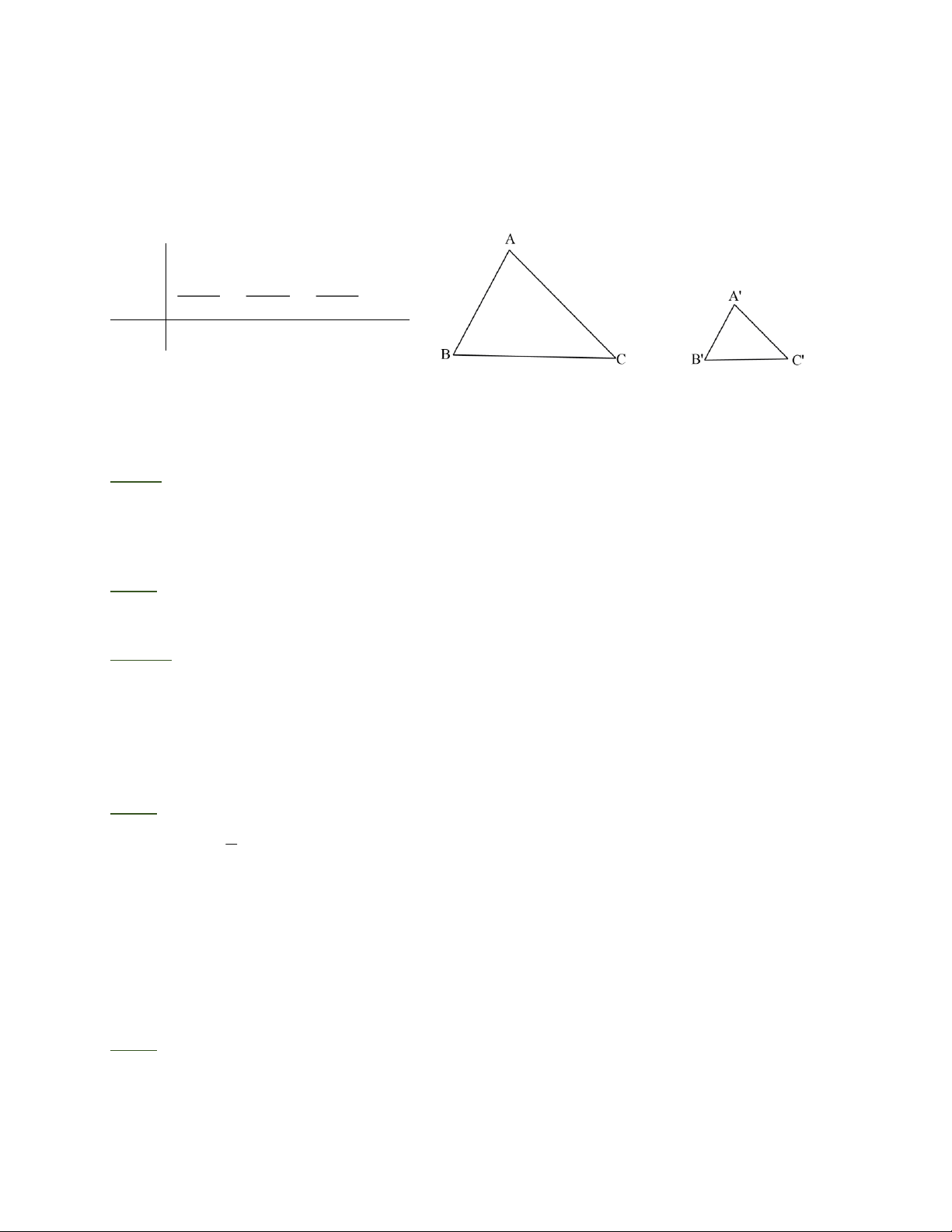
 Định lý: Nếu ba cạnh của tam giác này tỉ lệ với ba cạnh của tam giác kia thì hai tam giác đó đồng dạng.
DA BC , DA ' B 'C ' GT A B BC CA = = A ' B ' B 'C ' C ' A ' KL
DA BC ” DA ' B 'C ' II. BÀI TẬP
Bài 1: Hai tam giác mà các cạnh có độ dài như sau có đồng dạng không? Tại sao?
a) 4cm, 5cm, 6cm và 8mm, 1cm, 12mm.
b) Tam giác ABC vuông tại A, có AB = cm,AC = 8cm và tam giác A 'B'C' vuông tại A ' ,
có A ' B ' = 9cm, B 'C' = 16 cm .
Bài 2: Cho tam giác ABC có độ dài các cạnh tỉ lệ với 4 : 5 : 6 . Cho biết D DEF ” D A BC và
cạnh nhỏ nhất của D DEF là 0, 8m , hãy tính các cạnh còn lại của D DEF .
Bài 3: Cho tam giác ABC đồng dạng với tam giác A ' B 'C ' . Cho biết
BC = 24, 3cm,CA = 32, 4cm và A B = 16, 2cm , hãy tính độ dài các cạnh của tam giác
A ' B 'C ' nếu:
a) A B lớn hơn A ' B ' là 10 cm;
b) A ' B ' lớn hơn A B là 10 cm.
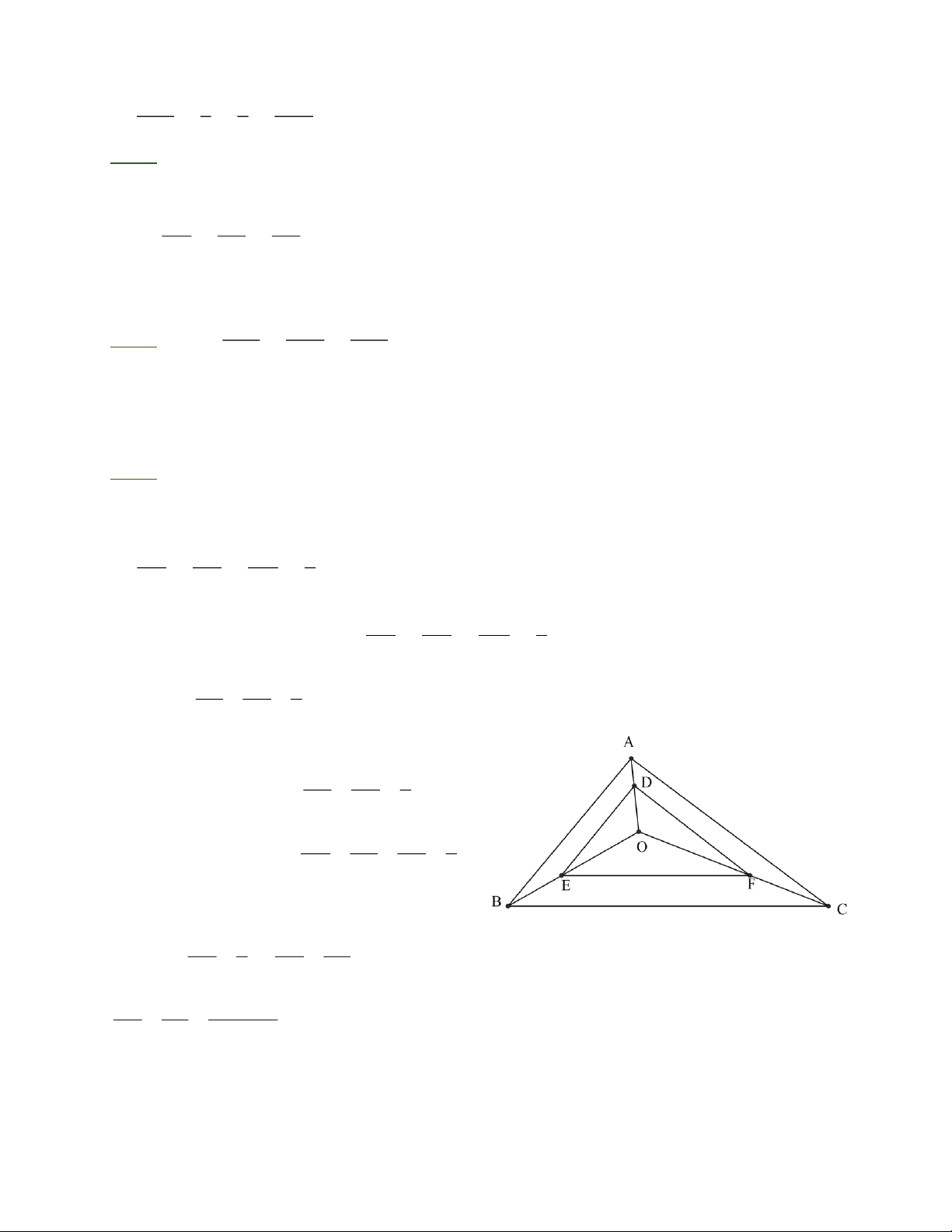
Bài 4: Cho tam giác ABC và một điểm O nằm trong tam giác đó. Trên cạnh OA lấy điểm D 2
sao cho OD = OA . Qua D vẽ các đường thẳng song song với AB, AC lần lượt cắt OB, OC 3 tại E và F
a) Chứng minh D DEF ” D A BC
b)Tính độ dài DE, AB biết hiệu độ dài hai cạnh đó là 12cm
c) Tính chu vi của  DEF, biết rằng tổng chu vi của  ABC và  DEF là 120cm.
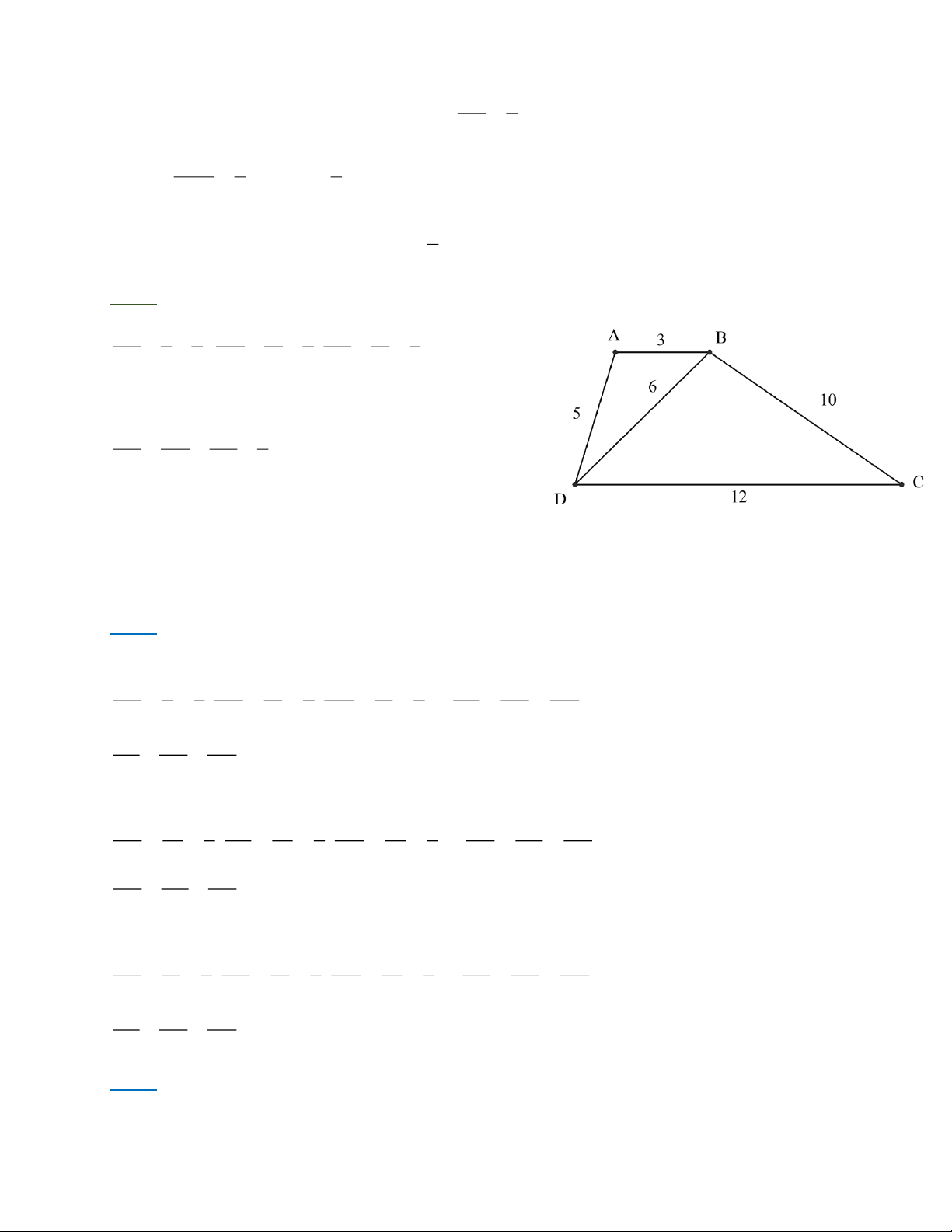
Bài 5: Cho tứ giác ABCD có A B = 3cm ; BC = 10cm ; CD = 12 cm ; A D = 5cm ;
BD = 6cm . Chứng minh rằng tứ giác A BCD là hình thang. Trang 1
Bài 6: Chứng minh 2 tam giác ABC và DEF đồng dạng và viết các cặp góc bằng nhau, nếu
biết một trong các trường hợp sau:
a) AB =4cm, BC = 6cm, AC = 5cm, DE = 10cm, DF = 12cm, EF = 8cm.
b) AB = 24cm, BC = 21cm, AC = 27cm, DE = 28cm, DF = 36cm, EF = 32cm.
c) AB = DE = 12cm, AC = DF = 18cm, BC = 27cm, EF = 8cm.
Bài 7: Cho D ABC vuông tại A và D DEF vuông tại D có BC = 10cm, AC = 8cm, EF = 5cm, DF = 4cm. a) Tính AB, DE. A B A C BD b) Chứng minh: = = . DE DF EF
c) Chứng minh: D A BC ” D DEF .
Bài 8: Cho tam giác ABC. Gọi A, B, C lần lượt là trung điểm của các cạnh AB, BC, CA. a) Chứng minh A B ¢ C ¢ ¢ D ” DCAB
b) Tính chu vi của D A ' B 'C ', biết chu vi của D A B C bằng 54cm. Tự luyện
Bài 1: Từ điểm D trên cạnh AB của tam giác ABC, kẻ một đường thẳng song song với BC,
cắt AC ở E và cắt đường thẳng qua C song song với AB tại F; BF cắt AC ở I. Tìm các cặp tam giác đồng dạng. DB 1
Bài 2: Cho tam giác ABC, lấy D trên cạnh BC sao cho =
. Qua D kẻ đường thẳng DC 2
song song với AC cắt AB tại D. Qua D kẻ đường thẳng song song với AB cắt AC tại E.
a) Tìm các cặp tam giác đồng dạng và tìm tỉ số đồng dạng.
b) Tính chu vi các tam giác DBD, EDC biết chu vi tam giác ABC bằng 24cm.
Bài 3: Cho tam giác ABC, kẻ A x song song với BC. Từ trung điểm M của cạnh BC, kẻ một PN QN
đường thẳng bất kỳ cắt Ax ở N, cắt AB ở P và cắt AC ở Q. Chứng minh = . PM QM
KẾT QUẢ - ĐÁP SỐ 40 50 60
Bài 1: a) Đổi sang đơn vị mm, ta lập được tỉ số: = = = 5 8 10 12
Từ đó kết luận hai tam giác đồng dạng.
b) Theo định lý Pytago, tính được BC = 10cm . Trang 2 A B 2 5 BC Vì = ¹ =
nên hai tam giác không đồng dạng. A B ¢ ¢ 3 8 B C ¢ ¢
Bài 2: Vì DDEF ” DA BC nên DDEF cũng có độ dài các cạnh tỉ lệ với 4 : 5 : 6.
Giả sử DE < EF < FD Þ DE = 0, 8m DE EF FD Ta có = = = 0, 2 4 4 6
Từ đó tính được EF = 1m và FD = 1, 2m . 16, 2 24, 3 32, 4 Bài 3: Ta có = = A B ¢ ¢ B C ¢ ¢ C A ¢ ¢
a) Tính được A ' B ' = 6, 2cm . Từ đó tính được B 'C ' = 9, 3cm và A 'C ' = 12, 4cm .
b) Tương tự câu a tính được A ' B ' = 26, 2cm , B 'C ' = 39, 3cm và A 'C ' = 52, 4cm . Bài 4:
a) Ta có: DE / / A B suy ra: D ODE ” D OA B OD OE DE 2 Þ = = = (1) OA OB A B 3 OD OF DF 2
Tương tự: D ODF ” D OA C Þ = = = (2) OA OC A C 3 OE OF 2 Do đó:  =
=  EF / / BC ( theo OB OC 3 định lí Ta let đảo) EF OF 2
 DOEF ” DOBC  = = (3) BC OC 3 DF EF DE 2 Từ (1) và (2); (3) suy ra = = = AC BC AB 3
Þ D DEF ” D A BC ( c.c.c) DE 2 DE AB b) Ta có: =  =
mà A B – DE = 12 . Theo tính chất dãy tỉ số bằng nhau có AB 3 2 3 DE AB AB − = = DE =12 2 3 3 − 2
 DE = 24(cm); AB = 36(cm)
c) Ta có tỉ số về chu vi bằng tỉ số đồng dạng Trang 3 AB 3
D A BC ” D DEF theo tỉ số đồng dạng k = = DE 2 P 3 3 Do đó: ABC  =  P = P A  BC  EF P 2 2 D  EF D 3
Mà theo giả thiết: P + P =120  P + P =120  P = 48(cm) ABC  E D F BED  E D F  E D F 2
Bài 5: Ta có: AB 3 1 AD 5 1 BD 6 1 = = ; = = ; = = BD 6 2 BC 10 2 BC 12 2 Do đó: AB AD BD 1 = = = BD BC BC 2
Þ D A BD ” D BDC (c.c.c)
 ABD = BDC Mà hai góc ở vị trí so le trong
Do đó suy ra: A B / / CD  Tứ giác ABCD là hình thang. Bài 6:
a) Ta chia các cặp cạnh theo thứ tự từ nhỏ đến lớn: AB 4 1 AC 5 1 BC 6 1 BA AC CB = = ; = = ; = =  = = EF 8 2 DE 10 2 DF 12 2 FE ED DF BA AC CB = =  B  AC” F
 ED  B = F, A = E,C = D FE ED DF
b) Ta chia các cặp cạnh theo thứ tự từ nhỏ đến lớn: BC 21 3 AB 24 3 AC 27 3 CB BA AC = = ; = = ; = =  = = DE 28 4 FE 32 4 DF 36 4 DE EF FD CB BA AC = =  C  BA” D
 EF  C = D, B = E, A = F DE EF FD
c) Ta chia các cặp cạnh theo thứ tự từ nhỏ đến lớn: AB 12 3 AC 18 3 BC 27 3 AB AC BC = = ; = = ; = =  = = EF 8 2 DE 12 2 DF 18 2 EF DE DF BA AC CB = =  B  AC” F
 ED  B = F, A = E,C = D FE ED DF Bài 7: a) Tính AB, DE. Trang 4 2 2 2 2 A B = BC - A C = 10 - 8 = 6cm 2 2 2 2 DE = EF - DF = 5 - 4 - 3cm AB 6 AC 8 BC 10 AB AC BC b) = = 2; = = 2; = = 2  = = DE 3 DF 4 EF 5 DE DF EF A B A C BC c) = =
Þ DA BC ” DDEF DE DF EF A 'B ' B 'C ' C ' A ' 1 Bài 8: a) = = = , suy ra ngay ABC  ” A
 ' B 'C ' (c-c-c) A B BC CA 2 1 A ' B ' B 'C ' C ' A '
A ' B '+ B 'C '+ C ' A ' P 1 b)
A ' B 'C ' = = = = = Þ P = .P = 27cm
A ' B 'C ' 2 A B BC CA
A B + BC + CA P 2 ABC A BC Trang 5